图1 双馈风电场与火电机组打捆经串补外送系统结构
Fig.1 Structure of wind-thermal bundled series compensated transmission system
摘要 双馈风电场接入含串补输电线路系统时，会对火电机组次同步谐振（SSR）产生影响，但其次同步控制互作用（SSCI）对火电机组SSR的影响尚未明确。该文针对风火打捆经串补外送系统，对各元件进行“模块化”建模，通过将火电机组复频域模型推广至双馈风机（DFIG），提出一种适用于含双馈风电场系统的分散消元式复转矩系数法。利用该方法从阻尼特性角度阐释系统引起多模态SSR机理，并分析主导振荡因素对SSR的影响。结果表明，串补是引发SSR的主导因素，不同串补度可能会引发不同模态的SSR，同时DFIG并网可能引入SSCI助增某个弱阻尼模态SSR分量，引发新的SSR模态失稳，当两者作用于不同模态时，将可能导致系统出现多模态SSR；在一定串补度范围内，降低串补度有利于SSR稳定性；串补输电线路电阻对不同模态阻尼产生的影响不同，合理的电阻值有利于降低SSR风险；随着双馈风电场容量的增加，火电机组阻尼增大，SSR稳定性提高；基于PSCAD/EMTDC的时域仿真和实际系统算例验证了所提理论分析的正确性。
关键词：双馈风电场 复转矩系数法 阻尼特性 次同步谐振 次同步控制相互作用
近年来，在“双碳”战略目标的引领下，以风电为代表的新能源发电发展迅猛，截至2023年12月底，我国风机装机容量约4.4亿kW，同比增长20.7%[1]。为提高风电的消纳和传输能力，风火打捆经串补外送系统成为近年来风电外送的主要形式之一。然而，大规模风电的接入会对系统的次同步振荡（Sub-Synchronous Oscillation, SSO）特性产生影响，甚至威胁系统中火电机组的安全稳定运行，如2015年新疆哈密SSO事故[2-6]。因此，有必要开展风电场并网对火电机组SSO影响的研究。
目前，针对双馈风电场与火电机组打捆经串补外送系统SSO稳定性的研究，主要围绕火电机组与串补之间交互作用产生的次同步谐振（Sub-Synchronous Resonance, SSR）问题展开。文献[7]研究了双馈风电场并网前后火电机组的阻尼特性，揭示双馈风电场并网时串补度、风速等因素对火电机组SSR的影响；文献[8]对含双馈风电电力系统次同步振荡的产生机理展开了分析，表明火电机组SSR可能通过线路激发双馈风机（Doubly-Fed Induction Generator, DFIG）的次同步控制相互作用（Sub-Synchronous Control Interaction, SSCI）。SSCI是指DFIG内部变流器与电力系统其余部分之间产生的相互作用。现有研究主要集中于DFIG和串补之间的SSCI展开分析。文献[9]对DFIG与串补之间的SSCI振荡模式展开分析，指出其SSCI频率主要受串补度影响；文献[10]分析了定子电流控制的DFIG与串补产生的SSCI风险性；文献[11-12]建立了考虑功率外环的DFIG阻抗模型，从阻抗特性角度阐述了DFIG与串补之间的交互作用机理。然而，双馈风电场SSCI与火电机组SSR之间的联系尚不清楚。因此，有必要在考虑SSCI的情况下，展开双馈风电场并网对火电机组次同步谐振影响的分析，弥补当前双馈风电场并网系统次同步振荡研究的不足。
现有次同步振荡分析的方法主要有模态分析法、阻抗分析法和复转矩系数法。模态分析法能获得系统较为全面的振荡信息，但具有“维数灾”问题，且物理意义不明确[13-14]；阻抗分析法多用于两个子系统间的交互作用分析，难以解释系统内部振荡模式间的耦合作用机理[15-17]；复转矩系数法具有明确的物理意义，从阻尼角度揭示系统SSO机理，被广泛应用于SSO的分析[18-19]。文献[20]基于时域仿真的测试信号法求取DFIG的复转矩系数，进而从电气阻尼的角度对其SSCI展开研究。文献[21]通过复转矩系数分析了IEEE第二标准模型火电机组SSR特性；文献[22-25]基于电力系统各元件的复频域端口导纳矩阵（Complex frequency domain Port-equivalence Conductance Matrix, CPCM）模型，通过一种分散消元式的复转矩系数法对复杂系统火电机组SSR问题展开分析，但未应用于新能源机组的研究；文献[26]通过基于CPCM的复转矩系数法对火电机组的阻尼特性展开分析，同时探究了大规模直驱风电场接入对火电机组的影响，但并未考虑直驱风机SSCI的影响。上述方法均局限于指定发电机组复转矩系数的求取，对兼有DFIG与火电机组的新能源并网系统不具有普适性。因此，若希望探究双馈风电场SSCI对火电机组SSR的影响，亟须对上述复转矩系数法进行推广，同时结合火电机组和DFIG的阻尼特性展开研究。
本文首先对双馈风电场与火电机组打捆经串补外送系统进行模块化建模，将火电机组复频域模型推广至DFIG。在文献[22]基础上，保留原有易于建模、克服“维数灾”问题和适应任意网络结构SSR分析的优势，将分散消元式复转矩系数法推广至含双馈风电场系统中。然后，利用该方法从阻尼角度阐释DFIG并网引起火电机组多模态SSR机理，通过时域仿真验证其正确性，并结合实际算例对结论和方法展开进一步验证。最后，分析串补及SSCI、串补输电线路电阻和风电场并网容量对系统SSR特性的影响。
双馈风电场与火电机组打捆经串补外送系统结构如图1所示。系统由火电机组、双馈风电场、串补输电线路和受端交流电网组成。
图1 双馈风电场与火电机组打捆经串补外送系统结构
Fig.1 Structure of wind-thermal bundled series compensated transmission system
火电机组、串补输电线路和交流电网采用IEEE第一标准模型参数，具体见文献[27]，火电机组、串补输电线路及交流电网参数见附表1和附表2。其中，火电机组电磁回路采用完整的六绕组模型，轴系部分采用含高压缸（HP）、中压缸（IP）、低压缸（LPA、LPB）、发电机（GEN）和励磁机（EXC）的六质量块模型。双馈风电场采用受控源输出倍乘的单机聚合法进行等值[28]，额定风速为11 m/s，DFIG网侧变流器（Grid Side Converter, GSC）和转子侧变流器（Rotor Side Converter, RSC）分别采用电网电压矢量定向和定子磁链矢量定向控制策略，主要参数见附表3。
图1中，is、ir、ig分别为DFIG的定子电流、转子电流和GSC电流；i1为DFIG输出电流；us、ur、ug分别为DFIG定子端电压，转子变流器端电压和网侧变流器端电压；Cdc、Udc、Idc分别为DFIG变流器直流电容、直流电压和电流；Rg、Lg分别为网侧变流器出口电阻、电感；uwt、iwt分别为双馈风电场端电压和输出电流；N为风电场受控源聚合放大倍数；usg、isg分别为火电机组端电压和输出电流；RC、LC、CC分别为输电线路电阻、电感和串补电容；Lsys为受端无穷大交流电网电感；下标d、q、dq表示变量在dq坐标系下对应的分量
适用于分散消元式复转矩系数法的系统交流网络、火电机组和DFIG模型介绍如下。
交流网络中变压器、输电线路和受端交流电网复频域导纳矩阵由式（1）阻抗支路CPCM模型表示[29-30]，串补电容矩阵由式（2）表示。
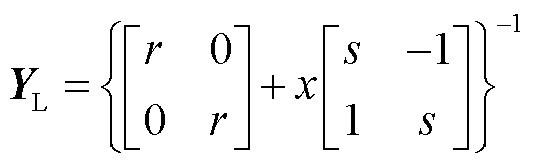（1）
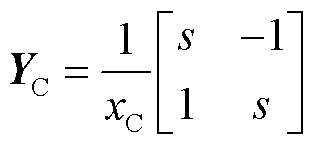（2）
式中，r、x分别为阻抗支路电阻和电抗；xC为串补电容容抗。
火电机组包括电气和机械两部分，其复频域模型分别如式（3）、式（4）所示[21,30]，其中机械部分由发电机轴系方程求得，具体见文献[30]。本节线性化传递函数方程中的变量与图1中变量意义相同。Δ表示变量的小扰动量。
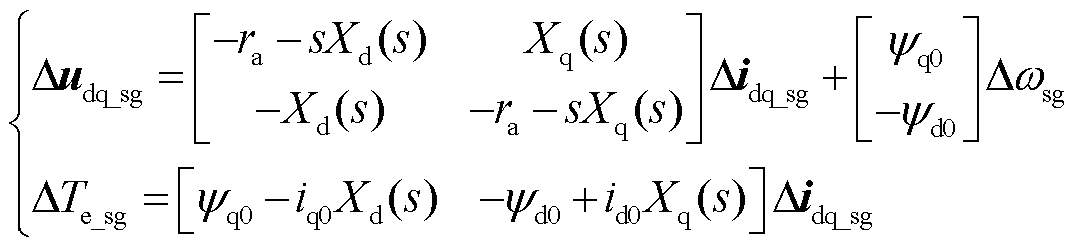（3）
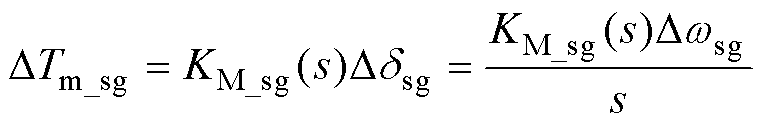（4）
其中
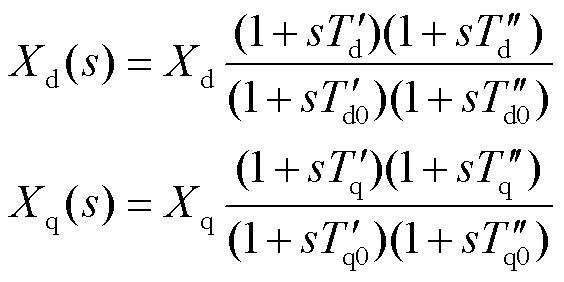
式中，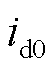
、
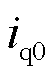分别为电流d、q轴分量稳态值；ra为发电机电枢电阻；ψd0、ψq0分别为磁链d、q轴分量稳态值；
、
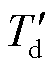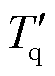为暂态短路时间常数；
、
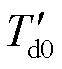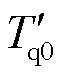为暂态开路时间常数；
、
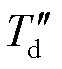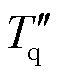为次暂态短路时间常数；
、
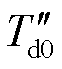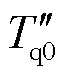为次暂态开路时间常数；wsg和δsg分别为火电机组转子转速和旋转角位移；Te_sg为火电机组电磁转矩；Tm_sg为火电机组机械转矩；KM_sg(s)为火电机组机械复转矩系数。
由DFIG磁链和转子电压方程[31]，可得转子电压关于转子电流和转速的线性化传递函数方程如式（5）。本文线性化传递函数方程表达式见附录。
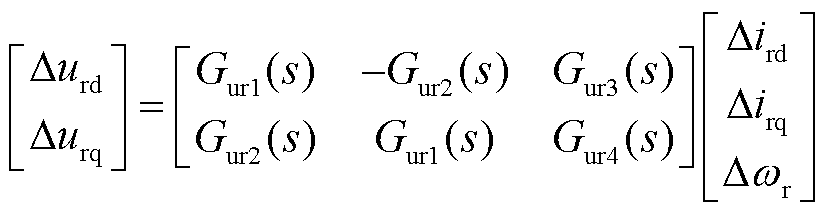（5）
式中，wr为发电机转速；Gur1(s)～Gur4(s)为该传递函数方程相应的系数。
双馈风机转子变流器采用双闭环控制策略，对RSC控制框图（图1蓝色点画线框图）电流内环进行线性化，并联立式（5）可得
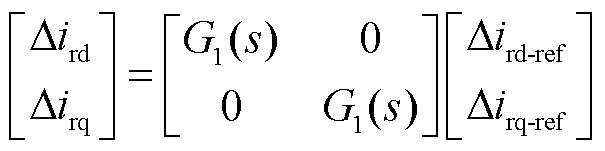（6）
式中，ird-ref、irq-ref分别为转子电流d、q分量参考值；G1(s)为该传递函数方程相应的系数。
DFIG采用MPPT控制，RSC有功功率和无功功率给定值分别为
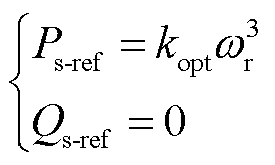（7）
式中，kopt为最大功率跟踪曲线比例系数。
结合式（7），RSC控制框图功率外环线性化传递函数方程为
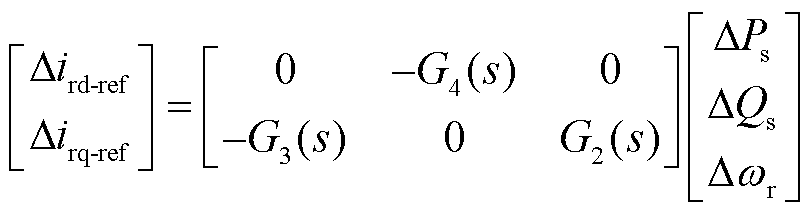（8）
式中，Ps、Qs分别为有功功率和无功功率；G2(s)～G4(s)为该传递函数方程相应的系数。
功率线性化传递函数方程为
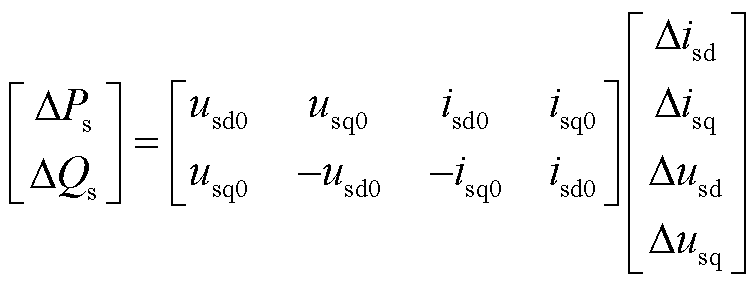（9）
式中，usd0、usq0分别为定子电压d、q轴分量稳态值；isd0、isq0分别为定子电流d、q轴分量稳态值。
由DFIG定子电压和磁链方程[31]，得到定子电压关于定转子电流的线性化传递函数方程为
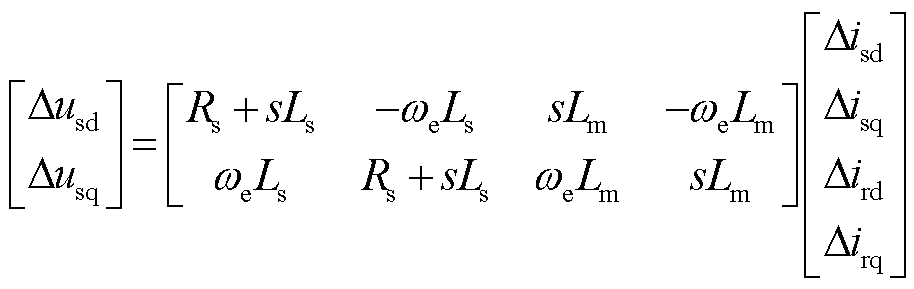（10）
式中，Ls、Lm分别为定子电抗和励磁电抗；Rs为定子电阻；we为同步转速。
DFIG电磁转矩线性化传递函数方程为
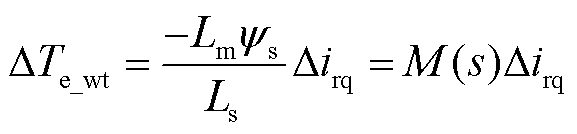（11）
式中，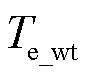
为DFIG的电磁转矩；ψs为按定子磁链定向后的定子磁链矢量幅值；M(s)为相应的系数。
联立式（6）、式（8）～式（11），将式（3）推广至DFIG，可得DFIG电气部分复频域模型，如图2所示。
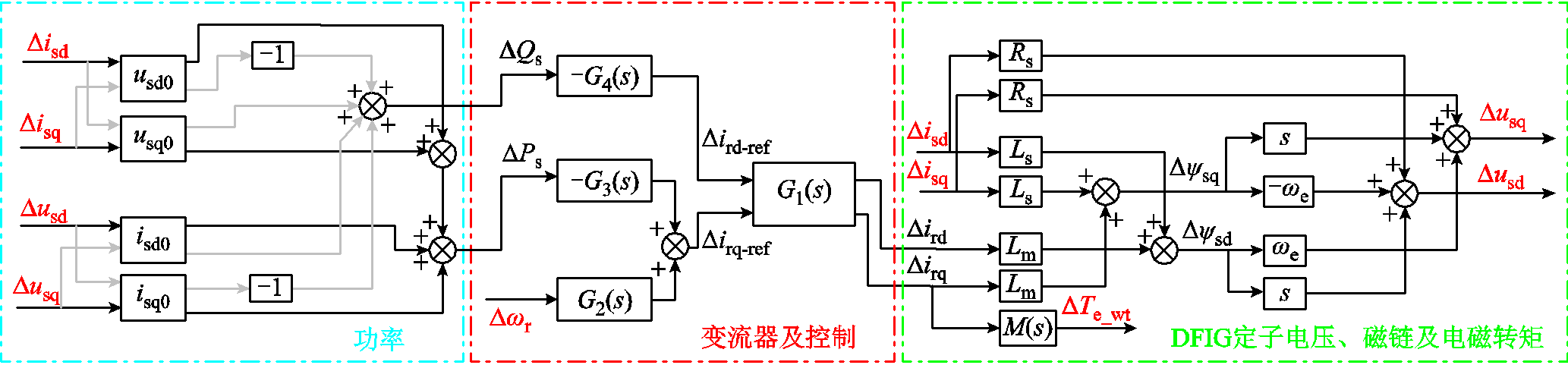
图2 DFIG电气部分复频域模型
Fig.2 Complex frequency domain model of DFIG electrical subsystem
图2说明DFIG电气部分模型同火电机组类似，可表示成以定子电流和转速为输入，定子电压和电磁转矩为输出的形式。整理图2所示DFIG各信号连接关系，可得式（12）所示DFIG电气部分模型的完整传递函数，具体表达式见附录。
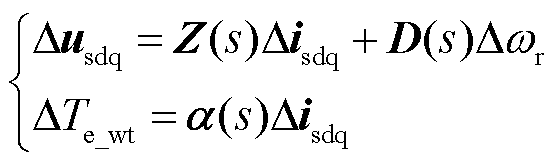（12）
式中，Z(s)、D(s)和α(s)为相应的系数矩阵。
DFIG轴系采用两质量块模型，动态过程[31]为
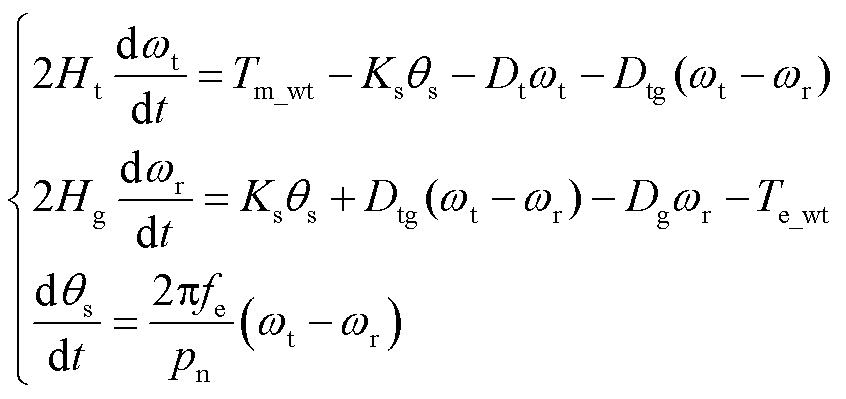（13）
式中，Ht、Hg分别为风轮和发电机惯性时间常数；Ks为轴系总刚度；wt、wr分别为风轮转速和发电机转速；θs为二质量块之间的相对位移角；Tm_wt为DFIG机械转矩；Dt、Dg和Dtg分别为风力机、发电机转子的阻尼系数及其互阻尼系数；fe为电网额定频率；pn为极对数。
对式（13）进行线性化，可得DFIG机械部分复频域模型为
（14）
其中
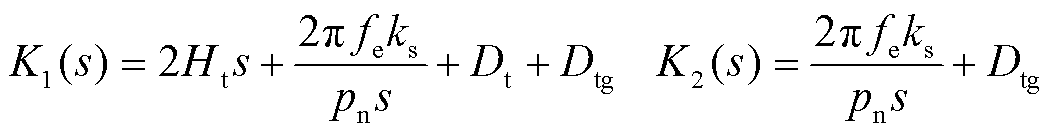
式中，δr为发电机转子旋转角位移；KM_wt(s)为DFIG机械复转矩系数。
复转矩系数法的核心在于从待研究发电机组处将系统划分为机械子系统和电气子系统。机械子系统为待研究发电机组的轴系，电气子系统为待研究发电机组的电气部分、外部交流网络和系统中其他发电机组。通过求取两个子系统转矩对于功角或转速的振荡响应，进而根据发电机的阻尼特性判断其SSO稳定性，这两种响应分别为“机械复转矩系数”和“电气复转矩系数”[30]，可由式（15）表示。
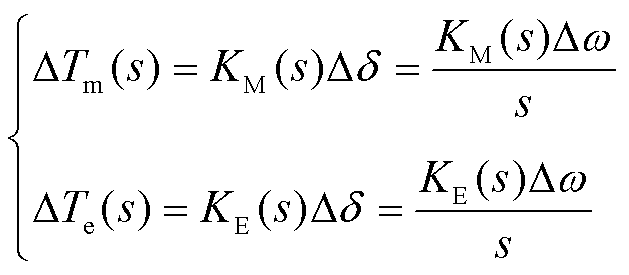（15）
式中，KM(s)和KE(s)分别为机械复转矩和电气复转距系数；Δδ、Δω分别为发电机转子旋转角位移和转速；ΔTm(s)、ΔTe(s)分别为发电机机械转矩和电磁转矩。
KM(s)和KE(s)均为算子s的函数，在频率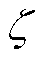
处将两个系数展开（
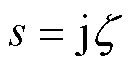），可得[32-33]
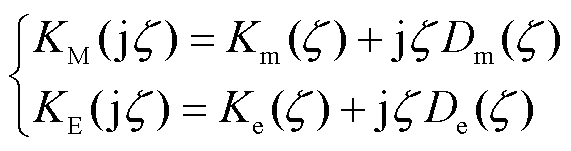（16）
式中，Km、Ke分别为机械弹性系数和电气弹性系数；Dm、De分别为机械阻尼系数和电气阻尼系数。
判断SSO失稳的准则为
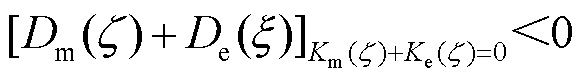（17）
由式（17）可知，当总弹性系数Km+Ke=0时，若总阻尼系数Dm+De＜0，系统存在发生SSO的风险。
因此，只要求得发电机组的KM(s)和KE(s)，即从阻尼特性的角度对SSO稳定性进行分析。
KM(s)仅与待研究发电机组的机械部分轴系（机械子系统）有关[30]，因此火电机组和DFIG的机械复转矩系数可分别由式（4）和式（14）求得。
下面重点介绍KE(s)的求取方法。
设系统有n个发电机节点，其中i台火电机组，j台风电机组，s个非发电机节点。基于第2节交流网络各元件模型，可列写式（18）所示全系统复频域节点电压方程（网络方程）为[22,30]
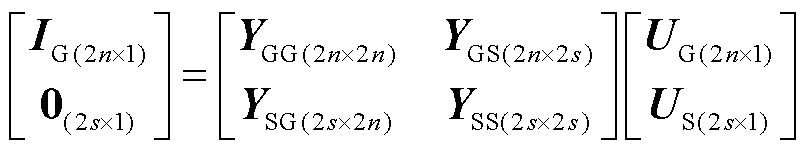（18）
式中，UG、IG分别为发电机节点电压和注入电流；US为非发电机节点电压；YGG、YSS分别为发电机节点自导纳矩阵和非发电机节点自导纳矩阵；YGS、YSG分别为发电机与非发电机节点之间的互导纳矩阵。
消去式（18）非发电机节点，对系统网络方程进行降阶并线性化，可得
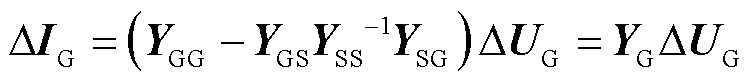（19）
式中，YG为消去非发电机节点后，只与发电机节点相关的导纳矩阵。
式（19）可具体展开为
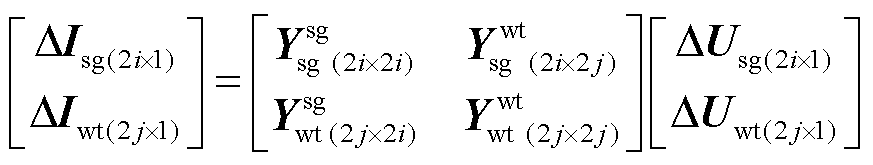（20）
式中，ΔI=Δixy=[Δix Δiy]T，ΔU=Δuxy=[Δux Δuy]T；Isg、Usg分别为火电机组节点的注入电流和节点电压；Iwt、Uwt分别为风电机组节点的注入电流和节点电压；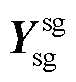
为火电机组节点自导纳；
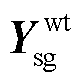和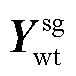
分别为火电机组节点和风电机组节点之间的互导纳；
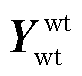为风电机组节点自导纳。
由第2节式（3）和式（12）可知，火电机组和DFIG电气部分复频域模型可表示为
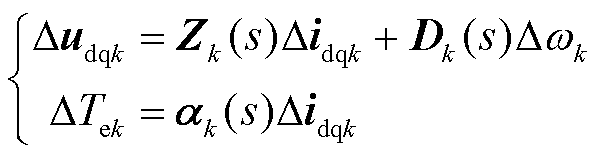（21）
式中，Δidq=[Δid Δiq]T；Δudq=[Δud Δuq]T；下标k表示系统中第k台发电机组，k=1,2,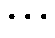
,n。
由于发电机方程和网络方程所在坐标系不同，需要进行坐标系的转换，如式（22）所示[21]。
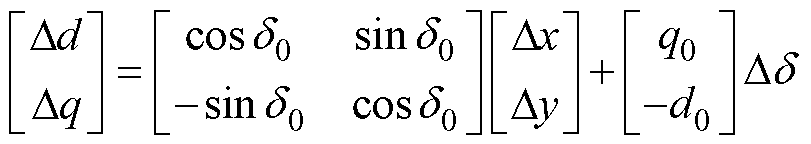（22）
式中，Δd、Δq分别为dq坐标系下的变量；Δx、Δy为xy坐标系下的变量；d0、q0分别为dq坐标系下变量的稳态值；δ0为稳态时d轴和x轴的夹角；Δδ为d轴和x轴的夹角，且Δδ=Δω/s，Δω为转速偏差。
同时，要求取待研究发电机组的电气复转矩系数，在考虑此机组电磁转矩增量时，应当认为此时其他发电机组的机械转矩与电磁转矩平衡，便可将其他发电机机械部分的影响计入待研究发电机组的电气复转矩系数[22]，此时其他发电机组满足
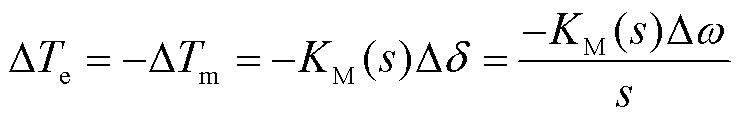（23）
式（23）中具体表达式可见式（4）和式（14）所示的火电机组和DFIG机械部分复频域模型。
联立式（20）～式（22），并将除待研究机组外的其他发电机组如式（23）所示的关系式代入，即可求得待研究发电机组的电气复转矩系数，其求取过程示意图如图3（电气子系统）所示。
通过上述方法即可分别求取风火打捆系统中火电机组和DFIG的机械和电气复转矩系数。
结合前文内容，含双馈风电场系统应用分散消元式复转矩系数法的步骤如下：
1）对系统各元件进行“模块化”建模，具体见本文第2节。需要说明的是，这里所述“模块化”建模指对系统各元件进行独立建模，无需对整个系统进行统一建模，大大降低了建模的复杂度。
2）基于交流网络元件模型建立系统网络方程，消去非发电机节点进行降阶，求取仅含发电机节点的系统网络方程。
3）结合发电机模型，对发电机节点网络方程进一步降阶，消去非待研究发电机节点，求取待研究发电机的复转矩系数，如图3所示。
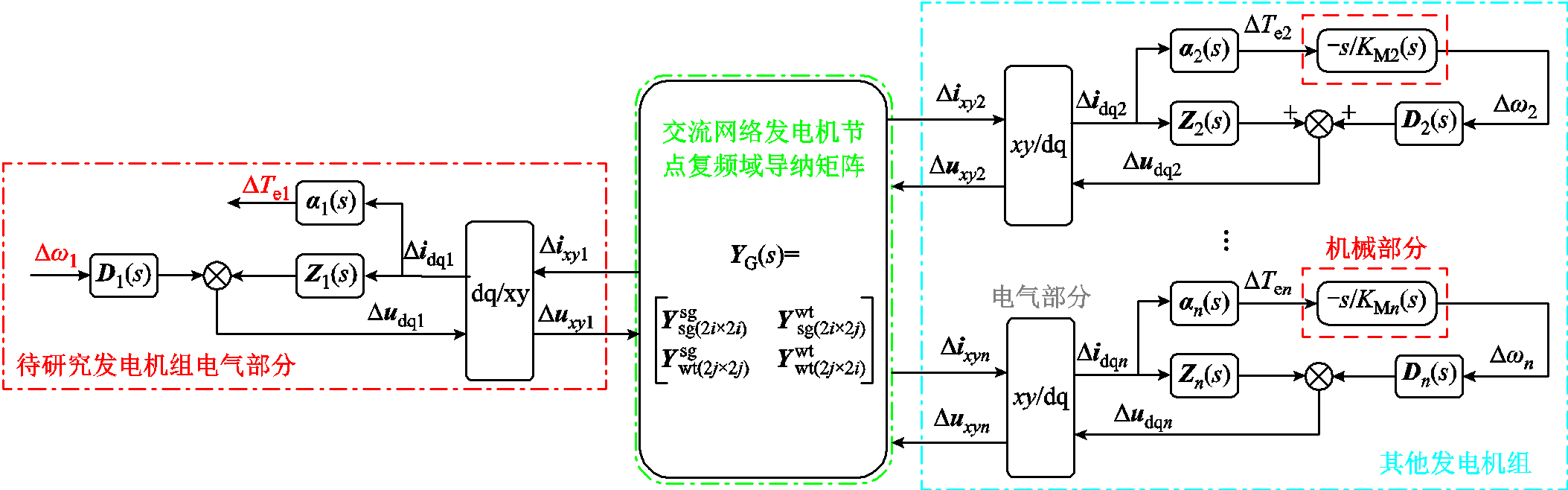
图3 待研究发电机组的电气复转矩系数求取示意图
Fig.3 The schematic diagram of the electrical complex torque coefficient of the generator set to be studied
4）根据式（17）分析系统次同步振荡稳定性，若系统阻尼为负值，说明系统不稳定，反之稳定。
相较于传统复转矩系数法，该方法能在一定程度上避免“维数灾”，而且实现系统各元件“模块化”，易于建模，通用性强，特别是系统结构发生变化时只需对系统网络方程进行修改即可，无需重新建模。
图3中，udq、idq分别为发电机在各自dq坐标系下的节点电压和电流；uxy、ixy为xy坐标系下发电机节点电压和电流；α(s)、Z(s)和D(s)为发电机电气部分复频域模型的系数矩阵；下标1代表待研究发电机组的相关变量；下标为2～n代表非待研究发电机组的相关变量。
本节基于第3节所述方法，分别求取火电机组和DFIG的复转矩系数，从阻尼角度阐述系统多模态SSR机理，通过时域仿真验证机理，并通过实际系统算例进一步验证分析结果与方法的正确性。系统SSR由发电机轴系与串补相互作用引发[4,34]，由于风电机组轴系的自然扭振频率较低，通常在1～10 Hz，实际工程中的串补度难以激发其轴系扭振，发生SSR的概率较小[34]。因此，本文重点对火电机组的SSR展开分析（后续所提SSR均指火电机组的SSR），揭示其产生机理。
由第3节可知，发电机Km和Ke之和为零处的频率为系统可能存在的SSR振荡频率。由于Km远大于Ke，可认为Km+Ke=0的频率点非常接近Km=0的频率点[32-33]，即轴系的自然扭振频率点。火电机组机械弹性系数如图4所示。
由图4可知，该系统中火电机组存在15.7 Hz、20.2 Hz、25.6 Hz和32.3 Hz四种振荡模态，分别对应称为模态一、模态二、模态三和模态四。
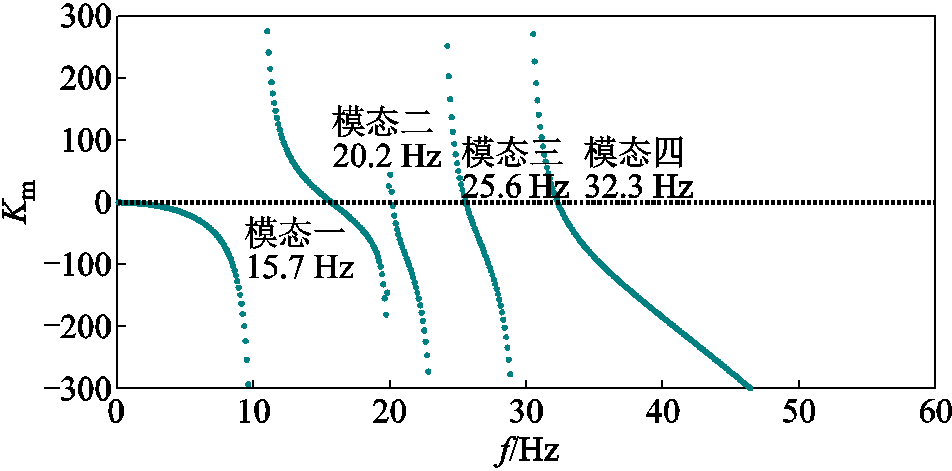
图4 火电机组机械弹性系数
Fig.4 Km of thermal power unit
复转矩系数法通过阻尼反映系统次同步振荡和发电机轴系扭振行为[30]，本节主要阐释图1所示系统SSR产生机理，因此分别对火电机组和DFIG阻尼特性展开分析。
首先分析系统火电机组阻尼特性（后续简称为SSR阻尼特性）。风电场由20台5 MW风机等值聚合而成，风速设置为11 m/s，分别设置串补度为48%、60%和74%三种工况，其他参数保持不变，其SSR阻尼特性如图5所示。为了便于直观判断系统总阻尼的大小，机械阻尼用实际值的负值表示。
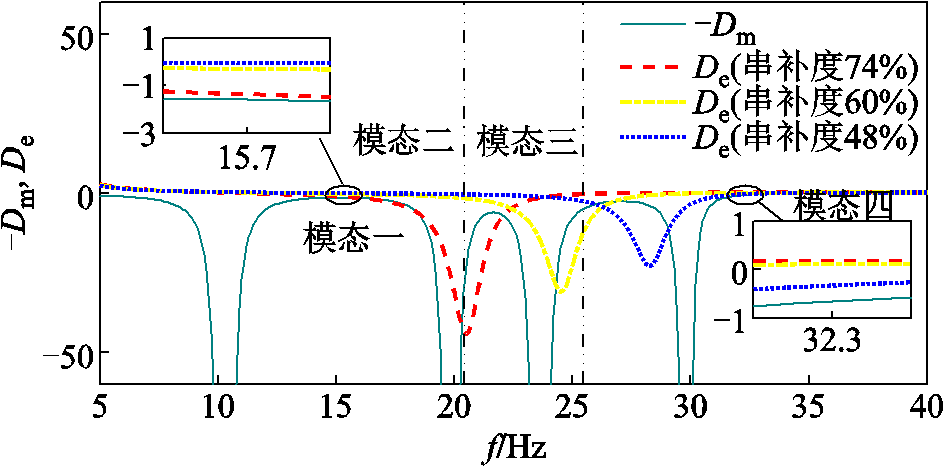
图5 不同串补度下SSR阻尼特性
Fig.5 SSR damping characteristics under different series compensation degrees
由图5可知，串补度为48%时，各模态总阻尼均大于0，不存在SSR失稳的风险；串补度为60%和74%时，火电机组分别在模态三和模态二处呈现出负阻尼，具有SSR失稳的风险，其余情况下阻尼均大于0，处于稳定。同时，可以看出各串补度下模态一和模态四虽处于正阻尼，但阻尼较弱，特别是串补度为74%时模态一总阻尼接近于0，处于稳定边缘，易受影响导致该模态SSR失稳，需重点关注串补度为74%时弱阻尼模态一的SSR情况。
综上所述，串补度在很大程度上影响火电机组的电气阻尼特性。串补度若设置不当，可能导致火电机组在某个模态呈现负阻尼从而引发SSR，且不同串补度可能激发出不同频率的SSR。
同时，DFIG与火电机组之间可能存在相互作用，进而对火电机组SSR造成影响。文献[35]指出双馈风电场参与的SSO可分为SSR、次同步扭振互作用（Sub-Synchronous Torsional Interaction, SSTI）和SSCI。其中SSR和SSTI均与DFIG轴系相关，其参与频率很低，因此本文重点考虑SSCI对火电机组SSR的影响。SSCI主要由双馈风电场控制系统与电力系统其余部分之间的交互产生，与其机械系统没有联系[35]，因此从DFIG电气阻尼特性角度揭示其SSCI。保持系统参数不变，火电机组采用单刚体模型，求取DFIG在48%、60%和74%三种串补度下的电气阻尼特性，如图6所示。
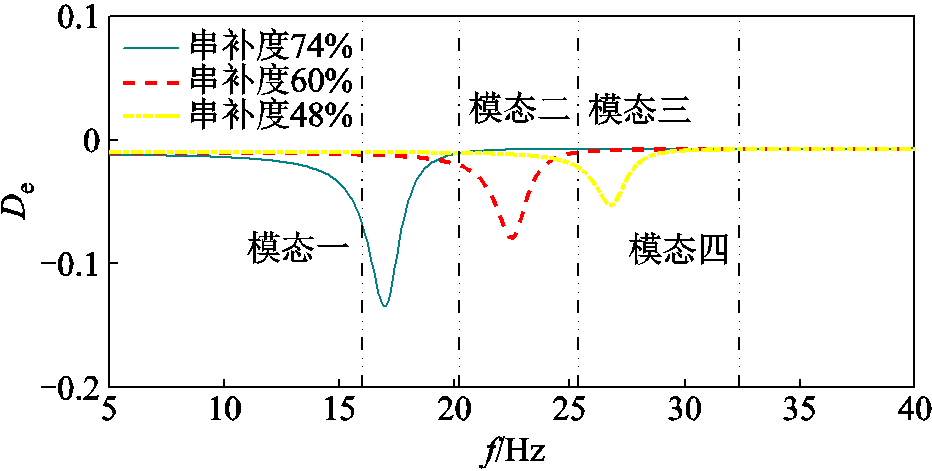
图6 不同串补度下DFIG电气阻尼特性
Fig.6 Electrical damping characteristics of DFIG under different series compensation degrees
由图6可知，串补度为74%时，DFIG在模态一频率处呈现较大的负阻尼，此时若系统存在该频率的次同步分量，在此负阻尼的作用下会助增该模态分量，从而导致该模态振荡加剧。而在其他情况下，DFIG负阻尼相对较小，产生的影响较小。
因此，在串补度为74%时，由于串补和双馈风电场的SSCI，可能导致系统呈现出“多SSR模态”的情况，产生过程如图7所示。
当串补度为74%时，系统受到小扰动后，由串补引起的电气谐振频率与模态二互补频率接近，电气阻尼接近负的峰值，导致总阻尼为负，激发20.2 Hz的模态二SSR，如图中红色（虚线）箭头所示。同时，由于火电机组模态一处于弱阻尼，存在较小的模态一SSR分量，从而在线路中产生与其频率互补的次同步电流分量。结合SSCI作用机理，该次同步电流分量经线路进入DFIG的控制环节，由于DFIG在该模态下表现为较大的负阻尼，会助增该次同步分量电流[8,20]，进而与火电机组轴系相互激励，导致火电机组在该模态下的SSR分量加剧，从而引起系统15.7 Hz的SSR失稳，作用过程如图中黑色（实线）箭头流程所示。需指出的是，以上双馈风电场SSCI并非DFIG与串补之间的相互作用，串补受扰产生的谐振频率对应模态二频率，而DFIG在模态二下的阻尼相对来说较大，不会与串补产生SSCI。此时双馈风电场SSCI是由于火电机组在线路侧产生与模态一对应的次同步扰动分量产生的，因此模态一SSR失稳的原因可归结为火电机组与DFIG之间的相互作用。
图7 多模态SSR产生过程
Fig.7 Multi-mode SSR generation process
综上所述，可得如下结论：不恰当的串补度是引发SSR的主导因素；同时DFIG并网可能引入SSCI，若DFIG在某个SSR弱阻尼模态下呈现较大负阻尼，将会助增该模态次同步分量电流，进而与火电机组轴系相互激励，引起新的SSR模态失稳。当串补和SSCI作用于不同模态时，将可能导致系统出现“多SSR模态失稳”的情况。
为了验证上述SSR机理分析结果的正确性，在PSCAD/EMTDC建立串补度为48%、60%和74%三种工况下系统的时域仿真。t=1.5 s时B点发生三相接地短路，故障持续0.075 s，并通过带通滤波器提取四种模态下的火电机组转速偏差次同步分量，仿真波形如图8所示。
由图8可知，串补度为48%时，火电机组各转速偏差模态基本趋于稳定，模态一和模态四存在振幅很小的等幅振荡；串补度为60%时，转速偏差模态二分量稳定，模态一和模态四出现振幅很小的等幅振荡，模态三振荡幅值逐渐发散，系统出现25.6 Hz的SSR失稳；串补度为74%时，转速偏差模态三趋于稳定，模态四为振幅很小的等幅振荡，模态一和模态二振荡发散，系统出现15.7 Hz和20.2 Hz的SSR失稳，与前述分析结果一致。
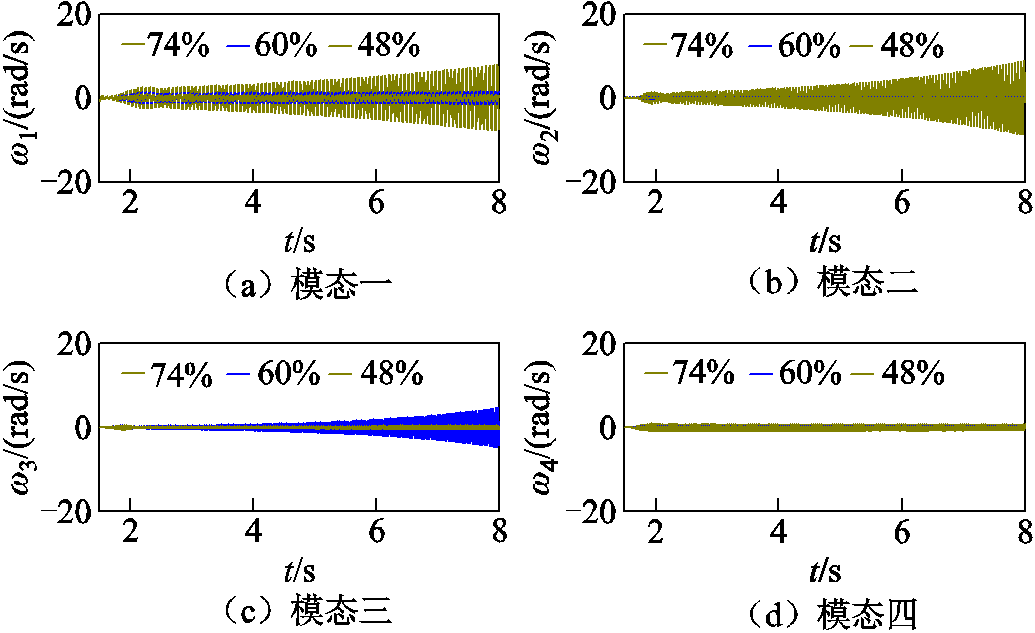
图8 不同串补度时各SSR模态仿真结果
Fig.8 The waveform of SSR mode under different series compensation degree
为了进一步验证上述分析结果与所提方法的正确性，分析图9所示我国华北某地区实际系统SSR特性。该地区主要以火电和风电为主，包括三个火电厂和三个风电场，其中火电厂A有2台额定容量为733 MV·A的机组，火电厂B和火电厂C各有2台额定容量为412 MV·A的机组；风电场机型为双馈风机，约250多台，额定容量均为1.5 MV·A。
图9 实际系统示意图
Fig.9 Schematic diagram of the practical system
风电场通过220 kV输电线路汇集到升压站后，与火电厂打捆通过500 kV含串补电容补偿的双回输电线路送出，串补电容为121 μF。该地区某一实际运行工况为：风电汇集区域出力约150 MW，火电厂A投运两台机组，火电厂B投运一台机组，火电厂C机组停运。在此工况下分析火电厂A和B机组的SSR特性。利用Km求取各机组SSR振荡模态，结果见表1。
表1 实际系统SSR振荡模态
Tab.1 SSR oscillation mode of practical system
火电厂模态振荡频率/Hz A模态1模态221.526.5 B模态323.4
由表1可知，该实际系统中火电厂A机组存在21.5 Hz和26.5 Hz两种振荡模态，火电厂B机组存在23.4 Hz的振荡模态，分别对应称为模态1、模态2和模态3。
利用所提方法求取各火电厂机组和双馈风电场阻尼特性。由于本文重点关注风电汇集区域对于各火电厂的影响，且各风电机组差别不大，因此将该风电汇集区域等值成一个具有N台机的风电场，等值过程见文献[36]。除该实际系统所配置的121 μF串补电容外，补充59 μF、66.5 μF和74 μF串补电容情况下系统的SSR风险分析。火电厂各机组和风电汇集区域阻尼特性，如图10～图12所示。
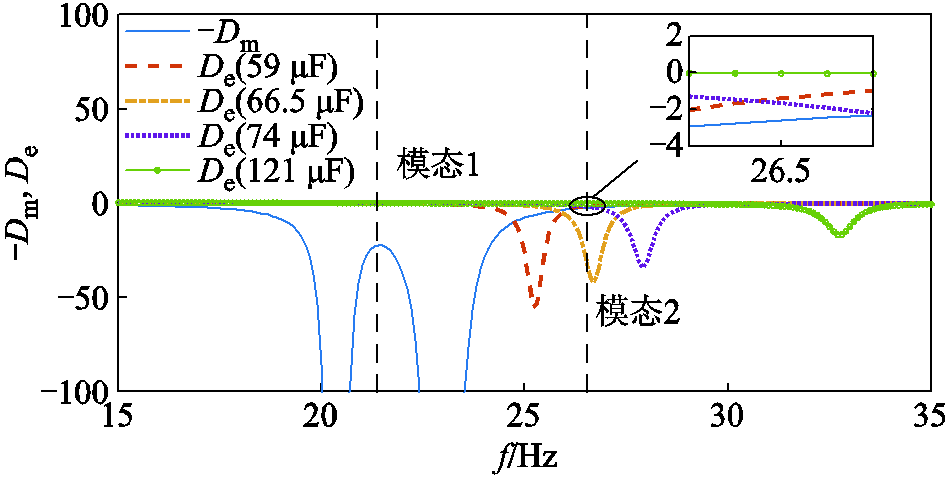
图10 火电厂A机组阻尼特性
Fig.10 Damping characteristics of unit in thermal power plant A
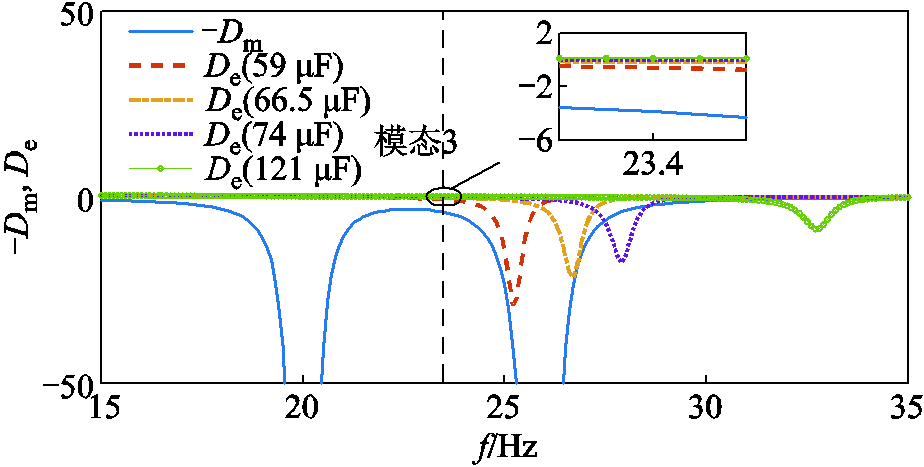
图11 火电厂B机组阻尼特性
Fig.11 Damping characteristics of unit in thermal power plant B
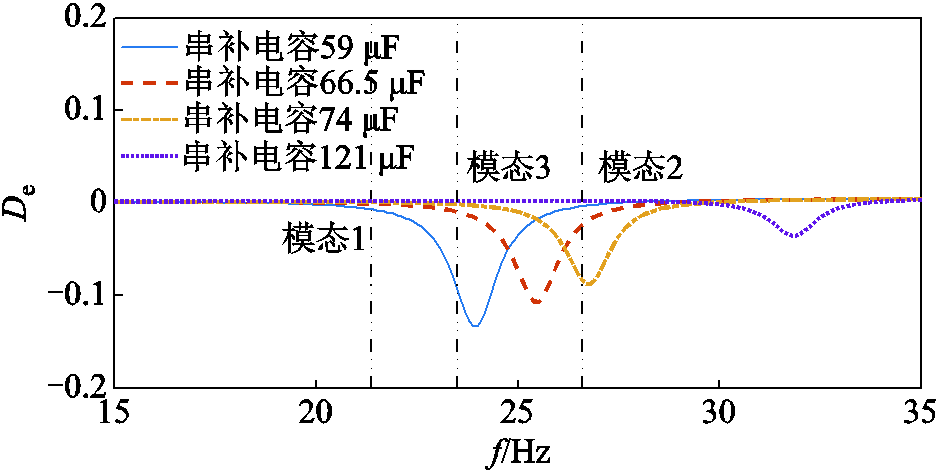
图12 风电汇集区域阻尼特性
Fig.12 Damping characteristics of wind power farm
由图10可知，火电厂A机组在串补电容为 66.5 μF时，模态2呈现较大的负阻尼，存在26.5 Hz的SSR失稳风险，而模态1具有较大的正阻尼，不具有SSR风险；在配置59 μF和74 μF串补电容时，火电厂A机组在模态1和模态2频率处均呈现正阻尼，但模态2阻尼较弱，易受影响。
由图11可知，火电厂B机组在四种不同的串补电容下，均呈现正阻尼，串补不会引起其SSR失稳，但其阻尼均较弱，可能受到风电场汇集区域SSCI的影响。
由图12可知，在串补电容为59 μF和74 μF时，风电汇集区域分别在模态3和模态2频率处呈现较大的负阻尼，此时由于DFIG的SSCI可能会助增对应模态的SSR分量，从而引起火电厂B机组23.4 Hz（模态3）的SSR失稳和火电厂A机组26.5 Hz（模态2）的SSR失稳，而其他情况下风电汇集区域阻尼均较小，对火电厂机组产生的影响较小。
同时，由图10～图12可知，在121 μF串补电容的情况下，火电厂A和B机组各模态阻尼均大于0，且风电汇集区域的阻尼在各模态下的阻尼均很小。因此，此时各火电厂机组均不存在SSR失稳的风险，这与该系统在此实际工况运行下所呈现的结果一致。
通过PSCAD/EMTDC建立该实际系统在上述四种工况下的时域仿真模型。在t=1.5 s设置扰动激发系统SSR，并提取系统各火电厂机组转速偏差次同步分量，仿真波形如图13所示。
由图13可知，串补电容为66.5 μF和74 μF时，火电厂A机组引发了模态2的SSR；串补电容为59 μF时，火电厂B机组引发了模态3的SSR；而其他情况下各机组处于稳定，与前述分析结果一致。
综上所述，在该实际系统算例中，串补和双馈风机SSCI同样可能引起SSR失稳，与4.2节所得结论一致，进一步验证了SSR机理分析的正确性，时域仿真对所得结论也进行了论证。同时，该算例也验证了本文方法在多机系统的适用性与可行性。
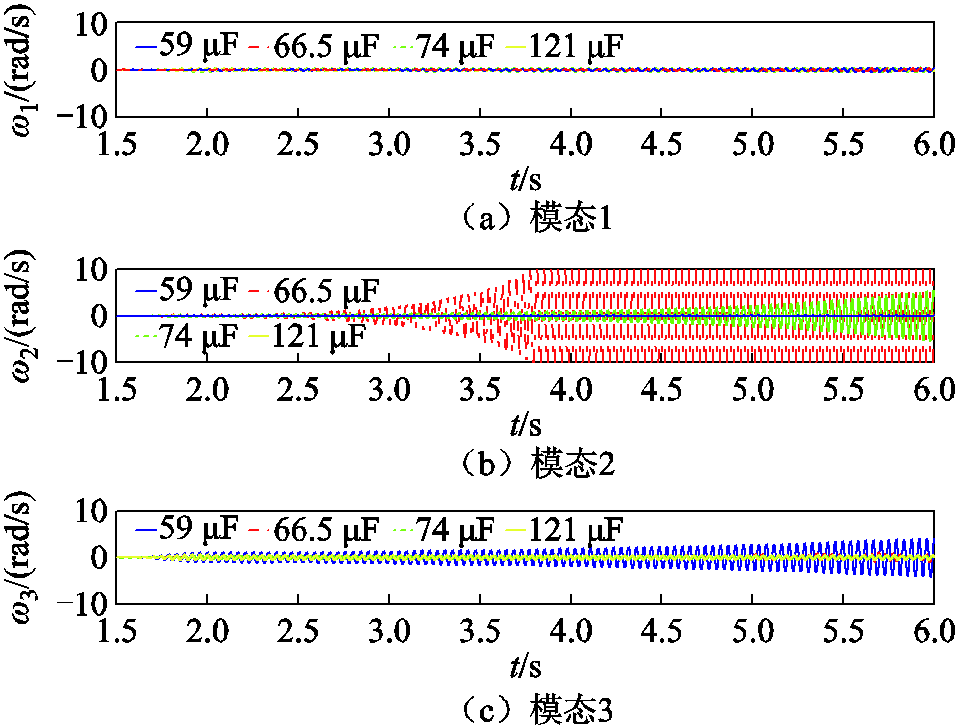
图13 不同串补电容时实际系统各SSR模态仿真结果
Fig.13 The waveform of SSR mode of the practical system under different series compensation capacitors
由于串补输电线路和DFIG共同影响系统的SSR稳定性。因此，本节重点分析串补及SSCI、串补输电线路电阻和双馈风电场并网容量对系统SSR阻尼特性的影响。
由第4节分析可知，串补度能够在很大程度上改变火电机组和DFIG的阻尼，从而使系统呈现出不同的SSR特性。为了进一步说明串补和SSCI对SSR的影响，以1%为步长，分析72%～75%串补度下系统的阻尼特性，风电场设置同4.2节。火电机组和DFIG阻尼特性如图14和图15所示。
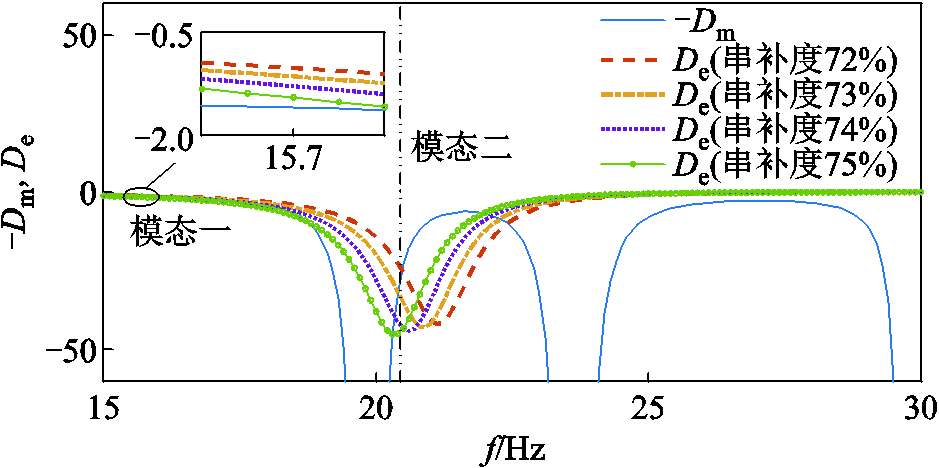
图14 72%～75%串补度时火电机组SSR阻尼特性
Fig.14 SSR damping characteristics of thermal power units under 72%～75% series compensation degree
由图14可知，在串补度为72%～75%范围内，模态一处于正阻尼，串补不会引起模态一的SSR；而模态二在串补度为73%～75%时处于负阻尼，即此时由于串补的作用，会引起火电机组模态二SSR失稳，模态二在串补度为72%阻尼接近0，处于临界稳定，且可以看出随串补度的增加，模态二阻尼降低，振荡加剧。
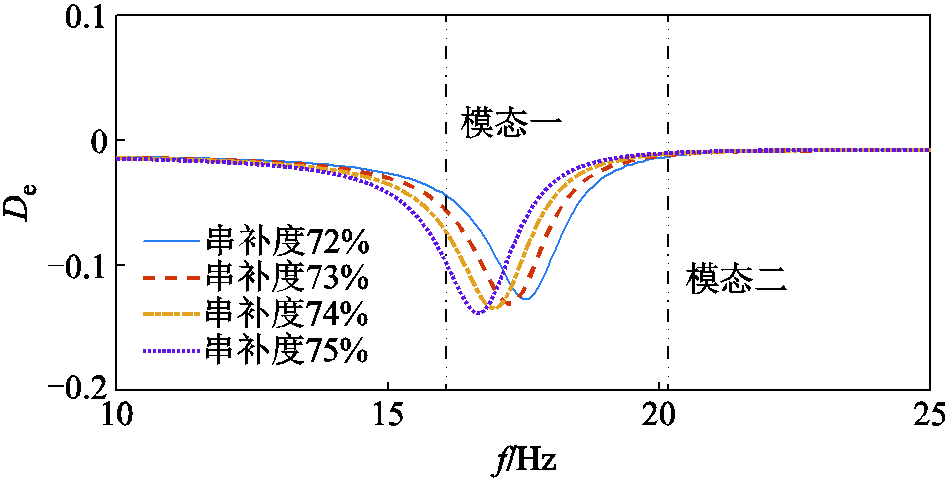
图15 72%～75%串补度时DFIG阻尼特性
Fig.15 Damping characteristics of DFIG under 72%～75% series compensation
由图15可知，在串补度为72%～75%范围内，DFIG在模态一呈现出负阻尼，此时DFIG可能会在该频率处产生SSCI，助增该模态SSR分量，进而引起火电机组在该频率下的SSR，且可以看出随串补度增加，DFIG的阻尼减小，即SSCI的作用越强，模态一SSR稳定性越低；而对于模态二来说，DFIG的阻尼相对来说很小，产生的影响很小。
综上所述，可以看出在一定串补度范围内，降低串补度有利于SSR稳定性。
在PSCAD/EMTDC建立上述各工况下各SSR模态的时域仿真模型，仿真波形如图16所示。
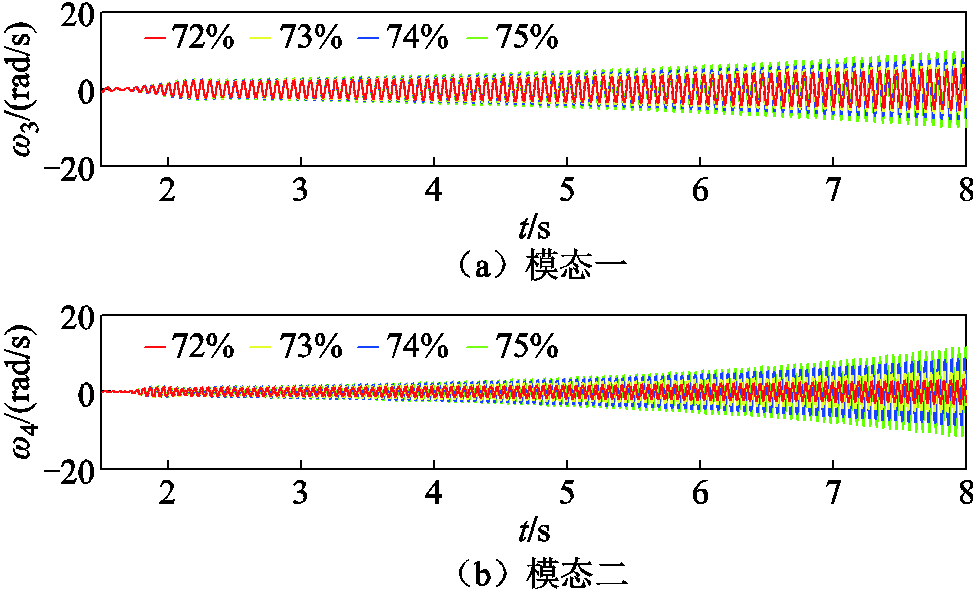
图16 72%～75%串补度时各SSR模态仿真结果
Fig.16 The waveforms of SSR mode under 72%～75% series compensation degree
由图16可知，在串补度为72%～75%范围内，随串补度的增加，由串补引起的模态一SSR逐渐加剧，而由双馈风电场SSCI引起的模态二SSR也逐渐加剧，与前述分析结果一致。
以串补度为74%为例，重点关注具有SSR风险的模态一和模态二。风电场容量为100 MW，串补输电线路电阻RC分别为0.01(pu)、0.02(pu)和0.04(pu)，其他参数保持不变，SSR阻尼特性如图17所示。PSCAD/EMTDC仿真平台不同Rc时各SSR模态的仿真结果如图18所示。
由图17可知，模态一阻尼随着串补输电线路电阻RC的减小而增加，模态二阻尼随RC的增加而增加。由此可知，串补输电线路电阻会对系统SSR阻尼特性造成影响，不同于串补度的是RC不会导致电气阻尼的峰值偏移，因此不同SSR模态的激发仍主要取决于串补度。
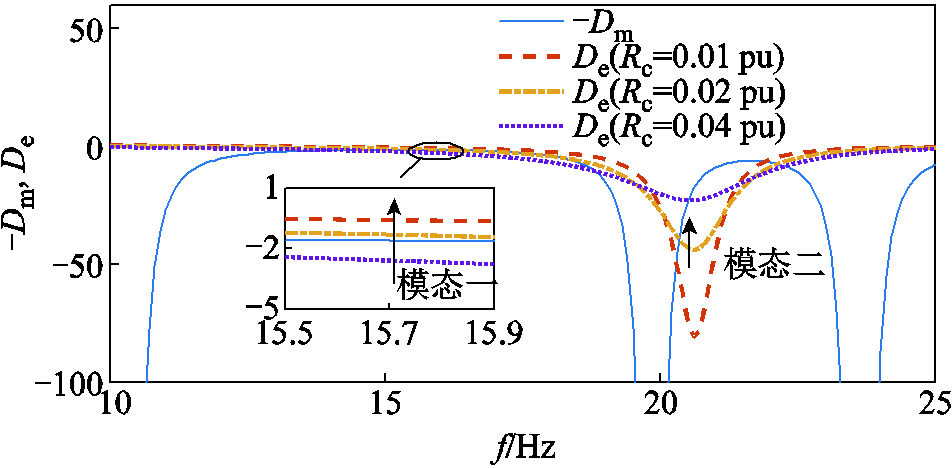
图17 不同RC时SSR阻尼特性
Fig.17 SSR damping characteristics under different RC
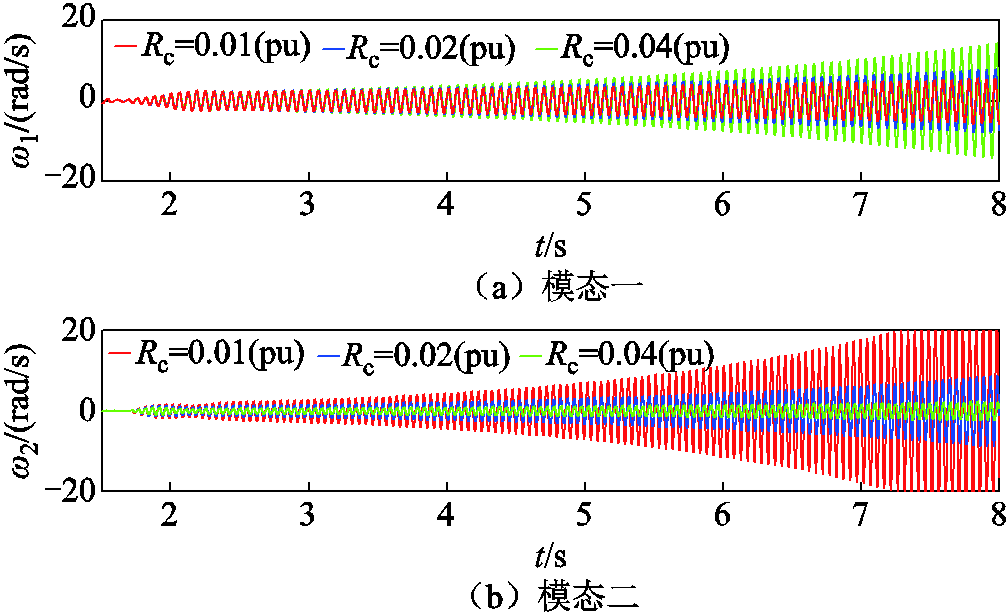
图18 不同RC时各SSR模态仿真结果
Fig.18 The waveforms of SSR mode under different RC
由图18可知，SSR模态一分量振幅随着RC的减小而减小，说明阻尼随RC的减小而增加；SSR模态二分量振幅随RC的增加而减小，说明阻尼随RC的增加而增加，验证了前述分析结果。
串补度为74%，RC=0.02(pu)时，风电场容量分别设置为50 MW、100 MW和150 MW，其他参数保持不变，重点关注具有SSR风险的模态一和模态二的情况，SSR阻尼特性如图19所示。PSCAD/EMTDC仿真平台仿真结果如图20所示。
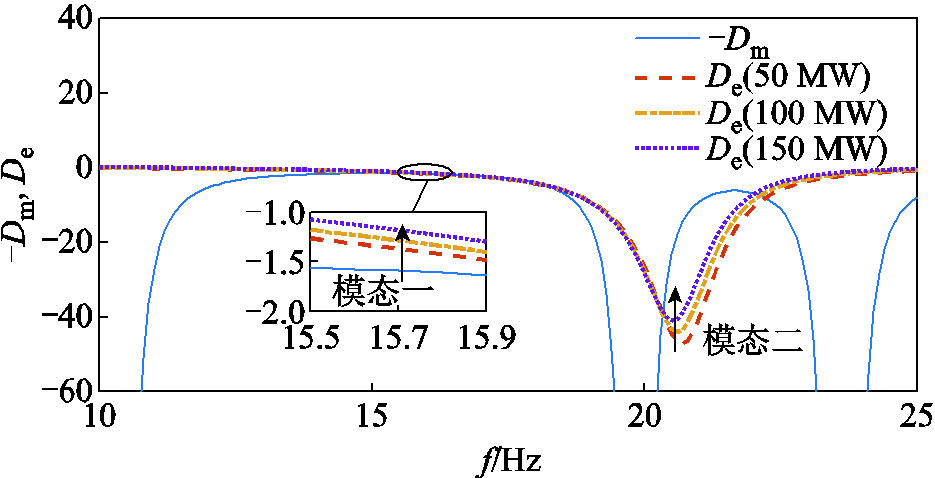
图19 不同风电场并网容量时SSR阻尼特性
Fig.19 SSR damping characteristics under different wind farm capacity
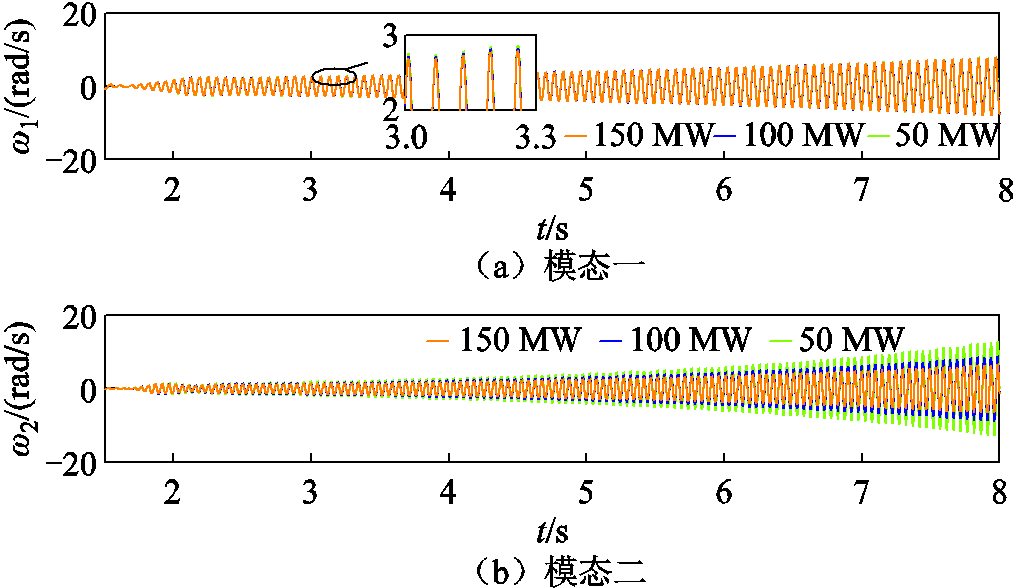
图20 不同风电场并网容量时各SSR模态仿真结果
Fig.20 The waveforms of SSR mode under different wind farm capacity
由图19可知，随风电场并网容量的增加，模态一阻尼略微增加，变化很小；而模态二阻尼得到较大的提升。由此可知，双馈风电场并网容量的提升有利于SSR稳定性。
由图20可知，随着风电场并网容量的增加，SSR模态一分量振幅略微有所减小，但变化不大；而SSR模态二分量振幅减小较为明显。说明模态一阻尼变化不大，而模态二阻尼随风电场并网容量增加得到较为明显的提升，验证了前述分析结果的正确性。
本文基于分散消元式复转矩系数法在含双馈系统的推广，从阻尼特性的角度阐释了双馈风电场并网引起火电机组多模态SSR失稳的机理，分析了相关因素对SSR阻尼特性的影响，主要结论如下：
1）基于火电机组复频域模型在DFIG的推广，提出了一种适用于含双馈风电场系统的分散消元式复转矩系数法。所提方法相较于传统复转矩系数法，能在一定程度上避免维数灾问题，实现各元件模块化，易于建模，通用性强。相较于时域仿真法，能够提供系统较多的振荡信息，阐述振荡机理与特性，计算速度快，且适用于多机系统。
2）不恰当串补度是导致系统SSR失稳的主导因素，不同串补度可能引发不同模态的SSR，同时DFIG并网可能引入SSCI，若DFIG在某个SSR弱阻尼模态下呈现较大负阻尼，将会助增该模态次同步分量电流，进而与火电机组轴系相互激励，引起新的SSR模态失稳。当两者作用于不同模态时，将可能导致系统出现多模态SSR失稳的情况。
3）串补度对阻尼特性的影响较大，在一定串补度范围内，降低串补度有利于提高SSR稳定性。串补输电线路电阻改变时，不同模态阻尼呈现的变化趋势不同，选取合理的串补输电线路电阻有利于降低SSR风险；双馈风电场容量增加时，火电机组阻尼会增大，SSR稳定性也会提高。
附 录
1. 系统参数
附表1 火电机组主要参数
App.Tab.1 Main parameters of thermal power unit
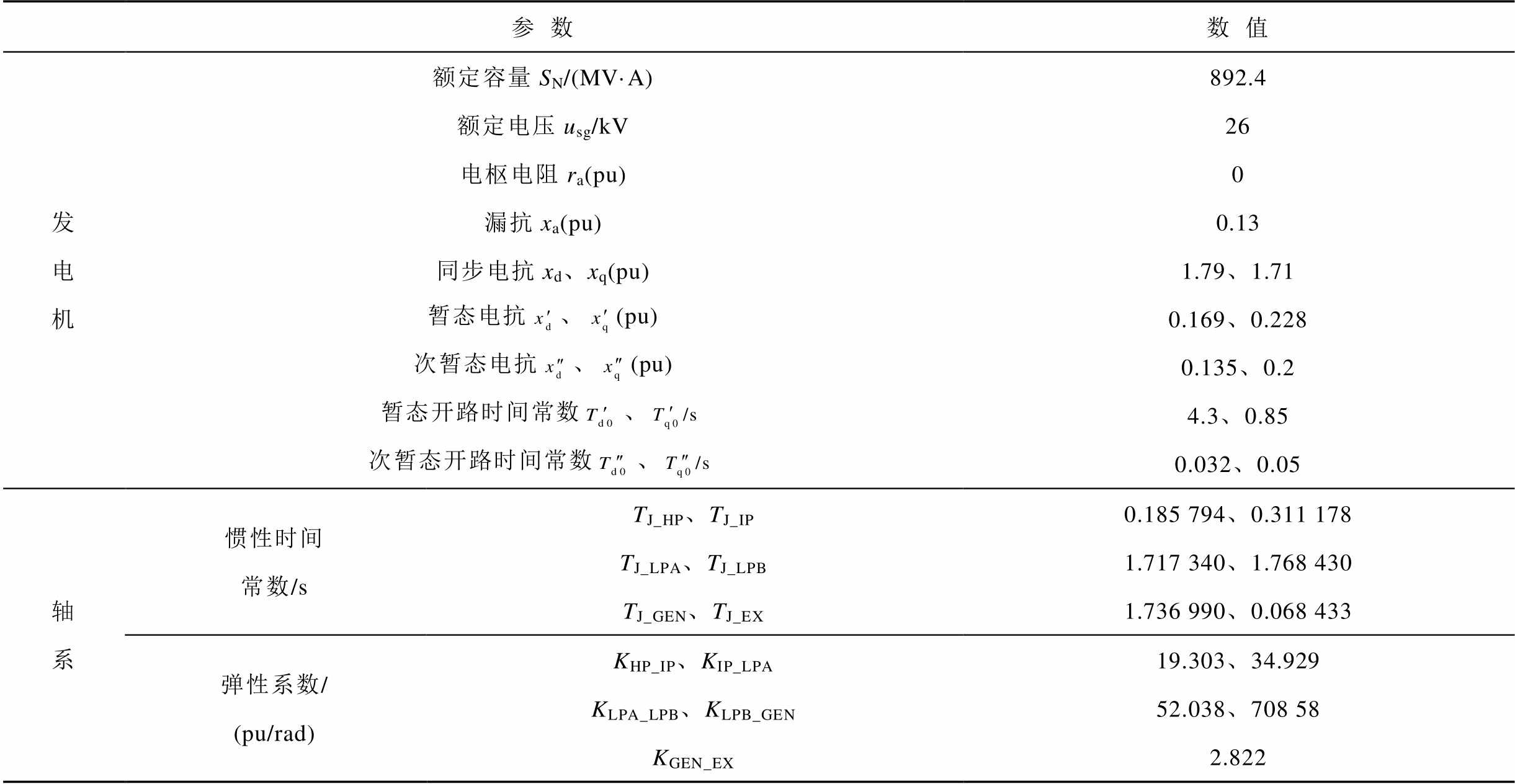
参数数值 发电机额定容量SN/(MV·A)额定电压usg/kV电枢电阻ra(pu)892.4260 漏抗xa(pu)0.13 同步电抗xd、xq(pu)暂态电抗、(pu)次暂态电抗、(pu)暂态开路时间常数、次暂态开路时间常数、1.79、1.710.169、0.2280.135、0.24.3、0.850.032、0.05 轴系惯性时间常数/sTJ_HP、TJ_IP0.185 794、0.311 178 TJ_LPA、TJ_LPB1.717 340、1.768 430 TJ_GEN、TJ_EX1.736 990、0.068 433 弹性系数/(pu/rad)KHP_IP、KIP_LPAKLPA_LPB、KLPB_GENKGEN_EX19.303、34.92952.038、708 582.822
附表2 输电线路及交流电网参数
App.Tab.2 Transmission line and AC grid parameters
参数数值 输电线路输电线路电阻RC/Ω输电线路电感LC/mH串补电容CC（串补度为74%时）/μF6.0832432.321.977 交流电网变压器T1电压比变压器T1漏抗(pu)26kV:539kV0.14 电感Lsys/mH51.78
附表3 DFIG主要参数
App.Tab.3 Main parameters of DFIG
参数数值 发电机额定功率PN_DFIG/MW额定电压us/kV极对数Pn定子电抗Ls(pu)50.6934.6 转子电抗Lr(pu)4.61 励磁电抗Lm(pu)4.5
（续）
参数数值 定子电阻Rs(pu)转子电阻Rr(pu)惯性时间常数Hg/s机械阻尼Dg(pu)出口变压器T2电压比0.005 40.006 0730.000 10.69 kV : 26 kV 机械部分风轮惯性时间常数Ht/s4.32 轴系总刚度Ks/(pu/rad)1.11 风力机与发电机互阻尼Dtg(pu)1.5 控制参数RSC有功外环Kp1, Ti1RSC无功外环Kp2, Ti2RSC电流内环Kp3, Ti3GSC直流电压外环Kp4, Ti4GSC无功外环Kp5, Ti5GSC电流内环Kp6, Ti62, 0.022, 0.051.2, 0.0250.4, 0.010.2, 0.051, 0.01
2. 双馈风机电气部分模型传递函数
式（5）中传递函数具体表达式为
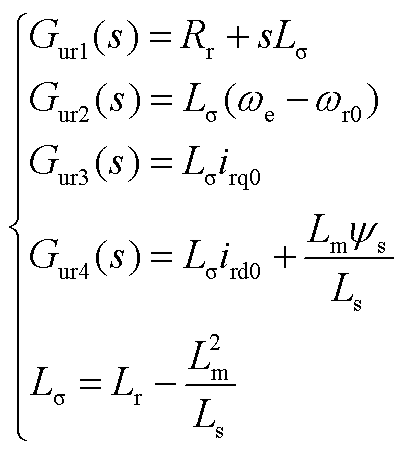（A1）
式中，Rr为转子电阻；we、wr0分别为同步转速和转子转速稳态值；ird0、irq0分别为转子电流dq轴分量稳态值；Ls、Lr、Lm分别为定、转子和励磁电抗。
式（6）中传递函数具体表达式为
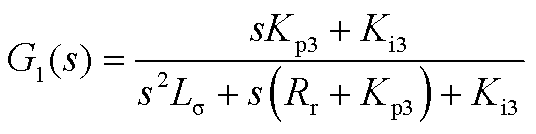（A2）
式（8）中传递函数具体表达式为
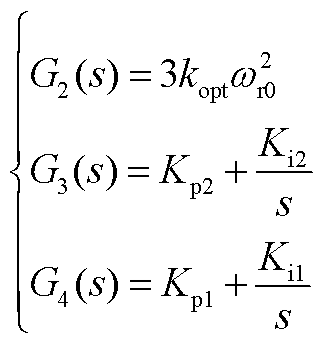（A3）
式（12）中传递函数具体表达式为
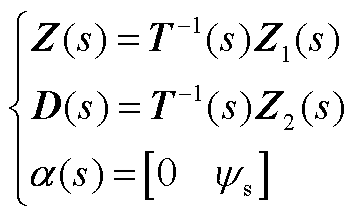（A4）
其中
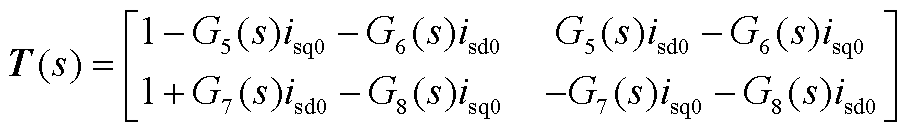
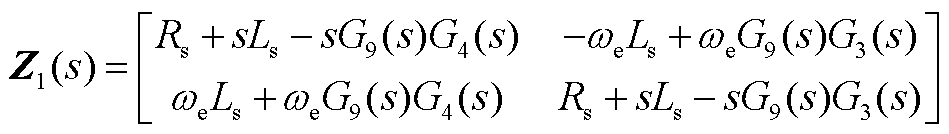
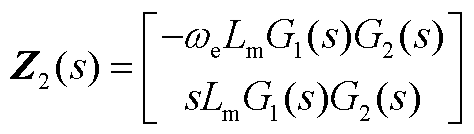
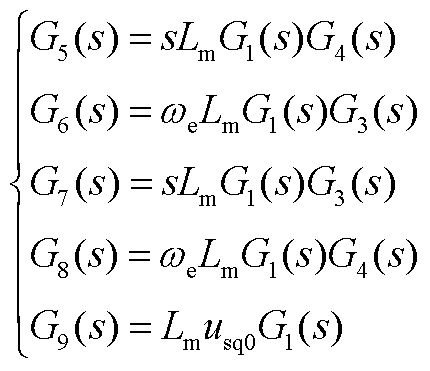
参考文献
[1] 国家能源局. 国家能源局发布2023年全国电力工业统计数据[EB/OL]. 2024-01-26[2023-02-03]. http: //www.nea.gov.cn/2024-01/26/c_1310762246.htm.
[2] 李明节, 于钊, 许涛, 等. 新能源并网系统引发的复杂振荡问题及其对策研究[J]. 电网技术, 2017, 41(4): 1035-1042. Li Mingjie, Yu Zhao, Xu Tao, et al. Study of complex oscillation caused by renewable energy integration and its solution[J]. Power System Technology, 2017, 41(4): 1035-1042.
[3] 谢小荣, 刘华坤, 贺静波, 等. 电力系统新型振荡问题浅析[J]. 中国电机工程学报, 2018, 38(10): 2821-2828, 3133. Xie Xiaorong, Liu Huakun, He Jingbo, et al. On new oscillation issues of power systems[J]. Proceedings of the CSEE, 2018, 38(10): 2821-2828, 3133.
[4] Shair J, Xie Xiaorong, Wang Luping, et al. Overview of emerging subsynchronous oscillations in practical wind power systems[J]. Renewable and Sustainable Energy Reviews, 2019, 99: 159-168.
[5] 郑泽天, 沈沉, 严鋆, 等. 直驱风电场多电压源型变流器控制耦合引发振荡的机理分析[J]. 电力系统自动化, 2023, 47(17): 14-26. Zheng Zetian, Shen Chen, Yan Jun, et al. Mechanism analysis of oscillations induced by control coupling of voltage source converters in wind farms with direct-driven turbines[J]. Automation of Electric Power Systems, 2023, 47(17): 14-26.
[6] 郑少明, 刘一民, 董鹏, 等. 张北工程风电柔直汇集系统次、超同步振荡分析[J]. 全球能源互联网, 2023, 6(6): 608-617. Zheng Shaoming, Liu Yimin, Dong Peng, et al. Analysis of sub/super-synchronous oscillation between wind farm and MMC in Zhangbei Project[J]. Journal of Global Energy Interconnection, 2023, 6(6): 608-617.
[7] 吴杨. 风火打捆经串补外送系统次同步振荡分析与抑制[D]. 北京: 华北电力大学, 2019. Wu Yang. Analysis and Suppression of Subsynchronous Oscillation in Wind-Fire Bundling System with Series Compensation[D]. Beijing: North China Electric Power University, 2019.
[8] 赵阳. 含双馈风电电力系统次同步振荡机理分析及抑制策略研究[D]. 重庆: 重庆大学, 2021. Zhao Yang. Analysis of sub-synchronous oscillation mechanism and research on suppression strategies of power system with dfig-based wind power generation[D]. Chongqing: Chongqing University, 2021.
[9] 赵书强, 李忍, 高本锋, 等. 双馈风电机组经串补并网的振荡模式分析[J]. 高电压技术, 2016, 42(10): 3263-3273. Zhao Shuqiang, Li Ren, Gao Benfeng, et al. Modal analysis of doubly-fed induction generator integrated to compensated grid[J]. High Voltage Engineering, 2016, 42(10): 3263-3273.
[10] 杜程茂, 杜雄, 苏婧媛, 等. 定子电流控制的双馈风机导纳建模与次同步振荡风险分析[J]. 电力系统自动化, 2023, 47(13): 159-167. Du Chengmao, Du Xiong, Su Jingyuan, et al. Admittance modeling and subsynchronous oscillation risk analysis of DFIG-based wind turbine with stator current control[J]. Automation of Electric Power Systems, 2023, 47(13): 159-167.
[11] 李光辉, 王伟胜, 张兴, 等. 双馈风电场并网次/超同步振荡建模与机理分析(一)：考虑功率外环的阻抗建模[J]. 中国电机工程学报, 2022, 42(7): 2438-2449. Li Guanghui, Wang Weisheng, Zhang Xing, et al. Modeling and suppression method of Sub/Super-synchronous oscillation of grid-connected dfig wind farms (part Ⅰ): sequence impedance modeling and analysis of dfig wind turbines considering power loop[J]. Proceedings of the CSEE, 2022, 42(7): 2438-2449.
[12] 李光辉, 王伟胜, 张兴, 等. 双馈风电场并网次/超同步振荡建模与机理分析(二)：阻抗特性与振荡机理分析[J]. 中国电机工程学报, 2022, 42(10): 3614-3627. Li Guanghui, Wang Weisheng, Zhang Xing, et al. Modeling and mechanism analysis of Sub/Super-synchronous oscillation of grid-connected dfig wind farms (part Ⅱ): analysis of impedance characteristic and oscillation mechanism[J]. Proceedings of the CSEE, 2022, 42(10): 3614-3627.
[13] 季一宁, 王海风. 包含串补的并网直驱风电场振荡稳定性及可行域分析[J]. 电工技术学报, 2024, 39(3): 686-698. Ji Yining, Wang Haifeng. Analysis of oscillation stability and feasible region of parameters in grid-connected direct-drive wind farm with series compensation[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 686-698.
[14] 吴翔宇, 张晓红, 尚子轩, 等. 基于频域阻抗网络建模分析的交直流微电网振荡问题研究[J]. 电工技术学报, 2024, 39(8): 2294-2310. Wu Xiangyu, Zhang Xiaohong, Shang Zixuan, et al. Research on the oscillation problem of AC-DC microgrids based on frequency domain impedance network modeling and analysis[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2294-2310.
[15] 刘芳, 刘威, 汪浩东, 等. 高比例新能源电力系统振荡机理及其分析方法研究综述[J]. 高电压技术, 2022, 48(1): 95-114. Liu Fang, Liu Wei, Wang Haodong, et al. Review on oscillation mechanism and analysis methods of high proportion renewable energy power system[J]. High Voltage Engineering, 2022, 48(1): 95-114.
[16] 高本锋, 邓鹏程, 梁纪峰, 等. 光伏电站与弱交流电网间次同步交互作用路径及阻尼特性分析[J]. 电工技术学报, 2023, 38(24): 6679-6694. Gao Benfeng, Deng Pengcheng, Liang Jifeng, et al. Analysis of path and damping characteristics of subsynchronous interaction between photovoltaic plant and weak AC grid[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6679-6694.
[17] 高本锋, 王义, 范辉, 等. 基于阻尼路径的新能源经LCC-HVDC送出系统次同步交互作用分析方法[J]. 电工技术学报, 2023, 38(20): 5572-5589. Gao Benfeng, Wang Yi, Fan Hui, et al. A sub-synchronous interaction analysis method of renewable energy generations integrated with LCC-HVDC system based on damping path[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5572-5589.
[18] 王一珺, 杜文娟, 王海风. 基于改进复转矩系数法的多风电场接入引发多机电力系统次同步振荡机理分析[J]. 中国电机工程学报, 2021, 41(7): 2383-2395. Wang Yijun, Du Wenjuan, Wang Haifeng. Analysis of subsynchronous oscillation in multi-machine power system caused by the integration of multiple wind farms based on improved complex torque coefficient method[J]. Proceedings of the CSEE, 2021, 41(7): 2383-2395.
[19] 郭春义, 刘晓颖, 吕乃航, 等. 风火打捆传统直流外送系统中控制环节对轴系-控制交互模式的影响机理研究[J]. 中国电机工程学报, 2024, 44(9): 3463-3476. Guo Chunyi, Lü Xiaoying, Lyu Naihang, et al. Research on the influence mechanism of control loops on shaft-control interactive mode for wind-thermal-bundled power transmission through LCC-HVDC system[J]. Proceedings of the CSEE, 2024, 44(9): 3463-3476.
[20] 高本锋, 李忍, 杨大业, 等. 双馈风电机组次同步振荡阻尼特性与抑制策略[J]. 电力自动化设备, 2015, 35(12): 11-20. Gao Benfeng, Li Ren, Yang Daye, et al. Damping characteristics and countermeasure of DFIG sub-synchronous oscillation[J]. Electric Power Automation Equipment, 2015, 35(12): 11-20.
[21] Guo Chunlin, Zhou Shuangya, Xu Kun, et al. The study of complex torque coefficient approach based on benchmark[C]//2011 International Conference on Electrical and Control Engineering, Yichang, China, 2011: 1374-1379.
[22] 朱鑫要, 孙海顺, 文劲宇, 等. 基于CPCM的复转矩系数法在复杂电力系统SSR问题研究中的应用[J]. 中国电机工程学报, 2013, 33(4): 77-84, 11. Zhu Xinyao, Sun Haishun, Wen Jinyu, et al. Application of complex torque coefficient basing on CPCM to SSR study of complex power system[J]. Proceedings of the CSEE, 2013, 33(4): 77-84, 11.
[23] Zhu Xinyao, Sun Haishun, Wen Jinyu, et al. A practical method to construct network state equations in multi-machine system SSR study[J]. Electric Power Systems Research, 2014, 107: 51-58.
[24] 王冠青. 电力系统次同步谐振的分析方法和抑制措施研究[D]. 武汉: 华中科技大学, 2013. Wang Guanqing. Research on methods of analysis for subsynchronous resonance of power systems and its countermeatures[D]. Wuhan: Huazhong University of Science and Technology, 2013.
[25] 毛俞杰, 孙海顺, 韩应生, 等. 采用STATCOM抑制多机系统次同步振荡的理论与仿真[J]. 电力系统保护与控制, 2022, 50(6): 23-32. Mao Yujie, Sun Haishun, Han Yingsheng, et al. Theory and simulation of STATCOM for damping subsynchronous oscillation of a multi-machine system[J]. Power System Protection and Control, 2022, 50(6): 23-32.
[26] 毛俞杰. 火电机组次同步振荡阻尼特性分析及大规模风电场接入对其影响研究[D]. 武汉: 华中科技大学, 2022. Mao Yujie. Analysis on damping characteristics of subsynchronous oscillation of thermal power unit and study on the influence of large-scale wind farms connected to the grid on it[D]. Wuhan: Huazhong University of Science and Technology, 2022.
[27] IEEE SSR Working Group. First benchmark model for computer simulation of subsynchronous resonance[J]. IEEE Transactions on Power Apparatus and Systems, 1977, 96(5): 1565-1572.
[28] 高本锋, 刘培鑫, 刘王锋, 等. 直驱风电场并网对火电机组次同步谐振影响[J]. 电工技术学报, 2024, 39(11): 3308-3322. Gao Benfeng, Liu Peixin, Liu Wangfeng, et al. Influence of grid connected direct drive wind farm on subsynchronous resonance of thermal power units[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3308-3322.
[29] 倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社, 2002.
[30] 程时杰, 曹一家, 江全元. 电力系统次同步振荡的理论与方法[M]. 北京: 科学出版社, 2009.
[31] 王毅, 朱晓荣, 赵书强. 风力发电系统的建模与仿真[M]. 北京: 中国水利水电出版社, 2015.
[32] Canay I M. A novel approach to the torsional interaction and electrical damping of the synchronous machine. part I: theory[J]. IEEE Power Engineering Review, 1982, PER-2(10): 24.
[33] Canay I M. A novel approach to the torsional interaction and electrical damping of the synchronous machine. part I: theory[J]. IEEE Power Engineering Review, 1982, PER-2(10): 24.
[34] 高本锋, 刘晋, 李忍, 等. 风电机组的次同步控制相互作用研究综述[J]. 电工技术学报, 2015, 30(16): 154-161. Gao Benfeng, Liu Jin, Li Ren, et al. Studies of sub-synchronous control interaction in wind turbine generators[J]. Transactions of China Electrotechnical Society, 2015, 30(16): 154-161.
[35] 王一珺, 杜文娟, 陈晨, 等. 基于复转矩系数法研究并网双馈风电场引发电力系统次同步振荡问题综述[J]. 发电技术, 2018, 39(3): 195-203. Wang Yijun, Du Wenjuan, Chen Chen, et al. A review of investigations on sub-synchronous oscillations in power systems caused by DFIG wind farms based on the complex torque coefficients method[J]. Power Generation Technology, 2018, 39(3): 195-203.
[36] 杨博闻, 占颖, 谢小荣, 等. 双馈风电场接入串补输电系统引发次同步谐振的研究模型[J]. 电力系统保护与控制, 2020, 48(8): 120-126. Yang Bowen, Zhan Ying, Xie Xiaorong, et al. A study model for subsynchronous resonance in DFIG based wind farms connected to a series-compensated power system[J]. Power System Protection and Control, 2020, 48(8): 120-126.
Abstract With the implementation of the "carbon peaking and carbon neutrality goals", the wind-thermal bundled system has become the main form of wind power transmission in recent years. However, when the doubly-fed wind farm is integrated into power system with series compensated transmission lines, it may have an impact on the subsynchronous resonance (SSR) of the thermal power unit and threaten the safe and stable operation of the system. Therefore, the oscillation problem cannot be ignored. The influence of sub-synchronous control interaction (SSCI) caused by doubly-fed wind farms on SSR of thermal power units is not clear.
Firstly, the 'modular' modeling of each component is carried out for the doubly-fed wind farm and the thermal power unit bundled series compensated transmission system. By extending the complex frequency domain model of the thermal power unit to the doubly fed induction generator (DFIG), a complex torque coefficient method with decentralized elimination of variables suitable for the system with doubly-fed wind farm is put forward. Secondly, the complex torque coefficients of the thermal power unit and DFIG in classical example are obtained by using the proposed method. The mechanism of multi-mode SSR caused by the system is explained from the perspective of damping characteristics, and the SSR mechanism is verified by time-domain simulation. Then, the conclusions and methods are further verified by the actual system examples in North China. Finally, the influence of dominant oscillation factors including series compensation degree, SSCI, series compensation transmission line resistance and wind farm grid-connected capacity on SSR is analyzed.
The mechanism analysis of SSR generation in the system shows that, after the system is subjected to small disturbances, if the electrical resonance frequency caused by series compensation is close to the SSR modal frequency, the electrical damping of the thermal power unit will show a large negative value, resulting in SSR instability. At the same time, when the system has a weak damping SSR mode, the generated small SSR component will enter the control link of the DFIG through the line. If the DFIG shows a large negative damping in this mode, it will help to increase the subsynchronous component current corresponding to the weak damping mode, and then stimulate each other with the shaft of the thermal power unit, resulting in the aggravation of the SSR component in this mode, thus causing SSR instability.
The main conclusions of this paper are as follows: (1) Compared with the traditional complex torque coefficient method, the proposed method can avoid the dimension disaster problem to a certain extent, realize the modularization of each component, and is easy to model and versatile. Compared with the time domain simulation method, it can provide more oscillation information of the system, explain the oscillation mechanism and characteristics, and calculate quickly. It is suitable for multi-machine systems. (2) The inappropriate series compensation degree is the dominant factor causing SSR instability of the system, and different series compensation degrees may lead to different modes of SSR. At the same time, DFIG grid connection may introduce SSCI. If the DFIG presents a large negative damping in a SSR weak damping mode, it will help to increase the subsynchronous component current of the mode, and then stimulate each other with the shaft of the thermal power unit, causing new SSR mode instability. When the two act on different modes, it may lead to multi-mode SSR instability in the system. (3) The series compensation degree has a great influence on the damping characteristics. Within a certain range of series compensation degree, reducing the series compensation degree is beneficial to the stability of SSR. When the resistance of the series compensated transmission line changes, the change trend of different mode damping is different. Selecting a reasonable series compensated transmission line resistance is beneficial to reduce the risk of SSR. With the increase of the capacity of the doubly-fed wind farm, the damping of the thermal power unit increases and the stability of the SSR increases.
keywords：Doubly-fed wind farm, complex torque coefficient method, damping characteristic, sub-synchronous resonance(SSR), sub-synchronous control interaction (SSCI)
DOI: 10.19595/j.cnki.1000-6753.tces.240366
中图分类号：TM712
收稿日期 2024-03-06
改稿日期 2024-06-12
马燕峰 女，1978年生，副教授，研究方向新能源电力系统分析、运行与控制。E-mail：ma_yanfeng01@163.com
程有深 男，1999年生，硕士研究生，研究方向为新能源电力系统稳定性分析。E-mail：1500903459@qq.com(通信作者)
（编辑 赫 蕾）