（1）
摘要 准确评估并合理利用风电机组的调频能力是目前研究亟须解决的问题。为此，提出一种基于可用调频能量的风电机组综合虚拟惯性控制参数整定方法。首先，推导了风电机组机械能损失和可用转子动能与风速之间的数学模型，根据模型揭示了风速变化对二者的影响，实现了风电机组调频能力的有效评估；其次，建立了风电机组调频能量与控制参数的关系表达式，计及风电机组可用调频能量、系统的频率变化量和频率变化率，考虑不同场景下的调频优先等级，设计了模糊控制规则，并基于模糊控制规则采用模糊逻辑控制方法得到了综合控制效果最优时的控制参数整定值；最后，通过算例验证了所提方法的有效性。
关键词：风电机组 综合虚拟惯性控制 可用调频能量 参数整定
在能源结构改革和“双碳”目标的驱动下，可再生能源正逐渐取代火电等传统能源在电力系统中占据主要地位[1]。而风电由于其易获得、经济性好、技术成熟等优势成为了目前应用最广、规模最大的可再生能源。风电的大规模并网有助于构建新型电力系统，却也威胁着电力系统的安全稳定运行，近几年国内外发生的频率失稳引发的停电事故与风电等可再生能源的占比升高密切相关[2-6]。
传统电力系统的频率安全依赖于同步机，在电力系统发生扰动导致频率变化时，同步机因为其转速和系统频率之间具有耦合关系，可通过惯性响应和一次调频使系统频率恢复到正常允许范围[7]。然而风电机组通过变流器等电力电子器件与电网相连，故与系统频率完全解耦[8]。为充分利用风能，风电机组通常处于最大风功率跟踪（Maximum Power Point Tracking, MPPT）状态，因此无法主动提供有功支撑，在系统层面表现为等效惯量降低，调频能力变弱。为减弱风电并网给电网带来的冲击，国内外开展了大量研究，通过附加控制使风电机组模拟同步机的频率响应特性。
风机调频方法根据能量来源的不同，主要分为功率备用控制和综合虚拟惯性控制[9]。功率备用控制通过超速控制或变桨控制使风电机组减载运行，留出备用支持调频，因此无法最大化利用风能资源，降低了经济效益。综合虚拟惯性控制可以充分利用风机自身的转子动能，无需减载运行，经济性更好，是目前主流的风机调频方法。文献[10]首次提出综合虚拟惯性控制，证明了采用该控制的风电机组具备参与电网调频的能力。但较小的控制参数不能充分发挥机组的调频能力，较大的参数会造成频率的二次跌落、转子转速越限问题[11]。故研究学者根据不同目标相继提出了一系列参数整定方法，文献[12]以兼顾风机运行的经济性和一次调频需求为目标，根据自身储能荷电状态修正虚拟惯性与下垂系数；文献[13]以风机转速不超过限值为目标，实现根据扰动的大小在线调整下垂参数；文献[14]以兼顾抑制系统频率二次跌落和转速恢复性能为目标，依据风机实时工况调整下垂系数和虚拟惯性系数。
上述文献中的参数整定方法都未考虑和评估风电机组的调频能力，选取的控制参数容易与机组实际调频能力不匹配，一方面可能对机组的调频能力利用不充分，造成资源浪费；另一方面可能导致过度调频，引起系统安全隐患。文献[15]定量分析了风机转子动能的惯量支撑能力，提出一种转子动能与超级电容储能的协调频率控制策略；文献[16]以风机转子动能表征调频能力，并根据调频能力大小调节下垂系数和虚拟惯性系数；但是以上文献均未考虑风机偏移MPPT造成的机械能损失。在此基础上，文献[17]计及机械能损失参考同步机能量分配机制调节下垂系数和虚拟惯性系数。但是未给出风机调频能力的量化表达式，并且在能量分配时缺少对系统实际运行场景的考虑。
针对上述问题，本文提出一种基于可用调频能量的风电机组综合虚拟惯性控制参数整定方法。首先推导风电机组机械能损失和可用转子动能与风速之间的数学模型，根据模型揭示风速对二者的影响，从而有效评估风电机组在不同风速下的调频能力；其次通过建立调频能量与控制参数的关系表达式，计及风电机组可用调频能量、系统的频率偏差和频率变化率，考虑不同场景下的调频优先等级，设计模糊控制规则，并基于模糊控制规则采用模糊逻辑控制方法得到综合控制效果最优时的控制参数整定值；最后通过算例验证所提方法的有效性。
风电机组的风能捕获功率Pm为
（1）
式中，ρ为空气密度；R为风轮半径；v为风速；Cp为风能利用系数；λ为风机叶尖速比；β为风机桨距角；ωr为风机转速。
在不同风速下，由于R是常数，故只需ωr与v始终保持在最佳比值，即最佳叶尖速比，就可以实现风电机组最大风能捕获。图1为Cp-λ-β的关系特性曲线。
在风电机组的MPPT控制基础上附加综合虚拟惯性控制后可使风机具备类似于同步机的频率支撑能力，结构框图如图2所示。原理是在风机有功控制环节同时引入频率偏差和频率变化率，当频率变化时，风机释放转子中蕴含的旋转动能，参与系统调频，维持频率稳定。因为该方法的调频能量源自风机自身的转子动能，故又称为转子动能控制。
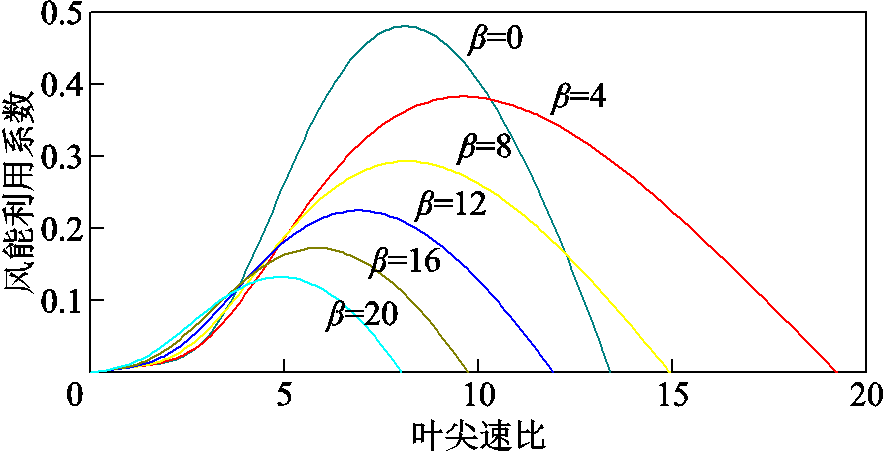
图1 Cp-λ-β的关系特性曲线
Fig.1 Relation characteristic curve of Cp-λ-β
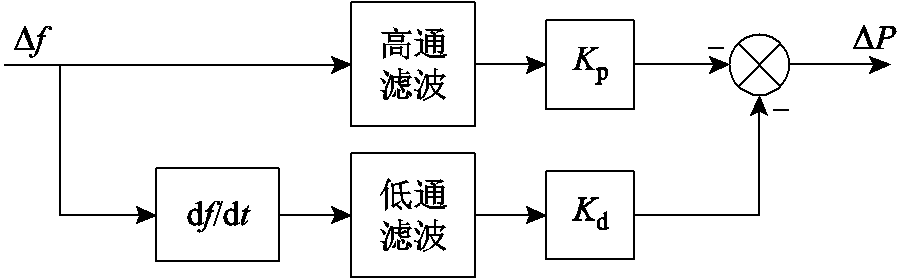
图2 综合虚拟惯性控制结构框图
Fig.2 Structure of integrated virtual inertia control
风电机组的有功功率增量表达式为
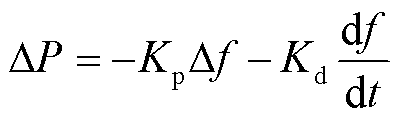（2）
式中，Kp为下垂系数；Kd为虚拟惯性系数；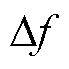
为频率变化量；df/dt为频率变化率。
风机附加综合虚拟惯性控制是通过提取风机内部储存的转子动能，使风机有能力提供有功支撑，参与系统调频。因此无论综合虚拟惯性控制参数如何选取，调频效果本质上都取决于调频能量的多少，故需要从能量角度量化评估风电机组综合虚拟惯性控制的调频能力。本节以双馈风机为例，通过推导风电机组机械能损失和可用转子动能与风速之间的数学模型，揭示风速变化对二者的影响，有效评估风电机组在不同风速下的调频能力。
由于综合虚拟惯性控制能量的来源是风电机组转子蕴含的转子动能，当风机参与调频时，释放转子动能会导致风机的转子转速发生变化，风机不再保持MPPT运行，会损失一部分的机械能。因此，释放的转子动能需要有一部分补偿风机偏移MPPT运行点产生的机械能损失。
由于式（1）所示的风电机组的机械功率计算式十分复杂，而且无法直观地看出转子转速与机械功率的关系，因此需要对机械功率表达式进行简化。将风电机组在不同风速下的最优功率、转子转速分为四个区间[18]。区间划分如图3所示，起动区内的风机转速为最低转速ωrmin，此时风机不能再降低转速，故无法通过释放转子动能参与调频；MPPT区内的风机转速为MPPT模式下的最优转速ωrmppt，风机可实现最大风功率捕获；恒转速区内的风机转速接近最高转速ωrmax，输出功率接近额定功率PN；恒功率区内的风机转速为最高转速ωrmax，输出功率为额定功率，并可通过增大桨距角维持功率输出，此时风机虽有充足的转子动能，但因输出功率不能超过功率上限，所以也无法参与调频。因此，只需评估处于MPPT区间和恒转速区间的风机的调频能力，本节只针对这两个区间进行机械功率表达式化简。
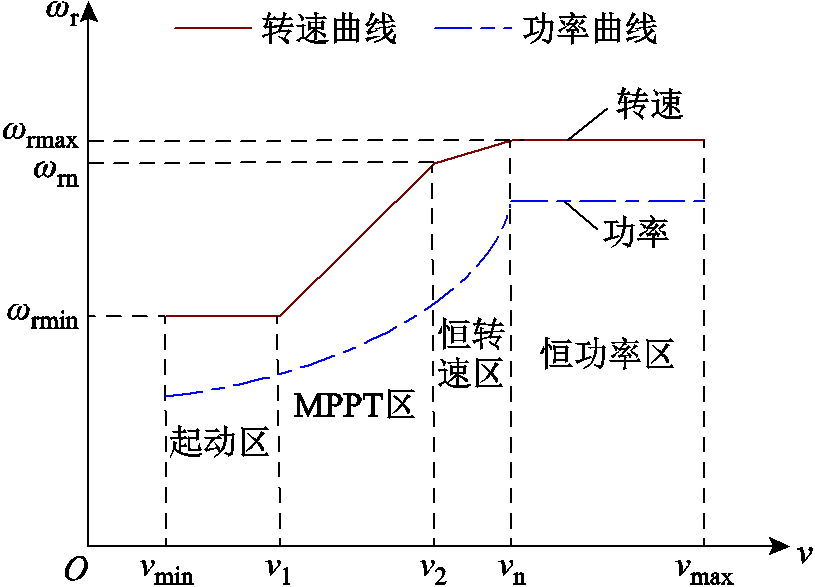
图3 风电机组的风速分区
Fig.3 Wind speed partiton diagram of wind turbine
针对MPPT区间，以二次函数曲线近似风机的机械功率曲线。曲线经过点(ωrmin, Pmin)和点(ωrmppt, Pmppt)，可得解析式为
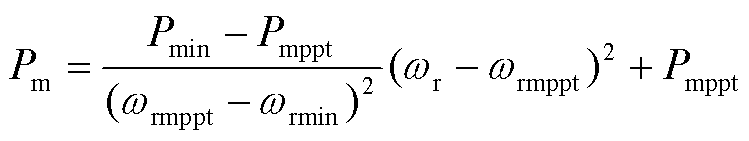（3）
式中，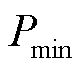
为风电机组最低转速对应的输出功率；
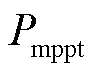为最优转速对应的输出功率。上述参数均取标幺值。
不同风速区间的曲线拟合效果如图4所示，图中实线为机械功率实际曲线，虚线为机械功率拟合曲线。在MPPT区间内的曲线拟合效果如图4a所示，可以看出Pm的拟合曲线与实际曲线几乎重合，拟合效果良好。同理针对恒转速区间，以二次函数曲线近似风机的机械功率曲线，拟合效果如图4b所示。Pm的拟合曲线与实际曲线几乎重合，拟合效果良好。
风电机组的机械功率损失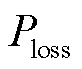
计算式为
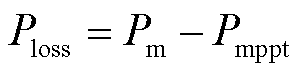（4）
将式（3）中的Pm化简式代入式（4）得
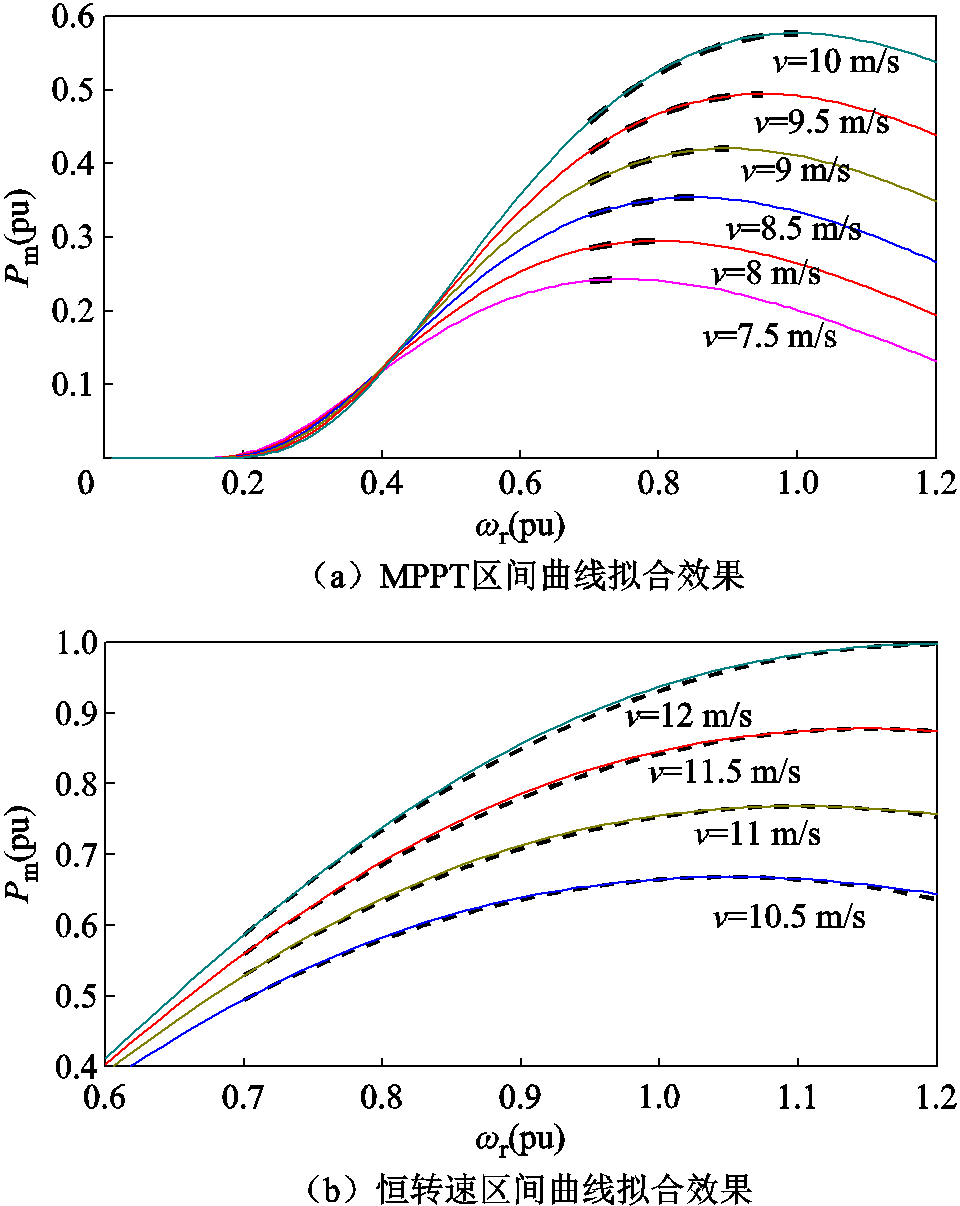
图4 不同风速区间的曲线拟合效果
Fig.4 Curve fitting effect of different wind speed partitons
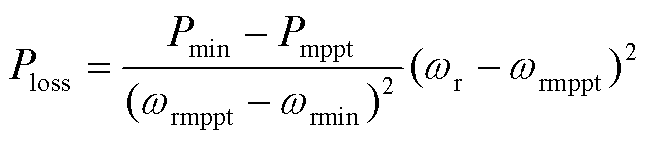（5）
本文将风电机组最低转速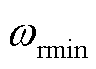
取值为0.7(pu)，根据式（5），只要风电机组选定，机组的机械功率损失就是关于转速的二次函数，从而可以求取不同风速下的机械功率损失。
风电机组的可用调频能量为机组释放的转子动能减去机械能损失，即
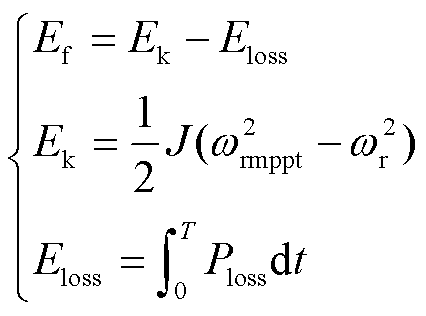（6）
式中，Ef为风电机组的可用调频能量；Ek为释放的转子动能；Eloss为机械能损失；J为转动惯量，T为平均调频时间，T=25 s。
由于能量变化不易量测，在实际工程中，获取和利用的通常是风电机组的功率，故本节给出风电机组可用调频功率Pf的标幺值计算式为
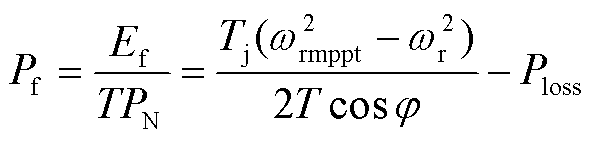（7）
式中，Tj为转子惯性时间常数，s；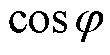
为风电机组的功率因数；PN为额定功率。
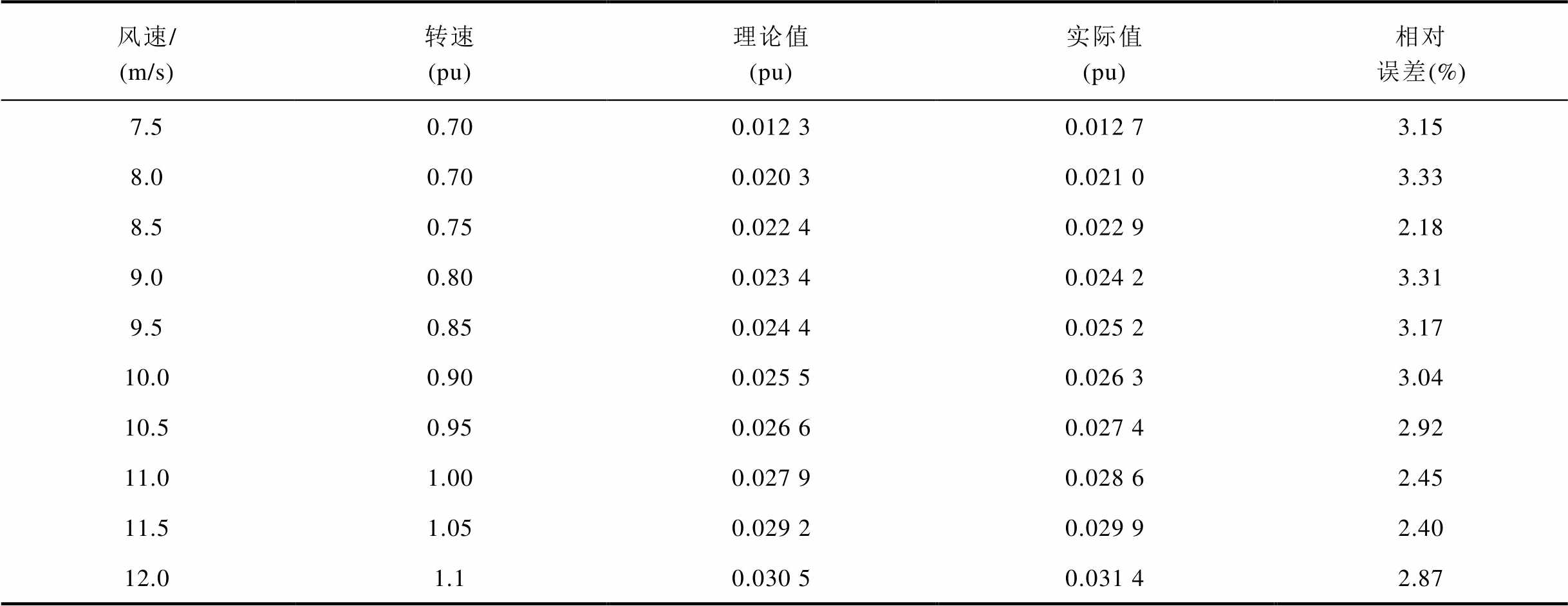
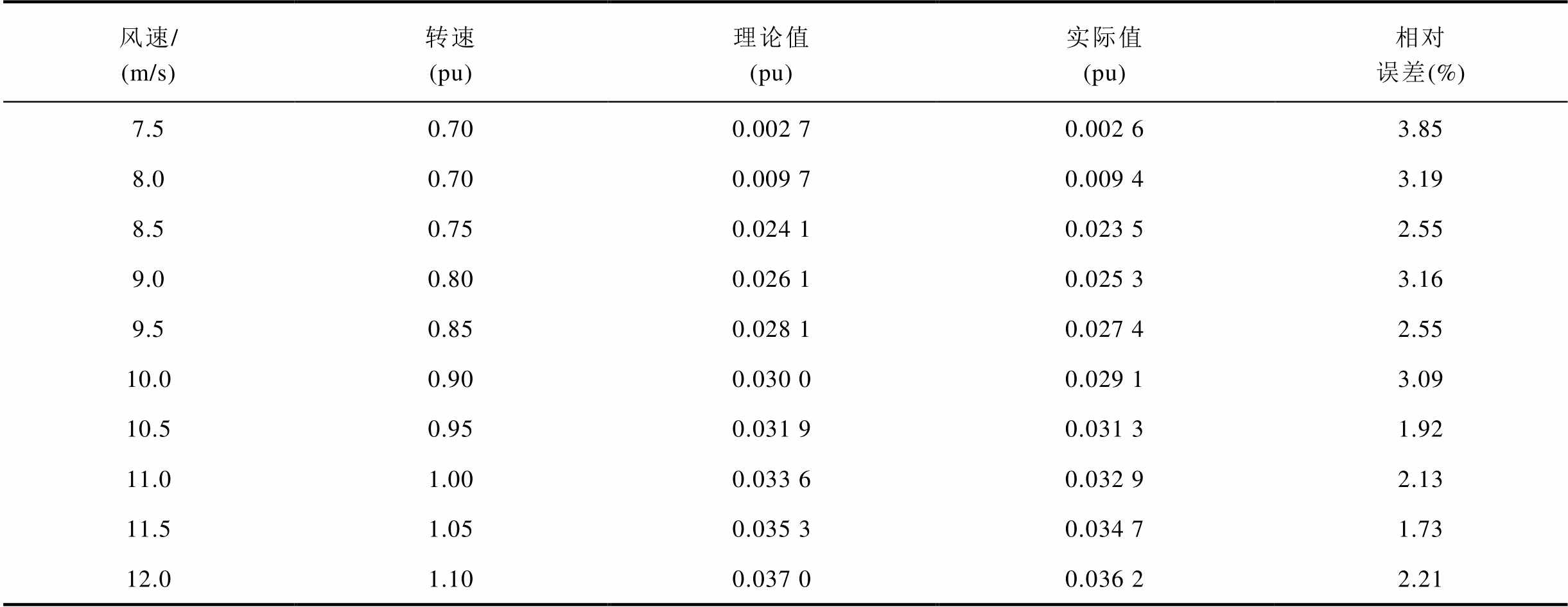
结合式（6）和式（7）可知，当风电机组选定时，可用调频能量只与风电机组的转速ωr有关。某2 MW双馈风机在不同风速下的最大可用调频功率的理论值和实际值对比及对应转子转速见表1，该风机在不同风速下的最大可用调频功率对应的机械功率损失见表2。
表1 某2 MW双馈风机的最大可用调频功率及转子转速
Tab.1 Maximum available frequency regulation power and corresponding rotor speed of a 2 MW doubly-fed induction generator
风速/(m/s)转速(pu)理论值(pu)实际值(pu)相对误差(%) 7.58.08.59.00.700.700.750.800.012 30.020 30.022 40.023 40.012 70.021 00.022 90.024 23.153.332.183.31 9.510.010.511.011.512.00.850.900.951.000.024 40.025 50.026 60.027 90.025 20.026 30.027 40.028 63.173.042.922.45 1.051.10.029 20.030 50.029 90.031 42.402.87
表2 某2 MW双馈风机的最大机械功率损失
Tab.2 Maximum mechanical power loss of a 2 MW doubly-fed induction generator
风速/(m/s)转速(pu)理论值(pu)实际值(pu)相对误差(%) 7.58.08.59.00.700.700.750.800.002 70.009 70.024 10.026 10.002 60.009 40.023 50.025 33.853.192.553.16 9.510.010.511.011.512.00.850.900.951.000.028 10.030 00.031 90.033 60.027 40.029 10.031 30.032 92.553.091.922.13 1.051.100.035 30.037 00.034 70.036 21.732.21
通过计算，表1中的理论值和实际值的绝对误差均不超过0.001(pu)，相对误差均不超过3.5%，说明所提出的可用调频功率与风速间的数学模型是合理的。同时由表1可知，风速越大，风电机组的最大可用调频功率越大，且对应的转速越高，意味着转速可变化范围越小。即使在12 m/s的额定风速下，可用调频功率最多也只有风机额定功率的3%。
通过计算，表2中的理论值和实际值的绝对误差均不超过0.001(pu)，相对误差均不超过4%，说明所提出的机械功率损失与风速间的数学模型是合理的。同时由表2可知，随着风速的增大，风电机组最大可用调频功率所对应的机械功率损失也逐渐增大，在12 m/s的额定风速下，机械功率损失可达风机额定功率的3.7%。
本节基于第2节的评估结果，建立了调频能量与控制参数的关系表达式，以频率最低点和频率平均变化率为优化对象，采用模糊逻辑控制方法得到综合控制效果最优时的控制参数整定值。
附加综合虚拟惯性控制的风机具备参与系统调频的能力，但是Kp、Kd取值不同，调频效果不同。
图5是当Kd为定值时，系统频率在不同Kp下的响应情况。由图5可知，随着Kp的增大，发生扰动后频率的最低点上升，频率变化率几乎没有变化；在第30 s进入转速恢复阶段后，频率二次跌落程度随着Kp的增大而加深，这是因为Kp越大，风机用于参与一次调频的转子动能越多，导致退出调频时系统的不平衡功率越大，从而加剧了频率二次跌落。
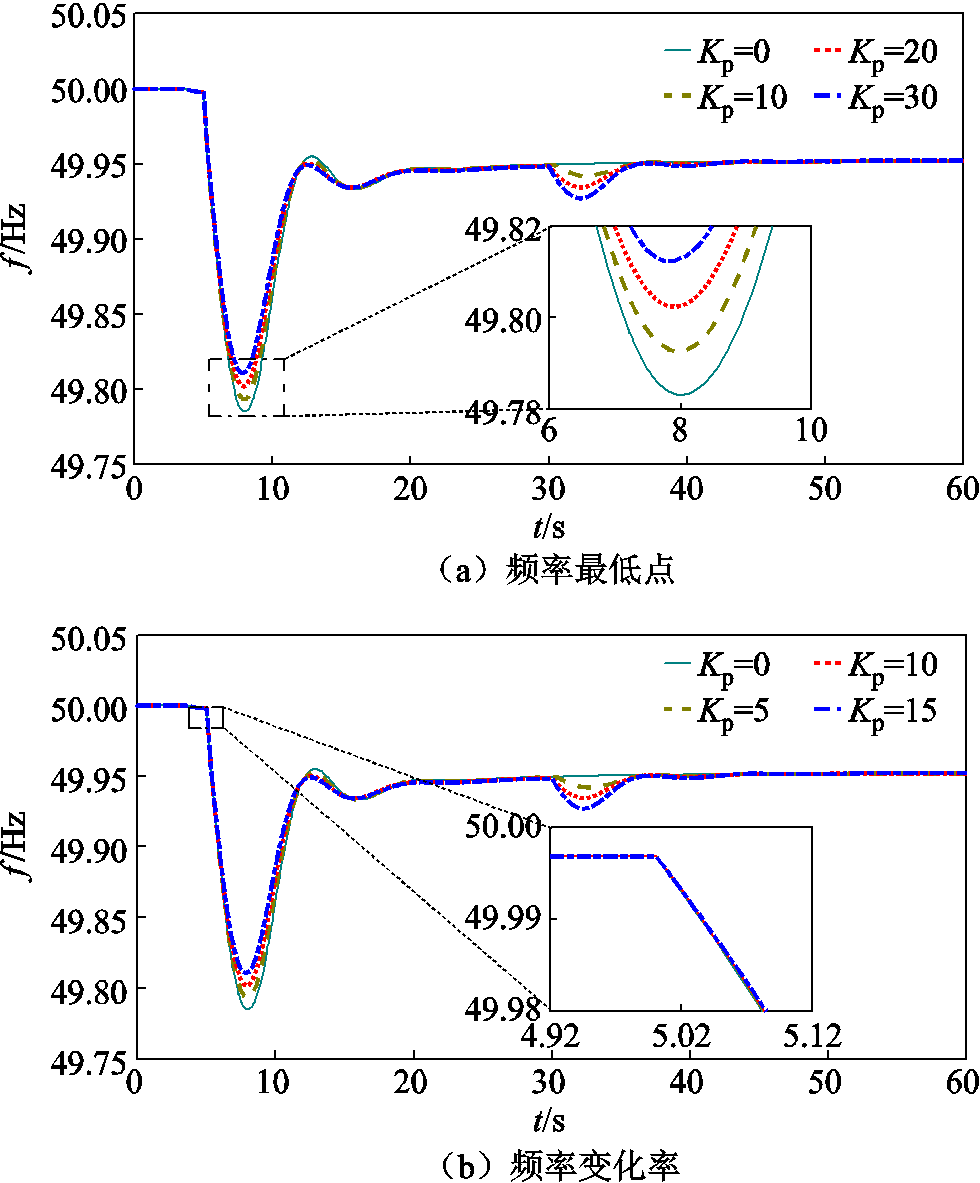
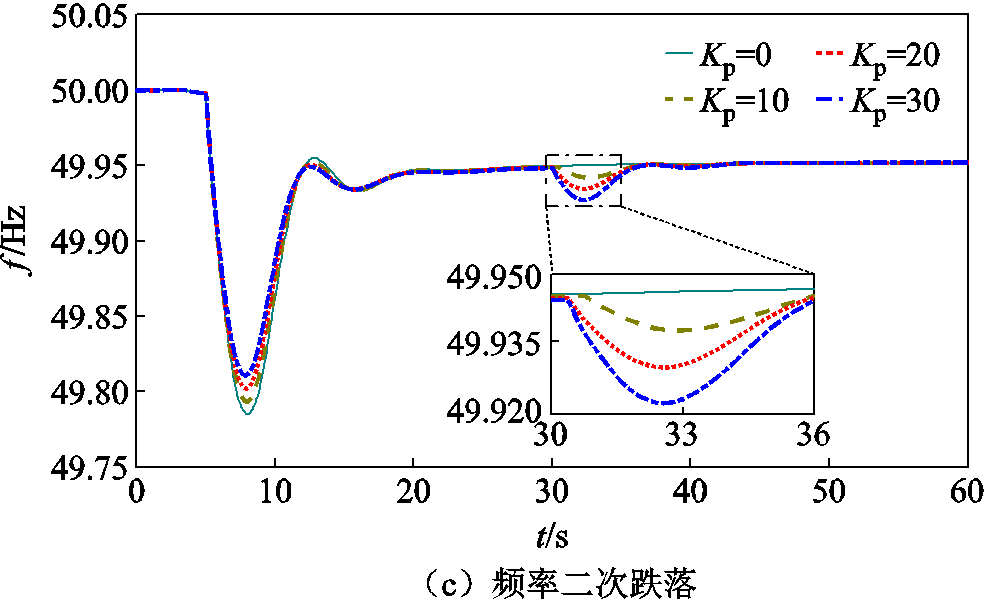
图5 不同Kp下的频率响应曲线
Fig.5 Frequency response curves for different Kp
图6是当Kp为定值时，系统频率在不同Kd下的响应情况。由图6可知，随着Kd的增大，发生扰动后频率的最低点上升，频率变化率降低，频率二次跌落的最低值几乎不受影响，频率响应特性得到有效改善。但Kd取值不易过大，这是为了避免风电机组参与调频时因增加的功率过多而导致变流装置容量越限。
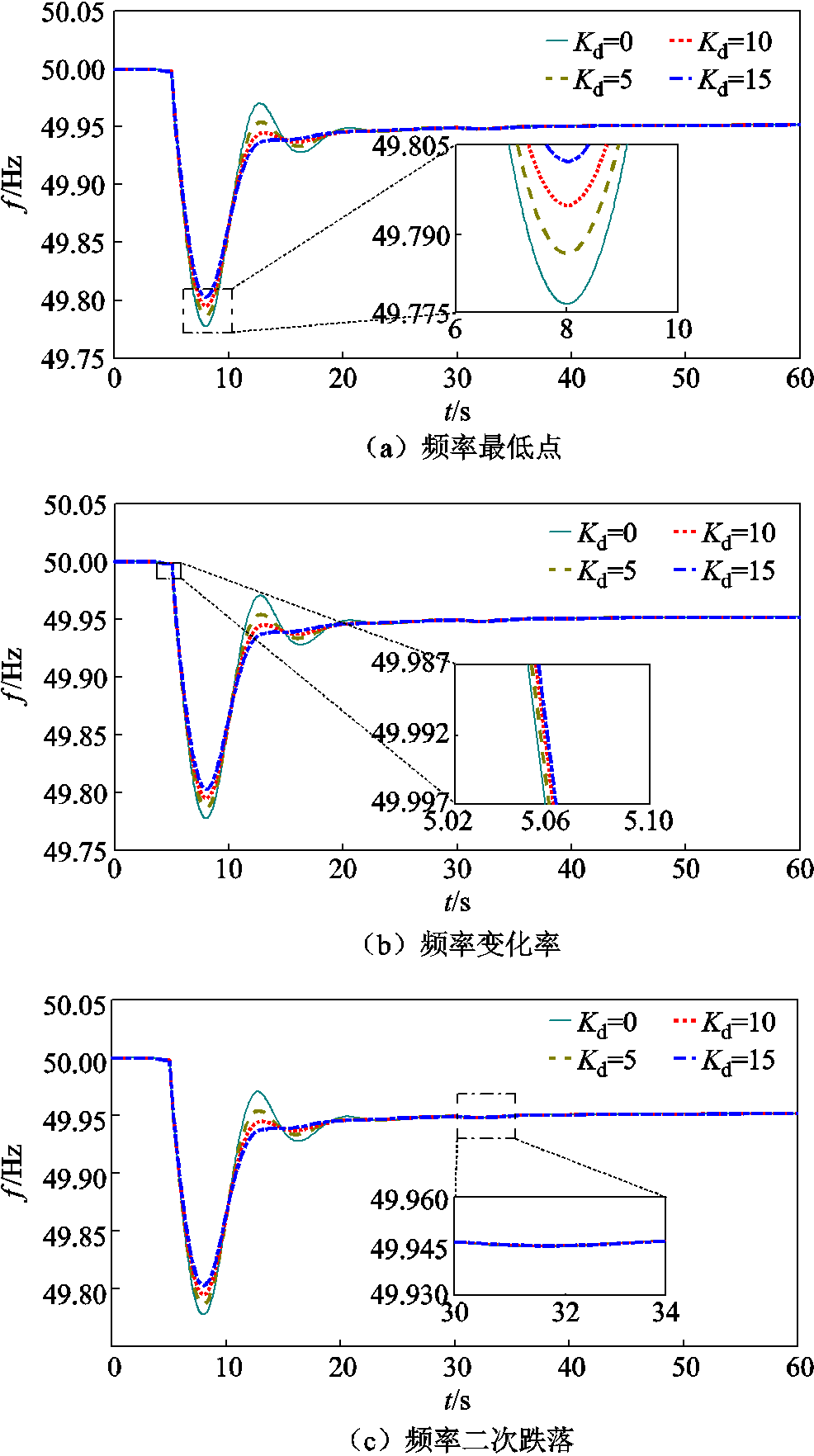
图6 不同Kd下的频率响应曲线
Fig.6 Frequency response curves for different Kd
不同的Kp、Kd取值对频率的调节效果不同，由第1节可知，调频效果本质上取决于调频能量的多少，因此需构建调频能量与控制参数之间的关系表达式。
3.2.1 调频能量与控制参数的关系表达式
同步机的频率调节效应系数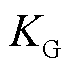
的含义是单位频率变化时的功率增量[17]，即
（8）
式中，ΔPG为同步机的调频功率增量；PGN为同步机的额定功率；fN为额定频率。
同步机惯量常数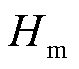
的物理意义是额定转速下转子具有的动能与额定容量的比值[19]，即
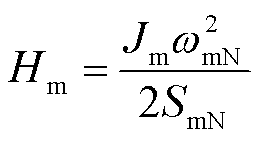（9）
式中，Jm为同步机的转动惯量；ωmN为额定转速；SmN为额定容量。
分别参照同步机的频率调节效应系数和惯量常数，定义风电机组的Kp和Kd [20-21]为
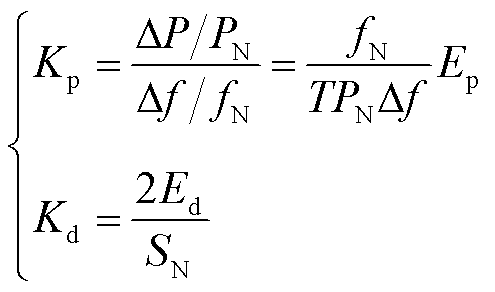（10）
式中，Ep为下垂控制分配到的能量；Ed为虚拟惯量控制分配到的能量；SN为风电机组额定容量。
对于综合虚拟惯性控制而言，风机的调频能量来源只有风机自身蕴含的转子动能，是分配给下垂控制和虚拟惯性控制的能量之和，即
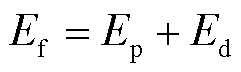（11）
联立式（10）和式（11）可得
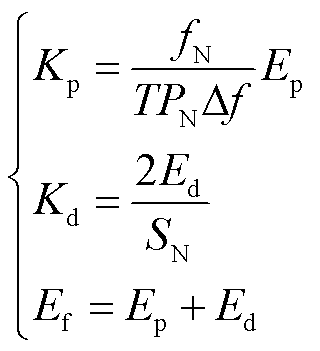（12）
发生扰动时，若调频时间T和频率变化量Δf确定，则Kp、Kd的取值只取决于风机能够提供的调频能量，且成正比。为方便计算，将式（12）转换成功率表示的计算式，有
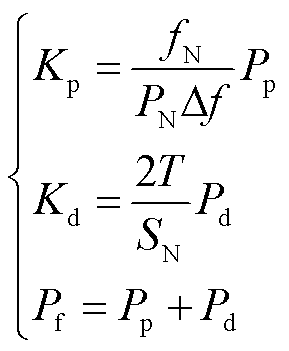（13）
式中，PP为下垂控制分配到的功率；Pd为虚拟惯性控制分配到的功率。
3.2.2 基于模糊逻辑控制的参数整定方法
电力系统运行情况多变，不同时间下系统对惯量响应和一次调频阶段的要求不一样，导致下垂系数和虚拟惯性系数选择存在差异。模糊逻辑控制使用语言方便、鲁棒性强，适用于时变、模型不完全、非线性的系统[22-24]。本节根据场景的不同需求，改变模糊控制规则，采用模糊逻辑控制整定控制参数。
当系统发生扰动而导致频率跌落时，通常将频率变化率、频率最低点和稳态频率作为系统频率响应特性的评价指标。由于风电机组只能提供短时有功支撑，后期需要进行转速恢复，故风电机组只参与系统的惯量响应和一次调频阶段，无法改善系统稳态频率，因此本文以系统频率变化率df/dt和频率最低点fmin为优化对象，而不考虑稳态频率。
从电网运行角度，当扰动很大时，频率下降很快，容易触发相应的保护装置。故本文对Kd采用模糊控制，将可用调频功率Pf、频率变化量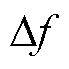和频率变化率df/dt作为模糊控制器输入，将Kd作为模糊控制器输出，模糊控制器的结构如图7所示。
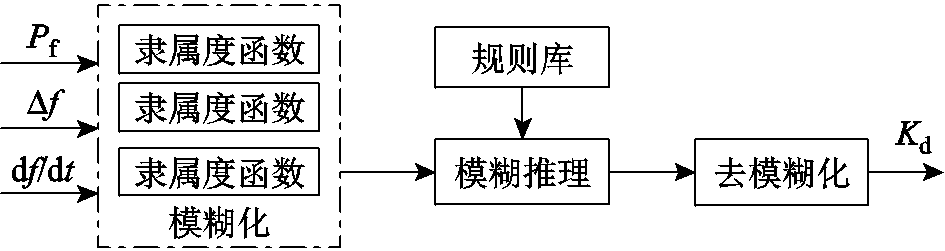
图7 模糊控制器的结构
Fig.7 Structure of fuzzy logic controller
本文只考虑发生功率扰动导致频率跌落的事件，依据2.2节计算得到的可用调频能量数值设置Pf的论域为[0, 0.03]，根据一次调频死区、低频减载第一道防线等工程实际要求设置Δf的论域为[-1, -0.033]，df/dt的论域为[-0.6, 0]，Kd的论域为[5, 20]。其中，Pf的模糊集为{RS(较小), M(中), RB(较大)}，Δf、df/dt、Kd的模糊集均为{VS(很小), RS(较小), M(中), RB(较大), VB(很大)}，以上各输入、输出量的隶属度函数曲线如图8所示。
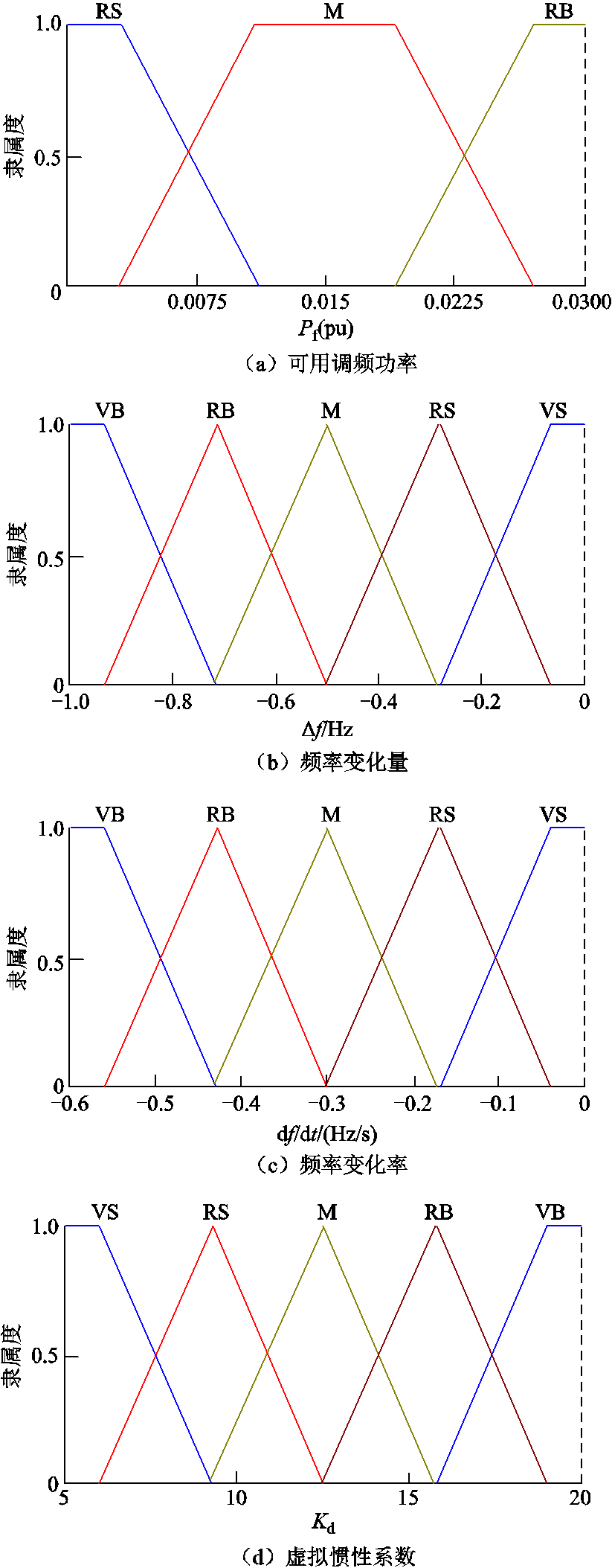
图8 输入、输出变量的隶属度函数
Fig.8 Membership function of input and output variables
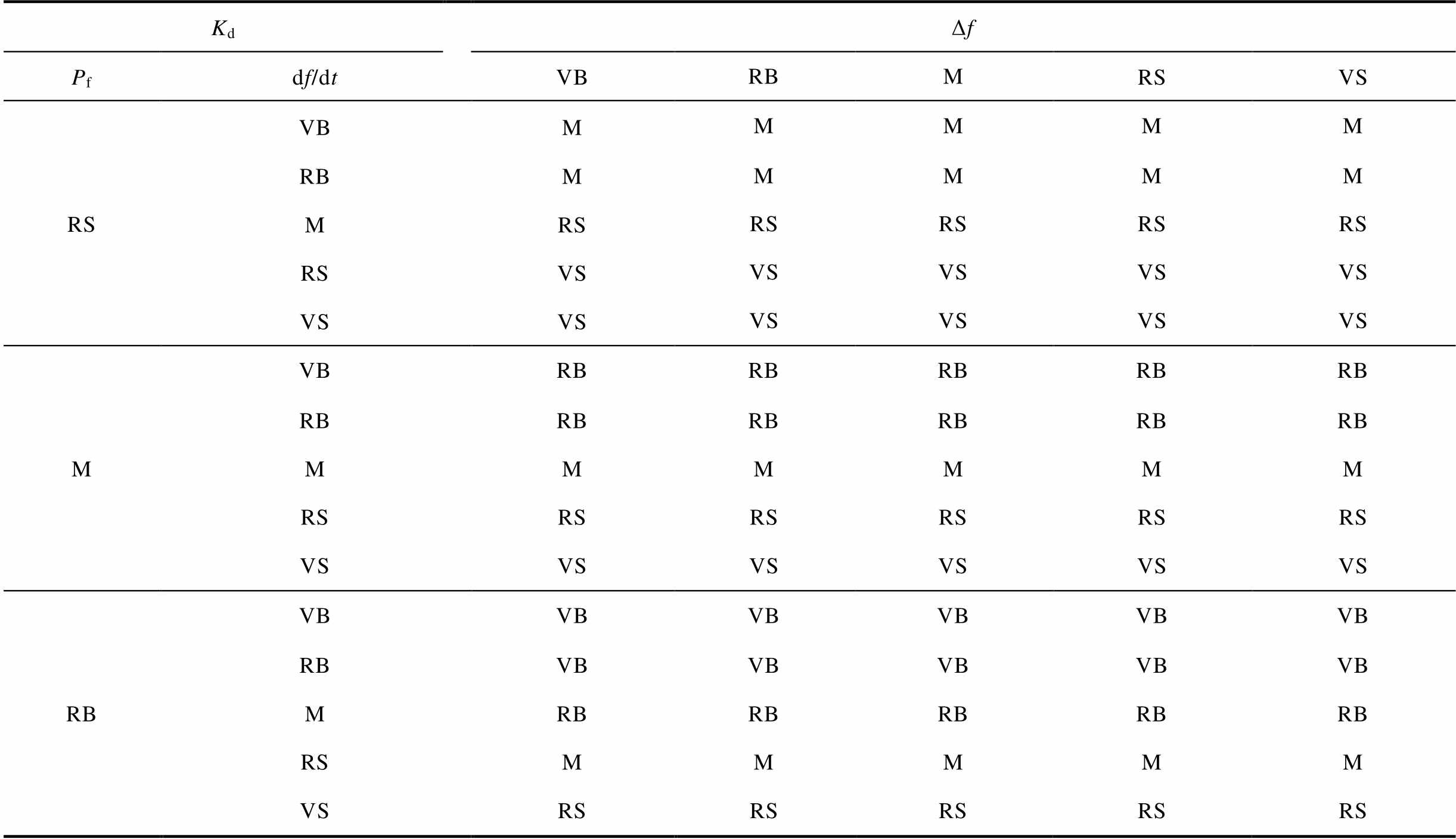
考虑不同场景下的调频优先等级，建立模糊控制规则见表3，模糊控制器实时判断风电机组可用调频功率Pf、系统的频率变化量Δf和频率变化率df/dt的大小，选定当前的模糊规则。当df/dt变化得快时，应尽量将有限的调频能量用于减缓频率的快速变化，即Kd取值偏大一些；若df/dt变化得慢，则尽量将有限的调频能量用于提升频率最低点，即Kd取值偏小一些。采用重心法去模糊化，可以得到不同情况下的虚拟惯性系数Kd的整定值，继而由式（13）能够计算出虚拟惯性控制分配到的功率Pd，进一步计算出下垂控制分配到的能量Pp以及下垂系数Kp的整定值。
表3 模糊逻辑规则
Tab.3 Fuzzy control rule
KdΔf Pfdf/dtVBRBMRSVS RSVBMMMMM RBMMMMM MRSRSRSRSRS RSVSVSVSVSVS VSVSVSVSVSVS MVBRBRBRBRBRB RBRBRBRBRBRB MMMMMM RSRSRSRSRSRS VSVSVSVSVSVS RBVBVBVBVBVBVB RBVBVBVBVBVB MRBRBRBRBRB RSMMMMM VSRSRSRSRSRS
为验证本文所提出的基于可用调频能量的风电机组综合虚拟惯性控制参数整定方法的有效性和可行性，在Matlab/Simulink仿真平台搭建3机9节点系统如图9所示。系统包含2台同步机组G1、G2，1个由50台2 MW双馈风机构成的风电等值机组G3，双馈风机均施加了综合虚拟惯性控制，系统风电渗透率为38.5%，仿真系统参数详见附表1。在仿真时间5 s时，负荷Load1突增40 MW，仿真时长为40 s。
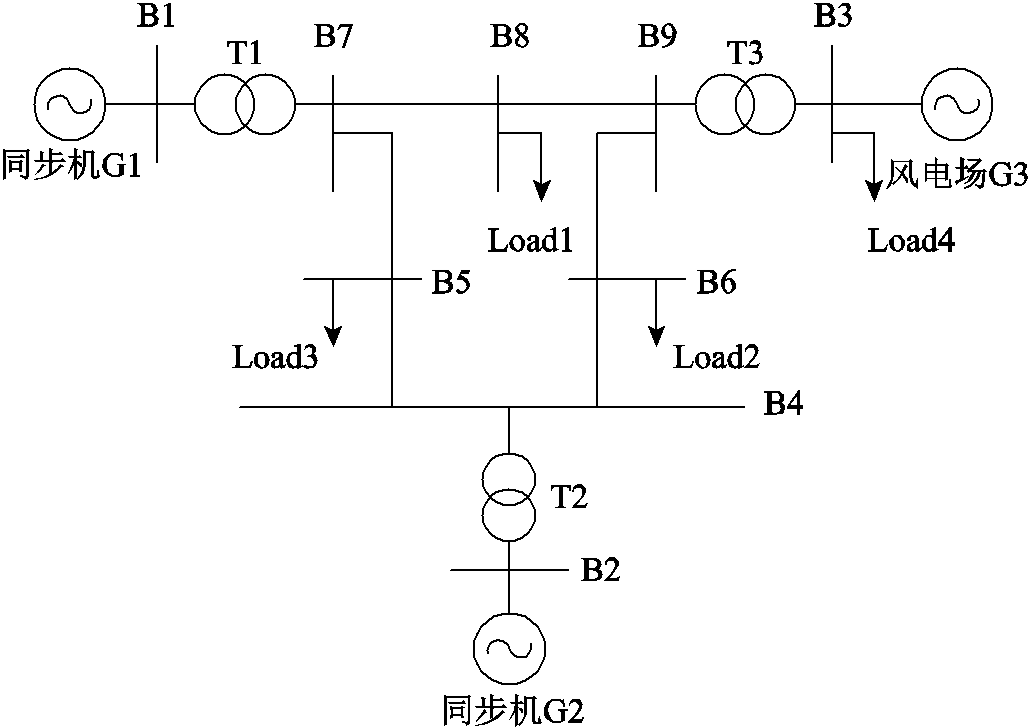
图9 仿真系统
Fig.9 Simulation system
设置如下四个算例，并在MPPT区间和恒转速区间内的不同风速下进行验证。
算例1：风电机组无任何附加控制，始终运行在MPPT状态。
算例2：风电机组附加定系数综合虚拟惯性控制，其中Kp=20、Kd=5。
算例3：风电机组附加变系数综合虚拟惯性控制，采用文献[17]提出的根据同步机能量分配机制分配调频能量的方法整定Kp、Kd。
算例4：风电机组附加变系数综合虚拟惯性控制，采用本文提出的方法整定Kp、Kd。
设置风电等值机组的初始风速为9 m/s。根据3.2.1节设置，算例3中Kp=17.98、Kd=3.83，算例4中Kp=15.35、Kd=4.78。四个算例对应的频率响应过程和风机转速变化如图10所示，仿真结果见表4。
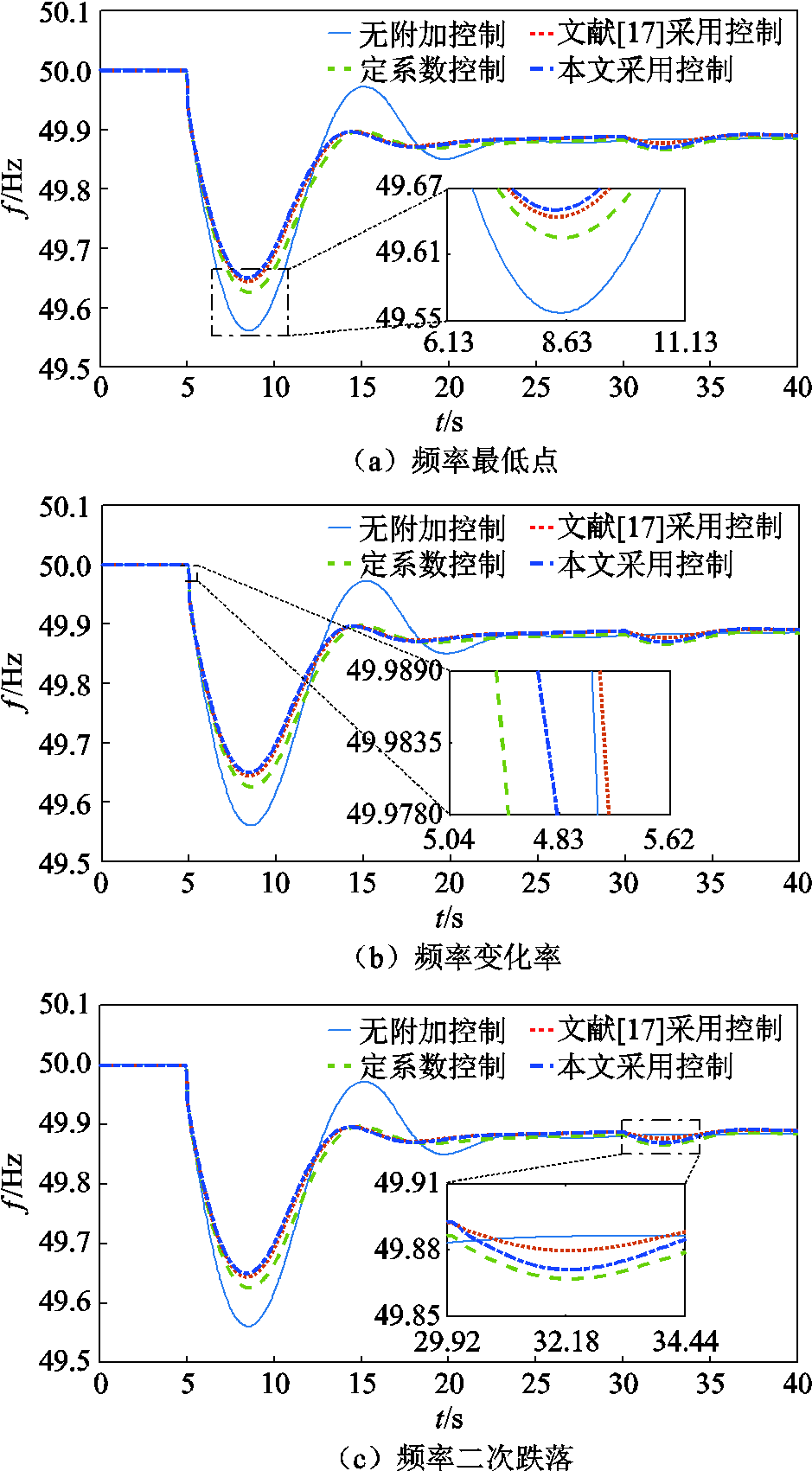
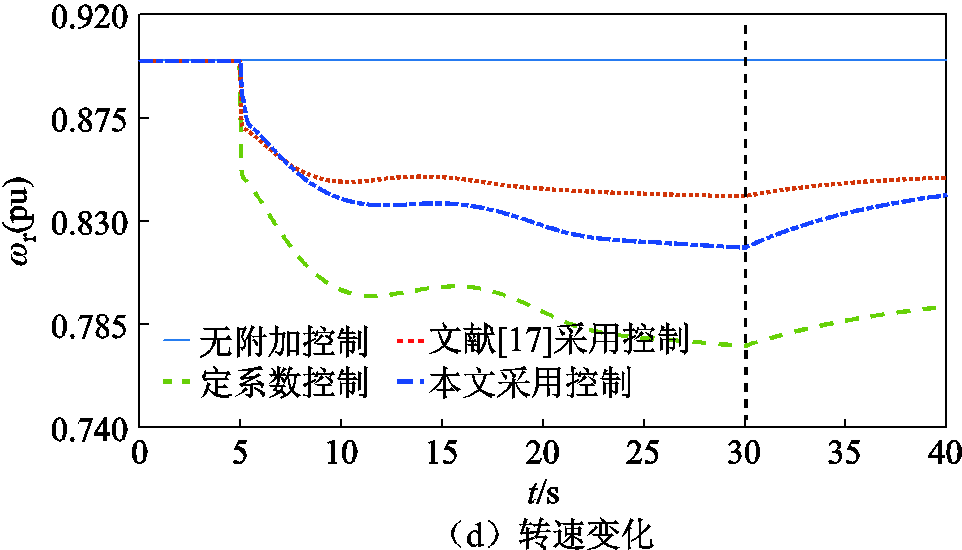
图10 9 m/s下不同算例的仿真曲线
Fig.10 Simulation curves for different examples at 9 m/s
表4 9 m/s风速下的仿真结果
Tab.4 Simulation results at 9 m/s wind speed
算例频率最低点/Hz频率变化率/(Hz/s)频率二次跌落/Hz转速(pu) 149.5610.324—0.9 249.6260.2790.018 20.776 349.6440.2750.015 20.841 449.6510.2410.016 70.819
对比图10及表4中的四个算例可以发现，无附加控制的风机转速会维持在0.9(pu)，保持MPPT运行状态，不响应系统频率变化。其余三个算例中的风机均通过释放转子动能参与了频率调节过程，频率最低点和频率变化率都得到了明显改善。其中，相比于算例2中的定系数控制，考虑了可用调频能量的算例3和算例4的频率最低点上升得更多，频率变化更缓慢，因而频率调节效果更好。
当风机采用定系数控制时，由于控制参数未与风机当前运行状态下的实际调频能力相匹配，参数过大导致风机转速下降至0.776(pu)，超出9 m/s风速下最大可用调频能量对应的转速0.8(pu)，不仅调频效果变差，还因过度释放转子动能而加剧了频率二次跌落，不利于后期风机的转速恢复。由图10和表4可知，本文提出的基于可用调频能量的参数整定方法可以弥补这一缺陷，在最大可用调频能量对应的转速约束下，最大程度地利用了转子动能改善频率最低点和频率变化率。同时相比于文献[17]中所采用的同步机能量分配机制，本文提出的基于模糊逻辑控制的调频能量分配规则能够根据系统的实际运行场景确定调频优先等级，更合理地分配提供给惯量响应和一次调频阶段的能量，转子动能释放程度更深，对可用调频能量的利用更充分，调频效果更好。
设置风电等值机组的初始风速为11 m/s。根据3.2.1节设置，算例3中Kp=28.42、Kd=12.55，算例4中Kp=30.07、Kd=10.12。四个算例对应的频率响应过程和风机转速变化过程如图11所示，仿真结果见表5。
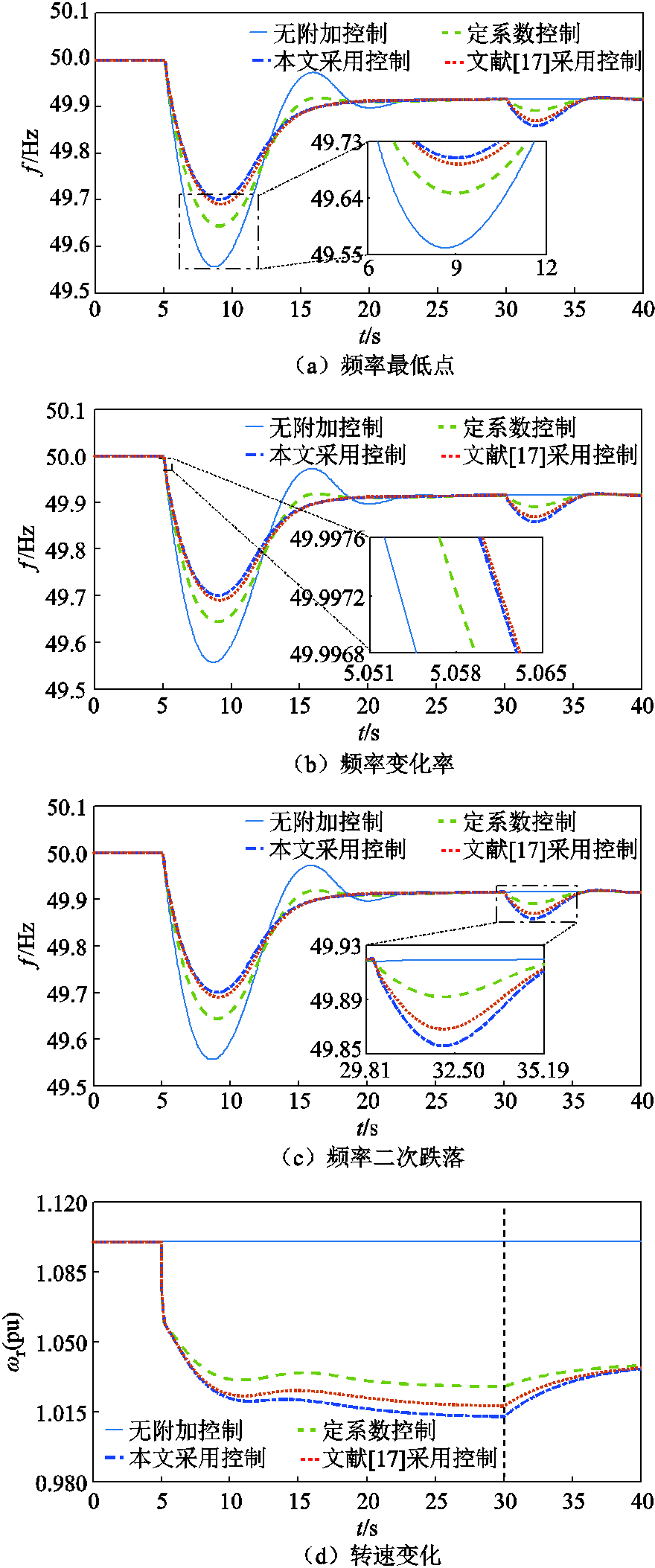
图11 11 m/s下不同算例的仿真曲线
Fig.11 Simulation curves for different examples at 11 m/s
对比图11及表5中的四个算例可以发现，无附加控制的风机转速会维持在1.1(pu)，保持MPPT运行状态，不响应系统频率变化。其余三个算例中的风机均通过释放转子动能参与了频率调节过程，频率最低点和频率变化率都得到了明显改善。其中，相比于算例2中的定系数控制，考虑了可用调频能量的算例3和算例4的频率最低点上升得更多，频率变化更缓慢，因而频率调节效果更好。
表5 11 m/s风速下的仿真结果
Tab.5 Simulation results at 11 m/s wind speed
算例频率最低点/Hz频率变化率/(Hz/s)频率二次跌落/Hz转速(pu) 149.5570.327—1.1 249.6450.2860.0241.029 349.6910.2290.0451.019 449.7010.2340.0561.013
当风机采用定系数控制时，同样由于控制参数未与风机当前运行状态下的实际调频能力相匹配，参数设置过小导致风机释放的转子动能较少，没有充分利用风机的调频能量，造成了调频资源浪费，调频效果不理想。由图11和表5可知，本文提出的基于可用调频能量的参数整定方法可以弥补这一缺陷，在不超出最大可用调频能量对应的转速范围内，能够最大程度地利用转子动能，有效地改善频率最低点和频率变化率。同时相比于文献[17]中所采用的同步机能量分配机制，本文提出的基于模糊逻辑控制的调频能量分配规则能够根据系统的实际运行场景确定调频优先等级，更合理地分配提供给惯量响应和一次调频阶段的能量，转子动能释放程度更深，对可用调频能量的利用更充分，调频效果更好。
因此，在不同的风速区间内，本文提出的基于可用调频能量的风电机组综合虚拟惯性控制参数整定方法均能够匹配控制参数与风机实际调频能力，根据系统扰动和频率响应情况合理地分配提供给惯量响应和一次调频阶段的能量，最大程度地利用可用转子动能，改善频率最低点和频率变化率，验证了本文所提参数整定方法在不同风速下均具有较强的适应性。
本文从能量角度有效地评估了附加综合虚拟惯性控制的风电机组在不同风速下的调频能力，并采用模糊逻辑控制提出一种基于可用调频能量的风电机组综合虚拟惯性控制参数整定方法，经过算例验证得到以下结论：
1）综合考虑风电机组释放的转子动能和机械能损失，提出风电机组调频能力的评估方法。根据推导的风电机组机械能损失和可用转子动能与风速之间的数学模型发现，风速越大，最大可用调频能量越大且对应的转速越高，转速变化范围越小，机械能损失越多。
2）基于可用调频能量，综合考虑频率最低点和频率变化率，采用模糊逻辑控制整定控制参数的方法可以使得综合调频效果最好，最大程度地利用风电机组的调频能力。同时可为如何制定风电机组综合虚拟惯性控制的能量分配机制提供研究思路。
本文提出的参数整定方法主要从能量角度匹配综合虚拟惯性控制参数与风电机组的实际调频能力，只关注惯量响应和一次调频阶段，缺少对转速恢复阶段的频率二次跌落问题的考虑，后续工作会针对该问题进行深入研究。
附 录
附表1 仿真算例系统参数
App.Tab.1 Simulation example system parameters
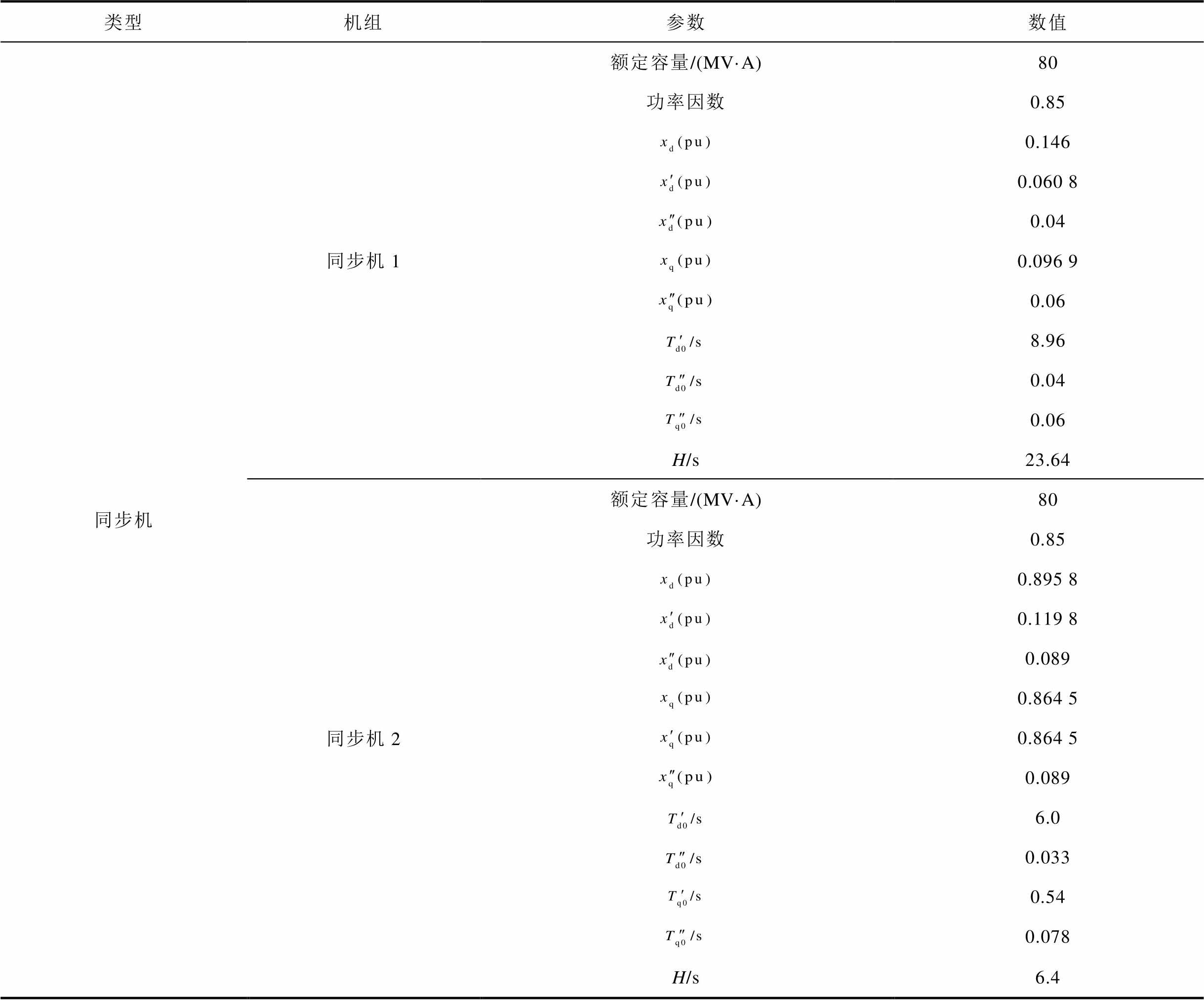
类型机组参数数值 同步机同步机1额定容量/(MV·A)80 功率因数0.85 0.146 0.060 8 0.04 0.096 9 0.06 8.96 0.04 0.06 H/s23.64 同步机2额定容量/(MV·A)80 功率因数0.85 0.895 8 0.119 8 0.089 0.864 5 0.864 5 0.089 6.0 0.033 0.54 0.078 H/s6.4
（续）
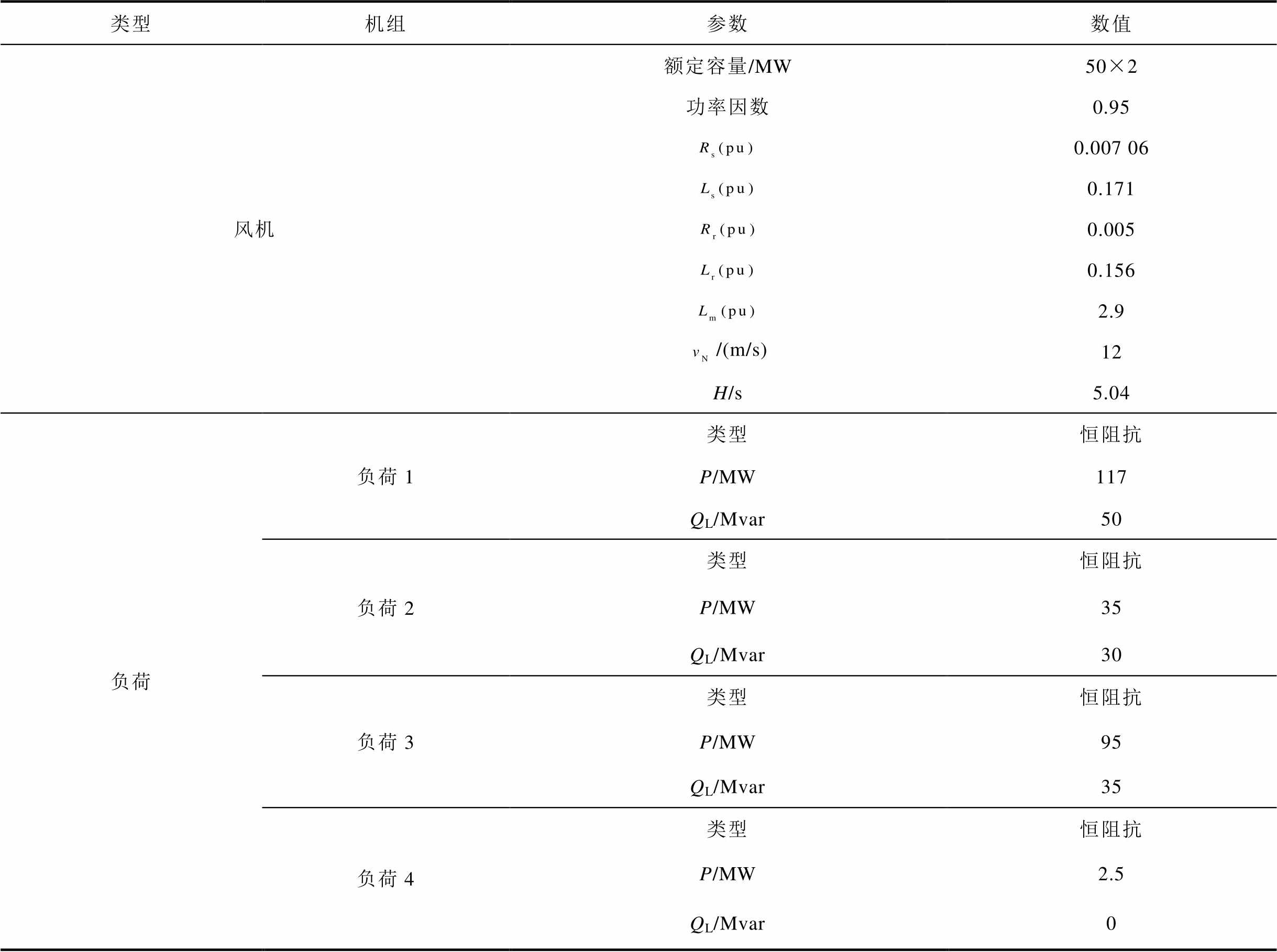
类型机组参数数值 风机额定容量/MW功率因数/(m/s)H/s50×20.950.007 060.1710.0050.1562.9125.04 负荷负荷1类型恒阻抗 P/MW117 QL/Mvar50 负荷2类型恒阻抗 P/MW35 QL/Mvar30 负荷3类型恒阻抗 P/MW95 QL/Mvar35 负荷4类型恒阻抗 P/MW2.5 QL/Mvar0
参考文献
[1] 李军徽, 安晨宇, 李翠萍, 等. 计及调峰市场交易的储能-新能源-火电多目标优化调度[J]. 电工技术学报, 2023, 38(23): 6391-6406. Li Junhui, An Chenyu, Li Cuiping, et al. Multi-objective optimization scheduling method considering peak regulating market transactions for energy storage-new energy-thermal power[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6391-6406.
[2] 安军, 周永超, 周毅博, 等. 考虑风荷不确定性的电源无功电压调差系数整定方法研究[J]. 东北电力大学学报, 2023, 43(4): 30-38. An Jun, Zhou Yongchao, Zhou Yibo, et al. Optimization method for var-voltage adjustment CoefficientConsidering wind power and load uncertainty[J]. Journal of Northeast Electric Power University, 2023, 43(4): 30-38.
[3] Fradley J, Preece R, Barnes M. The influence of network factors on frequency stability[J]. IEEE Transactions on Power Systems, 2020, 35(4): 2826-2834.
[4] 李兆伟, 吴雪莲, 庄侃沁, 等. “9·19”锦苏直流双极闭锁事故华东电网频率特性分析及思考[J]. 电力系统自动化, 2017, 41(7): 149-155. Li Zhaowei, Wu Xuelian, Zhuang Kanqin, et al. Analysis and reflection on frequency characteristics of East China grid after bipolar locking of “9·19” Jinping-Sunan DC transmission line[J]. Automation of Electric Power Systems, 2017, 41(7): 149-155.
[5] 方勇杰. 英国“8·9”停电事故对频率稳定控制技术的启示[J]. 电力系统自动化, 2019, 43(24): 1-5. Fang Yongjie. Reflections on frequency stability control technology based on the blackout event of 9 August 2019 in UK[J]. Automation of Electric Power Systems, 2019, 43(24): 1-5.
[6] 孙华东, 许涛, 郭强, 等. 英国“8·9”大停电事故分析及对中国电网的启示[J]. 中国电机工程学报, 2019, 39(21): 6183-6192. Sun Huadong, Xu Tao, Guo Qiang, et al. Analysis on blackout in great Britain power grid on August 9th, 2019 and its enlightenment to power grid in China[J]. Proceedings of the CSEE, 2019, 39(21): 6183-6192.
[7] 谢震, 杨曙昕, 代鹏程, 等. 构网型全功率风电机组网侧变流器耦合分析及抑制策略[J]. 电工技术学报, 2023, 38(14): 3745-3758, 3768. Xie Zhen, Yang Shuxin, Dai Pengcheng, et al. Grid-side coupling analysis and suppression strategy of grid-forming full-power wind turbines[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3745-3758, 3768.
[8] 王勤赫, 边竞, 齐文博, 等. 大规模风电经VSC-HVDC接入的电网频率控制策略[J]. 东北电力大学学报, 2023, 43(4): 74-81. Wang Qinhe, Bian Jing, Qi Wenbo, et al. The frequency control strategy of the grid connected to large-scale wind power via VSC-HVDC[J]. Journal of Northeast Electric Power University, 2023, 43(4): 74-81.
[9] 张冠锋, 杨俊友, 孙峰, 等. 基于虚拟惯量和频率下垂控制的双馈风电机组一次调频策略[J]. 电工技术学报, 2017, 32(22): 225-232. Zhang Guanfeng, Yang Junyou, Sun Feng, et al. Primary frequency regulation strategy of DFIG based on virtual inertia and frequency droop control[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 225-232.
[10] Morren J, de Haan S W H, Kling W L, et al. Wind turbines emulating inertia and supporting primary frequency control[J]. IEEE Transactions on Power Systems, 2006, 21(1): 433-434.
[11] 胡正阳, 高丙团, 张磊, 等. 风电机组双向支撑能力分析与自适应惯量控制策略[J]. 电工技术学报, 2023, 38(19): 5224-5240. Hu Zhengyang, Gao Bingtuan, Zhang Lei, et al. Bidirectional support capability analysis and adaptive inertial control strategy of wind turbine[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5224-5240.
[12] 颜湘武, 崔森, 常文斐. 考虑储能自适应调节的双馈感应发电机一次调频控制策略[J]. 电工技术学报, 2021, 36(5): 1027-1039. Yan Xiangwu, Cui Sen, Chang Wenfei. Primary frequency regulation control strategy of doubly-fed induction generator considering supercapacitor SOC feedback adaptive adjustment[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 1027-1039.
[13] 王同森, 程雪坤. 计及转速限值的双馈风机变下垂系数控制策略[J]. 电力系统保护与控制, 2021, 49(9): 29-36. Wang Tongsen, Cheng Xuekun. Variable droop coefficient control strategy of a DFIG considering rotor speed limit[J]. Power System Protection and Control, 2021, 49(9): 29-36.
[14] 王鑫, 杨德健. 基于变系数PI控制的双馈风电机组自适应转速恢复策略[J]. 电工技术学报, 2023, 38(15): 4120-4129. Wang Xin, Yang Dejian. Adaptive speed recovery strategy of doubly-fed induction generator based on variable PI control coefficient[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4120-4129.
[15] 颜湘武, 孙雪薇, 崔森, 等. 基于转子动能与超级电容器储能的双馈风电机组惯量和一次调频改进控制策略[J]. 电工技术学报, 2021, 36(增刊1): 179-190. Yan Xiangwu, Sun Xuewei, Cui Sen, et al. Improved control strategy for inertia and primary frequency regulation of doubly fed induction generator based on rotor kinetic energy and supercapacitor energy storage[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 179-190.
[16] Lee J, Muljadi E, Srensen P, et al. Releasable kinetic energy-based inertial control of a DFIG wind power plant[J]. IEEE Transactions on Sustainable Energy, 2016, 7(1): 279-288.
[17] 张峰, 李柏慷, 丁磊. 考虑风电调频能量联动分配的时变调频参数设定方法[J]. 电力系统自动化, 2022, 46(16): 188-197. Zhang Feng, Li Baikang, Ding Lei. Parameter setting method of time-varing frequency regulation considering linked energy distribution of wind power for frequency regulation[J]. Automation of Electric Power Systems, 2022, 46(16): 188-197.
[18] 彭勃, 张峰, 梁军. 考虑风速分区的风-储系统短期频率响应协同控制策略[J]. 电力系统自动化, 2018, 42(8): 57-65. Peng Bo, Zhang Feng, Liang Jun. Coordinated control strategy for short-term frequency response of wind-energy storage system considering wind speed partition[J]. Automation of Electric Power Systems, 2018, 42(8): 57-65.
[19] 闵勇, 陈磊, 刘瑞阔, 等. 电力系统频率动态中惯量与惯量响应特性辨析[J]. 中国电机工程学报, 2023, 43(3): 855-868. Min Yong, Chen Lei, Liu Ruikuo, et al. Analysis on characteristics of inertia and inertial response in power system frequency dynamics[J]. Proceedings of the CSEE, 2023, 43(3): 855-868.
[20] 张祥宇, 胡剑峰, 付媛, 等. 风储联合系统的虚拟惯量需求与协同支撑[J]. 电工技术学报, 2024, 39(3): 672-685. Zhang Xiangyu, Hu Jianfeng, Fu Yuan, et al. Virtual inertia demand and collaborative support of wind power and energy storage system[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 672-685.
[21] 安军, 盛帅, 周毅博, 等. 基于量测数据的风电场等效虚拟惯量评估方法[J]. 电网技术, 2023, 47(5): 1819-1829. An Jun, Sheng Shuai, Zhou Yibo, et al. Evaluation of equivalent virtual inertia of wind farm based on measured data[J]. Power System Technology, 2023, 47(5): 1819-1829.
[22] 郭慧, 汪飞, 顾永文, 等. 基于电压分层控制的直流微电网及其储能扩容单元功率协调控制策略[J]. 电工技术学报, 2022, 37(12): 3117-3131. Guo Hui, Wang Fei, Gu Yongwen, et al. Coordinated power control strategy for DC microgrid and storage expansion unit based on voltage hierarchical control[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3117-3131.
[23] 林莉, 林雨露, 谭惠丹, 等. 计及SOC自恢复的混合储能平抑风电功率波动控制[J]. 电工技术学报, 2024, 39(3): 658-671. Lin Li, Lin Yulu, Tan Huidan, et al. Hybrid energy storage control with SOC self-recovery to smooth out wind power fluctuations[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 658-671.
[24] 毛志宇, 李培强, 郭思源. 基于自适应时间尺度小波包和模糊控制的复合储能控制策略[J]. 电力系统自动化, 2023, 47(9): 158-165. Mao Zhiyu, Li Peiqiang, Guo Siyuan. Control strategy of composite energy storage based on wavelet packet with adaptive time scale and fuzzy control[J]. Automation of Electric Power Systems, 2023, 47(9): 158-165.
Abstract The additional integrated virtual inertia control of wind turbine is an important measure to improve the frequency stability of new type power system. It is of great significance to evaluate the frequency regulation capability of wind turbine under this control effectively and make full use of the frequency regulation capability by setting control parameters reasonably, hence, an integrated virtual inertia control parameter setting method for wind turbine based on available frequency regulation energy is proposed.
Firstly, considering the mechanical energy loss, a mathematical model describing the relationship between available rotor kinetic energy and rotor speed is constructed from the perspective of energy, and the effect of wind speed on available rotor kinetic energy is discovered. Secondly, the available frequency regulation energy is converted into available frequency regulation power, so that the relationship between the available frequency regulation power and wind speed can be described intuitively. On this basis, in order to make full use of the available frequency regulation power, the relational expression between the frequency regulation power and the control parameters is established. Considering the frequency regulation requirements in different scenarios, the fuzzy control rules are designed, and the control parameter setting values are obtained by using the fuzzy logic control method when the comprehensive effect of the system frequency change rate and the lowest frequency is optimal. Finally, the proposed method is applied to a 3-machines 9-nodes system, and the effectiveness of the proposed method is verified by simulation.
It is found that the maximum available frequency regulation power of wind turbine increases with the increase of wind speed. Under rated wind speed, the maximum available frequency regulation power of 2 MW wind turbine is 3% of rated power. In the simulation example, the proposed parameter setting method is compared with those without additional control, constant coefficient control and the parameter setting method of energy distribution mechanism of synchronous machine. The simulation results show that, at low wind speed, the method that does not consider the available frequency regulation energy exceeds the rotor speed limit corresponding to the maximum available frequency regulation energy due to the large parameter setting, and not only the frequency regulation effect becomes worse, moreover, the secondary frequency drop is aggravated due to excessive release of kinetic energy of rotor. At high wind speed, the parameter setting is too small, so the kinetic energy of the rotor is not fully utilized. When the available frequency regulation energy is considered, the rotor kinetic energy can be utilized to the maximum extent within the rotor speed limit of the wind turbine, and the frequency regulation effect is better. At the same time, compared with the energy distribution mechanism of synchronous machine, the proposed parameter setting method based on fuzzy control can consider the adjustment requirements of the frequency change rate and the lowest frequency under different scenarios, and determine the priority of frequency regulation, so as to optimize the comprehensive control effect of the system.
The following conclusions can be obtained through the analysis and verification: (1) The mathematical model of available frequency regulation power of wind turbine considering mechanical energy loss can directly describe the relationship between available frequency regulation power of wind turbine and wind speed. (2) Considering the frequency regulation requirements under different scenarios, the proposed parameter setting method can flexibly adjust the integrated virtual inertia control parameters, and maximize the frequency regulation capability of wind turbine on the basis of ensuring operation safety.
keywords：Wind turbine, integrated virtual inertia control, available frequency regulation energy, parameter setting
DOI:10.19595/j.cnki.1000-6753.tces.240400
中图分类号：TM614
国家自然科学基金重点资助项目（52337004）。
收稿日期 2024-03-14
改稿日期 2024-04-25
李可心 女，2000年生，硕士研究生，研究方向为含新能源电力系统运行与控制。E-mail：lkx18941799539@163.com
安 军 男，1978年生，教授，博士生导师，研究方向为含新能源电力系统运行与控制。E-mail：anhuianjun@163.com（通信作者）
（编辑 赫 蕾）