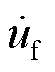，并使其幅值和频率跟踪给定值。GSVSC采用定直流电压控制使风电-柔直并网系统输出有功功率Pg动态跟踪Pw，同时保持直流线路电压Udc为给定值。摘要 为优化风电场经柔性直流输电接入受端电网的惯性响应动态特性，该文提出一种在风电-柔直并网系统中实现无通信协调惯量支撑的关键参数设计方法。基于风机变比例系数调速和柔直网侧换流站附加直流电压-频率下垂控制建立风电-柔直系统实现无通信频率响应的传递函数，明确了下垂系数和调速系数对并网系统惯性响应的调节作用。采用协同控制理论，通过选取频率和直流电压偏差、风电-柔直系统虚拟惯量构造宏变量，设计了下垂系数自适应频率变化调节、调速系数自适应直流电压和风机转速变化调节的协同控制律，实现并网系统利用电容储能和差异化转子动能协同提供惯量支撑。最后在Matlab/Simulink中建立风电-柔直并网模型，利用受端电网频率负荷扰动验证了协同控制律的有效性。仿真研究表明，所提策略能够优化风电场和柔直系统惯量支撑的协同配合，改善受端电网惯性响应动态特性，同时具有优化直流电容电压及风机转速恢复动态过程的优势。
关键词：风电场 柔性直流输电（VSC-HVDC） 惯性响应 协同控制
我国可再生能源与负荷中心的逆向分布，使可再生能源基地经柔性直流向负荷中心输电成为一种主要运行方式[1-2]。由于风机和柔性直流无法像同步发电机一样为电网提供旋转惯量支撑，因此，风电-柔直系统的并网不仅使受端电网的转动惯量因同步发电机开机规模的压缩而下降，而且使受端电网频率对扰动响应变化幅度的阻尼能力下降[3-4]。同时，由于直流输电使风电场侧柔直换流站（Wind Farm Voltage Source Converter, WFVSC）的换流母线电压频率与受端电网频率解耦[5]，在无通信或弱通信条件下风电场不能快速感知受端电网的频率扰动，从而无法利用附加快速调频控制为受端电网提供惯量支撑和频率响应，以改善其频率动态调节特性[6-7]。
为实现风电场经柔性直流输电对受端电网频率变化的协同主动频率支撑，同时避免风电场利用通信感知受端电网频率扰动引起的控制时延问题[8-9]，有学者研究通过耦合风电场侧换流母线电压频率调节跟随网侧换流站（Grid Side Voltage Source Converter, GSVSC）直流电压调节变化，实现风电-柔直系统的无通信协调频率支撑控制[10]。文献[11]利用此无通信耦合控制方式，通过联立直驱风机并网变流器直流母线并联超级电容的充放电功率与同步机摇摆方程，研究了风电-柔直系统基于超级电容电压调节实现惯性响应的控制策略，但该策略没有考虑风机惯量支撑能力的利用。与此同时，利用风机转子动能与直流电容储能实现风电-柔直系统主动频率支撑也得到了研究[12]。文献[13]利用上述无通信耦合控制方式研究了风电场和柔直网侧换流站实现各自虚拟惯性时间常数的惯量支撑控制，但未考虑二者控制之间的配合。文献[14]将同步发电机惯性响应和频率下垂控制引入风机有功调节和柔直直流电容充放电控制以协调提供主动频率支撑，但实现协同控制的GSVSC频率偏差放大因子、WFVSC频率-直流电压下垂系数和风机有功-频率下垂系数均采用固定值，使得并网系统的惯量支撑不能自适应风电场和直流电容储能的可用容量而变化，并且未对参数的控制效果影响进行讨论。文献[15-16]定性讨论了不同GSVSC直流电压-频率下垂系数和风机附加有功-频率下垂控制系数对并网系统无通信协调惯量支撑效果、直流电压和风机转速动态响应过程的影响。分析表明，由于直流电压调节量正比于下垂系数，虽然较小的下垂系数取值能够保证极端情况下的直流电压调节不越限，但也限制了GSVSC利用电容储能提供惯量支撑的作用；同时，较小的风机附加调频下垂系数也会限制风电场发挥惯量支撑的作用，较大的下垂系数则会引起风机转速恢复导致的频率二次跌落，但该文献并未进一步研究提升协同惯量支撑的系数整定方法。文献[17]考虑频率、直流电压和风机转速偏移限值，通过将调节系数设置为与上述限值的固定比例，实现了风电-柔直系统基于差异化转子动能和直流电容储能提供惯量支撑的协调控制，但固定比例不能根据并网系统实时状态进行风机动能和电容储能的自适应调节。文献[18]考虑转子可释放动能和直流电容储能的实时变化，基于惯量和下垂综合控制设计了风电-柔直系统利用可用能量实现自适应惯量支撑的控制参数设计方法，但对如何避免风机转速恢复中的频率二次扰动缺乏考虑。
为优化风电-柔直系统提供惯量支撑的动态特性，本文基于风机变比例系数调速和GSVSC附加直流电压-频率下垂控制，建立了风电-柔直并网系统的无通信频率响应传递函数，明确了利用直流电压-频率下垂系数和调速系数实现协调惯量支撑的可行性；然后，采用协同控制理论设计了下垂系数自适应频率变化调节、调速系数自适应直流电压和风机转速变化调节的协同控制律，所设计的协同控制策略能够充分挖掘风电-柔直系统的惯量支撑能量以实现惯量支撑，并且能够充分利用频率恢复阶段的发电机调频能力，在避免产生频率二次扰动情况下优化直流电压和风机转速的恢复动态特性；最后在Matlab/Simulink中建立风电场经柔直并网模型，通过与典型控制策略比较验证了所提策略的有效性。
双馈风电场经柔性直流输电接入受端电网并网运行的原理如图1所示。图中双馈风电场在风机转速控制、转子变流器功率外环和电流内环控制的相互作用下，可利用最大功率跟踪（Maximum Power Point Tracking, MPPT）运行方式向柔直输送有功功率Pw。WFVSC采用定交流电压控制构建风电场并网电压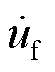，并使其幅值和频率跟踪给定值。GSVSC采用定直流电压控制使风电-柔直并网系统输出有功功率Pg动态跟踪Pw，同时保持直流线路电压Udc为给定值。
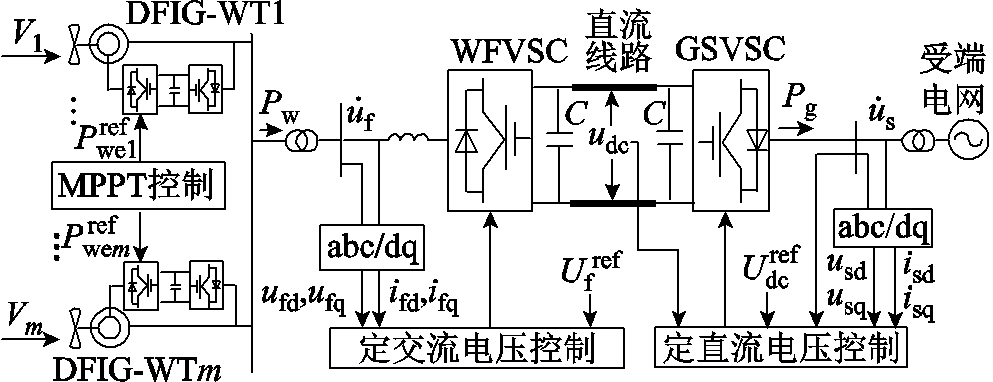
图1 风电场经柔直并网系统的原理
Fig.1 Schematic diagram of wind farms integration to grid via VSC-HVDC
当受端电网发生负荷频率扰动时，由发电机转子运动方程可得受端电网频率变化表达式为
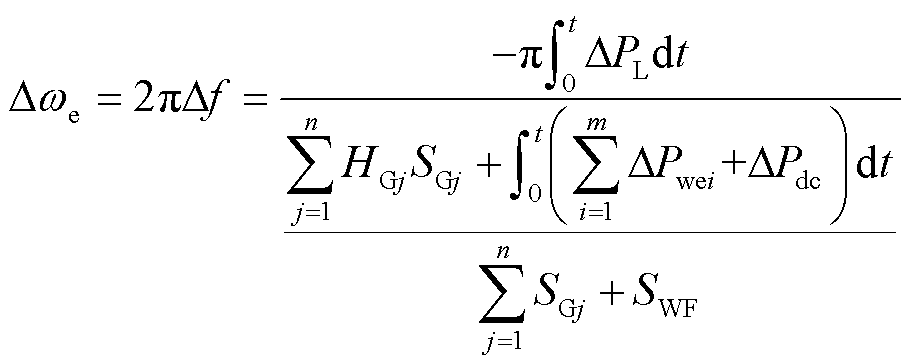（1）
式中，Dwe和Df分别为受端电网同步电气角速度和频率变化量；m、n分别为并网风机和同步发电机数量；HGj和SGj分别为同步发电机j的惯性时间常数和容量；DPL为扰动负荷有功；DPwei为风机i参与调频的有功增量；DPdc为柔直参与调频的有功增量；SWF为风电场的装机容量；t为调频时间。
由式（1）可知，当风电-柔直并网系统在受端电网发生频率扰动时，通过快速调节风机和柔直的有功输出可为系统提供频率支撑。该频率响应有助于减小受端电网的频率变化幅度，减少新能源并网对受端电网频率响应动态的不利影响。
当WFVSC采用定交流电压控制时，由电压源型变流器实现电压-电流双环级联逆变电压控制原理可知，WFVSC能根据Udc变化动态调节脉宽调制比，实现逆变电压模值Uf保持给定值，忽略WFVSC逆变电压调节对Udc调节的暂态响应以及直流线路的有功损耗，即可认为风电场输出有功功率Pw对GSVSC的Udc调节保持不变。WFVSC和GSVSC的协调运行使得在GSVSC定直流电压控制设定值附加Udc/f下垂控制补偿分量，就可以在不影响风电场输出功率情况下，使柔直利用直流线路电容储能为受端电网频率扰动提供频率响应。当GSVSC调制电压基波分量按照网侧换流母线电压d轴分量定向，且GSVSC采用前馈补偿实现输出有功无功解耦控制时，GSVSC附加Udc/f下垂控制后的频率响应的传递函数框图如图2所示。
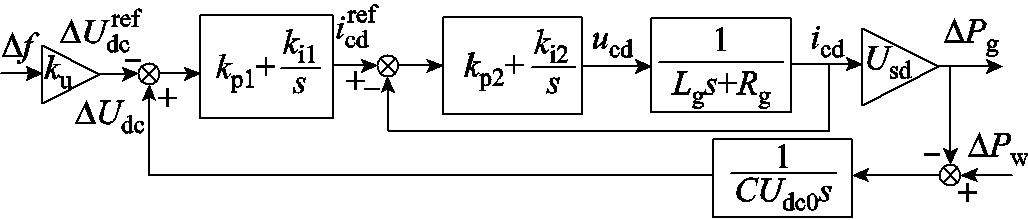
图2 柔直附加Udc/f下垂控制的频率响应框图
Fig.2 Frequency response block diagram of GSVSC using additional Udc/f droop control
图2中，Lg和Rg分别为GSVSC交流侧等效连接阻抗；C为直流线路等效电容；上标ref表示参考值；Usd为网侧换流母线电压d轴分量；Udc0为系统稳态运行时的直流电压；ku为直流电压-频率下垂系数；kp1、ki1、kp2和ki2分别为GSVSC功率外环和电流内环PI控制的比例和积分控制参数。考虑∆Pw=0，依据叠加原理化简框图可得
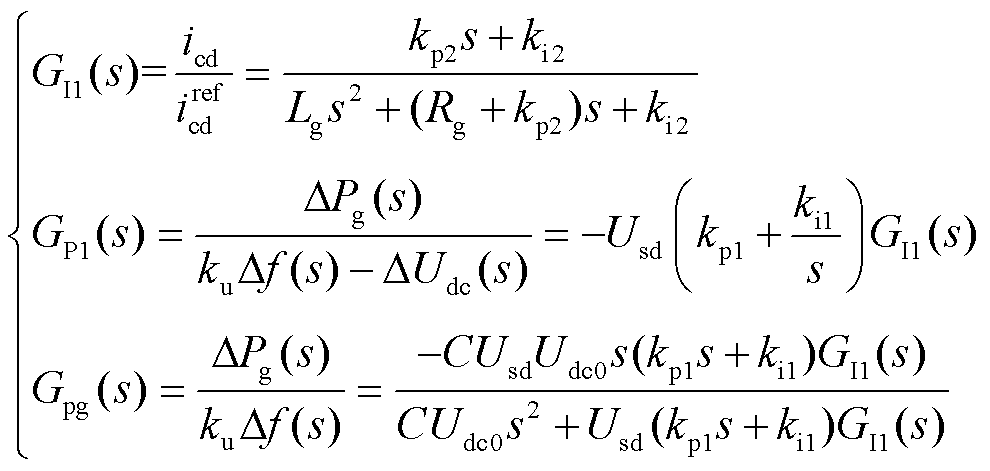（2）
式中，GI1(s)为柔直电流内环传递函数；GP1(s)为柔直频率响应开环传递函数；Gpg(s)为柔直频率响应闭环传递函数。
由式（2）可知，Gpg(s)分子项包含微分算子，因此附加Udc/f下垂控制使GSVSC能够响应Df变化率，表明Udc/f下垂控制使GSVSC的频率响应控制具有利用电容储能提供惯量支撑的作用。
双馈风机利用转子和定子间背靠背电压源型变流器将捕获的风能转换为电能。文献[19]讨论了在桨距角不变的情况下，双馈风机利用转速控制和转子侧变流器电压-电流双环级联控制，调节风机电磁功率Pwe使机组转速ωr跟踪转速给定值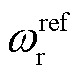
，并针对上述控制使ωr与we解耦问题，研究了使风机转子动能耦合电网频率的变比例调速控制，以实现风机对频率扰动的虚拟惯量支撑。当双馈风机采用定子磁链d轴定向，结合文献[20]中DPwe(s)/
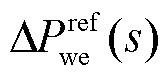传递函数，在当前转速可建立双馈风机变比例调速频率响应框图如图3所示。
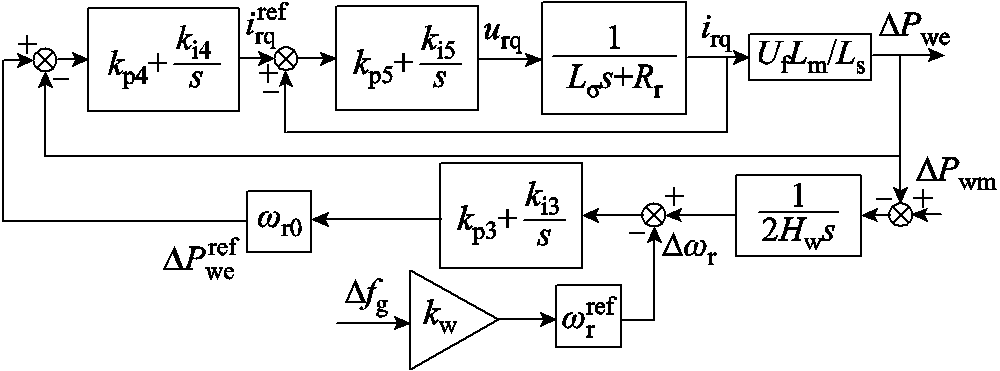
图3 双馈风机基于变比例调速的频率响应框图
Fig.3 Frequency response block diagram of DFIG-WT using variable proportional speed regulation
图3中，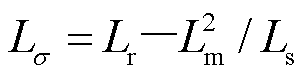
，Ls、Lr、Lm分别为双馈风机定、转子绕组的自感和互感；Rr为转子绕组电阻；ωr0为转子稳态转速；∆Pwe和∆Pwm分别为风机电磁和机械功率增量；kw为调速系数；∆fg为WFVSC逆变电压频率变化量；Hw为风机转子惯性时间常数；kp3和ki3分别为转速PI控制的比例和积分参数；kp4、ki4、kp5和ki5分别为双馈风机转子侧变流器功率外环和电流内环PI控制的比例和积分参数。考虑∆Pwm=0，依据叠加原理化简框图可得
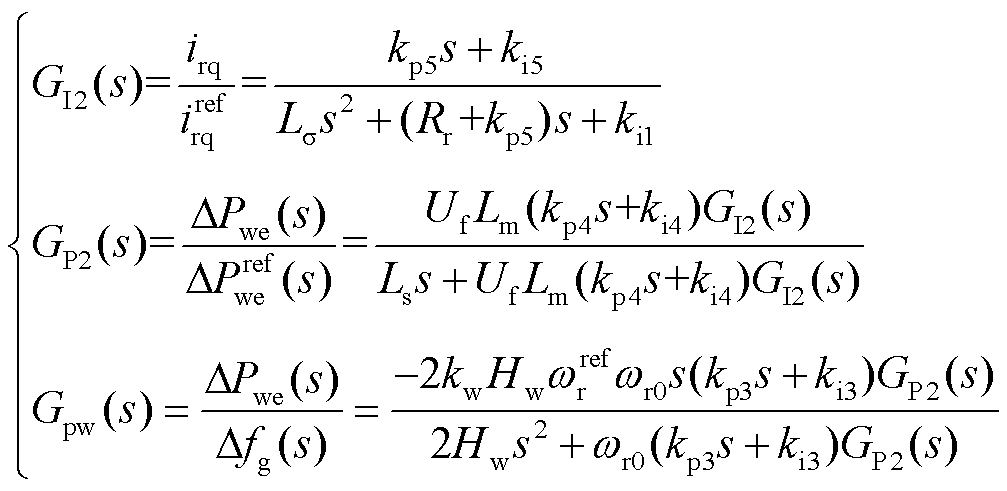（3）
式中，GI2(s)为风机电流内环传递函数；GP2(s)为风机输出功率传递函数；Gpw(s)为风机频率响应闭环传递函数。
因为Gpw(s)分子项包含微分算子，因此风机采用变比例调速能够响应∆fg变化率，表明变比例调速使风机的频率响应具有利用转子动能提供惯量支撑的作用。
为使风电场在无通信条件下能感知受端电网频率扰动并提供惯量支撑，在GSVSC附加Udc/f下垂控制的基础上，利用∆Udc调节WFVSC逆变电压频率fg，可建立图4所示风电-柔直并网系统无通信协调惯性响应传递函数框图。图4中kf为惯性协调系数，化简框图可建立并网系统的协调惯性响应传递函数为
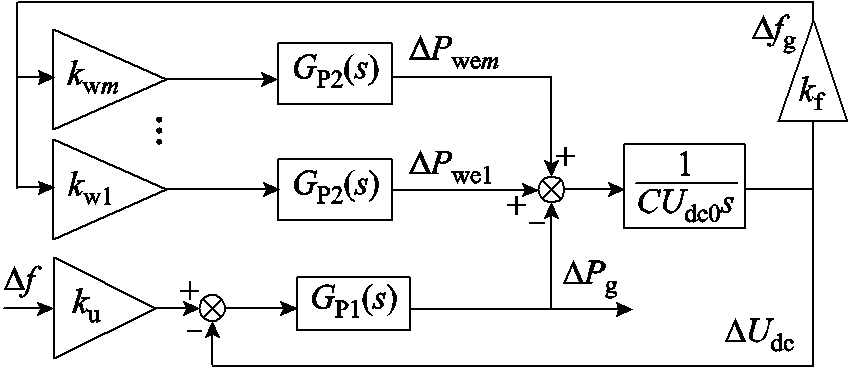
图4 风电-柔直系统无通信协调惯性响应框图
Fig.4 Non-communication coordinated inertia response block diagram of wind farms integration to grid via VSC-HVDC
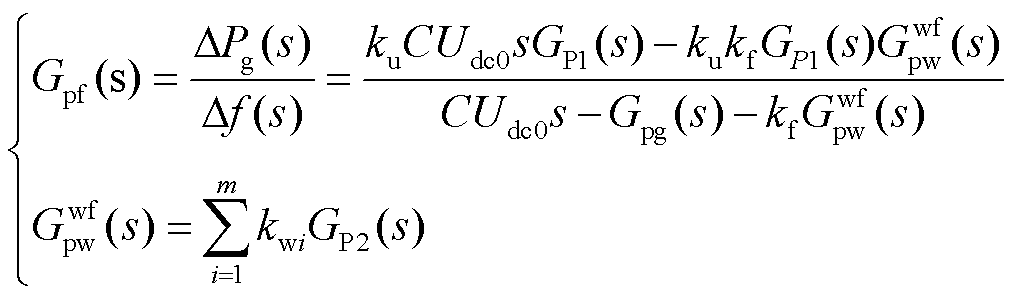（4）
式（4）分子表明，利用惯性协调系数实现风电场和柔性直流的无通信协调惯性响应，包含直流电容储能提供的惯性响应和风电场经柔直提供的惯性响应两部分。由于协调惯性响应过程中，风电场作用分量的kuGp1(s)会随Df变化，因此如何使kwi根据kuGp1(s)的动态变化进行自适应调整，对于提高风电-柔直并网系统的惯性响应效果具有重要作用。同时，由于两个分量符号相反，因此利用kwi调节不仅可以起到增强或阻尼直流电容惯性响应的作用，而且能够使风电-柔直并网系统在惯量支撑后根据受端电网实际调频能力快速恢复直流电压和风电场MPPT运行，避免恢复过程对电网频率产生二次扰动。
由第1节分析可知，实现风电-柔直并网系统无通信协调惯性响应的关键，一是自适应调节下垂系数ku实现直流电容储能提供的惯量随受端电网频率偏差变化；二是自适应调节调速系数kwi实现风电场提供的惯量随直流电容储能动态变化。因此，可以采用具有良好鲁棒性的协同控制理论进行两参数的优化设计。协同控制理论是基于协同学和自组织理论发展的状态空间控制理论[21]。其基本方法为：对于系统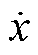
=f(x,u,t)，利用状态变量x线性组合构成宏变量y(x)，基于式（5）约束宏变量趋于流形y(x)=0，求解式（5）并代入
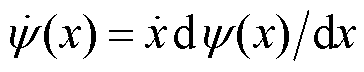得到控制输入u的控制规律，使系统在u的作用下由初始状态沿着流形稳定运行达到稳定状态。
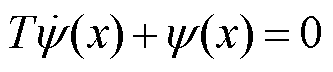（5）
式中，T为协同运动系数，表示系统从初始状态变量收敛到流形的速度。与使用近似线性化处理的经典控制理论不同，协同控制不用近似线性化，而是直接使用非线性模型，使得协同控制器控制更简单。
由式（2）可知，采用Udc/f下垂控制的GSVSC能响应受端电网∆f变化率，结合图2有功控制框图，直流电容储能对受端电网频率变化的惯性响应为
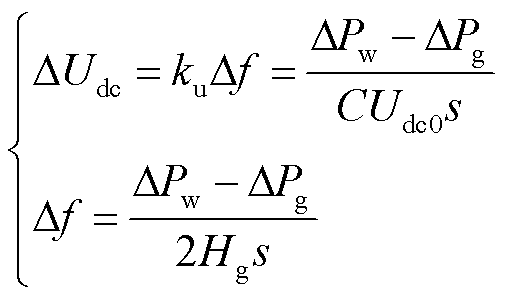（6）
式中，Hg为柔性直流提供的虚拟惯性时间常数。
因此，为使直流电容自适应受端电网频率偏差提供惯量支撑并协同直流电压自身恢复，基于协同控制原理，选取系统频率偏差Δf与直流电容虚拟惯量时间常数Hg为宏变量，即
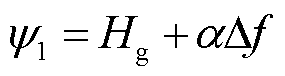（7）
式中，α为y1沿流形趋于目标位置时∆f方向位移变化的调节权重。在设计时选择α值越大，流形中αΔf所占比重则越大，宏变量的流形约束会使GSVSC直流电容释放出更多能量来提供更大的虚拟惯量支撑。
对式（6）中的Hg及宏变量ψ1求导并代入式（5），得到柔性直流提供的虚拟惯量Hg的控制律为
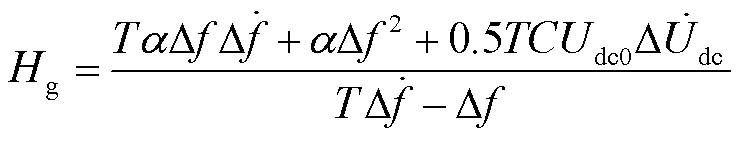（8）
在此控制律下，直流电容储能自适应系统频率偏差参与惯性响应，系统从初始状态运行到流形ψ1=0，并沿着流形稳定到稳定状态。
结合式（6）可得下垂系数ku的控制律为
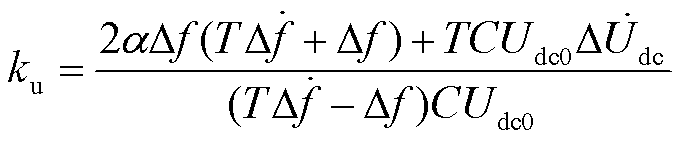（9）
观察式（9）可知，ku控制律分子第一部分与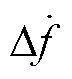
、∆f有关，表明直流电容能自适应系统频率及其变化率的变化。在系统频率受扰初期，频率变化率和直流电压变化率较大，ku迅速增大使直流电容快速释放能量提供更大的惯量支撑。ku控制律分子第二部分与直流电压变化率有关，表明直流电容储能调节能自适应直流电压变化率的变化。随着直流电容快速释放储能进行惯量支撑，直流电压迅速减小，直流电容电压变化率增大，ku逐渐减小，有助于提供阻尼∆Udc过度调节的分量，以避免惯性响应过程中的直流电压超调，同时能够在惯量支撑后恢复直流电容电压的过程中提供优化动态恢复过程，避免电容充电有功功率引起频率二次扰动的阻尼分量。
由式（3）可知，双馈风机采用基于变比例系数转子调速的有功控制，结合图3有功控制框图，双馈风机的转子运动方程及相应的惯性响应为
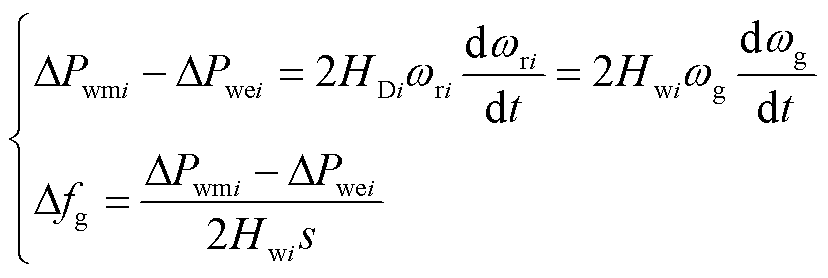（10）
式中，wg为WFVSC侧电气角速度；HDi和Hwi分别为风机i自身固有的惯性时间常数和阻尼fg变化的虚拟惯性时间常数。
式（4）中，两个作用分量符号相反，因此风电场基于协同控制自适应调节kwi提供协同惯量支撑，能阻尼直流电容储能变化并快速恢复系统直流电压。基于此，对于直流电容考虑其直流电压约束，取风电场虚拟惯性时间常数、系统频率偏差和直流电压变化量的线性组合来构造宏变量，即
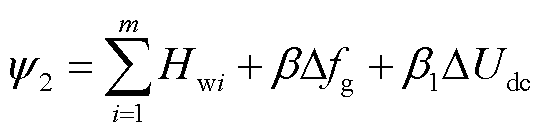（11）
式中，β和β1分别为y2沿流形趋于目标位置时∆fg和∆Udc方向位移变化的调节权重。选择较大的β和β1能够使风电场提供的虚拟惯量支撑更大，有利于风机参与惯性响应以及协助直流电压恢复。
对式（10）中的Hwi及宏变量ψ2求导并联立式（5）得到风机i的虚拟惯性时间常数为
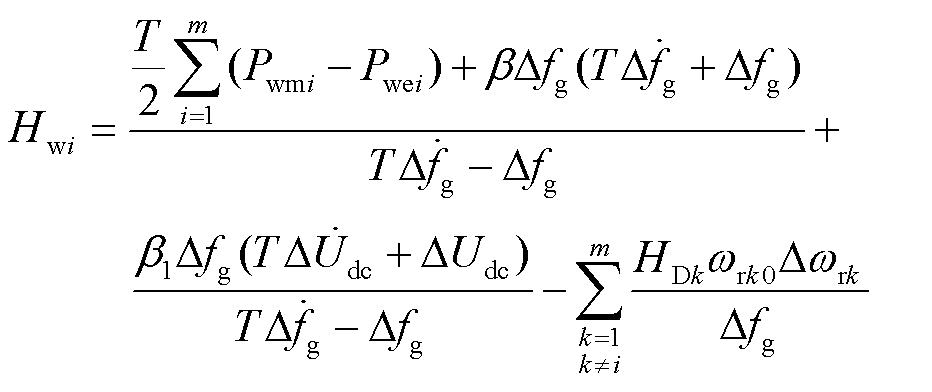（12）
结合图3和式（10）可得风机i的kwi控制律为
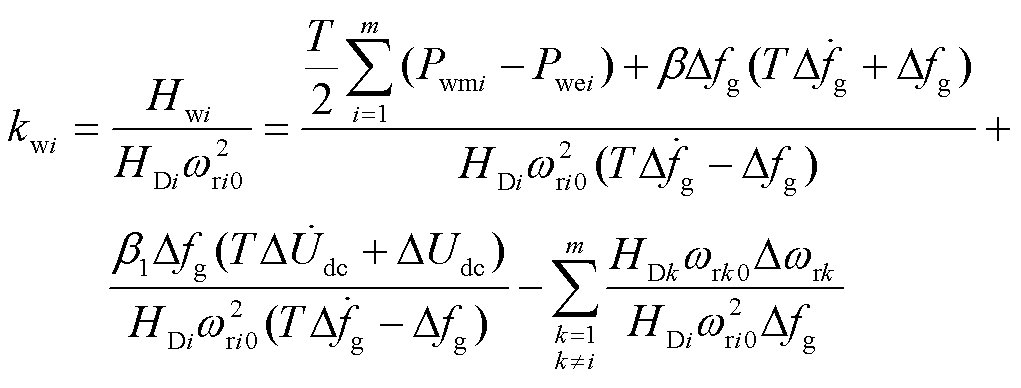（13）
观察式（13）可知，kwi控制律第一部分与WFVSC侧频率偏差及其变化率有关，表明kwi能自适应系统频率偏差变化。在扰动初期，WFVSC侧频率偏差及其变化率跟随直流电压变化较大，kwi迅速增大使风电场提供大量虚拟惯量支撑。控制律第二部分与直流电压及其变化率有关，表明kwi能自适应直流电容储能的动态变化。在直流电压偏差过大、直流电容逐渐退出惯量支撑并开始吸收功率恢复电压过程中，kwi继续增大以阻尼直流电容继续释放储能，协助直流电压恢复，同时风电场增大输出功率来响应频率变化，恢复系统频率。随着风机快速释放转子动能进行惯性响应，WFVSC侧频率与直流电压偏差及其变化率减小，kwi控制律的第一、二部分逐渐减小，使得风机逐渐减小输出功率并在提供惯量支撑后利用受端电网调频能力优化转速恢复过程，有利于恢复MPPT运行并避免给电网频率造成二次扰动。风电场与柔直协同完成对受端电网的惯性响应。同时，kwi的第三部分为其余风机提供的惯量之和除以风机i的初始动能，高风速区初始动能大的风机该分量小，其kwi较低风速区风机的kwi更大，以实现不同风速的风机基于差异化转子动能协同调节惯性响应。
以上控制过程分析以频率跌落为对象进行讨论，同理可分析上述协同惯量控制对频率上升扰动的作用过程，这里不再赘述。
因此，本文基于协同控制理论，设计了下垂系数ku和调速系数kwi的协同控制律，提出图5所示的风电-柔直并网系统协同惯性控制策略，提高受端电网惯性响应动态特性。
在Matlab/Simulink中搭建图6所示含风电场经柔性直流并网的WSCC-9 bus模型进行所提策略有效性的验证。模型中，采用风机等值建模方法[22]，将风电场参考文献[23]按风速等效为三台风机，输入风速分别为11、10、9 m/s。母线5、6和8分别接入(0.5+j0.15)(pu)、(0.3+j0.1)(pu)和(0.4+j0.2)(pu)的负荷L1、L2和L3（基准容量为100 MV·A）。同步发电机调速器参数参考文献[24]仿真算例，柔性直流和线路参数分别参考文献[25-26]。
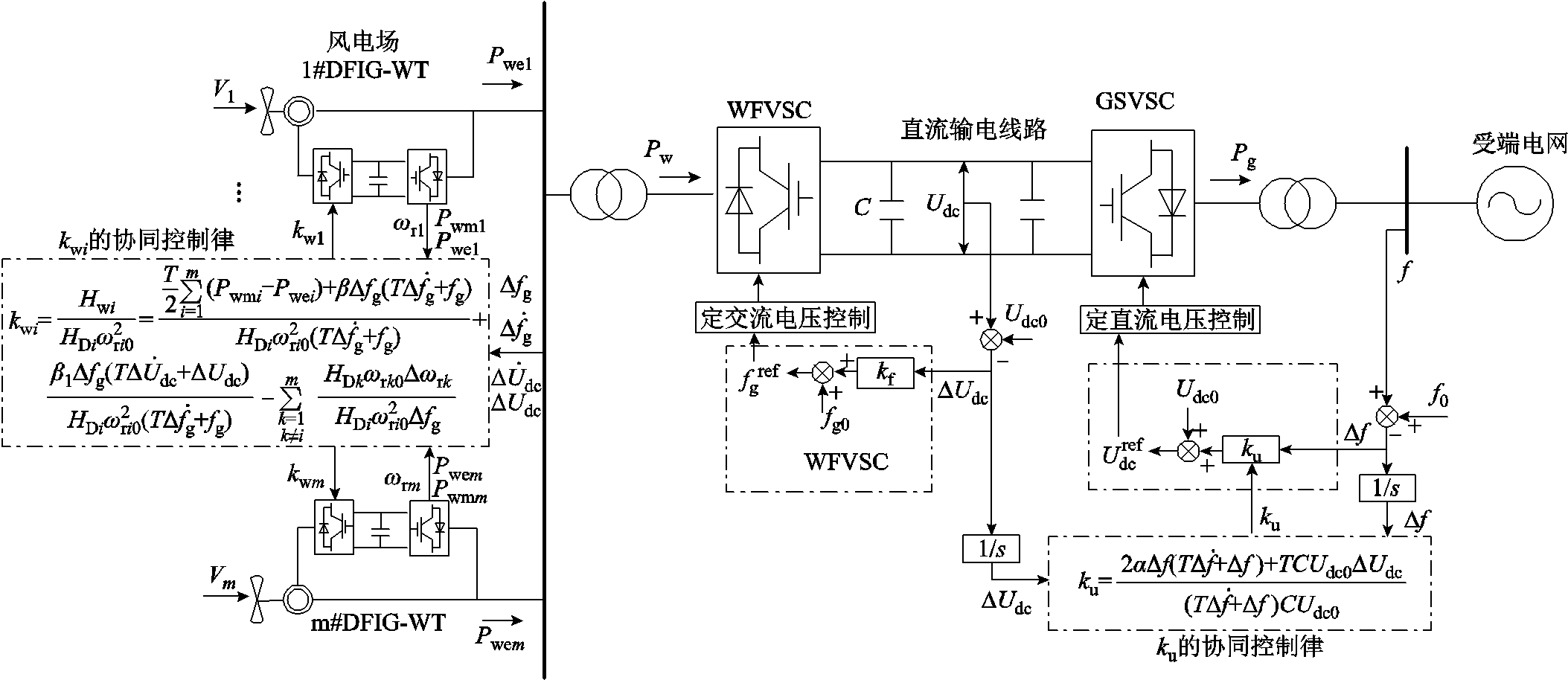
图5 风电场柔直并网系统的协同惯性控制策略原理图
Fig.5 Synergetic inertia regulation strategy schematic diagram of wind farms integrating to grid via VSC-HVDC
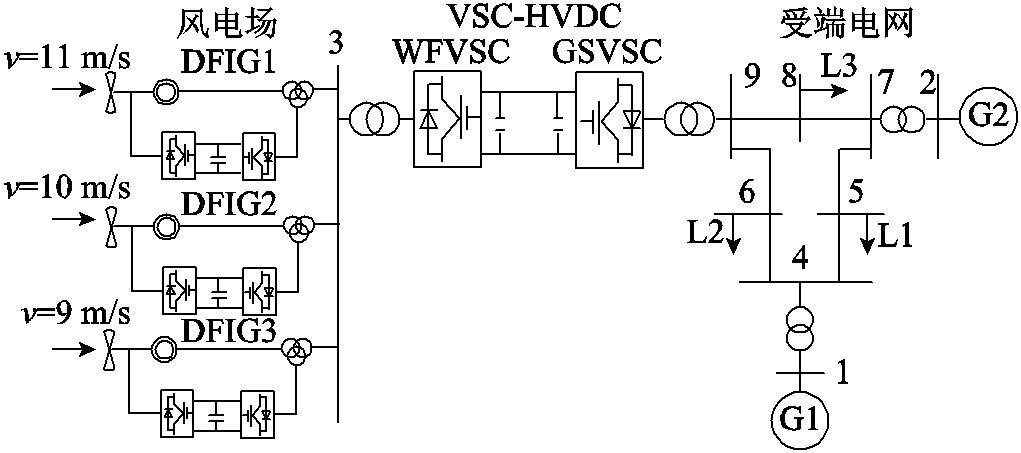
图6 含风电场经柔直并网的WSCC-9 bus受端电网
Fig.6 WSCC-9 bus receiving grid integrated with wind farms via VSC-HVDC
设置t=5.0 s时受端电网母线8有功负荷增加 0.2(pu)，对比受端电网在风电-柔直并网系统无附加惯性响应、仅GSVSC采用附加Udc/f下垂控制、风电场及GSVSC采用定系数协调惯性响应控制和所提协同变系数控制作用下的响应动态特性。仿真中，GSVSC下垂控制中设置下垂系数ku=10，定系数协调控制中设置ku=10、惯性协调系数kf=0.1、风机调速系数kwi=3，协同控制中kf=0.1、ku和kwi控制律如式（9）和式（13），式中T=0.02 s、α=16、β=14、β1=30。
不同控制下系统频率响应相关指标对比见表1，其中fmin为系统频率最低点，t为频率恢复时间。图7对比了四种策略作用下的系统频率、GSVSC输出功率、风电场输出功率及受端电网同步发电机输出功率曲线。无附加控制时，风电场及VSC-HVDC的输出功率不变，频率跌落至最低点49.773 Hz，表明其无法感应受端电网频率变化，不提供惯量支撑。采用GSVSC控制时直流电压释放能量提供惯量支撑使得频率最低点升高为49.799 Hz。而对于同一扰动，采用定系数协调控制及本文所提协同控制时，频率最低点分别升高至49.812 Hz和49.822 Hz，说明在柔直附加下垂控制可以使风电场经直流电压变化感应受端电网频率跌落，从而有效地提高风电-柔直并网系统的惯量支撑能力。在本文策略作用下，系统频率更早恢复至额定值，具有更优的频率恢复动态过程。观察GSVSC、风电场及同步机输出功率曲线，扰动产生瞬间，频率和并网母线电压迅速跌落导致柔直输出功率减小，而风电场输出功率不变，直流电压增大。在柔直附加下垂控制下，直流电压参考偏差正比于系统频率偏差，因此直流电容开始释放能量提供惯量支撑，直流电压下降，经WFVSC附加下垂控制风电场侧感知频率跌落，释放转子动能提供惯量支撑。所提控制能够在频率跌落期间使风电-柔直系统输出功率最大、同步机组输出功率最小，在频率恢复阶段更加充分地利用同步机对受端电网频率调节的支撑能力，协助直流电容电压及风机转速恢复。
表1 不同控制下系统频率响应相关指标对比
Tab.1 Comparison of the relative indexes of system frequency response under different controls
控制方式fmin/Hz频率变化率/(Hz/s)t/s 无附加控制49.773-0.30012.612 GSVSC控制49.799-0.28712.648 定系数协调控制49.812-0.28713.550 协同控制49.822-0.28413.241
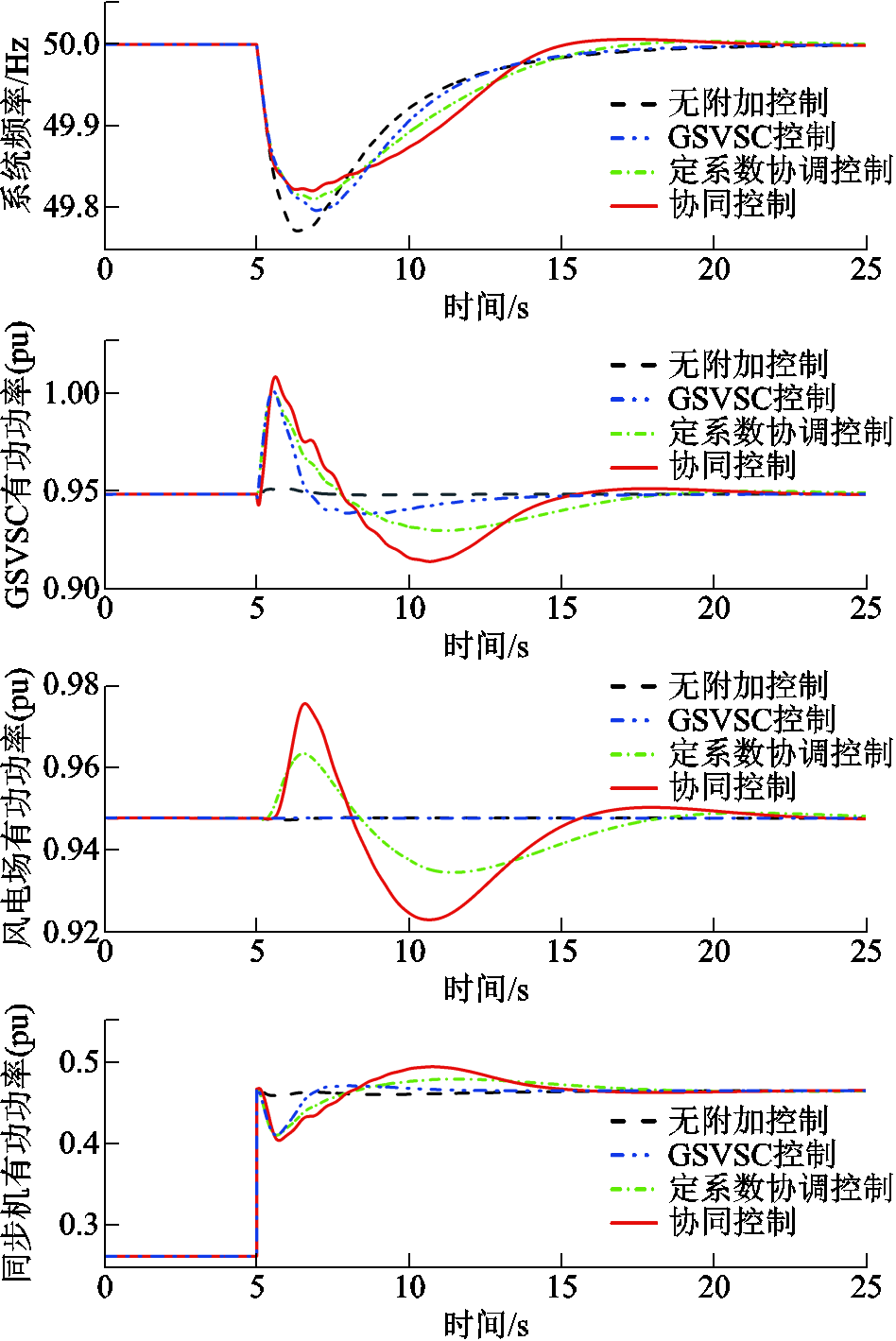
图7 不同控制下的系统频率响应
Fig.7 Frequency response under different controls
图8为四种控制下直流电容电压、ku及Hg的变化曲线。在附加控制下，直流电容能以ku正相关速率快速释放能量为受端电网提供虚拟惯量以减缓频率变化。在GSVSC下垂控制及定系数协调控制下，直流电容在扰动期间提供一个较大的惯性时间常数，达5 s，但这会导致直流电容快速释放能量，电压迅速减小，其恢复所需的能量增大，不利于直流电容电压恢复。本文所提控制下ku初期迅速增大，虚拟惯性时间常数达5.668 s，随着系统频率恢复，ku逐渐减小至零，说明协同控制下GSVSC能按照式（9）自适应地调节ku，其在频率扰动初期提供较大的惯量支撑并随着系统频率恢复而减小，使得暂态情况下的直流电压偏差减小，减小直流电容电压恢复所需的能量，更快地恢复电压至额定值。直流电压恢复时间较定系数协调控制减小31.3%，从而优化直流电压的动态恢复过程。
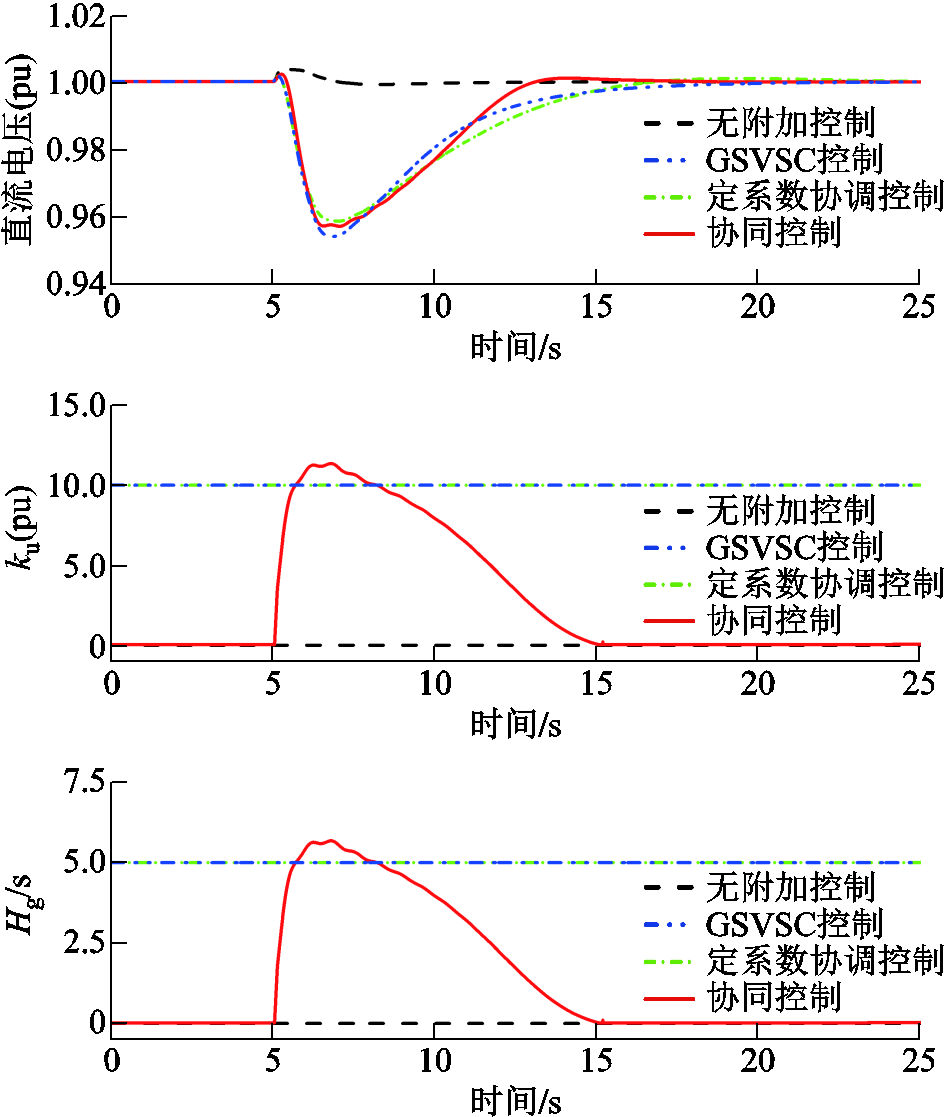
图8 不同控制下的柔直惯性响应
Fig.8 Inertia response of VSC-HVDC under different controls
风电场各风机转速及kwi的变化情况如图9所示。无附加控制下，风机无法感应受端电网频率变化，转子转速不变；而附加控制下风机可以响应受端电网频率变化，释放转子动能，提供惯量支撑。与定系数协调控制相比，所提协同控制下kwi初期迅速达到峰值并随着系统频率恢复逐渐减小至零，说明协同控制下各风机kwi能按照式（13）自适应系统频率偏差及直流电容电压偏差变化，在扰动初期迅速达到峰值，使风机迅速释放转子动能，以提供最大的惯量支撑。随着频率恢复和直流电容电压恢复，kwi在控制律作用下逐渐减小以避免过多地释放转子动能，风机转速恢复时间减小18.7%，表明所提策略能优化风机转速恢复过程，在避免产生二次扰动的情况下协助风机快速恢复转子动能及MPPT运行方式。同时，各风机的kwi在式（13）控制下自适应转子动能差异，高风速区的风机kwi大，承担更大的惯量支撑任务。
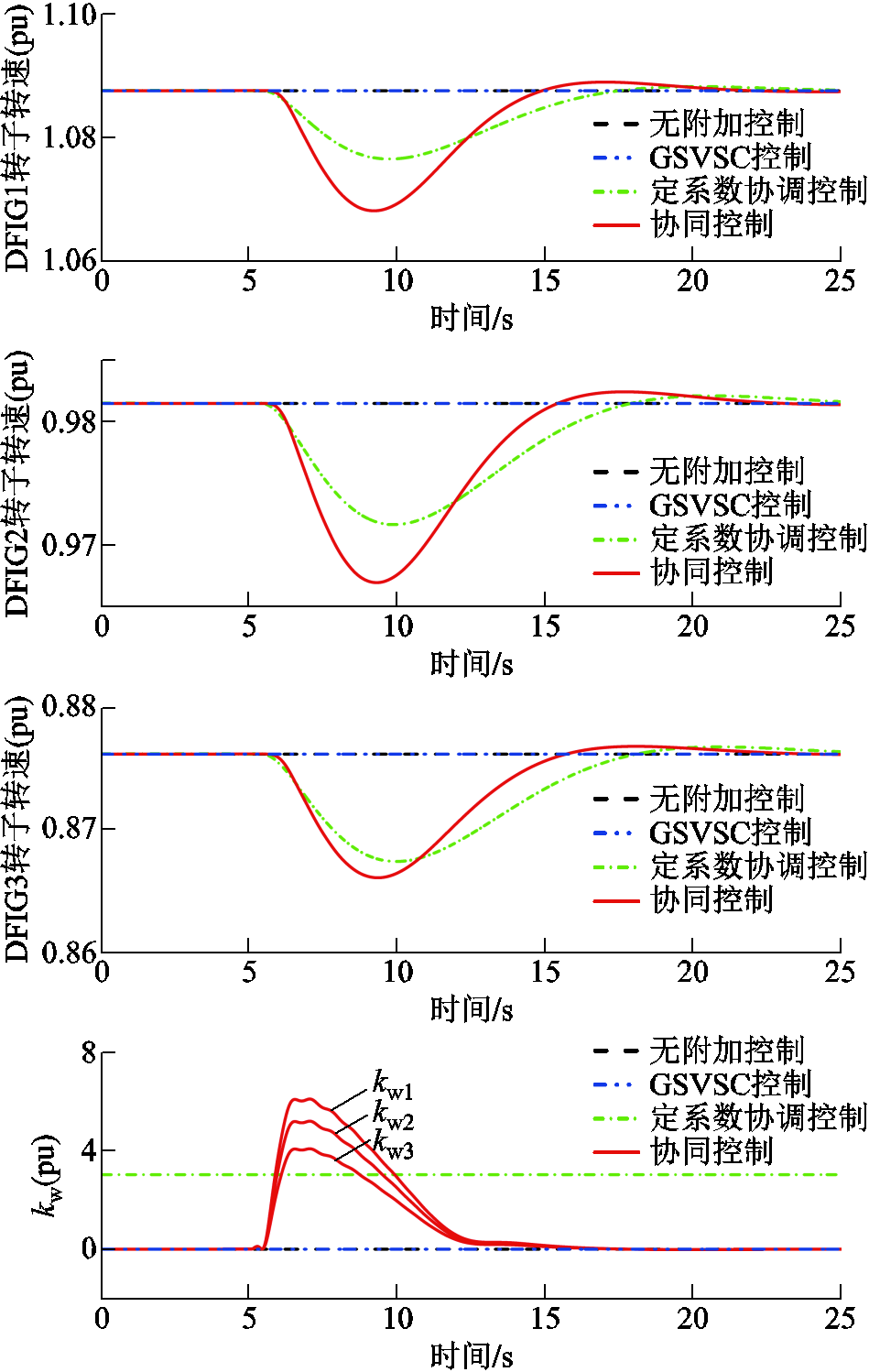
图9 不同控制下的风电场惯性响应
Fig.9 Inertia response of the wind farm under different controls
协同控制构建的宏变量ψ1、ψ2的变化曲线如图10所示。可以看出，在频率扰动初期，宏变量突变，然后在协同控制律的作用下调节ku和kwi，使风电-柔直系统增大有功功率的输出，响应频率变化提供惯量支撑，ψ1、ψ2收敛并保持在流形ψ=0上，实现协同控制。
图10 宏变量的变化曲线
Fig.10 The variation curve of macro variables
设置GSVSC下垂控制及定系数协调控制中ku=30，协同控制式（9）中α=60。图11对比了三种控制下柔直惯性响应曲线。结果表明，GSVSC下垂控制和定系数协调控制中的ku过大会使直流电容因过度释放储能导致电压下降超过限值，从而使柔直在提供惯量支撑后需要更多能量恢复初始直流电容电压。而本文所提的ku协同控制，因为能自适应直流电压变化率，在直流电压偏差及其变化率过大时，通过控制律式（9）第二部分阻止ku继续增大，从而避免直流电容过多释放能量而带来直流电压调节越限。
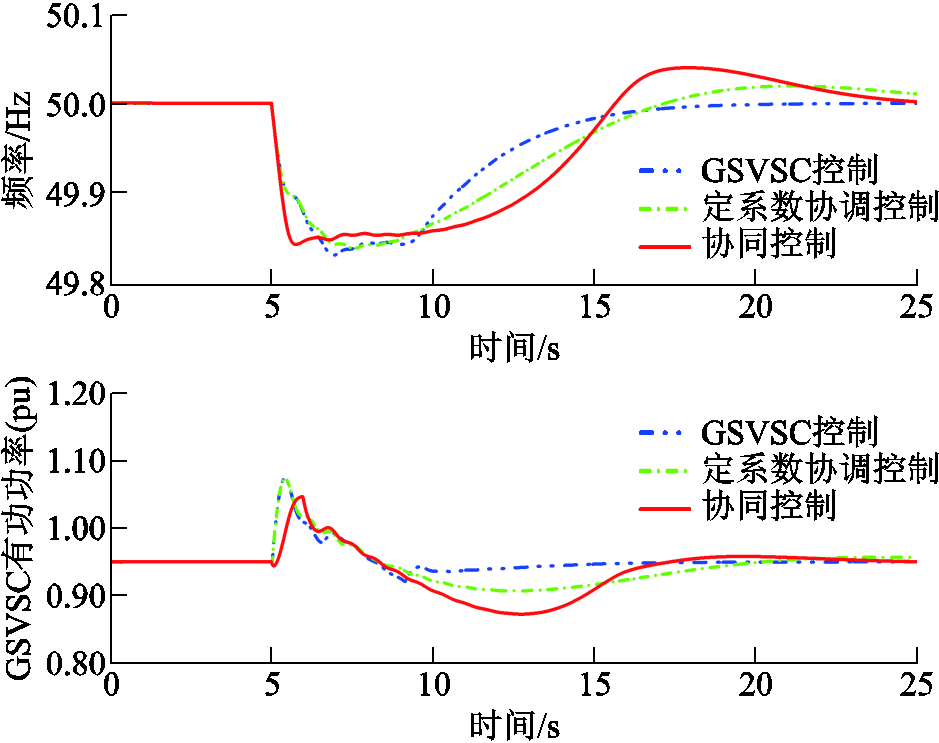
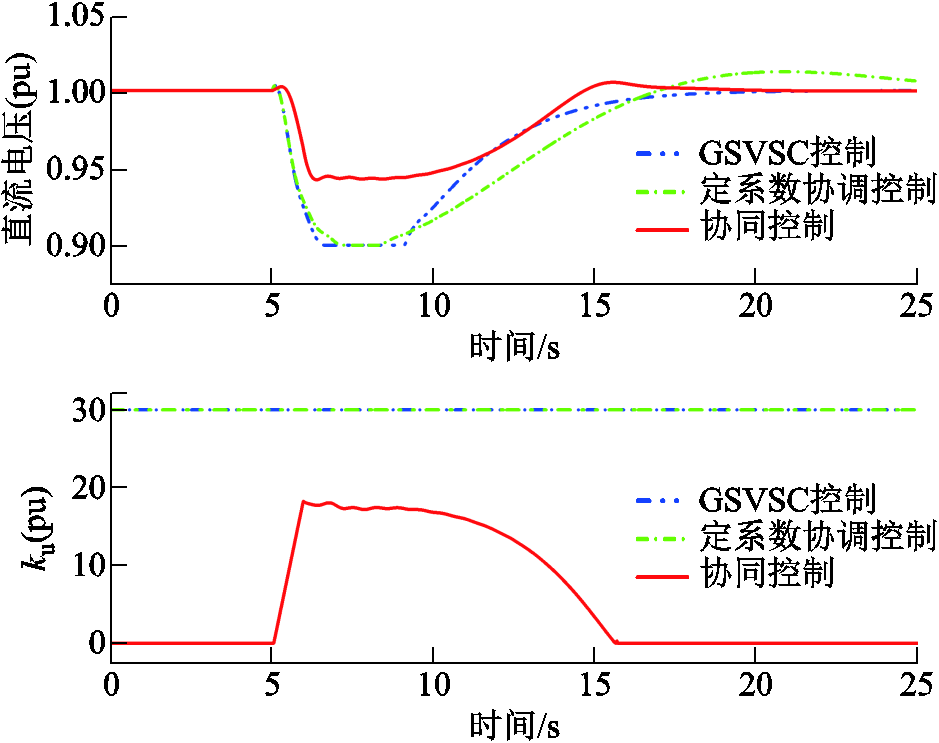
图11 协同控制对直流电压调节越限的抑制作用
Fig.11 The inhibitory effect of synergetic control on exceeding the limit of DC voltage
为考察kf取值对所提协调策略的影响，分别设置kf=0.05、0.1、0.2，在t=5.0 s时模拟受端电网频率跌落扰动，图12展示了kf对系统惯性响应的影响。随着kf的增大，风电-柔直并网输出功率增加，直流电容电压最低点和系统频率最低点上升，说明高的kf取值能使风电场经柔直提供更大的惯量支撑。但是当kf=0.2时，风电场侧频率跌落进一步增大，kwi在控制律式（13）的作用下进一步增大，使风电场释放更多转子动能，此动能一部分作用于阻尼系统频率跌落，另一部分作用于阻尼直流电压跌落。因此扰动初期系统频率与直流电压跌落减小，但直流电容储能未能充分利用，同时过多挖掘风机转子动能使得转子恢复时所需能量更多，受端电网同步机释放更多能量来恢复风机转速，导致系统频率出现二次跌落，直流电压恢复时间加长，对转子转速恢复及直流电容恢复产生不利影响。因此可以考虑在kf =1/ku附近适当选取较大的kf值，以获得更优的惯量支撑效果。
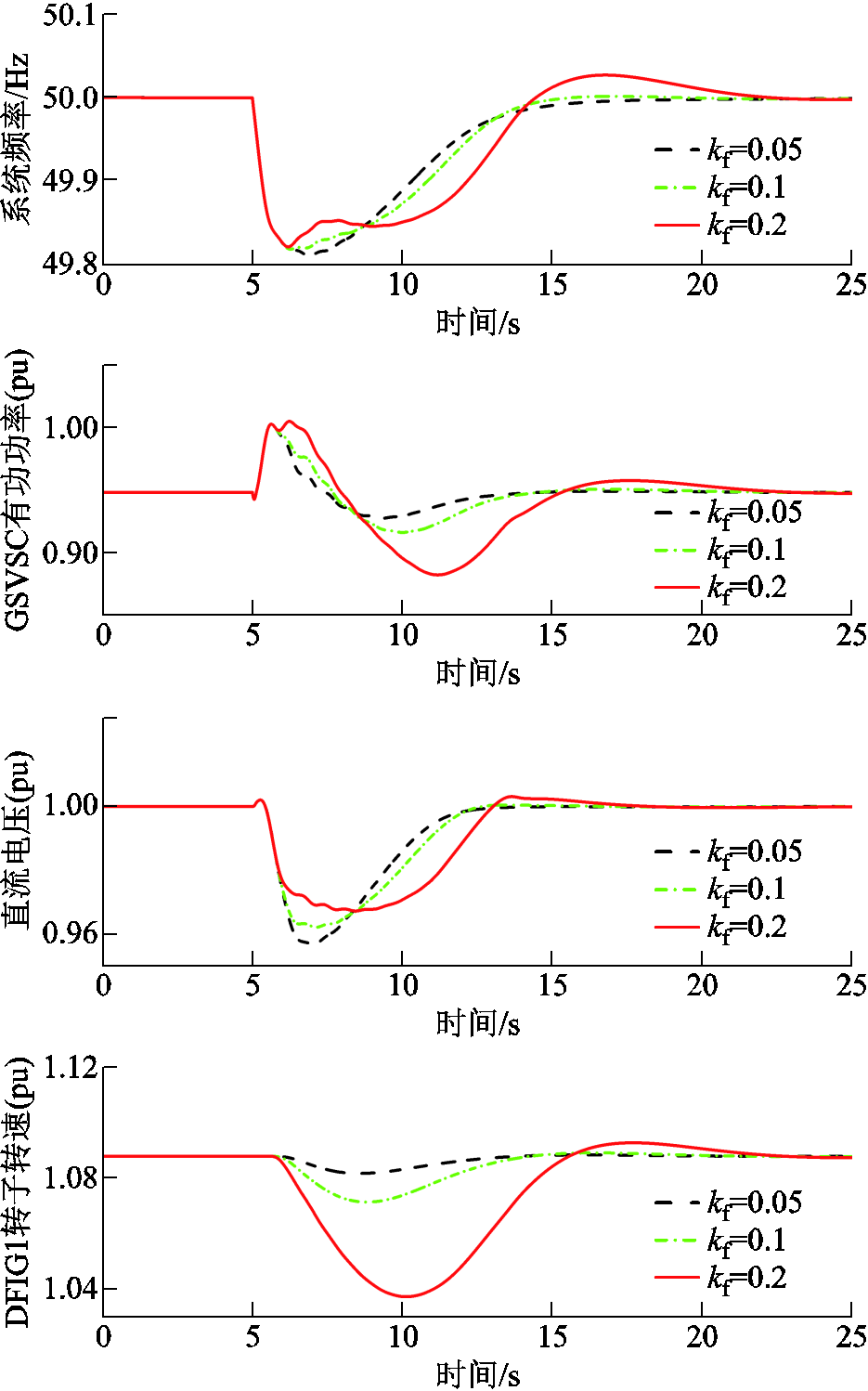
图12 kf对系统惯性响应的影响
Fig.12 The influence of kf on system inertia
为验证随机风速下所提协同策略的有效性，设置风电场的随机风波动如图13所示，基本风速分别为11、10、9 m/s，阵风峰值为0.2 m/s，周期为5 s，渐变风峰值为0.2 m/s，持续时间为15 s，随机风波动峰值为0.1 m/s。图13展示了四种控制在随机风速下的系统惯性响应曲线。结果表明，风速随机变化时，系统频率在额定频率附近范围波动。当受端电网发生频率跌落时，相对于无附加控制、GSVSC控制及定系数协调控制，所提策略下风电场输出功率增大，频率偏差幅度减小，表明所提策略能在风速波动下为受端电网的频率扰动提供有效的惯量支撑。
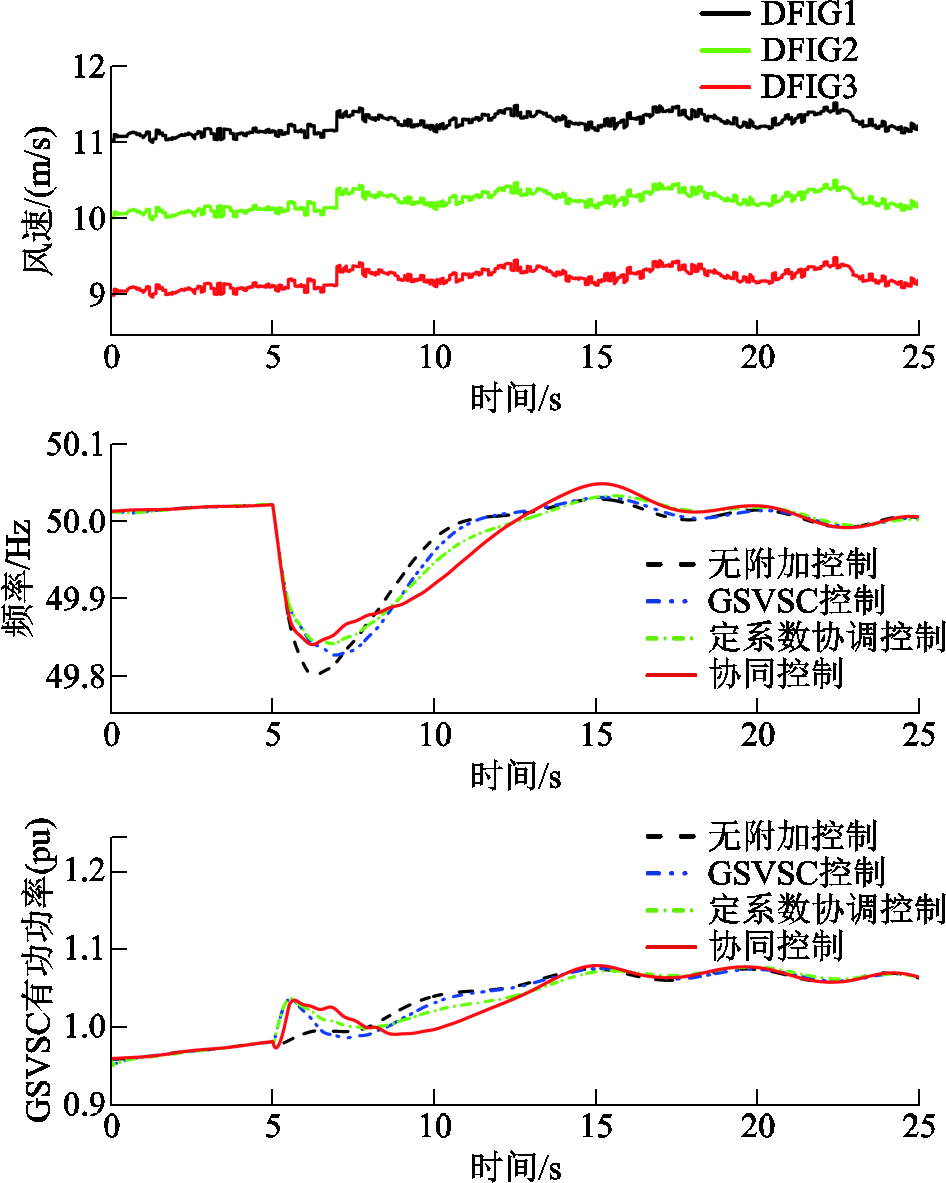
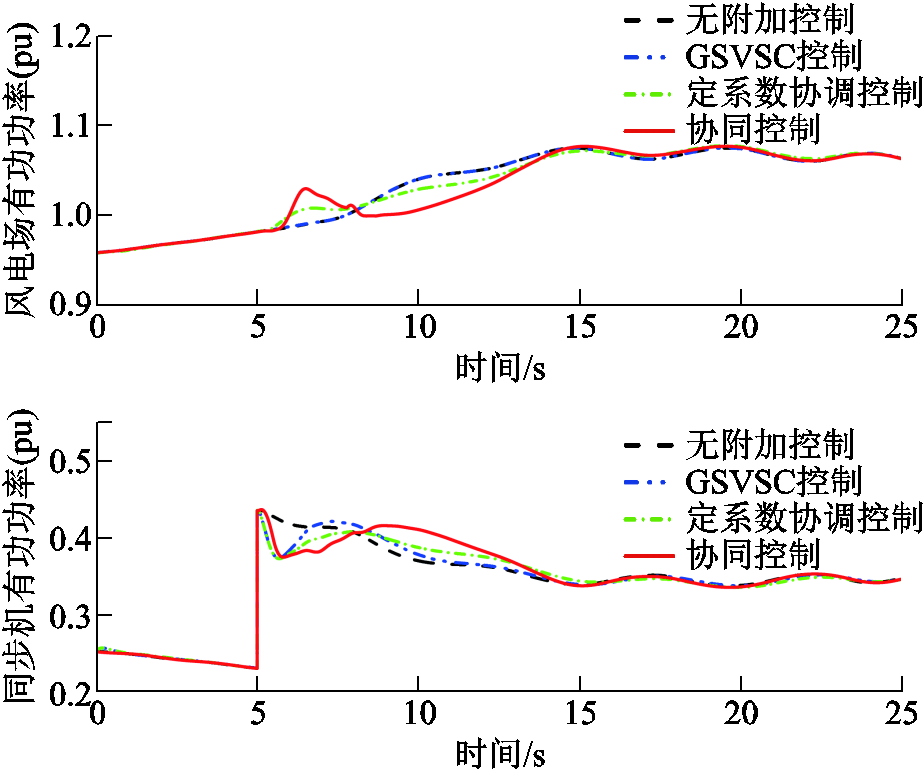
图13 随机风速下的系统惯性响应
Fig.13 System inertia response under random wind speeds
图14对比了四种控制在随机风速下的柔直惯性响应曲线。可以看出，当直流电容电压偏离额定值时，所提策略通过自适应调整ku维持直流电容电压在额定值附近，直流电容电压波动更小。在系统频率受扰后直流电容仍能释放能量提供惯量支撑，且所提策略的直流电压偏差更小，动态恢复过程更优。
图14 随机风速下的柔直惯性响应
Fig.14 Inertia response of VSC-HVDC under random wind speeds
图15为四种控制在随机风速下的风电场惯性响应曲线。附加阵风时，各风机转子转速增加。在系统频率受扰后，定系数协调控制与所提策略中各风机仍能释放转子动能提供惯量支撑，但所提策略提供的惯量支撑更大。同时所提策略下kwi仍能自适应转子动能差异，增大高风速风机kwi以提供更大的惯量支撑，减小低风速风机kwi以提供较小的惯量支撑。仿真结果验证了所提策略在风速随机波动运行场景的适用性。
图15 随机风速下的风电场惯性响应
Fig.15 Inertia response of the wind farm under random wind speeds
本文提出一种基于协同控制优化的风电-柔直并网惯性响应控制策略，主要结论如下：
1）构建风电-柔直并网无通信协调频率响应模型，通过推导其传递函数可知，利用GSVSC下垂系数与风机调速系数能实现电容储能和差异化转子动能协同提供惯量支撑。
2）基于协同控制理论，提出下垂系数与调速系数的优化设计方法，实现柔直虚拟惯量自适应频率偏差、风电场虚拟惯量自适应直流电压偏差及转子动能差异，从而优化风电-柔直系统并网的协调惯性响应特性。
3）恒定风速和波动风速下的频率扰动仿真表明，本文策略相较于定系数控制使系统频率偏差减小5.4%，频率变化率减小1.1%，直流电压恢复时间减小31.3%，风机转速恢复时间减小18.7%。本文策略能在频率受扰时提高转子动能差异化风机和柔直惯量支撑的协同配合，并在惯量支撑后优化直流电压及风机MPPT运行恢复动态过程。
后续可以进一步深入研究惯性协调系数kf与本文下垂系数和调速系数间的协调优化，以及所提策略在大规模实际风电-柔直并网系统中的可行性应用。
参考文献
[1] 蔡旭, 杨仁炘, 周剑桥, 等. 海上风电直流送出与并网技术综述[J]. 电力系统自动化, 2021, 45(21): 2-22. Cai Xu, Yang Renxin, Zhou Jianqiao, et al. Review on offshore wind power integration via DC transmission [J]. Automation of Electric Power Systems, 2021, 45(21): 2-22.
[2] 马富艺龙, 辛焕海, 刘晨曦, 等. 新能源基地柔性直流送出系统小扰动电压支撑强度评估[J]. 电工技术学报, 2023, 38(21): 5758-5770, 5938. Ma Fuyilong, Xin Huanhai, Liu Chenxi, et al. Small-disturbance system voltage support strength assessmentmethod for renewables VSC-HVDC delivery system[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5758-5770, 5938.
[3] 韩民晓, 翟冬玲, 唐晓骏. 连接低惯量系统的柔性直流输电模型预测控制[J]. 电工技术学报, 2017, 32(22): 198-206. Han Minxiao, Zhai Dongling, Tang Xiaojun. Model predictive control of voltage source converter-HVDC connected to low inertia system[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 198-206.
[4] 束洪春, 邵宗学, 赵伟, 等. 含柔性直流的交直流混联电力系统紧急频率控制研究[J]. 电工技术学报, 2023, 38(20): 5590-5604. Shu Hongchun, Shao Zongxue, Zhao Wei, et al. Research on emergency power control of AC-DC hybrid power system with flexible DC[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5590-5604.
[5] 邵冰冰, 贾焦心. 弱受端交流电网下VSC-HVDC系统的功率解耦控制设计[J]. 电机与控制学报, 2022, 26(10): 56-65. Shao Bingbing, Jia Jiaoxin. Power decoupling control design of the VSC-HVDC under the weak receiving AC grid conditions[J]. Electric Machines and Control, 2022, 26(10): 56-65.
[6] 孙华东, 王宝财, 李文锋, 等. 高比例电力电子电力系统频率响应的惯量体系研究[J]. 中国电机工程学报, 2020, 40(16): 5179-5192. Sun Huadong, Wang Baocai, Li Wenfeng, et al. Research on inertia system of frequency response for power system with high penetration electronics[J]. Proceedings of the CSEE, 2020, 40(16): 5179-5192.
[7] 王博, 杨德友, 蔡国伟. 高比例新能源接入下电力系统惯量相关问题研究综述[J]. 电网技术, 2020, 44(8): 2998-3007. Wang Bo, Yang Deyou, Cai Guowei. Review of research on power system inertia related issues in the context of high penetration of renewable power generation[J]. Power System Technology, 2020, 44(8): 2998-3007.
[8] Andreasson M, Wiget R, Dimarogonas D V, et al. Distributed frequency control through MTDC transmission systems[J]. IEEE Transactions on Power Systems, 2017, 32(1): 250-260.
[9] Liu Hongzhi, Chen Zhe. Contribution of VSC-HVDC to frequency regulation of power systems with offshore wind generation[J]. IEEE Transactions on Energy Conversion, 2015, 30(3): 918-926.
[10] 谢小荣, 苏开元, 邱银锋, 等. 海上风电-柔直送端系统频率控制研究现状及建议[J]. 中国海上油气, 2023, 35(1): 136-147. Xie Xiaorong, Su Kaiyuan, Qiu Yinfeng, et al. Frequency control of VSC-HVDC transmission system for offshore wind farms: research status and suggestions[J]. China Offshore Oil and Gas, 2023, 35(1): 136-147.
[11] 朱介北, 史美琦, 张利, 等. 基于超级电容的海上风电柔直送出系统协调惯量支撑策略[J]. 电网技术, 2022, 46(8): 2938-2952. Zhu Jiebei, Shi Meiqi, Zhang Li, et al. Supercapacitor-based coordinated inertia support strategy for offshore wind farms integration via VSC-HVDC[J]. Power System Technology, 2022, 46(8): 2938-2952.
[12] Lin C H, Wu Yuankang. Overview of frequency-control technologies for a VSC-HVDC-integrated wind farm[J]. IEEE Access, 2829, 9: 112893-112921.
[13] 杨仁炘, 张琛, 蔡旭. 具有频率实时镜像和自主电网同步能力的风场–柔直系统控制方法[J]. 中国电机工程学报, 2017, 37(2): 496-506. Yang Renxin, Zhang Chen, Cai Xu. Control of VSC-HVDC with real-time frequency mirroring and self-synchronizing capability for wind farm integration[J]. Proceedings of the CSEE, 2017, 37(2): 496-506.
[14] Liu Xudan, Lindemann A. Control of VSC-HVDC connected offshore windfarms for providing synthetic inertia[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(3): 1407-1417.
[15] 李宇骏, 杨勇, 李颖毅, 等. 提高电力系统惯性水平的风电场和VSC-HVDC协同控制策略[J]. 中国电机工程学报, 2014, 34(34): 6021-6031. Li Yujun, Yang Yong, Li Yingyi, et al. Coordinated control of wind farms and VSC-HVDC to improve inertia level of power system[J]. Proceedings of the CSEE, 2014, 34(34): 6021-6031.
[16] Li Yujun, Xu Zhao, Østergaard J, et al. Coordinated control strategies for offshore wind farm integration via VSC-HVDC for system frequency support[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 843-856.
[17] 江守其, 徐亚男, 李国庆, 等. 提升海上风电经柔直联网系统频率稳定性的协调控制策略[J]. 电力自动化设备, 2023, 43(9): 194-201. Jiang Shouqi, Xu Yanan, Li Guoqing, et al. Coordinated control strategy for improving frequency stability of MMC-HVDC connecting offshore wind power[J]. Electric Power Automation Equipment, 2023, 43(9): 194-201.
[18] Lu Zongxiang, Ye Yida, Qiao Ying. An adaptive frequency regulation method with grid-friendly restoration for VSC-HVDC integrated offshore wind farms[J]. IEEE Transactions on Power Systems, 2019, 34(5): 3582-3593.
[19] Peng Xiaotao, Yao Wei, Yan Cai, et al. Two-stage variable proportion coefficient based frequency support of grid-connected DFIG-WTs[J]. IEEE Transactions on Power Systems, 2020, 35(2): 962-974.
[20] 周际城, 彭晓涛, 罗鹏, 等. 基于复转矩系数法的双馈风机次同步控制相互作用阻尼特性研究[J]. 电网技术, 2020, 44(4): 1247-1257. Zhou Jicheng, Peng Xiaotao, Luo Peng, et al. Study on sub-synchronous control interaction damping characteristics of doubly-fed induction generator based on complex torque coefficient method[J]. Power System Technology, 2020, 44(4): 1247-1257.
[21] Kolesnikov A, Veselov G, Popov A, et al. A synergetic approach to the modeling of power electronic systems[C]//COMPEL 7th Workshop on Computers in Power Electronics, Blacksburg, VA, USA, 2000: 259-262.
[22] 李龙源, 付瑞清, 吕晓琴, 等. 接入弱电网的同型机直驱风电场单机等值建模[J]. 电工技术学报, 2023, 38(3): 712-725. Li Longyuan, Fu Ruiqing, Lü Xiaoqin, et al. Single machine equivalent modeling of weak grid connected wind farm with same type PMSGs[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 712-725.
[23] Miller N W, Sanchez-Gasca J J, Price W W, et al. Dynamic modeling of GE 1.5 and 3.6 MW wind turbine-generators for stability simulations[C]//2003 IEEE Power Engineering Society General Meeting, Toronto, ON, Canada, 2003: 1977-1983.
[24] Kundur P, Balu N J, Lauby M G. Power System Stability and Control[M]. New York: McGraw-Hill, 1994.
[25] Zhou Guoliang, Shi Xinchun. Research on the model and control strategy of one multi-module-converter based VSC-HVDC[C]//2007 IEEE International Symposium on Industrial Electronics, Vigo, Spain, 2007: 759-763.
[26] Anderson P M, Fouad A A. Power System Control and Stability[M]. 2nd ed. Piscataway: IEEE Press, 2003.
Abstract Wind farms integrating into receiving grid via voltage sourced converter based high voltage direct current (VSC-HVDC) has become a main operating mode. However, VSC-HVDC causes the decoupling of the wind farm side VSC (WFVSC) frequency from the receiving grid frequency and, hence, wind farms cannot quickly perceive frequency disturbances in the receiving power grid without communication and use additional frequency regulation control to provide inertia support and frequency response. Recently, some non-communication methods were presented to couple the frequency of wind farms with the receiving power grid to provide inertia support, but most of them didn’t discuss how to design parameters. To address this issue, this paper proposes a key parameter design method for wind farms integrating into receiving grid via VSC-HVDC to provide non-communication coordinated inertia support and optimize the dynamic characteristics of inertial response.
Firstly, based on the variable proportion coefficient rotor speed regulation of doubly fed induction generators (DFIGs) and the additional DC voltage-frequency droop control of the grid side VSC (GSVSC) station, the non-communication coordinated frequency response transfer functions of VSC-HVDC connected wind farm are derived. The role of the droop coefficient ku of GSVSC and speed regulation coefficient kwi of DFIGs in providing inertia response for receiving grid is analyzed. Then select frequency deviation, DC voltage deviation and virtual inertia of wind farms connected to VSC-HVDC as macro variables according to synergetic control theory. Further, synergistic control law of ku is designed to adapt to frequency change while synergistic control law of kwi is designed to adapt to DC voltage change and rotor speed change, which makes the coordinated inertia provided by capacitor energy storage and differential rotor kinetic energy.
Simulation results in WSCC-9 bus system show that, the lowest frequency increases to 49.822 Hz and the rate of change of frequency (RoCoF) decreases to -0.284 Hz/s under the proposed strategy. Compared with fixed coefficient controls, the system frequency deviation is reduced by 5.4% and RoCoF is reduced by 1.1%, which verifies the effectiveness of the proposed strategy in improving the inertia support ability and optimizing the dynamic response characteristics.Furthermore, ku in proposed strategy rapidly increases in the early stage and provides significant support with a virtual inertia of 5.668 s. As the system frequency recovers, ku gradually decreases to zero, reducing the DC voltage deviation and the energy required for DC capacitor voltage recovery. The voltage is restored to the rated value faster, and the DC voltage recovery time is reduced by 31.3%. In the early stage of frequency disturbance, kwi quickly reaches its peak, and DFIGs quickly release the rotor kinetic energy to provide maximum inertia support. As the frequency recovers, kwi gradually decreases to zero to avoid excessive release of rotor kinetic energy, and the rotor speed recovery time decreases by 18.7%. At the same time, kwi of DFIGs in high wind speeds are larger than those in low wind speeds, which meanseach DFIG adapts to the difference in rotor kinetic energy to provide appropriate inertia support. Finally, considering the randomness of wind power, random fluctuations are added to the input wind speeds. The results show that the proposed strategy is applicable under random wind speeds.
The following conclusions can be drawn from the simulation analysis: (1) Compared with fixed coefficient controls, the proposed strategy can not only improve the collaborative cooperation inertia support between VSC-HVDC and wind farms with differential rotor kinetic energy when suffering frequency disturbances, but also optimize the dynamic characteristics of the receiving grid inertia response. (2) The proposed strategy can optimize the dynamic recovery process of DC capacitor voltage after inertia support, and help wind farms quickly recover rotor kinetic energy and maximum power point tracking (MPPT) operation mode while avoiding secondary disturbances.
keywords：Wind farm, voltage source converter based high voltage direct current transmission (VSC-HVDC), inertia response, synergetic control
DOI: 10.19595/j.cnki.1000-6753.tces.240238
中图分类号：TM722
国家自然科学基金项目（52237004）和国家电网公司总部科技项目（1400-202235243A-1-1-ZN）资助。
收稿日期 2024-02-04
改稿日期 2024-06-26
谭珺敉 女，2000年生，硕士研究生，研究方向风电经柔性直流输电并网控制。E-mail：2018302070222@whu.edu.cn
彭晓涛 男，1971年生，副教授，博士生导师，研究方向为新能源并网控制及其优化等。E-mail：pengxiaotao@whu.edu.cn（通信作者）
（编辑 赫 蕾）