图1 电磁轨道发射原理及二维简化模型
Fig.1 Schematic diagram of electromagnetic rail launch and its 2D simplified model
摘要 速度趋肤效应是影响电磁轨道发射性能的重要因素，数值计算是研究速度趋肤效应的重要手段。然而，基于有限差分法、有限元法和有限体积法的传统数值算法，难以满足电磁轨道发射实时模拟和数字孪生场景下对速度趋肤效应的快速计算需求。为此，该文提出一种基于深度算子网络（DeepONet）的电磁轨道发射速度趋肤效应快速计算方法。首先，基于传统有限元法求解获得不同速度和电流条件下轨道区域内的磁感应强度，构建训练数据集；其次，构建非堆叠型深度算子网络，包含分支网络和主干网络，分别用于对变化参数和时空坐标进行编码，并将电枢和导轨的磁感应强度数据输入网络中进行训练；最后，通过对比不同速度和电流条件下有限元法和深度算子网络获得的结果，验证深度算子网络方法的有效性。算例实验结果表明，以有限元法的结果为基准，基于深度算子网络的电磁轨道发射模型在训练条件区间内的相对L2误差为0.43%，在训练条件区间外的相对L2误差为0.74%，平均预测时长为0.865 s，验证了所提方法的准确性和实时性。
关键词：电磁轨道发射 速度趋肤效应 深度算子网络 数据驱动
不同于传统火炮的发射过程，电磁轨道发射装置利用发射系统产生精确可控的电磁力对携带电枢的弹丸进行加速，其发射初速度一般可达1～3 km/s[1-2]。发射装置的主要构成部分是发射系统中的平行滑轨、脉冲功率电源、弹丸和电枢。处于发射状态时，由电源向其中一条导轨供电，电流通过电枢流向另外一条导轨，流经两条平行导轨的巨大电流会产生方向相反的强线性磁场，进而与电枢相互作用产生巨大的电磁力，驱动电枢和弹托沿着滑轨轴向加速，瞬间获得极大的初速度，使弹丸高速打击目标[3-4]。目前制约电磁轨道发射的关键技术包括电源小型化、发射器长寿命、制导弹药抗过载等[5]。而电流和磁场的分布特性与发射性能及发射器寿命息息相关[6-7]，其中速度趋肤效应是影响电流和磁场分布的重要物理效应[5]，因此关于速度趋肤效应和电流磁场分布特性的相关研究大量涌现。
考虑到有限元网格差分精度的限制，文献[8]提出了提升趋肤效应计算精度的改进模型。在此基础上，文献[9]采用有限差分法建立了电磁轨道发射的三维瞬态模型，研究了电磁轨道发射装置的速度趋肤效应。与此同时，文献[10]也发现了速度趋肤效应引起的高温烧灼现象，为避免转捩发生和抑制灼烧提供了理论依据。文献[11]为分析电枢膛内运动以及炮口电弧回流两个阶段绝缘体的热损伤情况，建立了“电-磁-热”耦合的三维瞬态模型。随后，文献[12]利用有限元计算模型对速度趋肤效应中速度的影响开展了深入研究，获得了相对速度与磁场分布的关系。而文献[13]则从磁场特性的角度对电枢运动进行分析，阐释了电枢运动产生瞬变磁场的根本原因，并对瞬变磁场进行了频谱分析。由于对动态条件下电磁场分布特性的研究相对缺乏，文献[14]针对该问题提出了一种有限元计算方法，可有效地计算轨道炮智能炮弹部位的感应电场和磁场。基于对上述方法的改良，文献[15]通过有限元-边界元模拟方法，研究了当轨道发射中增稳轨道的几何形状发生变化时轨道发射装置电气参数和机械参数的变化。针对电枢-钢轨接触特性的研究需求，文献[16]推导了消除感应电动势影响的电枢-钢轨接触电阻解析公式，揭示了电枢轨道的接触电阻和物理参数之间的相关性。文献[17]则提出基于Fluent UDS二次开发的数值计算方法，为建立电磁轨道发射膛内多物理场耦合模型奠定了基础。在上述研究的基础上，为了提高计算效率，文献[18]采用有限差分法的两种数值格式对速度趋肤效应进行了计算分析，并总结了求解特点和应用范围。为了具体研究速度趋肤效应和接触电阻对电磁轨道发射性能的影响，文献[19]采用有限元法仿真研究了轨道发射装置的电流分布特性，并根据有限元模型中影响因素的不同，建立了速度趋肤效应模型、接触电阻模型以及两者都包含的综合模型。
综上所述，目前关于电磁轨道发射速度趋肤效应的研究主要采用有限元法对磁场分布特性开展分析，且相关研究聚焦于电磁轨道的单次发射和单影响因素分析[20-22]，对于实时模拟以及参数变化场景的考虑有所欠缺。然而在实际应用中，电磁轨道发射参数（如速度、电流等）需反复调整和测试，与之对应的基于有限元法的仿真模型在参数变化后需重新计算，大大降低了电磁轨道发射参数的优化设计效率，也无法为电磁轨道发射的数字孪生建模提供高效的仿真模型。由此可见，发展一种能够在电磁发射参数实时变化情况下高效求解磁场分布特性的方法非常必要。
因此，本文提出了一种基于深度算子网络（Deep Operator Network, DeepONet）的电磁轨道发射速度趋肤效应快速求解方法。通过构建包含主干网络和分支网络的深度算子模型，对变化参数和时空坐标进行解耦式编码，实现了在电磁轨道发射参数（速度和电流）变化条件下磁场暂稳态分布的高效高精度求解。相关数值计算结果也进一步验证了该方法的有效性。
在研究过程中假设导轨为无限长，且电枢与导轨间接触良好，忽略导轨与电枢间高速运动产生的非线性作用。此外，不考虑摩擦，假设物性参数均为各向同性，且输入电流在轨道高度上平均分布。
电磁轨道发射时，电枢相对导轨向前运动，可以看作运动的磁场源，与此同时产生反向电动势。为了求解方便，本文以电枢作为参照物，导轨则以恒定速度vx沿-x方向高速运动。
电磁轨道发射原理如图1a所示，装置高度为25 mm。脉冲电流从导轨一侧流入，通过电枢后从导轨另一侧流出，由此在炮膛中产生磁场，该磁场与电流作用产生洛伦兹力推动电枢运动。由安培定则可知，炮膛内磁场方向是-z轴，故本文以磁感应强度Bz为模型自变量，将三维模型简化为在xOy平面上的二维模型，如图1b所示。由于轨道和电枢模型关于xOz平面对称，故可选取该二维模型的一半作为研究对象，简化模型如图1c所示。
图1 电磁轨道发射原理及二维简化模型
Fig.1 Schematic diagram of electromagnetic rail launch and its 2D simplified model
如图1所示，本文设定导轨宽度S1=20 mm，导轨间距为2S3=25 mm，电枢长度S4=17.4 mm，令S2= 120 mm，S6=175 mm。选择导轨的材质为铜，电枢的材质为铝。设定轨道区域的电导率为2×107 S/m，磁导率为4π×10-7 H/m；电枢区域的电导率为3.6× 107 S/m，磁导率为4π×10-7 H/m。
由于电磁轨道发射系统的尺寸远小于电磁场的波长，故可以忽略位移电流，从而将电磁轨道发射作为准静态系统进行研究[23]，该系统满足的麦克斯韦控制方程组表示为
（1）
式中，H为磁场强度；J为电流密度；E为电场强度；B为磁感应强度；v为速度；D为电位移矢量；ρ为电荷密度。
结合欧姆定律
（其中σ为电导率）与法拉第电磁感应定律、高斯磁通定律，以及材料本构关系
和
（其中ε和μ分别为介电常数和磁导率），可得到磁扩散方程为
（2）
式中，μ0为真空磁导率。
由于本文将电枢作为参考系，故式中速度扩散项
，则电枢的磁扩散方程可以表示为
（3）
设置整个计算域的初始条件为
（4）
设置边界条件为
（5）
式中，
为电流线密度。本文设置电流线密度
，I为电磁轨道输入电流。
由式（5）可知，当电枢相对导轨进行高速运动时，速度趋肤效应会使磁场与电流集中于导轨内侧边缘与电枢后边缘处[24]，因此本文设置S2和S3的边界条件为
。
为了在电磁发射参数（速度和电流）发生变化时高效求解上述电磁发射模型，本文基于算子回归的思想，构建了面向电磁轨道发射速度趋肤效应快速求解的深度算子模型。下面分别阐述深度算子网络（DeepONet）的基本原理以及基于深度算子网络的电磁轨道发射计算模型。
根据神经网络的通用近似定理，神经网络不仅可以逼近任意连续函数，还可以近似连续非线性泛函或算子[25-26]，即逼近从一个函数空间到另一个函数空间的映射。基于该定理，文献[27]设计了一种特殊的网络架构，称为深度算子网络。该网络既可学习显式算子（如积分算子、拉普拉斯算子等），也可学习隐式算子（如常微分方程和偏微分方程）。相关实验结果也证明，深度算子网络在解决算子逼近问题上比其他现有的主流神经网络架构具有更好的泛化能力[26]。
定义为
在紧集K上的所有连续函数f的Banach空间，且其范数
。设κ(·)是一个连续的非多项式函数，X是一个Banach空间，
和
是两个紧集，V是
中的一个紧集，G是将V映射到
的非线性连续算子，则对任意δ＞0，有正整数n, p, m，常数
，
，
，
，
，
，使得
（6）
式（6）适用于任意
和
。
以式（6）为理论基础，通过将
作为权重，
和s作为输入特征，n, p, m作为节点，构建如图2所示的网络，即为深度算子网络。与传统神经网络（如全连接网络和卷积网络）相比，深度算子网络由两个子网络组成[28]，其中分支网络（Branch net）以离散点的形式将含参函数作为输入，用于在固定数量的传感器上对输入函数进行编码；主干网络（Trunk net）则用于对时空坐标域进行编码。与其他算子学习方法（如傅里叶神经算子）相比[25]，深度算子网络在分支网络的功能和结构选择上更具灵活性。
图2 非堆叠型深度算子网络结构
Fig.2 Structure of unstacked DeepONet
深度算子网络具有拟合非线性泛函或算子的强大能力。如果以电磁发射参数（速度和电流）为输入，以电磁发射过程中的磁场分布为输出，可以构建面向电磁轨道发射速度趋肤效应快速计算的深度算子模型。
以速度到磁感应强度的非线性映射
为例，构建深度算子模型如图3所示。其中，分支网络以导轨相对电枢的速度vx为输入，并在离散点上编码输入函数vxj。vxj的采样间隔没有限制，可以随机采样，也可以等间隔采样。本文通过等间隔采样的方式对vx进行编码。主干网络以电枢和导轨内磁场分布的时空坐标s(x, y, t)为输入，并依据网格节点对时空坐标进行采样。分支网络和主干网络分别输出相同维度的张量[b1b2…bp]和[g1g2…gp]，以便获得最终输出，表示为
（7）
图3 基于深度算子网络的电磁轨道发射速度趋肤效应快速计算
Fig.3 Fast calculation of velocity skin effect in electromagnetic rail launch based on DeepONet
本文构建的深度算子网络采用全连接网络架构，并根据问题类型（稳态和暂态仿真）以及数据量设定网络的规模，具体参数在第3节中给出。
在网络设计的基础上，通过传统有限元法[29]获得电磁轨道发射模型在不同速度、电流条件下的稳态磁场和暂态磁场分布特性，并根据深度算子网络输入和输出张量的维度构建训练数据集。有限元模型根据导轨和电枢区域的磁扩散方程并结合其边界条件和初始条件设计。
训练数据以三元组形式表示，即(vx, s, Bz(vx) (s))。其中，前两项表示模型的输入，最后一项表示模型的输出。若输入n1个函数样本，对于每个输入
，采样n2个时空坐标
以评估网络的输出功能，则训练样本的总数为n1×n2，损失函数为所有样本上的均方误差，即
（8）
式中，
为网络预测值；
为对应的标签数据。
为了验证深度算子模型的有效性，本文以第1节所述电磁轨道发射简化模型为例，首先采用传统有限元法对该模型进行磁场建模和计算，将计算获得的数据作为训练集和测试集；然后对深度算子网络进行训练，对比不同计算条件下深度算子模型和传统有限元法的结果，同时对深度算子网络开展超参数敏感性分析。所有计算过程均在深度学习服务器上进行，处理器为Intel Xeon Gold 6226R，显卡为NVIDIA RTX 3090，软件框架采用Pytorch 1.10。
1）异常数据处理：受有限元计算精度的影响，有限元模型产生的磁感应强度数据存在极少数异常点（B＜0且量级在1×10-40 T左右），在构建数据集时将它们剔除，以免影响深度算子模型的预测精度。
2）数据归一化处理：为了避免数据量级的巨大差异导致小量级数据被淹没造成模型精度下降，本文采用min-max标准对数据集进行归一化处理，通过线性变换将所有数据约束在[0, 1]，即
（9）
式中，
为归一化后的值；
和
分别为样本数据的最小值和最大值。
为了验证深度算子模型的准确性，本文首先基于传统有限元法获得的电磁轨道发射稳态结果训练深度算子网络。
在稳态情况下，深度算子模型的分支网络采用4层隐藏层和每层300个神经元的网络架构，网络输入为由导轨相对速度和电流线密度组成的二维数据；主干网络采用7层隐藏层和每层700个神经元的网络结构，输入为由模型空间坐标组成的二维数据。
为了生成训练稳态模型的数据集，本文在0～500 m/s的速度区间，以50 m/s为间隔进行均匀采样；在1.0×107～2.0×107 A/m的电流密度区间，以0.1×107 A/m为间隔进行均匀采样。将速度和电流密度组合，作为传统有限元法的建模参数，从而获得121组训练数据。为了生成验证模型有效性的测试数据集，本文在训练区间内从25～475 m/s每隔150 m/s采样速度数据，在训练区间外取点525 m/s；对于电流密度则在训练区间内从1.35×107～1.95×107 A/m每隔0.3×107 A/m进行采样，在训练区间外取点0.9×107 A/m和2.1×107 A/m，共组合得到25组测试数据。
图4展示了测试集中深度算子网络与传统有限元法在不同速度条件下求解获得的磁感应强度稳态分布及其误差云图，其中电流密度均为1.5×107 A/m。从图4中两种方法的结果对比可知，深度算子模型预测的稳态磁场分布情况与有限元方法的结果基本一致，均表现为导轨内侧后边缘和电枢前进方向后边缘磁场较为集中，磁感应强度较大，即呈现明显的趋肤效应。随着速度增大，轨道内部趋肤效应扩散区域逐渐被压缩至一个薄层内。 图4的结果表明，深度算子模型能够有效地模拟不同速度条件下的复杂磁场分布及其速度趋肤效应。
图4 不同速度条件下深度算子模型与传统有限元法的稳态结果对比
Fig.4 Comparison of steady solution between the DeepONet model and the traditional finite element method at different conditions of velocity
由图4的误差云图可以看出，深度算子模型预测的稳态磁场误差主要集中分布在导轨的内侧后边缘和电枢后边缘侧。虽然误差随着速度的提高而有所增加，但整体而言依然很小，在训练条件区间内的相对L2误差为0.337%，在训练条件区间外的相对L2误差为0.758%。在计算效率方面，稳态条件下深度算子模型的平均预测时长为0.86 s。上述对比结果表明，深度算子模型不仅能够预测电磁发射过程中的稳态磁场分布，而且在速度条件发生变化时也具有较高的求解精度和计算效率。
在暂态情况下，深度算子模型的分支网络采用4层隐藏层和每层400个神经元的网络架构，网络输入为由导轨相对速度和电流线密度组成的二维数据；主干网络采用4层隐藏层和每层200个神经元的网络架构，输入为由模型时空坐标组成的三维数据。
为了生成训练暂态模型的数据集，本文将电流密度固定为1.5×107 A/m，对导轨相对速度在0～500 m/s区间内每隔50 m/s进行采样，共获得11组训练数据；对时间序列在0～3.5 ms区间进行采样，间隔0.05 ms，共计71个时刻。对于暂态模型的测试数据集，本文在训练区间内从25～475 m/s每隔150 m/s进行采样，在训练区间外取点525 m/s，共得到5组测试数据。
图5展示了深度算子网络与传统有限元法在不同速度条件下求解获得的磁感应强度暂态分布及其误差云图，其中电流密度为1.5×107 A/m，误差云图为2.1 ms时刻的结果。两种方法均选取10个相同时刻下的磁感应强度等位线进行对比。从图5中两种方法的结果对比可知，深度算子模型预测的暂态磁场分布情况与有限元方法的结果基本一致。
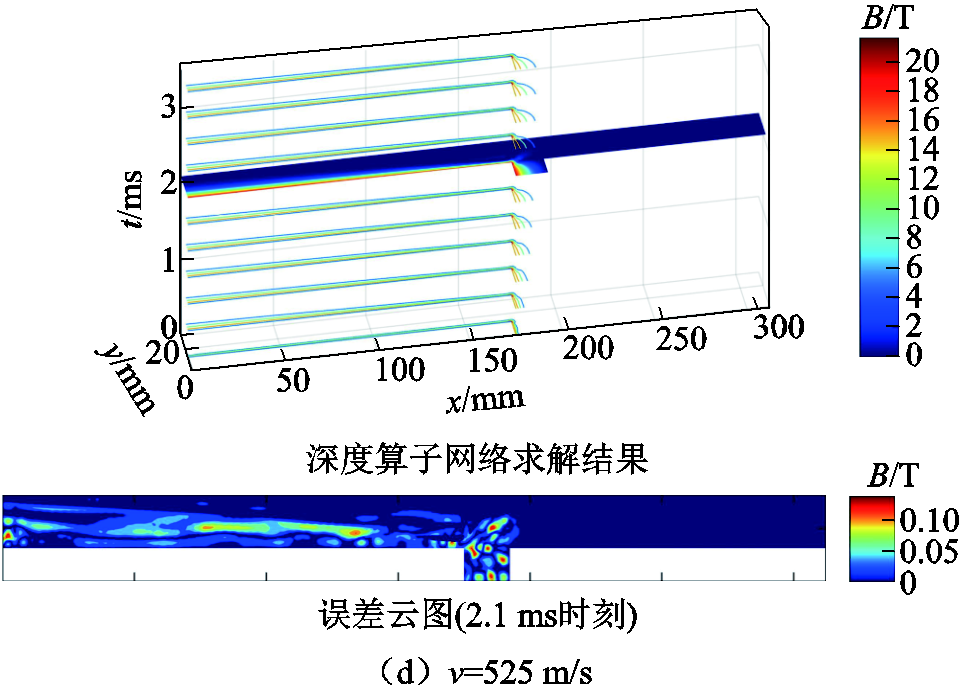
图5 不同速度条件下深度算子模型与传统有限元法的暂态结果对比（误差云图为2.1 ms时刻的结果）
Fig.5 Comparison of transient solution between the DeepONet model and the traditional finite element method at different conditions of velocity (the error maps are determined at the time of 2.1ms)
由图5的误差云图可知，深度算子模型预测的暂态磁场误差集中分布在相对电枢前进方向的导轨后边缘和电枢区域。在训练条件区间内的相对L2误差为0.526%，在训练条件区间外的相对L2误差为0.724%，模型的平均预测时长为0.87 s。这表明深度算子模型能够以较高的精度预测电磁发射过程中的暂态磁场分布，而且在速度条件发生变化时无需重新训练，而是仅仅通过网络的前向推理完成计算，计算效率较高。
此外，由于暂态问题相比于稳态问题有更高的复杂度，传统有限元法需要消耗更多计算资源和计算时间，但暂态条件下的深度算子模型的计算消耗并未因所求问题复杂度的上升而增加，其平均预测时间与稳态模型相当。这也表明深度算子网络可较好地满足电磁发射模型实时性或准实时性的计算要求，在未来数字孪生应用中有较大潜力。
考虑到深度算子网络的性能受网络结构和规模的影响较大，本文进一步通过调整深度算子网络中主干网络和分支网络的隐藏层层数和每层神经元数量，对深度算子模型进行参数敏感性分析。由于网络规模庞大且算力有限，每层神经元数的调整步长设置为100。模型性能通过式（8）中的LMSE指标来评估。测试结果见表1～表4。
表1和表2分析了稳态情况下主干网络和分支网络规模对深度算子模型性能的影响。模型训练轮数（Epoch）均为10 000次，主干网络的训练批次大小为977，分支网络的训练批次大小为121。从表1中可知，稳态情况下主干网络的最优网络层数为7层，分支网络的最优网络层数为4层。从表2中可知，稳态情况下主干网络每层神经元的最优数量为700，分支网络每层神经元数的最优数量为300。
表1 稳态情况下网络层数对深度算子模型的影响
Tab.1 Influence of network layers on the DeepONet model in the steady-state case
网络层数LMSE/10-3 主干网络分支网络 20.581.81 31.360.12 41.010.11 51.551.15 60.090.74 70.08— 80.13— 90.58—
表2 稳态情况下网络每层神经元数对深度算子模型的影响
Tab.2 Influence of network neurons on the DeepONet model in the steady-state case
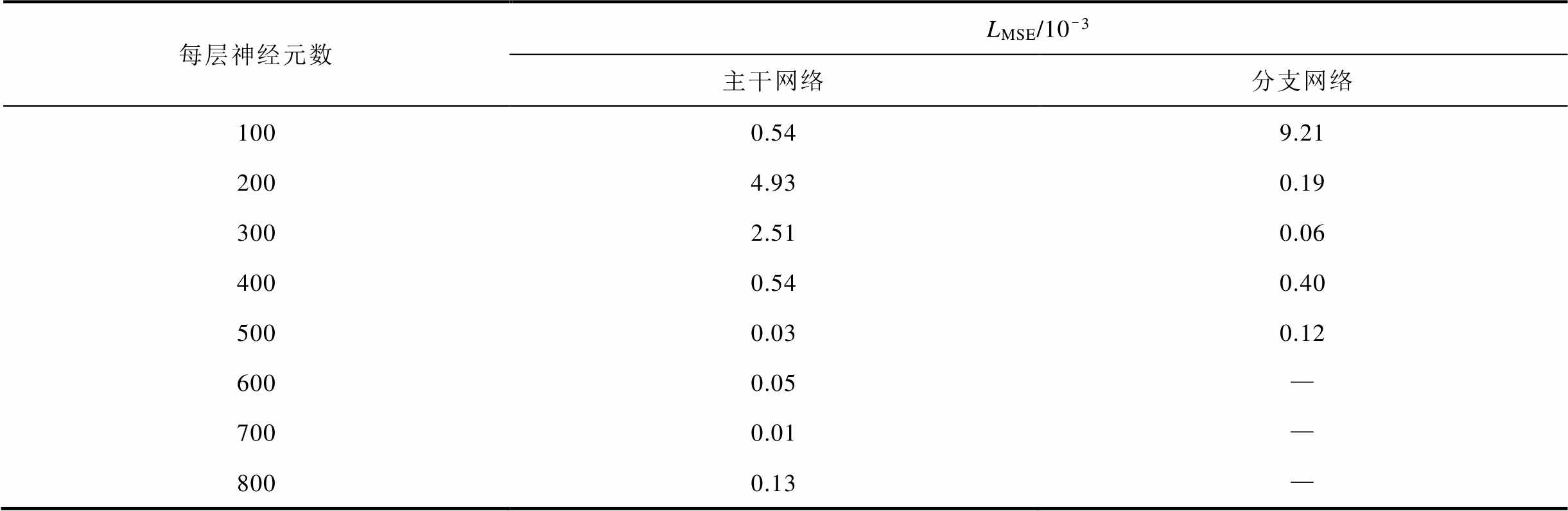
每层神经元数LMSE/10-3 主干网络分支网络 1000.549.21 2004.930.19 3002.510.06 4000.540.40 5000.030.12 6000.05— 7000.01— 8000.13—
表3 暂态情况下网络层数对深度算子模型的影响
Tab.3 Influence of network layers on the DeepONet model in the transient-state case
网络层数LMSE/10-3 主干网络分支网络 22.070.88 31.072.28 40.870.42 52.020.65 61.310.56 7—2.85
表4 暂态情况下网络每层神经元数对深度算子模型的影响
Tab.4 Influence of network neurons on the DeepONet model in the transient-state case
每层神经元数LMSE/10-3 主干网络分支网络 1003.916.14 2000.830.52 3000.930.54 4008.80.11 5001.61.13
类似地，表3和表4分析了暂态情况下主干网络和分支网络规模对深度算子模型性能的影响。模型训练轮数（Epoch）均为10 000次，主干网络的训练批次大小为69 367，分支网络的训练批次大小为11。从表3中可知，暂态情况下主干网络和分支网络的最优网络层数均为4层。从表4中可知，暂态情况下主干网络每层神经元的最优数量为200，分支网络每层神经元数的最优数量为400。
上述分析结果显示，适当地增加主干网络和分支网络的规模（即网络层数和每层网络的神经元）可以提升模型的学习效果、降低学习误差。然而，当网络规模过于庞大时，学习误差会随之增加，出现过拟合情况，这也进一步突出了在深度算子模型设计中平衡网络复杂度与性能的重要性。因此，合理地选择网络结构和规模对于保证模型的预测精度和泛化能力至关重要。
本文针对电磁轨道发射实时模拟和数字孪生场景下对速度趋肤效应的快速计算需求，提出了一种基于深度算子网络的电磁轨道发射速度趋肤效应快速计算方法。该方法的主要优点及性能提升包括：
1）针对电磁发射参数（如发射速度和电流大小）实时变化的应用场景，本文提出的深度算子模型通过引入分支网络和主干网络，分别对电磁发射参数和时空计算域进行解耦式编码，能够以相比有限元法更高的计算效率获得电磁发射过程中的磁场分布，而不需要针对每个电磁发射条件重新进行有限元计算，且计算精度较高、泛化能力较强。以有限元法的结果为基准，基于深度算子网络的电磁轨道发射模型在训练条件区间内进行预测时，在稳态和暂态情况下的相对L2误差分别为0.337%和0.526%，总平均相对L2误差为0.43%；在训练条件区间外进行预测时，在稳态和暂态情况下的相对L2误差分别为0.758%和0.724%，总平均相对L2误差为0.74%。
2）在电磁轨道发射暂态磁场计算中，深度算子模型通过在分支网络中引入时间变量，实现了对电磁发射暂态过程的有效模拟。算例结果显示，深度算子网络相比传统有限元方法的相对L2误差为0.724%，表明其具有较高的计算精度。而深度算子网络在暂态模型中的平均预测时长为0.87 s，与稳态模型相当，表明即使在问题复杂度提高的情况下，深度算子网络的前向推理效率依然较高。
3）对深度算子模型的敏感性分析显示，网络规模对深度算子模型的性能有较大影响，且主干网络和分支网络的最优网络规模可能不尽相同。虽然在一定范围内增加网络规模可以提升模型的学习能力，降低学习误差，但也容易出现过拟合的情况。因此，合理地选择网络结构和规模对于深度算子模型的实际应用至关重要。后续工作将进一步研究通过自动机器学习技术开展深度算子模型的超参数调优。
参考文献
[1] 马伟明, 鲁军勇. 电磁发射技术的研究现状与挑战[J]. 电工技术学报, 2023, 38(15): 3943-3959. Ma Weiming, Lu Junyong. Research progress and challenges of electromagnetic launch technology[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 3943-3959.
[2] 李兵, 李卫超, 荆从凯. 电磁发射系统研究现状及应用展望[J]. 兵器装备工程学报, 2023, 44(10): 173-181. Li Bing, Li Weichao, Jing Congkai. Research status and application prospects of electromagnetic launch system[J]. Journal of Ordnance Equipment Engineering, 2023, 44(10): 173-181.
[3] 马晓平, 廖欣, 陈兵. 电磁发射超高速制导炮弹国内外研究现状综述[J]. 空天防御, 2021, 4(2): 87-92. Ma Xiaoping, Liao Xin, Chen Bing. Research review of hypervelocity projectile by electromagnetic launch at home and abroad[J]. Air & Space Defense, 2021, 4(2): 87-92.
[4] Mao Weiwei, Pang Teng, Guo Zhirong, et al. Analysis of the research progress of electromagnetic railgun based on CiteSpace[J]. IEEE Access, 2024, 12: 3499-3513.
[5] 李军, 严萍, 袁伟群. 电磁轨道炮发射技术的发展与现状[J]. 高电压技术, 2014, 40(4): 1052-1064. Li Jun, Yan Ping, Yuan Weiqun. Electromagnetic Gun technology and its development[J]. High Voltage Engineering, 2014, 40(4): 1052-1064.
[6] 阮景煇, 陈立学, 夏胜国, 等. 电磁轨道炮电流分布特性研究综述[J]. 电工技术学报, 2020, 35(21): 4423-4431. Ruan Jinghui, Chen Lixue, Xia Shengguo, et al. A review of current distribution in electromagnetic railguns[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4423-4431.
[7] Engel T G, Neri J M, Veracka M J. Characterization of the velocity skin effect in the surface layer of a railgun sliding contact[J]. IEEE Transactions on Magnetics, 2008, 44(7): 1837-1844.
[8] Hsieh K T, Stefani F, Levinson S J. Numerical modeling of the velocity skin effects: an investigation of issues affecting accuracy in railguns[J]. IEEE Transactions on Magnetics, 2001, 37(1): 416-420.
[9] Li Xin, Weng Chunsheng. Three-dimensional investigation of velocity skin effect in U-shaped solid armature[J]. Progress in Natural Science, 2008, 18(12): 1565-1569.
[10] 李昕, 翁春生. U形电枢非稳态电磁场二维数值模拟[J]. 火炮发射与控制学报, 2009, 30(1): 1-4. Li Xin, Weng Chunsheng. Two dimension numerical simulation of unsteady electromagnetic field in U-shaped solid armature[J]. Journal of Gun Launch & Control, 2009, 30(1): 1-4.
[11] 胡鑫凯, 鲁军勇, 李白, 等. 瞬态条件下电磁轨道发射装置绝缘体热损伤分析[J]. 电工技术学报, 2023, 38(21): 5673-5681. Hu Xinkai, Lu Junyong, Li Bai, et al. Thermal damage analysis of insulator in electromagnetic rail launcher under transient conditions[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5673-5681.
[12] 王刚华, 谢龙, 王强, 等. 电磁轨道炮电磁力学分析[J]. 火炮发射与控制学报, 2011, 32(1): 69-71, 76. Wang Ganghua, Xie Long, Wang Qiang, et al. Analysis on electromagnetic mechanics in electromagnetic railgun[J]. Journal of Gun Launch & Control, 2011, 32(1): 69-71, 76.
[13] 耿轶青, 申泽军, 袁建生. 电磁轨道炮电枢运动产生的磁场特性分析与计算方法[J]. 高电压技术, 2016, 42(9): 2876-2881. Geng Yiqing, Shen Zejun, Yuan Jiansheng. Characteristic analysis and calculation method of magnetic field produced by moving armature of electromagnetic railgun[J]. High Voltage Engineering, 2016, 42(9): 2876-2881.
[14] 殷强, 张合, 李豪杰. 动态条件下电磁轨道炮膛内磁场和电场分析[J]. 兵工学报, 2017, 38(6): 1059-1066. Yin Qiang, Zhang He, Li Haojie. Analysis of In-bore magnetic and electric fields in electromagnetic railgun under dynamic condition[J]. Acta Armamentarii, 2017, 38(6): 1059-1066.
[15] Naga Praneeth S R, Singh B. Finite element-boundary element method based simulations of electromagnetic railgun in augmented configurations[J]. IEEE Journal on Multiscale and Multiphysics Computational Techniques, 2022, 7: 320-327.
[16] Ge Xia, Cao Bin, Wang Zhao, et al. Research on the contact characteristics between armature and rail of the enhanced electromagnetic rail Gun based on the new aluminum alloy armature[J]. IEEE Transactions on Plasma Science, 2023, 51(12): 3703-3708.
[17] 李湘平, 鲁军勇, 谭赛, 等. 基于Fluent二次开发的电磁轨道发射运动磁场仿真[J]. 中国电机工程学报, 2020, 40(19): 6364-6370. Li Xiangping, Lu Junyong, Tan Sai, et al. Simulation on moving magnetic field of electromagnetic rail launch based on fluent secondary development[J]. Proceedings of the CSEE, 2020, 40(19): 6364-6370.
[18] 周鹏飞, 栗保明. 两种数值格式对电磁轨道炮速度趋肤效应的计算与分析[J]. 高电压技术, 2022, 48(6): 2418-2424. Zhou Pengfei, Li Baoming. Calculation and analysis of velocity skin-effect of electromagnetic railgun by two numerical forms[J]. High Voltage Engineering, 2022, 48(6): 2418-2424.
[19] 王增基, 陈立学, 尤彭昊, 等. 考虑速度趋肤效应与接触电阻影响的枢轨界面电流分布特性[J]. 电工技术学报, 2022, 37(19): 5003-5010. Wang Zengji, Chen Lixue, You Penghao, et al. Current distribution characteristics of armature-rail interface under velocity skin effect and contact resistance[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 5003-5010.
[20] 翟小飞, 邹锟, 李配飞, 等. 身管外壳对电磁轨道发射装置发射性能影响分析[J]. 电工技术学报, 2024, 39(2): 333-342. Zhai Xiaofei, Zou Kun, Li Peifei, et al. Analyzing influence of barrel shell on launching performance of electromagnetic rail launcher[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 333-342.
[21] 张嘉炜, 鲁军勇, 谭赛, 等. 考虑初始接触压力的滑动电接触界面磁扩散模型[J]. 电工技术学报, 2022, 37(2): 488-495. Zhang Jiawei, Lu Junyong, Tan Sai, et al. A magnetic diffusion model of electromagnetic launcher considering initial contact pressure[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 488-495.
[22] 彭之然, 汪光森, 翟小飞, 等. 电磁轨道发射装置时变电感梯度建模与分析[J]. 电工技术学报, 2020, 35(23): 4843-4851. Peng Zhiran, Wang Guangsen, Zhai Xiaofei, et al. Modeling and analysis of time-varying inductance gradient for electromagnetic rail launcher[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4843-4851.
[23] 林庆华, 栗保明. 电磁轨道炮三维瞬态涡流场的有限元建模与仿真[J]. 兵工学报, 2009, 30(9): 1159-1163. Lin Qinghua, Li Baoming. Finite element analysis of 3D transient eddy field in electromagnetic railgun[J]. Acta Armamentarii, 2009, 30(9): 1159-1163.
[24] 李军. 电磁轨道炮中的电流线密度与膛压[J]. 高电压技术, 2014, 40(4): 1104-1109. Li Jun. Linear current density and bore pressure of electromagnetic railgun[J]. High Voltage Engineering, 2014, 40(4): 1104-1109.
[25] Chen Tianping, Chen H. Approximations of continuous functionals by neural networks with application to dynamic systems[J]. IEEE Transactions on Neural Networks, 1993, 4(6): 910-918.
[26] Chen Tianping, Chen Hong. Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to dynamical systems[J]. IEEE Transactions on Neural Networks, 1995, 6(4): 911-917.
[27] Lu Lu, Jin Pengzhan, Pang Guofei, et al. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators[J]. Nature Machine Intelligence, 2021, 3: 218-229.
[28] Lu Lu, Meng Xuhui, Cai Shengze, et al. A comprehensive and fair comparison of two neural operators (with practical extensions) based on FAIR data[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 393: 114778.
[29] 孟洲恬, 淡淑恒. 基于有限元和神经网络方法的电磁斥力机构结构优化设计[J]. 高压电器, 2021, 57(6): 196-202. Meng Zhoutian, Dan Shuheng. Structural optimization design of electromagnetic repulsive mechanism with finite element method and neural network method[J]. High Voltage Apparatus, 2021, 57(6): 196-202.
Abstract Electromagnetic rail launch is a technology that uses precisely controlled magnetic forces to accelerate the armature to a very high speed. The distribution characteristics of magnetic fields are closely related to the launch performance, and one of the physical effects that have an important impact on the magnetic field distribution is the velocity skin effect. However, the traditional numerical algorithms based on finite difference, finite element and finite volume methods are difficult to perform fast calculation of velocity skin effect in real-time simulation and digital twin scenarios of electromagnetic rail launch. Therefore, a fast calculation method based on deep operator network (DeepONet) is proposed in this paper, which can accurately and efficiently solve the velocity skin effect of electromagnetic rail launch.
DeepONet, as a powerful deep learning model that can learn nonlinear operators based on the general approximation theorem of operators, has been proven to have better generalization ability in solving calculus problems than other neural network architectures. DeepONet consists of two subnetworks, one with functions as inputs in the form of discrete points for encoding input functions on a fixed number of sensors, called Branch Net, and another for encoding domains of output functions, called Trunk Net.
In order to verify the performance of DeepONet-based method, this paper solves the magnetic field distribution of electromagnetic rail launch under different velocity and current conditions. Firstly, the magnetic induction intensity in the rail region is obtained based on the traditional finite element method, and the training data set is constructed accordingly. Then, a non-stacked DeepONet is constructed, including branch network and trunk network, which are used to encode the variable parameters and space-time coordinates, respectively. The magnetic induction intensity data of armature and rail are then fed into DeepONet for training. Finally, the results obtained by finite element method and DeepONet are compared under different conditions of velocity and current to verify the effectiveness of DeepONet-based method. The experimental results show that, the relative L2 error between the DeepONet-based method and the finite element method is 0.43% within the training conditions, and 0.74% outside the training conditions, and the average prediction time reaches 0.865 s.
The following conclusions can be drawn: (1) Compared with the finite element method, the proposed DeepONet-based method introduces branch and trunk networks to decouple the electromagnetic launch parameters and the space-time computational domain, which can obtain the magnetic field distribution in the electromagnetic rail launch with higher computational efficiency. It does not need to redo finite element calculation for each electromagnetic launch condition. (2) In the transient calculation, the DeepONet-based method realizes the effective simulation of electromagnetic rail launch by introducing time variable into the branch network. The average prediction time in the transient model is 0.87 seconds, which is equivalent to the steady-state model, indicating that even with an increase in problem complexity, the inference efficiency of the DeepONet-based method is still relatively high. (3) The sensitivity analysis shows that network size has a significant impact on the performance of the DeepONet-based method, and the optimal network size for branch and trunk networks may not be the same. Although increasing the network size within a certain range can improve the learning ability of the model and reduce learning errors, overfitting is also prone to occur. Therefore, a reasonable selection of network structure and scale is crucial for the practical application of the DeepONet-based method.
keywords：Electromagnetic rail launch, velocity skin effect, deep operator network (DeepONet), data driven
DOI: 10.19595/j.cnki.1000-6753.tces.240431
中图分类号：TM l53+.1
国家自然科学基金（92066106）、江苏省基础研究计划自然科学基金（BK20231427）、东南大学“至善青年学者”支持计划（中央高校基本科研业务费）（2242022R40022）资助项目。
收稿日期 2024-03-18
改稿日期 2024-03-27
魏 蓉 女，2002年生，硕士研究生，研究方向为人工智能技术在电气工程领域的应用、配电网韧性。E-mail：rongw.56@qq.com
仲林林 男，1990年生，副研究员，博士生导师，研究方向为高电压技术、放电等离子体技术、人工智能技术。E-mail：linlin@seu.edu.cn（通信作者）
（编辑 李 冰）