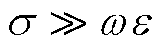），那么，由斯涅尔折射定律可得良导体内折射波的折射角θ满足关系式摘要 应用单一时域数值方法，在面对嵌入式导电薄层一类多尺度问题时，都面临着建模极为困难的挑战。该文提出了一种基于时域有限差分（FDTD）法和高阶时程精细积分（PITD）法的电磁波混合数值方法。该方法对导电薄层外部进行粗网格剖分并应用FDTD法，而对薄层内部进行一维细网格剖分并应用四阶PITD法，以实现不同网格尺度的同步时间推进。为了实现粗细网格之间的信息交换，在PITD域中引入过渡区域并应用二阶PITD法，通过等效本构参数来更新交界面处的切向电场。分析了该混合算法的数值稳定性和数值反射，并通过典型数值算例验证了所提方法的有效性和准确性。
关键词：时域有限差分法 四阶时程精细积分法 亚网格技术 矩阵指数
在计算电磁学的发展中，频域数值方法[1]在很长的一段时间内一直占据主导地位。在对电磁系统进行宽频带特性分析时，频域数值方法需要针对每个频率点重复计算复杂的方程组，而时域数值方法[2]可以直接分析电磁信号与电磁系统相互作用的动态过程，只需对一次计算获得的时域结果进行简单的傅里叶变换就可以得到其频域宽带特性，这是频域数值方法无法比拟的优点。时域有限差分（Finite-DifferenceTime-Domain, FDTD）法[3]是一种广泛应用的时域数值方法，然而其时间步长受到Courant-Friedrichs-Lewy（CFL）稳定性条件的限制。为克服这一缺点，马西奎教授团队率先提出了时程精细积分（Precise-Integration Time-Domain, PITD）法[4]。PITD法的核心思想是将Maxwell旋度方程中的时间和空间偏微分算子分开处理，首先应用Yee元胞对空间偏微分算子进行差分离散，然后采用精细积分技术处理时间偏微分算子。与FDTD法相比，PITD法不仅突破了CFL稳定性条件的限制，具有相当宽松的时间步长选取范围，且数值色散误差与时间步长几乎无关，从而保证了大时间步长下的计算精度。为了降低数值色散和提高计算精度，基于四阶空间中心差分格式的PITD法[5]被提出。这里，分别把基于二阶和四阶空间中心差分格式的PITD法简写为PITD(2)法和PITD(4)法。
嵌入式导电薄层在电磁系统的屏蔽中有着广泛的应用，如飞行器、汽车和金属机箱的外壳，其主要材料有碳纤维层、碳纳米管和金属涂层等[6]。在采用常规的FDTD法计算时，为了确保导电薄层建模的准确性，必须对整个计算空间进行细网格剖分，从而导致计算机资源消耗剧增。为解决这一问题，嵌入式薄层建模技术得到了广泛的研究，其主要分为三类。第一类是基于平均参数思想的等效参数模型法[7-8]，其仅适用于厚度小于或与趋肤深度相当的可穿透薄层。第二类是网络阻抗边界条件（Network ImpedanceBoundary Condition, NIBC）法[9]，通过频域阻抗矩阵关系来确定薄层两侧的切向电场和磁场，但是NIBC法存在后期不稳定的缺点。第三类是亚网格技术[10]，即在薄层外的电大尺寸区域进行粗网格剖分，在薄层内的电小尺寸区域进行细网格剖分。然而，这种非均匀网格的时间步长仍然受到最小网格尺寸的限制，导致需要极长的运行时间。
为了放宽亚网格技术中CFL稳定性条件的限制，已提出了多种时域混合数值方法，如基于FDTD法和时域Crank-Nicolson法的混合方法[11]，以及基于FDTD法和混合隐显式FDTD法的混合方法[12]等。受这些混合方法的启发，几乎无条件稳定的PITD法也特别适用于求解局部细网格上的场量，因此基于FDTD法和PITD法的混合方法的相关研究工作已经开展[13-15]。由于良导体薄层内的波沿着近似垂直于其表面的方向传播，这样就不需要考虑薄层内部的法向场分量，可以仅通过一维全波模拟来确定薄层两侧的切向电场[16]。因此，本文基于FDTD法和一维PITD(4)法提出了一种电磁波混合方法来对嵌入式导电薄层进行高效精确建模，在薄层内部采用一维PITD(4)法，而外部采用FDTD法，避免了时间步长的减小，能够快速准确地评估导电薄层的屏蔽效能。
假设角频率为ω的电磁波从理想介质（介电常数为ε0和磁导率为μ0）以入射角θ0斜入射到良导体表面（介电常数为ε、磁导率为μ和电导率为σ，满足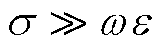），那么，由斯涅尔折射定律可得良导体内折射波的折射角θ满足关系式
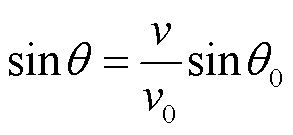（1）
式中，
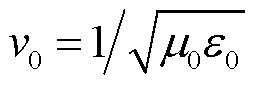和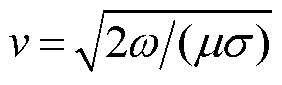
分别为理想介质和良导体内波的相速。对于一般非磁性媒质有μ≈μ0，则
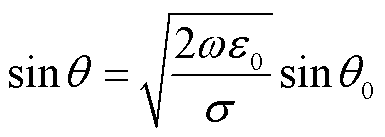（2）
如果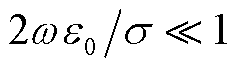
，则sinθ≈0或θ≈0。这表明，对于良导体而言，透入的电磁波都是近似地沿表面的法线方向传播，与入射波的方向无关。
空间网格尺寸由两个因素决定：①相关频带对应的最小波长（通常不超过最小波长的1/12）；②精细结构的几何尺寸。当导电薄层的厚度远小于波长时，薄层外部区域网格尺寸的主要限制因素是波长，而内部则取决于其几何尺寸。因此，本文首先从最小波长的角度考虑对整体区域进行粗网格剖分，再将导电薄层嵌入其中，模型示意图如图1a所示。由前述可知，在导电薄层内部可以沿其表面的法线方向进行一维细网格剖分，采用PITD法来突破细网格对时间步长的限制，以实现导电薄层内部和外部空间中时间步长的一致。同时，采用一维模拟能大大降低PITD法对内存的需求。与PITD(2)法相比，PITD(4)法具有更高的空间离散精度，并不会造成额外的内存负担[5]，因为它们两者矩阵指数规模和稀疏性的差异并不显著。嵌入式导电薄层建模横截面示意图如图1b所示，本文所提出的电磁波混合FDTD-PITD(4)方法基于导电薄层内外区域的特点，采用常规的FDTD法来求解导电薄层外部的粗网格区域，而采用一维PITD(4)法来求解薄层内部的细网格区域。
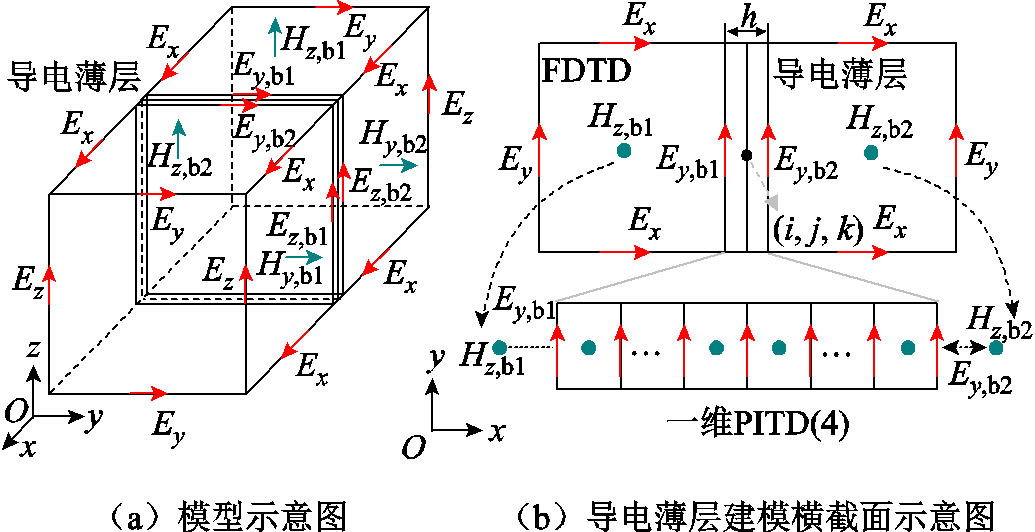
图1 嵌入式导电薄层建模示意图
Fig.1 Schematic diagram of embedded thin conductive layer modeling
假设薄层外部是介电常数为ε0和磁导率为μ0的理想介质，导电薄层是介电常数为ε、磁导率为μ和电导率为σ的良导体，且被离散成I个一维元胞，即薄层离散层数为I。
令Ur代表电场E和磁场H在直角坐标系中的某一分量，其在时间域和空间域的离散表示为
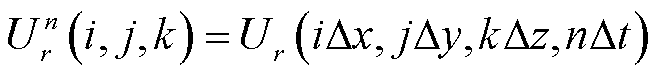（3）
式中，n为时刻标记；r表示x、y或z方向；Δx、Δy和Δz为空间步长；Δt为时间步长。
如图1所示，采用常规的FDTD法来更新导电薄层外部粗网格区域的场量。但是，与导电薄层相邻的切向磁场Hz,b1和Hz,b2需要特殊处理，其更新公式为
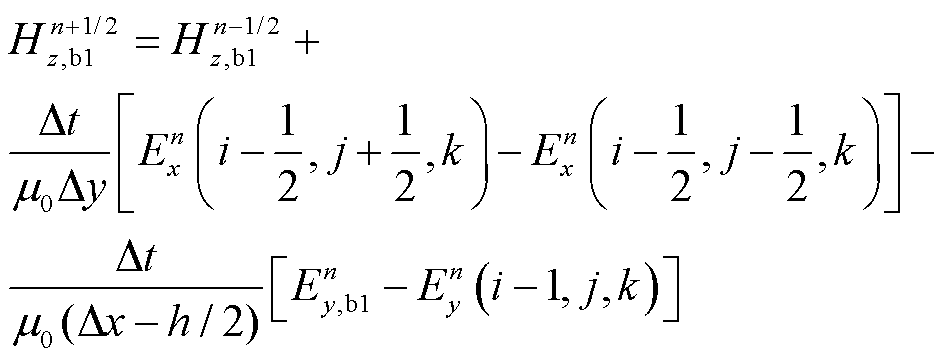(4)
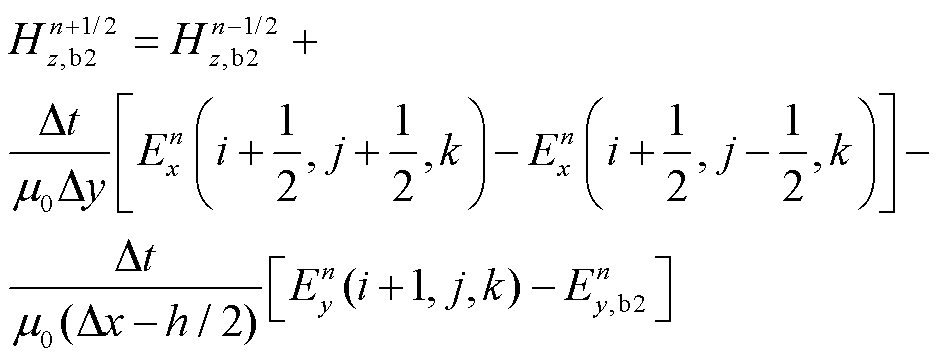(5)
式中，h为导电薄层的厚度；下标b表示边界处的场值。导电薄层两侧边界处的切向电场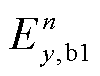
和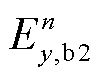
是通过薄层内部的一维全波模拟得到的，即
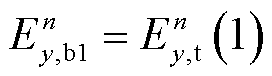（6）
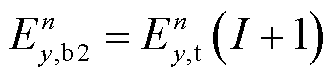（7）
式中，下标t表示导电薄层内部的场值。
2.3.1 导电薄层内部的空间离散
导电薄层内部空间离散示意图如图2所示，对导电薄层内部进行细网格离散，将其剖分为I个网格尺寸为Δxt的一维网格，即有I+1个电场分量Ey,t和I个磁场分量Hz,t。
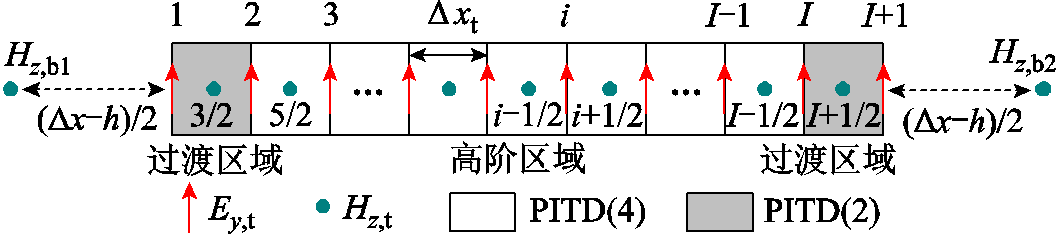
图2 导电薄层内部空间离散示意图
Fig.2 Schematic diagram of spatial discretization inside the thin conductive layer
如图2所示，在导电薄层内部的高阶区域中，采用四阶中心差分格式来对Maxwell旋度方程进行空间离散，得到PITD(4)法的半离散方程为
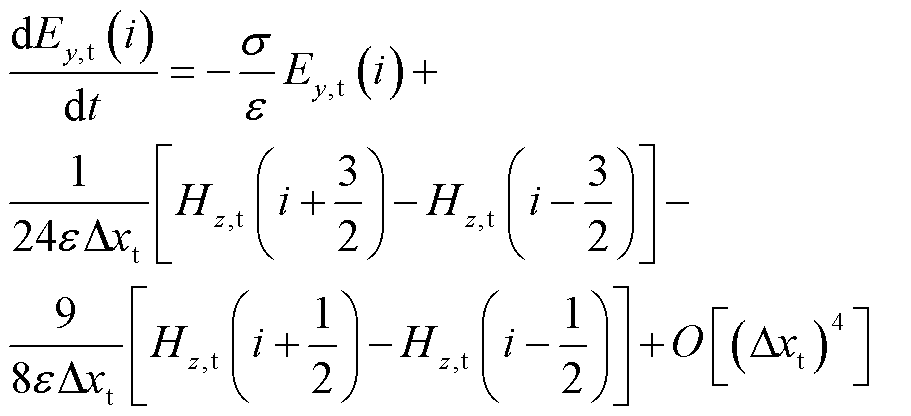(8)
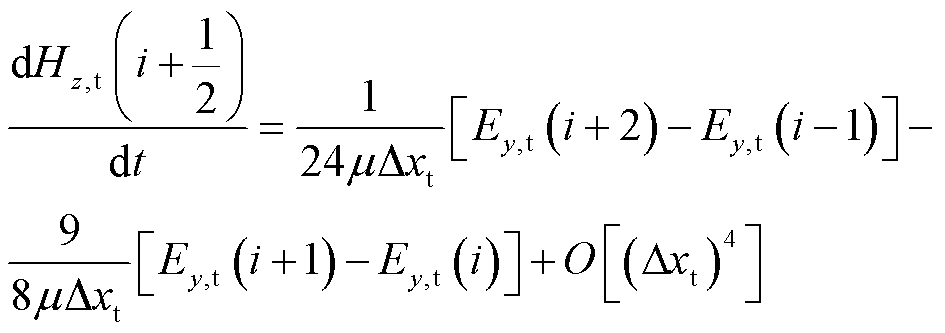(9)
式（8）和式（9）中的空间差分近似所产生的误差为O[(Δxt)4]，因此PITD(4)法在空间上具有四阶精度。在混合方法中，通过引入过渡区域[17]，实现FDTD区域和PITD(4)区域的信息交换。考虑到二阶空间中心差分格式执行简单，且不需要进行插值，因此在过渡区域中采用PITD(2)法，电场Ey,t(2)和Ey,t(I)的半离散方程为
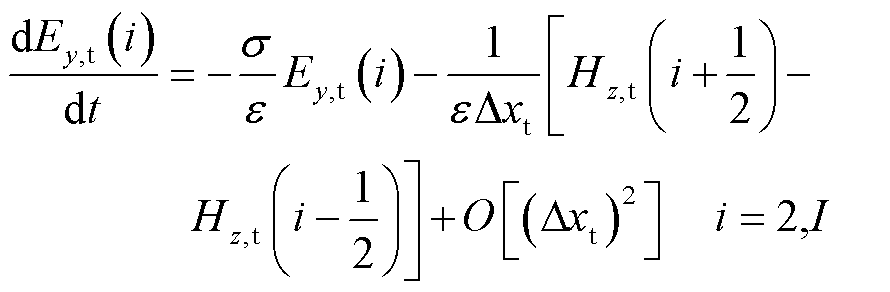(10)
在过渡区域中，磁场Hz,t(3/2)和Hz,t(I+1/2)的半离散方程为
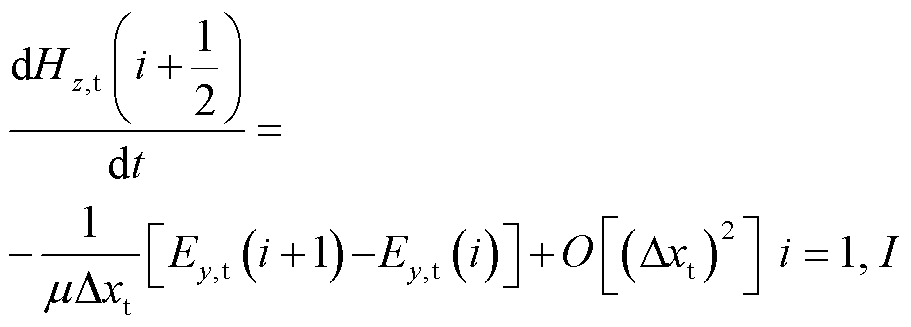(11)
此外，过渡区域的厚度选择应该遵循求解高阶区域所用到的未知量都位于薄层内的原则。然后，在粗细网格分界面处，将导电薄层外的磁场Hz,b1和Hz,b2作为薄层内PITD域的外加激励，可得分界面处的半离散方程为
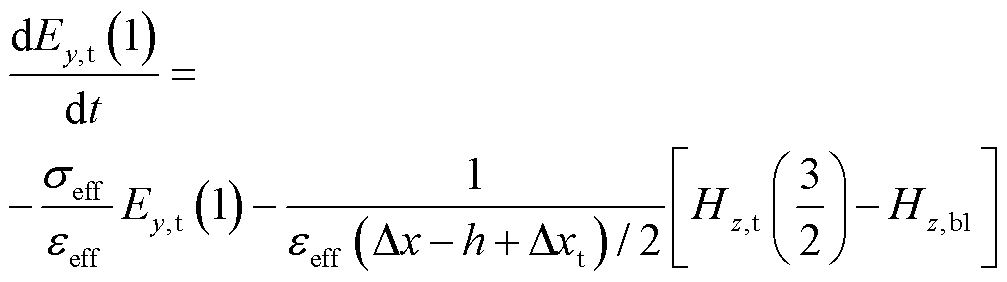（12）
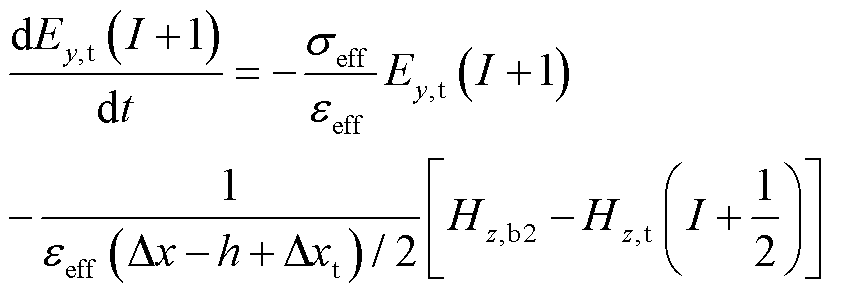(13)
式中，由于分界面处的元胞填充了两种介质，因此其等效介电常数εeff和等效电导率σeff分别为
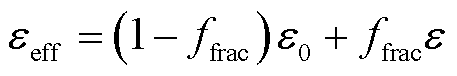（14）
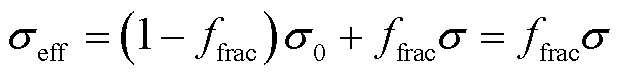（15）
式中，σ0为理想介质的电导率，有σ0=0；ffrac为分界面处元胞中良导体所占的比例，可表示为
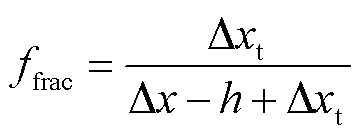（16）
2.3.2 精细积分技术
可以将导电薄层内部和边界处的所有常微分方程（式（8）～式（13））写为矩阵形式，即
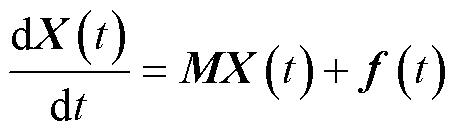（17）
式中，X(t)=[Ey,t(1)Hz,t(3/2)×××Hz,t(I+1/2)Ey,t(I+1)]T是一个由嵌入式导电薄层内部全部网格节点上电磁场分量组成的列向量；M为一维问题对应的系数矩阵；f(t)=Cnh[Hz,b10×××0−Hz,b2]T为由外加激励引入的非齐次项，Cnh=2/[εeff(Δx−h+Δxt)]。
根据常微分方程组理论，式（17）的解析解为
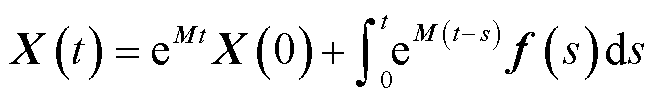（18）
对f(t)采用分段常数近似，即假设在采样区间[nΔt, (n+1)Δt]内有f(t)≈fn+1/2，其中fn+1/2由FDTD区域计算已知。因此，对式（18）进行时间离散，得到逐步递推公式为
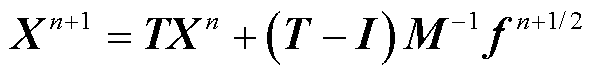（19）
式中，I为单位矩阵，T=eMΔt为矩阵指数。不难看出，矩阵指数T的精确计算是求解式（19）的关键。精细积分技术可以在计算机字长范围内精确计算矩阵指数[4]。下面简要给出精细积分技术计算矩阵指数T的过程。利用指数函数的加法定理，有
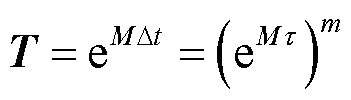（20）
式中，τ=Δt/m，m=2N，N为预选的整数。对于给定的时间步长Δt，总存在N使得τ为极小的时间区段，因此对eMτ进行四阶Taylor级数展开就可以具有极高的近似精度，即
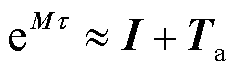（21）
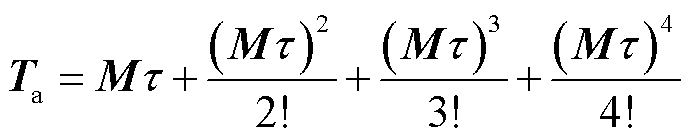（22）
显然，矩阵Ta是一个小量，当Ta与单位矩阵I相加时会成为尾数，在计算机的舍入操作下精度将丧失殆尽。为了避免丧失有效位数，T可分解为
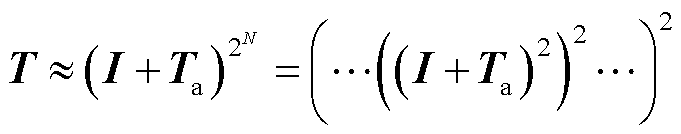（23）
所以，T的计算可以从(I+Ta)2开始，又因为
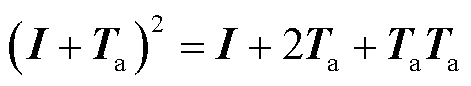（24）
因此，可通过如算法1所示的程序流程来计算矩阵指数T，再将其代入时间步进公式（19）中，即可获得各时刻电磁场的值。
算法1 精细积分技术计算矩阵指数T 1: 设置参数τ和N2: 初始化和创建矩阵M3: Ta=Mτ+(Mτ)2/2!+(Mτ)3/3!+(Mτ)4/4!4: for iter=1:N do5: Ta=2Ta+TaTa6: end for7: T=I+Ta
本文所提出的混合FDTD-PITD(4)方法的求解流程如图3所示。具体步骤如下：
（1）若已知前一时刻空间各处的电场和磁场，采用FDTD法计算导电薄层外(n+1/2)Δt时刻的磁场。
（2）通过式（4）和式（5）来更新导电薄层外部相邻的(n+1/2)Δt时刻的切向磁场。
（3）采用FDTD法来计算导电薄层外(n+1)Δt时刻的电场。
（4）将步骤（2）计算获得的外部切向磁场作为外加激励引入PITD域。
（5）采用一维PITD(4)法，通过式（19）来更新导电薄层内(n+1)Δt时刻的电场和磁场。
（6）通过式（6）和式（7）来更新导电薄层两侧边界处(n+1)Δt时刻的切向电场。
（7）重复上述步骤。
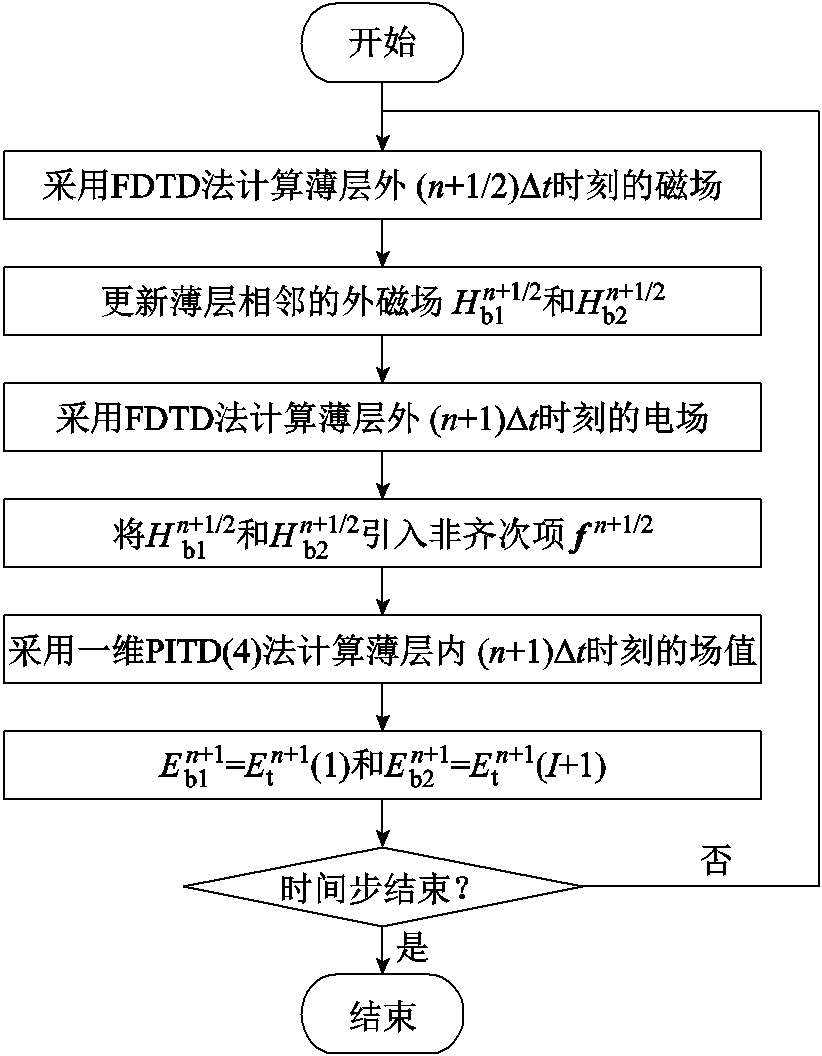
图3 混合算法求解流程
Fig.3 Solution flowchart of the hybrid algorithm
3.1.1 一维PITD(4)法和FDTD法的稳定性条件
对于一维情况（X(t)=[Ey,t Hz,t]T），矩阵M为
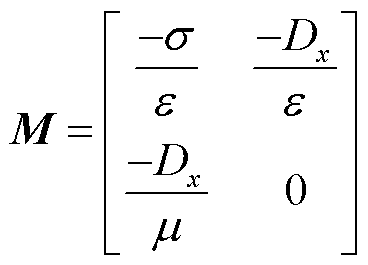（25）
式中，Dx为空间差分算子。
对于沿着x方向传播的正弦均匀平面波，在空间谱域中可以把电磁场的某一分量表示为[8]
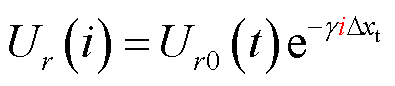（26）
式中，γ为数值传播常数，γ=α+jβ；α为数值损耗常数；β为数值相位常数。此时有
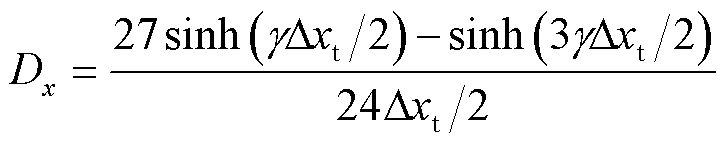（27）
不难看出，矩阵M的特征值λM满足
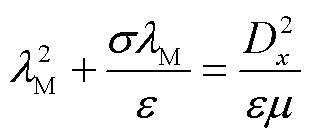（28）
矩阵指数T的特征值λT为
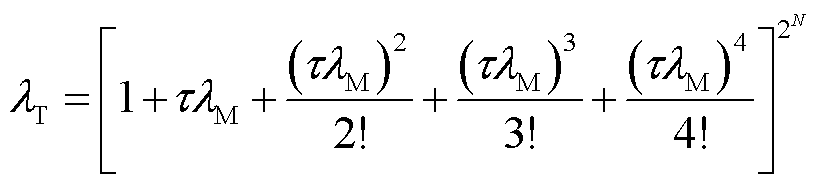（29）
根据Von Neumann稳定性分析法，要求|λT|≤1，可以得到有耗媒质中一维PITD(4)法的稳定性条件为
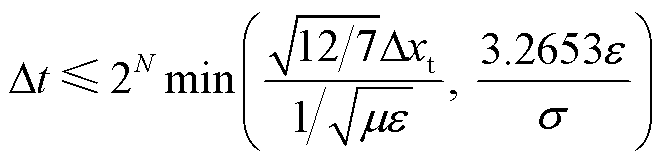（30）
由式（30）可知，通过调整N的取值可以使得一维PITD(4)法的时间步长选取更加灵活。而FDTD法则受到严格的CFL稳定性条件的限制，即
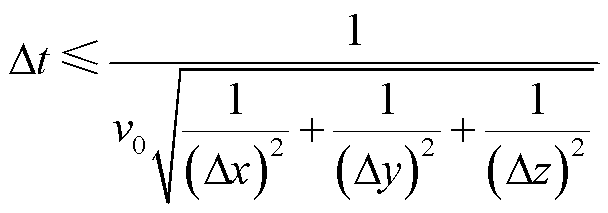（31）
通常情况下，只要N足够大，例如，N=30，就可以取一维细网格PITD(4)法的时间步长与粗网格FDTD法的时间步长相同，从而实现粗细网格区域同步推进。
3.1.2 矩阵稳定性的计算分析
上述一维 PITD(4)法和 FDTD法的稳定性分析没有考虑粗细网格分界面的影响。为了更好地证明混合方法的稳定性，这里对混合方法的全局矩阵稳定性进行计算分析。与所有线性时域方法一样，混合算法也可以用一个时间步进算子表示为[18]
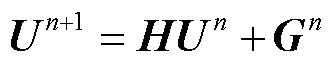（32）
式中，H为时间步进算子，也称为状态传递矩阵；U为包含所有未知量的列向量；G为表示源的列向量。这描述了一个线性有界输入有界输出系统，如果矩阵H的所有特征值λH都位于复平面的单位圆内或单位圆上，则该系统稳定。矩阵H可通过如下方法提取[16]：
（1）定义列向量Un包含所有未知量。
（2）将只有第p个元素为1的单位向量赋值给Un。
（3）将混合算法向前推进一个时间步长。
（4）得到的向量Un+1是矩阵H的第p列。
（5）完成p的所有取值迭代。
数值稳定性的测试如图4所示。用如图4a所示的测试算例来验证混合算法的稳定性。平面波正入射到无限大导电薄层，设置薄层的厚度为0.25 mm，电导率为104S/m，相对介电常数为1。粗细网格的尺寸分别为1 mm和5μm。定义S为FDTD区域的Courant常数，即S=v0Δt/Δx。从图4b不难看出，当S=1时经过106个时间推进步，算法依然稳定。通过上述方法提取矩阵H，得到矩阵H的特征值分布如图5所示。从图5可知，当S=1时，所有特征值都位于复平面的单位圆内或单位圆上，而当S=1.1时，存在单位圆外的特征值，此时算法不稳定。综上所述，考虑不同网格分界面的影响，混合算法的全局稳定性也只取决于粗网格FDTD法的CFL稳定性条件。
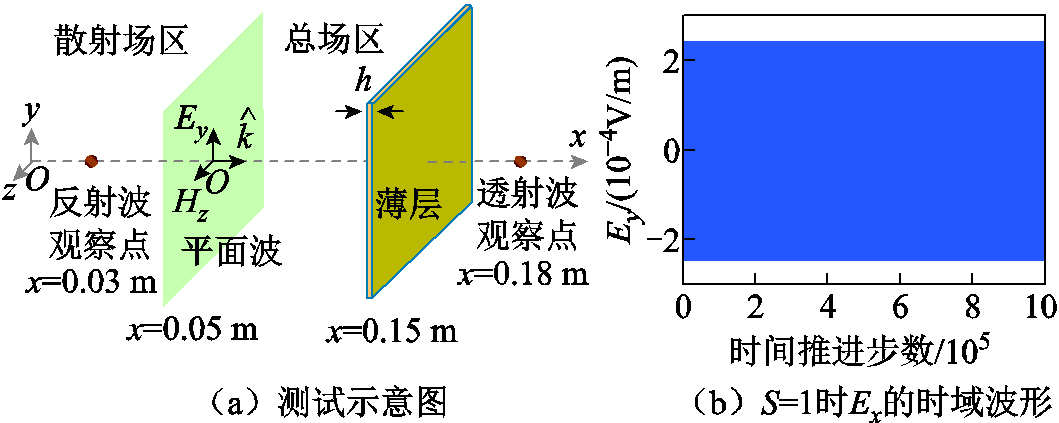
图4 数值稳定性的测试
Fig.4 Testing of numerical stability
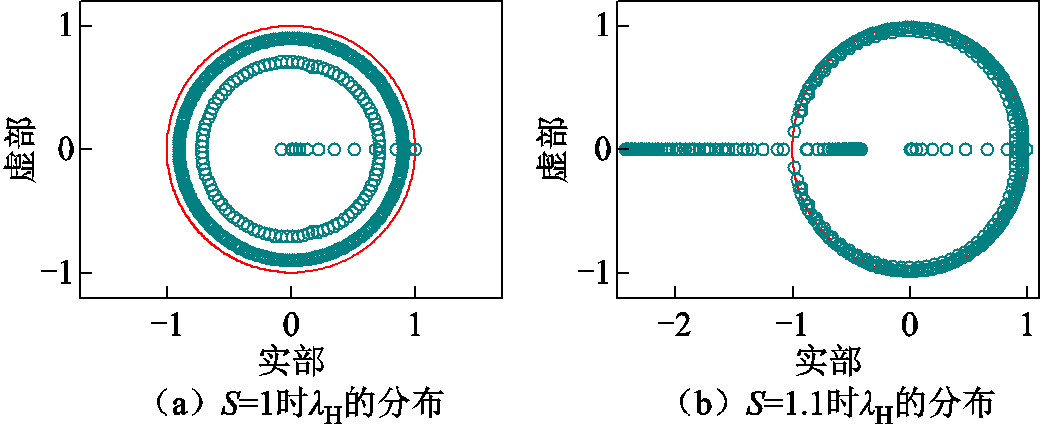
图5 不同S下的矩阵H的特征值分布
Fig.5 Eigenvalue distribution of matrix H under different S
为了进一步研究各种不同条件下混合算法的稳定性，对下面两种情形进行验证：
（1）情形1：将细网格尺寸减小为2.5μm，其他设置不变。如图6a所示，矩阵H的所有特征值都位于单位圆内或单位圆上，由此可知，即使减小细网格的尺寸，混合算法依然稳定。
（2）情形2：将薄层设置为双层导电薄层，其他设置不变。薄层1的厚度为0.1 mm，电导率为 104 S/m，相对介电常数为5，薄层2的厚度为0.15 mm，电导率为105 S/m，相对介电常数为1。如图6b所示，矩阵H的所有特征值都位于单位圆内或单位圆上，由此可知，对于这种复杂情形的导电薄层，混合算法依然表现出良好的稳定性。
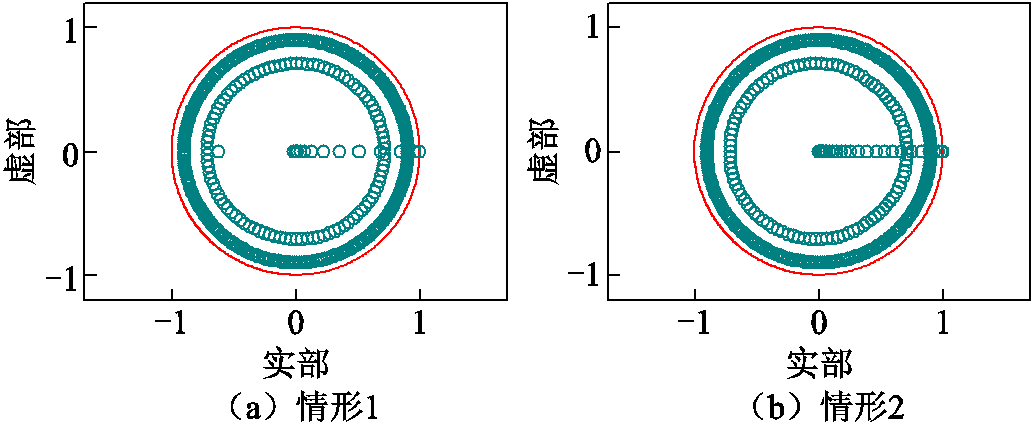
图6 不同情形下矩阵H的特征值分布
Fig.6 Eigenvalue distribution of matrix H under different scenarios
一般来说，不同的区域采用不同的数值方法，在其分界面处会产生数值反射[11]。这种虚假反射可以通过模拟平面波正入射于导电薄层的反射系数来量化。如图4a所示，设置该薄层与周围自由空间都是真空，理论上无物理反射，所以该仿真测量的就是非物理数值反射，其他设置保持不变。反射系数Γ的计算公式为
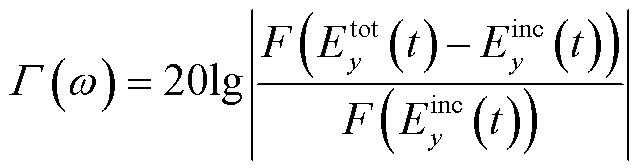（33）
式中，F(·)表示傅里叶变换；Eytot(t)和Eyinc(t)分别为总电场和入射电场强度。数值反射的量化结果如图7所示。从图7a不难看出，FDTD-PITD(2)法和FDTD-PITD(4)法的反射系数基本上是相同的，因此高阶区域的引入并不会增加分界面处的数值反射，这确保了高阶混合方法的精度。由图7b可知，数值反射基本上不受薄层离散层数I的影响。此外，根据2.4节中混合算法的求解流程可知，式（18）中积分项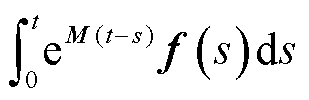
的计算精度直接影响数值反射的大小[16]，因此可以通过对f(t)采用更高次的分段多项
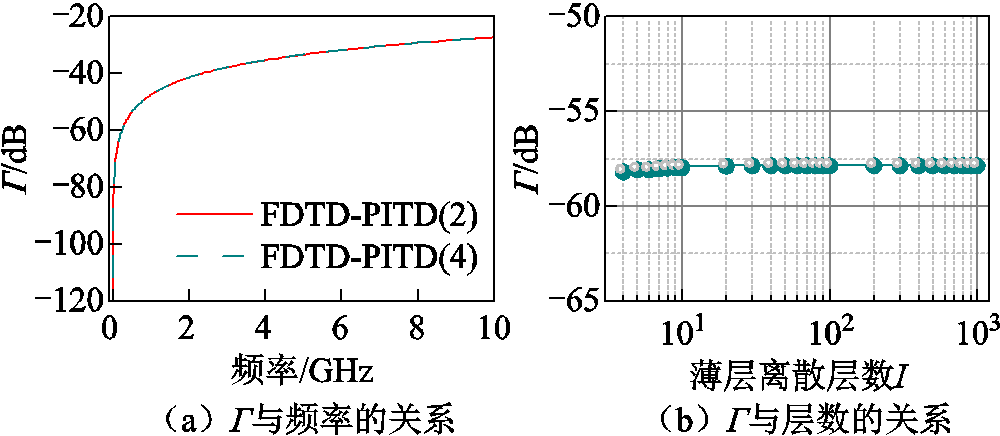
图7 数值反射的量化
Fig.7 Quantization of numerical reflection
式近似来提高积分项的计算精度，进而减小和管理数值反射。
通过图4a所示的典型算例来对本文方法的有效性、性能和趋肤深度进行验证，其中导电薄层的厚度为h、电导率为σ和相对介电常数为εr。自由空间采用1 mm的均匀网格离散，时间步长Δt=2.87 ps，激励采用调制高斯脉冲
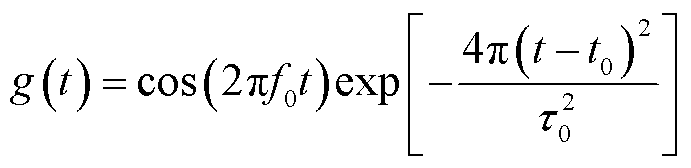（34）
式中，f0=2.1 GHz，τ0=0.238 ns，t0=0.8τ0。
屏蔽效能SE的计算公式为
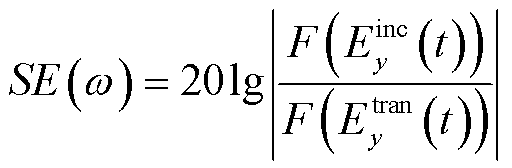（35）
式中，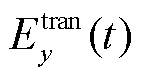
为透射电场。
4.1.1 有效性验证
无限大导电薄层嵌入特征阻抗为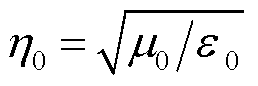
的媒质中，其屏蔽效能SE的解析解为
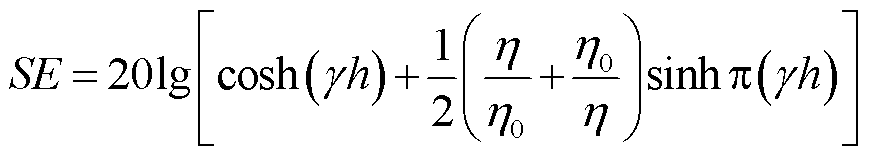（36）
式中，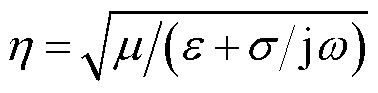
；
。
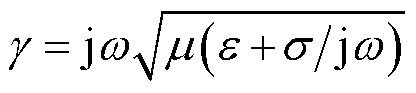设置薄层离散层数I=50。对薄层参数如图8所示的情形1和情形2进行仿真，仿真结果与解析解吻合。因此，本文所提方法的有效性得到验证。
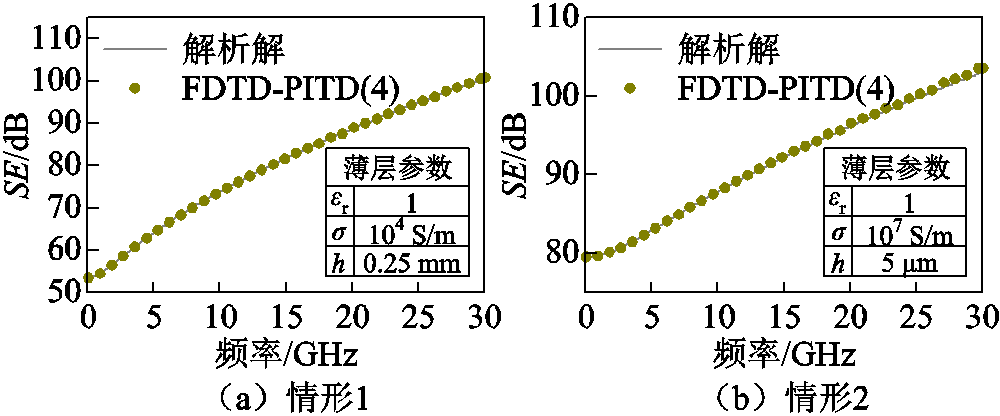
图8 导电薄层的屏蔽效能
Fig.8 Shielding effectiveness of the thin conductive layer
4.1.2 性能分析
设置薄层参数为h=0.25 mm，σ=104 S/m，εr=1，薄层内部的元胞尺寸为25 μm。将本文方法与其他几种导电薄层建模方法进行比较，其中电阻边界条件[7]和加权平均法[8]属于等效参数模型法。图9和表1分别给出了这几种不同导电薄层建模方法的仿真结果和计算信息。以解析解为参考值，相对误差的计算公式为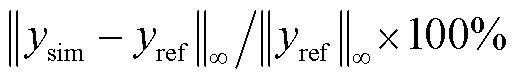
，其中ysim为仿真值，yref为参考值。如图9所示，电阻边界条件和加权平均法仅在薄层厚度小于趋肤深度的低频时有效，且相对误差都高达18.8%。此外，与其他方法相比，由于FDTD-PITD(4)法在空间离散过程中引入了四阶中心差分格式，其仿真结果最接近解析解，相对误差仅为0.31%。
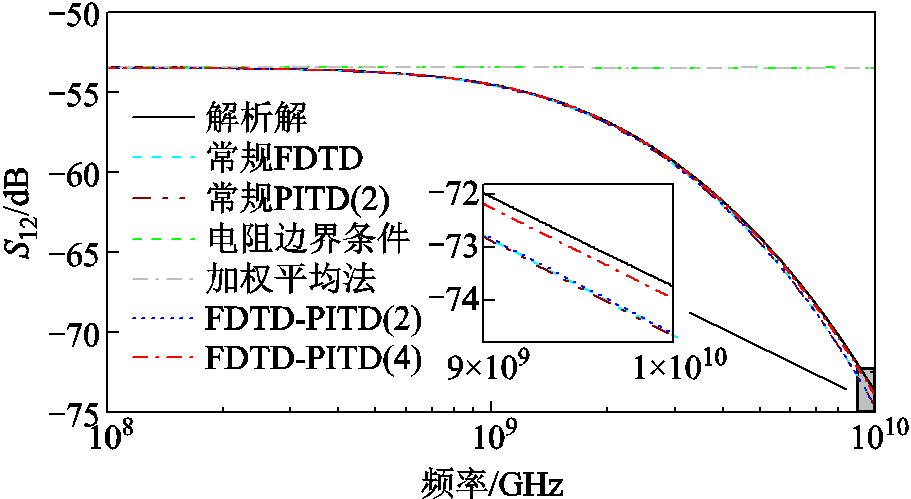
图9 不同方法的S12（S12=−SE）
Fig.9 S12 of different methods (S12=−SE)
表1 不同导电薄层建模方法的计算信息
Tab.1 Thecalculation information of different methods for the modeling of the thin conductive layer
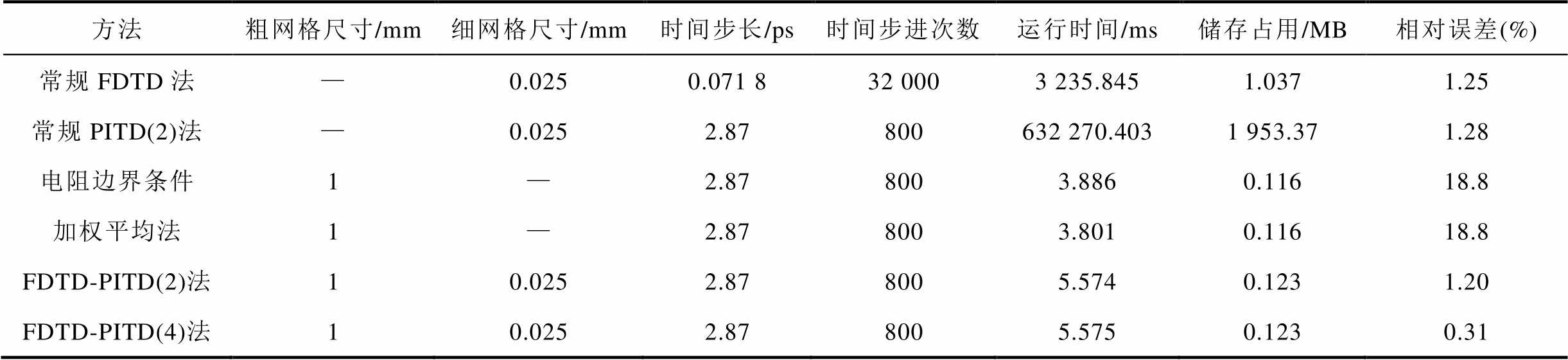
方法粗网格尺寸/mm细网格尺寸/mm时间步长/ps时间步进次数运行时间/ms储存占用/MB相对误差(%) 常规FDTD法—0.0250.071 832 0003 235.8451.0371.25 常规PITD(2)法—0.0252.87800632 270.4031 953.371.28 电阻边界条件1—2.878003.8860.11618.8 加权平均法1—2.878003.8010.11618.8 FDTD-PITD(2)法10.0252.878005.5740.1231.20 FDTD-PITD(4)法10.0252.878005.5750.1230.31
由表1可知，为了确保导电薄层建模的准确性，在采用常规FDTD法和常规PITD(2)法计算时，必须对整个计算空间进行细网格剖分，从而导致计算机资源消耗剧增。FDTD-PITD(2)法的运行时间约为常规FDTD法的0.17%，储存占用小于常规PITD(2)法的1/10000，因此结合两种方法对导电薄层进行建模，可以大大提高计算效率和减少计算机资源消耗。
此外，FDTD-PITD(4)法比FDTD-PITD(2)法具有更高的计算精度，而运行时间和储存占用基本相同。因此，在实际应用中，对导电薄层内部采用PITD(4)法可以在不牺牲计算效率的前提下，提高混合算法的计算精度。
4.1.3 趋肤深度
为了验证本文方法对导电薄层内部建模的准确性，设置薄层内部的元胞尺寸为5 μm。归一化电流密度分布如图10所示，通过仿真计算得到了784 MHz时薄层内部归一化电流密度的幅值，并采用最小二乘法对一个趋肤深度内的仿真数据点进行指数拟合。在该频率下，趋肤深度的理论值为17.971 μm。通过拟合曲线得到的趋肤深度为18.017 μm，相对误差为0.256%。
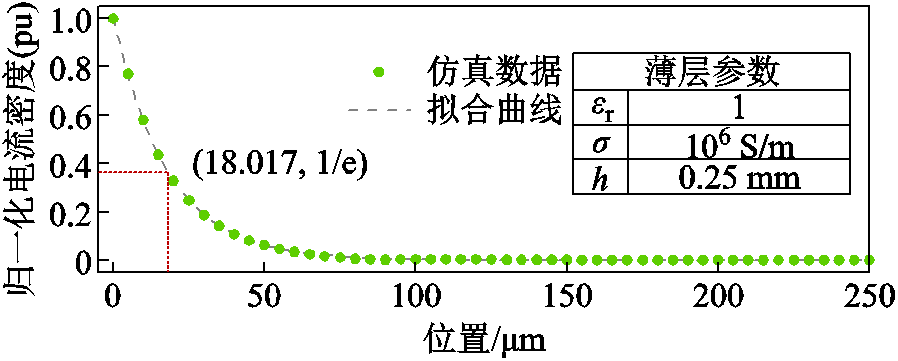
图10 归一化电流密度的分布
Fig.10 Distribution of normalized current density
为了进一步探究本文方法对更为复杂情形下导电薄层建模的有效性，从涂层结构和多层结构两个方面进行验证。仍然采用图4a所示的计算模型，薄层外部的元胞尺寸为1mm，时间步长Δt=2.87 ps。
4.2.1 薄涂层介质问题
假设导电薄层左侧是自由空间，右侧是相对介电常数为5的介质层，薄层内部的元胞尺寸为25 μm，其他设置保持不变。由图11所示的计算结果可知，本文方法在分析薄涂层介质问题时显示出良好的效果。
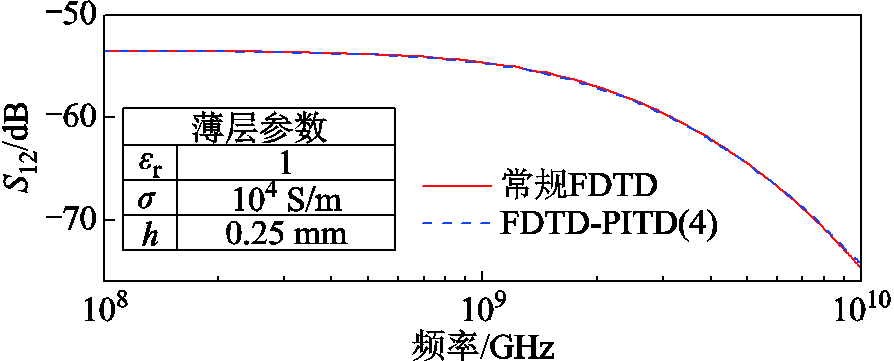
图11 涂层介质的S12（S12=−SE）
Fig.11 S12 of thecoating medium (S12=−SE)
4.2.2 双层导电薄层
将图4a所示的薄层设置为具有不同材料特性的双层导电薄层，薄层材料参数如图12所示，薄层内部的元胞尺寸为5μm，其他设置保持不变。由图12可知，本文方法与常规FDTD法的计算结果吻合良好。
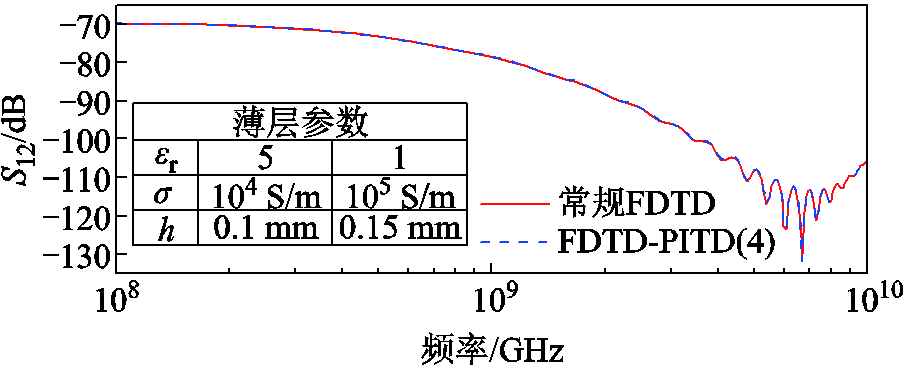
图12 双层导电薄层的S12（S12=−SE）
Fig.12 S12 of thedouble-layer thin conductive layer (S12=−SE)
由上述两个算例可以看出，本文方法对多种复杂情况下的导电薄层算例都显示出了良好的效果。
以图13a所示的屏蔽腔体模型为例，对本文方法在求解三维电磁屏蔽问题时的适用性进行说明。如图13a所示，封闭腔体的尺寸为50 cm×50 cm× 50cm，其左面为铜薄层，其余五面均为理想导电体（Perfect Electric Conductor, PEC）。铜薄层的厚度为5 μm，其电导率为5.8×107 S/m和相对介电常数为1。沿z方向的电偶极子源位于铜薄层左侧20 cm处，观察点则位于封闭腔体的中心。采用0.5 μm的一维细网格对铜薄层进行剖分，其余区域采用5 cm的粗网格进行剖分。时间步长Δt=83.39 ps。屏蔽效能如图13b所示，本文方法得到的结果与NIBC法的结果吻合良好，可决系数R2=0.983 9。可决系数R2可以描述仿真结果与参考结果之间的拟合程度，R2越接近1，拟合程度越好，其计算公式为
图13单面铜薄层封闭腔的计算模型及屏蔽效能
Fig.13 Calculation model and shielding effectiveness of closed cavity with single-sided copper thin-layer
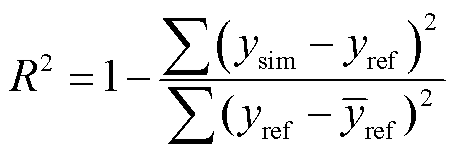（37）
式中，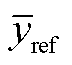
为参考结果的平均值。
为了验证本文方法在处理大规模计算问题时的有效性，以图14a所示模型为例，模拟计算铜薄层方舱内人体的比吸收率（Specific Absorption Rate, SAR）分布。SAR是评估电磁场对人体健康影响的最重要的参数，定义为单位质量的人体组织所吸收的功率，计算公式为
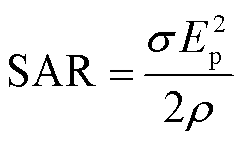（38）
式中，σ和ρ分别是人体组织的电导率和质量密度；Ep为电场强度的峰值。整个计算域的尺寸为632 mm×424 mm×2010mm，其中粗网格的尺寸为 4 mm×4 mm×6 mm，一维细网格的尺寸为0.5 μm。本算例的自由度为35814896，时间步长为Δt=6.67 ps。计算得到的SAR如图14b和图14c所示，本文方法得到的结果与NIBC法的结果相吻合。因此，对于实际应用中的大规模复杂电磁问题，本文方法依然表现出良好的计算效果。
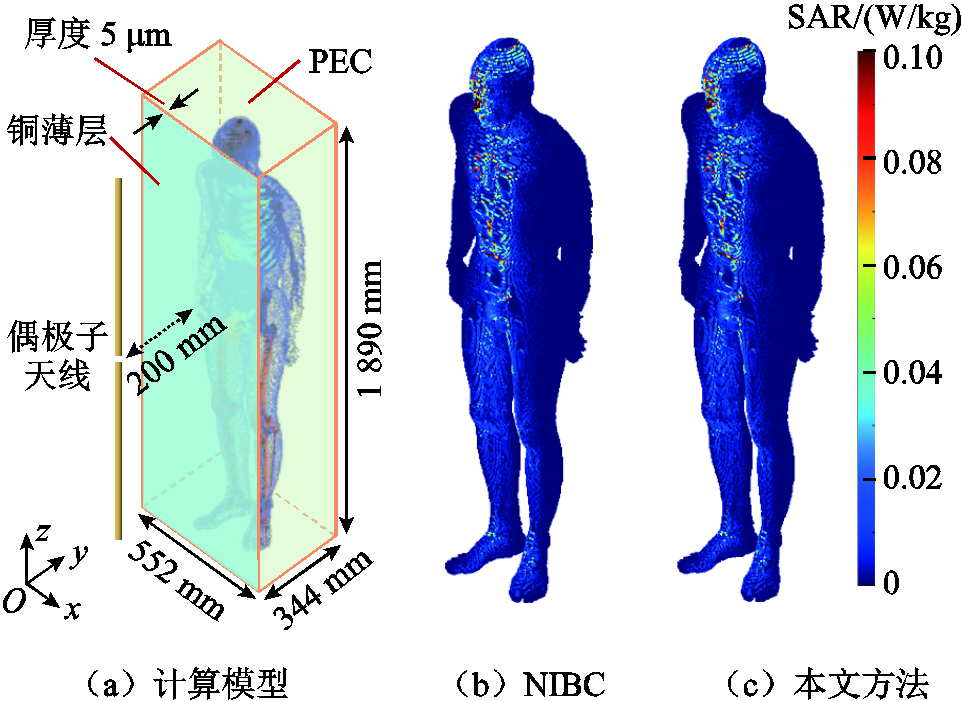
图14计算模型及人体SAR分布
Fig.14 Computational model and SAR distributionsofhumanbody
本文提出了一种适用于嵌入式导电薄层建模的高阶电磁波混合FDTD-PITD方法，不仅避免了薄层厚度的模糊性，并且摆脱了细网格对时间步长的限制，提高了算法的计算效率。数值计算结果表明，该方法能够高效精确地预测导电薄层的屏蔽效能。与单一数值方法相比，混合方法将FDTD法和PITD法结合起来协同处理多尺度问题，兼顾了两种方法的优点，同时弥补了不足，并且很容易在现有的FDTD代码中实现，是一种极具潜力的嵌入式导电薄层建模方法。
参考文献
[1] 赵志刚, 张学增. LLC平面变压器绕组损耗与漏感改进有限元计算方法[J]. 电工技术学报, 2022, 37(24): 6204-6215. Zhao Zhigang, Zhang Xuezeng. Improved finite element method of winding loss and leakage inductance for planar transformer used in LLC converter[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6204-6215.
[2] 魏鹏, 陈龙, 贲彤, 等. 一种考虑动态磁滞效应的高效稳定时域有限元计算方法[J]. 电工技术学报, 2023, 38(21): 5661-5672. Wei Peng, Chen Long, Ben Tong, et al. An efficient and stable time domain finite element method considering dynamic hysteresis effect[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5661-5672.
[3] 胡亚楠, 包家立, 朱金俊, 等. 纳秒电脉冲对肝脏组织不可逆电穿孔消融区分布的时域有限差分法仿真[J]. 电工技术学报, 2021, 36(18): 3841-3850. Hu Yanan, Bao Jiali, Zhu Jinjun, et al. The finite difference time domain simulation of the distribution of irreversible electroporation ablation area in liver tissue by nanosecond electrical pulse[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3841-3850.
[4] 迟明珺, 马西奎, 马亮, 等. 一种适用于有源区域电磁波时程精细积分仿真的大时间步长矩阵数值积分方法[J]. 电工技术学报, 2024, 39(21): 6604-6613+6895. Chi Mingjun, Ma Xikui, Ma Liang, et al. A large Time step size matrix numerical integral method for precise integration time domain simulation of electromagnetic waves in active regions [J]. Transactions of China Electrotechnical Society, 2024, 39(21): 6604-6613+6895.
[5] Kang Zhen, Ma Xikui, Yang Fang, et al. Stability condition and numerical dispersion of fourth-order compact precise-integration time-domain method[J]. IEEE Transactions on Magnetics, 2019, 55(6): 7200804.
[6] 孟雪松, 张瀚, 鲍献丰, 等. 碳纤维增强复合材料薄层高效建模方法研究[J]. 电波科学学报, 2019, 34(1): 19-26. Meng Xuesong, Zhang Han, Bao Xianfeng, et al. High efficient modeling techniques of carbon fiber reinforced composite thin layer[J]. Chinese Journal of Radio Science, 2019, 34(1): 19-26.
[7] 王力, 谭振杰, 曾祥君, 等. 基于改进等效电路模型的直流微电网大信号稳定性分析[J].电工技术学报, 2024, 39(5): 1284-1299. Wang Li, Tan Zhenjie,Zeng Xiangjun, et al. Large-signal stability analysis for DC microgrids based onthe improved equivalent circuit model[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1284-1299.
[8] Shao Jinghui, Ma Xikui, Yin Shuli, et al. Conformal precise-integration time-domain method for analyzing electromagnetic fields in fine-structured device with moving 3-D part[J]. IEEE Transactions on Microwave Theory and Techniques, 2018, 66(7): 3200-3209.
[9] Lei Qi, Wang Jianbao, Shi Lihua. Shielding analysis of uniaxial anisotropic multilayer structure by impedance network boundary condition method[J]. IEEE Transactions on Antennas and Propagation, 2019, 67(4): 2462-2469.
[10] 张泽华,宋桂英,张晓璐,等.考虑恒功率负载的直流微电网稳定性与鲁棒性控制策略[J].电工技术学报, 2023, 38(16): 4391-4405.Zhang Zehua, Song Guiying, Zhang Xiaolu, et al. Stability and robustness control strategy of DC microgrid considering constant power load[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4391-4405.
[11] Ruiz Cabello M, Diaz Angulo L, Alvarez J, et al. A hybrid crank–Nicolson FDTD subgridding boundary condition for lossy thin-layer modeling[J]. IEEE Transactions on Microwave Theory and Techniques, 2017, 65(5): 1397-1406.
[12] Van Londersele A, De Zutter D, VandeGinste D. A new hybrid implicit–explicit FDTD method for local subgridding in multiscale 2-D TE scattering problems[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(8): 3509-3520.
[13] 康祯, 杨方, 张瑞祥, 等. 用于电磁波多尺度问题求解的高效FDTD-PITD混合算法[J]. 微波学报, 2022, 38(3): 46-52. Kang Zhen, Yang Fang, Zhang Ruixiang, et al. An efficient hybrid FDTD-PITD formulation for solving multiscale electromagnetic wave problems[J]. Journal of Microwaves, 2022, 38(3): 46-52.
[14] Chi Mingjun, Ma Xikui, Ma Liang. A switched-Huygens-subgridding-based combined FDTD-PITD method for fine structures[J]. IEEE Microwave and Wireless Technology Letters, 2023, 33(7): 947-950.
[15] Ma Liang, Ma Xikui, Chi Mingjun, et al. A nonoverlapping hybrid FDTD-PITD method using upwind conditions for multiscale problems[J]. IEEE Transactions on Microwave Theory and Techniques, 2024, 72(5): 2961-2972.
[16] Ma Liang, Ma Xikui, Chi Mingjun, et al. Toward the modeling of thin conductive layer with hybrid FDTD-PITD method[J]. IEEE Transactions on Magnetics, 2024, 60(12): 1-4.
[17] Zhou Longjian, Yang Feng, Long Rui, et al. A hybrid method of higher-order FDTD and subgriddingtechnique [J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 1261-1264.
[18] 孙东阳,李爽,王俊武,等.基于虚拟直流电机控制的船舶高频高峰值脉冲负载冲击平抑控制策略研究[J].电工技术学报, 2024, 39(20): 6328-6344. Sun Dongyang, Li Shuang, Wang Junwu, et al. Study on virtual DC generator-based ship high-frequency and high-peakpower pulsed loads impact damping control strategy[J]. Transactions of China Electro-technical Society, 2024, 39(20):6328-6344.
Abstract For wideband characteristic analysis, frequency-domain numerical methods need to calculate complicated equations at each frequency point repeatedly. However, time-domain numerical methods only need to perform the Fourier transform on time-domain results of one calculation to obtain the wideband frequency-domain information. The finite-difference time-domain (FDTD) method is the most widely used time-domain method, but its time step size is limited by the Courant-Friedrichs-Lewy (CFL) stability condition. To overcome this shortcoming, the precise-integration time-domain (PITD) method is proposedto be free from the CFL restriction by discretizing the spatial derivatives with difference and solving the ordinary differential equations about time by using the precise integration technique, designated as the second-order PITD [PITD(2)]. For the improvement of the numerical dispersion characteristics, the fourth-order PITD [PITD(4)] method is proposed by using the fourth-order spatial central difference scheme. The difference in memory requirements between PITD(2) and PITD(4), merely reflected in the size and sparsity of the matrix exponential, is not significant.
Thin conductive layers, as typical multiscale problems, exist widely in electromagnetic (EM) systems for shielding, posing challenges to any single numerical algorithm. For suchproblems, the cell size of FDTD must be sufficiently small to capture the thickness and skin effect of the thin conductive layer, requiring significant resources. To describe their EM properties more effectively, the subgridding technology is introducedto employ high-density sampling only for the local thin layer and coarse-grid divisions for the remaining areas. Since the waves inside thegood conductor propagate nearly perpendicular to its surfaces, the thin conductive layer is divided into fine grids only along the vertical direction and itsinternalEM fieldscan be found by one-dimensional (1-D) full-wave simulation. To relax the CFL restriction of fine grids, PITD can be used to synchronize the time step sizeforfine grids with that forcoarsegrids. Meanwhile, 1-D simulation can greatly reduce the memory requirement of PITD. Compared with PITD(2), PITD(4) has higher accuracy without additional memory burden. Therefore, the high-order hybrid FDTD-PITD method is proposed to model the embedded thin conductive layer, which is asynergetic combination of FDTD and 1-D PITD(4). FDTD is adopted for coarse grids outside the thin conductive layer, while 1-D PITD(4) is used for fine grids inside the thin conductive layer.
Conventional FDTD is used to update the EM fields outside the thin conductive layer, and the magnetic fields adjacent to the boundariesofthe thin conductive layer need to be specially treated by using the boundary electric fields obtained by 1-D PITD(4) inside the thin conductive layer. For the PITD domain, the transition region is introduced between the high-order region and the interface of different grids. The fourth-order spatial central difference is used for the high-order region and the second-order for the transition region. The thickness of the transition region is selected following the principle that all unknowns used to solve the high-order region arelocatedinsidethe thin conductive layer. The tangential electric field components at the interface are updated by using effective permittivity and conductivity, thereby connecting coarse and fine grids. Finally, the numerical stability and numerical reflection of the hybrid method are analyzed, and several canonical numerical examples are presented to verify the effectiveness and accuracy of the proposed method.
keywords：Finite-difference time-domain method, fourth-order precise-integration time-domain method, subgridding technology, matrix exponential
DOI: 10.19595/j.cnki.1000-6753.tces.240355
中图分类号：TM15
国家自然科学基金资助项目（52177008）。
收稿日期 2024-03-06
改稿日期 2024-10-06
马 亮 男，1997年生，博士研究生，研究方向为时程精细积分法在求解多尺度电磁问题中的应用。E-mail：3120104254@stu.xjtu.edu.cn（通信作者）
马西奎 男，1958年生，教授，博士生导师，研究方向为电气工程中的多种物理场的耦合理论及其数值分析和软件技术，通信与电子系统中的电磁场与电磁波，非线性电路与系统中的分歧与混沌，混沌的控制、同步及其应用等。E-mail：maxikui@mail.xjtu.edu.cn
（编辑 郭丽军）