 为电网的中性点。图中,vx(x=a, b, c)为电网相电压,ix为相电流。vxy和ixy(y=p, n)为每个桥臂的电压和电流,p表示上桥臂,n表示下桥臂。icir,x为x相的桥臂环流。vxyj和vC,xyj(x=1,…, N)为分别为SM的交流端口电压和电容电压,C为电容值,其额定电压VC= Vdc/N。vC,xy为一个桥臂内所有SM的电容电压之和。
为电网的中性点。图中,vx(x=a, b, c)为电网相电压,ix为相电流。vxy和ixy(y=p, n)为每个桥臂的电压和电流,p表示上桥臂,n表示下桥臂。icir,x为x相的桥臂环流。vxyj和vC,xyj(x=1,…, N)为分别为SM的交流端口电压和电容电压,C为电容值,其额定电压VC= Vdc/N。vC,xy为一个桥臂内所有SM的电容电压之和。摘要 光伏模块利用模块化的特点,可以分布集成在模块化多电平变换器子模块的直流侧,构成基于模块化多电平变换器的光伏系统(MMC-PVS)。由阴影遮挡、损坏等问题引起的光伏模块功率不平衡会使子模块的调制信号存在显著差异,严重降低现有共模电压抑制方案的抑制效果。为了解决这些问题,该文提出一种脉冲衔尾排布调制,能够在光伏模块功率不平衡工况下抑制MMC-PVS的共模电压。通过分析光伏模块功率不平衡工况下MMC-PVS,实现零共模电压的条件,表明理论上子模块的调制信号具备实现零共模电压的能力,而由调制策略生成的子模块驱动脉冲是产生共模电压的关键因素。脉冲衔尾排布调制能将子模块驱动脉冲依次衔尾排布,即后一子模块的上升沿时刻与前一子模块的下降沿时刻对齐,在每个开关周期内保证三相上桥臂总电压与三相下桥臂总电压的形状相同,达到理论上零共模电压的效果,实现共模电压抑制。最后,通过仿真与实验验证了脉冲衔尾排布调制在光伏模块功率不平衡工况下抑制共模电压的可行性与理论分析的正确性。
关键词:模块化多电平变换器 光伏系统 光伏功率不平衡 共模电压 脉冲衔尾排布调制
模块化多电平变换器(Modular Multilevel Con- verter, MMC)具有低电压应力、低谐波含量、高效率和模块化等特点[1-4]。利用MMC模块化的特点,光伏(Photovoltaic, PV)模块可以分布集成在MMC子模块(Sub-Module, SM)的直流侧,构成基于MMC的光伏系统(MMC-based Photovoltaic System, MMC-PVS),使每个PV模块实现独立的最大功率点跟踪控制,提升光伏系统的发电效率[5-6]。由于MMC-PVS以MMC拓扑为核心,利用MMC拓扑的交流端口连接电网,脉冲宽度调制(Pulse Width Modulation, PWM)策略会在MMC拓扑的三相交流端口产生明显的高频共模电压(Common Mode Voltage, CMV),在寄生电容上产生高频的共模电流,造成严重的电磁干扰,影响系统的正常运行[7]。因此,为了MMC-PVS的安全运行,消除或抑制共模电压是一个亟待解决的问题。
针对共模电压抑制问题,空间矢量调制[8-10]通过选择零CMV矢量消除共模电压,但MMC电平数较多,显著增加了空间矢量调制的复杂性[11]。相较而言,基于载波的调制方案实现简单且更加适用于MMC。文献[11]将三相调制波转化为伪调制波,利用载波层叠调制获得三相伪脉宽信号,再将伪脉宽信号成对相减并求平均,得到具有零CMV特征的三相脉宽信号,消除调制引起的CMV。文献[12]利用载波层叠调制获得初始桥臂投入SM数目,随后按照三相调制波的大小关系重新确定桥臂投入SM数目,使三相上(下)桥臂投入SM数目之和保持桥臂SM数目的1.5倍,实现CMV消除。类似于文献[12],文献[13]基于最近电平调制提出一种最近零CMV向量选择的CMV抑制方法。利用三相SM调制信号的对称性,文献[14-15]提出了一种基于载波移相调制(Carrier-based Phase-Shift PWM, CPS-PWM)的脉冲顺接CMV消除方案。按照传统的CPS-PWM生成SM的脉冲波形,以六个SM为一组将三相上(下)桥臂的SM分组并按照指定规律排序。每组内,将上一个SM的脉冲下降沿作为下一个SM的脉冲上升沿,使三相上(下)桥臂导通的SM数目始终保持在桥臂SM数的1.5倍,以达到消除CMV的目的。
上述CMV抑制策略是以传统的两端口MMC为基础进行研究的。对于MMC-PVS,阴影遮挡、PV故障等[16]原因会使相应的PV模块输出功率显著下降,导致PV模块间功率不平衡。PV功率不平衡会使桥臂内高功率PV的SM调制比升高而出现过调制,造成桥臂电压和电流畸变,甚至影响系统的稳定运行[17-20]。为此,基于独立电压平衡控制,文献[17-20]提出了谐波补偿调制(Harmonic Com- pensation Modulation, HCM),将高功率PV的SM调制比上限提升至1.273,增加了SM的功率传输能力,大幅扩展了MMC-PVS在PV功率不平衡工况的安全工作域。
然而,文献[11-13]是基于排序平衡控制实现SM的电容电压平衡及产生SM驱动脉冲生成,无法适配HCM以扩展MMC-PVS在PV功率不平衡工况的安全工作域。文献[14-15]的脉冲顺接方案采用独立电压平衡控制实现SM的电容电压平衡,可与HCM配合提高MMC-PVS在PV功率不平衡下的安全工作域。但是,脉冲顺接方案需要修改SM的驱动脉冲宽度,这会使MMC的系统调制比降低为给定值的86.6%,严重降低了MMC交流端口电压的可调范围。同时,PV功率不平衡会使功率不同的PV模块对应的SM调制信号存在显著差异,导致三相SM调制信号失去对称性,严重影响脉冲顺接方案在PV功率不平衡工况中的抑制效果。另外,脉冲顺接方案只适用于MMC的桥臂模块数为偶数的情况。
为了在PV功率不平衡工况下抑制MMC-PVS的CMV,本文提出一种脉冲衔尾排布调制方案。本文分析PV功率不平衡工况下MMC-PVS实现零CMV的理论基础,介绍HCM的基本原理,阐述所提出的脉冲衔尾排布调制方案的实现原理,给出仿真和实验验证结果。
图1a为MMC-PVS电路结构,图1b为其MMC侧控制框图。MMC-PVS由三相六个桥臂构成,每个相单元由上桥臂、下桥臂和两个桥臂电感L0构成,相单元中点通过交流滤波电感Lg与电网相连。每个桥臂由N个半桥型SM串联构成,每个SM的直流侧通过DC-DC变换器集成PV模块。Vdc为MMC-PVS直流侧电压,O为直流侧的中点,idc为直流电流,交流侧为三相平衡电网, 为电网的中性点。图中,vx(x=a, b, c)为电网相电压,ix为相电流。vxy和ixy(y=p, n)为每个桥臂的电压和电流,p表示上桥臂,n表示下桥臂。icir,x为x相的桥臂环流。vxyj和vC,xyj(x=1,…, N)为分别为SM的交流端口电压和电容电压,C为电容值,其额定电压VC= Vdc/N。vC,xy为一个桥臂内所有SM的电容电压之和。
为电网的中性点。图中,vx(x=a, b, c)为电网相电压,ix为相电流。vxy和ixy(y=p, n)为每个桥臂的电压和电流,p表示上桥臂,n表示下桥臂。icir,x为x相的桥臂环流。vxyj和vC,xyj(x=1,…, N)为分别为SM的交流端口电压和电容电压,C为电容值,其额定电压VC= Vdc/N。vC,xy为一个桥臂内所有SM的电容电压之和。
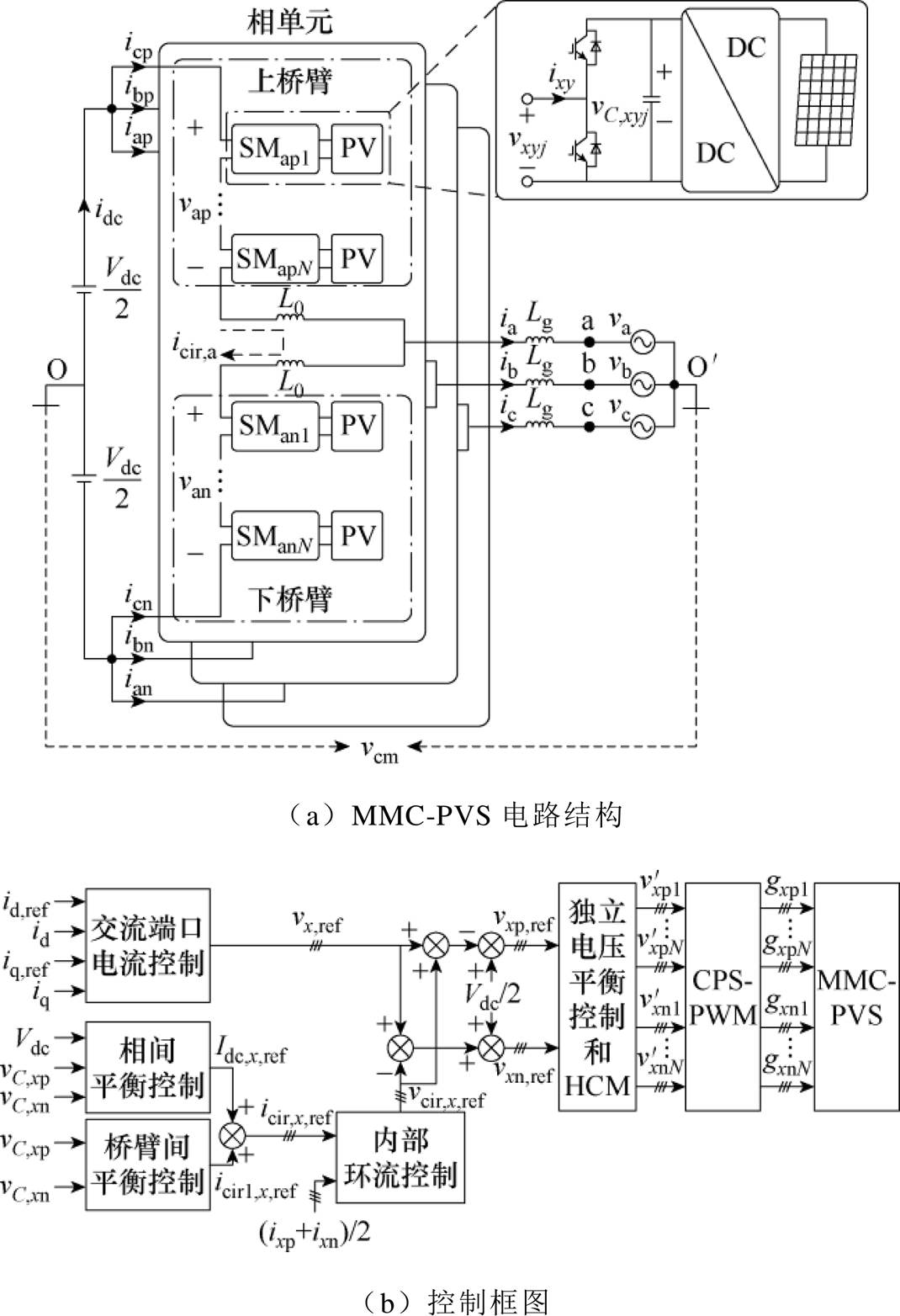
图1 MMC-PVS的电路结构及控制框图
Fig.1 Structure and control diagram of MMC-PVS
根据图1a及基尔霍夫电压和电流定律,MMC- PVS的桥臂电压vxy和桥臂电流ixy可分别表示为
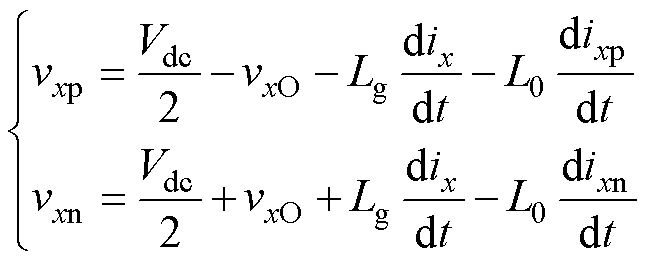 (1)
(1)
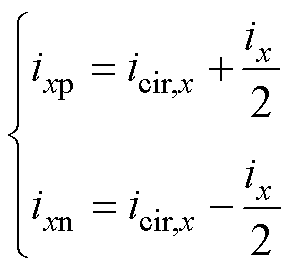 (2)
(2)
式中,vxO为MMC-PVS每相输出与直流侧中点O之间的电压。
根据文献[11],MMC的共模电压vcm表示为
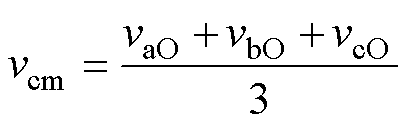 (3)
(3)
将式(1)和式(2)代入式(3),vcm可表示为
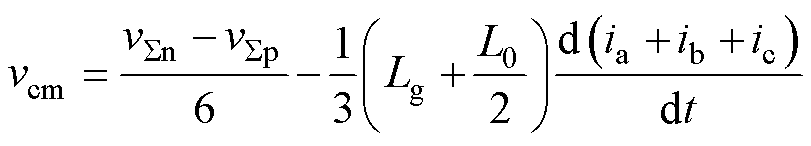 (4)
(4)
式中,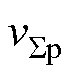 和
和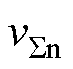 分别为MMC三相上桥臂总电压和下桥臂总电压,即
分别为MMC三相上桥臂总电压和下桥臂总电压,即
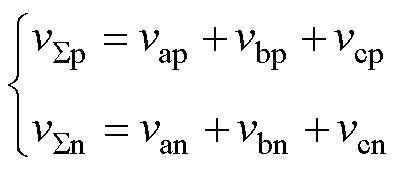
考虑MMC-PVS的交流端口三相电流平衡工况,ia+ib+ic=0,式(4)可以重写为
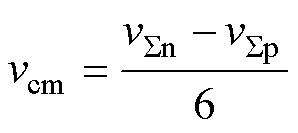 (5)
(5)
由式(5)可知,MMC-PVS的CMV由三相上桥臂和三相下桥臂的桥臂电压差决定。为了消除CMV,需要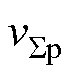 和
和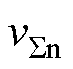 在任意时刻都相等,即
在任意时刻都相等,即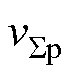 和
和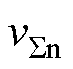 波形完全相同。
波形完全相同。
在实际的MMC-PVS控制中,桥臂电压vxy是由桥臂电压参考值vxy,ref和调制策略共同确定的。由式(1)和式(2)可知,桥臂电压与MMC-PVS的交流端口电压和电流以及内部环流相关,桥臂电压参考值vxy,ref需由MMC-PVS的交流端口控制、内部平衡控制及内部环流控制共同确定,如图1b的MMC- PVS控制框图所示。交流端口电流控制产生交流端口电压参考值vx,ref;内部环流参考值icir,x,ref的直流分量Idc,x,ref和基频分量icir1,x,ref由相间和桥臂间平衡控制产生,并经内部环流控制后生成内部环流控制电压vcir,x,ref[21];随后,由vx,ref、vcir,x,ref和Vdc计算出桥臂电压参考值vxy,ref,并经独立电压平衡控制、HCM和CPS-PWM环节生成SM驱动信号gxyj,用于控制MMC-PVS,保证SM电容电压平衡。因此,桥臂电压参考值vxy,ref可以表示[22]为
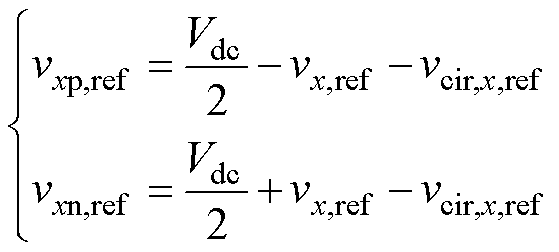 (6)
(6)
且vx,ref满足
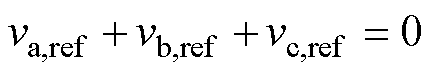 (7)
(7)
vxy,ref无法直接施加到SM中,需要由调制策略转化为SM的驱动信号使SM的交流端口输出对应的电压脉冲vxyj,叠加后产生桥臂电压vxy。根据PWM的面积等效原理[23],在一个开关周期内,vxy,ref和vxy满足
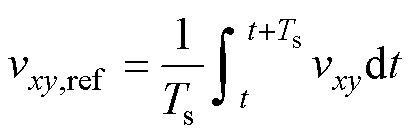 (8)
(8)
式中,Ts为开关周期。
将式(6)~式(8)代入式(5),一个开关周期内vcm的平均值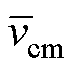 为
为
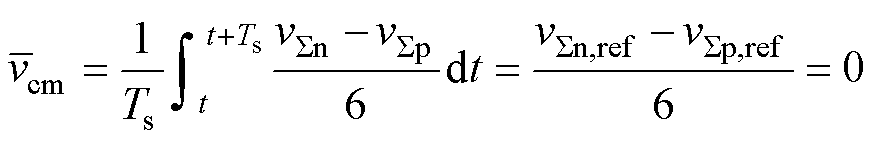 (9)
(9)
其中
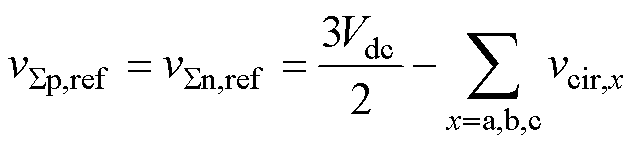
根据式(9)可知,一个开关周期内,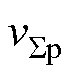 和
和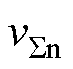 的伏秒积是相同的。
的伏秒积是相同的。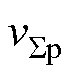 和
和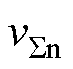 由三相上桥臂和下桥臂的所有SM输出电压脉冲叠加形成,且SM电压幅值均为VC,式(9)中,
由三相上桥臂和下桥臂的所有SM输出电压脉冲叠加形成,且SM电压幅值均为VC,式(9)中,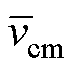 =0表明三相上桥臂所有SM的脉冲宽度之和与三相下桥臂所有SM的脉冲宽度之和是相同的,
=0表明三相上桥臂所有SM的脉冲宽度之和与三相下桥臂所有SM的脉冲宽度之和是相同的,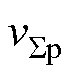 和
和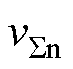 的脉冲宽度具有一致性,是
的脉冲宽度具有一致性,是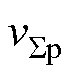 和
和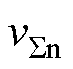 波形相同的一个必要条件。
波形相同的一个必要条件。
PWM策略不仅是将调制波转化为脉冲信号,还决定了脉冲信号的上升沿时刻和下降沿时刻,即脉冲信号在一个开关周期内的位置。这是实现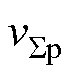 和
和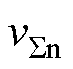 波形相同的另一个必要条件。
波形相同的另一个必要条件。
图2为N=3时,一个开关周期内CPS-PWM产生的CMV时序。根据式(9)可知,CPS-PWM的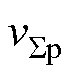 和
和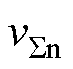 的平均值都是4.5VC,但是CPS-PWM产生的脉冲信号位置无法使
的平均值都是4.5VC,但是CPS-PWM产生的脉冲信号位置无法使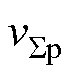 和
和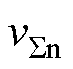 波形保持一致,因而存在较大幅值的CMV。
波形保持一致,因而存在较大幅值的CMV。
由于阴影遮挡、故障等原因,MMC-PVS会出现PV功率不平衡的现象。由于SM的串联结构,流经每个SM的电流均相同,为保证每个SM的交流端口功率与相应的PV模块功率匹配,需对SM交流端口电压vxyj进行调整。SM的交流端口电压vxyj由直流分量和基频分量组成,可分别表示为
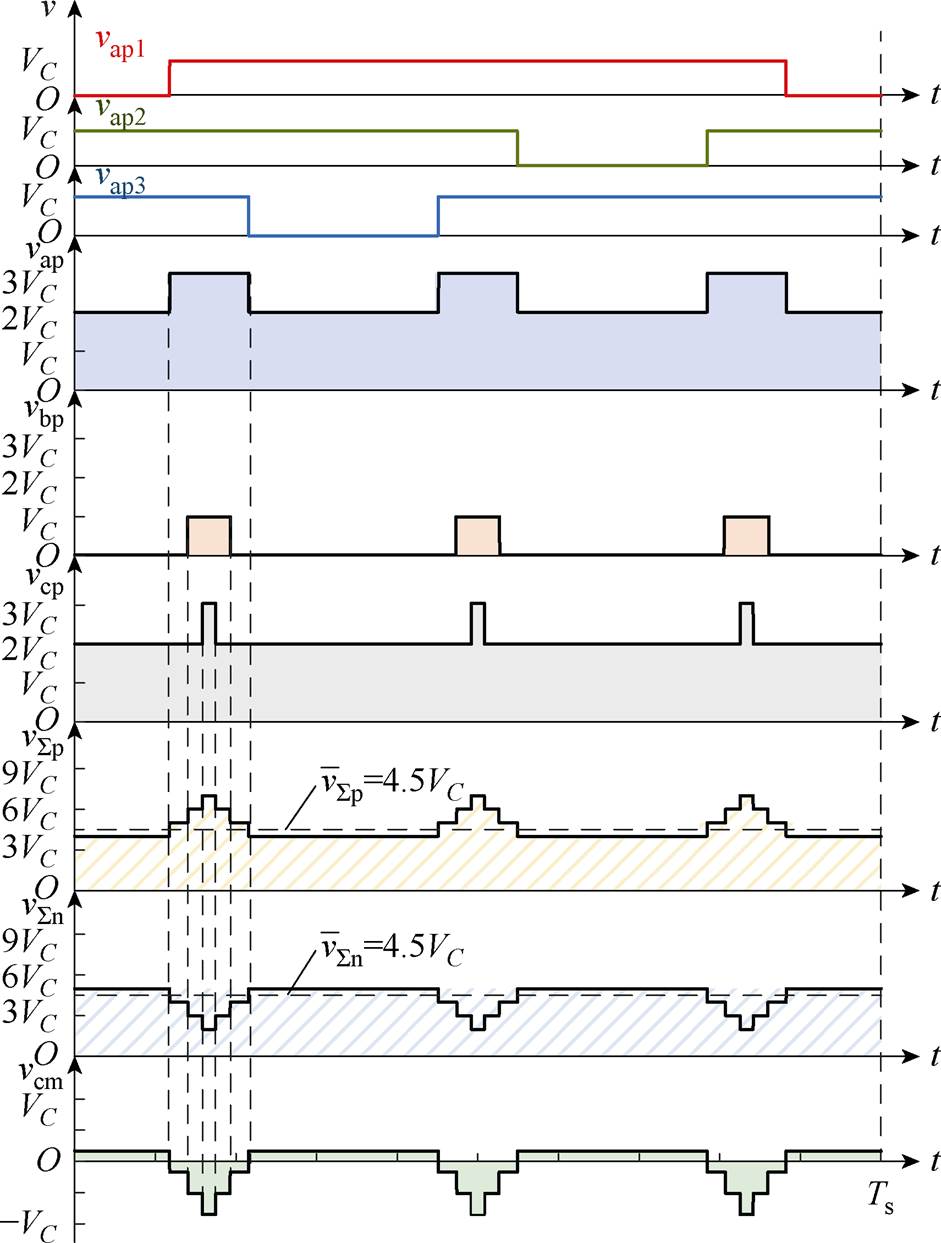
图2 CPS-PWM时序
Fig.2 Sequence of CPS-PWM
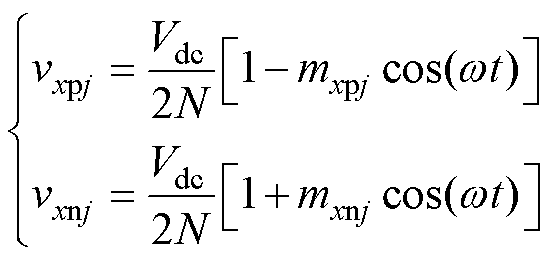 (10)
(10)
式中,mxyj为子模块的调制比;w 为基频角频率。
桥臂电流ixy中只有直流和基频分量与有功功率传输相关,ixy可表示为
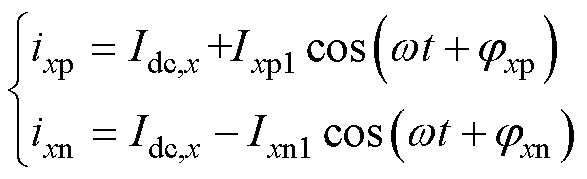 (11)
(11)
式中,Idc,x为每相桥臂电流的直流分量幅值;Ixy1和jxy分别为桥臂电流中的基频分量的幅值和相位,表示为
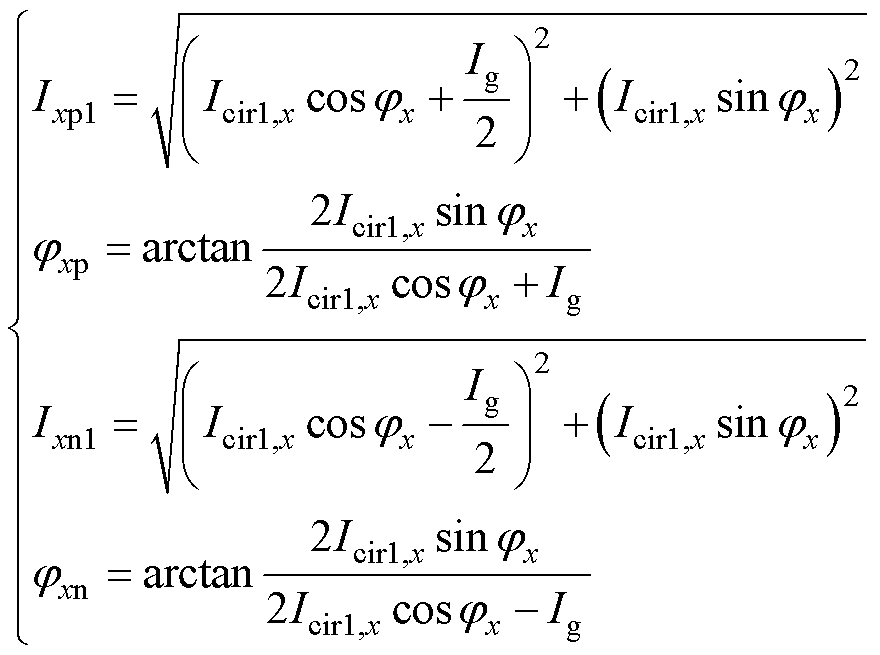
式中,Icir1,x和jx分别为桥臂环流icir,x的基频分量幅值和相位;Ig为MMC-PVS交流端口的相电流幅值。
根据式(10)和式(11),SM交流端口的平均功率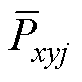 为
为
 (12)
(12)
为保持SM电容电压稳定,PV模块的有功功率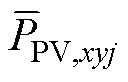 与SM交流端口的平均有功功率满足功率平衡关系,即
与SM交流端口的平均有功功率满足功率平衡关系,即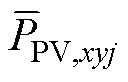 +
+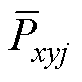 =0。结合式(12),SM的调制比mxyj可表示为
=0。结合式(12),SM的调制比mxyj可表示为
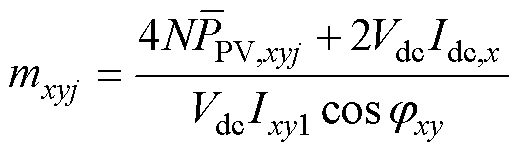 (13)
(13)
由式(13)可知,当同一桥臂内PV功率不平衡时,高功率PV模块的SM调制比会升高,而一旦SM调制比mxyj>1,SM会出现过调制,这不仅会增加系统谐波,还会造成SM电容电压升高和电容电压不平衡,甚至导致系统失稳。同时,低功率PV模块的SM调制比会降低,使同一开关周期中SM的占空比存在明显差异。
为保证MMC-PVS在PV功率不平衡下稳定运行,文献[17-21]提出了谐波补偿调制,将SM的调制比上限值由1扩大至1.273,其基本原理如下。
定义一个桥臂内出现过调制的SM(Over- Modulation SM, OMSM)数目为nOM,xy,剩余SM为正常SM(Normal SM, NRSM)。假定桥臂内SM的序号按照SM调制比降序排列,桥臂内过调制SM的序号为j=1,…, nOM,xy,正常SM的序号为j= nOM,xy+1,…, N。根据式(10),OMSM和NRSM的调制波vxyj可分别表示为
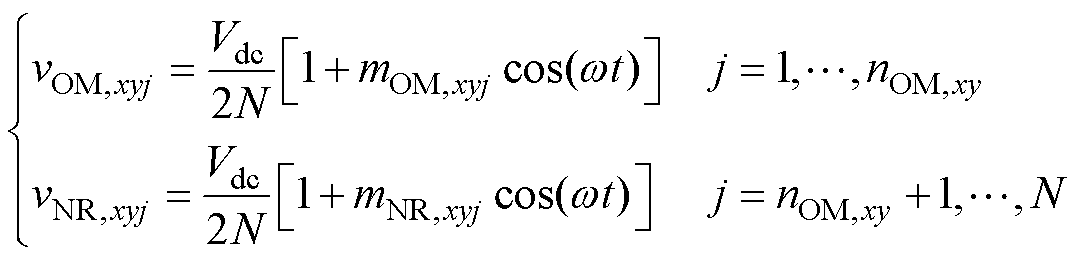 (14)
(14)
式中,mOM,xyj和mNR,xyj分别为OMSM和NRSM对应的调制比,mOM,xyj>1、mNR,xyj≤1。
桥臂电压vxy为桥臂内所有SM交流端口电压之和,可表示为
 (15)
(15)
将式(14)代入式(15),则mOM,xyj和mNR,xyj满足
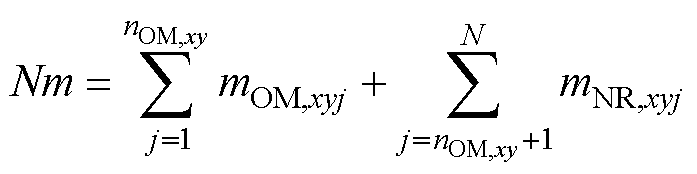 (16)
(16)
式中,m为MMC-PVS的交流端口系统调制比。
为了避免OMSM出现过调制,可向OMSM的调制波vOM,xyj中注入一定的谐波hOM,xyj,构成如图3a所示的OMSM调制波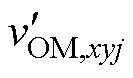 ,在不改变SM调制比mOM,xyj的基础上,降低OMSM调制波的幅值,避免过调制。基于文献[18],
,在不改变SM调制比mOM,xyj的基础上,降低OMSM调制波的幅值,避免过调制。基于文献[18],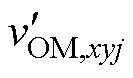 时域表达式为
时域表达式为
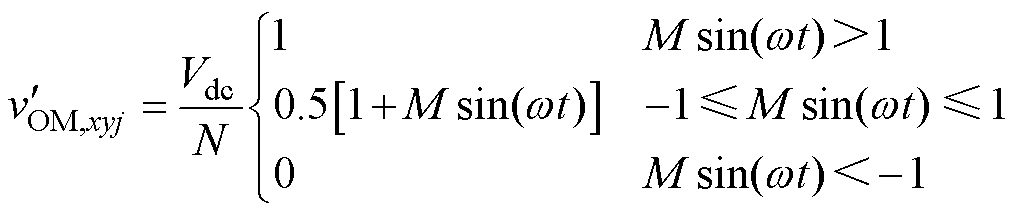 (17)
(17)
式中,M与OMSM调制比mOM,xyj满足
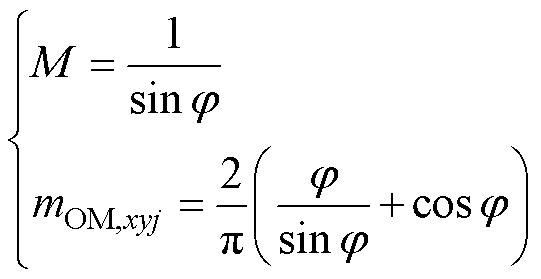 (18)
(18)
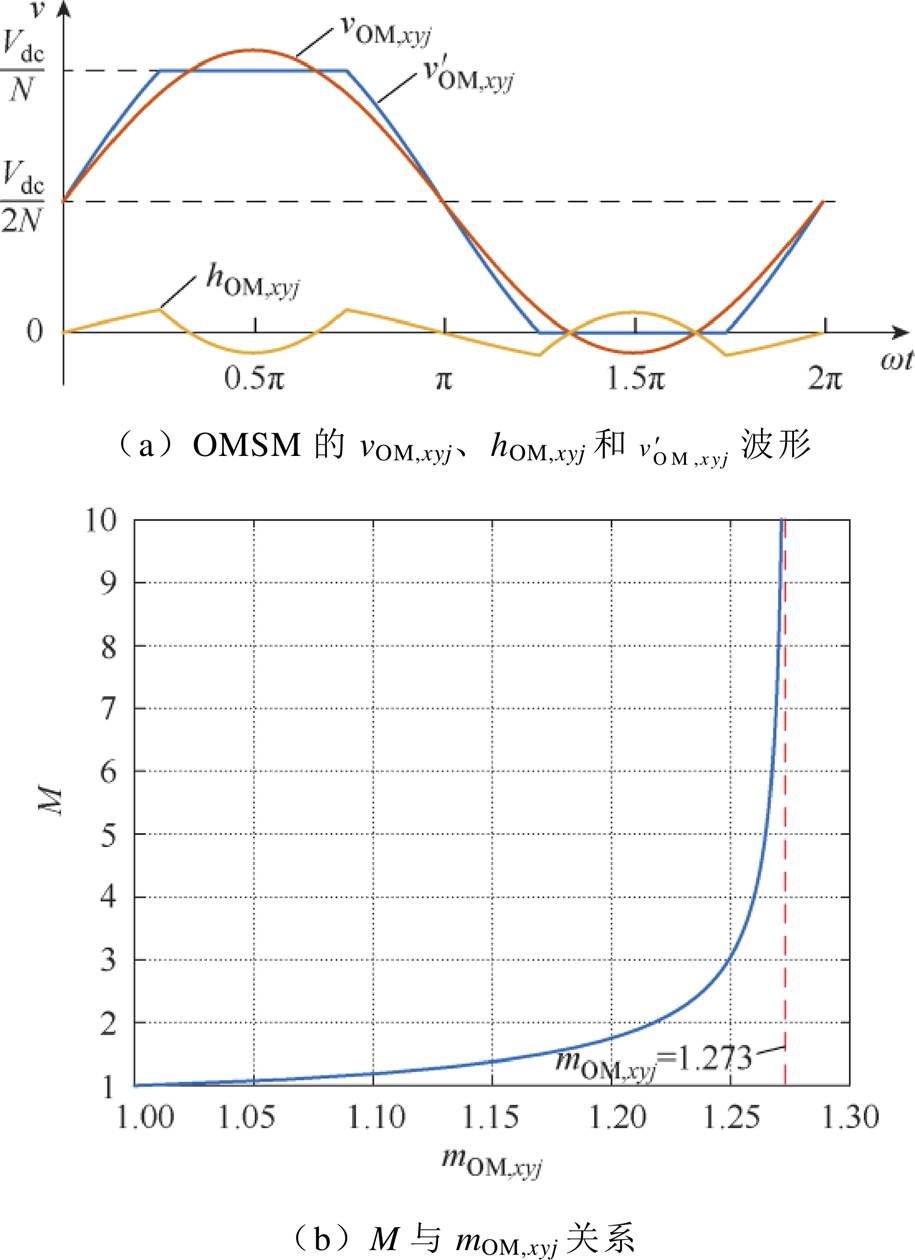
图3 文献[18]的HCM策略
Fig.3 HCM strategy of reference Ref.[18]
根据式(18),图3b给出了M与mOM,xyj的关系曲线。这表明,通过调节系数M,可调节OMSM调制波的调制比,最大可达1.273。
同时,为避免注入的谐波造成桥臂电压畸变,NRSM需完全补偿注入OMSM的谐波。因此,注入谐波后OMSM调制波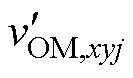 及补偿谐波后NRSM调制波
及补偿谐波后NRSM调制波 可表示为
可表示为
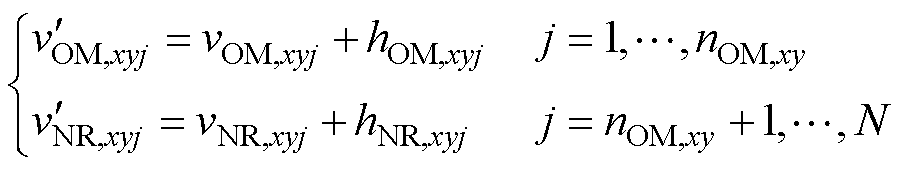 (19)
(19)
式中,hNR,xyj为每个NRSM补偿的谐波。
由于NRSM需要完全补偿同一桥臂内所有注入OMSM的谐波,将式(19)代入式(15),桥臂内所有NRSM需要补偿的谐波hNR,xy为
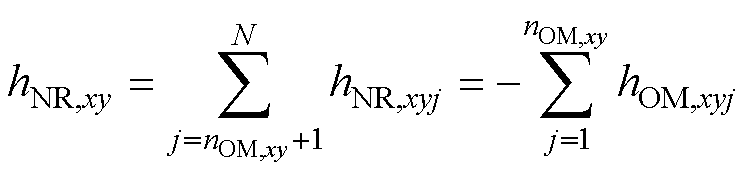 (20)
(20)
根据文献[18],每个NRSM补偿的谐波hNR,xyj按照式(21)的规律进行分配,并结合式(19)即可得到NRSM的调制波 。
。
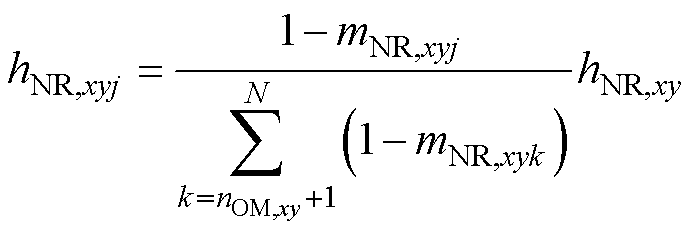 (21)
(21)
以桥臂子模块数目N=3为例,图4给出了采用HCM策略时,PV功率不平衡下桥臂内OMSM和NRSM的调制波波形。可知,PV功率不平衡时,SM的调制波存在显著差异,使每个开关周期子模块的占空比不相同。
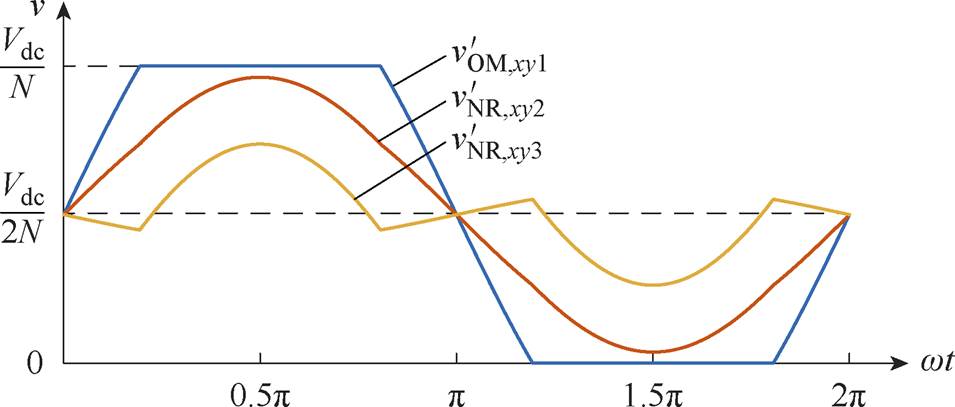
图4 PV功率不平衡下HCM策略的SM调制波波形
Fig.4 SM modulation waveforms of HCM strategy under PV power imbalance
由第1节分析可知,MMC的控制环路产生的桥臂电压参考值vxy,ref保证了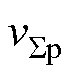 和
和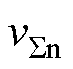 脉冲宽度的一致性,调制策略只需要对SM的输出电压脉冲进行合理的排布就能使
脉冲宽度的一致性,调制策略只需要对SM的输出电压脉冲进行合理的排布就能使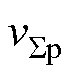 和
和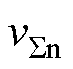 波形相同,实现波形对消,达到抑制CMV的目的。
波形相同,实现波形对消,达到抑制CMV的目的。
本节提出一种脉冲衔尾排布调制,能够将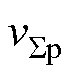 和
和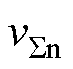 排布成相同的形状,实现CMV消除。以N=3为例,图5给出了所提脉冲衔尾排布调制消除CMV的基本原理。
排布成相同的形状,实现CMV消除。以N=3为例,图5给出了所提脉冲衔尾排布调制消除CMV的基本原理。
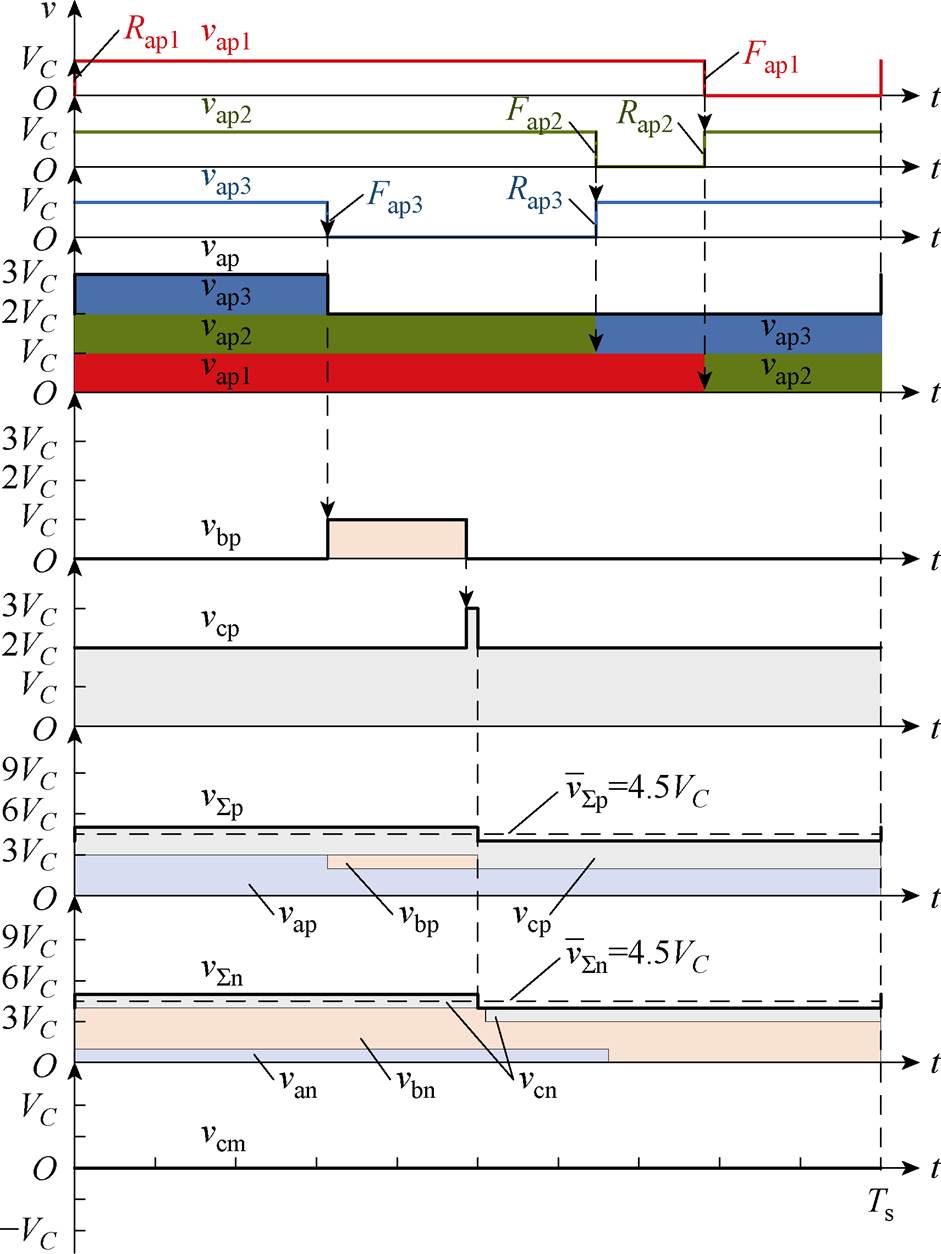
图5 脉冲衔尾排布原理
Fig.5 Principle of nose-to-tail pulse arrangement
由于PV功率不平衡,HCM会使SM的调制信号存在差异。在图5所示的开关周期中,SMap1、SMap2和SMap3的占空比满足Dap2>Dap1>Dap3。三相上桥臂所有SM的输出电压脉冲按照SMap1—SMap2—SMap3—SMbp1—SMbp2—SMbp3—SMcp1—SMcp2—SMcp3的顺序依次排布,前一个SM交流端口电压脉冲的下降沿时刻为后一个SM交流端口电压脉冲的上升沿时刻,其中,SMap1的上升沿时刻为0,即每个开关周期的起始时刻。依照上述规律,三相下桥臂所有SM的输出电压脉冲按照SMan1—SMan2—SMan3—SMbn1—SMbn2—SMbn3—SMcn1—SMcn2—SMcn3的顺序依次排布,SMan1的上升沿时刻为0。
由式(9),每个开关周期三相上桥臂所有SM脉冲宽度之和与三相下桥臂所有SM脉冲宽度之和是相同的。按照图5规律排布SM输出电压脉冲后,SMap1和SMan1的上升沿时刻相同,SMcp3和SMcn3的下降沿时刻相同,使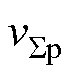 和
和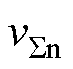 具有相同的波形,如图5所示,满足
具有相同的波形,如图5所示,满足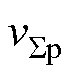 和
和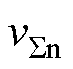 完全对消的条件,达到了使vcm恒等于零而抑制CMV的目的。
完全对消的条件,达到了使vcm恒等于零而抑制CMV的目的。
所提脉冲衔尾排布调制的实现方法分为以下步骤,实现流程如图6所示。

图6 脉冲衔尾排布调制实现流程
Fig.6 Flow chart of implementation of nose-to-tail pulse arrangement modulation
(1)获取所有SM的占空比Dxyj。在每个开关周期,根据MMC-PVS的交流端口控制、相间和桥臂间平衡控制、内部环流控制、独立电压平衡控制和HCM,可获得所有SM的调制波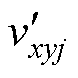 。利用SM的额定电压VC对
。利用SM的额定电压VC对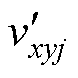 进行归一化,可得到SM的占空比Dxyj为
进行归一化,可得到SM的占空比Dxyj为
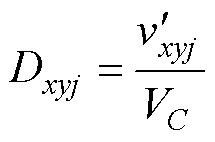 (22)
(22)
(2)根据占空比Dxyj确定每个SM电压脉冲的上升沿时刻Rxyj和下降沿时刻Fxyj。由图5可知,在每个开关周期,三相上桥臂所有SM电压脉冲按照SMap1—SMap2—SMap3—SMbp1—SMbp2—SMbp3—SMcp1—SMcp2—SMcp3的顺序依次排布。上桥臂SMap1的上升沿时刻为 的上升沿时刻,设定该上升沿时刻为起始时刻,即Rap1=0。保持SMap1的占空比不,SMap1的下降沿时刻应为Fap1=Rap1+Dap1。依据相同的规律,三相上桥臂其余SM的上升沿时刻和下降沿时刻可由式(23)计算得到,其中,rem( · ) 为取余函数。同样地,三相下桥臂所有SM输出电压脉冲按照SMan1—SMan2—SMan3—SMbn1—SMbn2—SMbn3—SMcn1—SMcn2—SMcn3的顺序依次排列,SMan1的上升沿时刻为
的上升沿时刻,设定该上升沿时刻为起始时刻,即Rap1=0。保持SMap1的占空比不,SMap1的下降沿时刻应为Fap1=Rap1+Dap1。依据相同的规律,三相上桥臂其余SM的上升沿时刻和下降沿时刻可由式(23)计算得到,其中,rem( · ) 为取余函数。同样地,三相下桥臂所有SM输出电压脉冲按照SMan1—SMan2—SMan3—SMbn1—SMbn2—SMbn3—SMcn1—SMcn2—SMcn3的顺序依次排列,SMan1的上升沿时刻为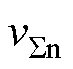 的上升沿时刻,需与
的上升沿时刻,需与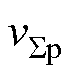 的上升沿时刻对齐,因此,Ran1应与Rap1相同,设定为Ran1=Rap1。保持SMan1的占空比不变,SMan1的下降沿时刻应为Fan1=Ran1+Dan1,而三相下桥臂其余SM的上升沿时刻和下降沿时刻可由式(23)确定。
的上升沿时刻对齐,因此,Ran1应与Rap1相同,设定为Ran1=Rap1。保持SMan1的占空比不变,SMan1的下降沿时刻应为Fan1=Ran1+Dan1,而三相下桥臂其余SM的上升沿时刻和下降沿时刻可由式(23)确定。
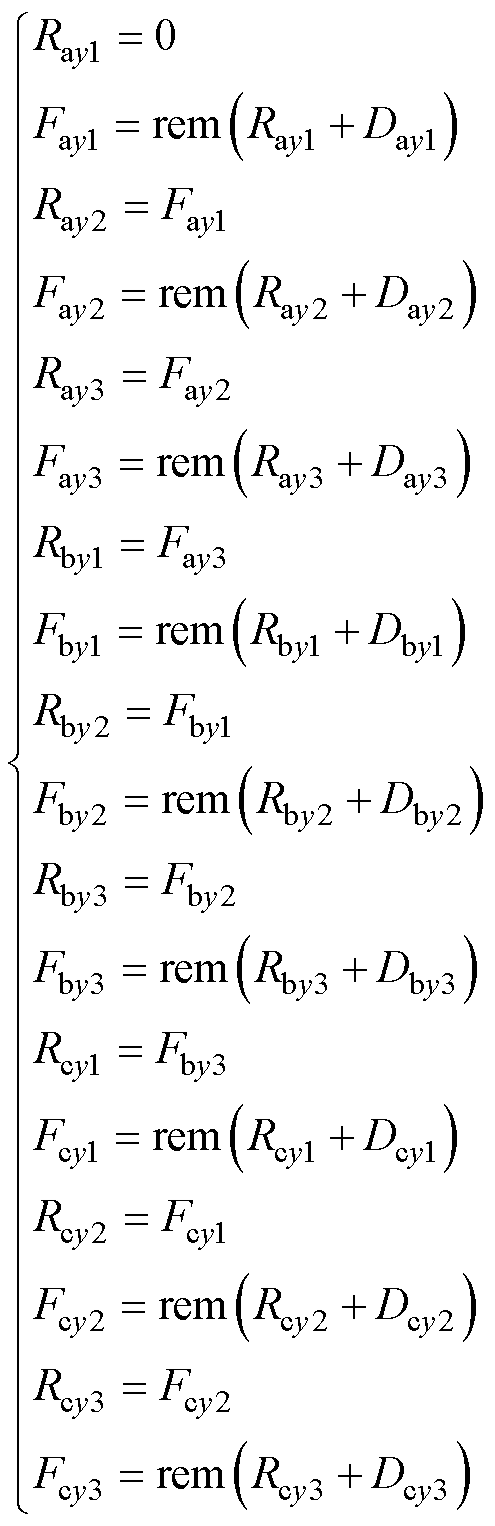 (23)
(23)
当桥臂SM数目扩展为N时,SMap1的上升沿时刻依旧设定为Rap1=0,且SMan1的上升沿时刻与SMap1对齐,Ran1设定为Ran1=Rap1,三相SM的上升沿时刻和下降沿时刻由式(24)确定。
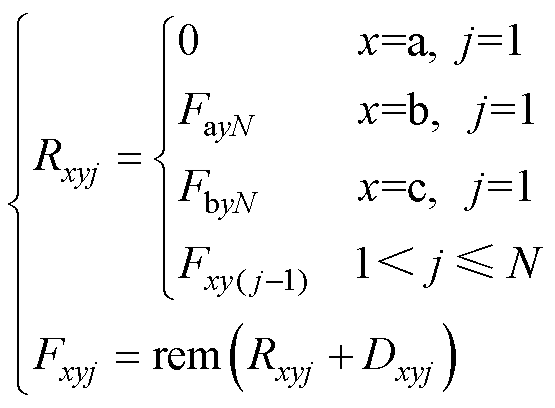 (24)
(24)
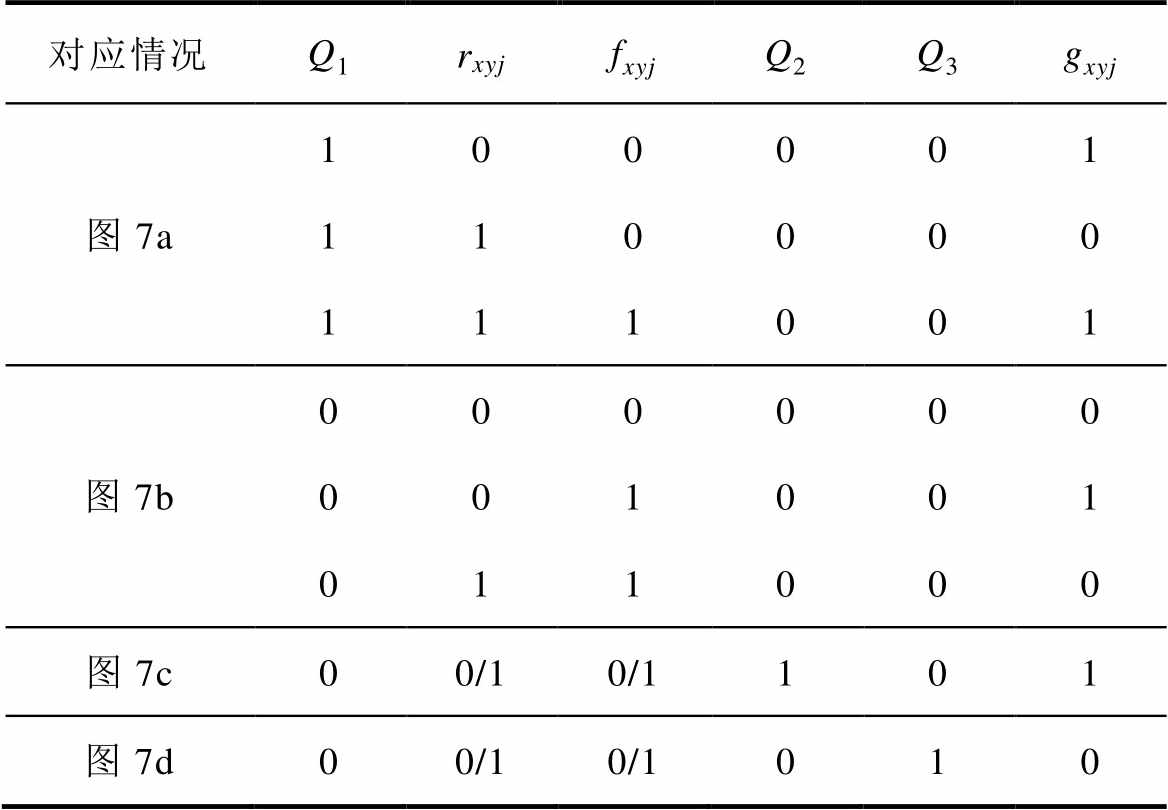
(3)根据Dxyj、Rxyj和Fxyj生成SM驱动信号gxyj。根据Rxyj和Fxyj的大小关系及Dxyj的取值,SM的驱动信号存在如图7所示的四种情况。图中,Rxyj和Fxyj分别与锯齿型载波比较后可得到脉冲形式的中间变量rxyj和fxyj,用以确定SM驱动信号的上升沿和下降沿位置。
当0<Dxyj<1且Q1=1时(见图7a),SM驱动信号gxyj分布在开关周期的中间部分;当0<Dxyj<1且Q1=0时(见图7b),SM驱动信号gxyj分布在开关周期的两端;当Dxyj=1时,由式(24)计算可知,Rxyj=Fxyj,且SM驱动信号在整个开关周期都为高电平;当Dxyj=0时,Rxyj=Fxyj,且SM驱动信号在整个开关周期都为低电平。
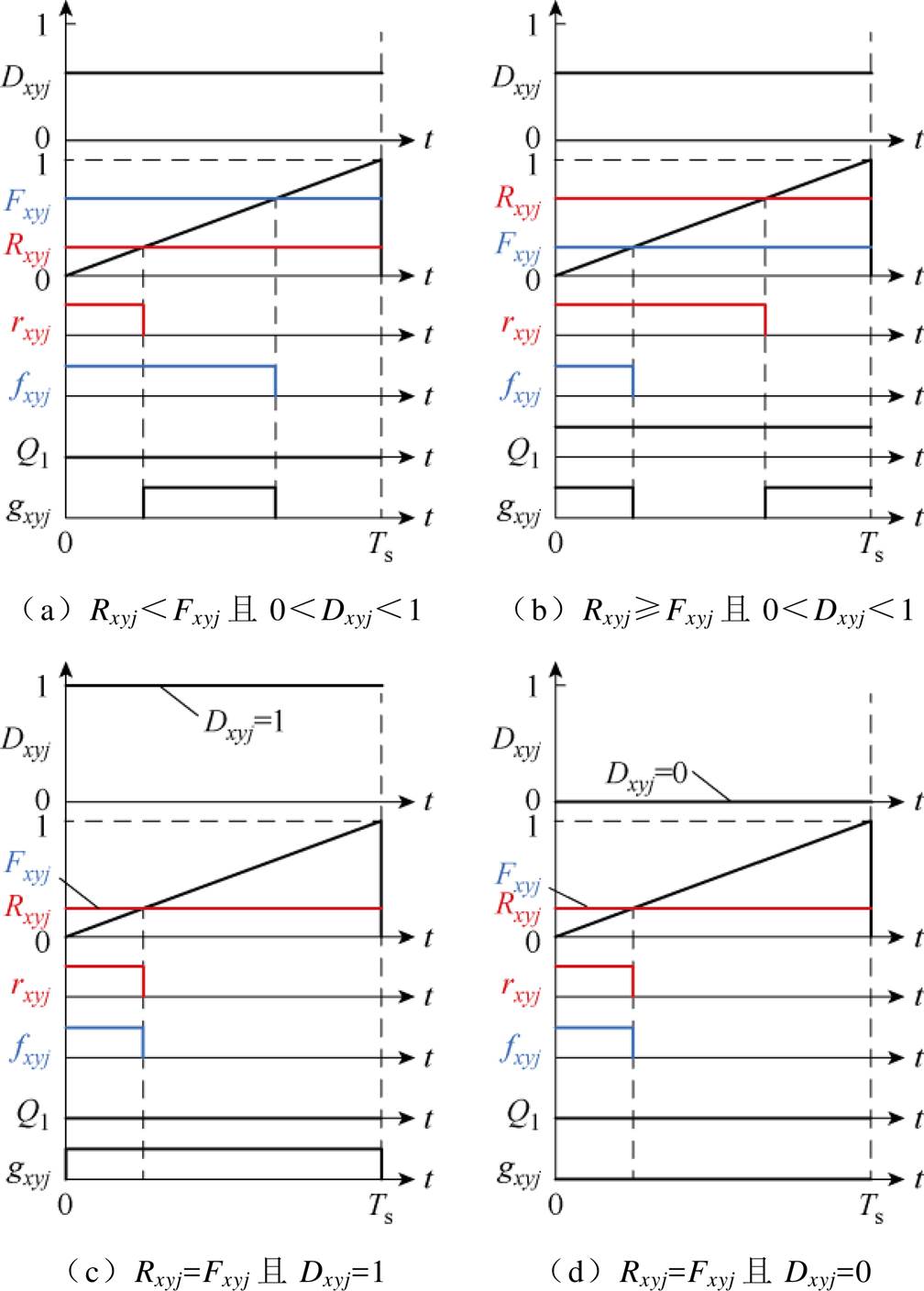
图7 不同Dxyj、Rxyj和Fxyj组合的gxyj
Fig.7 gxyj with different combinations of Dxyj, Rxyj and Fxyj
为了能够通过逻辑关系式生成SM驱动信号,定义Q1表示Rxyj和Fxyj的大小关系,Q2表示Dxyj与1的大小关系,Q3表示Dxyj与0的大小关系,分别为
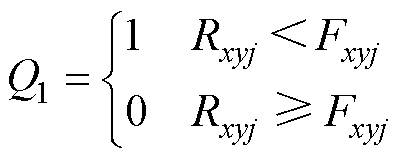 (25)
(25)
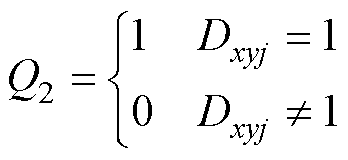 (26)
(26)
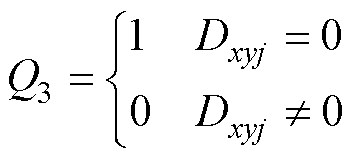 (27)
(27)
结合图7和式(25)~式(27),gxyj的真值见表1,由此得到gxyj的逻辑表达式为
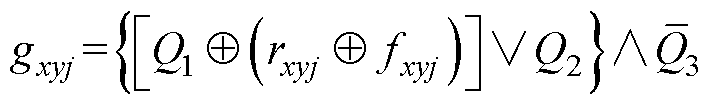 (28)
(28)
根据式(28),由Dxyj、Rxyj和Fxyj生成SM驱动信号gxyj的逻辑电路如图8所示。
表1 gxyj真值
Tab.1 Truth of gxyj
对应情况Q1rxyjfxyjQ2Q3gxyj 图7a100001 110000 111001 图7b000000 001001 011000 图7c00/10/1101 图7d00/10/1010
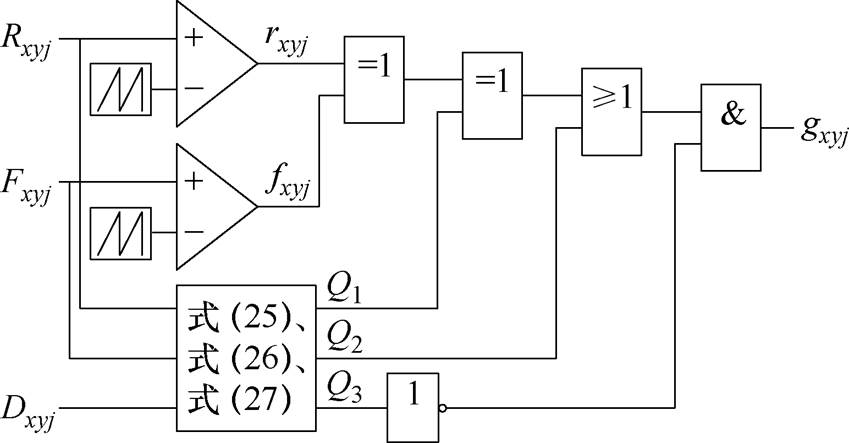
图8 生成gxyj的逻辑电路
Fig.8 Logic circuit for generating gxyj
综上所述,所提脉冲衔尾排布调制通过对SM驱动脉冲进行平移和分割,将SM电压脉冲按照指定规律依次排布,重塑了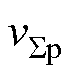 和
和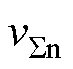 的波形形状,使
的波形形状,使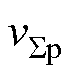 和
和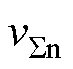 满足vcm=0的条件。同时,所提调制保持每个开关周期SM的占空比不变,不会影响MMC-PVS的SM调制比和系统调制比,能够满足HCM调制信号在[0, 1]范围变化的需求。
满足vcm=0的条件。同时,所提调制保持每个开关周期SM的占空比不变,不会影响MMC-PVS的SM调制比和系统调制比,能够满足HCM调制信号在[0, 1]范围变化的需求。
本文在Matlab/Simulink中搭建了如图1a所示的MMC-PVS仿真模型,系统仿真参数见表2。由第2节原理分析可知,所提脉冲衔尾排布调制不需修改SM的脉冲宽度,不存在将MMC-PVS交流端口系统调制比降低为给定值的0.866的问题。本文选取系统调制比为m=0.8和m=0.9的两种仿真设置,验证在系统调制比为m<0.866和m>0.866时,所提脉冲衔尾排布调制对MMC-PVS的共模电压抑制效果,以表明所提脉冲衔尾排布调制对共模电压的抑制能力不受系统调制比m限制。同时,在每种系统调制比设置下,分别对PV功率平衡和PV功率不平衡两种工况进行了仿真验证。图9给出了基于所提脉冲衔尾排布调制的MMC-PVS控制框图。
表2 MMC-PVS仿真参数
Tab.2 Simulation parameters of MMC-PVS

参 数数 值 直流侧电压幅值Vdc/kV6 交流侧单相额定功率Pr/kW400 桥臂SM数目N4 桥臂电感L0/mH2 交流侧滤波电感Lg/mH2 SM电容C/mF10 载波频率/kHz10
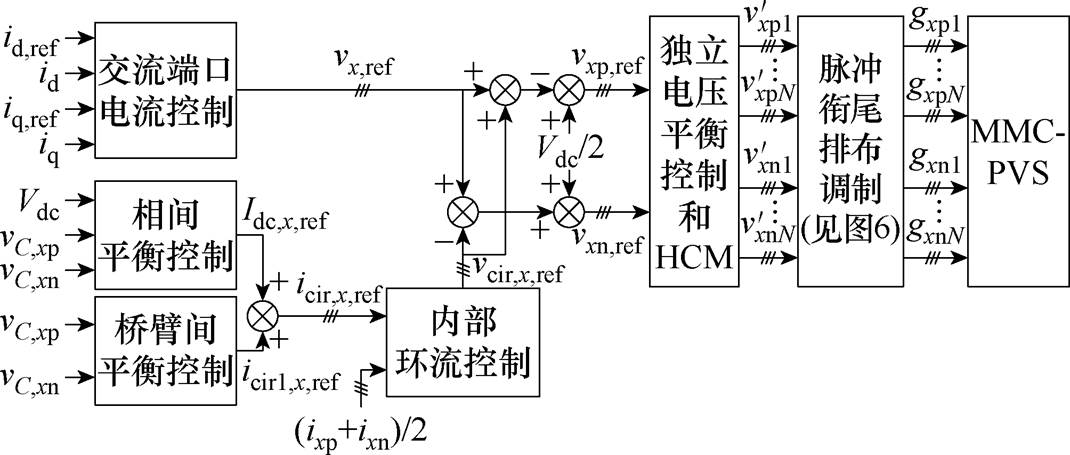
图9 基于脉冲衔尾排布调制的MMC-PVS控制框图
Fig.9 Control diagram of MMC-PVS based on nose-to-tail pulse arrangement modulation
当m=0.8时,图10和图11分别为MMC-PVS在PV功率平衡和PV功率不平衡条件下采用CPS- PWM和所提脉冲衔尾排布调制的仿真波形。图10中,所有PV模块功率都是50 kW;图11中,a相上桥臂PV模块功率为47.5、45、20、10 kW,其余PV模块功率为50 kW。当m=0.9时,图12和图13分别为MMC-PVS在PV功率平衡和PV功率不平衡条件下采用CPS-PWM和所提脉冲衔尾排布调制的仿真波形。图12中,所有PV模块功率都是50 kW;图13中,a相上桥臂PV模块功率为47.5、45、30、20 kW,其余PV模块功率为50 kW。图10a~图13a中的波形依次为a相上桥臂SM调制信号波形、SM电容电压波形、CMV波形、a相上桥臂电压vap波形、a相上下桥臂电压差模分量(van-vap)/2的波形和三相交流电流ix的波形,图10b~图13b为稳态时一个开关周期的放大波形,依次为a相上桥臂SM输出电压vapj的波形、三相桥臂电压vxy的波形、 的波形及CMV波形。
的波形及CMV波形。
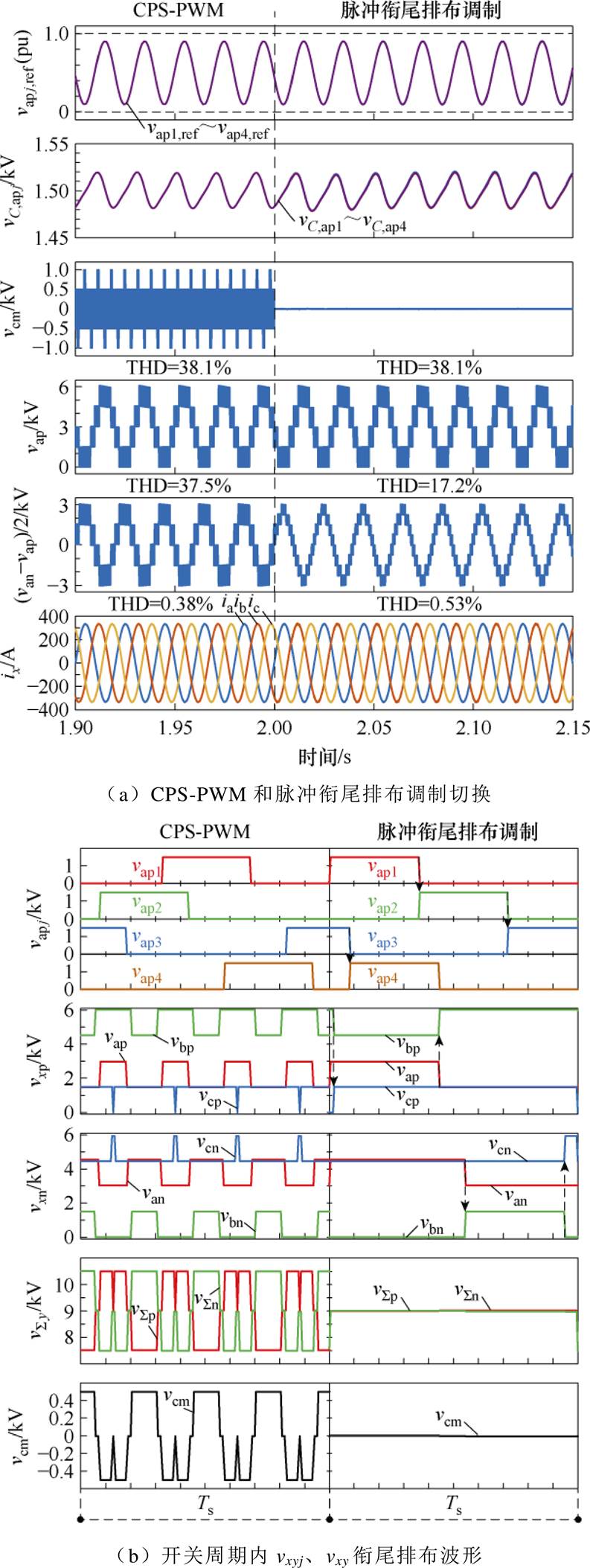
图10 m=0.8时PV功率平衡仿真波形
Fig.10 Simulation waveforms of balanced PV power under m=0.8
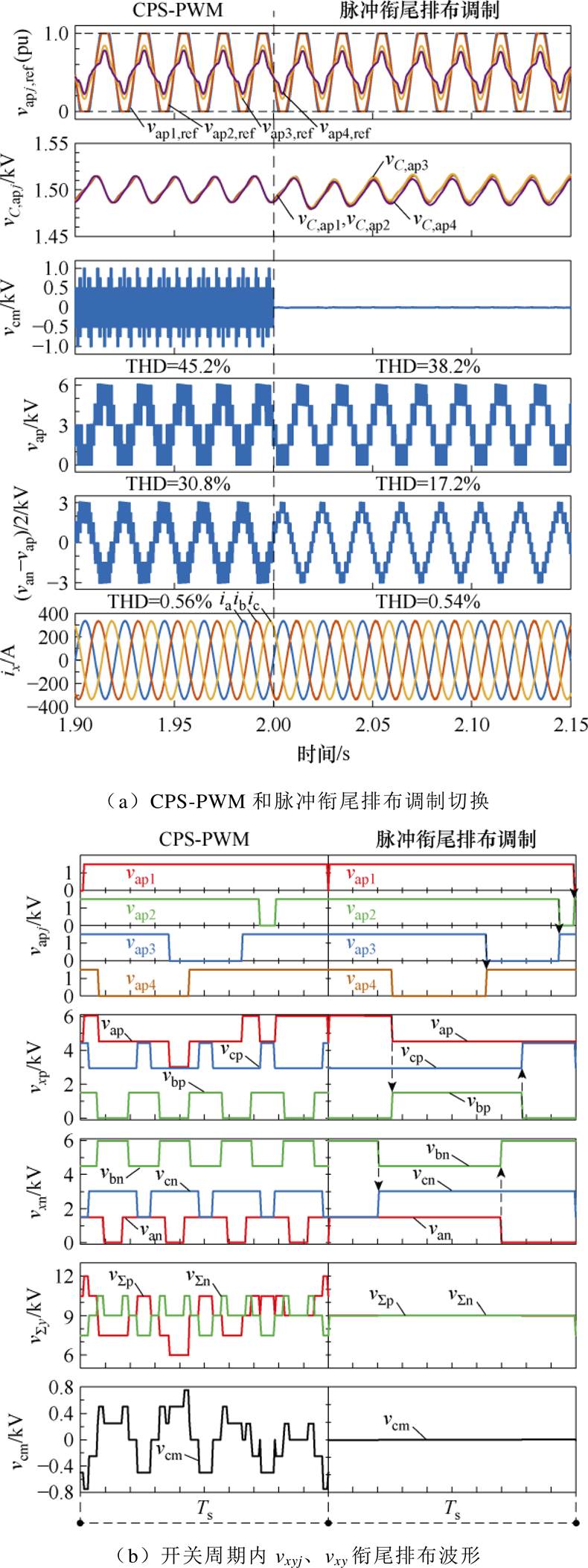
图11 m=0.8时PV功率不平衡仿真波形
Fig.11 Simulation waveforms of unbalanced PV power under m=0.8
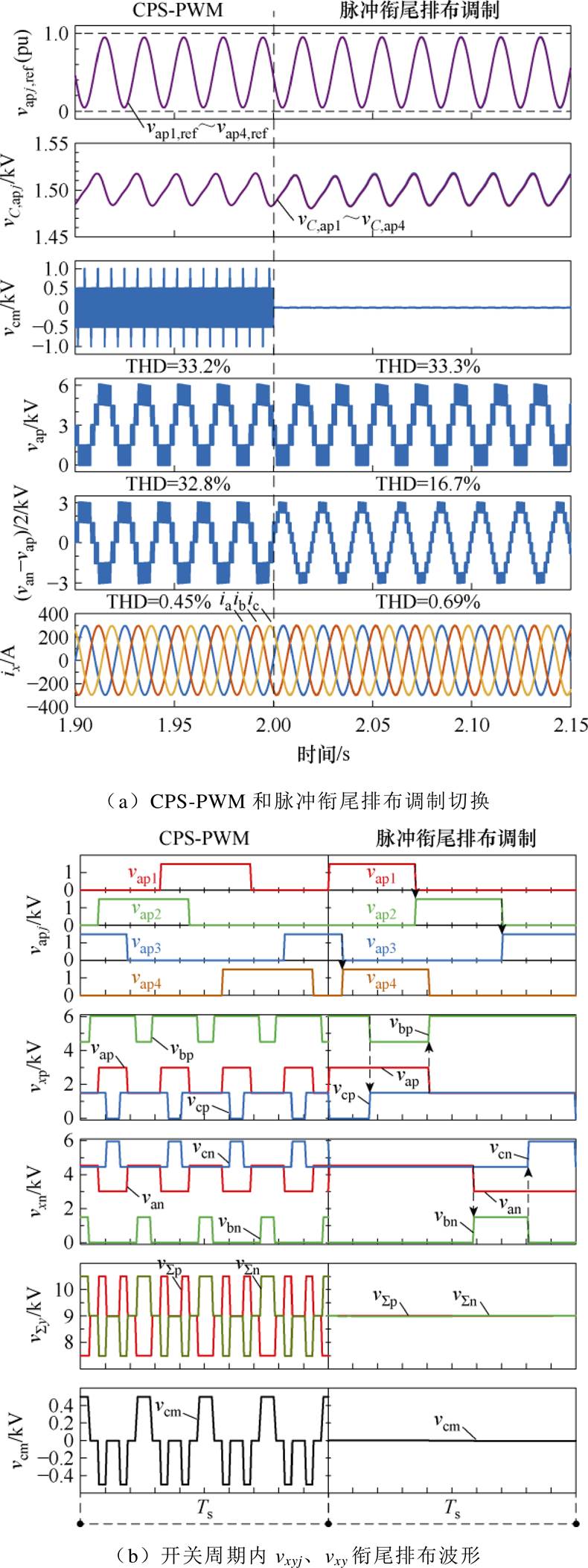
图12 m=0.9时PV功率平衡仿真波形
Fig.12 Simulation waveforms of balanced PV power under m=0.9

图13 m=0.9时PV功率不平衡仿真波形
Fig.13 Simulation waveforms of unbalanced PV power under m=0.9
由图10a~图13a可知,在PV模块功率平衡和功率不平衡两种工况下,所提脉冲衔尾排布调制都有效地抑制了MMC-PVS的CMV。在m=0.8和m= 0.9两种系统调制比下,所提调制都能正常运行,说明所提脉冲衔尾排布调制不受系统调制比m的限制。由图10a~图13a可知,调制策略由CPS-PWM切换至所提脉冲衔尾排布调制的过程中,MMC- PVS的SM电容电压都能保持平衡,且稳态时SM的电容电压波动基本保持不变。针对桥臂电压vap,当PV功率平衡时,CPS-PWM和所提脉冲衔尾排布调制的桥臂电压总谐波畸变率(Total Harmonic Distortion, THD)基本一致,而当PV功率不平衡时,所提脉冲衔尾排布调制的桥臂电压THD略低于CPS- PWM。针对于上、下桥臂电压差模分量(van-vap)/2,无论是PV功率平衡还是PV功率不平衡,所提脉冲衔尾排布调制产生的THD都明显小于CPS-PWM。另外,CPS-PWM和所提脉冲衔尾排布调制产生的交流端口电流THD基本一致,都具有良好的电能质量。
在图10b~图13b中,同一桥臂内,后一个SM的输出电压上升沿时刻与前一个SM的输出电压下降沿时刻保持一致;b相桥臂电压的上升沿时刻与a相桥臂电压的上升沿时刻保持一致,c相桥臂电压的上升沿时刻与b相桥臂电压的上升沿时刻保持一致。这使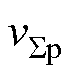 和
和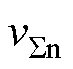 在一个开关周期内具有相同的形状,满足了vcm=0的条件,有效抑制了CMV,与图5的脉冲衔尾排布调制的基本原理一致。
在一个开关周期内具有相同的形状,满足了vcm=0的条件,有效抑制了CMV,与图5的脉冲衔尾排布调制的基本原理一致。
为了验证脉冲衔尾排布调制在模块功率平衡与不平衡工况下高频共模电压的抑制效果,本文搭建了三相MMC实验样机,实验平台参数见表3,实验平台如图14所示。本实验中,实验样机采用dSPACE MicroLabBox作为MMC控制器,实验平台的控制信息可以通过上位机实时观测与修改。MMC的a相上桥臂SMap3通过DC-DC变换器与模拟光伏的直流电源相连,并通过CAN总线与上位机通信。直流电源注入SMap3的功率为50 W,其余SM直流侧无DC-DC变换器相连,功率为零。MMC直流侧连接直流电源作为MMC的直流母线,交流侧连接三相电阻负载。
表3 实验平台参数
Tab.3 Experimental parameters of prototype

参 数数 值 直流侧电压幅值Vdc/V300 交流侧电阻负载/W16 SM数目N3 桥臂电感L0/mH8 交流侧滤波电感Lg/mH2 SM电容C/mF4.5 载波频率/kHz6.67

图14 三相MMC实验平台
Fig.14 Experimental prototype of three-phase MMC
图15为m=0.8时,在模块功率平衡和模块功率不平衡两种工况下,采用所提脉冲衔尾排布调制的同一桥臂内SM交流端口电压波形和三相上桥臂电压波形。由图15可知,模块功率平衡时,同一桥臂内SM交流端口电压脉冲宽度一致,而模块功率不平衡时,同一桥臂内SM交流端口电压脉冲宽度存在差异。两种工况下,所提脉冲衔尾排布调制都能够使同一桥臂内SM交流端口电压和三相桥臂电压按照衔尾排布方式工作,实现CMV波形重塑。
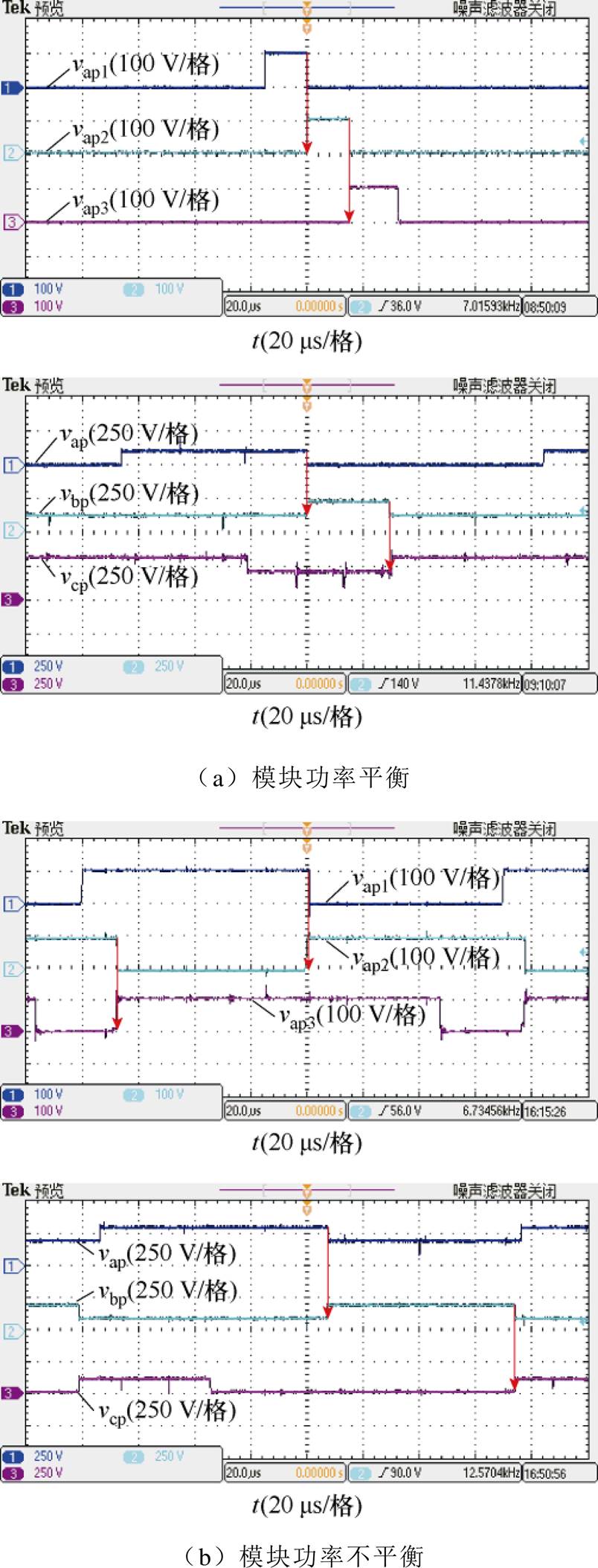
图15 m=0.8时脉冲衔尾排布调制实验波形
Fig.15 Experimental waveforms with balanced SM power when m=0.8
当m=0.8时,采用CPS-PWM和所提脉冲衔尾排布调制,图16a和图17a分别为模块功率平衡和模块功率不平衡工况下输出相电压和CMV的波形,图16b和图17b为相应的CMV频谱图。根据图16和图17,在模块功率平衡和模块功率不平衡两种工况下,所提脉冲衔尾排布调制都能有效抑制CMV峰值。通过对比频谱图,所提脉冲衔尾排布调制对等效开关频率(20 kHz)及其倍频和边带频率处的高频CMV分量有显著的抑制作用。相较于CPS- PWM,当模块功率平衡时,所提脉冲衔尾排布调制会略微增加开关频率处CMV谐波幅值,仅有1 V左右;当模块功率不平衡时,CPS-PWM在开关频率处CMV谐波幅值会增加,而所提脉冲衔尾排布调制会对此处CMV谐波产生抑制作用。
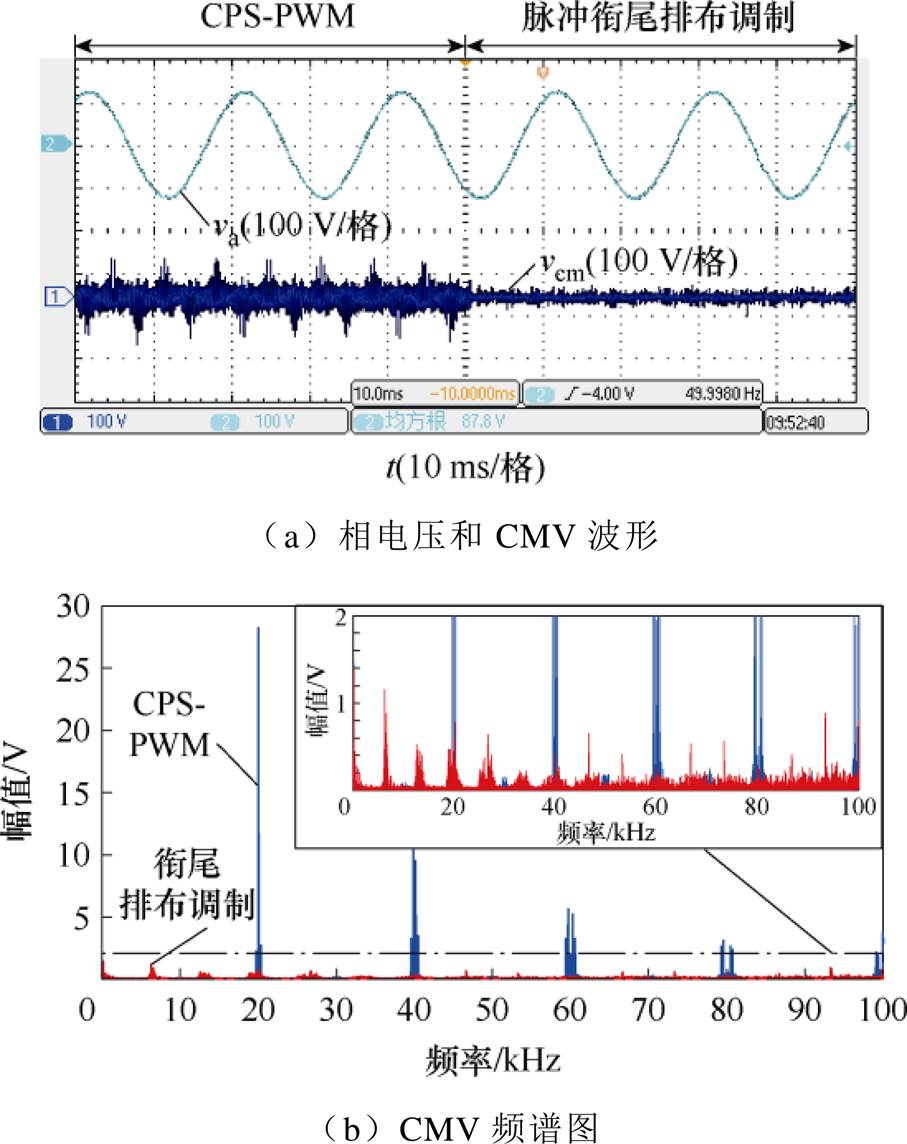
图16 m=0.8时模块功率平衡实验波形
Fig.16 Experimental waveforms with balanced SM power when m=0.8
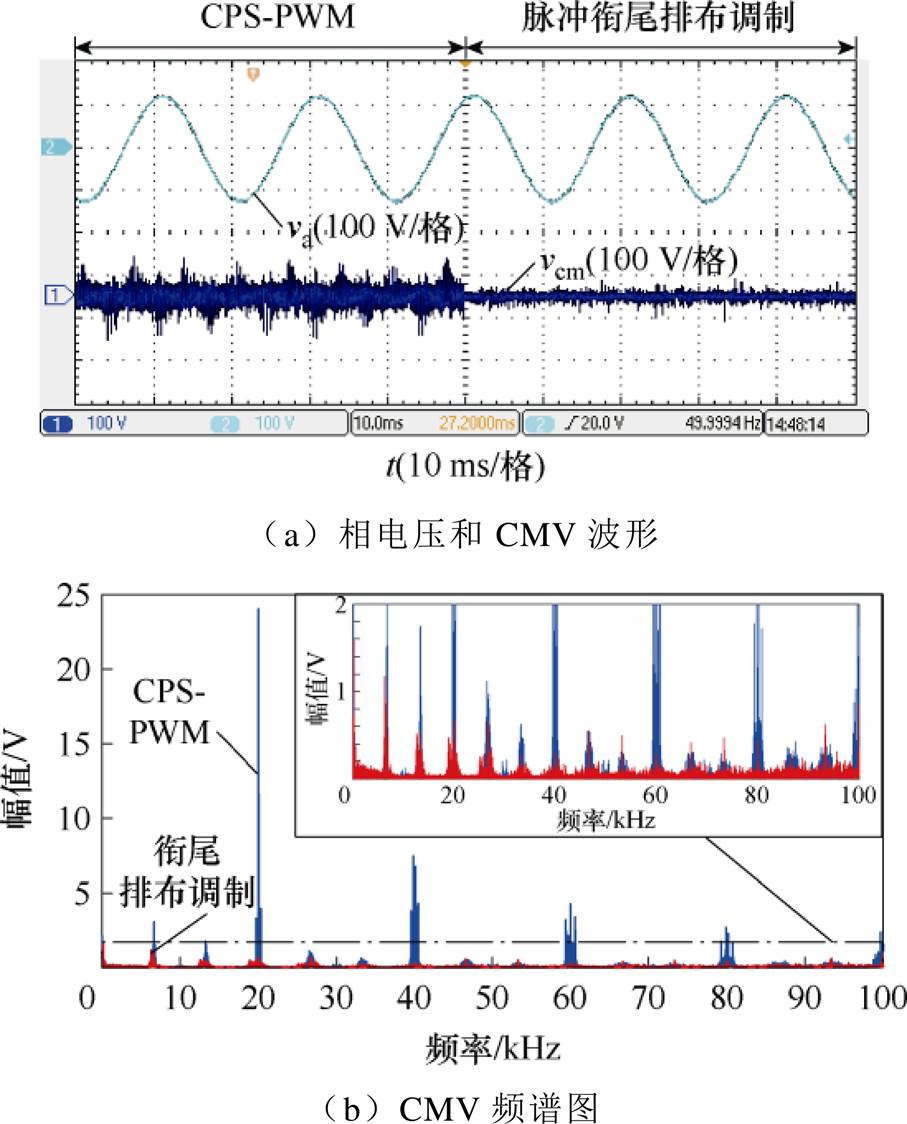
图17 m=0.8时模块功率不平衡实验波形
Fig.17 Experimental waveforms with unbalanced SM power when m=0.8
图18和图19为m=0.9时,采用CPS-PWM和所提脉冲衔尾排布调制的实验波形。可以发现,当m=0.9时,在模块功率平衡和模块功率不平衡工况下,所提脉冲衔尾排布调制都能够有效抑制CMV,抑制效果分析结果与m=0.8时类似。实验结果表明,所提脉冲衔尾排布调制能够在系统调制比m>0.866时正常运行,说明所提脉冲衔尾排布调制不受系统调制比m的限制。
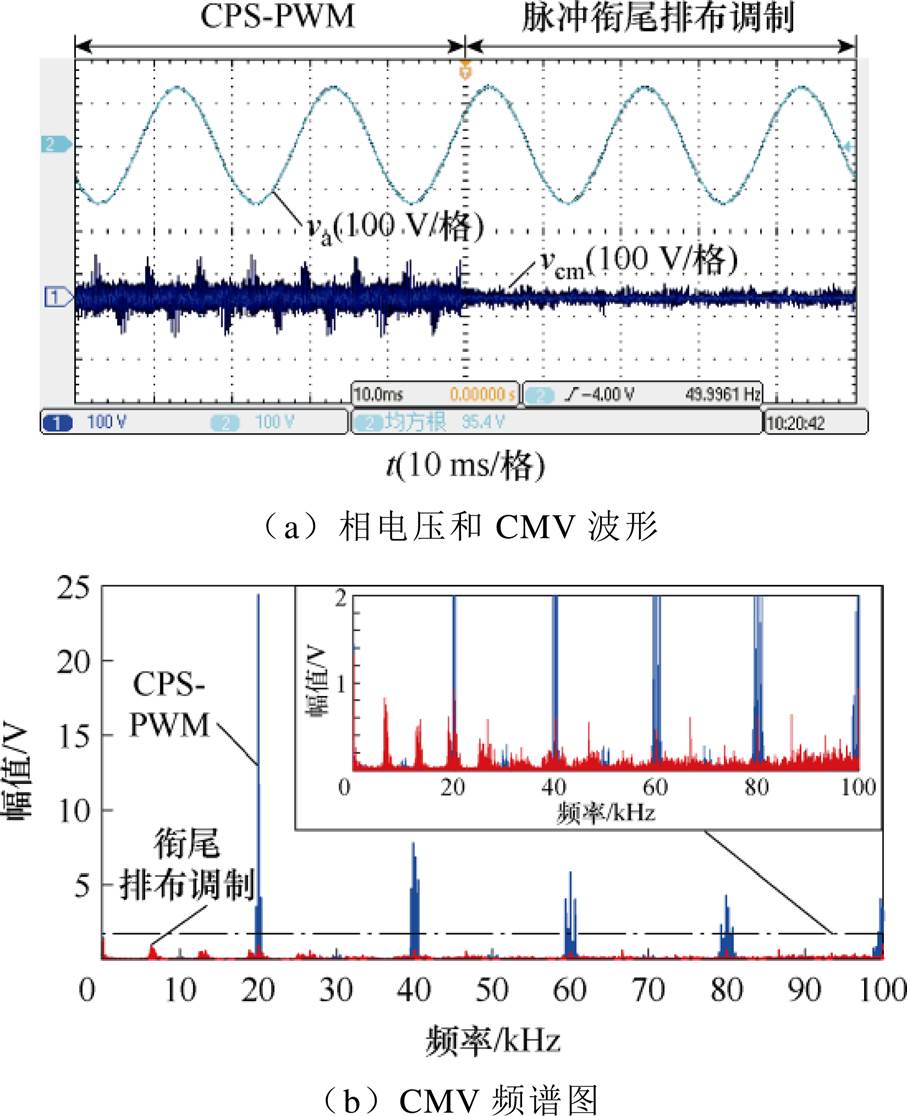
图18 m=0.9时模块功率平衡实验波形
Fig.18 Experimental waveforms with balanced SM power when m=0.9
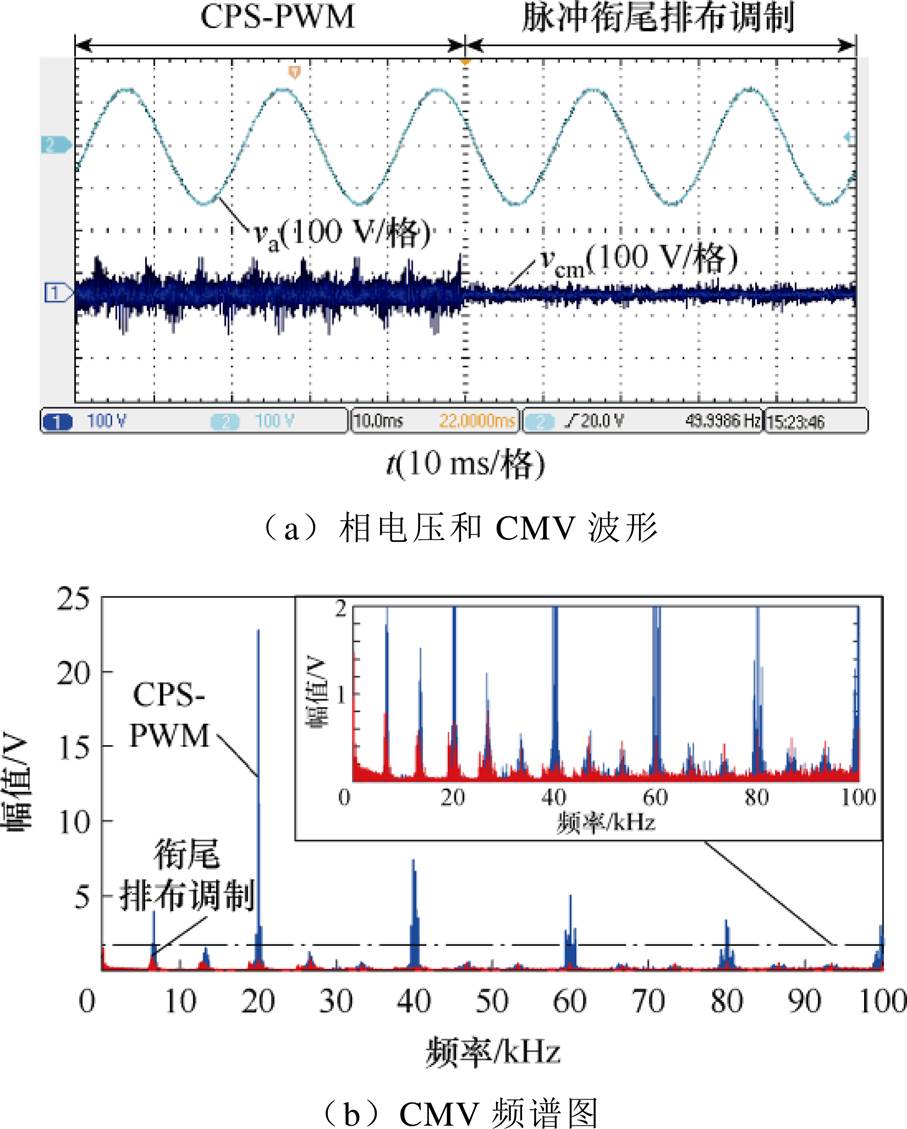
图19 m=0.9时模块功率不平衡实验波形
Fig.19 Experimental waveforms with unbalanced SM power when m=0.9
本文提出了一种脉冲衔尾排布调制,在PV功率平衡和PV功率不平衡工况下都能有效抑制MMC- PVS的共模电压。文中分析了PV功率不平衡工况下MMC-PVS实现零CMV的条件,指出理论上子模块的调制信号具备实现零CMV的能力。在此基础上,脉冲衔尾排布调制不仅能将同一桥臂内SM电压依次衔尾排布,即后一子模块的上升沿时刻与前一子模块的下降沿时刻对齐,还能将三相上桥臂电压和三相下桥臂电压分别依次衔尾排布,使三相上桥臂总电压和三相下桥臂总电压的形状相同,达到了理论上零CMV的效果。通过仿真和实验验证,无论是PV模块功率平衡,还是PV功率不平衡工况,在保证子模块电容电压平衡的基础上,脉冲衔尾排布调制都能实现良好的CMV抑制效果。同时,脉冲衔尾排布调制无须修改SM的调制比,也不会受到系统调制比过高的限制,并且在桥臂子模块数目为奇数和偶数情况下都能正常运行。
参考文献
[1] 任鹏, 涂春鸣, 侯玉超, 等. 考虑异质器件混用与输出电平倍增的混合型MMC及其调控方法[J]. 电力系统自动化, 2024, 48(5): 128-136.
Ren Peng, Tu Chunming, Hou Yuchao, et al. Hybrid MMC considering heterogeneous device mixing and output level multiplication and its regulation method[J]. Automation of Electric Power Systems, 2024, 48(5): 128-136.
[2] 武鸿, 王跃, 刘熠, 等. 基于广义电容电压不平衡度的MMC子模块开路故障诊断策略[J]. 电工技术学报, 2023, 38(14): 3909-3922.
Wu Hong, Wang Yue, Liu Yi, et al. Open circuit fault diagnosis strategy of MMC sub-module based on generalized capacitor voltage unbalance[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(14): 3909-3922.
[3] 盛景, 陈聪, 向鑫, 等. 模块化多电平谐振变换器多自由度调压控制及子模块电容均压方法[J]. 电工技术学报, 2022, 37(24): 6216-6229.
Sheng Jing, Chen Cong, Xiang Xin, et al. Multiple- degree-of-freedom control and capacitor voltage balancing method of modular multilevel resonant converter[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6216-6229.
[4] 滕甲训, 潘禹卓, 卜泽敏, 等. 基于谐振式推挽结构的三端口MMC-SST波动功率耦合方案研究[J]. 中国电机工程学报, 2022, 42(6): 2308-2320.
Teng Jiaxun, Pan Yuzhuo, Bu Zemin, et al. Research on fluctuating power coupling scheme of three-port MMC-SST based on resonant push-pull structure[J]. Proceedings of the CSEE, 2022, 42(6): 2308-2320.
[5] Teng Jiaxun, Sun Xiaofeng, Liu Xinlei, et al. Power mismatches elimination strategy for MMC-based photovoltaic system and lightweight design[J]. IEEE Transactions on Power Electronics, 2023, 38(9): 11614-11629.
[6] Barcellona S, Barresi M, Piegari L. MMC-based PV three-phase system with distributed MPPT[J]. IEEE Transactions on Energy Conversion, 2022, 37(3): 1567-1578.
[7] Wang Zuoxing, Li Hong, Chu Zhaoyi, et al. A review of EMI research in modular multilevel converter for HVDC applications[J]. IEEE Transactions on Power Electronics, 2022, 37(12): 14482-14498.
[8] Guo Xiaoqiang, Du Senyu, Xing He, et al. A new modulation for leakage current reduction of modular multilevel converter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(1): 722-731.
[9] Li Wuhua, Wang Yuxiang, Hu Jiawei, et al. Common- mode current suppression of transformerless nested five-level converter with zero common-mode vectors[J]. IEEE Transactions on Power Electronics, 2019, 34(5): 4249-4258.
[10] Nguyen T K T, Nguyen N V. An efficient four-state zero common-mode voltage PWM scheme with reduced current distortion for a three-level inverter[J]. IEEE Transactions on Industrial Electronics, 2018, 65(2): 1021-1030.
[11] 陈嘉楠, 蒋栋, 孙伟, 等. 一种抑制奇数多电平变换器共模噪声的通用调制策略[J]. 中国电机工程学报, 2022, 42(13): 4695-4705.
Chen Jianan, Jiang Dong, Sun Wei, et al. A general modulation strategy for suppressing common-mode noise of odds multilevel converter[J]. Proceedings of the CSEE, 2022, 42(13): 4695-4705.
[12] Li Hong, Wang Jiaxin, Yang Zhichang. Common- mode voltage reduction of modular multilevel converter based on six-segment carrier level shifted sinusoidal pulse width modulation[C]//2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 2020: 807-811.
[13] Chen Jianan, Jiang Dong, Sun Wei, et al. Common- mode voltage reduction scheme for MMC with low switching frequency in AC-DC power conversion system[J]. IEEE Transactions on Industrial Infor- matics, 2022, 18(1): 278-287.
[14] Wang Jiaxin, Li Hong, Wang Zuoxing, et al. A novel common-mode voltage reduction method of MMC: pulse sequential connection carrier phase-shifted SPWM[C]//2021 IEEE International Joint EMC/SI/PI and EMC Europe Symposium, Raleigh, NC, USA, 2021: 89-93.
[15] Teng Jiaxun, Sun Xiaofeng, Wang Zizhe, et al. Nose-to-tail modulation of three-phase 12N switching- cells inverter for zero common mode voltage[J]. IEEE Transactions on Power Electronics, 2023, 38(11): 13555-13560.
[16] 李桐, 韩学山. 时变追踪并网光伏电站最大输出功率的无功优化方法[J]. 电工技术学报, 2023, 38(11): 2921-2931.
Li Tong, Han Xueshan. Reactive power optimization method for maximum output power of time-varying tracking grid-connected photovoltaic power station[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2921-2931.
[17] Wang Mingda, Zhang Xing, Zhao Tao, et al. Harmonic compensation strategy for single-phase cascaded H-bridge PV inverter under unbalanced power conditions[J]. IEEE Transactions on Industrial Electronics, 2020, 67(12): 10474-10484.
[18] 潘尧, 孙孝峰, 蔡瑶, 等. 一种拓展模块化多电平变换器的光伏系统稳定运行范围的谐波补偿调制策略[J]. 电工技术学报, 2024, 39(4): 1132-1146.
Pan Yao, Sun Xiaofeng, Cai Yao, et al. A harmonic compensation modulation strategy to expand the stable operation range of photovoltaic system with modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1132- 1146.
[19] Zhao Tao, Zhang Xing, Mao Wang, et al. Harmonic compensation strategy for extending the operating range of cascaded H-bridge PV inverter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1341-1350.
[20] 李金玉, 陈杰, 龚春英, 等. 一种提高级联H桥逆变器功率不平衡运行能力的控制策略[J]. 电工技术学报, 2023, 38(10): 2731-2743.
Li Jinyu, Chen Jie, Gong Chunying, et al. A control strategy for improving the power unbalanced operation capability of cascaded H-bridge inverter[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2731-2743.
[21] Soong T, Lehn P W. Internal power flow of a modular multilevel converter with distributed energy resources[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(4): 1127-1138.
[22] Tu Qingrui, Xu Zheng, Xu Lie. Reduced switching- frequency modulation and circulating current suppression for modular multilevel converters[J]. IEEE Transactions on Power Delivery, 2011, 26(3): 2009-2017.
[23] 王兆安, 刘进军. 电力电子技术[M]. 5版. 北京: 机械工业出版社, 2009.
Abstract In modular multilevel converter-based photovoltaic systems (MMC-PVSs), the PV power imbalance caused by shadowing leads to differences among modulation signals of sub-modules (SMs) and further changes the characteristics of the high-frequency common mode voltage (CMV) of the MMC-PVS AC port. Thus, the existing high-frequency CMV suppression methods can not eliminate the high-frequency CMV of MMC-PVS.
This paper analyzes the elimination condition of the high-frequency CMV. That is, the sum of the upper arm voltages of three phases is always the same as that of the lower arm voltages of three phases at any time. According to the control loop, the sum of pulse widths of all SMs in the three phases’ upper arm and lower arm are equal, illustrating that zero-CMV is feasible from the aspect of the control loop. Thus, the key is to shape the arm voltages using the modulation method to satisfy the zero-CMV condition. Then, the principle of SM modulation signal difference caused by PV power imbalance is revealed and illustrated: a high PV module power results in a high SM modulation index and a high risk of over-modulation.
This paper proposes a nose-to-tail pulse arrangement modulation to eliminate the high-frequency CMV of MMC-PVS under PV power imbalance conditions. The basic principle of nose-to-tail pulse arrangement modulation is to arrange the SM pulse voltages in sequence; namely, the rising edge time of the current SM pulse voltage is aligned with the falling edge time of the previous SM pulse voltage. Accordingly, the shapes of the sums of the three-phase upper arm voltages and the three-phase lower arm voltages are the same during one switching period, and the condition of zero-CMV is satisfied. Compared with the sawtooth carrier, the rising time and falling time of each SM are determined by the duty cycle of the SM during each switching period to obtain the rising and falling edges of the SM pulse voltage. Then, according to the derived logical expression, the SM switching function can be generated. With the generated switching function of each SM, high-frequency CMV elimination can be achieved on the premise of SM capacitor voltage balance.
The simulation and experimental results are as follows. When the system modulation index m is set as 0.8, the proposed nose-to-tail pulse arrangement modulation can eliminate the high-frequency CMV on both the PV power balance and imbalance conditions via arranging the SM pulse voltages with the given orders, maintaining the SM capacitor voltage balance. From the simulation and experimental results of m=0.9, it can be concluded that the proposed method can operate under m larger than 0.866 under both PV power balance and imbalance conditions on the premises of SM capacitor voltage balance and system stability.
keywords:Modular multilevel converter, photovoltaic system, imbalanced PV power condition, common- mode voltage, nose-to-tail pulse arrangement modulation
DOI: 10.19595/j.cnki.1000-6753.tces.240077
中图分类号:TM464
河北省重点研发计划项目(19214405D)和河北省自然科学基金重点项目(E2021203162)资助。
收稿日期 2024-01-11
改稿日期 2024-01-31
潘 尧 男,1993年生,博士研究生,研究方向为多电平变换器控制。E-mail: 798968001@qq.com
孙孝峰 男,1970年生,教授,博士生导师,研究方向为变流器拓扑及波形控制技术、功率因数校正与有源滤波技术、新能源发电与组网技术。E-mail: sxf@ysu.edu.cn(通信作者)
(编辑 陈 诚)