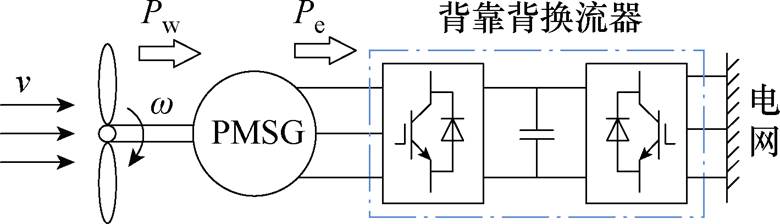
图1 永磁直驱风力发电系统结构
Fig.1 Permanent magnet direct drive wind system structure
摘要 对风电功率进行平滑处理能够有效降低风电波动对电网造成的负面影响。相较于其他方法，通过转子动能平滑风电功率，具有成本低、响应快的优势。该文提出一种计及功率指令和积分周期优化的新型风电机组转子动能功率平滑方法。首先，从风电机组的传递函数出发，推导出新型平滑参考功率，通过改变参数，能够实现对该功率指令平滑程度和波动均值大小的解耦调节。其次，通过转速闭环控制实现对功率指令的间接精准跟踪，分析了其中的关键参数积分周期Dt对功率跟踪效果产生影响的数学机理，并提出了Dt的优化整定方法。最后，以永磁直驱风电机组为研究对象，通过建立仿真模型及搭建实验平台，验证了所提新型功率平滑控制策略的可行性及有效性。
关键词：风电机组 功率平滑 转子动能 积分周期 小扰动线性化
风力发电是一种成熟的可再生能源发电方式，可有效减缓温室效应，近年来得到了广泛的应用和快速的发展[1]。在风电并网渗透率越来越高的背景下，风电的随机性、不确定性导致输出功率存在强波动性，对电网安全[2-3]、频率稳定[4-6]等产生影响，对风电出力进行一定的平滑处理能够降低风电波动对电网的冲击。目前，主流风电机组单机容量在6～10 MW左右，新发布海上风电机组单机容量则普遍在12 MW及以上，大容量风电机组规模化投产的背景下，单台机组的输出特性对电网的影响增大，对单台机组的功率特性进行改善是实现风电场多机组功率平滑的基础，能够为平抑风电场并网点功率波动提供研究参考，因此对单台机组的功率进行平滑处理有显著的研究意义。
常见的单台机组功率平滑方案可分为采用外接储能的间接法和利用机组自身资源的直接法[7]。前者主要通过电化学储能装置、飞轮、超级电容等实现风电出力的“多退少补”[8-11]；后者则是利用风电机组本身的特性和控制结构的优化实现对风电出力的平滑，相对而言成本更为低廉，主要有桨距角控制和转子动能控制两种途径。桨距角控制通过改变捕获风功率实现对输出功率的平滑，但桨距角变化速度有限，无法平抑高频功率波动，且频繁调节易增加变桨机构疲劳载荷，降低寿命[12-14]；转子动能控制通过控制转子的加减速来吸收或释放功率，平抑功率波动，其优势在于仅需控制转速便能实现对功率的平滑，无需额外成本，且不会对机组寿命产生明显影响[15-23]。众多文献针对其平滑功率的效果及控制过程中的稳定性展开了研究。文献[15]研究了风电机组参考功率为转速线性量和恒定常数两种情况下的风电机组运行情况，推导了风速到功率的传递函数。文献[16]将一阶低通滤波器（First- Order Filter, FOF）引入功率控制回路，在平抑风电功率高频波动的同时放大了低频风速段的功率波动，普适性欠佳。文献[17]提出了一种基于功率曲线查表法的转速优化控制策略，但平滑尺度过小。文献[18]在额定风速以下的转速区间引入变桨调节，但桨距角长期非零导致其风能捕获效率较传统方法降低明显。文献[19]在转矩控制回路引入二阶滤波器（Second-Order Filter, SOF），但缺乏通用的参数配置原则，且未考虑平滑策略下的机组稳定性。文献[20]对机组期望参考功率和实际参考功率做出了明确区分，但变流器的功率指令表达式繁琐，实际输出并未有效跟踪功率指令。文献[21-22]通过在功率指令中引入积分补偿项实时平滑输出功率，但关键参数计算方法复杂，且存在明显的功率损失。文献[23]将二阶滤波器引入功率控制回路，并利用稳定约束系数降低功率输出，但通过该方法防止机组失稳的可靠性未得到充分验证，不同风况下的机组稳定性难以得到有效保障。此外，上述研究中实现功率控制所采用的控制结构也有所不同，主要包括转速闭环控制[16-18]和功率/转矩闭环控制[19-23]。功率闭环控制结构的优点在于控制精准度高，但由于缺乏对转速的直接有效调控，在功率平滑策略下存在失稳风险。相比之下，转速闭环控制由于采用了主动变速的控制逻辑[24]，在优化转速运行区间、确保机组稳定运行方面更具优势。
综上所述，上述研究通过设计参考功率指令[15-16, 20-23]、优化控制器结构[17-19]实现了功率平滑，但存在以下两个方面的问题：①平滑策略的可靠性和普适性欠佳，部分方法功率指令表达式繁琐，计算复杂。②上述文献大都通过设置恒定转速下限来防止机组失速失稳，当转速达到下限时切换功率指令或参考转速使机组工作至最大功率点跟踪（MaximumPower Point Tracking, MPPT）运行状态，但功率指令的强行切换会引起电磁功率的大幅跌落，对机组载荷造成冲击，且当转速下限设置较低时将造成风能利用率下降。
针对上述问题，本文提出了一种计及功率指令和积分周期优化的新型风电机组转子动能功率平滑方法，该方法创新性如下：首先，设计了基于传递函数模型的新型功率指令，该功率指令表达式简洁，普适性高，实现了输出功率平滑程度和功率大小的解耦调节，并通过基于滑动均值滤波算法的风电机组稳态运行点选取方法进一步优化平滑效果。其次，对传统转子动能控制框架中的重要参数——积分周期Dt影响功率跟踪效果的数学机理进行了定量分析和推导，以精准控制功率为目标，首次提出了Dt的优化整定方法，从而利用转速闭环结构间接精准控制机组输出功率。同时，本文所提方法将MPPT转速设置为转速下限，当转速持续降低时，风电机组能够在平滑模式和MPPT模式间平稳过渡和切换，在最大化风能利用率的同时确保了任意风况下机组的稳定运行，提高了功率平滑策略的普适性和可靠性。
本文以永磁直驱风力发电系统为研究对象，研究基于转子动能的风电功率平滑控制策略。典型的永磁直驱风力发电系统的结构如图1所示，该系统由风力机、永磁同步发电机（Permanent Magnet Synchronous Generator, PMSG）、背靠背换流器、直流电容等组成。PMSG与风力机通过传动轴直接相连，风力机捕获风能并输出机械转矩作为PMSG的输入，PMSG发出电功率并由换流器送入电网。
图1 永磁直驱风力发电系统结构
Fig.1 Permanent magnet direct drive wind system structure
根据贝茨理论，风力机捕获机械功率可表示为
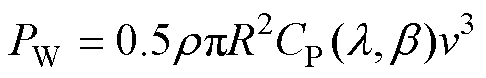（1）
式中，r 为空气密度；R为风力机叶轮半径；v为风速；CP为风能利用系数，是关于叶尖速比l 和桨距角b 的函数，当桨距角b 为0时，可将CP近似为关于l 的二次函数[25]，即
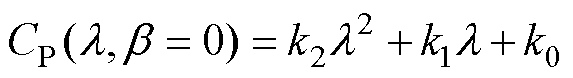（2）
式中，k2、k1、k0为常数。
叶尖速比l 定义为
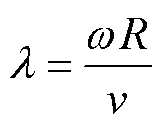（3）
式中，w 为风机机械转速。
联立式（1）～式（3），可得机械功率为
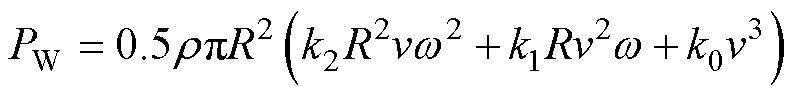（4）
由此可得机械转矩为
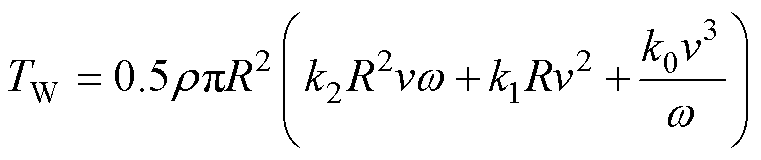（5）
PMSG电磁转矩Te与电磁功率Pe的关系为
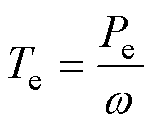（6）
永磁同步电机的运动方程为
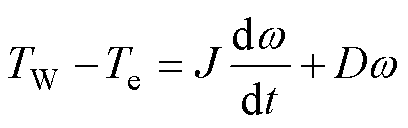（7）
式中，J为风力机和永磁同步电机的整体等效转动惯量；D为阻尼系数。
下面对风电机组从风速到转速、输出功率的传递函数进行推导。设风电机组的稳态运行点（Steady State Operating Point, SSOP）为（w0, v0, Pe0），采用小扰动分析法，对式（7）在（w0, v0, Pe0）处进行线性化处理并经Laplace变换，可得
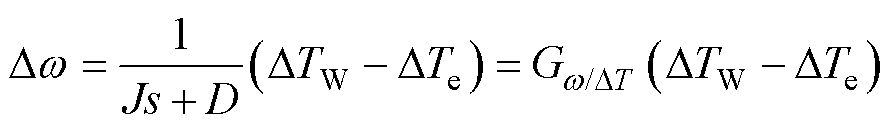（8）
式中，D为各量相对于稳态参考值的增量；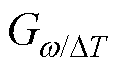
为合转矩到转速的传递函数。根据式（5）、式（6），分别对TW、Te在（w0, v0, Pe0）处进行全微分可得
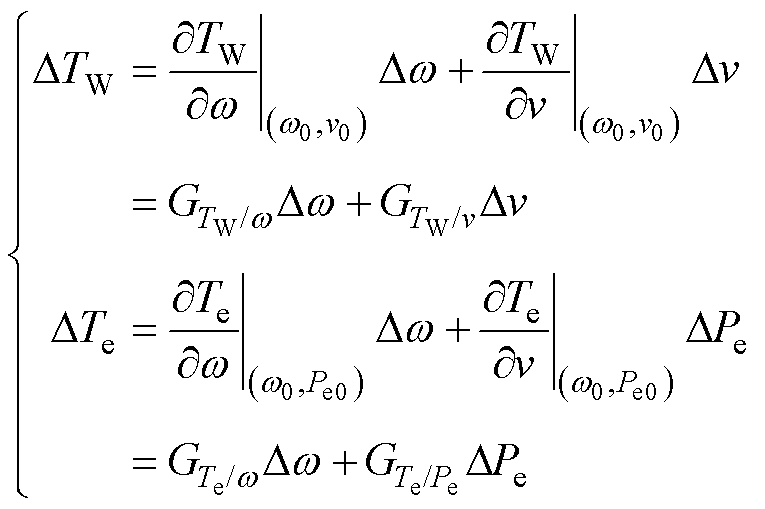（9）
式中，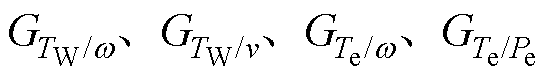
分别为转速到机械转矩、风速到机械转矩、转速到电磁转矩、电磁功率到电磁转矩的传递函数。
考虑到控制器的参数优化并非本文重点，因此假定风电机组的各个控制环节参数均为最优参数，变流器能够实时响应参考功率的变化[23]，即认为在MPPT策略下，机组电磁功率满足
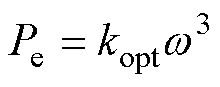（10）
式中，kopt为与风机自身参数相关的常数。
因此，在MPPT策略下，有
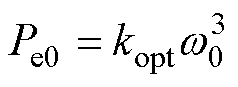（11）
对式（10）进行线性化处理，得到MPPT策略下转速到功率的传递函数关系为
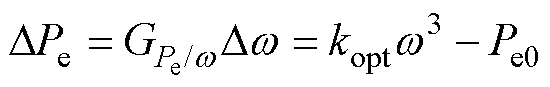（12）
式（8）、式（9）、式（12）共同组成MPPT策略下风电机组的传递函数模型，如图2所示。进一步联立可得到风速与转速、功率的传递函数关系为
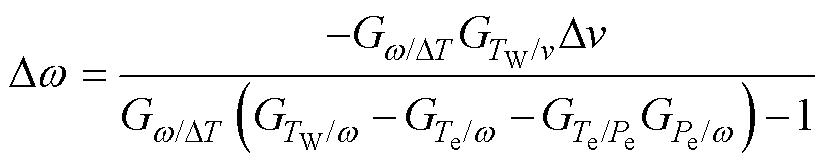（13）
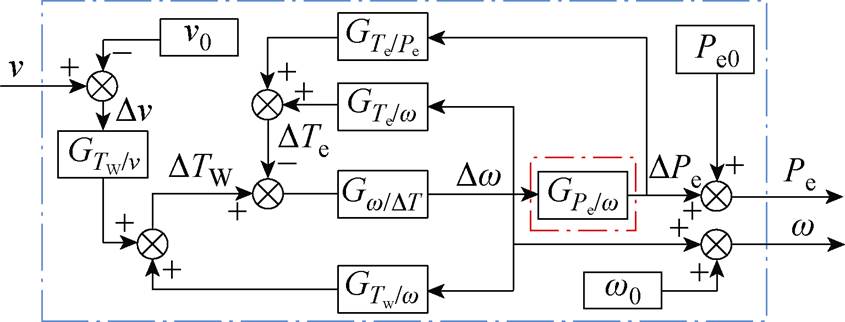
图2 风电机组传递函数模型
Fig.2 Transfer function modeling of wind turbines
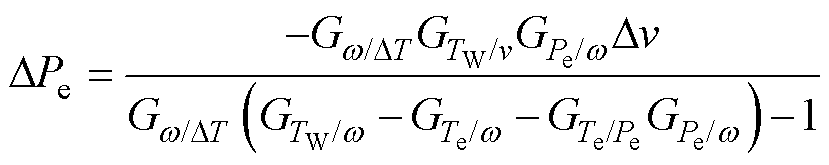（14）
1.1节给出了风电机组的传递函数模型，本节从该模型出发对风电机组的新型功率平滑指令进行设计，实现对输出功率平滑程度和波动均值大小的解耦调节。式（12）中，DPe为MPPT策略下的功率输出扰动量，该功率经过一阶LPF后得到平滑模式下的理想输出功率波动DPhope为
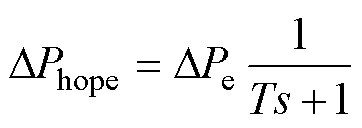（15）
式中，T为一阶LPF的时间常数。
通过改变Dw 至DPe的传递函数，能够在传递函数模型中实现式（15）的功率平滑要求[23]。其方法是在原传递函数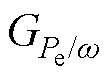
后增加一个二阶滤波环节GF(s)，从而使
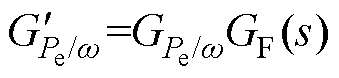，实现增加GF(s)后的输出
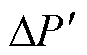恰好满足式（15），即
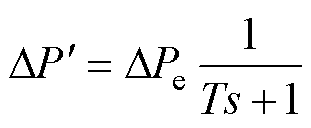（16）
引入GF(s)后，相同的风速扰动所引起的转速变化将与MPPT模式下有所不同。在式（13）中用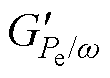
替代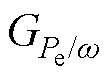，得到引入GF(s)后的转速波动变为
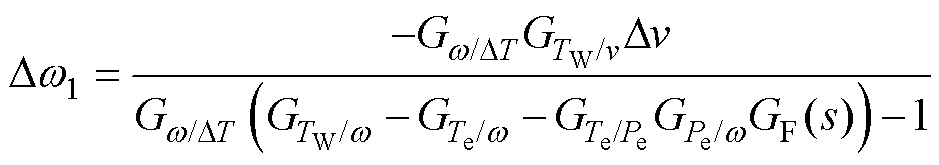（17）
在式（12）中用w1代替w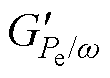，代替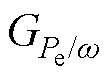，得到引入GF(s)的功率波动为
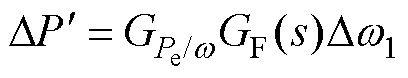（18）
联立式（14）、式（16）～式（18），化简可得
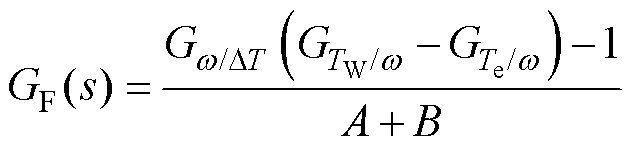（19）
其中
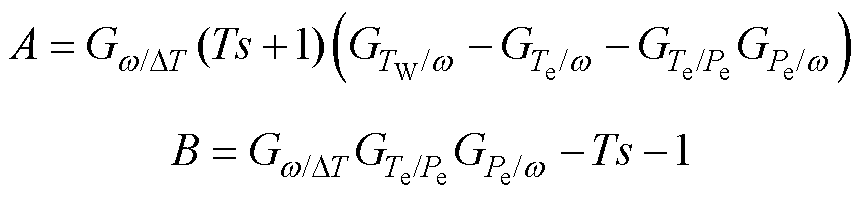
在传递函数模型中引入GF(s)能够实现对输出功率的平滑，但该模型中变量均为扰动量，实现的是对Pe关于w 的导函数的改变。对实际风电机组进行功率控制需要准确的平滑参考功率，即Pe与w 的具体数学关系。实现该方案的一种思路是直接在转速立方曲线后级联GF(s)，即Pref=koptw3GF(s)。值得注意的是，传递函数模型中的扰动量均是相对于稳态点（w0, v0, Pe0）而言的，对GF(s)表达式的推导前提是引入GF(s)前后的稳态运行点（w0, v0, Pe0）不发生改变。若直接采用Pref=koptw3GF(s)，会导致同样的稳态点（w0, v0）对应的功率稳态值发生改变，由Pe0变为Pe0GF(s)，二阶滤波环节GF(s)往往会导致整体功率水平下降，因此该方法实际上与式（14）～式（19）的推导矛盾。考虑到这一点，下面给出一种新型的功率指令设计方案。
将式（12）中的w 替换为w1，代入式（18），有
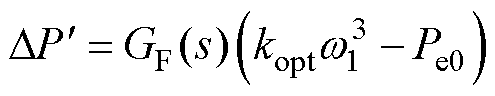（20）
将式（20）代入式（16），可得
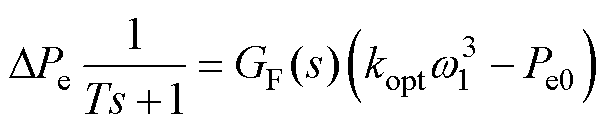（21）
平滑策略的目标是对式（10）给出的MPPT策略输出功率进行平滑，设理想输出功率为
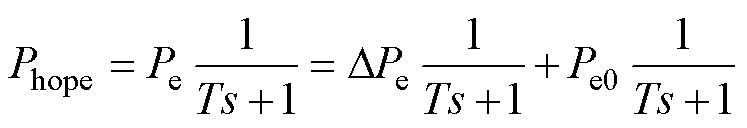（22）
将式（21）代入式（22），可得含实时转速项的平滑功率指令为
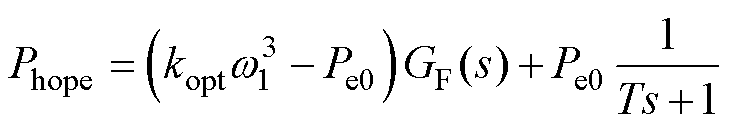（23）
采用该平滑指令后，（w0, v0）对应的功率稳态值为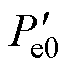
，将w1=w0, v=v0代入式（23），得到
（24）
式中，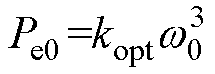
为常数，当机组处于长时间稳态运行时，由一阶传递函数的特性可知，存在
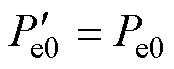，可认为机组的稳态运行点仍然为（w0, v0, Pe0），未发生变化，因此该平滑指令不与GF(s)的推导过程矛盾。
式（23）所示平滑功率指令可看作两部分，第一部分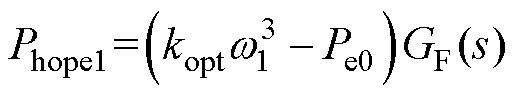
为与转速相关的波动量，表征了参考功率的平滑程度，可通过调节GF(s)对应的滤波参数
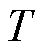进行控制。第二部分Phope2= Pe0/(Ts+1)近似为一个常量，表征了参考功率的整体取值水平。引入功率等级系数K（0＜K＜1），令Phope2=KPe0/(Ts+1)，通过调整K以满足不同情况下风电机组的减载需求，最终采用的功率平滑指令为
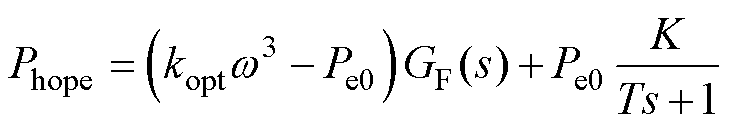（25）
上述参考功率指令将输出功率分解成表征功率平滑度的波动量和表征功率整体大小的波动均值，并实现对二者的解耦调节，同时，相较于直接对最大风功率进行滤波作为功率参考值，该功率指令由于含有实时转速反馈，抗扰动能力更强。
为使式（25）中参考功率的平滑效果足够理想，满足式（22）的理想条件，GF(s)的取值要足够准确。式（19）表明GF(s)的取值与传递函数模型的参数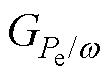
、
、
、
、
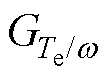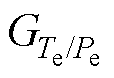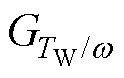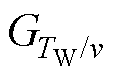有关，上述参数均由稳态运行点（w0, v0, Pe0）决定，因此稳态运行点的合理选取能够优化参考功率的平滑效果。如何选取在已有的研究中提及较少，本文对此展开了研究。
小扰动线性化建模中通常采用一段时间内风速的均值（Averages, AVG）作为v0，v0风速下机组进入稳态运行后的各个变量值w、Pe作为w0、Pe0，以此来进行传递函数建模，为方便描述，称上述方法为AVG-SSOP方法。然而实际运行过程中难以对一段时间内的风速变化准确预知，v0难以准确取值，从而无法获得合理的稳态运行点。因此，本文提出了一种基于滑动均值滤波（Moving Average Filtering, MAF）算法的风电机组稳态运行点选取方法，以下简称MAF-SSOP方法。
设实时风速为v(t)，对v(t)进行滑动均值滤波，其滤波输出作为t时刻风电机组的风速稳态运行点，即
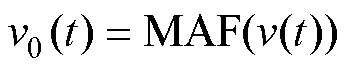（26）
当风电机组工作在稳态运行点时，转子保持匀速，其转子吸收功率为0，忽略摩擦等损耗，可认为捕获风功率与输出电磁功率相等，即
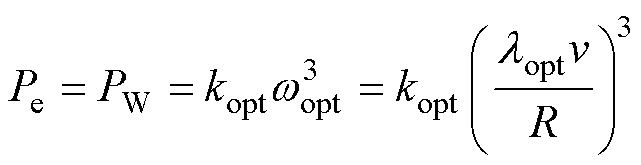（27）
式中，v为机组的稳态运行风速；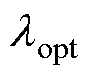
为最佳叶尖速比；wopt为风速对应的稳态运行转速。令v=v0(t)，可得v0(t)下处于MPPT策略下机组的w0、Pe0分别为
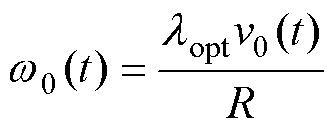（28）
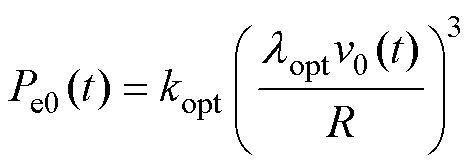（29）
为验证MAF-SSOP方法的有效性，本文以6 MW永磁直驱风电机组为研究对象，在Matlab/ Simulink中分别搭建风电机组详细模型和传递函数等效模型，机组仿真参数见表1，仿真所用的风速曲线如图3所示，平均风速va=6.456 m/s。对采用以下四种参数取值方法的传递函数模型进行仿真对比，并与风电机组详细模型的MPPT功率输出进行比较。
表1 永磁直驱风电机组仿真参数
Tab.1 Simulation parameters of the permanent magnet direct drive wind turbine
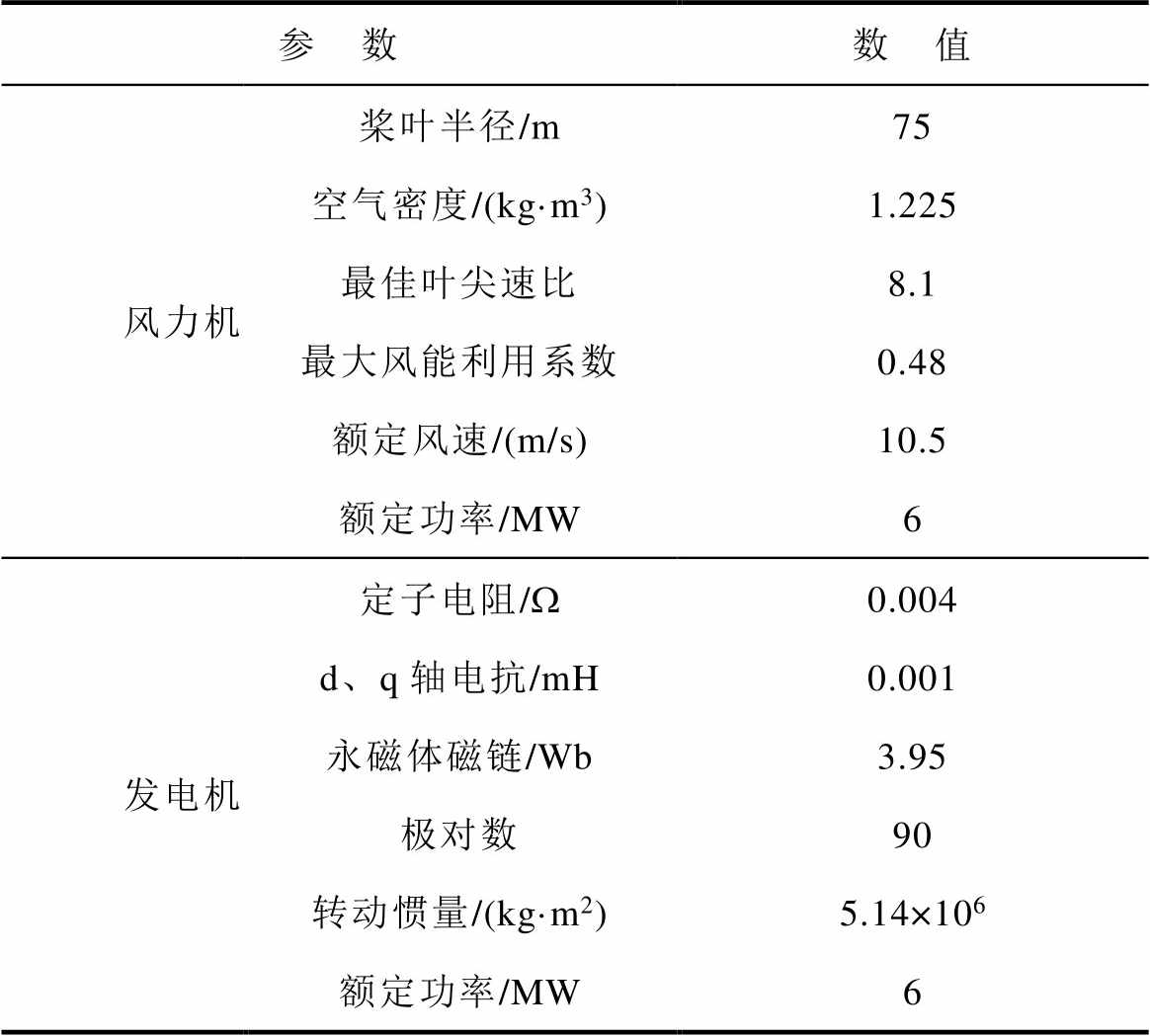
参 数数 值 风力机桨叶半径/m75 空气密度/(kg·m3)1.225 最佳叶尖速比8.1 最大风能利用系数0.48 额定风速/(m/s)10.5 额定功率/MW6 发电机定子电阻/W0.004 d、q轴电抗/mH0.001 永磁体磁链/Wb3.95 极对数90 转动惯量/(kg·m2)5.14×106 额定功率/MW6
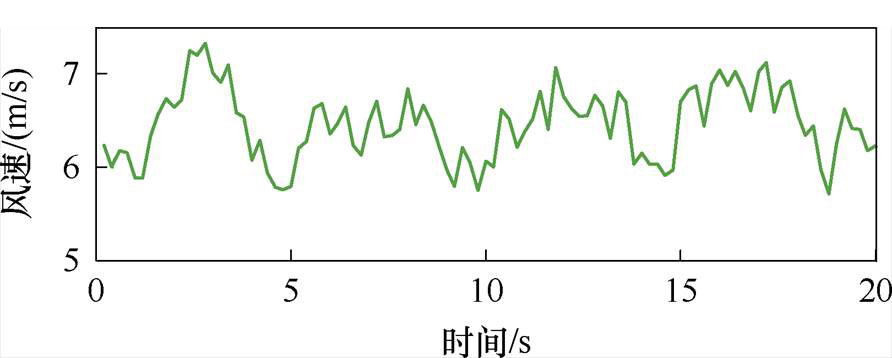
图3 验证MPPT传递函数模型所用风速
Fig.3 Wind speed used to validate the MPPT transfer function model
（1）AVG-SSOP方法，v0=va。
（2）AVG-SSOP方法，v0=1.2va，即v0取值偏大。
（3）AVG-SSOP方法，v0=0.8va，即v0取值偏小。
（4）MAF-SSOP方法，v0=MAF(v(t))。
仿真结果如图4所示，采用MAF-SSOP方法、AVG-SSOP方法（v0=va）的传递函数模型和风电机组详细模型的输出功率波形几乎重合，验证了MAF- SSOP方法的有效性。此外，图4显示采用AVG- SSOP方法时，若v0取值偏大或偏小，均会大大降低传递函数模型的准确性。
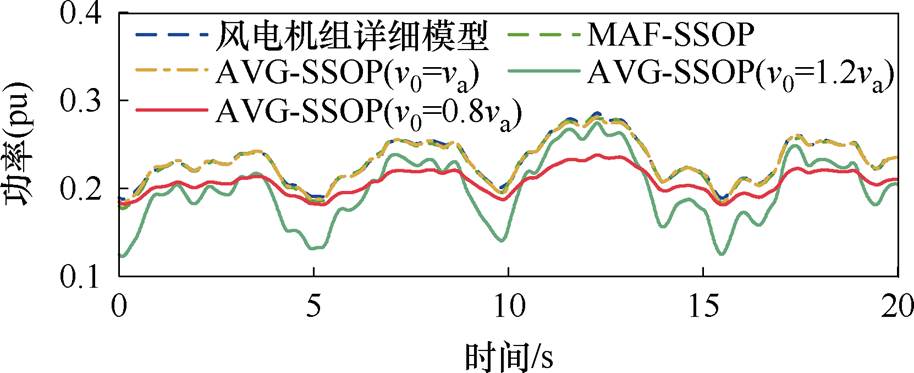
图4 MPPT传递函数模型仿真功率
Fig.4 Output power of the MPPT transfer function model
当转子减速释放动能参与功率平滑时，存在失速失稳的风险。风机的失稳是由转速过低引起的，相较于对参考电磁功率进行处理来防止失稳，对转速进行直接控制要更直观和可靠，因此本文采用转速闭环控制的方法间接实现对功率指令的跟踪。
风机运行过程中转子变速吸收的功率为
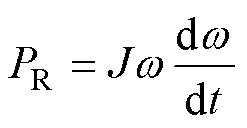（30）
根据功率守恒，转子吸收功率PR、风力机捕获机械功率PW以电磁功率Pe满足
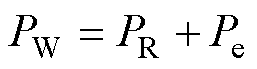（31）
因此有
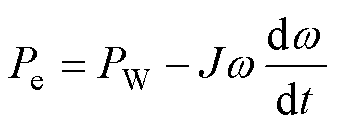（32）
式中，PW、Pe均可看作转速w 的函数，因此控制转速w 便能实现对电磁功率Pe的准确控制。现控制目标是使其跟踪参考功率Pref，即Pe=Pref，设t时刻转子转速为w1，经过Dt后t+Dt时刻的转速为w2，由能量守恒有
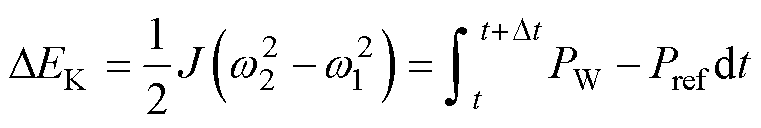（33）
解得
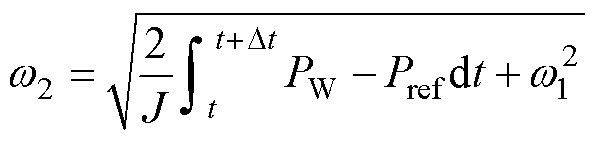（34）
因此，欲使电磁功率跟踪Pref，转速必须满足式（34）的关系，由此可得风机运行过程中的参考转速取值为
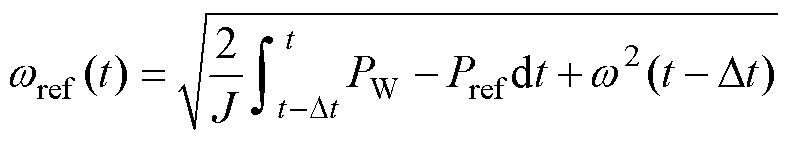（35）
式中，参数Dt为积分周期。值得注意的是，按照上述推导流程所得到的参考转速仅仅是Pe=Pref的必要条件，而非充分条件。在风机运行过程中，式（32）始终成立，对其在[t-Dt, t]进行积分并化简，得到
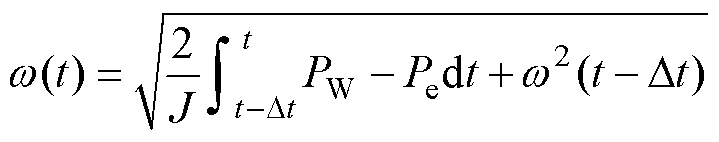（36）
式（36）在风机任意运行策略下均保持成立。当转速w 跟踪式（35）给出的参考转速，即w(t)=wref(t)时，联立式（35）、式（36）得到
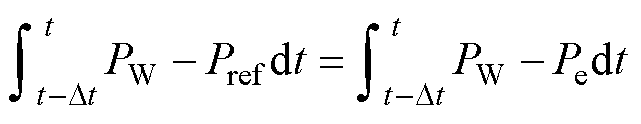（37）
即
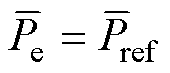（38）
式中，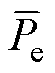
为电磁功率在Dt内的均值；
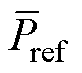为参考功率均值。
可见，让转速跟踪wref仅能实现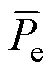
对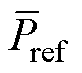的跟踪。仅当Dt很小时，才能近似得到Pe=Pref，因此，Dt取值不宜过大。
由上述分析可知，通过跟踪式（35）给定的参考转速实现对功率Pref的跟踪，Dt取值应尽可能小，其原因在于转速表达式中含有积分项。但该推导建立在w 与wref在数值上完全等价的基础上。考虑到实际机组的转速-电流双闭环控制系统的性能和机组本身的惯量影响，实际转速无法在数值上完全准确跟踪参考转速，二者之间存在一定偏差，设定当满足式（39）时，认为电机已成功跟踪参考转速。
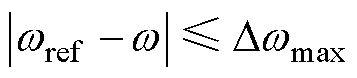（39）
式中，Dwmax为由于转速环、电流环的特性导致的转速跟踪过程中实时转速w 和实时参考转速wref的最大差值。
对参考转速wref的数学表达式（35）进行分析，在大容量风电系统中，机组转动惯量J可达百万级，因此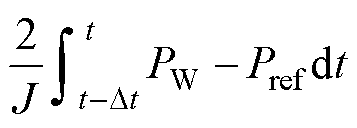
项相较于w2(t-Dt)项是很小的，Dt的取值大小实际上反映了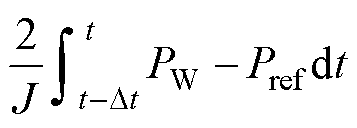项相对于w2(t-Dt)项的数学尺度。当Dt过小时，若Pe≠Pref，即电磁功率没有成功跟踪参考功率，由于
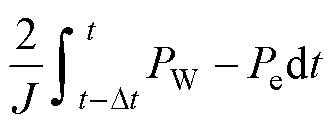项在整个w 构成（即式（36））中占比极小，会导致w 与wref在数值上差异很小，甚至小于转速闭环控制的固有偏差Dwmax，因此依然存在|wref-w|≤Dwmax，即工程上仍然认为w=wref。由上述分析可知，尽管转速能成功跟踪参考值wref，但电磁功率却无法跟踪Pref，因此，Dt的取值不宜过小，存在下限值。
从2.1节的分析可知，Dt的取值有一定的范围，但当前已有研究中对此提及甚少，往往通过经验对其进行取值。下面根据2.1节的分析提出一种可行的Dt整定方案。对风电机组转速控制的最终目标是精准响应参考功率，定义功率跟踪最大允许偏差DPmax，当机组功率Pe满足|Pe-Pref|≤DPmax时认为成功对参考功率实现跟踪，因此，本文所希望的通过控制转速实现功率精准控制的目标能够简化成以下数学命题始终成立。
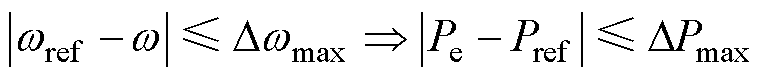（40）
其逆否命题为
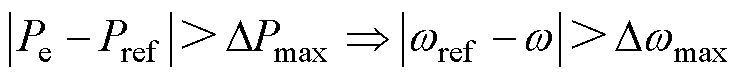（41）
式（40）和式（41）等价，因此，只要使得式（41）成立，便能实现对功率的精准控制。令Pe= Pref+DPmax，则由式（40）、式（41）可得
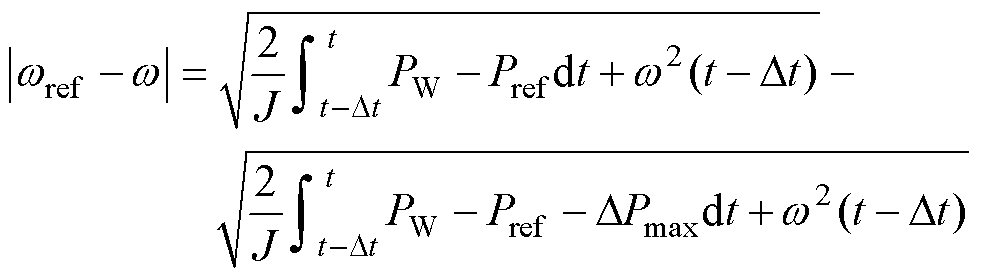（42）
对式（42），由拉格朗日中值定理，可得
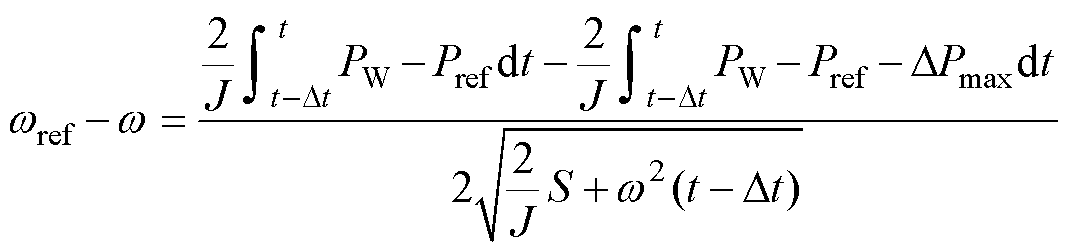（43）
式中，S为中间变量，满足
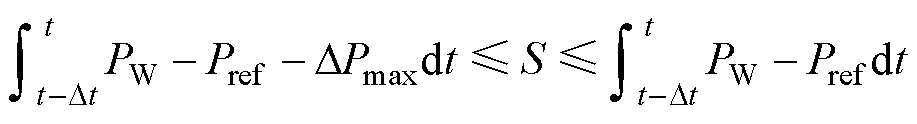（44）
结合式（35）、式（36）、式（44），可知
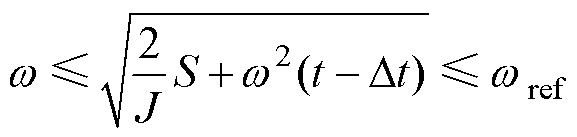（45）
令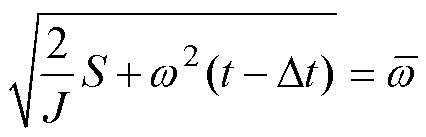
（
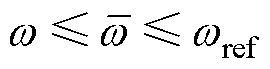），代入式（43）并进一步化简可得
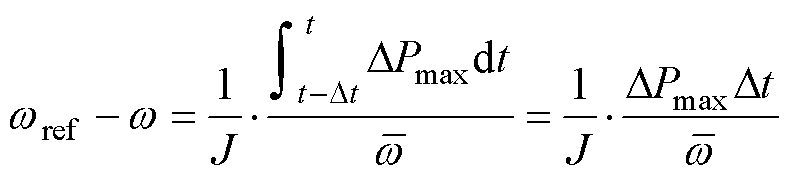（46）
结合式（41），有
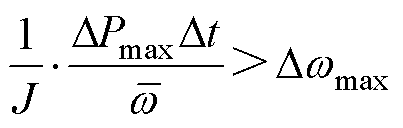（47）
因此，Dt的取值下限为
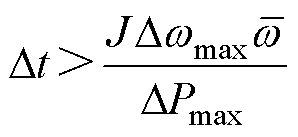（48）
式（48）揭示出为使机组跟踪参考功率，由于转速跟踪偏差的影响，Dt取值存在下限。在MPPT策略下参考功率Pref=koptw3，定义功率跟踪偏差比DP=|Pref-Pe|/Pref，DP越小说明功率跟踪效果越好，设DP最大值为DPmax，则有
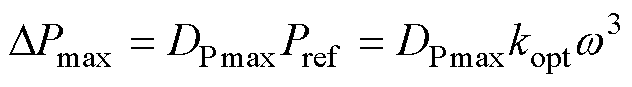（49）
同样地，定义转速跟踪偏差比Dw=|wref-w|/wref，Dw越小说明转速跟踪能力越强，设Dw最大值为Dwmax，有
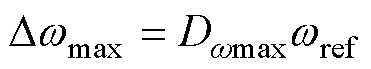（50）
联立式（48）～式（50），得到MPPT策略下Dt的取值下限为
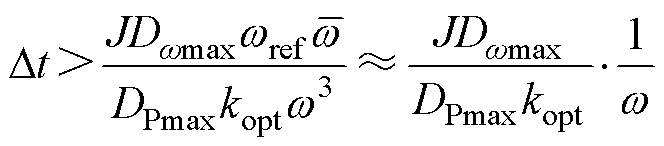（51）
在风机运行过程中Dt为固定参数值，为使式（51）始终成立，令式中w 为转速运行过程中的最小值wmin，因此，Dt的整定值为
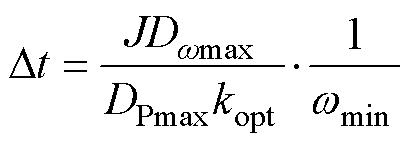（52）
尽管对式（52）中整定值的推导是在MPPT策略下进行，但由2.1节分析可知，Dt的取值实际上决定了式（35）中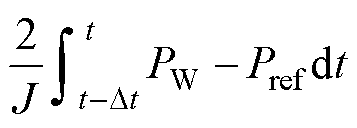项对整体w 值的影响程度，在Dt的时间尺度下可近似认为PW-Pref是常数，因此同样的整定值在采用其他参考功率指令时也可适用。
在风机运行过程中，通过转子变速能够响应式（25）得到的平滑功率指令，然而转子大范围变速的过程中存在低速失稳的风险。因此，本文采用以下原则来确定风机运行过程中的参考转速的实际取值。
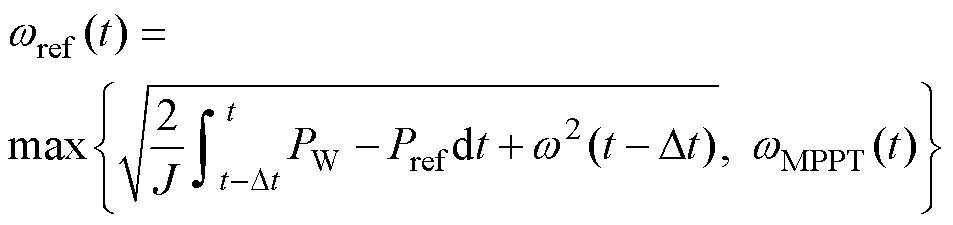（53）
式中，wMPPT(t)为MPPT策略下风电机组的实时转速，可由实时风速v(t)通过式（13）得到，通过将转速下限设置成wMPPT(t)，能够在机组释放转子动能补偿功率缺额导致转速降低后防止机组失稳，同时让机组平稳地过渡到MPPT模式实现最大风能跟踪。若后续风速增大，当MPPT输出大于平滑功率指令时，机组加速，由MPPT模式恢复至平滑模式。
本节提出了响应参考功率的转速闭环控制策略，并对参考转速中的参数Dt进行优化整定，使得通过转速闭环控制间接实现对参考功率的精准跟踪，实现了与功率闭环控制相同的效果，且由于采用转速闭环，可方便设定转速下限，防止机组失速失稳。
综上所述，本文提出的计及功率指令和积分周期优化的新型风电机组转子动能功率平滑控制策略下的永磁直驱风机机侧控制框图如图5所示，其中，图5a给出了本控制策略所采用的基于空间矢量脉宽调制（Space Vector Pulse Width Modulation, SVPWM）的转速闭环矢量控制结构。图中，ids、iqs和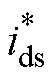
、
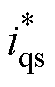分别为两相旋转坐标系下d轴和q轴的实际电流与参考电流值；
、
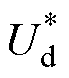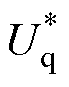分别为两相旋转坐标系下的d轴和q轴参考电压；
、
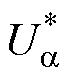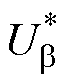分别为两相静止坐标系下的a 轴和b 轴参考电压；ia、ib、ic为发电机三相电流；q 为发电机转子电角度。图5b为本文所提出的功率平滑控制策略的功率指令和参考转速的计算流程，平滑功率指令获取、参考转速计算及Dt整定方法已在1.1、1.2、2.1和2.2节中进行了详细表述。
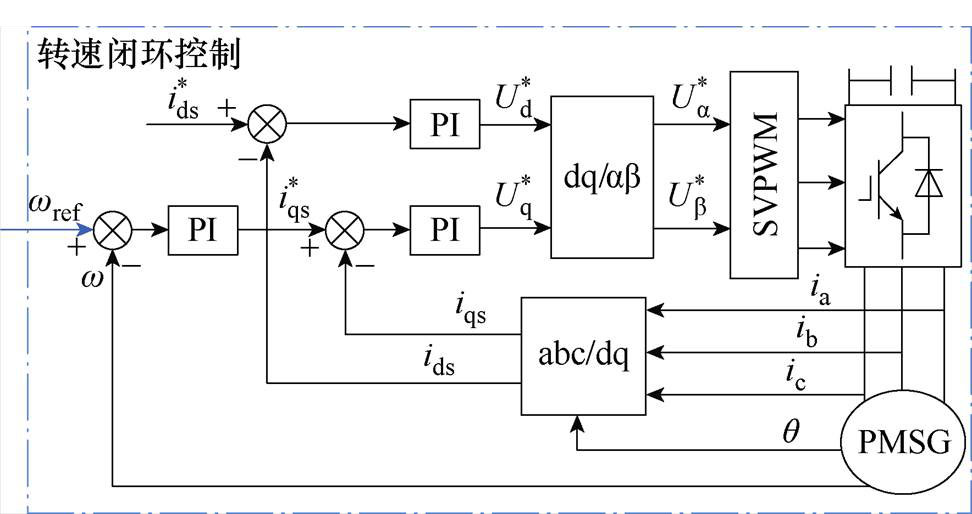
（a）PMSG机侧控制结构
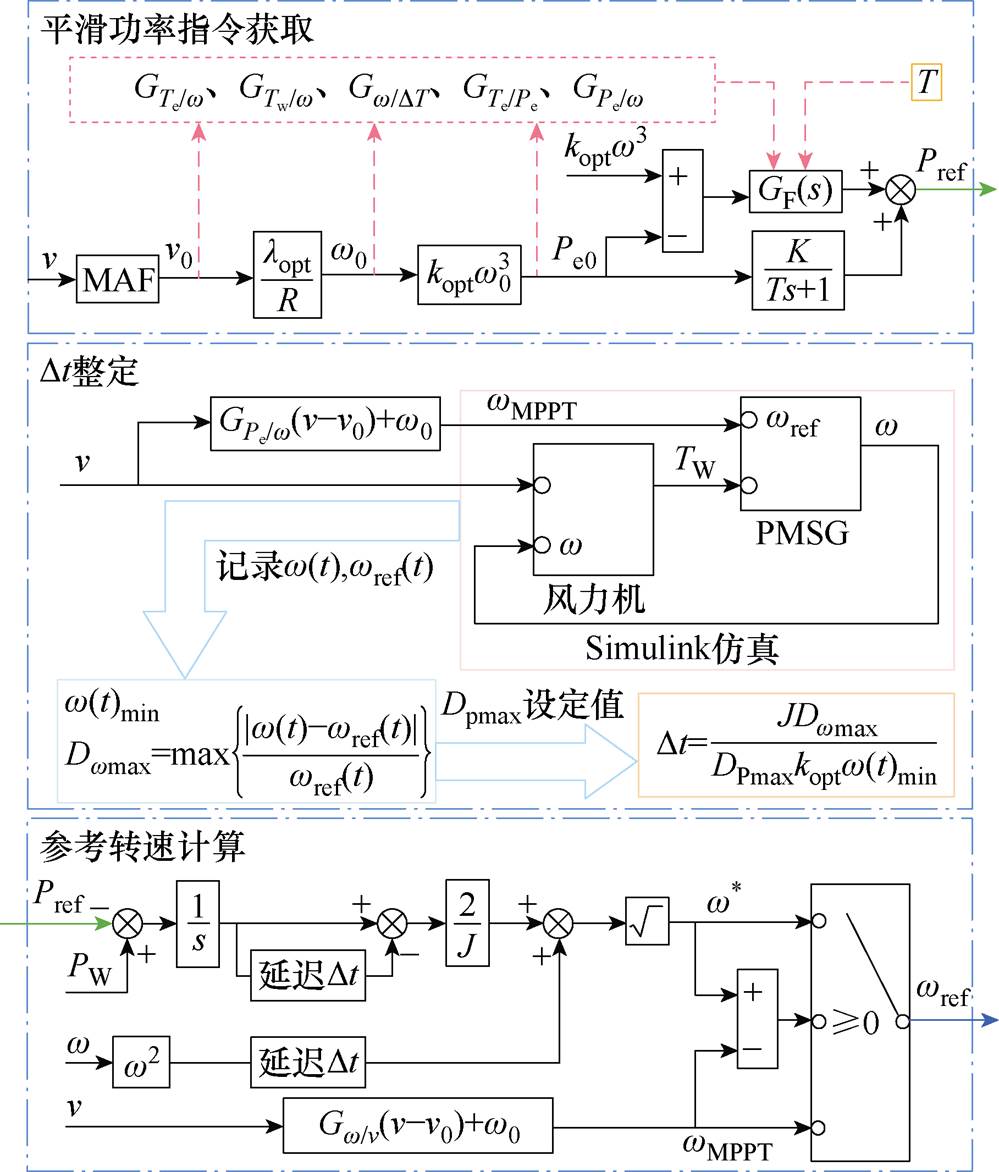
（b）平滑参考功率指令和参考转速计算
图5 基于改进功率平滑控制的永磁直驱风机控制框图
Fig.5 Control strategy for the permanent magnet direct drive wind generator based on the improved power smoothing control
本文在第2节中给出了精准响应参考功率的转速控制策略以及相应积分周期Dt的整定原则，下面以6 MW永磁直驱风电机组为例验证该转速控制策略的有效性。仿真参数见表1，选取风速为图6所示的正弦形风速进行仿真，功率跟踪目标为MPPT功率。将wMPPT设置为参考转速，对机组进行转速跟踪仿真，得到运行过程中的转速跟踪偏差比Dw和转速w 的波形如图7所示。
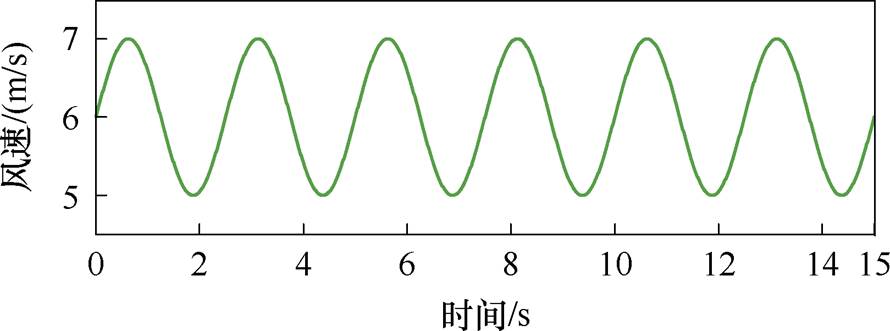
图6 15 s正弦风速
Fig.6 15 s sinusoidal wind speed
由转速跟踪仿真结果可知，MPPT策略下wmin= 0.586 rad/s，Dwmax=1.76×10-3，分别将允许最大功率跟踪偏差比DPmax设定为不同值，计算得到不同的Dt取值，此外，增设一组Dt=0.000 01 s，即Dt极端小的仿真作为对比。取式（35）中Pref=koptw3，并进行仿真，相应的输出功率波形如图8所示，记录机组的实际DPmax，见表2。
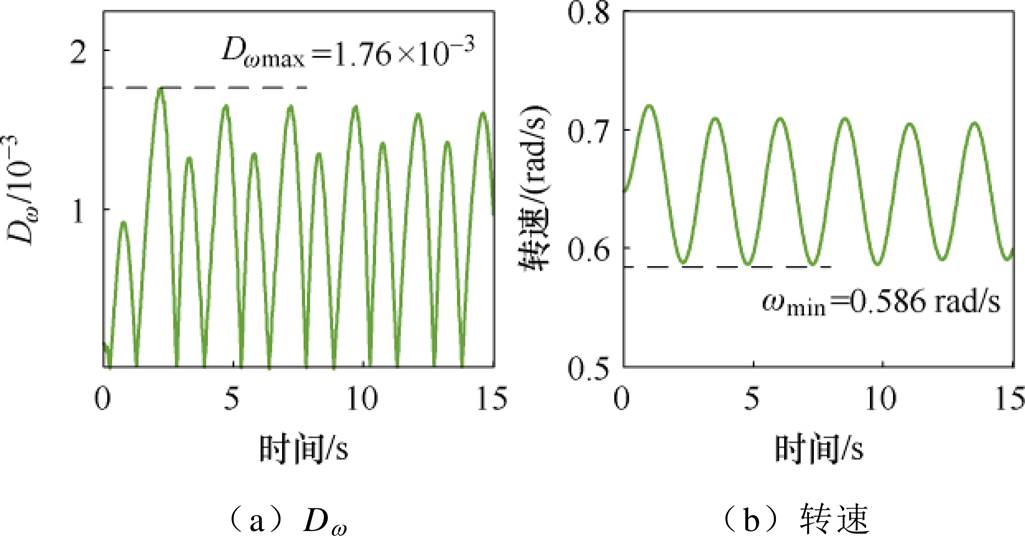
图7 MPPT策略下的转速跟踪偏差比Dw和转速w
Fig.7 Speed tracking deviation ratio Dw and speed wunder MPPT control strategy
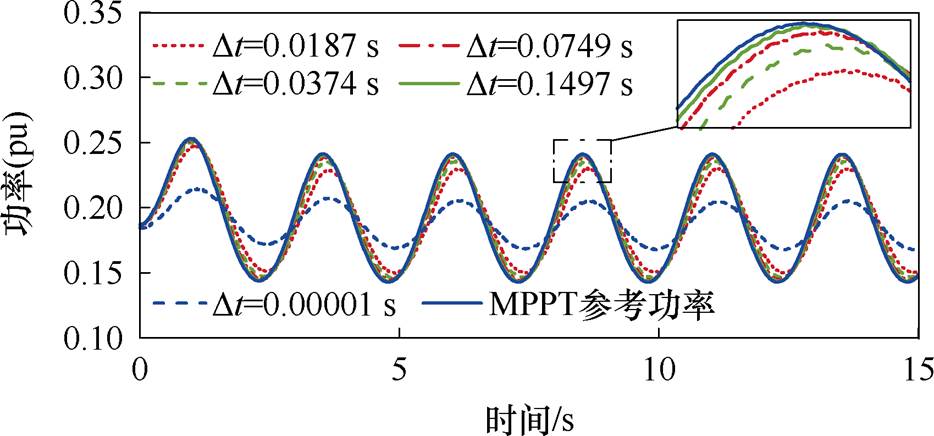
图8 不同Dt取值下的输出功率对比
Fig.8 Comparison of output power under different Dt
表2 Dt整定方法有效性仿真验证结果
Tab.2 Simulation validation results of the effectiveness of the Dt -setting method
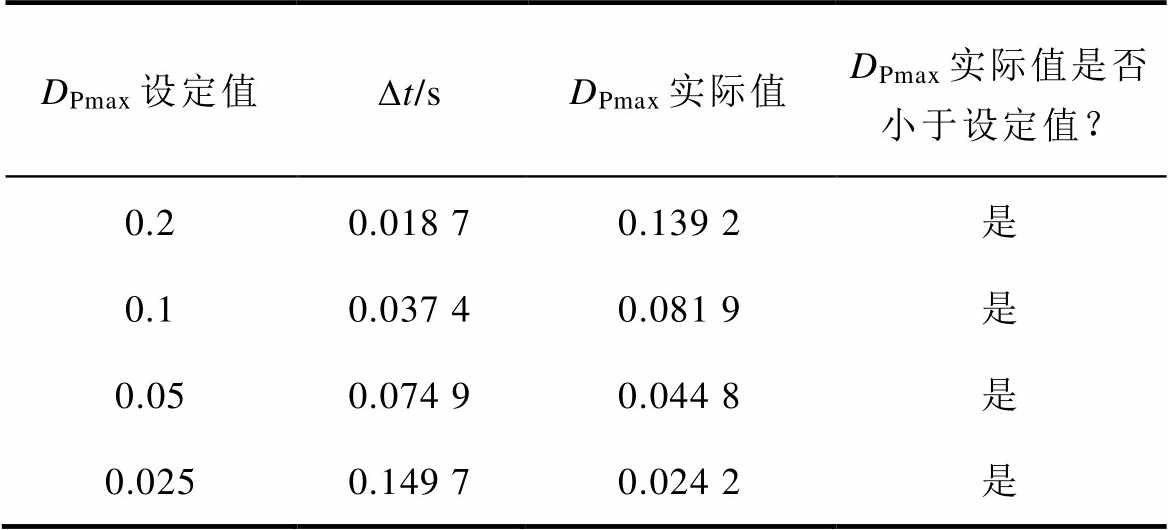
DPmax设定值Dt/sDPmax实际值DPmax实际值是否小于设定值？ 0.20.018 70.139 2是 0.10.037 40.081 9是 0.050.074 90.044 8是 0.0250.149 70.024 2是
从图8可看出，随着Dt的取值的减小，风机对MPPT参考功率的跟踪能力逐渐变差。当Dt极端小时，机组输出功率为图8中蓝色虚线，跟踪效果极差，事实上已脱离MPPT运行模式。其他四组Dt取值下的输出功率尽管存在跟踪效果的差异，但在正弦波形的平滑处差异较小，可认为处于MPPT模式。表2表明，实际DPmax均小于设定值，通过转速闭环控制实现了对参考功率在允许偏差范围内的跟踪，可见2.2节所提出的Dt整定原则是有效的。
风速波形如图9所示。在图9所示的60 s风速下进行仿真。为对功率平滑策略效果进行量化分析，本文采用平滑策略下输出电磁功率的标准差
来衡量其平滑度，越小表明输出功率越平滑。定义相对均值
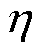来衡量平滑策略下相对MPPT模式的输出效率，有
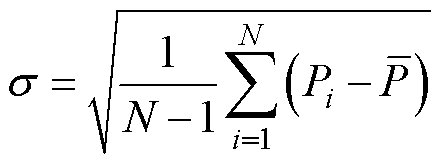（54）
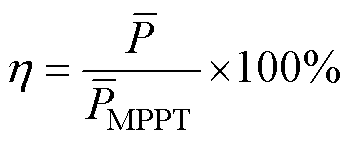（55）
式中，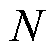
为功率曲线采样点个数；
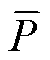为平滑策略下输出功率的均值；
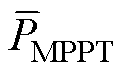为MPPT策略下输出功率的均值。
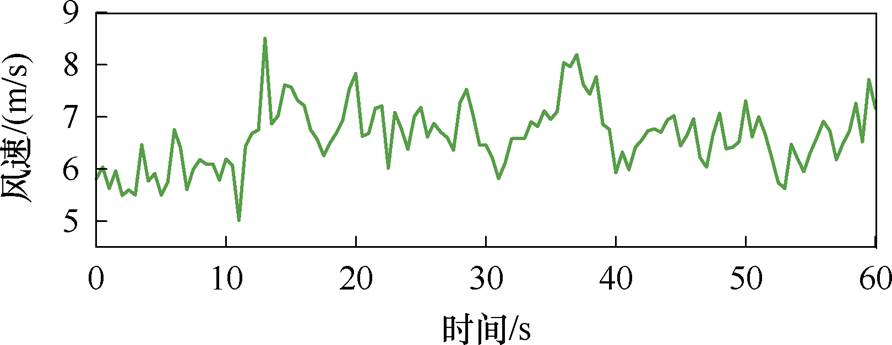
图9 风速波形
Fig.9 wind speed waveform
定义相对MPPT模式的平滑度提高程度sP为
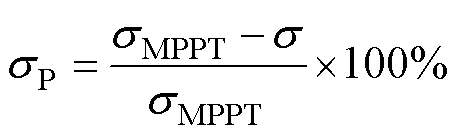（56）
式中，sMPPT为MPPT输出功率的标准差。由于本文所提出的功率平滑策略在s级的时间尺度上对风电机组输出功率进行平滑，因此不妨将计算平滑度的采样时间设置为1 s，即
。
为支撑本文中所述功率平滑策略的有效性，将本文所提平滑策略与文献[16]中的FOF方法、文献[19]中的SOF方法进行比较，仿真结果如图10所示，相应的输出功率量化指标见表3。可见本文所提出的平滑策略在全风速段的整体平滑效果更加优异，且造成的功率损失更少。
进一步对本文所提策略的功率平滑能力进行验证，分别取不同的滤波参数T计算GF(s)并进行仿真，输出功率和转速波形如图11所示，相应的输出功率量化指标见表4。
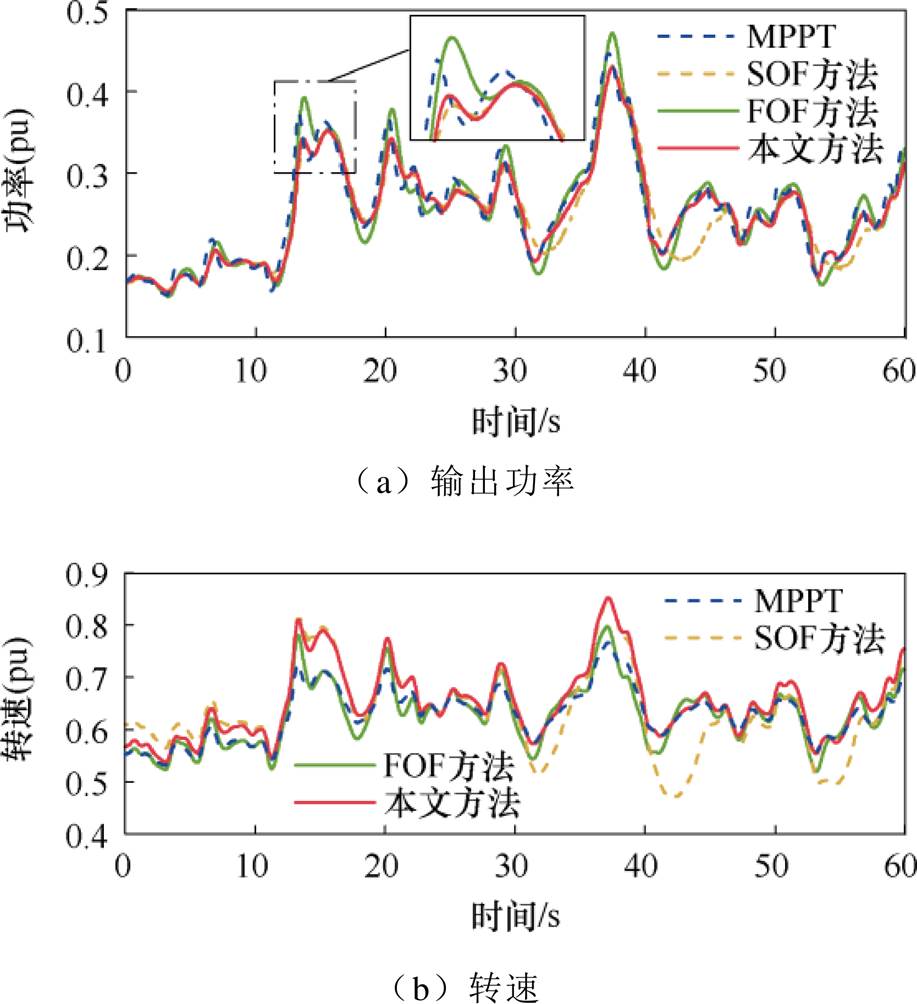
图10 功率平滑能力对比
Fig.10 Comparison of power smoothing capabilities
表3 不同平滑策略下机组输出功率统计数据
Tab.3 Statistical data of unit output power under different smoothing strategies
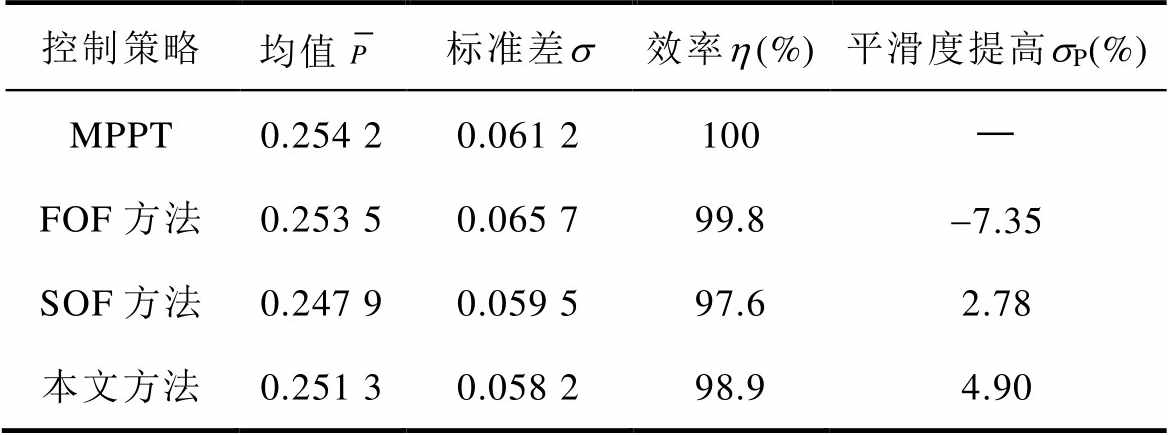
控制策略均值标准差s效率h(%)平滑度提高sP(%) MPPT0.254 20.061 2100— FOF方法0.253 50.065 799.8-7.35 SOF方法0.247 90.059 597.62.78 本文方法0.251 30.058 298.94.90
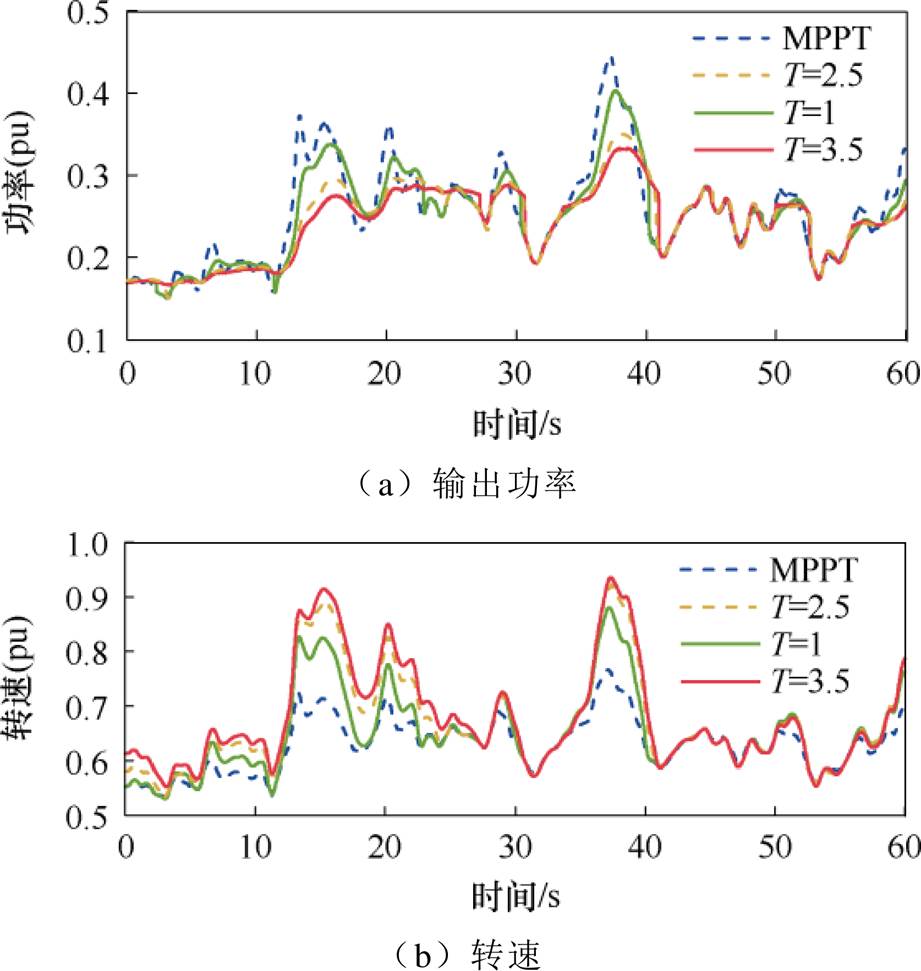
图11 不同T值下的功率平滑效果（K=1）
Fig.11 Power smoothing effect at different values of T (K=1)
表4 不同T值下机组输出功率统计数据（K=1）
Tab.4 Statistical data of unit output power at different T (K=1)
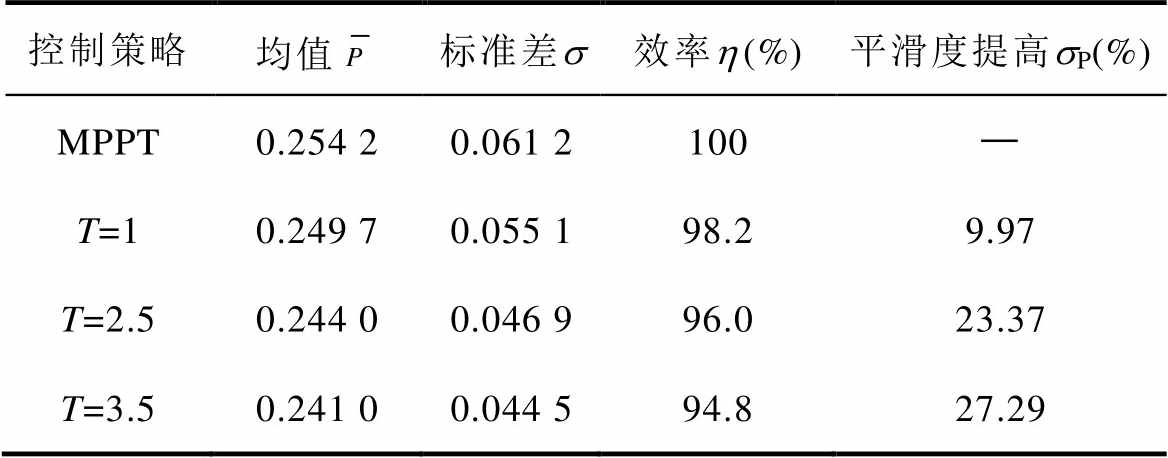
控制策略均值标准差s效率h(%)平滑度提高sP(%) MPPT0.254 20.061 2100— T=10.249 70.055 198.29.97 T=2.50.244 00.046 996.023.37 T=3.50.241 00.044 594.827.29
从图11、表4可以看出，本文所提出的基于转速闭环控制的功率平滑策略能够较大程度地提高输出功率的平滑程度，同时保持一定的风能捕获效率。在第30、40 s附近存在电磁功率向MPPT输出功率跌落，这是由于转速持续减小进入MPPT转速引起的。随后由于风速逐渐增大，当MPPT输出功率增大到超过平滑指令时，转子加速，脱离MPPT模式，继续响应功率平滑指令。尽管存在功率跌落的现象，但转速限制策略有效防止了机组失稳，利于风机长时间稳定运行。
除滤波参数T外，式（25）中功率等级系数K也影响整体的功率平滑效果。以T=2.5为例，对不同K取值下的机组输出功率进行对比，仿真结果如图12所示，统计数据见表5。
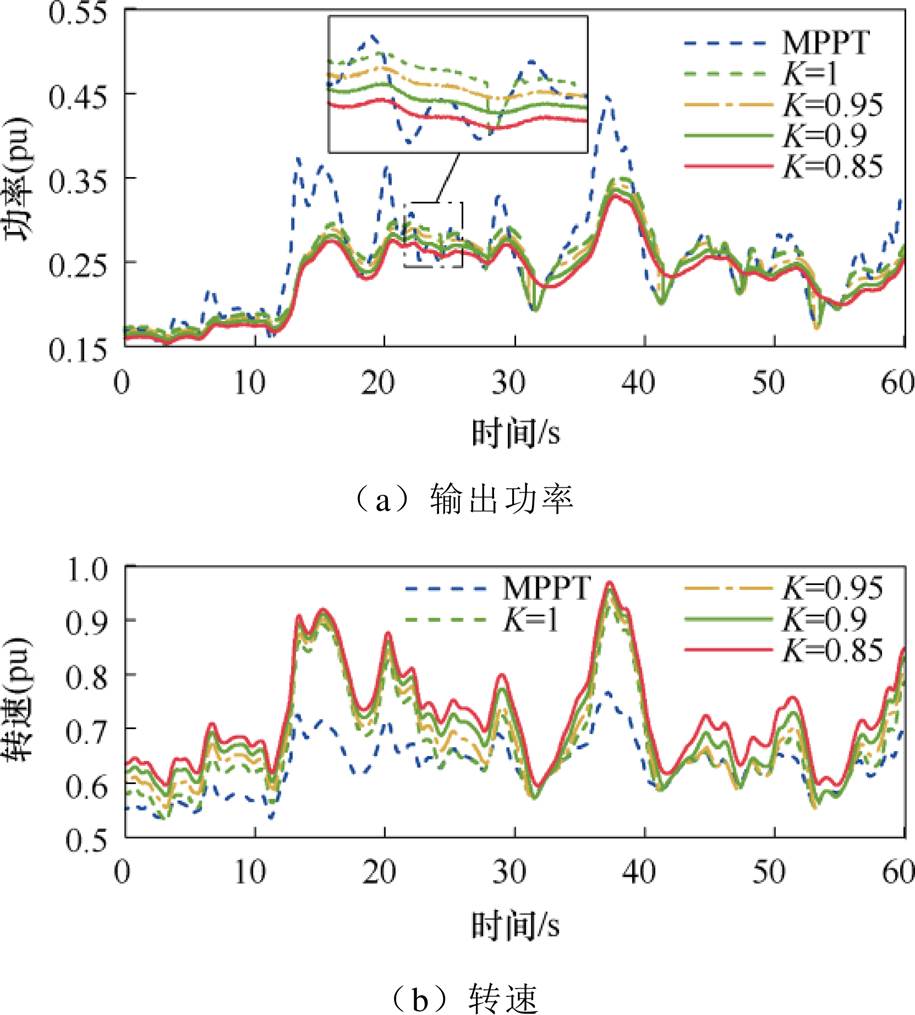
图12 不同K值下的功率平滑效果（T=2.5）
Fig.12 Power smoothing effect at different values of K (T=2.5)
表5 不同K值下机组输出功率统计数据（T=2.5）
Tab.5 Statistical data of unit output power at different K (T=2.5)
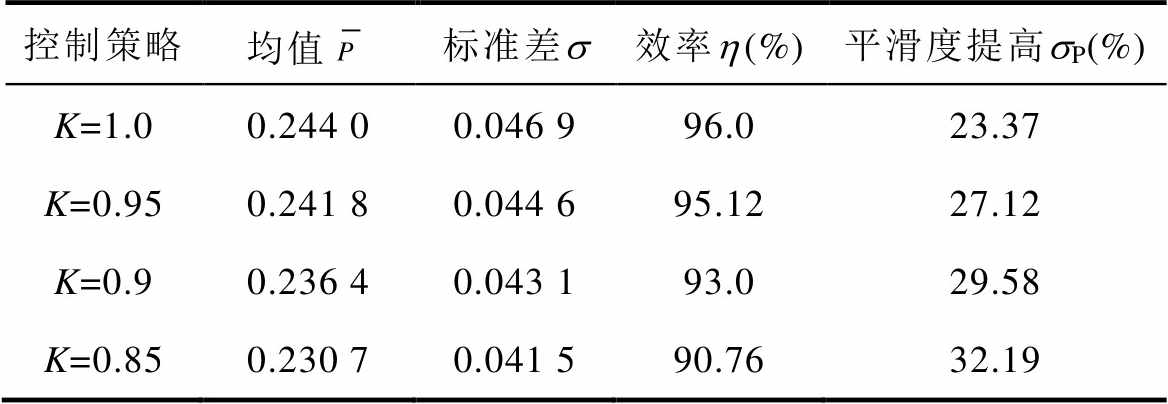
控制策略均值标准差s效率h(%)平滑度提高sP(%) K=1.00.244 00.046 996.023.37 K=0.950.241 80.044 695.1227.12 K=0.90.236 40.043 193.029.58 K=0.850.230 70.041 590.7632.19
仿真结果表明，随着K取值的减小，整体参考功率水平下降，风机转速整体运行在更高的区间，越过转速下限而发生功率模式切换的概率越小，平滑效果越优异。T=2.5的条件下，当K=0.85时，机组始终运行在平滑模式，平滑效果显著。此时平滑度较MPPT模式提高了32.19%，输出效率仅降至MPPT模式的90.76%，该结果在以平滑为主要目标时是可以接受的。实际工况下应结合具体的要求对K进行取值，当功率平滑度为首要目标时，使K尽可能小，实现最大限度的平滑；当需要综合考虑机组效率和平滑度时，应灵活选取K，使其在具有一定平滑功能的基础上拥有足够的输出效率。
为了验证所提控制策略在实际工程应用的可行性，搭建了小功率等级的永磁直驱风电系统模拟实验平台，该实验平台基于RTU-BOX204控制器构建，如图13所示。实验参数见表6。
图13 永磁直驱风电机组实验平台
Fig.13 Permanent magnet direct-drive wind power system experimental platform
表6 永磁直驱风电机组实验参数
Tab.6 Experimental parameters of permanent magnet direct-drive wind power system
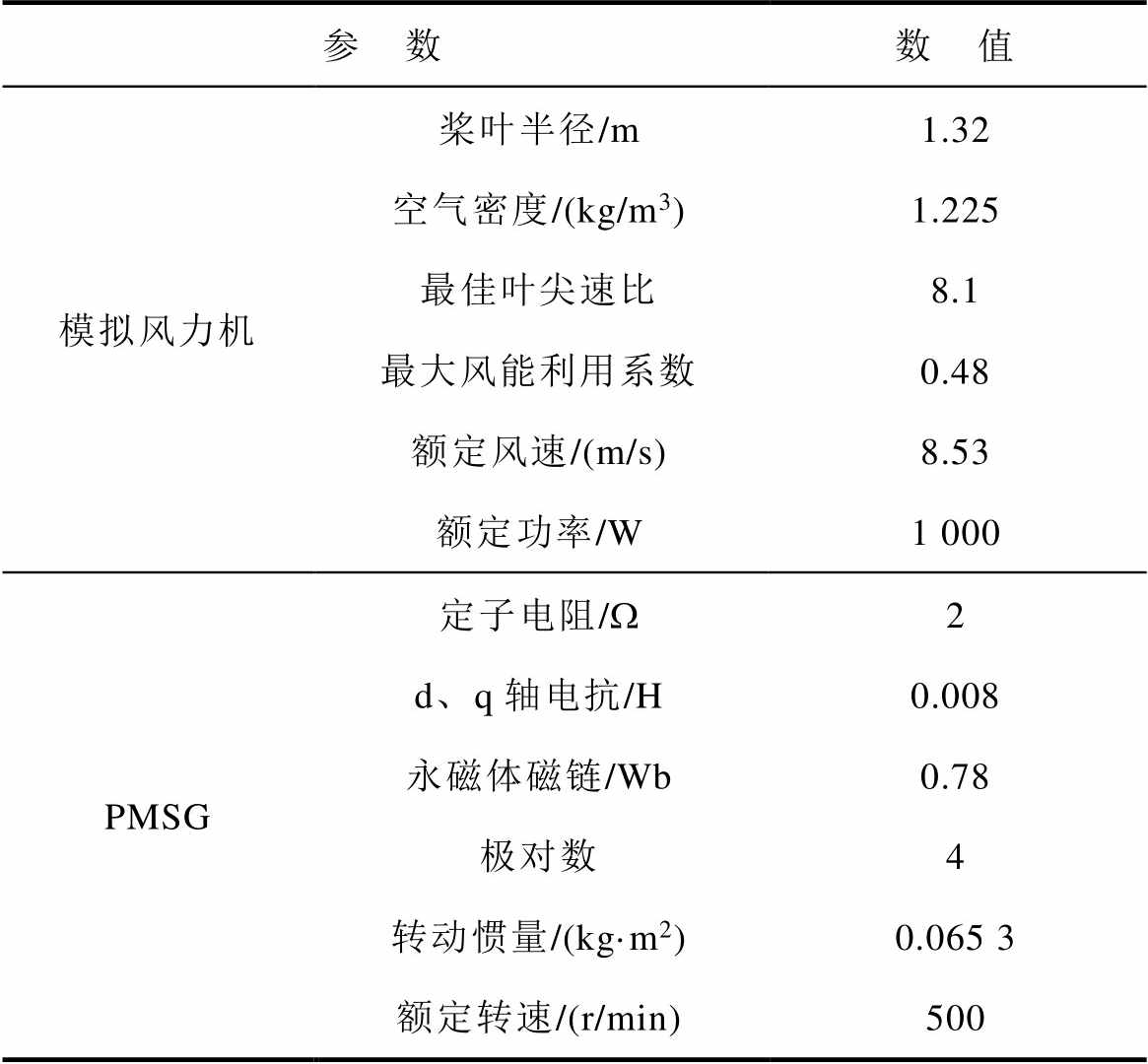
参 数数 值 模拟风力机桨叶半径/m1.32 空气密度/(kg/m3)1.225 最佳叶尖速比8.1 最大风能利用系数0.48 额定风速/(m/s)8.53 额定功率/W1 000 PMSG定子电阻/W2 d、q轴电抗/H0.008 永磁体磁链/Wb0.78 极对数4 转动惯量/(kg·m2)0.065 3 额定转速/(r/min)500
采用图14所示的正弦风速段对2.2节提出的积分周期Dt整定方法进行实验验证。将参考功率设定为MPPT功率Pref=koptw3，分别将允许最大功率跟踪偏差比DPmax设定为不同值，计算得到不同的Dt取值。此外，增设一组Dt=2×10-5 s，即Dt极端小的实验作为对比，不同Dt取值下的功率变化如图15所示，记录机组的实际最大功率跟踪偏差比DPmax见表2。实验结果表明，机组的功率跟踪效果随Dt的减小逐渐降低。当Dt=2×10-5 s，即Dt取极端小时，机组的电磁功率已经无法跟踪参考功率。同时，由表7可知，不同Dt设定值下的实际DPmax均小于设定值，与仿真结果基本一致。可见2.2节所提出的Dt整定方法是可行有效的。
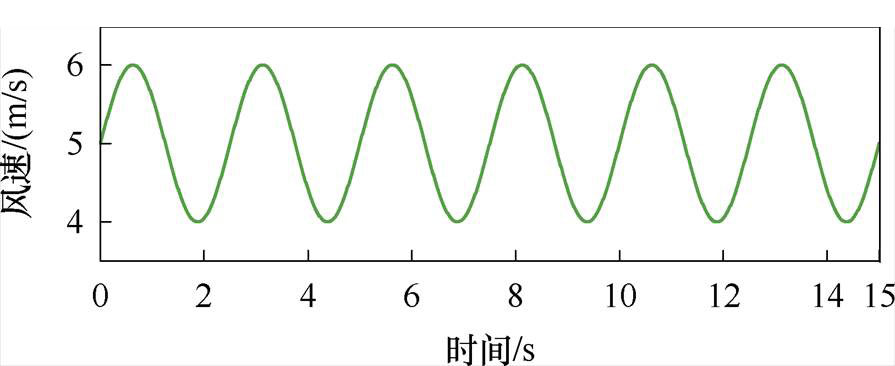
图14 实验用正弦风速
Fig.14 Experimental sinusoidal wind speed
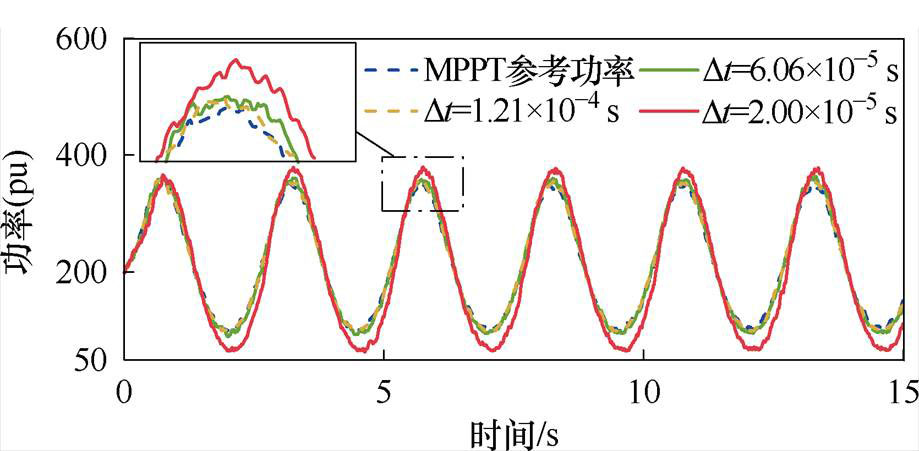
图15 Dt整定策略的实验验证
Fig.15 Experimental validation of the Dt-setting strategy
表7 Dt整定方法有效性实验验证结果
Tab.7 Experimental validation results of the effectiveness of the Dt-setting method
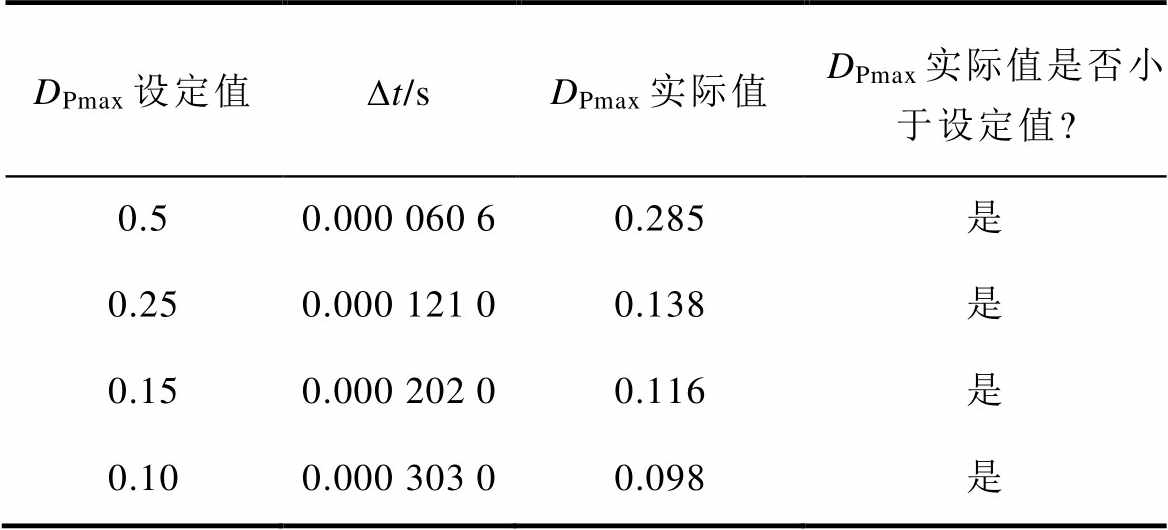
DPmax设定值Dt/sDPmax实际值 DPmax实际值是否小于设定值? 0.50.000 060 60.285是 0.250.000 121 00.138是 0.150.000 202 00.116是 0.100.000 303 00.098是
实验所用的风速与仿真风速相似，波形如图16所示。考虑到实验机组惯量极小，平滑能力有限，因此滤波参数T取值不宜太大，取T=0.3、0.6、0.9,分别进行实验，实验过程中的功率和转速波形如图17所示。由图17可知，在12 s处，风速急剧增大，转子通过加速吸收风功率，实现对输出电磁功率的平滑。在57～58 s处，风速减小，转子通过减速释放功率弥补此时风功率的缺额，实现对平滑参考功率的跟踪。当平滑功率参考值小于MPPT功率时，转子加速吸收功率，同时转子的提速会造成捕获风功率减小，最终使机组运行在某一稳态运行转速，该转速下机组的捕获风功率与平滑参考功率相等。当平滑功率参考值大于MPPT功率时，转子减速释放功率，但由于捕获风功率始终小于平滑参考功率，因此不存在稳态运行转速，当转速达到下限时便停止平滑，因此该情景对平滑功率的支撑主要通过转子减速释放功率实现，其持续时间较短。
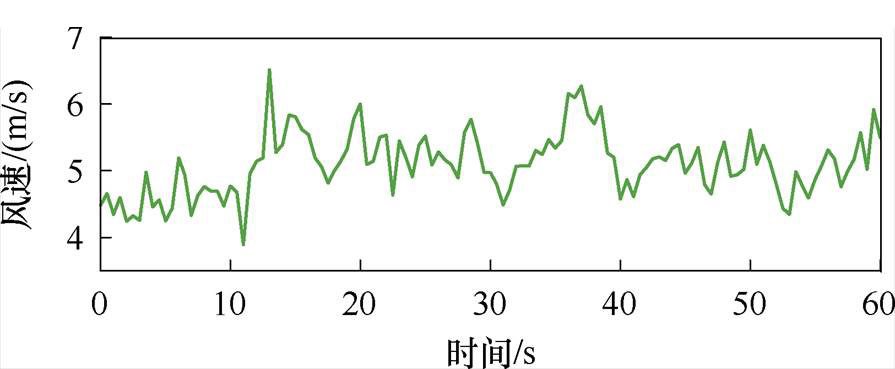
图16 实验用60 s风速
Fig.16 Experimental wind speed of 60 s
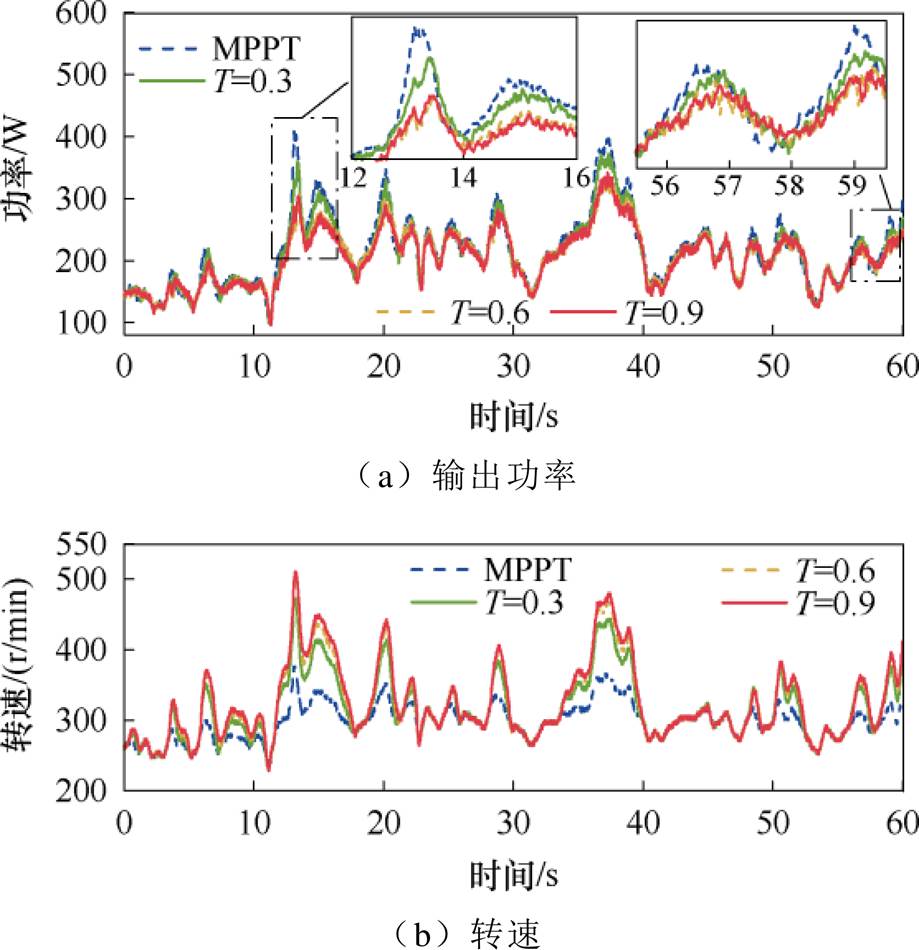
图17 功率平滑策略的实验波形
Fig.17 Experimental waveforms for power smoothing strategy
由上述分析可知，12～14 s的功率平滑效果实际有两个来源：其一是转子加速过程吸收一部分捕获风功率；其二是转子提速造成捕获风功率减小。而57～58 s期间的功率平滑效果则主要由转子减速的动态过程实现，其持续时间与转子变速的快慢有关。实验所用机组转动惯量小，额定转速高，其惯性时间常数远小于典型实际直驱风电机组，因此变速过程容易实现且持续时间短。实际直驱风电机组的转动惯量很大，往往能够达到百万级，从而动态响应缓慢，变速过程持续时间长，针对风速骤降情景下的平滑效果将更显著，由此验证了本文所提功率平滑策略的可行性。
本文以永磁直驱风电系统为研究对象，提出了一种计及功率指令和积分周期优化的风电机组转子动能平滑功率控制策略，本文主要贡献和结论如下：
1）提出了一种利用传递函数模型辅助建立的新型功率平滑指令，并针对传递函数模型的建模和参数取值进行了分析，提出了基于滑动均值滤波的稳态运行点选取方法，通过调整各独立参数实现了对输出功率平滑度和水平高低的灵活调节。
2）推导了转速闭环结构中重要积分周期Dt影响功率跟踪效果的数学机理，并首次提出了Dt的整定原则。进而通过转速闭环间接实现了对电磁功率的精准跟踪，并通过将MPPT转速设定为转速下限，确保了任意时刻、任意风况下机组的稳定运行，极大地程度提高了功率平滑策略的普适性和可靠性。
仿真和实验结果验证了本文所提控制策略中功率平滑指令优化及积分周期Dt整定的有效性，表明了改进功率平滑控制策略在保证风能利用率的同时能够有效提高输出功率的平滑度，并避免了变速过程中机组可能存在的失稳现象。
参考文献
[1] 胡正阳, 高丙团, 张磊, 等. 风电机组双向支撑能力分析与自适应惯量控制策略[J]. 电工技术学报, 2023, 38(19): 5224-5240.
Hu Zhengyang, Gao Bingtuan, Zhang Lei, et al. Bidirectional support capability analysis and adaptive inertial control strategy of wind turbine[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(19): 5224-5240.
[2] 孔贺, 侯山, 赵弋菡, 等. 低电压穿越控制诱导的陆上风电场电压振荡的分岔分析及其判据研究[J/OL]. 中国电机工程学报: 1-20 [2024-04-28]. https://doi.org/10.13334/j.0258-8013.pcsee.230763.
Kong He, Hou Shan, Zhao Gehan. Bifurcation analysis and criteria of voltage oscillation induced by low voltage ride through control in onshore wind farm[J/OL]. Proceedings of the CSEE: 1-20 [2024- 04-28]. https://doi.org/10.13334/j.0258-8013.pcsee.23073.
[3] 周伟波, 黄伟. 基于云边协同架构的海上风电场公共连接点电压控制方法[J]. 电气工程学报, 2023, 18(1): 169-180.
Zhou Weibo, Huang Wei. Voltage control method for common connection point of offshore wind farm based on cloud edge collaborative architecture[J]. Journal of Electrical Engineering, 2023, 18(1): 169- 180.
[4] 颜湘武, 孙雪薇, 崔森, 等. 基于转子动能与超级电容器储能的双馈风电机组惯量和一次调频改进控制策略[J]. 电工技术学报, 2021, 36(增刊1): 179-190.
Yan Xiangwu, Sun Xuewei, Cui Sen, et al. Improved control strategy for inertia and primary frequency regulation of doubly fed induction generator based on rotor kinetic energy and supercapacitor energy storage[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 179-190.
[5] 张宇博, 杨松浩, 郝治国. 最大化电力系统频率最低点的并网风电机组频率支撑控制[J]. 电力系统自动化, 2024, 48(8): 141-151.
Zhang Yubo, Yang Songhao, Hao Zhiguo. Frequency support control of grid-connected wind turbines to maximize frequency nadir of power systems[J]. Automation of Electric Power Systems, 2024, 48(8): 141-151.
[6] 李京华, 王德林, 孙浩宁, 等. 双馈风电并网后系统的惯量特性研究及其最小惯量评估方法[J/OL]. 电气工程学报: 1-13 [2024-04-28]. http://kns.cnki.net/ kcms/detail/10.1289.TM.20230705.1705.002.html.
Li Jinghua, Wang Delin, Sun Haoning, et al. Research on inertia characteristics and minimum inertia evaluation method of doubly-fed wind power system after grid connection[J/OL]. Journal of Electrical Engineering: 1-13[2024-04-28]. http://kns.cnki.net/kcms/ detail/10.1289.TM.20230705.1705.002.html.
[7] 朱瑛, 高云波, 臧海祥, 等. 风电机组输出功率平滑技术综述[J]. 电力系统自动化, 2018, 42(18): 182-191.
Zhu Ying, Gao Yunbo, Zang Haixiang, et al. Review of output power smoothing technologies for wind turbine[J]. Automation of Electric Power Systems, 2018, 42(18): 182-191.
[8] 林莉, 林雨露, 谭惠丹, 等. 计及SOC自恢复的混合储能平抑风电功率波动控制[J]. 电工技术学报, 2024, 39(3): 658-671.
Lin Li, Lin Yulu, Tan Huidan, et al. Hybrid energy storage control with SOC self-recovery to smooth out wind power fluctuations[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 658-671.
[9] 赵靖英, 乔珩埔, 姚帅亮, 等. 考虑储能SOC自恢复的风电波动平抑混合储能容量配置策略[J]. 电工技术学报, 2024, 39(16): 5206-5219.
Zhao Jingying, Qiao Hengpu, Yao Shuailiang, et al. Hybrid energy storage system capacity configuration strategy for stabilizing wind power fluctuation considering SOC self-recovery[J]. Transactions of China Electrotechnical Society, 2024, 39(16): 5206- 5219.
[10] 周皓, 李军徽, 葛长兴, 等. 改善风电并网电能质量的飞轮储能系统能量管理系统设计[J]. 太阳能学报, 2021, 42(3): 105-113.
Zhou Hao, Li Junhui, Ge Changxing, et al. Research on improving power quality of wind power system based on energy management system of flywheel energy storage system[J]. Acta Energiae Solaris Sinica, 2021, 42(3): 105-113.
[11] 李忠瑞, 聂子玲, 艾胜, 等. 一种基于非线性扰动观测器的飞轮储能系统优化充电控制策略[J]. 电工技术学报, 2023, 38(6): 1506-1518.
Li Zhongrui, Nie Ziling, Ai Sheng, et al. An optimized charging control strategy for flywheel energy storage system based on nonlinear disturbance observer[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1506-1518.
[12] 汤雪松, 殷明慧, 李冬运, 等. 变速与变桨协调的风电机组平滑功率控制[J]. 电力系统自动化, 2019, 43(2): 112-120.
Tang Xuesong, Yin Minghui, Li Dongyun, et al. Power smoothing control of wind turbine generator via coordinated rotor speed and pitch angle regulation[J]. Automation of Electric Power Systems, 2019, 43(2): 112-120.
[13] Van T L, Nguyen T H, Lee D C. Advanced pitch angle control based on fuzzy logic for variable-speed wind turbine systems[J]. IEEE Transactions on Energy Conversion, 2015, 30(2): 578-587.
[14] Senjyu T, Sakamoto R, Urasaki N, et al. Output power leveling of wind turbine Generator for all operating regions by pitch angle control[J]. IEEE Transactions on Energy Conversion, 2006, 21(2): 467-475.
[15] Luo Changling, Banakar H, Shen Baike, et al. Strategies to smooth wind power fluctuations of wind turbine generator[J]. IEEE Transactions on Energy Conversion, 2007, 22(2): 341-349.
[16] Jia Feng, Cai Xu, Li Zheng. Fluctuating characteristic and power smoothing strategies of WECS[J]. IET Generation, Transmission & Distribution, 2018, 12(20): 4568-4576.
[17] Qin Zian, Blaabjerg F, Loh P C. A rotating speed controller design method for power leveling by means of inertia energy in wind power systems[J]. IEEE Transactions on Energy Conversion, 2015, 30(3): 1052-1060.
[18] 陈载宇, 沈春, 殷明慧, 等. 面向AGC的变速变桨风电机组有功功率控制策略[J]. 电力工程技术, 2017, 36(1): 9-14.
Chen Zaiyu, Shen Chun, Yin Minghui, et al. Review of active power control strategy for variable-speed variable-pitch wind turbine participating in AGC[J]. Electric Power Engineering Technology, 2017, 36(1): 9-14.
[19] 周银, 林桦. 平滑永磁同步风电系统功率波动的改进最佳转矩控制策略[J]. 电力系统自动化, 2013, 37(9): 13-17, 73.
Zhou Yin, Lin Hua. Improved optimal torque control strategy for smoothing power fluctuations of permanent magnet synchronous generator for wind turbine[J]. Automation of Electric Power Systems, 2013, 37(9): 13-17, 73.
[20] Lü Xue, Zhao Jian, Jia Youwei, et al. Coordinated control strategies of PMSG-based wind turbine for smoothing power fluctuations[J]. IEEE Transactions on Power Systems, 2019, 34(1): 391-401.
[21] Zhao Xianxian, Yan Zuanhong, Xue Ying, et al. Wind power smoothing by controlling the inertial energy of turbines with optimized energy yield[J]. IEEE Access, 2017, 5: 23374-23382.
[22] 王海旗, 晋涛, 刘星廷, 等. 基于转子动能控制的风电机组功率平滑控制结构及优化策略研究[J]. 太阳能学报, 2022, 43(9): 251-257.
Wang Haiqi, Jin Tao, Liu Xingting, et al. Research on wind turbine power smooth control structure and optimization strategy based on rotor kinetic energy control[J]. Acta Energiae Solaris Sinica, 2022, 43(9): 251-257.
[23] Liao Kai, Lu Dingwen, Wang Min, et al. A low-pass virtual filter for output power smoothing of wind energy conversion systems[J]. IEEE Transactions on Industrial Electronics, 2022, 69(12): 12874-12885.
[24] 殷明慧, 顾伟, 陈载宇, 等. 面向风电机组有功功率控制的风轮变速运行模式比较研究[J]. 中国电机工程学报, 2022, 42(12): 4419-4430.
Yin Minghui, Gu Wei, Chen Zaiyu, et al. Comparative study of rotor speed variation modes for active power control of wind turbine generators[J]. Proceedings of the CSEE, 2022, 42(12): 4419-4430.
[25] Lin Jin, Sun Yuanzhang, Song Yonghua, et al. Wind power fluctuation smoothing controller based on risk assessment of grid frequency deviation in an isolated system[J]. IEEE Transactions on Sustainable Energy, 2013, 4(2): 379-392.
Abstract With the yearly growth of the stand-alone capacity of wind turbines, the negative impact of wind power fluctuations on the quality and frequency stability of the power grid is becoming increasingly severe. A novel control strategy for smoothing wind turbine output power is proposed using rotor kinetic energy. Specifically, the following work is included. (1) A novel smoothing reference power command is designed. (2) The influence of the key parameter in the rotor kinetic energy control framework and the integration period Dt on power tracking is analyzed. An optimization method for setting Dt is proposed. (3) The maximum power point tracking (MPPT) speed is set as the lower limit of the rotational speed, and the generator is allowed to output the reference power precisely through the speed closed-loop control structure.
Firstly, the transfer function model of the wind turbine is established, and the steady-state operating point is determined according to the moving average filtering algorithm. The novel smooth reference power command is calculated, which decouples and adjusts the output power’s smoothness and average value by changing the values of parameters T and K. The larger the value of T, the more pronounced the power smoothing effect. The smaller the value of K, the lower the average output power. Then, through speed tracking simulation on the wind turbine, the speed tracking error caused by controller delay and other factors is recorded and analyzed to determine the optimal value of the integration period Dt. Finally, the precise response to power command is achieved through the speed closed-loop control structure, effectively avoiding the instability problem that may occur during the large-scale variable speed operation of the wind turbine.
Compared with the traditional MPPT control strategy under 60s turbulent wind conditions in the simulation, the standard deviation of the output power using the proposed method is decreased by 9.97% when T=1, while the average value is only reduced by 1.2%. When T=3.5, the standard deviation is decreased by 27.29%, greatly improving waveform smoothness, and the average value is decreased by 5.2%. Since the MPPT speed is set as the lower speed limit, the wind turbine may cross the lower speed limit during operation and cause the power to fall. Therefore, reducing the value of K can reduce the average output power value, so the turbine operates in a high-speed interval. The turbine decelerating probability to the lower speed limit can be reduced. In the case of T=2.5 and K=0.85, the unit speed is always higher than the lower limit value, and the standard deviation of the output power is reduced by 32.19% compared with the MPPT strategy. The smoothness of output power is significantly improved, and the average value is only reduced to 90.76%.
The simulation and experimental results show that after optimizing the integral period parameter, the speed closed-loop control structure can achieve the same effect as the power closed-loop control structure and accurately respond to the reference power command, which helps set the speed limit to prevent unit instability. The proposed power smoothing control strategy can effectively suppress wind power fluctuations while ensuring sufficient wind energy utilization efficiency. By setting the MPPT speed as the lower speed limit, the stable operation of the wind turbine can be ensured under turbulent wind conditions.
keywords：Wind turbine, power smoothing, rotor kinetic energy, integration period, small disturbance linearization
DOI: 10.19595/j.cnki.1000-6753.tces.240172
中图分类号：TM315
国家自然科学基金资助项目（U1966025）。
收稿日期 2024-01-25
改稿日期 2024-03-25
朱 瑛 女，1987年生，博士，副教授，研究方向为风力发电及其并网控制技术、风电场优化布局及新型永磁电机控制技术等。E-mail: yingzhu@hhu.edu.cn（通信作者）
李 斌 男，2000年生，硕士研究生，研究方向为风力发电机系统及其控制。E-mail: binlihhu@163.com
（编辑 崔文静）