图1 AMBs系统结构
Fig.1 The structure of AMBs system
摘要 随着磁悬浮轴承(AMB)在工业各领域的应用,其受到的关注与日俱增,而随着工业各领域技术的不断进步,对AMB的设计和优化也提出了更高的需求。该文提出一种基于多物理场的AMBs系统自适应多目标优化(MOO)方法,通过自适应MOO方法与多物理场分析方法相结合,解决两者分别存在的参数合理性和迭代收敛性问题。通过仿真与传统多目标优化方法对比证明了该方法的可行性。最后根据优化后的AMBs参数,搭建200 kW,30 000 r/min高速永磁同步电机(HPMSM)驱动下的AMBs系统验证了所提方法的有效性。
关键词:磁悬浮轴承 多目标优化 高速永磁同步电机 遗传算法
主动磁悬浮轴承(Active Magnetic Bearing, AMB)由于具有无接触、低噪声、可主动控制和高功率密度等特点,在工业领域有着广泛的应用,如飞轮储能、电主轴、离心压缩机等[1-9]。在实际应用时通常由径向磁悬浮轴承(Radial Active Magnetic Bearing, RAMB)和轴向磁悬浮轴承(Axial Active Magnetic Bearing, AAMB)以各种形式组成AMBs系统使用,以满足应用工况的各种需求。对AMBs系统的合理设计不仅能降低其本身的控制难度,更能提高其配合部件的使用寿命从而间接降低使用成本。
由于AMBs系统多工作在中高速工况下,因此多物理场优化方法对其适配度很高。文献[10]提出了一种全局多物理场优化方法,同时优化AMBs系统及其驱动电机,并将这种方法推广至复杂物理机械的设计中。然而,其并未提及多物理场优化方法中普遍存在的迭代收敛性问题,在现有文献中也鲜有提及[11]。
遗传算法[12]作为最常用的智能优化方法之一,同样在AMB优化设计领域有着广泛的应用,其通常会与优化目标一同展开讨论,优化目标的变化同样也反映了优化方法的变化。文献[13-15]已经针对体积、承载力等优化目标进行了单目标优化(Single Objective Optimization, SOO)。相比较于SOO方法,多目标优化(Multi-Objective Optimization, MOO)方法能够实现优化后AMB性能的相对平衡。文献[16]同时优化了两自由度混合励磁AMB的体积、质量和涡流损耗以及静态负载能力。文献[17]对高速压缩机用混合励磁AMB进行了优化,同时以总体积、轴向长度和涡流损耗为优化目标。如今已有更多学者对此展开研究[18-20],可见MOO方法在AMBs系统中已成为主流。
在AMBs系统中常用的MOO遗传算法主要有向量评估遗传算法[21](Vector-Evaluated Genetic Algorithm, VEGA)、多目标遗传算法[22](Multi- Objective Genetic Algorithm, MOGA)及由MOGA衍生出的强度Pareto进化算法[23](Strength Pareto Evolutionary Algorithm, SPEA)和非支配排序遗传算法[24](Non-dominated Sorting Genetic Algorithms, NSGA)四种。其中,VEGA最早被提出,也是首个通过一组非支配解来逼近Pareto前沿的遗传算法;MOGA是最早使用基于Pareto排序和小生境技术来搜索Pareto前沿并保持群体多样性的遗传算法;SPEA则是一种兼顾非支配排序与种群多样性且加入精英保留策略的遗传算法;NSGA系列遗传算法提出至今已有三代,其中以NSGA-Ⅰ为基础,NSGA-Ⅱ最为通用而NSGA-Ⅲ对于复杂优化问题的处理能力最强。
VEGA与NSGA相比在优化过程中将MOO问题转化为SOO问题,以提高整体的计算效率,但在面对MOO问题时最终结果会明显倾向于其中一个目标函数,无法做到全局最优。MOGA的优化过程与NSGA-Ⅰ类似,然而其种群多样性保护机制导致其需要指定大量参数,进而降低收敛速度。SPEA的优化过程与NSGA-Ⅱ类似,但其计算成本远远高于NSGA-Ⅱ。
本文提出了一种基于多物理场辅助优化的应用于AMBs系统的自适应NSGA-Ⅱ。首先,介绍了AMBs系统的基本结构并给出其常规设计流程。其次,介绍了所提出自适应NSGA-Ⅱ的实现过程,并给出了与AMBs系统相对应的约束条件和优化目标。然后,给出了对于所提出的自适应NSGA-Ⅱ的仿真分析过程。最后,通过实验证明了本文所提出方法的可行性和通过其得出的优化结果的有效性。
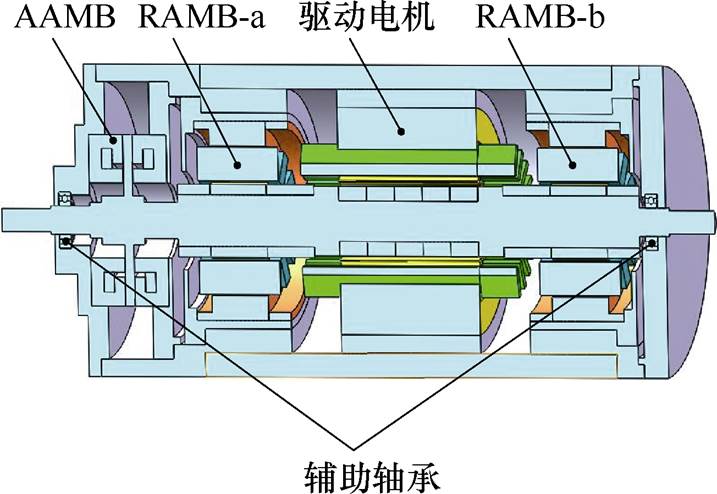
本文所研究的AMBs系统主要由AMBs和驱动电机两部分组成。其中,AMBs部分主要由位于转轴两端的两个RAMBs和一个AAMB组成,具体结构如图1所示。

图1 AMBs系统结构
Fig.1 The structure of AMBs system
本文所用驱动电机类型为高速永磁同步电机(High-speed Permanent Magnet Synchronous Motor, HPMSM),其额定转速为30 000 r/min,空载反电动势为288 V,额定转矩为65 N·m,额定功率为200 kW,额定电压为320 V。AMBs的设计要求见表1。
表1 AMBs的设计要求
Tab.1 The design requirements for AMBs

参 数RAMB需求AAMB需求 AMB气隙长度/mm<0.8<1 辅助轴承气隙长度/mm<0.4— 最大电磁力/N>400>500
在AMBs系统中,RAMB采用十二极结构设计,其具体结构如图2所示。图2中,bz为主磁极宽度,bf为副磁极宽度,ar为主-副磁极中线夹角。由于十二极结构AMB既具备四极和八极结构的电磁力数量级,同时又可以兼顾十六极和更高磁极数AMB的精密控制能力,因此是中小体积被控对象下提供磁性支撑的最佳选择。
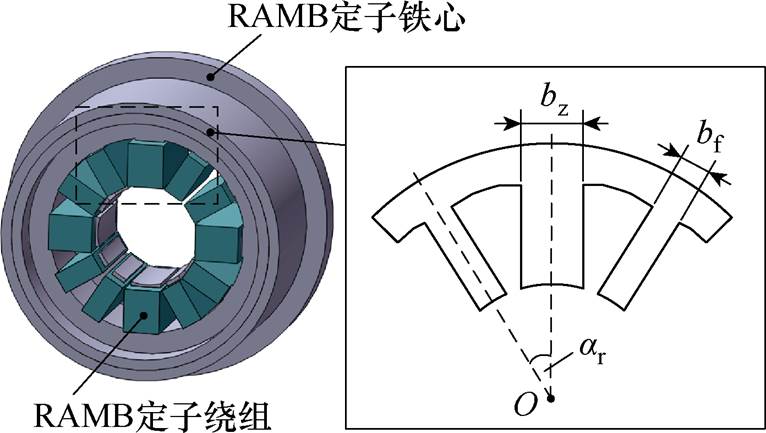
图2 RAMB基本结构
Fig.2 The basic structure of RAMB
在AMBs系统中,对于AAMB采用单环结构设计,其具体结构如图3所示,在磁路上为穿过单侧气隙的同极性结构。图3中,tas1为定子大环宽度,tas2为定子小环宽度,hacu为线圈腔高度,lsa为定子轴向长度,tas3为轴向截面宽度。这种AAMB的结构组成相对简单,不易造成磁路的局部饱和,且制造简易、成本低,也更具代表性。
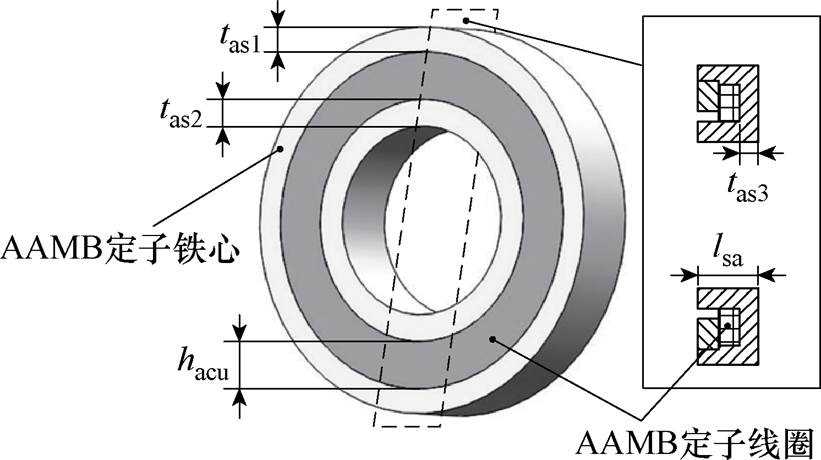
图3 AAMB基本结构
Fig.3 The basic structure of AAMB
AMBs系统结构设计的本质是根据负载条件和使用条件的要求,协调线圈腔面积和等效磁极面积。优化设计是在结构设计的基础上实现的,AAMB和RAMB在结构设计上有相似也有不同,两者的结构设计流程如图4所示。
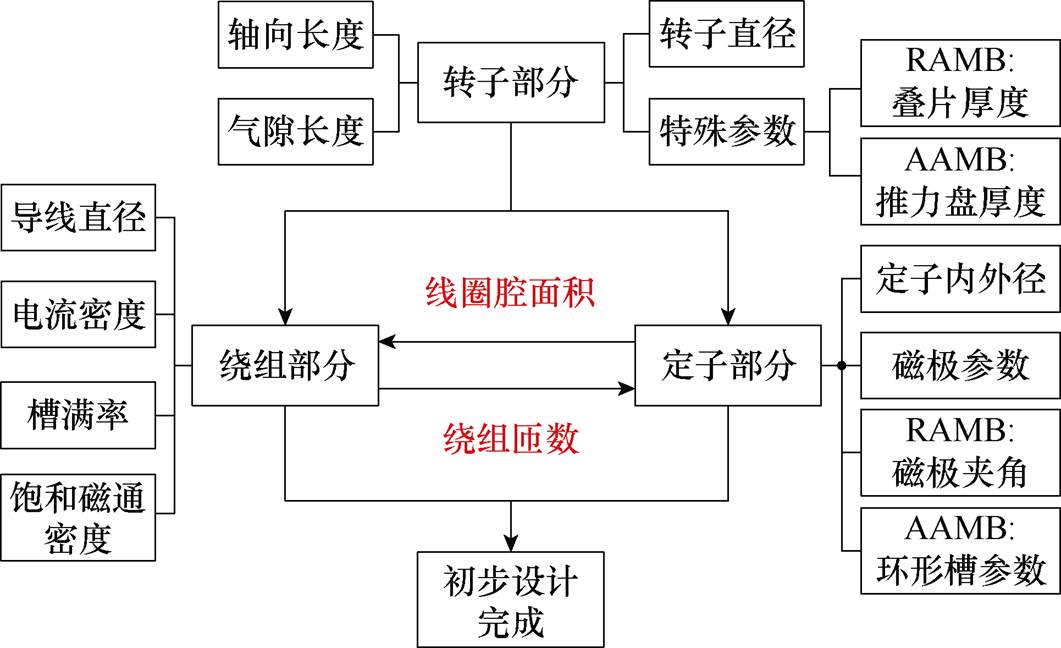
图4 AMB设计流程
Fig.4 The design process of AMB
由图4可知,AMB结构设计中通常可以分为三个部分,即转子、定子和绕组部分;三部分没有明确的计算先后顺序,但是定子和绕组部分会有数据交互。其中,转子部分两者共有的参数主要有气隙长度和轴向长度;绕组部分两者共有的参数主要有饱和磁通密度、电流密度、工作电流、匝数和槽满率;定子部分两者共有的参数主要有线圈腔面积和定子外径。
以下给出AMB结构设计时的重要公式。对于RAMB,由于其磁极结构相对不规则,因此在设计时磁极夹角ar尤为重要。为表示ar需引入磁极宽度比ka,可以表示为
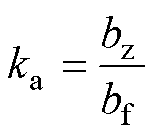 (1)
(1)
同时,引入结构系数kr用于将电磁力折算到直角坐标系下以便于计算,可以表示为
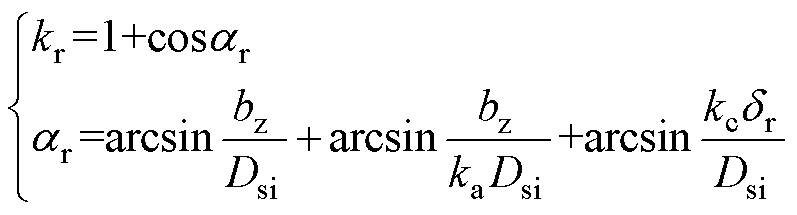 (2)
(2)
式中,kc为主副磁极间距与气隙长度的比值系数;Dsi为RAMB的定子内径;dr为RAMB的气隙长度。
对于AAMB,其槽型结构参数的计算更加重要。同心单环结构的典型设计方法是假定tas1和tas3相等,则槽宽hacu可以表示为
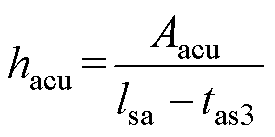 (3)
(3)
式中,Aacu为AAMB的线圈腔面积。
特殊地,tas2需要通过解方程的方式来得到,可以表示为
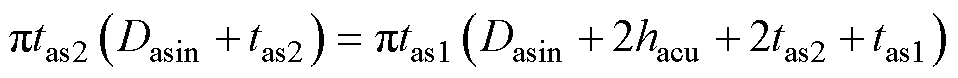 (4)
(4)
式中,Dasin为AAMB的定子内径。
本文提出的优化设计方法其实现过程如图5所示。首先,由图4给出的AMB设计流程和表1给出的设计要求来确定优化设计方法中的设计参数取值范围,同时确定HPMSM和AMBs之间的结构布局。其次,根据设计需求设立目标函数,使用MOO方法对诸多设计结果进行筛选,得到范围内的相对最优设计解集。
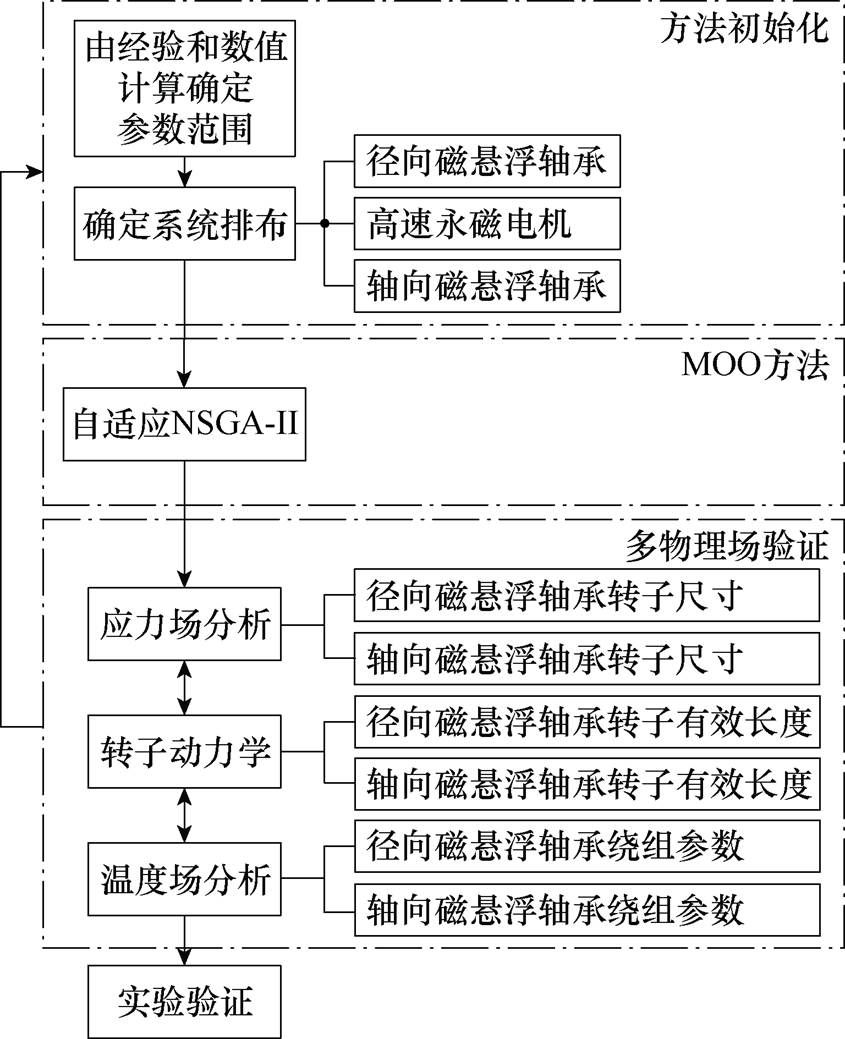
图5 多物理MOO方法基本流程
Fig.5 Basic process of multi-physics MOO method
然后,根据初步得到的相对最优设计解集在各自场下建立相对应的参数化有限元模型。根据多物理场仿真结果针对性地调整设计参数的取值范围,并根据调整后的取值范围继续使用MOO方法得到新范围内的相对最优设计解集。多次重复上述流程,不断缩小大部分设计参数的取值范围但保留少数设计参数的取值范围,以维持设计解集多样性。保留参数的选择取决于目标函数。
最后,在迭代中不断减少相对最优设计解集的数量,从而选出满足设计要求的相对最优解。
多物理场分析中的各个步骤之间需保持数据交互且严格按照顺序执行仿真过程,各步骤中互相关联的结构尺寸参数在图4中有所体现。
本文对提出的多物理MOO方法的核心:NSGA- Ⅱ进行了改进,提出了一种自适应NSGA-Ⅱ,其具体流程如图6所示。
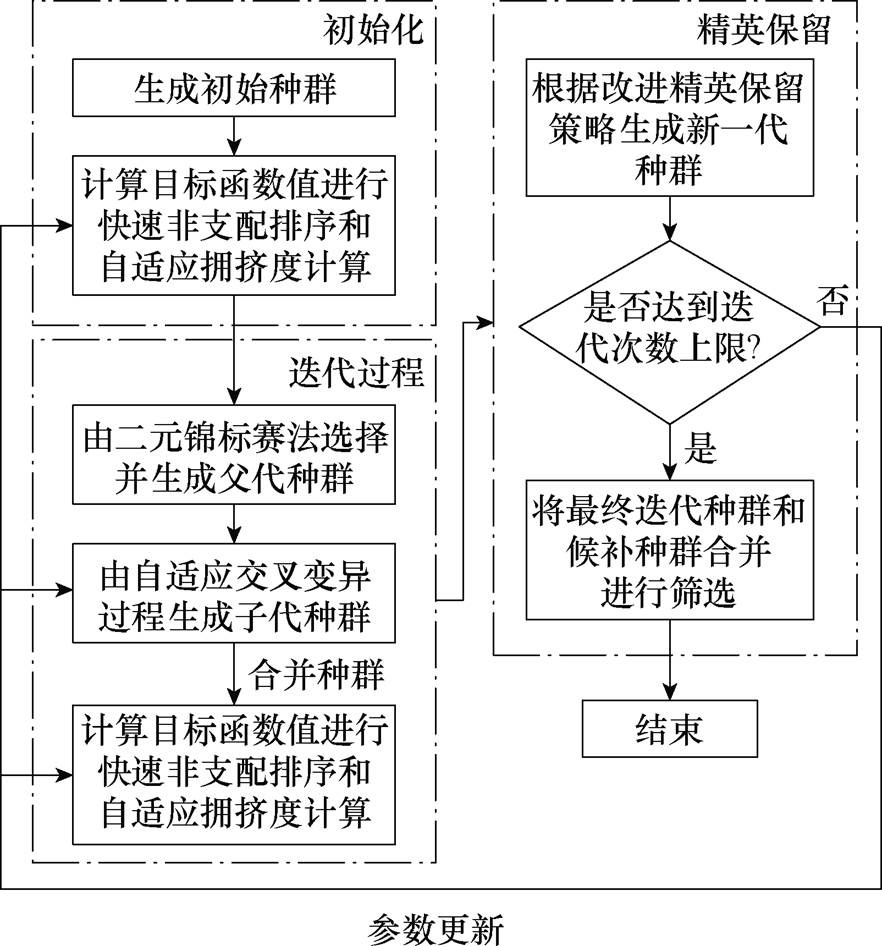
图6 自适应NSGA-Ⅱ基本流程
Fig.6 Basic process of adaptive NSGA-Ⅱ
在本文提出的自适应NSGA-Ⅱ中,选择过程、交叉变异过程和精英保留过程中的部分参数会随着迭代次数和非支配排序等级的变化而变化,改进主要体现在以下几个方面。
2.2.1 非支配排序方法和选择过程改进
本文采用一种效率更高的“倒序”非支配排序方法[25]。其具体步骤为,首先从种群所有个体构成的集合中的第1个个体x1开始,将x1与其之后个体进行“超级支配”比较。一轮比较之后将集合分成两部分,一部分为被x1支配的个体,这部分个体必不为当前种群的非支配个体;另一部分为“超级支配”x1的个体,这部分个体组成新集合。若x1不被新集合中的个体所支配,则x1为当前种群的非支配个体,将其并入非支配解集中。在新集合中重复上述操作,直至其中只有1个个体。最后,将旧集合中属于当前非支配解集的个体删除,重复上述操作,直至所有个体的非支配等级都分配完毕。
本文对根据拥挤度选择个体的选择方式进行了改进。传统NSGA-Ⅱ在填充种群时,在相同非支配等级下会优先选择拥挤度大的个体进行填充。然而,在实际优化中应该尽量避免选择拥挤度为无穷大的个体。随着迭代次数的增加,种群的变化范围也越来越小,受到种群多样性的制约也越来越小。因此,迭代次数越大,对于多样性的需求相对越低,也就越不需要大拥挤度的个体;反之,在迭代次数很低时,需要扩大搜索范围,对于大拥挤度个体的需求就远大于迭代后期时。
综上所述,本文引入一个概率函数,在高迭代次数时,增加选择小拥挤度个体的概率;而在低迭代次数时,增加选择高拥挤度个体的概率。这样就能在保证合理性的同时维持种群的多样性,具体表示为
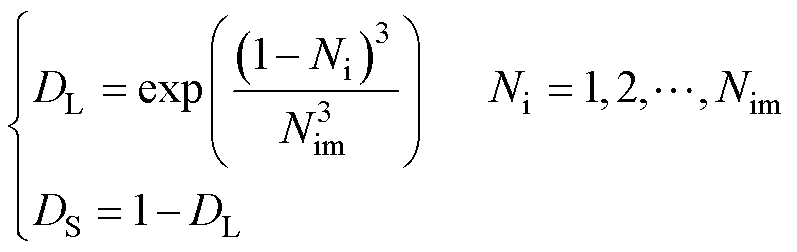 (5)
(5)
式中,DL为选择排位等级在中位数以上的拥挤度所对应的相同非支配等级下个体的概率;DS为选择排位等级在中位数以下的拥挤度所对应的相同非支配等级下个体的概率;Ni为实时更新的迭代次数;Nim为设定的最大迭代次数。
值得补充的是,在计算拥挤度选择概率之前,需首先对父代和子代组成的新种群中所有拥挤度按照由小到大的顺序进行排序,并选取其排序中位数;然后再根据迭代次数计算拥挤度选择概率;最后应用随机遍历采样方法结合实际选择合适拥挤度的个体加入新的种群。
2.2.2 交叉、变异过程改进
本文的交叉变异算子采用模拟二进制交叉(Simulated Binary Crossover, SBX)算子。与拥挤度选择过程类似,随着迭代次数的增加,对于交叉和变异程度的需求会逐渐降低,但仍需保持在一个合理的范围内。研究表明[26],为避免算法搜索过程变成随机搜索,变异率不宜超过0.1,交叉率的范围应为[0.9, 1]。而与拥挤度选择过程不同的是,交叉和变异程度的变化还与其本身的非支配等级有关,非支配等级越高,对于交叉和变异的需求越大,需要以相对较大的交叉变异率来促进种群的进化;而当非支配等级很高时,则恰好相反。为此,本文提出一种自适应交叉变异率,可以表示为
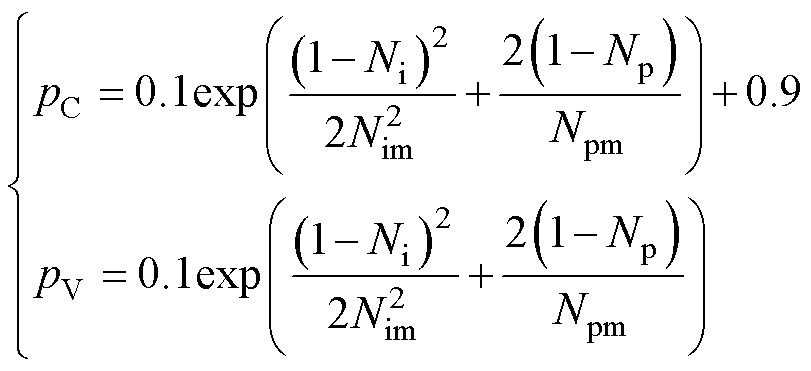
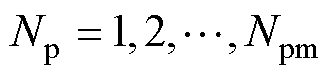 (6)
(6)
式中,pC为交叉概率;pV为变异概率;Np为个体对应的非支配排序等级;Npm为最大非支配排序等级。分析式(6)可知,优化目标越复杂,迭代次数越多,采用自适应交叉变异率时的效果就越好。
2.2.3 精英保留策略改进
传统的精英保留策略通过非支配关系与拥挤度保留父代与子代合并种群中的前Nm个个体作为新一代种群,而本文首先在选择个体填充新种群的方式上,选择2.2.1节中所提及的拥挤度选择方式,同时对于保留策略进行改进,建立“额外”的大小为Nm的候补种群;从没有进入新种群的“淘汰”种群中按照一定比例选择个体加入候补种群中,且只从非支配等级为1的个体所组成的临时种群中选取,而当候补种群中的个体数量达到或超过2Nm时,会在候补种群内部进行同样的精英保留操作,使得候补种群内部的个体数量恢复为Nm。最后,在最后一次迭代结束后,从新种群和候补种群中共同选择出最终种群。每次迭代候补种群增加的个数可以表示为
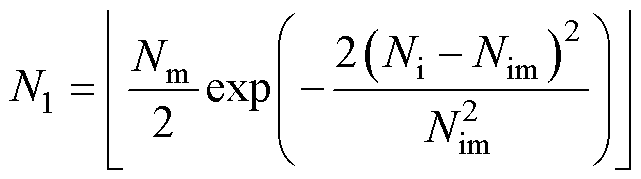 (7)
(7)
由于AMBs系统的优化设计是在固定参数的HPMSM基础上进行的,因此必定会存在体积V的约束Vmax,有
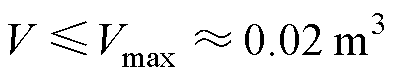 (8)
(8)
在RAMB的设计中,需要对高速工况下的转子套筒做塑性变形校验。应用第三强度理论,径向叠片强度约束可以表示为
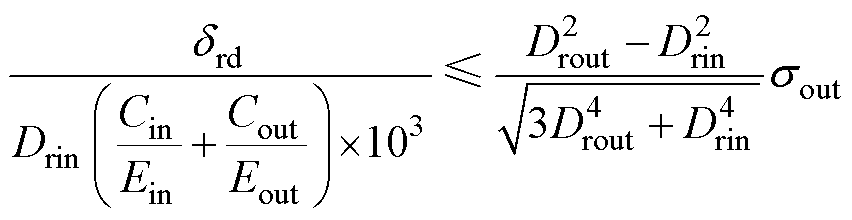 (9)
(9)
式中,Drout、Drin分别为转子叠片的外径和内径;sout为转子叠片的理论屈服极限;drd为过盈量;Ein, Eout、Cin, Cout分别为转轴和转子叠片的弹性模量和刚性系数。
在AAMB的设计中,一般需要对推力盘的变形量进行校核。根据相关标准[27],认为其变形量应不超过气隙本身数值的10%。如果将推力盘等效为均匀载荷环形板模型,则其强度约束可以表示为
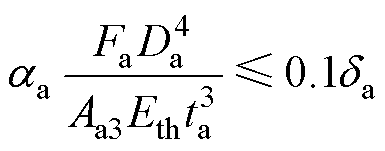 (10)
(10)
式中,aa为无量纲挠度系数,通过查询环形板模型经验计算曲线获得;Fa为AAMB的电磁力;da为AAMB的气隙长度;Eth为推力盘材料的弹性模量;Da为AAMB的定子外径;ta为推力盘宽度;Aa3为推力盘的环形面积。
本文设定三个优化目标,分别是电磁力体密度、总损耗和临界转速。
电磁力体密度rF为单位体积下AMBs系统提供的电磁力大小,可以表示为径向和轴向电磁力的体积加权形式,有
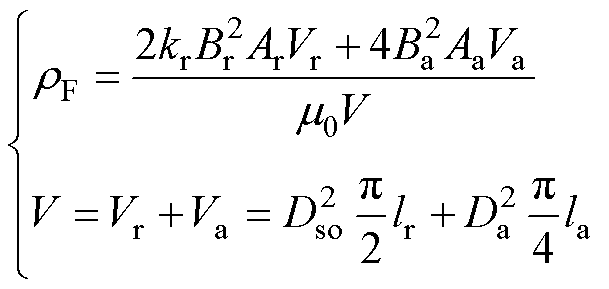 (11)
(11)
式中,Ar为RAMB的主磁极面积;Aa为AAMB的环形磁极面积;Br和Ba分别为RAMB和AAMB的气隙磁通密度;Vr和Va分别为RAMB和AAMB的总体积;Dso为RAMB的定子外径;lr和la分别为RAMB和AAMB轴向总长。
AMBs系统的损耗主要包括三部分,铜耗PCu、铁耗PFe和风摩耗Pf。系统的总损耗P可以表示为
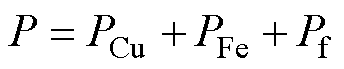 (12)
(12)
其中
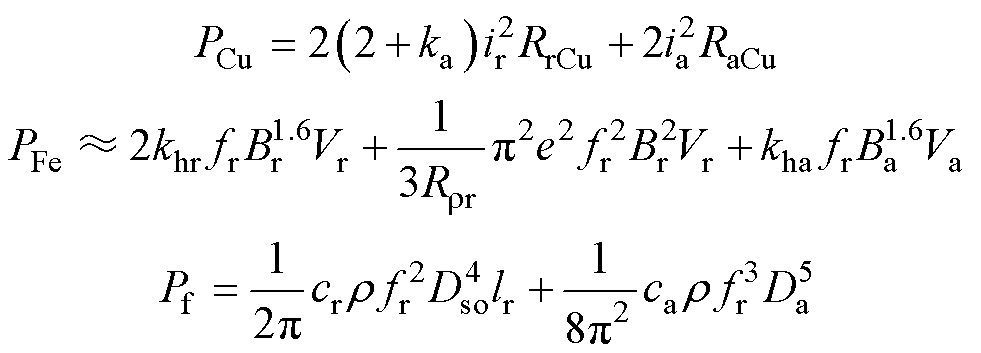
式中,RrCu和RaCu分别为RAMB和AAMB的总电阻;khr和kha分别为RAMB和AAMB的磁滞损耗系数,通过磁化曲线确定;fr为HPMSM的工作频率,根据实际情况设定;e为单位叠片的厚度;Rρr为叠片的电阻率;cr和ca分别为径向和轴向磁悬浮轴承的拖曳系数;r 为气体密度。AAMB由于结构原因近似认为没有涡流损耗而只有磁滞损耗。对于风摩耗,AAMB可用圆盘结构公式进行计算,而RAMB可用圆柱结构进行计算。
根据两端自由杆件固有频率近似计算公式[28]计算转轴自由模态下的一阶临界转速ffre1,可以表示为
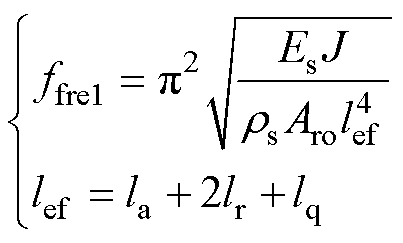 (13)
(13)
式中,Aro为转子等效面积;rs为转轴等效密度;Es为转子等效弹性模量;J为等效截面积相对中性轴的惯性矩;lef为转子总长度;lq为HPMSM转子轴向长度。
RAMB和AAMB的耦合特性可以在式(11)~式(13)中得到直观体现。在径向上体现在对于损耗的影响,尤其是风摩耗;在轴向上体现在对于临界转速的影响;在体积上,也就是同时包含轴向和径向上,主要体现在对于电磁力体密度的影响,这也是本文目标函数如此设置的原因。
本节将从优化算法仿真、电磁场仿真、应力场仿真、转子动力学仿真、温度场仿真五个方面,证明所提出的多物理MOO方法的可行性。
本文选择超体积(Hyper Volume, HV)指标和反世代距离(Inverted Generational Distance, IGD)指标两种综合性指标作为MOO方法的评价标准。
反世代距离IGD计算的是Pareto近似前沿P上每个参考点到解集中相距最近的解的平均距离,可以表示为
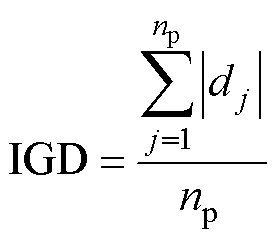 (14)
(14)
式中,dj为参考点到解集中最近解距离的绝对值;np为参考点数量,数量与解集中的个体数量相同。按照近似前沿面定义,参考点是均匀分配的。同时,在计算IGD时一般使用欧式距离,IGD越小代表解集S的综合性能越好。
超体积指标HV衡量的是解集中个体所支配的空间和,主要用于算法收敛性和多样的综合性评价。可以表示为
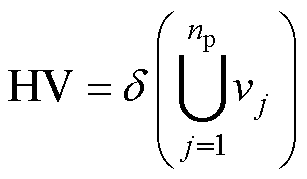 (15)
(15)
式中,vj为解集中的指定个体与参考点形成的超体积;d(· )为Romberg测度。
与IGD不同,HV越大,说明解集的综合性能越好。同时,HV对应的参考点中元素数量与目标函数数量相同。在分析ZDT(Zitzler-Deb-Thiele test functions)相关问题时,本文采用各目标函数值中的最大值所对应的点作为参考点;而在分析磁悬浮轴承优化问题时,选用最小目标函数值所对应的点作为参考点。
为选定更为适配的种群规模和迭代次数,本文以ZDT1为例,应用提出的自适应NSGA-Ⅱ方法分析几种典型组合下的具体表现,并以IGD和HV两种指标进行量化,具体结果如图7所示。需要补充的是,对于ZDT1问题,变量个数设为30。
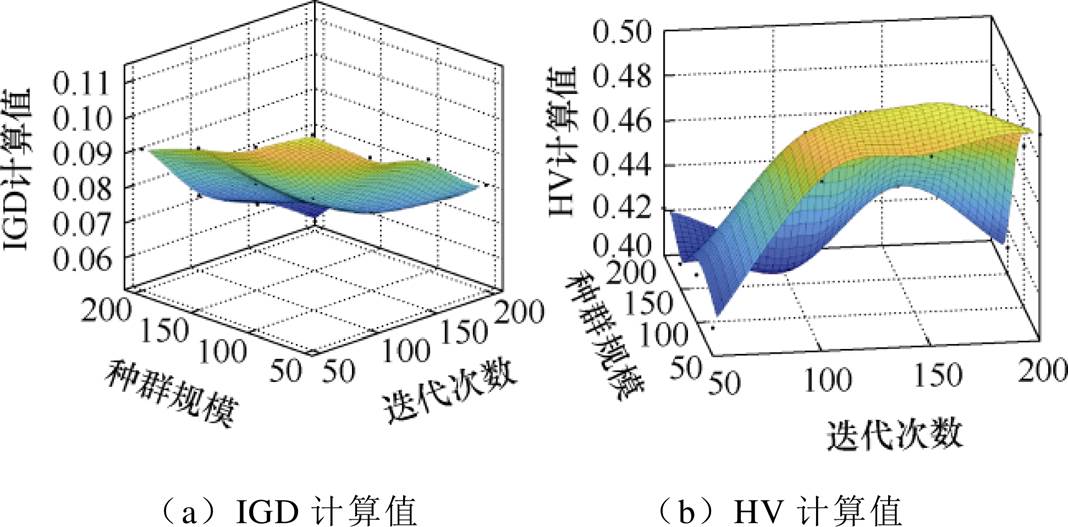
图7 ZDT1问题下自适应NSGA-Ⅱ的性能表现
Fig.7 Performance of adaptive NSGA-Ⅱ in ZDT1
由图7可知,两种指标都存在各自的相对最优“区域”,应选择两“区域”重合的部分,为了方便,本文选取种群规模为100,迭代次数为150。
本文应用自适应NSGA-Ⅱ对AMBs系统进行优化并与传统NSGA-Ⅱ进行了对比,主要对比在种群规模为100、不同迭代次数时两种优化方法在两种评价指标下的表现,结果如图8所示。传统NSGA-Ⅱ的交叉概率设为0.9,变异概率设为0.1,SBX算子的变异分布系数设为10。
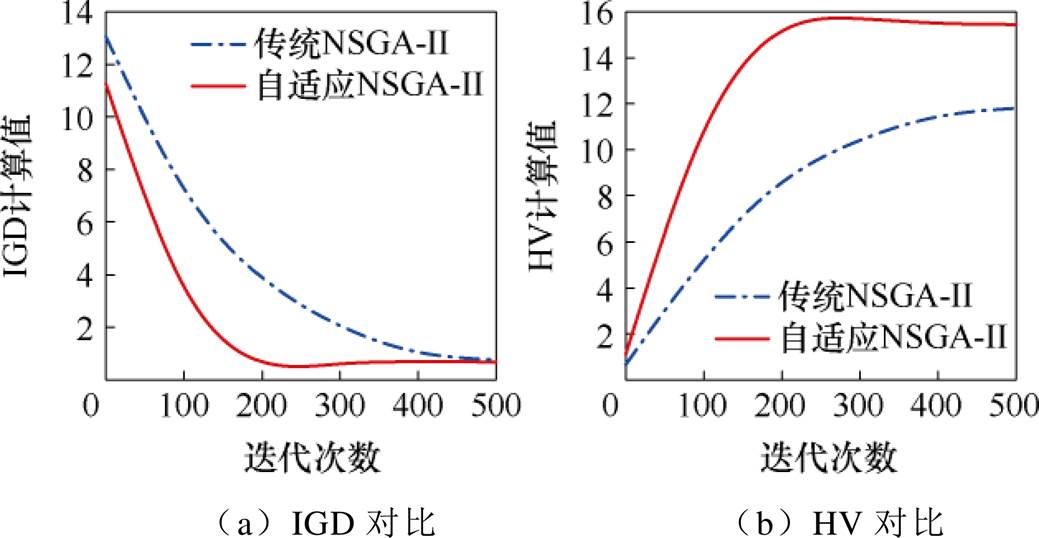
图8 两种NSGA-Ⅱ的性能对比
Fig.8 Comparison of performance between two types of NSGA-Ⅱ
图8由每间隔20次迭代次数对两种评价指标计算一次的采样点的集合拟合而成,反映了两种NSGA-Ⅱ随迭代次数不断增加,其对应的两种评价指标的变化趋势。由图8可知,自适应NSGA-Ⅱ的收敛速度远大于传统NSGA-Ⅱ,且两者均收敛时的两种评价指标也好于传统NSGA-Ⅱ。而从时间复杂度的角度来看,自适应NSGA-Ⅱ的O(300×lg300)也要明显优于传统NSGA-Ⅱ的O(3×1002)。
在自适应NSGA-Ⅱ优化得到的最终种群中取非支配等级为1的个体进行多物理场有限元验证,最后保留6个相对最优个体,其设计变量详见表2,表中参数均保留两位有效数字。表2首行中的数字为个体序号,排序无先后顺序。表2中,Jr和Ja分别为RAMB和AAMB的电流密度;lmr和lma分别为RAMB和AAMB的槽满率;tr为RAMB的转子叠片厚度;Daout为推力盘转轴外径。
表2 相对最优个体的设计变量
Tab.2 Design variables of relatively optimal individuals (单位: mm)
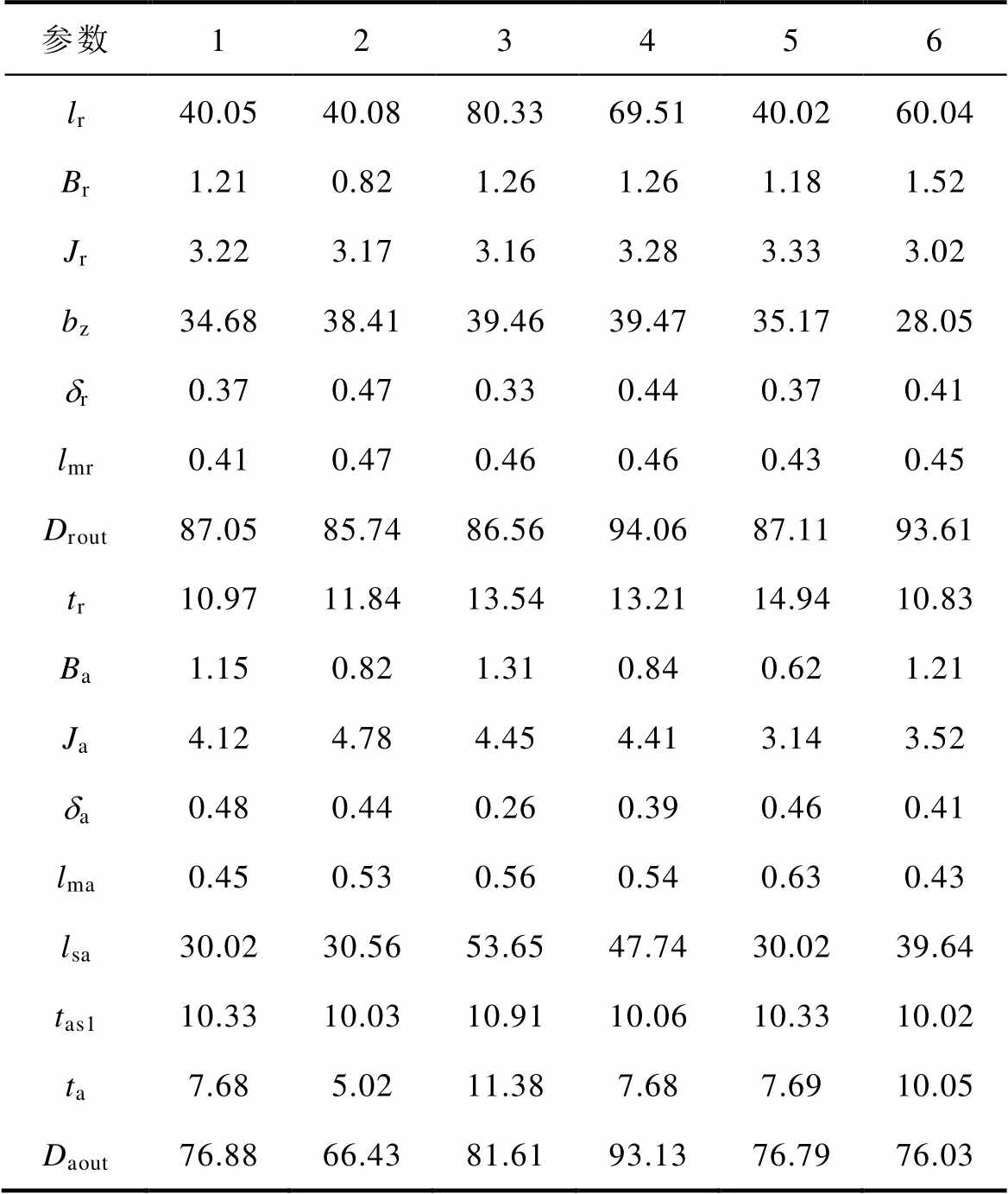
参数123456 lr40.0540.0880.3369.5140.0260.04 Br1.210.821.261.261.181.52 Jr3.223.173.163.283.333.02 bz34.6838.4139.4639.4735.1728.05 dr0.370.470.330.440.370.41 lmr0.410.470.460.460.430.45 Drout87.0585.7486.5694.0687.1193.61 tr10.9711.8413.5413.2114.9410.83 Ba1.150.821.310.840.621.21 Ja4.124.784.454.413.143.52 da0.480.440.260.390.460.41 lma0.450.530.560.540.630.43 lsa30.0230.5653.6547.7430.0239.64 tas110.3310.0310.9110.0610.3310.02 ta7.685.0211.387.687.6910.05 Daout76.8866.4381.6193.1376.7976.03
对相对最优个体单独进行两种评价指标的计算。将计算结果进行整理,相对最优个体的性能对比如图9所示。
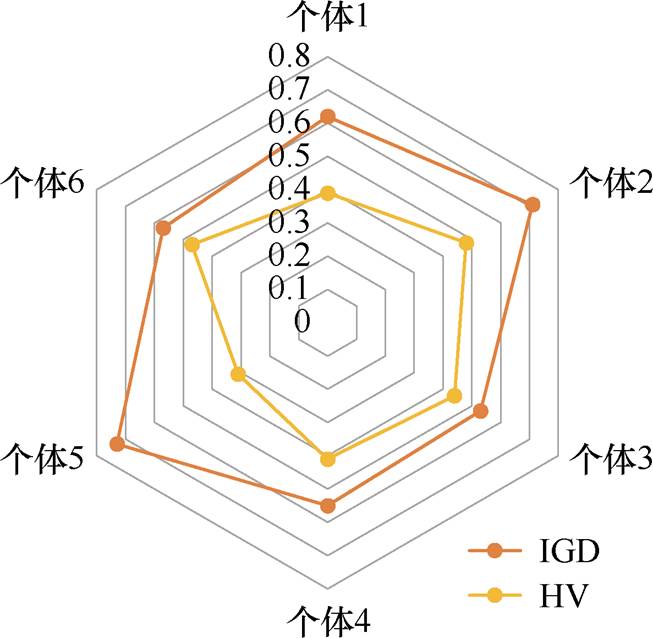
图9 相对最优个体的性能对比
Fig.9 Comparison of performance between relatively optimal individuals
由图9可知,个体6的两项指标都到了最优,所以本文将个体6作为后续小节中多物理场仿真对比分析和实验验证时的参考数据。最后,给出经过150次迭代后的优化结果如图10所示,图中的坐标值为经过归一化后的目标函数值。
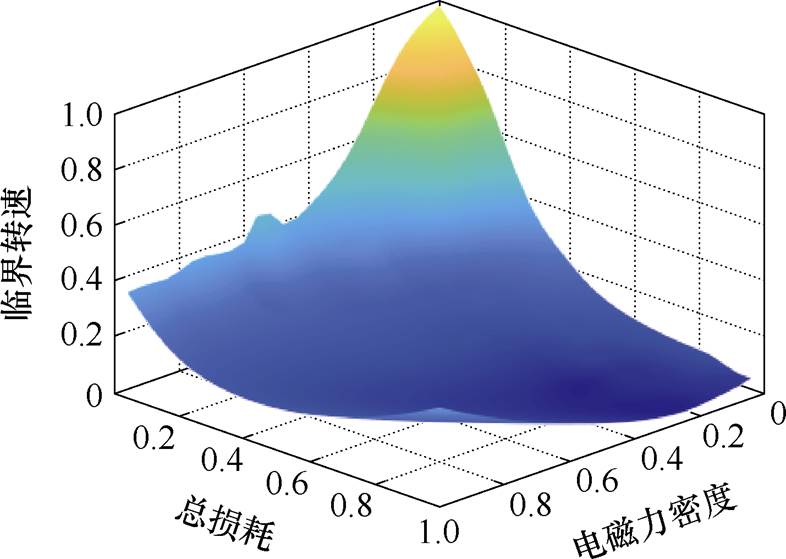
图10 自适应NSGA-Ⅱ的Pareto前沿面
Fig.10 The Pareto frontier of adaptive NSGA-Ⅱ
本小节分别对RAMB和AAMB优化前后的电磁性能进行仿真分析。对于RAMB,由于其结构与传统径向磁通电机类似,因此需在瞬态电磁场且考虑轴向长度的前提下进行计算。RAMB的电磁仿真需分析驱动电机额定转速情况下,仅存在偏置电流时的磁通密度分布情况,仿真所需参数见表3,电磁场仿真结果如图11所示。
表3 RAMB电磁仿真参数
Tab.3 Electromagnetic simulation parameters of RAMB

参 数优化前优化后 主磁极匝数14080 主-副磁极匝数比3:24:3 槽满率(%)4045 偏置电流/A43 气隙长度/mm0.60.4 绕组等效电阻/W2.92.2
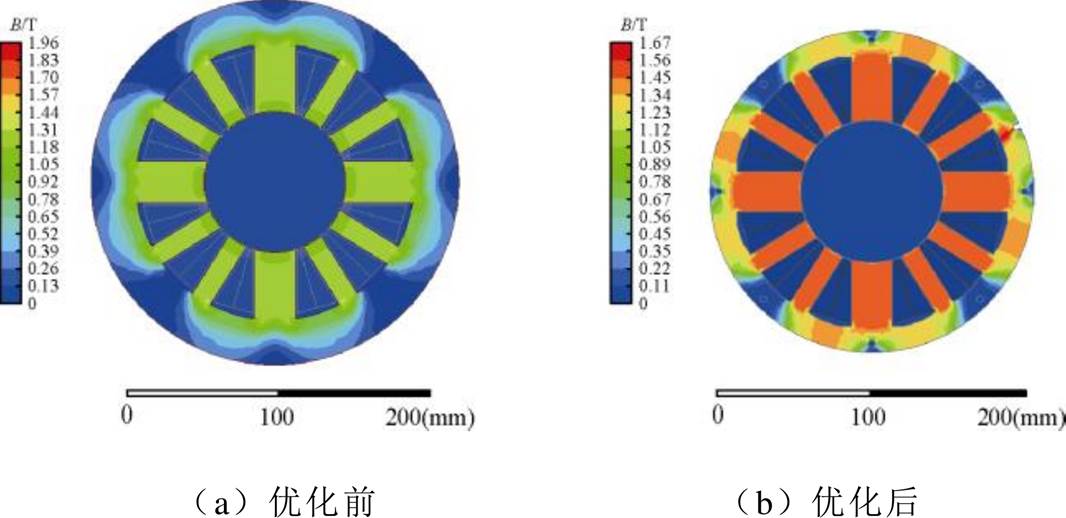
图11 优化前后RAMB的磁通密度云图
Fig.11 Magnetic flux density nephogram of RAMB before and after optimization
RAMB的定子铁心材料为B35A250。由图11和表3可知,优化前后主-副磁极匝数比由3 2变为4
2变为4 3,总体积和总电阻均有所降低;最大磁通密度由1.9 T降低为1.6 T,小于材料的饱和磁通密度;虽然由于体积变化导致的定子平均磁通密度变高,但局部饱和磁通密度降低,因此优化后RAMB的电磁性能得到了提高。
3,总体积和总电阻均有所降低;最大磁通密度由1.9 T降低为1.6 T,小于材料的饱和磁通密度;虽然由于体积变化导致的定子平均磁通密度变高,但局部饱和磁通密度降低,因此优化后RAMB的电磁性能得到了提高。
对于AAMB,由于其无需考虑轴向长度,因此只需在静态电磁场下进行计算。AAMB电磁仿真所需参数见表4,优化前后的仿真结果如图12所示。
表4 AAMB电磁仿真参数
Tab.4 Electromagnetic simulation parameters of AAMB
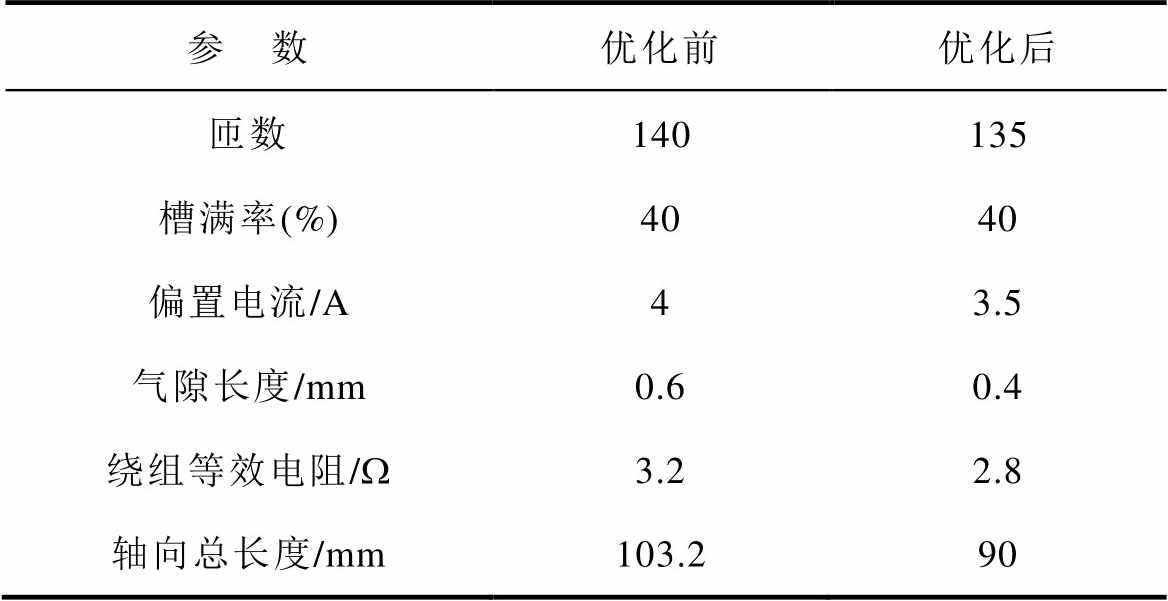
参 数优化前优化后 匝数140135 槽满率(%)4040 偏置电流/A43.5 气隙长度/mm0.60.4 绕组等效电阻/W3.22.8 轴向总长度/mm103.290
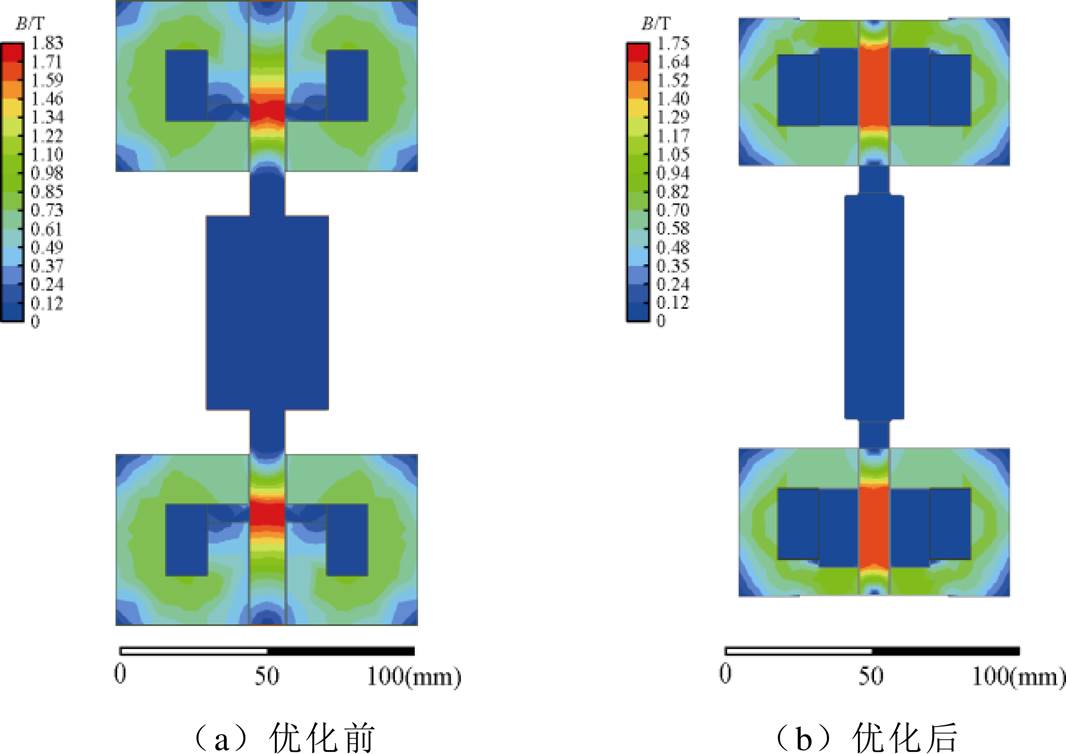
图12 优化前后AAMB的磁通密度云图
Fig.12 Magnetic flux density nephogram of AAMB before and after optimization
AAMB的定子铁心材料为DT4C,与RAMB类似,AAMB优化前后的匝数、体积和绕组电阻均有所降低。由图12可知,优化后的AAMB虽然饱和磁通密度辐射区域有所扩大,但AAMB定子利用率得到了提高,且最大磁通密度由1.82 T降低为1.75 T,可知优化后AAMB的电磁性能同样有所 提高。
应力场仿真主要用于验证2.3节中的两种强度约束,RAMB和AAMB的应力场仿真参数见表5。
表5 RAMB和AAMB应力仿真参数
Tab.5 Stress simulation parameters of RAMB and AAMB (单位: mm)
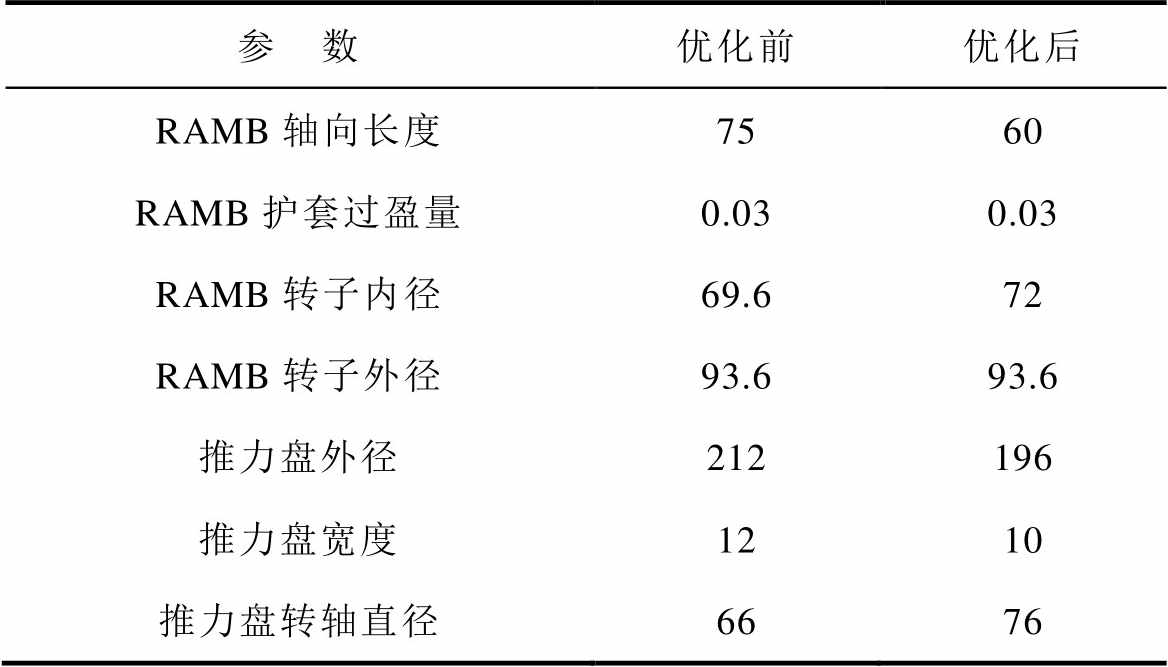
参 数优化前优化后 RAMB轴向长度7560 RAMB护套过盈量0.030.03 RAMB转子内径69.672 RAMB转子外径93.693.6 推力盘外径212196 推力盘宽度1210 推力盘转轴直径6676
对于RAMB,需对其对应的护套部分进行强度校核,假设各面均为有摩擦非理想约束,得到优化前后RAMB的应力场仿真结果如图13所示。
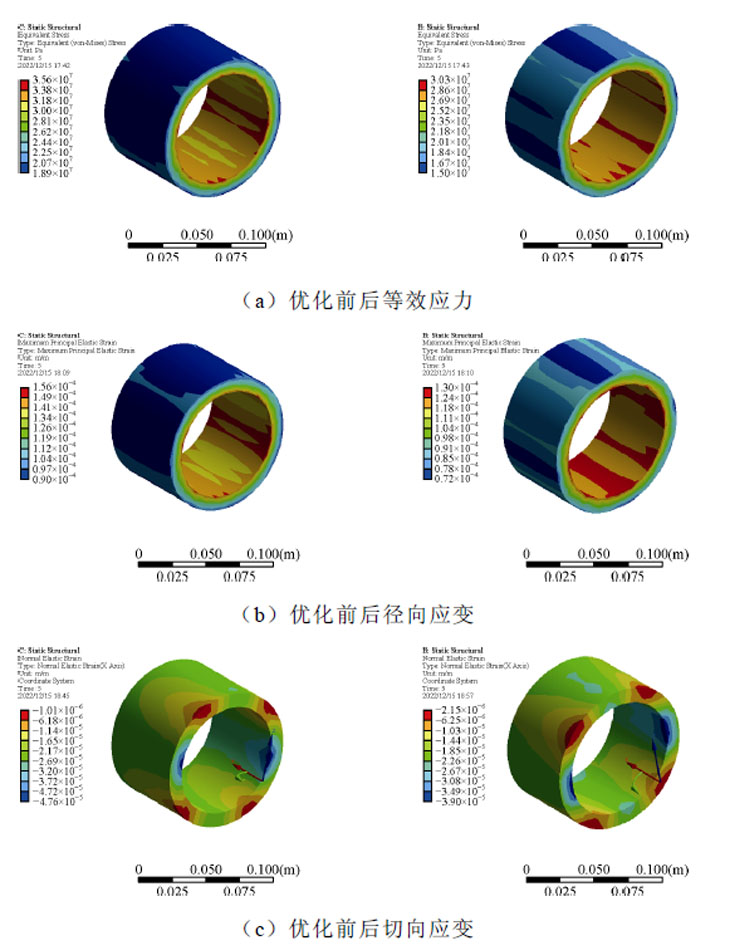
图13 RAMB应力分析对比
Fig.13 Stress analysis and comparison of RAMB
RAMB的应力场仿真条件设定为加载转速在10 s内达到额定转速。由图13a可知,优化后护套所受等效应力由35 MPa降低为30 MPa,远小于护套材料本身的屈服强度。由图13b可知,优化后的护套额定转速下的径向应变最大值由0.16 mm降低为0.13 mm,其形变量在除去辅助轴承后仍在可接受范围内。由图13c可知,优化后的铁心护套额定转速下的切向应变由47 mm减小为39 mm。综上所述,优化后的护套其受力环境得到了改善,且径向应变有所减小,给辅助轴承预留了更多的设计余量。
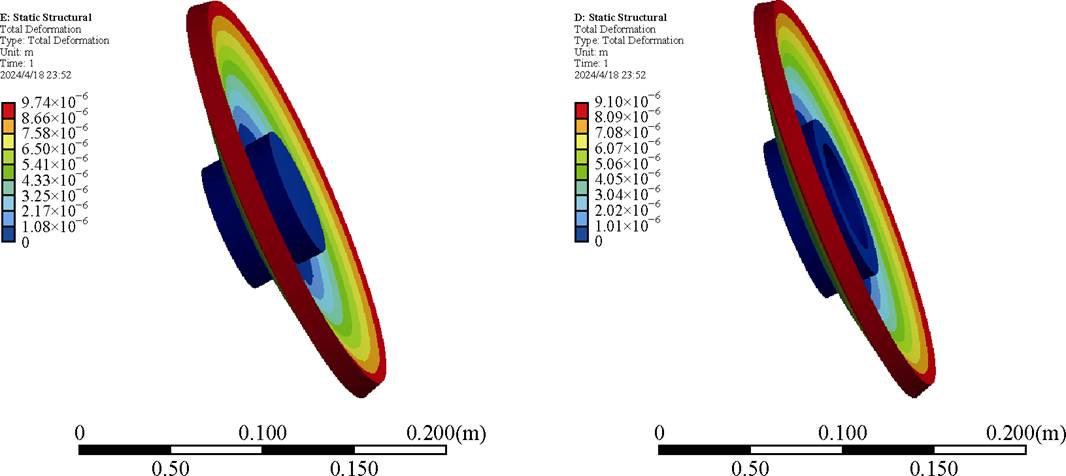
对于AAMB,本文将电磁仿真算得的最大轴向电磁力作为载荷加到推力盘上,同时在推力盘与转轴连接处附加圆柱约束,优化前后的仿真结果如图14所示。
(a)优化前 (b)优化后
图14 AAMB应力分析对比
Fig.14 Stress analysis and comparison of AAMB
由图14可知,优化前后推力盘在额定转速下的最大变形量由9.7 mm减小为9.1 mm,远小于轴向磁轴承本身的气隙长度,因此经过优化后的推力盘其抗压性能得到了提高。
AMBs系统的坎贝尔图和转子动力学仿真对比如图15和图16所示。
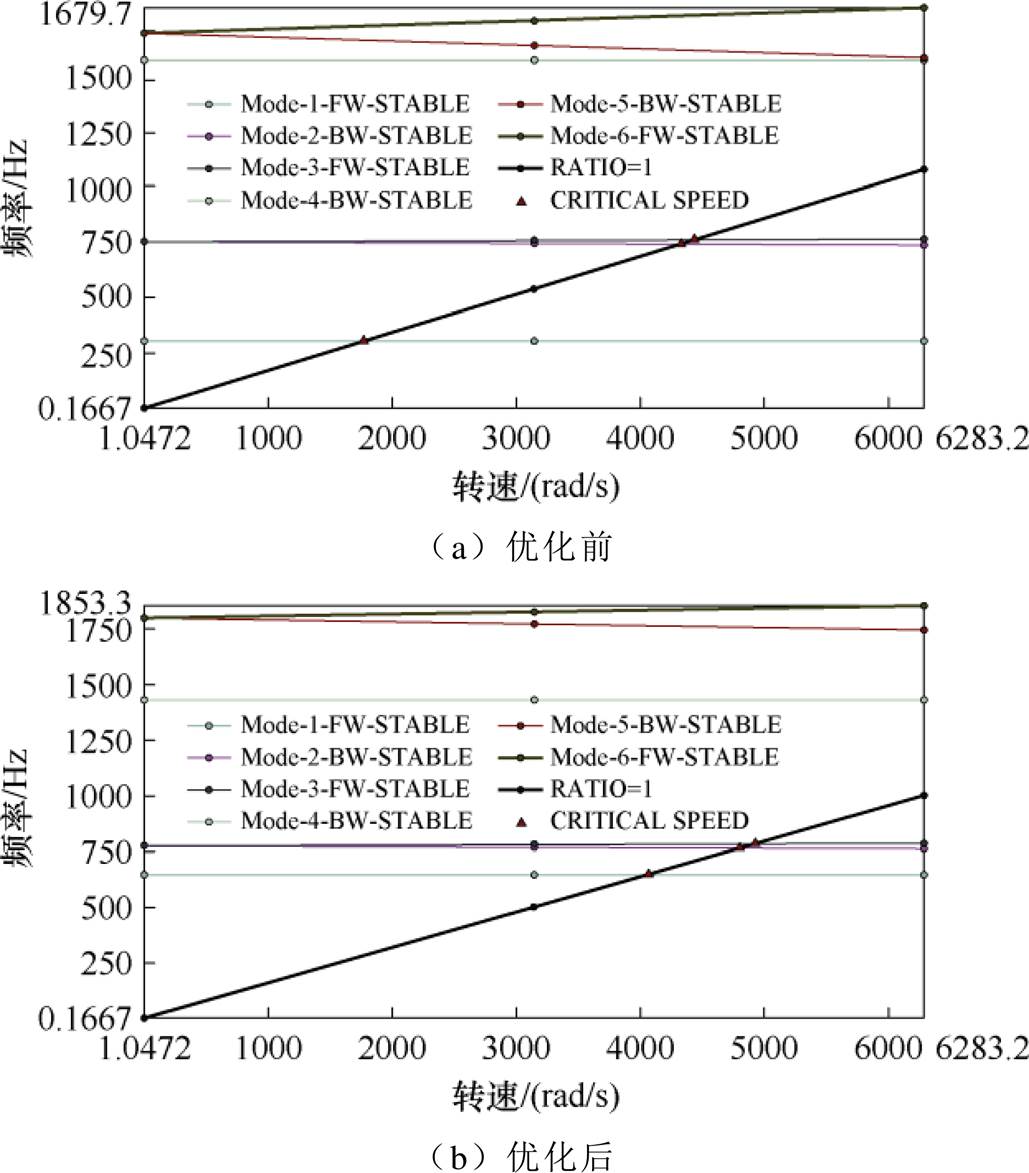
图15 AMBs系统的坎贝尔图
Fig.15 Campbell diagram of AMBs system
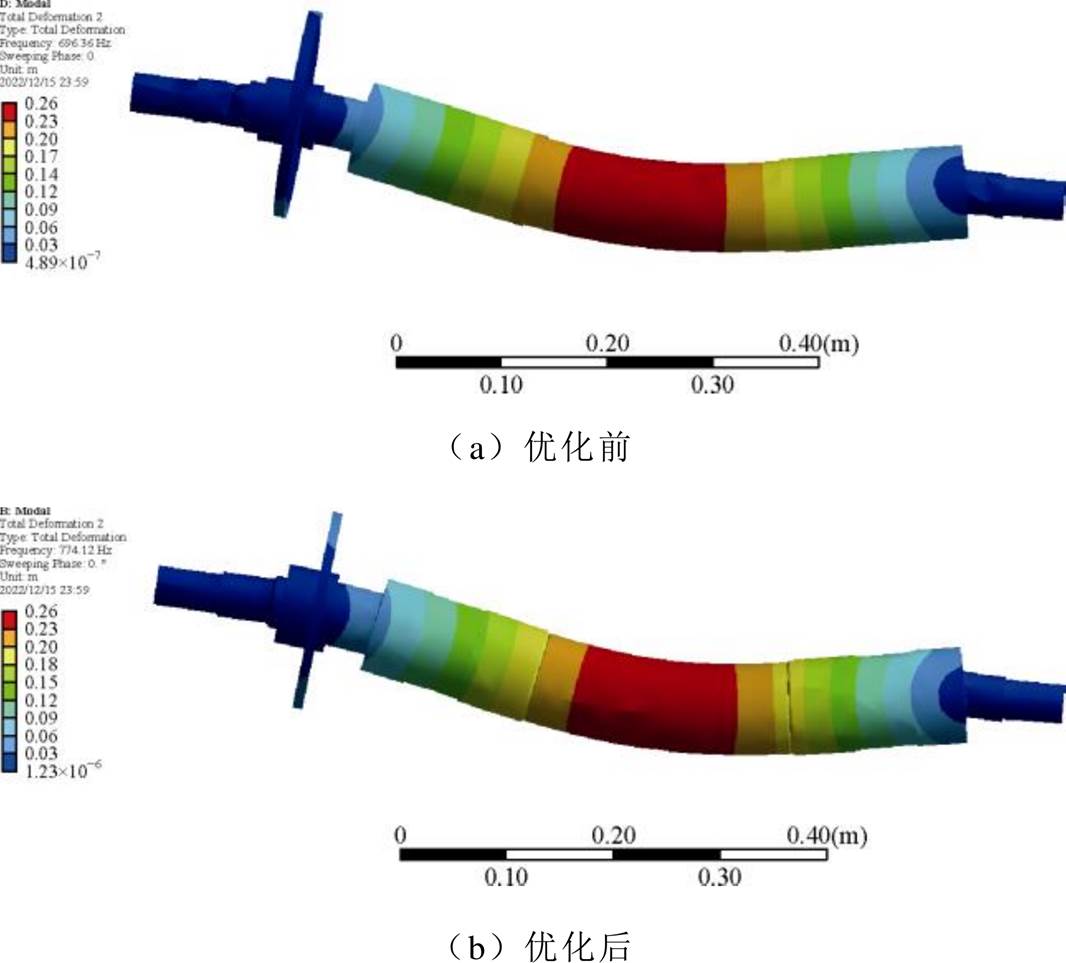
图16 转子动力学仿真对比
Fig.16 Comparison of rotor dynamics simulation
本文的转子动力学仿真主要考虑在RAMB和AAMB都仅处在偏置电流作用下时AMBs提供的电磁力对转子模态带来的影响。转轴材料为42CrMo,优化前后转子轴向总长度由948 mm减少至910 mm。
在仿真时,应如2.3节,一般考虑偏移量不超过气隙长度10%的前提下根据电磁场仿真结果得出的偏置等效电磁力分别计算RAMB和AAMB的等效刚度。不仅如此,本文还在软件中加入与等效刚度相对应的弹性约束,同时在实际辅助轴承所在转轴处的位置增加位移约束。
由图15可知,优化前后转子的平动模态频率由282 Hz提升至647 Hz。由图16可知,优化前后在偏置电流作用下转子一阶模态由696 Hz提升为774 Hz,远大于额定转速,此时AMBs系统全速域均为刚性转子结构。综上所述,本文所提出优化方法可以大幅改善AMBs系统的动力学性能。
由于AMB发热量较同体积驱动电机小得多,因此常采用自然冷却或强迫风冷;且由于与驱动电机共同冷却风道,因此冷却结构上无需额外的设计。与此同时,受轴向长度的影响,驱动电机本身的发热对AMB的影响较小,因此可考虑仅在稳态温度场下分别对RAMB和AAMB进行仿真分析。
温度场仿真中的材料属性除绕组部分选择纯铜以外其余均与转子动力学和应力场仿真相同。在添加热源时需根据电磁场仿真时的损耗结果进行折算,优化前后主要仿真参数见表6,温度场仿真结果如图17所示。
表6 RAMB和AAMB温度场仿真主要参数
Tab.6 Main parameters of temperature field simulation in RAMB and AAMB (单位: kW/m3)
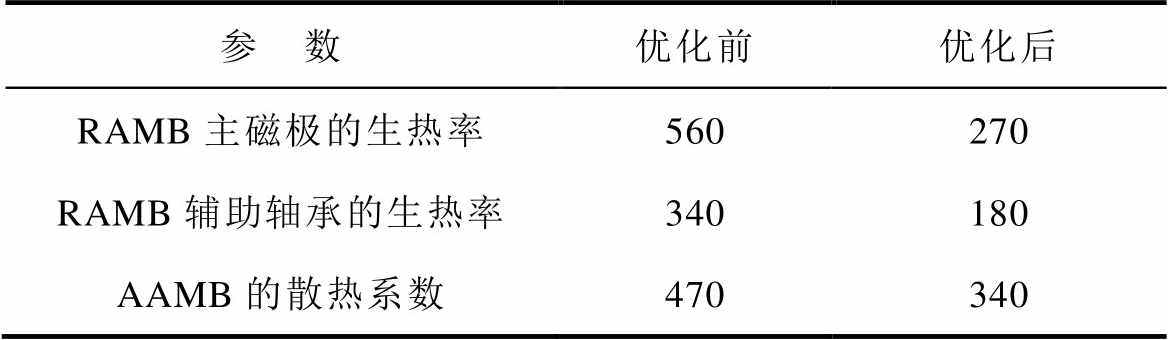
参 数优化前优化后 RAMB主磁极的生热率560270 RAMB辅助轴承的生热率340180 AAMB的散热系数470340
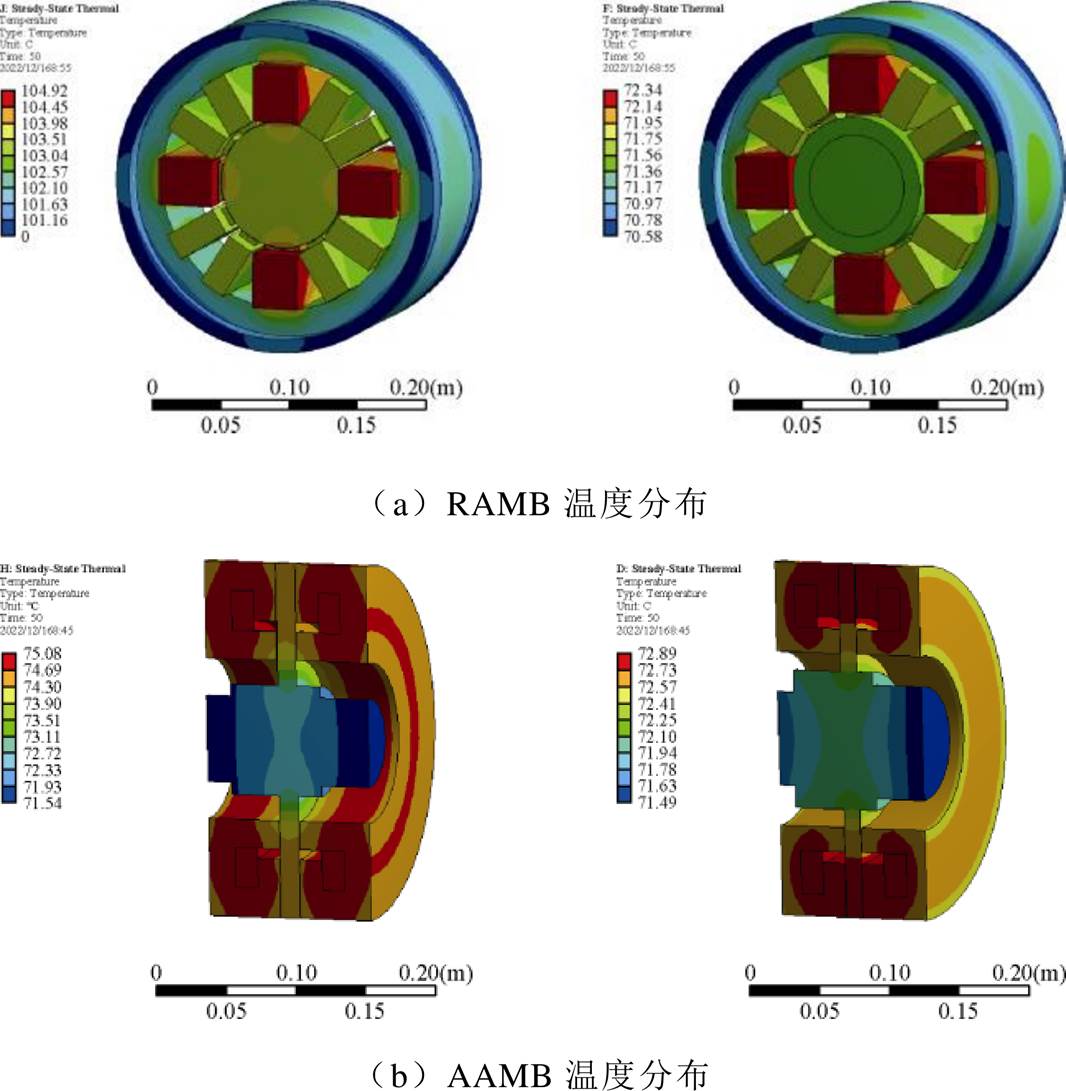
图17 温度场结果对比
Fig.17 Comparison of temperature field Results
由图17可知,优化前后相同时间内RAMB最高温度由105℃降低为72℃,AAMB的最高温度由75℃降低为73℃,经过优化后AMBs的温升均有所降低且在绕组承受范围内。
根据优化后的最终结果制造AMBs样机,与HPMSM组成AMBs系统,并配备各自的控制器搭建了AMBs实验平台。实验平台和AMBs各部件的实物结构如图18所示。

图18 AMBs样机和实验平台
Fig.18 The prototype of AMBs and experimental platform
实验平台中的AMBs控制器采用DSP+FPGA双芯片架构。DSP主要起算法计算和实现作用,FPGA作为开关信号发生器,根据DSP输出的占空比信号实时高效地输出开关信号。
在驱动电机停机状态下,调节控制器参数,使AMBs系统实现由跌落状态到静态悬浮状态的转变,并在稳定悬浮状态下采样至10 s。本文主要通过位移变化反映AMBs的设计结果,RAMB各自由度的位移变化情况如图19所示。
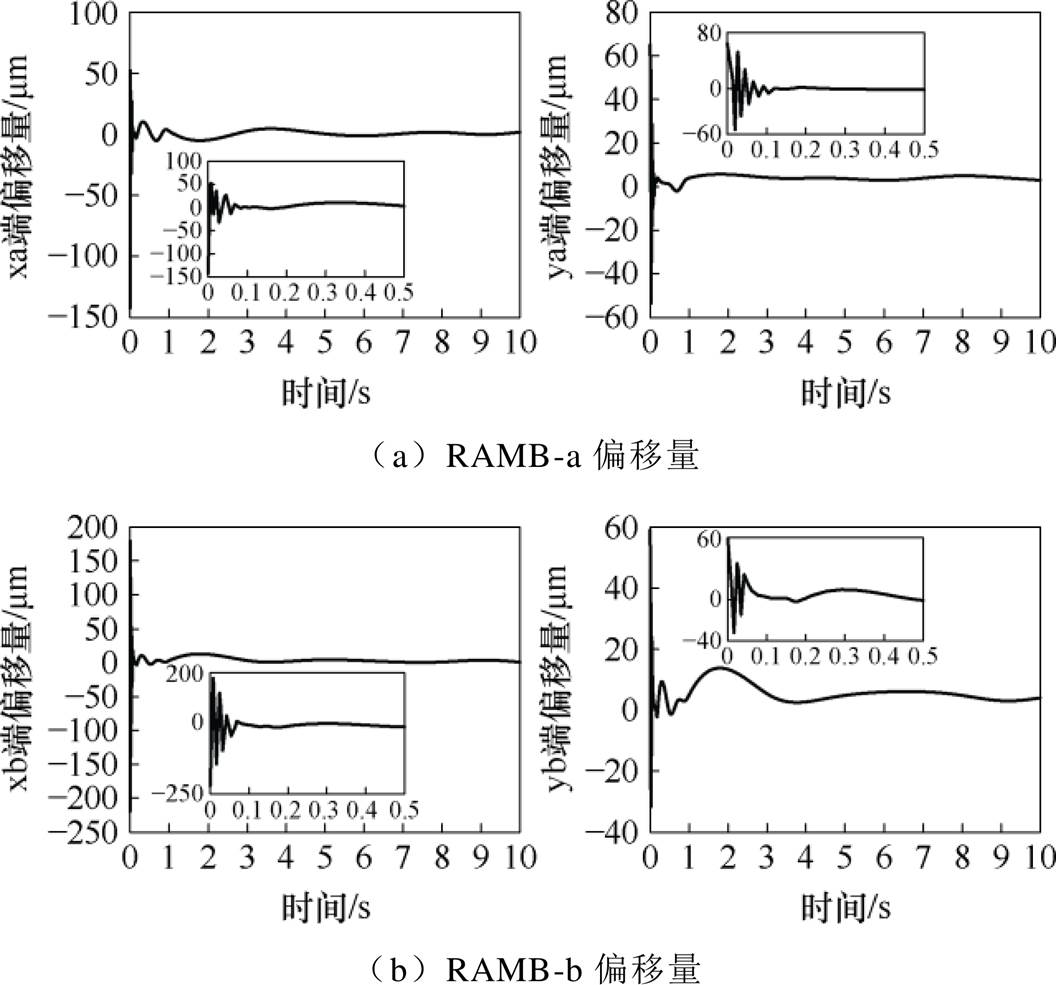
图19 RAMBs位移参数
Fig.19 Displacement parameters of RAMBs
由图19可知,各径向自由度均有一定的初始偏移量,这主要取决于辅助机械轴承由于油膜间隙和生产误差影响所预留的气隙尺寸。本文给出的位移变化情况由电感式传感器实时采样后,提取数据并折算后获得。
由图19的局部放大图可知,各径向自由度均可在0.2 s内达到等幅振荡或衰减振荡的相对稳定状态,且在采样到达10 s时位移波纹较小,这说明所设计的AMBs系统可以实现快速、稳定的静态起浮,且具备良好的静态特性。
本文采用专用环形力传感器测量转子的径向受力情况,并以此得出AMBs系统的静态刚度特性。力传感器测量结果同样表征合力的变化情况,以匹配电感式位移传感器的测量结果。同时由于辅助轴承将占据气隙长度中的0.2 mm,因此计算和实际测量结果中的位移范围将小于设计气隙长度。在保证转子稳定悬浮的前提下,测量转子在不同位移和电流下的刚度特性,同时与优化前的设计结果相对比,对比结果如图20所示。
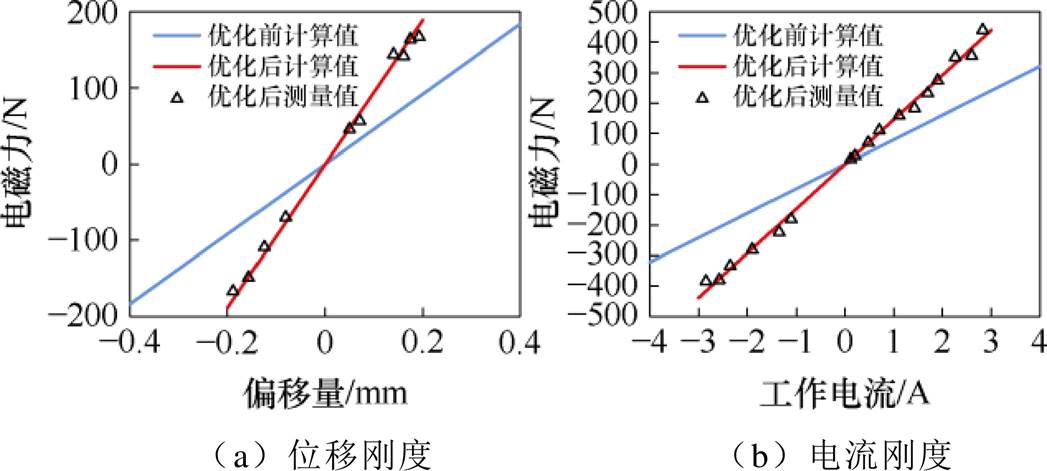
图20 AMBs刚度特性测量结果
Fig.20 Measurement results of stiffness characteristics of AMBs
由图20可知,AMBs在起浮4 s后达到相对稳定阶段,优化前后的偏置电流分别为4 A和3 A。优化后的位移刚度特性和优化前相比由459 N/mm变为943 N/mm,提高了105.4%。与此同时,电流刚度由80.4 N/A变为146 N/A,提高了81.6%。将刚度参数代入,可算得优化后电磁力体密度约为318 572 N/m3。两种类型的刚度特性优化后的测量值和计算值相比误差分别为位移刚度5.8%、电流刚度7.3%。综上所述,所提出的优化方法对于AMBs系统的刚度特性有着显著提升。
本文采用热像仪分别在HPMSM驱动频率为0、50、100、150和200 Hz时测量AMBs的温升,采样点为RAMB-b所在转轴端部,实验结果如图21所示。
由图21可知,在HPMSM驱动频率为200 Hz时转轴端部温度为83℃,在允许范围内,即经过优化后AMBs系统的总损耗在合理范围内。
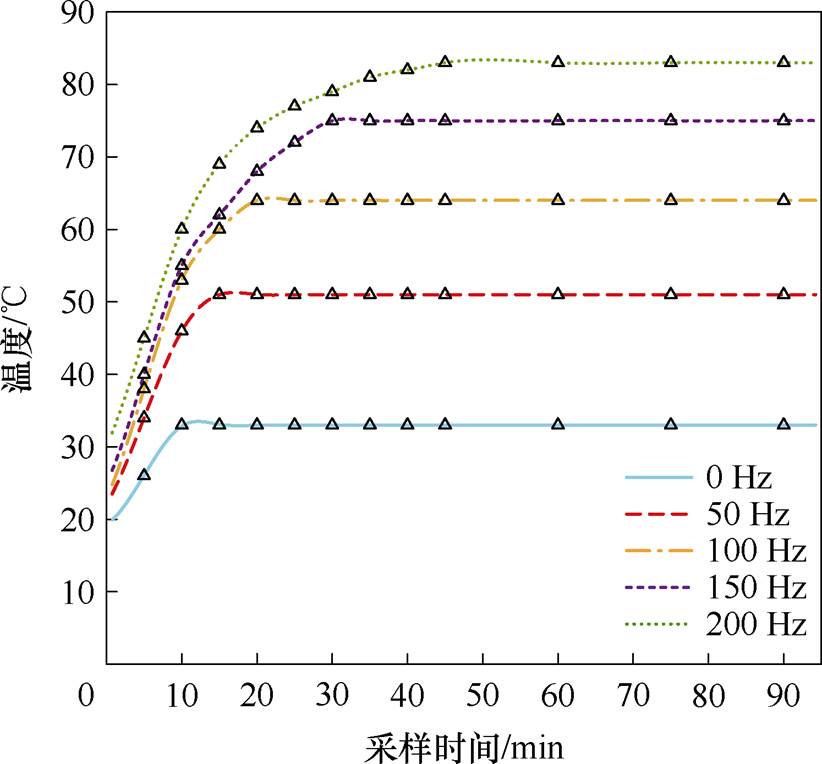
图21 AMBs系统温升测量结果
Fig.21 Temperature rise measurement results of AMBs system
本文针对AMBs系统的优化设计问题进行研究,为解决多物理场分析方法难以收敛以及多目标优化方法的参数合理性问题,提出了一种多物理场的AMBs系统自适应NSGA-Ⅱ。首先,通过改进传统NSGA-Ⅱ,对其选择、交叉变异以及精英保留过程赋予自适应特性,使其随迭代次数等算法参数变化而变化,达到了算法上的全局最优。其次,将所提出自适应NSGA-Ⅱ与多物理优化方法相结合,使得参数始终处在合理范围内,并使得算法本身快速接近相对最优结果,提高了计算效率的同时也极大提升了收敛速度,为混合励磁AMB和无轴承电机的优化设计提供了参考。
参考文献
[1] 李万杰, 张国民, 王新文, 等. 飞轮储能系统用超导电磁混合磁悬浮轴承设计[J]. 电工技术学报, 2020, 35(增刊1): 10-18.
Li Wanjie, Zhang Guomin, Wang Xinwen, et al. Integration design of high-temperature super- conducting bearing and electromagnetic thrust bearing for flywheel energy storage system[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 10-18.
[2] 陈信维, 李红伟, 任宗强, 等. 基于模和阻抗角的自感式位移传感器阻抗建模[J]. 电工技术学报, 2025, 40(2): 387-391.
Chen Xinwei, Li Hongwei, Ren Zongqiang, et al. Improved impedance modeling of self-inductive displacement sensor based on the modulus and angle of the coil impedance[J]. Transactions of China Electrotechnical Society, 2025, 40(2): 387-391.
[3] 刘奇, 苏振中, 姜豪, 等. 基于Bang-Bang+前馈策略的磁轴承执行器失效故障容错控制[J]. 电工技术学报, 2023, 38(1): 177-189.
Liu Qi, Su Zhenzhong, Jiang Hao, et al. Fault tolerant control of magnetic bearing actuator failure based on Bang-Bang + feedforward strategy[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 177-189.
[4] 刘奇, 苏振中, 姜豪, 等. 考虑部分通道故障的磁轴承系统动态承载力分析[J]. 电工技术学报, 2023, 38(10): 2625-2636.
Liu Qi, Su Zhenzhong, Jiang Hao, et al. Dynamic capacity analysis of active magnetic bearing system with partial channel failure[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2625-2636.
[5] 戈宝军, 杨子豪, 陶大军, 等. 计及磁路分布特性的电磁轴承解析模型建立与支撑性能影响因素研究[J]. 电工技术学报, 2023, 38(8): 2025-2035, 2085.
Ge Baojun, Yang Zihao, Tao Dajun, et al. Establish- ment of analytical model of active magnetic bearing considering magnetic circuit distribution characteri- stics and study on influencing factors of support performance[J]. Transactions of China Electro- technical Society, 2023, 38(8): 2025-2035, 2085.
[6] Le Yun, Wang Di, Zheng Shiqiang. Design and optimization of a radial magnetic bearing considering unbalanced magnetic pull effects for magnetically suspended compressor[J]. IEEE/ASME Transactions on Mechatronics, 2022, 27(6): 5760-5770.
[7] Jastrzebski R P, Liukkonen O. Analysis of a segmented axial active magnetic bearing for multi- MW compressor applications[J]. IEEE/ASME Transa- ctions on Mechatronics, 2023, 28(5): 2799-2809.
[8] Han Xue, Liu Gang, Le Yun, et al. Unbalanced magnetic pull disturbance compensation of magnetic bearing systems in MSCCs[J]. IEEE Transactions on Industrial Electronics, 2023, 70(4): 4088-4097.
[9] 胡余生, 李立毅, 郭伟林, 等. 磁悬浮制冷离心压缩机停机气流冲击抑制研究[J]. 电机与控制学报, 2022, 26(1): 24-31.
Hu Yusheng, Li Liyi, Guo Weilin, et al. Study on suppression of airflow impact during shutdown of magnetic suspension refrigeration centrifugal com- pressor[J]. Electric Machines and Control, 2022, 26(1): 24-31.
[10] Wang Kun, Ma Xin, Liu Qiang, et al. Multiphysics global design and experiment of the electric machine with a flexible rotor supported by active magnetic bearing[J]. IEEE/ASME Transactions on Mechatro- nics, 2019, 24(2): 820-831.
[11] 戴睿, 张岳, 王惠军, 等. 基于多物理场近似模型的高速永磁电机多目标优化设计[J]. 电工技术学报, 2022, 37(21): 5414-5423.
Dai Rui, Zhang Yue, Wang Huijun, et al. Multi- objective optimization design of high-speed per- manent magnet machine based on multi-physics approximate model[J]. Transactions of China Elec- trotechnical Society, 2022, 37(21): 5414-5423.
[12] 孙超, 张昆仑. 基于遗传算法的悬浮电磁铁磁热耦合参数优化[J]. 电气工程学报, DOI: 10.11985/2024. 02.037.
Sun Chao, Zhang Kunlun. Optimization of magneto- thermal coupling parameters of suspension electro- magnet based on genetic algorithm[J]. Journal of Electric Engineering, DOI: 10.11985/2024.02.037.
[13] Moser R, Sandtner J, Bleuler H. Optimization of repulsive passive magnetic bearings[J]. IEEE Transactions on Magnetics, 2006, 42(8): 2038-2042.
[14] Lijesh K P, Hirani H. Optimization of eight pole radial active magnetic bearing[J]. Journal of Tribo- logy, 2015, 137(2): 024502.
[15] Cheng Shanbao, Olles M W, Burger A F, et al. Optimization of a hybrid magnetic bearing for a magnetically levitated blood pump via 3-D FEA[J]. Mechatronics, 2011, 21(7): 1163-1169.
[16] Liu Xu, Han Bangcheng. The multiobjective optimal design of a two-degree-of-freedom hybrid magnetic bearing[J]. IEEE Transactions on Magnetics, 2014, 50(9): 8101914.
[17] Han Bangcheng, Xu Qinjie, Yuan Qian. Multiobje- ctive optimization of a combined radial-axial mag- netic bearing for magnetically suspended com- pressor[J]. IEEE Transactions on Industrial Electro- nics, 2016, 63(4): 2284-2293.
[18] Jin Zhijia, Sun Xiaodong, Chen Long, et al. Robust multi-objective optimization of a 3-pole active magnetic bearing based on combined curves with climbing algorithm[J]. IEEE Transactions on Indu- strial Electronics, 2022, 69(6): 5491-5501.
[19] Singh S S, Kumar P. Finite element analysis and optimization of active magnetic bearings for contra- rotating coaxial rotor system[J]. Indian Journal of Engineering and Materials Sciences, 2022, 29(4): 470-480.
[20] Yadav V K, Kumar P, Bhushan G. A novel approach for design optimisation of radial active magnetic bearing[J]. Australian Journal of Mechanical Engin- eering, 2023, 21(5): 1461-1473.
[21] Schaffer J D. Some experiments in machine learning using vector evaluated genetic algorithms[D]. Tenne- ssee: Vanderbilt University Electrical Engineering, 1984.
[22] Fonseca C M, Fleming P J. Genetic algorithm[C]// Proceedings of the Fifth International Conference, San Mateo, USA, 1993: 416-423.
[23] Zitzler E, Thiele L. Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach[J]. IEEE Transactions on Evolu- tionary Computation, 1999, 3(4): 257-271.
[24] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.
[25] 郑金华. 多目标进化算法及其应用[M]. 北京: 科学出版社, 2007: 57-63.
[26] 王嵘冰, 徐红艳, 郭军. 自适应的非支配排序遗传算法[J]. 控制与决策, 2018, 33(12): 2191-2196.
Wang Rongbing, Xu Hongyan, Guo Jun. Adaptive non-dominated sorting genetic algorithm[J]. Control and Decision, 2018, 33(12): 2191-2196.
[27] Mechanical vibration-vibration of rotating machinery equipped with active magnetic bearings-part 2: evaluation of vibration: ISO 14839-2-2004[S]. 2004.
[28] 倪振华. 振动力学[M]. 西安: 西安交通大学出版社, 1989.
Abstract Active magnetic bearing is a widely used supporting component in the industrial field. With the arrival of the wave of economic recovery, the trend of “high-speed” and “high-efficiency” in the industrial field has become increasingly apparent, which undoubtedly puts higher requirements on the performance of supporting components such as active magnetic bearings. Among numerous active magnetic bearing optimization design methods, traditional finite element methods generally suffer from high model complexity and slow calculation speed. On the other hand, although traditional multi-objective optimization methods have improved computational speed, they are prone to convergence issues due to the algorithm being trapped in local optima. Therefore, after careful consideration, an adaptive multi-objective optimization method based on the multi-physics field is proposed.
Firstly, the electromagnetic design process of a high-speed permanent magnet synchronous motor provides the basic design process of an active magnetic bearings system. In addition, taking the twelve-pole radial active magnetic bearing and the concentric single-ring axial active magnetic bearing as examples, specific formulas related to the design process are provided.
Secondly, comprehensive optimization is carried out on NSGA-Ⅱ, and the optimized NSGA-Ⅱ is combined with multi-physics fields to achieve a cyclic optimization process of real-time variable range correction. During the sorting process, the improved “super dominated” sorting method is chosen. Different adaptive rules with non-dominated levels and iteration times as variables are proposed in the selection process, crossover and mutation process, and retention process to ensure population diversity and adaptability in optimization.
Then, based on the operating conditions of the active magnetic bearings system, four main constraint forms were proposed: volume constraint, stiffness constraint, rotor strength constraint of radial active magnetic bearing, and thrust disc strength constraint of axial active magnetic bearing. Furthermore, the electromagnetic force density, total loss of the active magnetic bearings system, and critical speed are regarded as optimization objectives.
Then, using hypervolume and inverted general distance as performance indicators, the two optimization methods are compared, taking the ZDT problem as an example. The results show that compared with traditional NSGA-Ⅱ, the adaptive multi-objective optimization method not only converges faster but also reduces the time complexity from O(3×1002) to O(300×lg300).
Finally, the results before and after optimization are compared through multi-physics field simulation, and an experimental platform is built to compare the parameter changes of each optimization objective. Taking radial active magnetic bearing as an example, the optimized displacement stiffness coefficient increases by 105.4% from 459 N/mm to 943 N/mm. At the same time, the current stiffness coefficient increases from 80.4 N/A to 146 N/A with an increase of 81.6%. The error between the measured and calculated values after optimizing the displacement stiffness coefficient is 5.8%, and the error after optimizing the current stiffness coefficient is 7.3%. The simulation and experimental results demonstrate that the proposed adaptive multi-objective optimization method can ensure global optimization and fast convergence in active magnetic bearings systems.
keywords:Active magnetic bearings, multi-objective optimization, high-speed permanent magnet synchronous motor, genetic algorithm
DOI: 10.19595/j.cnki.1000-6753.tces.240207
中图分类号:TH133.3;TM351
收稿日期 2024-01-30
改稿日期 2024-02-29
徐煜昊 男,1993年生,博士研究生,研究方向为磁悬浮轴承优化设计及控制。E-mail: yuhao_xu@tju.edu.cn(通信作者)
王晓远 男,1962年生,教授,博士生导师,研究方向为电机及其系统设计、电机电磁场分析及计算、永磁电机及其应用、特种电机设计等。E-mail: xywang62@tju.edu.cn
(编辑 崔文静)