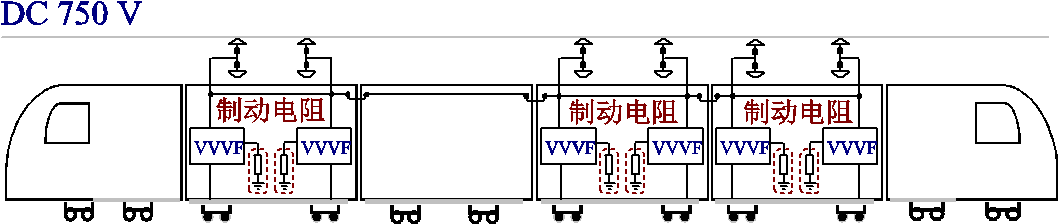
图1 车载制动电阻安装示意图
Fig.1 Installation of on-board braking resistors
摘要 传统的基于网压或者人工智能算法的控制策略虽然可以使车载储能装置制动能量具有一定的回收效果，但是却存在忽略了储能元件自身充放电特性、模型建立复杂、难以求解最优策略的解析解等问题。为此，该文提出基于等效面积法的车载储能装置控制策略。在储能装置的充电阶段，为了保证最优的节能效果，以储能装置的功率作为状态变量，通过选取最优的初始电压和充电电流，使列车制动功率曲线与储能装置充电功率曲线所围面积最大。储能装置的放电阶段，在保证储能装置的放电截止电压在列车牵引结束时达到最优充电初始值的前提下，选取合适的放电电流使列车牵引功率曲线与储能装置放电功率曲线面积差的最大高度最小，此时车载储能装置的“填谷”效果最佳。该策略从列车的牵引制动特性出发，不仅充分考虑了储能元件的充放电特性，而且模型简单、计算量小、且易于求解得到最优控制策略的解析解，从而可以充分发挥储能装置的充放电能力。算例分析结果表明，相较于传统的基于网压的双环PI控制策略，所提的控制策略可以进一步提升储能装置的充放电量，节能效果显著。
关键词：城市轨道交通 车载储能装置 制动能量回收 控制策略 等效面积法
近年来随着城市轨道交通线网规模的快速扩大，其能耗问题也日益突出。据不完全统计，2022年全国城市轨道交通总电能耗为227.92亿kW×h，其中牵引能耗为113.15亿kW×h，两项数据均创历史新高[1]。而北京、上海的城市轨道交通年耗电量已超过20亿kW×h。在我国积极推进“碳达峰·碳中和”目标的大背景下，深入挖掘城市轨道交通节能减排的潜力将极大地促进低碳交通运输体系建设，助力“双碳”目标的实现[2-3]。
由于城市轨道交通具有运量大、发车间隔短、列车启停频繁等特点，城轨列车在制动时会产生大量的制动能量，约占列车牵引能耗的50%左右[4]。因此高效利用列车的制动能量是降低城市轨道交通系统总能耗的有效手段之一[5]。然而，目前城市轨道交通牵引变电站普遍采用二极管单向整流方式，列车的再生制动能量无法反馈到交流电网[6-7]。为避免发生再生失效，制动列车往往采取投入车载制动电阻吸收再生制动能量的措施。此时，制动能量将通过制动电阻以热能的形式进行耗散。这种方式不仅无法有效利用列车的再生制动能量，造成能量的浪费，还会由于增加发热量导致隧道内的温升[8]。
随着储能技术及电力电子技术的发展，利用储能装置高效回收城轨列车的再生制动能量成为近年来的研究热点[9-10]。通过将列车制动时的能量先存储在超级电容、电池等储能介质中，而后在列车牵引时进行释放，由此实现高效回收利用列车再生制动能量的目的[11]。
与将储能装置安装在变电站（即地面储能）的方式不同，文献[12]提出在不额外增加质量和体积的前提下，利用车载储能装置取代原有车载制动电阻的设计方案。该方案不仅可以有效避免前述所提的投入车载制动电阻的各种弊端，还可以使储能装置更好地匹配列车的运行特性，消除地面储能装置在能量传输时因线路电阻引起的损耗，高效回收列车再生制动能量[13]。此外，在牵引供电系统发生故障时，车载储能装置还可对列车进行应急牵引，将乘客运送至临近的车站，提高城轨系统运营的可靠性和安全性[14]。因此，该方案具有很好的应用前景。
利用储能装置回收城轨列车再生制动能量的一个关键问题是储能装置的控制策略。科学合理的控制策略可以充分发挥储能装置的充放电能力，实现良好的节能稳压效果。有学者对车载储能装置控制策略进行了相关研究。文献[15]针对车载超级电容储能系统，提出了一种间接电流控制策略。在传统电压电流双闭环控制结构的基础上，通过控制线网电流来间接给定充放电电压阈值。该策略虽然可以在一定程度上抑制列车受电弓处的电压波动，但是却无法保证达到的节能稳压效果最优。文献[16]以车载储能装置及制动电阻的输出功率作为决策变量，通过建立优化模型来最小化列车受电弓处的电压波动。文献[17]利用混合整数线性规划模型同时优化列车运行曲线和车载储能装置充放电功率，以实现系统净能耗最低。然而上述两个模型均直接以储能装置功率作为优化变量，忽略了储能元件自身的充放电特性，因此模型中关于储能装置功率的约束与实际情况存在偏差。文献[18]同时考虑列车能耗、受电弓电流、列车速度波动、超级电容SOC、超级电容充放电电流及充放电次数六个目标，通过划分区段将运行过程离散化，并采用动态规划求解最优的列车运行模式以及超级电容工作模式。由于该模型的求解精度取决于对运行区间以及决策变量的离散化程度，因而模型的精细解的求解时间较长。文献[19]基于对城轨列车能耗数据的短期及长期预测，采用Takagi-Sugeno模糊控制器结合差分进化算法，对车载超级电容的输出功率进行优化。文献[20]则针对混合储能系统提出了一种基于深度强化学习在线序列决策的动态功率分配策略，旨在降低系统能耗的同时延长储能系统寿命。上述基于智能算法的控制策略虽然能在一定程度上实现节能稳压效果，但是却无法给出特定工况下储能装置最优控制策略的解析解。
为此，本文从城轨列车牵引制动特性的角度出发，以车载储能装置的初始电压和充放电电流作为优化变量，提出一种基于等效面积法的车载储能装置控制策略。充电过程通过建立数学优化模型使车载储能装置的节能量最大，即最大化列车制动功率曲线与车载储能装置充电功率曲线所围成的面积；放电策略则是在保证车载储能装置电压在列车牵引结束达到预设值的前提下，使两条功率曲线面积差的最大高度最小，即“填谷”效果最好。与其他策略相比，该优化模型不仅充分考虑了列车的牵引制动特性以及储能元件的充放电特性，而且结构简单、计算量小，并且易于求解得到最优控制策略的解析解。
目前常用的储能装置有超级电容、锂离子电池和飞轮。与其他储能元件相比，超级电容具有循环寿命长、功率密度大、安全性能高等优势。为了匹配城轨列车牵引制动功率大，频繁启停的运行特性并满足对车载储能装置安全性的要求，本文选用超级电容作为车载储能元件。
以三动三拖编组列车为研究对象，其编组形式如图1所示，每节动车上安装两套车载制动电阻。在利用车载储能装置替代原有的车载制动电阻时，为了减少对列车原有布局的改动，采用分散式安装方案，即以单套车载制动电阻的质量和体积为约束条件，分别将每套储能装置安装在原制动电阻箱的位置，如图2所示[4]。具体的设计步骤可参照文献[4]，此处不再赘述。
图1 车载制动电阻安装示意图
Fig.1 Installation of on-board braking resistors
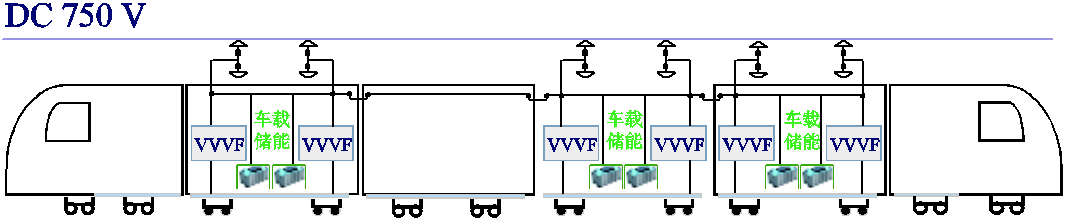
图2 车载储能装置分散安装示意图
Fig.2 Decentralized installation of on-board energy storage systems
典型的城轨列车牵引制动特性曲线如图3所示。列车牵引时，电机主要经历恒转矩区、恒功区和自然特性区三个阶段[21]。恒转矩区电机的牵引力为恒定值，牵引功率随着速度的增加而逐渐增大；当功率达到最大值后，电机进入恒功区，此时电机功率为恒定值，其转矩与速度成反比；当处于自然特性区时，电机转矩与速度二次方成反比。而列车的制动特性曲线通常只包括恒转矩区和自然特性区两部分，且转折速度V3接近列车的最高设计时速[22]。
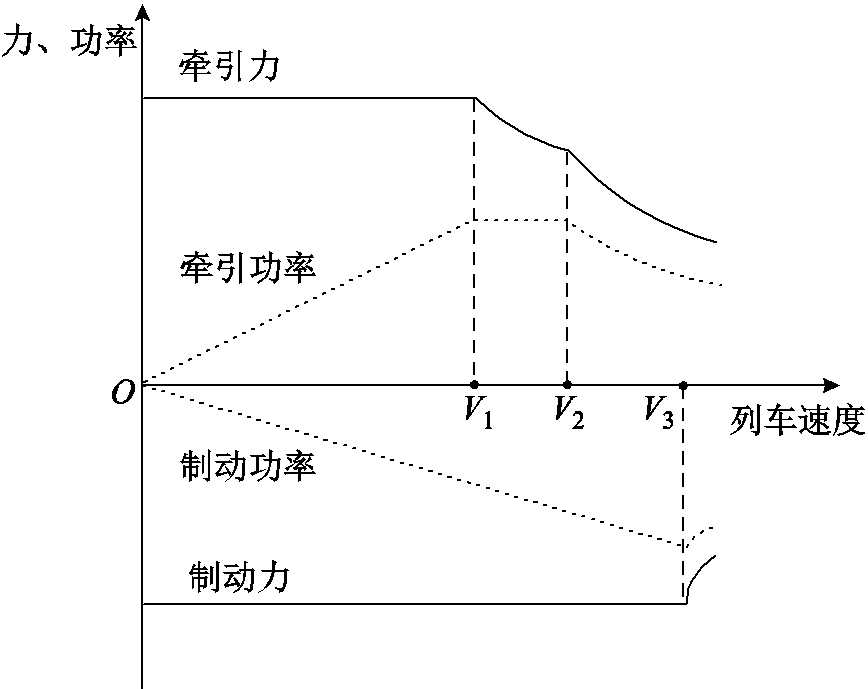
图3 列车牵引制动特性曲线
Fig.3 Traction and braking characteristic curves of urban rail trains
对于电容C而言，通过的电流i与电压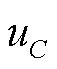
的变化率成正比[23]，即。
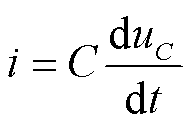（1）
若电流i为恒定值，由式（1）可得电容电压与电流关系为
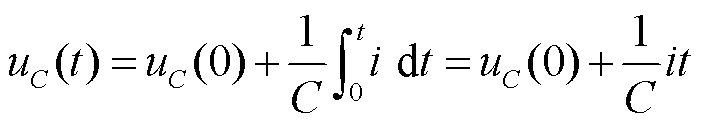（2）
在电流和电压关联参考方向下，电容在时刻t的功率为
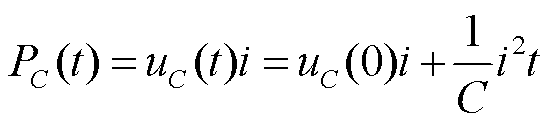（3）
在0～t时段，电容吸收的能量为
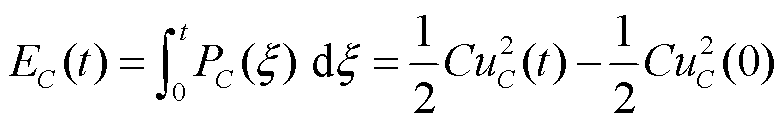（4）
由式（3）和式（4）可知，对于超级电容而言，在截止电压一定的条件下，其功率与可吸收的能量是相互矛盾的。若超级电容的初始电压低，其对应的功率也低，但是可吸收的能量大；反之，若超级电容的初始电压高，其对应的功率也高，但是可吸收的能量小。因此，在利用车载储能装置回收城轨列车的再生制动能量时，如何设置合理的初始电压及充放电电流来平衡超级电容的功率与可吸收能量，以达到最优的节能效果，是一个值得研究的问题。
车载储能装置在列车牵引时进行放电，在列车制动时进行充电。本文将列车功率曲线分割为“制动”+“牵引”两部分，对储能装置的充放电过程分别进行研究。
列车实际运行时的最高速度一般低于图3中的V3，因而列车制动过程中电机一直运行于恒转矩区，此时制动功率与时间近似呈线性关系。由图3及式（3）可得列车制动功率曲线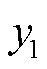
以及超级电容充电功率曲线f1如图4所示，其对应的表达式分别为
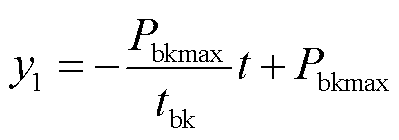（5）
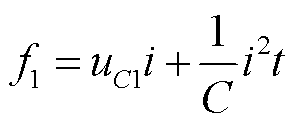（6）
式中，Pbkmax为列车的峰值制动功率；tbk为制动时长；uC1为制动开始时超级电容的初始电压；i为超级电容的充电电流。
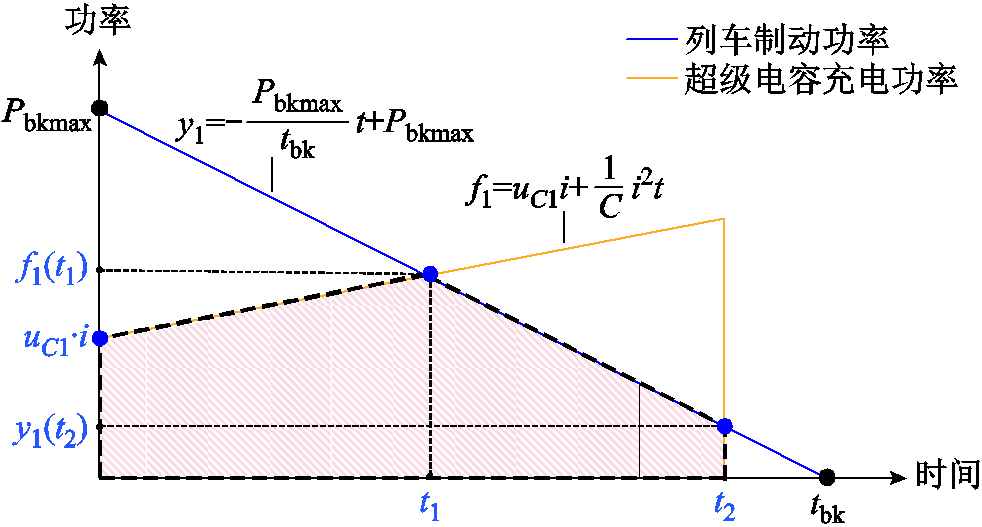
图4 制动过程中列车及超级电容的功率曲线
Fig.4 Power profiles of the train and the supercapacitor during braking
图4中，t1为超级电容功率等于列车制动功率的时刻，令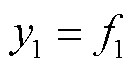
，可求得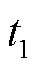
的表达式见式（7）。t2为超级电容充电结束的时刻，由式（2）可得其表达式为式（8）。
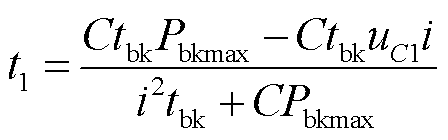（7）
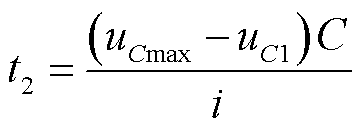（8）
式中，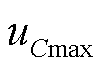
为超级电容的截止电压。
当t＜t1时，列车的制动功率大于超级电容的充电功率，此时系统属于“供大于求”的阶段；当 t1＜t＜t2时，列车的制动功率小于超级电容的充电功率，此时系统属于“供小于求”的阶段。为了保证最优的节能效果，在此过程中，超级电容应尽可能地多充电。换言之，应选取合适的初始电压uC1及充电电流i，使图4中两条曲线围成的阴影面积最大。
列车牵引时，由图3及式（3）可得列车以及超级电容的功率曲线如图5所示，其对应的表达式为
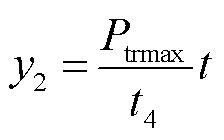（9）
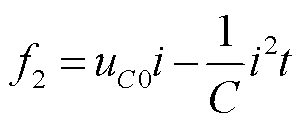（10）
式中，Ptrmax为列车的峰值牵引功率；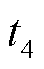
为列车牵引恒转矩区时长；uC0为牵引开始时超级电容的初始电压。令y2=f2，可求得t3的表达式为
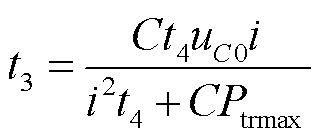（11）
式中，t3为超级电容功率等于列车牵引功率的时刻。
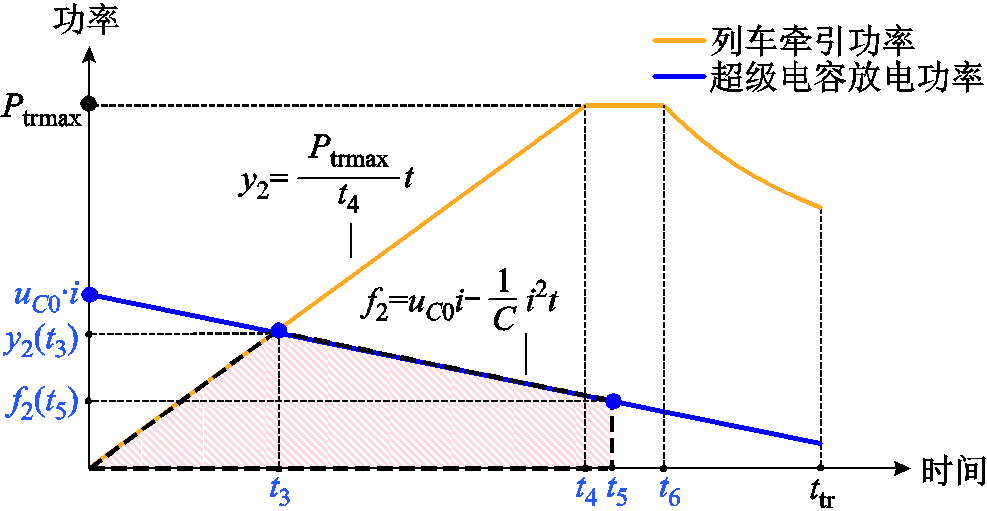
图5 牵引过程中列车及超级电容的的功率曲线
Fig.5 Power profiles of the train and the supercapacitor during accerating
t5为超级电容放电结束的时刻，t6为恒功区-自然特性区的转换时刻，ttr为总牵引时长。当t＜t3时，列车的牵引功率小于超级电容的放电功率，此时系统属于“供大于求”的阶段；当t3＜t＜t5时，列车的牵引功率大于超级电容的放电功率，此时系统属于“供小于求”的阶段。为了保证后续制动阶段储能装置的节能效果，列车牵引结束时超级电容的电压应为前述所求得的制动阶段开始时的初始电压uC1。
由2.3节分析可知，超级电容充电策略优化即选取合适的初始电压uC1及充电电流i，使其功率曲线f1与列车制动功率曲线y1围成的面积最大。
当选取的初始电压及充电电流不同时，两条功率曲线所围的形状也有所不同。
令f1(t2)=y1(t2)，可得关于i的一元二次方程，即
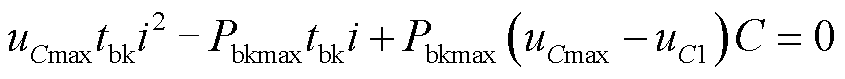（12）
其判别式为
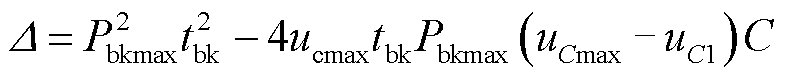（13）
当
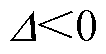，即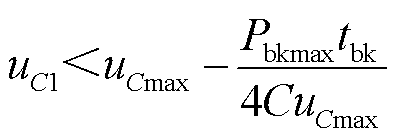
时，不存在临界电流值使曲线f1与y1恰好相交于t2时刻，如图6a所示。此时两条曲线围成的面积有两种形状。
同理，当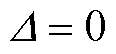
，即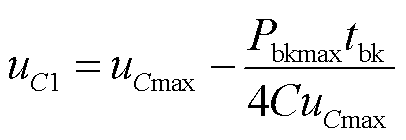
时，只存在1个临界电流值使曲线f1与y1恰好相交于t2时刻，如图6b中点A所示。此时两条曲线围成的面积有三种形状。
当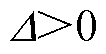
，即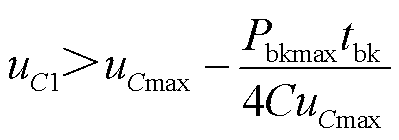
时，存在两个临界电流值使曲线f1与y1恰好相交于t2时刻，如图6c 中点B、C所示。此时两条曲线围成的面积有三种形状。
图6 不同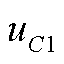
及i下两条功率曲线所围面积的形状
Fig.6 Shapes of the area enclosed by two power curves with different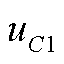 and i
对于图6a不存在临界电流值的情形，分别对其可能产生的两种形状进行分析。
3.1.1 形状①
当超级电容的初始电压较低，且充电电流较小时，会存在当列车制动结束，超级电容电压仍未达到截止电压的情形，即t2≥tbk。此时两条功率曲线围成的形状为四边形，如图7中阴影部分所示。
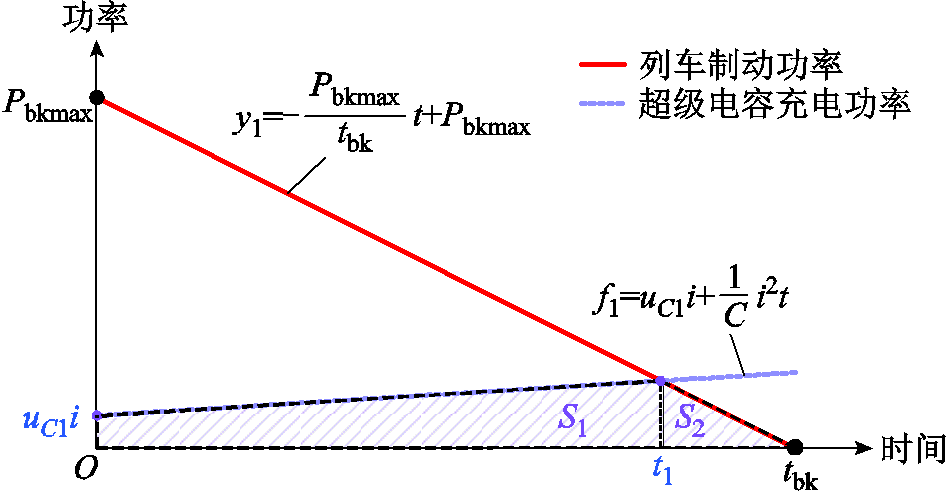
图7 形状①示意图
Fig.7 Schematic diagram of Shape ①
由t2≥tbk可以求得该情形下对应的电流范围为
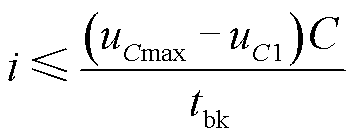（14）
阴影部分的面积计算式为
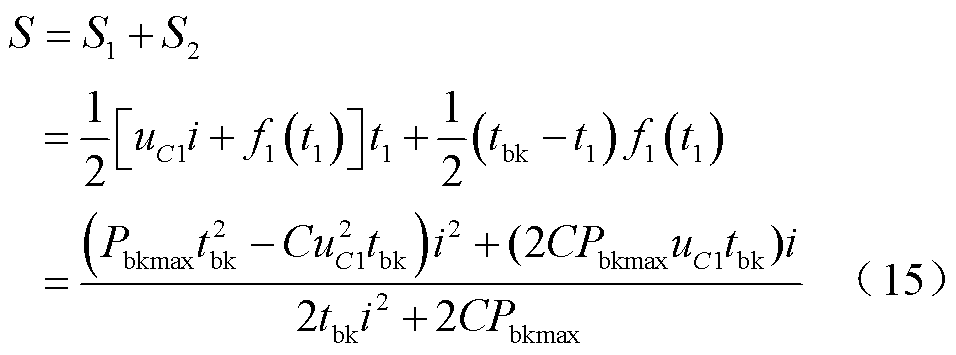
此时超级电容的充电策略优化问题即转化为以uC1和i为决策变量的面积最大化问题，即
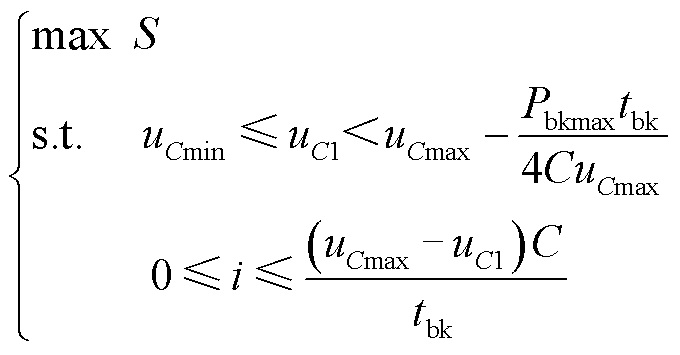（16）
式中，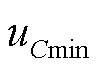
为允许的超级电容电压下限。
3.1.2 形状②
当超级电容的初始电压较低，但充电电流较大时，会存在列车还未制动结束，超级电容电压已达到截止电压的情形，即t2＜tbk。此时两条功率曲线围成的形状为五边形，如图8中阴影部分所示。
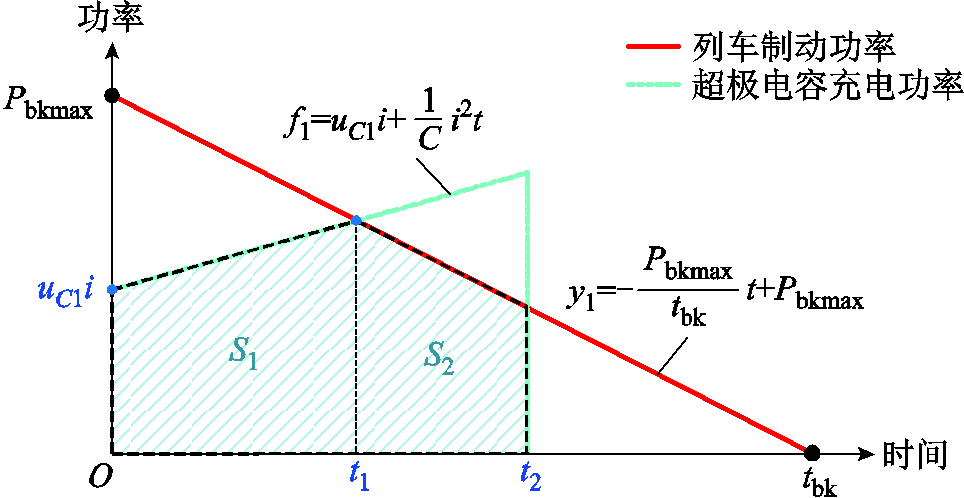
图8 形状②示意图
Fig.8 Schematic diagram of Shape ②
该情形下对应的电流范围为
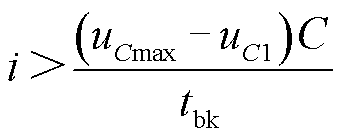（17）
阴影部分的面积计算式为
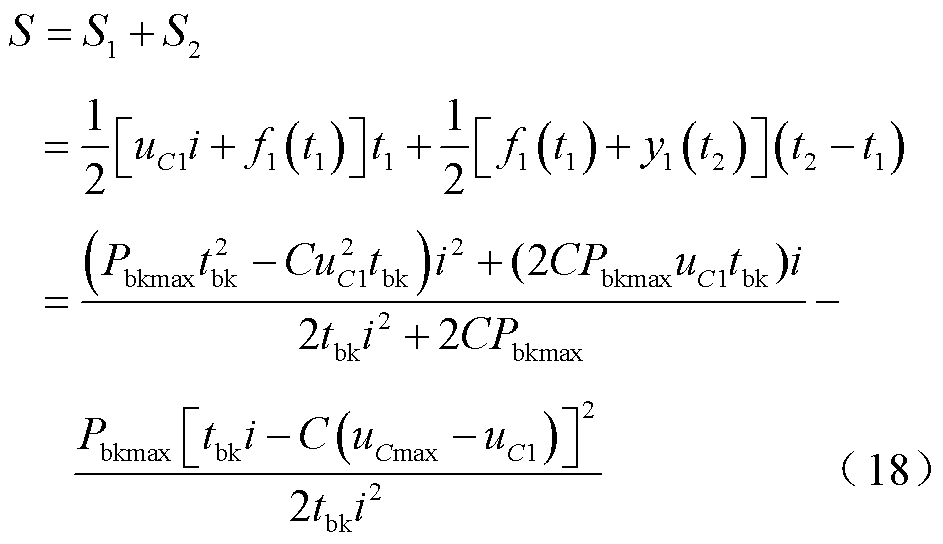
此时对应的优化模型为
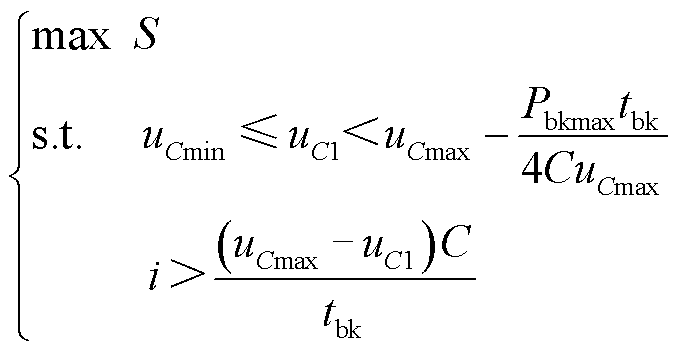（19）
对于图6b、图6c存在临界电流值的情形，同样分别对各个形状进行分析。
3.2.1 形状①
该情形下的形状①面积计算与3.1.1节完全相同，只是电压范围有所不同，如式（20）所示。
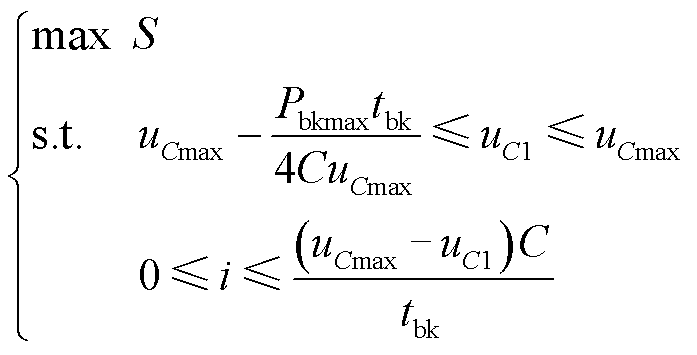（20）
3.2.2 形状②
该情形下超级电容的功率始终小于列车的制动功率，此时两条功率曲线围成的形状为梯形，其面积只与超级电容初始电压相关，即
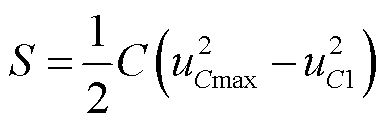（21）
对应的电流范围为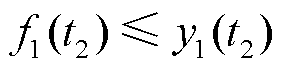
，即
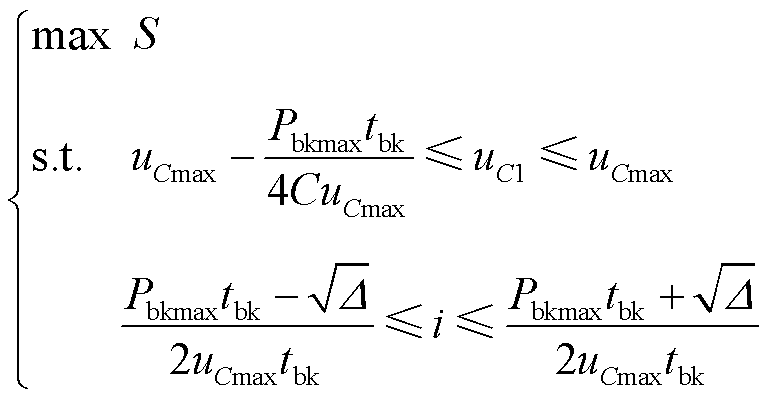（22）
3.2.3 形状③
该情形下形状③的面积计算与3.1.2节完全相同，只是电压电流范围有所不同，即
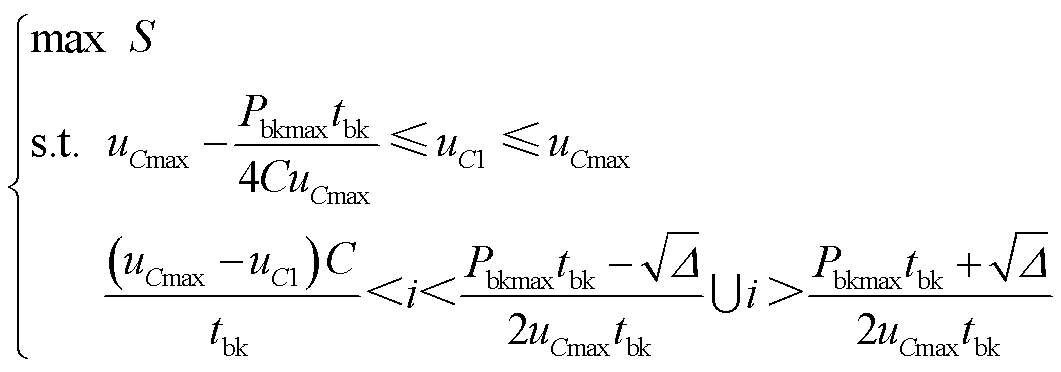（23）
对于放电过程而言，超级电容的初始及截止电压均已确定。因此放电策略设计的目标便是选取合适的放电电流i，使超级电容在列车牵引结束时的电压为前述优化求解得到的制动阶段初始电压uC1。
运用面积等效的思想，上述目标即为使图5中阴影部分的面积S等于超级电容在列车牵引阶段释放的电量，即
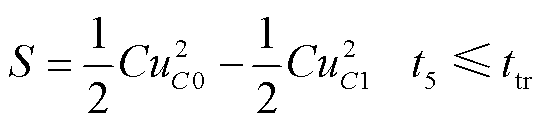（24）
其中
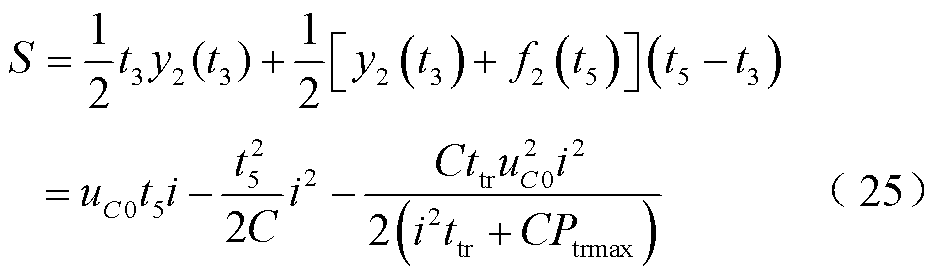
在保证超级电容电压在列车牵引结束时能达到uC1的前提下，使其可以兼顾“填谷”的功能，即降低列车从牵引网吸收的峰值功率。令t5=ttr，此时超级电容的电压刚好在列车牵引结束时达到uC1，列车从牵引网吸收的峰值功率则可以从图5中的Ptrmax降低至图9中的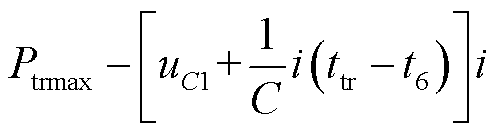
。
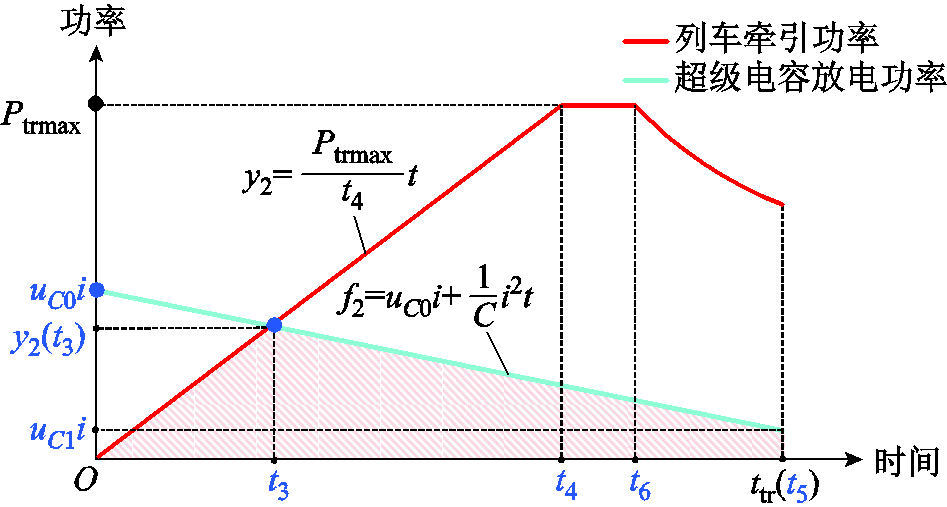
图9 牵引过程中列车及超级电容的的功率曲线
Fig.9 Power profiles of the train and the supercapacitor during accerating
以某地铁车辆段试车线作为试验场景，构建列车运行工况。该区间平直道长490 m，限速40 km/h。设计列车速度如图10所示，以最大牵引级位牵引至40 km/h，而后惰行至38 km/h，最终以最大级位制动至零速。
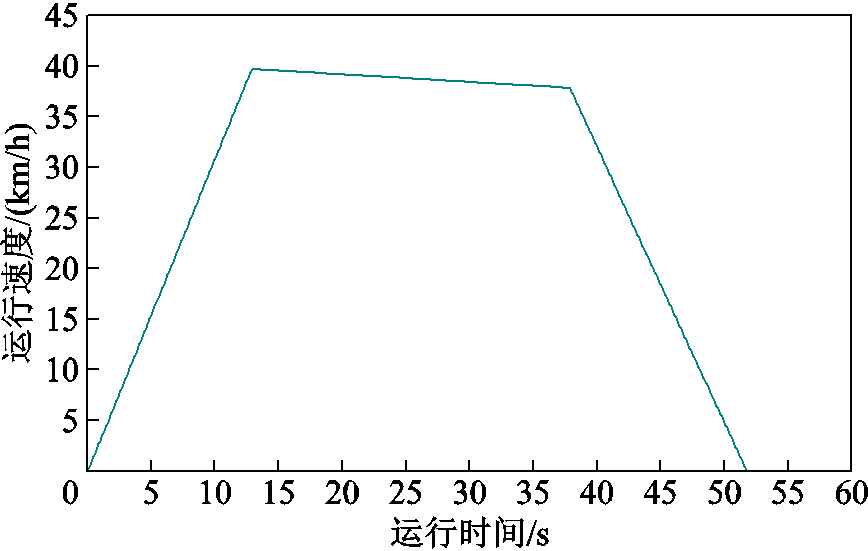
图10 列车速度曲线
Fig.10 Speed profile of the train
列车的牵引制动特性曲线如图11所示。在AW0工况下，利用牵引计算可得列车的功率曲线如图12所示。整个运行过程持续51.8 s，包括牵引阶段ttr=12.9 s，惰行阶段25 s，制动阶段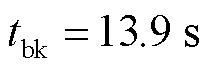
。在此过程中，电机均运行在恒转矩区，列车的峰值牵引功率Ptrmax=2 318.95 kW，峰值制动功率Pbkmax= 1 497.4 kW。
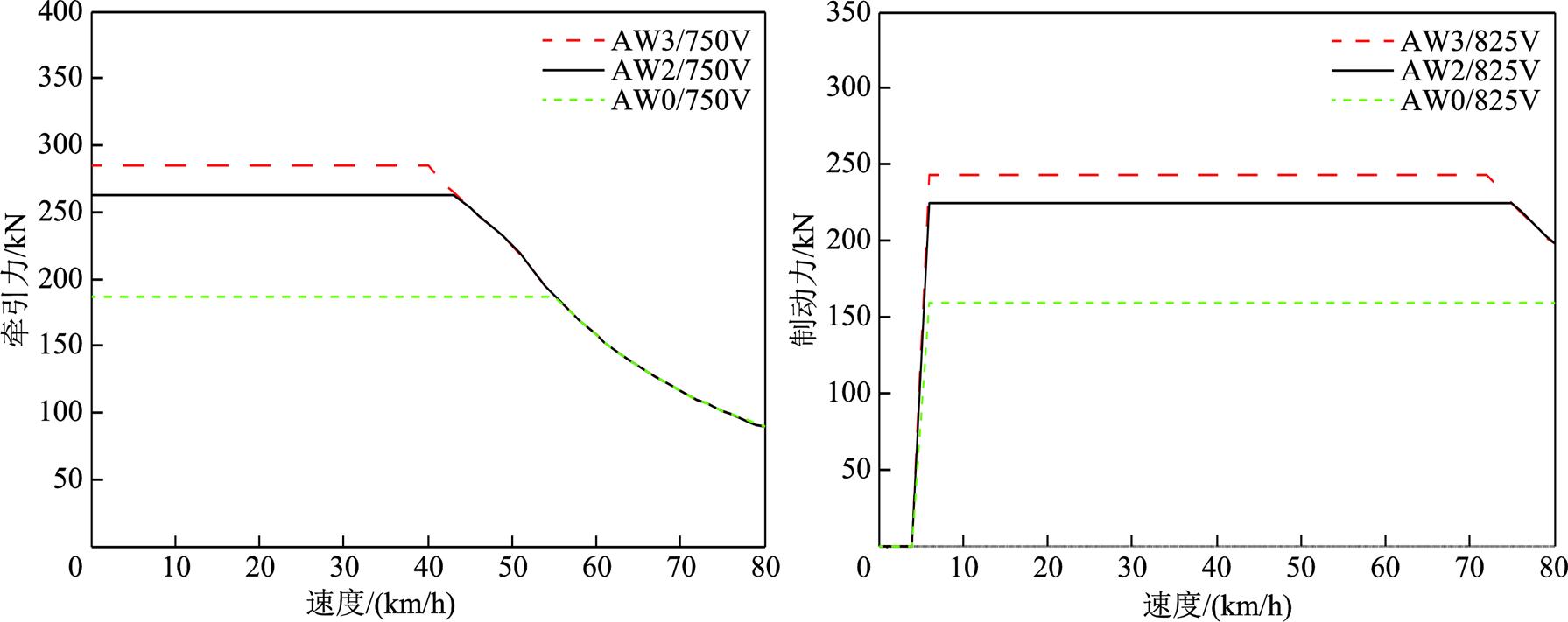
图11 列车牵引制动特性曲线
Fig.11 Traction and braking characteristic curves of the train
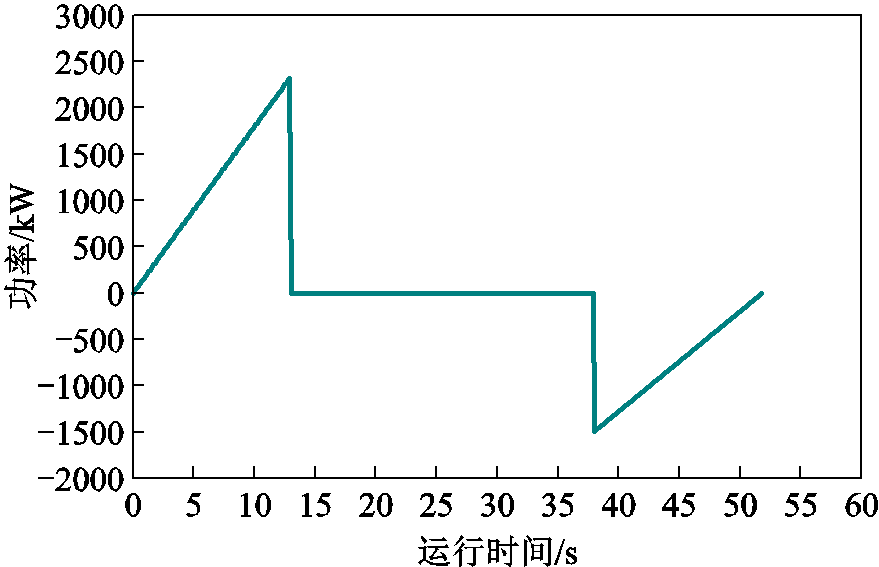
图12 列车功率曲线
Fig.12 Power profile of the train
列车原有的车载制动电阻参数见表1。在不超过原有车载制动电阻质量体积的前提下，选用国内某公司生产的9个54 V/166 F超级电容模组串联组成单套车载储能装置，其参数见表2。装置的电路拓扑如图13所示。
表1 车载制动电阻参数
Tab.1 Parameters of on-board braking resistors
参数数值 型号YBZZ40 数量/台6 安装方式车下吊装 额定阻值/Ω0.973 质量/kg197(±3%) 尺寸/(mm×mm×mm)754×720×660
表2 单套车载储能装置参数
Tab.2 Parameters of a single set on-board energy storage system
参数数值 容值/F166/9 模组构成1并9串 额定电压/V486 电压范围/V313.3～461.1 最大电流/A200 可用能量/(kW·h)0.293
图13 车载储能装置电路拓扑
Fig.13 Circuit topology of OESS
5.3.1 不存在临界电流值的情形
由式（13）可知，当超级电容的充电初始电压uC1＜359.128 V时，不存在电流值使曲线f1与y1恰好相交于t2时刻。此时两条功率曲线围成的面积有两种形状。
对于形状①而言，若不考虑实际应用中对车载储能装置最低电压以及最大电流的限制，模型式（16）对应的三维图如图14所示，当uC1=154 V, i=2 445 A时，两条功率曲线围成的面积最大，对应的最大充电量为1.812 kW×h。
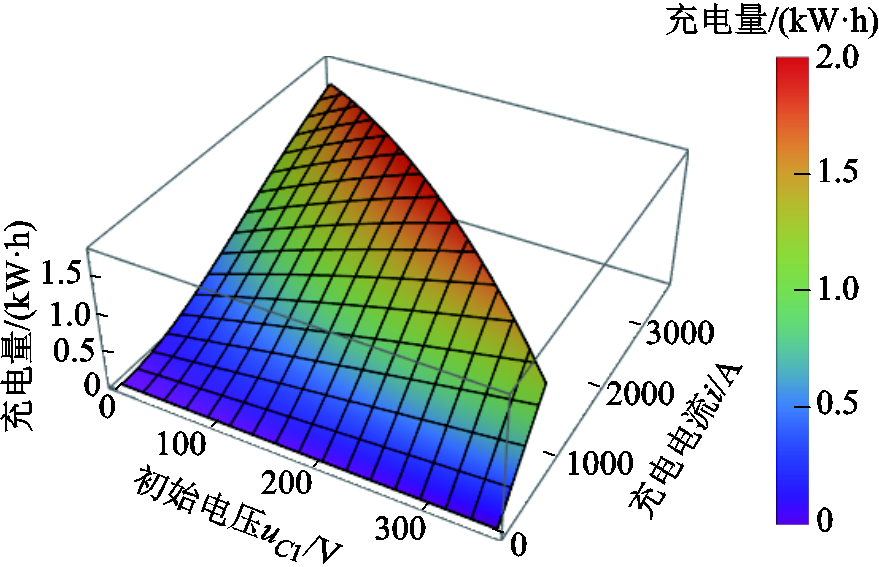
图14 形状①充电量三维图-不考虑实际应用限制时
Fig.14 3D diagram of charging energy with Shape ① without practical application limitations
实际应用中考虑到变流器效率以及开关管最大允许电流的限制，车载储能装置的最低电压为313.3 V，最大允许电流为1 200 A，见表2。此时，模型式（16）对应的三维图如图15所示，当uC1=313.3 V、i=1176.7 A时，两条功率曲线围成的面积最大，对应的最大充电量为1.4192 kW×h。
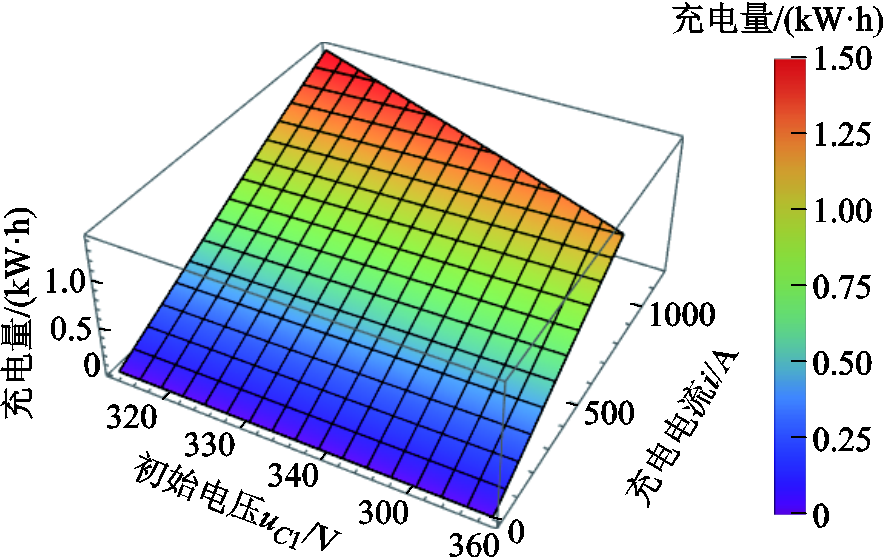
图15 形状①充电量三维图-考虑实际应用限制
Fig.15 3D diagram of charging energy with Shape ①with practical application limitations
对于形状②而言，在不考虑实际应用限制时，模型式（19）对应的三维图如图16所示。当uC1=162.84 V、i=3 452.79 A时，两条功率曲线围成的面积最大，对应的最大充电量为2.0452 kW·h。
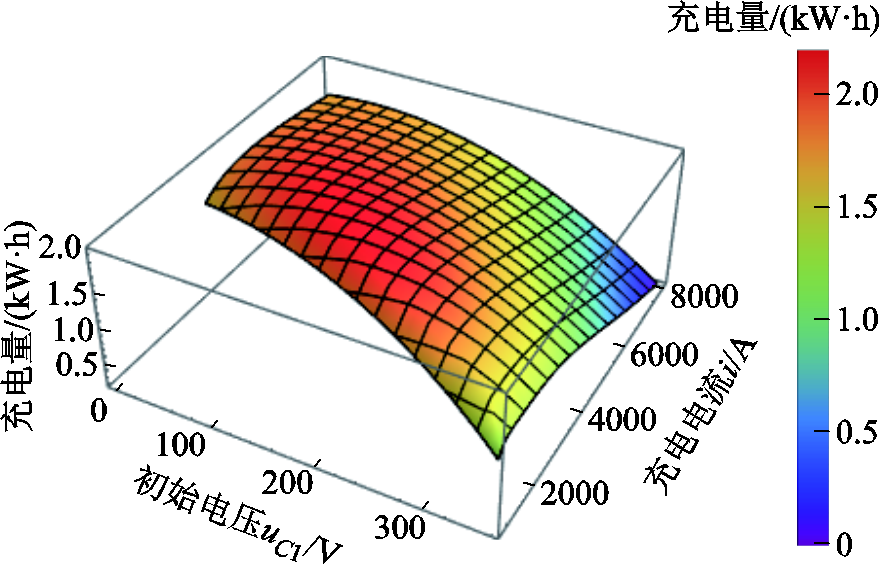
图16 形状②充电量三维图-不考虑实际应用限制
Fig.16 3D diagram of charging energy with Shape ②without practical application limitations
当考虑实际应用限制时，模型式（19）对应的三维图如图17所示。充电量最大值1.453 8 kW×h。
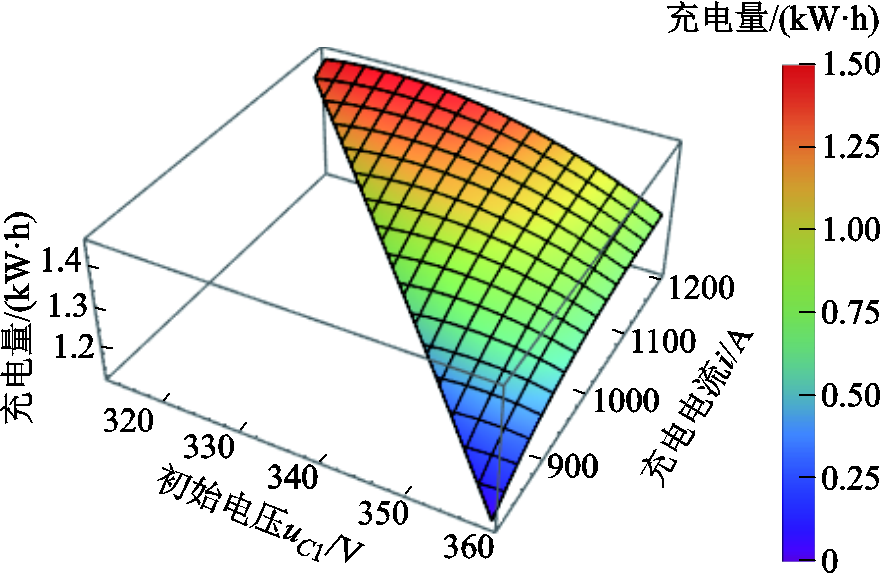
图17 形状②充电量三维图-考虑实际应用限制
Fig.17 3D diagram of charging energy with Shape ② with practical application limitations
在uC1=322.4 V、i=1 200 A时取得充电量最大值1.453 8 kW×h。
5.3.2 存在临界电流值的情形
当超级电容的充电初始电压uC1≥359.128 V时，存在电流值使曲线f1与y1恰好相交于t2时刻。此时两条功率曲线围成的面积有三种形状。
对于形状①而言，模型式（20）对应的三维图如图18所示。当uC1=359.128 V、i=811.863 A时，两条功率曲线围成的面积最大，对应的最大充电量为1.114 4 kW×h。
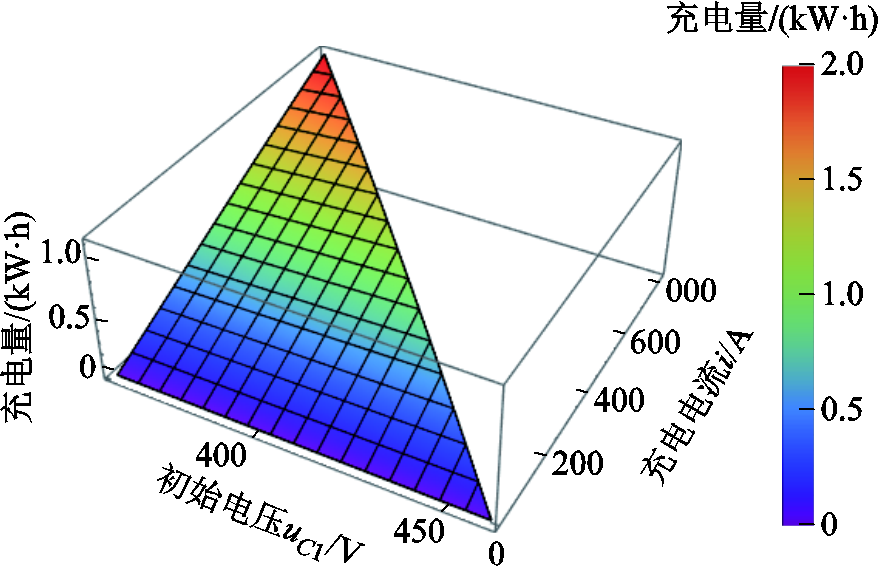
图18 形状①充电量三维图
Fig.18 3D diagram of charging energy with Shape ①
由式（21）可知，当初始电压取得允许范围内最低时，形状②面积最大。因此，若不考虑实际应用限制，当uC1=359.128 V、i=1 623.726 A时取得最大充电量1.285 6 kW×h。考虑开关管最大允许电流 1 200 A限制，其最大充电量降低为1.208 2 kW·h，此时u C1=366.072 V、i=1 200 A。
同理，不考虑实际应用限制时，模型式（23）对应的三维图如图19所示。当uC1=359.128 V、i= 1 623.726 A时，储能装置充电量最大，为1.285 6 kW×h。若考虑实际最大电流1 200 A约束，模型式（23）对应的最大充电量为1.280 1 kW×h ，在uC1=359.128 V、i=1 200 A时取得，与图20所示的三维图一致。
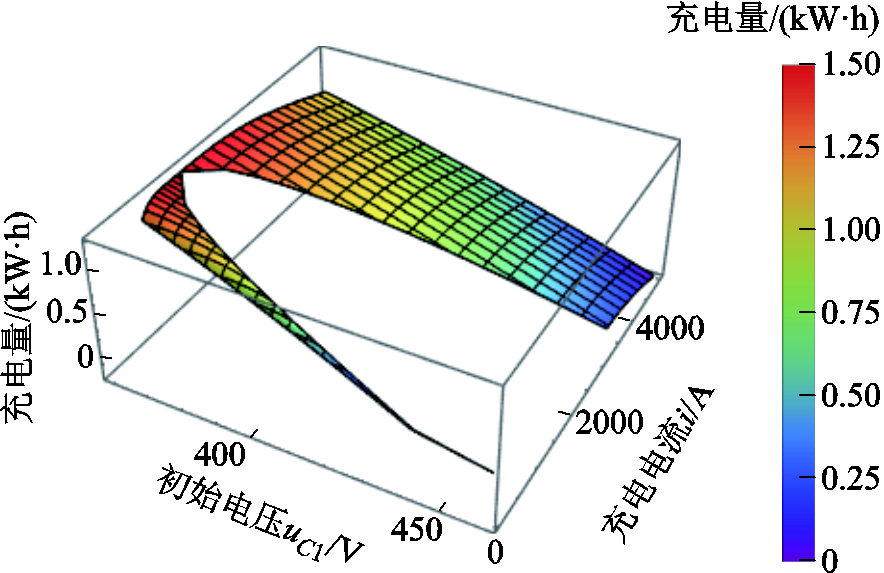
图19 形状③充电量三维图-不考虑实际应用限制
Fig.19 3D diagram of charging energy with Shape ③ without practical application limitations
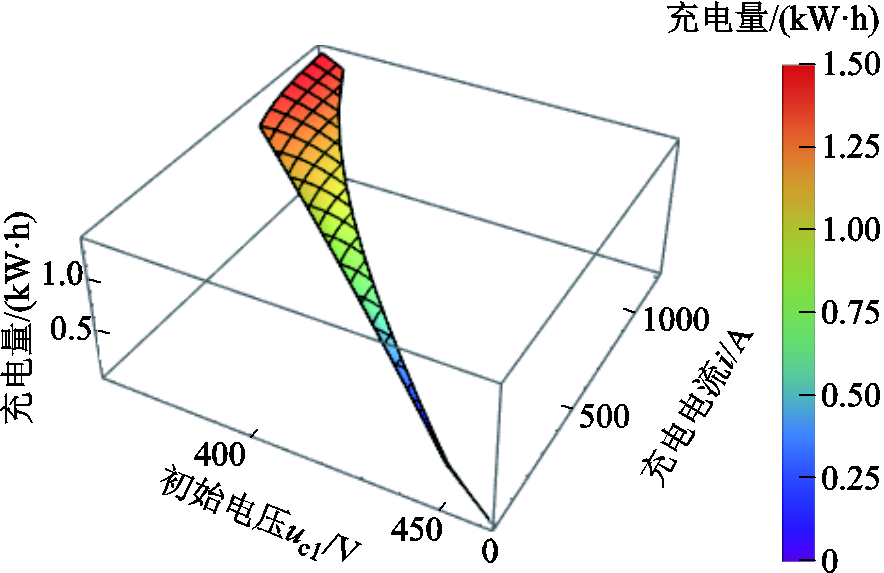
图20 形状③充电量三维图-考虑实际应用限制
Fig.20 3D diagram of charging energy with Shape ③ with practical application limitations
表3、表4分别列出在不考虑实际应用限制以及考虑实际应用限制的条件下，前述各种情形对应的最优充电初始电压及充电电流，以及相应的储能装置最大充电量。由此可以看出，若考虑实际约束，当uC1=322.423 V、i=1 200 A时，车载储能装置可以取得最优的节能效果，节能值为1.453 8 kW·h.
表3 最优充电策略-不考虑实际应用限制
Tab.3 Optimal charging strategy without practical application limitations
i最优充电策略 不存在临界电流值形状① 形状② 存在临界电流值形状① 形状② 形状③
表4 最优充电策略-考虑实际应用限制
Tab.4 Optimal charging strategy with practical application limitations
i最优充电策略 不存在临界电流值形状① 形状② 存在临界电流值形状① 形状② 形状③
假设列车牵引开始时，超级电容的初始电压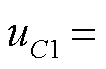
420 V。基于前述充电策略优化的结果，令t5=ttr，求解模型式（24），得到充电电流i=938.433 A。此时在列车牵引结束时，超级电容电压恰好为前述求解得到的最优充电起始电压
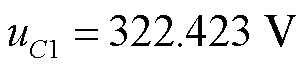。而列车从牵引网吸收的峰值功率也由2 318.95 kW降低至2 016.38 kW。
为了验证本文所提策略的有效性，针对图12所示的列车运行工况，进一步采用传统的电压电流双闭环PI控制策略对表2所示车载储能装置进行充放电管理。该策略的基本原理如图21所示。设置储能装置的充电阈值uch和放电阈值uds。当列车支撑电容电压uFC大于充电阈值uch时，储能装置进入充电模式；当uFC小于放电阈值uds时，储能装置进入放电模式。uFC与相应阈值的差值依次经过电压外环PI调节器、电流内环PI调节器后得到PWM占空比，输入DC-DC变换器便可控制储能装置进行充放电[23]。仿真相关参数见表5。考虑到列车牵引会将网压拉低，选取放电阈值uds等于空载电压-5 V。同时由于网压超过900 V时制动电阻会启动，因此选取充电阈值uch等于制动电阻启动阈值-5 V。具体建模及仿真过程见参考文献[24]，此处不再赘述。
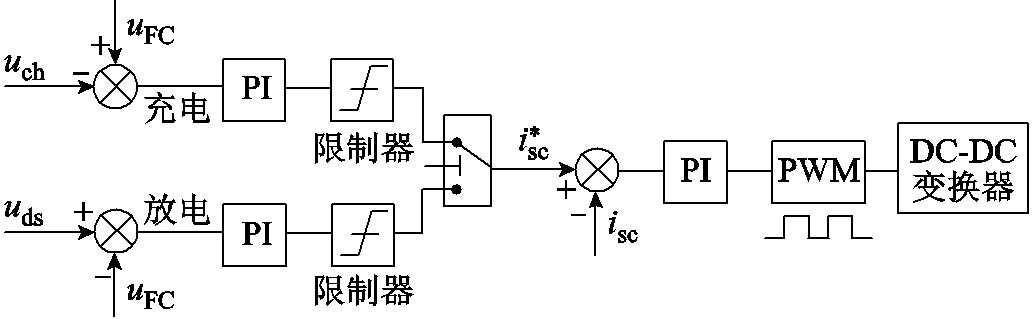
图21 电压电流双闭环控制策略
Fig.21 Voltage-current double closed loop control strategy
表5 仿真参数
Tab.5 Simulation parameters
参数数值 变电站空载电压us/V860 变电站内阻rs/Ω0.011 9 充电阈值uch/V895 放电阈值uds/V855 超级电容初始电压/V420 充电电压环P100 充电电压环I0.01 放电电压环P90 放电电压环I0.01 电流环P500 电流环I0.1
两种控制策略下车载储能装置的充放电效果对比见表6。可以看出，与双环PI控制策略相比，采用等效面积法的控制策略可以增加储能装置的充电量12.089%，提升放电量12.225%，更加充分地发挥了储能装置的充放电性能，由此证明了基于等效面积法的控制策略的有效性。
表6 不同策略充放电效果对比
Tab.6 Comparison of charging and discharging effect between different strategies
控制策略充放电电量/(kW×h)改进百分比（%） 基于双环PI控制基于等效面积法 充电1.2971.453 812.089 放电0.992 21.113 512.225
针对利用车载储能装置回收城轨列车再生制动能量的问题，本文提出了一种基于等效面积法的控制策略。为了保证最优的节能效果，将储能装置的充电策略转换为最大化列车及超级电容功率曲线所围面积的最优化问题。而放电策略目标则是使超级电容的电压在列车牵引结束时达到前述求解得到的最优值，同时最大化发挥其“填谷”功能。与基于网压或者人工智能算法的控制策略相比，本文所提策略可以给出特定工况下最优控制策略的解析解。最后以某地铁线路为例进行算例分析，验证了所提策略的有效性。
下一步将尝试在实际线路中应用该控制策略，同时将该策略运用至多站多车或者包含车载+地面储能装置等一些更复杂的工况。
参考文献
[1] 中国城市轨道交通协会. 城市轨道交通2022年度统计和分析报告[EB/OL]. (2023-03-31)[2024-01-01]. https: //www.camet.org.cn/tjxx/11944.
[2] 陈冲, 贾利民, 赵天宇, 等. 去碳化导向的轨道交通与新能源融合发展—形态模式、解决方案和使/赋能技术[J]. 电工技术学报, 2023, 38(12): 3321-3337.
Chen Chong, Jia Limin, Zhao Tianyu, et al. Decarbonization-oriented rail transportation and renewable energy integration development-configurations, solutions, and enabling/empowering technologies[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3321-3337.
[3] 程鹏, 刘文泉, 陈冲, 等. 面向电气化铁路牵引供电的光伏发电分相电流控制策略[J]. 电力系统自动化, 2022, 46(19): 145-153.
Cheng Peng, Liu Wenquan, Chen Chong, et al. Individual phase current control strategy of photovoltaic power generation for traction power supply of electrified railway[J]. Automation of Electric Power Systems, 2022, 46(19): 145-153.
[4] 赵荣华, 庞涛, 米佳雨, 等. 替代制动电阻的车载储能系统容量配置研究[J]. 机电工程技术, 2023, 52(9): 269-273.
Zhao Ronghua, Pang Tao, Mi Jiayu, et al. Study on capacity configuration of on-board energy storage systems substituting braking resistors[J]. Mechanical & Electrical Engineering Technology, 2023, 52(9): 269-273.
[5] 林锦杰, 李勇, 胡斯佳, 等. 计及再生制动能量的铁路潮流控制器功率柔性分配方法[J]. 电工技术学报, 2023, 38(22): 6121-6132.
Lin Jinjie, Li Yong, Hu Sijia, et al. Flexible power assignment method for railway power flow controller considering regenerative braking energy[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6121-6132.
[6] 钟志宏, 李炎, 米佳雨, 等. 基于牵引网电压和空载电压的多储能系统区间能量管理策略[J]. 电工技术学报, 2024, 39(15): 4583-4598.
Zhong Zhihong, Li Yan, Mi Jiayu, et al. Interval energy management strategy for multiple energy storage systems based on traction network voltage and no-load voltage[J]. Transactions of China Electrotechnical Society, 2024, 39(15): 4583-4598.
[7] 陈艳波, 刘宇翔, 田昊欣, 等. 基于广义目标级联法的多牵引变电站光伏-储能协同规划配置[J]. 电工技术学报, 2024, 39(15): 4599-4612.
Chen Yanbo, Liu Yuxiang, Tian Haoxin, et al. Collaborative planning and configuration of photovoltaic and energy storage in multiple traction substations based on generalized analytical target cascading method[J]. Transactions of China Electrotechnical Society, 2024, 39(15): 4599-4612.
[8] 刘宇嫣. 城市轨道交通地面式混合储能系统自适应能量管理策略与容量配置研究[D]. 北京: 北京交通大学, 2022.
Liu Yuyan. Adaptive energy management and capacity configuration of stationary hybrid energy storage system in urban rail transit[D]. Beijing: Beijing Jiaotong University, 2022.
[9] 李欣, 卢景涛, 肖林润, 等. 高速铁路列车长大坡道混合储能系统容量优化配置[J]. 电工技术学报, 2023, 38(20): 5645-5660.
Li Xin, Lu Jingtao, Xiao Linrun, et al. Capacity optimization configuration of hybrid energy storage system for long steep slope of high-speed railway[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5645-5660.
[10] 金勇, 黄先进, 石春珉, 等. 城市轨道交通地面储能技术应用综述[J]. 电工技术学报, 2024, 39(15): 4568-4582, 4642.
Jin Yong, Huang Xianjin, Shi Chunmin, et al. Review on wayside energy storage technology for urban rail transit[J]. Transactions of China Electrotechnical Society, 2024, 39(15): 4568-4582, 4642.
[11] Meishner F, Sauer D U. Wayside energy recovery systems in DC urban railway grids[J]. eTransportation, 2019, 1: 100001.
[12] Mi Jiayu, Yang Zhongping, Zhong Zhihong, et al. Optimal sizing of on-board and wayside energy storage systems for braking energy recovery[C]//2022 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Haining, China, 2022: 1-6.
[13] Khodaparastan M, Mohamed A A, Brandauer W. Recuperation of regenerative braking energy in electric rail transit systems[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(8): 2831-2847.
[14] 王虎高, 屈海洋, 陈中杰. 储能电源应用于地铁车辆应急牵引的设计研究[J]. 电力机车与城轨车辆, 2016, 39(1): 50-53.
Wang Hugao, Qu Haiyang, Chen Zhongjie. Design and research on energy storage power supply used on metro vehicle emergency traction[J]. Electric Locomotives & Mass Transit Vehicles, 2016, 39(1): 50-53.
[15] 赵坤, 王椹榕, 王德伟, 等. 车载超级电容储能系统间接电流控制策略[J]. 电工技术学报, 2011, 26(9): 124-129.
Zhao Kun, Wang Shenrong, Wang Dewei, et al. Indirect current control strategy of on-board supercapacitor energy storage system of railway vehicle[J]. Transactions of China Electrotechnical Society, 2011, 26(9): 124-129.
[16] Di Pasquale A, Fedele E, Iannuzzi D, et al. Centralised control strategy for an urban rail network in the presence of onboard storage systems[C]//2023 AEIT International Annual Conference (AEIT), Rome, Italy, 2023: 1-6.
[17] Wu Chaoxian, Lu Shaofeng, Tian Zhongbei, et al. Energy-efficient train control with onboard energy storage systems considering stochastic regenerative braking energy[J]. IEEE Transactions on Transportation Electrification, 2024, PP(99): 1.
[18] Liu Wei, Xu Jiaxuan, Tang Jingkun. Study on control strategy of urban rail train with on-board regenerative braking energy storage system[C]//IECON 2017 - 43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 2017: 3924-3929.
[19] Talla J, Streiť L, Peroutka Z, et al. Fuzzy energy management strategy for tram with supercapacitors [C]//IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 2015: 3963-3968.
[20] Wang Xin, Luo Yingbing, Qin Bin, et al. Power allocation strategy for urban rail HESS based on deep reinforcement learning sequential decision optimization[J]. IEEE Transactions on Transportation Electrification, 2023, 9(2): 2693-2710.
[21] 何晔, 胡彩凤, 吴能峰, 等. 地铁车辆牵引仿真计算[J]. 铁道机车车辆, 2015, 35(6): 63-68.
He Ye, Hu Caifeng, Wu Nengfeng, et al. Simulation calculations of metro tractions[J]. Railway Locomotive & Car, 2015, 35(6): 63-68.
[22] 杨中平, 林飞. 储能技术在地面式再生制动能量吸收和利用装置中的应用[J]. 都市快轨交通, 2021, 34(6): 1-8.
Yang Zhongping, Lin Fei. Application of energy storage technology in stationary regenerative braking energy absorption and utilization devices[J]. Urban Rapid Rail Transit, 2021, 34(6): 1-8.
[23] 周强, 王金全, 杨波. 超级电容器:性能优越的储能器件[J]. 电气技术, 2006, 7(6): 64-68.
Zhou Qiang, Wang Jinquan, Yang Bo. Supercapacitor: excellent energy storage element[J]. Electrical Engineering, 2006, 7(6): 64-68.
[24] 诸斐琴. 城市轨道交通地面式超级电容储能系统自适应协调控制与容量配置综合优化研究[D]. 北京: 北京交通大学, 2020.
Zhu Feiqin. Research on adaptive coordinated control and comprehensive optimization of capacity allocation of ground-based supercapacitor energy storage system in urban rail transit[D]. Beijing: Beijing Jiaotong University, 2020.
Optimal Control of On-Board Supercapacitor Energy Storage Systems for Regenerative Braking Energy Recovery Based on Area-Equivalent Principle
Abstract Conventional control strategies of on-board energy storage systems (OESSs) based on catenary voltage or artificial intelligence algorithms can achieve a certain level of regenerative braking energy recovery. However, they ignore the charging and discharging characteristics of energy storage elements and fail to provide an explicit analytical solution to the corresponding control parameters due to the complicated model. On the other hand, according to the characteristics of the supercapacitor, its power is at odds with the amount of energy it can absorb. If the initial voltage of the supercapacitor is low, the energy it can absorb would be large while the charging power would be low, and vice versa. Therefore, it is an issue worth studying how to set a reasonable initial voltage and charging/discharging current to balance the power and absorbable energy of a supercapacitor so that the best regenerative braking energy recovery effect can be achieved.
The OESS is charged when the urban rail train is braking and discharged when the train is in traction. The power profile of the train was divided into two parts in this paper: "braking" and "traction", and the charging and discharging processes of the OESS were studied, respectively.
When the train was braking, the OESS should be charged as much as possible to ensure the optimal energy-saving effect. By applying the area-equivalent principle, the problem of maximizing the charge of OESS could be transformed into a mathematical problem of maximizing the area enclosed by the braking power curve of the train and the power curve of the supercapacitor. When the initial voltage and charging current of the supercapacitor varied, the shape enclosed by the two power curves was also different. Therefore, the enclosed area with various shapes was modeled with respect to different initial voltages and charging currents. Finally, the optimal initial voltage and charging current corresponding to the largest enclosed area were picked out, and the energy-saving effect of the OESS was the best in this case.
As for the discharging process, the design principle of the OESS discharge strategy was to ensure that the voltage of the supercapacitor at the end of the train traction reached the optimal initial voltage of the braking stage obtained above. According to the area-equivalent principle, this goal could be achieved by making the area enclosed by the two power curves equal to the discharged energy of the supercapacitor during train traction. Furthermore, to maximize the "valley-filling" effect of the OESS, the charging time of the OESS was set equal to the traction time of the train to obtain the optimal discharge current. In this way, the maximum height of the area difference between the train traction power curve and the supercapacitor power curve could be cut down; in other words, the peak power absorbed by the train from the traction network could be reduced.
Finally, a case study was conducted based on the single-train operation scenario to verify the effectiveness of the proposed control strategy. The result shows that, compared with the traditional voltage-based double-loop PI control strategy, the control strategy proposed in this paper can further improve the charging and discharging capacity of OESS and thus have a more significant energy-saving effect.
Keywords：Urban rail transit, on-board energy storage system, regenerative braking energy recovery, energy management strategy, area-equivalent principle
中图分类号：TM922
DOI: 10.19595/j.cnki.1000-6753.tces.232198
国家重点研发计划资助项目（2022YFB4301203）。
收稿日期 2024-01-02
改稿日期 2024-05-06
米佳雨 女，1996年生，博士研究生，研究方向为城市轨道交通储能节能技术。
E-mail：20117033@bjtu.edu.cn
杨中平 男，1970年生，教授，博士生导师，研究方向为轨道交通节能技术、牵引传动技术、无线电能传输技术等。
E-mail：zhpyang@bjtu.edu.cn（通信作者）
（编辑 郭丽军）