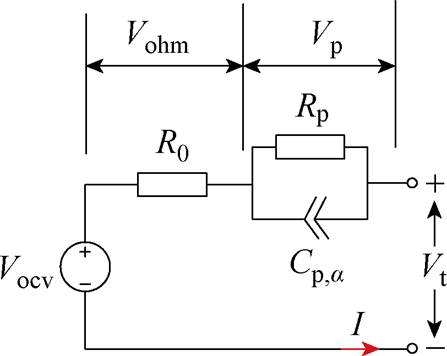
图1 一阶分数阶模型
Fig.1 First order fractional order model
摘要 锂离子电池作为储能系统的关键,准确的电池模型对提高状态估计精度至关重要。该文提出一种基于动量反向传播神经网络的锂离子电池分数阶模型建模与荷电状态估计方法。在分数阶等效电路模型的基础上,构建具有半物理意义的神经网络模型,并使用动量反向传播算法,实现了对包含模型分数阶阶数的模型参数优化以及状态估计。为了验证所提算法的可行性,分别通过理论推导与实验结果证明。通过理论推导,证明所提方法误差会收敛。实验结果显示,相比于扩展卡尔曼滤波与无迹卡尔曼滤波算法,所提方法具有更高的精度,能够准确地预测电池的电压响应。综上所述,基于动量反向传播神经网络在锂离子电池建模和荷电状态估计中具有良好的应用前景,可为电池的性能评估和管理提供有效支持。
关键词:锂离子电池 分数阶模型 参数辨识 荷电状态估计 动量反向传播神经网络
近年来,在“双碳”目标指引下,中国新能源电动汽车产业和电化学储能装机规模得以迅速发展。中汽协数据显示,2023年,我国新能源汽车产销量分别达958.7万辆和949.5万辆,同比分别增长35.8%和37.9%,市场占有率达31.6%。根据《2023年上半年度电化学储能电站行业统计数据》报告显示,2023年上半年,新增投运电化学储能电站227座、总功率7.41 GW、总能量14.71 GW×h,超过此前历年累计装机规模的总和。电池系统作为电动汽车和电化学储能的核心部件,起到能量存储与缓冲作用[1]。锂离子电池具有电压平台高、能量密度大、循环寿命长等优点,是电动汽车和电化学储能的首先方案[2]。然而,锂离子电池作为一种电化学储能器件,其行为具有典型的非线性特性,行为描述准确性对其状态估计与管理具有重要的意义[3]。
电化学模型(Electrochemical Model, EM)是根据电池工作机理抽象出来的一种等效模型,具有精度高、可解释性强等优点,被广泛用于电池老化机理、热故障诊断研究[4]。这类模型包括单粒子模型(Single Particle Model, SPM)[5]、准二维模型(Pseudo two Dimensions Model, P2DM)[6]。然而,EM包含大量偏微分方程,需要更多的计算资源,这就限制了该模型的适用性。相比而言,等效电路模型具有结构简单、易于辨识等优点,被广泛用于电池状态估计和均衡管理等方面[7]。常用的等效电路模型(Equivalent Circuit Model, ECM)包括一阶电阻-电容(Resistance-Capacitance, RC)模型、二阶RC模型、新一代汽车协商会(Partnership for a New Generation of Vehicles, PNGV)模型等,这些模型共性是采用RC网络近似描述电池极化过程。然而,受限于材料、制造工艺等影响,电池极化行为在频域特性方面并不完全服从整数阶RC网络特性[8]。分数阶积分在描述系统非线性特性方面具有显著优势。分数阶模型(Fractional Order Model, FOM)可以更加精准地描述电池电压和电流非线性特性[9]。典型的分数阶模型包括一阶分数阶模型,二阶分数阶模型、PNGV分数阶模型[10]。然而,分数阶模型离散化较为繁杂,限制了该模型在实际中的应用。神经网络具有强大的层次化特征提取能力,可以有效地描述电池输入从连续域到离散域的映射关系。文献[11]采用BP神经网络建立了ECM和等效热模型之间的非线性耦合关系。然而,这类方法将电池建立为“黑箱”模型,可解释性不强。
根据原理不同,电池荷电状态(State of Charge, SOC)估计方法可以归纳为以下几类:①直接测量法:通过内阻表、阻抗谱测试仪等专用仪器测量电池阻抗等信息[12],但是这类方法无法测量电池极化参数信息;安时积分法通过安时累计估算电池SOC,但是由于开环原理导致其测量结果容易受到噪声影响;②模型驱动法:这类方法在系统模型基础上,结合自适应滤波器或非线性观测器实现电池参数与状态估计[13],然而,这类方法估计效果依赖模型精度,并且需要算法调参,无疑增加了参数辨识和状态估计的难度;③数据驱动法:神经网络具有良好的非线性拟合能力和自学习能力,被广泛用于电池状态估计。大多的研究方法将电池SOC估计视为回归预测,即将通过神经网络学习历史SOC变化规律,从而预测SOC演变趋势[14]。这类方法忽略了电池工作原理,算法依赖样本工况,导致适应性较差。Li Chaoran等[21]提出了加权聚类-卷积神经网络长短期记忆方法,在小模型尺寸下实现了高精度的SOC估计,缩短了计算需要的时间。
本文提出的参数辨识与SOC联合估计算法,将电池工作机理融入神经网络中,增强了神经模型的可解释性。同时,利用神经网络的层次化特征提取能力,实现对分数阶电池模型分数阶阶数的优化,从而提高模型的精度。相较于传统深度学习方法,该方法构造的模型具有一定解释性,适合探究电池内部机理。同时,该算法解决了基于深度学习SOC估计方法计算量需求大的问题。因此,具有半物理意义的神经网络模型可以更好地描述电池行为特性。基于此,本文将神经网络与电池分数阶模型结合,建立了基于神经网络的分数阶模型,并利用神经网络参数自学习机制,实现电池模型参数辨识与状态估计。
分数阶模型具有结构简单、物理意义明确的优点[15],被广泛用于状态估计和故障诊断。数据驱动模型通过大数据训练模型,可以更好地提高模型精度,但目前应用于电池状态估计神经网络可解释性较差。将两者结合可以充分发挥两者的优势,有效地提高模型精度和数据驱动模型可解释性。
图1展示了一阶RC分数阶电路模型,该模型由一个非线性电压源、一个电阻和极化网络串联构成,如图1所示[9, 16],参数Rp和Cp,a分别代表电池极化电阻和极化电容,a代表Cp的阶数,Vohm和Vp分别为欧姆电压与极化电压。

图1 一阶分数阶模型
Fig.1 First order fractional order model
端电压Vt可以表示为
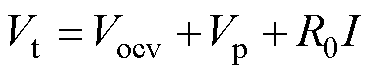 (1)
(1)
式中,Vocv为开路电压(Open Circuit Voltage, OCV),OCV和SOC满足[17]关系
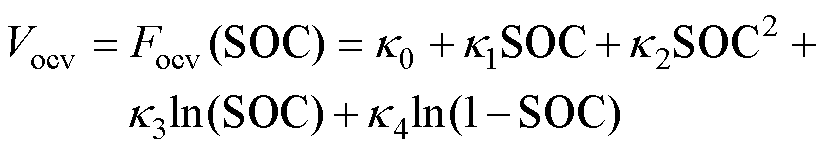 (2)
(2)
式中,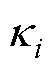 (
(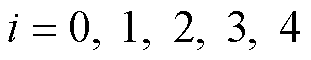 )为OCV-SOC函数系数;Focv( · )为OCV-SOC关系式。
)为OCV-SOC函数系数;Focv( · )为OCV-SOC关系式。
SOC被定义[18]为
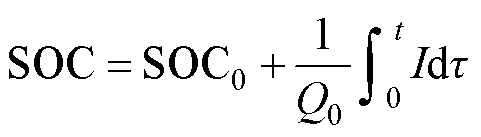 (3)
(3)
式中,I为电路电流;Q0为电池当前最大容量。
对于极化电压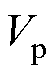 和欧姆电压
和欧姆电压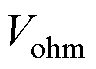 满足条件
满足条件
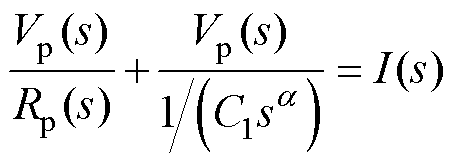 (4)
(4)
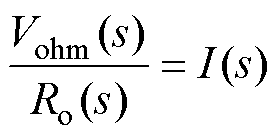 (5)
(5)
定义电压差 为
为
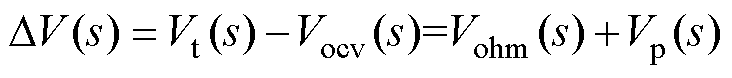 (6)
(6)
结合式(4)、式(5),则式(6)可以变换为
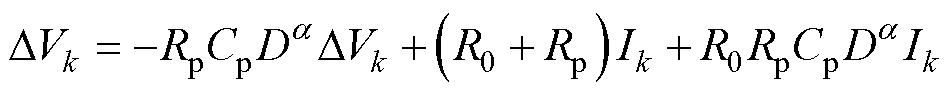 (7)
(7)
式中,D为欧拉记号,表示求导;k表示当前时间序列。
为了对分数阶模型进行优化,需要将式(7)从连续域转换为离散域。Grünwald-Letnikov(G-L)方法通过离散化的加权历史数据,为分数阶微积分提供了直观且实用的数值工具,成为复杂系统建模中的重要手段。采用G-L方法对式(7)进行离散化得到
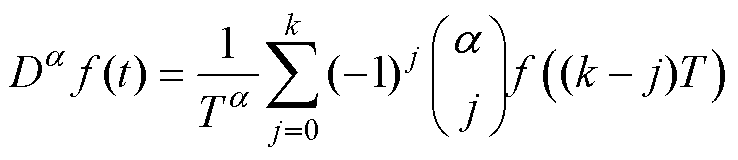 (8)
(8)
式中,T为采样时间,T=1 s;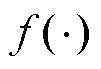 为待离散化函 数;j为离散化当前所使用数据与正在进行离散化的时间序列之差。
为待离散化函 数;j为离散化当前所使用数据与正在进行离散化的时间序列之差。
为了减少计算量,仅使用一定记忆空间内的数据进行离散化,式(8)近似为
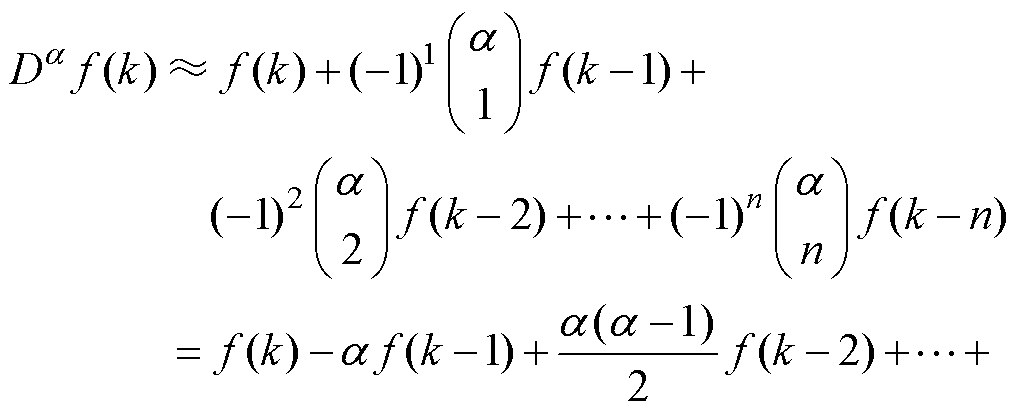
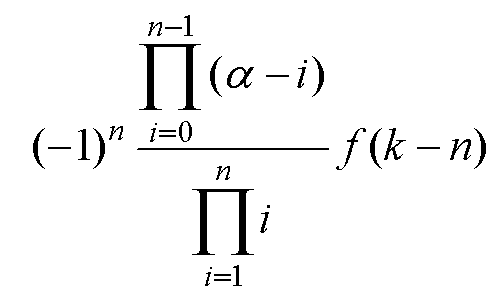 (9)
(9)
式中,n为记忆空间内包含数据的数量。根据式(9),式(7)可以转换为
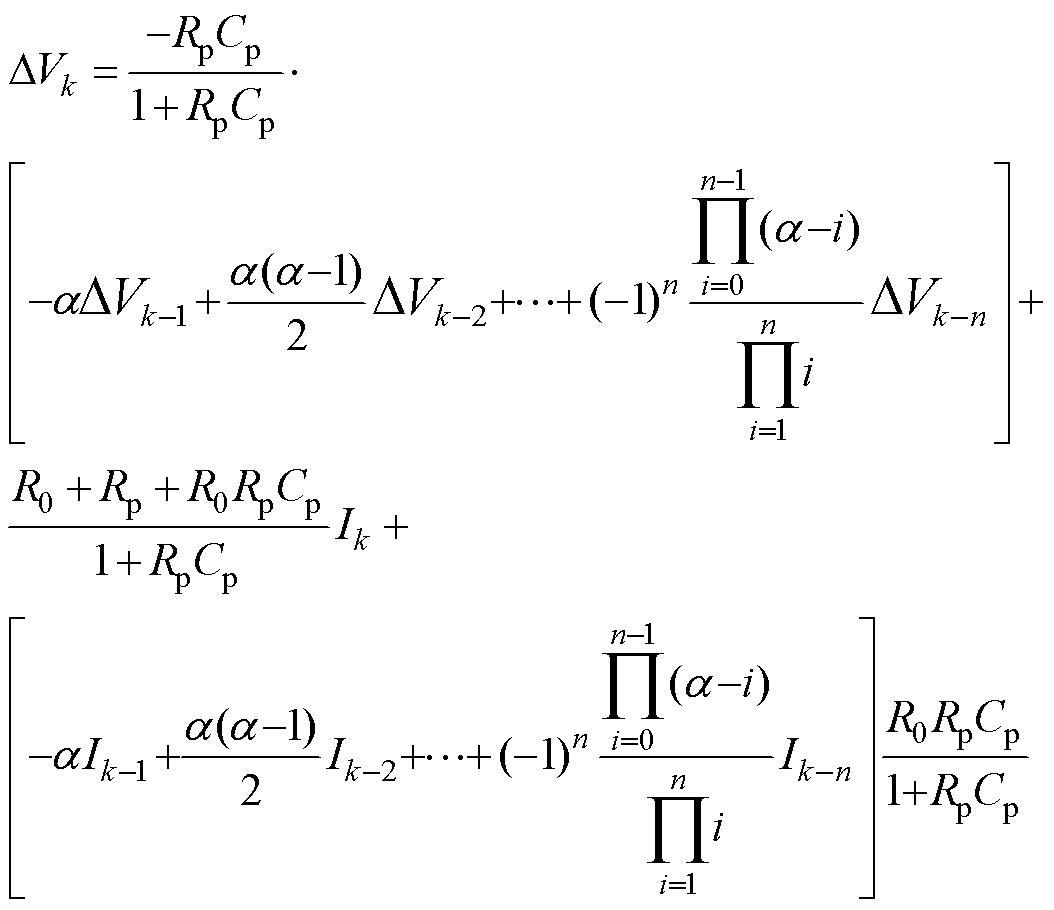 (10)
(10)
为了对电池的SOC进行状态估计,需要对式(2)进行线性化处理。通过使用泰勒公式,式(2)可以转换为
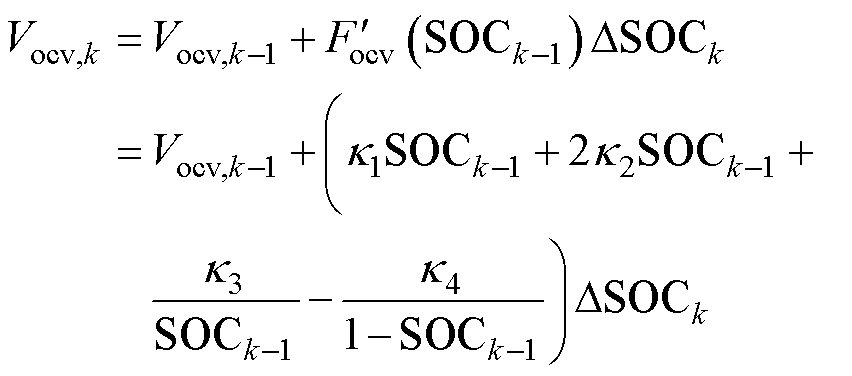 (11)
(11)
式中,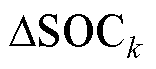 为k时刻先验
为k时刻先验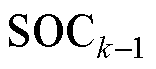 与k-1时刻后验
与k-1时刻后验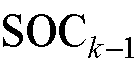 的差,即
的差,即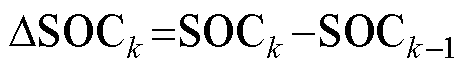 ;
;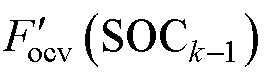 为对OCV-SOC关系式进行SOC求导。先验
为对OCV-SOC关系式进行SOC求导。先验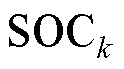 通过安时积分法获得,即
通过安时积分法获得,即
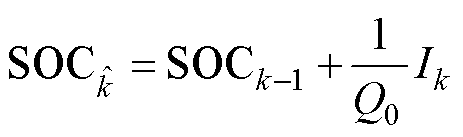 (12)
(12)
通过式(11),式(10)可以被转换为
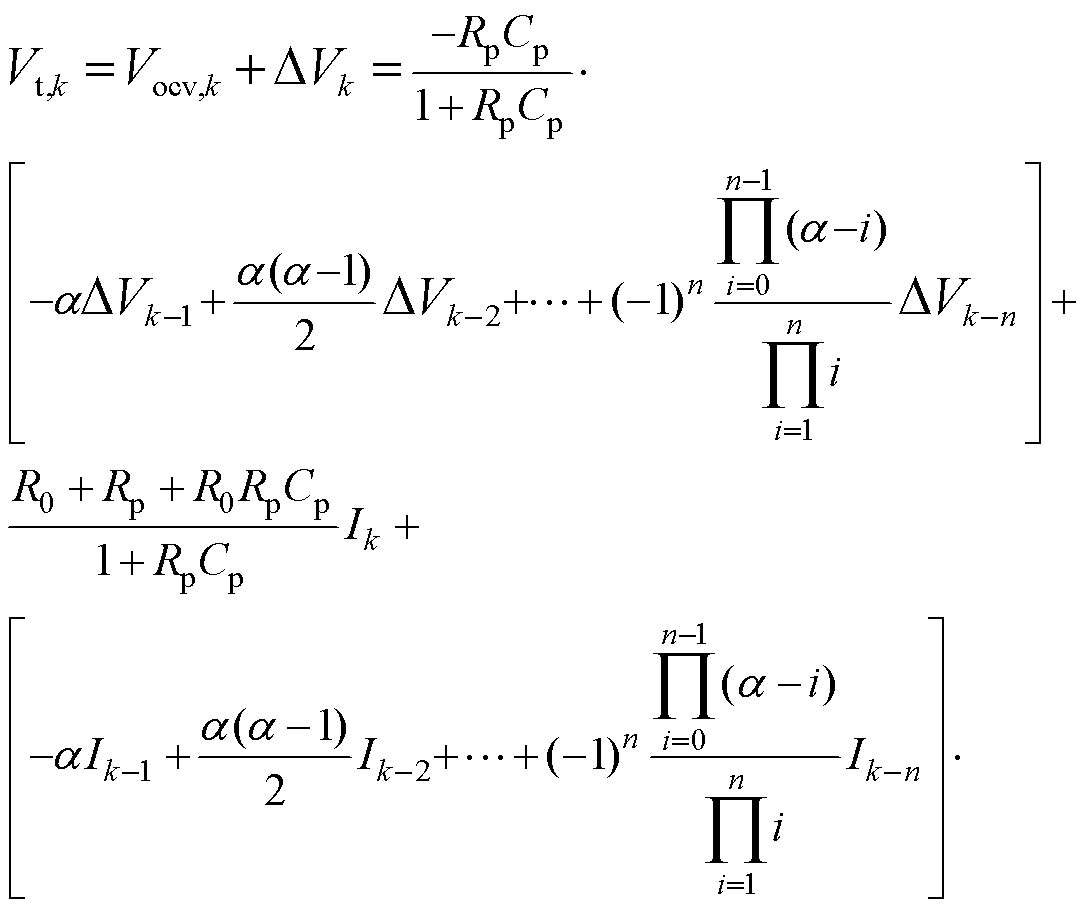
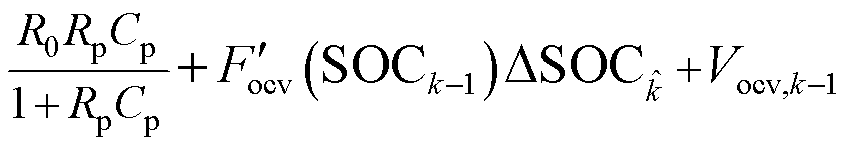 (13)
(13)
人工神经网络通过对神经元的信息传输、处理方式的模仿,具有并行协同处理能力强、信息处理能力快、自适应学习力强等有优点。数据驱动模型方法使用神经网络对电池进行建模,目前在状态估计方面得到了广泛应用。然而,这种方法将电池模型视为黑箱,无法得到电池模型参数的实际值,可解释性较差。
将分数阶模型与数据驱动模型结合,可以构建如图2所示的神经网络电池模型。该模型使用式(13)中的各项参数来定义神经网络中神经元以及传递权值。通过赋予物理意义,获取电池模型参数的实际值,提高模型的可解释性。在传统分数阶等效电路模型参数优化中,一般预先对测量数据进行离散化,然后再进行参数辨识。这会导致分数阶阶数a无法得到在线优化。基于神经网络的电池模型利用神经网络的层次化特征提取,将分数阶模型测量数据离散化的过程添加到参数优化中,实现了电池分数阶模型包含分数阶阶数在内的在线模型参数优化。
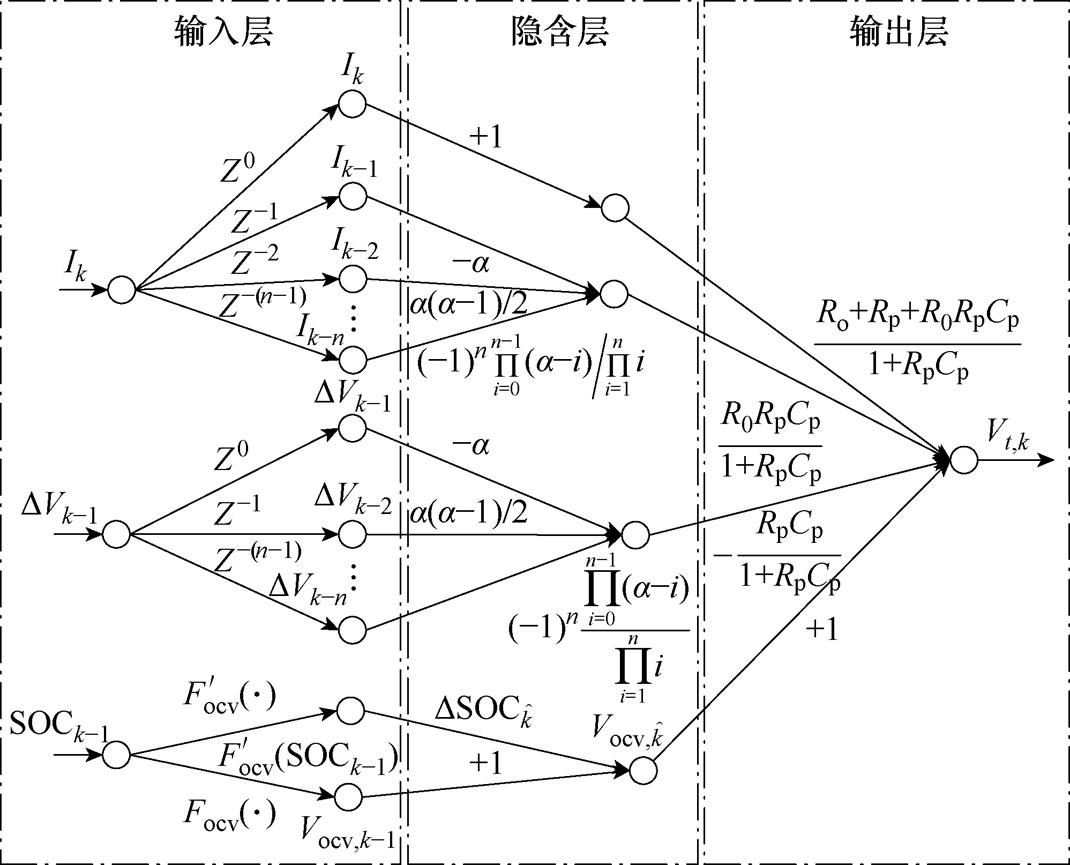
图2 分数阶神经网络模型
Fig.2 Fractional order neural network model
神经网络模型分为三层,包括输入层、隐藏层以及输出层。神经网络各神经元的激活函数设定为输入等于输出,即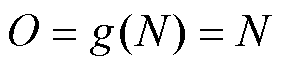 。
。
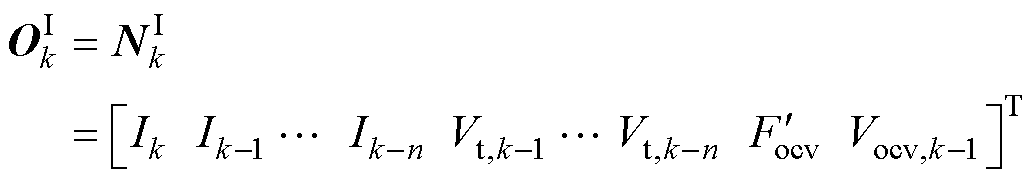 (14)
(14)
式中,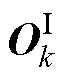 为输入层输出;
为输入层输出;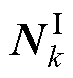 为输入层神经元;上标I表示输入层。输入层到隐藏层的传递权值描述为
为输入层神经元;上标I表示输入层。输入层到隐藏层的传递权值描述为
隐藏层H神经元 输出为
输出为 ,即
,即
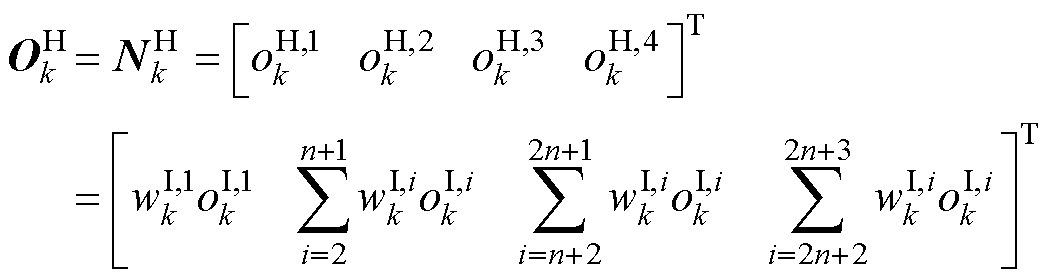 (16)
(16)
式中,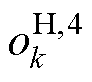 可以被视为电池的开路电压,即
可以被视为电池的开路电压,即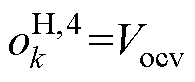 。
。
隐藏层H到输出层O的传递权值被设定为
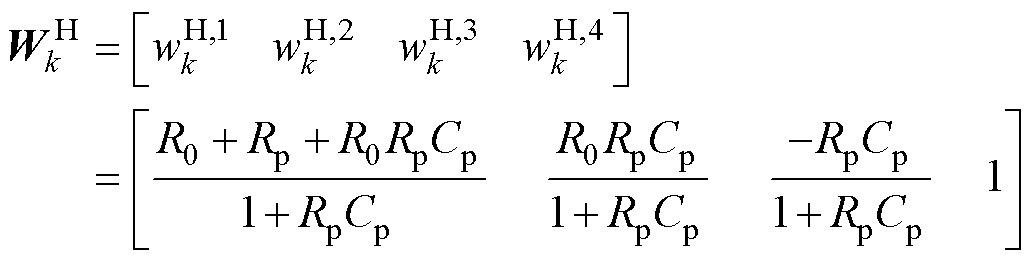 (17)
(17)
神经网络输出层输出为端口电压估计值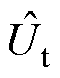 ,即
,即
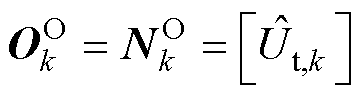 (18)
(18)
神经网络根据损失函数,对各层间传递权值进行优化。在电池的神经网络模型中,损失函数被定义为
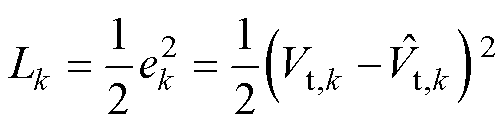 (19)
(19)
式中,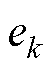 为电压预测值
为电压预测值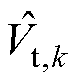 与测量值
与测量值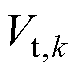 的偏差。
的偏差。
经过优化后,分数阶模型的欧姆电阻R0、极化电阻Rp、极化电容Cp、分数阶阶数a以及当前时刻DSOCk可根据式(20)求出。
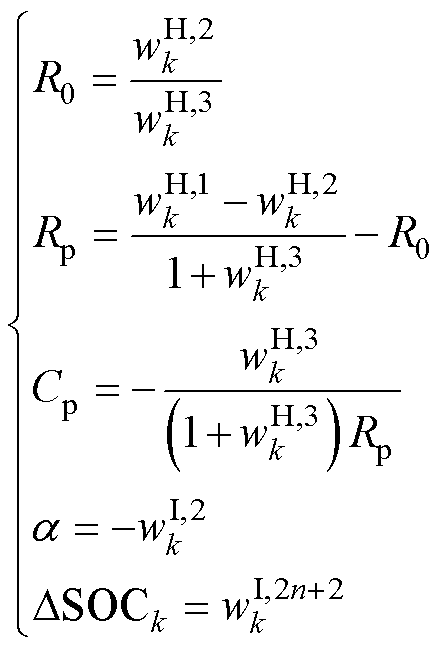 (20)
(20)
结合优化后DSOCk的,可以获得后验SOCk,即
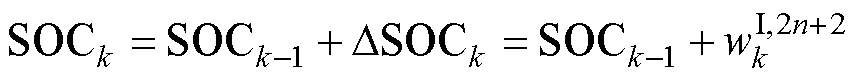 (21)
(21)
误差反向传播(Back Propagation, BP)算法使用神经网络误差函数Lk的向后传播来逐层修改权值。BP算法中引入动量项可以提高网络的收敛速度以及稳定性。带动量的误差反向传播算法(Back Propagation algorithm with Momentum, BPM)不仅考虑当前时刻误差,还考虑到上一个时刻的影响。图3构建了基于BPM电池参数辨识与SOC估计的框架。
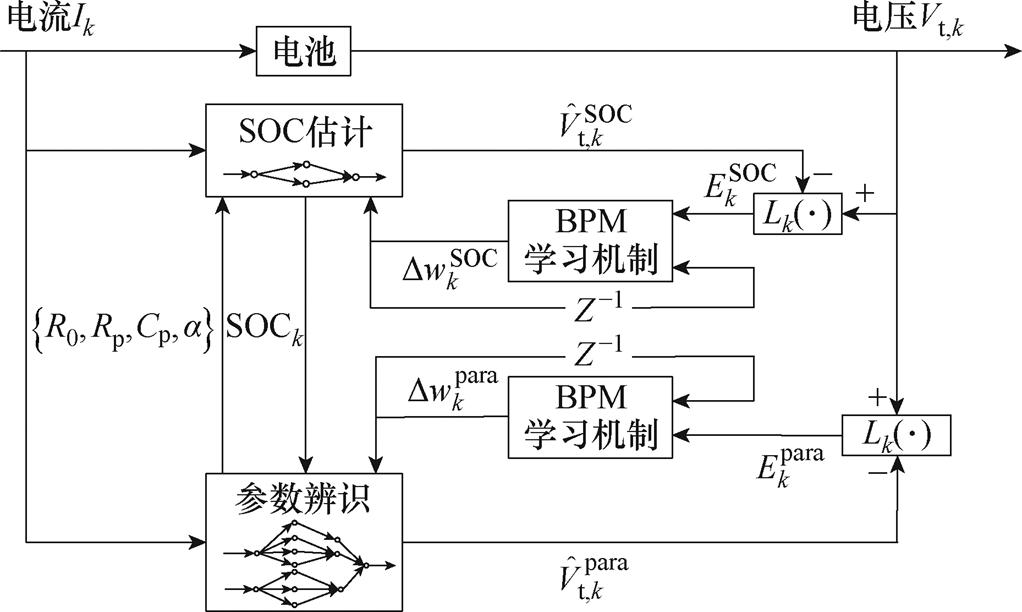
图3 基于BPM电池参数辨识与SOC估计框架
Fig.3 BPM-based battery parameter identification and SOC estimation framework
BP算法通过对传递权值W的优化,使损失函数Lk达到极小值。为此,一个被普遍使用的方法是梯度下降法。结合损失函数Lk,算法对传递权值进行多轮优化,直至到达截停条件完成优化。首先对隐藏层到输出层权值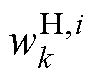 进行优化,通过式(22)和式(23)求得。
进行优化,通过式(22)和式(23)求得。
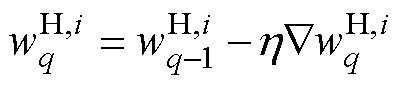 (22)
(22)
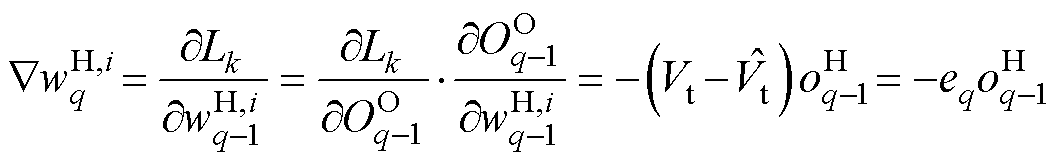 (23)
(23)
式中,h为学习速率;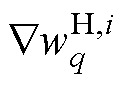 为隐藏层到输出层权值
为隐藏层到输出层权值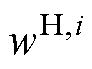 第q轮训练的下降梯度;q为当前训练轮数。
第q轮训练的下降梯度;q为当前训练轮数。
完成隐藏层到输出层的优化后,算法开始输入层到隐藏层的权值优化。优化规则为
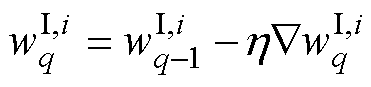 (24)
(24)
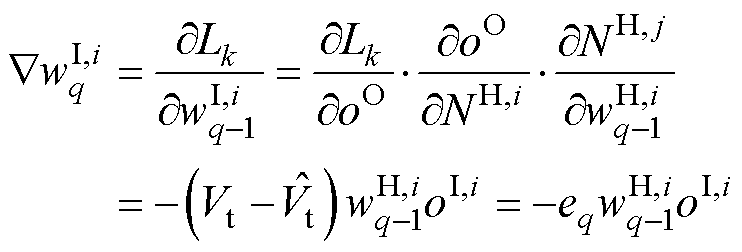 (25)
(25)
式中,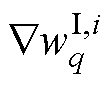 为输入层到隐藏层权值第q轮训练的下降梯度。
为输入层到隐藏层权值第q轮训练的下降梯度。
在BP算法中,学习速率h影响神经网络的收敛速度。较小的h使得神经网络的稳定性上升,但收敛速度极低。较大的h使得神经网络能够快速收敛,但网络权值变化量不稳定。BPM算法通过利用上一时刻权值变化DWk-1,在保持系统稳定的基础上加快收敛速度。BPM算法在权值的优化规则中增加动量项,如
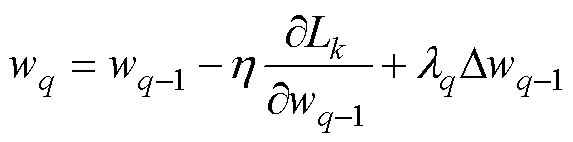 (26)
(26)
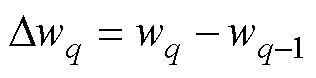 (27)
(27)
式中,l(k)为动量系数,决定算法的稳定性与收敛速度。其更新为
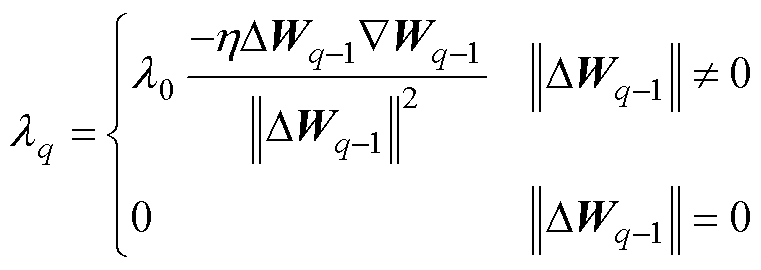 (28)
(28)
式中,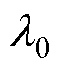 为常数且
为常数且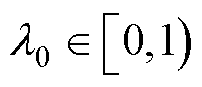 。从式(28)可以看出,动量项系数的大小由当前权值的梯度向量
。从式(28)可以看出,动量项系数的大小由当前权值的梯度向量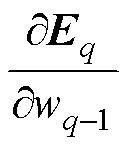 与上一时刻权值的更新向量
与上一时刻权值的更新向量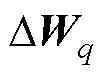 之间的夹角决定。当两个向量夹角大于90°时,动量系数为0。
之间的夹角决定。当两个向量夹角大于90°时,动量系数为0。
结合式(22)~式(28),可以推出BPM算法下,神经网络传递权值的更新依照规则为
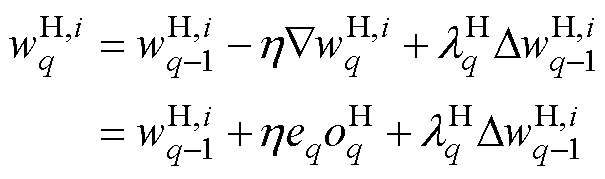 (29)
(29)
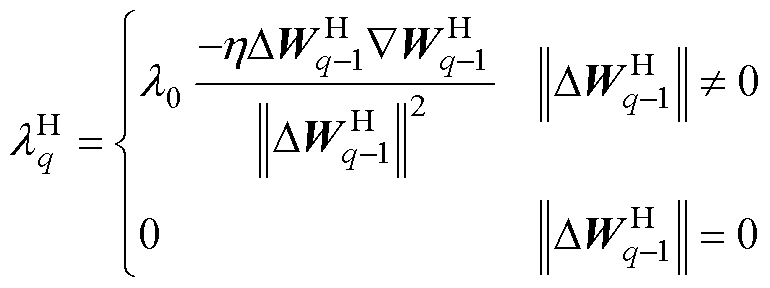 (30)
(30)
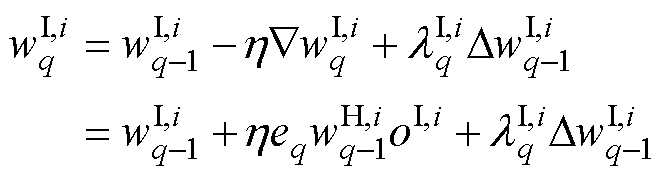 (31)
(31)
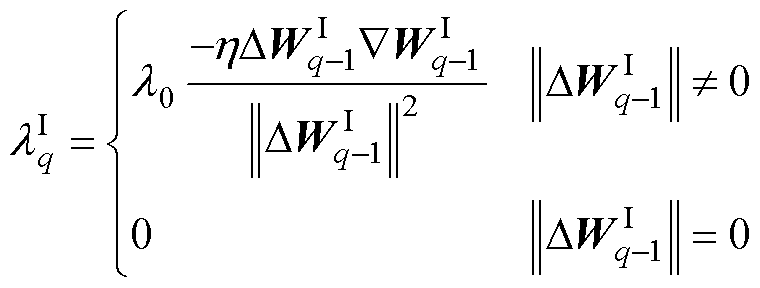 (32)
(32)
表1中给出了基于BPM的电池一阶分数阶模型参数辨识与SOC估计的伪代码。
表1 基于BPM电池模型参数辨识与SOC估计伪代码
Tab.1 Pseudo codes for parameter identification and SOC estimation of battery models using BPM

1. 初始化:网络结构,输入电流序列I,输出电压序列V,学习速率h,动量系数l0,序列长度T,迭代次数M,分数阶离散化记忆空间n等2. Fork=1→T3. Forq=1→M4. 由式(13)计算输出层输出。5. 由式(29)优化权值。6. 由式(31)优化权值。8. q=q+1;9. End10. 计算当前时刻SOCk如式(21);11. Forq=1→M12. 计算输出层输出如式(13);13. 优化权值、、如式(29);14. 优化权值如式(31);15. End16. 求解模型参数如式(20);17. k=k+118. End
为了验证基于BPM的参数辨识与SOC估计方法的收敛性,神经网络图2可以变化为如图4所示的收敛性分析模型。保持输入输出不变,将图2隐藏层中第二、三个神经元各自拆分为n个,第四个神经元化为两个。则隐层到输出层的传递权值被设定为
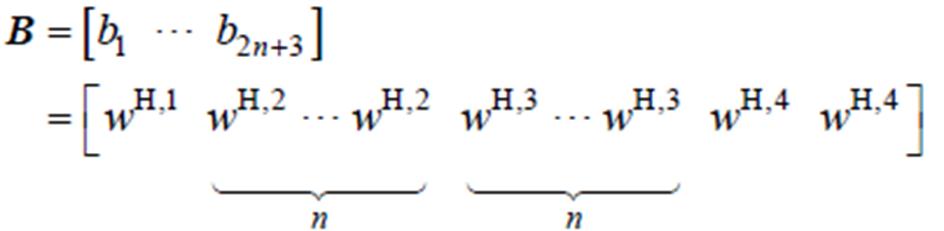 (33)
(33)
矩阵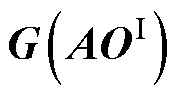 设定为
设定为
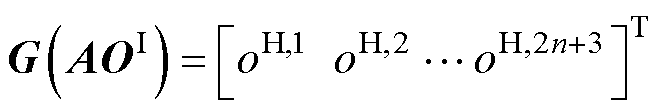 (34)
(34)
则有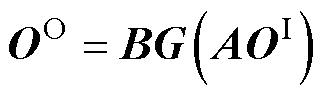 。
。
由于电池分数阶模型的神经网络具有物理意义且激活函数为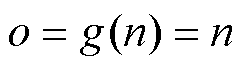 。所以有以下引理1、2成立。
。所以有以下引理1、2成立。
引理1: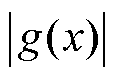 ,
,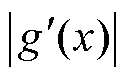 ,
,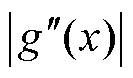 一致有界,
一致有界, 。
。
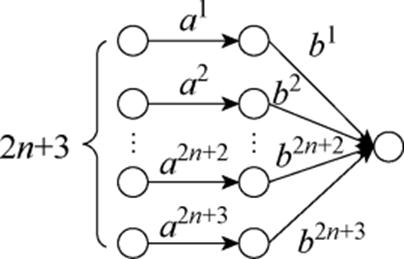
图4 收敛性分析模型
Fig.4 Convergence analysis model
引理2:传递权值 (
( )一致有界。
)一致有界。
由中值定理以及引理1,易证引理3成立。
引理3:存在常数C满足:
①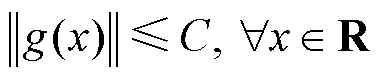 。
。
②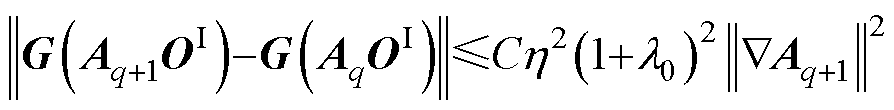 ,
,
 为第q+1次误差与第q次误差之差,即
为第q+1次误差与第q次误差之差,即
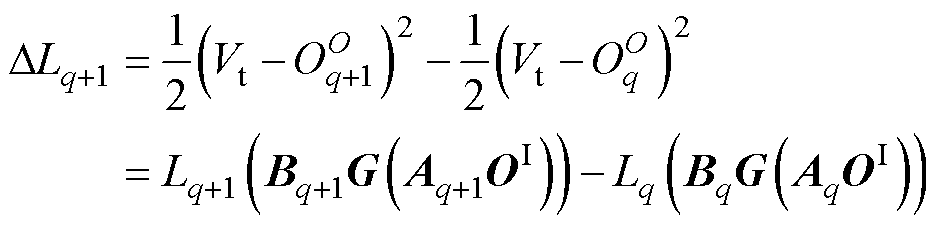 (35)
(35)
通过泰勒公式,式(35)可以转换为
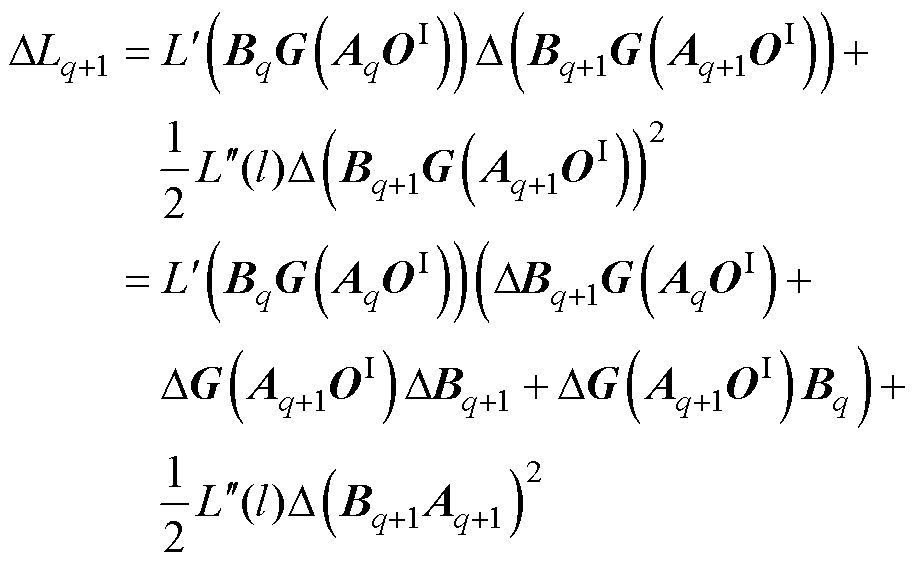 (36)
(36)
其中
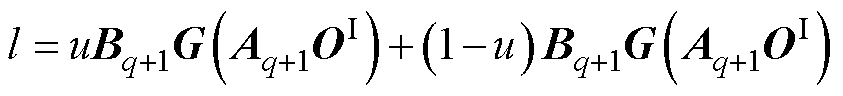
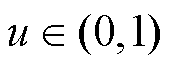
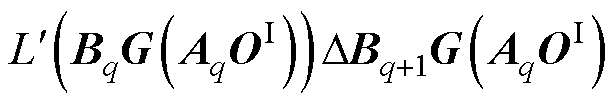
式中,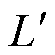 、
、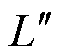 分别为函数
分别为函数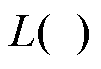 的一阶与二阶导数。结合式(23)可以转化为
的一阶与二阶导数。结合式(23)可以转化为
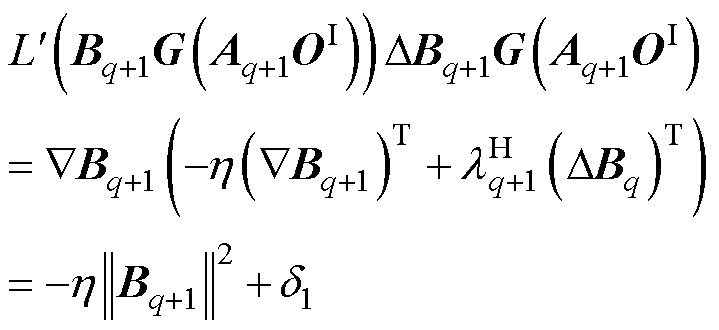 (37)
(37)
式中,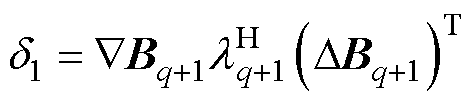 。通过泰勒公式,可以得到
。通过泰勒公式,可以得到
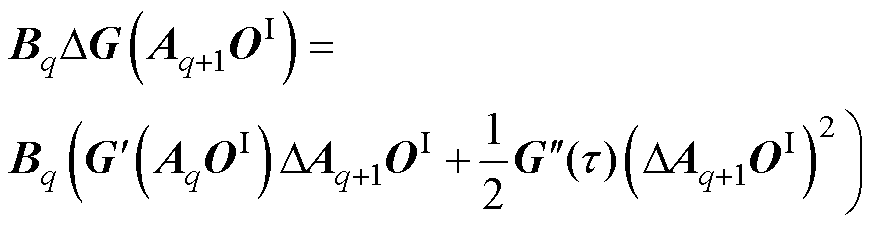 (38)
(38)
式中,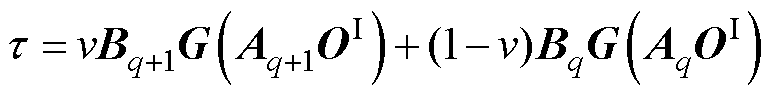 ,
,
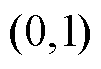 。
。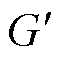 、
、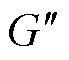 分别为函数
分别为函数 的一阶与二阶导数。将
的一阶与二阶导数。将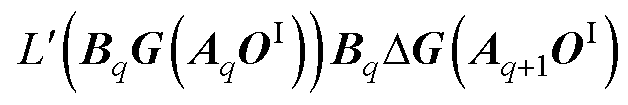 与式(25)、式(31)、式(38)结合可以得到
与式(25)、式(31)、式(38)结合可以得到
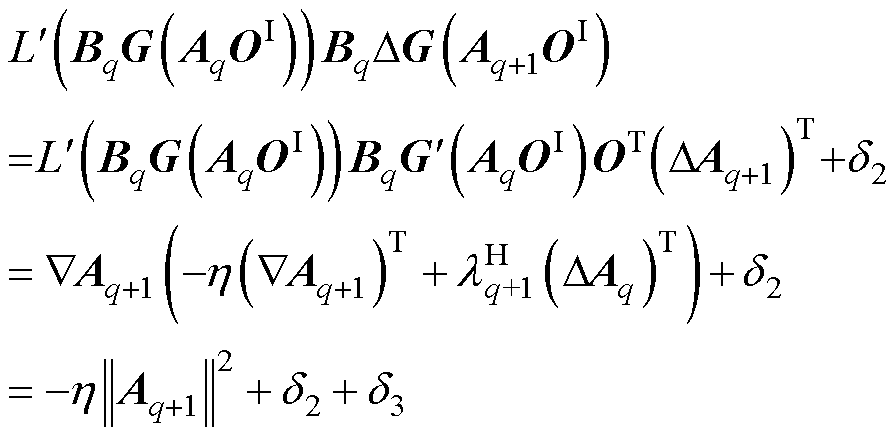 (39)
(39)
其中
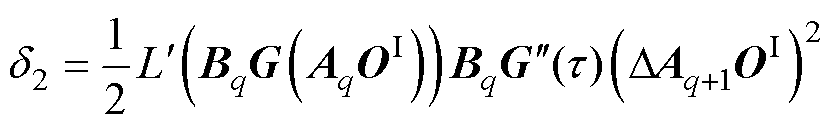
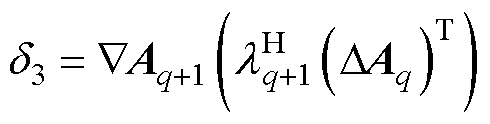
结合式(37)、式(39),式(36)可以转换为
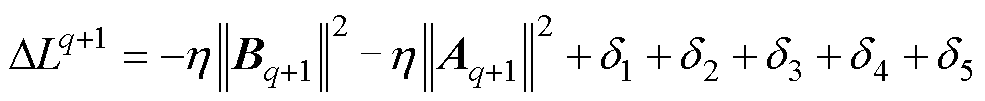 (40)
(40)
其中
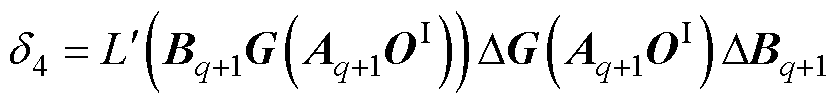
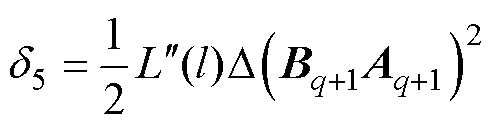
由式(29)~式(32)可得
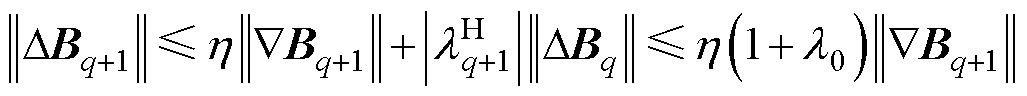 (41)
(41)
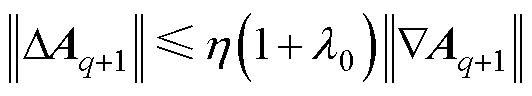 (42)
(42)
由式(30)可得
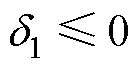 (43)
(43)
由引理1、2以及式(42)可以获得
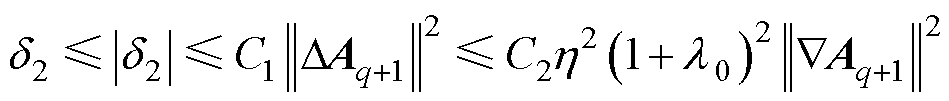 (44)
(44)
式中,C1、C2为正数常量。由式(32)可得
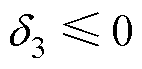 (45)
(45)
由式(41)和引理3以及Cauchy-Schwartz不等式可得
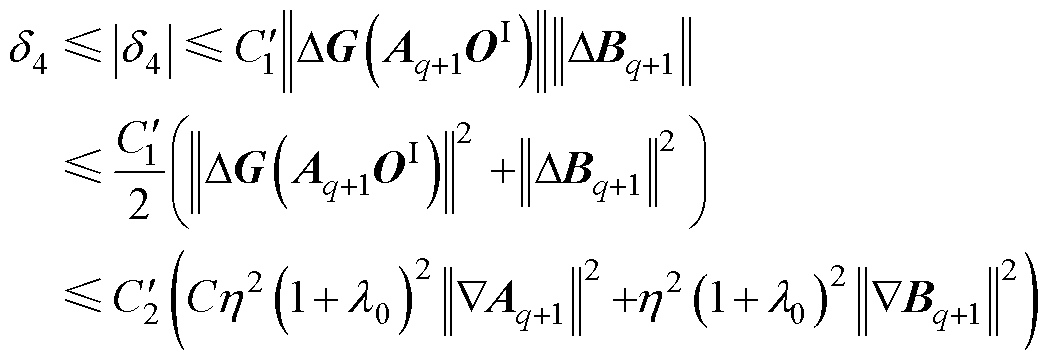
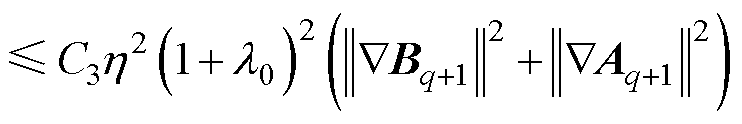 (46)
(46)
式中,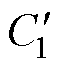 、
、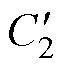 、
、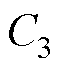 为正数常量。由引理2、3及式(41),有式(47)成立。
为正数常量。由引理2、3及式(41),有式(47)成立。
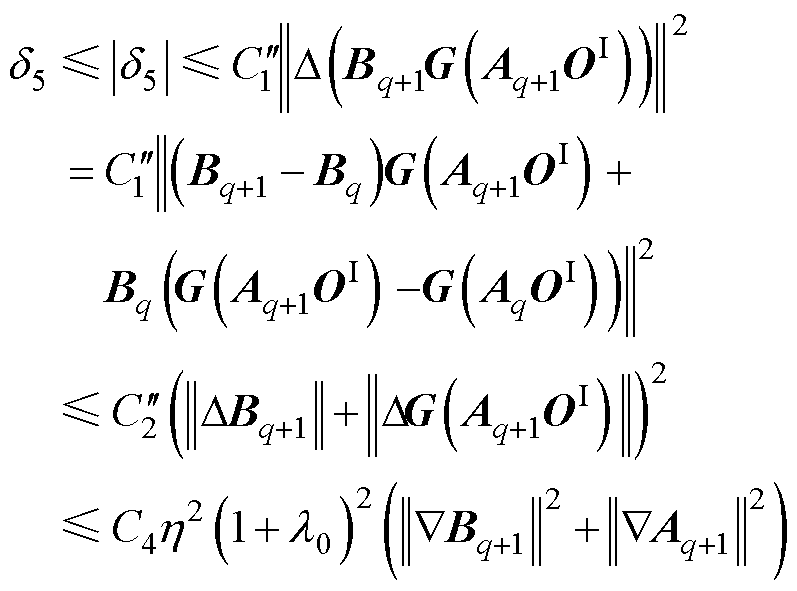 (47)
(47)
式中,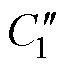 、
、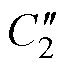 、
、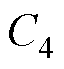 为正数常量。由式(40)、式(43)~式(47),可以得到
为正数常量。由式(40)、式(43)~式(47),可以得到
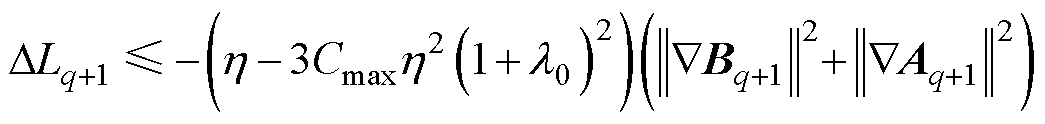 (48)
(48)
式中,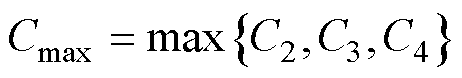 。则当
。则当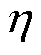 满足
满足
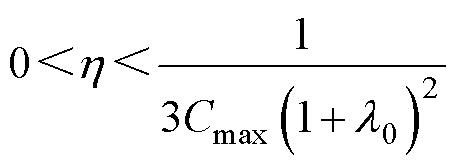 (49)
(49)
有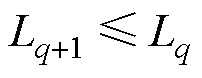 ,即神经网络损失函数为单调递减函数,同时由于
,即神经网络损失函数为单调递减函数,同时由于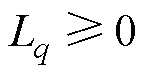 ,即损失函数有下界,则有
,即损失函数有下界,则有
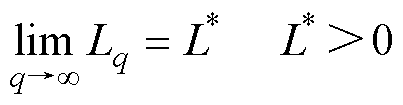 (50)
(50)
以上说明当神经网络学习速率满足式(49),即学习速率足够小时,神经网络的损失函数会下降收敛至某一正数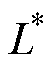 。
。
为了验证所建立电池模型与SOC估计算法的有效性,搭建了如图5所示实验平台,并开展了不同环境工况下的电池实验测试。实验平台为一台电池测试系统(NEWARE CT-4008Tn-5V12A-S1)、一台高低温恒温箱(Hongjin HJT-TH-150CHD)和一个工控机组成,实验电池参数见表2。
电池测试流程如图6所示,包括定容测试、OCV测试和动态工况测试。其中,定容测试以1C电流进行充放电,循环执行进行3次,测试结果的平均值作为实际容量,充电截止电压和截止电流分别为3.6 V和0.03C,放电截止电压为2.0 V。OCV实验采用恒流脉冲测试方案,以放电OCV测试为例,电池以-1C电流放电6 min,再搁置2 h,记录端电压,即为其开路电压,测试方案和工况如图6c和图7a所示。动态工况可以更好地反映电池内部特性,为此本实验分别对电池实施动态应力测试(Dynamic Stress Test, DST)和城市道路循环测试(Urban Dynamometer Driving Schedule, UDDS),动态电流工况如图7b~图7e所示。为了进一步验证所建立的神经网络模型和状态估计算法的鲁棒性,上述实验分别在温度-5℃、25℃和45℃下执行操作。

图5 实验平台
Fig.5 Experimental platform
表2 电池规格参数
Tab.2 Battery specification parameters
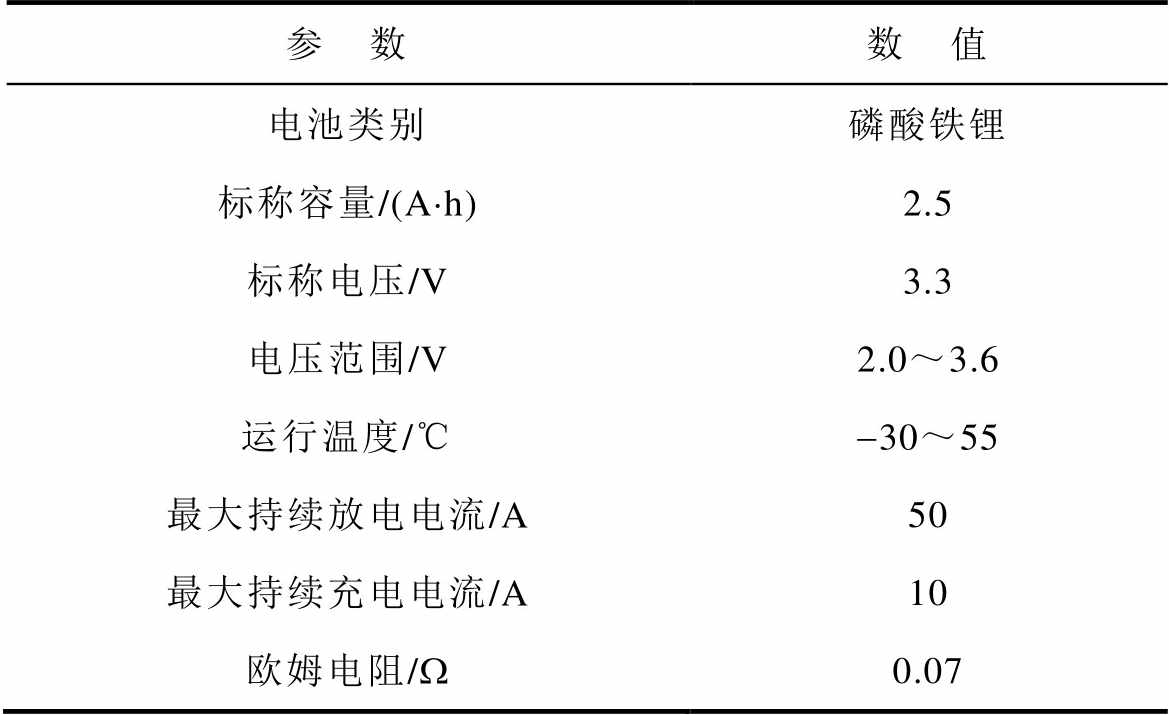
参 数数 值 电池类别磷酸铁锂 标称容量/(A×h)2.5 标称电压/V3.3 电压范围/V2.0~3.6 运行温度/℃-30~55 最大持续放电电流/A50 最大持续充电电流/A10 欧姆电阻/W0.07
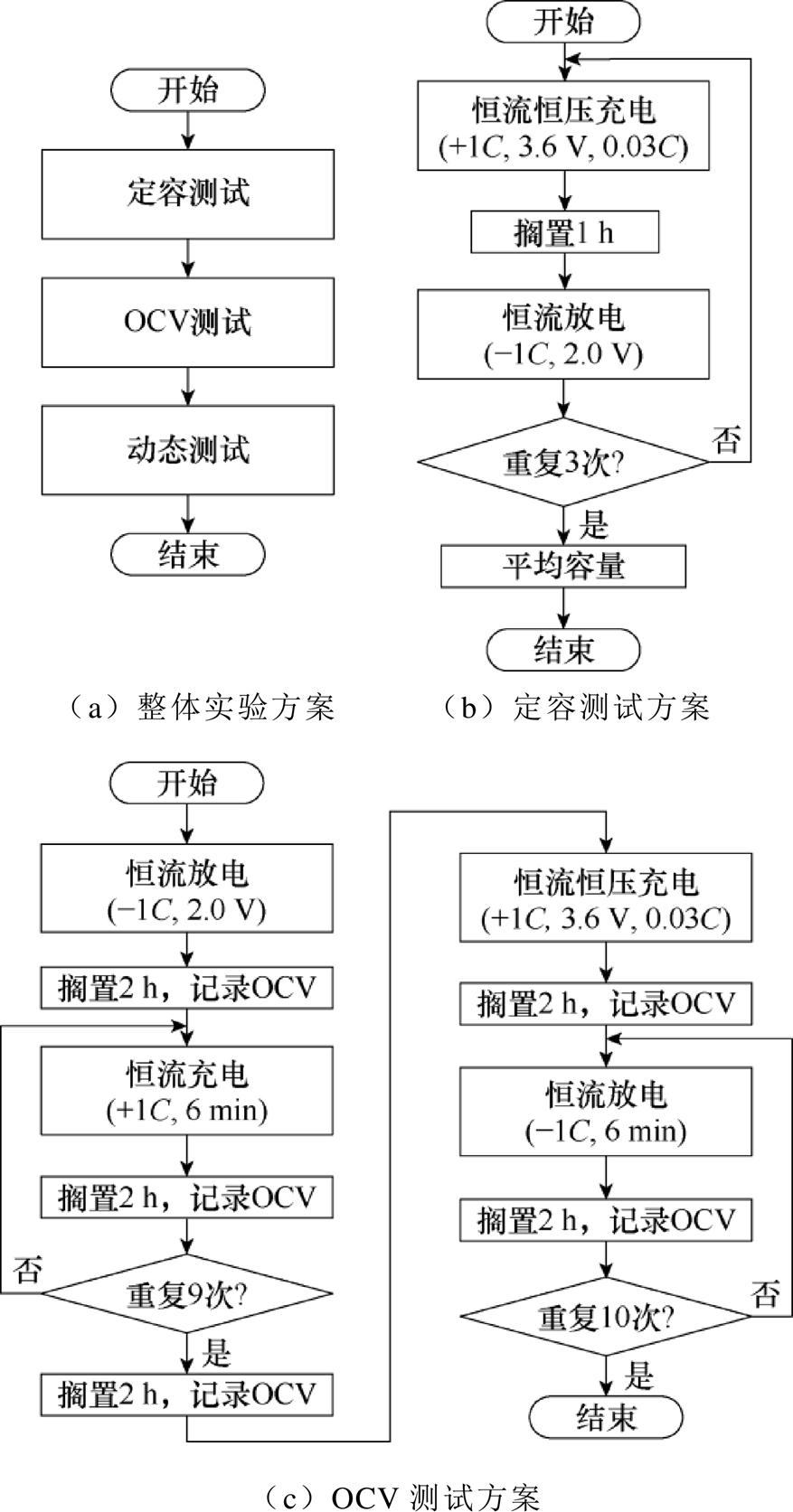
图6 实验方案
Fig.6 Experimental plan
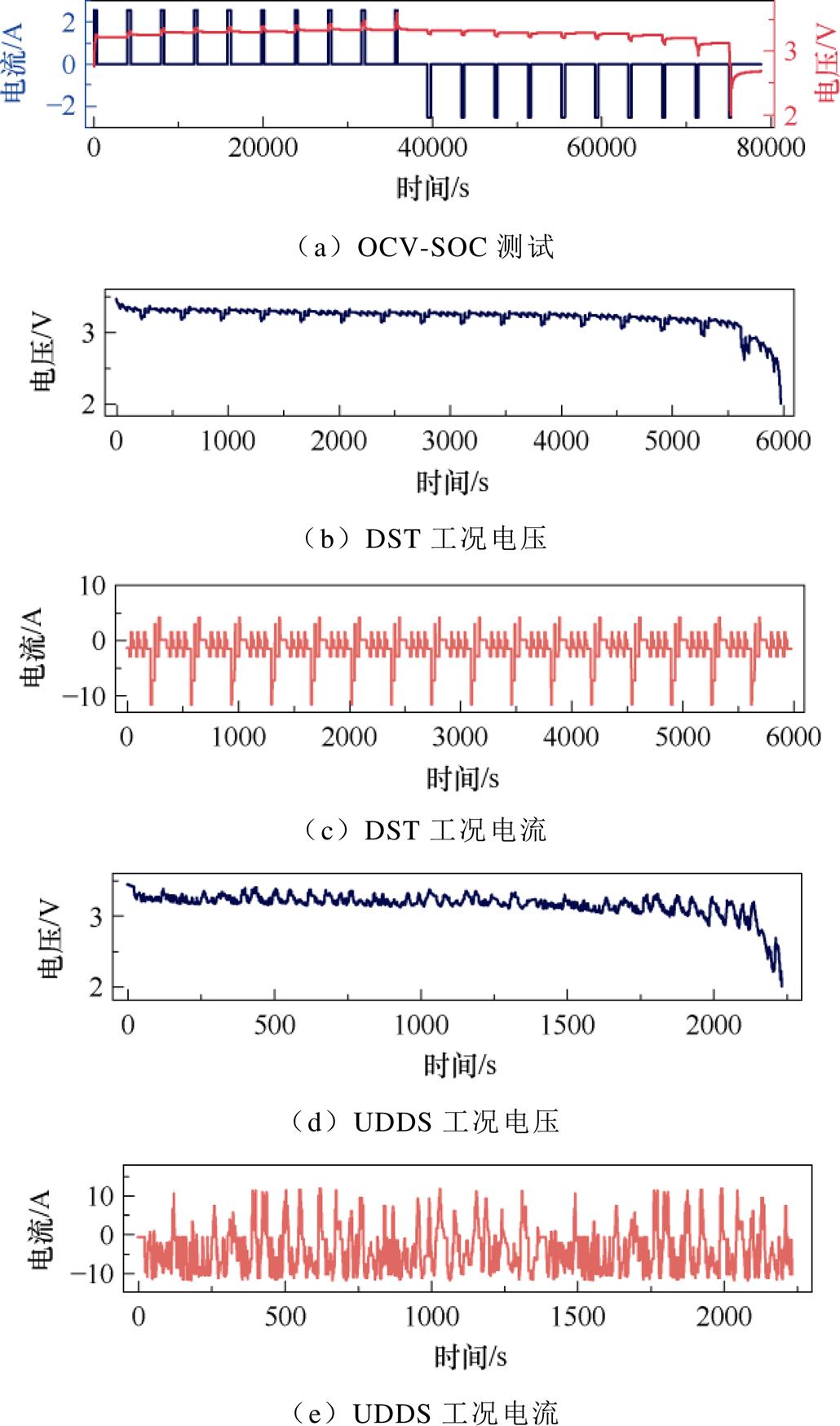
图7 实验工况
Fig.7 Experimental conditions
本节主要验证电池模型精度与状态估计精度。将所提出的BPM算法与扩展卡尔曼滤波(Extended Kalman Filter, EKF)、无迹卡尔曼滤波(Unscented Kalman Filter, UKF)[18-19]进行比较,计算输出电压验证模型精度。考虑到计算量,BPM算法分数阶离散的记忆空间设置为n=100。由于EKF与UKF算法无法对分数阶阶数a进行优化,两者统一设置为a=0.8。参考SOC通过安时积分法计算。在实验中,参考SOC的初始值为100%,SOC预测算法SOC初始值为90%。为了更好地量化对比不同算法的辨识精度,本研究采用平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)、平均绝对误差(Mean Absolute Error, MAE)等指标量化电压误差。
考虑外部温度会对电池产生较大的影响,提出算法将在低温、常温及高温三种温度环境下进行参数辨识与SOC,探讨温度对于由BPM算法建立的电池模型在模型参数、模型精度以及SOC估计精度的影响。图8~图10展示了一阶分数阶模型在-5℃、25℃以及45℃时的欧姆内阻、极化电阻、极化电容、SOC、分数阶阶数以及Ut、SOC误差的估计结果。
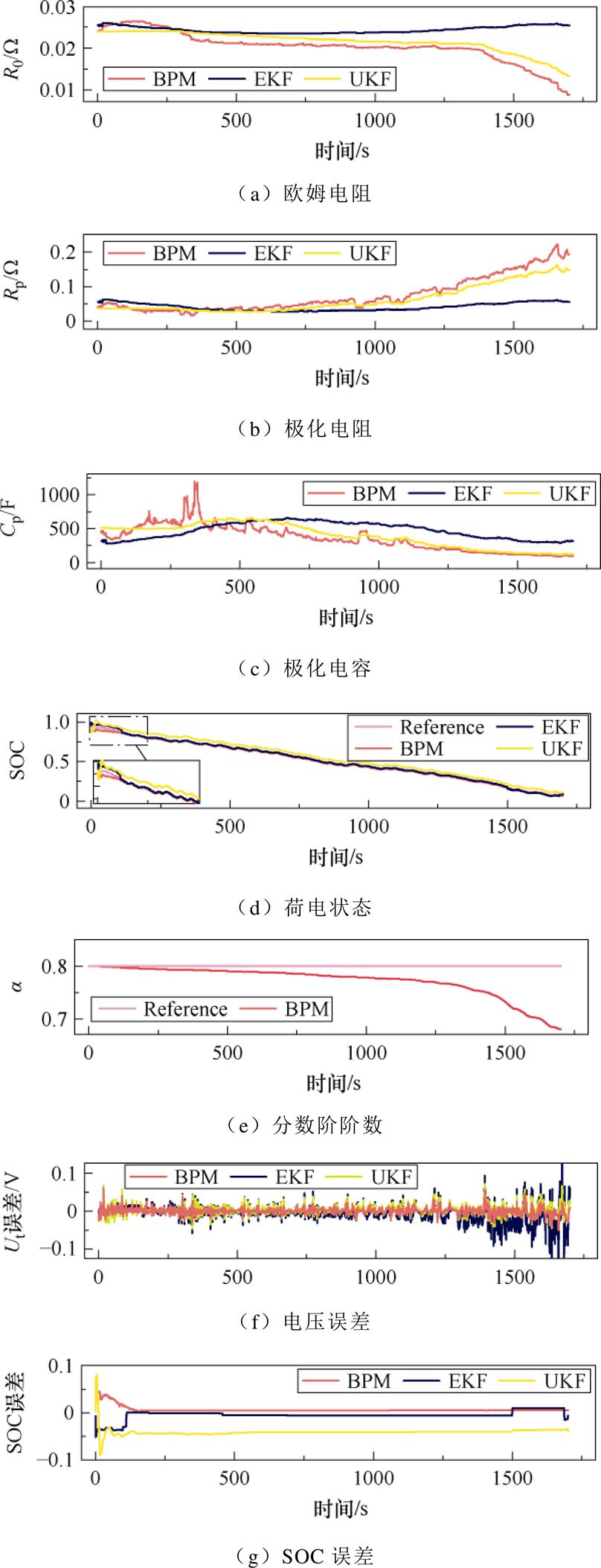
图8 -5℃下UDDS工况结果对比
Fig.8 Comparison of results with UDDS condition under -5℃
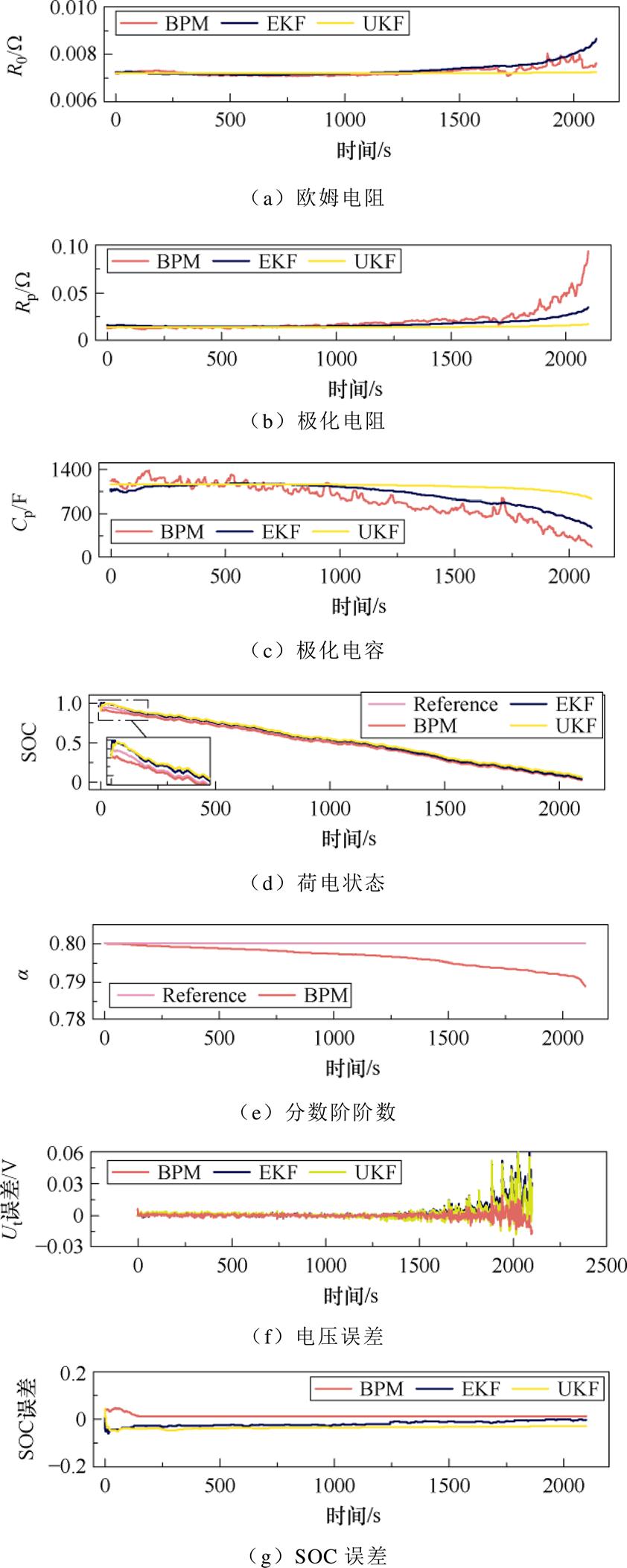
图9 25℃下UDDS工况结果对比
Fig.9 Comparison of results with UDDS condition under 25℃
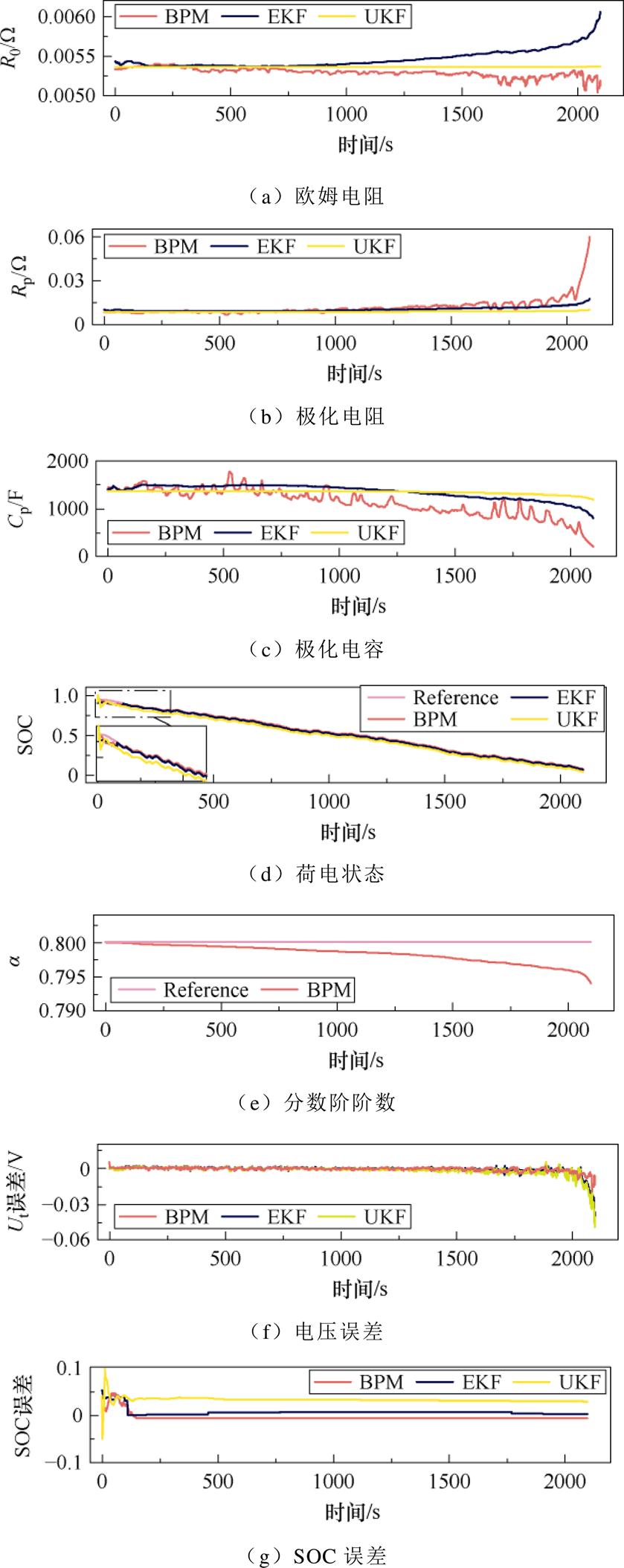
图10 45℃下UDDS工况结果对比
Fig.10 Comparison of results with UDDS condition under 45℃
随着温度的上升,欧姆电阻从-5℃时0.025 W下降到45℃时0.005 5 W。与欧姆电阻相反,极化电容从-5℃时500 F上升到45℃时1 500 F。极化电阻呈微弱下降趋势,从0.05 W附近降到0.01 W附近。通过对分数阶阶数曲线的分析,可以看出随着电池SOC的下降,a呈下降趋势且高温会使得其下降速度减缓。对比三种温度下的参数,低温环境会造成锂电池欧姆内阻的急剧上升,不利于锂电池安全高效的使用。
图8f、图9f、图10f展示了锂电池端电压估计的误差。对比三种算法可以看出,BPM算法在电池低SOC时的误差显著小于其他两种算法。图8g、图9g、图10g展示了锂电池SOC估计的误差,三种算法的收敛速度以及误差基本相同。表3给出了三种算法SOC估计结果的精度评估,三种指标的计算公式为
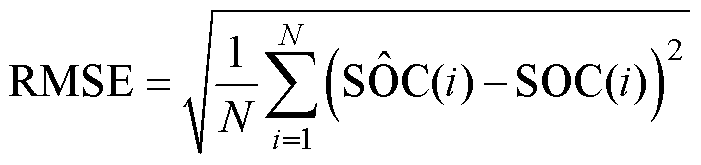 (51)
(51)
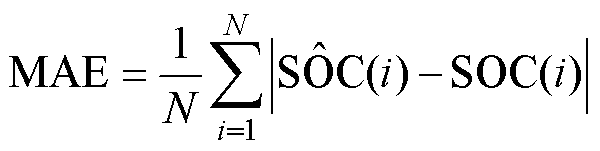 (52)
(52)
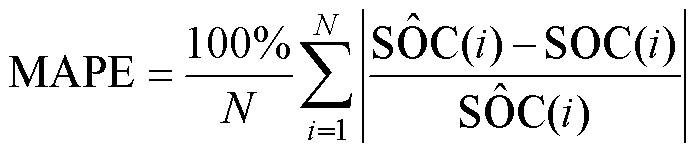 (53)
(53)
式中,N为总时间数;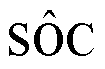 为参考SOC。
为参考SOC。
表3中的数据表明,使用BPM算法SOC估计的精度最高。根据表3中的RMSE指标,相较于EKF、UKF,BPM算法最高可以提高SOC估计精度的36.5%。对比各温度下SOC估计结果,可以看出温度对于SOC估计精度并无影响。
进一步地,使用模型估计电压作为模型精度的评估标准,见表4。实验结果显示,BPM算法使电池模型精度上有了大幅提高。在25℃效果最为突出,相较于EKF、UKF分别提高了约36%、61%。对比三种环境下的结果,可以看出低温环境对电池模型精度影响较大,高温对于电池模型精度影响较小。
表3 SOC估计结果对比
Tab.3 Comparison of SOC estimation
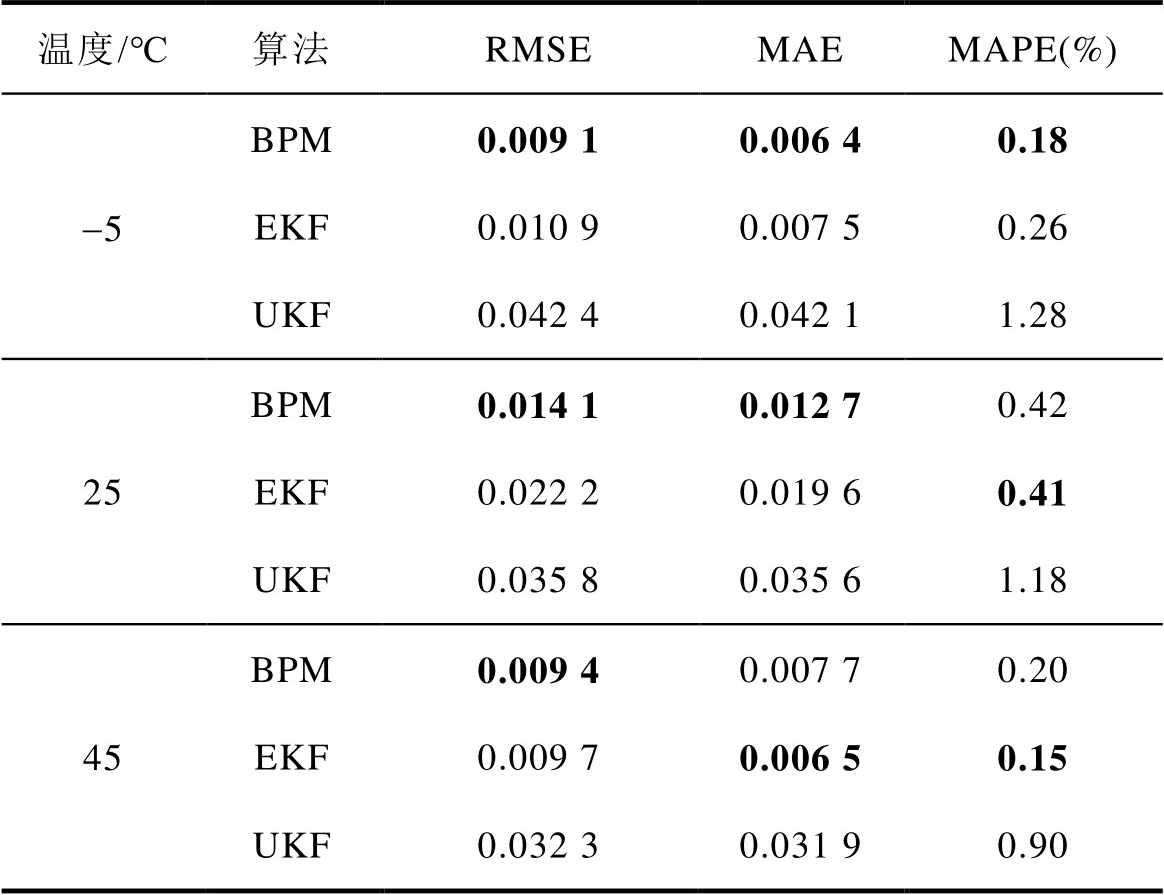
温度/℃算法RMSEMAEMAPE(%) -5BPM0.009 10.006 40.18 EKF0.010 90.007 50.26 UKF0.042 40.042 11.28 25BPM0.014 10.012 70.42 EKF0.022 20.019 60.41 UKF0.035 80.035 61.18 45BPM0.009 40.007 70.20 EKF0.009 70.006 50.15 UKF0.032 30.031 90.90
表4 电压估计精度对比
Tab.4 Comparison of voltage prediction accuracy
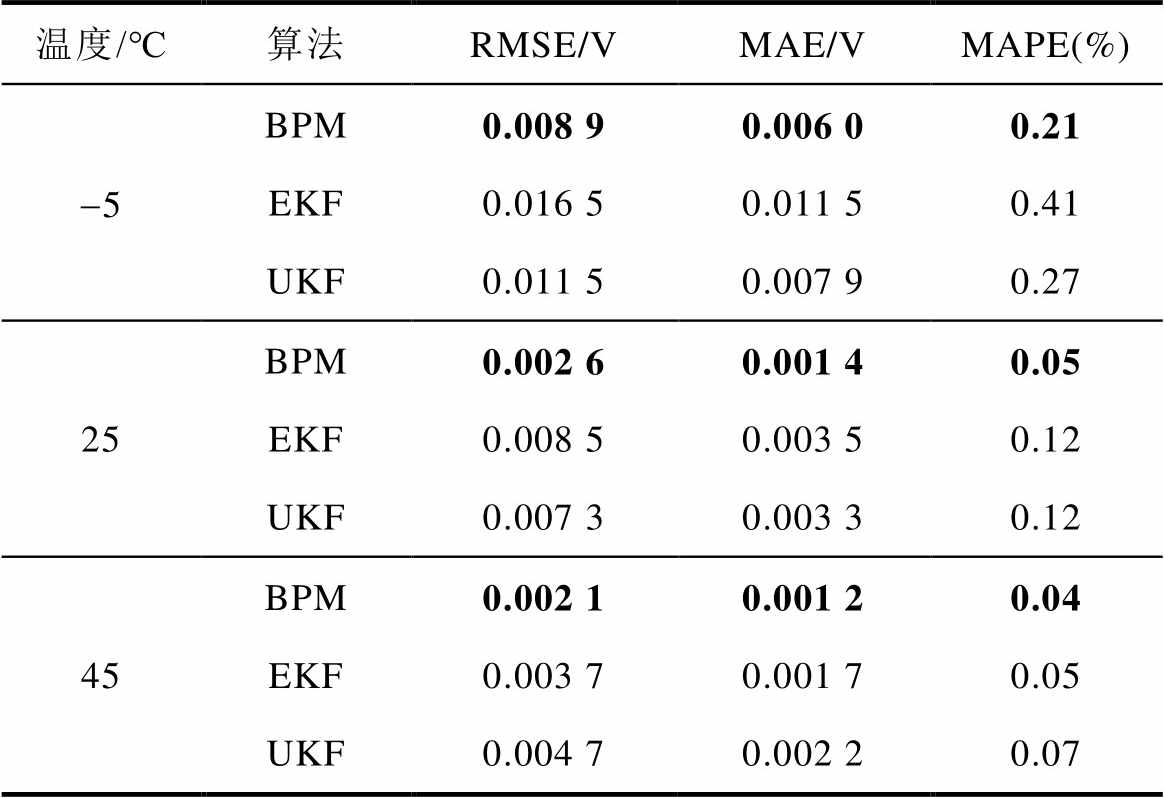
温度/℃算法RMSE/VMAE/VMAPE(%) -5BPM0.008 90.006 00.21 EKF0.016 50.011 50.41 UKF0.011 50.007 90.27 25BPM0.002 60.001 40.05 EKF0.008 50.003 50.12 UKF0.007 30.003 30.12 45BPM0.002 10.001 20.04 EKF0.003 70.001 70.05 UKF0.004 70.002 20.07
图11展示了锂电池在25℃ DST工况下参数辨识与SOC估计的结果。BPM算法所得参数曲线呈现出明显的周期性波动,这是由于DST工况的周期性电流所造成的。DST工况下分数阶模型的R0、Rp、Cp各自约为0.008 W、0.03 W、1 200 F。相比同情况下UDDS工况的结果,模型参数发生了增长。
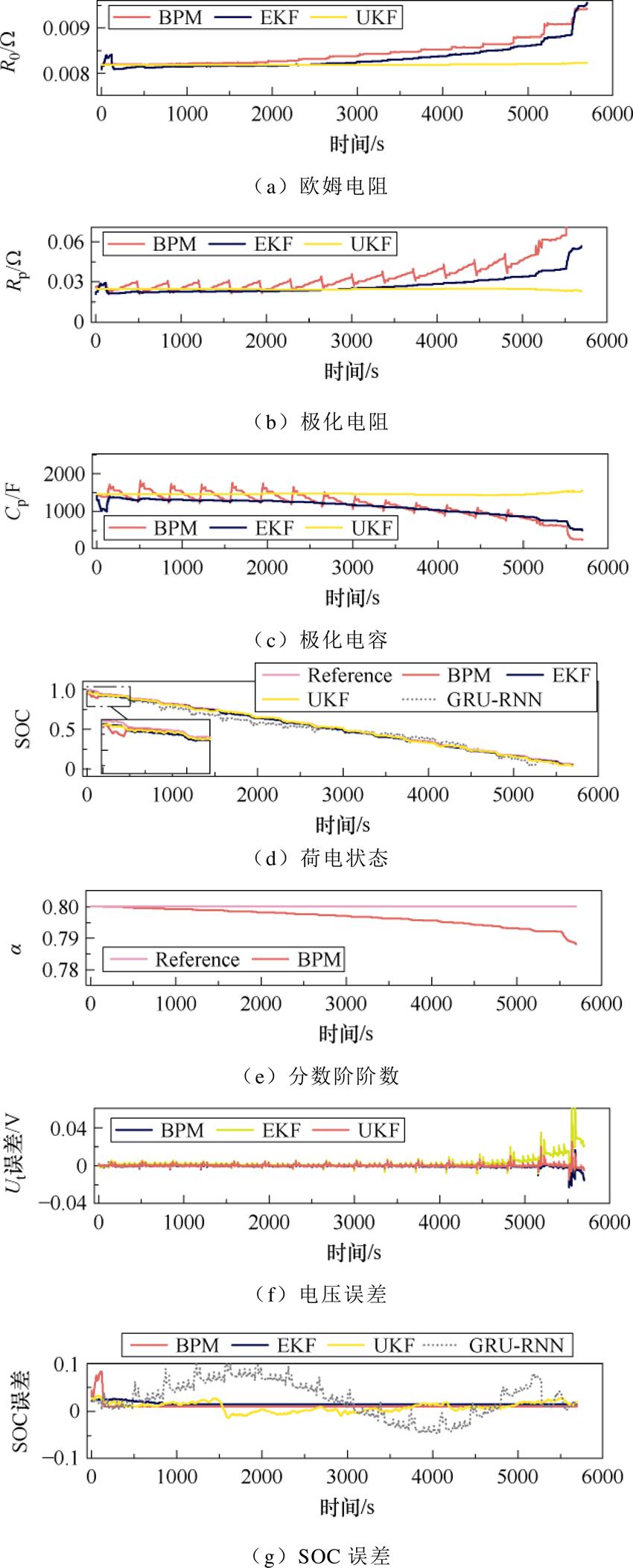
图11 25℃DST工况下结果对比
Fig.11 Comparison of results with DST condition under 25℃
在本对比中加入了基于门控循环单元递归神经网络(Gated Recurrent Unit-Recurrent Neural Net- work, GRU-RNN)的SOC深度学习估计方法[20]。GRU-RNN方法的SOC估计结果及误差在图11d、图11g中,从图中可以看出,深度学习方法估计得到的SOC误差较大,这是因为由于电池内部的各种反应会随着电池内部与外部的变化而变化。基于深度学习的SOC方法通过训练集构建的电池系统输入与输出关系,可能并不适用于测试集。同时,该系统在测试集中为开环系统,无法矫正外部干扰以及累计误差等。
表5为不同工况下电池模型的电压估计精度指标。相较于UDDS工况,DST工况下三种算法的精度均得到了提高。DST工况下的BPM算法与EKF算法的进度相当,高于UKF算法。从图11g中的SOC误差曲线可以看出,UKF算法SOC估计的结果较不稳定,BPM与EKF算法的SOC估计结果基本相同。
表5 不同工况下电压Ut估计精度对比
Tab.5 Comparison of voltage prediction accuracy under different conditions
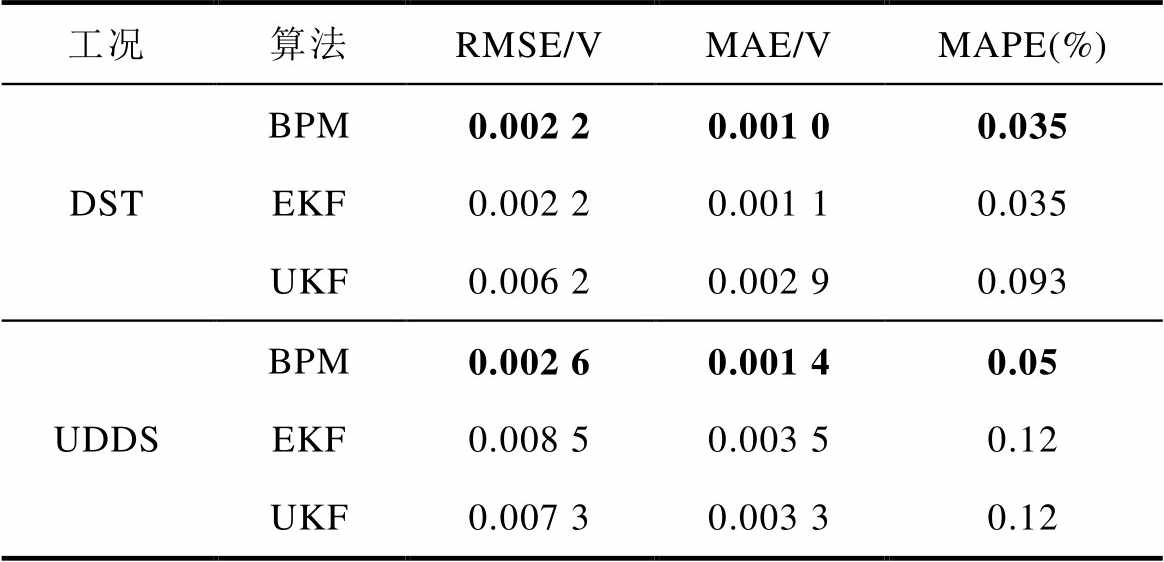
工况算法RMSE/VMAE/VMAPE(%) DSTBPM0.002 20.001 00.035 EKF0.002 20.001 10.035 UKF0.006 20.002 90.093 UDDSBPM0.002 60.001 40.05 EKF0.008 50.003 50.12 UKF0.007 30.003 30.12
在分数阶模型中,对数据进行离散化不仅需要当前时刻数据,还需要使用n个过去时刻的数据。记忆空间n的设定决定了分数阶模型的精度、计算量等性能。为了探讨记忆空间n对与分数阶模型的具体影响,具有不同记忆空间的BPM算法被用来进行对比。
图12展示的是25℃时UDDS工况在不同记忆空间下的评价结果。
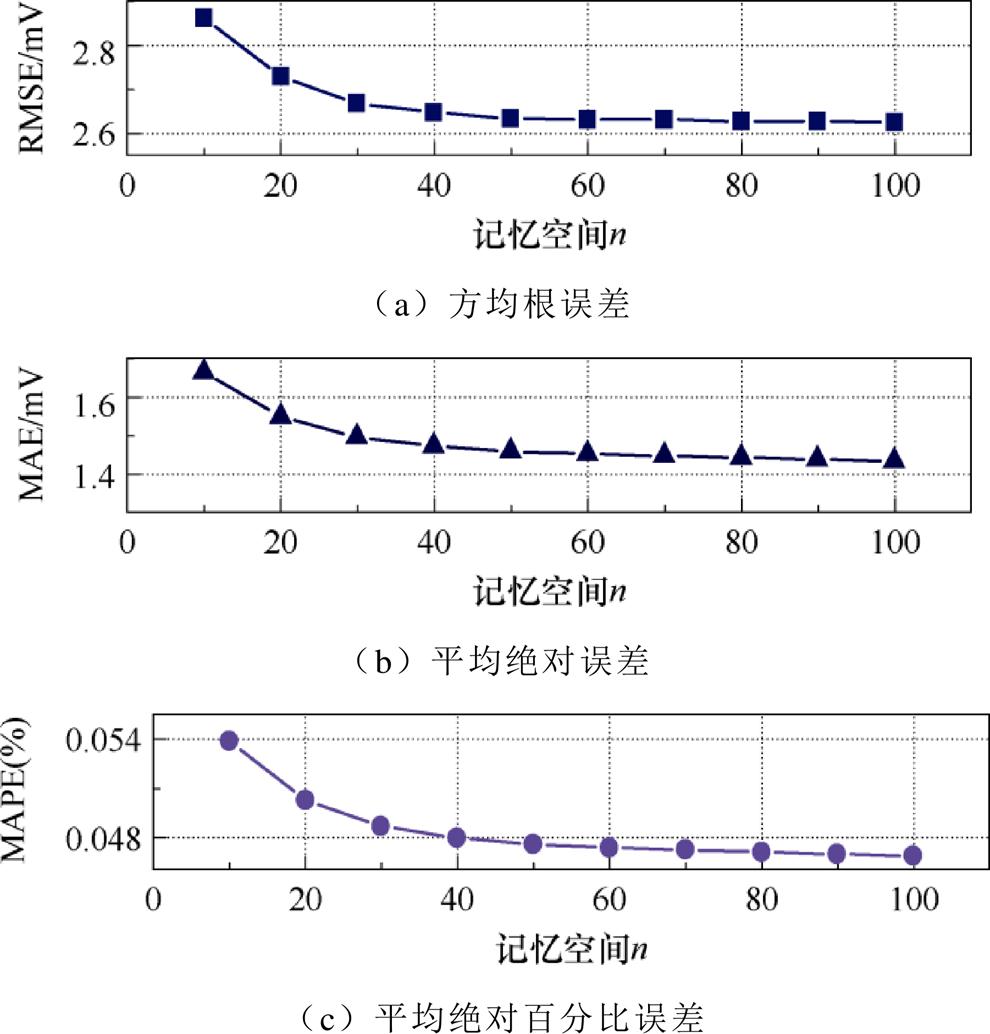
图12 不同记忆空间Ut估计对比
Fig.12 Comparison of Utestimation with different memory spaces
从结果分析,RMSE、MAE、MAPE随着n的增加而减小,模型精度上升。当n上升到50时,模型精度趋于稳定。考虑到大记忆空间带来的计算负担,当nÎ[50, 70]时,分数阶模型能在模型精度与计算负担之间达到平衡。
精确的电池模型对其状态估计、故障诊断和能量管理具有重要意义。本文提出的半物理意义的电池神经网络建模方法结合了分数阶等效电路模型和神经网络的优势,引入了模型分数阶阶数a的在线估计,有效提高了模型精度和可解释性。在神经网络优化算法方面,通过动量引入过去时刻的数据,从而提高模型的精度。实验结果表明,在不同环境温度和工况下,使用BPM进行参数辨识可以获得更准确的模型参数,进而实现更精确的电压预测。相比于EKF、UKF参数辨识与SOC估计算法,基于BPM算法具有更高的精度,模型的精度指标最高可提高61%,适用于需要高精度电压预测的应用场景。对比不同记忆空间n下的电池模型,结果表明,记忆空间n决定了分数阶模型的精度与计算负担。当nÎ[50, 70]时,分数阶模型可以实现模型精度与计算负担的平衡。神经网络在锂离子电池建模和状态估计中具有重要意义,可以为电池的性能评估和管理提供有效的支持。
参考文献
[1] 张程, 陆万林, 张东清, 等. 基于调节因子改进模糊熵融合加权法的锂电池状态联合估计[J/OL]. 电工技术学报, 1-13[2025-05-22]. https://doi.org/10. 19595/j.cnki.1000-6753.tces.242101.
Zhang Cheng, Lu Wanlin, Zhang Dongqing, et al. Joint estimation of lithium battery states based on improved fuzzy entropy fusion weighting method with regulation factors[J/OL]. Transactions of China Electrotechnical Society, 1-13[2025-05-22]. https:// doi.org/10.19595/j.cnki.1000-6753.tces.242101.
[2] Tian Jiaqiang, Fan Yuan, Pan Tianhong, et al. A critical review on inconsistency mechanism, evaluation methods and improvement measures for lithium-ion battery energy storage systems[J]. Renewable and Sustainable Energy Reviews, 2024, 189: 113978.
[3] 李弈, 张金龙, 漆汉宏, 等. 基于变分深度嵌入-带有梯度惩罚的生成对抗网络的锂离子电池老化特性建模[J]. 电工技术学报, 2024, 39(13): 4226-4239.
Li Yi, Zhang Jinlong, Qi Hanhong, et al. Ageing performance modeling of li-ion batteries based on variational deep embedding-wasserstein GAN with gradient penalty[J]. Transactions of China Electro- technical Society, 2024, 39(13): 4226-4239.
[4] Li Weihan, Demir I, Cao Decheng, et al. Data-driven systematic parameter identification of an electro- chemical model for lithium-ion batteries with artificial intelligence[J]. Energy Storage Materials, 2022, 44: 557-570.
[5] Tian Jiaqiang, Wang Yujie, Chen Zonghai. An improved single particle model for lithium-ion batteries based on main stress factor compensation[J]. Journal of Cleaner Production, 2021, 278: 123456.
[6] Appiah W A, Busk J, Vegge T, et al. Sensitivity analysis methodology for battery degradation models[J]. Electrochimica Acta, 2023, 439: 141430.
[7] 李建林, 李雅欣, 陈光, 等. 退役动力电池健康状态特征提取及评估方法综述[J]. 中国电机工程学报, 2022, 42(4): 1332-1347.
Li Jianlin, Li Yaxin, Chen Guang, et al. Research on feature extraction and SOH evaluation methods for retired power battery[J]. Proceedings of the CSEE, 2022, 42(4): 1332-1347.
[8] 刘旖琦, 雷万钧, 刘茜, 等. 基于双自适应扩展粒子滤波器的锂离子电池状态联合估计[J]. 电工技术学报, 2024, 39(2): 607-616.
Liu Yiqi, Lei Wanjun, Liu Qian, et al. Joint state estimation of lithium-ion battery based on dual adaptive extended particle filter[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 607-616.
[9] 赵靖英, 胡劲, 张雪辉,等. 基于锂电池模型和分数阶理论的SOC-SOH联合估计[J]. 电工技术学报, 2023, 38(17): 4551-4563.
Zhao Jingying, Hu Jin, Zhang Xuehui, et la. Joint estimation of the SOC-SOH based on lithium battery model and fractional order theory[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4551- 4563.
[10] Wang Yujie, Zhao Guanghui. A comparative study of fractional-order models for lithium-ion batteries using Runge Kutta optimizer and electrochemical impe- dance spectroscopy[J]. Control Engineering Practice, 2023, 133: 105451.
[11] 杜焕伦, 李哲帆, 石琼林, 等. 基于BP神经网络与DP等效电路的锂离子电池热电耦合模型构建[J/OL]. 电源学报, 1-12[2025-05-22]. http://kns. cnki.net/kcms/detail/12.1420.tm.20231219.1348.014.html.
Du Huanlun, Li Zhefan, Shi Qionglin, et al. Con- struction of a thermoelectric coupling model for Lithium-ion batteries[J/OL]. Journal of Power Supply, 2024: 1-12[2025-05-22]. http://kns.cnki.net/kcms/ detail/ 12.1420.tm.20231219.1348.014.html.
[12] 蔡黎, 何德伍, 代妮娜, 等. 锂离子电池测试仪的设计与实现[J]. 电池, 2019, 49(1): 83-85.
Cai Li, He Dewu, Dai Nina, et al. The design and implementation of a Li-ion battery testing instru- ment[J]. Battery Bimonthly, 2019, 49(1): 83-85.
[13] Wu Longxing, Lü Zhiqiang, Huang Zebo, et al. Physics-based battery SOC estimation methods: recent advances and future perspectives[J]. Journal of Energy Chemistry, 2024, 89: 27-40.
[14] Chai Xuqing, Li Shihao, Liang Fengwei. A novel battery SOC estimation method based on random search optimized LSTM neural network[J]. Energy, 2024, 306: 132583.
[15] 林鹏, 刘涛, 金鹏, 等. 基于多新息辨识算法的锂离子电池等效电路模型参数辨识[J]. 储能科学与技术, 2023, 12(10): 3155-3169.
Lin Peng, Liu Tao, Jin Peng, et al. Identification of lithium-ion battery equivalent circuit model para- meters based on the multi-innovation identification algorithm[J]. Energy Storage Science and Technology, 2023, 12(10): 3155-3169.
[16] 刘芳, 邵晨, 苏卫星, 等. 基于全新等效电路模型的电池关键状态在线联合估计器[J]. 控制与决策, 2023, 38(6): 1620-1628.
Liu Fang, Shao Chen, Su Weixing, et al. Online joint estimator of battery key states based on a new equivalent circuit model[J]. Control and Decision, 2023, 38(6): 1620-1628.
[17] Tian Jiaqiang, Zhang Qingping, Liu Xinghua, et al. Route planning-based active equalization of recon- figurable battery packs in electric vehicles[J]. IEEE Transactions on Intelligent Vehicles, 2024(99): 1- 14.
[18] 程泽, 杨磊, 孙幸勉. 基于自适应平方根无迹卡尔曼滤波算法的锂离子电池SOC和SOH估计[J]. 中国电机工程学报, 2018, 38(8): 2384-2393, 2548.
Cheng Ze, Yang Lei, Sun Xingmian. State of charge and state of health estimation of Li-ion batteries based on adaptive square-root unscented Kalman filters[J]. Proceedings of the CSEE, 2018, 38(8): 2384-2393, 2548.
[19] Hu Xiaosong, Yuan Hao, Zou Changfu, et al. Co- estimation of state of charge and state of health for lithium-ion batteries based on fractional-order calculus[J]. IEEE Transactions on Vehicular Technology, 2018, 67(11): 10319-10329.
[20] Yang Fangfang, Li Weihua, Li Chuan, et al. State- of-charge estimation of lithium-ion batteries based on gated recurrent neural network[J]. Energy, 2019, 175: 66-75.
[21] Li Chaoran, Zhu Sichen, Zhang Liuli, et al. State of charge estimation of lithium-ion battery based on state of temperature estimation using weight clustered-convolutional neural network-long short- term memory[J]. Green Energy and Intelligent Transportation, 2025, 4(1): 100226.
Modeling and State of Charge Estimation for Lithium-Ion Batteries Using Backpropagation Neural Network with Momentum
Abstract Boosting the adoption of new energy electric vehicles and energy storage technologies is pivotal in expediting the standardization of the “dual carbon” objectives. Lithium-ion batteries, serving as critical components in electric vehicles and energy storage systems, are indispensable for energy storage and buffering purposes. The precision of a battery model is vital for enhancing state estimation accuracy. Based on momentum back propagation neural networks, this paper introduces a fractional-order modeling and state- of-charge estimation technique for lithium-ion batteries, aiming to improve the interpretability of data-driven modeling.
Firstly, a BPM neural network (BPMNN)-based battery model is constructed, which incorporates the physical information of a first-order fractional-order model. The weights of the BPMNN-based model represent the model parameters, including resistance, capacitance, and fractional order. With the hierarchical feature extraction capability of neural networks, the novel battery model enables the online optimization of fractional order. Secondly, the OCV-SOC relationship is linearized using a Taylor expansion, and the linearized OCV-SOC relationship is employed to reconstruct the BPMNN-based battery model. Thirdly, a momentum gradient descent algorithm is utilized. Historical data is introduced using momentum, which improves the stability of the estimation. Moreover, the convergence of the proposed method is analyzed. The loss function of the BPMNN-based battery model converges to a positive value with a suitable learning rate. Finally, the proposed method is verified with a 2.55 A·h LiFePO4 battery. The influence of temperature is compared with a UDDS profile at -5℃, 25℃, and 45℃. The result shows that the external temperature influences the ohmic resistance, model accuracy, and fractional order. However, it seems to have no relationship with the SOC estimation. The fractional order descends faster as the temperature decreases. Compared to the EKF-based and UKF-based methods, the proposed method improves the model accuracy by up to 64%, and the SOC estimation accuracy is improved by up to 36.5%. Compared to the GRU-RNN-based SOC estimation method, the BPMNN-based method yields a better result in SOC estimation because the combination of physical information enables online optimization of the BPMNN-based battery model. As the memory space increases, the computational burden also grows, and the battery model becomes more accurate. The model achieves a balance between accuracy and computational burden when the memory space includes 50~70 steps.
The following conclusions can be drawn. (1) The BPMNN-based online estimation method converges with a suitable learning rate, significantly improving the accuracy of the battery model and SOC estimation. The BPMNN-based method estimates SOC more accurately than the GRU-RNN method. (2) The external temperature influences the variation of ohmic resistance and model accuracy, but the SOC estimation is not affected. The fractional order descends more rapidly as the temperature decreases. (3) The memory space influences the computational burden and model accuracy.
Keywords:Lithium-ion battery, fractional order model, parameter identification, SOC estimation, back propagation neural network with momentum
中图分类号:TM911
DOI: 10.19595/j.cnki.1000-6753.tces.241977
国家自然科学基金(62203352)、国家资助博士后研究人员计划(GZB20230001)和安徽省重点研发计划(202304a05020046)资助项目。
收稿日期 2024-11-05
改稿日期 2025-03-19
田佳强 男,1992年生,博士/博士后,讲师,研究方向为储能系统能源管理与节能技术、动力电池系统集成制造、退役电池梯次 利用。
E-mail: 23706@ahu.edu.cn
潘天红 男,1974年生,教授,博士生导师,研究方向为过程建模与系统优化、储能系统能源管理与节能技术等。
E-mail: thpan@ahu.edu.cn(通信作者)
(编辑 郭丽军)