表1 AA-CAES系统常用关键部件
Tab.1 Commonly used key components of the AA-CAES system
部件/容量压缩机透平储气室储热室换热器发电机电动机 小型活塞式压缩机向心透平储气罐单体储热罐管壳式换热器同步发电机同步电动机 中型离心式压缩机轴流透平储气岩穴储热罐 大型组合式压缩机轴流透平储气岩穴并联储热罐
摘要 先进绝热压缩空气储能（AA-CAES）技术是具有发展前景的大容量储能技术之一。建立AA-CAES系统动态模型并在此基础上开展动态特性研究，对AA-CAES系统优化设计、提升系统稳定性，具有一定的理论与工程意义。首先，提出多级组合式压缩机与多级轴流透平动力学建模方法，研究AA-CAES系统关键物理量相互影响机理，建立AA-CAES系统各关键部件动态模型，并进行有效性验证；其次，提出AA-CAES系统全工况动态仿真模型，研究各部件间参数耦合关系；最后，在所建动态模型上开展系统“压缩—停机—发电”全工况动态仿真，分析了系统启动、爬坡及停机等动态过程。仿真结果表明，所建模型可以反映AA-CAES系统动态特性，表征系统动态过程中各关键参数的耦合关系，为优化AA-CAES系统运行、改善调控策略提供支撑。
关键词：先进绝热压缩空气储能 动态建模 全工况仿真 动态特性 大容量
随着光伏、风电等新能源大规模并网，电力系统安全稳定问题愈发突出[1-2]。储能技术作为平衡能源供需的重要手段，可提高能源利用率与电网稳定性，是电力系统安全稳定问题的关键解决方案[3-5]。在当前已实现大规模应用的储能方式中，先进绝热压缩空气储能（Advance Adiabatic Compressed Air Energy Storage, AA-CAES）技术被认为是具有广阔发展前景的大容量储能技术之一[6]。
近年来，我国已投入建设多个大容量先进绝热压缩空气储能电站，建设规模从单机100 MW级向300 MW级推进。区别于小型AA-CAES系统，大容量压缩空气储能电站在设备选型、参数设计及应用场景方面均与小、中型系统有较大差异。AA- CAES系统工作过程为多部件非线性耦合过程，涉及多种复杂物理特性。为准确地把握大容量AA- CAES系统调控运行过程的动态响应与调节能力，对系统关键部件及整体进行建模仿真至关重要。
在系统建模方面，现有AA-CAES建模研究大多以模块化建模思想为基础，引申为静态模型与动态模型两种建模方式[7]。其中，静态模型大多研究不同状态参数下静态特性参数变化情况，多以入口参数为边界条件，通过热力学公式与能量损失公式计算出口参数[8-11]。例如，文献[8]建立了简化AA- CAES系统热力学模型，以发电效率与循环效率两个静态指标对AA-CAES系统与火电机组联合循环效率进行评估；文献[9]提出用于AA-CAES系统的离心压缩机一维损失模型，以热力学公式为基础，分析单级离心压缩机内部损失分布情况，完成离心压缩机参数设计。
动态模型则引入描述系统动态变化情况的微分方程，表征输入参数及内部参数动态变化情况下AA-CAES系统输出参数变化情况[12-18]。文献[14]对带有额外压缩机的7 MW级A-CAES系统进行参数分析，详细考虑储气室、储热室与换热器部件动态方程，得出各参数动态变化情况。文献[16]考虑了离心压缩机质量、动量与能量守恒方程，对具有中间冷却的多级压缩机结构进行动力学建模，在此基础上完成小型AA-CAES系统建模。文献[17]考虑压缩机通用经验公式与透平流通经验公式，在建立10 MW级压缩空气储能系统（CAES）模型基础上，对比研究压缩机、透平处在定压、滑压工况下储能效率与储能密度变化情况。由此可见，现有研究大多基于小型AA-CAES系统（10 MW及以下），鲜有针对大容量AA-CAES系统（单机300 MW级）动态建模及特性展开研究。而与小型AA-CAES系统相比，大容量AA-CAES系统在关键部件、系统参数及应用场景等诸多方面均存在很大差异，因此，其动态建模及特性分析方法亟须进一步深入研究，不能简单地套用低级别系统模型与方法。
综上所述，已有AA-CAES模型多为10 MW及以下小型机组模型，建模方法大多基于热力学公式，以经验公式或特性曲线反映压缩机与透平特性，且其研究大多针对AA-CAES系统静态特性与变工况特性。迄今为止，鲜有针对大容量AA-CAES机组的动力学建模及动态特性研究。鉴于上述问题，本文提出了AA-CAES系统关键部件动力学建模方法，详细研究了系统关键物理量影响机理，建立了300 MW级AA-CAES系统动态模型，并结合电网与AA-CAES耦合系统进行动态特性分析，研究了AA-CAES系统启动、停机、爬坡等动态性能。研究结果将为大容量AA-CAES系统设计与运行提供参考。
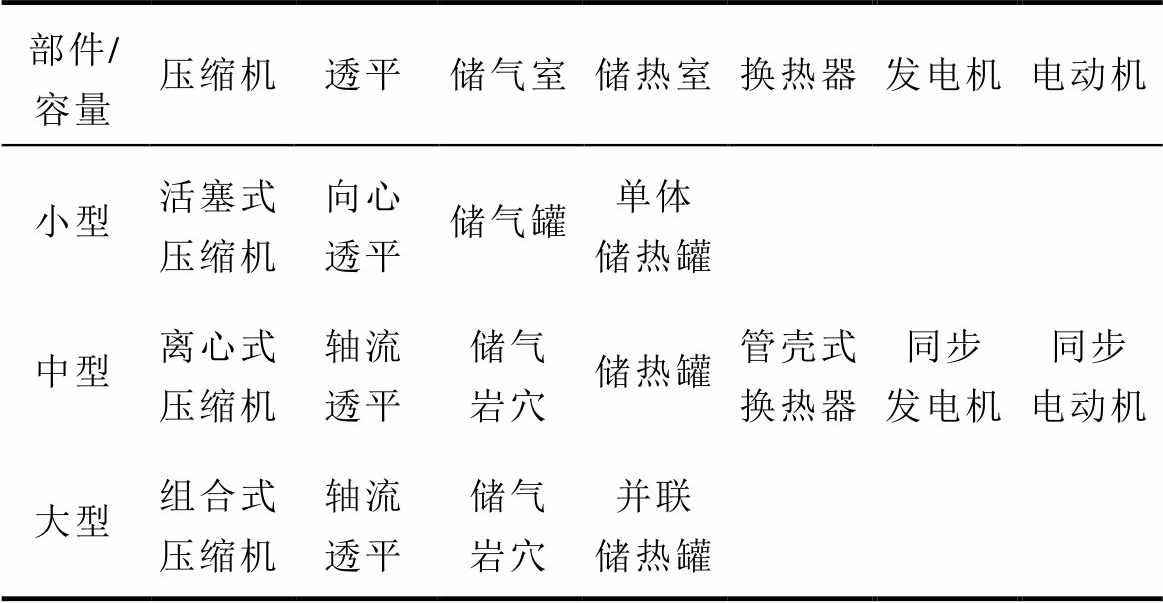
大容量压缩空气储能系统关键部件与小型系统存在较大差异，针对不同容量压缩空气储能系统特点，整理总结其常见部件使用情况见表1。表1中，小型、中型、大型压缩空气储能系统定义来自GB/T 43687—2024《电力储能用压缩空气储能系统技术要求》。
表1 AA-CAES系统常用关键部件
Tab.1 Commonly used key components of the AA-CAES system
部件/容量压缩机透平储气室储热室换热器发电机电动机 小型活塞式压缩机向心透平储气罐单体储热罐管壳式换热器同步发电机同步电动机 中型离心式压缩机轴流透平储气岩穴储热罐 大型组合式压缩机轴流透平储气岩穴并联储热罐
在压缩环节，现有典型大容量压缩空气储能电站多采用组合式压缩机。该压缩机采用轴流压缩机与离心压缩机组合运行方式。轴流压缩机中气体方向为轴向，便于建立多级式结构，可满足高压缩比与大功率需求；离心压缩机结构简单，单级可实现较大压比，与轴流压缩机组合可简化整体结构[19]。
在膨胀环节，多数大容量压缩空气储能电站的发电部件为高负荷轴流透平。高负荷情况下，轴流透平相比于离心透平在尺寸、质量等方面均有较大优势[20]。
在储气环节，地下岩穴具有天然密封性好、造腔工艺简单等特点[21]，大容量压缩空气储能电站均采用储气岩穴进行储气。
对于其他关键部件，综合考虑结构、成本及实际工程情况，考虑对管壳式换热器阵列、球形水罐、同步发电机与同步电动机进行动态建模。
1.2.1 组合式压缩机
组合式压缩机采用多级轴流压缩机在前、单级离心压缩机在后的组合策略。相较于单独采用离心压缩机或轴流压缩机，该方式可在提高效率时简化整体结构，保证系统安全性。本文以离心压缩机与轴流压缩机为研究对象，对其动力学模型展开研究。
1）轴流压缩机动力学建模
轴流压缩机多为多级结构，流动过程复杂。因此考虑将三维流动过程简化，考虑各级转子与静子出入口状态变量相互关系，采用守恒方程求解级间状态变量。轴流压缩机参数以下标a表示，其状态变量分布如图1所示。对于n级轴流压缩机，共有2n+1组状态变量。其中，ca.i、wa.i、ma.i、Ta.i分别代表第i组状态变量的绝对速度、相对速度、质量流量与温度参数。
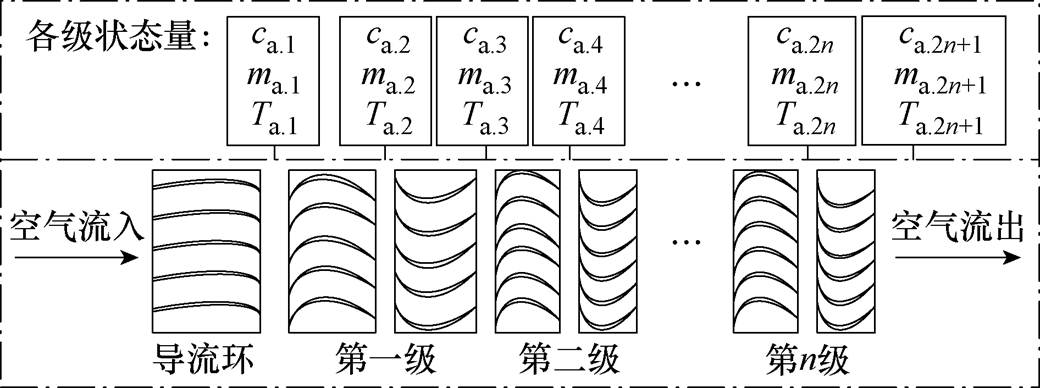
图1 轴流压缩机状态变量
Fig.1 Axial compressor state variables
基于转子转速与转子尺寸，可得出各级转子内径与外径轮周速度求解公式，即
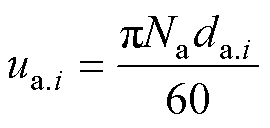（1）
式中，ua.i、da.i分别为第i组压缩机状态变量对应转子叶轮转速与叶轮直径；Na为压缩机转速。
考虑摩擦损失，以第一级为例，转子级相对速度wa.2和静子级绝对速度ca.3分别为
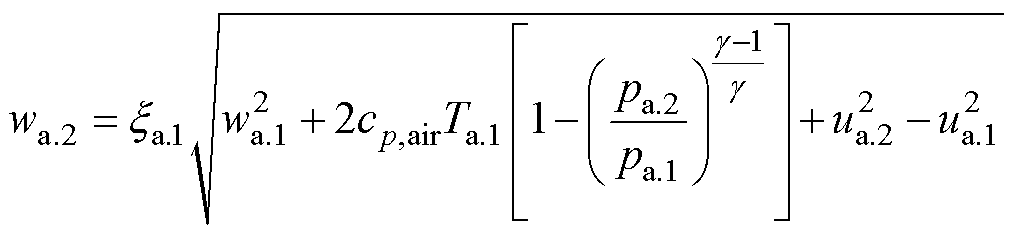（2）
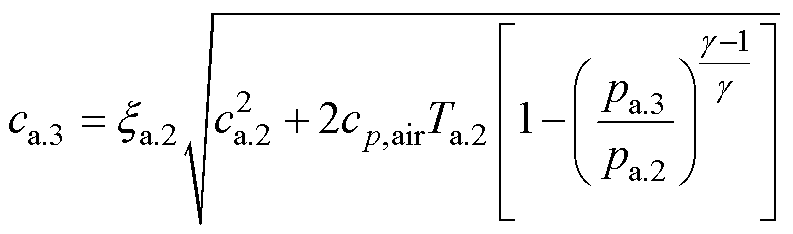（3）
式中，cp,air为空气比定压热容；xa.1、xa.2分别为第一级转子与第一级静子中的摩擦损失系数；g为比热比。
在第i级状态变量中，由余弦定理可得出wa.i、ca.i相互转化公式，转子级公式和静子级公式分别为
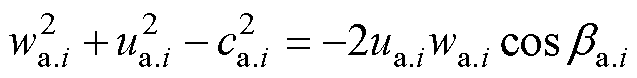（4）
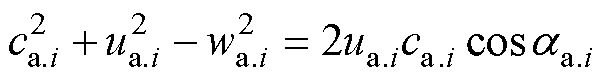（5）
式中，aa.i、ba.i分别为第i组状态变量中转子级叶轮速度与气体绝对速度、气体相对速度的夹角。
叶尖泄露导致的气压损失[22]为
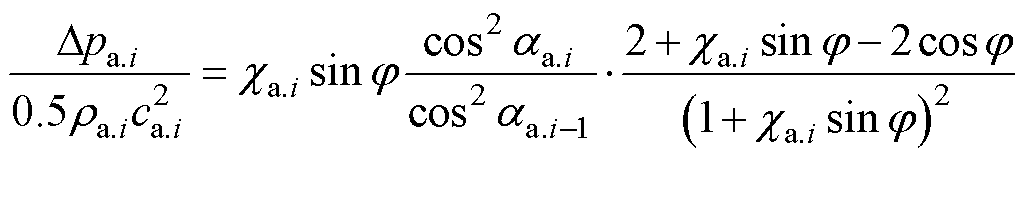（6）
式中，Dpa.i为第i组状态变量对应转子级叶尖泄露气压损失；ra.i为第i组状态变量对应位置气体密度；ca.i为叶尖泄露面积与总截面积之比；j为叶尖泄露流的方向角。
考虑该转子级气压损失后，级出口气压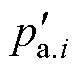
可由原出口气压pa.i与气压损失之差Dpa.i表示，即
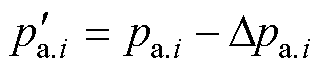（7）
基于威斯奈（Weisner）滑移系数公式的速度偏移量[22]为
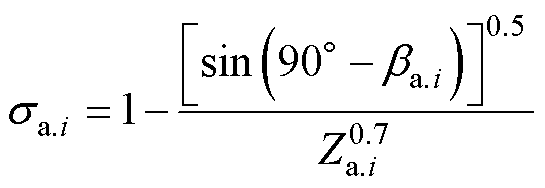（8）
式中，sa.i为第i组状态变量对应转子级的速度偏移量；Za.i为该级转子叶轮数目。
考虑滑移系数偏移量后，转子速度三角形发生变化，由三角函数推导可得，转子级气流相对速度在偏移后为
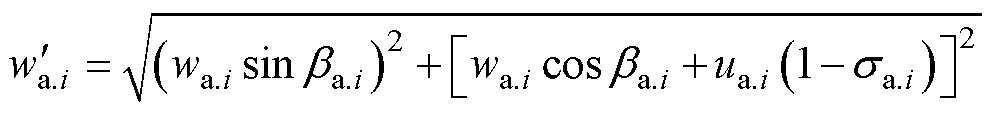（9）
轴流压缩机中各级空气质量流量为该级轴向流速与截面积、密度之积，其计算方法为
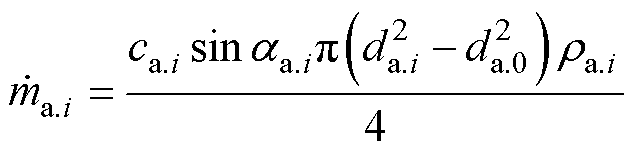（10）
式中，da.0为轴流压缩机转轴直径；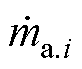
为质量流量变化率。
密度公式由理想气体状态方程得出，有
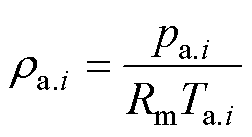（11）
式中，Rm为理想气体常数，Rm=8.314 J/(mol·K)。
综合式（10）和式（11）与转子、静子级计算公式，在已知空气质量流量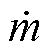
的基础上，可得如下各级状态参数关系式，即
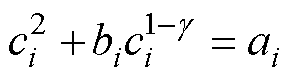（12）
式中，ai、bi、ci参数为自定义参数，分别为
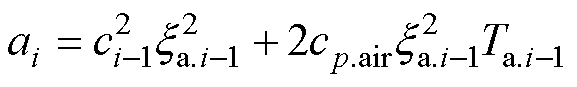（13）
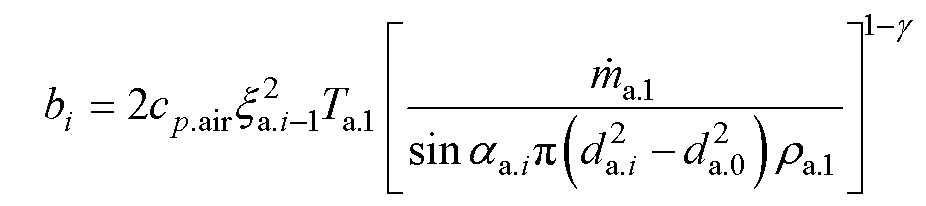（14）
综合各级公式，可用非线性方程组表示轴流压缩机流动过程。根据质量守恒定理，流过轴流压缩机各级静子与转子的气体质量流量应相等。因此，可将该非线性方程组转化为寻优问题求解。
2）离心压缩机动力学模型
离心压缩机多为单级系统，相较于轴流压缩机，其建模过程无多级级间参数耦合。离心式压缩机参数以下标c表示。
在构建压缩机数学模型时，主要考虑两种损失方式：①摩擦损失，包括压缩机定、转子中摩擦损失，以及级间摩擦损失；②冲角损失，主要为汽流进汽角与叶片进口几何角度不一致引起的附加 损失。
在离心压缩机压缩过程中，气体共经历四种状态：转子入口—转子出口—定子入口—定子出口，上述状态分别使用下标1～4表示。
转子出口处气体能量守恒公式与质量守恒公式分别为
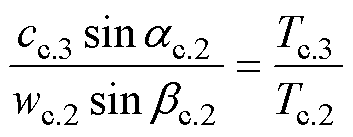（15）
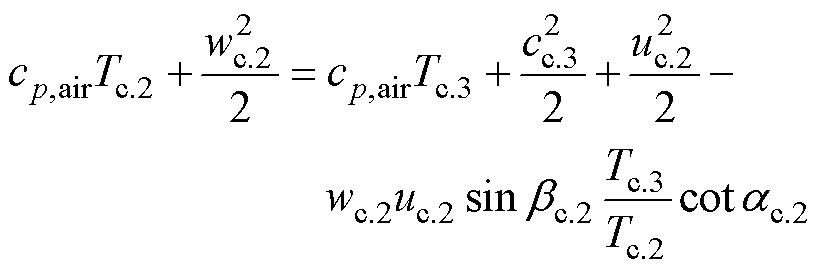（16）
综合考虑式（15）与式（16），可得出定子入口温度与绝对速度公式，分别为
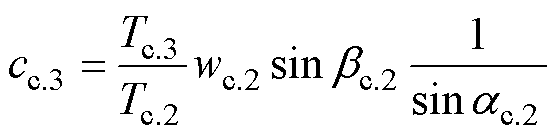（17）
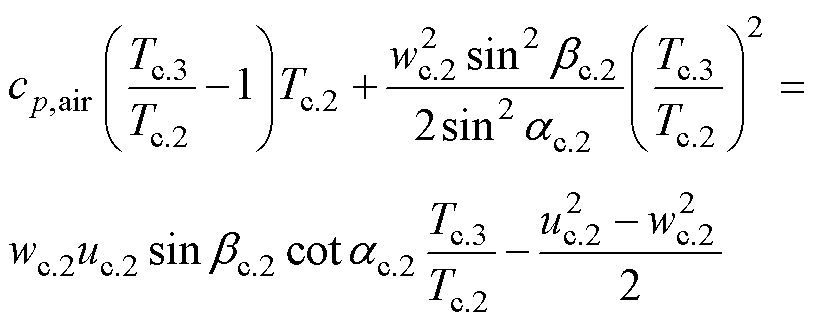（18）
根据质量守恒定理，流过离心压缩机转子与定子的气体质量流量应相等，据此可将该问题转化为寻优问题。
1.2.2 轴流透平
轴流透平与组合式压缩机均为叶轮机械，其建模原理类似。在本节轴流透平建模过程中，采用与轴流压缩机类似的建模方式，n级轴流透平共含有2n+1组状态变量。轴流透平变量以下标e表示。轴流透平公式符号意义与轴流压缩机部分相同，在此不再赘述。
以第一级为例，静子公式与转子公式分别为
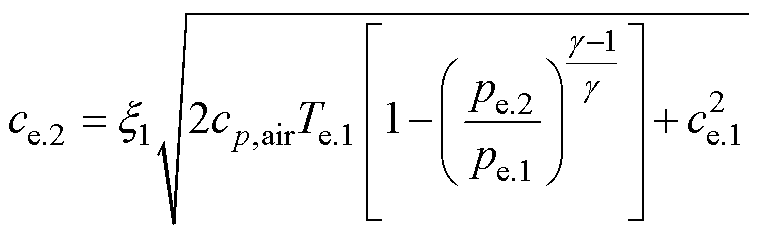（19）
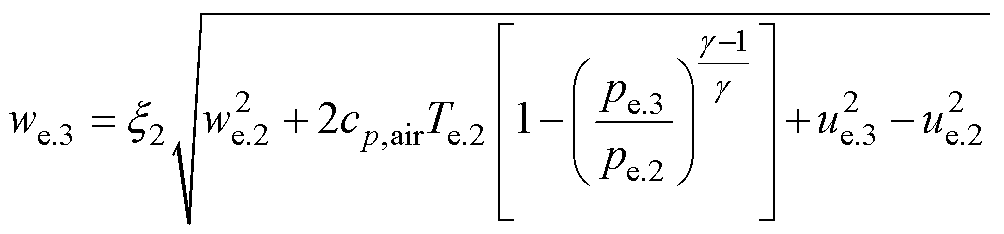（20）
轴流透平单位质量转矩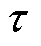
为
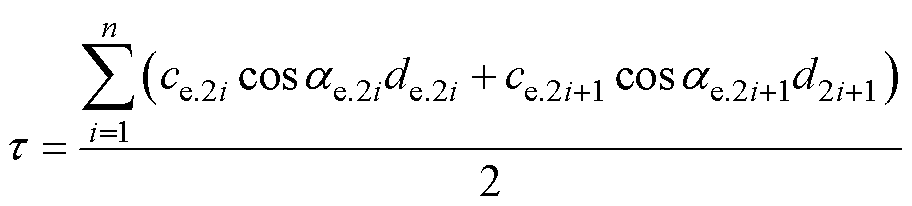（21）
根据质量守恒定理，流过定子和转子气体质量流量相等。据此可将该问题转化为寻优问题。
1.2.3 储气岩穴
储气岩穴动态模型以质量守恒方程及能量守恒方程为基础，不考虑质量损失。两种守恒公式[23]分别为
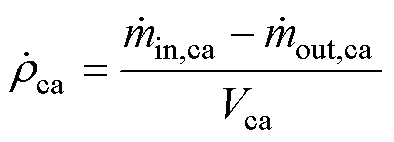（22）
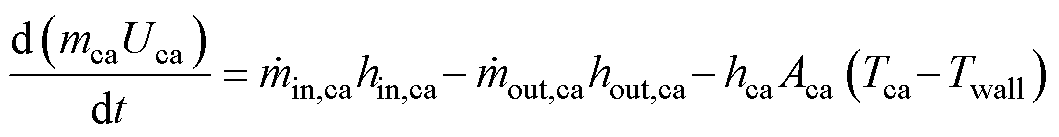（23）
式中，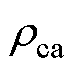
为岩穴气体密度；
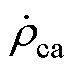为岩穴内气体密度变化率；
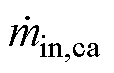和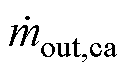
分别为某时刻流入、流出岩穴的气体质量流量；Vca为岩穴体积；mca为储气岩穴内气体总质量；Uca为岩穴内气体总内能；hin,ca和hout,ca分别为流入、流出气体的比焓；hca为岩穴与外界换热系数；Aca为岩穴表面积，即换热面积；Tca与Twall分别为岩穴内气体温度与内壁温度。
综合上述守恒公式，可得储气岩穴内部气压变化率表达式为
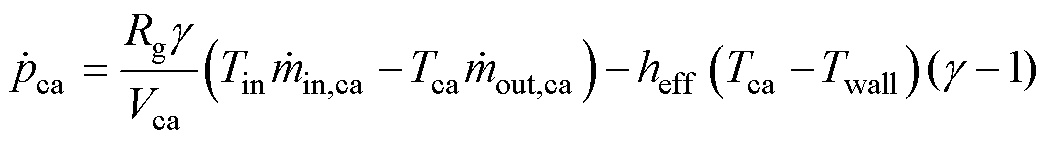（24）
式中，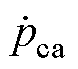
为岩穴气压变化率；heff为岩穴与外界等效换热系数，该换热系数计算式[23]为
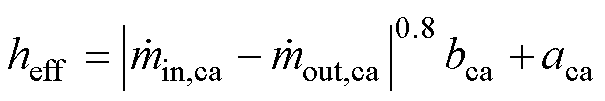（25）
式中，bca为表面传热系数；aca为强制表面传热系数。
1.2.4 管壳式换热器与水罐
作为AA-CAES系统换热环节关键部件，换热器通过余热回收提升系统效率。管壳式换热器包含壳程与管程，壳程流体下标为s，管程流体下标为t。壳程流体动态换热方程[24]为
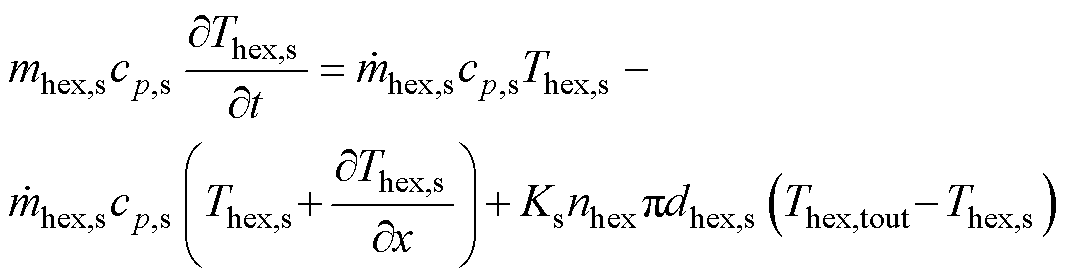（26）
式中，Thex,s为壳程流体温度；mhex,s与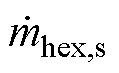
分别为单位长度壳程流体质量与质量流量；cp,s为壳程流体比定压热容；Thex,tout为外壁温度；dhex,s为换热管外径；nhex为换热管根数；Ks为壳程给热系数。
化简式（26）可得
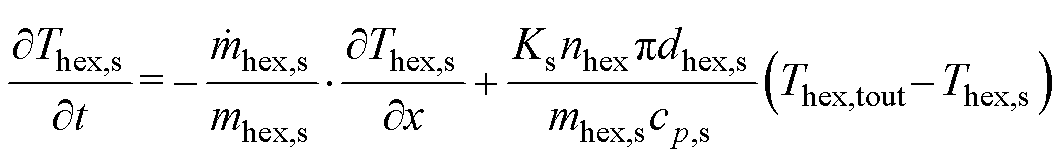（27）
同理，可列出管程流体温度的动态方程为
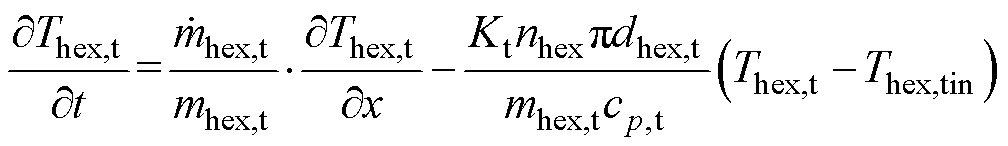（28）
式中，Thex,t为管程流体温度；Thex,tin为管内壁温度；mhex,t为管程流体单位长度的质量；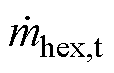
为流过管程的流体质量流量；Kt为管程给热系数；cp,t为管程流体比定压热容；dhex,t为换热管内径。
由能量守恒方程，可列出管外壁温度动态方程与管内壁温度动态方程，分别为
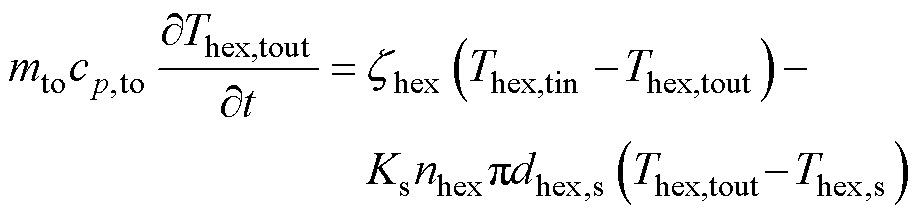（29）
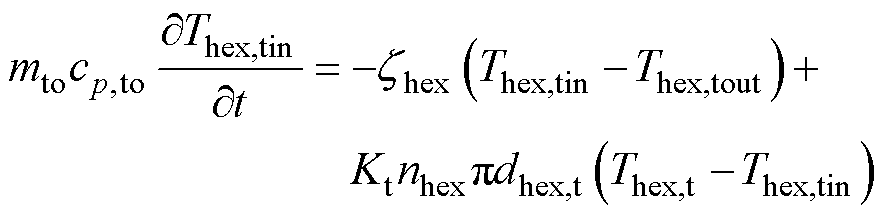（30）
式中，mto为换热管单位长度的质量；cp,to为换热管比定压热容；zhex为管侧等效传热系数。
本文使用球形水罐作为储水容器。水罐热量守恒公式为
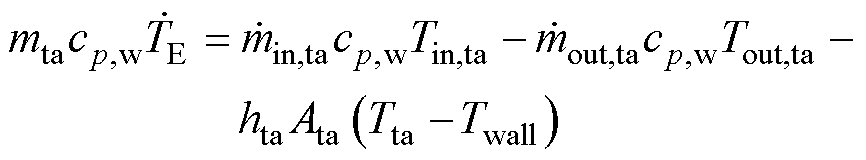（31）
式中，
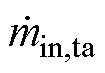与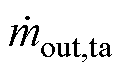
分别为流入与流出水罐的水流量；mta为水罐中水的质量；
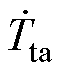为水罐中水的温度变化率；Tin,ta、Tout,ta分别为流入和流出水罐的水温；Tta为水罐中水温；Twall为水罐壁温度；hta为水罐换热系数；Ata为水罐中水与水罐壁接触面积。
1.2.5 同步发电机与同步电动机
当前同步电动机与同步发电机工程业绩已满足300 MW级AA-CAES系统需求（压缩侧采用双列并联方案）。其具体动态建模过程参考自文献[25-26]。
AA-CAES系统是多部件、非稳态、强非线性耦合的复杂系统，其复杂性较大程度取决于部件间耦合关系。本文按照AA-CAES系统各环节功率实际流动情况，以参数传递方式处理其耦合关系。各部件详细耦合机理与参数传递情况如图2所示。图2中，箭头指向方向为参数传递方向（由于本文未考虑AA-CAES系统短时特性，因此，文中参数传递过程均忽略延迟）。
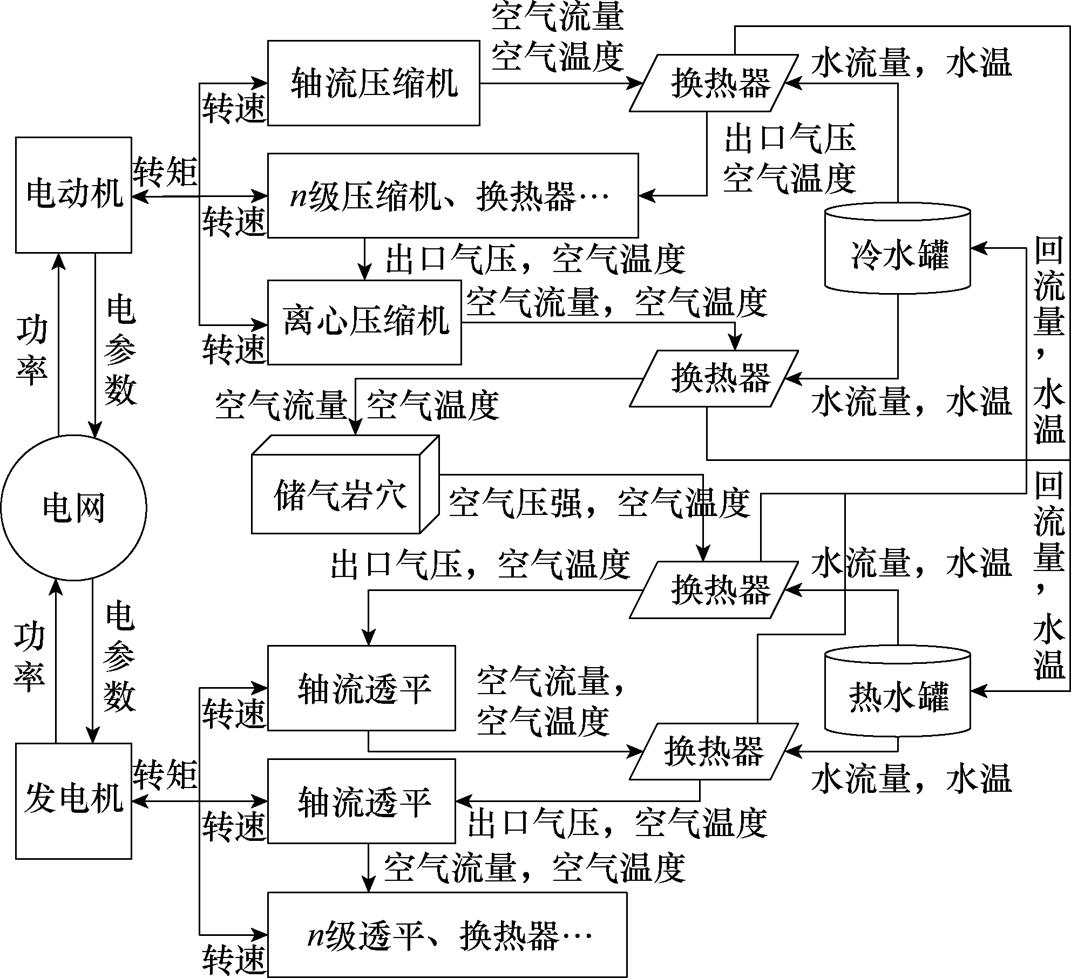
图2 AA-CAES系统部件关系
Fig.2 AA-CAES system component relationships
为验证AA-CAES系统关键部件数学模型的准确性，本文采用分体式验证方法：对各子系统模型进行独立校核，通过对比仿真数据与参考文献实测数据的吻合度，验证其数学表征的有效性。数据对比分析与验证过程详见附录。组合后整体模型如图3所示。
本文使用Simulink建立300 MW级AA-CAES系统动态模型。该300 MW级AA-CAES系统包含6级压缩机及4级膨胀机。压缩部分采用两段式压缩，每段由2级轴流压缩机与1级离心压缩机组合；膨胀部分采用4级轴流透平；同时，包含4个8 000 m3容量球形水罐与800 000 m3容量储气岩穴。
按照“压缩→储存→发电”过程进行300 MW级AA-CAES系统动态仿真。系统总仿真时间为15 h，包括：压缩过程8 h、停机过程1 h及膨胀过程6 h。岩穴内气压初始值为6.2 MPa，气温初始值为298 K。图4展示了系统动态过程仿真结果。
图4a描述仿真过程中岩穴气温、气压变化情况。压缩过程中，岩穴内压强平稳升高，温度升高趋势逐渐减缓，这是由于储气室输入气体温度基本保持恒定，随着高压气体进入储气室内，储气室内温度将逐渐接近输入气体温度。过程结束后储气岩穴内压力从6.2 MPa提升到8.09 MPa，岩穴内气体温度从298 K提升到303.3 K。停机过程储气岩穴内气压下降0.01 MPa，温度下降0.1 K。
图3 AA-CAES系统动态模型
Fig.3 Dynamic model of AA-CAES system
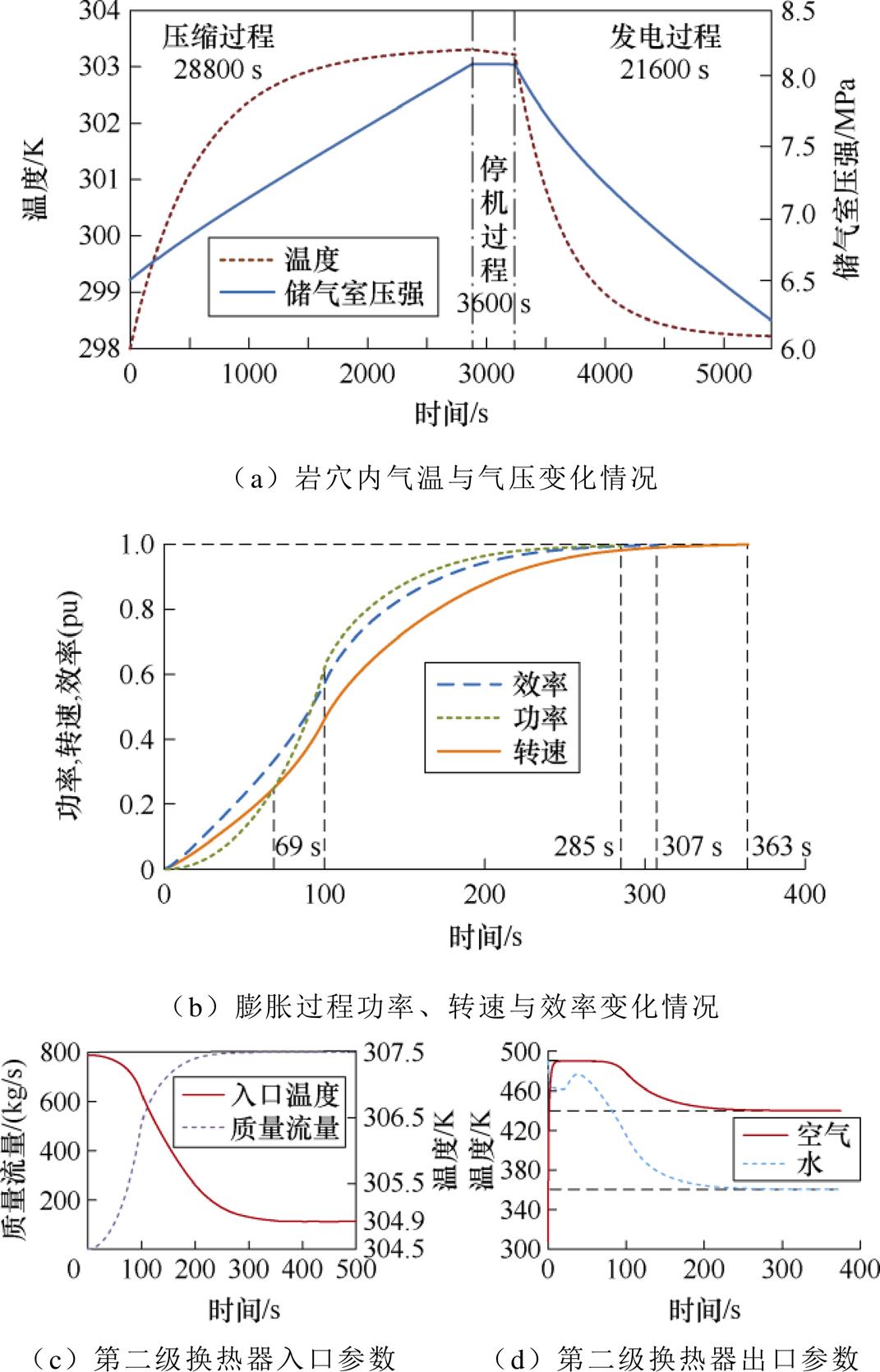
图4 AA-CAES系统全动态仿真结果
Fig.4 Dynamic simulation results of AA-CAES system
膨胀过程中，四级透平保持恒压比运行方式，除启动过程外，透平入口气压始终与储气岩穴内部气压相等，系统处于变工况运行状态。在6 h膨胀过程中，储气岩穴内压强迅速下降，气体温度降低。膨胀过程结束后，岩穴内气温为298.2 K，压力为6.21 MPa。岩穴内气温与气压相比全动态仿真过程执行前仅有微小变化，系统可重复执行该过程。
图4b描述膨胀机启动过程中机组功率、转速与效率标幺值变化情况，该过程中气压爬升率为0.8 Pa/s。根据膨胀机组数据，膨胀机输出功率于285 s达到额定功率，转速于363 s达到额定值，膨胀机输出功率先达到300 MW，转速达到额定值所需时间落后于功率达到额定值所需时间。这是由于惯性效应，透平启动过程中其入口气压爬升率为0.8 Pa/s，100 s时即可达到额定气压，其参数调整迅速，导致膨胀机输出功率接近300 MW时，发电机转速仍未达到额定转速。
膨胀机组输出效率达到稳定状态所需时间介于两者之间，于307 s达到稳定，这是由于膨胀机组输出效率由发电机转速与膨胀剂输出功率共同决定。
分析功率与转速变化情况可知，相比于膨胀机功率变化情况，转速变化更加平缓。在69 s前，功率标幺值低于转速标幺值，随后，功率标幺值高于转速标幺值。透平发电功率由透平转速、输入气压、透平参数等共同决定，因此，在透平启动初始过程中，功率爬升速度应落后于转速爬升速度。在运行过程中，效率与额定效率之比始终高于转速标幺值。
在100 s时，透平入口气压爬升至额定气压，此时图4b中三条曲线爬升速度均达到最大值。这是由于入口气压参数与气压爬升率参数可促进功率爬升与转速爬升速度，在气压爬升至额定值后，透平入口气压不再爬升，因此功率与转速趋于额定状态，带动效率逐渐趋向稳定值。
图4c描述膨胀过程第二级换热器入口气温与空气流量变化情况。在启动过程中，质量流量平稳爬升至800 kg/s，气温保持在306 K左右。
图4d描述第二级换热器出口气温与水温变化情况。第二级换热器输入水温恒为490 K，水的输入流量随启动时间逐渐爬升，50 s时其流量达额定值。由出口数据可知，在启动过程中，换热器出口气温首先爬升至490 K，随后达到稳定；在该过程中，水温逐渐升高。在50 s左右，随着空气与水输入质量上升，气温与水温均逐渐下跌，最终气温稳定于440 K，水温稳定于365 K。经分析可知，在0～50 s间，水的流量爬升速度高于空气流量爬升速度，空气得到充分换热，因此可达到水的额定温度；50 s后，水流量达额定值，空气流量仍然爬升，气温与水温换热逐渐充分，两换热介质温度均逐渐下跌，并随空气质量流量的稳定而趋于稳定。
为研究300 MW级AA-CAES系统面向电力系统响应特性，构建含AA-CAES的电力系统模型，其结构如图5所示，AA-CAES机组与较小厂用电负荷Ⅰ经变压器接入110 kV母线。
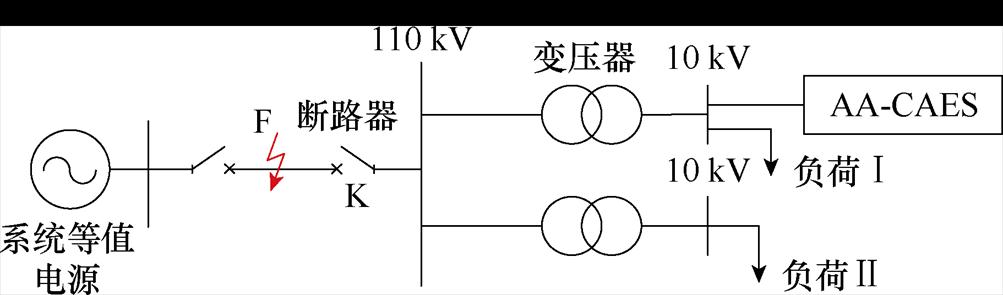
图5 AA-CAES系统接入电网整体结构
Fig.5 The overall structure of the network connected to CAES system
针对该情况设置三个场景，进行AA-CAES系统特性分析：
场景一：系统启动特性分析。40 s前，AA-CAES系统处于停机工况，40 s时，F处发生三相短路，随后F处对应断路器断开，AA-CAES系统以发电状态启动，为负荷供电。
场景二：系统爬坡特性分析。40 s前，AA-CAES系统输出功率低于额定输出功率，40 s时，F处发生故障，对应断路器断开，随后AA-CAES进入爬坡状态，逐渐增大出力至300 MW。
场景三：系统停机特性分析。F处发生故障，对应断路器断开后，AA-CAES机组达额定发电状态，达稳定状态150 s后，F处故障解除，系统重新并网，命令AA-CAES系统开始停机过程。
为详细分析各运行参数与AA-CAES系统启动过程的关系，引入启动过程性能指标。此处使用启动时间描述储能系统启动特性，并按照额定功率70%对启动时间进行划分，定义t1为发电机启动至功率达到额定功率70%对应时间，t2为发电机功率由额定功率70%达到额定功率100%所需时间。三者之间的关系为
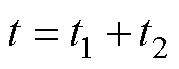（32）
随后分析多组惯性时间常数情况下AA-CAES系统启动特性，该算例中气压爬升率为0.8 Pa/s，惯性时间常数使用h表示。图6描述了AA-CAES系统功率变化情况与转速变化情况，由图6中数据可知：在惯性时间常数增大过程中，系统启动时间增大，其中t1小幅增加，t2大幅增加；当惯性时间常数为14 s时，系统启动时间达741 s，这说明AA- CAES系统作为一种能量性储能设备，其优势表现为储能容量大、发电时间长，启动过程相较功率型储能不具优势。
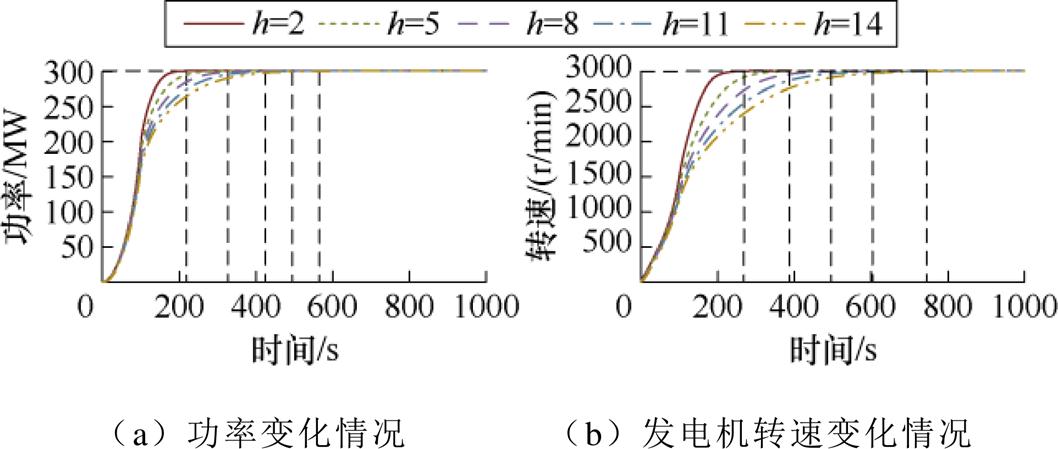
图6 不同惯性时间常数下仿真结果
Fig.6 Simulation results with different inertia time constants
在启动过程前半段，不同惯性时间常数下发电机功率与转速爬升速度基本保持一致，这是由于前半段启动过程中，气压爬升率对功率与转速起限制作用。
其次，分析多组气压爬升率情况下AA-CAES系统启动特性，该算例发电机惯性时间常数为5 s。图7a描述了AA-CAES系统功率变化与转速变化情况。可以看出，系统启动时间随出口气压爬坡率增加而减小，其中t2小幅减小，t1大幅减小。出口气压爬坡率在1.43 Pa/s时，系统启动时间最短，仅255 s。
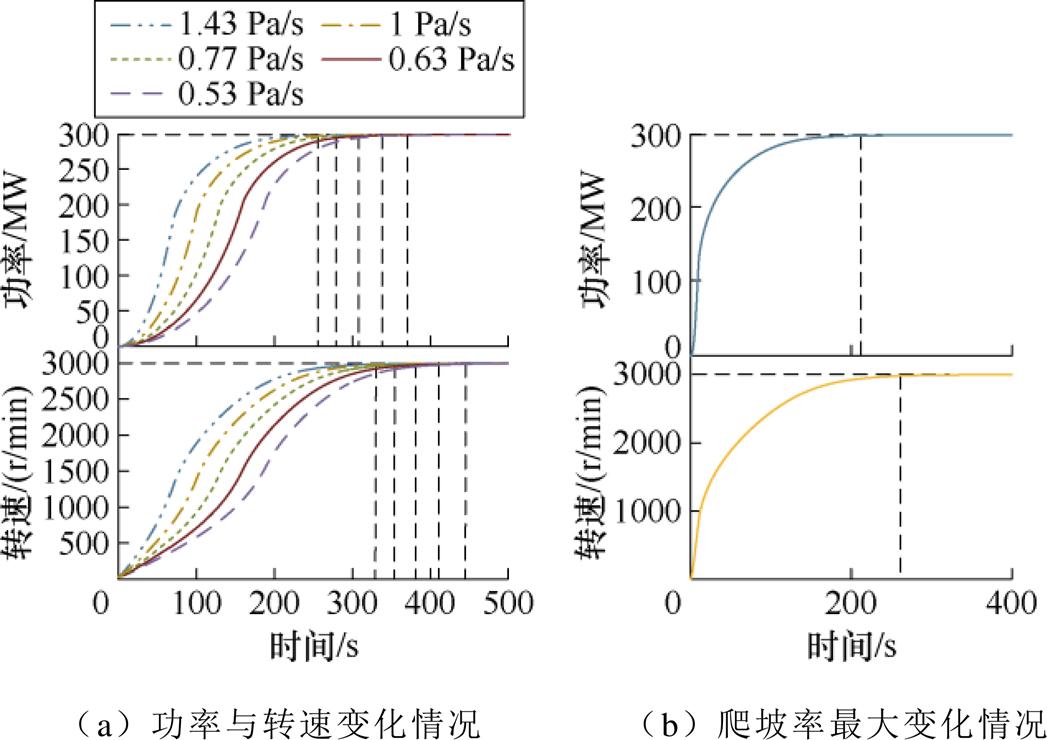
图7 储气室出口气压爬坡率变化情况下仿真结果
Fig.7 Simulation results under the change of air pressure ramp-up rate at the outlet of the gas storage chamber
由图7a易于看出，随着储气室气压爬坡率逐渐上升，发电机起动时间逐渐趋于某个定值，图7b描述了这个定值。当储气室出口气压爬升率为无穷大时，发电机转速仍需260 s达额定状态，这是由于系统具有惯性，大气压使发电机转速初始爬升速度极快，但很快收到惯性时间常数限制。需要注意的是，在AA-CAES机组发电状态实际启动过程中，膨胀机组入口气压不能直接达到额定值，这是由于过大气压将导致透平叶片和部分机械部件承受巨大应力，减少部件寿命，也易于导致透平失稳，产生失速现象。
由此可知，在透平启动过程中，惯性时间常数与气压爬升率均会影响透平启动时间。惯性时间常数越大，其对启动爬升速度限制越大，t1增加幅度越大；气压爬升率越大，其对启动过程促进效果越明显，t2增加幅度越大。惯性时间常数主要反映启动过程前期，与t1有关，气压爬升率主要反映在启动过程后期，与t2有关。
为详细分析各运行参数与AA-CAES系统启动过程的关系，引入爬坡过程性能指标。此处使用爬坡率、反调峰值功率衡量储能机组爬坡特性。
本文搭建的AA-CAES动态模型通过增大透平入口气压增大输出功率，不同透平入口气压对应不同额定工况输出功率。图8描述了AA-CAES系统在不同初始发电功率情况下功率与转速变化曲线。40 s前，四组算例对应透平发电功率各不相同；40 s时，F处发生故障，开始执行爬坡过程，阀门控制透平入口气压升高，在80 s达到300 MW对应额定气压。
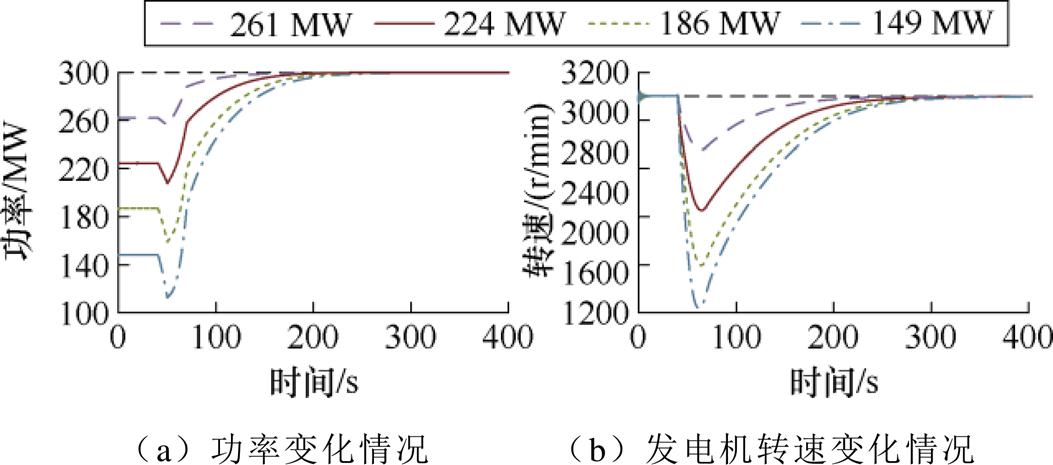
图8 不同初始发电功率下仿真结果
Fig.8 Simulation results at different initial power generation powers
由图8中曲线可知，系统进行工况转换时，转速将首先向下波动，进入反调峰过程，且随着系统初始发电功率减小，其爬坡过程中反调峰值功率增大，爬坡率减小。这是由于40 s时负载所需功率上升，导致初始阶段透平出力小于负载功耗与机械损耗功率的总和。随着转速向下波动，功率也将在小幅下降后上升，最终达到稳定状态。
随着初始功率降低，其爬坡初始阶段反调峰值功率上升，但其反调峰值时间基本不变。在150 MW级系统爬坡过程中，转速最小值可达1 230 r/min，功率最小值达128 MW，转速波动幅度达59%，功率波动幅度达14%，对发电机正常运行有较大影响。
由此可知，在入口气压达到额定气压时间恒定情况下，系统爬坡过程中，功率将发生反调峰现象，反调峰值功率取决于发电功率与额定功率的差值。因此，为保证系统正常运作，需保证系统最低功率、最低转速不越限，采用一定方式限制其波动幅度。
使用停机时间描述储能系统停机特性。在本算例中，系统于150 s开始执行停机程序。本文在停机过程中，通过减小阀门开度降低透平入口气压，从而降低负荷，完成停机。
图9描述了透平入口气压在不同阀门关闭时间情况下发电机功率与转速随时间变化情况。可以看出，透平停机时间与气压归零时间保持同步，这是由于气压降低后，难以为发电机提供足够转矩，在气压降低至1 Pa时，入口气压与出口气压相同，电动机将无法提供功率输出。
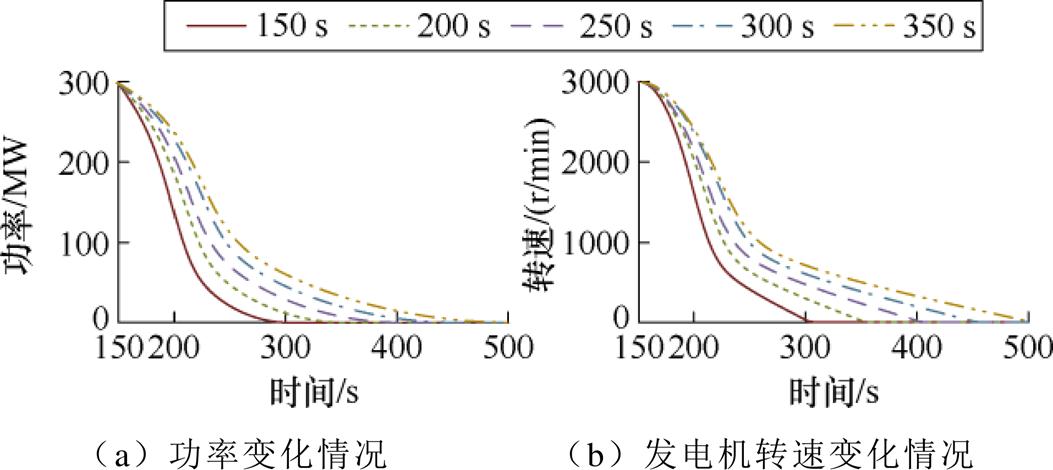
图9 不同阀门关闭速度下仿真结果
Fig.9 Simulation results at different valve closing speeds
由此可知，透平转速、功率参数取决于透平出入口气压差，其停机时间与气压差达谷时间吻合。需要注意的是，气压差变化率需要严格控制，较高的气压差变化率将严重影响设备机械寿命。
本文分析AA-CAES系统关键物理量相互影响机理，建立300 MW级AA-CAES系统各关键部件动态模型；在此基础上建立AA-CAES系统全动态模型，使用该模型开展系统全工况动态仿真研究；并针对系统启动特性、爬坡特性及停机特性进行动态仿真分析。得出以下结论：
1）以“部件搭建-部件验证-系统组合”为核心思路，构建了AA-CAES系统动态模型。首先，建立组合式压缩机与轴流透平动力学模型，在未使用特性曲线与经验公式的条件下，解决多级式压缩机与透平结构复杂、难以计算的问题；完成储气岩穴、换热器等其他关键部件动态模型。随后，使用现有文献中的实验数据验证各关键部件有效性。最后，组合各关键部件模型，完成AA-CAES系统动态模型搭建。
2）实现AA-CAES系统“压缩—停机—发电”全过程动态仿真，阐释了机组全动态过程中各参数耦合关系。仿真结果表明：在发电机起动过程中，功率初始爬升速度较慢，但随后其爬升速度将快于转速爬升速度；效率标幺值始终高于转速标幺值，惯性时间常数与起动时间成正比，透平输入气压爬升率与起动时间成反比。同时通过图像阐明不充分换热与充分换热过程换热器输入与输出气温变化 情况。
3）对AA-CAES系统起动、爬坡及停机过程进行动态仿真，建立动态过程性能指标体系，有效表征了机组多种动态过程中关键参数的变化规律。各阶段性能指标与输入参数间关系见表2，描述了各输入参数增加时，各对应参数变化情况。仿真结果表明：在起动过程中，惯性时间常数越大，对起动过程速度爬升率限制越大；气压爬升率越大，其启动初期转速加速度越大。在爬坡过程中，爬坡功率及气压爬坡率越大，其转速波动幅度与反调峰值功率越大，爬坡所需时间越长。在停机过程中，透平转速与功率由透平出入口气压差决定，停机时间与气压差达谷时间吻合。
表2 性能指标与输入参数对应关系
Tab.2 Correspondence between performance indicators and input parameters
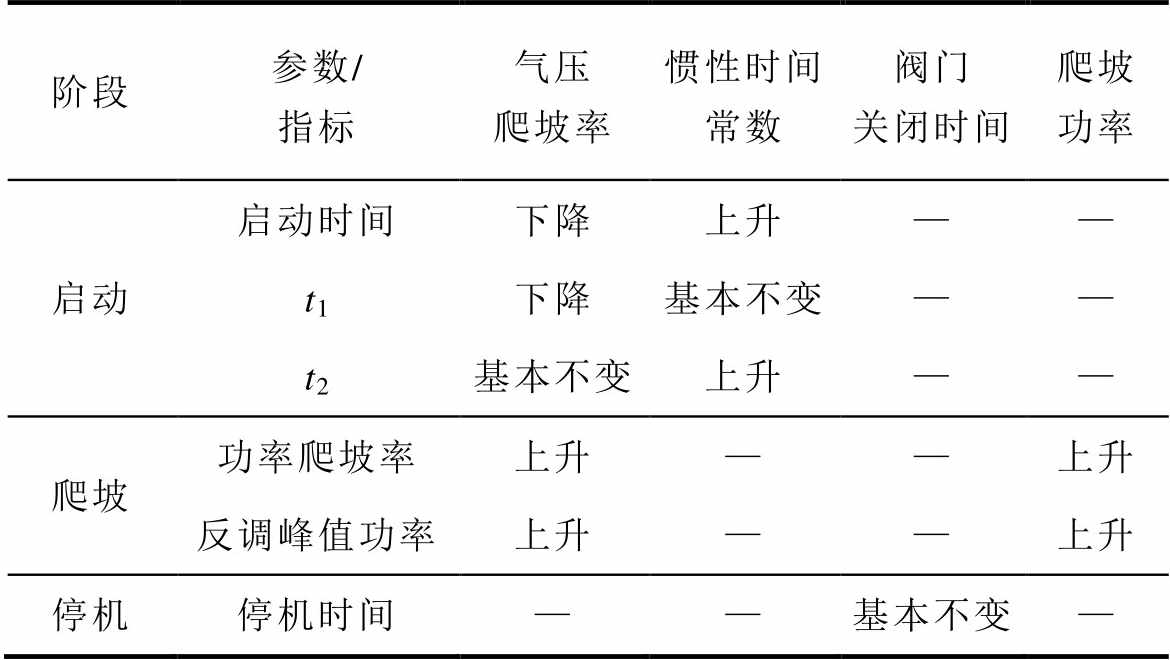
阶段参数/指标气压爬坡率惯性时间常数阀门关闭时间爬坡功率 启动启动时间下降上升—— t1下降基本不变—— t2基本不变上升—— 爬坡功率爬坡率上升——上升 反调峰值功率上升——上升 停机停机时间——基本不变—
附 录
AA-CAES系统关键部件模型验证如下。
1）离心压缩机与轴流压缩机
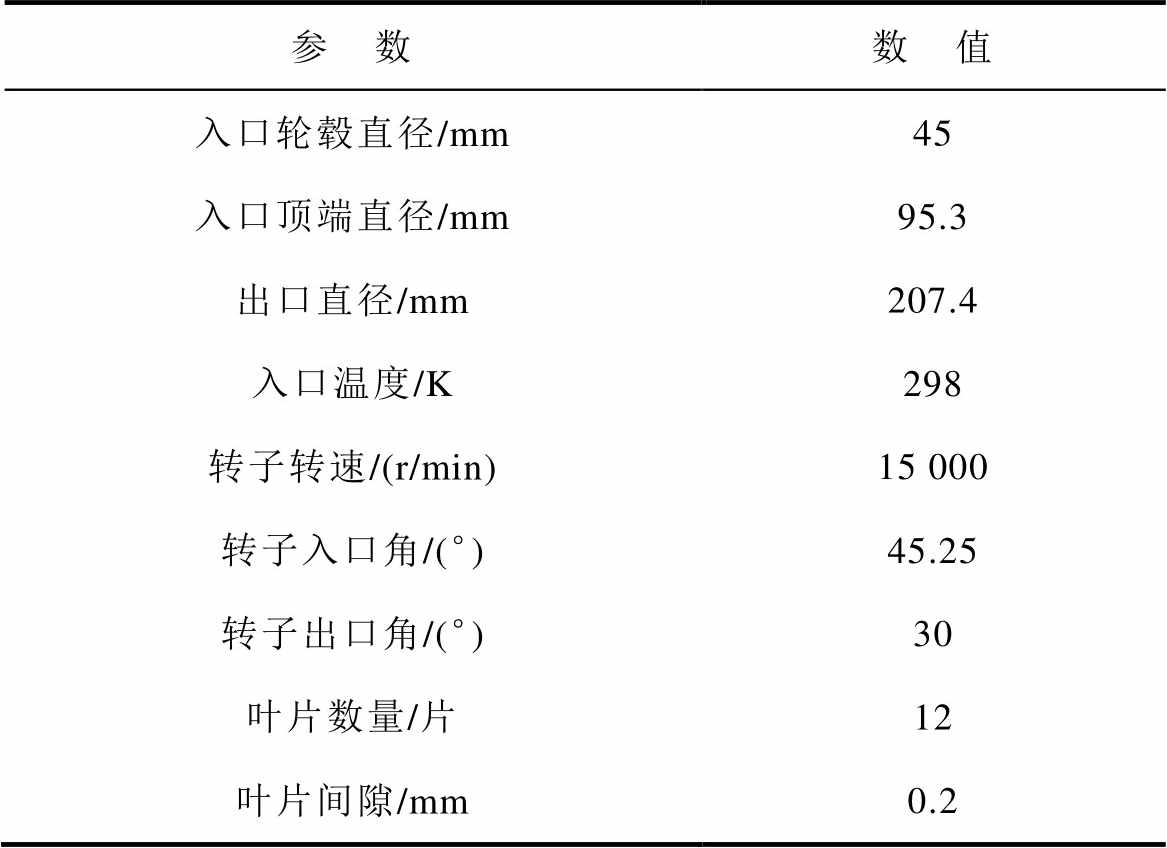
为了说明整体压缩方式可行性，本节分别验证离心压缩机与轴流压缩机动态模型。离心压缩机具体参数见附表1[27]，仿真结果如附图1所示。图中展示了五种不同转速情况下空气流量与压缩比变化情况，对比实验数据与仿真数据可知，该动态模型仿真数据与实验数据误差小，动态模型可反映离心式压缩机输出参数动态变化情况。
附表1 离心压缩机输入参数
App.Tab.1 Centifugal compressor input parameters
参 数数 值 入口轮毂直径/mm45 入口顶端直径/mm95.3 出口直径/mm207.4 入口温度/K298 转子转速/(r/min)15 000 转子入口角/(°)45.25 转子出口角/(°)30 叶片数量/片12 叶片间隙/mm0.2
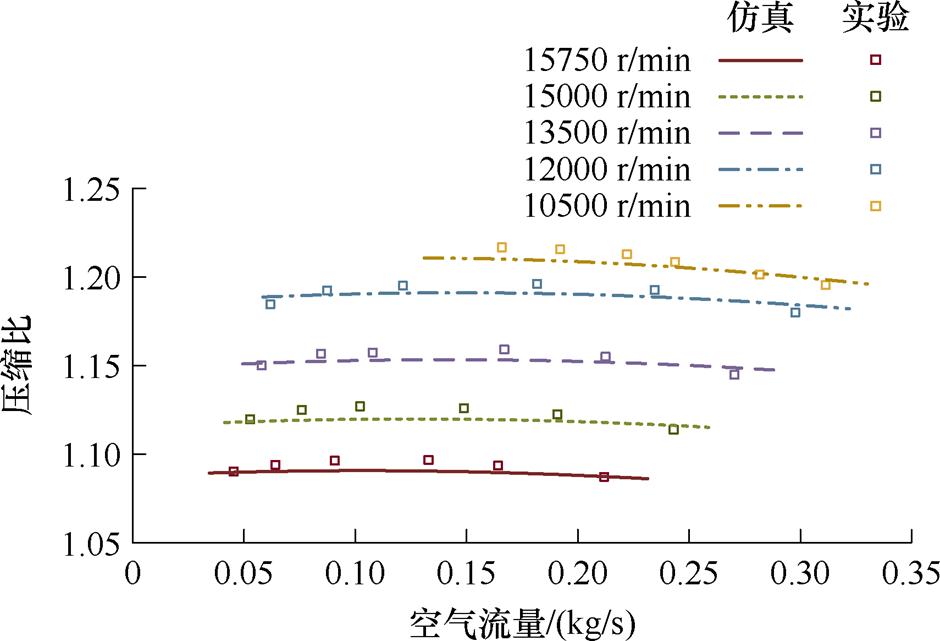
附图1 总压比随空气质量流量变化情况
App.Fig.1 Variation of pressure ratio with air mass flow rate
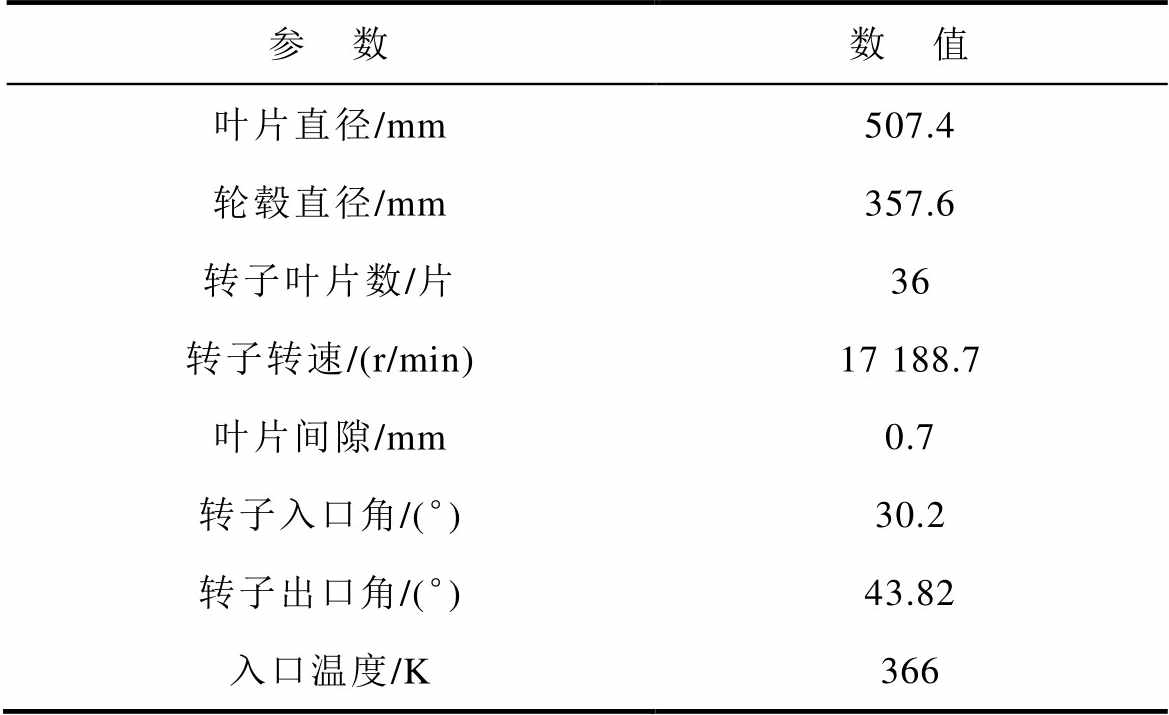
轴流式压缩机实验数据来源于文献[28]，输入参数见附表2。附图2展示了相同参数情况下压比与气体流量变化情况，对比可知，该轴流式压缩机动态模型能够反映轴流压缩机各参数实际变化情况。
附表2 轴流式压缩机输入参数
App.Tab.2 Axial compressor input parameters
参 数数 值 叶片直径/mm507.4 轮毂直径/mm357.6 转子叶片数/片36 转子转速/(r/min)17 188.7 叶片间隙/mm0.7 转子入口角/(°)30.2 转子出口角/(°)43.82 入口温度/K366
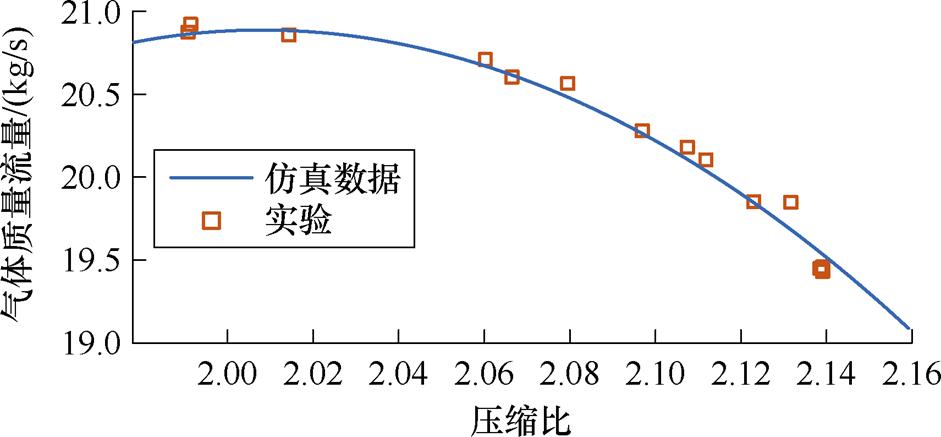
附图2 空气质量流量随总压比变化情况
App.Fig.2 Variation of air mass flow rate with pressure ratio
2）轴流透平
用于验证轴流透平的数据来源于文献[29]，具体数据见附表3。
该轴流透平采用两级轴流结构，附图3展示了总压比变化情况下轴流透平系统的输出功变化曲线，在工况下与实验结果基本相符。
附表3 轴流透平输入参数
App.Tab.3 Axial turbine input parameters
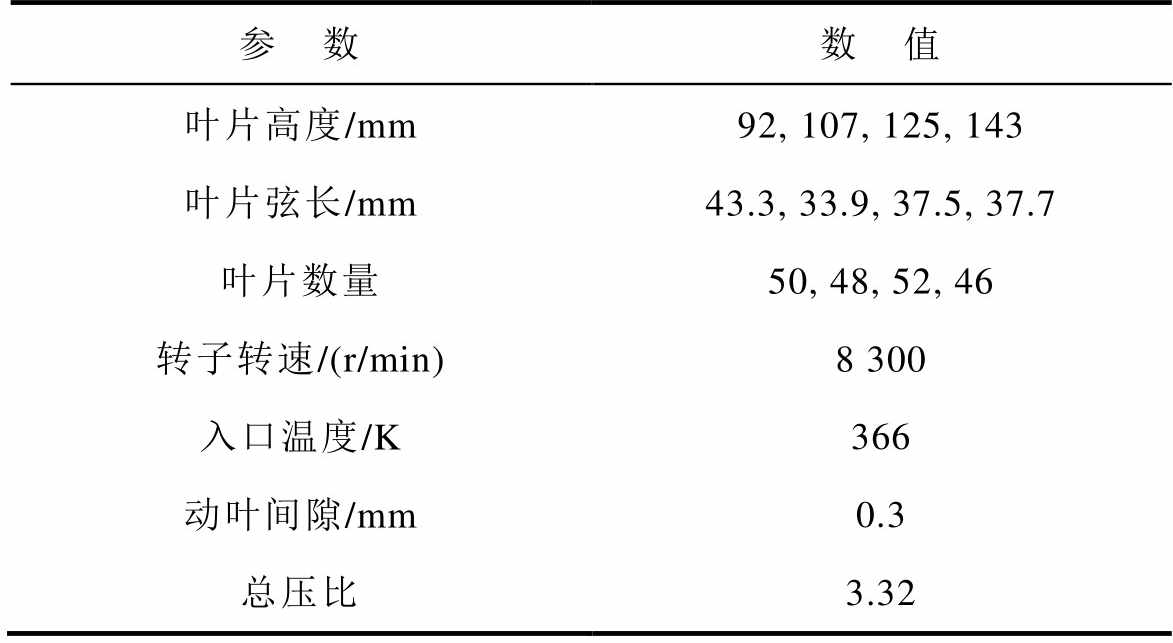
参 数数 值 叶片高度/mm92, 107, 125, 143 叶片弦长/mm43.3, 33.9, 37.5, 37.7 叶片数量50, 48, 52, 46 转子转速/(r/min)8 300 入口温度/K366 动叶间隙/mm0.3 总压比3.32
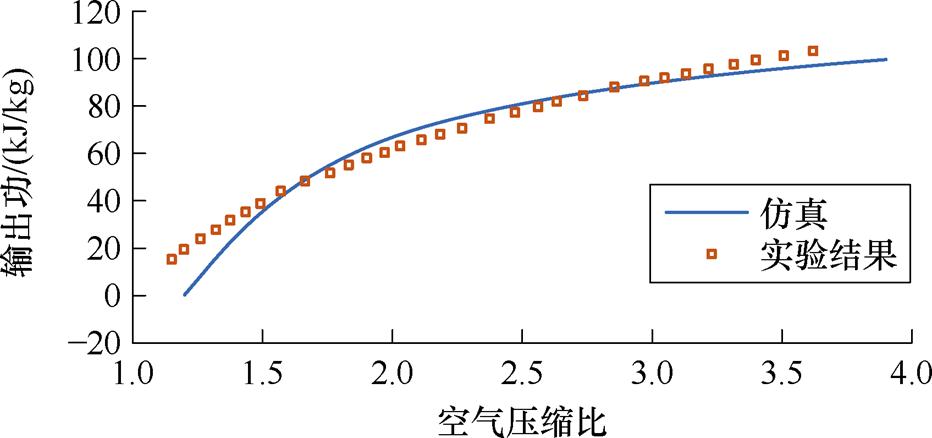
附图3 输出功随空气压缩机变化情况
App.Fig.3 Variation of output work with the compression ratio of air
3）管壳式换热器
管壳式换热器数据及验证过程参考文献[30]。
参考文献
[1] 赵冬梅, 宋晨铭, 冯向阳, 等. 100%新能源场景下考虑频率稳定约束的源网荷储一体化系统储能优化配置[J]. 电工技术学报, 2025, 40(7): 2146-2161.
Zhao Dongmei, Song Chenming, Feng Xiangyang, et al. The optimal configuration of energy storage in the source-grid-load-storage integrated system considering frequency stability constraints in 100% new energy scenarios[J]. Transactions of China Electrotechnical Society, 2025, 40(7): 2146-2161.
[2] 马富艺龙, 辛焕海, 刘晨曦, 等. 新能源基地柔性直流送出系统小扰动电压支撑强度评估[J]. 电工技术学报, 2023, 38(21): 5758-5770, 5938.
Ma Fuyilong, Xin Huanhai, Liu Chenxi, et al. Small-disturbance system voltage support strength assessment method for renewables VSC-HVDC deli- very system[J]. Transactions of China Electrotech- nical Society, 2023, 38(21): 5758-5770, 5938.
[3] 张祥宇, 邵孜建, 付媛. 风储并网发电系统的虚拟多段协同调速与频率安全支撑技术[J]. 电工技术学报, 2025, 40(15): 4677-4693.
Zhang Xiangyu, Shao Zijian, Fu Yuan. Virtual multi- stage coordinated speed regulation and frequency safety support technology of wind-storage grid- connected power generation system[J]. Transactions of China Electrotechnical Society, 2025, 40(15): 4677-4693.
[4] 军徽, 潘雅慧, 穆钢, 等. 高比例风电系统中储能集群辅助火电机组调峰分层优化控制策略[J]. 电工技术学报, 2025, 40(7): 2127-2145.
Li Junhui, Pan Yahui, Mu Gang, et al. Hierarchical optimal control strategy for storage cluster-assisted thermal unit peaking in high-ratio wind power system[J]. Transactions of China Electrotechnical Society, 2025, 40(7): 2127-2145.
[5] 何叶, 杨晓东, 吴红斌, 等. 面向新型配电系统灵活性提升的智能软开关与储能系统协调规划[J]. 电力系统自动化, 2023, 47(18): 142-150.
He Ye, Yang Xiaodong, Wu Hongbin, et al. Coor- dinated planning of soft open point and energy storage system for flexibility enhancement of new distribution system[J]. Automation of Electric Power Systems, 2023, 47(18): 142-150.
[6] 陈海生, 李泓, 徐玉杰, 等. 2023年中国储能技术研究进展[J]. 储能科学与技术, 2024, 13(5): 1359-1397.
Chen Haisheng, Li Hong, Xu Yujie, et al. Research progress on energy storage technologies of China in 2023[J]. Energy Storage Science and Technology, 2024, 13(5): 1359-1397.
[7] Cui Sen, Chen Laijun, Chen Siyuan, et al. Dynamic modeling and analysis of compressed air energy storage for multi-scenario regulation requirements[J]. Journal of Energy Storage, 2024, 100: 113227.
[8] 李佳佳, 李兴朔, 周国文, 等. 基于火-储联合循环的冷热电三联供系统多运行模式热力性能分析[J].中国电机工程学报, 2024, 44(9): 3598-3610.
Li Jiajia, Li Xingshuo, Zhou Guowen, et al. Thermo- dynamics analysis under different operation modes of trigenerative system based on CFPP-CAES combined cycle[J]. Proceedings of the CSEE, 2024, 44(9): 3598-3609.
[9] Ma Linrui, Zhang Xuelin, Zhang Zhao, et al. Appli- cation of the multi-stage centrifugal compressor 1D loss model in the adiabatic compressed air energy storage[J]. Energy Conversion and Management, 2023, 283: 116908.
[10] 张萱, 陈来军, 崔森, 等. 先进绝热压缩空气储能系统宽工况运行可行域分析[J/OL]. 电网技术, 1-10 [2025-05-28]. https://doi.org/10.13335/j.1000- 3673.pst.2024.1339.
Zhang Xuan, Chen Laijun, Cui Sen, et al. Feasible region analysis of advanced adiabatic compressed air energy storage system under wide operation con- dition[J/OL]. Power System Technology, 1-10 [2025- 05-28]. https://doi.org/10.13335/j.1000-3673.pst.2024.1339.
[11] 韩中合, 刘士名, 周权, 等. 恒壁温储气模型下先进绝热压缩空气储能系统性能分析[J]. 中国电机工程学报, 2016, 36(12): 3373-3381.
Han Zhonghe, Liu Shiming, Zhou Quan, et al. Per- formance analysis of AA-CAES system with constant wall-temperature air storage model[J]. Proceedings of theCSEE, 2016, 36(12): 3373-3381.
[12] Bu Shujuan, Yang Xinle, Sun Yue, et al. Thermo- dynamic performances analyses and process opti- mization of a novel AA-CAES system coupled with solar auxiliary heat and organic Rankine cycle[J]. Energy Reports, 2022, 8: 12799-12808.
[13] 郭欢, 徐玉杰, 张新敬, 等. 蓄热式压缩空气储能系统变工况特性[J]. 中国电机工程学报, 2019, 39(5): 1366-1377.
Guo Huan, Xu Yujie, Zhang Xinjing, et al. Off-design performance of compressed air energy storage system with thermal storage[J]. Proceedings of the CSEE, 2019, 39(5): 1366-1377.
[14] 李盼, 杨晨, 陈雯, 等. 压缩空气储能系统动态特性及其调节系统[J]. 中国电机工程学报, 2020, 40(7): 2295-2305, 2408.
Li Pan, Yang Chen, Chen Wen, et al. Dynamic characteristics of compressed air energy storage system and the regulation system[J]. Proceedings of the CSEE, 2020, 40(7): 2295-2305, 2408.
[15] Chen Longxiang, Zhang Liugan, Yang Huipeng, et al. Dynamic simulation of a re-compressed adiabatic compressed air energy storage (RA-CAES) system[J]. Energy, 2022, 261: 125351.
[16] Chen Wei, Bai Jianshu, Wang Guohua, et al. First and second law analysis and operational mode opti- mization of the compression process for an advanced adiabatic compressed air energy storage based on the established comprehensive dynamic model[J]. Energy, 2023, 263: 125882.
[17] 孙晓霞, 桂中华, 高梓玉, 等. 压缩空气储能系统动态运行特性[J]. 储能科学与技术, 2023, 12(6): 1840-1853.
Sun Xiaoxia, Gui Zhonghua, Gao Ziyu, et al. Dynamic characteristics of compressed air energy storage system[J]. Energy Storage Science and Tech- nology, 2023, 12(6): 1840-1853.
[18] 崔森, 陈来军, 陈思源, 等. 基于最优动态功率补偿的先进绝热压缩空气储能一次调频控制策略[J]. 高电压技术, 2024, 50(6): 2433-2441.
Cui Sen, Chen Laijun, Chen Siyuan, et al. Primary frequency modulation control of advanced adiabatic compressed air energy storage based on optimal dynamic power compensation[J]. High Voltage Engineering, 2024,50(6): 2433-2441.
[19] 清华大学热能工程系动力机械与工程研究所, 深圳南山热电股份有限公司. 燃气轮机与燃气－蒸汽联合循环装置[M]. 北京: 中国电力出版社, 2007.
[20] 桂幸民, 滕金芳, 刘宝杰, 等. 航空压气机气动热力学理论与应用[M].上海: 上海交通大学出版社, 2014.
[21] Liu Wei, Li Qihang, Yang Chunhe, et al. The role of underground salt Caverns for large-scale energy storage: a review and prospects[J]. Energy Storage Materials, 2023, 63: 103045.
[22] 王进, 周玲, 季路成. 轴流压气机一维特性计算方法简介及展望[J]. 实验流体力学, 2021, 35(2): 1-12.
Wang Jin, Zhou Ling, Ji Lucheng. Brief introduction and prospect of calculation methods for one- dimensional characteristics of axial flow com- pressor[J]. Journal of Experiments in Fluid Mechanics, 2021, 35(2): 1-12.
[23] Luo Xing, Dooner M, He Wei, et al. Feasibility study of a simulation software tool development for dynamic modelling and transient control of adiabatic compressed air energy storage with its electrical power system applications[J]. Applied Energy, 2018, 228: 1198-1219.
[24] 李显, 朱天宇, 徐小韵, 等. 1MW塔式太阳能电站蓄热系统模拟分析[J]. 太阳能学报, 2011, 32(5): 632-638.
Li Xian, Zhu Tianyu, Xu Xiaoyun, et al. Simulation of thermal storage system for 1MW solar power tower plant[J]. Acta Energiae Solaris Sinica, 2011, 32(5): 632-638.
[25] Li Yaowang, Miao Shihong, Luo Xing, et al. Dynamic modelling and techno-economic analysis of adiabatic compressed air energy storage for emergency back-up power in supporting microgrid[J]. Applied Energy, 2020, 261: 114448.
[26] 刘逸凡, 邹明, 王焱, 等. 面向海上风电仿真的永磁同步发电机电磁暂态等效建模方法[J]. 电工技术学报, 2024, 39(8): 2400-2411.
Liu Yifan, Zou Ming, Wang Yan, et al. equivalent modeling method for electromagnetic transient of permanent magnet synchronous generator for offshore wind power simulation[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2400-2411.
[27] Zhang Chaowei, Dong Xuezhi, Liu Xiyang, et al. A method to select loss correlations for centrifugal compressor performance prediction[J]. Aerospace Science and Technology, 2019, 93: 105335.
[28] Ji Ziqi, Du Gang. A tensor basis neural network-based turbulence model for transonic axial compressor flows[J]. Aerospace Science and Technology, 2024, 149: 109155.
[29] Xiong Jun, Zhu Yangli, Wang Xing, et al. Blade solidity optimization of axial turbine in compressed air energy storage system[J]. Journal of Energy Storage, 2023, 72: 108598.
[30] 孙宝芝, 曹民侠, 赵嘉明, 等. 管壳式换热器瞬态换热性能分析[J]. 哈尔滨工程大学学报, 2007, 28(12): 1332-1336.
Sun Baozhi, Cao Minxia, Zhao Jiaming, et al. Analysis of the transient heat transfer performance of shell-and-tube heat exchangers[J]. Journal of Harbin Engineering University, 2007, 28(12): 1332-1336.
Dynamic Modelling and Characterization of Large Capacity Advanced Adiabatic Compressed Air Energy Storage System
Abstract The intermittency and unpredictability of renewable energy sources, such as photovoltaic (PV) and wind power, pose significant challenges to grid stability. Advanced energy storage technologies have attracted considerable attention in both academic and industrial fields. Among them, advanced adiabatic compressed air energy storage (AA-CAES) is considered a promising solution for large-scale energy storage applications. Accurately characterizing the dynamic response and regulation capabilities of large-scale AA-CAES systems is essential. To this end, developing robust dynamic models and conducting systematic analyses are crucial.
To investigate the dynamic characteristics of the AA-CAES system, the interaction mechanisms of key physical parameters are analyzed. A dynamic modeling approach based on conservation laws and empirical formulas is employed to establish mathematical models for the multistage compressor and turbine. Additionally, dynamic models for other critical components, including the underground cavern, heat storage chamber, and heat exchanger, are systematically developed. Each component model is validated against experimental data from existing literature to ensure accuracy and reliability. By integrating the validated models of all critical components, a comprehensive dynamic model of the entire AA-CAES system is constructed. This model is then used to conduct full-condition dynamic simulations of the system's operational cycles, including “compression- shutdown-power generation” processes. The three dynamic characteristics of startup, shutdown, and ramp-up are also simulated for the system operating parameters.
The simulation analysis leads to the following conclusions. (1) The operating parameter variations of the key component models are consistent with actual conditions. The system's dynamic model accurately captures parameter variations under all operating conditions. (2) Through the dynamic analysis of the entire operation process, the evolution of multiple parameters in the ‘Compression-Stop-Generation’ process is determined. Specifically, during the generator startup process, the initial power ramp-up rate is relatively slow but eventually exceeds the rotor's ramp-up rate. The per-unit efficiency remains consistently higher than the per-unit speed. The inertia time constant is directly proportional to the startup time, whereas the rate of increase in turbine inlet air pressure is inversely proportional to the startup time. (3) Dynamic simulation of the AA-CAES system startup, climb, and shutdown processes. By establishing performance indices, the dynamic characteristics of the system are further clarified. During the startup process, a larger inertia time constant imposes greater limitations on the speed ramp-up rate. In contrast, a higher air pressure ramp-up rate results in a greater initial acceleration of speed. In the ramp-up phase, lower initial power generation results in larger fluctuations in rotor speed and output power, as well as longer ramp-up durations. During the shutdown process, turbine speed and power output are primarily determined by the pressure differential between the turbine inlet and outlet, with the shutdown time coinciding with the moment when the pressure differential reaches its minimum value.
Keywords：Advanced adiabatic compressed air energy storage (AA-CAES), dynamic modeling, full- operating-condition simulation, dynamic characteristics, large capacity
中图分类号：TM91
DOI: 10.19595/j.cnki.1000-6753.tces.242058
国家重点研发计划资助项目（2023YFB2406500）。
收稿日期 2024-11-14
改稿日期 2025-02-09
侯心宇 男，2002年生，硕士研究生，研究方向为压缩空气储能系统、电力系统建模与仿真等。
E-mail: houxinyu@hust.edu.cn
苗世洪 男，1963年生，教授，博士生导师，研究方向为电力系统继电保护及自动化、配电网与微网新技术、压缩空气储能系统等。
E-mail: shmiao@hust.edu.cn（通信作者）
（编辑 郭丽军）