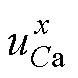 为a相中各个模块的电容电压,x=1, 2,…, Nm。usa、usb、usc为SVG三相电压,isa、isb、isc为SVG三相电流,un为三相连接点电压,Cm为各个模块中电容,Lf为交流测滤波电感。电网侧uga、ugb、ugc为三相电网电压,Zg为交流电网等效阻抗。
为a相中各个模块的电容电压,x=1, 2,…, Nm。usa、usb、usc为SVG三相电压,isa、isb、isc为SVG三相电流,un为三相连接点电压,Cm为各个模块中电容,Lf为交流测滤波电感。电网侧uga、ugb、ugc为三相电网电压,Zg为交流电网等效阻抗。摘要 级联H桥静止无功发生器(SVG)是改善电能质量、进行无功补偿的常用装备。然而,作为一种由控制主导动态特性的电力电子装备,必然存在振荡风险,对电力系统安全稳定运行造成威胁。针对上述问题,该文首先分析级联H桥SVG非线性、强耦合的内部动态特性,针对开关频率以下的低频段,建立考虑多控制环路作用的SVG谐波状态空间复矢量阻抗模型。然后,基于系统频率耦合关系,得到降维后的SVG阻抗模型及等效的单输入单输出阻抗模型,通过Matlab/Simulink仿真平台进行频率扫描,验证阻抗模型的正确性。在阻抗模型基础上,基于不同控制环以及其控制参数对SVG进行稳定性分析。分析发现,锁相环对系统稳定性影响显著,因此对其参数进行量化分析,为参数设计提供参考。而相间均压环对系统稳定性影响相对不显著。为解决SVG并网稳定性问题,该文针对主导控制环即锁相环引发的振荡风险,提出一种电压前馈阻抗重塑策略,有效减小锁相环带来的负阻问题,进而提高系统的并网稳定性。最后,基于RT-Lab建立SVG并网系统的硬件在环实验,验证该文所提的理论分析和振荡抑制策略的有效性。
关键词:静止无功发生器 谐波状态空间 频率耦合 稳定性分析 阻抗重塑
静止无功发生器(Static Var Generator, SVG)具备输出无功功率灵活可调、补偿效果好、响应速度快等优点,在改善电能质量和无功补偿方面成为了首选[1-4]。其中级联H桥SVG因其易于模块化扩展、各逆变单元独立,是目前常用的一种无功补偿装 置[5-6]。然而作为电力电子装置,级联H桥SVG的动态受到多个控制环路影响,必然存在振荡风险,对电力系统安全稳定运行造成威胁。例如,在我国新疆哈密地区含集成SVG的风电场和光伏电站中曾频繁出现振荡现象[2],英国也曾出现由于风电场配置的SVG而引发振荡的事故[3],由此引发了广泛关注。
针对振荡风险分析问题,阻抗分析法因其物理机理明确、分析过程简单,已成为强有力的工具。文献[7-8]在同步旋转坐标系中建立两电平SVG阻抗模型,但该方法不能直接推广至多变量、强耦合的级联H桥SVG。文献[9]基于级联H桥SVG建立同步旋转坐标系下的阻抗模型,实现电流解耦,然而该方法仅适用于所设计的自抗扰控制策略,不能推广至PI控制等经典控制方法。文献[10]在不同频域中应用Park变换建立多个旋转坐标系,从而将各次谐波转为相应的直流分量,得到可用于线性化的系统。然而,随着所考虑的谐波次数增加,该方法适用性较差。
线性周期(Linear Time Periodic, LTP)阻抗建模方法具有更好的兼容性,适用于多频率耦合系统。频率耦合现象即当施加某频率的电压扰动时,除了产生同频率的电流响应分量之外,还会产生其他不同频率的电流响应分量[11-12]。针对该现象,文献[2]提出一种采用双谐波线性化建模的SVG阻抗模型揭示频率耦合效应。与(多)谐波线性化序阻抗建模方法等效的谐波状态空间(Harmonic State Space, HSS)建模方法已在模块化多电平换流器(Modular Multilevel Converter, MMC)等设备中得到广泛应用并得到一定成果[13-16]。该方法能够在较宽的频率范围内体现谐波耦合特性,且物理意义更加明确,这是前述方法难以做到的。但其阻抗模型呈现出多输入多输出(Multiple-Inputs Multiple-Outputs, MIMO)特性,增加了阻抗测量与稳定性分析的复杂度。针对该问题,文献[17]将MMC阻抗模型降维至单输入单输出(Single-Input Single-Output, SISO)阻抗模型进行分析,文献[18]对换相换流器直流输电系统阻抗模型截断频次进行探究,得到等效SISO阻抗模型。
针对SVG引发的振荡问题,现有文献已开展了一定的研究。文献[19-20]研究了集成级联H桥SVG与风电场的振荡机理,从运行模式和控制器参数两方面分析其对直驱风场振荡的影响。文献[21]探究SVG与直驱风机之间交互作用影响导致系统产生的次同步振荡现象,但未提出振荡抑制策略。文献[22]以控制参数的角度探究了SVG对风电场次同步振荡的影响,但将直流侧简化了。文献[23]提出了一种SVG参数设计方法,然而存在一定受限性。文献[24]提出了一种自适应控制参数设计方法。文献[25]针对含SVG的风电场,分析抑制风电场中频振荡风险策略。文献[7]提出一种基于电压前馈控制的方法,重塑SVG的负阻区从而抑制风电场高频振荡,但将SVG直流侧简化为恒定直流电压源,忽略了电压外环控制,同时只考虑高频振荡风险。文献[26]基于含级联H桥SVG的光伏电站,通过SVG高频相位补偿抑制光伏电站高频振荡,但未考虑其他频段。现有文献侧重于级联H桥SVG在系统中与其他电力电子设备的交互作用影响,且大多数只关注高频或者某一特殊频段,前提是该设备单独联网时是稳定的。但实际上,此设备本身作为电力电子装置,单独并网时也存在宽频振荡风险,而目前对此研究较少,振荡机理尚不明确,且缺乏相应的稳定性提升技术。鉴于上述问题,本文针对级联H桥SVG引发的振荡问题,聚焦产生机理及振荡抑制策略展开研究。基于HSS建模方法建立考虑频率耦合的阻抗平均模型并定量计算,通过Matlab/ Simulink仿真平台进行频率扫描验证,与理论分析结果进行对比,验证模型的正确性。
在此基础上,计及内部电流、输出电压以及三相电容电压的动态以及与电网阻抗的频率耦合,推导系统SISO阻抗模型。进而对控制环以及其控制参数可能引发的振荡风险进行探究,得到控制参数的优化设计方法,揭示锁相环是影响系统稳定性的主导控制环,基于振荡风险机理提出一种电压前馈阻抗重塑策略,有效减小锁相环带来的负阻问题,从而增强系统稳定性。最后,通过RT-Lab实时数字仿真平台验证理论分析和所提出控制策略的有效性。
级联H桥SVG主电路拓扑与控制框图如图1所示。SVG每个桥臂连接Nm个H桥(H-Bridge, HB)模块,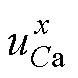 为a相中各个模块的电容电压,x=1, 2,…, Nm。usa、usb、usc为SVG三相电压,isa、isb、isc为SVG三相电流,un为三相连接点电压,Cm为各个模块中电容,Lf为交流测滤波电感。电网侧uga、ugb、ugc为三相电网电压,Zg为交流电网等效阻抗。
为a相中各个模块的电容电压,x=1, 2,…, Nm。usa、usb、usc为SVG三相电压,isa、isb、isc为SVG三相电流,un为三相连接点电压,Cm为各个模块中电容,Lf为交流测滤波电感。电网侧uga、ugb、ugc为三相电网电压,Zg为交流电网等效阻抗。
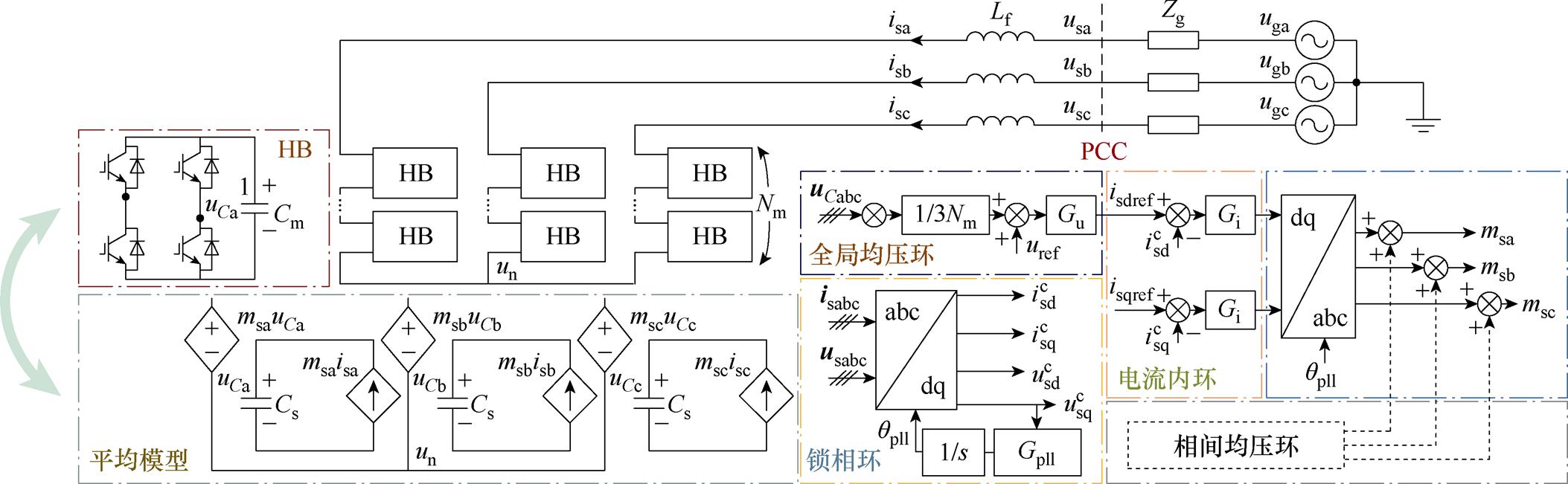
图1 级联H桥SVG主电路拓扑结构与控制框图
Fig.1 Topology of cascaded H-bridge SVG and control diagram
由于开关动作引发非线性影响的频率远高于本文探究的频率范围,因此本文不考虑开关频率,建立如图1所示平均模型进行分析[2, 27]。msa、msb、msc为三相调制信号,uCa、uCb、uCc为三相直流侧电容电压之和,Cs为每相子模块电容之和,Cs=Cm/Nm。
级联H桥SVG的闭环控制系统由电压环、电流环及锁相环(Phase-Locked Loop, PLL)组成。通常情况下,级联H桥SVG的电压控制采用分层控制的方法[28],即全局均压、相间均压及相内均压控制。其中,相内均压控制是在开关频率基础上对各子模块的电容电压进行调节,且正常运行时电容电压不平衡程度较小,而本文针对开关频率以下频段建立平均模型分析,因此将其忽略[2, 29]。全局均压环控制每相直流侧电容电压的平均值稳定,同时生成d轴电流基准值isdref。相间均压环保证三相电压均衡。锁相环通过测量公共耦合点(Point of Common Coupling, PCC)处电压生成qpll以实现SVG与电网的同步。Gu、Gi、Gpll分别为全局均压环、电流环、锁相环的PI调节器,表示为Gu=kpv+ kiv/s、Gi=kpi+kii/s、Gpll=kp_pll+ki_pll/s,kpv, kiv、kpi, kii、kp_pll, ki_pll分别为全局均压环、电流环、锁相环控制器的比例、积分系数。
由于本文涉及的变量与坐标系较多,在此做统一规定:下标“abc”、“dq”和“ab”分别表示三相静止坐标系、两相同步旋转坐标系和两相静止坐标系。例如,三相静止坐标系下PCC电压表示为usabc=[usausbusc]T,isabc、uCabc同理。下标“+、-、0”表示不同序分量,下标“h”表示h次谐波。锁相环动态引入由其输出相位确定的旋转坐标系,称作控制坐标系,用上标“c”表示和系统坐标系区别,系统坐标系与控制坐标系如图2所示。
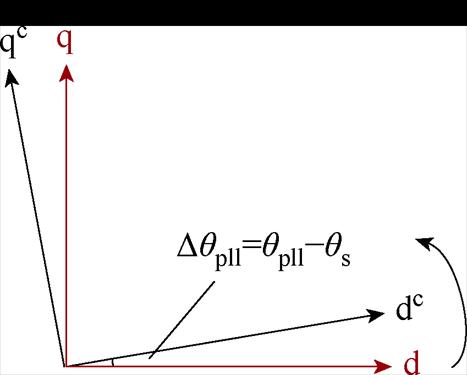
图2 系统坐标系与控制坐标系
Fig.2 The system and control frames
由图1可知,级联H桥SVG的主电路状态方程为
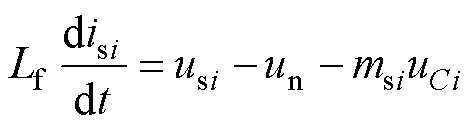 (1)
(1)
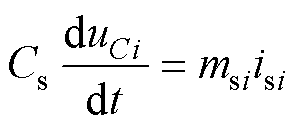 (2)
(2)
式中,i=a, b, c,表示a、b、c三相电路。
对于三相对称系统,中性点电压un表示为
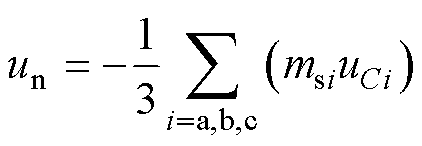 (3)
(3)
联立式(1)~式(3),将状态方程小信号线性化,可得
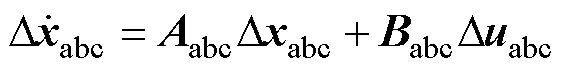 (4)
(4)
其中
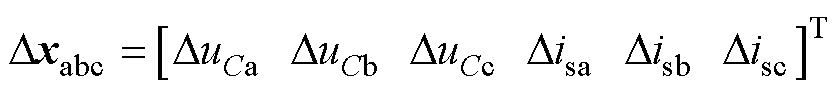 (5)
(5)
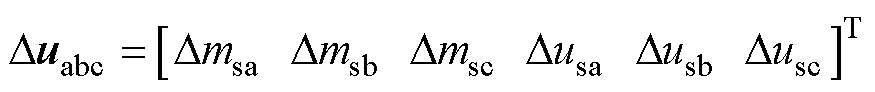 (6)
(6)
式中,Dxabc和Duabc分别为系统的状态向量和输入向量的小信号量;Aabc和Babc分别为状态矩阵和输入矩阵,具体形式参见附录第1节。
进一步地,通过坐标变换矩阵T,将小信号状态方程由abc三相静止坐标系转换至ab复矢量两相静止坐标系,得到
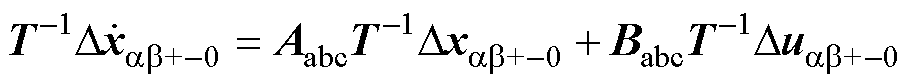 (7)
(7)
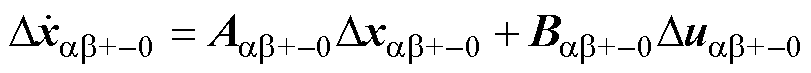 (8)
(8)
式中,Dxab+-0和Duab+-0分别为Dxabc和Duabc在ab坐标系中对应的复矢量。变换矩阵T=diag(T1T2, T1T2),具体为
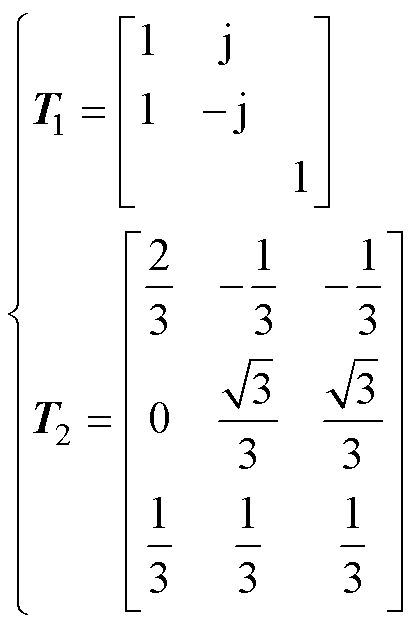 (9)
(9)
通过拉普拉斯变换得频域表达式(8),并利用HSS建模方法,可得主电路频域状态方程为
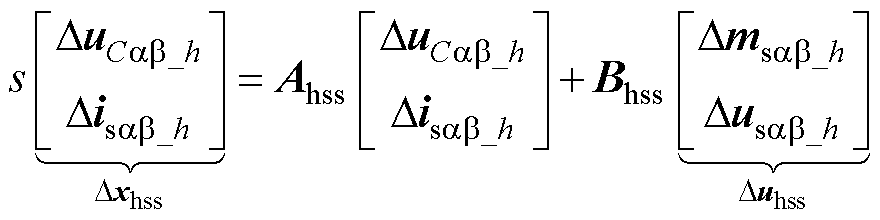 (10)
(10)
其中
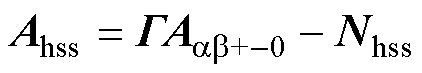 (11)
(11)
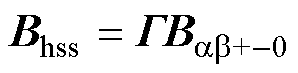 (12)
(12)
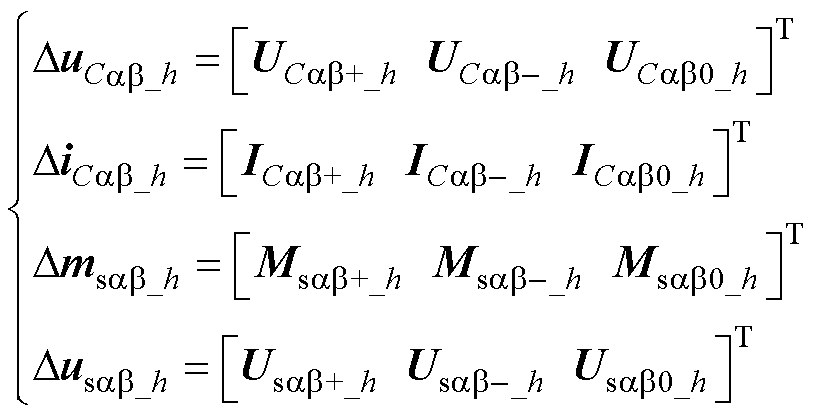 (13)
(13)
式中,所含矩阵具体形式参见附录第2节;Nhss为N的六阶对角矩阵,N=diag(-hjw0,…,-jw0, 0, jw0,…, hjw0);w0为基频;G为Toeplitz矩阵,即傅里叶系数组成的矩阵。
考虑锁相环动态的影响,系统坐标系与控制坐标系中变量的转换关系[30]可表示为
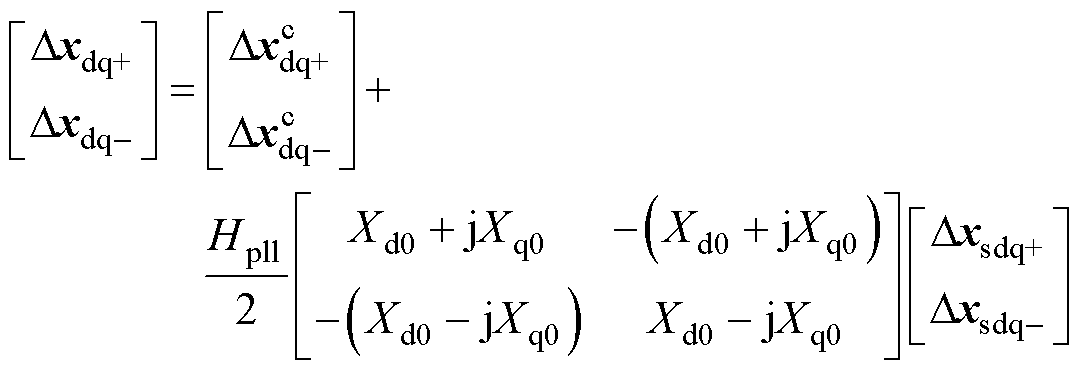 (14)
(14)
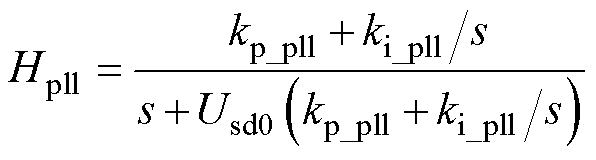 (15)
(15)
式中,Dx为该系统中的任意小信号量;Xd0、Xq0分别为其在d、q坐标系下的稳态值;Usd0为PCC电压的d轴稳态量。
电流控制环表示为
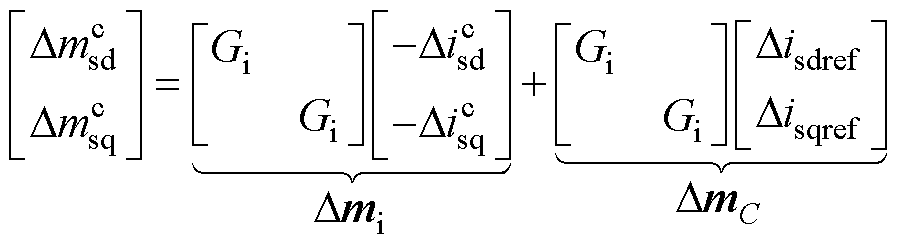 (16)
(16)
电流与调制函数的小信号量在系统坐标系与控制坐标系中的转换关系如式(14)所示。且有
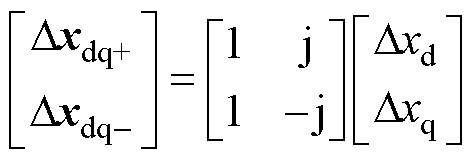 (17)
(17)
将式(14)、式(17)代入Dmi,可获得考虑锁相环动态的电流环模型为
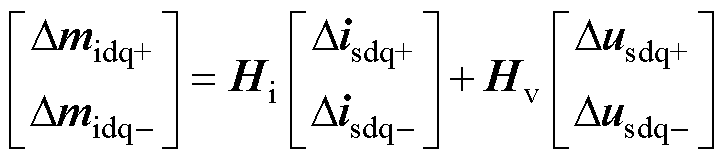 (18)
(18)
其中
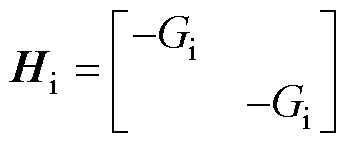 (19)
(19)
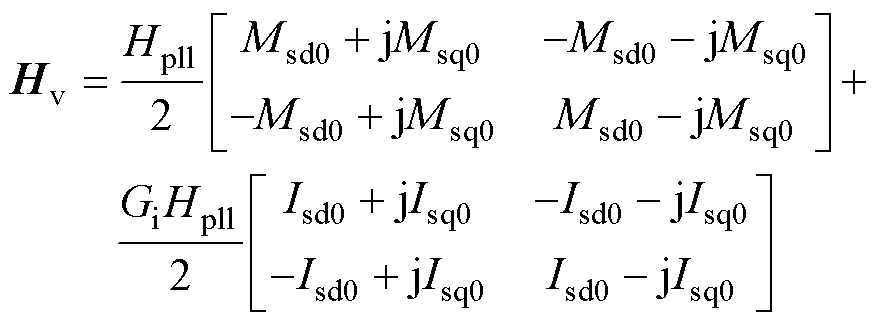 (20)
(20)
进一步地,将其转换为静止坐标系下的复矢量形式[17]为
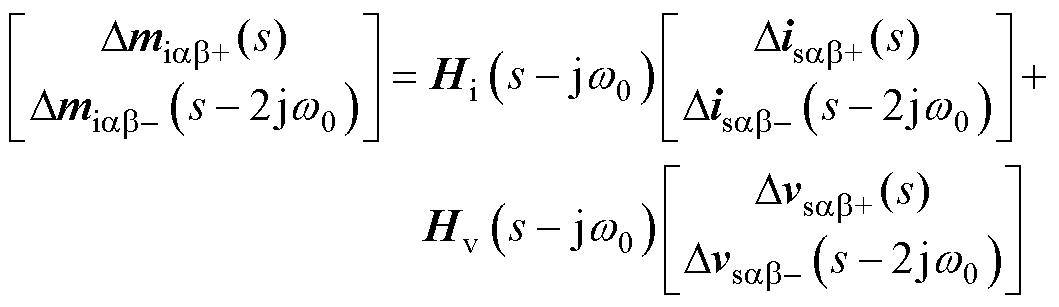 (21)
(21)
拓展至h次谐波后,可以得到含锁相环动态的电流环HSS模型为
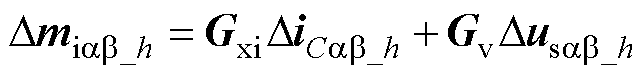 (22)
(22)
三相桥臂中,子模块电容电压平均值的小信号量表示为
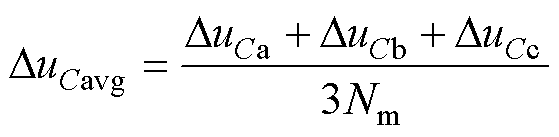 (23)
(23)
由控制框图得出全局均压控制输出d轴电流参考量,即
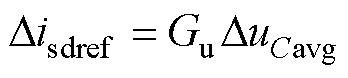 (24)
(24)
将式(23)、式(24)代入式(16)中的DmC,应用Park变换及式(8),获得全局均压环静止坐标系下复矢量形式的HSS模型为
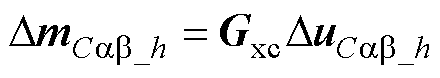 (25)
(25)
图3给出相间均压环控制框图。其中电流环的比例系数以及相间均压电压环的PI调节器分别表示为kp_cu、ki_cu、Gcu,其中Gcu=kp_cu+ki_cu/s。mua、mub、muc为相间均压控制产生的三相调制信号。
以a相为例,调制信号与电容电压以及电流的小信号关系表示为
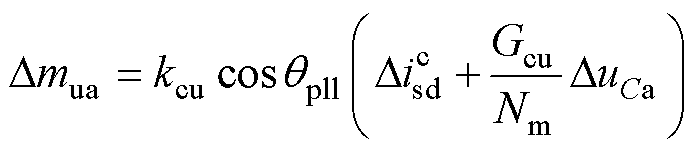 (26)
(26)
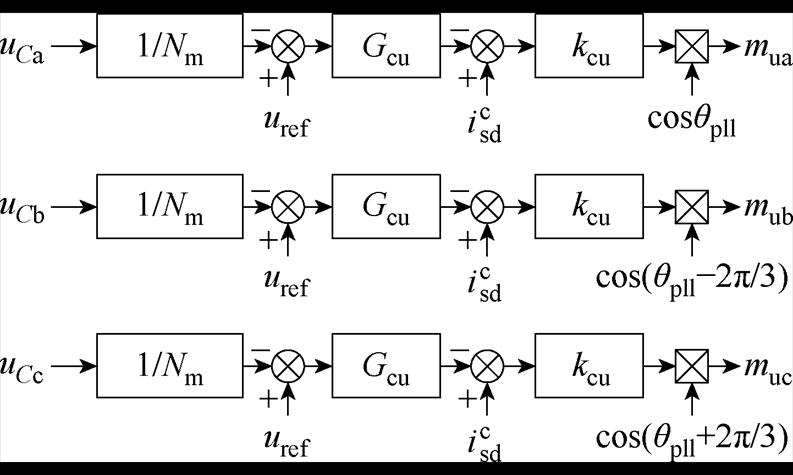
图3 相间均压环控制
Fig.3 Inter-phase balanced voltage control
其余两相同理。由于锁相角qpll小信号作用导致的影响较小,可以忽略不计,因此将其等效为系统坐标系下的旋转角。
将式(14)代入式(26),基于Park变换,得到相间均压环在静止两相坐标系下的复矢量HSS模型,表示为
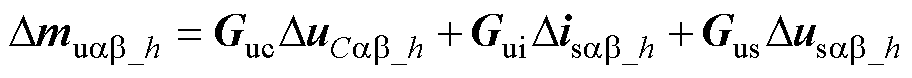 (27)
(27)
联立式(8)、式(22)、式(25)、式(27),可得级联H桥SVG的三相HSS模型为
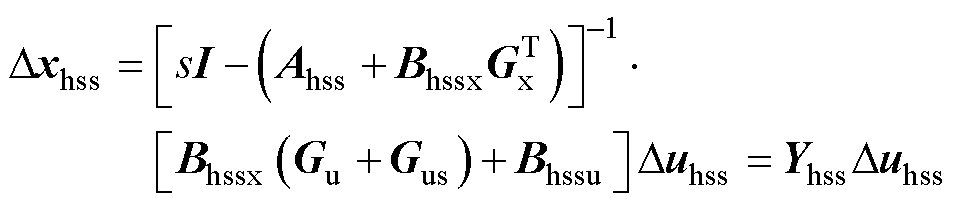 (28)
(28)
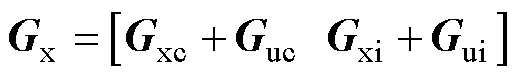 (29)
(29)
式中,Bhssx、Bhssu为Bhss的组成部分。
阻抗计算即扰动电压与响应电流之间的关系[14]计算,为此将式(28)按矩阵形式展开得
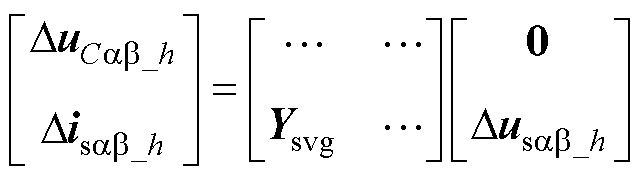 (30)
(30)
式中,0为零矩阵;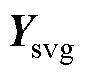 为导纳矩阵。
为导纳矩阵。
提取Disab+-0与Dusab+-0的输入输出关系,即获得SVG的导纳矩阵Ysvg,其阻抗矩阵为导纳矩阵的逆,如式(31)、式(32)及式(33)所示。以正序导纳矩阵为例,对角线项表示相同频率下的关系,非对角线项表示耦合频率下的关系。
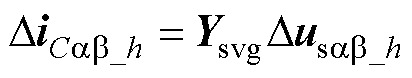 (31)
(31)
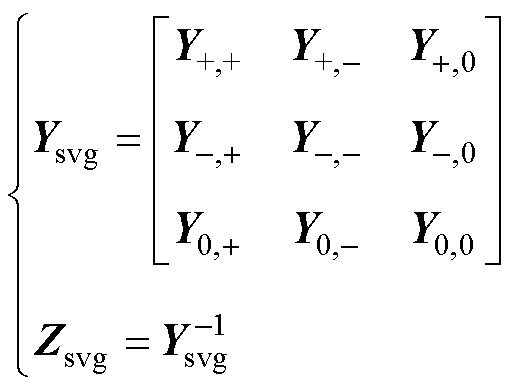 (32)
(32)
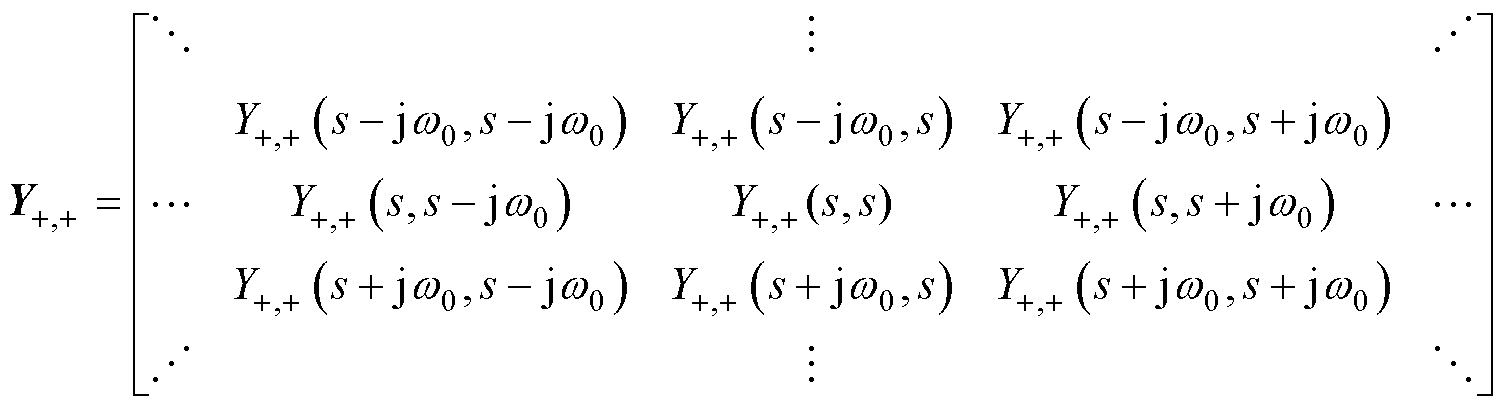 (33)
(33)
分别对级联H桥SVG中稳态量与小信号量讨论频率耦合现象,即对注入某特定频率的电压扰动时产生的响应进行分析,以此为依据将MIMO形式的HSS阻抗模型截断。
稳态运行时,三相桥臂调制信号的基频分量与三相交流电流的基频分量卷积,在桥臂电容电压上产生直流分量和负序二倍频分量。桥臂电容电压的二倍频分量与调制信号的基频分量卷积,在电流上产生零序三倍频分量,而在星形联结中零序电流分量无法流通。至此没有更多频率分量产生。因此稳态量的频率耦合如图4所示。
探究小信号量频率耦合现象时,讨论过程与稳态量频率耦合现象同理,f0为基频频率。
在稳态工作点叠加频率为fp的正序电压,电流和调制信号的小信号量分别与调制信号和电流的基频分量卷积,在桥臂电容电压上产生频率为fp-f0的零序小信号量和频率为fp+f0的负序小信号量。二者与调制信号基频分量卷积,在电流上产生频率为fp-2f0的负序小信号量。调制信号的小信号量与桥臂电容电压基频分量的卷积同理。在电压上产生的零序小信号量不会产生响应。接着,电流和调制信号的fp-2f0处负序小信号量分别与调制信号和电流的基频分量卷积,在桥臂电容电压上产生频率为fp-3f0的正序小信号量。其与调制信号的基频分量卷积,在电流上产生频率为fp-4f0的零序小信号量和频率为fp-2f0的负序小信号量。而所产生的零序电流分量无法流通。至此没有更多的频率分量产生。
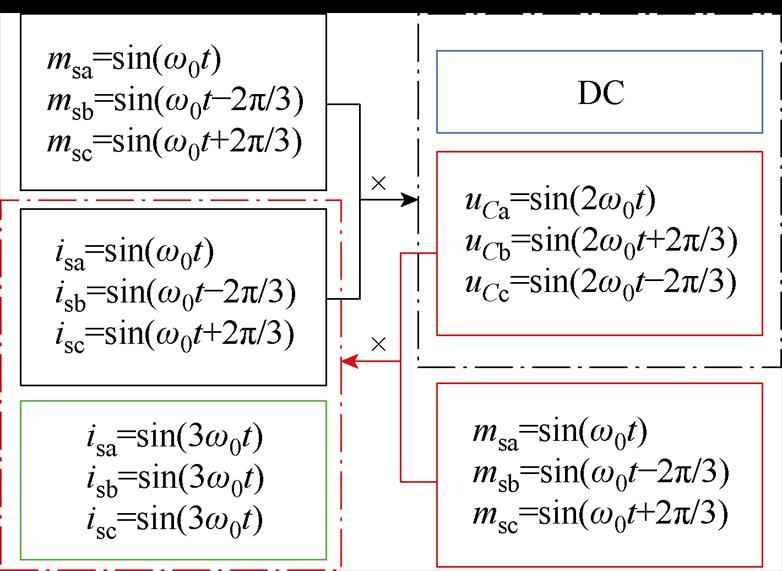
图4 稳态量的频率耦合
Fig.4 Diagram of frequency coupling in steady-state
探究负序扰动信号下的响应时,将正序扰动响应中的fp替换为-fp后,取各项的共轭获得。
根据上述分析,将HSS阻抗模型截断,保留稳态量的直流、基频和2次谐波分量以及小信号量的直流、基频、2次和3次谐波分量,截断后的三相SVG阻抗模型阶数为21。
以表1参数为例对阻抗模型定量分析,并对式(31)中MIMO阻抗模型测量,频率范围为1~1 000 Hz。为简化分析,忽略电网阻抗中的电阻。
理论计算与扫频结果如图5所示,通过数学计算得到的阻抗理论值与在仿真中测得的阻抗测量值高度吻合,所建模型的准确度得到验证。
表1 级联H桥SVG参数
Tab.1 Parameters of cascaded H-bridge SVG
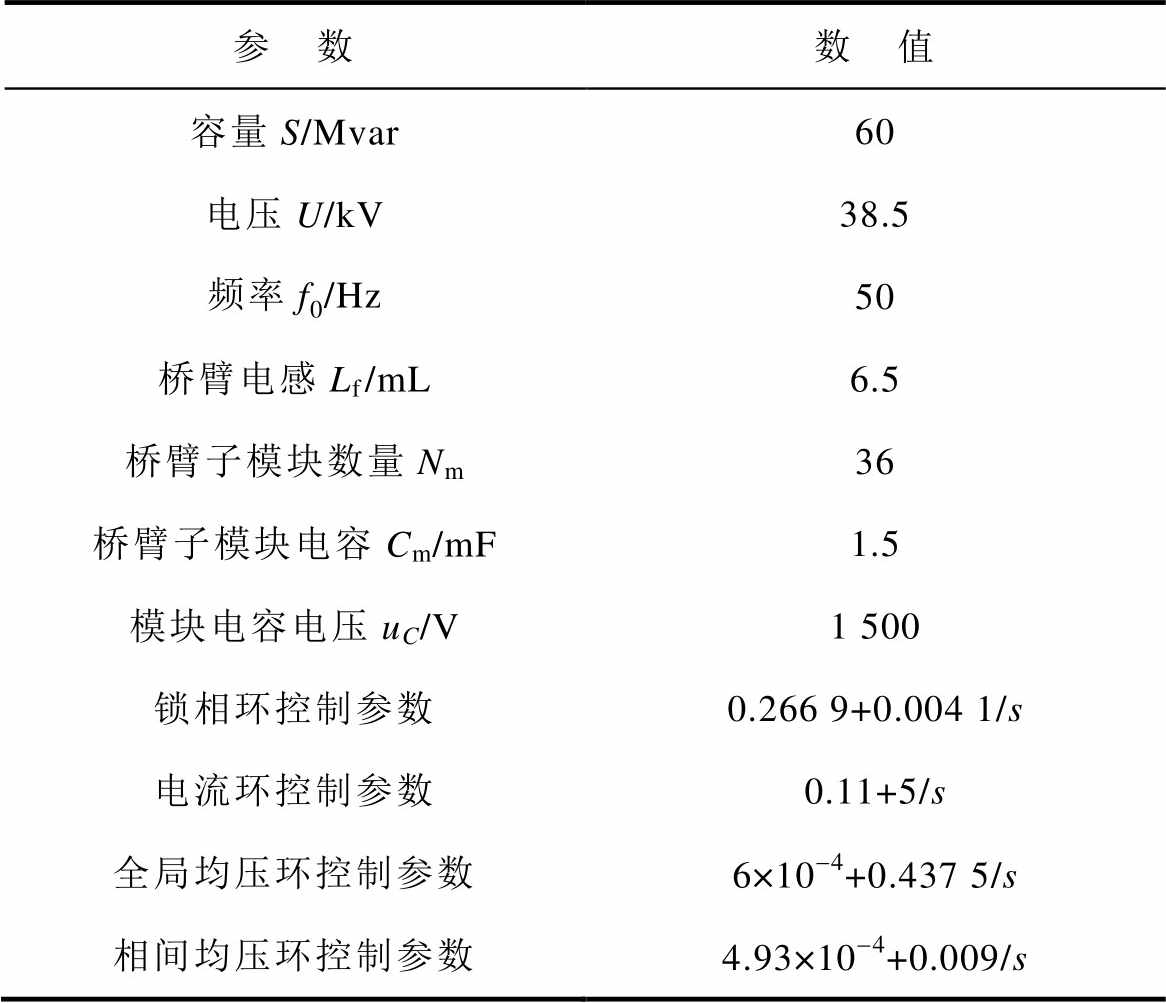
参 数数 值 容量S/Mvar60 电压U/kV38.5 频率f0/Hz50 桥臂电感Lf/mL6.5 桥臂子模块数量Nm36 桥臂子模块电容Cm/mF1.5 模块电容电压uC/V1 500 锁相环控制参数0.266 9+0.004 1/s 电流环控制参数0.11+5/s 全局均压环控制参数6×10-4+0.437 5/s 相间均压环控制参数4.93×10-4+0.009/s
级联H桥SVG的HSS阻抗模型呈现多输入多输出形式,且阶数较高。为了更方便和直观地分析振荡风险,可等效地将MIMO阻抗模型变换为SISO阻抗模型[31-32],降维前后系统参数恒定。
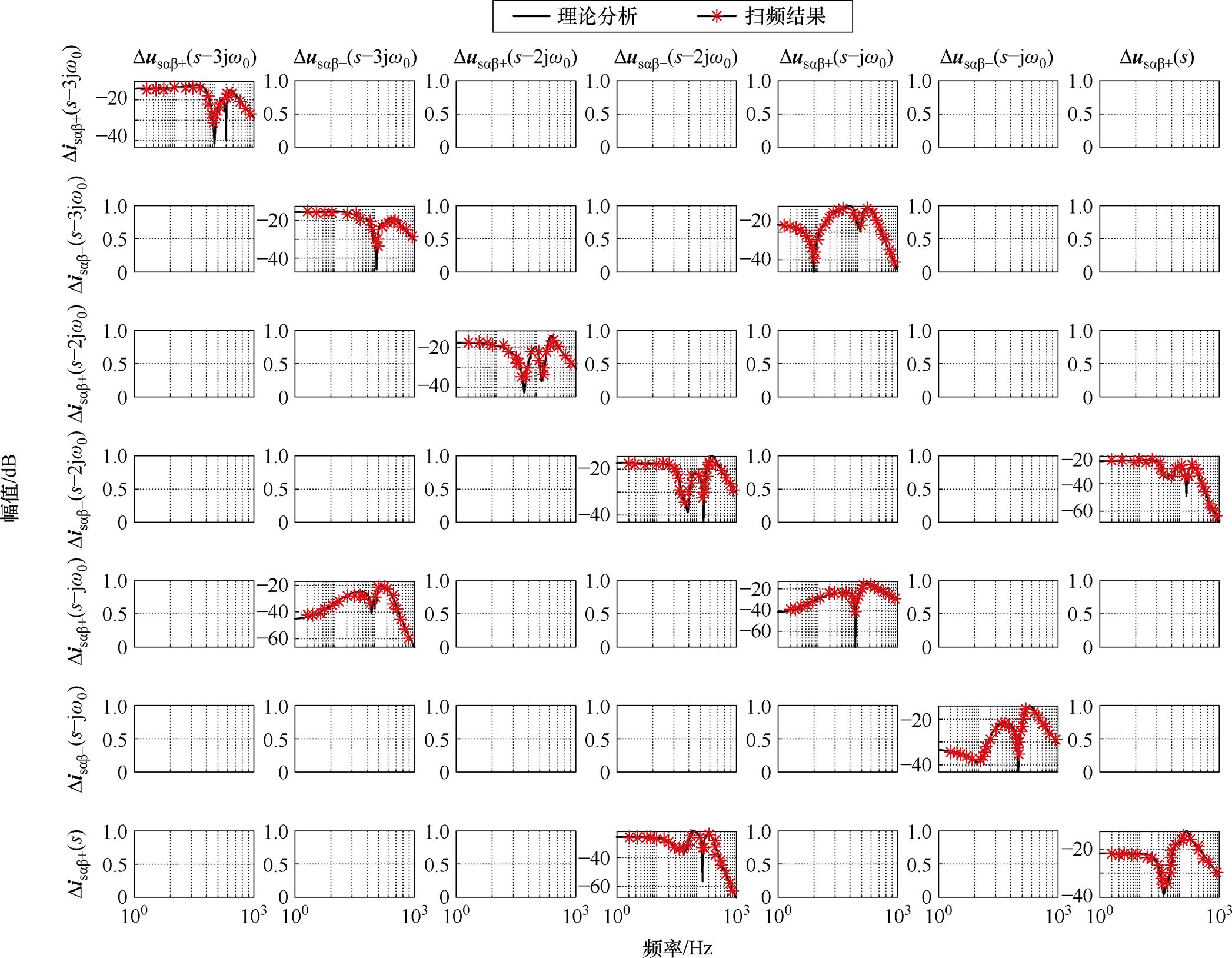
图5 HSS阻抗理论模型和仿真结果
Fig.5 Theoretical curves and simulation results of HSS impedance model
SVG并网系统的小信号模型如图6所示。
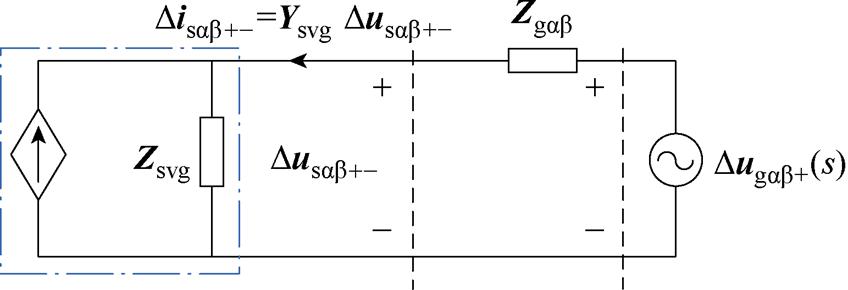
图6 小信号等效电路
Fig.6 Small-signal equivalent circuit
其中
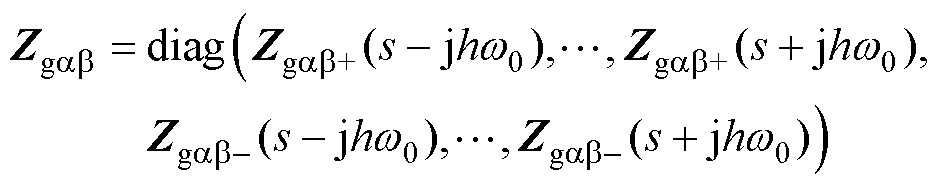 (34)
(34)
级联H桥SVG内部以及其与电网阻抗间的频率耦合关系如图7a所示,其等效示意图如图7b所示,有B=[O(1,3) 1 O(1,10)],C=BT,O为零矩阵。
由图7b获得Dugab+(s)与Disab+(s)之间的传递函数,计算过程见附录第3节。可得H桥SVG的SISO阻抗模型[17]为
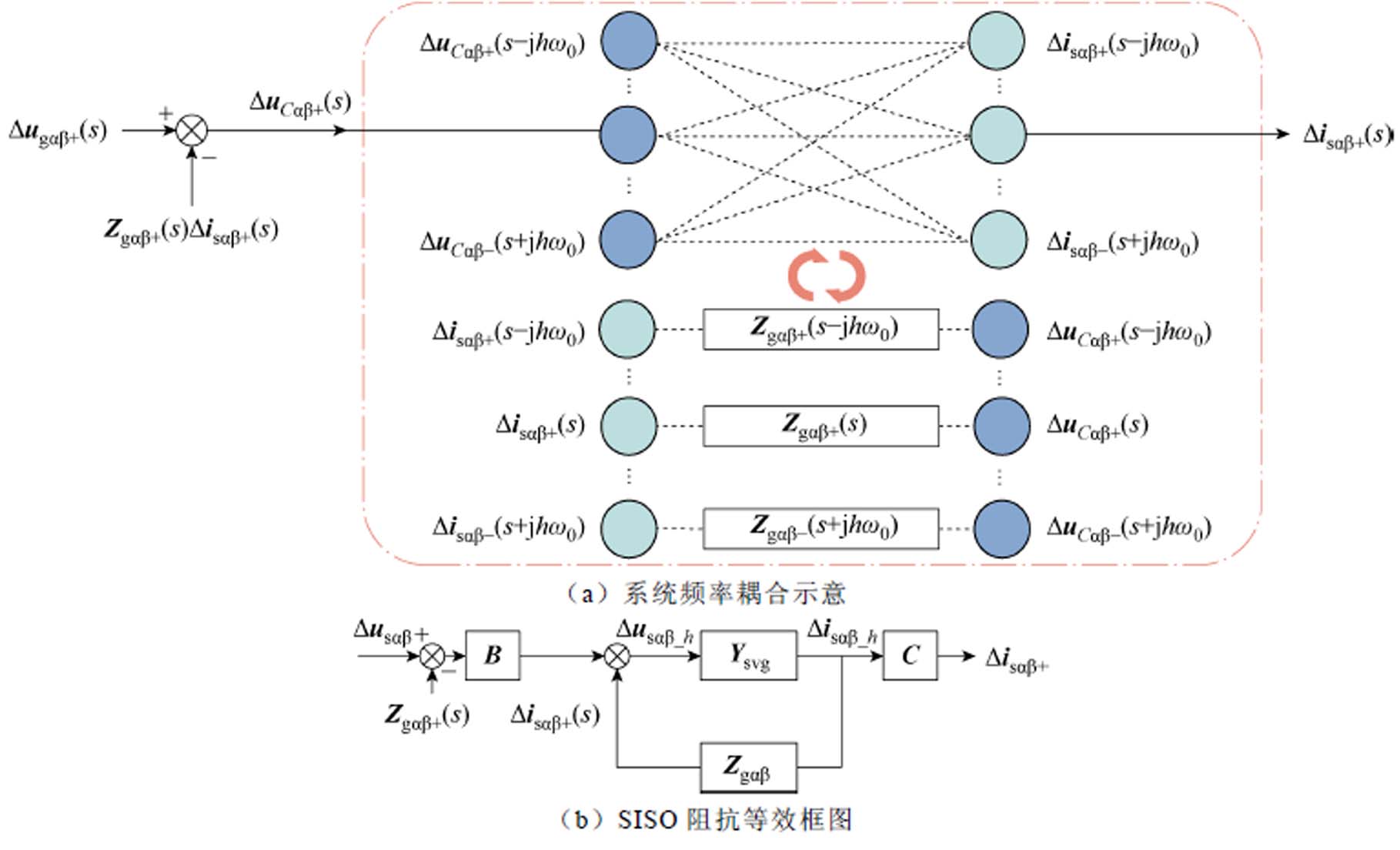
图7 考虑耦合的SISO阻抗
Fig.7 Diagram of SISO impedance with couplings
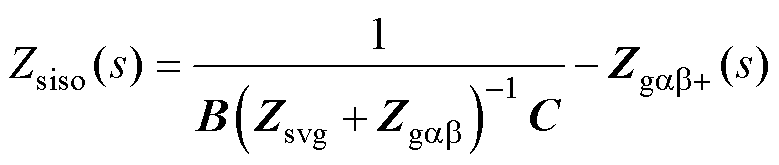 (35)
(35)
降维后的SISO阻抗模型包含MIMO阻抗矩阵中所有耦合关系,二者等价[17]。
值得注意的是,Zsiso(s)与Zp,p(s,s)并不相同,Zsiso(s)与Zp,p(s,s)的Bode图如图8所示。在中低频范围内,二者幅值和相位均有显著差异,因此简单地使用Zp,p(s,s)进行阻抗特性分析可能导致不准确的判断。
SVG的多个控制环路相互耦合,共同影响阻抗特性。本节基于阻抗模型分析SVG的振荡风险,确定影响阻抗特性的主导控制环,进而分析其对系统稳定性的影响。
图9对比考虑锁相环、相间均压环前后的阻抗特性。
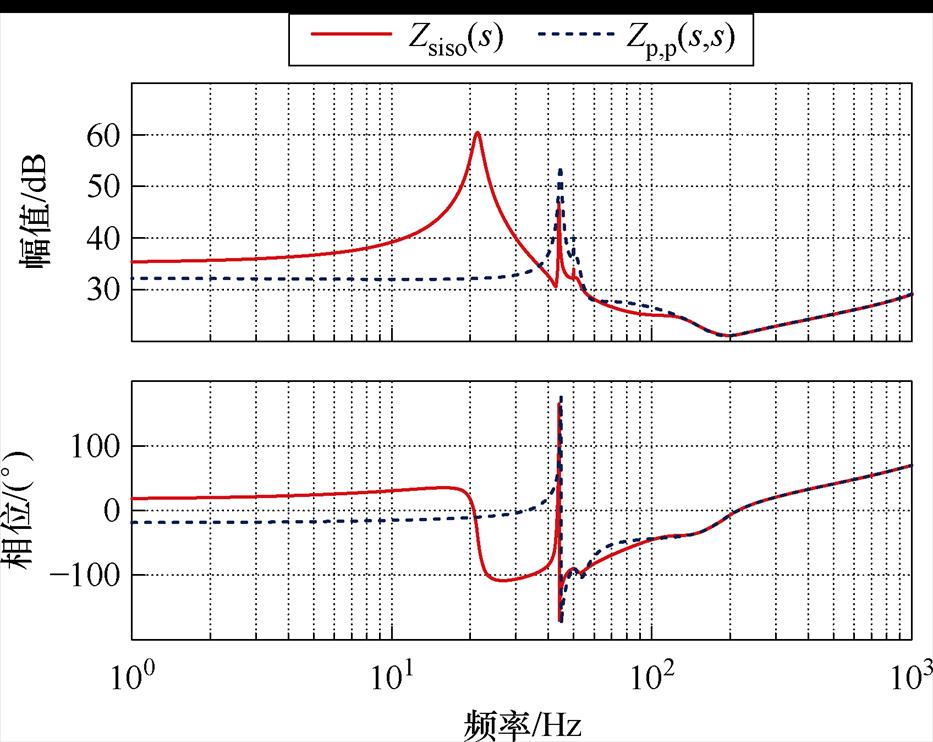
图8 Zsiso(s)与Zp,p(s,s)的Bode图
Fig.8 Bode diagrams of Zsiso(s) and Zp,p(s,s)
由图9可以看出,考虑锁相环前后,在150 Hz内系统阻抗具备明显差异,且锁相环是产生负阻区间和谐振峰的主要原因。考虑相间均压环前后对系统不产生显著影响,这是由于相间均压控制通常较慢,以避免与全局均压控制和电流控制产生冲突[28]。根据以上分析,锁相环是影响系统稳定性的主导控制环,有必要对其展开进一步研究。
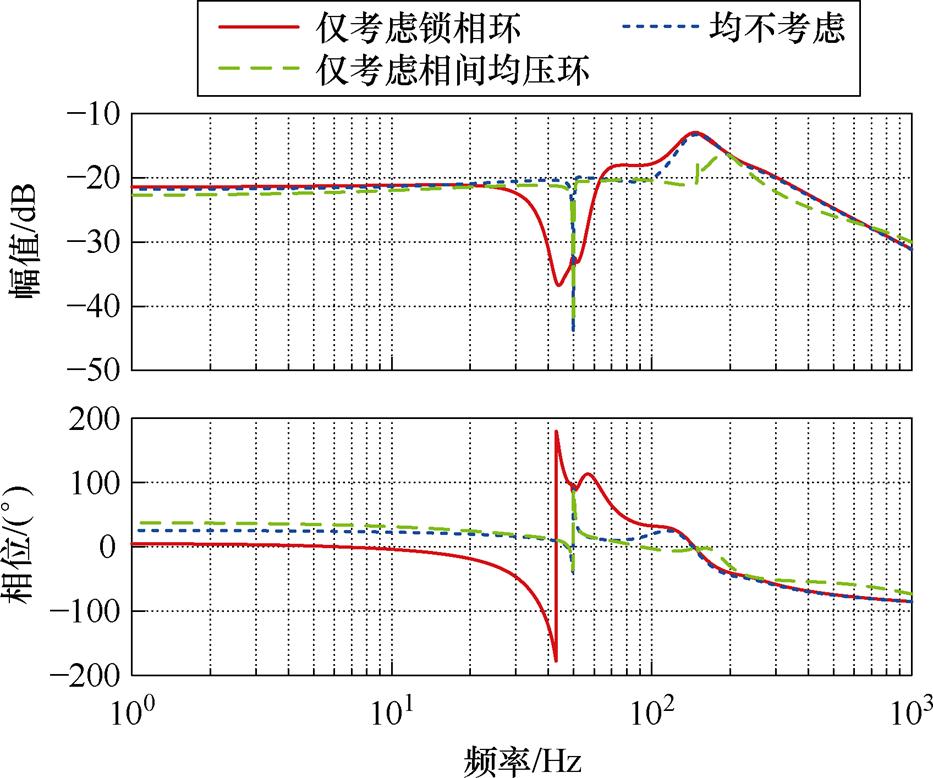
图9 不同控制环对SVG阻抗的影响
Fig.9 Impacts of different control loops on SVG impedance
为研究不同锁相环带宽对系统SISO阻抗的影响,改变锁相环带宽为10、20、30、80 Hz,对应的阻抗理论曲线如图10所示。
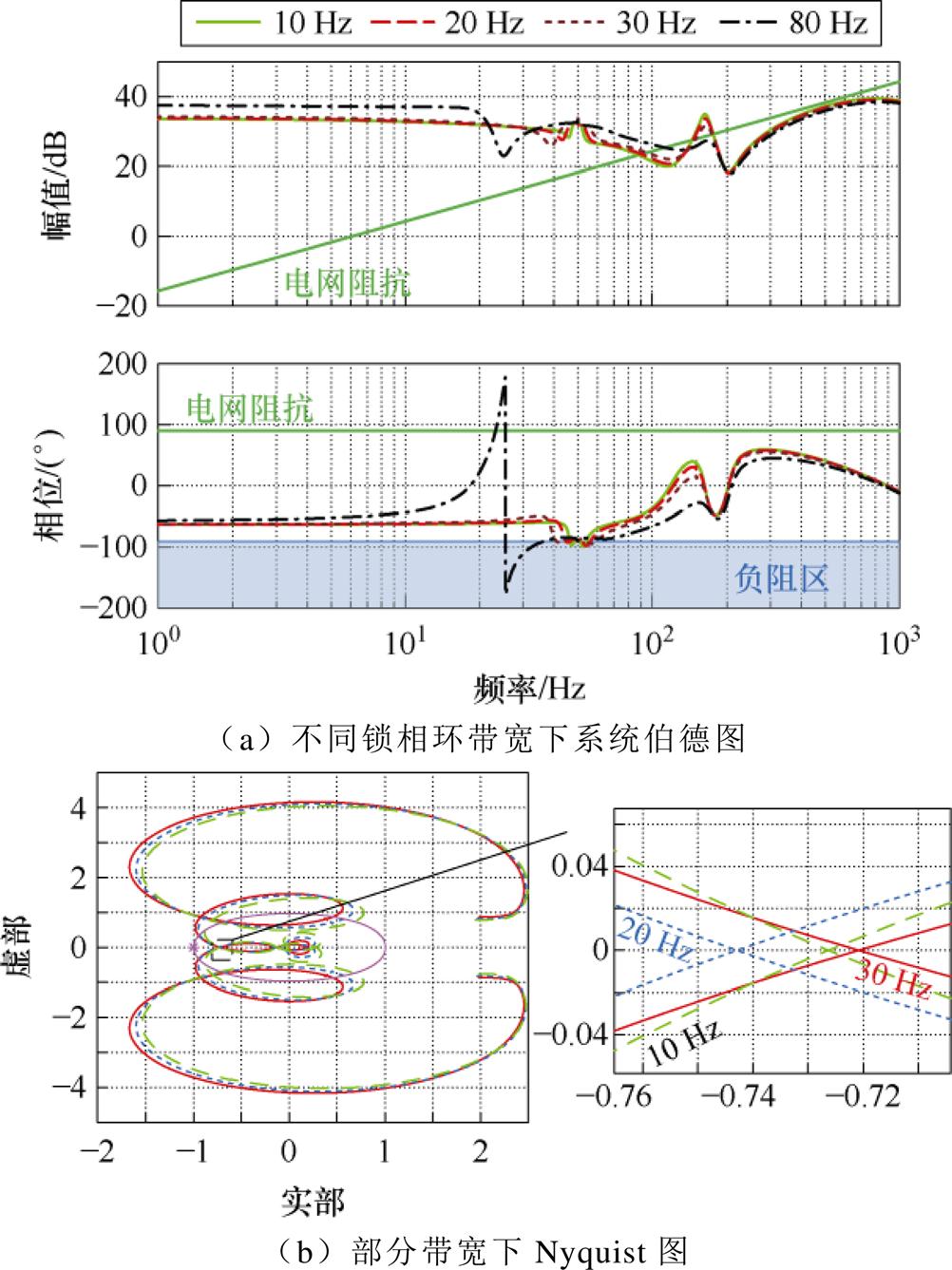
图10 不同锁相环带宽下系统稳定性分析
Fig.10 Stability analysis of impedance under different PLL bandwidths
设定全局均压环带宽为20 Hz,该值在带宽设计的合理范围内。同时,由控制器带宽设计规律,即遵循外环远小于内环带宽的原则以避免不同控制器交互作用,电流内环控制器与锁相环带宽差异较显著[21,27]。
由图10可知,锁相环带宽与引入负阻区间呈现非线性关系。由图10a,当锁相环带宽逐渐增大时,系统相位裕度减小,系统趋于不稳定。由图10b,锁相环带宽与全局均压环带宽相同时,二者易产生频率耦合,影响稳定性。
综上所述,锁相环带宽的选择应考虑两方面的因素:锁相环带宽与全局均压环带宽相同时,易发生耦合现象,系统趋于不稳定;锁相环带宽过大时,稳定裕度较小,系统也会趋于不稳定。
由第4节的机理分析可知,级联H桥SVG系统的系统稳定性由锁相环主导。因此在优化控制参数的基础上,还可以针对锁相环阻抗重塑提高系统稳定性。
级联H桥SVG系统控制器主要包括锁相环控制、电流环控制、全局均压环以及相间均压环控制。即
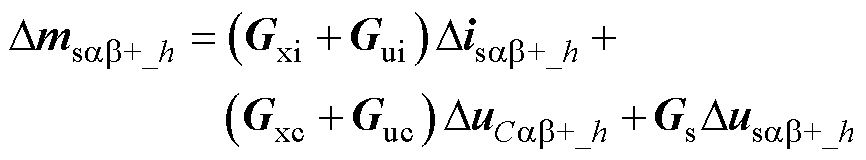 (36)
(36)
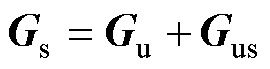 (37)
(37)
这里需引入电压前馈消除锁相环的影响,即消除式(36)的第三项。因此,分别加入Gf1、Gf2满足
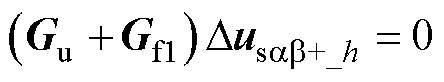 (38)
(38)
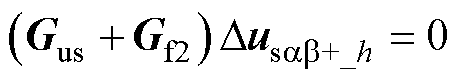 (39)
(39)
如此,锁相环引入的矩阵被电压前馈矩阵抵消,锁相环引入的负阻抗区间和耦合效应完全消除。这里以Gf1为例,假设Gf1为
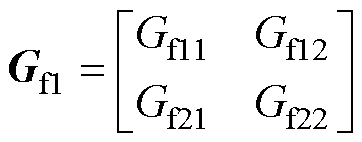 (40)
(40)
由于式(36)中其余项已知,可得Gf1的数值为
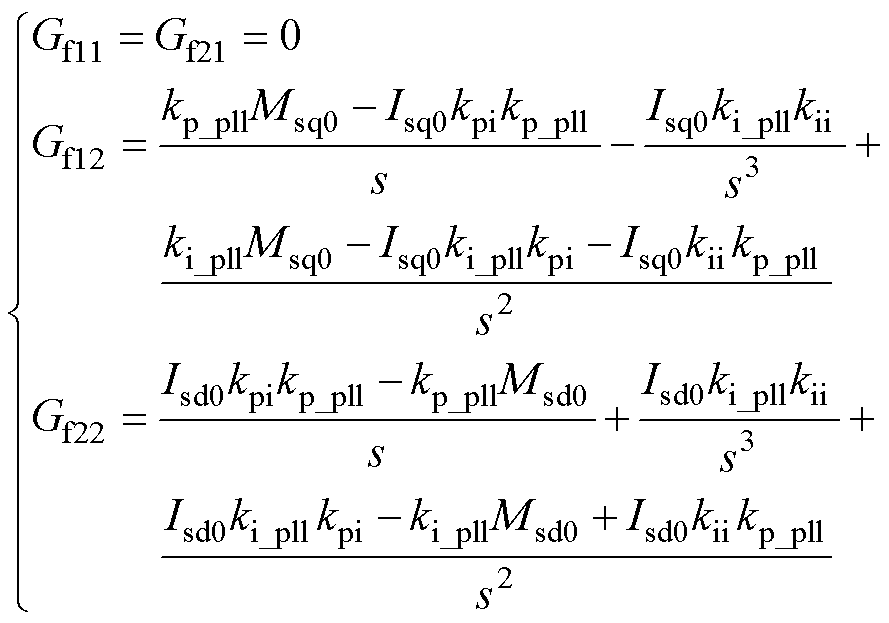 (41)
(41)
加入Gf1所示电压前馈后,静止坐标系下系统控制框图如图11所示。
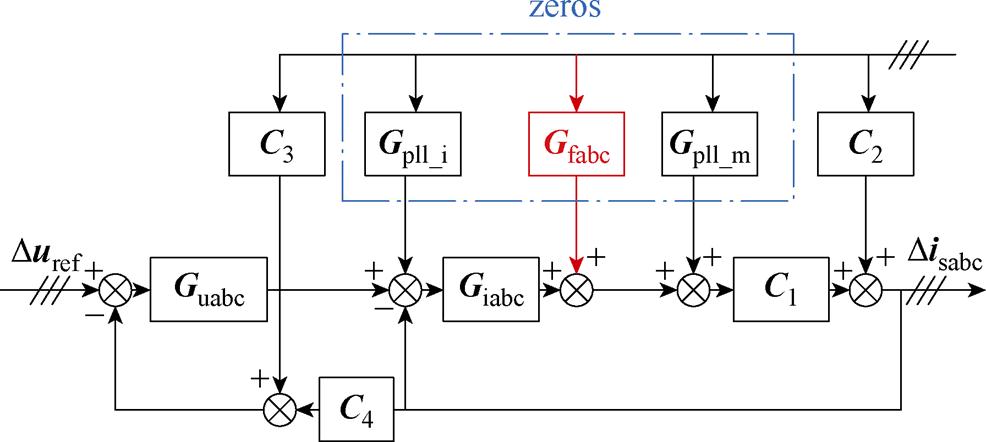
图11 加入电压前馈后SVG小信号控制框图
Fig.11 Small-signal control block diagram with voltage feedforward
图11中,Gpll_i、Gpll_m为锁相环引入矩阵,Giabc、Guabc分别为电流环与电压环的传递函数矩阵,Gfabc为电压前馈矩阵。矩阵C1、C2、C3、C4可通过图1所示主电路拓扑计算获得[7]。由控制框图11可知,通过引入电压前馈Gfabc抵消Gpll_i、Gpll_m,使得锁相环引入的影响完全消除。
然而,前馈系数中Gf12、Gf22均包含高次积分,在低频时相位滞后太多,极易造成系统发生不稳定振荡现象,因此有必要对其优化。在锁相环引入振荡风险的频率区间内,高次积分项影响较小,因此仅保留一次积分。此时前馈系数为
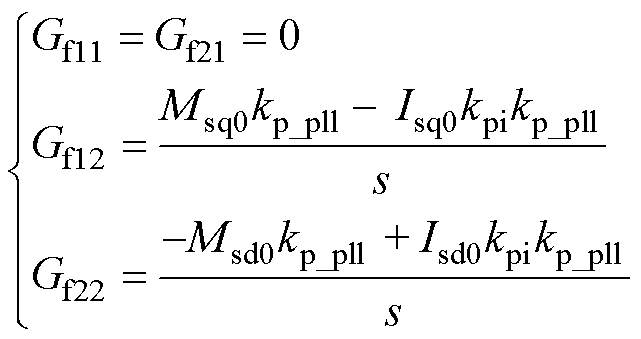 (42)
(42)
同理,前馈项Gf2的取值过程同式(38)~式(41),表示为
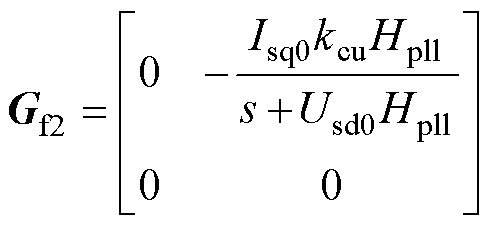 (43)
(43)
图12为分别考虑锁相环矩阵以及不同电压前馈控制的SISO阻抗Bode图。
对比Gs=Gs1、Gs=Gs3、Gs=Gs5三种前馈方式可知,接入Gf1和Gf2所示电压前馈时,其阻抗曲线与不考虑锁相环时的阻抗曲线完全重合,因此完全抵消了锁相环带来的影响,满足式(37)、式(38)所示关系,与理论分析结果一致。
对比Gs=Gs3、Gs=Gs4两种前馈方式,能够看出,考虑Gus前后阻抗曲线的变化较小,而阻抗模型的复杂程度却大幅提高。因此保留Gus,仅针对Gu采用电压前馈控制,从而消除其影响。
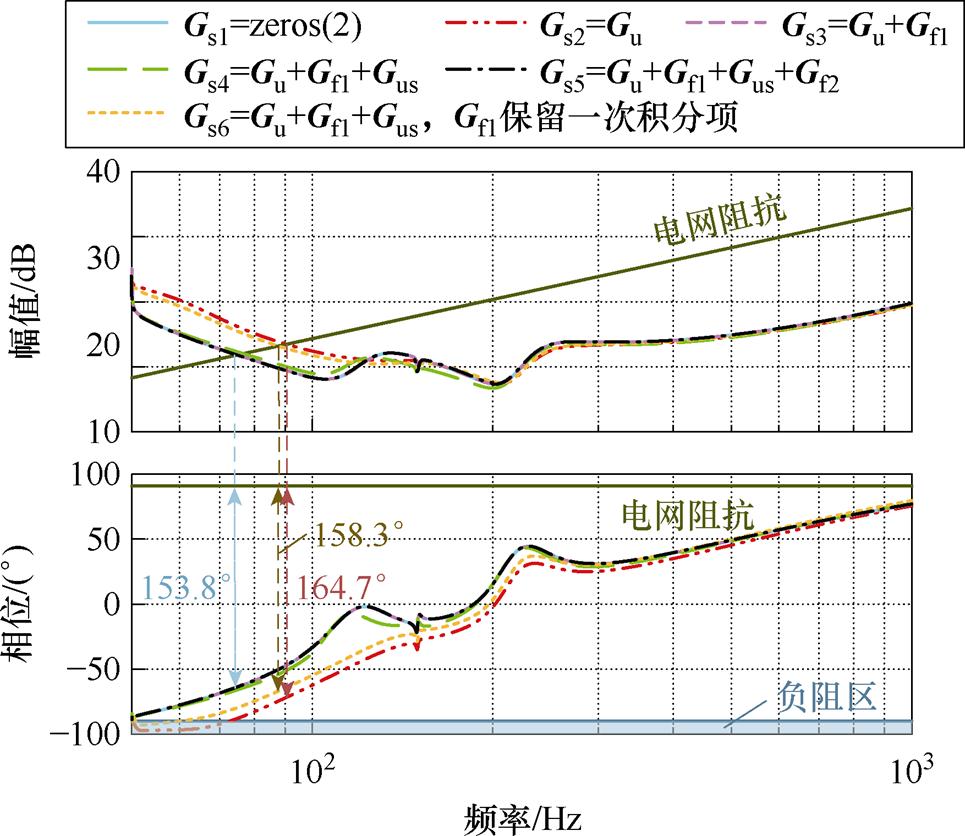
图12 不同电压前馈控制对系统阻抗的影响
Fig.12 Impacts of different voltage feedforward controls on system impedance
采用仅保留一次积分的前馈控制时,尽管不能完全消除Gu带来的影响,但也能显著减小锁相环引入的负阻区间,有效提升系统的稳定裕度。
改变系统SCR,绘制级联H桥SVG及电网阻抗Bode图,分析系统稳定性,如图13所示。可知,考虑抑制策略前后,阻抗相位差减小,系统稳定裕度提升,从而验证了该策略的鲁棒性。
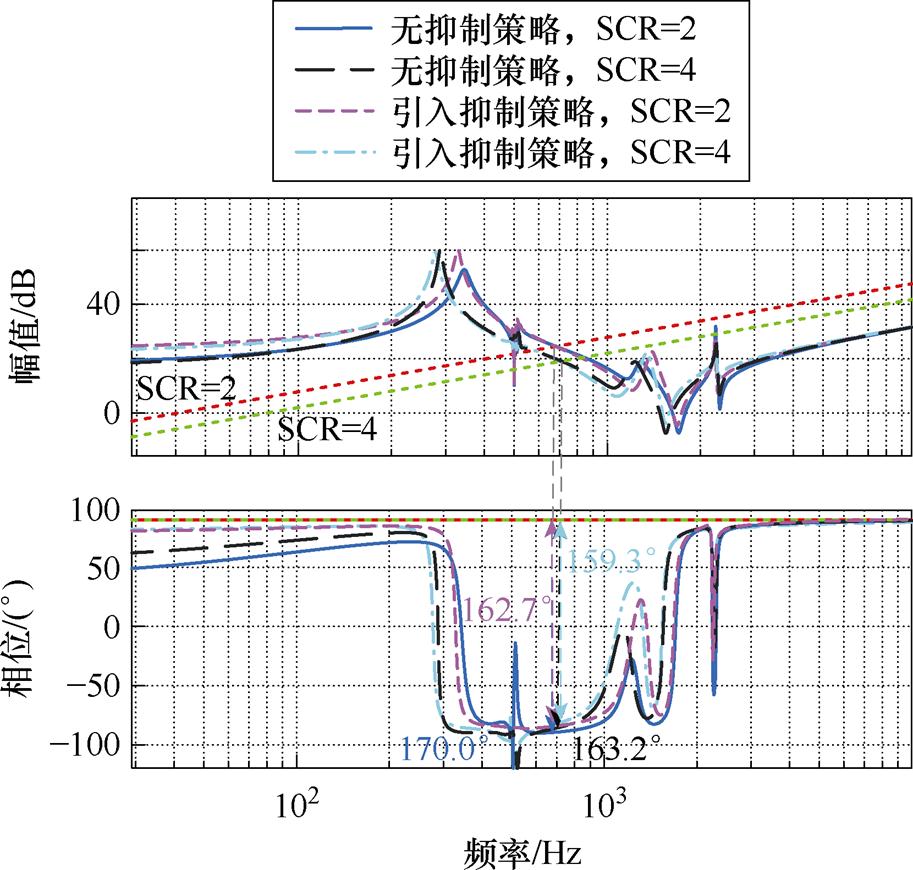
图13 不同SCR的阻抗Bode图
Fig.13 Bode diagrams under different SCR
本文基于RT-Lab实时数字仿真平台(OPAL- RT5600)和DSP(TMS320F28335)+FPGA(EP3C16)控制系统搭建实验平台,以验证提出策略有效性,RT-Lab实验平台如图14所示。实验中,算例参数见表1。系统中,级联H桥SVG、电缆以及所连接的电网由RT-Lab进行实时仿真,其仿真步长为20 ms。SVG的控制算法基于控制系统实现,其开关频率高于所设计带宽以及研究频率范围,因此不考虑开关频率导致的耦合。

图14 RT-Lab实验平台
Fig.14 RT-Lab experiment platform
初始时系统在额定功率稳定运行(SCR=3),3 s时增大锁相环带宽,系统发生振荡。t1时刻接入Gs5所示的电压前馈环节,实验结果如图15所示,系统振荡显著,无法达到抑制振荡的效果。
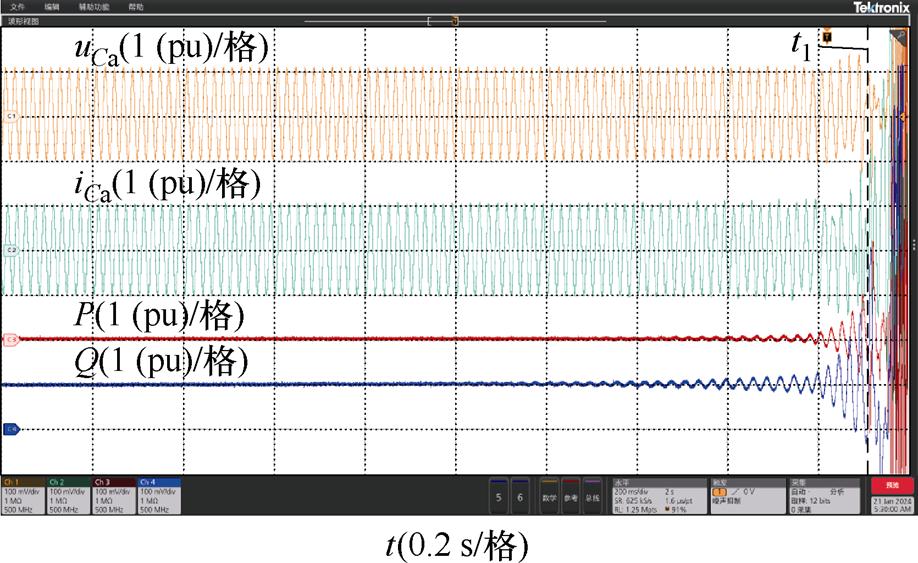
图15 接入前馈环节Gs5实验结果
Fig.15 Experimental results after SVG with Gs5 feedforward
在同样参数条件下,t1时刻接入Gs6所示的电压前馈环节,t2时刻改变SVG输出容量,实验结果如图16所示。图16a中,接入前馈后,系统趋于稳定,能够实现抑制振荡的效果。与图15对比可以看出,接入Gs6所示的电压前馈环节能够有效抑制振荡风险;图16b中,改变SVG输出容量时,系统能够快速跟踪响应并稳定运行,验证了该前馈策略的鲁棒性。因此,所提出的控制策略能够在输出容量发生变化时有效抑制振荡风险,改善系统稳定性问题。
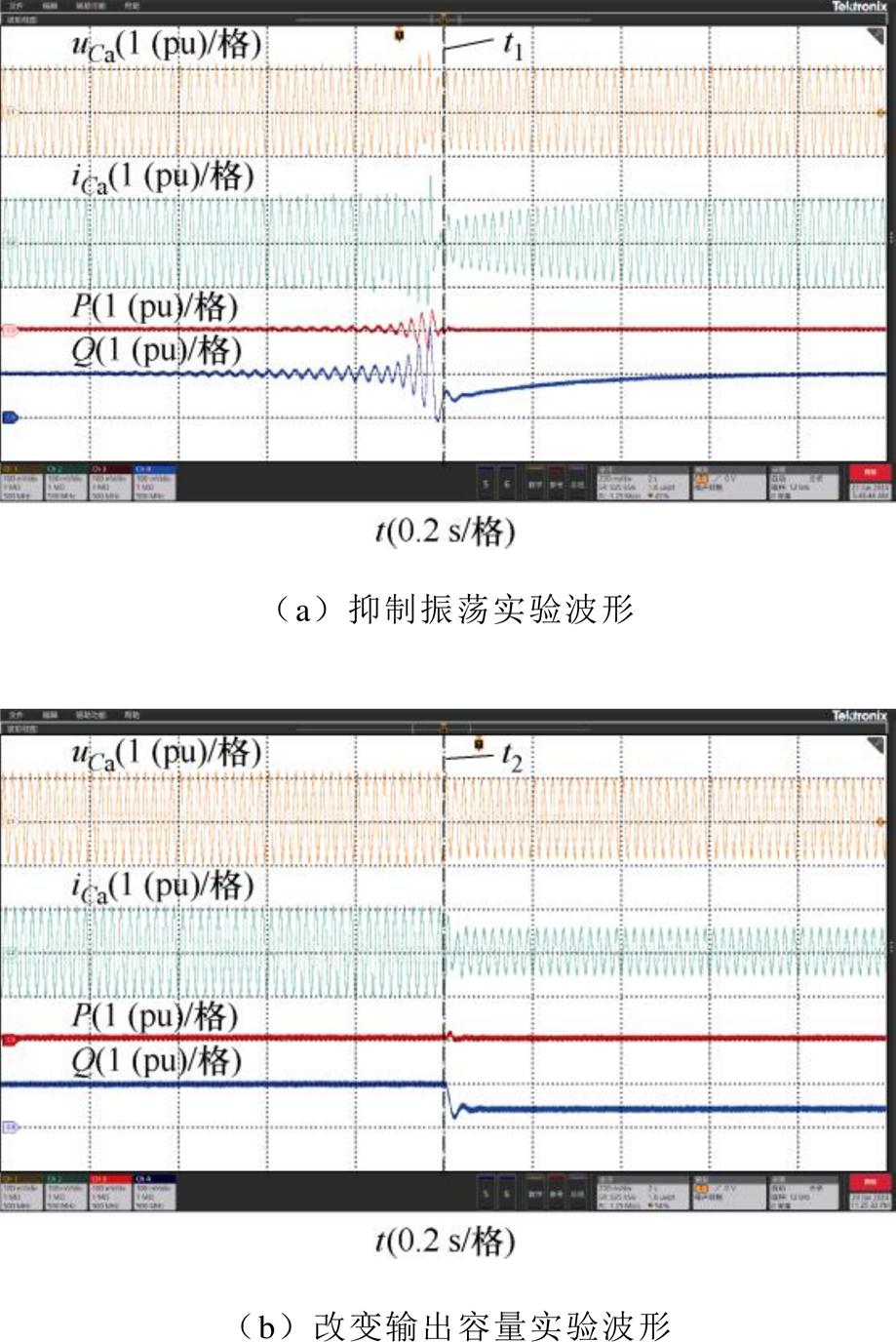
图16 接入前馈环节Gs6实验结果
Fig.16 Experimental results after SVG impedance with Gs6 feedforward
本文基于HSS建模方法建立级联H桥SVG的阻抗模型,针对开关频率以下的低频段,分析其内部向量的动态并揭示系统频率耦合机理。针对等效降维所得的SISO阻抗模型,分析控制环对系统振荡风险的影响,并针对主导控制环即锁相环提出基于电压前馈控制的阻抗重塑控制策略,从而降低系统振荡风险,提高系统的稳定性。得到结论如下:
1)基于所建立的考虑多频率耦合级联H桥SVG的HSS阻抗模型并分析可得,锁相环及其控制参数对系统振荡风险具备显著影响,而相间均压环及其控制参数影响较小。
2)锁相环带宽设计需考虑两方面因素,锁相环带宽过大会导致稳定裕度减小、锁相环带宽与全局均压环带宽相同时,易发生耦合现象,从而引入振荡风险。
3)针对主导控制环即锁相环引发的振荡风险问题,基于理论模型,提出一种基于电压前馈的阻抗重塑控制策略,能够有效减小锁相环导致的负阻区间,从而提高系统稳定性。
附 录
1.Aabc和Babc的具体形式为
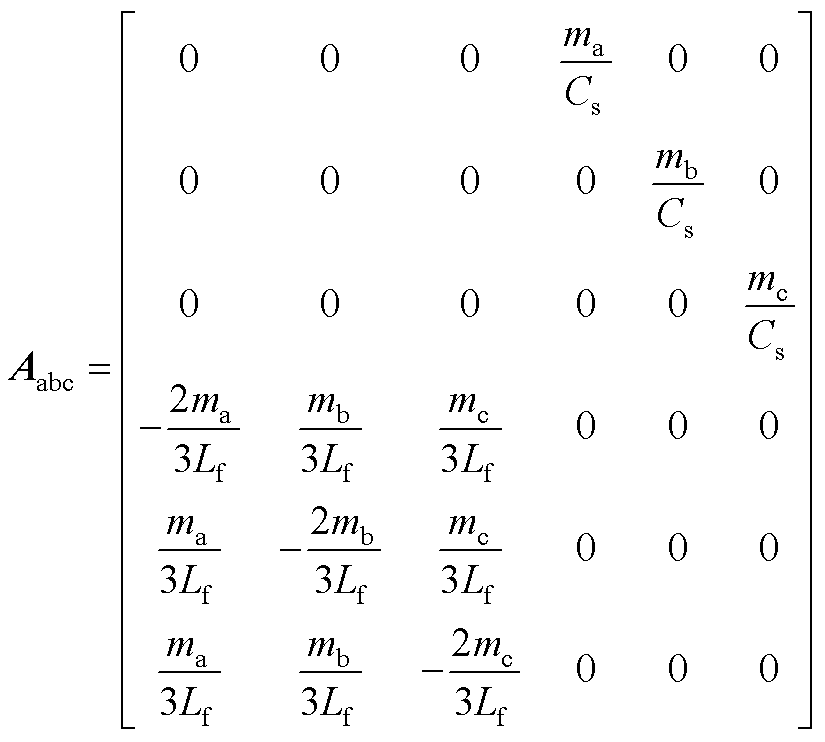 (A1)
(A1)
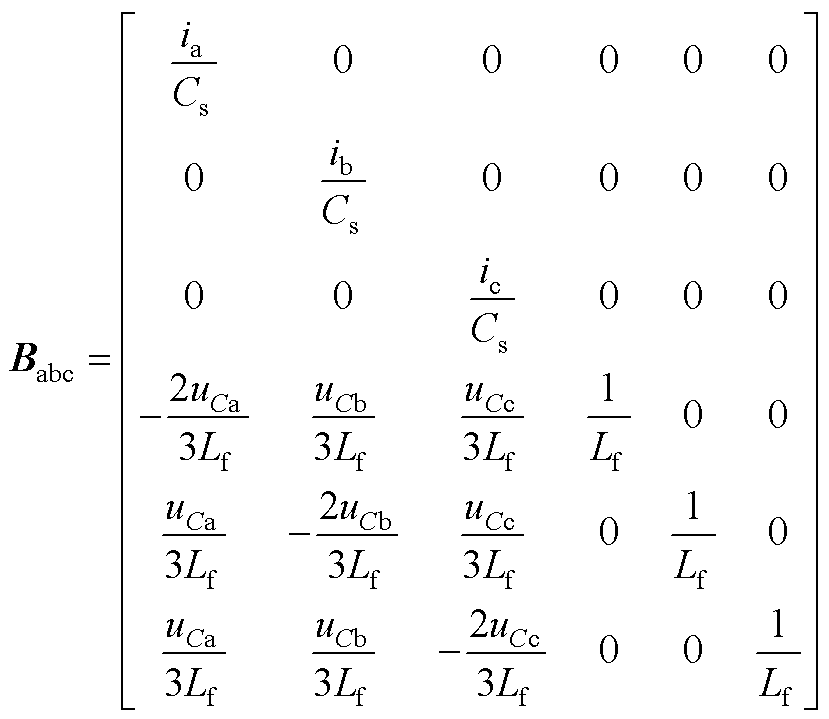 (A2)
(A2)
2.Toeplitz矩阵具体形式为
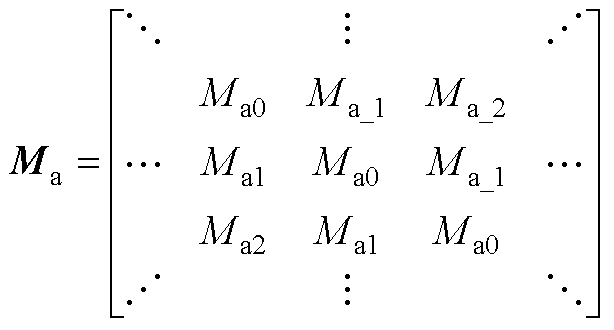 (A3)
(A3)
式中,稳态量下标“0、_1、1”分别代表0、-1、1次傅里叶系数,其余下标同理。
状态变量HSS展开后具体形式为
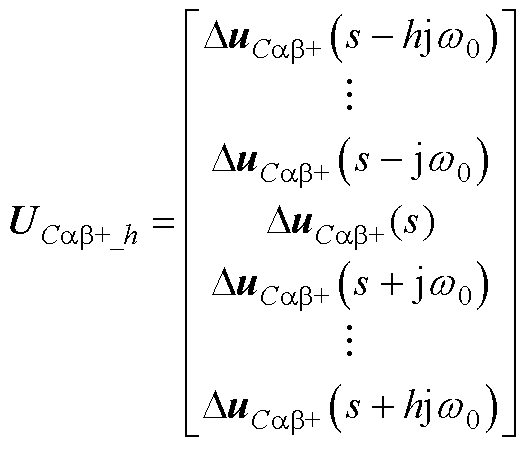 (A4)
(A4)
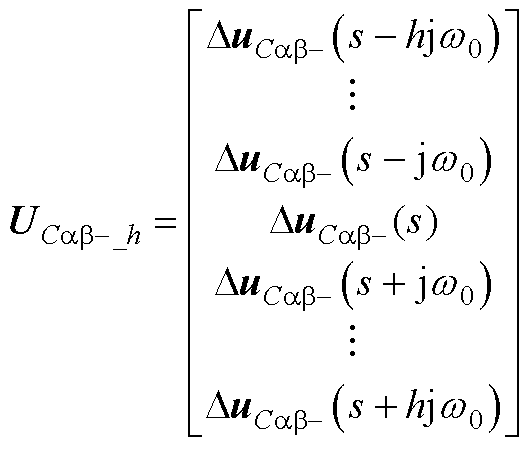 (A5)
(A5)
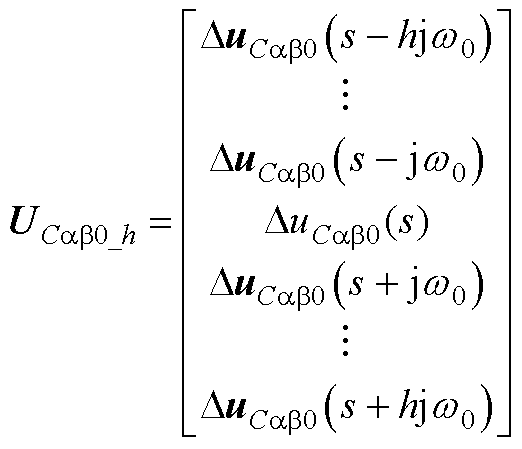 (A6)
(A6)
下标相同的Disab_h、Dmsab_h、Dusab_h同理。
3. Disab+到Dugab+的传递函数表示为
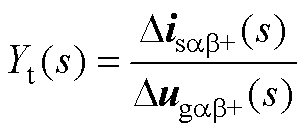 (A7)
(A7)
同理,将SVG和电网视为一个闭环系统,而不是受独立源扰动的子系统。根据图6所示,得
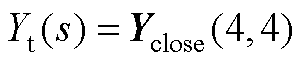 (A8)
(A8)
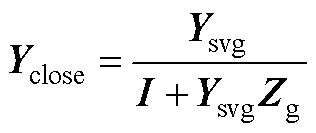 (A9)
(A9)
从Disab+到Dusab+的传递函数为
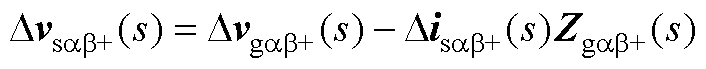 (A10)
(A10)
式(A10)两侧同时除以Diab+,等效SISO阻抗为
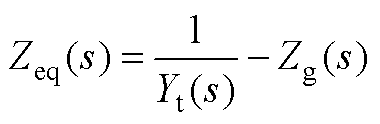 (A11)
(A11)
参考文献
[1] 王兆安,杨君,刘进军,等. 谐波抑制和无功功率补偿[M]. 2版. 北京: 机械工业出版社,2006.
[2] 张旸,沈梦娇,陈新,等. 基于双谐波线性化的级联H桥静止无功发生装置序阻抗建模与分析[J]. 电工技术学报,2019,34(20): 4334-4346.
Zhang Yang,Shen Mengjiao,Chen Xin,et al. Sequence impedance modeling and analysis of cascaded H-bridge static var generator based on double-harmonic linearization[J]. Transactions of China Electrotechnical Society,2019,34(20): 4334- 4346.
[3] 陈鸿琳,熊馨瑶,余浩,等. SVG对海上风电交流并网系统稳定性影响分析[J]. 电力系统保护与控制,2022,50(19): 119-129.
Chen Honglin,Xiong Xinyao,Yu Hao,et al. Analysis on the influence of an SVG on the stability of AC grid-connected offshore wind farms[J]. Power System Protection and Control,2022,50(19): 119-129.
[4] 杨铭,曹武,赵剑锋,等. 受控电压/电流源型变流器混合多机暂态电压支撑策略[J]. 电工技术学报,2023,38(19): 5207-5223,5240.
Yang Ming,Cao Wu,Zhao Jianfeng,et al. Transient voltage support strategy for hybrid multi-converter of controlled voltage/current source converter[J]. Transa- ctions of China Electrotechnical Society,2023,38(19): 5207-5223,5240.
[5] Akagi H. Classification,terminology,and application of the modular multilevel cascade converter (MMCC)[J]. IEEE Transactions on Power Electronics,2011,26(11): 3119-3130.
[6] 单庆晓,李永东,潘孟春. 级联型逆变器的新进展[J]. 电工技术学报,2004,19(2): 1-9.
Shan Qingxiao,Li Yongdong,Pan Mengchun. A review on cascaded inverter[J]. Transactions of China Electrotechnical Society,2004,19(2): 1-9.
[7] 熊小玲,罗博晨,刘京波,等. 计及SVG的双馈风电场高频阻抗建模及振荡分析[J]. 电网技术,2023,47(7): 2905-2917.
Xiong Xiaoling,Luo Bochen,Liu Jingbo,et al. High frequency impedance modeling and oscillation analysis of DFIG-based station considering SVG[J]. Power System Technology,2023,47(7): 2905-2917.
[8] 张前进,周林,李海啸,等. 考虑SVG补偿装置的大型光伏并网系统振荡分析与抑制[J]. 中国电机工程学报,2019,39(9): 2636-2644.
Zhang Qianjin,Zhou Lin,Li Haixiao,et al. Oscillation analysis and suppression of large-scale grid-connected photovoltaic system considering SVG equipment[J]. Proceedings of the CSEE,2019,39(9): 2636-2644.
[9] 于雁南,杨荣峰,严继池,等. 级联H桥静止无功发生器的多变量自抗扰解耦控制[J]. 中国电机工程学报,2016,36(8): 2233-2241.
Yu Yannan,Yang Rongfeng,Yan Jichi,et al. Multiple-input multiple-output decoupling control schemes of static var generator with cascaded H- bridge based on active disturbance rejection control[J]. Proceedings of the CSEE,2016,36(8): 2233-2241.
[10] Bergna-Diaz G,Freytes J,Guillaud X,et al. Generalized voltage-based state-space modeling of modular multilevel converters with constant equili- brium in steady state[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics,2018,6(2): 707-725.
[11] 年珩,朱茂玮,徐韵扬,等. 基于谐波传递矩阵的MMC换流站频率耦合特性建模与分析[J]. 电力系统自动化,2020,44(6): 75-83.
Nian Heng,Zhu Maowei,Xu Yunyang,et al. Modeling and analysis of frequency coupling characteristic for MMC station based on harmonic transfer matrices[J]. Automation of Electric Power Systems,2020,44(6): 75-83.
[12] 刘欣,郭志博,贾焦心,等. 基于序阻抗的虚拟同步发电机并网稳定性分析及虚拟阻抗设计[J]. 电工技术学报,2023,38(15): 4130-4146.
Liu Xin,Guo Zhibo,Jia Jiaoxin,et al. Stability analysis and virtual impedance design of virtual synchronous machine based on sequence impe- dance[J]. Transactions of China Electrotechnical Society,2023,38(15): 4130-4146.
[13] 高本锋,沈雨思,宋瑞华,等. 虚拟同步机控制模块化多电平变流器阻抗建模及次/超同步振荡稳定性分析[J]. 电工技术学报,2025,40(2): 559-573.
Gao Benfeng,Shen Yusi,Song Ruihua,et al. Impedance modeling and sub/super synchronous oscillation stability analysis of modular multilevel converter under virtual synchronous generator control[J]. Transactions of China Electrotechnical Society,2025,40(2): 559-573.
[14] 宗皓翔,张琛,吕敬,等. MMC多入多出阻抗及其在不对称小扰动稳定分析中的应用[J]. 中国电机工程学报,2022,42(15): 5649-5664.
Zong Haoxiang,Zhang Chen,Lü Jing,et al. MMC MIMO impedance and its application in the asymmetric small-signal stability analysis[J]. Pro- ceedings of the CSEE,2022,42(15): 5649-5664.
[15] Zhang Chen,Molinas M,Føyen S,et al. Harmonic- domain SISO equivalent impedance modeling and stability analysis of a single-phase grid-connected VSC[J]. IEEE Transactions on Power Electronics,2020,35(9): 9770-9783.
[16] Wu Heng,Wang Xiongfei,Kocewiak Ł H. Impedance- based stability analysis of voltage-controlled MMCs feeding linear AC systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics,2020,8(4): 4060-4074.
[17] Wu Heng,Wang Xiongfei. Dynamic impact of zero-sequence circulating current on modular multilevel converters: complex-valued AC impedance modeling and analysis[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics,2020,8(2): 1947-1963.
[18] 王杨,夏菲,田旭,等. 基于谐波状态空间的高压直流输电系统SISO阻抗建模及稳定性分析[J]. 中国电机工程学报,2024,44(5): 1985-1999.
Wang Yang,Xia Fei,Tian Xu,et al. SISO impedance modeling and stability analysis of HVDC system based on harmonic state space[J]. Proceedings of the CSEE,2024,44(5): 1985-1999.
[19] 张旸,孙龙庭,陈新,等. 集成静止无功发生装置的直驱风场序阻抗网络模型与稳定性分析[J]. 中国电机工程学报,2020,40(9): 2877-2891.
Zhang Yang,Sun Longting,Chen Xin,et al. Sequence impedance network model and stability analysis for direct-drive wind farm with static var generator[J]. Proceedings of the CSEE,2020,40(9): 2877-2891.
[20] 任必兴,杜文娟,王海风. 静止同步补偿器与直驱永磁风机的次同步控制交互研究[J]. 电工技术学报,2018,33(24): 5884-5896.
Ren Bixing,Du Wenjuan,Wang Haifeng. Analysis on sub-synchronous control interaction between static synchronous compensator and permanent magnet synchronous generator[J]. Transactions of China Electrotechnical Society,2018,33(24): 5884-5896.
[21] 周佩朋,李光范,宋瑞华,等. 直驱风机与静止无功发生器的次同步振荡特性及交互作用分析[J]. 中国电机工程学报,2018,38(15): 4369-4378,4637.
Zhou Peipeng,Li Guangfan,Song Ruihua,et al. Subsynchronous oscillation characteristics and intera- ctions of direct drive permanent magnet synchronous generator and static var generator[J]. Proceedings of the CSEE,2018,38(15): 4369-4378,4637.
[22] 胡鹏,艾欣,肖仕武,等. 静止无功发生器序阻抗建模及对次同步振荡影响因素的分析[J]. 电工技术学报,2020,35(17): 3703-3713.
Hu Peng,Ai Xin,Xiao Shiwu,et al. Sequence impedance of static var generator and\r analysis of influencing factors on subsynchronous oscillation[J]. Transactions of China Electrotechnical Society,2020,35(17): 3703-3713.
[23] Zhang Yang,Yang Yongheng,Chen Xin,et al. Intelligent parameter design-based impedance opti- mization of STATCOM to mitigate resonance in wind farms[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics,2021,9(3): 3201-3215.
[24] 邢纪奎,袁辉,代江,等. 抑制新能源次/超同步振荡的SVG鲁棒自适应控制参数设计方法[J]. 电力自动化设备,2024,44(8): 160-167.
Xing Jikui,Yuan Hui,Dai Jiang,et al. Design method of robust adaptive control parameter of SVG to suppress sub/sup-synchronous oscillation caused by new energy[J]. Electric Power Automation Equipment,2024,44(8): 160-167.
[25] 陈继开,郝鑫,常旗峰,等. 考虑SVG控制模式的风电场系统中频谐振分析与抑制[J]. 电力自动化设备,2023,43(9): 39-46.
Chen Jikai,Hao Xin,Chang Qifeng,et al. Analysis and suppression of medium frequency resonance of wind farm system considering SVG control modes[J]. Electric Power Automation Equipment,2023,43(9): 39-46.
[26] 张东辉,陈新,杨舒婷,等. 含静止无功补偿装置的光伏电站高频谐振分析及抑制策略研究[J]. 中国电机工程学报,2023,43(24): 9580-9594.
Zhang Donghui,Chen Xin,Yang Shuting,et al. Analysis of high-frequency resonance and suppression strategy of photovoltaic power plant with static reactive power compensation device[J]. Proceedings of the CSEE,2023,43(24): 9580-9594.
[27] Zhang Yang,Chen Xin,Sun Jian. Sequence impe- dance modeling and analysis of MMC in single-star configuration[J]. IEEE Transactions on Power Elec- tronics,2020,35(1): 334-346.
[28] Akagi H,Inoue S,Yoshii T. Control and performance of a transformerless cascade PWM STATCOM with star configuration[J]. IEEE Transactions on Industry Applications,2007,43(4): 1041-1049.
[29] Sun Jian,Liu Hanchao. Sequence impedance modeling of modular multilevel converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics,2017,5(4): 1427-1443.
[30] Wen Bo,Boroyevich D,Burgos R,et al. Analysis of D-Q small-signal impedance of grid-tied inverters[J]. IEEE Transactions on Power Electronics,2016,31(1): 675-687.
[31] Zhang Chen,Cai Xu,Rygg A,et al. Sequence domain SISO equivalent models of a grid-tied voltage source converter system for small-signal stability analysis[J]. IEEE Transactions on Energy Conversion,2018,33(2): 741-749.
[32] 王震,程鹏,贾利民. 基于对称控制的三相并网变流器单输入单输出阻抗建模与分析[J]. 电工技术学报,2024,39(6): 1777-1791.
Wang Zhen,Cheng Peng,Jia Limin. Single-input single-output impedance modeling and analysis of three-phase grid-tied converter based on symmetric control[J]. Transactions of China Electrotechnical Society,2024,39(6): 1777-1791.
Analysis of Static Var Generator Considering the Impacts of Internal Dynamics and Frequency Coupling
Abstract Due to its compensation capabilities and fast dynamic response times,the cascaded H-bridge static var generator (SVG) has become widely adopted for enhancing power quality and providing reactive power in modern power systems. However,as a power electronic device predominantly governed by control-driven dynamics,the SVG faces the risk of oscillations. In addition,the mechanisms of wideband oscillations in SVG systems remain insufficiently understood,and effective stability enhancement techniques are lacking.
This paper analyzes the cascaded H-bridge SVG's nonlinear and strongly coupled internal dynamic characteristics. Focusing on the low-frequency range below the switching frequency,a harmonic state-space (HSS) complex vector impedance model is developed,incorporating the influence of multiple control loops. A detailed time-domain model is constructed to simulate the system's behavior,and frequency scanning is conducted using Matlab/Simulink. Furthermore,considering the system's frequency coupling relationships,the dynamic interactions of internal currents,output voltages,and three-phase capacitor voltages and their coupling grid impedance are examined. Accordingly,an equivalent single-input single-output impedance model is constructed. A stability analysis of the SVG is performed to evaluate the impact of various control loops and their associated parameters on system stability.
The phase-locked loop (PLL) is critical in determining system stability. Consequently,a quantitative analysis of the PLL parameters is conducted for parameter design and optimization. In contrast,the inter-phase voltage balancing loop has a minor influence on system stability. This paper proposes a voltage feedforward impedance reshaping strategy to mitigate the stability challenges associated with SVG grid integration. This approach targets the oscillations introduced by the dominant control loop (the PLL),which can offset its impact. However,since this method involves high-order integration,it is prone to causing system instability. Therefore,an optimized control strategy is proposed,effectively reducing the negative resistance region caused by the PLL,thereby enhancing the overall stability of the grid-connected system. A hardware-in-the-loop experiment is implemented using the RT-LAB platform. The experimental results verify the effectiveness of the proposed methods in improving system stability.
The key conclusions of this study are as follows. (1) The PLL and its control parameters significantly influence the system's oscillation risk based on the developed HSS impedance model for multi-frequency coupling in the cascaded H-bridge SVG. In contrast,the inter-phase voltage balancing loop and its control parameters exhibit a negligible impact. (2) The design of the PLL bandwidth needs to consider two critical factors: a considerable PLL bandwidth that reduces stability margins and a PLL bandwidth that aligns with the global voltage balancing loop bandwidth. As a result,additional oscillations from coupling are introduced. (3) A voltage feedforward-based impedance-shaping control strategy is proposed. This strategy mitigates the negative resistance region caused by the PLL,significantly improving the stability of the SVG system. This paper provides measures for the design and optimization of SVG systems.
Keywords:Static var generator (SVG),harmonic state space,frequency coupling,stability analysis,impedance reshaping
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.242145
国家自然科学基金资助项目(52277176)。
收稿日期 2024-11-29
改稿日期 2025-02-16
李龙灿 女,2000年生,硕士研究生,研究方向为电力系统稳定性分析。
E-mail: longcanlee@126.com
熊小玲 女,1984年生,副教授,博士生导师,研究方向为电力电子化电力系统的建模与稳定性、先进高压直流输电技术等。
E-mail: xiongxl1102@ncepu.edu.cn(通信作者)
(编辑 陈 诚)