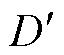 =D与载波相位依次相差Tsw/3的PS-PWM比较生成,在输出节点sw处产生幅值差为Vdc/6的四电平波形。调制信号D<0时,对应图2中T/2~T区间,S1、S3保持关断,S2、S4保持开通状态,飞跨电容多电平级调制信号为
=D与载波相位依次相差Tsw/3的PS-PWM比较生成,在输出节点sw处产生幅值差为Vdc/6的四电平波形。调制信号D<0时,对应图2中T/2~T区间,S1、S3保持关断,S2、S4保持开通状态,飞跨电容多电平级调制信号为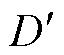 = 1+D,经PS-PWM生成SA、SB、SC及其互补器件动作信号,输出节点sw处负极性的四电平波形,在满调制范围内节点sw输出七电平波形,负载侧等效开关频率为3fsw。
= 1+D,经PS-PWM生成SA、SB、SC及其互补器件动作信号,输出节点sw处负极性的四电平波形,在满调制范围内节点sw输出七电平波形,负载侧等效开关频率为3fsw。摘要 七电平有源中点钳位式(ANPC)拓扑能有效降低滤波电感需求,有望实现更高的功率密度和效率,但移相脉冲宽度调制(PS-PWM)下飞跨电容的电压调节能力有限,而飞跨电容电压不平衡会恶化变换器的可靠性和输出电能质量。为此,该文基于PS-PWM技术提出一种飞跨电容电压调控方法,该方法通过修正飞跨单元PWM信号相位以调节电感电流纹波形状,从而改变飞跨电容充/放电电流,原理上不受负载电流极性影响,不改变变换器输出等效占空比。在0~1/3与2/3~1占空比下,源侧飞跨电容和载侧飞跨电容存在独立充/放电区域,改变对应PWM信号相位,可以改变飞跨电容充/放电状态下的电感电流幅值而不改变充/放电时间,定向调整飞跨电容电压;在1/3~2/3占空比下,PWM相位变化同时影响飞跨电容充/放电电流幅值及时间,推导相关数学模型确定单一PWM相位自由度下两级飞跨电容的充/放电状态,采用飞跨电容电压迟滞比较控制可以改善此占空比范围内的电压偏移情况。因此,所提修正PWM相位方法可在0~1占空比范围内改善飞跨电容的电压不平衡问题。
关键词:七电平 有源中点钳位 飞跨电容 移相脉冲宽度调制 电压调控
近年来,飞跨电容多电平(Flying Capacitor Multi-Level, FCML)拓扑的应用已不再局限于高压大功率场景,随着半导体器件如碳化硅(Silicon Carbide, SiC)和氮化镓(Gallium Nitride, GaN)[1-3],以及电容技术(如多层陶瓷电容)的进步,FCML在低电压、低功率应用中也展现了巨大潜力[4]。尤其是FCML拓扑在有源中点钳位(Active Neutral- Point-Clamped, ANPC)型变换器中的应用,在移相脉冲宽度调制(Phase-Shifted Pulse Width Modu- lation, PS-PWM)下,相比传统FCML,可以减少一半以上的电容器体积及部分高频开关器件,且对输出滤波器的要求保持不变[5]。得益于这些优势,可以在800~1 000 V平台中应用高品质因数的低压硅器件或氮化镓器件,有望实现更高的效率和功率密度。
然而,多电平ANPC拓扑的控制策略较复杂,仍有一些控制难题未解决,限制了其广泛应用,其中,飞跨电容电压平衡控制是一个关键问题。不平衡的飞跨电容电压会导致输出电压多电平波形的畸变,恶化电感电流纹波,进而引发磁件产生额外损耗、磁心饱和、开关器件损耗变大以及阻断电压升高等问题,这可能抵消多电平ANPC拓扑的优势。
目前,已有多种飞跨电容电压调控方法被提出,但都存在一定局限性。最常见的方法是通过调节飞跨电容前后级开关PWM信号的脉冲宽度差DD[6-11],来改变飞跨电容的充放电平衡。然而,在轻载条件下,DD对充放电时间的影响可能弱于对充放电电流幅值的影响,在此状态下飞跨电容充放电动态可能反转,如飞跨电容前后级脉宽差DD为正时,飞跨电容放电而非充电,电压控制失去稳定性[12]。非线性控制方案能够缓解这一问题,此外,基于三角载波的双边沿非连续PWM方案可以改善低占空比下的稳定性[13],并通过线性补偿器实现全调制范围内的电压控制,但这对数字电路的计算能力和分辨率提出了更高要求。通过调节调制信号宽度来实现飞跨电容电压控制是可行的,但其电压控制机制仍待完善,同时前后级脉宽差DD会影响飞跨单元的等效输出占空比,可能恶化系统的输出电压波形 质量。
基于输出电平冗余开关状态的电压调控方法能缓解脉宽差DD方法的局限性。按是否改变单一器件开关时序可分为两类:第一类通过不同的开关组合实现相同的电压输出,在不同开关组合下飞跨电容存在不同充放电状态,以实现飞跨电容电压控制,如文献[14-19]所述,但该方法不适用于PS-PWM控制,飞跨单元的器件开关频率并不一致,变换器输出侧等效开关频率较低;第二类则保证一个开关周期的等效输出占空比不变,通过调整所选开关状态的持续时间,并修改PS-PWM的开关时刻来补偿电容电压的偏差[20-24],这种方法有效规避了脉宽差DD的局限性,不改变PS-PWM下变换器的输出高等效开关频率特性,但需要同时控制PWM脉宽和相位,实施起来较为复杂。
前两种方法在飞跨电容电压调整方面的能力多依赖于负载电流,主要通过调节飞跨电容的充放电时间来实现。当负载电流较小时,调节效果较弱。同时,在飞跨电容电压控制中忽视飞跨电容充放电流中电感电流纹波的影响是不合理的。PWM信号的变化不仅影响充放电时间,还会影响电感电流的大小,从而影响飞跨电容的充放电电流幅值。虽然文献[23-24]考虑了这一机制,但其所建立的控制模型较为模糊,未能清晰定量地描述控制变量与飞跨电容电压调节能力之间的关系。文献[25]则提出了一种方法,利用飞跨电容充/放电电流的纹波特性,调整飞跨电容前后级器件PWM信号的相位,在不改变充放电时间宽度的前提下,改变充放电区间内电感电流的纹波幅值,进而定量调整飞跨电容电压,但该方案仅针对简单的三电平FCML拓扑,未扩展到更高电平中。
受上述内容启发,本文针对七电平ANPC拓扑中的两级飞跨电容,提出了一种基于PS-PWM移相调制的电容电压调控方法。该方法以PWM信号相位为控制自由度,通过改变PWM信号相位以改变电感电流纹波形状,间接控制飞跨电容充放电电流大小与时间,实现飞跨电容电压调节。所提飞跨电容电压调控方法不受负载电流极性及其他稳定性问题的干扰,同时不改变变换器等效输出占空比。
七电平ANPC型变换器拓扑如图1所示,对应不同开关组合状态下的节点sw处输出对地多电平电压见表1,其中开关S1~S4以输出电压基波频率动作,为飞跨电容多电平级提供±Vdc/2的输入电压,SA、SB、SC及其互补导通器件以开关频率fsw动作,两级飞跨电容电压额定值分别为Vdc/3与Vdc/6,当参考调制信号D为正时,对应图2中0~T/2区间,ANPC级开关S1、S3开通,S2、S4关断,飞跨电容多电平级SA、SB、SC由调制信号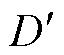 =D与载波相位依次相差Tsw/3的PS-PWM比较生成,在输出节点sw处产生幅值差为Vdc/6的四电平波形。调制信号D<0时,对应图2中T/2~T区间,S1、S3保持关断,S2、S4保持开通状态,飞跨电容多电平级调制信号为
=D与载波相位依次相差Tsw/3的PS-PWM比较生成,在输出节点sw处产生幅值差为Vdc/6的四电平波形。调制信号D<0时,对应图2中T/2~T区间,S1、S3保持关断,S2、S4保持开通状态,飞跨电容多电平级调制信号为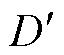 = 1+D,经PS-PWM生成SA、SB、SC及其互补器件动作信号,输出节点sw处负极性的四电平波形,在满调制范围内节点sw输出七电平波形,负载侧等效开关频率为3fsw。
= 1+D,经PS-PWM生成SA、SB、SC及其互补器件动作信号,输出节点sw处负极性的四电平波形,在满调制范围内节点sw输出七电平波形,负载侧等效开关频率为3fsw。
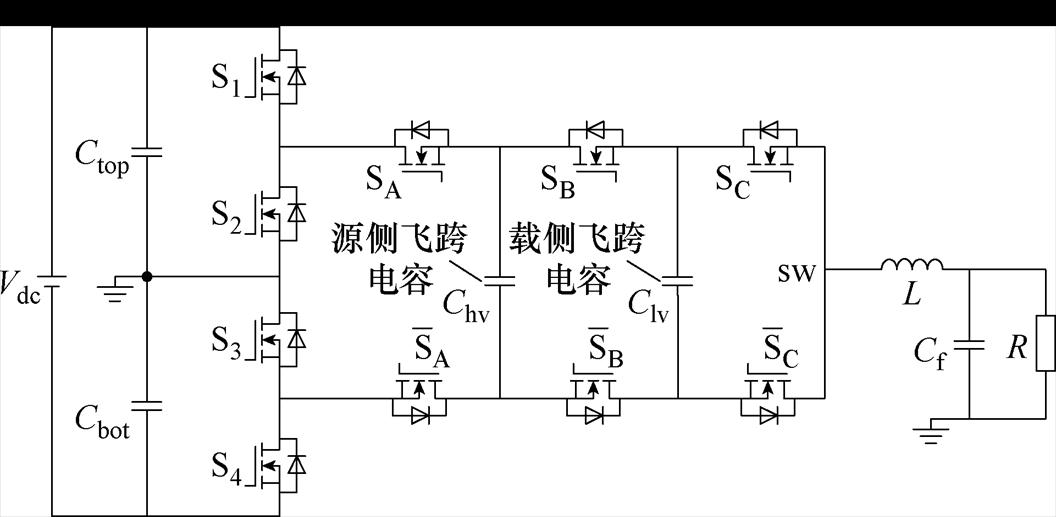
图1 七电平ANPC型变换器拓扑
Fig.1 7-level ANPC converter topology
表1 七电平ANPC开关状态对应电平
Tab.1 Output levels corresponding to switching states of the 7-level ANPC
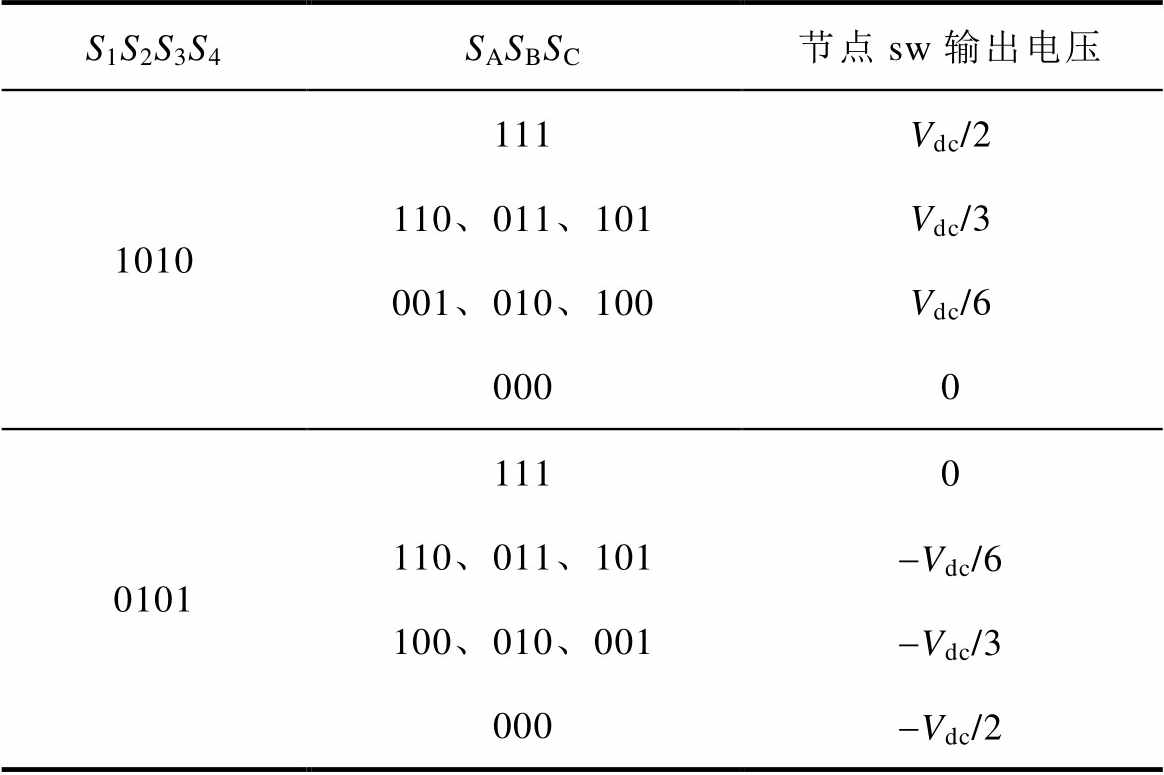
S1S2S3S4SASBSC节点sw输出电压 1010111Vdc/2 110、011、101Vdc/3 001、010、100Vdc/6 0000 01011110 110、011、101-Vdc/6 100、010、001-Vdc/3 000-Vdc/2
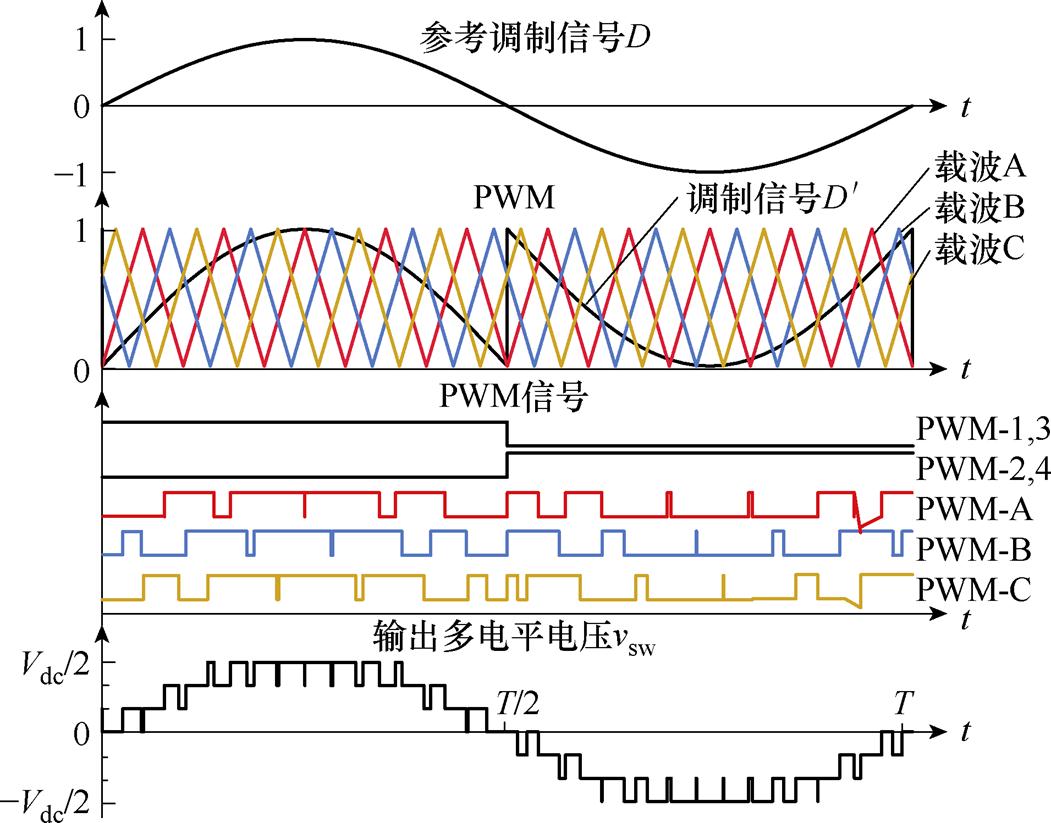
图2 七电平ANPC调制原理
Fig.2 Seven-level ANPC modulation principle
载波移相调制对飞跨电容电压有一定的自然调节能力,在系统输出电压稳定时,主要表现为两方面:一方面,飞跨电容电压为额定值时,开关周期内飞跨电容充放电平衡,电容电压不发生偏移;另一方面,飞跨电容电压偏移时,系统存在负反馈机制,飞跨电容之间相互反馈,调节飞跨电容电压向额定值收敛。
定义器件开通为“1”,关断为“0”,以0~1/3占空比为例,PS-PWM下飞跨电容电流波形如图3所示。t0~t1时间段SA-SB>0,源侧飞跨电容处于充电状态;t2~t3时间段SA-SB<0,源侧飞跨电容处于放电状态;t3~t4时间段SB-SC>0,载侧飞跨电容处于充电状态;t4~t5时间段SB-SC<0,载侧飞跨电容处于放电状态。
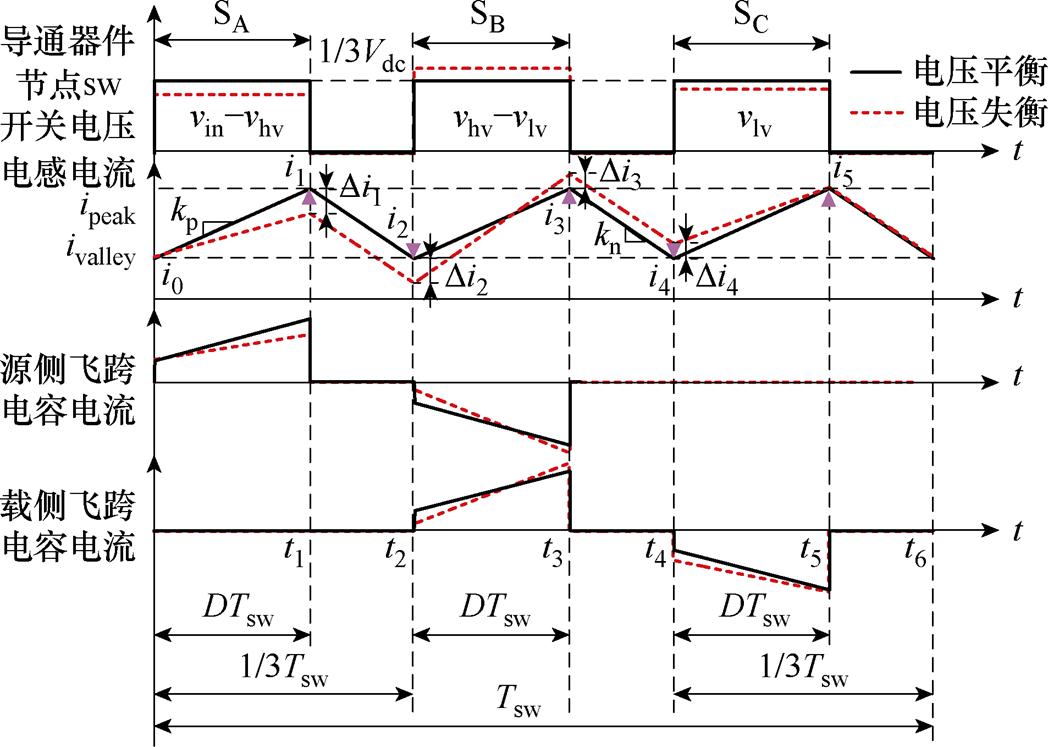
图3 PS-PWM下飞跨电容电流波形
Fig.3 Flying capacitor current waveforms under PS-PWM
由飞跨电容在充电、放电状态下的持续时间与对应电感电流的平均值,得到源侧、载侧飞跨电容在一个开关周期内的净充电电荷Qhv、Qlv分别为
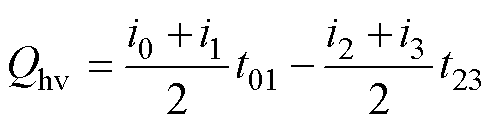 (1)
(1)
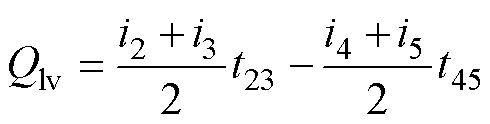 (2)
(2)
其组成部分系数为正表示充电;系数为负表示放电。
假设输出滤波电容在开关周期内保持输出为稳定电压vo,飞跨电容容值足够大,电容电压在开关周期内视为恒定值,当飞跨电容电压为额定值时,七电平ANPC系统中输出电压波形、电感电流、源侧飞跨电容与载侧飞跨电容电压如图3中黑色实线所示,电感电流纹波斜率为
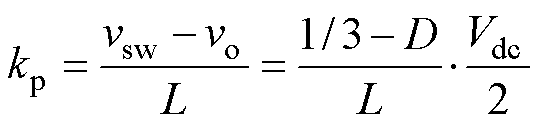 (3)
(3)
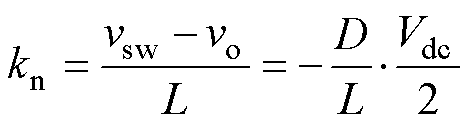 (4)
(4)
式中,vsw为节点sw处的多电平电压;L为滤波电感感值;Vdc为直流母线电压。
结合式(1)~式(4),开关周期内的电感电流纹波峰值、谷值分别保持一致,表示为ipeak、ivalley,每个飞跨电容在一个开关周期内的充、放电状态维持时间均为DTsw,充、放电平均电流为(ipeak+ivalley)/2,由于充放电均值电流及时间均相等,飞跨电容电压在开关周期前后不发生偏移,维持在额定值,即PS-PWM可以不改变系统稳定状态。
定义源侧飞跨电容电压偏移量为Dvhv,载侧飞跨电容电压偏移量为Dvlv,图3红色虚线为Dvhv>0、Dvlv<0且|Dvhv|>|Dvlv|时飞跨电容相关电压电流波形,系统输出开关电压的频率和脉宽不变,输出低电平电压保持为0 V,高电平电压偏离飞跨电容电压平衡工况下的Vdc/6,对应电感电流波形、飞跨电容电压充放电电流波形发生变化,对应开关周期内电容电压平均充电电流为
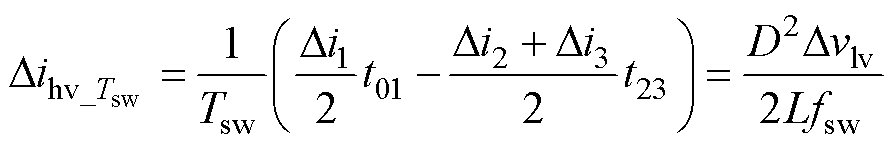 (5)
(5)
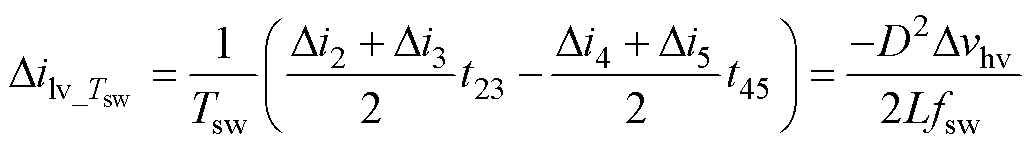 (6)
(6)
式中,fsw为FCML单元器件开关频率。结合源侧、载侧飞跨电容容值Chv、Clv与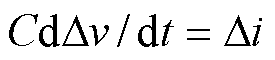 ,得到关于电压Dv的状态方程特征根为
,得到关于电压Dv的状态方程特征根为
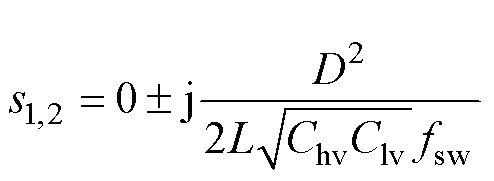 (7)
(7)
特征根为纯虚数,代表系统处于临界稳定状态时。在此状态下,飞跨电容电压会相互影响:当载侧飞跨电容电压降低时,会拉低源侧飞跨电容电压;反之,源侧飞跨电容电压降低会抬升载侧飞跨电容电压。然而,反馈系统的特征根没有负实部,缺乏足够的阻尼,导致飞跨电容电压振荡衰减不足,难以稳定在额定值上。
尽管从振荡周期的角度看,飞跨电容电压总体上是稳定的,但PS-PWM电压调节能力有限,在更小时间尺度下电压水平可能明显偏移额定值,如开关周期尺度下飞跨电容电压的平均值。
同理,可以得到在0~1满调制范围内,飞跨电容电压偏离额定值时,飞跨电容在开关周期内电容电压的平均充电电流为
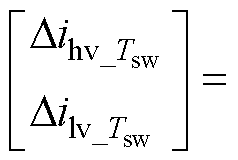
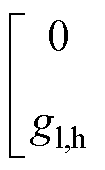
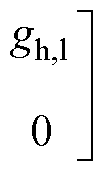
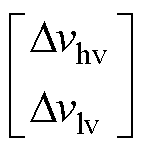 (8)
(8)
其中
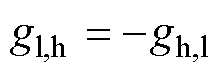 (9)
(9)
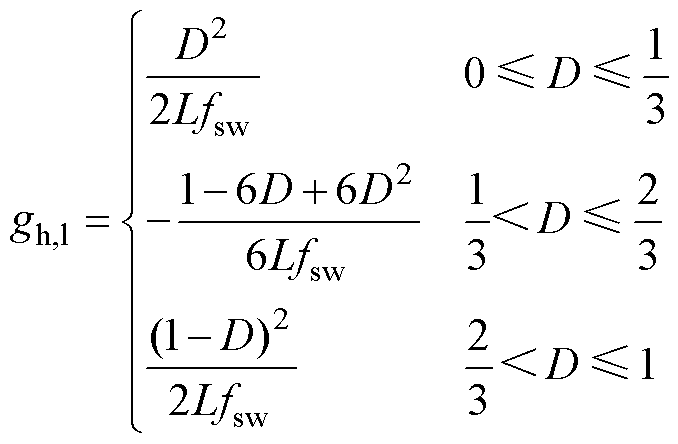 (10)
(10)
结合式(8)~式(10)可知,七电平ANPC飞跨电容电压在PS-PWM下有一定的自然调节能力,但对应的系统特征值均为纯虚数,系统处于临界稳定状态。
从物理角度看,单个开关周期内飞跨电容的电压偏移不会改变自身的充放电平衡,而会影响另一飞跨电容在充或放电状态的电流。不考虑不同开关模态下由飞跨电容与电感串联回路的等效电阻,负载电压视为恒定,飞跨电容电压偏移后,电感电流形状改变,进而影响飞跨电容电压的充/放电平衡过程仅有能量的转移而无能量的消耗,即自然平衡机制是无阻尼的,飞跨电容电压自然平衡系统处于临界稳定状态。被动电压控制在飞跨电容电压调控中的作用有限,需要通过主动调控飞跨电容电压来改善其偏移问题。
七电平ANPC拓扑中,流经飞跨电容的电流为电感电流纹波的一部分,改变有关PWM信号相位可以调整对应飞跨电容充/放电状态下的电感电流纹波形状,在0~1/3、2/3~1占空比下实现在不改变飞跨电容有效充/放电时间的前提下改变充/放电电流幅值,在1/3~2/3占空比下同时改变充/放电时间和电流幅值,在不同占空比范围下采用不同PS- PWM相位策略实现飞跨电容电压调控。
0~1/3占空比下,飞跨电容充放电状态如图4所示,定义“+、0、-”分别为单个飞跨电容的充电、旁路和放电三个状态,源侧、载侧飞跨电容的组合充放电状态存在(00)、(+0)/(0-)、(00)段,改变状态中的(+0)或(0-)状态对应电感电流纹波波形,如电感电流纹波(34)段,定义SA、SC器件PWM信号在PS-PWM基础上的相位偏移量为jA与jC,改变相应PWM信号相位,即可改变此段电感电流纹波幅值,而不影响其他时间段飞跨电容充放电电流,实现对指定飞跨电容电压的解耦控制,这一机制同样适用于2/3~1占空比下。
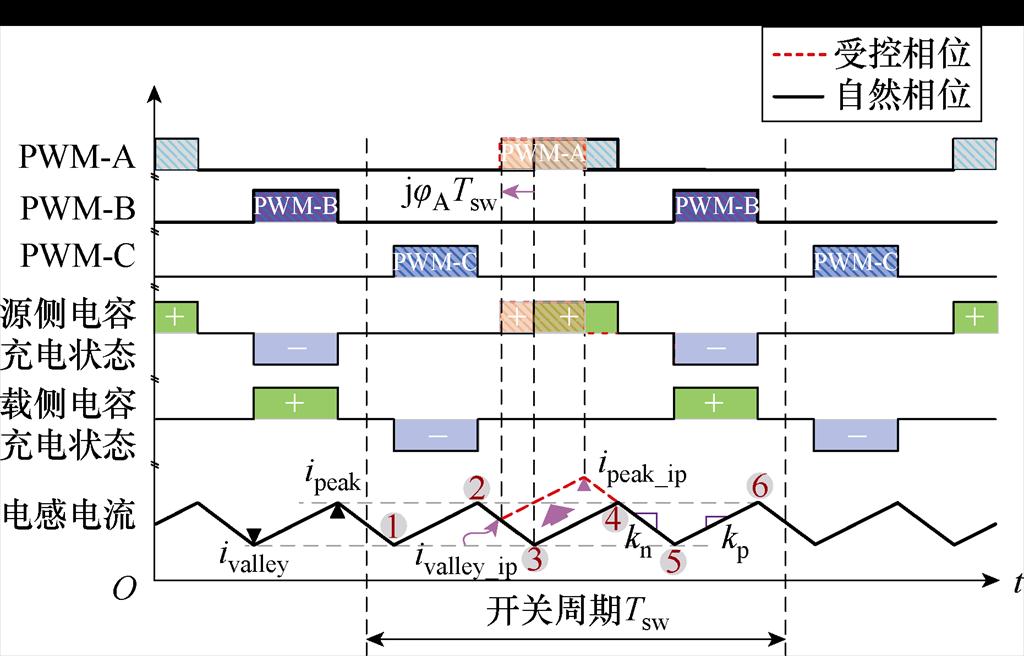
图4 0~1/3占空比下源侧飞跨电容电压调控原理
Fig.4 Principle of source side flying capacitor voltage control under 0 to 1/3 duty ratio
拓扑工作在1/3~2/3占空比下,PWM信号存在交叠,调整单一PWM信号相位会同时改变两级飞跨电容的充放电时间及电流幅值。建立开关周期下飞跨电容平均充电电流关于PWM信号相位jA、jC的完整模型,在一个自由度jA或jC作用下,即在jA置零时调整jC或在jC置零时调节jA,源侧、载侧飞跨电容所受充/放电作用是确定的。根据飞跨电容电压偏移程度,确定jA、jC控制方案,进而改善飞跨电容电压偏移现象。
因此,所提方法通过调整PWM信号相位可在满占空比范围实现七电平ANPC飞跨电容电压调控。控制量为PWM信号相位jA与jC,飞跨电容电压调整中不改变逆变器等效输出占空比,在0~1/3、2/3~1占空比下,所提方法通过调制PWM信号相位可在满占空比范围实现七电平飞跨电容电压调控。
当调制区间介于0~1/3内时,开关SA、SB、SC的PWM信号相互错开而不交叠,飞跨电容存在互不影响的独立充放电状态。如图4所示,源侧飞跨电容的充电状态仅与PWM-A信号高电平对应电感电流纹波有关,改变PWM-A信号相位,对应电流纹波幅值线性变化,而时间宽度不变。
以jA<0为例,将PWM-A信号在时间上右移jATsw,电感电流纹波段(34)随之右移jATsw,由于PWM-A脉宽未发生改变,结合式(4)可以得到自然相位下电流信息为
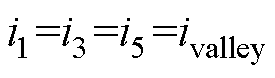 (11)
(11)
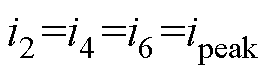 (12)
(12)
改变PWM-A相位前后载侧飞跨电容充放电,电流信息未发生改变,对应电感电流纹波(12)、(56)段。源侧飞跨电容在(34)段的平均充电电流增量为
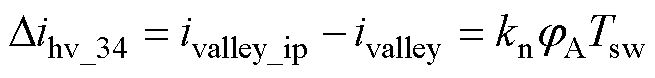 (13)
(13)
在飞跨电容有平衡状态的基础上,改变PWM-A相位后,源侧飞跨电容在开关周期内的平均充电电流为
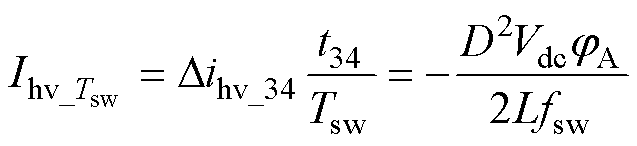 (14)
(14)
由式(14)可知,源侧飞跨电容的平均充电电流仅与调制信号D与PWM-A相位jA有关,而与负载电流无关。同时,开关周期的等效占空比(SA、SB、SC的占空比之和DA+DB+DC,3D)未发生改变,降低了逆变器等效输出电压矢量误差,从而将对系统级输出电压和电流控制的影响最小化。
调节PWM-A相位对于源侧和载侧飞跨电容电压的调节效果如图5所示,滞后调节PWM-A相位,jA>0,电容平均充电电流为负,飞跨电容电压降低;超前调节PWM-A相位,jA<0,平均充电电流为正,电容电压增大,相位改变对于载侧低压飞跨电容电压无影响。
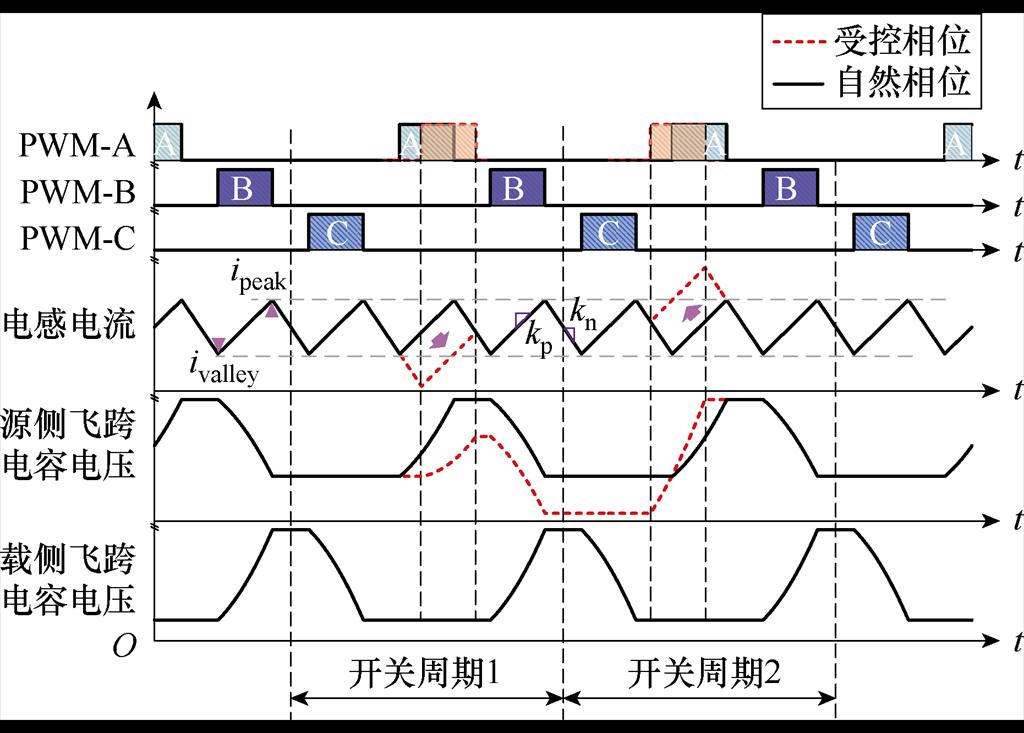
图5 0~1/3占空比下飞跨电容电压受PWM-A相位影响
Fig.5 Flying capacitor voltage affected by PWM-A phase under 0 to 1/3 duty ratio
同理,0~1/3占空比下,载侧飞跨电容放电状态仅与PWM-C高电平对应电感电流纹波有关,且此段电流纹波不对源侧飞跨电容进行充/放电。在调制中改变PWM-C相位,对应电感电流纹波幅值线性变化,而时间宽度不变。0~1/3占空比下载侧飞跨电容调节原理如图6所示,在开关周期1内,滞后调节PWM-C相位时,平均放电电流减小,开关周期内载侧飞跨电容净充电电荷增大,载侧飞跨电容电压水平提高;开关周期2内,超前调节PWM-C相位,放电电流平均值变大,载侧飞跨电容电压水平降低。相位jC引起载侧飞跨电容放电区间平均放电电流的增量为
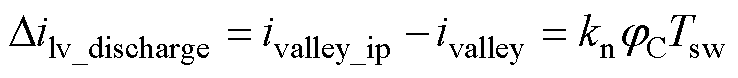 (15)
(15)
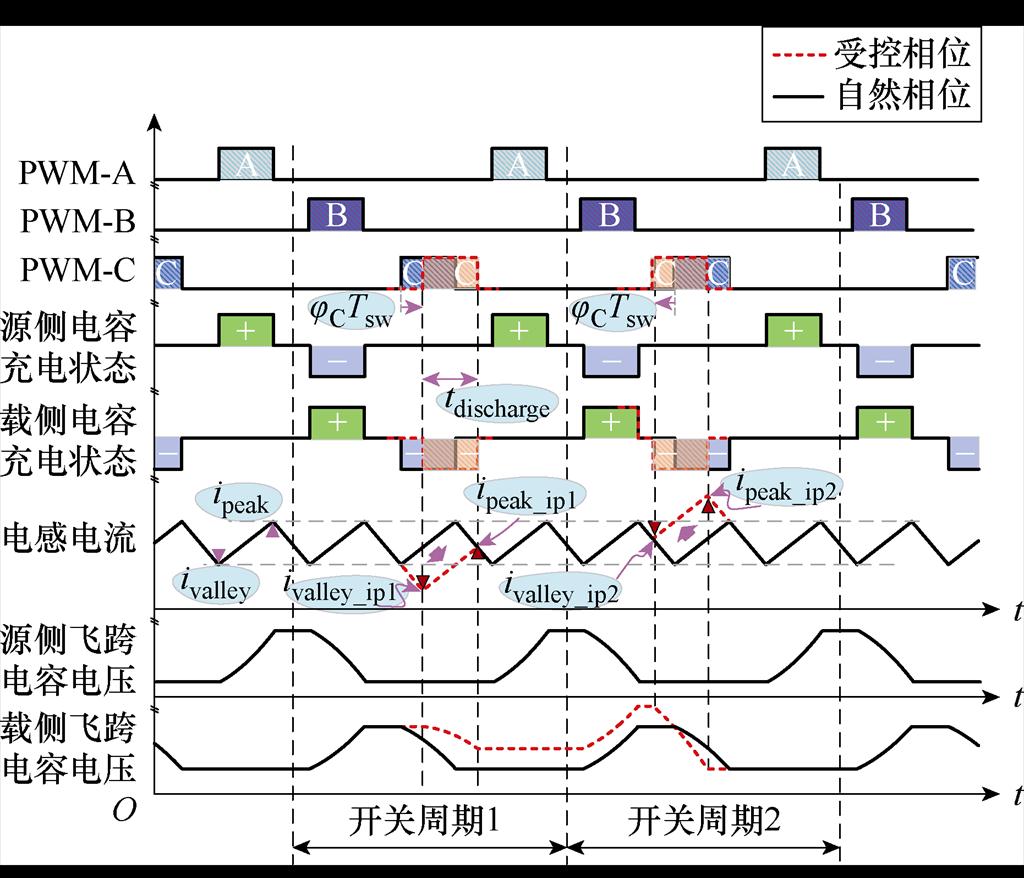
图6 0~1/3占空比下载侧飞跨电容调控原理
Fig.6 Load side flying capacitor regulation principle under 0 to 1/3 duty ratio
自然PS-PWM下,飞跨电容开关周期内的平均充电为零,相位jC作用下的平均充电电流为
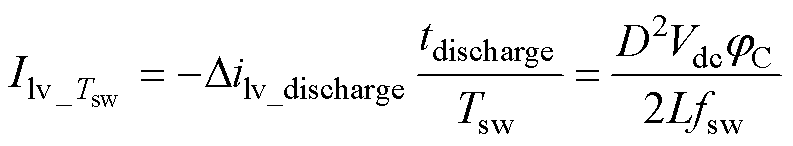 (16)
(16)
结合式(14)、式(16)和Q=it=CDv,飞跨电容电压调控中,源侧、载侧飞跨电容电压偏移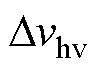 、
、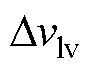 与SA、SC开关PWM信号移相角jA、jC的关系为
与SA、SC开关PWM信号移相角jA、jC的关系为
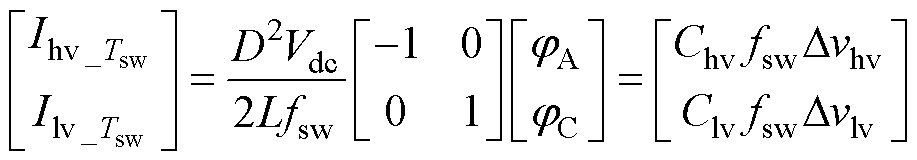 (17)
(17)
式(17)成立的前提条件为改变相位jA、jC后,不影响PWM信号的时序,即PWM信号保持无重叠状态,在此状态下调节jA、jC可以实现源侧、载侧飞跨电容电压的独立调控。
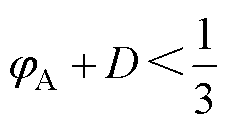 (18)
(18)
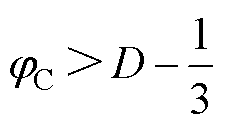 (19)
(19)
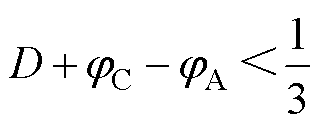 (20)
(20)
区别于0~1/3占空比下,1/3~2/3占空比下开关PWM信号区间内不存在独立的充/放电状态,如图7所示。改变任意PWM相位都会影响到连续三段电感电流纹波,而任意三段连续纹波中必同时包含两组飞跨电容的充/放电过程,即源侧飞跨电容的连续充/放电区间总伴随着载侧飞跨电容的充/放电。在此占空比下,移相引起的充放电时间与充放电电流的幅值变化都要考虑。
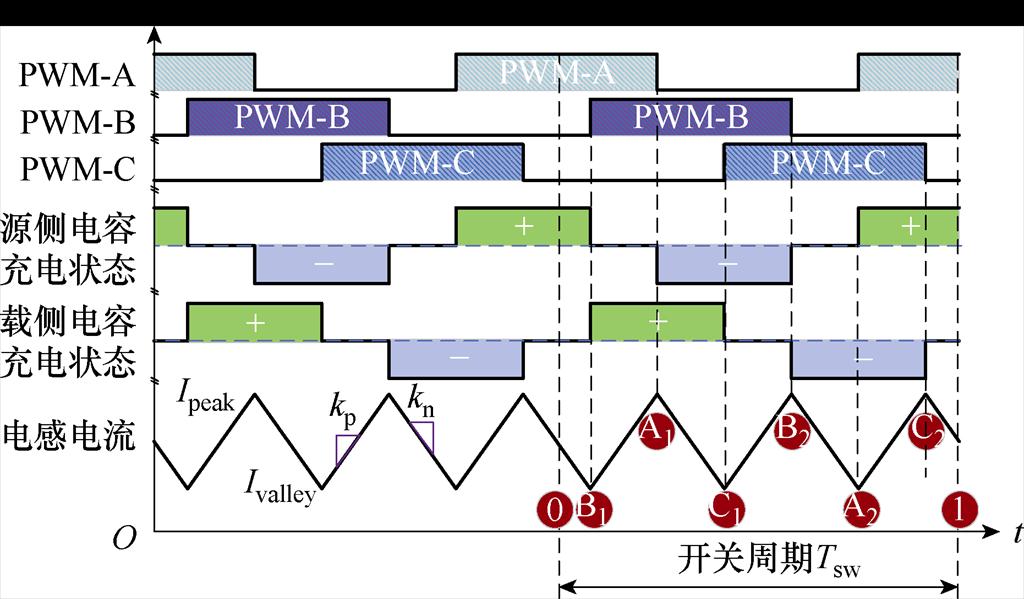
图7 1/3~2/3占空比下飞跨电容充放电信息
Fig.7 Flying capacitor charge and discharge information under 1/3 to 2/3 duty ratio
从简化模型考虑,若以解耦控制为目标,在调整源侧飞跨电容电压时,载侧飞跨电容的充放电平衡简单条件为
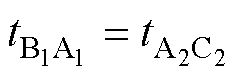 (21)
(21)
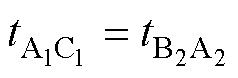 (22)
(22)
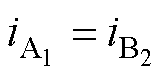 (23)
(23)
在此约束下PWM相位jA=jB=jC,对于源侧和载侧的电容电压均无调节能力,简单几何模型下的飞跨电容电压解耦控制不能实现,引入PWM相位影响飞跨电容电压的数学模型。
改变jA、jC下飞跨电容的充放电变化情况如图8所示,图8中展示了jA<0、jC<0的一种工况,在移相角不一致的情况下,飞跨电容充放电时间和充放电平均电流均发生改变,以开关周期1为例,改变PWM相位后,各纹波段时间长度为
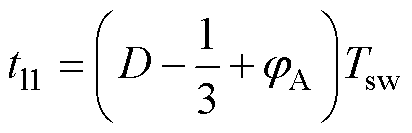 (24)
(24)
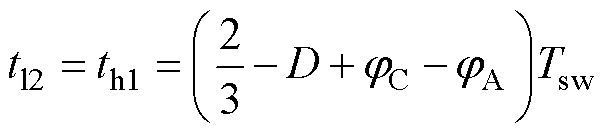 (25)
(25)
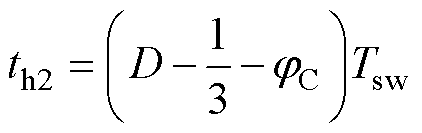 (26)
(26)
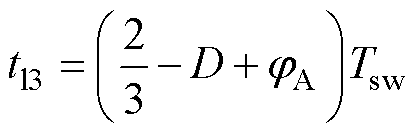 (27)
(27)
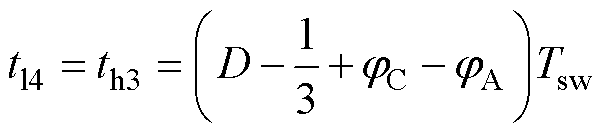 (28)
(28)
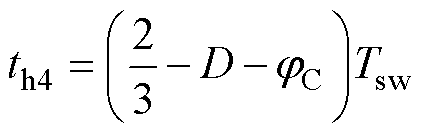 (29)
(29)
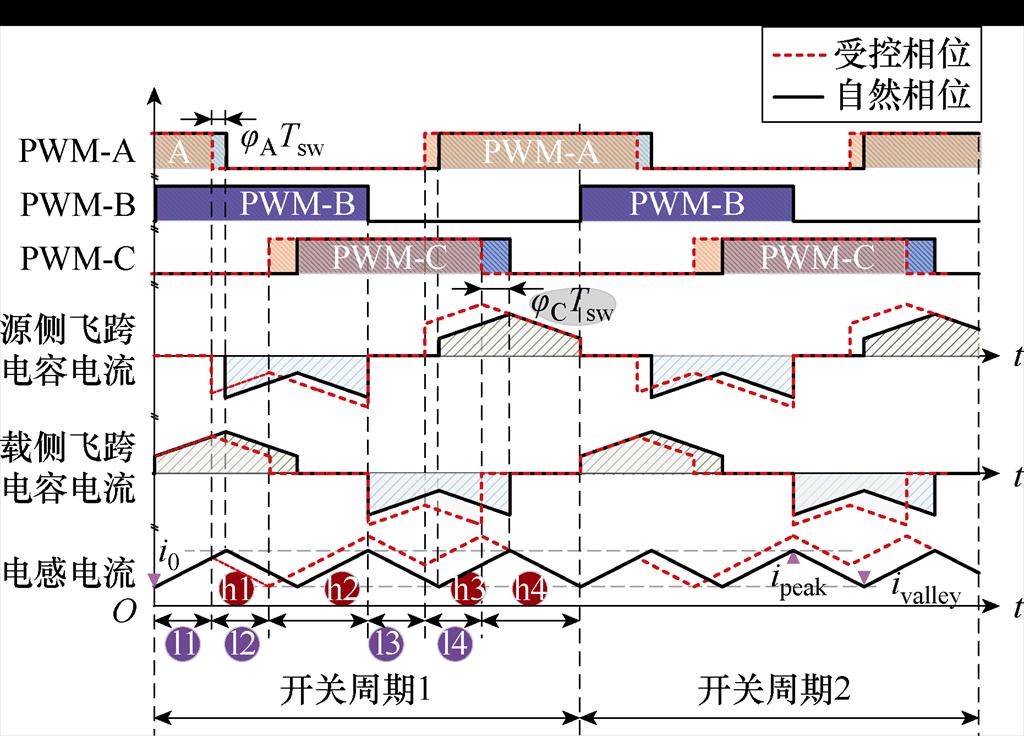
图8 1/3~2/3占空比下飞跨电容电流受移相角影响过程
Fig.8 The process of flying capacitor current being affected by phase shift angle under 1/3 to 2/3 duty ratio
对应纹波电流平均值为
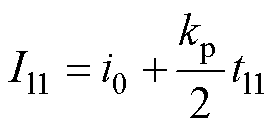 (30)
(30)
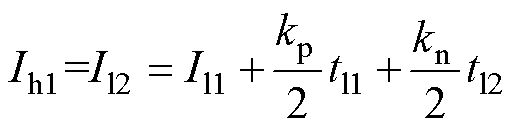 (31)
(31)
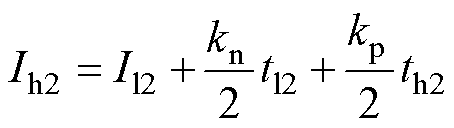 (32)
(32)
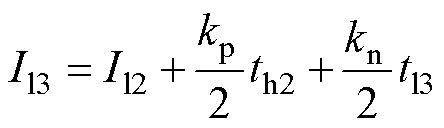 (33)
(33)
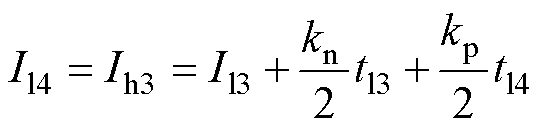 (34)
(34)
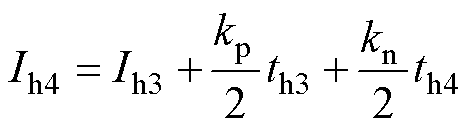 (35)
(35)
飞跨电容在开关周期内的平均充电电流为
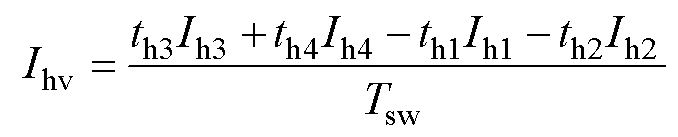 (36)
(36)
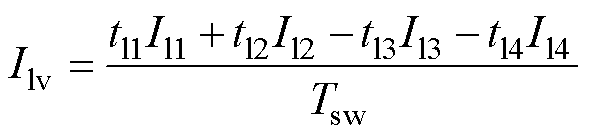 (37)
(37)
结合式(24)~式(37)可以得到飞跨电容平均充电电流与PWM信号相位的关系为
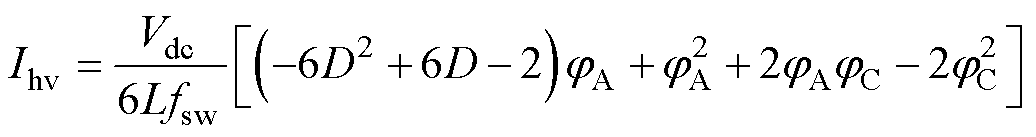 (38)
(38)
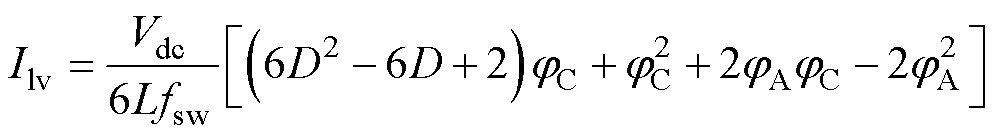 (39)
(39)
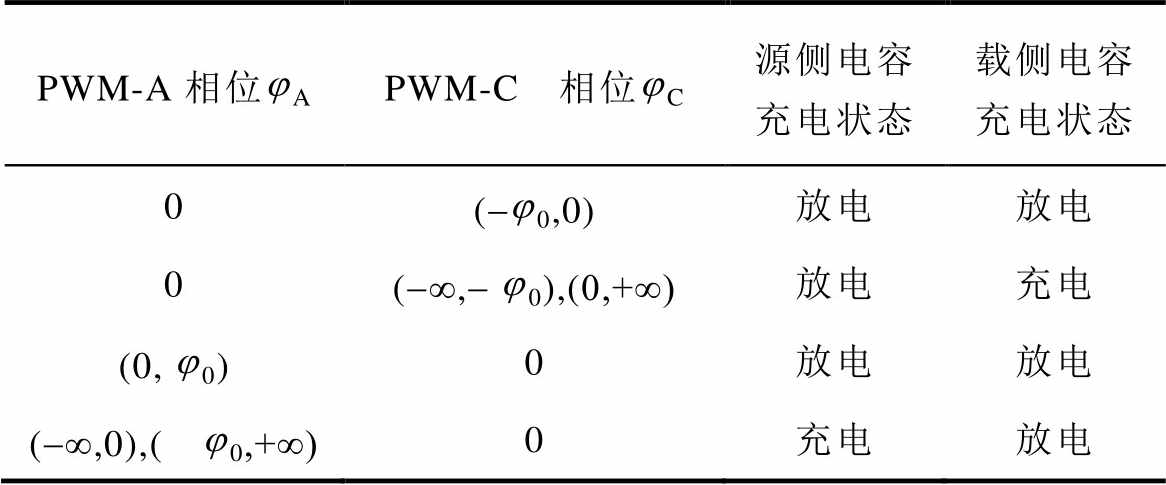
式(38)、式(39)中,在jA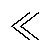 jC时,jC作用下源侧飞跨电容充电电流不可忽略,因此在飞跨电容电压调控中考虑完整数学模型而非降阶模型。简化电压调控策略,jA、jC单一调节变量下飞跨电容充电情况见表2,其中,jA置零,调节jC,源侧飞跨电容充电电流为负,载侧飞跨电容充电电流在不同jC下可正可负。同理,jC置零,调节jA,载侧飞跨电容充电电流为负,源侧飞跨电容充电电流在不同jC下可正可负。表2中,j0表示为
jC时,jC作用下源侧飞跨电容充电电流不可忽略,因此在飞跨电容电压调控中考虑完整数学模型而非降阶模型。简化电压调控策略,jA、jC单一调节变量下飞跨电容充电情况见表2,其中,jA置零,调节jC,源侧飞跨电容充电电流为负,载侧飞跨电容充电电流在不同jC下可正可负。同理,jC置零,调节jA,载侧飞跨电容充电电流为负,源侧飞跨电容充电电流在不同jC下可正可负。表2中,j0表示为
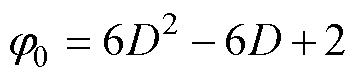 (40)
(40)
在1/3~2/3占空比下系统的调控策略不以同时调节所有飞跨电容电压为导向,优先调整恶劣级飞跨电容电压,定义权重k为
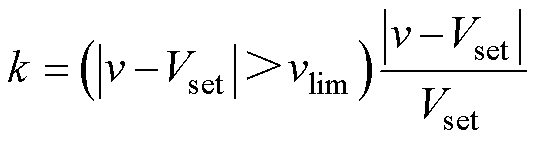 (41)
(41)
表2 飞跨电容充电状态
Tab.2 Flying capacitor charging status
PWM-A相位jAPWM-C相位jC源侧电容充电状态载侧电容充电状态 0(-j0,0)放电放电 0(-∞,-j0),(0,+∞)放电充电 (0, j0)0放电放电 (-∞,0),(j0,+∞)0充电放电
式中,Vset为飞跨电容电压额定值;v为飞跨电容电压测量值;vlim设定为动作阈值电压,飞跨电容电压偏移量低于vlim时视为正常工况,权重置零,不调整相关电容电压。
优先改善权重高的飞跨电容电压,以源侧飞跨电容电压调整为例,若源侧飞跨电容电压低于额定值,查阅表2,源侧飞跨电容电压充电,jC置零,调整jA,由飞跨电容电压偏移量可知其电压调整到额定值所需充电电荷量,结合式(38)可以得到
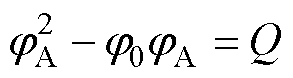 (42)
(42)
其中
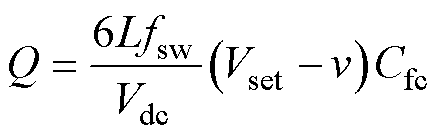 (43)
(43)
式中,Cfc为飞跨电容容值。式(42)、式(43)可以得到jA分别为正、负两个数值解,由式(39)可知,jC置零仅调整jA时,载侧飞跨电容持续放电,定义为调控源侧飞跨电容电压时伴随的寄生效果,一方面,较小的jA下载侧飞跨电容放电作用更小;另一方面,jA>0时源侧飞跨电容存在充、放电两个状态,应避免jA>0的解以确定源侧电容处于可靠的充电状态,因此,源侧电容充电策略下jA的数值解为
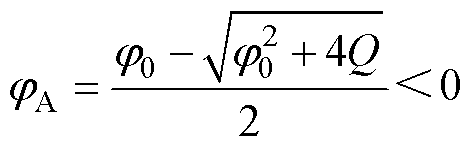 (44)
(44)
同理,在jA<0、jC<0的约束下,以式(41)确定目标调控对象并确定其充、放电需求,基于表2飞跨电容充电状态确定调节PWM-A或PWM-C相位,进而由式(38)、式(39)所示平均充电电流与电压偏移量联立求解得到jA或jC。对应不同调控目标下相位调节对象及其数值解见表3,其中H+、H-、L+、L-分别表示源侧、载侧飞跨电容充放电,单独引入一例H-、L-调控策略,提高飞跨电容电压调节速度。当式(24)~式(29)非负时,调节PWM相位可以调控飞跨电容电压,对应的相位调节临界条件为
表3 不同调整模式下受控相位数值解
Tab.3 Numerical solutions of controlled phase under different regulation modes
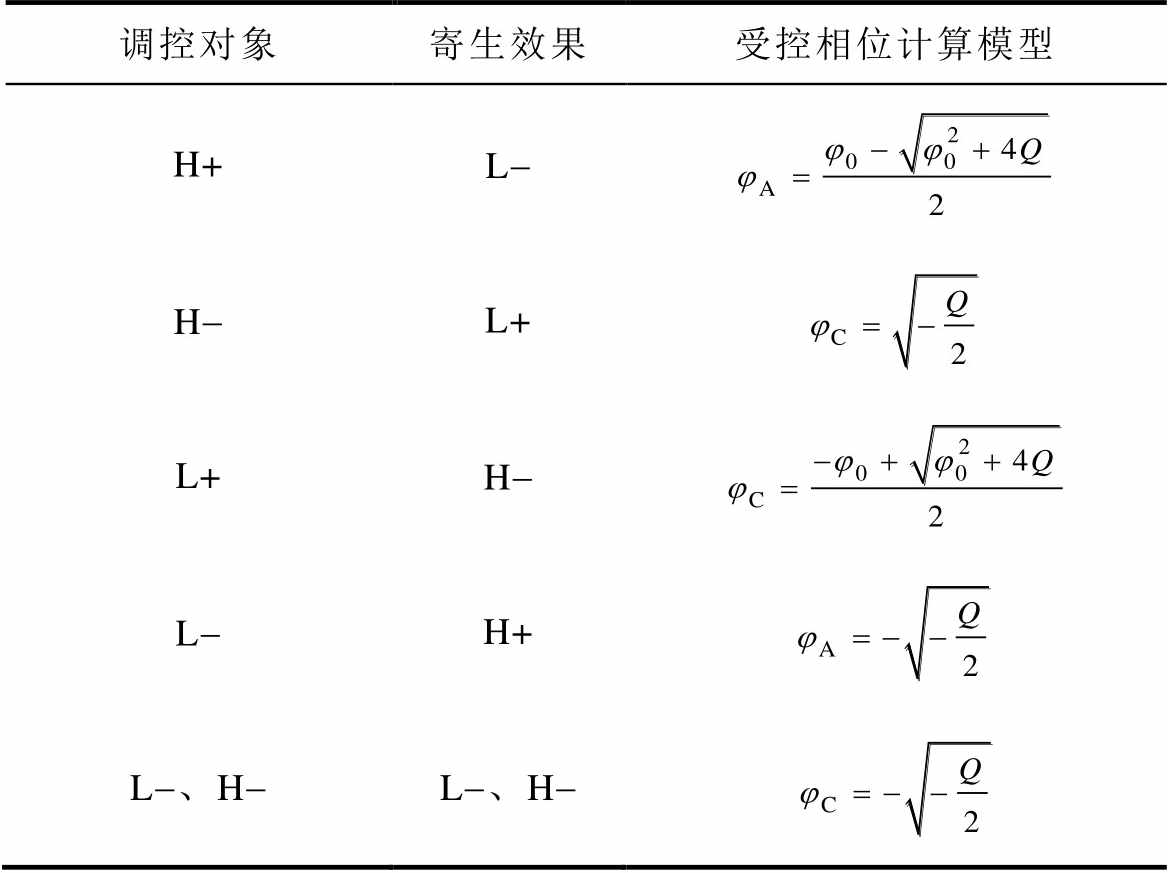
调控对象寄生效果受控相位计算模型 H+L- H-L+ L+H- L-H+ L-、H-L-、H-
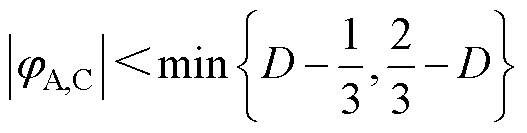 (45)
(45)
与0~1/3占空比下原理相同,调整PWM-A相位jA可以调节源侧飞跨电容开关周期内的放电段平均电流幅值,调整PWM-C相位jC可以线性调节载侧飞跨电容充电段平均电流幅值,2/3~1占空比下飞跨电容电压调控原理如图9所示。基于jA、jC的飞跨电容电压调控方法,在此占空比范围内,飞跨电容电压控制不存在耦合。

图9 2/3~1占空比下飞跨电容电压调控原理
Fig.9 Flying capacitor voltage control principle under 2/3 to 1 duty ratio
开关周期内飞跨电容平均充电电流为
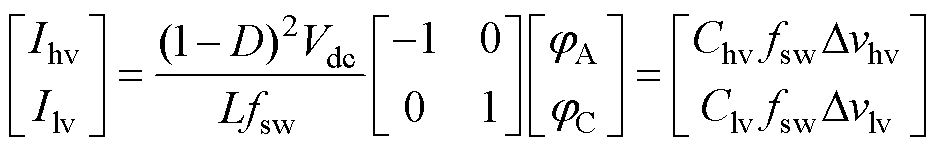 (46)
(46)
jA、jC的边界条件分别为
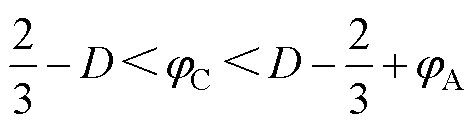 (47)
(47)
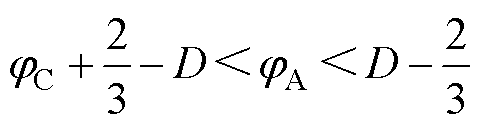 (48)
(48)
由式(17)、式(46)和表3所建立飞跨电容电压关于D、jA和jC的数学模型,得到0~1占空比范围下,飞跨电容电压的移相调控方法流程如图10所示,以频率fsw采样飞跨电容电压与占空比,由占空比所在区间调用不同的飞跨电容电压调控模型,飞跨单元等效占空比小于1/3时调用式(17)所示移相角模型,占空比高于2/3时调用式(46)所示移相角模型,占空比介于1/3~2/3之间时,根据飞跨电容电压偏移情况,基于权重确定控制对象为源侧或载侧飞跨单元,由充/放电需求选择调控移相角jA或jC,查阅表3调用有关移相角模型,进而在满占空比范围实现飞跨电容电压的移相调控。
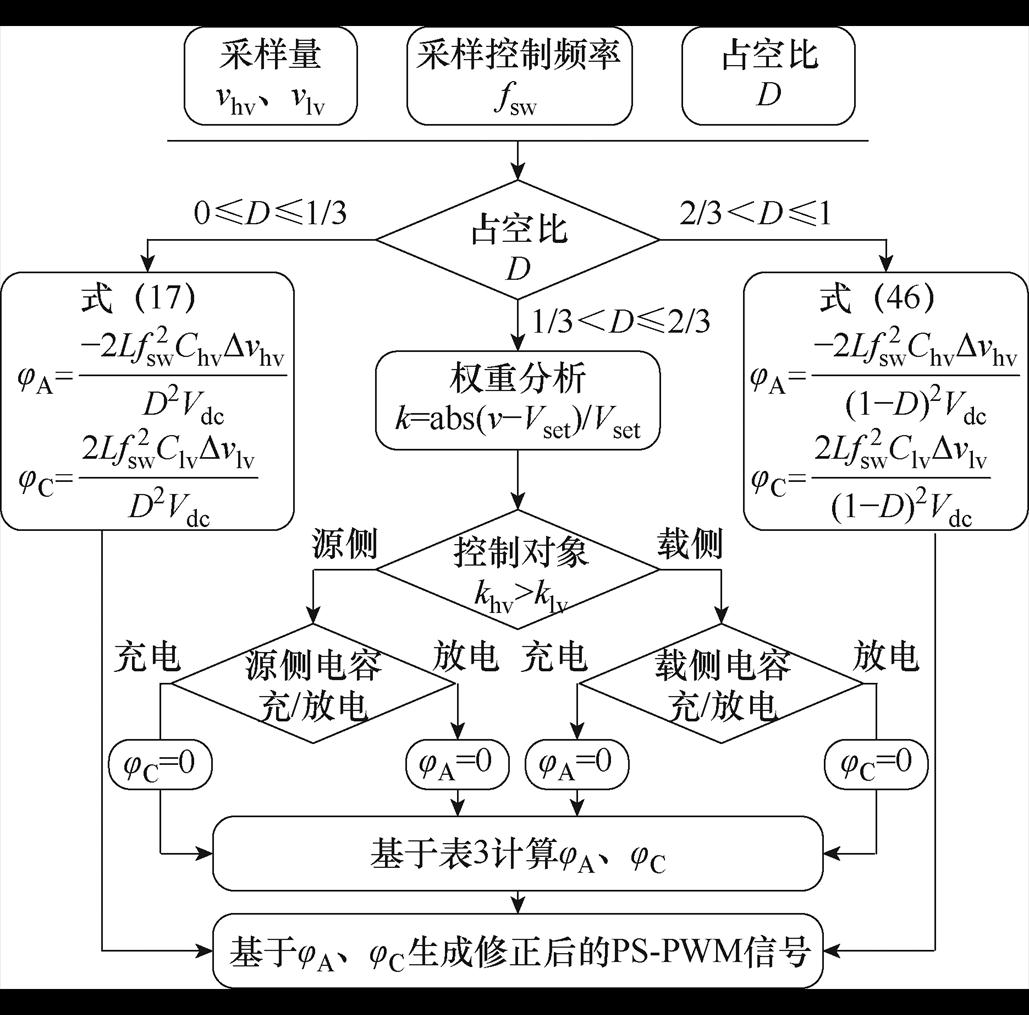
图10 满占空比范围下的飞跨电容电压移相调控框图
Fig.10 Block diagram of flying capacitor voltage phase shift control under full duty cycle range
基于图1拓扑搭建PLECS半实物仿真模型,选用TI TMS320F28379D作为DSP控制卡,以20 kHz的开关及控制频率生成PWM信号,具体PLECS仿真电路参数设置见表4。PLECS仿真关键波形如图11所示。
图11中,0.06~0.08 s为自然PS-PWM下的仿真波形,此工况下源侧飞跨电容电压峰、谷与平均值分别为324、231与255 V,载侧飞跨电容电压分别为186、85与129 V;0.08~0.1 s区间采用基于计算模型的改进PS-PWM方法后,源侧飞跨电容电压峰、谷与平均值分别为279、252与266 V,载侧飞跨电容电压156、112与132 V。
表4 仿真参数设置
Tab.4 Simulation parameter settings
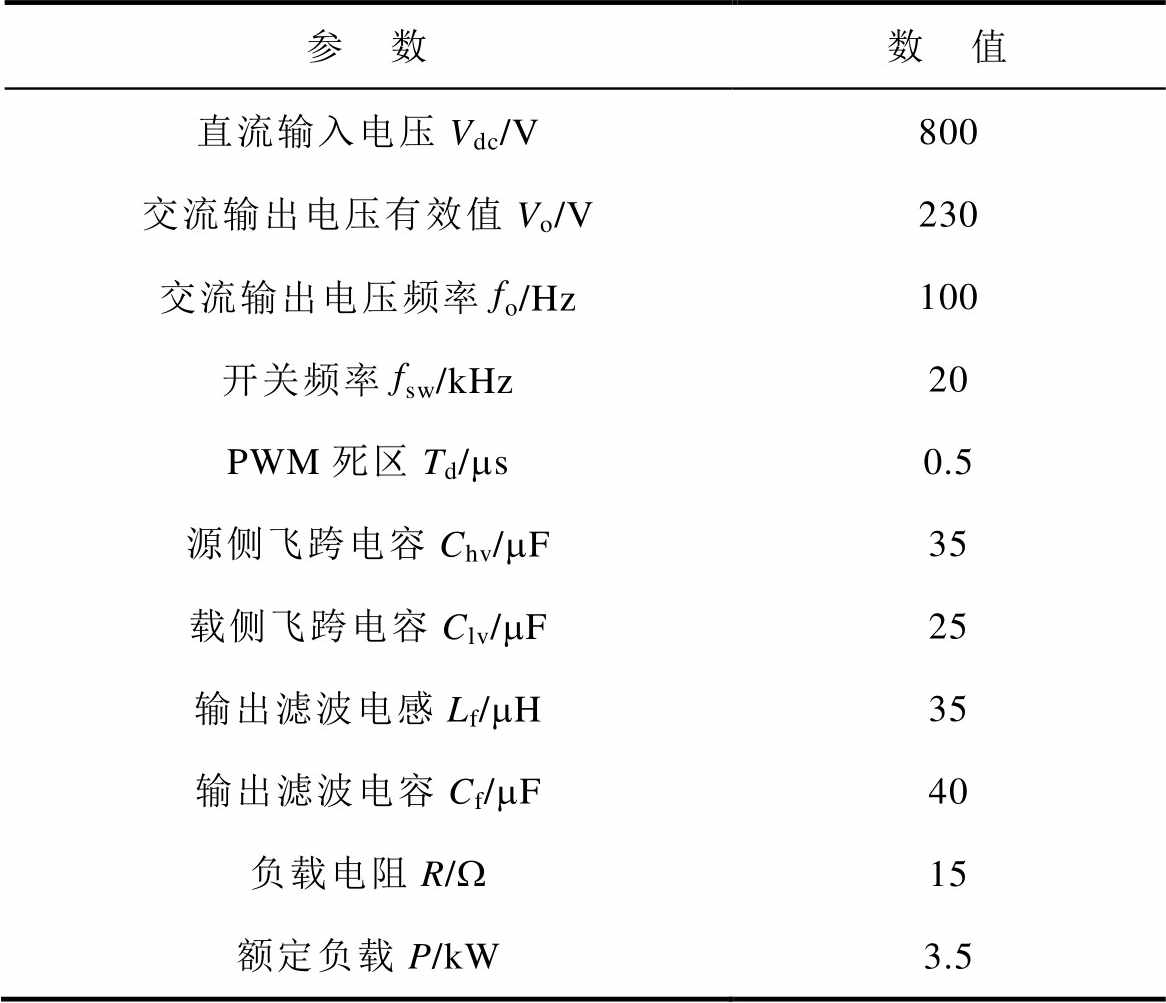
参 数数 值 直流输入电压Vdc/V800 交流输出电压有效值Vo/V230 交流输出电压频率fo/Hz100 开关频率fsw/kHz20 PWM死区Td/ms0.5 源侧飞跨电容Chv/mF35 载侧飞跨电容Clv/mF25 输出滤波电感Lf/mH35 输出滤波电容Cf/mF40 负载电阻R/W15 额定负载P/kW3.5
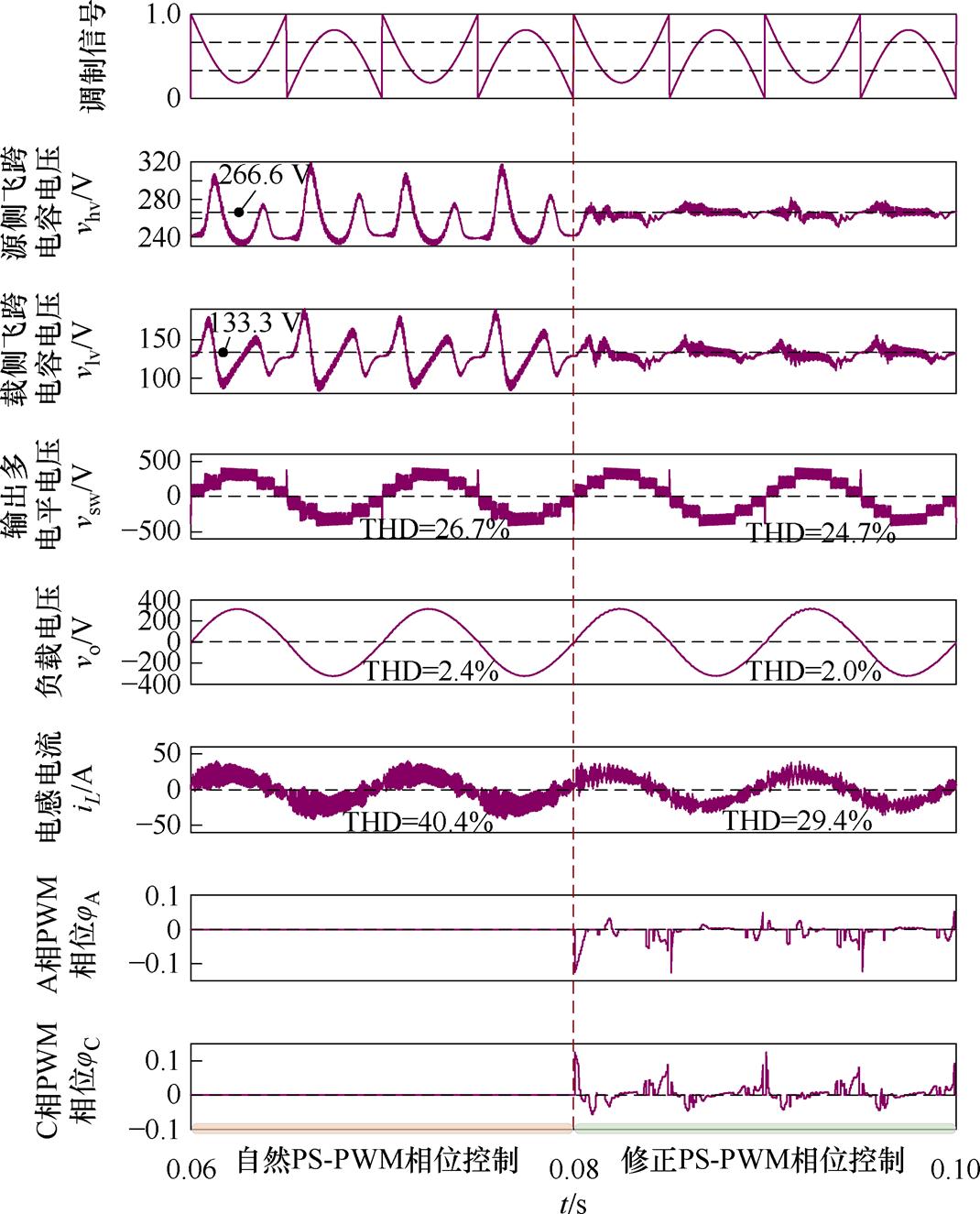
图11 PLECS仿真关键波形
Fig.11 PLECS simulation key waveforms
自然PS-PWM与改进PS-PWM下的飞跨电容电压与电感电流如图12所示,其中自然相位为图12中727~730 ms采用自然PS-PWM策略对应波形,受控相位对应图12中827~830 ms采用所提策略后对应波形,两组波形在时间上相差一个基频周期0.01 s。对比可知,采用修正PS-PWM策略后,通过修正PWM-A、C相位jA和jC,电感电流形状得到调整,飞跨电容充放电更趋于平衡,电压维持在其额定值附近。在PS-PWM下,飞跨电容电压波动大,输出多电平电压波动明显,电感电流纹波水平整体偏大,这可能导致磁件高频铁耗增大。采用改进PS-PWM后,飞跨电容电压稳定性更好,输出多电平波形更规律,部分电感电流纹波由于相位改变幅度变大,但电感电流纹波整体水平变低,电感电流总谐波畸变率(Total Harmonic Distortion, THD)由40.4%降到29.4%,输出电压总谐波含量由2.4%降为2%,系统运行更健康。
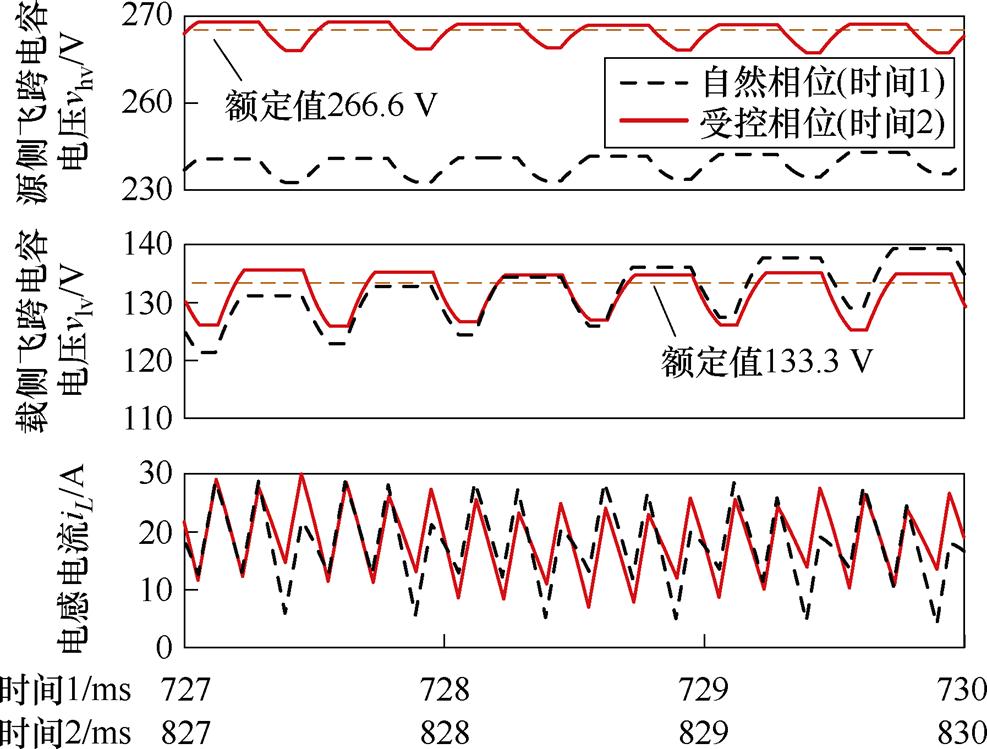
图12 策略前后电压电流波形对比
Fig.12 Comparison of voltage and current waveforms before and after the strategy
基于表4所示仿真参数,搭建测试平台如图13所示,变换器平台配置与控制参数设置与仿真保持一致,实验降额运行于240 V直流电压输入。
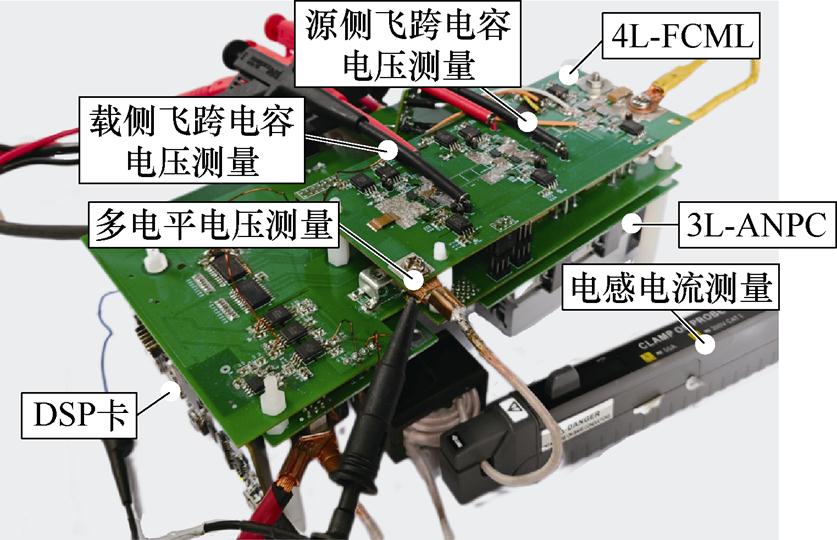
图13 实验平台
Fig.13 Experimental platform
源侧、载侧飞跨电容的额定值分别为80 V、40 V,不同调制深度M下飞跨电容电压电流波形如图14所示,其中图14a、图14d,图14b、图14e,图14c、图14f分别为调制深度M在0.3、0.6和0.81下采用改进PS-PWM策略前后波形。调制深度M=0.3时飞跨单元调制信号幅度在正、负极性调制信号下分别介于0~0.3、0.7~1区间,可以验证占空比在0~1/3和2/3~1下所提调控策略可行性;同理M=0.6时飞跨单元占空比介于0~0.6和0.4~1,覆盖了1/3~2/3占空比区间,图14e中输出开关节点电压最高/最低电平对应飞跨电容电压相较于图14b更收敛于额定值,可以验证所提1/3~2/3占空比区间改进PS-PWM策略的可行性。如图14a、图14d,图14b、图14e所示,改进PS-PWM策略下飞跨电容电压更趋近于额定值,波动幅度更小,所提策略分别在0~1/3、1/3~2/3、2/3~1占空比区间都可以改善飞跨电容电压。
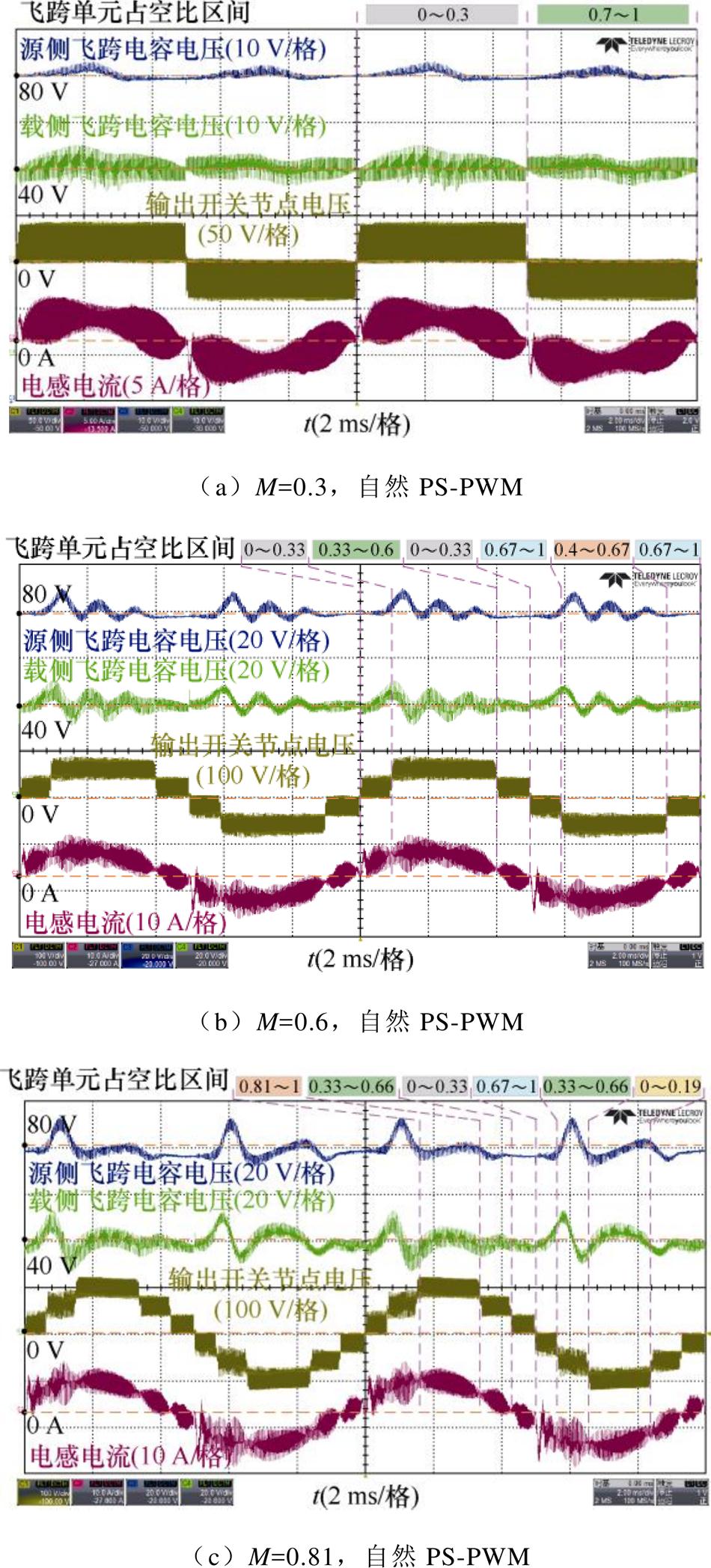
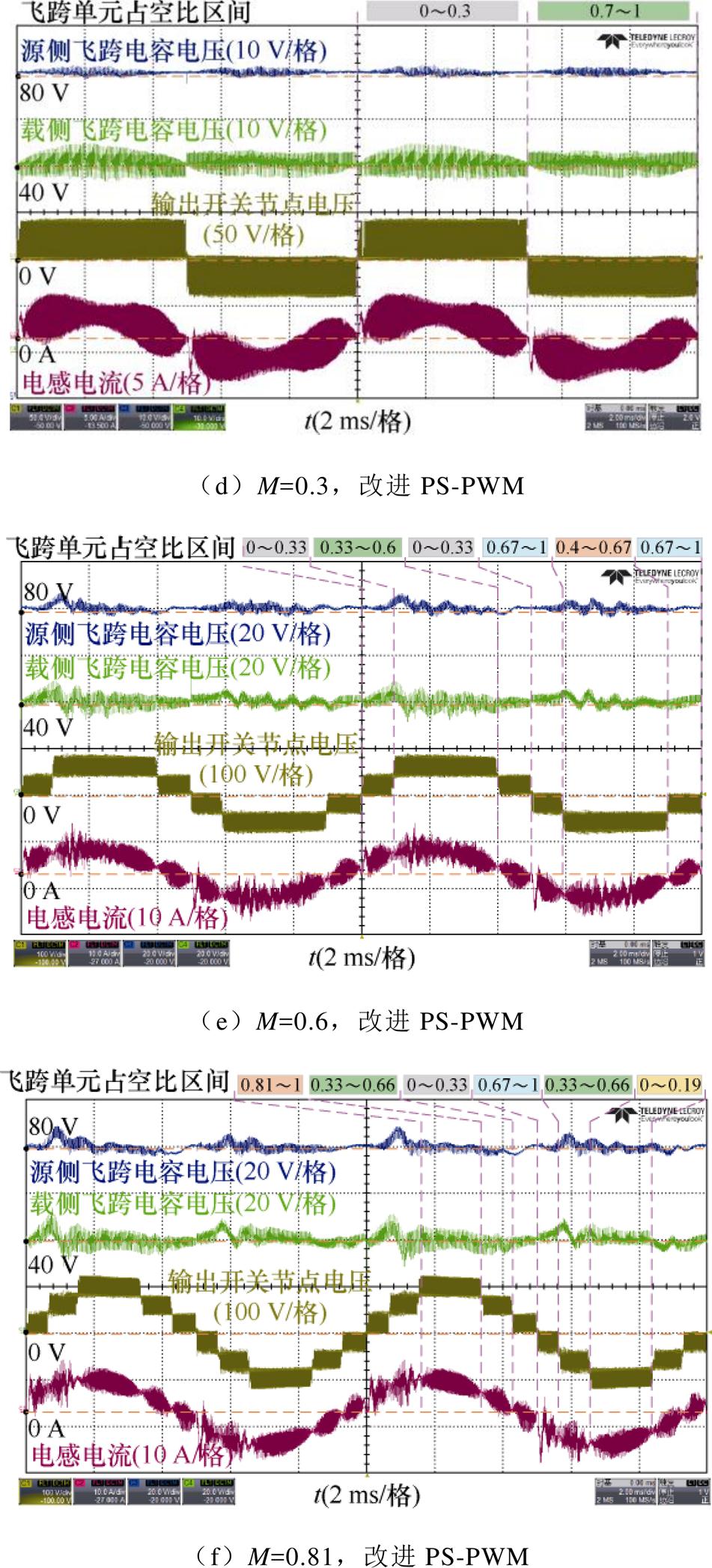
图14 240 V输入电压下不同占空比范围飞跨电容电压对比
Fig.14 Comparison of flying capacitor voltages under different modulation index ranges with 240 V input voltage
变换器正常运行时调制深度M常介于2/3~1区间,以图11仿真工况下调制深度M=0.81为例,自然PS-PWM策略下逆变器部分波形如图14c所示,载侧、源侧飞跨电容电压平均值为78.9 V、39.9 V,飞跨电容电压波动幅度的方均根值分别为3.8 V、3.7 V,电压偏移现象明显。采用基于数学模型的飞跨电容电压调控方法后,飞跨电容电压波形如图14f所示,输出电压基波周期下,相较于自然PS-PWM,载侧、源侧飞跨电容电压平均值水平相近,分别为79.5 V、40.5 V,但更集中在额定值附近,飞跨电容电压误差信号方均根分别为2.1 V、2.6 V,电压整体偏移水平有效降低,电感电流THD由29.1%降为27.6%。源侧/载侧飞跨电容电压纹波峰峰值也有所改善。
实验和仿真结果验证了所提基于计算模型的移相调制策略可以改善飞跨电容电压不平衡现象,利于提高变换器关键组件可靠性及输出电能质量。
针对七电平ANPC逆变拓扑中飞跨电容电压偏移问题,本文提出了一种基于改变飞跨单元PWM信号相位的电压调控方法,该方法不改变开关周期内输出等效占空比,有效改善输出多电平波形质量,通过仿真与实验验证了所提方法的可行性,基于理论推理和数据分析,可以得出如下结论:
1)七电平ANPC拓扑中飞跨电容电压有一定自调节能力,源侧和载侧飞跨电容的电压偏移量能够相互影响,从而改善彼此的电压偏移过程。但电压的被动调节能力有限,开关周期下飞跨电容电压均值偏移需要进一步抑制。
2)改变PWM相位可以改变电感电流形状,进一步调整飞跨电容充放电电流和充放电时间信息,间接实现飞跨电容电压控制。在0~1/3与2/3~1占空比下,飞跨电容间存在独立的充/放电区间,改变飞跨单元PWM相位可以调整独立充/放电区间电感电流纹波幅值,而不改变其充/放电区间宽度,实现飞跨电容电压线性调节;1/3~2/3占空比下改变飞跨单元PWM相位会同时改变飞跨电容充/放电电流幅值与时间,通过建立飞跨电容电流关于PWM相位的数学模型,简化控制变量,利用电压迟滞比较控制可以改善飞跨电容电压偏移现象。
本文采用的修正PS-PWM控制方法可以提高飞跨电容电压稳定性,降低开关器件阻断电压水平,降低电感电流THD含量,改善电能质量,但策略的相位基于数值计算得到,相位控制不连续时,电感电流纹波幅值或存在突变,引起输出电压波形局部畸变。同时,移相控制模型中未考虑飞跨电容电压偏移对纹波电流的影响,在基于简化数学模型的验证中存在电容电压调整量不足或过多,后续将继续完善电感电流纹波斜率变化下的移相调制模型。
参考文献
[1] 张少昆, 孙微, 范涛, 等. 基于分立器件并联的高功率密度碳化硅电机控制器研究[J]. 电工技术学报, 2023, 38(22): 5999-6014.
Zhang Shaokun, Sun Wei, Fan Tao, et al. Research on high power density silicon carbide motor controller based on parallel connection of discrete devices[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 5999-6014.
[2] 王议锋, 车超昌, 陈博, 等. 基于SiC器件的高压宽范围直流辅助电源研究与设计[J]. 电工技术学报, 2025, 40(3): 786-799.
Wang Yifeng, Che Chaochang, Chen Bo, et al. Research and design of high voltage and wide range DC auxiliary power supply based on SiC devices[J]. Transactions of China Electrotechnical Society, 2025, 40(3): 786-799.
[3] 佟强, 刘贺, 曲璐. 基于氮化镓的反激同步整流DC/DC变换器设计[J]. 电源学报, 2024, 22(2): 81-89.
Tong Qiang, Liu He, Qu Lu. Design of synchronous rectifier flyback DC/DC converter based on GaN[J]. Journal of Power Supply, 2024, 22(2): 81-89.
[4] Lei Yutian, Barth C, Qin Shibin, et al. A 2-kW single-phase seven-level flying capacitor multilevel inverter with an active energy buffer[J]. IEEE Transactions on Power Electronics, 2017, 32(11): 8570-8581.
[5] Anderson J A, Hanak E J, Schrittwieser L, et al. All-silicon 99.35% efficient three-phase seven-level hybrid neutral point clamped/flying capacitor inverter[J]. CPSS Transactions on Power Electronics and Applications, 2019, 4(1): 50-61.
[6] 宋磊, 段善旭, 米慧瑶, 等. 输入输出共地型三电平Buck/Boost变换器飞跨电容电压自平衡分析[J]. 中国电机工程学报, 2023, 43(15): 5983-5995.
Song Lei, Duan Shanxu, Mi Huiyao, et al. Self- balance mechanism analysis of the flying capacitor voltage in the three-level Buck/Boost converter with input and output sharing the ground[J]. Proceedings of the CSEE, 2023, 43(15): 5983-5995.
[7] 樊启高, 吕华阳, 毕恺韬, 等. 面向直流储能系统的飞跨电容三电平双向升降压变换器及其模型预测控制策略[J]. 电工技术学报, 2022, 37(16): 4169- 4179.
Fan Qigao, Lü Huayang, Bi Kaitao, et al. Flying capacitor three-level bi-directional buck-boost converter and its model predictive control strategy for DC energy storage system[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4169-4179.
[8] 高娜, 张宇, 关清心, 等. 基于有源中点钳位五电平电路的双有源桥DC/DC变换器[J]. 中国电机工程学报, 2023, 43(5): 1950-1960.
Gao Na, Zhang Yu, Guan Qingxin, et al. Five-level active neutral point clamed dual active bridge DC/DC converter[J]. Proceedings of the CSEE, 2023, 43(5): 1950-1960.
[9] 黄桢楠, 董纪清. 基于PI控制的飞跨电容均压环研究[J]. 电气开关, 2024, 62(3): 12-16.
Huang Zhennan, Dong Jiqing. Research on flying capacitor voltage balance based on PI control[J]. Electric Switchgear, 2024, 62(3): 12-16.
[10] 张琦, 李江江, 孙向东, 等. 单相级联七电平逆变器拓扑结构及其控制方法[J]. 电工技术学报, 2019, 34(18): 3843-3853.
Zhang Qi, Li Jiangjiang, Sun Xiangdong, et al. Topology and control method of single-phase cascaded seven-level inverter[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3843- 3853.
[11] 张元媛, 阮新波. 多电平直流变换器中飞跨电容电压的一种控制策略[J]. 中国电机工程学报, 2004, 24(8): 37-41.
Zhang Yuanyuan, Ruan Xinbo. A novel control strategy for the flying capacitor voltage of the multilevel converter[J]. Proceedings of the CSEE, 2004, 24(8): 37-41.
[12] Vukadinović N, Prodić A, Miwa B A, et al. Extended wide-load range model for multi-level DC-DC converters and a practical dual-mode digital controller[C]//2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 2016: 1597-1602.
[13] da Silva Carvalho S, Halamíček M, Vukadinović N, et al. Digital PWM for multi-level flying capacitor converters with improved output resolution and flying capacitor voltage controller stability[C]//2018 IEEE 19th Workshop on Control and Modeling for Power Electronics (COMPEL), Padua, Italy, 2018: 1-7.
[14] 刘苗, 洪峰, 尹培培, 等. 复合型级联双Buck飞跨电容五电平逆变器[J]. 电工技术学报, 2015, 30(18): 35-42.
Liu Miao, Hong Feng, Yin Peipei, et al. A hybrid cascaded dual Buck flying-capacitor five-level inverter[J]. Transactions of China Electrotechnical Society, 2015, 30(18): 35-42.
[15] Zhou Dehong, Quan Zhongyi, Li Yunwei. Simplified predictive duty cycle control of multilevel converters with internal identical structure[J]. IEEE Transactions on Power Electronics, 2020, 35(11): 12416-12428.
[16] 向超群, 杜京润, Zhang Xinan, 等. 电容电压平衡的四电平有源中性点钳位逆变器的改进模型预测电流控制[J]. 电工技术学报, 2024, 39(18): 5826- 5838.
Xiang Chaoqun, Du Jingrun, Zhang Xinan, et al. An improved model predictive control of four-level active neutral point clamped inverter with balanced capacitor voltage[J]. Transactions of China Elec- trotechnical Society, 2024, 39(18): 5826-5838.
[17] 刘苗, 洪峰, 王成华. 五电平飞跨电容型双降压逆变器[J]. 电工技术学报, 2011, 26(5): 83-87, 94.
Liu Miao, Hong Feng, Wang Chenghua. A novel flying-capacitor dual Buck five-level inverter[J]. Transactions of China Electrotechnical Society, 2011, 26(5): 83-87, 94.
[18] 郭小强, 贺冉, 张纯江. 高压大容量五电平逆变器共模电压抑制研究[J]. 电工技术学报, 2016, 31(3): 1-7.
Guo Xiaoqiang, He Ran, Zhang Chunjiang. Common- mode voltage reduction of high voltage high power five-level inverters[J]. Transactions of China Electro- technical Society, 2016, 31(3): 1-7.
[19] 严干贵, 刘文华, 穆钢, 等. 内蕴电压平衡控制的飞跨电容逆变器的PWM方法[J]. 中国电机工程学报, 2006, 26(4): 119-125.
Yan Gangui, Liu Wenhua, Mu Gang, et al. Flying capacitor multilevel inverter PWM method with intrinsic voltage balancing control[J]. Proceedings of the CSEE, 2006, 26(4): 119-125.
[20] Feng Chunmei, Liang Jun, Agelidis V G. Modified phase-shifted PWM control for flying capacitor multilevel converters[J]. IEEE Transactions on Power Electronics, 2007, 22(1): 178-185.
[21] Stillwell A, Lei Yutian, Pilawa-Podgurski R C N. A method to extract low-voltage auxiliary power from a flying capacitor multi-level converter[C]//2016 IEEE 17th Workshop on Control and Modeling for Power Electronics (COMPEL), Trondheim, Norway, 2016: 1-8.
[22] Stillwell A, Robert C N, Pilawa-Podgurski. A 5-level flying capacitor multi-level converter with integrated auxiliary power supply and start-up[C]//2017 IEEE Applied Power Electronics Conference and Expo- sition (APEC), Tampa, FL, USA, 2017: 2932-2938.
[23] Stillwell A, Candan E, Pilawa-Podgurski R C N. Constant effective duty cycle control for flying capacitor balancing in flying capacitor multi-level converters[C]//2018 IEEE 19th Workshop on Control and Modeling for Power Electronics (COMPEL), Padua, Italy, 2018: 1-8.
[24] Stillwell A, Candan E, Pilawa-Podgurski R C N. Active voltage balancing in flying capacitor multi- level converters with valley current detection and constant effective duty cycle control[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 11429-11441.
[25] da Silva Carvalho S, Vukadinovic N, Prodic A. Phase-shift control of flying capacitor voltages in multilevel converters[C]//2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 2020: 299-304.
Phase-Shift Method for Seven-Level Active Neutral Point Clamped Inverter Flying Capacitor Voltage Control
Abstract The 7-level active neutral point clamped (ANPC) topology effectively reduces the need for filter inductance, offering the potential for higher power density and efficiency. However, under phase-shifted pulse width modulation (PS-PWM), the voltage regulation capability of the flying capacitors is limited, and imbalances in flying capacitor voltage can degrade converter reliability and output power quality. This paper proposes a flying capacitor voltage regulation method based on PS-PWM. This method adjusts the PWM phase of the flying capacitor unit to modulate the ripple shape of the inductor current, thereby modifying the charging/discharging current of the flying capacitor. The method is fundamentally unaffected by load current polarity and does not alter the effective duty cycle of the converter output.
In the 0~1/3 modulation range, the charging current of the source-side flying capacitor is primarily related to the inductor current during the high-level period of the PWM-A signal near the source side. It is independent of the high-level periods of PWM-B and PWM-C signals. Moreover, the high-level period of the PWM-A signal does not affect the charging and discharging process of the load-side flying capacitor. Given a duty ratio D, adjusting the phase jA of the PWM-A signal can linearly modulate the average amplitude of the corresponding inductor current ripple without changing its ripple duration. This adjustment allows precise control of the source-side flying capacitor’s charge over the switching period, thereby regulating its voltage. During this process, the charging/discharging state of the flying capacitor only occurs during the high-level periods of the PWM-A, PWM-B, and PWM-C signals. By ensuring that the high-level periods of the PWM signals do not overlap, the source-side flying capacitor voltage can be independently controlled without affecting the load-side flying capacitor. Similarly, adjusting the phase jC of the PWM-C signal can linearly modulate the discharge current amplitude of the load-side flying capacitor. As long as the high-level periods of the PWM signals do not overlap, the load-side flying capacitor voltage can be independently controlled.
In the 1/3~2/3 modulation range, changes in the PWM signal phases affect the flying capacitor’s charging and discharging current amplitude and duration. By deriving the phase-shift modulation model of the average charging current of the source-side and load-side flying capacitors over the switching period concerning the PWM-A and PWM-C signal phases jA and jC, the charging/discharging states of the two-stage flying capacitors can be determined under the single PWM phase degree of freedom. An appropriate voltage modulation strategy can be selected depending on the degree of flying capacitor voltage offset. Subsequently, adjusting the phases of PWM-A or PWM-C can improve the voltage offset of the flying capacitors and optimize the voltage balance between the source and load-side flying capacitors.
In the 2/3~1 modulation range, the charging and discharging states of the flying capacitors occur during the low-level periods of the PWM-A, PWM-B, and PWM-C signals. The regulation principle in this range is similar to that in the 0~1/3 modulation range. In this case, adjusting the phases jA and jC of the low-level periods of PWM-A and PWM-C signals can achieve independent and linear voltage regulation for the source-side and load-side flying capacitors.
Thus, the proposed improved PS-PWM phase modulation method can effectively address the voltage imbalance in the flying capacitors over the entire 0~1 modulation range.
Keywords:Seven-level, active neutral point clamp (ANPC), flying capacitor, phase-shifted pulse width modulation (PS-PWM), voltage regulation
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.242148
国家重点研发计划资助项目(2024YFB4007504)。
收稿日期 2024-11-29
改稿日期 2025-03-03
李 祥 男,1999年生,硕士研究生,研究方向为多电平变换器调制方法及应用。
E-mail: lixiang@stu.cqu.edu.cn
丰 昊 男,1991年生,副教授,博士生导师,研究方向为宽禁带功率半导体器件及应用。
E-mail: hfeng6@cqu.edu.cn(通信作者)
(编辑 陈 诚)