图1 使用集成磁器件的两相交错并联Buck变换器拓扑
Fig.1 Topology of two-phase interleaved Buck converter with integrated magnetic device
摘要 为实现变换器效率、集成磁器件占地面积与体积的共同优化，该文基于两相交错并联Buck变换器，针对改进磁心结构和绕组布局后的异名端耦合磁器件，提出一种多维度建模与多目标优化方法。首先基于变换器电气参数模型和异名端耦合电感磁路特性，对磁心结构与绕组布局进行改进；其次建立变换器关于绕组匝数、磁柱气隙、磁柱边长以及开关频率的多维度模型，结合约束条件设计多目标优化流程，获取不同绕组匝数下变换器效率与磁器件占地面积、体积的非支配解，为磁器件参数设计提供可选范围；最后从工程实际出发选取最佳参数并制作集成磁器件。通过搭建28 V/12 V、168 W的实验样机对集成磁器件以及独立电感进行对比实验，得出优化后磁器件占地面积与体积缩减率分别为45.48%与43.66%，变换器额定效率提高0.9%，磁器件功率密度为8 020 W/in3（1 in3=1.638 71×10-5m3）的结果，验证了异名端耦合的优越性以及所提方案与设计流程的可行性。
关键词：交错并联Buck 异名端耦合 集成磁器件 多维度建模 多目标优化
航空航天、电动汽车、绿色数据中心等产业的快速发展，对中间级小功率非隔离降压开关电源的高效率、高功率密度、轻量小型化提出了新的要 求[1-3]。高效小型化开关电源不仅可以降低电源的体积和质量，也有利于提高能源利用效率。为了降低输出电流纹波，中间级变换器多采用多相交错并联Buck的拓扑结构，然而磁器件通常占据电源总体积的30%以上，是影响电源功率密度以及电源输出动态特性的重要因素[4-5]。为进一步减小磁器件的占地面积、体积和损耗，提高开关电源效率，科研人员对开关变换器中的磁器件展开了大量研究，其中，功率磁集成技术是一个有效的解决方案[6-8]。
将多个独立电感进行集成有利于提高变换器的效率和功率密度[9-10]。文献[11]通过分段式绕组将两个电感集成到一副EE型磁心上，减小了磁器件的体积、质量以及变换器的损耗，但该文献使用的是解耦的集成方式，相比独立电感，集成磁器件的体积和质量缩减程度有限。文献[12]利用电感的同名端耦合使开关管工作在零电压开通状态，减小了其导通损耗，但是会增大绕组的电流纹波以及其他的相关损耗，并不适用于小功率且绕组电流直流分量较大的场合。文献[13-14]对电感进行异名端耦合，实验表明异名端耦合在减小磁器件体积、提高变换器效率和相间均流度方面均有良好效果，但文献[13-14]所使用的磁心是在传统EE型磁心的基础上进行改进，因为磁心中柱的存在，集成磁器件相较独立电感的体积缩减还存在进一步提升的空间。
对于基于印制电路板（Printed Circuit Board, PCB）的变换器，平面集成磁器件的设计更加趋于规范化、流程化，其设计流程往往需要将占地面积等多种因素纳入考量范围[15]。在磁器件多目标优化设计中，文献[16-17]将多项参数作为变量，对集成磁器件的损耗进行建模与寻优，得到满足设计需求的参数数值，但并未考虑开关频率与耦合系数对损耗的影响。文献[18-20]将变换器效率作为约束条件，研究了集成磁器件体积与变换器效率之间的非支配解（Pareto front），但是忽略了绕组匝数对绕组损耗的影响以及绕组的交流损耗，导致损耗模型在高频下不够精确。因此，文献[16-20]由于损耗模型有关变量以及优化流程设计的局限性，并不能为磁器件的建模和优化提供理论指导。
为实现变换器效率、磁器件占地面积与体积的共同优化，本文基于两相交错并联Buck变换器，针对改进磁心结构与绕组布局后的异名端耦合磁器件，提出一种集成磁器件多维度建模与多目标优化方法。首先对变换器进行特性分析，得出其电气参数模型；其次基于异名端耦合电感的磁路特性分析，对其磁心结构以及绕组布局进行改进；再次围绕绕组匝数、磁柱气隙、磁柱边长以及开关频率建立变换器多维度模型，并结合约束条件设计多目标优化流程，获取变换器效率与磁器件占地面积、体积的非支配解；最后从工程实际的角度出发，选取最佳设计参数制作集成磁器件，并通过制作28 V/12 V、168 W的实验样机对集成磁器件以及独立电感进行对比实验，验证异名端耦合的优越性以及所提方案与设计流程的可行性。
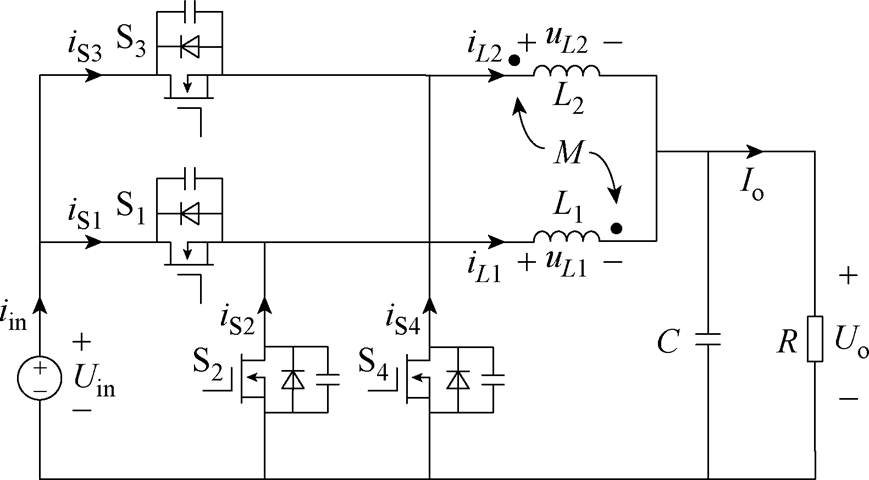
使用异名端耦合磁器件的两相交错并联Buck变换器拓扑如图1所示。图1中，Uin与Uo分别为输入、输出电压，vL1与vL2分别为集成磁器件的两相绕组电压，iL1与iL2为集成磁器件绕组电流，Io为负载电流，L1、L2为集成磁器件自感，M为互感，k为耦合系数。S1与S3为两相Buck变换器的主开关管，以180°相位差交错运行，S2和S4为同步整流管，R为变换器负载，C为变换器输出滤波电容。
图1 使用集成磁器件的两相交错并联Buck变换器拓扑
Fig.1 Topology of two-phase interleaved Buck converter with integrated magnetic device
当变换器工作在电感电流连续导通模式（Con- tinuous Conduction Mode, CCM）时，以D=0.5可将占空比划分为两个范围，两个范围内绕组电流以及主开关管驱动波形如图2所示。
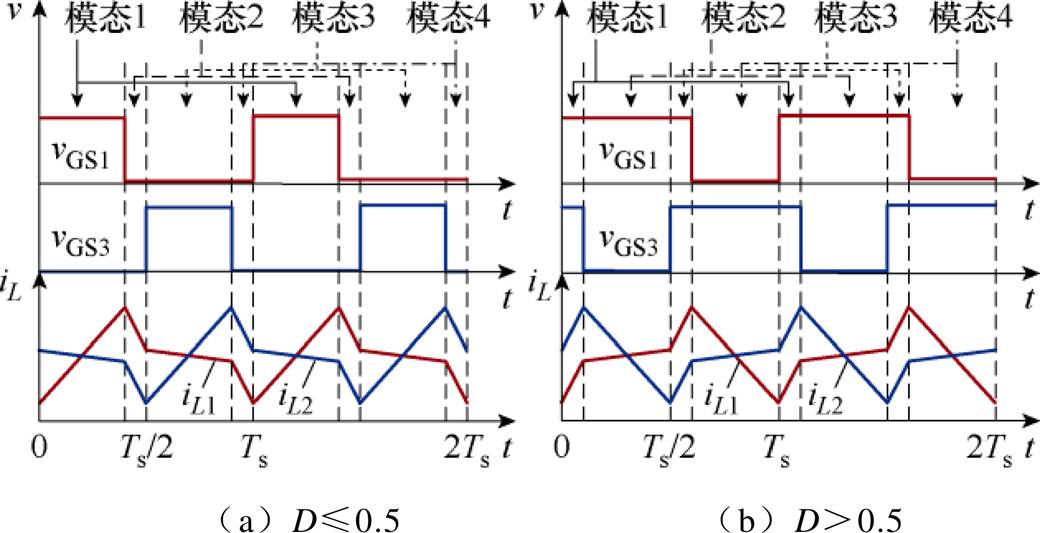
图2 不同占空比范围内驱动波形与电感电流波形
Fig.2 Driving waveforms and inductor current waveforms within different duty cycle ranges
由图2可见，每个占空比范围内变换器分为4个工作模态。当其中一相的主开关管开关状态发生变化时，另一相绕组电流由于异名端耦合的作用，其变化率会降低，进而电流纹波会减小。电流纹波的减小有利于降低集成磁器件的磁通密度和磁心损耗，以提高变换器的整体效率和功率密度。
当变换器工作在CCM时，磁器件绕组电压为
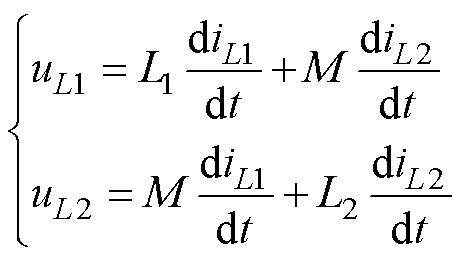（1）
假设自感L1=L2=L，定义等效模态电感等于模态绕组电压与电流变化率的比值，以两相耦合磁器件中的第一相为例，模态1～模态4分别对应4个等效模态电感，另一相情况相同。
由图2和式（1）可得，在不同的占空比范围内，耦合电感绕组一个开关周期内的等效稳态电感电流纹波分别取决于模态1～模态4的等效模态电感电流纹波，通过计算可得等效稳态电感表达式为
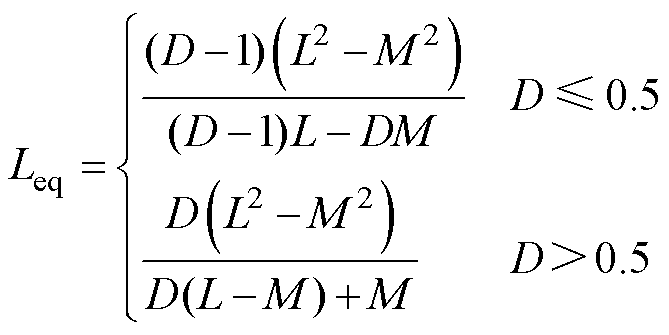（2）
同时可得绕组电流纹波为
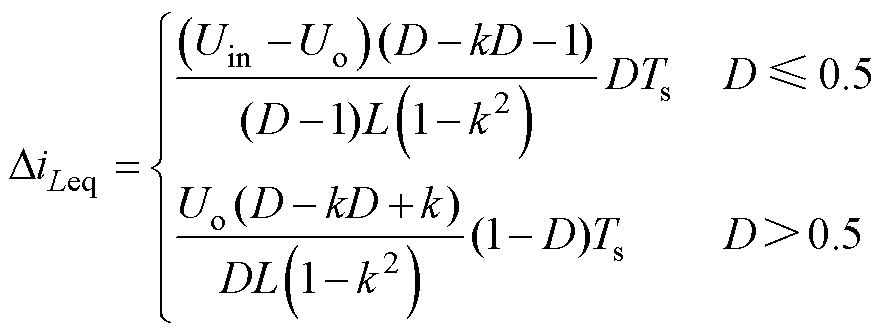（3）
式中，Ts为变换器开关周期。
当耦合系数k=0时，由式（3）可得非耦合电感L电流纹波的表达式，与式（3）对比可得耦合与非耦合电感绕组电流纹波之比为
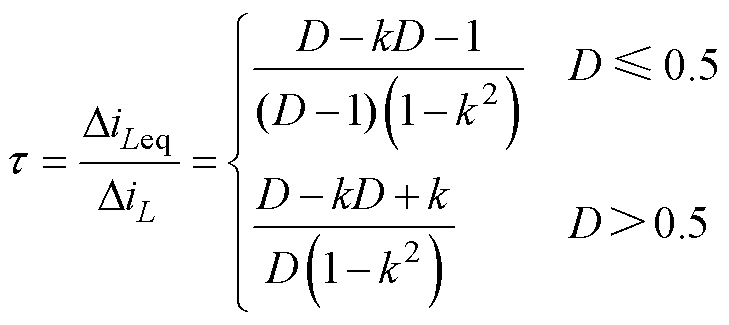（4）
式中，DiL为非耦合状态下电感绕组的电流纹波。
图3所示为不同占空比以及耦合系数下电流纹波比值t。图3中，在一定D和k的变化范围内t＜1，且t在k=-1，D=0.5时取最小值。可见异名端耦合在一定参数设计范围内能够减小电感绕组纹波，以降低纹波带来的损耗。
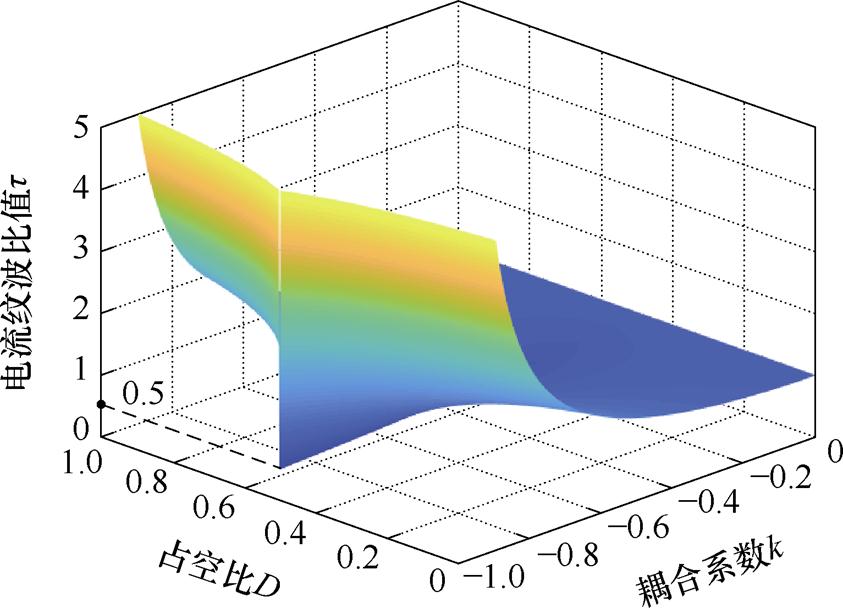
图3 不同占空比和耦合系数下耦合与否电流纹波之比
Fig.3 Current ripple ratio of coupled and uncoupled inductors in different duty cycles and coupling coefficients
同时，图3还可以表示不同占空比以及耦合系数下耦合前电感值L与耦合后等效稳态电感值Leq之比。
通过上述分析可知，对于异名端耦合的设计应使得稳态占空比接近0.5，同时耦合程度在条件允许时应尽量增大。对于使用耦合电感作为集成磁器件的Buck变换器，合理的参数设计在抑制电感电流纹波、降低磁器件损耗的同时，有利于减小开关器件的通态损耗、绕组匝数以及耦合电感体积，能够提高变换器的效率，实现更高的功率密度。
集成磁器件的优化包含结构性改进与参数寻优，为进一步减小磁器件的占地面积与体积，本文围绕一般EE型磁心展开分析，基于分析结果合理改进其磁心结构与绕组布局，得到新型磁器件设计。同时为了对改进后的磁器件进行进一步参数优化，本文对磁器件的各项特征数值进行多维度建模。
为了使结构改进设计和参数优化流程更具现实意义，本文给出两相交错并联Buck变换器的参数要求见表1，表1中，1 in3=1.638 71×10-5m3。
表1 两相交错并联Buck变换器参数要求
Tab.1 Parameter requirements for two-phase interleaved Buck converter
参 数数 值 输入电压Uin/V28 输出电压Uo/V12 额定负载电流Io/A14 参考独立电感Lsep/mH2.2 磁器件最低功率密度/(W/in3)5 000
2.2.1 磁阻模型与磁心结构改进
在平面磁器件的设计中，将气隙开在磁心两个边柱以及中柱的EE型磁心被广泛采用。如图4所示为基于传统EE型磁心的异名端耦合电感绕组结构与其磁通正方向示意图，L1与L2为绕制在边柱上的线圈与磁心构成的两相电感，iL1与iL2为两相电感的绕组电流，l为磁心窗口高度，磁柱有效截面是边长为le的正方形，gs为磁心两个边柱气隙长度，gm为磁心中柱气隙长度，F11与F22分别为L1和L2产生的磁通。
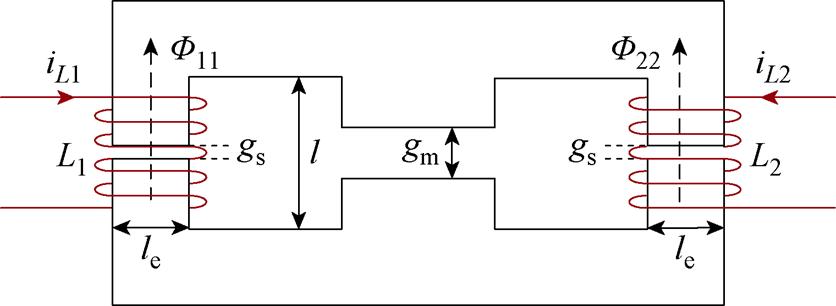
图4 EE型磁心电感绕组与磁通正方向示意图
Fig.4 Schematic diagram of EE-type magnetic core
根据图4可得使用EE型磁心的耦合电感等效磁路模型如图5所示。图5中，R1、R2与R3分别为磁心三个磁柱的等效磁阻，N1与N2为两个边柱上的绕组匝数，F1、F2与F3分别为绕组在三个磁柱上产生磁通的叠加，N1iL1与N2iL2分别为两个绕组在各自卷绕磁柱上产生的磁动势，两个磁心边柱的截面积为Ae，磁心中柱的截面积为2Ae。
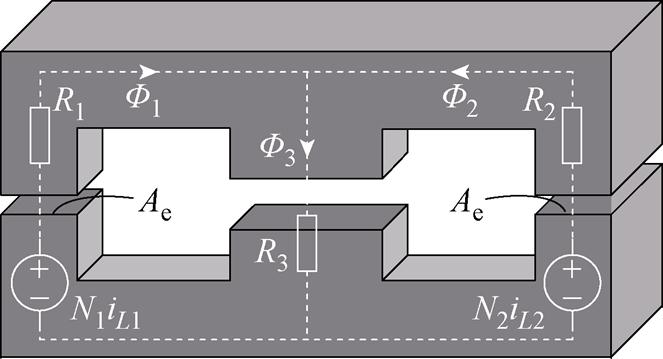
图5 EE型磁心耦合电感等效磁路模型
Fig.5 Equivalent magnetic circuit model of coupled inductor with EE-type magnetic core
结合图5与磁路的欧姆定律，可以得到两个磁心边柱上的磁通表达式为
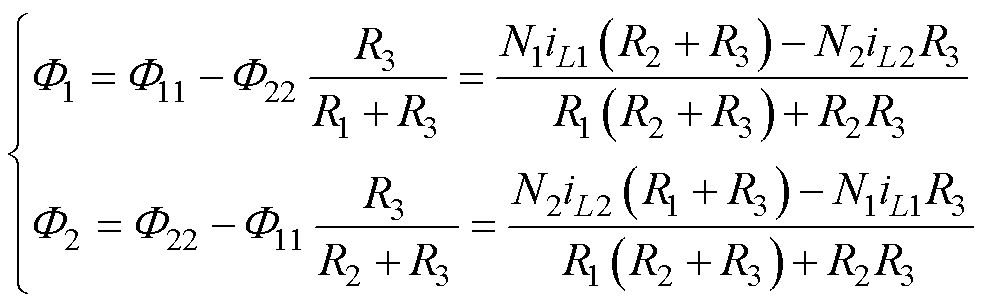（5）
将法拉第电磁感应定律应用到式（5）中，可得
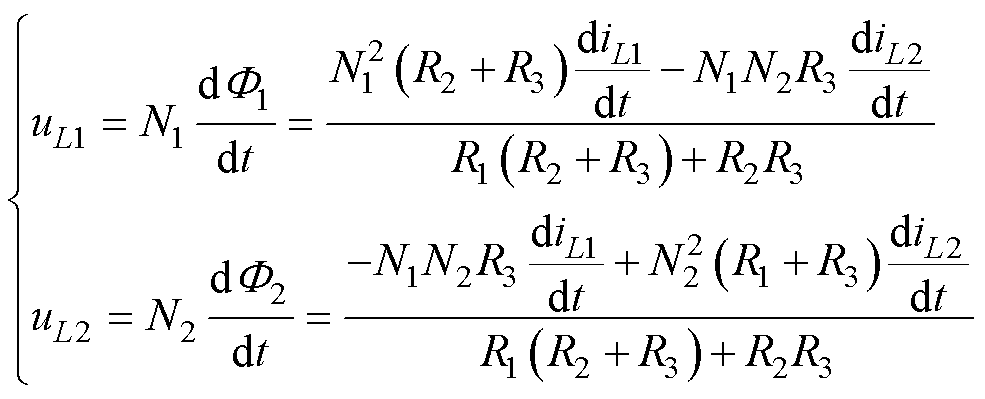（6）
为了设计方便，两个绕组的匝数设置为相同值N1=N2=N，如此两个磁心边柱的等效磁阻相同，即R1=R2=R。对比式（1）与式（6），可得两个绕组的自感与其之间互感表达式为
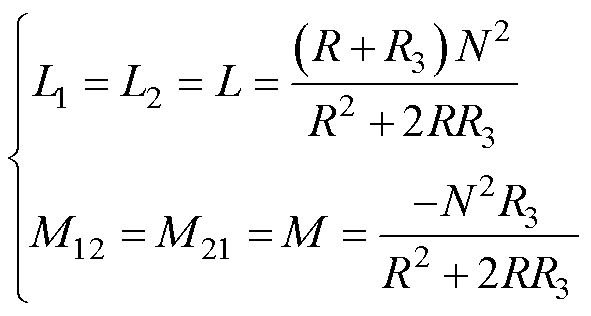（7）
参考图4和图5，可得磁柱磁阻为
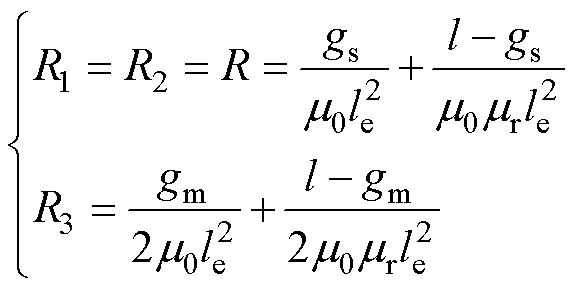（8）
式中，m0为真空磁导率；mr为磁心材料相对磁导率。
结合式（7）与式（8），可得耦合系数k为
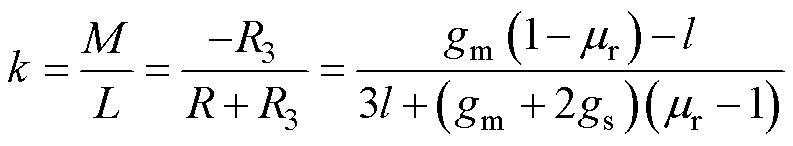（9）
考虑到集成磁器件等效稳态电感Leq的参考数值是独立电感Lsep，将Leq=Lsep代入式（2），结合式（7）～式（9），在一定的气隙变化范围内绘制耦合系数随两个气隙的变化率，如图6所示。本文采用的磁性材料为中国电科某研究所的CETC9R53，其相对磁导率可通过数据手册获取。
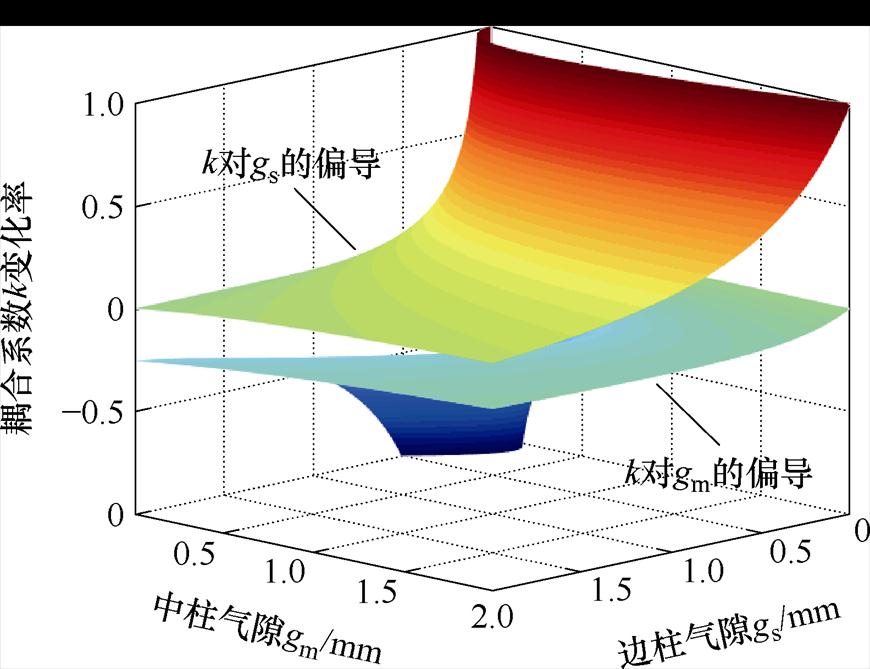
图6 耦合系数变化率随气隙变化
Fig.6 Image of coupling coefficient varying rate with air gap variation
由图6可见，在所有边柱气隙gs变化范围内，当中柱气隙gm＞0.75 mm时，耦合系数k随gm的变化率接近0，而一般PCB平面磁器件的气隙长度大于0.75 mm。因此，对于一般EE型平面磁器件而言，可以取消其磁心中柱，只将气隙开在两个磁心边柱上。同时为了减少高频工作时的漏磁通，将磁心上下平面周向延伸，形成能够覆盖绕组的磁心盖板。新型平面磁心设计如图7所示。
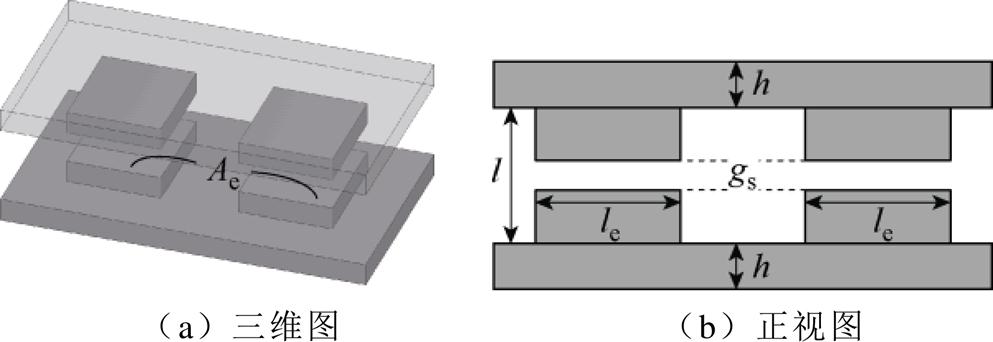
图7 新型平面磁心设计
Fig.7 Novel magnetic planar core design
对于图7所示新型平面磁心设计，每一相磁心磁路磁阻Rcore和气隙磁阻Rgap分别为
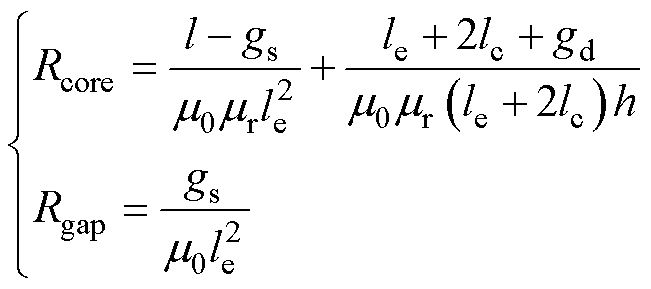（10）
式中，lc为平面PCB的绕组宽度；gd为两相电感的PCB绕组间距；h为磁心磁板厚度。
结合式（10）与磁路欧姆定律，可得新型平面磁心两相的自感与两相之间的互感表达式为
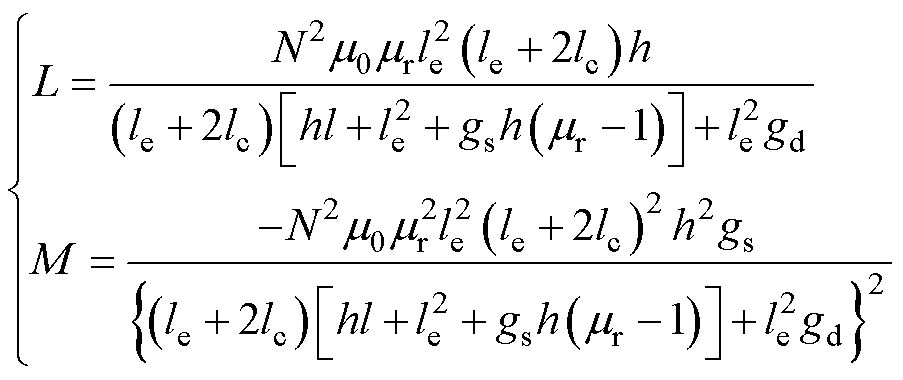（11）
利用有限元仿真软件在N=5、l=2 mm、le与gs在一定范围内变化的条件下，对式（11）进行仿真证明，结果如图8所示。由图8可见，仿真结果与式（11）计算所得数值误差小于0.5 mH，证明了式（11）的正确性，为优化流程提供可行的理论前提。
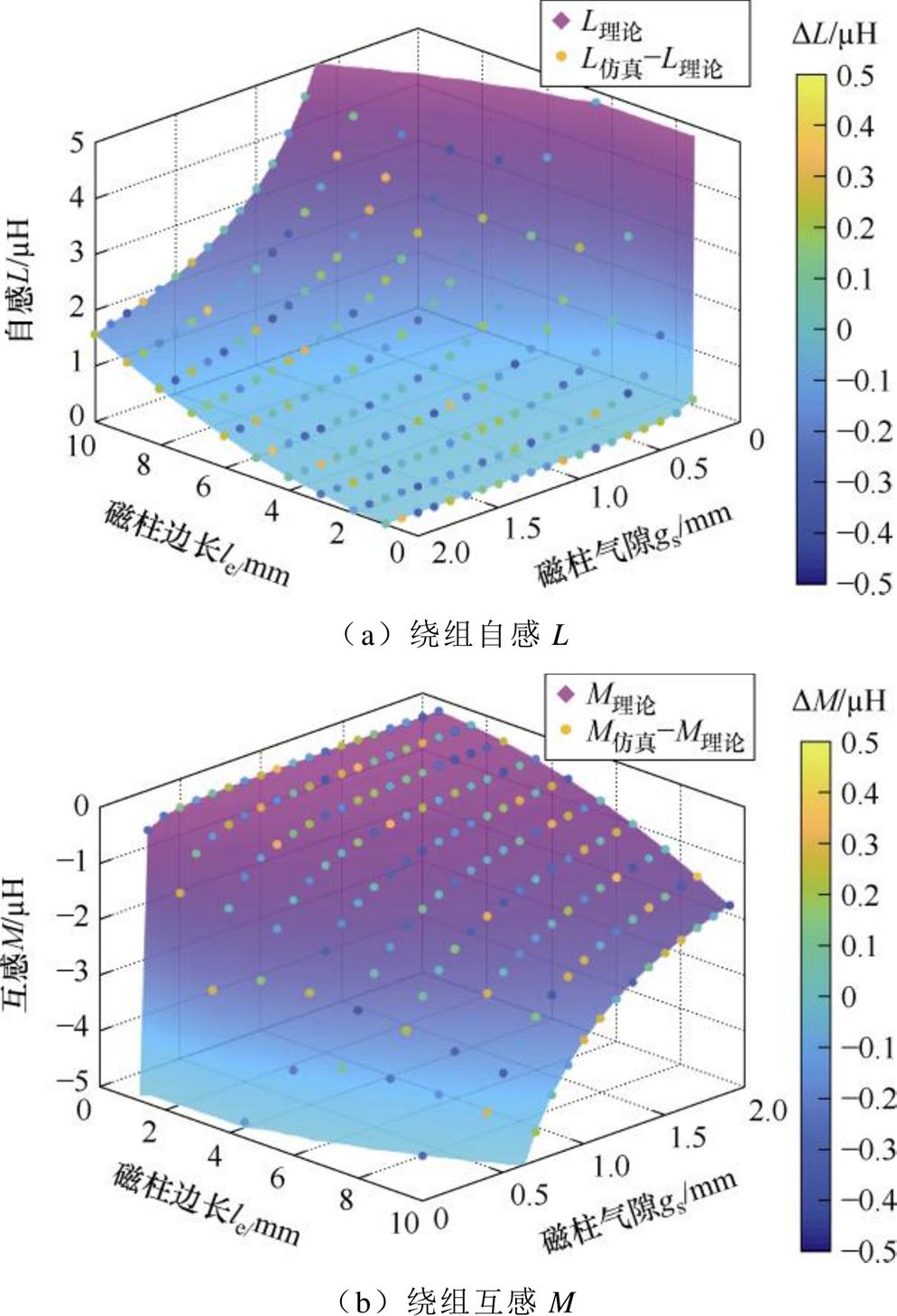
图8 新型平面磁心参数表达式仿真证明
Fig.8 Simulation verification of parameter expressions for new planar magnetic cores
2.2.2 集成磁器件体积与占地面积建模
为了更加符合新型磁心结构设计，增强磁屏蔽作用，在此进一步对绕组布局做一定的改进。区别于传统的绕组匝间连接布局设计，将绕组匝间连接过孔放置于磁心磁板覆盖范围内，改进后绕组PCB布局示例如图9所示。其中，为了简化绕组损耗建模与计算难度，考虑一定散热条件，将绕组宽度lc设计为1.5 mm，每层厚度2 oz（1 oz=0.035 mm），三层并联，同时设定gd=1.5lc。
经过对上述新型平面磁心以及改进后绕组布局设计进行分析，可得新型平面磁器件占地面积为
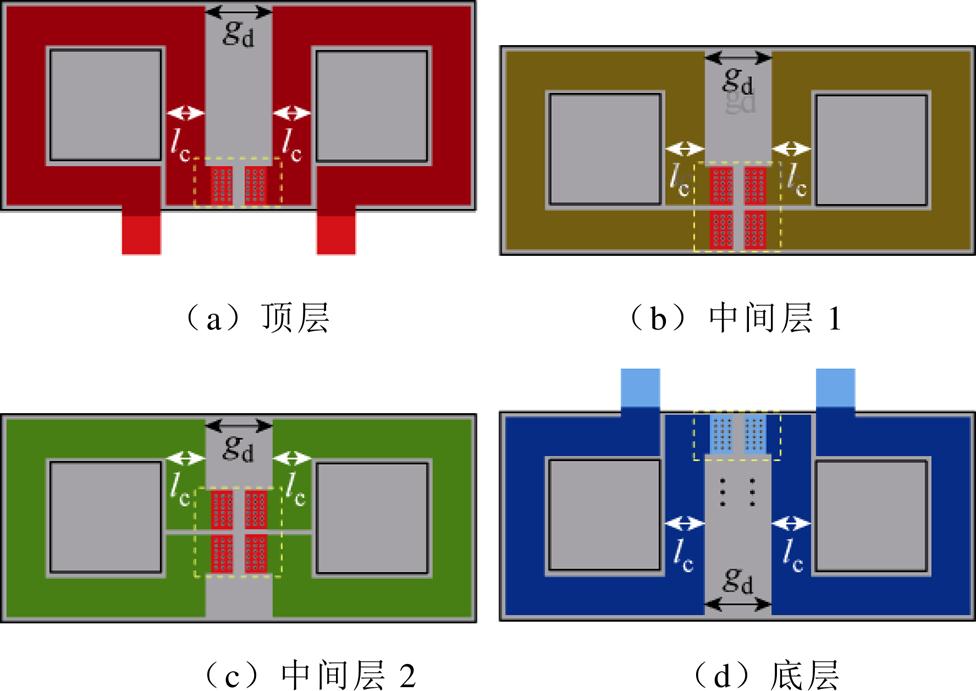
图9 改进后绕组PCB布局示例
Fig.9 Example of optimized winding PCB layout
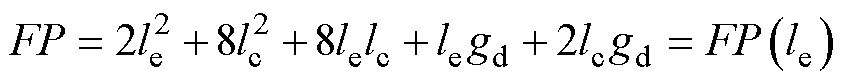（12）
结合式（12），对比图5与图7可得，当磁柱截面积为Ae时，新型平面磁器件与EE型平面磁器件占地面积FP的比值如图10所示。可见随磁柱边长le的变化，新型平面磁器件的占地面积较EE型磁器件减小明显，证明了新型平面磁器件设计在减小占地面积和提高功率密度方面的积极作用。
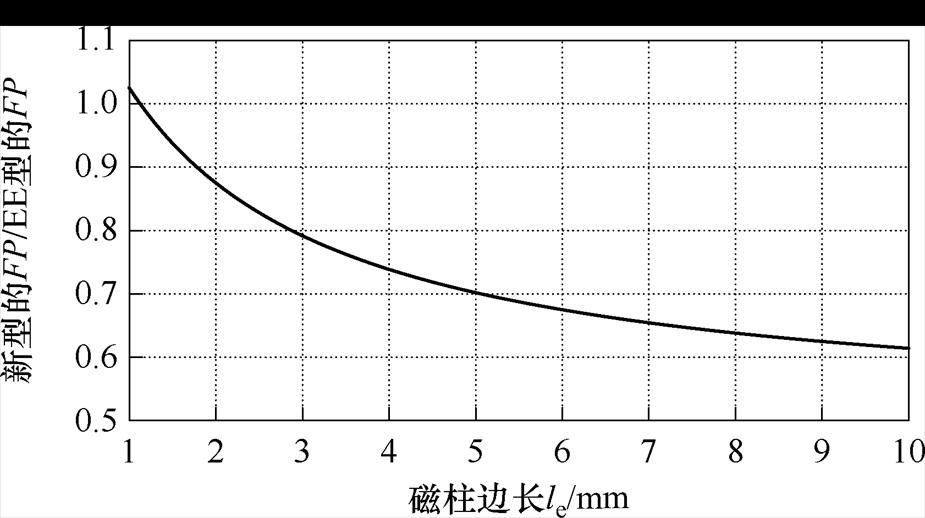
图10 新型平面磁器件与EE型平面磁器件FP比值
Fig.10 The ratio of footprint between novel planar magnetic device and EE-type planar magnetic device
根据图7、图9可得新型平面磁器件磁柱体积Vs、上下磁板体积Vb以及总体积Ve分别为
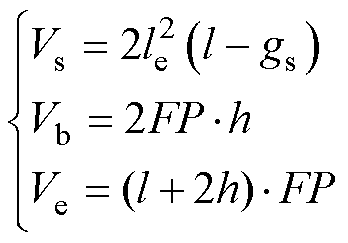（13）
所有的模型以新型平面磁器件结构和改进后绕组布局为基础构建，本文变换器的损耗主要包含新型平面集成磁器件的损耗和开关器件的损耗，其中集成磁器件的损耗由磁心损耗和PCB绕组损耗构成。
2.3.1 磁心磁通密度建模
由于变换器在高频工作时，磁心损耗与磁通密度的变化量有关联，同时磁通密度的大小也必须符合磁性材料的特性范围。因此，在对相关损耗进行建模之前，首先对磁心的磁通与磁通密度进行分析。
依据法拉第电磁感应定律，磁心两个磁柱中的直流磁通Fsdc与交流磁通DFs表达式分别为
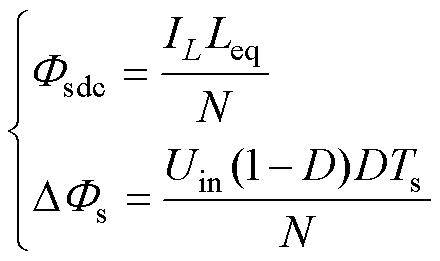（14）
式中，N为绕组匝数；IL为单相绕组电流平均值，IL=Io/2。
由式（14）可得，磁柱交流磁通密度峰值DBs、直流磁通密度Bs_dc以及最大磁通密度Bmax分别为
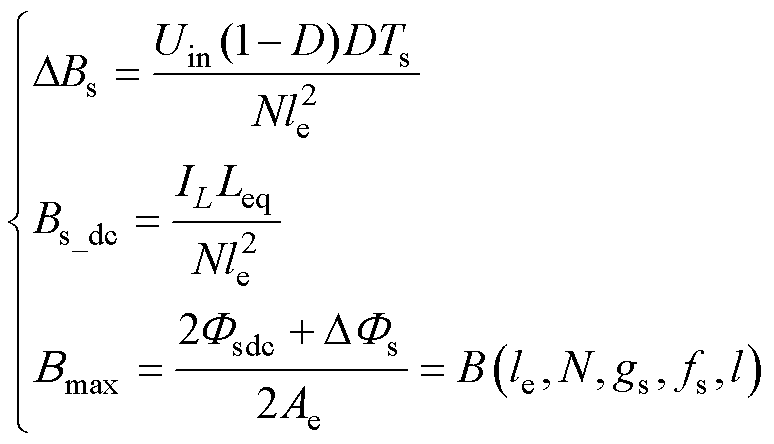（15）
在异名端耦合的作用下，两个绕组电流产生的磁通在上下磁板中因相互削减而呈不均匀分布。将边柱磁通进行交错作差，可以得到上下磁板的交流磁通DFb为
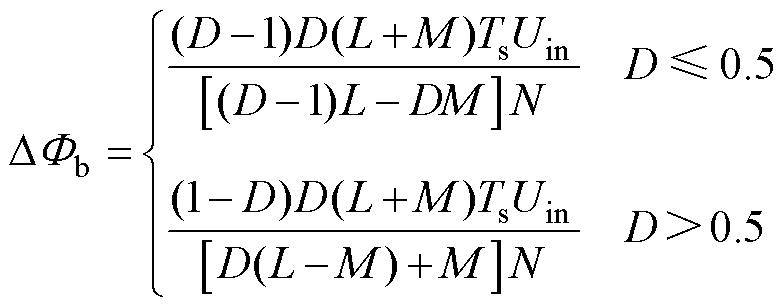（16）
在保证磁心不会饱和的前提下，为了使磁心磁通密度分布均匀，设计上下磁板的最大磁通密度DBb与磁柱的最大磁通密度一致，即DBb=Bmax，同时可得磁心磁板厚度h表达式为
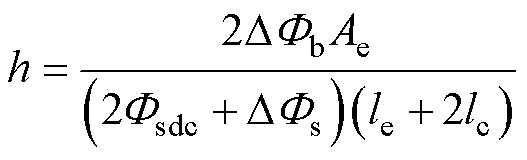（17）
2.3.2 损耗建模与效率计算
由于两相交错并联以及绕组异名端耦合的原因，绕组电流呈分段线性化，且叠加直流分量。因此，本文采用广义Steinmetz公式，通过分段积分的方式求解磁心损耗。
定义Ps_unit为单位体积的磁柱磁损，Zb为电流直流分量作用下的增量系数，Ki为非线性效应的修正系数，B(t)为磁通密度瞬时值，DBs为交流磁通密度幅值，K、a、b为Steinmetz公式系数，K1、K2为与磁材有关的常系数，经拟合得来。由此得磁心磁柱的单位体积损耗计算式为
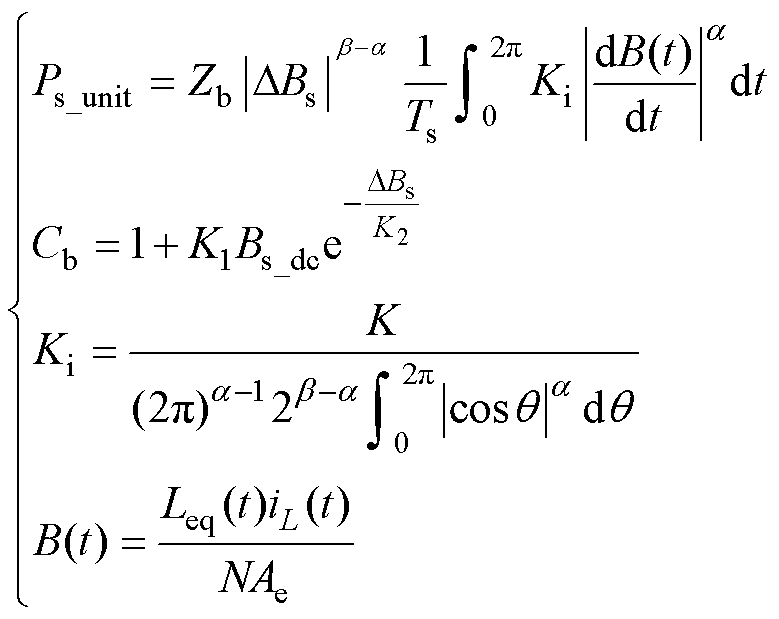（18）
磁心上下磁板单位体积的损耗Pb_unit计算方式与式（18）相似。
结合式（15）与式（18）可得，集成磁器件的磁心损耗为
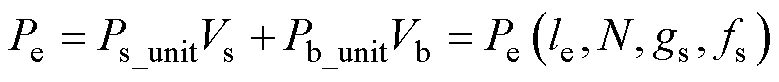（19）
对于PCB绕组而言，其直流损耗为
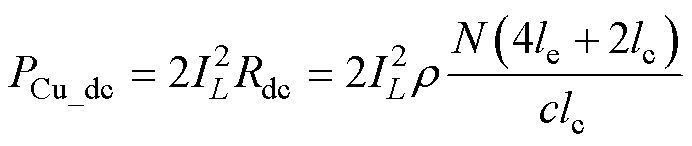（20）
式中，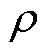
为铜的电阻率；c为每匝铜厚，c=6 oz= 210 mm。
除直流损耗外，由趋肤效应、邻近效应和气隙扩散引起的交流损耗也不可忽视。根据高频平面绕组二维损耗模型的相关分析，单位长度的绕组交流损耗表达式为
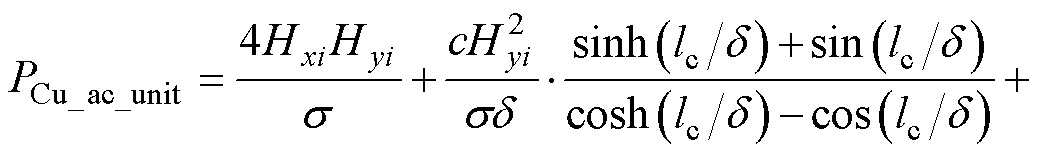
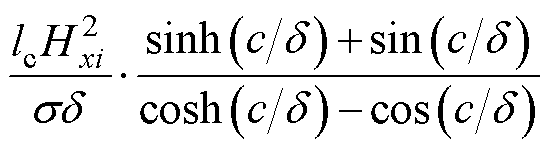（21）
其中，横纵坐标方向的两个边界条件与相关参数为
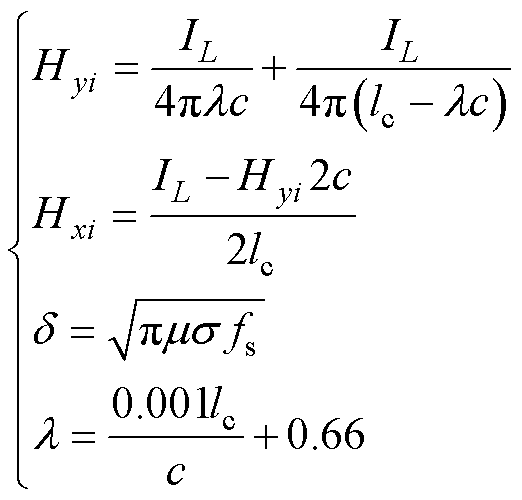（22）
式中，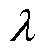
为一个通过拟合得到的比例系数；
为铜的电导率；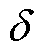
为趋肤深度；
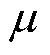为铜的磁导率。
结合式（20）～式（22）可得，集成磁器件的绕组损耗为
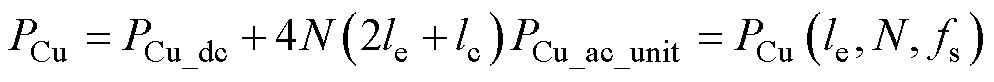（23）
变换器每相包含两个互补导通的开关管，高频工作时开关器件的损耗包含导通损耗Pon、关断损耗Poff、通态损耗Pds、输出电容损耗PCds以及驱动损耗Pdr。本文所使用的开关管为GaN Systems的GS61004B，变换器每相的开关器件损耗为
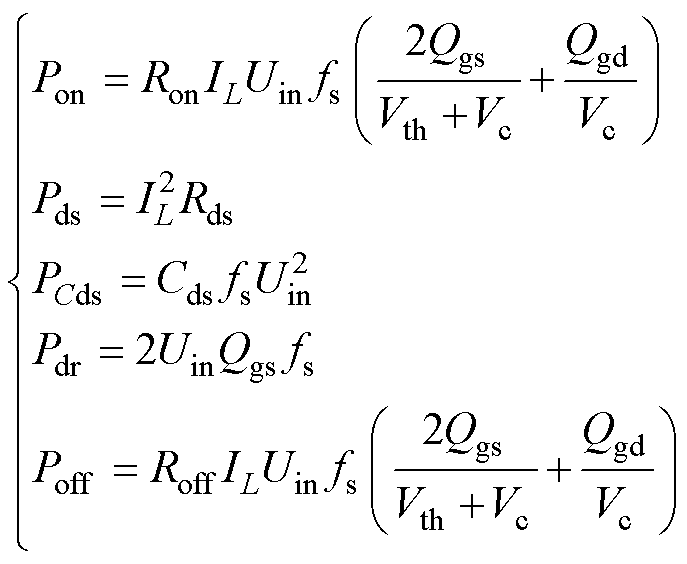（24）
式中，Ron为导通驱动电阻，Ron=2 W；Roff为关断驱动电阻，Roff=5 W；开关管寄生参数包含栅源电荷Qgs、栅漏电荷Qgd、阈值电压Vth、米勒平台电压Vc、输出电容Cds、通态电阻Rds，以上各项寄生参数的数值均可通过开关管数据手册获取。由式（24）可得，开关器件的损耗Pmos为
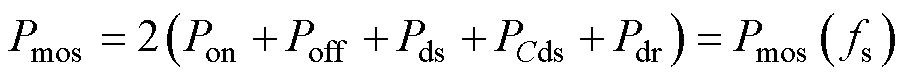（25）
基于式（19）、式（23）与式（25）可得，变换器额定的效率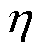
可以表示为
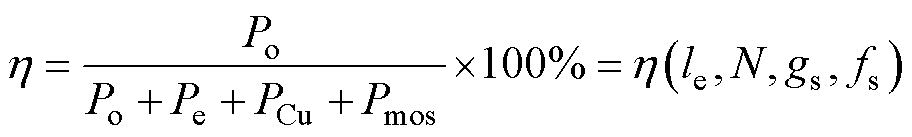（26）
在PCB平面磁器件设计中，往往需要就磁器件体积和占地面积、变换器效率以及磁心饱和度等外向特征进行综合考量。因此本文将集成磁器件的体积和占地面积按照需求进行加权求和，并通过不断调整额定最低效率约束，得到效率与加权求和结果的非支配解，最终根据实际情况选取最佳参数，实现三者共同优化，使参数权衡具有实际意义。
本文所使用的磁心磁材是中国电科某研究所提供的CETC9R53，该材料饱和磁通密度为0.45 T，为避免磁心饱和，在此取磁通密度限值Blim=0.35 T。
结合式（15）以及式（26）可得，磁器件占地面积和体积为优化目标，效率、磁通密度以及自感互感关系为约束条件。由于磁器件占地面积和体积的数值变化范围以及量纲不同，通过式（27）所示最小-最大归一化方法将两个函数值线性地映射到[0, 1]的范围内。
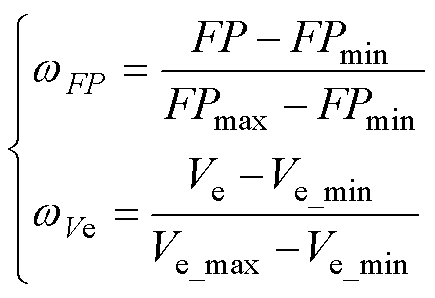（27）
式中，FPmin、FPmax、Ve_min、Ve_max分别为占地面积和体积在所有参数变化范围内的最小值和最大值，其值依次序为41 mm2、367 mm2、62 mm3、3 339 mm3。
在进行参数迭代时，第j次迭代效率约束下的集成磁器件优化函数为
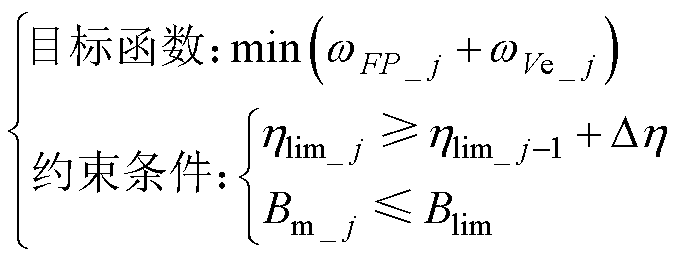（28）
式中，wFP_j与wVe_j为第j次效率约束下的磁器件的占地面积和体积的归一化加权值；Dh为效率约束的增量；Bm_j为第j次效率约束下的磁心最大磁通密度。
由函数表达式（12）、式（13）、式（15）、式（26）及式（28）可知，集成磁器件的设计目标函数以及约束函数是与磁柱截面积边长le、绕组匝数N、磁柱气隙gs以及开关频率fs相关联的。
由于绕组匝数N可变数量少，因此在固定N与效率约束hlim的情况下对余下3个参数进行迭代，获取当前效率约束下的最优目标函数，再对hlim和N进行迭代，获取不同匝数下效率约束与目标函数的非支配解。参数的迭代范围和增量见表2。
表2 参数的迭代范围和增量
Tab.2 Iteration range and increment of parameters
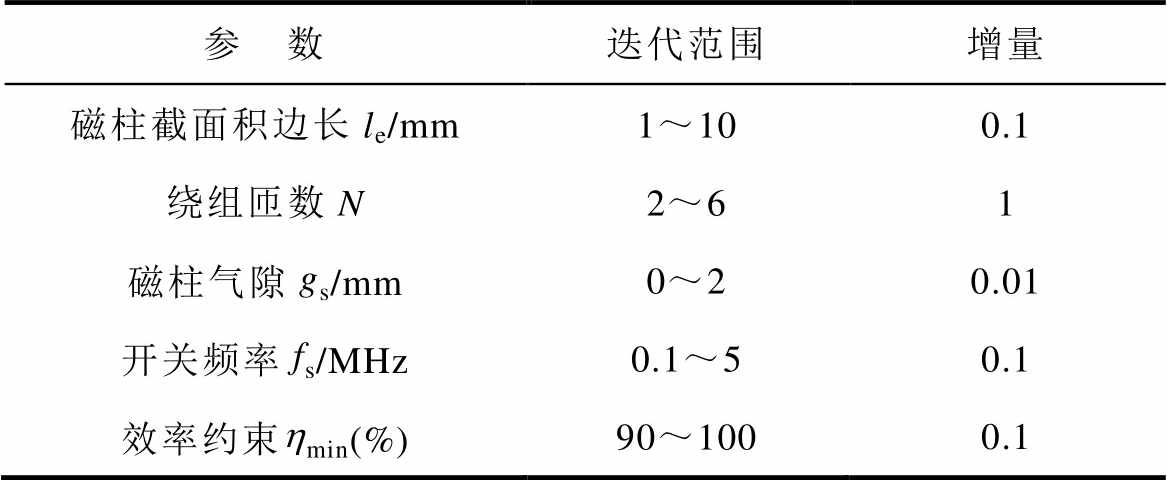
参 数迭代范围增量 磁柱截面积边长le/mm1～100.1 绕组匝数N2～61 磁柱气隙gs/mm0～20.01 开关频率fs/MHz0.1～50.1 效率约束hmin(%)90～1000.1
集成磁器件的多目标优化流程如图11所示。通过多个运算迭代回路，计算出每个绕组匝数与效率约束下符合各项约束条件的目标函数最小值，即非支配解，并记录各项参数数值。
如图12所示为多目标优化结果，图中展示了不同匝数下效率约束与占地面积和体积二者加权值的非支配解。由图12可见，相同效率约束下，目标函数值随着匝数的增大而减小，而且相较于N=2与N=3，N=3与N=4之间加权值的变化并不明显，同时N=5与N=6并不能实现更高的效率，考虑到PCB的设计难度与制作成本，选取绕组匝数N=3。
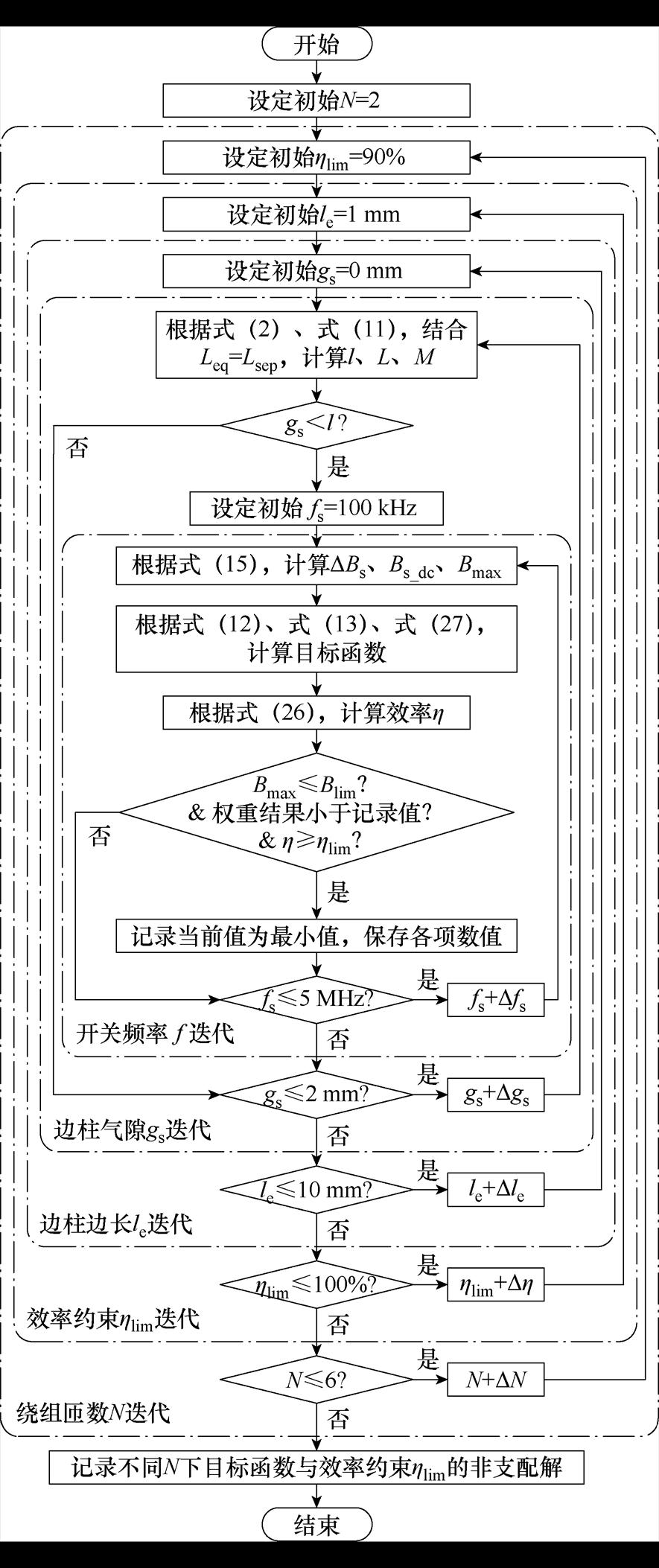
图11 集成磁器件多目标优化流程
Fig.11 Multi-objective optimization process for integrated magnetic device
进一步地，将N=3的变化曲线通过线性拟合划分为四个分区，可见在分区3、4中，目标函数值随效率约束的变化速率增大。综合考虑变换器效率、磁器件的占地面积与体积，选取效率约束hlim=94.4%、目标函数wFP+wVe=0.3的点进行磁器件的设计。
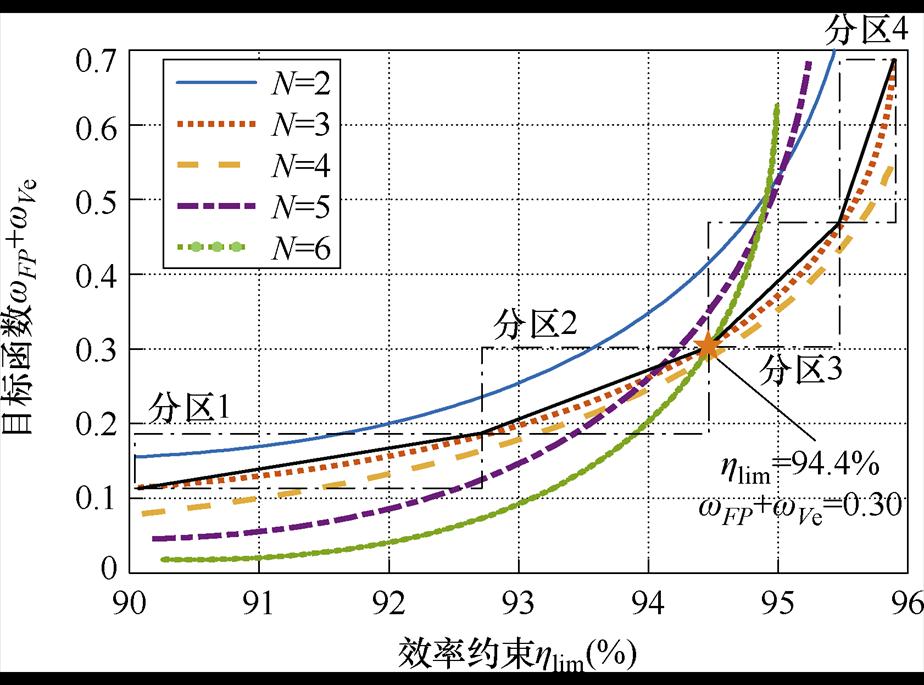
图12 不同匝数下效率约束与加权结果的非支配解
Fig.12 Pareto fronts of efficiency constraints and weighted results under different turns
图13所示为N=3、hlim=94.4%时所对应的全部设计结果。
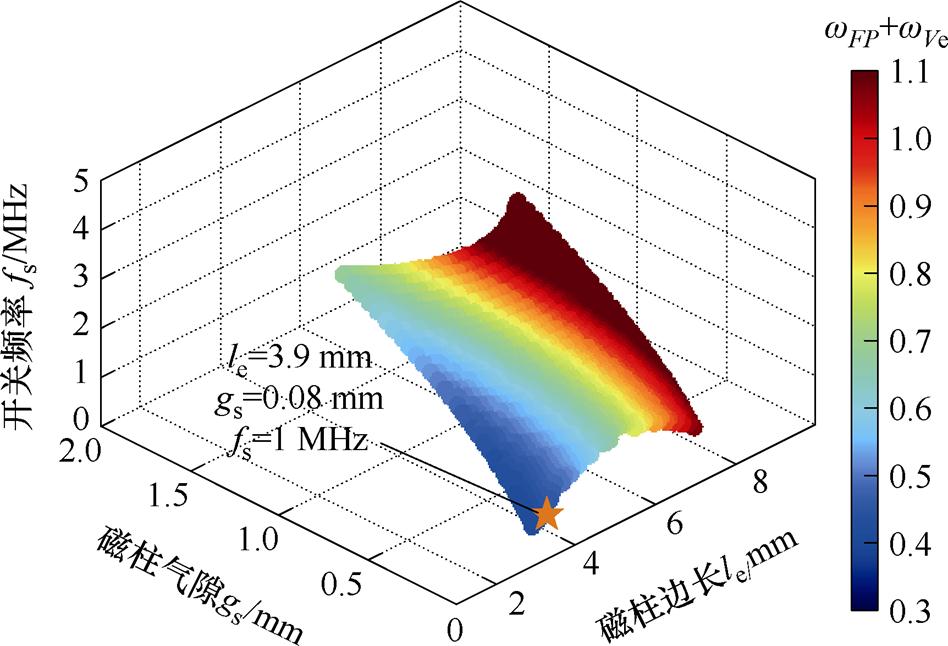
图13 选定匝数与效率约束下的加权值设计结果
Fig.13 Design results of weighted values under selected turns and efficiency constraints
图13中标注了匝数N=3、效率约束hlim=94.4%时所对应全部结果中的最小值点，在此基础上所得出的集成磁器件的关键参数见表3。
表3 集成磁器件关键参数设计结果
Tab.3 Design results of key parameters for integrated magnetic device
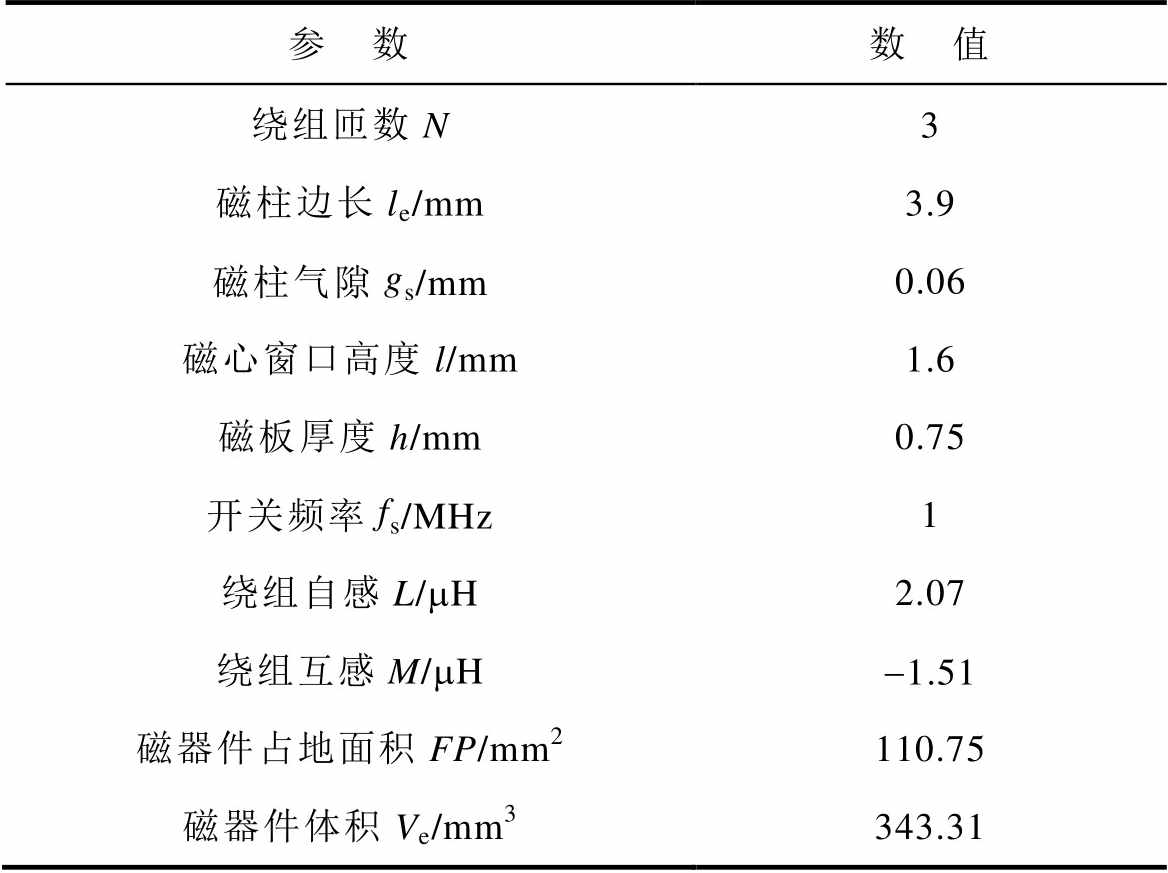
参 数数 值 绕组匝数N3 磁柱边长le/mm3.9 磁柱气隙gs/mm0.06 磁心窗口高度l/mm1.6 磁板厚度h/mm0.75 开关频率fs/MHz1 绕组自感L/mH2.07 绕组互感M/mH-1.51 磁器件占地面积FP/mm2110.75 磁器件体积Ve/mm3343.31
表3所示自感值L与Leq的比值符合图3描述，证明优化结果具有理论正确性。按照上述参数构建多目标优化后的磁器件模型，使用Ansys对磁器件进行有限元仿真，磁通密度分布如图14所示。可见其磁通密度分布较均匀，且不超过0.3 T，符合设计要求与磁通密度约束。
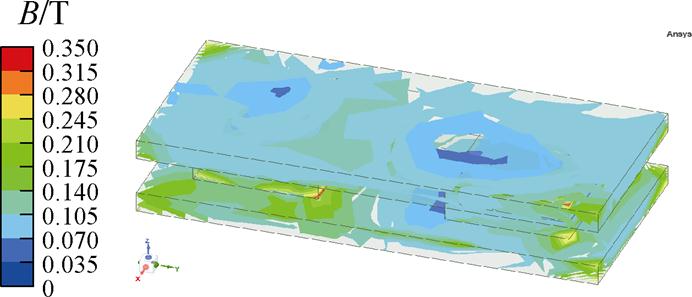
图14 优化后磁器件磁通密度有限元仿真结果
Fig.14 FEM simulation results of magnetic flux density in optimized magnetic core
观察磁板周向延伸与否情况下磁心附近的磁通密度分布，如图15所示。可见相较于磁板不延伸，延伸的磁板使得磁器件附近磁通密度有所减小，因此可以提高磁器件高频运行时的磁屏蔽作用，减小其对附近电子器件的影响，提高变换器工作稳定性。
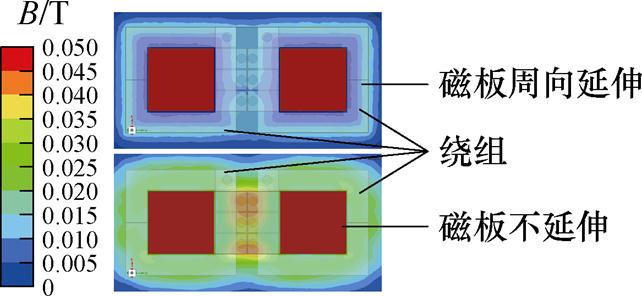
图15 磁板周向延伸与否时磁心附近磁通密度
Fig.15 Magnetic flux density near the magnetic core when the magnetic plate extends or not
图16所示为基于上述多目标优化所得参数制作的磁心与基于面积乘积（Area Product, AP）法设计的独立电感EQ磁心。
图16 独立电感EQ型磁心与多目标优化所得新型磁心
Fig.16 Independent inductance EQ-type magnetic core and novel magnetic core obtained by optimization
图16中两种磁心的最大磁通密度以及绕组参数设计均一致，设置独立电感磁心中柱开气隙，且独立电感Lsep=2.2 mH。经过对比可得，在相同工作条件下，优化后新型磁器件占地面积与体积缩减率分别为45.48%和43.66%，且优化后新型磁器件功率密度达到8 020 W/in3，符合参数设计要求，证明了异名端耦合的优越性和优化流程设计的合理性。
基于表1设计两相交错并联Buck变换器样机实验平台如图17所示。
图17 两相交错并联Buck变换器样机实验平台
Fig.17 Prototype of two-phase interleaved Buck converter
实验平台参数见表4。利用该样机对两种磁器件进行对比实验。
表4 实验平台参数
Tab.4 Parameters of the experimental platform
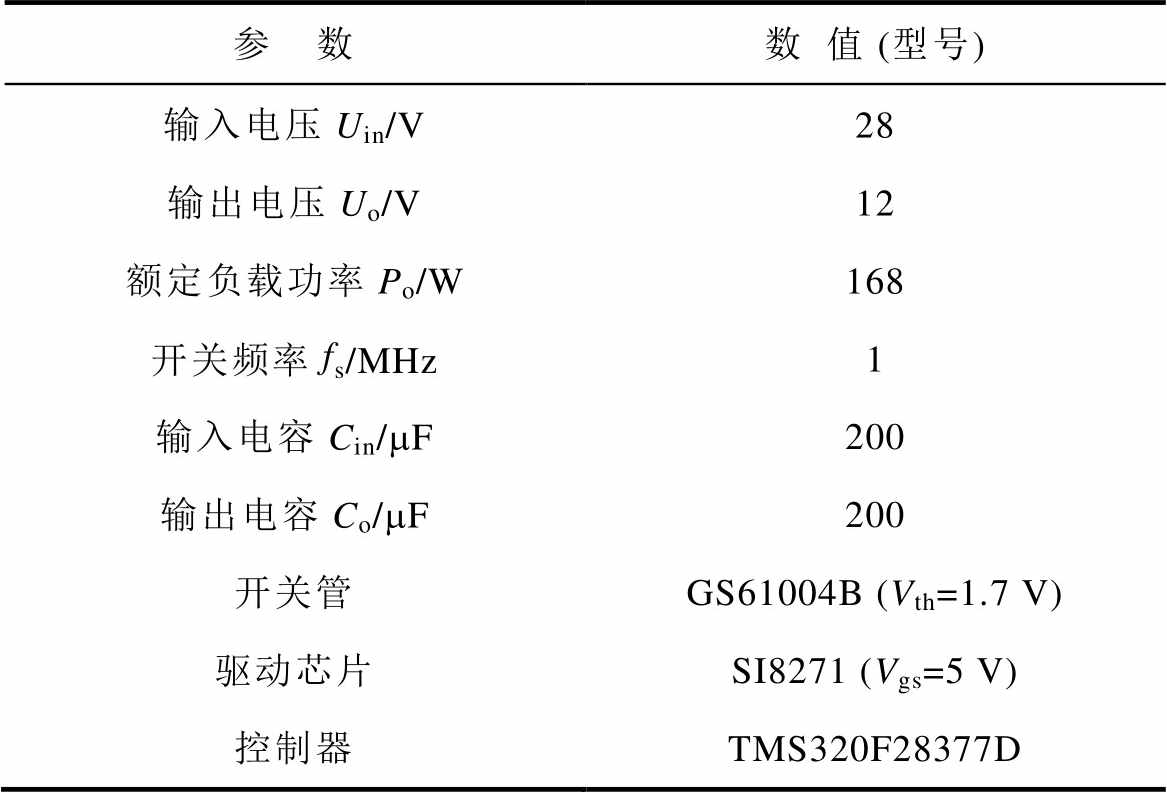
参 数数值 (型号) 输入电压Uin/V28 输出电压Uo/V12 额定负载功率Po/W168 开关频率fs/MHz1 输入电容Cin/mF200 输出电容Co/mF200 开关管GS61004B (Vth=1.7 V) 驱动芯片SI8271 (Vgs=5 V) 控制器TMS320F28377D
图18所示为使用两种磁器件时变换器的输出电压、输出电流以及两相绕组电流波形。由图18可见，两相电感电流以相位差180°交错运行，图18b中的绕组电流在异名端耦合的影响下分为4段，与图2所示相符，图18a与图18b中的绕组电流纹波DiL一致，均为3.15 A，符合变换器参数特性，同时符合集成磁器件的设计和优化目标。
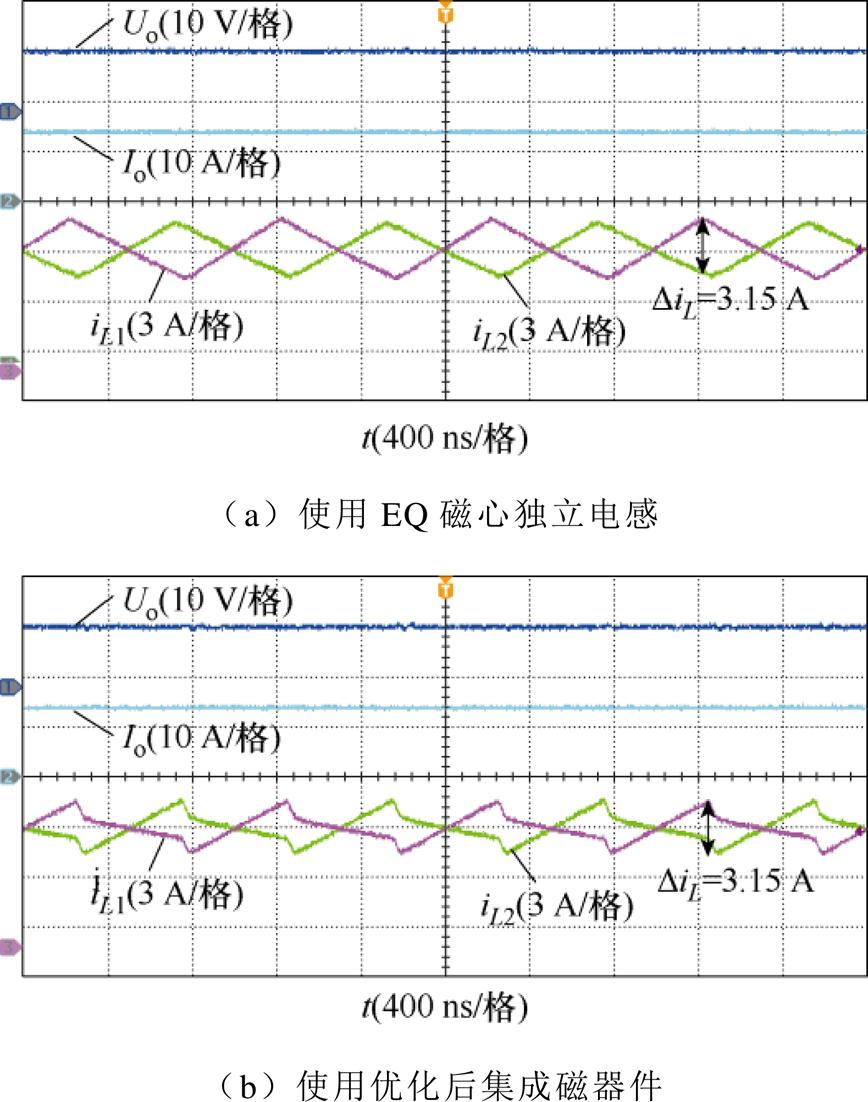
图18 两相交错并联Buck变换器满载实验波形
Fig.18 Full load experimental waveforms of two-phase interleaved Buck converter
在表3参数的基础上，分别对输入电压变为21 V以及气隙变为1 mm两种情况进行实验，波形如图19所示。可见，Vin=21 V时，稳态占空比D=0.57，两相电流纹波与Vin=28 V时相同，符合图3以及式（2）描述；集成磁器件气隙gs=1 mm时，相电流纹波为5.41 A，符合式（2）以及式（11）的理论计算。图19证明了集成磁器件相关理论表达式与推论的正确性和合理性。
图19 两种特殊情况下变换器实验波形
Fig.19 Experimental waveforms of converters under two special circumstances
使变换器按照表3参数运行，分别观察使用两种不同磁器件时变换器的效率，同时对集成磁器件在开关频率fs=0.5 MHz以及2 MHz时的效率进行记录，使用不同磁器件时两相交错Buck变换器效率如图20所示。
由图20可见，变换器按照表3参数工作在额定负载时使用两种磁器件均能满足所设计的效率约束，同时使用新型磁器件的效率略高于使用独立电感的效率，二者分别为95.2%和94.3%。
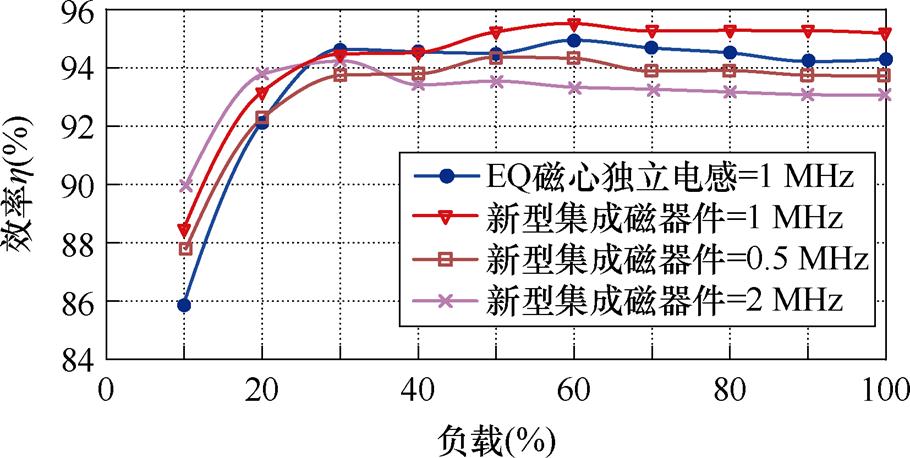
图20 使用不同磁器件时两相交错Buck变换器效率
Fig.20 Efficiency of two-phase interleaved Buck converter using different magnetic devices
此外由图20所示，使用优化后新型磁器件的效率总体上优于使用EQ型磁心的独立电感，这是因为虽然二者的绕组电流纹波相同，但在异名端耦合的作用下，新型磁器件的绕组电流有效值更小，其所带来的相关损耗更小，同时在相同的磁通密度工作情况下，新型磁器件的占地面积和有效体积更小，因此其磁心损耗也相对较小。相比之下，fs=0.5 MHz时磁器件绕组纹波较大，因此带来的损耗更大，fs= 2 MHz时，开关损耗的增大使得整体效率降低，这证明了多目标优化流程设计的合理性。
图16～图20通过对比和实验展示了对磁器件占地面积、体积和变换器效率的共同优化，实现了多目标优化的设计目标。体现了异名端耦合磁器件相较于非耦合电感在占地面积、体积、效率和功率密度方面的优势外，也验证了所改进的集成磁器件结构以及所设计的建模和多目标优化流程的正确性。
为使得异名端耦合电感的占地面积、体积以及变换器效率得到同步优化，本文在改进磁心结构的基础上，设计了一种针对新型集成磁器件的多维度建模与多目标优化流程。针对多目标优化所得的集成磁器件与AP法设计的独立电感，制作了168 W的实验样机，以验证所提建模和优化流程的可行性，所得结论如下：
1）为使耦合前后电感绕组电流纹波不变，应使得耦合后的等效稳态电感与独立电感值相同。
2）基于合理分析，对传统EE型磁器件的磁心结构与绕组布局进行改进，得到新型磁器件设计。相较于基于传统EE型磁心的磁器件，新型磁器件占地面积减小了35%。同时，新型磁器件磁心通过磁板周向延伸的方式提高了磁屏蔽性能，减小了对磁器件附近元器件的磁性干扰。
3）对于所设计的新型磁器件，异名端耦合降低了磁心磁板中交流磁通的幅值，同时削减了磁板中的直流磁通，有利于在磁心不饱和的前提下减小磁板厚度和磁器件体积，提高变换器功率密度。
4）通过所设计的集成磁器件多维度建模以及多目标优化流程，使得相较于独立电感，优化后的新型磁器件占地面积和体积的缩减率分别为45.48%和43.66%，新型磁器件功率密度达到8 020 W/in3，同时变换器额定效率提升了0.9个百分点，证明本文对磁器件所进行的改进、建模以及多目标优化与理论相符合，具有实用性。
参考文献
[1] 刘晓东, 董保成, 吴慧辉, 等. 基于并联变压器切换的LLC谐振变换器宽范围效率优化控制策略[J]. 电工技术学报, 2020, 35(14): 3018-3029.
Liu Xiaodong, Dong Baocheng, Wu Huihui, et al. Wide range efficiency optimization control strategy for LLC resonant converter based on parallel trans- former switching[J]. Transactions of China Electro- technical Society, 2020, 35(14): 3018-3029.
[2] 倪硕, 吴红飞, 陈君雨, 等. 交错并联临界导通模式Buck电感高密度集成与优化[J]. 电工技术学报, 2022, 37(18): 4688-4696.
Ni Shuo, Wu Hongfei, Chen Junyu, et al. Integration and optimization of a high power density inductor for an interleaved critical conduction mode Buck converter[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4688-4696.
[3] Lee F C, Wang Shuo, Li Qiang. Next generation of power supplies: design for manufacturability[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 9(6): 6462-6475.
[4] 程鹤, 徐恺, 李朋圣, 等. 三相CLLC谐振变换器磁集成平面变压器设计与优化[J]. 电工技术学报, 2024, 39(12): 3774-3786.
Cheng He, Xu Kai, Li Pengsheng, et al. Design and optimization of three-phase CLLC resonant converter with magnetic integrated planar transformer[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3774-3786.
[5] 高圣伟, 王浩, 刘晓明, 等. 新型磁集成双频DC/ DC变换器[J]. 中国电机工程学报, 2020, 40(24): 8131-8144, 8250.
Gao Shengwei, Wang Hao, Liu Xiaoming, et al. A novel double frequency DC/DC converter with magnetic integration[J]. Proceedings of the CSEE, 2020, 40(24): 8131-8144, 8250.
[6] Li Mingxiao, Wang Chang, Ouyang Ziwei, et al. Optimal design of a matrix planar transformer in an LLC resonant converter for data center applications[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(2): 1778-1787.
[7] Lee F C, Li Qiang, Nabih A. High frequency resonant converters: an overview on the magnetic design and control methods[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(1): 11-23.
[8] Liu Yue, Wu Hongfei, Ni Shuo, et al. Lower-height- oriented magnetic integration design for onboard power converter of electric vehicles[J]. IEEE Transa- ctions on Transportation Electrification, 2024, 10(1): 163-173.
[9] 苏冰, 王玉斌, 王璠, 等. 基于耦合电感的多相交错并联双向DC-DC变换器及其均流控制[J]. 电工技术学报, 2020, 35(20): 4336-4349.
Su Bing, Wang Yubin, Wang Fan, et al. Multi-phase interleaved bidirectional DC-DC converter with coupled inductors and current sharing control strategy[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4336-4349.
[10] Naseem N, Cha H. Triple-active-bridge converter with automatic voltage balancing for bipolar DC distribution[J]. IEEE Transactions on Power Elec- tronics, 2022, 37(7): 8640-8648.
[11] 高圣伟, 王博, 孙醒涛. 一种交错并联双向DC-DC变换器的新型磁集成技术[J]. 中国电机工程学报, 2023, 43(9): 3538-3549.
Gao Shengwei, Wang Bo, Sun Xingtao. A novel magnetic integration technology for interleaved parallel bidirectional DC-DC converters[J]. Pro- ceedings of the CSEE, 2023, 43(9): 3538-3549.
[12] Wang Shuo, Pham P H, Li Qiana, et al. PCB winding-based coupled inductor for a high-frequency DC/DC converter with 99% efficiency[C]//2023 IEEE Applied Power Electronics Conference and Expo- sition (APEC), Orlando, FL, USA, 2023: 420-425.
[13] 马小勇, 王萍, 王议锋, 等. 基于交错并联Boost变换器的耦合电感综合建模与多目标优化方法[J]. 电工技术学报, 2022, 37(24): 6399-6410.
Ma Xiaoyong, Wang Ping, Wang Yifeng, et al. Comprehensive modeling and multi-objective opti- mization method for coupled inductors of interleaved Boost converters[J]. Transactions of China Electro- technical Society, 2022, 37(24): 6399-6410.
[14] Zhu Feiyang, Li Qiang. Coupled inductors with an adaptive coupling coefficient for multiphase voltage regulators[J]. IEEE Transactions on Power Elec- tronics, 2023, 38(1): 739-749.
[15] 刘越, 吴红飞, 邹军, 等. CRM-PFC矩阵式低高度平面电感优化设计[J]. 中国电机工程学报, 2021, 41(19): 6760-6769.
Liu Yue, Wu Hongfei, Zou Jun, et al. Optimal design of CRM-PFC matrix low-height planar inductor[J]. Proceedings of the CSEE, 2021, 41(19): 6760-6769.
[16] Gadelrab R, Lee F C. PCB-based magnetic integration and design optimization for three-phase LLC[J]. IEEE Transactions on Power Electronics, 2023, 38(11): 14037-14049.
[17] 高圣伟, 李永宵, 田金锐, 等. 双频DC-DC变换器的磁集成技术[J]. 电工技术学报, 2024, 39(13): 4025-4036.
Gao Shengwei, Li Yongxiao, Tian Jinrui, et al. Magnetic integration of double frequency DC-DC converter[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 4025-4036.
[18] Stratta A, Gottardo D, Di Nardo M, et al. Optimal integrated design of a magnetically coupled inter- leaved H-bridge[J]. IEEE Transactions on Power Electronics, 2022, 37(1): 724-737.
[19] Li Zheqing, Hsieh E, Li Qiang, et al. High-frequency transformer design with medium-voltage insulation for resonant converter in solid-state transformer[J]. IEEE Transactions on Power Electronics, 2023, 38(8): 9917-9932.
[20] Kimura S, Itoh Y, Martinez W, et al. Downsizing effects of integrated magnetic components in high power density DC-DC converters for EV and HEV applications[J]. IEEE Transactions on Industry Appli- cations, 2016, 52(4): 3294-3305.
Multidimensional Modeling and Multi-Objective Optimization of Integrated Magnetic Device for Two-Phase Interleaved Buck Converter
Abstract The rapid development of industries such as aerospace, electric vehicles, and green data centers requires low-power, non-isolated buck-switching power supplies to achieve high efficiency, high power density, and lightweight miniaturization. The converter adopts a topology structure of multi-phase interleaved Buck to reduce the current ripple. However, magnetic components usually occupy more than 30% of the total volume of the power supply, which affects the power density and dynamic characteristics of the power output. Power magnetic integration technology has been studied to reduce magnetic components' footprint, volume, and losses and improve switching power supplies’ efficiency.
This paper proposes a multi-dimensional modeling and multi-objective optimization method based on a two-phase interleaved Buck converter for the negative-coupling magnetic devices with improved core structure and winding layout. Firstly, based on the electrical parameter model of the converter and the magnetic circuit characteristics of the negative-coupling inductor, the magnetic core structure and winding layout are improved and optimized. Secondly, multi-dimensional models of the converter are established regarding the winding turns, magnetic column air gap, magnetic column edge length, and switching frequency. Combining the model and constraint conditions, a multi-objective optimization process is designed to obtain non-dominated solutions for the transformer efficiency, magnetic device footprint and volume under different winding turns. Finally, the optimal parameters are selected, and integrated magnetic devices are manufactured.
A 28 V/12 V, 168 W experimental prototype has been built. Compared to independent inductors, the optimized magnetic device had a footprint reduction rate of 45.48%, a volume reduction rate of 43.66%, an increase in the rated efficiency of the converter by 0.9%, and a magnetic device power density of 8 020 W/in3. Simultaneously changing the input voltage of the converter and the air gap of the integrated magnetic device allows the converter to operate under different working conditions. By operating the converter and integrated magnetic devices at different switching frequencies and observing the efficiency of the converter, the feasibility of the multi-objective optimization process can be verified.
The following conclusions can be drawn. The equivalent steady-state inductance should be the same as the independent inductance value to keep the current ripple constant. The new magnetic device extends the magnetic core and plates in the circumferential direction, improving the magnetic shielding performance and reducing interference with other components. Negative-coupling reduces the AC magnetic flux in the magnetic core and offsets the DC magnetic flux in the magnetic plates. It is beneficial for reducing the magnetic plates’ thickness and the magnetic device’s volume, thereby improving the converter’s power density.
Keywords：Interleaved Buck converter, negative-coupling, integrated magnetic device, multidimensional modeling, multi-objective optimization
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.242241
国家自然科学基金资助项目（62271417）和四川省高效电源变换技术工程研究中心基金项目（2023-02）资助。
收稿日期 2024-12-13
改稿日期 2025-03-03
刘 泽 男，2000年生，博士研究生，研究方向为电力电子技术及其磁集成技术。
E-mail: liuze_swjtu@163.com
周国华 男，1983年生，教授，博士生导师，研究方向为电力电子调制与控制技术、数字控制技术、建模与稳定性分析、电力电子技术在新能源发电系统中的应用等。
E-mail: ghzhou-swjtu@163.com（通信作者）
（编辑 陈 诚）