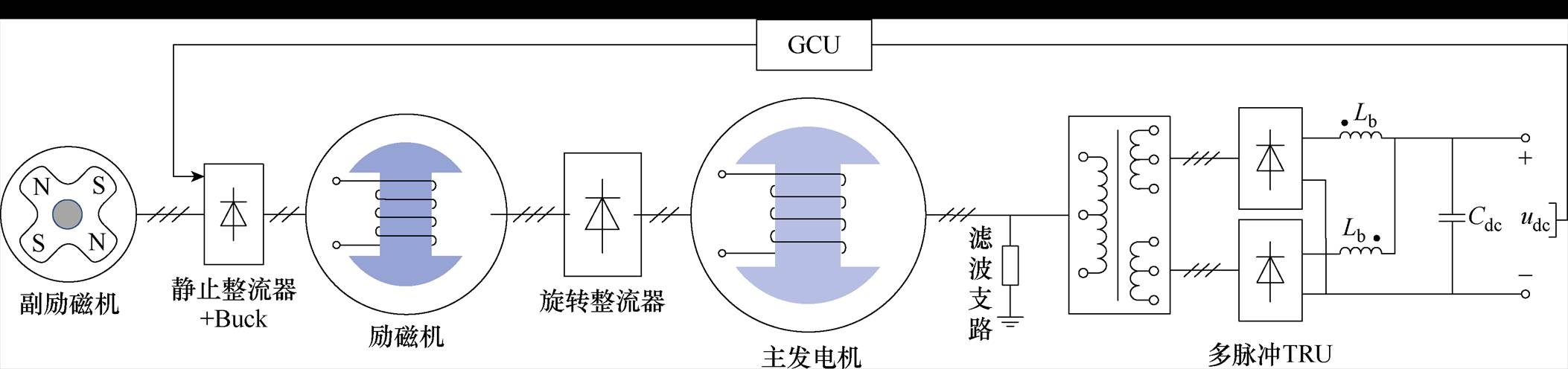
图1 TSG-HVDC电源系统架构
Fig.1 Architecture of TSG-HVDC-based power supply system
摘要 以三级式发电机为基础的机载高压直流（TSG-HVDC）电源系统具有结构复杂、非线性强等特点。建立TSG-HVDC电源系统低复杂度的阻抗模型是对机载电源系统开展稳定性分析与准确致稳设计的前提。该文考虑旋转/静止整流器、多脉冲变压整流器等不同部件的运行方式与处理差异，采用等效电路集成和子系统二端口H参数表征，完整地建立了TSG-HVDC电源系统输出阻抗模型。设计采用矢量拟合的二端口H参数降阶分析流程，推导宽频段方均根误差最优的降阶阻抗模型，明晰了TSG-HVDC各子系统与整体输出阻抗的内在关系及降阶影响规律。进而结合降阶阻抗的幅值和相位灵敏度，提出一种考虑负载阻抗区间描述的多参数协调整定方法。最后通过时域仿真、物理实验以及控制器硬件在环实验，验证了该文所建模型的准确性及所提参数整定方法的鲁棒性。
关键词：多电飞机 三级式发电机 高压直流电源系统 降阶阻抗模型 参数协调整定
多电飞机是当前航空技术发展的主要方向之一，其核心在于用电能替代液压能、气压能等二次能源，以简化飞机系统结构，实现技术与经济性能的全局优化[1]。随着机载用电设备数量与功率的不断增加，先后出现了低压直流、恒速恒频、变速恒频、变频交流以及高压直流（High Voltage Direct Current, HVDC）等多种架构的机载电源系统[2]。凭借在可靠性、维修性、费用、质量和供电质量方面的优势，HVDC更是成为美国三军军用飞机的首要选择，军机F-35、F-14A、S-3A、P-3C与F-22等均局部或全部采用270 V-HVDC作为供电架构[3]。然而，受限于飞机电气系统的体积和质量要求，电源容量一般和负载相当，供电裕度小，在HVDC电源系统源-荷两端高度电力电子化与负载功率等级提升的影响下，稳定性尤其是小干扰稳定问题将会极为突出[4]。
除时域仿真外，评估多电飞机电源系统小干扰稳定性的方法主要有状态空间法和阻抗分析法两 类[5]。文献[6]建立了6脉冲与12脉冲变压整流器单元（Transformer Rectifier Unit, TRU）的状态空间平均模型。在dq旋转坐标系下，文献[7]建立了同步发电机电源与感应电机操动机构构成的简单电气系统状态空间模型。针对永磁同步电机HVDC电源系统，文献[8]通过特征值灵敏度和参与因子分析了电机参数、控制参数和运行方式对系统稳定性的影响。文献[9]进一步设计了多电飞机复杂电气系统小信号模型的模块化建模方法。虽然状态空间法可清晰地分析系统小信号稳定性的时域特征，但其依赖统一建模，且模型维数灾问题会随着变换器组件数量的增加而极为突出[10]。考虑到机载电气系统存在内部参数部分或全部未知的灰/黑盒组件，阻抗分析法不依赖统一建模且可利用端口测量特性，稳定性分析实施过程会更为便捷和易于工况拓展，因而引起了广泛关注[11-13]。
究其本质，阻抗分析法是将系统稳定分割为组件与系统两个层级，即在组件单独运行稳定的前提下，通过系统稳定要求来约束组件的阻抗外特 性[14]，这也使得阻抗建模或测定成为阻抗分析法应用的前提。针对270 V单母线多永磁同步电机并联结构HVDC电源系统，文献[15]引入下垂控制建立了输出阻抗模型，并对恒功率负载接入的稳定性进行了分析。针对最为成熟的三级式发电机（Three- Stage Generator, TSG）结构HVDC电源系统。文献[16]提出了基于二端口与矢量拟合的电磁干扰（Electromagnetic Interference, EMI）宽频阻抗建模方法，但该方法依赖实测数据，受电机测试平台约束。文献[17]通过对二极管整流桥的直接二端口平均建模，导出了TSG的交流阻抗模型，但未涉及较常配置的多脉冲变压整流环节。
就完整的TSG-HVDC电源系统而言，除电机本体涉及副励磁机、励磁机、主发电机外，还含有旋转整流器、静止整流器、变压整流器等多个非线性环节[18]，导致阻抗建模的集成过程复杂，且高阶特性显著，因此，实际稳定性分析和设计亟须具备宽频段表征能力的简化阻抗模型。囿于TSG-HVDC电源系统的应用领域，关于其阻抗降阶模型及其适用范围的厘定工作，现有研究还相对分散，极易出现因模型简化而降低问题识别的准确性或因模型复杂而阻碍稳定机理的分析[19-20]。因此，为建立完备且低复杂度的TSG-HVDC电源系统阻抗模型，并在阻抗法范畴实现机载供电系统多工况的稳定性分析与致稳设计，本文主要贡献如下：
（1）针对旋转/静止整流器与多脉冲TRU运行方式差异，分别采用开关函数基波近似与平均电路等效两种建模方式，通过等效电路集成和二端口H参数表征完整建立了TSG-HVDC电源系统的输出阻抗模型。
（2）设计了采用矢量拟合的子系统二端口H参数降阶分析流程，推导了宽频段方均根误差最优的降阶阻抗模型，并明晰了副励磁机、励磁机、主发电机各子系统与整体输出阻抗的内在联系及降阶影响规律。
（3）基于降阶阻抗的幅值与相位灵敏度，提出了一种考虑负载阻抗区间描述的TSG-HVDC电源系统参数整定方法，可实现多负载工况的TSG- HVDC电源系统多参数协调整定。
最后，通过Matlab/Simulink时域仿真、分解系统物理实验以及控制器硬件在环实验，验证了本文所建阻抗模型的准确性及所提参数整定方法的鲁 棒性。
图1为TSG-HVDC电源系统的基本结构，TSG由副励磁机、励磁机、主发电机等同轴构成，端口可配置多脉冲TRU实现270 V或更高电压等级的直流输出。
图1 TSG-HVDC电源系统架构
Fig.1 Architecture of TSG-HVDC-based power supply system
TSG以同步发电机为主体，转子旋转和凸极效应使得发电机方程存在显著的时变非线性特征。为便于阻抗集成，选择在dq旋转坐标系下进行建模（q轴超前）。考虑到变换后有名值方程仍存在各绕组间互感参数不可逆、参数较多等问题，将励磁与阻尼绕组参数和状态变量折算至电枢侧。以主发电机为例，其简化模型[18]为
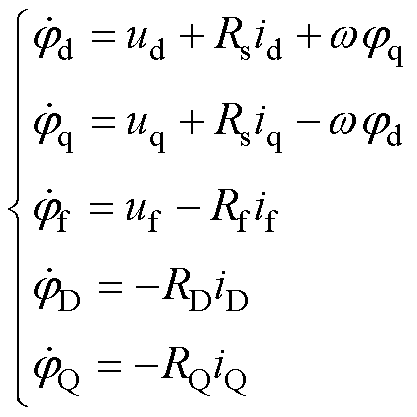（1）
式中，w为TSG旋转角速度；Rs为电枢绕组电阻；idq与udq分别为d、q轴电流与端电压；Rf、if与uf分别为励磁绕组电阻、电流与电压；RD、RQ与iDQ为D、Q阻尼绕组电阻与电流；jdq为dq电枢绕组磁链；jf为励磁绕组磁链；jDQ为DQ阻尼绕组磁链。jdq、jf、jDQ表示为
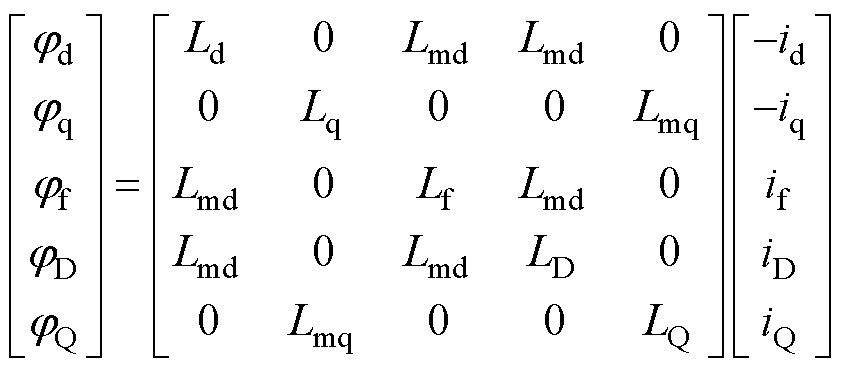（2）
式中，Ld=Lls+Lmd与Lq=Lls+Lmq分别为d、q电枢绕组自感，Lls为电枢绕组漏感，Lmd与Lmq为d轴与q轴磁化电感，由电枢绕组等效匝数与气隙磁通路径磁导表示[21]；Lf为励磁绕组自感，Lf=Llf+Lmd，Llf为励磁绕组漏感；LD与LQ为D、Q阻尼绕组自感，LD=LlD+Lmd，LQ=LlQ+Lmq，LlD与LlQ为D、Q阻尼绕组漏感。
由于三级式电机的复杂性，需根据参数与变量折算前后磁链守恒原则折合为单台电机，以d轴为例，励磁与阻尼绕组参数与变量的折算方式为
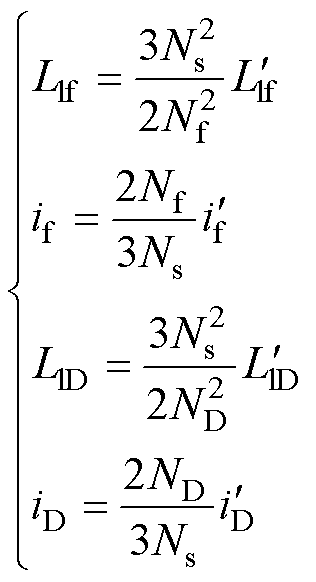（3）
式中，Ns、Nf与ND分别为电枢、励磁与D阻尼绕组的等效匝数，其中阻尼绕组等效匝数一般与励磁绕组相同；上标“'”表示折算前参数。
消去磁链状态量，式（1）与式（2）可重构为以电流为状态量的微分方程组。考虑到副励磁机、励磁机建模过程与主发电机类似，为便于区分，三者状态量与参数均采用上标“p、e、g”表示。相比于主发电机，励磁机和副励磁机一般不配置阻尼绕组，其中副励磁机主要考虑永磁同步电机。需要强调的是，在各级电机经整流装置互联时，需要按式（3）所示关系进行折算还原，其中电枢与励磁绕组的等效匝比可采用式（4）进行估计[21]。式（4）由无负载状态下磁链守恒导出，在电枢与励磁绕组等效电路中表现为理想变压器形式，正常范围工况变化可不考虑磁化电感、励磁绕组漏感等参数的变动，折算关系也将保持不变。
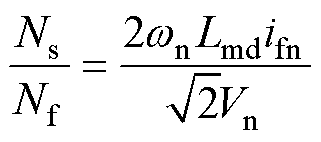（4）
式中，ifn为空载励磁电流；wn为额定旋转角速度；Vn为额定相电压幅值。
TSG中静止和旋转整流器为三相不控整流，主要用来提供直流励磁电流，区别是前者保持静止而后者随轴高速旋转。由于励磁电流连续且换相时间较短，换相重叠角m相对较小，三管工作的换相状态与两管工作的导通状态交替出现，如图2a所示。
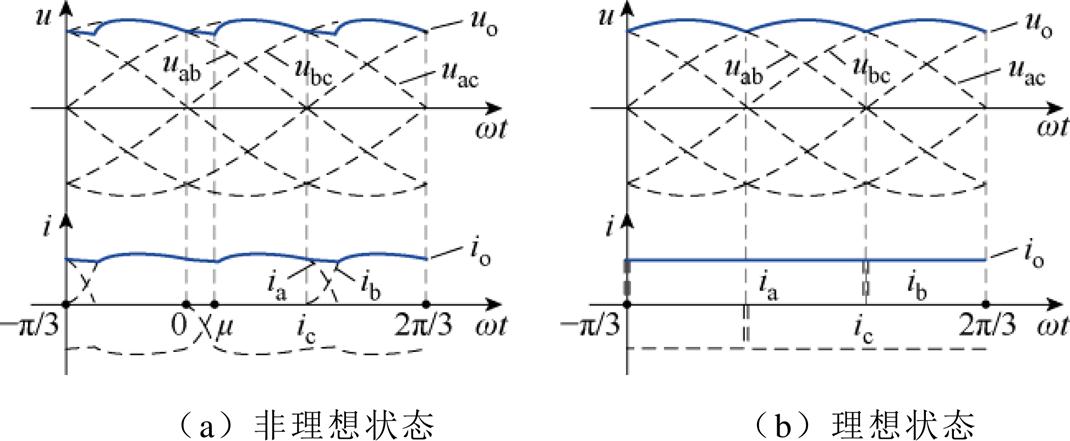
图2 静止/旋转整流器波形及其近似处理
Fig.2 Waveforms and approximate processing of static/rotating rectifier
若忽略静止或旋转整流器换相过程，即简化为换相点，则交流侧电压uabc和直流侧电压uo的关系可表述为uo=[SaSbSc]uabc，交流侧电流iabc和直流侧电流io的关系可表述为iabc=[SaSbSc]Tio，其中Sa、Sb和Sc为三相开关函数，取值为1、-1与0时，分别表示桥臂上管导通、下管导通与两管关断。图2b展示了开关函数描述的交、直流侧电压与电流波形。对开关函数取基波近似（傅里叶级数展开），并进行abc/dq变换（q轴与交流侧所接同步电机a相空载电动势重合），可得变换后开关函数的基波分量为[Sd Sq]=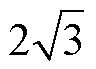
[sind cosd]/p，其中d为输入电压与q轴夹角，从而uo可改写为
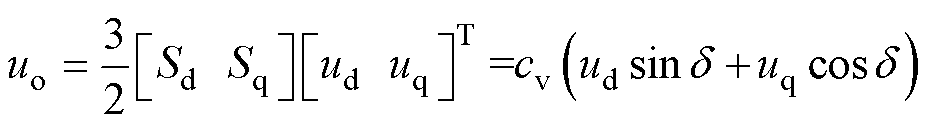（5）
式中，cv为电压增益，cv=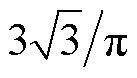
。
由图2a可见，若关注换相过程中的基波分量，则电流相位会出现滞后于电压相位的现象。因此，在开关函数与基波近似的基础上，引入相位差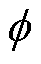
对交、直流侧电流关系进行修正，即
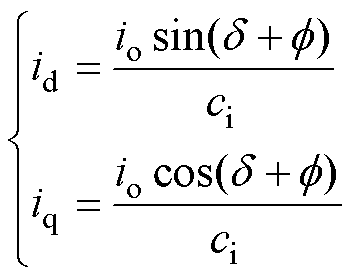（6）
式中，ci为电流增益，ci=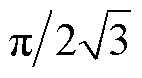
。
需要强调的是：
（1）上述建模方式仍忽略了电压与电流的换相重叠部分，从而导致式（5）、式（6）所示电压增益cv与电流增益ci存在微小的固有误差，可使用平衡点处交、直流侧电压电流平均值，修正cv、ci和相位差。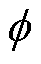
（2）旋转整流器连接励磁机与主发电机，在等效电路范畴相当于交、直流侧均直接与阻感支路相连，即交、直流两侧最关联的状态量均为电流。因此，式（5）与式（6）在表征旋转整流器特性嵌入系统整体模型时，交流侧电压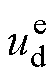
与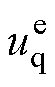
需要由旋转整流器交流侧其他状态量联合表示，这会导致交、直流状态量之间的进一步耦合。为降低模型结构的复杂度，考虑实际存在的微小机端寄生电容，通过引入寄生电容增加电压状态量，进而简化小信号模型的集成过程。
（3）静止整流器直流侧一般接Buck或H桥结构的调压器，且配有滤波电容。调压器部分可采用平均建模，若保留滤波电容电压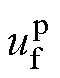
和交流侧电流
、
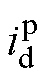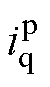为状态量，则交流侧电压
、
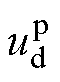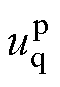与直流侧电流
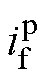分别为
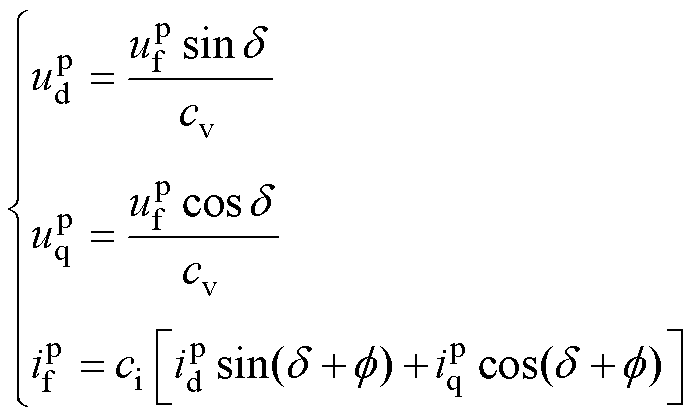（7）
常用的多脉冲TRU有12与18脉冲，两者原理类似。以12脉冲TRU为例，其主体由星形-星形-三角形变压器和上、下两组不控整流桥构成，下桥输入电压滞后上桥臂30°，从而实现交错输出降低脉动。为平衡上、下桥臂输入电压，星形-星形-三角形变压器电压比理论值应为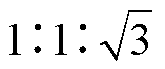
，则二次绕组等效参数一致。由于存在变压器漏感与较大负载电流，TRU电流换相过程较为显著，因而区别于旋转/静止整流器，需要对其进行详细建模。考虑到上、下桥臂运行方式的对称性，在上、下桥臂参数一致的前提下，可将平衡电抗器拆分，等效为两组含隔离变压器与输出电抗器的不控整流并联。
以上桥臂为例，令隔离变压器等效电阻与电感分别为Rt与Lt，其中Rt包含一次、二次绕组电阻和二极管内阻，Lt包含一次、二次绕组漏感；输出电抗器可用平衡电抗器单侧漏感Lb近似；Vg为主发电机机端电压幅值，即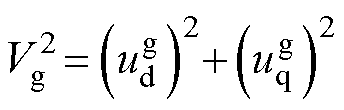
。由于TRU一般设计在换相与导通交替出现的工作模式中，因此选取cb换相与ac导通两个相邻阶段进行分析。换相阶段cb相间短路，并与a相构成回路，如图3a所示。假定a相电压初始相位
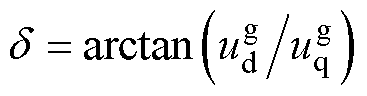，若已知交流侧电压
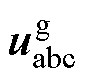与上桥直流侧电流
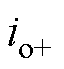，则交流侧电流
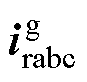与直流侧电压udc表示为
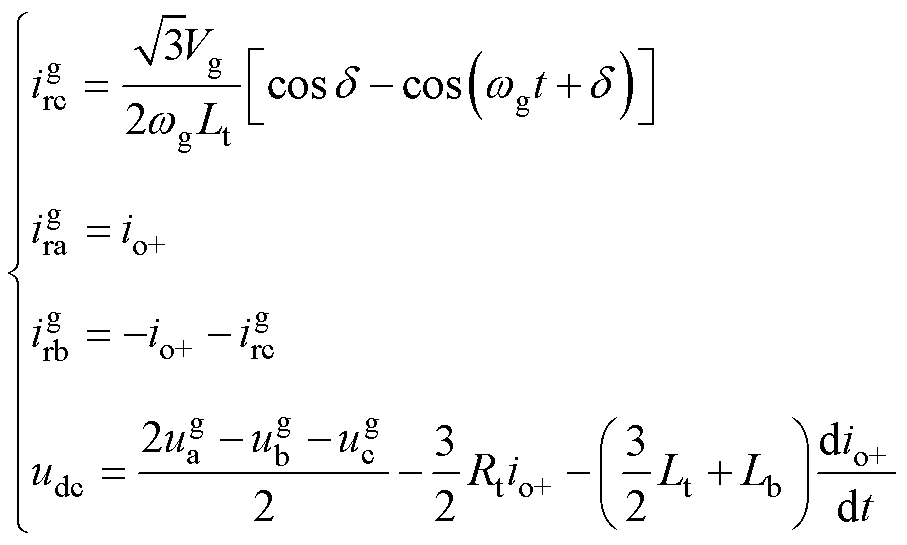（8）
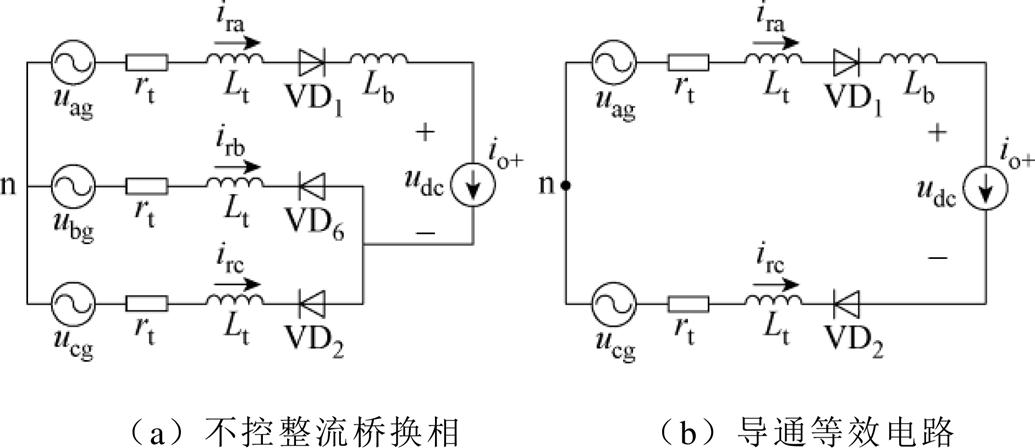
图3 不控整流桥换相与导通等效电路
Fig.3 Equivalent circuits of commutation and conduction of diode rectifier bridge
导通阶段a、c两相构成回路，如图3b所示，交流侧电流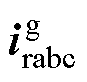与直流侧电压udc可表示为
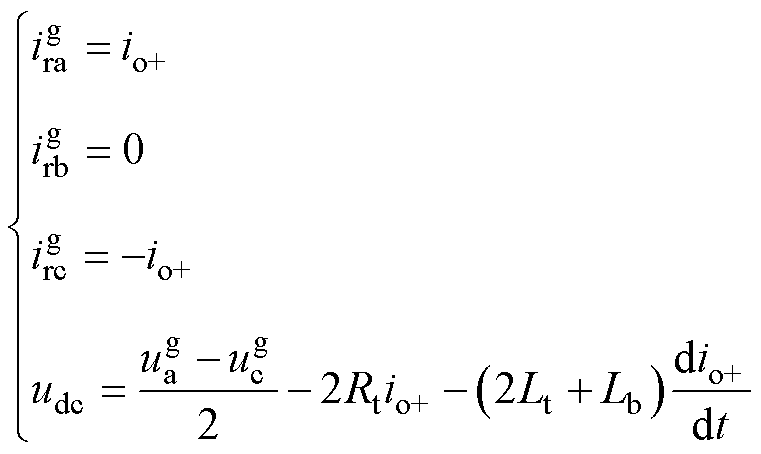（9）
由换相结束后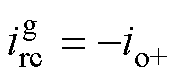
可得换相重叠角m与直流电流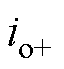的基本关系。若进一步假定
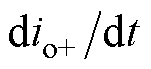在换相与导通阶段都保持不变，对式（8）与式（9）中的直流侧电压udc状态取平均，可得
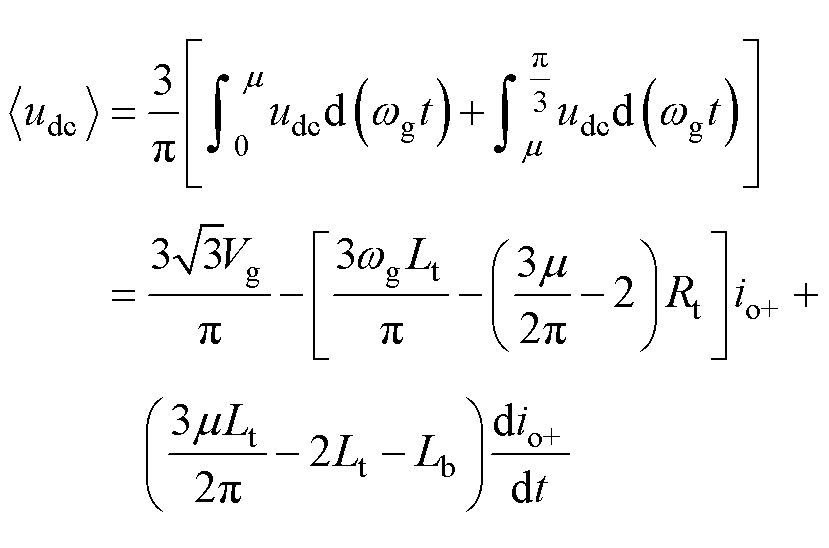（10）
式中，
表示平均算子，平均周期为p/3。
对换相阶段输入电流进行abc/dq变换，可得dq坐标系下输入电流表示为
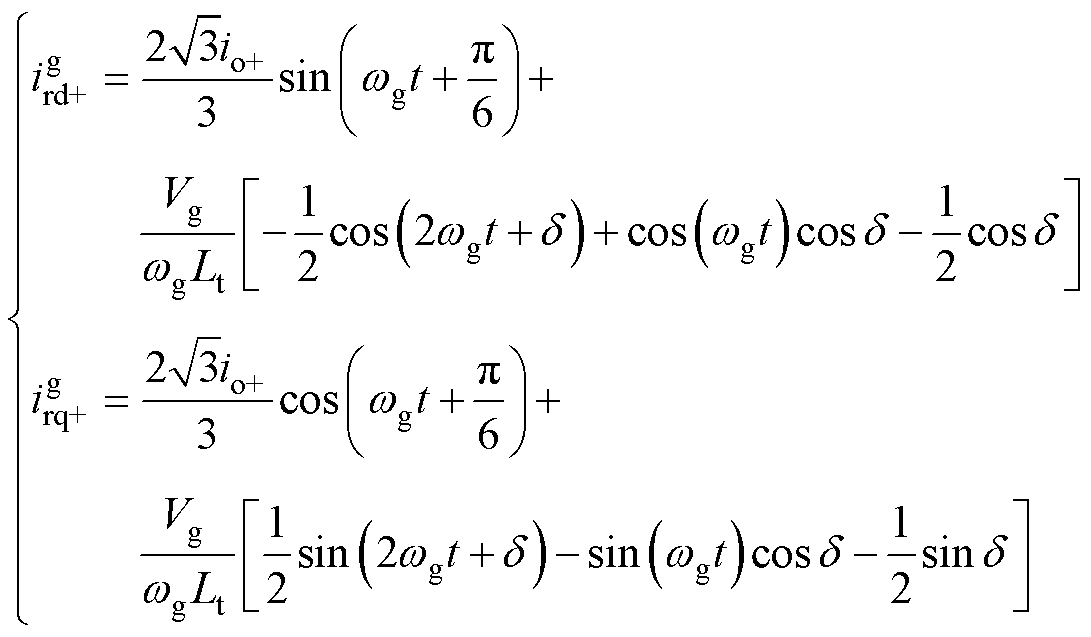（11）
导通阶段处理方式与换相阶段类似，则取状态平均后输入电流d轴分量为
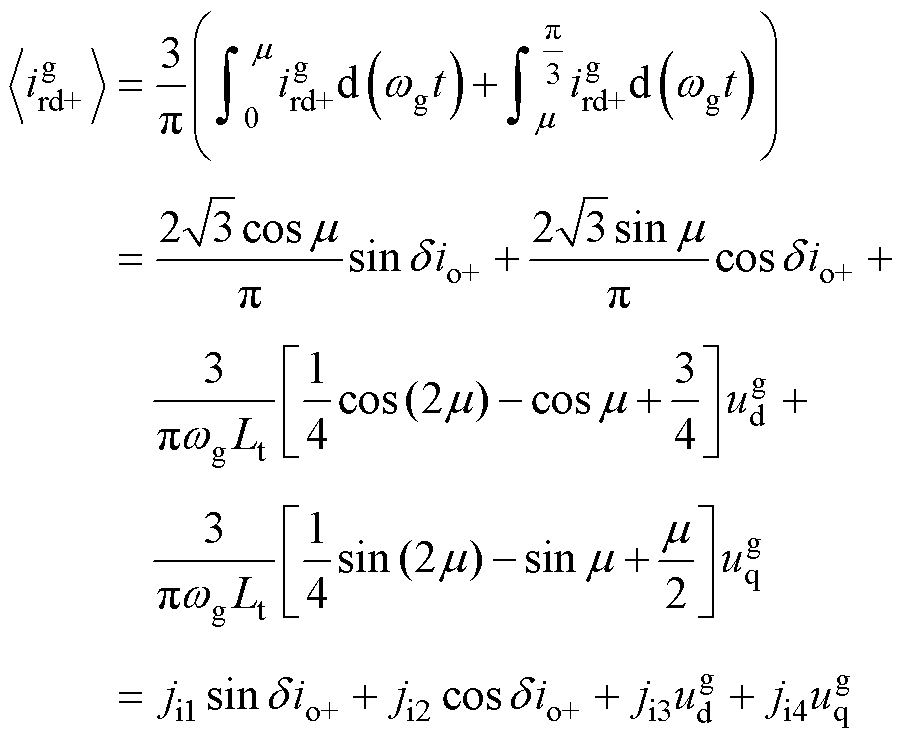（12）
类似地，输入电流q轴分量为
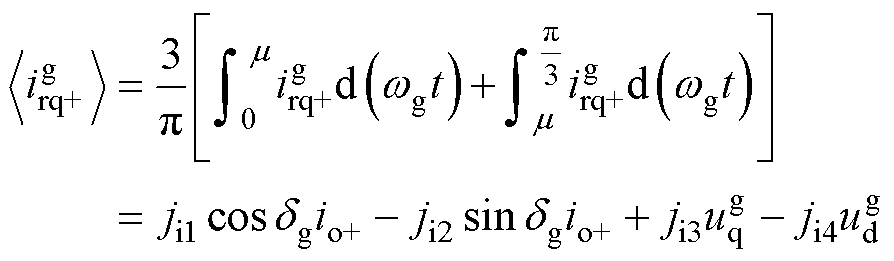（13）
由于采用分裂等效，TRU输入和输出电流应是上桥臂输入和输出的2倍，省略算子后，TRU及直流侧滤波电容Cdc的整体动态过程可表示为
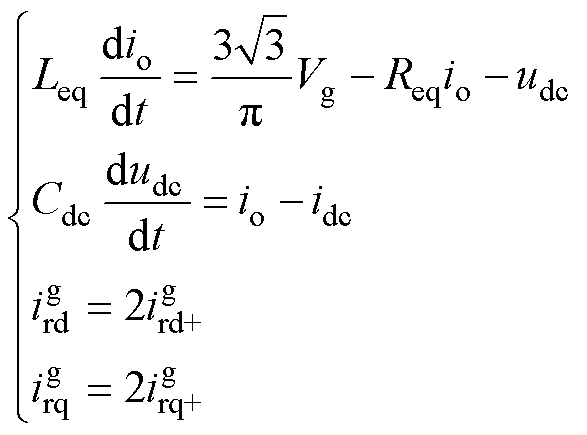（14）
式中，
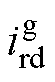与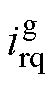
分别为d、q坐标系下TRU输入电流；idc为负载电流；Leq=0.5Lb+Lt(1-0.75m/p)；Req=1.5wgLt/p-Rt(0.75m/p-1)。
在等效电路集成的基础上，引入二端口网络H参数，对TSG-HVDC的阻抗模型进行了完整推导，并设计了采用矢量拟合的二端口H参数降阶分析流程，完成了TSG-HVDC阻抗降阶特性分析与低复杂度建模。
首先对静止/旋转整流器与多脉冲TRU进行线性化处理，并记下标“0”为平衡点处取值。对于静止整流器，考虑到实际相位差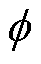变化范围极为微小，故线性化过程中直接按常值处理，进而令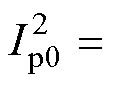
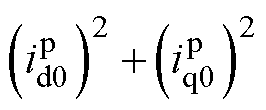，则式（8）所示静止整流器非线性方程可近似为
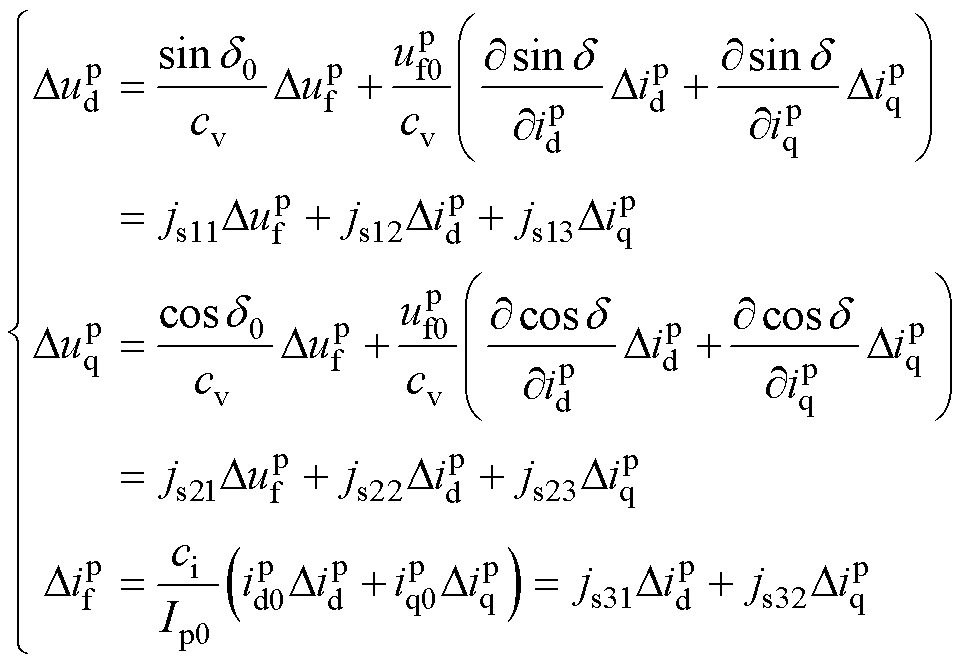（15）
类似地，旋转整流器可按同样方式处理，由于状态量选择差异，形式上会有所区别，具体为
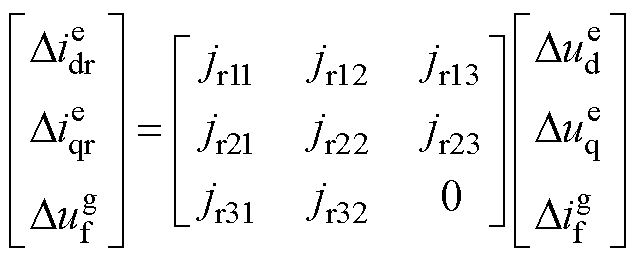（16）
对于12脉冲TRU，将换相重叠角m视为常值，其线性化模型为
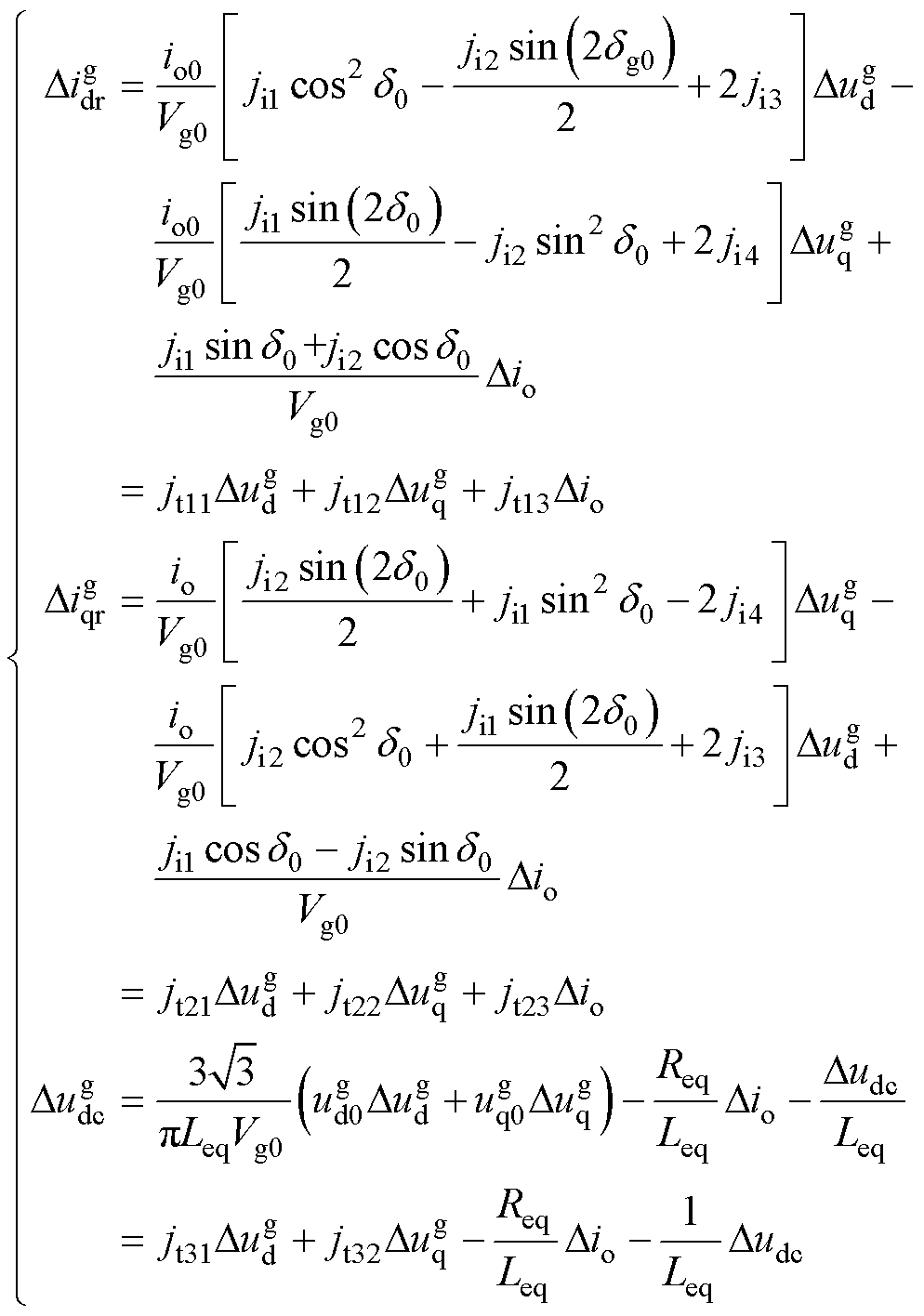（17）
式中，jr11～jr32为旋转整流器线性化模型状态变量等效常系数。
若调压器采用Buck电路，则集成后的TSG- HVDC电源系统小信号等效电路如图4所示。主电路部分可划分为主发电机、励磁机、副励磁机3个子系统。引入控制器Gc(s)与二端口网络H参数方程集中表征，从而整体小信号模型可分解如图5所示，其中主发电机子系统可由式（18）所示传递函数矩阵G(s)关联输入输出。
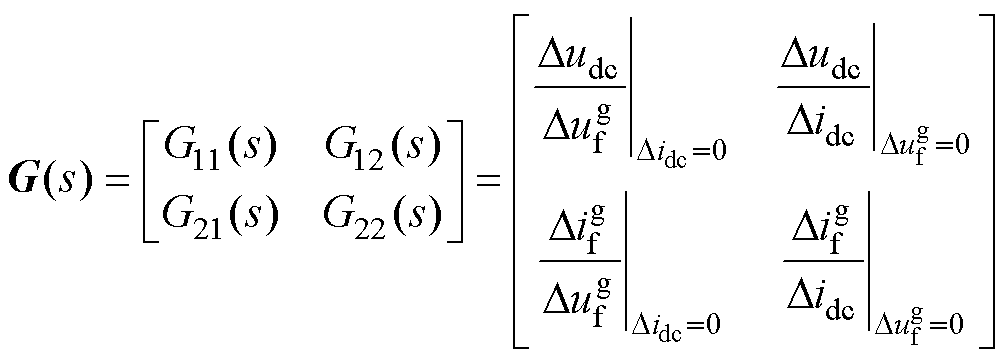（18）
类似地，励磁机和副励磁机子系统输入输出分别采用传递函数矩阵E(s)=[[E11(s) E12(s)]T [E21(s) E22(s)]T]T和Zp(s)进行关联。基于上述表示，TSG-HVDC电源系统直流侧阻抗可解析为
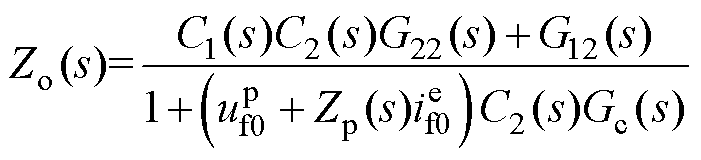（19）
其中
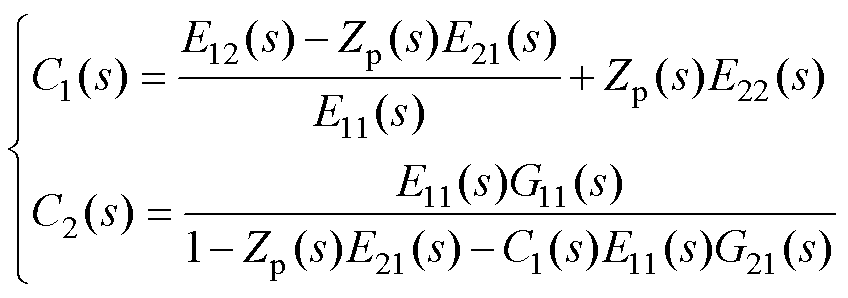（20）
式（19）所示阻抗模型依赖特定的稳态运行点，为保证建模的准确度，稳态点计算可通过机载供电系统潮流计算获得；对于过载运行等极端工况导致的三级式发电机等值参数偏移，可通过详细的电磁暂态模型和物理实验数据对参数偏差进行拟合和辨识，进而修正阻抗模型中的参数。
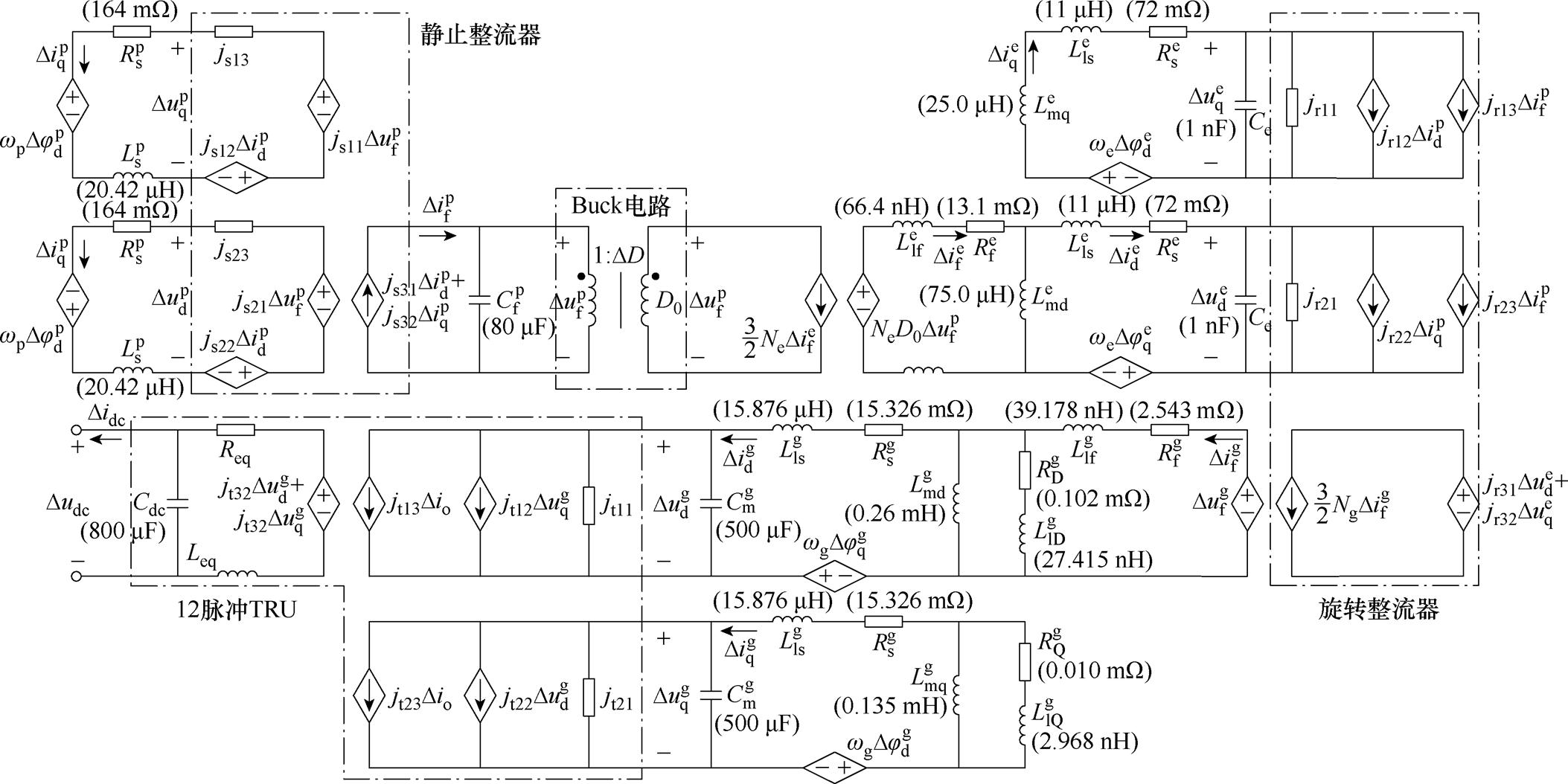
图4 TSG-HVDC电源系统小信号等效电路
Fig.4 Small signal equivalent circuit of TSG-HVDC-based power supply system
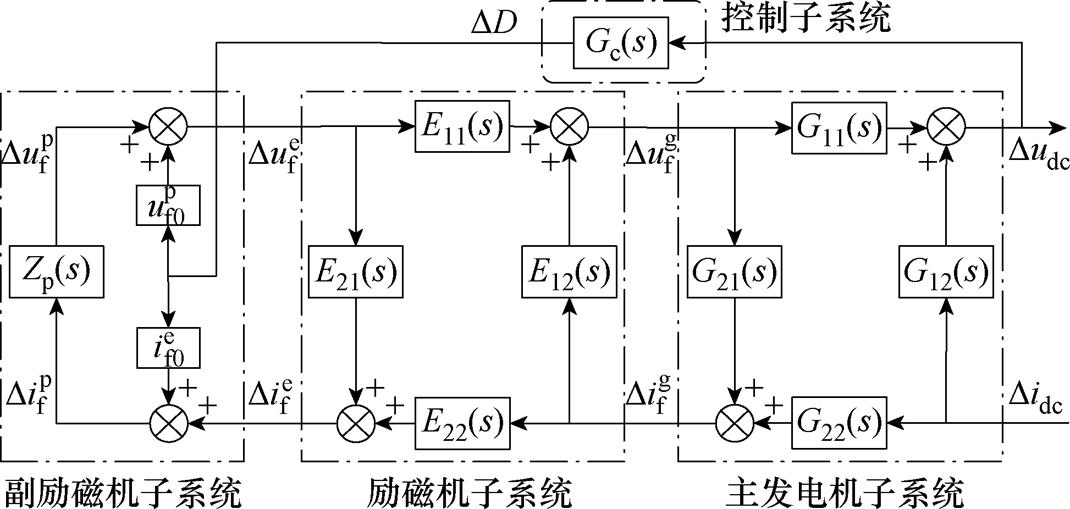
图5 基于二端口的TSG-HVDC电源系统小信号模型
Fig.5 Small-signal model of TSG-HVDC-based power supply system using two-ports
式（19）所示阻抗模型为19阶，为便于供电稳定性分析与设计，需对其进行降阶处理。考虑到直接截断法、奇异摄动法等经典降阶方法均存在欠拟合问题，且截断误差会随降阶程度的加深而增大，因此引入矢量拟合对各子系统进行降阶处理和特性分析。由式（18）和式（19）所示基本形式，假定传递函数矩阵某一元素可近似为f(s)，阶数为n，引入待定传递函数s(s)用于求解，其初始极点和留数分别为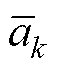
和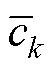
，
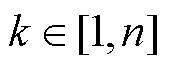，具体表达式为
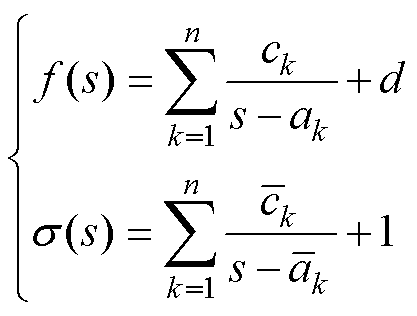（21）
式中，ck与ak分别为留数与极点；d为常数项。
将s(s)与f(s)相乘，则对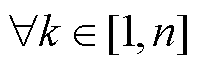
，当
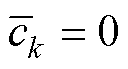且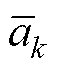接近ak时，满足
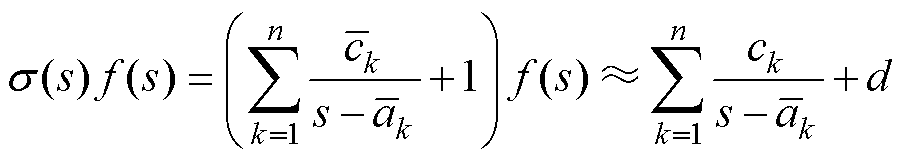（22）
令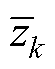
为s(s)的零点，则由式（21）的特殊构造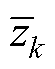，应满足
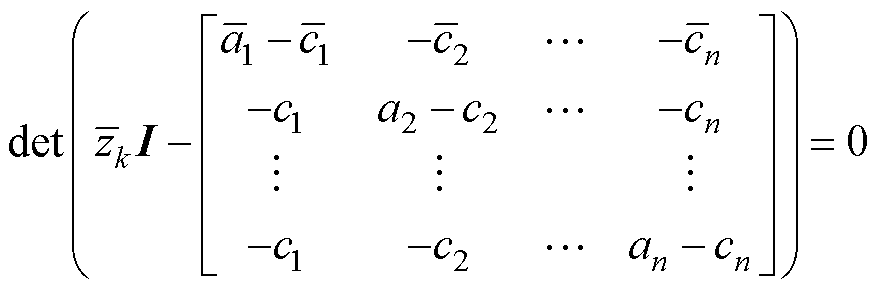（23）
从而，式（22）可转化为
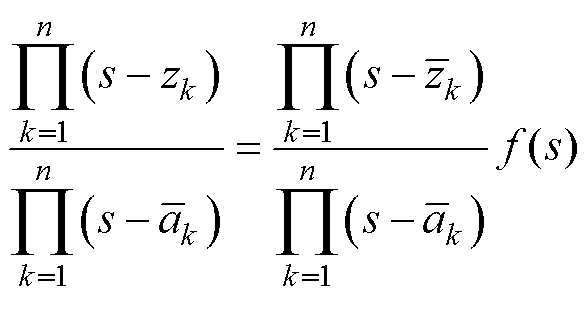（24）
式中，zk为s(s)f(s)的零点，则f(s)的极点最终可由待确定的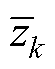构成，即
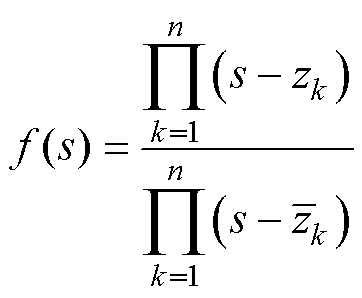
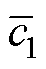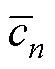关于矢量拟合参数的确定，可通过最小二乘法求解式（25）所示超定线性方程组来实现。由于式（25）是式（22）直接取等号近似而来，因而需要将求解得到的
～
和预设的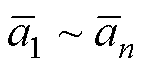
代入式（23），更新零点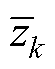后并替代初始极点代入式（25），通过如此反复求解直至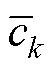收敛至0或小于某一阈值。
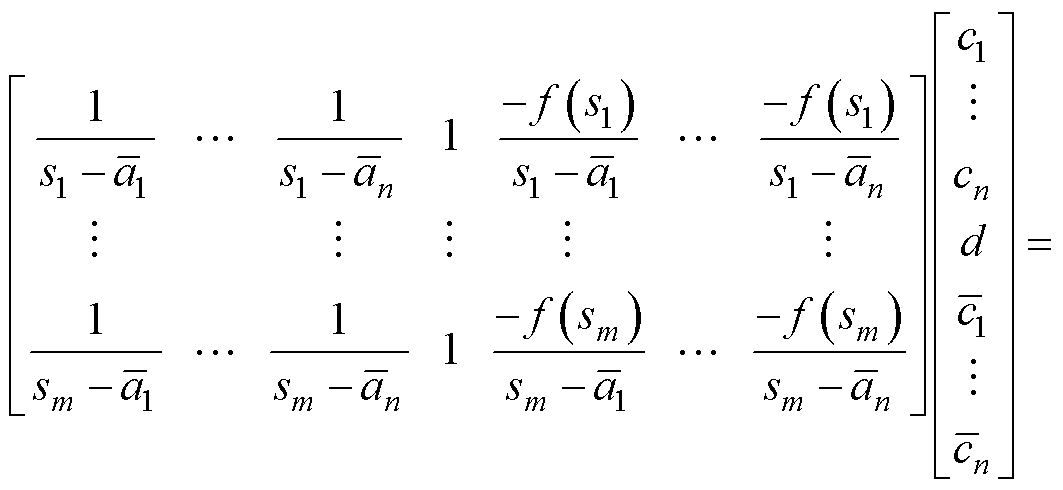
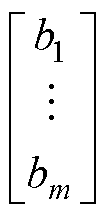（25）
式中，m为频率采样点数；b1～bm分别为频率w1～wm处待拟合传递函数矩阵元素幅值（相位）特性。
区别于单一传递函数的矢量拟合和降阶，在对图5所示主发电机和励磁机子系统传递函数矩阵实施降阶分析时，各元素极点需要统一校正，较为有效的处理方式是筛选传递函数矩阵各元素相似极点，取其均值作为进行二次矢量拟合的初始极点，从而确保降阶阻抗的零、极点分布的合理性与整体阶数。图6给出了完整的降阶分析流程，模型最低阶数由传递函数矩阵元素在各采样频率下的幅值（相位）特性拟合偏差方均根值ε确定。对于TSG-HVDC电源系统整体输出阻抗而言，9阶模型具备较宽频段范围内的准确表征能力，具体实施过程可见本文案例验证部分。
飞机在爬升、巡航、着陆等工况下负载运行方式多样，单一工况的电源系统致稳设计往往难以保证全工况适用性，而保守设计又会影响响应性能。因此，为进一步强化阻抗法稳定性设计的便捷性与鲁棒性，考虑负载阻抗特性宽范围变动，提出一种基于负载阻抗区间描述的TSG-HVDC电源系统多参数协调整定方法。
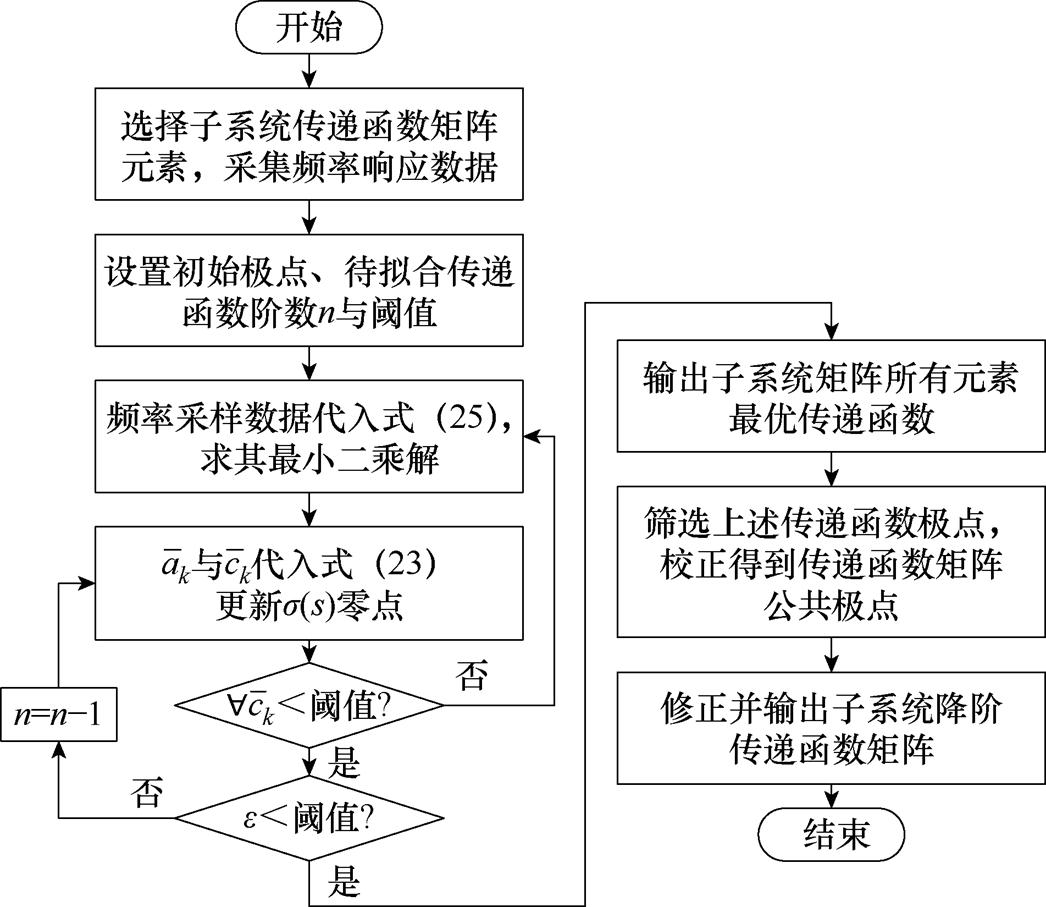
图6 基于矢量拟合的子系统传递函数矩阵降阶主流程
Fig.6 Main flowchart of vector fitting-based order reduction for sub-system function matrix
TSG-HVDC电源系统接入机载负载后可等效为级联系统，稳定性特征可通过输出阻抗Zo(s)和负载输入阻抗Zin(s)的交截情况来评估[22]。系统运行方式的多样性使得Zin(s)不再呈现为单一的幅相特性曲线，可采用图7所示阻抗区间进行一般性描述，其幅值上、下边界可分别记为Min+(w)、Min-(w)，相位上、下边界可表示为qin+(w)、qin-(w)。
当负载阻抗采用区间描述后，系统稳定的充分约束条件设计为Zo(jw)的幅频曲线|Zo(jw)|与Min-(w)不交截，即
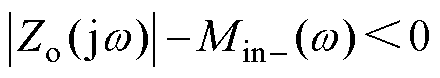（26）
|Zo(jw)|与Min-(w)存在交截频段[wA1, wA2]，但在该频段内∠Zo(jw)与qin-(w)的差均处于0°～180°之间，即对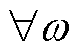
Î[wA1, wA2]有
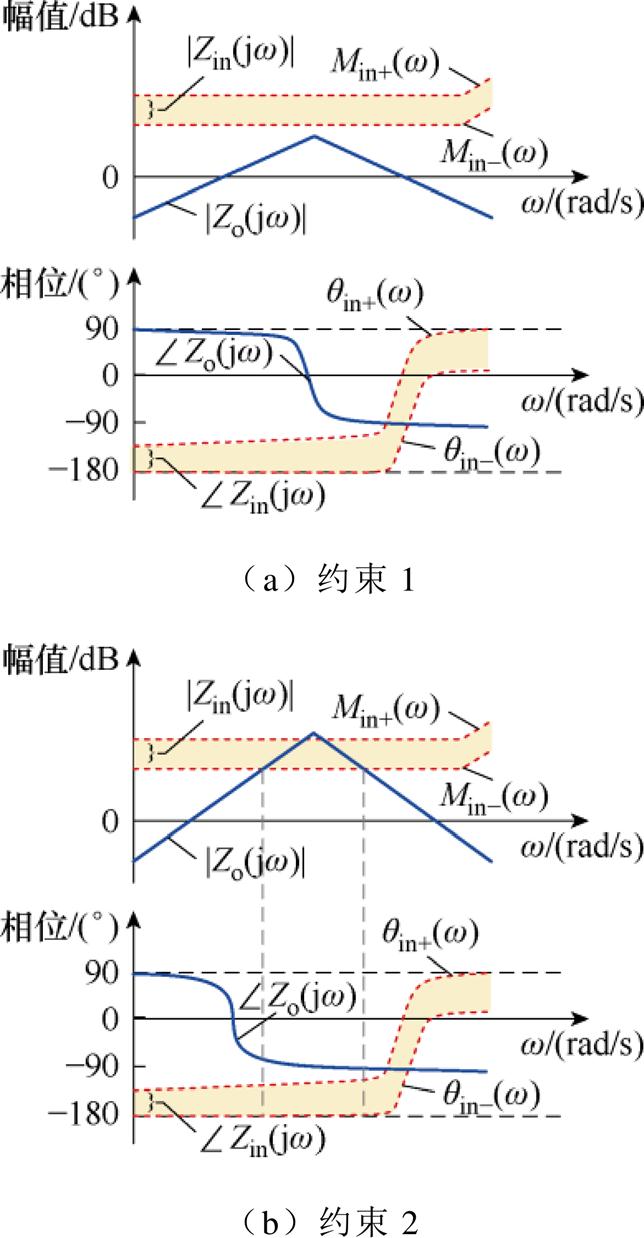
图7 基于阻抗区间描述的电源系统稳定性约束
Fig.7 Stability constraints of power system based on impedance interval description
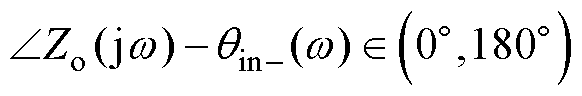（27）
若TSG-HVDC电源系统在考虑负载阻抗区间描述的情况下同时不满足式（26）和式（27），则意味着存在振荡失稳的风险，需以Min-(w)或qin-(w)为基准进行参数整定。
结合式（26）和式（27）所示两种稳定性约束，可提出分别基于幅值灵敏度和相位灵敏度的参数整定方法。
假定TSG-HVDC电源系统中待整定参数记为a，Zo(jw)=Ro(w)+jXo(w)，则有：
1）基于Zo(jw)幅值灵敏度的参数整定
考虑|Zo(jw)|=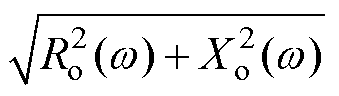
，构建Zo(jw)的幅值灵敏度SA,a(w)为
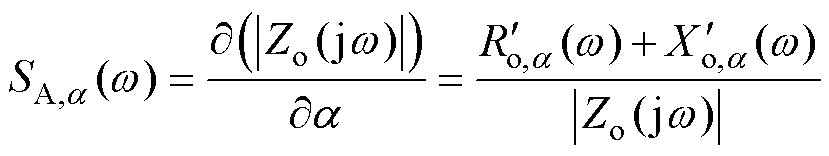（28）
式中，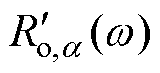
=∂Ro(w)/∂a；
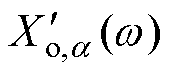=∂Xo(w)/∂a。
由于SA,a(w)反映参数a变化对|Zo(jw)|的影响，按|Zo(jw)|与Min-(w)不交截进行整定，调节量Da可估计为
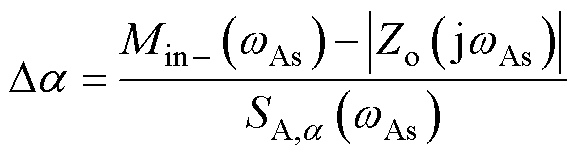（29）
式中，wAs为交截频段[wA1, wA2]内|Da|最大值对应的频率。
2）基于Zo(jw)相位灵敏度的参数整定
类似地，结合∠Zo(jw)=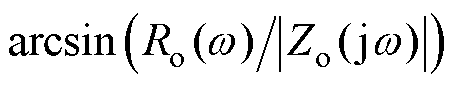
，构建Zo(jw)的相位灵敏度Sq,a(w)为
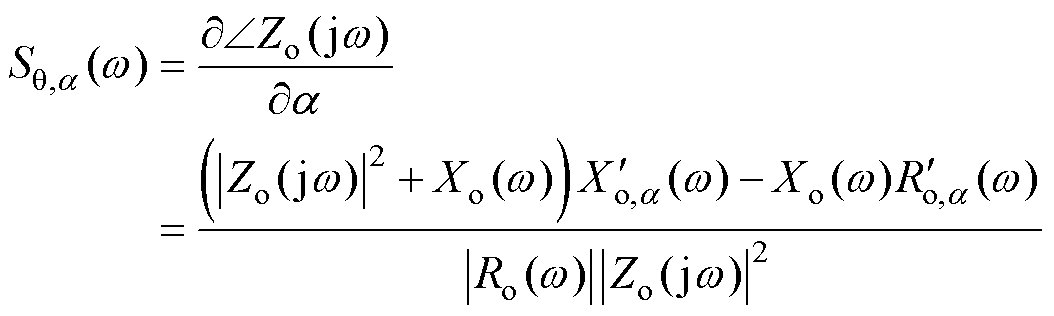（30）
结合图7和式（30），按∠Zo(jw)与qin-(w)之差始终处于0°～180°之间进行整定，调节量Da可估计为
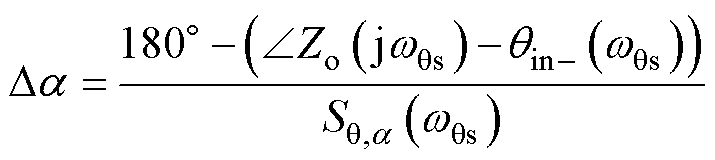（31）
式中，wqs表示在[wA1, wA2]内，且∠Zo(jw)-qin-(w)未处于0°～180°之间的频段[wq1, wq2]中，|Da|最大值对应的频率。
若整定过程中存在n个可调参数a1～an，各可调参数的量纲和数值差异会同时影响幅值/相位灵敏度的量纲和数值。按式（32）将各参数调节量转换为相对调节量。
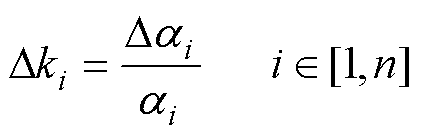（32）
以模值最小的相对调节量Dkj所对应的参数aj作为被调参数进行整定，从而保证多参数整定协同性，避免量纲差异导致整定过程中过分倾向[22]。当同时利用幅值和相位灵敏度进行参数整定时，仅需在分别得到两种灵敏度独立使用时的相对调节量后，选择其中幅值最小的相对调节量所对应的参数即可，具体整定流程如图8所示。需要指出，上述参数整定过程也可以使用TSG-HVDC电源系统的完整阻抗模型，但相应的灵敏度求解过程和复杂度也会提高。因此，从便捷性角度考虑，建议使用降阶阻抗计算灵敏度和整定参数，完整阻抗模型则用于整定结果的校验。
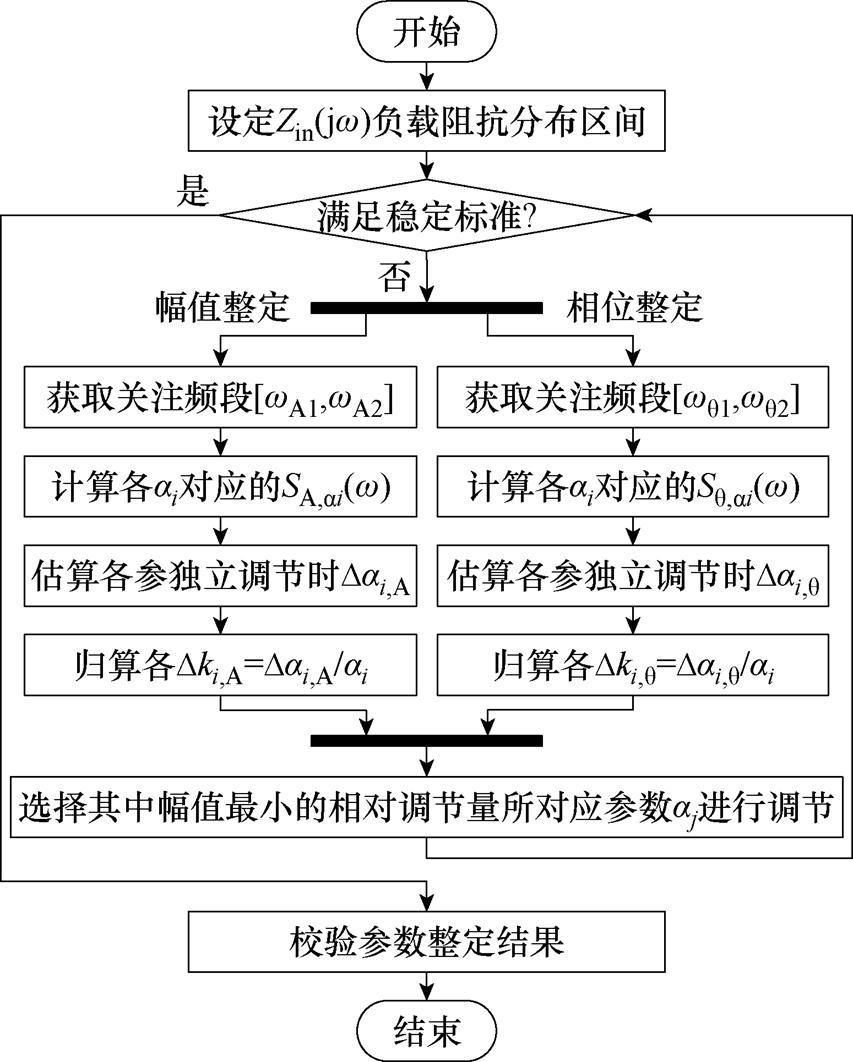
图8 考虑阻抗区间描述的多参数协调设计流程
Fig.8 Multi-parameter coordinated design process considering impedance interval distribution
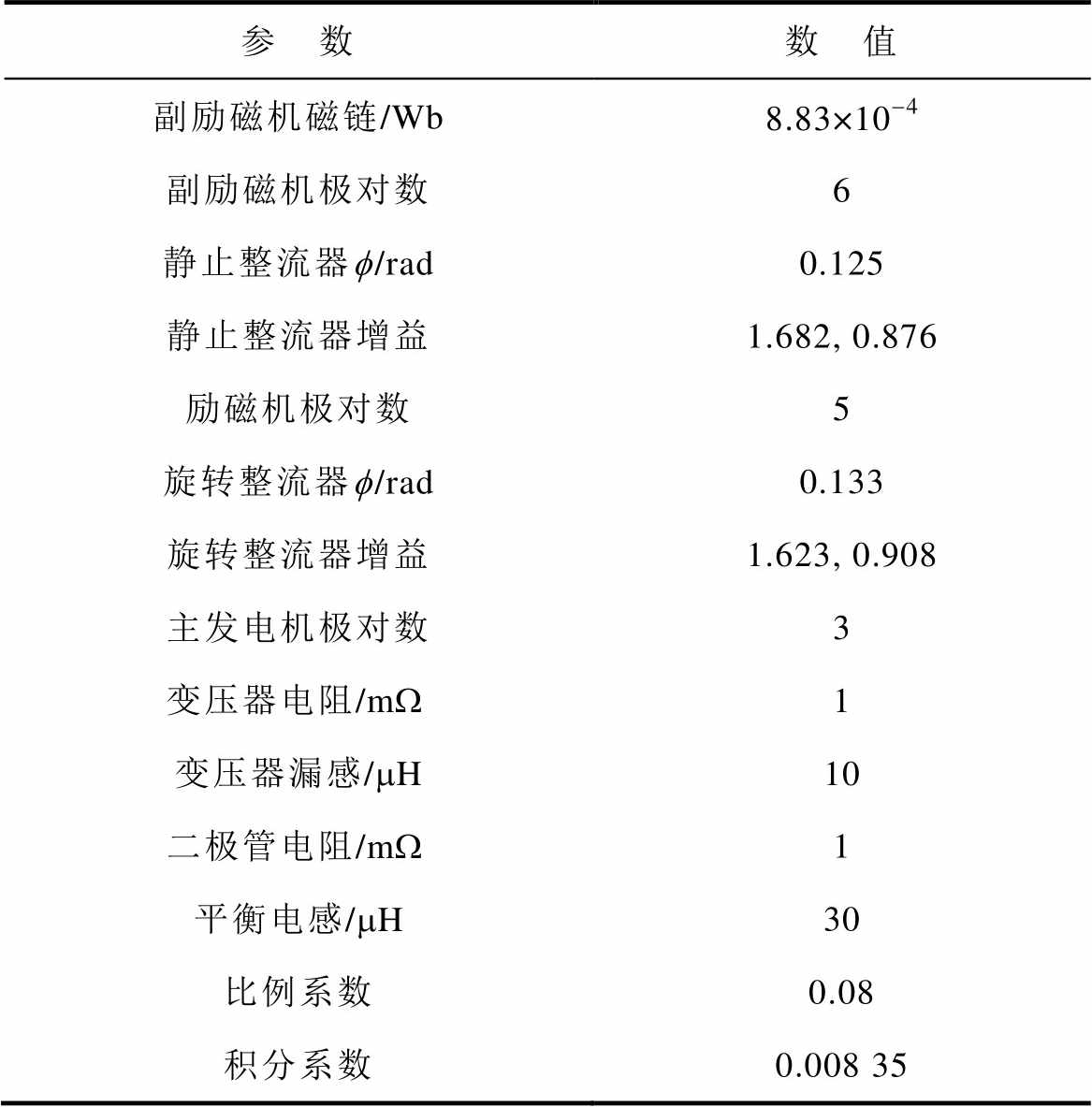
TSG-HVDC电源系统阻抗模型是小信号模型的传递函数表征。为验证模型的准确性，基于Matlab/ Simulink搭建了90 kW单电压环控制的TSG-HVDC电源系统仿真模型及相应小信号状态空间模型。输出电压270 V，系统参数如图4所示，其余参数见表1。
表1 TSG-HVDC电源系统参数
Tab.1 Parameters of TSG-HVDC power supply system
参 数数 值 副励磁机磁链/Wb8.83×10-4 副励磁机极对数6 静止整流器f/rad0.125 静止整流器增益1.682, 0.876 励磁机极对数5 旋转整流器f/rad0.133 旋转整流器增益1.623, 0.908 主发电机极对数3 变压器电阻/mW1 变压器漏感/mH10 二极管电阻/mW1 平衡电感/mH30 比例系数0.08 积分系数0.008 35
图9a与图9b分别展示了负载与电压参考指令扰动下小信号状态空间模型的响应，其中负载功率扰动由80 kW阶跃至90 kW，电压参考值由270 V变化为290 V。由时域仿真的对比结果表明，建模环节涉及的简化（如换相重叠角采用常值处理）尚未影响到保留TSG-HVDC电源系统动态特性，对小干扰或谐振稳定性分析可完全适用。
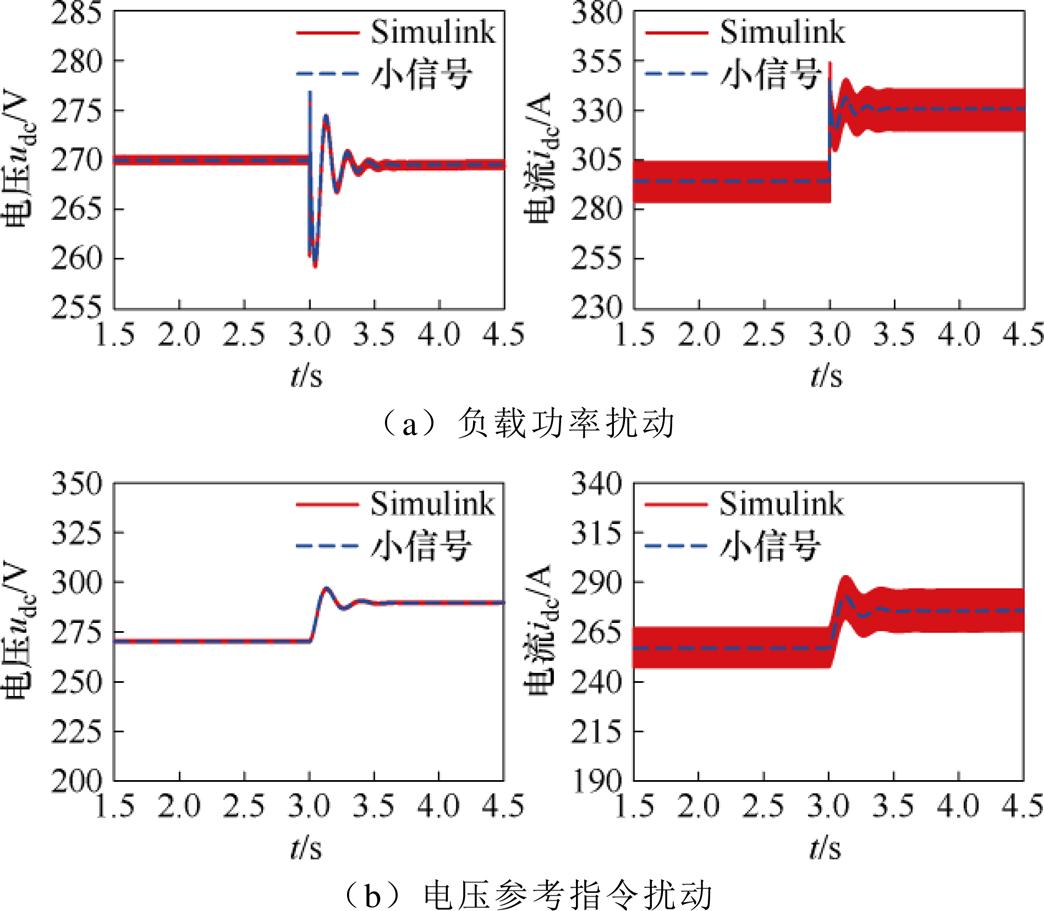
图9 小信号模型响应与电磁暂态仿真对比
Fig.9 Comparison of response between small-signal model and EMT simulation
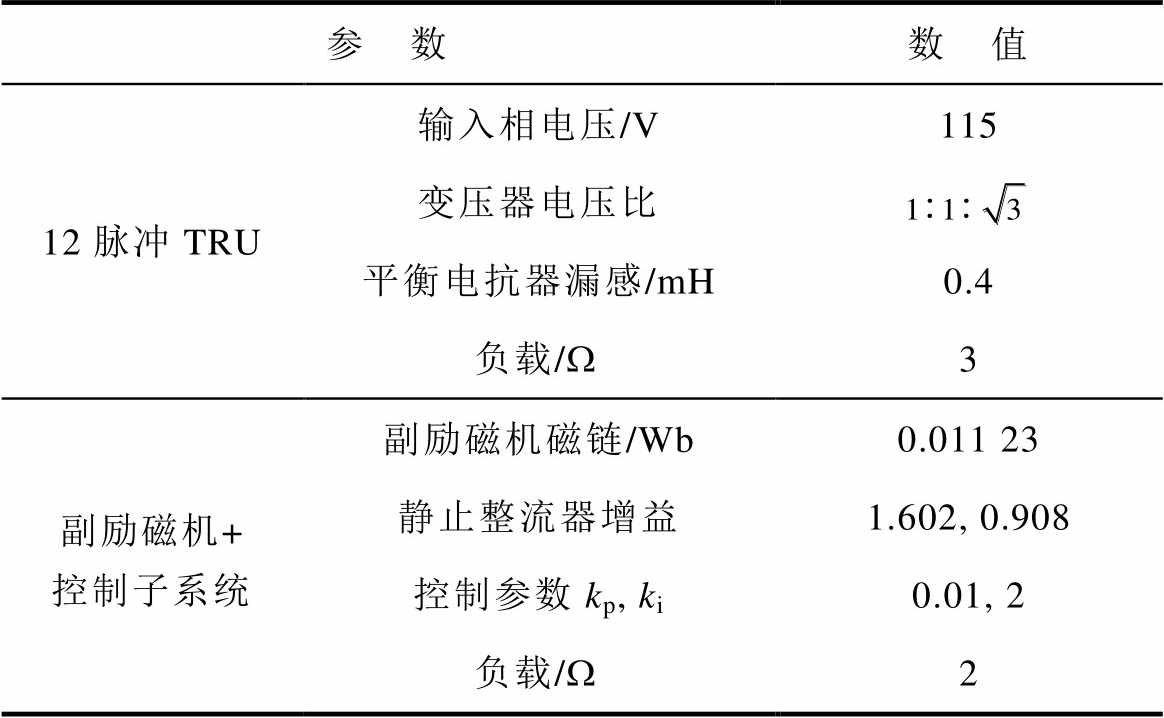
为进一步明确静止/旋转整流器和TRU建模方式的精度，避免其他部件模型偏差对建模有效性判断的干扰，搭建了如图10所示硬件平台对12脉冲TRU子系统与副励磁机子系统两个关键非线性环节进行分解实验验证，佐证建模对实际装置的适用性。测试系统的部分参数见表2，其中静止整流器增益可由不同负载状况下电压与电流变量的平均值代入式（7）计算得到。
图10 12脉冲TRU与副励磁机测试系统
Fig.10 Test systems of low power 12-pulse TRU and auxiliary exciter
表2 测试系统基本参数
Tab.2 Basic configuration of test systems
参 数数 值 12脉冲TRU输入相电压/V115 变压器电压比 平衡电抗器漏感/mH0.4 负载/W3 副励磁机+控制子系统副励磁机磁链/Wb0.011 23 静止整流器增益1.602, 0.908 控制参数kp, ki0.01, 2 负载/W2
图11对比了阶跃扰动下12脉冲TRU小信号模型响应与物理实验波形，图12则展示了含闭环控制副励磁机子系统的验证结果。动态过程的高度一致说明了整体小信号建模方法（尤其是静止整流器、TRU等非线性环节）的可靠性。
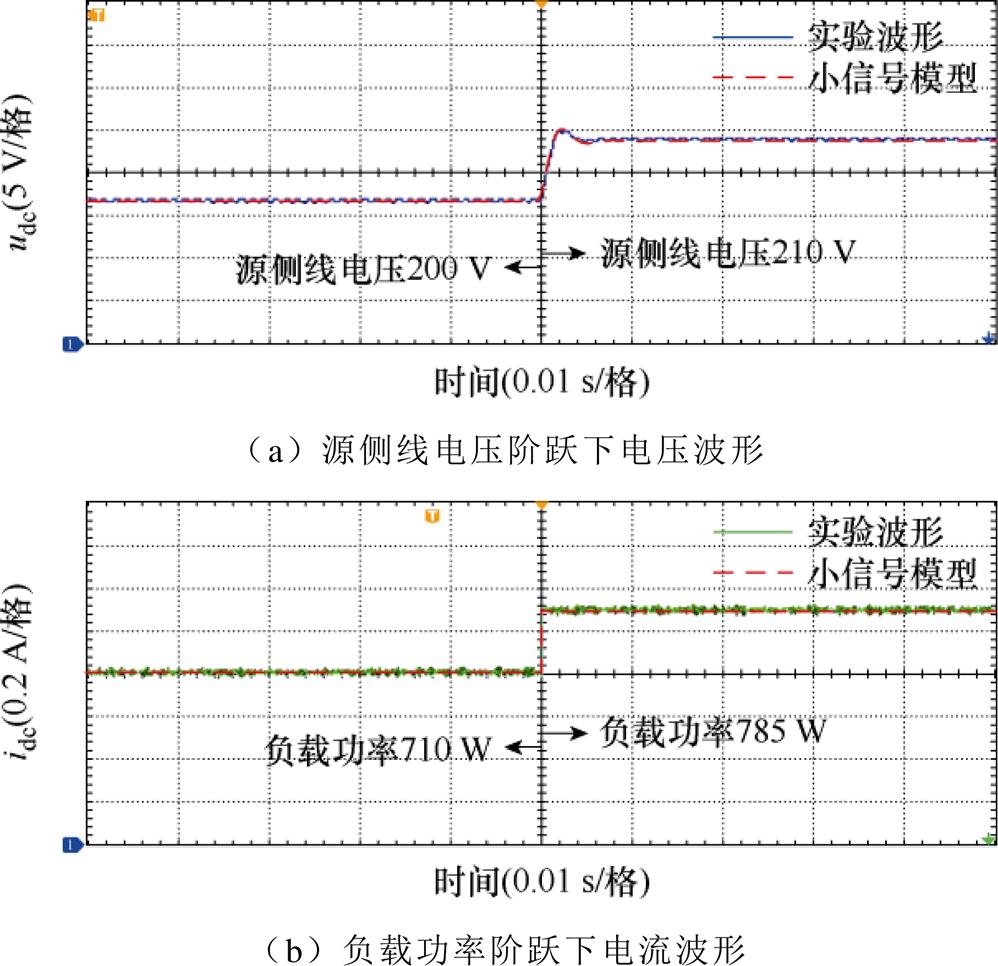
图11 12脉冲TRU小信号模型响应与物理实验对比
Fig.11 Response comparison between small-signal model of 12-pulse TRU and its physical experiment
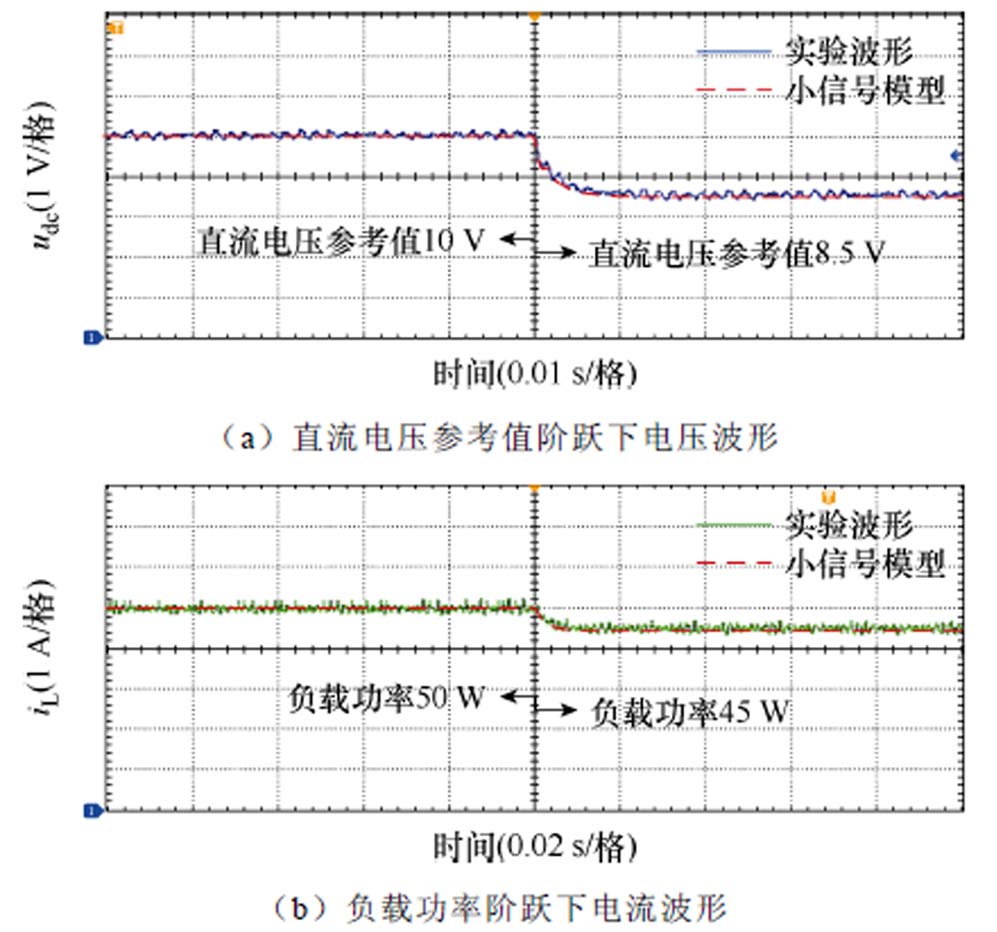
图12 副励磁机小信号模型响应与物理实验对比
Fig.12 Response comparison between small-signal model of auxiliary exciter subsystem and its physical experiment
按表1所示参数和式（19）所示结果，图13展示了TSG-HVDC电源系统阻抗模型幅频、相频特性，与仿真扫频结果高度吻合，验证了所建阻抗模型的准确性。
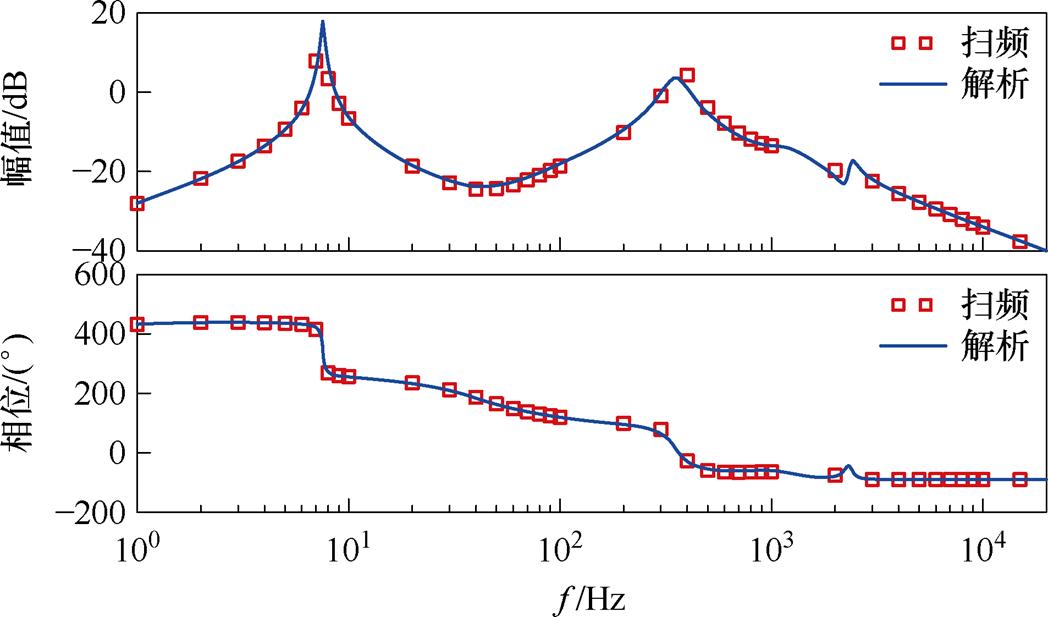
图13 阻抗模型与扫频结果对比
Fig.13 Comparison between impedance model and frequency sweep
为进一步明确各子系统参数对阻抗尖峰分布的影响，将副励磁与励磁处理为单位增益环节，并在图14中给出了阻抗简化模型与仿真扫频结果。对比图13可见，10 Hz附近的阻抗尖峰由励磁子系统产生，其余阻抗尖峰主要受主发电机子系统的影响。因此，在考虑低频振荡尤其是恒功率负载负阻尼引发的自激振荡问题时，阻抗建模须涉及励磁机子系统。
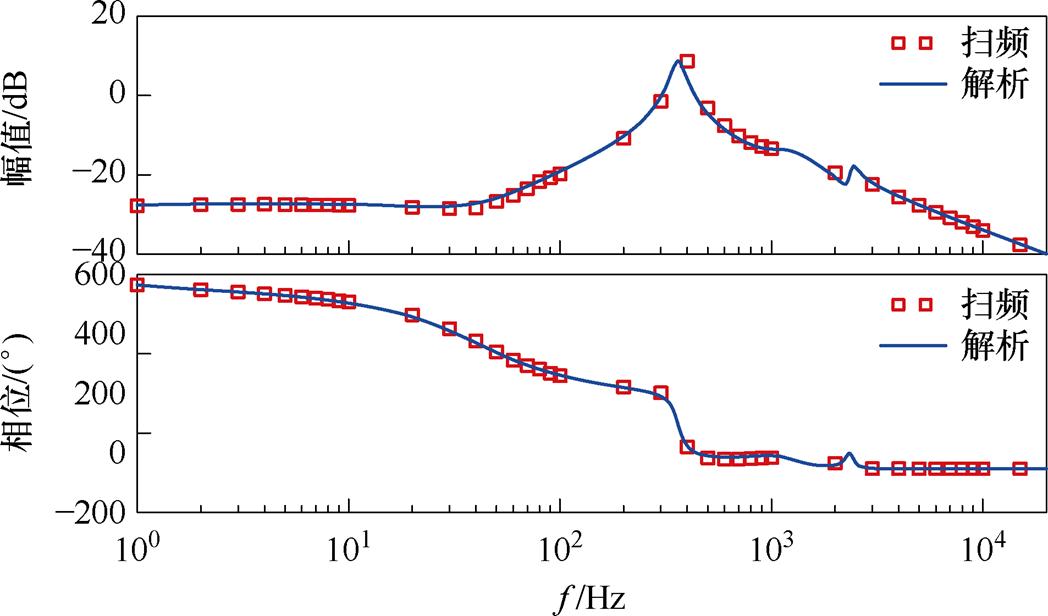
图14 仅配置主发电机的HVDC电源系统输出阻抗
Fig.14 Output impedance of HVDC power supply system with only configuration of main generator
现采用定数对数采样获取各子系统传递函数矩阵的幅值（相位）特性，最小采样频率1 Hz，最大采样频率10 kHz。对比原始小信号模型阶数，表3给出了各子系统传递函数矩阵矢量拟合降阶后的结果。在误差可接受范围内，副励磁机子系统Zp(s)可近似为增益环节，励磁机子系统E(s)各元素可用一阶惯性环节表征，等效时间常数约为0.591 s。表4进一步给出了G(s)中各元素的极点拟合结果，其中误差选取的是传递函数矩阵各元素降阶拟合的最大值。对比基于奇异摄动法的截断降阶结果（主导特征值及由参与因子分析得到的主要参与状态量），矢量拟合降阶虽然模糊了内部状态量的物理意义，但在相同阶数下具备更好的模型精度。
表3 各子系统传递函数矩阵降阶结果
Tab.3 Order-reduction results of transfer matrices for subsystems
子系统原始模型降阶后模型 e=1×10-10e=1×10-5 副励磁机Zp(s)320 励磁机E(s)531 主发电机G(s)977 整体阻抗19139
表4 主发电机子系统的两种降阶方法对比
Tab.4 Comparison of two reduced order modeling methods for the main generator subsystem
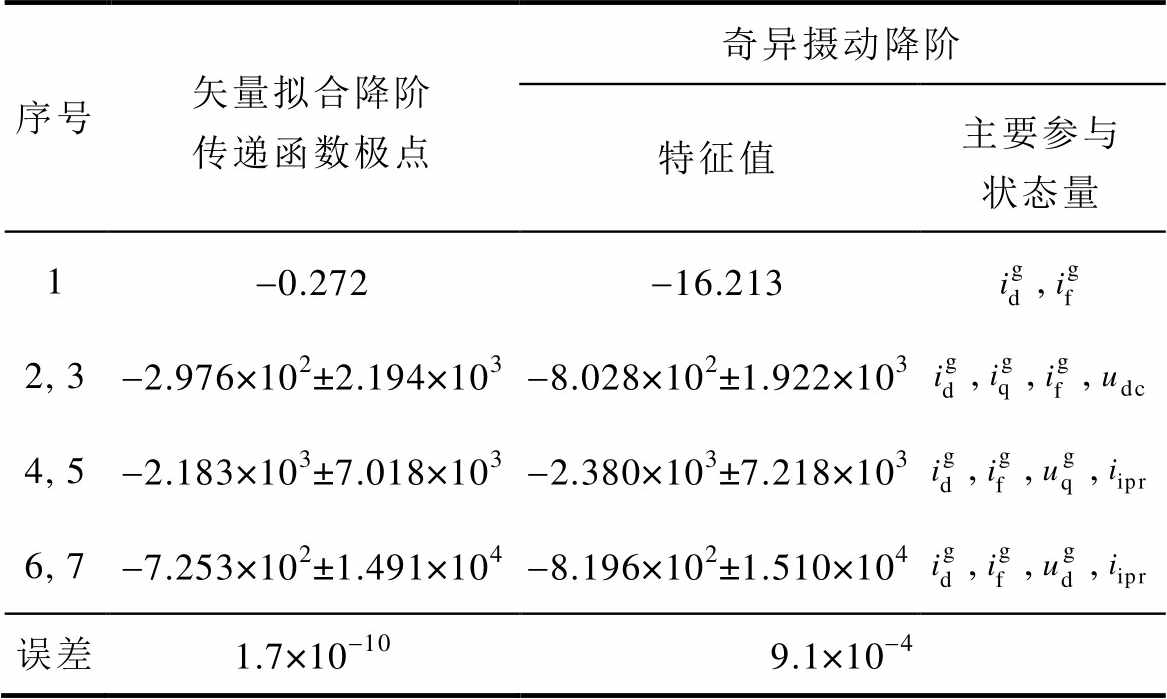
序号矢量拟合降阶传递函数极点奇异摄动降阶 特征值主要参与状态量 1-0.272-16.213, 2, 3-2.976×102±2.194×103-8.028×102±1.922×103,,, 4, 5-2.183×103±7.018×103-2.380×103±7.218×103,,, 6, 7-7.253×102±1.491×104-8.196×102±1.510×104,,, 误差1.7×10-109.1×10-4
以完整19阶阻抗模型为参照，图15对比了均为9阶时矢量拟合降阶与奇异摄动法截断降阶的阻抗幅频、相频特性，其中矢量拟合降阶阻抗模型由副励磁机子系统（0阶、比例环节）、励磁机子系统（1阶）、主发电机子系统（7阶）和电压控制器（1阶）构成，表明9阶模型能在较宽频段内表征TSG-HVDC电源系统动态特性，而截断类降阶分析与处理方法无法保证。在控制整体模型阶数的情况下，通过搜寻局部最优整合出整体最优，该9阶模型保留了各子系统的主导特性，符合三级式发电机的结构特点，便于工程应用中各子系统模型的移植，同时降低参数整定过程灵敏度求解的复杂度，提高了整定效率。
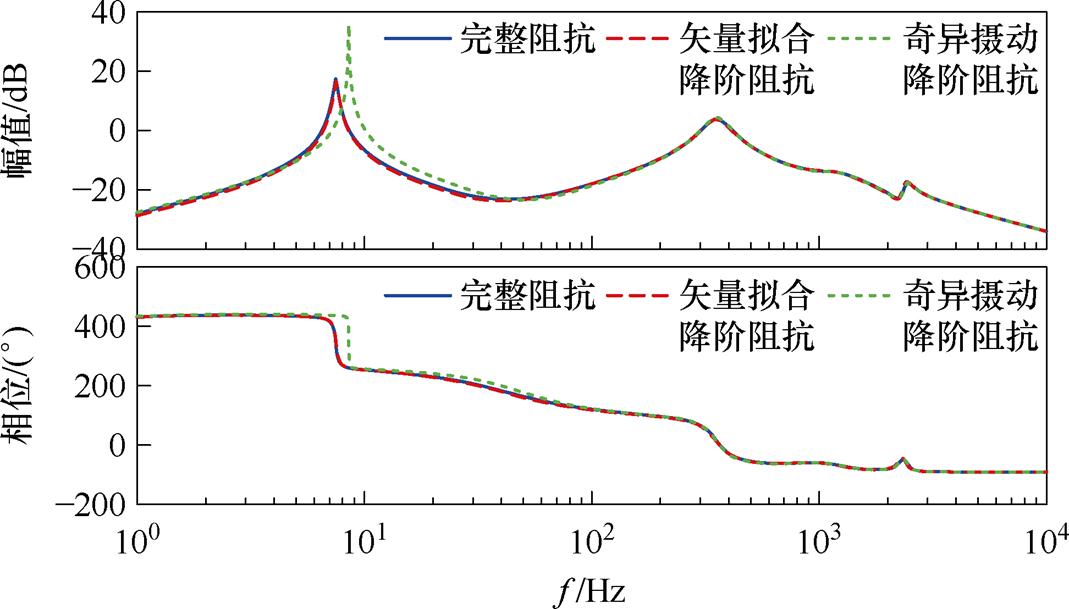
图15 矢量拟合与奇异摄动降阶阻抗结果对比
Fig.15 Comparison of impedances between order-reduction by vector fitting and singular perturbation
为验证所提区间描述的参数整定方法，设置了如图16所示测试系统。其中，Buck变换器采用单电压环控制，用于油泵、电嘴等设备，VSC采用定交流电压控制，主要对制冷风扇、窗加热等负载供电。TSG-HVDC电源系统额定功率为20 kW，负载功率随着巡航速度和高度的变化而变化，故Buck负载变换器消耗功率P1在0～2 kW范围内，VSC消耗功率P2在15～20 kW范围内。此时，即使负载消耗的总功率一致，也会因P1和P2分配的不同导致Zin(s)存在差异，故根据P1和P2所有可能的取值搭配给出Zin(s)的分布范围，最终得到考虑负载阻抗区间描述的系统阻抗交截情况如图17所示。
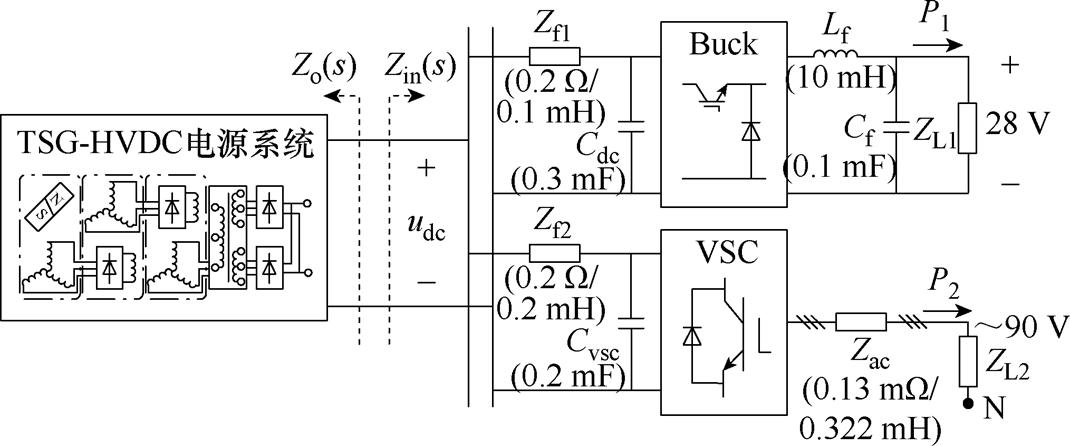
图16 基于TSG-HVDC电源的直流供电系统
Fig.16 DC distribution system based on TSG-HVDC
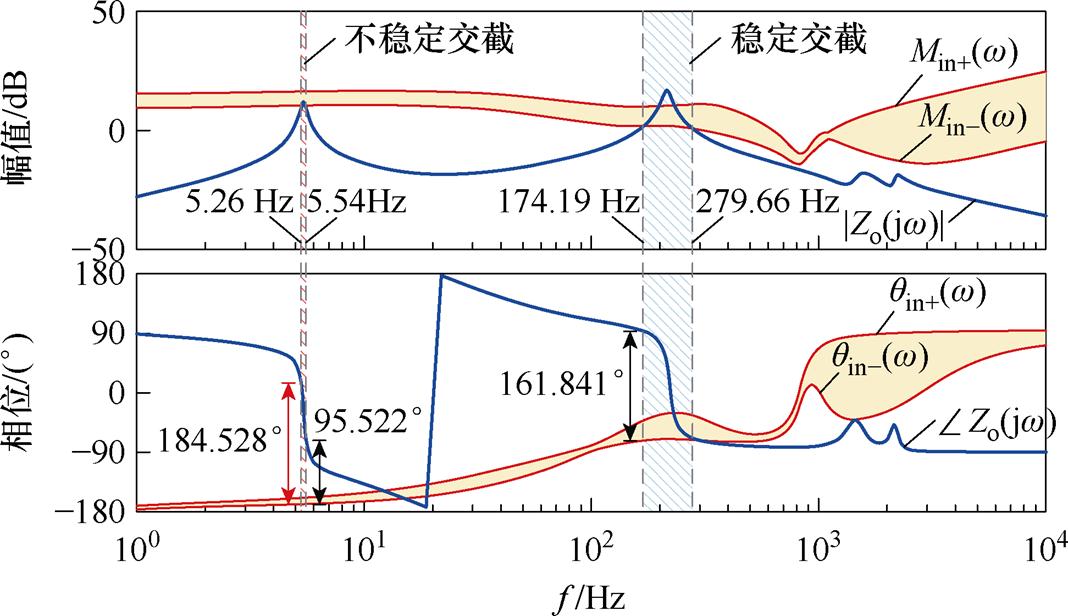
图17 考虑负载阻抗区间描述的系统阻抗交截情况
Fig.17 The system impedance intersection situation considering interval distribution of load impedance
结合式（26）和式（27）可知，Zo(s)在5.26～5.54 Hz频段内与区间描述的Zin(s)存在不稳定交截，系统存在振荡失稳风险。现利用阻抗和相位灵敏度，以Min-(w) 和qin-(w) 为基准对系统控制参数进行整定，整个过程见表5。累计比例系数Kp和积分系数Ki的调节量分别为DKp=0.043 9和DKi= -0.010 3，此时判别系统全工况稳定。
表5 TSG控制参数整定过程
Tab.5 The process of setting control parameters for TSG
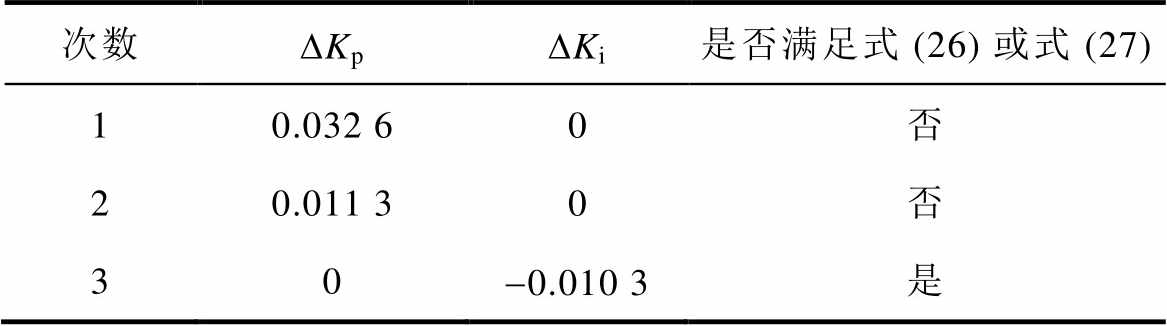
次数DKpDKi是否满足式 (26) 或式 (27) 10.032 60否 20.011 30否 30-0.010 3是
图18给出了两种极端工况下，考虑负载阻抗区间描述的参数整定前后的时域仿真验证结果。
1）P1=2 kW，P2=18 kW
图18a中，VSC负载变换器和Buck负载变换器在11 s分别设置了3 kW和2 kW负载阶跃，系统电压振荡发散。在13.5 s时，对TSG控制参数进行修正，振荡逐渐收敛，与理论分析一致。
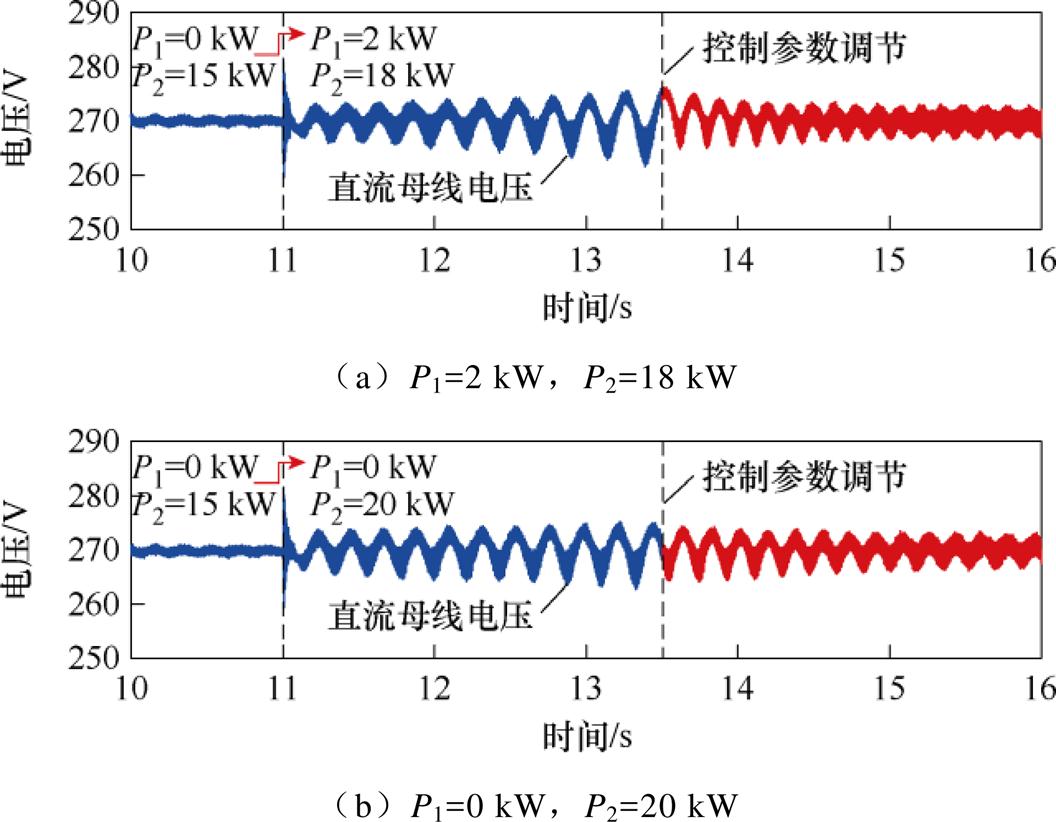
图18 考虑负载阻抗区间描述的参数整定效果
Fig.18 Parameter tuning effect considering interval distribution of load impedance
2）P1=0 kW，P2=20 kW
图18b中，仅VSC负载变换器在11 s设置5 kW负载阶跃，系统电压振荡失稳。当在13.5 s对TSG控制参数进行修正，振荡同样逐渐收敛。
若仅对P1=2 kW和P2=18 kW的单一工况进行控制参数设计，可得控制参数的调节量为DKp= 0.011。此时，两种极限工况在各自负载阶跃后，引入该控制参数调节量时的电压响应分别如图19a和图19b所示，P1=0 kW和P2=20 kW工况下母线电压无法收敛，且P1=2 kW和P2=18 kW工况的母线电压收敛速度变慢。
为进一步验证考虑负载区间描述的参数整定方法的有效性，基于远宽MT6020实时仿真器搭建了如图20所示控制器硬件在环实验平台，并复现了P1=0 kW和P2=20 kW工况下的测试系统。由于系统规模与电路模拟器的能力之间存在矛盾，主电路仿真步长设为20 ms，采样间隔设置为40 ms。图21为控制硬件在环实验参数整定前、后的实验结果，与时域仿真的稳定性特征一致，进一步佐证了参数整定结果的有效性。
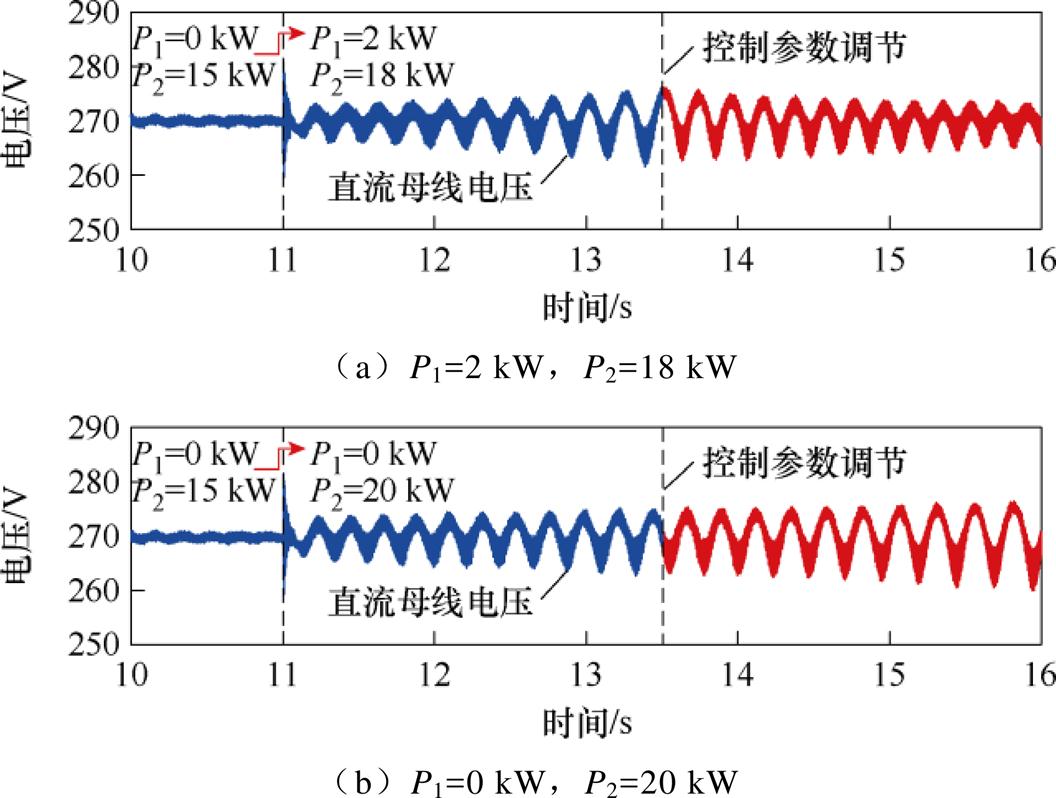
图19 考虑单一工况的参数整定效果
Fig.19 Parameter tuning effect considering a single operating condition
图20 控制器硬件在环实时仿真平台
Fig.20 Real-time simulation platform of control hardware-in-the-loop
通过等效电路集成和子系统二端口H参数表征，本文建立了TSG-HVDC电源系统完整输出阻抗，并基于矢量拟合获得了方均根误差最优的降阶阻抗模型，同时提出了一种考虑负载阻抗区间描述的参数整定方法。最后，结合时域仿真、子系统分解物理实验和控制器硬件在环实验，验证了阻抗模型的准确性和参数整定方法的鲁棒性，并得到结论如下：
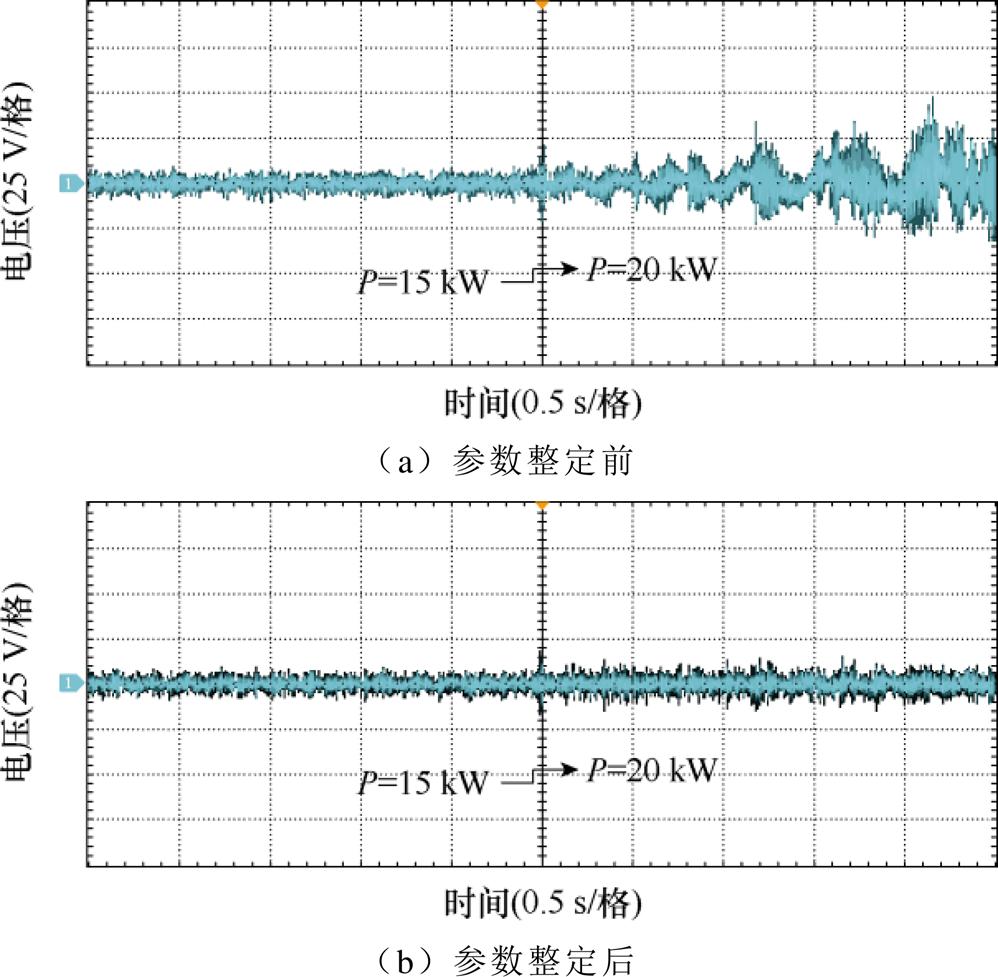
图21 控制硬件在环实验验证
Fig.21 Experimental verification of the control hardware-in-the-loop
1）TSG-HVDC电源系统完整输出阻抗模型原始阶数高达19阶，经矢量拟合降阶，最低9阶即可较为准确地进行描述。
2）TSG-HVDC电源系统降阶阻抗最终保留的动态过程涉及PI控制、励磁机励磁绕组暂态及忽略暂态凸极效应的电枢绕组暂态过程、忽略阻尼绕组的主发电机与TRU的动态过程。
3）所提参数整定方法可以计及负载阻抗分布范围，结合降阶阻抗和幅/相灵敏度，可对TSG-HVDC电源系统参数进行协调整定，具有很好的鲁棒性。
后续将针对TSG-HVDC电源系统的特殊与极端工况对系统参数的影响，提出误差修正方法，构建适用工况更多、适用频段更宽的TSG-HVDC电源系统阻抗模型。
参考文献
[1] Wheeler P, Bozhko S. The more electric aircraft: technology and challenges[J]. IEEE Electrification Magazine, 2014, 2(4): 6-12.
[2] Chen Jiawei, Wang Chengjun, Chen Jie. Investigation on the selection of electric power system architecture for future more electric aircraft[J]. IEEE Transactions on Transportation Electrification, 2018, 4(2): 563- 576.
[3] Nya B H, Brombach J, Schulz D. Benefits of higher voltage levels in aircraft electrical power systems[C]// 2012 Electrical Systems for Aircraft, Railway and Ship Propulsion, Bologna, Italy, 2012: 1-5.
[4] 李永东, 章玄, 许烈. 多电飞机高压直流供电系统稳定性研究综述[J]. 电源学报, 2017, 15(2): 2-11.
Li Yongdong, Zhang Xuan, Xu Lie. A survey on stability analysis for HVDC power system in MEA[J]. Journal of Power Supply, 2017, 15(2): 2-11.
[5] 吴翔宇, 张晓红, 尚子轩, 等. 基于频域阻抗网络建模分析的交直流微电网振荡问题研究[J]. 电工技术学报, 2024, 39(8): 2294-2310.
Wu Xiangyu, Zhang Xiaohong, Shang Zixuan, et al. Research on the oscillation problem of AC-DC microgrids based on frequency domain impedance network modeling and analysis[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2294- 2310.
[6] Han Liqiu, Wang Jiabin, Howe D. State-space average modelling of 6- and 12-pulse diode rectifiers[C]// 2007 European Conference on Power Electronics and Applications, Aalborg, Denmark, 2007: 1-10.
[7] Areerak K N, Wu T, Bozhko S V, et al. Aircraft power system stability study including effect of voltage control and actuators dynamic[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(4): 2574-2589.
[8] Gao Fei, Zheng Xiancheng, Bozhko S, et al. Modal analysis of a PMSG-based DC electrical power system in the more electric aircraft using eigenvalues sensitivity[J]. IEEE Transactions on Transportation Electrification, 2015, 1(1): 65-76.
[9] Xu Qianwen, Wang Peng, Chen Jiawei, et al. A module-based approach for stability analysis of complex more-electric aircraft power system[J]. IEEE Transactions on Transportation Electrification, 2017, 3(4): 901-919.
[10] 谢小荣, 李浩志, 张丹, 等. 新型电力系统稳定器研究初探[J]. 电力系统自动化, 2024, 48(23): 156- 166.
Xie Xiaorong, Li Haozhi, Zhang Dan, et al. Pre- liminary study on stabilizer for new power systems[J]. Automation of Electric Power Systems, 2024, 48(23): 156-166.
[11] 刘欣, 袁易, 王利桐, 等. 柔性直流输电系统三端口混合参数建模及其稳定性分析[J]. 电工技术学报, 2024, 39(16): 4968-4984.
Liu Xin, Yuan Yi, Wang Litong, et al. Three-port hybrid parameter modeling and stability analysis of MMC-HVDC system[J]. Transactions of China Elec- trotechnical Society, 2024, 39(16): 4968-4984.
[12] Cespedes M, Sun Jian. Impedance modeling and analysis of grid-connected voltage-source con- verters[J]. IEEE Transactions on Power Electronics, 2013, 29(3): 1254-1261.
[13] 陈鹏伟, 姜文伟, 阮新波, 等. 直流配电系统有源阻尼控制的阻抗释义与谐振点灵敏度参数调节方法[J]. 中国电机工程学报, 2021, 41(19): 6616-6630.
Chen Pengwei, Jiang Wenwei, Ruan Xinbo, et al. Impedance explanation and resonance point sensitivity- based parameter design method of active damping applied to DC distribution system[J]. Proceedings of the CSEE, 2021, 41(19): 6616-6630.
[14] 刘欣, 郭志博, 贾焦心, 等. 基于序阻抗的虚拟同步发电机并网稳定性分析及虚拟阻抗设计[J]. 电工技术学报, 2023, 38(15): 4130-4146.
Liu Xin, Guo Zhibo, Jia Jiaoxin, et al. Stability analysis and virtual impedance design of virtual synchronous machine based on sequence impe- dance[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4130-4146.
[15] Gao Fei, Bozhko S, Costabeber A, et al. Control design and voltage stability analysis of a droop- controlled electrical power system for more electric aircraft[J]. IEEE Transactions on Industrial Elec- tronics, 2017, 64(12): 9271-9281.
[16] 赵丹, 申科, 刘卫国, 等. 基于二端口理论的航空三级式起动/发电机宽频阻抗模型研究[J]. 中国电机工程学报, 2021, 41(22): 7841-7850.
Zhao Dan, Shen Ke, Liu Weiguo, et al. Two-port theory based wide frequency impedance modeling method for aircraft three-stage starter/generator[J]. Proceedings of the CSEE, 2021, 41(22): 7841-7850.
[17] Wang Shuang, Ruan Xinbo, He Yuying, et al. Small- signal impedance modeling and analysis of variable- frequency AC three-stage generator for more electric aircraft[J]. IEEE Transactions on Power Electronics, 2023, 38(1): 206-216.
[18] 徐子梁, 任小永, 吴玲燕, 等. 航空Vienna整流器缺相控制方法[J]. 电工技术学报, 2023, 38(20): 5560-5571.
Xu Ziliang, Ren Xiaoyong, Wu Lingyan, et al. A lack phase control strategy for aircraft Vienna rectifier[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5560-5571.
[19] 孙立政, 王丰, 许子怡, 等. 基于等效降阶模型的直流变换器虚拟直流电机控制参数设计[J]. 电力系统自动化, 2024, 48(24): 124-135.
Sun Lizheng, Wang Feng, Xu Ziyi，et al. Control parameter design of virtual DC machine for DC/DC converter based on equivalent reduced-order model[J]. Automation of Electric Power Systems, 2024, 48(24): 124-135.
[20] 付兴贺, 夏宏伟, 熊嘉鑫. 基于降阶动态相量模型的电感耦合式励磁系统间接励磁电流估计[J]. 电工技术学报, 2023, 38(19): 5152-5163.
Fu Xinghe, Xia Hongwei, Xiong Jiaxin. Indirect field current estimation algorithm for inductively coupled excitation systems based on reduced-order dynamic phasor model[J]. Transactions of China Electro- technical Society, 2023, 38(19): 5152-5163.
[21] Krause P C, Wasynczuk O, Sudhoff S D, et al. Analysis of Electric Machinery and Drive Systems[M]. Hoboken, New Jersey: John Wiley & Sons, Inc., 2013.
[22] Chen Pengwei, Jiang Wenwei, Ruan Xinbo, et al. Active damping control and parameter design method for ISOP-based load converter in DC distribution system[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(1): 465-477.
Reduced Impedance Modeling and Parameter Tuning Method of Three-Stage Generator-Based Airborne High Voltage DC Power Supply System
Abstract The three-stage generator-based airborne high voltage direct current (TSG-HVDC) power supply system has a complex structure and strong nonlinearity, leading to high impedance modeling and integration complexity. The low complexity impedance model of the TSG-HVDC power supply system is the premise of stability analysis and design. Existing research on the impedance reduction model and scope of application is relatively scattered, which hinders the stable theoretical analysis of the TSG-HVDC power supply system.
Considering the differences in operation and processing between rotating/stationary rectifiers and multi- pulse transformer rectifier units, this paper derives the output impedance model by integrating each subsystem's equivalent circuit and two-port H parameter. Then, a vector fitting-based order-reduction analysis process of the two-port H parameter is designed, and the reduced impedance model with optimal wideband root mean square error is obtained, as well as the impacts of each subsystem on the overall output impedance. Subsequently, a multi-parameter coordinated tuning method based on load impedance interval description is proposed by combining the amplitude and phase sensitivity of the reduced-order model. Finally, compared with the time-domain simulation, scaled-down physical experiments, and controller hardware-in-the-loop, the accuracy of the impedance model and the robustness of the parameter tuning method are verified.
The high consistency between the response of the small signal model under step disturbance and the dynamic process of the physical experimental waveform indicates the reliability of the overall small signal modeling method. Secondly, compared with the truncated order reduction results based on the singular perturbation method, the vector fitting order reduction has better model accuracy in the same order. Thirdly, the experimental results before and after parameter tuning are consistent with the stability characteristics of the time-domain simulation.
The conclusions of this paper are as follows. (1) The original order of the complete output impedance model of the TSG-HVDC power supply system is as high as the 19th order. After order reduction using vector fitting, the minimum order required to describe it accurately is 9. (2) The dynamic processes retained in the reduced- order impedance of the TSG-HVDC power supply system include the PI control, the transient process of the excitation winding of the exciter, the transient process of the armature winding with the transient salient pole effect ignored, and the dynamic processes of the main generator (excluding damper winding impacts) and the TRU. (3) The proposed parameter tuning method can consider the distribution range of the load impedance. Combining the reduced-order impedance and the amplitude/phase sensitivity can coordinate the TSG-HVDC power supply system's parameters.
Keywords：More electric aircraft, three-stage generator, high voltage direct current power supply system, reduced-order impedance model, parameters coordinated tuning
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.242282
国家自然科学基金项目（U2141227, 52377190）和江苏省自然科学基金面上项目（BK20231446）资助。
收稿日期 2024-12-28
改稿日期 2025-02-21
陈鹏伟 男，1992年生，副教授，硕士生导师，研究方向为直流供配电系统稳定性建模、分析与优化控制。
E-mail: chenpw2014@163.com
陈 杰 男，1982年生，教授，研究方向为电力电子变换装置的建模与控制技术、微电网与分布式发电技术、航空二次电源技术等。
E-mail: chen_jie@nuaa.edu.cn（通信作者）
（编辑 陈 诚）