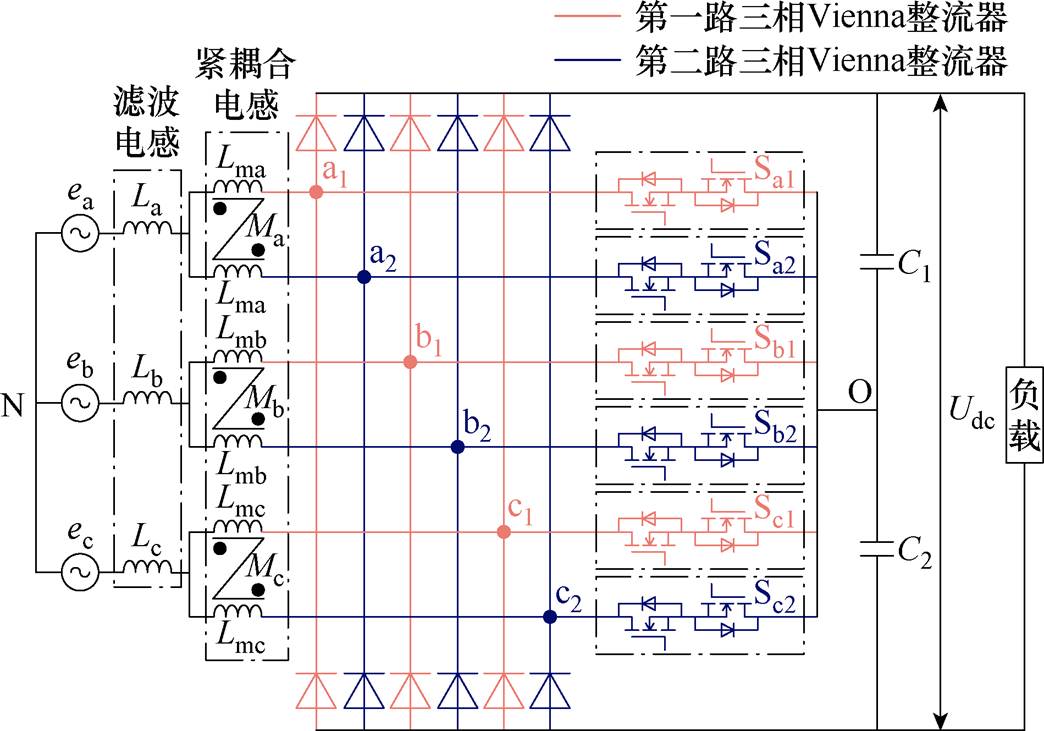
图1 两路交错并联三相Vienna整流器
Fig.1 Power circuit of two-channel interleaved three-phase Vienna rectifier
摘要 为衰减并网电流高频分量和抑制桥臂间环流，交错并联Vienna整流器每相需要滤波电感与紧耦合电感两个磁性器件，其中紧耦合电感对磁心的利用率较低，使变流器的效率和功率密度难以继续提高。该文针对此问题提出一种三绕组耦合电感，并建立其电路模型和磁路模型，进而提出一种三绕组耦合电感的设计方法。所提三绕组耦合电感通过磁心复用与绕组复用使磁心中的磁通均匀分布并减少绕组匝数，可以降低绕组损耗，尤其适用于大电流应用场景。与滤波电感串联紧耦合电感的传统方案相比，在滤波能力、磁心体积、磁心饱和度和绕组电流密度均不变的前提下，所提三绕组耦合电感使绕组的直流电阻降低了35%，进一步提高了装置的效率。最后，通过有限元仿真与40 kW样机实验的效率对比验证了所设计三绕组耦合电感的可行性和有效性。
关键词：Vienna整流器 交错并联 磁集成 耦合电感
三相Vienna整流器具有无桥臂直通风险、控制相对简单[1-2]等优点，电动汽车充电前端普遍采用该拓扑结构。随着近年来电动汽车的蓬勃发展，对直流充电桩功率等级的需求越来越高，而两路交错并联是增加功率输出能力、分散损耗分布、提高等效开关频率及减小网侧电流纹波的有效途径[3]，并已在实际工程中得到广泛应用。
交错并联技术在AC-DC变换[4-5]和DC-DC变 换[6-8]中均已有大量研究。AC-DC变换的桥臂调制波是工频正弦交流量，流过其电感的是工频正弦电流叠加幅值随工频相位变化的高频纹波电流；DC-DC变换（这里指Buck或Boost变换器）的桥臂调制波是直流量，流过其电感的是直流电流叠加幅值固定的高频纹波电流。虽然电流波形不同，但两种电能变换中的电感功能一致，因此两种电能变换中的交错并联磁集成思路是相通的，都是将分立电感集成为耦合电感，下面分别介绍DC-DC变换和AC-DC变换中用于交错并联的耦合电感研究现状。
对于交错并联DC-DC变换器，从磁心结构及绕组分布两个方面对耦合电感设计的研究现状进行介绍。在磁心结构方面，文献[9]提出一种“E王E”型耦合电感磁心结构，该结构中气隙远离绕组，可以减少绕组涡流损耗；文献[10]针对两路交错并联Buck变换器，提出一种四柱式磁心结构，实现了两路电感的平面化耦合集成，其主要目标是降低磁元件高度；文献[11]在文献[10]的基础上提出气隙分布优化方法，可进一步降低电感磁损和铜损。在绕组分布方面，文献[12]针对大功率交错并联Boost变换器，提出绕组均分的耦合电感方案，并提出了耦合电感综合建模与多目标优化方法；文献[13]采用分段式绕组的设计使磁心内磁通分布均衡，实现了交错并联DC-DC变换器两路电感的解耦集成，值得注意的是，该文献之所以选择进行解耦集成，是因为其拓扑中存在开关电容使两路电流实现自均衡，而不需要通过反向耦合电感抑制高频环流，因此该解耦集成方法并不适用于常规交错并联拓扑。
对于交错并联AC-DC变换器，现有方案通常需要滤波电感与紧耦合电感串联作为交流电网与变流器之间的连接电感，其中滤波电感可以对并网电流中的高频成分进行衰减，而紧耦合的反向耦合电感可以在桥臂环流通路中形成较大的等效电感，主要用来减小桥臂间环流的幅值[3]，本文将这种方案称为传统分立方案。在其磁元件集成设计方面，文献[14]提出一种四柱式磁心S型绕线的两路解耦集成电感，存在环流通路上电感较小的问题，与传统分立方案相比对高频环流的抑制能力较差；与交错并联DC-DC变换器中的耦合电感设计思路相同，文献[15]提出一种与文献[10]类似的四柱式磁心集成两路电感，也是通过增大磁元件占板面积来降低纵向高度，适用于平面化要求较高的场景；文献[16-17]分别基于EE型磁心、环形磁心提出了用于两路交错并联桥臂的弱耦合电感；文献[18]则基于立体式磁心结构提出了用于四路交错并联桥臂的弱耦合电感，虽然磁心结构和绕组数量不同，但其思路大致相同，均是利用同相绕组间弱耦合的特性形成滤波电感，通过控制绕组自感和绕组间的耦合度可以实现与传统分立方案相同的滤波性能，但并未给出具体设计过程。
本文以两路交错并联Vienna整流器为应用场景，针对传统分立方案中的紧耦合电感对磁心利用率较低的问题，提出一种三绕组耦合电感。所提三绕组耦合电感方案将滤波电感与耦合电感集成在一个EE型磁心上，相比于传统分立方案，所提方案通过磁心复用与绕组复用使磁心中的磁通均匀分布并减少绕组匝数，既可降低磁元件损耗，又可提升两路交错并联系统功率密度。相比于文献[16]中的EE型磁心两绕组弱耦合电感方案，本文所提方案具有更低的绕组直流电阻。首先，给出所提三绕组耦合电感的结构，分析其等效电路模型，得到其等效基波电感、等效环流电感与各绕组自感、互感之间的关系；其次，分析其磁路模型，得到各绕组自感、互感与各磁路磁阻之间的关系，随后给出考虑空气漏磁通路的三绕组耦合电感设计方法，并基于该方法设计了额定电流60 A（有效值）的三绕组耦合电感，通过有限元仿真证明了该设计的正确性；再次，在滤波能力、磁心体积、磁心饱和度和绕组电流密度均不变的前提下，与传统分立方案和两绕组弱耦合电感方案相比所提方案在绕组直流电阻与电感体积方面均有优势；最后，通过在40 kW样机上的效率对比实验验证了所设计三绕组耦合电感的可行性和有效性。
两路交错并联三相Vienna整流器如图1所示，由于同相两桥臂的驱动信号之间存在180°相位差，两桥臂中点会存在电位不等的情况，目前的主流做法是通过引入紧耦合的反向耦合电感以抑制同相两桥臂之间的高频环流[19]，传统分立方案中每相的连接电感由滤波电感与紧耦合电感串联组成。图1中，La、Lb、Lc分别为三相的滤波电感，Lma、Lmb、Lmc分别为三相的紧耦合电感的自感，Ma、Mb、Mc分别为三相的紧耦合电感的互感，ea、eb、ec分别为三相电网电动势，Sa1、Sa2、Sb1、Sb2、Sc1、Sc2分别为三相各路的双向可控开关，C1、C2分别为上、下半直流母线的支撑电容。
图1 两路交错并联三相Vienna整流器
Fig.1 Power circuit of two-channel interleaved three-phase Vienna rectifier
由于三相的对称性，可对单相进行独立分析。以a相为例，电感的连接方式及各处电流和磁通的分布分别如图2所示。图2中，ia为滤波电感绕组的实际电流，ia1、ia2分别为紧耦合电感两个绕组中的实际电流，icira为紧耦合电感两个绕组电流中大小相同、方向相反的环流成分。
由于a1、a2点为基波等电位点，可近似认为ia被a1和a2支路平分，由基尔霍夫电流定律可知ia、ia1、ia2、icira满足
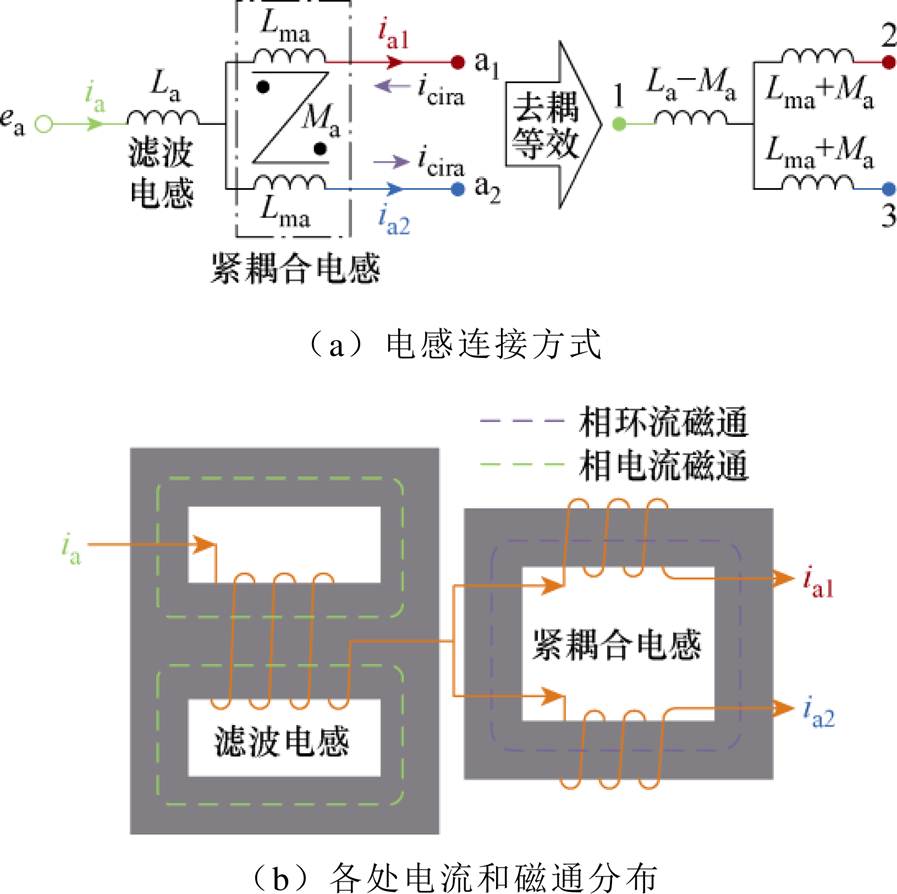
图2 传统分立方案的电路连接及各处磁通分布
Fig.2 Circuit connections and flux distribution in traditional separated scheme
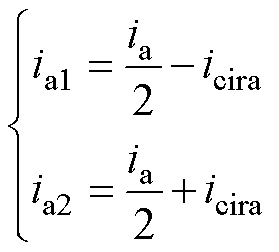（1）
如图2b所示，在滤波电感中，相电流ia产生相电流磁通；而在紧耦合电感中，由于其为反向紧耦合，因此其中近似只有相环流磁通。通常要求环流相比于相电流越小越好，因此紧耦合电感的磁心饱和度远低于滤波电感。由此可见，传统分立方案中的紧耦合电感没有实现对磁心的充分利用。
作为滤波器件，电感值应根据允许的电流纹波峰峰值进行设计。交错并联Vienna整流器需要同时关注网侧电流纹波和同相桥臂间的环流纹波，二者分别与等效基波电感与等效环流电感有关。等效基波电感与等效环流电感由图2a中的去耦等效电路获得，其定义分别为：等效基波电感为相电流通路上的电感，由于同相两桥臂采用相同的调制波，因此去耦等效电路中的2、3端子为基波等电位点，所以等效基波电感为1端子与2、3端子之间的总电感，即La-Ma与(Lma+Ma)//(Lma+Ma)的串联；等效环流电感为相环流通路上的电感，即2端子与3端子之间的总电感，即Lma+Ma与Lma+Ma的串联。若将滤波电感与紧耦合电感视为一个整体，则其电路上的外特性完全由等效基波电感与等效环流电感决定。
本文将每相的滤波电感与紧耦合电感集成在一个磁心上，提出了如图3所示的满足单相滤波需求的三绕组耦合电感结构，其磁心包括上轭、下轭和三个芯柱，三套绕组分别绕在三个芯柱上。定义绕在中间芯柱上的绕组为绕组1，其匝数为N1，自感为L1，电流为i1；绕在左侧芯柱上的绕组为绕组2，其匝数为N2，自感为L2，电流为i2；绕在右侧芯柱上的绕组为绕组3，其匝数为N3，自感为L3，电流为i3。三个绕组两两之间存在耦合，其中绕组1与绕组2、绕组1与绕组3均为正向耦合，互感分别为M12、M13；绕组2与绕组3为反向耦合，互感为M23。绕组1与传统分立方案中的滤波电感绕组功能相近，绕组2、绕组3与传统分立方案中的紧耦合电感的两个绕组功能相近。由于中间芯柱的存在，绕组2、绕组3耦合程度降低，所以磁心各部分均流过相电流磁通，各绕组均交链相电流磁通，达到磁心复用与绕组复用的目的，从而实现对磁心与绕组的充分利用。所提三绕组耦合电感关于中间芯柱轴对称，本文中与中间芯柱有关的变量以下标“c”表示，与左右两侧芯柱和上下轭有关的变量以下标“s”表示，如绕组1匝数记为Nc，绕组2、3匝数记为Ns。
图3 三绕组耦合电感结构
Fig.3 Structure of three-winding coupled inductor
根据图3中电流的正方向以及绕组的绕向，电感各绕组与某相电网及Vienna整流器桥臂之间的电路连接如图4所示。图4中，Udc为直流母线电压，O为直流母线电容中点，红色点画线框内为Vienna整流器桥臂1的4个开关器件，T1为其桥臂中点，蓝色点画线框内为Vienna整流器桥臂2的4个开关器件，T2为其桥臂中点。设某相电流为ic，记ic/2=is，并设该相环流为icir，其参考方向与i3相同，与i2相反，则i1=ic，i2=is-icir，i3=is+icir。根据交错并联Vienna整流器的运行原理，需要保证两路桥臂电感量相等，为此应保证磁路关于中间芯柱轴对称且N2=N3，因此L2=L3，M12=M13。
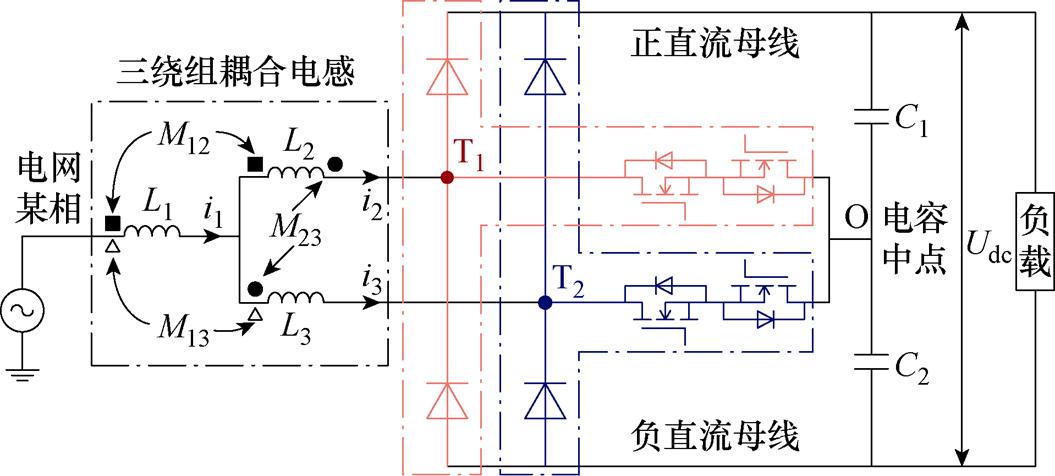
图4 三绕组耦合电感的电路连接
Fig.4 Circuit connection of three-winding coupled inductor
由于L2=L3且M12=M13，所以绕组1、绕组2之间的耦合系数与绕组1、绕组3之间的耦合系数是相等的，均为k1，同时绕组2和绕组3之间的耦合系数为k2，则
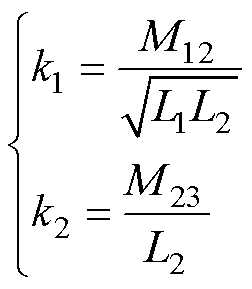（2）
绕组自感及绕组之间的互感与各磁路磁阻有关，将在第2.3节中详细分析。
三绕组耦合电感电路上的外特性亦由其等效基波电感与等效环流电感表示，为此应首先求出三绕组耦合电感的去耦等效电路，从而求得上述两个等效电感与各绕组自感及互感之间的关系，进而根据电流纹波的要求完成各个绕组自感值以及互感值的设计。本文所提三绕组耦合电感的三个绕组两两之间存在互感，对三组耦合电感M12、M13、M23分别进行去耦等效，可得其去耦等效电路如图5所示。
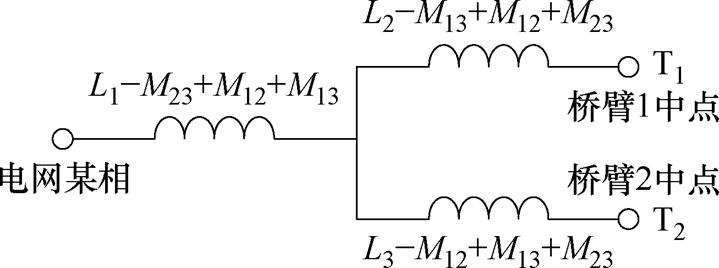
图5 三绕组耦合电感的去耦等效电路
Fig.5 Decoupling equivalent circuit of three-winding coupled inductor
根据图5可知，其等效基波电感Leq为L1-M23+ M12+M13与(L2-M13+M12+M23)//(L3-M12+M13+M23)的串联，其中(L2-M13+M12+M23)//(L3-M12+M13+M23)代表L2-M13+M12+M23与L3-M12+M13+M23的并联，由于L2=L3且M12=M13，则Leq的表达式为
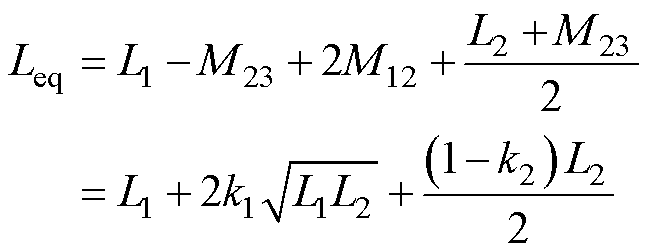（3）
其等效环流电感Lcir为L2-M13+M12+M23与L3-M12+M13+M23的串联，所以Lcir的表达式为
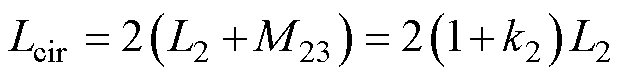（4）
磁路模型是计算自感与互感的前提，磁路中磁阻的大小与磁路长度、磁路横截面积及磁路材料的磁导率有关，磁心尺寸的定义如图6a所示。本文所提三绕组耦合电感的磁阻模型如图6b所示，根据磁阻的定义可知磁路中各磁阻的计算公式为
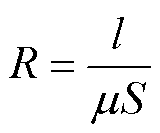（5）
式中，R为图6b中某一段磁路的磁阻；l为该段磁路的长度；m 为该段磁路的磁导率；S为该段磁路的横截面积。由此可知，R1、R2、R3、R4的表达式为
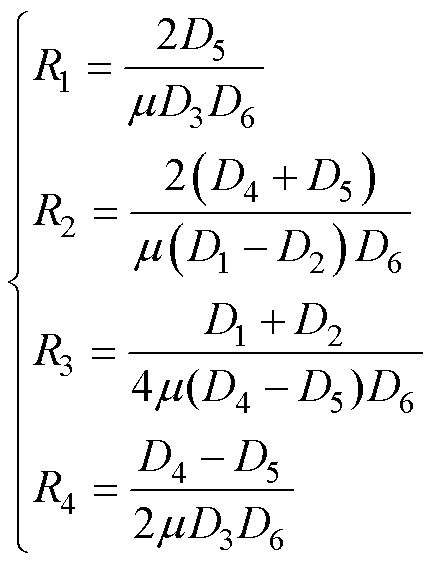（6）
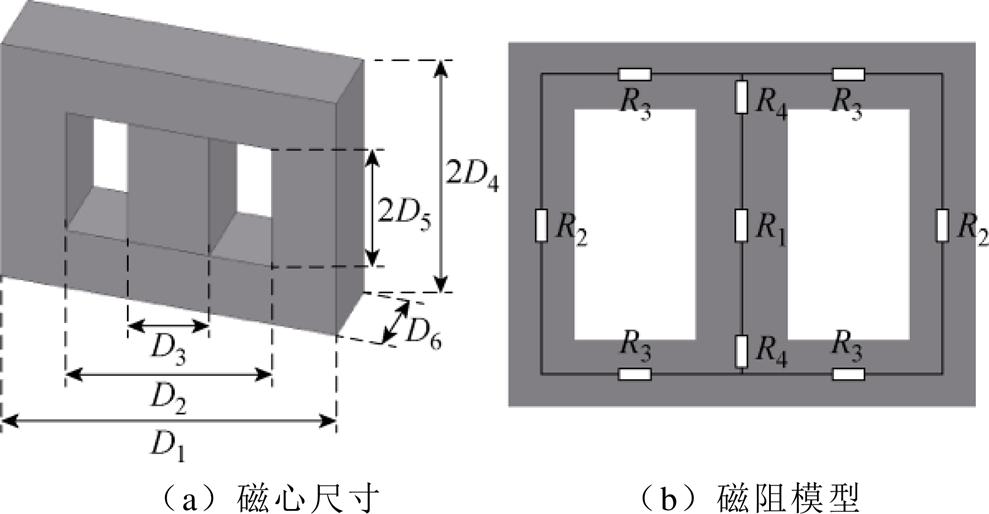
图6 磁心尺寸定义及磁阻模型
Fig.6 Definition of core size and reluctance model
将图6b中串联的磁阻合并，得到合并后的磁路模型如图7a所示。F1、F2、F3分别为受图中所示磁动势激励，中间芯柱、左侧芯柱、右侧芯柱中流过的磁通。考虑绕组中实际流过的电流波形，三绕组耦合电感磁路中的磁通可以分解为如图7b、图7c所示的相电流磁通和相环流磁通。Fs、Fc、Fcirc、Fcirs的含义与F1、F2、F3类似，亦代表受相应图中磁动势激励，不同段磁路中流过的磁通。
图7中的磁阻Rc、Rs与图6b中的磁阻R1、R2、R3、R4的关系为
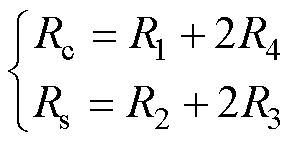（7）
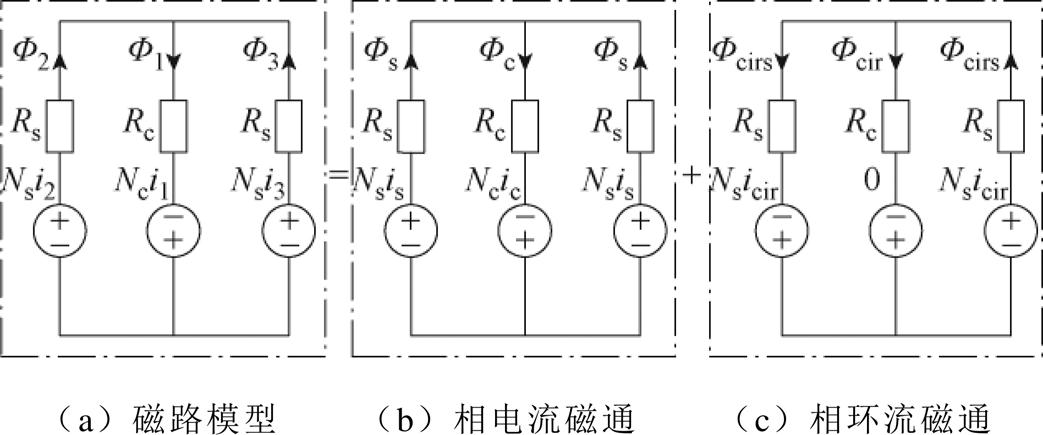
图7 三绕组耦合电感的磁路模型及磁通分解
Fig.7 Magnetic circuit model and flux decomposition of three-winding coupled inductor
则本文所提三绕组耦合电感各绕组自感与各磁路磁阻的关系为
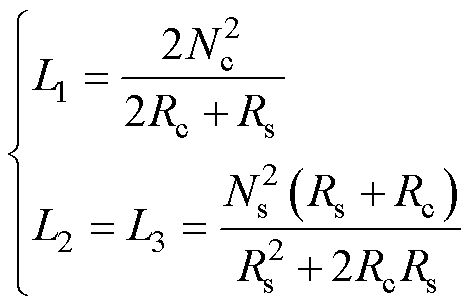（8）
电感设计时以式（8）为依据确定各磁路磁阻。下面分析互感，互感与电流大小无关，为便于推导，本节设定i2=i3=is。
忽略漏磁通，则三绕组耦合电感磁路中的磁通分布如图8所示。
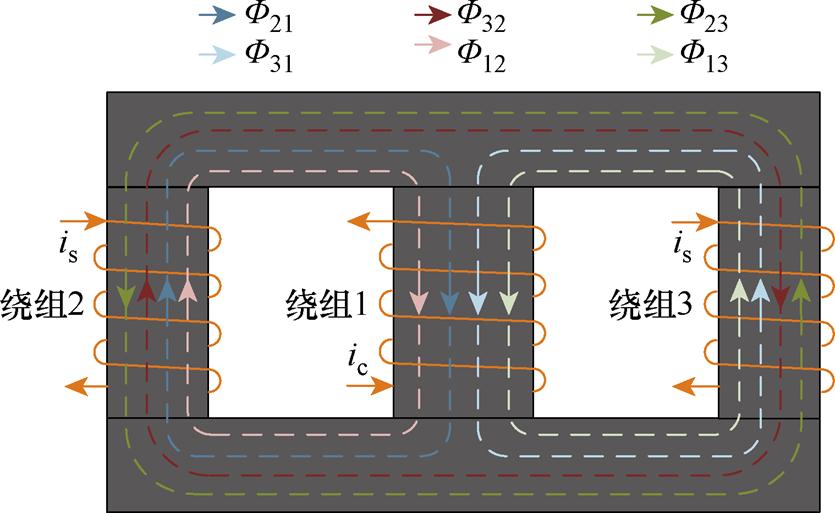
图8 三绕组耦合电感磁路中的磁通分布
Fig.8 Flux distribution in three-winding coupled inductor
图8中，Fij表示绕组j产生的与绕组i交链的磁通，i、j表示绕组编号。如F21代表绕组1产生的与绕组2交链的磁通，F31代表绕组1产生的与绕组3交链的磁通。其余符号的含义与此类似，此处不再赘述。图8中各磁通的表达式为
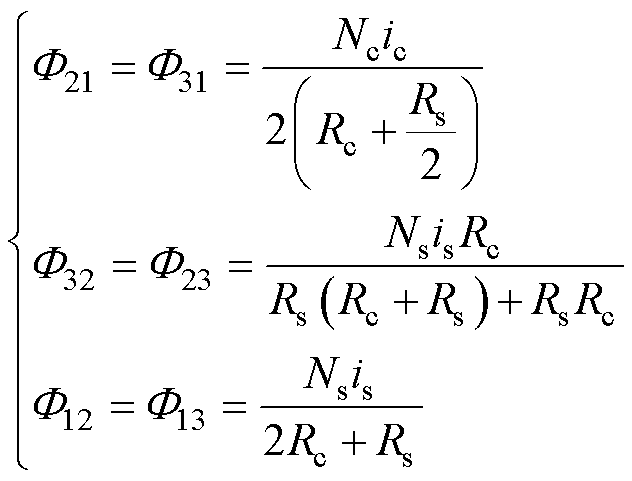（9）
基于各磁通表达式（9），即可计算出各绕组之间耦合系数k1、k2与各磁路磁阻Rc、Rs的关系。由互感的定义可知
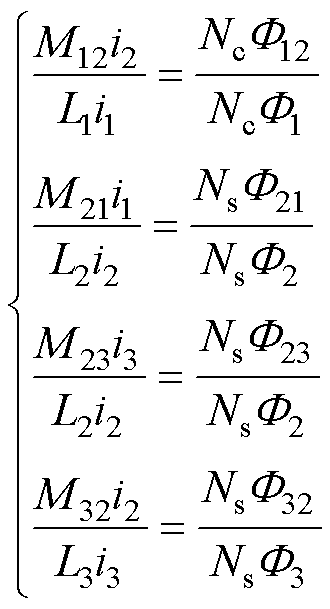（10）
将式（9）代入式（10）并与式（2）联立可 解得
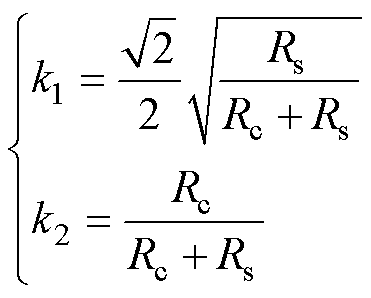（11）
由式（11）可知k1与k2之间的关系为
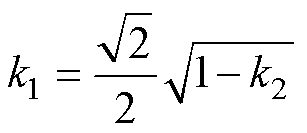（12）
当k2确定后，Rc与Rs之间的关系为
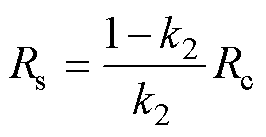（13）
当开关频率固定时，网侧电流的纹波峰峰值与等效基波电感Leq成反比，环流峰峰值与等效环流电感Lcir成反比。网侧电流的纹波峰峰值与调制比、调制波相位以及调制方式均有关，文献[20]中已有详细推导，由于该表达式较为复杂，此处不再赘述。交直流侧电压、调制方式确定后即可根据文献[20]确定网侧电流纹波最大峰峰值与等效基波电感Leq的关系。
交错并联桥臂之间的环流源自于两桥臂之间调制波相同而载波相位相差180°，调制波及载波如图9所示。定义两桥臂中点之间的电位差Udiff=UT1O- UT2O，若分析时认为上、下半直流母线的电容电压均为Udc/2，并以电容中点电位为电位参考点，则调制比为0.25、0.5、0.75时Udiff及icir的波形如图9所示。
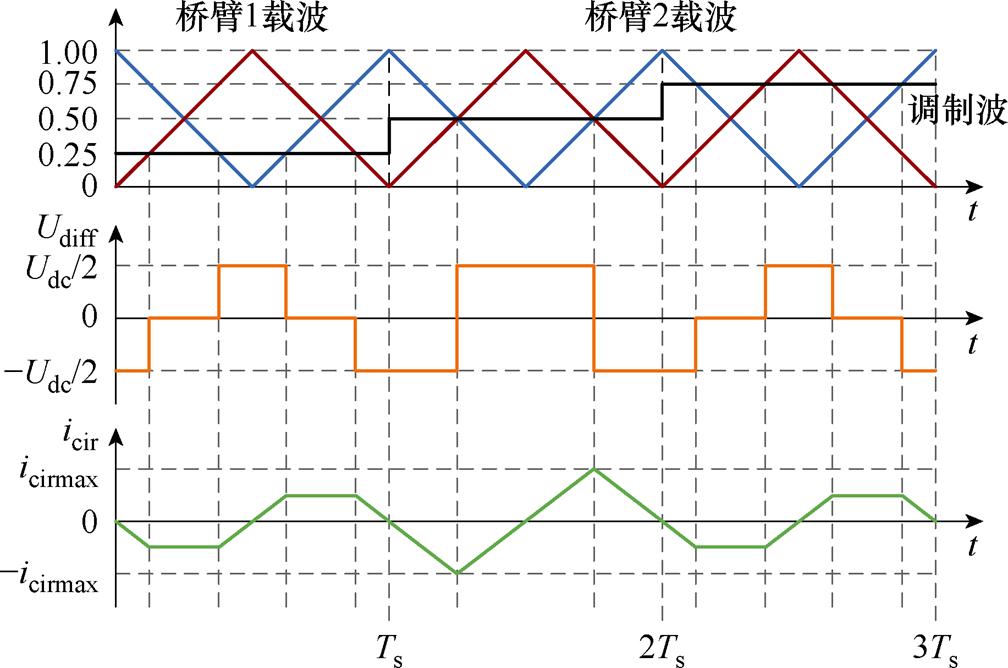
图9 交错并联调制的主要波形
Fig.9 Main waveforms of interleaved modulation
由图9可知，当占空比为0.5时环流峰峰值最大，设环流最大峰峰值为icirppmax，则
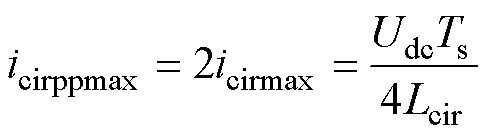（14）
式中，Ts为载波周期，根据式（14）即可确定环流最大峰峰值与等效环流电感Lcir的关系。
允许的网侧电流纹波最大峰峰值和环流最大峰峰值在电感设计前就已经确定，可以由此计算出所需的Leq和Lcir。由式（4）可知，L2与k2、Lcir之间的关系为
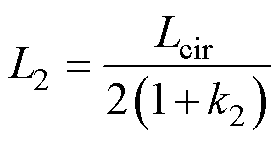（15）
由式（12）可知，当k2确定后，k1也可确定。由式（3）可知，L1与k2、Leq、Lcir之间的关系为
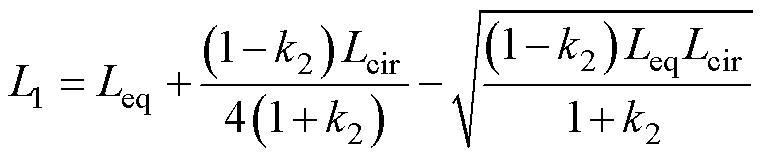（16）
联立式（8）中两个式子可以求得Ns与Nc的匝比n为
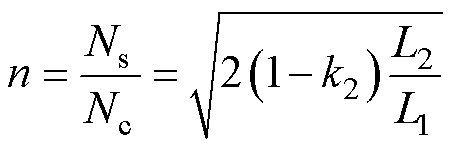（17）
由式（15）～式（17）可知，L2、L1、n的值由k2、Leq、Lcir决定，当Leq=60 mH、Lcir=550 mH时，L2、L1、n与k2的关系如图10所示。由图10可知，k2不应太小，否则，匝比n极大，使绕组2、3匝数过多无法绕制；k2也不应太大，因为k2越大则k1越小，绕组1与绕组2、3之间耦合程度越低，当k2=1时就变成了传统的滤波电感与耦合电感的串联。
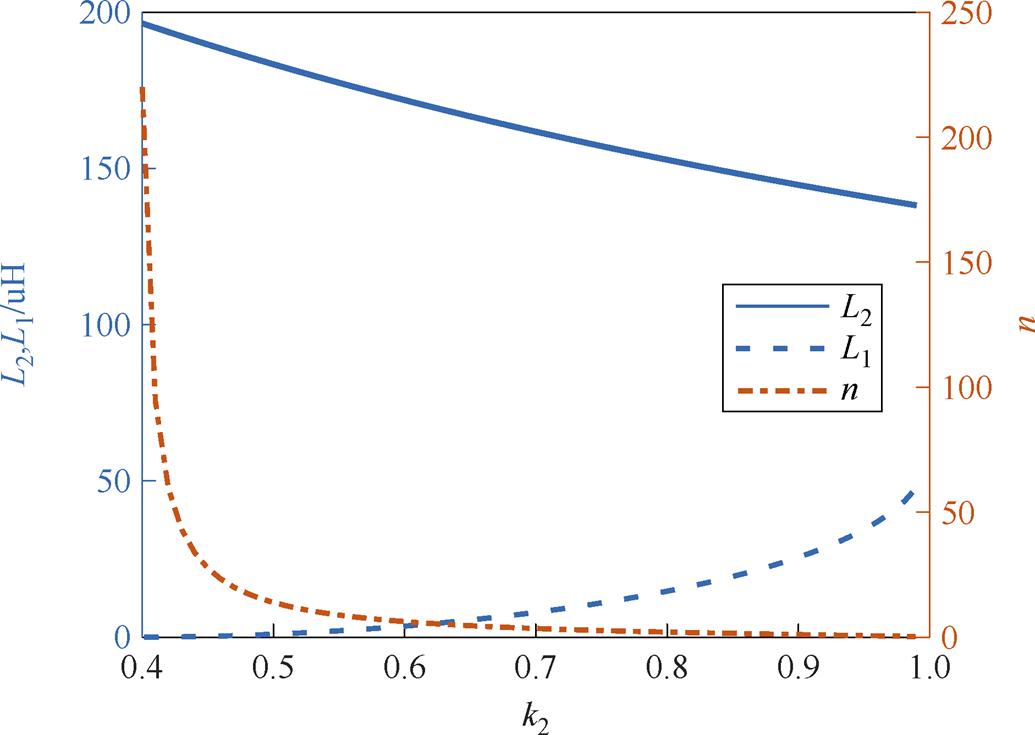
图10 电感、匝比与耦合系数间的关系
Fig.10 The relationship between sensitivity, turn ratio, and coupling coefficient
根据磁通大小确定磁路横截面积。考虑绕组中实际流过的电流波形，对图7b、图7c分别列写磁路基尔霍夫定律，可以求出各磁通的表达式为
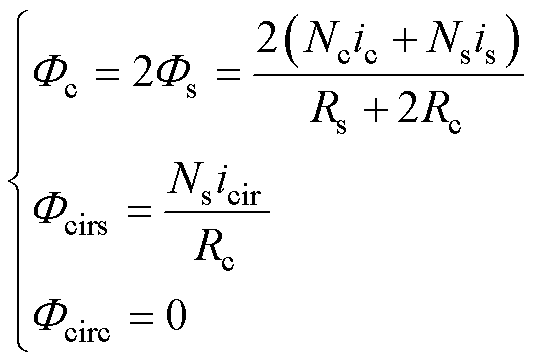（18）
由叠加定理可知，中间芯柱的最大磁通为Fc，两侧芯柱的最大磁通为Fs+Fcirs。设中间芯柱横截面积Sc，则Sc的表达式为
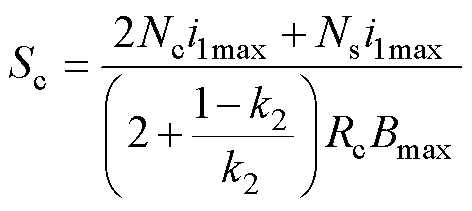（19）
对于磁粉芯电感，设计时需要考虑峰值电流处电感值的衰减度，因此磁通密度峰值Bmax是电感设计过程中的关键参数，一般取磁通密度峰值处电感量降额为50%左右[20]。以中间芯柱与两侧芯柱磁通密度峰值Bmax相同为原则设计两侧芯柱及上下轭横截面积Ss。为了留出一定裕量，认为绕组1电流达到峰值i1max时环流也达到最大值icirmax（实际上环流峰值的位置和大小与调制策略和桥臂间移相角有关，本文所提设计方法适用于马鞍波调制和180°移相），设r=icirmax/i1max，则
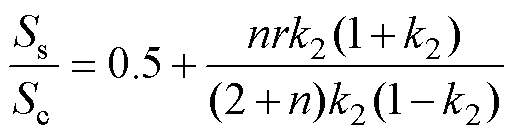（20）
从以上推导中不难发现，当Leq、Lcir、k2确定后，k1、L2、L1、n都可以确定下来，此时只要Nc确定，就可求出Ns、Rc、Rs、Sc、Ss的值，磁路各段的长度也随之确定，其中Ns、Rc、Sc三个变量是独立的，Ns、Rc、Sc与k2、Nc的关系分别如图11所示。
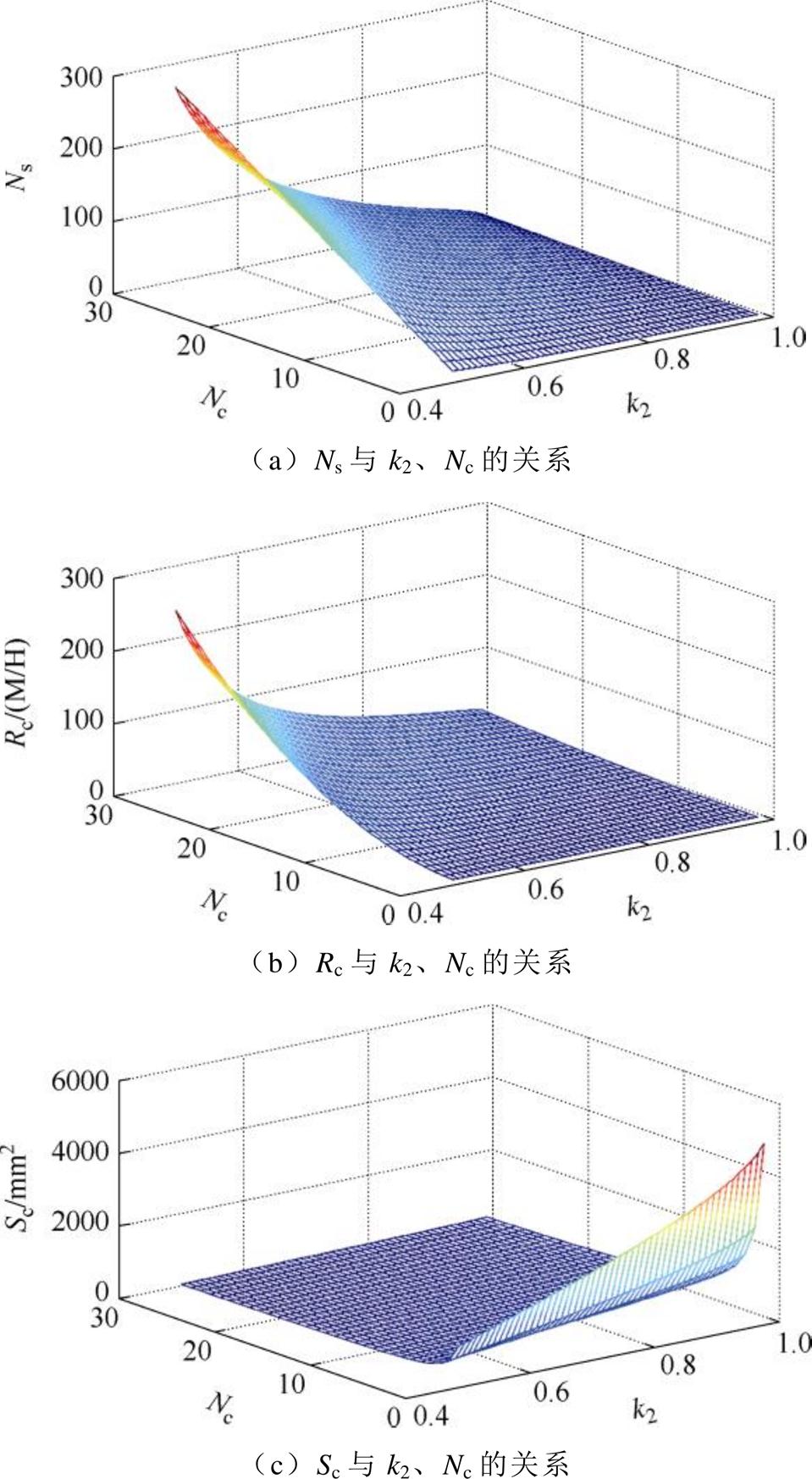
图11 Ns、Rc、Sc与k2、Nc的关系
Fig.11 The relationship between Ns, Rc, Sc and k2, Nc
由式（13）可知，当k2＞0.5时，Rs＜Rc，但由于Rs对应的磁路长度比Rc更长，且Rs对应的磁路横截面积比Rc更小，所以为满足磁阻关系，应采用图3所示的不同磁导率磁性材料组合式磁心。上下轭及两侧芯柱使用的磁性材料的相对磁导率为ms，中间芯柱使用的磁性材料的相对磁导率为mc，则为了在中柱磁路更短、横截面积更大的条件下获得更大的中柱磁阻，mc相比于ms越小越好。磁粉芯厂家一般只会提供几个特定的磁导率磁材，所以中柱选择其中磁导率最小的磁材，上下轭及侧柱选择其中磁导率最大的磁材即可。
由于磁粉芯的相对磁导率较低（通常小于150），因此应予以考虑漏磁通。文献[21]中已对绕组产生的外部空气磁场的建模方式进行了详细阐述，此处不再赘述。在图7a的基础上，考虑各个绕组的空气漏磁通路，本文所提三绕组耦合电感的改进磁路模型如图12所示。图12中，Rairc、Rairs分别为绕组1空气漏磁通路的磁阻、绕组2或3空气漏磁通路的磁阻，二者的表达式分别为
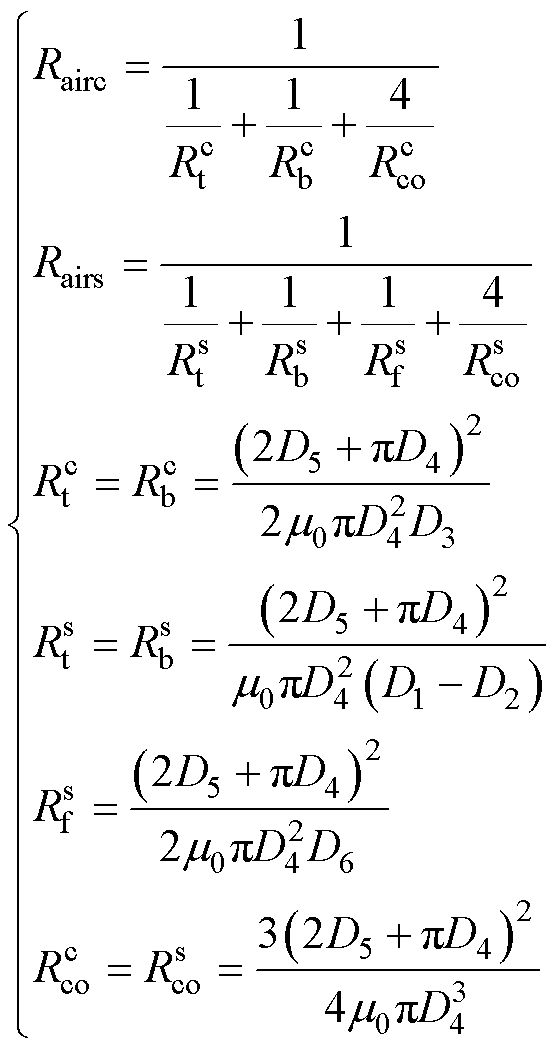（21）
式中，m0为真空磁导率，m0=4p×10-7 H/m；Rt、Rb、Rf分别为电感平放时上表面、下表面、侧面形成的半圆柱形状空气漏磁通路的磁阻；Rco为上述表面拐角处形成的1/4球体形状空气漏磁通路的磁阻。
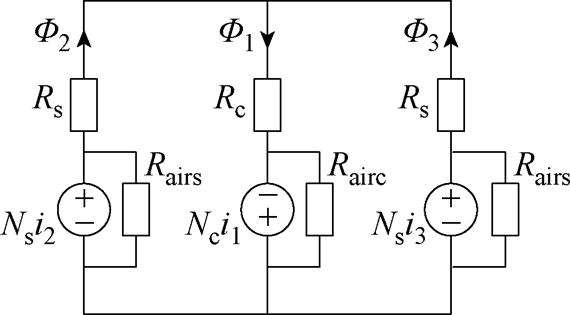
图12 三绕组耦合电感的改进磁路模型
Fig.12 Improved magnetic circuit model of three-winding coupled inductor
各个绕组的空气漏磁通路对应的空气磁阻Rairc、Rairs并联在对应绕组磁动势上，因此这些磁阻不会影响各绕组耦合磁通的分布，只影响各个绕组的自感磁通，因此各绕组互感不变、自感增大。
定义考虑空气漏磁通路后绕组1、绕组2、绕组3的自感分别为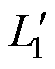
、
、
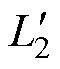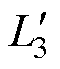，其表达式为
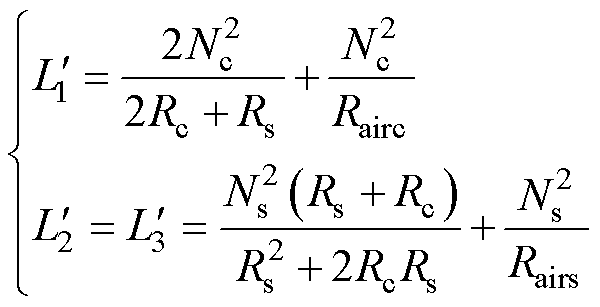（22）
定义考虑空气漏磁通路后三绕组耦合电感的等效基波电感和等效环流电感分别为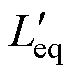
、
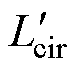，其表达式为
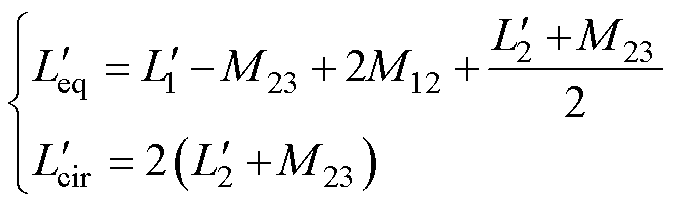（23）
三绕组耦合电感的设计流程如图13所示。首先，根据系统参数、允许的网侧电流纹波最大峰峰值和环流最大峰峰值以及电流峰值处允许的电感降额计算出所需的等效基波电感、等效环流电感及Bmax等关键参数。其次，基于不考虑空气漏磁通路的模型，以避免Ns过大为原则根据图11确定k2和Nc的范围，并在此范围内对k2和Nc进行遍历，求出每组k2和Nc对应的磁心尺寸并计算这组参数的窗口利用率，遍历完成后找到窗口利用率最接近0.4的设计方案[22]。最后，考虑之前计算过程中忽略的空气漏磁通路，并重新计算各磁路磁通密度峰值Bmaxreal，若Bmaxreal对应的电感降额满足要求，则设计完成；否则，需要对这组参数进行改进。改进方式有两种，改进方式2会对电感值造成影响，因此改进后需要判断改变后的电感值是否仍满足电流峰峰值的要求，而改进方式1基本不会对电感值产生影响，且考虑漏磁后自感增大，相当于增大了电感值设计裕度，因此无需该步验证过程。
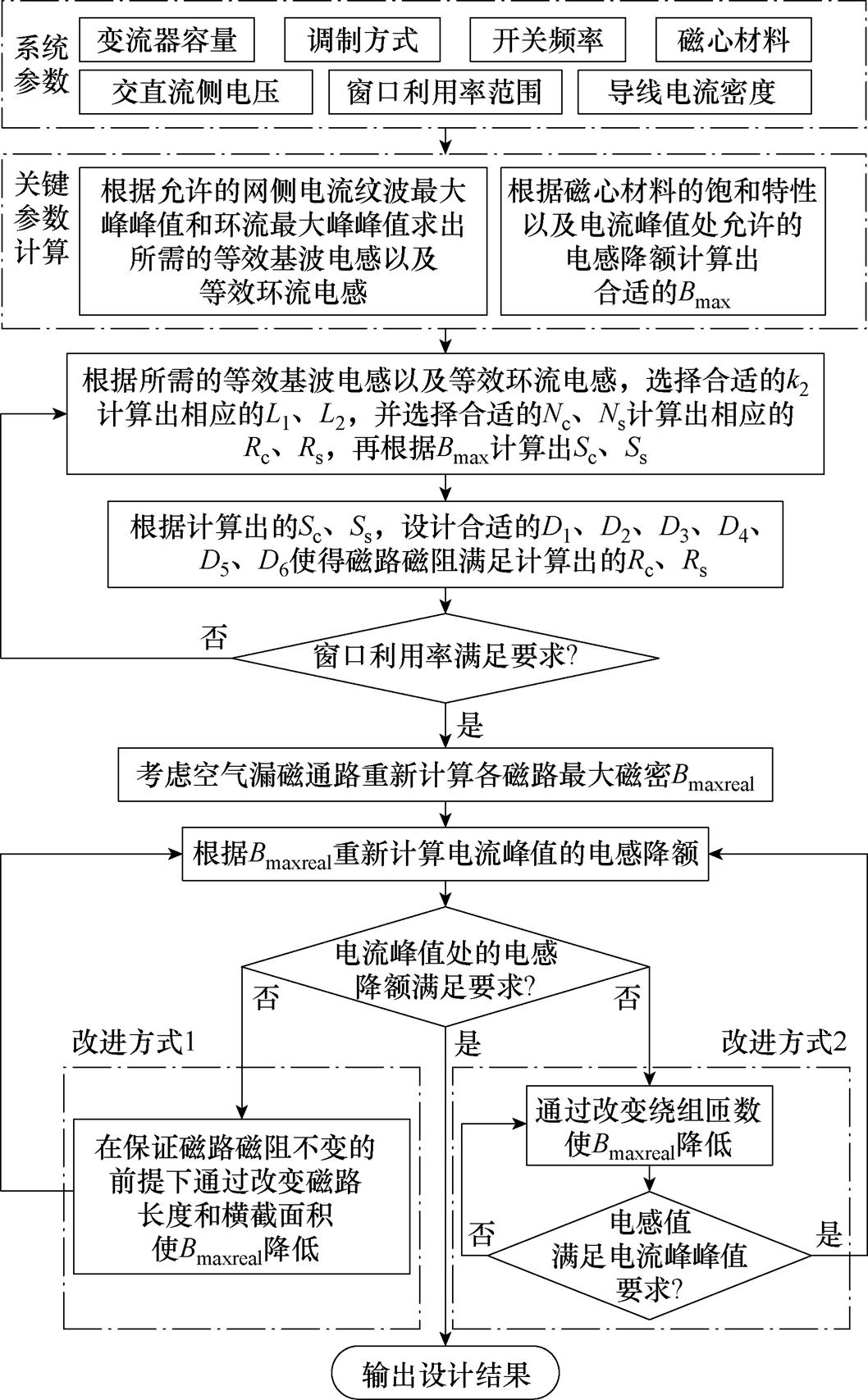
图13 三绕组耦合电感的设计流程
Fig.13 Design process of three-winding coupled inductor
按照上述设计方法，以Leq=60 mH，Lcir=550 mH为目标设计了额定电流60 A（有效值）的三绕组耦合电感，k2和Nc的遍历结果如图14所示。图14中，z坐标为窗口利用率（将窗口面积不足以绕制绕组的情况统一采用窗口利用率1），选择k2=0.54、Nc=3这组参数，其对应的窗口利用率为0.397，最终的设计结果见表1。
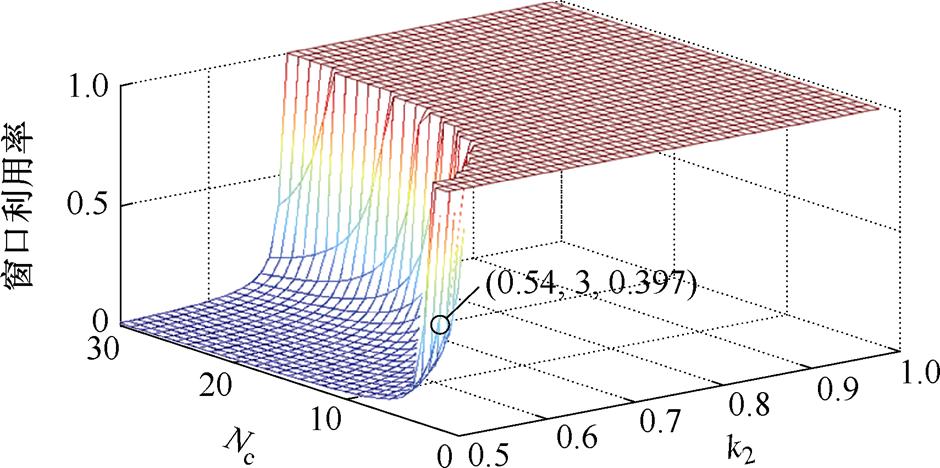
图14 k2和Nc的遍历结果
Fig.14 Traversal results of k2 and Nc
表1 三绕组耦合电感设计结果
Tab.1 Design result of three-winding coupled inductor
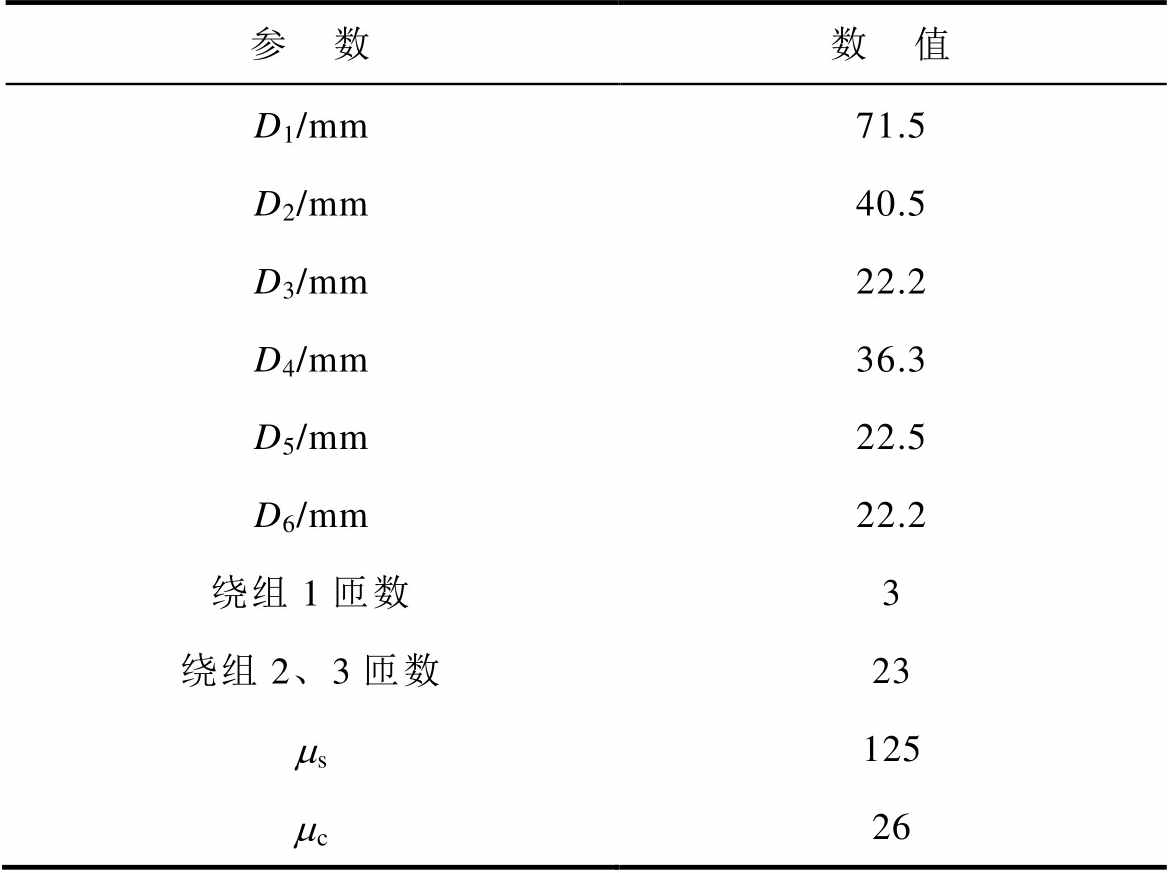
参 数数 值 D1/mm71.5 D2/mm40.5 D3/mm22.2 D4/mm36.3 D5/mm22.5 D6/mm22.2 绕组1匝数3 绕组2、3匝数23 ms125 mc26
按照表1中参数，在Ansys/Maxwell 3D软件中对所设计的三绕组耦合电感进行有限元仿真，磁心各处磁通密度分布如图15所示，中间芯柱的平均磁通密度为0.66 T，不叠加环流时左右两侧芯柱的平均磁通密度为0.63 T，叠加环流后左右两侧芯柱的最大平均磁通密度为0.69 T，磁心各部分磁通密度较为接近，实现了对磁心各部分的充分利用。结合所用铁硅铝材料的软饱和特性曲线，对两种磁心材料在峰值电流处的电感降额分别进行分析可知，中间芯柱磁心的磁导率降低为标定值的53.6%，左右两侧芯柱磁心的磁导率降低为标定值的51.5%，二者降幅近似相等且均在50%附近，与设计目标相符，证明了所提设计方法的可行性。
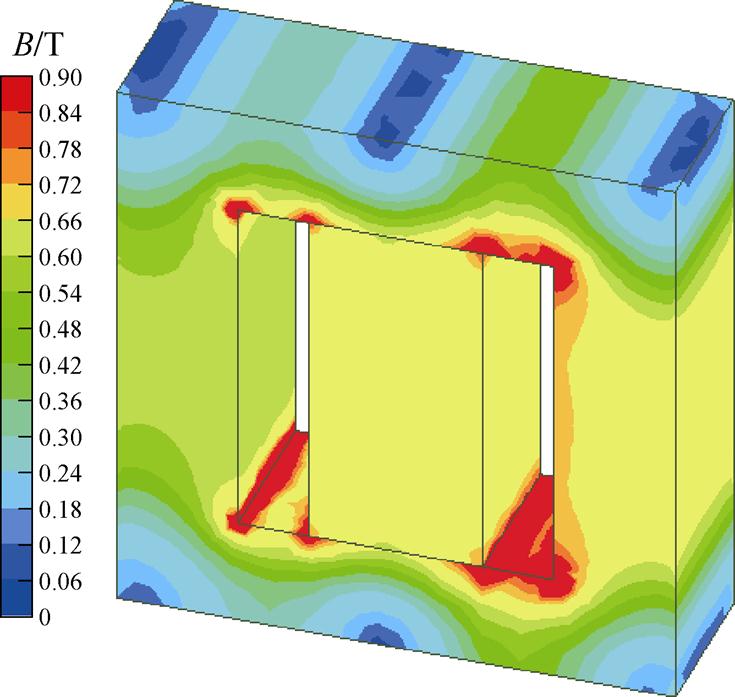
图15 三绕组耦合电感有限元仿真结果
Fig.15 Finite element simulation results of three-winding coupled inductor
将上述三绕组耦合电感各自感、互感的仿真值与基于磁路模型得到的计算值进行对比，结果见表2。由表2可知，计算值与仿真值之间的误差百分比均在6.5%以内，证明了所建磁路模型的准确性。
将表2中各自感、互感的仿真值代入式（23）中计算可得上述三绕组耦合电感的等效基波电感为63 mH，等效环流电感为562 mH。
表2 磁路模型解析计算与有限元仿真结果对比
Tab.2 Comparison of results between magnetic circuit model analysis calculation and finite element simulation
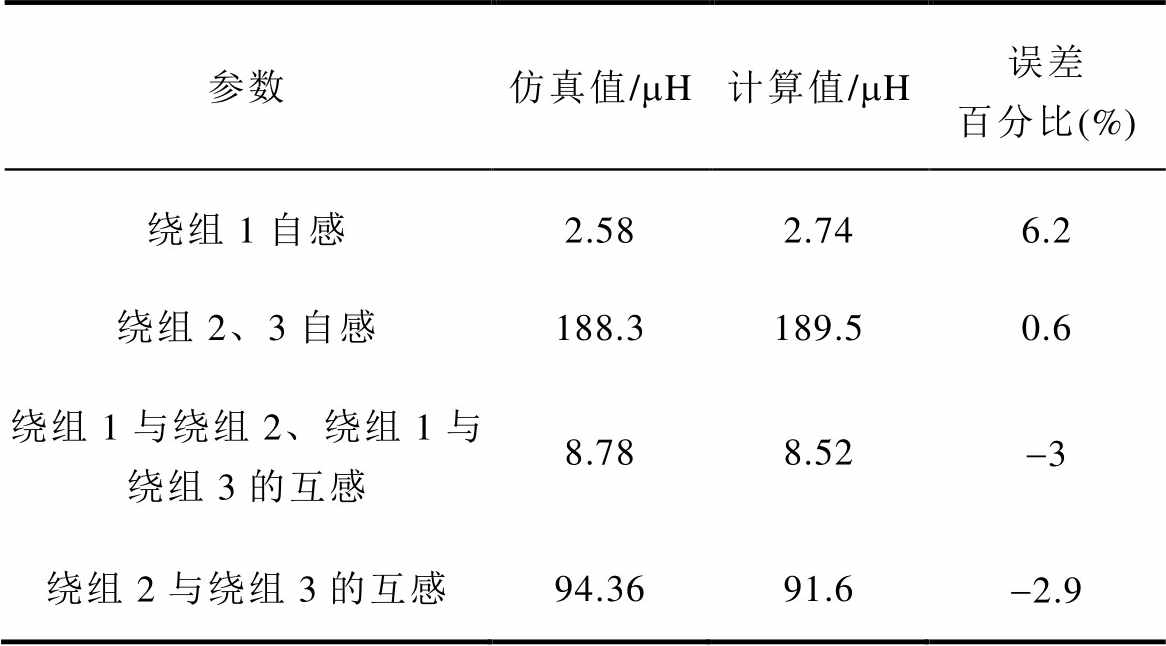
参数仿真值/mH计算值/mH误差百分比(%) 绕组1自感2.582.746.2 绕组2、3自感188.3189.50.6 绕组1与绕组2、绕组1与绕组3的互感8.788.52-3 绕组2与绕组3的互感94.3691.6-2.9
为了体现所提三绕组耦合电感的优势，需要将其与传统分立方案以及两绕组弱耦合电感方案进行对比。传统分立方案以及两绕组弱耦合电感方案的设计结果见表3。为了方案对比的公平性，设计时已保证三种方案的绕组电流密度相同（均为7 A/mm2），电路外特性和以及磁心最大平均磁通密度近似相同。
由表3可知传统分立方案、两绕组弱耦合电感方案的等效基波电感和等效环流电感与三绕组耦合电感方案近似保持相同。将三种方案在磁心体积、绕组直流电阻和电感体积三个维度进行对比，结果见表4。
表3 传统分立方案及两绕组弱耦合电感方案的设计结果
Tab.3 Design results of traditional separated scheme and two-winding weakly coupled inductor scheme
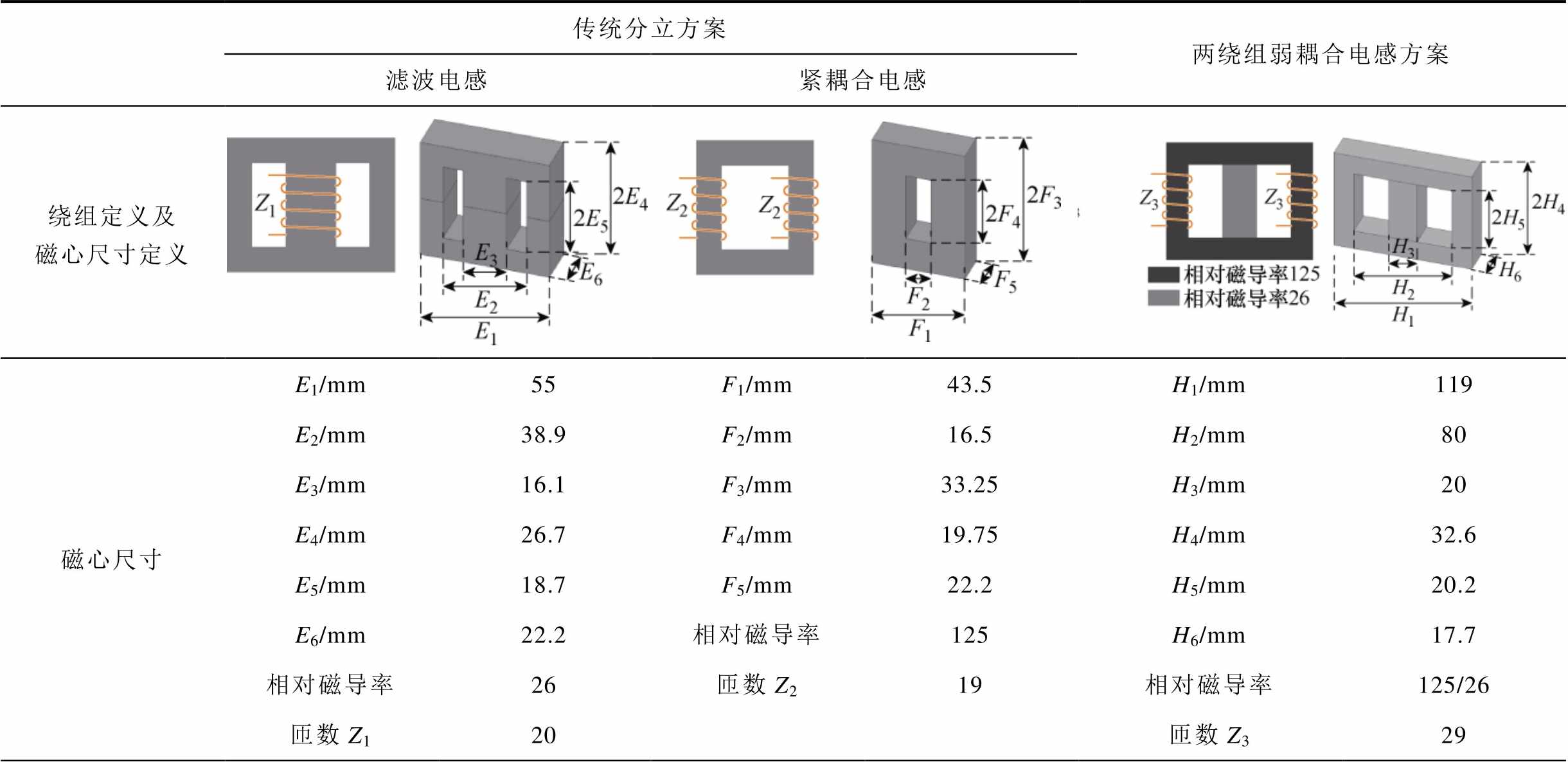
传统分立方案两绕组弱耦合电感方案 滤波电感紧耦合电感 绕组定义及磁心尺寸定义 磁心尺寸E1/mm55F1/mm43.5H1/mm119 E2/mm38.9F2/mm16.5H2/mm80 E3/mm16.1F3/mm33.25H3/mm20 E4/mm26.7F4/mm19.75H4/mm32.6 E5/mm18.7F5/mm22.2H5/mm20.2 E6/mm22.2相对磁导率125H6/mm17.7 相对磁导率26匝数Z219相对磁导率125/26 匝数Z120匝数Z329
（续）
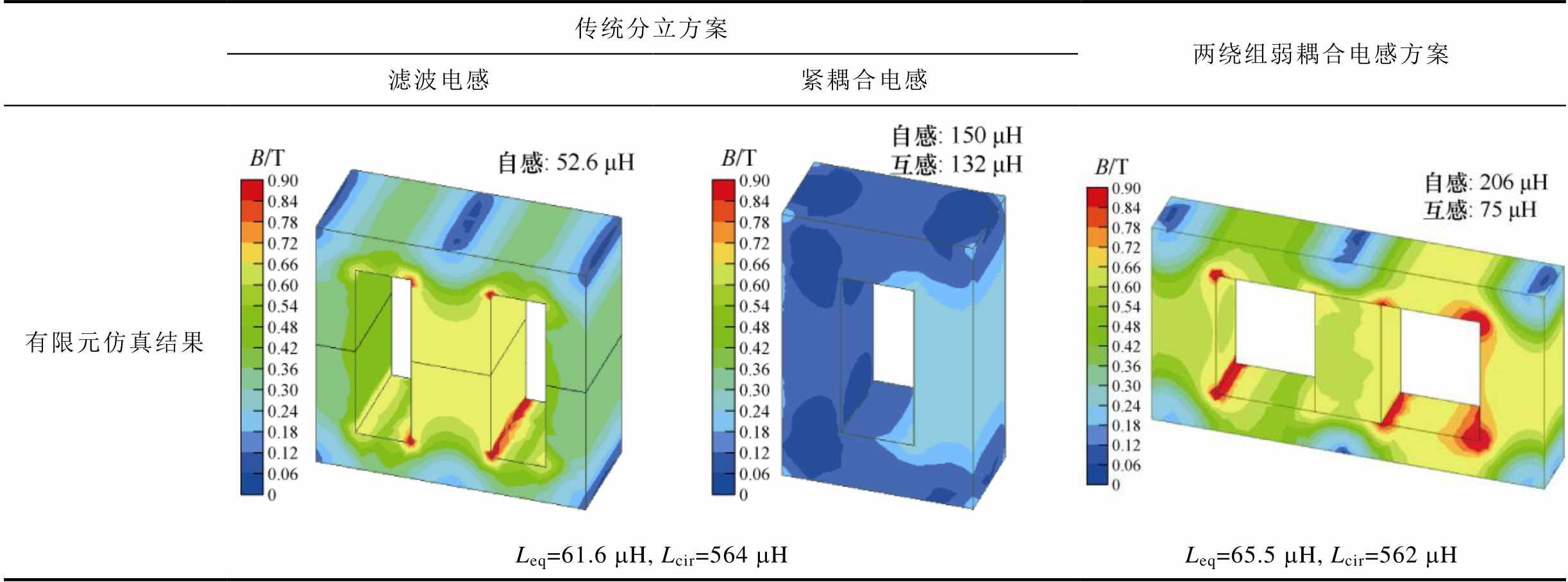
传统分立方案两绕组弱耦合电感方案 滤波电感紧耦合电感 有限元仿真结果 Leq=61.6 mH, Lcir=564 mHLeq=65.5 mH, Lcir=562 mH
表4 三种方案的对比
Tab.4 Comparison of three schemes
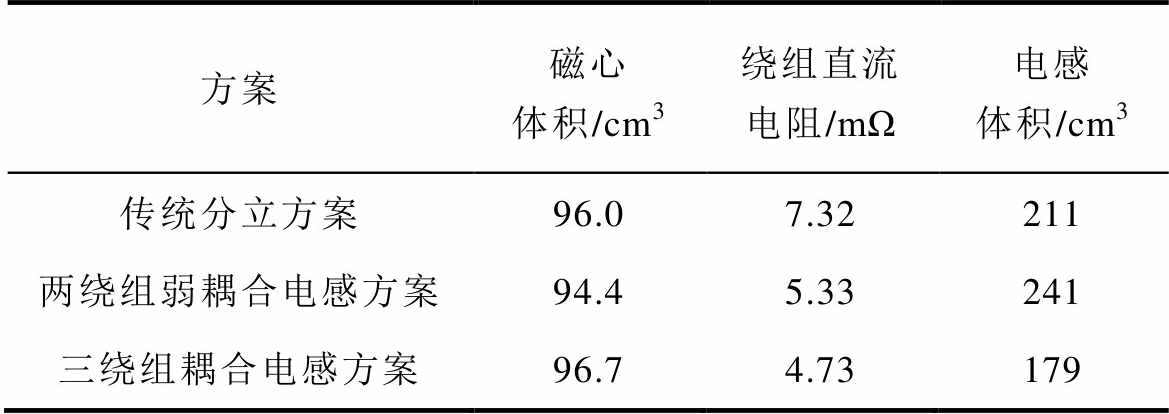
方案磁心体积/cm3绕组直流电阻/mΩ电感体积/cm3 传统分立方案96.07.32211 两绕组弱耦合电感方案94.45.33241 三绕组耦合电感方案96.74.73179
由表4可知，在三种方案的磁心体积相差无几的情况下，传统分立方案的绕组直流电阻最大，两绕组弱耦合电感方案次之，三绕组耦合电感方案最小。相比于传统分立方案和两绕组弱耦合电感方案，本文所提三绕组耦合电感的绕组直流电阻分别降低了35%和11%。绕组直流电阻与绕组损耗成正比，电流越大时电感铜损的减少越明显。由表4亦可知，所提方案可以减小磁元件的总体积，提升装置功率密度。
由表3可知，传统分立方案中滤波电感的中柱最大平均磁通密度为0.63 T，与三绕组耦合电感近似相同，而紧耦合电感的最大平均磁通密度仅为0.25 T左右，对磁心的利用不够充分，这也是表4中传统分立方案绕组直流电阻较大的原因：传统分立方案中，紧耦合电感的磁心中几乎只有环流磁通，这两个绕组近似只产生环流电感，所以需要滤波电感匝数较多才能产生足够的基波电感。而所提三绕组耦合电感中的绕组2、3既交链环流磁通也交链基波磁通，可以同时产生环流电感和基波电感，通过这样的绕组复用，绕组1只需提供较小的基波电感即可，因此可以大幅减少绕组1的匝数，即绕组长度大幅减少，在电流密度相同时可以实现绕组直流电阻的降低。
由表3可知，两绕组弱耦合电感方案的中间芯柱平均磁通密度为0.61 T，不叠加环流时左右两侧芯柱平均磁通密度为0.63 T，叠加环流后左右两侧芯柱最大平均磁通密度为0.69 T，与三绕组耦合电感方案近似相同。下面分析三绕组耦合电感的绕组直流电阻比两绕组弱耦合电感更小的原因。
三绕组耦合电感与两绕组弱耦合电感均采用EE型磁心，区别在于三绕组耦合电感增加了中间芯柱上的绕组1。分析式（18）第一个式子可知，由于ic/2=is，绕组1的一匝和绕组2、3各两匝产生的各磁路磁通完全相同，下面计算二者所形成的基波电感。
一匝绕组1形成的基波电感Lf1=L1，由式（8）第一个式子可知
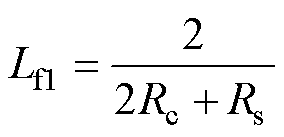（24）
绕组2、3各两匝形成的基波电感Lf2= (1-k2)L2/2，由式（8）第二个式子可知
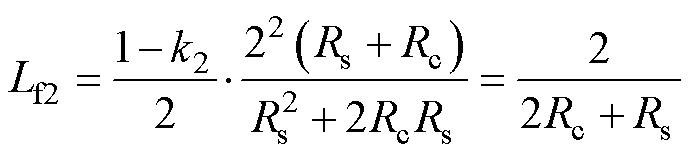（25）
式（24）、式（25）完全相同，所以在EE型磁心中，对于基波电感来说，绕组1的一匝等效于绕组2、绕组3各两匝。但这两种绕组分布产生的直流电阻是不同的，不同绕组分布对应的直流电阻如图16所示。
由于绕组1电流是绕组2、3电流的2倍，因此电流密度相同时两匝绕组2（或两匝绕组3）的横截面积与一匝绕组1相同，但一匝绕组1比两匝绕组2（或两匝绕组3）匝长更短，用一匝绕组1代替绕组2、3各两匝可以获得更小的直流电阻和更少的铜材用量。因此，中间绕组的引入使三绕组耦合电感的绕组直流电阻比两绕组弱耦合电感更小。
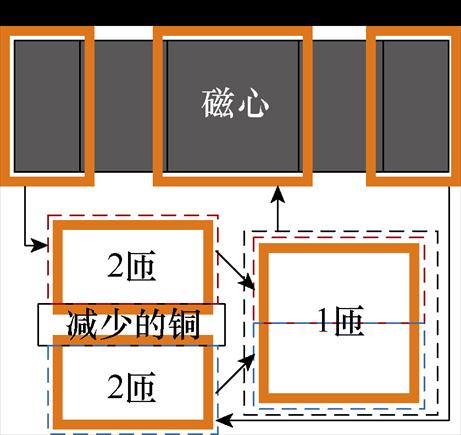
图16 不同绕组分布对应的直流电阻
Fig 16 DC resistance corresponding to different winding arrangements
为验证所提三绕组耦合电感在效率提升方面的有效性，按照表1及表3的设计结果分别制作了如图17所示不同方案的电感实物，所使用的磁心材料为瑞德磁电RS系列的铁硅铝，并搭建了如图18所示的功率等级40 kW的两路交错并联三相Vienna整流器样机。
图17 不同方案的电感实物
Fig.17 Inductors of different schemes
图18 40 kW交错并联三相Vienna整流器样机
Fig.18 40 kW interleaved three-phase Vienna rectifier prototype
三相Vienna整流器样机主要参数见表5，所采用的SiC MOSFET的型号为Infineon IMZA65R027M1H，所采用的SiC二极管的型号为Infineon IDWD40G120C5。在样机其他电路不变的情况下，连接电感部分分别使用传统分立方案、两绕组弱耦合电感方案和三绕组耦合电感方案，通过功率分析仪HIOKI PW3390测量整机效率来进行对比验证。
表5 三相Vienna整流器样机主要参数
Tab.5 Main parameters of three-phase Vienna rectifier prototype
参 数数 值 交流侧线电压/V380 直流母线电压Udc/V670 直流母线电容C1, C2/mF900 开关频率/kHz33.33
图19～图21分别为三相Vienna整流器的连接电感使用传统分立方案、两绕组弱耦合电感方案和三绕组耦合电感方案时与某相两路桥臂相连的两个绕组上的电流iBri1、iBri2，两个绕组电流之和isum及两个绕组电流作差的一半isub的波形，其中isum=i1，isub=icir。
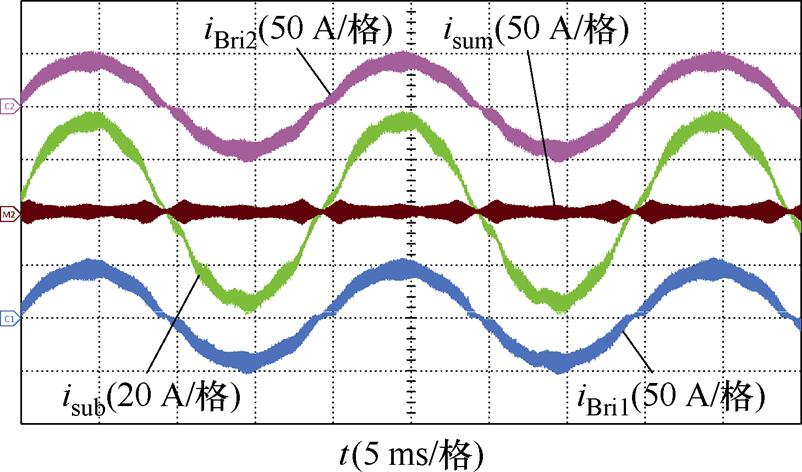
图19 传统分立方案实验波形
Fig.19 Experimental waveforms of traditional separated scheme
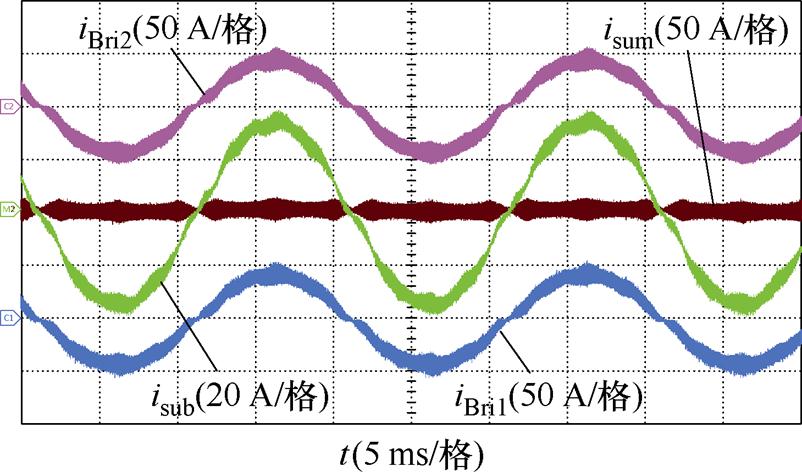
图20 两绕组弱耦合电感方案实验波形
Fig.20 Experimental waveforms of two-winding weakly coupled inductor
三种电感方案均可以使整流器稳定运行，且由于三种方案具有几乎相同的外特性，因此其绕组电流波形相差无几。但两种集成方案的环流波形与传统分立方案存在一定区别，这是由于两种集成方案的环流电感随基波电流增大出现电感衰减，而传统分立方案中的环流电感基本不随基波电流变化而变化，因此工频周期内，在正弦峰值和谷值附近，两种集成方案的环流幅值略大，而在其他区间内，三种方案的环流波形几乎相同。
图21 三绕组耦合电感方案实验波形
Fig.21 Experimental waveforms of three-winding coupled inductor
图22为不同电感方案在满载工况下的理论损耗分布。由图22可知，由于三种电感方案具有近似相同的磁心体积和磁通密度，所以三种方案的磁心铁损近似相同；由于三种电感方案具有近似相同的电路外特性，所以流过各开关器件的电流近似相同，三种方案的开关器件损耗也近似相同。三种电感方案的损耗差异主要源于电感绕组直流电阻不同带来的不同电感铜损。
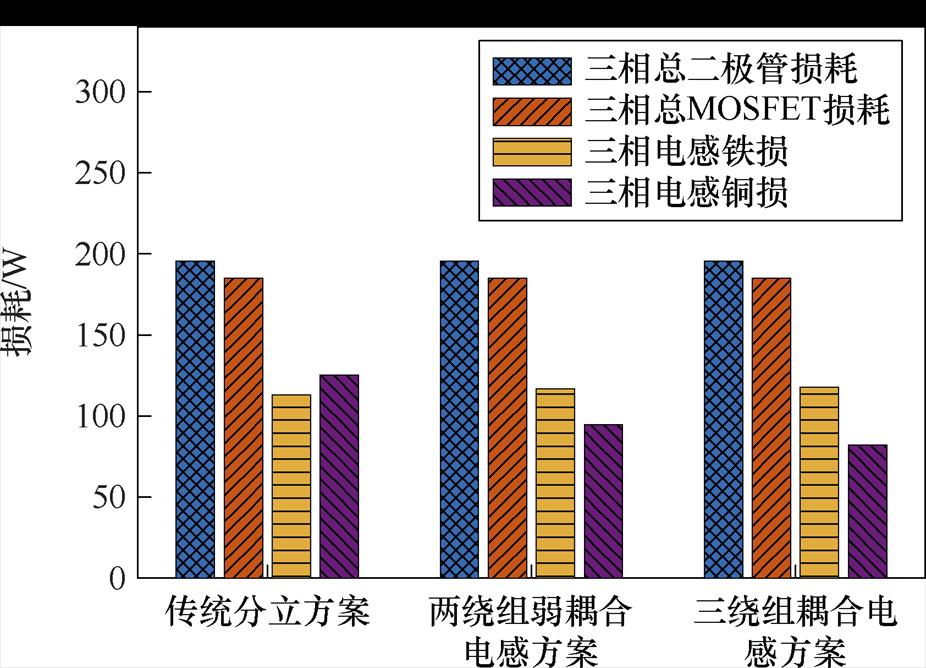
图22 不同电感方案在满载工况下的理论损耗分布
Fig.22 Theoretical loss distribution of different inductor schemes under full load condition
图23为不同电感方案实测的整机效率曲线。由图23可知，在全负载范围内，所提三绕组耦合电感方案的整机效率均高于传统分立方案和两绕组弱耦合电感方案，可见按照所提方法设计的三绕组耦合电感的损耗更小，证明了理论分析的正确性。
三绕组耦合电感方案的整机最高效率为98.5%，且负载越重即电流越大时，三绕组耦合电感方案的效率提升越明显，这是由于电流越大时铜损在损耗中的占比越大，而三绕组耦合电感通过减小绕组直流电阻降低了铜损，显示了所提三绕组耦合电感在大电流场景中的优势。
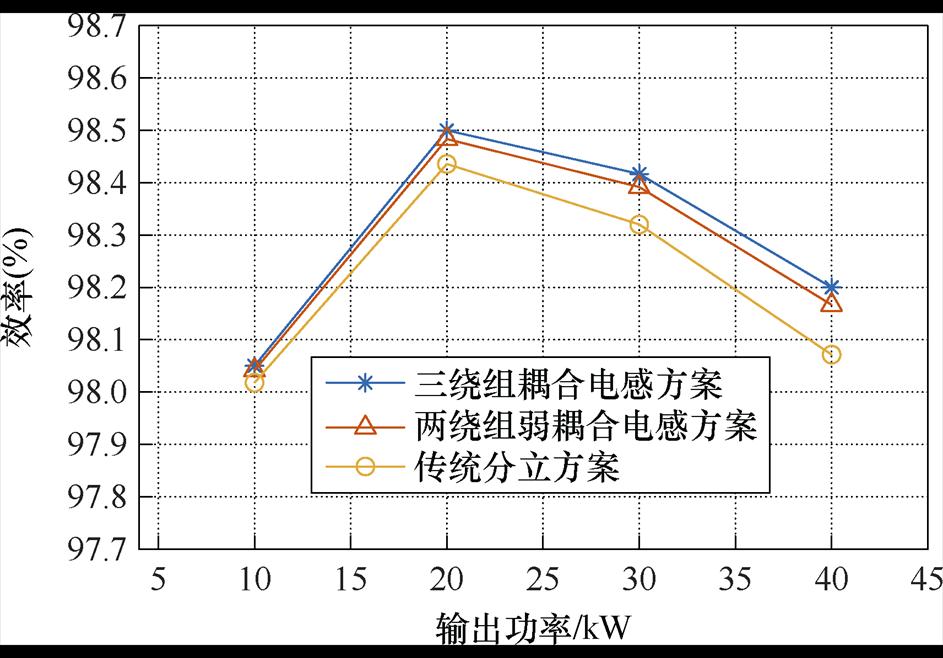
图23 效率曲线
Fig.23 Efficiency curves
针对两路交错并联Vienna整流器中紧耦合电感磁心利用率低的问题，本文提出一种三绕组耦合电感，并提出相应的设计方法。与滤波电感与紧耦合电感串联的传统分立方案相比，本文所提新型电感在保证电路外特性相同的前提下，采用磁集成技术将滤波电感与耦合电感集成在一个磁心上，通过绕组及磁路的复用，使得磁通密度分布更为均匀，并在磁心体积不变的情况下使得绕组匝数减少，因此，可在电流密度相同的情况下，降低铜材用量和绕组直流电阻。相比于两绕组弱耦合电感方案，本文所提三绕组耦合电感可以进一步降低绕组的直流电阻，电流越大时本文所提方案的效率优势越明显。所提新型电感在减小损耗的同时亦有利于装置功率密度的提升，仿真与实验均验证了本文所提三绕组耦合电感的可行性与有效性。
参考文献
[1] 姜卫东, 胡业波, 张庆岩, 等. 基于调制波分解的Vienna整流器的调制方法[J]. 电工技术学报, 2023, 38(16): 4339-4352.
Jiang Weidong, Hu Yebo, Zhang Qingyan, et al. Modulation method of Vienna rectifier based on modulation wave decomposition[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4339- 4352.
[2] 汪凤翔, 杨奥, 于新红, 等. 基于自适应超螺旋滑模观测器的三相Vienna整流器无模型预测电流控制[J]. 电工技术学报, 2024, 39(6): 1859-1870.
Wang Fengxiang, Yang Ao, Yu Xinhong, et al. Model-free predictive current control for three-phase Vienna rectifier based on adaptive super-twisting sliding mode observer[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1859-1870.
[3] 王涛, 陈昌松, 段善旭, 等. 用于改善电流过零点畸变的Vienna整流器空间矢量调制策略[J]. 电工技术学报, 2019, 34(18): 3854-3864.
Wang Tao, Chen Changsong, Duan Shanxu, et al. An improved space-vector modulation for Vienna rectifier to eliminating current distortion around zero-crossing point[J]. Transactions of China Elec- trotechnical Society, 2019, 34(18): 3854-3864.
[4] Choi H W, Lee K B. Reduction method of circulating current in parallel three-level inverters using modified discontinuous pulse-width modulation based on inter- leaving scheme[J]. IEEE Transactions on Power Electronics, 2024, 39(2): 2322-2333.
[5] 陈建良, 刘耀源, 张子旭, 等. 基于电流纹波预测的交错并联三相逆变器任意功率因数全范围软开关策略[J]. 中国电机工程学报, 2024, 44(22): 9003- 9014.
Chen Jianliang, Liu Yaoyuan, Zhang Zixu, et al. Current ripple prediction based full range soft switching method for two parallel interleaved three- phase inverters under any power factor[J]. Pro- ceedings of the CSEE, 2024, 44(22): 9003-9014.
[6] 苏冰, 王玉斌, 王璠, 等. 基于耦合电感的多相交错并联双向DC-DC变换器及其均流控制[J]. 电工技术学报, 2020, 35(20): 4336-4349.
Su Bing, Wang Yubin, Wang Fan, et al. Multi-phase interleaved bidirectional DC-DC converter with coupled inductors and current sharing control strategy[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4336-4349.
[7] 杨玉岗, 马杰, 马云巧, 等. 多相交错并联磁集成双向DC/DC变换器中耦合电感的通用设计准则[J]. 中国电机工程学报, 2015, 35(23): 6122-6134.
Yang Yugang, Ma Jie, Ma Yunqiao, et al. The universal design criterion of coupled inductors in multiphase interleaving and magnetically integrated bidirectional DC/DC converters[J]. Proceedings of the CSEE, 2015, 35(23): 6122-6134.
[8] 王议锋, 王忠杰, 陈博, 等. 基于耦合电感的交错Boost变换器性能优化[J]. 电工技术学报, 2022, 37(8): 2097-2106.
Wang Yifeng, Wang Zhongjie, Chen Bo, et al. Performance optimization of interleaved boost based on coupled inductors[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 2097-2106.
[9] Yang Yugang, Ma Jie, Ho C N, et al. A new coupled-inductor structure for interleaving bidire- ctional DC-DC converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(3): 841-849.
[10] 倪硕, 吴红飞, 陈君雨, 等. 交错并联临界导通模式Buck电感高密度集成与优化[J]. 电工技术学报, 2022, 37(18): 4688-4696.
Ni Shuo, Wu Hongfei, Chen Junyu, et al. Integration and optimization of a high power density inductor for an interleaved critical conduction mode Buck converter[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4688-4696.
[11] Liu Yue, Wu Hongfei, Ji Guosheng, et al. Optimized air-gap configuration for an integrated coupled inductor with lower height and reduced core/winding losses[J]. IEEE Transactions on Industry Applications, 2024, 60(2): 2980-2990.
[12] 马小勇, 王萍, 王议锋, 等. 基于交错并联Boost变换器的耦合电感综合建模与多目标优化方法[J]. 电工技术学报, 2022, 37(24): 6399-6410.
Ma Xiaoyong, Wang Ping, Wang Yifeng, et al. Comprehensive modeling and multi-objective opti- mization method for coupled inductors of interleaved Boost converters[J]. Transactions of China Elec- trotechnical Society, 2022, 37(24): 6399-6410.
[13] 高圣伟, 王博, 孙醒涛. 一种交错并联双向DC-DC变换器的新型磁集成技术[J]. 中国电机工程学报, 2023, 43(9): 3538-3549.
Gao Shengwei, Wang Bo, Sun Xingtao. A novel magnetic integration technology for interleaved parallel bidirectional DC-DC converters[J]. Pro- ceedings of the CSEE, 2023, 43(9): 3538-3549.
[14] Xu Yuhang, Yang Xu, Dong Suchen, et al. S-shaped coil, four column design based on interleaved parallel PFC uncoupled inductor[C]//2022 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Guangzhou, Guangdong, China, 2022: 1036-1040.
[15] Wang Shuo. PCB-based heterogeneous integration of PFC/Inverter[D]. Virginia Polytechnic Institute and State University, 2023.
[16] Zhang Di, Wang Fei, Burgos R, et al. Total flux minimization control for integrated inter-phase indu- ctors in paralleled, interleaved three-phase two-level voltage-source converters with discontinuous space- vector modulation[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1679-1688.
[17] Zhang Xuning, Boroyevich D, Burgos R. Design and integration of interphase inductors for interleaved three phase voltage-source-inverters in DC-fed motor drive systems[C]//2014 International Power Elec- tronics Conference (IPEC-Hiroshima 2014-ECCE ASIA), Hiroshima, Japan, 2014: 2626-2631.
[18] Gohil G, Bede L, Teodorescu R, et al. Magnetic integration for parallel interleaved VSCs connected in a whiffletree configuration[J]. IEEE Transactions on Power Electronics, 2016, 31(11): 7797-7808.
[19] 魏琪康. 多相交错并联逆变器耦合特性分析与容错运行方法[D]. 武汉: 华中科技大学, 2018.
Wei Qikang. Fault tolerant and coupling characteri- stics analysis for multiphase parallel interleaved inverter[D]. Wuhan: Huazhong University of Science and Technology, 2018.
[20] 王涛. 三相三电平整流器输入电流特性分析及优化[D]. 武汉: 华中科技大学, 2021.
Wang Tao. Analysis and optimization of input current for threephase three-level rectifier[D]. Wuhan: Huazhong University of Science and Technology, 2021.
[21] 杨玉岗, 万冬, 张凯强. “目”字形耦合电感器的设计及应用[J]. 电工技术学报, 2016, 31(5): 35-43.
Yang Yugang, Wan Dong, Zhang Kaiqiang. Design and application of the “UUUU” shape coupled inductor[J]. Transactions of China Electrotechnical Society, 2016, 31(5): 35-43.
[22] McLyman C. 变压器与电感器设计手册(第四版)[M]. 周京华, 龚绍文, 译. 北京: 中国电力出版社, 2014.
Three-Winding Coupled Inductor and Its Design Method for Interleaved Vienna Rectifiers
Abstract Interleaved Vienna rectifiers have been adopted extensively, enhancing power output capability, dispersing loss distribution, improving equivalent switching frequency, and reducing current ripple at the grid side. In the traditional separated scheme, the connecting inductor between the power grid and the converter generally comprises two magnetic components, a filter inductor and a tightly coupled inductor connected in series. The filter inductor is used to attenuate the high-frequency component of the grid current. The tightly coupled inductor forms a large equivalent inductance in the circulating current path to primarily reduce the amplitude of the circulating current between the bridge arms. Both are essential components of the interleaved Vienna rectifier. However, the utilization ratio of the tightly coupled inductor to the magnetic core is low, and two magnetic elements will occupy a larger PCB area. These two reasons make it difficult to improve the power density and efficiency of the interleaved system.
This paper proposes a three-winding coupled inductor that integrates the filter inductor and the coupled inductor on a single magnetic core. The flux in the magnetic core is evenly distributed, and the number of turns of the winding is reduced by reusing the magnetic core and the winding. Firstly, the structure of the proposed three-winding coupled inductor is given, and its equivalent circuit model is analyzed to obtain the relationship between its equivalent fundamental inductance, equivalent circulating inductance, and the self-inductance and mutual inductance of each winding. Secondly, the magnetic circuit model is analyzed to obtain the relationship between each winding’s self and mutual inductances and each magnetic circuit’s magnetic resistance. Then, the design method is given considering the air leakage path, and a three-winding coupled inductor with a rated current of 60 A (RMS value) is designed. Compared with the traditional separated scheme and the two-winding weakly coupled inductor scheme, the DC resistance of the designed three-winding coupled inductor is reduced by 35% and 11%, respectively, with the filter capacity, core volume, core saturation, and winding current density unchanged. The 40 kW three-phase Vienna rectifier using the three-winding coupled inductor achieves a maximum efficiency of 98.5%.
In view of the low utilization of the magnetic core of the tightly coupled inductor in the interleaved Vienna rectifier, this paper proposes a three-winding coupled inductor using integrated magnetic. The proposed inductor reduces losses and improves the power density of the device. Finite element simulation has proved the feasibility and effectiveness of the three-winding coupled inductor. The experiment on the prototype of an interleaved three-phase Vienna rectifier with a rated power of 40 kW proves that the designed three-winding coupled inductor has lower loss than the traditional separated scheme and the two-winding weakly coupled inductor scheme.
Keywords：Vienna rectifier, interleaved, magnetic integration, coupled inductor
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.242160
省部级重点实验室基金资助项目（6142217）。
收稿日期 2024-12-02
改稿日期 2025-02-28
王开国 男，1998年生，硕士研究生，研究方向为大功率磁元件的综合优化设计。
E-mail: wangkaiguo@whu.edu.cn
宫金武 男，1981年生，副教授，博士生导师，研究方向为高效率高功率密度电力电子变换技术、宽禁带半导体器件应用、电能质量分析与治理。
E-mail: gongjinwu@whu.edu.cn（通信作者）
（编辑 陈 诚）