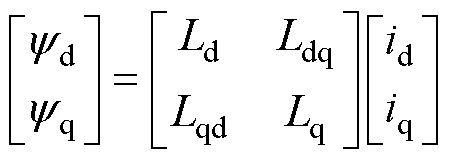（1）
摘要 同步磁阻电机无位置传感器控制能够极大地降低电机系统的复杂性和成本，在工业领域得到了越来越广泛的应用。其中，如何解决电机零低速域准确的位置观测是目前亟待解决的关键问题。然而，同步磁阻电机运行时存在显著的饱和及耦合现象，极大地影响了零低速域无传感器控制精度。针对上述问题，该文提出一种考虑饱和及耦合特性的同步磁阻电机零低速运行位置观测方法。首先，建立考虑电机饱和及耦合影响下的零低速无位置传感器角度误差观测模型。然后，提出基于虚拟轴系等效阻抗建模的零低速电机参数在线辨识方法，量化电机饱和及耦合特性在无传感器模型中的影响。最后，结合所辨识的参数对同步磁阻电机零低速运行高频有效磁链观测器中的饱和及耦合误差进行补偿，提高同步磁阻电机零低速运行位置观测精度。所提方法在3 kW同步磁阻电机对拖平台上进行实验验证，证明了其有效性。
关键词：同步磁阻电机 饱和及耦合特性 零低速 无位置传感器控制 在线参数辨识
同步磁阻电机（Synchronous Reluctance Motor, SynRM）采用无永磁体结构，具有高可靠性、高性价比等优点[1-2]。SynRM无位置传感器控制使得电机系统无须依赖传感器，从而避免了传感器故障导致的电机控制失效问题，有效地降低了维护成本，具有重要的应用价值[3-4]。SynRM高精度零低速无传感器控制一直是亟待解决的关键问题，电机存在的饱和及耦合现象极大地影响了零低速无位置传感器控制的精度[5]。所以，研究高精度的SynRM零低速运行位置观测方法十分重要[6]。
当SynRM运行于零低速域时，其感应磁链较小而难以实现高信噪比的磁链观测，所以SynRM常采用高频有效磁链观测器实现磁链观测并进行零低速无位置传感器控制。然而，观测器的精度依赖于电感，当忽略电机的饱和及耦合特性时，其观测精度将受到影响[7]。文献[8]设计了一种适用于SynRM零低速无位置传感器控制的高频磁链观测器，实现了低电流波动的位置观测，但未考虑SynRM饱和及耦合特性对观测精度的影响。文献[9]分析了电机饱和特性与耦合特性对SynRM无位置传感器控制的影响，并验证了在无位置传感器控制中考虑电机饱和及耦合特性的必要性。文献[10]从转矩方程角度探讨了电机饱和及耦合特性对无位置传感器控制的影响，并采用低频电流信号注入实现了位置误差辨识与补偿。文献[11]结合SynRM自感与互感的数值曲面改善了考虑电机饱和及耦合特性的零低速无位置传感器控制的观测效果，然而该方法需要通过有限元分析及微分计算获取电感曲面，限制了方法的通用性。虽然目前已有部分研究考虑了SynRM饱和及耦合特性对零低速无传感器控制的影响，但其精度仍需改进与提高。
电机饱和及耦合特性主要体现在电机电感矩阵的数值变化及耦合项上。因此，研究基于电感辨识的SynRM零低速无位置传感器控制模型饱和及耦合特性优化是常见的方法[12]。近年来，SynRM电感在线辨识受到国内外学者的关注，辨识所使用的模型可分为基频电压模型和高频模型[13-14]。基于基频电压模型的辨识方法主要通过构建新的方程实现电压方程组的满秩以获取电感参数。文献[15]通过不同观测轴系下的磁链观测器建立基频电压方程来求解电感，然而未考虑电机互感带来的耦合特性。相比之下，基于高频模型的辨识方法主要通过高频信号注入建立高频模型获取电感参数。该类方法算法简单、数据量少，具有更强的可靠性[16]。文献[17]在dq轴系注入高频电压信号并使用电流椭圆模型实现了同步磁阻电机dq轴电感的在线辨识，但该方法依赖电机工况，辨识精度受到dq轴电流的影响。文献[18]设计了高频信号异步旋转注入，利用电机dq轴高频等效阻抗模型实现了电机dq轴电感的在线辨识，其考虑了电机饱和及耦合特性影响下参数耦合问题，实现了辨识结果精度与工况的解耦。由于零低速无位置传感器控制位置观测多采用高频有效磁链观测器。因此，基于高频模型的辨识方法更适用于零低速下SynRM饱和及耦合特性的辨识。
为了提高同步磁阻电机零低速无传感器性能，降低电机复杂饱和及耦合影响下多类型的位置观测误差，本文提出一种基于饱和及耦合特性辨识的零低速运行位置观测方法。首先，分析SynRM饱和及耦合影响下的阻抗特性，阐述SynRM零低速运行位置观测模型，揭示电机饱和及耦合特性导致的零低速无传感器多类型观测误差产生机理。然后，提出基于虚拟解耦轴系高频信号注入的电感及耦合角辨识方法，结合对注入及感应高频信号的包络信息提取策略，实现对电机饱和及耦合特性的辨识。最后，研究零低速无传感器高频有效磁链观测器改进策略，对同步磁阻电机零低速无传感器位置观测误差进行修正与补偿。所提方法在3 kW同步磁阻电机平台进行了验证。
在SynRM饱和及耦合特性的作用下，电机磁场数值和空间分布会同时受到工况的影响，进而导致电机dq轴电感数值的变化以及互感（电感矩阵中互感项）的产生[19-20]。此时dq轴系下的磁链模型为
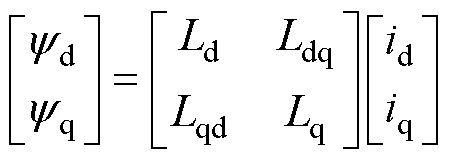（1）
式中，yd、yq分别为d、q轴系的磁链；Ld、Lq分别为d、q轴系的自感；Ldq和Lqd为dq轴系的互感；id、iq分别为d、q轴系的电流。
由于Ldq与Lqd数值相等，结合矩阵坐标变换可知，dq轴系所处的空间内总存在一个互感项为0的正交轴系，使得电机dq轴电感解耦。定义此轴系为解耦diqi轴系，且该轴系下磁链模型可以表示为
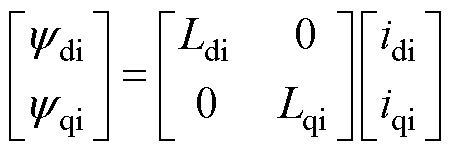（2）
式中，ydi、yqi分别为解耦di、qi轴系的磁链；Ldi、Lqi分别为解耦di、qi轴系的自感；idi、iqi分别为解耦di、qi轴系的高频电流。
由于矩阵坐标变换并未改变电机磁场的物理性质，所以此时式（1）与式（2）描述了同一个磁场。而两式分别基于dq轴和解耦diqi轴系建立，dq轴下的实际磁力线可通过解耦diqi轴系的虚拟磁链线描述，如图1所示。由于解耦diqi轴系互感为0，所以解耦diqi轴系下的等效磁场可以看作不存在耦合特性的电机磁场，同时定义解耦diqi轴系与dq轴系的夹角为耦合角qcp。
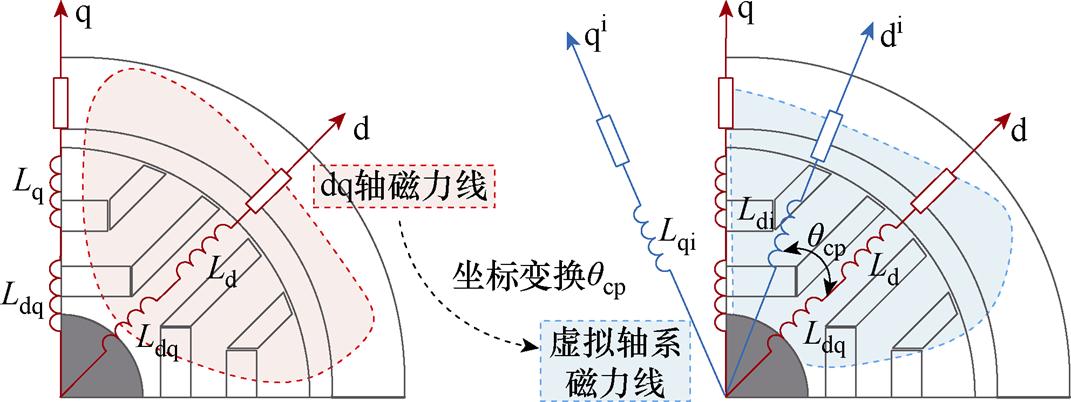
图1 解耦diqi轴系与dq轴系位置示意图
Fig.1 Schematic diagram of decoupling diqi axis and dq axis positions
根据矩阵坐标变换可以建立解耦diqi轴系与dq轴系之间的磁链模型关系为
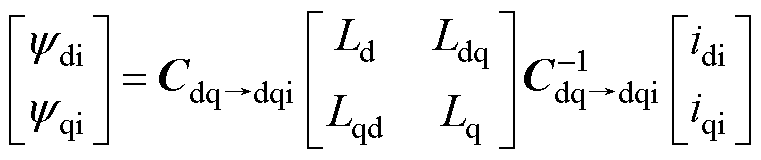（3）
其中
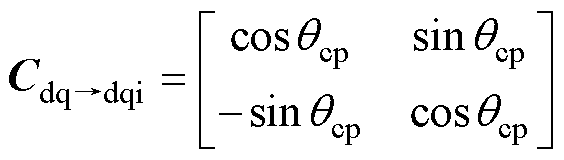
进而，可建立解耦diqi轴系与dq轴系之间的电感系数关系式为
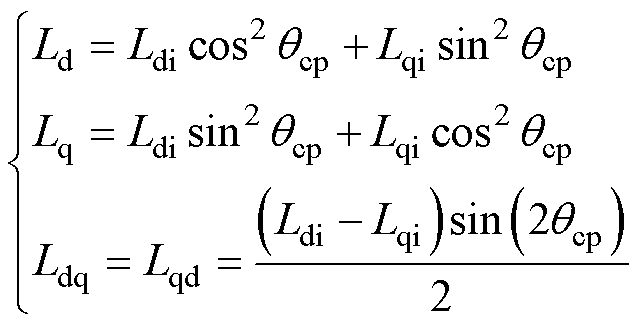（4）
由于电机饱和特性，解耦diqi轴系的电感系数与电流之间存在非线性关系。由于电机耦合特性，解耦diqi轴系下的qcp不可忽略，其可以反映dq轴系互感的变化。
高频有效磁链观测器通过定位与d轴同向的高频有效磁链矢量实现位置观测及无位置传感器控制。高频有效磁链矢量满足
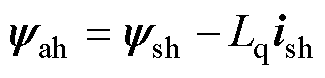（5）
式中，yah为高频有效磁链矢量；ysh为定子磁链高频量；ish为定子电流高频量。
已知电机饱和及耦合特性可以通过解耦diqi轴系电机模型中的电感数值及耦合角描述，结合式（5）可得饱和及耦合影响下高频有效磁链观测器的观测误差特性，如图2所示。
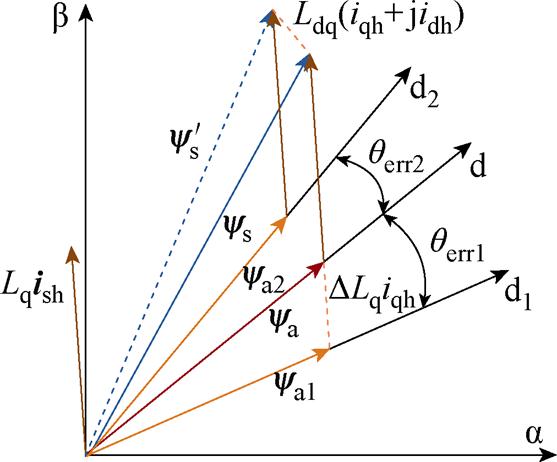
图2 与电机饱和及耦合特性相关的位置误差示意图
Fig.2 Schematic diagram of position errors related to motor saturation and coupling characteristics
电机饱和特性使得Lq随工况的变化而变化，若高频有效磁链观测器不考虑电机饱和特性，如图2所示，高频有效磁链矢量ya1与ya之间将存在着DLqiqh计算的误差，从而引起观测误差，具体为
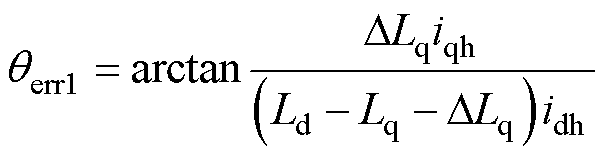（6）
式中，qerr1为电机饱和特性所引起的观测误差；idh、iqh分别为d、q轴的高频电流；DLq为电机饱和特性所带来的q轴电感误差。
电机耦合特性使得dq轴系互感不为0，如图2所示，定子磁链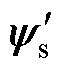
相对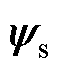
出现偏移。在解耦diqi轴系中，dq轴系互感可通过qcp描述。若忽略电机耦合特性影响，其观测误差角度即为qcp，具体表达式为
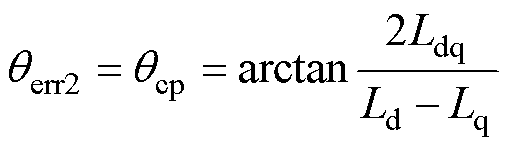（7）
式中，qerr2为电机耦合特性所引起的观测误差。
定义变量Lst辅助qerr1与qerr2的分析，当Lst为未考虑电机饱和及耦合特性的dq轴电感之差时，则式（6）和式（7）可修正为
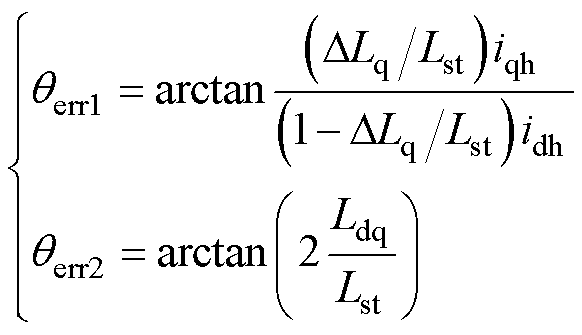（8）
根据式（8），可绘制出不同iqh、idh比值下的qerr1与qerr2变化曲线，如图3所示。
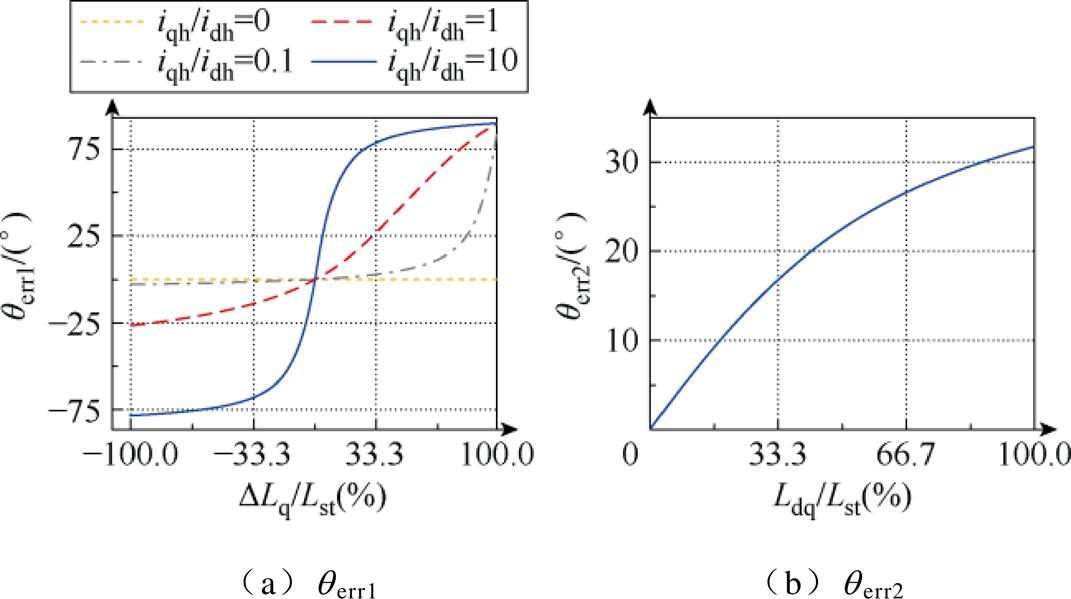
图3 电机饱和及耦合特性所引起的观测误差
Fig.3 Observation errors caused by motor saturation and coupling characteristics
考虑到电机饱和及耦合特性对零低速磁链观测器的影响，本文提出基于电感及耦合角自学习的电机饱和及耦合特性辨识方法，依次实现对qerr1与qerr2的补偿，进而达到高精度的SynRM零低速运行位置观测目标。
考虑饱和及耦合特性的SynRM零低速运行位置观测方法控制框图如图4所示。首先通过对电感及耦合角的自学习实现电机饱和及耦合特性的在线辨识，再结合辨识结果对高频有效磁链观测器的位置误差进行补偿（qerr1与qerr2），最终实现SynRM零低速运行位置的精准观测。在考虑饱和及耦合特性的SynRM零低速运行位置观测方法中，电机饱和及耦合特性的在线辨识可先于高频有效磁链观测器进行。
构建虚拟轴系，使其转速与dq轴系转速存在固定转速差，以固定周期实现对dq轴系所处转子空间的扫描。进而，在虚拟轴系下注入高频正弦电压信号，虚拟轴系中高频电压表达式为
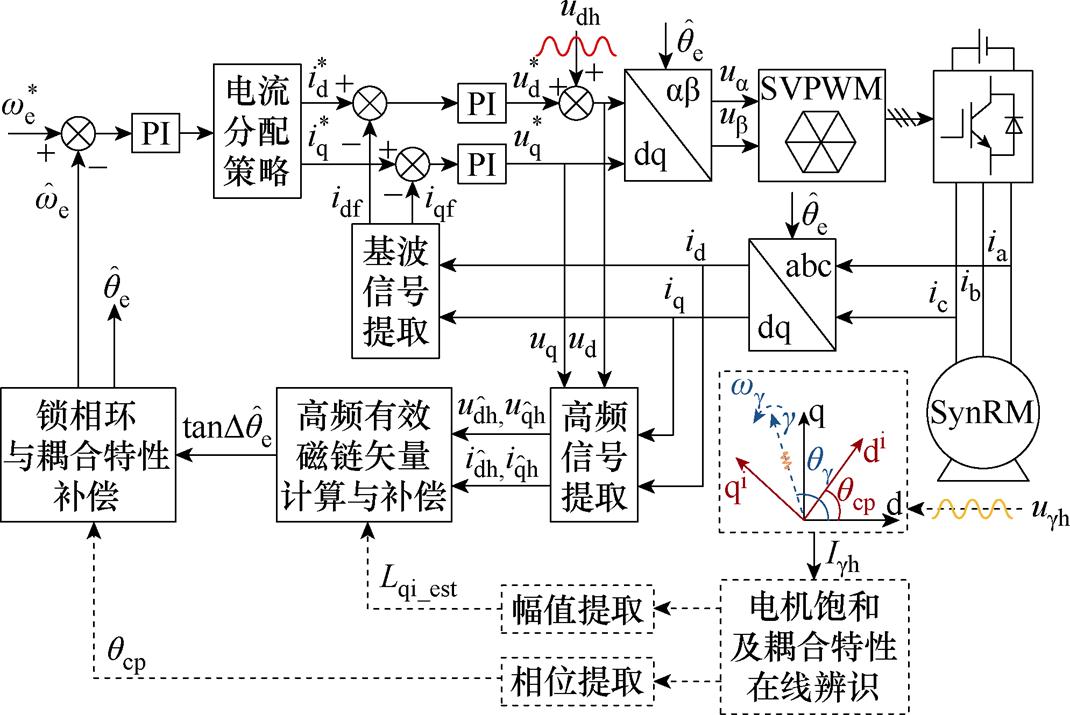
图4 考虑饱和及耦合特性的SynRM零低速运行位置观测方法控制框图
Fig.4 Sensorless control block diagram at zero and low speeds based on online identification of saturation and coupling characteristics of SynRM
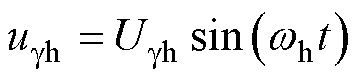（9）
式中，ugh为虚拟轴系g轴下的高频电压；Ugh为虚拟轴系g轴下的高频电压幅值；wh为注入高频正弦电压信号的电角频率。
根据解耦diqi轴系电机模型，可求得解耦diqi轴系下的高频电流分量，有
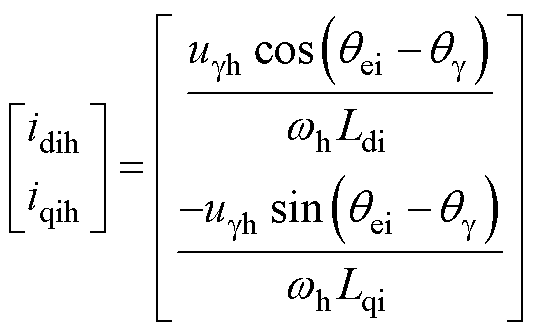（10）
式中，idih、iqih分别为解耦di、qi轴系下的高频电流分量；qei为解耦diqi轴系的电角度；qg为虚拟轴系g轴的电角度。
此时虚拟轴系等效阻抗模型中的高频电流为
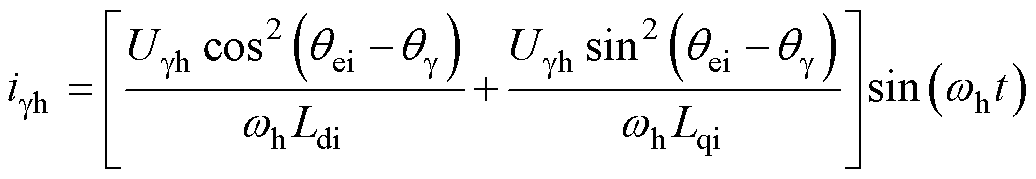（11）
式中，igh为虚拟轴系g轴下的高频电流。
由于虚拟轴系扫描dq轴系所在的空间，igh幅值会反映dq轴系所在空间内电感及耦合角的变化。此时通过离散傅里叶变换可以提取出igh包络曲线，即
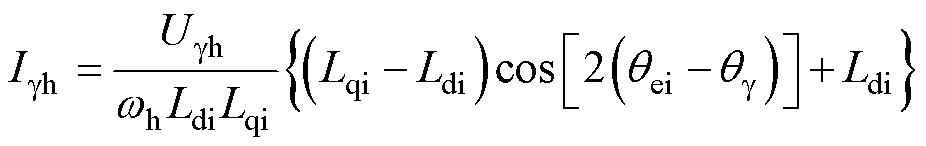（12）
式中，Igh为g轴高频电流igh的包络值。为实现电感及耦合角辨识，需采用离散傅里叶变换对注入信号的包络及相位进行提取，其计算公式为
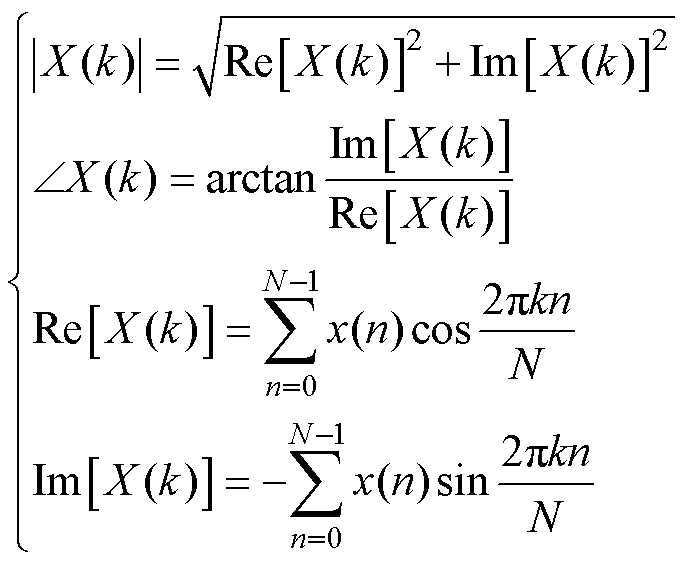（13）
式中，X(k)为离散周期序列，k为数据组数，k=0, 1,…, N-1；n为当前采样点；N为一个周期采样点数；“
”为相位信号。
图5为g轴高频电流信号包络曲线及重构曲线示意图，结合式（12）与图5的实线部分可得Igh波形为正弦变化，其极大值对应解耦diqi的q轴位置，数值为Ugh/(whLqi)，其极小值对应解耦diqi轴系d轴位置，数值为Ugh/(whLdi)。以式（12）为基础构建重构曲线，如图5的虚线部分所示，其表达式为
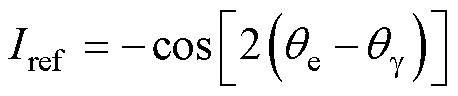（14）
式中，Iref为重构曲线；qe为传感器测量的dq轴系的电角度。
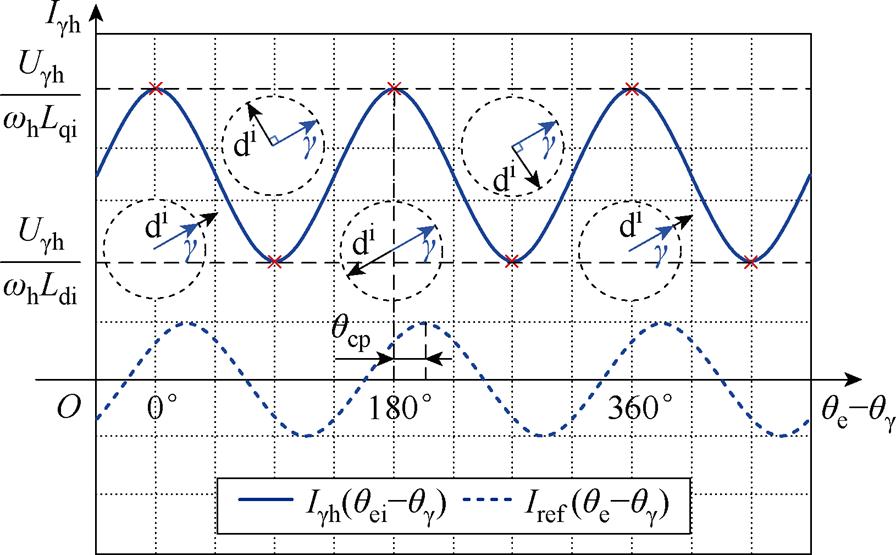
图5 g轴高频电流信号包络曲线及重构曲线示意图
Fig.5 Schematic diagram of envelope curve and reconstruction curve of g axis high-frequency current
因此，qcp可通过Igh与Iref的相位对比来获取，解耦diqi轴系电感可以通过与Igh有关的计算及幅值提取来获得，耦合角及电感辨识公式为
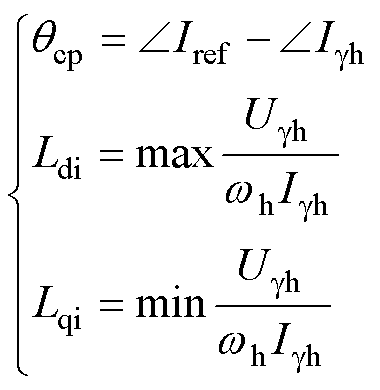（15）
式中，“max”和“min”分别为极大值和极小值。式（15）中g轴高频电压和电流的幅值Ugh、Igh，以及Igh与Iref的相位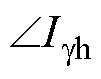
和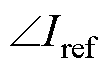
可通过式（13）计算获取。
图6为高频有效磁链矢量计算示意图，以测量dq轴系为观测基础来设计高频有效磁链观测器。测量dq轴系为与dq轴系同速的任意一轴系，高频有效磁链观测器需使测量dq轴系收敛至dq轴系所处的位置。
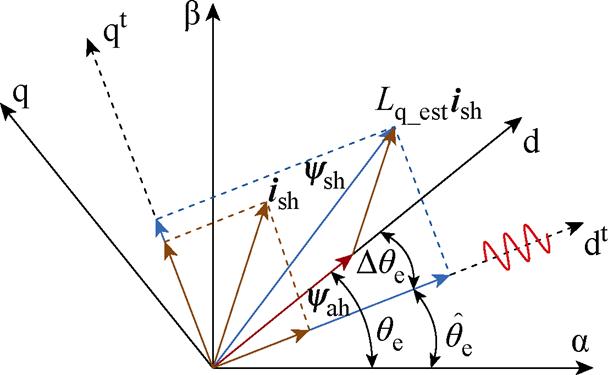
图6 高频有效磁链矢量计算示意图
Fig.6 Schematic diagram of high-frequency effective magnetic flux vector calculation
考虑电机的饱和特性时，由式（6）可知，代入解耦diqi轴系电感辨识值可消除qerr1。根据式（5）可计算出测量dq轴系的高频有效磁链分量为
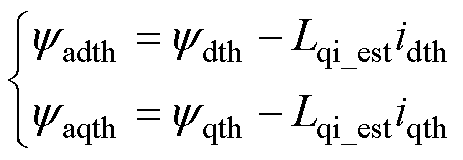（16）
式中，yadth、yaqth分别为测量dq轴系d轴、q轴的高频有效磁链分量；Lqi_est为Lqi的辨识值。
以解耦diqi轴系为基础，测量dtqt轴系与解耦diqi轴系的磁链模型，满足
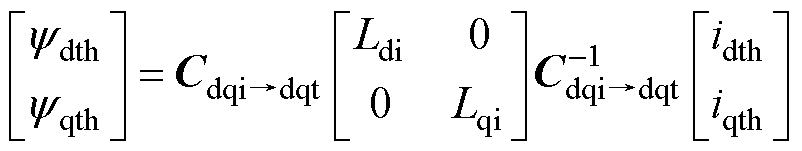（17）
其中
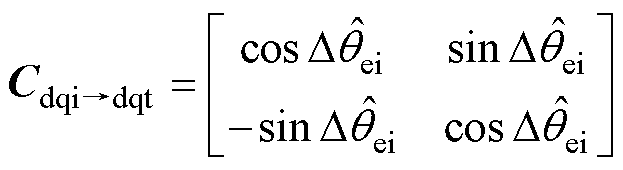
式中，上标“
”为测量值；Dqei为解耦diqi轴系与测量dq轴系之间的夹角。最终可计算出式（16）中的高频有效磁链分量满足
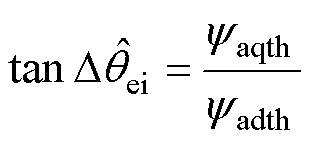（18）
根据式（18）设计锁相环，可实现SynRM零低速运行位置观测，如图7所示。当tanDqei收敛为0时，Dqei也收敛至0，高频有效磁链观测器可输出解耦diqi轴系的位置。对比文献[21]，本文的位置观测方法通过除法运算简化运算过程，可在取消低通滤波环节的基础上进一步提高位置观测精度。
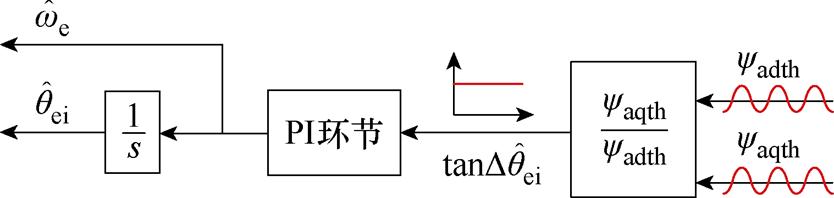
图7 高频有效磁链观测器的锁相环控制框图
Fig.7 Phase-locked loop control block diagram of high-frequency effective magnetic flux observer
为了进一步补偿式（7）中电机耦合特性所引起的观测误差，由于qcp=qerr2且为dq轴系与diqi轴系的夹角，考虑电机的耦合特性时，将辨识所得的qcp对高频有效磁链观测器输出位置进行直接补偿，便可消除qerr2，对电机饱和及耦合效应进行补偿后，准确的转子观测位置
表达式为
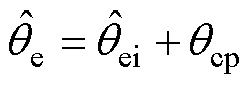（19）
综上所述，获取电机解耦diqi轴系下的电感及耦合角辨识结果，并通过辨识结果对电机饱和及耦合特性所引起的高频有效磁链观测器的qerr1与qerr2进行修正和补偿，可实现高精度的SynRM零低速位置观测。
所提方法测试采用的实验平台如图8所示，测试电机为3 kW的同步磁阻电机，负载机为永磁同步电机，电机驱动器采用ARM STM32F103芯片进行算法验证，开关频率为6 kHz，所测试的SynRM参数见表1。实验结果部分变量均用标幺值表示，其基值对应电机铭牌额定值。测试平台针对0～10%额定速度范围对无位置传感器位置观测展开设计，结合现有文献定义认为该速度范围为电机零低速域[22]。
图8 SynRM驱动系统实验平台
Fig.8 Experimental platform of SynRM drive system
基于虚拟轴系等效阻抗模型的电机饱和及耦合特性辨识波形如图9所示。图9a为虚拟轴系等效阻抗模型下的高频信号注入实验波形。电机运行频率为15 Hz，g轴转速为14 Hz，g轴始终以1 Hz转速差扫描dq轴平面。注入的高频电压信号幅值为0.1(pu)，频率为750 Hz。可知g轴高频电流信号为幅值变化的信号，其幅值包含解耦轴系耦合角及电感信息。图9b为g轴高频电流包络信号、重构参考信号及耦合角实验波形，其中耦合角通过g轴高频电流包络信号及重构参考信号的相位对比获得，如式（15）所示。图9c为所辨识的g轴电感曲线，其极大值和极小值分别对应Ldi和Lqi。
表1 同步磁阻电机实验参数
Tab.1 Experimental Parameters of SynRM
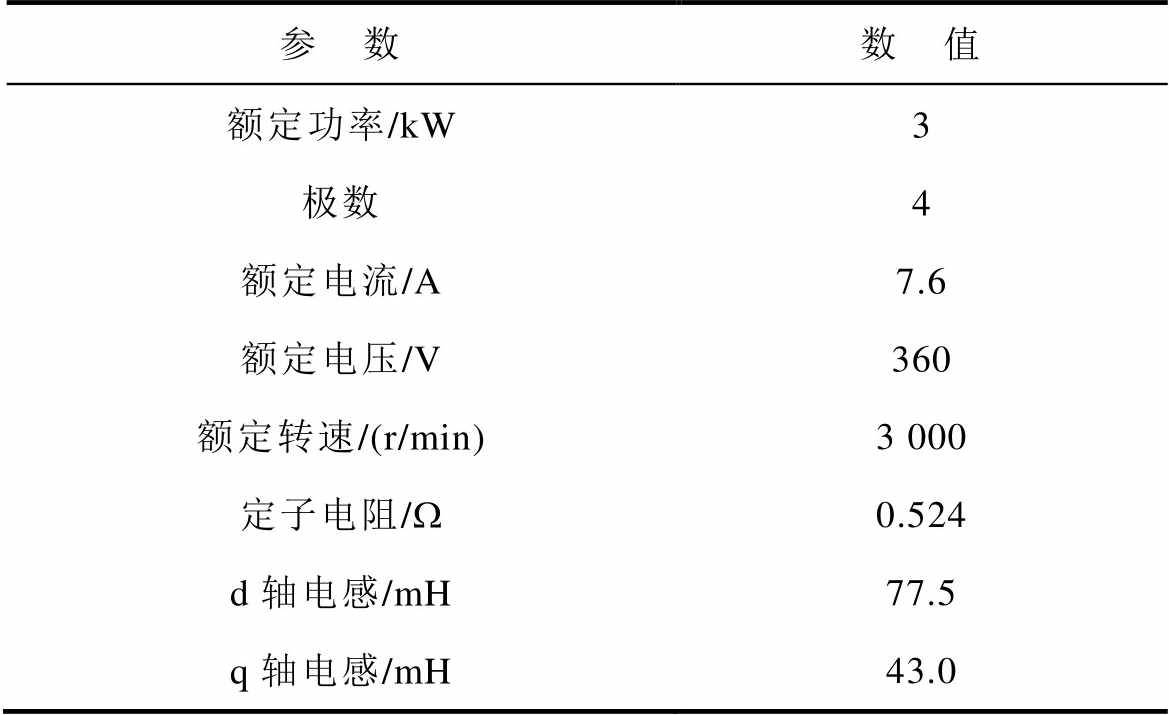
参 数数 值 额定功率/kW3 极数4 额定电流/A7.6 额定电压/V360 额定转速/(r/min)3 000 定子电阻/W0.524 d轴电感/mH77.5 q轴电感/mH43.0
图9 基于虚拟轴系等效阻抗模型的电机饱和及耦合特性辨识波形
Fig.9 Experimental waveforms of motor saturation and coupling characteristics identification
耦合角及电感可反映电机饱和及耦合特性，其中Ldi与Lqi描述电机饱和特性，qcp描述电机耦合特性。图10为耦合角和解耦diqi轴电感辨识结果曲面。图10a中，Ldi主要受id变化影响，其变化幅度可达65 mH，变化量可达76%。图10b中，Lqi主要受iq变化影响，其变化幅度可达50 mH，变化量可达83%。图10c反映了qcp的变化，其主要受到iq的影响，当id趋于0且iq趋于额定值时，qcp存在从0°突变为90°的情况。
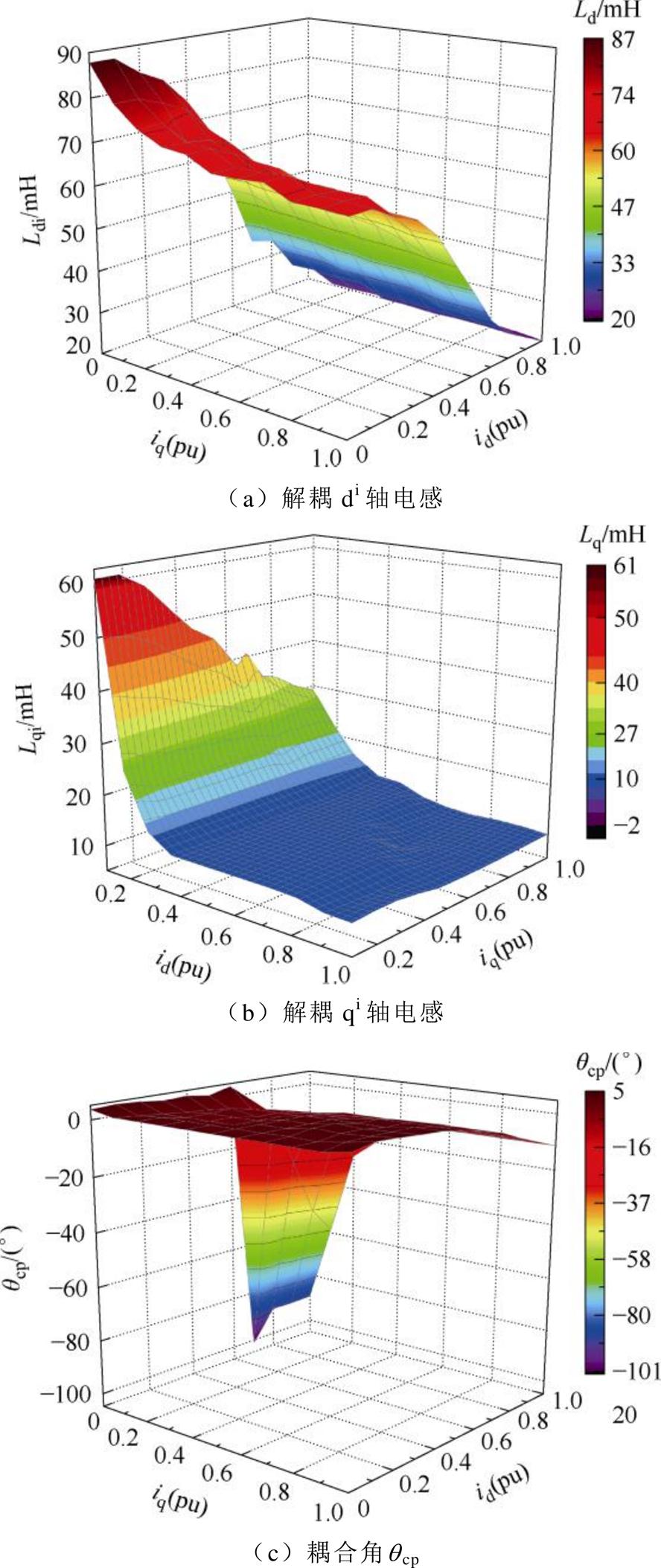
图10 耦合角和解耦diqi轴电感辨识结果曲面
Fig.10 Surface of coupling angle and diqi-axis inductance identification results
根据式（4）中解耦diqi轴系与dq轴系的电感关系，可以求出dq轴系电感曲面，如图11所示。由于SynRM中id提供励磁电流，当id趋于0且iq趋于额定值的情况下，从Ld＞Lq变化至Ld＜Lq。由dq轴饱和特性导致Ld＜Lq的现象，即为凸极转变现象。dq轴凸极转变前后，dq轴系电感曲面存在凸极比等于1的过渡工况曲线，在该曲线上Ld=Lq。由于额定电流的限制，在dq轴电流有效区间内，仅有小区域dq轴电流存在过渡工况曲线（id＜0.2(pu)，iq＞0.7(pu)）。由图11可得，所测试的SynRM在采用id=iq控制时不存在凸极转变现象。
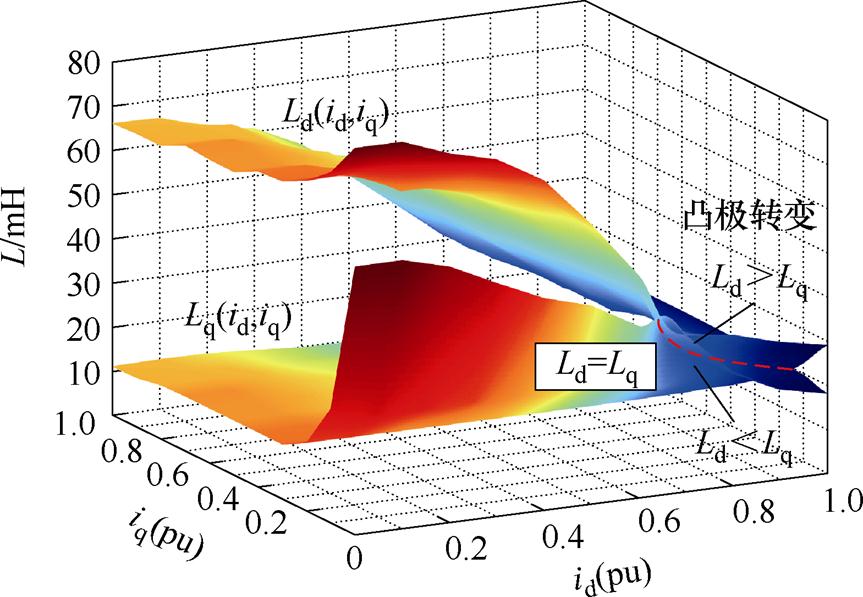
图11 dq轴系电感曲面及凸极转变现象
Fig.11 dq-axis inductance surface and convex pole transition phenomenon
图12为id=iq控制下的耦合角与解耦diqi轴系电感在线辨识值变化曲线。由于空载时的电流近乎为0，电机不存在耦合现象，此时qcp=0。当电机满载时，qcp随着电流的增大而增大，qcp增至11.7°。解耦diqi轴系电感随电流的增大而减小，空载时Ldi和Lqi分别为77.5 mH和43.0 mH，满载时Ldi和Lqi分别为46.8 mH和11.0 mH，Ldi和Lqi变化幅度分别为39.6%和74.4%。综合qcp、Ldi和Lqi的变化结果，SynRM饱和及耦合特性使得电机电感及耦合角产生明显变化，说明了零低速考虑电机饱和及耦合特性的必要性。
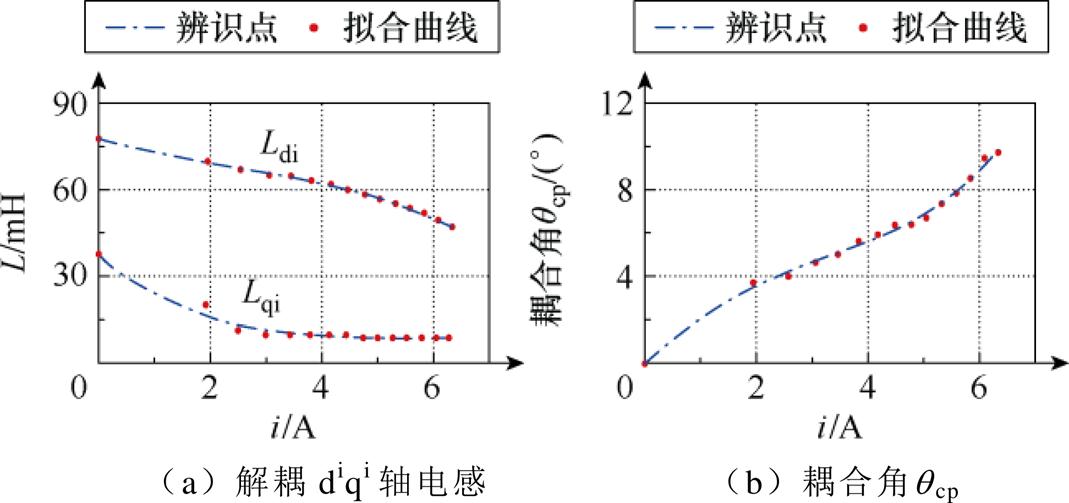
图12 id=iq控制下的耦合角与解耦diqi轴系电感在线辨识值变化曲线
Fig.12 Online identification variation curves of coupling angle and diqi-axis inductance
图13为SynRM在满载下转速从零速变化到300 r/min时的无位置传感器控制输出转速实验波形。注入的高频电压幅值为0.1(pu)，频率为750 Hz。电机转速从零速变化至150 r/min至300 r/min时转速均平稳变化，且转速观测误差接近于0。本文所提考虑电机饱和及耦合特性的同步磁阻电机零低速运行位置观测方法，可应用于SynRM零低速无位置传感器控制。
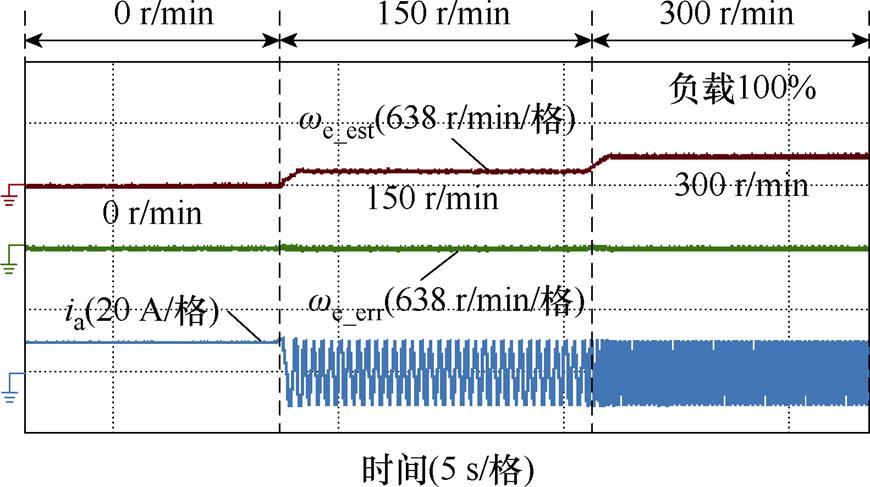
图13 满载下转速从零速变化到300 r/min时的无位置传感器控制输出转速实验波形
Fig.13 Experimental waveforms of sensorless control speed with speed changing from 0 r/min to 300 r/min under full load
为证明算法有效性，分别说明电机饱和及耦合（qerr1和qerr2）对零低速无传感器位置观测影响及其误差补偿的效果，设置对照组实验见表2。
表2 零低速无传感器测试工况
Tab.2 Zero-low speed sensorless test condition
测试分组测试内容 组1未补偿电机饱和及耦合误差 组2仅补偿饱和特性位置观测误差 (qerr1) 组3仅补偿耦合特性位置观测误差 (qerr2) 组4同时补偿饱和及耦合误差 (qerr1和qerr2)
图14为零速下的无位置传感器控制实验波形，保持零速时突加减负载，负载从空载至50%负载再至满载，后从满载至50%负载再至空载。可通过对比各个测试组的观测位置误差来分析qerr1和qerr2的补偿效果。
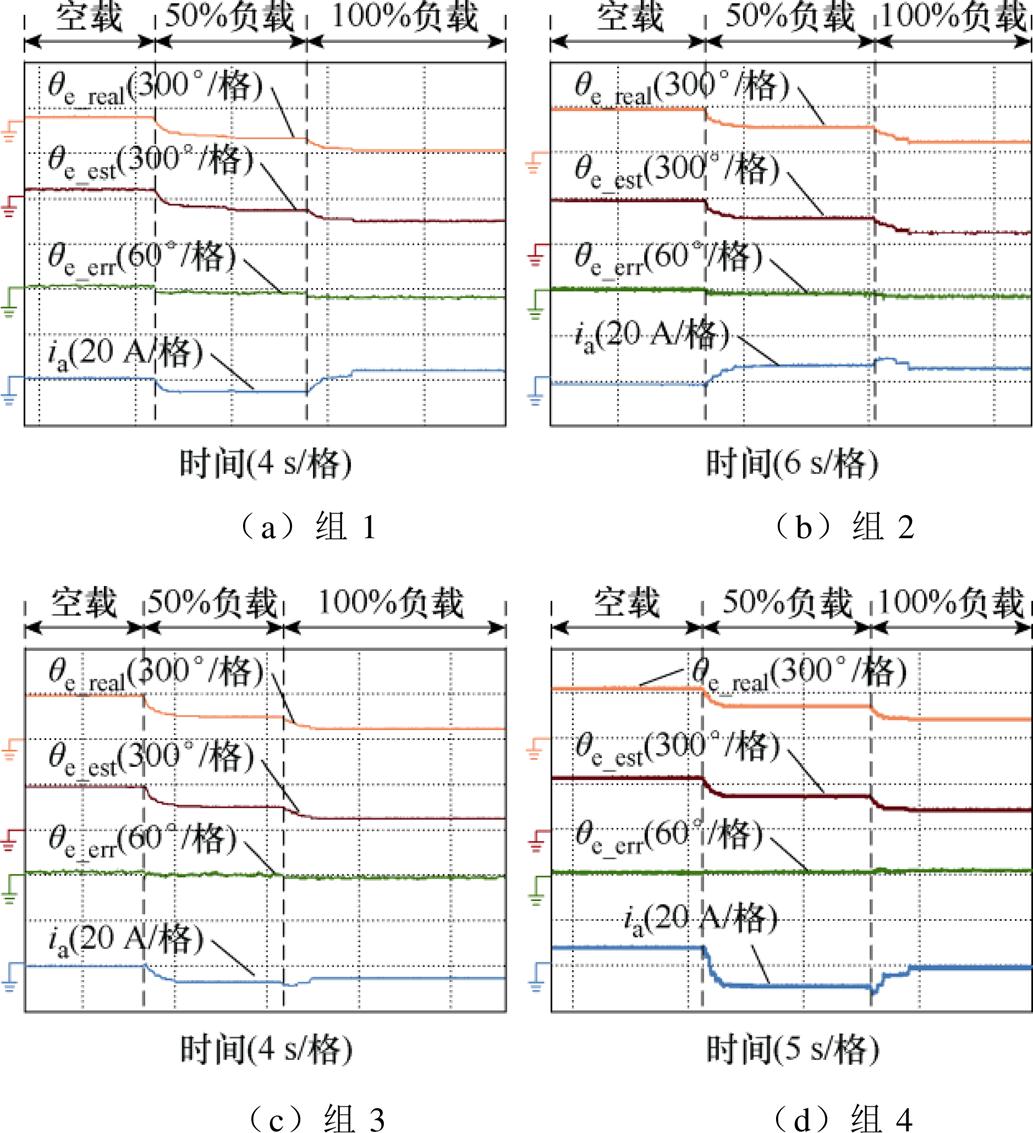
图14 零速下无位置传感器控制实验波形
Fig.14 Experimental waveforms of sensorless control at zero speed
低速实验以150 r/min和300 r/min为代表，结合零速实验，以验证所提方法在零低速工作域的鲁棒性。图15和图16分别为150 r/min与300 r/min转速下无位置传感器控制实验波形，保持转速时分别测试空载、半载和满载工况下的算法效果。
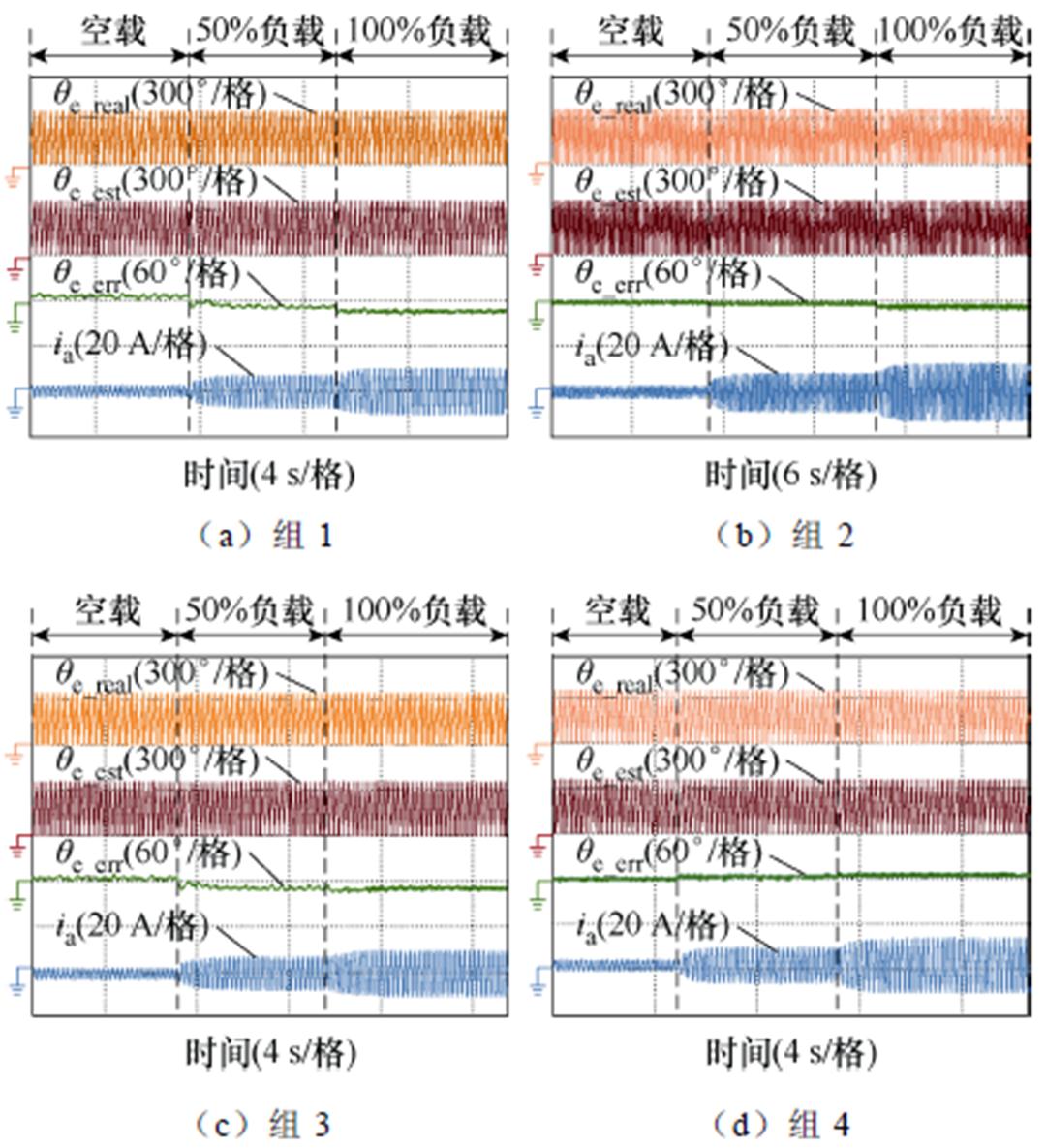
图15 150 r/min转速下无位置传感器控制实验波形
Fig.15 Experimental waveforms of sensorless control at 150 r/min
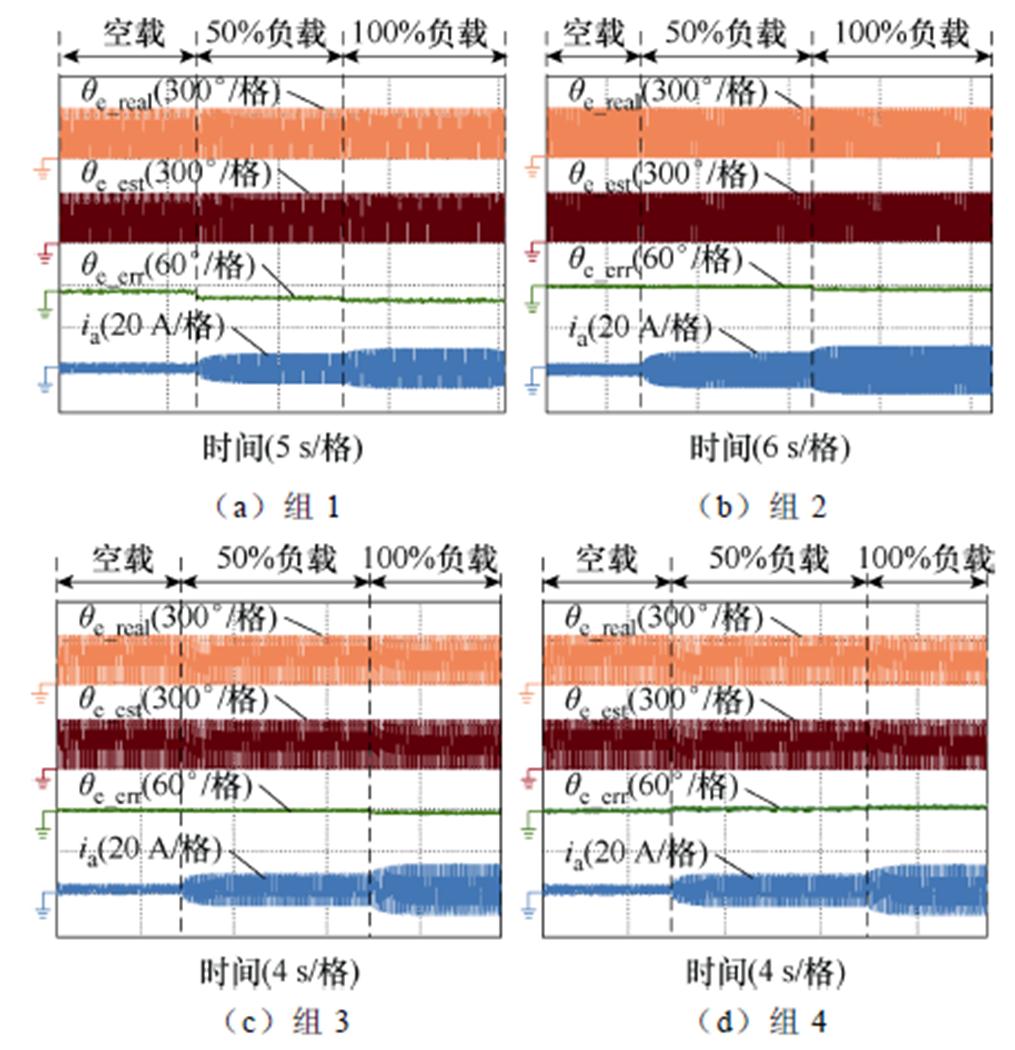
图16 300 r/min转速下无位置传感器控制实验波形
Fig.16 Experimental waveforms of sensorless control at 300 r/min
结合图14～图16的实验结果，零低速运行观测位置误差绝对值对比如图17所示。以未考虑饱和及耦合特性影响时的实验数据（组1）为参考，在考虑饱和及耦合特性影响（组4）时，零速下空载、半载和满载观测位置误差分别降低了85.7%、76.7%及80.8%，150 r/min转速下空载、半载和满载观测位置误差分别降低了98.2%、73.4%及80.4%，300 r/min转速下空载、半载和满载观测位置误差分别降低了99.1%、89.5%及91.0%。仅考虑饱和特性影响（组2）或者仅考虑耦合特性影响（组3）时，零低速下的观测位置误差会比同时考虑饱和及耦合特性影响时的观测位置误差更大。实验结果说明了所提方法的有效性。
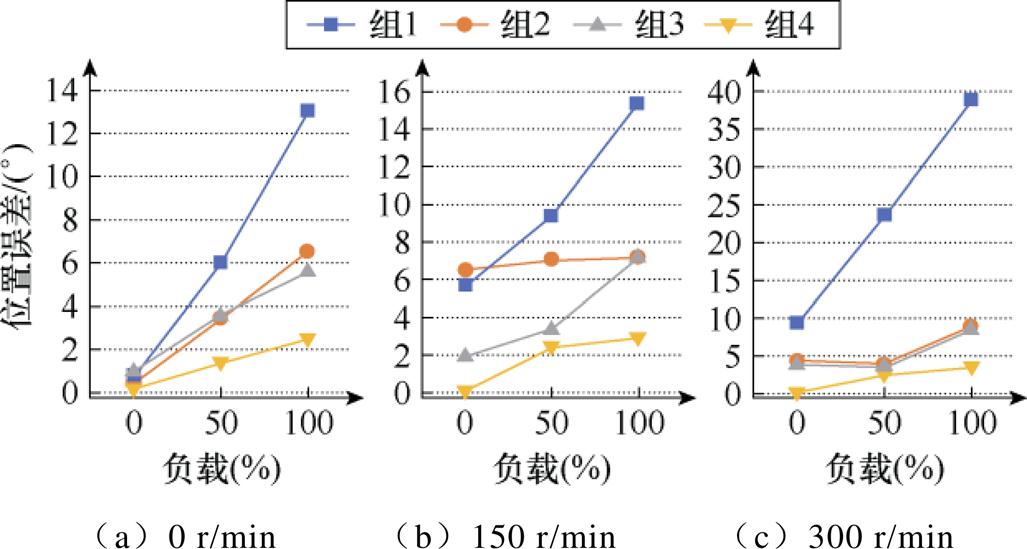
图17 零低速运行观测位置误差绝对值对比
Fig.17 Experimental waveforms of sensorless control at zero speed comparison diagrams of experimental data for observed position error at zero and low speeds
电机饱和及耦合特性可以通过解耦diqi轴系的电感及耦合角进行描述，且在电机饱和及耦合特性的影响下，电感呈现出随着电流增大而减小的变化趋势，耦合角呈现出随着电流减小而增大的变化趋势。电感及耦合角数值与电流有关，其可以反映出电机饱和程度及耦合程度。电机饱和及耦合特性仅与负载（id和iq）相关，基于所提方法在零低速应用工况下所获取的交直轴电感和耦合角同样可应用于高速工况无传感器位置观测器对于电机饱和及耦合特性的补偿[3, 19]。
本文提出了一种考虑饱和及耦合特性的SynRM零低速运行位置观测方法，提高了同步磁阻电机零低速位置观测精度。通过虚拟解耦轴系高频信号注入对电机零低速工况的电感及耦合角进行辨识，实现了对电机饱和及耦合特性的描述。基于辨识结果，对零低速无传感器高频有效磁链观测器进行修正，实现了对电机饱和及耦合导致多类型误差的补偿。本文方法充分考虑了电机多运行工况下非理想特性影响，提高了同步磁阻电机零低速无传感器控制的精度和鲁棒性。所提方法在3 kW同步磁阻电机进行了验证，证明了该方法的有效性。
参考文献
[1] 王建渊, 王海啸, 尹忠刚, 等. 基于一阶线性自抗扰控制器的同步磁阻电机无速度传感器控制[J]. 电工技术学报, 2024, 39(14): 4405-4421.
Wang Jianyuan, Wang Haixiao, Yin Zhonggang, et al. Sensorless control of synchronous reluctance motor based on first order linear active disturbance rejection controller[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4405-4421.
[2] Murataliyev M, Degano M, Di Nardo M, et al. Synchronous reluctance machines: a comprehensive review and technology comparison[J]. Proceedings of the IEEE, 2022, 110(3): 382-399.
[3] 张国强, 杜锦华. 永磁同步电机无位置传感器控制技术综述[J]. 电机与控制应用, 2024, 51(1): 1-13.
Zhang Guoqiang, Du Jinhua. Review of position sensorless control technology for permanent magnet synchronous motors[J]. Electric Machines & Control Application, 2024, 51(1): 1-13.
[4] Xu Yulei, Yao Ming, Sun Xiaodong. Overview of position-sensorless technology for permanent magnet synchronous motor systems[J]. World Electric Vehicle Journal, 2023, 14(8): 212.
[5] 王奇维, 李斌兴, 潘冠丞, 等. 基于转子位置误差解耦阻抗建模的永磁同步电机电感在线辨识方法[J]. 电工技术学报, 2025, 40(2): 439-451.
Wang Qiwei, Li Binxing, Pan Guancheng, et al. Impedance model based online inductance identi- fication method of permanent magnet synchronous motor decoupled from rotor position error[J]. Transa- ctions of China Electrotechnical Society, 2025, 40(2): 439-451.
[6] Accetta A, Cirrincione M, Pucci M, et al. Space- vector state dynamic model of the SynRM considering self, cross-saturation and iron losses and related identification technique[J]. IEEE Transactions on Industry Applications, 2023, 59(3): 3320-3331.
[7] Li Chengrui, Wang Gaolin, Zhang Guoqiang, et al. Review of parameter identification and sensorless control methods for synchronous reluctance machines[J]. Chinese Journal of Electrical Engineering, 2020, 6(2): 7-18.
[8] Hatanaka T, Kato S, Tomita M, et al. Position sensorless control of synchronous reluctance motors at low-speeds[C]//2019 IEEE 4th International Future Energy Electronics Conference (IFEEC), Singapore, 2019: 1-6.
[9] Tsujii Y, Morimoto S, Inoue Y, et al. Effect of inductance model on sensorless control performance of SynRM with magnetic saturation[C]//2022 Inter- national Power Electronics Conference (IPEC-Himeji 2022-ECCE Asia), Himeji, Japan, 2022: 2687-2693.
[10] Foti S, De Caro S, Scimone T, et al. Rotor position error compensation in sensorless synchronous relu- ctance motor drives[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 4442-4452.
[11] 王建渊, 李英杰, 景航辉, 等. 基于静止轴系改进高频方波注入同步磁阻电机无传感器控制[J]. 电工技术学报, 2024, 39(12): 3658-3669.
Wang Jianyuan, Li Yingjie, Jing Hanghui, et al. Sensorless control of high frequency square wave injection synchronous reluctance motor based on static axis system improvement[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3658- 3669.
[12] 曹恒佩, 艾萌萌, 王延波. 永磁辅助同步磁阻电机研究现状及发展趋势[J]. 电工技术学报, 2022, 37(18): 4575-4592.
Cao Hengpei, Ai Mengmeng, Wang Yanbo. Research status and development trend of permanent magnet assisted synchronous reluctance motor[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(18): 4575-4592.
[13] Mercorelli P. Identification of parameters and states in PMSMs[J]. Electronics, 2023, 12(12): 2625.
[14] 许爱德, 刘鑫, 李新宇, 等. 基于参数辨识的永磁辅助同步磁阻电机电流无差拍控制[J]. 电工技术学报, 2024, 39(18): 5626-5638.
Xu Aide, Liu Xin, Li Xinyu, et al. Current deadbeat control of permanent magnet-assisted synchronous reluctance motor based on parameter identification[J]. Transactions of China Electrotechnical Society, 2024, 39(18): 5626-5638.
[15] Jin Tong, Sun Wei, Wang Haowen, et al. Saturated dq-axis inductance offline identification method for SynRM based on a novel active flux observer orientation[J]. IEEE Transactions on Power Elec- tronics, 2024, 39(9): 10670-10674.
[16] Zhang Jindong, Peng Fei, Huang Yunkai, et al. Online inductance identification using PWM current ripple for position sensorless drive of high-speed surface- mounted permanent magnet synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2022, 69(12): 12426-12436.
[17] Berto M, Alberti L, Martin F, et al. Online incre- mental inductance identification for reluctance syn- chronous motors[C]//IECON 2021-47th Annual Con- ference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 2021: 1-6.
[18] Wang Qiwei, Wang Gaolin, Zhao Nannan, et al. An impedance model-based multiparameter identification method of PMSM for both offline and online con- ditions[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 727-738.
[19] 鲍晓华, 刘婕, 关博凯, 等. 考虑磁饱和的潜水感应电机励磁电感的解析计算[J]. 电工技术学报, 2025, 40(8): 2405-2417.
Bao Xiaohua, Liu Jie, Guan Bokai, et al. Analytical calculation of the magnetizing inductance of the submersible induction machine considering the mag- netic saturation[J]. Transactions of China Electro- technical Society, 2025, 40(8): 2405-2417.
[20] 刘小青, 王晋, 刘开元, 等. 基于高频注入法的同步磁阻电机无位置传感器控制[J]. 微电机, 2024, 57(5): 28-32.
Liu Xiaoqing, Wang Jin, Liu Kaiyuan, et al. Research on sensorless control of synchronous reluctance motor based on high frequency signal injection[J]. Micro- motors, 2024, 57(5): 28-32.
[21] 项润华. 基于有效磁链观测的同步磁阻电机无传感器控制策略[D]. 哈尔滨: 哈尔滨工业大学, 2022.
Xiang Runhua. Active flux observer based sensorless synrm drives srategy[D]. Harbin: Harbin Institute of Technology, 2022.
[22] Chen Guanren, Chen J Y, Yang S C. Implementation issues of flux linkage estimation on permanent magnet machine position sensorless drive at low speed[J]. IEEE Access, 2019, 7: 164641-164649.
Position Observation Method for Synchronous Reluctance Motor at Zero and Low Speeds Considering Saturation and Coupling Characteristics
Abstract The synchronous reluctance motor (SynRM) exhibits significant saturation and coupling phenomena, leading to noticeable position observation errors in sensorless control. To achieve high-precision sensorless control of SynRM at zero and low speeds, it is crucial to fully consider the motor's saturation and coupling characteristics, which are primarily reflected in nonlinear inductance changes and the coupling terms in the inductance matrix. Online inductance identification can acquire the motor's saturation and coupling characteristics, which are essential for optimizing sensorless control. This paper proposes a position observation method for synchronous reluctance motor at zero and low speeds, considering saturation and coupling characteristics. First, the influence of motor saturation and coupling characteristics on the high-frequency effective flux linkage observer in zero and low-speed sensorless control is analyzed. Then, a virtual axis equivalent impedance model is constructed to simplify the SynRM model by decoupling the axes. An online identification method for the decoupled axis model parameters is proposed to describe the saturation and coupling characteristics of the SynRM, thereby eliminating position observation errors. Finally, combined with the results of online identification, motor saturation and coupling error compensation are implemented in the sensorless control of the SynRM at zero and low speeds.
A 3 kW SynRM test platform was set up. The experimental results demonstrate that the proposed method enables high-precision sensorless control of SynRM at zero and low speeds. Full-load acceleration tests were conducted to verify the effectiveness of the high-frequency effective flux observer in the SynRM, where the speed variation remained stable and the steady-state error was close to zero. Additionally, zero and low speeds at 150 r/min were selected. Under constant speed conditions, load step change tests were conducted to verify the accuracy of the high-frequency effective flux observer. Experimental results show that correcting and compensating the high-frequency effective flux observer with the identified motor saturation and coupling characteristics can significantly improve the sensorless observation accuracy of the SynRM at zero and low speeds. The steady-state position observation error at zero speed was reduced by 85.7%, 76.7%, and 80.8% under no-load, half-load, and full-load conditions. At low speeds, the steady-state position observation error was reduced by 98.2%, 73.4%, and 80.4% under no-load, half-load, and full-load conditions.
The conclusions can be drawn. (1) SynRMs exhibit significant variations in saturation and coupling characteristics, which cannot be ignored in the design of sensorless control at zero and low speeds. (2) The proposed method simplifies the high-frequency effective flux observer, ensuring stable speed and position output without using a low-pass filter. (3) The proposed method reduces the steady-state error of the observed angle and improves the observation accuracy for sensorless control of the SynRM at zero and low speeds.
Keywords：Synchronous reluctance motor, saturation and coupling effects, zero/low-speed, sensorless control, online parameter identification
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.241720
国家自然科学基金青年科学基金项目（52307048）、黑龙江省自然科学基金联合引导项目（LH2024E047）、黑龙江省博士后资助项目（LBH-Z23022）和台达电力电子科教发展计划科研项目（DREG2024008）资助。
收稿日期2024-10-07
改稿日期 2025-01-14
王奇维 男，1993年生，讲师，硕士生导师，研究方向为精密电机控制，电机参数辨识、状态检测及故障诊断技术。
E-mail: wqwhit@hit.edu.cn
王高林 男，1978年生，教授，博士生导师，研究方向为电机高品质驱动控制技术、高性能电力电子技术等。
E-mail: WGL818@hit.edu.cn（通信作者）
（编辑 崔文静）