图1 不对称半桥功率变换器拓扑结构及其工作原理
Fig.1 Asymmetric half-bridge power converter topology and its operating principle
摘要 开关磁阻电机凭借其独特优势已成为电动汽车和多电飞机领域内最有竞争力的起发电机之一。然而，运行过程中的大转矩脉动成为了制约其进一步应用的主要障碍之一，而模型预测控制作为抑制开关磁阻电机转矩脉动的有效策略得到了广泛的应用，然而代价函数的设计依赖人为经验，影响其抑制效果。针对这一问题，该文提出一种基于二维数据插值的开关磁阻电机转矩脉动抑制策略。首先，采用PWM信号替代传统预测控制中的三种开关状态。然后，经在线运行区域调整，在单相区采用无差拍预测控制计算导通相最优占空比；换相区则采用模型预测控制计算励磁相和退磁相的最优占空比，即通过拉丁超立方抽样获取电机性能预测模型，提出利用二维线性插值法替代传统代价函数设计，以实现占空比在线寻优。实验结果表明，基于二维数据插值的方法可以在几乎不损失效率的情况下有效地抑制转矩脉动。
关键词：开关磁阻电机 转矩脉动 二维线性插值 模型预测控制 无差拍预测控制
开关磁阻电机（Switched Reluctance Machine, SRM）结构原理简单、成本低廉，具有可靠性高、耐高温能力强以及调速范围宽等优势，已经成为电动汽车和多电飞机领域内最有竞争力的起发电机之一[1-2]。SRM采用双凸极结构，具有高饱和磁路和非线性电磁特性，其输出转矩难以通过解析式和数学模型直接得到[3]。这导致在经典电流斩波控制下，SRM输出转矩将具有严重的波动，这种大转矩脉动将对电驱动系统的可靠性造成威胁[4]。
为有效地抑制转矩脉动，国内外学者提出了直接转矩控制、直接瞬时转矩控制、转矩分配函数以及模型预测控制（Model Predictive Control, MPC）等方法[5]。在文献[6]中，提出了一种应用于SRM的直接转矩控制方法，构建了用于减小转矩脉动的电压矢量表。文献[7]对电压矢量表进行改进，并提出通过转矩和磁链的估算误差确定最优电压矢量，进一步降低了转矩脉动。直接瞬时转矩控制的核心是基于实时反馈的瞬时转矩实现滞环控制，但产生的负转矩也造成了效率损失。为解决该问题，文献[8]提出了一种角度迭代优化方法，有效降低了换相过程中的电流脉冲，提升了系统效率。转矩分配函数的功能是将参考转矩合理地分配给每相，以保持总转矩恒定[9]。为提高转矩分配函数在高速下的转矩跟踪精度和对不同工况的通用性，在线转矩分配函数被提出。文献[10]基于引力搜索算法调节磁链曲线，在最优磁链曲线上推导出在线转矩分配函数，提高了磁链和转矩变化的平滑性。
基于精确预测模型，MPC通过预测目标变量在所有可能控制信号下的变化并基于预设的控制律实现控制信号的在线寻优。文献[11]提出了一种滑模控制器以取代传统MPC中的PI控制器来生成参考转矩，有效提高了动态性能和抗干扰能力。文献[12]提出了一种基于直接转矩控制的新型异步电机MPC策略，通过基于最小方均自适应算法实现谐波消除，并在线更新余弦和正弦信号的权重系数，有效地估计并消除谐波干扰分量，实现了对转矩脉动的有效抑制。文献[13]提出一种基于快速选择表的永磁同步电机模型预测转矩控制策略，减少了双矢量模型预测转矩控制中忽略的定子磁链波动，实现了同时抑制转矩脉动和磁链脉动。应用于SRM的模型预测转矩控制在文献[14]中被首次提出，未来控制周期的转矩和电流通过预测模型估算得到，进而通过代价函数选择能使转矩脉动最小的控制信号。由于其表现的出色性能，国内外学者在该方向进行了更深入的研究。为减少预测模型的存储量，文献[15]提出了一个四阶傅里叶模型来替代数据查找表，在保障转矩脉动抑制性能的同时提升了控制实时性。文献[16]采用简单的SRM线性模型建立预测模型，通过磁链和转矩的等效转化提高模型精度，该方法不仅能有效减少换相过程的转矩脉动，且提高了高速下的转矩控制性能。无差拍预测控制凭借其动态响应快的优势同样逐渐应用于SRM。通过在不同运行区域灵活选择不同预测控制方法，文献[17]提出一种SRM四象限运行控制方法，展现了出色的参考转矩跟随能力。
基于上述文献可以发现，现有研究中MPC代价函数的设计直接决定了控制系统的性能，难以仅凭人工经验生成最优控制序列；在有限控制信号集内选择出最优控制信号，限制了转矩脉动的抑制效果，没有充分利用MPC的灵活性。为解决以上问题，本文在将PWM控制信号引入MPC替代传统有限集预测方案的基础上，提出一种利用二维线性插值寻优代替传统代价函数的方法，避免繁琐低效的调参过程，降低SRM转矩脉动抑制效果对人为设计权重、约束和时域等参数的依赖，最大化MPC的潜力。
在以不对称半桥功率变换器为基础的传统SRM模型预测转矩控制中，每个控制周期下只有励磁、退磁以及零压续流三种开关状态被评估。
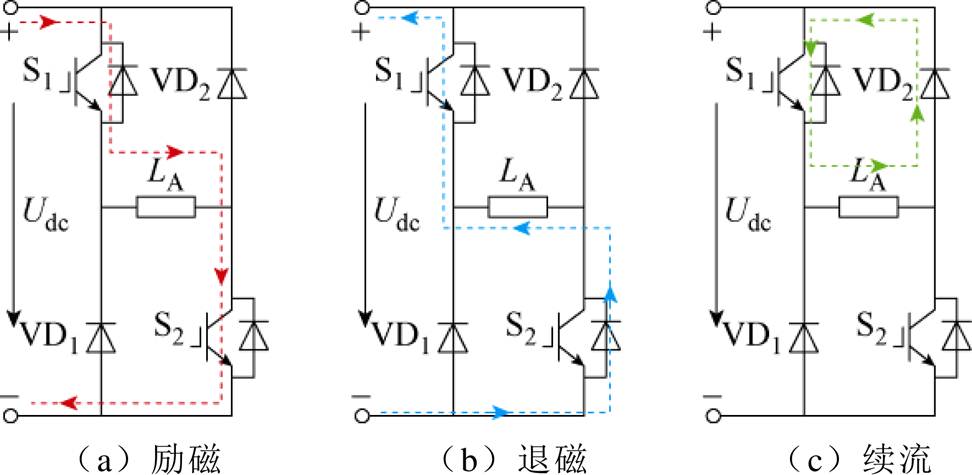
不对称半桥功率变换器拓扑结构及其工作原理如图1所示。励磁状态下，如图1a所示，两个开关管同时导通，相绕组电压即为母线电压。退磁状态下，如图1b所示，两个开关管同时关断，能量经两个二极管回馈至电源，此时相电压为负。零压续流状态即上下桥臂只有一个开关管导通，相电压等于零，如图1c所示。
图1 不对称半桥功率变换器拓扑结构及其工作原理
Fig.1 Asymmetric half-bridge power converter topology and its operating principle
在单相区，传统MPC对三种开关状态进行预测和评估，选择出最优开关状态。在换相区，两个导通相可能的开关状态进行排列组合，对组合得到的九种方案进行预测和评估，得到下一个控制周期的最优控制信号。
虽然传统MPC可以在有限的预测方案中选出最优开关状态，但由于其电磁特性呈现高度非线性，预测出的最优信号仍与实际最优解存在一定差距。同时，传统预测方案过于简单，也将造成处理器算力的损失。PWM控制通过电压斩波可以在固定周期内给相绕组施加给定的平均电压。将PWM信号与MPC相结合，预测出的最优控制信号可以在相同的计算频率下让电流与磁链的变化更加灵活，有效提高转矩控制的精确度。
当每相的预测信号从三种开关状态u∈{-1, 0, 1}拓展到占空比d∈[-1, 1]后，虽然可以像传统有限集MPC一样，通过选择固定间隔的占空比来组成预测方案[18-19]，但这限制了PWM控制的灵活性。拉丁超立方抽样（Latin Hypercube Sampling, LHS）是一种用于在多维空间内的均匀采样方法，它可以将每个维度划分为相等的间隔，然后在每个间隔内随机采样一次。拉丁超立方抽样示意图如图2所示，利用拉丁超立方抽样可以将范围为[-1, 1]的占空比分为n层，每层内抽取一个随机占空比，保障了采样的均匀性和随机性，为后续进行二维线性插值扩展样本数据提供了保障。
为将预测出的最优占空比转化为对应的开关管控制信号，在调制PWM信号时选用在[-1, 1]变化的三角波作为调制载波，比较值c1和c2与三角载波相比较以生成开关管S1和S2的控制信号[20]。比较值c1和c2与占空比d的数量关系为
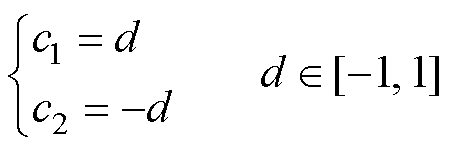（1）
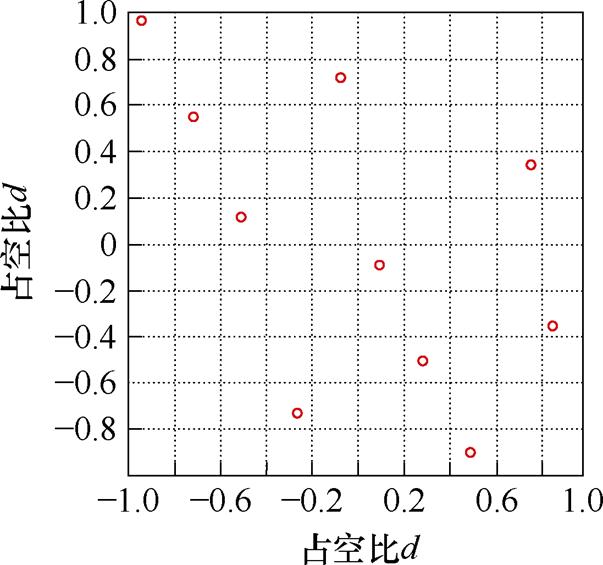
图2 拉丁超立方抽样示意图
Fig.2 Schematic of latin hypercube sampling
当三角载波小于c1时，开关管S1导通，大于c1时关断。对于开关管S2，当三角载波小于c2时开关管S2关断，大于c2时导通。通过该调制方法，每相在一个控制周期内被施加的平均电压范围为[-Udc, Udc]，其中，Udc为母线电压。
基于第1节的控制信号优化，本文提出基于PWM信号的SRM二维数据插值控制方法以抑制转矩脉动，其控制原理框图如图3所示。通过在线运行区域调整方法划分单相区和换相区，在单相区采用无差拍预测控制实时计算最优占空比，实现参考转矩的精确跟随，在换向区通过MPC得到励磁相和退磁相的最优占空比。
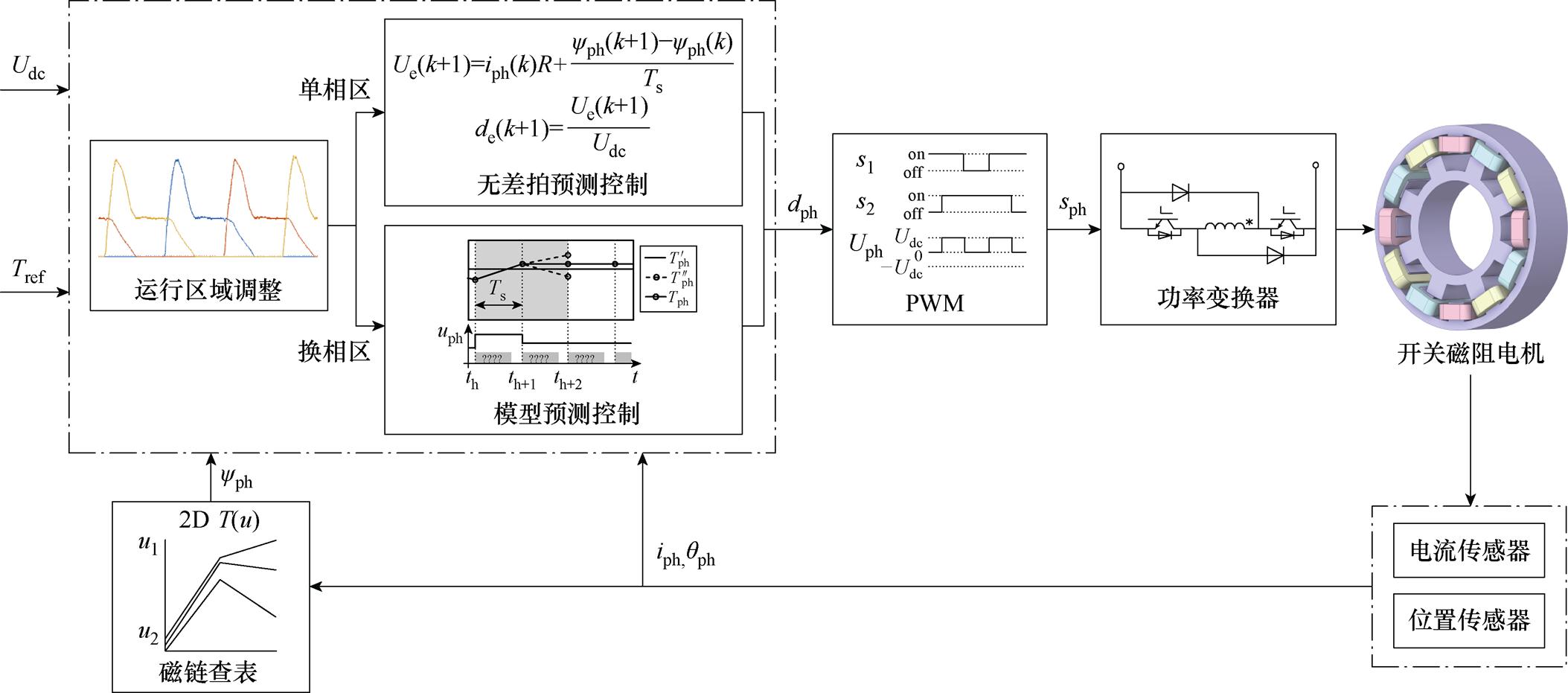
图3 基于二维数据插值的SRM转矩脉动抑制策略原理框图
Fig.3 Block diagram of SRM torque ripple suppression strategy based on 2D data interpolation
相电流规划、转矩分配函数等传统控制方法都采用人为设定的固定开关角来划分单相区和换相区，虽然简单方便但难以在所有工况下展现最优控制效果。
在换相区中，退磁相的完全关断时间可以通过磁链和实时转速估算。首先对SRM电压平衡方程进行离散化，有
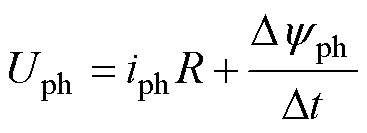（2）
式中，Uph为相电压；iph为相电流；R为相电阻；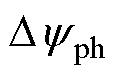
为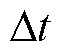
时间间隔内的离散相磁链。
因为始终有相电流iph≥0，可以得到
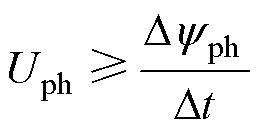（3）
假设此时退磁相的磁链和退磁时间分别为Dy和Dt。在关断阶段，相电压Uph近似等于母线电压的负值-Udc。因此，最长退磁时间tdmax为
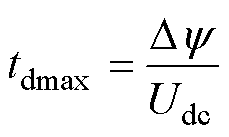（4）
通过转子位置qph和转速w可以得到退磁相此时距离进入负转矩区的时间tc为
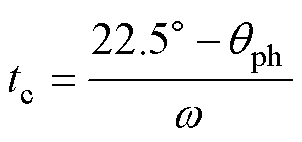（5）
在换相区中，当退磁相的最长退磁时间tdmax大于其进入负转矩区的时间tc时，需要迅速关断退磁相，此时电机进入单相区，避免了出现大转矩脉动和效率的损失。通过该在线运行区域调整方法可以根据电机此时运行状态计算出一个动态的关断角度，保证了退磁相不会过早或过晚关断。
在单相区，只有一相最优控制信号需要输出，因此该阶段MPC的预测方案较为单调，对单变量优化作用较小。而在无差拍预测控制中，最优输出由预测模型直接推导而出，不仅减少了稳态误差，且更适用于单目标控制。
在单相区中，两个关断相的相电压为母线电压的负值，基于离散化电压平衡方程可以预测这两相在k+1时刻的相磁链yph(k+1)为
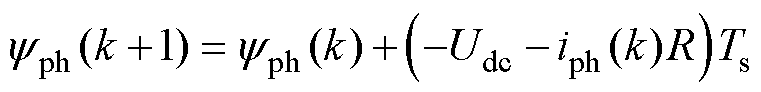（6）
式中，yph(k)为k时刻相磁链，可以通过预存的数据查找表yph(iph, qph) 得到，iph(k)和qph(k)分别为k时刻的相电流和转子位置；Ts为控制周期。在预测控制中，电机转速w可以被认为是恒定值，因此k+1时刻的转子位置qph(k+1) 可以预测为
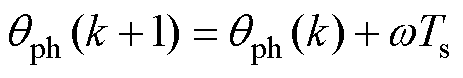（7）
导通相在k+1时刻的参考相转矩Teref(k+1)为
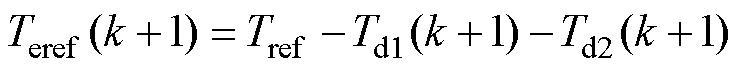（8）
式中，Tref为总参考转矩；Td1(k+1)、Td2(k+1)为两个关断相的预测转矩，可以通过数据查找表iph(yph, qph)和Tph(iph, qph) 得到[21]；Tph为相转矩。
基于参考相转矩，导通相在k+1时刻的参考相电流ieref(k+1)和磁链yeref(k+1)可以通过数据查找表iph(Tph, qph)和yph(iph, qph)得到，进而，导通相的在k+1时刻的参考电压和最优占空比为
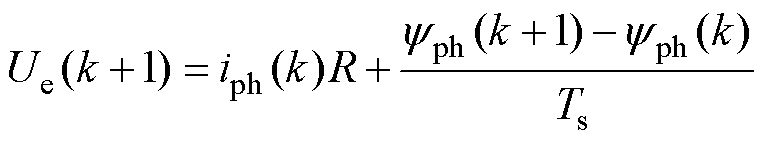（9）
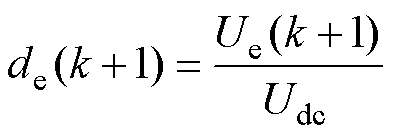（10）
在换相区，随着PWM信号在MPC中的应用，将有无穷多个占空比组合可以被应用，这无疑增加了控制灵活性。因此，控制核心是如何在这无穷多个组合中选择可以使转矩脉动最小化的最优占空比组合。基于第1节的预测方案获取和控制信号转化方法，为得到励磁相和退磁相的最优占空比，本文提出一种应用于换相区的MPC方法，其原理如图4所示。
首先，进行一次初步预测以判断下一个控制周期内输出转矩应该上升或下降。假设k+1时刻每相的磁链与当前时刻相同，k+1时刻的预测总转矩T0(k+1)可以通过数据查找表iph(yph, qph)和Tph(iph, qph)得到。然后，比较预测总转矩T0(k+1)与参考转矩Tref，比较结果将决定预测占空比方案的范围。
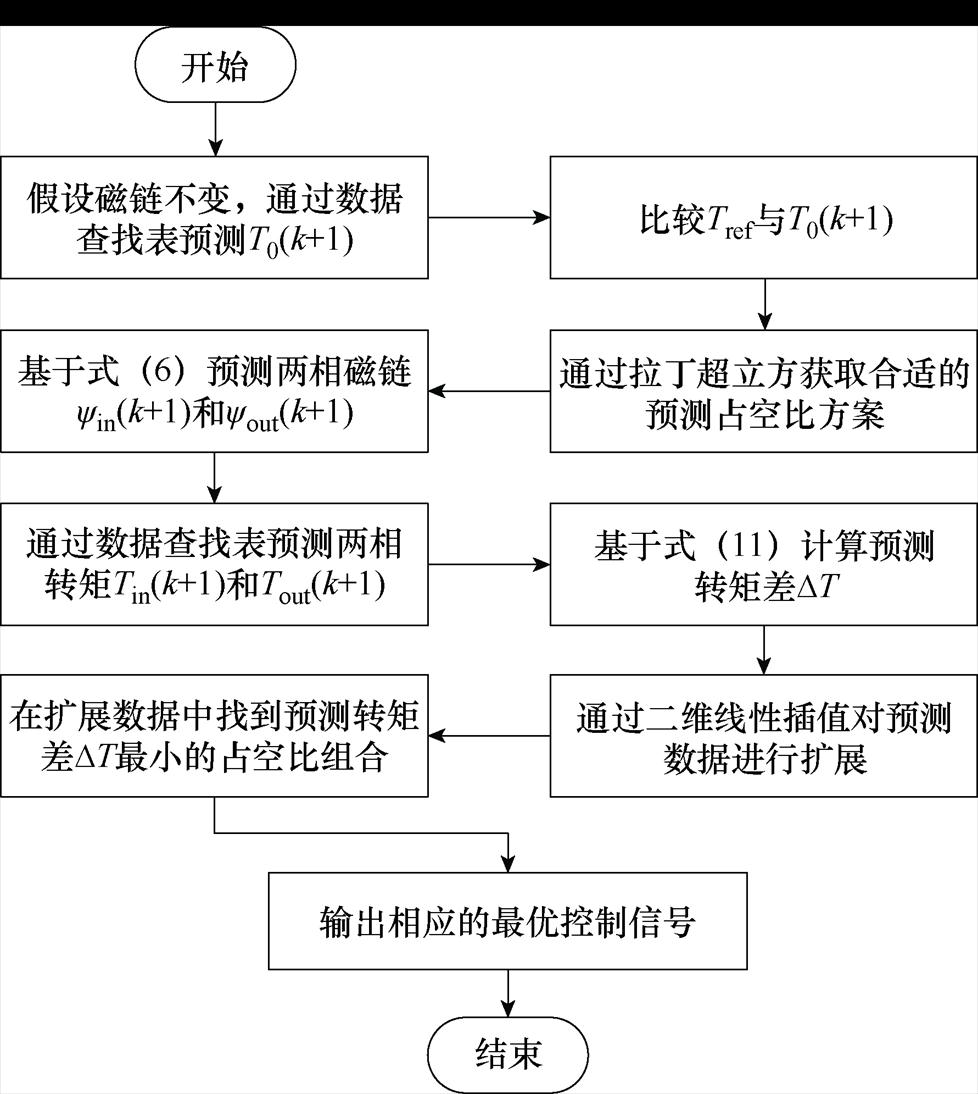
图4 MPC原理
Fig.4 Model predictive control schematic
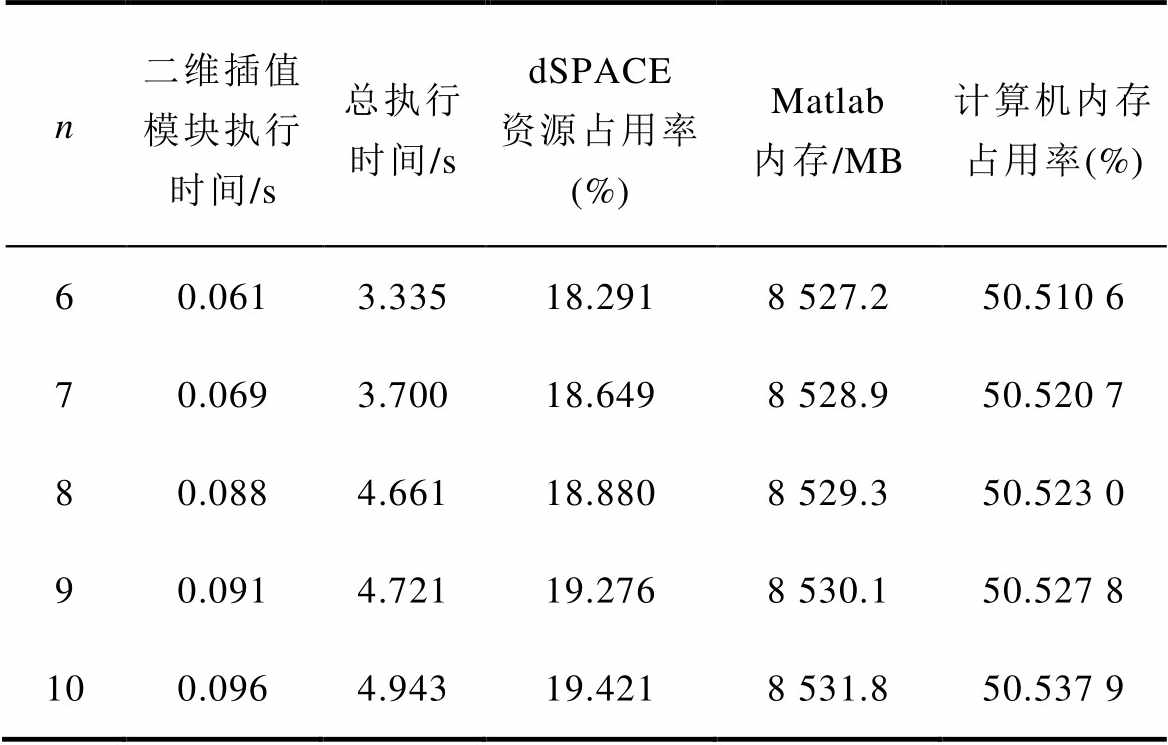
在SRM换相区，为避免大转矩脉动的出现，励磁相应迅速代替退磁相以输出转矩。因此，当Tref＞T0(k+1)时，各相输出的转矩不足以跟随参考转矩，为快速完成换相，由拉丁超立方抽样获得的励磁相预测占空比方案范围应该为[0, 1]，励磁相磁链在下一个控制周期需要进一步增大以输出更大的转矩，而退磁相的磁链变化仍不确定，需要通过进一步预测确定，其预测占空比方案范围为[-1, 1]。当Tref＜T0(k+1)时，各相输出的转矩超过参考转矩，退磁相磁链在下一个控制周期需要减少以减小输出转矩，由拉丁超立方抽样获得的退磁相预测占空比方案范围应为[-1, 0]，而励磁相的磁链变化仍不确定，其预测占空比方案范围为[-1, 1]。预测方案内的占空比数量为n。为获取其最优值，首先获取计算机上的物理内存随机存取存储器（Random Access Memory, RAM）总量为16 882 MB，该模型在不同占空比数量n的条件下编译后的内存占用情况见表1。同时为验证该方法的实时有效性，利用Profiler工具监测模型中各个模块的执行时间，间接了解CPU执行时的资源占用情况。
可以看到，随着n的不断增加，计算机内存占用率逐渐增加，模型中涉及到的主要模块即二维线性插值模块占用时间逐渐有小幅度的增加，且总体执行时间未受到大的影响。但增加至11时，模型运行时间过长甚至无法运行，且n=10时，模型控制性能相较于传统MPC已有显著提升，故综合考虑处理器的计算能力和模型的控制性能，本文将其设定为10。
表1 不同占空比资源占用情况
Tab.1 Resource occupancy at different duty cycles
n二维插值模块执行时间/s总执行时间/sdSPACE资源占用率 (%)Matlab内存/MB计算机内存占用率(%) 60.0613.33518.2918 527.250.510 6 70.0693.70018.6498 528.950.520 7 80.0884.66118.8808 529.350.523 0 90.0914.72119.2768 530.150.527 8 100.0964.94319.4218 531.850.537 9
在获得预测占空比方案后，基于离散化电压平衡方程和数据查找表建立预测模型。通过式（6）预测两个导通相在所有预测占空比下k+1时刻的相磁链。基于数据查找表iph(yph, qph)和Tph(iph, qph)可以得到这两相的预测输入相转矩Tin(k+1)与输出相转矩Tout(k+1)。进而，计算参考转矩与两相预测转矩差值的绝对值为
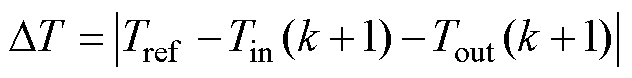（11）
此时，预测方案内n个励磁相和退磁相占空比组合对应n个转矩差绝对值。虽然可以直接从其中选择能使转矩差绝对值最小的占空比组合，但这没有充分利用PWM控制的灵活性。本文拟采用二维线性插值对预测数据进行扩展，为占空比寻优提供更多数据样本。
（1）首先，对上述预测方案内的导通相和退磁相占空比按升序进行排序，记为二维坐标(din_i, dout_j)，其中i, j∈[1, n]，每个二维坐标对应一个预测转矩差DTi,j，构建起一个n×n的二维数据集。
（2）根据由预测总转矩和参考转矩比较结果获得的预测方案范围确定待插值点(din_k, dout_l)，其中 k, l∈[1, m]，m为待插值点的数量，其值应大于预测数据n。
（3）对于每一个给定的待插值点(din_k, dout_l)，在二维数据集内寻找4个与其最近的相邻数据点，记为(din_i, dout_j)、(din_i+1, dout_j)、(din_i, dout_j+1)、(din_i+1, dout_j+1)，待插值点与数据集的坐标应满足
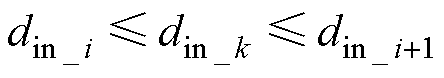（12）
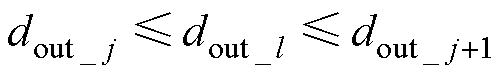（13）
（4）通过对4个相邻数据点对应的预测转矩差进行加权平均完成插值计算，待插值点对应的预测转矩差值DTk,l可以由式（14）得到。
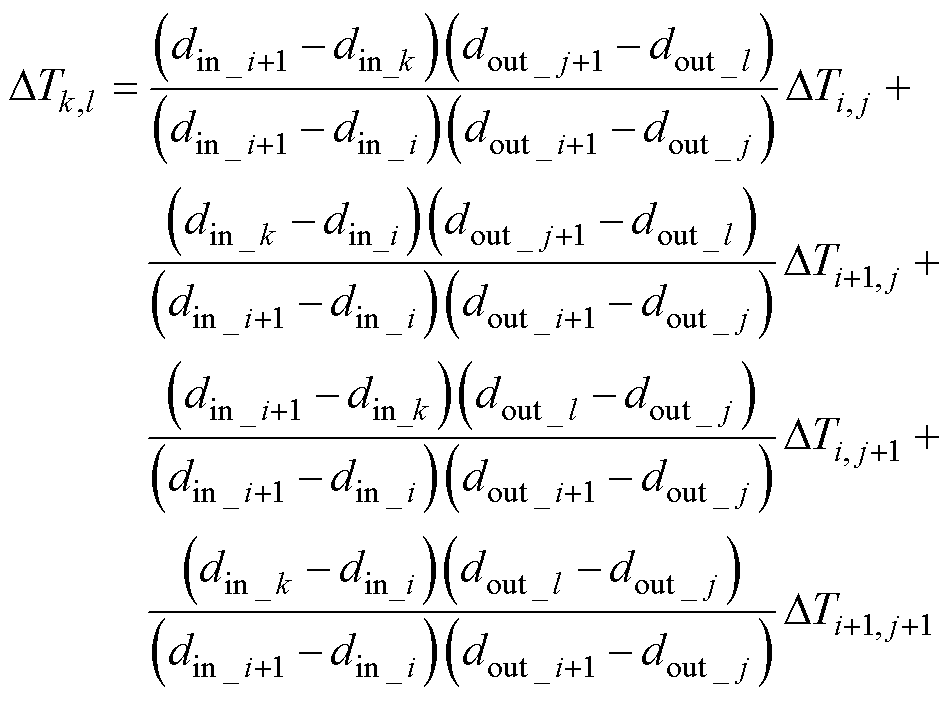（14）
（5）通过二维线性插值后，数据集扩展至m×m二维矩阵。此时，该矩阵中对应的最小预测转矩差值DTk,l的坐标 (din, dout) 即为能使转矩脉动最小的最优占空比。
最后，通过第1节中的PWM方法即可将最优占空比转化为功率变换器中开关管的控制信号，实现对相绕组平均电压的精确控制。
为进一步验证所提二维数据插值控制方法的性能，本文在一个三相12/8极SRM实验平台上对该方法的转矩脉动抑制效果进行评估，实验平台如图5所示，电机参数见表2。实验平台的机械部分主要由带编码器的SRM和永磁同步电机组成。电气部分主要包括dSPACE实时仿真平台、上位机、示波器、直流电源、不对称半桥功率变换器、母线电容、电流传感器、功率驱动电路、开关电源、控制电源与采样调理电路、信号转接板和测试点板等。以仿真验证模型中的控制算法模块为核心，添加dSPACE软件库中的A-D输入模块、旋变解码模块、PWM输出模块和D-A输出模块，结合外部硬件接口即可使得仿真平台和被控电机形成闭合回路。
设置母线电压为48 V，采样频率和控制频率为10 kHz，同样以传统模型预测转矩控制方法为对比，在两个工况下对所提二维数据插值控制方法进行性能验证，实验结果如图6和图7所示。从图中波形可以看出，所提方法有效地抑制了转矩脉动，转矩输出更加平滑，电机转矩输出性能明显得到优化。在换相区，由于PWM控制的应用，所提出的二维数据插值控制方法输出了更精确的控制信号，避免了大转矩脉动的出现。同时，通过对退磁相完全关断时间的实时计算，在保障电机转矩输出能力的同时避免了负转矩的出现。在单相区，基于无差拍预测控制的快速响应性，下一个控制周期能使转矩脉动最小的导通相占空比被精确计算出，这使得与传统有限集预测相比，输出的最优控制信号具有更多的选择，电流变化更加灵活，输出转矩可以更精确地跟踪参考转矩。
图5 SRM实验测试平台实物
Fig.5 SRM experimental test platform physical diagram
表2 SRM参数
Tab.2 SRM parameters
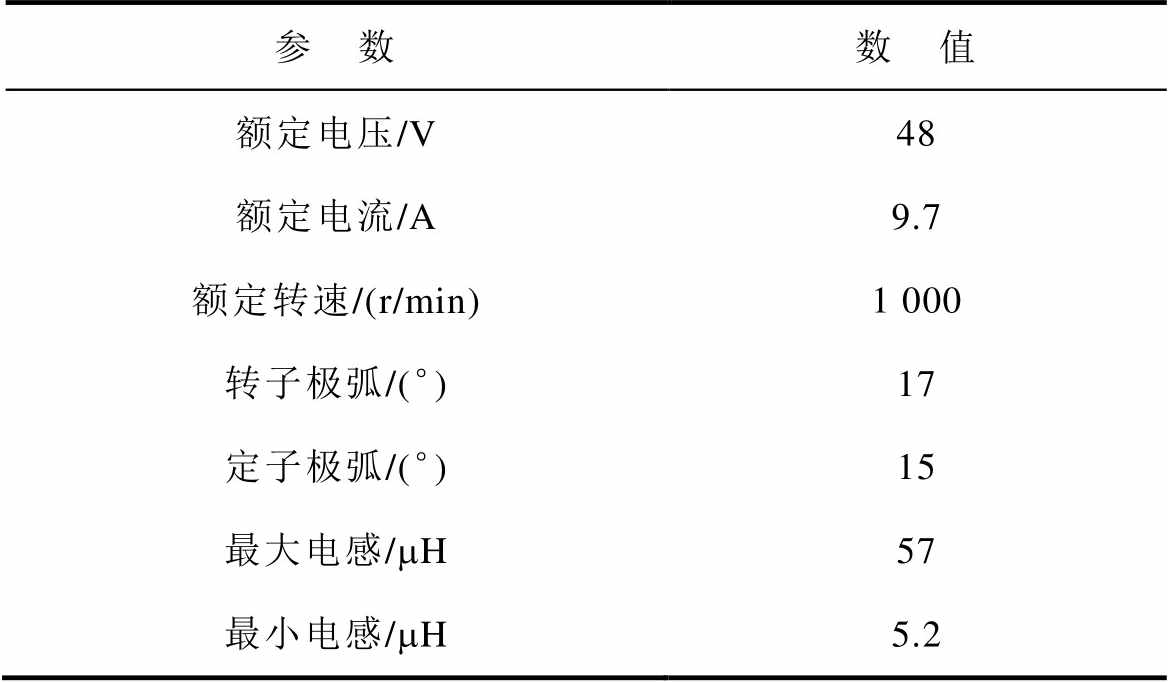
参 数数 值 额定电压/V48 额定电流/A9.7 额定转速/(r/min)1 000 转子极弧/(°)17 定子极弧/(°)15 最大电感/mH57 最小电感/mH5.2
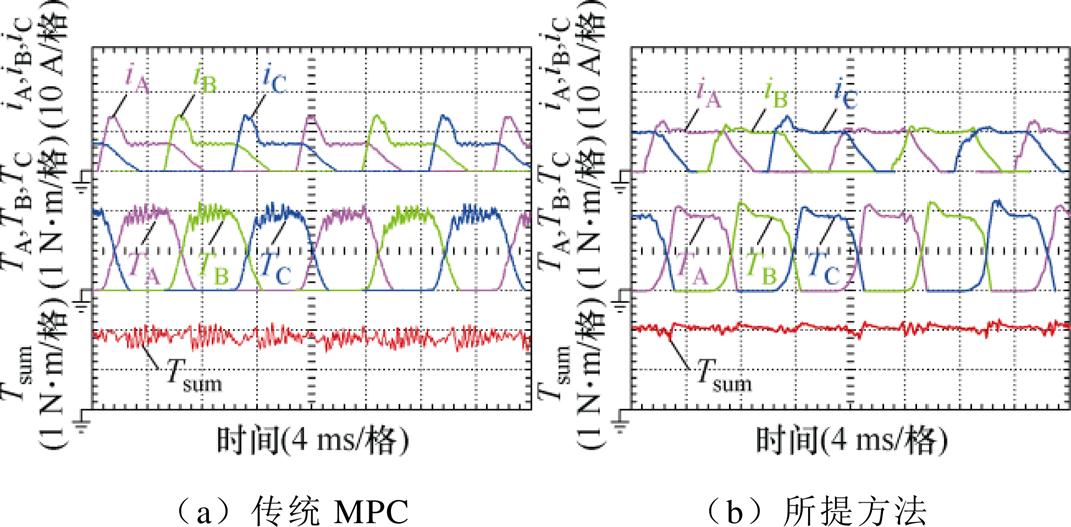
图6 转速为500 r/min，负载为2 N·m工况下的实验结果
Fig.6 Experimental results at 500 r/min and 2 N·m load condition
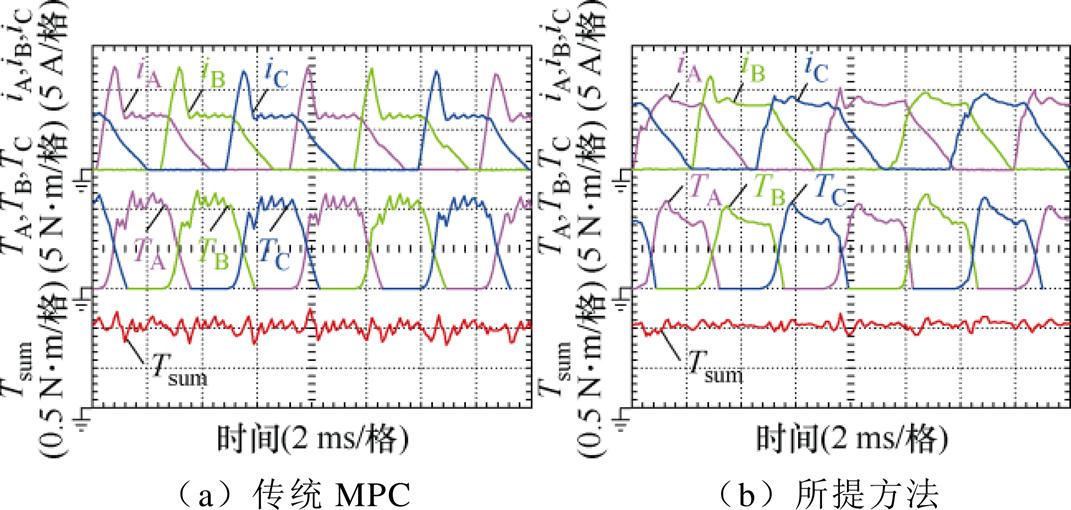
图7 转速为1 000 r/min，负载为1 N·m工况下的实验结果
Fig.7 Experimental results at 1 000 r/min and 1 N·m load condition
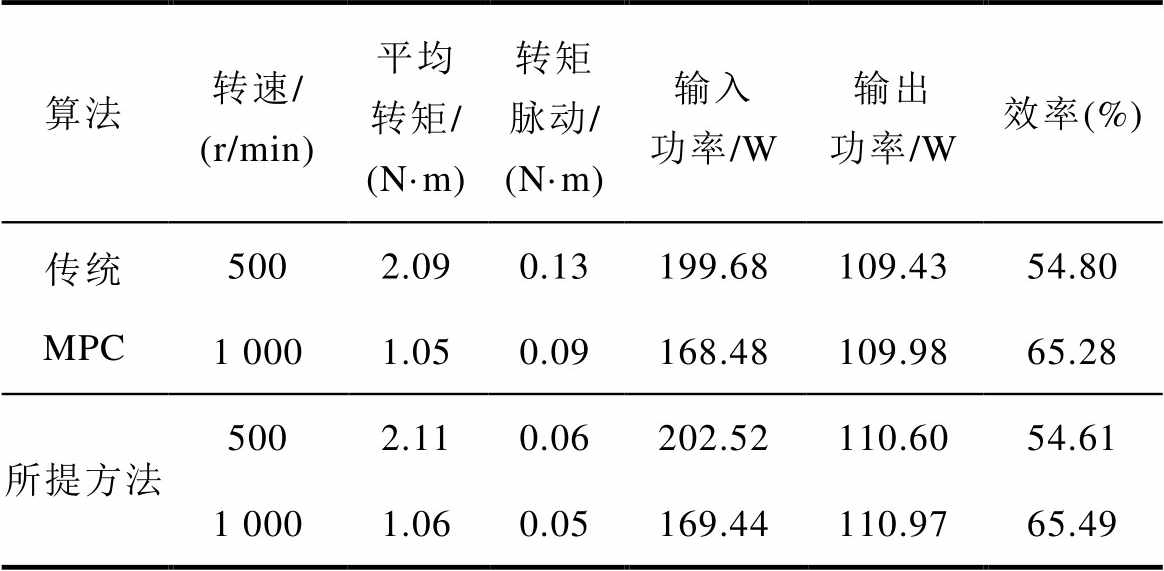
为进一步验证转矩脉动抑制效果，表3总结了这两种转矩控制方法在不同工况下的主要量化数据。其中，通过有效值计算量化SRM运行过程中的转矩脉动[22]，有
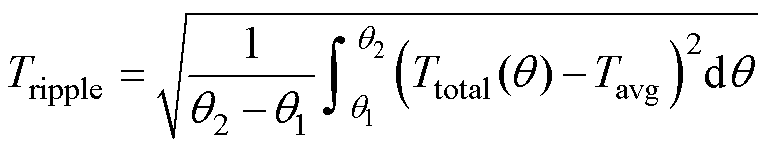（15）
其中
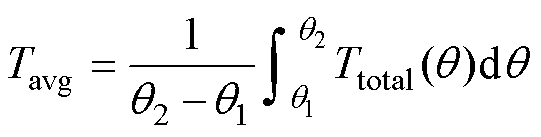（16）
式中，q1和q2分别为一个转子周期中的初始和末端转子位置；Ttotal(q)为当前位置的总转矩；Tavg为该周期内的平均转矩。可以看出，所提出的二维数据插值控制方法在不影响SRM效率的前提下可以使转矩脉动降低40%～50%。
表3 两种转矩控制方法的实验量化数据比较
Tab.3 Comparison of experimental quantitative data for two torque control methods
算法转速/ (r/min)平均转矩/ (N·m)转矩脉动/ (N·m)输入功率/W输出功率/W效率(%) 传统MPC5002.090.13199.68109.4354.80 1 0001.050.09168.48109.9865.28 所提方法5002.110.06202.52110.6054.61 1 0001.060.05169.44110.9765.49
为进一步验证所提二维数据插值控制方法的动态响应性能，分别在转速突变和负载突变两种工况下进行了实验验证，并记录了电机电流、转矩和转速的动态实验曲线，如图8所示。图8a展示了电机转速从500 r/min突变到1 000 r/min的动态过程，从实验波形可以看出，所提出的组合控制方法具有良好的转速跟踪能力，电机转速可以在120 ms内快速跟随上给定转速，转矩脉动也随着转速的稳定逐渐趋于平稳。图8b展示了负载转矩从1 N·m突变到2 N·m的动态过程，在输出转矩快速跟随参考转矩变化的同时转速也快速恢复稳定，证明了所提二维数据插值方法中转矩闭环的有效性。
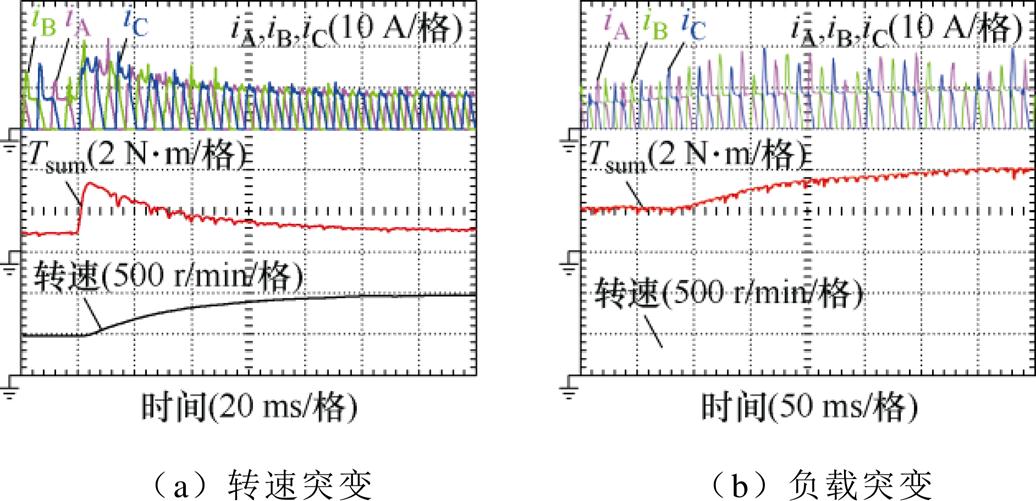
图8 转速和负载突变下的实验验证结果
Fig.8 Experimental validation results under abrupt speed and load changes
本文针对SRM运行过程中的大转矩脉动问题展开研究，提出了一种基于二维数据插值的控制方法，降低了MPC抑制转矩脉动效果对代价函数的依赖，实现了MPC策略对SRM低转矩脉动控制性能的有效提升。实验结果验证了所提方法相较于传统MPC具有更优的转矩脉动抑制性能。本文提出的方法具有以下优点：
1）通过应用PWM信号替代传统有限集预测信号，丰富了输出的最优控制信号，电流和转矩变化更加平滑，PWM信号的引入使得控制信号从离散的三个状态扩展到了连续的范围，能够更好地适应SRM复杂的非线性特性，使电机在不同工况下都能更精确地跟踪参考转矩。
2）提出以二维插值寻优代替传统的代价函数，不仅实现了PWM信号在MPC中的应用，也避免了复杂繁琐的调参过程，二维线性插值寻优方法能够更精细地调整励磁相和退磁相的占空比，使得电机在换相过程中能够更平稳地过渡，减少了因占空比突变导致的转矩脉动，最大化MPC的潜力。
参考文献
[1] Sayed E, Abdalmagid M, Pietrini G, et al. Review of electric machines in more-/ hybrid-/ turbo-electric aircraft[J]. IEEE Transactions on Transportation Electrification, 2021, 7(4): 2976-3005.
[2] 于丰源, 陈昊, 王星, 等. 不同定子绕组结构双定子轴向磁通开关磁阻电机性能对比研究[J]. 电工技术学报, 2024, 39(24): 7728-7741, 7776.
Yu Fengyuan, Chen Hao, Wang Xing, et al. Com- parative study on the double stator axial flux switched reluctance motors with different winding structures[J]. Transactions of China Electrotechnical Society, 2024, 39(24): 7728-7741, 7776.
[3] Ge Lefei, Ralev I, Klein-Hessling A, et al. A simple reluctance calibration strategy to obtain the flux- linkage characteristics of switched reluctance machines[J]. IEEE Transactions on Power Electronics, 2019, 35(3): 2787-2798.
[4] 韩国强, 韩颖, 贾政, 等. 基于超局部模型的开关磁阻电机无模型预测电流控制方法[J]. 电工技术学报, 2025, 40(18): 5931-5944.
Han Guoqiang, Han Ying, Jia Zheng, et al. Model- free predictive current control method for switched reluctance motor with ultralocal model[J]. Transa- ctions of China Electrotechnical Society, 2025, 40(18): 5931-5944.
[5] Fang Gaoliang, Scalcon F P, Xiao Dianxun, et al. Advanced control of switched reluctance motors (SRMs): a review on current regulation, torque control and vibration suppression[J]. IEEE Open Journal of the Industrial Electronics Society, 2021, 2: 280-301.
[6] Cheok A D, Fukuda Y. A new torque and flux control method for switched reluctance motor drives[J]. IEEE Transactions on Power Electronics, 2002, 17(4): 543- 557.
[7] 陈飞, 瞿遂春, 邱爱兵, 等. 一种改进的开关磁阻电动机直接转矩控制方法[J]. 微特电机, 2018, 46(5): 66-69.
Chen Fei, Qu Suichun, Qiu Aibing, et al. An improved direct torque control method for switched reluctance motor[J]. Small & Special Electrical Machines, 2018, 46(5): 66-69.
[8] 任浩天, 甘醇, 曲荣海, 等. 基于电流转矩协同控制的SRM新型直接瞬时转矩控制策略[J]. 中国电机工程学报, 2024, 44(19): 7794-7806.
Ren Haotian, Gan Chun, Qu Ronghai, et al. Current- torque coordinated control based direct instantaneous torque control strategy for switched reluctance motor[J]. Proceedings of the CSEE, 2024, 44(19): 7794-7806.
[9] 杨帆, 陈昊, 李晓东, 等. 一种优化开关磁阻电机换相区控制策略的高效率转矩分配函数[J]. 电工技术学报, 2024, 39(6): 1671-1683.
Yang Fan, Chen Hao, Li Xiaodong, et al. An efficient torque sharing function for optimizing the com- mutation zone control strategy of switched reluctance motors[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1671-1683.
[10] Ge Lefei, Fan Zizhen, Huang Jiale, et al. Model predictive control of switched reluctance machines with online torque sharing function based on optimal flux-linkage curve[J]. IEEE Transactions on Trans- portation Electrification, 2024, 10(3): 4990-5001.
[11] Zhang Yanqing, Yin Zhonggang, Li Wei, et al. Finite control set model predictive torque control using sliding model control for induction motors[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(3): 262-270.
[12] 韩硕, 张勇军, 肖雄, 等. 面向异步电机模型预测直接转矩控制的自适应谐波消除方法[J]. 电工技术学报, 2025, 40(4): 1078-1089.
Han Shuo, Zhang Yongjun, Xiao Xiong, et al. Adaptive harmonic elimination for model predictive direct torque control of asynchronous motor[J]. Transactions of China Electrotechnical Society, 2025, 40(4): 1078-1089.
[13] 兰志勇, 罗杰, 李延昊, 等. 基于快速选择表的永磁同步电机模型预测转矩控制[J]. 电工技术学报, 2023, 38(21): 5749-5757.
Lan Zhiyong, Luo Jie, Li Yanhao, et al. Model prediction torque control for permanent magnet synchronous motor based on the fast selection table[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5749-5757.
[14] Peyrl H, Papafotiou G, Morari M. Model predictive torque control of a switched reluctance motor[C]// 2009 IEEE International Conference on Industrial Technology, Churchill, VIC, Australia, 2009: 1-6.
[15] Ge Lefei, Zhong Jixi, Huang Jiale, et al. A novel model predictive torque control of SRMs with low measurement effort[J]. IEEE Transactions on Indu- strial Electronics, 2023, 70(4): 3561-3570.
[16] Fang Gaoliang, Ye Jin, Xiao Dianxun, et al. Computational-efficient model predictive torque control for switched reluctance machines with linear- model-based equivalent transformations[J]. IEEE Transactions on Industrial Electronics, 2022, 69(6): 5465-5477.
[17] Song Shoujun, Liu Jialiang, Zhao Yong, et al. High- dynamic four-quadrant speed adjustment of switched reluctance machine with torque predictive control[J]. IEEE Transactions on Industrial Electronics, 2021, 69(8): 7733-7743.
[18] Kouro S, Cortes P, Vargas R, et al. Model predictive control: a simple and powerful method to control power converters[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6): 1826-1838.
[19] Rodriguez J, Kazmierkowski M P, Espinoza J R, et al. State of the art of finite control set model predictive control in power electronics[J]. IEEE Transactions on Industrial Informatics, 2013, 9(2): 1003-1016.
[20] Ge Lefei, Guo Jixuan, Mao Shuai, et al. A composite model predictive control method of SRMs with PWM-based signal for torque ripple suppression[J]. IEEE Transactions on Transportation Electrification, 2024, 10(2): 2469-2478.
[21] Song Shoujun, Ge Lefei, Ma Shaojie, et al. Accurate measurement and detailed evaluation of static elec- tromagnetic characteristics of switched reluctance machines[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(3): 704-714.
[22] Fang Gaoliang, Ye Jin, Xiao Dianxun, et al. Low- ripple continuous control set model predictive torque control for switched reluctance machines based on equivalent linear SRM model[J]. IEEE Transactions on Industrial Electronics, 2022, 69(12): 12480- 12495.
Switched Reluctance Machine Torque Ripple Suppression Strategy Based on 2D Data Interpolation
Abstract The switched reluctance machine (SRM) has become one of the most competitive generator/ starter candidates in the field of electric vehicles and multi-electric aircraft. However, the torque ripple caused by the double-bump structure limits its applications. Realizing effective suppression of the torque ripple has become a research hotspot. Based on the accurate prediction model, model predictive control (MPC) can predict the variation of the target variable under all possible control signals and optimize the control signals online based on a predefined control law. However, the existing research only selects the optimal control signal within a limited set of control signals, which limits the suppression effect and does not fully utilize the flexibility of MPC. Moreover, the artificial setting of the parameters in the cost function affects the effectiveness of the MPC strategy. Thus, this paper proposes a torque ripple suppression strategy for the SRMs based on two-dimensional linear interpolation.
Firstly, PWM control signals are used to replace the three switching states in the conventional predictive control. The predicted optimal control signal can smooth the current and flux-linkage more flexibly under the same calculation frequency, which effectively enhances the accuracy of torque control. Latin hypercube sampling is proposed to divide the duty cycle in the range [-1, 1] into n strata, and one random duty cycle is drawn within each stratum to compose the predicted duty cycle scheme. To convert the predicted optimal duty cycle into the corresponding switching tube control signals, a PWM modulation method for the asymmetric half-bridge power converter is proposed.
Then, the operating region is divided into single-phase and commutation regions by online operating region adjustment, and different predictive control methods are used for each region. In the single-phase region, the deadbeat predictive control calculates the optimal duty cycle for the conduction phase to follow the phase torque reference. In the commutation region, the MPC predicts the optimal duty cycle for the incoming and outgoing phases. The expected duty cycle scheme is determined based on the SRM operation state, and the corresponding predicted torque is obtained using the prediction model. A two-dimensional linear interpolation method is proposed to expand the prediction dataset and find the optimal duty cycle that corresponds to the minimum predicted torque difference.
Experimental verification of the torque ripple suppression effect is carried out on a three-phase 12/8-pole SRM experimental platform. The results show that in the commutation region, the proposed combined predictive control method produces more accurate control signals and prevents the occurrence of a large torque ripple due to the application of PWM control. In the single-phase region, according to the deadbeat predictive control’s fast response, the duty cycle of the conduction phase that minimizes the torque ripple in the next control cycle is accurately calculated, and the output torque can track the reference torque precisely. The proposed method, based on 2D data interpolation, can reduce torque ripple by 40-50% while causing almost no efficiency loss.
The proposed method has the following advantages. (1) By applying PWM signals instead of the conventional finite-set predictive signals, the output optimal control signals are enriched, and the current and torque variations are smooth. (2) The proposed two-dimensional interpolation optimization, instead of the conventional cost function, not only realizes the application of PWM signals in MPC but also avoids the complicated and complex process of parameter tuning.
Keywords：Switched reluctance machine (SRM), torque ripple, two-dimensional linear interpolation, model predictive control (MPC), deadbeat predictive control
中图分类号：TM352
DOI: 10.19595/j.cnki.1000-6753.tces.241921
国家自然科学基金（52107055）、陕西省自然科学基础研究计划（2024JCYBQN-0753）、航空科学基金（20220040051002）和广东省基础与应用基础研究基金（2024A1515010657）资助项目。
收稿日期2024-10-28
改稿日期 2025-04-11
付倩娆 女，1990年生，博士，研究方向为开关磁阻电机转矩脉动抑制等。
E-mail: qfu@xauat.edu.cn
葛乐飞 男，1992年生，博士，研究方向为航空电驱动系统等。
E-mail: lge@nwpu.edu.cn（通信作者）
（编辑 崔文静）