 ~
~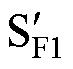 和
和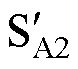 ~
~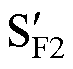 分别为逆变器单元1与逆变器单元2各桥臂的下管,isA~isF为SOEW- PMSM各相电流。
分别为逆变器单元1与逆变器单元2各桥臂的下管,isA~isF为SOEW- PMSM各相电流。摘要 针对六相开绕组永磁同步电机(SOEW-PMSM)驱动系统,该文提出了一种基于复杂矢量集优选的空间电压矢量脉宽调制(SVPWM)方法,从逆变器输出端避免了3次谐波的产生,同时通过矢量合成对5次谐波进行抑制,兼顾了电流谐波与转矩脉动的抑制。通过对SOEW-PMSM进行数学建模与平面分解,分析六相H桥逆变器不同开关组合产生的空间电压矢量,筛选出在3次谐波平面投影分量为零的空间电压矢量,将这些矢量作为SVPWM的备选矢量。分析备选矢量在5次谐波平面投影量之间的比例关系,通过比例关系分配各矢量的作用时间,以实现对3、5次谐波电流的高精度抑制。可以在摒弃谐波电流控制器的前提下,对3、5次谐波电流与转矩脉动进行有效抑制。最后,通过对比实验证明了所提谐波抑制方法的有效性。
关键词:空间电压矢量脉宽调制 六相开绕组永磁同步电机 空间电压矢量合成 谐波抑制
多相永磁同步电机具有功率密度大、转矩脉动低、可靠性高等优点,在动力牵引、电动汽车等大功率场合得到了广泛应用[1]。相较于多相永磁同步电机,开绕组多相永磁同步电机自由度更多、直流电压利用率更高且容错能力更强,更契合应用于船舶推进等交通电气化应用场合[2-4]。
已有诸多学者针对三相、五相和九相开绕组永磁电机开展建模、控制策略优化等研究[5-8],但国内外对于六相开绕组永磁同步电机(Six-phase Open- End Winding Permanent Magnet Synchronous Motor, SOEW-PMSM)驱动系统的研究甚少。
不同于传统永磁同步电机,SOEW-PMSM增加了相数,除了基波平面(ab)外,还存在多个谐波平面,如3次谐波平面(o1o2)与5次谐波平面(z1z2)。且由于电机绕组中性点的取消,定子绕组中存在3次谐波电流通路,3次谐波平面的电压分量会产生3次谐波电流,降低系统的运行效率与稳定性[9-11]。现有3次谐波电流抑制方法多以谐波电流环或谐波注入等外部手段为主[12-14],基于空间矢量脉冲宽度调制(Space Vector Pulse Width Modulation, SVPWM)在逆变器输出端进行谐波电流抑制的相关研究较少。本文针对多相开绕组永磁同步电机驱动系统研究基于SVPWM的谐波抑制方法,可以更高效、稳定地对谐波平面分量进行抑制。
传统的两矢量SVPWM算法是在幅值最大的电压矢量集合中选择两个相邻矢量进行参考电压矢量的合成。两矢量SVPWM算法由于只考虑了对ab平面的电压进行跟踪,没有考虑z1z2平面上的电压合成效果,将会在z1z2平面上产生不必要的谐波分量。四矢量SVPWM策略可以优化上述谐波,其在两矢量SVPWM算法的基础上增加两个基本电压矢量,通过增加的电压矢量来抵消在z1z2平面上形成的谐波分量,但对谐波电流的抑制效果仍然有 限[15-17]。文献[18]提出了基于重构电压矢量的控制方法,选择由基波平面幅值最大的空间电压合成的虚拟矢量,确保合成虚拟矢量z1z2平面内的投影为零,但随着电机相数增多,虚拟矢量的合成与作用时间计算太过复杂。文献[19-21]使用多个PI调节器,对每个谐波平面进行控制,大大增加了控制系统的复杂程度。文献[22-23]采用零序电压谐波注入方式,以抑制o1o2平面谐波分量。上述文献所提方法虽然对谐波抑制效果有所改善,但谐波注入或增加谐波电流环等方法侧重于通过外部手段进行谐波抑制,增大了控制系统的复杂程度与作用时间的计算难度。且多相开绕组永磁同步电机的3、5次谐波电感值往往较小,一个小的谐波电压也会引起电流较大的畸变。因此,对多相开绕组驱动系统而言,越复杂的谐波抑制方法稳定性越低,简单高效的谐波抑制方法可靠性更高。
针对上述不足,本文提出了一种基于复杂矢量集优选的SOEW-PMSM电流谐波与转矩脉动抑制方法,利用扇区相邻两边界上的4个次大矢量进行SVPWM,所选4个次大矢量在3次谐波平面投影为零,因此从逆变器输出端与电压矢量的选择上避免了3次谐波平面分量的产生,同时通过作用时间的计算,使5次谐波平面的合成分量为零,兼顾了电流谐波与转矩脉动的抑制。在不增加控制系统复杂程度与计算难度的前提下实现了3、5次谐波的高精度抑制。此外,提出了一种通适于开绕组驱动系统的双边调制方法,避免了在一个周期内开关管多次跳变的问题。
共直流母线型SOEW-PMSM驱动拓扑如图1所示。图1中,逆变器单元1与逆变器单元2均为两电平逆变器,Udc为直流母线电压。SA1~SF1和SA2~SF2分别为逆变器单元1与逆变器单元2各桥臂的上管, ~
~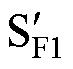 和
和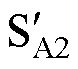 ~
~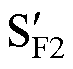 分别为逆变器单元1与逆变器单元2各桥臂的下管,isA~isF为SOEW- PMSM各相电流。
分别为逆变器单元1与逆变器单元2各桥臂的下管,isA~isF为SOEW- PMSM各相电流。
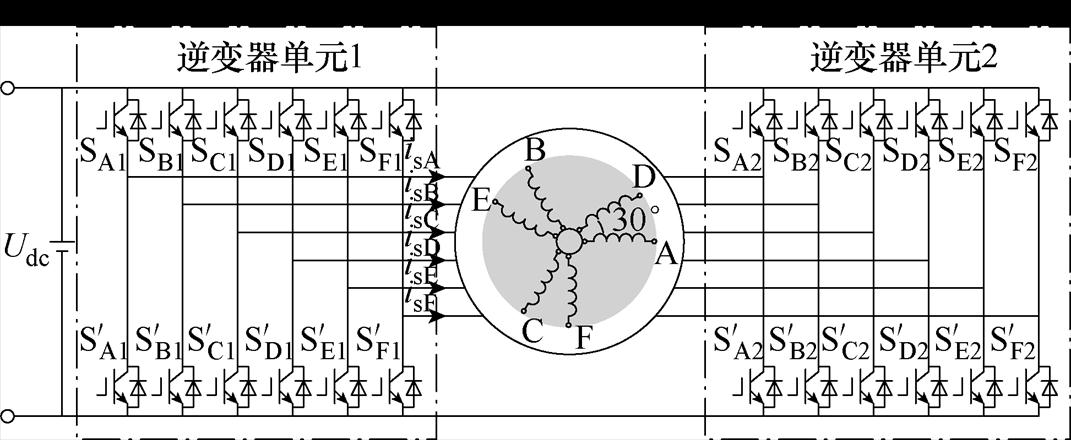
图1 共直流母线型SOEW-PMSM
Fig.1 Common DC bus type SOEW-PMSM
与传统多相永磁电机不同,SOEW-PMSM的3、5次谐波平面存在实际意义,因此在变换矩阵中3、5次谐波平面的变换式不可忽略[8]。为避免大篇幅公式推导出现,针对数学模型,本节只列出基本方程与解耦后的坐标变换矩阵。
在建立电机在自然坐标系下的数学模型之前,需做出以下假设:
(1)定子绕组和永磁体磁链在气隙中产生的磁场应按正弦分布。
(2)忽略铁心涡流和磁滞损耗。
(3)电机定子绕组参数对称。
则自然坐标系下,电机的电压、磁链、运动和转矩方程分别为
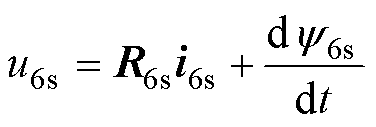 (1)
(1)
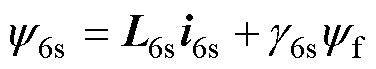 (2)
(2)
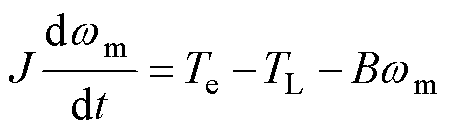 (3)
(3)
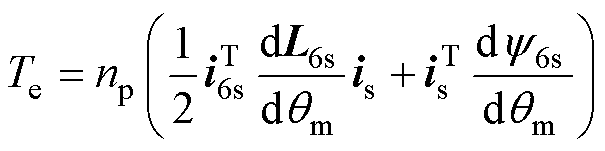 (4)
(4)
式中,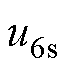 、
、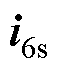 、
、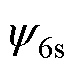 分别为定子相电压、定子相电流和定子每相磁链;
分别为定子相电压、定子相电流和定子每相磁链;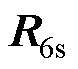 、
、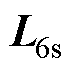 分别为电阻、电感系数矩阵;
分别为电阻、电感系数矩阵;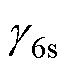 为磁链系数矩阵;Te为电磁转矩;TL为负载转矩;np为极对数;
为磁链系数矩阵;Te为电磁转矩;TL为负载转矩;np为极对数;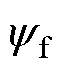 为转子磁链;
为转子磁链;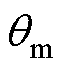 为机械角度;
为机械角度;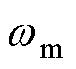 为转子机械角速度。
为转子机械角速度。
由于多相电机是一个强耦合系统,不利于控制,因此本文使用矢量空间分解(Vector Space Decom- position, VSD)方法对SOEW-PMSM的数学模型进行降阶解耦处理。解耦后可以得到3个子系统,以等幅值变换为前提,得到的Clarke变换矩阵为
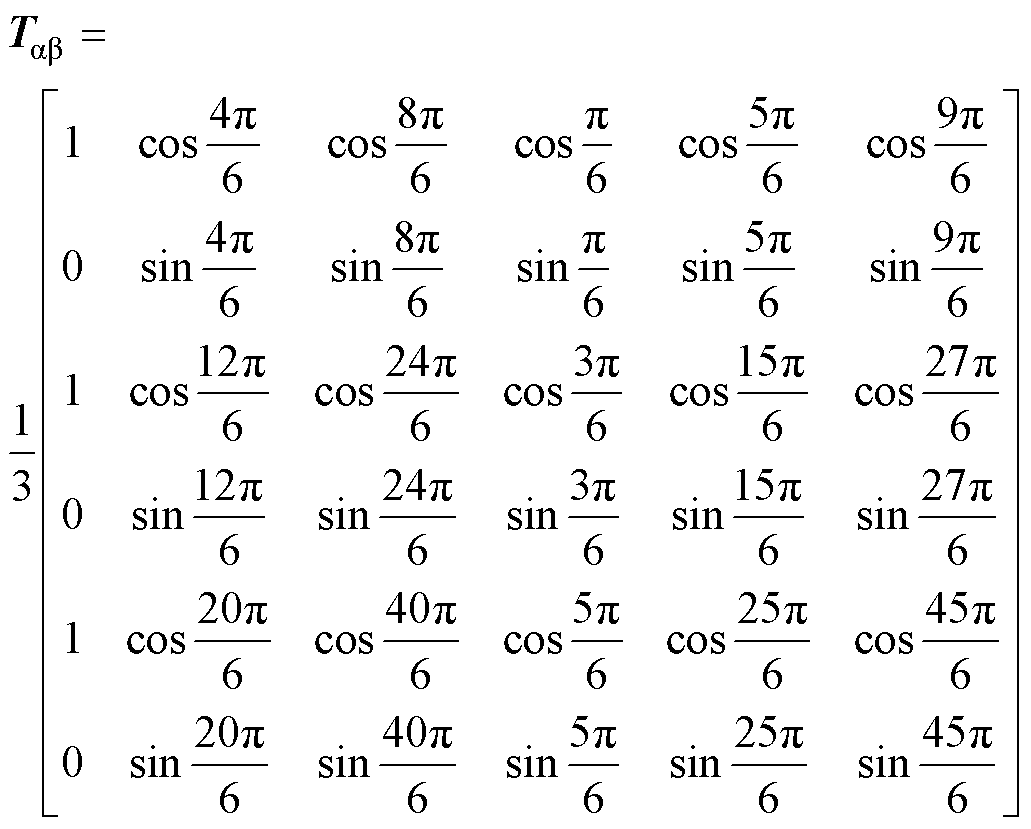 (5)
(5)
SOEW-PMSM由于3次谐波磁链的存在,零序电流会产生零序转矩。经过Clarke变换后,含有3次谐波磁链的电磁转矩可以简化[24]为
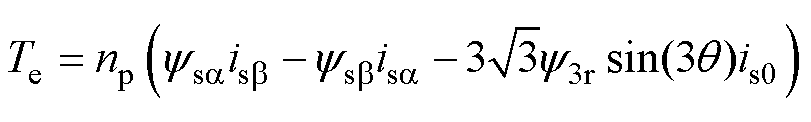 (6)
(6)
式中,ysa与ysb为静止坐标系下的定子磁链;isa与isb为静止坐标系下的定子电流;y3r为电机3次谐波磁链;is0为零序电流。
为了进一步分析,可以利用式(7)Park变换矩阵将静止坐标系下的数学模型变换到同步旋转坐标系下的数学模型。
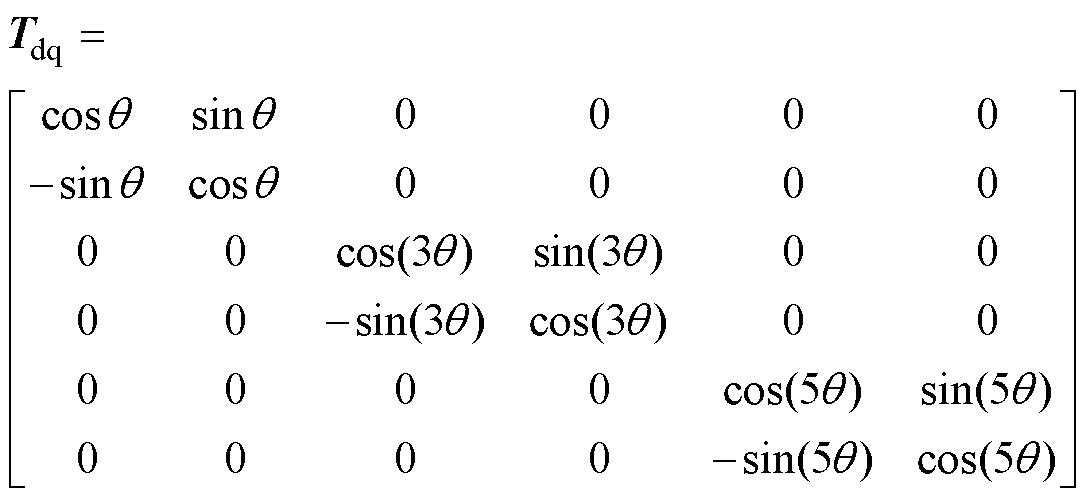 (7)
(7)
结合式(5)与式(7),可以将自然坐标系下的电机电压、磁链、运动和转矩方程转换到旋转坐标系,完成数学模型的搭建。
含有3次谐波磁链的电磁转矩表达式(6)经Park变换后可以简化为
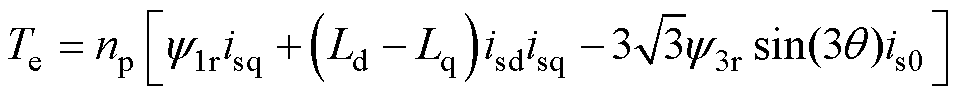 (8)
(8)
其中
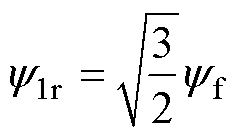
式中,isd与isq为旋转坐标系下定子电流;Ld与Lq分别为d、q轴电感。
此外,为了研究5次谐波对转矩脉动的影响,定义矢量旋转的正方向为:A[I1msin(wt)]→B[I1msin(wt-120°)]→C[I1msin(wt+120°)],则5次谐波的矢量旋转方向为A[I5msin5(wt)]→C[I5msin(5wt+120°)]→B[I5msin(5wt-120°)],其中,I1m、I5m分别为基波、5次谐波平面下电流,与基波矢量的旋转方向相反。因此,静止坐标系下的5次谐波电流经过Park变换后,在dq坐标系下会变为6倍于基波频率的谐波,式(8)中q轴电流包含6次谐波分量,对转矩计算产生影响。
综上分析,静止坐标系下的3、5次谐波电流会产生转矩脉动,因此对3、5次谐波电流进行抑制可以在减小谐波电流损耗的同时优化转矩脉动。
SOEW-PMSM经过VSD建模后,逆变器端输出的空间电压矢量可以被解耦到3个正交平面中,即ab平面、o1o2平面与z1z2平面。
基于VSD,将电压矢量定义为二进制值ui= SASBSCSDSESF,则空间电压矢量在各平面的投影为
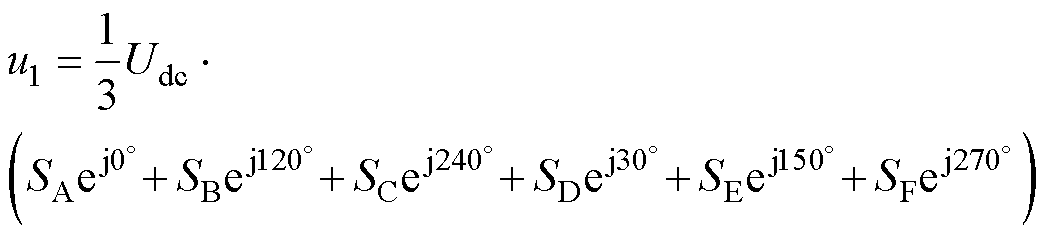 (9)
(9)
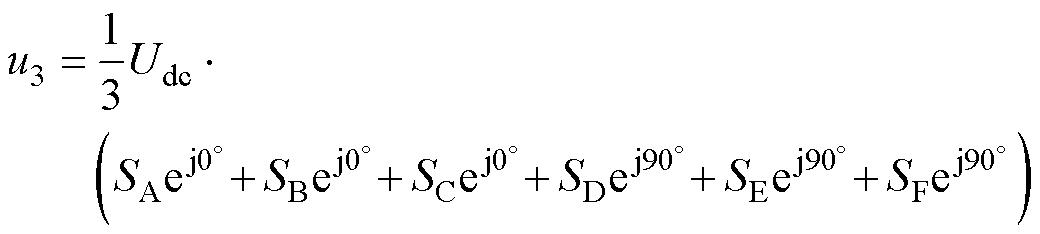 (10)
(10)
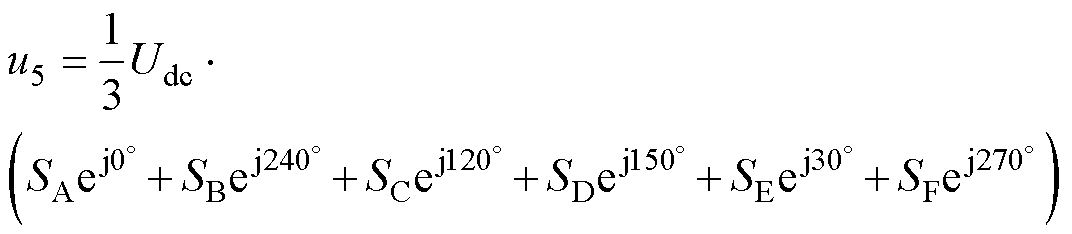 (11)
(11)
式中,SA~SF为各相开关管的导通状态,有0,1两种取值,当取值为1时表示此相上管导通下管关闭,当取值为0时表示此相上管关闭下管导通;Udc为直流电压源。
参考三相OEW-PMSM的电压矢量构建方法,SOEW-PMSM可以将6组H桥逆变器的左右桥臂分为左右两组六相逆变器单元,则H桥单侧六相逆变器在ab平面与z1z2平面上产生的空间电压矢量如图2a和图2b所示。空间电压矢量幅值见表1。H桥单侧逆变器可产生64个空间电压矢量,分别将H桥两侧六相逆变器空间电压矢量的ab平面分量相减则可以得到SOEW-PMSM空间电压矢量的ab平面分量,则SOEW-PMSM有(64)2=4 096个空间电压矢量(包含不同开关模态合成相同的电压矢量)。除去在规则角度边界上的电压矢量,还存在诸多角度为13°±15°k与17°±15°k的非规则角度电压矢量,由于非规则角度的电压矢量在进行硬件计算时,角度值的换算更加复杂,且在其他谐波平面的投影量难以准确估量,因此需要对ab平面的非规则角度电压矢量进行筛除。
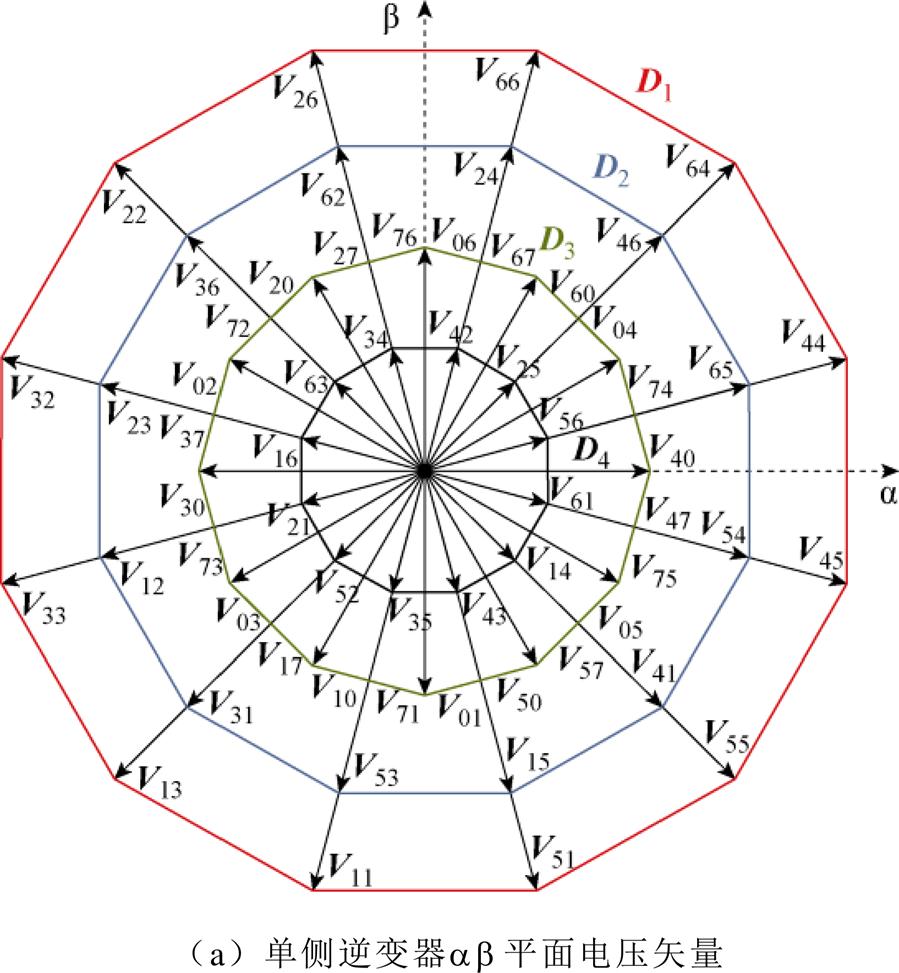
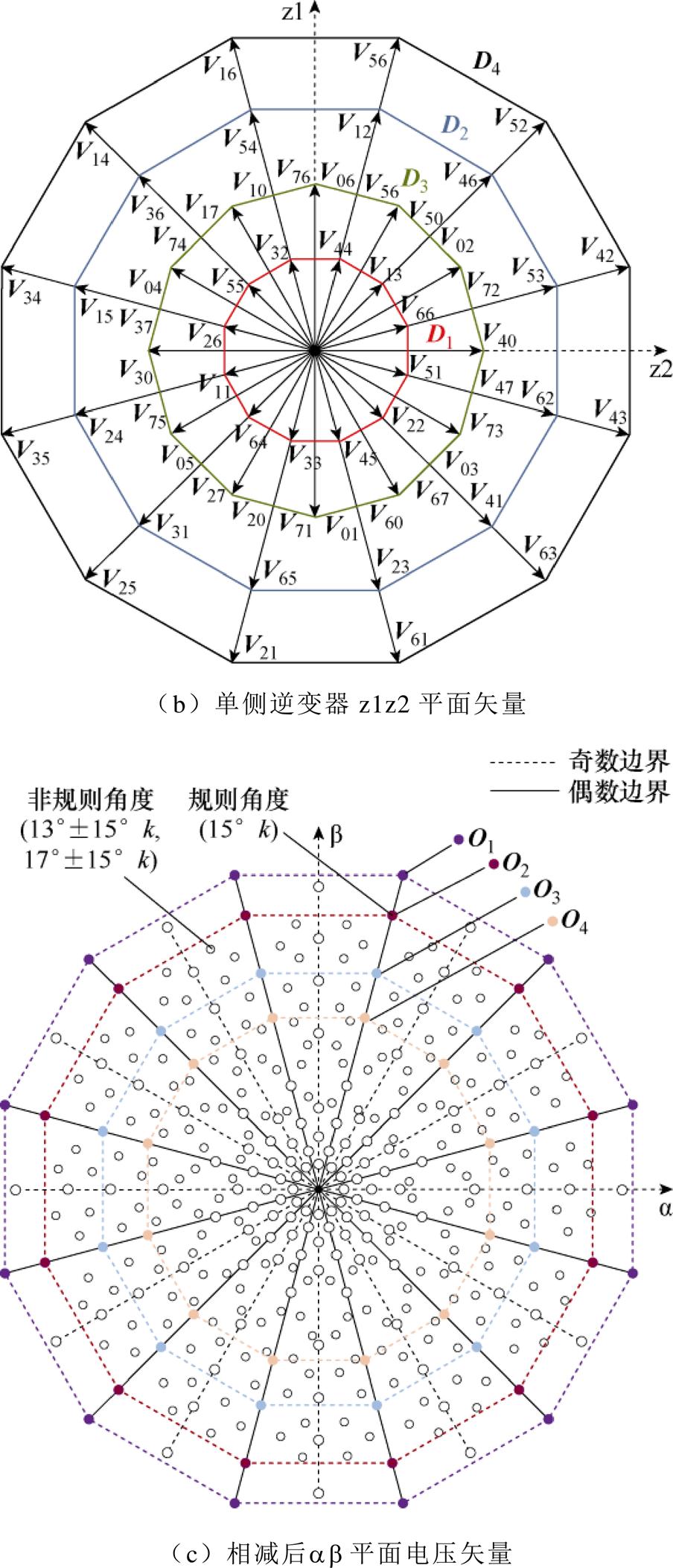
图2 SOEW-PMSM空间电压矢量ab平面分布
Fig.2 ab-plane spatial voltage vectors for SOEW-PMSM
表1 不同平面电压矢量大小
Tab.1 Voltage vector magnitudes in different planes

电压矢量组abz1z2 D1 D2 D3 D4
经过筛选后保留了角度为15°k的规则角度电压矢量,在ab平面的投影如图2c所示。依据电压矢量幅值大小区别扇区边界。其中实线扇区边界为H桥两侧六相逆变器在奇数边界上的合成矢量,最大电压矢量幅值为1.288Udc,虚线扇区边界为H桥两侧六相逆变器在偶数边界上的合成矢量,最大电压矢量幅值为1.244Udc(普通六相电机最大电压矢量幅值仅为0.644Udc,因此开绕组系统电压利用率高的优势明显)。后文所提调制方法所用电压矢量均位于奇数边界,考虑过小的电压矢量直流电压利用率较低,因此仅考虑使用电压矢量子集O1~O4进行调制。以奇数边界上最大矢量子集O1为例,由六相逆变器VD1边界上反向的电压矢量合成,如H桥左右两侧开关管分别为[1-0-0-1-0-0]44与[0-1-1-0-1-1]33时,通过相减可合成奇数边界上最大矢量。此外电压矢量子集O1~O4所对应的幅值大小包含多种冗余开关状态,因此在选择合适空间电压矢量进行调制时可根据开关组合进行优选。
为了减小SOEW-PMSM的空间电压矢量在各谐波平面中的投影量,还需要对ab平面中电压矢量在z1z2、o1o2平面的投影进行分析。z1z2平面的电压矢量与ab平面的电压矢量分布类似,除了幅值与角度的对应变换外,没有产生新的空间电压矢量。
除了5次谐波平面外,不同于普通六相永磁同步电机,SOEW-PMSM存在零序电流通路,o1o2平面的分量会产生零序电流。因此还需要对SOEW- PMSM的o1o2平面进行分析。
结合式(10),H桥单侧六相逆变器在o1o2平面的空间电压矢量仅分布在第一象限如图3a、图3b所示。o1o2平面的分量与桥臂开关管状态紧密相关,以电压矢量集D3为例,表示单侧逆变器有两个桥臂开关状态为“1”,因此包含多种开关组合,如[0-1-0-0-1-0]22、[0-0-1-0-0-1]11或[1-0-0-1-0-0]44。以电压矢量集D7为例,表示单侧逆变器有6个桥臂开关状态为“1”,因此仅包含一种开关组合,及[1-1-1-1-1-1]77。通过对D1~D7矢量集对应的开关组合分析,可得o1o2平面分量的幅值与开关管组合中桥臂开关状态为“1”的数量有关。同样将单侧6相逆变器在o1o2平面的分量相减,可以得到SOEW-PMSM在o1o2平面的分量如图3c所示。
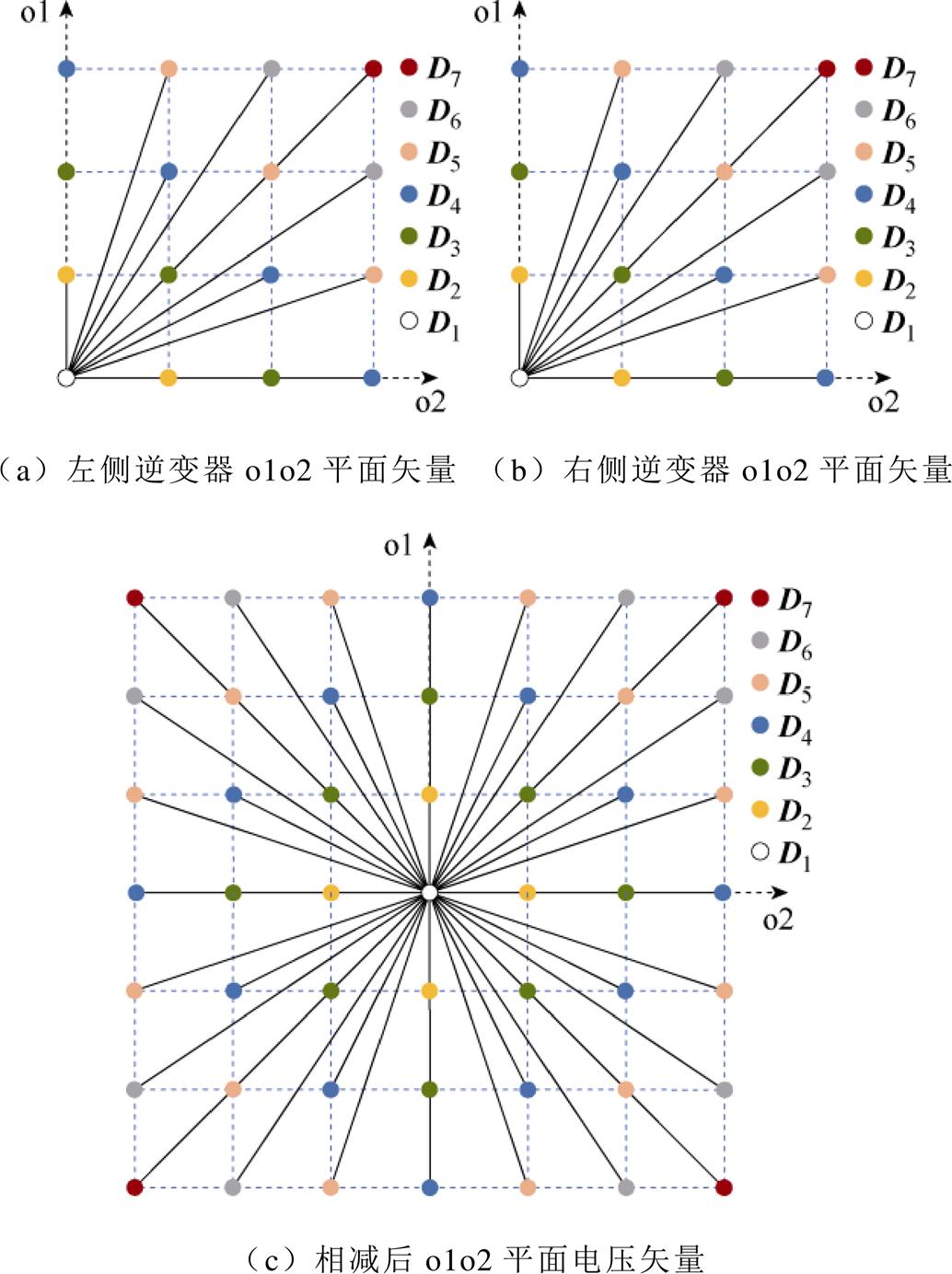
图3 SOEW-PMSM空间电压矢量o1o2平面分布
Fig.3 o1o2 plane spatial voltage vectors for SOEW-PMSM
完成各平面的电压矢量分析后,可以对调制方式开展研究,如何选择合适的矢量、如何减小谐波平面分量、如何保证在一个开关周期开关管只动作一次等都是在研究调制方式时需要考量的问题。
传统的两矢量法是在幅值最大的电压矢量集合中选择两个相邻矢量进行参考电压矢量的合成。在SOEW-PMSM的ab平面中,也就是奇数边界隔成的十二扇区,而电压矢量集O1就是最大合成空间电压矢量,如图4所示。
图4中,S1~S12为划分的十二扇区,各扇区相隔30°,图中电压矢量集O1的开关组合进行了标注,以第一扇区S1为例,上边界电压矢量为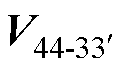 ,则左侧逆变器单元的开关管状态为[1-0-0-1-0-0],右边逆变器单元的开关管状态为[0-1-1-0-1-1];下边界电压矢量为
,则左侧逆变器单元的开关管状态为[1-0-0-1-0-0],右边逆变器单元的开关管状态为[0-1-1-0-1-1];下边界电压矢量为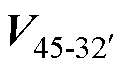 ,则左侧逆变器单元的开关管状态为[1-0-0-1-0-1],右边逆变器单元的开关管状态为[0-1-1-0-1-0],上下边界最大合成矢量的幅值均为1.288Udc。选用两个大矢量合成参考电压矢量,需要计算各矢量的作用时间,两矢量SVPWM算法如图5所示。
,则左侧逆变器单元的开关管状态为[1-0-0-1-0-1],右边逆变器单元的开关管状态为[0-1-1-0-1-0],上下边界最大合成矢量的幅值均为1.288Udc。选用两个大矢量合成参考电压矢量,需要计算各矢量的作用时间,两矢量SVPWM算法如图5所示。
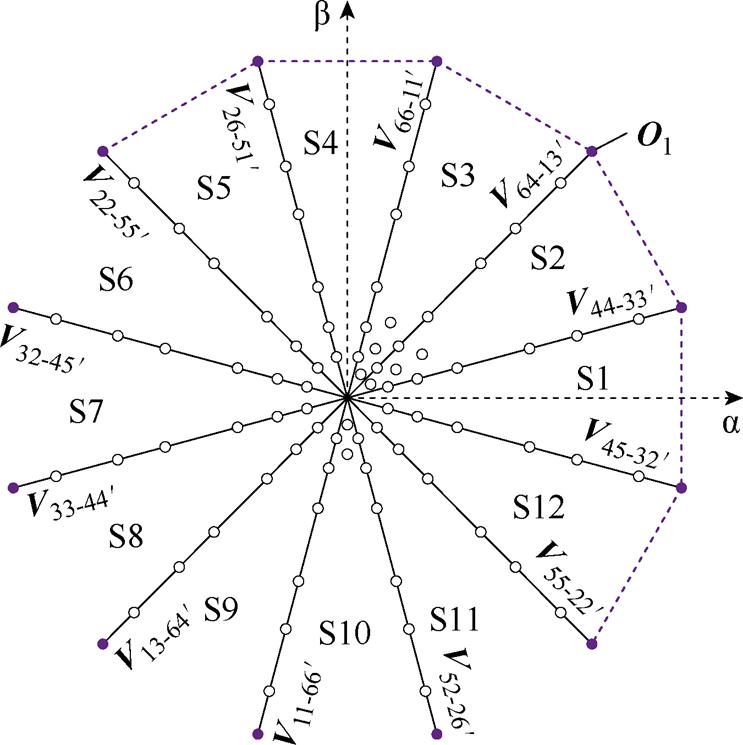
图4 最大电压矢量划分的十二扇区
Fig.4 Twelve sectors divided by the maximum voltage vector
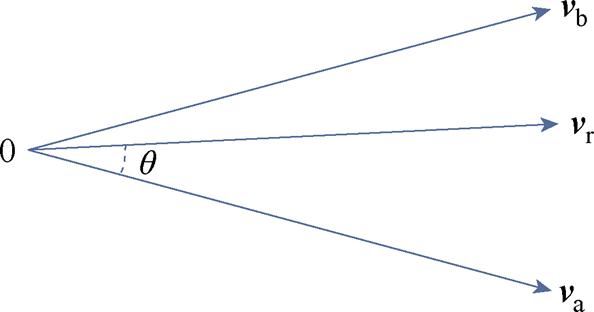
图5 两矢量SVPWM算法
Fig.5 Two vector SVPWM algorithm
以参考电压矢量vr位于第一扇区S1为例进行分析计算。假设基本矢量va、vb的作用时间分别为ta、tb,根据正弦定理与伏秒平衡原理可得基本矢量的作用时间为
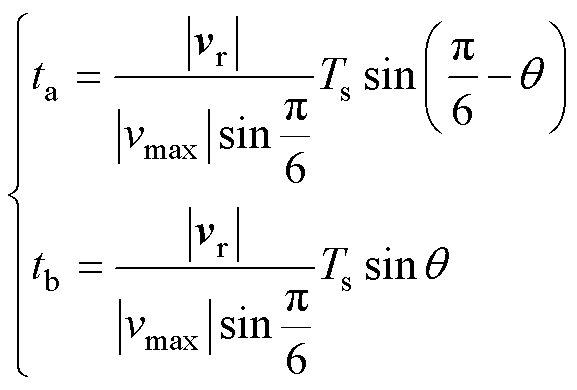 (12)
(12)
式中,q为vr与va之间的夹角;Ts为PWM开关周期;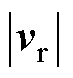 为参考电压矢量幅值;
为参考电压矢量幅值;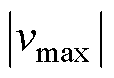 为所选两矢量的幅值。则零矢量作用时间为
为所选两矢量的幅值。则零矢量作用时间为
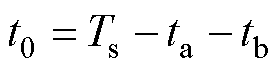 (13)
(13)
同理,当参考电压矢量位于第N(N=1, 2,…, 12)扇区时,可算出电压矢量作用时间的一般表达式为
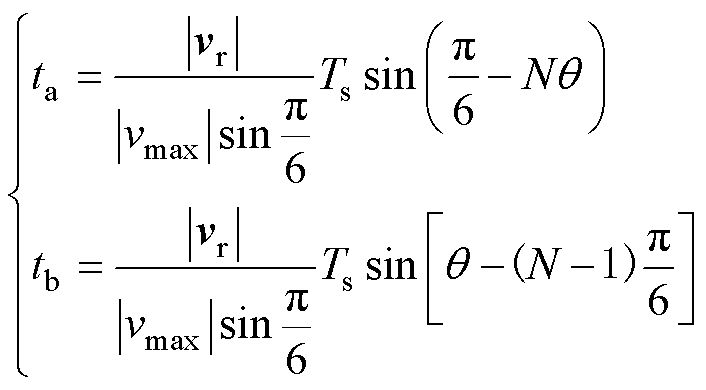 (14)
(14)
计算各扇区大矢量合成参考电压矢量的作用时间后,可进行相应SVPWM。两矢量SVPWM算法由于只考虑了对ab平面的电压进行跟踪,没有考虑z1z2平面上的电压合成效果,将会在z1z2平面上产生不必要的谐波损耗。
四矢量SVPWM策略可以优化上述谐波,四矢量SVPWM的电压矢量选取的标准为:在一个开关周期内,ab平面内合成的电压矢量最大,并且在z1z2平面内合成的电压矢量最小。四矢量SVPWM算法就是在两矢量SVPWM算法的基础上增加两个基本电压矢量,通过增加的电压矢量来抵消在z1z2平面上形成的电压作用效果。
为了简化四矢量SVPWM参考电压矢量的合成过程,选择ab子平面中3个相邻的大矢量合成新的基本矢量,称为虚拟矢量。
以电压矢量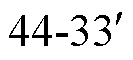 、
、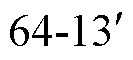 、
、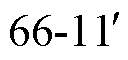 的合成过程为例。由电压矢量在z1z2平面的投影可以看出,若按一定的比例分配3个矢量作用的时间,可以使z1z2平面上伏秒电压作用为零,抑制5次谐波。
的合成过程为例。由电压矢量在z1z2平面的投影可以看出,若按一定的比例分配3个矢量作用的时间,可以使z1z2平面上伏秒电压作用为零,抑制5次谐波。
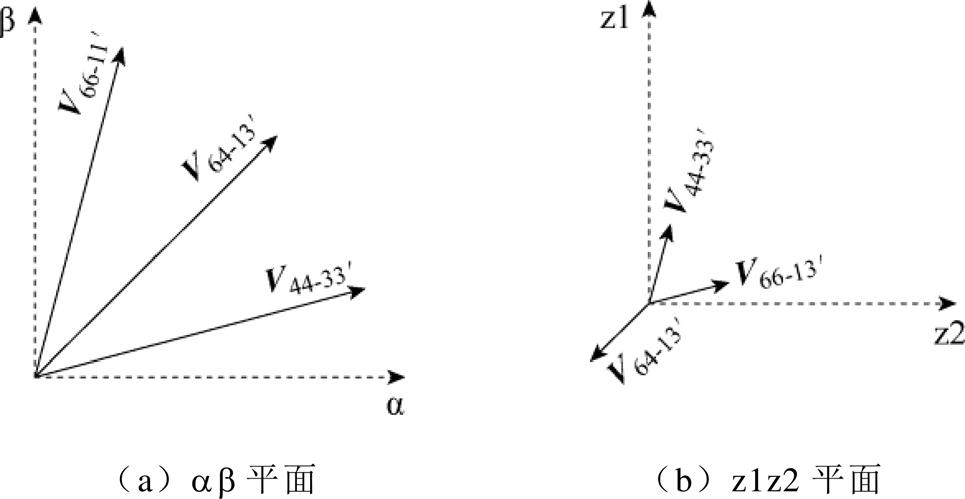
图6 虚拟矢量合成方法
Fig.6 Virtual vector synthesis method
每3个相邻的基本电压矢量均可合成一个新的虚拟电压矢量,虚拟电压矢量的方向与位于中间的基本电压矢量方向相同,这样可以得到12个虚拟电压矢量,同样将ab平面划分为十二扇区,如图7 所示。
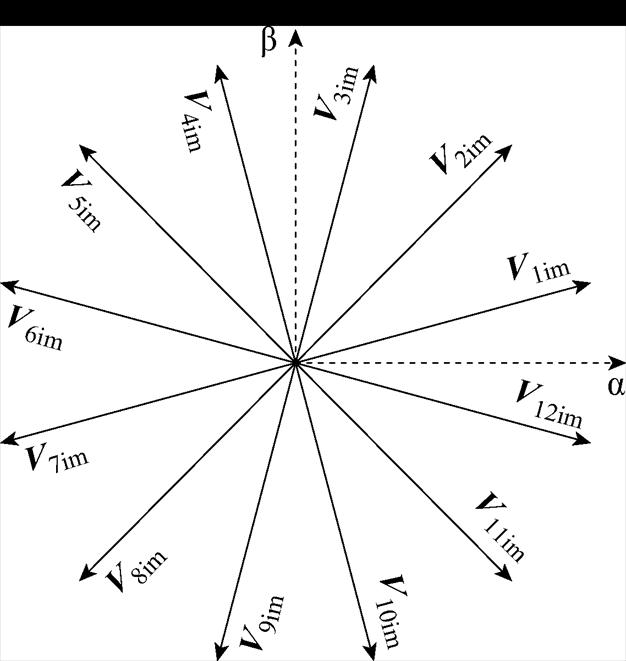
图7 虚拟电压矢量扇区划分
Fig.7 Virtual voltage vector sectorization
得到12个新的虚拟大矢量后,以第一扇区S1为例,选择虚拟大矢量V1im与V12im进行SVPWM,计算V1im与V12im合成参考矢量作用的时间,而虚拟大矢量V1im与V12im是通过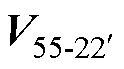 、
、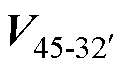 、
、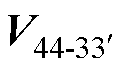 、
、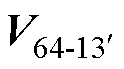 4个基本大矢量合成的,因此计算虚拟大矢量的作用时间等价于计算4个基本大矢量作用的时间。
4个基本大矢量合成的,因此计算虚拟大矢量的作用时间等价于计算4个基本大矢量作用的时间。
假设4个基本矢量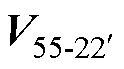 、
、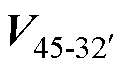 、
、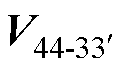 、
、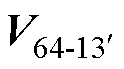 和零矢量作用时间分别为T1、T2、T3、T4、T0,作用时间表达式为
和零矢量作用时间分别为T1、T2、T3、T4、T0,作用时间表达式为
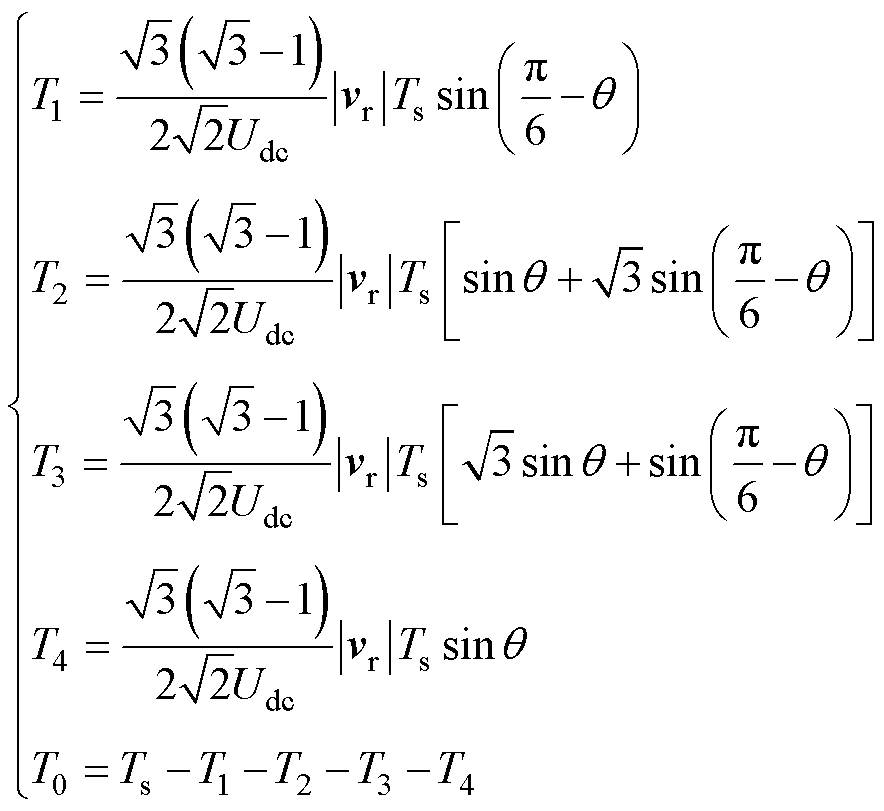 (15)
(15)
若T1+T2+T3+T4>Ts,则需进行过调制处理,有
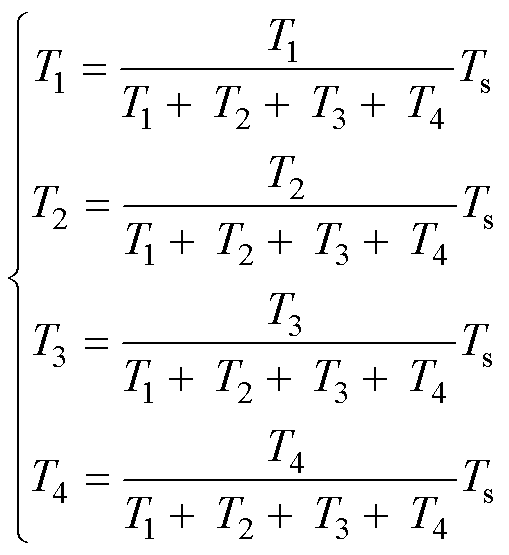 (16)
(16)
四矢量调制利用基本矢量合成12个虚拟矢量,再利用虚拟矢量进行两矢量调制,与两矢量SVPWM相比,相电流5次谐波含量有明显降低,但是抑制效果还有较大的优化空间,相电流3次谐波含量依然很大,在实际应用中如此大的3次谐波含量造成的影响远比5次谐波严重。因此,本文提出了无3次谐波输出的SOEW-PMSM SVPWM方法,可同时抑制3、5次谐波。
3.1节、3.2节所提的不论两矢量或是四矢量SVPWM方法对3、5次谐波的抑制效果并不理想,谐波的存在会使电机的相电流杂乱,电机在运动过程中产生噪声,此外,在实际应用过程中,逆变器单元的开关管会因为无法承受较大的3次谐波电流而被击穿。
所提电压矢量子集O1~O4在各平面的幅值见表2。
表2 各平面中电压矢量子集O1~O4的幅值
Tab.2 Amplitude of a subset of voltage vectors O1~O4 in each plane
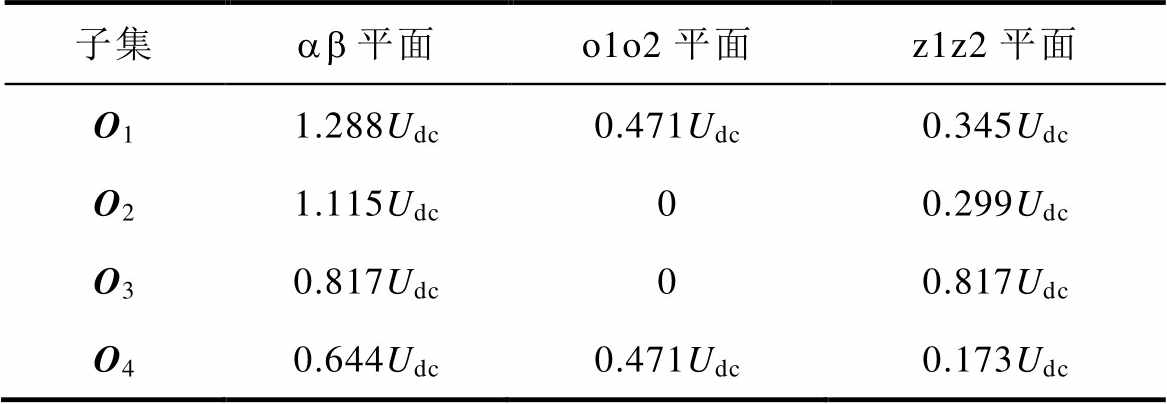
子集ab平面o1o2平面z1z2平面 O11.288Udc0.471Udc0.345Udc O21.115Udc00.299Udc O30.817Udc00.817Udc O40.644Udc0.471Udc0.173Udc
从表2中可以看到,电压矢量集O2与O3在o1o2平面的分量为零,因此若选择此电压矢量集中的电压矢量进行调制方法研究,可以从逆变器的输出端避免3次谐波的产生。
以第一扇区S1为例,罗列出偶数边界上O2与O3电压矢量集所有电压矢量及其开关管模态,如图8所示。
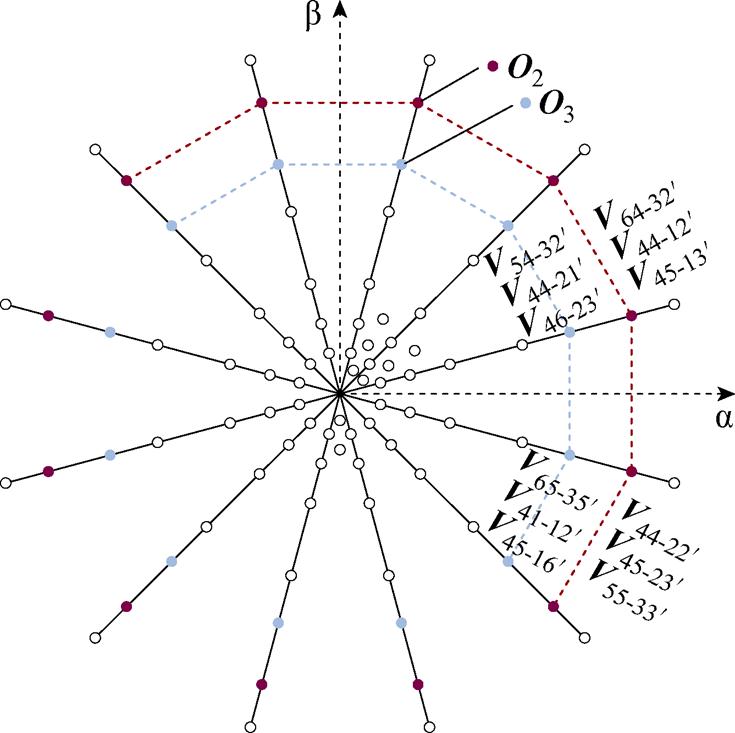
图8 扇区边界上电压矢量分布及开关管组合
Fig.8 Voltage vector distribution on sector boundary and switching tube combination
根据图8,奇数扇区边界上矢量集O2与O3对应多种开关管组合,且六相H桥单侧桥臂的每个开关管组合中开关状态为1的数量相同,因此单侧桥臂相减后在o1o2平面的合成分量为零,实现了从逆变器输出端与电压矢量的选择上避免3次谐波平面分量的产生。
以第一扇区S1为例,电压矢量集O2与O3在z1z2平面上的投影分量如图9所示。
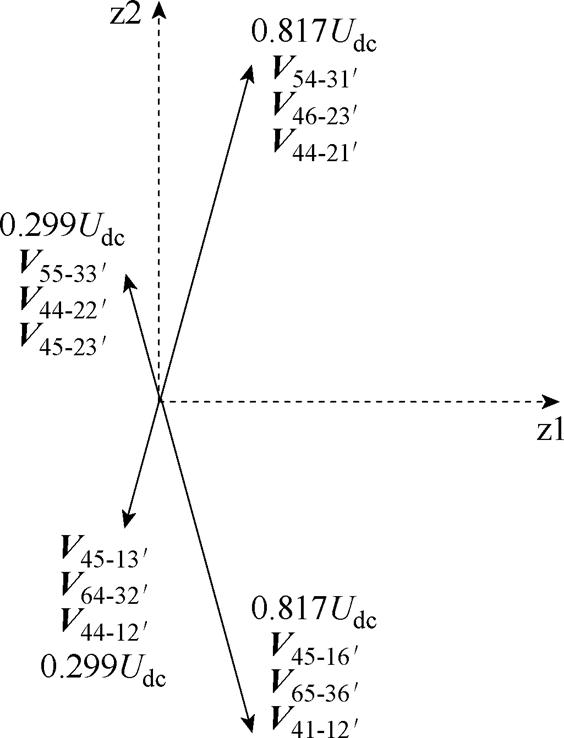
图9 电压矢量集O2与O3在z1z2平面上的投影
Fig.9 Projections of O2, O3 amplitude voltage vectors on z1z2 subspace
结合图8与图9,选择电压矢量集O2与O3不会从调制方式上引入3次谐波,且5次谐波可以通过计算作用时间使其合成为零。
以第一扇区S1为例的调制方法如图10所示。
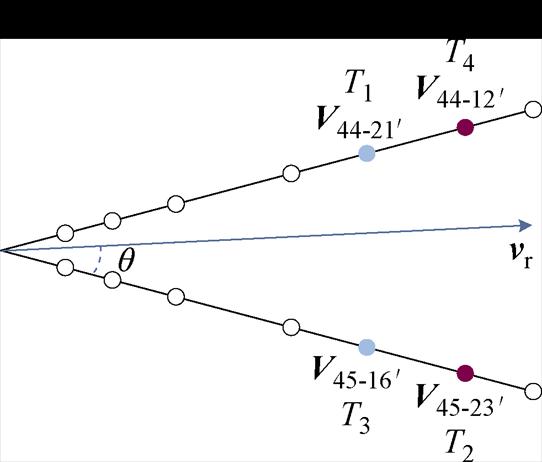
图10 基于SVPWM的谐波抑制方法
Fig.10 Harmonic suppression method based on SVPWM
如图10所示,在电压矢量集O2与O3的开关组合中,选择了开关组合为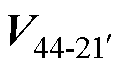 、
、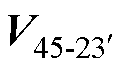 、
、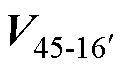 、
、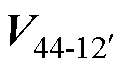 且作用时间分别为T1~T4,没有选择其他开关组合是因为经过测试,选其他开关组合在设计PWM波形时会出现开关管在一个开关周期内跳变多次的情况。确定开关组合后计算各矢量的作用时间,5次谐波平面的合成值为零是约束条件之一,因此可以列出作用时间的通式为
且作用时间分别为T1~T4,没有选择其他开关组合是因为经过测试,选其他开关组合在设计PWM波形时会出现开关管在一个开关周期内跳变多次的情况。确定开关组合后计算各矢量的作用时间,5次谐波平面的合成值为零是约束条件之一,因此可以列出作用时间的通式为
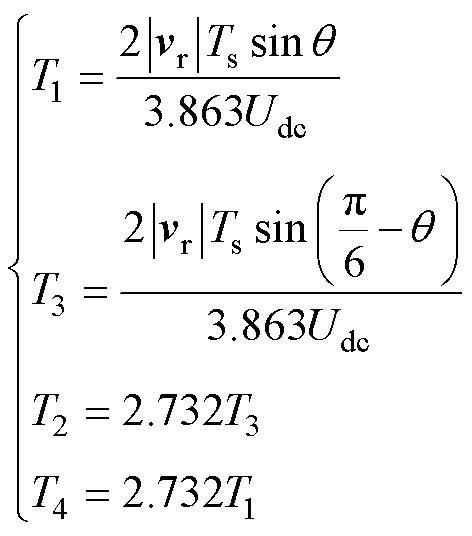 (17)
(17)
求出各矢量的作用时间后,绘制出第一扇区S1合适的桥臂PWM波形如图11所示,将左右两组开关管分别使用两组PWM波进行控制,可避免一个周期内开关管多次跳变的情况出现。

图11 第一扇区S1调制波形
Fig.11 First sector S1 modulation waveforms
同理,根据第一扇区S1的桥臂PWM波形与开关管切换时间点可以绘制出其他扇区的桥臂PWM波形与开关管切换时间点。
由H桥逆变器供电,且采用无3次谐波输出的SVPWM方法的SOEW-PMSM矢量控制系统框图如图12所示。
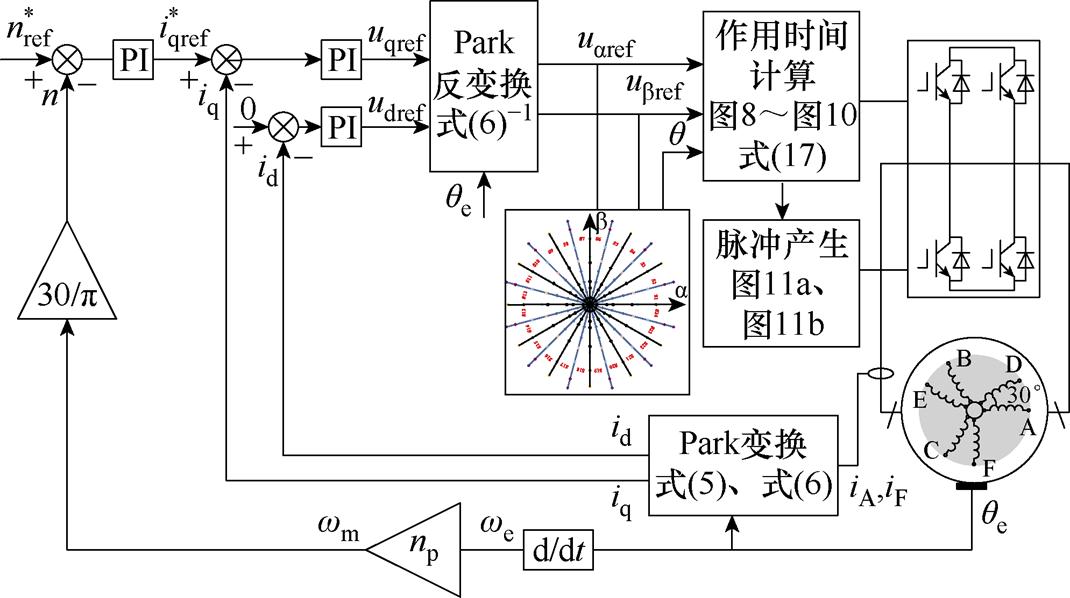
图12 SOEW-PMSM矢量控制系统框图
Fig.12 SOEW-PMSM vector control system block diagram
为了验证本文所提方法的有效性,搭建相应的SOEW-PMSM对拖实验平台,图13展示了用于实验测试的各个部分。50 kW级SOEW-PMSM由一个两电平逆变器供电,该逆变器由6个具有公共直流总线的智能功率模块组成。每个模块使用H桥为一个相绕组供电。主控电路板由STM32和FPGA(EP4CE115F29C8N)两块芯片组成,STM32主要通过与上位机网口的通信实现指令的接收与下发、数据的上传与接收工作,以及与FPGA的SPI通信。FPGA主要通过接收指令实现相应控制、上传采样数据、算法控制、PWM波形输出、采样芯片控制、大电流瞬时值保护等功能。SOEW-PMSM的轴连接到作为发电机的直流电机上。直流电机的电枢连接到消耗功率的可变无源电阻负载,因此负载转矩与速度有关。

图13 SOEW-PMSM对拖实验平台
Fig.13 SOEW-PMSM pair of tor experimental platforms
表3列出了系统参数,控制频率设定为25 kHz。由于永磁体是表面安装的,所以在各个平面中dq轴的电感相等。采用矢量控制进行调速,基于此平台验证文中SVPWM谐波抑制方法的谐波消除效果。
为了验证所提SOEW-PMSM SVPWM方法对电流谐波与转矩脉动的抑制效果,本节在转速300 r/min,负载1.6 kN·m的情况下将所提方法与传统两矢量SVPWM、四矢量SVPWM、谐波电流环抑制方法进行了实验比较。图14中,从上到下依次为三种方法的相电流波形与谐波含量分析。实验结果图14中相电流具体谐波幅值见表4。
表3 SOEW-PMSM参数
Tab.3 SOEW-PMSM parameters
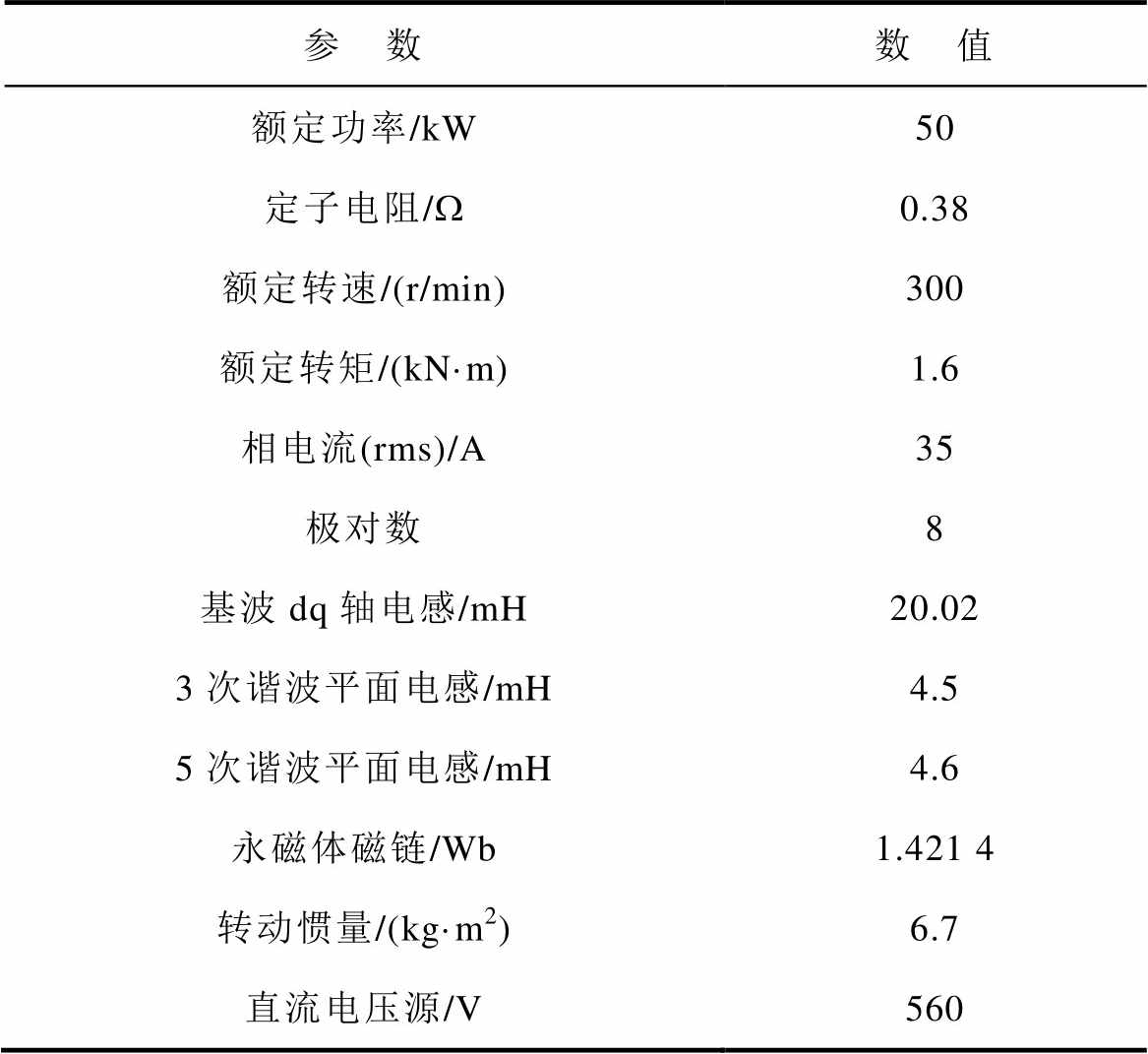
参 数数 值 额定功率/kW50 定子电阻/W0.38 额定转速/(r/min)300 额定转矩/(kN·m)1.6 相电流(rms)/A35 极对数8 基波dq轴电感/mH20.02 3次谐波平面电感/mH4.5 5次谐波平面电感/mH4.6 永磁体磁链/Wb1.421 4 转动惯量/(kg·m2)6.7 直流电压源/V560
传统两矢量调制方法3、5次谐波极大的原因在于,在调制时仅对参考电压矢量的基波平面进行了跟踪,没有考虑3、5次谐波平面的分量。虚拟四矢量调制考虑了5次谐波平面,因此对5次谐波平面有一定的抑制效果,但是此调制方式并未考虑针对3次谐波平面的抑制,且5次谐波平面的抑制效果也不够理想。而谐波电流环抑制方法可以较好地抑制5次谐波,但对危害更大的3次谐波的抑制效果较差,含量高达13.71%。本文所提基于复杂矢量集优选的SOEW-PMSM电流谐波与转矩脉动抑制方法可以很好地解决以上问题,在电压矢量的选择上已经选择使用在3次谐波平面合成分量为零的电压矢量,因此从根本上抑制了3次谐波的产生,效果较谐波电流环的抑制方法更优。
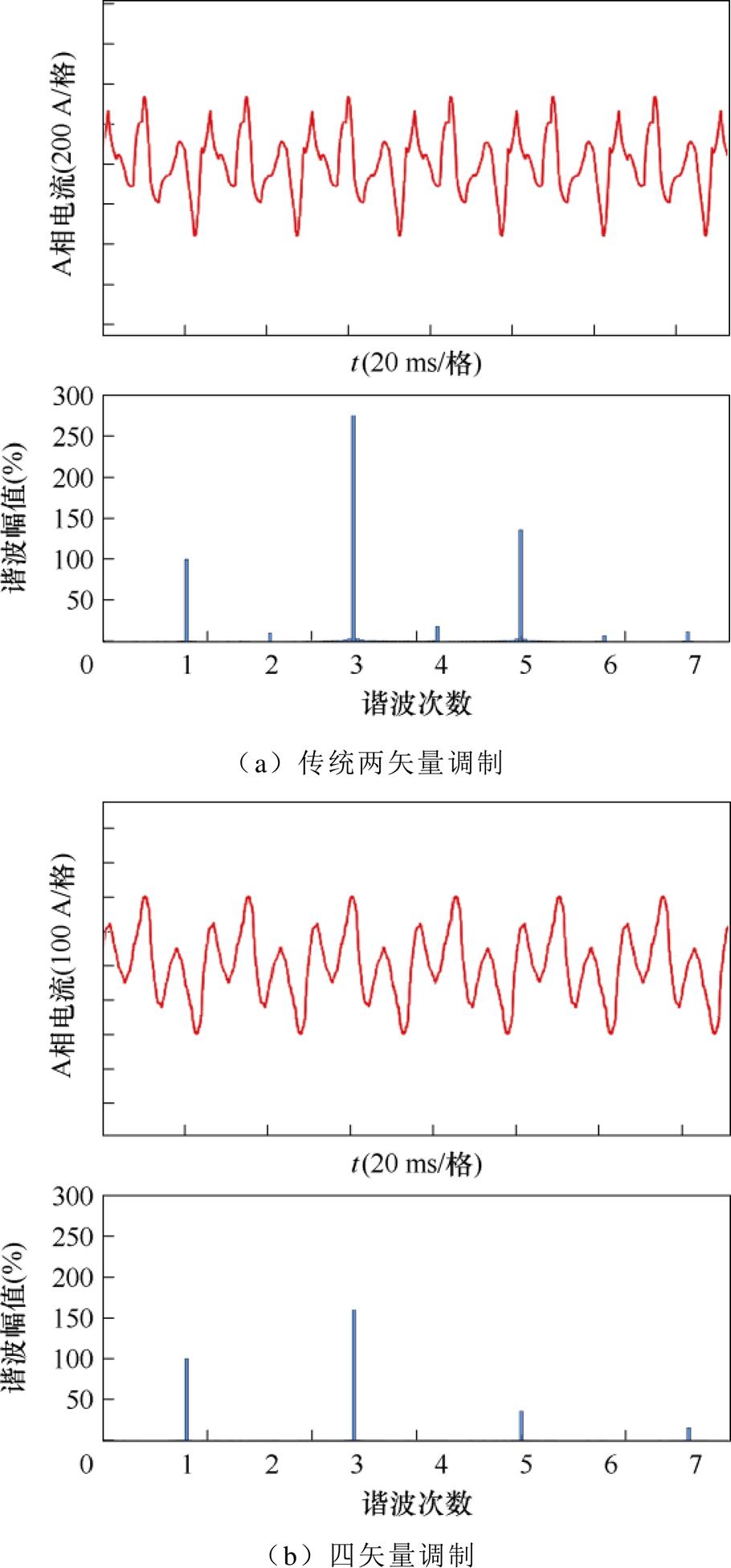
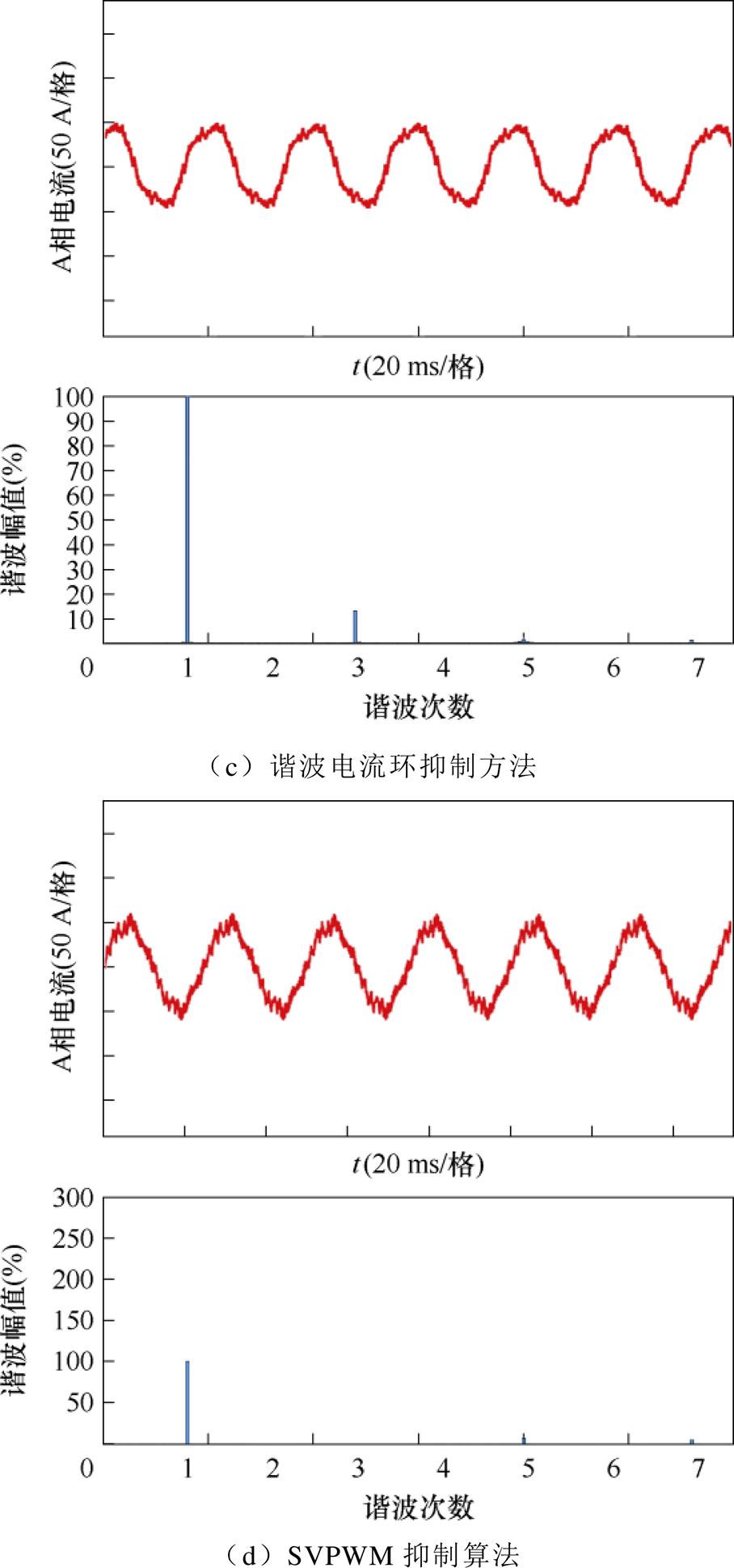
图14 相电流实验波形及谐波分析
Fig.14 Phase current simulation waveforms and harmonic analysis
表4 调制方法的实验结果对比
Tab.4 Comparison of simulation results of modulation methods
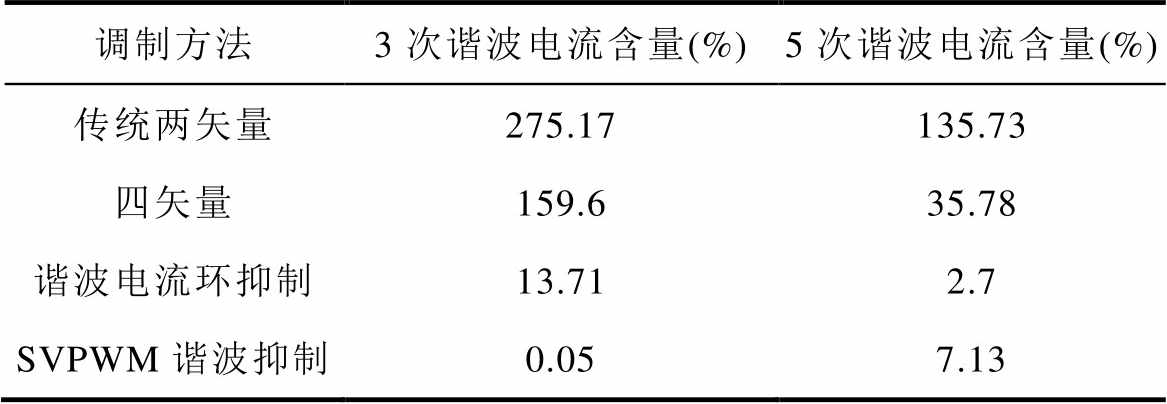
调制方法3次谐波电流含量(%)5次谐波电流含量(%) 传统两矢量275.17135.73 四矢量159.635.78 谐波电流环抑制13.712.7 SVPWM谐波抑制0.057.13
此外,除了电机谐波电流幅值,电磁转矩脉动同样是稳态运行的关键指标之一,本文所提SOEW- PMSM SVPWM谐波抑制方法在对电流谐波进行抑制的同时,对电机运行时的转矩脉动也能进行有效抑制。稳态电磁转矩脉动实验结果如图15所示。
根据图15的电机稳态转矩对比实验结果可知,传统两矢量调制方法的转矩纹波约为±50 N·m,转矩脉动约为3.28%。四矢量调制方法的转矩纹波与转矩脉动较两矢量基本无差别。本文所提无3次谐波输出的SOEW-PMSM SVPWM方法可以有效降低转矩纹波,约为±11 N·m,转矩脉动约为0.63%,对电机转矩脉动的优化效果也较明显。
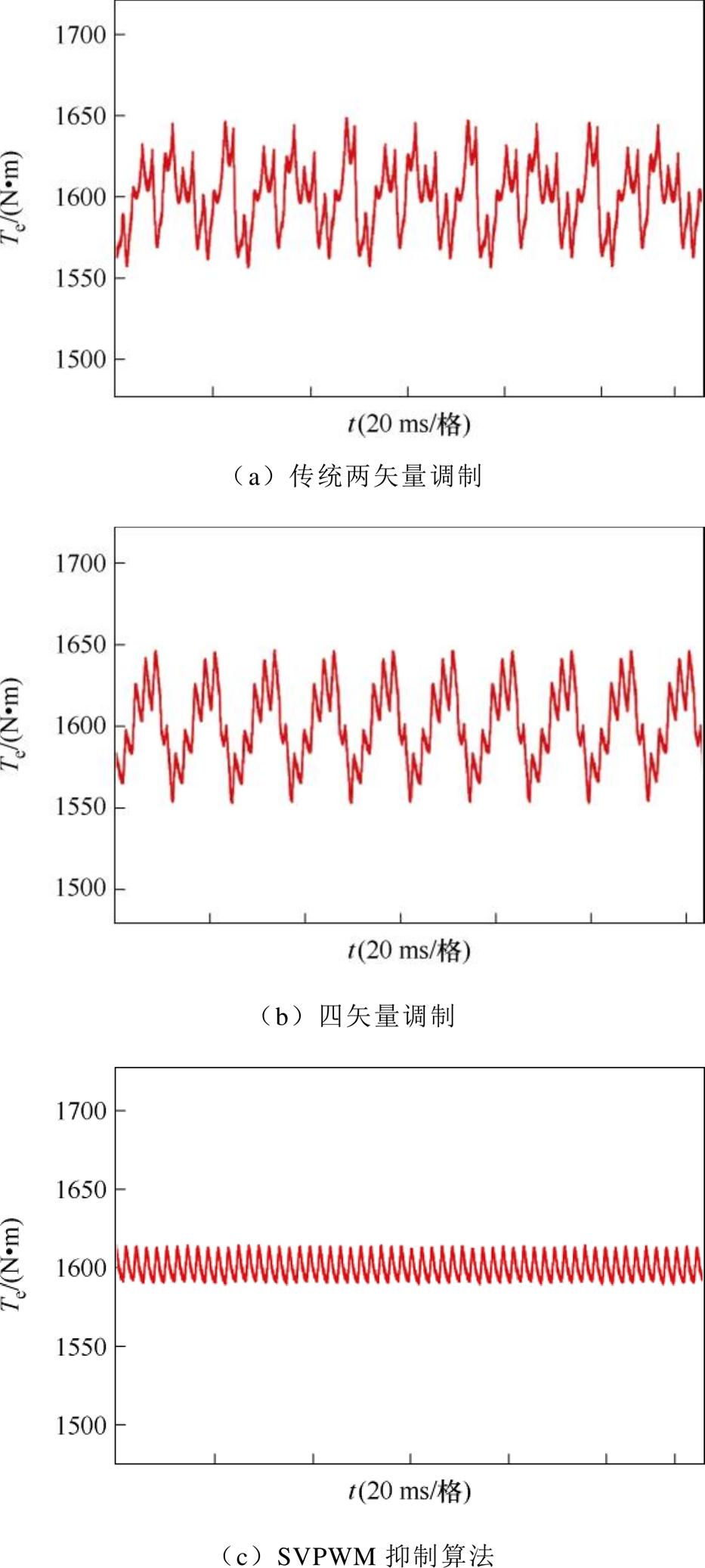
图15 电机稳态转矩对比
Fig.15 Motor steady state torque comparison
本文建立了SOEW-PMSM的数学模型,提出了一种基于复杂矢量集优选的SOEW-PMSM电流谐波与转矩脉动抑制方法,并在50 kW SOEW-PMSM对拖实验平台上验证了该方法的有效性和优越性。本研究的主要贡献归纳如下:
1)该方法在进行空间电压矢量选择时,选择在3次谐波平面合成分量为零的开关管组合及电压矢量,进行参考电压矢量的合成,并通过计算各矢量作用时间,可以较好地在抑制3次谐波的同时抑制5次谐波,使相电流3次谐波含量降低至0.05%,5次谐波含量降低至7.13%。此外,本文所提方法对转矩脉动的优化效果同样较好,在额定负载转矩为1 600 N·m的情况下,将转矩纹波降低至约±11 N·m,转矩脉动降至约为0.63%。极大地提升了电机运行的稳定性,降低了电机系统的损耗与噪声。
2)提出了一种适用于开绕组系统的双边调制脉冲产生方法,易于数字实现,可用于在线多矢量合成,为开绕组系统提供了一种通适性的脉冲产生 方案。
3)与基于谐波电流环的抑制方法相比,本文所提方法从逆变器输出端与电压矢量的选择上避免了3次谐波平面分量的产生,无需对PI或PIR控制器进行复杂的参数整定工作,因此更加简单有效。
参考文献
[1] 周华伟, 陈铖, 向小龙, 等. 基于扰动观测器的五相永磁同步电机开路和短路容错矢量控制[J]. 电工技术学报, 2024, 39(15): 4782-4793.
Zhou Huawei, Chen Cheng, Xiang Xiaolong, et al. Disturbance-observer-based field-oriented control of five-phase PMSM under open-circuit and short-circuit faults[J]. Transactions of China Electrotechnical Society, 2024, 39(15): 4782-4793.
[2] 王海峰, 吴新振. 九相开绕组永磁同步电机谐波电流模型预测控制[J]. 中国电机工程学报, 2024, 44(23): 9431-9442.
Wang Haifeng, Wu Xinzhen. A harmonic current model predictive control for nine-phase open-end winding permanent magnet synchronous motors[J]. Proceedings of the CSEE, 2024, 44(23): 9431-9442.
[3] 张晓光, 闫康, 张文涵. 开绕组永磁同步电机混合双矢量模型预测控制[J]. 电工技术学报, 2021, 36(1): 96-106.
Zhang Xiaoguang, Yan Kang, Zhang Wenhan. Hybrid double vector model predictive control for open- winding permanent magnet synchronous motor with common DC bus[J]. Transactions of China Elec- trotechnical Society, 2021, 36(1): 96-106.
[4] Song Zhanfeng, Hu Siyu, Zhang Ran. Performance improvement of open-winding PMSMs with a discrete- time designed zero-sequence current controller based on virtual three-phase expansion[J]. IEEE Transa- ctions on Industrial Electronics, 2020, 67(12): 10046-10054.
[5] 袁雷, 程剑波, 徐岸非, 等. 双三相永磁同步电机两相开路谐波抑制矢量容错控制[J]. 电工技术学报, 2025, 40(18): 5945-5958.
Yuan Lei, Cheng Jianbo, Xu Anfei, et al. Vector fault-tolerant control with harmonic suppression for a dual three-phase permanent magnet synchronous motor under two-phase open-circuit conditions[J]. Transactions of China Electrotechnical Society, 2025, 40(18): 5945-5958.
[6] 汪逸哲, 黄晟, 廖武, 等. 基于新型虚拟矢量调制方法的IPMSM模型预测电流控制方法[J]. 电工技术学报, 2024, 39(8): 2422-2433.
Wang Yizhe, Huang Sheng, Liao Wu, et al. IPMSM model predictive current control method based on a novel virtual vector modulation method[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(8): 2422-2433.
[7] 林潇锐, 和阳, 赵文祥, 等. 基于电流自适应的九相永磁同步电机开路容错控制[J]. 电气工程学报, 2025, 20(1): 26-36.
Lin Xiaorui, He Yang, Zhao Wenxiang, et al. Open- circuit fault-tolerant control of nine-phase PMSM based on current adaptation[J]. Journal of Electrical Engineering, 2025, 20(1): 26-36.
[8] 吴洪恒, 吴新振, 王海峰, 等. 九相开绕组永磁电机SVPWM谐波抑制方法[J]. 中国电机工程学报, 2022, 42(6): 2365-2375.
Wu Hongheng, Wu Xinzhen, Wang Haifeng, et al. SVPWM harmonic suppression method for nine phase open-end winding permanent magnet motor[J]. Pro- ceedings of the CSEE, 2022, 42(6): 2365-2375.
[9] 曾恒力, 年珩, 周义杰. 基于比例谐振控制的共直流母线开绕组永磁同步电机零序电流抑制技术[J]. 电工技术学报, 2016, 31(22): 35-44.
Zeng Hengli, Nian Heng, Zhou Yijie. Zero sequence current suppression for open winding permanent magnet synchronous motor with common DC bus based on proportional-resonant controller[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(22): 35-44.
[10] 孙全增, 张志锋, 刘伽. 一种新型双三相电机空间矢量脉宽调制方法[J]. 电机与控制学报, 2023, 27(7): 86-97.
Sun Quanzeng, Zhang Zhifeng, Liu Jia. Space voltage vector pulse width modulation method for dual three-phase permanent magnet synchronous motor[J]. Electric Machines and Control, 2023, 27(7): 86-97.
[11] Song Zhanfeng, Ma Xiaohui, Yu Yun. Design of zero-sequence current controller for open-end winding PMSMs considering current measurement errors[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 6127-6139.
[12] Hu Wei, Nian Heng, Zheng Taiying. Torque ripple suppression method with reduced switching frequency for open-winding PMSM drives with common DC bus[J]. IEEE Transactions on Industrial Electronics, 2019, 66(1): 674-684.
[13] Song Zhanfeng, Hu Siyu, Yu Yun, et al. Performance improvement of semicontrolled open-winding PMSGs based on virtual zero-crossing detection and segment injection of third-order harmonic current[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 12050-12063.
[14] 田明赫, 王勃, 于泳, 等. 基于谐振改进型单自由度自抗扰控制器的PMSM转速波动抑制策略[J]. 中国电机工程学报, 2024, 44(15): 6209-6219.
Tian Minghe, Wang Bo, Yu Yong, et al. Speed fluctuations suppression strategy for PMSM based on resonance-improved single-degree-of-freedom active disturbance rejection controller[J]. Proceedings of the CSEE, 2024, 44(15): 6209-6219.
[15] 沈宏源, 吴新振, 王海峰, 等. 九相开绕组永磁电机SPWM中的三次谐波抑制[J]. 中国电机工程学报, 2023, 43(5): 1992-2001.
Shen Hongyuan, Wu Xinzhen, Wang Haifeng, et al. Suppression of third harmonic caused by SPWM for a nine-phase open-end winding permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2023, 43(5): 1992-2001.
[16] 朱元, 朱醴亭, 肖明康, 等. 基于几何约束优化的重复控制器及PMSM电流谐波抑制应用[J]. 电工技术学报, 2024, 39(4): 1059-1073.
Zhu Yuan, Zhu Liting, Xiao Mingkang, et al. Repetitive controller based on geometric constraint optimization and its application to current harmonic suppression of PMSM[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1059-1073.
[17] Liu Cheng, Shang Jing. Sensorless drive strategy of open-end winding PMSM with zero-sequence current suppression[J]. IEEE Transactions on Energy Con- version, 2021, 36(4): 2987-2997.
[18] 孙丹, 赵琛, 柯伟煌, 等. 基于重构电压矢量的共直流母线型开绕组永磁同步电机改进直接转矩控制[J]. 电工技术学报, 2022, 37(7): 1644-1653.
Sun Dan, Zhao Chen, Ke Weihuang, et al. Recon- structed voltage vector based improved direct torque control strategy for open-winding permanent magnet synchronous motor with common DC bus[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1644-1653.
[19] 徐古轩, 赵峰. 基于零偏差型准比例谐振控制的高速永磁电机电流谐波抑制策略[J]. 兵工学报, 2025, 46(1): 247-257.
Xu Guxuan, Zhao Feng. Current harmonic suppression strategy of high-speed permanent magnet synchronous motor based on zero-deviation quasi-proportional resonant control[J]. Acta Armamentarii, 2025, 46(1): 247-257.
[20] 郭磊, 魏佳丹, 王艺威, 等. 基于开绕组电机的电动汽车双电池集成充电系统准直接功率控制[J]. 电工技术学报, 2024, 39(10): 3007-3020.
Guo Lei, Wei Jiadan, Wang Yiwei, et al. Quasi-direct power control of dual-battery electric vehicle integrated charging system based on an open-winding motor[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3007-3020.
[21] Li Guibin, Hu Jiefeng, Li Yongdong, et al. An improved model predictive direct torque control strategy for reducing harmonic currents and torque ripples of five-phase permanent magnet synchronous motors[J]. IEEE Transactions on Industrial Elec- tronics, 2019, 66(8): 5820-5829.
[22] 刘国海, 赵万祥, 周华伟, 等. 基于零序电压谐波注入式脉宽调制的五相永磁电机直接转矩控制[J]. 中国电机工程学报, 2017, 37(5): 1517-1527.
Liu Guohai, Zhao Wanxiang, Zhou Huawei, et al. Direct torque control of five-phase permanent magnet motor based on zero-sequence voltage harmonic injection pulse width modulation[J]. Proceedings of the CSEE, 2017, 37(5): 1517-1527.
[23] Zhou Yijie, Nian Heng. Current zero-crossing duration reduction of a semicontrolled open-winding PMSG system based on third harmonic current injection[J]. IEEE Transactions on Industrial Elec- tronics, 2016, 63(2): 750-760.
[24] Zhang Shuo, Zhou Ying, Li Xueping, et al. An improved modulation strategy with torque ripple suppression method for OEW-PMSM drives with common DC bus[J]. IEEE Transactions on Trans- portation Electrification, 2023, 9(2): 3095-3105.
Current Harmonics and Torque Ripple Suppression of Six-Phase Open-Winding Permanent Magnet Synchronous Motor Based on Complex Vector Set Preference
Abstract Multi-phase open-winding permanent magnet synchronous motors (OEW-PMSMs) have many advantages, such as small power-sharing per phase, high voltage utilization, and high fault-tolerance performance. However, the multiphase OEW-PMSM requires comprehensive suppression of multi-harmonic plane components and ZSC suppression. Conventional methods using harmonic current loops or harmonics are challenging to realize effective control when facing multiphase OEW-PMSM. This paper proposes a space vector pulse width modulation (SVPWM) method based on complex vector set preference for a six-phase open-winding permanent magnet synchronous motor (SOEW-PMSM) drive system, which avoids the generation of the third harmonic at the output and suppresses the fifth harmonic.
Firstly, the method considers the 3rd and 5th harmonics in the transformation matrix to achieve high- accuracy modeling of SOEW-PMSM. The plane decomposition is performed based on the vector space decomposition method. The space voltage vectors generated by different switching combinations of the 6-phase H-bridge inverter are analyzed. The spatial voltage vectors are projected to each harmonic plane. The spatial voltage vectors with zero projected components in the 3rd harmonic plane are filtered out as the alternative vectors for SVPWM. Secondly, the proportionality relationship between the alternative vectors in the 5th harmonic plane projection is analyzed, and the action time of each vector is assigned through the proportionality relationship. High-precision suppression of the 3rd and 5th harmonic currents is realized. After finding the action time of each vector, the appropriate bridge arm PWM waveforms for each sector are plotted, and the left and right switching tubes are controlled using two sets of PWM waves, avoiding multiple jumps of the switching tubes in one cycle. Finally, a 50 kW-class SOEW-PMSM pair-tow experimental platform was constructed to compare the proposed control method with the traditional vector control and harmonic current loop methods.
The experimental results indicate that the method selects switching tube combinations and voltage vectors with zero synthesized components in the 3rd harmonic plane for the space voltage vector selection. It can better suppress the 3rd harmonic while suppressing the 5th harmonic by calculating the action time of each vector. The 3rd harmonic content of the phase current can be reduced to 0.05%, and the 5th harmonic content can be reduced to 7.13%. In addition, the proposed method’s optimization effect on the torque pulsation is good. The torque ripple is reduced to about ±11 N·m, and the torque pulsation is reduced to about 0.63% in the case of the rated load torque of 1 600 N·m. (2) A bilateral modulation pulse generation method for open-winding systems is proposed, which is easy to implement digitally and can be used for online multi-vector synthesis. (3) Compared with the suppression method based on the harmonic current loop, the proposed method avoids the 3rd harmonic in terms of the inverter outputs and the selection of the voltage vectors. The method is more straightforward and does not require complex parameter tuning work for the PI or PIR controllers.
Keywords:Space voltage vector pulse width modulation, six-phase open-winding permanent magnet synchronous motor, space voltage vector, synthesis harmonic suppression
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.242102
收稿日期2024-11-24
改稿日期 2024-12-18
彭宇航 男,1998年生,博士研究生,主要研究方向为永磁同步电机智能控制算法。
E-mail: yuhang.peng@whu.edu.cn
宫金武 男,1981年生,副教授,博士生导师,主要研究方向为高效率高功率密度电力电子变换技术。
E-mail: gongjinwu@whu.edu.cn(通信作者)
(编辑 崔文静)