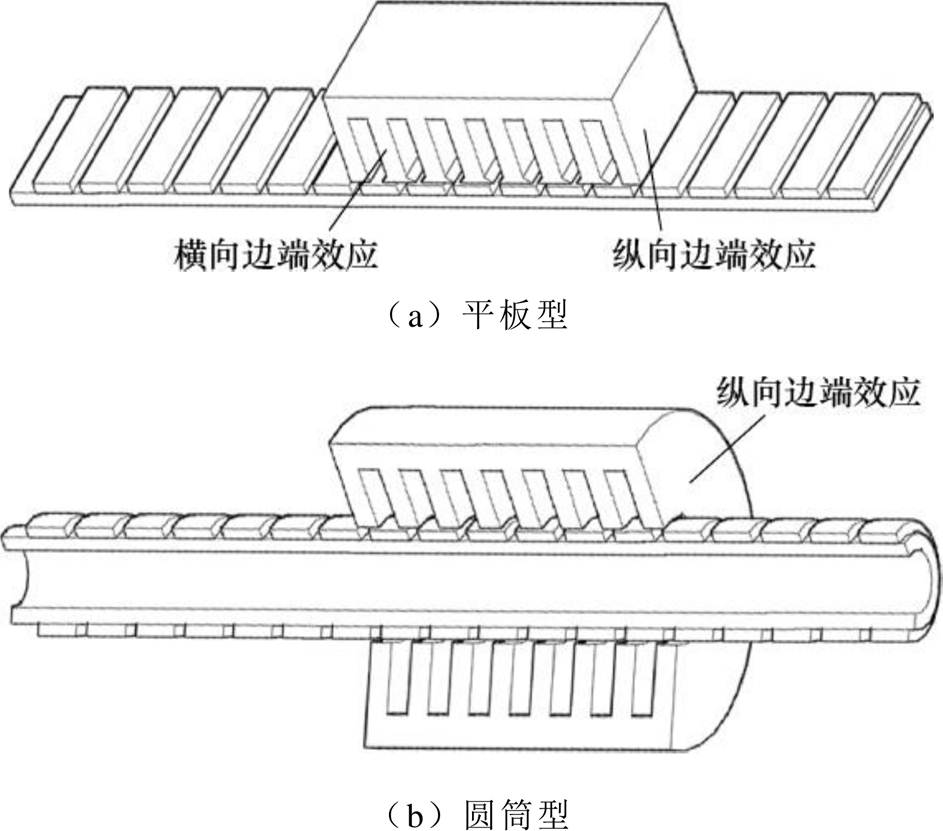
图1 常见的两种PMLSM类型
Fig.1 Two common typologies of PMLSM
摘要 有铁心永磁直线同步电机(PMLSM)推力密度高,广泛应用于半导体加工、精密机械加工与自动化加工等需要高性能直线运动的设备,但其推力波动大,给本体设计与驱动控制都带来了挑战。推力波动的主要分量是定位力,因此设计过程中通常将降低定位力作为优化目标。该文首先分析了定位力的特性,在此基础上对比了定位力计算的三种方法:解析法、磁网络法和有限元法,聚焦于这些方法对铁心饱和、齿槽效应和边端效应的处理方式,指出了精度与适用范围;其次围绕本体结构优化和控制补偿两方面综述了定位力的各种抑制方法,分析了本体结构优化时分离抑制法和直接抑制法的优缺点,对比了控制补偿时基于数学模型和观测器的特点;然后针对定位力抑制目前存在的问题和局限性,进一步总结了负载推力波动的抑制方法;最后展望了定位力研究的发展趋势。
关键词:永磁直线同步电机(PMLSM) 铁心 定位力 推力波动 抑制技术 优化设计
直线电机直接驱动负载做直线运动,无需丝杆、同步带等传统直线驱动系统中的传动机构,简化了系统结构,减小了系统体积,提高了系统效率,在轨道交通、工业制造及电磁弹射领域中都得到了应用[1-5]。常用的类型有直线感应电机和直线同步电机两种,前者次级通常为复合实心板,结构简单、成本低,但存在较大的转差率,效率、功率因数与推力密度低;后者次级采用电励磁或永磁结构,优缺点与前者正好相反,相对来说,电励磁结构需要给次级供励磁电流,所以次级结构会比较复杂,目前只在高速磁悬浮列车中有应用,而永磁直线同步电机(Permanent Magnet Linear Synchronous Motor, PMLSM)的次级结构非常简单,成为了目前研究与应用的热点。
PMLSM主要包括有铁心结构和空心结构,有铁心结构具有高推力、高推力密度、低成本等显著优点,在精密机床、半导体加工、智能制造等领域都得到了广泛关注[6]。有铁心PMLSM的缺点是推力波动大,影响了伺服运行的精度与稳定性,限制了其应用范围。若能有效抑制其推力波动,则可取代一些设备中的无铁心PMLSM,从而大幅降低成本与体积,拓宽应用范围,因此如何有效地抑制有铁心PMLSM(后续直接称为PMLSM)的推力波动成为了研究热点。
定位力是PMLSM推力波动的主要组成部分,也是需要被重点抑制的对象。定位力是指绕组开路条件下,永磁磁场与电枢铁心齿槽和铁心边端相互作用产生的磁阻力,二者又可分别称为齿槽力与边端力。前者与旋转电机齿槽转矩的产生原理相同,抑制方法也通用;后者是直线电机所特有的,其纵向边端导致磁路开断,使PMLSM的气隙磁场分布并非像旋转电机一样具有周期性,而是在边端处具有明显畸变,这被称为纵向边端效应,是造成PMLSM定位力比旋转电机更大的主要因素[7]。抑制定位力时,简单的方法是分别对边端力和齿槽力进行削弱抑制,缺点是不能达到最好的抑制效果,因此需要考虑边端力和齿槽力的耦合影响提出综合抑制措施[8]。
此外,在实际负载工况下,电枢电流不为零,推力波动不仅含有定位力,还增加了电枢磁场谐波分量引起的纹波推力。随着电枢电流逐渐增大,电枢磁动势谐波分量、磁路饱和度都增加,纹波推力逐渐增大,在推力波动中的占比提升,在过载运行条件下能超过50%,此时只将定位力抑制到最小,推力波动中还存在很大的纹波推力,不能保证推力波动是最小值,这也是目前定位力研究存在的局 限性。
学者们对PMLSM定位力进行了大量的研究[9],分析方法和抑制策略的研究成果非常丰富,但侧重点和适用范围各有不同,本文梳理和总结了目前PMLSM定位力已有的相关研究成果。首先分析了不同电机结构定位力的特性和影响因素,归纳了三种定位力的分析方法,对比了各自的优缺点;其次从电机结构优化和控制补偿策略两方面总结了现有的定位力抑制技术,探讨了不同方法的适用范围和应用效果;然后分析了目前定位力研究存在的不足,指出了对负载推力波动直接抑制的优势;最后展望了未来的发展趋势。
PMLSM的结构形式多样,有平板型、圆筒型、圆盘型和圆弧形,其中研究应用较多的是平板型和圆筒型,如图1所示。这两种结构在运动方向上的气隙磁场分布都具有非周期性,在边端处有明显的磁场畸变,即都受纵向边端效应的影响,存在较大的随定、动子相对位置变化而周期性变化的边端力。另外,平板型PMLSM在横向也具有端部畸变磁场,存在横向边端效应,但其对运动方向的磁场影响较小,因此在定位力抑制时通常被忽略。与圆筒型相比,平板型PMLSM制造工艺更简单,且行程不受限,散热条件好,推力密度更高,因此应用范围也更广。

图1 常见的两种PMLSM类型
Fig.1 Two common typologies of PMLSM
平板型PMLSM根据气隙数量还可进一步分为单边型与双边型,甚至也有多边型。单边型结构存在较大的单边磁拉力,一般为推力的5~10倍[10],对直线导轨的支撑强度要求较高。双边型和多边型结构推力密度高,并且可以抵消两边的磁拉力,在定位力抑制时拥有更多的优化参数,可采取的抑制方法也更多样。
PMLSM根据初、次级的相对长度可以分为短初级和短次级,前者初级的纵向端部处磁场畸变,此时定位力跟初级边端位置与尺寸紧密相关;后者次级的纵向端部处磁场畸变,定位力跟次级边端的磁极紧密相关,显然这两种结构定位力抑制的优化变量发生了变化。相比较而言,短初级PMLSM应用较普遍。
PMLSM的绕组通常采用分数槽集中绕组,具有相间耦合弱、端部短、容错能力强等优点,但反电动势谐波含量丰富,在绕组设计时也需要考虑抑制反电动势谐波的问题。根据初级每槽线圈数可进一步分为单层(半齿绕组)和双层(全齿绕组),半齿绕组具有线圈数量少、槽内无需层间绝缘、槽利用率高等优点,且初级铁心端部不需要增加附加槽,但不易制成短距线圈来抑制电动势高次谐波;而全齿绕组结构则正好相反,其反电动势谐波含量低,但需要增加附加槽,导致同样槽极配合时初级长度增加,两者定位力的大小与波形都不相同。
为了分析定位力特性,针对图1a所示的典型6槽5极短初级单边平板型PMLSM,基于有限元法建立了两种绕组结构的2D有限元模型,如图2所示,仿真得到空载定位力与额定推力,其波形如图3所示。由图3可知,对于全齿绕组来说,额定推力的平均值为51.26 N、波动峰峰值为5.26 N,定位力峰峰值为4.43 N;对于半齿绕组来说,额定推力的平均值为53.18 N、波动峰峰值为41.42 N,定位力峰峰值为41.38 N。定位力在额定推力波动中所占比重分别为84.2%、99.9%,可见定位力是推力波动的主要成分,削弱定位力能够明显改善推力波动。此外,由于半齿绕组比全齿绕组少一个附加槽,所以图2中两个PMLSM的初级铁心长度存在差异,图2a的左、右边端分别位于永磁前段和永磁后段,而图2b的左、右边端均位于永磁后段,边端力发生了变化,进而使两种绕组结构的定位力有明显差异。
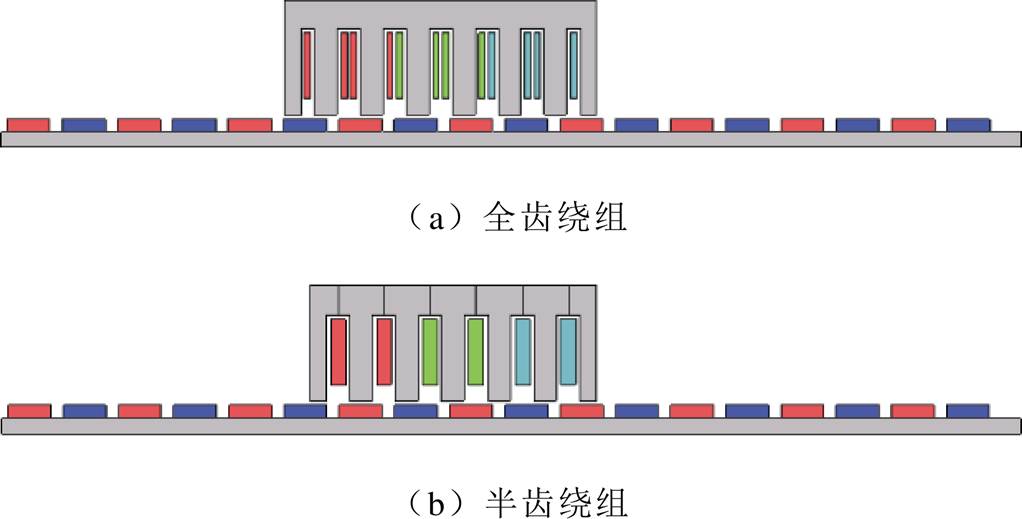
图2 短初级单边平板型PMLSM有限元模型
Fig.2 Finite element models of single-sided flat PMLSM with short primary
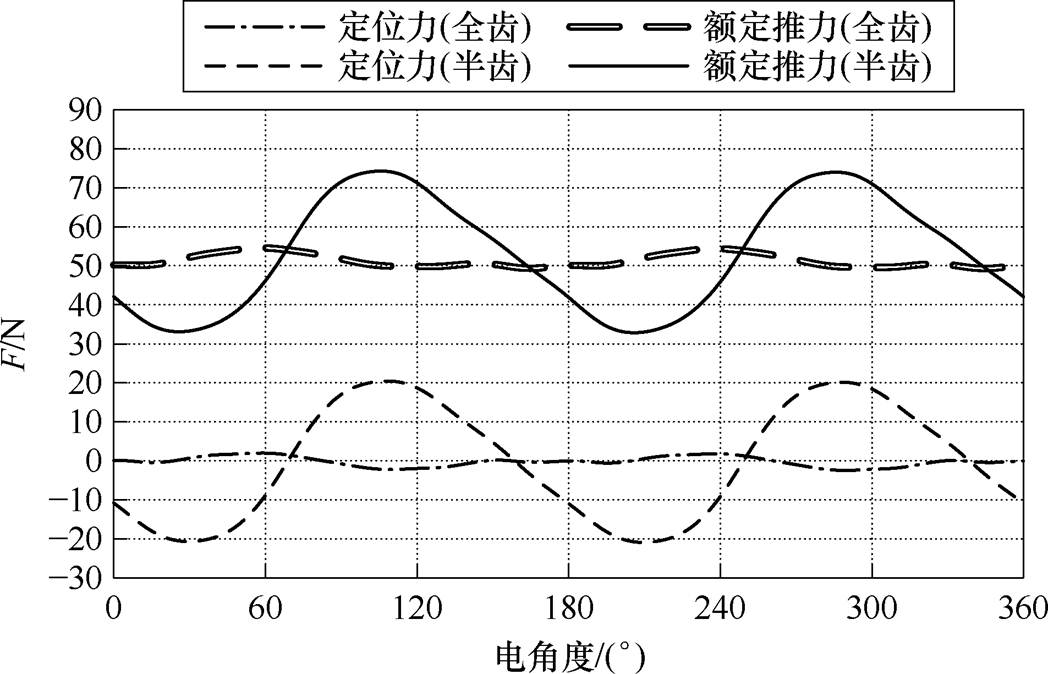
图3 短初级两种绕组结构定位力与额定推力的波形
Fig.3 Waveforms of the detent force and rated thrust force of different winding structure with short primary
为了进一步分析定位力各次谐波成分的来源,分离了定位力中齿槽力与边端力两个分量。基于有限元建立了如图4a所示的齿槽力分离模型和如图4b所示的边端力分离模型,前者初级铁心设置为纵向无限长,即没有初级端部;后者初级铁心设置为光滑表面,即没有齿槽。图5显示了求得的齿槽力与边端力波形。
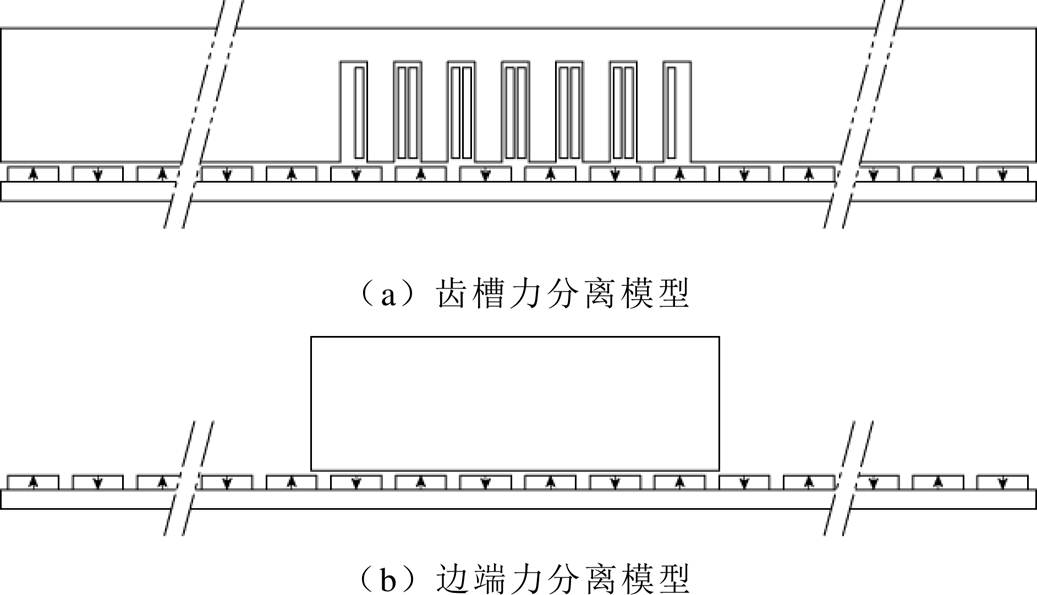
图4 短初级PMLSM齿槽力和边端力的分离模型
Fig.4 Separation models for the cogging force and end force of short primary PMLSM
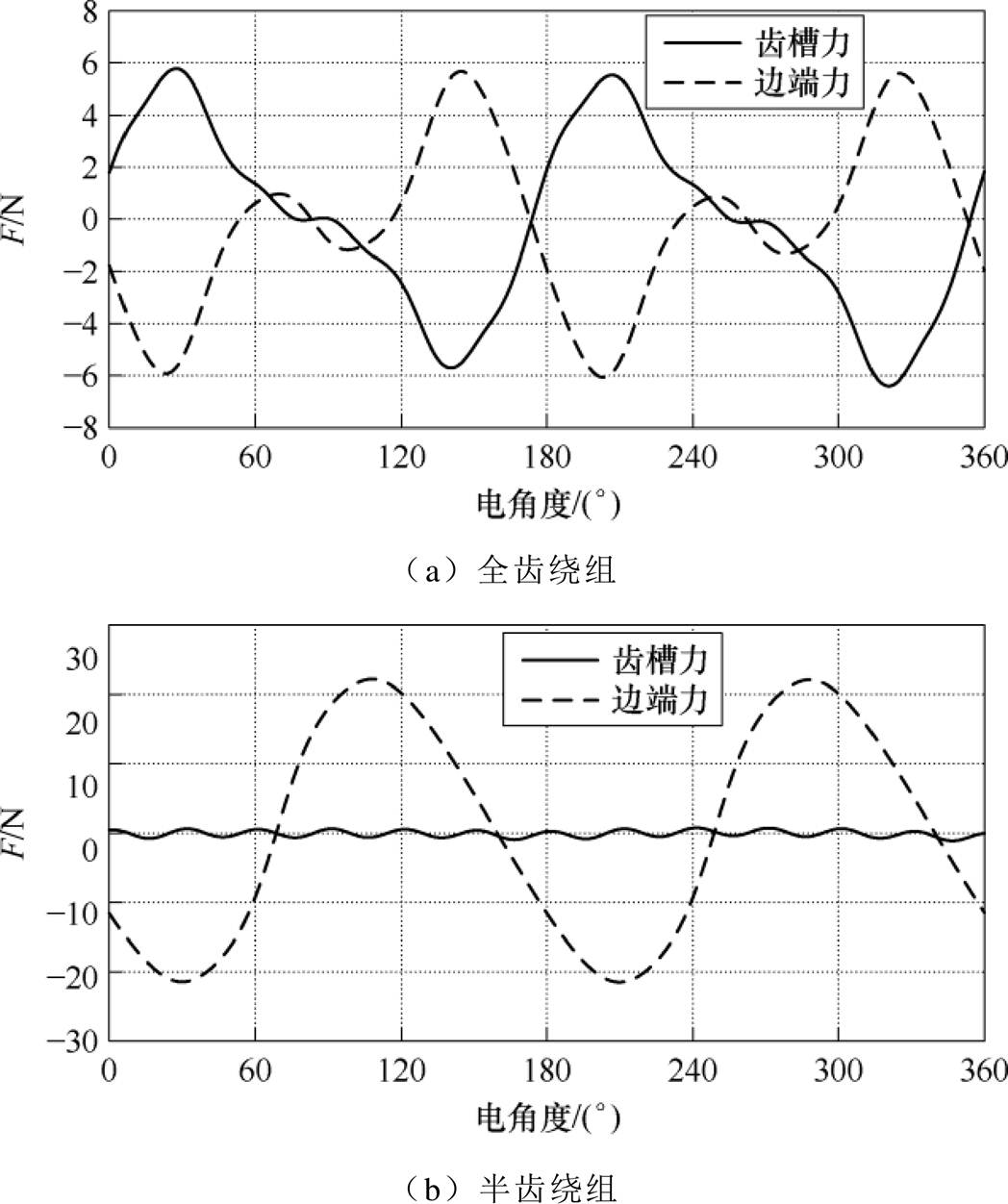
图5 短初级PMLSM齿槽力与边端力的波形
Fig.5 Waveforms of the cogging force and end force of short primary PMLSM
由图5可见,全齿绕组和半齿绕组在齿槽力的谐波成分上有所不同。半齿绕组的齿槽力与旋转电机齿槽力类似,主要成分为由极槽配合所决定的12次齿谐波分量,其幅值较小,而全齿绕组的齿槽力则额外含有较多的2倍次谐波分量,如2、4次谐波,这是由初级铁心增加的第7个附加槽所产生的,其幅值比半齿绕组的大。
由此可见,PMLSM齿槽力的一个分量与旋转电机类似,谐波次数为LCM(Ns,2p)/p(LCM(Ns,2p)为电机极数2p与槽数Ns的最小公倍数);另外,对于全齿绕组来说,还存在铁心开断导致绕组纵向非周期性分布而引入的附加槽所产生的多个低次谐波,如对于Ns槽2p极PMLSM,全齿绕组结构实 际具有Ns+1个槽,其齿槽力幅值会比半齿绕组结构 的大。
此外,无论是全齿绕组还是半齿绕组,其边端力均以2次谐波分量为主,由于两个模型中对应的初级铁心长度不同,因此边端力波形也不相同。边端力是初级铁心端部与次级磁场相互作用产生的,由于在分离模型中忽略了铁心开槽对边端磁场的影响,所以可进一步将边端力看作左、右边端各自产生的力之和。单个边端与次级磁场作用产生的力以一个磁极极距为周期,即主要包含2次谐波分量,且有一个直流分量,运动方向前侧的边端受力为正,运动方向后侧的边端受力为负。两个边端产生的力呈镜像对称关系,合成后的边端力中含有多个2倍次谐波分量,主要为2、4次谐波,其大小取决于左、右两个边端的相对位置。
综上所述,短初级PMLSM的定位力主要由2次谐波分量构成,这是区别于旋转电机齿槽转矩之处。
不同于短初级结构,短次级PMLSM的定位力与旋转电机的齿槽转矩类似,仍以齿谐波成分为主。以24槽20极双边平板型PMLSM为例,有限元模型如图6所示,图7显示了次级处于中间位置时的定位力与额定推力。定位力的峰峰值为153.9 N,额定推力波动的峰峰值为169.5 N,定位力占比90.8%,是推力波动的主要成分。此时定位力的谐波分量主要为12次齿谐波。另外,无论是短初级还是短次级结构,如果动子在长定子的边端处运行,会因定子端部的磁场畸变而产生局部的端部力,其不具有周期性,可单独通过优化长定子端部结构进行抑制。
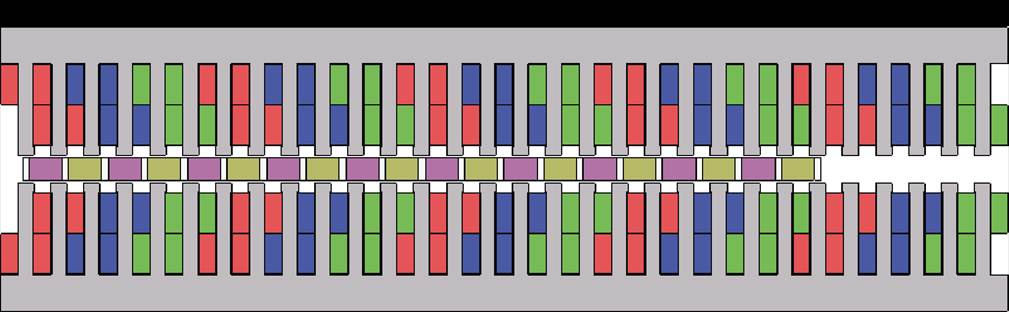
图6 短次级双边平板型PMLSM有限元模型
Fig.6 Finite element model of double-sided flat PMLSM with short secondary
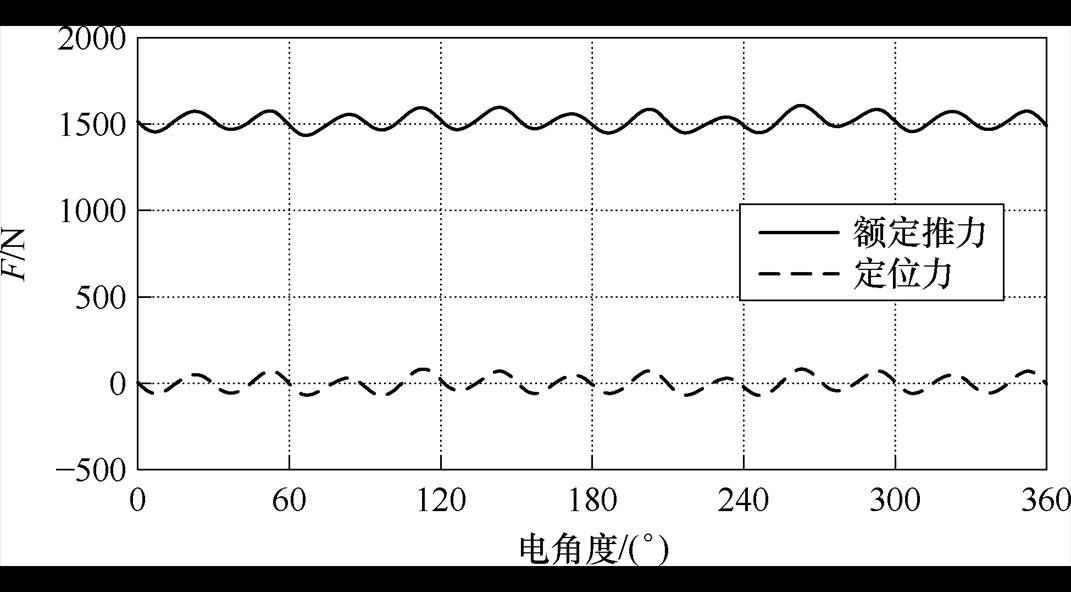
图7 短次级双边平板型PMLSM定位力与额定推力
Fig.7 The detent force and rated thrust force of double-sided flat PMLSM with short secondary
短初级结构制造成本与控制系统复杂度都远低于短次级结构,因此除了柔性物流、无绳电梯等特殊场合外一般都采用短初级结构,所以短初级PMLSM定位力所特有的2次谐波成分抑制方法成为一直以来的研究热点,本文综述的相关内容也聚焦在该方面。
PMLSM定位力抑制首先需要对定位力进行精确计算,常用的分析方法除了前述的有限元法,还有解析法和磁网络法[9]。
解析法通过建立磁场分布与电机结构参数之间的数学模型,直接关联了结构参数对磁场分布的影响,但需要通过适当的假设条件来简化模型,通常也不能考虑铁心饱和等非线性因素,从而计算结果准确性有所降低,但运算速度快,物理概念明确,对计算机的硬件要求也不高。
解析法有多种类型,其中精度较高的是子域法,多用于2D模型。一般先假设铁心磁导率为无穷大,忽略横向边端效应和涡流效应,且永磁的相对磁导率为固定常数。然后根据材料属性、激励类型以及场域形状,将电磁场求解区域划分为若干个简单几何形状的子域空间。图8显示了无槽圆筒型PMLSM的基础子域法解析模型,其子域划分情况为:永磁体子域1、气隙子域2和电枢绕组子域3,整个解析域的边界需满足周期边界条件。在各区域内,以标量磁位或矢量磁位建立拉普拉斯方程或泊松方程,其通解为傅里叶级数叠加的形式,各通解的待定系数则根据相邻子域的边界条件求解方程组得到。各区域内标量磁位或矢量磁位表达式确定后,磁场强度的分布也随之确定。由于基础子域法针对的是简单规则形状的子域空间,因此适用于无槽、无铁心或者可忽略齿槽效应、边端效应的场合,不适用于有铁心PMLSM,因为其齿槽效应和边端效应对磁场分布和电磁性能的影响不可忽略。需要采用衍生出的等效系数法、精确子域法和保角映射法等改进方法。表1对这些方法的优缺点进行了详细的对比:
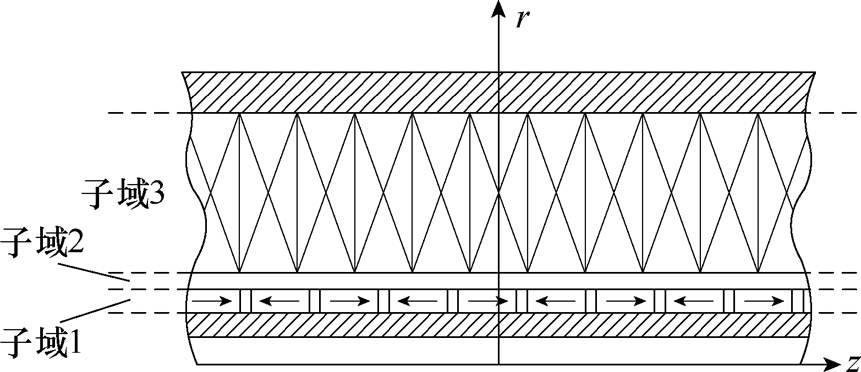
图8 无槽圆筒型PMLSM子域解析模型
Fig.8 Subdomain model of slot-less tubular PMLSM
表1 有铁心PMLSM子域法比较
Tab.1 Comparison of subdomain methods for iron-core PMLSM
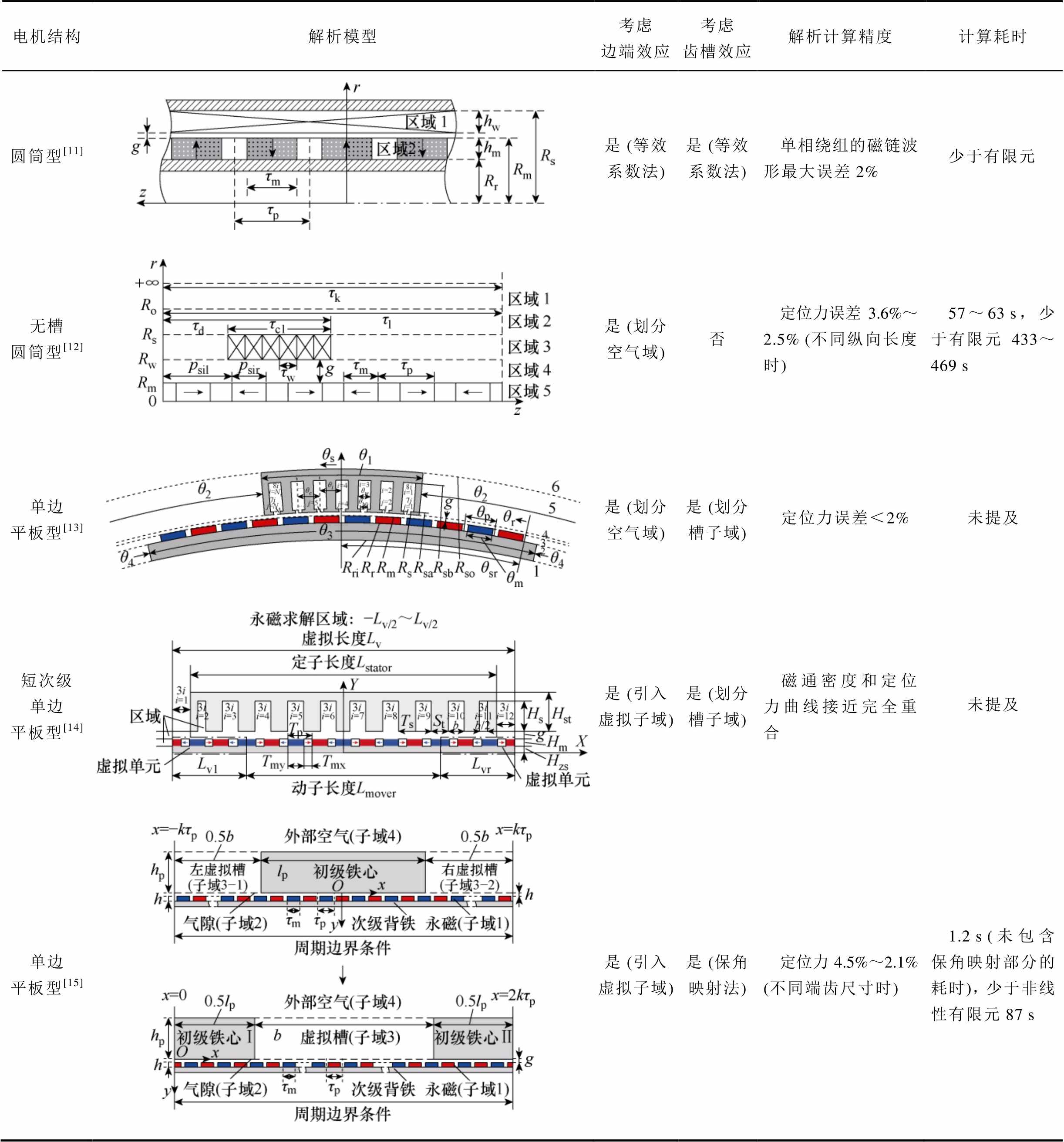
电机结构解析模型考虑边端效应考虑齿槽效应解析计算精度计算耗时 圆筒型[11]是 (等效系数法)是 (等效系数法)单相绕组的磁链波形最大误差2%少于有限元 无槽圆筒型[12]是 (划分空气域)否定位力误差3.6%~2.5% (不同纵向长度时)57~63 s,少于有限元433~469 s 单边平板型[13]是 (划分空气域)是 (划分槽子域)定位力误差<2%未提及 短次级单边平板型[14]是 (引入虚拟子域)是 (划分槽子域)磁通密度和定位力曲线接近完全重合未提及 单边平板型[15]是 (引入虚拟子域)是 (保角映射法)定位力4.5%~2.1% (不同端齿尺寸时)1.2 s (未包含保角映射部分的耗时),少于非线性有限元87 s
(1)等效系数法。文献[11]在图8基础子域法的基础上,引入卡特系数来等效齿槽效应对磁场的影响,并假定边端处的磁场分布为弧形磁力线,引入磁场外悬系数来等效边端效应对磁场的影响。计算准确性受等效系数的制约,与有限元相比,单相绕组的磁链波形最大误差为2%,优点是用时短。
(2)精确子域法。文献[12]在实平面中对电磁场空间进行了更细致的子域划分,增加了初级端部的空气子域来考虑无槽圆筒型PMLSM的边端效应,跟有限元相比,定位力误差可降至2.5%,用时只需有限元法的1/8左右。该方法适用于齿槽效应和边端效应同时存在的PMLSM。文献[13]对单边平板型结构详细划分了槽子域、槽开口子域和边端子域,通过坐标转换将直角坐标系转换到极坐标系,使两个边端域合并,减少了子域个数,降低了解析模型的复杂程度,定位力计算准确度较高,误差小于2%。由于高精度的前提是转换后的等效半径取值要尽可能大,提高了解析计算的时间成本。文献[14]针对的是短次级结构,同样采用了建立槽子域和边端子域的精确子域法来考虑齿槽效应和边端效应,在永磁区域段增加了虚拟单元,解析计算得到的磁通密度波形和定位力波形与有限元结果近乎完全重合。此方法将整个子域解析的长度视为基波周期,长度选得短会影响边端磁场分布,而选得长又会增加解析计算时长。
(3)保角映射法。通过保角映射法将形状不规则场域经过复平面中多次变换得到规则场域,再利用基础子域法进行求解,适用于PMLSM的齿槽效应分析[15-17]。文献[15]引入边端子域考虑边端效应,并采用模型重构法将引入的两个边端子域合二为一来减少子域个数,复杂开槽结构通过保角变换转变为简单无槽结构,求得的气隙磁场再采用复数相对气隙磁导系数进行修正,实现了同时考虑齿槽效应和边端效应的目的,计算结果精度高,其气隙磁通密度波形与有限元结果基本一致,定位力误差在2.1%。缺点是涉及保角变换,计算过程比较复杂。
子域法也可用于3D模型。文献[18]研究了圆形磁体PMLSM的子域解析模型,先在横向方向上假定为间隔较大的无限周期性铁磁平面,用傅里叶级数推导得到圆形磁体的磁场分布函数,再利用保角变换引入了考虑横向边端效应的调制函数,与3D有限元仿真结果相比,磁通误差小于3%。
子域法建模简单、灵活度高、计算时间短,主要问题是忽略了铁心的饱和效应,空载时磁路不饱和,因此空载磁场计算精度高,但负载时磁路通常在饱和状态,影响了负载磁场的计算精度,因此比较适用于结构参数敏感性分析、初始方案设计、优化设计等需要快速计算的场合。
磁网络法将永磁体和电枢绕组等效为磁动势源、复杂空间磁路等效为多段磁路,计算得到各段的磁阻和磁动势后,结合磁路欧姆定律和基尔霍夫定律得到各节点磁动势。各段磁阻可以在定义磁通管后借助公式计算,也可利用有限元法等数值方法,但后者需要借助额外工具,灵活度受限,因此多数采用前者。
磁网络法可以进行2D或3D建模。在求解空间等效分段时,常用分段方法如图9所示。图9a、图9b基于2D平面模型,分别为方形分段和正六边形分段,图9c基于3D模型,为方体分段,类似于有限元中的网格剖分,将网格确定好后,各单元节点位置也随之确定,各节点之间的磁导计算公式由形状和材料磁导率所决定。考虑到PMLSM同时存在齿槽效应和边端效应,气隙和边端处的磁场分布较为复杂,磁力线路径不像初级轭部和齿中段处的规整,所以通常会采用磁路规划法[19]或者网格化磁 阻[20-21]的方式来对气隙和边端处的磁力线进行处理。基于铁心材料的B-H曲线,采用迭代计算来考虑铁心的饱和效应。
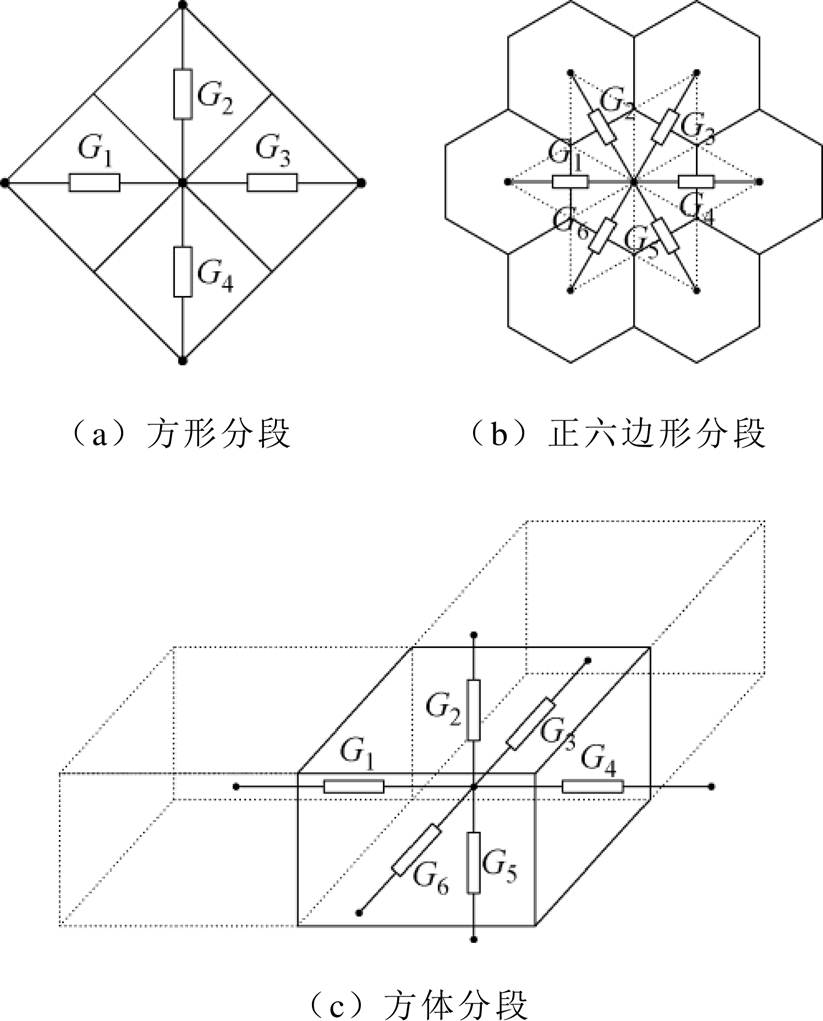
图9 磁网络法分段单元类型
Fig.9 Segment unit types of magnetic network
文献[19]结合有限元磁场分布,对边端、齿槽处的磁通路径用直线和半圆段弧线进行定义,如图10所示。与有限元结果相比,此方法计算得到的反电动势误差为2.7%,定位力误差为17.7%,定位力精度不高,模型节点总数488个,但计算仅需17 s,非常适合快速优化设计。
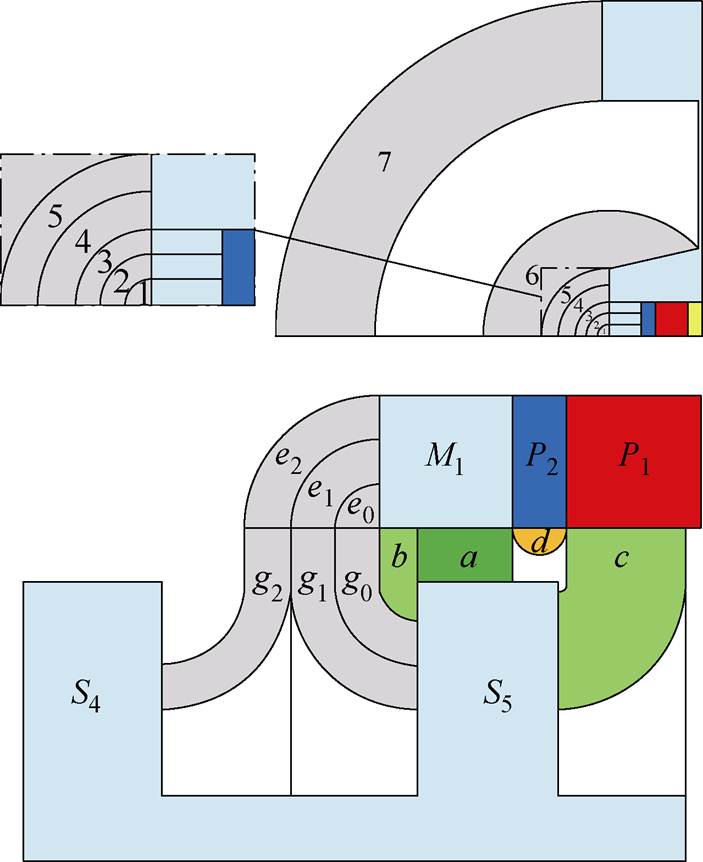
图10 磁路规划的磁网络模型[19]
Fig.10 Magnetic network model with flux path division[19]
为了提高磁网络法的计算精度,需要对磁场进行细化分段,因此有学者类比有限元的网格剖分提出了网格化磁阻的方式。文献[20]在气隙部分进行了网格加密剖分,如图11所示,并且比较了方形和正六边形两种单元划分的效果。为避免产生过多的节点增加时间成本,在边端处同样采用等效弧形磁路。与有限元结果相比,定位力误差为5.6%,用时为205 s,小于有限元的900 s。但是,磁网络模型建立时需要人为识别并设计磁通路径,进行各段磁导的推导,比有限元建模要复杂。
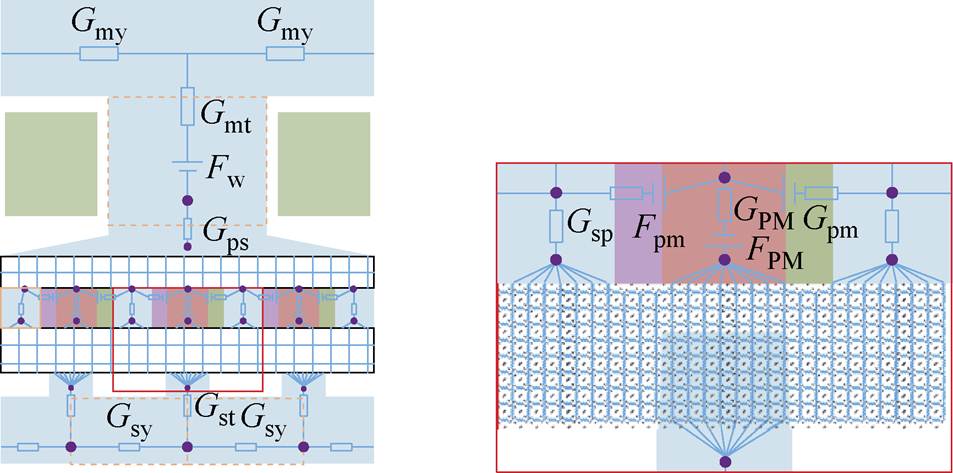
图11 网格化磁阻的磁网络模型[20]
Fig.11 Magnetic network model with meshing reluctance[20]
文献[21]则是针对PMLSM的横向边端效应进行3D建模分析,磁场全部划分为方块单元,根据每块的材料、形状得到每两个节点之间的磁导,并考虑了永磁退磁曲线。该方法具有通用性,不需要进行特定的磁路规划,随着网格密度增加,精度提高,但节点数会激增使得时间成本增加。由于定、动子之间的节点连接情况会随相对位置的变化而变化,不可避免地会引起误差波动,需要选择平滑算法或者滤波算法进行二次处理。
与解析法相比,磁网络法原理简单,能够考虑铁心饱和影响,通过磁路规划法或网格化磁阻的方式,可以同时考虑PMLSM齿槽效应和边端效应,磁路计算速度快,但需要将连续磁场进行空间节点化处理,定子与动子之间节点连接会变化,引入了计算误差,使得在空载条件下计算精度不如精确子域法,另外也存在建模过程复杂、灵活度低的缺点。
有限元法可以进行2D与3D建模,建模直接方便,模型中包括了PMLSM的边端和齿槽,并设置了铁心的B-H曲线,因此计算同时考虑了边端效应、齿槽效应与铁心饱和,得到的定位力计算精度高,也能够方便地进行边端力与齿槽力分离,逐渐成为PMLSM电磁性能分析与优化的主要手段[22],结果准确度获得了公认,成为解析法和磁网络法计算精度的对比标准。
但有限元法无法直接给出电磁性能与电机结构参数之间的关系,且计算精度与速度受网格剖分质量的影响大。电机模型越大,所需的网格数量越多,求解耗时越长。目前,有限元仿真软件性能不断提升,能够基于参数化建模采用遗传算法进行全局优化,获得优化方案,但耗时很久,尤其是在有多个优化变量时。为此,结合有限元模型与机器学习的优化算法获得了关注,其通过有限元模型建立样本库,再采用机器学习方法获得电机的代理模型,保证了电磁性能的计算精度与速度,再采用全局优化算法进行结构优化,优化时间大大缩短。
表2对以上三种PMLSM定位分析方法进行比较,主要对比了计算精度和时间成本。有限元建模方便直接,计算精度最高,但同时耗时也比较久,且受有限元仿真软件的限制,会增加一些研究成本;而解析法和磁网络法不需要专用软件,建模需要理论基础,并且需要合理的假设条件降低时间成本,但同时也不可避免地损失了一些精度。因此,在PMLSM分析与优化过程中,可根据不同的需求选择合适的计算方式,也可以选择两种方式进行组合。例如,为了提高优化设计的效率,通常会选择子域模型或磁网络模型进行快速分析来完成初步优化,再由有限元法进行验证和精密优化。
表2 三种PMLSM定位力分析方法比较
Tab.2 Comparison of three detent force analysis methods for PMLSM

子域法磁网络法有限元法 适用范围2D、3D 考虑铁心饱和的方法未考虑迭代计算设置材料B-H曲线 考虑齿槽效应的方法引入卡特系数[11]、划分槽子域[13-14]、保角变换[15-17]磁路规划 法[19]、网格化磁阻[20-21]建模后网格剖分 考虑边端效应的方法引入磁场外悬系数[11]、划分空气域[12-15]磁路规划 法[19-20]、网格化磁阻[21]建模后网格剖分 计算精度(与有限元对比)定位力误差2%以内[13]定位力误差5.6%[20]— 耗时均少于有限元法,但精度越高,耗时越多— 优点建模简单,灵活度高,空载磁场的计算精度高原理简单,可考虑铁心饱和效应,建模后求解速度快计算精度高,逼近真实磁场情况 缺点忽略了铁心饱和效应精度依赖模型,建模过程复杂,灵活度低受网格剖分质量影响大,仿真耗时久
PMLSM定位力抑制主要从电机本体结构优化和控制补偿两个方面进行。
削弱定位力的思路可分为两种:一种是分离抑制方法,其将定位力中的齿槽力和边端力分离,分别采取相应的抑制手段;另一种则是直接抑制,其直接削弱定位力,能考虑齿槽力和边端力之间的耦合影响。
分离抑制方法应用得较多,具体过程为:先分离定位力中的齿槽力和边端力两个分量,再分别采取相应的方式进行削弱。文献[23]采用端部铁心无限长的模型来消除边端效应的影响,如图4a所示。利用有限元仿真得到该模型的定位力即为齿槽力,再用原电机定位力减去齿槽力即可得到边端力。但实际上该模型端部由无槽到有槽的过渡过程中仍存在一定的磁场畸变,有边端效应的影响,因此这种分离方法存在一定的误差。文献[24]采用初级铁心无齿槽的模型来消除齿槽效应的影响,如图4b所示。利用有限元仿真得到该模型的定位力即为边端力,再用原电机的定位力减去边端力即得到齿槽力,但该方法忽略了端部齿、槽形状对边端力的影响。也就是说,无论采取哪种分离方法,齿槽力与边端力的耦合影响都被忽略了,这是分离抑制方法所存在的弊端。
将齿槽力和边端力分离出来后,可以分别采取相应的抑制方法,见表3。
在齿槽力抑制方面,其原理与旋转电机的齿槽转矩类似,所采用的方法也与之相似,常见的有以下几种[25]:
(1)优化极槽配合。当定、动子发生相对位移时,齿槽力会呈周期性变换,齿谐波的次数与极槽数相关,且齿谐波次数越大,幅值就越小,选择合适的极槽配合有利于降低齿槽力大小,因此绕组端部非重叠的近槽配合被广泛采用,其初级槽数与次级极数相差为1或2,分数槽结构大大降低了齿槽力。文献[26]将分数槽结构和整距绕组结构进行了对比,基于齿槽周期延拓模型,采用分数槽结构后的齿槽力峰值从20.5 N降到了0.22 N。文献[27]以PMLSM齿槽力最小化为目标,分析了不同极槽配合下的齿槽力大小,并得出了最优极槽组合为极槽数互质的结论。
表3 齿槽力和边端力的抑制方法
Tab.3 Suppression methods of cogging force and end force
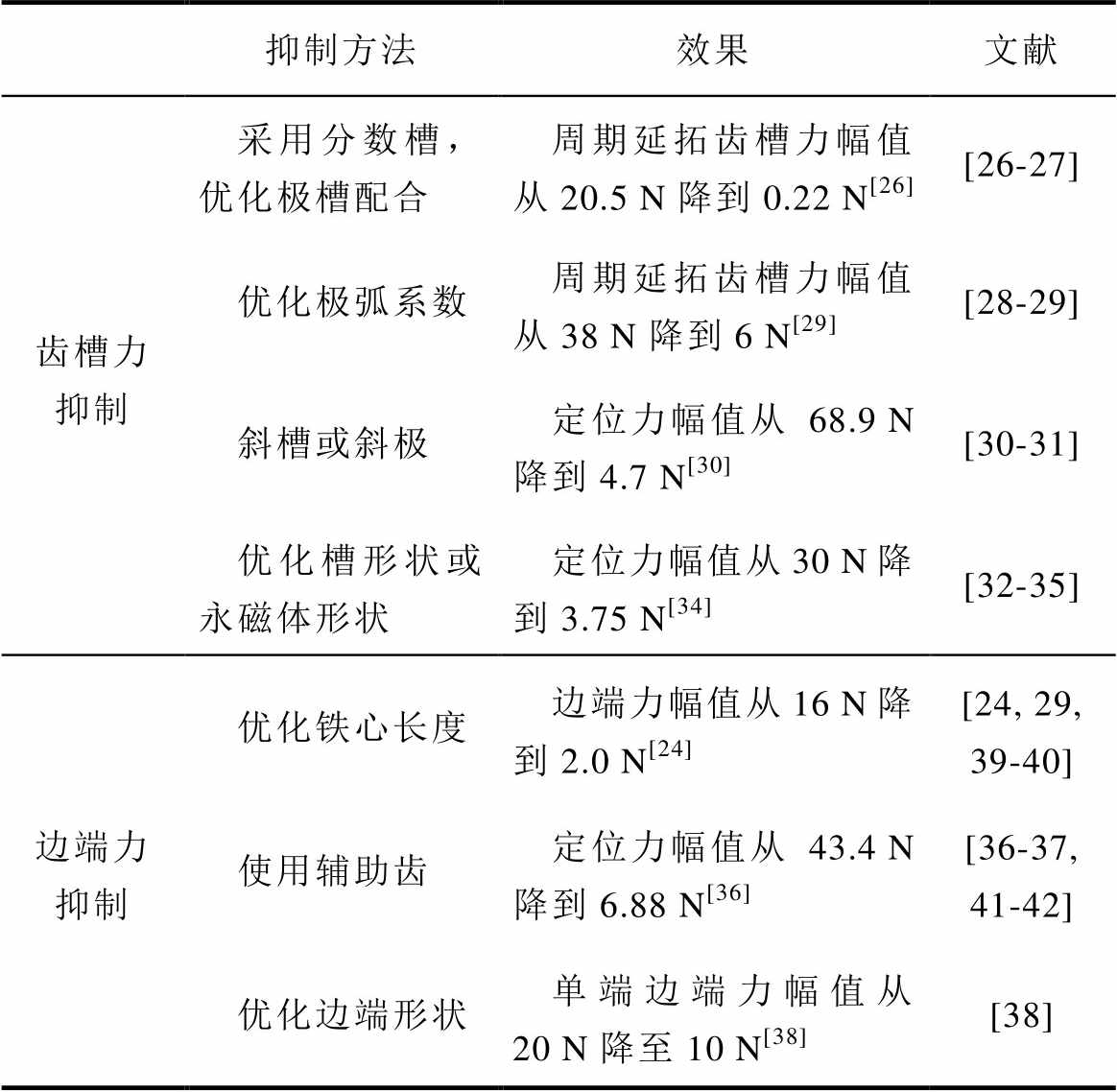
抑制方法效果文献 齿槽力抑制采用分数槽,优化极槽配合周期延拓齿槽力幅值从20.5 N降到0.22 N[26][26-27] 优化极弧系数周期延拓齿槽力幅值从38 N降到6 N[29][28-29] 斜槽或斜极定位力幅值从68.9 N降到4.7 N[30][30-31] 优化槽形状或永磁体形状定位力幅值从30 N降到3.75 N[34][32-35] 边端力抑制优化铁心长度边端力幅值从16 N降到2.0 N[24][24, 29, 39-40] 使用辅助齿定位力幅值从43.4 N降到6.88 N[36][36-37, 41-42] 优化边端形状单端边端力幅值从20 N降至10 N[38][38]
(2)优化极弧系数。极弧系数直接决定了永磁体提供的磁通密度大小,影响气隙磁通密度的分布,同时也影响着齿槽力的形状和各次谐波幅值,选择合适的极弧系数可有效降低齿槽力的谐波分量[28]。文献[29]基于周期延拓的齿槽力模型,发现随着永磁体宽度,即极弧系数的变化,齿槽力幅值呈周期性变化,对极弧系数进行优化可以使齿槽力幅值最小化。
(3)斜槽或斜极。文献[30]采用磁极的分段斜极来减小齿槽力,优化后的定位力峰峰值从68.9 N降至4.7 N。文献[31]对比了极弧系数、斜极和半闭口槽这三种方法对齿槽力的抑制效果,发现磁极斜极是减小齿槽力最有效的方法,但是斜极也会造成平均推力的下降。
(4)优化槽形状或永磁体形状。文献[32]提出了采用不等槽口宽配合的方法减小齿槽转矩,并给出了具体的匹配方法,不过只适用于偶数槽电机。文献[33]研究了磁极的宽度、高度以及磁极倒角的影响,发现选择合适的磁极倒角可以改善PMLSM的输出特性。文献[34]提出了三种不同的梯形磁极结构来改善气隙磁场分布,并与常规的矩形磁极比较,如图12所示,发现底部斜角的结构对齿槽力的抑制效果更佳。文献[35]采用Halbach磁极结构来减小永磁磁场的谐波,从而削弱齿槽力。
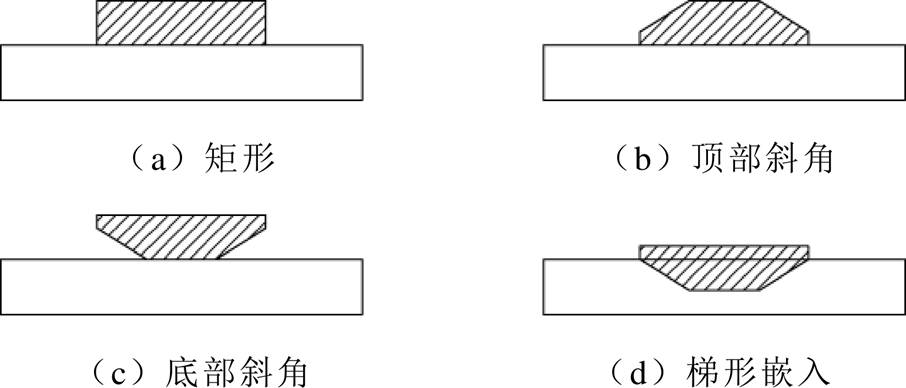
图12 不同磁极形状示意图
Fig.12 Schematic diagram of different magnet shapes
需要注意的是,方法(1)和方法(2)是将齿槽进行周期延拓后得到的齿槽力,并非采用图4分离模型得到的齿槽力,因此针对的是高次齿谐波的优化抑制,与旋转电机齿槽转矩原理相同。但对于采用全齿绕组的短初级PMLSM来说,齿槽力中还存在附加槽所产生的大量低次谐波,对此可采用方法(3)和方法(4)进行抑制。
在边端力抑制方面,主要采取的方法有优化铁心长度[24]、使用辅助齿[36-37]和优化边端形状[38]等。文献[39]中最先指出存在使边端力最小化的最佳铁心长度。文献[40]采用Fourier级数的形式表达单边磁吸力,进而推导出了端部力,通过优化初级铁心长度和端部齿形状削弱了切向力和法向力。文献[29]基于等效磁化电流法和Schwarz-Christoffel变换建立的电磁场解析模型上,结合有限元的仿真计算,讨论了边端力的周期特性,给出了最佳铁心长度的预测值。文献[36]研究了辅助齿结构对单边永磁直线同步电机定位力的影响,通过优化辅助齿的结构参数减小了边端力。文献[41]建立了边端力的解析模型,推导得到了辅助齿宽度和最优位置与永磁极距、初级槽宽之间的关系。文献[42]提出了带隔磁桥的辅助极设计,实现了电机初级与辅助极在机械上连接而在电磁上隔离的目的,并通过解析法推导出了辅助极的最优位置和最优宽度的表达式。文献[38]提出了凹型端齿的设计,可有效削弱边端力的主要谐波成分。
分离抑制方法具体应用于PMLSM结构优化时,需要根据结构类型以及优化需求来采取合适的齿槽力和边端力的抑制方法。以长初级短次级的PMLSM为例,由于纵向边端效应由短次级的两端开断引起,此时针对初级优化的方法如优化铁心长度、辅助齿等将不再适用,可采用的方法是优化次级结构,如斜极、优化永磁形状等[33]。由于长初级结构的制造成本和运行费用较高,因此应用研究最多的是长次级结构,可采用的抑制方法也更多样。文献[43]针对圆筒型PMLSM,分别采用优化齿槽形状和初级长度的方法削弱齿槽力和边端力,使得推力波动降低至5.04%。因铁心开断产生的边端力要远大于齿槽力,也有一些学者会侧重于边端力的分析,如文献[24]中,对单边平板型PMLSM建立了关于边端力的分析模型,并提出存在使边端力最小的最佳初级长度,但需要耦合迭代找到最优值,且进一步采取了如图13所示的分段倾斜辅助齿结构,优化后的定位力峰峰值从28 N削弱到了4.2 N。
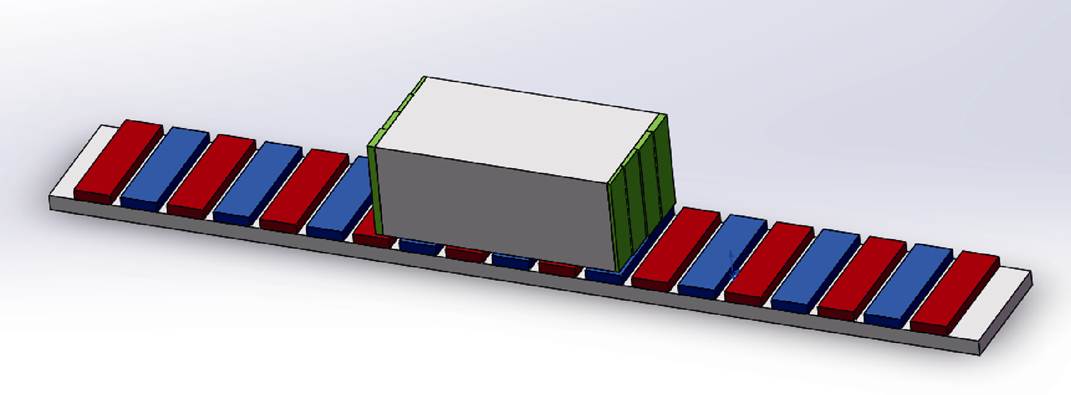
图13 分段倾斜的辅助齿结构示意图
Fig.13 Structure diagram of step-skewed auxiliary iron
分离抑制方法存在的问题是忽略了齿槽力与边端力之间的耦合影响,为了实现更好的定位力抑制效果,有很多研究者调整思路,采用直接抑制方法,也就是直接抑制PMLSM定位力。文献[44]研究了齿尖形状与边端齿形状对定位力的影响,并利用响应面函数对结构参数进行了优化,将定位力峰峰值从11.7 N降到2.7 N。文献[45]针对PMLSM定位力的主要谐波成分,提出了采用分段斜极时,区别于旋转电机的分段数和倾斜角的最优选取方法。
双边平板型PMLSM定位力抑制的结构调整方法更加多样。文献[46]提出了反向槽结构,优化了4个边端齿宽度,使得定位力峰峰值从17.5 N减小到7.6 N,另外还增加了两个补偿绕组,使推力波动进一步降低,小于4%,改善了推力性能。文献[47]提出了一种双边不对称的PMLSM结构,将双边电枢铁心错开90°电角度的距离,并重新排列绕组,对于18槽16极双边PMLSM,其定位力峰峰值可削弱到3.94 N,实验验证了此方法具有较好的定位力抑制效果。文献[48]设计了不等槽宽的结构,并结合斜极的方法,将双边PMLSM的定位力削弱了73%(峰峰值削弱到3.4 N),且没有牺牲其他性能。但上述这些方法使得电机结构复杂化,增加了加工制造成本。文献[8]利用边端槽宽去调节齿槽力,利用双初级共四个辅助齿宽去调节边端力,使得两者幅值相等、相位相反,从而达到相互抵消的目的,如图14所示,此方法将定位力削弱了95.5%,其峰峰值从334 N抑制到了15 N,且只更改了辅助齿的结构,加工成本低。类似的调制法思想也分别应用于圆筒型结构[49]和单边平板型结构[50],都可实现较好的定位力抑制效果。
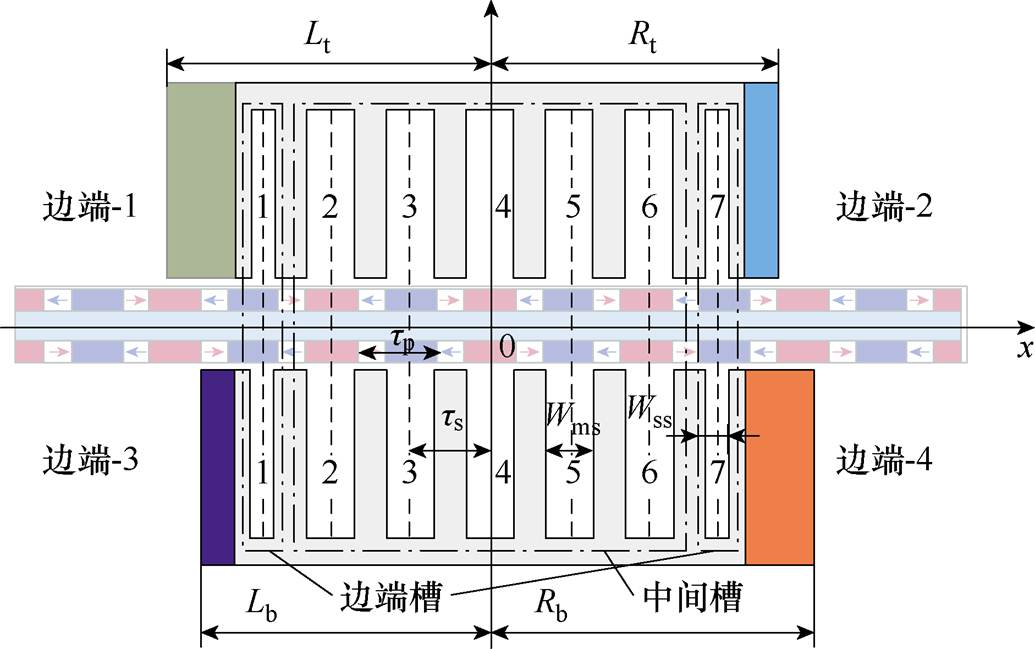
图14 双边PMLSM的调制法模型[8]
Fig.14 Modulation method model for double-sided PMLSM[8]
分离抑制和直接抑制定位力两种方法在PMLSM优化中的应用效果见表4。相比于将齿槽力和边端力进行分离抑制的方法,直接抑制定位力的方法可以将PMLSM定位力的峰峰值抑制得更小,且适用于双边平板型结构的抑制方法更多。这些抑制方法也存在各自的弊端,斜极是一种有效削弱PMLSM定位力的方法,但同时也牺牲了部分平均推力;特殊形状的齿槽或永磁结构会提高加工制造的难度;双边平板型PMLSM拥有很好的定位力抑制效果,但是结构复杂使得适用范围受限;辅助齿调制法在双、单边平板型以及圆筒型PMLSM中都适用,抑制效果好,但是此方法受加工精度的影响较大。实际在对PMLSM进行定位力抑制优化时,需要结合结构特点和设计需求,采取合适的抑制方法。
表4 两种定位力抑制方法的应用效果
Tab.4 Effectiveness of two detent force suppression methods

PMLSM类型抑制方法抑制效果文献 分离抑制单边平板型优化铁心长度+分段倾斜辅助齿定位力峰峰值从28 N降到4.2 N[24] 圆筒型优化极弧系数和槽形状+优化铁心长度推力波动从1.14 kN降到0.22 kN[43] 直接抑制单边平板型优化齿尖形状与边端齿形状定位力峰峰值从11.7 N降到2.7 N[44] 双边平板型反向槽结构+优化边端齿定位力峰峰值从17.5 N降到7.6 N[46] 双边平板型错齿结构定位力峰峰值从126.44 N降到3.94 N[47] 双边平板型不等槽宽结构定位力峰峰值从12.8 N降到3.4 N[48] 双边平板型辅助齿调制法定位力峰峰值从334 N降到15 N[8] 圆筒型辅助齿调制法定位力峰峰值从20.05 N降到3.24 N[49] 单边平板型辅助齿调制法定位力峰峰值从41.65 N降到0.94 N[50]
控制抑制方法主要可分为基于定位力数学模型的补偿方法和不基于定位力数学模型的补偿方法[51],见表5。
表5 两种控制补偿策略
Tab.5 Two kinds of control compensation strategies

补偿方法控制效果文献 基于定位力数学模型查表法速度响应波动从11.36%降到6.42%[52] Fourier级数曲线拟合法速度响应波动降低到补偿前的15%左右[54][53-56] 自适应控制搜索法定位误差0.001 m[57] 递推最小二乘法轨迹误差波动从17.9 mm降到1.1 mm[58] 不基于定位力数学模型降阶扰动观测器负载突变响应时间0.1 s[59] 斜极+线性观测器速度响应波动从2.5%降到0.5%[60] 前馈控制的观测器速度响应波动降低了36%[61] 比例谐振内膜扩张状态观测器速度波动的平均抑制率为68.7%[62]
基于定位力数学模型的抑制方法是通过有限元分析或实验采集得到定位力数据,然后采取查表或者数学建模的方法,将对应的补偿电流注入闭环控制系统中,抑制定位力扰动。这类方法比较依赖于定位力模型的准确性。文献[52]在实验校正的基础上,利用有限元方法建立以次级位置和给定电流为索引量的电流补偿模型和补偿表,在PMLSM运行时快速查找相应的电流补偿值,并通过实验验证了此补偿方法的有效性。
查表法占用了大量的存储空间,本身补偿表的长度和精度具有局限性,因此很多学者在定位力的数学模型构造方面进行了很多研究。文献[53-55]基于有限元仿真对定位力波形进行了傅里叶级数曲线拟合,并通过前馈电流补偿的方法使得定位力最小化。文献[56]在前者的基础上增加了扰动观测器进行前馈补偿,将波动降低到了补偿前的15%左右。文献[57]针对重复往返运行的工况,利用定位力与位置相关的周期性,采用自适应控制策略对系统控制器的参数做相应改变,但自适应控制需要耗费较长时间来调整参数。文献[58]在不改变系统结构的情况下,根据加速度计采集的定位力波动数据,利用递推最小二乘法得到定位力模型,并结合基于位置的补偿控制器和迭代学习控制器,降低了电机运行中的定位误差。
PMLSM运行中影响推力波动的因素不只是定位力,对所有扰动进行测量和精确建模是不现实的,所以有很多学者将包括定位力在内的所有扰动均看成外部扰动,不需要进行精确建模,只需利用观测器等方法观测出扰动的近似值,再进行在线的补偿,称为不基于定位力数学模型的控制补偿方法。文献[59]利用降阶扰动观测器对定位力进行补偿和抑制,通过仿真模拟验证了PMLSM不同工况下的观测器补偿的有效性。文献[60]则将电机结构优化和控制优化相结合,用斜极消除定位力的高频分量,再利用线性观测器补偿定位力的低次谐波分量,与无定位力补偿的控制效果相比,速度的响应波动从2.5%下降到了0.5%。此方法简单且能显著减小定位力对速度响应的影响,但是不能对非线性扰动进行补偿。此外,定位力与位置相关,在较高速度下,定位力的频率分量较高,而观测器带宽受测量噪声的限制,运行速度升高,扰动补偿的效果会变差。针对此问题,文献[61]设计了一种带前馈控制的观测器,与直接反馈的观测器相比,前者在高速情况下对扰动的补偿效果更好,但是由于此前馈控制是基于位置函数的,所以比较依赖初始位置估计算法的性能。文献[62]建立了考虑定位力模型的比例谐振内膜扩张状态观测器,在不同工况下对定位力具有明显的观测补偿作用,同时也可抑制其他扰动成分,动子速度波动的平均抑制率为68.7%。
现代控制策略或者智能控制策略也被很多学者应用于扰动抑制,如利用滑模控制替代传统的PI控制[63-64]、结合人工神经网络算法的自适应观测 器[65-66]、利用模糊控制改进的自适应滑模控制器[67-68]等。
定位力虽然是PMLSM推力波动的主要成分,但是在不同负载条件下其所占比重会有所变化。以图2a所示的6槽5极PMLSM为例,通过有限元仿真可得到不同电流时的推力波动峰峰值,结果如图15所示。由图15可见,空载推力波动(定位力)峰峰值为4.43 N,额定电流2.5 A时推力波动峰峰值为5.26 N,定位力的占比高达84.2%,此时抑制定位力能够有效地削弱推力波动。但在2倍和3倍过载电流时,定位力占比分别降至54.8%、42.6%,此时仅对定位力进行抑制并不能有效降低推力波动。
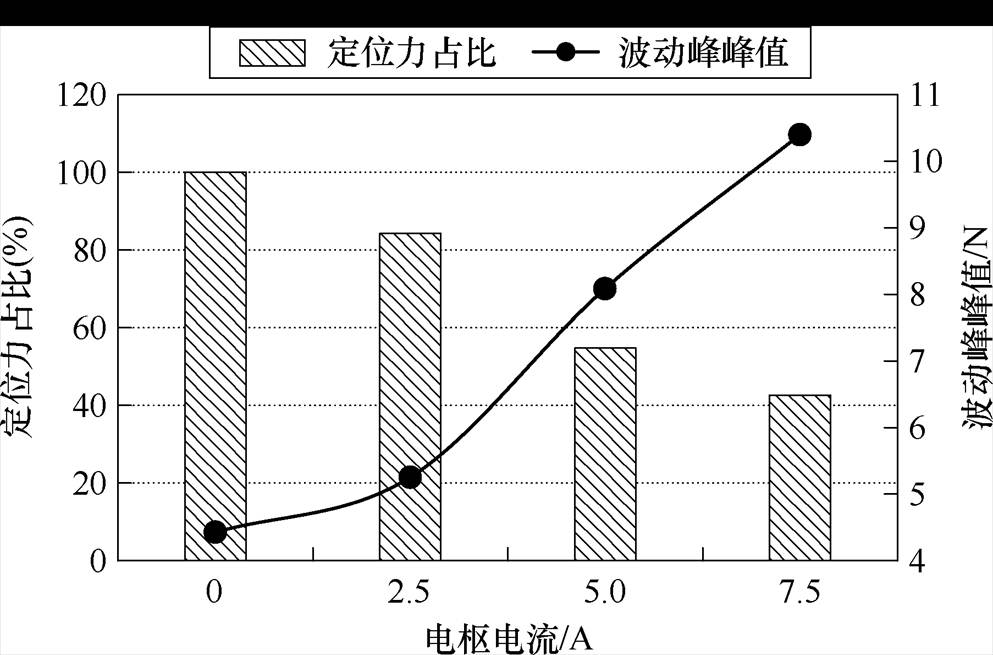
图15 不同电枢电流时定位力在推力波动中的比重
Fig.15 The proportion of detent force in thrust ripple at different armature currents
此外,以抑制定位力为优化目标得到的最优方案,对实际负载条件下运行时的推力波动并不一定是最优方案。以图2a所示6槽5极PMLSM为例,分别以空载和负载时的波动峰峰值最小为优化目标,利用遗传算法进行优化迭代,得到的最优辅助齿并不同,见表6。显然,负载推力波动达到最小的优化结构,其定位力并不是最小。因此,只对定位力进行抑制并不能确保负载推力波动也有同等的抑制效果。
为了将负载推力波动中电枢电流的影响也考虑在内,解析模型中需要设置负载电流,同时考虑铁心的饱和效应。目前,有部分学者针对考虑铁心饱和效应的子域法进行了研究,常用的两种方法分别为采取非同质的诺伊曼边界条件和引入傅里叶级数形式的磁导率函数[69],前者的精度更高,但耗时也更长,不过两者都是针对旋转电机的电磁场分析,还未有在PMLSM方面的应用。文献[70]则是基于能够通过迭代方式考虑铁心饱和效应的磁路法,并结合能够快速计算的子域法,提出了一种既能考虑边端效应和齿槽效应,又能考虑铁心饱和效应的混合解析模型,其推力的计算误差为4.2%,与有限元相比,用时缩短了28%。
表6 不同条件下的优化结果
Tab.6 Optimization results with different conditions
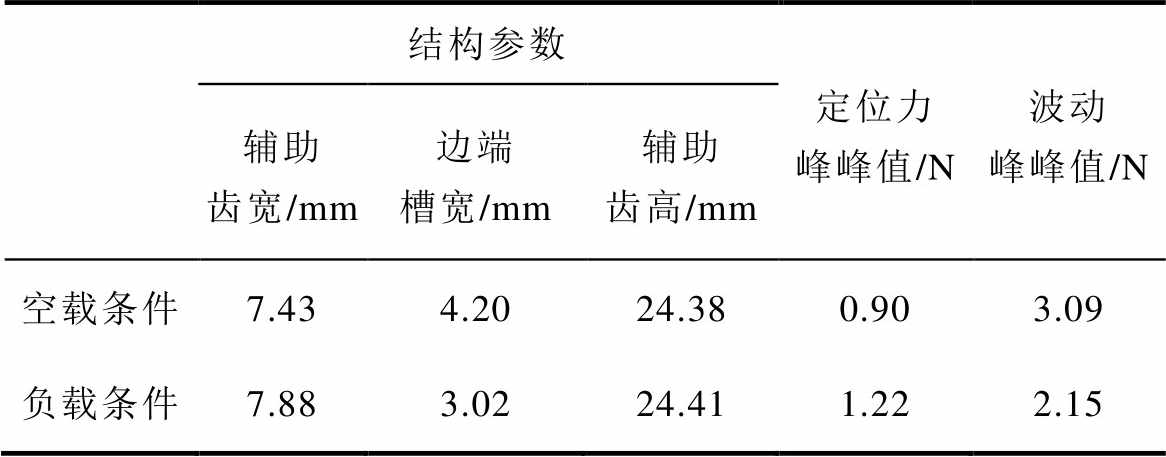
结构参数定位力峰峰值/N波动峰峰值/N 辅助齿宽/mm边端槽宽/mm辅助齿高/mm 空载条件7.434.2024.380.903.09 负载条件7.883.0224.411.222.15
目前,对负载推力波动的成分分离还存在一定的困难,部分学者仍旧采用定位力的抑制策略,只是在对结构参数进行优化调整时基于负载模型,以推力波动最小化为优化目标[45, 71]。也有学者对多速段的优化算法进行了研究。文献[72]采用梯形永磁,在对结构参数进行优化时,先得到不同速度下的最优参数集,再利用信噪比算法得到最终的多速段综合优化结果。而在电机控制方面,对不同负载条件下进行推力波动的抑制补偿需要进行快速有效的在线观测,对控制器和控制算法的性能要求较高。文献[73]提出了一种改进的预测电流控制,采用离散时间的线性观测器观测推力波动,通过此方法补偿后的速度曲线波动从4%降到了1%,但是该测试电机本体结构未进行优化,定位力较大,峰峰值在18 N左右。如果让PMLSM直驱控制系统实现更高的精度,在推力波动抑制方面应当结合电机本体结构和控制补偿策略两方面,从系统的角度采取抑制措施。
综上所述,实际运行时定位力在推力波动中的占比会有所变化,因此定位力抑制到最小并不代表运行时的推力波动也抑制到最优。为了实现更好的推力波动抑制效果,需要进一步考虑电枢电流的影响。有部分学者基于定位力的抑制策略,在优化过程中以负载推力波动为优化目标,优化在固定负载下进行,能把该负载下的推力波动降低到最小值,但不适用于全工况。为了实现全工况下的推力波动优化,可以采取在线的推力波动补偿控制,但对推力波动模型或观测器的精度要求高,提高了控制成本。未来可以采用结构优化和控制策略相结合的方式,分别优化推力波动的不同频次分量,从而实现更优的控制效果。
本文综述了目前PMLSM定位力的分析方法和抑制技术,并指出了定位力抑制存在的不足,进一步考虑不同负载条件下推力波动的分析方法及影响因素至关重要,未来相关研究将主要集中在以下几个方面:
1)考虑铁心饱和效应的精确解析模型。只对定位力进行优化并不能保证负载推力波动具有同样的抑制效果,因此需要建立负载条件下的推力波动解析模型,此时铁心的饱和效应不可忽略。目前已有的方法是考虑铁心非线性的精确子域法或混合解析模型。考虑铁心非线性的精确子域法目前应用于旋转电机,之后可拓展应用于PMLSM结构,但由于其特有的边端效应,模型会更为复杂,对此可采用局部非线性的方式,降低模型的复杂程度,提高计算效率;混合解析模型则结合子域法和磁网络法的优点,只在易饱和的铁心区域进行磁网络节点划分,但建模过程比较复杂,灵活度较低,可考虑参数化建模研究。
2)更高效的推力波动抑制措施。定位力抑制研究的目的是减小推力波动,为了实现更好的波动抑制效果,需要进一步考虑实际运行条件。可以从分析负载推力波动的组成和各谐波分量的影响因素着手,考虑定位力与纹波推力的调制抵消思路,实现对负载推力波动的直接抑制,从而实现更好的运行性能。此外,PMLSM优化设计时不仅可以采用传统分析方法,还可以采用基于数据驱动的代理模型,提高优化设计的效率。电机本体的优化除了常见的结构参数优化,还可以考虑进行拓扑结构优化,即网格化区域,对不同的网格进行材料分配,可以实现更多样的结构设计,具有更高的自由度和灵活 性[74]。除了以上确定性优化外,考虑到电机性能对结构参数的敏感度,需要进行考虑制造公差的鲁棒性优化[75],以提高产品批量生产的质量。
3)系统层面进行推力波动抑制。为满足高精度控制的需求,需要结合电机结构优化与控制补偿策略,不受负载影响的波动分量由电机本体结构优化予以抑制,从源头上削弱该部分推力波动;与负载电流相关的波动分量则由控制补偿策略来抑制,在深入分析变化规律与影响因素的基础上,通过高性能观测器在线实时观测扰动分量,实现快速补偿,从而获取更优的控制效果。
参考文献
[1] 吕刚. 直线电机在轨道交通中的应用与关键技术综述[J]. 中国电机工程学报, 2020, 40(17): 5665-5675.
Lü Gang. Review of the application and key tech- nology in the linear motor for the rail transit[J]. Proceedings of the CSEE, 2020, 40(17): 5665-5675.
[2] 鲁军勇, 柳应全. 电磁发射用直线电机及其控制技术综述[J]. 电工技术学报, 2024, 39(19): 5899-5913.
Lu Junyong, Liu Yingquan. Review on linear motor for electromagnetic launch and its control tech- nology[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5899-5913.
[3] 赵立华, 谭立杰, 黄卫国, 等. 直线电机在半导体设备中的典型应用分析[J]. 电子工业专用设备, 2019, 48(2): 16-19.
Zhao Lihua, Tan Lijie, Huang Weiguo, et al. Linear motor analysis in semiconductor equipment appli- cation[J]. Equipment for Electronic Products Manufa- cturing, 2019, 48(2): 16-19.
[4] 杨永康. 定子分段式永磁同步直线电机的控制方案及其在门控系统应用研究[D]. 济南: 山东大学, 2022.
Yang Yongkang. Research on control strategies of stator-segmented permanent magnet synchronous linear motor and its application to door system[D]. Jinan: Shandong University, 2022.
[5] 张美玉. 直线电机作动器在汽车悬架主动控制中的应用研究[D]. 长春: 吉林大学, 2022.
Zhang Meiyu. Research on application of linear motor actuator in active control of automobile suspen- sion[D]. Changchun: Jilin University, 2022.
[6] Kung Y S. Design and implementation of a high- performance PMLSM drives using DSP chip[J]. IEEE Transactions on Industrial Electronics, 2008, 55(3): 1341-1351.
[7] Danielsson O, Leijon M. Flux distribution in linear permanent-magnet synchronous machines including longitudinal end effects[J]. IEEE Transactions on Magnetics, 2007, 43(7): 3197-3201.
[8] Zhang Chi, Chen Feixue, Qiu Shuheng, et al. A low detent force DS-PMSLM based on the modulation of cogging and end forces[J]. IEEE Transactions on Industrial Electronics, 2023, 70(1): 721-730.
[9] Boff B H B, Eckert P R, Amara Y. A comprehensive review on the end effects of linear permanent magnet machines[C]//2021 13th International Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 2021: 1-6.
[10] 卢琴芬, 沈燚明, 叶云岳. 永磁直线电动机结构及研究发展综述[J]. 中国电机工程学报, 2019, 39(9): 2575-2588.
Lu Qinfen, Shen Yiming, Ye Yunyue. Development of permanent magnet linear synchronous motors structure and research[J]. Proceedings of the CSEE, 2019, 39(9): 2575-2588.
[11] Wang Jiabin, Jewell G W, Howe D. A general framework for the analysis and design of tubular linear permanent magnet machines[J]. IEEE Transa- ctions on Magnetics, 1999, 35(3): 1986-2000.
[12] 赵云涛, 卢琴芬, 李焱鑫. 无槽圆筒永磁直线同步电机推力波动的解析模型及抑制方法[J]. 中国电机工程学报, 2023, 43(16): 6453-6464.
Zhao Yuntao, Lu Qinfen, Li Yanxin. Analytical model and suppression method of thrust ripple in slot-less tubular permanent magnet linear synchronous machines[J]. Proceedings of the CSEE, 2023, 43(16): 6453-6464.
[13] Hu Hengzai, Zhao Jing, Liu Xiangdong, et al. No-load magnetic field and cogging force calculation in linear permanent-magnet synchronous machines with semi- closed slots[J]. IEEE Transactions on Industrial Electronics, 2017, 64(7): 5564-5575.
[14] Chen Feixue, Zhang Chi, Chen Jinhua, et al. Accurate subdomain model for computing magnetic field of short moving-magnet linear motor with halbach array[J]. IEEE Transactions on Magnetics, 2020, 56(9): 8200509.
[15] Lu Qinfen, Wu Bocheng, Yao Yihua, et al. Analytical model of permanent magnet linear synchronous machines considering end effect and slotting effect[J]. IEEE Transactions on Energy Conversion, 2020, 35(1): 139-148.
[16] Zhu Z Q, Howe D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors. Ⅱ. armature-reaction field[J]. IEEE Transa- ctions on Magnetics, 1993, 29(1): 136-142.
[17] Zhu Z Q, Howe D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors. Ⅲ. effect of stator slotting[J]. IEEE Transa- ctions on Magnetics, 1993, 29(1): 143-151.
[18] de la Barrière O, Hlioui S, Ben Ahmed H, et al. Three-dimensional analytical modeling of a permanent- magnet linear actuator with circular magnets[J]. IEEE Transactions on Magnetics, 2010, 46(9): 3608-3616.
[19] Liu Guohai, Ding Ling, Zhao Wenxiang, et al. Nonlinear equivalent magnetic network of a linear permanent magnet vernier machine with end effect consideration[J]. IEEE Transactions on Magnetics, 2018, 54(1): 8100209.
[20] Liu Guohai, Jiang Shan, Zhao Wenxiang, et al. Modular reluctance network simulation of a linear permanent-magnet vernier machine using new mesh generation methods[J]. IEEE Transactions on Indu- strial Electronics, 2017, 64(7): 5323-5332.
[21] Hur J, Yoon S B, Hwang D Y, et al. Analysis of PMLSM using three dimensional equivalent magnetic circuit network method[J]. IEEE Transactions on Magnetics, 1997, 33(5): 4143-4145.
[22] Boduroglu A, Demir Y, Cumhur B, et al. A novel track structure of double-sided linear PM synchronous motor for low cost and high force density appli- cations[J]. IEEE Transactions on Magnetics, 2021, 57(2): 8201305.
[23] Youn S W, Lee J J, Yoon H S, et al. A new cogging-free permanent-magnet linear motor[J]. IEEE Transactions on Magnetics, 2008, 44(7): 1785-1790.
[24] Hu Hengzai, Liu Xiangdong, Zhao Jing, et al. Analysis and minimization of detent end force in linear permanent magnet synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2018, 65(3): 2475-2486.
[25] Jahns T M, Soong W L. Pulsating torque minimi- zation techniques for permanent magnet AC motor drives-a review[J]. IEEE Transactions on Industrial Electronics, 1996, 43(2): 321-330.
[26] 徐月同, 傅建中, 陈子辰. 永磁直线同步电机推力波动优化及实验研究[J]. 中国电机工程学报, 2005, 25(12): 122-126.
Xu Yuetong, Fu Jianzhong, Chen Zichen. Thrust ripple optimization and experiment for PMLSM[J]. Proceedings of the CSEE, 2005, 25(12): 122-126.
[27] 程远雄. 永磁同步直线电机推力波动的优化设计研究[D]. 武汉: 华中科技大学, 2011.
Cheng Yuanxiong. Study on optimal design of thrust ripple of permanent magnetic synchronous linear motors[D]. Wuhan: Huazhong University of Science and Technology, 2011.
[28] 王秀和, 杨玉波, 丁婷婷, 等. 基于极弧系数选择的实心转子永磁同步电动机齿槽转矩削弱方法研究[J]. 中国电机工程学报, 2005, 25(15): 146-149.
Wang Xiuhe, Yang Yubo, Ding Tingting, et al. The method for reducing cogging torque by suitable selection of pole-arc coefficient in solid-rotor PM synchronous motors[J]. Proceedings of the CSEE, 2005, 25(15): 146-149.
[29] 张颖. 永磁同步直线电机磁阻力分析及控制策略研究[D]. 武汉: 华中科技大学, 2008.
Zhang Ying. Research on the analysis of detent force and control strategies of permanent magnetic synchronous linear motors[D]. Wuhan: Huazhong University of Science and Technology, 2008.
[30] Kim T W, Chang J H. Analysis of thrust characte- ristics considering step-skew and overhang effects in permanent magnet linear synchronous motor[J]. IEEE Transactions on Magnetics, 2015, 51(3): 8102104.
[31] Trapanese M, Cipriani G, Curto D, et al. Optimization of cogging force in a linear permanent magnet generator for the conversion of sea waves energy[C]// 2015 IEEE International Electric Machines & Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 2015: 769-773.
[32] 杨玉波, 王秀和, 陈谢杰, 等. 基于不等槽口宽配合的永磁电动机齿槽转矩削弱方法[J]. 电工技术学报, 2005, 20(3): 40-44.
Yang Yubo, Wang Xiuhe, Chen Xiejie, et al. A method for reducing cogging torque by different slot widths in permanent magnet motors[J]. Transactions of China Electrotechnical Society, 2005, 20(3): 40-44.
[33] Chi Song, Yan Jianhu, Shan Liang, et al. Detent force minimizing for moving-magnet-type linear synchronous motor[J]. IEEE Transactions on Magnetics, 2019, 55(6): 8102005.
[34] Kimoulakis N M, Kladas A G, Tegopoulos J A. Cogging force minimization in a coupled permanent magnet linear generator for sea wave energy extraction applications[J]. IEEE Transactions on Magnetics, 2009, 45(3): 1246-1249.
[35] Xu Xiaozhuo, Sun Zhen, Du Baoyu, et al. Pole optimization and thrust ripple suppression of new halbach consequent-pole PMLSM for ropeless elevator propulsion[J]. IEEE Access, 2020, 8: 62042- 62052.
[36] Zhu Yuwu, Lee Sanggun, Chung K S, et al. Investi- gation of auxiliary poles design criteria on reduction of end effect of detent force for PMLSM[J]. IEEE Transactions on Magnetics, 2009, 45(6): 2863-2866.
[37] Zhang Chao, Zhang Liwei, Huang Xianjin, et al. Research on the method of suppressing the end detent force of permanent magnet linear synchronous motor based on stepped double auxiliary pole[J]. IEEE Access, 2020, 8: 112539-112552.
[38] 彭兵, 刘铁法, 张囡, 等. 凹型端齿削弱永磁直线电机端部力波动方法[J]. 电工技术学报, 2015, 30(7): 119-124.
Peng Bing, Liu Tiefa, Zhang Nan, et al. A method for reducing the end effect force fluctuation by the concave profile end-tooth in permanent magnet linear motors[J]. Transactions of China Electrotechnical Society, 2015, 30(7): 119-124.
[39] Zhu Z O, Xia Z P, Howe D. Reduction of cogging force in slotless linear permanent magnet motors[J]. IEE Proceedings-Electric Power Applications, 1997, 144(4): 277-282.
[40] Inoue M, Sato K. An approach to a suitable stator length for minimizing the detent force of permanent magnet linear synchronous motors[J]. IEEE Transa- ctions on Magnetics, 2000, 36(4): 1890-1893.
[41] Zhang He, Kou Baoquan, Jin Yinxi, et al. Investi- gation of auxiliary poles optimal design on reduction of end effect detent force for PMLSM with typical slot-pole combinations[J]. IEEE Transactions on Magnetics, 2015, 51(11): 8203904.
[42] 寇宝泉, 张赫, 郭守仑, 等. 辅助极一体式永磁同步直线电机端部定位力抑制技术[J]. 电工技术学报, 2015, 30(6): 106-113.
Kou Baoquan, Zhang He, Guo Shoulun, et al. End effect detent force reduction for permanent magnet linear synchronous motors with auxiliary poles one-piece structure[J]. Transactions of China Elec- trotechnical Society, 2015, 30(6): 106-113.
[43] 杨岳. 低速大推力分数槽绕组圆筒型永磁直线电机设计与优化[D]. 哈尔滨: 哈尔滨理工大学, 2019.
Yang Yue. Design and optimization of cylindrical permanent magnet linear motor with low-speed and large-thrust fractional-slot winding[D]. Harbin: Harbin University of Science and Technology, 2019.
[44] Baatar N, Yoon H S, Pham M T, et al. Shape optimal design of a 9-pole 10-slot PMLSM for detent force reduction using adaptive response surface method[J]. IEEE Transactions on Magnetics, 2009, 45(10): 4562- 4565.
[45] Yao Yihua, Chen Yi, Lu Qinfen, et al. Analysis of thrust ripple of permanent magnet linear synchronous motor with skewed PMs[C]//2015 18th International Conference on Electrical Machines and Systems (ICEMS), Pattaya, Thailand, 2015: 1141-1146.
[46] Zhao Jing, Mou Quansong, Zhu Congcong, et al. Study on a double-sided permanent-magnet linear synchronous motor with reversed slots[J]. IEEE/ ASME Transactions on Mechatronics, 2021, 26(1): 3-12.
[47] Huang Xuzhen, Yu Hanchuan, Zhou Bo, et al. Detent-force minimization of double-sided permanent magnet linear synchronous motor by shifting one of the primary components[J]. IEEE Transactions on Industrial Electronics, 2020, 67(1): 180-191.
[48] Chung S U, Kim J M. Double-sided iron-core PMLSM mover teeth arrangement design for redu- ction of detent force and speed ripple[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3000-3008.
[49] Wu Qingle, Yang Guolai, Tang Enling, et al. A slotted double-primaries permanent magnet syn- chronous linear motor with a low thrust ripple[J]. IEEE/ASME Transactions on Mechatronics, 2024, 29(5): 3786-3798.
[50] Wu Lize, Li Yanxin, Lu Qinfen. Detent force fast optimization method of modular permanent-magnet linear synchronous motors[J]. IEEE Transactions on Industrial Electronics, 2024, 71(12): 16191-16199.
[51] 张晓文. 基于卡尔曼滤波器的永磁直线同步电机定位力补偿策略研究[D]. 哈尔滨: 哈尔滨工业大学, 2021.
Zhang Xiaowen. Research on compensation strategy of detent force of permanent magnet linear syn- chronous motor based on Kalman filter[D]. Harbin: Harbin Institute of Technology, 2021.
[52] 夏加宽, 董婷, 王贵子. 抑制永磁直线电机推力波动的电流补偿控制策略[J]. 沈阳工业大学学报, 2006, 28(4): 379-383, 400.
Xia Jiakuan, Dong Ting, Wang Guizi. Current compensation control strategy for restraining thrust fluctuation of PMLSM[J]. Journal of Shenyang University of Technology, 2006, 28(4): 379-383, 400.
[53] Zhu Yuwu, Cho Y H. Thrust ripples suppression of permanent magnet linear synchronous motor[J]. IEEE Transactions on Magnetics, 2007, 43(6): 2537-2539.
[54] Zhu Yuwu, Koo D H, Cho Y H. Detent force minimization of permanent magnet linear syn- chronous motor by means of two different methods[J]. IEEE Transactions on Magnetics, 2008, 44(11): 4345-4348.
[55] Zhu Yuwu, Jin Sangmin, Chung K S, et al. Control- based reduction of detent force for permanent magnet linear synchronous motor[J]. IEEE Transactions on Magnetics, 2009, 45(6): 2827-2830.
[56] 陆华才, 江明, 郭兴众, 等. 永磁直线同步电机推力波动约束[J]. 电工技术学报, 2012, 27(3): 128- 132.
Lu Huacai, Jiang Ming, Guo Xingzhong, et al. Thrust ripple suppression for permanent magnet linear syn- chronous motor[J]. Transactions of China Electro- technical Society, 2012, 27(3): 128-132.
[57] Ahn H S, Chen Yangquan, Dou Huifang. State- periodic adaptive compensation of cogging and Coulomb friction in permanent-magnet linear motors[J]. IEEE Transactions on Magnetics, 2005, 41(1): 90-98.
[58] 陈兴林, 杨天博, 刘杨. 直线电机定位力波动的辨识及迭代补偿方法[J]. 电机与控制学报, 2015, 19(2): 60-65.
Chen Xinglin, Yang Tianbo, Liu Yang. Method of cogging force compensation for linear motor based on model identification and iterative learning[J]. Electric Machines and Control, 2015, 19(2): 60-65.
[59] 唐明, 吴凯, 李龙, 等. 永磁直线同步电机端部效应补偿的扰动观测器设计与仿真[J]. 微电机, 2016, 49(5): 40-44, 67.
Tang Ming, Wu Kai, Li Long, et al. End effects disturbance observer design and simulation of per- manent magnet linear synchronous motor[J]. Micro- motors, 2016, 49(5): 40-44, 67.
[60] Wang Mingyi, Li Liyi, Pan Donghua. Detent force compensation for PMLSM systems based on structural design and control method combination[J]. IEEE Transactions on Industrial Electronics, 2015, 62(11): 6845-6854.
[61] Kim J, Cho K, Jung H, et al. A novel method on disturbance analysis and feed-forward compensation in permanent magnet linear motor system[C]//2014 5th International Conference on Intelligent Systems, Modelling and Simulation, Langkawi, Malaysia, 2014: 394-399.
[62] 张国强, 赵新茹, 张恒, 等. 基于比例谐振内模扩张状态观测器的PMLSM推力波动抑制策略[J]. 电工技术学报, 2024, 39(8): 2449-2458.
Zhang Guoqiang, Zhao Xinru, Zhang Heng, et al. Proportional resonant internal model extended state observer based thrust ripple suppression strategy of PMLSM drives[J]. Transactions of China Electro- technical Society, 2024, 39(8): 2449-2458.
[63] 赵鑫宇, 王丽梅. 永磁直线同步电机自适应分数阶终端滑模控制[J]. 电工技术学报, 2023, 38(20): 5434-5443.
Zhao Xinyu, Wang Limei. Adaptive fractional-order terminal sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5434-5443.
[64] 方馨, 王丽梅, 张康. 基于扰动观测器的永磁直线电机高阶非奇异快速终端滑模控制[J]. 电工技术学报, 2023, 38(2): 409-421.
Fang Xin, Wang Limei, Zhang Kang. High order nonsingular fast terminal sliding mode control of permanent magnet linear motor based on disturbance observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 409-421.
[65] Wang Yiming, Wang Xiuping, Xu X. Backstepping control of primary permanent magnet linear syn- chronous motor based on adaptive RBF obser- ver[C]//2021 IEEE International Conference on Power Electronics, Computer Applications (ICPECA), Shenyang, China, 2021: 957-961.
[66] 宋琳, 聂子玲, 孙军, 等. 基于参数辨识的永磁同步直线电机循环神经网络多维观测器[J]. 电工技术学报, 2024, 39(22): 7059-7072.
Song Lin, Nie Ziling, Sun Jun, et al. Multidi- mensional observer of permanent magnet synchronous linear motor recurrent neural network based on parameter identification[J]. Transactions of China Electrotechnical Society, 2024, 39(22): 7059-7072.
[67] 魏惠芳, 王丽梅. 永磁直线同步电机自适应模糊神经网络时变滑模控制[J]. 电工技术学报, 2022, 37(4): 861-869.
Wei Huifang, Wang Limei. Adaptive fuzzy neural network time-varying sliding mode control for per- manent magnet linear synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(4): 861-869.
[68] Guo Liang, Zheng Chao. Optimization of fuzzy sliding mode controller with improved genetic algo- rithm[C]//2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 2019: 1-5.
[69] Sun Che, Fang Youtong, Pfister P D. Comparison of two finite-permeability subdomain models for surface-mounted permanent-magnet machines con- sidering magnetic saturation[J]. IEEE Transactions on Energy Conversion, 2024, 39(4): 2758-2768.
[70] Li Zhaokai, Wu Lize, Li Yanxin, et al. Hybrid analytical model of permanent magnet linear motor considering iron saturation and end effect[J]. IEEE Transactions on Energy Conversion, 2024, 39(3): 2008-2017.
[71] Liu C T, Hwang C C, Li Pinglun, et al. Design optimization of a double-sided hybrid excited linear flux switching PM motor with low force ripple[J]. IEEE Transactions on Magnetics, 2014, 50(11): 8102704.
[72] Dong Fei, Zhao Jiwen, Song Juncai, et al. Optimal design of permanent magnet linear synchronous motors at multispeed based on particle swarm optimization combined with SN ratio method[J]. IEEE Transactions on Energy Conversion, 2018, 33(4): 1943-1954.
[73] Wang Mingyi, Li Liyi, Pan Donghua, et al. High-bandwidth and strong robust current regulation for PMLSM drives considering thrust ripple[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6646-6657.
[74] Yang Ye, Mizushima K, Matsuba S, et al. Topology optimization using a normalized Gaussian network of iron yoke for magnetic field design of an accelerator superconducting magnet[J]. IEEE Transactions on Applied Superconductivity, 2023, 33(5): 4000105.
[75] 龚夕霞, 李焱鑫, 卢琴芬. 模块化永磁直线同步电机考虑制造公差的推力鲁棒性优化[J]. 电工技术学报, 2024, 39(2): 465-474, 513.
Gong Xixia, Li Yanxin, Lu Qinfen. Thrust robustness optimization of modular permanent magnet linear synchronous motor accounting for manufacture tolerance[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 465-474, 513.
Overview on Analysis and Suppression Techniques of Detent Force for Iron-Core Permanent Magnet Linear Synchronous Motor
Abstract Iron core permanent magnet linear synchronous motor (PMLSM) is widely used in semicon- ductor processing, precision machine tools, and flexible logistics lines that require high-performance linear motions. It has the advantages of high speed, large thrust force, and high thrust force density. However, due to the two broken ends of the structure, the asymmetry of the magnetic circuit causes large thrust ripple, and reducing thrust ripple has become the main objective of optimization design. Usually, the thrust ripple at no-load (detent force) is chosen as the research object. This paper reviews the three methods for calculating the detent force and discusses how to consider the core saturation, cogging effect, and end effect. Then, the suppression methods of detent force are summarized from two aspects of motor structure optimization and control strategy. In addition, the existing problems and limitations of detent force research are pointed out. The development trends of detent force research are predicted.
Firstly, the characteristics and principal components of detent force for an iron-core PMLSM with short primary and short secondary are introduced. For short primary structure, the a-slot PMLSM with all-teeth wound contains a+1 slots due to the broken ends, resulting in the cogging force containing 2nd and 4th harmonic components when taking 2tp (tp is pole pitch) as the fundamental wavelength. The detent force of PMLSM with short secondary operating in the non-end region of the primary contains the teeth harmonic component, similar to the cogging torque of a rotating motor.
Secondly, three analysis methods of the detent force are introduced, which are the analytical method, the magnetic network method, and the finite element method. To consider the slotting and end effects, the exact subdomain method and the conformal mapping method are proposed based on the traditional subdomain method. However, the magnetic saturation is ignored. The magnetic network method considers the nonlinearity of iron properties by iterative calculation, taking into account slotting and end effects through the magnetic circuit division method and the mesh generation method. The finite element method is the most widely used numerical method. It has high accuracy, but needs a long computing time with accurate meshing.
Thirdly, the suppression technology for the detent force is summarized from two aspects: motor design and motor control. In motor design, the optimization methods can be divided into two kinds. One is separating and decreasing the cogging force and end force, and the other is directly weakening the detent force, considering the coupling effect between the cogging force and end force. The latter is more effective in suppressing the detent force. The methods include end-reversed slots, shifting one of the primary components, unequal slot width design, and auxiliary teeth modulation. Most of them are only suitable for double-sided PMLSM. For motor control, the optimization methods of weakening detent force can be divided into compensation methods with and without the mathematical model of detent force. However, the design with the optimal detent force is not optimal for thrust ripple at load, especially under overload conditions. Thus, taking the thrust ripple at load as an optimization objective is needed.
The development trends of detent force research for PMLSM are as follows: (1) Exact analytical model considering core saturation effect. (2) Efficient thrust ripple suppression technologies combined with actual load conditions. (3) System-level thrust ripple suppression optimization combined with structural design and control strategies for high precision control requirements.
Keywords:Permanent magnet linear synchronous motor (PMLSM), iron core, detent force, thrust ripple, suppression techniques, optimization design
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.242250
国家自然科学基金(52177061)和浙江省自然科学基金(LZ23E070002)资助项目。
收稿日期2024-12-16
改稿日期 2025-03-05
吴丽泽 女,1999年生,博士研究生,研究方向为高性能直线电机设计。
E-mail: wulize@zju.edu.cn
卢琴芬 女,1972年生,教授,博士生导师,研究方向为直线电机优化设计、驱动控制及应用技术等。
E-mail: luqinfen@zju.edu.cn(通信作者)
(编辑 崔文静)