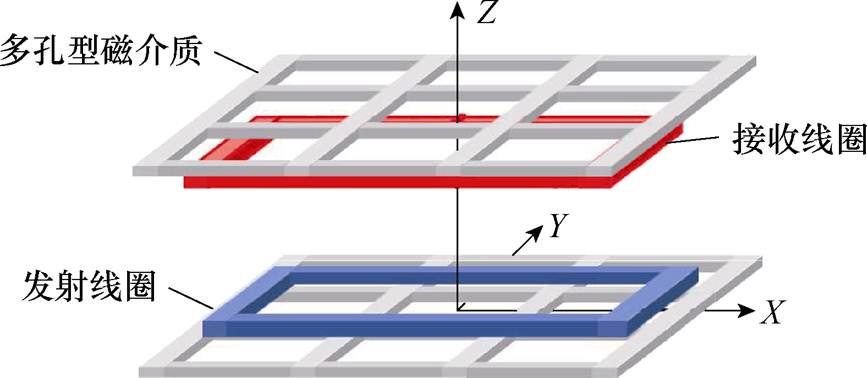
图1 双边有界多孔磁介质矩形线圈模型
Fig.1 Model diagram of a rectangular coil with bilateral bounded porous magnetic media
摘要 在无线电能传输技术中,互感是影响能量传输的关键因素之一。在线圈耦合结构中添加磁介质材料可以减少漏磁,显著提升互感。精确的互感计算模型能够为无线电能传输系统的线圈模型设计奠定可靠的理论基础,但现阶段仍缺乏针对多孔磁介质任意位置矩形线圈间互感的分析。该文首先通过空间截面分析法推导出二维截面各区域的磁矢势方程,再利用边界条件,将各二维平面的结果联结,得到了同轴时的互感计算公式。其次,进一步提出了一种镜像约束法,用镜像线圈来等效磁介质对线圈的作用,通过分析镜像系数的规律,得到了任意位置情况时的互感表达式,解决了任意位置线圈间的互感计算问题。最后,搭建了一套双边有界多孔型磁介质矩形线圈的系统实验装置,互感计算、实验和仿真值的最大误差为4.96%,验证了该文方法的有效性。在相同的参数下,所提模型比矩形磁介质结构节省材料56.25%。
关键词:无线电能传输 磁介质 互感计算 矩形螺旋线圈
无线电能传输(Wireless Power Transfer, WPT)技术通过非接触式电能输送方式,以安全可靠、灵活适配及低运维成本等优势,为现代设备供电提供了创新性解决方案。通过电磁感应、谐振技术等能够高效地为设备提供能量,是未来智能[1-3]供电技术的发展趋势之一。该技术也广泛应用于水下供电[4-6]、无人机技术[7-8]和生物医学[9-10]中。在实际应用时,接收与发射线圈间的位置难免会发生相对偏移,导致互感值变化,进而造成无线充电系统效率下降和电压不稳。因此,开发适用于位置动态变化的互感计算模型具有重要的理论价值和工程意义。
目前,线圈结构也各有不同,最常见的为圆形线圈[11]和矩形线圈。对于圆形线圈的互感计算方法研究已经有了许多成果,包括贝塞尔函数[12-13]、诺依曼公式[14]及毕奥-萨伐尔定律[15]等。
与圆形线圈相比,矩形线圈的互感问题研究较少。对于无磁介质的矩形线圈,文献[16]给出了基于二阶矢量位计算两个同轴平面螺旋矩形线圈之间互感的解析方法,但没有讨论水平偏移情况间的互感计算方法。文献[17]提出了一种使用线圈顶点坐标来建模互感的新方法,并求解了线圈发生水平偏移时的互感。文献[18]根据毕奥-萨伐尔定律,推导了直流带电导体在空间任意点产生的磁场方程,获得了计算两线圈之间任意位置互感的方法。文献[19-20]运用斯托克斯定理和毕奥-萨伐尔定律得到了六边形线圈任意位置的互感。尽管上述文献考虑了矩形线圈之间的各种相对位置,但都没有考虑磁介质材料对互感的影响。在无线电能传输系统中引入相应的磁介质材料[21-23]能够显著提升系统的传输效率和减少漏磁。目前,对于加入磁介质的矩形线圈互感计算方法研究较少,文献[24]在WPT系统中加入了磁介质材料,应用傅里叶-贝塞尔变换和双傅里叶变换,得到了圆形和矩形线圈的互感表达式。但该方法仅考虑了考虑磁介质厚度的有界性,且只考虑了一侧磁介质,因此并不满足实际应用的需要。文献[25]考虑了磁介质宽度的变化,通过对拉普拉斯方程和双曲函数的展开,得到了任意位置线圈互感的计算公式,但所建立的模型只考虑了单侧磁介质的情况。文献[26-27]采用分离变量法推导了具有双侧磁介质的矩形线圈的互感计算方法,将两个二维子域解析模型叠加,得到了有界磁介质的互感公式。但其并未分析发生角度偏转等任意位置的情况。上述文献研究了磁介质整体情况下的互感计算方法,但磁介质材料价格昂贵,且目前没有研究节省磁介质材料的互感计算方法。所以,对于具有双边有界多孔磁介质任意位置矩形线圈的互感计算需要深入分析。双边有界多孔磁介质矩形线圈模型如图1所示。

图1 双边有界多孔磁介质矩形线圈模型
Fig.1 Model diagram of a rectangular coil with bilateral bounded porous magnetic media
本文通过空间截面分析法得到了双边有界多孔磁介质矩形线圈间垂直和水平偏移时的互感表达式,进一步通过镜像约束法,用镜像线圈等效了接收线圈和发射线圈两侧的磁介质对线圈的影响,然后通过分析镜像系数的规律,得到了角度偏转等状况时的互感表达式。通过建模仿真和实验证实了本文方法的可行性。在模型参数一致的情况下,本文所提出的结构比矩形磁介质结构节省材料56.25%,互感值可以达到矩形磁介质的91%。
为了建立二维子域模型,本节根据材料特性将线圈结构划分为不同区域,构建了双边有界多孔磁介质矩形线圈模型的XZ截面示意图,如图2所示。图中,Tc为发射线圈,Rc为接收线圈,区域4b和4d为发射线圈的横截面,区域2b、2d、2f、2h、6b、6d、6f、6h分别为发射线圈和接收线圈两侧的磁介质截面,区域1a、2a、2c、2e、2g、2i、3a、4a、4c、4e、5a、6a、6c、6e、6g、6i、7a均为空气区域。w为线圈直径。b为线圈与磁介质之间的距离,其值为5 mm,保持不变。Dc为初始设定接收线圈与发射线圈间的距离,其为10 mm。
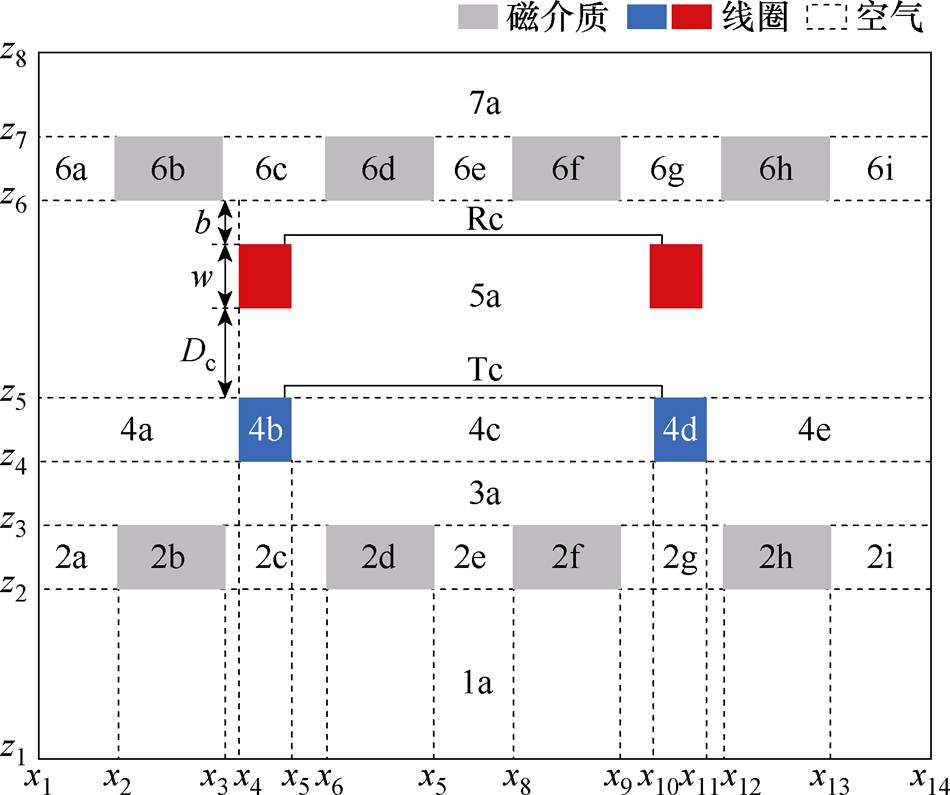
图2 双边多孔磁介质矩形线圈横截面示意图
Fig.2 Schematic diagram of the cross-section of a rectangular coil with bilateral porous magnetic medium
各区域的边界由二维XZ截面来划分,如图3所示,区域r在X轴的起始坐标为xpr,终点坐标为xqr,Z方向同理。Cr、Dr、Er和Fr为未知系数。
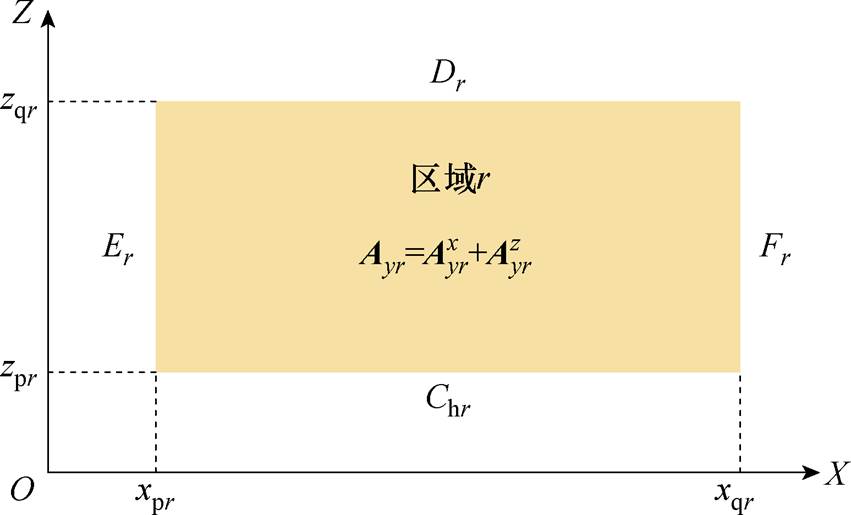
图3 各区域边界坐标
Fig.3 Boundary coordinate map of each region
泊松方程式(1)是求解磁矢势的关键,方程式(2)是通过分离变量法得到的,利用分离变量法并且结合各个区域的边界条件就可以得到各个区域的磁矢势的表达式。需要注意的是,Jr为线圈区域4b、4d的电流密度,Jr在其他区域中为零,所以其他区域的求解则利用拉普拉斯方程式(3)。XZ截面中磁矢势A仅具有y方向分量。
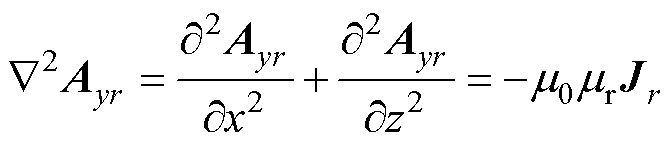 (1)
(1)
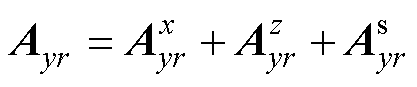 (2)
(2)
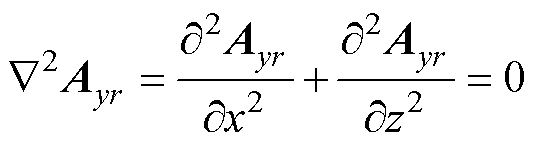 (3)
(3)
式中,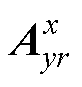 和
和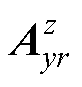 分别为模型Z边界和X边界的磁矢势分量;
分别为模型Z边界和X边界的磁矢势分量;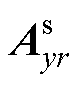 为线圈电流密度引起的磁矢势;
为线圈电流密度引起的磁矢势;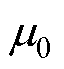 为真空磁导率;
为真空磁导率;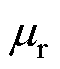 为磁介质区域的相对磁导率。
为磁介质区域的相对磁导率。
1)磁介质和导体区域
通过求解方程式(1)~式(3),并且结合其边界条件可以得到区域2b~6h的磁矢势表达式为
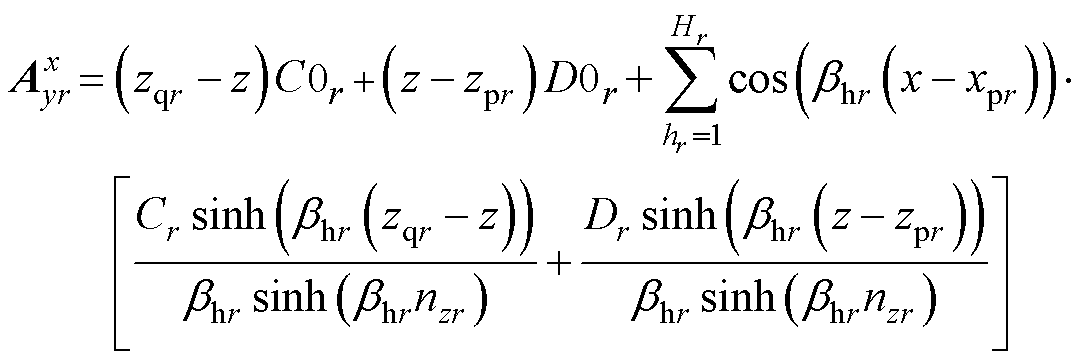 (4)
(4)
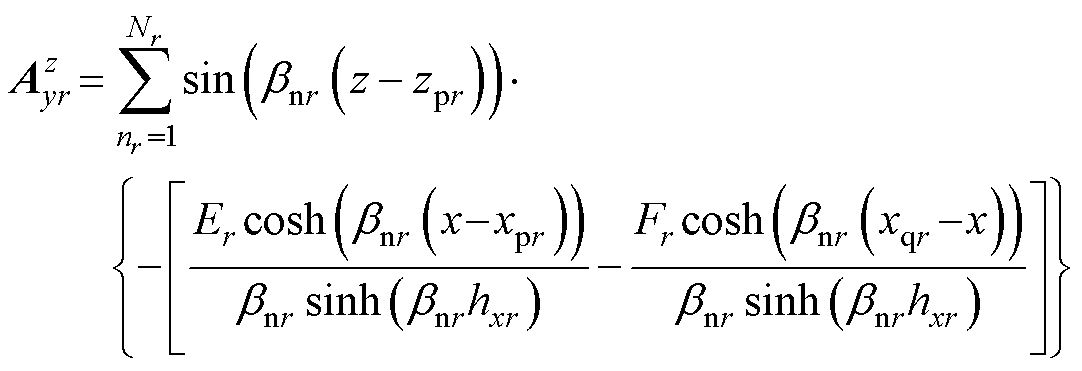 (5)
(5)
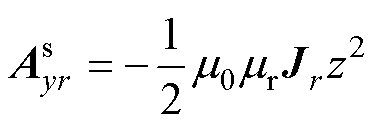 (6)
(6)
其中
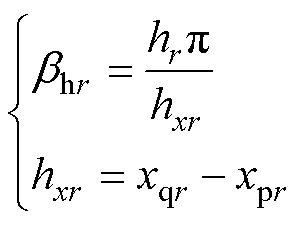 (7)
(7)
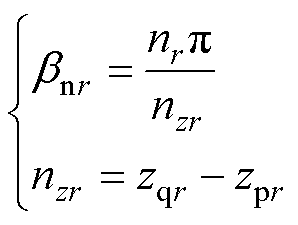 (8)
(8)
式中,C0r、D0r为未知系数;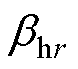 和
和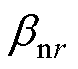 分别为
分别为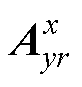 和
和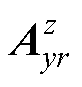 的各区域空间频率;hr和nr为空间谐波数。
的各区域空间频率;hr和nr为空间谐波数。
在磁介质区域中并不存在电流,因此电流密度引起的磁矢势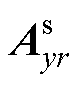 =0。
=0。
2)空气区域
通过求解方程式(3)可以得到空气区域的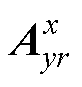 和
和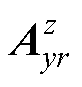 的表达式为
的表达式为
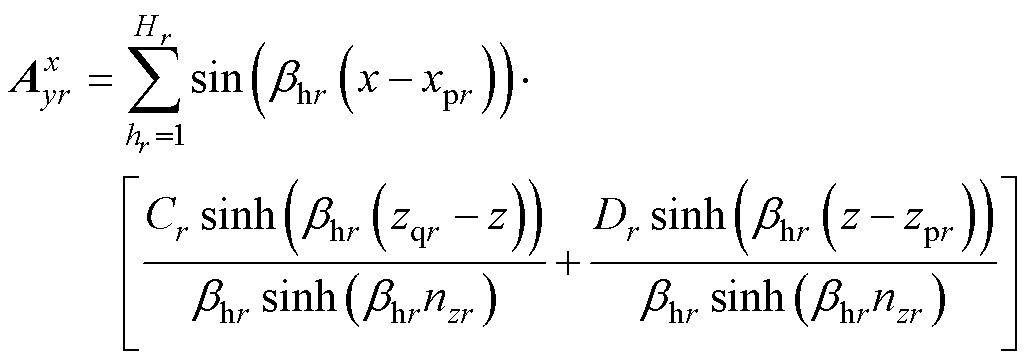 (9)
(9)
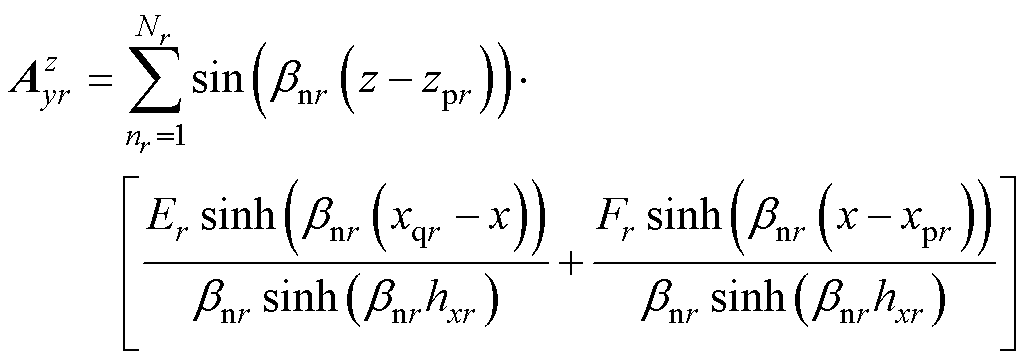 (10)
(10)
如图2所示,区域2a、4a、6a的左边界x=x1和区域2i、4e、6i的右边界x=x14与模型边界相接触,所以左侧和右侧空气区域的Er=Fr=0。
3)区域1a和7a
此区域不同于上述的空气区域。区域1a和7a的两侧边界与模型边界接触,因此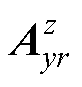 =0。
=0。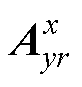 在若干区域中是连续的,因此可以获得区域1a和7a的磁矢势表达式为
在若干区域中是连续的,因此可以获得区域1a和7a的磁矢势表达式为
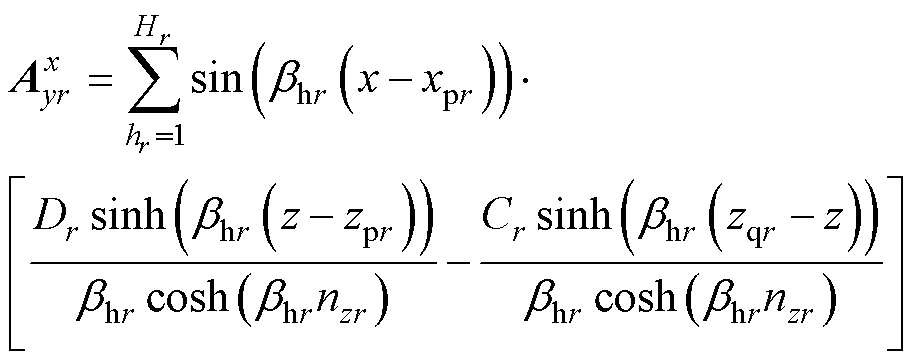 (11)
(11)
4)区域3a和5a
区域3a和5a类似于区域1a和7a。其两侧的边界与模型边界接触,因此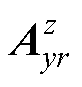 也为0。区域上下边界与线圈和磁介质两者的边界都有接触且
也为0。区域上下边界与线圈和磁介质两者的边界都有接触且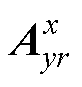 在接触的边界中是连续的,可得磁矢势为
在接触的边界中是连续的,可得磁矢势为
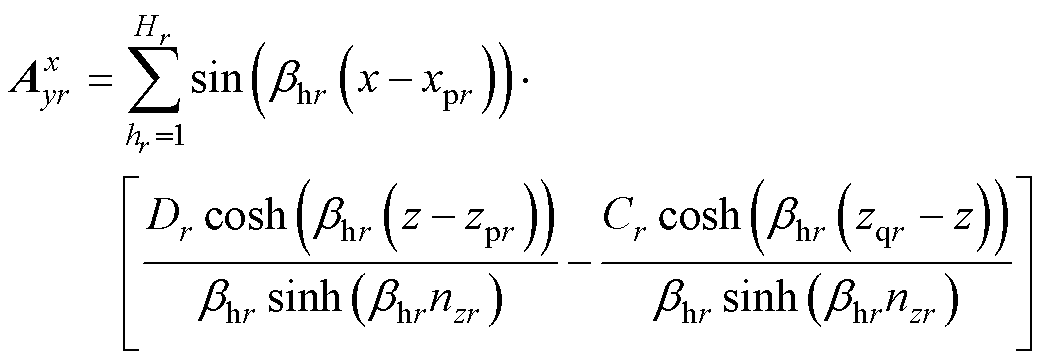 (12)
(12)
XZ截面的全部区域方程表达式如式(4)~式(12)所示,YZ截面的区域方程求解步骤与XZ截面同理。
磁介质的存在会影响磁矢势的分布,而磁矢势的分布很难用微分方程来描述,因此需要引入不同的边界条件。根据麦克斯韦边界条件,在不同介质的界面处,磁场强度H的切向分量和磁通密度B的法向分量于介质交界面处连续。B和H为
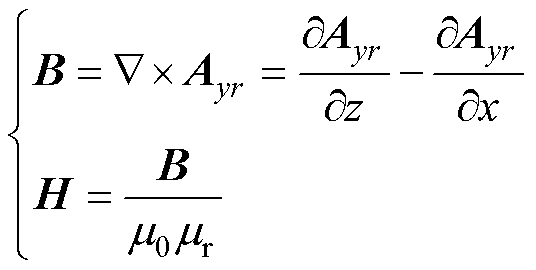 (13)
(13)
所有区域的边界条件可以分为三种情况,图4所示的例子解释了界面边界条件的应用。
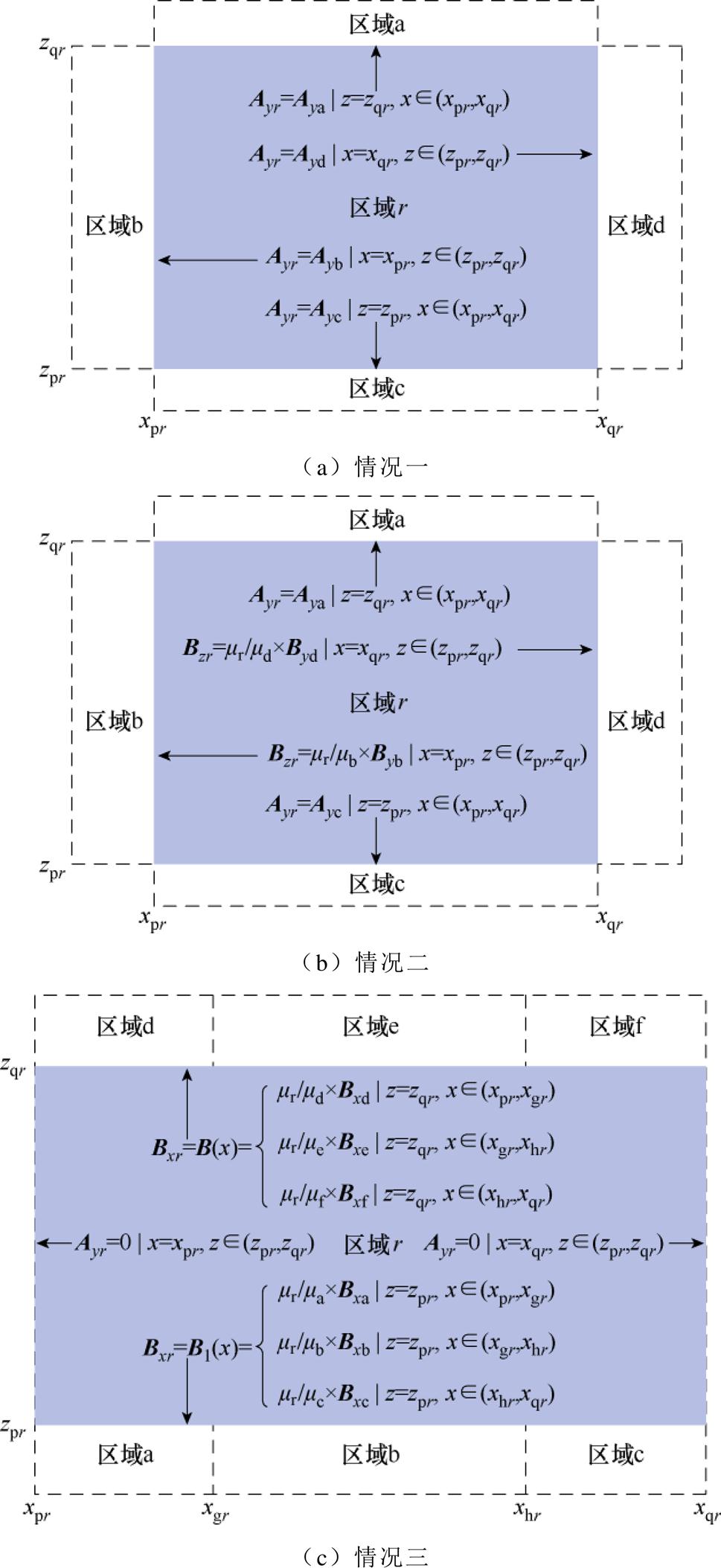
图4 边界条件
Fig.4 Boundary condition
Bxr、Bzr为B的x和z分量。空气区域应用图4a中的边界条件。需要注意的是,在区域2a、4a、6a的左边界处磁矢势为零,在区域2i、4e、6i的右边界处磁矢势为零。磁介质和导体区域应用图4b的边界条件。区域1a、3a、5a、7a应用图4c中的边界条件,需要考虑的是,此区域r的Z边界与多个区域相接触,因此Z边界上的边界条件的B(x)和B1(x)为分段函数。
未知系数的表达式可由线性方程组确定。基于1.2节的讨论,确定了每个区域的边界条件,便可以求得未知系数。为了演示用于计算待定系数的推导过程,以区域2b为例来展示基本方法。首先是同样位于z=z3边界上的区域3a,区域3a、2b的磁矢势为
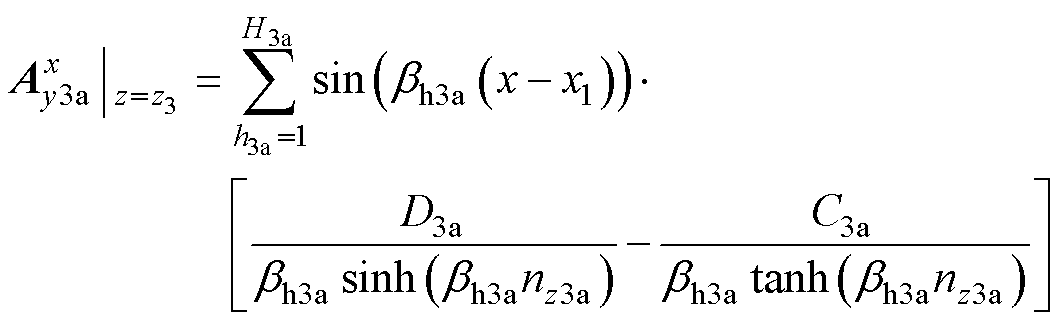 (14)
(14)
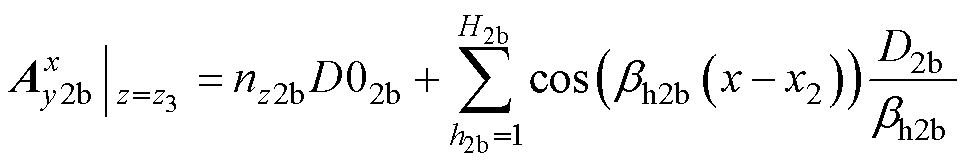 (15)
(15)
在z=z3的边界上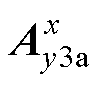 与
与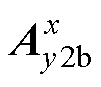 的磁矢势相等,展开方程式(15)通过傅里叶级数,得到区域2b中未知系数的表达式为
的磁矢势相等,展开方程式(15)通过傅里叶级数,得到区域2b中未知系数的表达式为
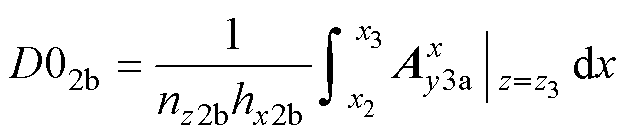 (16)
(16)
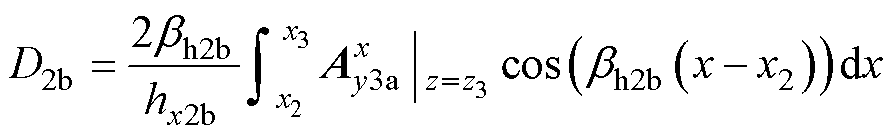 (17)
(17)
将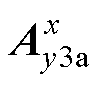 代入式(15)后化简可得式(16)和式(17)的表达式,由于两式的求解过程一致,因此本节仅分析式(16)的表达式。
代入式(15)后化简可得式(16)和式(17)的表达式,由于两式的求解过程一致,因此本节仅分析式(16)的表达式。
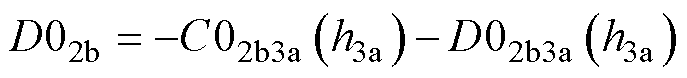 (18)
(18)
式中,C02b3a(h3a)和D02b3a(h3a)为式(16)的积分简化形式,只跟h3a有关。积分的上、下限主要取决于当前求解区域所处的xpr、xqr和zpr、zqr范围。
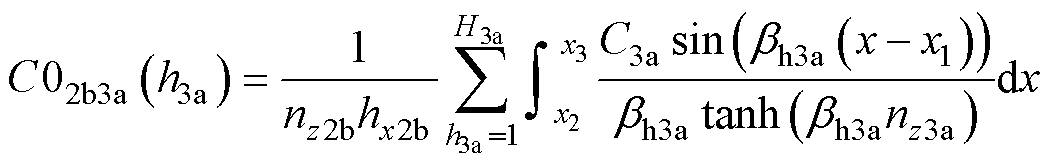 (19)
(19)
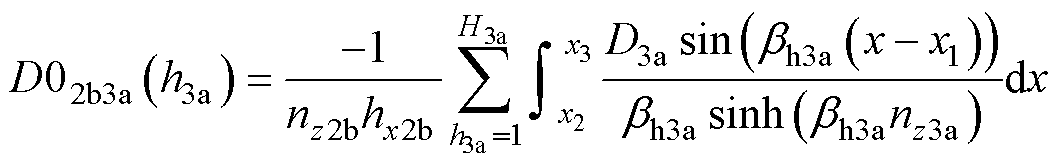 (20)
(20)
D2b的求解方法同D02b一致。对于其他区域,参考区域2b重复上述方法,得到矩阵形式为
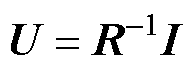 (21)
(21)
其中
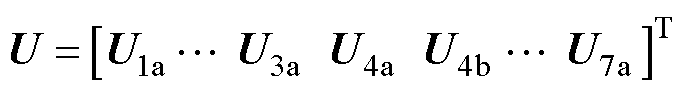 (22)
(22)
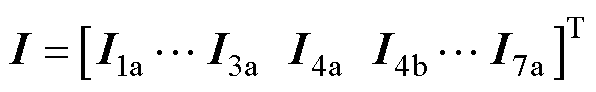 (23)
(23)
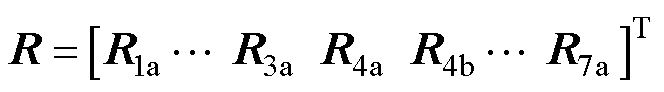 (24)
(24)
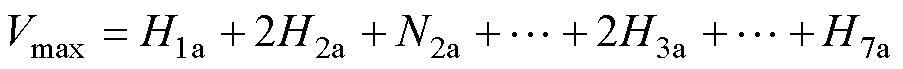 (25)
(25)
式中,U为未知系数矩阵;I为励磁电流矩阵;R为系统边界条件矩阵,整体维数为Vmax×Vmax;H1a~H7a为各区域的空间谐波数。
U中的每个元素都代表各区域磁矢势中的未知系数,其各项展开式为
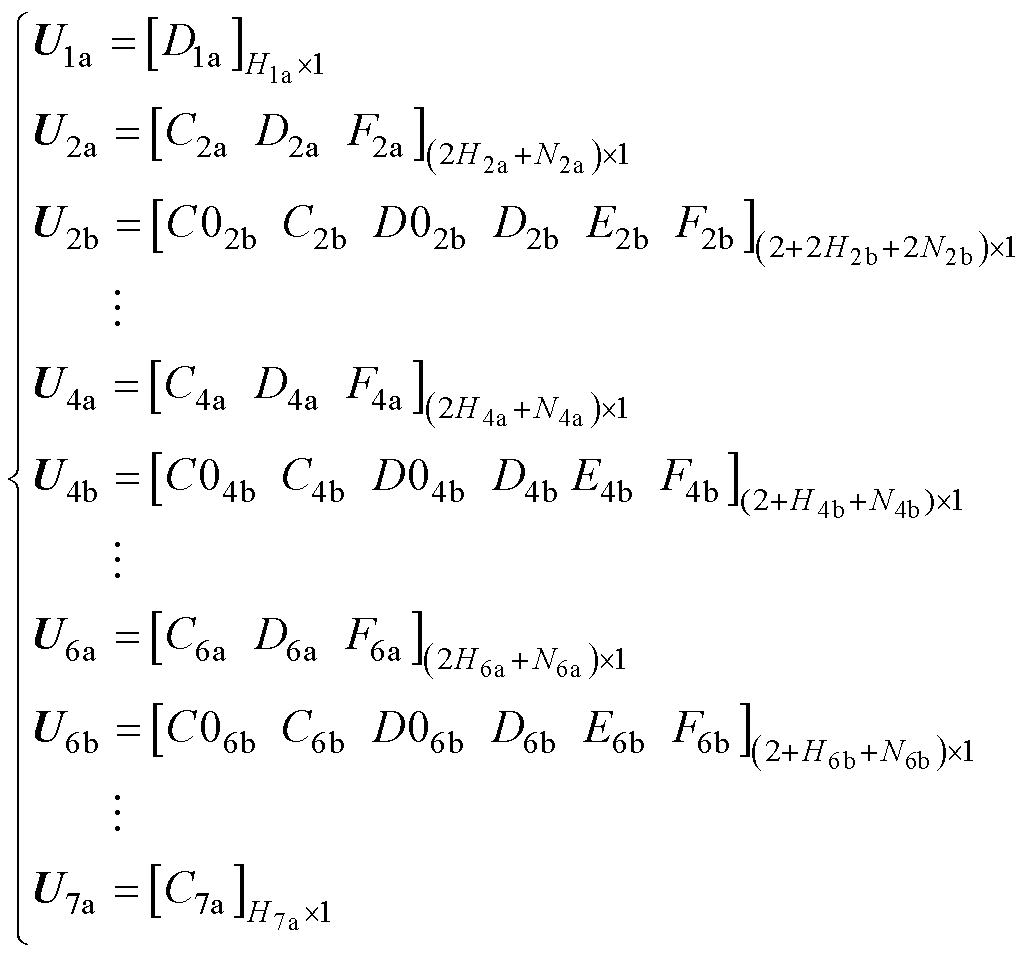 (26)
(26)
R1a~R7a的表达式为
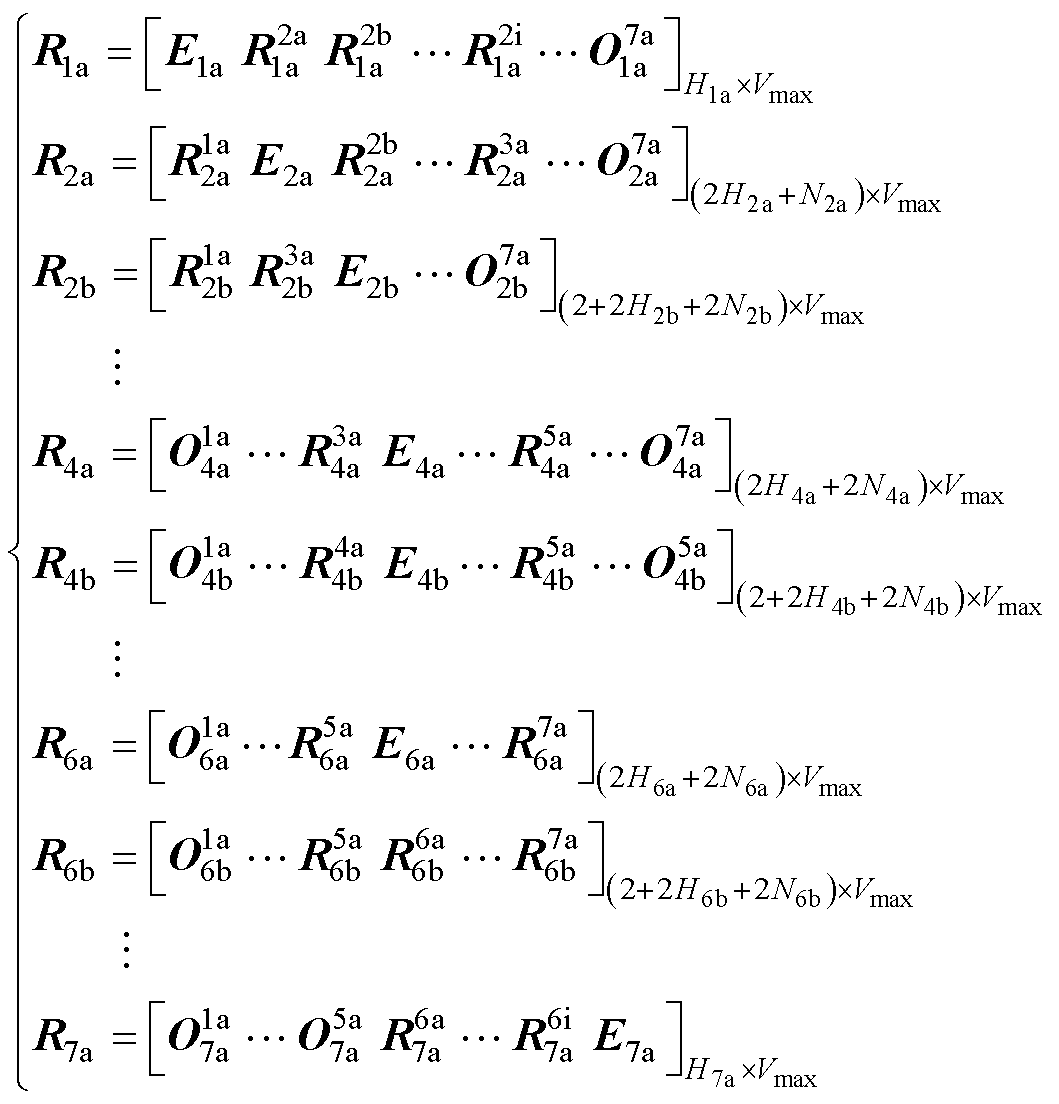 (27)
(27)
式中,E1a为单位矩阵,维数为H1a×H1a,E2a~E7a同理;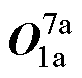 为零矩阵,维数为H1a×H7a,其余零矩阵同理。
为零矩阵,维数为H1a×H7a,其余零矩阵同理。
根据第1节的理论分析,可以计算出XZ截面的磁通密度。同理运用空间截面分析法可以得出YZ截面的磁通密度。由于二维模型在第三方向上被认为具有无限长度,但实际线圈系统的情况并非如此。为了解决这个问题,需要引入校正因子。根据毕奥-萨伐尔定律中无限长直导体磁通密度Binf与有限长直导体磁通密度Bf之比,可以获得模型在平面内的修正系数。
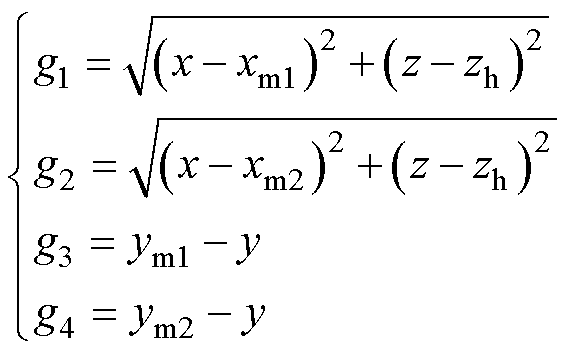 (28)
(28)
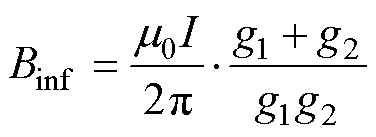 (29)
(29)
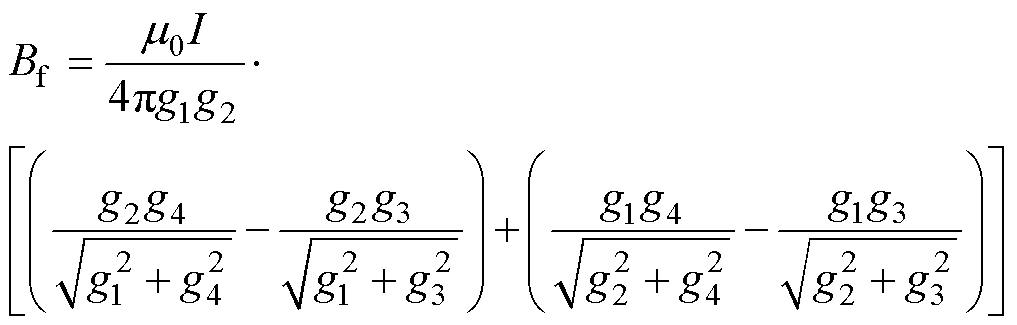 (30)
(30)
式中,g1、g2为XZ截面线圈中点到接收线圈面任意点的距离,且该任意点位于线圈间中点的延伸路径上;g3、g4为XY平面下线圈对应中点到线圈间中点在Y方向所涉任意点的距离。
如图2所示,YZ方向的坐标为ym1=(y4+y5)/2,ym2=(y10+y11)/2,XZ方向的坐标为xm1=(x4+x5)/2,xm2=(x10+x11)/2。Z方向上zh=z5-z4。
有限长导体与无线长导体的磁通密度之比的修正系数fxz(x, y, z)为
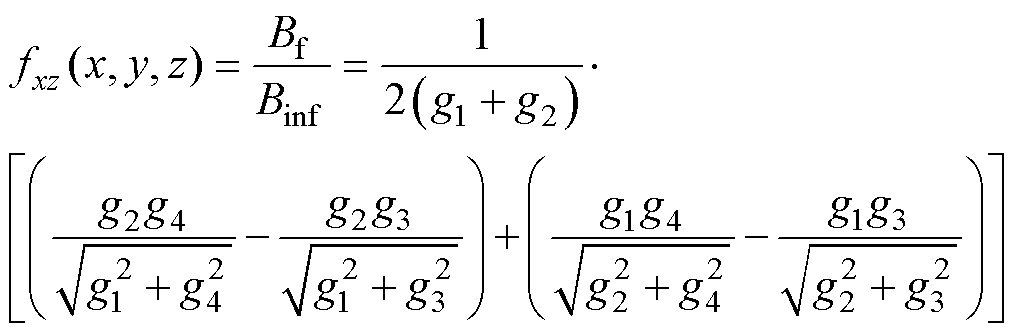 (31)
(31)
为了确定mr在2D到3D转换过程中的影响,文献[22]中提出了一个因子g(mr),适用于具有不同尺寸线圈的系统。
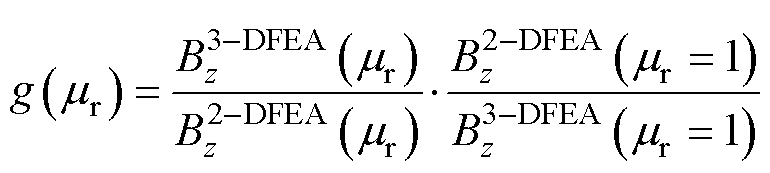 (32)
(32)
式中,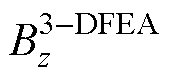 和
和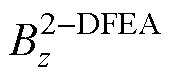 分别为从3D和2D有限元分析(Finite Element Analysis, FEA)仿真获得的磁导率为
分别为从3D和2D有限元分析(Finite Element Analysis, FEA)仿真获得的磁导率为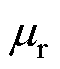 和
和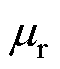 =1的磁场密度值。
=1的磁场密度值。
XZ截面最终修正系数表达式为
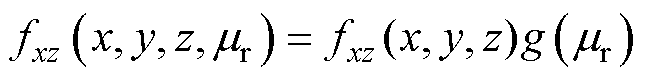 (33)
(33)
同理,YZ截面的表达式也可由此方法求出。
参考对于XZ截面互感的分析,可以得出YZ截面互感的分析过程。所以,对于整个系统的磁场,有
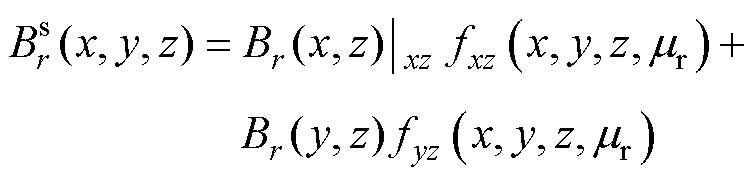 (34)
(34)
所提出的子域模型的互感表达式为
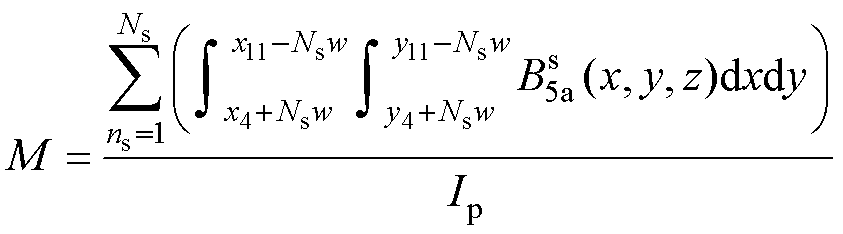 (35)
(35)
式中,Ns为接收线圈的匝数;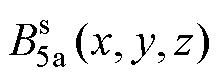 为区域5a的磁通密度。计算步骤如图5所示。
为区域5a的磁通密度。计算步骤如图5所示。

图5 互感计算步骤
Fig.5 Mutual inductance calculation steps
为求解任意位置时的互感,采用了镜像约束法,将发射侧和接收侧磁介质等效为两个镜像线圈用来代替多孔磁介质对磁场中线圈的影响效果,同轴镜像模型如图6所示。图中,l1和l2分别为发射线圈至接收侧磁介质和发射侧磁介质的距离。
发射线圈充当具有电流幅值Ip的激励线圈时,接收侧磁介质等效为镜像线圈3,且其电流幅值为x2mIp,其中,x2m为镜像系数。发射侧磁介质等效为镜像线圈4,电流幅值为x1Ip,其中,x1为镜像系数。当发生角度偏移时,镜像线圈3和4位置保持不变,所以镜像互感可以描述为
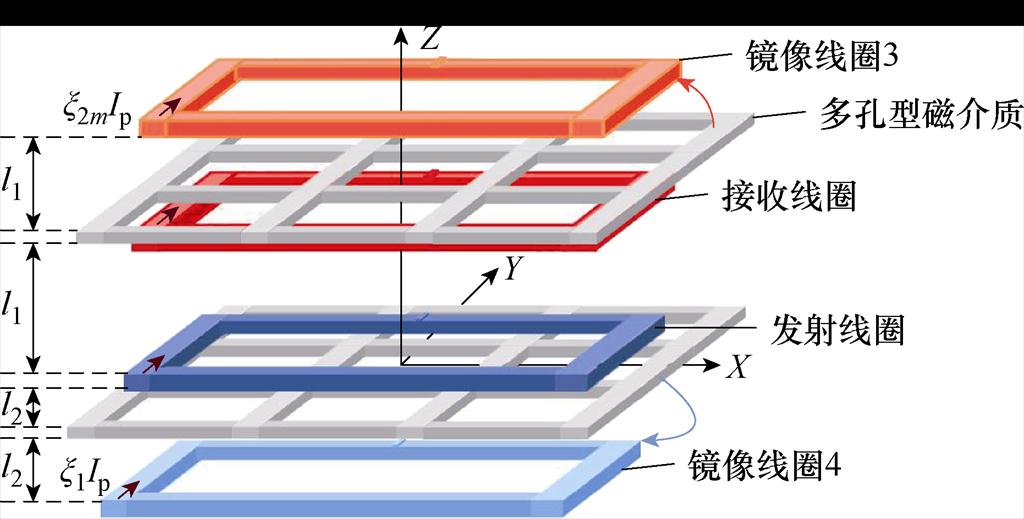
图6 镜像线圈示意图
Fig.6 Schematic diagram of mirrored coil
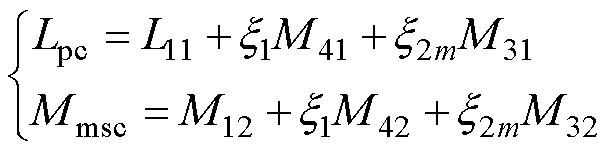 (36)
(36)
式中,Lpc和Mmsc分别为双边磁介质作用时的自感和互感;L11为线圈的自感;M12为发射线圈与接收线圈间的互感;M31、M41、M32和M42分别为镜像线圈3和4对发射线圈和接收线圈的互感。镜像线圈3对发射线圈产生的作用以接收线圈和发射线圈相距Dc=110 mm的角度偏转数据对比为例。偏转角度a的范围为-60°~60°。x2m有三种不同的情况,分别是:①x2ad表示接收线圈角度偏转情况;②x2ahp表示接收线圈角度偏转加同向水平偏移情况;③x2aho表示接收线圈角度偏转加负向水平偏移情况。
镜像系数变化曲线如图7所示。从图7中可以看出,镜像系数x1几乎没有变化,这是由于在角度偏转等情况中发射线圈位置保持不变,因此在后续的研究中x1可以用同轴系数来进行计算。
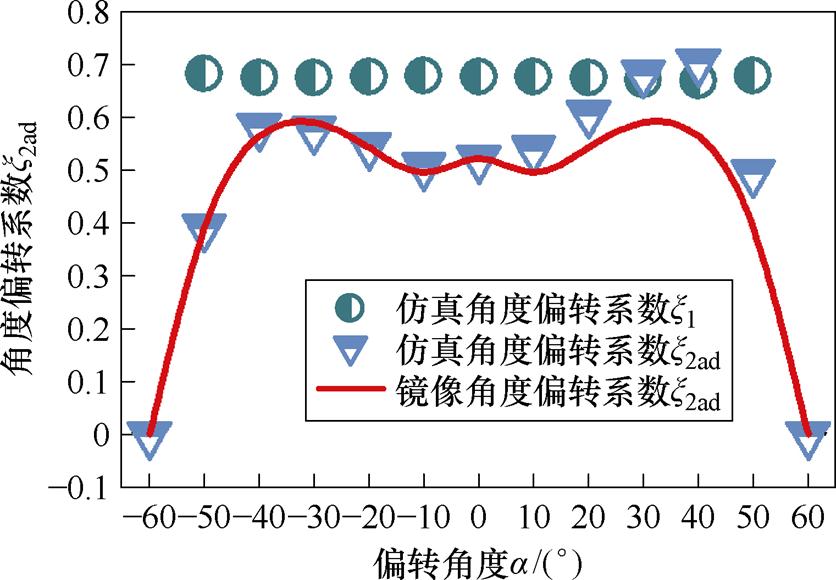
图7 镜像系数变化曲线
Fig.7 Mirror coefficient variation graph
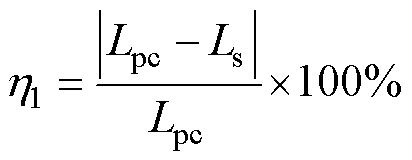 (37)
(37)
式中,Ls为线圈自感的仿真值;h1为镜像自感和仿真自感之间的误差。
接收线圈和发射线圈相距Dc=110 mm的角度偏转数据见表1。
表1 线圈间距110 mm角度偏转自感数据对比
Tab.1 Comparison of coil spacing 110 mm angular deflection self-sensing data
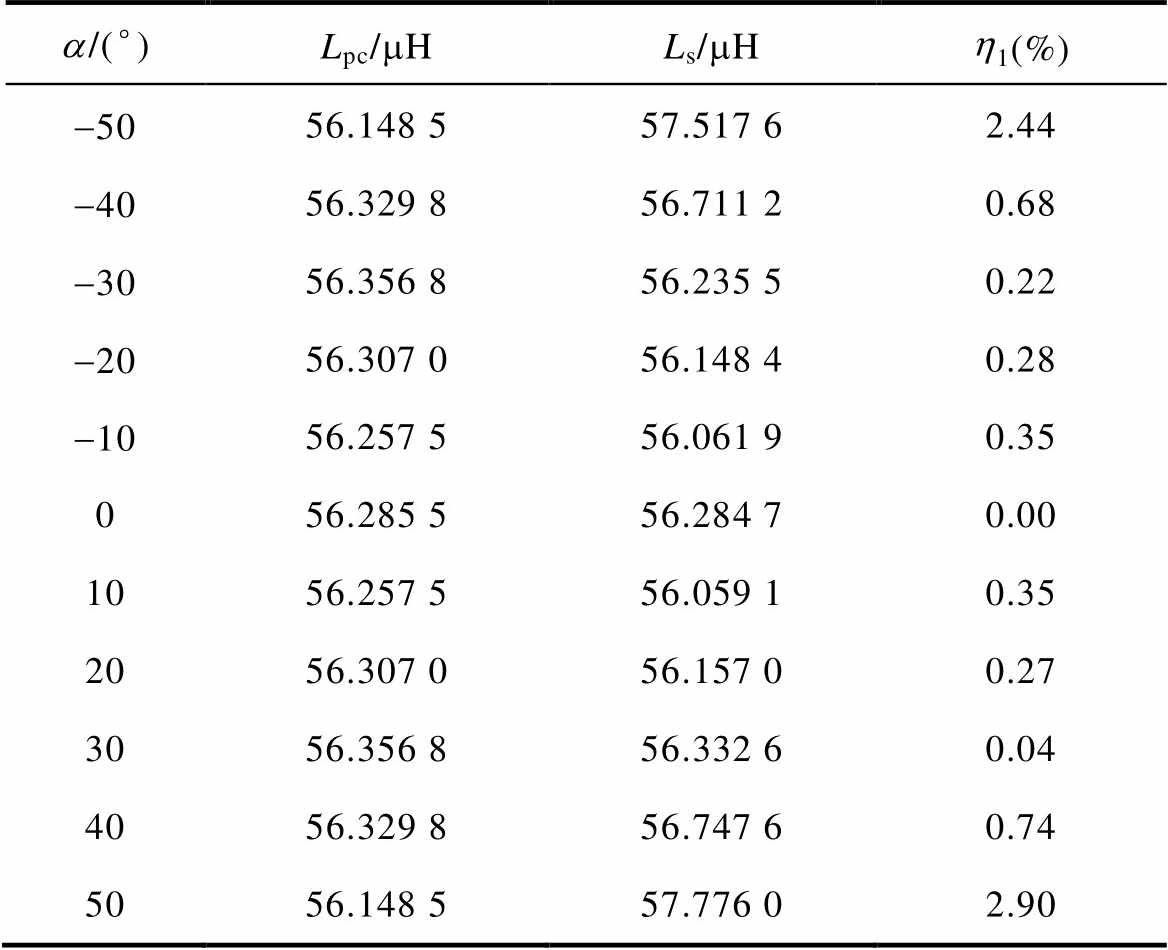
a/(°)Lpc/mHLs/mHh1(%) -5056.148 557.517 62.44 -4056.329 856.711 20.68 -3056.356 856.235 50.22 -2056.307 056.148 40.28 -1056.257 556.061 90.35 056.285 556.284 70.00 1056.257 556.059 10.35 2056.307 056.157 00.27 3056.356 856.332 60.04 4056.329 856.747 60.74 5056.148 557.776 02.90
根据表1的数据分析可知,Lpc和Ls之间的计算误差在大多数情况下均不超过0.74%,即使在偏转角度a=50°和a=-50°的情况下,误差也仅分别为2.90%和2.44%。这表明结果具有良好的一致性。接收端磁心的存在会对发射线圈的自感产生一定的影响,但该影响在实际情况下较为有限。为简化后续研究模型及计算过程,并更专注于主要影响因素,忽略该影响是合理且可行的。
接收侧同轴角度偏转示意图如图8所示,接收线圈位置为Dz=110 mm处,即Dc=120 mm处。图中,lc为中心距,偏转时保持不变。
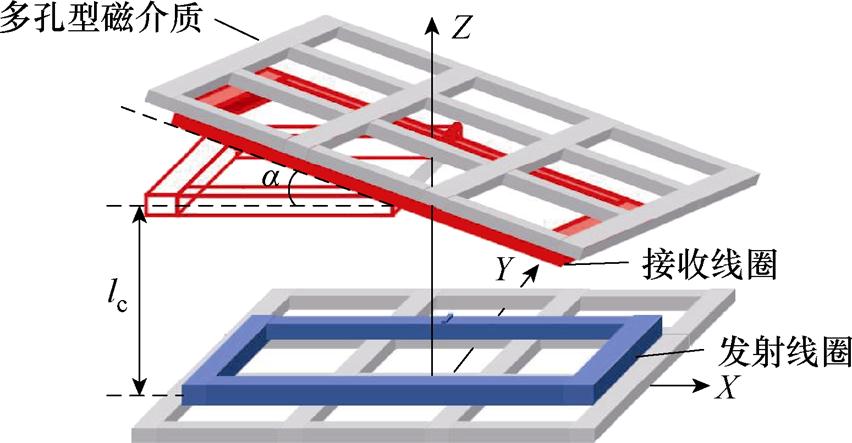
图8 接收侧同轴角度偏转示意图
Fig.8 Schematic diagram illustrating coaxial angular deflection at the receiving side component
将接收线圈分别以±10°的步长沿Y轴旋转。通过大量的FEA模拟,发现了x2ad在同轴角度偏转中的规律,a无论是在0°~60°还是-60°~0°的变化规律中,都呈3次函数的表达形式,在60°和-60°时x2ad衰减至0。
通过此规律得出镜像系数在同轴角度偏转的变化为
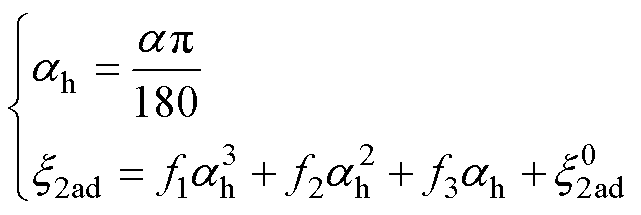 (38)
(38)
式中,f1、f2和f3为通过矩阵方程求解出的系数;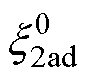 为当前位置同轴系数。
为当前位置同轴系数。
x2ad随垂直角度变化曲线如图9所示。图9中的镜像拟合系数由-60°~0°的数据结合式(38)得出。从图9中可以看出,在与0°~60°数据的对比中,x2ad也有较好的一致性。此方法适用于不同矩形线圈和磁介质结构的同轴角度偏转。
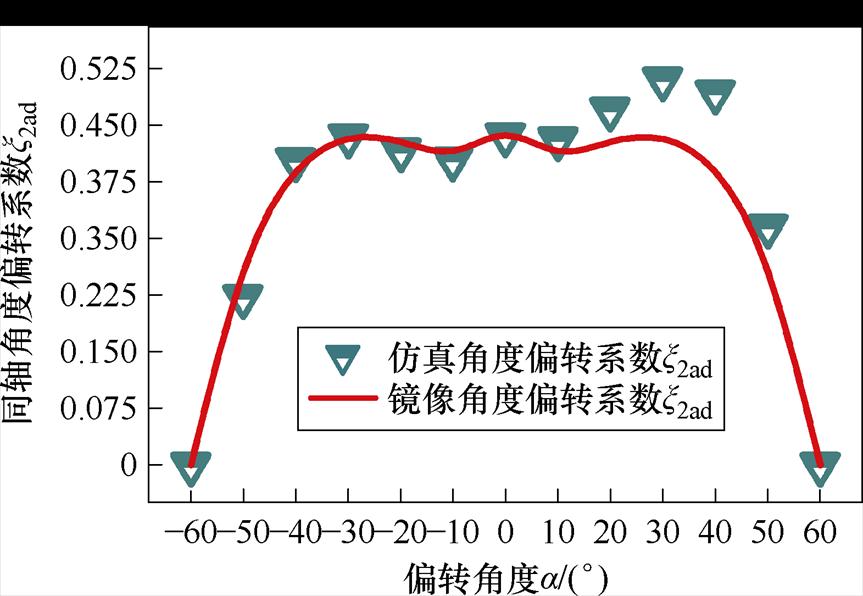
图9 x2ad随垂直角度变化曲线
Fig.9 Graph of x2ad varying with the vertical angle
3.2.1 角度偏转加同向水平偏移镜像系数
角度加水平偏移的情况要分为两种来讨论,本节为角度偏转加同向水平偏移。角度偏转加同向水平偏移包括接收侧线圈和磁介质的正角度水平右偏移和负角度水平左偏移,接收侧正角度水平右偏移如图10所示。接收线圈与发射线圈距离设定Dz=70 mm、lc=82 mm。接收侧绕Y轴旋转角度为a,设定a=30°和a=-30°,接收侧以Dx=±10 mm的步长沿X轴正负方向水平偏移,偏移范围为-50~50 mm。
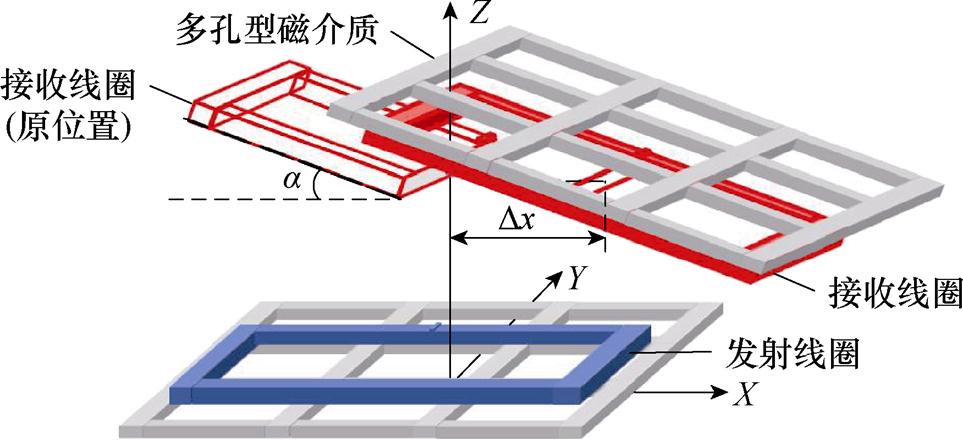
图10 接收侧正角度水平右偏移示意图
Fig.10 Receiving side positive angle horizontal right offset schematic
接收线圈在角度偏转加同向水平偏移的X轴正负方向水平偏移时其规律都为二次函数,根据此规律可以得出同向水平镜像系数x2ahp随水平偏移距离Dx的变化为
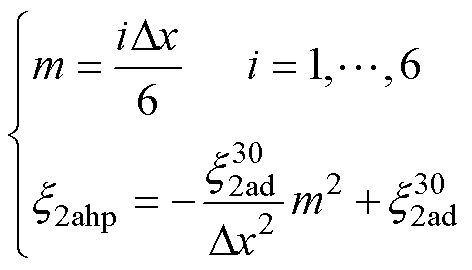 (39)
(39)
式中,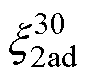 为同轴角度偏转30°的系数。x2ahp在Dx= 60 mm和Dx=-60 mm时系数衰减至0,图11中镜像同向水平系数由接收侧正角度水平右偏移的数据拟合。从图中可以看出,二者的规律具有较好的一致性。
为同轴角度偏转30°的系数。x2ahp在Dx= 60 mm和Dx=-60 mm时系数衰减至0,图11中镜像同向水平系数由接收侧正角度水平右偏移的数据拟合。从图中可以看出,二者的规律具有较好的一致性。
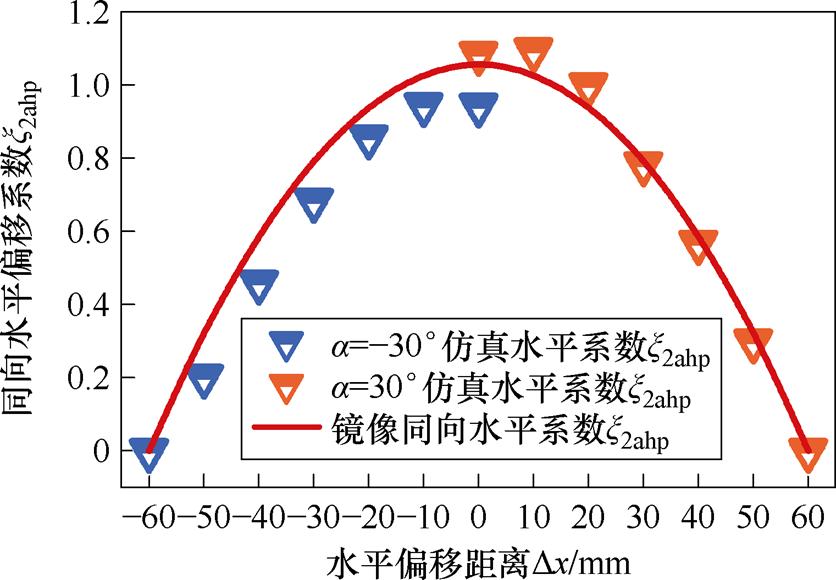
图11 x2ahp随水平距离变化曲线
Fig.11 Graph of x2ahp varing with horizontal distance
3.2.2 角度偏转加负向水平偏移镜像系数
接收线圈与发射线圈距离同样设定为lc= 82 mm。a设定同样为-30°和30°。接收侧偏移的步长设为Dx=±10 mm,沿X轴的正负方向水平偏移,偏移范围设为-50~50 mm。模型偏移状况如图12所示。
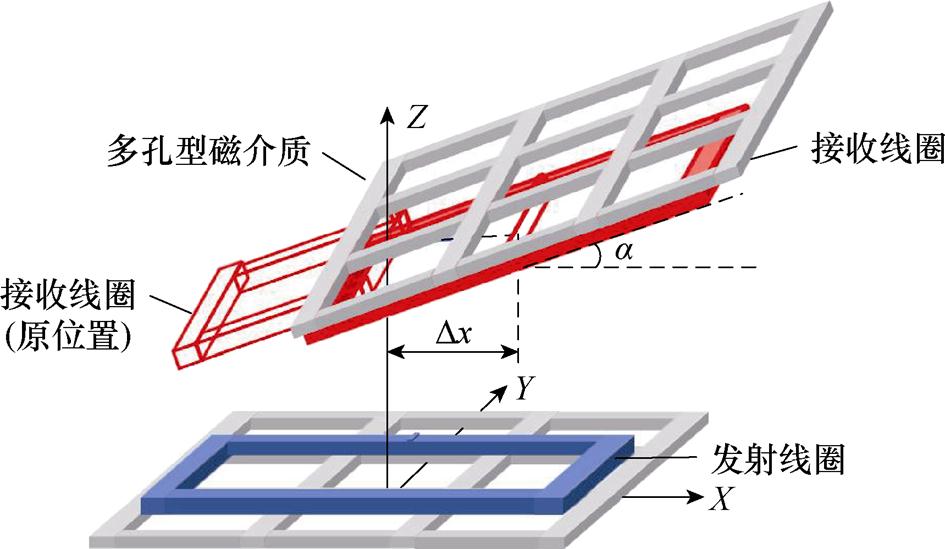
图12 接收侧负角度水平右偏移示意图
Fig.12 Negative angular horizontal rightward displacement schematic at receiving end
角度加负向水平偏移规律与角度加正向偏移规律都为二次函数的形式,但其衰减规律相比角度加正向水平偏移要快,在Dx=50 mm和Dx=-50 mm处时镜像系数已经衰减至负数,所以在此基础上要考虑Dx=50 mm或Dx=-50 mm时的x2aho。负角度水平右偏移在Dx=50 mm时其x2aho已经衰减至-0.211 4,用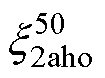 表示。其规律表达式为
表示。其规律表达式为
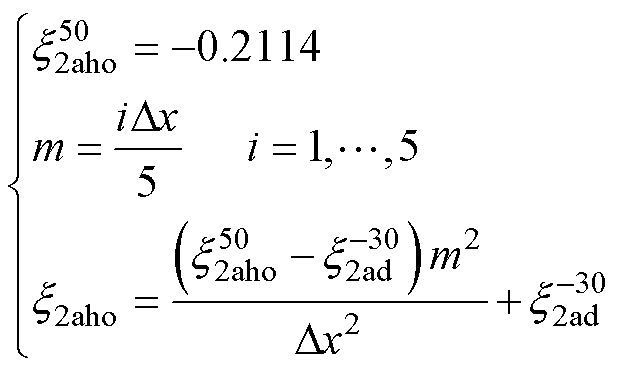 (40)
(40)
式中,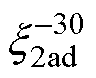 为同轴角度偏转-30°的系数。
为同轴角度偏转-30°的系数。
图13为提出的公式镜像负向水平系数与实际镜像系数的对比关系,可以看出,二者在Dx=0 mm之外具有良好的一致性。
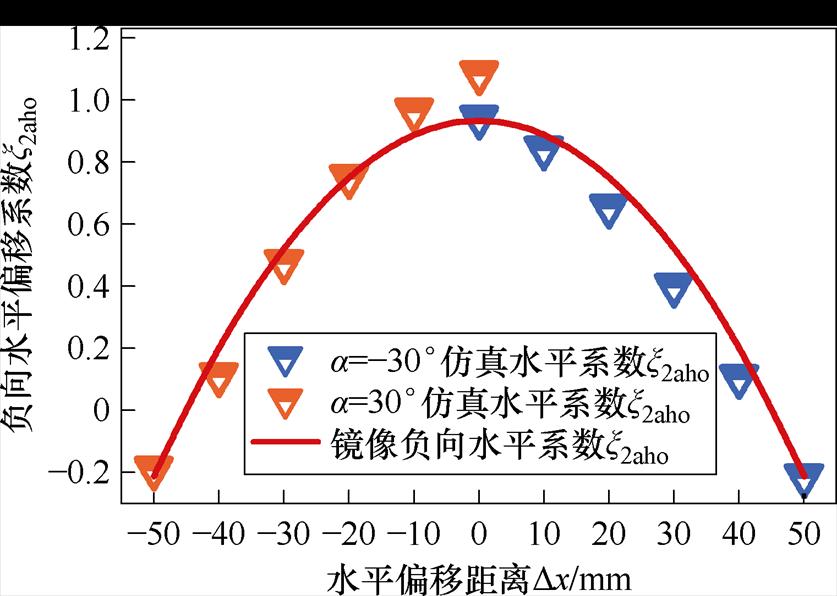
图13 x2aho随水平距离变化曲线
Fig.13 Graph of x2aho varing with horizontal distance
为了验证所提出的互感计算公式的有效性,采用Maxwell软件建模进行仿真验证。同时构建了一个双边多孔型磁介质矩形线圈无线电能传输系统的实验装置。通过操作亚克力实验台和三维运动平台实现线圈之间的相对位置变化,使用阻抗分析仪IM3536测量互感的实验值,电流频率设置为85 kHz。线圈和磁介质结构的具体参数见表2。
表2 线圈与磁介质材料参数
Tab.2 Coil and dielectric material parameters
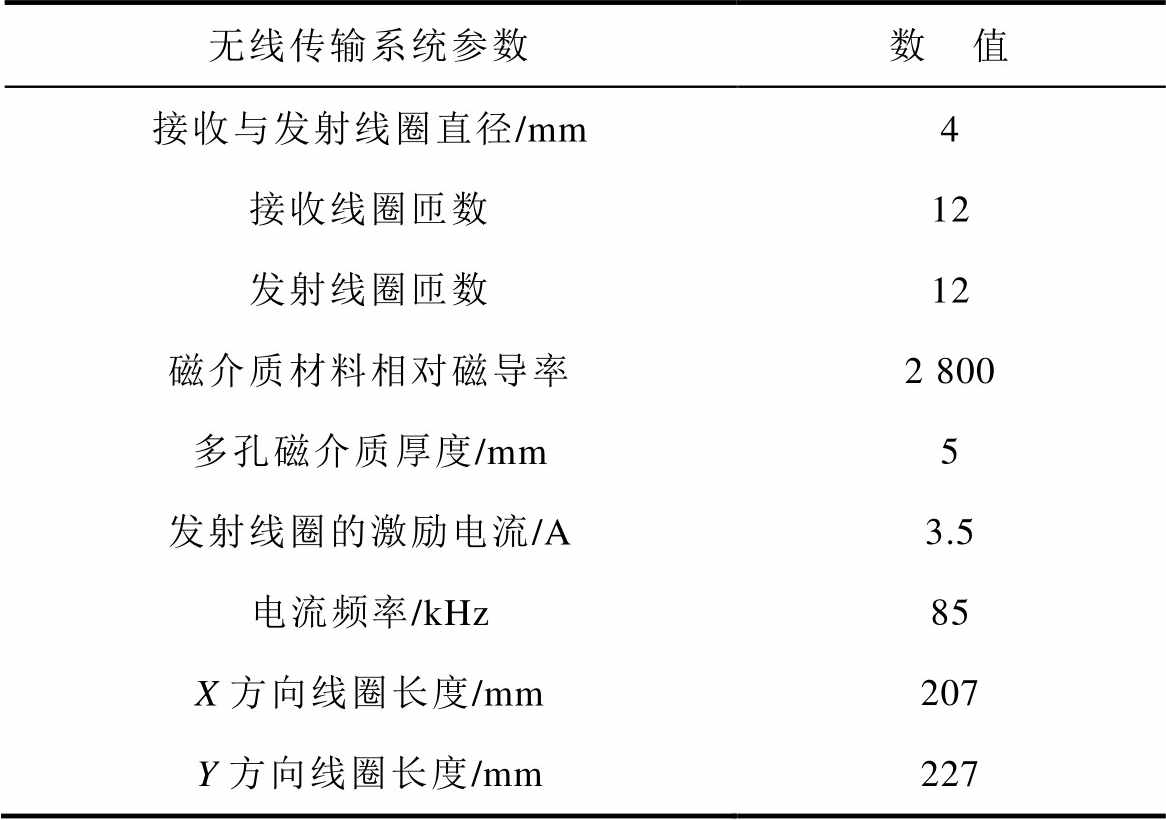
无线传输系统参数数 值 接收与发射线圈直径/mm4 接收线圈匝数12 发射线圈匝数12 磁介质材料相对磁导率2 800 多孔磁介质厚度/mm5 发射线圈的激励电流/A3.5 电流频率/kHz85 X方向线圈长度/mm207 Y方向线圈长度/mm227
每个区域采取的谐波数是不同的。对于大数量的谐波,线性系统会变得病态,并给出不准确的结果。较少数量的谐波数也会给出不准确的分析结果。本文中,区域5a的谐波数应采取为大数量,因为本区域用于计算互感。各个区域的谐波数设置见表3。
表3 区域谐波数
Tab.3 Regional harmonics
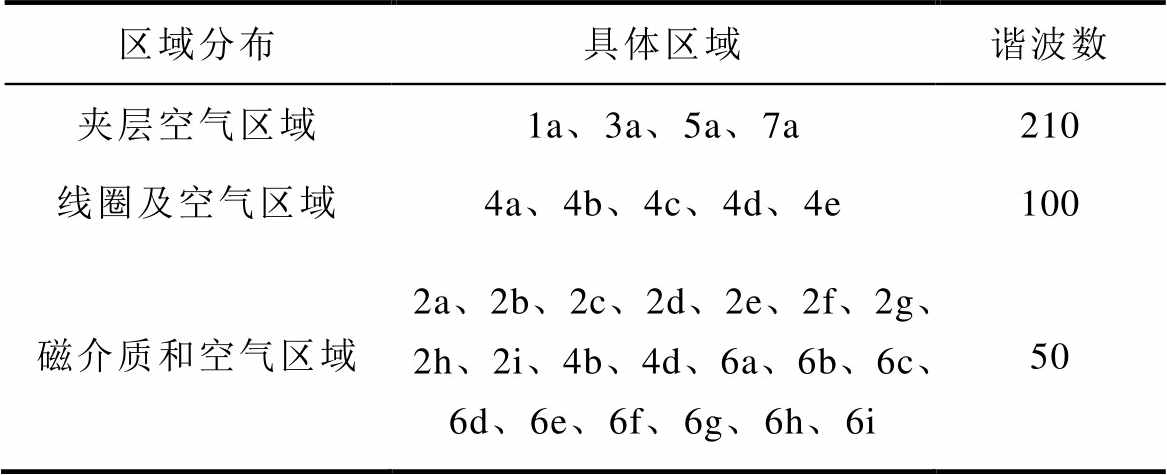
区域分布具体区域谐波数 夹层空气区域1a、3a、5a、7a210 线圈及空气区域4a、4b、4c、4d、4e100 磁介质和空气区域 2a、2b、2c、2d、2e、2f、2g、 2h、2i、4b、4d、6a、6b、6c、 6d、6e、6f、6g、6h、6i50
所构建的双边多孔磁介质矩形线圈三维模型的坐标参数见表4。
表4 三维坐标系参数
Tab.4 Parameters of three-dimensional coordinate system (单位: m)
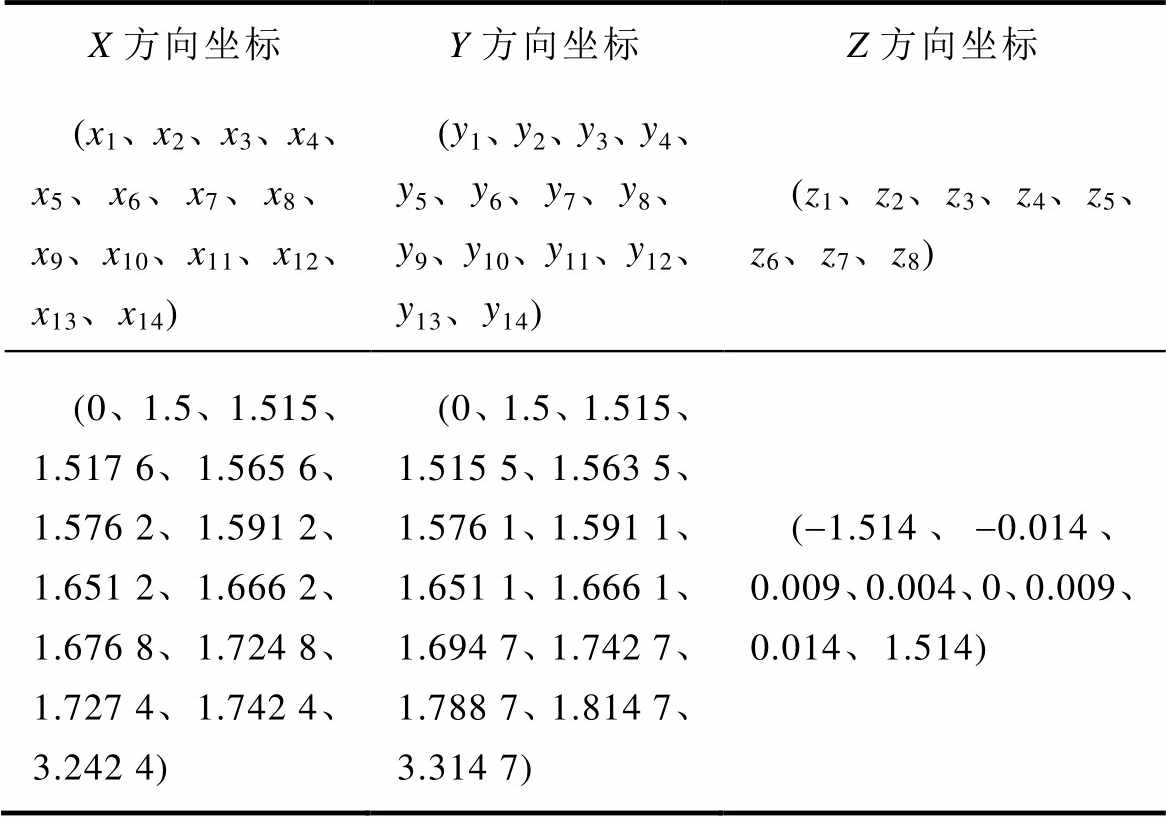
X方向坐标Y方向坐标Z方向坐标 (x1、x2、x3、x4、x5、x6、x7、x8、x9、x10、x11、x12、x13、x14)(y1、y2、y3、y4、y5、y6、y7、y8、y9、y10、y11、y12、y13、y14)(z1、z2、z3、z4、z5、z6、z7、z8) (0、1.5、1.515、1.517 6、1.565 6、1.576 2、1.591 2、1.651 2、1.666 2、1.676 8、1.724 8、1.727 4、1.742 4、3.242 4)(0、1.5、1.515、1.515 5、1.563 5、1.576 1、1.591 1、1.651 1、1.666 1、1.694 7、1.742 7、1.788 7、1.814 7、3.314 7)(-1.514、-0.014、0.009、0.004、0、0.009、0.014、1.514)
搭建的实验装置平台如图14所示,分别在亚克力刻度实验台和三维运动平台进行了四种线圈情况的实验。

图14 实验模型线圈相对位置变化
Fig.14 Relative position change of the experimental model coil
互感测量实验的技术接线示意图如图15所示。当发射与接收线圈间如图15a同向串联时,两端电感值为Ls1=L1+L2+2Me。当发射与接收线圈间如图15b反向串联时,两端电感值为Ls2=L1+L2-2Me。L1和L2为线圈的自感,系统接收线圈与发射线圈之间的互感Me可计算为Me=|Ls1-Ls2|/4。
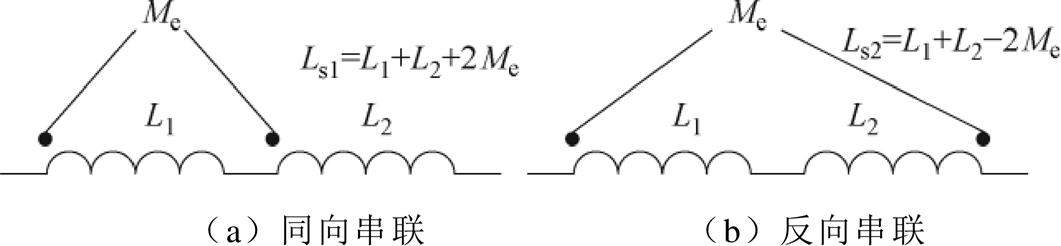
图15 互感测量实验的技术接线示意图
Fig.15 Technical wiring schematic for mutual inductance measurement experiment
垂直偏移实验中发射线圈和发射侧磁介质保持初始位置不变,接收线圈从初始固定位置Dc=10 mm处沿Z轴正方向以Dz=10 mm的步长间隔向上移动至Dc=120 mm处。接收侧磁介质也随着接收线圈一起沿Z轴正方向偏移。接收线圈垂直偏移如图16所示。蓝红色接收线圈表示线圈的初始时刻位置,红色接收线圈表示垂直偏移后的相对位置。
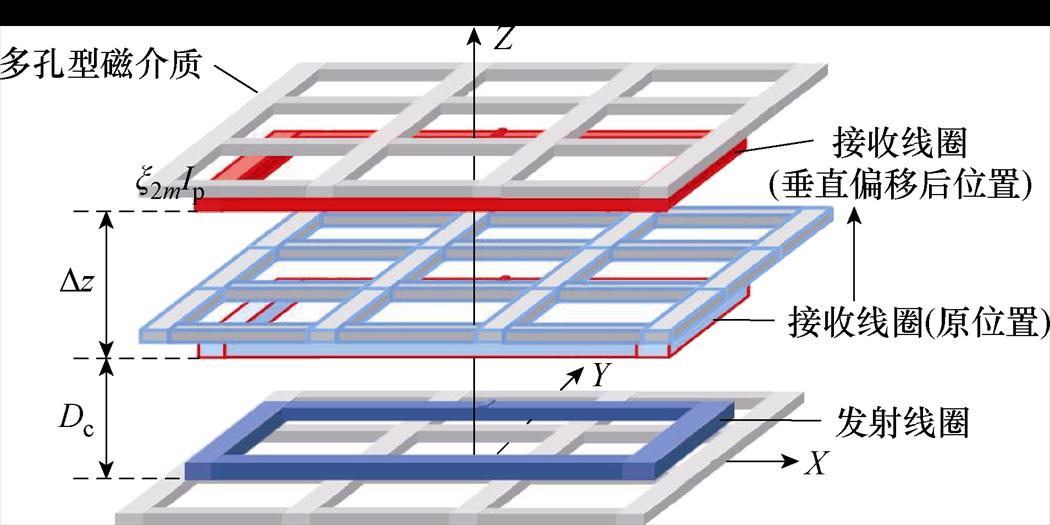
图16 接收侧垂直偏移示意图
Fig.16 Vertical displacement schematic at receiving side
表5展示了垂直偏移时互感的计算值、仿真值和实验值以及三者之间的误差。计算误差和实验误差g1、g2表达式分别为
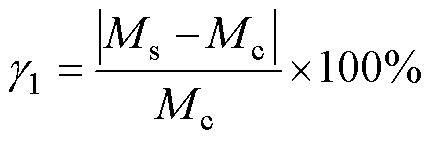 (41)
(41)
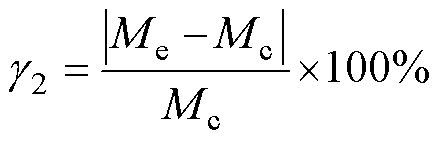 (42)
(42)
式中,Mc、Ms和Me分别为互感计算值、仿真值和实验值。
当发射线圈和接收线圈的垂直距离在Dz为10~ 110 mm的范围内,互感的计算误差g1在Dz=0 mm时为4.42%,其余误差均不大于2.73%。实验误差g2在Dz=110 mm时为4.15%,其余均不大于3.78%。互感的计算值、仿真值和实验值具有良好的一致性。综合表5数据可绘制出互感随垂直距离变化而变化的趋势如图17所示。
表5 垂直偏移时的互感及误差
Tab.5 Vertical offset-induced mutual inductance and error
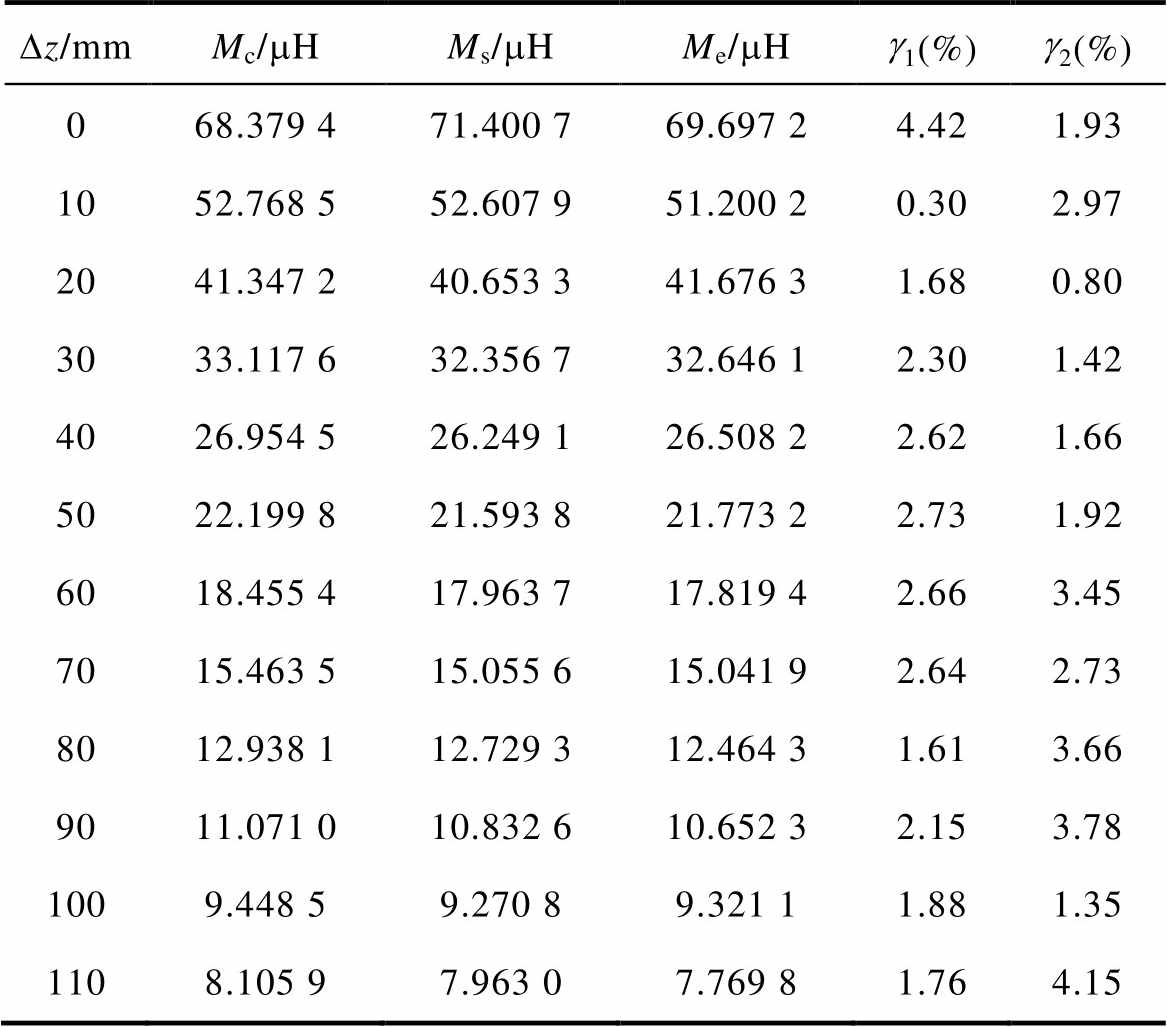
Dz/mmMc/mHMs/mHMe/mHg1(%)g2(%) 068.379 471.400 769.697 24.421.93 1052.768 552.607 951.200 20.302.97 2041.347 240.653 341.676 31.680.80 3033.117 632.356 732.646 12.301.42 4026.954 526.249 126.508 22.621.66 5022.199 821.593 821.773 22.731.92 6018.455 417.963 717.819 42.663.45 7015.463 515.055 615.041 92.642.73 8012.938 112.729 312.464 31.613.66 9011.071 010.832 610.652 32.153.78 1009.448 59.270 89.321 11.881.35 1108.105 97.963 07.769 81.764.15
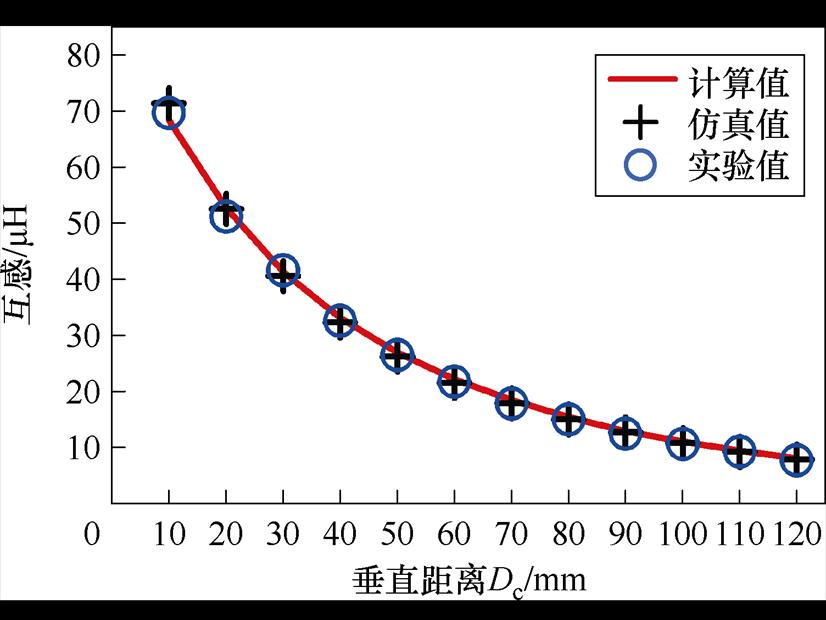
图17 互感随垂直距离变化曲线
Fig.17 Variation curve of mutual inductance with vertical distance
从图17中可以看出,发射线圈与接收线圈间距越小,其耦合效应越高,互感也随之增大。当沿Z轴正方向偏移时,耦合程度衰减,互感也随之减小,且衰减速率随垂直距离增大而逐渐趋缓。这是因为在相同步长间隔下,较大间距对应的磁通量变化幅度相对较小,使得互感衰减趋势趋缓。
水平偏移示意图如图18所示,发射线圈保持初始位置不变,接收线圈和接收侧磁介质分别沿Z轴正方向移动到Dz=50 mm,此时线圈之间距离Dc= 60 mm,然后将接收线圈和接收侧磁介质分别以Dx=±10 mm的步长向X正负轴方向移动,Dx范围为-50~50 mm。
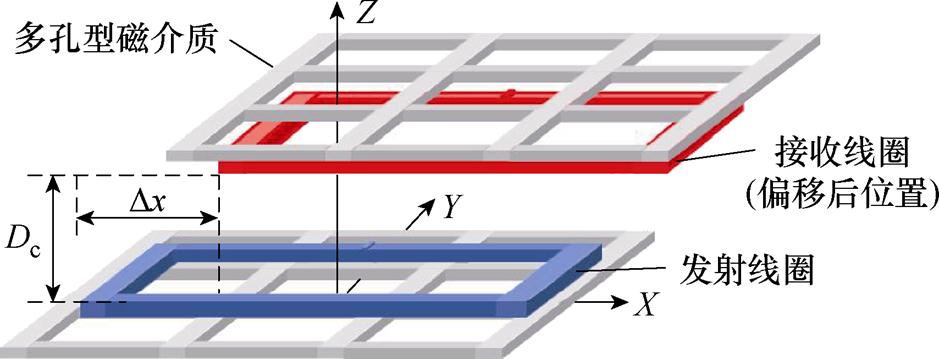
图18 接收侧水平偏移示意图
Fig.18 Horizontal offset diagram of the receiving side
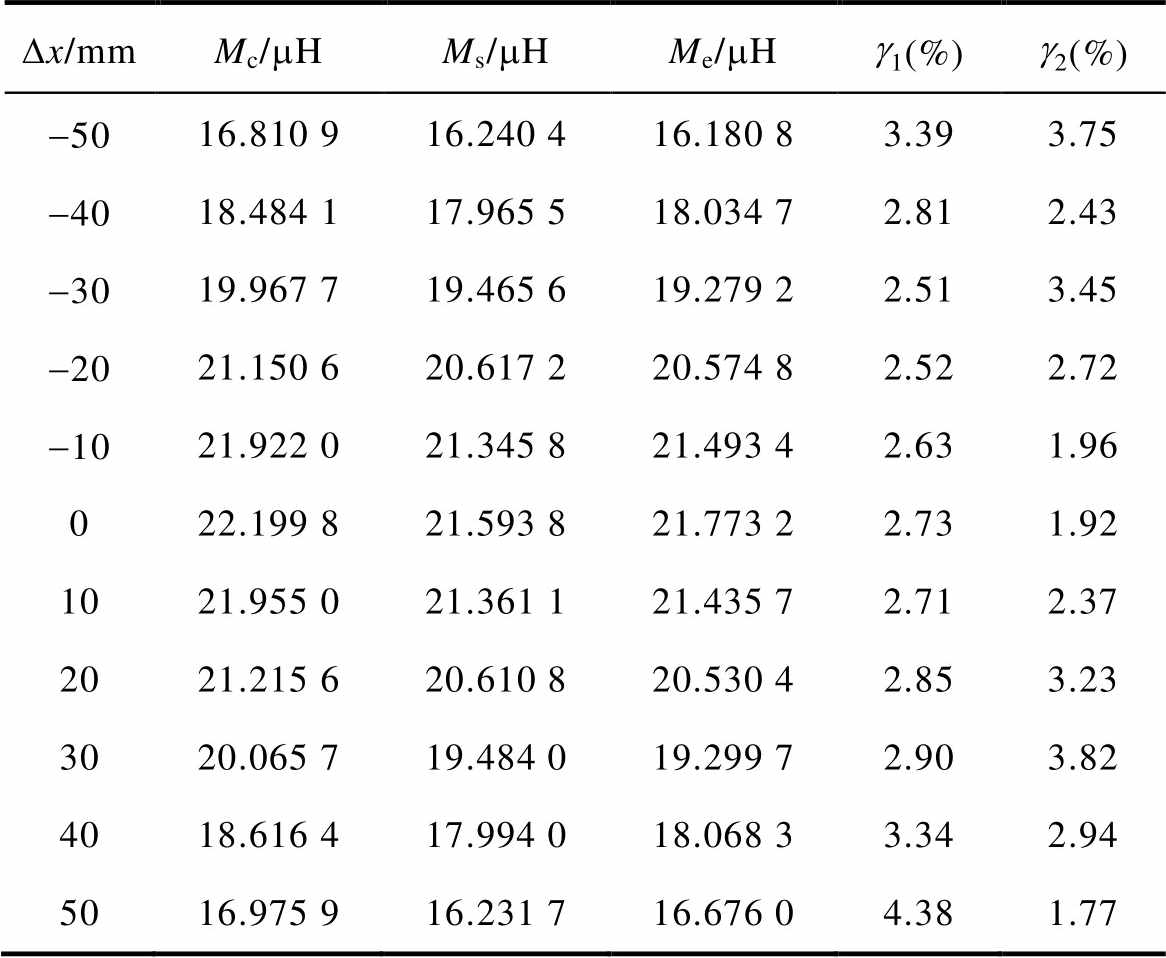
水平偏移装置如图14b所示,偏移时互感的计算值、仿真值和实验值及其误差见表6。通过分析其中的数据,在接收侧线圈和磁介质偏移Dx从-50~50 mm的过程中,最大计算误差和实验误差分别出现在接收线圈水平偏移至X轴50 mm处和30 mm处,分别是4.38%和3.82%。其余计算误差均小于3.39%,实验误差均小于3.75%。结果表明,互感的计算值、模拟值和实验值吻合良好。
表6 水平偏移时的互感及误差
Tab.6 Mutual inductance and errors during horizontal offset
Dx/mmMc/mHMs/mHMe/mHg1(%)g2(%) -5016.810 916.240 416.180 83.393.75 -4018.484 117.965 518.034 72.812.43 -3019.967 719.465 619.279 22.513.45 -2021.150 620.617 220.574 82.522.72 -1021.922 021.345 821.493 42.631.96 022.199 821.593 821.773 22.731.92 1021.955 021.361 121.435 72.712.37 2021.215 620.610 820.530 42.853.23 3020.065 719.484 019.299 72.903.82 4018.616 417.994 018.068 33.342.94 5016.975 916.231 716.676 04.381.77
依据表6的测试数据,绘制接收侧水平偏移条件下互感变化的关系曲线,如图19所示。
观察图19发现,接收线圈在Dx=0 mm时互感处于最大值,随着接收侧线圈和磁介质沿X轴左右水平偏移,互感随偏移距离的增大而减小,这是因为磁通量减少以致互感逐渐减小。
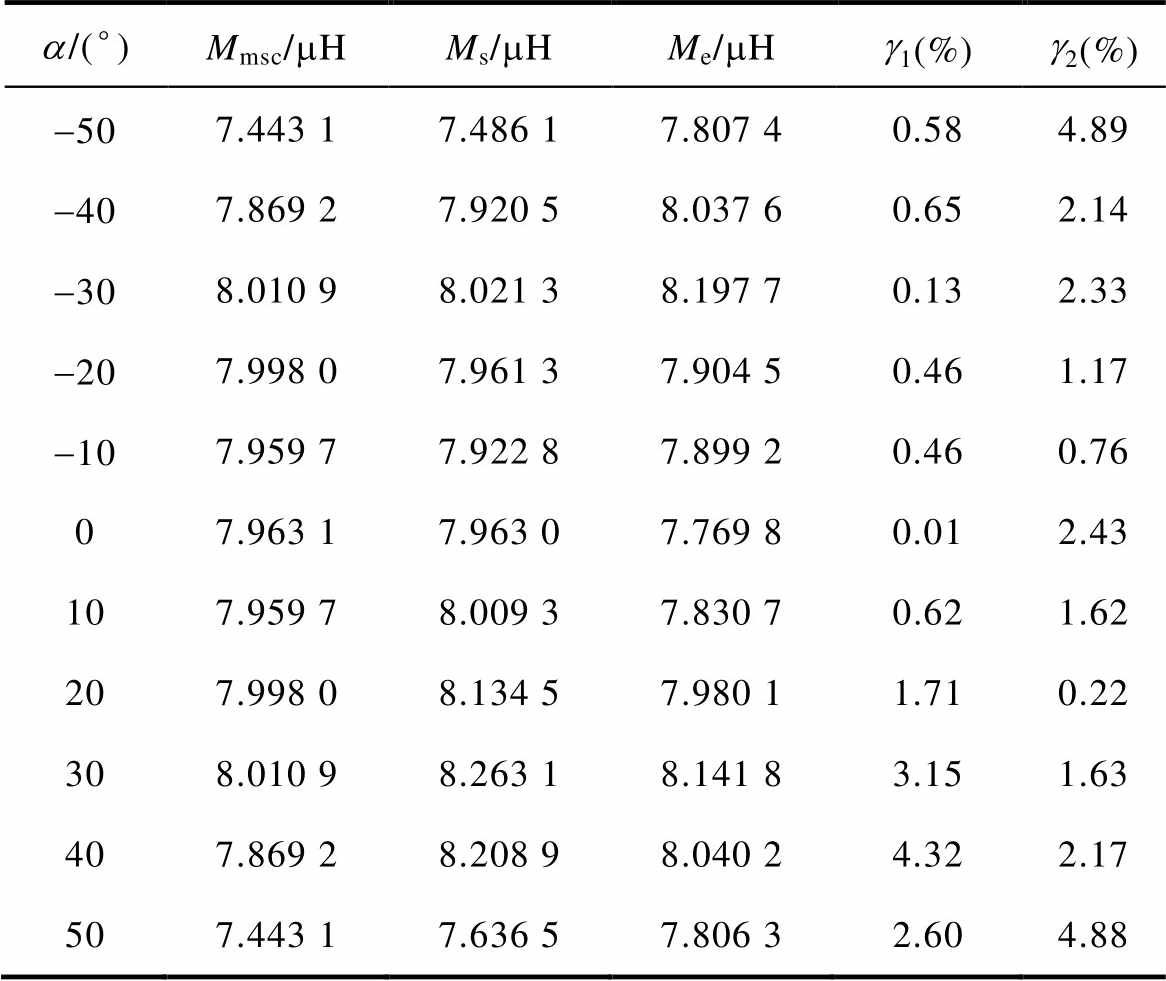
同轴角度偏转实验如图14c所示,接收侧线圈和磁介质分别以±10°的步长沿Y轴旋转,实验测试的a范围为-50°~50°。利用4.2节得到的同轴角度偏转镜像系数,结合式(36)计算出角度偏转时的互感值。同轴角度偏转时互感的各个数值及误差对比见表7。
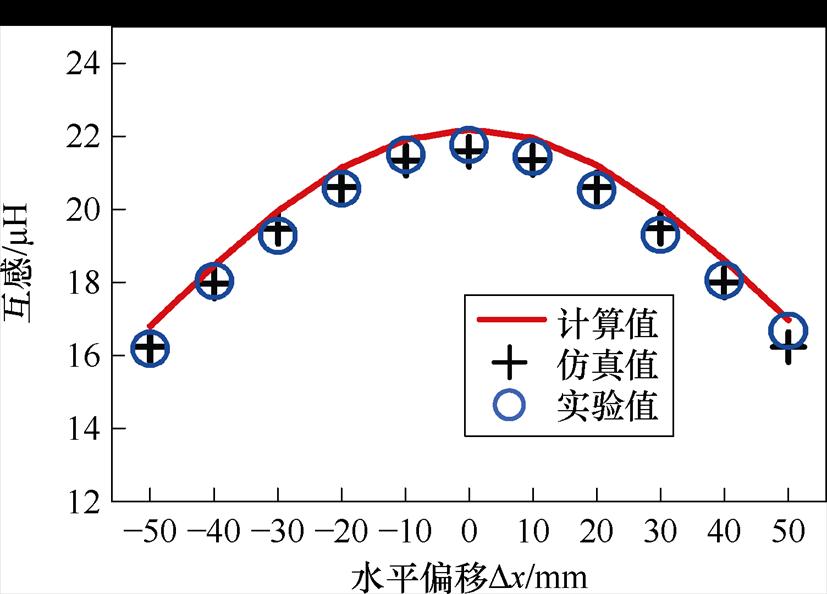
图19 互感随水平偏移距离变化曲线
Fig.19 Mutual inductance variation curve with horizontal offset distance
表7 同轴角度偏转时的互感及误差
Tab.7 Coaxial angular deflection-induced mutual inductance and error
a/(°)Mmsc/mHMs/mHMe/mHg1(%)g2(%) -507.443 17.486 17.807 40.584.89 -407.869 27.920 58.037 60.652.14 -308.010 98.021 38.197 70.132.33 -207.998 07.961 37.904 50.461.17 -107.959 77.922 87.899 20.460.76 07.963 17.963 07.769 80.012.43 107.959 78.009 37.830 70.621.62 207.998 08.134 57.980 11.710.22 308.010 98.263 18.141 83.151.63 407.869 28.208 98.040 24.322.17 507.443 17.636 57.806 32.604.88
基于表7数据的对比分析,镜像计算值与仿真值的计算误差g1除偏转a=40°时为4.32%外,其余误差均不大于3.15%。实验误差g2除a=-50°时为4.89%,其余误差均不大于4.88%。仿真、计算与实验结果的对比验证了三者数据呈现良好的一致性特征。根据表7的数据进行分析,可获得接收端同轴偏转过程中互感的变化规律,其对应关系曲线在图20中完整呈现。
从图20看出,接收线圈在垂直偏转角度0°~ 30°和-30°~0°时,互感会有微小的提升,这是因为线圈的有效投影面积增大且一侧的距离下降,增强了磁耦合程度。30°之后有效投影面积的减少占主导部分,互感开始减小。
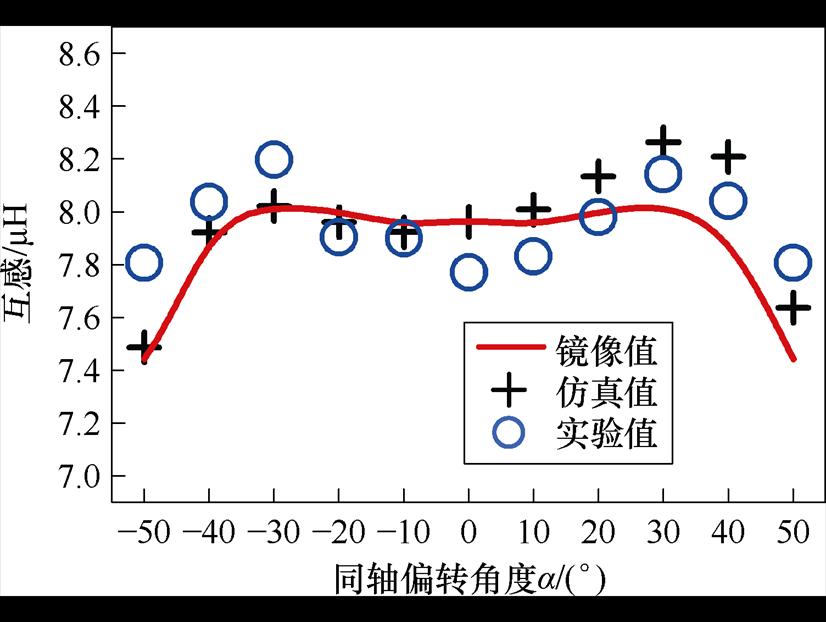
图20 互感随同轴角度偏转变化曲线
Fig.20 Mutual inductance variation curve with coaxial angular deflection
4.4.1 角度偏转加同向水平偏移
通过图14中的实验装置,测得当lc=82 mm时a=-30°和a=30°的角度偏转加同向水平偏移的Dx范围-50~50 mm的互感及误差见表8。
表8 角度偏转加同向水平偏移时的互感及误差
Tab.8 Mutual inductance and error characteristics under coupled angular displacement and co-directional lateral shift
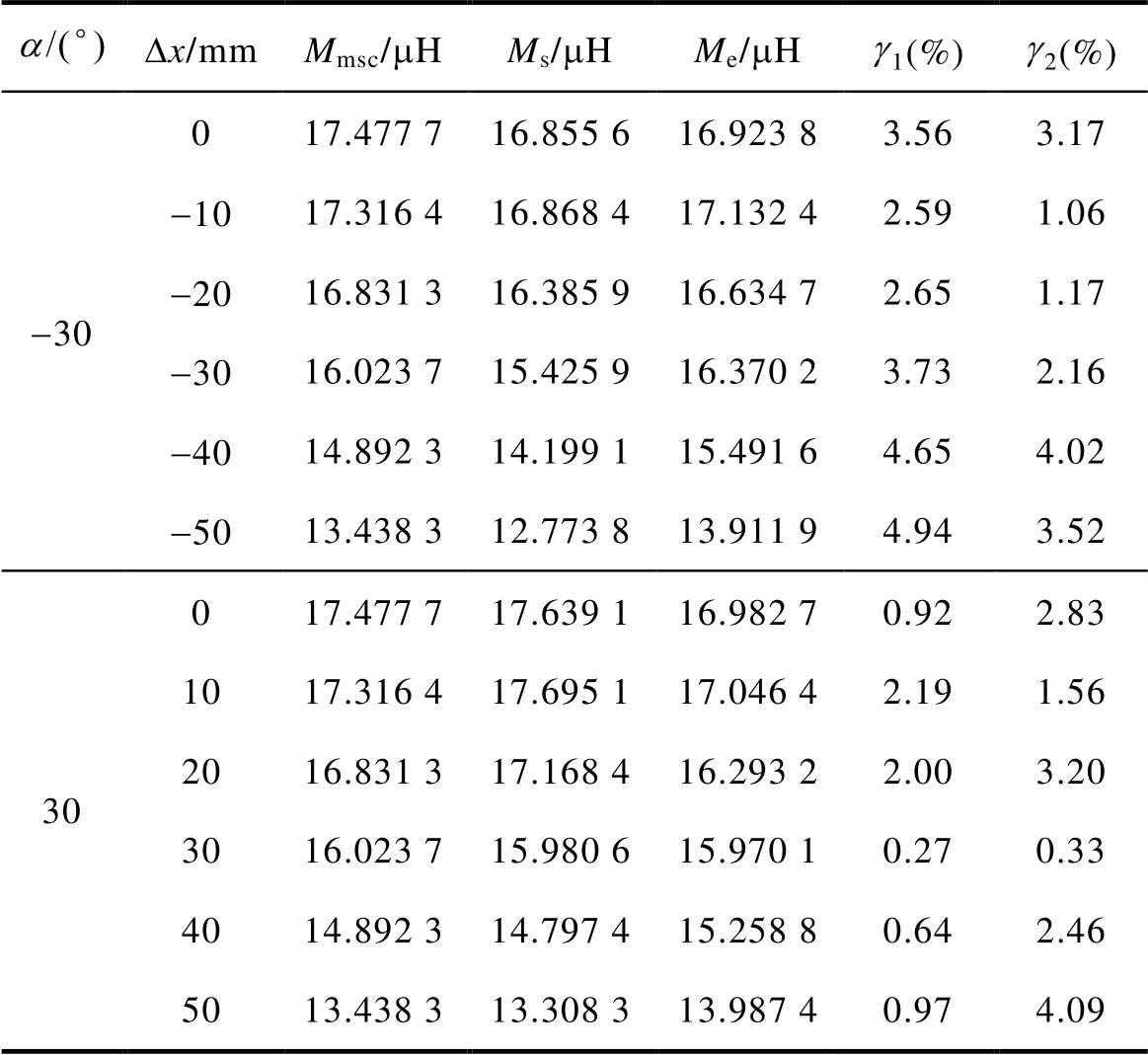
a/(°)Dx/mmMmsc/mHMs/mHMe/mHg1(%)g2(%) -30017.477 716.855 616.923 83.563.17 -1017.316 416.868 417.132 42.591.06 -2016.831 316.385 916.634 72.651.17 -3016.023 715.425 916.370 23.732.16 -4014.892 314.199 115.491 64.654.02 -5013.438 312.773 813.911 94.943.52 30017.477 717.639 116.982 70.922.83 1017.316 417.695 117.046 42.191.56 2016.831 317.168 416.293 22.003.20 3016.023 715.980 615.970 10.270.33 4014.892 314.797 415.258 80.642.46 5013.438 313.308 313.987 40.974.09
分析表8可知,镜像互感值和仿真值的计算误差g1在Dx(a=-30°)=-50 mm处为4.94%,其余误差均不大于4.65%。实验误差g2除Dx(a=30°)=50 mm时为4.09%,其余误差均不大于4.02%。仿真、计算与实验结果的对比分析表明,三者具有较高的一致性。角度加同向水平偏移下互感的变化曲线如图21所示。
分析图21可知,随着接收线圈水平偏移的距离增加,有效投影面积的磁通量逐渐降低,互感也随之减少。
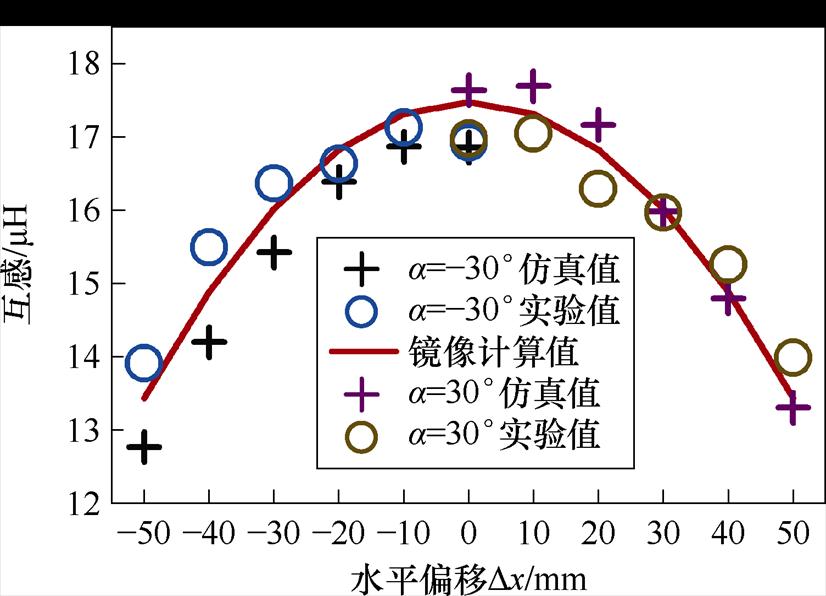
图21 角度偏转加同向水平偏移下互感变化曲线
Fig.21 Curve of mutual inductance variation under angular deflection and same-direction horizontal offset
4.4.2 角度偏转加负向水平偏移
实验的参数设置依旧是lc=82 mm和a=30°和a=-30°,Dx的范围为-50~50 mm,但其为角度偏转加负向水平偏移。测得实验数据见表9。
表9 角度偏转加负向水平偏移时的互感及误差
Tab.9 Mutual inductance and error during angular deflection with negative-directional horizontal offset
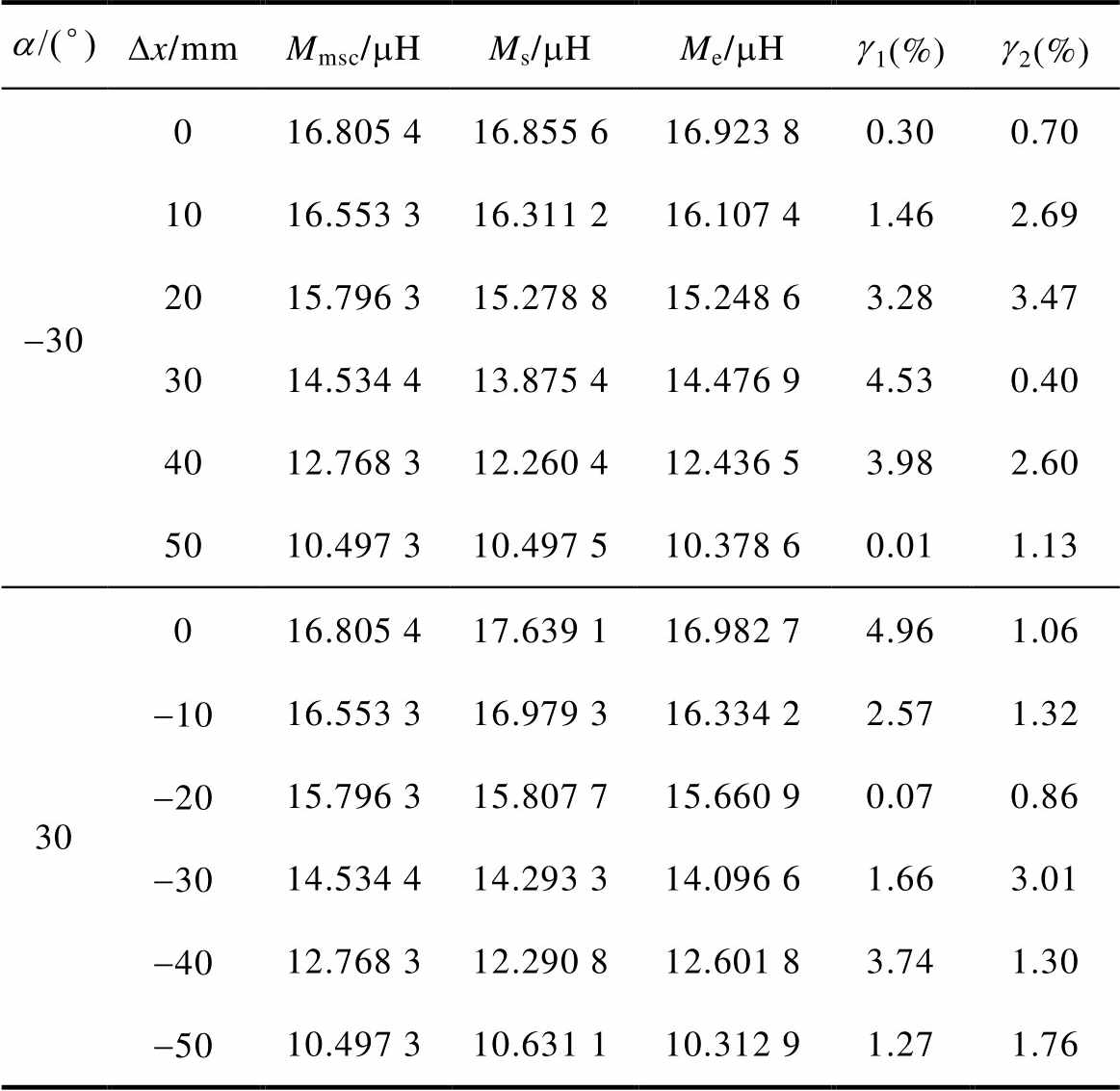
a/(°)Dx/mmMmsc/mHMs/mHMe/mHg1(%)g2(%) -30016.805 416.855 616.923 80.300.70 1016.553 316.311 216.107 41.462.69 2015.796 315.278 815.248 63.283.47 3014.534 413.875 414.476 94.530.40 4012.768 312.260 412.436 53.982.60 5010.497 310.497 510.378 60.011.13 30016.805 417.639 116.982 74.961.06 -1016.553 316.979 316.334 22.571.32 -2015.796 315.807 715.660 90.070.86 -3014.534 414.293 314.096 61.663.01 -4012.768 312.290 812.601 83.741.30 -5010.497 310.631 110.312 91.271.76
从表9数据来看,最大计算误差出现在Dx(a= 30°)=0 mm处,g1=4.96%,其余计算误差均不大于4.53%。最大实验误差出现在Dx(a=-30°)=20 mm处,g2=3.47%外,其余实验误差均小于3.01%。仿真、镜像计算与实验三者数据对比有着良好的一致性。此位置状况下互感变化曲线如图22所示。
分析图22可知,随着接收侧水平偏移距离的增加,磁通量减少,互感逐渐降低。当接收线圈绕Y轴顺时针偏转30°时,其沿X轴正方向水平位移所对应的有效磁通面积显著大于沿X轴负方向水平位移时的有效磁通面积。所以,角度加水平负向偏移的互感下降趋势比角度加水平同向偏移的情况快。
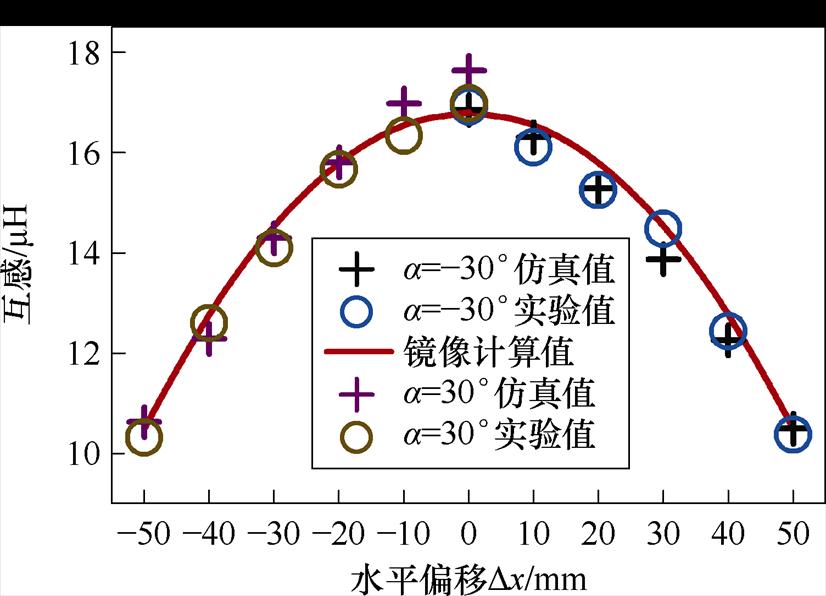
图22 角度偏转加负向水平偏移下互感变化曲线
Fig.22 Curve of mutual inductance variation under angular deflection and negative horizontal offset
以表1的参数将本文所提的多孔磁介质与相同规格下的矩形磁介质通过仿真数据来对比二者之间的互感数值。因为水平偏移具有对称性,所以本文仅绘出沿X轴负半轴水平偏移时两者的互感数据。水平偏移时矩形和多孔磁介质的互感仿真值对比见表10。可以看出,带多孔磁介质线圈间互感值可以达到带矩形磁介质线圈间互感值的91%。值得一提的是,多孔磁介质比矩形磁介质结构节省材料56.25%。
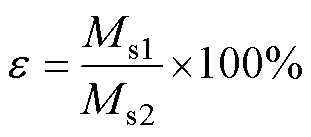 (43)
(43)
式中,Ms1为多孔磁介质的互感;Ms2为矩形磁介质的互感;e为多孔磁介质与矩形磁介质之间的比值。
表10 水平偏移时矩形和多孔磁介质的互感仿真值对比
Tab.10 Comparison of mutual inductance simulation values for rectangular and porous magnetic media under lateral offset
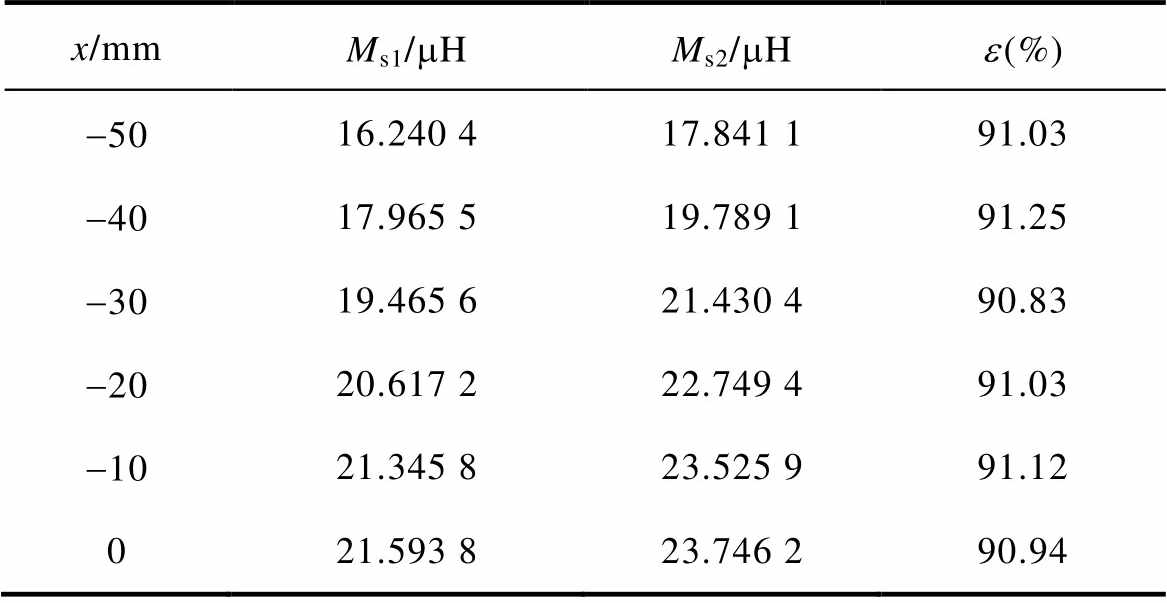
x/mmMs1/mHMs2/mHe(%) -5016.240 417.841 191.03 -4017.965 519.789 191.25 -3019.465 621.430 490.83 -2020.617 222.749 491.03 -1021.345 823.525 991.12 021.593 823.746 290.94
将本文所提方法与表11中文献的方法进行对比,表11中,LD为横向偏移(Lateral Displacement, LD),AP为任意位置(Arbitrary Position, AP),DMM为双边磁介质(Dual Magnetic Medium, DMM),BMM为有界磁介质(Bounded Magnetic Medium, BMM),SM为节省材料(Save Material, SM)。可以看出,只有本文所提出的空间截面分析法和镜像约束法能解决带非整块磁介质结构任意位置线圈间的互感计算难题。
表11 与其他文献的对比
Tab.11 Comparison with other literature
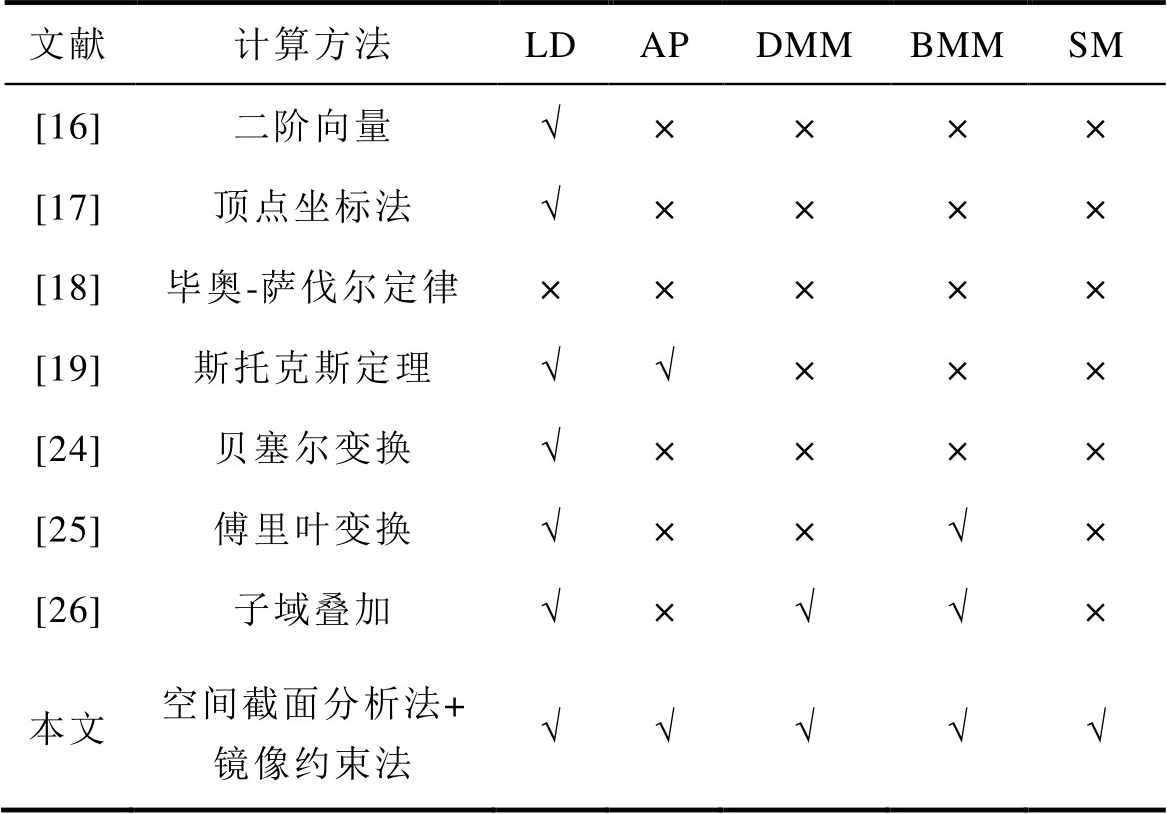
文献计算方法LDAPDMMBMMSM [16]二阶向量√×××× [17]顶点坐标法√×××× [18]毕奥-萨伐尔定律××××× [19]斯托克斯定理√√××× [24]贝塞尔变换√×××× [25]傅里叶变换√××√× [26]子域叠加√×√√× 本文空间截面分析法+镜像约束法√√√√√
本文提出了一种无线电能传输系统中双边有界多孔磁介质任意位置矩形线圈模型的互感计算方法。通过空间截面矢量分析法,将模型划分为XZ和YZ截面,通过分离变量法求解磁矢势的拉普拉斯方程、泊松方程,将各个区域的表达式求解出来,再利用麦克斯韦的边界磁场条件结合不同矢量合成的磁场修正因子得到互感的最终表达式。进一步地,提出了一种镜像约束法,将发射侧和接收侧磁介质等效为镜像线圈来代替磁介质对发射线圈和接收线圈的影响,通过分析不同情况下的镜像系数的变化规律得到了同轴偏转等情况时的互感表达式。通过对理论计算、实验测试和仿真结果的误差分析与对比,验证了所提方法的有效性。互感的计算误差g1均不大于4.96%,实验误差均不大于4.89%。在同等的结构参数下,本文所提出的模型结构比矩形磁介质节省了56.25%的材料,互感可以达到矩形磁介质互感的91%。本文提供的计算方法可为无线电能传输系统线圈结构的优化提供理论依据,对将来展开双边有界条形磁介质任意位置矩形线圈的建模具有一定的参考意义。
参考文献
[1] 杨庆新, 张献, 章鹏程. 电动车智慧无线电能传输云网[J]. 电工技术学报, 2023, 38(1): 1-12.
Yang Qingxin, Zhang Xian, Zhang Pengcheng. Intel- ligent wireless power transmission cloud network for electric vehicles[J]. Transactions of China Electro- technical Society, 2023, 38(1): 1-12.
[2] 胡俊杰, 潘羿, 徐成明, 等. 基于动态交通推演的电动汽车充电快速引导策略[J]. 电工技术学报, 2025, 40(9): 2880-2896.
Hu Junjie, Pan Yi, Xu Chengming, et al. Fast guidance strategy for electric vehicle charging based on dynamic traffic inference[J]. Transactions of China Electrotechnical Society, 2025, 40(9): 2880-2896.
[3] 陈渝, 李浩然, 朱玉玉, 等. 电动汽车无线电能传输系统参数优化研究[J]. 电力电子技术, 2024, 58(2): 51-54.
Chen Yu, Li Haoran, Zhu Yuyu, et al. Research on parameter optimization of electric vehicle wireless power transmission system[J]. Power Electronics, 2024, 58(2): 51-54.
[4] 闫争超, 胡谦宇, 赵晨旭, 等. 水下航行器感应式无线电能传输技术研究综述[J]. 中国电机工程学报, 2023, 43(24): 9668-9682.
Yan Zhengchao, Hu Qianyu, Zhao Chenxu, et al. Review on inductive wireless power transfer tech- nology for underwater vehicles[J]. Proceedings of the CSEE, 2023, 43(24): 9668-9682.
[5] 王得安, 张剑韬, 朱春波, 等. 海洋环境对水下无线电能传输系统的影响机理研究进展[J]. 电工技术学报, 2025, 40(3): 653-675.
Wang Dean, Zhang Jiantao, Zhu Chunbo, et al. Review of progress in the study of marine environ- ment effects on underwater wireless power transfer systems[J]. Transactions of China Electrotechnical Society, 2025, 40(3): 653-675.
[6] 祖建中, 赵进, 孙作民, 等. 具有恒功率特性的水下无线电能传输系统研究与设计[J/OL]. 电源学报, 2025: 1-15. (2025-03-27). https://kns.cnki.net/kcms/ detail/12.1420.tm.20250326.1743.030.html.
Zu Jianzhong, Zhao Jin, Sun Zuomin, et al. Research and design of underwater wireless power transfer system with constant power characteristic[J/OL]. Journal of Power Supply, 2025: 1-15. (2025-03-27). https://kns.cnki.net/kcms/detail/12.1420.tm.20250326. 1743.030.html.
[7] 张鑫, 杨帅鑫, 王文杰, 等. 电场耦合无人机无线电能传输系统轻量化抗偏无线输电耦合机构研究[J]. 电工技术学报, 2025, 40(14): 4343-4354.
Zhang Xin, Yang Shuaixin, Wang Wenjie, et al. Research on lightweight anti-bias wireless power transmission coupling mechanism for WPT system of UAV coupled with electric field[J]. Transactions of China Electrotechnical Society, 2025, 40(14): 4343- 4354.
[8] Krishna Chittoor P, Chokkalingam B. Wireless electrification system for photovoltaic powered auto- nomous drone charging[J]. IEEE Transactions on Trans- portation Electrification, 2024, 10(2): 3002-3011.
[9] 陈伟华, 刘岳鹏, 闫孝姮, 等. 心脏起搏器谐振式无线供能四匹配电容无功屏蔽[J/OL]. 电工技术学报, 2024: 1-11. (2024-09-05). https://link.cnki.net/ doi/10.19595/j.cnki.1000-6753.tces.241252.
Chen Weihua, Liu Yuepeng, Yan Xiaoheng, et al. Reactive shielding of four matching capacitors for resonant wireless power transfer in cardiac pace- makers[J/OL]. Transactions of China Electrotechnical Society, 2024: 1-11. (2024-09-05). https://link.cnki. net/doi/10.19595/j.cnki.1000-6753.tces.241252.
[10] Zhuang Haoyu, Wang Wei, Yan Guozheng. Ferrite concentrating and shielding structure design of wire- less power transmitting coil for inductively coupled capsule robot[J]. IEEE Transactions on Biomedical Circuits and Systems, 2023, 17(1): 45-53.
[11] 高鹏飞, 田晓盈, 杨志梁, 等. 非对称三线圈结构无线电能传输系统研究[J]. 电气工程学报, 2024, 19(4): 169-175.
Gao Pengfei, Tian Xiaoying, Yang Zhiliang, et al. Research on the wireless power transfer system with asymmetric three coils structure[J]. Journal of Elec- trical Engineering, 2024, 19(4): 169-175.
[12] 李中启, 林志远, 杨鹏, 等. 无线电能传输系统带双层有界磁屏蔽任意位置圆形线圈的耦合系数计算[J]. 电工技术学报, 2022, 37(24): 6306-6318.
Li Zhongqi, Lin Zhiyuan, Yang Peng, et al. Calculation of the coupling coefficient of an arbitrarily positioned circular coil for wireless power transfer system with a double-layered finite magnetic shield[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6306-6318.
[13] Dong Zifan, Li Xiaoming, Liu Sheng, et al. A novel all-direction antimisalignment wireless power transfer system designed by truncated region eigenfunction expansion method[J]. IEEE Transactions on Power Electronics, 2021, 36(11): 12456-12467.
[14] Qian Libo, Chen Mengfei, Cui Kexue, et al. Modeling of mutual inductance between two misalignment planar coils in wireless power transfer[J]. IEEE Microwave and Wireless Components Letters, 2020, 30(8): 814-817.
[15] Oliveira R, Lehn P. An improved mutual inductance electromagnetic model for inductive power transfer systems under misalignment conditions[J]. IEEE Transactions on Vehicular Technology, 2020, 69(6): 6079-6093.
[16] 吴德会, 何天府, 王晓红, 等. 感应电能传输中矩形螺线线圈互感耦合的解析建模与分析[J]. 电工技术学报, 2018, 33(3): 680-688.
Wu Dehui, He Tianfu, Wang Xiaohong, et al. Analytical modeling and analysis of mutual inductance coupling of rectangular spiral coils in inductive power transfer[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 680-688.
[17] Wu Dehui, Sun Qisheng, Wang Xiaohong, et al. Analytical model of mutual coupling between rectangular spiral coils with lateral misalignment for wireless power applications[J]. IET Power Electronics, 2018, 11(5): 781-786.
[18] Aydin Emrullah, Yildiriz Emin, et al. Analytical model of mutual coupling between rectangular spiral coils with lateral misalignment for wireless power applications[J]. IET Power Electronics, 2021, 103(3): 1769-1778.
[19] Altun H, Pirinççi N. A novel analytical model for mutual inductance calculations between two noni- dentical N-sided polygonal planar coils arbitrarily positioned in 3-D space for wireless power transfer[J]. IEEE Transactions on Power Electronics, 2023, 38(8): 10396-10411.
[20] 谭平安, 许文浩, 上官旭, 等. 无线电能传输系统中组合串绕六边形线圈的互感建模及参数优化[J]. 电工技术学报, 2023, 38(9): 2299-2309.
Tan Ping’an, Xu Wenhao, Shangguan Xu, et al. Mutual inductance modeling and parameter optimi- zation of wireless power transfer system with com- bined series-wound hexagonal coils[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2299-2309.
[21] Campi T, Cruciani S, Maradei F, et al. Magnetic field mitigation by multicoil active shielding in electric vehicles equipped with wireless power charging system[J]. IEEE Transactions on Electromagnetic Compatibility, 2020, 62(4): 1398-1405.
[22] Dai Zhongyu, Zhang Xian, Liu Tianqi, et al. Magnetic coupling mechanism with omnidirectional magnetic shielding for wireless power transfer[J]. IEEE Transa- ctions on Electromagnetic Compatibility, 2023, 65(5): 1565-1574.
[23] Zhu Lihua, Tian Zhongying, Li Yuan, et al. Analysis on new electromagnetic shielding structure and shielding effectiveness of electric vehicle wireless charging system[C]//2023 IEEE International Mag- netic Conference-Short Papers (INTERMAG Short Papers), Sendai, Japan, 2023: 1-2.
[24] Luo Zhichao, Wei Xuezhe. Analysis of square and circular planar spiral coils in wireless power transfer system for electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 331-341.
[25] Kushwaha B K, Rituraj G, Kumar P. 3-D analytical model for computation of mutual inductance for different misalignments with shielding in wireless power transfer system[J]. IEEE Transactions on Transportation Electrification, 2017, 3(2): 332-342.
[26] Kushwaha B K, Rituraj G, Kumar P. A subdomain analytical model of coil system with magnetic shields of finite dimensions and finite permeability for wire- less power transfer systems[J]. IEEE Transactions on Magnetics, 2020, 56(12): 8400511.
[27] Luo Zhichao, Nie Shuang, Pathmanathan M, et al. 3-D analytical model of bipolar coils with multiple finite magnetic shields for wireless electric vehicle charging systems[J]. IEEE Transactions on Industrial Elec- tronics, 2022, 69(8): 8231-8242.
Calculation of Mutual Inductance Between Rectangular Coils at Arbitrary Positions of Porous Magnetic Media for Wireless Energy Transmission Systems
Abstract For wireless power transfer (WPT) systems, mutual inductance is one of the core performance indicators. The system integration of magnetic medium materials can significantly enhance mutual inductance performance while effectively suppressing magnetic leakage phenomena. In practical engineering applications, relative positional deviations between transceiver devices of the system are inevitable, which directly affect energy transfer efficiency. Mutual inductance calculation methods that can save magnetic medium materials are rare. Therefore, studying the mutual inductance calculation method for rectangular coils with bilateral bounded porous magnetic media at arbitrary positions is of great significance.
This paper constructs a mutual inductance calculation model for rectangular coils integrated with porous magnetic media at arbitrary positions in a wireless power transfer (WPT) system. By leveraging spatial cross-sectional analysis, the magnetic vector potential equations for each region of the 2D cross-section were derived. Maxwell's boundary conditions were then applied to solve for the unknown coefficients in each area. Combining the results from individual 2D planes, the mutual inductance formula under coaxial conditions was ultimately obtained. Additionally, an image constraint method was proposed using image coils to represent the influence of magnetic media on the coils equivalently. Through analyzing the patterns of image coefficients, mutual inductance expressions for arbitrary positional scenarios were derived, thereby resolving the challenge of calculating mutual inductance between coils at arbitrary positions. Theoretical calculations, numerical simulations, and physical experiments confirmed the effectiveness of the proposed method across four positional configurations: vertical offset, horizontal offset, angular deflection, and combined angular-horizontal dis- placement.
The deviations between calculated mutual inductance values and simulated/experimental results under various relative positional configurations are presented below. (1) For vertical misalignment scenarios, maximum discrepancies observed between computational outcomes and experimental data, along with simulation results, reached 4.15% and 4.42% respectively. (2)For horizontal misalignment configurations, maximum discrepancies observed between computational outcomes and experimental data, along with computational outcomes and simulation results, were 4.38% and 3.82% respectively. (3) In the context of angular deflection, the maximum disparities between the computational results and the experimental findings, along with those between the computational results and the simulation outcomes, are 4.32% and 4.89% respectively. (4) In the case of angular deflection combined with horizontal offset in the same direction, compared with the experimental and simulation results, the calculation results’ maximum errors are 4.94% and 4.09%, respectively. (5) When angular deviation is accompanied by negative horizontal displacement, the maximum computational discrepancies to empirical findings and modeled predictions reach 4.96% and 3.47%.
The calculated, simulated, and experimental values exhibit good agreement, effectively validating the accuracy of the proposed calculation approach. Under the same parameter conditions, the model structure in this paper saves 56.25% of the materials compared with the traditional rectangular magnetic medium, and the mutual inductance can reach 91% of that of the rectangular magnetic medium.
Keywords:Wireless power transfer, magnetic medium, calculation of mutual inductance, rectangle spiral coil
中图分类号:TM724
DOI: 10.19595/j.cnki.1000-6753.tces.242196
国家重点研发计划项目(2022YFB3403200)、湖南省自然科学基金项目(2022JJ30226)和湖南省教育厅重点项目(23A0432)资助。
收稿日期 2024-12-05
改稿日期 2025-01-02
李中启 男,1985年生,博士,硕士生导师,研究方向为无线电能传输技术。
E-mail: lizhongqi@hnu.edu.cn
黄守道 男,1962年生,教授,博士,博士生导师,研究方向为特种电机控制、无线电能传输技术。
E-mail: hsd1962@hnu.edu.cn(通信作者)
(编辑 崔文静)