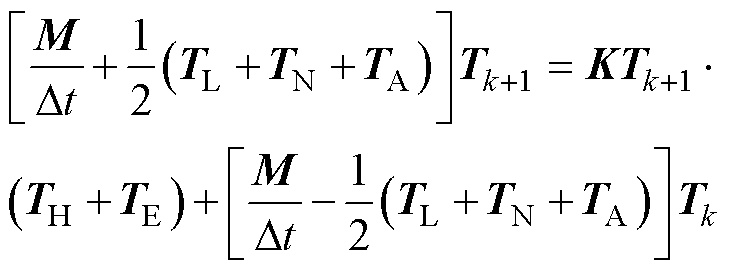 (1)
(1)
摘要 在构建变压器绕组温度场降阶模型时,现有方法普遍采用快照矩阵奇异值分解(SVD)后得到的恒定模态,模态发生变化会使降阶模型计算精度显著下降。该文基于矩阵低秩分解,提出一种低计算成本更新模态,进而更新降阶模型的方法。首先,在新快照矩阵可用时将其加入初始快照矩阵,并用矩阵低秩分解表示快照矩阵更新过程;然后,建立由初始快照矩阵SVD结果和新快照直接对模态进行更新的求解方式,无需再进行高计算成本的新快照矩阵SVD;之后,使用绕组温度的稀疏测量值确定了模态系数并形成动态降阶模型;最后,通过数值计算和变压器缩比样机实验开展了该方法有效性验证,结果表明:该文方法更新变压器绕组温度场模态的误差在10-8级别,百万级网格规模下单次更新耗时约0.71 s,比传统方法快239倍,所得动态降阶模型可有效避免变压器运行过程中模态变化导致的精度下降且计算速度为s级。研究可为当前降阶模型实现持续准确计算提供方案。
关键词:变压器 绕组温度场 降阶模型模态 低秩分解
目前,电力行业正加快构建和发展新型电力系统[1],电力装备的数字化、智能化转型是建设新型电力系统的关键环节和基础保障[2]。利用数字孪生等技术在数字空间中同步且全面地呈现电力装备状态是实现转型的重要手段[3],同时也对电力装备物理场高效计算方法提出了迫切需求。
绕组温度是变压器运维工作中关注的重点,其计算是一个涉及磁场-热场-流场耦合的复杂过程,因此关于变压器绕组温度场的高效计算方法被广泛研究[4-6]。所形成的方法可分为三类:基于模型简化的方法、基于场-路联合的方法、基于模型降阶的方法。模型简化法主要通过简化计算参数和网格来提升求解效率。文献[7]建立变压器绕组的等效热参数,得到计算绕组温度场的简化热模型,提升求解效率193倍。文献[8]在变压器的磁-热-流耦合计算中,以变压器油的流速为误差控制量进行网格自适应缩减,计算耗时减少36%。场-路联合法同样以降低网格规模为目标,把对计算有显著影响但又不关注场分布的区域等效为路模型。文献[9]以油温和流速为等效目标,建立变压器散热器和油路管道的路模型,将其与绕组的场计算模型进行联合求解。进一步地,文献[10]基于Modelica语言以方程的形式更为准确地对变压器传热过程中散热器等部件的热路进行建模。由于模型简化法和场路联合法的参数普适性较差,因此基于模型降阶的方法受到了广泛关注[11]。降阶模型(Reduced Order Model, ROM)根据是否需要修改控制方程可分为侵入式和非侵入式两类。基于本征正交分解(Proper Orthogonal Decom- position, POD)的降阶方法普适性好、计算效率高,应用最为广泛。文献[12]将变压器绕组温度场的热-流耦合场控制方程投影到POD模态张成的低维空间上,降低了控制方程的维度。受控制方程中非线性项的影响,原始基于POD的降阶方法对计算效率的提升有限。为提升求解效率,文献[13-14]通过离散经验插值的方法提高了刚度矩阵迭代过程中非线性项的形成效率。文献[15]加入混合变步长算法减少ROM计算步长中的冗余部分,进一步提升了计算效率。相比于前述的侵入式降阶,非侵入式降阶将待求场分布表示为已知模态和未知模态系数的组合,无需再对控制方程进行求解,将计算速度提升至s级。文献[16-18]进行大量数值计算及奇异值分解(Singular Value Decomposition, SVD)后,分别使用克里金代理模型、径向基函数、多层感知器,拟合了运行工况与模态系数间的关系。在线计算阶段可根据工况快速得到模态系数进而得到场分布,但该类方法在离线拟合阶段的计算成本过高。为此,文献[19-20]提出在线计算阶段使用绕组温度的部分监测值来确定模态系数,以避免离线阶段的高计算成本。
综上所述,当前研究主要关注如何提升ROM的求解速度,但普遍构建的是静态ROM,即基于快照矩阵得到POD模态后,保持模态不变并持续使用。变压器运行过程中,POD模态发生变化后,会出现初始的静态ROM计算精度的显著下降。在快照矩阵形成阶段就考虑所有工况难度较大且难以实现。当有新快照可用时,更新快照矩阵并重新进行SVD来更新模态是一种解决方案,但SVD极为耗时,又会使ROM失去原本的速度优势。
为此,本文提出一种仅使用初始SVD结果和可用的新快照直接低计算成本地更新模态,进而更新ROM的方法,无需再进行高耗时的新快照矩阵SVD运算。首先分析了静态ROM失效的原因,然后提出了由新快照和初始SVD结果直接更新模态的方法,同时利用绕组温度稀疏测量值计算模态系数,最后,建立动态ROM。最后通过数值实验和变压器缩比样机,验证了方法的有效性。
变压器绕组瞬态温度场控制方程的离散形式为
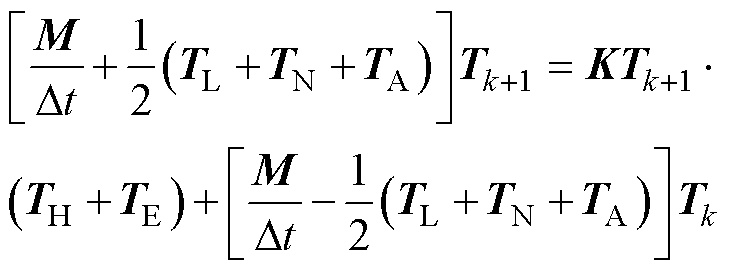 (1)
(1)
式中,K刚度矩阵,K=M/Dt+0.5(TL+TN+TA);Tk+1为第k+1个时间步的温度矩阵;Dt为离散的时间步长;各矩阵项M、TL、TN、TA、TH、TE详见文献[12]。
假设模型网格点数量为n,那么方程就是一个关于待求变量T的n维方程组。为降低待求方程的维度,现有研究普遍采用基于POD的模型降阶方法对式(1)进行处理。
首先,构造绕组温度场快照矩阵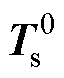 ,提取绕组温度场分布的主要特征。
,提取绕组温度场分布的主要特征。
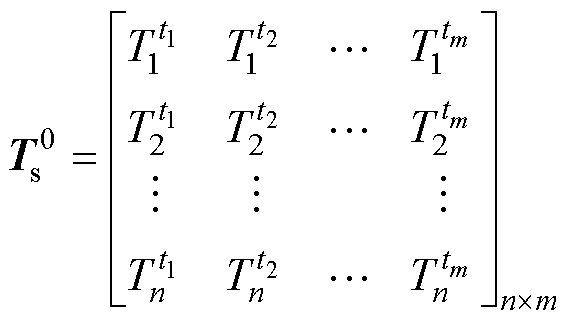 (2)
(2)
式中,m为快照数量;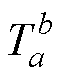 为b时刻网格点a处的温度。
为b时刻网格点a处的温度。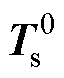 的每个列向量都是一个绕组温度场快照。
的每个列向量都是一个绕组温度场快照。
然后,对其进行SVD并根据奇异值大小进行截断,取前r n阶模态进行近似后可得
n阶模态进行近似后可得
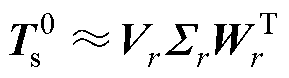 (3)
(3)
式中,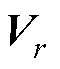 为左奇异矩阵,其列向量被称为POD模态,表征了绕组温度场分布的主要特征,
为左奇异矩阵,其列向量被称为POD模态,表征了绕组温度场分布的主要特征,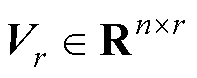 ;
;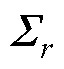 为奇异值矩阵,其对角线上元素为奇异值,
为奇异值矩阵,其对角线上元素为奇异值,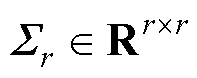 ;
;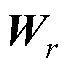 为右奇异矩阵,
为右奇异矩阵,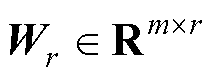 。任意ti时刻的绕组温度场
。任意ti时刻的绕组温度场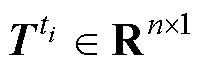 可由模态和模态系数表示为
可由模态和模态系数表示为
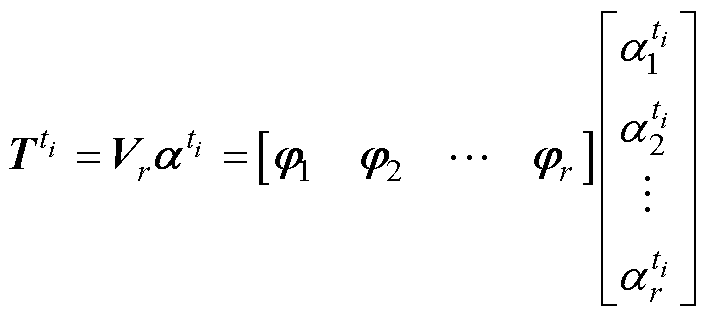 (4)
(4)
式中,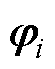 为模态,
为模态,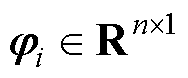 ;
;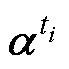 为模态系数,
为模态系数,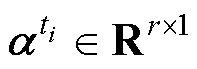 。
。
将式(4)代入式(1)并同时左乘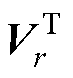 后,控制方程就可以表示为
后,控制方程就可以表示为
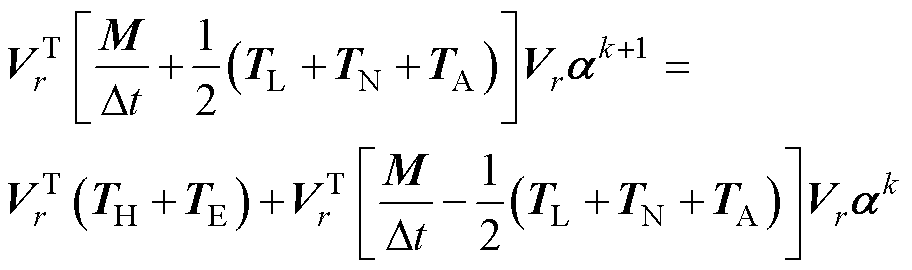 (5)
(5)
此时,控制方程被处理为r维的方程组,且待求变量也由n维的温度T转换为r维的变量模态系数a,由此就实现了控制方程的降阶。
前述的模态Vr是通过快照矩阵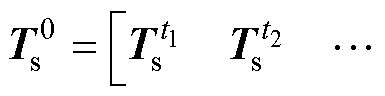
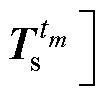 提取到的,该快照矩阵必然对应着一个参数空间D0。变压器运行过程中,当运行参数仍位于D0内时,ROM可以保持高计算精度。但变压器运行工况复杂多变,在形成快照集时,通常难以覆盖全部运行参数。当计算参数超出D0后,ROM会出现计算精度的显著下降。
提取到的,该快照矩阵必然对应着一个参数空间D0。变压器运行过程中,当运行参数仍位于D0内时,ROM可以保持高计算精度。但变压器运行工况复杂多变,在形成快照集时,通常难以覆盖全部运行参数。当计算参数超出D0后,ROM会出现计算精度的显著下降。
考虑运行工况发生变化或研究所感兴趣的参数域发生变化,导致参数域变化到D1的情况。假设在该时间段内,获得了某个时刻的温度场快照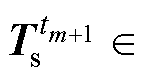
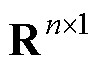 ,那么可构造新快照矩阵
,那么可构造新快照矩阵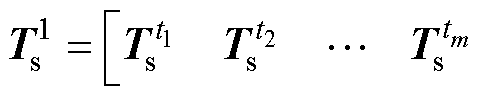
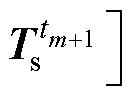 。此时POD模态实际上更新为由新快照矩阵
。此时POD模态实际上更新为由新快照矩阵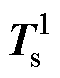 进行SVD运算后得到的Vr1,即此时在计算变压器绕组温度场时使用的ROM为
进行SVD运算后得到的Vr1,即此时在计算变压器绕组温度场时使用的ROM为
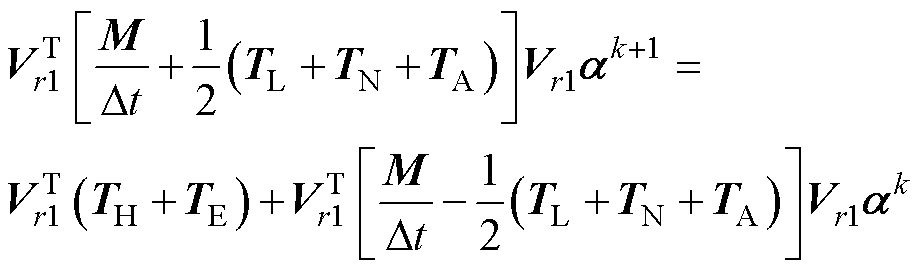 (6)
(6)
因此,在参数域D1下,如果仍使用参数域D0内构造的ROM即式(5)进行计算,而不对模态进行更新,就会导致计算精度的显著下降。
该问题有两种解决方案,其一是形成初始快照矩阵时就充分考虑各种工况,这将不可避免地形成一个超大规模的快照矩阵,导致离线阶段的计算成本过高,且由于运行参数域各异,也难以构造出如此全面的快照矩阵;其二是有新快照可用时,将其加入初始快照矩阵,即由初始快照矩阵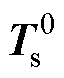 更新至新的快照矩阵
更新至新的快照矩阵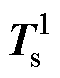 ,然后再对
,然后再对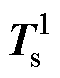 进行SVD更新POD模态,但SVD极耗时,如此操作又会使ROM失去原有的速度优势。
进行SVD更新POD模态,但SVD极耗时,如此操作又会使ROM失去原有的速度优势。
针对上述问题,本节旨在探索一种算法,能够在有新快照可用时,直接结合初始SVD结果快速计算出将新快照特征纳入考虑后的SVD结果,以较低的计算成本完成POD模态更新,无需再进行高计算成本的新快照矩阵SVD运算。
1.2.1 POD模态快速更新算法
假设在参数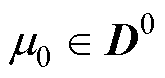 下已有绕组温度场快照矩阵Ts0,即
下已有绕组温度场快照矩阵Ts0,即
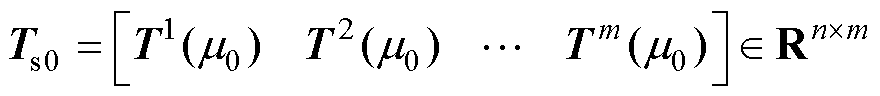 (7)
(7)
同时,添加全零列并将其写为
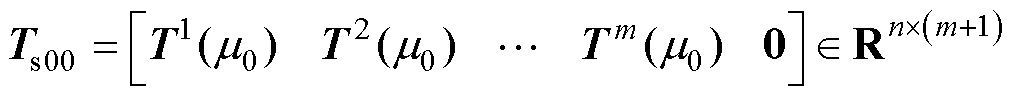 (8)
(8)
在参数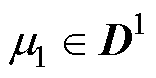 下有新快照
下有新快照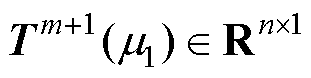 可用时,快照矩阵可更新为
可用时,快照矩阵可更新为
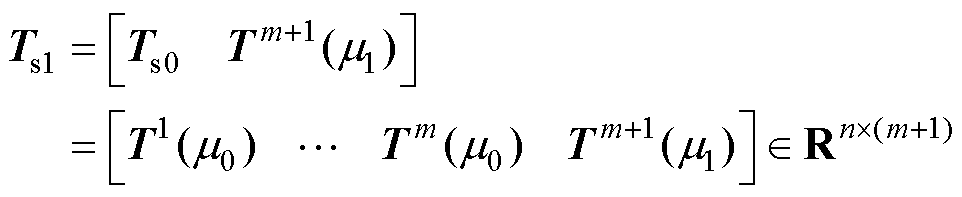 (9)
(9)
为快速得到更新后的POD模态,将Ts0到Ts1的更新用矩阵低秩分解的形式表达,即
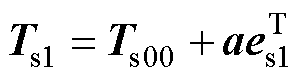 (10)
(10)
式中,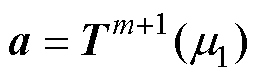 ,
,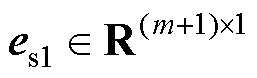 ,
,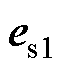 的第m+1个元素为1、其余元素为0;a和
的第m+1个元素为1、其余元素为0;a和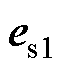 均是秩为1的矩阵。
均是秩为1的矩阵。
上述过程通过分解出两个秩为1的矩阵,表征了快照矩阵的更新。通过上述分解结果,式(10)可改写为
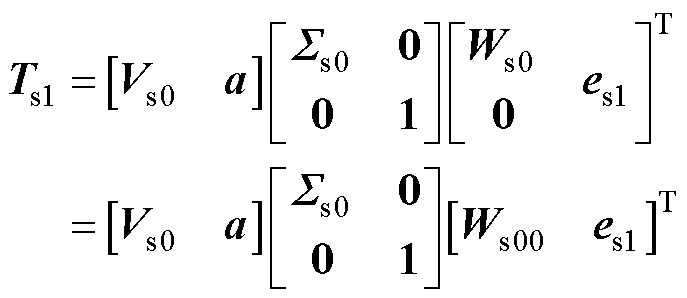 (11)
(11)
式中,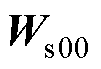 为
为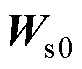 用全零行进行增广后的矩阵,
用全零行进行增广后的矩阵,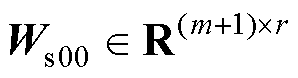 ;
;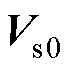 、
、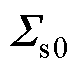 、
、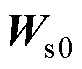 为初始快照矩阵
为初始快照矩阵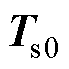 进行SVD并以r为截断数进行截断后的结果,
进行SVD并以r为截断数进行截断后的结果,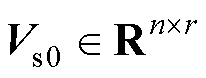 、
、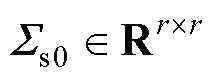 、
、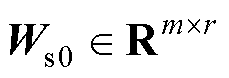 。即
。即
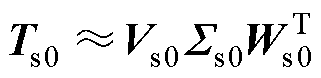 (12)
(12)
式(11)已将Ts1初步表示为预期的SVD形式,且是由式(12)所示的初始SVD结果和新快照直接表示。但这并不是最终的SVD结果,因为[Vs0 a]和[Ws00 es1]还不是列向量正交的矩阵。
因此,用式(13)对[Vs0 a]进行Gram-Schmidt正交化处理。
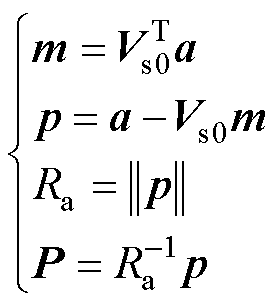 (13)
(13)
则有
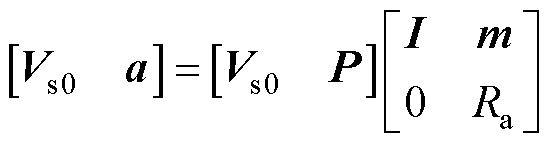 (14)
(14)
式中,I为单位矩阵;[Vs0 P]是列正交的。
同理,用式(15)对[Ws00 es1]进行正交化处理。
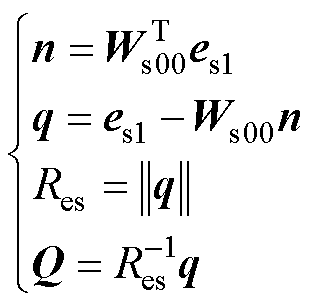 (15)
(15)
得到
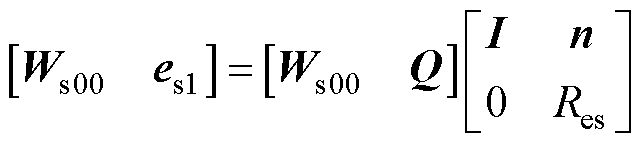 (16)
(16)
式中,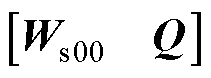 是列正交的。
是列正交的。
根据式(14)和式(16),可将式(11)改写为
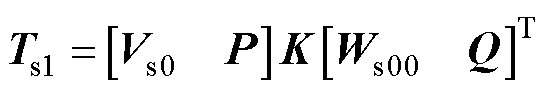 (17)
(17)
其中
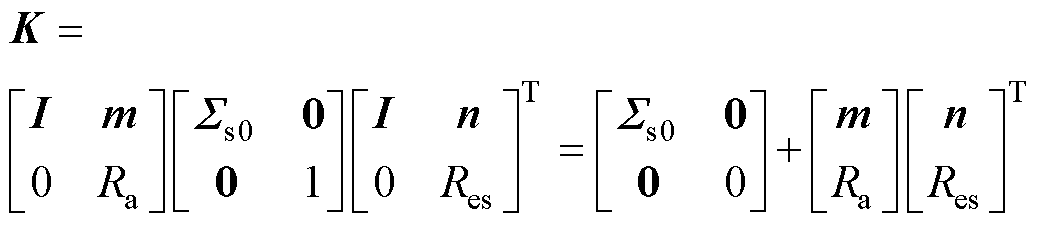 (18)
(18)
低维矩阵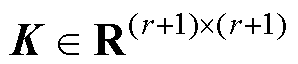 包含一个对角矩阵和两个秩1矩阵的乘积,截断数r通常为个位数,远小于百级规模的快照数m和百万甚至千万级规模的网格数n。因此,对K进行式(19)的SVD运算是低成本的。
包含一个对角矩阵和两个秩1矩阵的乘积,截断数r通常为个位数,远小于百级规模的快照数m和百万甚至千万级规模的网格数n。因此,对K进行式(19)的SVD运算是低成本的。
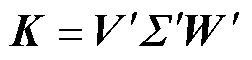 (19)
(19)
基于式(19),式(17)可表示为
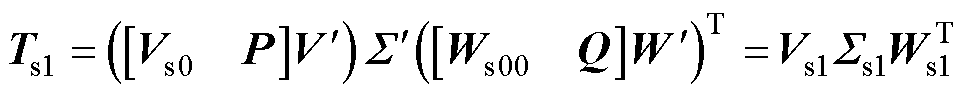 (20)
(20)
其中,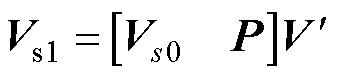 ,
,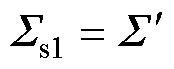 ,
,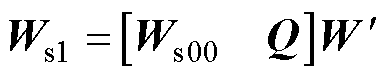 。
。
由于正交矩阵的乘积还是正交矩阵,所以通过上述变换,就由初始SVD运算结果和新快照得到了新快照矩阵的SVD结果。此时,无需对高维的新快照矩阵进行SVD,只需对低维矩阵K进行低成本的SVD,显著降低了更新POD模态时的计算成本。
综上所述,POD模态快速更新流程见表1。
表1 POD模态快速更新流程
Tab.1 The process of POD modesfastupdate

输入:更新前的SVD结果:Vs0、Ss0、Ws0;新快照:Tm+1(m1)。 输出:更新后的SVD结果:Vs1、Ss1、Ws1。 1. 使用矩阵低秩分解得到表示快照矩阵更新的a和es1。 2. 正交处理低秩分解后的左边项[Vs0 a],得到m、p、Ra、P。 3. 将低秩分解后的左边项用正交矩阵表示。 4. 正交处理低秩分解后的右边项[Ws00 es1],得到n、q、Res、Q。 5. 将低秩分解后的右边项用正交矩阵表示。 6. 计算矩阵低秩分解后的中间项K。 7. 对低维的中间项K进行SVD得到、、。 8. 计算更新后的快照矩阵的SVD结果Vs1、Ss1、Ws1。 9. 将更新后的SVD结果置为更新前的SVD结果,准备下一次计算。
1.2.2 误差来源和计算复杂度分析
得到POD模态快速更新算法后,本小节进一步分析其误差来源和计算的时间复杂度。
1)误差来源分析
在进行POD模态更新时,重复进行SVD运算得到的结果是准确的,故以此为参照,开展了本文方法的误差分析。表2中给出了对降阶模型的模态进行k次更新后,本文方法和传统重复进行SVD运算两种方式的误差来源对比。首先,两种方式均涉及式(3)中对初始快照矩阵Ts0进行SVD运算时的截断误差,即根据奇异值大小将其由m阶截断至r阶时所产生的误差。SVD通常以前r个奇异值在m个总奇异值中的占比达到99.99%以上作为截断判据,此时截断误差可以忽略。
表2 误差来源对比
Tab.2 Comparison of error sources

本文方法传统方法 ①初始快照矩阵Ts0进行SVD运算时的1次截断误差①初始快照矩阵Ts0进行SVD运算时的1次截断误差 ②k次Schmidt正价化的舍入误差②不断更新的快照矩阵Tsk进行k次SVD运算后的k个截断误差 ③低维矩阵K进行k次SVD运算后的k个截断误差
对于本文方法,其在进行式(13)和式(15)所示的正交化处理时,还会产生浮点数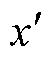 和原始数x之间的舍入误差
和原始数x之间的舍入误差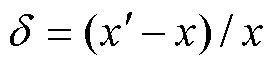 ,d取决于机器精度e。这个舍入误差会在后续不断地正交化过程中累积,使式(14)和式(16)的列向量间的正交性变差。对于Schmidt正交化的舍入误差,当且仅当式(21)成立,即各个正交向量的范数存在大的差异时,舍入误差的累积才不可以忽略[21]。
,d取决于机器精度e。这个舍入误差会在后续不断地正交化过程中累积,使式(14)和式(16)的列向量间的正交性变差。对于Schmidt正交化的舍入误差,当且仅当式(21)成立,即各个正交向量的范数存在大的差异时,舍入误差的累积才不可以忽略[21]。
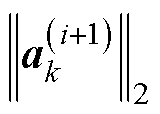

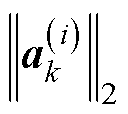 (21)
(21)
式中,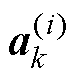 为本文方法第k次正交化后的第i个列向量。对于本文方法,各个列向量本质上是绕组温度场快照的标准正交基,由于绕组温度场是连续变化的,其标准正交基并不会出现式(21)的情形,且后续内容也验证了这一点,因此舍入误差可以忽略。
为本文方法第k次正交化后的第i个列向量。对于本文方法,各个列向量本质上是绕组温度场快照的标准正交基,由于绕组温度场是连续变化的,其标准正交基并不会出现式(21)的情形,且后续内容也验证了这一点,因此舍入误差可以忽略。
此外,对于本文方法所涉及式(19)所示的低维矩阵K的SVD运算,为避免迭代过程中矩阵K的维度不断增加,需按照式(22)对其进行截断。
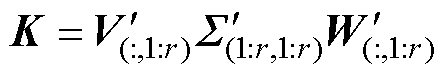 (22)
(22)
在第k次迭代时,本文方法进行的是奇异值由r+1阶到r阶的截断,传统方法进行的是奇异值由m+k阶到r阶的截断。由于奇异值的分布特性,前r阶奇异值的累计占比均是99.99%,所以尽管两者所截断的阶数存在差异,但此处两者的截断误差几乎相同。
综上所述,与传统重新进行SVD运算来更新模态的计算方式相比,本文方法额外的误差来源是每次Schmidt正交化时的舍入误差,但绕组温度场快照的各个标准正交基的范数并不会存在数量级的差异,因此舍入误差也是可以忽略的。
2)计算时间复杂度的定量分析
有新快照可用时,常规方法是将其加入初始快照矩阵后得到新快照矩阵,再通过SVD来重新求取POD模态。对于新快照矩阵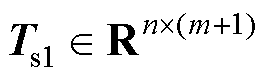 ,基于对
,基于对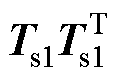 进行特征分解来求解Ts1的SVD运算结果的方式,存在舍入误差大导致数据信息丢失、矩阵条件数高导致数值稳定性差等问题。根据目前数值计算方法中进行SVD运算的主流方式[22-23],首先是对Ts1进行Golub-Kahan双对角化,计算成本为O(n(m+1)2),然后是对所得双对角矩阵应用引入隐式位移的QR算法(Implicit-shift QR algorithm)进而得到Ts1的SVD结果,计算成本为O((m+1)2)。作为对比,本文方法的耗时性主要发生在三个步骤,其一是根据式(18)计算得到矩阵K,计算成本为O(r)+O((r+1)2)≈O((r+1)2);其二是对特殊形式的低维矩阵
进行特征分解来求解Ts1的SVD运算结果的方式,存在舍入误差大导致数据信息丢失、矩阵条件数高导致数值稳定性差等问题。根据目前数值计算方法中进行SVD运算的主流方式[22-23],首先是对Ts1进行Golub-Kahan双对角化,计算成本为O(n(m+1)2),然后是对所得双对角矩阵应用引入隐式位移的QR算法(Implicit-shift QR algorithm)进而得到Ts1的SVD结果,计算成本为O((m+1)2)。作为对比,本文方法的耗时性主要发生在三个步骤,其一是根据式(18)计算得到矩阵K,计算成本为O(r)+O((r+1)2)≈O((r+1)2);其二是对特殊形式的低维矩阵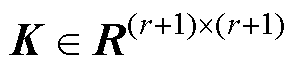 进行SVD运算,根据前述提及的数值计算中进行SVD运算的方式,计算成本为O((r+1)(r+1)2)+O((r+1)2)≈O((r+1)3);其三是计算
进行SVD运算,根据前述提及的数值计算中进行SVD运算的方式,计算成本为O((r+1)(r+1)2)+O((r+1)2)≈O((r+1)3);其三是计算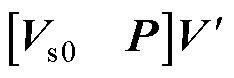 和
和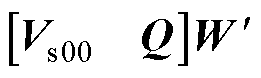 ,计算成本分别为O(nr2)和O(mr2)。
,计算成本分别为O(nr2)和O(mr2)。
对于变压器绕组温度场快照矩阵,n为网格点数量,通常在数千万级别;m为快照数量,通常在数百级别;r为奇异值截断数,通常小于数十级别。由此就比较出了两种方式的计算成本,如式(23)所示。
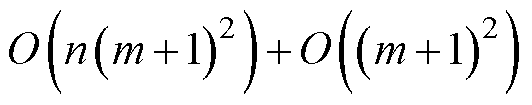
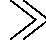
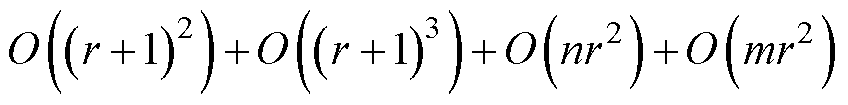 (23)
(23)
式中,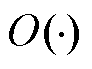 为计算成本的大O函数。
为计算成本的大O函数。
根据各项的数值规模,重点在于比较O(n(m+1)2)项和O(nr2)项,可以初步估计出本文方法通过矩阵的低秩分解能够至少降低2个数量级的计算成本,这一结论也将在后续实验中得到验证。
对于ROM,更新模态后还需要对模态系数进行求解。为了兼顾动态ROM对精度和速度的要求,本节使用绕组温度的稀疏测量值来确定模态系数,避免迭代刚度矩阵以提升计算效率。
假设使用测量矩阵C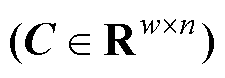 获得了ti时刻的绕组温度场
获得了ti时刻的绕组温度场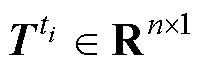 的稀疏测量值
的稀疏测量值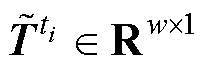 ,即
,即
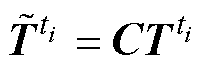 (24)
(24)
式中,w为所使用测温传感器的数量。若某个位置有传感器则其值为1;反之,则为0。
将场分布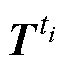 用模态
用模态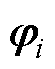 和模态系数
和模态系数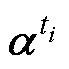 表示,有
表示,有
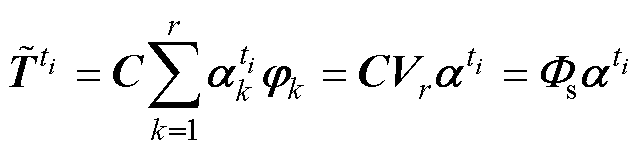 (25)
(25)
那么,就可由ti时刻的绕组温度稀疏测量值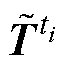 求得ti时刻的模态系数
求得ti时刻的模态系数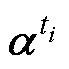 为
为
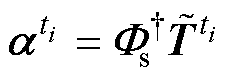 (26)
(26)
式中,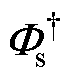 为
为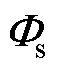 的伪逆。
的伪逆。
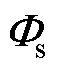 本质上是由测量矩阵C选择出的Vr中的特定行构成的,测量矩阵C直接决定了
本质上是由测量矩阵C选择出的Vr中的特定行构成的,测量矩阵C直接决定了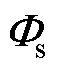 ,进而影响了模态系数
,进而影响了模态系数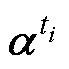 的求解结果,因此需要确定合理的测量矩阵C,即确定传感器的使用数量和放置位置。
的求解结果,因此需要确定合理的测量矩阵C,即确定传感器的使用数量和放置位置。
根据式(25),需满足方程个数不少于未知数个数,得到传感器的使用数量w应不少于截断模态的阶数r,即确定了传感器的使用数量。
确定放置位置时,目标是传感器测量误差对计算得到的模态系数影响最小,即最小化式(25)中矩阵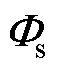 的条件数。因此,基于式(27)所示的QR- pivot方法来确定传感器放置位置。
的条件数。因此,基于式(27)所示的QR- pivot方法来确定传感器放置位置。
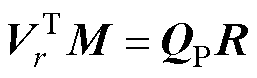 (27)
(27)
通过置换矩阵M不断进行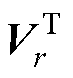 的列变换即Vr的行变换,使上三角矩阵
的列变换即Vr的行变换,使上三角矩阵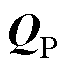 中对角线上元素从大到小依次排列,此时M的前w列就对应了测量矩阵C。
中对角线上元素从大到小依次排列,此时M的前w列就对应了测量矩阵C。
至此,就确定了测量矩阵C,可由式(26)求得模态系数,进而根据式(28)计算出变压器绕组温度场。
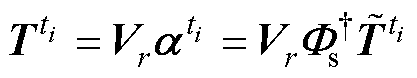 (28)
(28)
区别于传统静态ROM,此时POD模态矩阵Vr是动态更新的,更新方式如1.2节所述。进一步地,可定义动态的非侵入式降阶模型G为
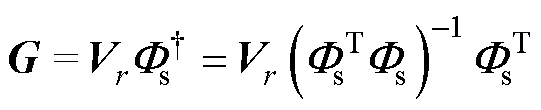 (29)
(29)
动态降阶模型G本质上是一个权值矩阵,对其输入绕组温度的稀疏测量值就可以得到完整的绕组温度场分布,且这个权值矩阵随着POD模态的更新而动态调整。
本节从POD模态更新的必要性、所提出方法更新POD模态时的精度和速度、所形成动态ROM计算场分布时的精度和速度开展了有效性验证。选择了基于主流的500 kV自耦变压器的数值实验和基于变压器缩比样机的真型试验。前者可探究负载率变化时变压器绕组温度场的POD模态是否变化,以及工程实际中的百万级网格规模下,所提方法更新POD模态的精度和效率;后者可从实测的角度直观地考察更新模态后所建立动态ROM的计算精度。
2.1.1 变压器磁-热-流耦合场仿真模型构建
建立了ODFS-334000 kV·A/500 kV型号变压器的磁-热-流耦合场仿真模型,计算了额定工况下达到稳态时的绕组温度场,并与6个验证点上的实测值进行对比,验证了仿真模型的准确性。
简化后的变压器几何模型如图1所示。几何模型的简化方式见表3。变压器主柱由内而外套装了低压绕组、公共绕组、串联绕组,旁柱由内而外套安装了励磁绕组和调压绕组。
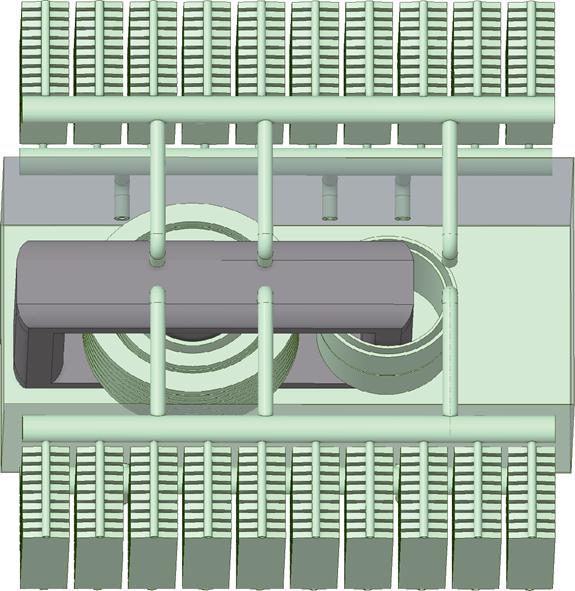
图1 简化后的变压器几何模型
Fig.1 The simplified geometric model of transformer
表3 几何模型简化方式
Tab.3 Simplification methods of geometric model
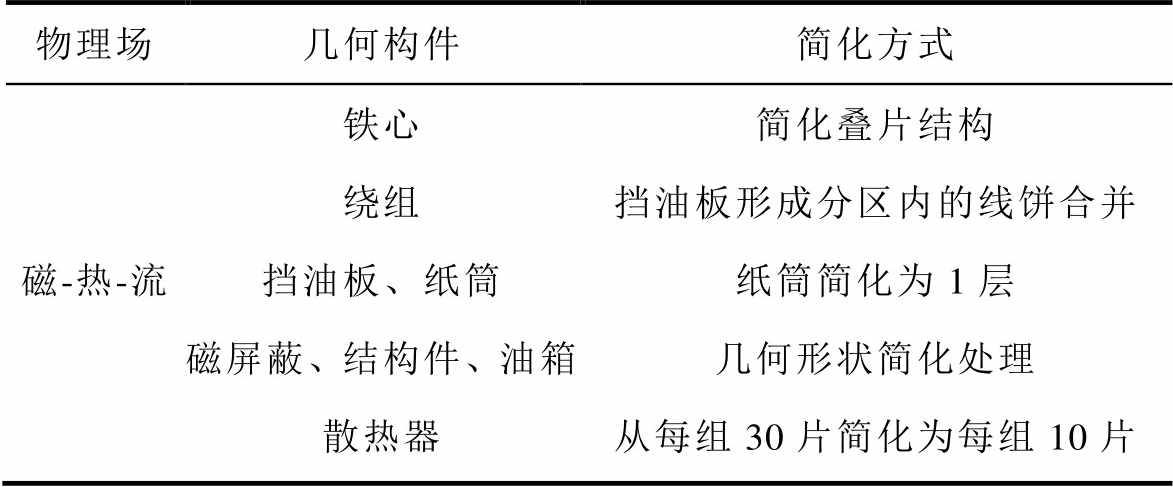
物理场几何构件简化方式 磁-热-流铁心简化叠片结构 绕组挡油板形成分区内的线饼合并 挡油板、纸筒纸筒简化为1层 磁屏蔽、结构件、油箱几何形状简化处理 散热器从每组30片简化为每组10片
计算时,各绕组的激励电流、匝数、线饼数见表4。得到该变压器在稳态情况下的温度场如图2所示,关注的是温度较高的串联绕组和公共绕组。
表4 激励源的参数
Tab.4 Parameters of excitation source
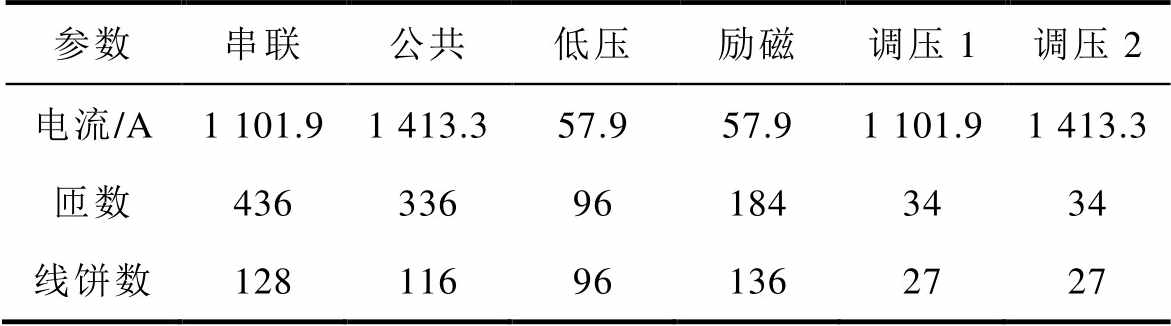
参数串联公共低压励磁调压1调压2 电流/A1 101.91 413.357.957.91 101.91 413.3 匝数436336961843434 线饼数128116961362727
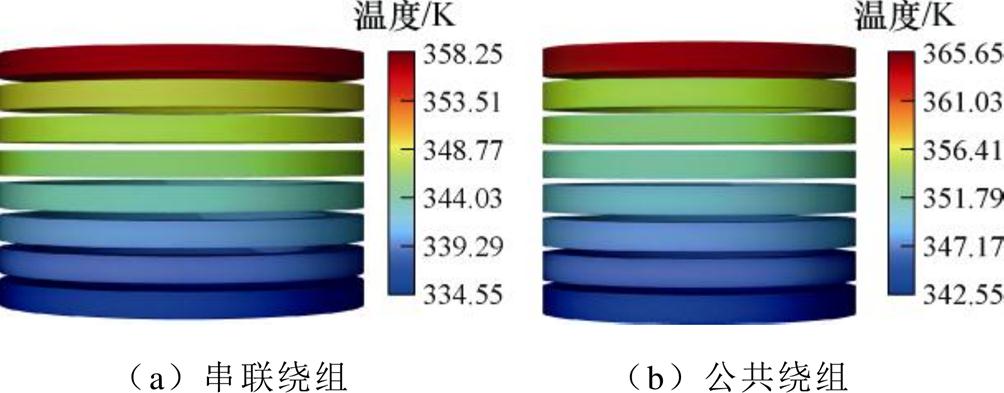
图2 达到稳态时的变压器绕组温度场分布
Fig.2 The temperature field distribution of transformer winding when reaching the steady state
上述计算中,散热器简化后的换热面积变为原来的1/3,因此为了散热功率的等效,将散热器的表面传热系数设置为正常情况下的3倍。该变压器在负载率低于70%时采用油浸自冷(Oil Natural Air Natural, ONAN)散热方式;反之,为自然油循环+强迫风冷(Oil Natural Air Forced, ONAF)散热方式。所以在仿真中,两种方式下的表面传热系数分别为42 W/(m2·K)和180 W/(m2·K)。
2.1.2 变负载下变压器绕组温度场的模态对比
验证前述仿真模型对绕组温度场计算的准确性后,进一步对其施加油浸式电力变压器负载导则中设定的变负载,如图3所示。
以公共绕组和串联绕组为整体,以5 s为时间间隔,导出整个过程的720张绕组温度场快照,每个负载率各180张。各负载率下的快照集分别命名为S1、S2、S3、S4,并分别进行SVD运算,求取了各快照集的奇异值分布和POD模态,分别如图4和图5所示。
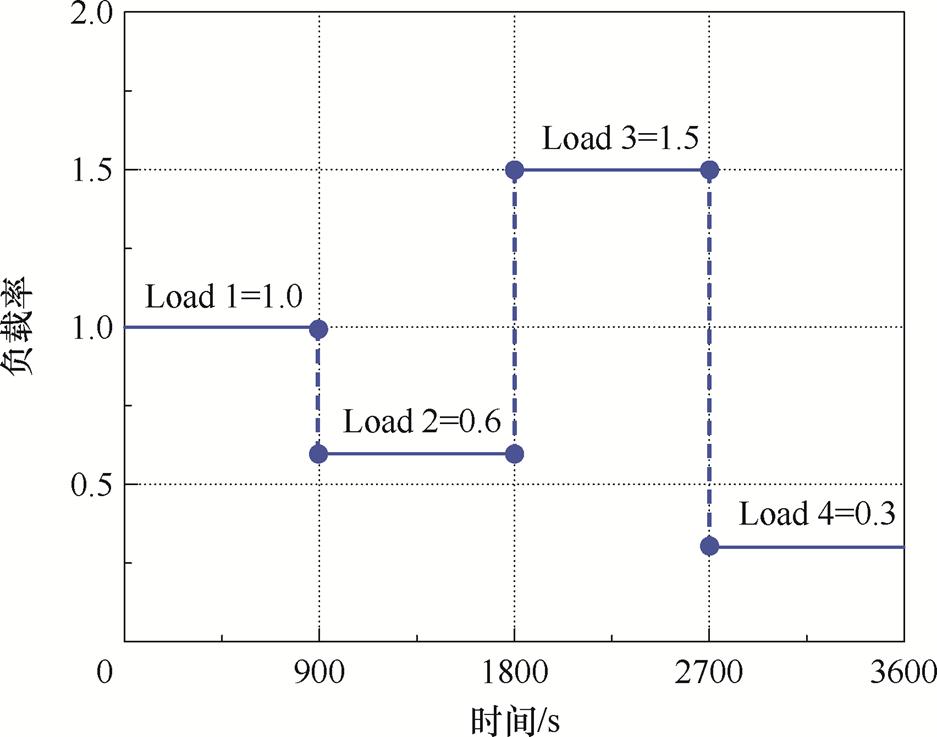
图3 施加的变负载
Fig.3 The applied variable load
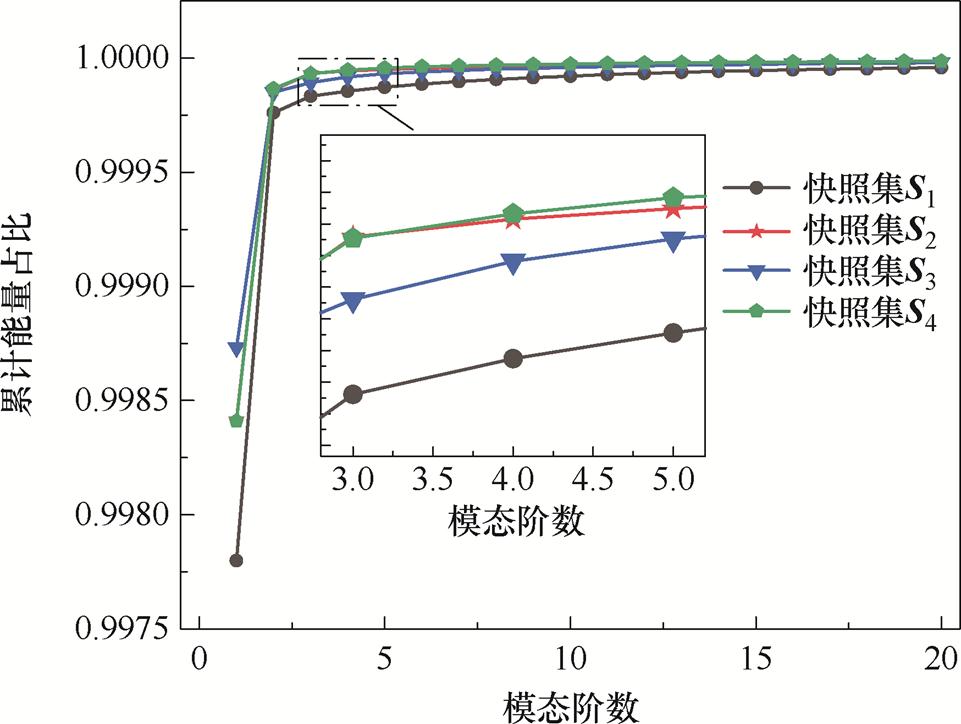
图4 不同负载率下绕组温度场快照集的奇异值分布
Fig.4 Singular value distribution of winding temperature field snapshots under different load rates
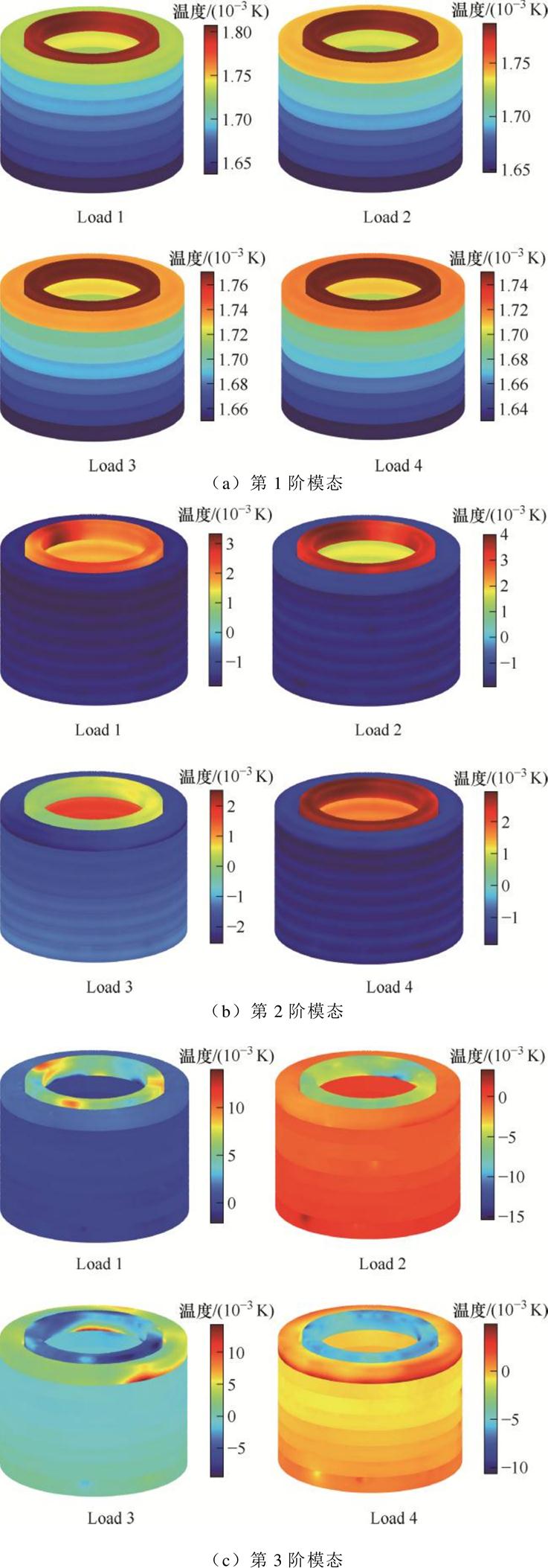
图5 不同负载率下的变压器绕组温度场各阶POD模态
Fig.5 POD modes of transformer winding temperature field under different load rates
因为奇异值表示所对应模态的能量,图4中的奇异值分布使用式(30)计算的各阶模态的累计能量占比来体现,即
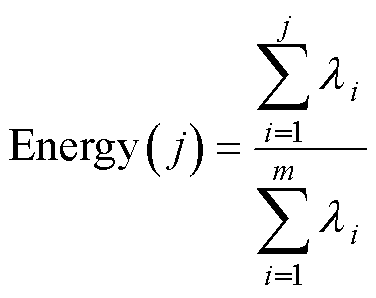 (30)
(30)
式中,Energy( j)为模态的累计能量占比,指前j阶模态的能量在总模态能量中的占比,也对应前j个奇异值在总奇异值中的占比;li为第i个奇异值;m为模态的阶数也是奇异值的个数。
从图4可以看出,由于各个负载率区间内变压器运行状态不同,因此,不同负载率快照集的奇异值分布也是不同的。此外,快照集S2和S4的奇异值分布非常接近,这是因为两者处于相同的风扇停止状态。相同阶数下,快照集S1的模态累计能量占比低于快照集S2、S3、S4,这是因为S1涉及温度场分布的建立过程。总体而言,四个快照集都是前三阶模态占主导地位,可达到约99.99%的能量占比。
图5进一步给出了前3阶主导模态在不同负载率下的直观对比,以云图的形式呈现了POD模态。通过图5可以明确看出,不同负载率下变压器绕组温度场的POD模态是不同的。变压器运行过程中,POD模态的变化必然会使传统保持POD模态不变的静态ROM出现计算精度的下降。因此,为了ROM能够保持计算的准确性,需要在有新快照可用时对模态进行更新。
2.1.3 模态更新的精度和耗时性
前述论证了更新POD模态的必要性,本小节则进一步分析了本文方法更新模态时的精度和耗时性。
1)本文方法更新POD模态时的精度
首先,对负载率Load 1下的快照矩阵S1进行SVD运算,有
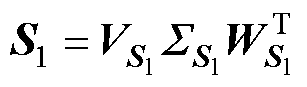 (31)
(31)
在某个时刻,有Load 2下的1张快照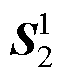 可用时,可形成新快照矩阵
可用时,可形成新快照矩阵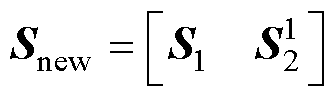 。传统方法通过对Snew进行一次SVD运算来更新POD模态;而本文方法则是根据S1的SVD结果和新快照
。传统方法通过对Snew进行一次SVD运算来更新POD模态;而本文方法则是根据S1的SVD结果和新快照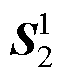 直接求得Snew的SVD结果,即得到更新后的模态。两种计算方式的数学表达式分别为
直接求得Snew的SVD结果,即得到更新后的模态。两种计算方式的数学表达式分别为
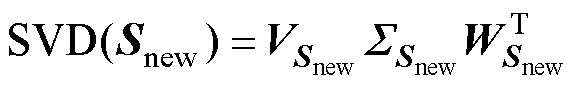 (32)
(32)
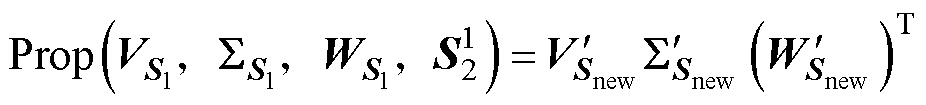 (33)
(33)
式中,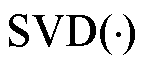 为进行SVD运算的函数;
为进行SVD运算的函数;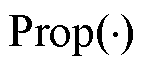 为本文方法对应的函数。
为本文方法对应的函数。
然后,对比了 和
和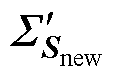 中的奇异值元素以及
中的奇异值元素以及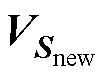 和
和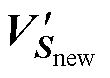 各个列向量即POD模态间的差异,以考察本文方法更新POD模态时的准确性。
各个列向量即POD模态间的差异,以考察本文方法更新POD模态时的准确性。
图6给出了两种方法所得奇异值的对比,由于前述计算结果得到前3个奇异值的累计能量比为99.99%,故在此只选择给出了前6个奇异值。
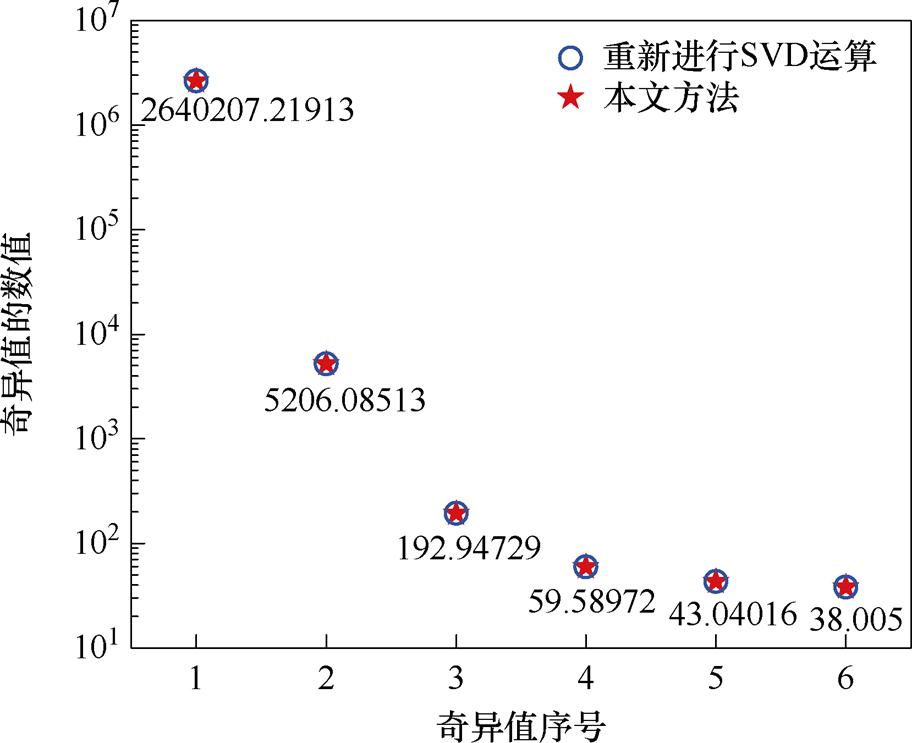
图6 两种计算方式所得奇异值对比
Fig.6 Comparison of singular values obtained by two calculation methods
从图6可以看出,本文方法计算得到的奇异值与重新进行SVD运算得到的奇异值是完全相同的。
进一步考察了对于POD模态计算的准确性,考察的是形成ROM时会用到的前三阶主导模态,误差统计使用的公式为
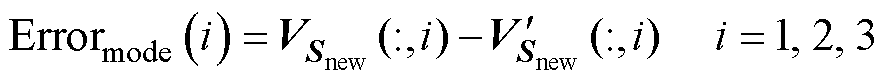 (34)
(34)
式中,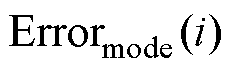 为第i阶模态的计算误差,
为第i阶模态的计算误差,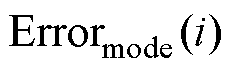
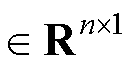 ;
; 为重新SVD运算后所得的第i阶模态;
为重新SVD运算后所得的第i阶模态; 为本文方法所得的第i阶模态。根据式(34)得到对POD模态的计算误差见表5。
为本文方法所得的第i阶模态。根据式(34)得到对POD模态的计算误差见表5。
表5 计算所得POD模态的误差
Tab.5 The errors in calculating POD modes

模态阶数最大计算误差平均计算误差 第1阶1.30×10-183.66×10-19 第2阶3.60×10-84.36×10-10 第3阶2.20×10-81.90×10-10
表5中,各阶模态的最大计算误差是Errormode(i)的最大值,平均计算误差是sum(Errormode(i))/n。在此,重点关注了本文方法的最大计算误差,可以看出其数值在10-8级别。所以从计算精度的角度考虑,在更新POD模态时,本文方法能够完全替代传统对新快照矩阵进行SVD运算的方式,因此可用于对POD模态的更新。
2)本文方法更新POD模态时的耗时性
对于实际运行的变压器,通常是在有新快照可用时才可以对模态进行更新,但何时有新快照可用往往并不确定。在此,为了研究的需要,假定新快照到达的时间间隔分别为Dt=900 s、Dt=450 s、Dt=225 s,不同Dt下更新模态时所引入的快照见表6。
表6 不同Dt下更新模态时所引入的快照
Tab.6 Snapshots introduced when updating modes under different Dt
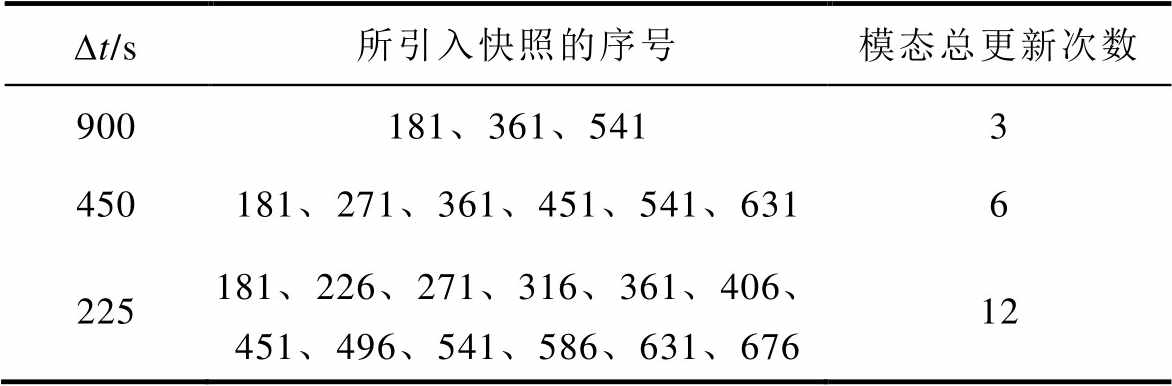
Dt/s所引入快照的序号模态总更新次数 900181、361、5413 450181、271、361、451、541、6316 225181、226、271、316、361、406、451、496、541、586、631、67612
首先,使用Load 1下的快照集S1即第1~180张快照提取POD模态并形成初始ROM。然后,在有新快照可用时就将其引入快照集以更新模态,完成更新后就持续用于计算,直至下一个可用的新快照出现,新快照出现的位置在表6中给出。传统方法每次更新POD模态都是通过对新快照矩阵进行SVD实现的,本文方法则是基于上一步的SVD结果和新快照直接计算。
于是,得到了不同Dt下本文方法与传统方法更新POD模态的耗时对比,如图7所示。在三种Dt下,对Load 2~Load 4区间内的绕组温度场进行计算时,POD模态总计更新了3次、6次、12次。
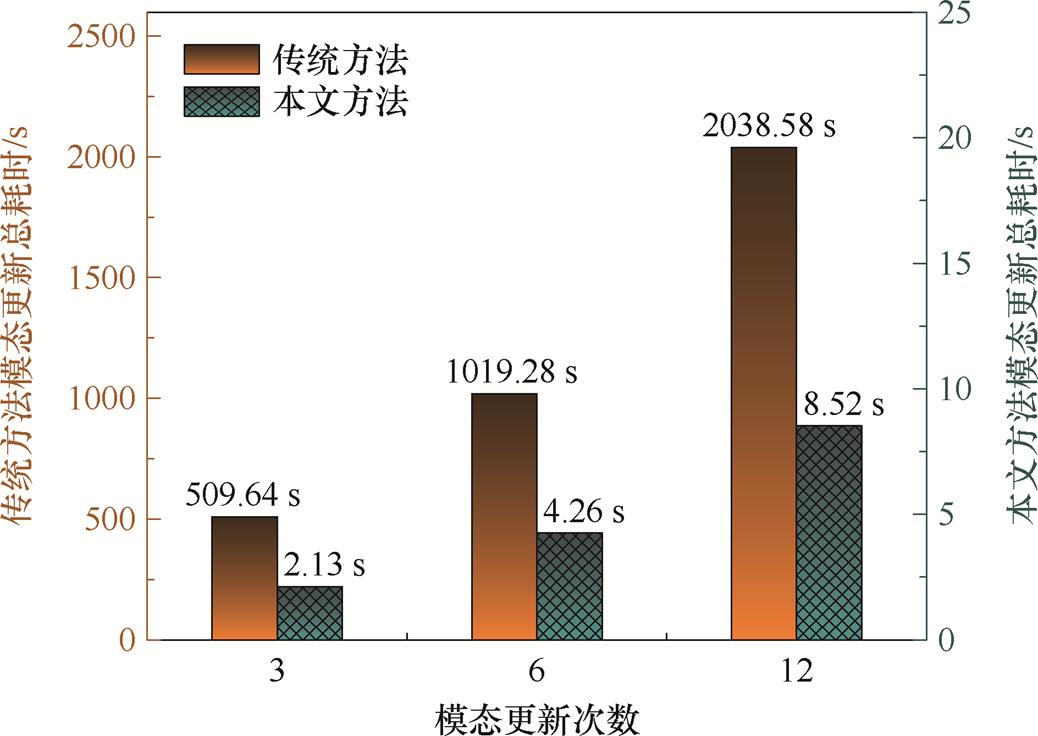
图7 更新POD模态时的效率提升情况
Fig.7 The efficiency improvement when updating the POD modes
从图7可看出,对于3 786 369网格规模的绕组温度快照数据,本文方法更新模态单次耗时为0.71 s,速度为传统方法的239倍,计算效率提升至少2个数量级。此外,随着Dt的减少即模态更新次数的增加,本文方法更新POD模态的速度优势更为明显。
2.1.4 动态降阶模型的计算精度和求解速度
在验证本文方法更新POD模态的精度和速度优势后,进一步考察了基于更新模态所形成动态ROM的计算精度和速度。
1)动态降阶模型计算精度分析
同样利用Load 1下的快照集S1提取得到初始模态,基于1.3节的方法确定模态系数,然后利用ROM计算出Load 2、Load 3、Load 4的绕组温度场数据,并与快照集S2、S3、S4进行比较,以考察ROM的计算精度。
前述研究确定了前三阶模态的累计能量占比为99.983%,利用1.3节的传感器放置方案确定算法,得到了传感器放置方案见表7。
表7 传感器放置方案
Tab.7 The sensor placement scheme
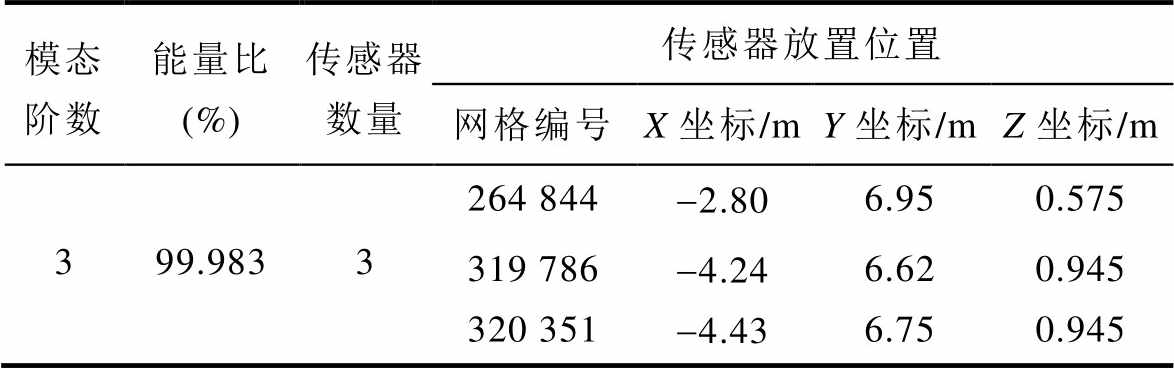
模态阶数能量比(%)传感器数量传感器放置位置 网格编号X坐标/mY坐标/mZ坐标/m 399.9833264 844-2.806.950.575 319 786-4.246.620.945 320 351-4.436.750.945
注:公共和串联绕组整体的X轴范围:-2.8~-5.4 m;Y轴范围:4.5~7.1 m;Z轴范围:-1.05~1.05 m。
根据坐标换算得到传感器的三个放置位置分别是:公共绕组自上而下第11饼且辐向由内至外第1匝、公共绕组自上而下第11饼且辐向由内至外第3匝、串联绕组自上而下第58饼且辐向由内至外第2匝的中间位置。
基于上述传感器放置方案,考察了模态累计更新3次、6次、12次,即在各负载率区间内模态分别更新1次、2次、4次,这三种情况下的动态ROM和传统静态ROM。对于动态ROM,引入快照更新模态的位置见表6,计算过程为从初始模态开始,当有新快照引入时对模态进行更新,然后持续用于计算,直到下一个新快照被引入,如此往复向前。
图8给出了静态和动态ROM的平均计算误差对比。
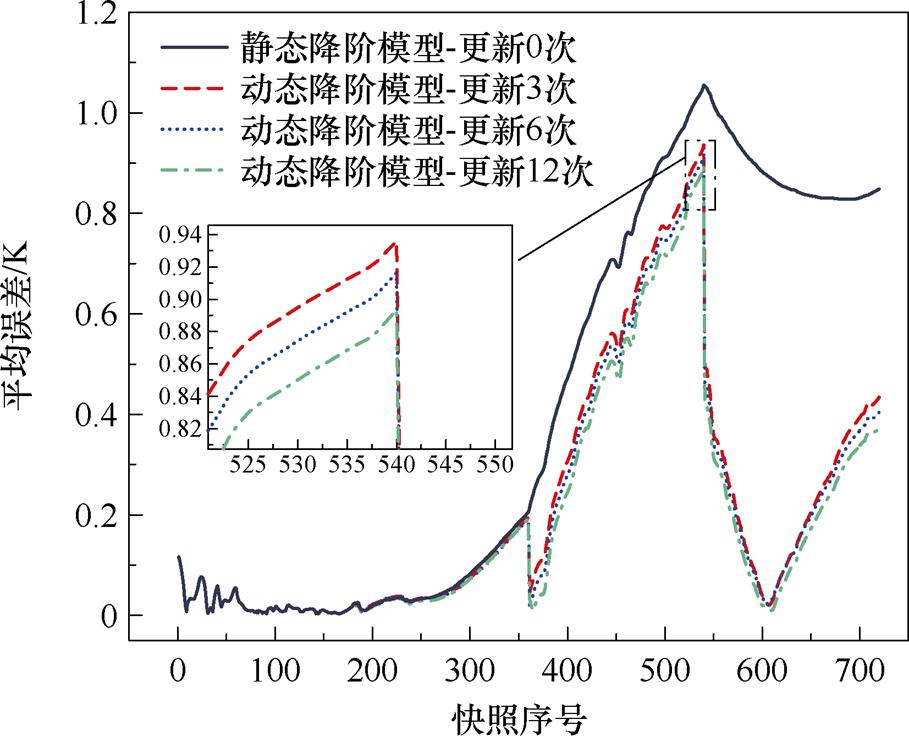
图8 不同降阶模型的平均计算误差
Fig.8 The average calculation error of different ROMs
图8中的平均计算误差为
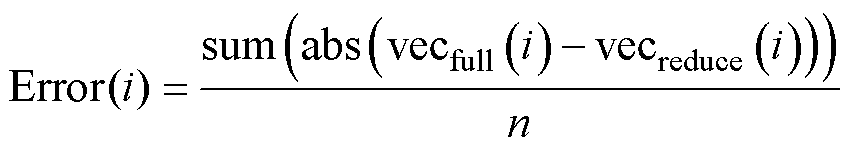 i=1~720(35)
i=1~720(35)
式中,Error(i)为ROM对第i个快照的平均计算误差;sum(·)为求和的函数,abs(·)为求绝对值的函数;vecfull(i)为全阶模型的计算结果;vecreduce(i)为ROM的计算结果。
从图8可以看出,动态ROM的计算误差是明显小于静态ROM的,说明了本文方法所得动态ROM的准确度优势。其次,在第361张快照和第541张快照位置处,动态ROM的计算误差较静态ROM出现了阶跃性下降,原因在于此处负载率调整,导致模态发生了变化,静态ROM未能更新模态所以误差较大,而动态ROM则引入快照更新了模态,所以误差出现阶跃式的下降。在第181张快照位置未出现误差阶跃下降的原因是0~180张快照区间内属于重构,误差接近于0,在第181张快照处模态的更新又刚好抑制了误差的增加。
此外,对于不同的动态ROM,随着更新次数的增加,计算误差会进一步减小,但增加更新次数产生的误差下降远小于模态由不更新转变为更新所产生的误差下降。
为更直观地呈现动态ROM和静态ROM在计算精度上的差异,以云图的形式给出了不同ROM在各个负载率区间内的计算误差,如附图1所示。附图1中,更新次数0次、1次、2次、4次表示对于静态ROM和三种Dt下的动态ROM,其模态在每个负载率区间内的更新次数。
进一步地,统计了各负载率区间内ROM计算所得场分布与真实快照的误差最大值,如图9所示。
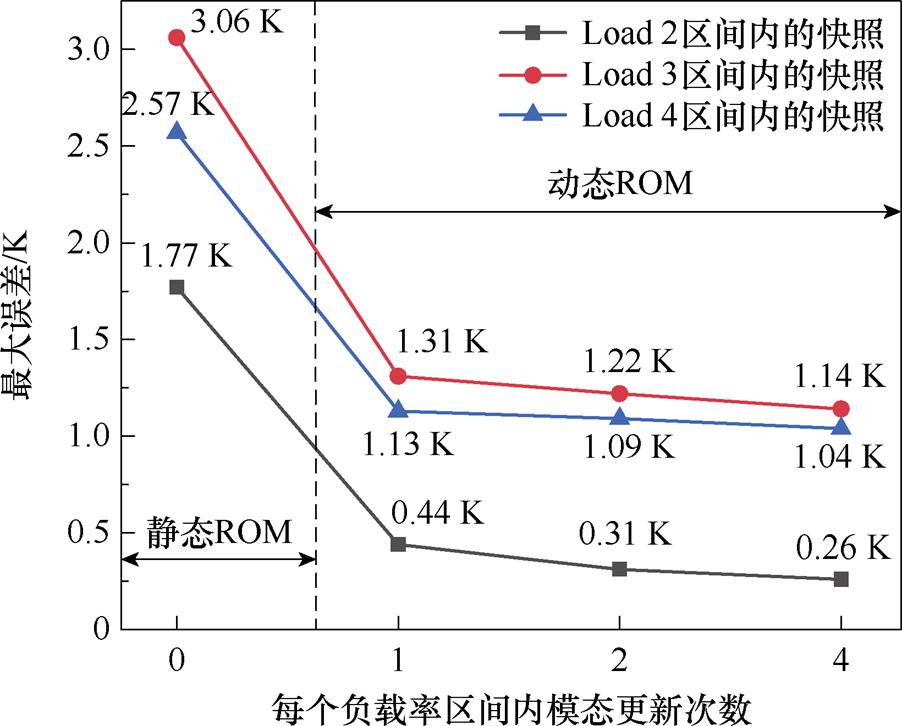
图9 不同降阶模型在各负载区间内的计算误差最大值
Fig.9 The maximum calculation error of different ROMs in each load interval
从附图1和图9可以看出,静态ROM在Load 2、Load 3、Load 4区间内的最大计算误差分别为1.77 K、3.06 K、2.57 K,出现了计算精度的显著下降,因为ROM如果仍然适用,该项误差应接近于0。对于动态ROM,如Dt=900 s,尽管只在计算到每个负载率区间内时引入1张快照来更新模态,但对于三个负载率区间的最大计算误差就分别降低了1.33 K、1.75 K、1.44 K,且增加所更新快照数量后,对于Dt=450 s和Dt=225 s的情况,进一步降低了计算误差。在本算例中,最大计算误差分别降低了1.51 K、1.92 K、1.53 K。所以,进行模态更新能够有效抑制静态ROM的计算精度下降的问题,增加更新次数能够进一步减小误差但减小程度将不再显著,因为可能会出现信息冗余。对于ROM而言,引入快照进行更新即可,无需增加大量快照来更新。因此,实际应用中,可通过将上一步的计算结果作为初始状态,将当前负载率作为边界条件,进行超短期的瞬态计算后,将获得的快照作为所需新快照,本文使用的仅是各负载区间内第5个时间步的快照。
前述确定了动态ROM应采用在每个负载率区间内更新一次模态的方式,进一步地,研究了该方式下传感器使用数量和放置位置对动态ROM计算精度的影响,如图10所示。
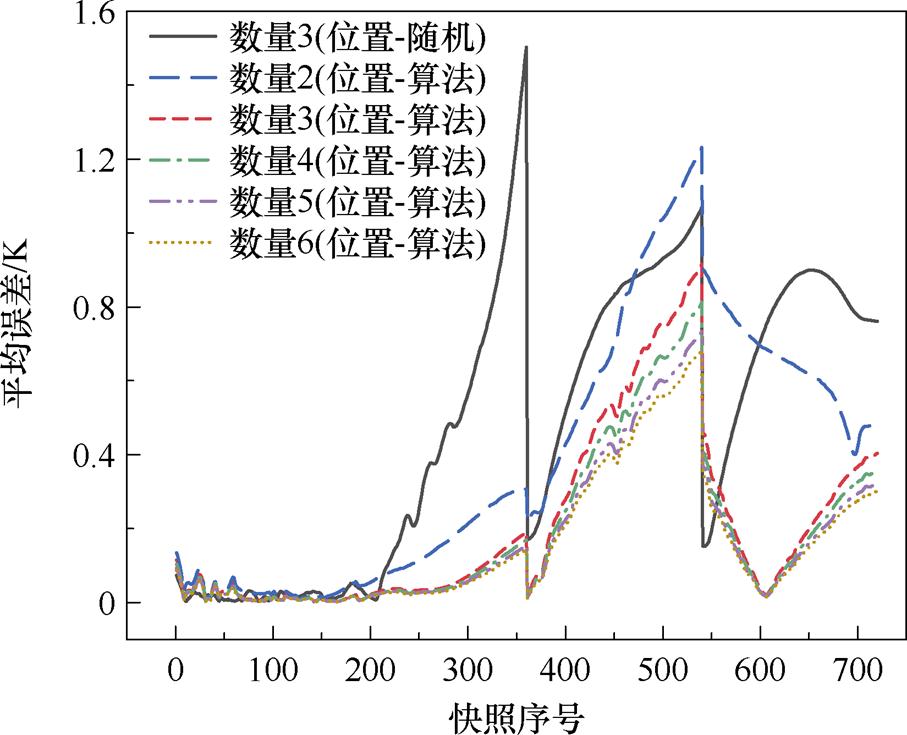
图10 传感器数量和位置对动态降阶模型精度的影响
Fig.10 The influence of the number and position of sensors on the accuracy of the dynamic ROM
由图10可以看出,传感器数量从2增加至3后计算误差会显著降低,但继续增加传感器使用数量后计算误差将不再显著降低,其对应了图4中快照集S1前三阶模态的累计能量占比达到约99.99%。此外,当传感器数量为3时,将其放置在本文方法确定的位置较随机放置也显著降低了平均误差,其中,位置随机放置的误差是100种随机放置情况的平均值。由此,验证了1.3节传感器放置方案确定方法的有效性,即基于模态累计能量占比确定传 感器需求数量,基于QR-pivot方法确定其放置位置。
2)动态降阶模型求解速度分析
验证动态ROM的精度优势后,进一步考察了其计算效率。图11统计了各种非侵入式ROM的计算耗时,这里非侵入式指1.3节根据稀疏测量值确定模态系数的计算方式。
图11中,序号1是非侵入式静态ROM,序号2~4是在单个负载率区间内分别进行1、2、4次模态更新的三种动态ROM。图11中比较的是在Load 1下的快照集S1上形成初始ROM后,基于前述四种方式对Load 2~Load 4区间内的温度场进行计算的耗时。总计算耗时是ROM计算得到Load 2~Load 4区间内540张快照的耗时,单步计算耗时是计算过程中单次计算的平均耗时,且重点应关注的是单步计算耗时。
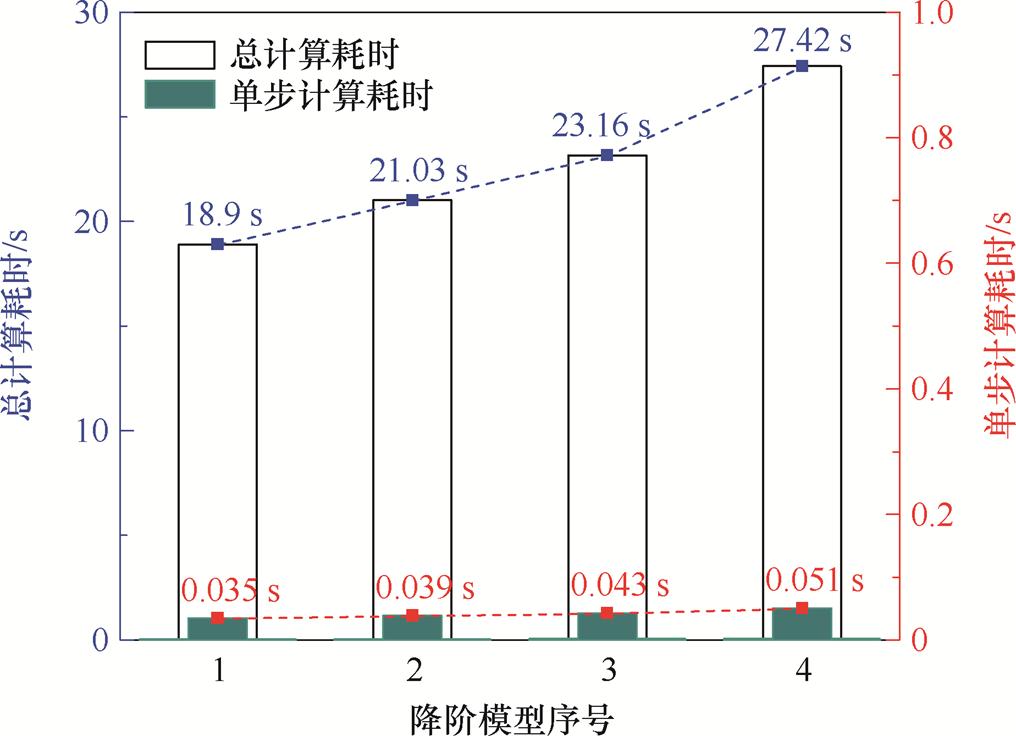
图11 不同降阶模型的耗时对比
Fig.11 Time-consuming comparison of different ROMs
1.1节所述的侵入式ROM的总计算耗时为22 982.4 s,单步计算耗时为42.56 s,而图11中的非侵入式ROM则有效地避免了高耗时问题,但是序号1的非侵入ROM不更新模态的计算方式会出现精度的显著下降,这在前述已经得到。序号2~4的动态ROM能够有效地抑制计算精度的下降,且通过图11可以看出,单步计算耗时并未明显增加。单步计算耗时最大增加0.016 s,仍能够在s级时间完成计算,证明了基于本文方法更新模态后形成的动态ROM能够兼顾保持高精度和计算速度。
上述比较的是ROM的计算耗时,由于ROM在形成时也涉及离线阶段生成快照集的时间消耗。为更全面地考察动态ROM的时间消耗情况,在表8中比较了不同方法的总耗时,其中本文方法的离线耗时同时包含了生成初始快照集的时间和生成用于模态更新的新快照的时间。
表8 不同方法的总时间消耗对比
Tab.8 Comparison of total time consumption of different methods
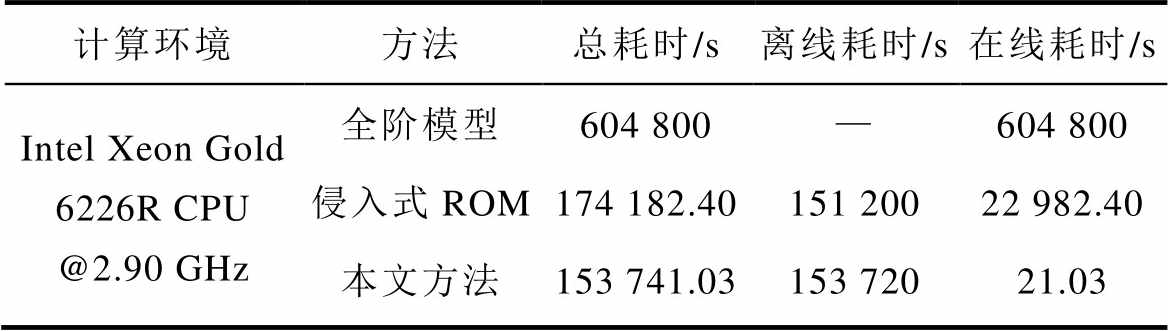
计算环境方法总耗时/s离线耗时/s在线耗时/s Intel Xeon Gold 6226R CPU @2.90 GHz全阶模型604 800—604 800 侵入式ROM174 182.40151 20022 982.40 本文方法153 741.03153 72021.03
本文方法的总耗时较全阶模型减少了75%,相比于侵入式ROM也实现了在线阶段的s级计算。
2.1节通过数值实验验证了本文方法的有效性,本节旨在进一步从试验测量的角度考察本文方法所形成动态ROM的计算精度和效率。
2.2.1 变压器缩比样机试验平台
变压器缩比样机的基本参数见表9,所建立的试验平台如图12所示,基于该试验平台开展了变压器的温升试验。
表9 变压器缩比样机参数
Tab.9 Parameters of transformer scale prototype
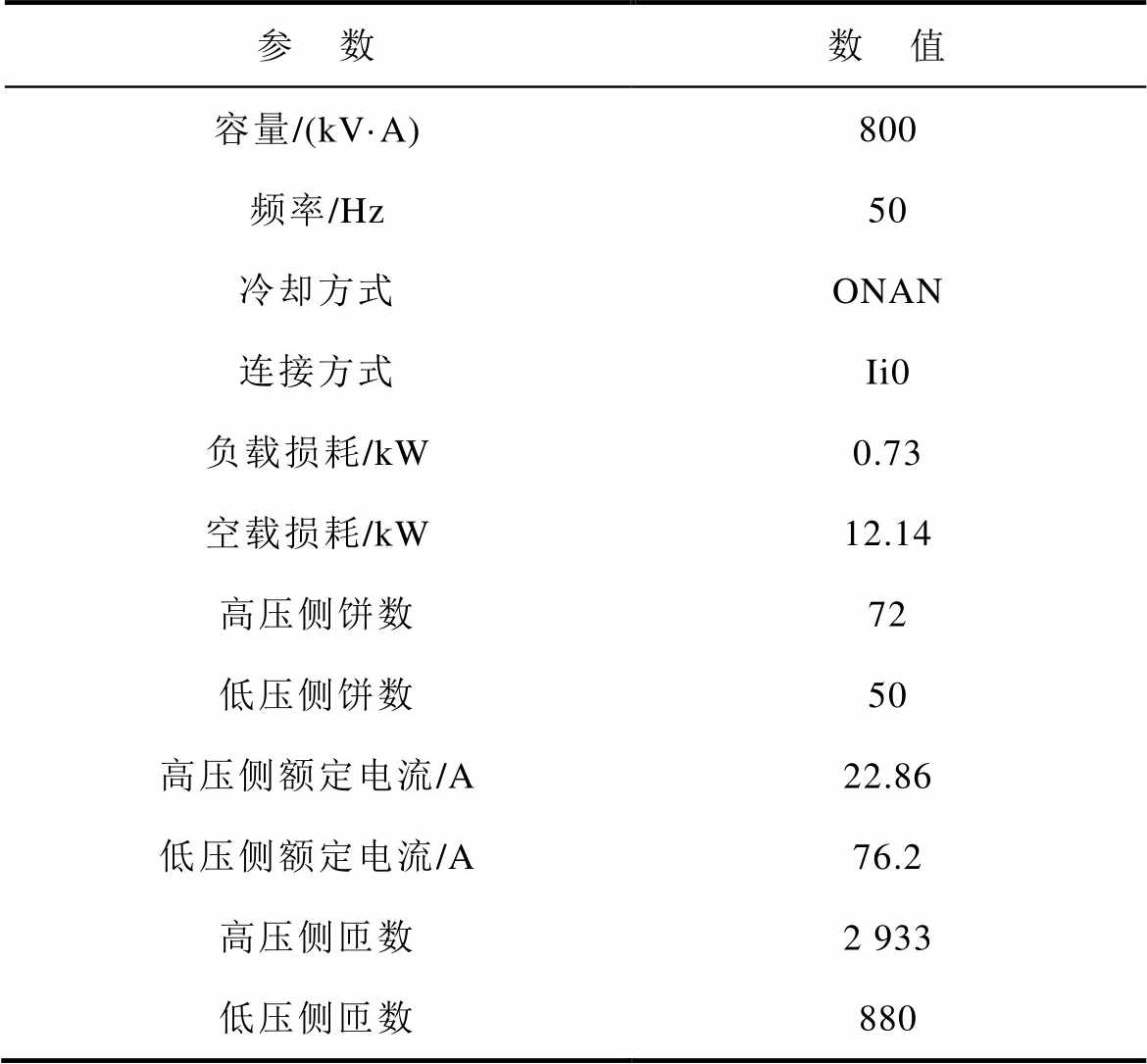
参 数数 值 容量/(kV·A)800 频率/Hz50 冷却方式ONAN 连接方式Ii0 负载损耗/kW0.73 空载损耗/kW12.14 高压侧饼数72 低压侧饼数50 高压侧额定电流/A22.86 低压侧额定电流/A76.2 高压侧匝数2 933 低压侧匝数880

图12 变压器缩比样机试验平台
Fig.12 Test platform of transformer scale prototype
试验是按照GB/T 1094.2—2013采用短路连接法进行的。功率分析仪记录了施加在高压绕组上的激励,包括功率、电压和电流。在第一阶段,总损耗被施加在变压器上,调整交流电源,直到功率分析仪显示损耗为12.87 kW。当顶油温升小于1 K/h时,认为顶油温升稳定,结束第一阶段。在第二阶段,由于变压器没有抽头开关,输入电流被减小到额定电流,直到功率分析仪显示施加在高压绕组上的电流为22.86 A。然后,直到绕组的热点温度变化小于1 K/h,结束第二阶段。光纤测温系统测量了整个温升过程中的绕组温度。
2.2.2 传感器放置方案确定
在2.2.1节的试验平台中,绕组上共计布置了6个光纤测温传感器,其中M1传感器用于为非侵入式动态ROM提供输入,V1~V5传感器分别放置在各个分区内温度最高的位置,用于将实测值与动态ROM在这些点的计算值进行对比,以考察计算的准确性。本节进一步给出了确定上述传感器布置方案的详细过程。
观测试验过程中绕组的温度数据后,得到第1~4 h区间内绕组温度上升较快,第4~7 h内绕组温度上升较慢。因此,建立了温升过程的绕组温度场计算模型,并以3 min为步长导出了前4 h的绕组温度场快照80张,用于提取模态后确定传感布置方案并形成初始ROM。
1)监测传感器的放置位置
对导出的80张快照进行SVD运算后,得到了各阶模态的累计能量占比,如图13所示。
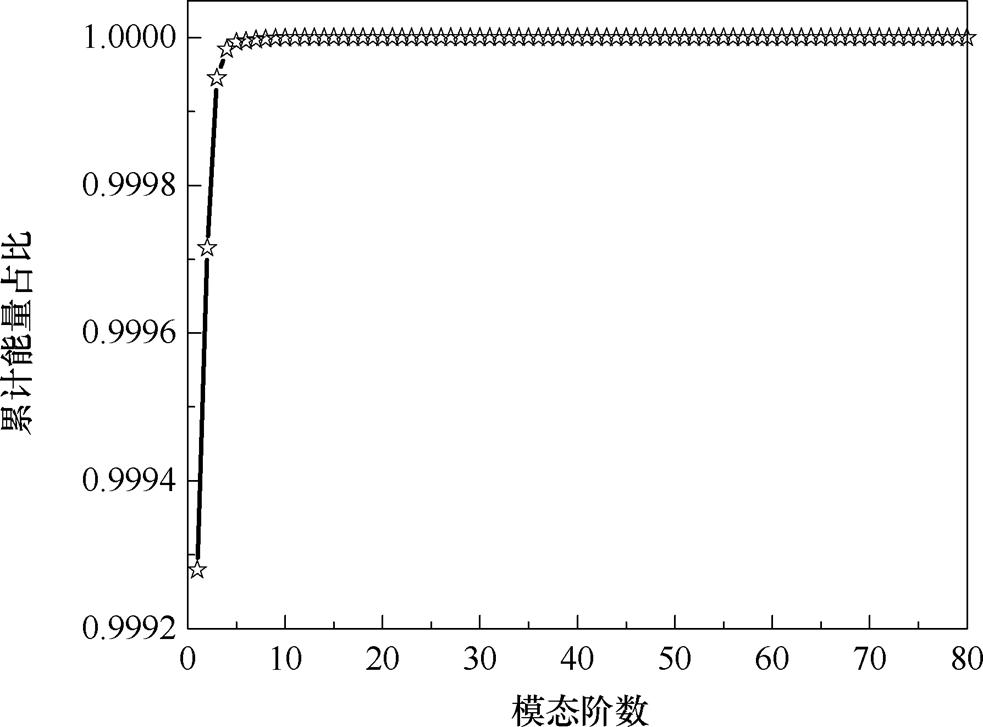
图13 各阶模态累计能量占比
Fig.13 The cumulative energy ratio of each modes
第一阶模态的累计能量占比大于99.92%,前三阶模态的累计能量占比大于99.99%,因此考察了三种传感方案下,计算得到的前4 h绕组温度场与前4 h绕组温度场快照的平均误差,不同传感方案下的计算误差如图14所示。显然,随着传感器数量的增加,计算精度会进一步提高,理想情况下应使用3个传感器,但考虑到使用1个传感器的计算精度也能够初步满足需求且其放置位置是热点区域,且结合在工程实际中也会获得热点温度且难以放置多个传感器为降阶模型提供输入,因此就采用了将1个传感器放置在62 760网格点即低压绕组第48饼位置,为降阶模型提供输入。
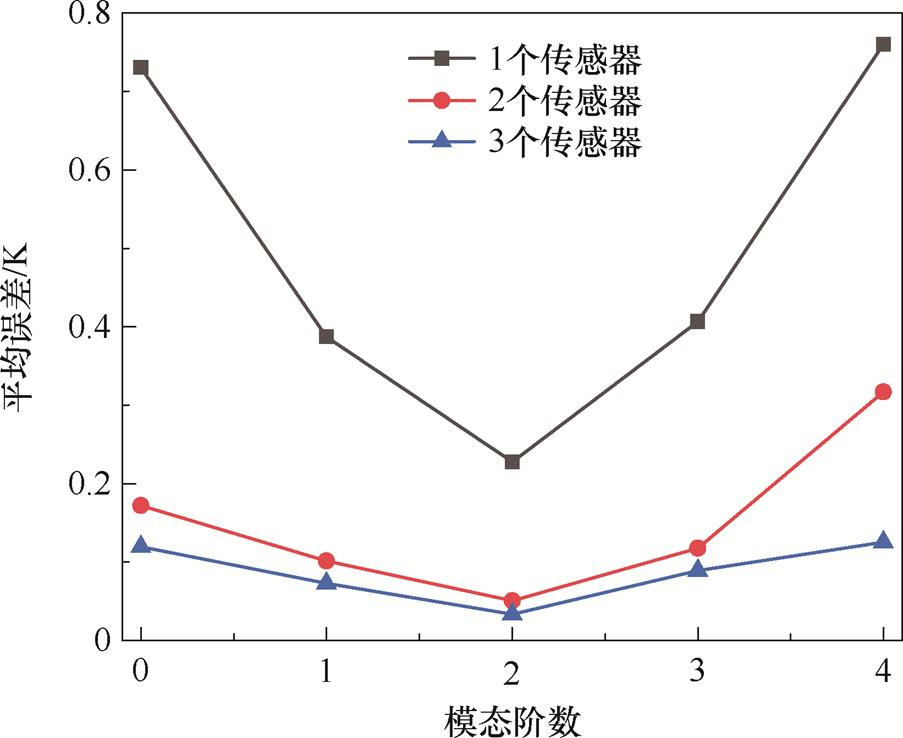
图14 不同传感方案下的计算误差
Fig.14 Calculation errors under different sensing schemes
2)验证传感器的放置位置
由于绕组各分区内温度最高的位置是较为关注的区域,故本节将传感器放置在此处进行验证。图15给出了t=7 h的绕组温度场快照及各线饼的温度。
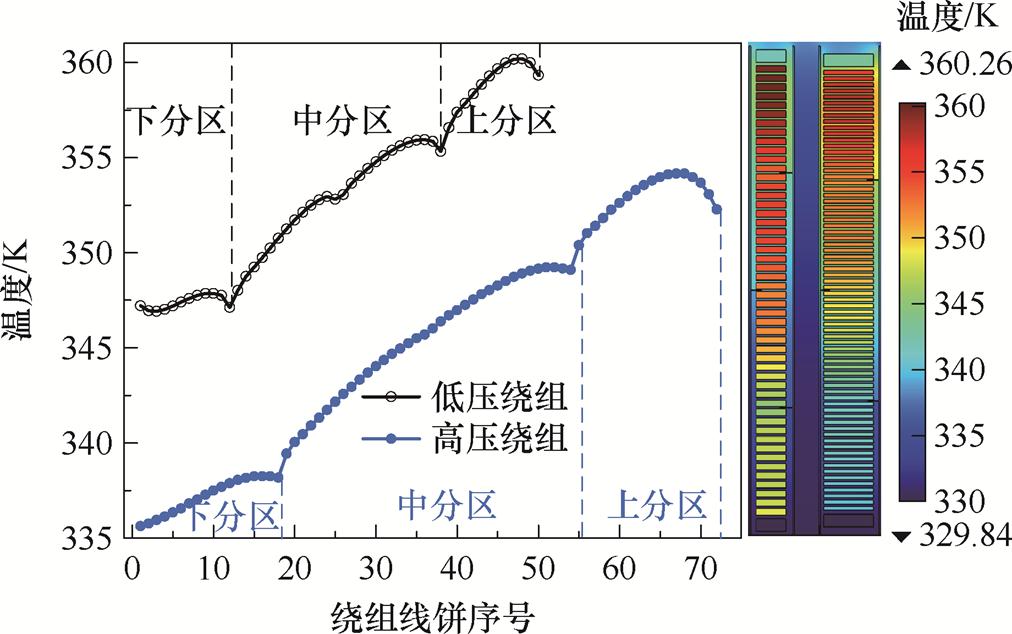
图15 热平衡时的绕组各线饼温度
Fig.15 The temperature of each disks of the winding at thermal equilibrium
基于图15就确定了5个验证传感器的放置位置,即低压绕组自下而上的第9饼、第36饼和高压绕组自下而上的第13饼、第52饼、第68饼。
2.2.3 动态降阶模型的计算精度和求解速度
采用上述传感方案,比较了保持初始ROM不变和仅使用4~7 h内的1张快照对初始ROM进行更新这两种方式下的计算精度,统计了ROM在4~7 h内的计算误差,如图16所示。
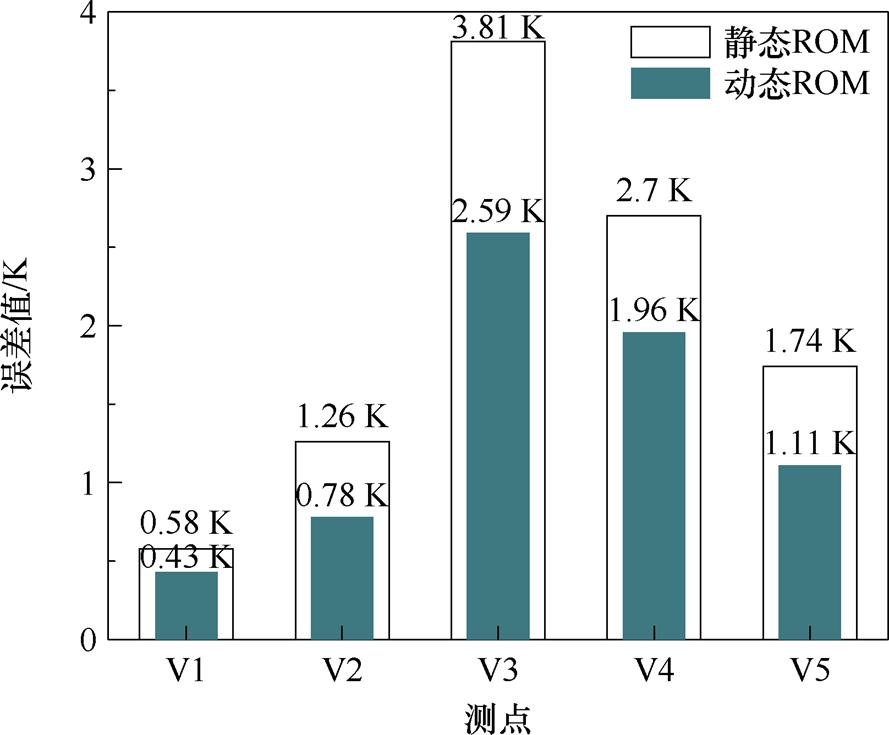
图16 降阶模型在4~7 h区间内的最大计算误差
Fig.16 The maximum calculation error of the ROM in the interval of 4~7 h
由图16可以看出,动态ROM在5个验证点上的计算值与实测值相比,误差最大为2.59 K,最小为0.43 K。对于该网格规模为69 725的动态ROM,传统方法与本文方法更新模态的耗时分别是1.513 5 s和0.032 9 s。本文方法在更新模态后,使单步计算耗时增加了0.000 48 s,现单步计算耗时为0.018 5 s。因此,动态ROM在几乎未增加计算耗时的情况下提高了计算精度。
ROM的模态是通过仿真模型的快照集提取得到的,因此,仿真模型的误差直接导致了ROM计算结果与实测值的差异。
前述2.1节和2.2节分别从500 kV变压器的数值实验和变压器缩比样机的试验开展了方法的有效性验证。两者在负载情况、网格规模方面均存在差异,因此进一步开展了实验数据对比分析,旨在得到上述负载情况和网格规模与模型性能间的关系。
在变负载的数值实验中,动态ROM相比于传统方法所降低平均计算误差的最大值和最小值分别为1.75 K和1.33 K;在负载率恒定的缩比样机试验中,动态ROM相比于传统方法所降低平均计算误差的最大值和最小值分别为1.22 K和0.15 K。从图5可以明确看出,变压器运行过程中,工况的变化会导致降阶模型的模态也发生相应变化,进而使传统静态ROM的计算精度下降、性能变差,而动态ROM则是通过模态的不断更新来抑制误差的增加。因此,当负载率的复杂性增大时,动态ROM相比于传统方法所形成静态ROM的精度优势会更加明显,即出现了上述两个实验中的精度对比情况。
在更新模态时,通常的做法是构建新快照集,然后重新进行SVD运算,但SVD的耗时特征将使ROM失去速度优势。在提升模态更新的效率方面,对于3 786 369网格规模的数值实验数据,动态ROM将计算速度提升至传统方法的239倍;对于69 725网格规模的缩比样机试验数据,动态ROM将计算速度提升至传统方法的46倍。原因可用1.2.2节的计算复杂度定量分析结果进行解释,前述得出动态ROM相比于传统方法的计算效率提升为O(n(m+1)2)-O(nr2),因此,随着网格规模n的增加,本文方法效率提升的优势将更加明显。
因此,本文方法相比于传统方法的精度提升和效率提升情况,与负载率变化的复杂性和模型的网格规模呈正相关。
本文提供了一种高效率更新POD模态进而更新降阶模型的方法,能够为当前降阶模型保持高精度且兼顾速度优势提供解决方案,研究结论如下:
1)变压器运行过程中,其POD模态是动态变化的,常规从快照集提取模态后保持其不变的方式会导致所形成的静态降阶模型出现计算精度的显著下降,需要在有新快照可用时对降阶模型的模态进行更新,从而抑制降阶模型的精度下降问题。
2)所提出的降阶模型模态快速更新方法,能够基于初始SVD运算结果和新的可用快照直接计算出新快照矩阵的SVD结果,进而完成POD模态更新,无需再对新快照矩阵进行SVD运算。对于百万级别的网格规模,更新POD模态的效率较传统方法提升了2个数量级且误差在10-8级别。
3)所构建的动态降阶模型能够实现高精度的变压器绕组温度场计算且在s级时间内完成。在数值实验中,其计算误差较静态降阶模型最大减少了1.92 K,单步计算耗时仅增加0.016 s;变压器缩比样机温升试验中,其计算误差最大为2.59 K,单步计算耗时0.018 5 s。
本文提出的动态降阶模型构建方法,是通过矩阵低秩分解的方式来更新POD模态进而更新降阶模型,因此在计算精度和效率方面具有普适性。未来可进一步将其应用到变压器运行过程中磁场、流场、应力场等的降阶计算中,服务于数字孪生场景下孪生模型与物理实体的物理场动态同步。
附 录
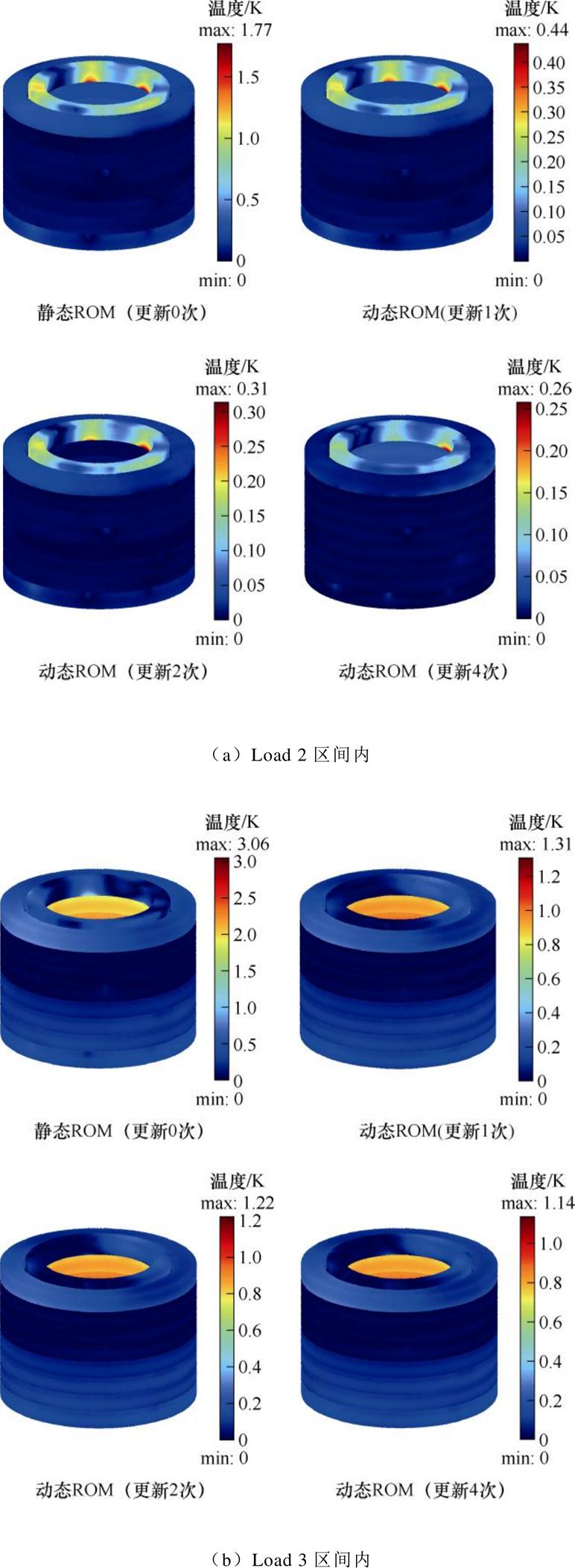
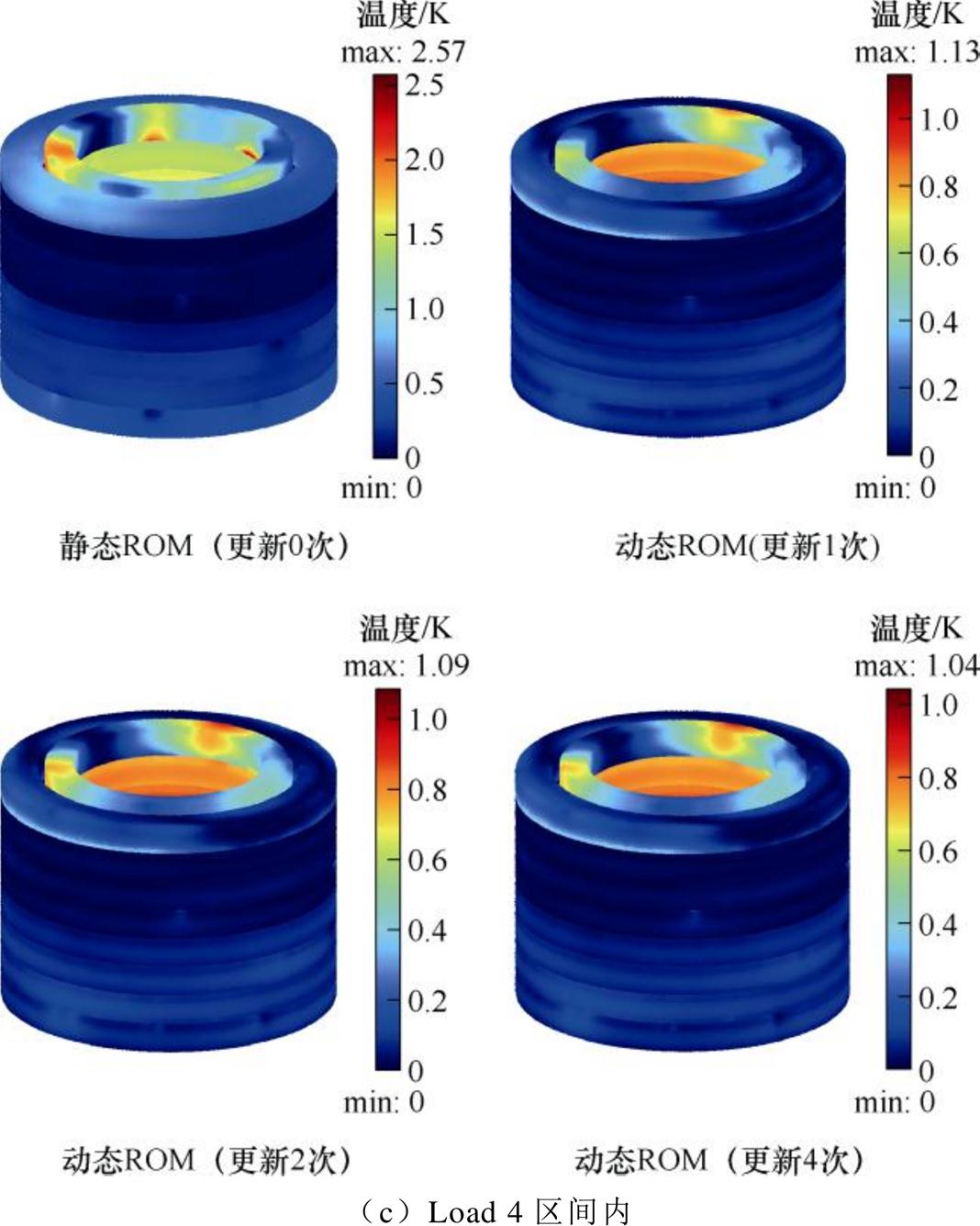
附图1 不同降阶模型在各个负载区间内的计算误差云图
App.Fig.1 Calculation error contour maps of different ROMs in each load interval
参考文献
[1] 吴珊, 边晓燕, 张菁娴, 等. 面向新型电力系统灵活性提升的国内外辅助服务市场研究综述[J]. 电工技术学报, 2023, 38(6): 1662-1677.
Wu Shan, Bian Xiaoyan, Zhang Jingxian, et al. A review of domestic and foreign ancillary services market for improving flexibility of new power system [J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1662-1677.
[2] 黄彦钦, 余浩, 尹钧毅, 等. 电力物联网数据传输方案: 现状与基于5G技术的展望[J]. 电工技术学报, 2021, 36(17): 3581-3593.
Huang Yanqin, Yu Hao, Yin Junyi, et al. Data transmission schemes of power Internet of Things: present and outlook based on 5G technology[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3581-3593.
[3] 罗豪, 成立, 杨丽君, 等. 虚实融合的变压器内绝缘状态孪生方法[J]. 电工技术学报, 2024, 39(23): 7628-7638.
Luo Hao, Cheng Li, Yang Lijun, et al. State twinning method of transformer internal insulation by virtual- real fusion[J]. Transactions of China Electrotechnical Society, 2024, 39(23): 7628-7638.
[4] 谭又博, 余小玲, 臧英, 等. 谐波电流对换流变压器绕组损耗及温度分布特性的影响[J]. 电工技术学报, 2023, 38(2): 542-553.
Tan Youbo, Yu Xiaoling, Zang Ying, et al. The influence of harmonic current on the loss and tempera- ture distribution characteristics of a converter transformer winding[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 542-553.
[5] 刘刚, 郝世缘, 朱章宸, 等. 基于动态模态分解-自适应变步长油浸式电力变压器绕组瞬态温升快速计算方法[J]. 电工技术学报, 2024, 39(12): 3895- 3906.
Liu Gang, Hao Shiyuan, Zhu Zhangchen, et al. Research on rapid calculation method of transient temperature rise of winding of dynamic mode decom- position-adaptive time stepping oil-immersed power transformer[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3895-3906.
[6] Yang Fan, Wu Tao, Jiang Hui, et al. A new method for transformer hot-spot temperature prediction based on dynamic mode decomposition[J]. Case Studies in Thermal Engineering, 2022, 37: 102268.
[7] 陈思, 盛戈皞, 张立静, 等. 基于绕组等效热参数的干式变压器温度场分布快速仿真方法[J]. 高电压技术, 2025, 51(1): 97-109.
Chen Si, Sheng Gehao, Zhang Lijing, et al. Fast simulation method of temperature field distribution for dry-type transformer based on equivalent thermal parameters of windings[J]. High Voltage Engineering, 2025, 51(1): 97-109.
[8] 邓永清, 阮江军, 董旭柱, 等. 基于自适应网格控制的10 kV油浸式变压器多物理场仿真计算[J]. 高电压技术, 2022, 48(8): 2924-2933.
Deng Yongqing, Ruan Jiangjun, Dong Xuzhu, et al. Simulation of multi-physical field of 10 kV oil-immersed transformer based on adaptive grid control [J]. High Voltage Engineering, 2022, 48(8): 2924-2933.
[9] Chi Cheng, Yang Fan, Xu Chong, et al. A multi-scale thermal-fluid coupling model for ONAN transformer considering entire circulating oil systems[J]. Interna- tional Journal of Electrical Power & Energy Systems, 2022, 135: 107614.
[10] 杨帆, 吴涛, 廖瑞金, 等. 数字孪生在电力装备领域中的应用与实现方法[J]. 高电压技术, 2021, 47(5): 1505-1521.
Yang Fan, Wu Tao, Liao Ruijin, et al. Application and implementation method of digital twin in electric equipment[J]. High Voltage Engineering, 2021, 47(5): 1505-1521.
[11] 田野, 卜凯阳, 李楚杉, 等. 用于IGBT模块温度观测的3-D降阶混合型热模型[J]. 电工技术学报, 2024, 39(16): 5104-5120.
Tian Ye, Bu Kaiyang, Li Chushan, et al. A hybrid 3-D reduced-order thermal model for temperature observa- tion of IGBT modules[J]. Transactions of China Electrotechnical Society, 2024, 39(16): 5104-5120.
[12] 刘刚, 荣世昌, 武卫革, 等. 基于混合有限元法和降阶技术的油浸式变压器绕组2维瞬态流-热耦合场分析[J]. 高电压技术, 2022, 48(5): 1695-1705.
Liu Gang, Rong Shichang, Wu Weige, et al. Two- dimensional transient flow-thermal coupling field analysis of oil-immersed transformer windings based on hybrid finite element method and reduced-order technology[J]. High Voltage Engineering, 2022, 48(5): 1695-1705.
[13] 刘刚, 胡万君, 郝世缘, 等. 油浸式变压器绕组瞬态温升降阶快速计算方法[J]. 电工技术学报, 2024, 39(3): 643-657.
Liu Gang, Hu Wanjun, Hao Shiyuan, et al. Reduced order calculation method of steady temperature rise of oil immersed power transformer[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 643-657.
[14] 刘刚, 胡万君, 郝世缘, 等. 包含快照选择策略的POD-QDEIM油浸式变压器绕组瞬态温升降阶算法研究及其实验验证[J]. 中国电机工程学报, 2024, 44(12): 4998-5011.
Liu Gang, Hu Wanjun, Hao Shiyuan, et al. Research and experimental verification of POD-QDEIM algorithm for transient temperature rise and reduced order of oil immersed transformer windings with snap- shot selection strategy[J]. Proceedings of the CSEE, 2024, 44(12): 4998-5011.
[15] 刘刚, 郝世缘, 胡万君, 等. 基于子循环自适应串行交错时间匹配算法的油浸式变压器绕组瞬态温升计算[J]. 电工技术学报, 2024, 39(4): 1185-1197.
Liu Gang, Hao Shiyuan, Hu Wanjun, et al. Transient temperature rise calculation of oil immersed trans- former winding based on sub cyclic adaptive staggered time matching algorithm[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1185-1197.
[16] 张志宇, 寇家俊, 张重远, 等. 基于本征正交分解和克里金代理模型的油浸式变压器绕组温度场快速计算方法[J]. 电工技术学报, 2025, 40(7): 2215- 2225.
Zhang Zhiyu, Kou Jiajun, Zhang Zhongyuan, et al. A fast calculation method for temperature field of oil immersed transformer windings based on proper orthogonal decomposition and Kriging surrogate model [J]. Transactions of China Electrotechnical Society, 2025, 40(7): 2215-2225.
[17] Liu Gang, Hu Wanjun, Hao Shiyuan, et al. A fast computational method for internal temperature field in oil-immersed power transformers[J]. Applied Thermal Engineering, 2024, 236: 121558.
[18] Liu Yunpeng, Zhao Qingxian, Liu Gang, et al. A real- time solution method for three-dimensional steady temperature field of transformer windings based on mechanism-embedded cascade network[J]. Case Studies in Thermal Engineering, 2024, 58: 104444.
[19] Wu Tao, Yang Fan, Farooq U, et al. Real-time calculation method of transformer winding tempera- ture field based on sparse sensor placement[J]. Case Studies in Thermal Engineering, 2023, 47: 103090.
[20] 刘刚, 胡万君, 刘云鹏, 等. 降阶技术与监测点数据融合驱动的油浸式变压器绕组瞬态温升快速计算方法[J]. 电工技术学报, 2024, 39(19): 6162-6174.
Liu Gang, Hu Wanjun, Liu Yunpeng, et al. A fast calculation method for transient temperature rise of oil immersed transformer windings driven by fusion of order reduction technology and monitoring point data[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 6162-6174.
[21] Björck Å. Numerics of Gram-Schmidt orthogonali- zation[J]. Linear Algebra and Its Applications, 1994, 197: 297-316.
[22] Peherstorfer B, Willcox K. Dynamic data-driven reduced-order models[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 291: 21-41.
[23] Trefethen L N, Bau D. Numerical Linear Algebra[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1997.
Fast Updating Method for Reduced-Order Model of Transformer Winding Temperature Field Based on Matrix Low-Rank Decomposition
Abstract The temperature state of transformer winding affects its operating life directly, so researchers have widely discussed how to achieve continuous and accurate calculations of the temperature field of transformer winding. The model orderreduction technique is currently the mainstream solution, and existing methods generally adopt singular value decomposition (SVD) of the initial snapshot matrix to obtain the modes, keeping the modes unchanged and continuously using them. During the operation of transformers, due to the dynamic changes in operating conditions, the modes will also change accordingly, resulting in a significant decrease in the computational accuracy of the static reduced order models (ROM).
It is difficult to fully consider various operating conditions when building the initial snapshot set, and it can lead to high computational costs in the offline phase. Continuously updating the initial snapshot matrix and performing SVD operations when new snapshots are available is a solution. Still, the high computational cost of SVD can cause ROM to lose its speed advantage. This paper proposed a low-cost method for updating modes and subsequently updating ROM based on matrix low-rank decomposition. Firstly, when a new snapshot is available, it is added to the initial snapshot matrix, and the snapshot matrix update is represented using matrix low-rank decomposition. Then, the solution of updating the modes directly from the SVD results of the initial snapshot matrix and the new snapshot was established. Only low computational cost SVD operation was required for low dimensional matrices, without the need for high computational cost SVD of the new snapshot matrix. Furthermore, sparse measurements of winding temperature were used to determine the modal coefficients and form a dynamic ROM. Finally, numerical calculations and transformer scaling prototype experiments verified the method’s effectiveness.
The results indicate that during the transformer’s operation, the proper orthogonal decomposition (POD) modes of its winding temperature field dynamically change, and it is necessary to update the modes of the ROM when new snapshots are available to suppress the increase in calculation errors of the ROM. The error of the proposed method for updating the temperature field modes of transformer winding is at the level of 10-8, and the single update takes 0.71 seconds for a grid-scaleofmillions, which is 239 times faster than traditional methods. In numerical experiments, the calculation error is reduced by a maximum of 1.92 K compared to the static ROM, with only a 0.016-second increase in single-step computation time. In the temperature rise test of the transformer scale prototype, the maximum computational error is 2.59 K, and the single-step computation time is 0.018 5 seconds, effectively avoiding the accuracy decline caused by modes change during transformer operation while maintaining computation speed at the second level. For calculating transformer winding temperature fields under varying load rates, only one mode update is required within each load rate interval. Increasing the number of mode updates will not lead to a further significant reduction in errors due to information redundancy. This research provides a solution for achieving continuous and accurate transformer winding temperature field calculations using ROMs.
Keywords:Transformer, winding temperature field, reduced order model, low-rank decomposition
中图分类号:TM411
DOI: 10.19595/j.cnki.1000-6753.tces.242353
国家重点研发计划资助项目(2021YFB2401700)。
收稿日期2024-12-25
改稿日期 2025-01-12
杨 帆 男,1980年生,教授,博士生导师,研究方向为输变电设备多物理场计算、电力装备数字孪生。
E-mail: yangfan@cqu.edu.cn
吴 涛 男,1993年生,博士研究生,研究方向为输变电设备多物理场计算、电力装备数字孪生。
E-mail: Bryant_Mentality@163.com(通信作者)
(编辑 郭丽军)