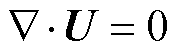（1）
摘要 为了应对非迎风有限元法在求解二维稳态不可压缩流体Navier-Stokes方程时可能引发的非物理振荡，以及有限差分法在复杂几何中因难以实现高精度网格划分而导致较大计算误差的挑战，同时克服基于结构化交错网格的有限体积法在处理复杂几何和边界条件时灵活性不足和计算复杂度高的难题，该文提出一种基于非结构化同位网格的有限体积法。采用延迟修正的高阶格式和二阶中心差分格式分别离散对流项和扩散项，以提高计算精度并避免数值振荡和耗散。同时，采用SIMPLE算法处理压力-速度耦合，确保了流场计算中的质量守恒。结合PARDISO求解器与COO存储格式，并引入欠松弛技术优化稀疏线性方程组的求解，提升了计算效率与收敛性。开发了适用于三角形网格和四边形网格的计算程序，比较了两者在相似节点数下的计算时长。通过优化欠松弛因子组合，对经典的方腔驱动流问题进行数值计算，并将结果与COMSOL有限元仿真软件及Ghia的涡量-流函数法进行了对比。结果表明，该方法在数值精度上优于有限元法，相较于结构化交错网格有限体积法在处理复杂几何与边界条件时，该方法具有更高的灵活性与适用性。最后，将该方法应用于油浸式换流变压器的油流场分析，并与COMSOL计算结果对比，验证了其在实际工程应用中的准确性与实用性。
关键词：非结构化同位网格 有限体积法 不可压缩N-S方程 SIMPLE算法 油浸式换流变压器
电力变压器作为电力系统中的关键设备，其运行状态直接影响电网的稳定性。电力变压器内部油流速度和温度分布是影响其绝缘和热性能的关键因素，因此，准确地预测和分析电力变压器内部的流热场对于设备优化设计和提高运行可靠性至关重要。近年来，随着电网容量的增加和设备运行复杂性的提升，流热场数值仿真的需求日益增加。为了应对国产化电力装备CAE软件在相关仿真技术中遇到的难题，并进一步提升自主仿真软件的核心能力，本文旨在为具有自主知识产权的高压电力装备多物理场仿真软件提供有效的计算方法支持，以满足电力变压器在设计与运行中的精确分析需求。
目前，针对电力变压器流热场问题的数值方法主要包含有限元法、有限差分法和有限体积法。有限元法在处理复杂几何时具有优势，但在模拟流动和传热时常遇到数值振荡问题。尤其是在分析油浸式变压器绕组温升和热点位置时，Galerkin有限元法的数值稳定性较差，容易产生非物理数值振荡，因此需要引入非对称迎风算子来提高计算稳定性[1]。有限差分法虽然在简单几何中具有较高的精度，但对网格要求较高，难以在大型变压器中实现高精度网格划分，容易导致较大的计算误差[2]。相比之下，有限体积法因其良好的守恒性和数值稳定性，被广泛应用于流动与传热问题。例如，文献[3-5]中，成功地将有限体积法用于变压器内部温度场和流速分布的模拟。然而，在采用有限体积法求解流体力学问题时，压力场与速度场的耦合计算可能会引发棋盘问题，进而影响计算精度与稳定性。为了有效避免棋盘问题，有限体积法通常采用交错网格和同位网格两种变量排列方式[6]。在基于结构化交错网格的有限体积法中，速度和压力存储在不同的网格位置。这种方法虽然有助于消除非物理振荡，但在处理复杂几何时，增加了数据结构的复杂性和插值操作的计算成本。此外，由于结构化网格通常由规则的四边形构成，因此在处理复杂几何形状和边界条件时，其灵活性和适应性会受到限制，从而影响了其在复杂流动问题中的应用[7-8]。
尽管现有方法在电力变压器流热场问题的研究中取得了一定的进展，但在处理复杂几何、提高计算精度、保持数值稳定性以及提升计算效率方面仍然存在诸多局限性。为了克服这些挑战，本文提出了一种基于非结构化同位网格的有限体积法，旨在解决现有方法在复杂流动问题中的不足。具体而言，该方法采用由不规则三角形构建的非结构化网格，从而在复杂流动几何的处理上展现出更高的灵活性和适应性[9-10]。为了简化数据结构并提升计算效率，采用同位网格排列速度和压力，以避免交错网格中因速度和压力存储在不同网格时的额外插值操作。其次，针对同位网格中可能因线性插值导致的棋盘问题，采用Rhie-Chow插值法来消除虚假压力振 荡[11-13]。此外，通过采用延迟修正的高阶格式和二阶中心差分格式分别离散对流项和扩散项，以提高计算精度。针对求解N-S方程的耦合算法在内存上计算成本高的问题，采用SIMPLE（semi-implicit method for pressure linked equations）分离算法优化求解过程，以降低内存和计算成本[14-19]。在稀疏矩阵存储方面，采用COO（coordinate list）格式，该格式相较于CSR（compressed sparse row）和CSC（compressed sparse column）格式更易编程实现，且无需额外计算就可恢复原始矩阵，从而节省存储空间[20-21]。与此同时，为了提高计算效率并避免迭代法的收敛性问题，采用基于超节点技术的并行稀疏直接求解器（Parallel sparse Direct Solver, PARDISO），其内存占用较少且支持单节点分解，优于MUMPS（multi-frontal massively parallel solver）和WSMP（web-based sparse matrix package）求解器[22-23]。最后，结合欠松弛技术优化收敛性能并确保数值求解的稳定性[24]。
基于上述方法，本文开发了适用于三角形网格和四边形网格的流场计算程序，并通过经典的方腔驱动流问题进行测试。最后，将该方法应用于油浸式换流变压器的油流场分析，以验证其在解决实际工程问题中的准确性与可行性。
在工程分析中，变压器油可以近似等效为不可压缩牛顿流体。稳态情况下不可压缩牛顿流体的质量守恒方程（也称连续性方程）及动量守恒方程[25]为
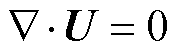（1）
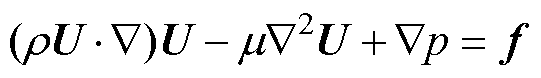（2）
式中，U为速度矢量（m/s）；r为流体密度（kg/m3）；m为流体动力黏度系数（N·s/m2）；p为流体压强（Pa）；f为外力密度矢量（N/m3）。在式（2）中，左端第一项为对流项，第二项为扩散项，第三项为压力梯度项。式（2）又称为控制流体流动的不可压缩Navier-Stokes方程。结合具体的应用场景，通过施加边界条件，并应用有限体积法等数值方法离散式（1）和式（2），即可得到不可压缩牛顿流体稳态情况下的速度分布。
根据矢量恒等式，存在关系[26]为
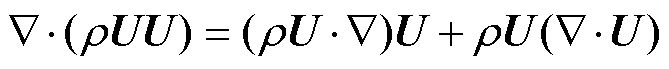（3）
采用有限体积法对对流项进行离散，结合式（1）将其在整个求解域上积分，并将积分转换为各个单元的积分之和[27]，可得
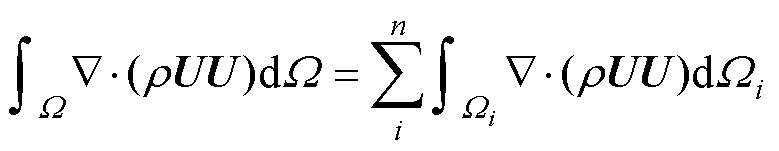（4）
式中，W为整个求解域；i表示第i个单元；n为单元总数；Wi为第i个单元的求解域。
利用高斯散度定理，在单元级别上的积分[27]可以表示为
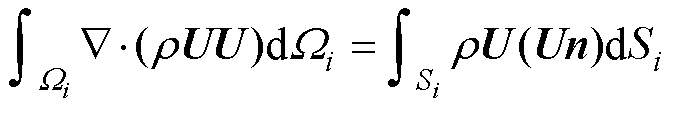（5）
式中，n为单元面法线方向单位矢量；Si为第i个单元的总面的面积。
将式（5）的对流项变为各个面的积分之和，并根据质量流公式mf=rUfSf[27]，可得
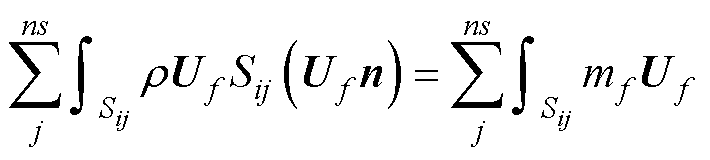（6）
式中，j为第j个面；ns为面总数；Sij为第i个单元中第j个面的面积；Uf为单元面f的速度。
1.1.1 高阶离散格式
在图1所示的非结构化网格中，对流项的高阶格式能够显著减少数值耗散，提高计算精度。本文主要考虑以下几种高阶格式，这些格式在已有研究中被证明能够有效处理复杂流场中的对流问题[27]。
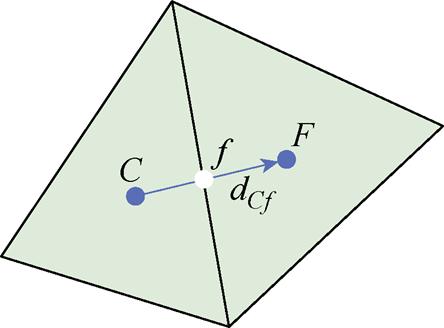
图1 非结构化网格中的单元
Fig.1 Elements in unstructured grids
1）中心差分格式
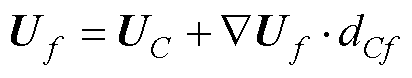（7）
2）二阶迎风格式
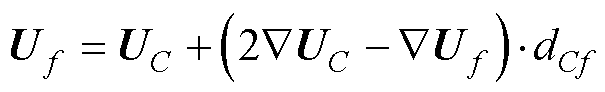（8）
3）FROMM格式
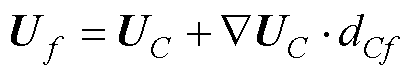（9）
4）QUICK格式
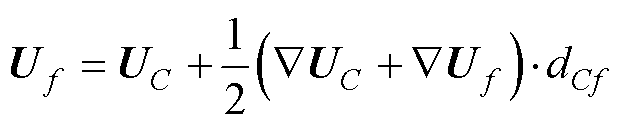（10）
式中，UC为单元C质心的速度值；dCf为单元C质心与面f中心的距离。
在非结构化网格上，采用上述高阶格式处理对流项显著提升了计算的准确性与稳定性。与低阶格式相比，高阶格式表现出更高的数值精度和更少的数值耗散。
1.1.2 延迟修正方法
为了进一步优化高阶格式的应用，本文引入了延迟修正方法[28]。该方法在不降低现有稳定性的前提下，成功地将高阶（High Order, HO）格式引入基于低阶格式编写的代码中。通过优化对流通量的计算，有效缓解了传统高阶格式在求解复杂流体问题时可能出现的数值稳定性问题，具体为
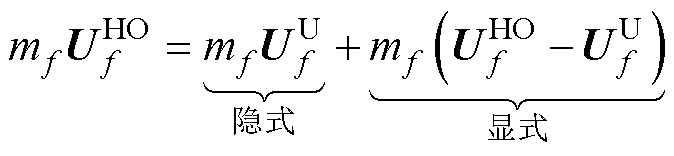（11）
式中，
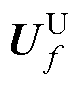和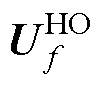
分别为采用一阶迎风格式和高阶格式计算得到的界面速度。在式（11）中，一阶迎风格式的对流通量采用隐式处理，以增强数值稳定性。同时，优化后的源项则通过显式处理，确保在求解过程中保持高阶精度。
1.1.3 刚度矩阵与边界处理
对流项的一阶迎风格式[27]为
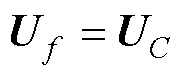（12）
传统的方程组装方法需逐个单元计算通量，导致在处理相邻单元分界面时出现重复计算，从而降低了效率并增加了计算量[29]。相比之下，本文在计算域内部的面上采用一阶迎风格式时，仅需计算一次质量流，并根据界面处的法向方向来区分上游和下游单元，从而优化了方程组装过程。一阶迎风格式示意图如图2所示。C单元和F单元在分界面的通量分别为rSfUfnCUC和rSfUfnFUC，Sf为单元面的法向面积；nC和nF分别为单元C和单元F的单位外法向。此外，通过直接在边界面使用给定边界值计算对流通量，并调整刚度矩阵K中的相关行和右端项，以准确反映对流边界条件。这一改进显著提升了计算效率。
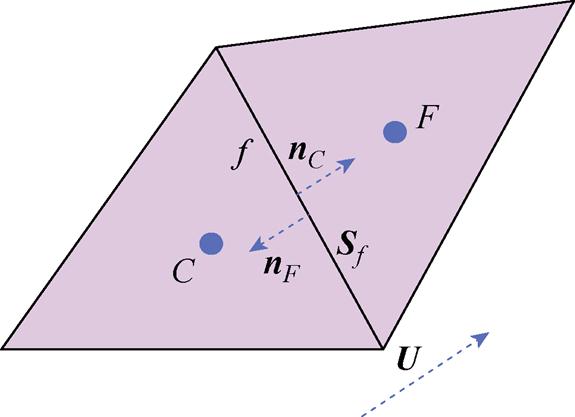
图2 一阶迎风格式示意图
Fig.2 Schematic diagram of first-order upwind format
采用有限体积法对扩散项进行离散，在整个求解域上进行积分，并转换为各个单元积分之和[27]，可得
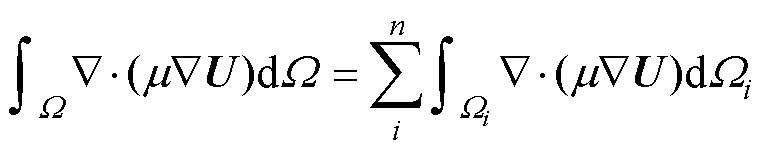（13）
在每个单元上，通过高斯散度定理将整个单元内的体积分转换成单元外表面上的面积分，并写成各个面的积分之和[27]为
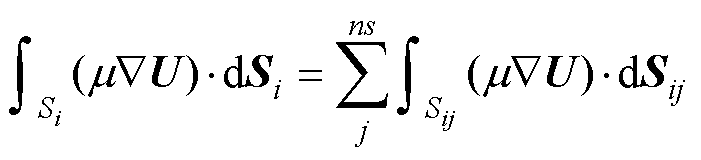（14）
式中，Sij为第i个单元中第j个面的面积。
在每个面上，采用单点积分。在四边形网格上，如图3所示[27]，可写为
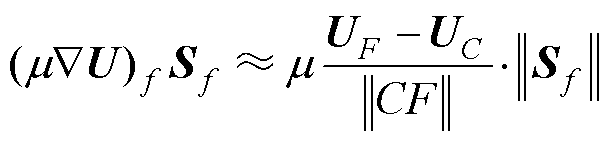（15）
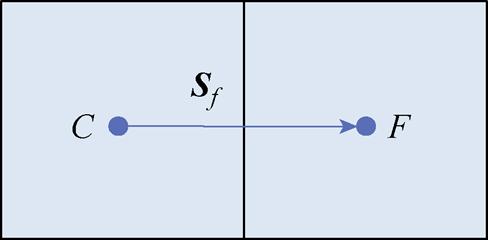
图3 四边形网格
Fig.3 Quadrilateral mesh
式中，UF为单元F质心的速度；||CF||为单元C质心与单元F质心间的距离。
在如图4所示三角形网格上[27]，有
（16）
式中，Ef为正交分量；Tf为非正交修正分量。
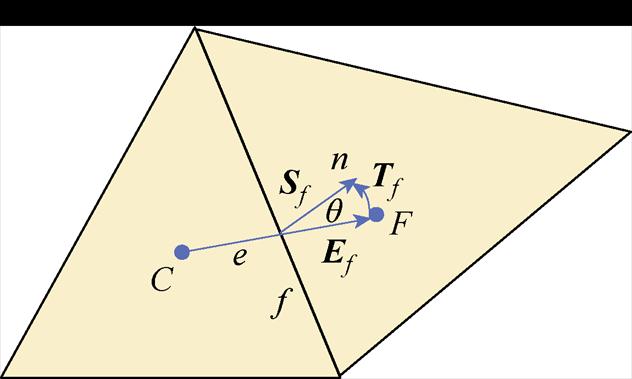
图4 三角形网格
Fig.4 Triangular mesh
关于Ef的计算，主要分析以下三种方法[27]：
1）最小修正法
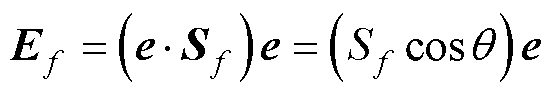（17）
式中，e为相邻单元中心连线的单位方向；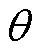
为Sf与e的夹角。
2）正交修正法
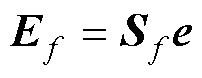（18）
3）过松弛法
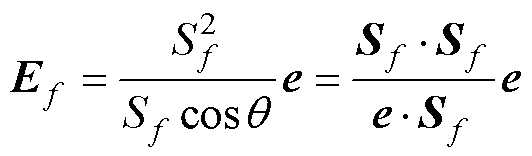（19）
通过比较三种方法在非正交网格上的精度和稳定性，结果表明，即使在网格高度非正交的情况下，过松弛的方法仍表现出最高的稳定性。因此，本文在三角形网格中优先采用过松弛法。
1.2.1 刚度矩阵的构建
在有限体积法中，传统的数据结构通常基于对每个单元的循环计算。这种方法在处理内部面通量时效率较低，且在应对复杂几何形状时边界处理较为复杂[29]。为了提高效率，本文提出了一种基于面-单元的数据结构。该结构通过对每个面进行循环计算，减少了通量计算的冗余，从而优化了刚度矩阵的组装效率。在此结构下，每个面只需计算一次通量，计算结果可同时用于相邻单元，避免了重复计算，显著提升了整体计算效率。
针对第一个单元，可写[27]为
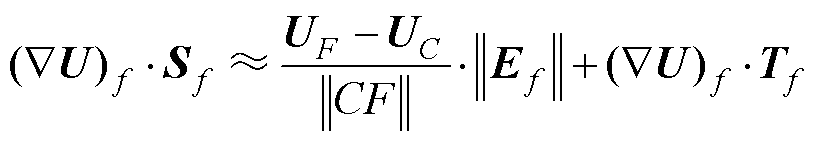（20）
针对相邻单元，可写[27]为
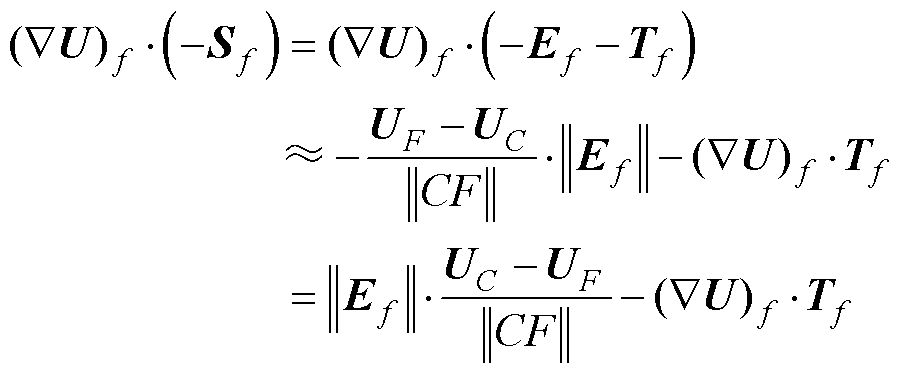（21）
1.2.2 边界的处理
在处理扩散项边界面时，需要考虑法向与梯度共线和不共线两种情况，如图5所示。针对这两种情况，分别采用相应的通量处理方法，以确保计算的准确性和稳定性。具体如下[27]：
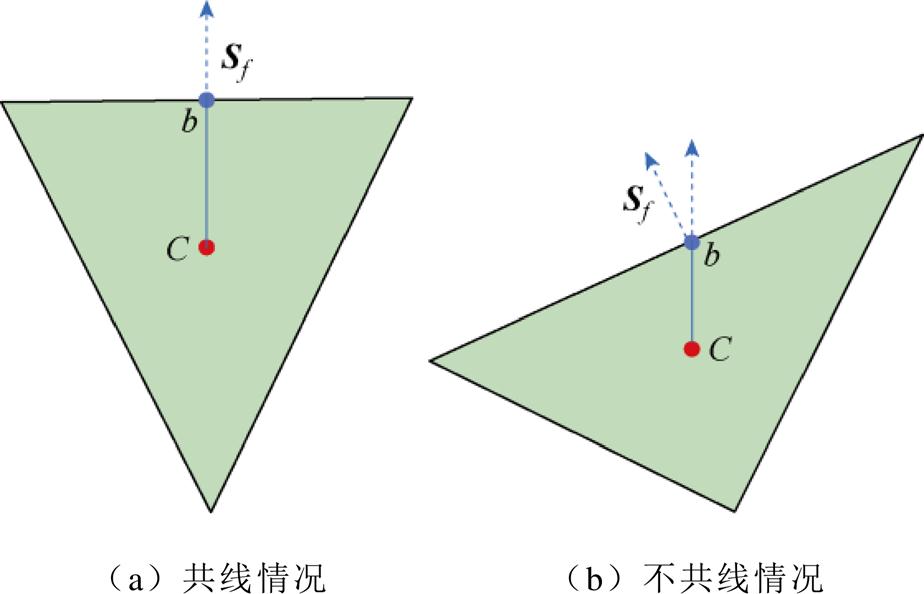
图5 非结构化网格边界处理
Fig.5 Unstructured grid boundary processing
1）针对共线情况边界面通量处理方法为
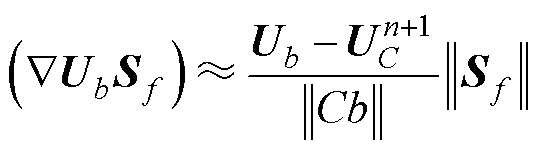（22）
式中，Ub为单元面中心处的速度；n表示前一迭代步骤；||Cb||为单元C质心与单元面中心b的距离。
2）针对不共线情况边界面通量处理方法为
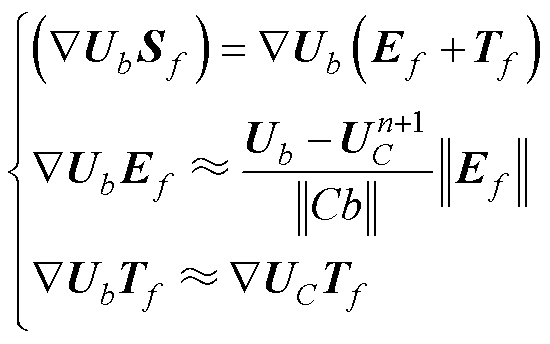（23）
在构建离散扩散方程组时，单元质心和单元面上的梯度离散化是关键步骤，格林高斯梯度计算方法在处理非结构化网格时面临灵活性和精度不足的局限性[27]。为此，本文采用最小二乘法计算非结构化网格单元质心的梯度，该方法在计算梯度时提供了更大的灵活性和更高的精度。此外，通过插值方法将该梯度传递至单元面，从而获得更准确的面梯度。这一优化方法提高了离散扩散方程组的稳定性与准确性。
利用前一迭代步骤的值来计算各个单元质心的梯度，具体如下[27]。
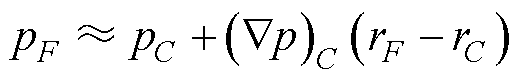（24）
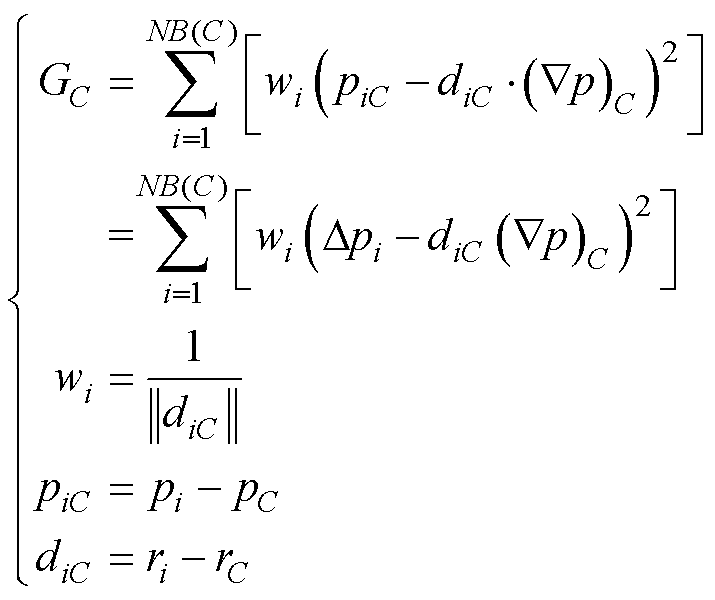（25）
式中，pC、pF分别为单元C和单元F的质心值；(Ñp)C为单元C质心的梯度；pi为第i个相邻单元质心的值；ri、rC、rF分别为第i个相邻单元质心、单元C质心和单元F质心的空间坐标位置；wi为权重因子；NB(C)表示单元C的相邻单元数量；piC为第i个相邻单元质心与单元C质心的差值；||diC||为第i个相邻单元质心与单元C质心间的距离。
采用优化程序计算质心梯度，该程序通过最小化定义为GC的目标函数来实现，将GC函数最小化[27]为
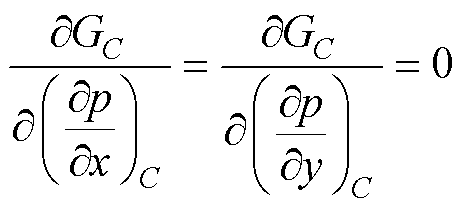（26）
其可写为矩阵的形式，即
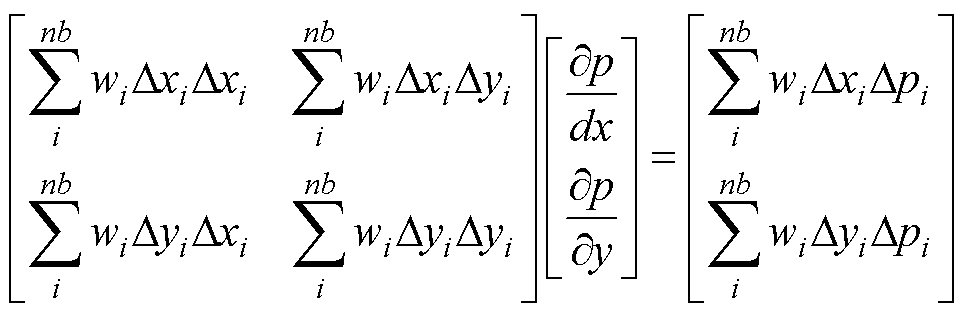（27）
式中，nb为相邻单元的数量；∂p/∂x、∂p/∂y分别表示质心沿x和y方向的压力梯度分量。这一方法提高了梯度计算的准确性，并增强了对非结构化网格的适应能力。
通过跨越界面相邻单元质心梯度的加权平均来得到单元面上的梯度，这种方法能够有效捕捉跨界面的变化。此方法基于对相邻单元之间梯度的合理估计，确保在非结构化网格中获得更高的计算精度。具体如下[27]。
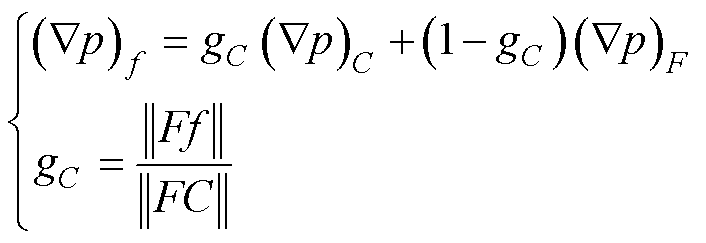（28）
式中，gC为界面f相对于质心C位置相关的几何加权因子；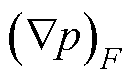
为单元F质心的梯度；
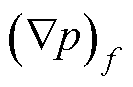为单元面f上的梯度；||Ff||为单元F质心与单元面f的距离；||FC||为单元F质心与单元C质心的距离。
SIMPLE算法的具体流程如图6所示。
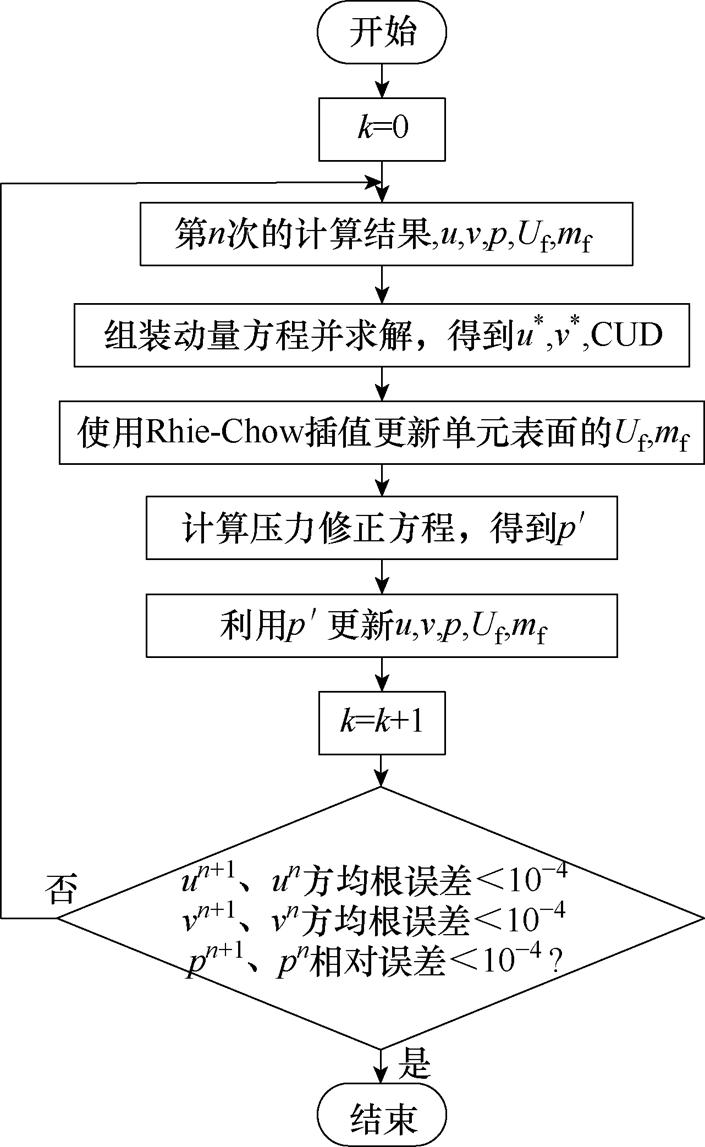
图6 SIMPLE算法流程
Fig.6 SIMPLE algorithm flowchart
为了计算第n+1次迭代的解，以第n次迭代时的速度、压力、单元面速度值及质量流作为初始值。采用SIMPLE算法对如下动量方程（不考虑外力影响）进行求解，从而计算得到u*和v*。
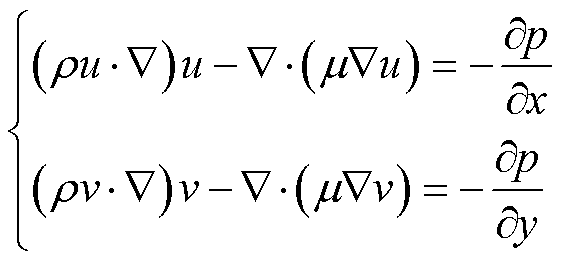（29）
式中，u和v分别表示x和y方向上的速度分量。
采用有限体积法离散的动量方程[27]可以写为
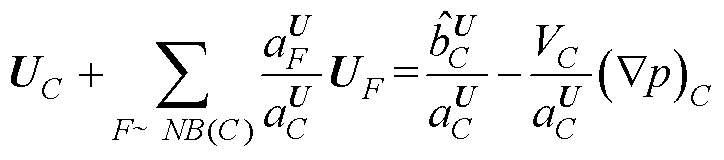（30）
式中，VC为单元外表面的面积；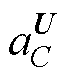
为单元C的离散化方程系数；
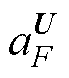为单元F的离散化方程系数；
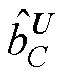为与单元C相关的源项。
令式（30）中
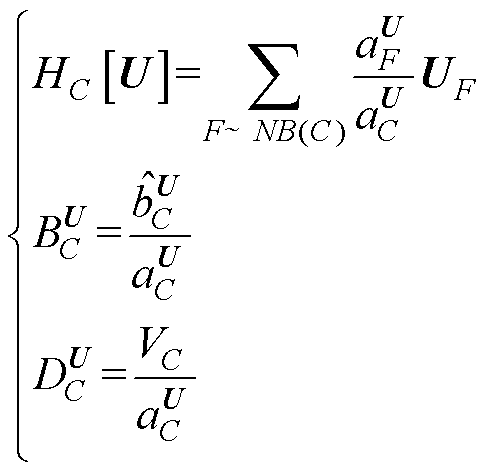（31）
式（30）经简化可写成
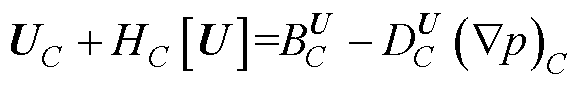（32）
从单元C和F离散x方向动量方程开始，可 写成
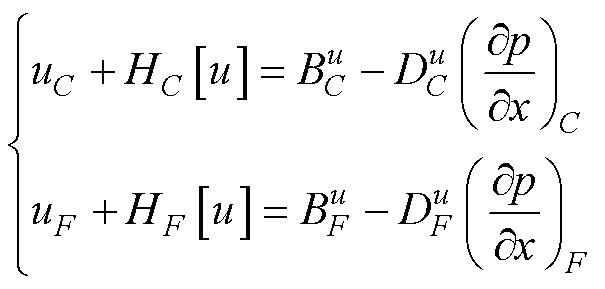（33）
与式（33）类似，uf速度方程中的压力梯度与局部相邻单元质心的压力值相关，其表达式为
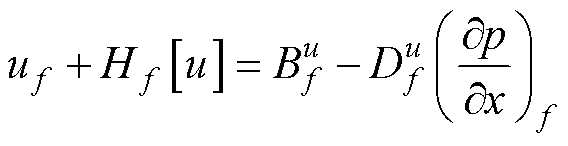（34）
式中，uf为x方向上的界面速度分量。
在同位网格中，直接计算该方程的系数存在困难。为此，采用线性插值法，从相邻单元质心的系数进行插值来近似计算。这些系数的计算式为
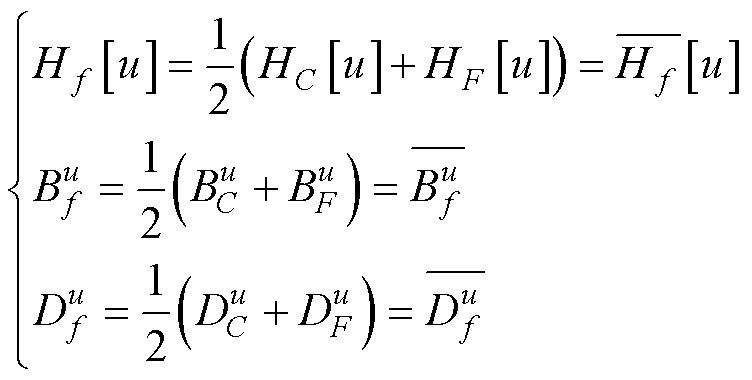（35）
采用式（35）中的值，式（34）变为
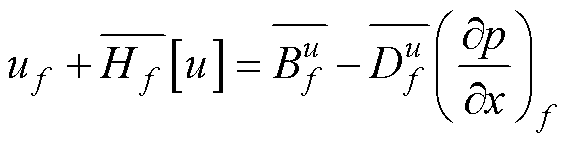（36）
在上述方程中，带有上划线“—”的值通过对质心C和质心F处的值进行线性插值得到，具体表达式为
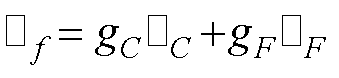（37）
式中，
为指带上划线的值；gC和gF分别为界面f相对于质心C和质心F位置相关的几何插值因子。
根据式（33）可以推导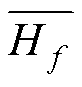
为
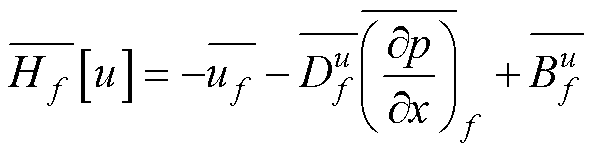（38）
将式（38）代入式（36）中，利用Rhie-Chow插值法，得到单元表面的速度为
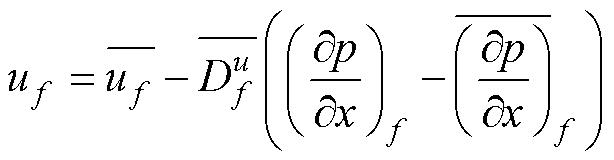（39）
式中，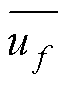
为初步计算的界面速度；
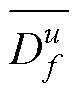为用于调整界面速度计算的系数；(∂p/∂x)f为相邻单元界面f上的压力梯度；
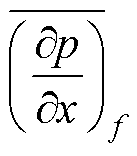为相邻单元界面f上压力梯度的平均值。
为适用于多维压力修正方程，将式（39）表示为矢量形式，即
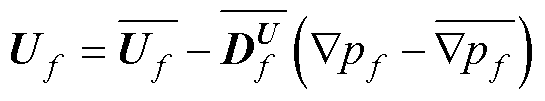（40）
其中，Ñpf的计算公式为
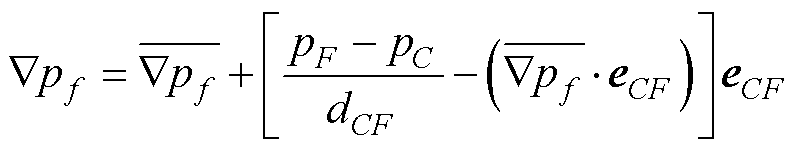（41）
式中，eCF表示从单元C到单元F的单位向量。
采用Rhie-Chow插值法相较于传统的线性插值法具有更强的适应性，能够灵活应用于不同类型的网格，尤其是能在复杂流场中更有效地捕捉界面流速的变化。此外，该方法避免了棋盘效应，从而确保了计算结果的物理合理性，因此在界面流速的计算中提供了更高的准确性和稳定性。
在动量方程计算得到的速度u*、v*尚未满足连续性方程，因此本文通过修正速度场和压力场来保证质量守恒。设速度和压力的修正量为U＇、p＇，精确场与计算场的关系为
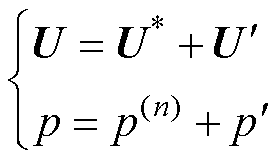（42）
将式（42）代入连续性方程后，得到
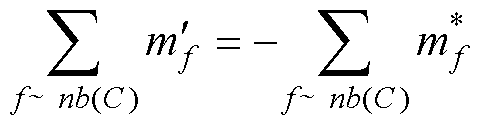（43）
式中，f～nb(C)为单元C的所有相邻面f；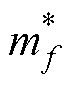
为通过动量方程得到的未修正的质量流；
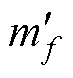为满足连续性方程而引入的修正项。
根据式（40），式（43）可重写为
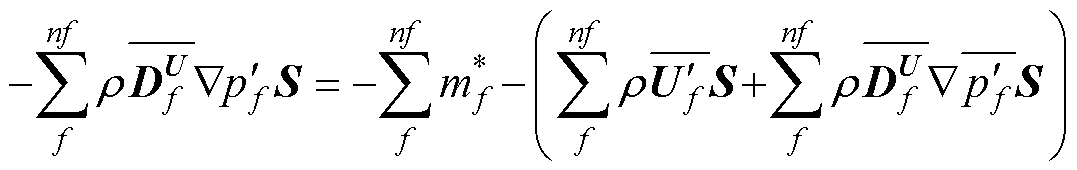（44）
式中，f为某个控制面的索引，nf为所有控制面的数量。
为了简化计算，在SIMPLE算法中忽略了式（44）右端括号中的项，使速度修正直接与压力修正相关联。由于此方程为修正方程，在收敛过程中修正项会趋于零，省略这些项不会影响最终解。具体形式为
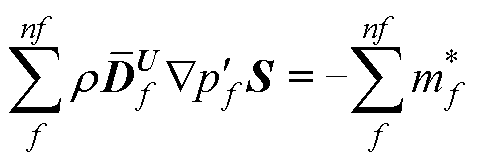（45）
修正后的方程简化为压力泊松方程，仅包含扩散项和源项。该简化方案在保证计算精度的同时提高了计算效率。
在SIMPLE算法中，忽略方程中的某些项可能导致较大的压力修正值，从而减缓收敛速度或引起发散[27]。为了提高稳健性并改善收敛行为，本文采用了一种改进的显式欠松弛策略。具体而言，从方程式（45）获得的压力修正值需要进行显式欠松弛，而更新速度时不使用欠松弛，因为压力修正将确保这些场的质量守恒。修正方程为
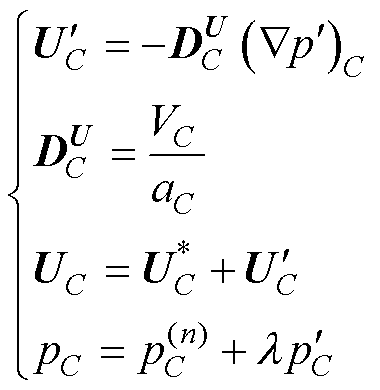（46）
式中，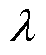
为欠松弛因子；aC为离散化方程C单元的系数。
在处理非正交网格上的扩散问题时，扩散系数可能作为未知因变量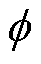
的函数，并且可能存在较大的交叉扩散项[27]。为了解决这一问题，本文引入了延迟修正方法进行处理。然而，在迭代过程中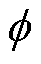，的较大变化可能导致源项和系数的较大变化，从而引起迭代求解过程的发散。这种发散通常源于系数和交叉扩散项引入的非线性，导致源项受到尚未收敛的当前解场影响[27]。为了促进收敛并稳定迭代求解过程，采用欠松弛技术以减缓迭代过程中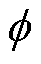的变化。
一般的离散化方程形式[27]为
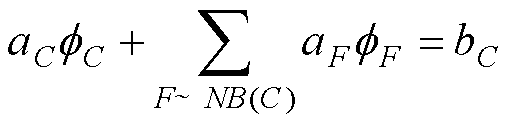（47）
式中，aC、aF分别为单元C与邻接单元F相关的系数；
、
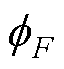分别为单元C与邻接单元F处的未知量；bC为与单元C相关的源项；F～NB(C)表示单元C的邻接单元集合。
式（47）可改写为
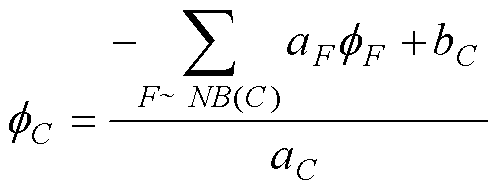（48）
利用上一次迭代的值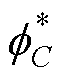
进行修正，式（48）可重写为
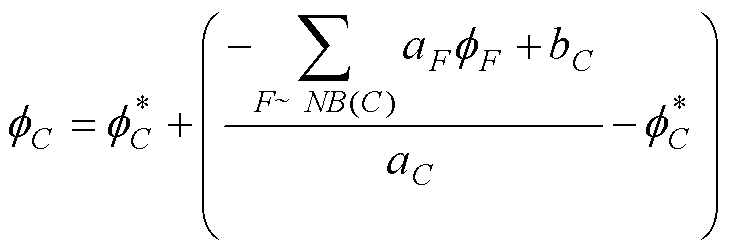（49）
式中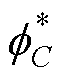，为前一次迭代的值。
式（49）中括号内的项表示当前迭代中的变化，该变化可通过松弛因子
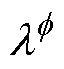加以调整，即
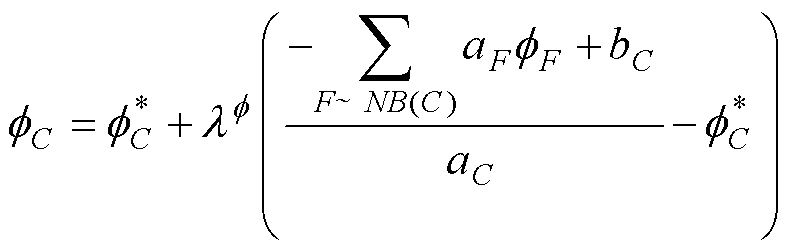（50）
式（50）经变换后可得
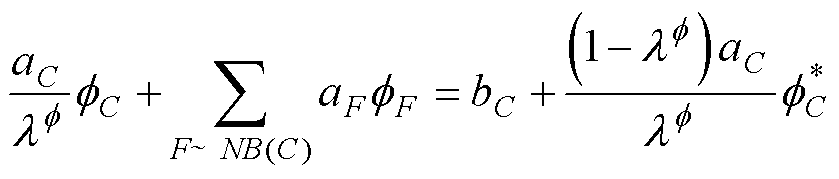（51）
在有限体积法中，物理量通常定义在单元质心处。为了提高单元节点物理量的计算精度，引入了反距离加权法[30]，该方法通过加权平均相邻单元质心的物理量来估算节点变量，其中权重与节点到单元质心距离的倒数成正比。为了避免误差累积和数值不稳定，针对原方法进行了改进，对权重进行归一化处理，使其总和为1。改进后的方法不仅有效提升了节点物理量的计算精度，还在处理复杂网格时展现了更高的稳定性。
将经典的方腔驱动流模型作为分析实例，采用非结构化同位网格有限体积法求解N-S方程。计算平台为基于Windows 11的PC，采用主频为2.10 GHz的Intel i7-12700十二核处理器，配备16 GB内存，开发环境为VS Code。为了验证所编写程序的有效性，将计算结果与COMSOL及Ghia应用的涡量-流函数法进行对比。
方腔驱动流模型及边界条件如图7所示，上边界为速度边界条件，入口速度值为1 m/s，左边界、右边界和下边界为壁面边界条件，速度值为u=0, v=0。为了确定压力场，将第一个单元设为压力参考点，即参考点位置处p=0。
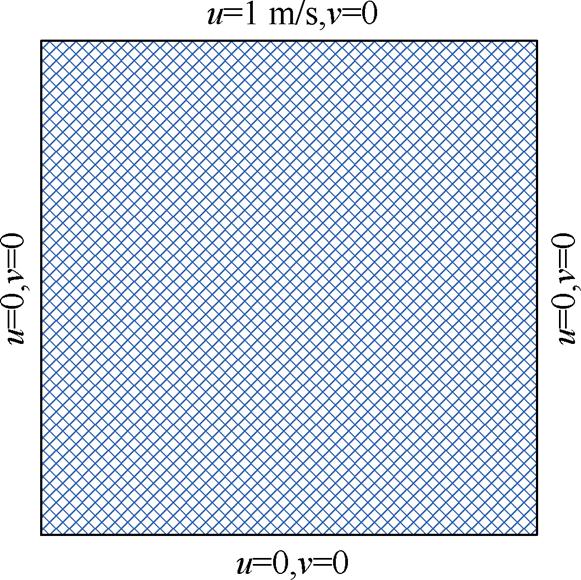
图7 方腔驱动层流模型
Fig.7 Square cavity driven laminar flow model
速度和压力的欠松弛因子与收敛迭代次数之间的关系如图8所示，可以看出，当速度的欠松弛因子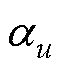
在0.1～0.6之间时，收敛迭代次数较多，收敛速度较慢。当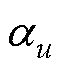=0.7时迭代次数较少，且相较于0.8和0.9时更为稳定。当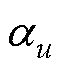=0.7时，压力的欠松弛因子
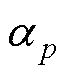＞0.7时，收敛迭代次数没有显著变化。因此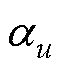=0.7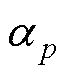，=0.7时是最优的欠松弛因子组合。
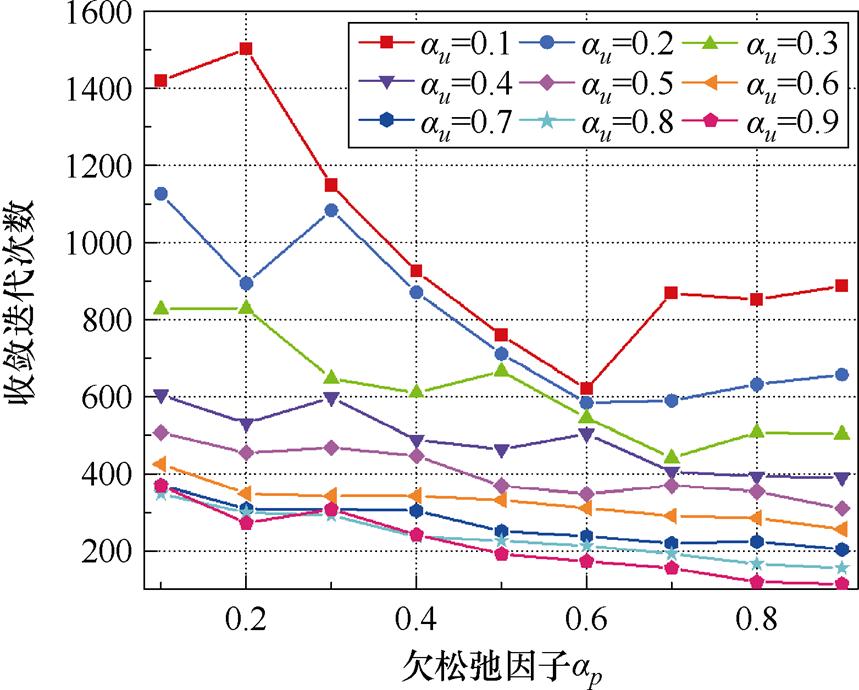
图8 欠松弛因子对迭代次数的影响
Fig.8 The influence of under relaxation coefficient on iteration times
本文采用最优的欠松弛因子组合，使用Frontal- Delaunay方法生成三角形网格和四边形网格，并对计算域进行离散化。网格示意图如图9a、图9b所示，其中，三角形网格包含1 856个单元和983个节点，四边形网格包含1 600个单元和1 681个节点。此外，本文使用的模型参数详见表1。
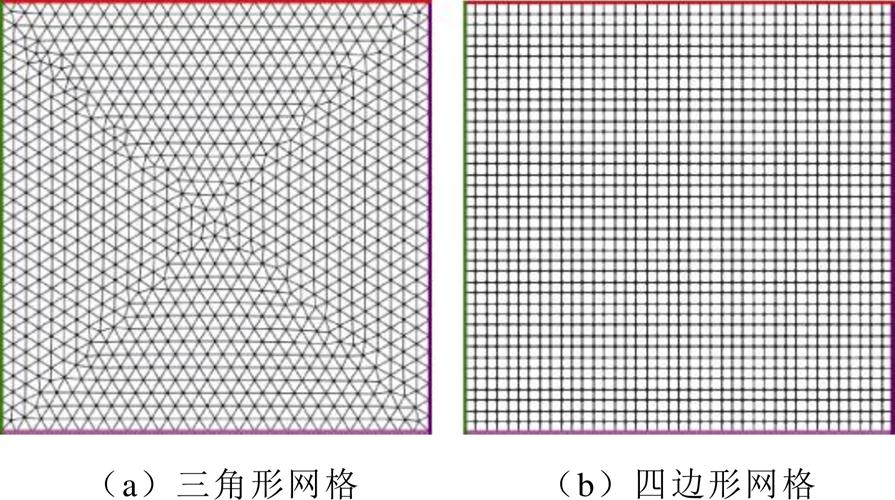
图9 网格示意图
Fig.9 Grid diagram
表1 模型参数[31]
Tab.1 Model parameters[31]
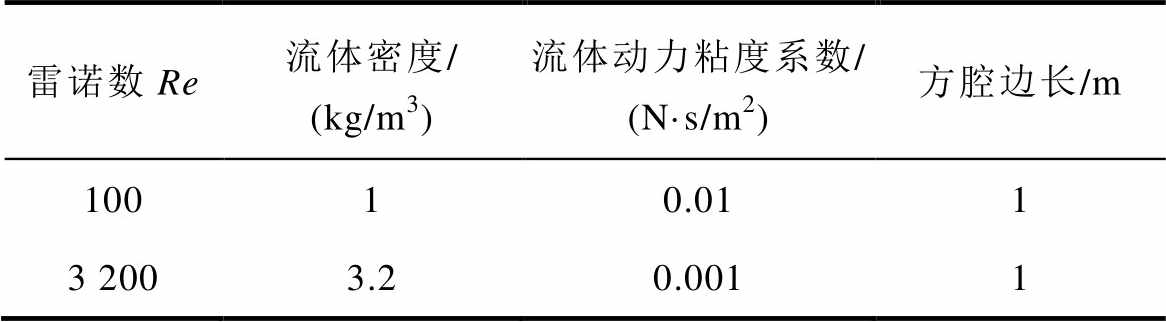
雷诺数Re流体密度/ (kg/m3)流体动力粘度系数/ (N·s/m2)方腔边长/m 10010.011 3 2003.20.0011
雷诺数Re为100对应典型的层流状态（Re≤2 300），此时流动结构清晰、稳定且受黏性力主导；而雷诺数Re为3 200则属于过渡流状态（2 300＜Re≤4 000），其流动特性复杂且不稳定，可能表现为层流与湍流交替出现[32]。通过选择这两个典型雷诺数值，本文方法的有效性验证不仅涵盖了层流状态，还扩展至过渡流状态，从而全面评估了该方法在不同流动状态下的表现，为其适用性提供了更有力的支持。
采用本文方法计算了在雷诺数Re为100和3 200时的稳态流体流动状态，结果如图10a、图10c和11a、图11c所示。相比之下，使用COMSOL得到的计算结果分别如图10b、图10d和11b、图11d所示。通过对比本文方法与COMSOL的计算结果，分析两种方法在不同网格配置下的数值精度。
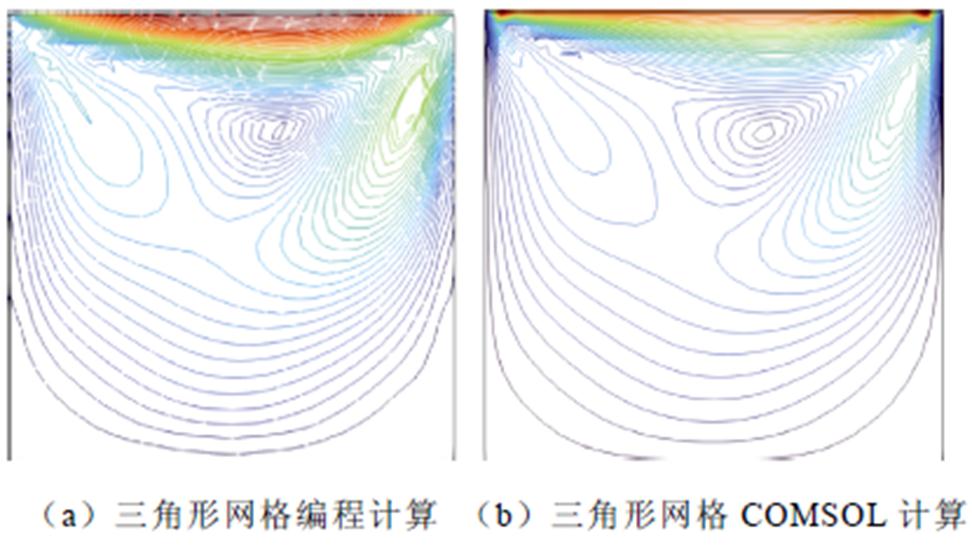
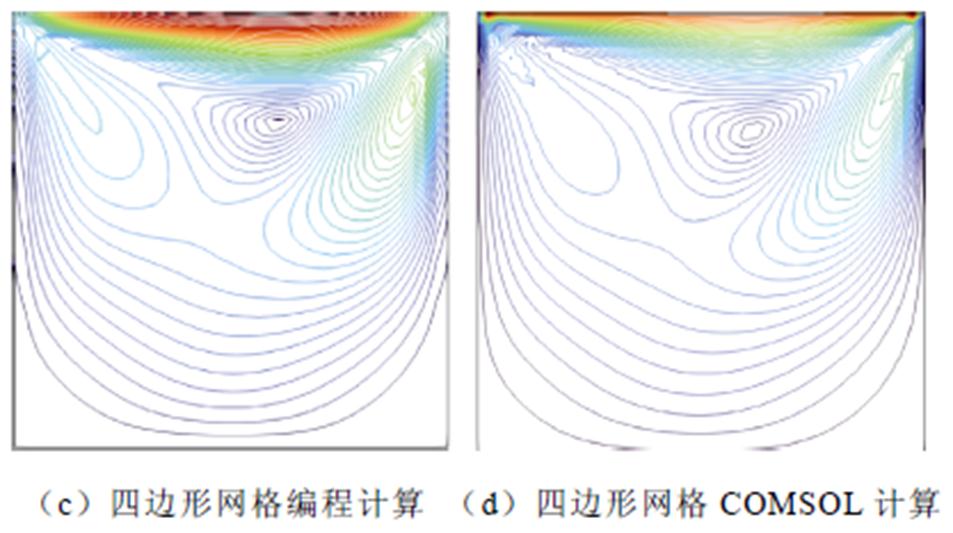
图10 流体流动流线图Re=100
Fig.10 Streamline diagram of fluid flow Re=100
图11 流体流动流线图Re=3 200
Fig.11 Streamline diagram of fluid flow Re=3 200
图10为雷诺数Re=100时，本文方法与COMSOL的流场流线图。图11为雷诺数Re=3 200时对应的流场流线图。从这些流线图可见，本文方法的计算结果与COMSOL基本一致，验证了算法的有效性。
为了进一步验证计算结果的准确性，本文分析了竖直和水平中心线上的速度分布。图12和图13分别显示了雷诺数Re=100和Re=3 200时竖直中心线上的水平速度分布与水平中心线上的竖直速度分布。结果表明，本文方法在两条中心线上的速度分布与Ghia的计算结果吻合度较高。与COMSOL采用的有限元法相比，本文方法能获得更高的计算精度，进一步验证了其有效性。
图14分别显示了在雷诺数Re=100和Re=3 200时，使用三角形与四边形网格计算时的所用时长。结果表明，在节点数基本相同的情况下，四边形网格的计算时长小于三角形网格的计算时长。
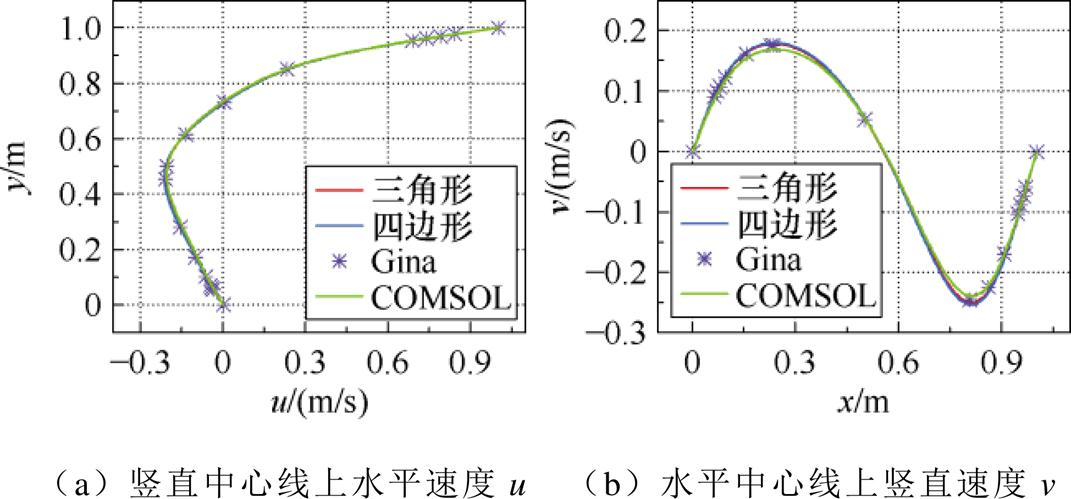
图12 模型中心线速度分量分布图Re=100[31]
Fig.12 Distribution diagram of velocity components along the centerline of the model Re=100[31]
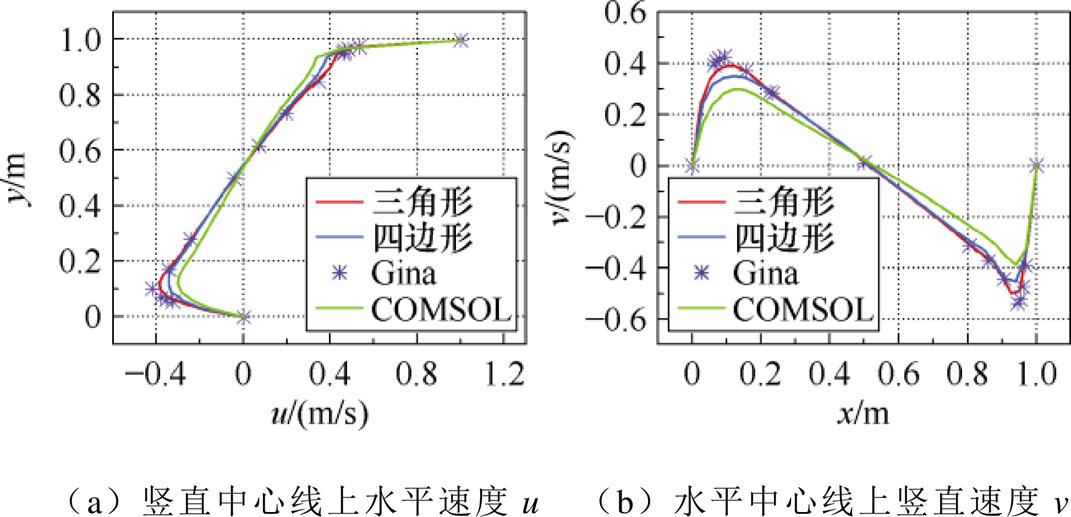
图13 模型中心线速度分量分布图Re=3 200[31]
Fig.13 Distribution diagram of velocity components along the centerline of the model Re=3 200[31]
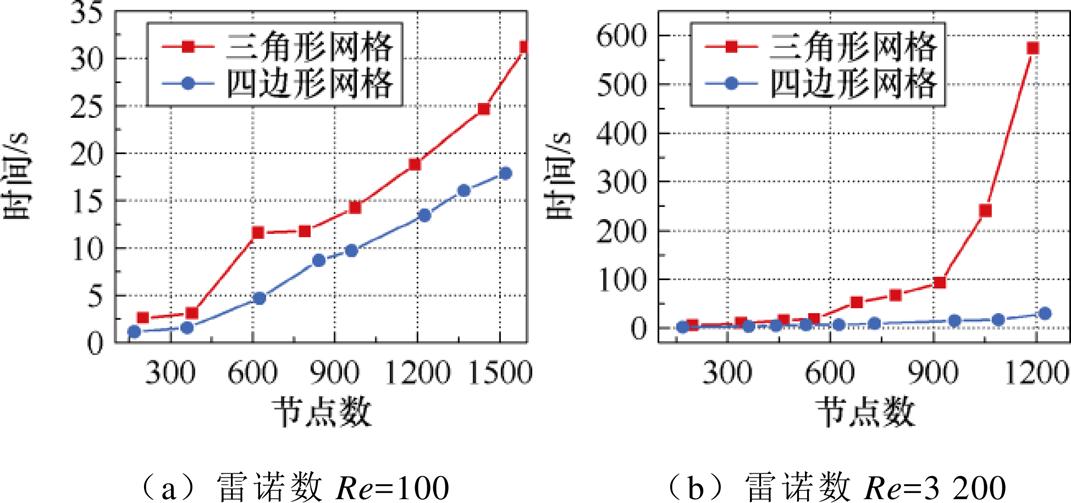
图14 网格节点数与计算时间关系图
Fig.14 Relationship between the number of grid nodes and computation time
本文采用基于非结构化同位网格的有限体积法，分析油浸式换流变压器的流场。由于该模型采用强迫油循环冷却方式，因此可以假定流场的物性参数保持不变，即不考虑温度的非线性影响[33]。
为了方便分析流场分布，对换流变压器的物理模型进行了简化。考虑到其空间对称性，采用了二维轴对称模型，并忽略了径向绕组油道的影响[34-35]。采用三角形网格对模型进行划分，简化模型及网格划分如图15所示，结构参数详见表2，该模型共有3 634个单元，1 901个节点。
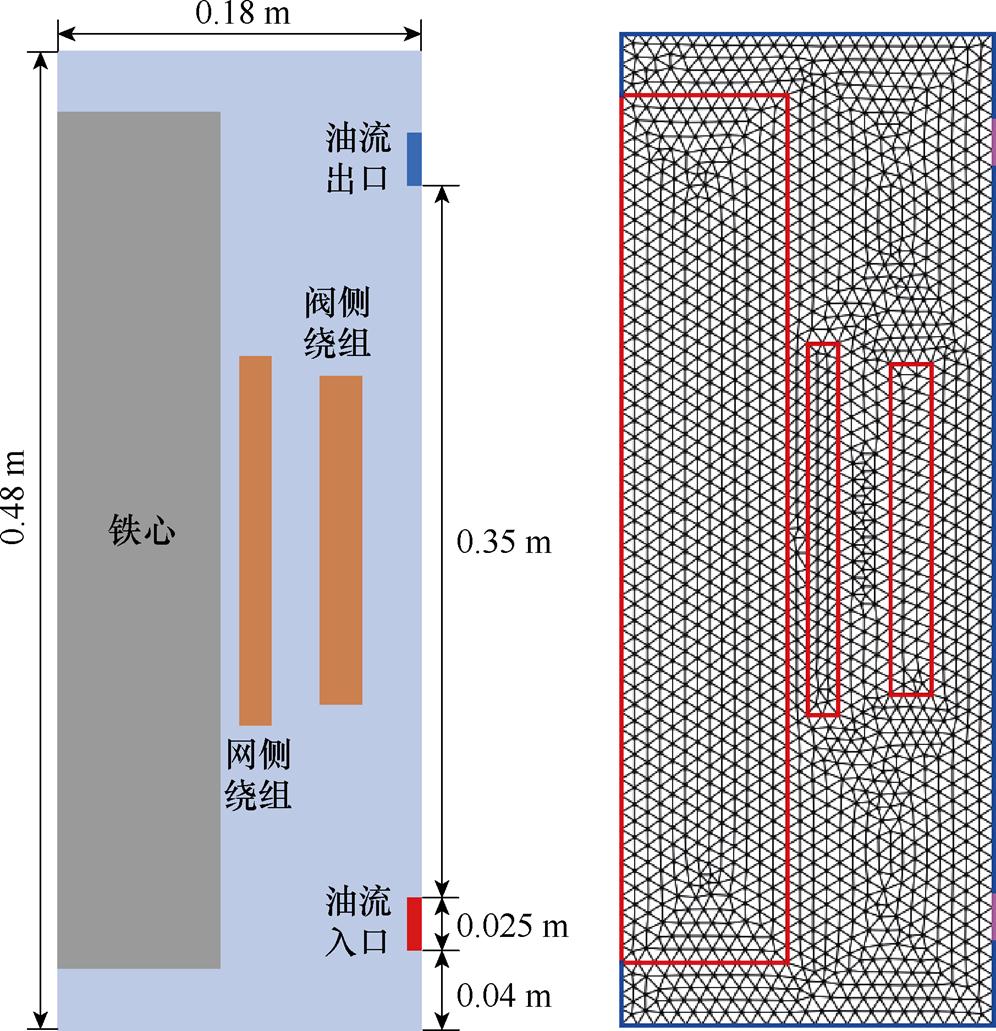
图15 换流变压器简化模型及网格划分图
Fig.15 Simplified model and grid division diagram of converter transformer
表2 模型结构参数[29]
Tab.2 Model structure parameters[29]
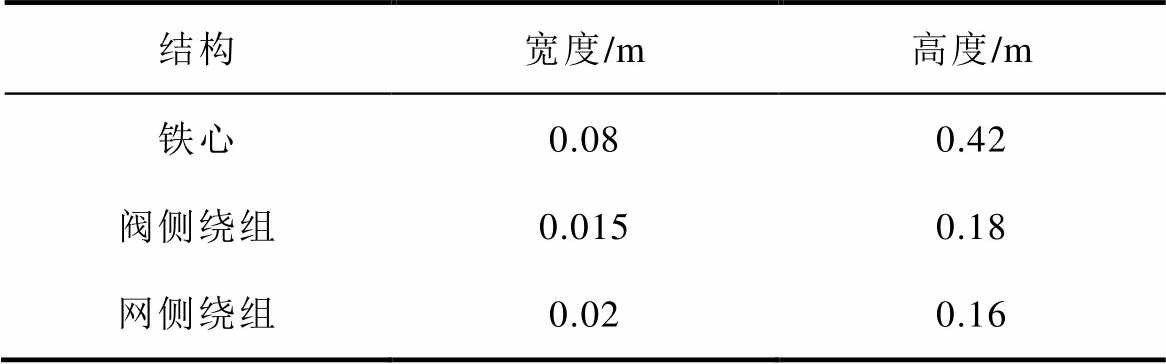
结构宽度/m高度/m 铁心0.080.42 阀侧绕组0.0150.18 网侧绕组0.020.16
在求解换流变压器流场问题时，仅需考虑变压器油中与流场计算相关的各项物性参数，忽略铁心及绕组的材料属性。变压器油的物性参数是温度的函数，见表3。为了简化模型，本文假设模型的整体油温T=330 K，因此可认为变压器油的物性参数为定值。
表3 材料物性参数[36]
Tab.3 Material properties parameters[36]
材料参数类型数 值 变压器油密度/(kg/m3)1098.72-0.712T 动力粘度系数/(N·s/m2)0.0846-4×10-4T+5×10-7T2
在求解流场分布时，首先将换流变压器仿真模型离散为不重叠的网格。边界条件设定为：①油入口：u=0.05 m/s，v=0 m/s；②油出口：v=0 m/s，p=0 Pa；③铁心、绕组及油箱壁：流-固耦合的无滑移壁面边界条件：u=0 m/s，v=0 m/s。
结合变压器油的流动特性，雷诺数Re被定义[27]为
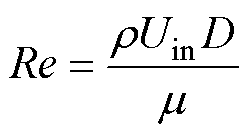（52）
式中，r为流体密度（kg/m3）；Uin为入口流速（m/s），D为特征长度（m）；m为流体动力粘度系数（N·s/m2）。
根据表2的物性参数与入口边界条件，计算得入口处的雷诺数Re≈153，远小于层流转变的临界值，表明流动处于层流状态。因此，在流场计算中采用层流模型，忽略湍流效应。文献[37]指出，自然油循环变压器中的油流通常处于层流状态，因此在模拟中采用层流模型。文献[38]也表明，强迫油循环变压器在入口处的雷诺数小于层流转变的临界值，因此同样采用层流模型。基于此，本文研究选用层流模型，以简化计算并确保数值求解的稳定性，符合实际流动特性。
为了验证本文方法的有效性，使用COMSOL对相同问题进行了分析。简化后的换流变压器内部二维模型的流场分布云图如图16所示。
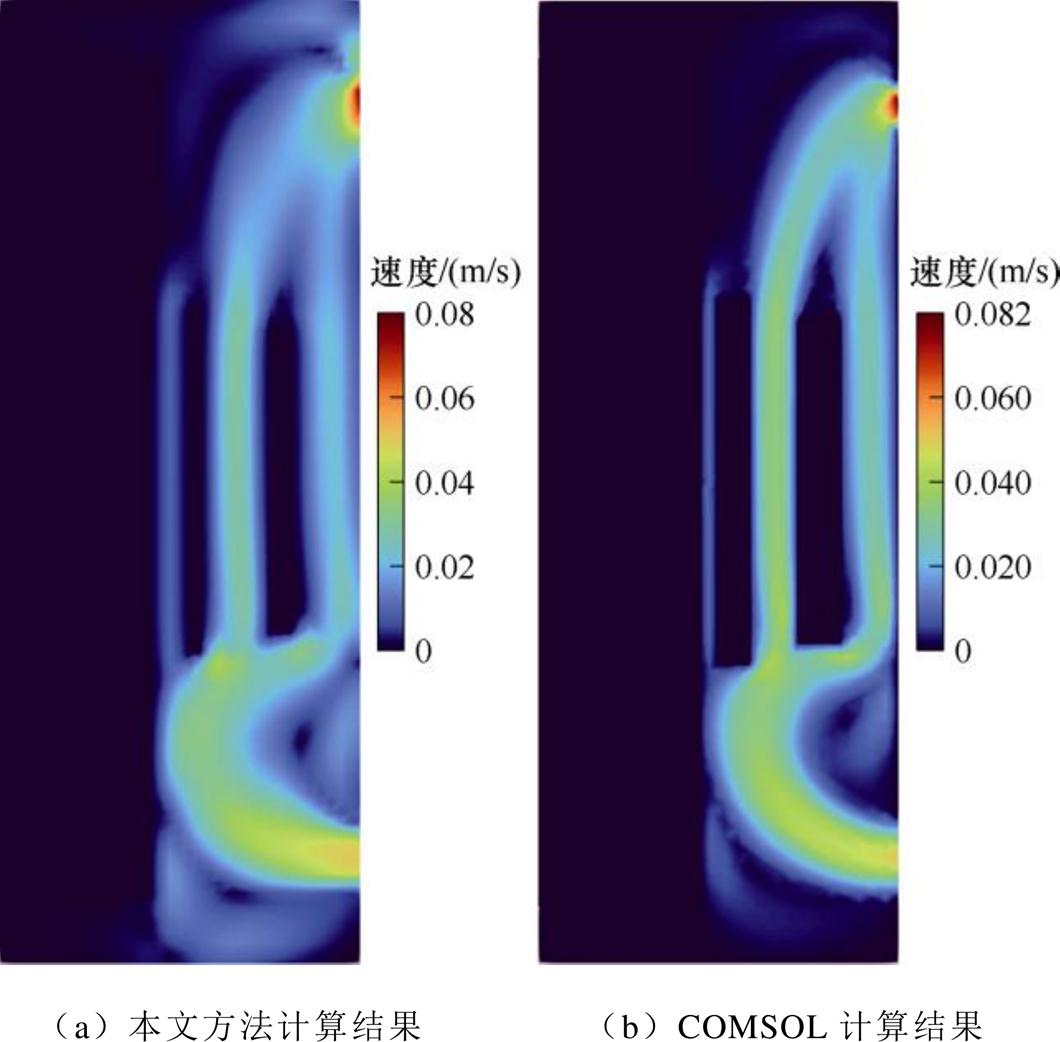
图16 换流变压器流场分布云图
Fig.16 Cloud map of flow field distribution in converter transformer
从图16中可见，本文方法的计算结果与COMSOL的速度分布差异较小，且入口流速略低于出口流速，满足液体的不可压缩性。同时，在入口下方形成了微小涡流，这是由于换流变压器内部铁心及绕组的影响所致，与流体力学理论相符，验证了模型和计算方法的有效性。
为了进一步验证计算方法的有效性，提取了水平中心线上的速度值进行分析。模型中心线速度分量分布如图17所示。由图17可见，本文方法计算得到的水平中心线上的竖直速度与COMSOL的计算结果存在一定偏差。这一偏差主要源于两个方面：一方面两种方法在离散偏微分方程上的原理上有所不同；另一方面本文方法在处理压力-速度耦合时采用了SIMPLE算法，而COMSOL则结合了变分法和牛顿-拉夫逊法。尽管结果存在一定的数值偏差，但从总体趋势上看，本文方法的计算结果与COMSOL较为接近，验证了所提方法的有效性。
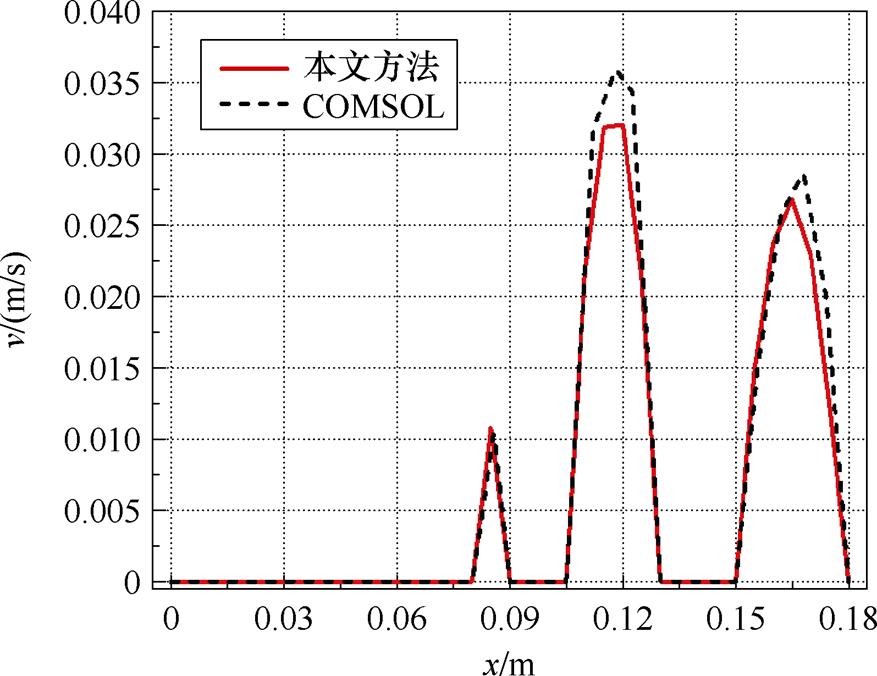
图17 模型中心线速度分量分布
Fig.17 Distribution diagram of velocity components along the centerline of the model
1）本文提出了一种基于非结构化同位网格的有限体积法，成功地应用于二维稳态不可压缩N-S方程的数值求解。该方法通过引入优化的高阶离散格式和高效求解技术，有效克服了非迎风有限元法在流体计算中可能引发的非物理振荡问题，同时解决了基于结构化交错网格有限体积法在处理复杂几何和边界条件时灵活性不足及计算复杂度高的问题，显著提升了计算的稳定性与适用性。此外，本文方法有效应对了当前CAE软件多物理场仿真中的挑战，推动了自主仿真软件的发展，为电力变压器的设计与优化提供了可靠的技术保障。
2）在经典的方腔驱动流数值计算中，通过优化欠松弛因子，确定了速度和压力的最佳欠松弛因子为0.7。数值结果显示，本文方法与Ghia的计算结果吻合度较高，且在精度上优于有限元法。此外，在节点数相近的情况下，四边形网格相较于三角形网格表现出更快的收敛速度。
3）该方法在油浸式换流变压器的油流场分析中得到了有效验证，尽管与COMSOL仿真结果在局部数值上存在一定偏差，但整体趋势一致，这表明了所提方法在实际应用中的可靠性和较强的工程应用潜力，为后续流-热耦合问题中的温升计算奠定了坚实的基础。
参考文献
[1] 谢裕清, 李琳, 宋雅吾, 等. 油浸式电力变压器绕组温升的多物理场耦合计算方法[J]. 中国电机工程学报, 2016, 36(21): 5957-5965, 6040.
Xie Yuqing, Li Lin, Song Yawu, et al. Multi-physical field coupled method for temperature rise of winding in oil-immersed power transformer[J]. Proceedings of the CSEE, 2016, 36(21): 5957-5965, 6040.
[2] 王永强, 马伦, 律方成, 等. 基于有限差分和有限体积法相结合的油浸式变压器三维温度场计算[J]. 高电压技术, 2014, 40(10): 3179-3185.
Wang Yongqiang, Ma Lun, Lü Fangcheng, et al. Calculation of 3D temperature field of oil immersed transformer by the combination of the finite element and finite volume method[J]. High Voltage Engin- eering, 2014, 40(10): 3179-3185.
[3] 刘刚, 胡万君, 郝世缘, 等. 油浸式变压器绕组瞬态温升降阶快速计算方法[J]. 电工技术学报, 2024, 39(3): 643-657.
Liu Gang, Hu Wanjun, Hao Shiyuan, et al. Reduced order calculation method of steady temperature rise of oil immersed power transformer[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 643-657.
[4] 刘刚, 胡万君, 刘云鹏, 等. 降阶技术与监测点数据融合驱动的油浸式变压器绕组瞬态温升快速计算方法[J]. 电工技术学报, 2024, 39(19): 6162-6174.
Liu Gang, Hu Wanjun, Liu Yunpeng, et al. A fast calculation method for transient temperature rise of oil immersed transformer windings driven by fusion of order reduction technology and monitoring point data[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 6162-6174.
[5] 唐智健, 邱志斌, 廖才波, 等. 外置式散热模块对配电变压器热点温升的影响[J]. 高压电器, 2024, 60(3): 135-143.
Tang Zhijian, Qiu Zhibin, Liao Caibo, et al. Influence of external cooling modules on hot-spot temperature rise of distribution transformer[J]. High Voltage Apparatus, 2024, 60(3): 135-143.
[6] Komen E M J, Hopman J A, Frederix E M A, et al. A symmetry-preserving second-order time-accurate PISO- based method[J]. Computers & Fluids, 2021, 225: 104979.
[7] Patankar S. Numerical Heat Transfer and Fluid Flow[M]. Boca Ration: CRC press, 2018.
[8] 刘刚, 靳艳娇, 马永强, 等. 基于非平均热源的油浸式变压器2维温度场分析[J]. 高电压技术, 2017, 43(10): 3361-3370.
Liu Gang, Jin Yanjiao, Ma Yongqiang, et al. Two- dimensional temperature field analysis of oil- immersed transformer based on non-uniformly heat source[J]. High Voltage Engineering, 2017, 43(10): 3361-3370.
[9] Gao Wei, Duan Yali, Liu Ruxun. The finite volume projection method with hybrid unstructured triangular collocated grids for incompressible flows[J]. Journal of Hydrodynamics, Ser B, 2009, 21(2): 201-211.
[10] 明平剑, 张文平. 计算多物理场: 有限体积方法应用[M]. 北京: 北京航空航天大学出版社, 2015.
[11] Rhie C M, Chow W L. Numerical study of the turbulent flow past an airfoil with trailing edge separation[J]. AIAA Journal, 1983, 21(11): 1525- 1532.
[12] Sirianni G, Re B, Abgrall R, et al. Momentum Weighted Interpolation for unsteady weakly com- pressible two-phase flows on unstructured meshes[J]. Journal of Computational and Applied Mathematics, 2023, 428: 115209.
[13] Zhang Wei, Uh Zapata M, Bai Xin, et al. An unstructured finite volume method based on the projection method combined momentum interpolation with a central scheme for three-dimensional non- hydrostatic turbulent flows[J]. European Journal of Mechanics - B/Fluids, 2020, 84: 164-185.
[14] Chen Yujie, Ling Kong, Zhang Xiaoyu, et al. Appli- cation of IDEAL algorithm based on the collocated unstructured grid for incompressible flows[J]. Com- putational Geosciences, 2024, 28(5): 907-923.
[15] Patankar S V, Spalding D B. A calculation procedure for heat, mass and momentum transfer in three- dimensional parabolic flows[J]. International Journal of Heat and Mass Transfer, 1972, 15(10): 1787-1806.
[16] Liu X L, Tao W Q, He Y L. A simple method for improving the SIMPLER algorithm for numerical simulations of incompressible fluid flow and heat transfer problems[J]. Engineering computations, 2005, 22(8): 921-939.
[17] Issa R I. Solution of the implicitly discretised fluid flow equations by operator-splitting[J]. Journal of Computational Physics, 1986, 62(1): 40-65.
[18] Latimer B R, Pollard A. Comparison of pressure- velocity coupling solution algorithms[J]. Numerical Heat Transfer, Part B: Fundamentals, 1985, 8(6): 635-652.
[19] Chorin A J. Numerical solution of the Navier-Stokes equations[J]. Mathematics of Computation, 1968, 22(104): 745-762.
[20] 尹孟嘉, 许先斌, 何水兵, 等. GPU稀疏矩阵向量乘的性能模型构造[J]. 计算机科学, 2017, 44(4): 182-206.
Yin Mengjia, Xu Xianbin, He Shuibing, et al. Performance model of sparse matrix vector multip- lication on GPU[J]. Computer Science, 2017, 44 (4): 182-206.
[21] ZhangMin, Li Linpeng, Wang Hai, et al. Optimized compression for implementing convolutional neural networks on FPGA[J]. Electronics, 2019, 8(3): 295.
[22] Puzyrev V, Koric S, Wilkin S. Evaluation of parallel direct sparse linear solvers in electromagnetic geophysical problems[J]. Computers & Geosciences, 2016, 89: 79-87.
[23] 苏朝阳, 沈金松, 罗辉. 基于PARDISO直接求解器的三维自然电位正反演[J]. 物探与化探, 2024, 48(2): 451-460.
Su Chaoyang, Shen Jinsong, Luo Hui. 3D forward and inverse modeling of self-potential data based on the PARDISO direct solver[J]. Geophysical and Geoche- mical Exploration, 2024, 48(2): 451-460.
[24] 柏威, 鄂学全. 基于非结构化同位网格的SIMPLE算法[J]. 计算力学学报, 2003, 20(6): 702-710.
Bai Wei, E Xuequan. Implement of SIMPLE algo- rithm based on unstructured colocated meshes[J]. Chinese Journal of Computational Mechanics, 2003, 20(6): 702-710.
[25] 刘刚, 高成龙, 胡万君, 等. 基于鲸鱼优化算法超参数优化的径向基函数响应面模型的油浸式变压器绕组挡板结构优化[J]. 电工技术学报, 2024, 39(17): 5331-5343.
Liu Gang, Gao Chenglong, Hu Wanjun,et al. Optimi- zation of winding block washer structure for oil immersed transformers based on radial basis function response surface model with whale optimization algorithm hyper-parameters optimization[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(17): 5331-5343.
[26] Anderson J D. Governing Equations of Fluid Dyna- mics[M]. Berlin, Heidelberg: Springer Berlin Heidelberg, 1992.
[27] Moukalled F, Mangani L, Darwish M. The Finite Volume Method in Computational Fluid Dynamics[M]. Cham: Springer International Publishing, 2016.
[28] Khosla P K, Rubin S G. A diagonally dominant second-order accurate implicit scheme[J]. Computers & Fluids, 1974, 2(2): 207-209.
[29] 彭丽丹. 电力变压器温度场数值计算研究[D]. 北京: 华北电力大学, 2016.
[30] 王立, 喻高明, 傅宣豪, 等. 基于反距离加权插值法的产量劈分新方法[J]. 断块油气田, 2018, 25(5): 617-621.
Wang Li, Yu Gaoming, Fu Xuanhao, et al. New method for production cleavage by inverse distance weighted interpolation[J]. Fault-Block Oil & Gas Field, 2018, 25(5): 617-621.
[31] Ghia U, Ghia K N, Shin C T. High-Re solutions for incompressible flow using the Navier-Stokes equ- ations and a multigrid method[J]. Journal of Com- putational Physics, 1982, 48(3): 387-411.
[32] 王衍, 葛云路, 黄国庆, 等. 干气密封旋转流场的宏观特性与介观速度场的逻辑关系研究[J]. 摩擦学学报, 2020, 40(3): 364-377.
Wang Yan, Ge Yunlu, Huang Guoqing, et al. The logic relationship between macroscopic characteristics and mesoscopic velocity field of high-speed rotating flow field of dry gas seal[J]. Tribology, 2020, 40(3): 364-377.
[33] Wu Hongbin, Zhang Qizhao, Wang Yifan, et al. Influence factors of converter transformer tempera- ture field with finite element method[C]//2021 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Chengdu, China, 2021: 1004- 1010.
[34] 谭又博, 余小玲, 臧英, 等. 谐波电流对换流变压器绕组损耗及温度分布特性的影响[J]. 电工技术学报, 2023, 38(2): 542-553.
Tan Youbo, Yu Xiaoling, Zang Ying, et al. The influence of harmonic current on the loss and temperature distribution characteristics of a converter transformer winding[J]. Transactions of China Elec- trotechnical Society,2023, 38(2): 542-553.
[35] 宋浩永, 黄青丹, 陈于晴, 等. 110 kV环保型天然酯绝缘油变压器绕组的温度场分析[J]. 高压电器, 2024, 60(5): 117-123.
Song Haoyong, Huang Qingdan, Chen Yuqing, et al. Temperature field analysis of windings of natural ester insulating oil-immersed transformer 110 kV environment friendly[J]. High Voltage Apparatus, 2024, 60(5): 117-123.
[36] 刘刚, 郝世缘, 胡万君, 等. 基于子循环自适应串行交错时间匹配算法的油浸式变压器绕组瞬态温升计算[J]. 电工技术学报, 2024, 39(4): 1185-1197.
Liu Gang, Hao Shiyuan, Hu Wanjun, et al. Transient temperature rise calculation of oil immersed trans- former winding based on sub cyclic adaptive staggered time matching algorithm[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1185- 1197.
[37] Garelli L, Ríos Rodriguez G A, Kubiczek K, et al. Thermo-magnetic-fluid dynamics analysis of an ONAN distribution transformer cooled with mineral oil and biodegradable esters[J]. Thermal Science and Engineering Progress, 2021, 23: 100861.
[38] Zhang Xiang, Wang Zhongdong, Liu Qiang. Predi- ction of pressure drop and flow distribution in disc- type transformer windings in an OD cooling mode[J]. IEEE Transactions on Power Delivery, 2017, 32(4): 1655-1664.
Abstract Non-physical oscillations may arise from the upwind finite element method when solving the two-dimensional steady-state incompressible Navier-Stokes equations, and mesh generation in complex geometries can cause large computational errors. In addition, the structured staggered-grid finite volume method has limitations for complex geometries and boundary conditions. Thus, this paper proposes a finite volume method based on unstructured collocated grids. The proposed method utilizes an unstructured mesh constructed from irregular triangles, which offers flexibility and adaptability in handling complex flow geometries. A collocated grid arrangement for velocity and pressure is adopted to avoid additional interpolation operations when velocity and pressure are stored on different grids in a staggered grid configuration. The Rhie-Chow interpolation method is employed to eliminate spurious pressure oscillations. Furthermore, delayed correction high-order schemes and second-order central difference schemes are used to discretize the convection and diffusion terms, respectively. The SIMPLE algorithm is employed to optimize the solution process, thereby reducing memory and computational costs. In terms of sparse matrix storage, the COO format is used. It does not require additional calculations to recover the original matrix, which is easier to implement than CSR and CSC formats, thus saving storage space. The PARDISO solver, based on super node technology, is employed to improve computational efficiency and avoid convergence issues with iterative methods. This solver requires less memory and supports single-node decomposition, outperforming MUMPS and WSMP solvers. Finally, under-relaxation techniques are incorporated to optimize convergence performance and ensure the stability of the numerical solution. Accordingly, a flow field calculation program was developed for triangular and quadrilateral meshes, and the computational time for both types of meshes with a similar number of nodes was compared. By optimizing the under-relaxation factor combination, numerical simulations were performed for the classical driven cavity flow problem, and the results were compared with those obtained from COMSOL finite element simulation software and Ghia's vorticity-stream function method. The results show that the proposed method agrees with Ghia's computation for the horizontal velocity distribution along the vertical centerline and the vertical velocity distribution along the horizontal centerline at Reynolds numbers Re=100 and Re=3 200. The proposed method provides higher computational accuracy than the finite element method. When handling complex geometries and boundary conditions, the proposed method demonstrates greater flexibility and applicability than the structured staggered grid finite volume method. Finally, the method is applied to the oil flow analysis in oil-immersed converter transformers, verifying its accuracy and practicality for real engineering applications.
Keywords：Unstructured collocated grid, finite volume method, incompressible Navier-Stokes equations, SIMPLE algorithm, oil-immersed power transformer
中图分类号：TM411
DOI: 10.19595/j.cnki.1000-6753.tces.242119
国家重点研发计划资助项目（2021YFB2401700）。
收稿日期 2024-11-25
改稿日期 2024-12-09
辛纪威 男，1995年生，博士研究生，研究方向电气设备多物理场耦合计算研究。
E-mail: xin291573287@vip.qq.com（通信作者）
李 琳 男，1962年生，教授，博士生导师，研究方向为电磁场理论及应用与先进输电技术。
E-mail: lilin@ncepu.edu.cn
（编辑 郭丽军）