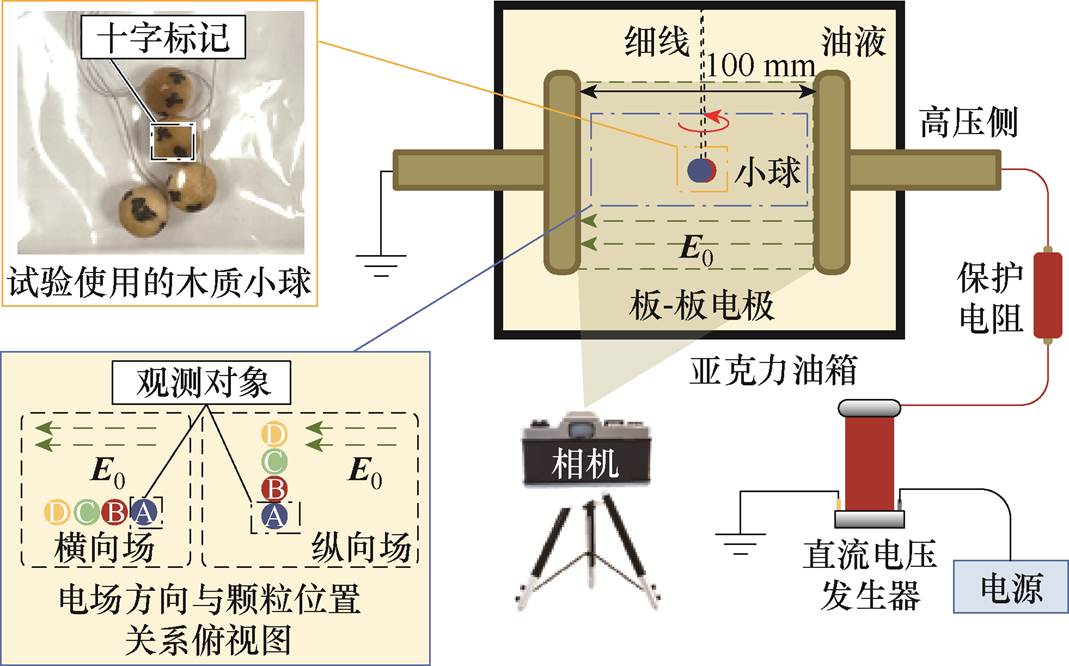
图1 颗粒在绝缘油中运动状态观测平台
Fig.1 Observing platform for motion of particles in insulating oil
摘要 变压器绝缘油中电介质杂质颗粒在电场作用下形成“小桥”是导致其绝缘性能下降的关键因素。当电介质颗粒间距较近时，极化相互作用力显著，会对颗粒运动成链过程产生重要影响，而颗粒成链过程及其形态变化是影响变压器绝缘油中电场畸变及局部放电的重要因素，但目前对于颗粒相互作用过程及其对颗粒运动状态的影响机制尚不明确，且缺乏有效的相互作用力分析模型。因此，该文搭建试验平台开展了颗粒相互作用对绝缘油中颗粒运动特性的影响研究，试验结果表明：当外加电场方向与颗粒球心连线平行时，颗粒在电场作用下相互吸引并排列成链；而当外加电场方向垂直于颗粒球心连线时，颗粒在沿电场线平移运动成链过程中存在奇异的“自转”现象，即呈现“吸引-自转-成链”的特殊运动模式，然而，经典点偶极子作用力模型无法解释和描述这一特殊试验现象。为此，该文考虑颗粒相互作用影响过程，提出电场作用下颗粒自偶极子与互偶极子极化等效思想，构建考虑颗粒相互作用的互偶极子作用力模型，成功地解释了颗粒相互作用引发的“吸引-自转-成链”现象。同时，利用该模型实现了不同电场及不同颗粒粒径条件下颗粒相互作用力和力矩的定量计算。研究结果可为电场环境下颗粒相互作用行为分析及绝缘油中电场优化提供新方法。
关键词：绝缘油 电介质颗粒极化 偶极矩 互偶极子模型 颗粒间相互作用力
大型电力变压器的绝缘多以油纸绝缘为主，理想的绝缘油纯净无杂质[1]。而在实际工程应用中，在变压器生产、运输、装配和绝缘油加注、维护等过程中，会不可避免地混入各类微小杂质颗粒[2-3]，而这些微小杂质颗粒被认为是威胁变压器绝缘油安全运行的重要因素之一[4-6]。
近年来，相关学者对变压器绝缘油中的杂质颗粒进行了大量研究，探讨其形成机理以及杂质颗粒对绝缘油电气性能的影响机制，以更好地识别污染物并完成对相关设备的维护[7-8]。绝缘油中的颗粒可按类型分为非金属颗粒和金属颗粒，金属颗粒以铜、铁等为主，非金属颗粒的典型代表物质是纸纤维或碳纤维。纸纤维主要是由于变压器运行时会产生大量热量，绝缘纸在高温下发生反应并受热而裂解，出现了脱落现象，这部分纤维散落在变压器油中所形成的，而且随着变压器油运行时间的增加，纸纤维含量也将大幅增加[9-10]。纤维颗粒在高压电场的作用下发生极化而运动至沿电场线排列[11-12]，引发局部放电进而导致绝缘失效。这种影响在直流电场[13]情况下更加严重，且纤维颗粒在形成颗粒小桥前后对绝缘油的影响不同[14-15]：在小桥结构形成前，由于纤维颗粒聚集成颗粒群后会使油中电场显著增强而导致绝缘油电离分解析出气体，气体在颗粒近旁产生气泡，电离使气泡随即增大；当小桥结构形成之后，纤维电导率较大，进而使得泄漏电流增大、发热增多，进一步促进了水分汽化，在颗粒近旁形成气泡，气泡则有可能排列成“气泡小桥”，导致放电发生。M. H. S. Zainoddin等通过探究直流电压下的绝缘油中纤维颗粒形成过程，分析了纤维小桥厚度与电压大小间的关系[16]。针对杂质颗粒的运动聚集、放电击穿等特性，国内外学者已开展了一系列研究，郝建等[17]对绝缘油中不同浓度与颗粒大小条件下的纤维颗粒、金属铜颗粒以及两种颗粒的混合物质在直流电压下的击穿场强进行了研究，揭示了不同颗粒物属性对绝缘油在直流电压下的击穿特性的影响；梁晨等[18]通过搭建交直流加压平台，对含碳纤维颗粒的绝缘油击穿特性进行了测试，探究了含颗粒的绝缘油在颗粒浓度、颗粒粒径和所受电压条件不同情况下击穿电压的变化情况，试验结果表明电压类型对绝缘油击穿电压的影响较为明显，随着颗粒浓度增加、颗粒粒径增大，绝缘油的绝缘性能下降，并说明了绝缘油电气性能下降的主要原因是碳颗粒在绝缘油中运动形成小桥；S. Mahmud等[19]建立了两个不同的试验装置分别研究了交流与直流条件下极板间两个不同电位处的桥接效应，发现交流与直流电压下的板间颗粒小桥堆积形态有所不同；王有元等[20]对交直流复合电压作用下的铜颗粒在绝缘油中的运动特性展开探究，研究了铜颗粒在绝缘油中的运动特性，以及铜颗粒对绝缘油油品绝缘性能的影响机理；李金忠等[21]设计油纸绝缘实验，分析了直流电压作用下小桥的形成原因及成分构成，以探究固相杂质颗粒的形成与发展机理；付守海等[22]给出了计算变压器绝缘油中导电颗粒的理论模型，表明电场力、惯性力等作用力的影响是油中颗粒运动的重要原因，并对极板间的导电颗粒运动轨迹进行计算，总结了颗粒粒径不同时颗粒的运动特点；M. Krins等[23]用实验的方法研究了绝缘棒在含碳颗粒的绝缘油中，当绝缘棒材料和表面结构不同时，碳颗粒对绝缘棒闪络电压的影响，实验现象表明油中碳颗粒的存在导致油隙的击穿强度及闪络电压降低，放电更易发生在电极表面。
综上可知，油中固体颗粒运动成桥的行为易导致绝缘油电气性能降低，虽然大量的研究已经表明了颗粒属性、电场类型等因素对颗粒运动成桥的影响效果，但实验均以研究颗粒群为主，且颗粒粒径较小，在研究运动特性时必须考虑颗粒荷电影响，针对颗粒在运动成链过程中颗粒相互作用对成链影响效果的研究较少，且用于分析颗粒间相互作用力的模型较少，难以做到对颗粒间相互作用力的定量计算。实际上，当颗粒相距较近时，显著的相互作用将使得颗粒周围电场发生变化，进而影响颗粒间相互作用力，且由于颗粒材质在电场中发生的极化类型不同[24]，电介质颗粒链和导体颗粒链中的个体在电场中可能呈现不同的运动现象。为得到颗粒相互作用对颗粒成链的影响机制，以及颗粒相互作用力对颗粒运动的影响效果，本文选择绝缘油中的电介质颗粒，搭建了考虑颗粒相互作用影响的颗粒运动特性试验平台，试验过程中发现在外加电场垂直于颗粒球心连线时，电介质颗粒在成链过程中存在“自转”现象。在使用点偶极子模型分析颗粒相互作用力时，由于该模型仅将颗粒近似等效为位于球心的一对点偶极子，得到的理论分析结果与试验现象不符。本文从电介质颗粒在电场中的极化过程出发，得到了颗粒自偶极子、互偶极子等效思路，提出了用于分析颗粒相互作用力的互偶极子模型，并用该模型计算且分析了不同间距条件下颗粒的相互作用力及粒径存在差异时的颗粒相互作用力，当颗粒间距D以颗粒粒径R为度量单位时，计算结果显示，若颗粒间距D在0.1R～0.5R之间，颗粒会受到显著的相互作用力影响，若在该范围内增大垂直方向外加电场的电场强度，颗粒将发生明显的自转现象。本文提出的模型对试验中电介质颗粒出现的自转现象提供了理论分析方法，揭示了颗粒相互作用对颗粒吸引-自转-成链的影响机制，同时为电介质颗粒在电场中的输运、排列等颗粒相互作用行为提供了一种新的理论分析方法。
为研究颗粒受到相互作用时其在绝缘油中的运动情况，本文搭建了颗粒运动轨迹观测平台，如图1所示。试验平台主要分为电压发生部分、外加电场区域、颗粒运动系统和观测系统四个部分。其中，电压发生部分包括电源、直流高压发生器、保护电阻；板-板电极、亚克力油箱组成外加电场区域；细线、小木球用于完成颗粒运动系统；将数码相机利用三脚架固定组成观测系统。试验中为确保颗粒在变压器油中保持运动状态并且不受外部条件干扰，初始状态将小球置于静止的绝缘油中。试验所用绝缘油选择25号长城变压器绝缘油，油温保持在室温29℃（±1℃），亚克力油箱尺寸为25 cm× 25 cm×30 cm（长×宽×高）。此外，板-板电极通过螺杆连接且全部浸于绝缘油中，试验时保持板间距为100 mm。试验中使用木质小球代替颗粒模型，小球半径R选择为3 mm，并在小球上做十字标记，以方便观测小球发生的自转现象，标记后的小球如图1中左上方插图所示。使用极细的棉线将木质小球穿起并悬挂于板-板电极间隙中，使得小球位于同一水平线，并且保持颗粒间距在0.1R～0.3R之间，尽可能地使其靠近而不接触，外加电场方向与颗粒球心连线方向相对位置排列俯视图如图1中左下方插图所示。试验时在亚克力油箱前侧放置相机拍摄并记录颗粒运动行为，每隔1 s使用相机拍摄并记录小球此时的位置情况，以得到小球在不同时刻的相对位置及单个小球的运动情况。
图1 颗粒在绝缘油中运动状态观测平台
Fig.1 Observing platform for motion of particles in insulating oil
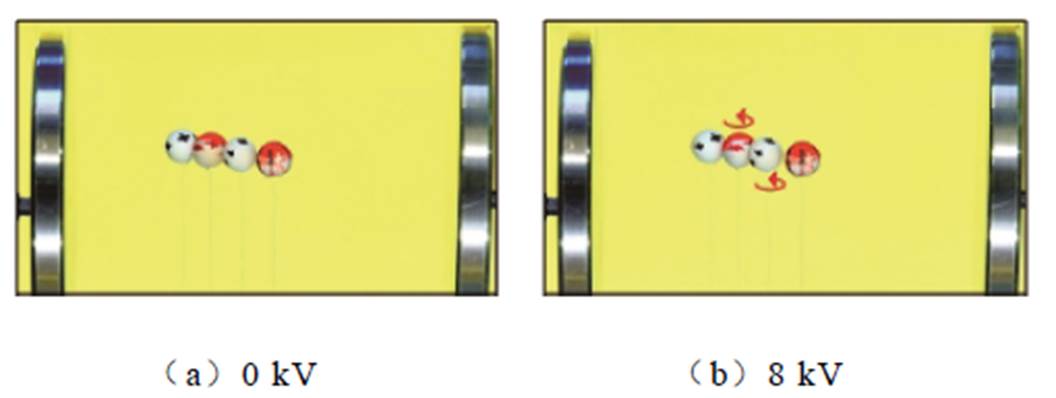
试验中为克服小球重力/浮力，选择轻质棉线将小球颗粒吊起，并保持小球悬挂在同一水平面及同一轴线方向，以方便观察相互作用力影响下小球的运动状态变化情况。当外加电场方向与颗粒球心连线方向平行时，外加电场为横向场。在该电场条件下，当电压由0 kV逐渐增大至40 kV时，观测平台拍摄到的颗粒运动情况如图2所示。
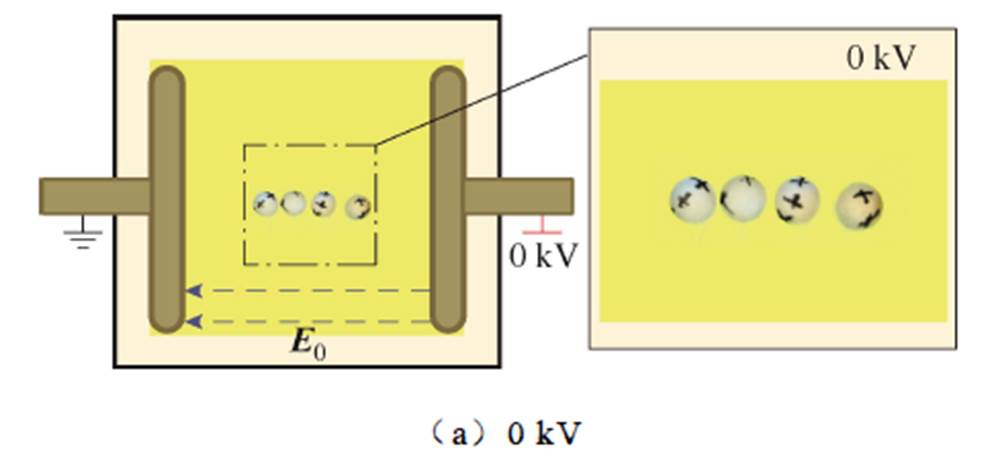
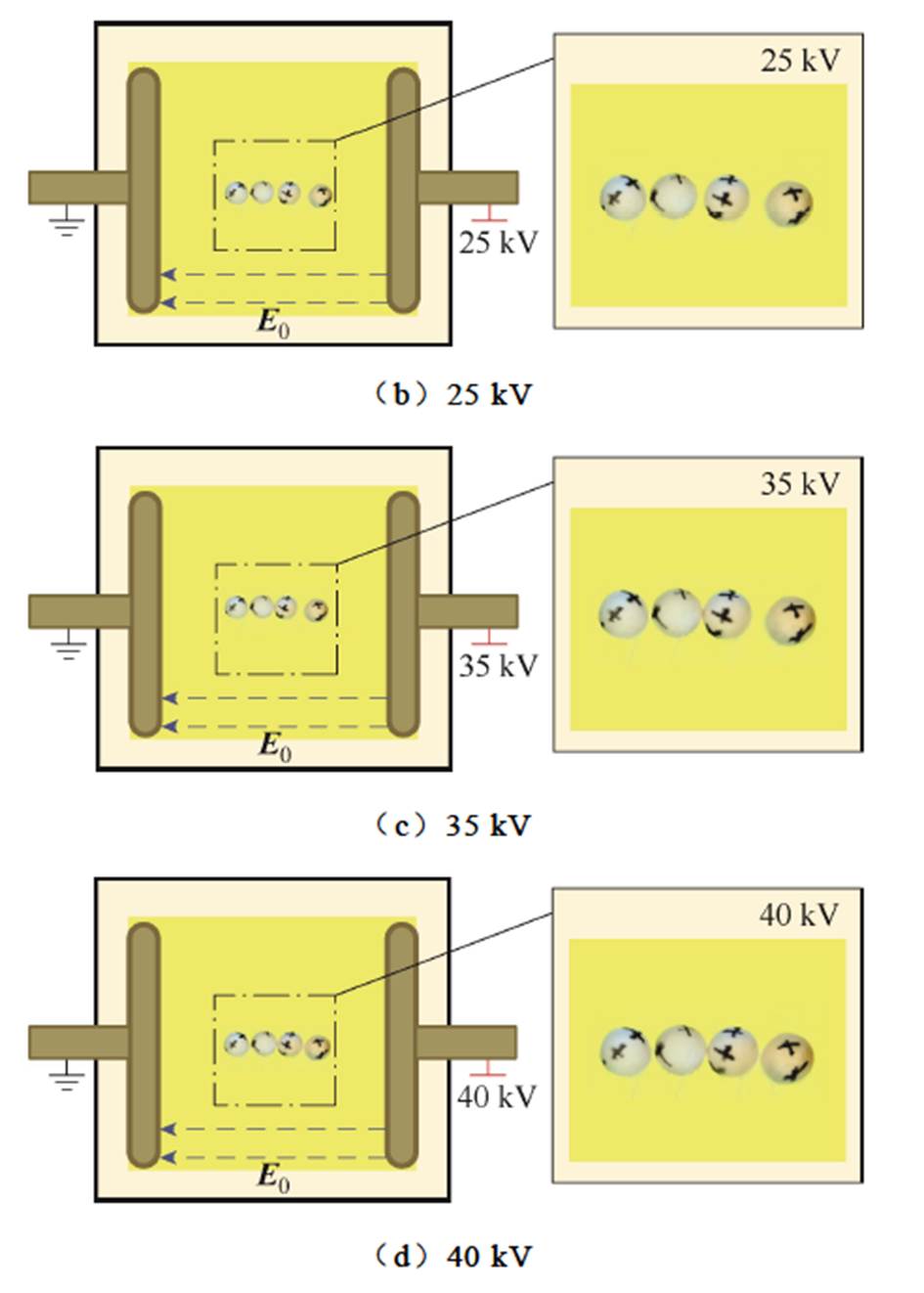
图2 横向场时的颗粒运动情况
Fig.2 The motion of particles in a transverse field
由图2可以看出，随着外施电压的增大，木质颗粒逐渐开始出现运动趋势，整体呈现“吸引-成链”的运动特性。对比图2a和图2d，相较于图2a中颗粒在初始状态下分散在绝缘油中的情况，当外加电压增大至40 kV时，图2d中颗粒最终相互吸引并排列成链。且颗粒在成链的过程中，颗粒球面的标记位置并未发生偏转，说明颗粒仅有在水平方向相互吸引的运动趋势。
当外加电场方向与颗粒球心连线方向垂直时，外加电场为纵向场。在该电场条件下，当电压从0 kV增大至40 kV时，颗粒运动情况如图3所示。由图3可以看出，随着外加电压增大至25 kV，颗粒开始发生沿电场线排列的相对运动，并伴随有逆时针旋转的运动趋势；直至电压增大至35 kV，图3c中颗粒沿电场线排列趋势较明显，且对比图3a和图3c可发现，位于颗粒链首端的颗粒A球面标记位置与最初的状态相比，发生约10°的逆时针偏转；当电压增大至40 kV时，由图3d可观察到颗粒呈现沿电场线排列的状态。并且由图3a～图3d的颗粒运动状态变化可知，在纵向场作用下颗粒呈现“吸引-自转-成链”的运动特性，即颗粒由最初的分散状态，逐渐相互吸引且伴随自转现象发生相对运动，直至最终形成沿电场线排列的链状结构。
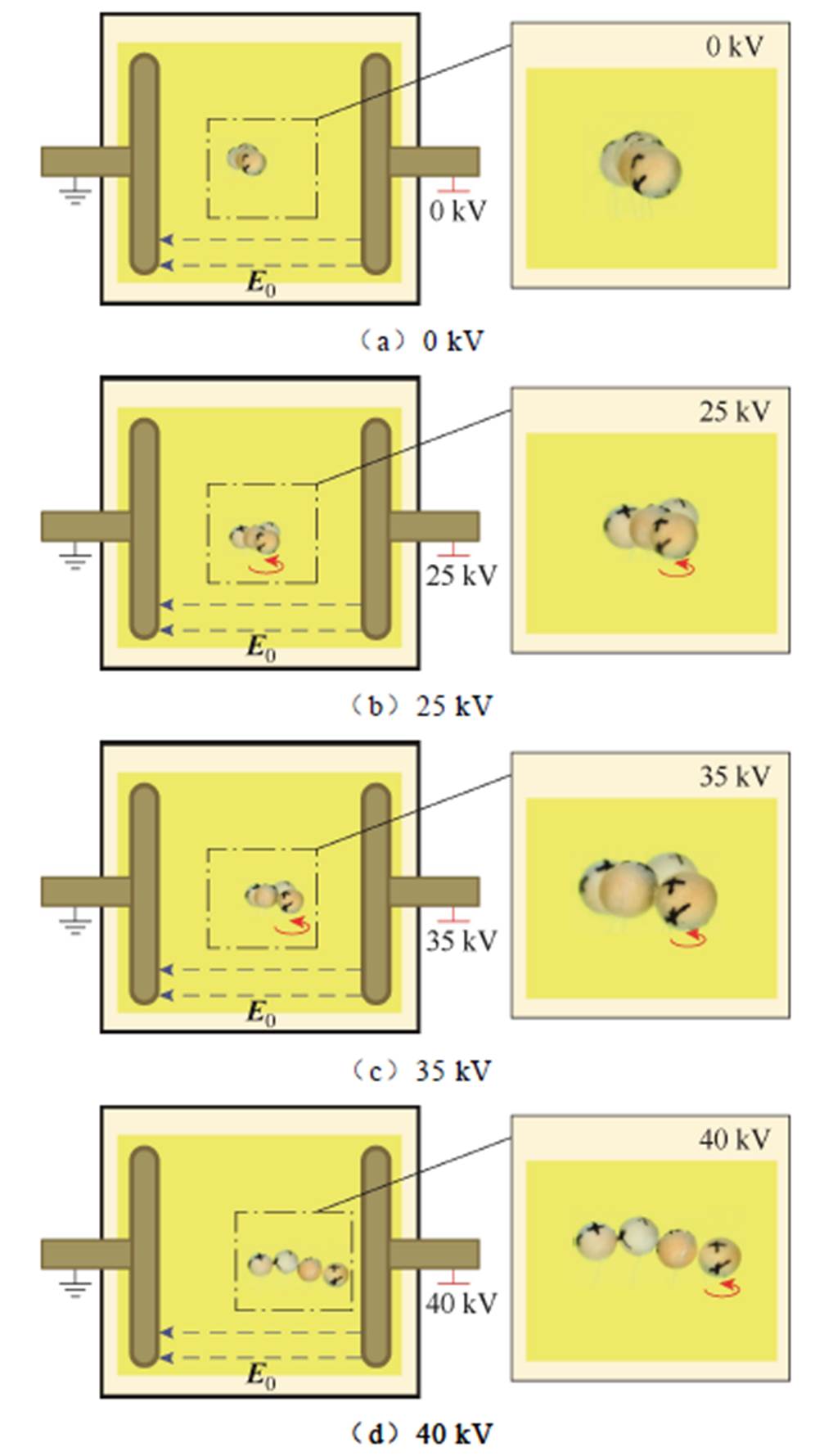
图3 纵向场时的颗粒运动情况
Fig.3 The motion of particles in a longitudinal field
对比颗粒在两种电场中的运动状态，横向场中颗粒仅存在相互吸引后成链的运动特性，即颗粒仅在水平方向发生平动；而纵向场中颗粒除平动运动外还发生自转运动。为分析相互作用对颗粒运动产生的影响，首先使用经典点偶极子模型对颗粒受到的相互作用力进行分析。
电偶极子模型是点电偶极子模型分析计算的基础，以下首先对电偶极子相互作用力进行分析，单电偶极子系统与远点P位置示意图如图4所示。电偶极子由一对处于坐标原点的等量异号点电荷+Q与-Q组成，如图4所示。图4中，r为远点P的位置矢量，q为r与z轴的夹角。位于坐标原点处的电偶极子对远点P产生的电场强度计算式[24]为
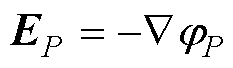（1）
式中，jP为点P的电势。
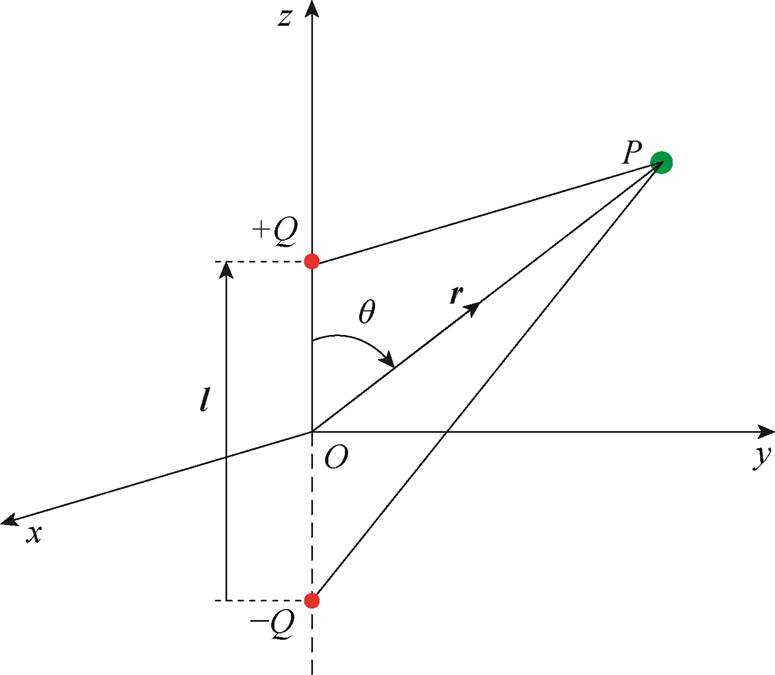
图4 单电偶极子系统与远点P位置示意图
Fig.4 Schematic diagram of single electric dipole system and far-point P
在计算远点P的电势时，可由点电荷电势叠加定理计算，即
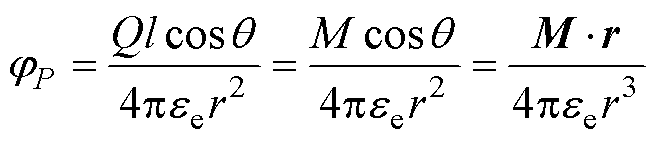（2）
式中，Q为单个点电荷的电荷量；M为点偶极子的有效偶极矩，M=Ql，l为两电荷间的路径，方向由负电荷指向正电荷，l为其长度；r为远点P到原点的距离；ee为环境介电常数。
联立式（1）与式（2），得到当电偶极子位于原点时，其对远点P产生的电场强度为
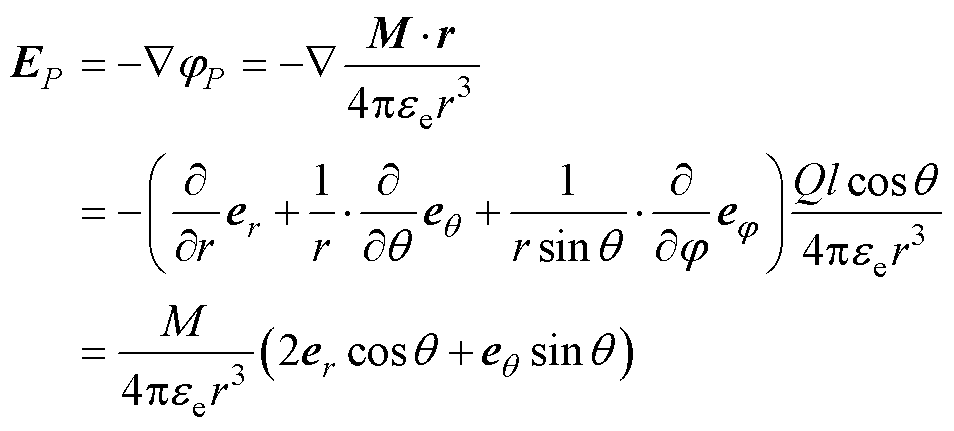（3）
式中， j为r在xOy平面上的投影与x轴的夹角，以逆时针方向为正；er、eq、ej分别为r、q、j方向对应的单位向量。
已知电荷体系的电偶极矩在外电场中的能量W计算式[25]为
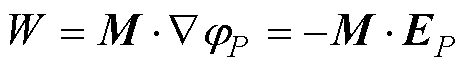（4）
由此得到电偶极子在外电场中所受的力F[24]为
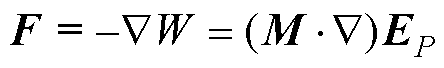（5）
在单个电偶极子远点P处引入偶极矩为M2的电偶极子P2，并且令位于原点处的电偶极子P1偶极矩为M1，得到两电偶极子系统，电偶极子P1与P2在球坐标系中的位置示意图如图5所示。图5中，a为M2与P2位置矢量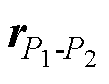
的夹角，b为电偶极子P1、P2偶极矩M1与M2之间的夹角。
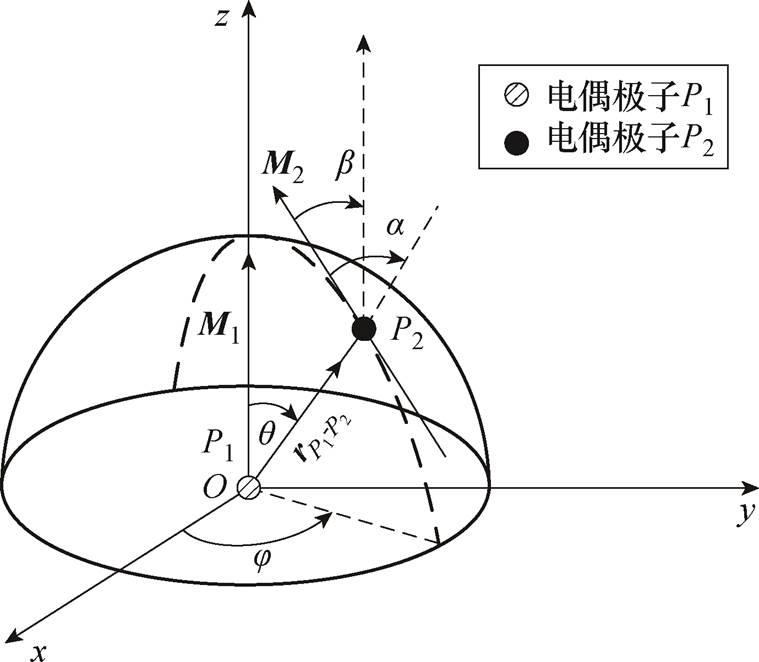
图5 电偶极子P1与P2在球坐标系中位置示意图
Fig.5 Position diagram of electric dipoles P1 and P2 in the spherical coordinate system
结合对远点P处电势计算的分析，由式（2）可得到两电偶极子系统中，电偶极子P1在远点P产生的电势为
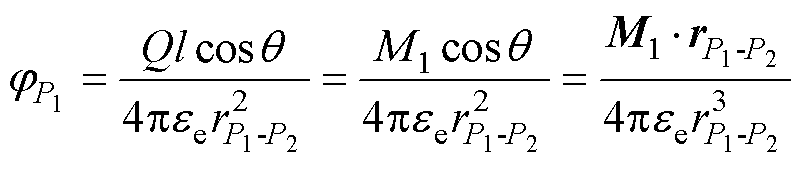（6）
当颗粒间距D远大于颗粒半径R时，颗粒间相互作用对颗粒物周围电场分布及相互作用力的影响可以忽略不计，此时使用点电偶极子模型能够近似地计算两颗粒系统周围电场分布与颗粒相互作用力。在计算两颗粒相互作用力时，可等效为两对电偶极子P1与P2之间相互作用力的计算。由此得到颗粒相互作用力为
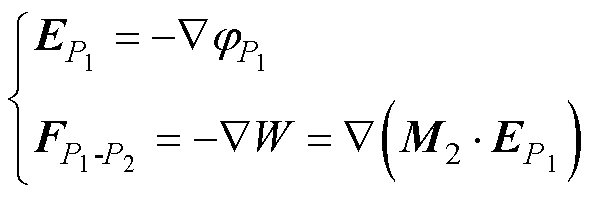（7）
由式（7）可得到当外加电场方向为横向场和纵向场时，使用点电偶极子模型计算的颗粒所受的相互作用力分别为
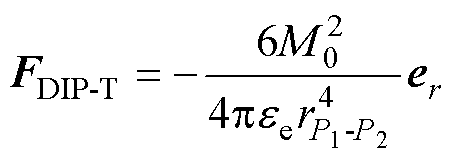（8）
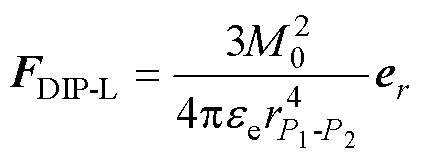（9）
式中，M0为颗粒的有效偶极矩；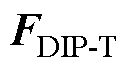
和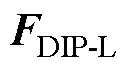
分别为点偶极子模型计算的横向场（用下角标中的T表示）和纵向场（用下角标中的L表示）下颗粒所受的相互作用力；负号表示两颗粒间的作用力为吸引力；
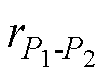为两颗粒球心距离。颗粒偶极矩在两种电场中的排列情况如图6所示。图6中，
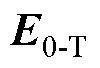和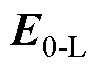
分别表示横向场和纵向场。
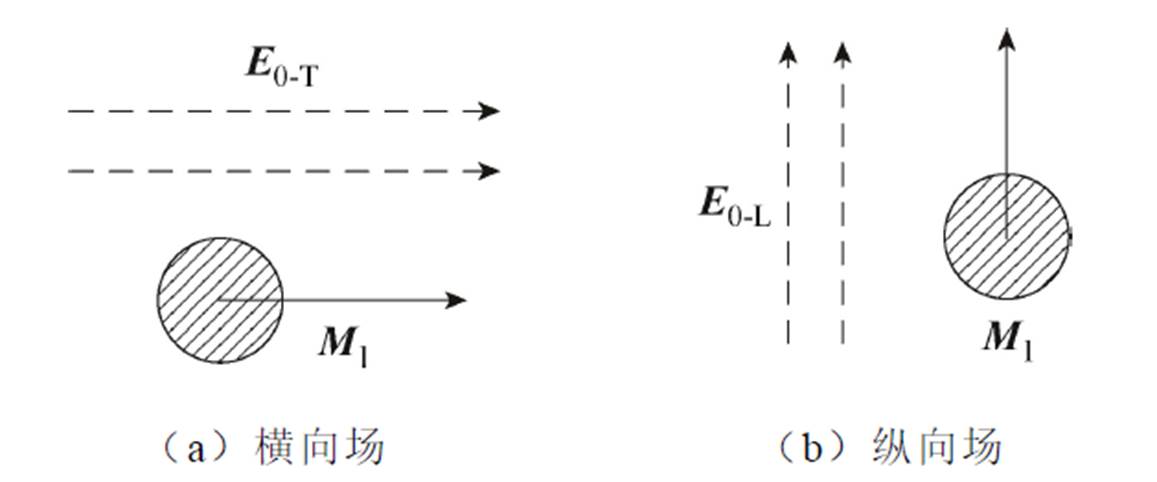
图6 颗粒偶极矩在两种电场中的排列情况
Fig.6 The arrangement of particle dipole moment in two kinds of electric fields
由式（8）、式（9）及图6可知，使用点偶极子模型分析颗粒相互作用力时，当外加电场方向与颗粒球心连线方向平行时，颗粒相互吸引；而当外加电场方向与颗粒球心连线方向垂直时，仅采用传统的颗粒相互作用力受力模型对颗粒进行分析时无法得到颗粒出现自转的力矩，说明经典的点偶极子模型在相互作用力分析时不能解释颗粒在纵向场中发生的“吸引-自转-成链”运动特性。
为了更好地描述颗粒在受到相互作用时发生的自转现象，首先分析其在电场环境下的极化特性：处于均匀外加电场E0中半径为R的单个电介质颗粒，会受到外加电场的作用发生极化，经典点偶极子模型在分析其极化效果时，认为此时单个电介质颗粒发生的极化是均匀的，即单个颗粒周围均匀分布着极化电荷，该情况可将电介质颗粒等效为一个位于颗粒球心的偶极矩，颗粒在电场作用下发生运动时，仅有位于球心的一个偶极矩；而若两个半径为R的颗粒同时置于外加电场中，当颗粒间间距较小、颗粒与环境相对介电常数较大时，颗粒间的相互作用显著增大，其中两颗粒边缘距离最近位置的相互作用最显著，此时对单个电介质颗粒产生极化作用的电场分为外加电场E0与另一颗粒的极化电场。因此，该情况下单个电介质颗粒应等效为两个不同的偶极矩。颗粒数量、颗粒间距与极化效果之间的关系如图7所示。
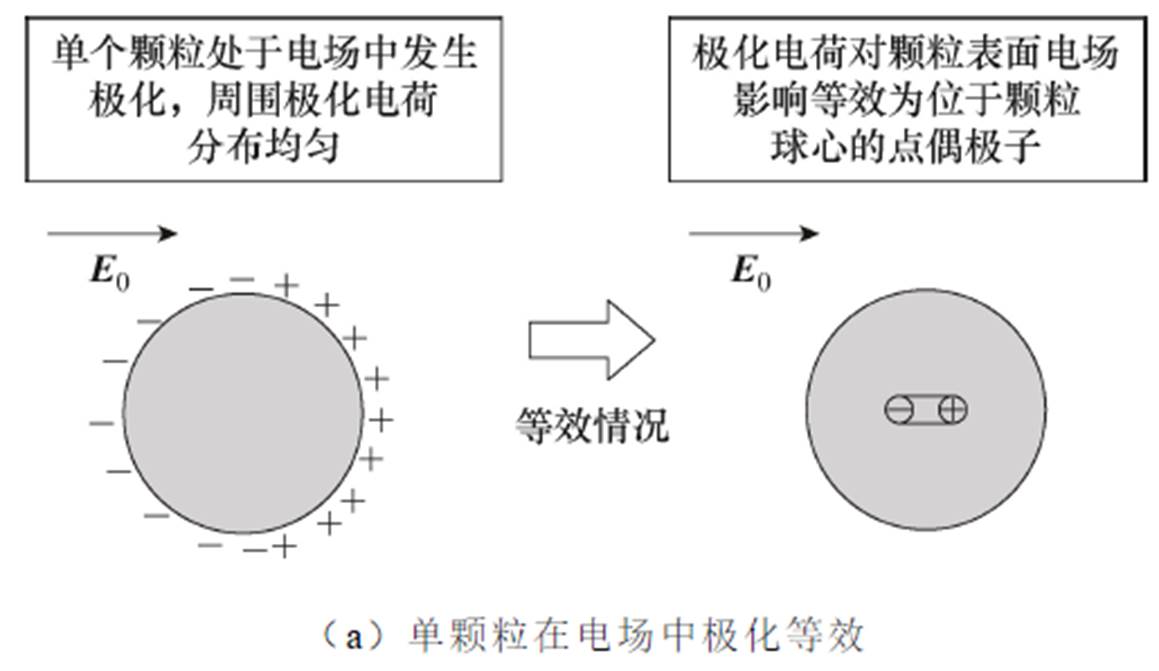
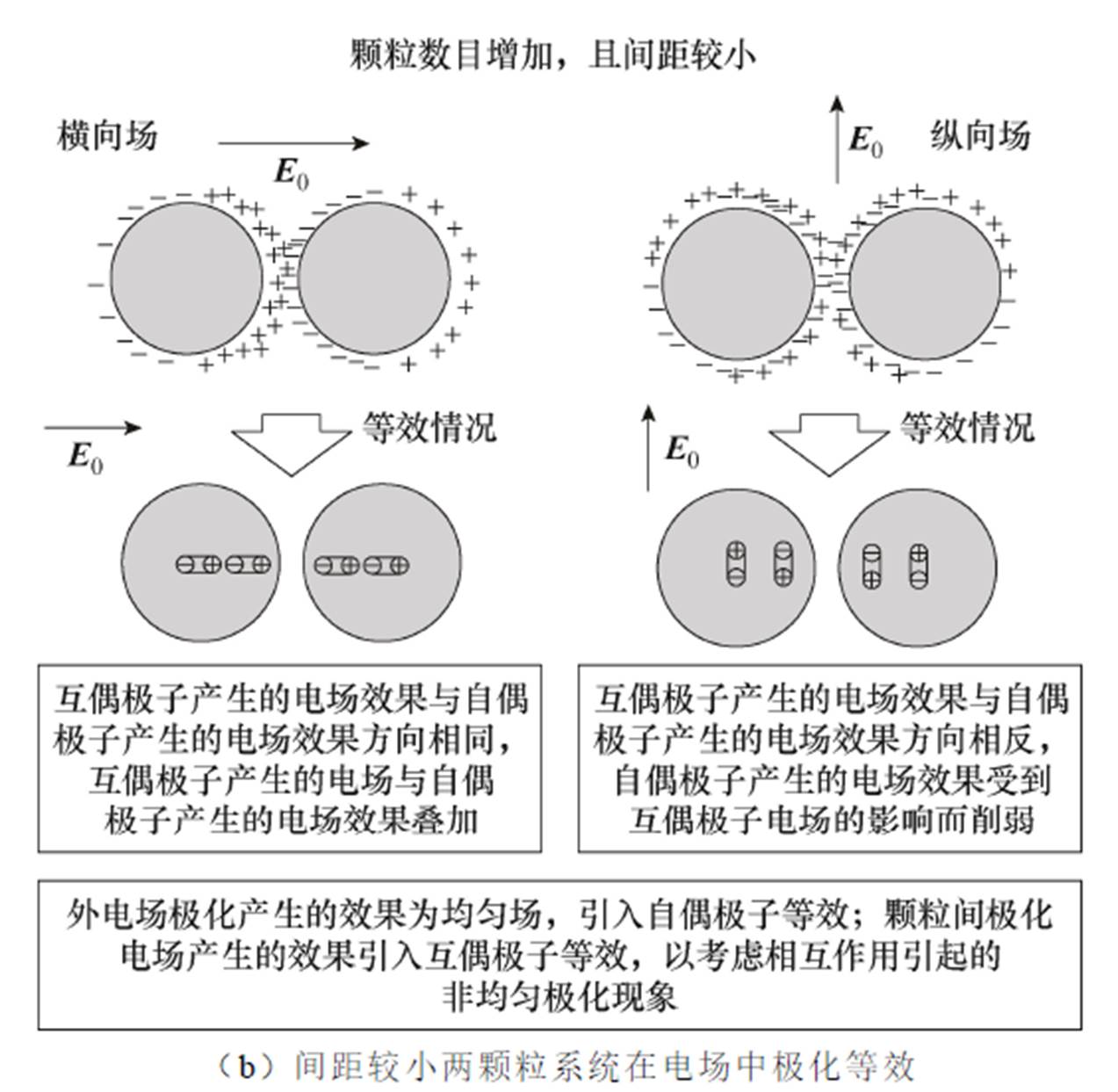
图7 电介质颗粒数量、颗粒间距与极化效果的关系
Fig.7 The relationship between the number of dielectric particles, particle spacing and polarization effect
在先前的研究中，已对柱体[26]以及旋转颗粒系统[27]的极化过程进行了分析，并分别建立了用于计算双柱体系统及旋转颗粒系统电场分布的互偶极子模型，且得到了较高的计算精度。颗粒球系统中的互偶极子等效思想如下：外加电场对颗粒的极化过程是均匀的，引入位于颗粒球心处的自偶极子进行等效，其极化产生的偶极矩为自偶极矩；与该颗粒靠近的另一颗粒的极化电场的极化是非均匀的，将该过程用偏离球心的互偶极子等效，其极化产生的偶极矩为互偶极矩。由此即可得到颗粒间距较近时考虑颗粒间相互作用的两颗粒系统互偶极子模型。
实际情况中颗粒半径可能存在差异，根据文献[26-27]中柱体及颗粒的互偶极矩和自偶极矩的求解思路，可分别得到两种电场条件下，不同半径颗粒系统的互偶极矩。
1）横向场
横向场条件下，颗粒互偶极矩为
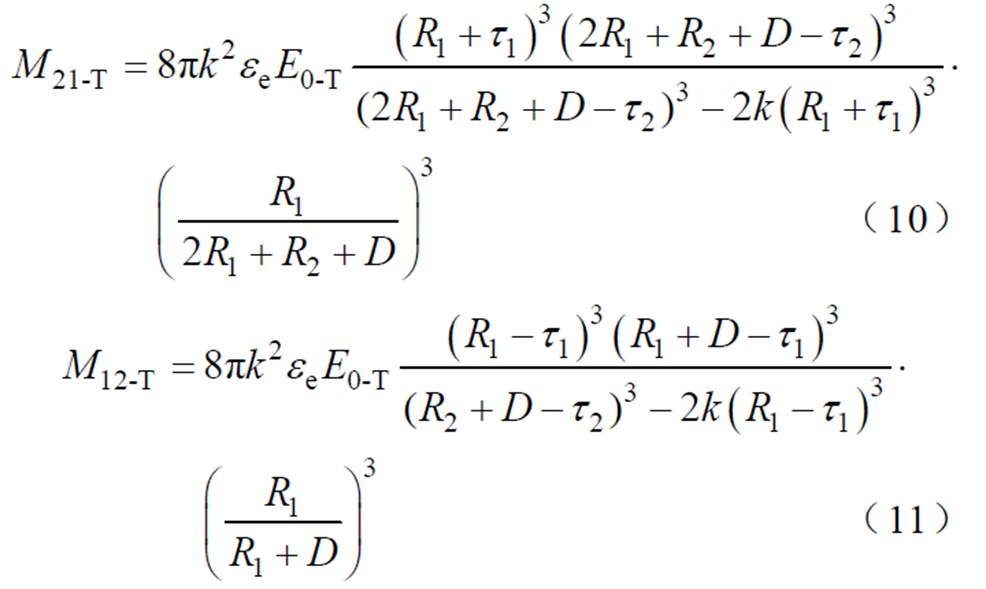
式中，M21为颗粒1的互偶极矩；M12为颗粒2的互偶极矩；k=(ep-ee)/(ep+2ee)，其中ep为颗粒介电常数；D为颗粒间距，本文中为两颗粒边缘到边缘的距离；R1和R2分别为颗粒系统中两颗粒对应的粒径；t1和t2分别为两颗粒互偶极子相对于颗粒球心的偏移距离。令s=R2/R1=t2/t1，s为常数，用于量化R2与R1的粒径差异。
联立式（10）与式（11），可得到横向场条件下两颗粒系统互偶极子偏移距离t满足关系为
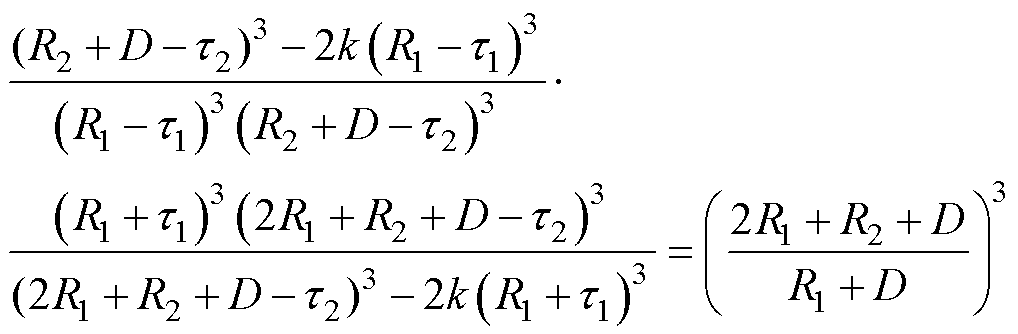（12）
2）纵向场
纵向场条件下，颗粒的互偶极矩为
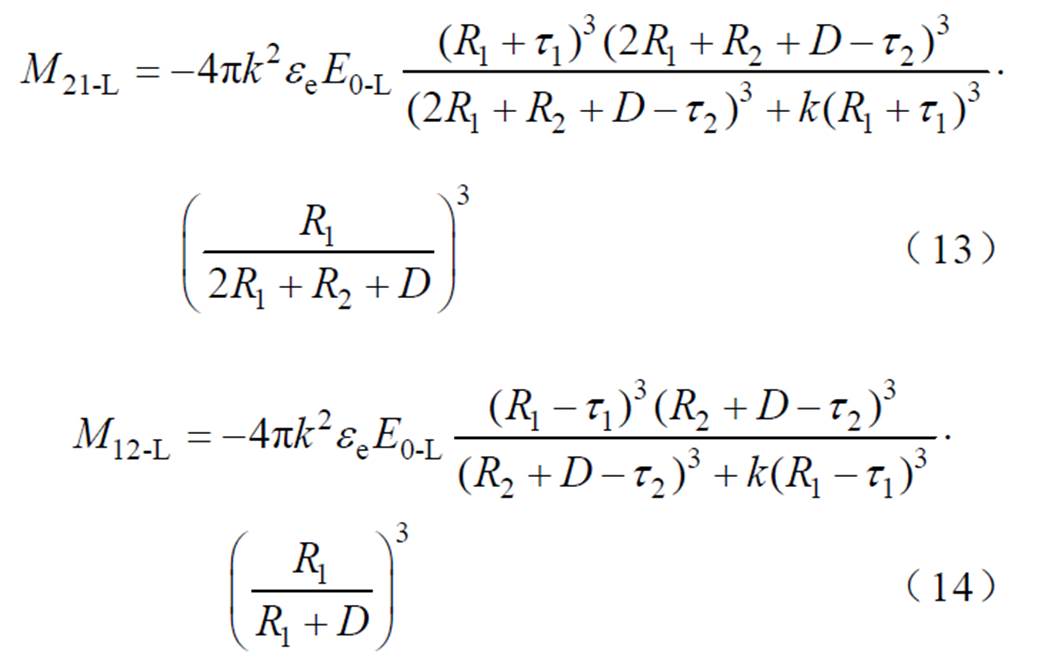
联立式（13）与式（14），可得到纵向场条件下两颗粒系统互偶极子偏移距离t满足关系为
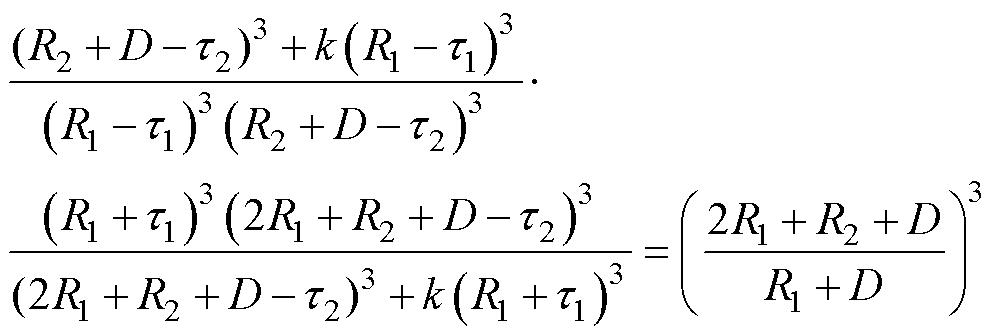（15）
在互偶极子模型建立过程中，当外加电场为纵向场时，认为互偶极子的互偶极矩与自偶极子的自偶极矩方向相反，即互偶极矩与自偶极矩产生的电场效果不同。
在实际情况中，颗粒相对位置易发生变化，电场方向可能与颗粒球心连线存在夹角，即颗粒系统在横向与纵向均含有分量。考虑外加电场是具有大小和方向的矢量，因此可对外加电场在规定的坐标系内进行矢量分解。即假定颗粒系统静止并建立原点位于颗粒1球心的直角坐标系，两颗粒球心连线为X轴，垂直于颗粒球心连线方向为Y轴，规定颗粒球心连线与外加电场的夹角为F；并且以外加电场方向为x轴，与电场垂直方向为y轴，建立另一坐标系，且该坐标系随着电场方向变化而旋转。电场任意角度时两颗粒系统截面示意图如图8所示，从图8中可知两坐标系相对位置，由此可对外加电场进行矢量分解，电场矢量分解过程为
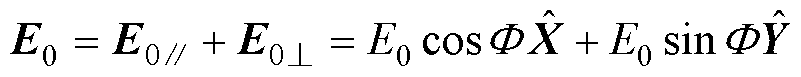（16）
式中，
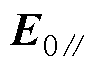和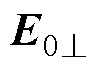
分别为电场E0在横、纵两个方向上的分量；
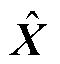和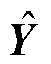
分别为X和Y方向上的单位向量。特别地，当E0仅包含横、纵向分量时，电场分别为横向场和纵向场。
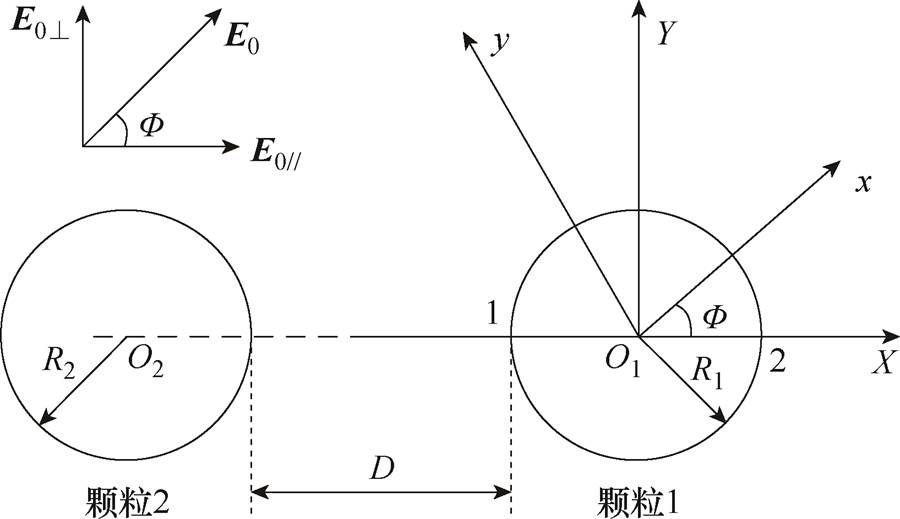
图8 电场任意角度时两颗粒系统截面示意图
Fig.8 Cross-section of a two-particle system at any angle of electric field
利用上述分解合成方法，当外加电场同时存在横向电场分量与纵向电场分量时，其效果同样能等同于一个合成电场。由此思路能够计算颗粒在任意位置下的相互作用力。颗粒系统在横纵电场联合作用下的运动轨迹如附图1所示。
由前述分析可知，当颗粒相互间距较近时，颗粒相互作用会影响颗粒周围的电场分布，进而影响颗粒周围相互作用力。由式（1）可知，准确地描述颗粒相互作用力的关键是得到其周围电场分布的精确计算值，点偶极子模型在计算电场时未充分考虑颗粒相互作用，可能存在计算误差。文献[26-27]中的计算结果误差对比已说明互偶极子模型能够得到精度较高的颗粒局部电场分布。因而，使用互偶极子模型在计算两颗粒相互作用力时，基于精度较高的电场计算结果，能够得到对颗粒间相互作用力的准确描述。使用互偶极子模型分析颗粒周围相互作用力的原理与点偶极子模型相同，基于点偶极子模型对颗粒相互作用力的分析原理，利用互偶极子模型对颗粒相互作用力分析如下。
位于颗粒2球心O2处的自偶极子在球心O1处产生的电势和颗粒2的互偶极子在球心O1处产生的电势分别为
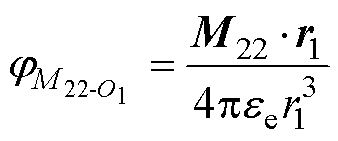（17）
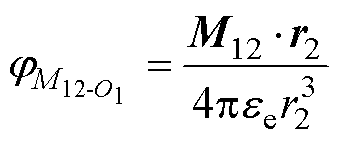（18）
式中，M22为颗粒2的自偶极矩；r1为颗粒2自偶极子到球心O1的距离；r1为颗粒1自偶极子指向颗粒2自偶极子的位置矢量；r2为颗粒2的互偶极子到球心O1的距离；r2为颗粒1自偶极子指向颗粒2互偶极子的位置矢量。
位于颗粒2球心O2处的自偶极子在颗粒1互偶极子处产生的电势和颗粒2的互偶极子在颗粒1互偶极子处产生的电势分别为
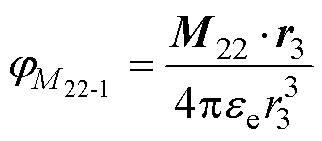（19）
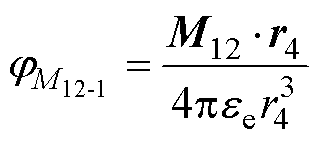（20）
式中，r3为颗粒2的自偶极子到颗粒1的互偶极子的距离；r3为颗粒1互偶极子指向颗粒2自偶极子的位置矢量；r4为颗粒2的互偶极子到颗粒1的互偶极子的距离；r4为颗粒1互偶极子指向颗粒2互偶极子的位置矢量。
根据式（1）中的电场强度计算式，对式（17）～式（20）进行求解，得到使用互偶极子模型计算的颗粒1球心O1处和颗粒1互偶极子处的电场强度为
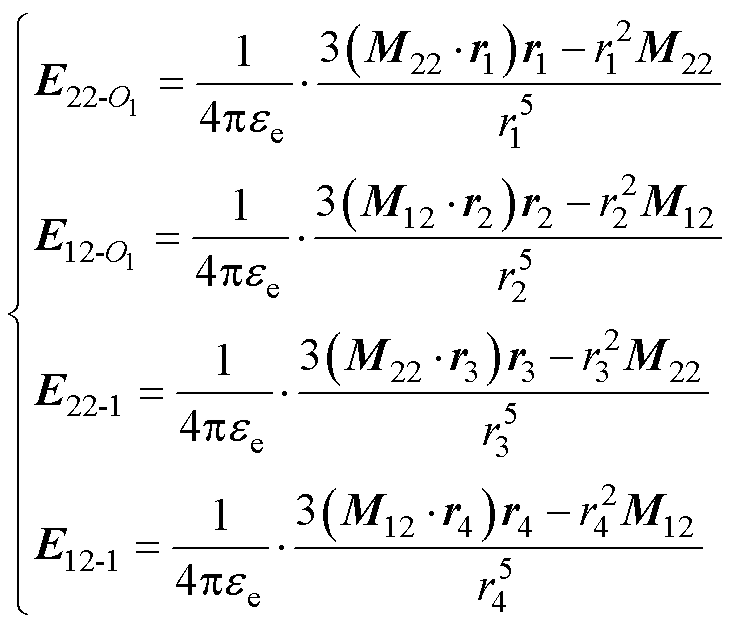（21）
式中，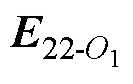
、
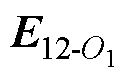分别为M22和M12在颗粒1球心O1处产生的电场强度；
、
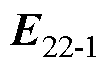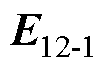分别为M22和M12在颗粒1互偶极子处产生的电场强度。
由式（7）对式（21）进行求解，得到互偶极子模型计算的颗粒1球心O1处和互偶极子处的颗粒间相互作用力为
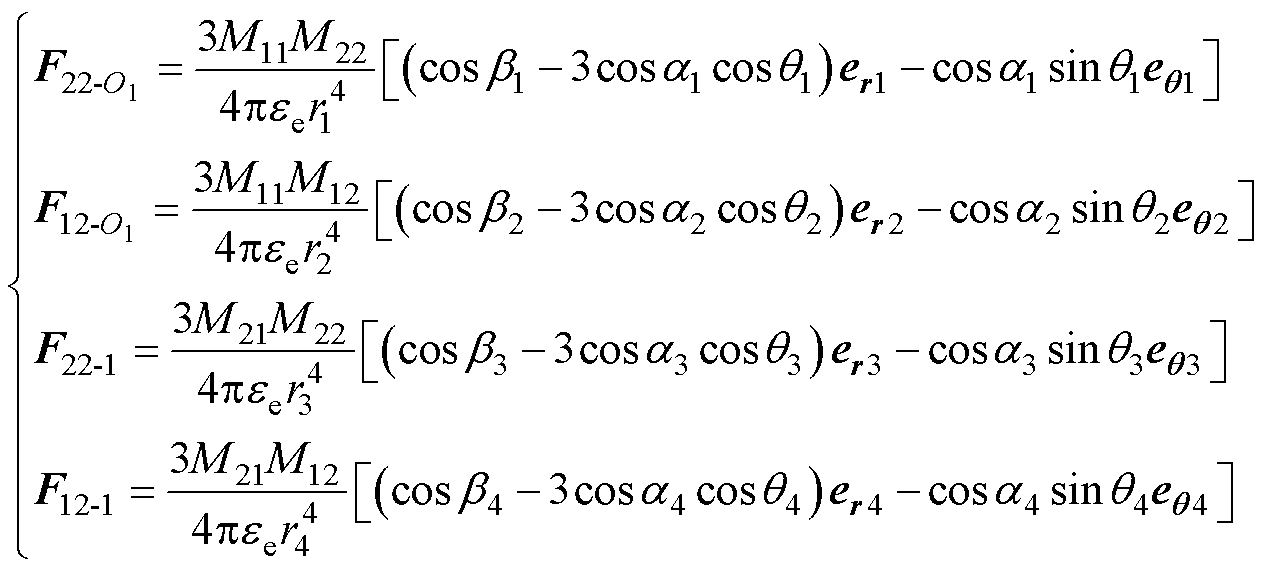（22）
式中，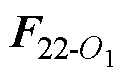
、
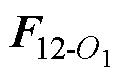分别为M22和M12与颗粒1球心O1处的相互作用力；
、
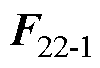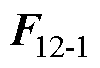分别为M22和M12与颗粒1互偶极子处的相互作用力；M11为颗粒1的自偶极矩；q1为颗粒2自偶极矩与位置矢量r1的夹角；a1为颗粒1自偶极矩与位置矢量r1的夹角；b1为颗粒2自偶极矩与颗粒1自偶极矩的夹角；q 2为颗粒2互偶极矩与位置矢量r2的夹角；a2为颗粒1自偶极矩与位置矢量r2的夹角；b2为颗粒2互偶极矩与颗粒1自偶极矩的夹角；q3为颗粒2自偶极矩与位置矢量r3的夹角；a3为颗粒1互偶极矩与位置矢量r3的夹角；b3为颗粒2自偶极矩与颗粒1互偶极矩的夹角；q4为颗粒2互偶极矩与位置矢量r4的夹角；a4为颗粒1互偶极矩与位置矢量r4的夹角；b4为颗粒2互偶极矩与颗粒1互偶极矩的夹角；ai、qi和bi（i=1, 2, 3, 4）以逆时针方向为正；er1、eq1、er2、eq2、er3、eq3、er4、eq4分别为各下标方向上的单位向量。
同时，由式（22）可知，颗粒的相互作用力可分为两部分：一部分由自偶极子产生，另一部分由互偶极子产生，且式（22）能够反映颗粒自偶极矩、互偶极矩与颗粒间相互作用力的关联关系。
由式（22）可得到，当外加电场为横向场时，使用互偶极子模型计算的颗粒1球心O1处和颗粒1互偶极子的相互作用力为
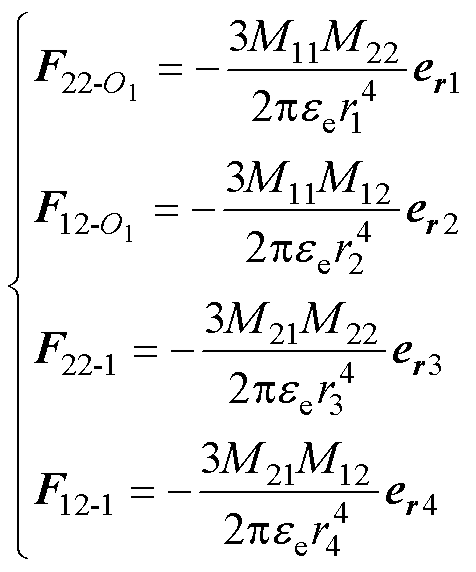（23）
同理可得外加电场为纵向场时，颗粒1球心O1处和颗粒1互偶极子的相互作用力为
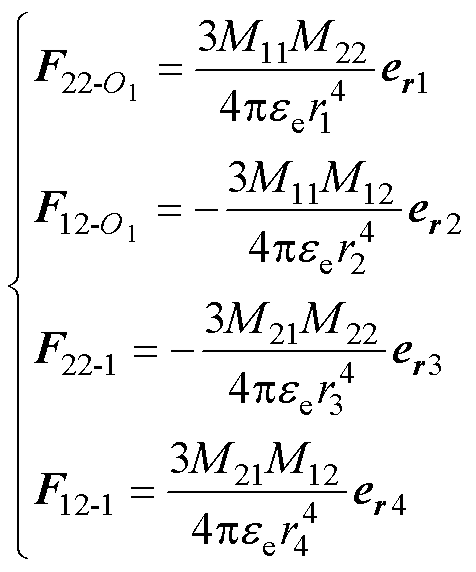（24）
使用互偶极子模型分析相互作用力时，颗粒1偶极矩在两种电场中的排列情况如图9所示。
图9 两种电场中颗粒1互偶极矩自偶极矩排列情况
Fig.9 The arrangement of mutual-coupling dipole moment and self-dipole moment of particle 1 in two electric fields
为更好地观测颗粒自转并验证颗粒互偶极子模型的正确性，本文对纵向场中三颗粒系统中中间颗粒的运动特性进行了观测记录，其自转运动特性示意图如附图2所示。由附图2a～附图2d可以观察到，位于中间的颗粒随两极板间电压增大发生了明显的自转行为。由附图2a可知，初始状态下中间颗粒保持静止，且标记A位于y轴负半轴；随着电压增加，中间颗粒的标记开始发生一定的偏转，到附图2d时能够看到中间颗粒发生了明显的自转变化，自转角度约为50°，这与本文中分析情况一致，证明了互偶极子模型能够正确地分析颗粒间相互作用造成的颗粒自转现象。
由式（24）及图9可知，若使用互偶极子模型分析颗粒相互作用力，当电场存在垂直分量时，互偶极子能够计算颗粒自偶极子相互作用力与互偶极子相互作用力。且互偶极子相对颗粒球心偏移，因而当存在垂直分量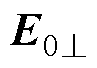
作用时，互偶极子相互作用力存在力矩，该力矩表达式[24]为
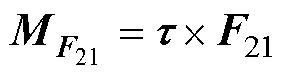（25）
式中，t为颗粒互偶极子相对球心的偏移矢量；F21为两颗粒间互偶极子作用力。
由式（25）可知，颗粒互偶极子相互作用力矩在外加电场为纵向场时最大，此时增大外加电场可使颗粒发生明显自转，有效地促进颗粒成链过程。利用互偶极子作用力模型计算分析得到的颗粒相互作用行为与试验中出现的“吸引-自转-成链”的运动特性一致，成功地解释并描述了这一特殊现象。
同时，使用互偶极子模型得到的颗粒在纵向场条件下的互偶极子相互作用力计算结果如图10所示，计算时外加电场E0=1×105 V/m。
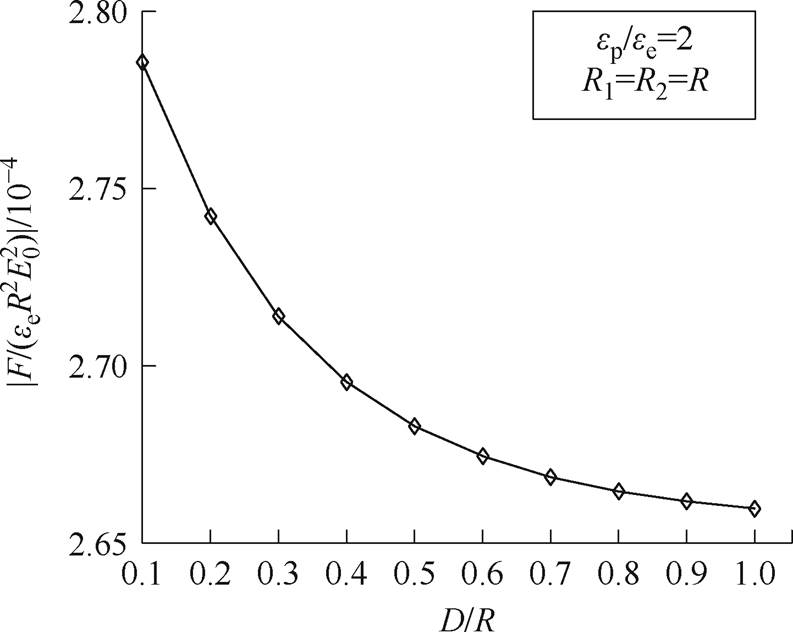
图10 颗粒互偶极子相互作用力随颗粒间距的变化
Fig.10 Variation of particle mutual-coupling dipole interaction with the particle spacing
互偶极子在外加电场的作用下相对球心存在偏移距离，当电场方向与颗粒球心连线方向存在夹角时，纵向分量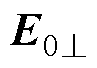影响互偶极矩在外加电场中的方向，使得互偶极子相互作用力与自偶极子相互作用力方向相反，且互偶极子相互作用力与自偶极子相互作用力无法合成，偏离颗粒球心的互偶极子相互作用力使得颗粒发生自转。
由图10可知，在颗粒间距较近时，颗粒间相互作用力较为显著，此时在相同电场条件下颗粒受到的互偶极子相互作用力也较大，颗粒在该力的作用下发生自转；随着颗粒间间距增大，颗粒间相互作用减弱，颗粒受到的互偶极子相互作用力也随之减小，即增大颗粒间距，颗粒自转行为将会减弱。
当颗粒1与颗粒2半径同时扩大倍数t由1变化为2时，颗粒1的互偶极子相互作用力如图11所示；颗粒2与颗粒1半径比R2/R1从1.1增大至2时，颗粒1的互偶极子相互作用力如图12所示。由图11可知，当颗粒2与颗粒1半径之比保持不变时，同时增大两个颗粒的半径，颗粒受到的互偶极子相互作用力逐渐增大，即随着颗粒半径的增大，颗粒相互作用力同时增大；而由图12可知，当颗粒1半径保持不变时，随着颗粒2半径的增大，即随着颗粒半径差异程度的增大，颗粒受到的互偶极子相互作用力逐渐减小。根据以上趋势，推测当两颗粒半径之比差距足够大时，相互作用对颗粒彼此的影响将变得很小。
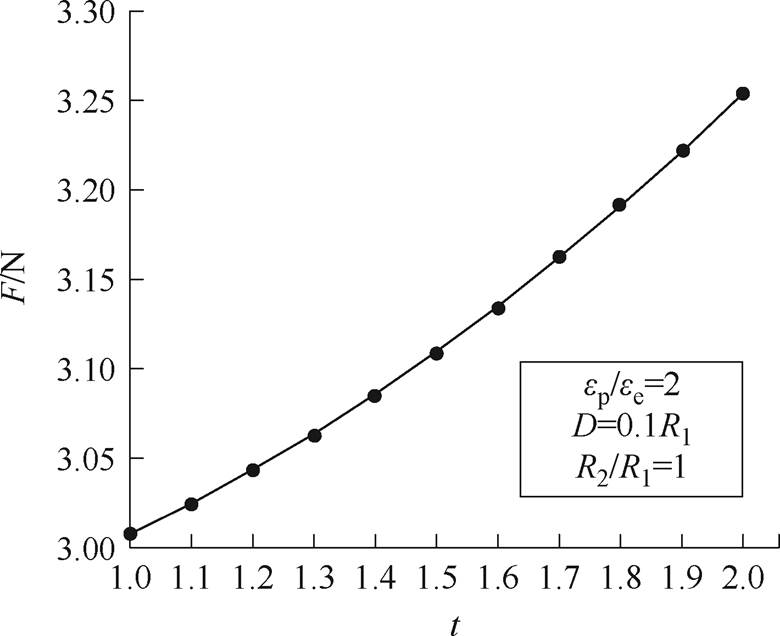
图11 颗粒2与颗粒1半径同时扩大t倍时，颗粒1互偶极子相互作用力变化曲线
Fig.11 The mutual-coupling dipole interaction force curve of particle 1 with changed by the radius of particle 2 and particle 1 increases by t times
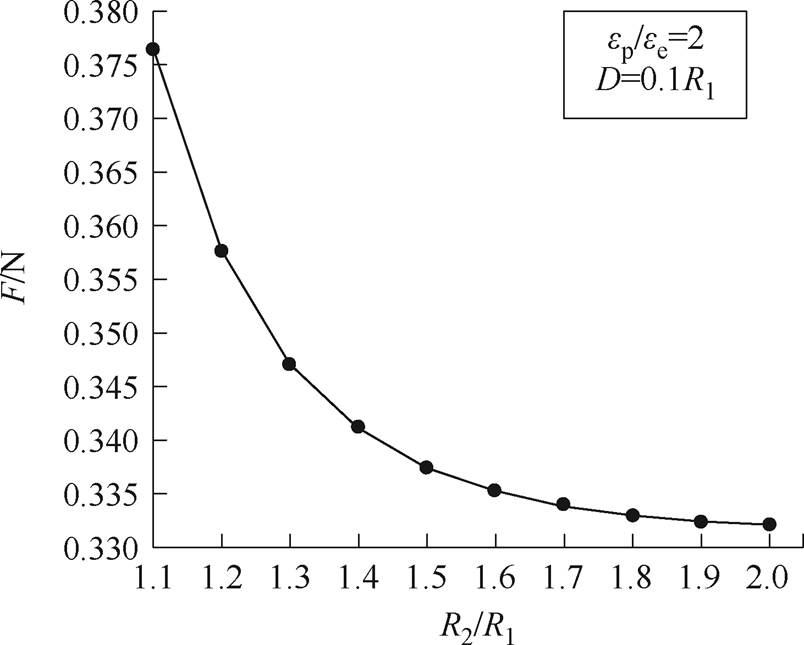
图12 颗粒2与颗粒1半径比R2/R1由1.1变化至2时，颗粒1互偶极子相互作用力变化曲线
Fig.12 The mutual-coupling dipole interaction force curve of particle 1 with the radius ratio R2/R1 between particle 2 and particle 1 changes from 1.1 to 2
由上述分析可知，经典的点偶极子模型在分析颗粒间相互作用力行为时，并不能解释颗粒在纵向场下的“自转”现象，而考虑颗粒相互作用的互偶极子模型方法，不仅解释了颗粒在绝缘油中的自转现象，同时实现了对颗粒自转时受到的相互作用力和力矩的定量计算。
本文在进行颗粒运动特性试验时发现，不同外加电场条件作用下，绝缘油中电介质颗粒呈现的运动特点不同：当电场方向与颗粒中心连线方向一致时，颗粒由于相互作用而呈现“吸引-成链”的运动趋势；而当电场方向与颗粒中心连线方向垂直时，颗粒呈现“吸引-自转-成链”的特殊运动模式。颗粒自转现象的机制是颗粒在电场环境下形成相互作用力矩的本质体现，而经典点偶极子作用力模型无法解释该现象。本文以试验结果为基础，根据颗粒在电场中的极化效果，考虑颗粒相互作用对颗粒周围电场分布及相互作用力的影响，提出了颗粒系统互偶极子与自偶极子的等效方法，获得了颗粒相互影响下电场分布及电偶极矩表达式，建立了用于考虑颗粒相互影响的互偶极子作用力模型，解释并描述了颗粒相互吸引-自转-成链的运动机制。对试验现象及模型计算结果分析得到如下结论：
1）颗粒的自转现象本质上是颗粒相互作用形成互偶极子等效力矩的结果，即偏离球心的互偶极子在纵向电场分量作用下形成偏转力矩，促使颗粒发生自转运动，且三颗粒系统的自转试验能够充分说明互偶极子概念在分析颗粒相互作用力时的正确性。
2）颗粒互偶极子相互作用力在外加电场与颗粒中心连线方向一致时最大，此时增大外加电场可使颗粒发生明显自转，且颗粒自转现象可有效地促进颗粒成链过程。
3）利用该模型计算了颗粒自转受到的相互作用力，以及颗粒粒径存在差异情况下的颗粒相互作用力。计算结果表明，若两颗粒粒径相同，当颗粒间距D在0.1R～0.5R之间时，颗粒之间存在显著的相互作用力，且颗粒相互作用力随着颗粒间距的增大而减小，随着颗粒粒径的增大而增大；对于粒径存在差异的颗粒系统，在颗粒半径比R2/R1增大的过程中，半径为R1的颗粒受到的相互作用力随半径比的增大而减小。
附 录
附图1 横纵电场联合作用时颗粒运动轨迹
App.Fig.1 Particle motion trajectory under the combined action of transverse and longitudinal electric fields
附图2 纵向场下三颗粒系统中间颗粒自转运动示意图
App.Fig.2 Rotation of the middle particles in a three-particle system in longitudinal field
参考文献
[1] 林智勇, 李荣华, 黄国泰, 等. 基于频域二次微分解谱法的油纸绝缘等效电路参数辨识[J]. 电工技术学报, 2025, 40(15): 4966-4975.
Lin Zhiyong, Li Ronghua, Huang Guotai, et al. Identification of dielectric response equivalent circuit of transformer’s oil-paper insulation based on quadratic differential decomposition spectroscopy of frequency domain spectroscopy[J]. Transactions of China Electro- technical Society, 2025, 40(15): 4966-4975.
[2] Butcher M, Neuber A A, Cevallos M D, et al. Conduction and breakdown mechanisms in transformer oil[J]. IEEE Transactions on Plasma Science, 2006, 34(2): 467-475.
[3] Kalantar A, Levin M. Factors affecting the dissolution of copper in transformer oils[J]. Lubrication Science, 2008, 20(3): 223-240.
[4] 刘云鹏, 赵家莹, 刘贺晨, 等. 低频电压下含纤维素颗粒变压器油绝缘特性及影响因素[J]. 电工技术学报, 2024, 39(4): 1198-1207.
Liu Yunpeng, Zhao Jiaying, Liu Hechen, et al. Insulation characteristics and influencing factors of transformer oil containing cellulose particles under low-frequency voltage[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1198-1207.
[5] 刘道生, 周春华, 丁金, 等. 变压器纳米改性油纸复合绝缘研究综述[J]. 电工技术学报, 2023, 38(9): 2464-2479, 2490.
Liu Daosheng, Zhou Chunhua, Ding Jin, et al. Research overview of oil-paper composite insulation modified by nano particles for transformer[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2464-2479, 2490.
[6] 田文锐, 任慧敏, 杨定乾, 等. 低温环境下油浸绝缘纸介电响应特性与温度归一化研究[J]. 电工技术学报, 2025, 40(11): 3630-3642.
Tian Wenrui, Ren Huimin, Yang Dingqian, et al. Study of dielectric response characteristics and temperature normalization of oil-paper insulation in low temperature[J]. Transactions of China Electro- technical Society, 2025, 40(11): 3630-3642.
[7] 张国治, 闫伟阳, 王堃, 等. 流动绝缘油中纤维杂质颗粒运动特性仿真研究[J]. 电工技术学报, 2023, 38(9): 2500-2509.
Zhang Guozhi, Yan Weiyang, Wang Kun, et al. Simulation research on movement characteristics of fiber impurity particles in flowing insulating oil[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2500-2509.
[8] 张宁, 王鹏, 刘智捷, 等. 流-电耦合场中金属颗粒群的荷电计算及影响因素研究[J]. 电工技术学报, 2024, 39(17): 5534-5544.
Zhang Ning, Wang Peng, Liu Zhijie, et al. Study on the charge calculation and influencing factors of metal particle groups in fluid-electric coupling field [J]. Transactions of China Electrotechnical Society, 2024, 39(17): 5534-5544.
[9] Ciuriuc A, Notingher P V, Jovalekic M, et al. Experimental study on vegetable and mineral trans- former oils properties[C]//2014 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Bran, Romania, 2014: 169-174.
[10] Yang Li jun, Sun Weidong, Gao Sihang, et al. Thermal aging test for transformer oil-paper insulation under over-load condition temperature[J]. IET Generation, Transmission & Distribution, 2018, 12(12): 2846-2853.
[11] 黄宇辰, 房俊龙, 闫伟阳. 不同电压类型下油流中纤维杂质颗粒运动特性仿真研究[J]. 高电压技术, 2022, 48(12): 4817-4828.
Huang Yuchen, Fang Junlong, Yan Weiyang. Simulation research on the motion characteristics of fiber impurity particles in oil flow under different voltage types[J]. High Voltage Engineering, 2022, 48(12): 4817-4828.
[12] 张宁, 刘士利, 郝建, 等. 变压器油中气泡杂质相局部放电特性研究综述[J]. 电工技术学报, 2023, 38(10): 2757-2776.
Zhang Ning, Liu Shili, Hao Jian, et al. Review on partial discharge characteristics of bubble impurity phase in transformer oil[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2757-2776.
[13] 李原, 张乔根, 赵毅. 直流电压下纤维小桥对油纸复合绝缘局部放电特性的影响[J]. 高电压技术, 2018, 44(11): 3611-3618.
Li Yuan, Zhang Qiaogen, Zhao Yi. Effect of cellulose bridge on characteristics of partial discharge in oil-paper insulation under DC voltage[J]. High Voltage Engineering, 2018, 44(11): 3611-3618.
[14] Lu Wu, Liu Qiang. Effect of cellulose particles on impulse breakdown in ester transformer liquids in uniform electric fields[J]. IEEE Transactions on Dielec- trics and Electrical Insulation, 2015, 22(5): 2554-2564.
[15] Pohl H A. The motion and precipitation of suspensoids in divergent electric fields[J]. Journal of Applied Physics, 1951, 22(7): 869-871.
[16] Zainoddin M H S, Zainuddin H, Aman A. Investigation of the dielectrophoresis effect on the electrical performance of dielectric liquid[J]. ARPN Journal of Engineering and Applied Sciences, 2017, 12(23): 7003-7007.
[17] 郝建, 但敏, 廖瑞金, 等. 颗粒属性对矿物绝缘油直流击穿特性的影响差异及原因分析[J]. 电工技术学报, 2019, 34(24): 5270-5281.
Hao Jian, Dan Min, Liao Ruijin, et al. Influence of particle properties on DC breakdown characteristics of mineral oil and its difference reason analysis[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5270-5281.
[18] 梁晨, 伍衡, 李原龙, 等. 油中碳颗粒对交直流复合电压下绝缘油击穿特性的影响[J]. 绝缘材料, 2018, 51(4): 21-27.
Liang Chen, Wu Heng, Li Yuanlong, et al. Effect of carbon particles on breakdown strength of insulating oil under AC/DC composite voltage[J]. Insulating Materials, 2018, 51(4): 21-27.
[19] Mahmud S, Chen G, Golosnoy I O, et al. Bridging in contaminated transformer oil under DC and AC electric field[J]. Journal of Physics: Conference Series, 2013, 472: 012007.
[20] 王有元, 李熙, 李原龙, 等. 交直流复合电压下铜颗粒在油中的分布及对绝缘油击穿特性的影响[J]. 电工技术学报, 2018, 33(23): 5581-5590.
Wang Youyuan, Li Xi, Li Yuanlong, et al. Distribu- tion of copper particle in insulating oil and its influenceon breakdown strength of insulating oil under combined AC and DC voltage[J]. Transactions of China Electro- technical Society, 2018, 33(23): 5581-5590.
[21] 李金忠, 张乔根, 李原, 等. 直流电压下油纸绝缘杂质小桥的形成过程[J]. 高电压技术, 2016, 42(12): 3901-3908.
Li Jinzhong, Zhang Qiaogen, Li Yuan, et al. Generation process of impurity bridges in oil-paper insulation under DC voltage[J]. High Voltage Engineering, 2016, 42(12): 3901-3908.
[22] 付守海, 王淑娟, 王景春. 变压器油中导电颗粒运动轨迹的计算[J]. 现代电力, 1999, 16(2): 30-37.
Fu Shouhai, Wang Shujuan, Wang Jingchun. Calculation of particles moving traces in transformer oil[J]. Modern Electric Power, 1999, 16(2): 30-37.
[23] Krins M, Borsi H, Gockenbach E. Impact of carbon particles on the electrical strength of different solid/liquid interfaces in a non-uniform field[C]// Conference Record of the 1998 IEEE International Symposium on Electrical Insulation, Arlington, VA, USA, 1998: 623-626.
[24] 张明月, 刘浩琦, 曹辉, 等. 金属颗粒极化中场激发双电层的电荷和电场特征研究[J]. 物探化探计算技术, 2023, 45(4): 531-541.
Zhang Mingyue, Liu Haoqi, Cao Hui, et al. Study on the charge and electric field characteristics of field- induced electric double layer in metal particles polarization[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2023, 45(4): 531-541.
[25] 郭硕鸿. 电动力学[M]. 3版. 北京: 高等教育出版社, 2008.
[26] 张嘉琳, 康永强, 蒲绪宏, 等. 双柱体系统局部电场计算的互偶极子模型[J]. 电工技术学报, 2024, 39(12): 3869-3883.
Zhang Jialin, Kang Yongqiang, Pu Xuhong, et al. The mutual-coupling dipole model in calculating the local electric field for two-cylinder system[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3869- 3883.
[27] Kang Yongqiang, Zhang Jialin, Shi Zhipeng, et al. A new method for calculating the electric field distribution in particle-particle rotating systems[J]. Journal of Electrostatics, 2024, 132: 103967.
Abstract The formation of small bridge by dielectric impurity particles in insulating oil under the action of electric field is the key factor that leads to the decrease of insulation performance. When the distance between dielectric particles is relatively close, the polarization interaction force is significant, which greatly affects the electric field distribution around dielectric particles and the chain process of particles in oil. The particle chain process and its morphological change are important factors affecting the distortion of electric field and partial discharge in transformer insulation oil. However, the mechanism by which the interaction between particles affects their motion is not well understood, and there is a lack of effective models for analyzing the interaction forces. Therefore, an experimental platform was established to study the effect of dielectric particle interaction on particle motion in insulating oil.
In the experiment, the electric field is uniform, and the field direction is changed to simulate the electric field in different directions. Dielectric particles are replaced by wooden balls and fixed with extremely fine cotton thread. The influence of their interaction on the particle chain process is mainly studied. The experimental results show that when the direction of the applied electric field is parallel to the line connecting the center of the particles, the particles attract each other and form a chain under the action of the electric field. However, when the direction of the external electric field is perpendicular to the line connecting the particle center, there will be a special “self-rotation” phenomenon in the process of the particle translation movement along the electric field line to form a chain, that is, the special motion mode of “attraction-self-rotation-chain”. However, the classical point dipole interaction model cannot explain and describe this special experimental phenomenon. Therefore, the process of particle interaction is considered in this paper, and the equivalent idea of self-dipole and mutual-coupling dipole polarization of particles under the action of electric field is proposed. On this basis, a model of mutual-coupling dipole interaction considering particle interaction is established, and the analytical expressions of particle self-dipole moment and mutual-coupling dipole moment are obtained, and the relationship between particle radius and “mutual-coupling dipole moment” is established.
The mutual-coupling dipole model is used to represent the result of particle interaction by the offset of the mutual-coupling dipole away from the center of the sphere, and successfully explains the “attraction- self-rotation-chain” phenomenon caused by particle interaction, that is, the particle self-rotation mechanism is the essential reflection of the interaction torque formation in the electric field environment. The self-rotation experiment of a three-particle system fully proves the validity of the concept of coupled dipoles in the analysis of the interaction force between particles. At the same time, the mutual-coupling dipole model can realize the quantitative calculation of particle interaction force and torque under different electric field angles and particle R. The calculation results show that when two particles have the same particle radius and particle spacing D is between 0.1R and 0.5R (D and R is the distance between the particles and the particle radius, respectively), there is a significant interaction force between particles, and the particle interaction force is inversely proportional to the particle spacing and proportional to the particle radius. The above analysis model provides a new method for analyzing the interaction behavior of particles in the electric field environment and optimizing the electric field in the insulating oil.
keywords：Insulating oil, dielectric particle polarization, dipole moment, mutual-coupling dipole model, interaction between particles
中图分类号：TM15
DOI: 10.19595/j.cnki.1000-6753.tces.242036
甘肃省青年科技基金（24JRRA754）和国网甘肃省电力公司科技项目（522722240003）资助。
收稿日期 2024-11-13
改稿日期 2025-01-22
包艳艳 女，1990年生，博士研究生，研究方向为超特高压电力设备状态检测、诊断与评价。E-mail: npuersbyy0930@163.com
陈 伟 男，1976年生，教授，博士生导师，研究方向为智能电网与智能电器、电能质量分析与状态评价等。E-mail: CW733000@163.com（通信作者）
（编辑 李 冰）