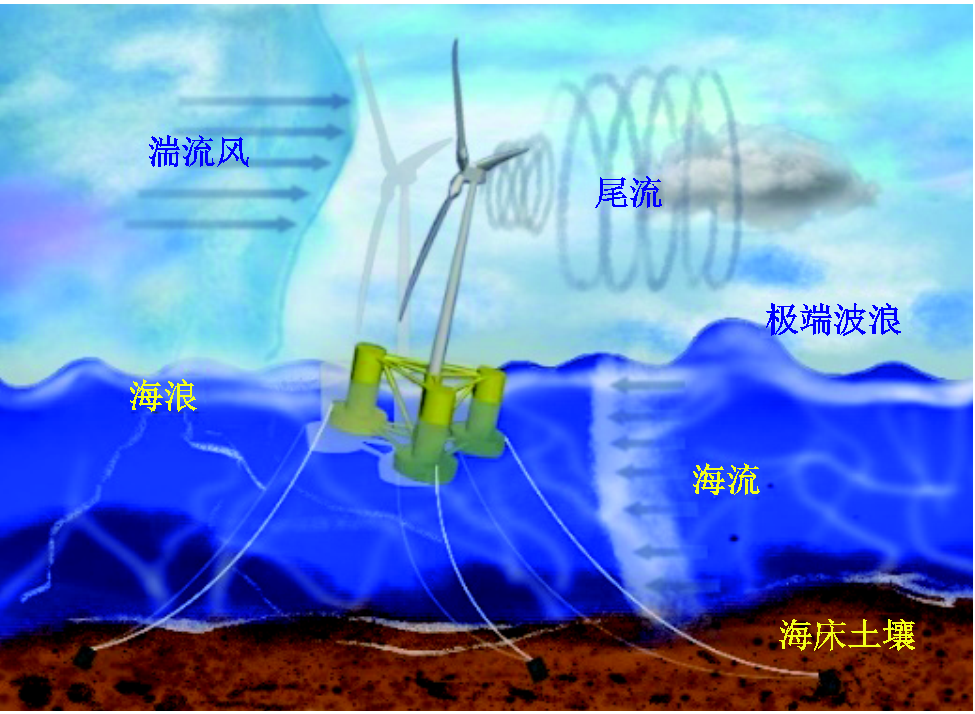
图1 半潜漂浮式海上风机运行环境
Fig.1 Operating environment of semi-submersible floating offshore wind turbine
摘要 针对漂浮式风机建模困难,风浪耦合输入下功率-载荷-运动多目标协调控制难度大,高湿高盐环境及独立变桨机制可能引发的变桨执行器故障率升高等问题,提出一种基于数据驱动的漂浮式风机被动容错独立变桨控制方法。首先,采用美国可再生能源实验室5 MW半潜漂浮式风机为参考机型,建立其液压变桨执行器正常及故障模型;其次,基于该漂浮式风机浮体纵摇模态阻尼特性对原统一变桨控制器进行改进,设计独立变桨控制器来降低不平衡叶根循环载荷,并在此基础上对变桨执行器故障敏感性进行分析,提出了基于叶根不平衡分离载荷的无模型自适应被动容错控制策略,为原变桨控制回路增加了容错控制功能;最后,在OpenFAST与Simulink联合仿真平台下进行多工况仿真测试表明,所提控制方法能实现风浪扰动输入下漂浮式风机的功率-载荷-运动多目标控制和变桨执行器带故障的容错运行控制。
关键词:漂浮式风机 负阻尼 数据驱动控制 独立变桨控制 容错控制
应用漂浮式风机是海上风电走向深远海发展的必由之路。漂浮式海上风电机组(Floating Offshore Wind Turbine, FOWT)变桨控制对机组发电性能、整机载荷安全和浮体运动控制等起着至关重要的作用,是亟须攻克的关键技术之一,因此,研究FOWT变桨控制具有重要的现实意义和工程应用价值[1]。
FOWT是气动-水动-伺服-弹性一体化耦合的非线性系统,在风浪流随机载荷输入下,平台自由度(Degree of Freedom, DOF)运动使得FOWT功率、载荷等发生较大波动,各子系统之间的耦合关系更加复杂,难以建立准确的面向控制的机理模型;同时,由于闭环变桨控制与平台纵摇运动的耦合作用,常规变桨控制可能出现纵摇运动“负阻尼”导致系统失稳问题。因此,FOWT变桨控制成为风浪流扰动输入下功率稳定-载荷降低-运动抑制的多目标优化控制问题[2-3]。此外,由于FOWT长期在高湿高盐强腐蚀海洋环境下运行,FOWT各部件的故障率上升,机组容错控制能力欠缺等问题凸显,故障容错控制需求不断上升[4]。
针对以上FOWT变桨控制问题,在统一变桨控制(Collective Pitch Control, CPC)方面,J. Jonkman等分析了常规CPC策略下驳船式FOWT平台纵摇运动可能出现负阻尼的原因,提出控制器增益重整定法、塔顶加速度反馈法和主动失速控制法,并将控制器增益重整定方法作为5 MW半潜式FOWT的基准控制器,该方法简单有效,但在高风速时FOWT功率跟踪性能变差[5-6];Hu Ruiqi等研究了10 MW张力腿式FOWT的主动失速控制策略,发现该控制策略虽能改善功率调节并避免纵摇模态负阻尼问题,但随风速增加机组载荷也成倍增加,难以适用于大兆瓦级FOWT[7];A. Fontanella等通过对不同阶跃风速下的FOWT动态响应对比和零极点分析发现,在12~17 m/s风速下,FOWT负阻尼问题较为明显,在18 m/s风速以上负阻尼问题基本消失,这表明在不同风速下FOWT的负阻尼问题严重程度不同[8];F. Lemmer等对FOWT控制器重整定法进行改良,提出了新的增益调度方法,在整个宽变桨工况下实现了半潜FOWT浮体纵摇振荡抑制和发电机转速跟踪的良好权衡[9]。以上研究主要关注单入单出CPC控制策略,具有简单易行的特点,但性能提升有限,无法兼顾多目标变桨控制需求。
在独立变桨控制(Individual Pitch Control, IPC)方面,针对大兆瓦级FOWT的降载需求,H. Namik和S. Sarkar等基于多入多出控制方法,分别提出基于线性状态反馈的IPC,实现了功率稳定调节和结构载荷降低[10-11];宋子秋和T. Wakui等分别提出了增益调度多模型预测和多回路反馈的CPC与转矩协同控制器,实现了FOWT功率和载荷的协调控制[12-13]。但以上IPC控制方法多基于模型控制,其控制性能对模型准确度具有强依赖性,而对于FOWT这样的复杂非线性模型,建模复杂度极高,且设备老化/故障等极易使得基于模型的控制方法出现模型失配,从而导致控制性能下降。对此,Qi Liangwen等提出变桨和尾缘襟翼联合的无模型自适应控制器(Model-Free Adaptive Control, MFAC),实现了半潜式FOWT叶片和浮体载荷的有效降低[14],该控制器设计摆脱了对线性化模型的依赖,只根据被控对象输入输出数据进行动态控制,规避了建模不准确、模型失配等问题,显示了数据驱动控制对FOWT这种复杂非线性系统的巨大优势。
IPC能够在CPC控制的基础上有效降低FOWT的叶根不平衡循环载荷,但也会加大变桨执行器动作频率,加速其老化、耗能和磨损。同时,长期恶劣的海上运行环境也亟须FOWT具备一定的故障容错运行控制能力。在容错控制方面,张艳峰等针对FOWT叶根传感器故障和变桨执行器故障问题,提出了基于卷积神经网络的故障诊断系统和基于无模型自适应主动容错控制的故障自适应补偿系统,能够较好地对传感器和执行器故障进行补偿,保持叶根载荷平衡[15];M. Mazare等针对变桨系统传感器和执行器故障提出了自适应滑模鲁棒主动容错控制,能够有效地隔离和适应故障的影响[16];H. Badihi等针对海上固定式风机变桨执行器故障问题提出了主动容错独立变桨控制(Active Fault-Tolerant Individual Pitch Control, AFTIPC)[17],主要由CPC、IPC及故障检测和诊断(Fault Detection and Diagnosis, FDD)模块组成,能够根据故障情况主动进行控制动作调整。以上三种主动容错控制方法是基于模型的容错控制方法,具有主动干预、针对性强的优势,但存在建模误差和难以建模的情况,控制性能和自适应能力受限,且设计内容较多,控制结构复杂。
为解决上述问题,本文提出一种基于数据驱动的漂浮式风电机组被动容错独立变桨控制(Passive Fault-Tolerant Individual Pitch Control, PFTIPC)方法。以美国可再生能源实验室(National Renewable Energy Laboratory, NREL)5 MW半潜式FOWT为参考风机,基于该FOWT平台纵摇阻尼特性对原变桨控制进行改进,提高其功率调节-载荷降低-运动抑制性能。同时,基于变桨执行器故障特性,设计叶根不平衡分离载荷的无模型自适应被动容错控制策略,为原有变桨控制回路增加容错控制功能,使其在变桨执行器故障情况下具备一定的容错控制能力。最后通过多种工况仿真验证了所提改进控制器及控制策略的有效性。
FOWT本体是由上部风机、下部浮体和系泊系统组成的气动-水动-伺服-弹性一体化非线性机电耦合系统,其在深远海运行环境下同时受到风-浪-流等多重复杂载荷作用。半潜式FOWT运行环境如图1所示。

图1 半潜漂浮式海上风机运行环境
Fig.1 Operating environment of semi-submersible floating offshore wind turbine
本文以NREL 5 MW半潜式FOWT[6]为参考机组,该机组集成于OpenFAST软件平台[18],平台遵循模块化设计原则,其中FOWT分为气动、水动、伺服、弹性四大模块,各模块子系统间耦合关系详见文献[18]。半潜式FOWT完全非线性模型可表示为
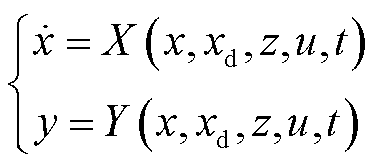 (1)
(1)
式中,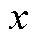 为FOWT气弹、电机、偏航、浮体等DOF的连续时间状态;
为FOWT气弹、电机、偏航、浮体等DOF的连续时间状态;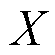 为DOF对应的非线性连续状态函数;
为DOF对应的非线性连续状态函数;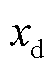 为离散时间状态;
为离散时间状态;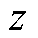 为约束状态;
为约束状态;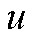 为发电机转矩、桨距角控制量输入和风-浪-流扰动量输入等;
为发电机转矩、桨距角控制量输入和风-浪-流扰动量输入等;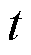 为时间;
为时间;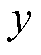 为系统输出;
为系统输出;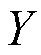 为非线性连续输出函数。
为非线性连续输出函数。
由于OpenFAST中无变桨执行器模型[19],在此建立FOWT的变桨执行器正常及故障模型。
1.2.1 变桨执行器正常模型
海上风机通常使用可靠性更高的液压变桨系统[20]。液压变桨执行器的系统结构示意图如图2所示。
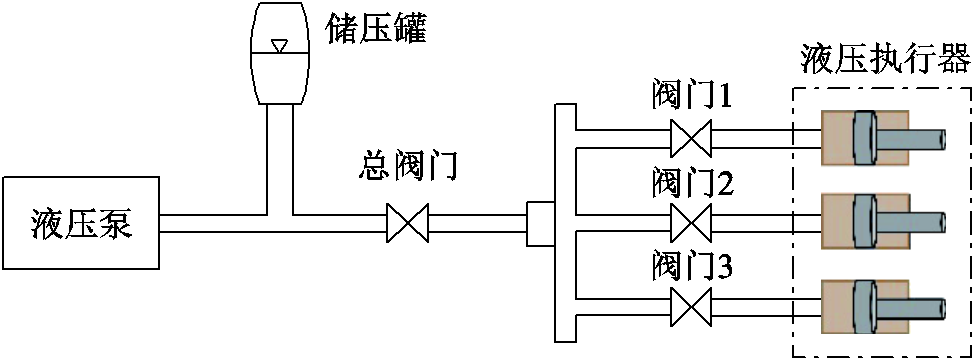
图2 液压变桨系统
Fig.2 Hydraulic pitch system
液压变桨执行器i的数学模型可等效为典型的二阶系统[20-21],即
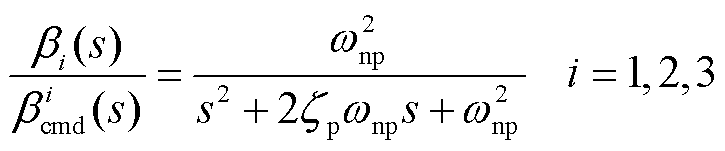 (2)
(2)
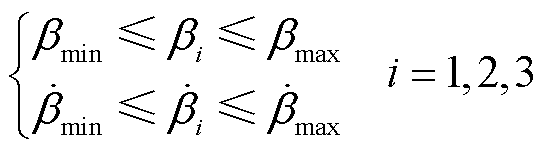 (3)
(3)
式中,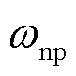 为液压变桨执行器固有频率;
为液压变桨执行器固有频率;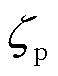 为阻尼比;
为阻尼比;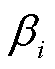 为实际变桨角;
为实际变桨角;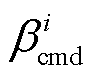 为变桨指令;
为变桨指令;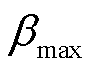 和
和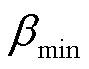 分别为变桨角幅值上、下限;
分别为变桨角幅值上、下限;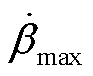 和
和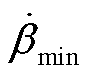 分别为变桨速率上、下限。变桨角幅值和速率约束范围分别为
分别为变桨速率上、下限。变桨角幅值和速率约束范围分别为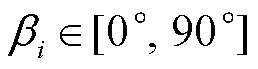 和
和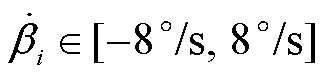 。
。
1.2.2 变桨执行器故障模型
FOWT液压变桨执行器易出现的故障问题可归结为三种主要类型:卡死(部分卡死或全部卡死,属于严重故障)、油中空气含量过高和液压下降。导致各类故障的原因可见文献[20-21]。三种类型故障的数学模型分别等同于常数、加性故障和乘性故障,FOWT液压变桨执行器故障模型见表1。
各类故障的发生将会使FOWT液压变桨执行器的固有频率、阻尼比和有效性发生变化,从而影响系统的闭环动态响应特性。根据以上建立的液压变桨执行器故障模型,可得不同运行工况下变桨执行器单位阶跃响应特性曲线如图3所示。
表1 FOWT液压变桨执行器故障模型
Tab.1 Fault models of FOWT hydraulic pitch actuators

故障类型系统参数故障模型严重程度影响时间 无故障,为故障变桨角无无 卡死,为常数高快 油中空气含量过高,为变桨偏差中慢 液压下降,为健康因子高中
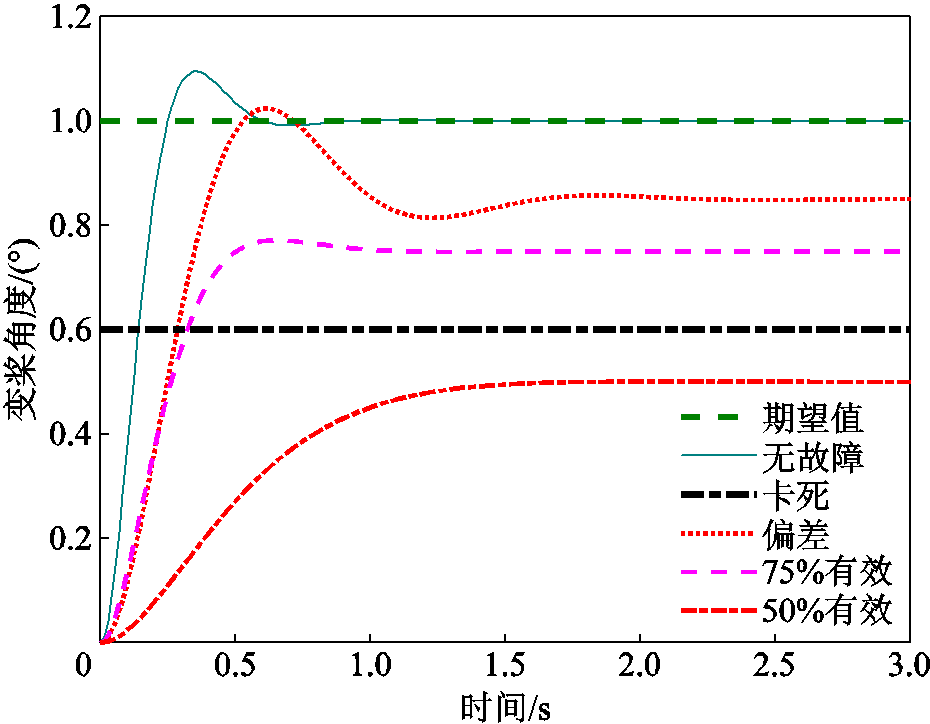
图3 不同运行工况下液压变桨执行器阶跃响应曲线
Fig.3 Step response curves of hydraulic pitch actuator under different operation conditions
与基于模型的控制方法相比,本文采用的PID和MFAC控制算法基于数据驱动,无需对FOWT进行面向控制的复杂精准建模和反向验证环节,不需要进一步的非线性系统多工况点的线性化过程,仅需选择合适的输入输出信号来设计控制器与被控对象进行交互。本文提出的基于数据驱动漂浮式风机PFTIPC方法的原理如图4所示。
该方法主要由三部分构成:
1)基于发电机转速误差的改进增益调度PI统一变桨控制器CPC:用于降低靠近额定风速区间的纵摇负阻尼影响,增强系统稳定性,并改善远离额定风速的更高风速区间FOWT功率调节性能。
2)基于转子方位角和叶根载荷反馈的双PI独立变桨控制器IPC:旨在降低由于风切变所造成的FOWT旋转周期内三叶片叶根不平衡循环载荷。
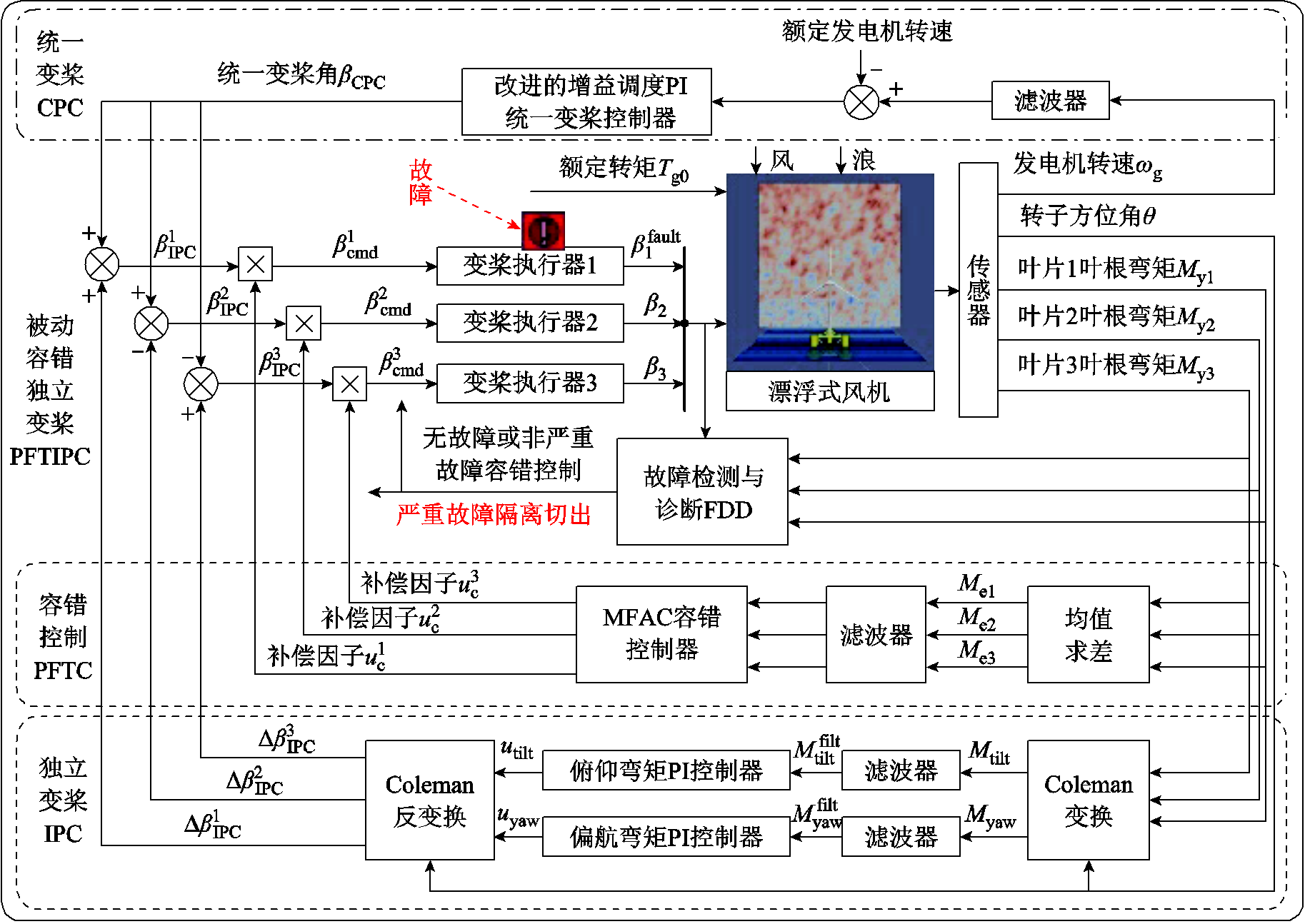
图4 基于数据驱动的漂浮式海上风电机组被动容错独立变桨控制原理
Fig.4 Schematic diagram of data-driven based passive fault-tolerant control of IPC for FOWT
3)基于叶根载荷误差反馈的无模型自适应被动容错控制器(Passive Fault Tolerant Control, PFTC):补偿由于各种原因造成的变桨角分离和三叶片叶根不平衡载荷分离故障,使得变桨执行器在非严重故障状态下具有容错控制运行能力。
最终FOWT变桨角控制指令为
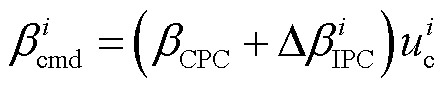 (4)
(4)
式中,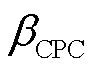 为统一变桨角;
为统一变桨角;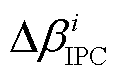 为叶片的独立变桨增量;
为叶片的独立变桨增量;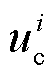 和
和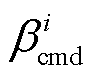 分别为变桨执行器的补偿因子和变桨指令。
分别为变桨执行器的补偿因子和变桨指令。
2.1.1 FOWT纵摇阻尼特性分析
FOWT闭环变桨控制与平台纵摇运动的耦合关系使其在特定风速区间可能出现负阻尼问题,从而严重影响控制性能。参照文献[22-23],建立半潜式FOWT纵摇运动方程,采用差分法对NREL 5 MW半潜式FOWT浮体平台纵摇阻尼比进行定量计算分析,最终可得NREL 5 MW半潜式FOWT开环(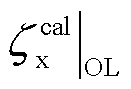 )和闭环(
)和闭环(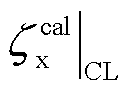 )情况下的纵摇模态阻尼特性变化曲线如图5所示。
)情况下的纵摇模态阻尼特性变化曲线如图5所示。
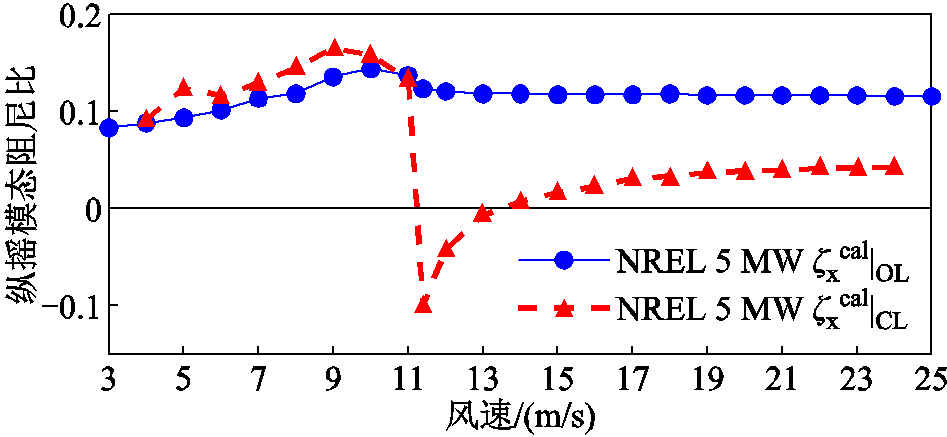
图5 NREL 5 MW半潜式FOWT平台纵摇运动阻尼比
Fig.5 Damping ratio of platform-pitch mode for NREL 5 MW semi-submersible FOWT
由图5可以看出,在靠近额定风速区间,NREL 5 MW半潜式FOWT平台纵摇模态呈现低阻尼甚至是负阻尼;但随着风速的继续增加,纵摇模态阻尼逐渐增大,负阻尼问题逐渐得到缓解。根据纵摇阻尼比变化趋势可得出负阻尼问题对FOWT稳定性的影响:FOWT负阻尼问题只在靠近额定风速区间时较为严重,要特别重视平台稳定性问题;而在远离额定风速的更高风速区间,FOWT纵摇模态阻尼比增大,要侧重于解决机组功率调节问题。
2.1.2 统一变桨控制回路改进
FOWT基准CPC控制器是基于变系数PI控制[24-25]的思想,采用递减型增益调度系数,其详细内容可见文献[6],关键推导步骤列于附录第1节。FOWT基准CPC控制策略使得FOWT在远离额定风速的更高风速区间发电功率波动增大。根据上述对FOWT平台纵摇运动阻尼特性的分析,应在靠近额定风速区间降低控制器增益,在远离额定风速区间适当提高控制器增益。
本文采取降低CPC控制器固有频率和改进增益调度函数相结合的控制策略对基准CPC控制器进行改进。选取较低的CPC控制器固有频率和二次函数型增益调度函数,其基本形式为
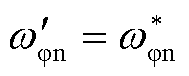 (5)
(5)
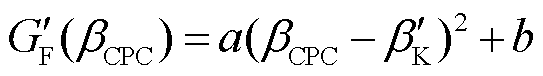 (6)
(6)
式中,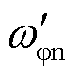 和
和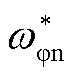 分别为选取的改进CPC控制器的固有频率和固有频率常数;
分别为选取的改进CPC控制器的固有频率和固有频率常数;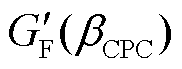 为改进的增益调度函数;a和b为待整定的二次函数常数值,且
为改进的增益调度函数;a和b为待整定的二次函数常数值,且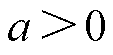 ,
,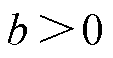 ;
;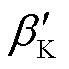 为改进的增益调度函数极小值点对应的桨距角,其通常选取FOWT纵摇模态阻尼比由负转正的风速点所对应的桨距角。因此,对于NREL 5 MW半潜式FOWT,
为改进的增益调度函数极小值点对应的桨距角,其通常选取FOWT纵摇模态阻尼比由负转正的风速点所对应的桨距角。因此,对于NREL 5 MW半潜式FOWT,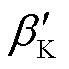 =6.60°(13 m/s对应的稳态桨距角)。
=6.60°(13 m/s对应的稳态桨距角)。
为保证FOWT的稳定性,CPC控制器固有频率要始终低于浮体纵摇模态固有频率;同时,为了使得改进CPC变桨控制器性能优于基准CPC控制器,控制器频率应低于基准CPC控制器频率;进一步,为提高远离额定风速的更高风速区间FOWT功率调节能力,本文设计改进的CPC控制器比例增益在纵摇阻尼比转折点风速处大于或等于基准CPC控制器比例增益,故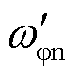 与
与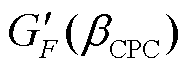 需满足的约束条件为
需满足的约束条件为
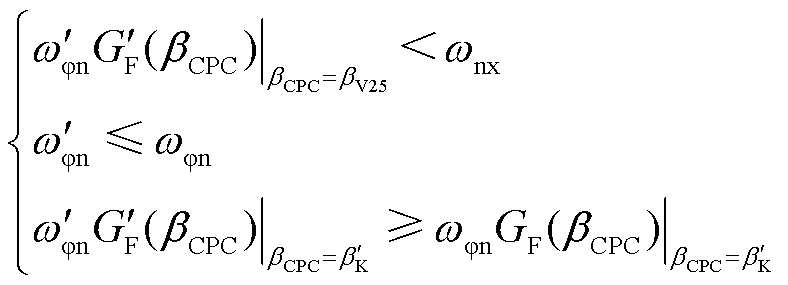 (7)
(7)
式中,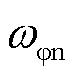 为FOWT统一变桨控制器的固有频率;
为FOWT统一变桨控制器的固有频率;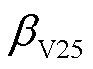 为风速为25 m/s时FOWT的稳态闭环变桨角,对于NREL 5 MW FOWT,
为风速为25 m/s时FOWT的稳态闭环变桨角,对于NREL 5 MW FOWT,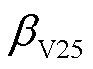 =23.47°。
=23.47°。
根据以上参数可解得所需整定的改进增益调度参数范围为:NREL 5 MW FOWT选取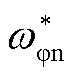 =0.1 rad/s,
=0.1 rad/s,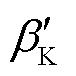 =6.60°,a≤0.528×10-3,b≥0.977且284.60a+b≤ 2.325。为便于仿真分析,本文改进的CPC控制策略选取边界值,即选取
=6.60°,a≤0.528×10-3,b≥0.977且284.60a+b≤ 2.325。为便于仿真分析,本文改进的CPC控制策略选取边界值,即选取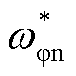 =0.1 rad/s,
=0.1 rad/s,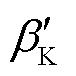 =6.60°,a=0.528×10-3,b=0.977。NREL 5MW半潜式FOWT基准和改进CPC控制策略的增益调度系数、比例增益及积分增益变化曲线对比如图6所示。
=6.60°,a=0.528×10-3,b=0.977。NREL 5MW半潜式FOWT基准和改进CPC控制策略的增益调度系数、比例增益及积分增益变化曲线对比如图6所示。
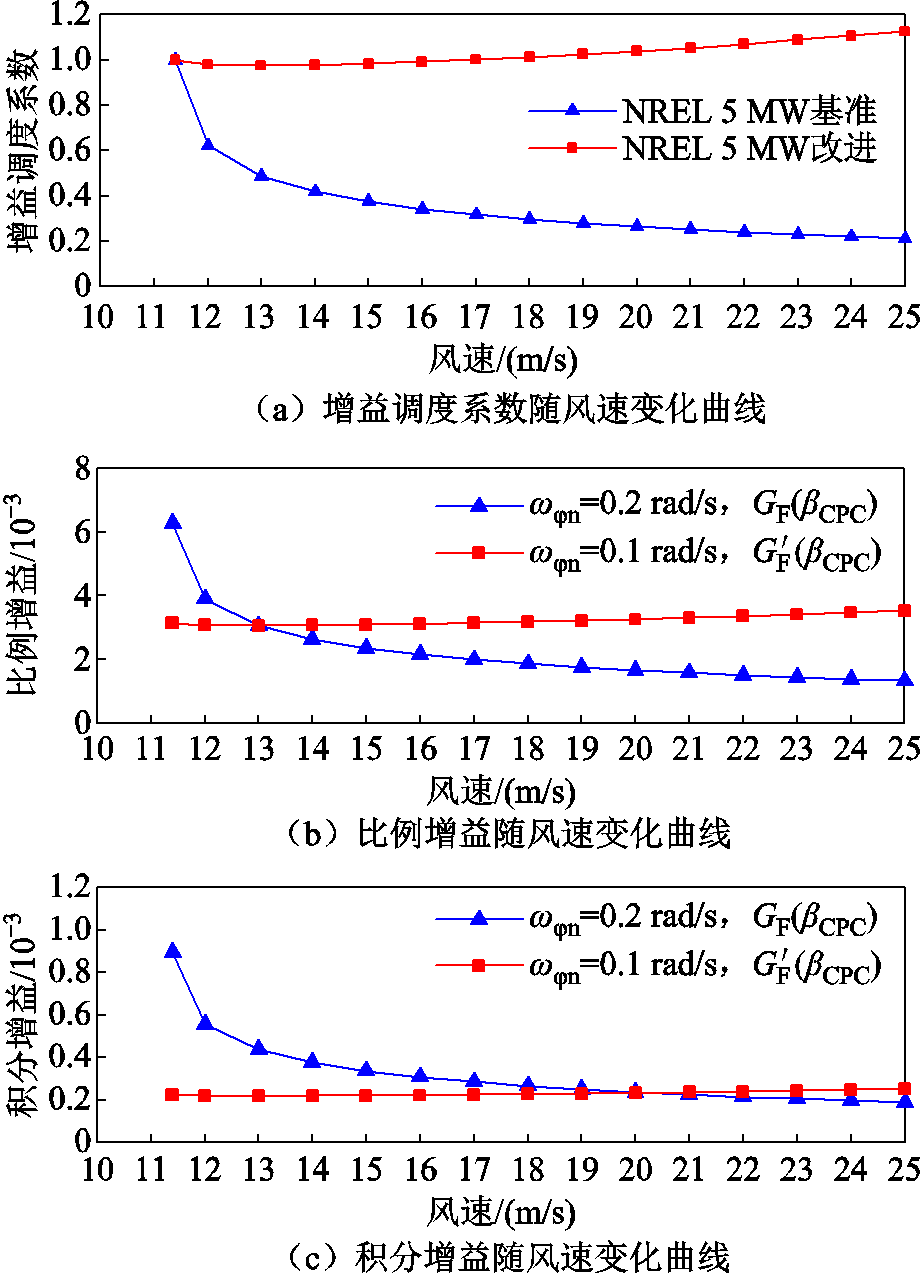
图6 改进的FOWT统一变桨控制器增益对比
Fig.6 Comparison of improved gains for FOWT collective pitch controller
大兆瓦级海上FOWT风轮转速低,风轮平面风速梯度大,IPC可以较好地适用于FOWT以降低机组载荷。IPC控制器的关键推导及参数列于附录第2节,经过IPC控制回路最终得到每只叶片的独立变桨角度增量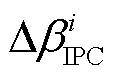 。
。
2.3.1 变桨执行器故障敏感性分析
根据液压变桨执行器故障模型分析,其乘性和加性故障数学模型可等效为
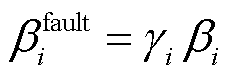 (8)
(8)
式中,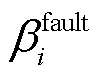 为故障变桨角;
为故障变桨角;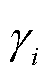 为变桨执行器健康因子,
为变桨执行器健康因子,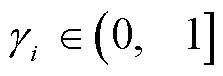 ,
,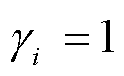 表示变桨执行器无故障。
表示变桨执行器无故障。
对于三叶片FOWT,在独立变桨机制下,变桨执行器正常工作时三叶片叶根载荷在每个旋转周期内因风切变的影响而呈现相位差为120°的交替变化趋势,且变化幅值基本一致。但由于当各类故障而导致的三叶片变桨执行器健康状态不同时,变桨角可能发生分离,从而导致叶片气动受力不均衡,最终使得三叶片叶根载荷波动发生分离,导致叶根载荷严重不平衡。
根据变桨执行器故障建模分析,各类故障可能导致个别变桨执行器或全部执行器故障。由叶根载荷分离特性又可将故障整体分为两类:不平衡叶根载荷分离类故障和叶根载荷不分离类故障。对于三叶片液压变桨执行器健康状态不同的情况,液压变桨执行器故障可以用FOWT叶根载荷波动程度来量化,定义叶根弯矩与平均值误差分别为
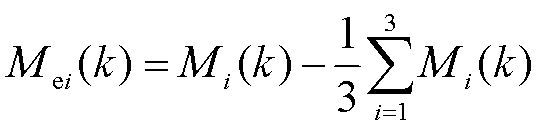 (9)
(9)
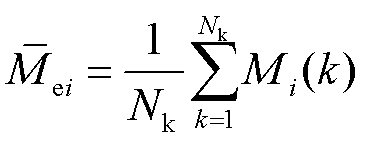 (10)
(10)
式中,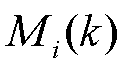 为k时刻第i只叶片的叶根载荷;
为k时刻第i只叶片的叶根载荷;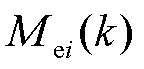 为k时刻第i只叶片与三只叶片叶根载荷均值的差值;
为k时刻第i只叶片与三只叶片叶根载荷均值的差值;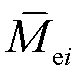 为
为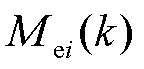 的均值;
的均值;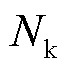 为采样点数。
为采样点数。
仿真模拟NREL 5 MW半潜式FOWT液压变桨执行器发生各类故障时变桨角和叶根载荷响应的分离情况,结果如附录第3节所示。结果表明:当某一变桨执行器发生故障时,该变桨执行器不能及时准确地跟踪给定变桨指令,故障变桨执行器变桨角输出下降,同时影响其他两个变桨执行器动作,使得三叶片变桨角发生分离,且随故障类型的严重程度不同而分离程度不同。同时,三叶片变桨角度的分离导致叶片气动受力发生变化,对应叶片叶根载荷也发生明显分离,且随故障类型的严重程度不同叶根载荷分离程度也不同,其分离特征与变桨角分离特征相反,变桨角度小的承受不平衡载荷更大。
用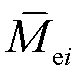 来量化各种故障状态下叶根不平衡载荷的分离程度,不同故障下
来量化各种故障状态下叶根不平衡载荷的分离程度,不同故障下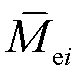 的值如图7所示。可以看出,无故障情况下,
的值如图7所示。可以看出,无故障情况下,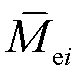 基本为零;对于卡死故障,在以上工况设置下
基本为零;对于卡死故障,在以上工况设置下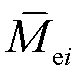 虽然较小,但由于卡死故障导致叶片变桨角不可调节,在风速变化剧烈工况下
虽然较小,但由于卡死故障导致叶片变桨角不可调节,在风速变化剧烈工况下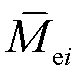 值将大大增加,从而产生严重影响,故属于严重故障。油中空气含量过高故障(偏差3°)、液压下降(75%有效)、液压下降(50%有效)的
值将大大增加,从而产生严重影响,故属于严重故障。油中空气含量过高故障(偏差3°)、液压下降(75%有效)、液压下降(50%有效)的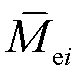 依次增大,即故障影响程度越来越大。
依次增大,即故障影响程度越来越大。

图7 不同故障下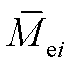 的值
的值
Fig.7 The value of 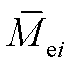 under different fault conditions
under different fault conditions
2.3.2 无模型自适应被动容错控制策略设计
基于紧格式动态线性化的无模型自适应控制(Compact Form Dynamic Linearization-based Model Free Adaptive Control, CFDL-MFAC)理论[26],利用FOWT输入输出数据,构建被动容错变桨控制器。
1)紧格式动态线性化模型
根据液压变桨执行器故障情况下三叶片叶根载荷的分离特征,考虑故障状态下三叶片叶根不平衡载荷与变桨执行器健康因子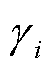 的关系,可建立基于FOWT叶根载荷误差的多入多出非线性离散时间液压变桨执行器故障补偿系统模型为
的关系,可建立基于FOWT叶根载荷误差的多入多出非线性离散时间液压变桨执行器故障补偿系统模型为
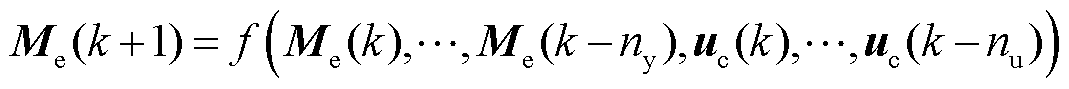 (11)
(11)
式中,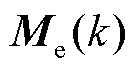 为k时刻每只叶片叶根载荷与三只叶片叶根载荷均值的差值向量,
为k时刻每只叶片叶根载荷与三只叶片叶根载荷均值的差值向量,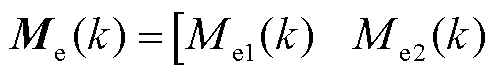
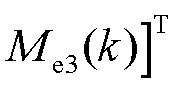 ;
;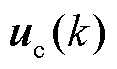 为变桨执行器健康因子为
为变桨执行器健康因子为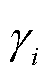 时容错控制器对变桨执行器的补偿因子,
时容错控制器对变桨执行器的补偿因子,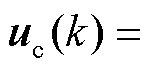
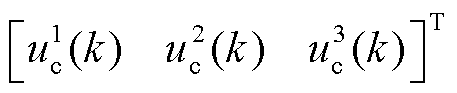 ;
;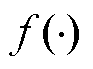 为未知非线性函数;
为未知非线性函数;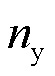 和
和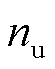 为未知整数。
为未知整数。
针对本文研究的FOWT变桨执行器故障问题,该系统满足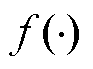 为连续光滑函数,控制输入信号
为连续光滑函数,控制输入信号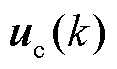 每一个分量有连续偏导数的约束条件,且叶根载荷误差的差分变化率有界,满足广义Lipschitz 条件,即本文研究的系统满足MFAC理论的假设条件[25]。对满足MFAC假设条件的变桨执行器系统,当
每一个分量有连续偏导数的约束条件,且叶根载荷误差的差分变化率有界,满足广义Lipschitz 条件,即本文研究的系统满足MFAC理论的假设条件[25]。对满足MFAC假设条件的变桨执行器系统,当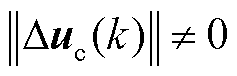 时,一定存在一个时变矩阵(也称伪雅可比矩阵)
时,一定存在一个时变矩阵(也称伪雅可比矩阵)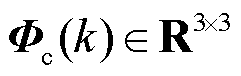 ,使得变桨执行器故障补偿系统模型式(12)可以等价转换为CFDL数据模型式(13)。
,使得变桨执行器故障补偿系统模型式(12)可以等价转换为CFDL数据模型式(13)。
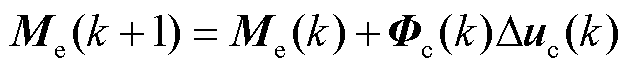 (12)
(12)
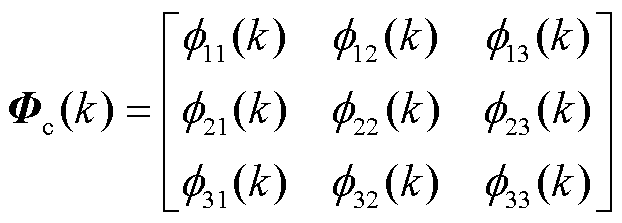 (13)
(13)
式中,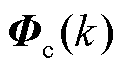 对任意时刻k是有界的,同时
对任意时刻k是有界的,同时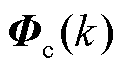 还需满足
还需满足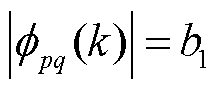 ,
,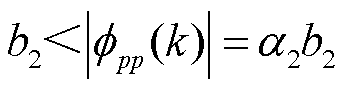 。其中,b1、b2和
。其中,b1、b2和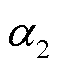 为常数,
为常数,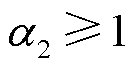 ,
,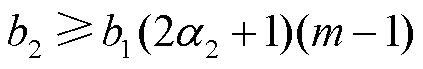 ,
,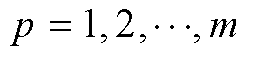 ,
,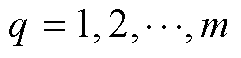 ,
,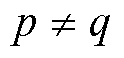 ,且
,且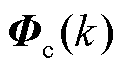 中所有元素符号对任意时刻k保持不变。
中所有元素符号对任意时刻k保持不变。
2)容错控制器设计
基于以上构建的CFDL数据模型,考虑控制目标的代价函数为
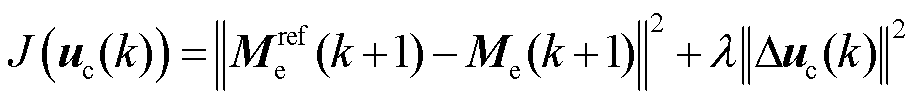 (14)
(14)
式中,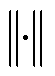 表示范数;
表示范数;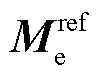 为叶根载荷误差参考值;
为叶根载荷误差参考值;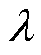 为补偿因子的权重系数,用来惩罚过大的控制量变化,
为补偿因子的权重系数,用来惩罚过大的控制量变化,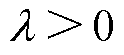 。将式(11)代入代价函数式(14)中并对
。将式(11)代入代价函数式(14)中并对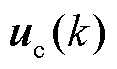 求导,求极小值点可得到
求导,求极小值点可得到
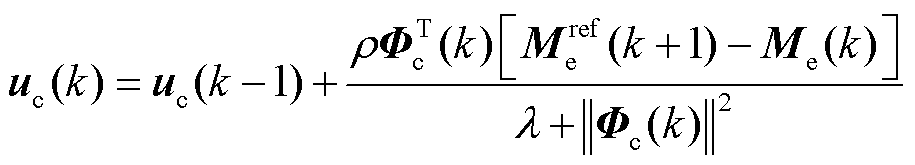 (15)
(15)
式中,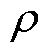 为步长因子,
为步长因子,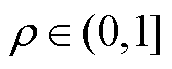 。由于伪雅可比矩阵
。由于伪雅可比矩阵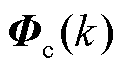 是未知时变矩阵,需对其参数进行估计。
是未知时变矩阵,需对其参数进行估计。
3)伪雅可比矩阵估计
根据变桨执行器故障补偿系统的CFDL数据模型,设计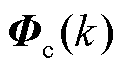 的参数估计代价函数为
的参数估计代价函数为
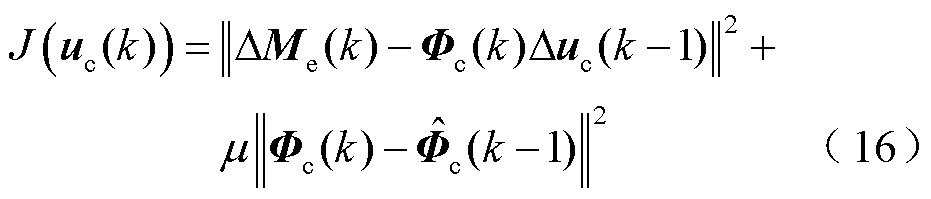
式中,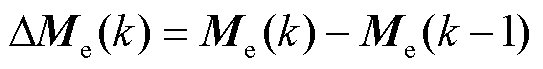 ;
;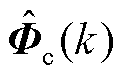 为
为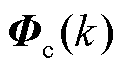 的估计值;
的估计值;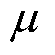 为
为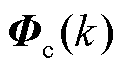 的权重系数,用于惩罚过大的
的权重系数,用于惩罚过大的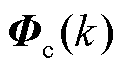 估计值变化,
估计值变化,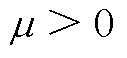 。对
。对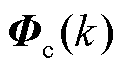 的参数估计代价函数求极小值可得
的参数估计代价函数求极小值可得
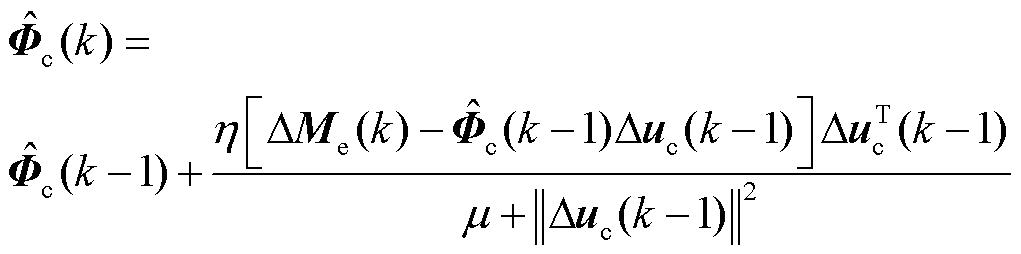 (17)
(17)
式中,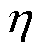 为伪雅可比矩阵估计的步长因子,
为伪雅可比矩阵估计的步长因子,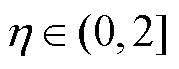 。
。
为使伪雅可比矩阵估计算法具有更强的跟踪能力,设置如下重置机制:
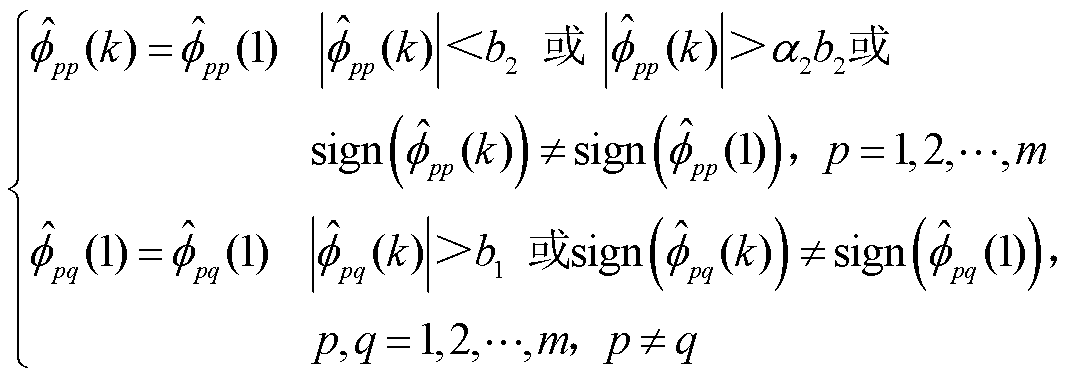 (18)
(18)
式中,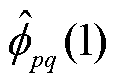 为
为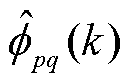 的初值;本文中,
的初值;本文中,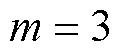 。
。
以NREL 5 MW半潜式FOWT为参考机组,在OpenFAST和Matlab/Simulink联合仿真平台上进行仿真,仿真模型如图8所示。联合仿真中激活NREL 5 MW半潜式FOWT所有可用自由度,仿真环境的硬件配置为CPU i5-13500H、2.60 GHz、32 GB内存的计算机。为了验证所提改进控制器及控制策略效果,仿真实验设置了阶跃风下无故障、突变风下无故障、湍流风下不平衡叶根载荷分离类故障及湍流风下叶根载荷不分离类故障四种场景,每种场景下对比以下五种控制器。
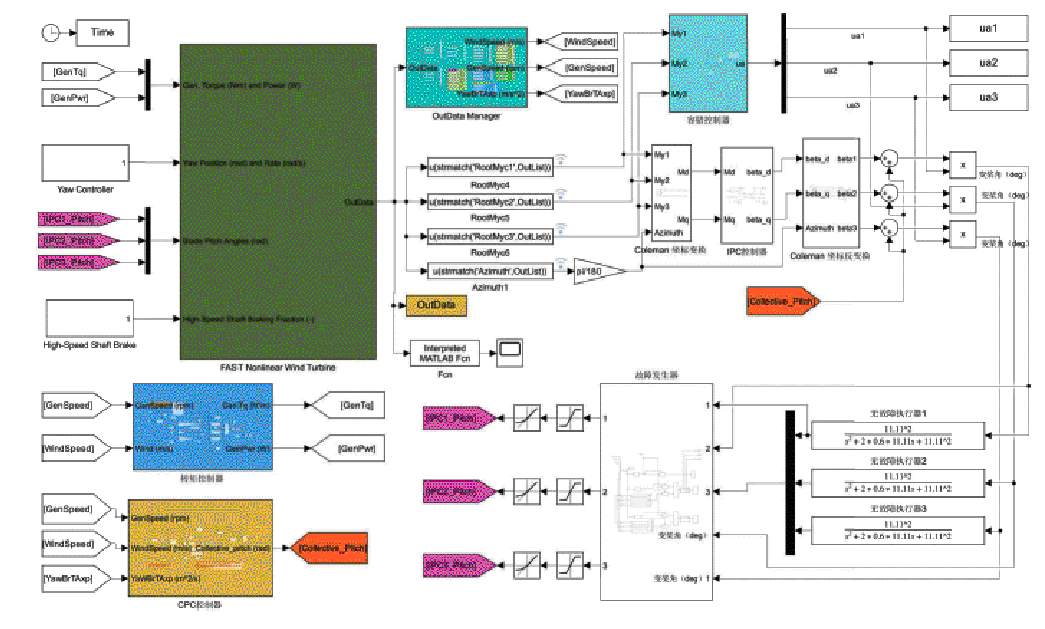
图8 OpenFAST与Matlab/Simulink联合仿真模型
Fig.8 Joint simulation model of OpenFAST and Matlab/Simulink
控制器0:线性变参数模型预测控制(Linear Parameter Varying-Model Predictive Control, LPV-MPC)CPC控制器[27],该控制器基于两质块传动链模型设计,不同模型精度响应对比见附录第4节。LPV-MPC控制器的权重矩阵Q=diag(0.1, 0.1, 1.0, 0, 0, 0.01),Ru=0和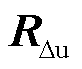 =0.05。
=0.05。
控制器1:基准CPC控制器,其中,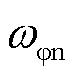 =0.2 rad/s,
=0.2 rad/s,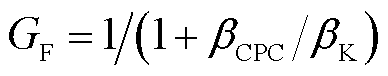 ,
,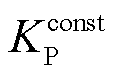 =6.28×10-3 s,
=6.28×10-3 s,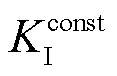 =8.97× 10-4,
=8.97× 10-4,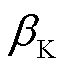 =6.302 336°。
=6.302 336°。
控制器2:基准IPC控制器(即基准CPC控制器+IPC控制器)。其中,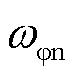 =0.2 rad/s,
=0.2 rad/s,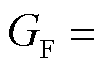
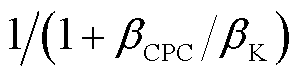 ,
,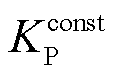 =6.28×10-3 s,
=6.28×10-3 s,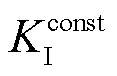 =8.97×10-4,
=8.97×10-4,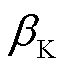 =6.302 336°,
=6.302 336°,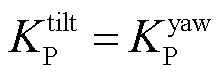 =5×10-6,
=5×10-6,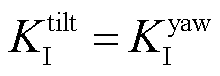 =1× 10-6。
=1× 10-6。
控制器3:改进IPC控制器(即改进CPC控制器+IPC控制器)。其中,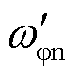 =0.1 rad/s,
=0.1 rad/s,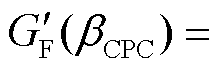
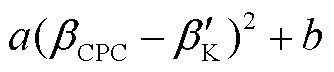 ,a=0.528×10-3,b=0.977,
,a=0.528×10-3,b=0.977,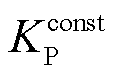 = 3.14×10-3 s,
= 3.14×10-3 s,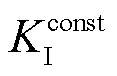 =2.24×10-4,
=2.24×10-4,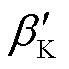 =6.60°,
=6.60°,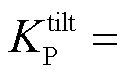
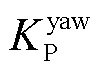 =5×10-6,
=5×10-6,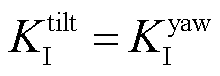 =10-6。
=10-6。
控制器4:所提出的基于数据驱动的被动容错独立变桨控制器PFTIPC(改进CPC控制器+IPC控制器+PFTC被动容错控制)。PFTIPC控制器的CPC控制参数由机组本体参数计算得出,IPC和PFTC相关控制参数经仿真实验整定得出,详见表2。
表2 PFTIPC控制器参数
Tab.2 Parameters of PFTIPC controller

控制器参数 改进CPC控制器=0.1 rad/s,,a=0.528×10-3,b=0.977,=3.14×10-3 s,=2.24×10-4,=6.60° IPC控制器=5×10-6 s,=1×10-6 =5×10-6 s,=1×10-6 PFTC被动容错控制器=8 000, ,, ,
通过设置宽范围连续阶跃变化风速来验证本文所提出的PFTIPC控制器对FOWT的功率稳定调节-机组载荷降低-平台运动抑制的多目标控制性能,并检验在变桨执行器无故障状态下被动容错控制器PFTC的控制效果。按照标准IEC 61400—3和文献[5]设置12:2:24 m/s(从12 m/s开始,以2 m/s为步长,每次变化间隔200 s,直至24 m/s的风速序列)阶跃变化的风速和有义波高为3.673 m、峰值谱周期为13.376 s的不规则JONSWAP谱波浪作为环境载荷输入。以基准CPC控制器、基准IPC控制器、改进IPC控制策略为对比,仿真结果如图9所示。基于图9结果,采用不同阶跃风速分段求取平均值和标准差的方式对控制器性能指标进行量化分析,结果如图10所示。
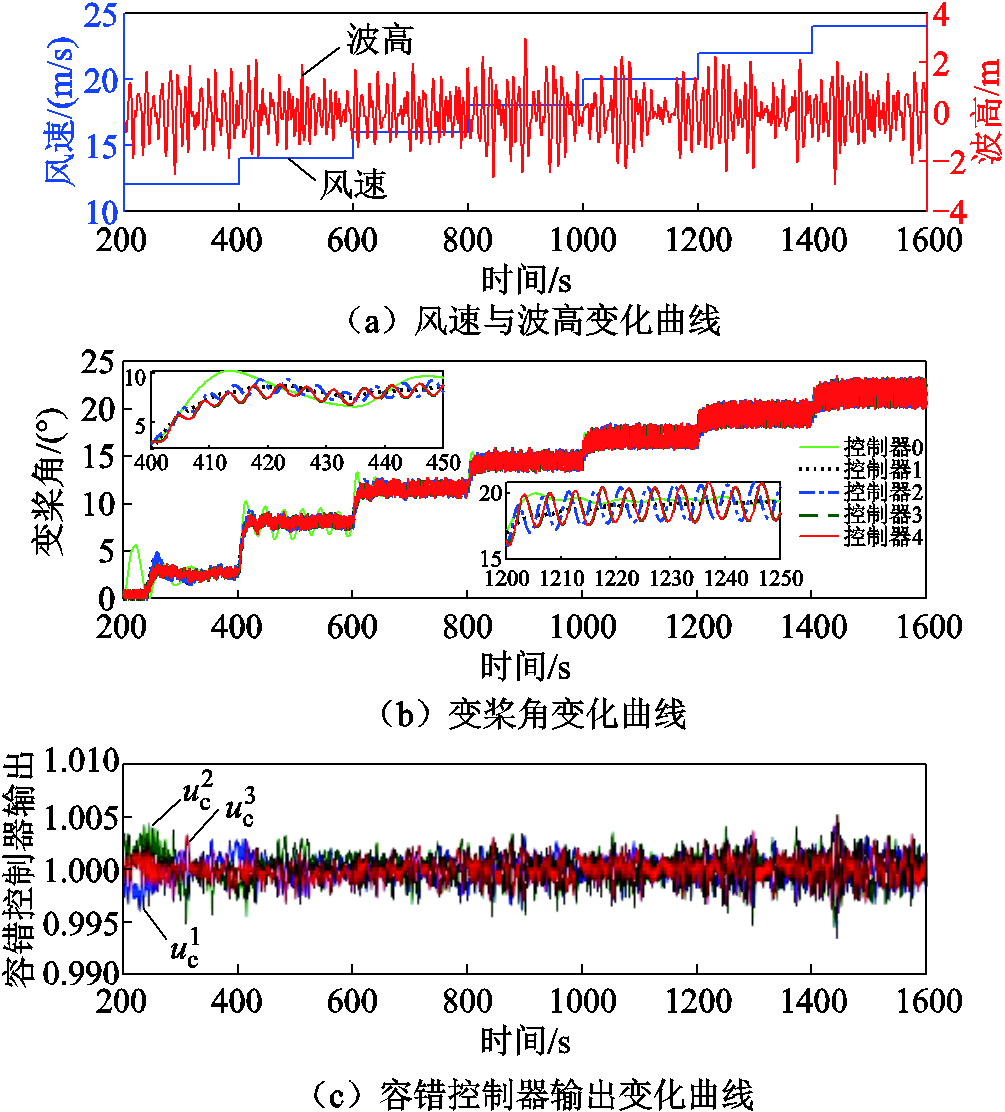

图9 阶跃风下FOWT PFTIPC控制器性能对比
Fig.9 Performance and comparison diagram of FOWT PFTIPC controller under step wind
根据图9和图10可以看出,相较于数据驱动的控制器1~4,基于模型驱动的LPV-MPC CPC控制器在靠近额定风速区间(12~18 m/s)控制性能较差,主要原因是在该风速区间模型精度较差,而在远离额定风速区间,模型精度较高,其控制性能与基准CPC控制器相当。对于数据驱动型控制,相较基准CPC控制器与基准IPC控制器,NREL 5 MW半潜式FOWT的改进IPC控制器在靠近额定风速区间,纵摇波动降低,系统稳定性增强;在远离额定风速的更高风速区间,功率波动降低,功率调节能力增强,其兼顾了平台稳定性和功率调节性能。此外,还可以看出,独立变桨能够显著降低风轮转子在旋转周期内的不平衡循环载荷。
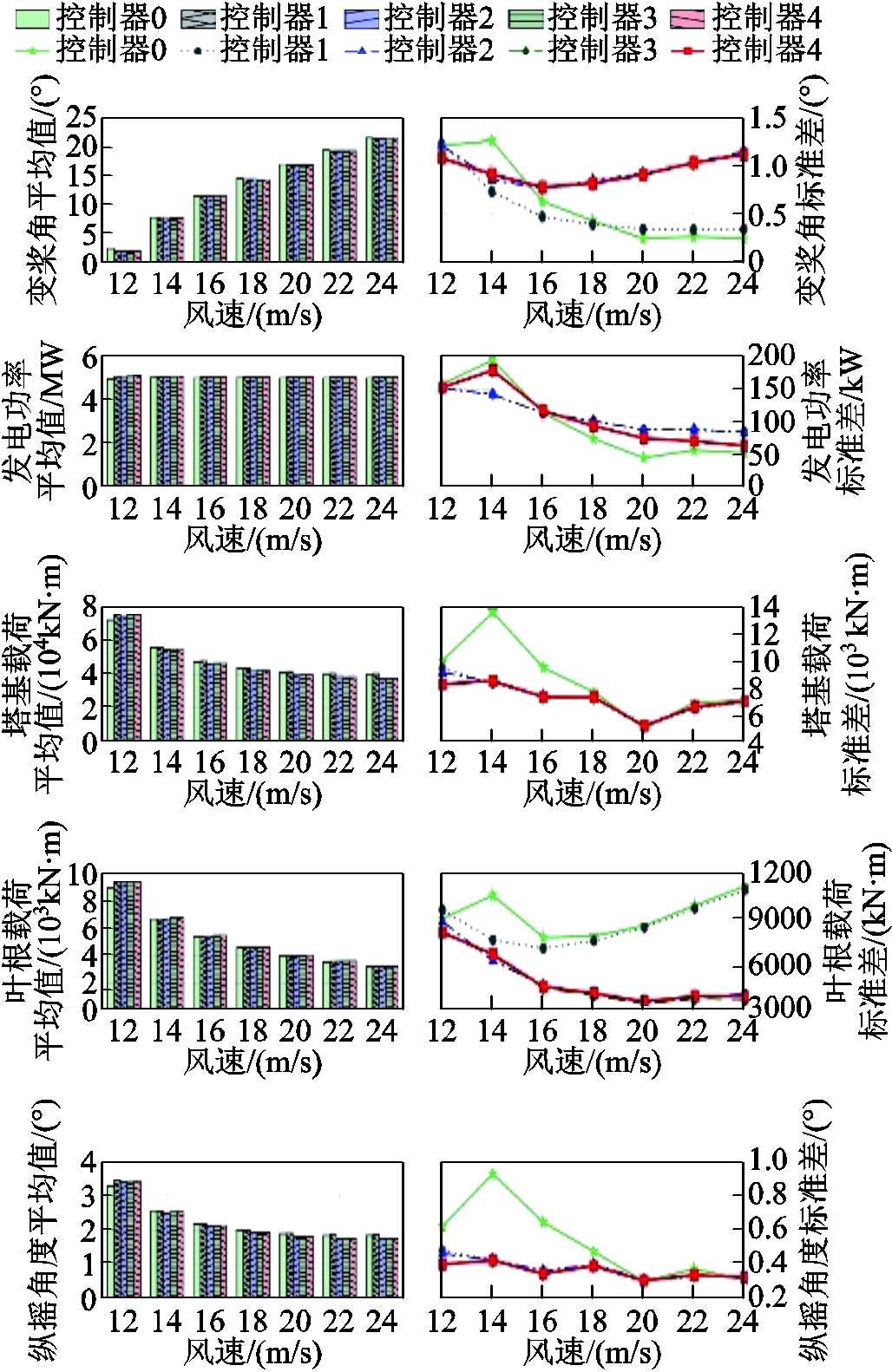
图10 阶跃风下FOWT系统性能指标量化图
Fig.10 Quantitative performance indicators of FOWT system under step wind
PFTIPC控制器对FOWT的功率波动、塔基/叶根载荷和浮体纵摇角度控制性能与改进IPC基本一致,且被动容错控制器PFTC的输出基本等于1,最大波动不超过1%。这说明在变桨执行器无故障情况下,三叶片叶根载荷几乎不发生分离,此时被动容错控制器PFTC的输出值近乎于1,即对CPC和IPC控制回路的增益近乎为1,表明无故障情况下PFTC控制器几乎不影响变桨控制回路的正常作用,此时PFTIPC控制效果等同于改进IPC控制器。
设置多个阶段的突变风速和有义波高为3.673 m、峰值谱周期为13.376 s的不规则JONSWAP谱波浪验证本文所提出的PFTIPC控制器对FOWT的功率稳定调节-机组载荷降低-平台运动抑制的多目标控制能力,并检验在变桨执行器无故障状态下被动容错控制器PFTC的控制效果。仿真结果如图11所示。对三个突变风速区间分段求取平均值和标准差进行对比分析,结果如图12所示。
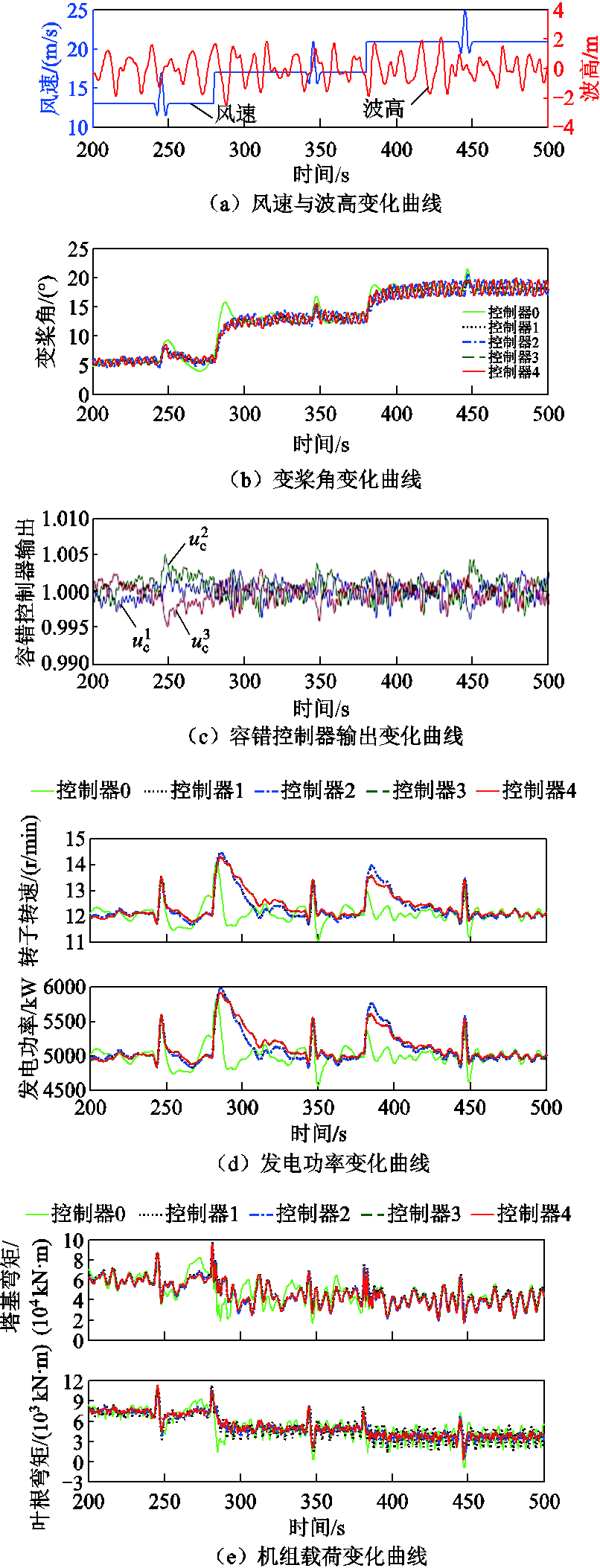
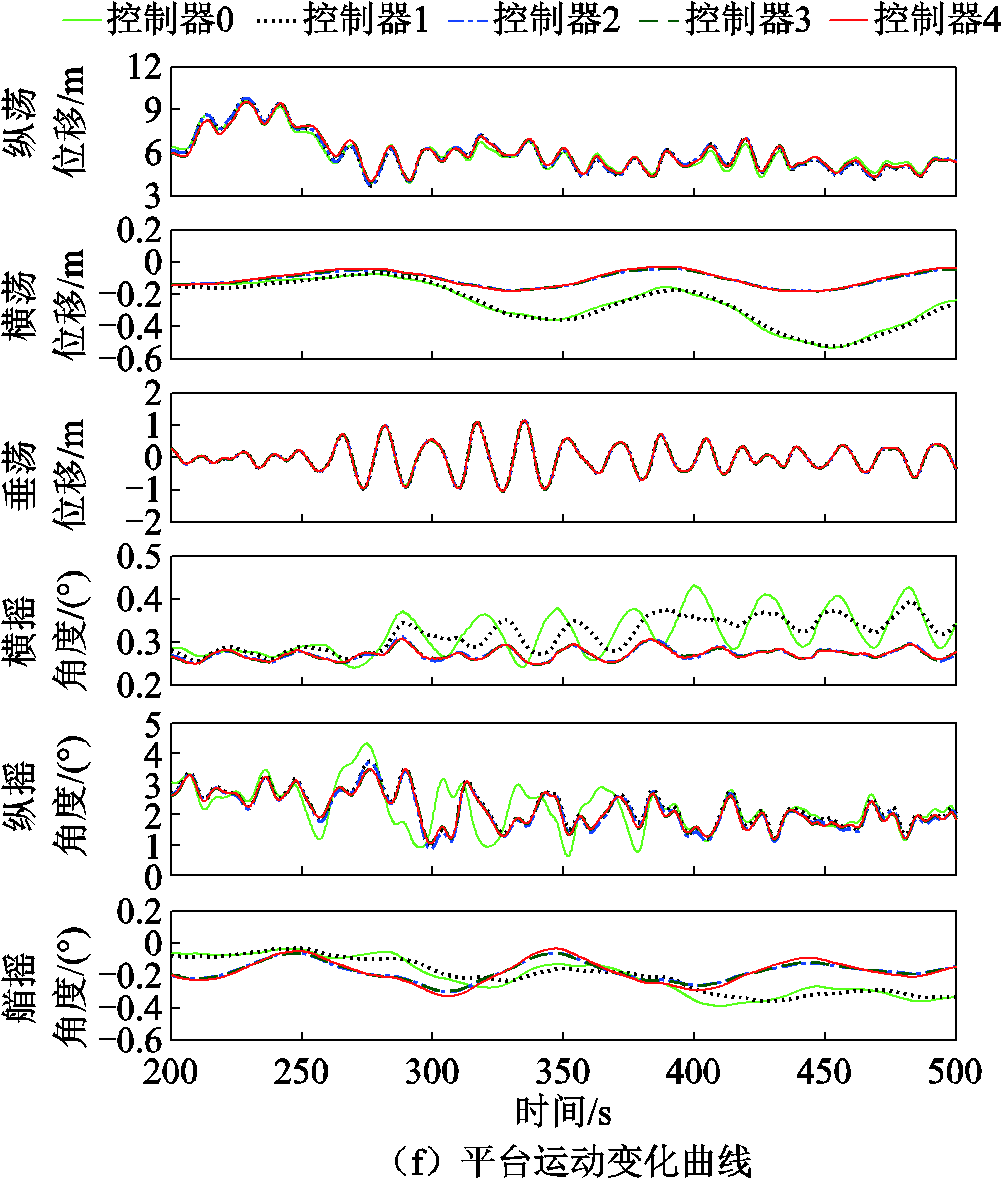
图11 突变风下FOWT PFTIPC控制器性能及对比
Fig.11 Performance and comparison diagram of FOWT PFTIPC controller under gust wind
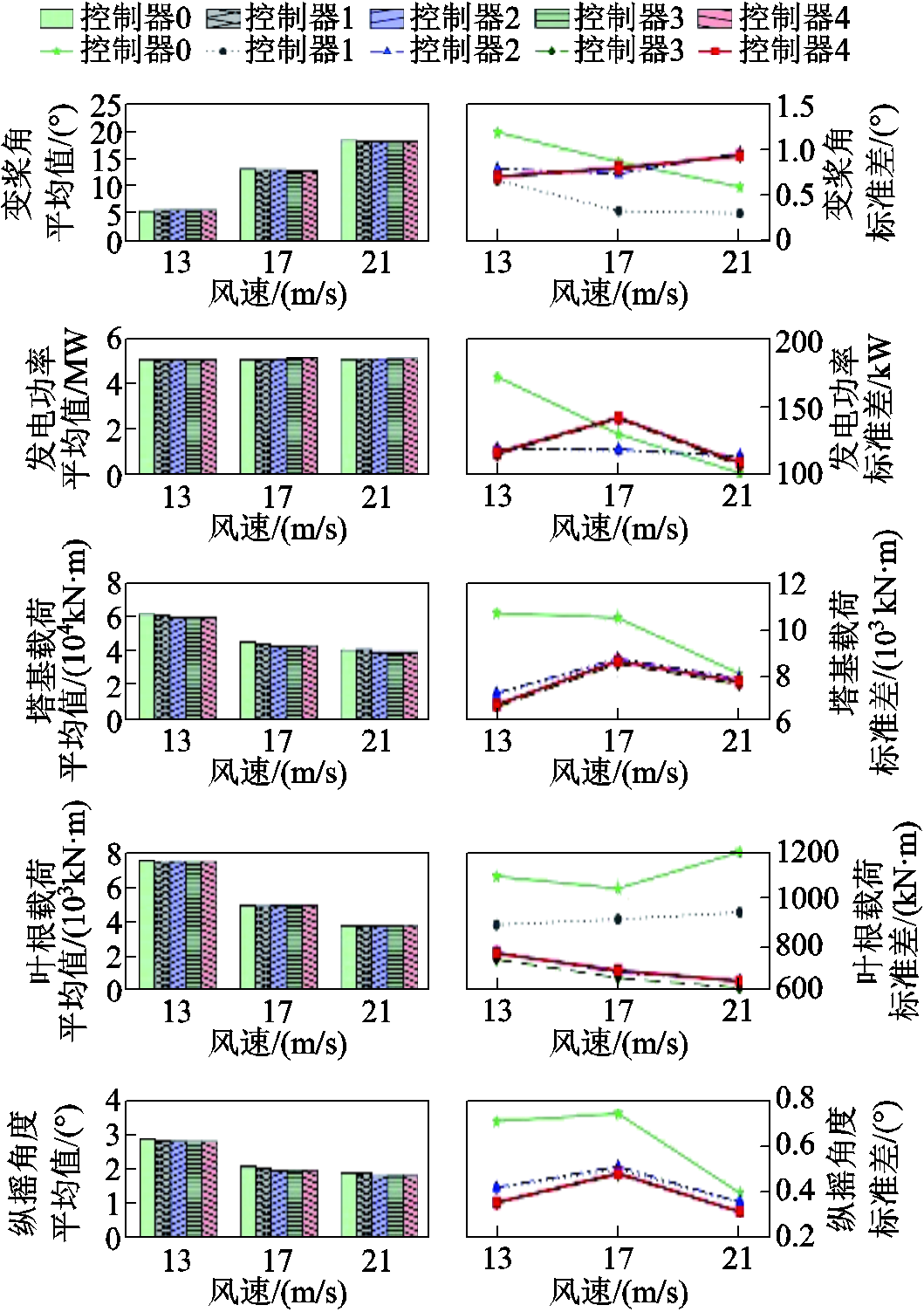
图12 突变风下FOWT系统性能指标量化图
Fig.12 Quantitative performance indicators of FOWT system under gust wind
由图11和图12可以看出,相较于模型驱动控制器LPV-MPC CPC,数据驱动的控制器1~4在突变风发生区间功率-载荷-运动控制性能更优,尤其是在靠近额定风速区间时,波动明显减弱。主要原因是在突变风速区间(尤其是在靠近额定风速区间)模型精度较差,且随突变风速快速变化,LPV-MPC模型需要不断切换,可能产生切换波动,相比之下数据驱动型IPC控制器对FOWT功率调节性能有一定的改善。同样,在突变风下独立变桨能够显著降低风轮转子在正常旋转周期内的不平衡循环载荷。在数据驱动控制器1~4对比方面,突变风下可得到与阶跃风下一致的结论,PFTIPC控制效果与改进IPC控制器相当。
本节设置湍流风和不规则波浪载荷验证PFTIPC控制器对FOWT叶根载荷不平衡的各类故障的容错控制能力。不同类型的单一故障工况对FOWT的影响结果见附录第3节。本节根据标准IEC 61400—3,采用轮毂高度处平均风速为18 m/s、湍流强度为12.7%、风切变指数为0.14、风模型为IEC Kaimal谱的湍流风速和有义波高为3.061 m、峰值谱周期为8.047 s的不规则JONSWAP谱波浪作为环境载荷输入。同时,设置半潜式FOWT叶片1的液压变桨执行器在100 s时刻发生油中空气含量过高故障(变桨执行器偏差3°),叶片2的液压变桨执行器在200 s时刻发生液压下降故障(变桨执行器75%有效),叶片3的液压变桨执行器在300 s时刻发生液压下降故障(变桨执行器50%有效)。以改进IPC控制器作为对比,仿真结果如图13所示。
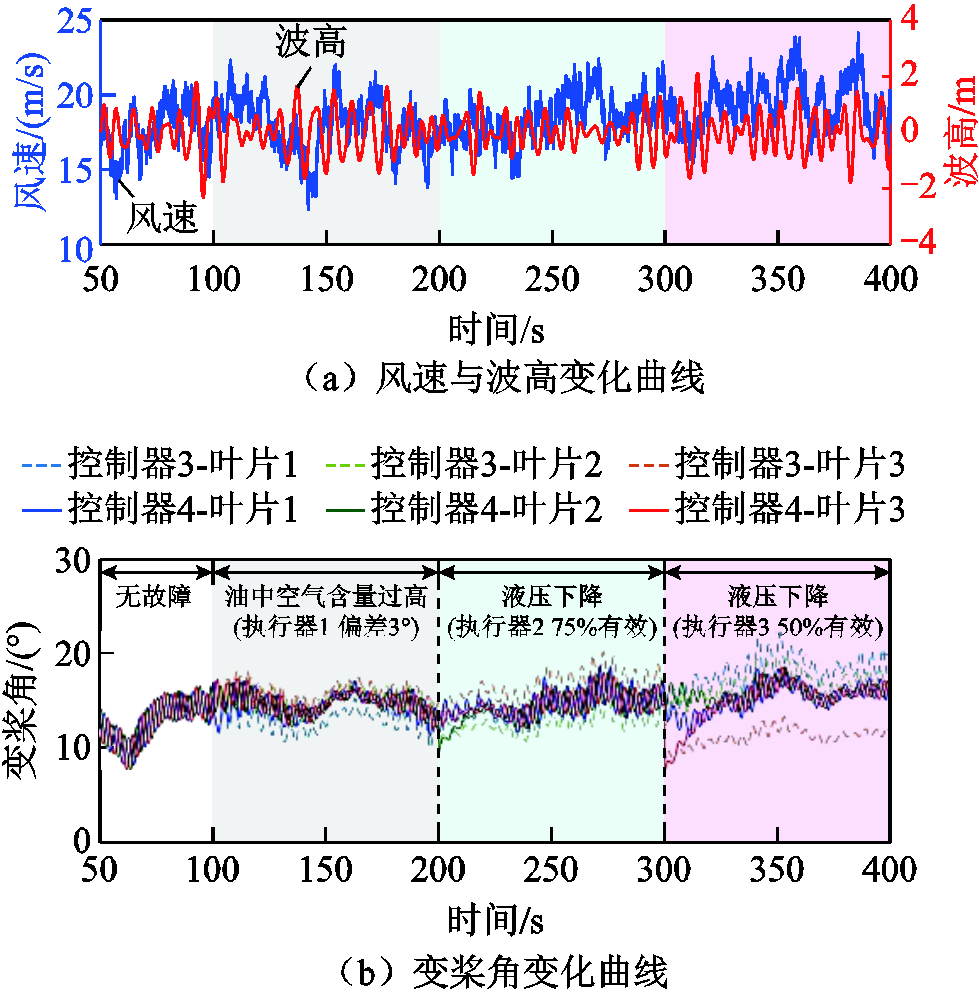
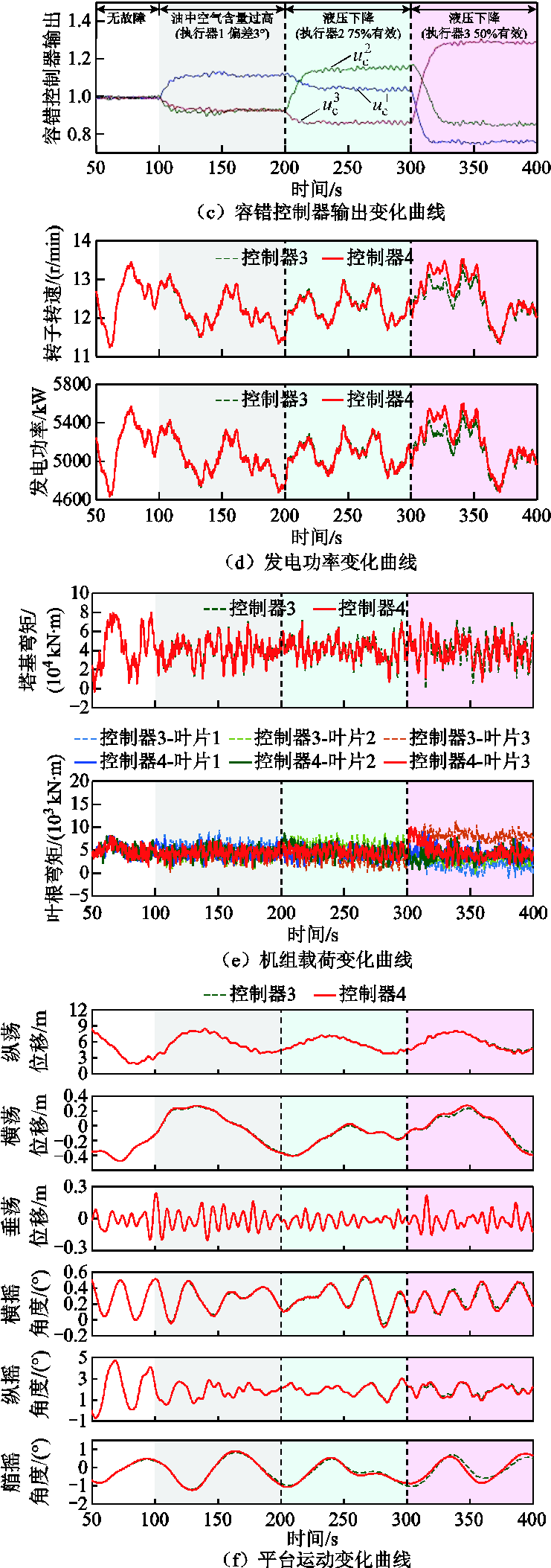
图13 湍流风不平衡叶根载荷分离类故障下FOWT PFTIPC控制器性能及对比
Fig.13 Performance and comparison diagram of FOWT PFTIPC controller under turbulent wind-induced unbalanced blade root loads and separation-type faults
根据以上仿真结果,对控制器性能指标进行量化分析,结果见表3。
表3 湍流风不平衡叶根载荷分离类故障下各控制器性能指标量化
Tab.3 Quantification of performance indicators for each controller under turbulent wind-induced unbalanced blade root loads and separation-type faults

参数性能指标控制器3控制器4 变桨角度/(°)平均值14.5714.62 标准差2.481.74 发电功率/kW平均值5 095.905 113.00 标准差191.66210.60 叶根载荷/(kN·m)平均值4 584.304 538.00 标准差1 994.501 258.30 塔基弯矩/(kN·m)平均值4.17×1044.13×104 标准差1.39×1041.34×104 纵荡位移/m平均值5.605.56 标准差1.591.61 纵摇角度/(°)平均值1.931.91 标准差0.810.82
由图13和表3可以看出,在本节设置的载荷工况和故障工况下,改进IPC控制器(无容错能力)的叶片1、2、3的变桨执行器在100、200和300 s时刻叶片桨距角分别发生跌落,随后叶片1、2、3的变桨角发生分离且无法恢复正常的幅值交替变化趋势。此外,随着故障严重程度的加深,变桨角变小,三叶片桨距角的分离使得对应叶片叶根载荷也发生明显分离,且随故障类型的严重程度不同叶根载荷分离程度也不同,其分离特征与变桨角分离特征相反,变桨角度小的承受不平衡载荷更大。
相比之下,PFTIPC控制器在叶片1、2、3的变桨执行器分别于100、200和300 s时刻桨距角发生跌落后,能够根据叶根载荷分离程度立刻自动调整补偿因子进行输出,及时恢复变桨角响应至正常趋势。此外,若其中一个变桨执行器故障,而另外两个变桨执行器健康状态相同,则相同状态变桨执行器的补偿因子相同;若三个变桨执行器健康状态皆不相同则输出的补偿因子也皆不相同,且补偿因子的变化幅度与故障程度成正比。由于PFTIPC控制器补偿因子对变桨角的调节作用能够使叶片变桨角在发生不平衡叶根载荷故障时及时恢复至正常水平,其叶根载荷也将由分离逐渐恢复至正常水平,避免了因叶根载荷的严重不平衡振荡而造成的叶片损坏。因此,PFTIPC控制器对各种原因所导致的不平衡叶根载荷分离类故障(三叶片变桨执行器健康状态不同)具有良好的补偿效果。
本节设置湍流风和不规则波浪载荷验证PFTIPC控制器对FOWT叶根载荷平衡的各类故障(即发生相同程度故障从而导致三个变桨执行器健康状态相同)的容错控制能力。采用3.3节所设置的风浪工况作为外部环境载荷输入,同时,设置半潜式FOWT叶片1、2、3的液压变桨执行器在100 s时刻都发生油中空气含量过高故障(变桨执行器偏差3°);叶片1、2、3的液压变桨执行器在200 s时刻都发生液压下降故障(变桨执行器75%有效);叶片1、2、3的液压变桨执行器在300 s时刻都发生液压下降故障(变桨执行器50%有效)。以改进IPC控制器为对比控制器,仿真结果如图14所示。根据仿真结果,对控制器性能指标进行量化分析,结果见表4。
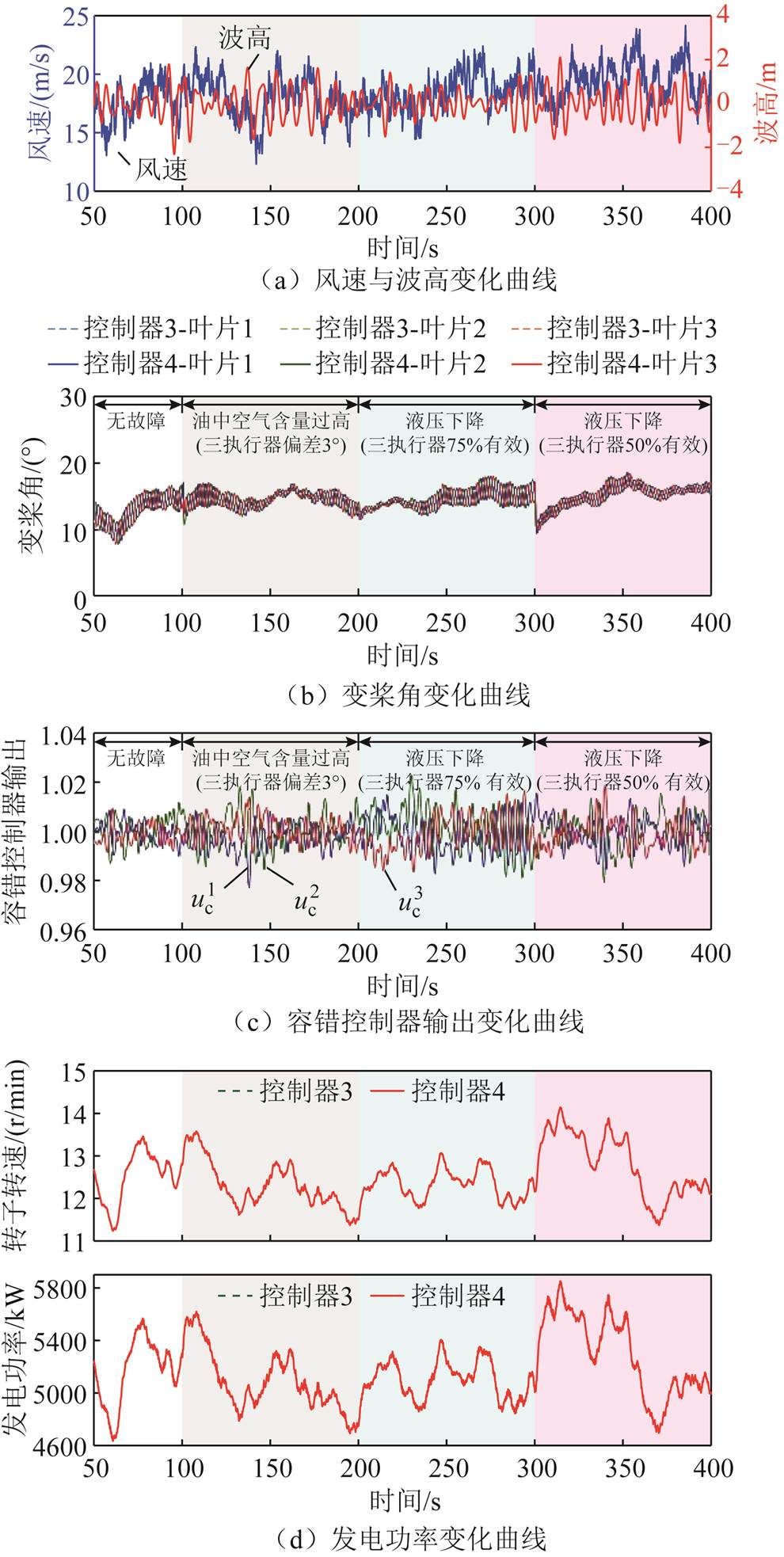
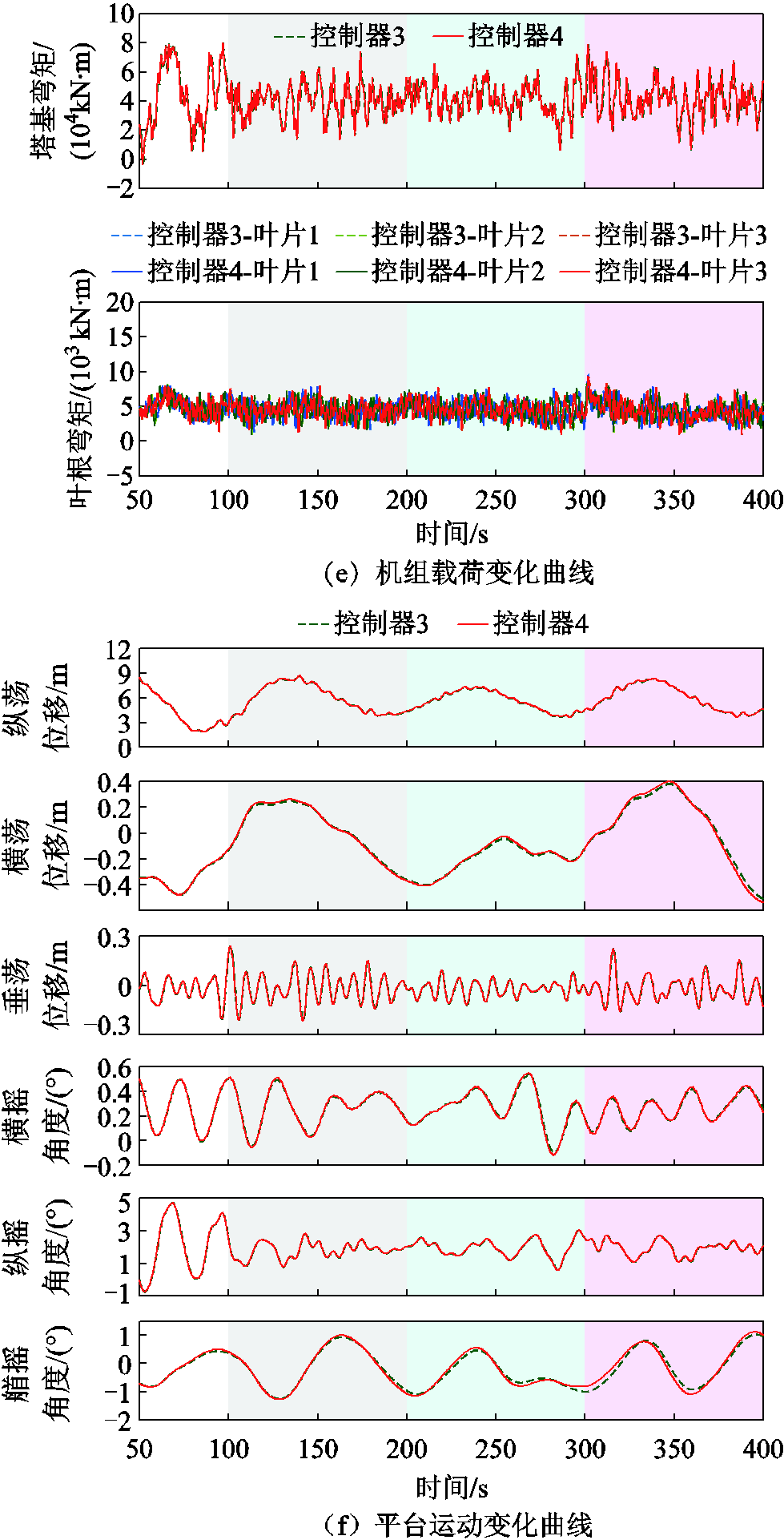
图14 湍流风叶根载荷不分离类故障下FOWT PFTIPC控制器性能及对比
Fig.14 Performance and comparison diagram of FOWT PFTIPC controller under turbulent wind-induced blade root loads and non-separation faults
表4 湍流风叶根载荷不分离类故障下各控制器性能指标
Tab.4 Quantification of performance indicators for each controller under turbulent wind-induced blade root loads and non-separation faults

参数性能指标控制器3控制器4 变桨角度/(°)平均值14.4914.49 标准差1.681.69 发电功率/kW平均值5 162.205 162.30 标准差251.73251.96 叶根载荷/(kN·m)平均值4 586.604 586.50 标准差1 202.701 215.60
(续)

参数性能指标控制器3控制器4 塔基弯矩/(kN·m)平均值4.16×1044.16×104 标准差1.33×1041.33×104 纵荡位移/m平均值5.585.58 标准差1.681.68 纵摇角度/(°)平均值1.931.93 标准差0.800.80
根据图14和表4可以看出,在本节设置的载荷工况和故障工况下,改进IPC控制器(无容错能力)的叶片1、2、3的变桨执行器在100、200、300 s时刻叶片桨距角皆同时发生跌落,随后叶片1、2、3的变桨角同时调节恢复至正常的幅值交替变化趋势,在发生跌落时叶根载荷发生较大振荡,随即恢复至正常水平。
相比之下,本文所提出的PFTIPC控制器在叶片1、2、3的变桨执行器分别于100、200、300 s时刻桨距角发生同样故障后,其控制效果与改进IPC控制器(无容错能力)基本相同,其容错控制模块输出的补偿因子低于3%,说明此时容错控制器基本不发挥补偿作用。这是由于PFTIPC控制器是基于三叶片叶根载荷与其均值的差值的平均数来进行设计补偿的,当三叶片同时发生相同故障(即三叶片健康状态相同)时,其叶根载荷变化也基本相同,并不会因发生分离而导致较大不平衡载荷,故补偿因子基本接近于1。此外,还可以看出在两种变桨控制器作用下液压变桨执行器故障对功率波动和平台六自由度运动的影响较小。
本文针对漂浮式风机负阻尼影响下的多目标变桨控制与故障容错控制需求,提出一种基于数据驱动的被动容错独立变桨控制方法。具体结论如下:
1)所改进的被动容错独立变桨控制器 PFTIPC基于PID和MFAC控制理论,均为数据驱动控制策略,无需对 FOWT 进行面向控制的复杂精细化建模及线性化过程,控制器设计及参数整定更为简单,控制性能良好。
2)改进的CPC控制策略既能在靠近额定风速区间提高漂浮式风机系统的稳定性,同时又能在远离额定风速的更高风速区间降低功率调节误差,独立变桨控制器则进一步降低了风切变带来的叶轮旋转周期内叶根不平衡循环载荷。
3)基于叶根不平衡载荷误差的无模型自适应被动容错控制策略对由各种原因所导致的不平衡叶根载荷分离类故障具有良好的故障补偿作用,同时在无故障和叶根载荷不分离类故障情况下不影响其他控制回路作用。
附 录
1. 统一变桨控制器
FOWT增益调度CPC控制器PI增益计算公式为
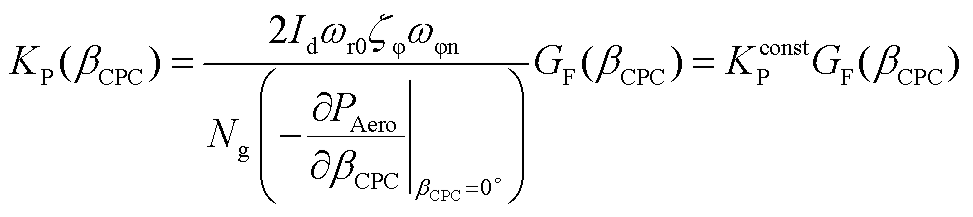 (A1)
(A1)
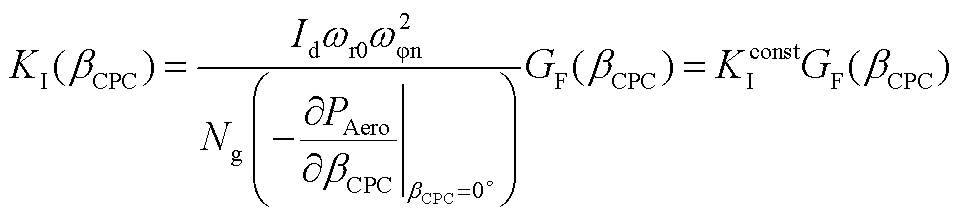 (A2)
(A2)
式中,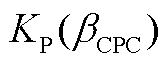 和
和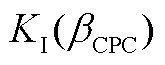 分别为CPC控制器的比例和积分增益;
分别为CPC控制器的比例和积分增益;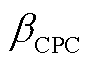 为统一变桨角;
为统一变桨角;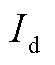 为低速轴的传动链惯性,
为低速轴的传动链惯性,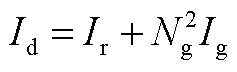 ,
,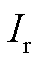 为转子惯性;
为转子惯性;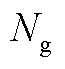 为齿轮箱增速比;
为齿轮箱增速比;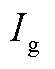 为发电机惯性;
为发电机惯性;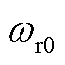 为额定转子转速;
为额定转子转速;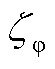 为FOWT统一变桨控制器的阻尼比;
为FOWT统一变桨控制器的阻尼比;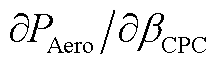 为变桨灵敏度;
为变桨灵敏度;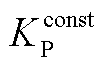 、
、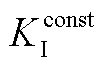 分别为变桨角为0°时的控制器比例增益和积分增益,
分别为变桨角为0°时的控制器比例增益和积分增益,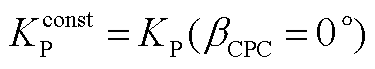 ,
, ;
;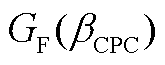 为无量纲增益调度系数,其计算公式为
为无量纲增益调度系数,其计算公式为
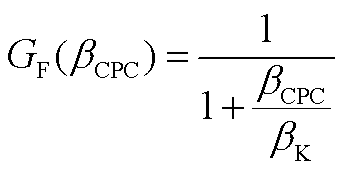 (A3)
(A3)
式中,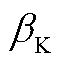 为变桨灵敏度从额定风速处的值翻了一倍的叶片桨距角,即
为变桨灵敏度从额定风速处的值翻了一倍的叶片桨距角,即
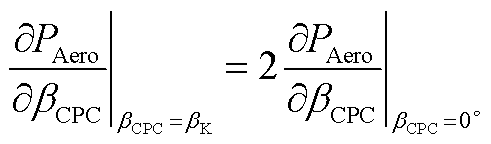 (A4)
(A4)
2. 独立变桨控制器
1)Coleman坐标变换
Coleman坐标变换基于转子方位角将三叶片叶根部载荷转换为轮毂俯仰弯矩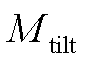 和偏航弯矩
和偏航弯矩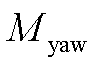 ,有
,有
 (A5)
(A5)
式中,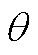 为风轮转子方位角;
为风轮转子方位角;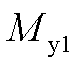 、
、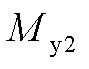 和
和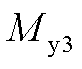 分别为测量的叶片1、2、3叶根载荷。
分别为测量的叶片1、2、3叶根载荷。
2)俯仰与偏航载荷双PI控制器设计
将滤波后的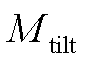 和
和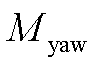 通过两个独立的PI载荷控制器可得到俯仰和偏航桨距角控制量
通过两个独立的PI载荷控制器可得到俯仰和偏航桨距角控制量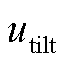 和
和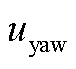 为
为
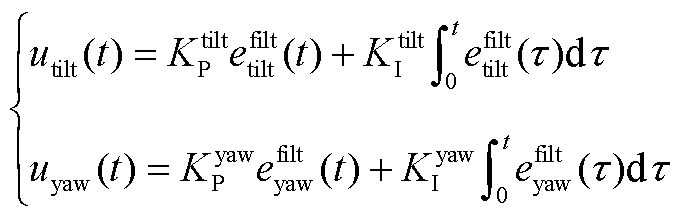 (A6)
(A6)
式中,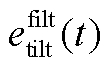 为俯仰弯矩误差,
为俯仰弯矩误差,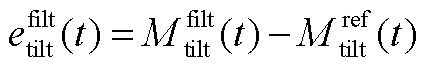 ;
;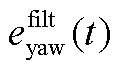 为偏航弯矩误差,
为偏航弯矩误差,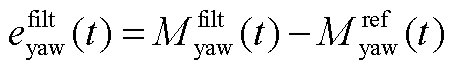 ;
;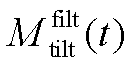 、
、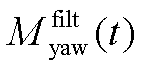 分别为滤波后的俯仰弯矩、偏航弯矩;
分别为滤波后的俯仰弯矩、偏航弯矩;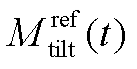 、
、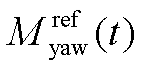 分别为给定的俯仰、偏航弯矩参考值;
分别为给定的俯仰、偏航弯矩参考值;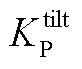 、
、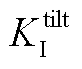 分别为俯仰弯矩PI控制的比例、积分增益;
分别为俯仰弯矩PI控制的比例、积分增益;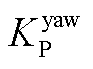 、
、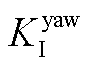 分别为偏航弯矩PI控制的比例、积分增益。
分别为偏航弯矩PI控制的比例、积分增益。
3)Coleman坐标反变换
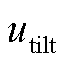 和
和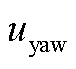 通过Coleman反变换得到每只叶片的独立变桨角度增量
通过Coleman反变换得到每只叶片的独立变桨角度增量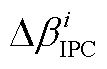 为
为
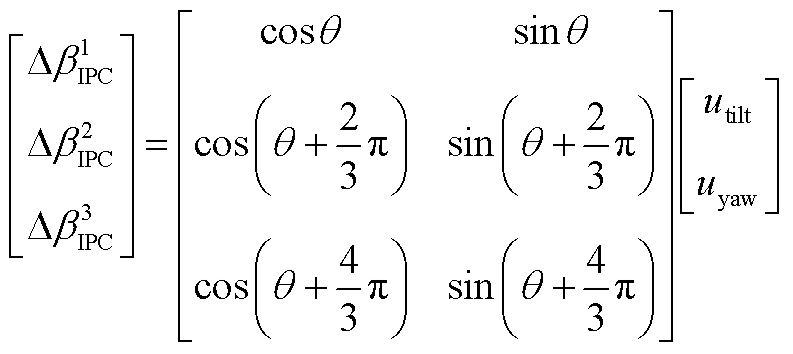 (A7)
(A7)
3. 不同故障下风机状态响应
根据标准IEC 61400—3,采用轮毂高度处平均风速为18 m/s、湍流强度为12.7%、风切变指数为0.14、风模型为IEC Kaimal谱的湍流风速和有义波高为3.061 m、峰值谱周期为8.047 s的不规则JONSWAP谱波浪作为环境载荷输入。仿真模拟NREL 5 MW半潜式FOWT叶片1的液压变桨执行器在100 s时刻发生各类故障时变桨角和叶根载荷响应。变桨控制器采用漂浮式基准IPC控制器(即基准CPC控制器+IPC控制器)(无容错功能),仿真结果如附图1所示。
4. 不同模型精度的响应对比
采用多阶跃变化风速和有义波高为3.673 m、峰值谱周期为13.376 s的不规则JONSWAP谱波浪作为环境载荷输入。NREL 5 MW半潜式FOWT风机模型、两质块非线性模型和线性变参数(Linear Parameter-Varying, LPV)模型的开环阶跃响应对比结果如附图2所示。
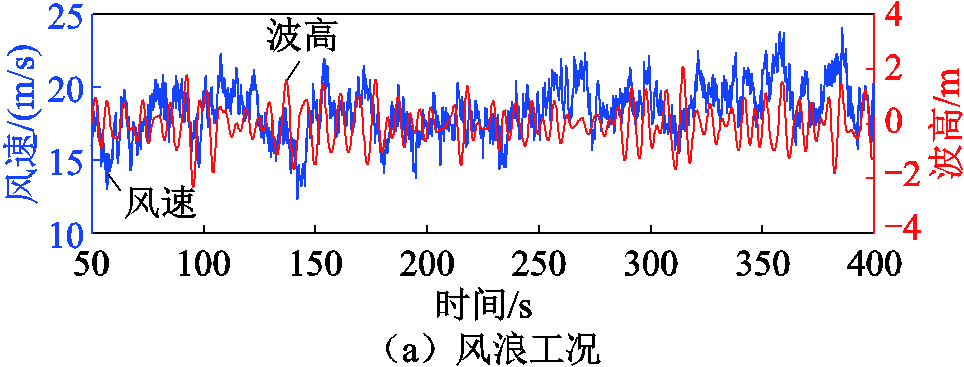
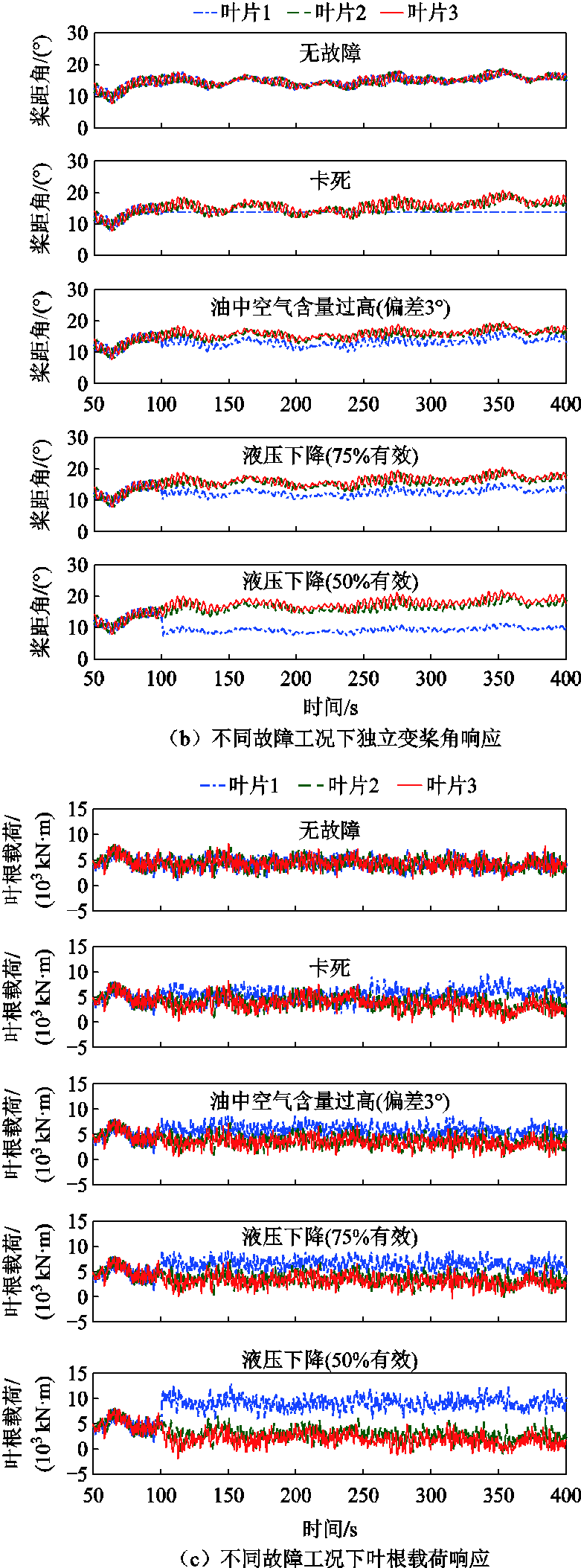
附图1 不同故障对FOWT系统的影响
App.Fig.1 The impact of different faults on FOWT system
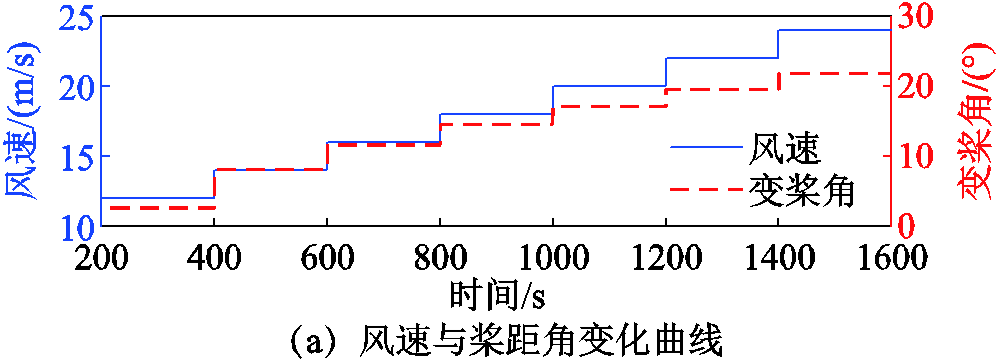
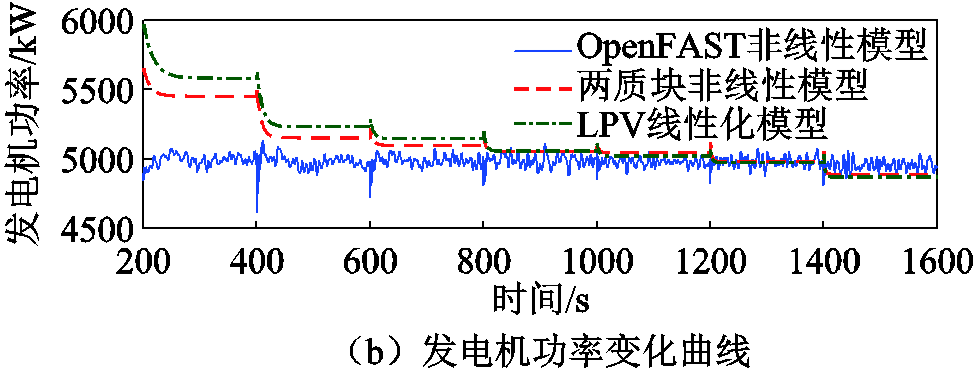
附图2 不同模型开环阶跃响应对比
App.Fig.2 Comparison diagram of open-loop step responses for different models
参考文献
[1] 潘俊良, 王明渝. 适用于大型海上风电的谐振型飞跨电容式模块化升压变换器[J]. 电工技术学报, 2024, 39(12): 3746-3760.
Pan Junliang, Wang Mingyu. Resonant flying capacitor modular boost converter for large scale offshore wind power[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3746-3760.
[2] 周腊吾, 杨彬佑, 韩兵, 等. 漂浮式风机气-水动力耦合下的独立变桨控制方法[J]. 电工技术学报, 2019, 34(17): 3607-3614.
Zhou Lawu, Yang Binyou, Han Bing, et al. The individual blade pitch control for the floating offshore wind turbines bearing the air-hydrodynamic coupling loads[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3607-3614.
[3] Ali Shah K, Meng Fantai, Li Ye, et al. A synthesis of feasible control methods for floating offshore wind turbine system dynamics[J]. Renewable and Sustainable Energy Reviews, 2021, 151: 111525.
[4] 高晨, 赵勇, 汪德良, 等. 海上风电机组电气设备状态检修技术研究现状与展望[J]. 电工技术学报, 2022, 37(增刊1): 30-42.
Gao Chen, Zhao Yong, Wang Deliang, et al. Research status and prospect of condition based maintenance technology for offshore wind turbine electrical equipment[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 30-42.
[5] Jonkman J. Influence of control on the pitch damping of a floating wind turbine[C]//46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 2008: 1306.
[6] Robertson A N, Jonkman J, Masciola M, et al. Definition of the semisubmersible floating system for Phase II of OC4[R]. National Renewable Energy Laboratory, 2014.
[7] Hu Ruiqi, Le Conghuan, Gao Zhen, et al. Implementation and evaluation of control strategies based on an open controller for a 10 MW floating wind turbine[J]. Renewable Energy, 2021, 179: 1751-1766.
[8] Fontanella A, Bayati I, Belloli M. Linear coupled model for floating wind turbine control[J]. Wind Engineering, 2018, 42(2): 115-127.
[9] Lemmer F, Yu Wei, Schlipf D, et al. Robust gain scheduling baseline controller for floating offshore wind turbines[J]. Wind Energy, 2020, 23(1): 17-30.
[10] Namik H, Stol K. Individual blade pitch control of a spar-buoy floating wind turbine[J]. IEEE Transactions on Control Systems Technology, 2014, 22(1): 214-223.
[11] Sarkar S, Fitzgerald B, Basu B. Individual blade pitch control of floating offshore wind turbines for load mitigation and power regulation[J]. IEEE Transactions on Control Systems Technology, 2021, 29(1): 305-315.
[12] 宋子秋, 冯翰宇, 余照国, 等. 基于模型预测控制的半潜漂浮式风机协调控制方法研究[J]. 中国电机工程学报, 2022, 42(12): 4330-4339.
Song Ziqiu, Feng Hanyu, Yu Zhaoguo, et al. Coordinated control of semi-submersible floating turbine with model predictive control strategy[J]. Proceedings of the CSEE, 2022, 42(12): 4330-4339.
[13] Wakui T, Yoshimura M, Yokoyama R. Multiple-feedback control of power output and platform pitching motion for a floating offshore wind turbine-generator system[J]. Energy, 2017, 141: 563-578.
[14] Qi Liangwen, Cao Huijing, Zhang Yinan, et al. Data-driven control of the coupled loads for floating wind turbine systems based on deformable trailing edge flaps[J]. Ocean Engineering, 2022, 250: 111083.
[15] 张艳峰, 杨锡运, 徐恩慧. 漂浮式海上风电机组无模型自适应容错控制策略[J]. 太阳能学报, 2024, 45(10): 467-477.
Zhang Yanfeng, Yang Xiyun, Xu Enhui. Model-free adaptive fault-tolerant control strategy for floating offshore wind turbines[J]. Acta Energiae Solaris Sinica, 2024, 45(10): 467-477.
[16] Mazare M, Taghizadeh M, Ghaf-Ghanbari P. Pitch actuator fault-tolerant control of wind turbines based on time delay control and disturbance observer[J]. Ocean Engineering, 2021, 238: 109724.
[17] Badihi H, Zhang Youmin, Pillay P, et al. Fault-tolerant individual pitch control for load mitigation in wind turbines with actuator faults[J]. IEEE Transactions on Industrial Electronics, 2021, 68(1): 532-543.
[18] Jonkman J. The new modularization framework for the FAST wind turbine CAE tool[C]//51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Grapevine (Dallas/Ft. Worth Region), Texas, 2013: 202.
[19] Jonkman J, Butterfield S, Musial W, et al. Definition of a 5-MW reference wind turbine for offshore system development[J]. Contract, 2009(2): 1-75.
[20] 王磊, 高瑞贞, 陈柳, 等. 风电系统故障诊断与容错控制[M]. 北京: 科学出版社, 2016.
[21] Odgaard P F, Stoustrup J, Kinnaert M. Fault tolerant control of wind turbines–a benchmark model[J]. IFAC Proceedings Volumes, 2009, 42(8): 155-160.
[22] Jonkman J. Calculation of negative damping in pitch mode of OC4 semi-5MW[EB/OL]. (2024-05-09)[2024-05- 22]. https://github.com/OpenFAST/openfast/discussions/ 2192.
[23] 张超, 文云峰, 黎婧娴, 等. 考虑抑制二次跌落的风电自适应频率支撑控制策略及其参数整定[J/OL].电工技术学报, 2025: 1-16. [2025-06-10]. https://link. cnki.net/doi/10.19595/j.cnki.1000-6753.tces.250393.
Zhang Chao, Wen Yunfeng, Li Jingxian, et al. An adaptive frequency support control strategy and parameter configuration method of wind power considering the mitigation secondary drop[J/OL]. Transactions of China Electrotechnical Society, 2025: 1-16. [2025-06-10]. https://link.cnki.net/doi/10.19595/j. cnki.1000-6753.tces.250393.DOI:10.19595/j.cnki.1000- 6753.tces.250393.
[24] 王鑫, 杨德健. 基于变系数PI控制的双馈风电机组自适应转速恢复策略[J]. 电工技术学报, 2023, 38(15): 4120-4129.
Wang Xin, Yang Dejian. Adaptive speed recovery strategy of doubly-fed induction generator based on variable PI control coefficient[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4120-4129.
[25] 兰飞, 潘益丰, 时萌, 等. 双馈风电机组变系数虚拟惯量优化控制[J]. 电力系统自动化, 2019, 43(12): 51-59.
Lan Fei, Pan Yifeng, Shi Meng, et al. Optimal variable-coefficient virtual inertia control for DFIG-based wind turbines[J]. Automation of Electric Power Systems, 2019, 43(12): 51-59.
[26] 侯忠生, 金尚泰. 无模型自适应控制: 理论与应用[M]. 北京: 科学出版社, 2013.
[27] 梁栋炀, 宋子秋, 刘亚娟. 基于LPV-MPC的风电机组功率-载荷协调控制策略[J]. 可再生能源, 2024, 42(1): 38-44.
Liang Dongyang, Song Ziqiu, Liu Yajuan. Coordinated power-load control strategy for wind turbine based on LPV-MPC[J]. Renewable Energy Resources, 2024, 42(1): 38-44.
Abstract Pitch control is related to the stable and efficient power generation and overall safety of floating offshore wind turbine (FOWT). However, the pitch control technology of FOWT faces several challenges such as difficulty in modeling, difficulty in coordinating power-load-motion multi-objective control under wind-wave coupling inputs, and the potential increase in the failure rate of pitch actuators caused by individual pitch mechanism and high humidity-salt environment. To address these issues, this paper proposes a data-driven passive fault-tolerant individual pitch control (PFTIPC) method for FOWT.
Firstly, the completely nonlinear 5 MW semi-submersible FOWT of National Renewable Energy Laboratory (NREL) is used as the reference model. The normal and fault model of hydraulic pitch actuator is established. Then, based on the damping characteristics of the platform-pitch mode of the FOWT, the traditional collective pitch controller (CPC) is improved to enhance power regulation capability. And individual pitch controller (IPC) is designed to reduce the imbalanced blade root cyclic load. On this basis, further analysis is conducted on the sensitivity of the fault pitch actuators, and a model free adaptive passive fault-tolerant control strategy (MFAC-FTC) based on blade root imbalance-separation load is proposed, which added fault-tolerant control function to the traditional pitch control loop. Finally, multi-condition simulation tests are conducted on the OpenFAST and Simulink joint simulation platform.
Simulation results on the different working conditions illustrate that, the data-driven control method has significant advantages in nonlinear FOWT pitch control. Under step wind and gust wind conditions with no faults in the three pitch actuators, improved CPC enhances system stability and power regulation capability in the range above the rated wind speed, and IPC effectively reduces imbalanced cyclic load at the blade root. The output of the fault-tolerant controller loop is close to 1, indicating that the fault-tolerant controller is basically ineffective and doesn’t affect the CPC and IPC loop without faults for pitch actuators. Under turbulent wind conditions where three pitch actuators experience varying degrees of failure, the fault-tolerant controller outputs corresponding compensation factors based on the degree of failure, avoiding root and tower load oscillations. Under turbulent wind conditions where three pitch actuators experience the same degree of failure, the fault-tolerant controller outputs close to 1. And at this situation, the IPC loop performs adjustment actions.
The following conclusions can be drawn from the simulation analysis: (1) The improved passive fault-tolerant individual pitch controller (PFTIPC) is based on data-driven control theory, which does not require complex and refined modeling and linearization processes for FOWT. The controller design and parameter tuning are simpler, and the control performance is good. (2) The improved CPC control strategy can improve the stability of the FOWT near the rated wind speed range, and reduce power regulation errors in higher wind speed ranges far from the rated wind speed. The IPC controller further reduces the imbalanced cyclic load at the blade root. (3) The model-free adaptive passive fault-tolerant control strategy based on blade root imbalanced load error has a good fault compensation effect on imbalanced blade-root load separation faults. At the same time, the model-free adaptive passive fault-tolerant control strategy doesn’t affect other control loop functions for no fault working condition and blade-root load non-separation fault working condition.
keywords:Floating offshore wind turbine, negative damping, data-driven control, individual pitch control, fault-tolerant control
中图分类号:TM614
DOI: 10.19595/j.cnki.1000-6753.tces.241566
国家自然科学基金(62373148)和国家重点研发计划子课题(2020 YFB1506601)资助项目。
收稿日期 2024-09-02
改稿日期 2025-07-22
梁栋炀 男,1998年生,硕士,工程师,研究方向为新能源发电与并网控制技术。E-mail:ldyang9828@163.com
石 鑫 男,1988年生,博士,副研究员,研究方向为新能源发电与并网控制、人工智能在电力系统中的应用等。E-mail:xinshi_bjcy@163.com(通信作者)
(编辑 赫 蕾)