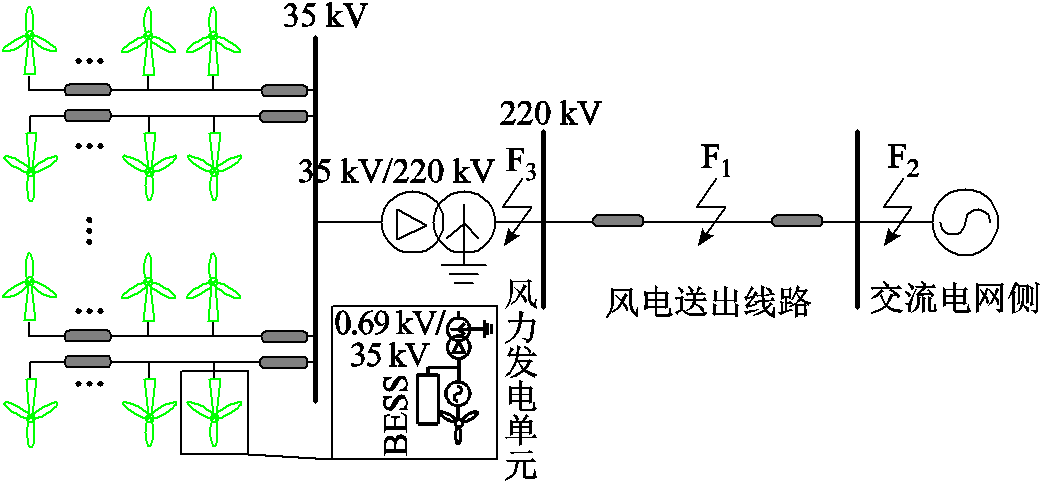
图1 风场集中送出线路拓扑结构
Fig.1 Schematic diagram of wind power outgoing line
摘要 双馈风机受换流器控制策略的影响,其故障电流呈现幅值受限、相位受控等特点,使得基于同步电源电流特性的传统纵联差动保护性能下降。为此,该文提出一种基于故障区域拟合系数的电流差动保护方案。首先,根据线路两端电流幅值系数构造虚拟制动电流,利用系统侧及风场侧电流相量的复数域关系建立动作边界模型,得出在区内外故障下故障点在复平面的分布特征;其次,推导了边界模型与过渡电阻及制动系数的偏微分方程,通过拟合暂态时域故障点下的故障边界自适应调整保护判据;最后,基于实时数字仿真器进行验证,结果表明所提方案可在暂态时域内自适应调整动作方程,耐受过渡电阻能力可达300 Ω,其暂态时域内的灵敏度显著高于传统纵联差动保护,并对转换性故障具有更强的适应性。
关键词:风电场送出系统 电流差动保护 暂态时域 故障边界模型 故障区域拟合系数
双馈风力发电机(Doubly Fed Induction Generator, DFIG)具有性能高、成本低、运行稳定及技术成熟等优点,广泛应用于陆上风电场系统[1-5]。然而,DFIG的故障特征取决于换流器的控制策略及响应特性[6],导致双馈风场侧故障电流具有幅值受限和相位受控等特点[7-11]。纵联差动保护通常作为新能源送出系统中的主保护[12-13],风场侧故障电流特征的不确定性会导致其灵敏性、可靠性下降,甚至可能引起保护装置拒动或误跳闸,因此研究适用于DFIG接入的风电场送出线路纵联差动保护新原理具有重要意义。
纵联差动保护仅利用区内电流相量平衡状态进行整定,对单一测量值的误差敏感度较低,具有受非工频分量影响较小的优点,因此已有许多学者提出了适用于风电场送出线路的纵联差动保护新原理。文献[14]提出了利用正序电流自适应调整阈值的差动保护方案,减小了风电“T”型接入对传统电流差动保护的影响。文献[15]利用电流幅值比构造虚拟电流,减轻了DFIG侧弱馈性造成的差动死区问题,但耐过渡电阻能力受限。文献[16-18]基于故障序网络进行保护整定,提高了保护在故障稳态下的适用性。然而,上述方法仅考虑DFIG故障稳态下的输出特性,考虑到纵联差动保护可能在暂态响应阶段就识别故障,暂态时域内电流的波动将导致上述方法的性能下降。
针对差动保护性能下降的问题,诸多研究针对双馈风电场的故障特征提出了改进的纵联保护方法。文献[19]提出了一种基于时域信息的距离纵联保护,减少了距离纵联保护受频偏特性以及过渡电阻的影响,但未考虑非工频分量对工频测量阻抗的影响。文献[20-22]针对风电场接入下基于工频量的传统纵联保护性能下降的问题,提出了基于波形相似度的纵联保护。文献[23]提出了基于5G通信的纵联保护,显著减弱了异常数据对波形相似度的判断,但增加了丢包率和通信费用。文献[24-25]利用模型对比的天然选择性,提出了基于状态估计的纵联保护,减少了对双端量测同步性的依赖。上述方案虽无需考虑动作边界适用性问题,但是对通信要求高,需要额外硬件支撑,保护建设难度较大。
综上所述,现有风场送出线路保护易受过渡电阻、电流暂态波动等因素干扰,且大多需要引入额外变量或增加通信通道建设复杂度。本文利用故障后的暂态电流信息,提出了一种基于故障区域拟合系数的纵联差动保护方案。首先引入虚拟制动电流,消除DFIG侧电流弱馈性造成的差动死区问题。其次,基于含虚拟电流的差动方程,构建了可以表征暂态电流波动特征的动作边界模型,并通过边界模型分析了区内外故障复平面内故障点的分布特征。然后,利用偏微分方程推导了边界模型基本参数随制动系数、双端电流幅值比的变化关系。在此基础上,利用暂态故障点拟合曲线与边界圆的临界相切关系,得到了关于自适应拟合系数的求解方程,并基于此调整差动方程的制动水平,将故障点锁定为动作区域内部。最后,在实时数字仿真器(Real Time Digital Simulation, RTDS)中验证了所提保护方案在各类故障工况下的有效性。
双馈风场集中送出系统通过汇集风电机组的电能,将其输送到风电场升压变电站,其系统拓扑结构如图1所示。

图1 风场集中送出线路拓扑结构
Fig.1 Schematic diagram of wind power outgoing line
在实际工程应用中,风电机组的出口电压一般为0.69 kV,与配套的升压变压器构成一个发电变电单元。先通过变压器将电压升至35 kV,并汇总至35 kV母线,然后经主变压器提高至220 kV,并通过送出线路接入主网。
DFIG定子绕组直接连接定频三相电网,转子绕组则通过双向背靠背换流器进行控制。其中,换流器可实现与电网的双向功率交换。
风电机组在交流系统并网运行时,其整体故障输出特性主要受限幅控制、低电压穿越控制(Low Voltage Ride Through, LVRT)的影响。其中,限幅控制主要影响DFIG的输出电流幅值,LVRT主要影响DFIG的输出电流相位。
当DFIG侧发生近距离故障时,为保证电力电子器件不因电流热效应而损坏,往往采用限幅系数来限制其输出电流的幅值。限幅环节往往位于低电压穿越控制之前,DFIG的限流控制框图如图2所示。

图2 DFIG限流控制框图
Fig.2 The diagram of current limiter
图2中限流控制可表示为将三相电流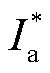 、
、 、
、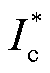 输入FFT模块得到幅值最大值,根据式(1)获得限幅系数。
输入FFT模块得到幅值最大值,根据式(1)获得限幅系数。
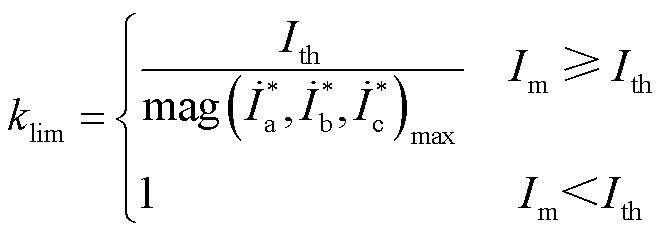 (1)
(1)
式中,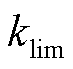 为限幅系数,
为限幅系数,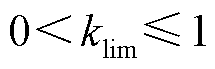 ,
,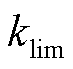 越小表示故障越严重;
越小表示故障越严重;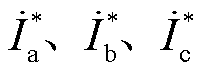 分别为a、b、c三相电流;
分别为a、b、c三相电流;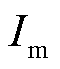 为电流幅值的最大值;
为电流幅值的最大值;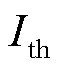 为电流阈值;mag(·)max为取幅值最大值。
为电流阈值;mag(·)max为取幅值最大值。
限幅控制位于DFIG转子换流器侧,由于定子电流与转子电流之间存在电磁耦合关系,换流器对转子电流的限制也会间接限制定子电流的幅值。因此DFIG侧输出的故障电流受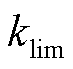 限制,而主网侧故障电流很大,将导致故障后DFIG侧电流呈现明显的弱馈性。
限制,而主网侧故障电流很大,将导致故障后DFIG侧电流呈现明显的弱馈性。
此外,根据新能源并网技术的低电压穿越控制标准[26-27],要求DFIG在故障时能为电网提供足够多的无功支持。因此,故障后DFIG转子侧的d、q轴电流参考值满足式(2)~式(4)。
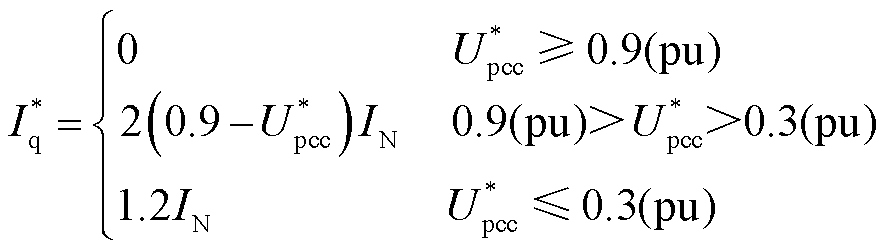 (2)
(2)
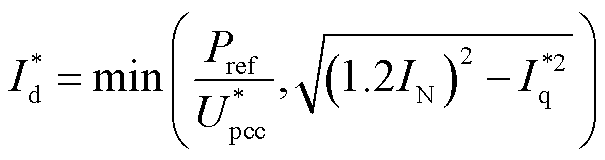 (3)
(3)
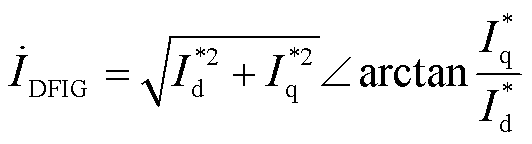 (4)
(4)
式中,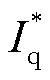 和
和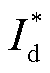 分别为DFIG的有功参考电流和无功参考电流;
分别为DFIG的有功参考电流和无功参考电流;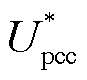 为公共并网点(Point of Common Coupling, PCC)的电压;
为公共并网点(Point of Common Coupling, PCC)的电压;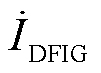 为DFIG侧电流;
为DFIG侧电流;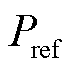 为有功功率参考值;
为有功功率参考值;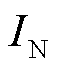 为DFIG额定运行电流。
为DFIG额定运行电流。
在低电压穿越过程中,DFIG不能按照正常运行时的标准输出电流。根据式(2)~式(4),低电压穿越过程中DFIG输出电流分量的变化曲线如图3所示。
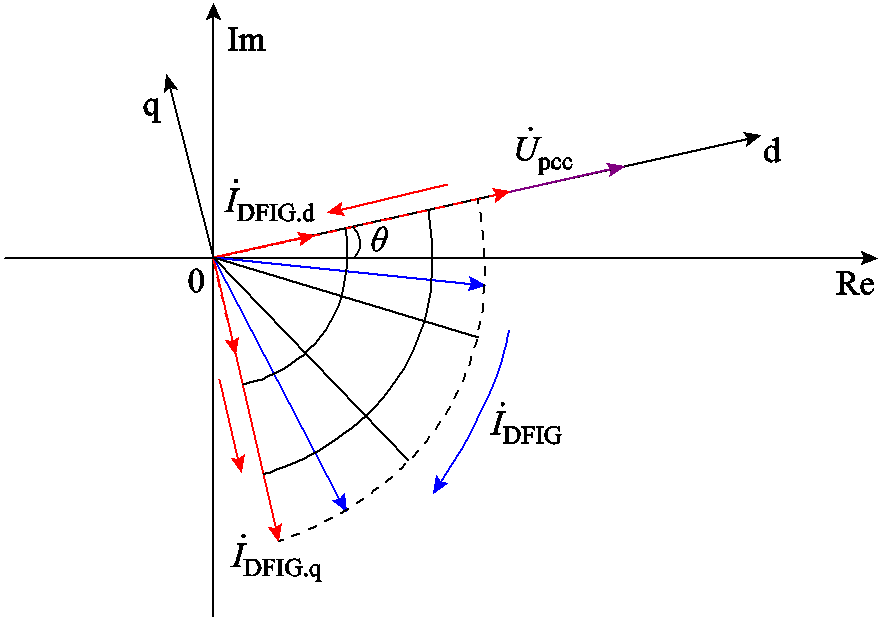
图3 LVRT过程中DFIG输出电流的变化曲线
Fig.3 The variation of the DFIG current during the LVRT
如图3所示,极端工况下相位的变化情况为:故障发生前,DFIG处于单位功率因数状态,只产生有功功率,电流只含d轴分量。当PCC电压降至30%以下时,DFIG产生的电流仅包含q轴分量。因此,故障电流在DFIG侧的相位将移动90°。
考虑到电流参考方向和电流相位的受控程度,即使未发生非高阻故障,故障馈线两侧电流的相位差也可能超过90°,即呈现“高阻相位特征前移性”。
在110 kV及以上系统中,往往配置电流差动保护作为主保护,同时配合光纤通信以提高速动性及可靠性。当大规模风电接入系统后,DFIG故障特性会影响线路两侧的电流幅值和相位关系,对依赖电流相量进行判定的电流差动保护构成挑战。
传统电流差动保护的动作方程为
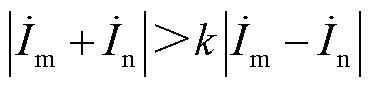 (5)
(5)
式中, 和
和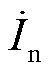 分别为故障馈线两侧的电流;k为制动系数。
分别为故障馈线两侧的电流;k为制动系数。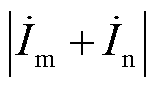 为动作量,
为动作量,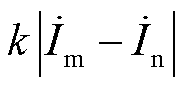 为制动量。
为制动量。
当风场侧电流表现为弱馈性时,电流差动保护的动作特性如图4所示。
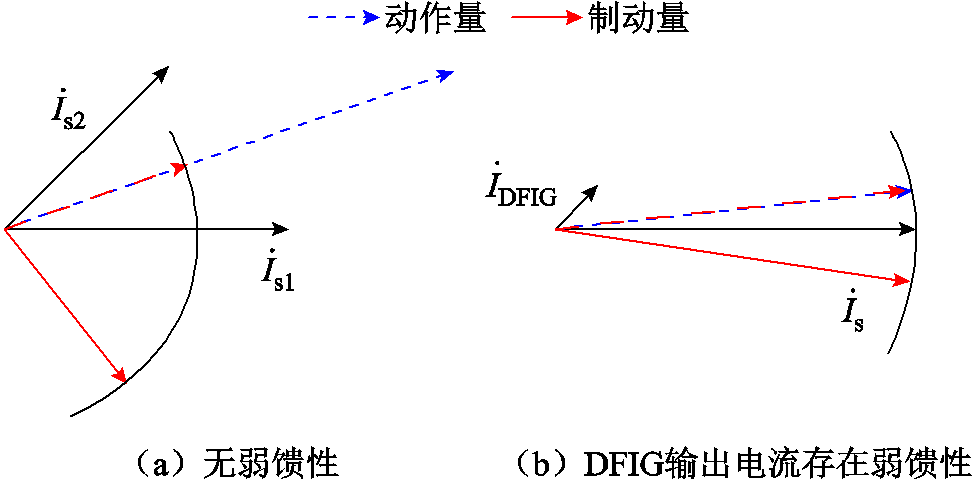
图4 弱馈性对电流差动保护动作特性的影响
Fig.4 The influence of weak infeed on the operating characteristics of current differential protection
如图4所示,当线路两侧均为传统同步电源时,保护能够可靠动作;当DFIG接入使得故障线路一侧电流表现为弱馈性时,制动量与动作量差值较小,在这种情况下,保护存在拒动风险。
当故障电流在高阻相位特征下时,保护的动作特性如图5所示。
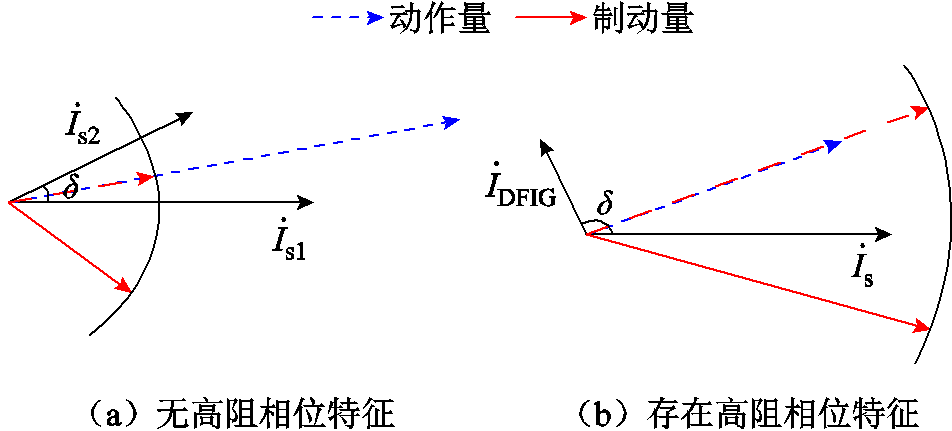
图5 “高阻相位特征”对电流差动保护动作特性的影响
Fig.5 Operating characteristic when the current exhibits phase characteristics under high-resistance faults
如图5所示,DFIG接入后,风场侧电流的相位控制对制动电流的幅值影响较大,在“高阻相位特征”下,制动量将大于动作量,保护无法区分故障,传统电流差动保护存在保护死区。
引入虚拟制动电流的差动保护故障判据式(6)。
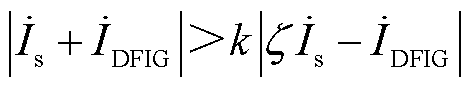 (6)
(6)
式中,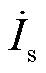 为系统侧电流;
为系统侧电流;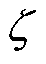 为电流幅值系数,
为电流幅值系数,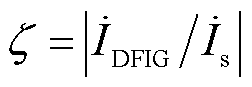 。
。
引入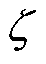 后,纵联差动保护的动作特性如图6所示。
后,纵联差动保护的动作特性如图6所示。
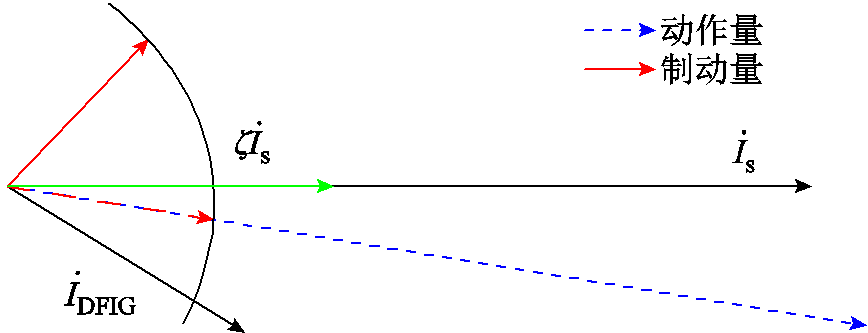
图6 引入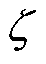 后保护的动作特性
后保护的动作特性
Fig.6 Operating characteristic after introducing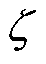
由式(6)附加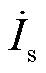 与
与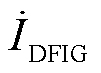 的关系为
的关系为
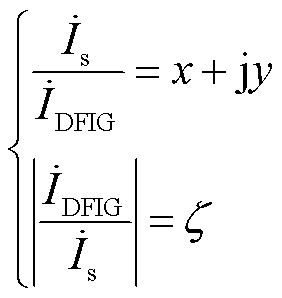 (7)
(7)
将式(7)代入式(6),使方程转入复平面,可得
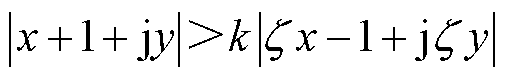 (8)
(8)
对式(8)两侧取幅值可得
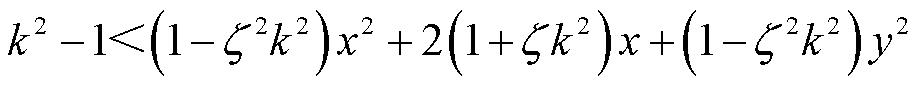 (9)
(9)
将式(9)两边同时除以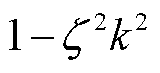 ,式(6)的动作边界模型可表示为
,式(6)的动作边界模型可表示为
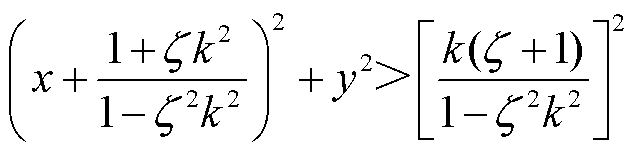 (10)
(10)
式中,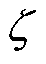 的取值范围为0~1,
的取值范围为0~1,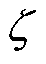 的取值与故障位置和故障类型有关。同时,边界模型的圆心和半径为
的取值与故障位置和故障类型有关。同时,边界模型的圆心和半径为
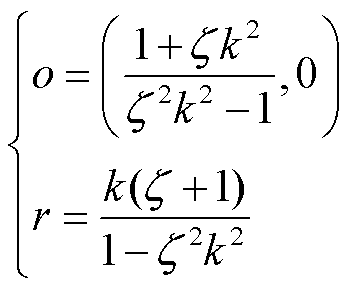 (11)
(11)
式中,o为动作边界圆的圆心;r为半径。
定义圆心到原点的距离d为
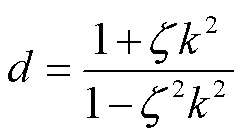 (12)
(12)
分别令d和r对k和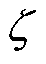 求偏导,可得
求偏导,可得
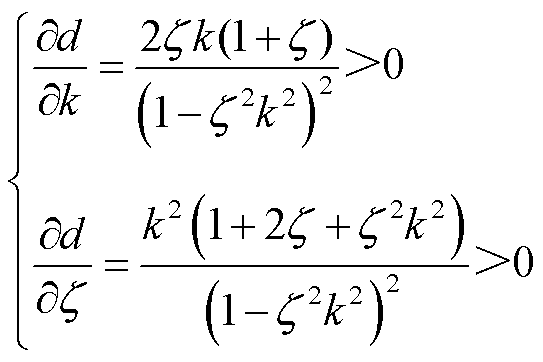 (13)
(13)
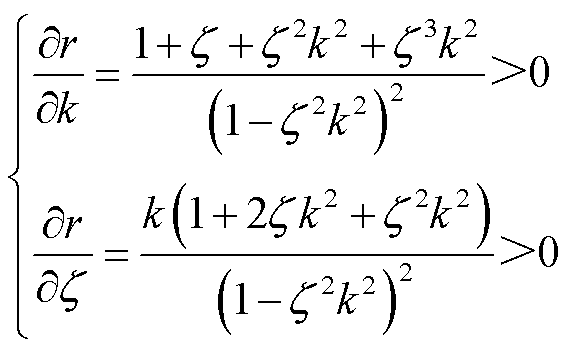 (14)
(14)
由式(13)和式(14)可知,d和r随着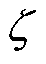 和k的增大而增大。为进一步获取边界模型的精确变化范围,令
和k的增大而增大。为进一步获取边界模型的精确变化范围,令
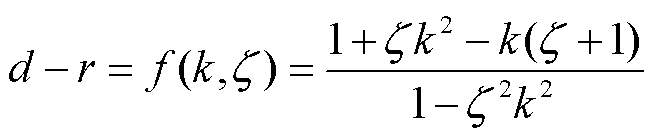 (15)
(15)
由式(15)可得d-r随k和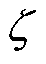 的变化曲线如图7所示。由图7可知,在d和r随
的变化曲线如图7所示。由图7可知,在d和r随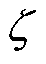 和k的增大而增大的过程中,d始终大于r,动作边界仅在复平面第二、三象限变化。保护动作边界模型如图8所示。正常运行以及区外故障时,故障点位于制动区域内部,保护不会误动。
和k的增大而增大的过程中,d始终大于r,动作边界仅在复平面第二、三象限变化。保护动作边界模型如图8所示。正常运行以及区外故障时,故障点位于制动区域内部,保护不会误动。
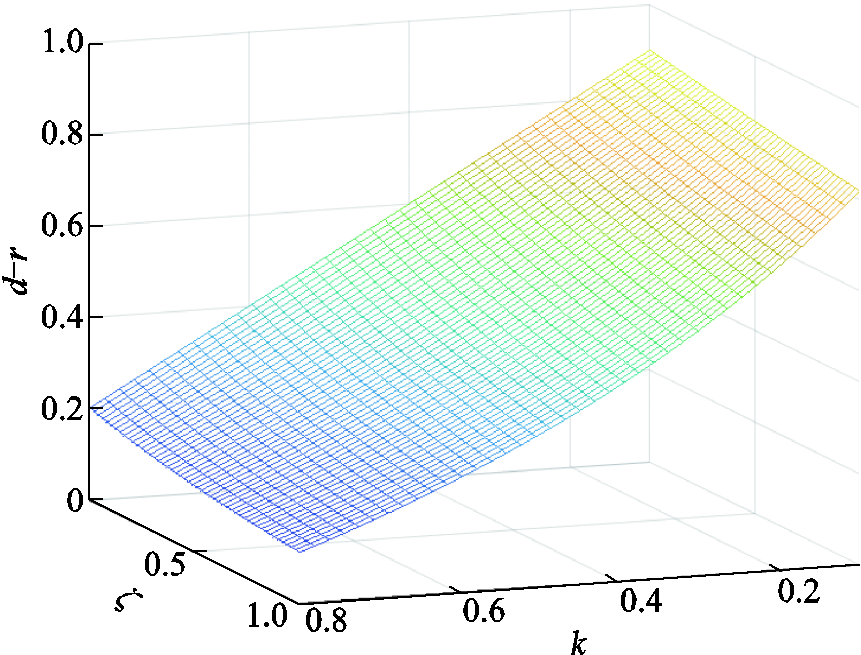
图7 d-r取值范围
Fig.7 The variation curves of d-r
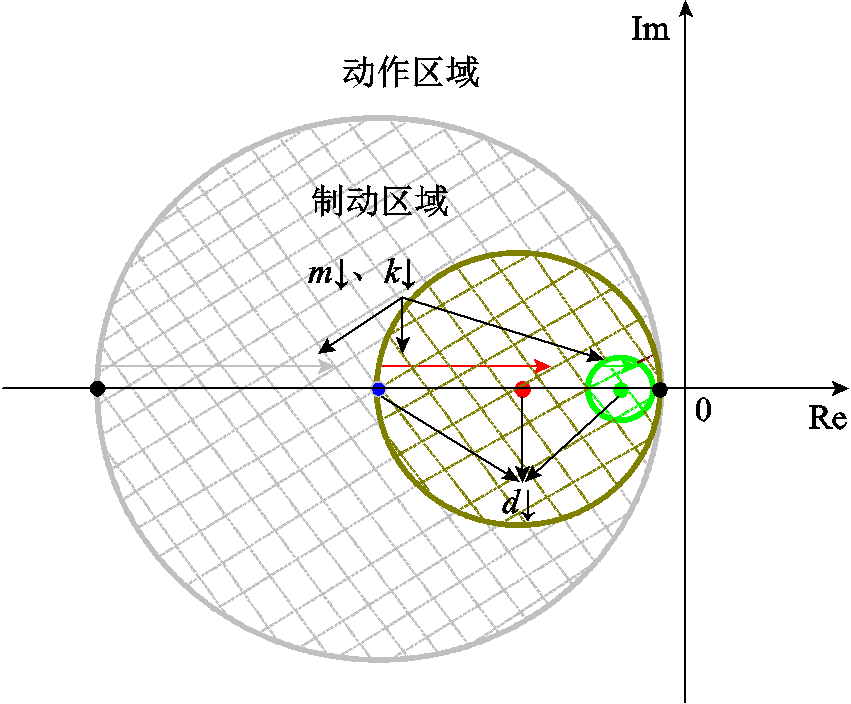
图8 保护动作边界模型
Fig.8 Operating boundary model of the scheme
基于动作边界模型随参数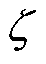 、k的变化趋势,本节将根据不同区内故障工况下故障点与边界圆的位置关系,对制动系数k进行自适应整定。
、k的变化趋势,本节将根据不同区内故障工况下故障点与边界圆的位置关系,对制动系数k进行自适应整定。
当故障电阻升高时,线路两侧电流参考相位差增大,故障点将进入第二象限,在暂态波动的影响下临界故障点易落入非动作区,在该类工况下故障点分布区域如图9所示。
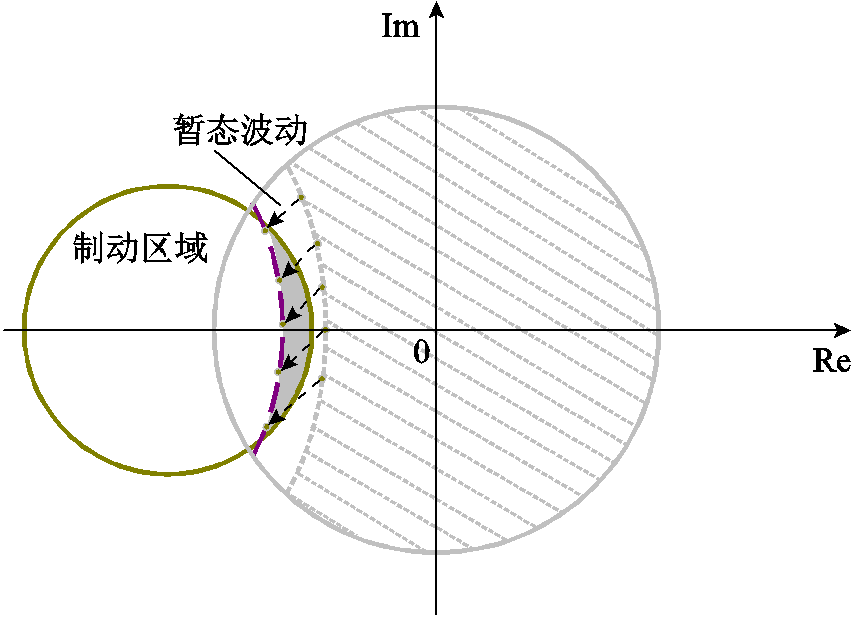
图9 故障点分布区域
Fig.9 The distribution area of fault point
由于电感等非线性元件的存在,系统无法从正常运行状态瞬间过渡到故障稳态状态,两种稳态时域之间存在暂态响应过程,而暂态响应过程中电流相位会产生波动。如图9所示,故障点在动作边界外的临界区域时,易在相位暂态波动的影响下形成保护盲区。
为避免所检测故障点进入保护死区内,根据线路两侧故障电流信息自适应调整保护判据,临界故障关系如图10所示。
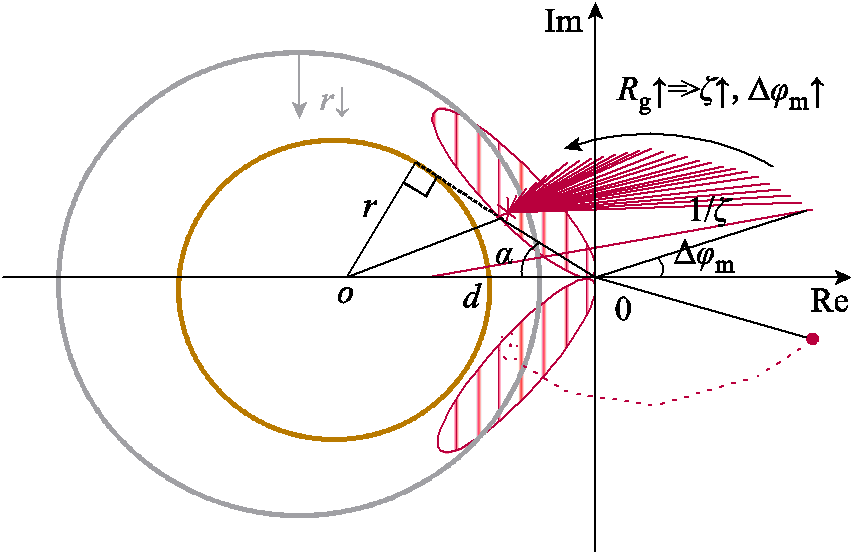
图10 临界故障关系
Fig.10 The critical positional relationship
图10中,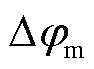 为故障点极角,表示故障线路两侧电流相位差。当故障电阻升高时,线路两侧电流幅值差减小,相位差增大,故障点由第一、四象限向第二、三象限偏移,当故障点落入制动区域内部时,保护产生死区。通过引入一个额外的拟合系数,使故障边界圆与故障点拟合曲线相切,关系式为
为故障点极角,表示故障线路两侧电流相位差。当故障电阻升高时,线路两侧电流幅值差减小,相位差增大,故障点由第一、四象限向第二、三象限偏移,当故障点落入制动区域内部时,保护产生死区。通过引入一个额外的拟合系数,使故障边界圆与故障点拟合曲线相切,关系式为
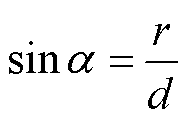 (16)
(16)
将式(11)、式(12)代入式(16)可得
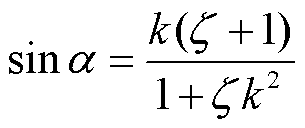 (17)
(17)
 (18)
(18)
通过求解方程(18),可得附加拟合系数为
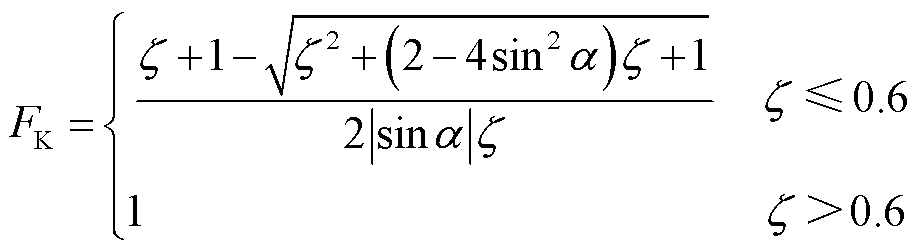 (19)
(19)
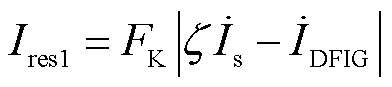 (20)
(20)
式中,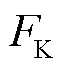 为故障区域拟合系数;
为故障区域拟合系数;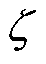 的阈值为0.6。
的阈值为0.6。
正常运行时,由于线路分布电容吸收电容电流导致系统侧电流幅值高于风场侧,而区外故障时由于电流升高以及电容电流的释放,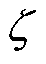 会高于阈值,因此利用设定
会高于阈值,因此利用设定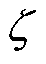 阈值来判断
阈值来判断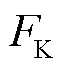 是否启动,以此避免区外故障下保护误动作。
是否启动,以此避免区外故障下保护误动作。
由于在系统侧发生区外故障后,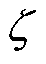 可能在电流暂态波动下低于阈值,因此在该工况下,同样需要判据来增加暂态时域内保护的可靠性,因此构造辅助制动电流为
可能在电流暂态波动下低于阈值,因此在该工况下,同样需要判据来增加暂态时域内保护的可靠性,因此构造辅助制动电流为
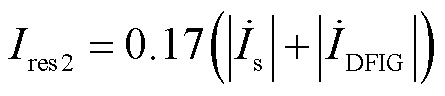 (21)
(21)
在引入辅助判据后,联合制动判据可表示为
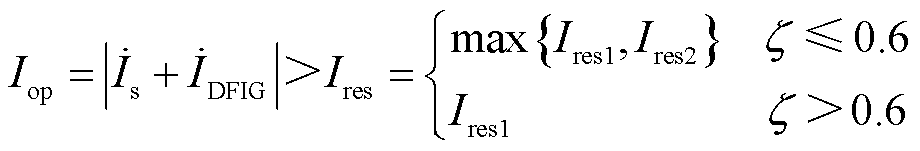 (22)
(22)
由式(22)可知,方案可通过协同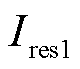 和
和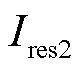 ,使FK与
,使FK与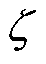 共同确保方案在区内故障时灵敏动作,以及区外故障时可靠不动作。
共同确保方案在区内故障时灵敏动作,以及区外故障时可靠不动作。
所提保护方案的流程如图11所示。
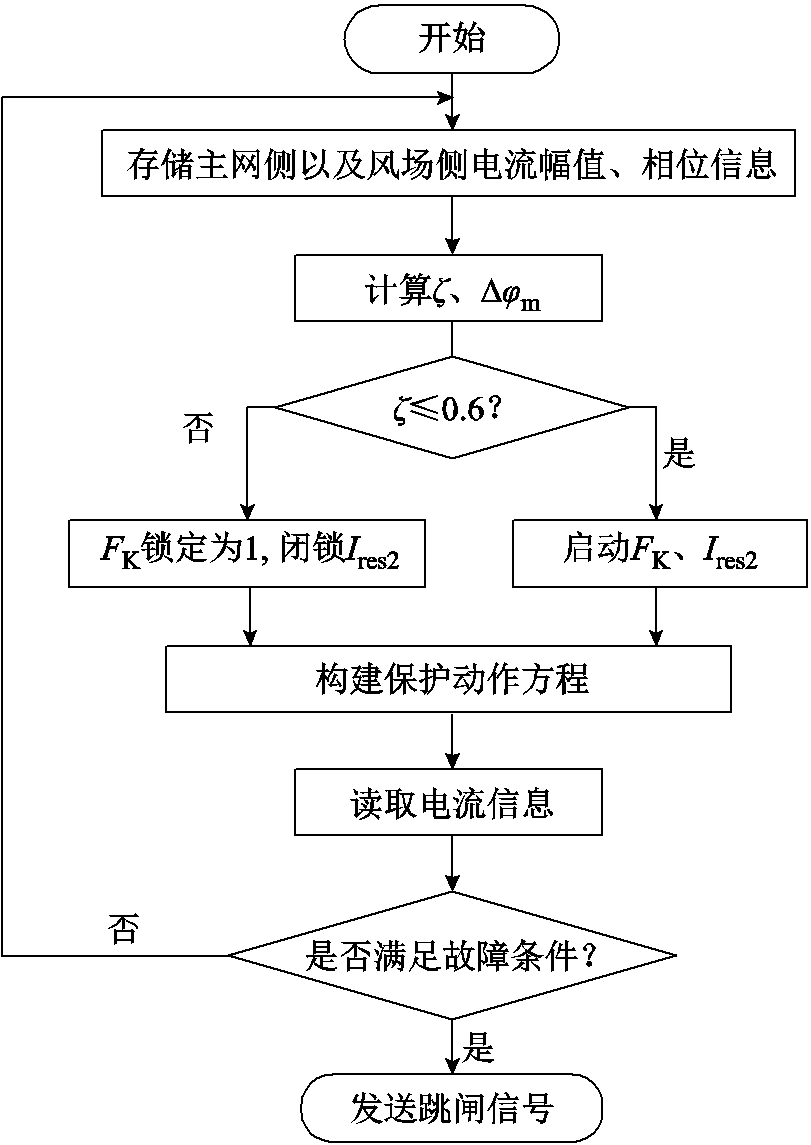
图11 所提保护方案流程
Fig.11 Flow chart of the proposed scheme
保护启动后,分别提取送出线路系统侧及风场侧的电流幅值及相位数据,并计算 、
、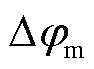 ,基于此生成虚拟制动电流。若
,基于此生成虚拟制动电流。若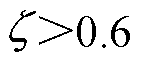 ,则将FK锁定为1,闭锁Ires2;若
,则将FK锁定为1,闭锁Ires2;若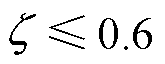 ,则启动FK、Ires2。根据式(19)生成故障区域拟合系数。若送出线路两侧量测数据满足式(22),即自适应电流差动保护方程,则保护判定为区内故障,此时继电器发出跳闸信号;否则,判定为非故障或区外故障,保护复归。
,则启动FK、Ires2。根据式(19)生成故障区域拟合系数。若送出线路两侧量测数据满足式(22),即自适应电流差动保护方程,则保护判定为区内故障,此时继电器发出跳闸信号;否则,判定为非故障或区外故障,保护复归。
为验证本方案在暂态时域的可靠性以及在不同故障情况下的适应性,在RTDS中搭建如图1所示的风电场送出系统模型。单个风电机组的额定容量以及额定电压分别为5 MW和0.69 kV,风电场总容量为75 MW。它通过35 kV/220 kV升压变压器连接到220 kV母线,并通过200 km的单回路线路输送至主网。主变压器的容量为200 MV·A,其阻抗电压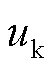 %为10.5%。
%为10.5%。
设置在送出线路50%处发生BC两相短路故障,设置故障电阻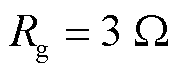 ,故障后风场侧以及主网侧的电流波形变化曲线如图12所示。
,故障后风场侧以及主网侧的电流波形变化曲线如图12所示。
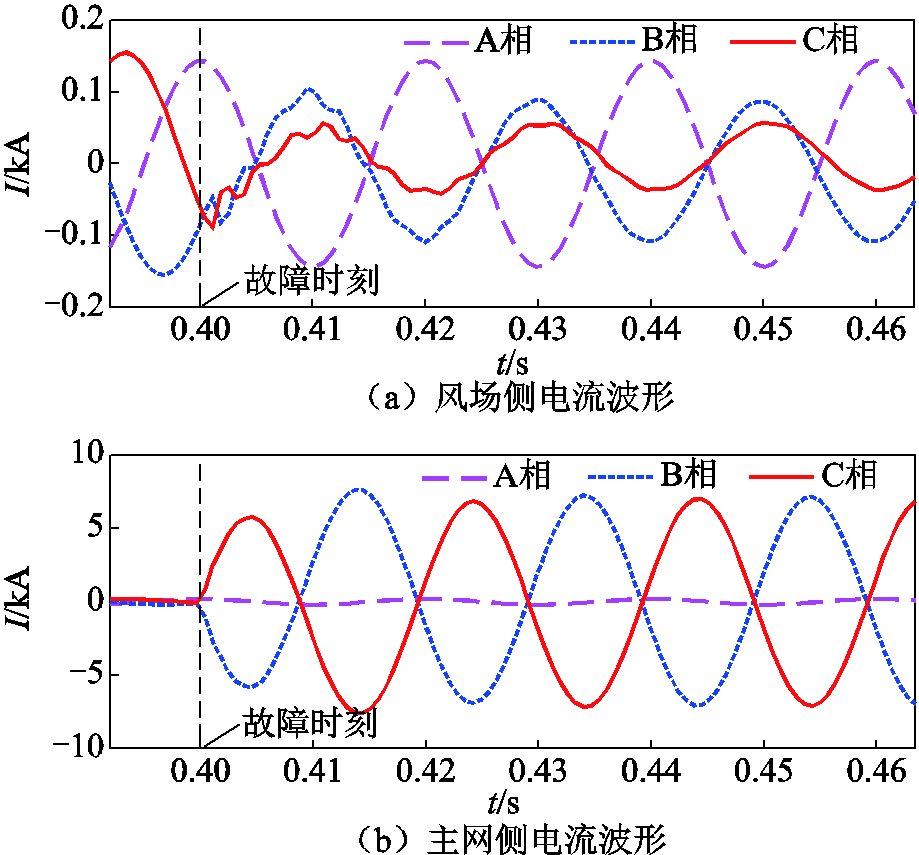
图12 BC两相短路下线路两侧电流波形变化曲线
Fig.12 The current variation for BC two-phase fault with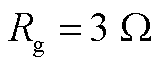
如图12所示,由于没有限幅环节,主网侧电流故障后可表现出明显的短路水平;而风场侧由于自身电流幅值受限,在故障后出现短路电流下降的特征,从而呈现明显的弱馈性。
对BC两相短路故障下的录波数据进行傅里叶提取,得到双端电流幅值及相位差变化曲线如图13所示。
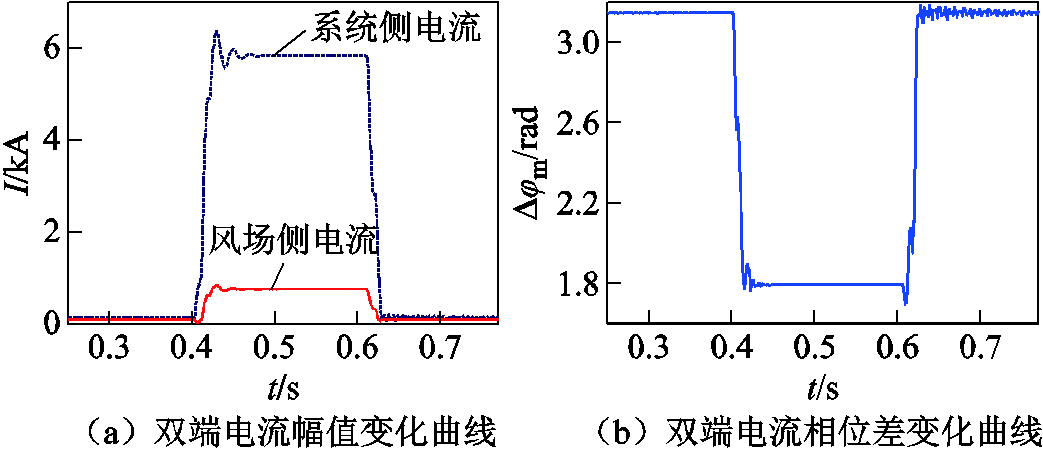
图13 双端电流幅值及相位差变化曲线
Fig.13 The amplitude and phase difference after fault
如图13a所示,由于定子直接向电网提供电流,导致故障后DFIG的输出电流高于1.2倍额定电流。然而,由于转子电流对定子电流的间接控制作用,定子侧直接向电网提供的电流幅值受限。因此,尽管DFIG的输出电流高于1.2倍额定电流,相比于系统侧电流,风场侧电流幅值依然表现出明显的弱馈特性。如图13b所示,在低阻故障下,由于换流器的控制策略,DFIG侧相位受控特征将影响双侧电流相位差,使其在低阻故障下可能呈现高阻故障下的相位特征。
选取C相为故障相,当送出线路50%处发生不同故障类型时,C故障相两侧电流相位差变化过程如图14所示。
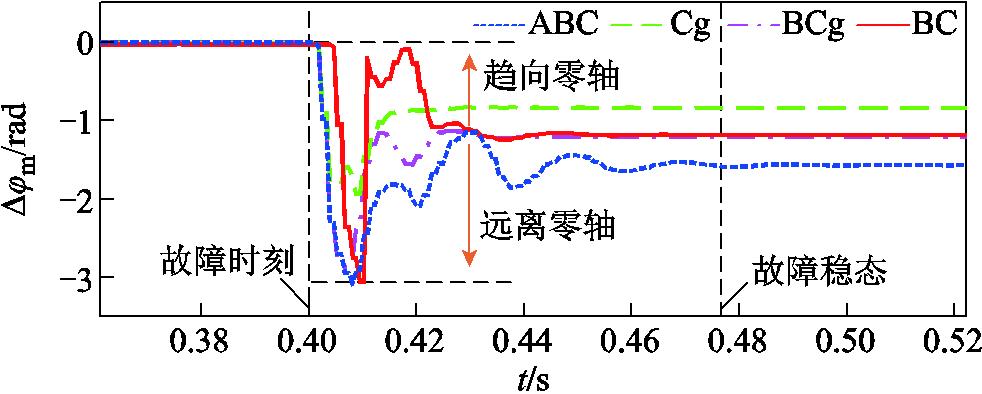
图14 不同故障类型下电流相位的暂态变化过程
Fig.14 The transient stage of current phase with different fault type
不同故障类型下,C相电流相位差的暂态波动情况均存在差异。发生三相短路时,相位的暂态响应过程最长,可达77 ms,这是由于三相短路引起的电压及电流波动最大,电感储存能量最大。由于电流幅值仅在故障后10~20 ms内呈现短路特性,因此电流相位的暂态波动易使故障点“趋向”零轴,从而使传统纵差保护产生死区。
以BC两相接地短路为例,分别设置不同过渡电阻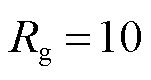 、50、
、50、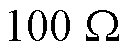 ,C相两侧电流相位差如图15所示。
,C相两侧电流相位差如图15所示。
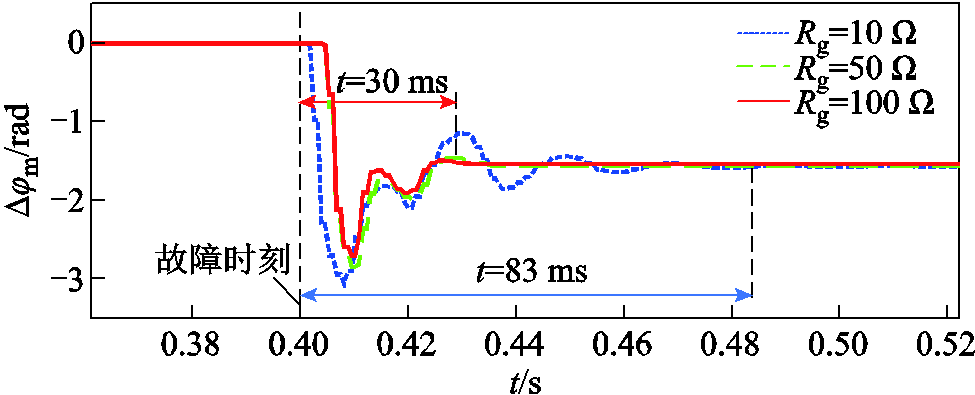
图15 不同过渡电阻下电流相位的暂态变化过程
Fig.15 The transient stage of current phase with different resistance
不同过渡电阻下,C相电流相位波动趋势相似,但波动时间以及波动幅度均存在差异。随着过渡电阻的升高,电感能量衰减较快,故障后的暂态响应过程也将缩短。
因此,由于短路类型以及过渡电阻无法提前预知,故障后电流相位的暂态特性具有不可预测性,基于故障稳态特性的保护在暂态时域内难以满足灵敏性要求。
设置区外故障位置F1(系统侧)和F3(风场侧),当发生C相接地短路时,幅值修正系数的变化曲线如图16所示。
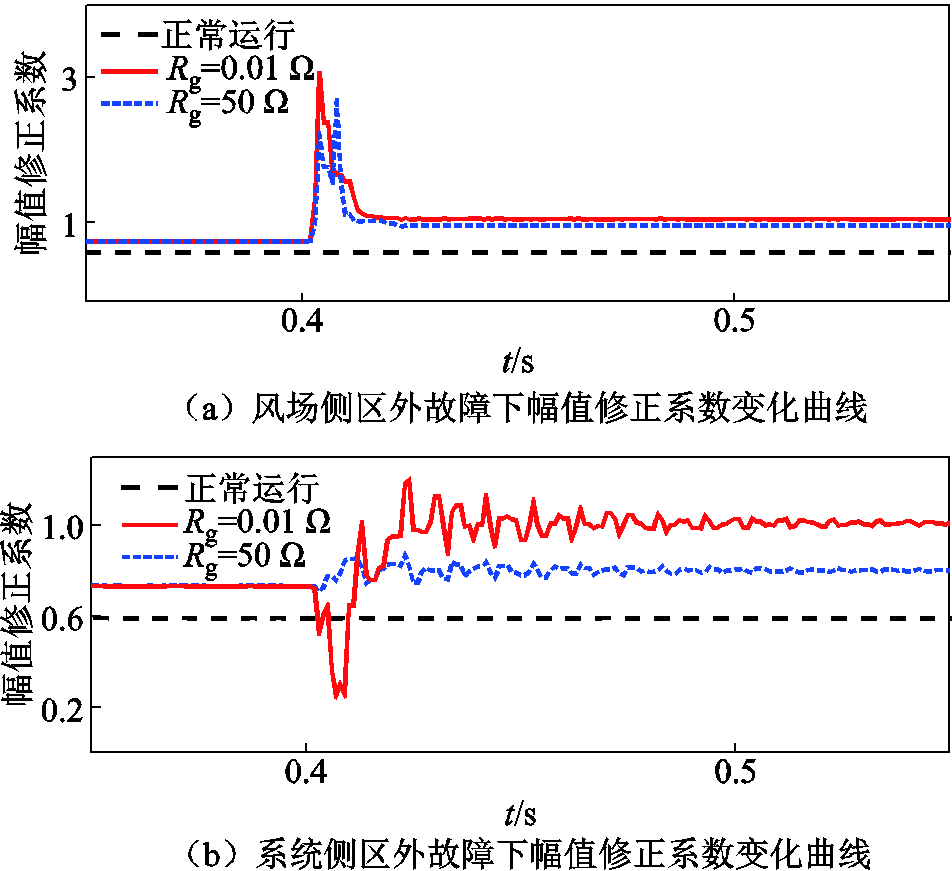
图16 区外故障下幅值修正系数变化曲线
Fig.16 The curves of under external faults
under external faults
在区外故障后的一段时间内,幅值修正系数几乎均高于阈值。这是因为在正常运行时,由于线路的分布式电容会吸收一部分容性电流,使得风场侧的电流幅值略低于系统侧的电流幅值。当主网侧发生故障时,分布电容将释放容性电流,由于短路电流由风场侧提供,短路水平较低,因此将出现幅值修正系数大于1的情况。而当风场侧发生区外故障时,短路电流由系统侧提供,短路水平较大,此时电容效应不明显,幅值修正系数趋近于1。
F1及F3处区外故障时,所提方案的动作曲线如图17所示。图17中,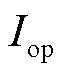 为动作电流,
为动作电流,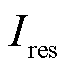 为本文所提方案的制动量,
为本文所提方案的制动量,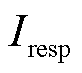 为传统电流差动保护的制动量。当发生区外故障低阻故障时,本文所提方案以及传统电流差动保护均可以保证不误动。同时相比于传统电流差动保护,本文所提方案在区外故障下的制动效果更加明显,因此能够在区外故障下具备更好的可靠性。
为传统电流差动保护的制动量。当发生区外故障低阻故障时,本文所提方案以及传统电流差动保护均可以保证不误动。同时相比于传统电流差动保护,本文所提方案在区外故障下的制动效果更加明显,因此能够在区外故障下具备更好的可靠性。
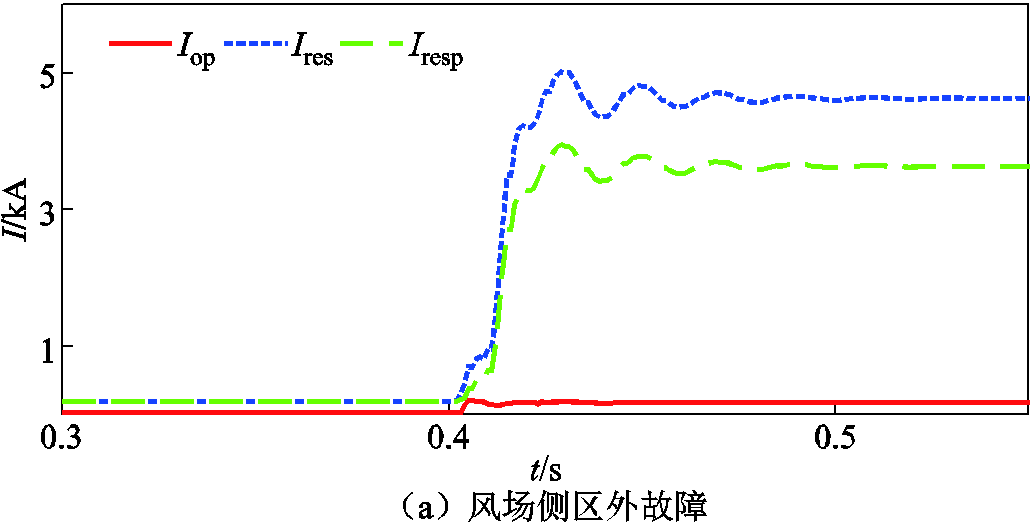
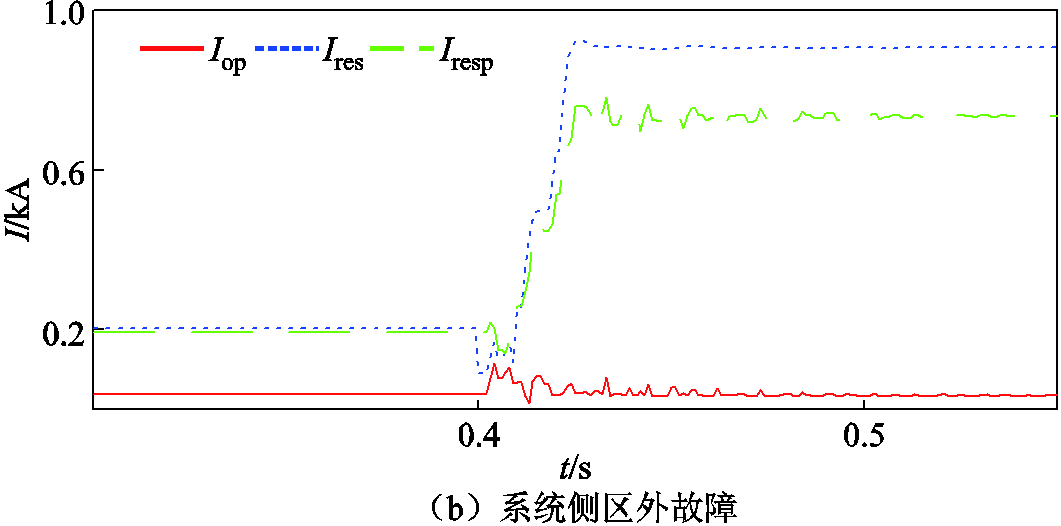
图17 区外故障下不同方案的动作曲线
Fig.17 Operating curves of the scheme under external faults
为进一步验证所提方案的性能,设置转换性故障,0.35 s时区外F1发生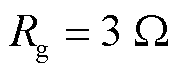 的BC两相接地短路,持续100 ms,0.4 s时F1处发生
的BC两相接地短路,持续100 ms,0.4 s时F1处发生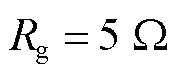 的C相接地短路,故障持续时间200 ms,在该工况下,幅值修正系数和保护动作曲线如图18所示。
的C相接地短路,故障持续时间200 ms,在该工况下,幅值修正系数和保护动作曲线如图18所示。
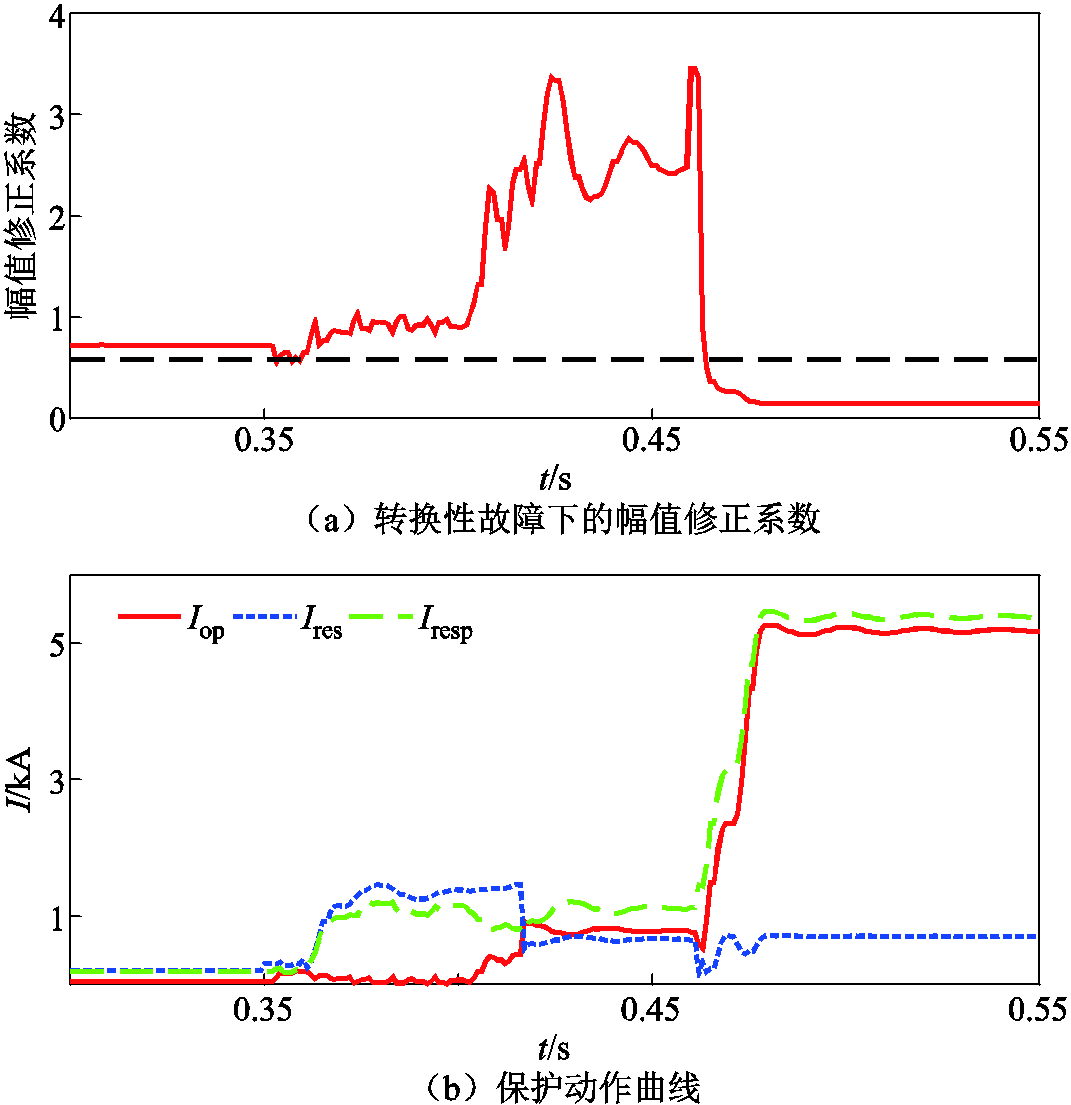
图18 转换性故障下幅值修正系数变化曲线
Fig.18 The curve of  and operation results under translational fault
and operation results under translational fault
如图18所示,当在区外与区内同时发生转换性故障时,由于本文所提方案能够在暂态时域内自适应整定,因此可以及时调整制动量,实现故障的快速切除。而对于传统电流差动保护,由于风场侧电流的弱馈性以及相位受控特性,在区内发生故障后将无法识别故障,对系统稳定性造成不利影响。
进一步设置区内故障,在位置F2处发生不同过渡电阻的C相接地短路,幅值修正系数的变化曲线如图19所示。
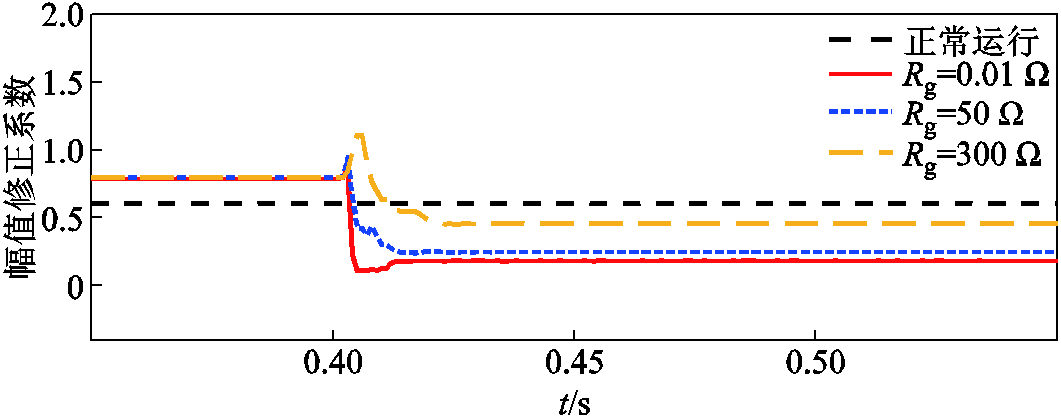
图19 区内故障下幅值修正系数变化曲线
Fig.19 The curves of under internal faults
under internal faults
当发生区内故障时,本文所提方案在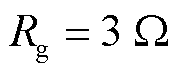 以及
以及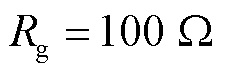 下的幅值修正系数显著低于阈值;在
下的幅值修正系数显著低于阈值;在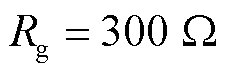 下的修正系数在故障后的短时间内高于阈值,此时FK不启动,由Ires2作为制动电流,保护仍然具备自适应调整能力。因此不同过渡电阻仅影响附加拟合系数的启动时效,保护仍能正确动作。
下的修正系数在故障后的短时间内高于阈值,此时FK不启动,由Ires2作为制动电流,保护仍然具备自适应调整能力。因此不同过渡电阻仅影响附加拟合系数的启动时效,保护仍能正确动作。
为验证本文所提方案的性能,选取传统纵联差动保护(Conventional Current Differential Protection, CCDP)作为对照实验,制动系数选取k=0.6。
区内金属性短路下本文所提方案与CCDP的动作曲线如图20所示。
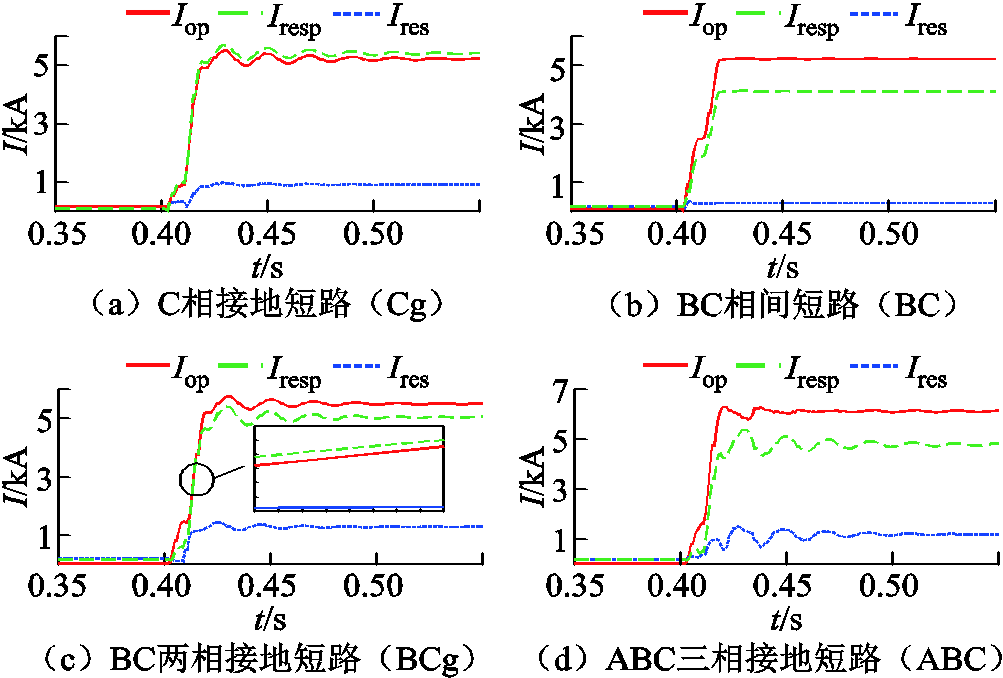
图20 区内金属性故障下保护方案动作曲线
Fig.20 Operating curves for internal metallic faults
如图20所示,虽然理论上传统电流差动保护在相间短路下能够动作,但是制动量和动作量相差不大,易受电流互感器测量误差等因素影响;在接地短路下,传统电流差动保护在故障稳态下动作,但在暂态时域下,动作量小于制动量,保护无法动作,灵敏性能不佳。而本文所提方案对于不同类型下的故障均能在暂态时域下可靠动作,同时相较于传统电流差动保护,在故障后本文所提方案能够自适应地调整制动量,使其显著区别于动作量。
为进一步验证所提方案在不同故障类型下的适用性,定义灵敏度系数为动作量和制动量之比。当灵敏度系数大于1时,保护动作;当灵敏度系数小于1时,保护不动作。区内故障灵敏度系数越大,保护灵敏度越高;区外故障灵敏度越小,保护可靠性越高。测试得到不同故障类型下本文方案与传统差动方案的灵敏度曲线如图21所示。图21中,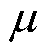 为本文所提方案的灵敏度系数,
为本文所提方案的灵敏度系数,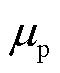 为传统差动方案的灵敏度系数。
为传统差动方案的灵敏度系数。
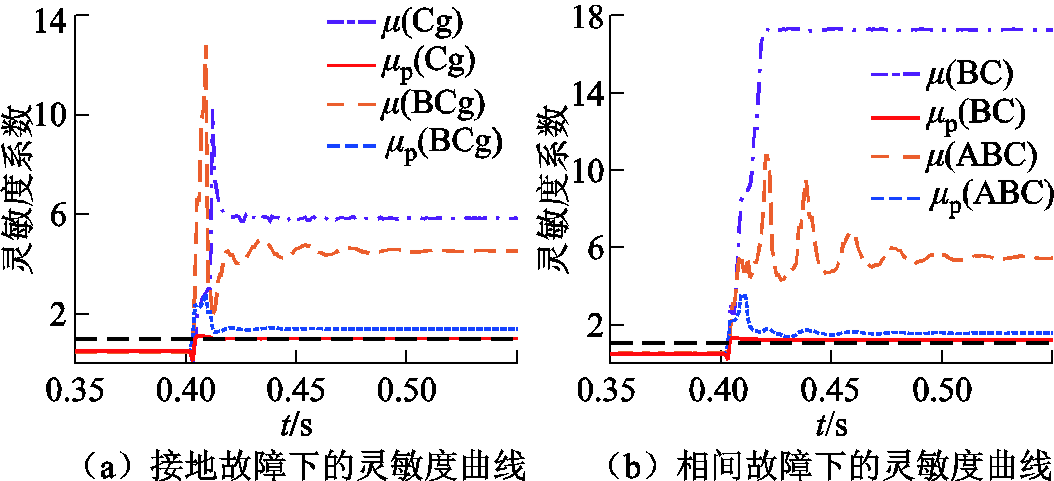
图21 区内金属性故障下保护方案的灵敏度曲线
Fig.21 Sensitivity curve for internal metallic faults
如图21所示,在故障稳态时域下,CCDP的灵敏度系数略高于1,这是因为在金属性故障时,风场侧电流幅值远小于系统侧,因此在制动系数的作用下,CCDP能够在故障稳态下识别故障。相比之下,本文所提方案在区内故障下的灵敏度系数显著高于CCDP,同时在BC相间短路时具有最高的灵敏度。因此本文所提方案在金属性故障下的性能优于CCDP。
暂态时域8 ms时间窗口处CCDP与本文方案的测试结果见表1、表2。
表1 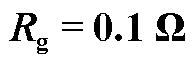 下CCDP测试结果
下CCDP测试结果
Tab.1 Test results of CCDP with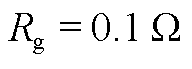

故障类型IopIres动作情况 BC2.008 21.058 8动作 Cg0.960 80.976 2不动作 BCg1.173 61.198 7不动作 ABC1.331 70.666 3动作
表2 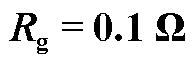 下本文方案测试结果
下本文方案测试结果
Tab.2 Test results of the adaptive scheme with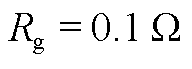

故障类型IopFKIres动作情况 BC2.008 20.394 80.288 0动作 Cg0.960 80.638 70.362 9动作 BCg1.173 60.281 00.124 8动作 ABC1.331 70.544 00.128 7动作
由表1、表2可见,在暂态时域8 ms处,CCDP无法识别接地故障,而本文所提方案对于不同过渡电阻均有良好适应性。
由于在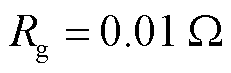 下风场侧电流对CCDP动作判据影响较小,因此将故障电阻升高至
下风场侧电流对CCDP动作判据影响较小,因此将故障电阻升高至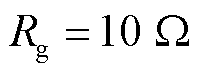 。在BC两相接地短路下,保护方案的动作情况与灵敏度系数变化曲线如图22所示。
。在BC两相接地短路下,保护方案的动作情况与灵敏度系数变化曲线如图22所示。
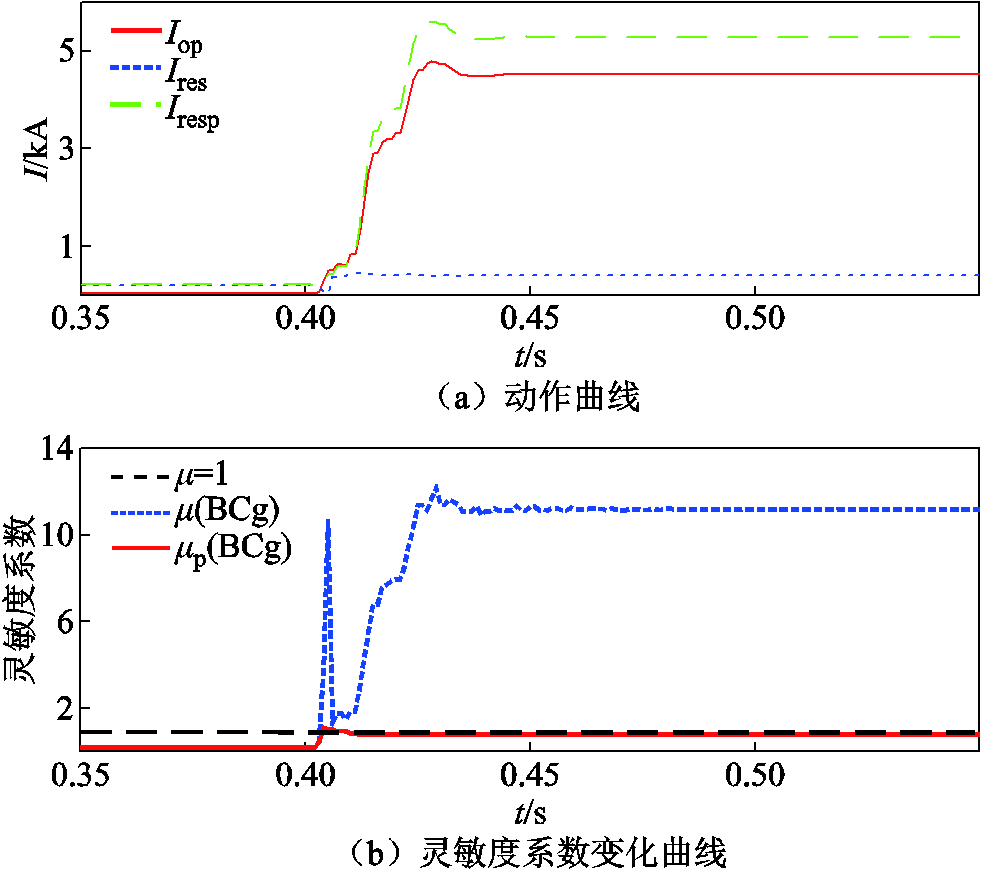
图22 BC两相接地短路保护方案的动作与灵敏度曲线
Fig.22 The operating and sensitivity curves for BC grounding fault
如图22所示,当过渡电阻升高至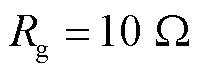 时,由于双端电流幅值差距缩小且风场侧电流仍然存在弱馈性,CCDP在暂态时域以及故障稳态下均无法识别故障,而本文所提方案依然具备可靠性。
时,由于双端电流幅值差距缩小且风场侧电流仍然存在弱馈性,CCDP在暂态时域以及故障稳态下均无法识别故障,而本文所提方案依然具备可靠性。
由于高阻故障往往发生于接地故障中,因此选取C相接地及BC两相接地短路工况来测试所提方案的耐过渡电阻能力。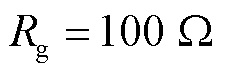 下保护方案的动作情况如图23所示。图23中,Ivres为FK不启动下本文所提方案的制动量。当过渡电阻升高后,CCDP在故障后的全过程中均无法识别故障,同时由于幅值修正系数无法立即低于阈值,拟合系数FK不会立即启动,但
下保护方案的动作情况如图23所示。图23中,Ivres为FK不启动下本文所提方案的制动量。当过渡电阻升高后,CCDP在故障后的全过程中均无法识别故障,同时由于幅值修正系数无法立即低于阈值,拟合系数FK不会立即启动,但 仍可作用,如在C相接地短路下,本文所提方案在故障后的4~6 ms内仍满足动作条件。
仍可作用,如在C相接地短路下,本文所提方案在故障后的4~6 ms内仍满足动作条件。
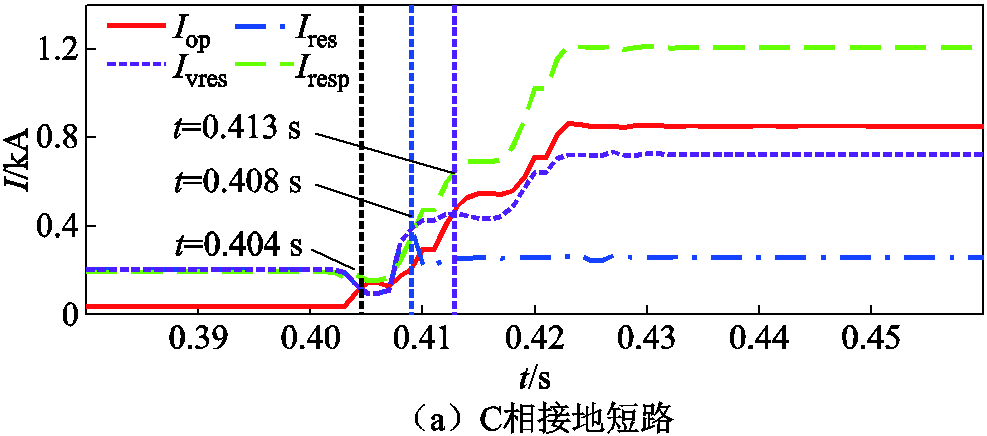
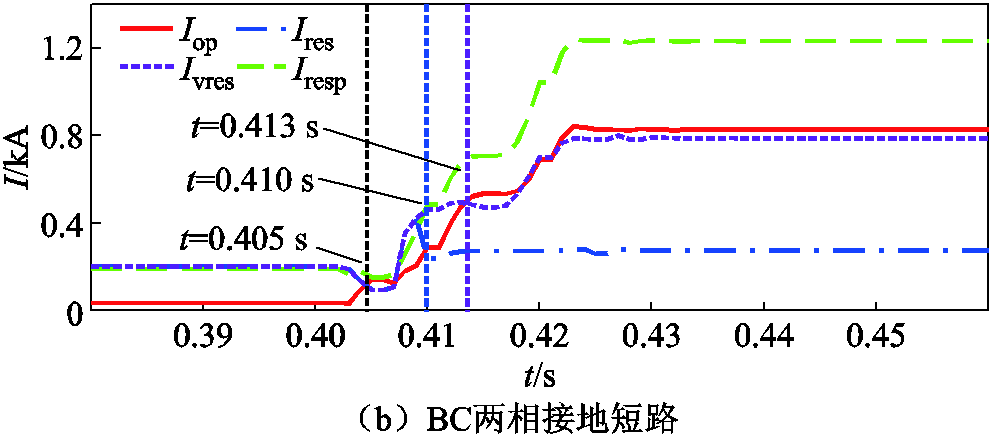
图23 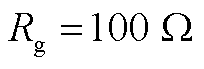 下保护方案的动作曲线
下保护方案的动作曲线
Fig.23 Operation curves of grounding faults with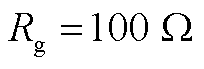
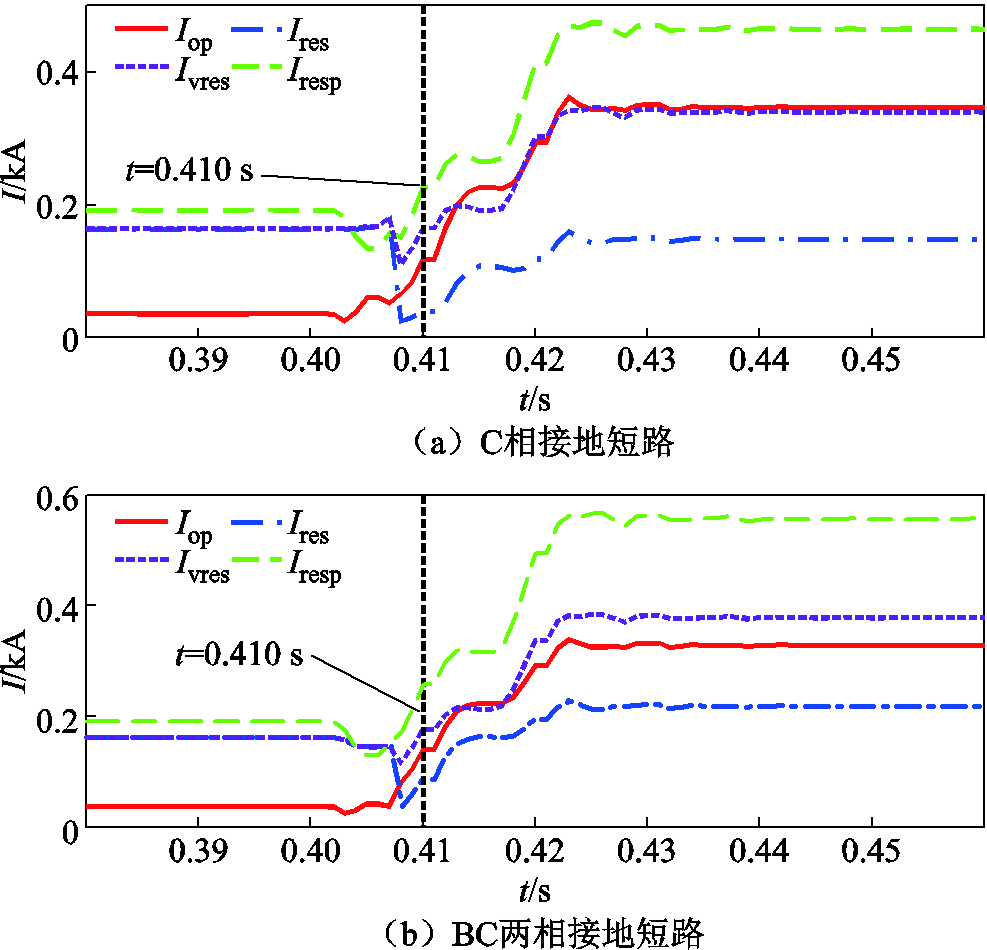
图24 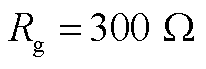 下保护方案的动作曲线
下保护方案的动作曲线
Fig.24 Operating curves of grounding faults with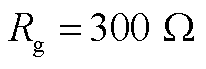
当过渡电阻升至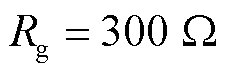 时,保护方案的动作情况如图24所示。由图24可知,当过渡电阻升高至
时,保护方案的动作情况如图24所示。由图24可知,当过渡电阻升高至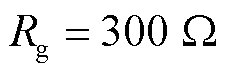 后,风场侧弱馈性不明显,依靠
后,风场侧弱馈性不明显,依靠 保护已无法切除故障,而当FK启动后,本文所提方案在故障后10 ms内仍可识别故障。因此本文所提方案在
保护已无法切除故障,而当FK启动后,本文所提方案在故障后10 ms内仍可识别故障。因此本文所提方案在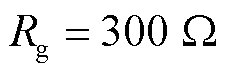 的高阻接地故障下,仍满足暂态时域切除故障的要求。
的高阻接地故障下,仍满足暂态时域切除故障的要求。
为解决风电场送出线路传统电流差动保护面临的低阻弱馈死区以及高阻暂态死区问题,本文提出了一种基于故障区域拟合系数的风电场送出线路电流差动保护原理。经过测试验证,所得主要结论如下:
1)对短路水平依赖低。本文引入双端电流幅值比来调节制动电流,弱化了风场侧故障电流弱馈性所造成的差动死区问题,提高了区内故障时电流平衡定律的适用性。
2)可同时兼顾速动性与可靠性。保护的动作方程可根据暂态电气信息自适应整定,仅利用暂态时域内10 ms内的故障电流信息即可切除故障,并且在300 Ω过渡电阻下仍能保持较高的可靠性。
3)保护整定方案不依赖精确的控制参数,对于换流器采用主流控制策略的机组具有良好的适应性。同时本方法仅利用电流信息,不需要额外增设电压互感器,因此具有较高的经济性。
本文所提方案为双端量保护,在后续的研究中,将进一步分析直驱风机接入的海上风电场中所提方案的适应性,并进一步研究保护方案的双端同步对时方法以及配套的后备保护方案。
参考文献
[1] 国家能源局. 国家能源局发布2022年全国电力工业统计数据[J]. 电力勘测设计, 2023(1): I0021.
National Energy Administration. National energy administration released statistical data of national electric power industry in 2022[J]. Electric Power Survey & Design, 2023(1): I0021.
[2] 贾科, 顾晨杰, 毕天姝, 等. 大型光伏电站汇集系统的故障特性及其线路保护[J]. 电工技术学报, 2017, 32(9): 189-198.
Jia Ke, Gu Chenjie, Bi Tianshu, et al. Fault characteristics and line protection within the collection system of a large-scale photovoltaic power plant[J]. Transactions of China Electrotechnical Society, 2017, 32(9): 189-198.
[3] 闫晨光, 张芃, 徐雅, 等. 换流变压器有载分接开关级间短路故障差动保护动作特性[J]. 电工技术学报, 2023, 38(21): 5878-5888, 5912.
Yan Chenguang, Zhang Peng, Xu Ya, et al. Differential protection performance for converter transformer intertap short-circuit faults in on-load tap changers[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5878-5888, 5912.
[4] 肖繁, 夏勇军, 张侃君, 等. 含新能源接入的配电网网络化保护原理研究[J]. 电工技术学报, 2019, 34(增刊2): 709-719.
Xiao Fan, Xia Yongjun, Zhang Kanjun, et al. Research on a principle of networked protection in distribution network with renewable energy sources[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 709-719.
[5] 李君, 何敏, 黄守道, 等. 基于相位差的小电阻接地有源配电网接地故障保护算法[J]. 电工技术学报, 2024, 39(23): 7418-7429.
Li Jun, He Min, Huang Shoudao, et al. Grounding fault protection algorithm of small resistance earthing active distribution network based on phase difference [J]. Transactions of China Electrotechnical Society, 2024, 39(23): 7418-7429.
[6] 李毅, 谢铁兵, 雷阳, 等. 新能源电站非直接接地系统电缆端部单相接地保护方法探讨[J]. 电气技术, 2023, 24(1): 76-80.
Li Yi, Xie Tiebing, Lei Yang, et al. Analysis and discussion on the protection method of single-phase grounding at the end of the cable of non-grounded power system[J]. Electrical Engineering, 2023, 24(1): 76-80.
[7] 王晨清, 宋国兵, 刘凯, 等. 突变量保护对风电接入系统的适应性分析[J]. 中国电机工程学报, 2014, 34(31): 5485-5492.
Wang Chenqing, Song Guobing, Liu Kai, et al. Adaptability analysis of fault component protection of power systems with wind farms[J]. Proceedings of the CSEE, 2014, 34(31): 5485-5492.
[8] 王涛, 诸自强, 年珩. 非理想电网下双馈风力发电系统运行技术综述[J]. 电工技术学报, 2020, 35(3): 455-471.
Wang Tao, Zhu Ziqiang, Nian Heng. Review of operation technology of doubly-fed induction generator-based wind power system under nonideal grid conditions[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 455-471.
[9] 褚旭, 刘琦, 吕昊泽, 等. 基于控保协同海底观测网供电系统保护方案[J]. 电工技术学报, 2023, 38(7): 1780-1792.
Chu Xu, Liu Qi, Lü Haoze, et al. Protection scheme for subsea observatory power supply system based on control and protection coordination[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1780-1792.
[10] 束洪春, 刘力滔, 唐玉涛, 等. 基于行波暂态能量的半波长输电线路高灵敏增强型纵联保护方案[J]. 电工技术学报, 2022, 37(24): 6372-6387.
Shu Hongchun, Liu Litao, Tang Yutao, et al. Highly sensitive enhanced pilot protection of half-wavelength transmission line based on directional traveling wave energy[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6372-6387.
[11] 马富艺龙, 辛焕海, 刘晨曦, 等. 新能源基地柔性直流送出系统小扰动电压支撑强度评估[J]. 电工技术学报, 2023, 38(21): 5758-5770, 5938.
Ma Fuyilong, Xin Huanhai, Liu Chenxi, et al. Small-disturbance system voltage support strength assessment method for renewables VSC-HVDC delivery system [J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5758-5770, 5938.
[12] 李彦宾, 贾科, 毕天姝, 等. 电流差动保护在逆变型新能源场站送出线路中的适应性分析[J]. 电力系统自动化, 2017, 41(12): 100-105.
Li Yanbin, Jia Ke, Bi Tianshu, et al. Adaptability analysis of current differential protection of outgoing transmission line emanating from inverter-interfaced renewable energy power plants[J]. Automation of Electric Power Systems, 2017, 41(12): 100-105.
[13] Zhang Fan, Mu Longhua, Guo Wenming. An integrated wide-area protection scheme for active distribution networks based on fault components principle[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 392-402.
[14] 黄方能, 梅勇, 周剑, 等. 基于正序电流的风电接入电网自适应阈值差动保护方案[J]. 电力系统保护与控制, 2022, 50(6): 117-124.
Huang Fangneng, Mei Yong, Zhou Jian, et al. Adaptive threshold differential protection scheme for wind power integration based on positive sequence current[J]. Power System Protection and Control, 2022, 50(6): 117-124.
[15] 李会新, 王兴国, 谢俊, 等. 一种基于虚拟电流制动量的电流差动保护[J]. 电力系统保护与控制, 2018, 46(9): 75-79.
Li Huixin, Wang Xingguo, Xie Jun, et al. A transmission line current differential protection based on virtual brake current[J]. Power System Protection and Control, 2018, 46(9): 75-79.
[16] 乔一达, 吴红斌, 吴通华, 等. 含逆变型分布式电源的配电网分区域电流保护[J]. 电工技术学报, 2022, 37(增刊1): 134-144.
Qiao Yida, Wu Hongbin, Wu Tonghua, et al. A partitioned current protection scheme of distribution network with inverter interfaced distributed generator [J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 134-144.
[17] 黄涛, 陆于平, 蔡超. DFIG等效序突变量阻抗相角特征对故障分量方向元件的影响分析[J]. 中国电机工程学报, 2016, 36(14): 3929-3940.
Huang Tao, Lu Yuping, Cai Chao. Analysis of phase angle characteristics of DFIG equivalent sequence superimposed impedances and its impact on fault components based direction relay[J]. Proceedings of the CSEE, 2016, 36(14): 3929-3940.
[18] 牛伟民, 樊艳芳, 侯俊杰, 等. 基于正序阻抗幅值比的风电场送出线路纵联保护[J]. 电力系统保护与控制, 2023, 51(16): 179-187.
Niu Weimin, Fan Yanfang, Hou Junjie, et al. Pilot protection of wind farm transmission lines based on the positive sequence impedance amplitude ratio[J]. Power System Protection and Control, 2023, 51(16): 179-187.
[19] 王春又, 孙士云, 毛肖, 等. 适应于双馈风电场送出线的时域距离纵联方向保护[J]. 电力系统保护与控制, 2021, 49(13): 82-94.
Wang Chunyou, Sun Shiyun, Mao Xiao, et al. Longitudinal direction protection of time domain distance applicable to the outgoing line of a double-fed wind farm[J]. Power System Protection and Control, 2021, 49(13): 82-94.
[20] Zheng Liming, Jia Ke, Bi Tianshu, et al. A novel structural similarity based pilot protection for renewable power transmission line[J]. IEEE Transactions on Power Delivery, 2020, 35(6): 2672-2681.
[21] 胡勇, 郑黎明, 贾科, 等. 基于Tanimoto相似度的光伏场站送出线路纵联保护[J]. 电力系统保护与控制, 2021, 49(3): 74-79.
Hu Yong, Zheng Liming, Jia Ke, et al. Pilot protection based on Tanimoto similarity for a photovoltaic station transmission line[J]. Power System Protection and Control, 2021, 49(3): 74-79.
[22] Zheng Liming, Jia Ke, Yang Bin, et al. Singular value decomposition based pilot protection for transmission lines with converters on both ends[J]. IEEE Transactions on Power Delivery, 2022, 37(4): 2728-2737.
[23] 李铁成, 范辉, 张卫明, 等. 基于5G通信的有源配电网新能源送出线路纵联保护[J]. 中国电力, 2024, 57(11): 139-150.
Li Tiecheng, Fan Hui, Zhang Weiming, et al. Pilot protection of new energy transmission line in active distribution network based on 5G communication[J]. Electric Power, , 2024, 57(11): 139-150.
[24] Liu Yu, Sakis Meliopoulos A P, Fan Rui, et al. Dynamic State Estimation based protection of microgrid circuits[C]//2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 2015: 1-5.
[25] 聂铭, 李猛, 和敬涵, 等. 基于状态估计的大规模新能源送出线路纵联保护[J]. 电网技术, 2024, 48(5): 2189-2198.
Nie Ming, Li Meng, He Jinghan, et al. Pilot protection of large-scale renewable energy transmission lines based on state estimation[J]. Power System Technology, 2024, 48(5): 2189-2198.
[26] 潘学萍, 黄文婷, 郭金鹏, 等. 考虑LVRT特性的新能源送端系统功角稳定与电压稳定交互影响分析[J]. 电力自动化设备, 2024, 44(10): 24-31.
Pan Xueping, Huang Wenting, Guo Jinpeng et al. Analysis of interaction between power angle stability and voltage stability for sending-end system with renewable energy considering LVRT characteristics [J]. Electric Power Automation Equipment, 2024, 44(10): 24-31.
[27] 徐可寒, 张哲, 刘慧媛, 等. 光伏电源故障特性研究及影响因素分析[J]. 电工技术学报, 2020, 35(2): 359-371.
Xu Kehan, Zhang Zhe, Liu Huiyuan, et al. Study on fault characteristics and its related impact factors of photovoltaic generator[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 359-371.
Abstract Doubly fed induction generators (DFIGs) are widely used in onshore wind farms. Fault currents in DFIGs are characterized by amplitude limitation and phase angle control, degrading conventional current differential protection based on synchronous power source characteristics. This paper proposes a differential protection scheme using fault region fitting coefficient. It constructs virtual restraint current based on double-end current amplitude coefficients to balance amplitude. An operating boundary model is built using complex domain current vector relationships, determining fault point distribution in the complex plane under internal and external faults. The scheme then constructs the fault boundary in the transient time-domain by deriving trends with transition resistance and restraint coefficient, and adaptively adjusts protection criteria.
Firstly, a pilot differential protection scheme based on the fitting coefficient of the fault area is proposed using the transient current information after the fault. To eliminate the differential dead zone problem caused by the weak infeed current on the DFIG side, a virtual restraint current is introduced. Then, based on the differential equation containing the virtual current, a boundary model that can characterize the fluctuation characteristics of the transient current is constructed, and the distribution characteristics of the fault point on the complex plane under both internal and external faults are analyzed through the boundary model. Subsequently, the relationship between the basic parameters of the boundary model and the restraining coefficient, as well as the ratio of the current amplitudes at both ends, is derived using partial differential equations. On this basis, the critical tangential relationship between the transient fault point fitting curve and the boundary circle is utilized to obtain the solving equation for the adaptive fitting coefficient. This equation is used to adjust the restraint level of the differential equation, thereby locking the fault point within the operating region. Finally, the effectiveness of the proposed protection scheme under various fault conditions is verified using a real-time digital simulator (RTDS).
The following conclusions can be drawn from the simulation analysis: (1) Compared to traditional models, the proposed protection scheme has low dependence on short-circuit levels. By introducing the ratio of the current amplitudes at both ends to regulate the restraining current, the scheme weakens the differential dead zone problem caused by the weak infeed current on the wind farm side, thereby improving the applicability of the current balance law during internal faults. (2) The proposed model can also simultaneously ensure high-speed operation and reliability. The protection operating equation is adaptively set based on transient electrical information, allowing for fault clearance using only 8 ms of fault current information during the transient time domain. It maintains high reliability even with a 300 Ω transition resistance. (3) The protection setting scheme employs a qualitative rather than quantitative analysis method, providing good adaptability for converter units using mainstream control strategies. Additionally, this method relies solely on current information, eliminating the need for additional voltage transformers, and thus offers high economic efficiency.
keywords:Renewable energy transmission systems, current differential protection, transient stage, fault boundary model, fault region fitting coefficient
中图分类号:TM773
DOI: 10.19595/j.cnki.1000-6753.tces.242062
国家自然科学基金青年基金资助项目(52207100)。
收稿日期 2024-11-15
改稿日期 2025-01-20
侯 冰 男,2001年生,硕士研究生,研究方向为新能源电力系统保护与控制。E-mail:_hb9@ncepu.edu.cn
李轶凡 男,1994年生,博士,副教授,研究方向为新能源独立电力系统保护与控制、输电线路保护在军事背景下的交叉应用等。E-mail:ivanlee_lyf@ncepu.edu.cn(通信作者)
(编辑 赫 蕾)