
图1 面向网络-光伏爬坡协同攻击的辨识模型示意图
Fig.1 Schematic diagram of the identification model of cyber-ramping coordinated attacks for PV
摘要 光伏爬坡事件的不确定性对网络攻击检测方法的准确度和时效性提出更高要求。现有研究忽视光伏爬坡事件与网络攻击事件的耦合特性,导致网络-光伏爬坡协同攻击难以精准辨识。该文提出一种基于张量分解个性化联邦学习的网络-光伏爬坡协同攻击辨识方法,首先,分析网络-光伏爬坡协同攻击路径,构建网络-光伏爬坡协同攻击模型并分析攻击原理;其次,提出基于张量分解的个性化联邦学习(TDPFed)方法进行网络-光伏爬坡协同攻击辨识,在保证不同电网分区数据隐私安全的同时进行快速低成本通信,实现本地数据的隐私保护和全局共享模型的高效训练;最后,通过算例分析证明所提方法相较于轻梯度提升机方法(LightGBM)、传统联邦平均方法(FedAvg)和基于Moreau envelopes策略的个性化联邦学习方法(pFedMe),在辨识准确度、收敛速度等指标上均有较大提升,能够突破辨识方法因通信条件制约导致联邦学习训练难的瓶颈。
关键词:光伏爬坡事件 网络-光伏爬坡协同攻击 虚假数据注入攻击 张量分解 联邦学习
光伏发电是近年来发展前景好、发展速度快的可再生能源之一[1-2]。我国通过建设大量光伏示范工程解决偏远地区用电紧张问题,促进电网绿色转型[3-5]。但随着光伏渗透率的不断提高,光伏爬坡事件导致功率大幅波动的问题日渐突出[6],对电网的调控能力提出了更高的要求[7-8]。别有用心的攻击者可能在光伏爬坡阶段同时发动虚假数据注入攻击,试图操纵电力市场价格以谋取不正当利益,或恶意破坏电力系统造成恶劣的社会影响[9-10]。
网络-光伏爬坡协同攻击是指在发生光伏爬坡事件的同时实施虚假数据注入攻击(False Data Injection Attack, FDIA)。攻击者通过设计满足线路拓扑和潮流约束的虚假数据避开不良数据检测机制,同时利用光伏爬坡的随机性来掩盖虚假数据注入的事实,操作状态估计结果并改变潮流走向,造成停电或设备损坏[11],或通过干扰电力经济调度,进行电力市场投资,获取非法利益[12]。文献[13]和文献[14]分别使用基于无迹卡尔曼滤波器和增强隐藏移动目标防御的方法,通过状态估计检测FDIA。文献[15]提出一种基于极端梯度提升结合无迹卡尔曼滤波的FDIA检测方法,通过数据预测检测FDIA。为了充分利用历史数据,文献[16]提出一种基于历史数据的无监督异常检测算法;文献[17]考虑数据的时空特性并在卷积神经网络中加入门控循环单元进行检测;文献[18]提出了提取电力负荷数据中非线性和非平稳特征,基于区间状态估计的防御机制的电网攻击防御策略。虽然现有的FDIA检测都表现出了较好的性能,但仍缺乏对于光伏爬坡过程存在随机波动的考虑,以及鉴别伪装成光伏波动的FDIA的研究。
同时,随着电力物理信息系统对于数据隐私保护提出更高要求,不同机构间的数据因隐私保护限制无法共享。由于单一机构遭受的FDIA攻击类型较为片面,导致训练的模型仅能辨识特定的攻击类型,难以对其他攻击做出反应。联邦学习是一种先进的分布式机器学习方法[19],在训练过程中,各用户不上传本地数据,仅上传模型参数,通过与服务器进行模型参数交互的方式更新和优化全局模型[20]。联邦学习可以充分保护各用户的数据隐私,但也存在因通信条件制约导致模型训练速度缓慢的问题。为了提高训练速度,文献[21]提出多标准选择模型用于挑选网络状态和计算能力更优的客户端参与联邦学习;文献[22]将传统压缩方法应用于联邦学习以提高通信效率。虽然上述算法在一定程度上缓解了通信效率低的负面影响,但由于降低了收敛速度,对于整体训练效率的提高并不显著。
针对上述问题,本文提出基于张量分解个性化联邦学习(Tensor Decomposition based Personalized Federated learning, TDPFed)的网络-光伏爬坡协同攻击辨识方法,在保护数据隐私的同时实现对各类网络-光伏爬坡协同攻击的辨识。首先,分析网络-光伏爬坡协同攻击路径,构建网络-光伏爬坡协同攻击模型并分析攻击原理;其次,使用张量分解对传统联邦学习进行改进,提出一种张量分解个性化联邦学习方法用于网络-光伏爬坡协同攻击辨识,实现面向海量数据的高效训练;然后,基于光伏出力特点和不同攻击方式提出10种网络-光伏爬坡协同攻击的典型场景,并生成大量样本用于仿真验证;最后,通过大量算例分析证明了本文方法具有收敛速度快、FDIA辨识准确度高、误报率低的优势,能够有效地减少通信资源需求,为大电网多节点系统进行联邦学习和解决网络-光伏爬坡协同攻击辨识问题提供有效方案。
网络-光伏爬坡协同攻击的辨识模型示意图如图1所示。多类型光伏终端通过公用互联网接入电力系统,若用户侧接入公用互联网的设备遭受攻击,攻击者可能跨越电力专网边界,通过注入病毒等方式发起网络-光伏爬坡协同攻击。针对该问题,本文采用个性化张量联邦学习训练辨识模型,通过学习光伏爬坡历史数据的特点和规律进行FDIA辨识。不同电网客户端收集到各自电网分区的数据后,在中央服务器的协调下训练全局模型。首先电网客户端通过储存在本地数据库的隐私数据训练个性化模型;其次训练张量化本地模型并与中央服务器进行通信,中央服务器则通过聚合不同电网分区的张量化本地模型得到通用性较好的全局模型;最后下发全局模型作为下次客户端训练的初始模型,完成一次训练过程。在这个过程中,相较于传统的联邦学习,个性化张量联邦学习由于采用了张量分解压缩模型,因此具有通信效率高的特点,可以突破通信瓶颈对训练效率的限制。

图1 面向网络-光伏爬坡协同攻击的辨识模型示意图
Fig.1 Schematic diagram of the identification model of cyber-ramping coordinated attacks for PV
鉴于文献[23-24]针对自动发电控制和负荷预测数据网络攻击,本文构建了网络-光伏爬坡协同攻击的缩放攻击、脉冲攻击、斜坡攻击和随机攻击模型。
缩放攻击可以描述为
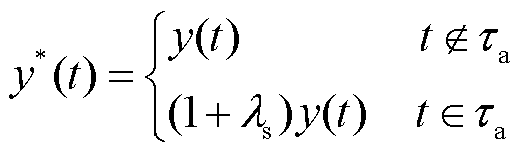 (1)
(1)
式中,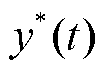 为被网络攻击篡改后的数据;
为被网络攻击篡改后的数据;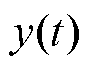 为真实数据;
为真实数据;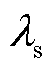 为缩放攻击的攻击参数;
为缩放攻击的攻击参数;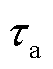 为缩放攻击持续的时间段。
为缩放攻击持续的时间段。
脉冲攻击可以描述为
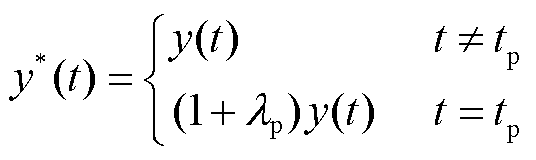 (2)
(2)
式中,λp为脉冲攻击参数;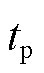 为脉冲攻击时刻。
为脉冲攻击时刻。
斜坡攻击分为Ⅰ型斜坡攻击和Ⅱ型斜坡攻击,Ⅰ型斜坡攻击仅考虑上升阶段的部分,Ⅱ型斜坡攻击则考虑上升和下降两个部分。Ⅰ型斜坡攻击可以描述为
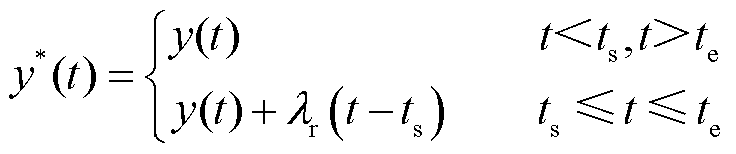 (3)
(3)
Ⅱ型斜坡攻击可以描述为
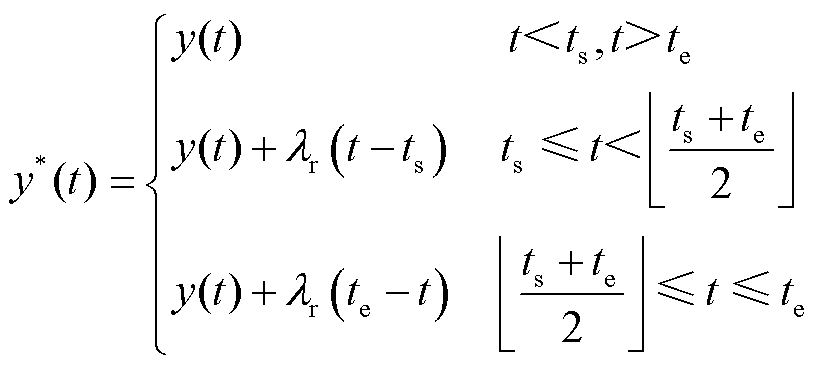 (4)
(4)
式中,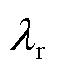 为斜坡攻击参数;
为斜坡攻击参数;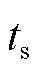 为攻击开始时刻;
为攻击开始时刻;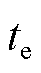 为攻击结束时刻;
为攻击结束时刻;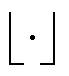 为向下取整符号。因为电网控制中心接收到离散的采样数据,所以此处用向下取整的方式将数据向下取整到最近的一个取样点,以此近似表示斜坡攻击的中间时刻。
为向下取整符号。因为电网控制中心接收到离散的采样数据,所以此处用向下取整的方式将数据向下取整到最近的一个取样点,以此近似表示斜坡攻击的中间时刻。
随机攻击可以描述为
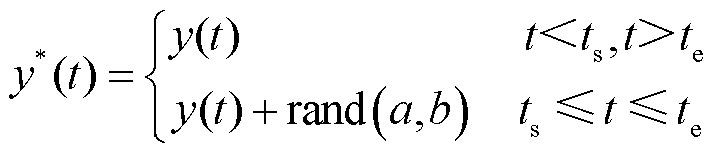 (5)
(5)
式中,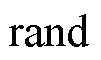 (·)为均匀随机函数;a为均匀随机函数的下界;b为均匀随机函数的上界。
(·)为均匀随机函数;a为均匀随机函数的下界;b为均匀随机函数的上界。
其他攻击是指不属于上述四种的攻击方式,如其他攻击中平滑曲线攻击[25]是通过将原始数据中的一组点替换成由多项式生成的平滑曲线上的点,以此避免产生突变数据的攻击方式。攻击者也可能使用上述攻击策略中的两种或多种进行组合使用,产生新的攻击曲线。为了模拟现实中可能出现新的攻击方式,“其他攻击”并非一种特定的攻击,而是未分类攻击单独出现或多种攻击组合出现的情况。
为进一步欺骗电网中的不良数据检测机制,可以令攻击向量 满足
满足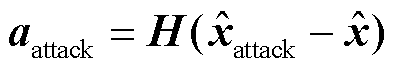 ,其中
,其中 为量测雅可比矩阵,
为量测雅可比矩阵, 为攻击下的状态估计值,
为攻击下的状态估计值,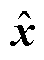 状态变量估计值。此时残差检测无法识别FDIA[26],攻击者可以通过此方法将量测数据改为任意值且不被不良数据检测机制发现[27]。
状态变量估计值。此时残差检测无法识别FDIA[26],攻击者可以通过此方法将量测数据改为任意值且不被不良数据检测机制发现[27]。
正则平行(CANDECOMP/PARAFAC, CP)分解为将张量分解为一系列秩1张量的方法,使用的主要符号及其含义见表1。
表1 主要符号及其含义
Tab.1 Main symbols and their meanings

符号含义 张量 ai向量a的第i个元素 ai, j矩阵的元素(i,j) 矩阵的第r列向量 矩阵与矩阵的Kronecker积 矩阵与矩阵的Khatri-Rao积 张量的模态n展开 客户端总数 因子矩阵 客户端k的本地数据集 参与联邦学习的样本总数 本地样本数量 节点功率的时间序列向量 第k个客户端的个性化模型 第k个客户端使用本地数据进行辨识时,个性化模型损失函数的期望 第k个客户端的因子矩阵 张量化本地模型
对于N维张量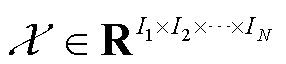 和正整数R,CP分解的目标是将其表示为
和正整数R,CP分解的目标是将其表示为
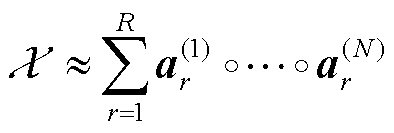 (6)
(6)
式中,向量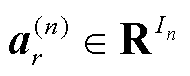 ,
,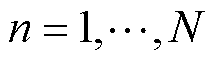 ,
,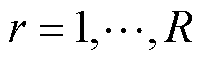 ,存在的最小可能的R作CP秩。这些向量形成了因子矩阵
,存在的最小可能的R作CP秩。这些向量形成了因子矩阵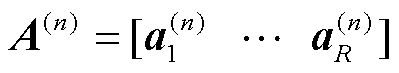 。使用Kruskal算子,CP分解可以写为
。使用Kruskal算子,CP分解可以写为
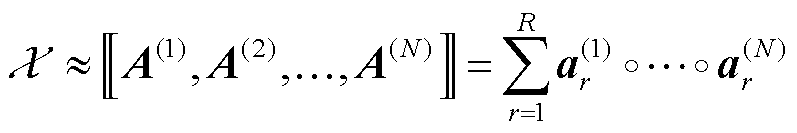 (7)
(7)
网络-光伏爬坡协同攻击辨识模型由很多层组成,以全连接层的张量解耦表示方法为例,其他部分与全连接层类似,不再赘述。全连接层权重矩阵的维数与输入向量和输出向量的维数相关,全连接层的输出向量 用于表示网络-光伏爬坡协同攻击辨识模型的输出,表示为
用于表示网络-光伏爬坡协同攻击辨识模型的输出,表示为
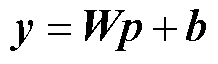 (8)
(8)
式中,p为输入向量,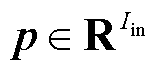 ,表示待辨识节点的历史功率数据,
,表示待辨识节点的历史功率数据,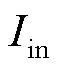 为输入到该层的神经元数量;W为权重矩阵,
为输入到该层的神经元数量;W为权重矩阵,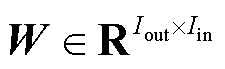 ,
,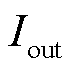 为从该层输出的神经元数量;b为偏置参数向量,
为从该层输出的神经元数量;b为偏置参数向量, 。
。
通过CP分解,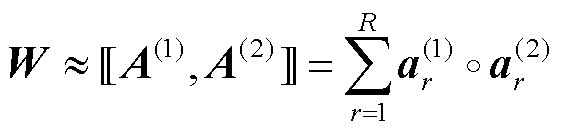 ,其中
,其中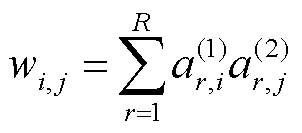 ,可以将式(8)中的权重矩阵重写为因子的矩阵乘积,即
,可以将式(8)中的权重矩阵重写为因子的矩阵乘积,即
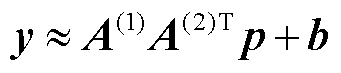 (9)
(9)
式(9)通过张量分解将高维网络-光伏爬坡协同攻击辨识模型投影到低维子空间,在几乎不损失有效信息的前提下减少模型所需的数据总量,提高网络-光伏爬坡协同攻击辨识模型的传输效率。
针对本文提出的基于CP分解的个性化张量联邦学习方法,将压缩率定义为原始网络的参数数量与张量分解后网络的全部参数数量之比。如对于网络-光伏爬坡协同攻击辨识模型的全连接层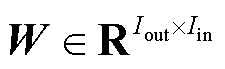 。进行张量分解前的参数数量为
。进行张量分解前的参数数量为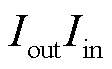 ,进行张量分解后的参数数量为
,进行张量分解后的参数数量为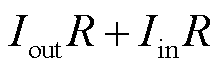 ,由此可以定义全连接层的压缩率为
,由此可以定义全连接层的压缩率为
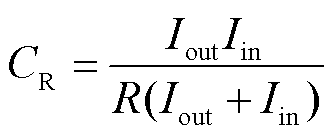 (10)
(10)
为了评估不同方法在实际应用中的耗时情况,根据文献[28-29]将联邦学习方法的训练总时间概括为通信时间和计算时间,并由此定义通信-计算时间比为
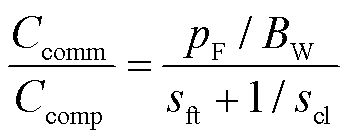 (11)
(11)
式中, 为通信时间;
为通信时间;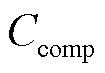 为计算时间;
为计算时间;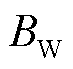 为带宽;
为带宽;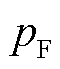 为长度为
为长度为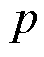 的向量所需要的位数;根据文献[30]提出的梯度计算时间的移位-指数模型,
的向量所需要的位数;根据文献[30]提出的梯度计算时间的移位-指数模型,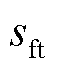 和
和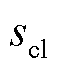 分别为移位指数分布的移位参数和尺度参数。
分别为移位指数分布的移位参数和尺度参数。
图2为由K个客户端和一个中央服务器组成个性化张量联邦学习框架的示意图,每个客户端训练两种模型,分别为个性化模型和张量化本地模型。
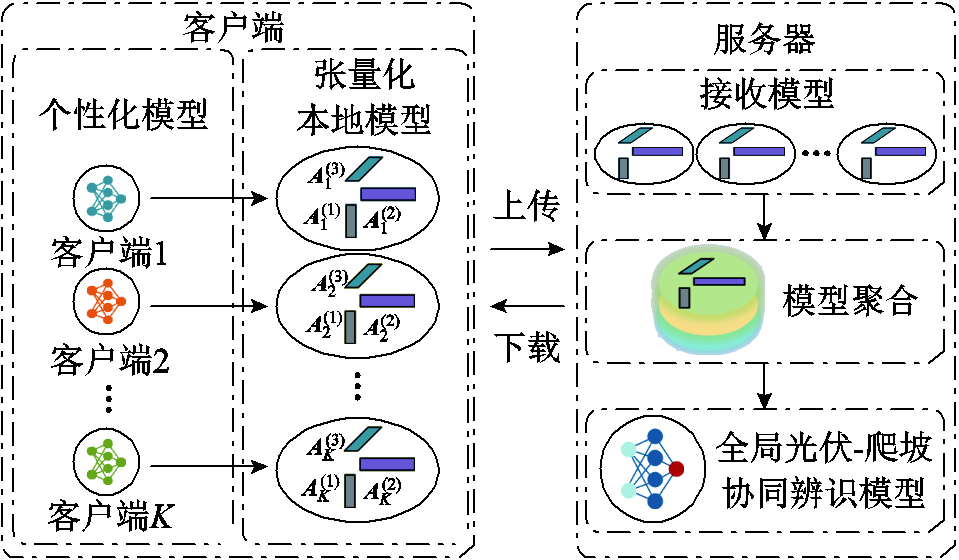
图2 张量分解个性化联邦学习示意图
Fig.2 The schematic of the tensor decomposition based personalized federated learning
1)个性化模型:每个电网分区客户端使用本地光伏爬坡和网络攻击数据集训练的模型,并将数据保存在本地。
2)张量化本地模型:通过将个性化模型的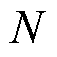 维权重参数矩阵分解为因子矩阵
维权重参数矩阵分解为因子矩阵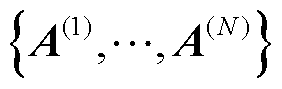 后得到的模型。张量化本地模型接近个性化模型,并用于与服务器通信以聚合全局模型。该模型目的是将高维权重参数压缩到低维子空间,从而降低通信成本和对于网络环境的要求。
后得到的模型。张量化本地模型接近个性化模型,并用于与服务器通信以聚合全局模型。该模型目的是将高维权重参数压缩到低维子空间,从而降低通信成本和对于网络环境的要求。
在定义第k个客户端的本地目标函数之前,为了防止模型过度拟合训练数据而导致对陌生数据识别效果下降,定义一个惩罚项为
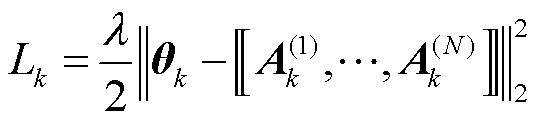 (12)
(12)
式中,λ为正则化项的系数。
客户端k的本地目标函数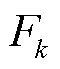 定义为
定义为
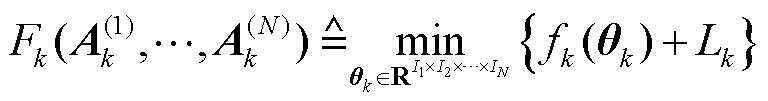 (13)
(13)
式(13)表示客户端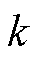 的目标是通过调整个性化模型
的目标是通过调整个性化模型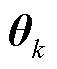 ,同时满足模型损失函数
,同时满足模型损失函数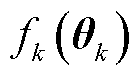 较小和
较小和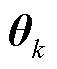 到张量化本地模型
到张量化本地模型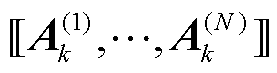 之间距离较小,使得模型既对现有数据具有良好的预测效果,又具有良好的泛化能力。
之间距离较小,使得模型既对现有数据具有良好的预测效果,又具有良好的泛化能力。
定义个性化张量联邦学习总体目标函数为
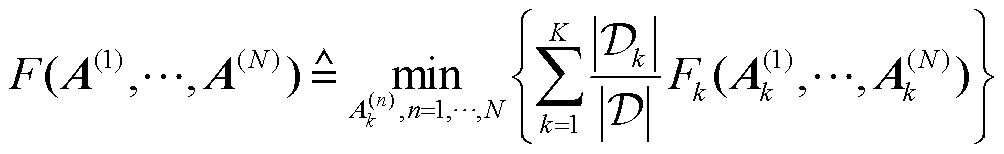 (14)
(14)
式(14)表示个性化张量联邦学习的总体目标为通过调整所有电网客户端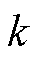 的因子矩阵
的因子矩阵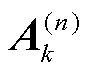 ,使得所有电网客户端的本地目标函数
,使得所有电网客户端的本地目标函数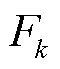 的加权和达到最小值,从而获得在所有独立电网分区都能准确进行网络-光伏爬坡协同攻击辨识的模型。其中
的加权和达到最小值,从而获得在所有独立电网分区都能准确进行网络-光伏爬坡协同攻击辨识的模型。其中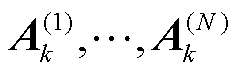 由
由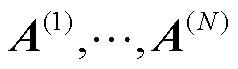 通过迭代得到,在2.4节中有详细说明。
通过迭代得到,在2.4节中有详细说明。
基于张量分解的个性化联邦学习训练策略整体思路如下。
1)第k个客户端的最优个性化模型表示为
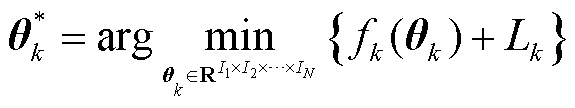 (15)
(15)
式中,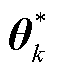 为第
为第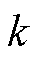 个客户端的最优个性化模型。
个客户端的最优个性化模型。
2)为了与服务器交互,客户端需要训练张量化本地模型以减少通信成本。客户端可以通过令局部目标函数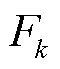 在
在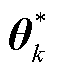 条件下最小来得到张量化本地模型
条件下最小来得到张量化本地模型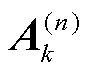 ,此时
,此时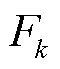 为
为
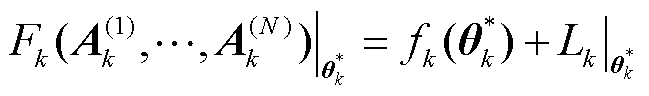 (16)
(16)
由此可以得到个性化模型和张量化本地模型。通过传输张量化本地模型以减少通信负载,加快训练速度,同时保留个性化模型以提高对本地光伏数据的辨识性能。
在电网客户端训练过程中,首先使用张量化本地模型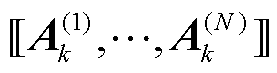 作为参考中心点,并以最小化式(13)中的目标函数
作为参考中心点,并以最小化式(13)中的目标函数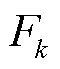 为目标训练个性化模型,然后在最优个性化模型的基础上训练张量化本地模型,并将因子矩阵上传到服务器。服务器首先聚合这些因子矩阵,然后向电网客户端提供聚合后的向量和因子矩阵,分别作为下次训练的初始个性化模型和张量化本地模型,重复该过程直到收敛。具体流程如下。
为目标训练个性化模型,然后在最优个性化模型的基础上训练张量化本地模型,并将因子矩阵上传到服务器。服务器首先聚合这些因子矩阵,然后向电网客户端提供聚合后的向量和因子矩阵,分别作为下次训练的初始个性化模型和张量化本地模型,重复该过程直到收敛。具体流程如下。
1)全局初始化和广播。首先,中央服务器初始化一个全局模型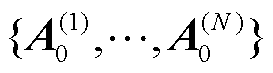 并将其广播给所有电网客户端,等待后续训练。
并将其广播给所有电网客户端,等待后续训练。
2)第t次全局通信。假设整个训练过程包含t次与服务器全局通信,在第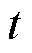 次(
次(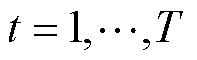 )全局通信时,每个电网客户端共计进行
)全局通信时,每个电网客户端共计进行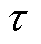 轮本地更新,并依次使用各自的光伏爬坡数据和FDIA攻击数据训练个性化模型和张量化本地模型。在第
轮本地更新,并依次使用各自的光伏爬坡数据和FDIA攻击数据训练个性化模型和张量化本地模型。在第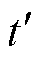 次(
次(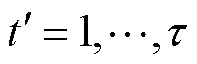 )更新时,第
)更新时,第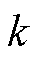 (
(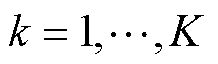 )个电网客户端首先使用
)个电网客户端首先使用 作为参考中心点,根据本文2.3节中的策略训练自己的个性化模型
作为参考中心点,根据本文2.3节中的策略训练自己的个性化模型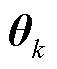 ,然后使用该模型根据本文2.4节中的策略训练张量化本地模型
,然后使用该模型根据本文2.4节中的策略训练张量化本地模型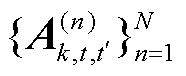 。
。
3)客户端选择和模型聚合。在联邦学习的过程中,由于通信负载大或者信号受到干扰等情况的出现会导致连接状况的不稳定,服务器有可能无法接收到所有上传的数据。因此,通常会选择一个大小为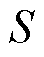 的客户端子集
的客户端子集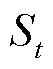 用于模型聚合,并广播更新后的全局模型。在客户端侧,每一个被选中的客户端上传其更新的张量化本地模型
用于模型聚合,并广播更新后的全局模型。在客户端侧,每一个被选中的客户端上传其更新的张量化本地模型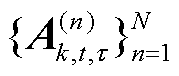 ,
,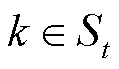 到服务器。在服务器侧,使用聚合因子矩阵或聚合向量组的方式进行模型聚合,然后将聚合后的向量和因子矩阵分发给各服务器分别作为下次训练的初始个性化模型和张量化本地模型。以聚合因子矩阵的个性化张量联邦学习为例展示个性化张量联邦学习训练模型的过程。
到服务器。在服务器侧,使用聚合因子矩阵或聚合向量组的方式进行模型聚合,然后将聚合后的向量和因子矩阵分发给各服务器分别作为下次训练的初始个性化模型和张量化本地模型。以聚合因子矩阵的个性化张量联邦学习为例展示个性化张量联邦学习训练模型的过程。

TDPFedAFM方法:基于聚合因子矩阵的个性化张量联邦学习方法 输入:客户端数据集,全局通信次数,本地更新轮次,个性化模型迭代次数,张量化模型迭代次数,个性化张量联邦学习的超参数、、等。输出:用于进行网络-光伏爬坡协同耦合攻击辨识的模型。服务器端:for do:for in parallel do: ClientUpdateend(选取的客户端集合St)endClientUpdate:for do:(抽取一个大小为的样本)ifendreturn
在每次本地迭代中随机选取小批量样本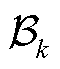 ,定义一个
,定义一个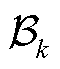 上的新目标函数为
上的新目标函数为
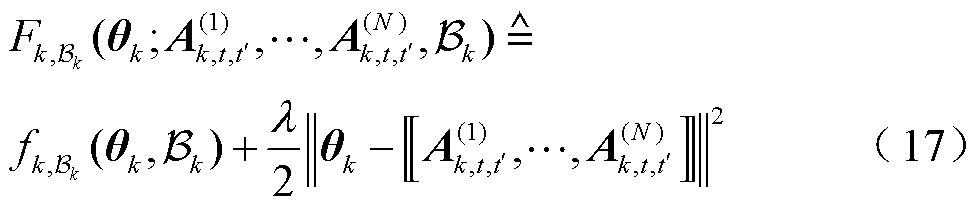
假设选择的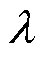 使得
使得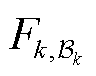 是强凸的,模型在小批量样本
是强凸的,模型在小批量样本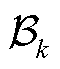 上的损失梯度
上的损失梯度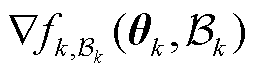 作为对整个数据集损失梯度
作为对整个数据集损失梯度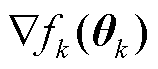 的无偏估计,所期望的准确度水平是
的无偏估计,所期望的准确度水平是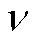 。此时应用Nesterov加速梯度下降方法,经过
。此时应用Nesterov加速梯度下降方法,经过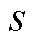 次迭代计算后获得新的个性化模型
次迭代计算后获得新的个性化模型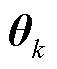 。如果
。如果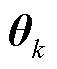 满足式(18)的条件,则使用新获得的
满足式(18)的条件,则使用新获得的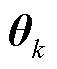 替换最优解
替换最优解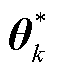 ,有
,有
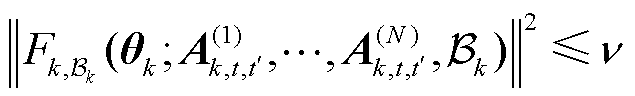 (18)
(18)
在训练得到最优个性化模型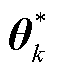 的基础上,本文方法基于梯度下降训练张量化本地模型。客户端
的基础上,本文方法基于梯度下降训练张量化本地模型。客户端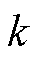 的因子矩阵
的因子矩阵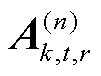 的梯度
的梯度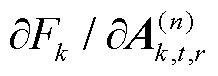 可以表示为
可以表示为
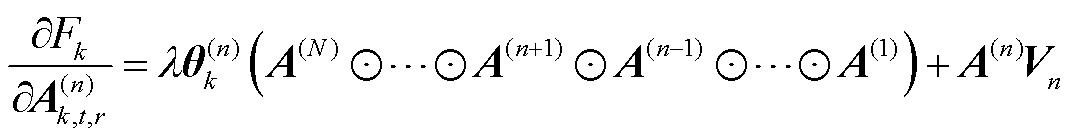 (19)
(19)
基于梯度下降,张量化本地模型的因子矩阵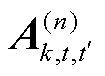 的更新公式为
的更新公式为
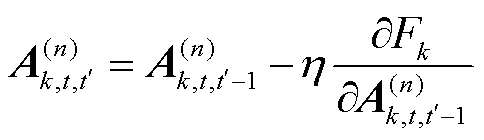 (20)
(20)
式中,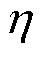 为张量化本地模型的学习率。在
为张量化本地模型的学习率。在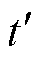 次本地更新轮次中,训练
次本地更新轮次中,训练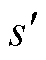 次以获得近张量化本地模型
次以获得近张量化本地模型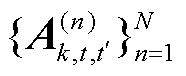 。
。
为了解决不同电网客户端对应的因子矩阵在梯度下降过程中迭代方向不同的问题,本文采用基于聚合因子矩阵的个性化张量联邦学习(记作TDPFedAFM)和基于聚合向量组的个性化张量联邦学习(记作TDPFedACT)这两种不同策略进行全局模型聚合。
1)聚合因子矩阵(Aggregating Factor Matrix, AFM):服务器根据训练时选取小批量样本的数量计算全局模型每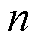 阶
阶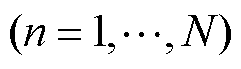 平均因子矩阵
平均因子矩阵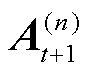 为
为
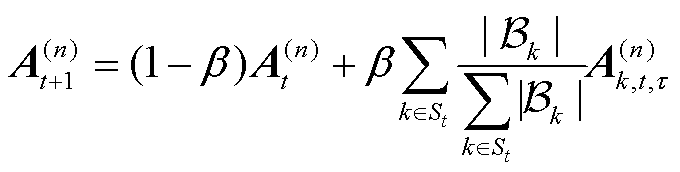 (21)
(21)
式中,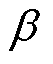 为聚合系数,用于控制全局模型更新率。
为聚合系数,用于控制全局模型更新率。
2)聚合向量组(Aggregating Composed Tensor,ACT):服务器首先将经过张量化压缩的因子矩阵还原为完整的本地模型,即
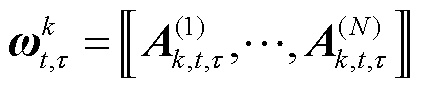 (22)
(22)
然后根据客户端本地样本数量计算更新后的全局模型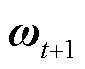 为
为
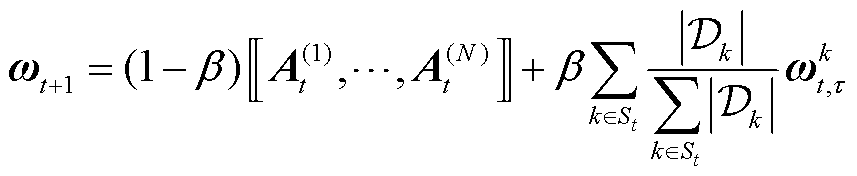 (23)
(23)
聚合后的完整全局模型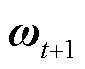 与张量化的全局模型
与张量化的全局模型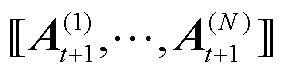 近似相等,即
近似相等,即
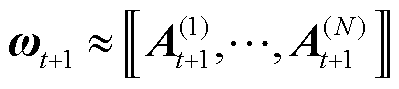 (24)
(24)
为解决实际应用过程中因电网运行时长较短导致数据不足,极端场景数据比例过低等问题,本节对光伏出力进行特征分析,并基于分析结果生成数据。生成的数据不仅可以模拟大量电网分区合作训练的场景,也可以为针对光伏爬坡的数据增强提供借鉴。
光伏发电的出力受地球自转的影响较大,呈现出明显的日周期特性。总体来看,光伏出力的大小与接收到的太阳辐射量密切相关,主要受两方面因素的影响[31-32]。
1)太阳辐射能量与大气层的衰减作用。大气层外的太阳辐射能量主要受地球和太阳之间的相对运动影响,呈现昼夜与季节性的周期变化,大气层则通过吸收、散射和反射减少了实际到达地表的太阳辐射能量。太阳辐射能量决定了光伏出力趋势,大气层的衰减作用在趋势不变的条件下降低了光伏出力的理论最大值。
2)天气状况。局部云层的扰动通过遮挡、散射和反射太阳辐射,导致光伏发电出力出现短时间内的剧烈波动。不同类型和高度的云层会对光伏出力的强度和稳定性产生不同影响,尤其在多云天气中,光伏出力往往呈现“锯齿状”波动。云层的移动、聚集和消散导致min级和h级的出力波动,增加了光伏出力的不确定性。
因此,将光伏出力曲线描述为
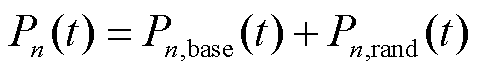 (25)
(25)
式中,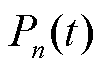 为第
为第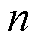 天的光伏实际出力;
天的光伏实际出力;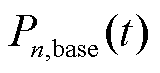 为第
为第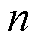 天的光伏出力基准曲线,主要表征太阳辐射能量与大气层的衰减作用;
天的光伏出力基准曲线,主要表征太阳辐射能量与大气层的衰减作用; 为第
为第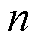 天的光伏出力随机分量,主要表征天气状况对实际出力的影响。
天的光伏出力随机分量,主要表征天气状况对实际出力的影响。
光伏出力的基准曲线是不考虑天气情况、云层扰动情况下光伏电站的出力曲线。虽然该曲线可以通过日地模型模拟,但光伏电站的实际出力还受当地气象条件、光伏板的安装方式等因素影响,日地模型误差较大[32]。为此,本文使用以下步骤对光伏出力的基准曲线进行提取。
1)数据归一化。由于不同光伏电站的装机容量和发电功率不同,为统一基准日的选取标准,首先对6个光伏电站的数据逐天进行了归一化,有
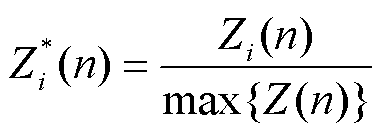 (26)
(26)
式中,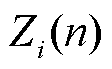 为第
为第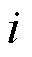 天第
天第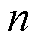 个功率的测量值;
个功率的测量值;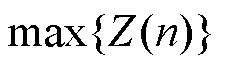 为该电站数据库中光伏出力的最大值;
为该电站数据库中光伏出力的最大值;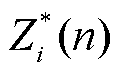 为归一化后的功率测量值。
为归一化后的功率测量值。
2)提取基准日曲线。基于归一化后的数据,通过筛选全天光伏出力较为平滑的曲线得到受天气状况影响较小的基准日,筛选依据为光伏出力的二阶差分绝对值小于扰动阈值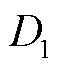 ,即
,即
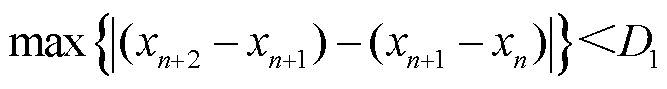 (27)
(27)
式中,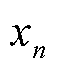 为当日第
为当日第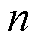 个采样点光伏出力的功率;扰动阈值
个采样点光伏出力的功率;扰动阈值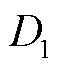 取0.003(pu)。
取0.003(pu)。
此外,为了避免选择阴雨天作为基准日曲线,增加了对当日最大功率的限制,此时的最大功率阈值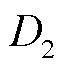 =0.2(pu)。
=0.2(pu)。
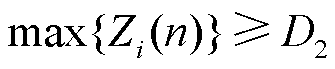 (28)
(28)
最后通过快速傅里叶变换并保留前7次谐波,得到基准日出力曲线所对应的解析化出力曲线。
光伏出力的随机分量主要来源于天气状况和云层扰动的影响,但随机分量的概率分布特征有待研究。为了对随机分量进行定量描述,根据式(25)得到随机分量的表达式为
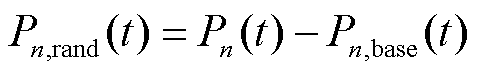 (29)
(29)
通过将扰动阈值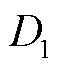 提高到0.008(pu),可以得到更多组基准日曲线与对应的解析化曲线,进而通过式(29)得到对应的随机分量。本文对6个电站3年的数据进行了统计,并使用正态分布、Logistic分布、广义极值分布、t location-scale(TLS)分布与拉普拉斯分布进行对比,发现拉普拉斯分布更适合描述随机分量的概率分布。拉普拉斯分布的表达式为
提高到0.008(pu),可以得到更多组基准日曲线与对应的解析化曲线,进而通过式(29)得到对应的随机分量。本文对6个电站3年的数据进行了统计,并使用正态分布、Logistic分布、广义极值分布、t location-scale(TLS)分布与拉普拉斯分布进行对比,发现拉普拉斯分布更适合描述随机分量的概率分布。拉普拉斯分布的表达式为
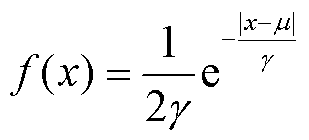 (30)
(30)
式中,x为随机变量;γ为尺度参数;μ为位置参数,且方差为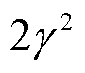 。
。
图3展示了6座电站3年数据提取的随机分量概率分布直方图和不同概率分布函数的拟合结果。可以看出,相比于其他概率分布函数,拉普拉斯分布拟合效果最好。
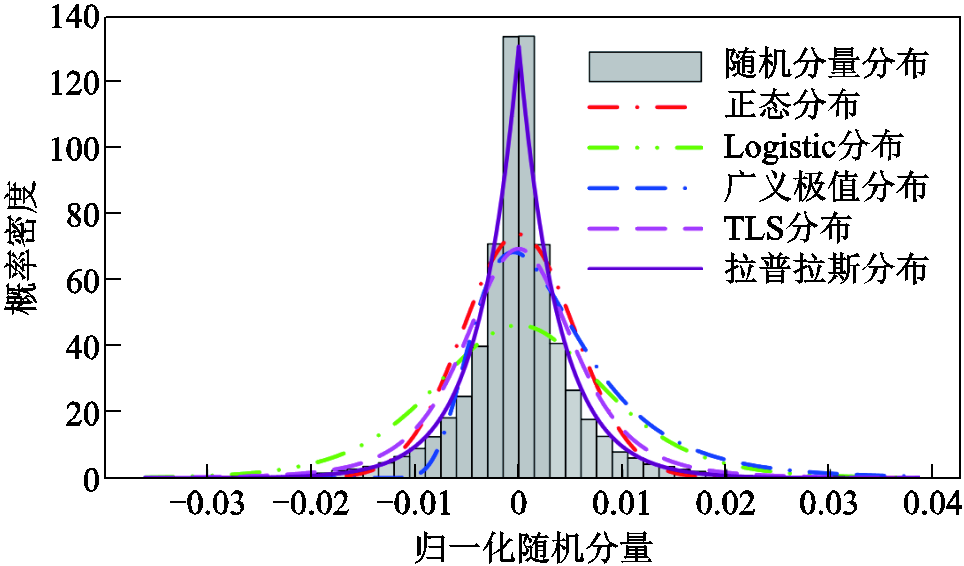
图3 随机分量的概率分布拟合
Fig.3 Fitting of probability distribution for random components
光伏出力曲线由两种方式生成:一种是基于基准日生成的出力曲线;另一种是基于非基准日生成的出力曲线。在光伏出力数据的基础上叠加网络攻击函数得到被攻击的数据曲线。
1)基于基准日生成的出力曲线
由于基准日对于程序理解光伏出力的规律至关重要,而实际数据中基准日数量较少,因此利用3.1节中提取的基准日曲线,采用线性插值的方式可以计算得到两个基准日之间缺失的曲线,有
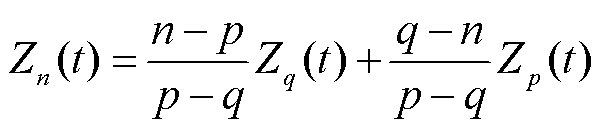 (31)
(31)
式中,Zn(t)为待计算缺失曲线的某日的功率;Zq(t)为第n日后最近基准日的功率;Zp(t)为第n日前最近基准日的功率;n为两个基准日之间待计算缺失曲线的某日;p为第n日前最近的基准日;q为第n日后最近的基准日。
得到基准日曲线之后,可以通过在曲线上叠加符合拉普拉斯分布的随机分量的方式生成更多数据用于后续程序的训练。图4a展示了实测数据与基于基准日生成的出力曲线。
2)基于非基准日生成的出力曲线
选取非基准日实际光伏出力数据并叠加满足拉普拉斯分布的随机分量,可以得到基于非基准日生成的出力曲线,如图4b所示。由于在实际生产中非基准日占比更高,因此选择基准日与非基准日为1:5的比例生成基于非基准日的出力曲线。
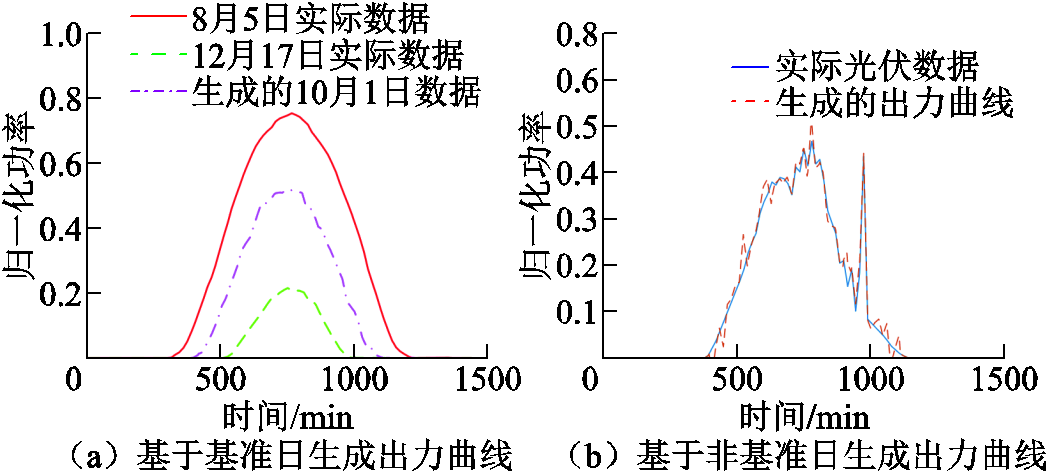
图4 光伏出力曲线生成
Fig.4 Generation of photovoltaic output curves
3)攻击数据集生成
基于实际光伏数据和生成的光伏出力曲线,按照1.1节中网络攻击方式对不同位置、不同时间的光伏数据进行恶意攻击,得到攻击后的部分数据如图5所示。
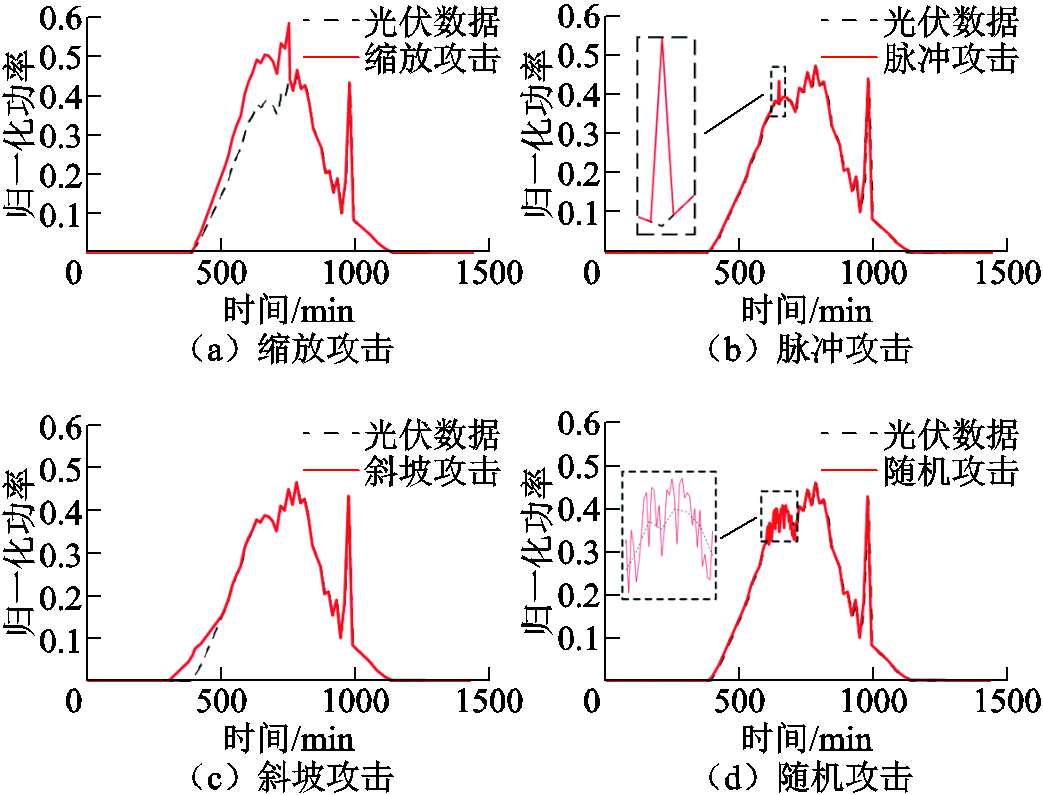
图5 网络-光伏爬坡协同攻击数据集
Fig.5 Datasets for cyber-ramping coordinated attacks for PV
由此生成的攻击数据和实际数据汇总形成数据集,作为个性化张量联邦学习训练网络-光伏爬坡协同攻击辨识模型的训练集和测试集。为了方便描述,根据不同时间段的光伏数据和攻击方式,定义不同场景的含义见表2。
由于实际网络受攻击时刻远小于正常运行时刻,正常样本数量会远远大于攻击样本数量,从而构成不平衡数据集。此时辨识方法大量学习正常运行数据,难以学习到网络攻击的特征,导致模型最终会偏向正常样本而忽视攻击样本[33-34]。为解决上述问题,采取本节的策略生成攻击样本,按照相同比例随机选取不同月份的正常样本构造平衡数据集。
表2 不同场景和对应含义
Tab.2 Different scenarios and corresponding meanings
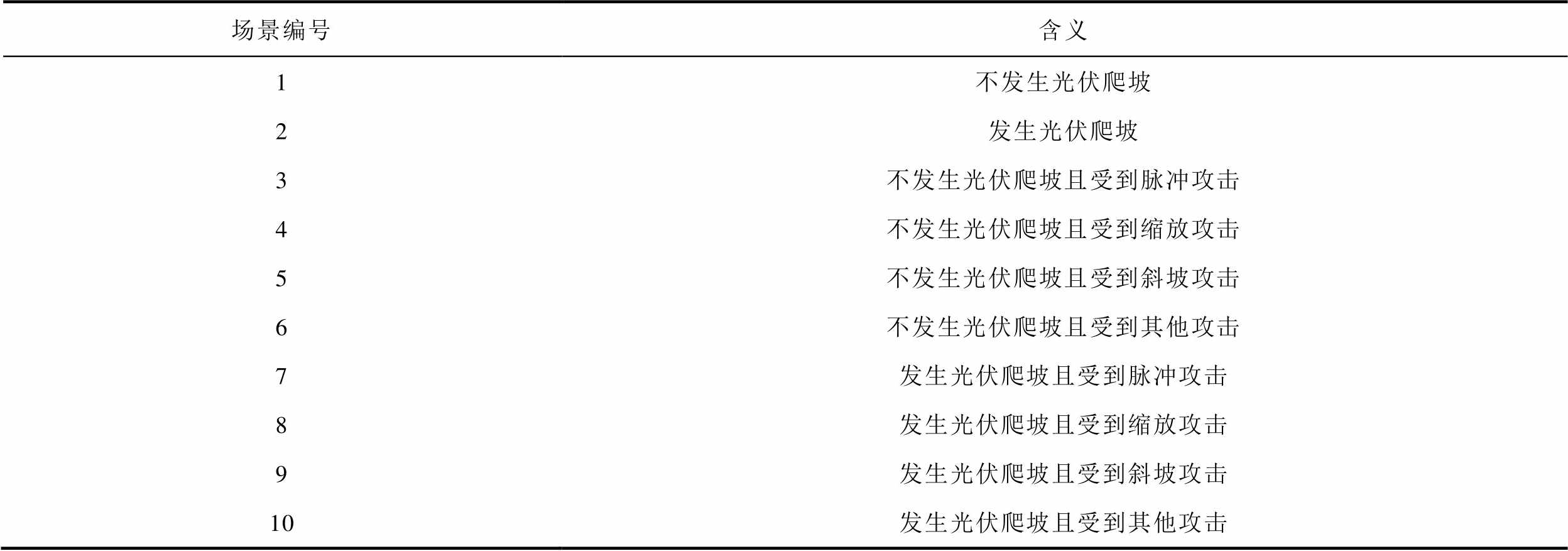
场景编号含义 1不发生光伏爬坡 2发生光伏爬坡 3不发生光伏爬坡且受到脉冲攻击 4不发生光伏爬坡且受到缩放攻击 5不发生光伏爬坡且受到斜坡攻击 6不发生光伏爬坡且受到其他攻击 7发生光伏爬坡且受到脉冲攻击 8发生光伏爬坡且受到缩放攻击 9发生光伏爬坡且受到斜坡攻击 10发生光伏爬坡且受到其他攻击
实验采用的软件为Pycharm,解释器版本为Python 3.10,所使用的计算机CPU配置为Intel Core i9-13900HX(2.20 GHz),RAM为16.0 GB,显卡采用NVIDIA GeForce RTX 4060 Laptop GPU。
实验采用IEEE 33节点系统作为测试案例,如图6所示。选取分辨率为3 min,周期为3年的实际负荷和光伏数据,攻击节点设置为13、18和29。
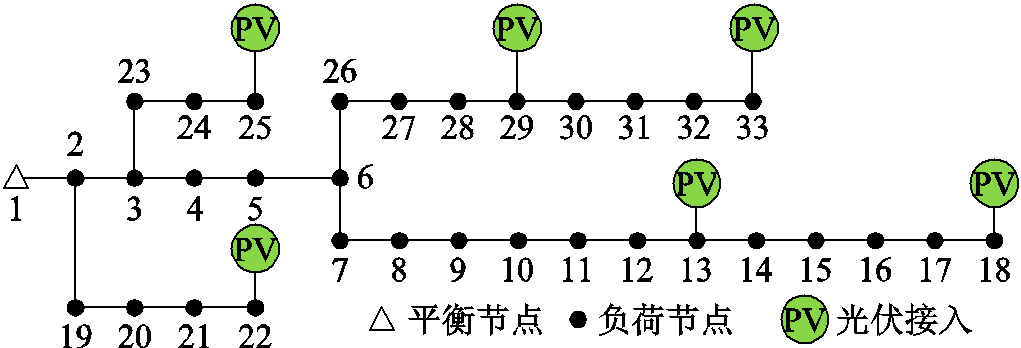
图6 IEEE 33节点系统示意图
Fig.6 Schematic of the IEEE 33-bus system
在实际数据的基础上根据光伏出力分析结果生成更多数据用于训练,其中训练集正常样本3 360个,攻击样本13 440个,全部样本16 800个。测试集正常样本1 400个,攻击样本5 600个,全部样本7 000个。采用深度神经网络(Deep Neural Network, DNN)训练数据集,通过多次试验确定个性化张量联邦学习模型参数见表3。
表3 张量分解个性化联邦学习参数
Tab.3 Parameters of tensor decomposition based personalized federated learning

参数数值 迭代总次数T1 000 客户端总数K20 聚合系数1.8
(续)

参数数值 正则化项的系数2.0 每次迭代使用的样本数量20 客户端的学习率0.000 8 个性化模型使用的学习率0.02 张量化模型的迭代次数5 个性化模型的迭代次数s15
为了体现本文方法的有效性,设置了以下方法进行对比:选取LightGBM(light gradient Boosting machine)方法作为集中式算法的对照组,选取未压缩的FedAvg(federated averaging)方法和pFedMe(personalized federated learning with moreau envelopes)方法作为联邦学习方法对照组。对传统的FedAvg方法采取随机选择与压缩率相同比例的参数进行传输,将修改后的方法记为FedAvg-Ⅱ来模拟通信资源不足的情况,未经修改的方法记为FedAvg-Ⅰ。将使用AFM和ACT聚合策略的个性化张量联邦学习分别记为TDPFedAFM和TDPFedACT,用于对比不同聚合策略的方法性能差异,并按照压缩率比例减少传输的信息量。
不同方法在不同压缩率下全局准确率和损失函数的变化情况如图7所示。在收敛速度方面,LightGBM、FedAvg-Ⅰ、pFedMe、FedAvg-Ⅱ方法在700次迭代时仍未收敛或收敛后准确率较低,本文方法在70次迭代时已经收敛,并且在准确率方面具有较大优势。随着压缩率的提高,FedAvg-II由于缺乏有效的数据压缩方法,无论是从无压缩到1.5倍压缩率还是从1.5倍压缩率到2倍压缩率,训练效果下降幅度均超过5%。TDPFedAFM和TDPFedACT方法由于使用张量分解对联邦学习进行改进,可以在减少参数传输的同时保持较高性能,因此仍能快速收敛且训练效果下降幅度在0.7%以内。此外,TDPFedAFM、TDPFedACT方法在不同压缩率的训练过程中均未出现因陷入局部最优导致准确率难以上升的问题,可以迅速学习不同场景的特征,从而快速收敛。
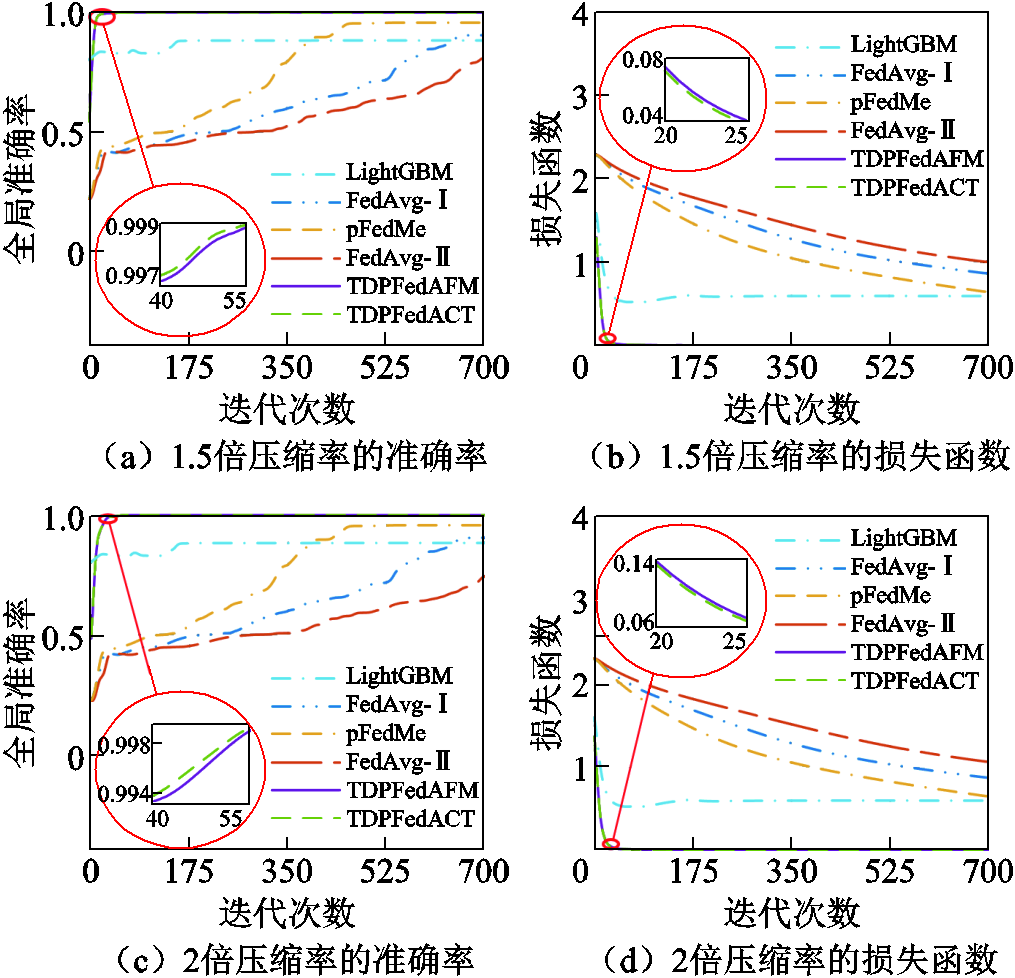
图7 准确率与损失函数
Fig.7 Accuracy ratio and loss function
首先给出辨识结果的表示方法见表4。
表4 事件辨识结果的表示方法
Tab.4 Representation of identification result

类型事件观测真事件观测假总计 事件辨识为真TPFP辨识为真 事件辨识为假FNTN辨识为假 总计观测真观测假
针对单一场景,根据表4给出精确率(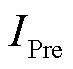 )、召回率(
)、召回率(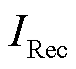 )、F1分数(
)、F1分数( )、特异度(
)、特异度(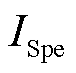 )和Matthews相关系数(
)和Matthews相关系数(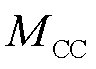 )五种分类性能评估指标,其表达式分别为
)五种分类性能评估指标,其表达式分别为
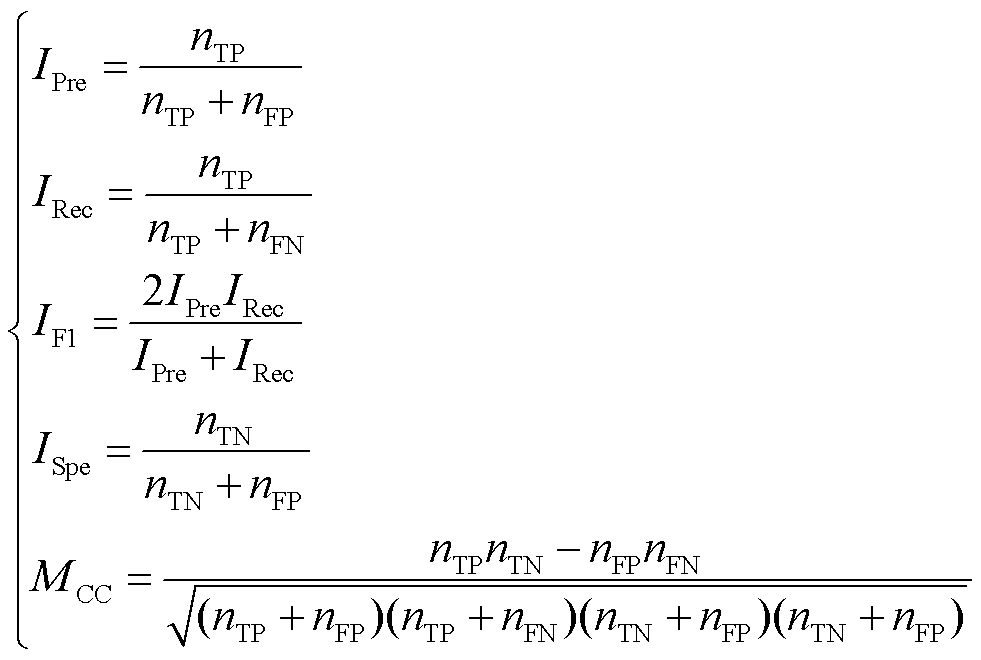 (32)
(32)
式中,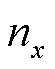 为x事件出现的次数,x=TP, FP, FN, TN。
为x事件出现的次数,x=TP, FP, FN, TN。
针对算法整体性能,根据式(32)给出宏平均精确率(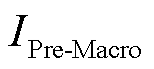 )、宏平均召回率(
)、宏平均召回率(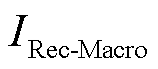 )、宏平均F1分数(
)、宏平均F1分数(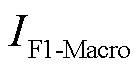 )、Kappa系数(
)、Kappa系数(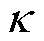 )和Hamming损失(
)和Hamming损失(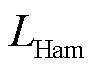 )五种评价指标,其表达式分别为
)五种评价指标,其表达式分别为
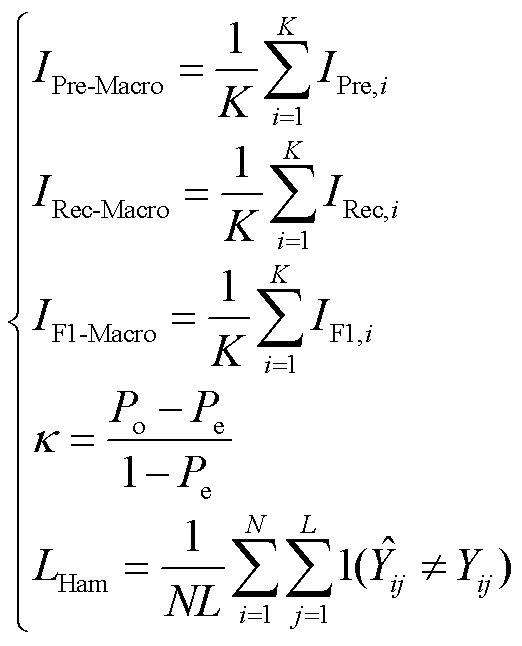 (33)
(33)
式中,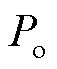 为观测一致性;
为观测一致性;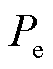 为预期一致性;
为预期一致性;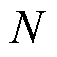 为样本数量;
为样本数量;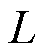 为样本标签;
为样本标签;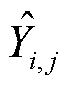 为第i个样本第j个标签的辨识结果;
为第i个样本第j个标签的辨识结果;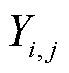 为第i个样本第j个标签的真实情况。
为第i个样本第j个标签的真实情况。
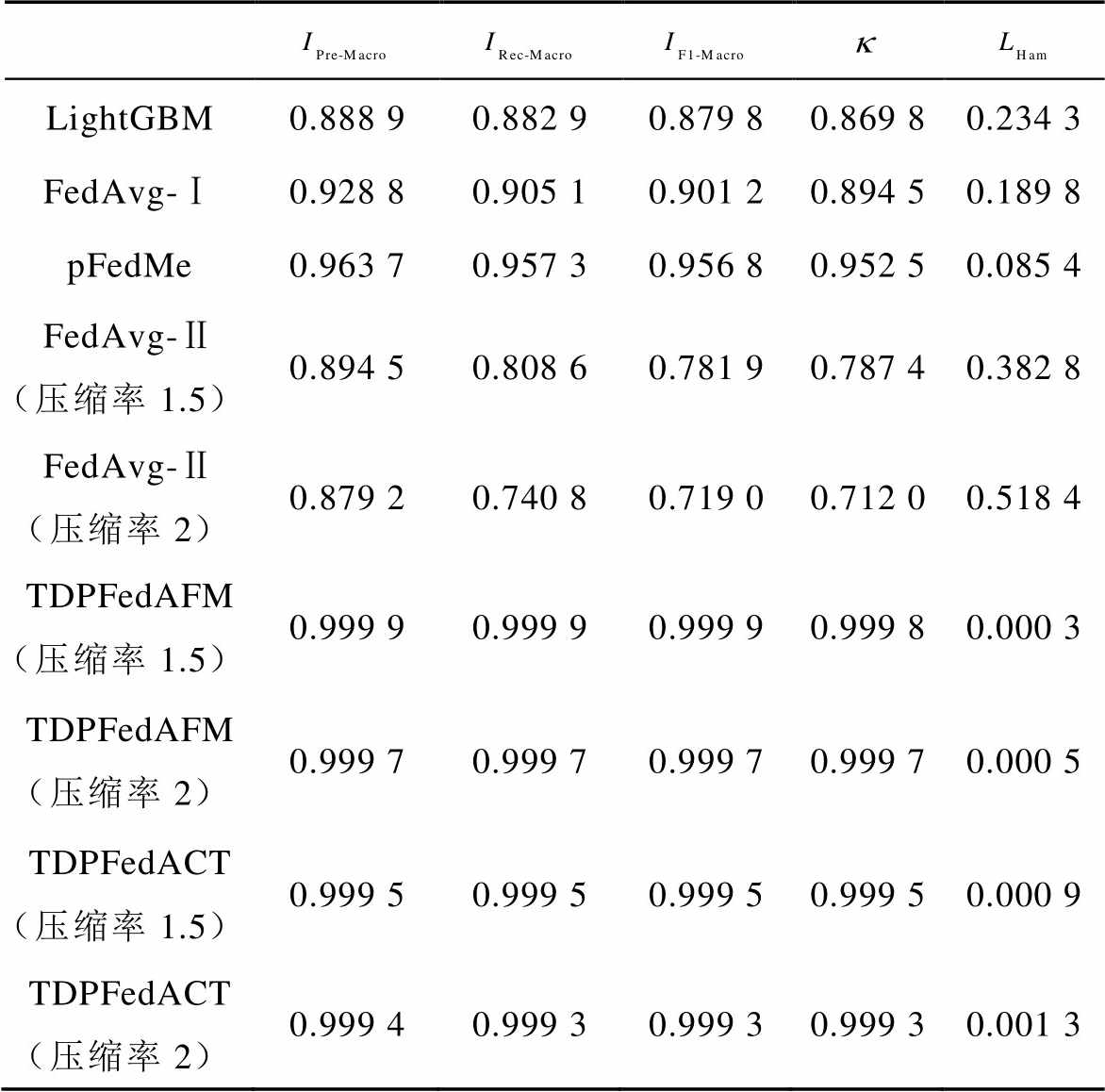
各方法性能比较见表5。表5中的指标主要表征算法的整体性能。可以看出,在宏平均精确率、宏平均召回率、宏平均F1分数、Kappa系数方面,传统的对比方法均在0.97以下,TDPFedAFM和TDPFedACT方法均大于0.999。Hamming损失方面,TDPFedAFM和TDPFedACT方法与其他方法产生了1~3个数量级的差距,证明两种聚合策略的个性化张量联邦学习都可以更有效地学习光伏爬坡和不同FDIA攻击场景的特征。在参数压缩方面,随着压缩率的提高,FedAvg-Ⅱ方法的辨识性能出现大幅下降。本文采用的TDPFedAFM和TDPFedACT方法在提升压缩率后辨识性能基本不变,说明本文方法使用的基于张量分解压缩的方式可以在提高通信效率的同时保证辨识的可靠性。
图8通过预测性能图直观展示五种方法对于不同场景的辨识效果。其中等高线为临界成功指数,左下角到右上角的虚线为偏差值,基于张量分解的个性化联邦学习使用AFM聚合策略。相较于其他方法,本文方法辨识结果更接近于右上角且分布集中,辨识效果更好。
表5 各方法性能比较
Tab.5 Performance comparison of each algorithm
LightGBM0.88890.88290.87980.86980.2343 FedAvg-Ⅰ0.92880.90510.90120.89450.1898 pFedMe0.96370.95730.95680.95250.0854 FedAvg-Ⅱ(压缩率1.5)0.89450.80860.78190.78740.3828 FedAvg-Ⅱ(压缩率2)0.87920.74080.71900.71200.5184 TDPFedAFM(压缩率1.5)0.99990.99990.99990.99980.0003 TDPFedAFM(压缩率2)0.99970.99970.99970.99970.0005 TDPFedACT(压缩率1.5)0.99950.99950.99950.99950.0009 TDPFedACT(压缩率2)0.99940.99930.99930.99930.0013
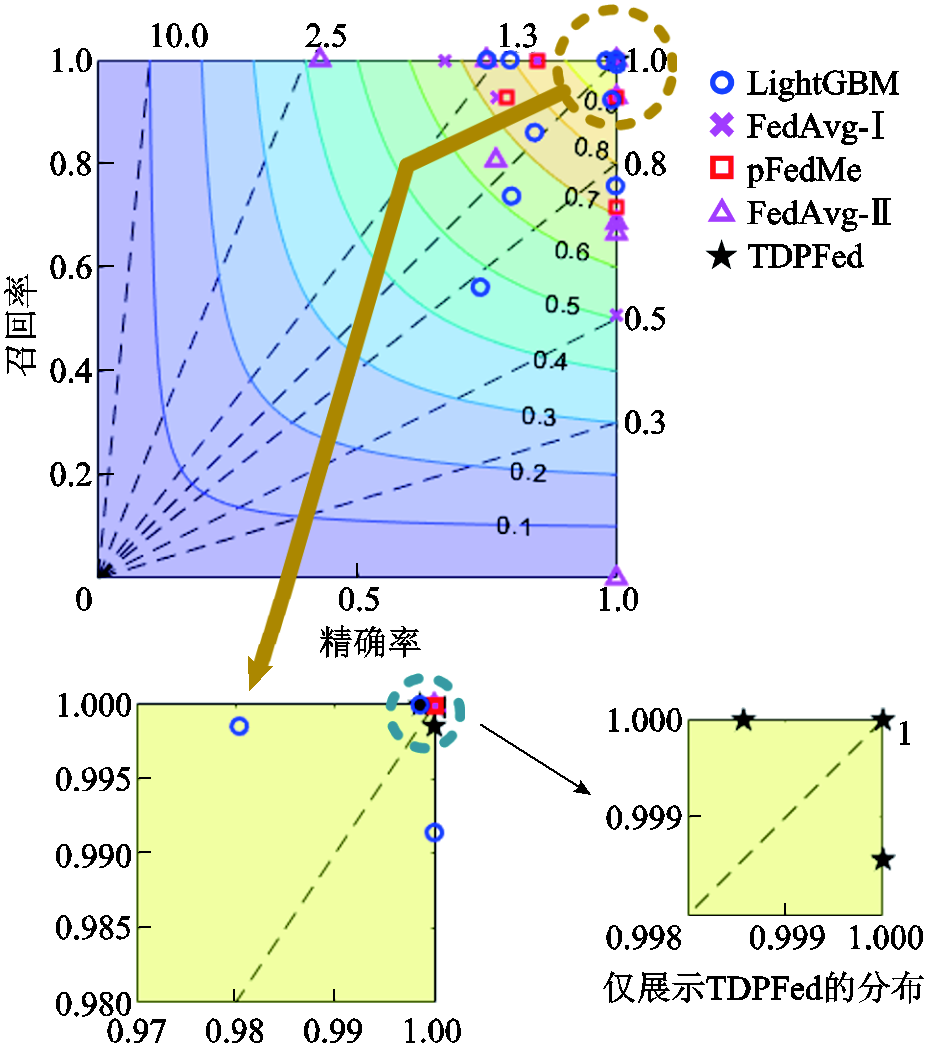
图8 预测性能
Fig.8 Prediction performance
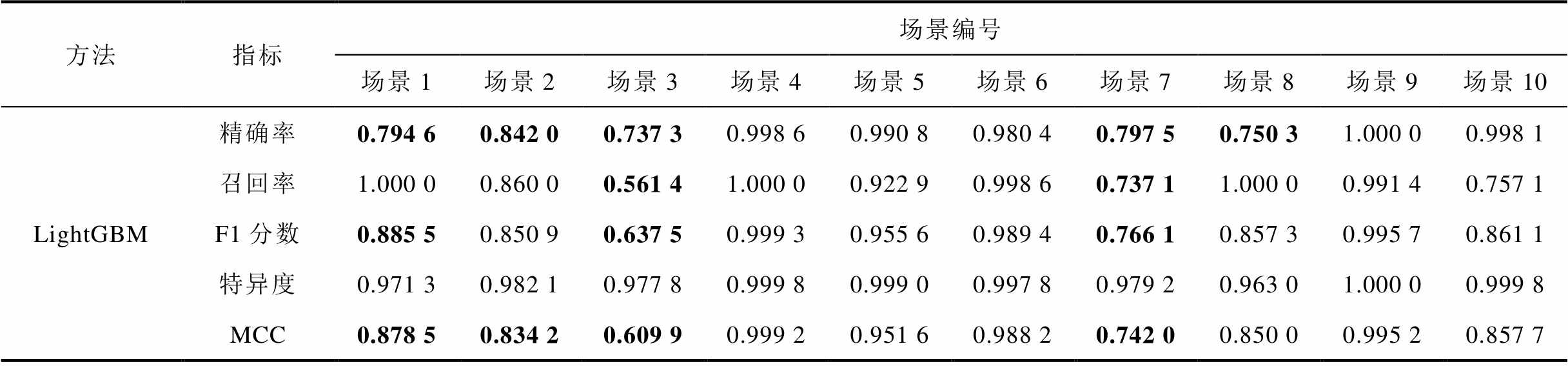
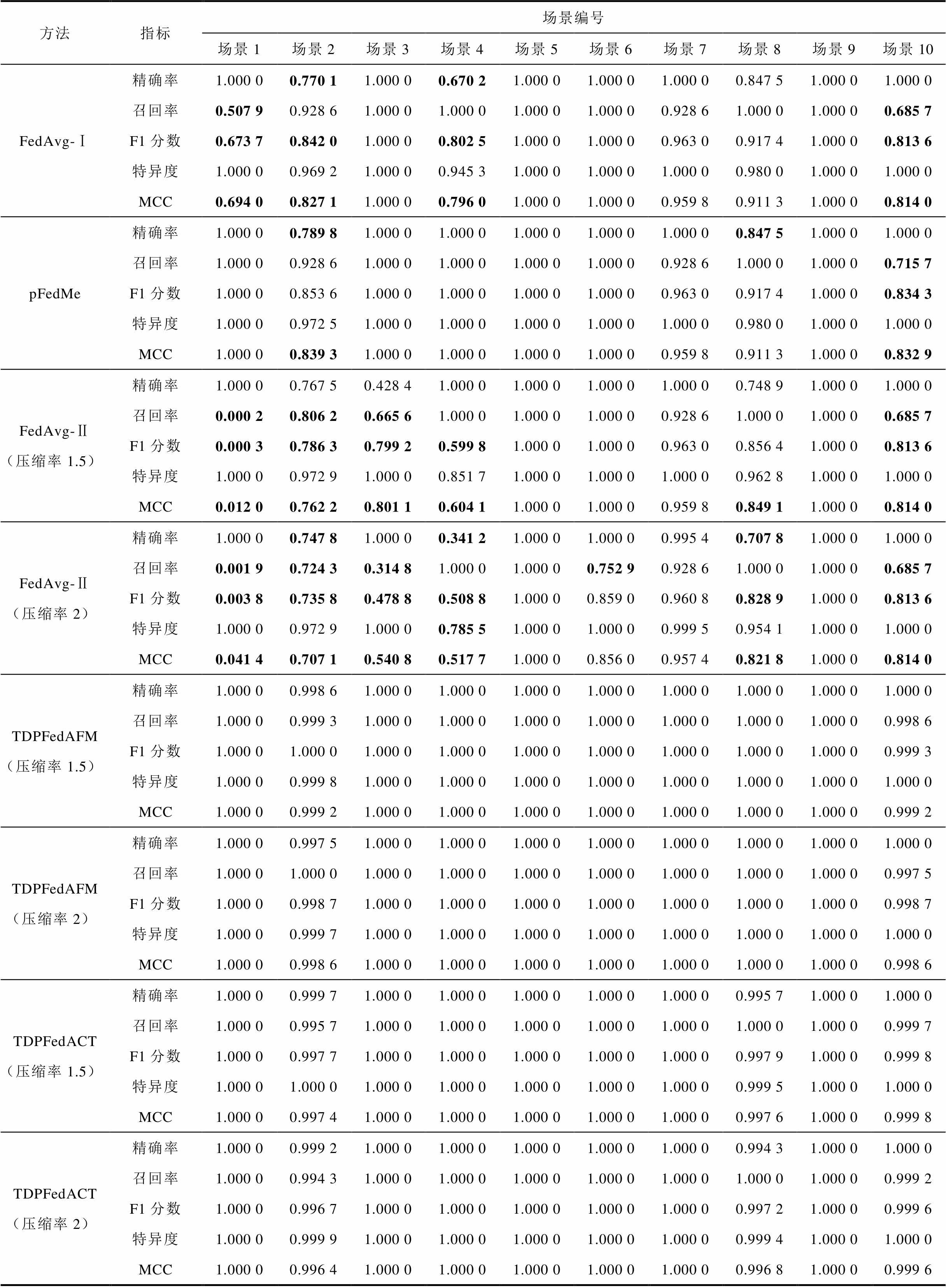
表6展示了不同场景下各方法的辨识效果,并加粗了辨识效果不佳的数据。其中pFedMe、FedAvg-Ⅰ和两种压缩率下的FedAvg-Ⅱ方法普遍对于场景1、2、3、4、8、10辨识效果不佳,且混淆了受攻击场景和无攻击场景;LightGBM方法对于场景1、2、3、7、8辨识效果不佳,相比之下个性化张量联邦学习方法在所有场景下都保持了较高的辨识准确率。
此外,对比FedAvg-Ⅰ和不同压缩率的FedAvg-Ⅱ可以看出,随着压缩率的提升,FedAvg方法因上传参数减少影响模型完整性,导致辨识效果大幅下降。然而本文所提方法可以在提升压缩率的同时保证各场景各指标均大于0.99,在减少通信成本的同时保证了模型完整性和辨识准确性。
表6 不同场景下各方法辨识效果评估
Tab.6 Evaluation of algorithm prediction performance in different scenarios
方法指标场景编号 场景1场景2场景3场景4场景5场景6场景7场景8场景9场景10 LightGBM精确率0.79460.84200.73730.998 60.990 80.980 40.79750.75031.000 00.998 1 召回率1.000 00.860 00.56141.000 00.922 90.998 60.73711.000 00.991 40.757 1 F1分数0.88550.850 90.63750.999 30.955 60.989 40.76610.857 30.995 70.861 1 特异度0.971 30.982 10.977 80.999 80.999 00.997 80.979 20.963 01.000 00.999 8 MCC0.87850.83420.60990.999 20.951 60.988 20.74200.850 00.995 20.857 7
(续)
方法指标场景编号 场景1场景2场景3场景4场景5场景6场景7场景8场景9场景10 FedAvg-Ⅰ精确率1.000 00.77011.000 00.67021.000 01.000 01.000 00.847 51.000 01.000 0 召回率0.50790.928 61.000 01.000 01.000 01.000 00.928 61.000 01.000 00.6857 F1分数0.67370.84201.000 00.80251.000 01.000 00.963 00.917 41.000 00.8136 特异度1.000 00.969 21.000 00.945 31.000 01.000 01.000 00.980 01.000 01.000 0 MCC0.69400.82711.000 00.79601.000 01.000 00.959 80.911 31.000 00.8140 pFedMe精确率1.000 00.78981.000 01.000 01.000 01.000 01.000 00.84751.000 01.000 0 召回率1.000 00.928 61.000 01.000 01.000 01.000 00.928 61.000 01.000 00.7157 F1分数1.000 00.853 61.000 01.000 01.000 01.000 00.963 00.917 41.000 00.8343 特异度1.000 00.972 51.000 01.000 01.000 01.000 01.000 00.980 01.000 01.000 0 MCC1.000 00.83931.000 01.000 01.000 01.000 00.959 80.911 31.000 00.8329 FedAvg-Ⅱ(压缩率1.5)精确率1.000 00.767 50.428 41.000 01.000 01.000 01.000 00.748 91.000 01.000 0 召回率0.00020.80620.66561.000 01.000 01.000 00.928 61.000 01.000 00.6857 F1分数0.00030.78630.79920.59981.000 01.000 00.963 00.856 41.000 00.8136 特异度1.000 00.972 91.000 00.851 71.000 01.000 01.000 00.962 81.000 01.000 0 MCC0.01200.76220.80110.60411.000 01.000 00.959 80.84911.000 00.8140 FedAvg-Ⅱ(压缩率2)精确率1.000 00.74781.000 00.34121.000 01.000 00.995 40.70781.000 01.000 0 召回率0.00190.72430.31481.000 01.000 00.75290.928 61.000 01.000 00.6857 F1分数0.00380.73580.47880.50881.000 00.859 00.960 80.82891.000 00.8136 特异度1.000 00.972 91.000 00.78551.000 01.000 00.999 50.954 11.000 01.000 0 MCC0.04140.70710.54080.51771.000 00.856 00.957 40.82181.000 00.8140 TDPFedAFM(压缩率1.5)精确率1.000 00.998 61.000 01.000 01.000 01.000 01.000 01.000 01.000 01.000 0 召回率1.000 00.999 31.000 01.000 01.000 01.000 01.000 01.000 01.000 00.998 6 F1分数1.000 01.000 01.000 01.000 01.000 01.000 01.000 01.000 01.000 00.999 3 特异度1.000 00.999 81.000 01.000 01.000 01.000 01.000 01.000 01.000 01.000 0 MCC1.000 00.999 21.000 01.000 01.000 01.000 01.000 01.000 01.000 00.999 2 TDPFedAFM(压缩率2)精确率1.000 00.997 51.000 01.000 01.000 01.000 01.000 01.000 01.000 01.000 0 召回率1.000 01.000 01.000 01.000 01.000 01.000 01.000 01.000 01.000 00.997 5 F1分数1.000 00.998 71.000 01.000 01.000 01.000 01.000 01.000 01.000 00.998 7 特异度1.000 00.999 71.000 01.000 01.000 01.000 01.000 01.000 01.000 01.000 0 MCC1.000 00.998 61.000 01.000 01.000 01.000 01.000 01.000 01.000 00.998 6 TDPFedACT(压缩率1.5)精确率1.000 00.999 71.000 01.000 01.000 01.000 01.000 00.995 71.000 01.000 0 召回率1.000 00.995 71.000 01.000 01.000 01.000 01.000 01.000 01.000 00.999 7 F1分数1.000 00.997 71.000 01.000 01.000 01.000 01.000 00.997 91.000 00.999 8 特异度1.000 01.000 01.000 01.000 01.000 01.000 01.000 00.999 51.000 01.000 0 MCC1.000 00.997 41.000 01.000 01.000 01.000 01.000 00.997 61.000 00.999 8 TDPFedACT(压缩率2)精确率1.000 00.999 21.000 01.000 01.000 01.000 01.000 00.994 31.000 01.000 0 召回率1.000 00.994 31.000 01.000 01.000 01.000 01.000 01.000 01.000 00.999 2 F1分数1.000 00.996 71.000 01.000 01.000 01.000 01.000 00.997 21.000 00.999 6 特异度1.000 00.999 91.000 01.000 01.000 01.000 01.000 00.999 41.000 01.000 0 MCC1.000 00.996 41.000 01.000 01.000 01.000 01.000 00.996 81.000 00.999 6
联邦学习训练过程中每次更新都涉及大量参数的上传与下载,在大电网系统中由于不同节点间参数上传和下载速度不一致、部分节点带宽不足等原因导致通信时间远超计算时间[35],通信时间成为制约训练效率的主要瓶颈。提高通信效率的方式有两种,分别为通过减少通信参数来减少单次通信所需时间,以及通过减少通信总轮次减少通信时间。因此,文本采取在客户端训练张量化本地模型的方式对模型进行压缩,减少单次上传所需的数据;同时采用了先进的模型聚合策略大幅提高模型收敛速度,减少训练所需轮次。
本文选择20个客户端,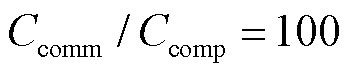 的条件下模拟电网系统中的通信瓶颈[35],并假设所有算法测试时网络环境一致,首先得到FedAvg-Ⅰ的通信时间并以此作为基准,其他方法依据通信所需的数据总量计算所需的通信时间。其中FedAvg-Ⅰ和pFedMe作为对比算法不进行参数压缩,FedAvg-Ⅱ、TDPFedAFM和TDPFedACT均采取2倍压缩率进行参数压缩,训练总时间包括本地训练时间、传输时间和模型聚合时间。通信-计算时间比为100时的耗时情况如图9所示。由图9可以看出,达到相同准确率时FedAvg-Ⅰ所需迭代次数少于FedAvg-Ⅱ,但在总耗时方面FedAvg-Ⅰ却高于FedAvg-Ⅱ,说明通过压缩单次传输所需要的数据量可以减少通信时间,进而缩短训练所需总时间。此外还可以看出,达到相同准确率时TDPFedAFM和TDPFedACT方法所需时间相较于其他方法小两个数量级,证明本文所使用方法在减少通信成本方面具有较大优势。
的条件下模拟电网系统中的通信瓶颈[35],并假设所有算法测试时网络环境一致,首先得到FedAvg-Ⅰ的通信时间并以此作为基准,其他方法依据通信所需的数据总量计算所需的通信时间。其中FedAvg-Ⅰ和pFedMe作为对比算法不进行参数压缩,FedAvg-Ⅱ、TDPFedAFM和TDPFedACT均采取2倍压缩率进行参数压缩,训练总时间包括本地训练时间、传输时间和模型聚合时间。通信-计算时间比为100时的耗时情况如图9所示。由图9可以看出,达到相同准确率时FedAvg-Ⅰ所需迭代次数少于FedAvg-Ⅱ,但在总耗时方面FedAvg-Ⅰ却高于FedAvg-Ⅱ,说明通过压缩单次传输所需要的数据量可以减少通信时间,进而缩短训练所需总时间。此外还可以看出,达到相同准确率时TDPFedAFM和TDPFedACT方法所需时间相较于其他方法小两个数量级,证明本文所使用方法在减少通信成本方面具有较大优势。
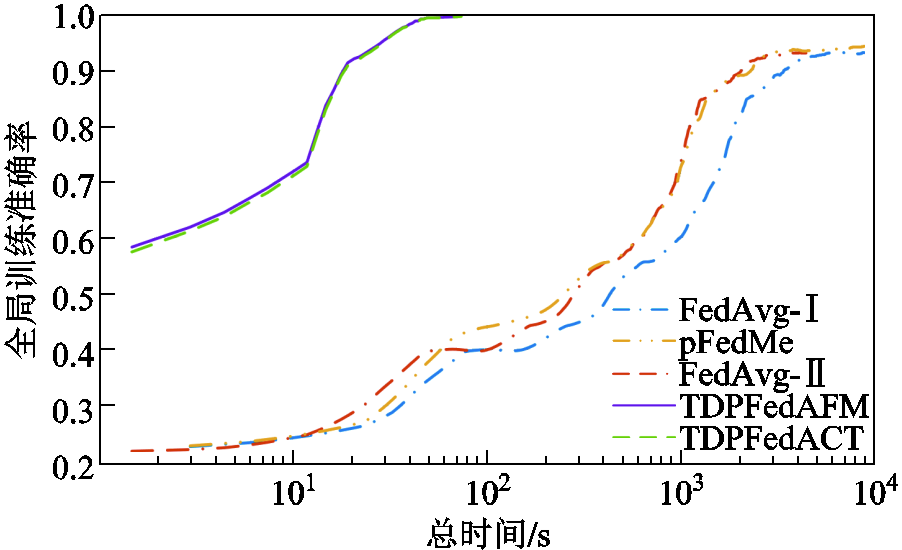
图9 通信-计算时间比为100时的耗时情况
Fig.9 The time consumption analysis with the communication-computing ratio of 100
使用文献[36]中介绍的快速符号梯度算法(Fast Gradient Sign Method, FGSM)生成光伏-爬坡协同对抗攻击数据并实施FDIA时,通过在攻击数据中添加精心设计的扰动使LightGBM方法的辨识准确率由88.3%下降至56%。相较于LightGBM方法,联邦学习算法表现出更强的鲁棒性,pFedMe算法辨识准确率由95.7%下降至89.1%,FedAvg方法辨识准确率由90.9%下降至82.2%。对抗攻击前后两种方法辨识结果如图10和图11所示。图10和图11为混淆矩阵,其中对角线上的元素表示辨识正确的样本,其余位置均为辨识错误的样本,红色越深代表辨识错误的比例越高,辨识效果越差。

图10 对抗攻击前后LightGBM方法辨识结果
Fig.10 Identification results of LightGBM method before and after adversarial attacks
由于本文方法能够学习到数据深层次抽象特征且训练过程中使用多种正则化技术提高模型泛化能力,不同聚合策略的TDPFed方法在不同压缩率下辨识准确率均高于96.7%,在各算法中表现出了较强的鲁棒性。

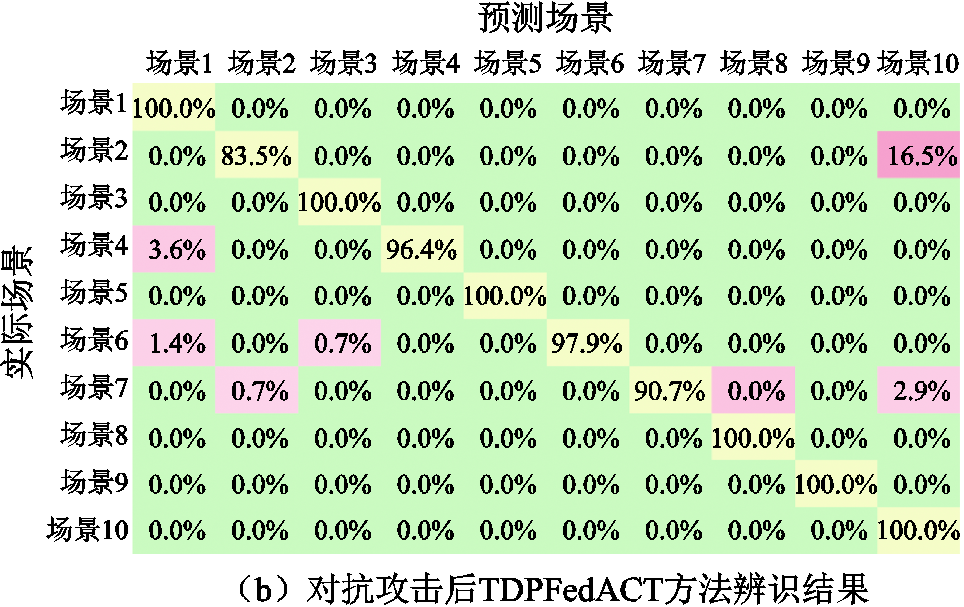
图11 对抗攻击前后TDPFedACT方法辨识结果
Fig.11 Identification results of TDPFedACT method before and after adversarial attacks
此外,文献[37]提出可以根据电网历史数据的FDIA通过对抗攻击添加特定扰动,并将生成的FDIA加入训练集重新训练来提高检测方法对噪声的鲁棒性。该方法可以进一步提高算法对于特定对抗攻击的辨识效果,但也需要更高的通信成本和更长的训练时间,与本文方法降低通信成本和快速收敛的思路存在一定冲突。在实际应用时可以先通过本文方法快速训练出具有较高检测能力的辨识模型,在此基础上通过上述方法增强辨识模型的鲁棒性,达到兼顾效率与准确率的目标。
针对光伏爬坡面临的虚假数据注入攻击,本文提出了一种基于张量分解个性化联邦学习的网络-光伏爬坡协同攻击的辨识方法,得到如下结论:
1)在模型训练过程中使用双层目标模型、合适的训练策略和聚合策略,可有效地提高网络-光伏爬坡协同攻击辨识的准确率,加快模型收敛速度。
2)通过张量分解压缩需要上传的参数数量,降低了联邦学习对于通信资源的要求,改进了传统联邦学习在大电网多节点系统中因通信资源不足导致训练困难的问题,明显地缩短了训练时间。
3)基于历史数据提取基准日曲线和光伏随机分量,通过实际数据生成网络-光伏爬坡协同攻击数据集,可以解决训练数据不足的问题。
4)通过算例分析,本文提出的个性化张量联邦学习与传统的LightGBM、FedAvg和pFedMe方法相比,整体辨识效果明显提高,在传统方法难以辨别的特定场景中依然具有较高的辨识精确率。
参考文献
[1] 陈艳波, 刘宇翔, 田昊欣, 等. 基于广义目标级联法的多牵引变电站光伏-储能协同规划配置[J]. 电工技术学报, 2024, 39(15): 4599-4612.
Chen Yanbo, Liu Yuxiang, Tian Haoxin, et al. Collaborative planning and configuration of photovoltaic and energy storage in multiple traction substations based on generalized analytical target cascading method [J]. Transactions of China Electro-technical Society, 2024, 39(15): 4599-4612.
[2] 陈明昊, 朱月瑶, 孙毅, 等. 计及高渗透率光伏消纳与深度强化学习的综合能源系统预测调控[J]. 电工技术学报, 2024, 39(19): 6054-6071, 6103.
Chen Minghao, Zhu Yueyao, Sun Yi, et al. The predictive-control optimization method for park integrated energy system considering the high penetration of photovoltaics and deep reinforcement learning[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 6054-6071, 6103.
[3] 孔令国, 王嘉祺, 韩子娇, 等. 基于权重调节模型预测控制的风-光-储-氢耦合系统在线功率调控[J]. 电工技术学报, 2023, 38(15): 4192-4207.
Kong Lingguo, Wang Jiaqi, Han Zijiao, et al. On-line power regulation of wind-photovoltaic-storage-hydro-gen coupling system based on weight adjustment model predictive control[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4192-4207.
[4] 李俊涛, 贾科, 董学正, 等. 网侧故障下光伏直流并网系统不平衡功率快速平抑方法[J]. 电工技术学报, 2024, 39(5): 1340-1351.
Li Juntao, Jia Ke, Dong Xuezheng, et al. A fast method for suppressing unbalanced power in photovoltaic DC grid-connected system under grid-side faults[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1340-1351.
[5] 张波, 高远, 李铁成, 等. 计及IGBT结温约束的光伏高渗透配电网无功电压优化控制策略[J]. 电工技术学报, 2024, 39(5): 1313-1326.
Zhang Bo, Gao Yuan, Li Tiecheng, et al. Reactive voltage optimization control strategy for high penetration photovoltaic distribution network consi-dering IGBT junction temperature constraint[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1313-1326.
[6] 戚永志, 刘玉田. 风光储联合系统输出功率滚动优化与实时控制[J]. 电工技术学报, 2014, 29(8): 265-273.
Qi Yongzhi, Liu Yutian. Output power rolling optimization and real-time control in wind-photovoltaic-storage hybrid system[J]. Transactions of China Electrotechnical Society, 2014, 29(8): 265-273.
[7] 乐健, 郎红科, 谭甜源, 等. 新型配电系统分布式经济调度信息安全问题研究综述[J]. 电力系统自动化, 2024, 48(12): 177-191.
Le Jian, Lang Hongke, Tan Tianyuan, et al. Review of research on information security problems in distributed economic dispatch for new distribution system[J]. Automation of Electric Power Systems, 2024, 48(12): 177-191.
[8] 韩晓, 王涛, 韦晓广, 等. 考虑阵列间时空相关性的超短期光伏出力预测[J]. 电力系统保护与控制, 2024, 52(14): 82-94.
Han Xiao, Wang Tao, Wei Xiaoguang, et al. Ultrashort-term photovoltaic output forecasting considering spatiotemporal correlation between arrays [J]. Power System Protection and Control, 2024, 52(14): 82-94.
[9] Cui Mingjian, Wang Jianhui. Deeply hidden moving-target-defense for cybersecure unbalanced distribution systems considering voltage stability[J]. IEEE Transa-ctions on Power Systems, 2021, 36(3): 1961-1972.
[10] 郭庆来, 辛蜀骏, 孙宏斌, 等. 电力系统信息物理融合建模与综合安全评估: 驱动力与研究构想[J]. 中国电机工程学报, 2016, 36(6): 1481-1489.
Guo Qinglai, Xin Shujun, Sun Hongbin, et al. Power system cyber-physical modelling and security assess-ment: motivation and ideas[J]. Proceedings of the CSEE, 2016, 36(6): 1481-1489.
[11] Mohsenian-Rad A H, Leon-Garcia A. Distributed internet-based load altering attacks against smart power grids[J]. IEEE Transactions on Smart Grid, 2011, 2(4): 667-674.
[12] 张程彬, 崔明建, 张梓枭, 等. 考虑攻击偏好的三相不平衡配电系统分布式FDIA检测[J]. 电力系统保护与控制, 2024, 52(24): 109-119.
Zhang Chengbin, Cui Mingjian, Zhang Zixiao, et al. Distributed FDIA detection for three-phase unbalanced distribution systems[J]. Power System Protection and Control, 2024, 52(24): 109-119.
[13] Živković N, Sarić A T. Detection of false data injection attacks using unscented Kalman filter[J]. Journal of Modern Power Systems and Clean Energy, 2018, 6(5): 847-859.
[14] Tian Jue, Tan Rui, Guan Xiaohong, et al. Enhanced hidden moving target defense in smart grids[J]. IEEE Transactions on Smart Grid, 2019, 10(2): 2208-2223.
[15] 刘鑫蕊, 常鹏, 孙秋野. 基于XGBoost和无迹卡尔曼滤波自适应混合预测的电网虚假数据注入攻击检测[J]. 中国电机工程学报, 2021, 41(16): 5462-5476.
Liu Xinrui, Chang Peng, Sun Qiuye. Grid false data injection attacks detection based on XGBoost and unscented Kalman filter adaptive hybrid prediction[J]. Proceedings of the CSEE, 2021, 41(16): 5462-5476.
[16] Mohammadpourfard M, Sami A, Weng Yang. Identification of false data injection attacks with considering the impact of wind generation and topology reconfigurations[J]. IEEE Transactions on Sustainable Energy, 2018, 9(3): 1349-1364.
[17] 李元诚, 曾婧. 基于改进卷积神经网络的电网假数据注入攻击检测方法[J]. 电力系统自动化, 2019, 43(20): 97-104.
Li Yuancheng, Zeng Jing. Detection method of false data injection attack on power grid based on improved convolutional neural network[J]. Automation of Electric Power Systems, 2019, 43(20): 97-104.
[18] Wang Huaizhi, Ruan Jiaqi, Wang Guibin, et al. Deep learning-based interval state estimation of AC smart grids against sparse cyber attacks[J]. IEEE Tran-sactions on Industrial Informatics, 2018, 14(11): 4766-4778.
[19] 韩一宁, 崔明建, 罗光浩, 等. 基于自适应联邦学习的输配网动-静态综合状态估计方法研究[J/OL]. 中国电机工程学报, 1-15[2025-03-17]. http://kns. cnki.net/kcms/detail/11.2107.tm.20250124.1046.010.html.
Han Yining, Cui Mingjian, Luo Guanghao, et al. An integrated dynamic-static state estimation method for transmission and distribution networks based on self-adaptive federated learning[J/OL]. Proceedings of the CSEE, 1-15[2025-03-17]. http://kns.cnki.net/kcms/ detail/11.2107.tm.20250124.1046.010.html.
[20] 王健宗, 孔令炜, 黄章成, 等. 联邦学习算法综述[J]. 大数据, 2020, 6(6): 64-82.
Wang Jianzong, Kong Lingwei, Huang Zhangcheng, et al. Research review of federated learning algorithms[J]. Big Data Research, 2020, 6(6): 64-82.
[21] Abdulrahman S, Tout H, Mourad A, et al. FedMCCS: multicriteria client selection model for optimal IoT federated learning[J]. IEEE Internet of Things Journal, 2021, 8(6): 4723-4735.
[22] Konečný J, Mcmahon H B, Yu F X, et al. Federated learning: strategies for improving communication efficiency[J]. arXiv preprint arXiv: 1610. 05492, 2016.
[23] Sridhar S, Govindarasu M. Model-based attack detection and mitigation for automatic generation control[J]. IEEE Transactions on Smart Grid, 2014, 5(2): 580-591.
[24] Cui Mingjian, Wang Jianhui, Yue Meng. Machine learning-based anomaly detection for load forecasting under cyberattacks[J]. IEEE Transactions on Smart Grid, 2019, 10(5): 5724-5734.
[25] Yue Meng. An integrated anomaly detection method for load forecasting data under cyberattacks[C]//2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 2017: 1-5.
[26] 苏向敬, 邓超, 栗风永, 等. 基于MGAT-TCN模型的可解释电网虚假数据注入攻击检测方法[J]. 电力系统自动化, 2024, 48(2): 118-127.
Su Xiangjing, Deng Chao, Li Fengyong, et al. Interpretable detection method for false data injection attack on power grid based on multi-head graph attention network and time convolution network model[J]. Automation of Electric Power Systems, 2024, 48(2): 118-127.
[27] 杨玉泽, 刘文霞, 李承泽, 等. 面向电力SCADA系统的FDIA检测方法综述[J]. 中国电机工程学报, 2023, 43(22): 8602-8622.
Yang Yuze, Liu Wenxia, Li Chengze, et al. Review of FDIA detection methods for electric power SCADA system[J]. Proceedings of the CSEE, 2023, 43(22): 8602-8622.
[28] Reisizadeh A, Taheri H, Mokhtari A, et al. Robust and communication-efficient collaborative learning[J]. Advances in Neural Information Processing Systems, 2019, 32.
[29] Berahas A S, Bollapragada R, Keskar N S, et al. Balancing communication and computation in distributed optimization[J]. IEEE Transactions on Automatic Control, 2019, 64(8): 3141-3155.
[30] Lee K, Lam M, Pedarsani R, et al. Speeding up distributed machine learning using codes[J]. IEEE Transactions on Information Theory, 2018, 64(3): 1514-1529.
[31] 程礼临, 臧海祥, 卫志农, 等. 考虑多光谱卫星遥感的区域级超短期光伏功率预测[J]. 中国电机工程学报, 2022, 42(20): 7451-7465.
Cheng Lilin, Zang Haixiang, Wei Zhinong, et al. Ultra-short-term forecasting of regional photovoltaic power generation considering[J]. Proceedings of the CSEE, 2022, 42(20): 7451-7465.
[32] 夏泠风, 黎嘉明, 赵亮, 等. 考虑光伏电站时空相关性的光伏出力序列生成方法[J]. 中国电机工程学报, 2017, 37(7): 1982-1993.
Xia Lingfeng, Li Jiaming, Zhao Liang, et al. A PV power time series generating method considering temporal and spatial correlation characteristics[J]. Proceedings of the CSEE, 2017, 37(7): 1982-1993.
[33] Japkowicz N, Stephen S. The class imbalance problem: a systematic study[J]. Intelligent Data Analysis, 2002, 6(5): 429-449.
[34] Kim M, Hwang K B. An empirical evaluation of sampling methods for the classification of imbalanced data[J]. PLoS One, 2022, 17(7): e0271260.
[35] Reisizadeh A, Mokhtari A, Hassani H, et al. Fedpaq: a communication-efficient federated learning method with periodic averaging and quantization[C]// International conference on artificial intelligence and statistics, Online, 2020: 2021-2031.
[36] 陈晓霖, 昝道广, 吴炳潮, 等. 面向纵向联邦学习的对抗样本生成算法[J]. 通信学报, 2023, 44(8): 1-13.
Chen Xiaolin, Zan Daoguang, Wu Bingchao, et al. Adversarial sample generation algorithm for vertical federated learning[J]. Journal on Communications, 2023, 44(8): 1-13.
[37] 黄冬梅, 丁仲辉, 胡安铎, 等. 低成本对抗性隐蔽虚假数据注入攻击及其检测方法[J]. 电网技术, 2023, 47(4): 1531-1540.
Huang Dongmei, Ding Zhonghui, Hu Anduo, et al. Low-cost adversarial stealthy false data injection attack and detection method[J]. Power System Technology, 2023, 47(4): 1531-1540.
Abstract Photovoltaic (PV) power has emerged as one of the most promising and rapidly developing renewable energy sources in recent years, significantly facilitating the green transition of power grids. However, the uncertainty of PV ramping events imposes higher demands on the accuracy and timeliness of cyber attack detection methods. Existing studies overlook the coupling characteristics between PV ramping events and cyber attack events, making it challenging to accurately identify cyber-ramping coordinated attacks. Besides, as the scale of the power grid continues to expand, strict privacy protection requirements between different grid partitions hinder data sharing. Traditional distributed algorithms are constrained by communication conditions, resulting in low training efficiency, which further limits the development of cyber-ramping coordinated attack detection methods. To address these issues, this paper proposes a cyber-ramping coordinated attack identification method based on tensor decomposition-based personalized federated learning (TDPFed).
Firstly, the attack pathways of cyber-ramping coordinated attacks are analyzed, and a corresponding attack model is constructed by integrating common cyber attack methods with the characteristics of PV ramping to elucidate the attack mechanisms. Secondly, tensor decomposition is employed to enhance traditional federated learning by compressing the communication parameters, effectively reducing communication cost while preserving nearly all information. Thirdly, a two-layer objective model is constructed, consisting of a tensorized local model and a personalized model. The personalized model is retained to enhance the identification performance on local data, while the tensorized local model is transmitted to alleviate communication load and accelerate training. Fourthly, training strategies for the personalized model and tensorized local model are formulated, and two different global aggregation strategies are introduced to improve upon the traditional federated averaging method. Finally, the characteristics of PV power output are analyzed, and a dataset generation method is proposed.
To validate the effectiveness of the proposed method, a power grid-communication network model based on the IEEE 33-bus system was constructed. Cyber-ramping coordinated attack identification was performed using traditional light gradient boosting machine (LightGBM), federated averaging (FedAvg), personalized federated learning with moreau envelopes (pFedMe), an improved FedAvg method, and the proposed TDPFed method. In terms of macro-averaged precision, the traditional methods achieved 0.888 9, 0.928 8, 0.963 7, and 0.894 5, respectively. The TDPFed algorithm, utilizing the aggregating factor matrix strategy and the aggregating composed tensor strategy, achieved 0.999 9 and 0.999 5, demonstrating its superior capability in accurately identifying various cyber-ramping coordinated attacks. When the compression ratio increased from 1.5 to 2, the macro-averaged precision of the improved FedAvg method decreased by 1.53%, whereas the proposed method exhibited only minor declines of 0.02% and 0.01%. This result indicates that the proposed approach effectively reduces the required transmission parameters while preserving nearly all information. In terms of communication cost, the four traditional methods required computation times that were two orders of magnitude higher than that of the proposed method. Furthermore, under adversarial attacks, the proposed method demonstrated the highest robustness among all evaluated approaches.
The following conclusions can be drawn from the above results: (1) The use of a two-layer objective model, appropriate training strategies, and aggregation strategies during model training effectively improves the accuracy of cyber-ramping coordinated attack identification and accelerates model convergence. (2) Tensor decomposition can compresses the parameters that need to be uploaded, reducing the communication resource requirements of federated learning. This improvement addresses the issue of insufficient communication resources in large-scale multi-node power grid systems, significantly shortening the training time. (3) By generating a cyber-ramping coordinated attack dataset using baseline curves and photovoltaic random components from historical data, the issue of insufficient training data is mitigated. (4) Through case analysis, the proposed TDPFed method demonstrates a significant improvement in overall identification performance compared to traditional methods such as LightGBM, FedAvg, and pFedMe. It maintains a high identification accuracy even in specific scenarios where traditional methods struggle.
Keywords:PV ramping, cyber-PV ramping coordinated attack, false data injection attack, tensor decomposition, federated learning
中图分类号:TM73;TM769
DOI: 10.19595/j.cnki.1000-6753.tces.241896
国家自然科学基金资助项目(52207130)。
收稿日期 2024-10-24
改稿日期 2025-03-21
崔沛然 男,2001年生,硕士研究生,研究方向为电力系统网络安全、联邦学习、配电网规划。E-mail:peirancui@tju.edu.cn
崔明建 男,1987年生,教授,博士生导师,研究方向为电力系统优化运行等。E-mail:mj_cui@tju.edu.cn(通信作者)
(编辑 赫 蕾)