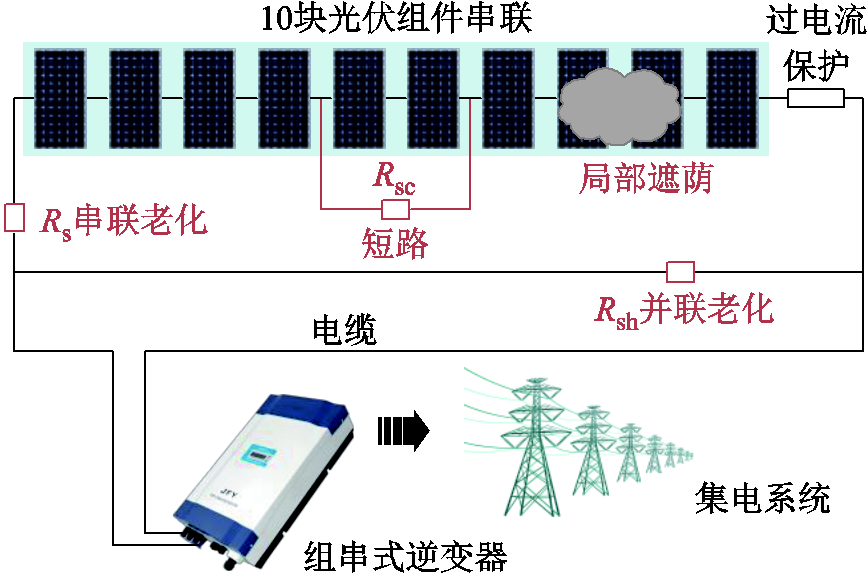
图1 光伏组串故障示意模型
Fig.1 Schematic model of PV module fault
摘要 为提高光伏系统自动化运维水平，该文提出一种基于I-V曲线全局特征提取的光伏组串Swin-Transformer故障诊断方法，以实现准确可靠的智能化光伏状态监测。首先，通过校正与归一化预处理提升I-V曲线数据的规范性；其次，采用格拉姆角场、递归图和相对位置矩阵多维度刻画I-V曲线的动态特性，提取表征光伏组串状态信息的I-V全局特征；然后，针对特征图的局部区域周期性重复等特点，提出Swin Transformer故障诊断模型，采用分层结构聚合局部特征实现层次化表示，设计移位窗口机制融合局部与全局特征，通过局部自注意力计算实现高效故障诊断；最后，3.75 kW光伏系统的仿真和现场实验表明，所提方法在相对位置矩阵特征变换下性能最佳，可精确诊断不同条件和严重程度的多种故障。在每类样本数低至25个时模型准确率为99.67%，在30 dB噪声干扰下模型准确率为99.56%。采用多种特征数据与不同算法进行消融实验，验证了所提特征提取法与故障诊断模型的优越性，该研究为光伏组串稳定运行提供了可靠的技术支持。
关键词：光伏组串 故障诊断 I-V曲线 全局特征 Swin-Transformer
近年来光伏发电并网装机容量迅猛增长，截至2023年底已达5.6亿kW，同比增长49.9%[1]。光伏组串的健康运行对光伏电站系统的安全稳定至关重要。但随着沙戈荒、山地光伏基地的建设，恶劣的室外运行环境导致故障频发，致使整体功率下降甚至发生火灾事故。因此，快速准确的光伏故障诊断对确保光伏基地可靠安全运行至关重要。
光伏故障诊断方法包括视觉成像法和电气参数分析法[2]。视觉成像法依赖光学成像技术，通常需要配备昂贵的设备，且成像质量易受环境影响；电气参数分析法是通过测量I-V曲线、电压、电流和功率等来诊断故障，其中I-V曲线能综合反映光伏组串的电气特性，清晰显示关键参数的变化趋势，相较于其他电气量能提供更丰富的故障信息，因此基于I-V曲线的光伏组串故障诊断是一项研究热点。
利用I-V曲线的光伏故障诊断包括局部特征阈值法、模型仿真对比法和人工智能故障分类法。局部特征阈值法通过选取关键电气特征参数，设置合适的阈值来判断故障类型。文献[3-4]通过检测I-V曲线凹凸性，以及阶梯处斜率判断拐点位置和特征实现故障识别。文献[5]从I-V曲线关键采样点中提取开路电压VOC、最大功率点电压VMPP、电流IMPP和串联电阻Rs五维特征，分类短路、阴影和老化故障。文献[6]通过阈值分析VMPP和I-V曲线上的压降来诊断阴影故障。尽管局部特征阈值法计算复杂度低但阈值设置困难，且仅靠I-V曲线局部参数难以处理不规则曲线。模型仿真对比法则通过光伏系统仿真模型生成的I-V曲线与实测I-V曲线进行对比。文献[7]根据I-V曲线建立智能模型计算并比较光伏模块参数，以检测阴影、短路和接地故障。文献[8]建立自然衰减模型，通过健康参数权重分析光伏组件故障程度。尽管此类方法能有效地评估光伏组串运行状态，但其精度严重依赖仿真模型的准确性，且仅能识别有限的故障类型[9]。
对于人工智能故障分类法，除常见的神经网络[10]、极限学习机[11]、CatBoost[12]外，文献[13]构建了基于改进证据相似度的数据融合模型以检测异常老化故障。文献[14]结合人工蜂群算法和极限学习机检测光伏组串非均匀污损故障。这两项研究虽然实现了较高的诊断精度，但可检测故障类型单一。文献[15]基于I-V曲线局部特征，提出了变量预测模型可检测五种光伏故障，其准确率最高可达98.6%。文献[16]将I-V曲线、辐照度和模块温度合并为特征矩阵，利用改进ResNet模型分类四种光伏故障，虽然该方法准确率达到98.8%，但存在特征冗余且计算复杂的问题。文献[17]提出了基于人工神经网络（Artifical Neural Network, ANN）的光伏故障分类方法，其模型训练和验证要求大量数据样本。综上所述，现有光伏故障诊断研究通常利用局部电气特征，难以充分挖掘I-V曲线蕴含的动态特性和故障信息，导致诊断精度有待提高；另一方面，人工智能模型的训练和测试往往依赖大量标记样本，且未考虑工程应用中可能存在的噪声干扰，因而在实际部署中面临较大挑战。
为此，本文提出了一种基于I-V曲线全局特征提取的光伏组串Swin-Transformer故障诊断方法。针对不同故障条件和严重程度，利用校正、归一化和特征变换获取的全局特征可多维度刻画I-V曲线动态特性。针对特征图局部周期性重复等特点，设计具有多尺度特征提取能力的Swin-Transformer故障诊断模型，并通过移位窗口机制和局部自注意力提高计算效率。实验结果表明，所提方法能准确诊断多种光伏组串故障，具有噪声鲁棒性，支持小样本学习，为光伏系统状态监测和自动化运维提供了重要的技术支撑。
光伏组串故障示意模型如图1所示。短路、局部遮荫和老化是最常见的光伏组串故障类型，这些故障在实际应用中发生频率高、危害重，且在仿真实验条件下具有较好的可再现性。
图1 光伏组串故障示意模型
Fig.1 Schematic model of PV module fault
1）短路：短路故障指光伏组串中两个不同电位点发生意外短接，通常由组件之间的意外连接、制造缺陷、表面污染或不良交联导致的模块分层引起，并致使输出功率急剧下降。本文通过控制并联电阻Rsc研究光伏组串中10%～50%的模块短路，即五种短路故障，分别记为SC1、SC2、SC3、SC4、SC5。
2）局部遮荫：局部遮荫指部分组件因外部物体遮挡而无法接收到阳光，导致光伏模块输出电流不均匀，并降低整体发电效率。本文通过控制输入辐照度研究10%～50%的光伏模块遮荫，即五种局部遮荫故障，分别记为PS1、PS2、PS3、PS4、PS5。
3）老化：老化故障指组串由于长期使用而逐渐退化，导致内部串联电阻增大，并联电阻减小，分为并联老化和串联老化。本文通过控制串联电阻Rs和并联电阻Rsh的大小来实现两种老化故障，分别记为De_Rs和De_Rsh。
I-V特性曲线蕴含表征光伏组串运行状态的丰富信息，可通过光伏测试仪便捷获取[18]，常用于光伏系统运维，具有较高的诊断效率和准确性。
图2展示了在相同环境条件下（辐照度Ir=900 W/m2，环境温度Tm=40℃），健康、局部遮荫、串并联老化和短路故障下光伏组串的I-V曲线。正常运行光伏组串的I-V曲线只有一个最大功率点（Maximum Power Point, MPP）。局部遮荫下I-V曲线出现了多个MPP，MPP个数与被遮挡的组件数量、遮挡的分布模式、光伏组件串并联配置等有关。串联老化时MPP左移，电压轴附近斜率变平缓；并联老化时MPP下移，电压轴附近斜率变陡峭。短路故障下VOC显著下降，由于电压瞬间降低而电流下降较为缓慢，I-V曲线几乎垂直从短路电流（ISC）水平迅速降到零。
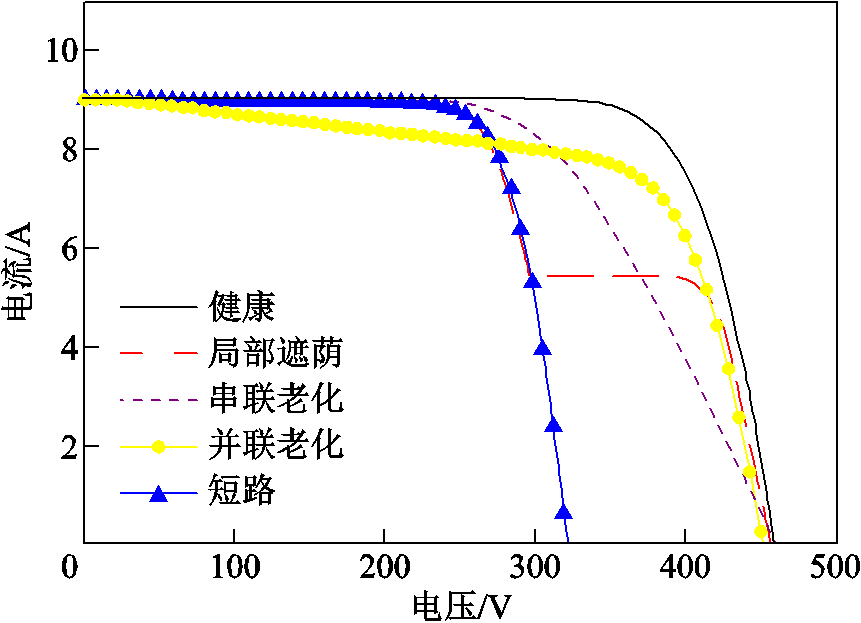
图2 不同运行情况下的I-V曲线
Fig.2 I-V curves under different conditions
提取全局特征以充分利用I-V曲线动态特性。I-V曲线受环境影响较大，为避免将环境因素引起的曲线变化误认为故障特征，首先将曲线校正到标准试验条件（Standard Test Conditions, STC）；其次，校正后由于采样点数不同且分布不均，进行归一化预处理提升I-V曲线数据的规范性；最后，分别采用不同的特征变换法提取表征光伏组串状态信息的全局I-V特征。
1.2.1 校正
采用IEC 60891标准中的程序2[19]进行STC校正，该方法能在本文所研究故障类型下实现更好的整体校正性能，I-V曲线校正方法为
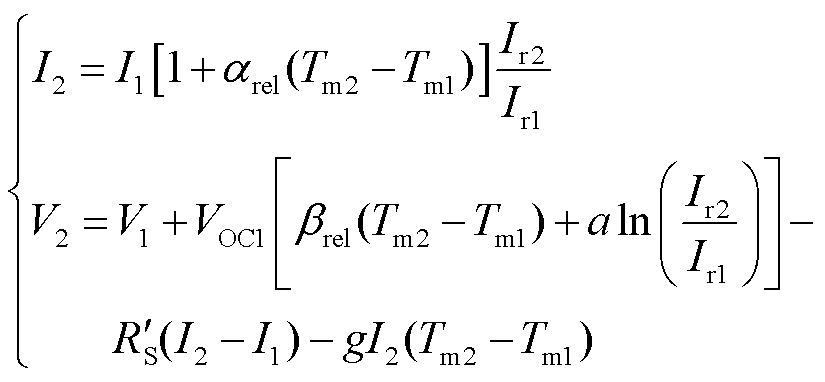（1）
式中，I1和V1、I2和V2分别为校正前、后的电流和电压；Tm1、Ir1分别为测量环境温度和辐照度；Tm2、Ir2分别为校正后环境参数（STC：Tm2 = 25℃、Ir2= 1000 W/m2）；αrel、βrel分别为ISC、VOC的相对温度系数；a为辐照度校正因子；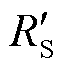
为内部电阻；g为温度系数。
1.2.2 归一化
由于不同曲线可能包含不同数量的采样点，且采样点在曲线上的分布可能不均匀，本文提出一种基于线性插值法的重采样方法对曲线归一化，有
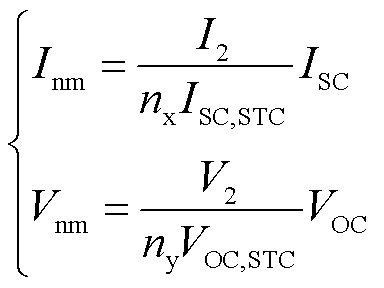（2）
式中，Inm、Vnm分别为归一化后的电流和电压；ISC,STC、VOC,STC分别为STC下单个光伏模块的额定ISC、VOC；nx为并联组串数量；ny为每一组串中光伏模块数量。
设计一种方法确定重采样点数G，采用面积误差EArea作为量化指标。
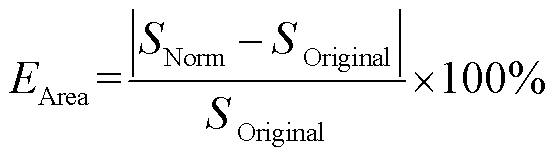（3）
式中，SOriginal为原始曲线与坐标轴所包围面积；SNorm为归一化后曲线与坐标轴所包围面积。当面积误差较小且趋于稳定时，对应的取值G即为重采样点数。
经过数据的校正和归一化预处理，不仅提升了I-V曲线数据规范性，还降低了模型训练复杂度。
1.2.3 特征变换
数据归一化后，Vnm和Inm为曲线上离散采样点。使用电压和电流作为坐标轴构建二维特征平面，采用格拉姆角场（Gramian Angular Field, GAF）、递归图（Recurrence Plot, RP）、相对位置矩阵（Relative Position Matrix, RPM）特征变换法充分提取表征光伏组串状态信息的全局I-V特征，多维度刻画I-V曲线的动态特性。同时进行数据增强，获取更丰富的空间特征信息，利用机器学习在图像处理上的优势建立分类模型，更直观、可视化地理解数据。
1）格拉姆角场
GAF分为格拉姆角差场（Gramian Angular Difference Fields, GADF）和格拉姆角正弦场（Gramian Angular Summation Fields, GASF）[20]，分别使用时间序列的差值与和值。对于I-V曲线的时间序列I= it，（t =1, 2, …, N1），具体步骤如下[21]。
（1）使用最小-最大定标器（Min-Max Scaler）将原始时间序列数据缩放到[-1,1]或[0,1]范围内。
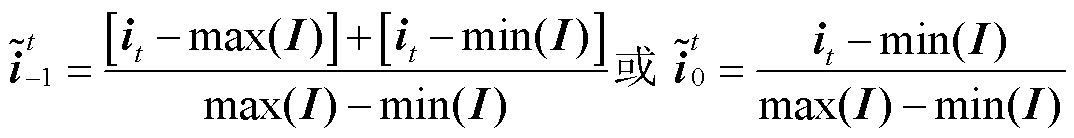（4）
（2）将缩放后的数据转换为极坐标，得到每一个点对应的半径和角度为
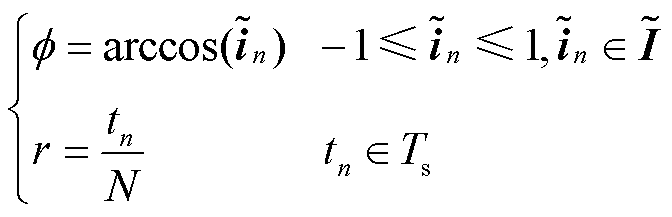（5）
式中，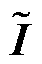
为缩放后的时间序列集合；tn为时间戳；N为常数；Ts为时间戳的集合。
（3）利用和角和差角关系，得到对应的GASF图和GADF图，其中X是一个单位行向量[1 1 … 1]。
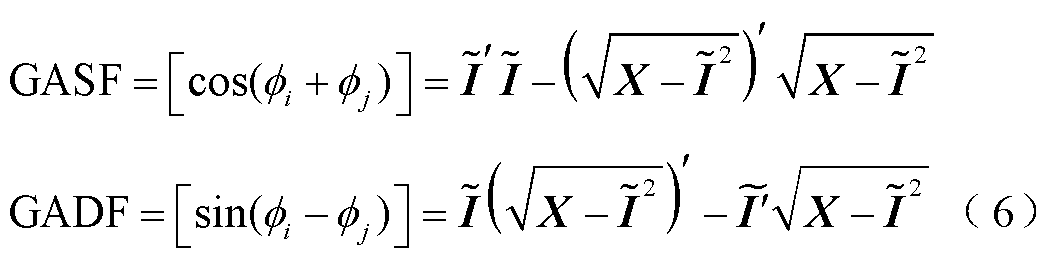
2）递归图
RP能使动态系统的递归特性可视化，由于对相空间中轨迹随时间演化的规律非常敏感，能将重构的相空间上的点以二维图的方式直观展示出来[22]。
将时间序列时域空间中的每个点xi变换到相空间的对应状态xi，计算每个状态（向量）间的距离得到向量范数，阈值二值化后得到递归图中对应两个状态之间的特征，用一系列递归矩阵表示递归图。
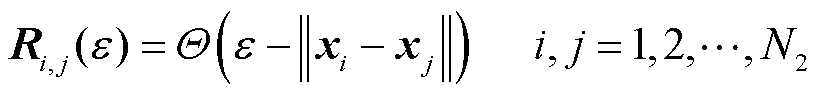（7）
式中，Ri, j为N2×N2的方阵；‖‖为向量范数，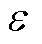
为距离阈值，使得Ri, j∈{0,1}；
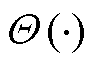为Heaviside函数。
3）相对位置矩阵
RPM包含原始时间序列的冗余特征，使变换后的图像更易显现类间和类内的相似度信息。对于一个时间序列T = tn（n=1, 2,…, N3），其中N3是时间长度，通过以下步骤得到RPM图[23]。
（1）原始时间序列归一化得到标准正态分布Z为
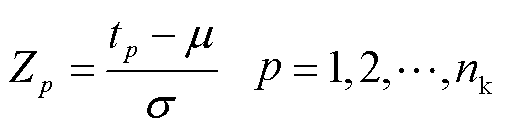（8）
式中，μ为时间序列T的平均值；σ为T的标准差。
（2）采用分段聚合近似法，选择合适的缩减因子k生成新的平滑时间序列X2 = {x1, x2,…,xm}，通过计算一个分段常数的平均值，将Z的维数从n降至m维，同时保持原始序列的近似趋势，其中m是X2的长度。
（9）
（3）计算xi之间的相对位置，将预处理后的时间序列X转换为m×m的二维矩阵M，矩阵M的每一行和列都以tn为参考点，包含整个时间序列的信息。
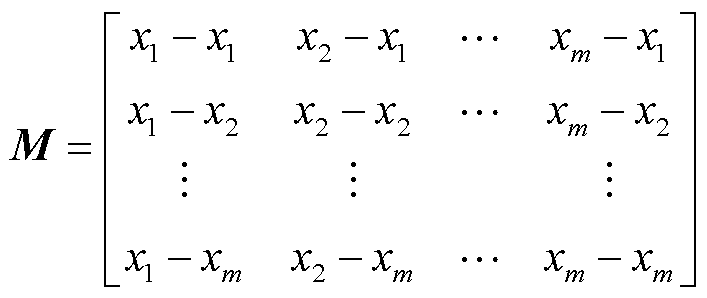（10）
（4）利用最小-最大归一化将M转换为灰度值矩阵，得到相对位置矩阵F为
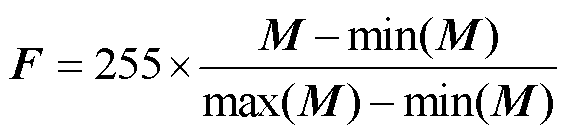（11）
运用上述特征变换技术处理I-V曲线，选取四种运行状态下的原始I-V曲线及相应转换结果对比如图3所示。
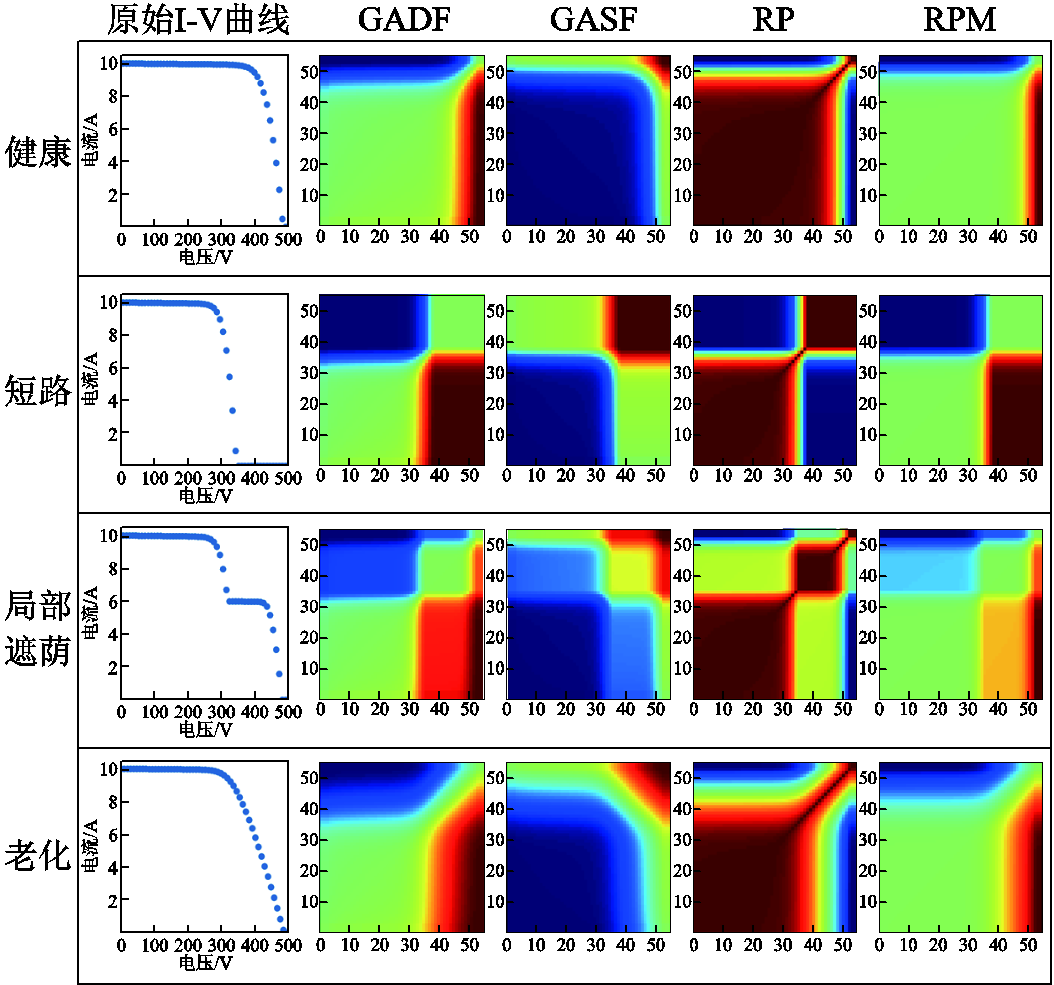
图3 I-V曲线应用不同特征变换法的结果
Fig.3 Transformation results for I-V curves
GAF、RP和RPM特征变换法将数据转换为图像，采用计算机视觉领域模型进行处理和分析。基于Transformer[24]设计Swin Transformer（Shifted Window Transformer）深度学习模型，创新性地采用分层结构、移位窗口和局部自注意力机制，能有效捕捉图像局部区域的周期性与全局特征，具有较强的图像处理能力，克服传统视觉Transformer模型[25]计算复杂度过高的问题。
Swin-Transformer将输入图像划分为不重叠的窗口，并在每个窗口内应用自注意力机制，通过移位窗口方式跨窗口融合特征，实现信息的全局交互。具有多尺度特征提取能力的Swin-Transformer减少了计算复杂度，且不需要提供大量数据集，提高了模型的效率和性能。
2.1.1 整体架构
图4展示了Swin-Transformer的总体模型架构及故障诊断流程。GAF、RP和RPM图为红绿蓝（RGB）三通道图像，模型使用P×P=4×4大小作为输入图像块，图像块展平后向量维度为P×P×3=48，通过图像块拆分层将输入为H×W×3的RGB图像分割为等尺寸不重叠的(H/4)×(W/4)×48图像块。图像块应用线性嵌入层将原维度的张量投射到任意维度C，此时维度为(H/4)×(W/4)×C，然后将图像块序列输入两个连续的Swin-Transformer块中：首先进行层归一化（Layer Normalization, LN）和基于窗口的多头自注意力（Window Multi-head Self Attention, W-MSA）；其次经过LN后对多层感知机（Multilayer Perceptron, MLP）进行非线性变换；最后应用基于移位窗口的多头自注意力（Shifted Window Multi-head Self Attention, SW-MSA）实现窗口间的通信，通过MLP得到输出结果，输出与输入序列数一致，由此完成第一阶段。
为实现层次化特征表示，第二阶段图像块合并层将相邻2×2个图像块的特征拼接以减少图像块序列量，通过模型块进行特征转换后输出为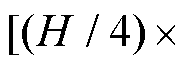
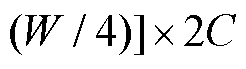。第三和第四阶段重复第二阶段的过程，每一阶段都会改变维度，从而形成具有层次性的特征图。
在Swin-Transformer主干网络的第四阶段后加入LN、自适应池化层（Adaptive Avg-pool）和全连接层（Linear），最终输出并诊断光伏组串故障类型。
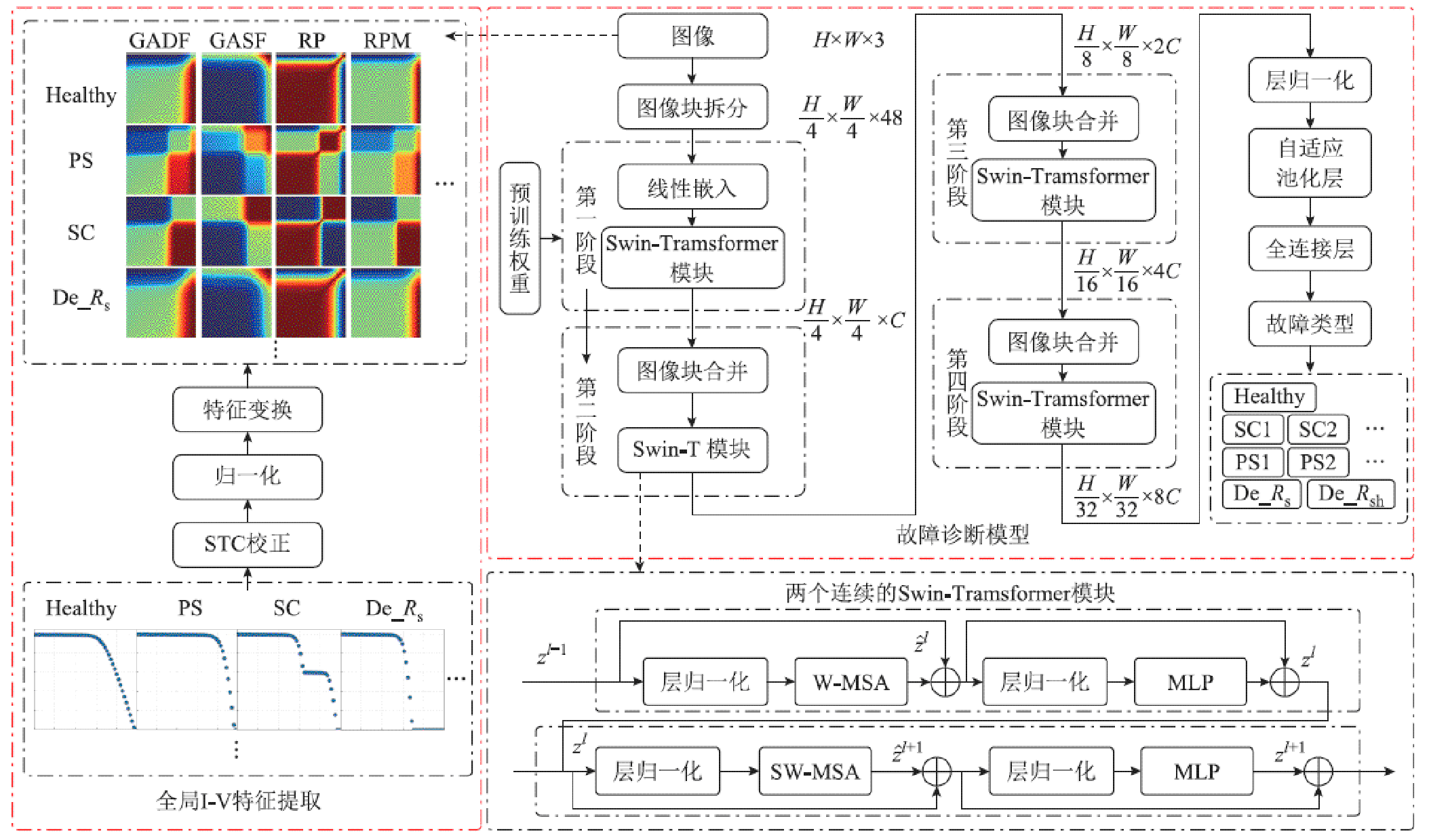
图4 Swin Transformer总体模型架构及故障诊断流程
Fig.4 Swin Transformer overall model architecture and fault diagnosis process
2.1.2 移位窗口机制
GAF将数据映射到极坐标系生成具有对称性和全局结构的矩阵，RP和RPM图通过显示时间序列中重复的模式，具有局部重复周期性。由此设计Swin-Transformer移位窗口机制，将局部与全局特征融合，自适应处理不同尺寸的窗口实现多尺度建模。图5所示为自注意力层之间的窗口分区移位法，在第l层中进行常规窗口分区，在每个窗口内进行自注意力计算，在l+1层中窗口分区移位产生新窗口，从而达到全局建模的能力，这对于GAF、RP、RPM图中的全局趋势、局部周期特征均非常有效。
Swin-Transformer将图像块合并，通过相邻图像块构建具有层次性的特征图，通过设计的移位窗口法将自注意计算限制在不重合的局部窗口内，窗口之间不进行信息传递，以降低运算量。每个窗口中图像块的数量固定，因此复杂度与图像大小成线性关系。所设计移位窗口法建模能力与现有滑动窗口法（Sliding Window, SW）[26]建模能力相似，但延迟有大幅降低。
图5 移位窗口分区法
Fig.5 The shifted window approach
2.1.3 自注意力计算
假设每个窗口包含M×M个图像块，以不重叠的方式均匀分割图像，一个多头自注意力（Multi-head Self Attention, MSA）模块和一个h×w的图像块的窗口的自注意力计算复杂度W 为
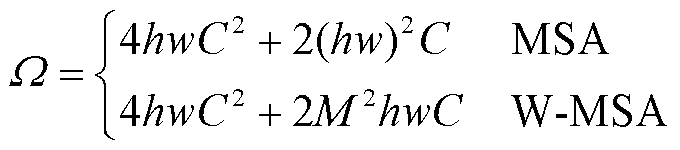（12）
采用跨窗口连接方式在Swin-Transformer块中的两个分区配置之间交替进行，两个连续的Swin-Transformer模块计算输出特征为
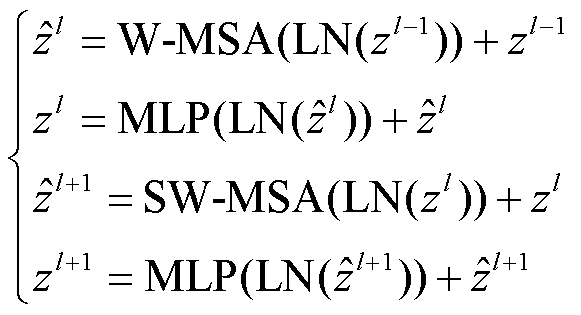（13）
式中：
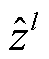和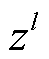
分别为W-MSA模块和MLP模块的输出特征。
为减少移位窗口分割时产生更多窗口使窗口尺寸过小，设计一种更有效的批量计算法，高效的批量计算法如图6所示，通过不断向左上方循环移位，使用屏蔽机制（Masked MSA）将自注意力计算限制在每个子窗口内，通过逆循环移位方法将每个窗口的自注意力结果返回。
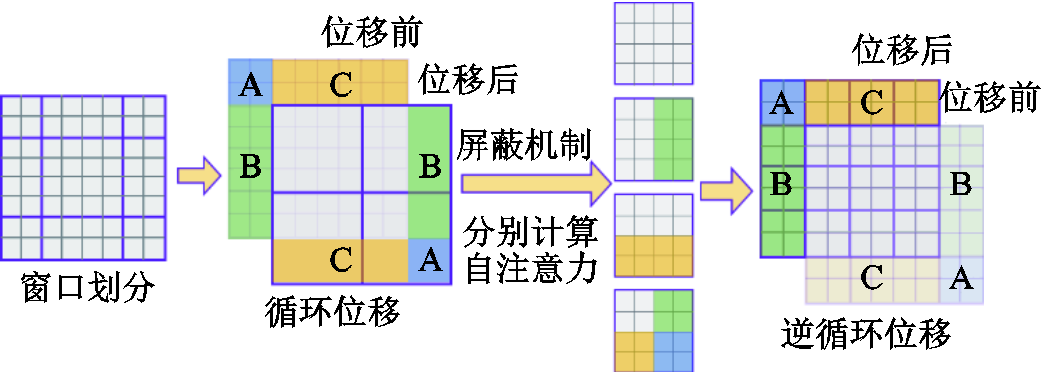
图6 高效的批量计算法
Fig.6 An efficient batch computation approach
传统Transformer模型在计算自注意力时，输入由Q（query）、K（keys）、V（values）组成，采用softmax函数获取V的权重，本文所提Swin-Transformer在计算自注意力时加入相对位置偏差B，输出矩阵为
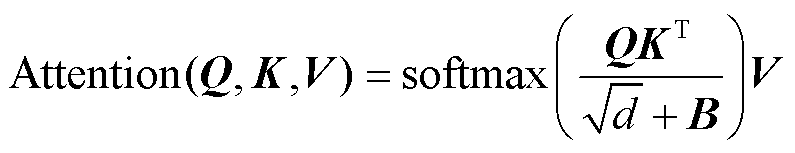（14）
式中，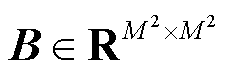
；
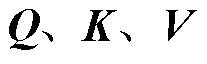分别为Query、Key和Value矩阵，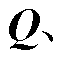
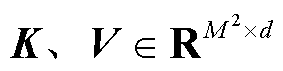，M2为局部窗口内的图像块数；d为Query和Key的维度。由于沿各轴的相对位置均处于[−M+1,M−1]范围内，将一个更小尺寸的位置偏差矩阵
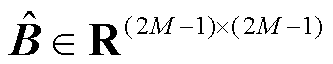参数化，式（14）中B的取值为
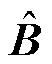。现有ViT（Vision Transformer）[27]使用绝对位置嵌入，而加入相对位置偏差的Swin-Transformer的性能有明显提升[24]。预训练中学习到的相对位置偏差也可用于初始化模型，通过双立方插值微调不同的窗口大小。
Swin-Transformer利用移位窗口进行局部自注意力计算，有效地减少计算量并提升模型效率；分层结构使模型可以逐步聚合局部特征，进而表示全局特征，层次化的特征提取方式更适合处理图像数据，同时保持高效的特征提取能力和分类精度；模型能适应不同大小和分辨率的图像输入，不需要提供大量样本，具有较高的灵活性，并能扩展应用于多种视觉任务，对于光伏场站智能运维有显著优势。
Swin-Transformer在基于Pytorch框架的Python语言中实现，硬件平台设置：CPU为Intel Core i9-12900H 2.50GHz，GPU为NVIDIA GeForce RTX 3070 8GB。在大规模数据集上预训练以加速收敛，提高泛化能力，减少过拟合，提升训练效率。
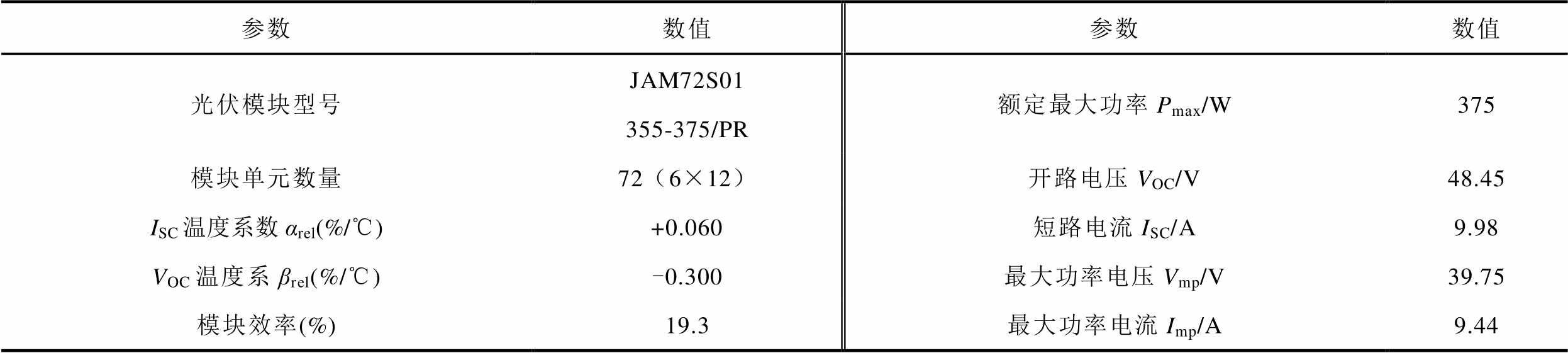
在Matlab/Simulink搭建一个如图1配置和表1详细参数的光伏组串仿真模型，在仿真模型中设置故障得到原始I-V曲线。为了更真实地模拟实际环境，加入噪声确保模型在应对实际的不确定性和数据噪声等仍具有鲁棒性和高效性，引入信噪比（Signal-to-Noise Ratio, SNR）作为噪声量化指标，信噪比越小，噪声负面影响越大。
表1 光伏模块在STC条件下的电气参数
Tab.1 Electrical parameters of PV modules under STC
参数数值参数数值 光伏模块型号JAM72S01355-375/PR额定最大功率Pmax/W375 模块单元数量72（6×12）开路电压VOC/V48.45 ISC温度系数αrel(%/℃)+0.060 短路电流ISC/A9.98 VOC温度系βrel(%/℃)-0.300最大功率电压Vmp/V39.75 模块效率(%)19.3最大功率电流Imp/A9.44
加入轻微噪声以模拟真实测量环境，根据现场实验数据、文献和报告[28-29]，确定在数据集中加入35 dB噪声。以一条局部遮荫故障I-V曲线为例，如1.2节步骤提取全局I-V特征，如图7所示。
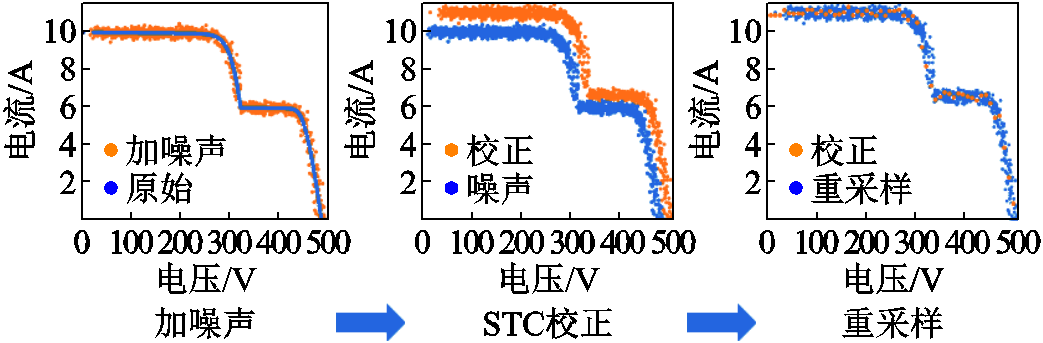
图7 全局I-V特征提取
Fig.7 Global I-V feature extraction
曲线归一化时需确定重采样点数，所有曲线面积误差平均值随采样点数的变化如图8所示。
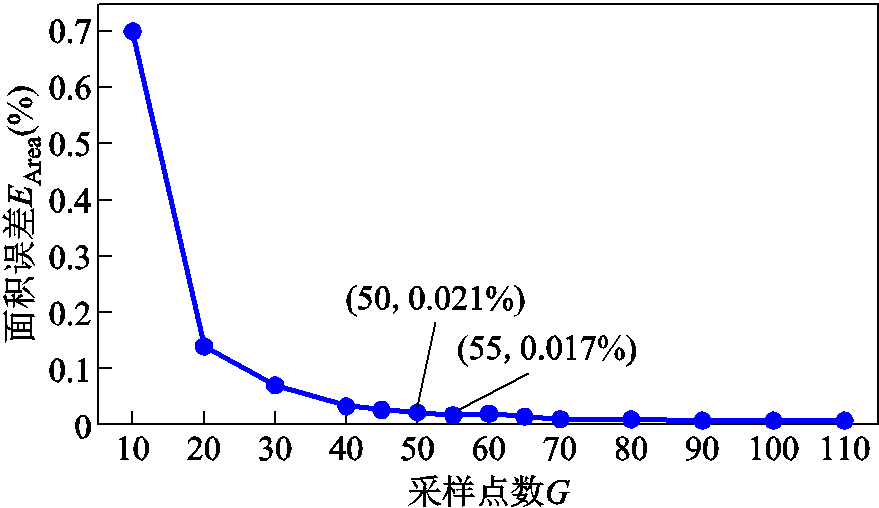
图8 面积误差随采样点数的变化
Fig.8 Variation of EAreawith number of resample points
随着G的增大，EArea逐渐减小且趋于稳定，当G＞50时，误差相对较小（约为0.021%）且几乎稳定。由于采样点数的增加会使后续训练模型复杂度提升，为保证良好的重采样性能并降低计算成本，设置重采样点数G为55。
重采样后的特征变换如图9所示。经全局I-V特征提取后，选取13种运行状态下、环境温度在15～45℃之间、辐照度在200～1 200 W/m2之间变化的仿真数据集。为覆盖更广泛的故障场景，考虑故障严重程度的变化，当发生局部遮荫故障时，通过改变增益值改变遮荫程度；老化故障时，通过串联5、10、15 W的电阻Rs、并联450、300、150W的电阻Rsh分别模拟轻微、正常、严重老化。最终仿真数据集包含16 500条仿真I-V曲线。
图9 全局I-V特征变换
Fig.9 Global I-V feature transformation
在实际工程应用中，大规模故障数据往往不易收集，若模型在小样本条件下能保持高诊断准确率，不仅能够降低数据采集成本，还能提高模型在复杂环境下的适应性和实用性。
在每类故障数据集中随机抽取不同数量的样本，采用递增方式逐步扩展训练集，根据准确率确定模型最小样本需求。表2显示了不同特征变换法下不同样本数量对应的模型准确率，每类样本数量增加到25个时，四种方法准确率均稳定在99.3%以上，由此确定模型的最小样本需求为每类25个。其中采用RPM时性能最佳，准确率达99.67%，证明所提模型在处理小样本故障数据时具有可行性，并能维持高诊断精度。图10为表2的直观显示。
表2 不同样本数量下模型准确率
Tab.2 The accuracy under different sample sizes
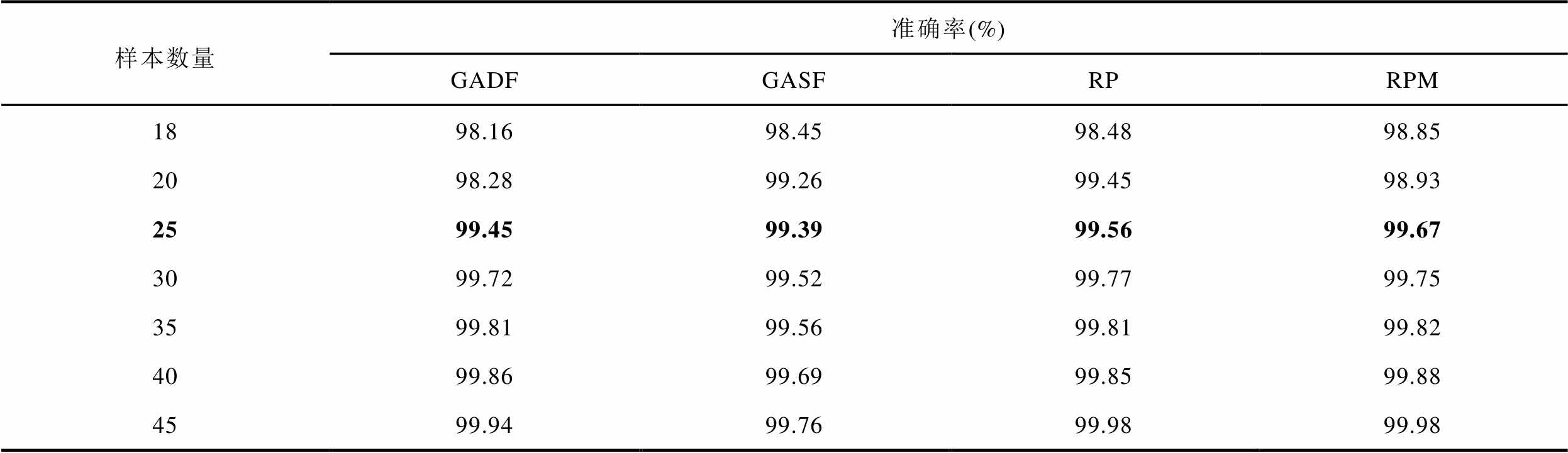
样本数量准确率(%) GADFGASFRPRPM 1898.1698.4598.4898.85 2098.2899.2699.4598.93 2599.4599.3999.5699.67 3099.7299.5299.7799.75 3599.8199.5699.8199.82 4099.8699.6999.8599.88 4599.9499.7699.9899.98
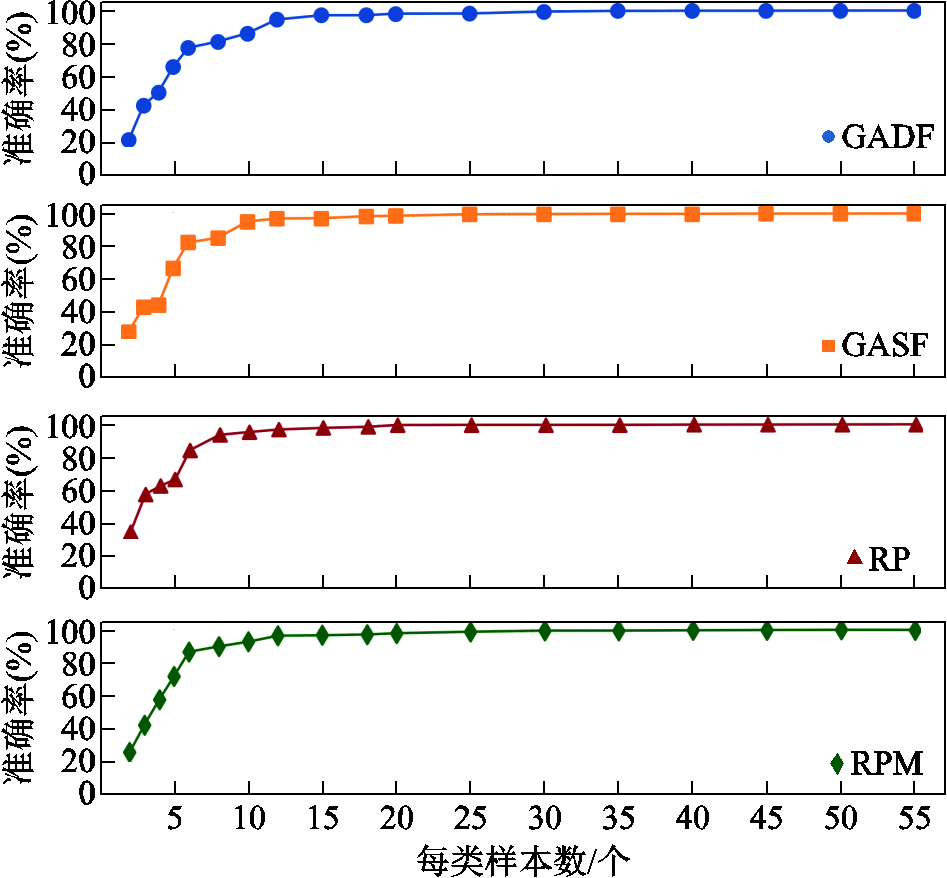
图10 模型准确率随训练样本数的变化
Fig.10 Variation of accuracy with the number of samples
在实际工程应用中，传感器等测量设备易受噪声干扰，影响故障诊断模型的准确率。通过分析噪声对模型性能的影响，了解模型在不同信噪比下的鲁棒性，可有针对性地优化算法，提升模型在噪声环境下的诊断精度。
基于模拟噪声环境的35dB SNR的数据集进行训练，然后在不同信噪比条件（45、40、35、30 dB）下测试模型性能，逐步降低SNR模拟噪声逐渐增强的场景，从而评估模型鲁棒性。
不同信噪比下模型准确率见表3。随着SNR的降低，各特征变换法下模型准确率均下降，当SNR低于30dB时，四种方法准确率均超过98.7%，模型整体分类正确率高。不同特征变换技术下的抗噪能力存在差异，表现效果依次为RPM＞GADF＞RP＞GASF。这表明所提模型在30 dB SNR下有较强鲁棒性，混淆矩阵如图11所示。其中采用RPM时性能最佳，准确率达99.56%，能在强噪声影响下高精度识别故障类型。
表3 不同信噪比下模型准确率
Tab.3 The accuracy under different SNRs （%）
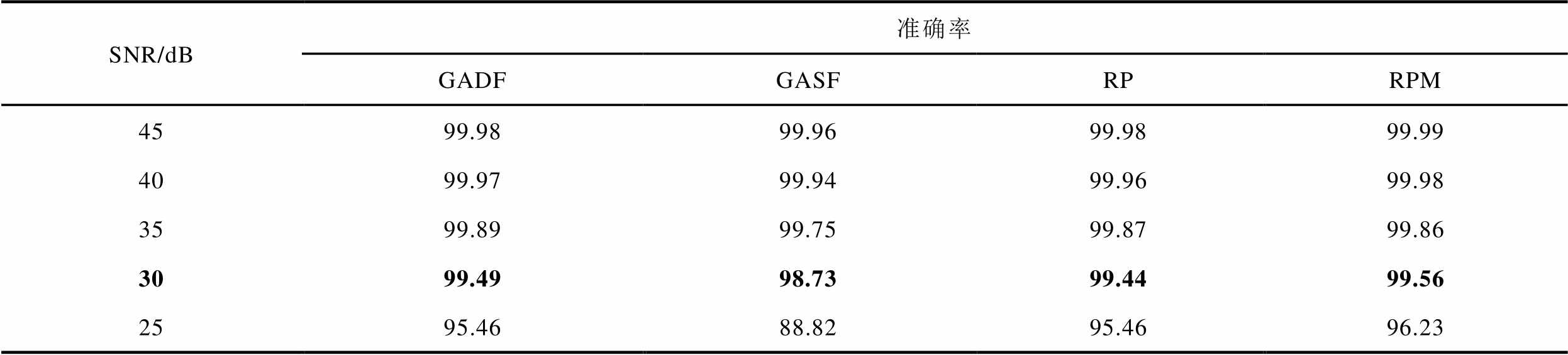
SNR/dB准确率 GADFGASFRPRPM 4599.9899.9699.9899.99 4099.9799.9499.9699.98 3599.8999.7599.8799.86 3099.4998.7399.4499.56 2595.4688.8295.4696.23
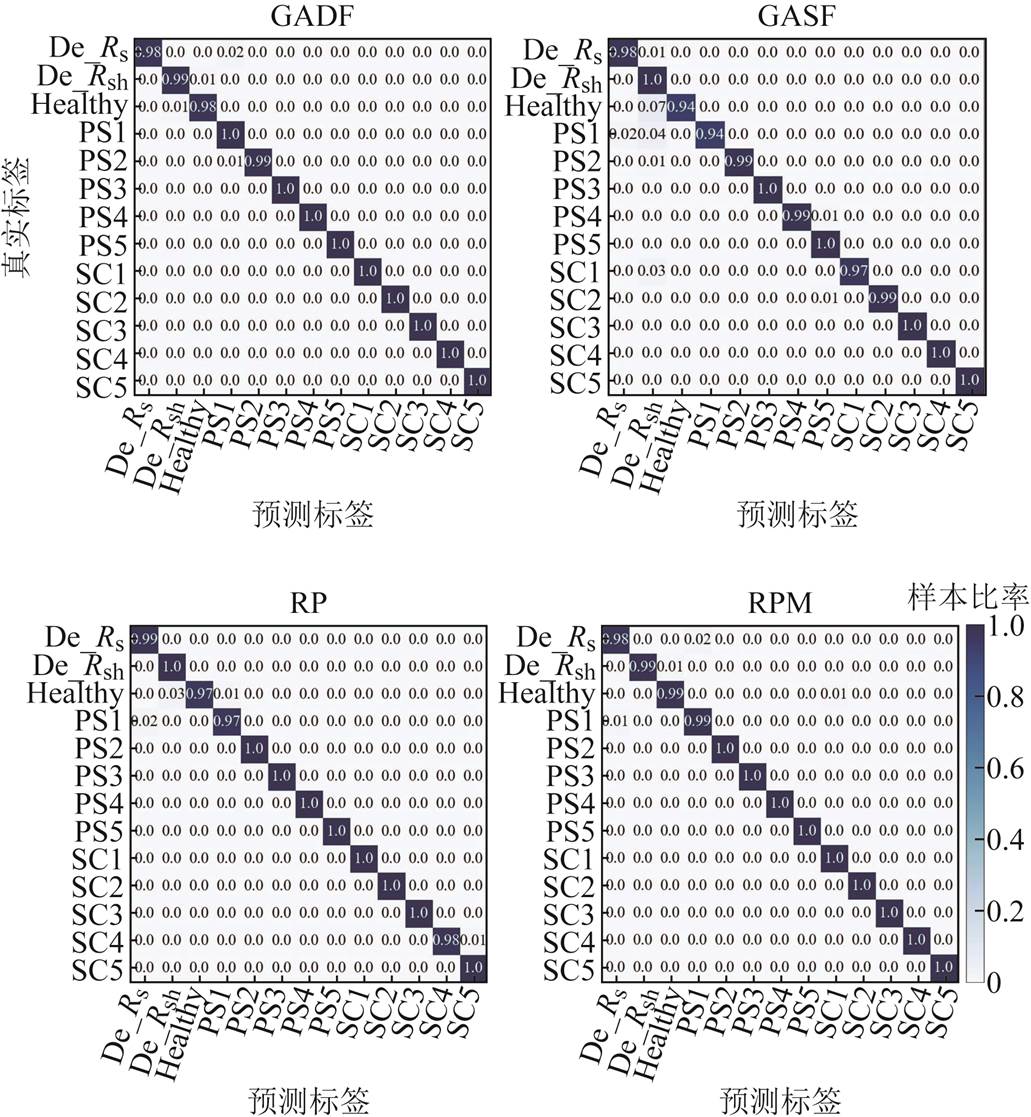
图11 不同特征变换方法在30 dB SNR的混淆矩阵
Fig.11 Confusion matrix of different feature extraction methods at 30 dB SNR
传统的I-V曲线故障诊断法主要依赖一维数据分类，将I-V曲线数据特征转换为二维图像，通过对比一维数据与二维图像数据在传统分类算法和机器学习模型中的表现，验证特征转换的有效性；通过对比所提Swin-Transformer与同类算法的表现，验证所提算法在光伏故障诊断中的优越性。
所有对比实验均在相同I-V曲线故障数据集和相同噪声影响下进行，通过在相同数据集上进行多模型、多方法的对比实验，确保实验结果的可靠性。
3.4.1 基于一维数据与传统分类算法的故障诊断
从原始I-V曲线和环境参数中提取Ir、Tm、VMPP、IMPP、VOC、ISC、Rs和Rsh八个局部电气参数进行训练，将采用八个局部电气参数和和采用所提方法提取的全局I-V曲线数据进行对比，使用故障诊断文献[30]中逻辑回归（Logistic Regression, LR）、朴素贝叶斯（Naive Bayes, NB）及支持向量机（Support Vector Machine, SVM）和ANN算法进行光伏组串故障诊断，得到模型准确率见表4。
表4 一维数据下模型准确率
Tab.4 Model accuracy with one-dimensional data （%）
数据类型准确率 LRNBSVMANN 原始I-V数据（全局）86.6586.5089.7392.77 8个电气参数（局部）78.1983.4688.6389.98
结果表明，采用全局I-V特征的效果普遍优于采用电气参数局部特征的效果。传统算法在一定程度上能够处理一维数据中的线性或简单非线性特征，如健康、老化故障，但由于一维数据缺乏足够的空间结构信息，在处理如短路、局部遮荫等复杂的非线性曲线时模型的分类能力存在局限性。
3.4.2 基于特征转换与机器学习模型的故障诊断
为验证将I-V曲线数据特征转换为二维图像后机器学习模型的表现，将使用原始I-V曲线数据和通过特征变换（GADF、GASF、RP、RPM）后的二维图像数据进行对比，基于Vision Transformer（ViT）、Data-efficient Vision Transformer（Dei-T）、卷积神经网络（Convolutional Neural Networks, CNN）和所提Swin-Transformer进行训练，得到不同变换方法下不同模型的准确率如图12所示。
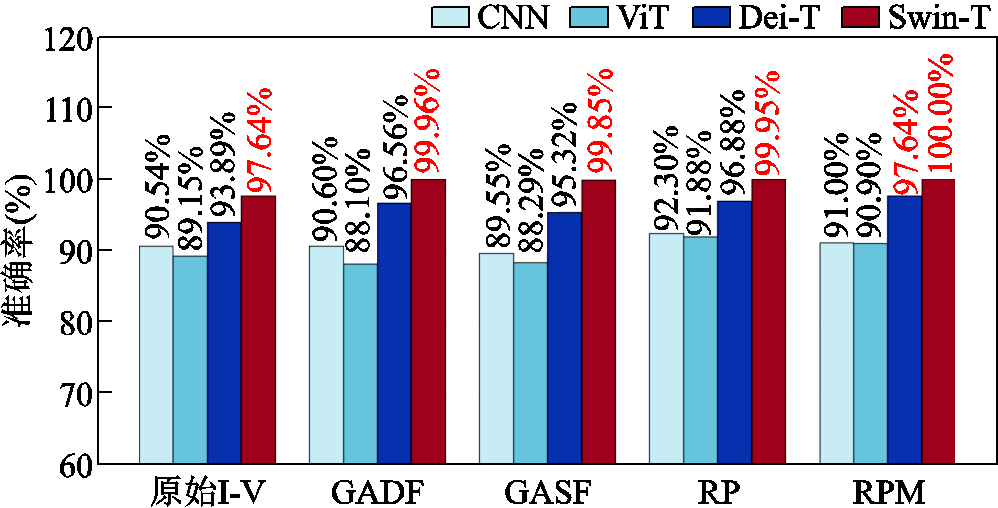
图12 二维图像下模型准确率
Fig.12 Model accuracy with two-dimensional images
一维数据与二维图像的模型准确率对比见表5。可见，基于使用原始I-V图像数据的准确率普遍高于基于一维数据的传统分类算法，说明二维图像能更有效提取I-V曲线的动态特性和多维特征，从而提高故障诊断准确性。
表5 一维数据与二维图像的模型准确率对比
Tab.5 Comparison of model accuracy between 1D data and 2D images （%）
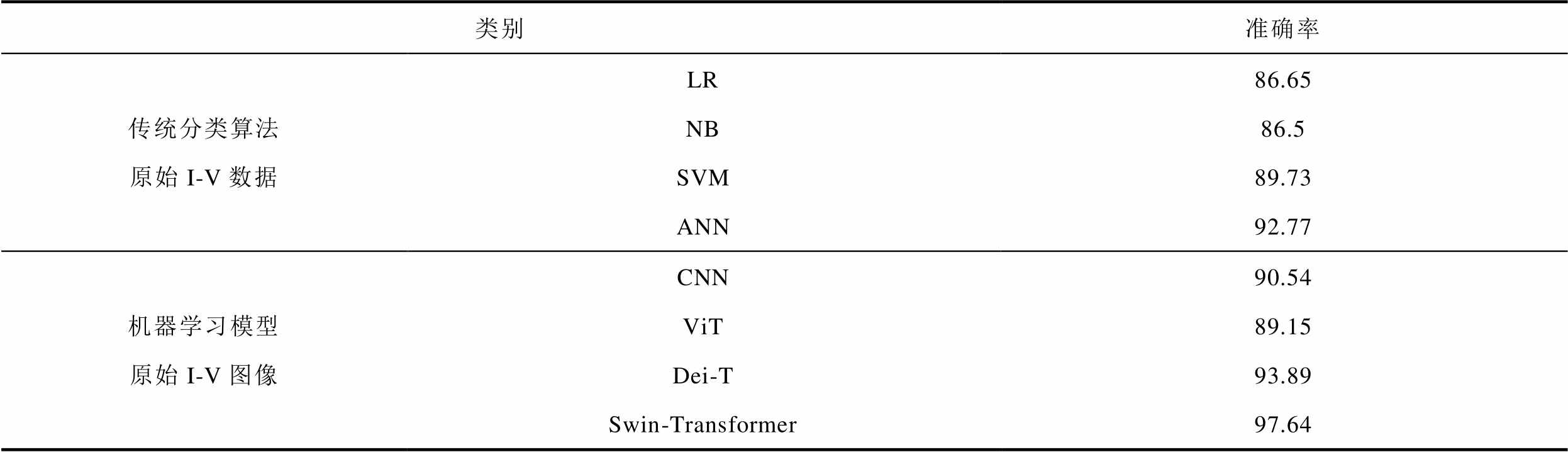
类别准确率 传统分类算法原始I-V数据LR86.65 NB86.5 SVM89.73 ANN92.77 机器学习模型原始I-V图像CNN90.54 ViT89.15 Dei-T93.89 Swin-Transformer97.64
从图12可以看出，分别应用四种特征转换法后的故障诊断准确率普遍高于使用原始I-V图像的数据。其中采用RPM性能最佳，这表明通过合适的特征转换方法，可以更好地增强模型对故障特征的感知能力，提升分类性能。
采用任一特征变换方法时，由于数据量规模不大，ViT出现轻微过拟合现象；Dei-T的准确率较ViT有所提升，但其知识蒸馏技术增加了训练时长和计算复杂度；Swin-Transformer的准确率均最高，其中采用RPM特征变换技术的故障诊断方法实现了100%的准确率。Swin-Transformer通过分层自注意力机制，在局部范围内有效提取特征，在全局范围内保持较低的计算复杂度，相比传统CNN和其他同类模型（ViT和Dei-T），在处理故障特征时表现出了更高的分类精度和更强的鲁棒性。由此证明了基于RPM特征变换法和Swin-Transformer的光伏组串故障诊断方法的优越性。
在重庆市搭建光伏组串现场实验平台如图13所示。采用3.75 kW光伏系统和工业级光伏板，参与现场实验的光伏组串由10个光伏模块JAM72S01串联组成，组串各参数配置与第3节中的仿真模型一致。采用辐照度仪实时测量环境辐照度，采用温度传感器实时测量环境温度，采用光伏测试仪得到I-V曲线数据。
图13 光伏组串实验平台
Fig.13 PV module field experiment platform
测量得到的I-V曲线经全局I-V特征提取后，选取13种运行状态、环境温度在34.77～42.79 ℃之间、辐照度在507.25～789.34 W/m2之间变化的实验数据集。为覆盖更广泛的故障场景，考虑故障严重程度的变化，不同故障类型的参数设置同仿真一致。综合考虑现场实验的可行性，故障示例如图14所示，最终实验数据集包含1 700条I-V曲线，每种条件对应100～300条曲线。
图14 故障示例
Fig.14 Example of faults
为验证最小样本需求的可靠性及所提全局I-V特征提取法和模型在实际应用中的可行性，在实验数据上应用四种特征变换方法（GADF、GASF、RP、RPM），特征提取过程和模型与仿真阶段一致以确保结果的可比性。
为验证模型最小样本需求，选取每类25个样本的训练权重，将处理后的实验数据作为测试集，表6展示了现场实验中不同特征提取方法的模型准确率，并在相同条件下与仿真结果对比。
表6 最小样本需求下仿真与实验准确率结果对比
Tab.6 Comparison of accuracy between simulation and experimental under minimum sample requirement
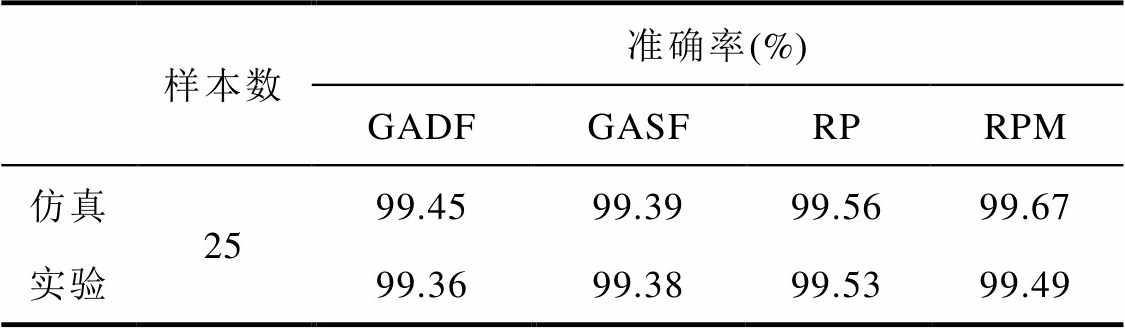
样本数准确率(%) GADFGASFRPRPM 仿真2599.4599.3999.5699.67 实验99.3699.3899.5399.49
实验结果显示，所提模型在实际数据中仍有较高准确率，模型可以承受最少为每类25个训练样本。为评估光伏组串故障检测模型在仿真结果和实验结果间的差异，采用方均根误差作为误差分析的定量指标，综合四种特征变换方法的方均根误差为0.005%，表明所提方法可准确诊断常见故障类型，具有实际可行性。
为验证仿真结果对承受噪声能力的可靠性及所提全局I-V特征提取法和模型在实际应用中的可行性，在实验数据上应用四种特征变换方法，特征提取过程和模型与仿真阶段相同。为验证模型噪声承受能力，将处理后的实验数据作为测试集，表7展示了现场实验中不同特征提取方法的模型准确率结果，并在相同条件下与仿真结果对比。
表7 噪声影响下仿真与实验准确率结果对比
Tab.7 Comparison of accuracy between simulation and experimental at different SNR
SNR/dB准确率(%) GADFGASFRPRPM 仿真3099.4998.7399.4499.56 实验99.4597.6599.4299.53
实验结果显示，模型可以承受最强为30 dB的噪声，综合四种特征提取方法的方均根误差为0.005%，表明所提模型在实际数据中表现出与仿真结果一致的鲁棒性，可准确诊断常见故障类型。
为多维度衡量模型性能，在30 dB噪声干扰下应用RPM变换技术，采用损失值、准确率函数（图15）、精确率、召回率、F1值（表8）作为模型性能评价指标。
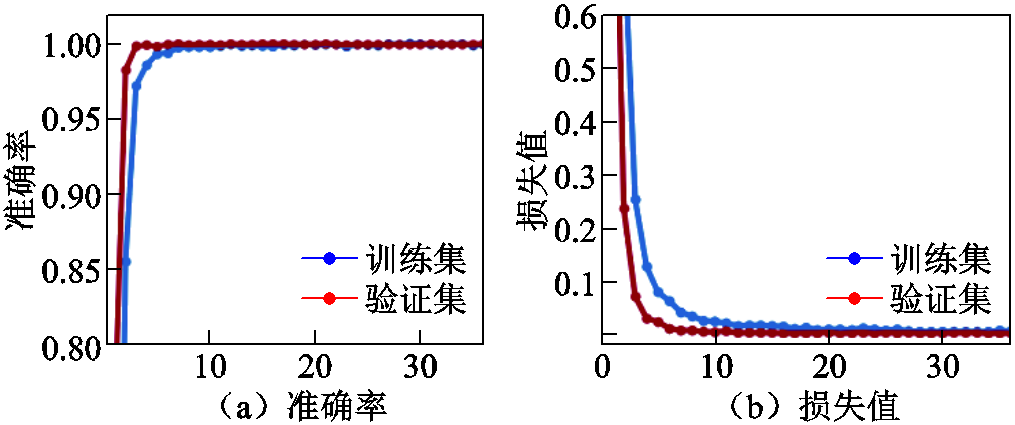
图15 SNR 30 dB下准确率和损失值
Fig.15 Accuracy and loss function at 30 dB SNR
表8 模型各项评价指标参数
Tab.8 Parameters of evaluation indicators
方法精确率召回率F1值 GADF0.9760.9720.973 GASF0.9790.9730.974 RP0.9810.9760.985 RPM0.9960.9960.996
在模型训练初期，训练集和验证集的损失函数曲线都迅速下降，模型正在学习训练数据的特征，参数迅速调整。随着训练的进行，损失值的下降逐渐趋于平缓，模型正逐渐收敛。在训练后期损失函数曲线基本保持平稳，模型达到相对最优状态，参数的进一步调整对误差的影响已经较小，模型成功收敛，未出现过拟合现象。
由于数据集不完全平衡，通过加权召回率和F1值等可以更好地评估模型在不同类别尤其是少样本下的表现，30 dB噪声干扰下应用RPM变换技时模型各项评价指标参数见表8。
结果显示模型能准确地识别故障类型，在精确率和召回率之间有较好的平衡，在训练集和验证集上都具备良好的泛化能力，在光伏组串故障诊断中性能良好，且适用于对分类准确度要求较高的应用场景。
本文提出了一种基于I-V曲线全局特征提取的光伏组串Swin-Transformer故障诊断方法，通过STC校正、归一化和维度变换从I-V曲线中提取全局特征，提出的Swin-Transformer模型可准确诊断三类常见光伏组串故障，最小样本需求仅为每类25个、且能承受30 dB的噪声，具体结论如下：
1）所提故障诊断方法采用四种特征变换技术对比，在RPM特征变换下性能最佳。
2）设计的机器学习模型最小标记样本需求为每类25个，采用RPM特征变换技术进行故障诊断准确率达99.67%，通过实验验证具有可行性，可以应用在光伏组串故障诊断中。
3）所提方法在30 dB的强噪声干扰下应用RPM特征变换技术进行故障诊断具有99.56%的准确率，通过实验验证具有较强鲁棒性，可准确诊断常见故障类型，为光伏组串的长期稳定运行提供了可靠的技术支持。
参考文献
[1] 吴春华, 易苑, 李智华, 等. 考虑参数权重与分层映射的光伏组件健康程度检测[J]. 电工技术学报, 2024, 39(15): 4856-4867.
Wu Chunhua, Yi Yuan, Li Zhihua, et al. Health detection of photovoltaic modules considering parameter weights and hierarchical mapping[J]. Transactions of China Electrotechnical Society, 2024, 39(15): 4856-4867.
[2] 王小宇, 刘波, 孙凯, 等. 光伏阵列故障诊断技术综述[J]. 电工技术学报, 2024, 39(20): 6526-6543.
Wang Xiaoyu, Liu Bo, Sun Kai, et al. A review of photovoltaic array fault diagnosis technology[J]. Transactions of China Electrotechnical Society, 2024, 39(20): 6526-6543.
[3] Zhang Zhixiang, Ma Mingyao, Ma Wenting, et al. A data-driven photovoltaic string current mismatch fault diagnosis method based on I-V curve[J]. Microelectronics Reliability, 2022, 138: 114705.
[4] 刘恒, 马铭遥, 张志祥, 等. 热斑晶硅光伏组件I-V曲线分析及特征模拟研究[J]. 太阳能学报, 2021, 42(4): 239-246.
Liu Heng, Ma Mingyao, Zhang Zhixiang, et al. Study on i-v curve analysis and characteristic simulation of silicon photovoltaic module with hot spot[J]. Acta Energiae Solaris Sinica, 2021, 42(4): 239-246.
[5] Huang Junming, Wai R J, Gao Wei. Newly-designed fault diagnostic method for solar photovoltaic generation system based on IV-curve measurement[J]. IEEE Access, 2019, 7: 70919-70932.
[6] Dhimish M, Chen Zhicong. Novel open-circuit photovoltaic bypass diode fault detection algorithm [J]. IEEE Journal of Photovoltaics, 2019, 9(6): 1819-1827.
[7] Bonsignore L, Davarifar M, Rabhi A, et al. Neuro-fuzzy fault detection method for photovoltaic systems[J]. Energy Procedia, 2014, 62: 431-441.
[8] 王尧, 马桐桐, 赵宇初, 等. 基于电磁辐射时延估计的串联光伏直流电弧故障定位方法[J]. 电工技术学报, 2023, 38(8): 2233-2243.
Wang Yao, Ma Tongtong, Zhao Yuchu, et al. Series DC arc-fault location method based on electromagnetic radiation delay estimation for photovoltaic systems[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2233-2243.
[9] Ren Bo, Wang Qianggang, Zhou Niancheng, et al. Fault diagnosis of photovoltaic strings based on SiamMN networks and panoramic I-V features[J]. IEEE Transactions on Industrial Electronics, 2025, 72(3): 3172-3182.
[10] 涂彦昭, 高伟, 杨耿杰. 一种基于卷积神经网络和长短期记忆网络的光伏系统故障辨识方法[J]. 电气技术, 2022, 23(2): 48-54.
Tu Yanzhao, Gao Wei, Yang Gengjie. A photovoltaic system fault identification method based on convolutional neural network and long short-term memory network[J]. Electrical Engineering, 2022, 23(2): 48-54.
[11] 赵靖英, 吴晶晶, 张雪辉, 等. 基于萤火虫扰动麻雀搜索算法-极限学习机的光伏阵列故障诊断方法研究[J]. 电网技术, 2023, 47(4): 1612-1625.
Zhao Jingying, Wu Jingjing, Zhang Xuehui, et al. Fault diagnosis of photovoltaic arrays based on sparrow search algorithm with firefly perturbation-extreme learning machine[J]. Power System Technology, 2023, 47(4): 1612-1625.
[12] 顾崇寅, 徐潇源, 王梦圆, 等. 基于CatBoost算法的光伏阵列故障诊断方法[J]. 电力系统自动化, 2023, 47(2): 105-114.
Gu Chongyin, Xu Xiaoyuan, Wang Mengyuan, et al. CatBoost algorithm based fault diagnosis method for photovoltaic arrays[J]. Automation of Electric Power Systems, 2023, 47(2): 105-114.
[13] 陈凌, 韩伟, 张经炜. 基于数据融合的光伏组件故障诊断[J]. 电网技术, 2017, 41(6): 1864-1873.
Chen Ling, Han Wei, Zhang Jingwei. PV module fault diagnosis based on data fusion[J]. Power System Technology, 2017, 41(6): 1864-1873.
[14] Huang Junming, Wai R J, Yang Gengjie. Design of hybrid artificial bee colony algorithm and semi-supervised extreme learning machine for PV fault diagnoses by considering dust impact[J]. IEEE Transactions on Power Electronics, 2019, 35(7): 7086-7099.
[15] Liu Yongjie, Ding Kun, Zhang Jingwei, et al. Intelligent fault diagnosis of photovoltaic array based on variable predictive models and I-V curves[J]. Solar Energy, 2022, 237: 340-351.
[16] Chen Zhicong, Chen Yixiang, Wu Lijun, et al. Deep residual network based fault detection and diagnosis of photovoltaic arrays using current-voltage curves and ambient conditions[J]. Energy Conversion and Management, 2019, 198: 111793.
[17] Li Baojie, Delpha C, Migan-Dubois A, et al. Fault diagnosis of photovoltaic panels using full I-V characteristics and machine learning techniques[J]. Energy Conversion and Management, 2021, 248: 114785.
[18] 曾祥超, 张鹤仙, 王水威, 等. 双面光伏组件I-V测试方法研究[J]. 太阳能学报, 2021, 42(3): 370-374.
Zeng Xiangchao, Zhang Hexian, Wang Shuiwei, et al. Research on testing methods of I-V characteristics of bifacial PV modules[J]. Acta Energiae Solaris Sinica, 2021, 42(3): 370-374.
[19] Standard IEC 60891. Photovoltaic Devices. Procedures for Temperature and Irradiance Corrections to Measured I-V Characteristics[S]. Britain: International Electro-technical Commission, 2009.
[20] Wang Zhiguang, Oates T, Wang Zhiguang, et al. Imaging time-series to improve classification and imputation[C]//Proceedings of the 24th International Conference on Artificial Intelligence, Buenos Aires, Argentina, 2015: 3939-3945.
[21] Zhiguang Wang, Tim Oates. Encoding time series as images for visual inspection and classification using tiled convolutional neural networks[C]//Workshops at the Twenty-Ninth AAAI conference on Artificial Intelligence, USA, 2015: 40-46.
[22] Marwan N, Carmen Romano M, Thiel M, et al. Recurrence plots for the analysis of complex systems[J]. Physics Reports, 2007, 438(5/6): 237-329.
[23] Chen Wei, Shi Ke. A deep learning framework for time series classification using Relative Position Matrix and Convolutional Neural Network[J]. Neurocomputing, 2019, 359: 384-394.
[24] Liu Ze, Lin Yutong, Cao Yue, et al. Swin transformer: hierarchical vision transformer using shifted windows [C]//2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 2021: 9992-10002.
[25] Ashish Vaswani, Noam Shazeer, Niki Parmar, et al. Attention is all you need[J]. Advances in Neural Information Processing Systems, 2017, 30: 5998-6008.
[26] Hu Han, Zhang Zheng, Xie Zhenda, et al. Local relation networks for image recognition[C]//2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea (South), 2019: 3464-3473.
[27] Dosovitskiy A. An image is worth 16x16 words: Transformers for image recognition at scale[C]//The Ninth International Conference on Learning Represe-ntations, California, 2021.
[28] Dirnberger D, Kräling U. Uncertainty in PV module measurement: part I: calibration of crystalline and thin-film modules[J]. IEEE Journal of Photovoltaics, 2013, 3(3): 1016-1026.
[29] Pvps I, Driesse A, Razongles G, et al. Uncertainties in PV system yield predictions and assessments[R]. Report IEA-PVPS T13-12, 2018.
[30] Eskandari A, Milimonfared J, Aghaei M. Fault detection and classification for photovoltaic systems based on hierarchical classification and machine learning technique[J]. IEEE Transactions on Industrial Electronics, 2021, 68(12): 12750-12759.
Abstract The installed capacity of grid-connected photovoltaic power generation has grown rapidly, and the healthy operation of PV strings is crucial to the safety and stability of the PV power plant system. However, with the construction of PV bases in deserts, Gobi wastelands, and mountainous areas, the harsh outdoor operating environment has led to frequent failures, resulting in a decline in the overall power and even fire accidents. Therefore, fast and accurate PV fault diagnosis is crucial to ensure the reliable and safe operation of PV bases. In order to improve the automated operation and maintenance level of PV system, a swin-transformer fault diagnosis method for PV strings based on global feature extraction of I-V curves is proposed to realize accurate and reliable intelligent PV condition monitoring.
Firstly, global I-V feature extraction is carried out to make full use of the dynamic characteristics of the I-V curve, which is greatly affected by the environment, and in order to avoid misidentifying the changes in the curve caused by environmental factors as fault characteristics, the curve needs to be calibrated to the standard test conditions (STC). After calibration, normalization preprocessing is performed due to the different sampling points and uneven distribution. The normality of the I-V curve data is improved by the correction and normalization preprocessing. Then, the dynamic characteristics of I-V curves are portrayed multidimensionally using the Gram angle field (GAF), recurrence plot (RP) and relative position matrix (RPM) feature transformations, and the global I-V features characterizing the state information of PV arrays are extracted.
The GAF, RP and RPM feature extraction methods transform the data into images for processing and analysis using models in the field of computer vision, and for the characteristics of periodicity and repetitiveness of local areas of the image, a fault diagnosis model based on swin transformer is proposed, which adopts a hierarchical structure to progressively aggregate the local features, and then represents the global features, and the hierarchical feature extraction is more suitable for dealing with the image data; a shift window is designed to extract global I-V features characterizing the state information of PV arrays. The hierarchical feature extraction method is more suitable for processing image data; a shift window mechanism is designed to fuse local and global features across the window, which has strong image processing capability; local self-attention computation using the shift window can adapt to image inputs with different resolutions without providing a large number of samples, which effectively reduces the amount of computation and improves the efficiency of the model, and realizes high-precision fault diagnosis.
Simulations and field experiments on a 3.75 kW PV system show that the proposed method performs best under the relative position matrix feature transformation, and can accurately diagnose multiple faults with different conditions and severities. The model accuracy is 99.67% with as low as 25 samples per class and 99.56% with 30dB noise interference. Ablation experiments using multiple feature data with different algorithms validate the superiority of the proposed feature extraction method and fault diagnosis model. This study provides reliable technical support for the stable operation of PV strings.
Keywords：PV strings, fault diagnosis, I-V curve, global feature, Swin-Transformer
中图分类号：TM615
DOI: 10.19595/j.cnki.1000-6753.tces.242073
国家自然科学基金集成项目资助（U22B6006）。
收稿日期 2024-11-17
改稿日期 2025-02-18
昌千琳 女，2001年生，硕士研究生，研究方向为直流保护、故障检测与诊断、人工智能在新能源系统中的应用。E-mail：qianlinchang@stu.cqu.edu.cn
王强钢 男，1987年生，博士，教授，博士生导师，研究方向为电力系统保护与控制、电能质量、新能源发电运行与控制。E-mail：qianggang1987@cqu.edu.cn（通信作者）
（编辑 赫 蕾）