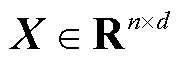 ,用
,用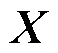 ~
~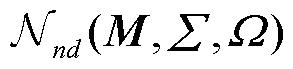 表示
表示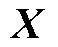 服从均值矩阵
服从均值矩阵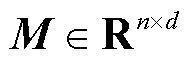 ,协方差矩阵为
,协方差矩阵为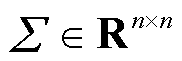 和
和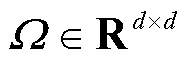 的矩阵变量高斯分布。其中
的矩阵变量高斯分布。其中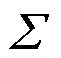 包含行向量之间的相关性信息,为列协方差矩阵;
包含行向量之间的相关性信息,为列协方差矩阵;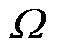 包含列向量之间的相关性信息,为行协方差矩阵,两者均为半正定矩阵[19]。此时随机矩阵
包含列向量之间的相关性信息,为行协方差矩阵,两者均为半正定矩阵[19]。此时随机矩阵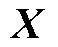 的概率密度函数为
的概率密度函数为摘要 数据驱动谐波源建模方法采用谐波电信号的幅值和相位数据训练模型,本质上是一种针对复信号的分析处理过程。传统数据驱动算法的设计与实现多在实数域上进行,在进行复信号回归时存在信息丢失的问题。对此该文首先提出一种基于矩阵变量高斯分布的多元高斯过程回归算法,借助行协方差矩阵刻画目标复信号实部虚部间的相关性信息,根据多类型谐波源的谐波发射影响因素选取特征变量建立复信号谐波源模型;其次,针对当前数据驱动谐波源建模方法对全局样本学习效果差的问题,该文提出一种模型全局性提升方法,采用基于密度的空间聚类算法划分历史样本数据并建立相应的谐波源子模型,根据待回归样本的输入特征量选择最接近的子模型进行回归;最后,算例表明该文所提算法的复信号回归效果优于高斯过程回归法和复线性最小二乘法,所选建模特征变量能够准确地反映多类型谐波源的谐波发射特性,所述全局性提升方法能够提高模型对全局样本的回归精度并减少算法的训练时间。
关键词:多元高斯过程回归 谐波源建模 谐波分析 电能质量 聚类
随着各类电力电子装备的规模化应用,电力系统中谐波污染源的种类和数量快速增长,谐波广分布、强耦合的特征越发显著,背景谐波电压水平不断恶化,严重威胁新型电力系统的安全稳定和优质高效运行[1-2]。我国新实行的《电能质量管理办法(暂行)》加强了对电能质量的监管力度[3],对新型电力系统谐波水平管理提出了更高的要求,谐波分析与治理刻不容缓。
谐波源建模在谐波责任划分、谐波交互影响分析和谐波潮流计算等方面均具有重要作用[4-6]。现有谐波源建模方法主要分为机理驱动建模和数据驱动建模两大类,其中机理驱动建模方法依据电路原理推导谐波源解析函数表达式[7],物理意义明确,但在实际工程中有时难以完全知晓电路拓扑和元件参数等信息,导致该方法应用受限;数据驱动谐波源建模方法仅以测量数据构建模型,具有更强的实用性和普适性[8-9]。这种建模方法借助数据驱动学习算法构建代理模型,挖掘谐波源物理特征之间的数学联系。文献[10-12]采用神经网络、支持向量机等机器学习算法对谐波源谐波电压与谐波电流之间的耦合关系进行非线性映射,实现了谐波电流幅值的确定性回归。文献[13]提出一种基于高斯过程回归(Gaussian Processes Regression, GPR)的不确定性谐波源模型,其谐波电流幅值回归结果是一个高斯分布,可以从概率意义上反映估计结果的不确定性。完整的谐波源建模涉及谐波电信号的幅值与相位信息,是一种针对复信号的分析与处理过程,然而上述数据驱动算法的设计与实现均在实数域上进行,在以复信号为回归目标时需要将其转换为实部和虚部后进行两次独立的模型训练,既丢失了目标信号实部与虚部之间的相关性信息,也增加了建模的工作量[14-15]。文献[16-17]采用复线性最小二乘法(Complex Least Squares, CLS)对谐波源线性化等值模型进行辨识,能够直接获取模型中的复参数,但受算法本身的限制其拟合非线性谐波源模型的精度有限,且无法刻画实际电力系统中谐波源谐波发射行为的随机性与波动性特征。
数据驱动方法对谐波源物理特征的拟合效果与学习样本息息相关。受限于有限场景下的数据样本,目前数据驱动谐波源模型仅能对谐波源设备部分运行状态下的局部谐波发射特征进行描述,难以做到全局性的学习与回归[18]。为保证算法模型参数能够适应电力系统运行状态变化以及复杂网络中谐波源设备的投切变动等情况,文献[13]提出不确定性谐波源模型的在线更新策略,在模型回归结果的命中率低于阈值时采用实时监测数据重新训练模型;文献[17]以供电电压变化程度作为更新判据,在供电电压相似度低于阈值时动态更新模型参数。上述动态更新的方法虽然提高了模型的实时回归效果,却无法保存历史样本数据中包含的谐波源历史运行状态信息,当谐波源切换到与历史样本相似的运行状态时仍需重新训练模型,模型的全局性学习效果差。
综合上述分析,针对传统数据驱动算法进行复信号回归时存在的信息丢失问题,本文首先提出一种基于矩阵变量高斯分布的多元高斯过程回归(Multivariate Gaussian Process Regression, MV-GPR)算法,引入行协方差矩阵来刻画目标复信号实部虚部的相关性信息,推导多元高斯过程的后验分布计算和参数估计方法,实现了对复信号的不确定性回归。然后,基于各类型谐波源的谐波发射特性影响因素选取三相不平衡条件下的复信号谐波源建模特征变量,并采用主成分分析法对输入特征变量进行降维,以保证算法的收敛性。针对当前数据驱动谐波源建模方法全局学习效果差的问题,本文根据MV-GPR算法在小规模样本回归中表现更好的特点提出一种模型全局性提升方法,首先采用基于密度的空间聚类算法(Density-Based Spatial Clustering of Applications with Noise, DBSCAN)将历史样本数据划分为代表谐波源不同运行状态的子样本集。其次基于各子样本集建立相应的谐波源子模型,再根据待回归样本与各子样本集的距离选择最接近的子模型进行回归,从而提高谐波源模型对全局样本的学习与回归效果。最后,本文基于仿真和实测数据算例,采用GPR算法和CLS算法对比验证MV-GPR算法对复信号的回归效果;采用不同输入特征变量对比验证本文所选复信号谐波源建模特征变量对多类型谐波源等值拟合的准确性;采用多运行状态样本集验证所提模型全局性提升方法的有效性。
对于高斯变量组成的随机矩阵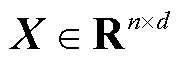 ,用
,用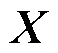 ~
~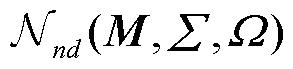 表示
表示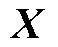 服从均值矩阵
服从均值矩阵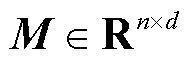 ,协方差矩阵为
,协方差矩阵为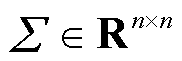 和
和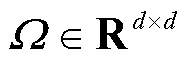 的矩阵变量高斯分布。其中
的矩阵变量高斯分布。其中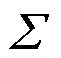 包含行向量之间的相关性信息,为列协方差矩阵;
包含行向量之间的相关性信息,为列协方差矩阵;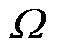 包含列向量之间的相关性信息,为行协方差矩阵,两者均为半正定矩阵[19]。此时随机矩阵
包含列向量之间的相关性信息,为行协方差矩阵,两者均为半正定矩阵[19]。此时随机矩阵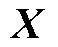 的概率密度函数为
的概率密度函数为
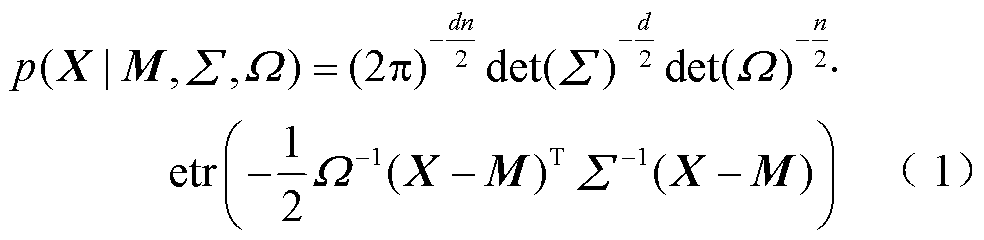
如果多维变量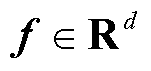 是
是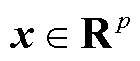 上的多元高斯过程
上的多元高斯过程 ,具有向量均值函数
,具有向量均值函数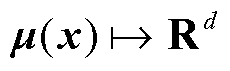 ,核函数
,核函数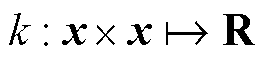 和半正定参数矩阵
和半正定参数矩阵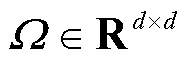 ,则任何向量变量
,则任何向量变量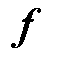 的有限集合服从一个联合的矩阵变量高斯分布[20],即
的有限集合服从一个联合的矩阵变量高斯分布[20],即
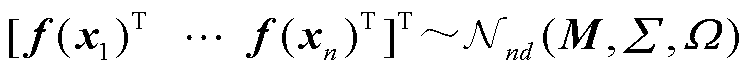 (2)
(2)
式中,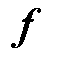 为行向量;均值矩阵
为行向量;均值矩阵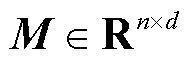 中的元素满足
中的元素满足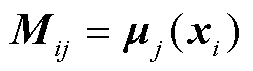 ;列协方差矩阵
;列协方差矩阵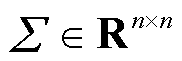 中的元素满足
中的元素满足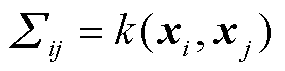 ;行协方差矩阵
;行协方差矩阵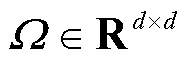 为待估计参数矩阵,用于保存多维变量
为待估计参数矩阵,用于保存多维变量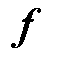 之间的相关性信息。
之间的相关性信息。
给定n组观测值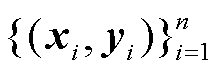 作为多元高斯过程回归的训练集。考虑到实际的观测值中总是包含噪声值,将噪声项纳入核函数中,则有
作为多元高斯过程回归的训练集。考虑到实际的观测值中总是包含噪声值,将噪声项纳入核函数中,则有
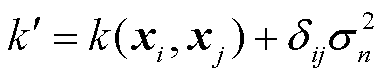 (3)
(3)
式中,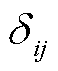 为克罗内克函数;
为克罗内克函数;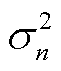 为随机噪声的方差。
为随机噪声的方差。
设多元高斯过程向量值均值函数的先验分布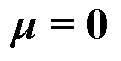 ,此时变量集
,此时变量集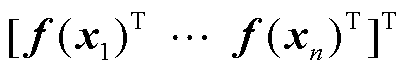 服从的矩阵变量高斯分布变为
服从的矩阵变量高斯分布变为
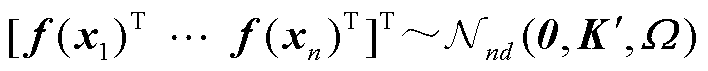 (4)
(4)
式中,列协方差矩阵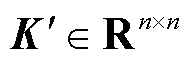 中的元素满足
中的元素满足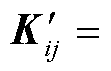
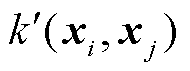 。
。
为实现由测试集输入变量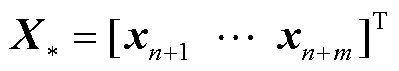 到对应输出变量
到对应输出变量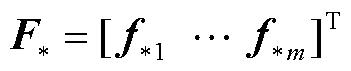 的映射回归,首先给出训练集输出变量
的映射回归,首先给出训练集输出变量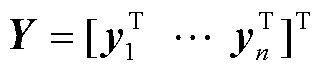 与测试集输出
与测试集输出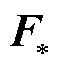 的联合分布形式为
的联合分布形式为
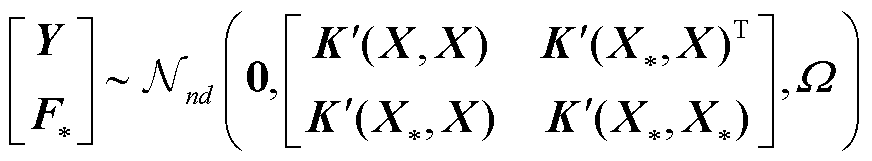 (5)
(5)
式中,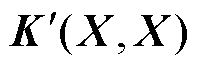 为
为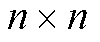 矩阵,元素满足
矩阵,元素满足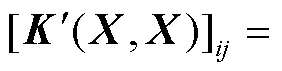
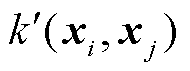 ;
;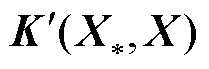 为
为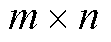 矩阵,元素满足
矩阵,元素满足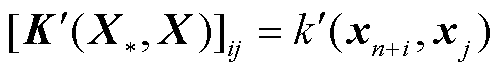 ;
;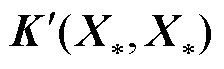 为
为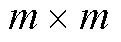 矩阵,元素满足
矩阵,元素满足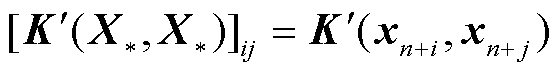 。利用多元高斯过程的条件分布,可求出测试集输出
。利用多元高斯过程的条件分布,可求出测试集输出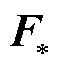 后验分布的期望和协方差分别为
后验分布的期望和协方差分别为
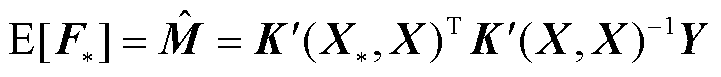 (6)
(6)
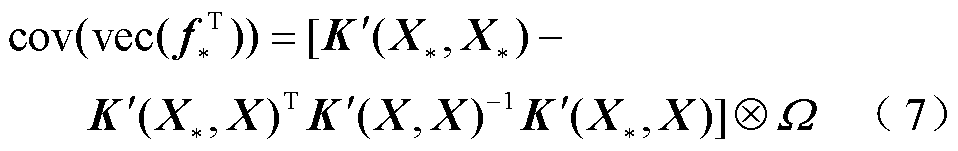
式中,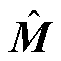 为M的估计值;vec(·)为列向量转换函数;
为M的估计值;vec(·)为列向量转换函数;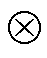 表示矩阵的克罗内克积。
表示矩阵的克罗内克积。
定义MV-GPR的列协方差矩阵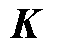 为核,矩阵元素取值与样本输入变量相关联,用于反映样本之间的接近度和相似性。最常采用的核函数是平方指数核函数,因为它的形式简单,具有平滑性和与其他函数的可积性。当输入为多维时,则需采用自相关平方指数核函数[21],即
为核,矩阵元素取值与样本输入变量相关联,用于反映样本之间的接近度和相似性。最常采用的核函数是平方指数核函数,因为它的形式简单,具有平滑性和与其他函数的可积性。当输入为多维时,则需采用自相关平方指数核函数[21],即
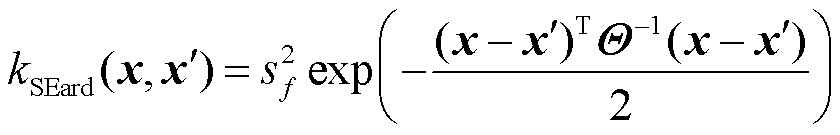 (8)
(8)
式中,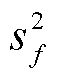 为信号方差;
为信号方差;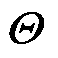 为p维对角矩阵,其元素分量
为p维对角矩阵,其元素分量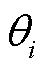 为每个相应输入特征的长度尺度。
为每个相应输入特征的长度尺度。
核函数中的未知参数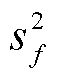 、
、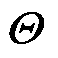 、噪声方差
、噪声方差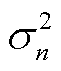 和MV-GPR的行协方差矩阵
和MV-GPR的行协方差矩阵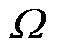 均需基于训练数据借助参数估计方法得出,本文使用极大似然法进行参数估计。与传统的GPR模型相比,
均需基于训练数据借助参数估计方法得出,本文使用极大似然法进行参数估计。与传统的GPR模型相比,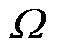 是一个额外的待估计参数矩阵。由于
是一个额外的待估计参数矩阵。由于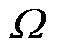 为半正定矩阵,可以将其划分为
为半正定矩阵,可以将其划分为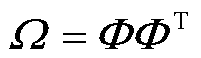 ,其中
,其中
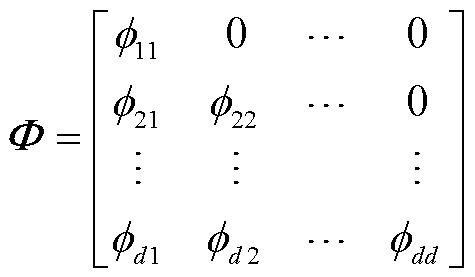 (9)
(9)
为保证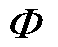 的唯一性,限制其对角元素必须为正数,并定义
的唯一性,限制其对角元素必须为正数,并定义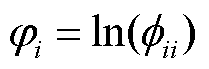 ,
,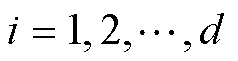 。
。
根据矩阵变量高斯分布,观测值的负对数边际似然为
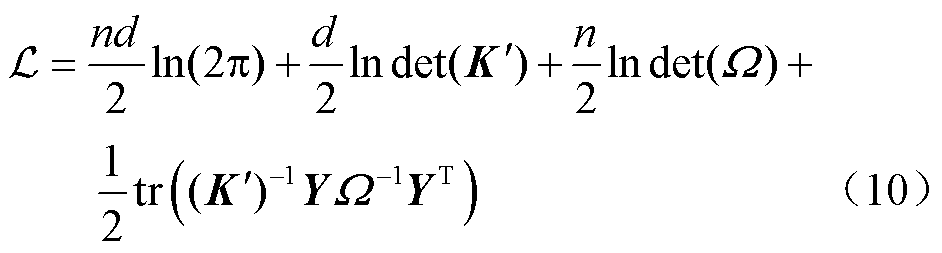
分别求取负对数边际似然函数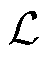 对超参数
对超参数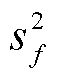 、
、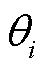 、
、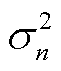 、
、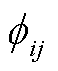 和
和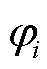 的导数,然后采用共轭梯度法最小化负对数边际似然函数,即可获得所有超参数的估计值,从而完成算法的训练。
的导数,然后采用共轭梯度法最小化负对数边际似然函数,即可获得所有超参数的估计值,从而完成算法的训练。
数据驱动谐波源建模方法从谐波源的外特性出发,基于谐波源端口量测数据借助数据驱动算法等值拟合输入输出物理特征量。数据驱动谐波源模型的通用表达形式为
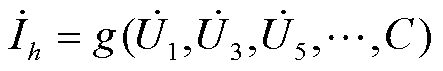 (11)
(11)
式中,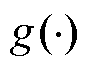 为描述输入变量与输出变量对应关系的函数,表示输入对输出的映射,其具体形式与谐波源建模时所用的数据驱动学习算法相关联;
为描述输入变量与输出变量对应关系的函数,表示输入对输出的映射,其具体形式与谐波源建模时所用的数据驱动学习算法相关联;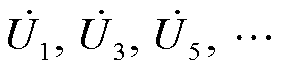 为端口量测数据中的基波电压和各次谐波电压;C为其余物理特征量。目前对于谐波源输入物理特征量的确定还没有统一、规范的方法,本文从各类型谐波源的谐波发射特性影响因素出发选取建模特征。
为端口量测数据中的基波电压和各次谐波电压;C为其余物理特征量。目前对于谐波源输入物理特征量的确定还没有统一、规范的方法,本文从各类型谐波源的谐波发射特性影响因素出发选取建模特征。
不同类型谐波源的谐波电流发射特性影响因素各不相同。光伏、风电等新能源发电设备以及非线性电弧炉负荷的谐波电流发射量与基波电流关联性强[22]。以光伏发电设备为例,在白天输出功率较高时,并网点的各次谐波电流与基波电流呈现正相关变化趋势;在夜间光伏不出力阶段,各次谐波电流与基波电流往往同时为零,对于此类设备采用基波电流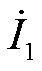 能够较好地描述其谐波发射特性。
能够较好地描述其谐波发射特性。
电力机车和直流输电换流器等电力电子设备受供电电压畸变的影响较大,现有研究多采用开关函数对电力电子设备各次电压与电流的调制关系进行推导,将其归纳整理为矩阵形式即谐波源的交叉频率导纳矩阵,其基本结构为
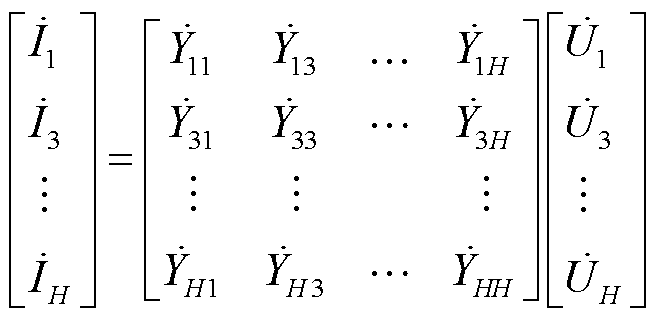 (12)
(12)
式中,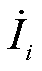 和
和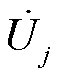 分别为第i次谐波电流复信号和第j次谐波电压复信号;H为所考虑谐波的最高次数;
分别为第i次谐波电流复信号和第j次谐波电压复信号;H为所考虑谐波的最高次数;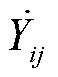 为第i次谐波电流和第j次谐波电压之间的耦合导纳,表明相应频次的谐波电流与谐波电压之间存在耦合关系,因此在构建谐波源模型时应考虑各次谐波电压
为第i次谐波电流和第j次谐波电压之间的耦合导纳,表明相应频次的谐波电流与谐波电压之间存在耦合关系,因此在构建谐波源模型时应考虑各次谐波电压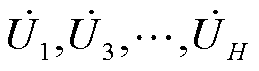 对谐波电流的影响。
对谐波电流的影响。
上述对各谐波源特发射特性影响因素的分析均是在三相平衡的理想条件下进行的。在实际电力系统中,由于电力机车和电弧炉等不平衡负荷的广泛接入以及网络结构并非严格三相对称,电力系统往往运行在三相不平衡条件下。此时各相谐波电压呈现差异化特征,经控制系统影响电力电子设备的触发时间及导通时间,从而进一步影响其谐波发射特性。三相不平衡电压除了会改变电力电子设备的特征谐波电流发射量以外,还导致其产生非特征谐波,增加了谐波分析的复杂度和困难度[23]。现有研究基于开关函数建立附加谐波耦合导纳矩阵[24],刻画了电压不平衡分量对谐波电流产生的影响。以A相各次电压作为基准值,则B、C相各次电压不平衡分量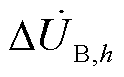 和
和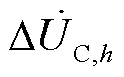 为
为
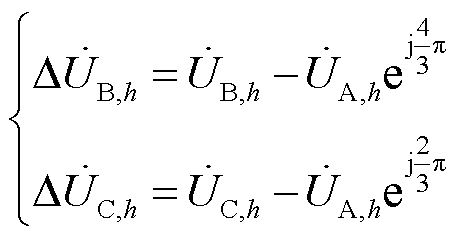 (13)
(13)
将B、C相各次电压不平衡分量加入建模输入特征集中,此时谐波源模型变更为三相形式。MV-GPR为多输入多输出算法,但输入输出特征量均要求为实数形式,因此本文将上述各类型谐波源的谐波发射相关复信号特征量分解为实部虚部形式,并作为输入特征,如此也可以考虑到各复信号特征量的共轭形式对谐波电流输出造成的影响。最终构建的MV-GPR复信号谐波源模型为
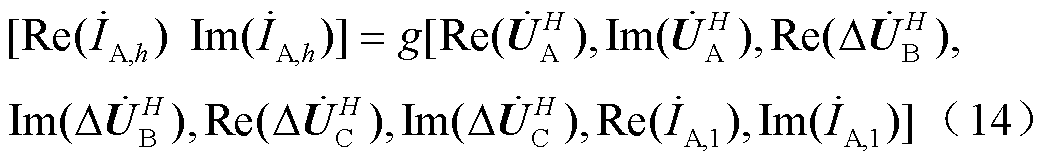
式中,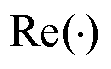 和
和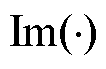 分别为复信号的实部和虚部;
分别为复信号的实部和虚部;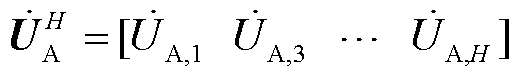 为A相各次电压复信号;
为A相各次电压复信号;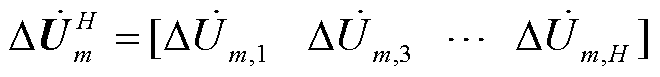 (
(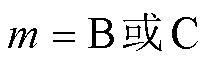 )为B相和C相各次电压复信号的不平衡分量;
)为B相和C相各次电压复信号的不平衡分量;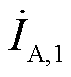 为A相基波电流复信号。
为A相基波电流复信号。
考虑到输入特征过多会导致算法训练时间过长及难以收敛,本文采用主成分分析法[25-26]对输入特征变量进行降维。主成分分析法为常用的变量降维方法,通过线性变换将原始数据映射到一个新的坐标系中,使得数据在新坐标系下的方差最大化,从而减少数据的维度并尽量保留原始数据的信息。本文将重新组合后的主成分分量按方差从小到大的方式进行排列,选取方差贡献率之和大于95%的主成分作为模型输入变量。
MV-GPR的行协方差矩阵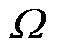 能够刻画多维输出变量
能够刻画多维输出变量 各维度之间的相关性。基于2.1节构建的MV-GPR复信号谐波源模型,采用谐波源端口测量数据进行一次算法训练,即可完成MV-GPR复信号谐波源建模,其建模流程如图1所示。
各维度之间的相关性。基于2.1节构建的MV-GPR复信号谐波源模型,采用谐波源端口测量数据进行一次算法训练,即可完成MV-GPR复信号谐波源建模,其建模流程如图1所示。
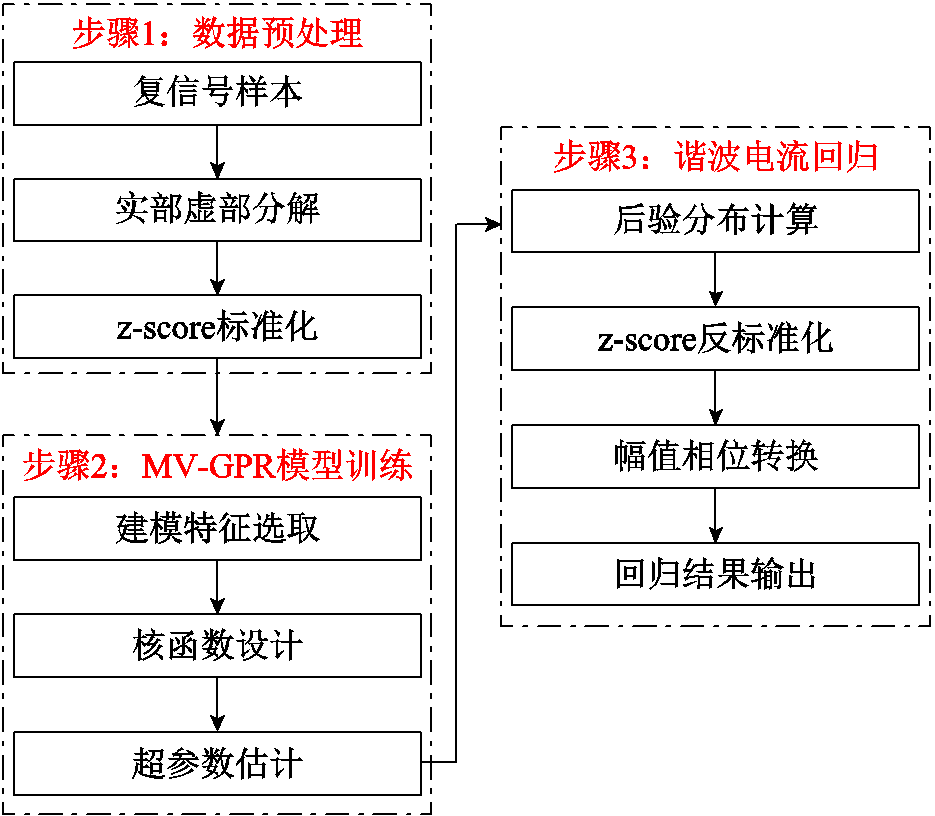
图1 基于MV-GPR的复信号谐波源建模流程
Fig.1 Complex signal modeling process for harmonic source based on MV-GPR
主要包括以下步骤:
1)数据预处理。对于仿真或实测得到的各次电压电流复信号样本,首先将其分解为实部、虚部形式,然后采用z-score标准化方法[27],根据数据序列的均值和标准差对实部虚部数据进行处理。如式(15)所示,对均值为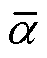 的序列
的序列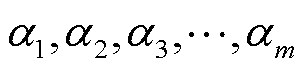 进行z-score变换,得到新序列
进行z-score变换,得到新序列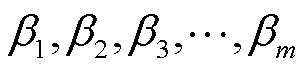 的均值为0,方差为1,且无量纲。其中m为待处理样本总数。
的均值为0,方差为1,且无量纲。其中m为待处理样本总数。
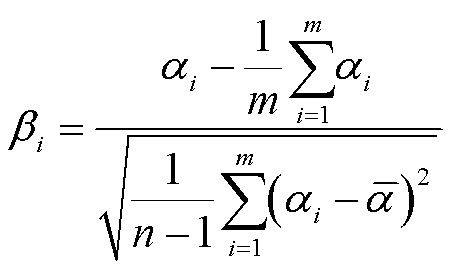 (15)
(15)
2)MV-GPR模型训练。首先根据MV-GPR复信号谐波源模型选取特征输入变量,包括各次谐波电压实部虚部、各次电压不平衡分量实部虚部和基波电流实部虚部等,采用主成分分析法对输入变量进行降维。然后对算法核函数进行设计,本文采用如式(8)所示的自相关平方指数核函数。最后采用极大似然法对算法模型中涉及的超参数进行估计。
3)谐波电流回归。获取模型超参数以后,根据待回归样本的输入特征变量计算相应谐波电流输出的后验分布。将回归结果进行z-score反标准化,再将谐波电流实部虚部转换为对应的幅值相位形式,得到谐波电流的幅值相位回归结果。
本文采用方均根误差(Root Mean Square Error, RMSE)和平均相对误差(Mean Relative Error, MRE)对回归的准确性进行评价,其表达式为
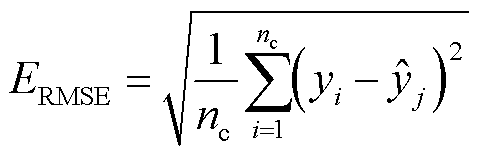 (16)
(16)
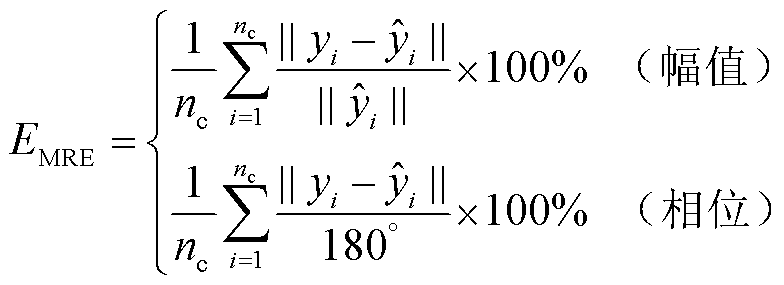 (17)
(17)
式中,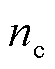 为测试集样本数;
为测试集样本数;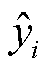 为回归值;
为回归值;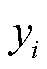 为真实值。
为真实值。
MV-GPR算法的回归结果服从高斯分布。为进一步评价该算法的不确定性回归效果,引入命中率和保守率两种不确定性回归效果指标。其中命中率表示谐波电流的真实值落在置信区间的个数m与测试集样本数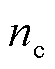 的比例,反映算法不确定性回归的准确程度,其表达式为
的比例,反映算法不确定性回归的准确程度,其表达式为
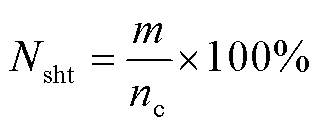 (18)
(18)
保守率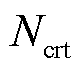 表示置信区间宽度L占真实值大小的百分比,值越小则回归结果分布的离散程度越小,不确定性回归效果越好,其表达式为
表示置信区间宽度L占真实值大小的百分比,值越小则回归结果分布的离散程度越小,不确定性回归效果越好,其表达式为
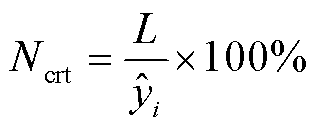 (19)
(19)
DBSCAN是一种基于密度的聚类算法,它将簇定义为密度相连的点的最大集合,把具有足够高密度的区域划分为簇。该算法无需预先指定聚类的数量,并可在有噪声的空间数据库中发现任意形状的聚类,这一特性使其在处理具有复杂结构和噪声的实际测量数据时具有更高的性能[28]。DBSCAN聚类的具体步骤包括:
1)选定聚类特征向量和DBSCAN聚类参数Eps和MinPts。其中Eps为聚类距离度量,用于定义任意点的邻域半径;MinPts为聚类在一起的点的最小数目,超过这一阈值才可算作一个簇。
2)通过距离度量的方式,找到所有样本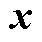 的Eps邻域子样本集。如果某样本
的Eps邻域子样本集。如果某样本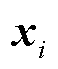 的邻域子样本集中样本个数大于等于MinPts,则将样本
的邻域子样本集中样本个数大于等于MinPts,则将样本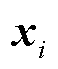 加入核心对象样本集A;否则将样本
加入核心对象样本集A;否则将样本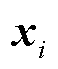 判定为边界点或噪声点。
判定为边界点或噪声点。
3)从核心对象集A中随机选择一个核心对象样本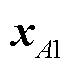 ,建立新簇的样本集
,建立新簇的样本集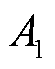 ,并将其Eps邻域中的所有样本都划入簇
,并将其Eps邻域中的所有样本都划入簇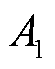 中。接着检查簇
中。接着检查簇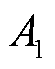 中所有样本Eps邻域内的样本,将其划入簇
中所有样本Eps邻域内的样本,将其划入簇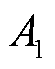 ;重复检查,直到没有新的样本可以划入。更新核心对象集
;重复检查,直到没有新的样本可以划入。更新核心对象集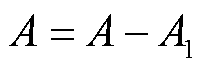 。
。
4)在更新后的核心对象集A中随机选择一个样本核心对象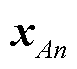 ,重复步骤3),直至核心对象集合A为空,输出最终聚类结果
,重复步骤3),直至核心对象集合A为空,输出最终聚类结果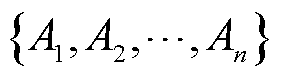 。
。
受限于样本数据的质量和规模,数据驱动谐波源模型只能对谐波源的有限运行状态进行描述,难以达到机理驱动方法全局统一分析的效果。MV-GPR是基于贝叶斯理论的回归算法,其回归效果在很大程度上取决于对均值函数和协方差函数中超参数的估计结果。当样本数量过多时,所估超参数将很难同时适用于所有的训练样本,反而会降低其回归精度。此外,MV-GPR的核心运算涉及逆矩阵的计算,对于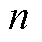 个训练样本,算法训练的计算复杂度为
个训练样本,算法训练的计算复杂度为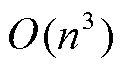 。当样本数量过多时,算法训练所需时间和收敛难度会迅速增加,导致其实用性变差。因此,MV-GRP更适用于小规模样本的回归场景,而这也意味着其面临运行状态复杂多变的谐波源设备时很难直接学习到谐波源的全局谐波发射特性。
。当样本数量过多时,算法训练所需时间和收敛难度会迅速增加,导致其实用性变差。因此,MV-GRP更适用于小规模样本的回归场景,而这也意味着其面临运行状态复杂多变的谐波源设备时很难直接学习到谐波源的全局谐波发射特性。
为提升MV-GPR复信号谐波源模型的全局性,本文首先基于DBSCAN聚类算法将历史样本数据划分为代表谐波源不同运行状态的子样本集。以2.1节中所述经z-score标准化和主成分分析降维后的建模输入特征变量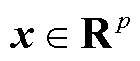 作为聚类特征向量;为保证聚类簇中的样本数量足够MV-GPR算法训练,MinPts取值为10;采用式(20)对Eps的取值进行预估计[29];采用欧式距离对样本间的距离进行度量。
作为聚类特征向量;为保证聚类簇中的样本数量足够MV-GPR算法训练,MinPts取值为10;采用式(20)对Eps的取值进行预估计[29];采用欧式距离对样本间的距离进行度量。
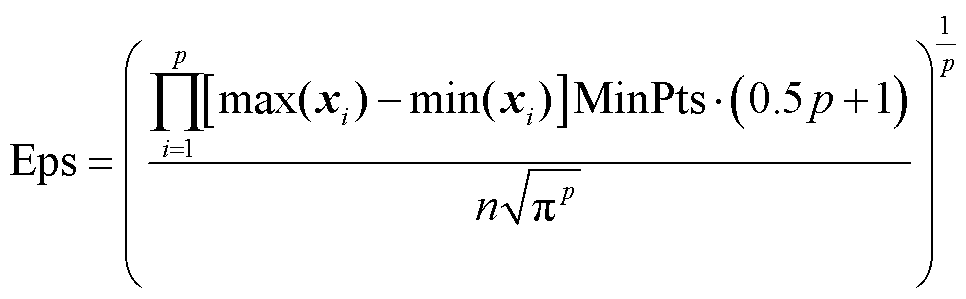 (20)
(20)
式中,p为输入特征变量维数。
其次,对于不同运行状态下的子样本集,采用MV-GPR算法学习并建立多个谐波源子模型,将其储存在模型数据库中。当需要进行回归计算时则根据待回归样本的输入特征变量与历史子样本集的距离选择最接近的谐波源子模型进行回归,从而在保证MV-GPR算法训练收敛性和回归准确性的前提下提升其用于多运行状态谐波源等值拟合时的全局性。上述模型全局性提升方法思路如图2所示。
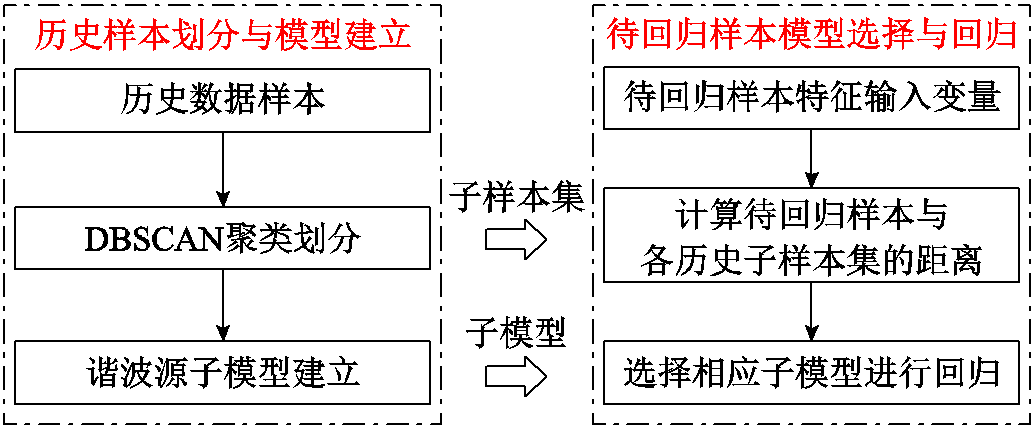
图2 模型全局性提升方法
Fig.2 Global enhancement method for models
4.1.1 算例设置
基于Matlab/Simulink仿真平台搭建包含三相交流电弧炉负荷和工业电解铝负荷的多类型谐波源设备仿真模型。两类负荷由同一等效电源供电,仿真模型如附图1所示。电弧炉负荷模型基于能量平衡方程以及混沌随机理论动态数学模型建立[30],所发射特征谐波次数为2~7次,模型参数为湖北某地区典型交流电石炉厂电压、电流数据的辨识结果;工业电解铝负荷模型由调压变压器、移相变压器、整流变压器、二十四脉波整流器组和直流电解槽负荷构成,属于电力电子型负荷设备,所发射特征谐波次数为23、25、47和49等。两类谐波源负荷的模型参数见附表1和附表2。
设置等效供电电源的基准值为220 kV,初始电压在基准值的90%~110%范围内随机变化。在此基础上向等效供电电源B、C相基波电压的幅值和相位随机添加一定的不平衡量,以模拟背景电压三相不平衡情况,各样本三相基波电压不平衡度在0%~3%范围内变化。采样点设置在等效供电电源出口的公共连接点处,共采集200组三相谐波电压电流数据。为模拟随机噪声和监测装置测量误差等因素对实际电力系统中谐波监测装置造成的干扰,向采集到的所有仿真数据中添加方差为0.1的随机高斯噪声。标记该组数据为状态1样本集。
为模拟谐波源设备群运行状态变化和设备投切情形,在原有仿真模型的基础上分别额外设置两个运行状态:在220 kV公共连接点处再添加一个相同的三相交流电弧炉负荷,此为状态2;修改工业电解铝负荷直流电解槽电压为300 V,此为状态3。采用与状态1相同的仿真设置方式分别获取状态2和状态3情形下的200组三相谐波电压电流数据。
4.1.2 算法有效性验证
为验证所提MV-GPR算法用于谐波电流复信号回归的有效性,采用该算法对状态1数据集中的7次和23次谐波电流进行不确定性回归。如无特殊说明,本文算法训练与验证方式均为从相应样本集中随机抽取160个样本数据作为训练集对算法进行训练,40个样本数据作为测试集用于回归验证,各样本后验分布的概率特性采用95%概率区间表示。测试集7次和23次谐波电流幅值相位的回归结果分别如图3和图4所示。
由图3、图4可见,MV-GPR算法回归得到的谐波电流幅值和相位均值都贴近真实值,各样本95%概率回归区间的宽度虽有一定差异,但并未出现宽度过大的情况,基本能以较低的保守率命中样本的真实值,有效地从概率意义上反映估计结果的不确定性,满足部分情况下的保守估计需求。
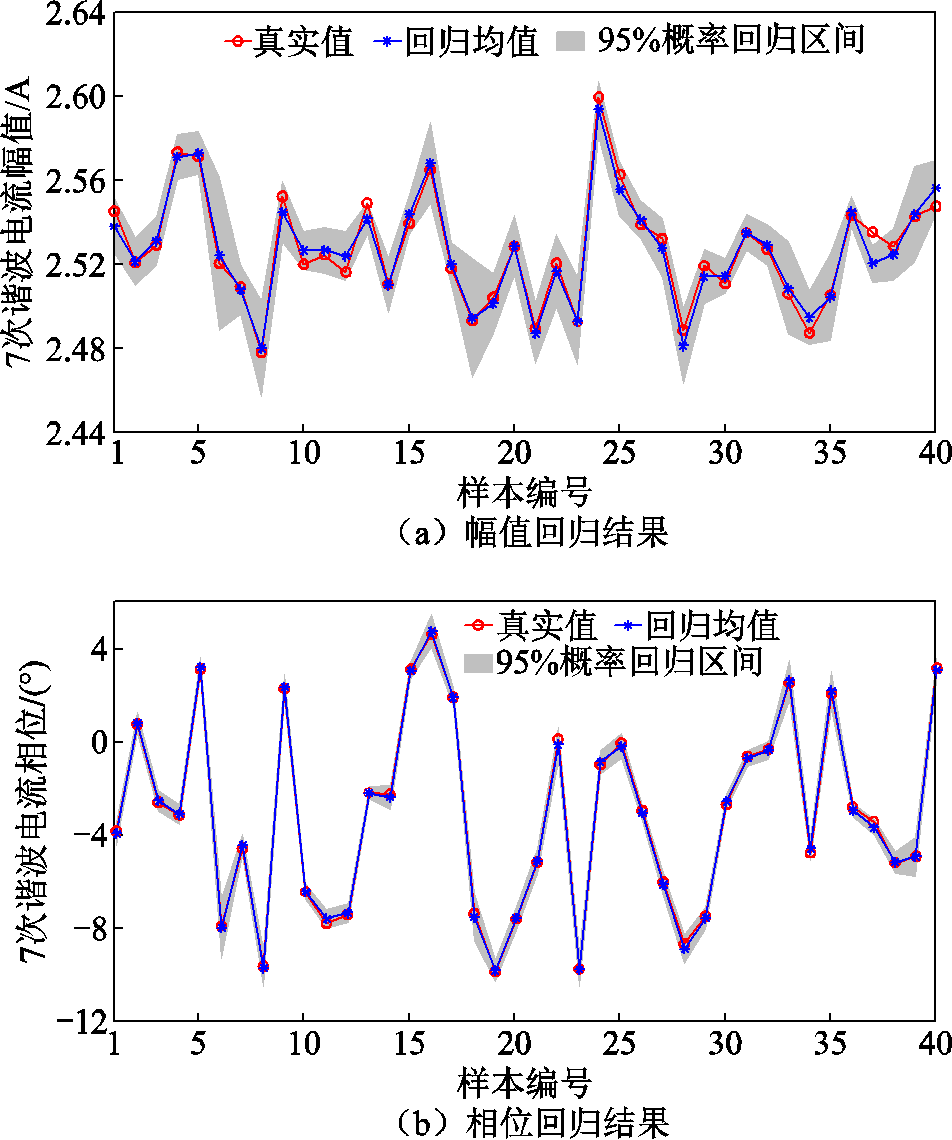
图3 测试集7次谐波电流回归结果
Fig.3 Regression results of 7th harmonic current of test set
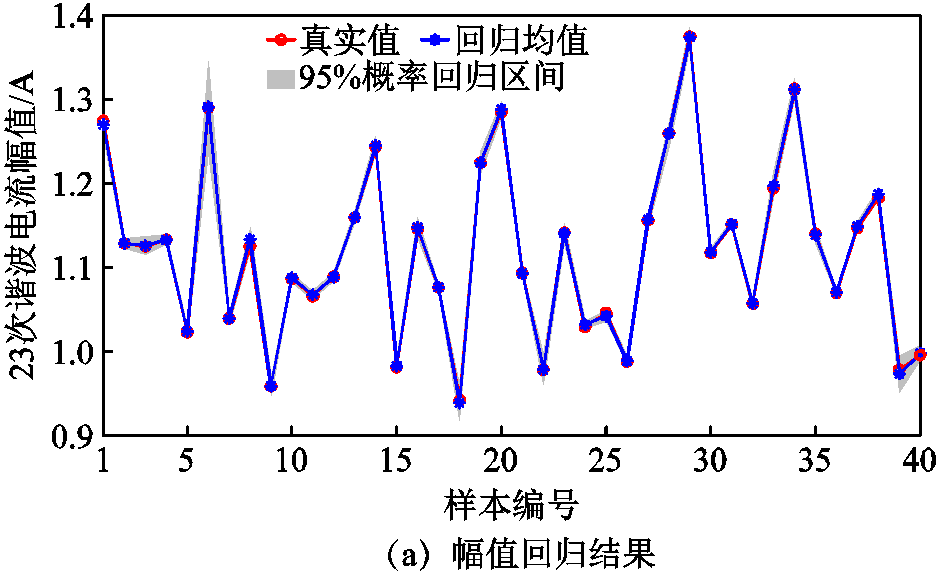
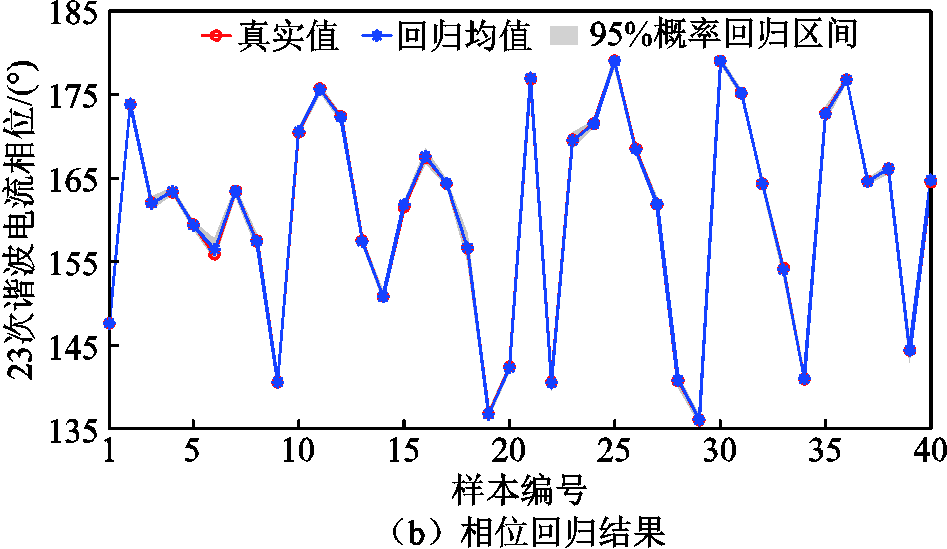
图4 测试集23次谐波电流回归结果
Fig.4 Regression results of 23rd harmonic current of test set
为进一步验证所提MV-GPR算法用于复信号回归时相对于传统数据驱动算法的优越性,另采用GPR算法和CLS算法对状态1样本集中的7次和23次谐波电流进行回归。其中GPR算法用于谐波电流复信号回归时需对分解成实部和虚部的目标值分别进行两次独立的训练与回归,CLS算法则直接采用复数数据进行训练和回归。不同算法回归结果的评价指标对比情况如图5和图6所示。
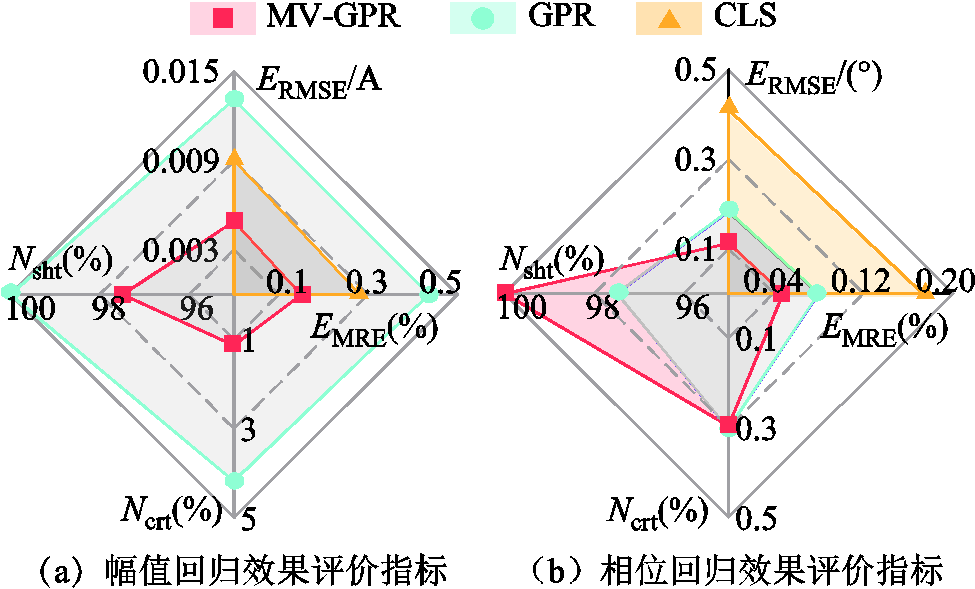
图5 测试集7次谐波电流回归效果评价指标
Fig.5 Evaluation indicators for the regression effect of 7th harmonic current of test set
由图5、图6可见,考虑到谐波电流实部虚部关联性的MV-GPR算法对谐波电流幅值和相位的回归误差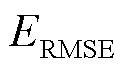 和
和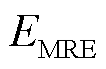 均小于GPR算法,且能以相对更低的保守率
均小于GPR算法,且能以相对更低的保守率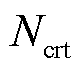 实现高命中率水平的区间回归,不确定性回归效果更好。相比于CLS算法,MV-GPR算法中的平方指数核函数能够更好地刻画谐波源模型输入输出特征量在高维层面的非线性关系,且由于核函数中噪声项的存在,MV-GPR算法能够在一定程度上对噪声水平进行学习与评估,从而降低噪声的影响,最终所表现出的回归准确度更高。
实现高命中率水平的区间回归,不确定性回归效果更好。相比于CLS算法,MV-GPR算法中的平方指数核函数能够更好地刻画谐波源模型输入输出特征量在高维层面的非线性关系,且由于核函数中噪声项的存在,MV-GPR算法能够在一定程度上对噪声水平进行学习与评估,从而降低噪声的影响,最终所表现出的回归准确度更高。
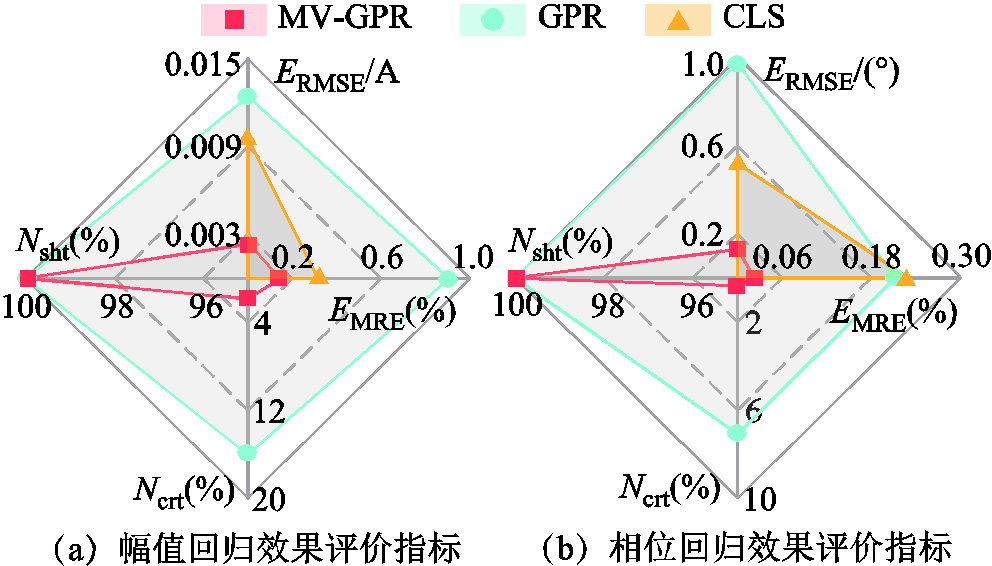
图6 测试集23次谐波电流回归效果评价指标
Fig.6 Evaluation indicators for the regression effect of 23rd harmonic current of test set
4.1.3 建模特征选取效果验证
为验证本文所选各建模特征变量用于谐波源等值拟合时的有效性,分别采用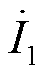 (特征集合1)、
(特征集合1)、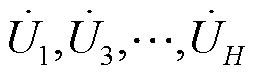 (特征集合2)和本文2.1节中选取的复信号谐波源模型输入变量(特征集合3),基于MV-GPR算法对状态1样本集中的7次和23次谐波电流进行回归验证,计算采用不同输入特征集合时算法对7次和23次谐波电流幅值和相位回归结果的
(特征集合2)和本文2.1节中选取的复信号谐波源模型输入变量(特征集合3),基于MV-GPR算法对状态1样本集中的7次和23次谐波电流进行回归验证,计算采用不同输入特征集合时算法对7次和23次谐波电流幅值和相位回归结果的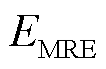 见表1。
见表1。
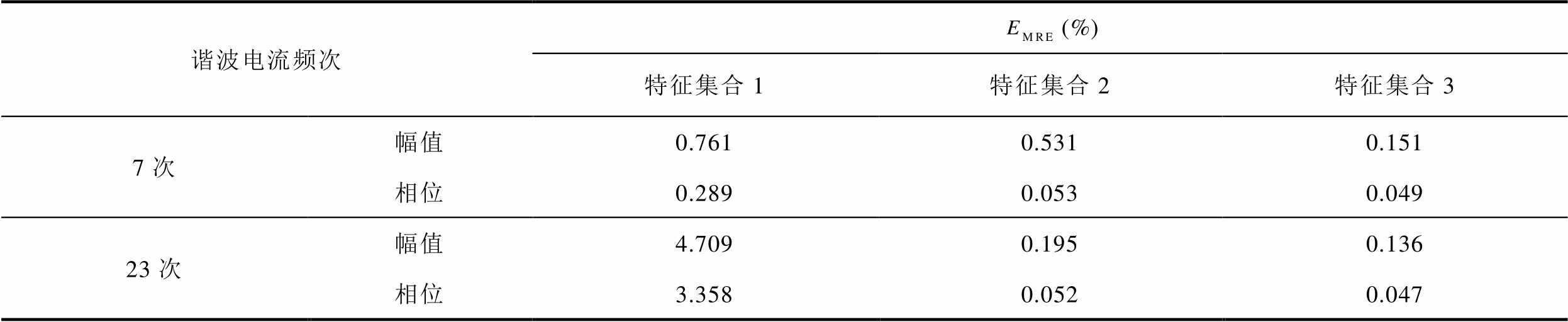
表1 仿真数据谐波电流回归结果平均相对误差
Tab.1 The MRE of harmonic current regression results of simulation data
谐波电流频次(%) 特征集合1特征集合2特征集合3 7次幅值0.7610.5310.151 相位0.2890.0530.049 23次幅值4.7090.1950.136 相位3.3580.0520.047
由表1可见,特征集合1对7次和23次谐波电流的拟合误差相对最大,特征集合2次之,特征集合3拟合误差均最小。这表明本文所选建模特征变量能够准确拟合电弧炉和电力电子型负荷设备所发射的特征谐波电流,具有通用性。值得一提的是,各特征集合对不同频次谐波电流拟合效果的差异也有所不同。7次谐波电流为电弧炉的特征谐波发射电流,采用基波电流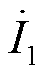 对其进行拟合时也能取得很好的回归结果,各等值模型拟合误差差异不大;23次谐波电流为工业电解铝负荷的特征谐波发射电流,该负荷模型中存在电力电子整流器元件,因此能够考虑到不同频次谐波交互影响的特征集合2和特征集合3相比特征集合1能更好地描述其谐波发射特性,拟合误差相对更小。这一结果与本文在2.1节中对不同谐波源设备谐波发射特性影响因素的分析结论相吻合。
对其进行拟合时也能取得很好的回归结果,各等值模型拟合误差差异不大;23次谐波电流为工业电解铝负荷的特征谐波发射电流,该负荷模型中存在电力电子整流器元件,因此能够考虑到不同频次谐波交互影响的特征集合2和特征集合3相比特征集合1能更好地描述其谐波发射特性,拟合误差相对更小。这一结果与本文在2.1节中对不同谐波源设备谐波发射特性影响因素的分析结论相吻合。
4.1.4 全局性提升效果验证
为验证本文所提聚类算法对历史样本集的划分效果,首先对各运行状态仿真数据样本进行编号。状态1样本编号1~200,状态2样本编号201~400,状态3样本编号401~600。然后采用DBSCAN算法对以上所有样本进行聚类,聚类结果如图7所示。
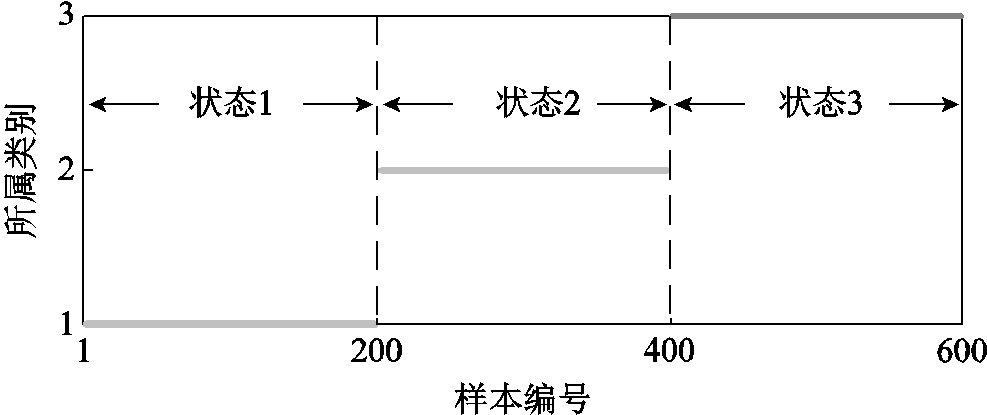
图7 各状态仿真样本聚类结果
Fig.7 Clustering results of simulation samples in various states
由图7可见,DBSCAN对所有样本的聚类结果与仿真所设谐波源设备群运行状态变化情况完全一致,表明本文所提聚类算法能够有效识别谐波源的不同运行状态,并对相应数据样本进行聚类与划分。
进一步地,为验证所提全局性提升方法的效果,从各聚类类别的样本集中分别随机抽取160个样本作为训练集训练子模型,剩下的样本作为相应的测试集用于检验各子模型对不同类别测试集的回归效果。另采用所有聚类类别的训练集集合来训练模型,以验证不进行聚类划分而直接用所有样本训练模型时的回归效果。各训练集训练所得模型对7次和23次谐波电流的回归结果分别见表2和表3。
表2 各训练集对应模型对7次谐波电流的回归相对误差
Tab.2 The MRE of models corresponding to each training set for 7th harmonic current

测试集(%) 类别1类别2类别3所有类别 类别1幅值0.1551.081.90.29 相位0.050.670.320.07 类别2幅值45.860.0746.260.57 相位1.250.011.130.14
(续)
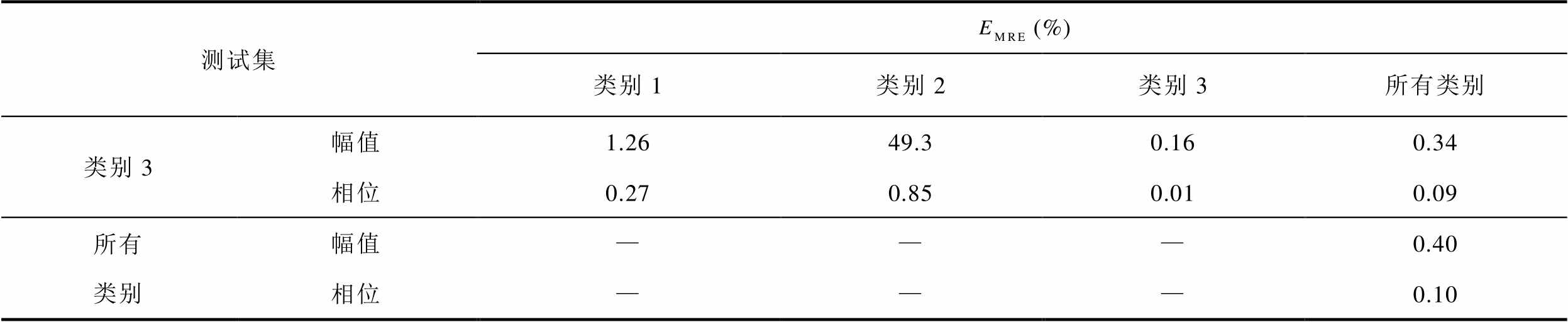
测试集(%) 类别1类别2类别3所有类别 类别3幅值1.2649.30.160.34 相位0.270.850.010.09 所有类别幅值———0.40 相位———0.10
表3 各训练集对应模型对23次谐波电流的回归相对误差
Tab.3 The MRE of models corresponding to each training set for 23rd harmonic current
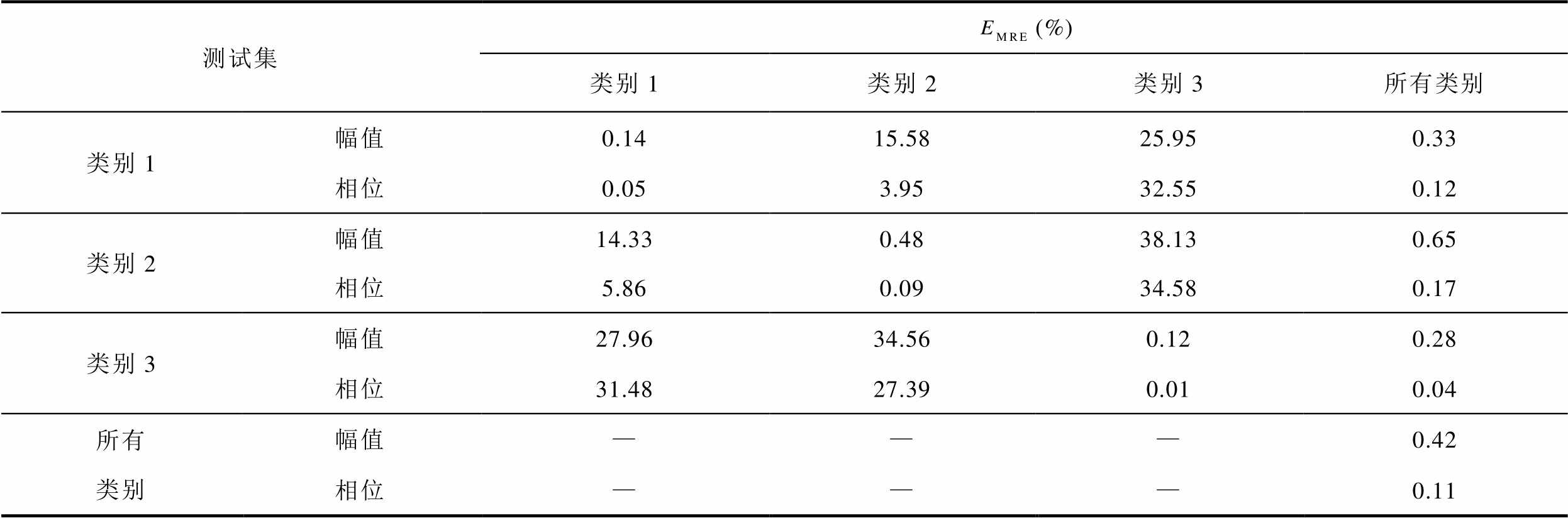
测试集(%) 类别1类别2类别3所有类别 类别1幅值0.1415.5825.950.33 相位0.053.9532.550.12 类别2幅值14.330.4838.130.65 相位5.860.0934.580.17 类别3幅值27.9634.560.120.28 相位31.4827.390.010.04 所有类别幅值———0.42 相位———0.11
由表2和表3可见,聚类划分样本集以后,各类别训练集训练出的子模型对本类别测试集的谐波电流回归误差最小,而对其他类别测试集的谐波电流回归误差明显增大;不进行聚类划分而直接用所有训练集样本集合训练出的模型对各测试集的谐波电流回归误差也明显大于各子模型对相应类别测试集的回归误差。
此外,本文采用Matlab中的tic&toc函数对各模型的训练时长进行了计时,测得训练三个子模型的全部时长为91.08 s,而训练所有聚类类别集合模型的时长达到了326.37 s,这表明本文所提全局性提升方法不仅能够有效提升模型对全局样本的回归精度,还大大缩减了模型训练的总时长。在所提方法的实际应用中,当新的训练样本到来以后,可根据样本聚类结果仅对发生变化的子样本集对应的子模型进行重新训练,这同样能够有效地减少模型训练对计算资源的占用。
4.2.1 算例设置
为验证本文所提回归算法和全局性提升方法用于实际电力系统谐波源设备群建模时的有效性,基于南方电网某500 kV变电站出线处宽频监测装置的实测三相谐波电压电流数据进行算例验证。该500 kV变电站地理接线如图8所示,周边谐波源设备类型包括电力机车牵引站、光伏电站、电解铝厂和常规直流换流站。
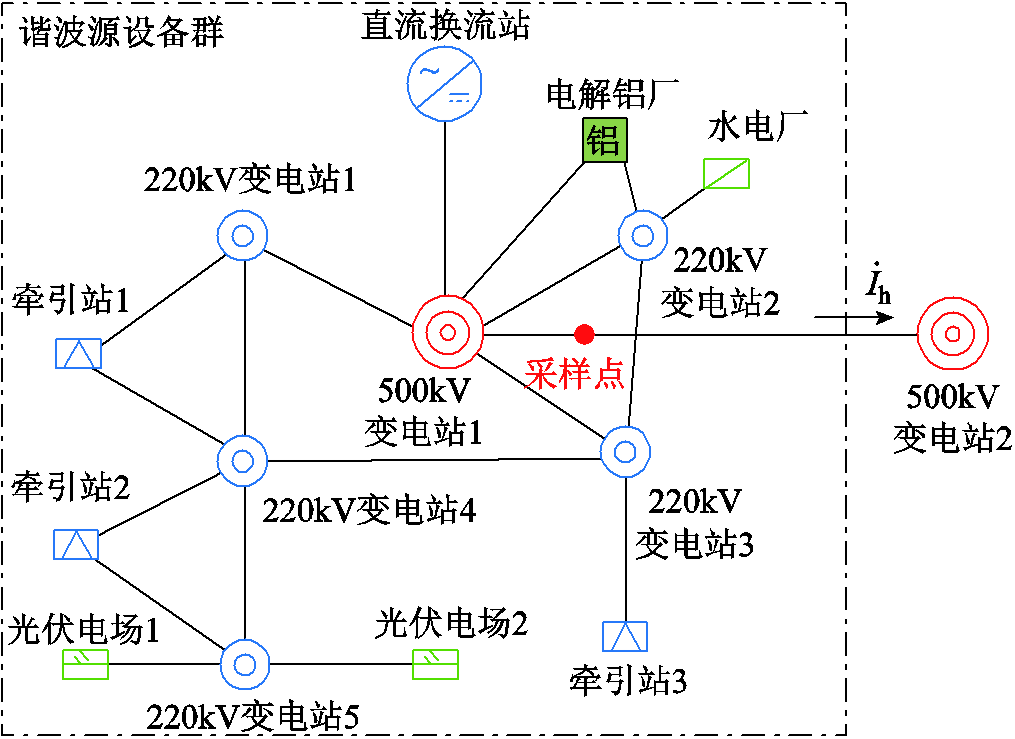
图8 某500 kV变电站周边地理接线
Fig.8 Geographical wiring diagram of the surrounding area of the 500 kV substation
该监测装置的宽频谐波数据记录周期为1 s,记录频率范围为50~2 500 Hz。本文每隔10 min连续收集300组(即300 s)三相谐波电压电流数据,收
集4次共1 200组数据。采样点处5、7、11、13、23和25次谐波含量相对较高,其中A相各频次谐波电流的平均幅值如图9所示,本文以幅值最大的5次谐波电流作为回归目标。
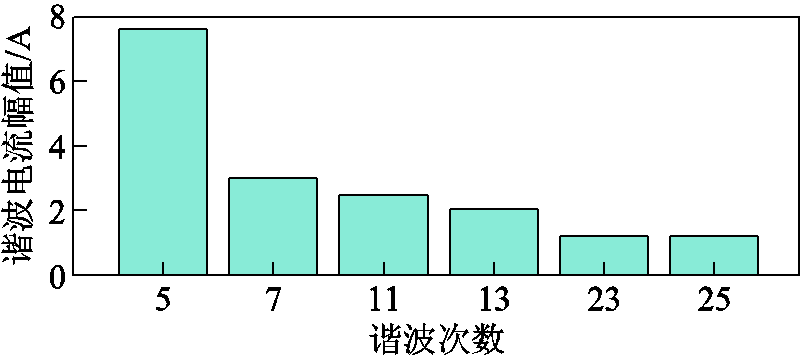
图9 实测数据A相各频次谐波电流平均幅值
Fig.9 The average amplitude of harmonic currents at various frequencies in phase A of measured data
4.2.2 算法有效性验证
从实测数据前200个样本中随机选取160个样本作为训练集,剩下40个样本作为测试集,采用MV-GPR算法对5次谐波电流进行不确定性回归验证,幅值相位回归结果如图10所示。
由图10可见,相较于仿真数据,MV-GPR算法对部分实测数据谐波电流样本的回归精度有所下降,但均值回归结果仍能反映出真实值的变化趋势。个别样本幅值的95%概率回归区间出现了宽度过大的情况。为进一步验证本算法对实测数据的不确定性回归效果,采用蒙特卡洛模拟法对实测数据前200个样本的5次谐波电流幅值进行多次随机抽样,抽样所得95%概率区间宽度为1.7 A。图10a中大部分样本的幅值95%概率回归区间宽度均小于1.7 A,且能够有效地命中真实值,反映测试集样本中的不确定性信息。
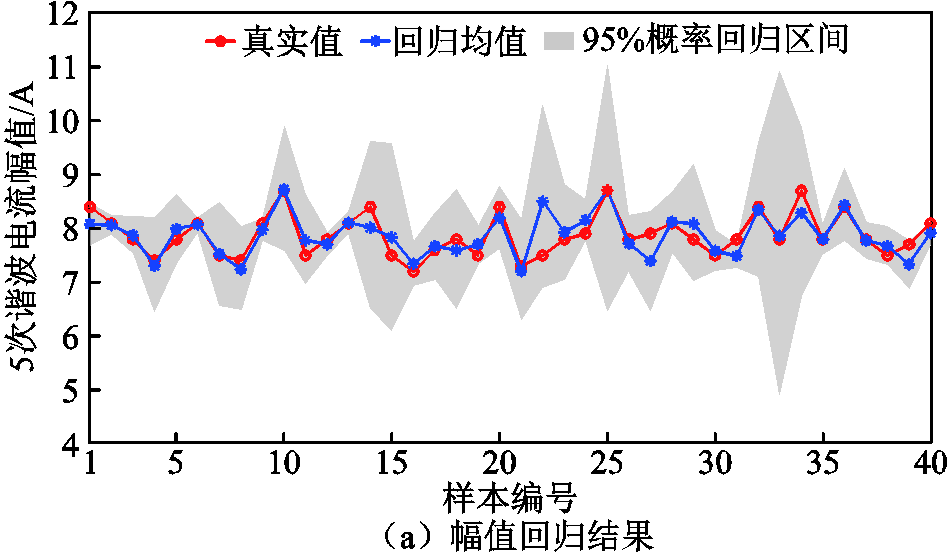
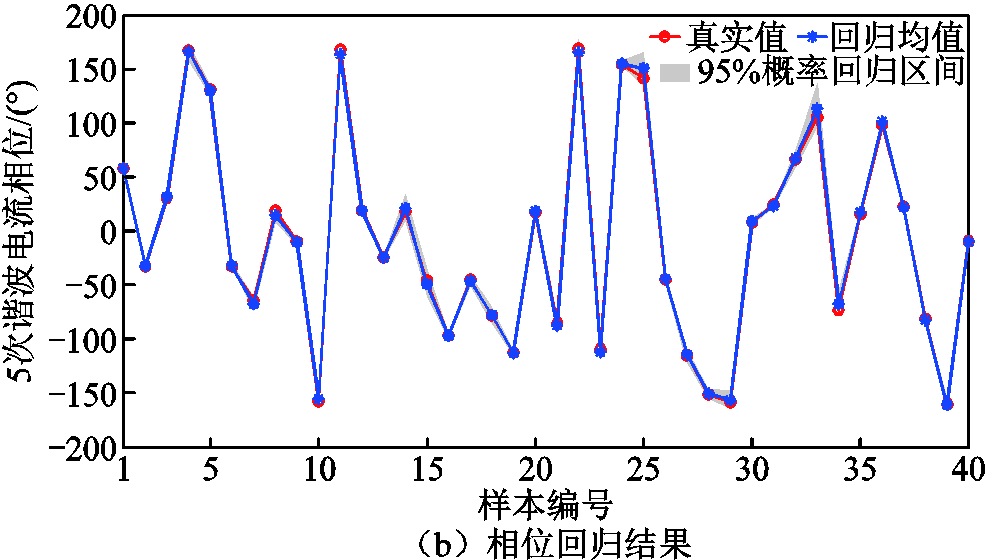
图10 测试集5次谐波电流回归结果
Fig.10 Regression results of 5th harmonic current of test set
不同算法对实测数据5次谐波电流的回归结果评价指标如图11所示。由图11可见MV-GPR算法对谐波电流幅值和相位回归结果的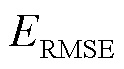 和
和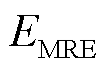 明显低于GPR算法和CLS算法,同时在高命中率水平下区间回归的保守率
明显低于GPR算法和CLS算法,同时在高命中率水平下区间回归的保守率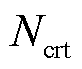 也远低于GPR算法,表明在实测数据谐波电流回归中MV-GPR算法相对另外两种算法更具优越性,不确定性回归效果更好。
也远低于GPR算法,表明在实测数据谐波电流回归中MV-GPR算法相对另外两种算法更具优越性,不确定性回归效果更好。
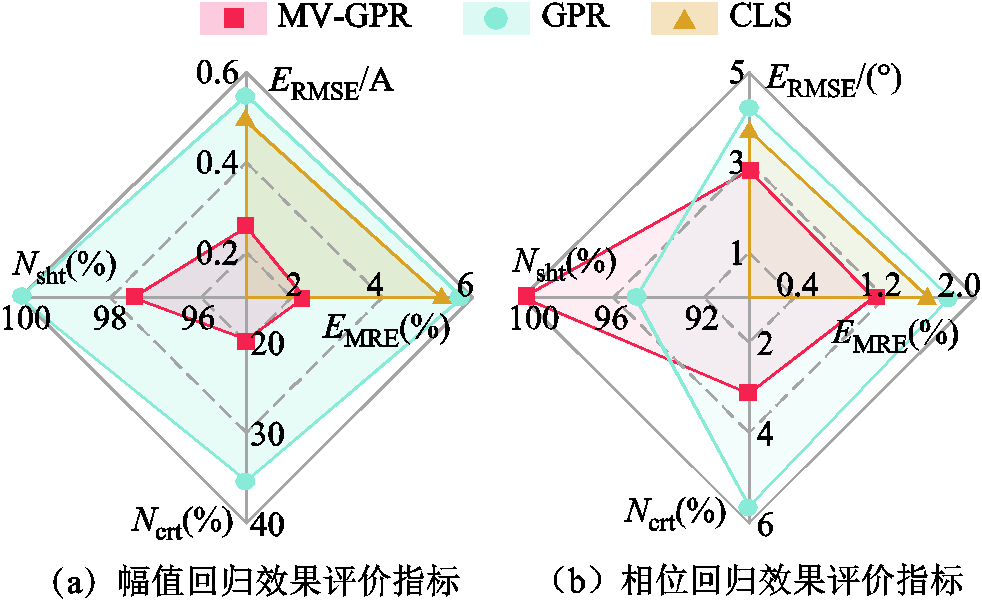
图11 测试集5次谐波电流回归效果评价指标
Fig.11 Evaluation indicators for the regression effect of 5th harmonic current of test set
4.2.3 建模特征选取效果验证
基于同样的训练集和测试集,采用不同输入特征集合时实测数据5次谐波电流幅值相位回归结果的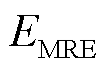 见表4。
见表4。
表4 实测数据5次谐波电流回归结果平均相对误差
Tab.4 The MRE of 5th harmonic current regression results of measured data

谐波电流(%) 特征集合1特征集合2特征集合3 幅值30.8494.0102.278 相位19.9921.3791.100
在实测数据算例中,所监测的500 kV变电站周边谐波源设备数量较多,种类丰富,存在牵引站和电解铝等三相不平衡冲击性负荷,此时特征集合1难以准确刻画该谐波源设备群的谐波发射特性,对幅值和相位的拟合误差都比较大;特征集合2考虑到同相各频次谐波电压对谐波电流的影响,拟合误差有所降低;考虑了三相不平衡分量影响的特征集合3对谐波电流幅值和相位的拟合误差小于特征集合1和特征集合2,在实际电力系统谐波源设备群的等值建模中表现最好。
4.2.4 全局性提升效果验证
采用DBSCAN算法对所有实测样本进行聚类的结果如图12所示。
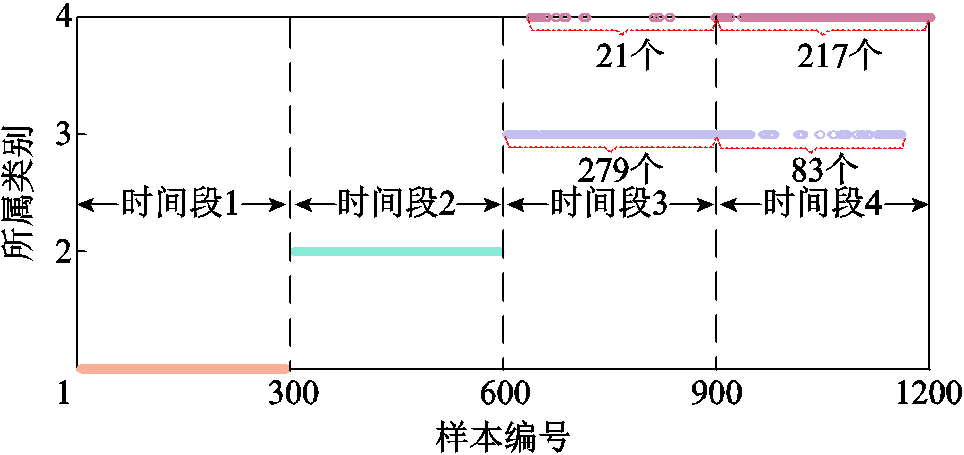
图12 实测样本聚类结果
Fig.12 Clustering results of measured samples
从图12可以看出,样本聚类结果与其所属时间段有较强的关联性,每300 s连续采集的样本基本属于同一类别,这表明在同一时间段内谐波源设备群的运行状态基本一致,文献[13,17]采用最新监测样本动态更新模型来保证其回归精度的做法存在合理性。但值得一提的是,在时间段3中存在少量聚类类别为4的样本,时间段4中存在少量聚类类别为3的样本。若将这两部分样本分别选作测试集样本,从动态更新的角度看,应选择同时间段其余样本作为训练集,而从聚类的角度看,应以同聚类类别其余样本作为训练集。根据上述两种思路分别进行算法训练与回归,得到测试集5次谐波电流幅值相位回归结果的相对误差见表5。
表5 各训练集对应模型对5次谐波电流的回归相对误差
Tab.5 The MRE of models corresponding to each training set for 5th harmonic current

测试集(%) 时间段3类别3时间段4类别4 时间段4类别3幅值3.667.44 相位1.540.71 时间段3类别4幅值3.342.58 相位0.910.64
由表5可见,除测试集时间段4类别3中的相位回归结果外,对同一测试集样本采用同类别样本训练所得算法模型的回归误差总体上小于采用同时间段样本训练所得算法模型的回归误差,这表明本文所提全局性提升方法也能够根据实际电力系统的时序监测数据有效地划分子样本集,建立高全局性和高回归精度的谐波源子模型。
本文针对传统数据驱动算法存在的复信号回归信息丢失问题和数据驱动谐波源模型全局性学习能力不足的问题,提出了一种基于多元高斯过程回归和DBSCAN聚类的复信号谐波源建模方法。采用仿真和实测算例对所提MV-GPR算法、建模特征以及全局性提升方法进行验证,得出以下结论:
1)所提MV-GPR算法能够在矩阵变量高斯分布框架基础上借助行协方差矩阵刻画谐波电流复信号实部虚部的关联性,对复信号回归的准确度高于GPR算法和CLS算法,且能以更低的保守率实现高命中率水平的不确定性回归。
2)所选择的MV-GPR复信号谐波源模型输入特征变量综合考虑了不同谐波源设备的谐波发射特性及三相不平衡因素的影响,能够准确地反映多类型谐波源的谐波发射特性,在谐波源设备群场景中的等值拟合精度明显更高。
3)所提DBSCAN聚类算法能够有效地将不同运行状态下的历史样本集划分为多个子样本集;采用子样本集训练子模型的方法能够有效地提升谐波源模型对全局样本的回归精度,且能够明显减少算法的训练时间。
附 录
1. 仿真模型图
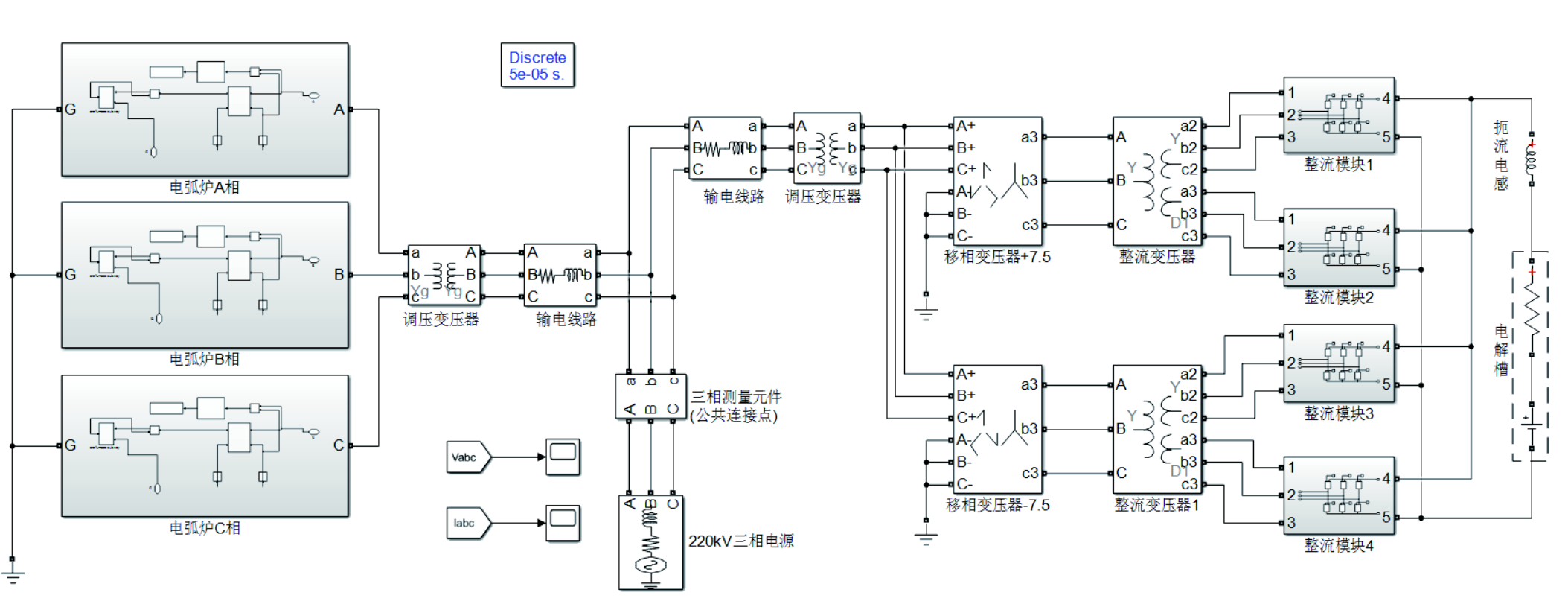
附图1 多类型谐波源设备仿真模型
App.Fig.1 Simulation model of multi type harmonic source equipment
2. 仿真模型参数
附表1 电弧炉仿真模型参数
App.Tab.1 Parameters of electric arc furnace simulation model

参数数值 等效供电电压/kV50.6 一次侧串联电阻/Ω0.346 一次侧串联电抗/Ω3.077 变压器额定功率/(MV·A)60 一次侧额定电压/kV46 二次侧额定电压/V700 绕组电阻(pu)0.002 绕组电感(pu)0.55
附表2 工业电解铝负荷仿真模型参数
App.Tab.2 Parameters of industrial electrolytic aluminum load simulation model

参数数值 等效供电电压/kV110 移相变压器额定功率/(MV·A)100 移相变压器一次侧额定电压/kV108.7 移相变压器二次侧额定电压/kV90.8 整流变压器额定功率/(MV·A)54 整流变压器一次侧额定电压/kV83.3 整流变压器二次侧额定电压/kV1.0 电解槽电阻/mΩ2.29 电解槽电压/V450
参考文献
[1] 李戎, 李建文, 李永刚, 等. 结合特征根及模态分析法的逆变器多机并网系统谐波扰动响应分析[J]. 电工技术学报, 2024, 39(14): 4519-4534.
Li Rong, Li Jianwen, Li Yonggang, et al. Analysis of harmonic disturbance response of multi-inverter grid-connected system combining characteristic root and modal analysis method[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4519-4534.
[2] 李建闽, 曹远远, 姚文轩, 等. 基于自适应移频滤波的电力系统谐波分析方法[J]. 电工技术学报, 2024, 39(13): 4015-4024.
Li Jianmin, Cao Yuanyuan, Yao Wenxuan, et al. Power system harmonic analysis method based on adaptive frequency-shift filtering[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 4015-4024.
[3] 国家发展和改革委员会. 电能质量管理办法(暂行) [EB/OL]. https://www.gov.cn/gongbao/2024/issue_ 11226/202403/content_6940055.html.
[4] 丁同, 陈红坤, 吴斌, 等. 多谐波源定位及谐波责任量化区分方法综述[J]. 电力自动化设备, 2020, 40(1): 19-30.
Ding Tong, Chen Hongkun, Wu Bin, et al. Overview on location and harmonic responsibility quantitative determination methods of multiple harmonic sources [J]. Electric Power Automation Equipment, 2020, 40(1): 19-30.
[5] 王杨, 田旭, 赵劲帅, 等. 基于相移原理的LCC-HVDC降维谐波状态空间建模[J]. 电力系统保护与控制, 2023, 51(14): 11-22.
Wang Yang, Tian Xu, Zhao Jinshuai, et al. Dimension-reduced harmonic state space modeling of an LCC-HVDC based on the phase shift principle[J]. Power System Protection and Control, 2023, 51(14): 11-22.
[6] 邵振国, 黄伟达. 考虑出力不确定性的分布式电源谐波传播计算[J]. 电工技术学报, 2019, 34(增刊2): 674-683.
Shao Zhenguo, Huang Weida. A calculation method of harmonic propagation considering the uncertainty of distributed generation[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 674-683.
[7] Fauri M. Harmonic modelling of non-linear load by means of crossed frequency admittance matrix[J]. IEEE Transactions on Power Systems, 1997, 12(4): 1632-1638.
[8] Hu Zhe, Han Yang, Zalhaf A S, et al. Harmonic sources modeling and characterization in modern power systems: a comprehensive overview[J]. Electric Power Systems Research, 2023, 218: 109234.
[9] 张逸, 孟祥亮, 刘必杰. 谐波源建模现状及新型电力系统下的发展趋势[J]. 电力系统及其自动化学报, 2022, 34(8): 139-149.
Zhang Yi, Meng Xiangliang, Liu Bijie. Current situation of harmonic source modeling and development trend under novel power system[J]. Proceedings of the CSU-EPSA, 2022, 34(8): 139-149.
[10] 李湘, 陈民铀, 郑永伟, 等. 基于稳健偏最小二乘法的谐波发射水平估计[J]. 电力系统及其自动化学报, 2016, 28(6): 86-90.
Li Xiang, Chen Minyou, Zheng Yongwei, et al. Assessing harmonic emission level based on robust partial least squares regression[J]. Proceedings of the CSU-EPSA, 2016, 28(6): 86-90.
[11] Moreno M A, Usaola J. A new balanced harmonic load flow including nonlinear loads modeled with RBF networks[J]. IEEE Transactions on Power Delivery, 2004, 19(2): 686-693.
[12] 郑连清, 吴萍, 刘小龙. 基于遗传算法的LS-SVM在谐波源建模中的应用[J]. 电力系统保护与控制, 2011, 39(3): 52-56.
Zheng Lianqing, Wu Ping, Liu Xiaolong. Application of least squares support vector machine to harmonic sources modeling based on genetic algorithm[J]. Power System Protection and Control, 2011, 39(3): 52-56.
[13] 张逸, 刘必杰, 邵振国, 等. 基于高斯过程回归的谐波源不确定性通用模型[J]. 中国电机工程学报, 2022, 42(3): 992-1002.
Zhang Yi, Liu Bijie, Shao Zhenguo, et al. General and uncertain harmonic source model based on Gaussian process regression[J]. Proceedings of the CSEE, 2022, 42(3): 992-1002.
[14] Xia Yili, Mandic D P. Widely linear adaptive frequency estimation of unbalanced three-phase power systems[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(1): 74-83.
[15] 张行. 面向非圆复数的自适应估计算法性能分析及其应用研究[D]. 南京: 东南大学, 2021.
Zhang Xing. Performance analysis and application research of adaptive estimation algorithm for noncircular complex numbers[D]. Nanjing: Southeast University, 2021.
[16] 贾秀芳, 华回春, 曹东升, 等. 基于复线性最小二乘法的谐波责任定量划分[J]. 中国电机工程学报, 2013, 33(4): 149-155, 20.
Jia Xiufang, Hua Huichun, Cao Dongsheng, et al. Determining harmonic contributions based on complex least squares method[J]. Proceedings of the CSEE, 2013, 33(4): 149-155, 20.
[17] 李亚辉, 孙媛媛, 王庆岩, 等. 基于源荷谐波耦合模型的数据驱动概率谐波潮流计算[J]. 中国电机工程学报, 2024, 44(11): 4323-4335.
Li Yahui, Sun Yuanyuan, Wang Qingyan, et al. Data-driven probabilistic harmonic power flow calculation based on source and load harmonic coupling model[J]. Proceedings of the CSEE, 2024, 44(11): 4323-4335.
[18] 李峰, 王琦, 胡健雄, 等. 数据与知识联合驱动方法研究进展及其在电力系统中应用展望[J]. 中国电机工程学报, 2021, 41(13): 4377-4390.
Li Feng, Wang Qi, Hu Jianxiong, et al. Combined data-driven and knowledge-driven methodology research advances and its applied prospect in power systems[J]. Proceedings of the CSEE, 2021, 41(13): 4377-4390.
[19] Thompson G Z, Maitra R, Meeker W Q, et al. Classification with the matrix-variate-t distribution [J]. Journal of Computational and Graphical Statistics, 2020, 29(3): 668-674.
[20] Chen Zexun, Wang Bo, Gorban A N. Multivariate Gaussian and Student-t process regression for multi-output prediction[J]. Neural Computing and Applications, 2020, 32(8): 3005-3028.
[21] Boloix-Tortosa R, Murillo-Fuentes J J, Payan-Somet F J, et al. Complex Gaussian processes for regression[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(11): 5499-5511.
[22] 陈少伟, 卢镇江, 沈渊彬, 等. 基于典型关联分析算法的恒流源型谐波用户识别[J]. 供用电, 2020, 37(11): 34-41.
Chen Shaowei, Lu Zhenjiang, Shen Yuanbin, et al. A method of constant current source type harmonic users identification based on typical association analysis[J]. Distribution & Utilization, 2020, 37(11): 34-41.
[23] 刘博, 杜正春. 含VSC-HVDC交直流混联电力系统三相谐波潮流统一算法[J]. 中国电机工程学报, 2018, 38(8): 2284-2293, 2538.
Liu Bo, Du Zhengchun. Unified Newton’s solution to three-phase harmonic power flow of VSC-HVDC based AC/DC power systems[J]. Proceedings of the CSEE, 2018, 38(8): 2284-2293, 2538.
[24] 李亚辉, 孙媛媛, 李可军, 等. 不平衡供电条件下多脉动整流器的谐波特性分析[J]. 电力系统自动化, 2021, 45(23): 152-161.
Li Yahui, Sun Yuanyuan, Li Kejun, et al. Harmonic characteristic analysis of multi-pulse rectifier under unbalanced power supply condition[J]. Automation of Electric Power Systems, 2021, 45(23): 152-161.
[25] 姜雅男, 于永进, 李长云. 基于改进TOPSIS模型的绝缘纸机-热老化状态评估方法[J]. 电工技术学报, 2022, 37(6): 1572-1582.
Jiang Yanan, Yu Yongjin, Li Changyun. Evaluation method of insulation paper deterioration status with mechanical-thermal synergy based on improved TOPSIS model[J]. Transactions of China Electro-technical Society, 2022, 37(6): 1572-1582.
[26] 吕俊超, 丁志远, 傅琪雯. 一种海上风电场柔直送出线单端保护方案[J]. 电气技术, 2024, 25(4): 47-51.
Lü Junchao, Ding Zhiyuan, Fu Qiwen. A single-end protection scheme for voltage source converter based high voltage DC transmission line of offshore wind farm[J]. Electrical Engineering, 2024, 25(4): 47-51.
[27] 陈光宇, 袁文辉, 徐晓春, 等. 基于残差图卷积深度网络的电网无功储备需求快速计算方法[J]. 电工技术学报, 2023, 38(17): 4683-4700.
Chen Guangyu, Yuan Wenhui, Xu Xiaochun, et al. Fast calculation method for grid reactive power reserve demand based on residual graph convolutional deep network[J]. Transactions of China Electro-technical Society, 2023, 38(17): 4683-4700.
[28] 刘征宇, 郭乐凯, 孟辉, 等. 基于改进DBSCAN的退役动力电池分选方法[J]. 电工技术学报, 2023, 38(11): 3073-3083.
Liu Zhengyu, Guo Lekai, Meng Hui, et al. A sorting method of retired power battery based on improved DBSCAN[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 3073-3083.
[29] 周国亮, 宋亚奇, 王桂兰, 等. 状态监测大数据存储及聚类划分研究[J]. 电工技术学报, 2013, 28(增刊2): 337-344.
Zhou Guoliang, Song Yaqi, Wang Guilan, et al. Research of condition monitoring big data storage and clustering[J]. Transactions of China Electrotechnical Society, 2013, 28(S2): 337-344.
[30] 胡畔, 陈红坤, 孙志达, 等. 一种交流电弧炉通用性模型[J]. 电工技术学报, 2016, 31(8): 172-180.
Hu Pan, Chen Hongkun, Sun Zhidang, et al. A versatility model of AC electric arc furnace[J]. Transactions of China Electrotechnical Society, 2016, 31(8): 172-180.
Abstract The data-driven harmonic source modeling method uses amplitude and phase angle data of harmonic electrical signals to train the model, which is essentially an analysis and processing process for complex signals. The design and implementation of traditional data-driven algorithms are mostly carried out in the real number field, and there is a problem of information loss when performing complex signal regression. In addition, the fitting effect of data-driven methods on harmonic source models is closely related to the learning samples. Due to limited data samples in certain scenarios, the current data-driven harmonic source model can only describe the local harmonic emission characteristics of harmonic source equipment under partial operating conditions, making it difficult to achieve global learning and regression.
To solve the problem of information loss in traditional data-driven algorithms for complex signal regression, this paper first proposed a multivariate gaussian process regression (MV-GPR) algorithm based on matrix variable Gaussian distribution. The MV-GPR algorithm uses the covariance matrix to characterize the correlation information between the real and imaginary parts of the target complex signal. The posterior distribution calculation and parameter estimation methods of multivariate Gaussian process were derived to achieve uncertainty regression of complex signals. Next, based on the influencing factors of harmonic emission characteristics of various types of harmonic sources, the modeling characteristic variables of complex signal harmonic sources under three-phase unbalance conditions were selected, and the principal component analysis method was used to reduce the dimensionality of the input characteristic variables to ensure the convergence of the algorithm.
To solve the problem of poor global learning performance in current data-driven harmonic source modeling methods, this paper proposed a model global improvement method according to the better performance of MV-GPR algorithm in small-scale sample regression. Firstly, the density-based spatial clustering of applications with noise (DBSCAN) algorithm was used to divide historical sample data into sub sample sets representing different operating states of harmonic sources. Then, sub harmonic source models were established based on each sub sample set, and the closest sub model was selected for regression according to the distance between the sample to be regressed and the historical sub sample set, thereby improving the learning and regression effect of the harmonic source model on global samples.
Based on simulation data from multiple types of harmonic sources model and actual measurement data from a 500kV substation of Southern Power Grid, the MV-GPR algorithm, modeling feature selection results and model global improvement method proposed in this paper were compared and verified. The following conclusions can be drawn: (1) The MV-GPR algorithm has higher accuracy in complex signal regression than GPR and CLS algorithms, and can achieve high hit rate uncertainty regression with lower conservatism. (2) The selected MV-GPR complex signal harmonic source model input characteristic variables can accurately reflect the harmonic emission characteristics of multiple types of harmonic sources, and the equivalent fitting accuracy is significantly higher in harmonic source equipment group scenarios. (3) The DBSCAN algorithm can effectively divide historical sample sets under different operating states into multiple sub sample sets. The method of using sub sample set to train sub models can effectively improve the regression accuracy of the harmonic source model on global samples, and can significantly reduce the training time of the algorithm.
keywords:Multivariate Gaussian process regression, harmonic source modeling, harmonic analysis, power quality, cluster
中图分类号:TM714
DOI: 10.19595/j.cnki.1000-6753.tces.242151
中国南方电网有限责任公司科技项目资助(0000002023030101FK 00007)。
收稿日期 2024-11-29
改稿日期 2025-03-10
褚昱麟 男,2001年生,硕士研究生,研究方向为电能质量分析与评估。E-mail:1252002047@qq.com
陈红坤 男,1967年生,教授,博士生导师,研究方向为电能质量分析、电力系统优化规划等。E-mail:chkinsz@163.com(通信作者)
(编辑 赫 蕾)