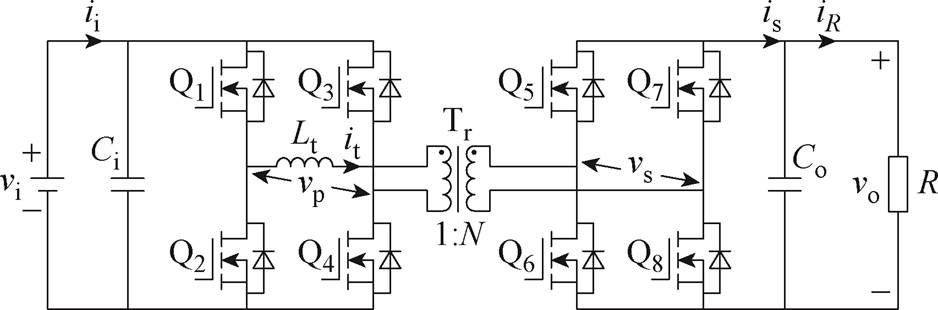
图1 DAB变换器拓扑结构
Fig.1 Topology of DAB converter
摘要 模型预测电压控制(MPVC)策略已广泛应用在双有源全桥(DAB)变换器中,以实现快速、准确的输出电压调节。然而,传统MPVC策略的电压控制性能对DAB系统模型参数变化较为敏感,若系统模型参数与实际参数存在误差,将影响DAB变换器的稳态及动态性能。为此,该文提出一种基于龙格库塔的DAB变换器鲁棒预测电压控制(RPVC)策略,以消除参数对DAB变换器输出电压控制的影响,提高系统参数的鲁棒性。首先,建立DAB变换器的龙格库塔数据模型;其次,结合拉格朗日插值法,实现龙格库塔数据模型的实时更新,消除系统参数的影响;然后,计算DAB变换器移相比范围,并通过价值函数评估下一时刻的最优移相比;最后,通过实验验证所提方法的有效性。
关键词:双有源全桥变换器 模型预测电压控制 龙格库塔 拉格朗日插值法 参数鲁棒性
近年来,直流微电网的规模与应用不断扩大[1-2]。相较于传统交流系统,直流微电网具有更高的效率、更强的电流承载能力和更快的动态响应[3-4]。这些优势使得直流微电网在可再生能源系统、电动汽车充电站、船舶和飞机等领域的应用日益增加。在直流微电网中,隔离型双向直流-直流电能变换器起着关键作用,其不仅可以实现储能系统与直流微电网间的能量交换,还可以通过连接固态变压器,完成直流微电网与配电网之间电力流动的管理。其中,双有源全桥(Dual Active Bridge, DAB)变换器拓扑结构是极具前景的拓扑之一,其不仅能够自动调节双向功率流动,还具备宽电压转换增益范围[5-7]。
为了保证DAB变换器的动态性能和电压追踪性能,同时提高其多目标控制能力,模型预测电压控制(Model Predictive Voltage Control, MPVC)近年来被广泛应用于DAB变换器系统[8-11]。MPVC方法根据系统采样信息和已知的离散模型预测其下一步开关状态,实现快速动态响应和多目标优化[12]。文献[13]提出一种基于单移相(Single-Phase-Shift, SPS)调制的MPVC,提升了DAB变换器的动态性能。文献[14-15]将多移相调制与MPVC相结合,进一步优化了系统效率和电流应力。然而,MPVC的性能依赖精确的建模和参数,系统模型和参数误差会降低MPVC的控制性能,并增加DAB变换器的电应力和热应力,降低系统的可靠性,甚至会在偏差持续累积的情况下损坏系统[16]。
为降低MPVC对建模和参数精度的依赖性,已有学者提出了基于扰动观测器的鲁棒MPVC方法以及基于在线参数辨识的鲁棒MPVC方法。基于扰动观测器的鲁棒MPVC方法利用设计的观测器估计模型与实际系统之间的偏差,并对偏差进行补偿。在这类研究中,文献[17]利用扩展状态观测器对DAB变换器进行整体不确定性估计;文献[18]提出了一种用于鲁棒电压跟踪控制的扰动观测器。然而,上述方法需要在不同工况下调整观测器增益,以保证观测器的性能。此外,基于在线参数辨识的鲁棒MPVC方法通过精确估计系统参数,降低了参数不匹配带来的影响。文献[19-20]利用递归最小二乘法进行漏感在线辨识,从而提高控制精度;文献[21]利用梯度下降法对漏感进行辨识。然而,上述方法的漏感辨识准确性易受系统测量噪声及DAB系统工况变化的影响,并且忽略了电容参数误差的影响。因此,基于参数辨识的MPVC方法很难完全消除参数扰动。
针对上述问题,本文针对DAB变换器提出了一种基于龙格库塔的鲁棒预测电压控制(Robust Predictive Voltage Control, RPVC)方法。首先,分析当漏感和电容模型参数与其实际参数存在误差时,DAB变换器在传统MPVC控制下的输出电压性能;其次,建立DAB变换器超局部模型,并结合龙格库塔和拉格朗日插值法实现超局部模型的实时更新,进而替代传统预测模型;然后,计算DAB变换器自适应移相比;最后,利用价值函数实现最优移相比的评估与应用。所提RPVC方法的主要贡献如下:①与传统MPVC方法[13-15]相比,所提RPVC方法消除了预测计算对建模和参数精度的依赖性;②与传统鲁棒MPVC方法[17-21]相比,所提RPVC方法完全消除了参数扰动的影响。
DAB变换器具有双向潮流、电流隔离和高效电压转换等优点,其典型拓扑结构如图1所示。由图1可知,DAB变换器由8个开关管Q1~Q8、1个高频变压器Tr、输入电源vi、输入电容Ci、输出电容Co、串联漏感Lt及负载电阻R组成。其中,高频变压器Tr通过电流隔离系统的输入侧和输出侧,并通过漏感Lt实现能量存储,N为高频变压器的匝数比。此外,ii为输入电流,is为输出电容Co的电流与负载电阻R的电流iR之和,vp和it分别为变压器输入侧的电压和电流,vs为变压器输出侧电压,vo为输出电压。

图1 DAB变换器拓扑结构
Fig.1 Topology of DAB converter
SPS调制通过改变输入、输出侧变压器电压的移相比D,从而控制输出电压、电流及功率。基于SPS调制,DAB变换器的变压器输入、输出侧电压及电流波形如图2所示。图中,Ts为控制周期。
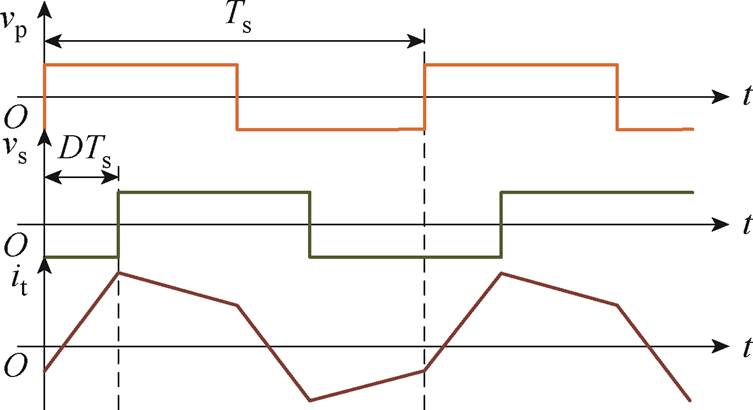
图2 SPS调制下DAB变换器的电压及电流波形
Fig.2 Waveforms of voltage and current under SPS modulation for DAB converter
MPVC方法已广泛应用于DAB变换器,以实现准确、快速的输出电压控制。传统DAB变换器MPVC控制框图如图3所示。该方法主要包括移相比计算、预测电压计算、价值函数评估三个部分[13]。
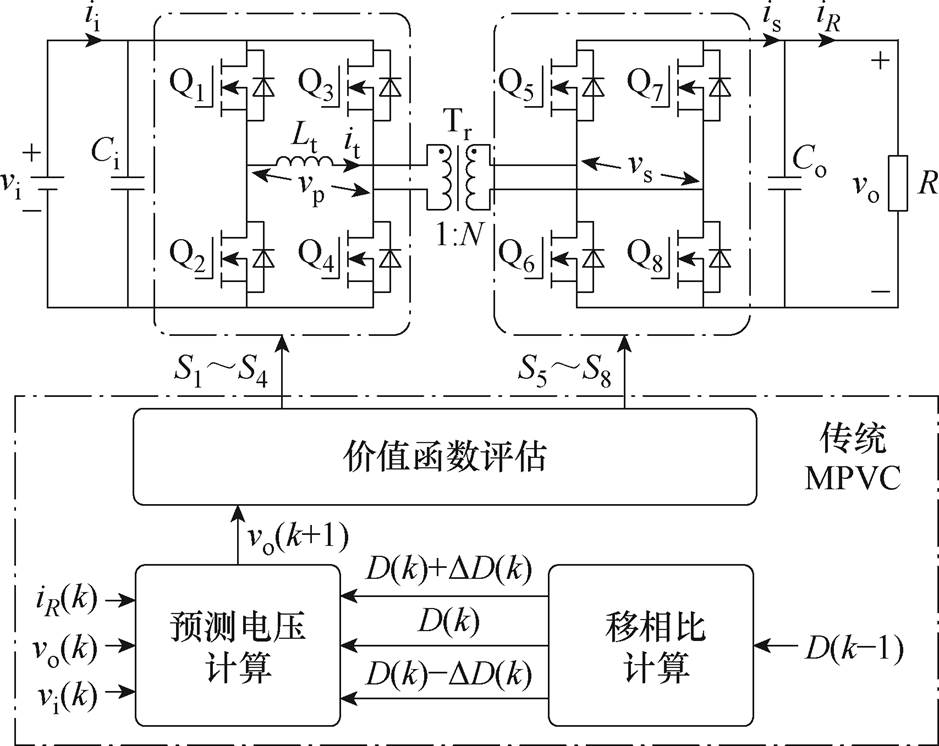
图3 传统DAB变换器MPVC控制框图
Fig.3 Control diagram of conventional MPVC for DAB converter
根据图3可以得到DAB变换器输出电压vo[13]为
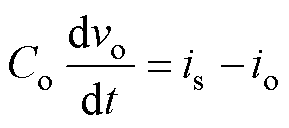 (1)
(1)
其中
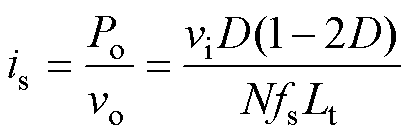 (2)
(2)
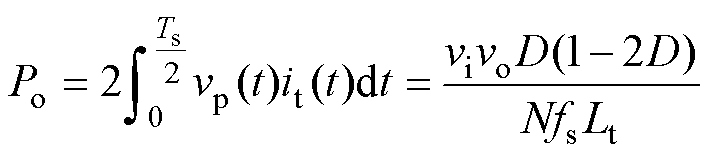 (3)
(3)
式中,Po为DAB变换器在SPS调制下的传输功率;fs为开关频率。
根据前向欧拉法,将式(1)离散化可以得到k+1时刻的输出电压为
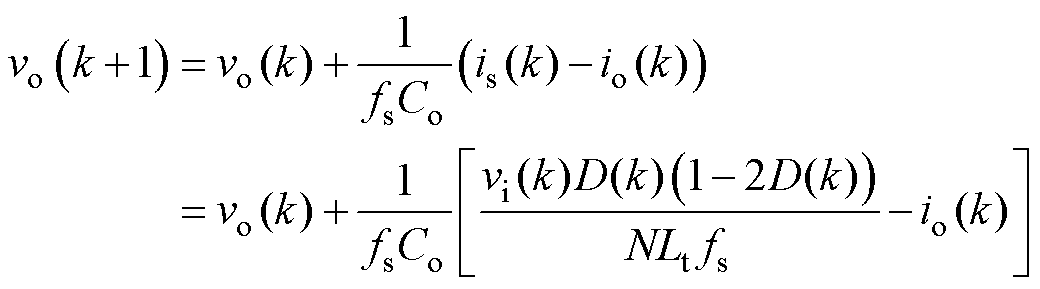 (4)
(4)
根据式(4)可以得到,k+1时刻的输出电压vo(k+1)由变压器漏感Lt和输出电容Co决定。当MPVC中变压器漏感模型参数Ltm及输出电容模型参数Com与其实际参数Lt和Co分别存在误差DLt和DCo时,会导致不准确的输出电压预测vom(k+1),其可以表示为
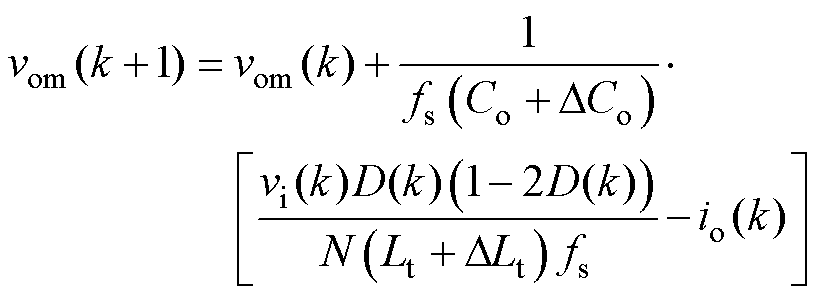 (5)
(5)
其中
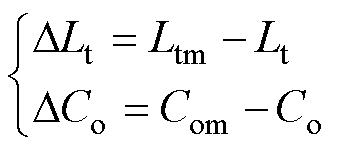
将式(5)与式(4)做差可以得到输出电压预测误差voerr,表示为
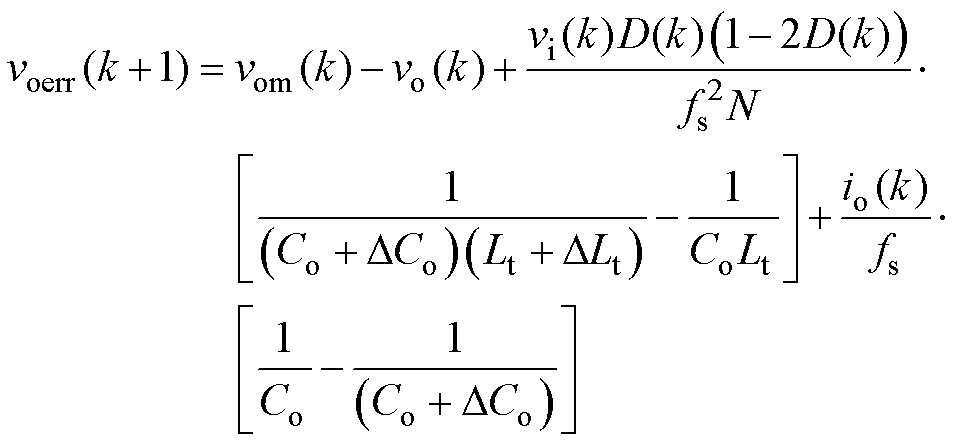 (6)
(6)
图4显示了存在参数误差DLt和DCo时的输出电压预测误差voerr。根据图4可知,当参数误差DLt和DCo增加时,输出电压预测误差voerr随之增加,进而影响DAB变换器的输出电压性能。
图5显示了不同参考电压下,存在参数误差DLt和DCo时的输出电压预测误差voerr。图5中,m为误差系数,DLt=mLt, DCo=mCo。根据图5可知,在不同的参考电压下,当参数误差DLt和DCo增加时,输出电压预测误差voerr随之增加。当参数误差DLt= -0.5Lt且DCo=-0.5Co时,电压误差绝对值在输出参考电压voref为40、50、60、70、80 V时的占比分别为4.75%、4.6%、4.67%、4.57%、4.63%,导致DAB输出功率分别降低14.8、22.5、32.8、43.8、57.9 W,效率分别降低9.3%、9%、9.1%、8.9%、9.1%。

图4 存在参数误差时传统MPVC预测电压误差
Fig.4 Prediction voltage error of conventional MPVC when parameter errors are existing
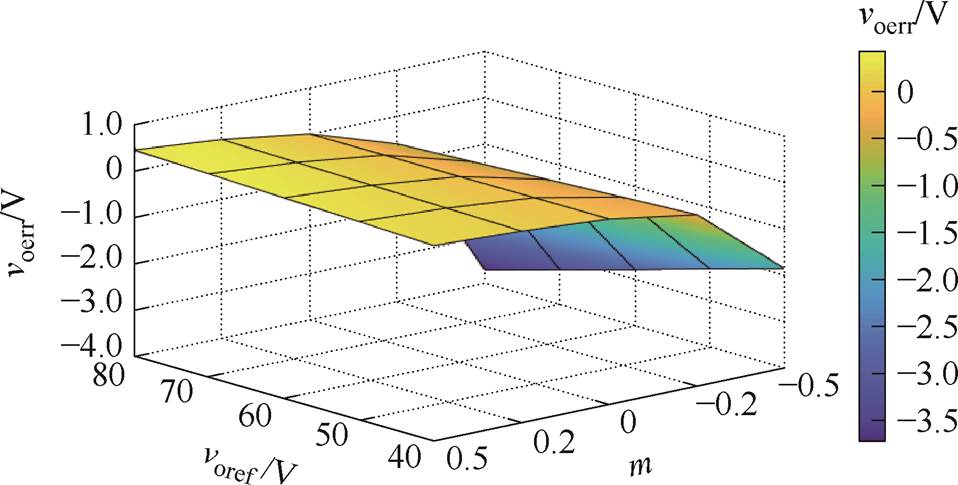
图5 不同参考电压下传统MPVC预测电压误差
Fig.5 Prediction voltage error of conventional MPVC under different voltage reference
为解决上述问题,本文针对DAB变换器提出一种基于龙格库塔的RPVC方法,控制框图如图6所示,其主要由超局部模型更新、鲁棒预测电压计算、移相比计算及价值函数评估四部分组成。
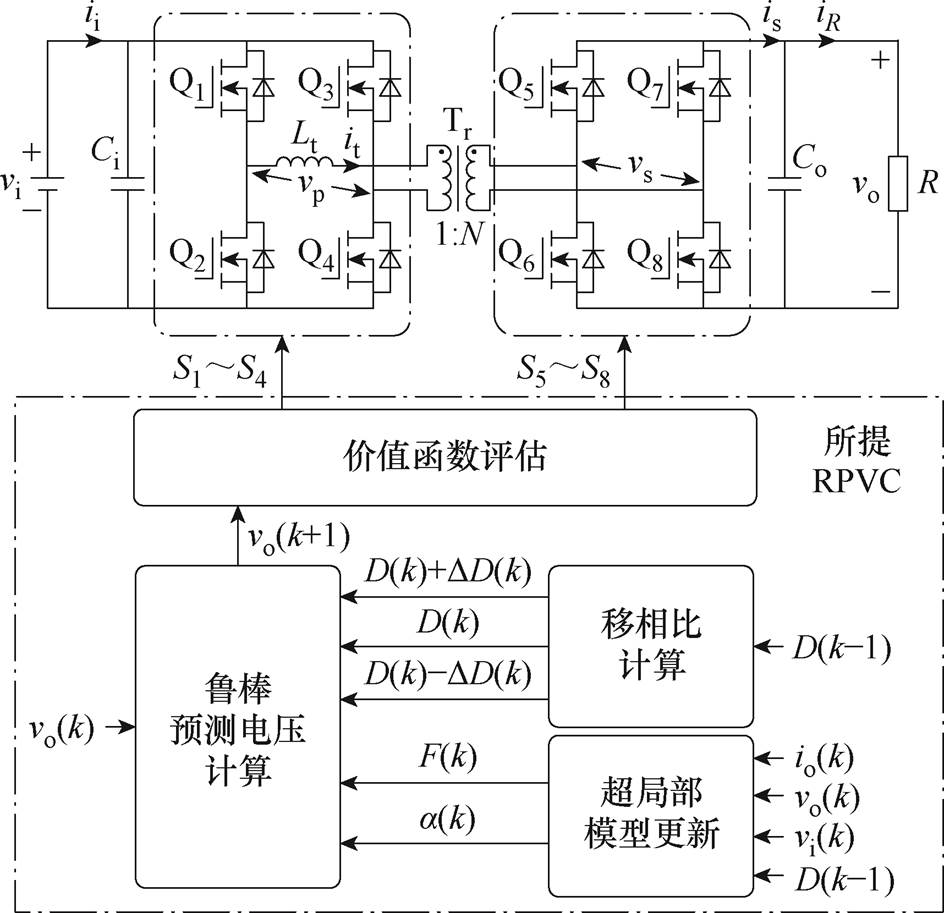
图6 所提DAB变换器RPVC控制框图
Fig.6 Control diagram of proposed RPVC for DAB converter
3.1.1 DAB变换器超局部数据模型建立
根据式(1)所示的DAB变换器数学模型,可以建立DAB变换器超局部数据模型[22-23]为
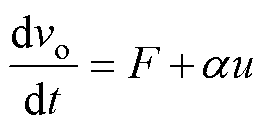 (7)
(7)
其中
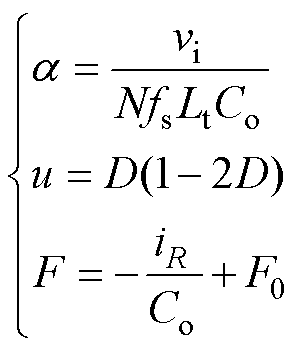 (8)
(8)
式中,a为超局部增益;u为超局部输入变量;F为超局部模型的集中扰动;F0为DAB变换器参数失配引起的非线性扰动。当DAB中模型参数与实际参数存在误差时,超局部模型增益a将存在误差,集中扰动F中的电容参数Co也将存在误差,该误差集合可通过非线性扰动F0表示。因此,通过实时估计超局部模型集中扰动F,即可消除参数对系统模型的影响。
3.1.2 基于四阶龙格库塔的超局部数据模型更新
龙格库塔法可以有效地求解微分方程,该方法将时间步长分解成若干子步长,并结合各子步长的斜率求解微分方程。为了在每个控制周期中准确地估计集中扰动F,本节利用四阶龙格库塔法对集中扰动F进行建模和估计,其可以表示为
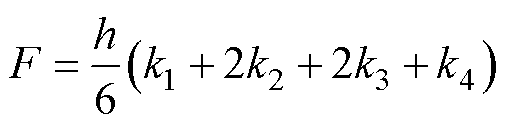 (9)
(9)
其中
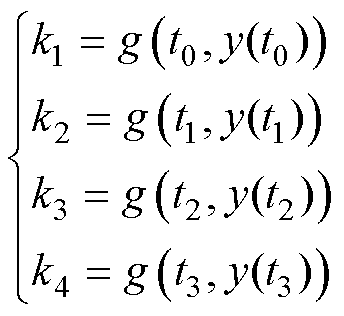 (10)
(10)
式中,h为时间步长;k1~k4为一个时间步长中的四个斜率;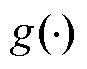 为斜率计算公式;t0~t3为一个时间步长中的四个时刻;y为不同时刻对应的值。然后,引入拉格朗日插值法[24],通过对t0~t3时刻的电压进行采样,计算四个历史时刻的电压斜率,并将龙格库塔法中k1~k4近似为四个历史时刻采样点处的斜率来估算集总扰动F。
为斜率计算公式;t0~t3为一个时间步长中的四个时刻;y为不同时刻对应的值。然后,引入拉格朗日插值法[24],通过对t0~t3时刻的电压进行采样,计算四个历史时刻的电压斜率,并将龙格库塔法中k1~k4近似为四个历史时刻采样点处的斜率来估算集总扰动F。
根据拉格朗日插值法,同时经过t0、t1、t2、t3四个历史时刻采样点的拉格朗日多项式可以表示为
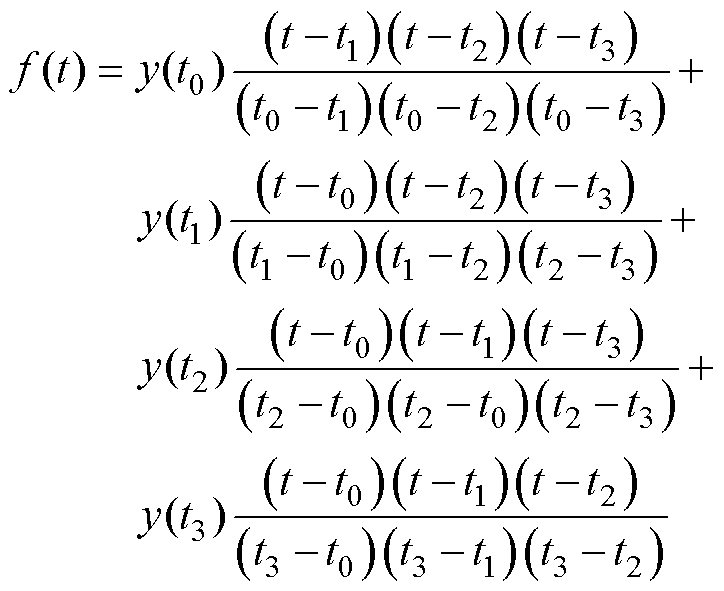 (11)
(11)
本文中,将时间步长h与控制周期Ts设为一致,并将四个历史时刻的时间间隔均设为Ts。因此,式(11)中t和ti(i=1~3)可以分别表达为
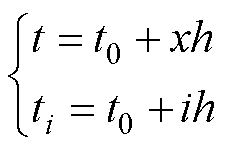 (12)
(12)
式中,x为时间步长h的系数变量,x=0~3。
将式(12)代入式(11),可以得到
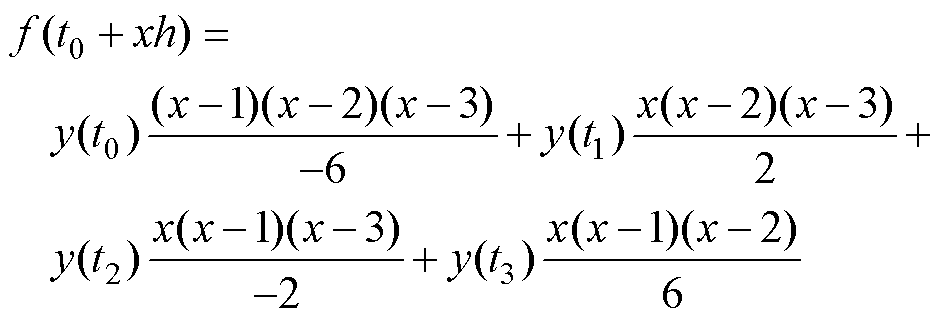 (13)
(13)
对式(13)求导可以得到
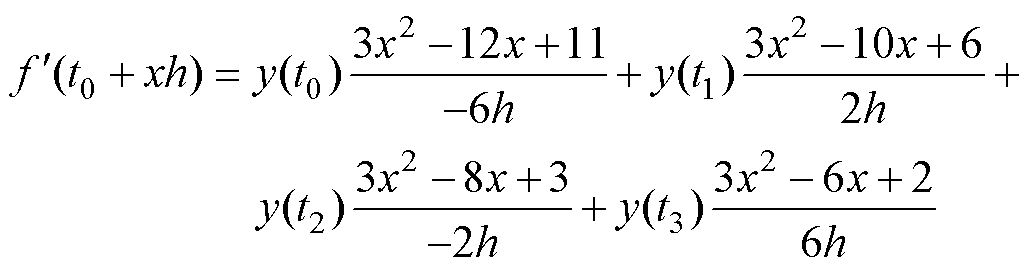 (14)
(14)
将x分别等于0~3并代入式(14)可以得到龙格库塔法中四个历史时刻的电压斜率k1~k4分别为
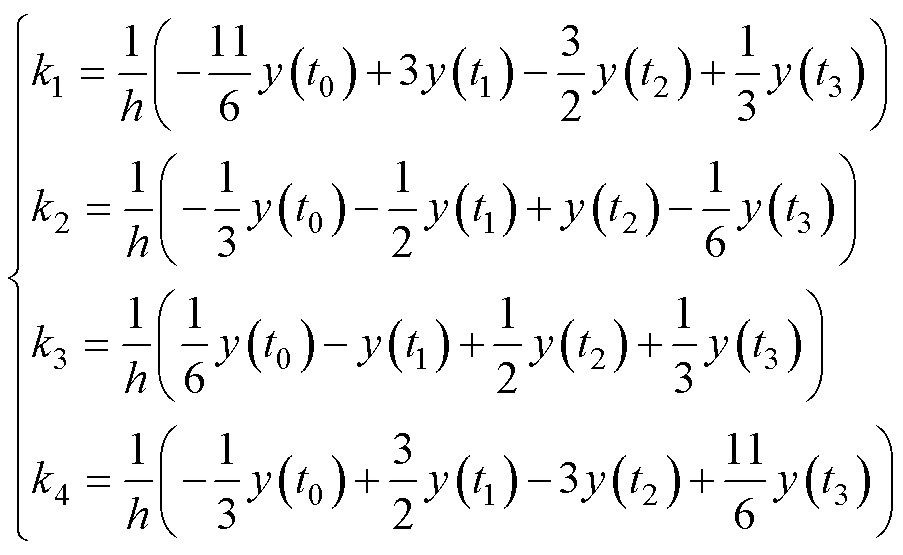 (15)
(15)
将式(15)得到的四个斜率k1~k4代入式(9)即可实时估计超局部集中扰动F,消除了参数误差的影响。
在单向功率传输的DAB变换器系统中,移相比范围为0~0.5,其离散形式可以表示为{0, DF, 2DF, 3DF, …, 0.5-2DF, 0.5-DF, 0.5},其中,DF为控制器可以应用的最小离散相移角。为了降低计算量,可将移相比范围设置为{D(k)-DD(k), D(k), D(k)+ DD(k)}。其中,D(k)为上一控制周期的最优移相比,DD(k)为自适应移相比,其可以表示为
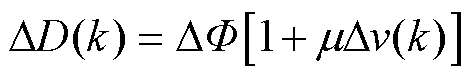 (16)
(16)
其中
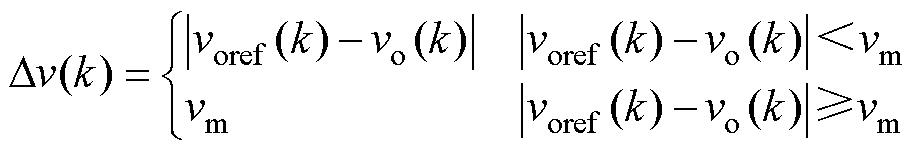 (17)
(17)
式中,m为误差增益;vm为最大电压误差;voref为输出电压参考;Dv为电压误差。
基于3.1节获得的超局部模型集中扰动F和超局部模型增益a,以及3.2节获得的移相比{D(k)-DD(k), D(k), D(k)+DD(k)},可以得到k+1时刻不同移相比对应的输出电压voj(k+1)(j=1~3)为
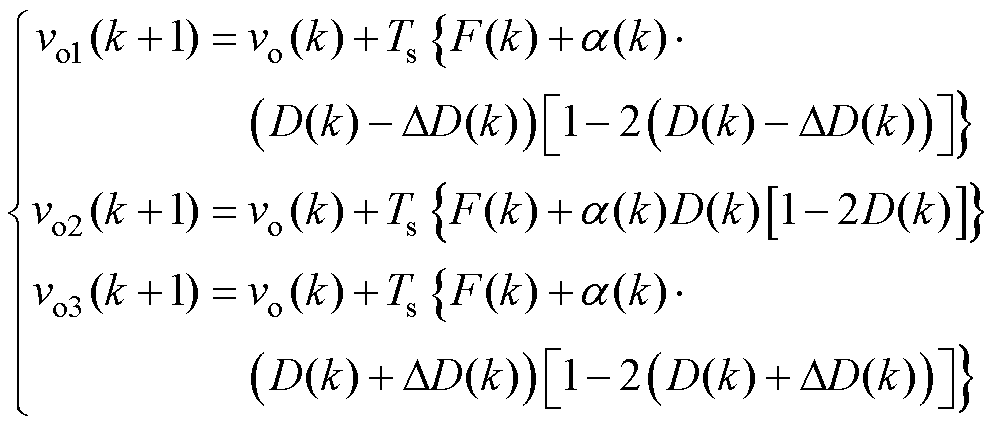 (18)
(18)
如式(18)所示,所提DAB变换器鲁棒预测电压计算通过实时计算超局部集中扰动F消除了参数误差对预测计算的影响,提高了预测控制的参数鲁棒性。
为了在移相比{D(k)-DD(k), D(k), D(k)+DD(k)}中选择最优的移相比并应用在下一控制周期,本节定义价值函数[13]为
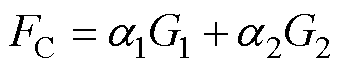 (19)
(19)
其中
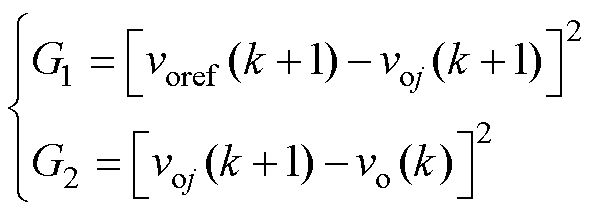 (20)
(20)
式中,G1用于追踪参考电压;G2用于提高DAB变换器稳态性能;a1和a2分别为G1和G2的权重因子,其中,a1负责动态追踪,a2负责稳态性能。
图7显示了不同控制周期中DAB变换器鲁棒预测电压计算及价值函数评估过程。如图7所示,在第k-2个控制周期中,采样的电压为vo(k-2),为了追踪参考电压voref,设置移相比范围为{D(k-2)-DD(k-2),D(k-2), D(k-2)+DD(k-2)},移相比D(k-2)+ DD(k-2)对应的鲁棒预测电压计算值vo3(k-1)与参考电压voref的误差最小,进而选择移相比D(k-2)+ DD(k-2)作为最优移相比;然后,在第k-1个控制周期中,采样的电压为vo3(k-1),为了追踪参考电压voref,设置移相比范围为{D(k-1)-DD(k-1), D(k-1), D(k-1)+DD(k-1)},移相比D(k-1)+DD(k-1)对应的鲁棒预测电压计算值vo3(k)与参考电压voref的误差最小,进而选择移相比D(k-1)+DD(k-1)作为最优移相比;最后,在第k个控制周期中,采样的电压为vo3(k),为了追踪参考电压voref,设置移相比范围为{D(k)-DD(k), D(k), D(k)+DD(k)},移相比D(k)对应的鲁棒预测电压计算值vo2(k+1)与参考电压voref的误差最小,进而选择移相比D(k)作为最优移相比。
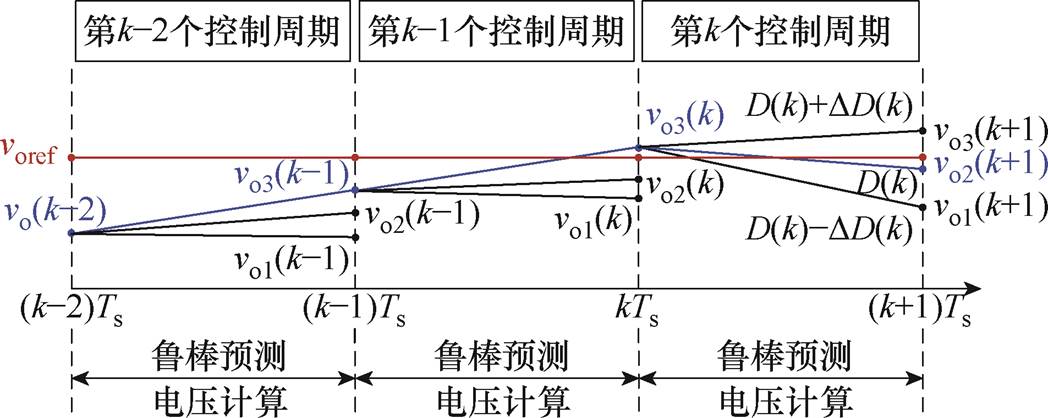
图7 所提鲁棒预测寻优评估示意图
Fig.7 Schematic diagram of optimization evaluation in proposed robust prediction
所提RPVC方法的流程如图8所示。首先,采样获得vi(k)和vo(k),将其代入式(8)计算超局部增益a;其次,根据式(15)计算电压斜率k1~k4,并根据式(9)计算超局部集中扰动F;然后,根据式(16)和式(17)得到{D(k)-DD(k), D(k), D(k)+ DD(k)},并将其代入式(18)计算voj (k+1);最后,根据式(19)选择最优移相比并应用在下一个控制周期。
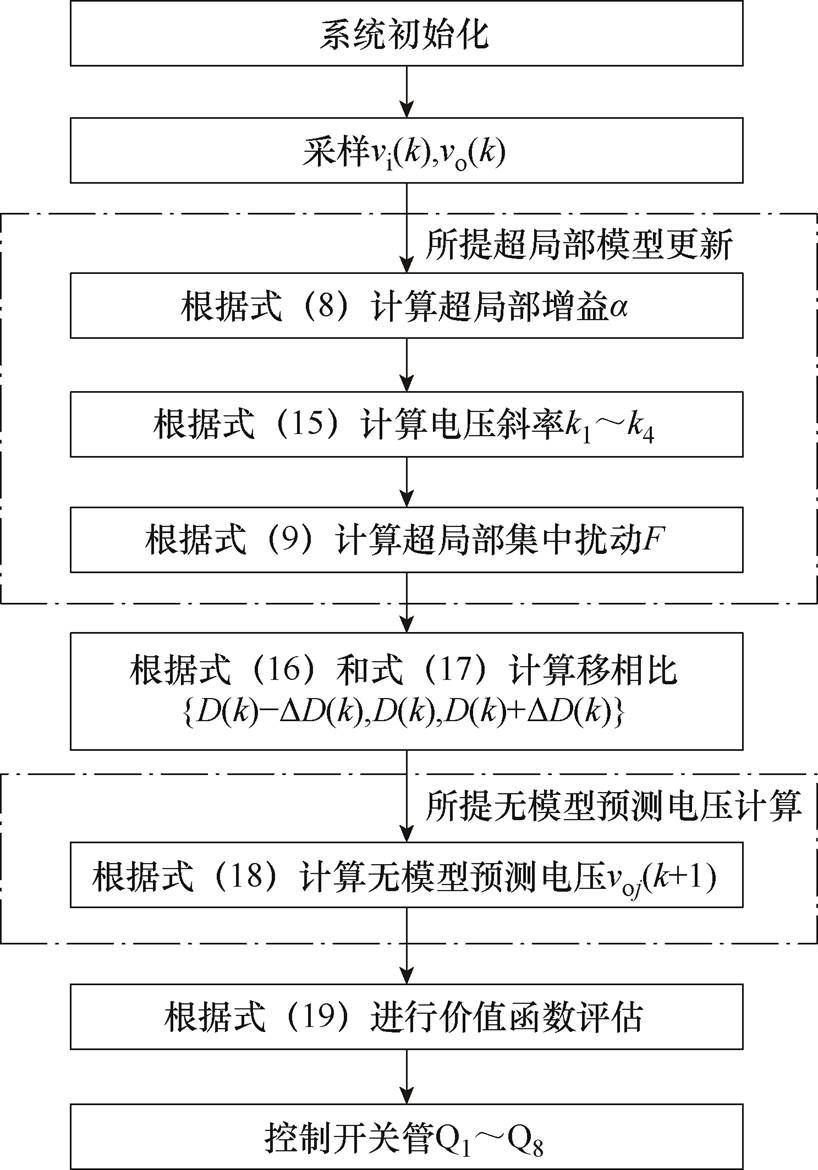
图8 所提DAB变换器RPVC流程
Fig.8 Flow chart of proposed RPVC for DAB converter
为了验证所提RPVC方法的有效性,本节搭建了DAB变换器实验平台如图9所示,比较了不同工况下传统MPVC方法[13]、传统鲁棒MPVC方法[19]与所提RPVC方法的稳态及动态电压性能。其中,实验平台控制器采用TMS320C28346,系统控制参数见表1。
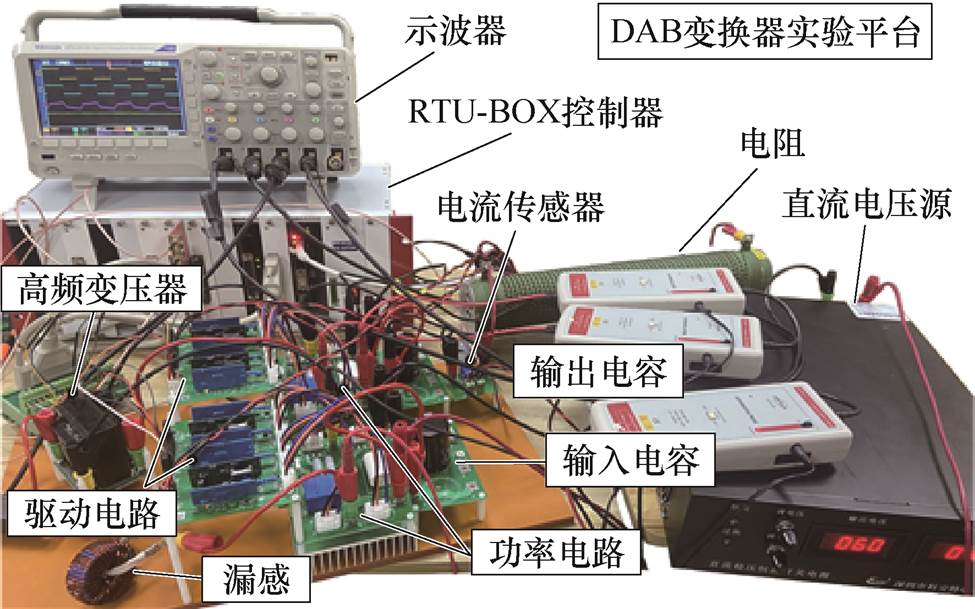
图9 DAB变换器实验平台
Fig.9 Experimental platform of DAB converter
表1 DAB变换器系统参数
Tab.1 System parameters of DAB converter

参 数数 值 输入电压vi/V80 输出电压参考voref/V60, 80 变压器漏感Lt/mH61.15 输出电容Co/mF820 负载电阻R/W10, 20 控制周期Ts/ms50 匝数比N1
4.1.1 参数准确实验对比
当漏感模型参数Ltm与输出电容模型参数Com准确时,传统MPVC方法、传统鲁棒MPVC方法及本文所提RPVC方法的稳态性能实验对比如图10所示。
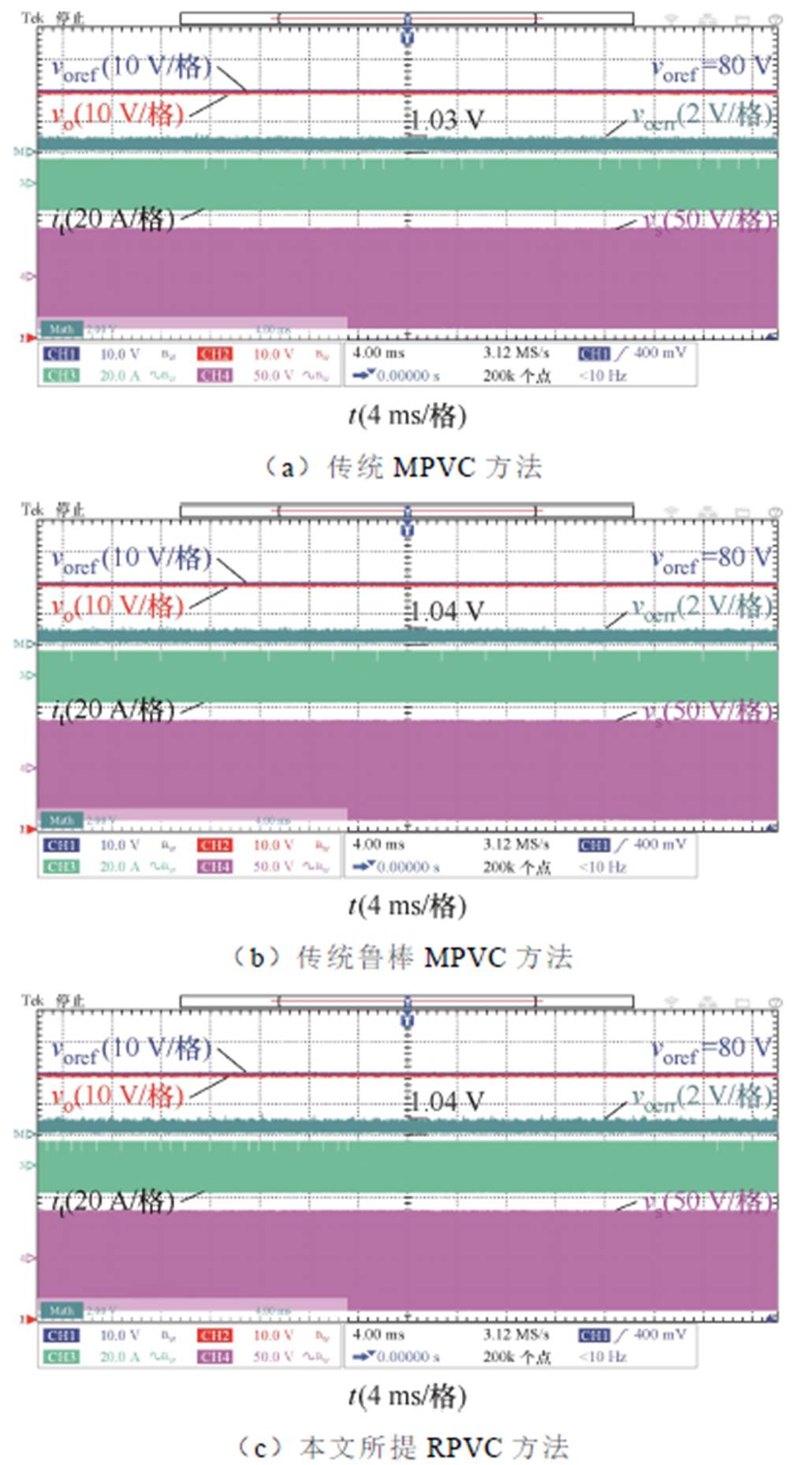
图10 参数准确时稳态性能实验对比
Fig.10 Experimental comparison of steady-state performance under accurate parameters
如图10a所示,当应用传统MPVC方法时,准确的模型参数保证了良好的输出电压性能,输出电压误差绝对值为1.03 V。如图10b所示,当应用传统鲁棒MPVC方法时,其利用最小二乘法实时在线辨识系统漏感模型参数,保证了良好的输出电压性能,输出电压误差绝对值为1.04 V。如图10c所示,当应用本文所提RPVC方法时,其利用龙格库塔法和拉格朗日插值法实时计算系统超局部模型集中扰动,保证了良好的输出电压性能,输出电压误差绝对值为1.04 V,验证了所提方法在参数准确时的有效性。
4.1.2 参数失配实验对比
当漏感模型参数Ltm与其实际参数Lt失配、输出电容模型参数Com与其实际参数Co失配时,传统MPVC方法、传统鲁棒MPVC方法以及本文所提RPVC方法的稳态性能实验对比如图11所示。
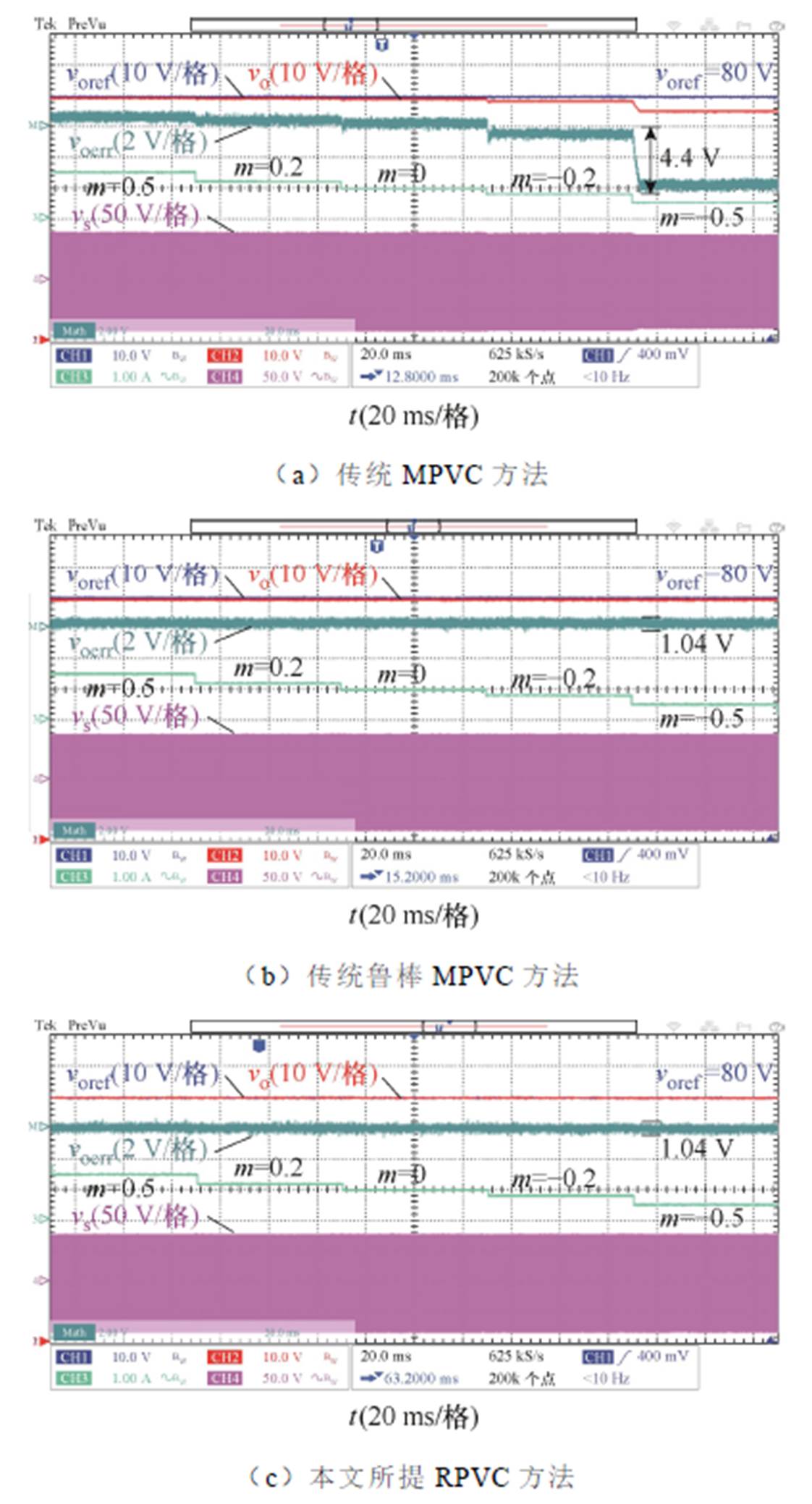
图11 参数失配时稳态性能实验对比
Fig.11 Experimental comparison of steady-state performance under mismatched parameters
如图11a所示,由于传统MPVC方法依赖准确的模型参数,当参数误差增加时,输出电压误差随之增大,在0.5倍参数误差时,输出电压误差达到4.4 V。如图11b所示,当应用传统鲁棒MPVC方法时,其利用最小二乘法辨识DAB系统漏感模型参数,改善了输出电压的鲁棒性。如图11c所示,当应用本文所提RPVC方法时,其利用龙格库塔法和拉格朗日插值法实时计算系统超局部模型集中扰动,保证了输出电压性能不受参数失配影响,拥有良好的鲁棒性。
4.1.3 稳态性能对比总结
表2总结了传统MPVC方法、传统鲁棒MPVC方法及本文所提RPVC方法的稳态性能。如表2所示,当参数准确时(m=0),传统MPVC方法、传统鲁棒MPVC方法及本文所提RPVC方法的稳态性能相近,输出电压误差绝对值分别为1.03、1.04、1.04 V。当参数失配时,本文所提RPVC方法和传统鲁棒MPVC方法动态性能相近,而传统MPVC方法受到误差系数m的影响,当m分别为0.5、0.2、-0.2及-0.5时,其输出电压误差分别为1.44、1.22、1.5、4.4 V。
表2 稳态性能总结
Tab.2 Steady-state performance summary
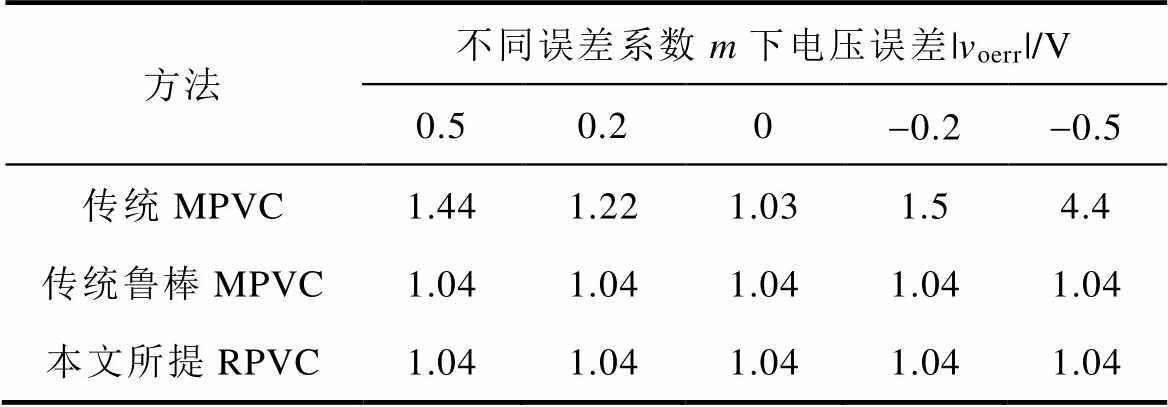
方法不同误差系数m下电压误差|voerr|/V 0.50.20-0.2-0.5 传统MPVC1.441.221.031.54.4 传统鲁棒MPVC1.041.041.041.041.04 本文所提RPVC1.041.041.041.041.04
4.2.1 参数准确实验对比
当漏感模型参数Ltm与输出电容模型参数Com准确并且参考电压突变时,传统MPVC方法、传统鲁棒MPVC方法以及本文所提RPVC方法的动态性能实验对比如图12所示。其中,参考电压voref分别为60 V和80 V。
如图12a所示,当应用传统MPVC方法时,在参考电压突增时,其响应时间为24.8 ms;在参考电压突减时,其响应速度为18 ms。如图12b所示,当应用传统鲁棒MPVC方法时,其响应速度与传统MPVC方法相近,在参考电压突增和突减时,响应时间分别为25.8 ms、17.2 ms。如图12c所示,当应用本文所提RPVC方法时,在参考电压突增时,其响应时间为24.1 ms;在参考电压突减时,其响应时间为18.2 ms。其响应速度与传统MPVC方法及传统鲁棒MPVC方法相近,验证了本文所提方法的有效性。
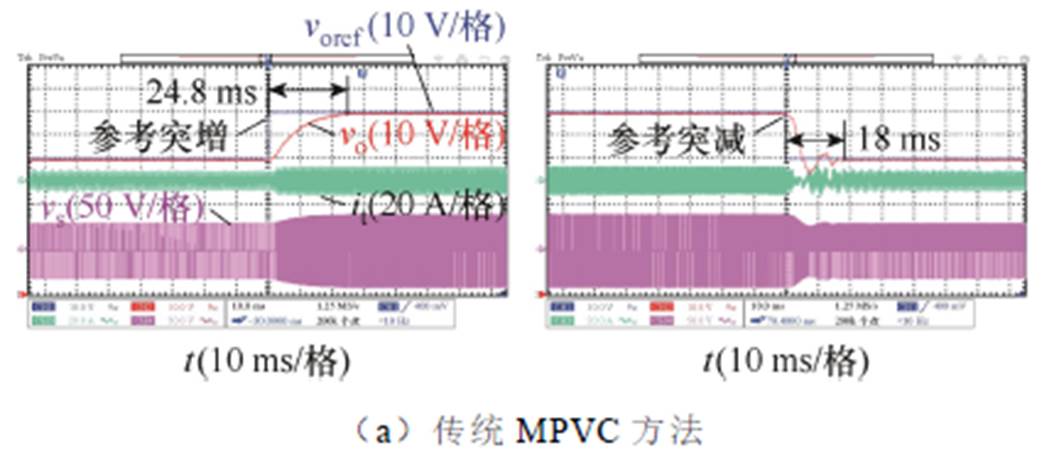
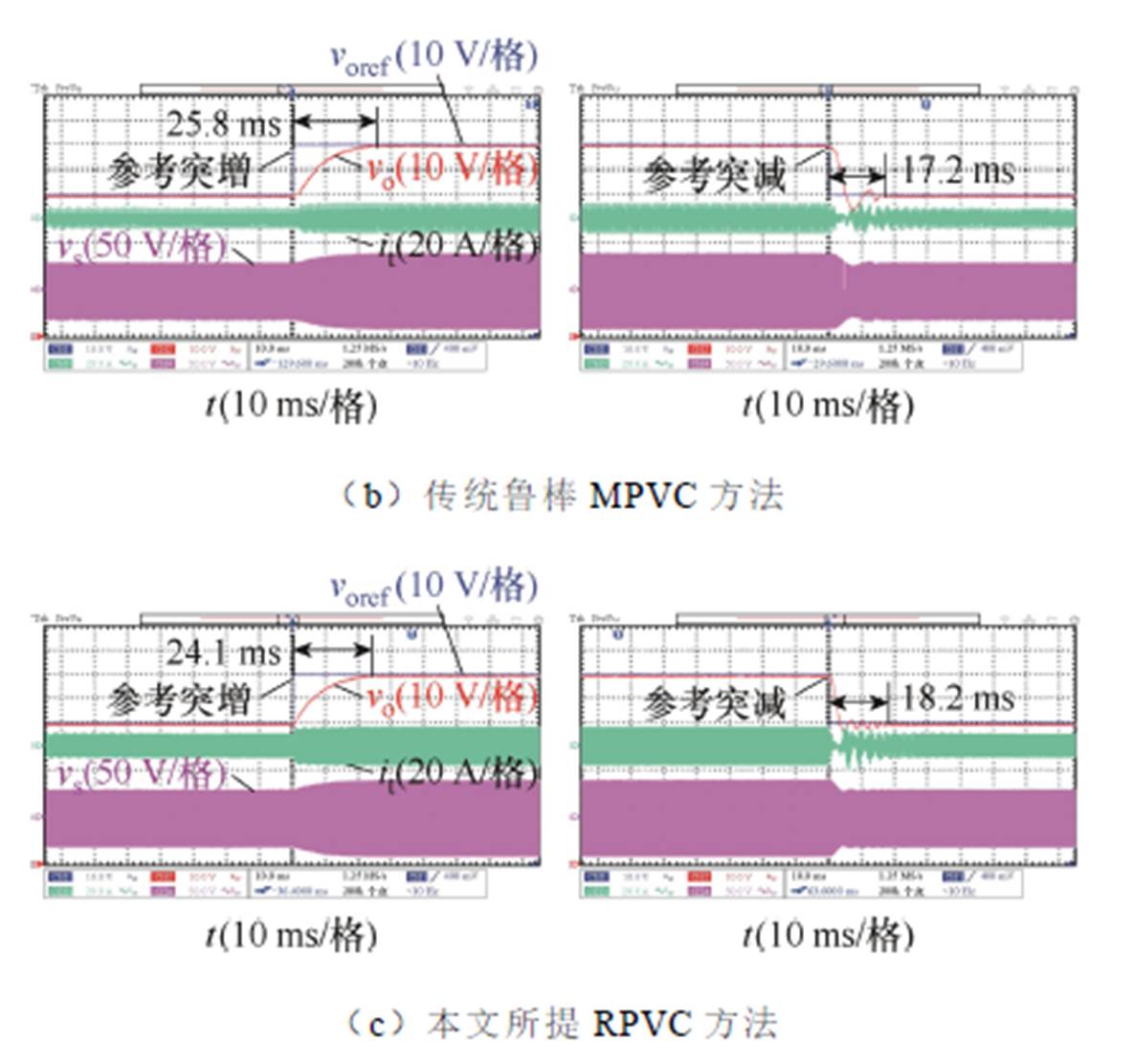
图12 参数准确及参考电压突变时动态性能实验对比
Fig.12 Experimental comparison of dynamic-state performance under accurate parameters and changed reference voltage
4.2.2 参数失配实验对比
当漏感模型参数Ltm和输出电容模型参数Com与其实际参数存在误差并且参考电压突变时,传统MPVC方法、传统鲁棒MPVC方法及本文所提RPVC方法的动态性能实验对比如图13所示。其中,在图13a~图13c中,参数误差DLt和DCo分别设置为-0.5Lt和-0.5Co;在图13d~图13f中,参数误差DLt和DCo分别设置为0.5Lt和0.5Co。
如图13a所示,当应用传统MPVC方法时,参数误差DLt和DCo导致其输出电压始终偏离输出电压参考,无法追踪电压参考。如图13b所示,当应用传统鲁棒MPVC方法时,其响应速度受参数误差影响较小。如图13c所示,当应用本文所提RPVC方法时,其响应速度不受参数误差影响,在参考突增和突减时响应时间分别保持为24.1 ms、18.2 ms,验证了本文所提方法在参考突变时的鲁棒性。
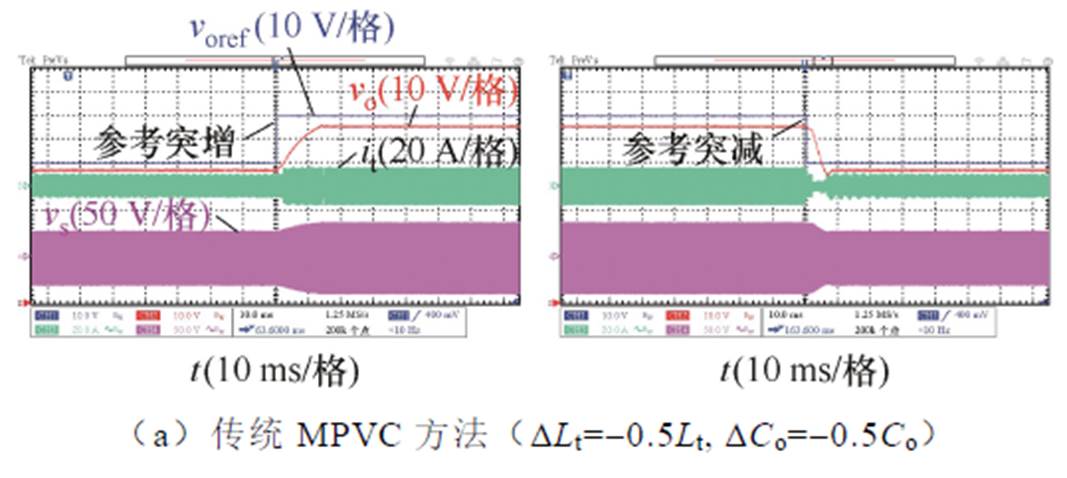
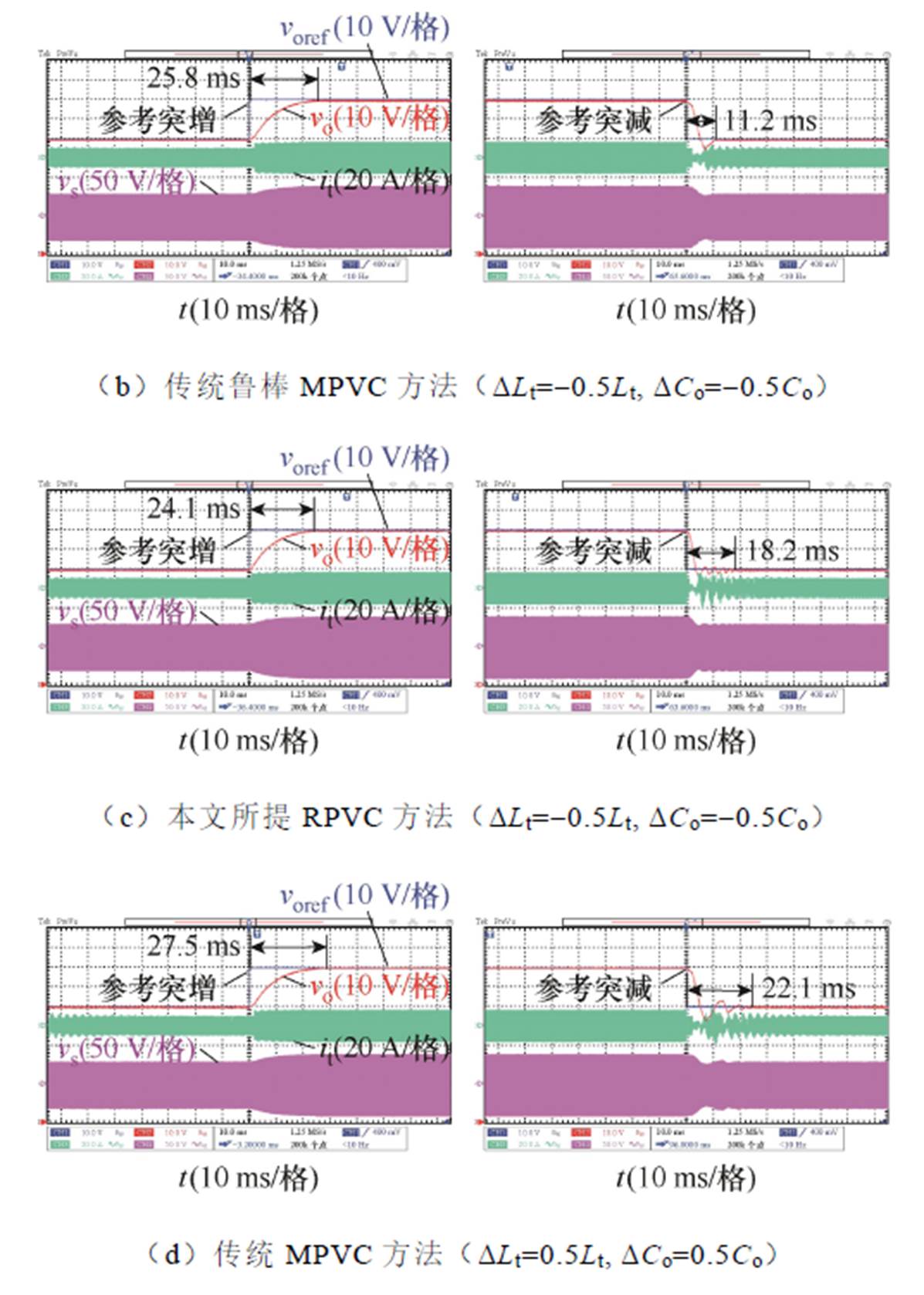
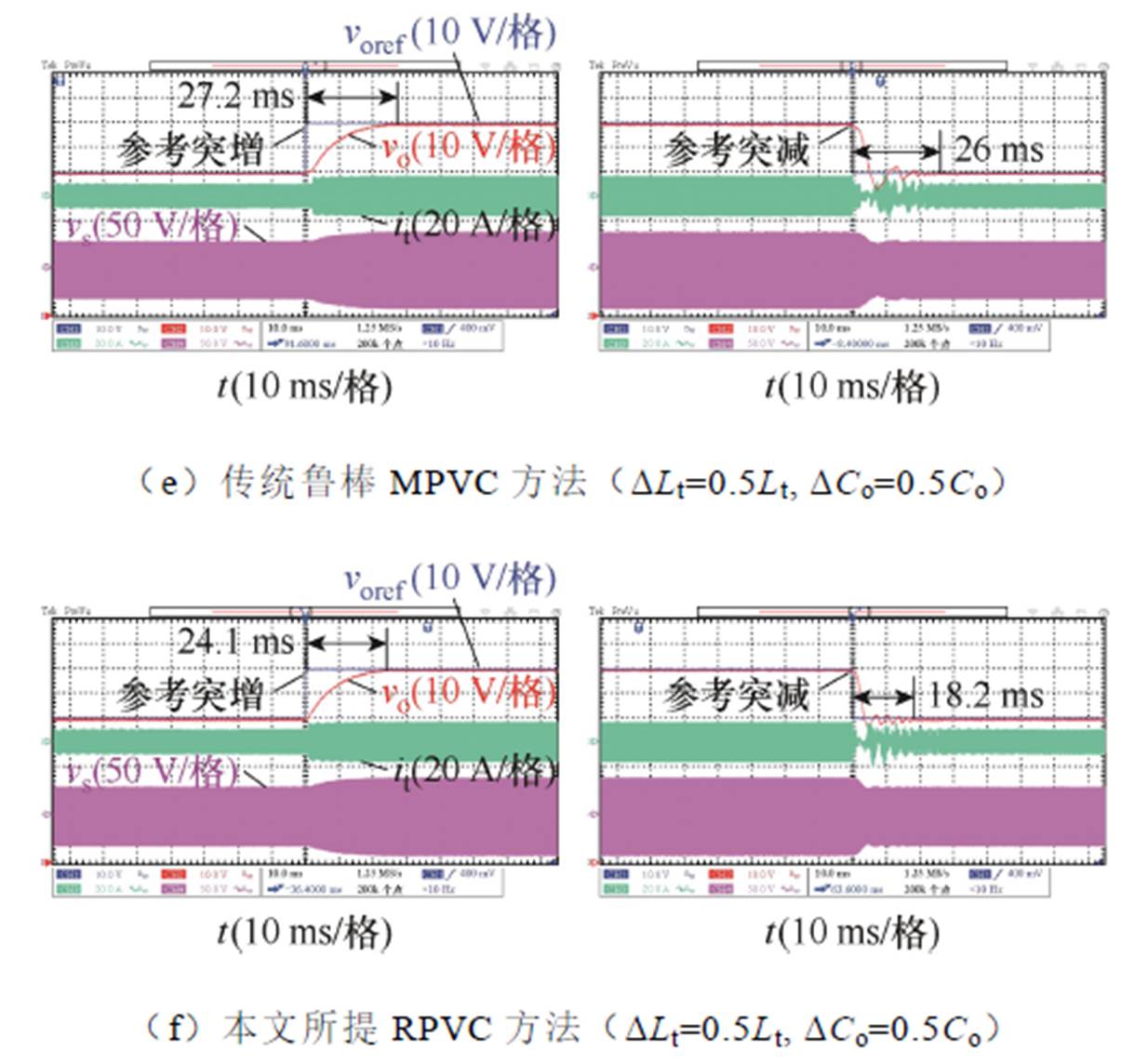
图13 参数失配及参考电压突变时动态性能实验对比
Fig.13 Experimental comparison of dynamic-state performance under mismatched parameters and changed reference voltage
如图13d所示,当应用传统MPVC方法时,参数误差DLt和DCo导致其动态性能降低,在参考突增和突减时响应时间分别为27.5 ms、22.1 ms,与参数准确时相比分别增加2.7 ms、4.1 ms。如图13e所示,当应用传统鲁棒MPVC方法时,其响应时间也受参数误差的影响,与参数准确时相比分别增加1.4 ms、8.8 ms。如图13f所示,当应用本文所提RPVC方法时,其响应时间不受参数误差影响,在参考突增和突减时分别保持为24.1 ms、18.2 ms,验证了所提方法在参考突变时的鲁棒性。
4.2.3 参考突变时动态性能对比总结
表3总结了本文所提RPVC方法、传统鲁棒MPVC方法及传统MPVC方法在参考突变时的动态性能。如表3所示,当参数准确时(m=0),本文所提RPVC方法、传统鲁棒MPVC方法及传统MPVC方法的动态性能相近。当参数失配时,传统MPVC方法受到误差系数m影响,当m=0.5时,其响应时间在参考突增和突减情况下相比参数准确时分别增加2.7 ms、4.1 ms;当m=-0.5时,其输出电压偏离参考值。传统鲁棒MPVC方法相比传统MPVC方法受到参数失配的影响有所降低;而本文所提RPVC方法的动态性能则完全不受参数失配影响,在参考突增和突减时响应时间分别保持为24.1 ms和18.2 ms。
表3 参考突变时动态性能总结
Tab.3 Dynamic-state performance summary under changed reference
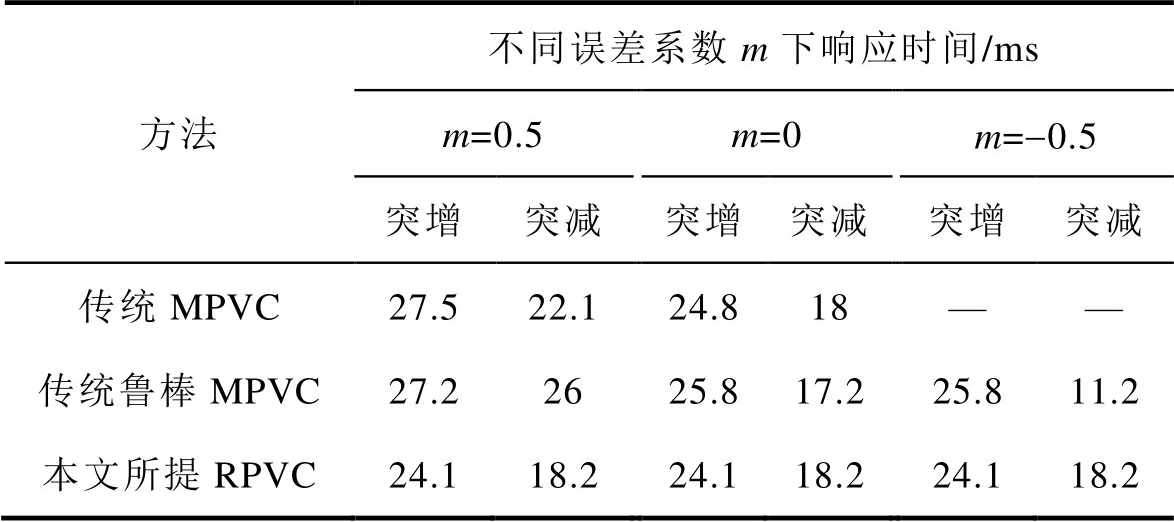
方法不同误差系数m下响应时间/ms m=0.5m=0m=-0.5 突增突减突增突减突增突减 传统MPVC27.522.124.818—— 传统鲁棒MPVC27.22625.817.225.811.2 本文所提RPVC24.118.224.118.224.118.2
注:“—”表示偏离参考值。
4.3.1 参数准确实验对比
当漏感模型参数Ltm与输出电容模型参数Com准确并且负载电阻突变时,传统MPVC方法、传统鲁棒MPVC方法及本文所提RPVC方法的动态性能如图14所示。其中,负载电阻R分别为10 W和20 W。
如图14a所示,当应用传统MPVC方法时,在负载突减时,其响应时间为11.9 ms;在负载突增时,其响应时间为12 ms。如图14b所示,当应用传统鲁棒MPVC方法时,其响应速度与传统MPVC方法相近,在负载电阻突减和突增时,响应时间分别为14.2 ms、9.8 ms。如图14c所示,当应用本文所提RPVC方法时,在负载突减时,其响应时间为10.1 ms;在负载突增时,其响应时间为7.2 ms。本文所提RPVC方法的响应速度优于传统MPVC方法和传统鲁棒MPVC方法,验证了所提方法的有效性。

图14 参数准确及负载电阻突变时动态性能实验对比
Fig.14 Experimental comparison of dynamic-state performance under accurate parameters and changed load resistance
4.3.2 参数失配实验对比
当漏感模型参数Ltm和输出电容模型参数Com与其实际参数存在误差并且负载电阻突变时,传统MPVC方法、传统鲁棒MPVC方法以及本文所提RPVC方法的动态性能如图15所示。其中,在图15a~图15c中,参数误差DLt和DCo分别设置为-0.5Lt和-0.5Co;在图15d~图15f中,参数误差DLt和DCo分别设置为0.5Lt和0.5Co。
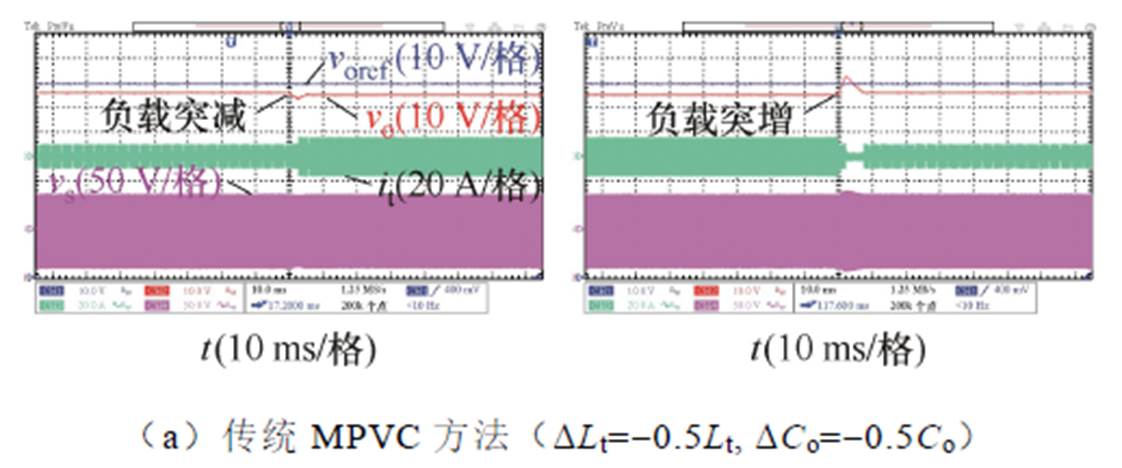

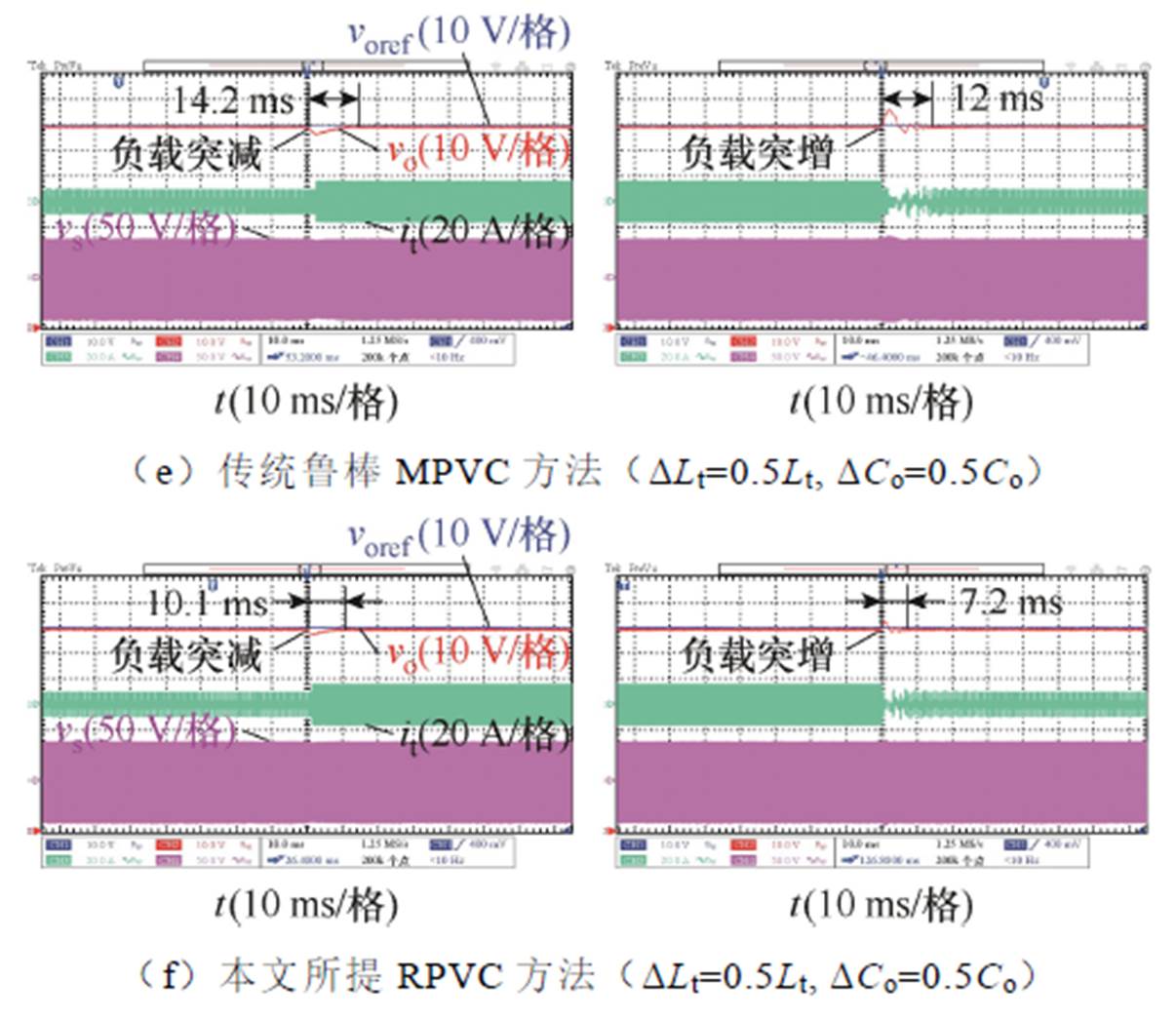
图15 参数失配及负载电阻突变时动态性能实验对比
Fig.15 Experimental comparison of dynamic-state performance under mismatched parameters and changed load resistance
如图15a所示,当应用传统MPVC方法时,参数误差DLt和DCo导致其输出电压始终偏离参考值,无法追踪电压参考。如图15b所示,当应用传统鲁棒MPVC方法时,其负载突增时响应时间也受到参数误差影响,与参数准确时相比增加6 ms。如图15c所示,当应用本文所提RPVC方法时,其响应时间不受参数误差影响,在负载突增和突减时分别保持为10.1 ms、7.2 ms,验证了本文所提方法在负载电阻突变时的鲁棒性。
如图15d所示,当应用传统MPVC方法时,参数误差DLt和DCo导致其动态性能降低,在负载突减和突增时响应时间分别为18.5 ms、18 ms,与参数准确时相比分别增加6.6 ms、6 ms。如图15e所示,当应用传统鲁棒MPVC方法时,其负载突增时响应时间也受到参数误差影响,与参数准确时相比增加2.2 ms。如图15f所示,当应用本文所提RPVC方法时,其响应时间不受参数误差影响,在负载突减和突增时保持为10.1 ms、7.2 ms,验证了本文所提方法在负载电阻突变时的鲁棒性。
4.3.3 负载突变时动态性能对比总结
表4总结了所提RPVC方法、传统鲁棒MPVC方法及传统MPVC方法在负载突变时的动态性能。如表4所示,当参数准确时(m=0),本文所提RPVC方法、传统鲁棒MPVC方法及传统MPVC方法的动态性能相近。当参数失配时,传统MPVC方法受到误差系数m影响,当m=0.5时,其响应时间在负载突减和突增相比参数准确时分别增加6.6 ms、6 ms;当m=-0.5时,其输出电压偏离参考值。传统鲁棒MPVC相比传统MPVC方法,其受到参数失配的影响有所降低;本文所提RPVC方法的动态性能则完全不受参数失配影响,在负载突减和突增时响应时间分别保持为10.1 ms和7.2 ms。
表4 负载突变时动态性能总结
Tab.4 Dynamic-state performance summary under changed load
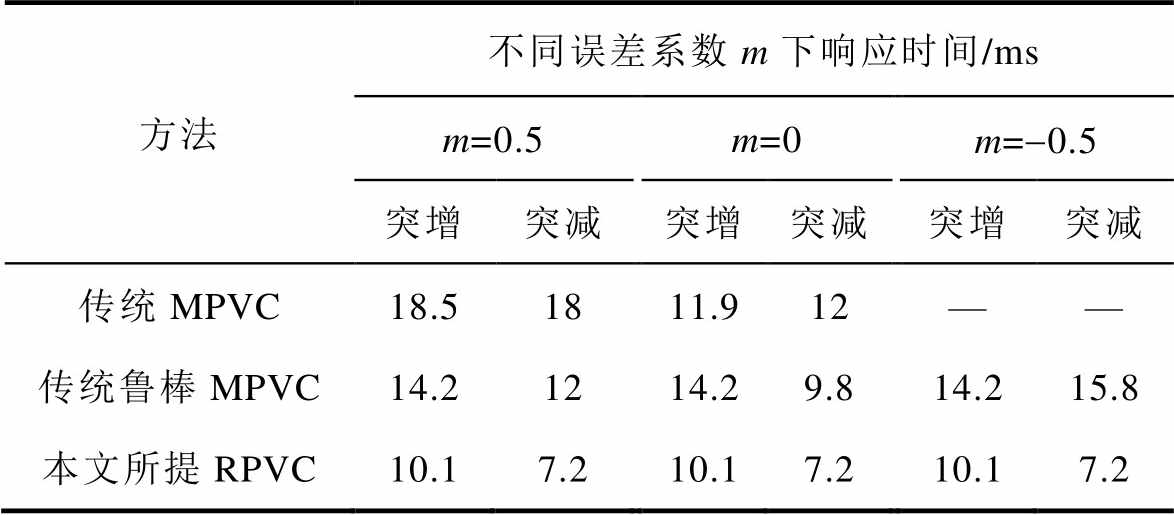
方法不同误差系数m下响应时间/ms m=0.5m=0m=-0.5 突增突减突增突减突增突减 传统MPVC18.51811.912—— 传统鲁棒MPVC14.21214.29.814.215.8 本文所提RPVC10.17.210.17.210.17.2
注:“—”表示偏离参考值。
本文针对DAB变换器提出了一种基于龙格库塔的鲁棒预测电压控制策略。所提方法建立了DAB变换器超局部模型,并结合龙格库塔法和拉格朗日插值法对超局部模型的集中扰动进行实时估计,消除了参数误差对输出电压预测的影响,提高了系统的鲁棒性。实验结果表明,当参数准确时,本文所提RPVC方法与传统MPVC方法、传统鲁棒MPVC方法相比,拥有相近的稳态和动态性能;当参数存在误差时,本文所提RPVC方法与传统MPVC方法、传统鲁棒MPVC方法相比,其稳态和动态性能不受参数影响,保证了DAB变换器的系统运行性能。
参考文献
[1] 马立红, 梁亚峰, 程西, 等. 计及构网型储能稳定拓展的微电网群优化运行[J]. 电力工程技术, 2024, 43(6): 214-222.
Ma Lihong, Liang Yafeng, Cheng Xi, et al. Optimal operation of microgrids considering stabilized expansion of grid-forming energy storage[J]. Electric Power Engineering Technology, 2024, 43(6): 214-222.
[2] 杨建, 刘笑, 董密, 等. 基于深度学习的恒功率负荷直流微电网稳定性分析[J]. 电力系统自动化, 2023, 47(15): 188-197.
Yang Jian, Liu Xiao, Dong Mi, et al. Deep learning based stability analysis of DC microgrid with constant power loads[J]. Automation of Electric Power Systems, 2023, 47(15): 188-197.
[3] 孔惠文, 马静, 程鹏, 等. 基于子网优先级驱动的交直流混合微电网集群双向互联变流器分散式控制策略[J]. 电工技术学报, 2024, 39(9): 2667-2681.
Kong Huiwen, Ma Jing, Cheng Peng, et al. Decentralized control strategy for hybrid microgrid cluster bidirectional interlinking converters based on sub-grid priority drive[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2667-2681.
[4] 苗晓阳, 李冰然, 傅洪全. 适用于DFIG连接到直流微网的双变换器设计与实现[J]. 电源学报, 2024, 22(5): 170-181.
Miao Xiaoyang, Li Bingran, Fu Hongquan. Design and implementation of dual-converter for connecting DFIG to DC microgrid[J]. Journal of Power Supply, 2024, 22(5): 170-181.
[5] 李文辉, 杨世华, 龚邻骁, 等. 基于励磁电流补偿与混合移相调制的高频DAB变换器全范围ZVS运行策略[J]. 中国电机工程学报, 2024, 44(10): 4050- 4062.
Li Wenhui, Yang Shihua, Gong Linxiao, et al. A full range ZVS operation strategy for high-frequency DAB Converters based on magnetizing current compensa- tion and hybrid phase shift modulation[J]. Proceedings of the CSEE, 2024, 44(10): 4050-4062.
[6] 李嘉进, 马翔, 谢宇帆, 等. 输入串联输出并联型三电平双有源桥变换器功率与电压平衡控制策略[J]. 电工技术学报, 2024, 39(10): 3082-3092.
Li Jiajin, Ma Xiang, Xie Yufan, et al. Power and voltage balance control strategy of series input parallel output type three-level dual active bridge converter[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3082-3092.
[7] 高祎韩, 周子航, 张欣, 等. 双有源桥串联欠谐振变换器的最小回流电流控制[J]. 电工技术学报, 2024, 39(14): 4480-4494.
Gao Yihan, Zhou Zihang, Zhang Xin, et al. Minimum backflow current control of under-resonant-dual-bridge- series-resonant converter[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4480-4494.
[8] 尹政, 邓富金, 詹昕, 等. 双有源桥变换器无电流传感器调制模型预测控制[J]. 电机与控制学报, 2025, 29(1): 49-57.
Yin Zheng, Deng Fujin, Zhan Xin, et al. Current- sensorless modulated model predictive control for dual-active-bridge converters[J]. Electric Machines and Control, 2025, 29(1): 49-57.
[9] 杨鸣, 汪小丰, 司马文霞, 等. 基于模型预测与复合占空比的双有源全桥变换器电压电流暂稳态调控方法[J]. 电工技术学报, 2025, 40(4): 1203-1220.
Yang Ming, Wang Xiaofeng, Sima Wenxia, et al. Transient-and steady-state optimization of voltage and current for dual active bridge converters based on model predictive control and composite duty modulation [J]. Transactions of China Electrotechnical Society, 2025, 40(4): 1203-1220.
[10] Deng Yaru, Song Wensheng, Yin Shuai, et al. A model predictive control scheme without current sensor of dual active bridge DC-DC converters: improving dynamic performance and reducing hardware cost[J]. IEEE Transactions on Transportation Electrification, 2023, 9(2): 2916-2928.
[11] 尹政, 胡存刚, 芮涛, 等. LC滤波型电压源逆变器无模型预测电压控制策略[J]. 电工技术学报, 2023, 38(14): 3723-3732.
Yin Zheng, Hu Cungang, Rui Tao, et al. Model-free predictive voltage control strategy for LC-filtered voltage source inverter[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3723-3732.
[12] Chen Linglin, Shao Shuai, Xiao Qian, et al. Model predictive control for dual-active-bridge converters supplying pulsed power loads in naval DC micro- grids[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 1957-1966.
[13] Tarisciotti L, Chen Linglin, Shao Shuai, et al. Finite control set model predictive control for dual active bridge converter[J]. IEEE Transactions on Industry Applications, 2022, 58(2): 2155-2165.
[14] Chen Linglin, Lin Lyuyi, Shao Shuai, et al. Moving discretized control set model-predictive control for dual- active bridge with the triple-phase shift[J]. IEEE Trans- actions on Power Electronics, 2020, 35(8): 8624-8637.
[15] 王攀攀, 徐泽涵, 王莉, 等. 基于三重移相的双有源桥DC-DC变换器效率与动态性能混合优化控制策略[J]. 电工技术学报, 2022, 37(18): 4720-4731.
Wang Panpan, Xu Zehan, Wang Li, et al. A Hybrid Optimization control strategy of efficiency and dynamic performance of dual-active-bridge DC-DC converter based on triple-phase-shift[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4720-4731.
[16] 尹政, 邓富金, 王青松, 等. 双有源桥变换器移动离散控制集无模型预测电压控制策略[J]. 电工技术学报, 2025, 40(6): 1853-1863.
Yin Zheng, Deng Fujin, Wang Qingsong, et al. Model-free predictive voltage control with moving- discrete-control-set for dual active bridge converters [J]. Transactions of China Electrotechnical Society, 2025, 40(6): 1853-1863.
[17] Zhang Hang, Li Yaohua, Li Zixin, et al. Extended- state-observer based model predictive control of a hybrid modular DC transformer[J]. IEEE Transactions on Industrial Electronics, 2022, 69(2): 1561-1572.
[18] Wu Yuheng, Mahmud M H, Zhao Yue, et al. Uncertainty and disturbance estimator-based robust tracking control for dual-active- bridge converters[J]. IEEE Transactions on Transportation Electrification, 2020, 6(4): 1791-1800.
[19] Guo Zhiqiang, Luo Yong, Sun Kai. Parameter identi- fication of the series inductance in DAB converters[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 7395-7399.
[20] Li Xuming, Dong Zheng, Cao Yan, et al. Model- predictive control with parameter identification for multi-dual-active-bridge converters achieving accurate power balancing[J]. IEEE Transactions on Power Electronics, 2023, 38(9): 10880-10894.
[21] Zhu Yi, Yang Yong, Wen Huiqing, et al. Model predictive control with a novel parameter identification scheme for dual-active-bridge converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(5): 4704-4713.
[22] Fliess M, Join C. Model-free control[J]. International Journal of Control, 2013, 86(12): 2228-2252.
[23] 刘兴, 阳辉, 王逸飞, 等. 基于拓展控制集的PMSM有限控制集无模型预测电流控制策略[J]. 电力工程技术, 2024, 43(5): 91-99.
Liu Xing, Yang Hui, Wang Yifei, et al. Finite-control- set model-free predictive current control strategy based on extended control set of PMSM[J]. Electric Power Engineering Technology, 2024, 43(5): 91-99.
[24] Yang Guanglu, Xiao Han, Sun Yifeng, et al. A model- free current prediction control with Runge-Kutta algorithm for grid-connected inverter[C]//IEEE Interna- tional Conference on Predictive Control of Electrical Drivesand Power Electronics, Jinan, China, 2021: 698-702.
Abstract In recent years, the scale and application of DC microgrids have continuously expanded. Within DC microgrids, isolated bidirectional DC/DC power converters play a pivotal role, enabling not only energy exchange between energy storage systems and DC microgrids but also power flow management between DC microgrids and distribution networks through solid-state transformer integration. Among various topologies, the dual active bridge (DAB) converter stands out as one of the most promising configurations due to its inherent capability for automatic bidirectional power flow regulation and wide voltage conversion gain range.
To ensure dynamic performance and voltage tracking accuracy of DAB converters while enhancing multi-objective control capabilities, model predictive voltage control (MPVC) has been widely adopted in DAB converter systems. However, the performance of MPVC critically relies on precise system modeling and parameter identification. Discrepancies between theoretical model parameters and actual system characteristics can degrade control effectiveness, increase electrical and thermal stresses on DAB converters, reduce system reliability, and potentially cause system failures under sustained error accumulation.
Addressing these challenges, this paper proposes a robust predictive voltage control (RPVC) strategy based on the Runge-Kutta method for DAB converters. Firstly, the impact of leakage inductance and capacitance parameter deviations on output voltage performance under conventional MPVC is systematically analyzed. Subsequently, an ultra-local model of the DAB converter is established and dynamically updated in real-time through the integration of Runge-Kutta discretization and Lagrange interpolation, effectively replacing traditional predictive models. Then, adaptive phase-shift ratios are calculated through model updating. Finally, an optimal phase-shift ratio is determined and implemented via a value function-based optimization process.
To validate the effectiveness of the proposed RPVC methodology, an experimental DAB converter prototype was developed for comparative analysis of voltage regulation performance under multiple operational conditions. Systematic evaluations were conducted among three control frameworks: conventional MPVC, traditional robust MPVC, and the proposed RPVC approach, with particular emphasis on steady-state precision and dynamic transient response. The control platform employed a TMS320C28346 DSP-based digital controller. Experimental results demonstrate that the proposed RPVC achieves comparable steady-state and dynamic performance to conventional MPVC and traditional robust MPVC methods under parameter-accurate conditions. Notably, under parameter mismatch scenarios, the RPVC maintains unaffected steady-state and dynamic characteristics, outperforming both conventional MPVC and traditional robust MPVC approaches. This parameter-independent performance ensures reliable system operation of DAB converters under practical implementation conditions.
For subsequent investigations, the proposed methodology could be systematically expanded to multi-port active bridge (MAB) converter architectures, facilitating detailed exploration of load distribution characteristics and system-wide parametric robustness under dynamic operational scenarios. This extension would enable quantitative evaluation of the framework’s scalability and adaptability in complex multi-terminal energy networks.
keywords:Dual active bridge converter, model predictive voltage control, Runge-Kutta, Lagrange interpolation method, parameter robustness
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.241890
国家重点研发计划“政府间国际科技创新合作”重点专项资助项目(2022YFE0196300)。
收稿日期 2024-10-22
改稿日期 2024-11-15
尹 政 男,1996年生,博士研究生,研究方向为新能源变换器预测控制。E-mail: zyin@seu.edu.cn
邓富金 男,1983年生,教授,博士生导师,研究方向为模块化多电平变流器。E-mail: fdeng@ seu.edu.cn(通信作者)
(编辑 李 冰)