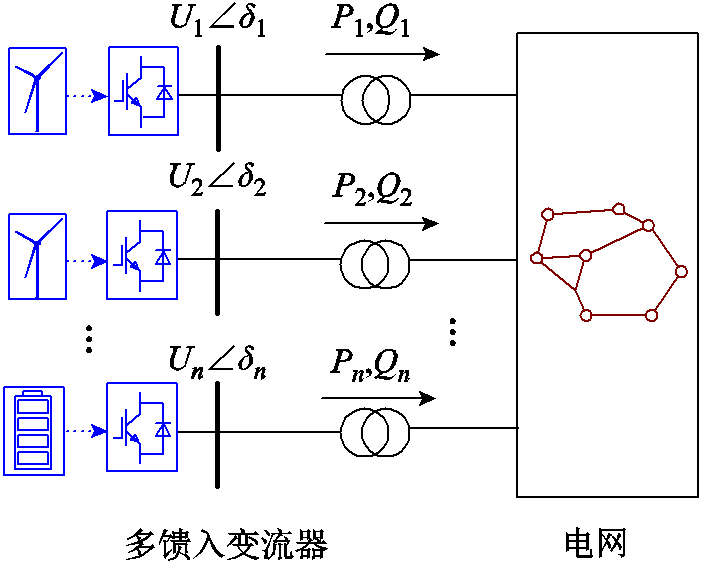
图1 多馈入系统示意图
Fig.1 Schematic diagram of a multi-infeed power system
摘要 新能源装备以电力电子变流器为接口并网,系统电压支撑强度(简称系统强度)表征了电力电子变流器多馈入系统受扰后节点电压抵抗失稳或偏移的能力。工程上大多从单一电网视角间接表征系统强度。然而,受扰后节点电压响应是系统整体的动态行为,以往方法可能忽视了多变流器的影响。为此,该文首先引入变流器多样性的概念,以便描述多变流器在运行功率因数、运行状态或跟网型/构网型控制方式等方面的差异化特征对系统强度的影响;其次,回顾了计及多变流器-电网闭环动态特性的系统强度量化方法,并从电压稳定、同步稳定与抗扰性能分析维度建立了相应的评估指标;然后,对比分析了单一化或多样化变流器运行工况、控制方式等因素对不同维度下系统强度评估指标的影响作用,论证了变流器多样性对系统强度的若干提升规律;最后,通过仿真算例验证了所提结论的有效性。
关键词:系统强度 静态电压稳定 小扰动同步稳定 抗扰性能 多馈入系统
构建以新能源为主体的新型电力系统是实现“碳达峰、碳中和”目标的重要途径[1]。在传统电力系统向新型电力系统的转型过程中,风电、光伏等新能源以电力电子变流器为接口大规模馈入电网,替代常规同步支撑电源,导致交流电网相对变弱[2-3],保障电力电子多馈入电力系统(简称“多馈入系统”)的安全稳定性面临严峻挑战。为了筛查多馈入系统潜在的失稳风险,学术界和工业界依据长期电力系统运行经验,引入了系统电压支撑强度(简称“系统强度”)的概念[2]。它可表征受扰后节点电压抵抗失稳或抵抗偏移的能力。系统强度低表明系统抵抗外界扰动冲击的能力弱,电压响应性能差,甚至可能引发系统失稳。
系统强度评估最早在常规直流馈入系统中开展,由于常规直流的特性相对固定,所以采用不计入装备作用的电网强度方法来间接地简化系统强度评估[4]。短路比(Short Circuit Ratio, SCR)是最常用的电网强度指标。SCR的优势在于计算简单,并衍生出一系列适用于新能源多馈入场景的SCR指标,例如,CIGRE多馈入短路比(Multi-infeed SCR, MSCR)[2]、新能源多场站短路比(Multiple Renewable energy station SCR, MRSCR)[5]等。实际上,系统强度所关注的受扰后节点电压响应是系统整体的动态行为,电网强度方法忽视了多馈入装备的特性,可能难以准确地评估系统强度。为此,文献[6-7]提出了基于广义短路比(generalized SCR, gSCR)的系统强度量化方法,从静态电压稳定、小扰动同步稳定与电压抗扰性能等维度实现装备-电网协同的系统强度评估;文献[8-9]通过建立计及变流器动态的系统宽频阻抗模型提出了系统强度评估方法。
然而,现有系统强度相关的研究主要关注如何评估系统强度,对系统强度影响因素的分析相对较少,且主要集中在电网阻抗及其网架研究[10],对多馈入变流器特性关注不足。由于多变流器存在交互作用,且多样化的变流器控制方式、运行状态等因素也增加了分析的复杂度,现有工作尚未阐明多变流器特性对系统强度存在何种一般性的影响规律。例如,文献[11]考虑了多馈入新能源场站有功出力的交互作用对系统强度的影响,但未计及新能源场站运行在非单位功率因数时的情形,也未考虑构网型变流器的影响;文献[8]基于两机并联运行系统仿真分析了跟网型/构网型变流器控制参数对系统强度的影响,但未针对一般性的电网拓扑给出解析的结论。这使得从装备层面提升系统强度的路径不明,普遍依赖工程经验而缺乏理论依据,且不利于发挥电力电子变流器运行控制的灵活性,给系统规划运行与网源协调带来困扰。
为此,本文针对一般性的多馈入系统并网拓扑,从小扰动视角解析了多变流器运行工况、控制方式等因素对系统强度的影响作用。首先,回顾了量化多馈入系统强度的基本方法,并从电压稳定、同步稳定(如不特殊说明,本文均指静态电压稳定与小扰动同步稳定)与抗扰性能等维度建立了相应的系统强度评估指标;其次,分析了多变流器在运行功率因数、运行状态或跟网型/构网型控制方面的差异化特征对不同维度下系统强度的作用,并基于变流器多样性概念总结了影响规律。研究结果有望为多馈入系统规划与运行提供理论指导。
多馈入系统示意图如图1所示,新能源等装备经变流器接口并网,它们由交流网络互联组成了多馈入系统。考虑到新能源等装备在弱电网下的多类稳定问题主要由它们的网侧变流器动态主导,故以下将这些装备统一抽象建模为变流器[3],且不涉及如双馈风机等同时具有变流器与电机并网接口的装备。考虑多馈入系统运行期间图1中风、光等新能源的强波动性可能引入功率扰动,导致节点电压失稳或偏离运行点[2]。这一功率扰动-电压响应过程可基于功率-电压灵敏度矩阵,即由变流器与电网的雅可比传递函数矩阵描述[6]。多馈入系统功率扰动-电压闭环响应框图如图2所示。

图1 多馈入系统示意图
Fig.1 Schematic diagram of a multi-infeed power system
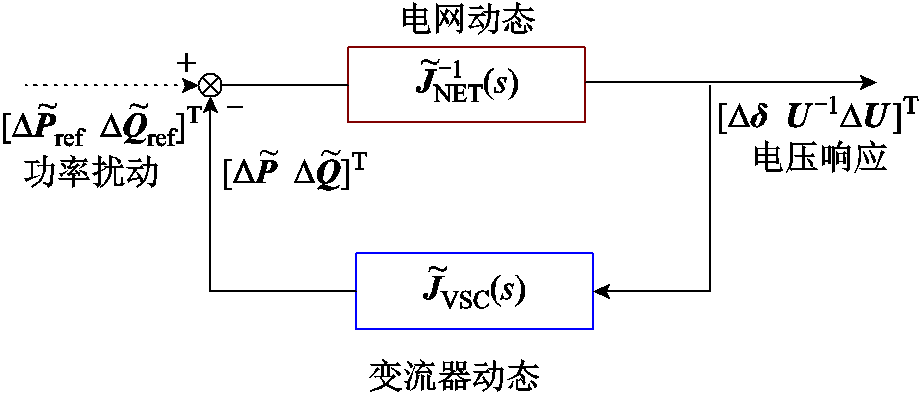
图2 多馈入系统功率扰动-电压闭环响应框图
Fig.2 Block diagram of voltage closed-loop response for a multi-infeed system under power disturbances
具体地,图2中闭环系统以多变流器功率扰动为输入变量,以系统节点电压为输出变量。其中,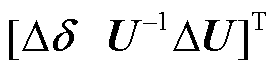 表示极坐标下节点电压相角和幅值动态;
表示极坐标下节点电压相角和幅值动态;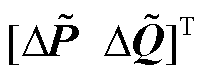 表示n个变流器馈入的归一化有功功率和无功功率动态[12],即
表示n个变流器馈入的归一化有功功率和无功功率动态[12],即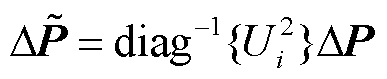 ,
,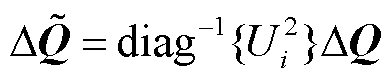 ;
;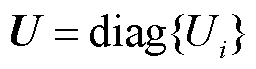 表示节点电压矩阵,
表示节点电压矩阵, 表示第i个变流器节点电压幅值,
表示第i个变流器节点电压幅值,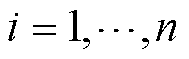 ;
;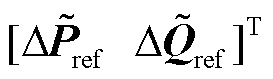 表示变流器馈入功率扰动向量,描述由于风、光条件变化而导致多变流器功率给定值发生偏离或波动;
表示变流器馈入功率扰动向量,描述由于风、光条件变化而导致多变流器功率给定值发生偏离或波动;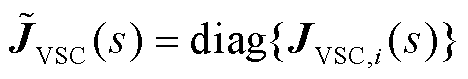 表示多变流器的雅可比传递函数矩阵,计及从交流端口看进去的n个馈入变流器的动态;
表示多变流器的雅可比传递函数矩阵,计及从交流端口看进去的n个馈入变流器的动态; 表示电网雅可比传递函数矩阵,计及变流器出口线路以及与变流器之间联络线路的动态,特别地,当s=0时
表示电网雅可比传递函数矩阵,计及变流器出口线路以及与变流器之间联络线路的动态,特别地,当s=0时 即为静态下电网潮流雅可比矩阵。频域传递函数矩阵
即为静态下电网潮流雅可比矩阵。频域传递函数矩阵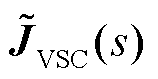 与
与 的具体推导思路与文献[6]一致。
的具体推导思路与文献[6]一致。
系统强度主要从稳定性与抗扰性(鲁棒性)两个方面对受扰后节点电压的响应性能提出要求[7],即要求图1中的多馈入系统具有抵抗电压失稳或抵抗电压偏移的能力。以下分别从这两个方面论述量化多馈入系统强度的基本方法,为后续分析变流器特性对系统强度的影响规律提供理论基础。
为了便于后文表述,将图2中多馈入系统闭环传递函数模型抽象表示为
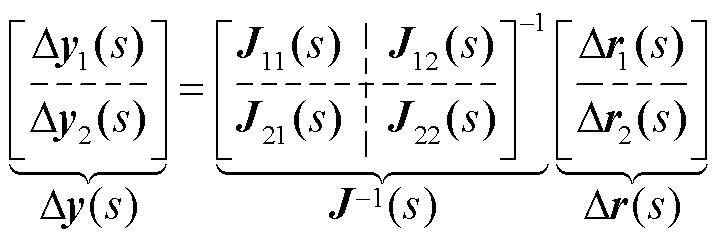 (1)
(1)
式中,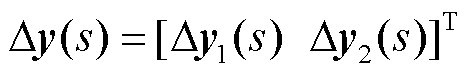 为任一坐标系下的输出电压向量,如图2中极坐标系下的电压响应
为任一坐标系下的输出电压向量,如图2中极坐标系下的电压响应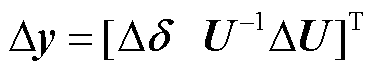 ;
;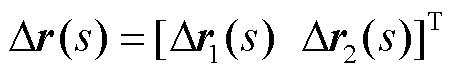 为任一坐标系下的输入扰动向量,如图2中直角坐标系下的功率扰动
为任一坐标系下的输入扰动向量,如图2中直角坐标系下的功率扰动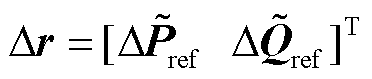 ;
;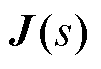 为闭环传递函数矩阵的逆,反映了扰动-响应之间的灵敏度,如图2中功率扰动-电压响应之间的闭环传递函数矩阵
为闭环传递函数矩阵的逆,反映了扰动-响应之间的灵敏度,如图2中功率扰动-电压响应之间的闭环传递函数矩阵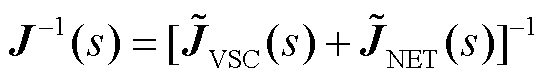 ;
;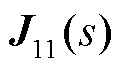 、
、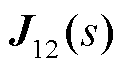 、
、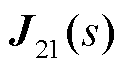 、
、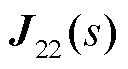 为对
为对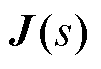 分块后的子矩阵。
分块后的子矩阵。
首先,稳定性是对多馈入系统动态性能的最基本要求,从稳定性维度评估系统强度即检验受扰后电压响应的有界性[13]。具体地,为了保证图2中多馈入系统输出电压响应向量有界,由式(1),考察任一频率点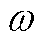 下
下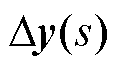 (令
(令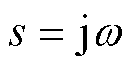 )的模态分量为
)的模态分量为
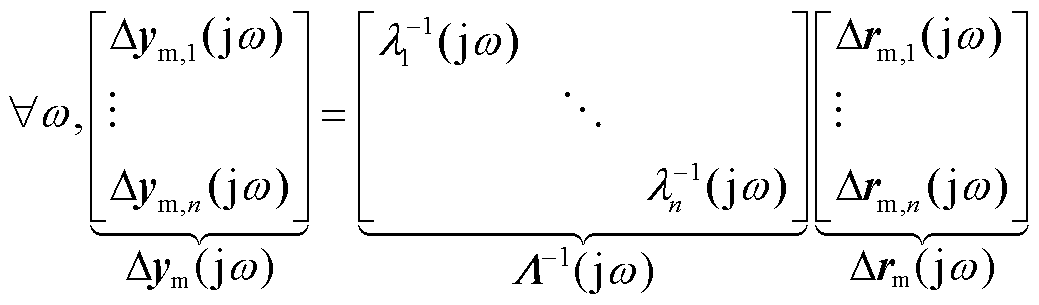 (2)
(2)
式中,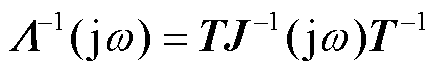 为对角矩阵,其对角元是
为对角矩阵,其对角元是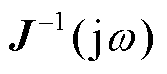 的特征(值)轨迹
的特征(值)轨迹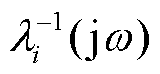 ;
;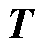 为非奇异坐标变换矩阵,它将电压响应向量与功率扰动向量分别变换到模态坐标系中,即得
为非奇异坐标变换矩阵,它将电压响应向量与功率扰动向量分别变换到模态坐标系中,即得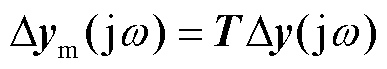 与
与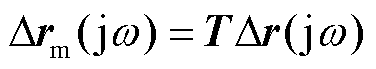 ;
;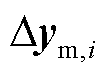 与
与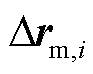 分别为模态
分别为模态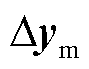 和
和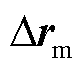 的第i个分量。
的第i个分量。
式(2)中特征(值)轨迹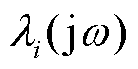 (
(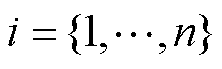 )表示了模态坐标系下各节点电压响应对功率扰动的灵敏度的倒数。若要避免受扰后电压响应的无限变化,则应使得最小模特征(值)轨迹(记作
)表示了模态坐标系下各节点电压响应对功率扰动的灵敏度的倒数。若要避免受扰后电压响应的无限变化,则应使得最小模特征(值)轨迹(记作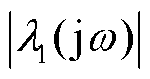 )远离原点,即
)远离原点,即
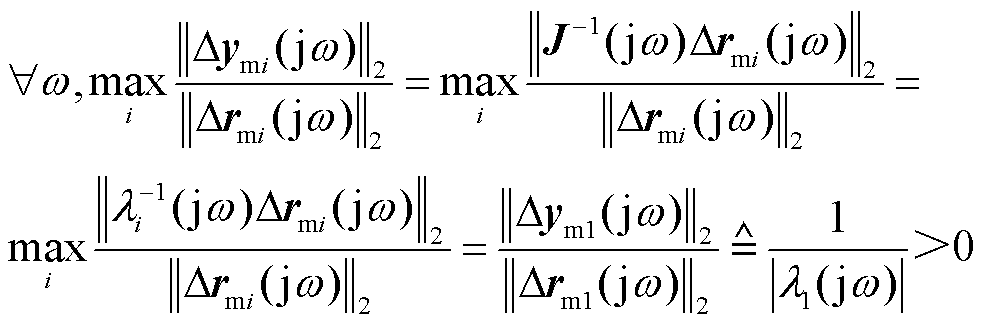 (3)
(3)
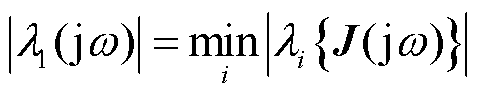 (4)
(4)
式中,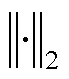 表示向量的
表示向量的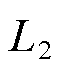 范数[13]。
范数[13]。
因此,由式(3)、式(4)可知,闭环传递函数矩阵逆的最小模特征(值)轨迹提供了从稳定性维度量化系统强度的方法,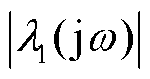 的物理意义是闭环主导特征(值)轨迹到原点的最近距离,其越小、越接近于零,则稳定裕度越小[13]。值得一提的是,稳定性维度下的系统强度分析并不一定基于式(1)中的全阶雅可比传递函数矩阵,还可基于其降阶后的传递函数矩阵分析,不影响判稳结果。例如,利用Q-V灵敏度法分析静态电压稳定问题时采用了无功功率扰动-电压幅值响应之间的降阶传递函数矩阵[14];利用P-δ灵敏度法分析功角稳定问题时采用了有功功率扰动-电压相角响应之间的降阶传递函数矩阵[14]。
的物理意义是闭环主导特征(值)轨迹到原点的最近距离,其越小、越接近于零,则稳定裕度越小[13]。值得一提的是,稳定性维度下的系统强度分析并不一定基于式(1)中的全阶雅可比传递函数矩阵,还可基于其降阶后的传递函数矩阵分析,不影响判稳结果。例如,利用Q-V灵敏度法分析静态电压稳定问题时采用了无功功率扰动-电压幅值响应之间的降阶传递函数矩阵[14];利用P-δ灵敏度法分析功角稳定问题时采用了有功功率扰动-电压相角响应之间的降阶传递函数矩阵[14]。
需要说明的是,本文探讨变流器特性对系统强度的影响,关注弱电网中变流器电压幅值/相角失稳模态,对应通常所说的电压稳定性或同步稳定问题(将分别在第2节与第3节具体分析);而串联补偿电容参与的次同步谐振,以及并联补偿电容等滤波器参与的谐波不稳定等问题与系统强度之间并没有强相关性[15],本文不做讨论。
另一方面,相较于稳定性,抗扰性能是对多馈入系统动态性能更为严苛的要求,不仅要求受扰后电压响应有界不失稳,还要求其偏移量小[7]。具体地,为了保证图2中多馈入系统的电压抗扰性,由式(1),单位扰动下的输出电压响应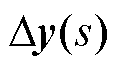 应尽量小,即应降低电压响应对外界扰动的最大灵敏度,有
应尽量小,即应降低电压响应对外界扰动的最大灵敏度,有
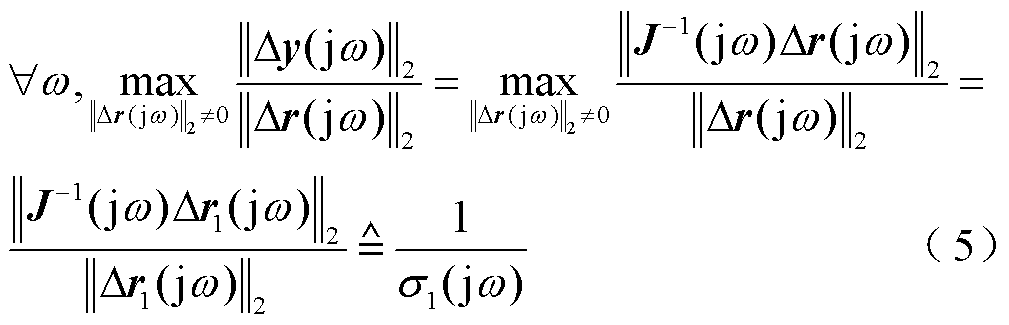
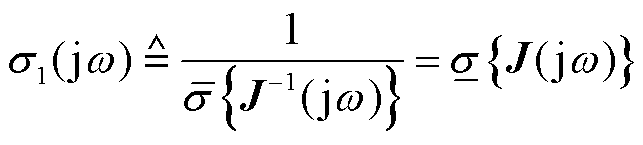 (6)
(6)
式中,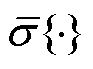 和
和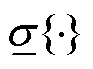 分别为最大和最小奇异值;
分别为最大和最小奇异值;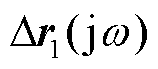 为矩阵
为矩阵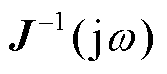 关于其最大奇异值(即
关于其最大奇异值(即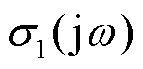 的倒数)的奇异向量。
的倒数)的奇异向量。
由式(5)、式(6)可知,闭环传递函数矩阵逆的最小奇异值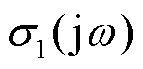 反映了受到所有可能方向扰动后输出电压的最大偏移程度,
反映了受到所有可能方向扰动后输出电压的最大偏移程度,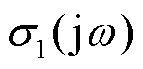 越小,受扰后电压偏移越剧烈。因此,它表征了系统抵抗电压失稳的能力,提供了从抗扰性能维度量化系统强度的方法。
越小,受扰后电压偏移越剧烈。因此,它表征了系统抵抗电压失稳的能力,提供了从抗扰性能维度量化系统强度的方法。
值得一提的是,最小奇异值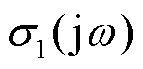 在数学上还指示了闭环传递函数矩阵逆的奇异性,
在数学上还指示了闭环传递函数矩阵逆的奇异性,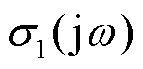 是否为零可表征系统是否对扰动具有无限增益,进而也可构成稳定性判据[14],式(4)中最小模特征值是其近似,它们的关系为
是否为零可表征系统是否对扰动具有无限增益,进而也可构成稳定性判据[14],式(4)中最小模特征值是其近似,它们的关系为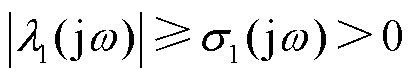 。
。
多馈入系统强度是变流器-电网所构成闭环系统动态性能的综合表征,但多变流器经网络相互耦合,往往难以厘清多变流器特性对系统强度存在何种影响规律。因此,为了便于描述与总结后续影响分析结果,首先引入电力电子变流器多样性(简称“变流器多样性”)的概念。
定义1:变流器多样性指通过电网互联的多馈入电力电子变流器的运行工况、控制方式等方面非同质化。例如,笔者认为至少有以下三种表现形式。
1)变流器功率因数多样性:指多变流器以其灵活的有功功率和无功功率调节能力,可运行于不相同的功率因数(Power Factor, PF),而不均以额定单位功率因数运行。
2)变流器运行状态多样性:指多变流器既可运行于发电状态,如作为新能源并网接口的变流器(Converter Interfaced Generator, CIG),也可运行于充电状态,如作为储能并网接口的变流器(Converter Interfaced Load, CIL)[2],而不是均运行于发电状态。
3)变流器控制方式多样性:指多变流器中既有采用跟网型(Grid-Following, GFL)控制的变流器,也有采用构网型(Grid-Forming, GFM)控制的变流器[2],而不均采用单一控制方式。
需要说明的是,本文关注的变流器多样性主要是多变流器在运行工况、控制方式等层面的内在差异,而不是表面上变流器种类或型号的差异,例如不同类型的风机变流器或光伏变流器。
此外,所引入的变流器多样性概念在内涵上借鉴了复杂系统中的“多样性”概念,其讨论个体多样性对复杂系统功能或性能的作用规律。例如,大量研究表明,保障生态系统的“物种多样性”有利于保障和提升生态系统鲁棒性和稳定性[16]。基于类似理念,引入变流器多样性概念更有利于理解与总结多变流器特性对电力系统动态性能的影响规律,进而有望帮助工程人员深入认识多馈入系统的动态性能需求,为多馈入系统规划运行提供基础理论指导。
由变流器多样性概念引出本文所关注的问题是:多变流器在运行控制方面的多样性如何影响系统强度?是否存在规律?
为此,本文的解决思路是:
1)1.1节、1.2节中多馈入系统闭环建模与强度量化方法计及了多变流器特性,在此基础上建立更具物理意义的系统强度评估指标。
2)对比分析均一化或多样化变流器特性对系统强度指标的作用,由指标的数学性质论证影响规律。
基于上述思路,第2节、第3节将分别论证变流器功率因数多样性与运行状态多样性对稳定性维度下系统强度的影响规律;第4节论证变流器控制方式多样性对抗扰性维度下系统强度的影响规律;第5节对理论分析结果作仿真验证。
本节由第1.2节中系统强度基本量化方法,进一步聚焦电压稳定问题,建立系统强度评估指标,解析变流器功率因数多样性对系统强度的提升规律。
为保证平衡点存在性或潮流可解性,多馈入系统必须保证静态电压稳定[14]。考虑到新能源变流器多采用跟网型控制,其有功-无功外环控制作用使得变流器静态下呈恒功率源特性[6],即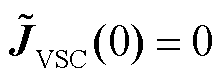 (取
(取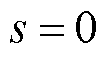 表示分析零频段处的传递函数特性),故以下重点关注图2中电网潮流雅可比矩阵
表示分析零频段处的传递函数特性),故以下重点关注图2中电网潮流雅可比矩阵 。基于文献[6]中的假设(如不特别说明,本文所有推导分析的假设均与文献[6]相同),
。基于文献[6]中的假设(如不特别说明,本文所有推导分析的假设均与文献[6]相同), 表达式为
表达式为
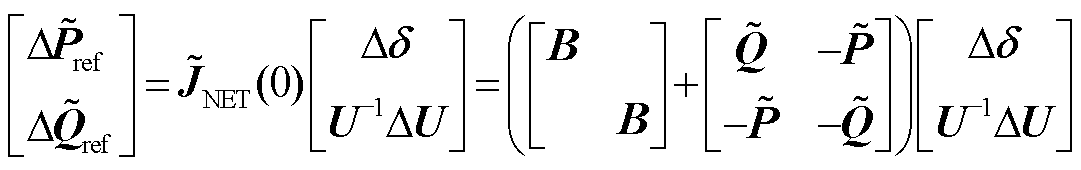 (7)
(7)
式中,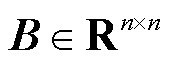 为保留n馈入变流器节点并删去无穷大节点所在行列的网络电纳矩阵[6],该电纳矩阵是通用的,不局限于多变流器并列运行等特殊的网络拓扑,这使本文分析结果能适应更一般性的多馈入系统;
为保留n馈入变流器节点并删去无穷大节点所在行列的网络电纳矩阵[6],该电纳矩阵是通用的,不局限于多变流器并列运行等特殊的网络拓扑,这使本文分析结果能适应更一般性的多馈入系统;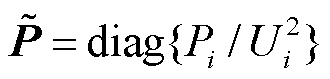 与
与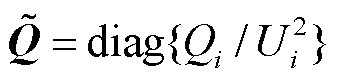 分别为变流器归一化有功功率与无功功率矩阵,
分别为变流器归一化有功功率与无功功率矩阵,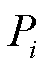 和
和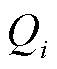 分别为第i个变流器馈入的有功功率和无功功率稳态值(取馈入电网为正方向)。
分别为第i个变流器馈入的有功功率和无功功率稳态值(取馈入电网为正方向)。
式(7)描述了静态时多馈入系统的功率扰动-电压响应过程。基于Q-V灵敏度的经典电压稳定分析方法是由电网无功功率与电压的强相关性,考虑系统受无功功率扰动下(即式(7)中扰动向量选取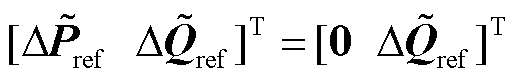 )节点电压幅值的响应结果[14]。而本节为分析新能源变流器运行于多种功率因数对系统强度的影响,拟分析复功率扰动形式下的电压响应,可视为经典Q-V灵敏度法在电力电子多馈入系统中的推广。
)节点电压幅值的响应结果[14]。而本节为分析新能源变流器运行于多种功率因数对系统强度的影响,拟分析复功率扰动形式下的电压响应,可视为经典Q-V灵敏度法在电力电子多馈入系统中的推广。
将式(7)作等价变换得
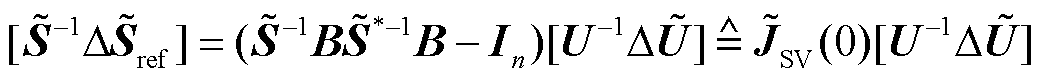 (8)
(8)
其中
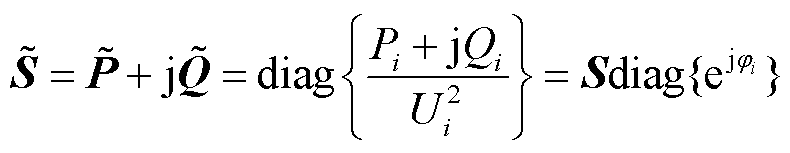 (9)
(9)
式中,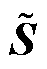 为归一化复功率矩阵[12];
为归一化复功率矩阵[12];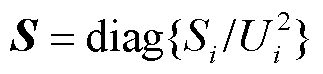 为归一化视在功率矩阵,
为归一化视在功率矩阵,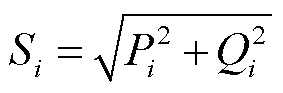 为第i个变流器的视在功率;
为第i个变流器的视在功率;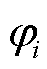 为第i个变流器的功率因数角,
为第i个变流器的功率因数角,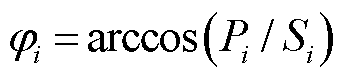 ,
,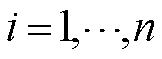 ;
;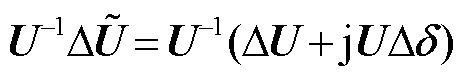 为受扰后的电压向量;
为受扰后的电压向量;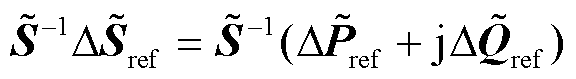 为按当前馈入功率水平规范化后的复功率扰动向量;
为按当前馈入功率水平规范化后的复功率扰动向量;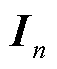 为n阶单位阵;*为矩阵的共轭转置[17];
为n阶单位阵;*为矩阵的共轭转置[17];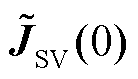 为静态时复功率扰动和节点电压响应之间的灵敏度矩阵。式(8)、式(9)的推导过程见附录。
为静态时复功率扰动和节点电压响应之间的灵敏度矩阵。式(8)、式(9)的推导过程见附录。
结合式(3),电压稳定维度下的系统强度可由灵敏度矩阵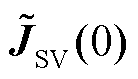 的最小(模)特征值
的最小(模)特征值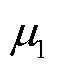 评估(注意到
评估(注意到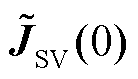 相似于一实对称阵,且电压稳定时模态电压与模态功率的变化方向一致[14],
相似于一实对称阵,且电压稳定时模态电压与模态功率的变化方向一致[14],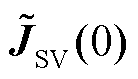 特征值均大于零,最小特征值即为最小模特征值,证明参照后文命题1),且等价于
特征值均大于零,最小特征值即为最小模特征值,证明参照后文命题1),且等价于
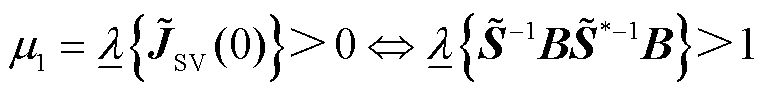 (10)
(10)
式中,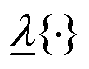 为求矩阵最小特征值。
为求矩阵最小特征值。
式(10)说明了最小特征值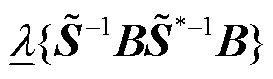 接近于1的程度(即
接近于1的程度(即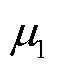 接近于0的程度)可表征电压稳定裕度,当
接近于0的程度)可表征电压稳定裕度,当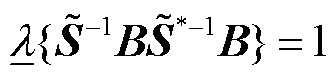 (即
(即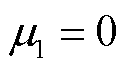 )时,矩阵
)时,矩阵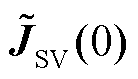 奇异,任何方向的功率扰动都将导致主导模态电压的无限变化,而引发电压崩溃。因此,由式(10)建立如下系统强度指标。
奇异,任何方向的功率扰动都将导致主导模态电压的无限变化,而引发电压崩溃。因此,由式(10)建立如下系统强度指标。
定义2:电压稳定维度下的系统强度指标定义为最小特征值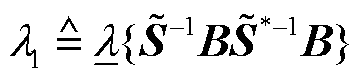 ,物理上反映了静态下多馈入系统的功率-电压灵敏度。电压稳定判据为:
,物理上反映了静态下多馈入系统的功率-电压灵敏度。电压稳定判据为: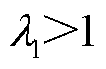 时判定电压稳定,
时判定电压稳定,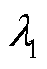 越大,受扰后系统抵抗静态电压失稳的能力越强;
越大,受扰后系统抵抗静态电压失稳的能力越强;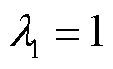 对应临界稳定。
对应临界稳定。
值得一提的是,定义2中的强度指标是广义短路比[6]或运行广义短路比(Operational gSCR, OgSCR)[18]在任意功率因数场景下的推广,且它们的临界阈值都是1。具体依据为:当所有变流器都运行于额定工况或单位功率因数时,式(9)中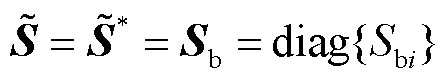 或
或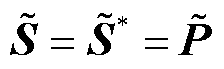 成立,其中
成立,其中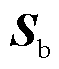 表示变流器容量矩阵,
表示变流器容量矩阵,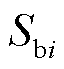 表示第
表示第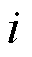 个变流器的容量,进而基于最小特征值
个变流器的容量,进而基于最小特征值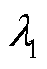 的电压稳定判据退化为基于gSCR或OgSCR的判据,即
的电压稳定判据退化为基于gSCR或OgSCR的判据,即
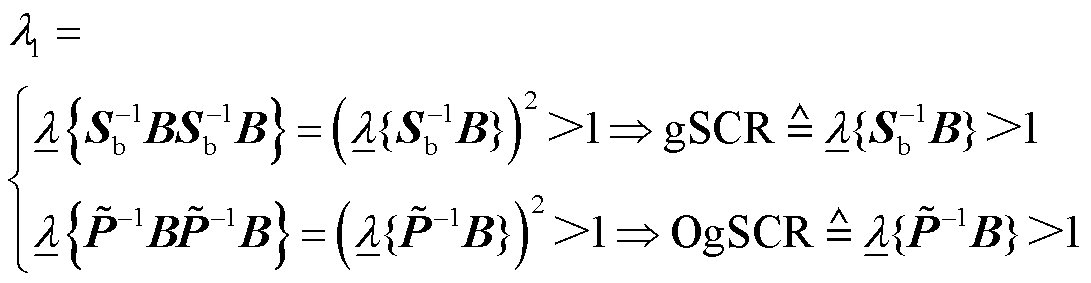 (11)
(11)
基于式(11)的gSCR或OgSCR指标可计及多变流器容量与有功出力的差异,前期工作说明了非均一化地调整多变流器容量与有功出力可最大程度地提升系统强度[11],本文在此基础上将重点关注功率因数的非均一化影响。
本节基于2.1节中所提指标的数学性质,进一步论证1.3节中的变流器功率因数多样性可从电压稳定维度提升系统强度。
考虑到变流器功率因数具有均一性与多样性两种运行场景(分别记为场景1和场景2),如图3所示,即场景1中各变流器复功率矢量的功率因数角相同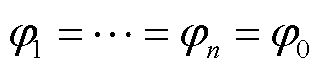 ,而场景2中功率因数角
,而场景2中功率因数角 则不完全相同,即具有多样性。
则不完全相同,即具有多样性。
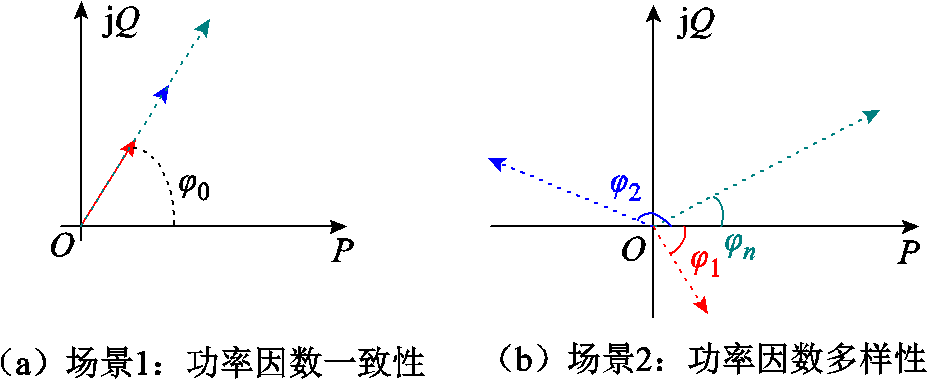
图3 多变流器功率因数一致性与多样性示意图
Fig.3 Diagram of multi-converter power factor consistency and diversity
场景1和场景2中各变流器节点电压幅值 (正常运行要求在额定值1.0(pu)附近)、视在功率
(正常运行要求在额定值1.0(pu)附近)、视在功率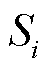 以及网络参数(即导纳矩阵B)均保持相同。场景1与场景2的区别仅在于上述变流器运行功率因数角
以及网络参数(即导纳矩阵B)均保持相同。场景1与场景2的区别仅在于上述变流器运行功率因数角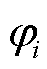 的性质不同。在此基础上,功率因数多样性对系统强度的影响有如下命题。
的性质不同。在此基础上,功率因数多样性对系统强度的影响有如下命题。
命题1:其他条件相同时,系统在运行场景2下的静态电压稳定性优于运行场景1,即在两种场景下系统强度指标满足
 (12)
(12)
证明:首先将矩阵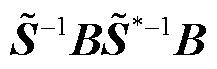 作以下相似变换,不影响其特征值
作以下相似变换,不影响其特征值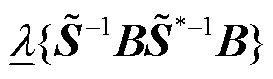 。
。
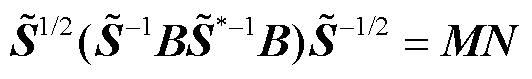 (13)
(13)
其中
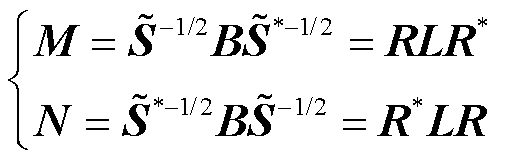 (14)
(14)
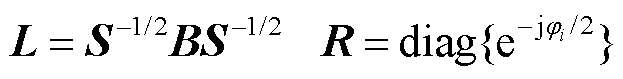 (15)
(15)
由于视在功率矩阵和网络导纳矩阵都是正定矩阵(即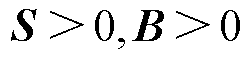 ),故
),故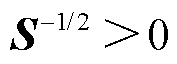 ,L是正定的;注意到
,L是正定的;注意到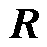 是酉矩阵,有
是酉矩阵,有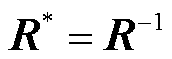 ,故矩阵M和N也是正定的(即
,故矩阵M和N也是正定的(即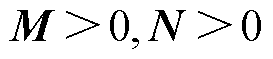 )。还可推知
)。还可推知
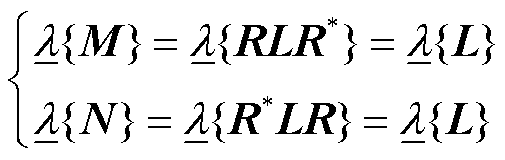 (16)
(16)
进一步,考虑场景1中多变流器功率因数角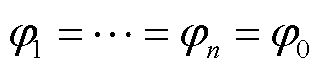 ,使得
,使得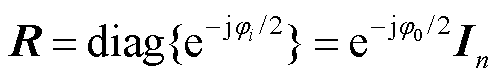 ;再结合式(13)~式(16),系统强度指标为
;再结合式(13)~式(16),系统强度指标为
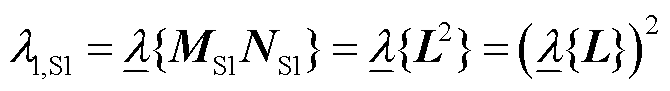 (17)
(17)
而考虑场景2中多变流器功率因数角 不完全相同,此时系统强度指标为
不完全相同,此时系统强度指标为
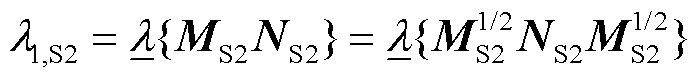 (18)
(18)
注意到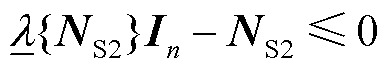 ,有矩阵不等式
,有矩阵不等式
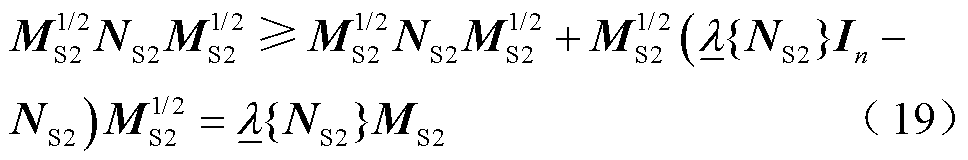
结合式(17)~式(19),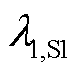 和
和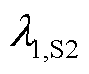 满足
满足
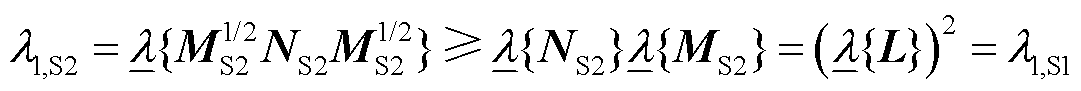 (20)
(20)
证毕。
由命题1可知,从电压稳定维度看,变流器功率因数多样性有助于增大最小特征值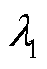 到临界阈值1的距离,进而相比于变流器均一化功率因数运行时提升了系统强度。上述命题也从理论上说明了新能源等装备都运行于同一功率因数下不一定最好,从功率因数多样性角度制定的协调措施可提升系统强度。
到临界阈值1的距离,进而相比于变流器均一化功率因数运行时提升了系统强度。上述命题也从理论上说明了新能源等装备都运行于同一功率因数下不一定最好,从功率因数多样性角度制定的协调措施可提升系统强度。
本节由第1.2节中量化系统强度的基本方法,进一步聚焦同步稳定问题,建立系统强度评估指标,解析变流器运行状态多样性对系统强度的提升规律。
相比于同步发电机基于转子运动的“物理同步”机制,CIG或CIL等变流器一般采用基于锁相环(Phase-Locked Loop, PLL)的跟网型“控制同步”机制[19]。为了分析PLL动态主导的小扰动同步稳定性,考虑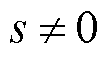 时的雅可比频域传递函数模型,仍依据图2中所描述的功率扰动-电压响应关系推导得到
时的雅可比频域传递函数模型,仍依据图2中所描述的功率扰动-电压响应关系推导得到
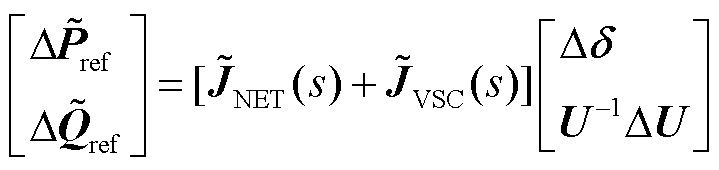 (21)
(21)
其中
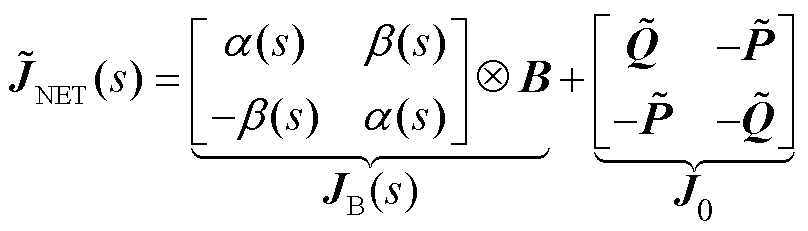 (22)
(22)
式中,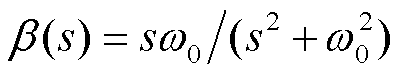 ,
,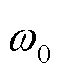 为同步旋转角频率,
为同步旋转角频率,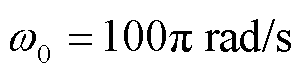 ;
;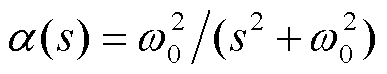 ;
;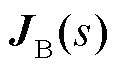 为网络侧雅可比传递函数矩阵
为网络侧雅可比传递函数矩阵 中与电网阻抗动态特性相关的部分;
中与电网阻抗动态特性相关的部分;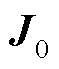 为
为 中与稳态馈入功率相关的部分。
中与稳态馈入功率相关的部分。
考虑锁相环带宽内的小扰动同步稳定问题时,变流器呈现电流源特性,可忽略电流环与滤波电路等快尺度动态而主要聚焦锁相环动态[20],故其传递函数矩阵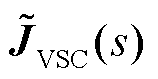 可简化为
可简化为
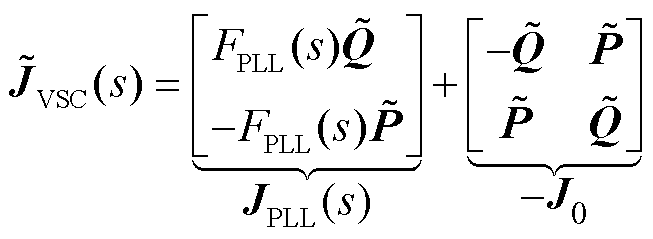 (23)
(23)
式中,传递函数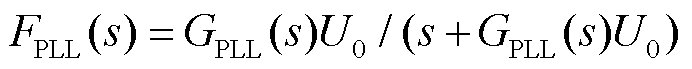 ,U0为各变流器并网点电压稳态值,U0≈1.0(pu),
,U0为各变流器并网点电压稳态值,U0≈1.0(pu),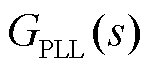 为PLL的PI控制传递函数。
为PLL的PI控制传递函数。
由于本节聚焦运行点影响,为简化分析,假设各变流器PLL参数相同,即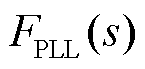 相同。
相同。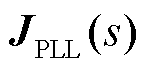 记为变流器侧雅可比传递函数矩阵
记为变流器侧雅可比传递函数矩阵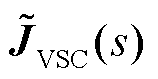 中与PLL动态相关的部分;
中与PLL动态相关的部分;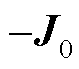 记为
记为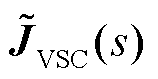 中与稳态馈入功率相关的部分。此外,从式(21)所示的闭环响应来看,
中与稳态馈入功率相关的部分。此外,从式(21)所示的闭环响应来看,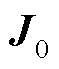 项可消去,故关注
项可消去,故关注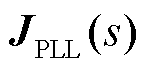 和
和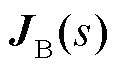 的性质。
的性质。
式(21)描述了计及PLL动态的多馈入系统功率扰动-电压响应过程。考虑到基于PLL的变流器同步本质是受功率因数角驱动下的功率平衡过程[19-20],故进一步推导功率因数角扰动-电压相角回路方程(即φ-δ灵敏度关系),以获得更具有物理意义的分析模型,可视为传统同步机电力系统中的P-δ灵敏度方法在电力电子多馈入系统的推广[14]。具体地,将式(21)中的功率扰动向量变换至极坐标系,有
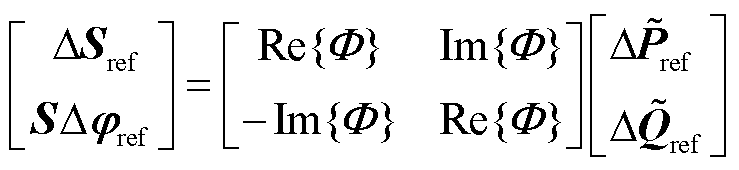 (24)
(24)
式中,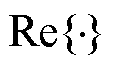 和
和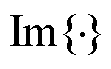 分别为取实部与虚部;
分别为取实部与虚部;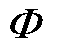 为功率因数角矩阵,
为功率因数角矩阵,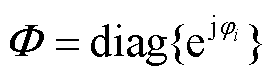 ;
;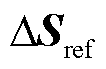 、
、 分别为视在功率和功率因数角组成的扰动向量,
分别为视在功率和功率因数角组成的扰动向量,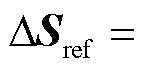
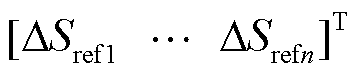 ,
,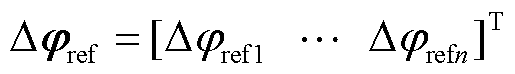 。
。
图4说明了经上述变换过程所得的系统功率因数角扰动-电压相角响应回路,是图2中雅可比传递函数模型降阶后的结果,用于同步稳定分析。其中,前向通路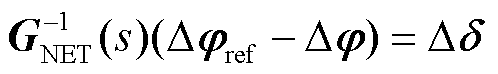 描述了功率因数角扰动由网络传递到各节点电压相角动态的过程,它与电网拓扑参数以及变流器馈入功率相关;反馈通路
描述了功率因数角扰动由网络传递到各节点电压相角动态的过程,它与电网拓扑参数以及变流器馈入功率相关;反馈通路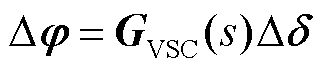 描述了通过跟踪电压相角的多变流器PLL动态。对应闭环特征方程为
描述了通过跟踪电压相角的多变流器PLL动态。对应闭环特征方程为
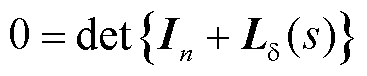 (25)
(25)
式中,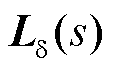 为开环回路传递函数,
为开环回路传递函数,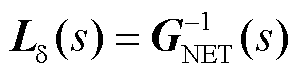
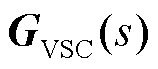 ,
,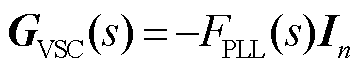 ,
,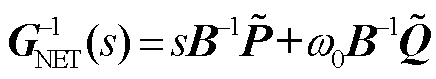 。式(25)的推导过程详见附录。
。式(25)的推导过程详见附录。
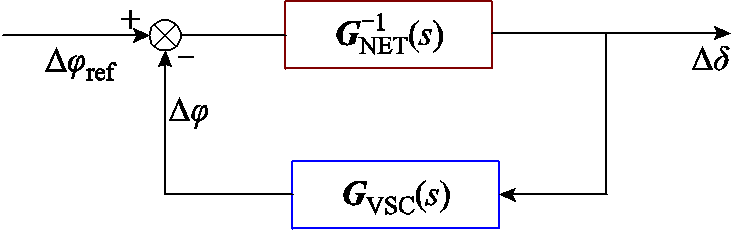
图4 多馈入系统相角回路模型
Fig.4 Phase loop model of multi-infeed system
结合第1.2节,为了保证图4中相角回路的稳定性且有一定裕度,应使其闭环特征轨迹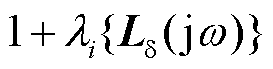 远离原点,即
远离原点,即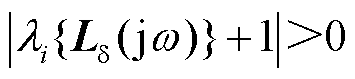 。进一步,该数学条件还可转换为电力系统中的正阻尼判据[21],其中特征轨迹在穿越频率处的实部反映了特征轨迹到原点的距离,即
。进一步,该数学条件还可转换为电力系统中的正阻尼判据[21],其中特征轨迹在穿越频率处的实部反映了特征轨迹到原点的距离,即
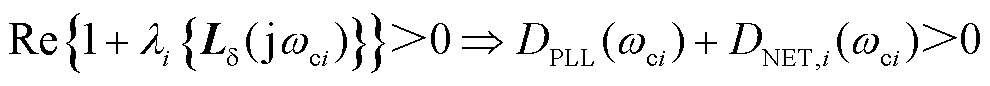 (26)
(26)
式中,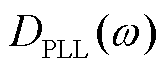 为变流器侧PLL的等效阻尼系数,
为变流器侧PLL的等效阻尼系数,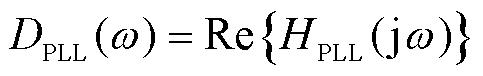 ,
,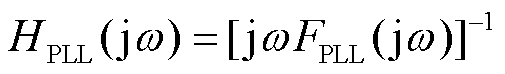 ;
; 为第i个闭环特征轨迹中电网侧等效阻尼系数,i=1,
为第i个闭环特征轨迹中电网侧等效阻尼系数,i=1, ,n,
,n,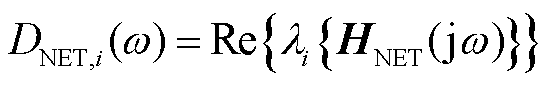 ,
,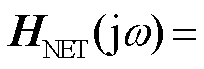
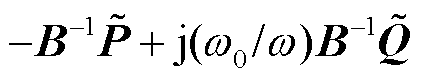 ;
;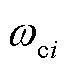 为第i个闭环特征轨迹的穿越角频率,即系统振荡频率满足
为第i个闭环特征轨迹的穿越角频率,即系统振荡频率满足
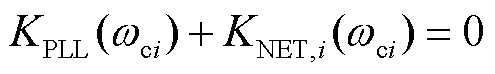 (27)
(27)
式中,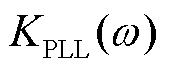 为变流器侧PLL等效弹性系数,
为变流器侧PLL等效弹性系数,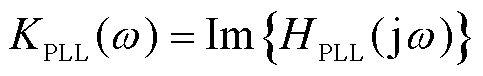 ;
;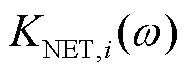 为第i个闭环特征轨迹中电网侧等效弹性系数,
为第i个闭环特征轨迹中电网侧等效弹性系数,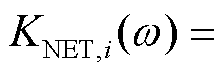
 。
。
式(26)、式(27)说明通过比较各特征轨迹在振荡频率处的PLL和网络等效阻尼系数的相对大小(即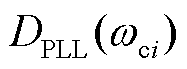 和
和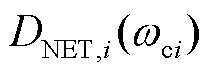 ),可判定图4中相角回路的稳定性。特别地,当变流器侧PLL参数给定时(即
),可判定图4中相角回路的稳定性。特别地,当变流器侧PLL参数给定时(即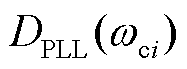 不变),具有最小网络阻尼系数的闭环特征轨迹即为主导特征轨迹,它决定了受扰后电压相角的稳定程度,因此,由式(26)建立如下系统强度指标。
不变),具有最小网络阻尼系数的闭环特征轨迹即为主导特征轨迹,它决定了受扰后电压相角的稳定程度,因此,由式(26)建立如下系统强度指标。
定义3:同步稳定维度下的系统强度指标定义为频率响应函数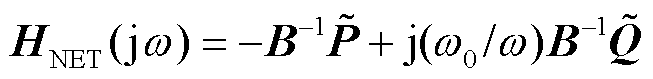 的最小网络阻尼系数
的最小网络阻尼系数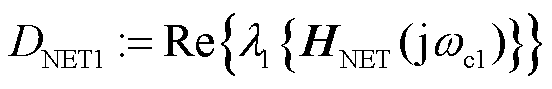 。它在物理上反映模态坐标下系统电压相角对功率因数角扰动的最大灵敏度,可量化同步稳定裕度:当
。它在物理上反映模态坐标下系统电压相角对功率因数角扰动的最大灵敏度,可量化同步稳定裕度:当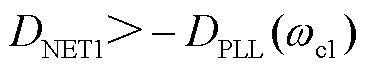 时判定同步稳定,
时判定同步稳定, 越大,受扰后系统抵抗小扰动同步失稳的能力越强;当
越大,受扰后系统抵抗小扰动同步失稳的能力越强;当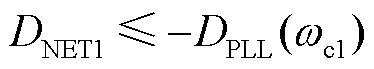 时判定阻尼不足导致同步失稳。
时判定阻尼不足导致同步失稳。
值得一提的是,定义3中的强度指标是广义短路比[6]或运行广义短路比[18]在任意功率因数场景下的推广,且阈值也与PLL动态密切相关[18]。具体依据为:当所有变流器都运行于额定工况或单位功率因数时,有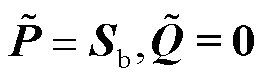 ,进而最小网络阻尼系数退化为gSCR或OgSCR,即
,进而最小网络阻尼系数退化为gSCR或OgSCR,即
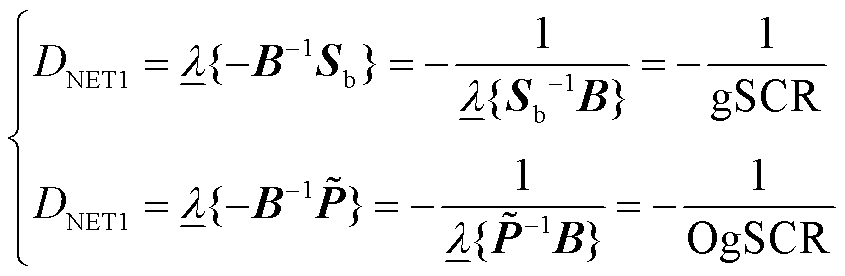 (28)
(28)
此时gSCR或OgSCR越小意味着 越小,变化趋势一致,均反映系统同步稳定性越弱,故
越小,变化趋势一致,均反映系统同步稳定性越弱,故 可视为gSCR或OgSCR的推广。
可视为gSCR或OgSCR的推广。
基于3.1节所提指标,本节进一步论证1.3节中的变流器运行状态多样性可从小扰动同步稳定维度提升系统强度。
为此,首先构建所有n馈入变流器均运行为CIG状态的场景1;并基于场景1,保持n1个变流器CIG运行状态不变而将n2个变流器切换为CIL状态,构建场景2(n1+n2=n)。多变流器运行状态均一性与多样性示意图如图5所示。场景1和场景2常见于新能源发电-储能变流器混联运行的系统中,差别在于储能变流器作为CIG(或CIL)运行时,变流器向电网注入有功功率(或从电网吸收有功功率),使得场景2具备变流器运行状态多样性。因此,相比于场景1,场景2中n2个CIL变流器吸收有功功率,数值为负,在节点电压幅值近似维持在额定值附近不变的前提下,场景1和场景2对应的变流器归一化有功功率矩阵满足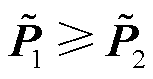 的不等关系。
的不等关系。
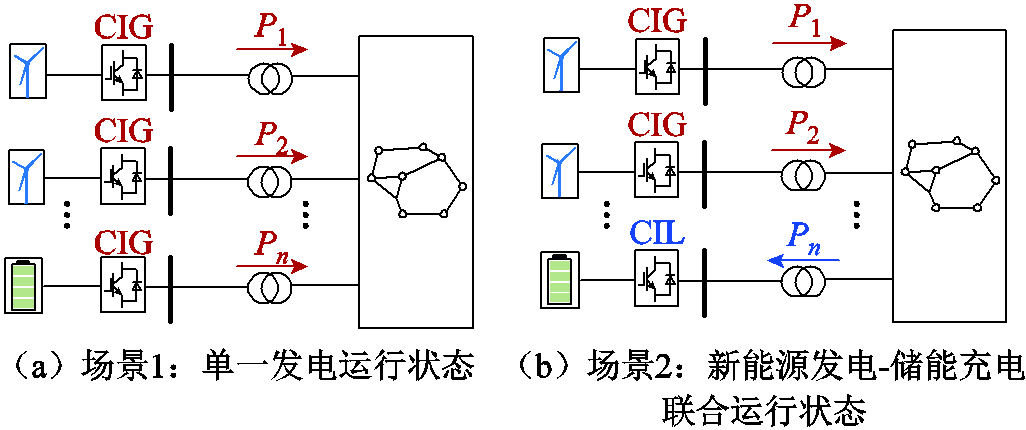
图5 多变流器运行状态均一性与多样性示意图
Fig.5 Diagram of multi-converter operation mode consistency and diversity
在此基础上,进一步考察场景1和场景2的小扰动同步稳定性差异,即有功功率变化对同步稳定维度下的系统强度指标的影响。有以下引理与命题:
引理1:作为小扰动同步稳定指标,最小网络阻尼系数 可表示为变流器归一化有功功率矩阵
可表示为变流器归一化有功功率矩阵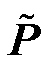 的Hermite二次型,即
的Hermite二次型,即
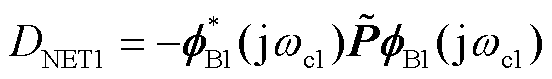 (29)
(29)
式中,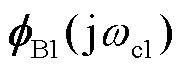 为矩阵
为矩阵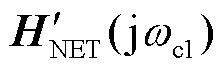 的归一化特征向量,即满足
的归一化特征向量,即满足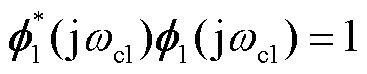 ,
,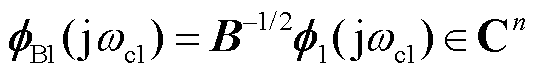 且
且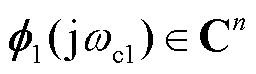 ;
;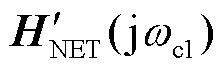 为网络频响函数矩阵
为网络频响函数矩阵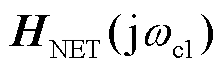 的相似矩阵,有
的相似矩阵,有
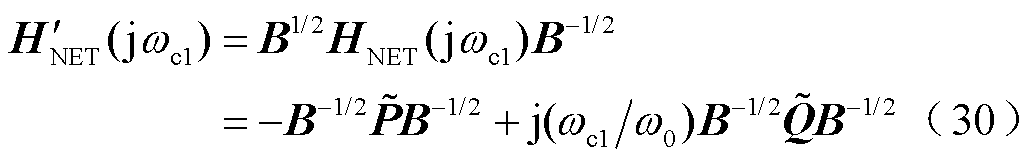
证明:见附录。
命题2:其他条件相同时,系统在运行场景2下的小扰动同步稳定性优于运行场景1,即二者的小扰动同步稳定指标满足
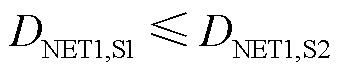 (31)
(31)
式中, 、
、 分别为场景1、场景2的最小网络阻尼系数。
分别为场景1、场景2的最小网络阻尼系数。
证明:由引理1将场景1与场景2的小扰动同步稳定指标分别写为Hermite二次型形式,即
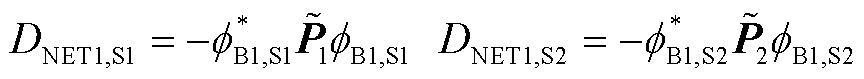 (32)
(32)
考虑到式(29)中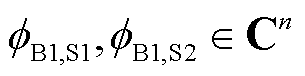 均通过归一化特征向量导出,满足
均通过归一化特征向量导出,满足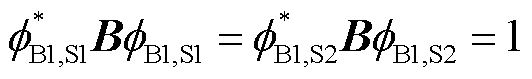 ,则存在一酉矩阵R使得
,则存在一酉矩阵R使得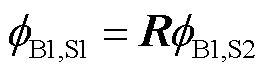 。式(32)可写为
。式(32)可写为
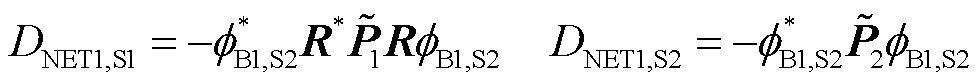 (33)
(33)
由于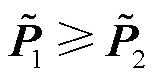 ,故它们的特征值满足不等关系:
,故它们的特征值满足不等关系: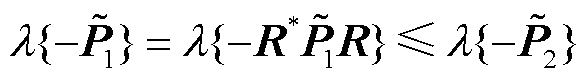 。再由文献[17]定理8.11可知,式(33)中的二次型也有不等关系
。再由文献[17]定理8.11可知,式(33)中的二次型也有不等关系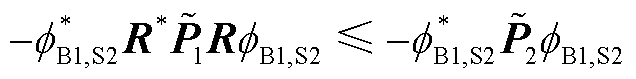 ,证毕。
,证毕。
由命题2可知,从小扰动同步稳定性维度看,变流器运行状态多样性有助于增大最小网络阻尼系数 ,进而相比变流器均处于发电运行状态时提升了系统强度。上述命题也从理论上说明了协调新能源场站中跟网型储能的运行状态有助于减轻馈入断面上的有功功率,提升同步稳定性,这与目前治理新能源场站次同步振荡的相关工程经验相互印证[22]。尽管实际工程环境中可能存在多种不确定性因素相互作用而使得有功-无功调节对稳定水平的改善机制更为复杂,但是本节所提出的影响规律是基于相角回路的机理模型导出的,该模型在分析锁相环主导的同步失稳模式时具有一定的鲁棒性[23],因此导出规律对工程实践仍具有一定的指导意义。
,进而相比变流器均处于发电运行状态时提升了系统强度。上述命题也从理论上说明了协调新能源场站中跟网型储能的运行状态有助于减轻馈入断面上的有功功率,提升同步稳定性,这与目前治理新能源场站次同步振荡的相关工程经验相互印证[22]。尽管实际工程环境中可能存在多种不确定性因素相互作用而使得有功-无功调节对稳定水平的改善机制更为复杂,但是本节所提出的影响规律是基于相角回路的机理模型导出的,该模型在分析锁相环主导的同步失稳模式时具有一定的鲁棒性[23],因此导出规律对工程实践仍具有一定的指导意义。
本节由第1.2节中量化系统强度的基本方法,进一步聚焦电压抗扰性能,建立系统强度评估指标,解析变流器控制方式多样性对系统强度的提升规律。
尽管1.2节已说明多馈入系统闭环传递函数矩阵逆的最小奇异值可反映电压抗扰性,但直接求解高维矩阵的奇异值轨迹较难[7],仍需要进一步建立实用化的系统强度指标来反映系统电压抵抗偏移的能力。为此,首先引入以下命题,为后续利用电网SCR直观表征电压抗扰性能提供理论基础。
命题3:无论基于图2中功率-电压为输入-输出变量的多馈入系统雅可比传递函数,还是基于图6中电流-电压为输入-输出变量的多馈入系统导纳传递函数(图6中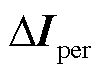 表示电流扰动向量,
表示电流扰动向量,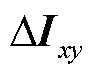 表示同步旋转xy坐标系下的电流向量,
表示同步旋转xy坐标系下的电流向量,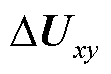 表示同步旋转xy坐标系下的节点电压向量),从抗扰性能维度评估系统强度的结果等价,即
表示同步旋转xy坐标系下的节点电压向量),从抗扰性能维度评估系统强度的结果等价,即
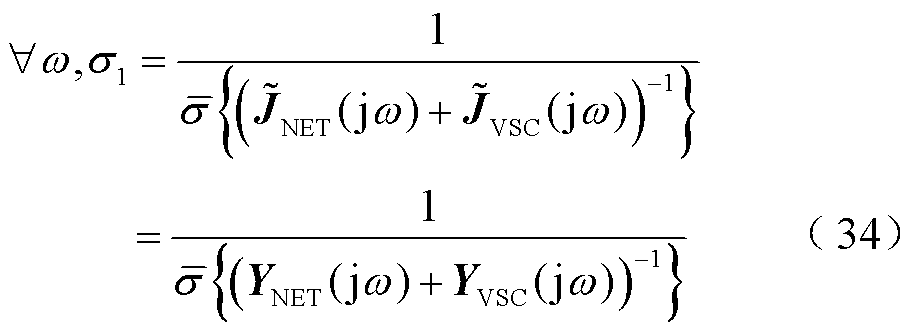
式中,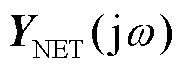 为电网导纳频域传递函数矩阵;
为电网导纳频域传递函数矩阵;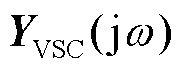 为多变流器导纳频域传递函数矩阵。
为多变流器导纳频域传递函数矩阵。
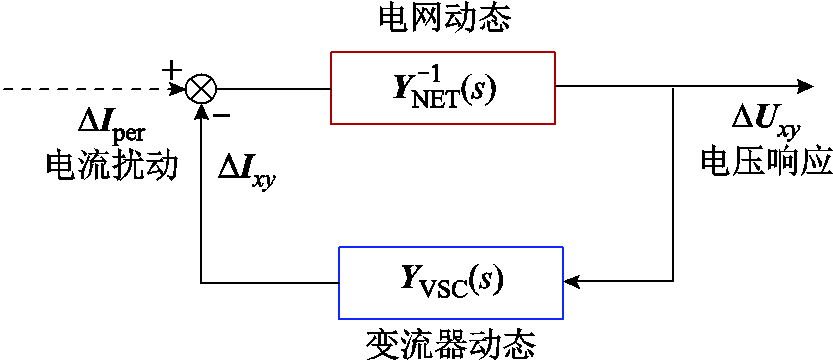
图6 多馈入系统电流扰动-电压闭环响应框图
Fig.6 Block diagram of voltage closed-loop response for a multi-infeed system under current disturbances
证明:见附录。
命题3将抗扰性能评估转换为考察图6所示系统电压对电流扰动的灵敏度,可在所关注的频段范围内取其峰值综合量化宽频段上的系统抗扰性,有
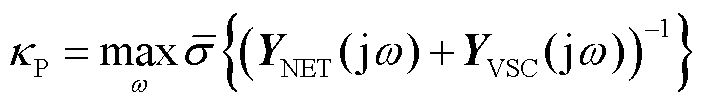 (35)
(35)
式中,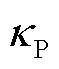 为闭环系统互补灵敏度峰值[13],
为闭环系统互补灵敏度峰值[13],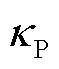 越小,说明系统输出电压对电流扰动的影响越不敏感。
越小,说明系统输出电压对电流扰动的影响越不敏感。
下面基于命题3说明电网导纳(或SCR)可作为抗扰性能维度下GFL或GFM变流器多馈入系统强度指标。为不失一般性,本文所考虑的GFM控制方式参照目前广泛使用的虚拟同步控制结构[24],其控制参数不依赖于广域设备。
具体地,考察图7a所示场景1(GFL变流器多馈入)与场景2(GFM变流器多馈入)的抗扰性,并采用式(6)中的最小奇异值量化,有
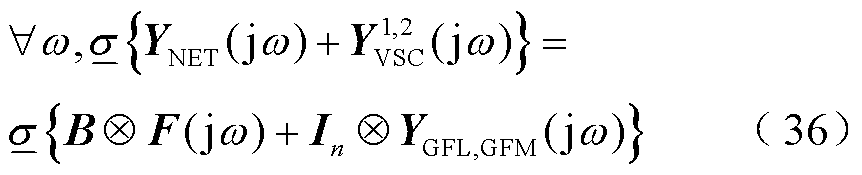
式中,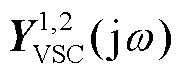 为场景1或场景2中的多变流器导纳传递函数,
为场景1或场景2中的多变流器导纳传递函数,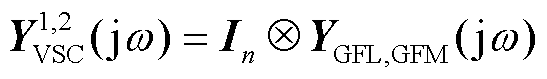 ,
, 为GFL或GFM变流器的单机导纳传递函数,所采用的具体控制结构与详细表达式见文献[24];
为GFL或GFM变流器的单机导纳传递函数,所采用的具体控制结构与详细表达式见文献[24];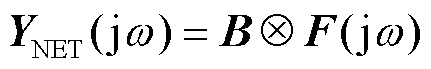 表示电网导纳传递函数;
表示电网导纳传递函数;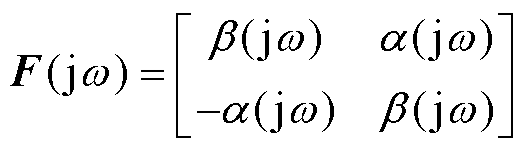 。
。
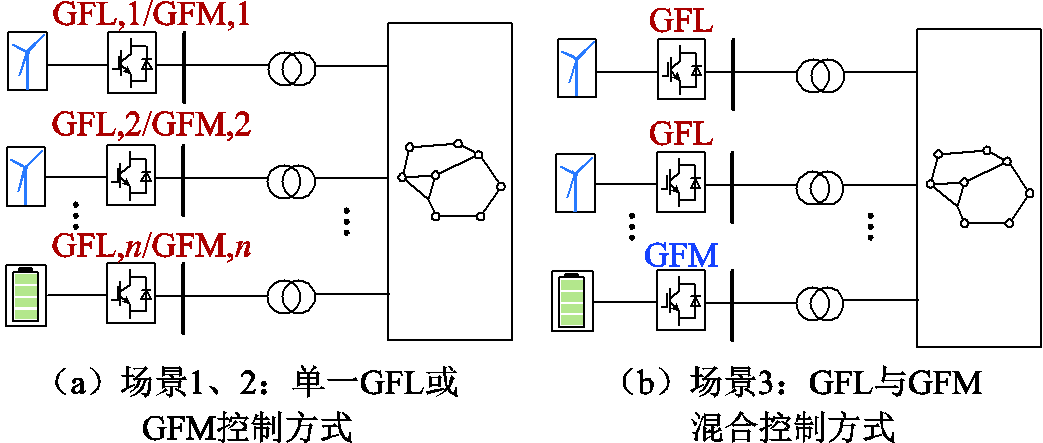
图7 多变流器控制方式一致性与多样性示意图
Fig.7 Diagram of multi-converter control scheme consistency and diversity
注意到,电网导纳矩阵B为正定矩阵,可酉相似对角化,有
 (37)
(37)
式中,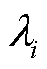 为矩阵B的特征值,
为矩阵B的特征值,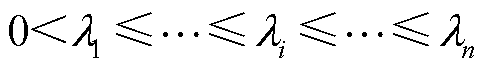 ;
;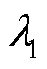 、
、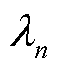 分别为矩阵B的最小特征值、最大特征值,
分别为矩阵B的最小特征值、最大特征值,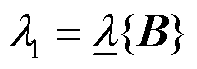 和
和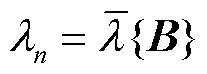 。当取变流器额定容量与系统容量基准一致时,
。当取变流器额定容量与系统容量基准一致时,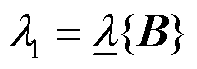 即为gSCR[6]。
即为gSCR[6]。
由奇异值对式(37)中酉变换的不变性[17],式(36)可进一步写为(为简洁起见,以下推导省略变量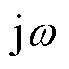 )
)
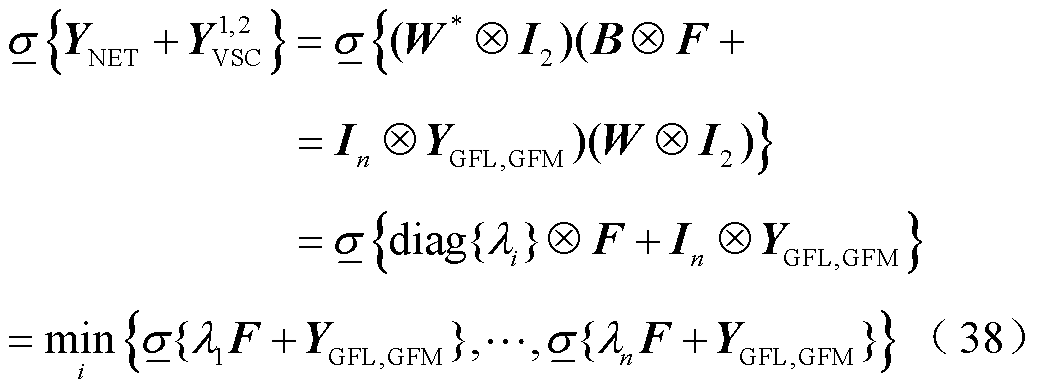
式(38)的物理含义是:场景1和场景2中的多馈入系统均可从抗扰性分析维度严格解耦为n个单馈入子系统;第i个单馈入子系统中的变流器接入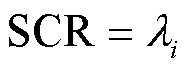 的等效电网;其中,抗扰性最差的单馈入子系统即决定了系统整体的抗扰性。考虑到GFL变流器接入低SCR的电网,系统抗扰性能差;而GFM变流器接入高SCR的电网,系统抗扰性能差[24]。因此,场景1和场景2中多馈入系统抗扰性分别由最小特征值
的等效电网;其中,抗扰性最差的单馈入子系统即决定了系统整体的抗扰性。考虑到GFL变流器接入低SCR的电网,系统抗扰性能差;而GFM变流器接入高SCR的电网,系统抗扰性能差[24]。因此,场景1和场景2中多馈入系统抗扰性分别由最小特征值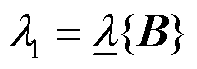 对应的GFL变流器单机子系统和最大特征值
对应的GFL变流器单机子系统和最大特征值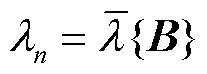 对应的GFM变流器单机子系统决定。
对应的GFM变流器单机子系统决定。
电网导纳矩阵最小与最大特征值(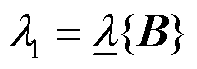 和
和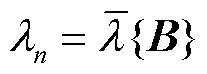 )可分别作为GFL与GFM变流器多馈入系统抗扰性能维度下的强度指标,其与场景1和场景2的闭环互补灵敏度峰值的关系分别为
)可分别作为GFL与GFM变流器多馈入系统抗扰性能维度下的强度指标,其与场景1和场景2的闭环互补灵敏度峰值的关系分别为
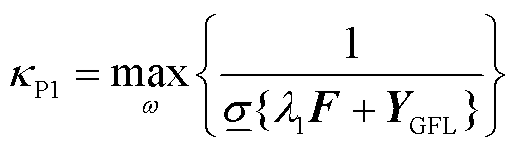 (39)
(39)
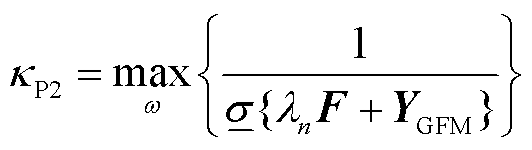 (40)
(40)
本节进一步关注跟网型与构网型变流器混联多馈入系统的抗扰性能,论证1.3节中的变流器控制方式多样性可从抗扰性能提升系统强度。
首先,考察图7b所示场景3(GFL与GFM变流器混联多馈入)的抗扰性,由式(6)得
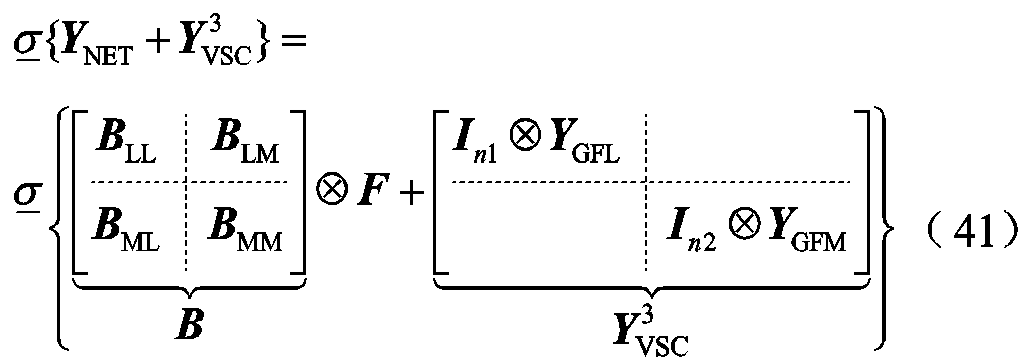
式中,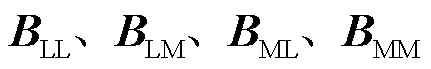 分别为电网导纳矩阵
分别为电网导纳矩阵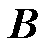 按GFL与GFM变流器接入节点分块后的子矩阵(令GFL变流器接入前n1个节点,GFM接入n1+1~n1+n2个节点,n1+n2=n);
按GFL与GFM变流器接入节点分块后的子矩阵(令GFL变流器接入前n1个节点,GFM接入n1+1~n1+n2个节点,n1+n2=n);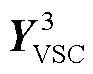 为场景3中多变流器导纳传递函数矩阵。
为场景3中多变流器导纳传递函数矩阵。
考虑式(41)中的最小奇异值在数学上反映了传递函数矩阵的亏秩程度[14],故以下可利用行列式为零的条件等价地反映最小奇异值的性质。式(41)的传递函数矩阵行列式可写为
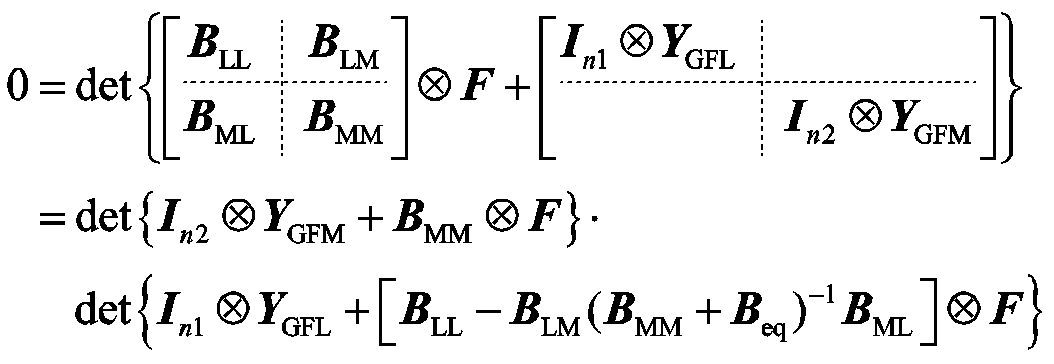 (42)
(42)
式中,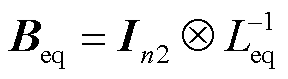 为GFM变流器的等效电纳矩阵;Leq为GFM变流器的等值电感[24-25],
为GFM变流器的等效电纳矩阵;Leq为GFM变流器的等值电感[24-25],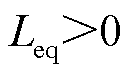 ,使等效电纳矩阵
,使等效电纳矩阵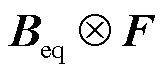 可近似所关注频段上GFM变流器的频域导纳矩阵
可近似所关注频段上GFM变流器的频域导纳矩阵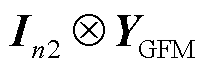 ;
;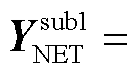
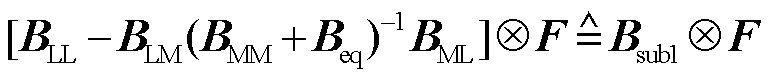 和
和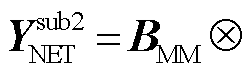
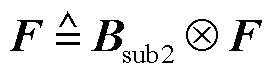 分别可视作仅有GFL变流器或仅有GFM变流器的等效多馈入子系统的电网导纳传递函数。
分别可视作仅有GFL变流器或仅有GFM变流器的等效多馈入子系统的电网导纳传递函数。
式(42)表明了场景3中GFL-GFM变流器混联系统可从抗扰性能分析的角度解耦为两个仅有GFL或GFM变流器的等效多馈入子系统。这是因为GFL-GFM变流器混联系统传递函数矩阵(即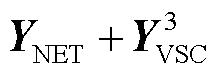 )的奇异性取决于GFL或GFM变流器等效多馈入子系统传递函数矩阵(即,
)的奇异性取决于GFL或GFM变流器等效多馈入子系统传递函数矩阵(即,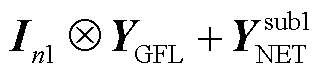 与
与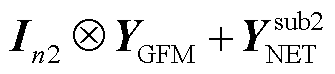 )的奇异性,具体由二者传递函数矩阵最接近奇异的那一个决定。因此,场景3中GFL-GFM变流器混联系统及其两个子系统的抗扰性能满足
)的奇异性,具体由二者传递函数矩阵最接近奇异的那一个决定。因此,场景3中GFL-GFM变流器混联系统及其两个子系统的抗扰性能满足
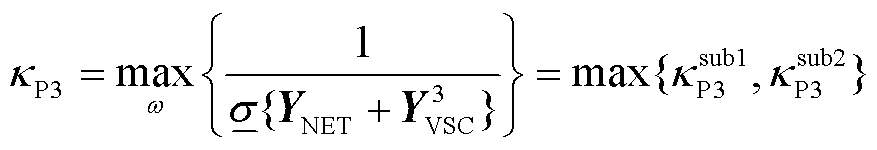 (43)
(43)
式中,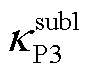 和
和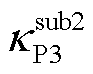 分别为GFL和GFM变流器等效多馈入子系统的互补灵敏度峰值,即
分别为GFL和GFM变流器等效多馈入子系统的互补灵敏度峰值,即
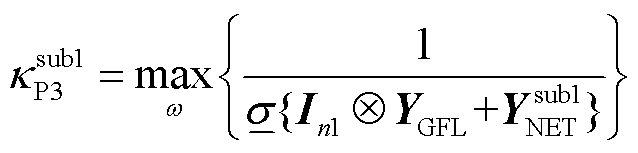 (44)
(44)
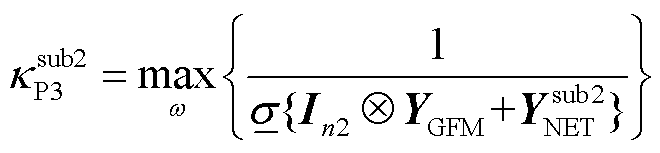 (45)
(45)
进一步地,由4.1节的分析,仅有GFL和GFM变流器的等效多馈入子系统的抗扰性能分别由其等效单机子系统的SCR,即电网等效导纳矩阵的最小/最大特征值表征。
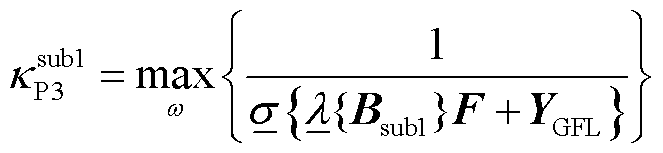 (46)
(46)
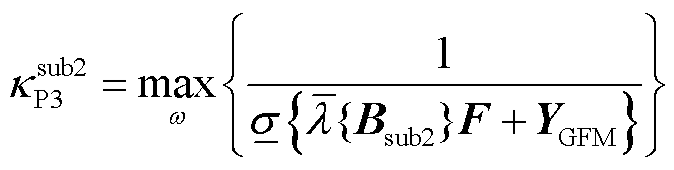 (47)
(47)
结合式(39)、式(40)与式(46)、式(47),若要从抗扰性能维度比较场景3(GFL-GFM变流器混联多馈入)与场景1、场景2(仅GFL或GFM变流器多馈入)的系统强度,探究变流器控制方式多样性的影响,则可转换为比较它们等效单机子系统的SCR如何变化,即考察各场景对应的电网导纳矩阵最小/最大特征值如何变化。为此,有下述引理。
引理2:场景1(仅GFL变流器多馈入)的电网导纳矩阵为B,场景3中GFL变流器等效多馈入子系统的电网导纳矩阵为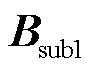 ,它们的最小特征值满足
,它们的最小特征值满足
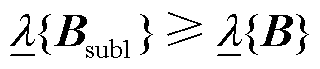 (48)
(48)
证明:见附录。
引理3:场景2(仅GFM变流器多馈入)的电网导纳矩阵为B,场景3中GFM变流器等效多馈入子系统的电网导纳矩阵为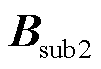 ,它们的最大特征值满足
,它们的最大特征值满足
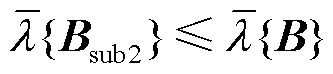 (49)
(49)
证明:见附录。
结合引理2和引理3,有下述命题。
命题4:其他条件相同时,系统运行于场景3(GFL-GFM变流器混联多馈入情形)的电压抗扰性能优于场景1(仅GFL变流器多馈入)或场景2(仅GFM变流器多馈入),即它们的互补灵敏度峰值满足
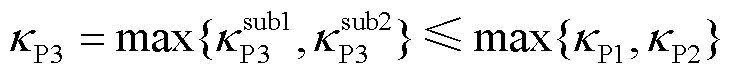 (50)
(50)
证明:由引理2,场景3中GFL变流器等效多馈入子系统的电网导纳矩阵最小特征值更大,意味着对于同一GFL变流器,所接入电网的SCR更高,系统互补灵敏度峰值下降,抗扰性增强,由式(39)和式(46)有
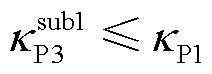 (51)
(51)
同理,由引理3可知,场景3中GFM变流器等效多馈入子系统的电网导纳矩阵最大特征值更小,意味着对于同一GFM变流器,所接入电网的SCR更小,系统互补灵敏度峰值下降,抗扰性增强,由式(40)和式(47)可得
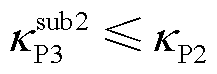 (52)
(52)
结合式(43)与式(51)、式(52),命题即证。
由命题4可知,从抗扰性能维度看,变流器控制方式多样性有助于降低多馈入系统的互补灵敏度峰值,进而相比于采用单一跟网型或构网型控制方式的多馈入系统具有较高的系统强度。上述分析也从系统强度的视角说明了将新能源场站中所有变流器均配置为构网型未必是最好的选择,多变流器中混合使用跟网型-构网型控制方式更有利于适应多变的并网环境,提升电压抗扰性能。这一结果可为新能源场站内跟网型-构网型设备配比规划等问题提供依据。
不失一般性,基于Matlab/Simulink搭建如图8所示的三馈入系统仿真模型,以验证所提出的变流器多样性影响规律。测试系统包含3台变流器,分别接入节点1~节点3,各变流器均具备功率因数四象限运行能力,可作为CIG或CIL变流器运行,也可采用GFL或GFM控制方式;节点4~节点6为中间节点;节点7~节点9接外部电网等值电源。变流器控制参数见附表1、附表2;系统线路参数见附表3。
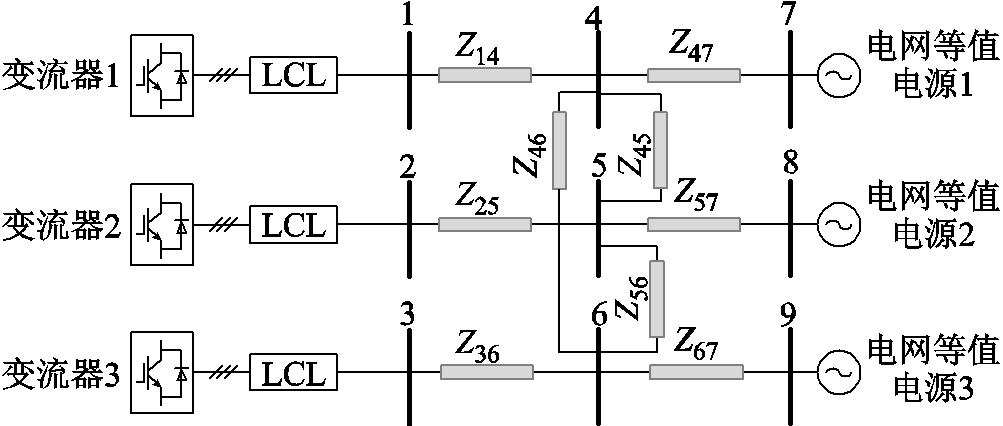
图8 三馈入测试系统单线图
Fig.8 Single-line diagram of the three-infeed test system
为了验证第2节所提出的变流器功率因数多样性对静态电压稳定维度下系统强度的提升作用,分别设置新能源变流器1~3采用GFL控制方式,以功率因数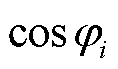 (i=1,2,3)运行在两组场景下。其中,场景1中各变流器功率因数保持一致(即cosφ1= cosφ2=cosφ3=0.9);场景2具备功率因数多样性(即cosφ1=0.8, cosφ2=0.5, cosφ3=1.0)。场景1和场景2中各变流器除运行功率因数外,其他运行工况均设置一致,即变流器1~3的视在功率与并网点电压幅值均为额定值1.0(pu)。
(i=1,2,3)运行在两组场景下。其中,场景1中各变流器功率因数保持一致(即cosφ1= cosφ2=cosφ3=0.9);场景2具备功率因数多样性(即cosφ1=0.8, cosφ2=0.5, cosφ3=1.0)。场景1和场景2中各变流器除运行功率因数外,其他运行工况均设置一致,即变流器1~3的视在功率与并网点电压幅值均为额定值1.0(pu)。
基于上述参数,设置场景1和场景2中各变流器有功功率指令值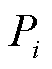 (
(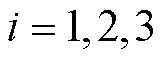 )按相同的速率随时间增加直至系统发生电压崩溃,这一过程中保持各变流器功率因数为上述设定值不变。解析计算场景1和场景2中电压稳定维度系统强度指标
)按相同的速率随时间增加直至系统发生电压崩溃,这一过程中保持各变流器功率因数为上述设定值不变。解析计算场景1和场景2中电压稳定维度系统强度指标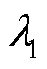 (详见定义2)随时间变化曲线,如图9所示;观察各变流器有功功率和并网点电压,时域波形如图10所示。
(详见定义2)随时间变化曲线,如图9所示;观察各变流器有功功率和并网点电压,时域波形如图10所示。
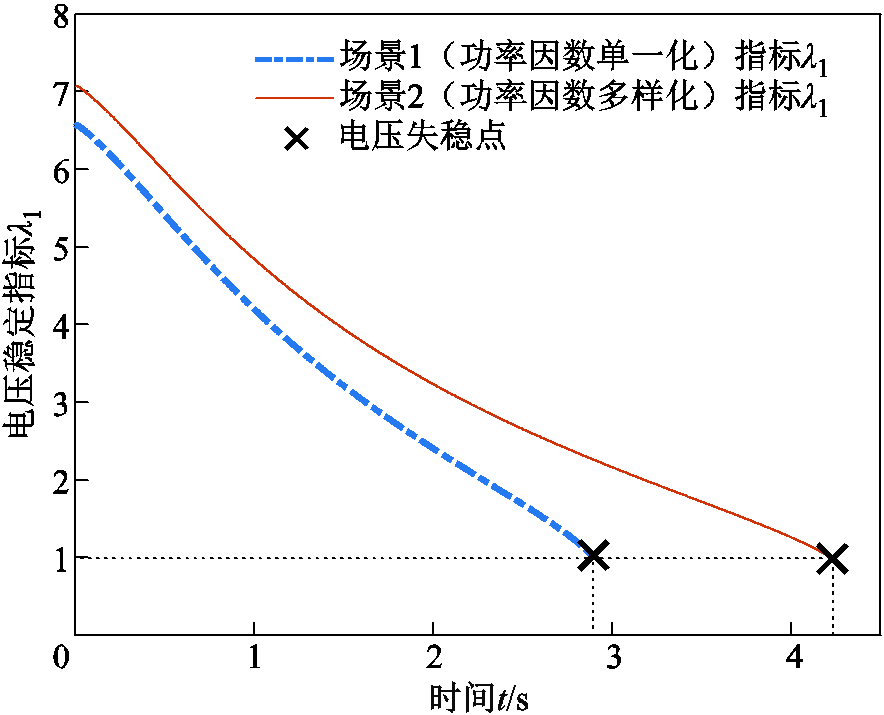
图9 不同功率因数运行场景下系统强度指标变化曲线
Fig.9 System strength indicator curves under different power factor operating scenarios
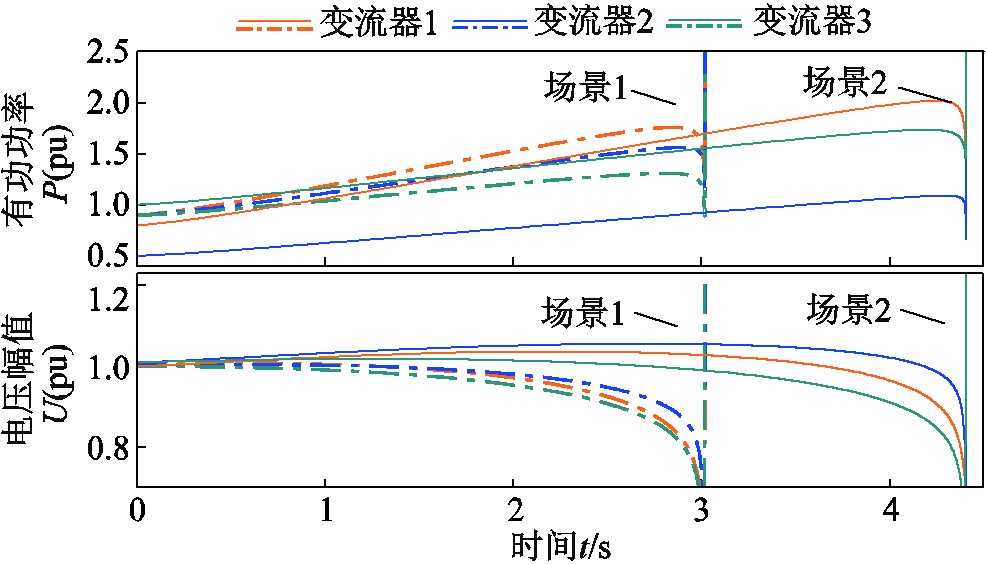
图10 不同功率因数运行场景下多变流器有功功率与节点电压时域波形
Fig.10 Active power and nodal voltage curves of converters under different power factor operating scenarios
对比图9的解析计算结果与图10的时域仿真结果可验证所提出的变流器功率因数多样性对系统强度的提升作用。具体地,图9显示了在保证功率因数一定而逐渐增大各变流器馈入功率的过程中,场景2中的系统强度指标λ1始终较大,说明了功率因数多样性使系统更加远离静态电压失稳边界;图10的时域仿真曲线也说明了这一点,按场景1运行的系统约在t=3.0 s电压失稳,相比于场景2更快地到达电压失稳点。因此,图10的时域仿真与图9的解析结果吻合,验证了变流器功率因数多样性有助于从静态电压稳定维度提升系统强度。
为了验证第3节所提出的变流器运行状态多样性对同步稳定维度下系统强度的提升作用,分别设置变流器1~3采用GFL控制方式,并作为CIG或CIL运行于场景1或场景2,两组场景下各变流器的发电-储能运行状态见表1。其中,场景1中变流器1~3均作为CIG运行;场景2中变流器1运行在CIG状态,而变流器2、3切换为CIL。
表1 两组场景下各变流器的发电-储能运行状态
Tab.1 CIG-CIL operating conditions of converters in two scenarios (pu)

场景变流器1变流器2变流器3 1P1=0.9,Q1=0.2(CIG)P2=0.8,Q2=0.2(CIG)P3=1,Q3=0(CIG) 2P1=0.9,Q1=0.2(CIG)P2=-0.3,Q2=0.2(CIL)P3=-0.3,Q3=0(CIL)
基于上述参数,解析计算场景1和场景2下系统等效阻尼-弹性模量曲线,以及同步稳定维度下的系统强度指标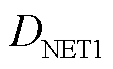 (详见定义3),如图11所示。再于t=2.0 s时在变流器1处施加0.02(pu)有功阶跃扰动,观察场景1和场景2中多变流器电压响应波形,分别如图12与图13所示。
(详见定义3),如图11所示。再于t=2.0 s时在变流器1处施加0.02(pu)有功阶跃扰动,观察场景1和场景2中多变流器电压响应波形,分别如图12与图13所示。
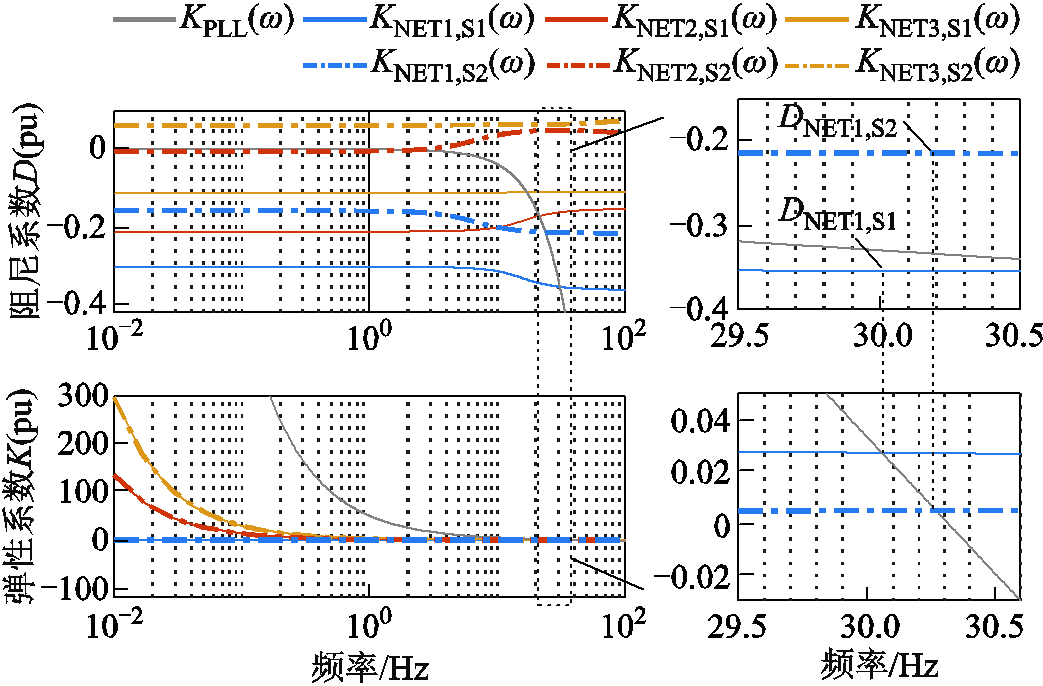
图11 不同运行状态下变流器与网络的阻尼-弹性曲线
Fig.11 Damping-spring curves of converters and networks under different operating conditions
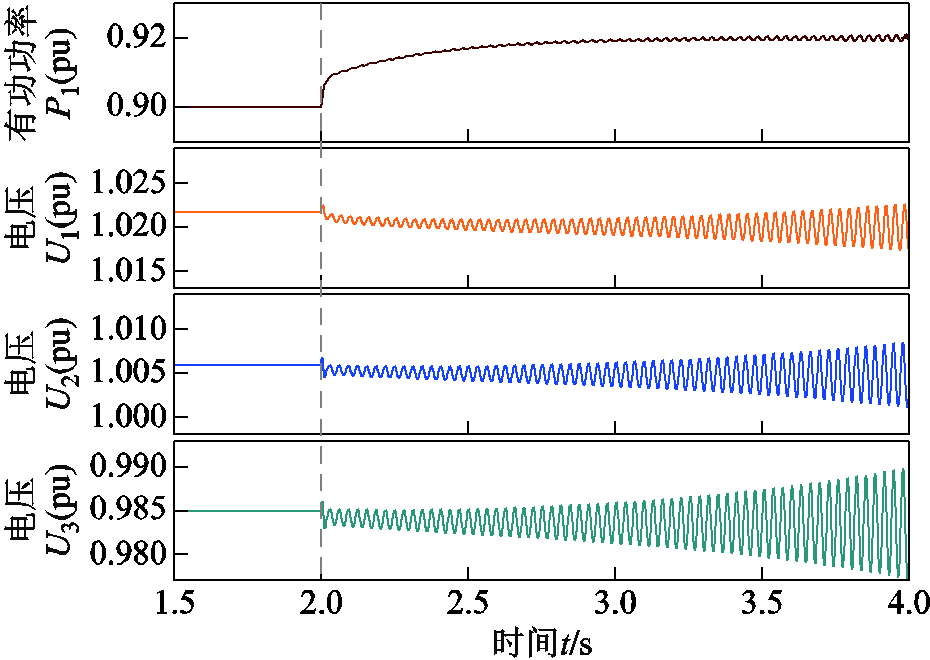
图12 场景1运行状态下变流器电压响应曲线(振荡频率fc = 30.2 Hz)
Fig.12 Voltage response curves of converters under scenario 1 operating conditions (oscillation frequency fc = 30.2 Hz)
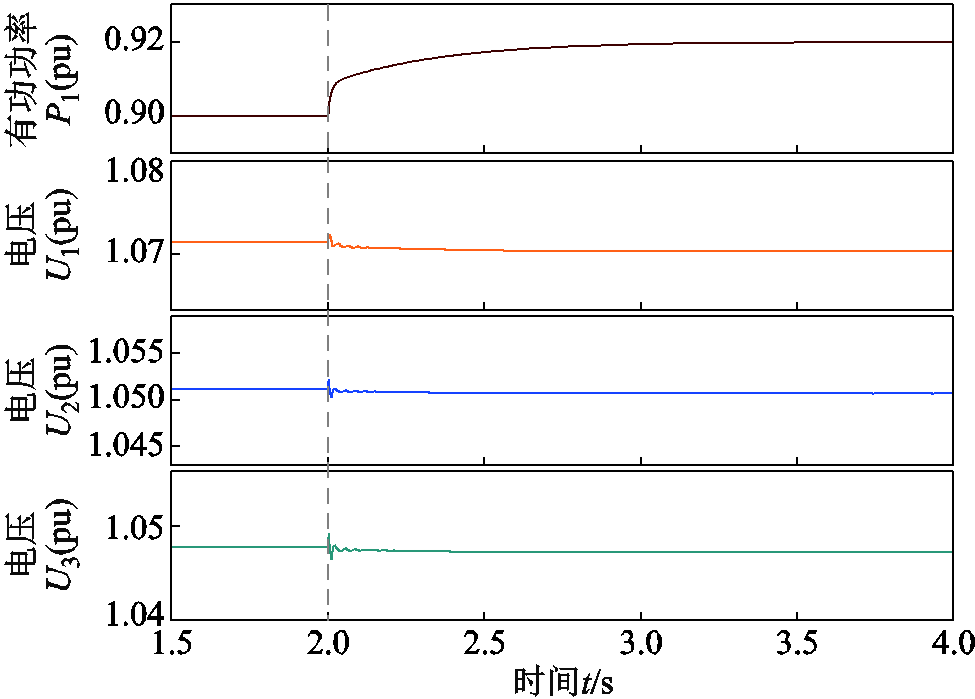
图13 场景2运行状态下变流器电压响应曲线
Fig.13 Voltage response curves of converters under scenario 2 operating conditions
对比图11的解析结果与图12和图13的时域仿真结果可验证运行状态多样性对系统强度的提升作用。具体地,由图11可知,系统在场景2下的最小网络阻尼曲线相比在场景1下,从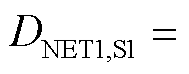
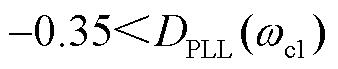 提升到
提升到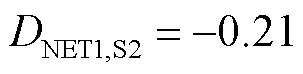 ,说明了CIG与CIL联合运行状态有助于增强网络侧等效阻尼,进而增强系统的小扰动同步稳定性。图12、图13的时域仿真曲线也说明了这一点,在相同的功率变动下,场景1中系统受扰后出现了锁相环带宽频率附近的功率发散振荡,频率为fc=30.2 Hz,而场景2中系统受扰后仍然稳定运行。因此,图11的理论分析与图12、图13的时域仿真结果相吻合,验证了变流器运行状态多样性有助于从小扰动同步稳定维度提升系统强度。
,说明了CIG与CIL联合运行状态有助于增强网络侧等效阻尼,进而增强系统的小扰动同步稳定性。图12、图13的时域仿真曲线也说明了这一点,在相同的功率变动下,场景1中系统受扰后出现了锁相环带宽频率附近的功率发散振荡,频率为fc=30.2 Hz,而场景2中系统受扰后仍然稳定运行。因此,图11的理论分析与图12、图13的时域仿真结果相吻合,验证了变流器运行状态多样性有助于从小扰动同步稳定维度提升系统强度。
为了验证第4节提出的变流器控制方式多样性对电压抗扰性能维度下系统强度的提升作用,分别设置如下场景:①场景1:变流器1~3均采用GFL控制;②场景2:变流器1~3均采用GFM控制;③场景3:变流1、2采用GFL控制,变流器3采用GFM控制。对于各场景,还分别构造了弱电网和强电网两种并网环境,具体通过引入比例系数k缩放各线路阻抗,k=1表示弱电网场景,k=0.5表示强电网场景(即各线路阻抗等比例减小为原参数的1/2)。
在保持场景1~3中各GFL变流器和GFM变流器的所有参数对应相同的前提下,解析计算弱电网和强电网环境下场景1~3中系统互补灵敏度函数最大奇异值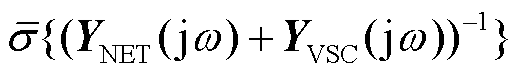 ,以反映抗扰性能,如图14a和图14b所示。再于t=2.0 s时在变流器1处施加0.1(pu)有功阶跃扰动,分别在弱电网或强电网环境下对比场景1与场景3或场景2与场景3的多变流器电压响应波形,分别如图15与图16所示。
,以反映抗扰性能,如图14a和图14b所示。再于t=2.0 s时在变流器1处施加0.1(pu)有功阶跃扰动,分别在弱电网或强电网环境下对比场景1与场景3或场景2与场景3的多变流器电压响应波形,分别如图15与图16所示。
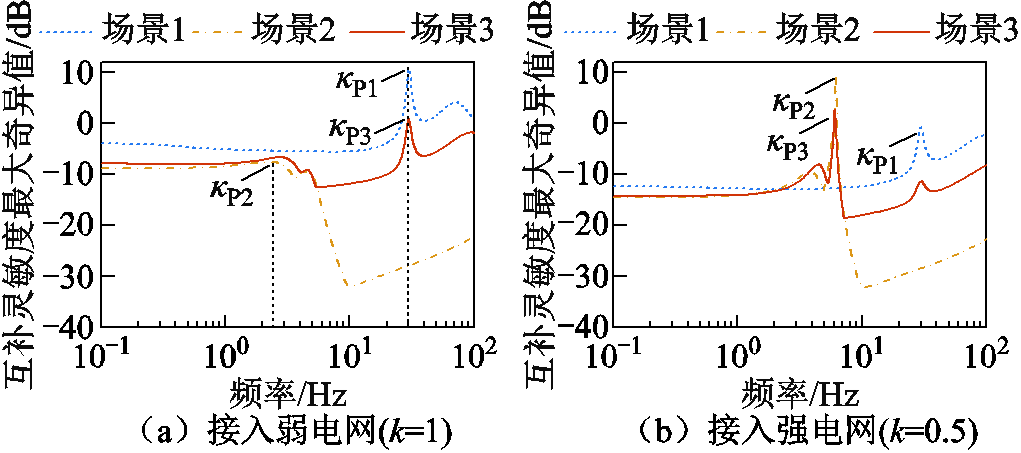
图14 不同变流器控制方式下互补灵敏度的最大奇异值
Fig.14 Maximum singular value curves of complementary sensitivity under different converter control combinations
对比图14的解析结果与图15、图16的时域仿真结果,可验证所提出的变流器控制方式多样性对系统强度的提升规律。具体地,由图14a可知,弱电网下场景1~3的互补灵敏度峰值分别为: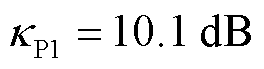 ,
,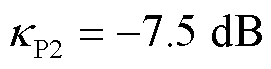 ,
,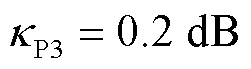 ,它们满足4.2节中
,它们满足4.2节中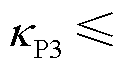
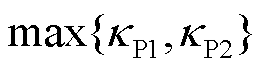 的不等关系;同理,由图14b可知强电网下场景1~3的互补灵敏度峰值仍然满足
的不等关系;同理,由图14b可知强电网下场景1~3的互补灵敏度峰值仍然满足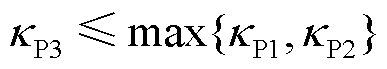 的关系,说明了在电网强弱变化时,GFL与GFM变流器混联多馈入场景相比于仅GFL变流器或GFM变流器多馈入场景具有较好的电压抗扰性能。图15和图16的时域仿真结果也说明了这一点,图15显示弱电网下场景3相比场景1具有更小的电压幅/相波动;图16显示强电网下场景3相比场景2具有更小的电压幅/相波动。因此,图14的理论分析与图15、图16的时域仿真结果相吻合,验证了变流器控制方式多样性有助于从抗扰性能维度提升系统强度。
的关系,说明了在电网强弱变化时,GFL与GFM变流器混联多馈入场景相比于仅GFL变流器或GFM变流器多馈入场景具有较好的电压抗扰性能。图15和图16的时域仿真结果也说明了这一点,图15显示弱电网下场景3相比场景1具有更小的电压幅/相波动;图16显示强电网下场景3相比场景2具有更小的电压幅/相波动。因此,图14的理论分析与图15、图16的时域仿真结果相吻合,验证了变流器控制方式多样性有助于从抗扰性能维度提升系统强度。
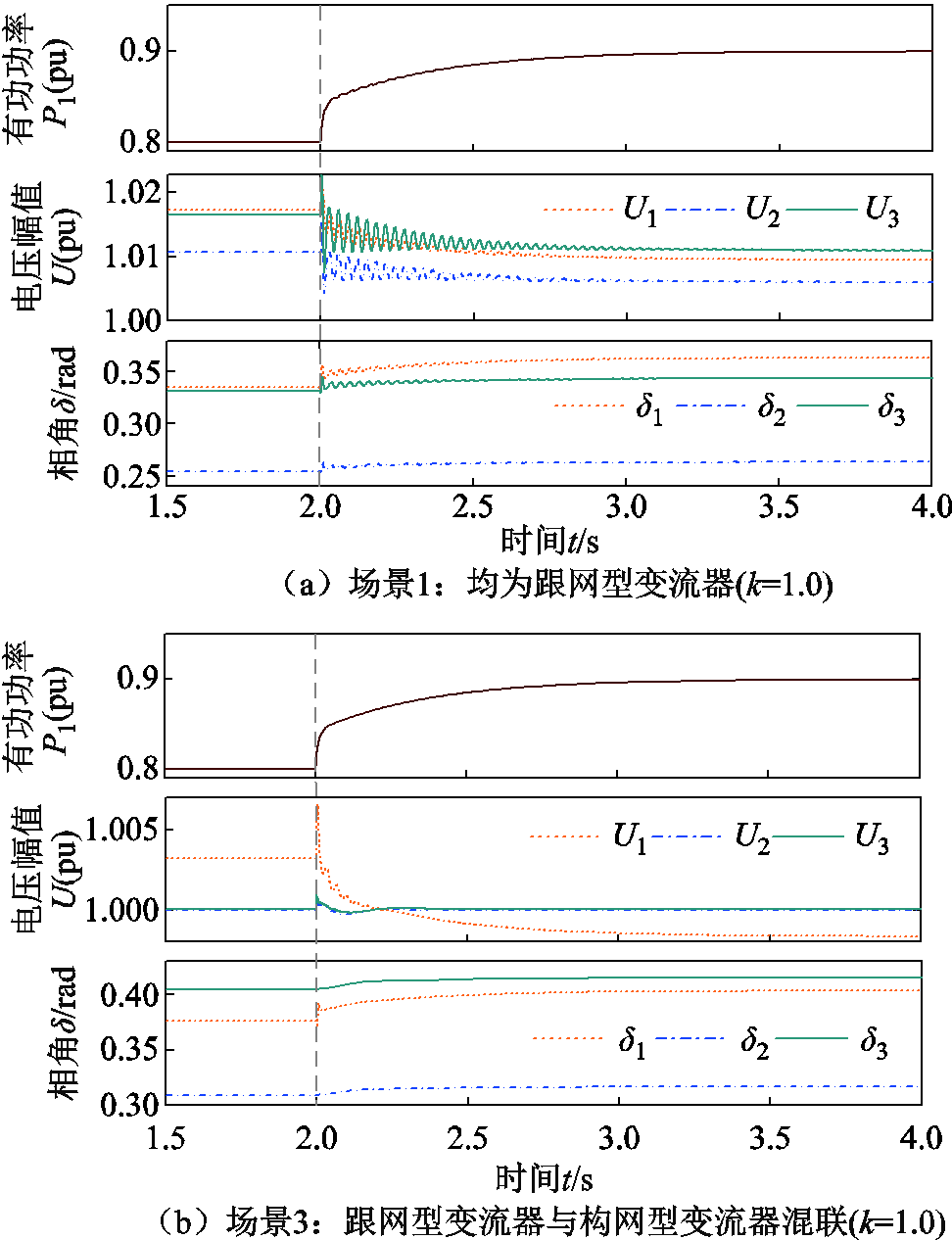
图15 弱电网下场景1和场景3变流器电压响应对比
Fig.15 Comparison of voltage response curves of converters in scenario 1 and scenario 3 in weak grid
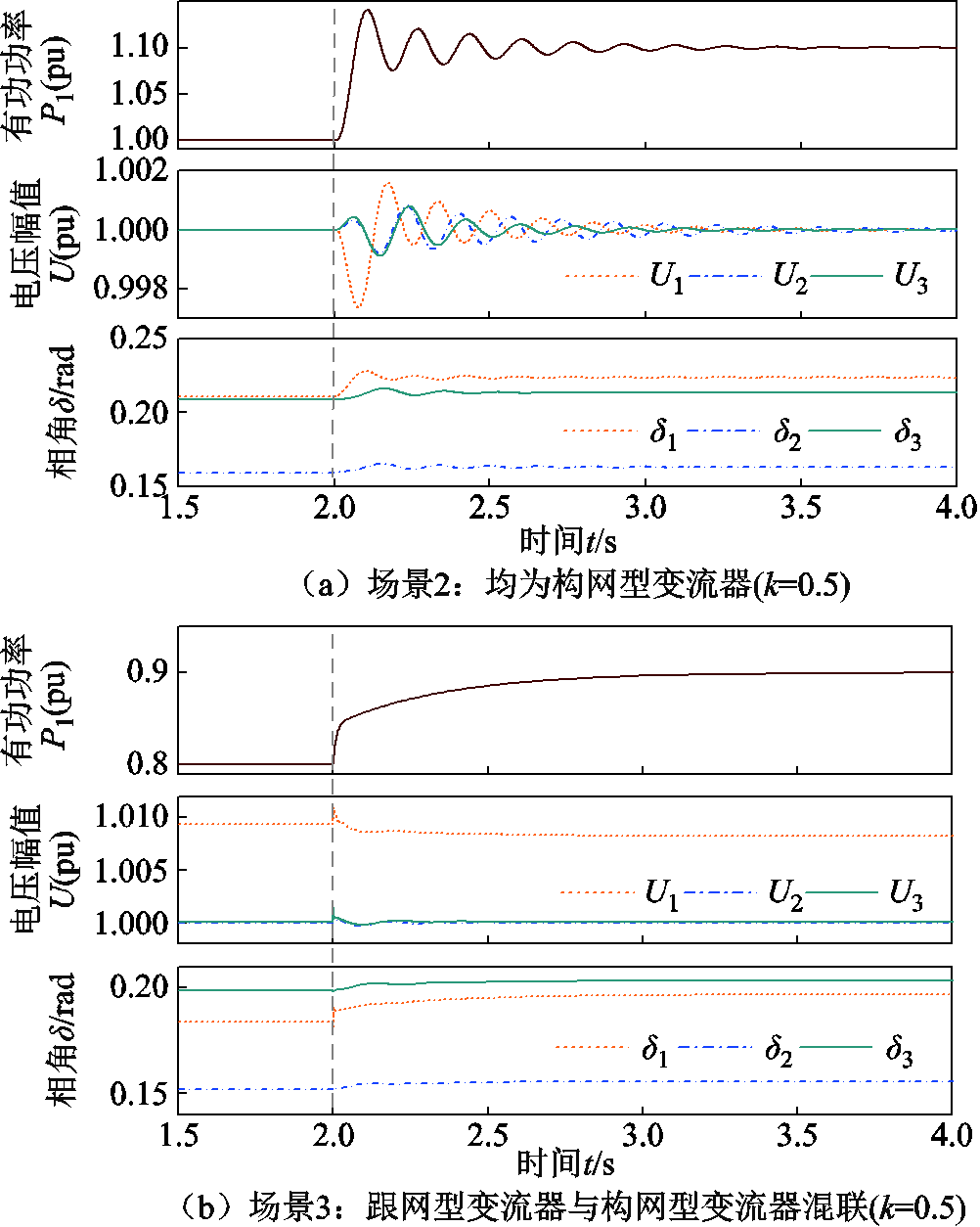
图16 强电网下场景2和场景3变流器电压响应对比
Fig.16 Comparison of voltage response curves of converters in scenario 2 and scenario 3 in strong grid
本文聚焦多变流器特性对系统强度的影响,论述了多变流器非均一化功率因数、运行状态、控制方式等多样性特征对系统强度的若干提升规律。具体结论如下:
1)相比于多跟网型变流器均运行于同一功率因数的场景,采取不完全相同的功率因数,即功率因数多样性有助于从电压稳定维度提升系统强度。
2)跟网型多变流器采取发电状态与充电状态(如作为储能馈入电网)联合的运行工况,有助于从同步稳定维度提升系统强度,相比于跟网型多变流器均运行于发电状态(如均作为新能源馈入电网)的场景,更能保障系统的小扰动同步稳定。
3)跟网型与构网型多变流器联合运行时有助于从电压抗扰性能维度提升系统强度,相比于单一类型的跟网型或构网型多变流器运行场景更能适应电网强弱的变化。
探究控制参数等其他因素的多样性对系统强度的提升规律,以及为新能源-储能联合运行、新能源场站内构网型装备的规划配置等工程实践问题提供优化方案将是后续的研究工作。
附 录
1. 推导与证明
1)式(8)、式(9)的推导过程
式(7)两边左乘单模矩阵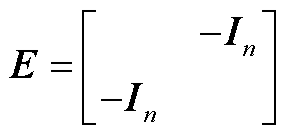 得到
得到
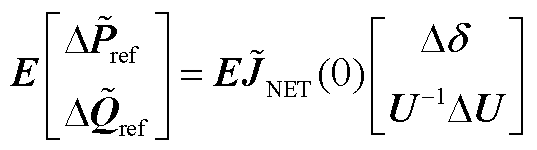 (A1)
(A1)
然后,作酉变换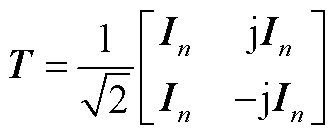 得到
得到
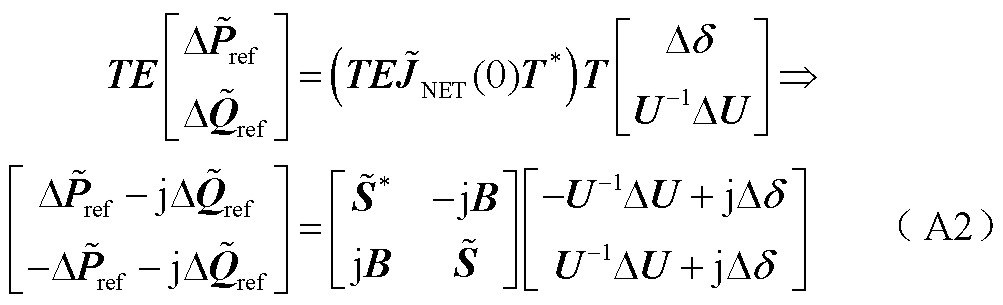
考虑复功率扰动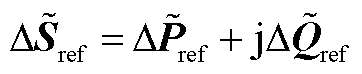 时(即(A2)中
时(即(A2)中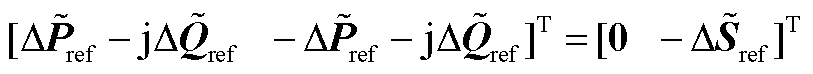 ),式(A2)降阶为
),式(A2)降阶为
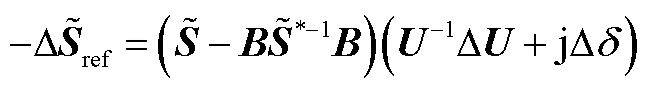 (A3)
(A3)
式(A3)等式两边左乘矩阵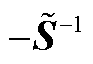 整理得
整理得
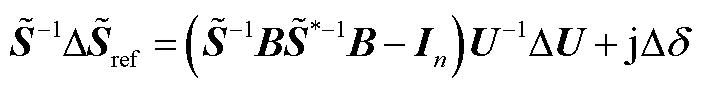 (A4)
(A4)
即推得式(8)。
2)式(25)的推导过程
首先,推导变流器侧传递函数。利用式(24)将式(23)变换到极坐标系得到
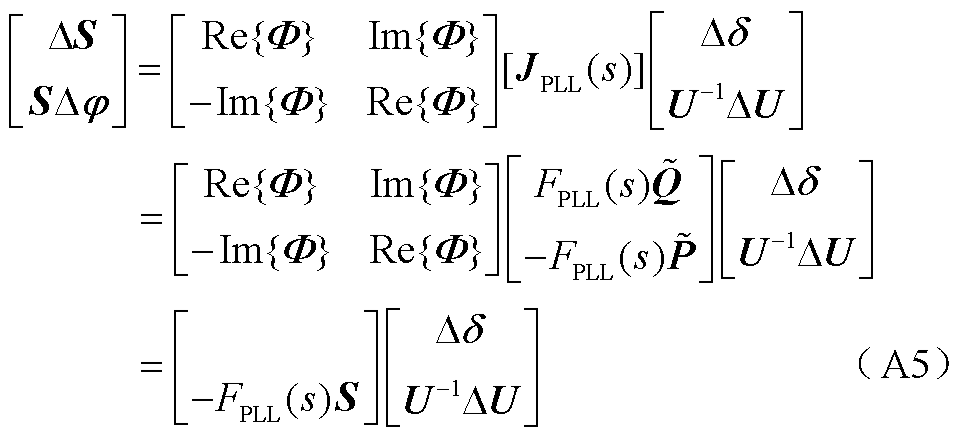
由式(A5)推出相角回路中变流器侧传递函数为
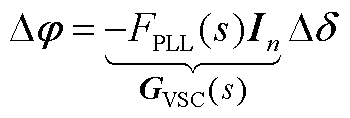 (A6)
(A6)
其次,推导电网侧传递函数为
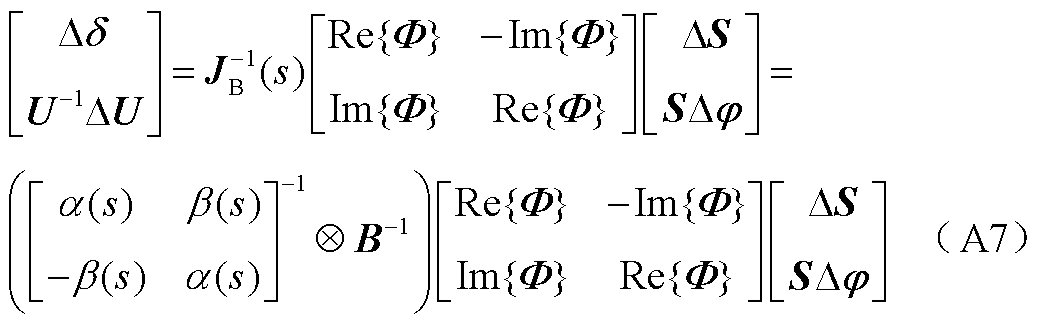
式(A7)作酉变换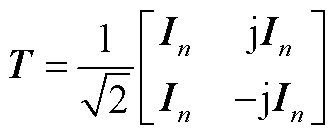 得到
得到
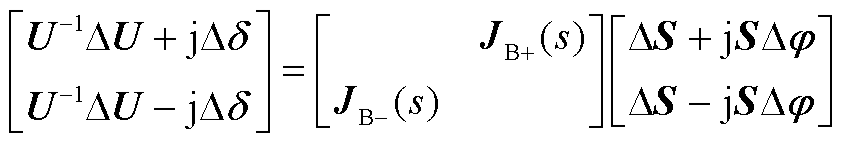 (A8)
(A8)
式中,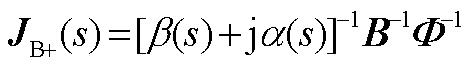 ,
,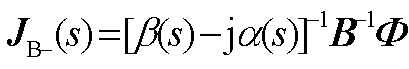 。
。
设扰动向量以功率因数角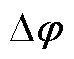 形式出现,其幅值分量为零(
形式出现,其幅值分量为零(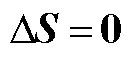 ),进而式(A8)降阶后得到相角回路中电网侧传递函数为
),进而式(A8)降阶后得到相角回路中电网侧传递函数为
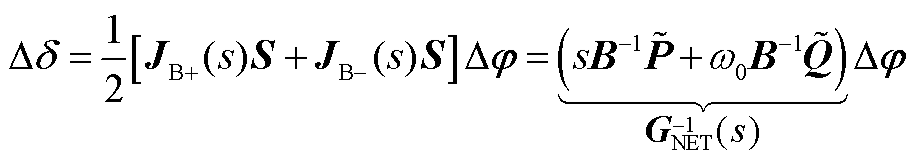 (A9)
(A9)
3)引理2证明
由于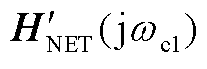 是式(26)中网络频响函数矩阵
是式(26)中网络频响函数矩阵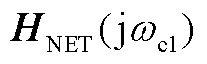 的相似矩阵,故
的相似矩阵,故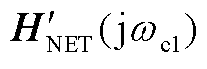 具有与
具有与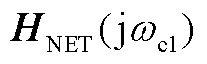 一致的特征值,即对于特征值
一致的特征值,即对于特征值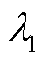 满足(为简洁起见,以下省略
满足(为简洁起见,以下省略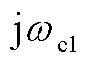 )
)
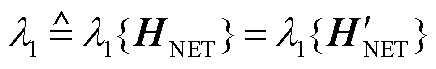 (A10)
(A10)
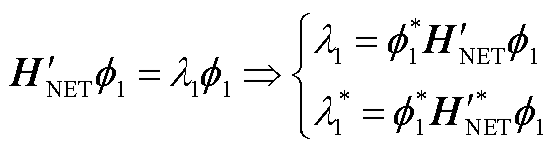 (A11)
(A11)
式中,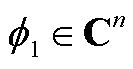 是矩阵
是矩阵 的归一化特征向量,即满足
的归一化特征向量,即满足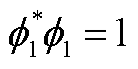 。
。
进一步考察该特征值实部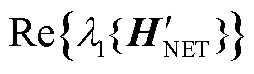 为
为
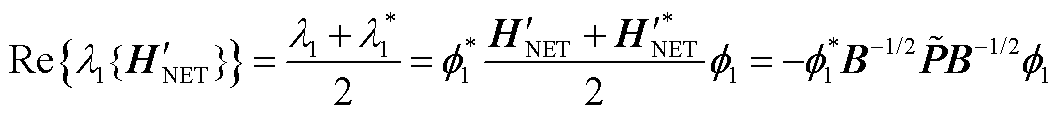 (A12)
(A12)
再令式(A12)中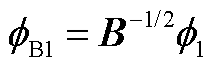 ,结合式(A10)得
,结合式(A10)得
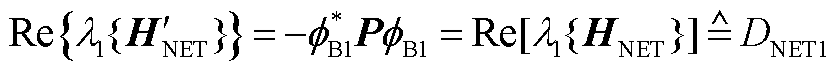 (A13)
(A13)
证毕。
4)命题3证明
首先,由文献[6]可得,第i个馈入变流器的归一化功率向量可基于变流器导纳传递函数表示为
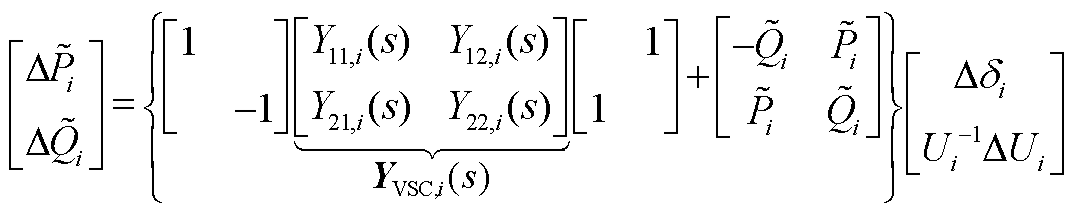 (A14)
(A14)
式中,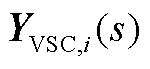 为第i个变流器的在同步旋转坐标系下的2×2导纳传递函数矩阵,是
为第i个变流器的在同步旋转坐标系下的2×2导纳传递函数矩阵,是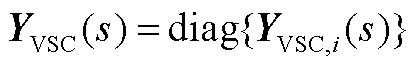 的第i个对角块;
的第i个对角块;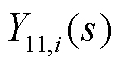 、
、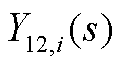 、
、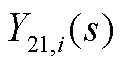 、
、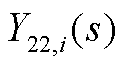 为矩阵
为矩阵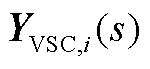 的元素;
的元素;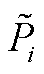 、
、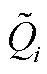 分别为第i个变流器馈入的归一化有功功率和无功功率,
分别为第i个变流器馈入的归一化有功功率和无功功率,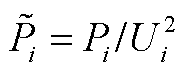 、
、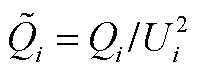 。
。
将式(A14)推广到多馈入系统,写为
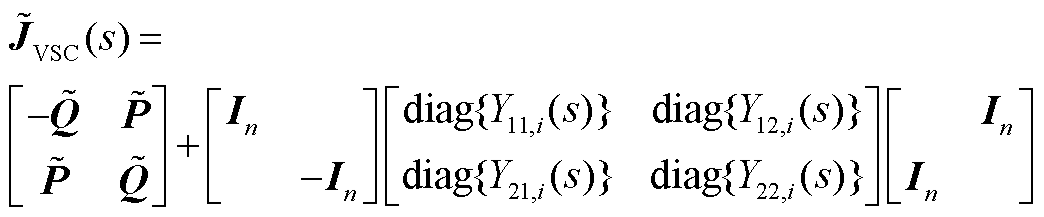 (A15)
(A15)
结合式(A15)与式(22)中的电网雅可比矩阵传递函数矩阵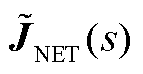 得到
得到
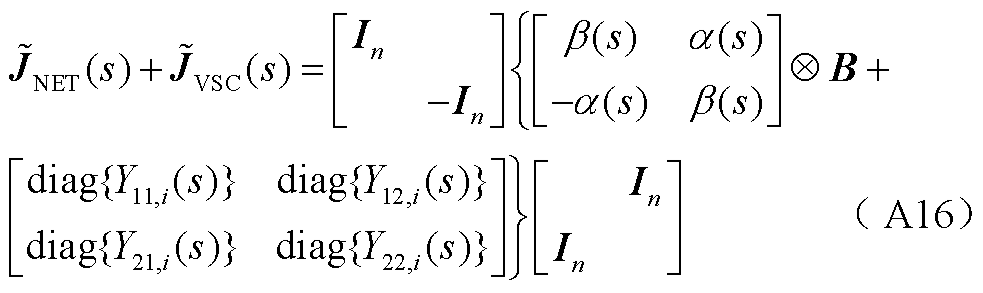
注意到,式(A16)中矩阵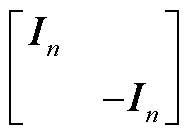 和
和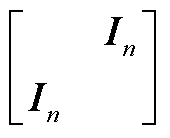 均为酉矩阵,左/右乘任意矩阵不影响其奇异值,故在任意频率点处有
均为酉矩阵,左/右乘任意矩阵不影响其奇异值,故在任意频率点处有
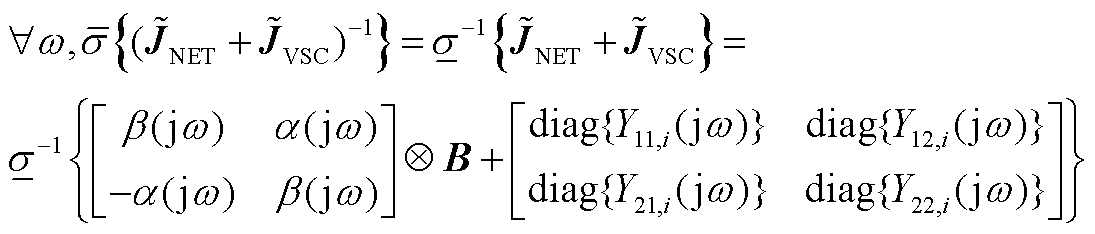 (A17)
(A17)
对式(A17)作初等行、列变换亦不影响奇异值,有
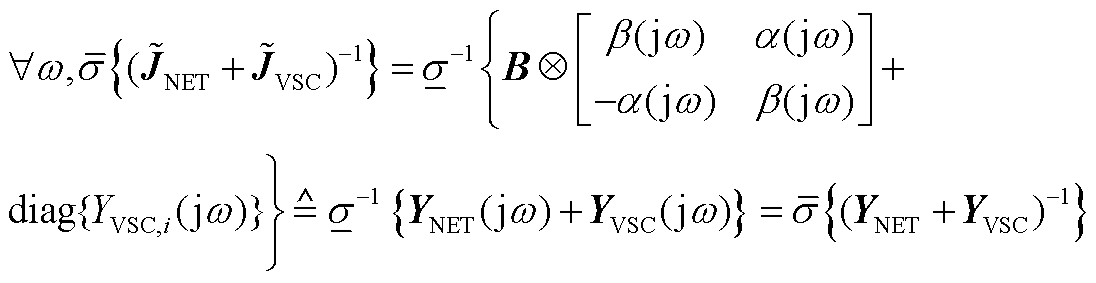 (A18)
(A18)
证毕。
5)引理2证明
首先,注意到利用构网型变流器等值电感修正前后的电网导纳矩阵B与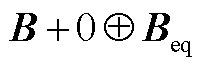 均是正定的(
均是正定的( 表示直和)。由文献[17]定理8.12,它们的最小特征值满足
表示直和)。由文献[17]定理8.12,它们的最小特征值满足
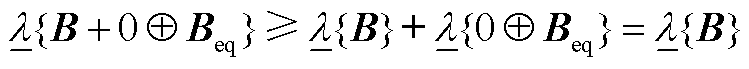 (A19)
(A19)
其次,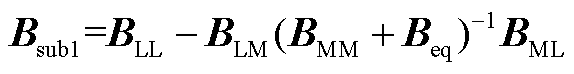 可看作矩阵
可看作矩阵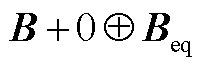 关于
关于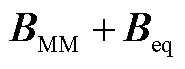 的Schur补,由文献[26]定理2.1可知,它们的最小特征值满足
的Schur补,由文献[26]定理2.1可知,它们的最小特征值满足
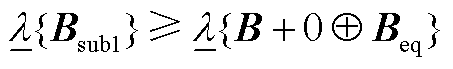 (A20)
(A20)
结合式(A19)、式(A20),可知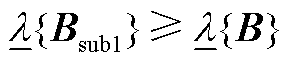 ,证毕。
,证毕。
6)引理3证明
由于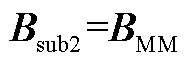 是电网导纳矩阵B的主子阵,二者均为Hermite矩阵。由文献[17]定理8.10(特征值交织定理)可知,它们的最大特征值满足
是电网导纳矩阵B的主子阵,二者均为Hermite矩阵。由文献[17]定理8.10(特征值交织定理)可知,它们的最大特征值满足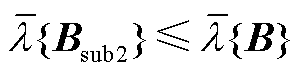 ,证毕。
,证毕。
2. 算例参数
附表1 跟网型变流器控制参数
App.Tab.1 Parameters of grid-following converter

参数数值 系统容量基值Sb/(kV·A)1 500 基准电压Ub/V690 直流电压基值Ubdc/V1 150 直流电容Cdc(pu)0.038 滤波电感Lf(pu)0.05 滤波电容Cf(pu)0.05 功率因数运行范围[-1, 1] 有功-无功功率外环PI参数0.5, 8
(续)

参数数值 电流内环PI参数0.3, 10 电压前馈滤波时间常数/s0.001 锁相环PI参数41, 34 690
附表2 构网型变流器控制参数
App.Tab.2 Parameters of grid-forming converter

参数数值 系统容量基值Sb/(kV·A)1 500 基准电压Ub/V690 直流电压基值Ubdc/V1 150 直流电容Cdc(pu)0.038 滤波电感Lf(pu)0.05 滤波电容Cf(pu)0.05 交流电压外环PI参数2, 30 电流内环PI参数0.3, 10 电压前馈滤波时间常数/s0.002 虚拟同步机控制参数(pu)J=2, D=20
附表3 三馈入系统线路参数
App.Tab.3 Network parameters of three-infeed system

阻抗数值(pu)阻抗数值(pu)阻抗数值(pu) Z140.04+j0.05Z250.04+j0.05Z360.04+j0.05 Z450.02+j0.38Z460.02+j0.45Z560.02+j0.52 Z470.02+j0.52Z570.02+j0.19Z670.02+j0.45
参考文献
[1] 舒印彪, 陈国平, 贺静波, 等. 构建以新能源为主体的新型电力系统框架研究[J]. 中国工程科学, 2021, 23(6): 61-69.
Shu Yinbiao, Chen Guoping, He Jingbo, et al. Building a new electric power system based on new energy sources[J]. Strategic Study of CAE, 2021, 23(6): 61-69.
[2] IEEE. IEEE Standard for Interconnection and Interoperability of Inverter-Based Resources (IBRs) Interconnecting with Associated Transmission Electric Power Systems: IEEE Standard 2800TM-2022[S]. IEEE 2022.
[3] 高磊, 吕敬, 马骏超, 等. 基于电路等效的并网逆变器失稳分析与稳定控制[J]. 电工技术学报, 2024, 39(8): 2325-2341.
Gao Lei, Lü Jing, Ma Junchao, et al. Instability analysis and stability control of grid-connected inverter based on impedance circuit equivalent[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2325-2341.
[4] Davies J. CIGRE WG B4.41 report: systems with multiple DC infeed[R]. Paris: CIGRE, 2007.
[5] 孙华东, 徐式蕴, 许涛, 等. 新能源多场站短路比定义及指标[J]. 中国电机工程学报, 2021, 41(2): 497-506.
Sun Huadong, Xu Shiyun, Xu Tao, et al. Definition and index of short circuit ratio for multiple renewable energy stations[J]. Proceedings of the CSEE, 2021, 41(2): 497-506.
[6] 辛焕海, 董炜, 袁小明, 等. 电力电子多馈入电力系统的广义短路比[J]. 中国电机工程学报, 2016, 36(22): 6013-6027.
Xin Huanhai, Dong Wei, Yuan Xiaoming, et al. Generalized short circuit ratio for multi power electronic based devices infeed to power systems[J]. Proceedings of the CSEE, 2016, 36(22): 6013-6027.
[7] 周瑀涵, 辛焕海, 鞠平. 基于广义短路比的多馈入系统强度量化原理与方法: 回顾、探讨与展望[J]. 中国电机工程学报, 2023, 43(10): 3794-3811.
Zhou Yuhan, Xin Huanhai, Ju Ping. System strength quantification principle and method of multi-infeed systems based on generalized short-circuit ratio: reviews, discussions and outlooks[J]. Proceedings of the CSEE, 2023, 43(10): 3794-3811.
[8] Henderson C, Egea-Alvarez A, Kneuppel T, et al. Grid strength impedance metric: an alternative to SCR for evaluating system strength in converter dominated systems[J]. IEEE Transactions on Power Delivery, 2024, 39(1): 386-396.
[9] Zhu Yue, Green T C, Zhou Xiaoyao, et al. Impedance margin ratio: a new metric for small-signal system strength[J]. IEEE Transactions on Power Systems, 2024, 39(6): 7291-7303.
[10] Huang Liang, Wu Chao, Zhou Dao, et al. Impact of grid strength and impedance characteristics on the maximum power transfer capability of grid-connected inverters[J]. Applied Sciences, 2021, 11(9): 4288.
[11] Yuan Hui, Xin Huanhai, Wu Di, et al. Assessing maximal capacity of grid-following converters with grid strength constraints[J]. IEEE Transactions on Sustainable Energy, 2022, 13(4): 2119-2132.
[12] He Xiuqiang, Häberle V, Dörfler F. Complex-frequency synchronization of converter-based power systems[J]. IEEE Transactions on Control of Network Systems, 2025, 12(1): 787-799.
[13] Skogestad S, Postelethwaite I. Multivariable Feedback. Control[M]. New York: Wiley Publishing, 1996.
[14] 周双喜. 电力系统电压稳定性及其控制[M]. 北京: 中国电力出版社, 2004.
[15] Wang Xiongfei, Blaabjerg F. Harmonic stability in power electronic-based power systems: concept, modeling, and analysis[J]. IEEE Transactions on Smart Grid, 2019, 10(3): 2858-2870.
[16] Liang Maowei, Baiser B, Hallett L M, et al. Consistent stabilizing effects of plant diversity across spatial scales and climatic gradients[J]. Nature Ecology & Evolution, 2022, 6(11): 1669-1675.
[17] Zhang Fuzhen. Matrix Theory: Basic Results and Techniques[M]. 2nd ed. New York: Springer, 2011.
[18] Liu Chenxi, Xin Huanhai, Wu Di, et al. Generalized operational short-circuit ratio for grid strength assessment in power systems with high renewable penetration[J]. IEEE Transactions on Power Systems, 2024, 39(4): 5479-5494.
[19] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994.
Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters [J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[20] Yang Ziqian, Zhan Meng, Liu Dan, et al. Small-signal synchronous stability of a new-generation power system with 100% renewable energy[J]. IEEE Transactions on Power Systems, 2023, 38(5): 4269-4280.
[21] Harnefors L. Proof and application of the positive-net-damping stability criterion[J]. IEEE Transactions on Power Systems, 2011, 26(1): 481-482.
[22] Cheng Yunzhi, Fan Lingling, Rose J, et al. Real-world subsynchronous oscillation events in power grids with high penetrations of inverter-based resources[J]. IEEE Transactions on Power Systems, 2023, 38(1): 316-330.
[23] 杨超然, 辛焕海, 宫泽旭, 等. 变流器并网系统复电路分析与广义阻抗判据适用性探讨[J]. 中国电机工程学报, 2020, 40(15): 4744-4758.
Yang Chaoran, Xin Huanhai, Gong Zexu, et al. Complex circuit analysis and investigation on applicability of generalized-impedance-based stability criterion for grid-connected converter[J]. Proceedings of the CSEE, 2020, 40(15): 4744-4758.
[24] Xin Huanhai, Liu Chenxi, Chen Xia, et al. How many grid-forming converters do we need? a perspective from small signal stability and power grid strength[J]. IEEE Transactions on Power Systems, 2025, 40(1): 623-635.
[25] 马富艺龙, 辛焕海, 刘晨曦, 等. 新能源基地柔性直流送出系统小扰动电压支撑强度评估[J]. 电工技术学报, 2023, 38(21): 5758-5770, 5938.
Ma Fuyilong, Xin Huanhai, Liu Chenxi, et al. Small-disturbance system voltage support strength assessment method for renewables VSC-HVDC delivery system [J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5758-5770, 5938.
[26] Zhang F. The Schur Complement and Its Applications (Numerical Methods and Algorithms)[M]. New York: Springer Science and Business Media, 2005.
Abstract Renewable energy and other devices are connected to the grid through the power electronic converter. The system voltage support strength (refferd to as “system strength”) characterizes the ability of power electronic converter-based multi-infeed systems (refferd to as “multi-infeed systems”) to resist voltage instability or deviation at nodes after disturbances. However, in most engineering practice and existing research, the system strength is often indirectly characterized from a single grid perspective, with limited investigation into the influence from grid impedance and network topology. In fact, the post-disturbance node voltage response represents a dynamic behavior of the entire system, and conventional methods may overlook the influence patterns of multi-converter characteristics on system strength. Also, existing studies fail to establish generalized impact mechanisms through which multi-converter characteristics influence system strength, due to the complex interactions among multiple converters. These limitations introduce challenges for planning, operation, and source-grid coordination of multi-infeed systems.
To fill this gap, this paper first introduces the concept of converter diversity to describe how differentiated features of multi-infeed converters—including operating power factors, operational states, and grid-following/grid-forming control strategies—affect system strength. Secondly, we review quantification methods for system strength of the multi-infeed system that consider closed-loop dynamic characteristics of multiple converters and the grid, establishing corresponding evaluation metrics for system strength from three analytical dimensions: voltage stability, synchronization stability, and disturbance rejection capability. Furthermore, we comparatively analyze the impacts of uniform versus diversified converter operating conditions and control strategies on system strength metrics across different dimensions. Through mathematical analysis of the evaluation metrics, we analytically demonstrate several enhancement mechanisms by which converter diversity improves system strength. Finally, simulation cases validate the effectiveness of the analytical results.
The key conclusions can be summarized as follows: (1) Implementing diversified power factor settings among grid-following multiple converters enhances system strength in the static voltage stability demension. This configuration provides superior static voltage stability margin in multi-infeed systems when compared to homogeneous power factor operation scenarios. (2) The diversified operation of grid-following multiple converters in hybrid generation-charging modes (e.g., co-deployment of renewable generation and energy storage systems) enhances system strength in the small-signal synchronization stability demension. This operational strategy achieves improved small-signal synchronization stability margins in multi-infeed systems relative to exclusive generation-mode operation paradigms (e.g., pure renewable energy integration). (3) The diversified control schemes of multiple converters in hybrid grid-following and grid-forming modes enhances system strength in the voltage disturbance rejection capability demension. Compared to homogeneous converter configurations, this heterogeneous converter architecture exhibits enhanced operational adaptability, particularly under varying grid conditions.
Future research will focus on investigating the enhancement patterns of system strength through diversity in control parameters and other factors. This will involve developing optimization strategies for practical engineering applications such as configuration of grid-forming equipment in renewable energy stations.
keywords:System strength, static voltage stability, small-signal synchronization stability, disturbance rejection performance, multi-infeed system
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.242168
国家自然科学基金联合基金资助项目(U22B6008, U24B6008)。
收稿日期 2024-12-02
改稿日期 2025-03-14
马富艺龙 男,1996年生,博士研究生,研究方向为新能源并网稳定分析与控制。E-mail:12210001@zju.edu.cn
辛焕海 男,1981年生,教授,博士生导师,研究方向为交直流系统稳定分析与控制、新能源并网稳定分析与控制。E-mail:xinhh@zju.edu.cn(通信作者)
(编辑 赫 蕾)