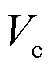 为换流器端口电压,即等效电压源内电动势,
为换流器端口电压,即等效电压源内电动势,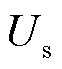 为并网点母线电压;构网型电源注入交流系统的有功功率和无功功率分别为
为并网点母线电压;构网型电源注入交流系统的有功功率和无功功率分别为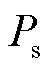 、
、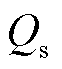 ,以复功率形式表示;忽略传输线路电阻、对地电容。为简化分析,以接入无穷大交流系统为例,假设母线电压幅值
,以复功率形式表示;忽略传输线路电阻、对地电容。为简化分析,以接入无穷大交流系统为例,假设母线电压幅值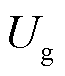 为恒定值1(pu),相角
为恒定值1(pu),相角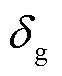 为0。
为0。摘要 异构新能源场站的大规模并网导致系统的电压稳定形态及稳定边界发生了重大变化。为此,该文基于电压稳定边界特性构建适用于异构新能源多馈入系统的潮流数学模型,并提出一种能够反映运行状态影响的多馈入系统静态电压稳定性量化评估方法。首先分析了构网型电源无功电压响应的两阶段变化特性,基于非线性环节约束条件实现控制系统与潮流关系的解耦,揭示了构网型电源节点类型转换特性,并明确了其电压支撑能力及运行边界的临界条件;其次,基于潮流雅可比矩阵自反馈项特征信息构造奇异判据,量化分析集中式和分布式异构新能源多馈入系统的送出能力及电压稳定形态;最后,从系统结构和新能源控制环节两个层面分析了影响多馈入系统静态电压稳定性的关键因素,并通过仿真验证了所提出机理与分析的正确性。研究结果表明,构网型电源的电压支撑能力存在明确的边界,且新能源的送出能力受到控制方式和运行方式的显著影响,为异构新能源多馈入系统的规划设计和运行优化提供了理论依据。
关键词:静态电压稳定性 多馈入电力系统 异构新能源 系统雅可比矩阵
静态电压稳定是电力系统能够稳定运行的重要约束条件。随着新能源占比的迅速提升[1-2],以同步机为支撑的常规电源占比逐步减少[3-4],电力系统静态电压稳定裕度不断下降,安全稳定面临严峻挑战[5-6]。大多数新能源场站采用跟网型换流器并入交流电网,其外部特性表现为电流源特性[7-8]。近年来,具有电压源特性的构网型换流器因具备支撑作用而应用于多个工程[9-11],跟网和构网控制并存使得电力系统呈现异构新能源多馈入特性[12]。对异构新能源多馈入系统而言,其电压稳定性与控制方式、系统结构等因素间耦合关系复杂[13]。因此,揭示异构新能源系统的静态电压稳定性机理,并给出量化评估方法对保证电力系统安全稳定运行至关重要。
目前,针对构网型控制在提高新能源场站主动支撑能力方面的研究已有大量结论。文献[14]总结了典型构网型控制在储能、静止无功补偿设备等不同控制主体下的适用情况。文献[15]研究了构网型控制应用于新能源基地经柔性直流送出场景下的系统强度评估方法。文献[16]基于临界短路比指标量化构网型电源的接入对新能源场站弱电网运行能力的提升作用。文献[17-18]总结了现有构网型变流器控制方法及稳定性分析成果。文献[19-20]研究了构网型无功补偿装置及构网型储能对系统电压稳定性的影响。
然而,针对构网型新能源潮流数学模型的分析较为缺失,使得在异构新能源多馈入系统中,如何计及关键特征量对静态电压稳定形态进行定性与定量分析已成为亟须解决的问题。已有文献中关于新能源多馈入系统静态电压稳定问题的研究缺少对控制方式和运行方式等多因素约束的考虑,且鲜有针对异构新能源并网送出能力及异构新能源多馈入系统静态电压稳定边界进行量化分析所得的研究结论,如文献[21]以雅可比矩阵最小奇异值为指标评估系统静态电压稳定性,文献[22-24]研究了新能源送出系统电压稳定裕度指标的适用条件,但都未考虑不同控制方式下新能源无功电压特性对评估过程产生的影响。
为解决上述问题,本文首先针对构网型电源的无功电压响应特性进行研究,揭示其节点类型转换特性,明确构网型电源电压支撑边界及送出能力边界;其次基于潮流雅可比矩阵奇异条件量化评估不同控制方式、不同运行方式下异构新能源多馈入系统的送出能力及静态电压稳定边界,从控制、系统参数方面分析了静态电压稳定性影响因素;最后仿真验证了所提出机理与分析的正确性。
常规的新能源场站电压支撑能力较弱,且有功送电距离长,随着出力的增加易出现电压失稳。为了明确构网型电源的电压支撑机理进而对其运行边界进行研究,本节首先建立构网型电源拓扑如图1所示。构网型电源通过功率同步控制策略模拟传统同步发电机的调频调压特性,从而独立构建并网点电压幅值和相角,本质上可以等效为图1b中的受控电压源[25-26],其中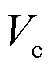 为换流器端口电压,即等效电压源内电动势,
为换流器端口电压,即等效电压源内电动势,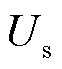 为并网点母线电压;构网型电源注入交流系统的有功功率和无功功率分别为
为并网点母线电压;构网型电源注入交流系统的有功功率和无功功率分别为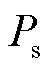 、
、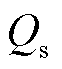 ,以复功率形式表示;忽略传输线路电阻、对地电容。为简化分析,以接入无穷大交流系统为例,假设母线电压幅值
,以复功率形式表示;忽略传输线路电阻、对地电容。为简化分析,以接入无穷大交流系统为例,假设母线电压幅值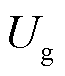 为恒定值1(pu),相角
为恒定值1(pu),相角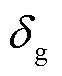 为0。
为0。
根据图1a所示的构网型电源拓扑结构,在d-q轴下列写换流器机端与并网点间稳态电路方程为
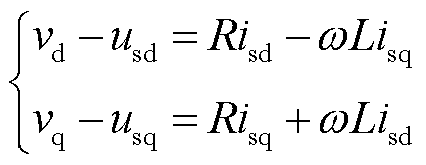 (1)
(1)
式中,R和L分别为包含滤波电阻电感及换流器损耗的等效电阻和电感;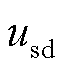 、
、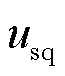 分别为并网点电压d、q轴分量;
分别为并网点电压d、q轴分量;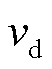 、
、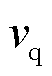 分别为等效电压源内电动势的d、q轴分量。假设内电动势向量与d轴重合,且在电压外环控制中,电压参考值q轴分量
分别为等效电压源内电动势的d、q轴分量。假设内电动势向量与d轴重合,且在电压外环控制中,电压参考值q轴分量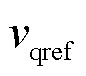 通常为0,换流器输出电压q轴分量
通常为0,换流器输出电压q轴分量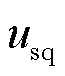 跟踪参考电压,则可认为稳态下
跟踪参考电压,则可认为稳态下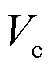 与
与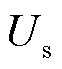 同相位,并有
同相位,并有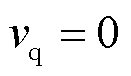 ,
,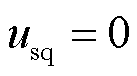 。进一步简化得到换流器输出电流d-q轴分量为
。进一步简化得到换流器输出电流d-q轴分量为
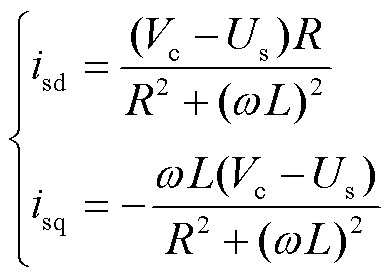 (2)
(2)
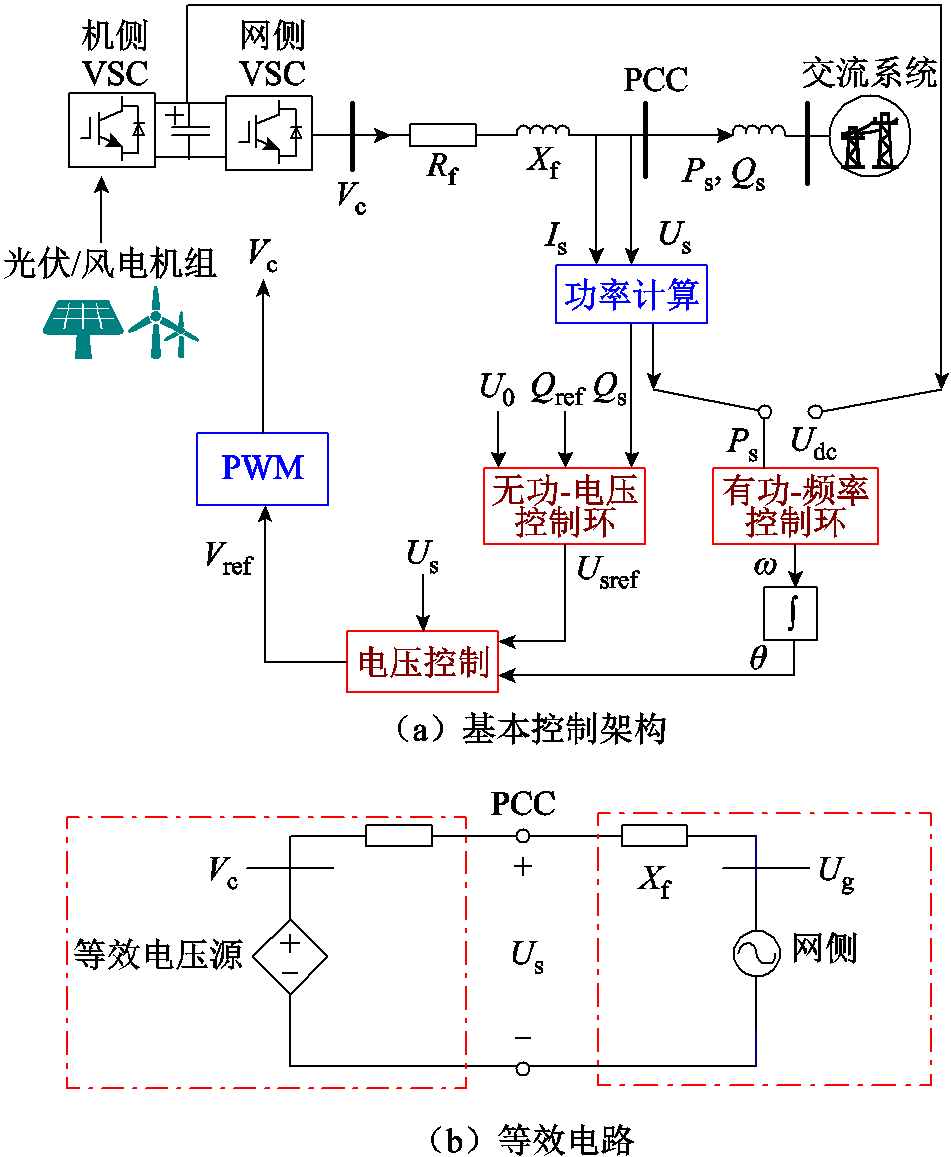
图1 构网型电源拓扑结构
Fig.1 Grid-forming power source topology structure
VSC输出电压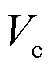 受调制上限约束,在附录第5节中进行说明。由式(2)可知构网型电源具有电流跟随电压形成的特性,得到输出电流
受调制上限约束,在附录第5节中进行说明。由式(2)可知构网型电源具有电流跟随电压形成的特性,得到输出电流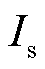 幅值表达式为
幅值表达式为
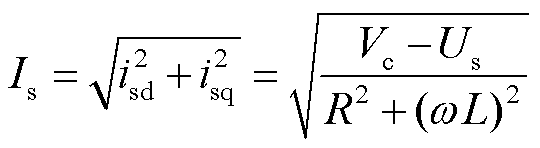 (3)
(3)
由d-q轴分量表示的换流器输出有功、无功功率[27]为
 (4)
(4)
将式(2)中的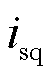 表达式代入式(4),进一步得到电压控制下的无功功率表达式为
表达式代入式(4),进一步得到电压控制下的无功功率表达式为
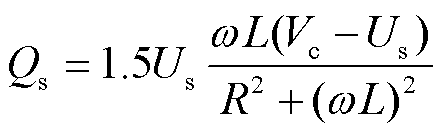 (5)
(5)
可知换流器输出无功功率是受机端电压及并网点电压影响的量。
由图1b中的等效电路,输出功率与并网点电压幅值和相角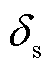 间关系[28]为
间关系[28]为
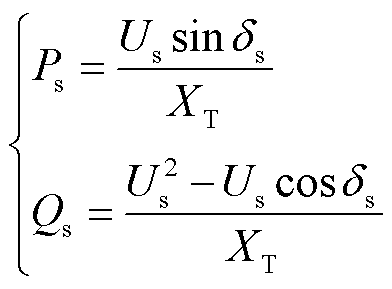 (6)
(6)
式中,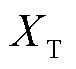 为包含联接变压器的并网线路等效电抗。消去相角
为包含联接变压器的并网线路等效电抗。消去相角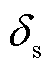 ,可以得到并网点电压有效值为
,可以得到并网点电压有效值为
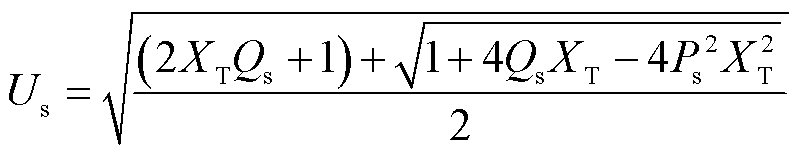 (7)
(7)
逐渐增加构网型电源有功出力,线路上流过的电流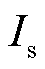 增大,稳态时并网点电压受控维持恒定。由式(3)可知,等效电压源内电动势
增大,稳态时并网点电压受控维持恒定。由式(3)可知,等效电压源内电动势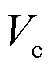 会增加,以补偿换流器端口与并网点间产生的电压降。而系统运行状态变化时,有功功率
会增加,以补偿换流器端口与并网点间产生的电压降。而系统运行状态变化时,有功功率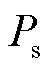 的变化量远大于无功功率
的变化量远大于无功功率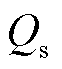 ,联立式(3)与式(4)得到简化后
,联立式(3)与式(4)得到简化后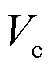 与输出有功功率间近似线性关系为
与输出有功功率间近似线性关系为
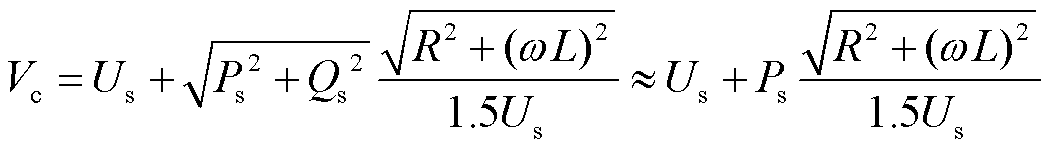 (8)
(8)
根据式(5),构网型电源输出无功功率由并网点母线电压及内电动势决定。当换流器输出有功功率不断增加时,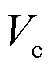 也线性增长,因此
也线性增长,因此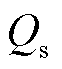 增加。由式(7)可知,
增加。由式(7)可知,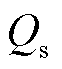 的增加为系统电压提供了支撑,可使
的增加为系统电压提供了支撑,可使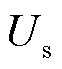 维持在额定值,直到
维持在额定值,直到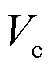 受调制上限约束变为恒定值,再增加有功功率,
受调制上限约束变为恒定值,再增加有功功率,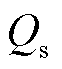 将不再继续增长,并网点母线电压会大幅下降,因此构网型电源稳态下的无功电压响应呈现明显的两阶段变化特性。得到换流器端口电压、网侧交流母线电压和电流以及输出无功功率随有功功率变化的曲线如图2所示。
将不再继续增长,并网点母线电压会大幅下降,因此构网型电源稳态下的无功电压响应呈现明显的两阶段变化特性。得到换流器端口电压、网侧交流母线电压和电流以及输出无功功率随有功功率变化的曲线如图2所示。
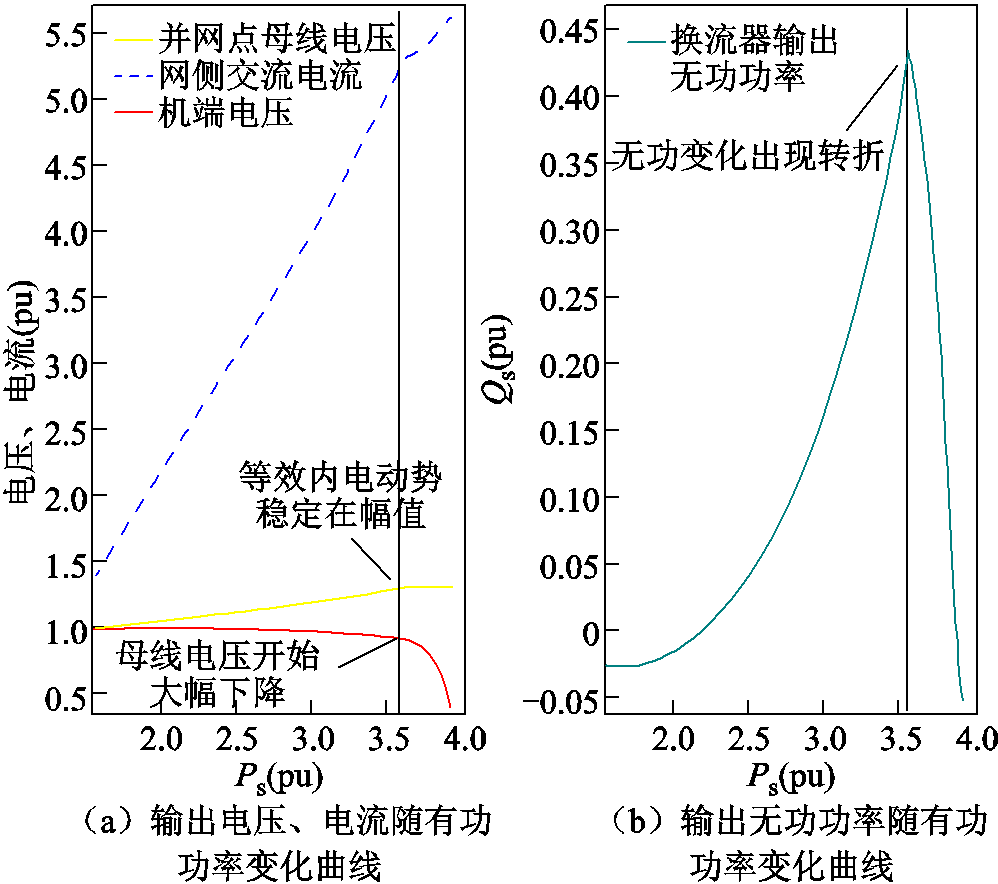
图2 构网型电源输出电压、电流及无功变化曲线
Fig.2 Output voltage、current and reactive power variation curves of grid-forming power source
附录第1节中展示了控制器输出参数随有功功率变化的响应全过程。结合上述内容对构网型电源两阶段的无功电压响应过程总结如下:
1)无功响应上升阶段
随着有功功率的增加,换流器输出电流及机端电压均上升,直至换流器最终达到调制上限,此后构网型电源输出的无功功率只随并网点电压变化。从初始运行点至达到限幅状态的过程中,构网型电源输出无功功率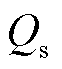 由控制器及并网点电压共同决定,输出无功功率持续增加,因此形成了无功电压变化曲线中的第一阶段。
由控制器及并网点电压共同决定,输出无功功率持续增加,因此形成了无功电压变化曲线中的第一阶段。
2)无功响应下降阶段
并网点电压变化趋势在控制器达到限幅状态后将由外部电路决定。考虑并网点与交流系统间传输线上的功率流动,由式(5)、式(7)及图2可知,越过第一阶段运行拐点后,随着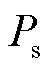 持续增加,
持续增加,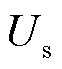 大幅下降,
大幅下降,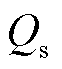 与
与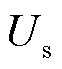 变化方向相同。故在这一阶段中,随着
变化方向相同。故在这一阶段中,随着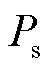 的增大,电压会不断下降直至系统崩溃,同时并网点母线电压幅值和相角满足
的增大,电压会不断下降直至系统崩溃,同时并网点母线电压幅值和相角满足
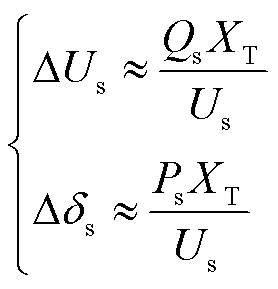 (9)
(9)
式中,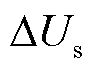 和
和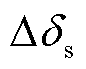 分别为并网点母线电压降落的横分量及纵分量,有
分别为并网点母线电压降落的横分量及纵分量,有
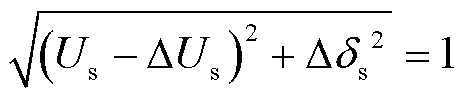 (10)
(10)
单馈入系统中,构网型电源所接入的无穷大交流系统母线电压保持不变(1(pu)),传输线上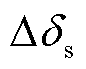 响应
响应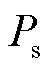 的变化而增加,
的变化而增加,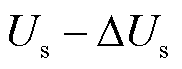 随主导变量
随主导变量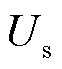 的变化而减小。由式(10)得到并网点母线电压幅值和相角对应的相量关系如图3所示。
的变化而减小。由式(10)得到并网点母线电压幅值和相角对应的相量关系如图3所示。
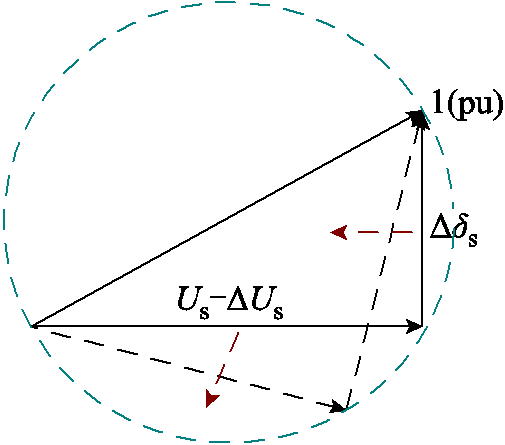
图3 并网点母线电压幅值和相角对应相量关系
Fig.3 Phase relationship diagram of the voltage fall stage of the point of common coupling bus
在线路功率传输极限的约束条件下,构网型电源输出功率与并网点母线电压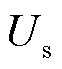 满足式(9)、式(10)所得关系,即随着输出有功功率的增加,
满足式(9)、式(10)所得关系,即随着输出有功功率的增加,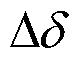 持续增大,而
持续增大,而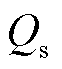 、
、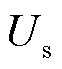 不断减小。因此并网点母线电压幅值和相角的端点构成的解空间形成了以无穷大交流系统母线电压幅值为直径的圆。
不断减小。因此并网点母线电压幅值和相角的端点构成的解空间形成了以无穷大交流系统母线电压幅值为直径的圆。
从电压、无功响应的两阶段变化曲线及图3可以得到结论,构网型电源可为系统起到一定的电压支撑作用,但其电压支撑能力受到换流器调制环节约束条件的影响,在达到约束条件后网侧电压、输出无功功率将由构网型电源所接入的外部系统决定。
在1.1节的分析中,构网型电源在无功响应上升阶段控制环节中输出的无功功率是与并网点电压及控制参数呈现强耦合关系的时变量,如式(5)所述,在潮流计算中应当作本节点的待求解量,此时构网型电源与同步发电机具有相似的电压源特性[29-30],应看作电压已知的PV节点。进一步由式(4)可以推导出由控制参数表示的有功、无功功率解析式为
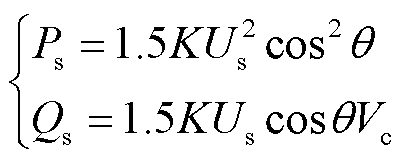 (11)
(11)
式中,K为网侧交流电流随VSC输出有功变化的增长系数,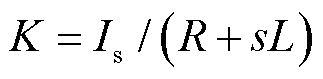 。由附图1a可知,有功控制环节输出的电压相角余弦值变化幅度较小,为分析简便将其按常数处理,有
。由附图1a可知,有功控制环节输出的电压相角余弦值变化幅度较小,为分析简便将其按常数处理,有
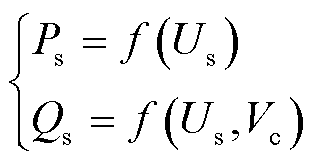 (12)
(12)
在图1b所示的等效系统中将公共连接点(Point of Common Coupling, PCC)看作PV节点,无穷大交流系统为平衡节点,描述构网型电源单馈入系统的非线性方程为
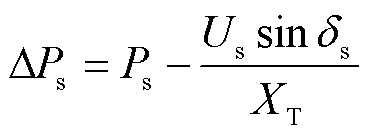 (13)
(13)
此时单馈入系统的雅可比矩阵中只有一个元素,即
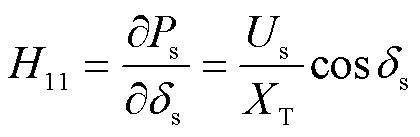 (14)
(14)
随着构网型电源输出功率的增加,换流器逐渐达到调制上限,式(12)中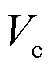 变为常数,输出无功功率不再受时变的控制量影响,从而易于求解。功率增长的过程实际上是将并网点电压采样值馈入控制系统从而对功率迭代求解的过程,即
变为常数,输出无功功率不再受时变的控制量影响,从而易于求解。功率增长的过程实际上是将并网点电压采样值馈入控制系统从而对功率迭代求解的过程,即
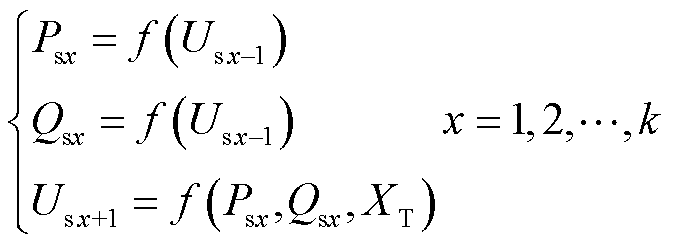 (15)
(15)
因此在第x步进行潮流计算时,PCC的给定量为有功功率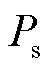 及无功功率
及无功功率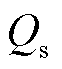 ,即PCC的类型由PV节点转换为PQ节点。对应式(14)有无功功率满足的非线性方程为
,即PCC的类型由PV节点转换为PQ节点。对应式(14)有无功功率满足的非线性方程为
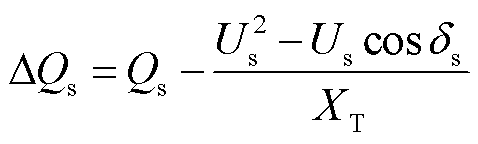 (16)
(16)
进一步得到其雅可比矩阵为
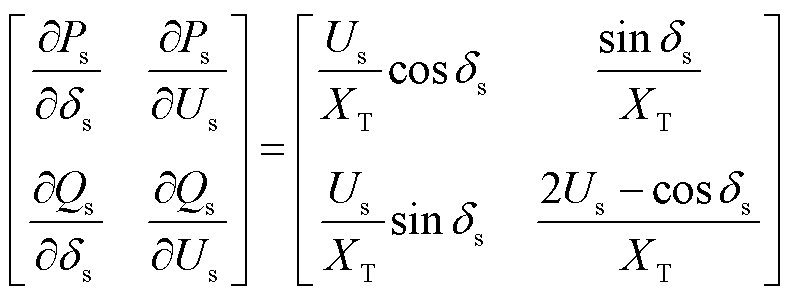 (17)
(17)
基于单馈入系统相量测量单元(Phasor Measurement Unit, PMU)在线运行数据计算潮流雅可比矩阵,分别得到PV节点转换为PQ节点及PV节点不转换时雅可比矩阵行列式与构网型电源送出功率、并网点电压间的关系,如图4所示。
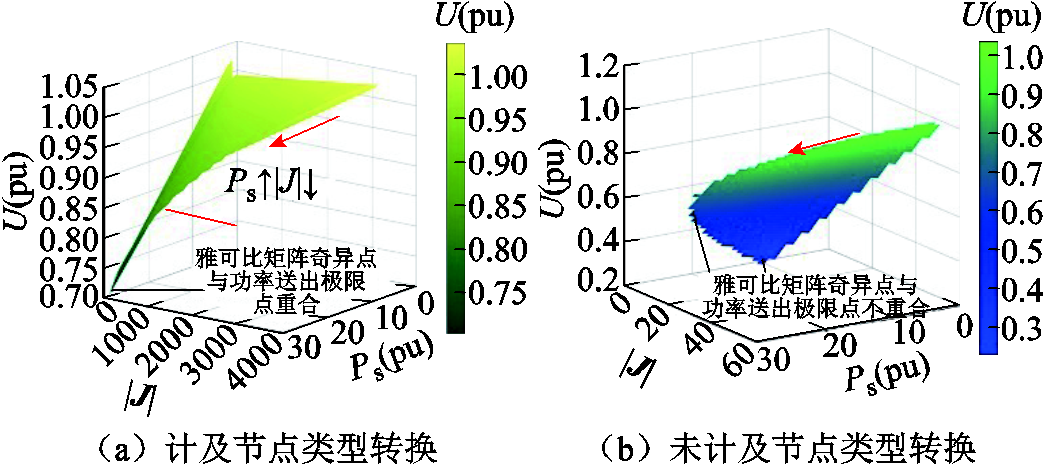
图4 不同并网点节点类型下雅可比矩阵奇异值与送出功率间关系
Fig.4 Relationship between the singular values of the Jacobian matrix and output power under different types of PCC nodes
在未到节点转换前,雅可比矩阵行列式与构网型电源送出功率、并网点电压间的关系是一定的。PV节点的电压幅值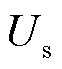 确定,列写雅可比矩阵时与无功功率相关的项会被简化。而当节点转换后,无功功率
确定,列写雅可比矩阵时与无功功率相关的项会被简化。而当节点转换后,无功功率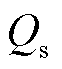 重新并入矩阵,电压幅值
重新并入矩阵,电压幅值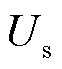 成为待求量,因此雅可比矩阵的所有元素都会参与计算。而在新能源系统中,
成为待求量,因此雅可比矩阵的所有元素都会参与计算。而在新能源系统中,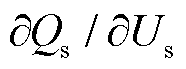 和
和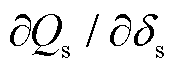 的非线性特性会显著增加矩阵的复杂度。随着有功出力持续增加,越过无功响应转折点后电压幅值急剧下降,
的非线性特性会显著增加矩阵的复杂度。随着有功出力持续增加,越过无功响应转折点后电压幅值急剧下降,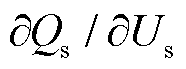 和
和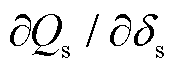 的值会逐渐增大。随着系统运行接近极限点,
的值会逐渐增大。随着系统运行接近极限点,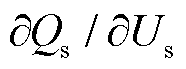 的非线性特性会进一步放大,导致雅可比矩阵行列式det(J)大幅变化。而在PV节点未转换的情况下,电压幅值始终是已知量,雅可比矩阵中不包含与无功功率相关的导数项,因此其行列式变化相对平稳。节点转换过程中,与无功功率相关的导数项的变化导致行列式剧烈变化,这一现象也反映了高比例新能源系统的非线性及复杂性。由图4可知,若不计及构网型电源节点类型转换,依然将其当作PV节点处理,则系统雅可比矩阵奇异点将出现在构网型电源送出功率极限点之后,此时系统静态电压稳定临界点将无法表征传输功率极限值,导致构网型电源并网系统静态电压稳定性量化评估及送出能力分析出现较大误差。因此,为精确评估送出能力,需在潮流模型中计及节点类型转换的影响。
的非线性特性会进一步放大,导致雅可比矩阵行列式det(J)大幅变化。而在PV节点未转换的情况下,电压幅值始终是已知量,雅可比矩阵中不包含与无功功率相关的导数项,因此其行列式变化相对平稳。节点转换过程中,与无功功率相关的导数项的变化导致行列式剧烈变化,这一现象也反映了高比例新能源系统的非线性及复杂性。由图4可知,若不计及构网型电源节点类型转换,依然将其当作PV节点处理,则系统雅可比矩阵奇异点将出现在构网型电源送出功率极限点之后,此时系统静态电压稳定临界点将无法表征传输功率极限值,导致构网型电源并网系统静态电压稳定性量化评估及送出能力分析出现较大误差。因此,为精确评估送出能力,需在潮流模型中计及节点类型转换的影响。
构网型电源输出无功功率受控制器约束条件影响,随功率变化存在先增后降拐点,且节点类型也会发生转换,对其运行边界的分析由两部分构成:电压支撑能力边界及功率送出能力边界。
由上述分析可以得到当内电动势达到幅值后,并网点电压迅速下降,此时即运行至电压支撑能力边界,内电动势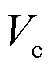 变为常数,
变为常数,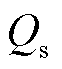 变化曲线出现拐点,得到表征电压支撑能力边界的条件为
变化曲线出现拐点,得到表征电压支撑能力边界的条件为
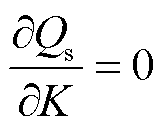 (18)
(18)
同时可由式(18)推导出并网点电压在构网型电源提供电压支撑情况下所能达到的最大值为
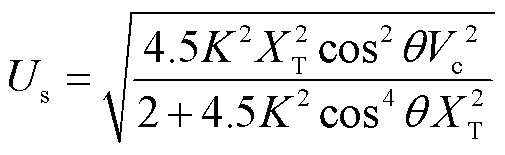 (19)
(19)
式(19)的推导过程在附录第2节中给出。
接下来分析功率传输能力边界,根据式(17),系统潮流雅可比矩阵奇异的条件为
 (20)
(20)
将式(11)中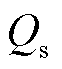 的解析式代入式(20)并求解,得到满足雅可比矩阵奇异条件时的并网点电压为
的解析式代入式(20)并求解,得到满足雅可比矩阵奇异条件时的并网点电压为
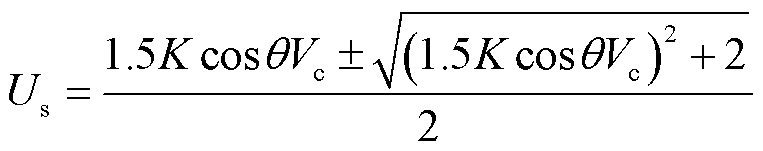 (21)
(21)
迭代过程中将式(21)代入式(11)进行潮流求解,当系统达到功率输出极限时,有
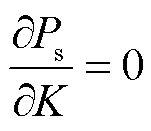 (22)
(22)
对应同步机在无功越限后由PV节点转换为PQ节点的特性,构网型电源在达到VSC内电动势约束条件后也将由PV节点转换为PQ节点。得到构网型电源的运行边界图如附录第3节所示。
在新能源汇集系统中,新能源场站外送功率增加会导致并网点母线电压降低,直至达到静态电压稳定临界点,接近临界点时可能造成系统发生电压崩溃,临界点对应场站的最大送出功率。由于新能源场站的无功电压特性受不同控制方式影响呈现复杂的耦合性,可能导致新能源场站并网系统在到达临界点前便已失稳[31],对于新能源多馈入系统,其失稳机理与新能源场站控制方式有关,将在下面进行详细分析。
设高比例新能源电网有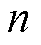 个节点,其中大部分电源为非同步机电源,少部分电源为传统同步机电源,系统简化拓扑如图5所示。
个节点,其中大部分电源为非同步机电源,少部分电源为传统同步机电源,系统简化拓扑如图5所示。
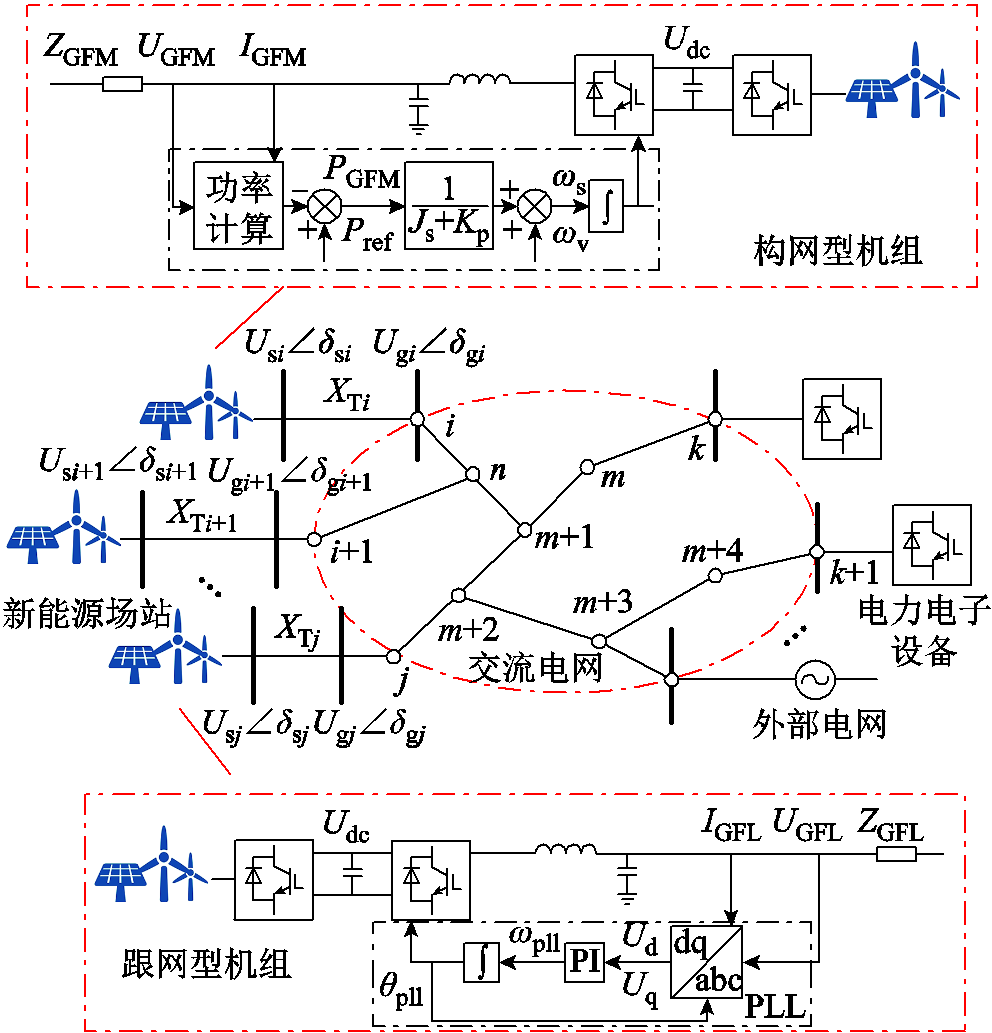
图5 多馈入系统简化拓扑
Fig.5 Simplified topology diagram of a multi-feed system
对应节点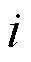 的注入功率用
的注入功率用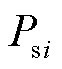 、
、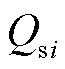 表示,节点
表示,节点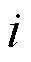 的负荷用
的负荷用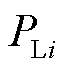 、
、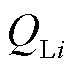 表示,则电网节点
表示,则电网节点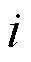 的功率平衡方程[32]为
的功率平衡方程[32]为
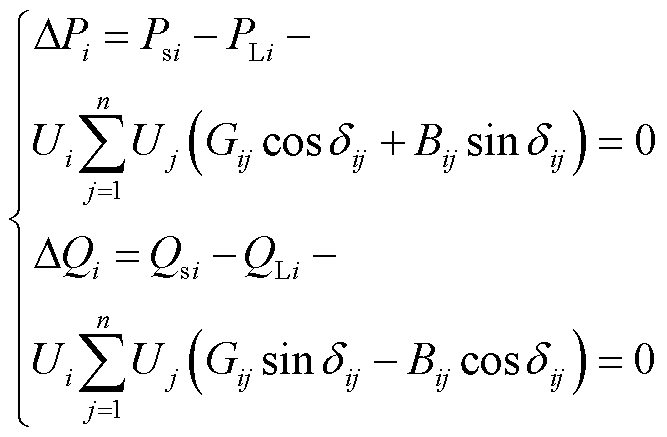 (23)
(23)
式中,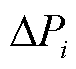 、
、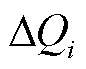 分别为节点
分别为节点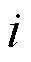 的有功和无功不平衡量;
的有功和无功不平衡量;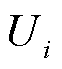 、
、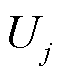 分别为节点
分别为节点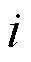 与
与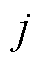 的电压幅值;
的电压幅值;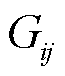 、
、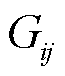 分别为节点
分别为节点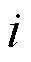 与
与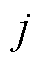 之间的电导和电纳;
之间的电导和电纳;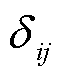 为节点
为节点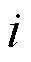 与
与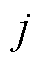 之间的相位差。
之间的相位差。
对于同步发电机节点,通常将其处理为平衡节点或PV节点,负荷模型采用恒阻抗(ZIP)模型,通常处理为PQ节点,从而得到交流侧雅可比矩阵为
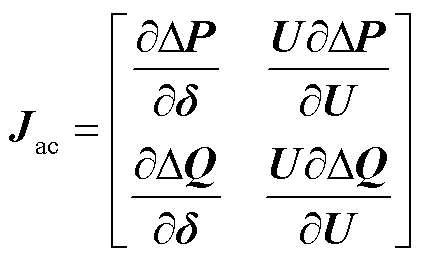 (24)
(24)
新能源多馈入系统的雅克比矩阵包括交流系统测雅克比矩阵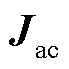 以及设备侧雅克比矩阵
以及设备侧雅克比矩阵 ,根据多馈入系统的潮流模型,可将其展开为
,根据多馈入系统的潮流模型,可将其展开为
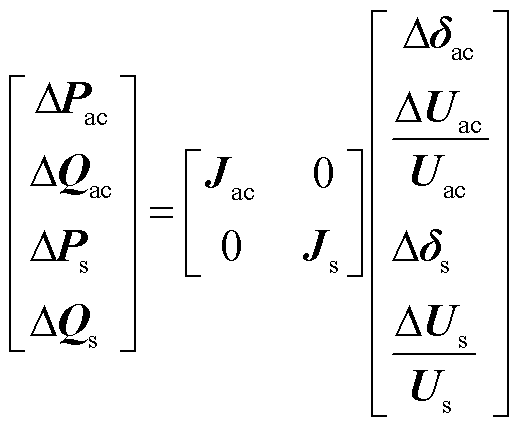 (25)
(25)
式中,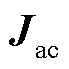 包含了交流系统中所有发电机、负荷及其联络节点;
包含了交流系统中所有发电机、负荷及其联络节点; 包含了所有新能源节点以及与之相连的交流系统侧并网节点。根据图5,新能源节点对应的雅可比矩阵元素表达式见附录第4节。
包含了所有新能源节点以及与之相连的交流系统侧并网节点。根据图5,新能源节点对应的雅可比矩阵元素表达式见附录第4节。
对于非同步机电源节点,需考虑不同新能源控制类型,对相应雅克比矩阵中元素进行修改。
2.2.1 跟网型新能源节点
跟网型新能源注入交流系统无功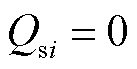 ,通常处理为PQ节点,令式(6)中无功功率为0,得到
,通常处理为PQ节点,令式(6)中无功功率为0,得到
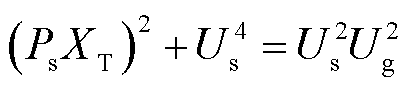 (26)
(26)
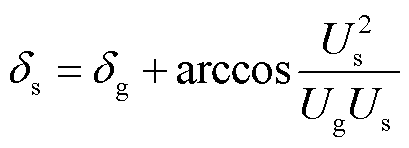 (27)
(27)
解得并网点电压的有效值为
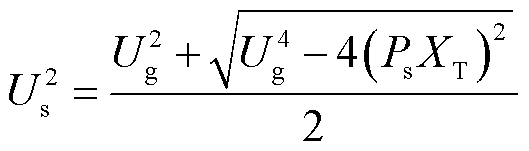 (28)
(28)
将式(27)代入雅可比矩阵元素表达式,有
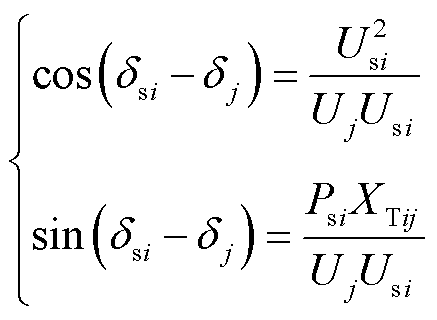 (29)
(29)
对雅可比矩阵中的相应元素进行修改可得
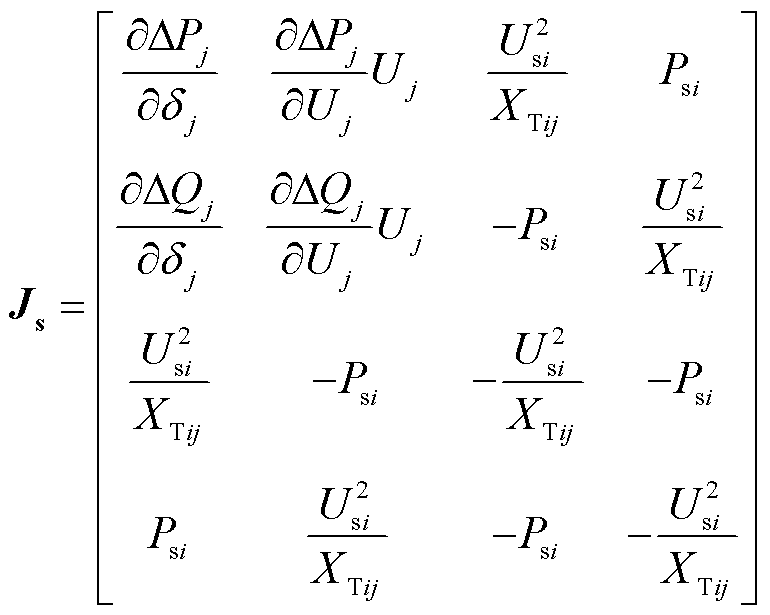 (30)
(30)
将采用恒电压控制下的跟网型新能源节点处理为PV节点,并网点电压幅值、相角与节点注入有功功率间关系与式(6)相同,代入雅可比矩阵元素表达式,则有
 (31)
(31)
对雅可比矩阵中的相应元素进行修改时,只需将与新能源节点输出有功功率相关的元素修改为
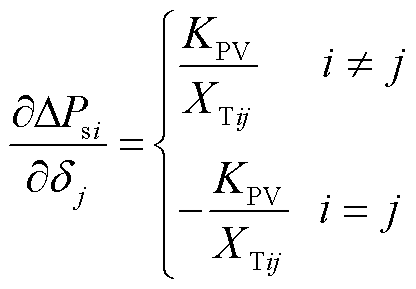 (32)
(32)
其中
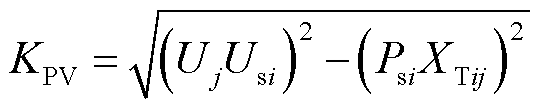 (33)
(33)
而与新能源节点输出无功功率相关的元素为0,其余元素的处理与式(30)相同,由此即可得到降阶的雅可比矩阵。
2.2.2 构网型新能源节点
由上述分析可知,构网型电源的节点类型在达到控制器调制上限时将发生转换,因此在对雅可比矩阵进行修改时,应考虑控制器变量,分阶段进行处理。在VSC内电动势达到限幅前将构网型新能源处理为PV节点,且Qsi = f (Usi,Vsi),得到控制器参数表示的并网点电压解析式为
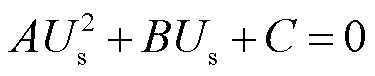 (34)
(34)
其中
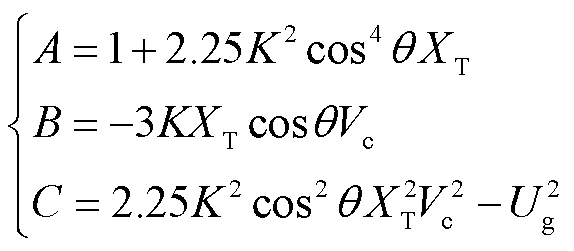 (35)
(35)
此时对雅可比矩阵元素的修改同式(31),只需将式(34)的方程解代入具体元素中。
VSC内电动势达到限幅值后,构网型新能源节点类型转换为PQ节点,且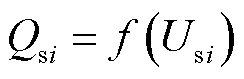 。令式(35)中Vc为常数,将式(34)的计算结果代入式(31)的雅可比矩阵元素中,则与新能源节点输出无功功率相关的元素修改为
。令式(35)中Vc为常数,将式(34)的计算结果代入式(31)的雅可比矩阵元素中,则与新能源节点输出无功功率相关的元素修改为
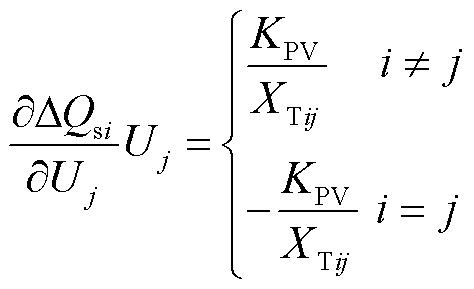 (36)
(36)
其余元素的处理与式(31)相同。由此得到不同控制方式下新能源节点部分在多馈入系统潮流雅可比矩阵中的元素表达式。
根据式(25)所述多馈入系统雅可比矩阵形式,分块矩阵结构忽略了外设备与不相连的交流系统节点间的耦合性,因此可将多馈入系统的雅可比矩阵简化为对角矩阵进行分析。在对角矩阵的奇异性分析中,如果某个主对角块是奇异的或接近奇异,整个矩阵也将趋近奇异,即系统达到静态电压稳定边界的条件为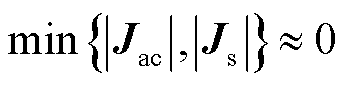 。由于
。由于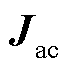 在交流系统侧运行方式不变的情况下近乎为系统的固有特性,因此重点考虑外设备侧的雅可比矩阵
在交流系统侧运行方式不变的情况下近乎为系统的固有特性,因此重点考虑外设备侧的雅可比矩阵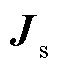 奇异性。
奇异性。
在2.2节的分析中得到了不同新能源控制方式下的系统潮流雅可比矩阵形式,其中与新能源并网点直接相关的主对角线元素与非对角线元素包含了传输功率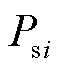 、
、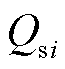 ,节点电压
,节点电压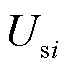 、
、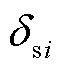 等信息。系统潮流雅可比矩阵中的主对角线元素
等信息。系统潮流雅可比矩阵中的主对角线元素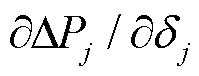 、
、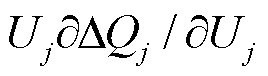 代表系统中的自反馈项,反映了系统的功率平衡和传输能力。由于矩阵奇异的充要条件是其为悬空矩阵[33],即其对角元素与非对角元素和为零,如果非对角线元素接近对角线元素,矩阵可能出现线性相关性,进而导致雅可比矩阵奇异值为零或接近零,表明矩阵可能是奇异的,此时系统接近不稳定状态。
代表系统中的自反馈项,反映了系统的功率平衡和传输能力。由于矩阵奇异的充要条件是其为悬空矩阵[33],即其对角元素与非对角元素和为零,如果非对角线元素接近对角线元素,矩阵可能出现线性相关性,进而导致雅可比矩阵奇异值为零或接近零,表明矩阵可能是奇异的,此时系统接近不稳定状态。
参考4.1节中系统结构参数得到不同控制方式下单新能源场站送出有功功率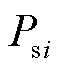 、雅可比矩阵自反馈项相关量及与之相连的交流系统侧节点电压Uj间关系,如图6所示。
、雅可比矩阵自反馈项相关量及与之相连的交流系统侧节点电压Uj间关系,如图6所示。
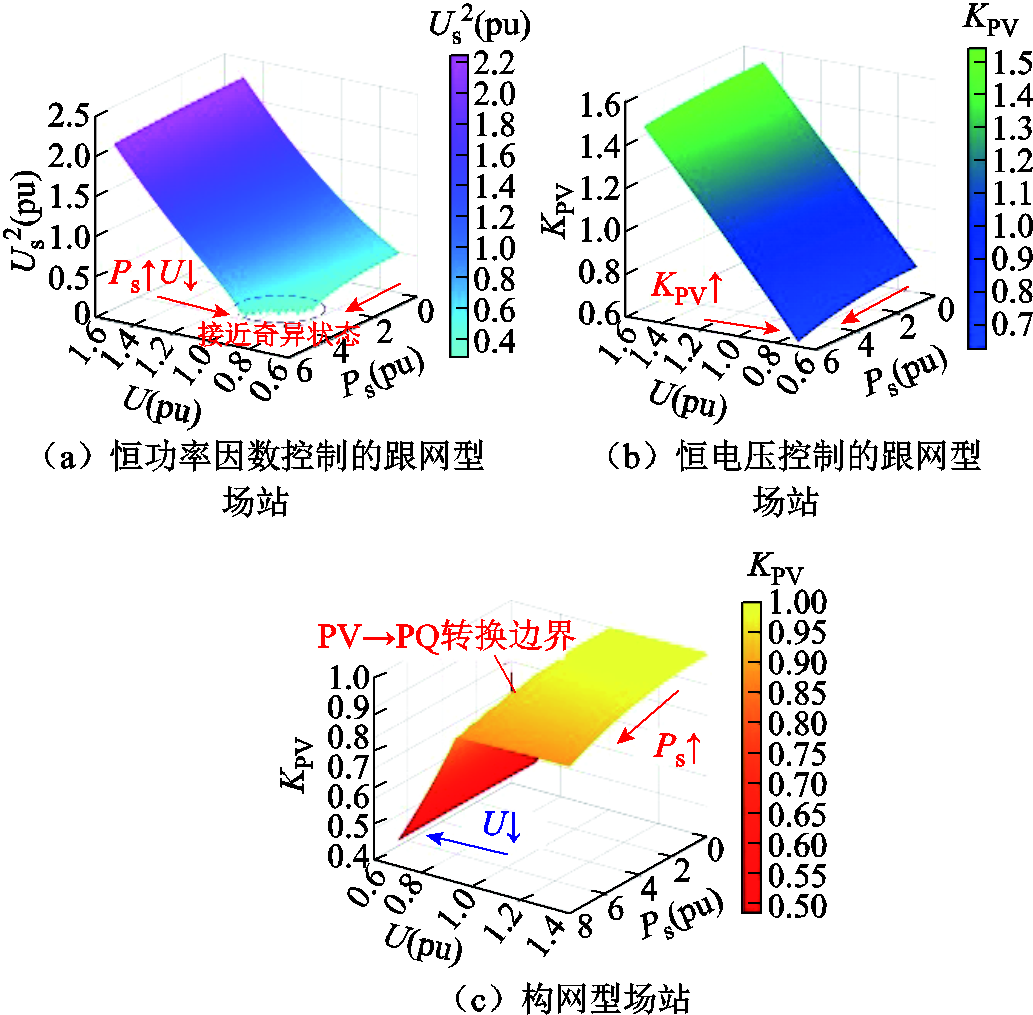
图6 不同控制方式下新能源场站送出能力示意
Fig.6 Diagram of the output capacity of the new energy plant under different control methods
对于恒功率因数控制下的跟网型新能源,如图6a所示,其雅可比矩阵接近奇异的条件为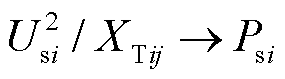 。随着送出功率的增加,各节点电压不断下降,直至达到静态电压稳定临界点,所对应的
。随着送出功率的增加,各节点电压不断下降,直至达到静态电压稳定临界点,所对应的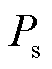 即为极限送出功率;对于恒电压控制下的跟网型新能源,系统潮流雅克比矩阵接近奇异的条件为
即为极限送出功率;对于恒电压控制下的跟网型新能源,系统潮流雅克比矩阵接近奇异的条件为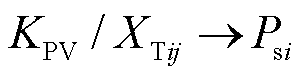 ,得到新能源送出有功功率、反映送出功率与电压耦合关系的系数
,得到新能源送出有功功率、反映送出功率与电压耦合关系的系数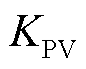 及与之相连的交流系统侧节点电压
及与之相连的交流系统侧节点电压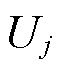 间关系如图6b所示。与恒功率因数控制的跟网型电源相比,此时奇异点所对应的
间关系如图6b所示。与恒功率因数控制的跟网型电源相比,此时奇异点所对应的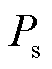 略大于图6a中的极限值。
略大于图6a中的极限值。
考虑构网型电源控制器环节约束条件,在刻画其送出功率关系时考虑电压支撑边界的临界条件,得到Psi、KPV及Uj间关系如图6c所示。分析可得,随着送出功率的增加,电压在响应初始阶段可维持在一定水平,直至达到电压支撑能力边界后出现明显转折,此时构网型电源节点类型发生转换。与跟网型电源相比,由于构网型电源具有阶段电压维持能力,因此在功率扰动下系统母线电压并不会直接大幅下降,从而提升了新能源送出极限。
需要说明的是,目前恒功率因数控制是跟网型电源并网运行的主要控制方式,其通过内外环的配合实现目标功率输出,而恒电压控制则多应用于需要主动调节电压的孤岛系统或微电网场景,通过对储能或静止无功补偿等设备控制模式的切换来协同调节新能源场站无功电压,因此本文选择恒功率因数控制策略作为后续跟网型电源的研究基础;对于构网型电源,其通过调节公共耦合点电压的幅值和相角控制注入功率[34],不同的构网型控制架构在具体实现细节上有所区别,但设计理念都与同步机原理类似,本文着重分析稳态运行情况下的系统等效结构及电气特征,对于同步控制策略中的具体控制方式并不过多涉及,综合认为其能够实现基本控制效果,对外呈现为电压源。
以上分析均是针对新能源单点送出系统,而在多馈入系统中,由于电源的多样性和耦合机理的复杂叠加,系统雅可比矩阵更容易接近奇异状态,接下来将考虑异构新能源不同并网运行方式,对系统静态电压稳定性进行分析。
2.5.1 多机单馈入场景
在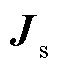 中令交流系统侧节点与本节点电压相角和幅值信息所对应的矩阵块为
中令交流系统侧节点与本节点电压相角和幅值信息所对应的矩阵块为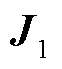 ,交流系统侧节点与新能源节点信息对应的矩阵块为
,交流系统侧节点与新能源节点信息对应的矩阵块为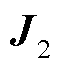 ,新能源节点与交流系统侧节点信息对应的矩阵块为
,新能源节点与交流系统侧节点信息对应的矩阵块为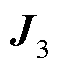 ,新能源节点自身信息所对应的矩阵块为
,新能源节点自身信息所对应的矩阵块为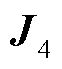 ,以构网型电源的外设备侧雅可比矩阵为例,有
,以构网型电源的外设备侧雅可比矩阵为例,有
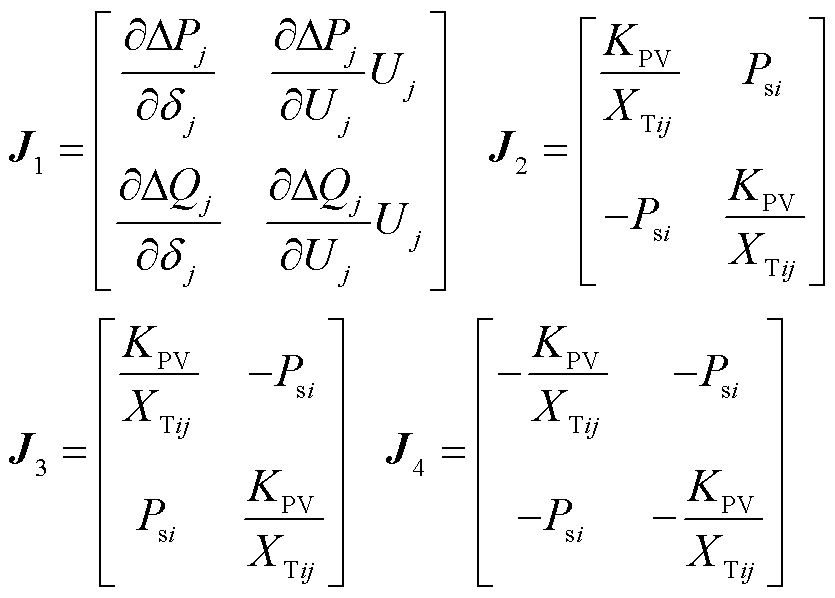 (37)
(37)
得到多机单馈入系统外设备侧雅可比矩阵的通用表达式为
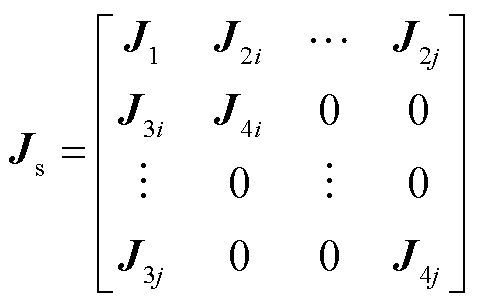 (38)
(38)
式中,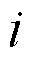 、
、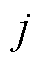 分别为不同新能源场站。
分别为不同新能源场站。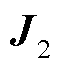 与
与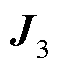 满足
满足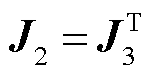 ,即对于多机单馈入新能源系统,其雅可比矩阵依然是对称矩阵。与新能源送出功率、并网点电压直接相关的主对角线元素为
,即对于多机单馈入新能源系统,其雅可比矩阵依然是对称矩阵。与新能源送出功率、并网点电压直接相关的主对角线元素为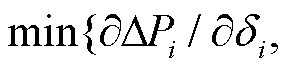
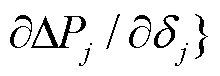 ,非对角线元素为
,非对角线元素为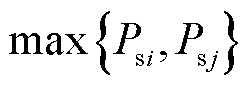 ,得到系统潮流雅克比矩阵接近奇异的简化条件为
,得到系统潮流雅克比矩阵接近奇异的简化条件为
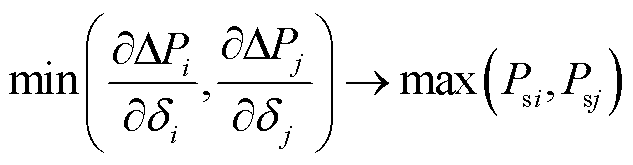 (39)
(39)
以异构新能源集群并网场景为例,场站送出功率与交流系统母线电压、雅可比矩阵奇异性判据间的关系如图7a所示,随着有功出力的增加,构网型新能源场站在达到电压支撑能力边界后电压大幅下降直至趋近静态电压稳定极限点,左侧为低电压解对应的不稳定运行区域。与异构新能源并网场景相比,在仅有跟网型场站的新能源系统中,其送出功率极限下降,如图7b所示,因此在新能源系统中以构网型场站替换部分跟网型场站可提升新能源送出能力。
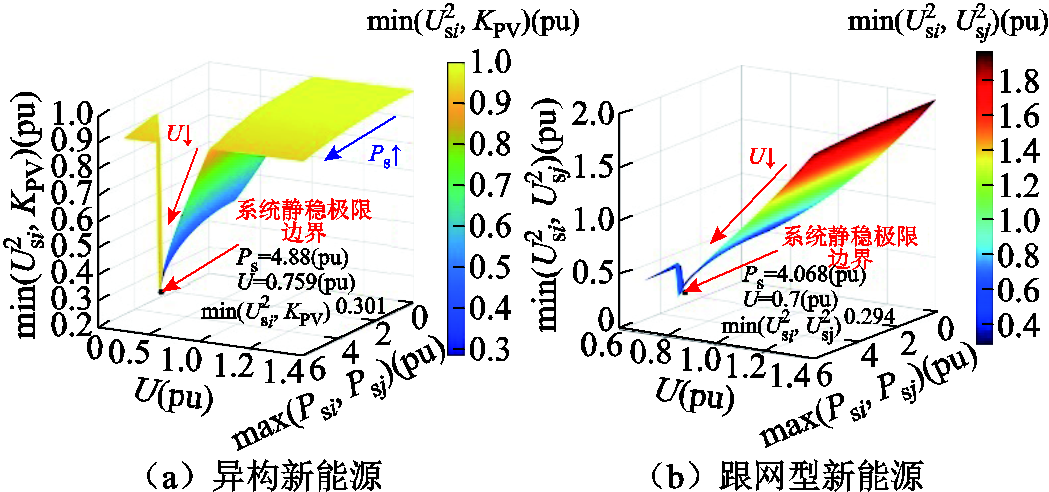
图7 不同控制方式下新能源集群并网送出能力示意图
Fig.7 Diagram of the output capacity of the collected new energy plant under different control methods
对于多机单馈入新能源系统,由于场站间电气距离较近,存在节点电压、功率耦合关系,可能制约其新能源送出能力,下面将在多机多馈入系统中进行分析。
2.5.2 多机多馈入场景
下面将对图5所示多机多馈入系统进行分析,类比式(38)推导得到多机多馈入系统外设备侧雅可比矩阵的通用表达式为
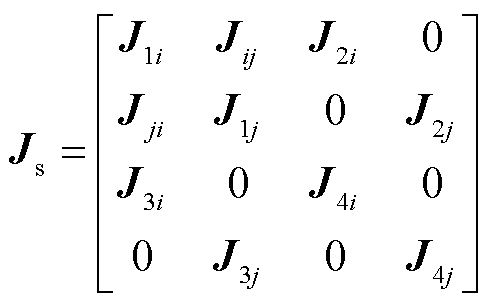 (40)
(40)
根据交流系统中潮流雅可比矩阵的一般性质,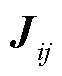 和
和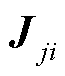 满足
满足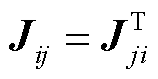 ,因此,交流系统自相关的左上角雅可比矩阵块为对称矩阵,新能源节点自相关的右下角的矩阵块为对角矩阵,考虑外设备侧特性,此时系统雅可比矩阵奇异性条件为
,因此,交流系统自相关的左上角雅可比矩阵块为对称矩阵,新能源节点自相关的右下角的矩阵块为对角矩阵,考虑外设备侧特性,此时系统雅可比矩阵奇异性条件为
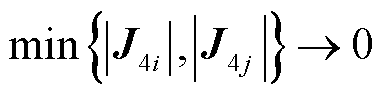 (41)
(41)
式(39)本质上为式(41)的简化推广,其外设备侧可等效为单点送出的电源。以新能源分布并网场景为例,计算得到场站送出功率与交流系统母线电压、雅可比矩阵块最小行列式间的关系如图8a所示。
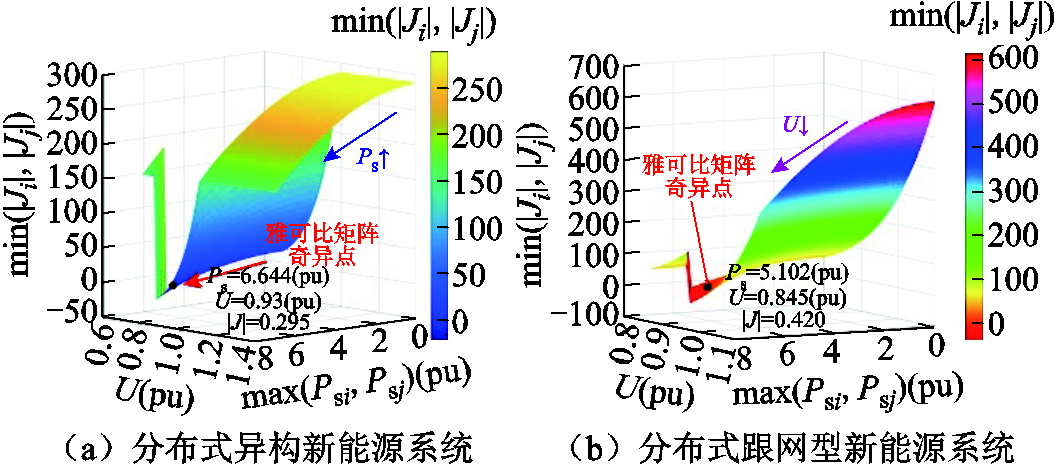
图8 不同控制方式下新能源分布并网送出能力示意图
Fig.8 Diagram of the output capacity of the distributed new energy plant under different control methods
与集群并网场景相比,异构新能源分布式接入交流系统时最大送出功率增加。在仅有跟网型场站分布式接入的新能源系统中,如图8b所示,其送出功率极限下降,因此在新能源场站分布式接入的系统中,以构网型场站替换部分跟网型场站对新能源送出能力的提升作用会更强。
本文所讨论的临界点均指系统达到静态电压稳定极限时的运行边界,实际上具备一定低电压穿越能力的新能源机组在低电压穿越状态下的有功输出迅速降低,在结束低电压穿越状态后,有功输出会缓慢恢复,系统运行在静稳极限边界内[35];而不具备低电压穿越能力的机组将在电压水平偏低时动作跳闸,也运行在静稳极限边界内。同时在实际系统中进行分析时,可能会出现外设备侧雅可比矩阵达到奇异条件前系统潮流就已不收敛的现象。以新能源馈入点附近的负荷节点为例,其非线性方程为
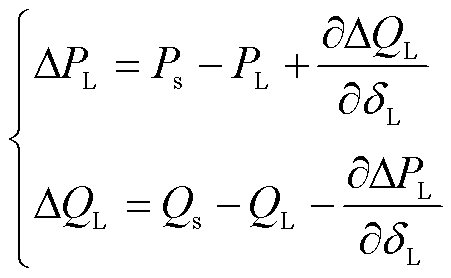 (42)
(42)
式中,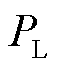 、
、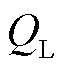 分别为负荷的有功功率及无功功率。由式(42)可知负荷节点自反馈项受外设备传输功率影响。在多机多馈入系统中,与新能源相连的节点数量增多,式(42)中的参数信息将被并入外设备侧雅可比矩阵中,增加式(40)所述的矩阵阶数维度,提高了奇异性分析的复杂程度。为分析多机多馈入系统中潮流收敛性与新能源渗透程度之间的关系,引入负荷节点电压灵敏度用以指示外设备变化时该点电压的响应情况。分别在单新能源及多新能源馈入系统中进行分析,得到外设备有功功率扰动值与负荷节点电压灵敏度、雅可比矩阵奇异判据间的关系如图9所示。在多机多馈入场景下,各负荷节点电压灵敏度分布范围较大,表明此时系统中节点更易受外设备功率波动的影响,在奇异判据未趋于0前系统就已运行至临界状态。
分别为负荷的有功功率及无功功率。由式(42)可知负荷节点自反馈项受外设备传输功率影响。在多机多馈入系统中,与新能源相连的节点数量增多,式(42)中的参数信息将被并入外设备侧雅可比矩阵中,增加式(40)所述的矩阵阶数维度,提高了奇异性分析的复杂程度。为分析多机多馈入系统中潮流收敛性与新能源渗透程度之间的关系,引入负荷节点电压灵敏度用以指示外设备变化时该点电压的响应情况。分别在单新能源及多新能源馈入系统中进行分析,得到外设备有功功率扰动值与负荷节点电压灵敏度、雅可比矩阵奇异判据间的关系如图9所示。在多机多馈入场景下,各负荷节点电压灵敏度分布范围较大,表明此时系统中节点更易受外设备功率波动的影响,在奇异判据未趋于0前系统就已运行至临界状态。
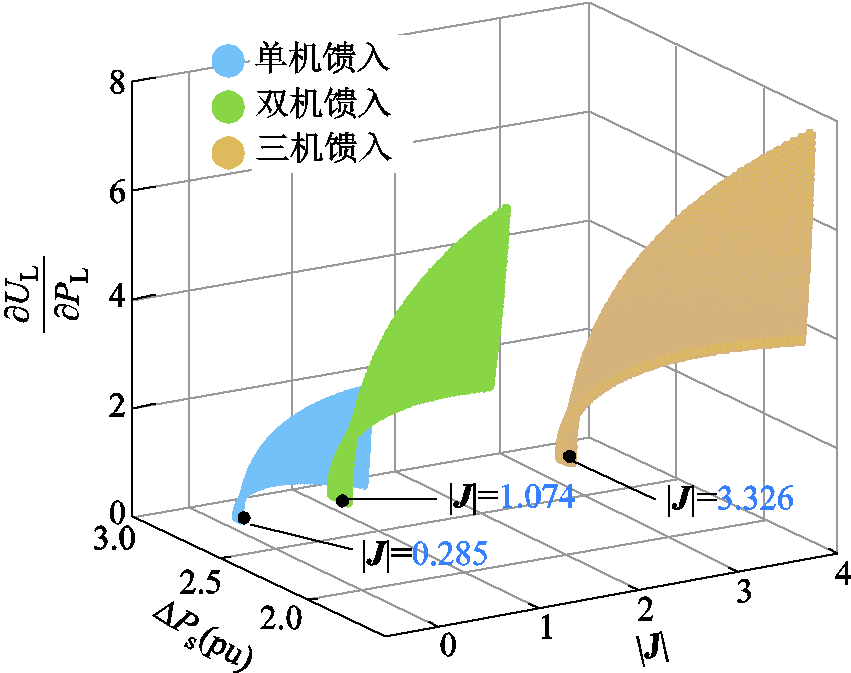
图9 不同新能源渗透程度与负荷节点电压灵敏度分布关系
Fig.9 Distribution relationship between different levels of renewable energy penetration and load node voltage sensitivity
由于实际系统中的复杂因素(如设备控制策略的切换、外部扰动等)与奇异边界存在强耦合性,外设备侧雅可比矩阵相关节点功率、电压变化时将引起交流系统整体的变化,系统中的电压薄弱节点(如重负荷节点)会先跌落至电压崩溃状态,从而导致系统可能在到达理论上的静态电压稳定临界点之前便已失稳,这种特性在新能源渗透率高的多机多馈入系统中将会更加明显。
因此,本文计算的稳定边界相较实际工况会更加保守,能确保系统的安全裕度弹性,因此具有更广泛的适用性。系统的运行状态等因素在不同应用场景下会有所变化,该方法能够适用于各类丰富场景的系统,可在面对实际工况复杂性时进行稳定性评估。
综上所述,针对新能源多馈入系统静态电压稳定问题的分析流程如图10所示。
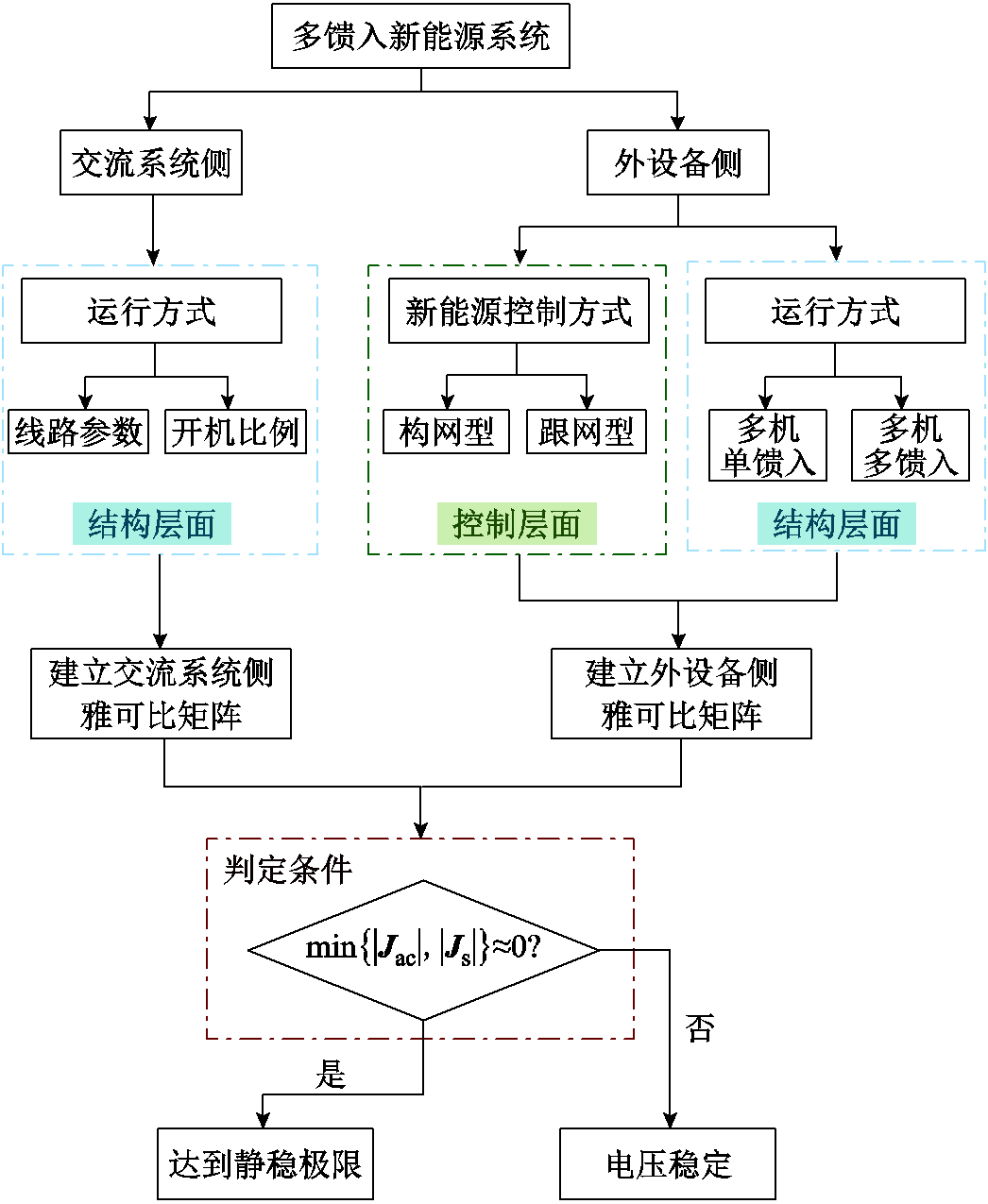
图10 新能源多馈入系统静态电压稳定性分析流程
Fig.10 Process for static voltage stability analysis of a new energy multi-feed system
新能源多馈入系统的雅克比矩阵建立过程考虑了系统结构和控制两方面,因此对多馈入系统静态电压稳定影响因素的分析也将从这两方面入手。
首先考虑系统结构的影响。在2.3节所述的雅可比矩阵中,主对角线元素大小与外设备接入交流系统的电气距离成反比,即增大新能源送出距离,并网线路阻抗XT增大,外设备侧雅可比矩阵主对角线元素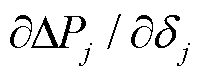 减小,将使得系统运行点向奇异点趋近,静稳极限边界偏移。
减小,将使得系统运行点向奇异点趋近,静稳极限边界偏移。
在异构新能源多馈入系统中改变新能源送出距离,得到不同送出距离下场站出力与系统雅可比矩阵行列式间的关系,如图11所示。在计算中分别设置送出距离为100、115、130、145 km,对应的线路阻抗XT为0.06(pu)、0.07(pu)、0.08(pu)、0.09(pu)。
分析图11所示结果可知,随着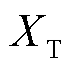 增加,新能源场站送出功率极限不断减小,静稳极限点随新能源送出距离的增加向左偏移。
增加,新能源场站送出功率极限不断减小,静稳极限点随新能源送出距离的增加向左偏移。
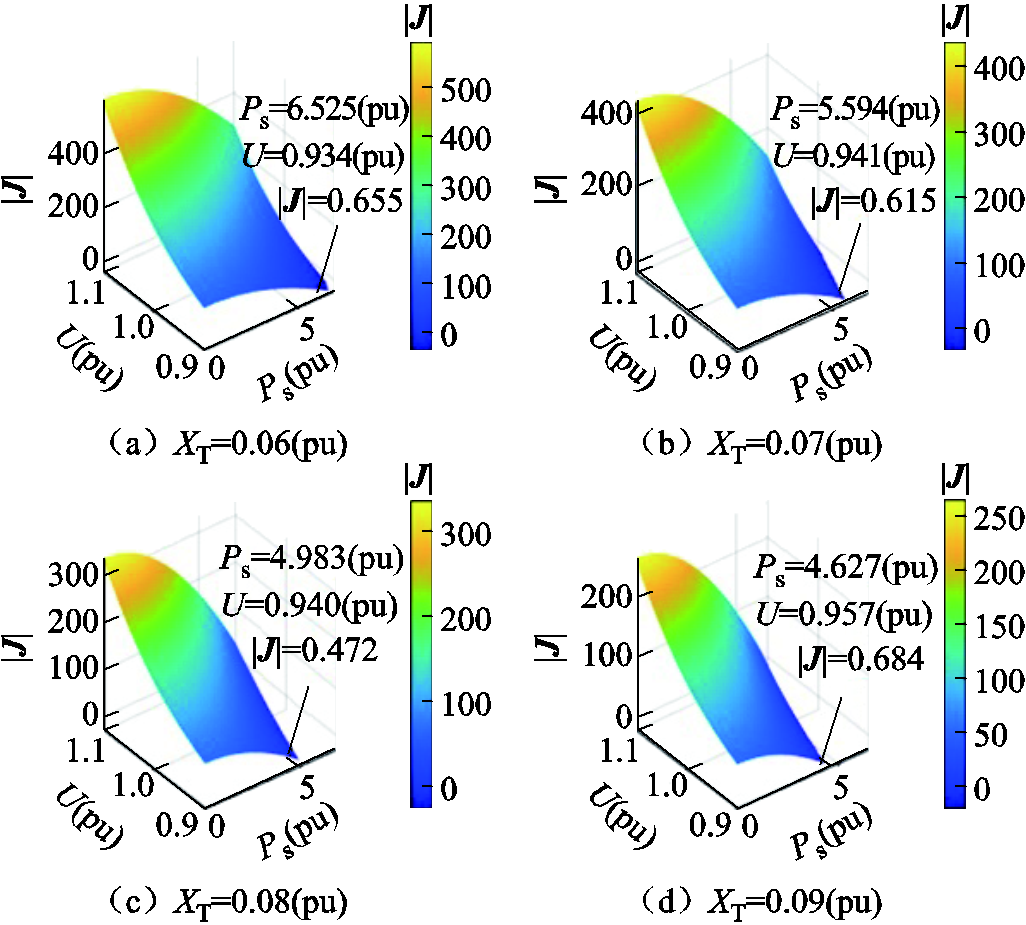
图11 不同新能源送出距离下系统静态电压稳定临界点
Fig.11 Static voltage stability critical points of the system under different new energy transmission distances
接下来考虑新能源场站控制方式的影响。在2.4节中已对不同控制方式下的非同步机电源功率送出能力进行了分析,并得到构网型电源的接入可提升新能源送出能力的结论。由于构网型电源的电压支撑能力与控制器调制环节有关,因此在计算中分别设置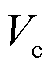 限幅值为1.0(pu)、1.2(pu)、1.4(pu)、1.6(pu),得到不同内电动势限幅值下系统静态电压稳定临界点,如图12所示。
限幅值为1.0(pu)、1.2(pu)、1.4(pu)、1.6(pu),得到不同内电动势限幅值下系统静态电压稳定临界点,如图12所示。
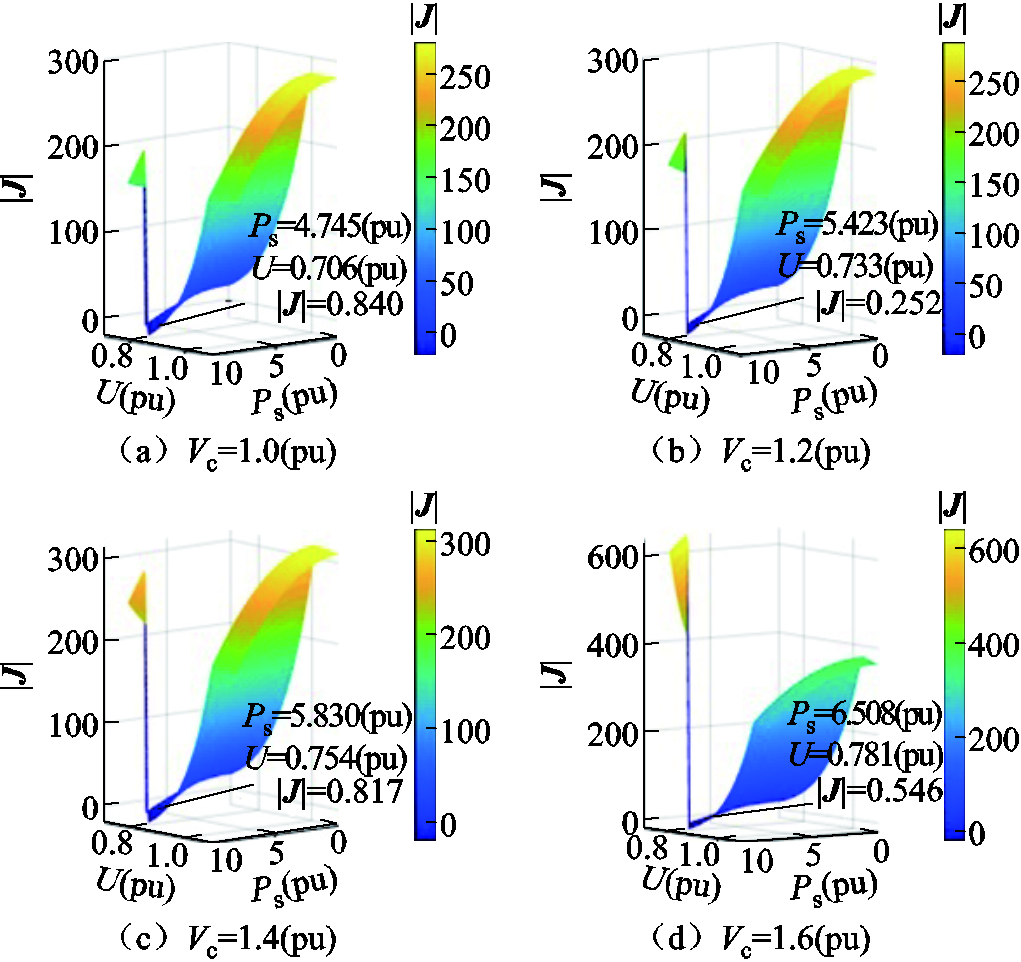
图12 不同内电动势限幅值下系统静态电压稳定临界点
Fig.12 Static voltage stability critical points of the system under different internal voltage limit values
从图12可以看出,随着送出功率的增加,构网型场站在最初运行时可提供一定的电压支撑,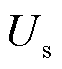 并不会直接跌落,直至达到调制环节上限后作为PQ节点运行到静态电压稳定临界点。因此,提升控制器调制环节上限值可在一定程度上提高新能源场站送出功率极限,静稳极限点随Vc的增加向左偏移,但同时,提升调制环节上限也会导致系统不稳定运行区域的扩大,即图12中左侧低电压解对应的运行区域,随Vc的增加不断扩大,可能会引起整个系统的电压崩溃。
并不会直接跌落,直至达到调制环节上限后作为PQ节点运行到静态电压稳定临界点。因此,提升控制器调制环节上限值可在一定程度上提高新能源场站送出功率极限,静稳极限点随Vc的增加向左偏移,但同时,提升调制环节上限也会导致系统不稳定运行区域的扩大,即图12中左侧低电压解对应的运行区域,随Vc的增加不断扩大,可能会引起整个系统的电压崩溃。
构网型新能源有功控制环节的数学模型为
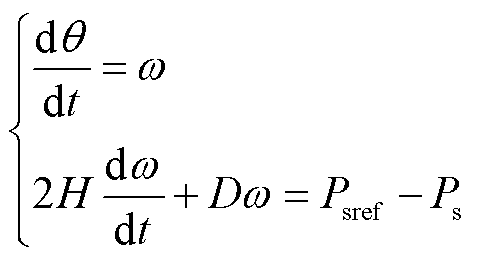 (43)
(43)
式中,H、D分别为与虚拟同步发电机(Virtual Synchronous Generator, VSG)惯性时间常数及阻尼有关的控制参数;Psref为给定的有功功率参考值。有功控制环节模拟了同步发电机的频率调节特性,通过调整控制参数大小可改变频率随输出有功功率变化的响应速度。但由于控制器在机电暂态时间尺度下的响应速度较快(见附录第5节),因此该控制环节对最终稳态相角的影响较小,如附图1a中红色曲线所示。实际上,行业相关规程已对VSG的有功调频响应能力相关指标做出了规定[36],其H、D等控制参数应尽量取值在公共范围内,由于控制器的参数优化并非本文研究重点,故不在此赘述。在分析系统静态电压稳定性时,研究的重点在于与潮流相关的节点功率、电压等物理量,而换流器输出功率分量中并不包含有功环控制参数的显著耦合项。因此,有功控制参数不会直接影响与静态电压稳定性相关的关键指标,可依据这一特性对构网型电源潮流数学模型进行简化,有助于降低分析静态稳定性时的模型复杂度。
接下来分析无功控制环的控制参数是否会对静态电压稳定性产生影响。对于构网型控制,目前得到广泛应用的主要是下垂控制及VSG控制策略,其无功控制环结构见附录第6节。其中VSG控制模拟了同步发电机的无功调压特性,Dq和Kq分别为无功控制下垂系数及惯性系数,根据下垂系数定义有
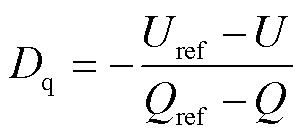 (44)
(44)
式中,Uref为额定电压值;Qref为给定的无功功率参考值。
当并网点电压受扰出现跌落时,功率控制环节会动态响应增发无功功率,且Dq决定了无功功率变化量与电压变化量之间的比例关系。在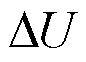 相同的情况下增加Dq可调整增发更多无功功率,同时,换流器会延缓达到调制上限的时间,但系统运行极限点依然与外电路相关,故增加Dq可在一定程度上提升构网型电源的电压支撑能力,维持电压水平,但并不会改变支撑边界。
相同的情况下增加Dq可调整增发更多无功功率,同时,换流器会延缓达到调制上限的时间,但系统运行极限点依然与外电路相关,故增加Dq可在一定程度上提升构网型电源的电压支撑能力,维持电压水平,但并不会改变支撑边界。
无功控制环中的积分响应环节使得系统能够逐步调整至理想状态,最终消除稳态误差。然而,由前述有功环控制系数的分析可知,采用机电暂态分析方法时采样时间步长通常在10-2 s数量级,积分器响应速度较快,稳态误差小,因此在稳态工况下,积分响应环节的时间常数并不会对系统的电压稳定性极限点产生显著影响。假设系统能够在足够短的时间内消除误差,实际值可以有效地跟踪参考值,Kq增大虽然改善了响应的平滑度,但主要影响的是暂态下的动态响应速度,即系统对突发大扰动后的恢复时间。它并不影响系统中的功率平衡关系,因此不会改变电压稳定极限点。
在IEEE 39节点中设置BUS2为新能源节点,分别采用多馈入系统静态电压稳定评估方法及传统潮流迭代求解PV曲线的方法,以多种指标分析系统的极限边界,得到图13所示结果。首先,本文基于雅可比矩阵奇异条件构造了评估指标R,定义为自反馈项最小值与互反馈项最大值之比,以系统失稳标志位来指示实际失稳点,稳态下其值为0,值为1时表明系统已失稳。
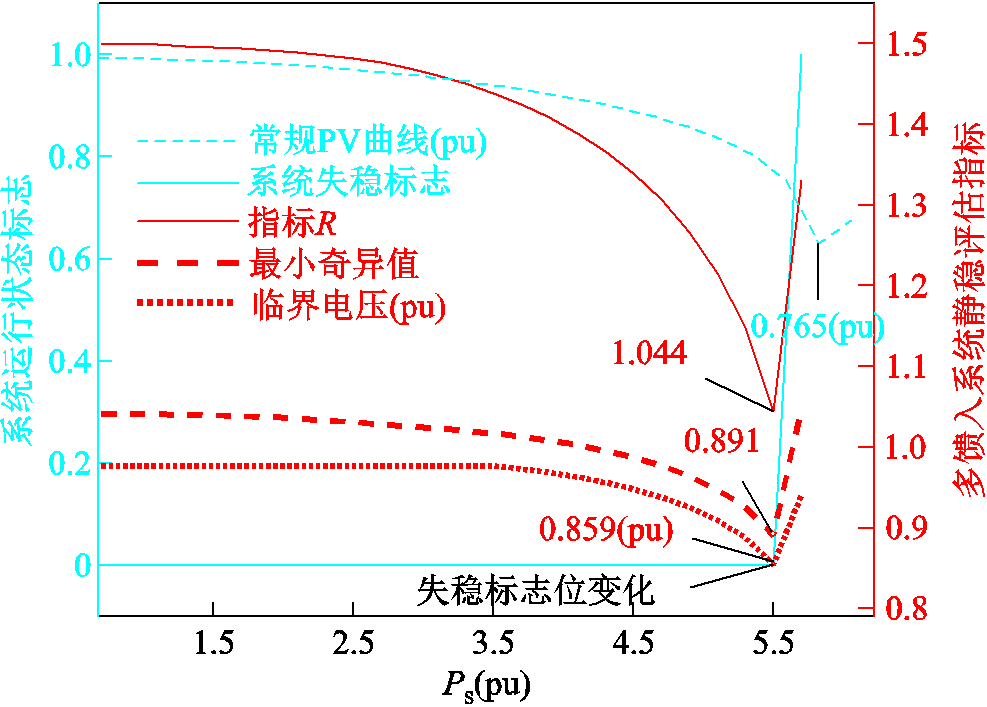
图13 评估方法与常规PV曲线计算得到失稳边界对比
Fig.13 Comparison of the proposed evaluation method with the instability boundary obtained from conventional PV curve calculations
由图13可知,功率为5.5(pu)时系统正处于临界点,即将失稳。在临界点R会趋近于1,计算得到的最小奇异值为0.891,表明系统电压崩溃早于数学意义上的分岔点出现,对应的临界电压为0.859(pu),而传统计算方法得到的PV曲线拐点所对应的电压极值为0.765(pu),系统已经失稳。以标志位为1时的运行点为实际失稳点,本文所提方法计算得到的极限边界比实际失稳边界更“窄”,说明本文所提量化方法能够反映高灵敏度区域内的系统状态变化,为复杂工况下的电压稳定性提供更高的安全裕度,不会将实际失稳的工况判定为稳定。且相比理论临界点的分析,这种方法能更敏感地捕捉到实际系统的失稳特性,因此具有更广泛的适用性。
4.2.1 多机单馈入场景
本算例基于改进3机系统,将发电机G3替换为含跟网型、构网型控制的新能源场站,如图14所示,设置新能源场站送出距离为100 km。
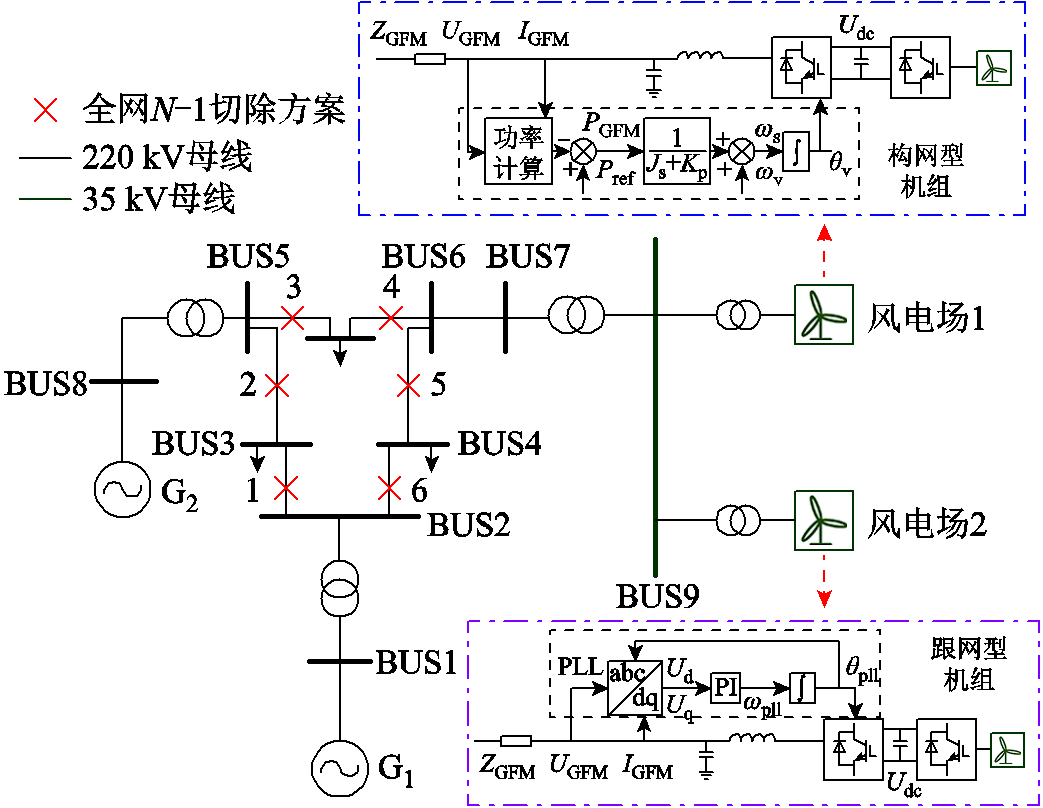
图14 多机单馈入的改进3机9节点系统拓扑
Fig.14 Topology diagram of the modified 3 machines and 9 buses system with multi-machine single-feed
设置场站出力增长并进行多组仿真,得到新能源出力与雅可比矩阵奇异条件的关系如图15所示。在构网型新能源电压支撑的作用下,随着场站出力的增加,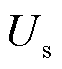 在响应之初具有一定的维持能力,对应的主对角线元素增加;当达到支撑边界后节点类型转换,随着
在响应之初具有一定的维持能力,对应的主对角线元素增加;当达到支撑边界后节点类型转换,随着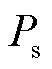 增加,新能源节点相关的电压大幅下降直至系统失稳,主对角线元素持续减小,趋近副对角线元素最大值时得到极限送出功率为4.8(pu)。
增加,新能源节点相关的电压大幅下降直至系统失稳,主对角线元素持续减小,趋近副对角线元素最大值时得到极限送出功率为4.8(pu)。
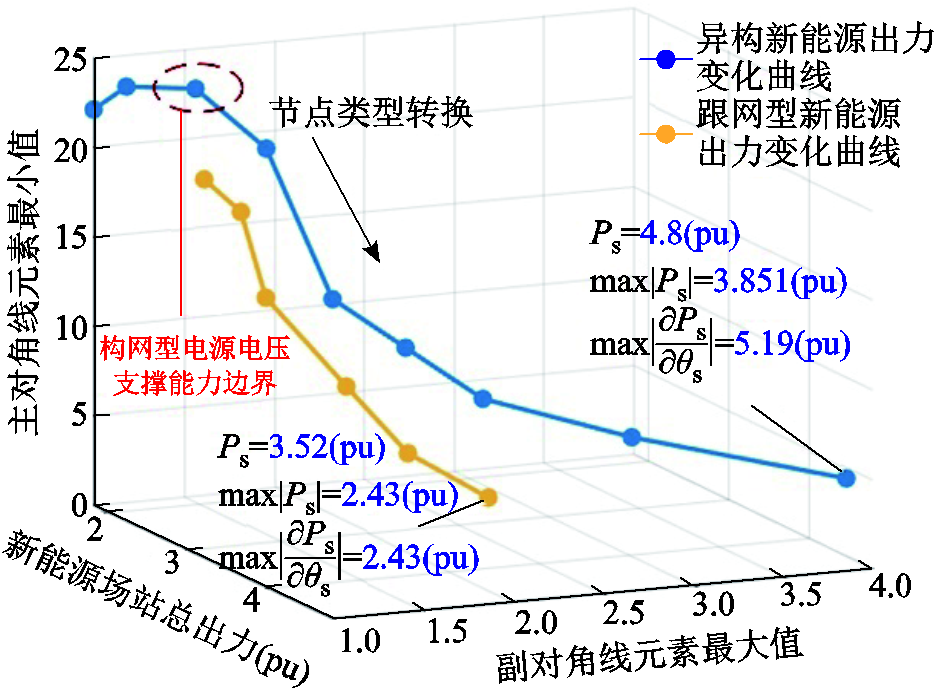
图15 多机单馈入系统各场站出力情况与雅可比矩阵奇异判据值关系
Fig.15 Relationship diagram between the output of each power plant in a multi-machine single-feed system and the singular criterion values of the Jacobian matrix
若在仅有跟网型新能源的场站中进行相同实验,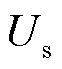 将随场站出力的增加而持续下降,系统失稳时对应的极限送出功率为3.52(pu),验证了2.5节所得结论,即将跟网型场站替换为构网型场站可提高新能源送出能力,且替换单个场站能提升约30%送出功率。
将随场站出力的增加而持续下降,系统失稳时对应的极限送出功率为3.52(pu),验证了2.5节所得结论,即将跟网型场站替换为构网型场站可提高新能源送出能力,且替换单个场站能提升约30%送出功率。
分析多机单馈入场景下各种配置的场站出力及雅可比矩阵奇异判据的结果可得,在达到系统临界点时,其雅可比矩阵趋近奇异,未完全满足奇异条件,即主对角线元素仍然较副对角线元素稍大,这也证明了在实际运行过程中,新能源与交流系统间存在复杂的耦合机制,导致系统可能在未达静态电压稳定临界点前便已失稳。
同时,在上述多机单馈入场景中开展了N-1故障场景下的静态电压稳定分析。切除方案如图14中所示,包括所有的主网交流线路。分析表1所列的切除结果可知,跟网型场站在出力达到2.0(pu)时已不满足系统N-1校核,若将其中部分场站替换为构网型控制的新能源场站则可提高系统的静态安全裕度。
表1 全网N-1切除结果
Tab.1 N-1 contingency removal results for the entire grid

场站配置场站总出力(pu)不收敛方案 跟网型新能源1.52.0—2,3 异构新能源2.543.09—3,4
4.2.2 多机多馈入场景
进一步改造3机9节点系统,将异构新能源场站分布接入系统中节点5、9处并保持系统参数不变,基于搭建的多机多馈入系统模拟新能源分布式并网场景对上述理论分析进行仿真验证。
同样设置场站出力增长并进行多组实验,得到总出力与外设备侧雅可比矩阵的行列式间变化关系如图16所示,同时引入雅可比矩阵最小奇异值作为辅助判据。与集群并网场景相似,在构网型场站电压支撑的作用下,雅可比矩阵奇异判据值在无功电压初始响应阶段可维持在一定水平;越过电压支撑能力边界后场站出力继续增加,新能源节点相关电压开始下降,雅可比矩阵行列式减小,最小奇异值将趋近于0,得到的新能源极限出力为5.04(pu),较集群并网场景更大。若在仅有跟网型新能源的场站中进行相同实验,系统失稳时对应的极限送出功率为3.62(pu),验证了2.5节所得结论,即新能源分布式并网场景下送出能力得到提高。

图16 多机多馈入系统各场站出力情况与雅可比矩阵奇异判据值关系
Fig.16 Relationship diagram between the output of each power plant in a multi-machine multi-feed system and the singular criterion values of the Jacobian matrix
但在分布式并网场景下,电压失稳时对应的外设备侧雅可比矩阵奇异判据差值会更大,同样验证了第2节所得结论,即在新能源渗透率高的多机多馈入系统中,新能源对并网系统的影响将更显著,系统更容易在未达静态电压稳定临界点前失稳。
4.3.1 新能源送出距离的验证
基于上述异构新能源多馈入系统对影响因素进行仿真验证。保持系统其他参数不变,分别设置送出距离为100、130、160 km,对应的线路阻抗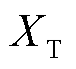 为0.06(pu)、0.08(pu)、0.10(pu),得到场站总出力与外设备侧雅可比矩阵的行列式间变化关系如图17所示。
为0.06(pu)、0.08(pu)、0.10(pu),得到场站总出力与外设备侧雅可比矩阵的行列式间变化关系如图17所示。
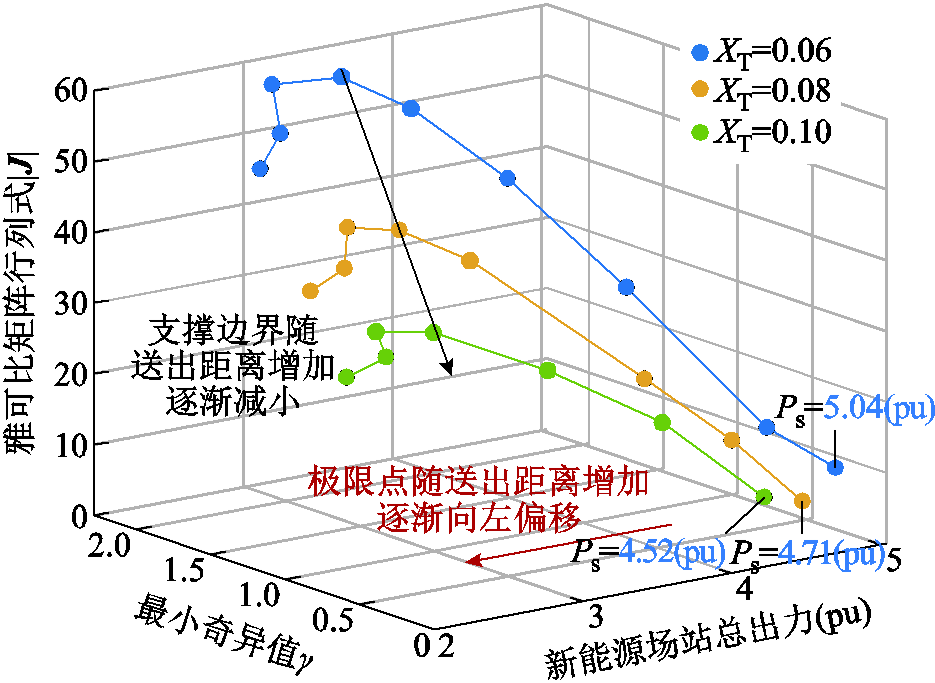
图17 不同新能源送出距离下场站出力与雅可比矩阵奇异判据值关系
Fig.17 Relationship diagram between the output of power plants and the singular criterion values of the Jacobian matrix under different new energy transmission distances
由仿真结果可知,随着送出距离的增大,场站出力极限值不断减小,与3.1节分析所得结论相同,随着送出距离的增加,新能源场站送出功率极限不断减小,静稳极限点随新能源送出距离的增加向左偏移。
4.3.2 控制器调制参数的验证
保持系统其他参数不变,分别设置Vc限幅值为1.00(pu)、1.25(pu)、1.50(pu),得到场站总出力与外设备侧雅可比矩阵的行列式间变化关系如图18所示。
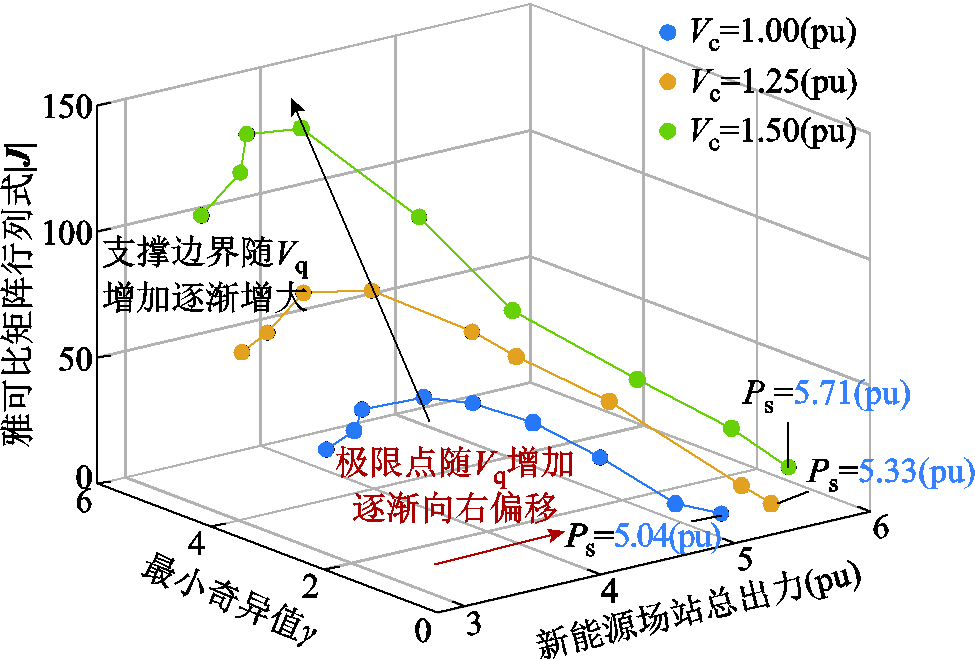
图18 不同内电动势限幅值下场站出力与雅可比矩阵奇异判据值关系
Fig.18 Relationship diagram between power plant output and the singular criterion values of the Jacobian matrix under different internal voltage limit values
由仿真结果可知,提升控制器调制环节上限值可在一定程度上提高新能源场站送出功率极限,静稳极限点随Vc的增加向左偏移,与3.2节分析所得结论相同。此时电压失稳点对应的外设备侧雅可比矩阵奇异判据差值更大,也验证了提升调制环节上限会导致系统不稳定运行区域的扩大。
4.3.3 功率同步环控制参数的验证
在构网型电源等效系统中设置惯性时间常数与阻尼系数的乘积分别为1(pu)、2(pu)及3(pu),步长Ts为0.01 s,得到不同系数下有功控制环中角频率的变化曲线如图19所示,其中HD为有功频率环控制系数。
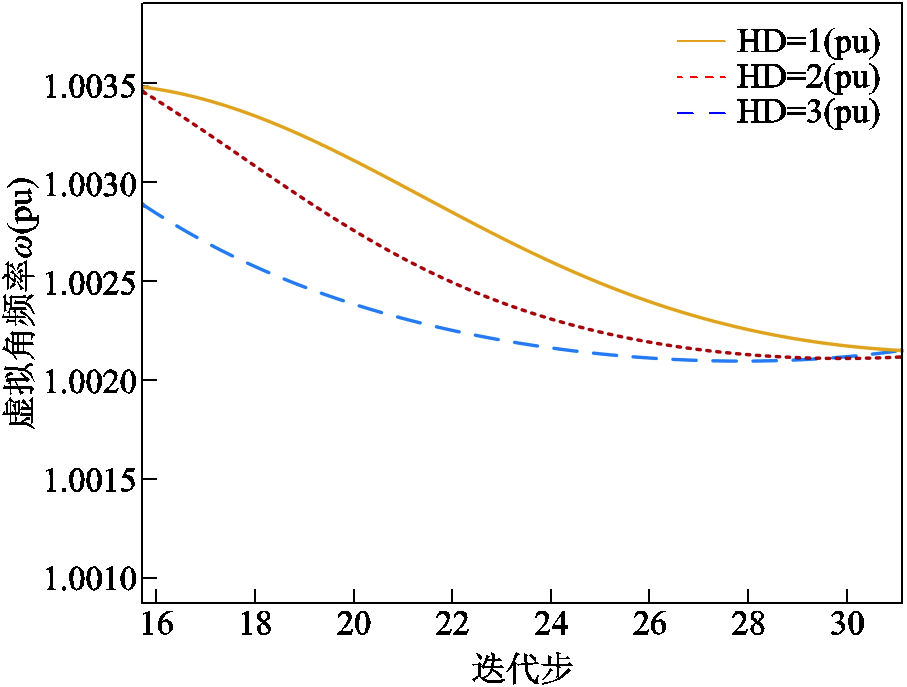
图19 不同有功环控制参数下角频率响应曲线
Fig.19 The angular frequency response curve under different active loop control parameters
由图19可知,控制系数越大,角频率回落到稳态时所用迭代步数越少,即响应速度越快。但由于系统额定角速度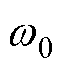 保持不变,因此控制环最终输出的相角稳态值也不变,验证了有功控制参数不会直接影响与静态电压稳定性相关的关键指标。
保持不变,因此控制环最终输出的相角稳态值也不变,验证了有功控制参数不会直接影响与静态电压稳定性相关的关键指标。
在系统中分别改变无功控制环节下垂系数及惯性系数,得到不同控制参数下换流器输出Q-V曲线如图20所示。
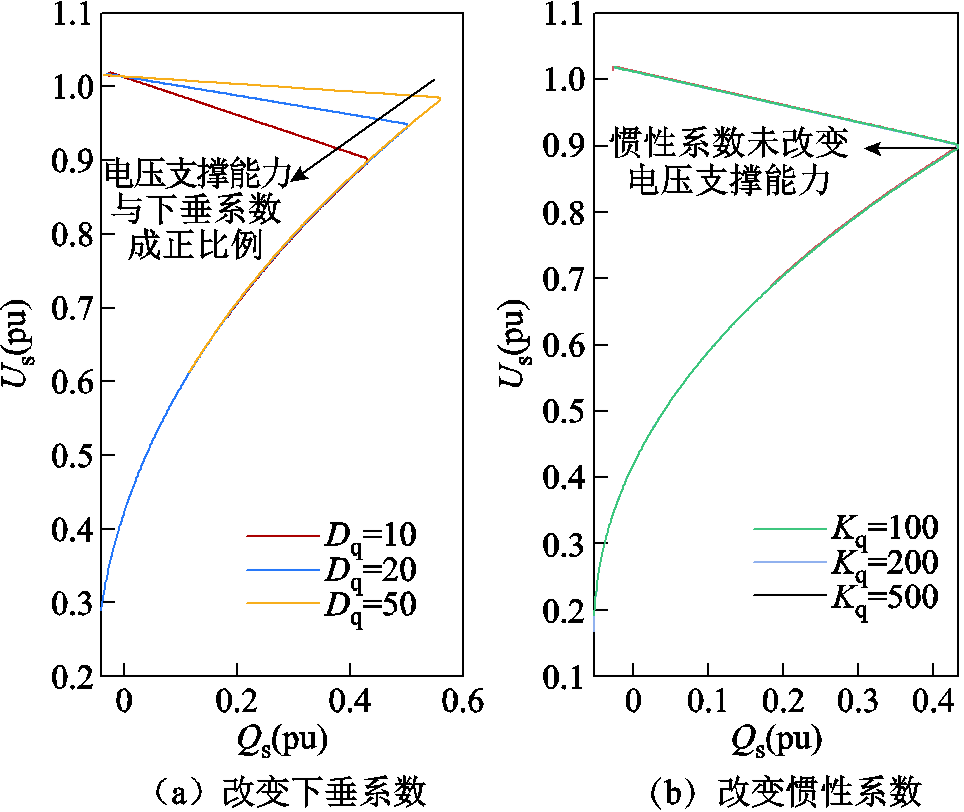
图20 不同控制参数下Q-V曲线
Fig.20 Q-V curves under different control parameters
由图20a观察到,增大Dq时,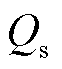 增加,
增加,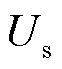 的下降趋势变缓,验证了增大下垂系数后,换流器根据电压波动情况调整增发无功功率补偿量来支撑电压,但其支撑边界变化并不大,因此不会对系统的稳定点产生太大影响。
的下降趋势变缓,验证了增大下垂系数后,换流器根据电压波动情况调整增发无功功率补偿量来支撑电压,但其支撑边界变化并不大,因此不会对系统的稳定点产生太大影响。
由图20b可知,增加惯性系数时,无功-电压支撑能力几乎没有发生变化,其稳定边界也不变,验证了上述分析的正确性。
本文首先针对构网型电源的无功电压特性进行分析,阐明了构网型电源节点类型转换机理,在此基础上建立了异构新能源多馈入系统潮流模型,并基于雅可比矩阵提出了面向异构新能源多馈入系统静态电压稳定极限边界的量化评估方法,从系统结构层面及新能源控制层面入手对影响多馈入系统静态电压稳定性的关键因素进行分析,主要结论如下:
1)构网型电源的电压支撑能力存在一定边界,主要受控制器限幅环节影响,且构网型电源的节点类型将在达到电压支撑能力边界后由PV节点转换为PQ节点。
2)静态电压稳定约束下,新能源极限送出能力与跟/构网机组配置比例和机组并网场景相关,提高构网型机组占比能够显著提升场站极限送出能力,且新能源场站分布式并网场景下场站极限送出能力较集群并网下得到提升。
3)在实际工况中,新能源多馈入系统有可能在达到系统静态电压稳定临界点前便已失稳,这种特性在新能源渗透率高的多机多馈入系统中将会更加明显。
4)新能源场站送出功率极限与送出距离呈负相关,与构网型电源内电势限幅值呈正相关,但提升调制环节上限同时会导致系统不稳定运行区域的扩大;同时构网型电源功率同步控制环中控制参数对静态电压稳定边界的影响较小。
附 录
1. 控制器输出参数响应曲线
随着有功功率的增加,图1中主要控制环节的输出参数变化曲线如附图1所示。
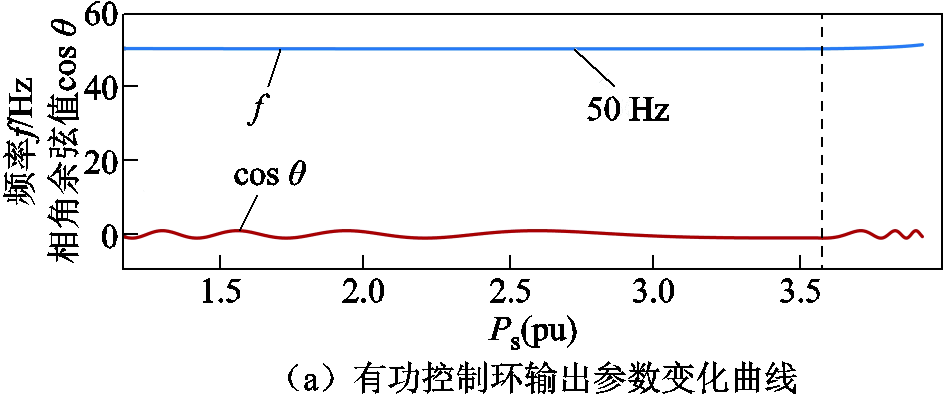
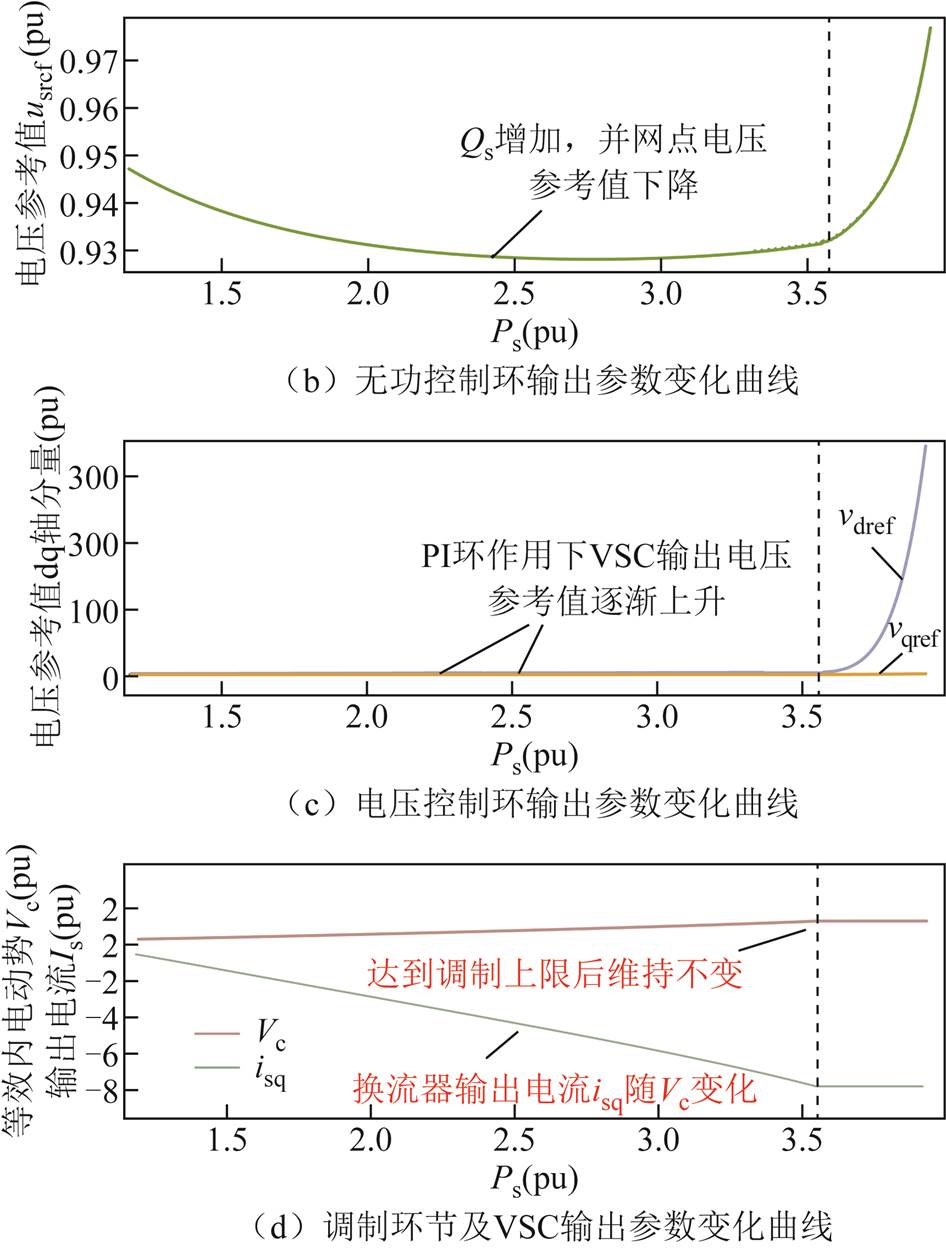
附图1 控制器输出参数随有功功率变化曲线
App.Fig.1 Controller output parameter variation curves with active power
由附图1可知,在各控制环节的作用下,最终会使换流器达到调制上限。
2. 式(19)推导过程
由式(11)有
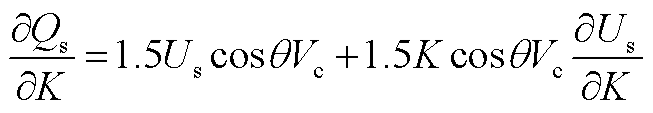 (A1)
(A1)
将式(12)代入式(7)并求导得到
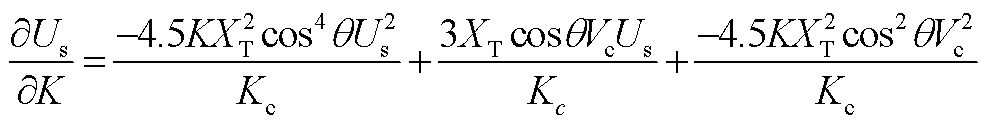 (A2)
(A2)
其中
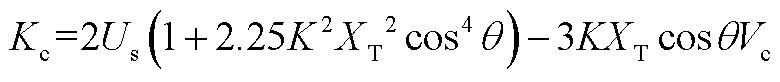 (A3)
(A3)
将式(A2)代入式(A1),并令表达式为0,化简即得到电压支撑边界对应的并网点电压最大值为式(19)。
3. 构网型电源运行边界
构网型电源运行边界示意图如附图2所示。附图2中,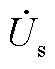 表示构网型电源并网点的电压相量,电压相量与横轴形成的角度
表示构网型电源并网点的电压相量,电压相量与横轴形成的角度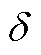 表示交流电压和电流之间的相位差,
表示交流电压和电流之间的相位差,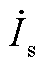 表示系统的电流相量。不同颜色的虚线表示在不同有功出力条件下系统的运行极限。随着构网型电源输出功率的变化,运行点由
表示系统的电流相量。不同颜色的虚线表示在不同有功出力条件下系统的运行极限。随着构网型电源输出功率的变化,运行点由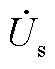 变为
变为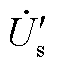 ,处于无功响应上升阶段,相角由
,处于无功响应上升阶段,相角由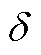 变为
变为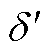 ,运行边界由黑色虚线向红色虚线偏移;当达到电压支撑能力边界后,随着有功功率的增加,系统将运行在无功响应下降阶段,运行点由
,运行边界由黑色虚线向红色虚线偏移;当达到电压支撑能力边界后,随着有功功率的增加,系统将运行在无功响应下降阶段,运行点由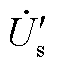 变为
变为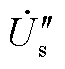 ,相角由
,相角由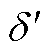 变为
变为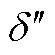 ,运行边界变为绿色虚线。附图2中功率极限曲线刻画了构网型电源在不同运行阶段下的功率传输能力,其中无功响应上升阶段边界指示了构网型电源的电压支撑能力边界,而无功响应下降阶段边界则指示了构网型电源的功率传输能力边界,考虑构网型电源功率变化的全过程得到实线部分即表示了整体运行边界。
,运行边界变为绿色虚线。附图2中功率极限曲线刻画了构网型电源在不同运行阶段下的功率传输能力,其中无功响应上升阶段边界指示了构网型电源的电压支撑能力边界,而无功响应下降阶段边界则指示了构网型电源的功率传输能力边界,考虑构网型电源功率变化的全过程得到实线部分即表示了整体运行边界。
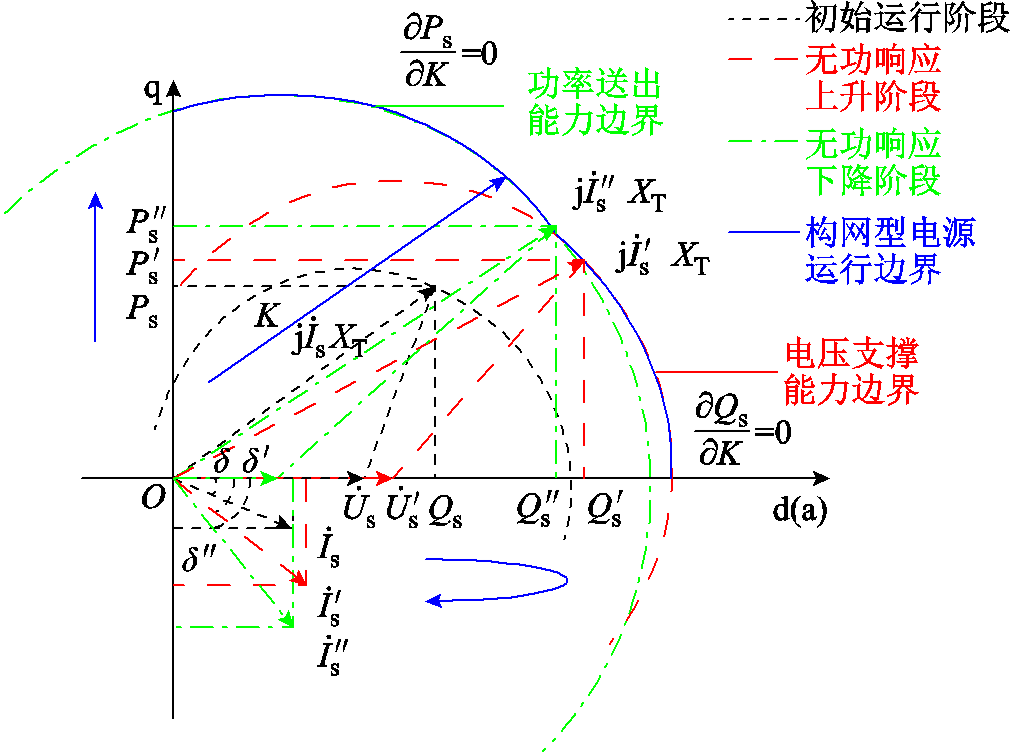
附图2 构网型电源运行边界示意图
App.Fig.2 Schematic diagram of the operating boundary of a grid-forming power source
4. 雅可比矩阵元素表达式
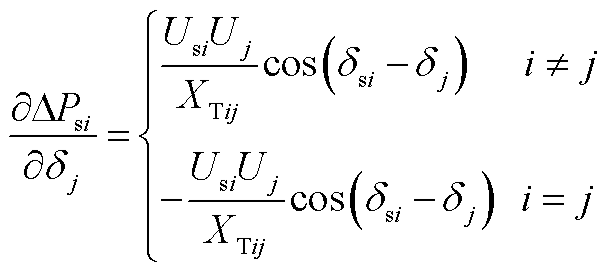 (A4)
(A4)
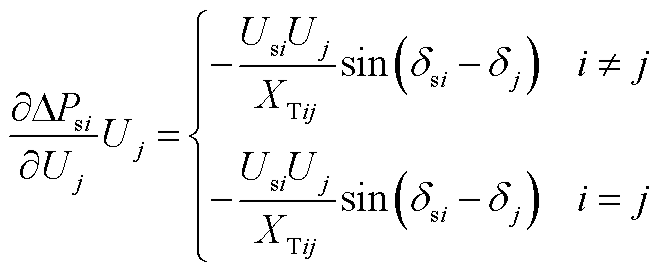 (A5)
(A5)
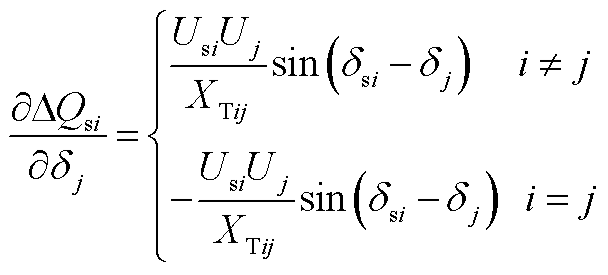 (A6)
(A6)
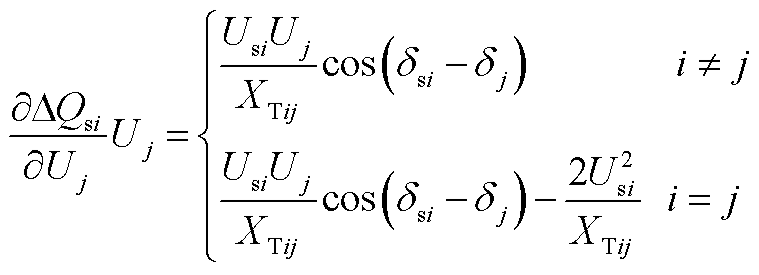 (A7)
(A7)
5. 换流器调制限幅
本文中的调制上限值基于系统稳定性要求和设计规范的约束,首先有电流内环输出的电压参考值与经调制环节后输出的电压间约束关系为
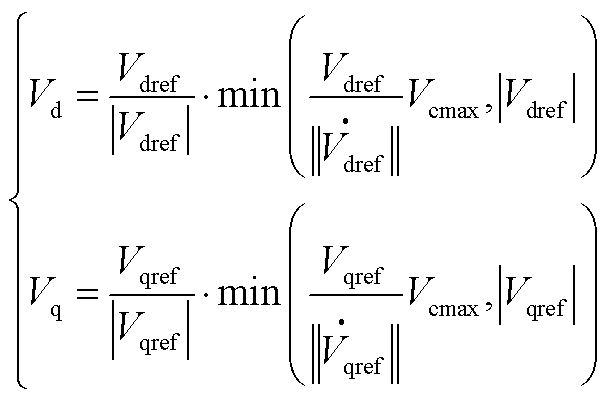 (A8)
(A8)
式中, 表示相量幅值。
表示相量幅值。
在调制环节中限幅器取值上下限构成了换流器输出内电动势的约束条件。实际应用时,限幅值Vcmax通常会设定在接近1.0 (pu),并留有一定的裕度。考虑到换流器在暂态下需具有一定的过电流能力,Vcmax可设定为1.1 (pu)或者1.2 (pu),以确保系统在异常情况下仍具有较强的响应能力和稳态恢复能力。
典型的跟网型换流器调制环节输出参数依然满足式(A8)的约束关系,用以确保换流器能够正常工作。然而,跟网型电源的无功电压响应机制与构网型电源存在本质区别。由附图3可知在机电暂态时间尺度下,电流内环响应远快于电压外环,因此可假设电流经较短时间即可有效跟踪其参考值,有isq=isqref =0。跟网型电源输出值随有功功率变化曲线如附图4所示。当有功出力增加时,电流Is随之增大,线路上的电压降增加,导致换流器端口电压及母线电压下降。而无功电流跟随其参考值维持0,且端口电压呈现下降趋势,不会达到限幅值,因此跟网型电源的调制上限仅能确保换流器正常工作,而并未改变其电流源的特性,调制上限不会对静态电压稳定性产生影响。
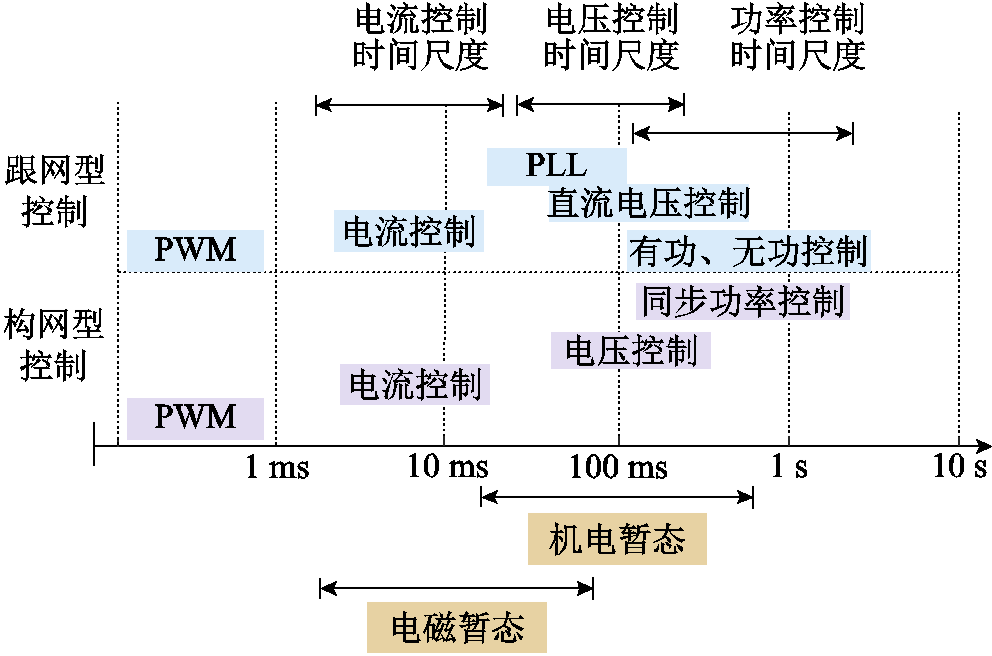
附图3 典型非同步机电源控制环节时间尺度
App.Fig.3 Time scales of control loops for typical non-synchronous generators
6. 不同构网型控制中无功电压环
典型构网型控制架构有VSG控制及下垂控制。根据附图5,其无功控制环节的主要部分是Q-V下垂控制,而在上述分析中已得到下垂系数本身并不会影响系统的稳定边界,因此,采用不同无功控制策略对构网型电源的电压支撑能力没有显著影响,系统的运行状态在静态电压稳定性方面是相似的。
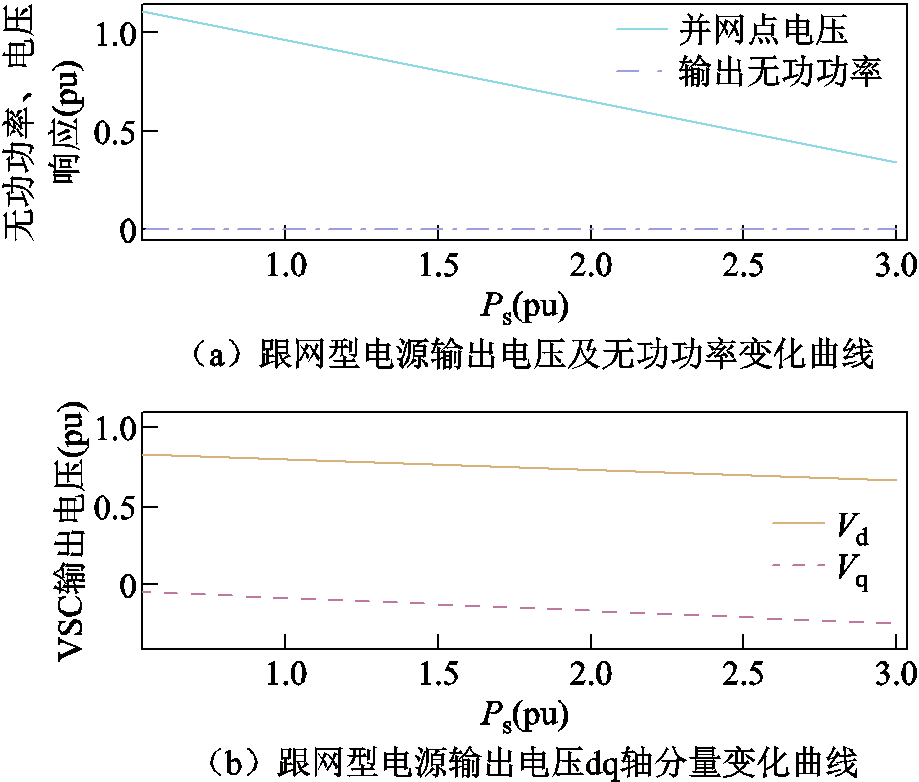
附图4 跟网型电源输出值随有功功率变化曲线
App.Fig.4 The output value curves of grid-following power sources with respect to active power variation
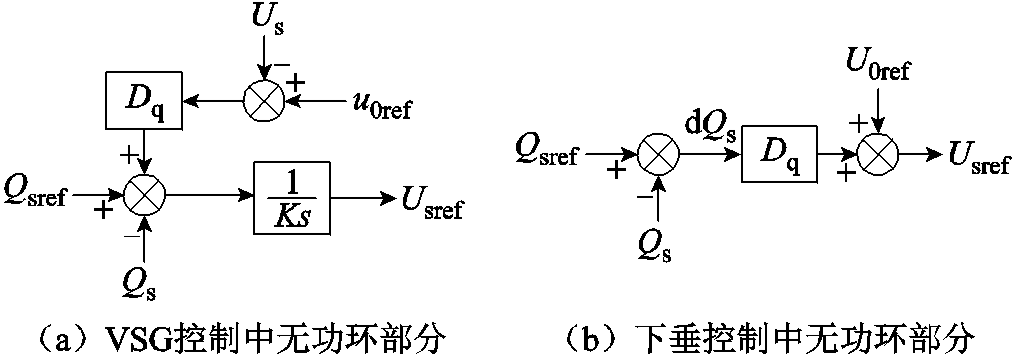
附图5 换流器无功控制环节框图
App.Fig.5 Block diagram of the reactive power control module of the converter
在构网型电源中分别采用VSG控制及下垂控制得到有功出力增加时换流器输出参数的响应情况,如附图6所示。由附图6可知,在不同控制策略下,换流器的输出值并没有发生明显变化,误差较小,因此无功控制策略对系统静态电压稳定的影响程度较低。
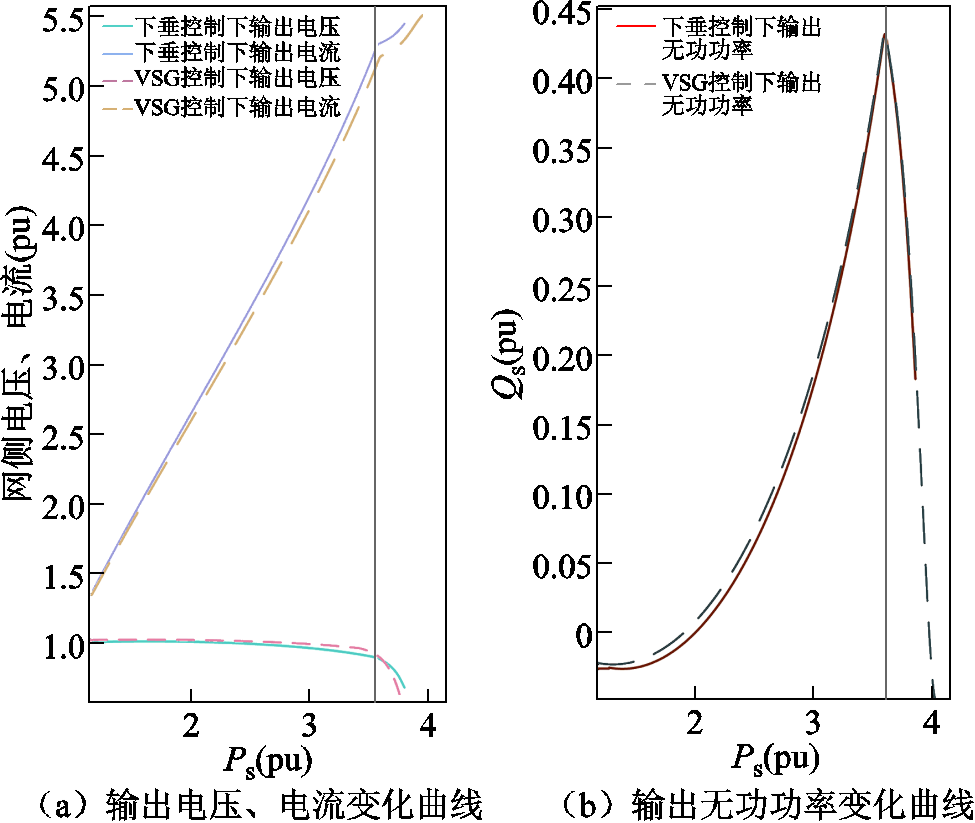
附图6 不同无功控制策略下换流器输出参数曲线
App.Fig.6 Output parameters of the converter under different reactive power control strategies
参考文献
[1] 周孝信, 陈树勇, 鲁宗相, 等. 能源转型中我国新一代电力系统的技术特征[J]. 中国电机工程学报, 2018, 38(7): 1893-1904, 2205.
Zhou Xiaoxin, Chen Shuyong, Lu Zongxiang, et al. Technology features of the new generation power system in China[J]. Proceedings of the CSEE, 2018, 38(7): 1893-1904, 2205.
[2] 王彤, 王潇桐, 韩梓畅, 等. 分布式调相机暂态特性分析与暂态功角稳定性机理研究[J]. 电工技术学报, 2025, 40(1): 36-51.
Wang Tong, Wang Xiaotong, Han Zichang, et al. Research on transient characteristic analysis and transient stability mechanism of distributed condenser [J]. Transactions of China Electrotechnical Society, 2025, 40(1): 36-51.
[3] 陈国平, 李明节, 许涛, 等. 关于新能源发展的技术瓶颈研究[J]. 中国电机工程学报, 2017, 37(1): 20-26.
Chen Guoping, Li Mingjie, Xu Tao, et al. Study on technical bottleneck of new energy development[J]. Proceedings of the CSEE, 2017, 37(1): 20-26.
[4] 郑超, 马世英, 申旭辉, 等. 强直弱交的定义、内涵与形式及其应对措施[J]. 电网技术, 2017, 41(8): 2491-2498.
Zheng Chao, Ma Shiying, Shen Xuhui, et al. Definition, connotation and form of strong HVDC and weak AC and countermeasures for stable operation of hybrid power grid[J]. Power System Technology, 2017, 41(8): 2491-2498.
[5] 袁小明, 程时杰, 胡家兵. 电力电子化电力系统多尺度电压功角动态稳定问题[J]. 中国电机工程学报, 2016, 36(19): 5145-5154, 5395.
Yuan Xiaoming, Cheng Shijie, Hu Jiabing. Multi-time scale voltage and power angle dynamics in power electronics dominated large power systems[J]. Proceedings of the CSEE, 2016, 36(19): 5145-5154, 5395.
[6] 吴林林, 赵伟, 徐曼, 等. 考虑风电机组故障穿越特性的电压反复波动机理分析与抑制[J]. 全球能源互联网, 2022, 5(3): 290-297.
Wu Linlin, Zhao Wei, Xu Man, et al. Mechanism analysis and suppression of repeated voltage fluctuation considering fault ride through characteristics of the wind turbine[J]. Journal of Global Energy Interconnection, 2022, 5(3): 290-297.
[7] Musca R, Gonzalez-Longatt F, Gallego Sánchez C A. Power system oscillations with different prevalence of grid-following and grid-forming converters[J]. Energies, 2022, 15(12): 4273.
[8] Mararakanye N, Bekker B. Renewable energy integration impacts within the context of generator type, penetration level and grid characteristics[J]. Renewable and Sustainable Energy Reviews, 2019, 108: 441-451.
[9] 徐政. 高比例非同步机电源电网面临的三大技术挑战[J]. 南方电网技术, 2020, 14(2): 1-9.
Xu Zheng. Three technical challenges faced by power grids with high proportion of non-synchronous machine sources[J]. Southern Power System Technology, 2020, 14(2): 1-9.
[10] 徐政. 新型电力系统背景下电网强度的合理定义及其计算方法[J]. 高电压技术, 2022, 48(10): 3805-3819.
Xu Zheng. Reasonable definition and calculation method of power grid strength under the background of new type power systems[J]. High Voltage Engineering, 2022, 48(10): 3805-3819.
[11] 刘辉, 于思奇, 孙大卫, 等. 构网型变流器控制技术及原理综述[J]. 中国电机工程学报, 2025, 45(1): 277-297.
Liu Hui, Yu Siqi, Sun Dawei, et al. An overview of control technologies and principles for grid-forming converters[J]. Proceedings of the CSEE, 2025, 45(1): 277-297.
[12] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994.
Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[13] 刘昊霖, 贾科, 毕天姝, 等. 计及新能源耦合特性的柔直换流站短路电流解析[J]. 电工技术学报, 2025, 40(15): 4835-4844.
Liu Haolin, Jia Ke, Bi Tianshu, et al. Analysis of short-circuit current in flexible DC converter stations considering the coupling characteristics of new energy sources[J]. Transactions of China Electrotechnical Society, 2025, 40(15): 4835-4844.
[14] 高洁, 王彤, 赵伟, 等. 提升电力系统安全稳定水平的风电光伏场站主动支撑技术发展及展望综述[J]. 新型电力系统, 2024(2): 201-222.
Gao Jie, Wang Tong, Zhao Wei, et al. Review on the development and prospect of active support technologies for wind power and photovoltaic stations to improve the security and stability level of power system[J]. New Type Power Systems, 2024(2): 201-222.
[15] 王祥宇, 辛焕海, 傅闯, 等. 考虑实际工况的新能源经MMC-HVDC送出系统强度评估方法[J]. 电工技术学报, 2025, 40(15): 4708-4721.
Wang Xiangyu, Xin Huanhai, Fu Chuang, et al. System voltage support strength evaluation method for renewables MMC-HVDC transmission system considering operating condition[J]. Transactions of China Electrotechnical Society, 2025, 40(15): 4708-4721.
[16] 马子涵, 黄萌, 付熙坤, 等. 构网型电源接入下新能源场站的稳定运行能力评估[J]. 电力系统自动化, 2025, 49(1): 38-46.
Ma Zihan, Huang Meng, Fu Xikun, et al. Stable operation capability evaluation for renewable energy station with grid-forming power sources[J]. Automation of Electric Power Systems, 2025, 49(1): 38-46.
[17] 詹长江, 吴恒, 王雄飞, 等. 构网型变流器稳定性研究综述[J]. 中国电机工程学报, 2023, 43(6): 2339-2359.
Zhan Changjiang, Wu Heng, Wang Xiongfei, et al. An overview of stability studies of grid-forming voltage source converters[J]. Proceedings of the CSEE, 2023, 43(6): 2339-2359.
[18] 郭小龙, 杨桂兴, 张彦军, 等. 构网型储能变流器并网系统SISO环路增益建模与重塑控制[J]. 电气技术, 2023, 24(2): 24-31, 51.
Guo Xiaolong, Yang Guixing, Zhang Yanjun, et al. Modeling and reshaping control of single input and single output loop gain of the grid-forming energy storage converter grid-connected system[J]. Electrical Engineering, 2023, 24(2): 24-31, 51.
[19] 尚磊, 唐王倩云, 苏适, 等. 构网型无功补偿抑制新能源送端暂态过电压[J]. 电力工程技术, 2024, 43(2): 83-93.
Shang Lei, Tang Wangqianyun, Su Shi, et al. Suppression of transient overvoltage in renewable energy transmission terminal by grid-forming based reactive power compensation[J]. Electric Power Engineering Technology, 2024, 43(2): 83-93.
[20] 王聪, 葛景, 汪莹, 等. 构网型储能提升系统电压稳定作用研究[J]. 电工技术, 2023(12): 183-185, 189.
Wang Cong, Ge Jing, Wang Ying, et al. Research on grid-forming BESS in improving voltage stability[J]. Electric Engineering, 2023(12): 183-185, 189.
[21] Wang Yinqiao, Li Zhimin, Lu Fang. Research on the impact of wind power integration on power system voltage stability[C]//2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Chengdu, China, 2019: 1683-1687.
[22] 易俊, 林伟芳, 余芳芳, 等. 受静态电压稳定约束的新能源临界渗透率计算方法[J]. 电网技术, 2020, 44(8): 2906-2912.
Yi Jun, Lin Weifang, Yu Fangfang, et al. Calculation method of critical penetration of renewable energy constrained by StaticVoltage stability[J]. Power System Technology, 2020, 44(8): 2906-2912.
[23] 吴林林, 李蕴红, 于思奇, 等. 基于短路比指标的风电汇集系统稳定性分析[J]. 电力自动化设备, 2022, 42(8): 72-78.
Wu Linlin, Li Yunhong, Yu Siqi, et al. Stability analysis of dense wind power area based on short circuit ratio index[J]. Electric Power Automation Equipment, 2022, 42(8): 72-78.
[24] 徐式蕴, 周玢玥, 彭龙, 等. 评估新能源多场站送出系统静态电压稳定的裕度比指标研究[J]. 电网技术, 2023, 47(10): 4026-4035.
Xu Shiyun, Zhou Fenyue, et al. Study on margin ratio index of static voltage stability of multiple renewable energy stations delivery system[J]. Power System Technology, 2023, 47(10): 4026-4035.
[25] 迟永宁, 江炳蔚, 胡家兵, 等. 构网型变流器: 物理本质与特征[J]. 高电压技术, 2024, 50(2): 590-604.
Chi Yongning, Jiang Bingwei, Hu Jiabing, et al. Grid-forming converters: physical mechanism and characteristics[J]. High Voltage Engineering, 2024, 50(2): 590-604.
[26] Pattabiraman D, Lasseter R H, Jahns T M. Comparison of grid following and grid forming control for a high inverter penetration power system[C]//2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 2018: 1-5.
[27] 徐政, 肖晃庆, 张哲任, 等. 柔性直流输电系统[M]. 2版. 北京: 机械工业出版社, 2017.
[28] 许晓菲, 牟涛, 贾琳, 等. 大规模风电汇集系统静态电压稳定实用判据与控制[J]. 电力系统自动化, 2014, 38(9): 15-19, 33.
Xu Xiaofei, Mu Tao, Jia Lin, et al. Practical criteria of static voltage stability in power systems with high wind penetration[J]. Automation of Electric Power Systems, 2014, 38(9): 15-19, 33.
[29] Rosso R, Wang Xiongfei, Liserre M, et al. Grid-forming converters: control approaches, grid-synchronization, and future trends: a review[J]. IEEE Open Journal of Industry Applications, 2021, 2: 93-109.
[30] Cole S, Beerten J, Belmans R. Generalized dynamic VSC MTDC model for power system stability studies [J]. IEEE Transactions on Power Systems, 2010, 25(3): 1655-1662.
[31] 叶希, 鲁宗相, 乔颖, 等. 大规模风电机组连锁脱网事故机理初探[J]. 电力系统自动化, 2012, 36(8): 11-17.
Ye Xi, Lu Zongxiang, Qiao Ying, et al. A primary analysis on mechanism of large scale cascading trip-off of wind turbine generators[J]. Automation of Electric Power Systems, 2012, 36(8): 11-17.
[32] 于琳, 孙华东, 赵兵, 等. 新能源并网系统短路比指标分析及临界短路比计算方法[J]. 中国电机工程学报, 2022, 42(3): 919-929.
Yu Lin, Sun Huadong, Zhao Bing, et al. Short circuit ratio index analysis and critical short circuit ratio calculation of renewable energy grid-connected system [J]. Proceedings of the CSEE, 2022, 42(3): 919-929.
[33] 王冲, 庞榕泽, 杨晓雷, 等. 考虑设备外特性影响的多馈入电力系统静态电压稳定分析[J]. 中国电机工程学报, 2025, 45(10): 3813-3826.
Wang Chong, Pang Rongze, Yang Xiaolei, et al. Static voltage stability analysis of multi-infeed power systems considering the influence of external characteristics of equipment[J]. Proceedings of the CSEE, 2025, 45(10): 3813-3826.
[34] 谢震, 杨曙昕, 代鹏程, 等. 构网型全功率风电机组网侧变流器耦合分析及抑制策略[J]. 电工技术学报, 2023, 38(14): 3745-3758, 3768.
Xie Zhen, Yang Shuxin, Dai Pengcheng, et al. Grid-side coupling analysis and suppression strategy of grid-forming full-power wind turbines[J]. Transactions of China Electrotechnical Society, 2023, 38(14).
[35] 孔贺, 侯山, 赵弋菡, 等. 低电压穿越控制诱导的陆上风电场电压振荡的分岔分析及其判据研究[J]. 中国电机工程学报, 2024, 44(21): 8475-8488.
Kong He, Hou Shan, Zhao Yihan, et al. Bifurcation analysis and criteria of voltage oscillation induced by low voltage ride through control in onshore wind farms[J]. Proceedings of the CSEE, 2024, 44(21): 8475-8488.
[36] 中关村储能产业技术联盟. 《构网型储能变流器技术规范》征求意见稿[R]. 北京: 中关村储能产业技术联盟, 2023.
Abstract With the rapid increase in the integration of heterogeneous new energy sources into the power grid, significant changes have occurred in the voltage stability characteristics and stability boundaries of the system. This shift has presented new challenges for power system stability. In response, this paper proposes a power flow mathematical model tailored for multi-feed-in systems incorporating heterogeneous new energy sources, focusing on the characteristics of voltage stability boundaries. Additionally, a method is introduced to quantitatively assess the static voltage stability of these systems under varying operational conditions.
First, the two-stage reactive power voltage response characteristics of grid-forming power sources are analyzed. By employing nonlinear constraints, the decoupling of the control system and power flow relationship is achieved. This analysis reveals the node type conversion behavior of grid-forming power sources. As a result, identifies the critical conditions for their voltage support capability and operational boundaries.
Secondly, a singularity criterion is developed from the self-feedback characteristics of the system power flow Jacobian matrix. This criterion allows for a comprehensive quantification and analysis of both the power delivery capacity and the voltage stability characteristics of the centralized and the distributed heterogeneous new energy multi-feed-in systems.
Finally, the paper investigates key factors that influence the static voltage stability of multi-feed-in systems, considering both system architecture and control methods of renewable energy. Simulation results are presented to validate the accuracy and effectiveness of the proposed analysis method.
The main contributions of the paper are as follows: (1) The voltage support capability of network-type power sources has certain boundaries, primarily influenced by the limitations imposed by the controller's clipping mechanisms. Additionally, when the voltage support capability reaches its boundary, the node type of network-type power sources will change from a PV node to a PQ node. (2) The transmission capacity of renewable energy is affected by different control strategies and operational conditions. Replacing a single grid-following station with a network-type station can improve the transmission capacity by approximately 30%. Moreover, distributed integration of renewable energy stations into the system offers enhanced transmission capacity compared to clustered integration scenarios. (3) In practical conditions, a multi-feed-in renewable energy system may become unstable before reaching the system's static voltage stability critical point. This characteristic becomes more pronounced in multi-machine, multi-feed-in systems with high renewable energy penetration. (4) The limit of the renewable energy station's transmission power exhibits a negative feedback relationship with the transmission distance and a positive feedback relationship with the voltage clipping value within the network-type power source. However, increasing the upper limit of the modulation stage will simultaneously expand the domain of system instability.
Keywords:Static voltage stability, multi-infeed power systems, heterogeneous new energy, system Jacobian matrix
中图分类号:TM721
DOI: 10.19595/j.cnki.1000-6753.tces.242028
国家电网有限公司总部管理科技项目资助(5100-202499006A-1-1-ZN)。
收稿日期 2024-11-12
改稿日期 2025-06-08
王 彤 女,1985年生,教授,博士生导师,研究方向为新能源电力系统稳定分析与控制。 E-mail:hdwangtong@126.com(通信作者)
肖熠涵 女,2000年生,硕士研究生,研究方向为新能源电力系统稳定分析与控制。 E-mail:rwreyeewy@163.com
(编辑 赫 蕾)