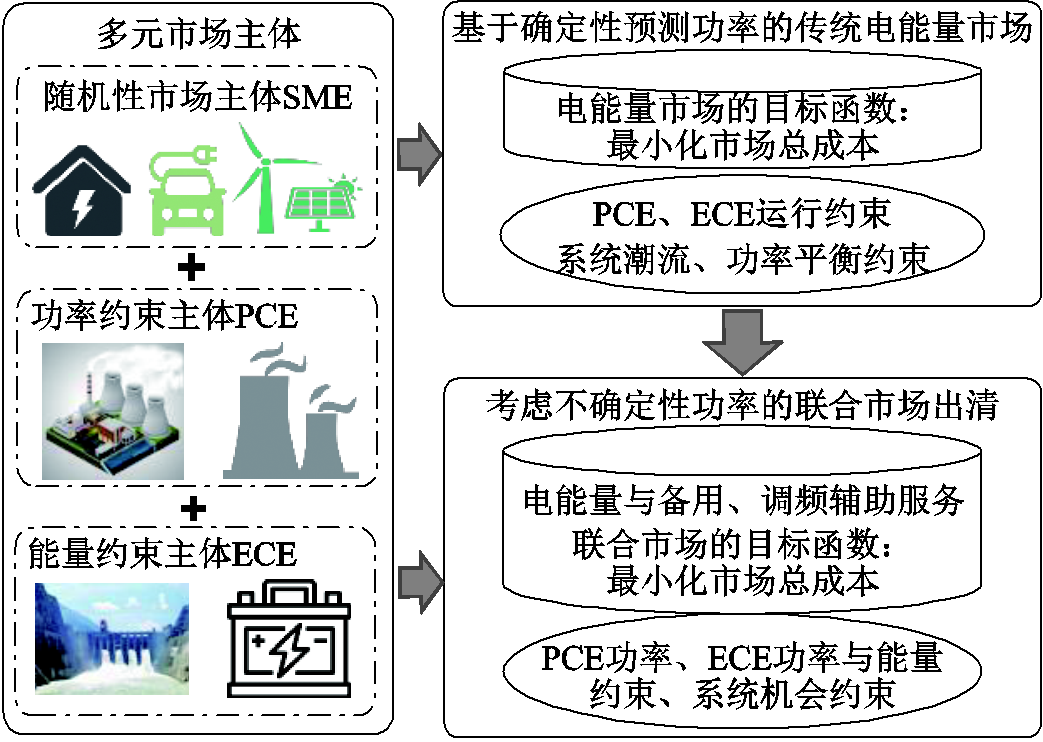
图1 多元市场主体参与的出清模型
Fig.1 Clearing model with multiple market entities
摘要 风光能源的持续并网显著增加了电力市场的不确定性。为引导强随机性市场主体降低不确定性,鼓励确定性市场主体参与系统平衡调节,设计科学合理的多品类电价机制是未来电力市场建设的关键所在。该文基于不确定性功率的统计矩信息构建了源荷模糊集,提出了基于分布鲁棒双边机会约束的电能量与辅助服务联合市场出清模型。在模型求解上,通过凸重构将分布鲁棒双边机会约束转换为混合整数二阶锥规划。基于边际定价原理,推导了电能量、备用与调频的节点边际价格,并提出衡量不确定性功率的系统和节点边际价格,用来反映强随机性市场主体产生不确定性功率的市场代价。在算例分析中,采用IEEE 39节点系统验证了出清定价模型的有效性,分析了不确定性电价机制的实际应用价值。对比传统出清模型,所提出清定价模型为联合市场的长效运营提供了抑制不确定性的价格激励信号。
关键词:联合市场 定价机制 分布鲁棒机会约束 不确定性
随着我国“双碳”战略目标的推进,风光电源渗透率的快速增长给电力系统带来强不确定性,对电网安全可靠运行提出了严峻挑战。由于风光电源与负荷功率预测不准确会引发源荷电力不平衡,导致系统灵活调节能力不足,备用和调频容量需求持续增加,给电力市场出清带来了巨大挑战[1]。
近年来,我国电力市场建设稳步有序推进,多元市场主体格局初步形成[2]。根据市场参与主体的特性,可划分为两类:确定性市场主体(Deterministic Market Entities, DME)和随机性市场主体(Stochastic Market Entities, SME)。具体地,DME指输出功率确定可控的市场主体;SME指输出功率随机性波动性强的市场主体,SME一般为风光能源发电企业、传统负荷的售电公司、电动汽车等柔性负荷聚合商。其中,DME可划分为两类:功率约束主体(Power Constraint Entities, PCE)和能量约束主体(Energy Constraint Entities, ECE)。PCE在参与市场时只需申报每个时间段内的功率范围和电价曲线,无需申报能量约束范围,一般为燃煤、燃气等发电企业。ECE受限于容量、一次能源供应不稳定等诸多因素,在参与市场时不仅需要申报功率范围,更着重考虑时段耦合的能量范围约束。ECE一般为大容量电化学储能、虚拟电厂等企业,在系统中充当电力平衡、功率存储、能量时空转移的角色,对维持系统的安全稳定运行起到了关键作用。显然,在强不确定性环境下,不同市场主体对系统功率平衡的贡献程度存在明显差异。
在市场规则与定价机制的设计上,应允许储能等ECE平等地参与电能量和辅助服务联合市场[3-4]。传统电力市场出清模型是基于源荷两侧的预测功率建立的,系统不确定性则通过备用与调频辅助服务市场解决。由于系统的强不确定性逐年增大,可能导致电能量与辅助服务市场的独立出清结果执行率不高甚至无法执行。电能量与辅助服务联合优化的市场出清模式能同时处理预测功率与不确定性功率,降低所有市场运行的总成本,联合优化将逐渐发展成为成熟市场的出清方法[5]。此外,电能量与辅助服务的联合市场能考虑机组不同产品的容量耦合约束。然而,当前联合市场的设计主要面向PCE,而对系统安全运行起重要作用的ECE参与者优待不足。目前,我国电力现货市场仍处于建设初期,虽然多省区已允许储能参与辅助服务市场,但尚未建立多元市场主体参与的联合市场出清协调机制[6]。
为进一步缓解风光电源对市场出清造成的影响,联合市场出清模型中亟须考虑系统不确定性程度。在求解含不确定随机变量优化问题的算法上,主要包含随机优化(Stochastic Optimization, SO)、鲁棒优化(Robust Optimization, RO)、分布鲁棒优化(Distributionally Robust Optimization, DRO)[7]等方法。具体地,作为SO方法中的一类,机会约束(Chance Constraint, CC)是指当优化问题中参数为随机变量时,在以一定概率满足约束条件的情况下进行优化。然而,SO通常需要了解不确定性的真实分布,而RO的结果往往又过于保守。基于随机变量的期望、方差、协方差等矩信息的DRO方法不需要已知随机变量的概率分布,而通过构建随机变量隶属的模糊集解决变量概率分布不确定的优化问题。分布鲁棒机会约束(Distributionally Robust Chance Constraint, DRCC)方法将CC与DRO相结合,不依赖随机变量的实际概率分布信息,同时能通过调节参数灵敏性决定决策结果的保守程度,避免了最优解的保守性问题[8-10]。
通过联合市场出清模型实现对备用与调频的协同定价,将引导灵活调节资源的优化配置[11]。此外,对不确定性功率定价可以为市场提供价格激励,有助于促进风光电源场站等SME降低自身的不确定性。与节点边际价格类似,不确定性功率的节点边际价格(Uncertainty Locational Marginal Prices, ULMP)定义为某节点实际功率偏离预测功率单位增量引起系统边际成本的变化量。在数学上,ULMP由不确定性功率的均值与标准差来表示;在物理意义上,ULMP描述市场主体的不确定性功率变化对市场总成本的影响。文献[12]构建了考虑风电和负荷需求时空相关性的最优潮流模型,并推导了含不确定性功率成分的电能量节点边际价格,但未明确将不确定性功率区别出来。文献[13]建立了涉及不确定性的市场出清模型,探索了含不确定性的节点边际价格和备用边际价格之间的关系,但缺乏考虑将储能作为一种特殊主体参与市场,以共同解决系统不确定性的问题。文献[14]提出了基于DRCC算法的蓄电池参与市场的日前调度计划模型,并对蓄电池提供的负荷功率转移、实时平衡、一次频率控制等多种服务进行定价。文献[13-14]所研究的对象仅限于虚拟电厂、储能类市场主体,并未对涉及多元市场主体协同解决强不确定性功率的联合市场出清问题进行宏观建模。
现有研究在联合市场出清和不确定性定价方向仍存在以下不足:①文献[7,12]对源荷两侧的不确定性建模多采用一致的模糊集,缺乏考虑新能源与负荷预测技术在准确度上的差异;②文献[8,13]对机会约束一般仅考虑单边机会约束,并不适用于市场出清模型中约束存在上下限的情况;③文献[13-14]对联合市场出清模型的构建缺乏考虑多元主体的协同优化,基于传统出清模型的定价方法未充分体现不同类型企业对系统功率实时平衡贡献程度不均衡的影响,导致对储能这类重要的灵活调节型企业的优待不足,同时缺乏对功率强不确定性主体的市场收益惩罚,未能充分体现市场公平性。总之,现有研究中对目前电力市场的价格机制设计尚不完善,对多元主体共同参与联合市场的效益分析不够深入,无法解决源荷强不确定性给市场运营带来的问题。
鉴于此,本文综合考虑系统源荷两侧的不确定性功率,构建了涵盖PCE、ECE和SME多元市场主体参与的电能量与辅助服务联合市场出清模型。考虑到源荷不确定性功率的差异性,将负荷不确定性功率建模为基于确定性矩信息的模糊集,新能源不确定性功率建模为考虑场站相关性的椭球模糊集,构建了基于系统不确定性功率椭球模糊集的分布鲁棒双边机会约束的联合市场优化出清模型,再通过凸重构将其转换为混合整数二阶锥规划模型。基于边际定价原理,推导了联合市场出清模型的电能量、备用、调频的节点边际价格,提出了不确定性功率的系统边际价格和节点边际价格。本文的创新性贡献凝练如下:
1)设计了基于联合市场出清模型的多品类价格机制,实现了电能量、备用、调频,以及不确定性功率的协同定价,为市场长效运营提供了技术保障。
2)量化了SME产生不确定性功率的市场惩罚成本,以及ECE参与调节系统功率平衡市场主体的市场收益,促进了多元市场主体参与联合市场的市场公平性。
3)所提联合市场出清模型能够降低功率强不确定性与波动性对市场的影响,相较于传统基于确定性预测功率的电能量市场独立出清模型,降低了市场总运行成本。
1.1节中首先基于统计矩信息构建了随机变量的模糊集,作为随机变量的概率分布集合。1.2节建立了考虑不确定性功率的电能量与辅助服务联合市场出清模型。为便于模型对照,附录第1节中建立了基于预测功率的传统电能量市场出清优化模型,本文多元市场主体参与的出清模型如图1所示。

图1 多元市场主体参与的出清模型
Fig.1 Clearing model with multiple market entities
不确定性功率定义为SME的实际功率与预测功率出现偏差的部分,有
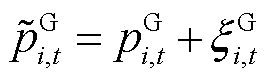 (1)
(1)
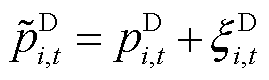 (2)
(2)
式中,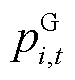 、
、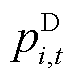 分别为i节点t时段新能源、负荷预测功率;
分别为i节点t时段新能源、负荷预测功率;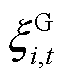 、
、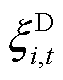 分别为新能源、负荷不确定性功率;
分别为新能源、负荷不确定性功率;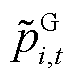 、
、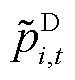 分别为新能源、负荷实际功率。文中考虑的不确定性功率特指由于新能源和负荷功率预测不准确所导致的,并不包括机组跳闸、线路断线等系统突发故障。
分别为新能源、负荷实际功率。文中考虑的不确定性功率特指由于新能源和负荷功率预测不准确所导致的,并不包括机组跳闸、线路断线等系统突发故障。
由于分布鲁棒优化模型中随机变量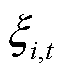 不遵循特定的概率分布,其所依赖的模糊集也没有明确的边界分布,仅需基于历史统计数据获得随机变量的均值和协方差。因此,首先需要通过历史数据确定随机变量的矩信息,构建基于均值和协方差矩阵的负荷不确定性功率的模糊集[15],如式(3)所示。考虑到各节点负荷功率的独立性,负荷不确定性功率的协方差矩阵为对角矩阵。
不遵循特定的概率分布,其所依赖的模糊集也没有明确的边界分布,仅需基于历史统计数据获得随机变量的均值和协方差。因此,首先需要通过历史数据确定随机变量的矩信息,构建基于均值和协方差矩阵的负荷不确定性功率的模糊集[15],如式(3)所示。考虑到各节点负荷功率的独立性,负荷不确定性功率的协方差矩阵为对角矩阵。
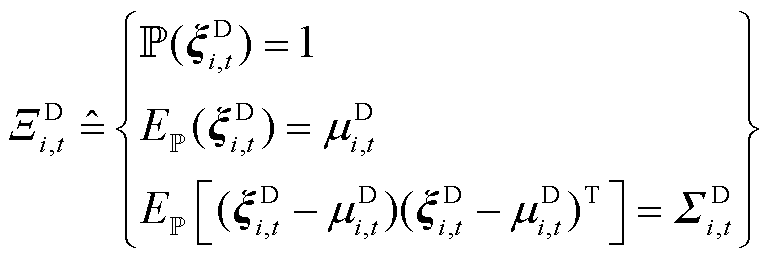 (3)
(3)
式中,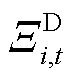 为t时段i节点负荷不确定性功率
为t时段i节点负荷不确定性功率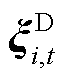 的模糊集;
的模糊集;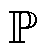 为概率分布函数,
为概率分布函数,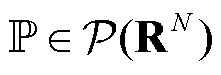 ,
,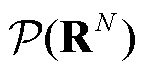 为随机变量的所有概率分布集合;N为随机变量的维数;
为随机变量的所有概率分布集合;N为随机变量的维数;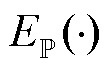 为概率分布的期望值;
为概率分布的期望值;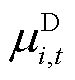 为i节点负荷不确定性功率的一阶矩,即
为i节点负荷不确定性功率的一阶矩,即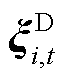 的均值,表征其位置;
的均值,表征其位置;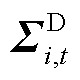 为i节点负荷不确定性功率的二阶矩,即
为i节点负荷不确定性功率的二阶矩,即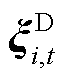 的协方差矩阵,表征其散度。
的协方差矩阵,表征其散度。
相比负荷预测的准确度,由于新能源固有的不确定性程度更大,新能源功率的预测精度远小于负荷功率。因此,采用不确定性矩信息的模糊集更能反映新能源功率的特性[16],如式(4)所示。
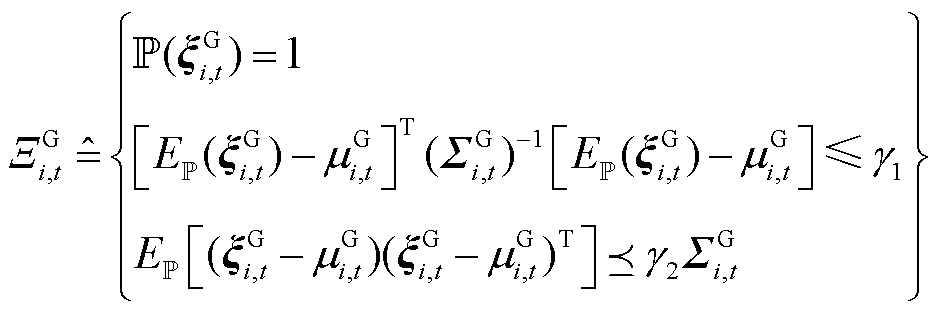 (4)
(4)
式中,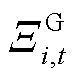 为t时段i节点新能源场站不确定性功率
为t时段i节点新能源场站不确定性功率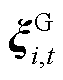 的模糊集;
的模糊集;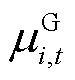 为i节点新能源场站不确定性功率的一阶矩;
为i节点新能源场站不确定性功率的一阶矩;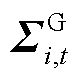 为i节点新能源场站不确定性功率的二阶矩;
为i节点新能源场站不确定性功率的二阶矩;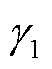 为椭球不确定集半径的限制参数,
为椭球不确定集半径的限制参数,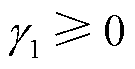 ;
;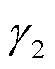 为半定锥不确定集的限制参数,
为半定锥不确定集的限制参数,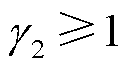 ;
;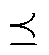 为半正定锥空间意义上的小于或等于。考虑到邻近新能源场站的预测功率偏差存在时空相关性,新能源不确定性功率处于一个椭球模糊集内,协方差矩阵表示为矩阵不等式限定的半定锥模糊集。椭球模糊集的构建需要借助期望及协方差矩阵这两个重要矩信息,可通过历史数据统计、预测模型、数据驱动等方式获得。
为半正定锥空间意义上的小于或等于。考虑到邻近新能源场站的预测功率偏差存在时空相关性,新能源不确定性功率处于一个椭球模糊集内,协方差矩阵表示为矩阵不等式限定的半定锥模糊集。椭球模糊集的构建需要借助期望及协方差矩阵这两个重要矩信息,可通过历史数据统计、预测模型、数据驱动等方式获得。
考虑到系统功率平衡公式中新能源功率与负荷功率是相减的关系,为运算方便,将系统不确定性功率定义为所有节点新能源与负荷不确定性功率之差,如式(5)所示。此外,新能源不确定性功率与负荷不确定性功率为两个相互独立的随机变量,因此二者的协方差矩阵为零。由此,系统不确定性功率的一阶矩与二阶矩分别如式(6)、式(7)所示。
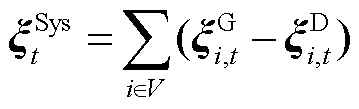 (5)
(5)
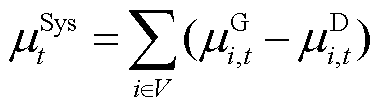 (6)
(6)
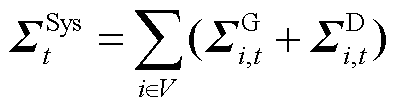 (7)
(7)
式中,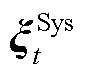 为系统不确定性功率;
为系统不确定性功率;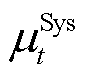 为系统不确定性功率的一阶矩;
为系统不确定性功率的一阶矩;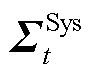 为系统不确定性功率的二阶矩。
为系统不确定性功率的二阶矩。
将系统不确定性功率的二阶矩表达为标准差的形式,如式(8)所示。
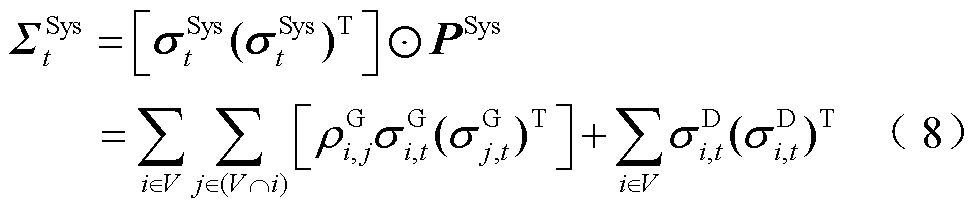
式中,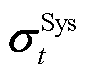 为系统不确定性功率的标准差;
为系统不确定性功率的标准差;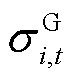 为i节点新能源不确定性功率的标准差;
为i节点新能源不确定性功率的标准差;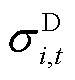 为i节点负荷不确定性功率的标准差;
为i节点负荷不确定性功率的标准差; 为矩阵中对应元素相乘运算;
为矩阵中对应元素相乘运算;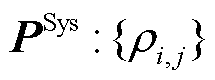 ,
,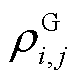 为新能源i节点和j节点输出功率的Pearson相关系数;
为新能源i节点和j节点输出功率的Pearson相关系数;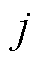 为
为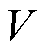 中不包含i节点的节点。
中不包含i节点的节点。
系统不确定性功率的模糊集为所有节点负荷与新能源不确定性功率模糊集的并集。由于负荷不确定性功率的矩信息是确定的,新能源场站不确定性功率的矩信息是不确定的,系统不确定性功率的模糊集同样为椭球模糊集。因此,随机变量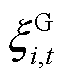 与
与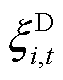 的联合概率分布满足式(9)所示的模糊集。
的联合概率分布满足式(9)所示的模糊集。
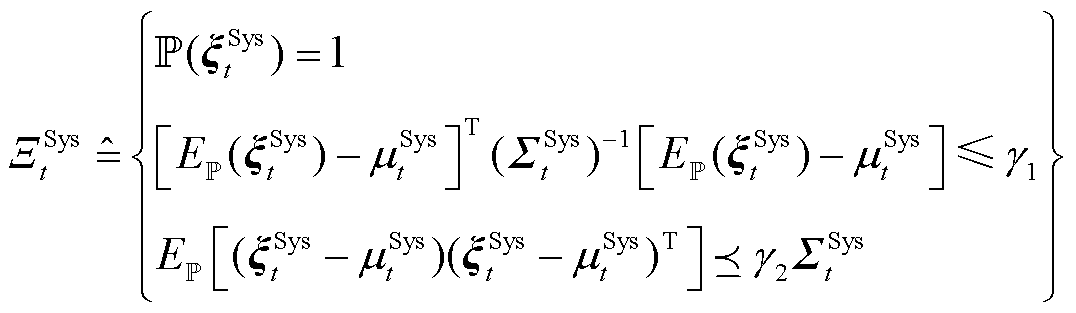 (9)
(9)
1.2.1 联合市场出清目标函数
联合市场中PCE和ECE均可以承担电能量、调频与运行备用辅助服务,其中,运行备用主要解决负荷曲线中几分钟内至几小时内的新能源与负荷功率爬坡与滑坡时的平衡问题;调频主要用于解决负荷曲线中每分钟随机、连续的新能源与负荷波动的频率稳定问题。特别地,本文所提调频交易标的只涉及调频容量,调频里程标的出清及定价机制详见文献[17]。多元市场主体参与的电能量、备用与调频辅助服务联合市场,以市场总运行成本C最小为出清优化目标[18],如式(10)所示。
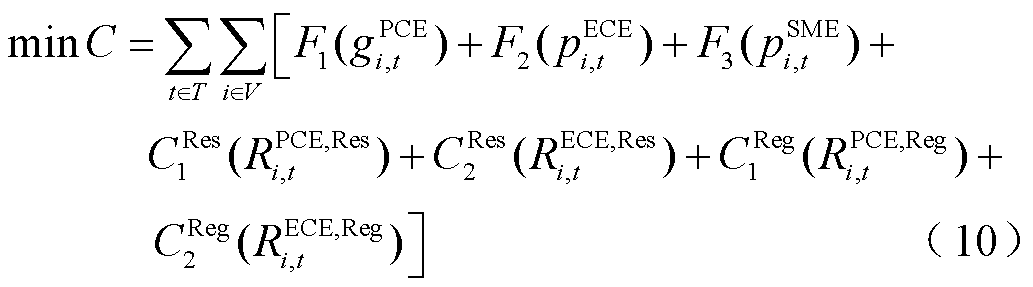
式中,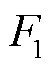 、
、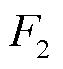 、
、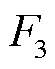 分别为PCE、ECE和SME参与电能量市场的报价函数;
分别为PCE、ECE和SME参与电能量市场的报价函数;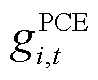 、
、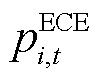 、
、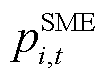 分别为t时段i节点PCE、ECE和SME申报的功率;
分别为t时段i节点PCE、ECE和SME申报的功率;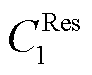 、
、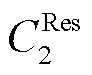 分别为PCE和ECE的备用报价;
分别为PCE和ECE的备用报价;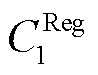 、
、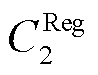 分别为PCE和ECE的调频报价;
分别为PCE和ECE的调频报价;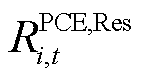 、
、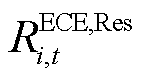 分别为由PCE和ECE申报的运行备用;
分别为由PCE和ECE申报的运行备用;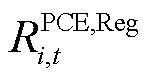 、
、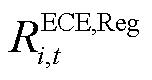 分别为PCE和ECE申报的调频功率;T为出清时段集合。
分别为PCE和ECE申报的调频功率;T为出清时段集合。
1.2.2 约束条件
1)考虑不确定性功率的PCE运行约束
考虑不确定性功率后,PCE运行功率约束为式(11)、式(12),爬坡约束为式(13)。此外,PCE投标的备用容量与调频功率也需要满足爬坡约束,如式(14)所示。下文约束条件右侧括号内为该约束条件的拉格朗日乘子,即对偶问题的对偶乘子变量,表征当约束中现有资源增加一个单位量对应目标函数的增量。
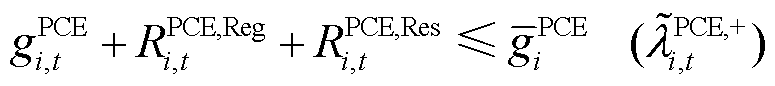 (11)
(11)
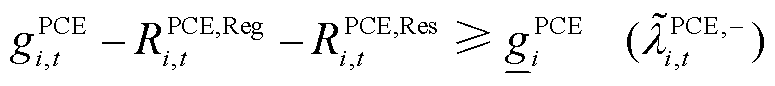 (12)
(12)
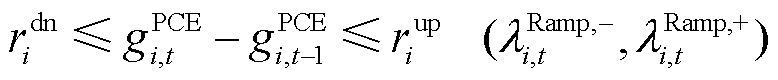 (13)
(13)
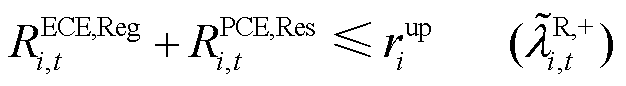 (14)
(14)
式中,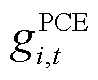 为t时段i节点机组有功出力;
为t时段i节点机组有功出力;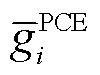 、
、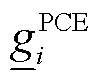 分别为机组有功出力上、下限;
分别为机组有功出力上、下限;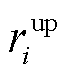 、
、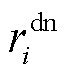 分别为机组在单位出清时段的向上、向下爬坡速率。
分别为机组在单位出清时段的向上、向下爬坡速率。
2)考虑不确定性功率的ECE运行约束
ECE运行功率约束为式(15)、式(16)。ECE的最终功率、运行状态、始末能量约束分别为式(17)~式(20)。考虑不确定性功率后ECE的能量约束如式(21)所示。
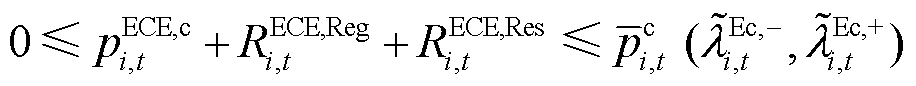 (15)
(15)
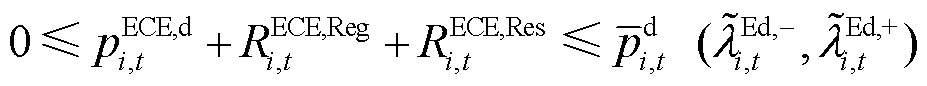 (16)
(16)
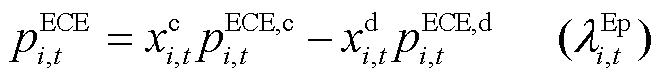 (17)
(17)
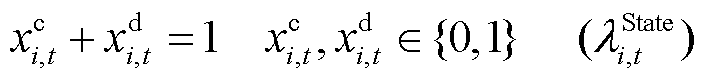 (18)
(18)
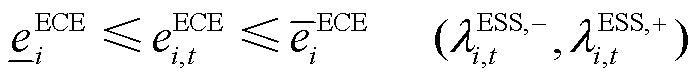 (19)
(19)
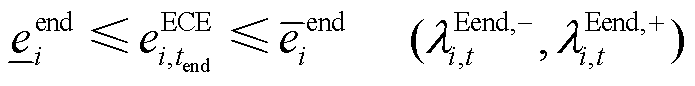 (20)
(20)
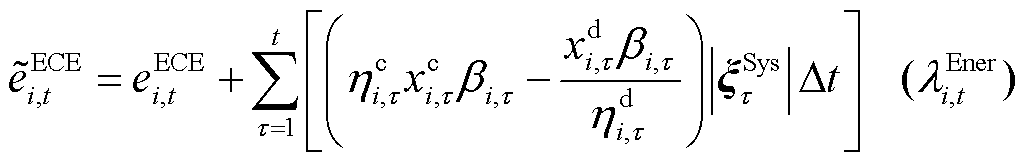 (21)
(21)
式中,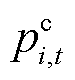 和
和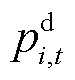 分别为t时段i节点ECE的有功充电和放电功率;
分别为t时段i节点ECE的有功充电和放电功率;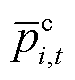 和
和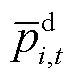 分别为t时段i节点储能ECE的有功充电和放电功率上限;
分别为t时段i节点储能ECE的有功充电和放电功率上限;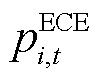 为t时段i节点ECE参与电能量市场的功率;
为t时段i节点ECE参与电能量市场的功率; 和
和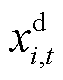 分别为t时段i节点ECE有功充电和放电功率的0-1变量;
分别为t时段i节点ECE有功充电和放电功率的0-1变量;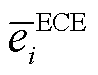 与
与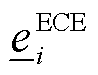 分别为ECE能量上、下限;
分别为ECE能量上、下限;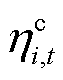 与
与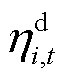 分别为ECE充电和放电损耗系数;
分别为ECE充电和放电损耗系数;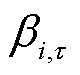 为
为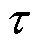 时段i节点ECE平衡系统不确定性功率的贡献因子;
时段i节点ECE平衡系统不确定性功率的贡献因子;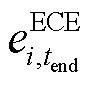 为末尾时段tend的ECE能量;
为末尾时段tend的ECE能量;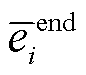 、
、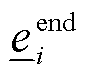 分别为末尾时段tend的ECE能量上、下限;
分别为末尾时段tend的ECE能量上、下限;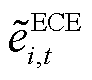 为考虑不确定性功率后t时段i节点ECE的能量;
为考虑不确定性功率后t时段i节点ECE的能量;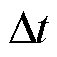 为市场出清时间间隔。
为市场出清时间间隔。
3)考虑不确定性功率的系统机会约束
系统总不确定性功率由PCE和ECE中标的备用容量与调频功率联合应对,如式(22)、式(23)所示。PCE和ECE共同分担系统备用容量的贡献因子,如式(24)所示;PCE和ECE共同分担系统调频功率的贡献因子,如式(25)所示。
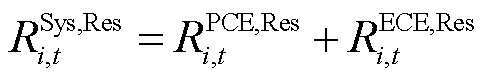 (22)
(22)
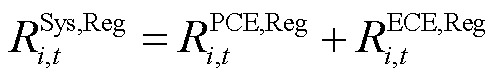 (23)
(23)
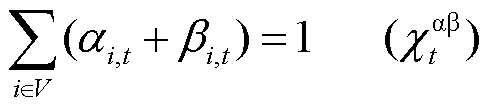 (24)
(24)
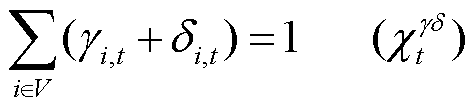 (25)
(25)
式中,![]() 、
、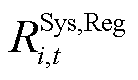 分别为t时段i节点PCE与ECE所能提供的备用容量、调频功率;
分别为t时段i节点PCE与ECE所能提供的备用容量、调频功率;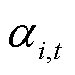 、
、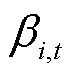 分别为t时段i节点PCE、ECE的备用容量平衡系统不确定性功率的贡献因子;
分别为t时段i节点PCE、ECE的备用容量平衡系统不确定性功率的贡献因子;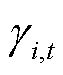 、
、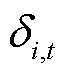 分别为t时段i节点PCE、ECE的调频功率平衡系统不确定性功率的贡献因子。
分别为t时段i节点PCE、ECE的调频功率平衡系统不确定性功率的贡献因子。
考虑不确定性功率后,系统功率平衡约束为
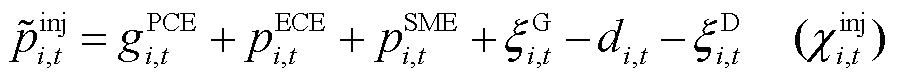 (26)
(26)
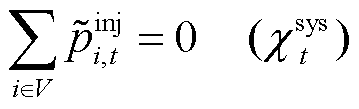 (27)
(27)
式中,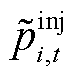 为考虑不确定性功率后的t时段i节点的净注入功率;
为考虑不确定性功率后的t时段i节点的净注入功率;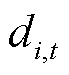 为t时段节点i处的负荷功率预测值。
为t时段节点i处的负荷功率预测值。
考虑不确定性功率后,ECE能量的机会约束见式(28);线路潮流的机会约束见式(29)。
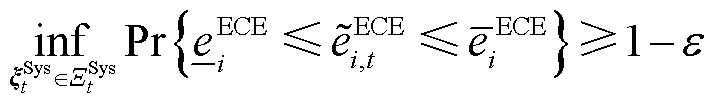 (28)
(28)
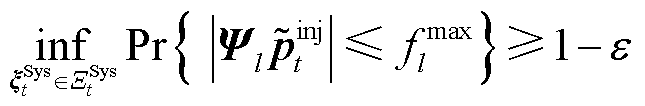 (29)
(29)
特别地,将系统备用容量需求与系统不确定性功率的均值相联系,解决长时间尺度上系统功率不平衡;将调频功率与系统不确定性功率的标准差相联系,解决更短时间尺度上系统功率波动。备用容量和调频需求的机会约束分别如式(30)、式(31)所示,保证约束成立的概率不小于 。
。
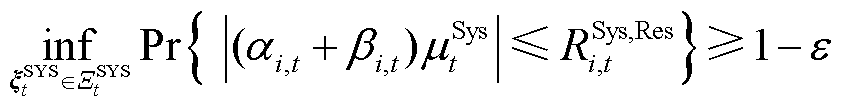 (30)
(30)
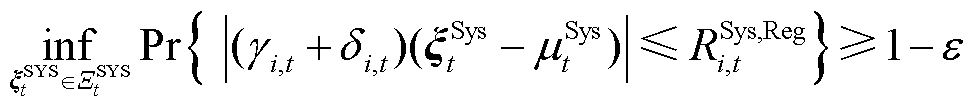 (31)
(31)
式中,ε为机会约束的风险容忍阈值;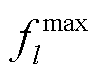 为线路l的潮流传输极限;
为线路l的潮流传输极限;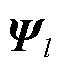 为所有节点对线路l的功率转移分布因子构成的行向量。
为所有节点对线路l的功率转移分布因子构成的行向量。
相比基于预测功率建立的电能量市场出清模型,基于不确定性功率模糊集的联合市场出清模型中引入了随机变量,模型求解较为复杂。1.2节建立的考虑双边机会约束的电能量、备用与调频辅助服务联合市场出清的分布鲁棒优化模型为非凸问题。为不失一般性,该优化模型的紧凑数学形式如式(32)所示。
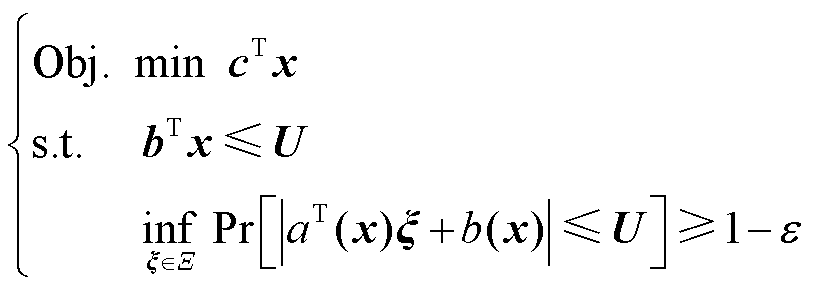 (32)
(32)
式中,c为目标函数系数;b为不等式约束系数;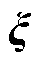 为随机变量;
为随机变量;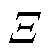 为随机变量
为随机变量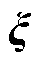 的模糊集;
的模糊集;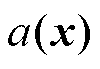 、
、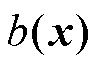 为优化变量x的仿射映射;
为优化变量x的仿射映射; 为约束限值;
为约束限值; 为机会约束成立的最小概率。
为机会约束成立的最小概率。
考虑到式(28)~式(31)中的双边机会约束均含有不确定性功率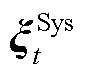 ,为非凸约束,需对其凸重构。首先,将其转换为两个单边的机会约束,可得
,为非凸约束,需对其凸重构。首先,将其转换为两个单边的机会约束,可得
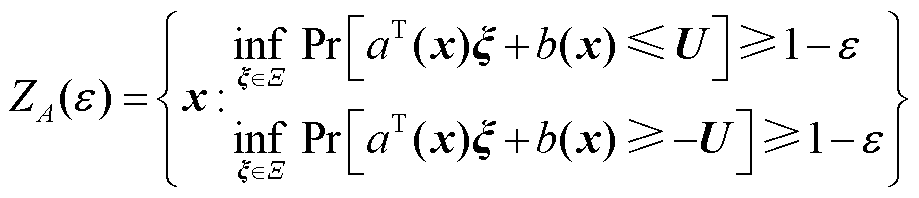 (33)
(33)
通过凸重构将双边机会约束转换为二阶锥规划(Second Order Cone Program, SOCP)[19],有
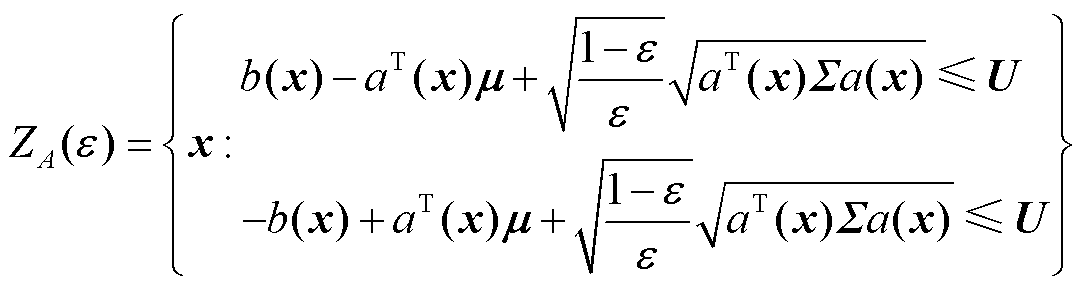 (34)
(34)
式中,μ为随机变量的均值;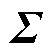 为随机变量
为随机变量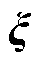 的协方差矩阵。
的协方差矩阵。
根据式(35),将分布鲁棒双边机会约束表达为一组确定性不等式约束。
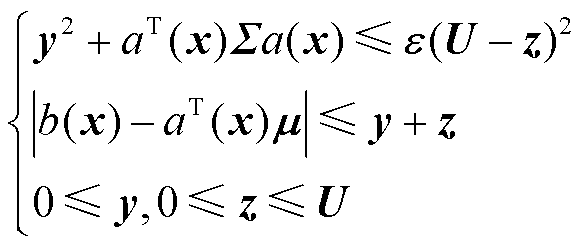 (35)
(35)
式中,y和z为辅助变量。
式(35)中的第一个不等式为二次约束,将其转换为二阶锥约束,有
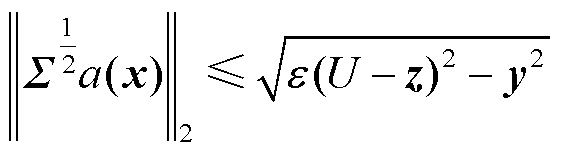 (36)
(36)
式中,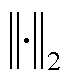 为二范数。
为二范数。
引入新的辅助分量来表示式(36)的二阶锥约束和式(35)中的第二个不等式中的列向量,如式(37)所示。
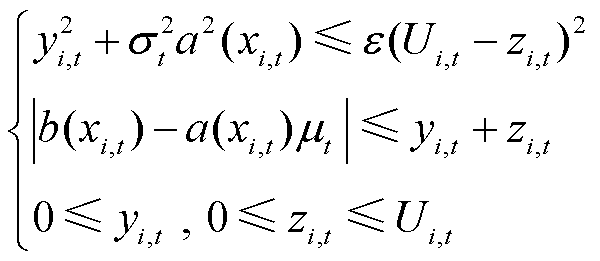 (37)
(37)
式中,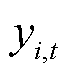 、
、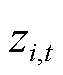 、
、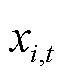 、
、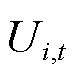 分别为列向量y、z、x、U的分量。
分别为列向量y、z、x、U的分量。
此后,采用分段线性函数或线性近似的方法来近似式(37)中的二次项函数和绝对值函数。同时,现成的商业求解器Gurobi、Cplex均可以求解含二次方项和绝对值的约束问题。由此,式(28)~式(31)被转换为附录第2节所示的四组凸性含非线性的不等式约束。
为促进不同市场主体参与联合市场的公平性,确保DME与SME均根据自身价值获取对等的收益,需区分DME提供确定性功率和SME产生不确定性功率的价格。因此,本文主张对两类功率分别定价,有助于引导系统中灵活调节资源与不确定性功率互相匹配。其中,确定性功率价格包括PCE与ECE的电能量、备用、调频定价,不确定性功率价格包括系统电价与节点电价。
电能量的节点电价定义为满足某节点负荷单位增量的系统边际成本增量,也称节点边际电价[20]。附录第1节中基于预测功率的电能量市场出清模型的拉格朗日函数详见附录第3节。根据包络定理和KKT(Karush-Kuhn-Tucker)条件,电能量的分时节点边际价格为拉格朗日函数对节点负荷需求功率的偏导数为零,如式(38)所示。系统各节点边际电价由电能量成本和系统阻塞成本两部分组成,即为式(39)。
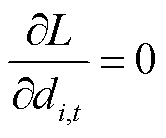 (38)
(38)
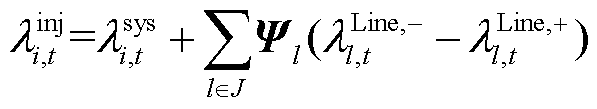 (39)
(39)
式中,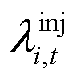 为t时段i节点电能量的节点边际价格;J为系统中所有支路的集合。
为t时段i节点电能量的节点边际价格;J为系统中所有支路的集合。
在1.2节基于电能量与备用、调频联合市场出清模型中,系统备用容量和调频功率的需求约束如式(40)、式(41)所示,不等式右侧即为最小需求量。
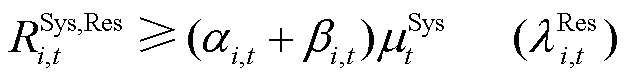 (40)
(40)
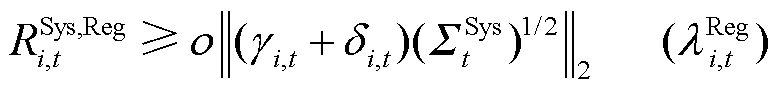 (41)
(41)
式中,o为考虑到不确定性功率的协方差而额外需要预留调频容量的裕度系数;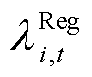 、
、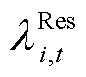 分别为t时段i节点备用容量、调频功率的节点边际价格。
分别为t时段i节点备用容量、调频功率的节点边际价格。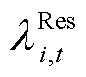 与PCE、ECE的平衡因子变量
与PCE、ECE的平衡因子变量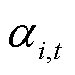 、
、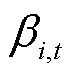 直接相关,
直接相关,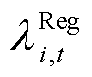 与PCE、ECE的平衡因子变量
与PCE、ECE的平衡因子变量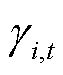 、
、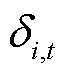 直接相关。
直接相关。
备用与调频的节点边际价格定义为每增加单位需求容量所对应的系统运营成本的增量。式(40)和式(41)约束条件对应的拉格朗日乘子即分别为备用与调频边际价格。附录第4节中联合市场出清模型的拉格朗日函数对备用、调频的需求量求偏导数即可得备用、调频的节点边际出清价格表达式,分别为
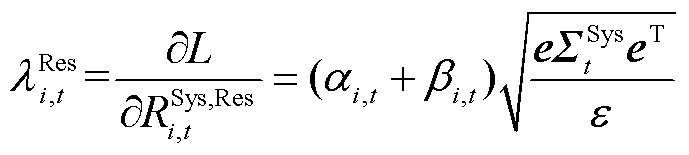 (42)
(42)
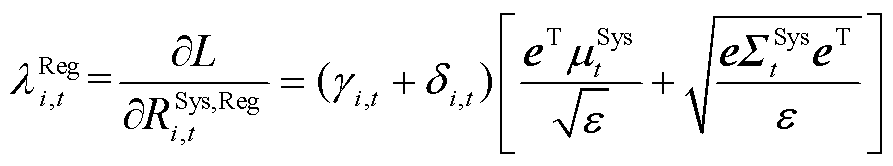 (43)
(43)
式中,e为单位列向量。
不确定性功率的系统边际价格(Uncertainty System Marginal Prices, USMP)定义为满足系统不确定性功率单位增量导致的系统边际成本变化量,具体包括单位均值增量和标准差增量导致系统运行成本的增加。在数学上,表示为拉格朗日函数对系统不确定性功率均值和标准差的偏导数,分别为
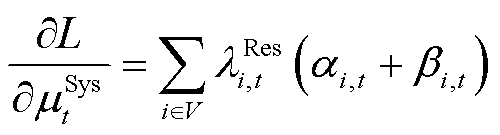 (44)
(44)
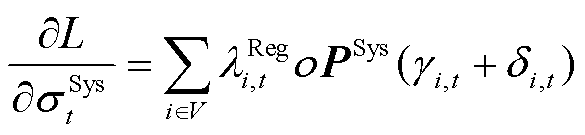 (45)
(45)
系统不确定性功率的边际价格与其对应的灵活调节资源的稀缺程度直接相关。
基于边际定价原理,ULMP定义为节点不确定性功率单位标准差增量导致的系统边际成本增量,数学上表示为拉格朗日函数对节点不确定性功率标准差的偏导数,即

式中,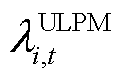 为不确定功率的节点边际价格;
为不确定功率的节点边际价格;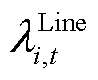 为需要线路预留可用传输功率的边际成本;
为需要线路预留可用传输功率的边际成本;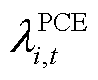 为需要PCE预留功率的边际成本;
为需要PCE预留功率的边际成本;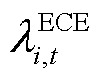 为需要ECE预留功率和能量的边际成本;
为需要ECE预留功率和能量的边际成本;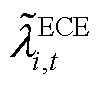 为需要ECE预留能量的边际成本。不确定性功率节点边际价格存在三个分量,各分量的具体表达式见附录第3节。
为需要ECE预留能量的边际成本。不确定性功率节点边际价格存在三个分量,各分量的具体表达式见附录第3节。
由式(46)可知,SME自身产生不确定性功率需要向PCE与ECE支付预留备用容量与调频功率的运行成本,以及向电网公司支付预留线路可用传输功率成本,以确保备用容量和调频功率在日内实时时间尺度能安全调度。由于系统不确定性功率的来源包括用户侧负荷功率与电源侧的新能源发电功率,根据“谁造成的成本谁承担”原则,产生不确定性的成本应该由两者共同承担。传统零散分散负荷的随机波动由售电公司统一承担。因此,SME中的新能源发电企业产生不确定性功率的市场惩罚成本计算公式如式(47)所示,SME中的售电公司因传统零散分散负荷产生随机波动功率的市场惩罚成本计算公式如式(48)所示。
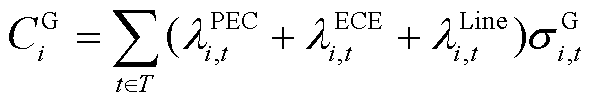 (47)
(47)
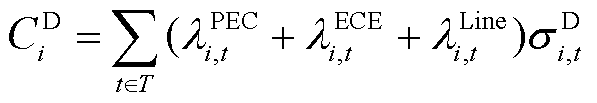 (48)
(48)
式中,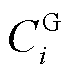 为i节点新能源发电企业因产生不确定性功率需要支付的成本;
为i节点新能源发电企业因产生不确定性功率需要支付的成本;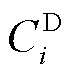 为i节点传统负荷的售电公司因产生不确定性功率需要支付的成本。
为i节点传统负荷的售电公司因产生不确定性功率需要支付的成本。
本节验证考虑不确定性功率的联合市场出清模型和定价方法的有效性。4.1节介绍了测试系统与参数设置。4.2节中展示了联合市场出清结果,并与传统电能量市场进行了对比分析。4.3节详细分析了备用、调频以及不确定性功率的定价结果对比分析。4.4节分析了不同市场主体的成本与收益分析。
采用IEEE 39节点系统对出清模型和定价方法进行算例分析,其拓扑结构以及PCE、ECE和SME在系统中的接入节点如附图1所示。具体地,PCE为传统火电机组,ECE为储能,SME为风电场(Wind Power Farm, WPF)和售电公司(Electricity Retail Company, ERC),各市场主体的功率范围见表1。特别的,假设该系统只有一家ERC,该售电公司需要承担所有负荷节点不确定性功率造成的成本。各市场主体的电能量、备用、调频报价见附表1。以1 h为周期进行市场出清,出清的总时段数为24。发电机组与风电场功率范围见表1。假设新能源与负荷的不确定性功率符合正态分布。各SME不确定性功率的均值设置为其预测功率的20%,标准差设置为其预测功率的30%;负荷不确定性功率的均值设置为其预测功率的5%,标准差设置为其预测功率的10%。机会约束的风险容忍阈值ε取5%。
表1 各市场主体的功率范围
Tab.1 Power range of market entities

SME序号功率范围/MWPCE序号功率范围/MWECE序号功率范围/MW能量范围/(MW·h) SME10~400PCE140~260ECE1-100~1000~200 SME20~400PCE260~350ECE2-50~500~200 SME30~200PCE360~350ECE3-80~800~80 SME40~200PCE440~260ECE4-40~400~80 SME50~300PCE560~300ECE5-100~1000~100 SME60~300PCE660~300ECE6-50~500~100
4.2.1 联合市场出清结果
联合市场中电能量、备用与调频的出清结果如图2所示。由于系统负荷需求不变,联合市场与传统市场的电能量出清总量一样。对比附录第1节中传统电能量市场的出清模型,所提联合市场出清模型考虑了各个市场主体发电系统的电能量、备用与调频之间的耦合关系。在同样的算例设置下,电能量、备用与调频三类市场的独立运行成本之和比联合市场的运行总成本高出25.5%。因此,联合市场能有效地降低市场运行总成本。
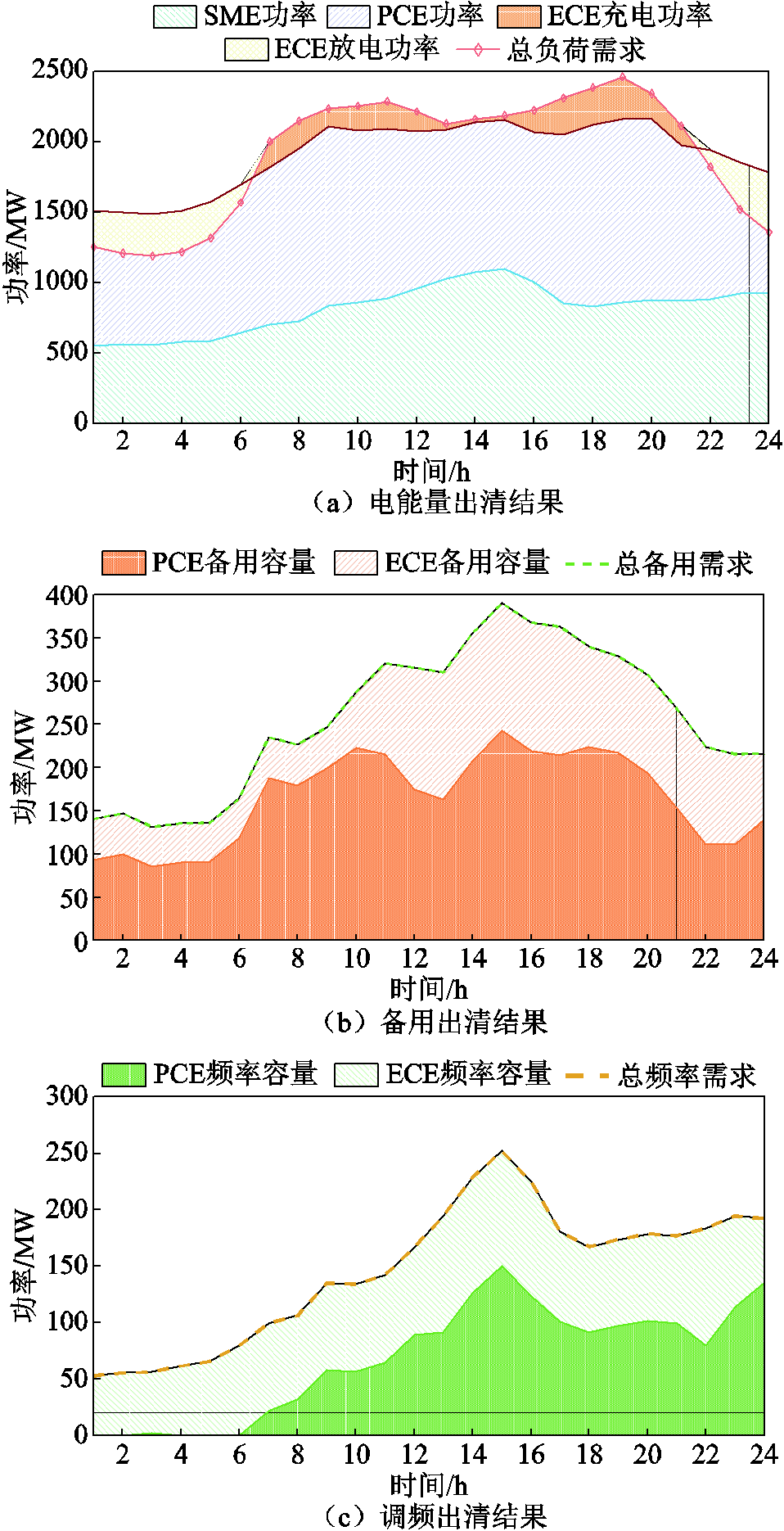
图2 联合市场的出清结果
Fig.2 Clearing results of joint market
4.2.2 不同风险容忍水平下联合市场出清结果
在不同风险容忍水平下,ECE3能量变化曲线如图3所示,图中红色虚线表示基于SME的预测功率得到的ECE3能量曲线,黑色实线表示1 000条ECE3可能的实际能量变化曲线。当风险容忍水平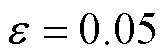 时,ECE3所有实际能量变化曲线都位于能量边界之内;当
时,ECE3所有实际能量变化曲线都位于能量边界之内;当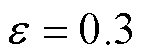 时,ECE3的实际能量变化曲线可能会出现能量越限,存在实际运行不能按照出清结果执行的情况。相比基于预测功率的电能量市场出清模型,考虑不确定性功率后ECE的能量约束缩小,进一步增大了市场运行成本。分析表明:对机会约束的风险容忍水平越高,ECE突破能量边界的可能性越大,ECE中标结果越激进,系统安全运行的风险越高。
时,ECE3的实际能量变化曲线可能会出现能量越限,存在实际运行不能按照出清结果执行的情况。相比基于预测功率的电能量市场出清模型,考虑不确定性功率后ECE的能量约束缩小,进一步增大了市场运行成本。分析表明:对机会约束的风险容忍水平越高,ECE突破能量边界的可能性越大,ECE中标结果越激进,系统安全运行的风险越高。

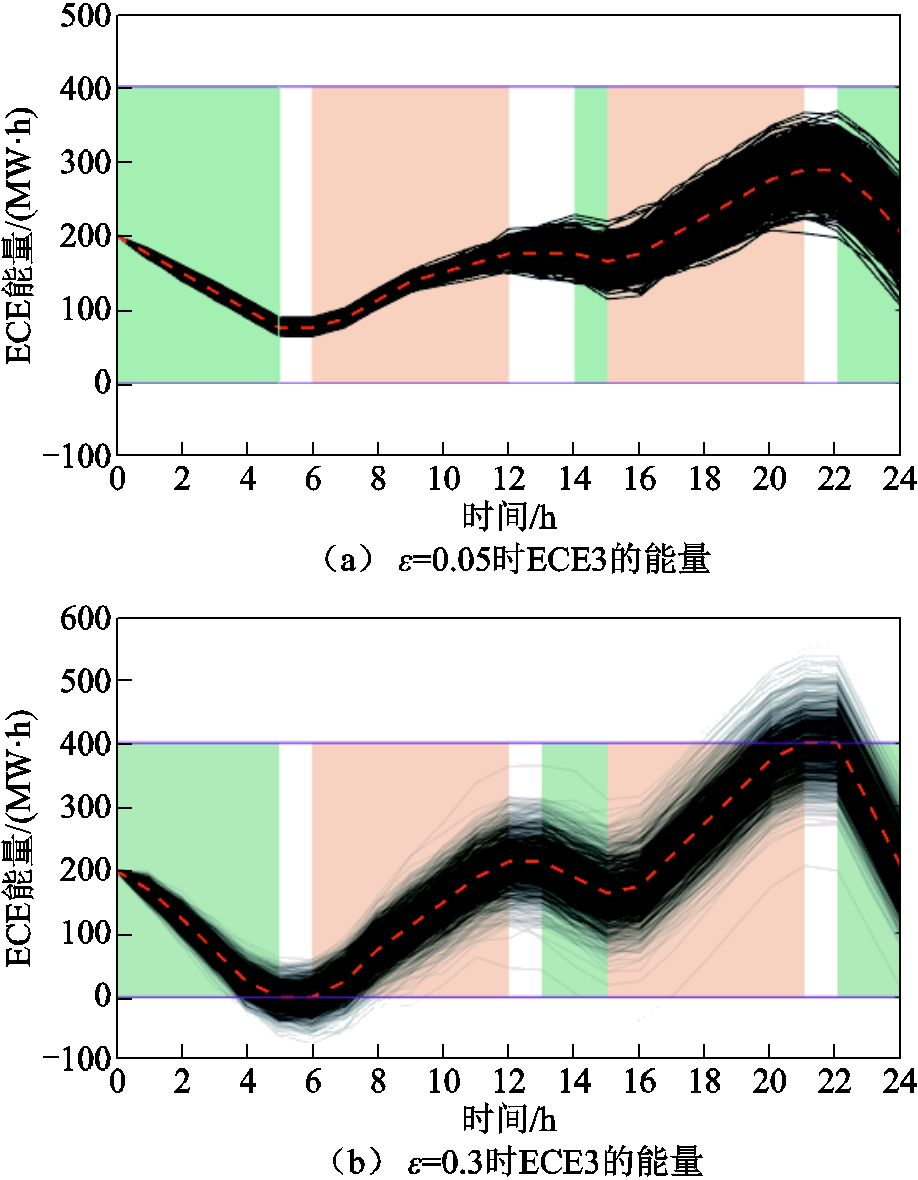
图3 ECE3预测及实际的能量变化曲线
Fig.3 ECE3 predicted and actual energy change curve
图4给出了联合市场中电能量、备用容量与调频功率的节点边际电价,为灵活调节资源提供价格激励。其中,电能量的节点边际电价与传统基于预测功率的市场出清模型所获得的电能量节点价格一致。由于系统线路容量较大,存在阻塞的线路较少,因此,在各分图中只列出了存在价格差异的节点,其他节点的价格与各分图中所列节点电价一致。大部分节点的电能量电价与节点15的价格一致,表明该电网线路容量充裕。

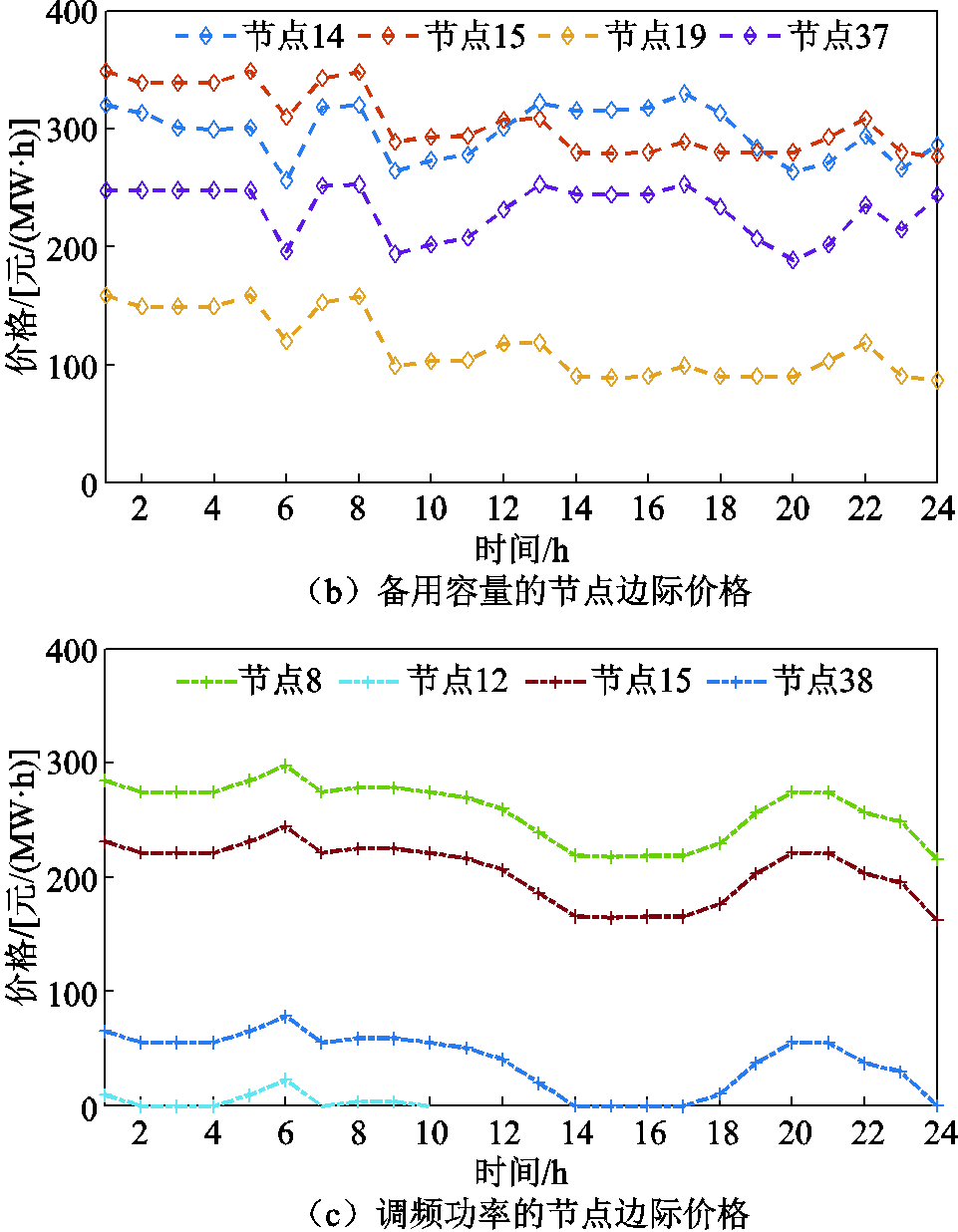
图4 电能量、备用容量与调频功率的节点边际价格
Fig.4 Locational marginal price of energy, reserve capacity and frequency regulation power
从图4b、图4c可看出,各节点备用与调频边际价格的变化趋势相对一致。其中,节点37、38为PCE所在节点,其备用与调频价格相对较低。节点8的调频价格较高,保证了ECE参与调频的公平性。此外,附图2和附图3展示了系统不确定性功率的均值与标准差对备用容量和调频容量市场成交价格的影响,整体上备用与调频出清价格随着不确定性水平的增加而增加。具体的,系统不确定性功率的均值增加到1.5倍,备用出清价格增加22.9%,系统不确定性功率的标准差增加到1.5倍,调频出清价格增加30.6%。
风电场所在节点的ULMP如图5所示。由于风电场所在节点没有负荷功率,通过ULMP可以直接反映风电场产生不确定性功率对市场运营造成的边际成本。
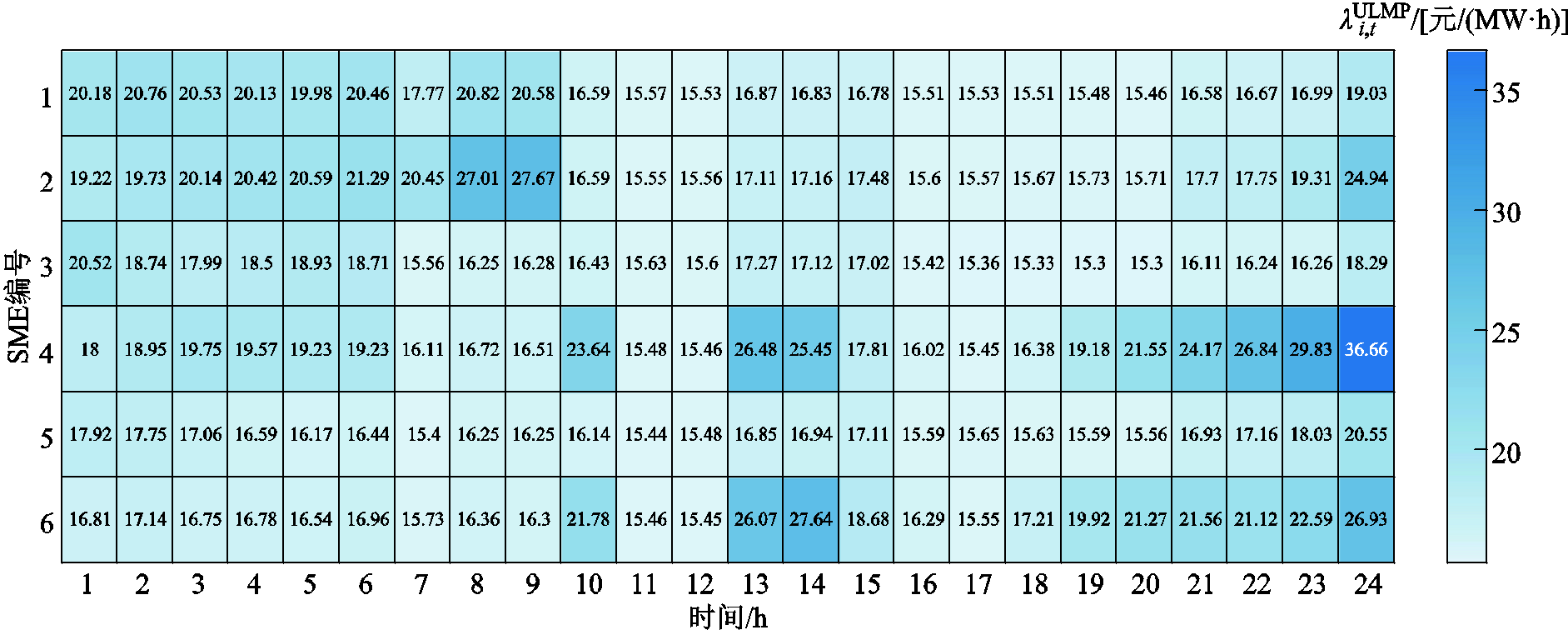
图5 不确定性功率的节点边际价格
Fig.5 Locational marginal price of uncertain power
分析可得以下结论:
1)在线路潮流不存在阻塞的情况下,各个节点的ULMP直观体现各个节点不确定性功率的水平。
2)由于风电场所在节点的负荷功率被设置为0,可直接根据风电场所在节点的ULMP对新能源企业产生的不确定性功率收取费用。
3)考虑到ECE的能量在时间上连续耦合,因此,在达到临界能量时刻前的所有时段中,ULMP中均会存在由于能量约束造成的成分。在实际市场运行时,可采用每4 h核算ECE的剩余能量,以降低对ECE补偿费用的频繁支付。
随着系统不确定性功率波动水平变化,SME和PCE市场主体的总收益与系统总成本的变化曲线如图6所示。由于ECE的收益和PCE、SME的收益并不在同一个量级,因此图6中并未展示ECE的收益。从图6可看出,整体上SME的收益随着不确定性水平的增加而降低;PCE的收益随着不确定性水平的增加而增加;随着不确定性水平的增加,联合市场出清总成本增大。分析表明:当系统不确定性功率的标准差低于0.7倍的原定标准差时,ECE能量、系统潮流以及备用容量、调频功率的机会约束未受到SME不确定性功率的影响。此外,附图4展示了市场主体的总收益与系统总成本随系统不确定性功率均值的变化曲线。市场主体与系统运行成本的变化趋势与图6整体上一致。从附图4可看出,随着不确定性功率均值增大,PCE市场主体的总收益逐渐趋向稳定,是因为PCE提供的备用和调频容量逐渐饱和,因而系统的调节需求转向成本更高的ECE,导致系统成本的快速上涨。
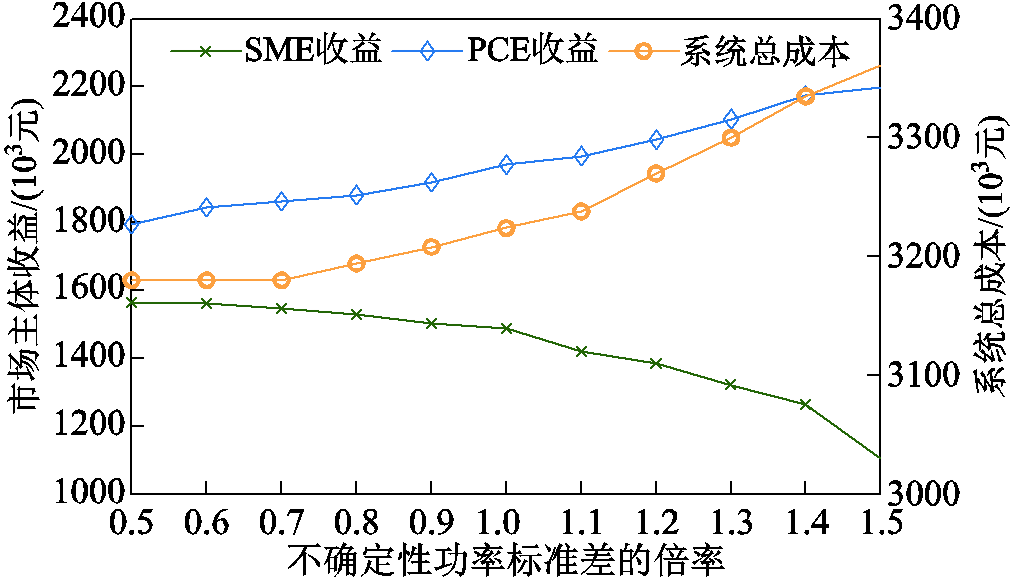
图6 不同标准差下市场主体收益与系统总成本曲线
Fig.6 Market entities benefit and system total cost curves under different standard deviations
表2给出了不同风险容忍水平下联合市场总成本以及各市场主体的收益统计。观察表2中数据可得,第4、5、7、8、9列之和与第11、12列之和相等。通过表2的数据,验证了以下结论:①在一个存在线路阻塞的系统中,SME产生不确定性功率的总成本等于PCE、ECE提供备用和调频的总收入,以及电网预留线路容量带来的收入总和;②随着风险容忍水平的增大,PCE和ECE提供备用容量和调频功率的收入减少,SME支付不确定性功率的成本也相应降低,市场总成本减少,但不可避免地提高了系统风险水平。
表2 不同风险容忍水平下联合市场成本对比
Tab.2 Comparison of joint market costs under different risk tolerance levels (单位:103元)

ε市场总成本PCE电能量收入PCE备用收入PCE调频收入ECE电能量收入ECE备用收入ECE调频收入电网线路容量收入SME电能量收入SME不确定性支付ERC不确定性支付 0.053 312.461 839.0383.0362.9516.3363.0355.4343.031 632.97145.06162.44 0.103 246.071 879.9576.0959.0918.1056.4951.2638.661 698.92132.34149.26 0.203 110.491 959.4070.0550.5522.9549.7547.9431.941 741.95124.37125.87 0.303 067.322 052.8862.8042.8225.2842.8039.8225.121 785.25107.14106.23
特别地,若在算例中将线路容量放大数十倍,即式(28)对应的线路潮流不起约束,则可以得到以下结论:在一个线路容量完全充裕的系统中,DME提供辅助服务的总收益与SME产生不确定性功率的总成本相等,以此确保市场运营商的收支平衡和市场运行的经济性。具体在表2中,第9列数据为0,第4、5、7、8列之和与第11、12列之和相等。
本文提出了一种考虑不确定性功率的电能量与辅助服务联合市场出清方法,实现了电能量、备用、调频容量以及不确定性功率的协同定价。本文主要结论与建议如下:
1)所提USMP和ULMP明确了不确定性源的市场代价,导致SME产生不确定性功率的惩罚成本金额主要流向了提供备用容量与调频功率的PCE和ECE企业。在周围线路阻塞严重的节点,SME还要向电网支付阻塞成本。系统不确定性功率的均值增加到1.5倍,备用出清价格增加22.9%,SME收益减少25.4%,PCE收益增加0.76%,市场运行成本增大4.46%;系统不确定性功率的标准差增加到1.5倍,调频出清价格增大30.6%,SME收益减少27.3%,PCE收益增加11.6%,市场运行成本增加3.75%。
2)所提多元产品联合的市场出清模型综合考虑了多类市场主体参与,兼顾了源荷不确定性功率,可获得不同风险容忍水平的出清结果。相较于传统基于预测功率的市场出清模型,新能源企业降低18.5%的收益,储能企业提高26%的收益,通过市场联合降低总运行成本25.5%。
3)随着我国风光电源功率占比不断增大,建议在中国现有电力产品价格机制的基础上,增加对不确定性功率的定价,这将有助于促使新能源等强随机性企业降低自身不确定性。鼓励引导储能等市场主体平等参与到市场中,提升系统灵活调节能力,同时要努力保障储能等调节型企业获得相对可观的收益。
后续研究将进一步考虑不确定性功率在实时市场中的平衡问题,即日前出清的备用与调频容量如何在实时市场实际调出,以及平衡成本如何在市场主体之间的分摊问题。
附 录
1. 传统市场出清优化模型
1.1 基于预测功率的传统市场出清优化模型
传统电能量市场基于SME的预测功率建立出清模型,以市场总成本最小为出清优化目标,电能量市场出清目标函数如式(A1)所示。
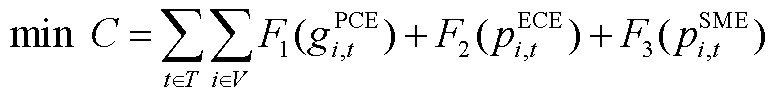 (A1)
(A1)
1.2 约束条件
1)PCE参与电能量市场的运行约束
PCE参与电能量市场的运行约束包括机组功率约束和爬坡约束,分别如式(11)、式(12)所示。
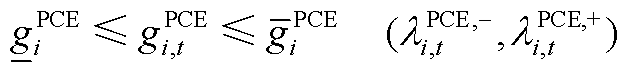 (A2)
(A2)
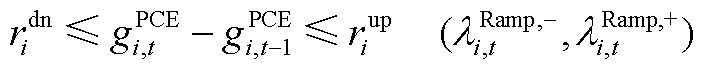 (A3)
(A3)
2)ECE参与电能量市场的运行约束
ECE参与电能量市场不仅需要输出功率、运行状态进行约束,还需要额外考虑能量限制、始末能量约束。ECE的运行约束如式(A4)~式(A10)所示。
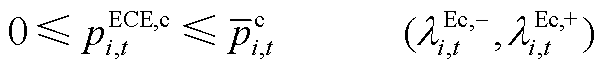 (A4)
(A4)
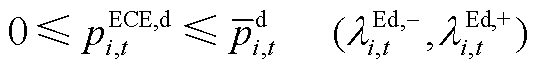 (A5)
(A5)
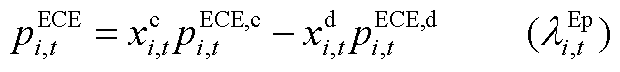 (A6)
(A6)
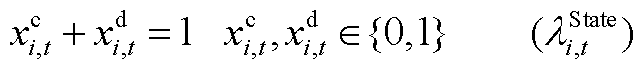 (A7)
(A7)
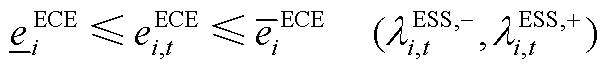 (A8)
(A8)
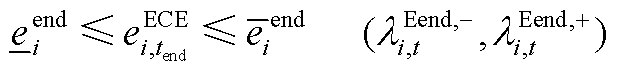 (A9)
(A9)
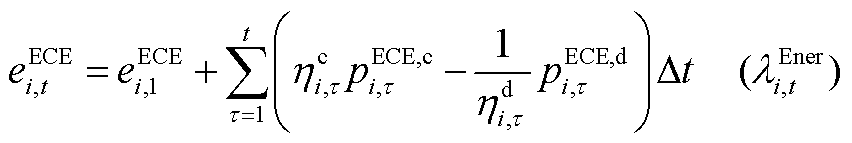 (A10)
(A10)
3)基于预测功率的系统约束
基于预测功率构建系统功率平衡的约束如式(A11)、式(A12)所示,各支路潮流约束如式(A13)所示。
 (A11)
(A11)
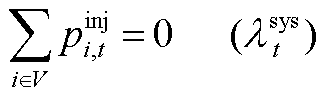 (A12)
(A12)
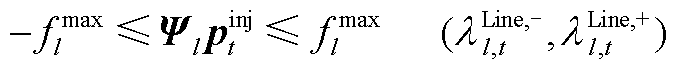 (A13)
(A13)
式中,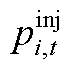 为t时段i节点的净注入功率;
为t时段i节点的净注入功率;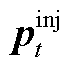 为t时段所有节点净注入功率
为t时段所有节点净注入功率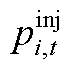 构成的列向量。
构成的列向量。
由此,基于SME确定性预测功率建立的电能量市场出清模型为混合整数线性规划(Mixed Integer Linear Programming, MILP)问题,如式(A14)所示。
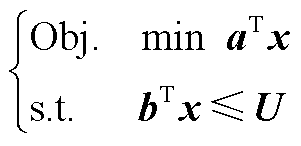 (A14)
(A14)
式中,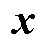 为决策变量,
为决策变量,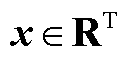 ;
;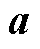 为成本向量;
为成本向量;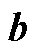 为系数向量;
为系数向量;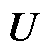 为限值,均为确定值。
为限值,均为确定值。
2. 双边机会约束转换为凸约束
将式(27)~式(30)的四组双边机会约束的数学表达转换成式(A15)~式(A18)所示四组凸性约束的形式,其中,各组的第一个式子为二阶锥(Second Order Cone, SOC)约束。
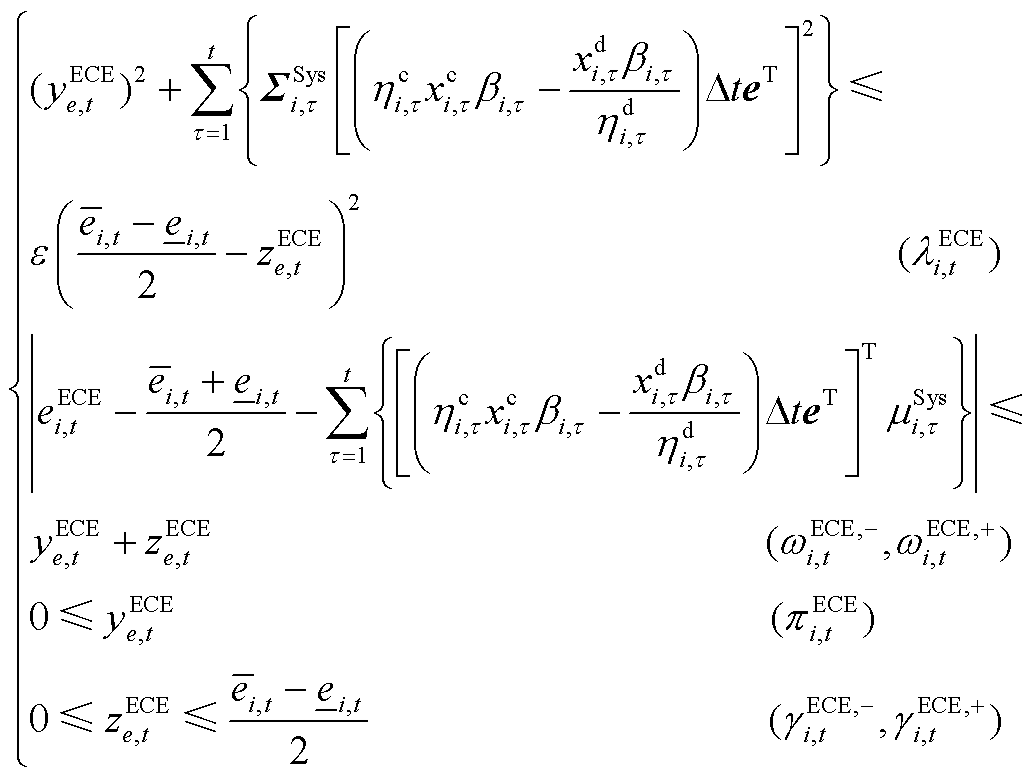 (A15)
(A15)
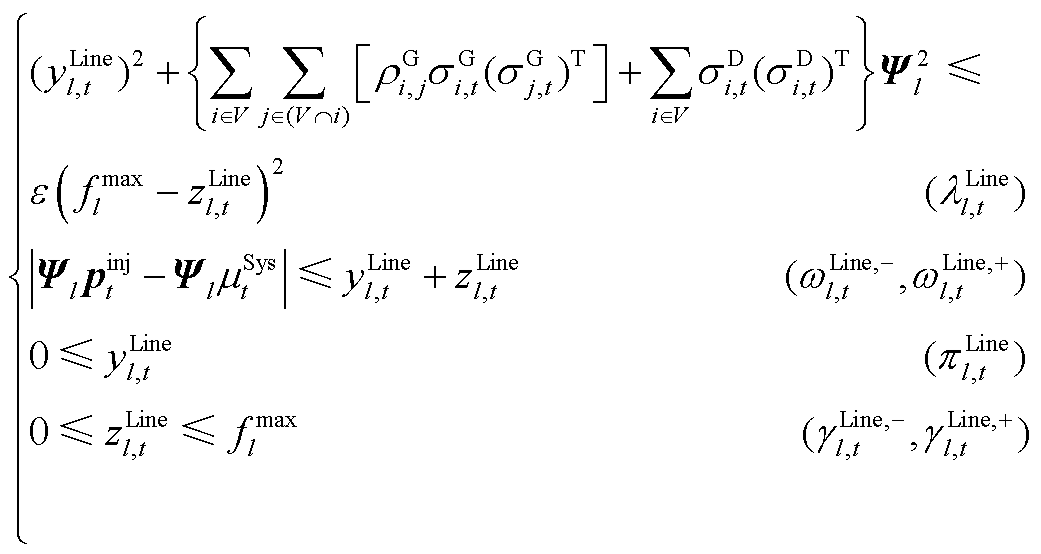 (A16)
(A16)
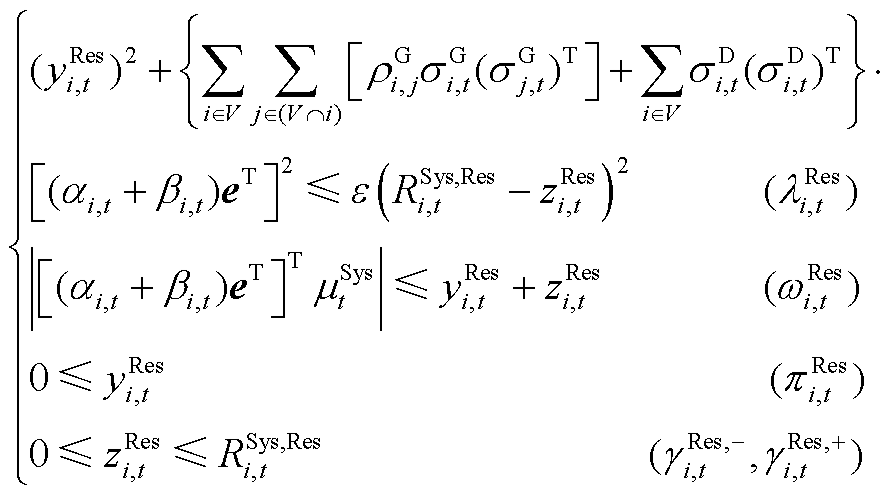 (A17)
(A17)
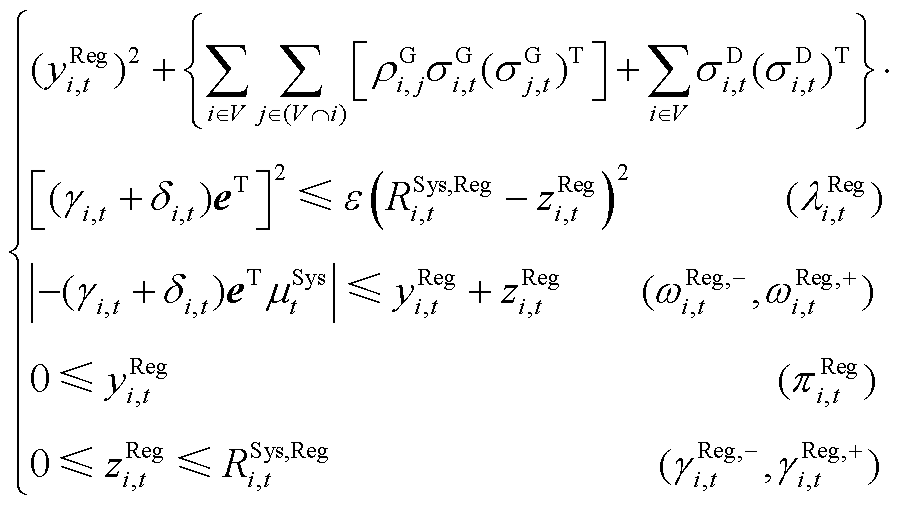 (A18)
(A18)
式中,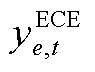 、
、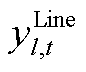 、
、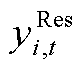 、
、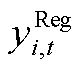 与
与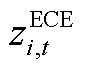 、
、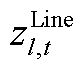 、
、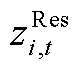 、
、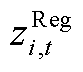 分别为ECE能量的机会约束、系统潮流安全的机会约束及备用容量需求的机会约束、调频容量的机会约束的辅助变量。由式(A17)和式(A18)可推出系统备用与调频的需求如式(A19)和式(A20)所示。
分别为ECE能量的机会约束、系统潮流安全的机会约束及备用容量需求的机会约束、调频容量的机会约束的辅助变量。由式(A17)和式(A18)可推出系统备用与调频的需求如式(A19)和式(A20)所示。
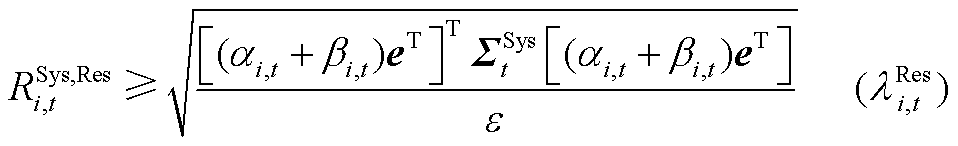 (A19)
(A19)
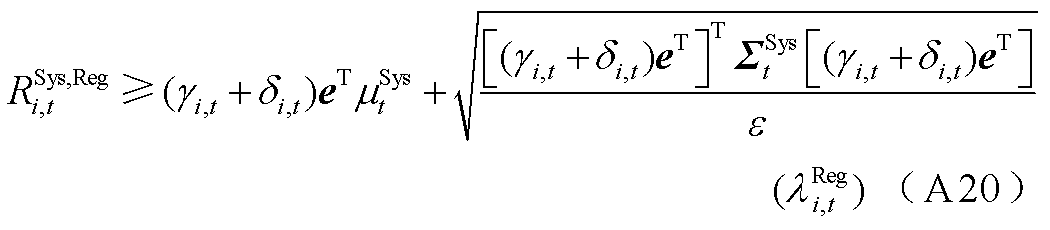
3. 电能量市场出清模型的拉格朗日函数
基于预测功率的电能量市场出清模型,其拉格朗日函数为
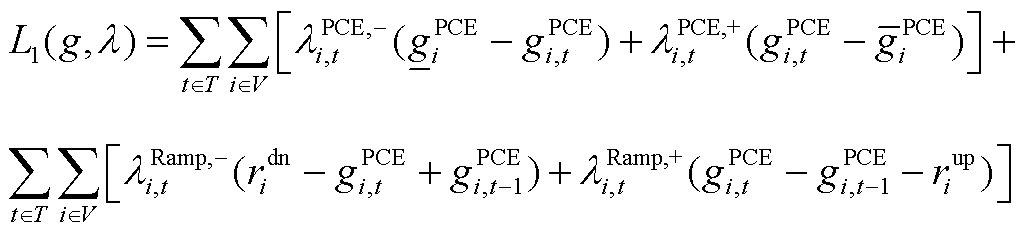 (A22)
(A22)
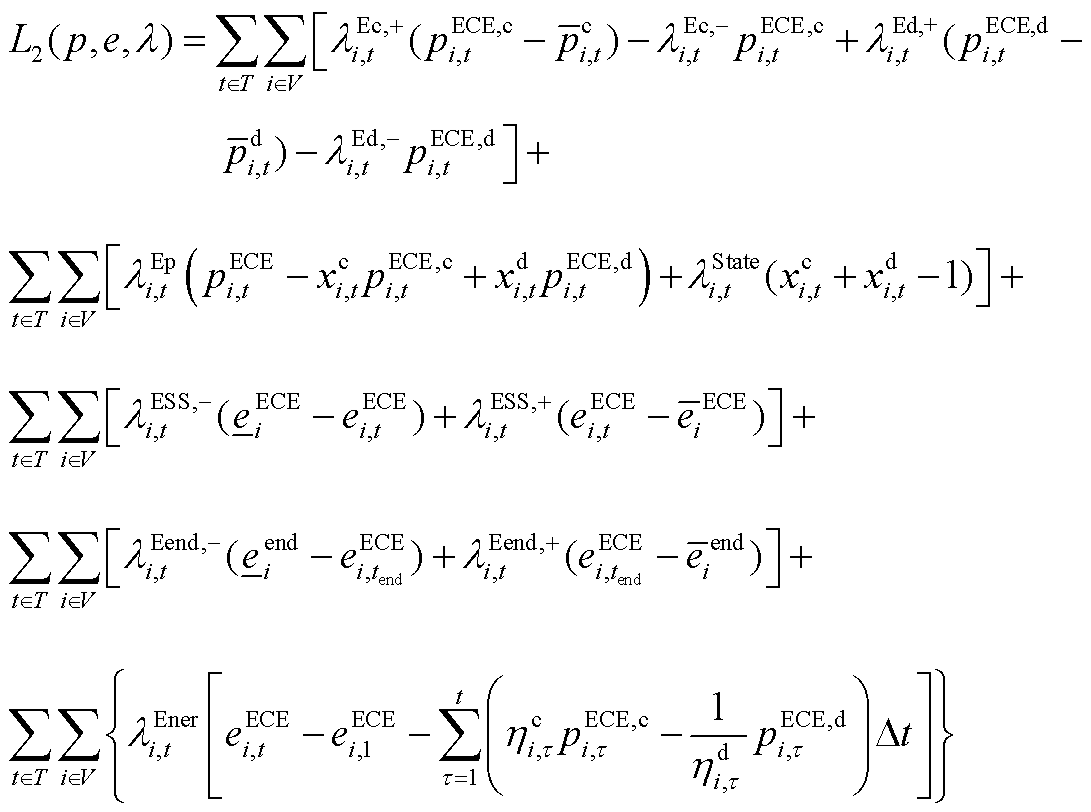 (A23)
(A23)
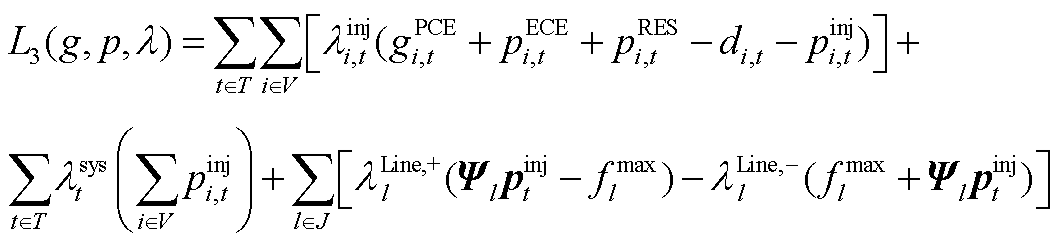 (A24)
(A24)
4. 联合市场出清模型的拉格朗日函数
考虑不确定性功率的联合市场优化出清模型的拉格朗日函数如式(A25)所示,属于混合整数二阶锥规划问题。
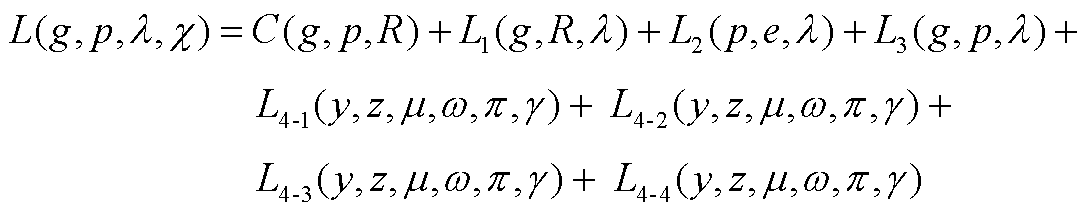 (A25)
(A25)
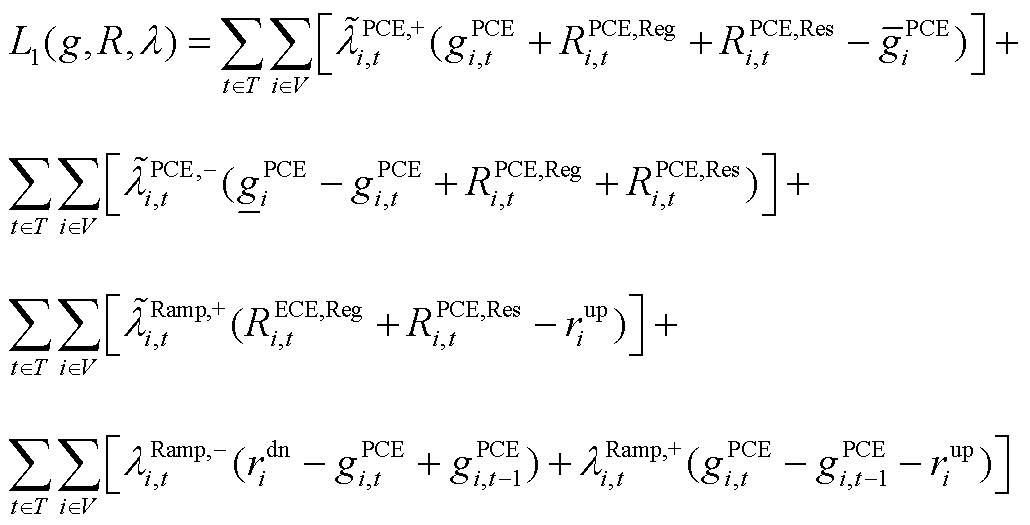 (A26)
(A26)
 (A27)
(A27)
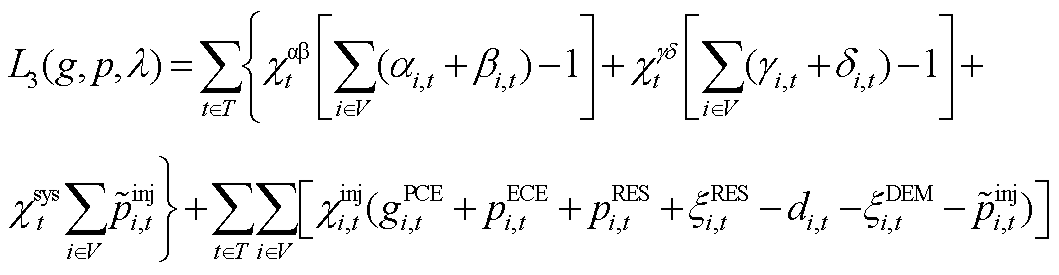 (A28)
(A28)
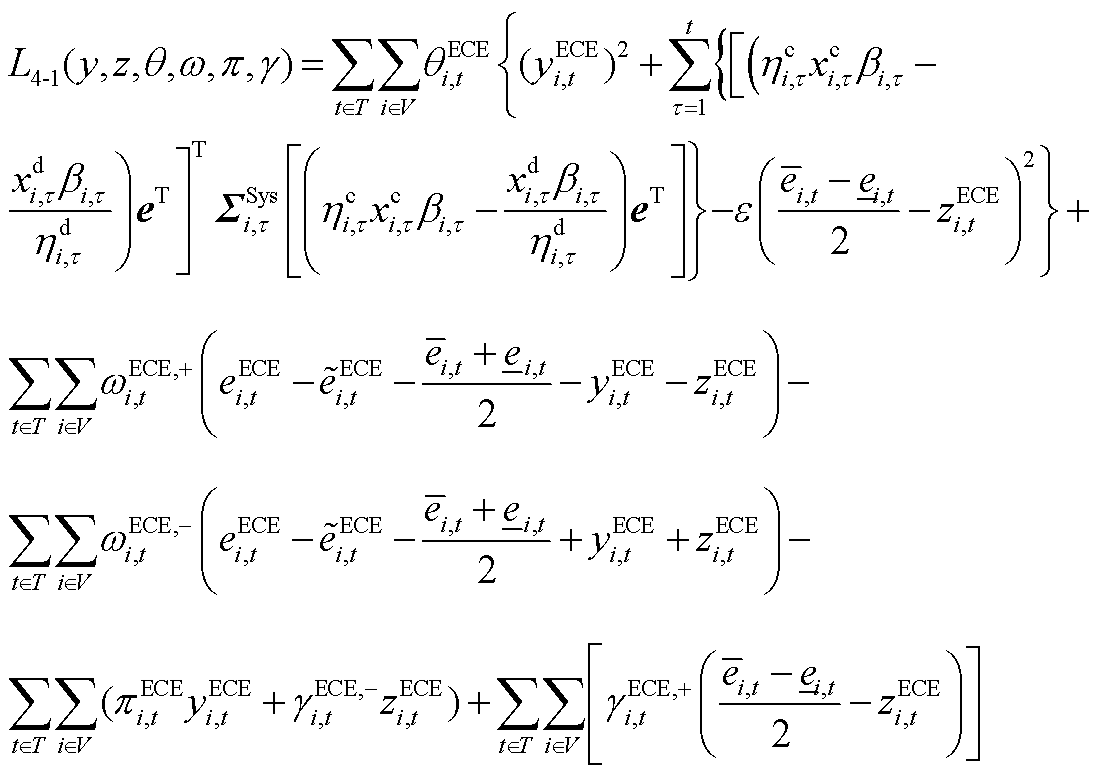 (A29)
(A29)
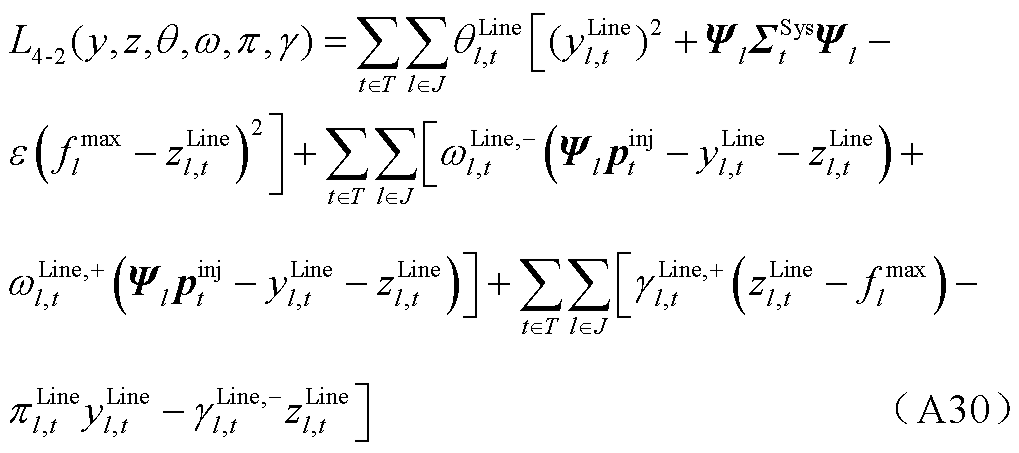
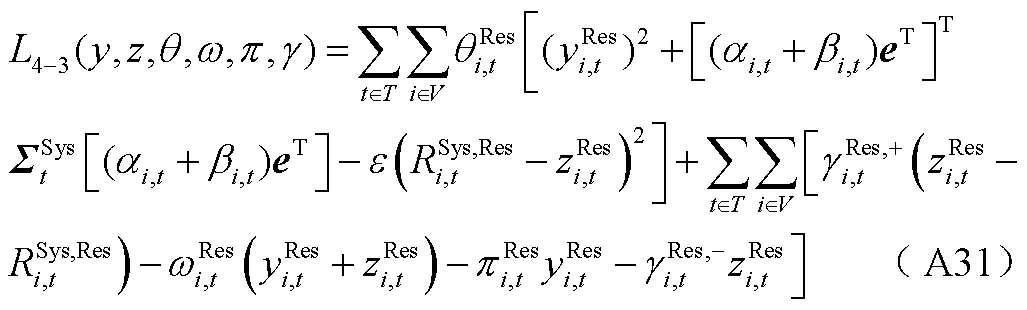
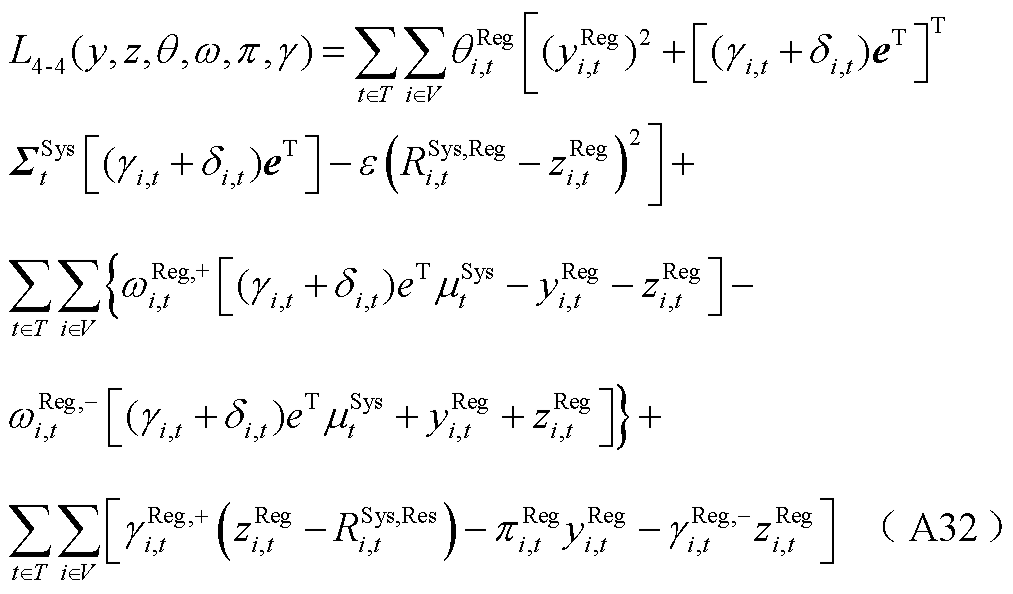
5. 不确定性功率的价格表达式
假设在理想的市场条件下(即排除市场中的非理性因素、政策干预等影响),联合市场中确定性市场主体DME(传统火电发电机组、抽水蓄能、储能等)提供辅助服务的总收益与新能源发电等随机性市场主体SME产生不确定性功率的总成本基本相等。从数学上给出了证明:
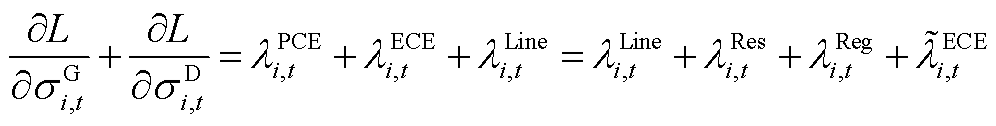 (A33)
(A33)
式中,由于存在不确定性功率,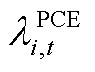 为需要PCE预留功率的边际成本;
为需要PCE预留功率的边际成本;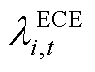 为需要ECE预留能量约束的边际成本;
为需要ECE预留能量约束的边际成本;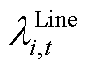 为需要线路预留可用传输功率的边际成本。
为需要线路预留可用传输功率的边际成本。
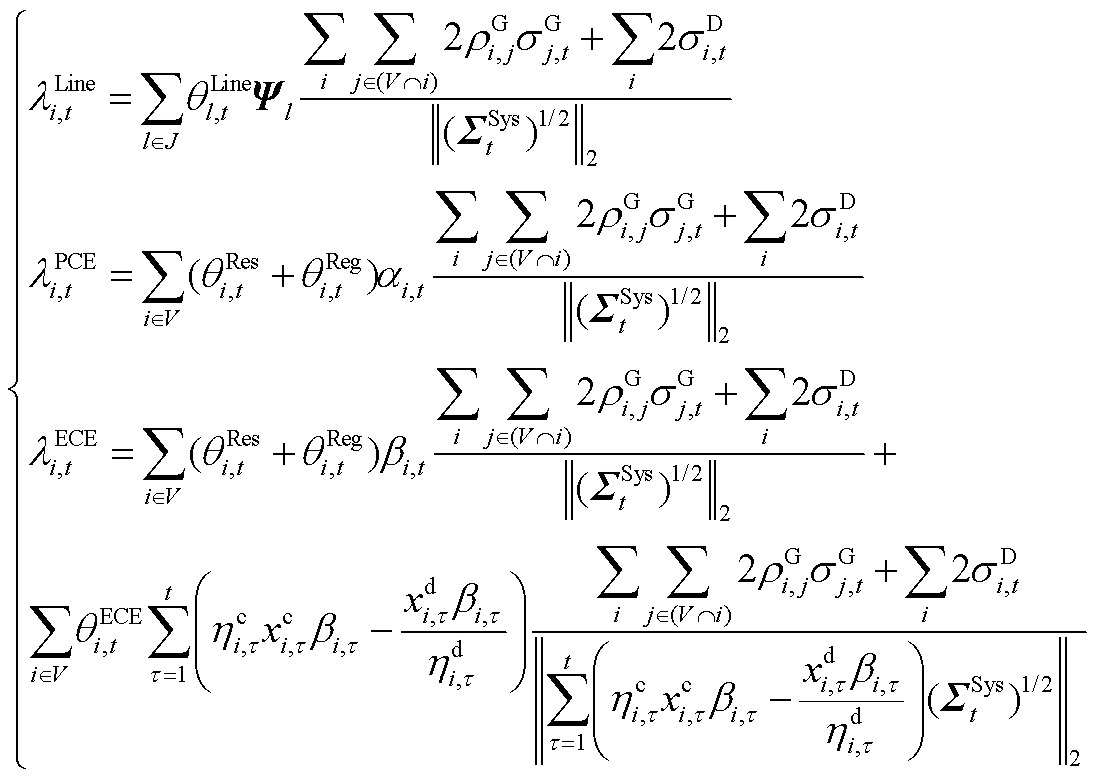 (A34)
(A34)
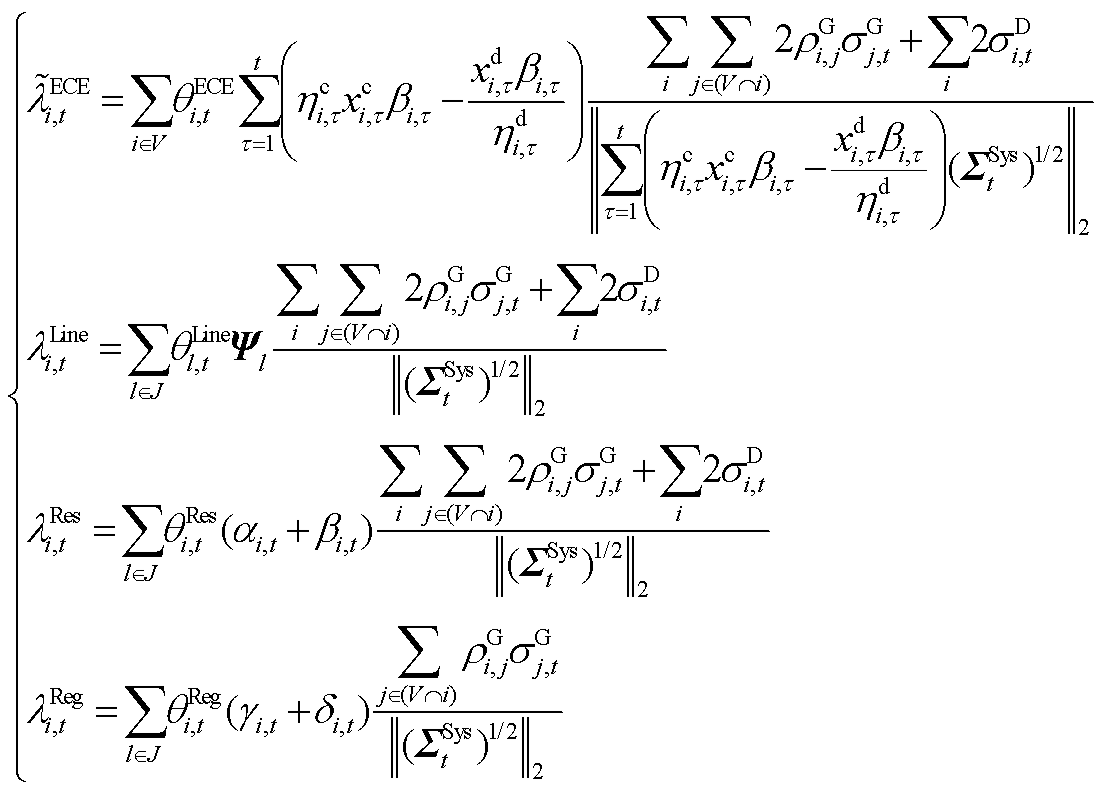 (35)
(35)
式中,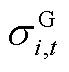 为i节点的新能源在t时段的不确定性功率标准差;
为i节点的新能源在t时段的不确定性功率标准差;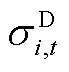 为i节点负荷不确定性功率的标准差。
为i节点负荷不确定性功率的标准差。
6. 表格与图
附表1 各市场主体的报价参数
APP.Tab.1 Quotation parameters of each market entity (单位:元/(MW·h))

SME序号电能量申报价格PCE序号电能量申报价格备用申报价格调频申报价格ECE序号电能量申报价格备用申报价格调频申报价格 SME1191.0PCE1628.0261.9120ECE1291.0123.4100 SME2162.5PCE2582.2218.3115ECE2242.5120.395 SME3188.6PCE3588.8214.8110ECE3238.695.990
(续)

SME序号电能量申报价格PCE序号电能量申报价格备用申报价格调频申报价格ECE序号电能量申报价格备用申报价格调频申报价格 SME4171.9PCE4612.5271.8118ECE4301.988.6105 SME5182.5PCE5573.5260.2126ECE5289.1118.1110 SME6166.0PCE6592.0234.0107ECE6260.0126.798
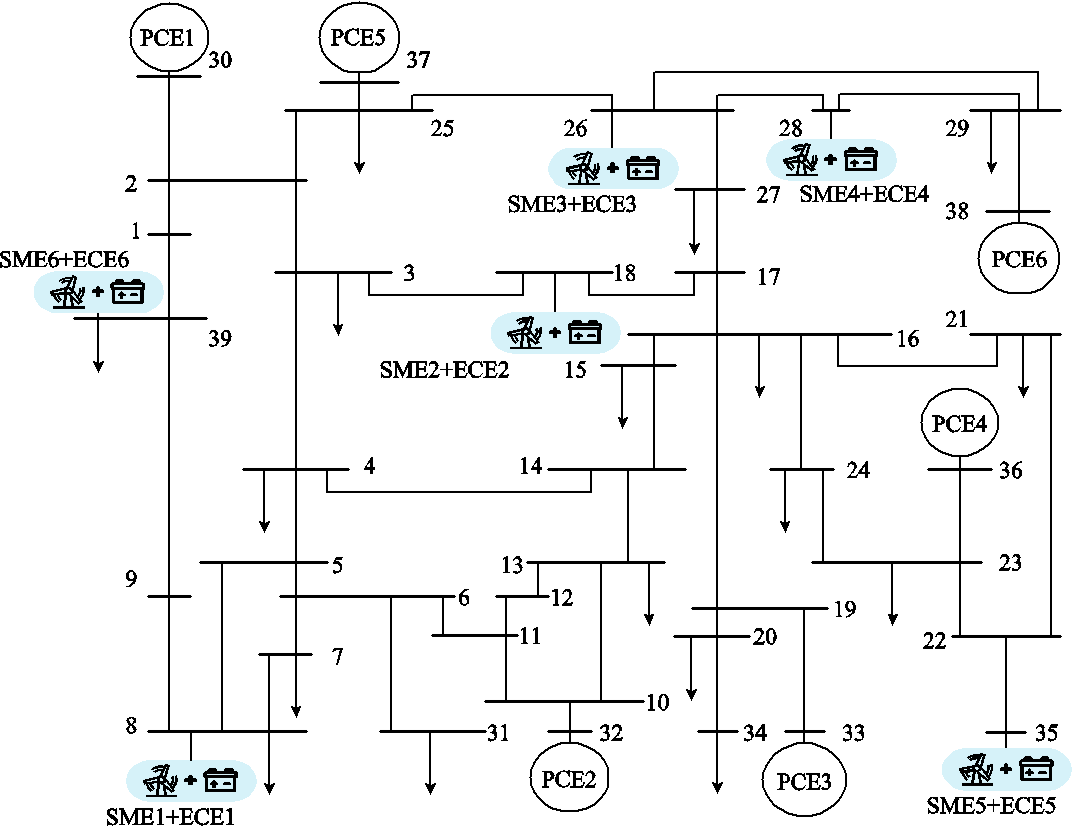
附图1 测试系统的拓扑结构及各市场主体的接入位置
App.Fig.1 Test system topology and access locations of various market players
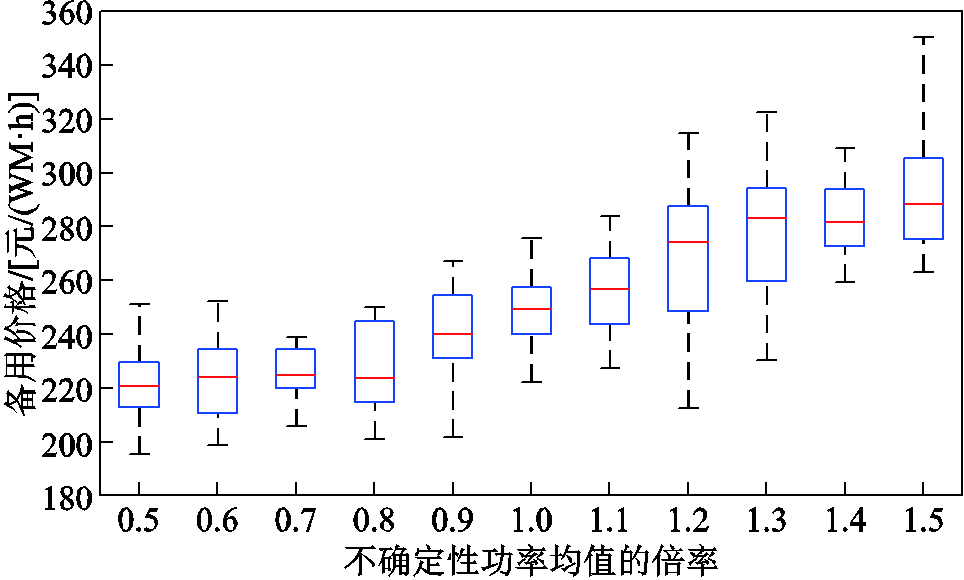
附图2 不同均值下备用出清价格的箱型图
App.Fig.2 Box diagram of reserve clearing prices with different means
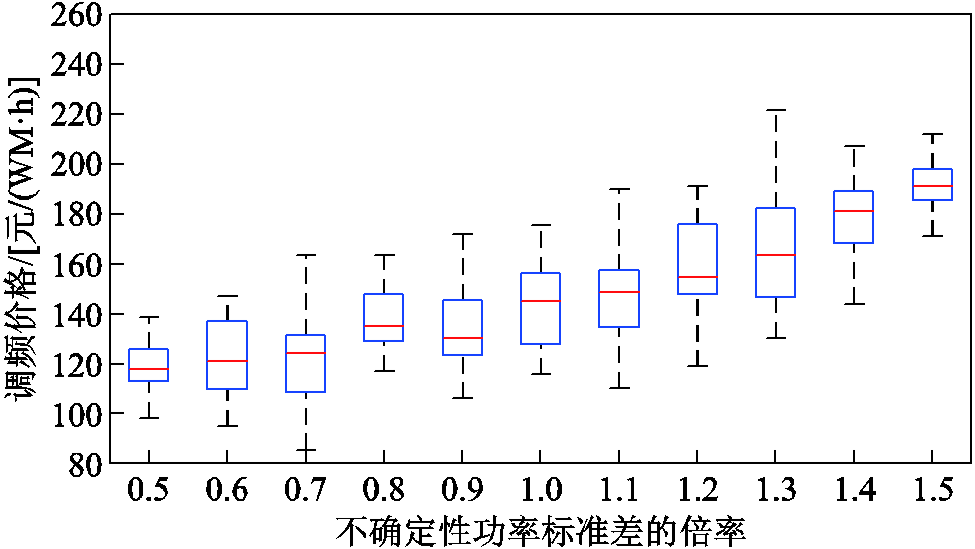
附图3 不同标准差下调频出清价格的箱型图
App.Fig.3 Box diagram of reserve clearing prices with different standard deviations
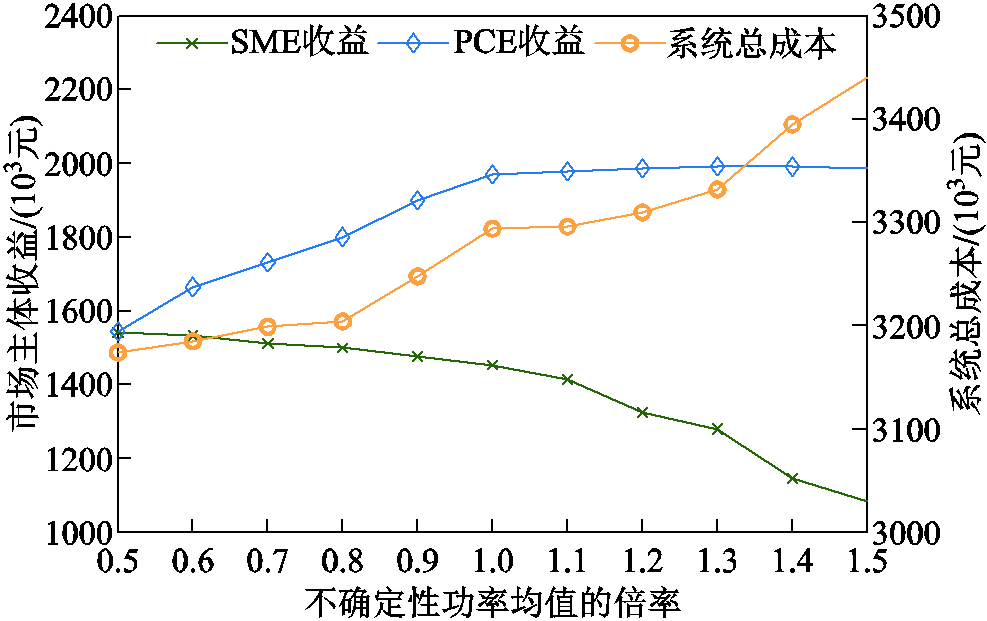
附图4 不同均值下市场主体收益与系统总成本曲线
App.Fig.F4 Market entities benefit and system total cost curves under different means
参考文献
[1] 刘映尚, 马骞, 王子强, 等. 新型电力系统电力电量平衡调度问题的思考[J]. 中国电机工程学报, 2023, 43(5): 1694-1705.
Liu Yingshang, Ma Qian, Wang Ziqiang, et al. Cogitation on power and electricity balance dispatching in new power system[J]. Proceedings of the CSEE, 2023, 43(5): 1694-1705.
[2] 向明旭, 陈泓霏, 曹晓峻, 等. 省间电力中长期交易出清问题多解顺次寻优的高效计算方法[J]. 电工技术学报, 2025, 40(11): 3545-3559.
Xiang Mingxu, Chen Hongfei, Cao Xiaojun, et al. Efficient sequential optimization method for inter-provincial medium- and long-term power transaction clearing problem under multiple-solution scenarios [J]. Transactions of China Electrotechnical Society, 2025, 40(11): 3545-3559.
[3] Fang Xichen, Guo Hongye, Zhang Xian, et al. An efficient and incentive-compatible market design for energy storage participation[J]. Applied Energy, 2022, 311: 118731.
[4] Thomas D, Kazempour J, Papakonstantinou A, et al. A local market mechanism for physical storage rights[J]. IEEE Transactions on Power Systems, 2020, 35(4): 3087-3099.
[5] 石剑涛, 郭烨, 孙宏斌, 等. 备用市场机制研究与实践综述[J]. 中国电机工程学报, 2021, 41(1): 123-134, 403.
Shi Jiantao, Guo Ye, Sun Hongbin, et al. Review of research and practice on reserve market[J]. Proceedings of the CSEE, 2021, 41(1): 123-134, 403.
[6] 肖云鹏, 张兰, 张轩, 等. 包含独立储能的现货电能量与调频辅助服务市场出清协调机制[J]. 中国电机工程学报, 2020, 40(增刊1): 167-180.
Xiao Yunpeng, Zhang Lan, Zhang Xuan, et al. Coordination mechanism of spot electric energy with independent energy storage and market clearing of FM auxiliary service[J]. Proceedings of the CSEE, 2020, 40(S1): 167-180.
[7] 周安平, 杨明, 翟鹤峰, 等. 计及风电功率矩不确定性的分布鲁棒实时调度方法[J]. 中国电机工程学报, 2018, 38(20): 5937-5946.
Zhou Anping, Yang Ming, Zhai Hefeng, et al. Distributionally robust real-time dispatch considering moment uncertainty of wind generation[J]. Proceedings of the CSEE, 2018, 38(20): 5937-5946.
[8] 董雷, 李扬, 陈盛, 等. 考虑多重不确定性与电碳耦合交易的多微网合作博弈优化调度[J]. 电工技术学报, 2024, 39(9): 2635-2651.
Dong Lei, Li Yang, Chen Sheng, et al. Multi-microgrid cooperative game optimization scheduling considering multiple uncertainties and coupled electricity-carbon transactions[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2635-2651.
[9] Fang Xin, Sedzro K S, Yuan Haoyu, et al. Deliverable flexible ramping products considering spatiotemporal correlation of wind generation and demand uncertainties [J]. IEEE Transactions on Power Systems, 2020, 35(4): 2561-2574.
[10] Fang Xin, Hodge B M, Li Fangxing, et al. Adjustable and distributionally robust chance-constrained economic dispatch considering wind power uncertainty [J]. Journal of Modern Power Systems and Clean Energy, 2019, 7(3): 658-664.
[11] 房欣欣, 杨知方, 余娟, 等. 节点电价的理论剖析与拓展[J]. 中国电机工程学报, 2020, 40(2): 379-390.
Fang Xinxin, Yang Zhifang, Yu Juan, et al. Theoretical analysis and extension of locational marginal price[J]. Proceedings of the CSEE, 2020, 40(2): 379-390.
[12] Fang Xin, Hodge B M, Du Ershun, et al. Introducing uncertainty components in locational marginal prices for pricing wind power and load uncertainties[J]. IEEE Transactions on Power Systems, 2019, 34(3): 2013-2024.
[13] Majumder S, Khaparde S A, Agalgaonkar A P, et al. Chance-constrained pre-contingency joint self- scheduling of energy and reserve in VPP[J]. IEEE Transactions on Power Systems, 2024, 39(1): 245-260.
[14] Zhong Weifeng, Xie Kan, Liu Yi, et al. Chance constrained scheduling and pricing for multi-service battery energy storage[J]. IEEE Transactions on Smart Grid, 2021, 12(6): 5030-5042.
[15] Wei Wei, Liu Feng, Mei Shengwei. Distributionally robust co-optimization of energy and reserve dispatch[J]. IEEE Transactions on Sustainable Energy, 2016, 7(1): 289-300.
[16] Wang Haoyuan, Bie Zhaohong, Ye Hongxing. Locational marginal pricing for flexibility and uncertainty with moment information[J]. IEEE Transactions on Power Systems, 2023, 38(3): 2761-2775.
[17] 陈中飞, 荆朝霞, 陈达鹏, 等. 美国调频辅助服务市场的定价机制分析[J]. 电力系统自动化, 2018, 42(12): 1-10.
Chen Zhongfei, Jing Zhaoxia, Chen Dapeng, et al. Analysis on pricing mechanism in frequency regulation ancillary service market of United States[J]. Automation of Electric Power Systems, 2018, 42(12): 1-10.
[18] 宋永华, 包铭磊, 丁一, 等. 新电改下我国电力现货市场建设关键要点综述及相关建议[J]. 中国电机工程学报, 2020, 40(10): 3172-3187.
Song Yonghua, Bao Minglei, Ding Yi, et al. Review of Chinese electricity spot market key issues and its suggestions under the new round of Chinese power system reform[J]. Proceedings of the CSEE, 2020, 40(10): 3172-3187.
[19] Xie Weijun, Ahmed S. Distributionally robust chance constrained optimal power flow with renewables: a conic reformulation[J]. IEEE Transactions on Power Systems, 2018, 33(2): 1860-1867.
[20] 王怡, 杨知方, 余娟, 等. 从优化视角剖析电力市场的定价问题[J]. 电工技术学报, 2023, 38(17): 4729-4745.
Wang Yi, Yang Zhifang, Yu Juan, et al. Analyzing pricing problem in electricity market from an optimization perspective[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4729-4745.
Abstract The continuous grid connection of wind and solar energy has significantly increased the uncertainty of the power system. Due to the inaccurate prediction of new energy and load power, the imbalance power results in insufficient flexible adjustment capacity, further leading to the continuous increase in demand for reserve and frequency regulation capacity, which brings huge challenges to the clearing of the power market.
The traditional clearing model of independent markets of electric energy and ancillary service is established based on the predicted power. However, the clearing results of the traditional market have a lower execution rate since the increasing strong uncertainty of the system net load power. Therefore, this paper proposes a joint market clearing model of electric energy and ancillary services constructed by distributed robust bilateral chance constraints (DRBCC) approach that is based on two types fuzzy sets of uncertain power. For the model solving, DRBCC are converted into mixed integer second-order cone programming for solving through convex reconstruction. Considering that the prediction accuracy of new energy power is much lower than that of load power, an ellipsoid fuzzy set is constructed to sketch the uncertainty of new energy power, while uncertainty of load power is described by deterministic fuzzy sets based on the statistical moment information. In order to classify different market participants, participants are divided into stochastic market entities (SME) and deterministic market entities (DME). Besides, DME are divided into two categories: power constraint entities (PCE) and energy constraint entities (ECE).
A scientific and reasonable electricity price mechanism and is the key to the construction of the future power market, which will guide market players to reduce uncertainty, reflecting the scarcity of flexible adjustment resources. Based on the marginal pricing principle, the node marginal prices of electric energy, reserve, frequency regulation and uncertain power are derived. The proposed USMP and ULMP clarify the market cost of uncertainty sources, resulting in the penalty cost of SME generating uncertain power mainly flowing to PCE and ECE enterprises that provide backup capacity and frequency regulation power. To ensure that both DME and SME obtain equal benefits based on their own value, it is necessary to distinguish the prices of deterministic power provided by DME and uncertain power generated by SME. Therefore, this paper advocates pricing the two types of power separately, which helps guide the matching of flexible adjustment resources and uncertain power in the system. The main contributions are illustrated as follows:
(1) A multi-category coordinated pricing mechanism is proposed based on the marginal pricing principle, the locational marginal prices (LMP) of electric energy, reserve and frequency regulation capacity are derived. Moreover, the uncertainty system marginal prices (USMP) and uncertainty locational marginal prices (ULMP) is designed to provide price signal for market operation.
(2) The market fairness is quantified by market returns, which is reflected in the SMEs’ market penalty cost for generating uncertain power, and the PCEs’ and ECEs’ market rewards for participating in regulating system power balance. The penalty cost encourage SMEs to reduce uncertainty, while the rewards promote DMEs to participate in the joint market.
(3) The proposed joint market clearing model is constructed by DRBCC based on two types fuzzy sets of uncertain power with consideration of the differences in prediction accuracy of new energy and load. Compared with the traditional model, the proposed model reduce the impact of strong uncertainty and volatility of power on the market.
Finally, case analysis verify the feasibility and practical application value of the proposed joint clearing model and uncertain power pricing mechanism the IEEE 39-node system. Compared with the traditional market clearing model, SMEs reduce their profits by 18.5% for uncertain payment, ECEs increase their profits by 26% for providing the reserve and frequency regulation service and the total operation costs are reduced by 25.5% for market cooperation. In conclusion, the proposed joint market clearing and pricing model provides technical support and incentives for the long-term operation of the strong uncertainty market.
keywords:Joint market, pricing mechanism, distributed robust chance constraint, uncertainty
中图分类号:TM732; F426
DOI: 10.19595/j.cnki.1000-6753.tces.241936
国家自然科学基金资助项目(52407089)。
收稿日期 2024-10-29
改稿日期 2024-12-05
蔡钦钦 女,1996年生,博士研究生,研究方向为电力市场和新型电力系统优化调度。E-mail:caiqinqin@stu.hit.edu.cn
徐 英 男,1980年生,教授,博士生导师,研究方向为电力系统优化与控制、寒地新型电力系统等。E-mail:ying.xu@hit.edu.cn(通信作者)
(编辑 赫 蕾)