表1 硅钢片规格
Tab.1 Specification of silicon steel sheet

硅钢型号长度/mm宽度/mm厚度/mm片数 GT-1006001000.0951
摘要 在频域有限元分析中,考虑材料磁滞特性对提高电工装备电磁特性的模拟精度具有重要意义。针对耦合磁滞特性频域有限元分析中存在的收敛不稳定问题,该文提出一种改进定点磁阻率计算策略。首先,基于测量得到的同心磁滞回环辨识逆Everett函数,采用Preisach磁滞模型构建静态磁滞模型,并结合损耗分离理论构建动态磁滞模型。其次,基于谐波平衡的思想建立频域有限元矩阵方程,考虑到大多数电气设备为电压励磁,建立场路耦合方程;并在有限元方程中引入定点磁阻率,针对出现的不稳定点问题进行了分析,并提出解决方案;提出一种局部松弛因子计算方法,进一步提高了有限元迭代的稳定性与收敛速度。最后,对直流偏磁激励下的卷铁心干式变压器进行测量,将计算结果与实验结果进行比较,验证了所提方法在模拟直流偏磁工况下电磁特性的有效性与可行性。
关键词:Preisach磁滞模型 频域有限元 定点磁阻率 松弛法
随着电力电子技术的发展与直流输电技术的逐渐普及,由于电力电子器件本身的特性与一些无法避免的客观自然条件,变压器等一些重要的电气设备常出现直流偏磁的现象,使变压器铁心处于半饱和或饱和状态[1-3]。直流偏磁现象的出现给变压器等电气设备与电网的稳定运行带来了极大的影响[4-7]。因此,对铁磁材料的磁特性的深入研究以及数值计算方法的优化对于电工装备在直流偏磁等激励条件下的优化设计具有重要意义。
目前,国内外学者对磁滞现象进行了深入的研究,其中常见的静态磁滞模型主要有J-A模型[8-9]和Preisach模型[10-12]。在对电气设备进行有限元计算时,以上两种模型通常需要结合涡流损耗与异常损耗的计算公式形成动态磁滞模型。针对有限元计算,E. Dlala提出了一种简化计算过程的逆Preisach模型[13]。然而,这种方法在计算一些对称工况与磁通密度较大的工况时效果较好,但对于非对称的直流偏磁工况,计算效果较差。针对这一问题,本文使用了改进的磁滞模型。
目前,对于铁心磁场分布的有限元计算可分为两类:一类是在时域内利用时间步进行有限元迭代计算[14-16],这种方法在计算正弦交流工况时通常需要迭代数十个时间周期才能收敛,对于直流偏磁这种非对称工况所需要的迭代次数甚至更多;另一类有限元计算方法利用傅里叶变换将磁场迭代计算转换到频域[17-18],但目前的方法主要使用磁化曲线描述电磁特性,未考虑磁滞效应的影响,因而对损耗的分析不够深入。文献[19]将定点技术引入频域有限元计算中,提高了有限元计算的速度。文献[20]将松弛法与有限元技术进行结合,提高了算法的稳定性与收敛速度。
本文将磁滞模型与频域有限元算法结合,对损耗进行了较全面的考虑。为提高频域有限元的计算精度与损耗计算能力,本文利用在实验平台测得的硅钢片数据,结合Preisach模型与损耗分离理论构建了动态磁滞模型,并将构建的动态磁滞模型与有限元算法结合,在频域下构建矩阵方程,实现了对铁心各位置磁特性的模拟。针对磁通密度零点附近的间断点,优化了定点磁阻率的计算,提高了算法的稳定性。此外,本文还改进了松弛法,进一步提高了算法的稳定性与收敛速度。
为了建立较为准确的磁滞模型并验证模型的准确性,基于BROCKHAUS测量系统中的单片测量仪(Single Sheet Test, SST),对超薄硅钢片的静态与动态磁滞特性进行测量。实验采用的硅钢片规格见表1。分别设定交流电压激励频率为5 Hz和400 Hz。为检验算法的有效性,本文设定励磁电流的直流分量为1.3 A、2.6 A与5.2 A。偏磁电流为1.3 A时的测量结果如图2和图3所示。
表1 硅钢片规格
Tab.1 Specification of silicon steel sheet

硅钢型号长度/mm宽度/mm厚度/mm片数 GT-1006001000.0951

图1 硅钢片磁特性测量平台
Fig.1 Magnetic property measurement platform for silicon steel sheet
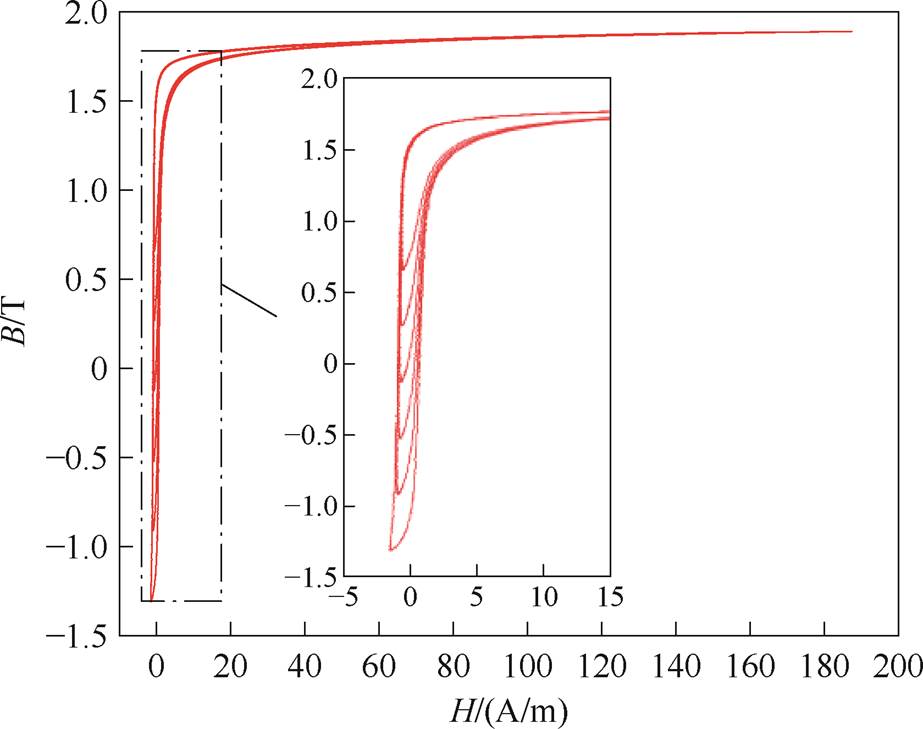
图2 静态磁滞回线测量结果(Idc=1.3 A)
Fig.2 Measurement results of static hysteresis loop(Idc=1.3 A)
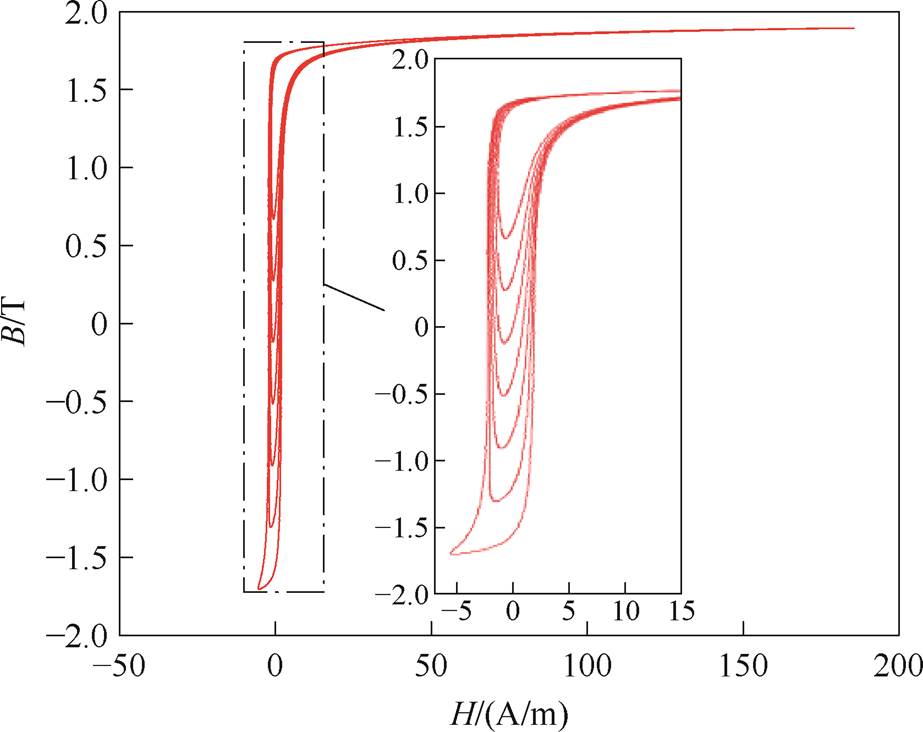
图3 动态磁滞回线测量结果(Idc=1.3 A)
Fig.3 Dynamic hysteresis loop measurement results(Idc=1.3 A)
为提高非线性工况下静态磁滞模型的模拟精度,本文采用Preisach模型模拟偏磁激励下的磁滞特性。该模型的关键为逆Everett函数的辨识。为建立较为精确的静态磁滞模型,本文基于准静态同心磁滞回环簇辨识逆Everett函数。
该模型假设铁磁材料由多个磁偶极子构成,每个磁偶极子的磁滞特性通过一个如图4所示的矩形磁滞算子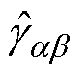 描述,即
描述,即
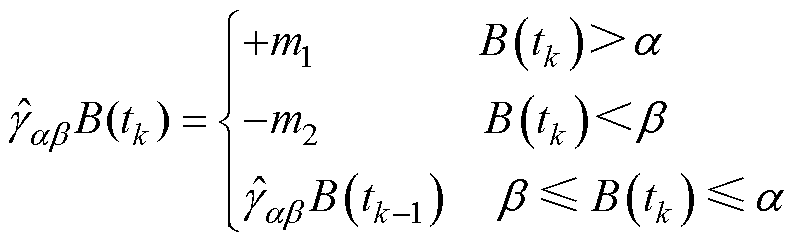 (1)
(1)
式中,B(tk)为磁化过程tk时刻输入值;a、b为对应于输入B(tk)的正、负向切换值;tk为输入时刻;m1和m2的取值为
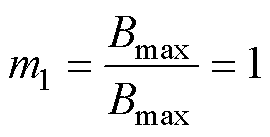 (2)
(2)
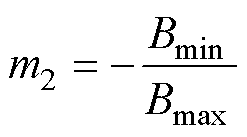 (3)
(3)
式中,Bmax、Bmin分别为输入B(t)的最大值、最小值。
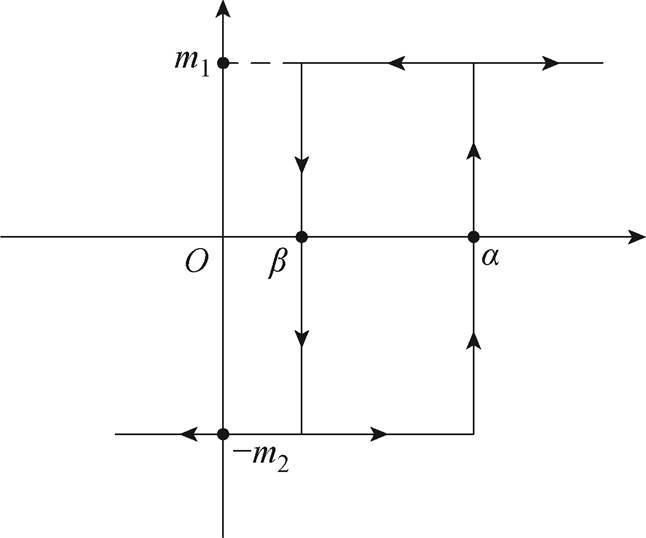
图4 矩形磁滞单元
Fig.4 Rectangular hysteresis element
整个铁磁材料的磁滞特性表达式为
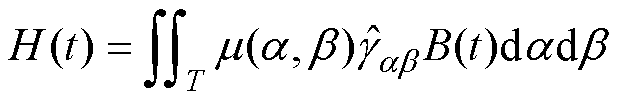 (4)
(4)
式中,T为Preisach平面区域;B(t)为磁化过程的输入值;H(t)为与B(t)对应的输出值;m(a, b)为磁偶极子的分布函数,即为Preisach模型的分布函数。
为简化式(4)中的积分计算,常引入逆Everett函数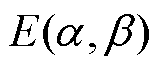 ,则有
,则有
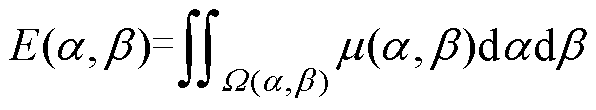 (5)
(5)
同心磁滞回环辨识方法及其对应Preisach平面示意图如图5所示。基于测量得到的同心磁滞回环,通过插值的方法构建Everett函数,以每条磁滞回线上磁通密度的最大值与最小值作为节点,在不同的磁滞回环上利用线性插值法计算各个节点的磁场强度,再利用这些磁场强度的数值计算逆Everett函数值,计算公式为
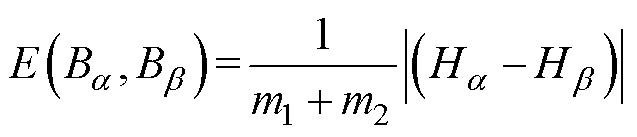 (6)
(6)
式中,Ba、Bb 和Ha、Hb 分别为a、b两点的磁感应强度和磁场强度。
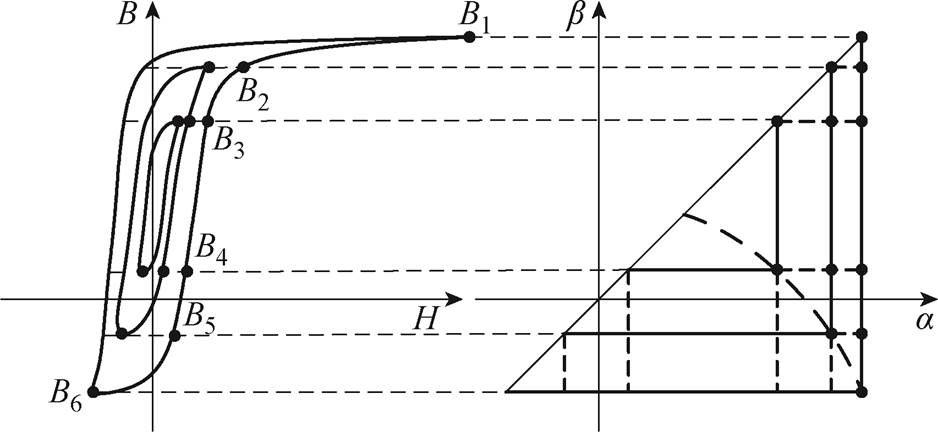
图5 同心磁滞回环辨识方法及其对应Preisach平面示意图
Fig.5 Identification method of concentric hysteresis loop and its corresponding Preisach plane schematic diagram
式(6)对于上升支、下降支均适用,a、b两点须位于同一磁滞回线上,且其中一点须为磁滞回线的磁通密度最小值或最大值,如图5中B1~B6所示。
与基于一阶回转曲线的构建方法相比,基于多条同心磁滞回线的方法无需计算一阶回转曲线,更好地利用了已知的测量数据,简化了计算过程。并且,在低磁通密度幅值处依旧有较高的精确度。与极限磁滞回线相比,内部同心磁滞回环的测量相对更加精确,因而更适用于求解非线性电磁场的计算问题。
根据上述方法辨识的逆Everett函数值,可计算得到一个周期内不同磁通密度幅值下硅钢片的静态磁滞回线,实验用取向硅钢的准静态磁滞回线测量结果和模型计算结果对比如图6所示。由图6可知,本文所构建的逆Preisach模型在不同的激励下均有良好的适应性,可准确模拟不同磁通密度幅值下的准静态磁滞回线,为进一步考虑动态磁滞特性的有限元计算提供了可靠的模型基础。
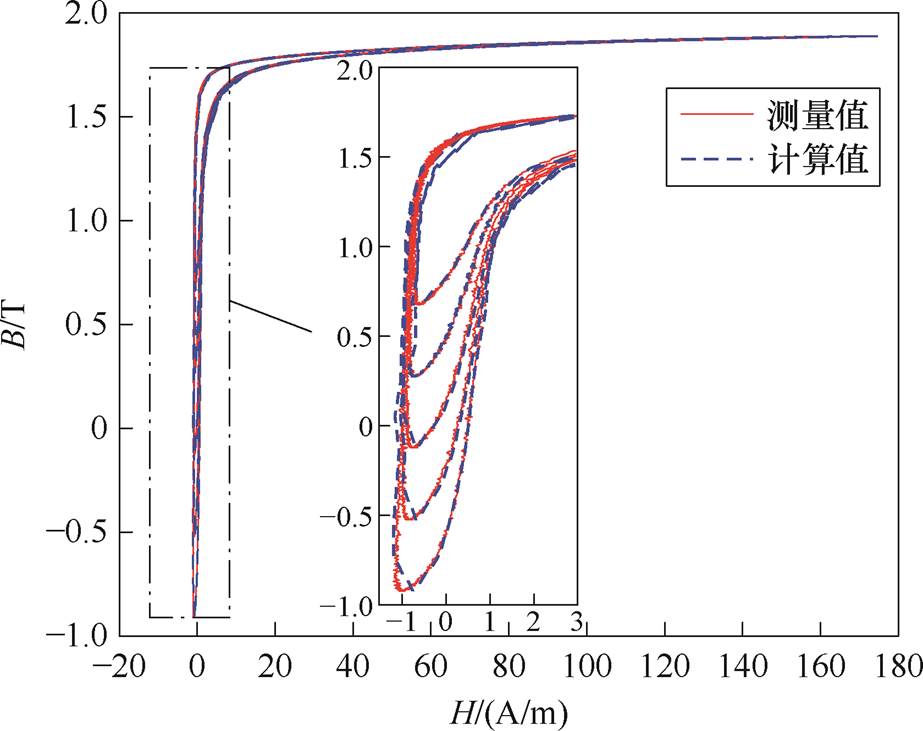
图6 静态磁滞回线测量值与计算值对比(Idc=1.3 A)
Fig.6 Comparison between measured and calculated values of static hysteresis loop(Idc=1.3 A)
根据Bertotti提出的损耗分离理论[21],铁磁材料单位体积的总损耗可分为磁滞损耗、异常损耗与涡流损耗。其中,磁滞损耗及其对应磁场强度可通过上述静态磁滞模型计算得到,异常损耗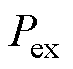 计算公式为
计算公式为
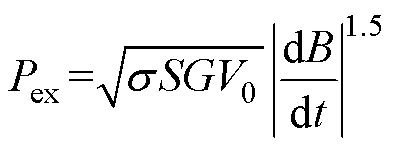 (7)
(7)
式中,s为铁磁材料的电导率;S为铁磁材料的横截面积;G为无量纲常数,其值为0.135 6;V0为与材料内部磁性单元有关的统计参数,与磁通密度幅值和频率相关,可通过不同磁通密度幅值下的磁滞回线实验数据拟合得到。
结合铁磁材料单位体积的总损耗P与B、H之间的关系式为
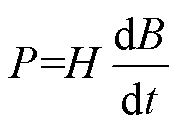 (8)
(8)
可以得到与异常损耗相关的磁场强度的计算公式为
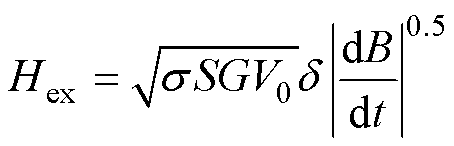 (9)
(9)
式中,d为符号函数,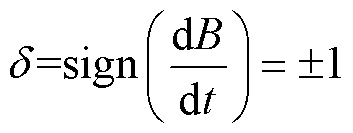 。
。
针对涡流损耗对应磁场强度,文献[22]给出了一种较为精确的算法。该方法主要采用分段线性的方式对基本磁化曲线进行逼近,并结合麦克斯韦方程分别对每个线性段进行了公式推导,最终得到了涡流损耗对应磁场强度的计算方法。具体推导与计算过程本文不再赘述。
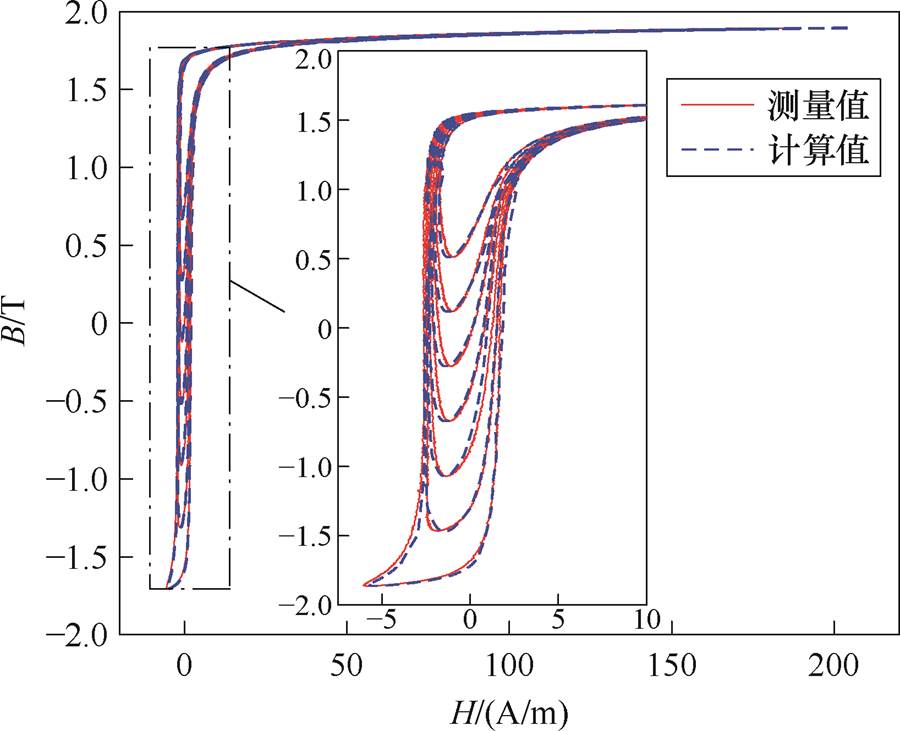
图7 动态磁滞回线测量值与计算值对比(Idc=1.3 A)
Fig.7 Comparison between measured and calculated values of dynamic hysteresis loop(Idc=1.3 A)
在非线性磁场的计算过程中,通常引入磁位来简化计算或提高计算效率,并结合麦克斯韦方程组建立非线性方程。
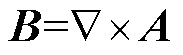 (10)
(10)
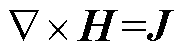 (11)
(11)
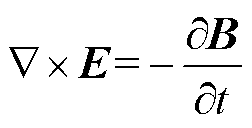 (12)
(12)
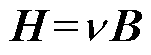 (13)
(13)
式中,n为磁阻率。
不动点法是一种常见的求解非线性方程的方法,该方法通过引入定点磁阻率 将磁场强度与磁通密度的本构关系拆分成两部分,即
将磁场强度与磁通密度的本构关系拆分成两部分,即
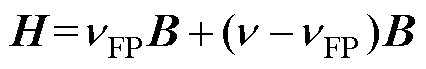 (14)
(14)
根据不动点定理,若迭代过程收敛,则满足
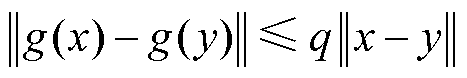 (15)
(15)
式中,g(x)为迭代函数;q为收缩数,迭代过程中通常使其尽可能小。
文献[23]提出了一种以范数为标准评价定点磁阻率选取的标准。
 (16)
(16)
式中,C为接近1的常数,其大小不依赖于定点磁阻率 ;
;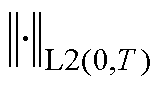 表示L2范数。
表示L2范数。
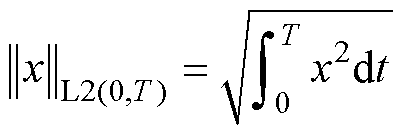 (17)
(17)
由式(16)和式(17)可知,定点磁阻率 和比值磁阻率
和比值磁阻率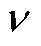 的相对误差影响着收缩数q的大小,进而影响整个迭代过程,故本文采用基于比值磁阻率的计算方法。
的相对误差影响着收缩数q的大小,进而影响整个迭代过程,故本文采用基于比值磁阻率的计算方法。
根据定点法的本构关系式和麦克斯韦方程,可得基于磁矢量磁位A的控制方程为
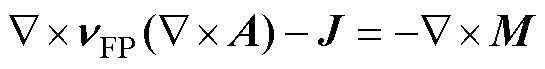 (18)
(18)
式中,M为与磁阻率相关的类磁化余量,在待求解域W内,利用Galerkin有限元法将式(18)展开成二维积分形式为
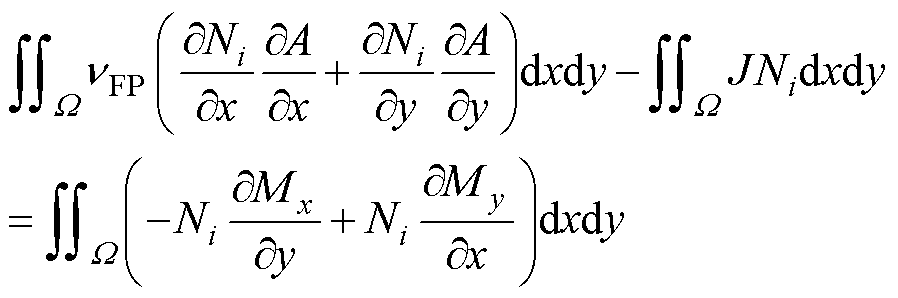 (19)
(19)
式中,Ni为各单元节点的插值函数。
在稳态激励下,场中各相关物理量均具有周期性,因此磁矢位A、磁阻率n和励磁电流均可用复指数函数的级数形式近似表示为
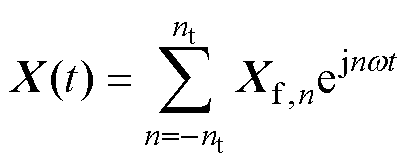 (20)
(20)
式中,X(t)为相关周期变量;n为谐波次数;w为基波角频率;Xf,n为X(t)的第n次谐波分量;nt为实际计算中截断的谐波次数。
将各物理量的谐波表达式代入式(19),按谐波次数对方程两端进行整理。由复指数函数的正交性,可得基于定点磁阻率的谐波平衡有限元矩阵方程为
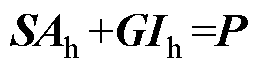 (21)
(21)
式中,S为与定点磁阻率相关的矩阵;Ah为磁矢位谐波向量;G为常系数矩阵;Ih为励磁电流谐波向量;P为与类磁化余量M相关的向量。
算法中涡流损耗与异常损耗对应的磁场强度均归算到定点磁阻率中。通过这种方式,只需计算每次迭代的有关磁阻率的矩阵,可以减少每次迭代的计算量,但给迭代过程带来了一定的扰动。
鉴于变压器等电气设备的励磁绕组大多为电压源,因此需要考虑电路与磁路的耦合关系,将励磁电流与磁矢位同时进行求解。从电路的角度建立方程,若忽略励磁线圈漏磁与匝间电容,端口电压方程为
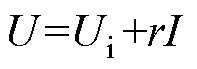 (22)
(22)
式中,U为励磁电压;Ui为绕组上的感应电动势;r为线圈电阻;I为励磁电流。
由电磁感应定律,绕组感应电动势Ui的表达式为
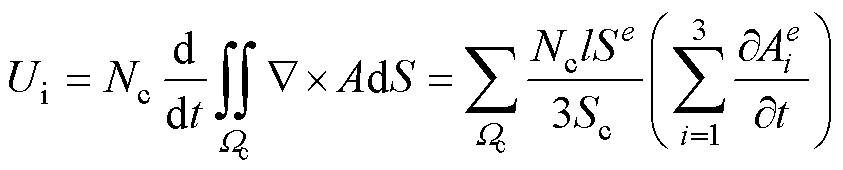 (23)
(23)
式中,Nc为线圈匝数;Wc为线圈内区域;l为线圈沿z方向的长度;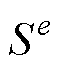 为单元e的面积;Sc为绕组横截面积;
为单元e的面积;Sc为绕组横截面积;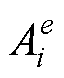 为三角形单元e顶点i的矢量磁位。
为三角形单元e顶点i的矢量磁位。
将式(20)所示励磁电压、磁矢位等物理量的复指数展开形式代入式(23),由复指数函数的正交性,得到谐波平衡有限元矩阵方程为
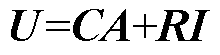 (24)
(24)
式中,U为励磁电压谐波向量;C为场路耦合矩阵;R为线圈电阻矩阵。
将式(21)与式(24)联立,可得电压激励下铁心的二维非线性频域有限元方程为
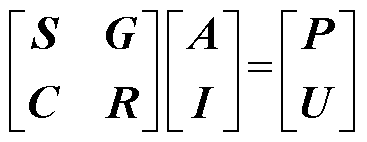 (25)
(25)
定点磁阻率的选择对算法的稳定性和收敛性具有重要影响。在有限元计算过程中,若定点磁阻率选取不当,可能导致计算过程中出现数值不稳定、振荡或发散等问题,使得计算结果无法收敛到真实解。文献[23]给出了一种基于比值磁阻率的定点磁阻率计算方法,并通过数学推导的形式证明了这种方法的收敛性。
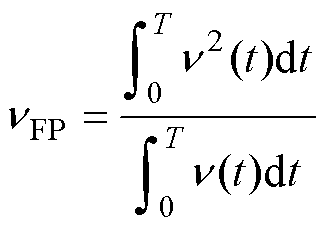 (26)
(26)
式中,n(t)为比值磁阻率,即磁场强度与磁通密度的比值。本文采用了相同的定点磁阻率计算方式,并结合磁滞回线的特点对其进行了改进。
基于上述基于比值磁阻率的定点磁阻率的计算方法,本文分析了磁滞回线的比值磁阻率曲线特点。
磁通密度与比值磁阻率示意图(Bm=1.4 T, Idc= 5.21 A)如图8所示。图8中,当磁通密度过零点时,其对应比值磁阻率图像中常出现跳跃间断点,主要由比值磁阻率的定义引起,这种现象会影响后续的傅里叶变换与有限元迭代。
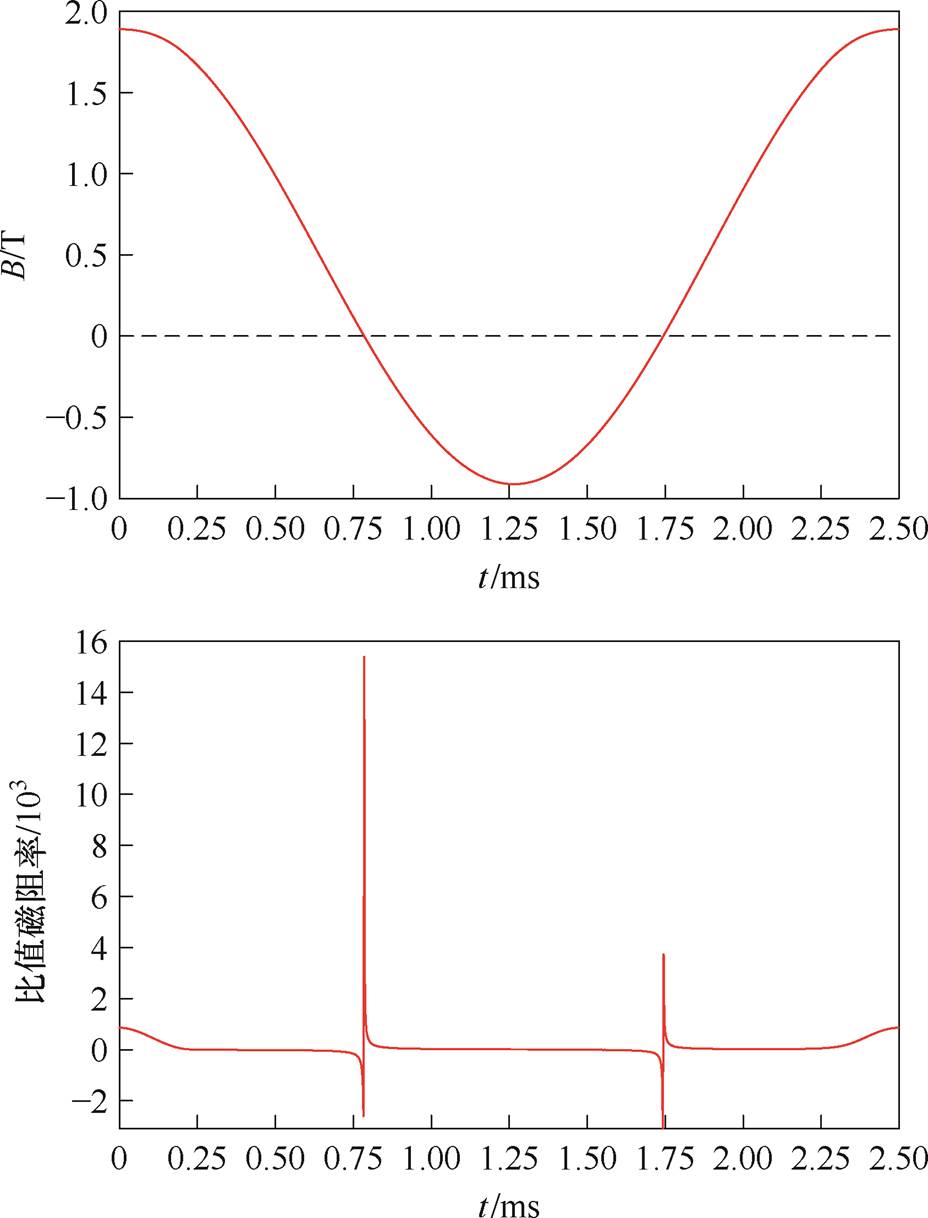
图8 磁通密度与比值磁阻率示意图(Bm=1.4 T, Idc=5.21 A)
Fig.8 Schematic diagram of magnetic induction intensity and specific reluctance(Bm=1.4 T, Idc=5.21 A)
迭代过程相对误差变化如图9所示。若在频域有限元迭代过程中直接使用如图8所示含有跳跃间断点的比值磁阻率,迭代过程中的最大相对误差与平均相对误差减小的速度较慢且不稳定,通常需要较多的迭代次数才能实现预先设定的收敛效果。
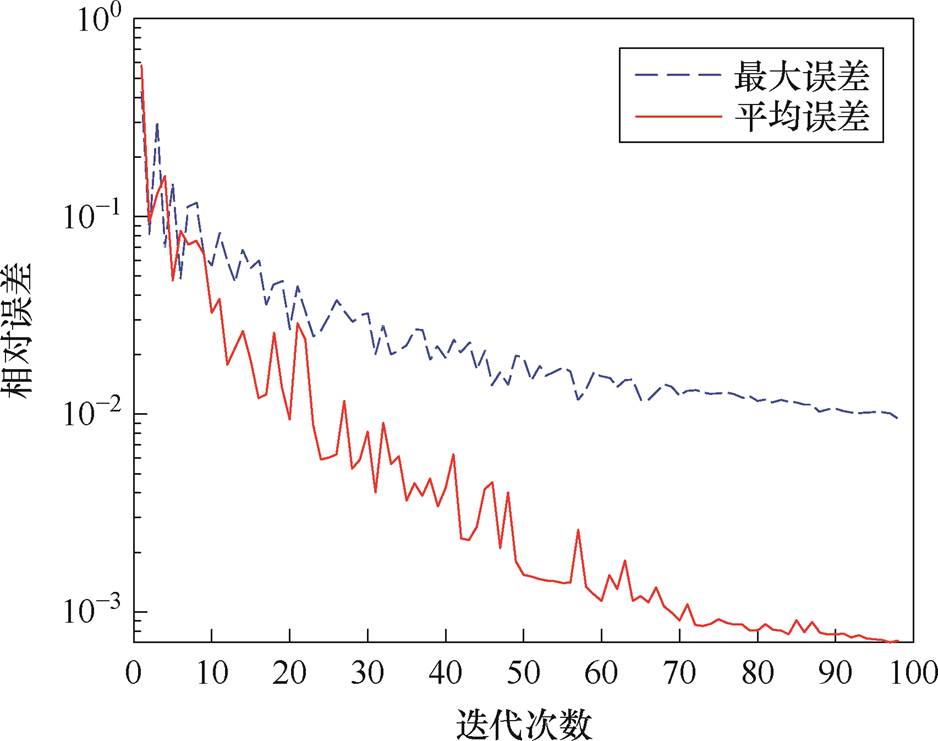
图9 迭代过程相对误差变化
Fig.9 Variation of relative error in iterative process
直流偏磁下励磁电流比较(Uac=100 V, Idc= 5.21 A)如图10所示。受磁通密度过零点位置磁阻率影响,最终迭代得到的励磁电流在数值接近零时的波形极不稳定。尽管上述问题可以通过提高谐波截断次数进行解决,但提高谐波截断次数将大大提升频域有限元迭代方程的阶数,进而提升每步的计算量与计算时间,而定点磁阻率的引入克服了提升谐波截止次数带来的不足[17]。针对上述问题,本文提出一种基于DBSCAN(Density-Based Spatial Clustering of Applications with Noise)的聚类算法[24]与概率分布的不稳定点筛查方法。
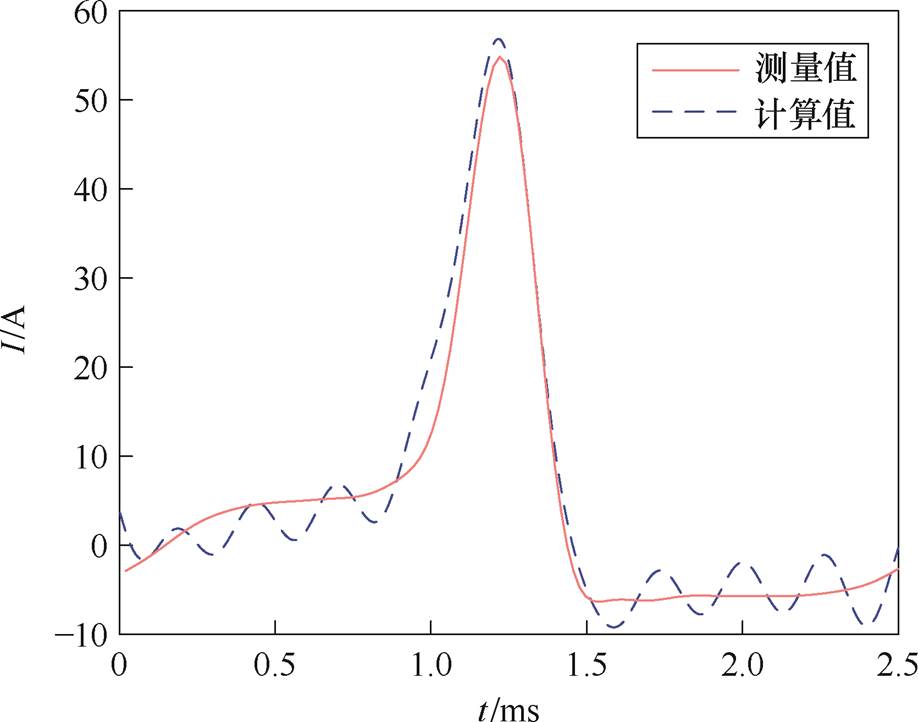
图10 直流偏磁下励磁电流比较(Uac=100 V, Idc=5.21 A)
Fig.10 Comparison of excitation current under DC bias(Uac=100 V, Idc=5.21 A)
比值磁阻率频数直方图如图11所示。比值磁阻率接近正态分布。根据概率论的相关知识,本文将聚类算法中搜索半径设定为数据集的标准差,最少点数设定为数据总数的2%。
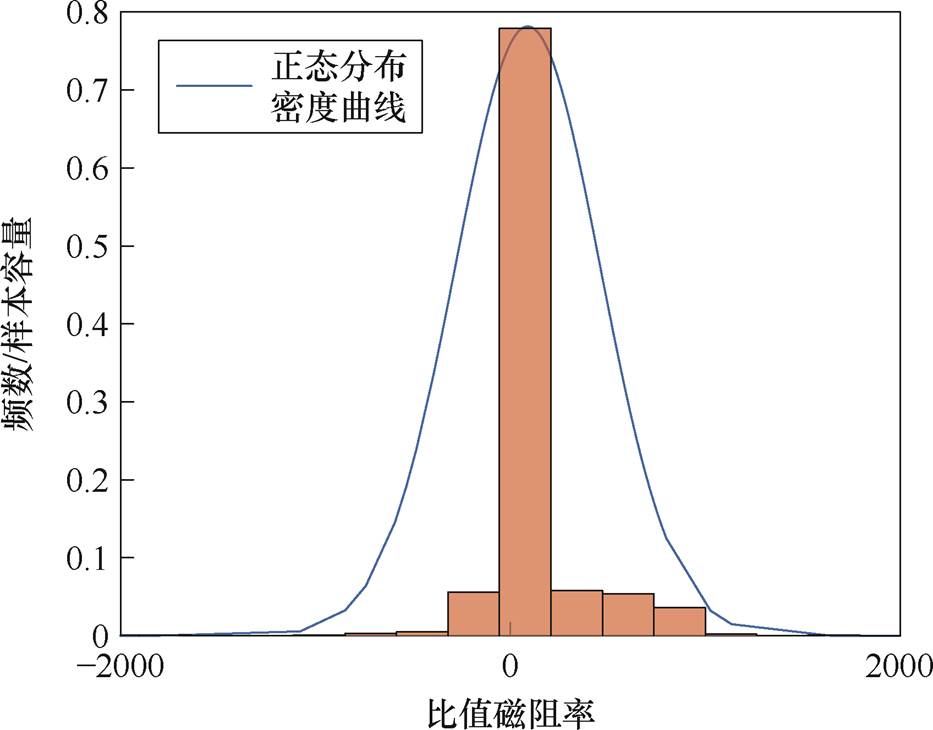
图11 比值磁阻率频数直方图
Fig.11 Frequency histogram of ratio magnetic reluctance
通过上述方法筛选出一个周期内比值磁阻率的不稳定点后,为保证数据点为等间隔采样,以便后续进行傅里叶变换,需利用不稳定点之前或之后的同号的数据对不稳定点位置的数据进行拟合。
按照上述方法得到的定点磁阻率能更好地满足傅里叶变换的狄利克雷条件中有关第一类间断点的约束条件,降低算法对傅里叶变换谐波截断次数的要求,有效提高算法的收敛性与精度。
由于上述方法中涡流损耗与异常损耗对应的磁场强度未在整体的有限元矩阵方程中进行直接计算,而是基于磁矢位的迭代结果与磁滞模型在计算过程中归于磁阻率矩阵中进行计算,这部分非线性的磁场关系为迭代过程带来了一定的扰动,故本文考虑使用松弛法降低其带来的数值扰动并提高算法的稳定性与收敛速度,计算公式为
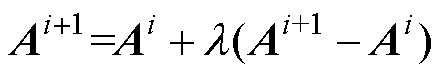 (27)
(27)
式中,i为迭代次数;l为松弛因子。
磁通密度分布是磁场有限元计算与分析的关键参数,也是电气设备优化设计的关键参数之一,目前已有一些软件利用磁通密度分布来调整网格的细化程度并设置优化边界条件。由上述矩阵方程,可根据各节点的磁矢量位A与各有限元的插值函数Ni计算得到各单元的磁通密度幅值。
基于此,本文尝试利用节点附近单元的磁通密度分布调整该节点的松弛因子取值,以提高算法的收敛性与计算速度,松驰因子计算流程如图12所示。
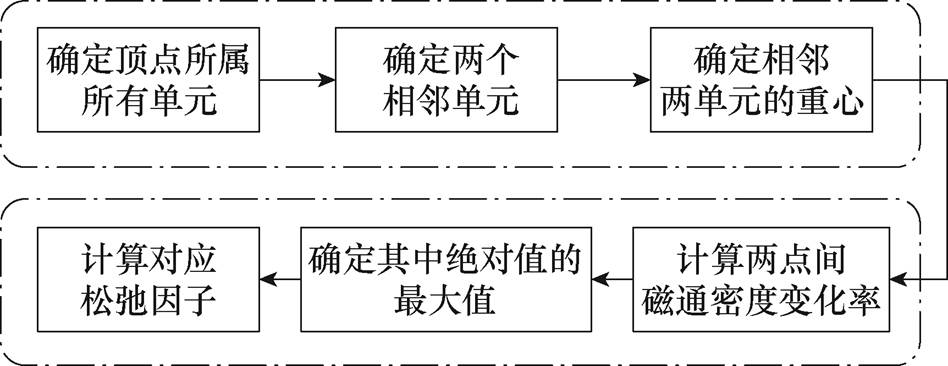
图12 松弛因子计算流程
Fig.12 Relaxation factor calculation process
图12中所述节点、节点所属单元、相邻的两个单元、单元重心与单元重心连线方向,即磁通密度幅值变化方向,如图13所示。由于迭代过程中有限元剖分不变,故流程中前三步仅需确定一次,而流程中后三步需随磁通密度分布变化。
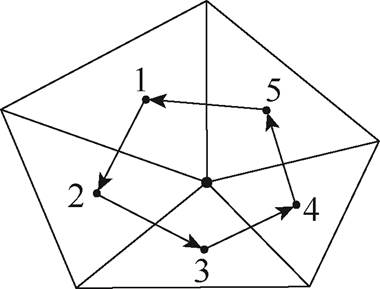
图13 节点、所属单元及单元的重心示意图
Fig.13 Schematic diagram of the finite element node, corresponding elements and their foci
通过式(28)计算可得两重心间磁通密度幅值变化率的绝对值。
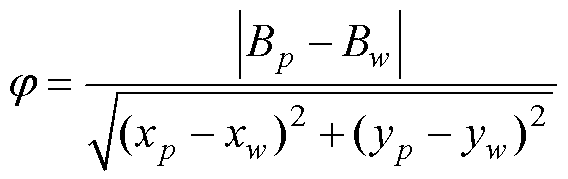 (28)
(28)
式中,Bp、Bw为两点的磁通密度幅值;xp、xw和yp、yw分别为两点横、纵坐标。对于如图13所示结构,若p取值为1、2、3、4、5,对应的w为5、1、2、3、4。
基于梯度模值与方向导数绝对值的大小关系,选取其中绝对值最大的变化率作为确定该节点松弛因子的依据。对于磁场变化相对剧烈的区域应采用较小的松弛因子,减小每次迭代的调整量,提高迭代的稳定性;对于磁场变化较平缓的区域,应当增大松弛因子,提高收敛速度,故构造两者关系式为
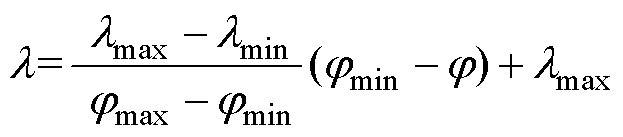 (29)
(29)
式中,l为该节点的松弛因子;lmax为设置的最大松弛因子;lmin为设置的最小松弛因子;j为被选定的磁通密度变化率;jmax为所有相邻单元重心间函数变化率绝对值的最大值;jmin为所有相邻单元重心间函数变化率绝对值的最小值。为平衡算法稳定性与计算速度,松弛因子的取值一般在0.3~0.9之间。
若电气设备工作在较恶劣的工况下,磁通密度在空间分布上存在很强的差异性,可将松弛因子的取值范围取得大一些,以尽可能地考虑各点的计算收敛情况;在正常工况下,磁通密度整体分布较为均匀,可适当缩小松弛因子的取值范围。
非线性迭代过程中,本文选择磁通密度的相对平均误差emean与最大误差emax作为判断收敛的标准,如式(30)所示,相邻两次迭代的相对误差均小于初始设定值时,迭代截止。
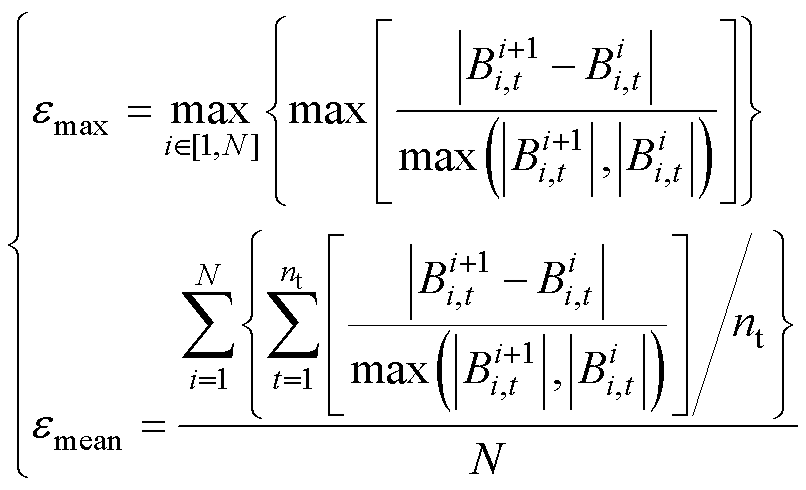 (30)
(30)
式中,N为待求解区域的节点数;i为迭代次数;nt为一周期时间点个数。文中最大截止误差与平均截止误差分别设置为0.01与0.001,完整的频域有限元迭代过程如图14所示。
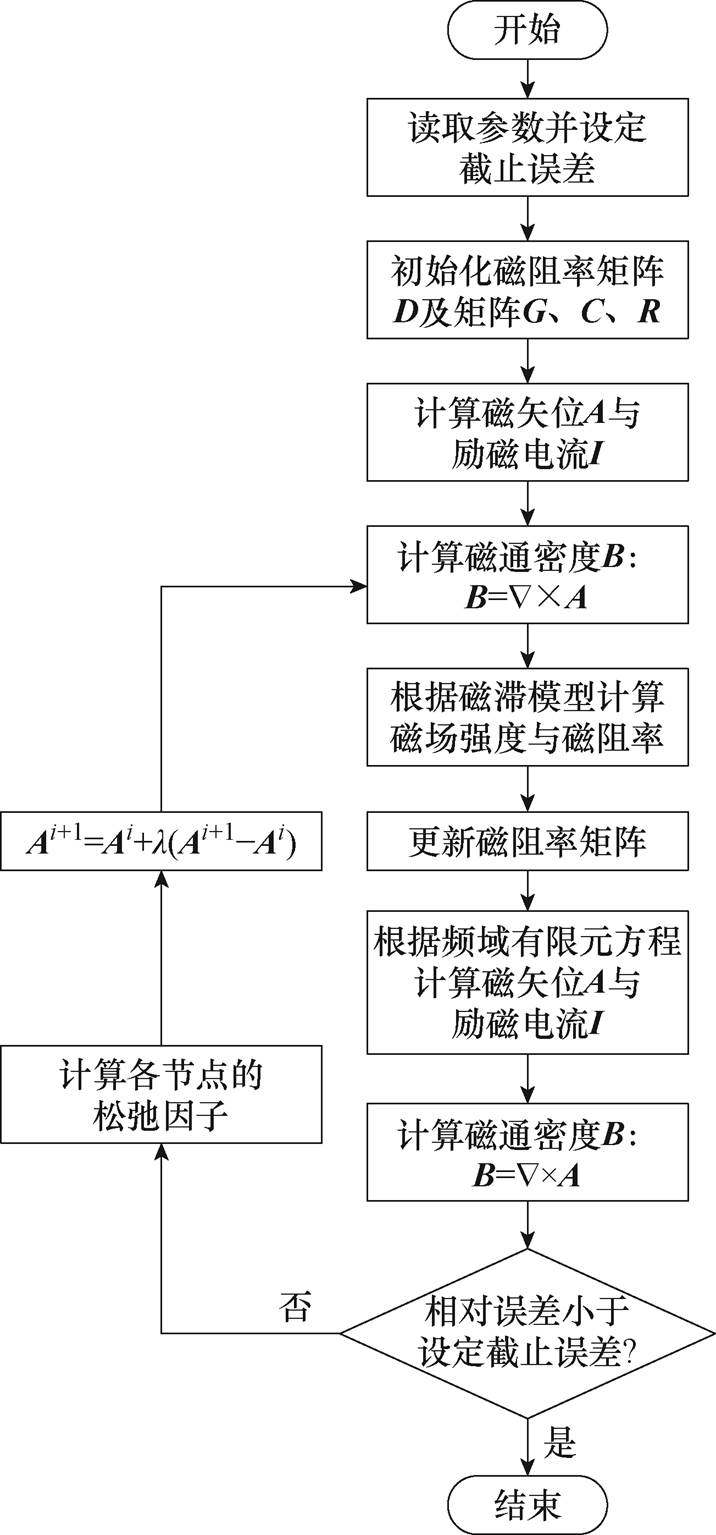
图14 考虑磁滞特性的频域有限元流程
Fig.14 Frequency domain finite element process considering hysteresis characteristics
为验证算法有效性,本文对中频(400 Hz)偏磁激励下由超薄硅钢片组成的如图15所示的卷铁心干式变压器进行了计算,所用超薄硅钢片型号为GT-100。一次、二次绕组匝数分别为64和8,二次侧空载。根据对称性,对铁心四分之一区域进行了剖分。如图16所示,共得到391个三角形单元,224个节点,559条公共边,55条边界边。
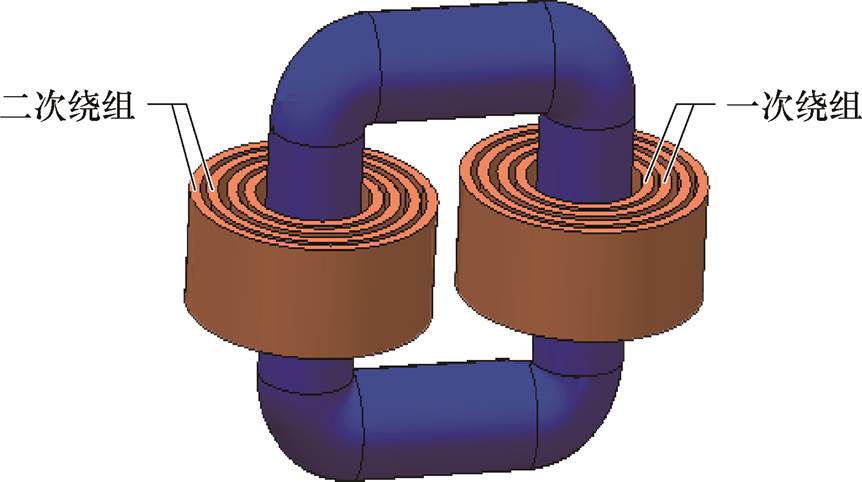
图15 卷铁心干式变压器示意图
Fig.15 Dry-type transformer model with rolled iron core
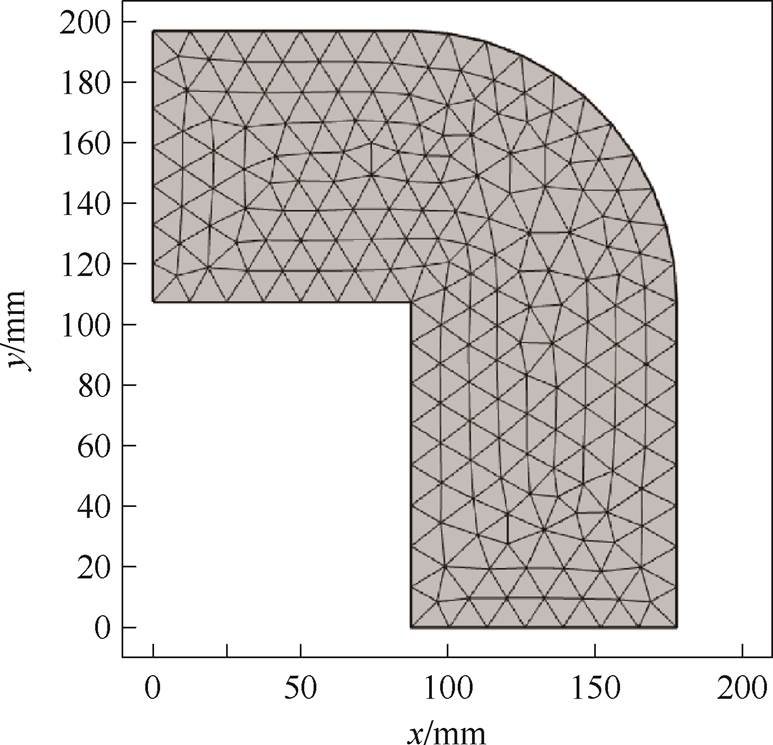
图16 铁心网格剖分图
Fig.16 The mesh diagram of the iron core
迭代过程最大误差和平均误差变化如图17与图18所示,本文算法在迭代过程中,相对误差随迭代次数增加稳定地减小直至低于初始设定值,该过程说明算法具有较好的收敛性。此外,通过对比可知,加入全局式松弛因子之后,迭代过程相对误差减小,算法的稳定性得到了加强,收敛速度也增快了,采用分布式的松弛因子后,算法的稳定性与收敛速度得到了进一步加强。
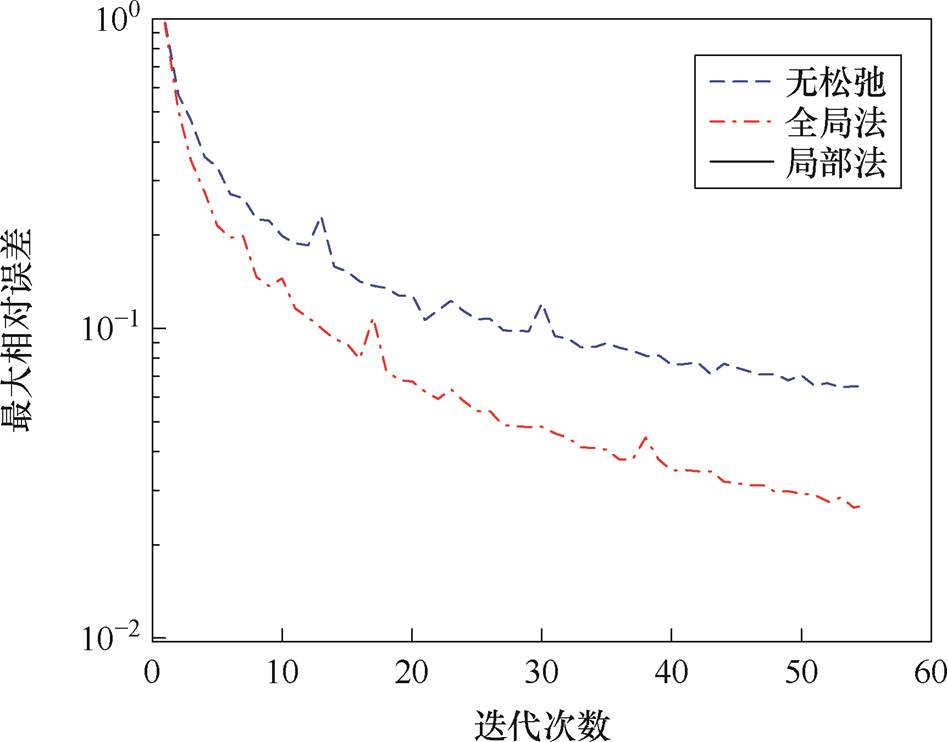
图17 迭代过程最大误差变化
Fig.17 Maximum error variation curves
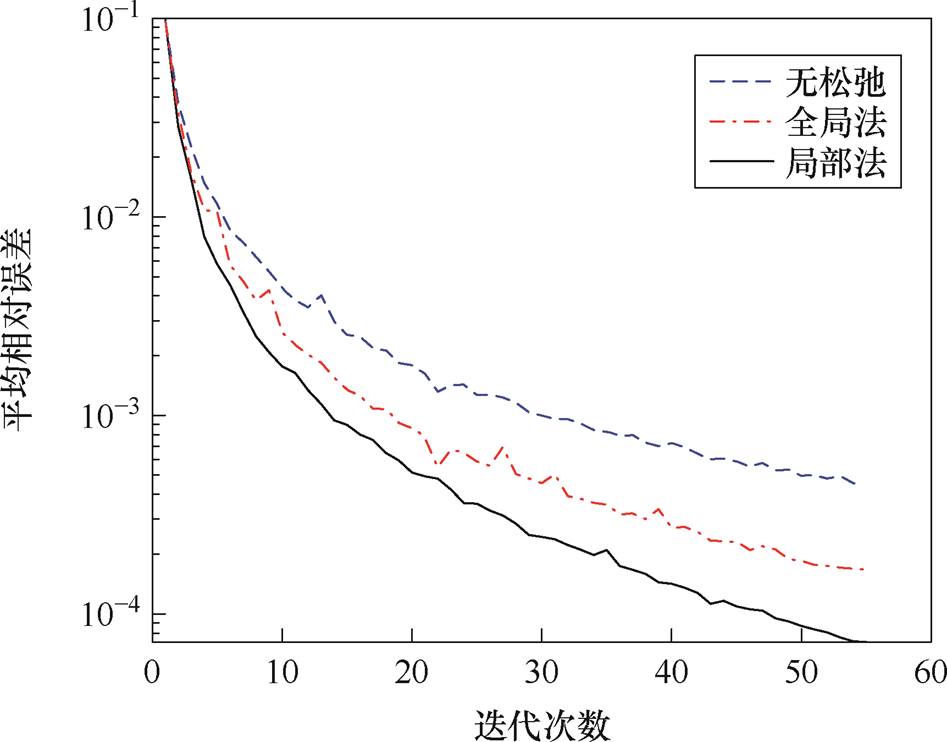
图18 迭代过程平均误差变化
Fig.18 Average error variation curves
考虑到铁心不同的磁饱和程度,本文对相同交流电压不同偏磁电流激励下模型的励磁电流进行了测量与计算。为验证使用磁滞模型对计算结果的影响,分别使用磁滞模型与单值磁化曲线的方法[18]对实验模型进行了计算。
不同条件(Idc=1.26 A、2.62 A、5.21 A)下励磁电流的比较如图19~图21所示,算法具有一定的有效性。造成计算存在一定误差的原因主要在于拐角处的硅钢片受内部应力的影响,磁畴排列和磁化过程与测量时存在一定的差异。
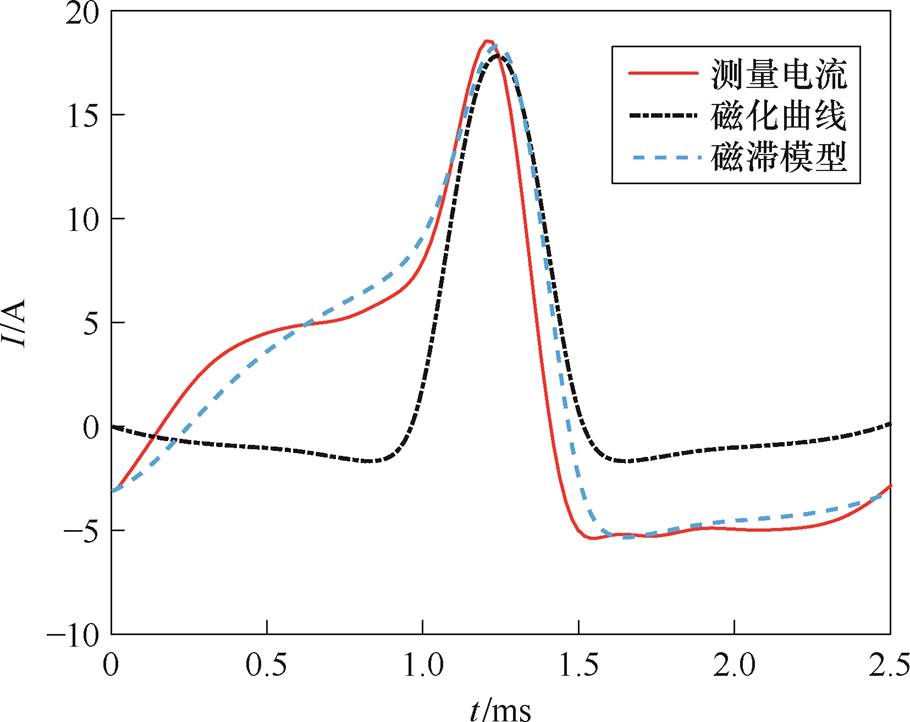
图19 直流偏磁下励磁电流比较(Uac=100 V, Idc=1.26 A)
Fig.19 Comparison of excitation current under DC bias(Uac=100 V, Idc=1.26 A)
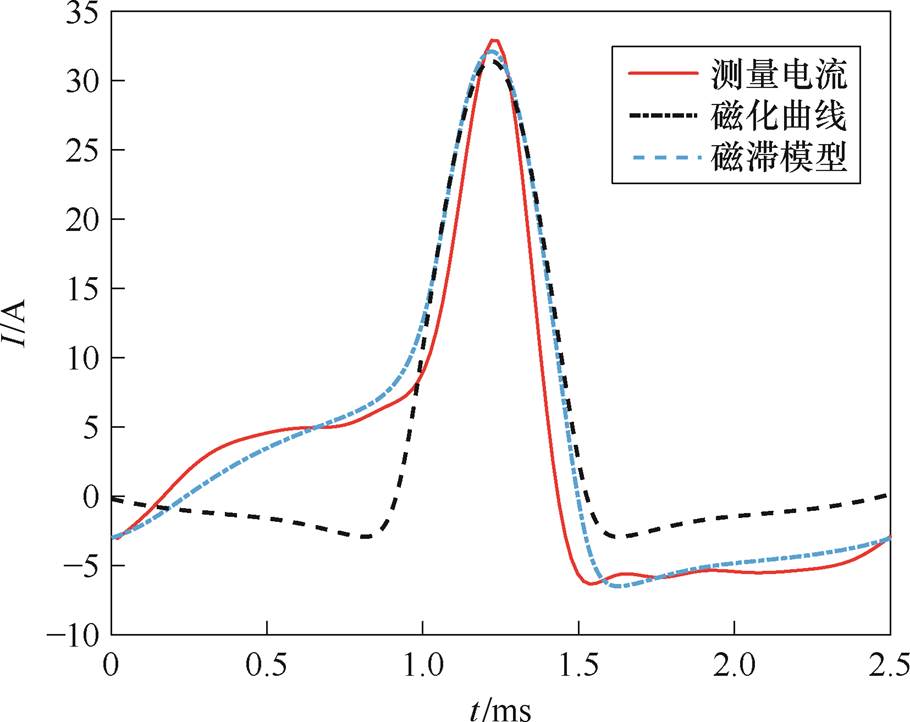
图20 直流偏磁下励磁电流比较(Uac=100 V, Idc=2.62 A)
Fig.20 Comparison of excitation current under DC bias(Uac=100 V, Idc=2.62 A)
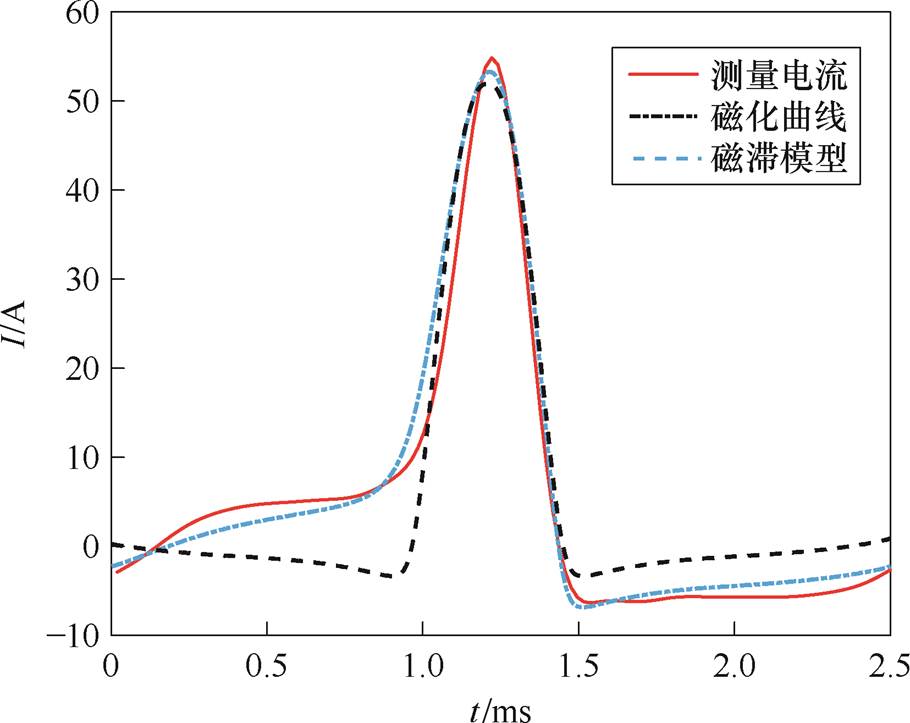
图21 直流偏磁下励磁电流比较(Uac=100 V, Idc=5.21 A)
Fig.21 Comparison of excitation current under DC bias(Uac=100 V, Idc=5.21 A)
与利用如图22所示直流偏磁激励下铁心磁化曲线的频域有限元算法进行对比可知,引入磁滞模型使频域有限元算法对励磁电流的计算精度得到了提高。其原因在于利用磁化曲线的算法默认上升支与下降支完全重合,简化了磁化过程,给最终的计算结果带来了一定误差。
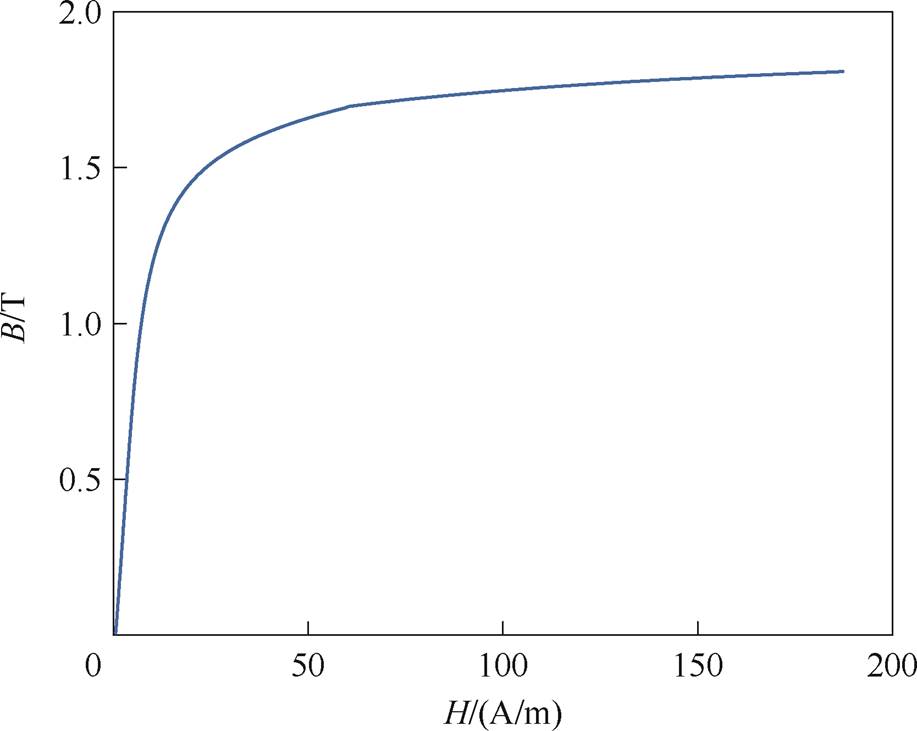
图22 直流偏磁激励下铁心磁化曲线(400 Hz)
Fig.22 DC magnetization curve of iron core(400 Hz)
为进一步验证算法的有效性,本文利用上述算法对如图15所示的卷铁心干式变压器模型内部磁场分布进行了模拟。磁通密度分布计算结果如图23所示,铁心内部磁通密度分布较为平均,转角处磁通密度分布不均,转角内部磁通密度较大,边缘较小。
根据每一个单元的磁滞回线计算结果,积分可得每一个单元的铁心损耗,再将各单元的损耗累加求和就得到了整个铁心的总铁损。
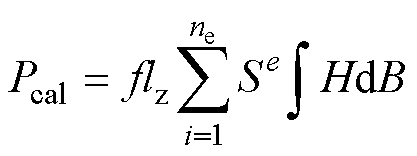 (31)
(31)
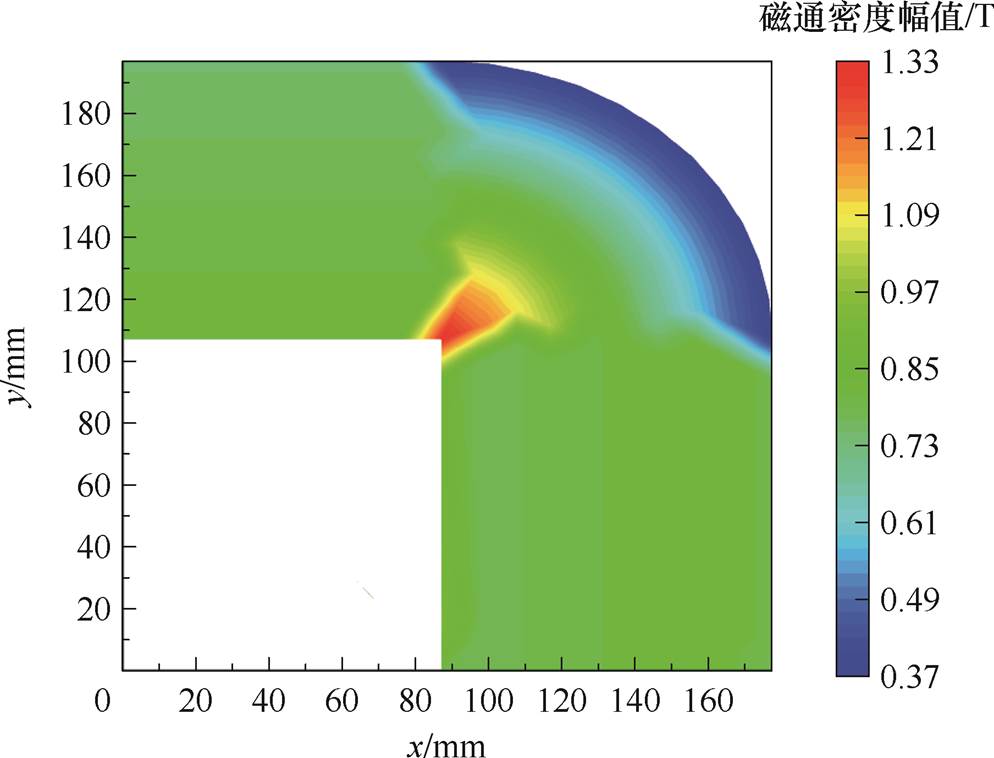
图23 铁心中磁通密度分布(Uac=83 V, Idc=1.3 A)
Fig.23 Flux density distribution in laminated core(Uac=83 V, Idc=1.3 A)
式中,f为激励的频率;lz为铁心等效厚度;ne为有限元个数;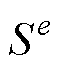 为单元e的面积。计算结果见表2~表4,根据本文提出的有限元算法计算得到的铁心损耗与实际测量结果基本一致。
为单元e的面积。计算结果见表2~表4,根据本文提出的有限元算法计算得到的铁心损耗与实际测量结果基本一致。
表2 直流偏磁激励下损耗对比(Idc=1.3 A)
Tab.2 Comparison of losses under DC bias excitation(Idc=1.3 A)
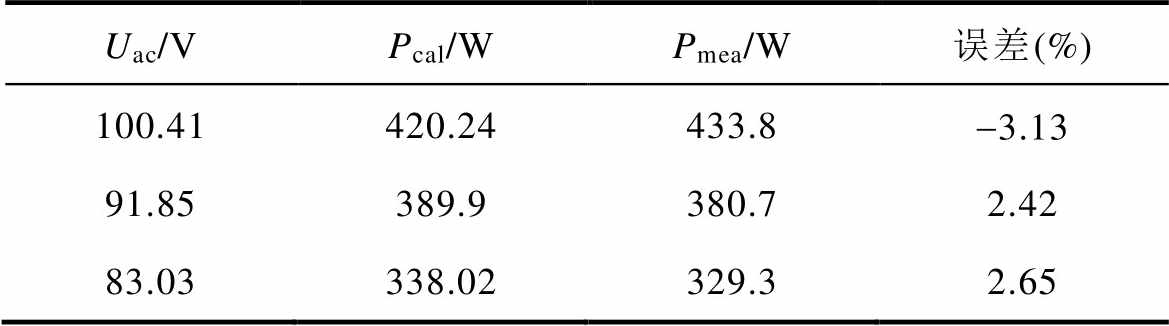
Uac/VPcal/WPmea/W误差(%) 100.41420.24433.8-3.13 91.85389.9380.72.42 83.03338.02329.32.65
表3 直流偏磁激励下损耗对比(Idc=2.6 A)
Tab.3 Comparison of losses under DC bias excitation(Idc=2.6 A)
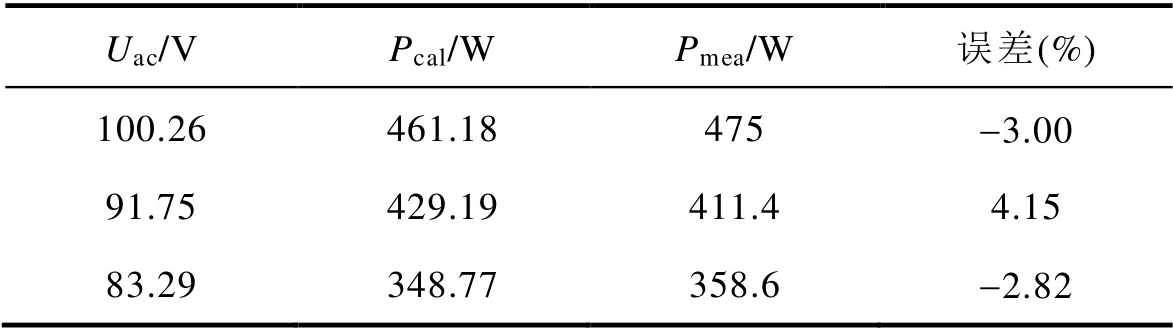
Uac/VPcal/WPmea/W误差(%) 100.26461.18475-3.00 91.75429.19411.44.15 83.29348.77358.6-2.82
表4 直流偏磁激励下损耗对比(Idc=5.2 A)
Tab.4 Comparison of losses under DC bias excitation(Idc=5.2 A)
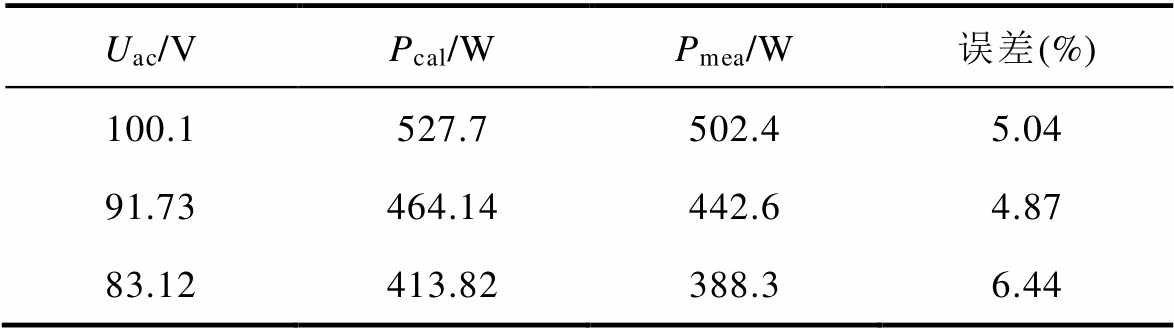
Uac/VPcal/WPmea/W误差(%) 100.1527.7502.45.04 91.73464.14442.64.87 83.12413.82388.36.44
为提高直流偏磁下电工设备电磁特性的模拟精度,本文将基于同心磁滞回环的磁滞模型与有限元计算结合。为提高迭代的稳定性与精度,本文提出了基于比值磁阻率的定点磁阻率计算方法,并考虑将松弛法引入其中。最终实现了对直流偏磁下中频变压器的计算,并通过与实验测量结果对比,验证了算法的有效性。
1)通过分析考虑磁滞回环相关比值磁阻率的特征,提出了基于比值磁阻率的固定点迭代策略,并有效地解决了磁通密度过零点时比值磁阻率引起的算法计算精度不高且易引起迭代不稳定的问题。
2)在采用固定点迭代策略的基础上,本文还考虑了松弛法的运用。通过与其他松弛法对比,根据磁通密度分布计算局部松弛因子,有效地提高了算法的稳定性与收敛速度,将收敛速度提高了40% 左右。
3)本文充分考虑了磁滞效应对有限元励磁电流与损耗计算结果的影响。与利用磁化曲线的频域有限元算法相比,励磁电流的计算精度得到了提高。此外,本文还利用磁滞模型对铁心损耗进行了计算,并与实验测量结果进行了对比,最大相对误差不超过7%,证明了算法的有效性。
参考文献
[1] 童轶, 祝全乐, 贺立, 等. 直流偏磁对换流变压器运行影响分析[J]. 高电压技术, 2021, 47(6): 2206- 2213.
Tong Yi, Zhu Quanle, He Li, et al. Analysis on DC bias impact on converter transformers operation[J]. High Voltage Engineering, 2021, 47(6): 2206-2213.
[2] 李晓辉, 刘海娟, 吴传奇, 等. 陕湖直流岗上湾接地极周边220 kV变压器直流偏磁噪声的试验研究[J]. 高压电器, 2022, 58(2): 111-118.
Li Xiaohui, Liu Haijuan, Wu Chuanqi, et al. Experimental study on 220 kV transformer DC bias noise around the grounding pole in Gangshangwan of Shaanxi-Hubei HVDC project[J]. High Voltage Apparatus, 2022, 58(2): 111-118.
[3] 谢志成, 林湘宁, 李正天, 等. 基于隔直装置全局优化投切的直流偏磁治理方法[J]. 中国电机工程学报, 2017, 37(24): 7133-7142, 7427.
Xie Zhicheng, Lin Xiangning, Li Zhengtian, et al. Suppression method for DC bias based on global optimal switching method of blocking devices[J]. Proceedings of the CSEE, 2017, 37(24): 7133-7142, 7427.
[4] 王振, 张艳丽, 张殿海, 等. 直流偏磁下单相变压器铁心实验模型局部磁致形变测量与模拟[J]. 中国电机工程学报, 2021, 41(12): 4316-4325.
Wang Zhen, Zhang Yanli, Zhang Dianhai, et al. Measurement and modelling of local deformation caused by magnetism in the single-phase transformer core experimental model under DC bias[J]. Proceedings of the CSEE, 2021, 41(12): 4316-4325.
[5] 宋奇珂, 王丰华. 大型变压器直流偏磁下电磁振动特征研究[J]. 高压电器, 2023, 59(10): 129-139.
Song Qike, Wang Fenghua. Research on electro- magnetic vibration features of large-scaled transformer under DC bias [J]. High Voltage Apparatus, 2023, 59(10): 129-139.
[6] 党存禄, 马雄文. 基于复杂网络理论的变电站直流偏磁治理研究[J]. 高压电器, 2024, 60(4): 193-198.
Dang Cunlu, Ma Xiongwen. Research on DC bias control of substation based on complex network theory [J]. High Voltage Apparatus, 2024, 60(4): 193-198.
[7] 黄天超, 王泽忠, 李宇妍. 换流变压器直流偏磁对油箱涡流损耗的影响[J]. 电工技术学报, 2023, 38(8): 2004-2014.
Huang Tianchao, Wang Zezhong, Li Yuyan. The influence of converter transformer DC bias on eddy current loss of tank[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2004-2014.
[8] 刘任, 顾朝阳, 孙江东, 等. Jiles-Atherton磁滞模型的改进与非正弦激励下软磁材料复杂磁滞准确模拟[J]. 中国电机工程学报, 2025, 45(5): 2016-2027.
Liu Ren, Gu Chaoyang, Sun Jiangdong, et al. Modified Jiles-Atherton hysteresis model and accurate simulation of complex hysteresis characteristics of soft magnetic materials under non-sinusoidal excitation [J]. Proceedings of the CSEE, 2025, 45(5): 2016- 2027.
[9] 朱育莹, 李琳. 考虑各向异性和模型参数应力依赖关系的改进Sablik-Jiles-Atherton磁滞模型[J]. 电工技术学报, 2023, 38(17): 4586-4596.
Zhu Yuying, Li Lin. An improved Sablik-Jiles- Atherton hysteresis model considering anisotropy and stress dependence of model parameters[J]. Trans- actions of China Electrotechnical Society, 2023, 38(17): 4586-4596.
[10] Zhao Xiaojun, Xu Huawei, Li Yongjian, et al. Improved preisach model for the vector hysteresis property of soft magnetic composite materials based on the hybrid technique of SA-NMS[J]. IEEE Transactions on Industry Applications, 2021, 57(5): 5517-5526.
[11] 陈彬, 王川源, 刘洋, 等. 基于磁导-电容类比法和解析Preisach模型的铁心动态磁滞建模方法[J]. 电工技术学报, 2024, 39(18): 5576-5587.
Chen Bin, Wang Chuanyuan, Liu Yang, et al. Dynamic hysteresis modeling method for iron core based on permeance-capacitance analogy and analytic Preisach model [J]. Transactions of China Electro- technical Society, 2024, 39(18): 5576-5587.
[12] 刘任, 杜莹雪, 李琳, 等. 解析逆Preisach磁滞模型[J]. 电工技术学报, 2023, 38(10): 2567-2576.
Liu Ren, Du Yingxue, Li Lin, et al. Analytical inverse Preisach hysteresis model[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2567-2576.
[13] Dlala E. Efficient algorithms for the inclusion of the Preisach hysteresis model in nonlinear finite-element methods[J]. IEEE Transactions on Magnetics, 2011, 47(2): 395-408.
[14] 王帅兵, 李琳, 赵小军, 等. 定点时间周期有限元法及其在变压器直流偏磁特性分析中的应用[J]. 中国电机工程学报, 2017, 37(17): 5198-5205, 5240.
Wang Shuaibing, Li Lin, Zhao Xiaojun, et al. Fixed-point time-periodic finite element method and its application for DC bias characteristics of transformer[J]. Proceedings of the CSEE, 2017, 37(17): 5198-5205, 5240.
[15] 孙佳安, 李琳, 王亚琦. 考虑次同步分量的变压器时间并行有限元及铁心动态损耗分析[J]. 中国电机工程学报, 2023, 43(6): 2426-2438.
Sun Jia’an, Li Lin, Wang Yaqi. Finite element method for transformers using parareal and core dynamic loss analysis considering subsynchronous components[J]. Proceedings of the CSEE, 2023, 43(6): 2426-2438.
[16] 魏鹏, 陈龙, 贲彤, 等. 一种考虑动态磁滞效应的高效稳定时域有限元计算方法[J]. 电工技术学报, 2023, 38(21): 5661-5672.
Wei Peng, Chen Long, Ben Tong, et al. An efficient and stable time domain finite element method considering dynamic hysteresis effect[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5661-5672.
[17] 高圣泽, 赵小军, 刘兰荣, 等. 基于棱边元的三维定点谐波平衡有限元法及其在非线性问题中的应用[J]. 中国电机工程学报, 2024, 44(增刊1): 332-341.
Gao Shengze, Zhao Xiaojun, Liu Lanrong, et al. 3-D fixed-point harmonic balance finite element method based on edge elements and its applications on nonlinear problems[J]. Proceedings of the CSEE, 2024, 44(S1): 332-341.
[18] 赵小军, 晋志明, 王刚, 等. 采用复指数的频域分解算法及其在三相变压器非对称直流偏磁分析中的应用[J]. 中国电机工程学报, 2019, 39(4): 1206-1215.
Zhao Xiaojun, Jin Zhiming, Wang Gang, et al. Analysis of three-phase transformer under asymmetrical DC bias by using frequency-domain decomposition based on complex exponential[J]. Proceedings of the CSEE, 2019, 39(4): 1206-1215.
[19] Dlala E, Belahcen A, Arkkio A. Locally convergent fixed-point method for solving time-stepping nonlinear field problems[J]. IEEE Transactions on Magnetics, 2007, 43(11): 3969-3975.
[20] O’ Dwyer J, O’ Donnell T. Choosing the relaxation parameter for the solution of nonlinear magnetic field problems by the Newton-Raphson method[J]. IEEE Transactions on Magnetics, 1995, 31(3): 1484-1487.
[21] Bertotti G. General properties of power losses in soft ferromagnetic materials[J]. IEEE Transactions on Magnetics, 1988, 24(1): 621-630.
[22] 赵小军, 武欣怡, 章轩源, 等. 高频多谐波激励下计及趋肤效应的软磁带材磁滞及损耗特性预测[J]. 中国电机工程学报, 2024, 44(22): 9039-9048.
Zhao Xiaojun, Wu Xinyi, Zhang Xuanyuan, et al. Predicting hysteresis and loss characteristics of soft magnetic tape material considering skin effect under high frequency multi-harmonic magnetization[J]. Proceedings of the CSEE, 2024, 44(22): 9039-9048.
[23] Koczka G, Auberhofer S, Biro O, et al. Optimal convergence of the fixed-point method for nonlinear eddy current problems[J]. IEEE Transactions on Magnetics, 2009, 45(3): 948-951.
[24] 申秋萍, 张清华, 高满, 等. 基于局部半径的三支DBSCAN算法[J]. 计算机科学, 2023, 50(6): 100-108.
Shen Qiuping, Zhang Qinghua, Gao Man, et al. Three-way DBSCAN algorithm based on local eps[J]. Computer Science, 2023, 50(6): 100-108.
Abstract In the frequency domain finite element analysis, considering the hysteresis properties of materials is of great significance in improving the simulation accuracy of electromagnetic characteristics of electrical equipment under DC bias excitation. Aiming at the problems of excessive number of iterations anddivergence in the frequency domain finite element calculation, this paper proposes an improved fixed point iteration strategy based on the ratio magnetic reluctivity. It is applied to the frequency domain finite element analysis under DC bias excitationbased on the loss separation model. After the problem of discontinuity point is solved, the finite element algorithm proposed in this paper has better convergence speed and higher accuracy by using the fixed-point reluctivity and the improved relaxation factor.
Compared with the inverse Preisach model based on the analytical first-order reversal curves, the hysteresis model based on the concentric hysteresis loops makes more comprehensive use of the measured data, simplifies the calculation process, and achieves higher accuracy at low flux density amplitude. Therefore, this paper uses the hysteresis model based on the concentric hysteresis loops to describe the static hysteresis characteristics of the iron core. Because the excitation system of transformers and other electrical equipment mostly imposesa voltage source, this paper considers the electromagnetic coupling and solves the excitation current and magnetic vector potential in the frequency domain at the same time. When the magnetic flux density passes through zero, the corresponding ratio reluctivity often appears jumping breakpoints, which will greatly affect the following finite element iteration. To solve the problem, this paper uses density-based spatial clustering of applications with the noise algorithm to identify the discontinuities, and then uses the data close to the discontinuities to supplement the points. Because the magnetic field strength corresponding to eddy current loss and exclusive loss in the method is not directly expressed in the finite element matrix equation, which is calculated based on the iterative results of the magnetic vector potential and hysteresis model in the calculation process, the non-linear magnetic field relationship brings some disturbance to the iterative process. this paper considers using relaxation method to reduce the numerical disturbance and improve the stability and convergence speed of the algorithm. Based on the value range of gradient modulus and artificially set range of relaxation factor, the relaxation factor of each node is differentiated to improve the stability and convergence speed of the algorithm.
Finally, the excitation current, magnetic field distribution and loss characteristics of the dry-type transformer model with rolled iron core excited by 400 Hz AC and DC bias excitation are tested and simulated by the finite element method. The hysteresis model based on the concentric hysteresis loops is used to describe thehysteresis characteristics of GT-100 silicon steel. The dynamic hysteresis loops simulated by the model are of high accuracy. In the two-dimensional calculation model, the limb-yoke area is selected as ancalculation domain. The calculated excitation current is compared with the measured data whose bias excitation current is 1.3 A, 2.6 A, and 5.2 A, respectively. After one period of computation, the total iron loss is calculated by integrating the dynamic hysteresis loop area of each element. Comparing the total iron loss with the measured data, the maximum relative error is less than 7%, which proves the effectiveness of the algorithm.
Through the simulation analysis, the following conclusions can be obtained: (1) By analyzing the characteristics of the ratio reluctivity about the hysteresis loops, the problem of large error and unstability caused by the ratio reluctivity when the flux density crosses zero is effectively solved. (2) Compared with other relaxation methods, the local relaxation method proposed effectively improves the stability and convergence speed of the algorithm and improves the convergence speed by about 40%. (3) In this paper, the influence of the hysteresis effect on the calculation results of excitation current and iron loss is fully considered. Compared with the frequency domain finite element method using a magnetization curve, the calculation accuracy of excitation current is improved. In addition, the hysteresis model is also used to calculate the core loss, and the results are compared with the measured results to verify the effectiveness of the algorithm.
keywords:Preisach hysteresis model, frequency-domain finite element, fixed-point reluctance, relaxation method
中图分类号:TM153
DOI: 10.19595/j.cnki.1000-6753.tces.242094
国家自然科学基金(52177006)、国家重点研发计划(2021YFB 2401703)和中央引导地方科技发展资金(236Z4508G)资助项目。
收稿日期 2024-11-21
改稿日期 2025-12-05
赵小军 男,1983年生,教授,博士生导师,研究方向为电磁场理论及其应用、频域数值计算方法等。E-mail: zxjncepu@ncepu.edu.cn(通信作者)
肖玉辰 男,2000年生,硕士研究生,研究方向为电磁场频域数值计算方法。E-mail: 2315735277@qq.com
(编辑 郭丽军)