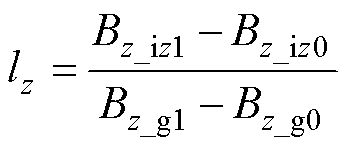（1）
摘要 地磁模拟法是船舶消磁中获取船舶垂向感应磁场的一种有效测量方法，但测量精度受模拟地磁场均匀度制约。为在有限的工程实施条件下尽限地提高地磁模拟均匀度以满足测量需求，必须对垂向地磁模拟线圈进行优化设计。首先，根据地磁模拟法测量原理，借助有限元法定量研究均匀度对地磁模拟法获取船舶垂向感应磁场精度的影响规律，再根据船舶结构并结合实际条件，建立针对模拟磁场均匀度、线圈尺度及其安匝量的多目标优化模型，并采用遗传优化算法进行优化求解，最后设计并搭建实验平台进行验证。结果表明，当模拟磁场均匀度达到89.05%时，船舶垂向感应磁场可获得高于94%的精度；与单目标优化结果相比，多目标优化结果在满足均匀度设计指标的同时，使线圈总长度减少了30%，所需安匝量减小了19%，可同时满足多个目标期望和设计指标，为在工程实际中推广应用地磁模拟法测量船舶垂向感应磁场提供参考。
关键词：地磁模拟法 船舶感应磁场 均匀度 有限元法 遗传优化算法
船舶感应磁场特征是非常重要的船舶物理场特征之一[1]。为抵御水中磁性兵器攻击和空中磁性探测，提高船舶的磁防护能力，必须对船舶实施磁性防护措施[2-4]，而准确掌握船舶感应磁场是实施磁性防护措施的重要前提。
船舶感应磁场是由外加地磁场作用在船体上诱发产生的附加场。目前船舶消磁工作中，主要采用磁传感器测量方法来直接获取船舶感应磁场特征，包括两航向测量法[5]、两地测量法和地磁模拟法[6]。其中，地磁模拟法具有不需调换航向、测磁速度快、测量效率高等诸多优点，能够解决船舶垂向感应磁场难以准确获取的难题，满足消磁技术指标不断提高的需求。唐申生等[7]较早地提出用地磁补偿线圈模拟地磁场，从而实现单航向上舰船垂向感应磁场的测量，但是线圈磁场均匀度较低，导致感应磁场获取精度不足。地磁模拟法获取的船舶感应磁场精度与所模拟的地磁场空间均匀度高度相关，要满足一定的精度需求，就必须提高模拟磁场均匀度。朱武兵等[8]针对纵向均匀磁场的建立，采用切比雪夫级数对多边形线圈磁场进行建模，开展了以均匀度最优为目的的线圈优化设计；郭成豹等[9]通过地磁模拟法测量舰船垂向感应磁场时，采用数值分析法对模拟线圈的电流进行整定，在一定程度上提高了地磁模拟法测量精度；何保委等[10]采用多目标模拟退火算法对四层模拟线圈的垂向高度和安匝比进行优化，使其能够用于获取高精度的舰艇垂向感应磁场；王锴松等[11]借助COMSOL多物理场有限元仿真平台，定量分析了地磁模拟法测量舰船感应磁场的精度受模拟地磁场均匀度影响的变化规律，提出持续增加均匀度，感应磁场测量精度提升效果变缓，工程效费比降低。因此，通过地磁模拟法获取船舶感应磁场时，在提高模拟磁场均匀度的同时还要考虑实际应用中的可实施性要求，从而降低推广应用的成本，提高效费比。
本文在以地磁模拟法获取高精度的舰船感应磁场为应用背景下，提出了一种地磁模拟线圈多目标优化设计方法。考虑实际测量中垂向感应磁场较难获取，且磁性处理时主要考虑船舶各磁性磁场的垂向分量，本文以船舶垂向感应磁场垂向分量Bz_iz作为分析对象。首先简述了垂向感应磁场地磁模拟法测量原理；其次借助COMSOL Multiphysics有限元分析平台，通过某船型数值算例，定量研究了均匀度对地磁模拟法获取船舶Bz_iz精度的影响规律；然后结合工程实际，根据船舶结构并采用遗传优化算法，在满足Bz_iz获取精度的条件下，对垂向地磁模拟线圈的尺度及安匝量等参数进行优化求解；最后设计并搭建了实验平台，对垂向地磁模拟线圈优化设计方法的有效性与可行性进行检验。
为便于描述船舶磁场，规定船舶坐标系如下：坐标系原点为船体几何中心；x轴平行于船体艏艉线，x轴正向指向船艏，称该方向为纵向；y轴平行于甲板面且与艏艉线垂直，y轴正向指向船体右舷侧，称该方向为横向；z轴垂直于甲板面且以向下为正向，称为垂向。铁磁性船舶在地磁场中磁化可以看作一种瞬时线性磁化效应，产生的感应磁场是一种瞬时效应磁场。地磁模拟线圈可以模拟不同地磁场对船舶的磁化作用，并通过磁传感器测量不同磁化作用下的船舶磁场，即可实现船舶感应磁场的分解。
在地磁模拟法中，设z方向上的线性磁化系数为lz，有
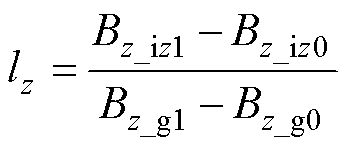（1）
式中，Bz_gk为地磁模拟场垂向分量；Bz_izk为由Bz_gk引起的船舶垂向感应磁场垂向分量，k=0或k=1，表示前后两次不同状态的地磁模拟场；Bz_iz1与Bz_iz0的差值一般通过磁传感器测得的磁场z分量差值得出。根据垂向磁化系数lz，又可直接求得船舶垂向感应磁场z分量，即
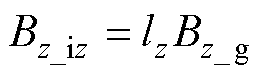（2）
式中，Bz_g为当地地磁场垂向分量。
根据地磁模拟法测量船舶垂向感应磁场的原理可知，当船舶周围空间的模拟地磁场越均匀，磁场的变化规律越接近原始地磁场时，船舶感应磁场的获取精度就会越高。为了分析模拟磁场均匀度对Bz_iz获取精度的影响，针对某船型应用背景，设计了如图1所示的垂向线圈系统有限元数值模型。图1中，线圈结构为布设于船体下方的单层矩形线圈及其组合，船模网格选用了软件平台预定义的“较细化”单元进行自动剖分。图1没有示出的部分是包络船模及整个线圈系统的有限截断边界，这里用一个半径为400 m的球体作为空气域进行分析，此外还设置了厚度为100 m的球层作为无限元域，包裹在空气域外层，无限元域网格通过用户自定义为固定单元数为3的扫掠分布。然后，通过AC-DC模块的“磁场”接口添加磁场激励及适应的边界条件。最后，根据问题类型选用稳态求解器进行迭代即可。
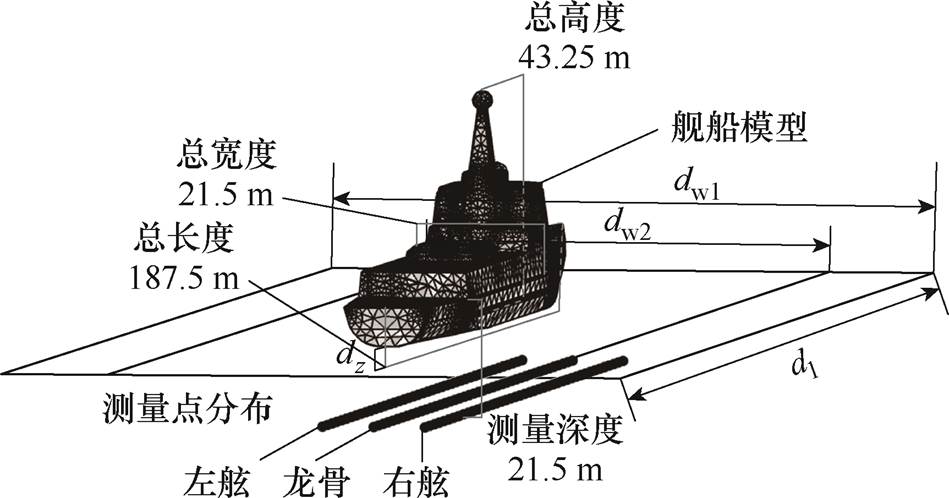
图1 船舶垂向地磁模拟线圈测量系统
Fig.1 Vertical geomagnetic analog coils measuring system for ship model
结合实际场地条件，设置垂向地磁模拟线圈系统的船舶有限元数值模型基本参数见表1。
表1 有限元分析模型参数设置
Tab.1 Parameter setting of the finite element analysis model
参 数数 值 地磁场垂向分量Bz_g/T4×10-5 船壳材料相对磁导率mr150 船壳厚度ts/mm100 线圈平面距船底面距离dz/m1 线圈长度dl/m340 外层线圈宽度dw1/m120 内层线圈宽度dw2/m79
基于地磁模拟法测量原理，船体区域模拟地磁场均匀度直接决定了船舶感应磁场测量精度，为了简化建模，该船模暂不考虑内部铁磁物质对磁场测量的影响，且上层舰桥由于磁性结构有限、铁磁性远弱于下方主船体，又与龙骨线测量点距离较远，因此在选取均匀度考察区域时可以忽略上层舰桥结构，以包裹船模主体的长方体空气域（尺寸190 m× 30 m×30 m）为均匀度考察区，区域内间距为10 m的320个等距截点作为均匀度考察点。于是对线圈系统模拟磁场均匀度的定义，有
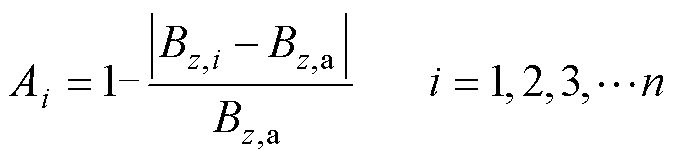（3）
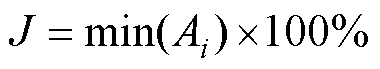（4）
式中，n为测量点总数；i为在一定区域内均匀分布的点的个数；Bz,i为任一点的磁感应强度垂向分量；Bz,a为所有点的磁感应强度垂向分量平均值；J为均匀度，定义为Ai的最小值，反映空间区域的最大不均匀性。根据该均匀度定义，计算可得表1参数下垂向地磁模拟线圈系统的磁场均匀度为89.05%。
本研究中对感应磁场计算值的准确性评估，考虑实际应用中船舶结构复杂，测量点数多，有时需要考量其局部测量点计算误差，因此引入相对方均根误差（Root-Mean-Square Error, RMSE）来定义船模感应磁场测量精度Jd，即
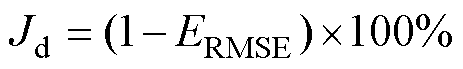（5）
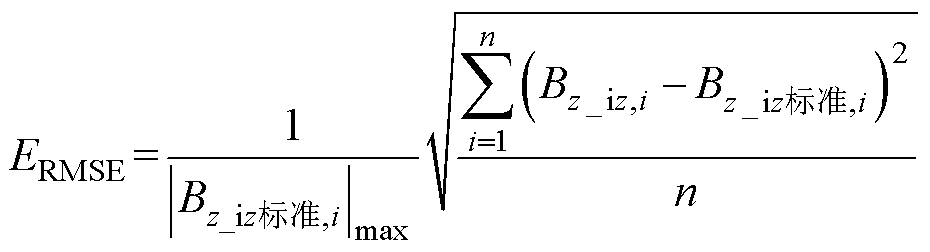（6）
式中，
为舰船受到均匀度为100%的地磁模拟场作用下，第i个测量点处舰船垂向感应磁感应强度垂向分量。测量点选取了水线下21.5 m（1倍总宽）龙骨线（x=-105～105 m, y=0）的43个等距点。
由式（3）和式（4）可知，模拟磁场均匀度主要与船体在模拟场中的相对位置、产生模拟场的方式相关，为了便于分析，在前期的建模工作中已经确定船体在模拟场中的位置，使得船模重心尽量接近模拟场的均匀分布中心。结合船舶实际，在考虑宽度方向满足均匀度的情况下，以线圈长度为单一变量设置不同均匀度的实验组，同步改变内外层线圈长度dl获得10组不同均匀度的地磁模拟场，再根据地磁模拟法原理解算每组线圈作用对应的Bz_iz数值解。通过AC-DC磁场接口中的约化场求解直接施加大小为40 000 nT的均匀背景场，即均匀度达到100%的垂向地磁场分量，计算Bz_iz标准值。均匀度对地磁模拟法测量Bz_iz精度的影响规律如图2所示。
从图2中曲线可知，随着均匀度的提升，Bz_iz精度呈递增趋势，当模拟磁场均匀度达到89.05%时，船模龙骨下方测量点的Bz_iz获取精度均优于94%，当均匀度提升12.18%后，龙骨下Bz_iz获取精度有了7.84%的增量，均匀度对地磁模拟法测量船舶感应磁场的影响程度高于64%。
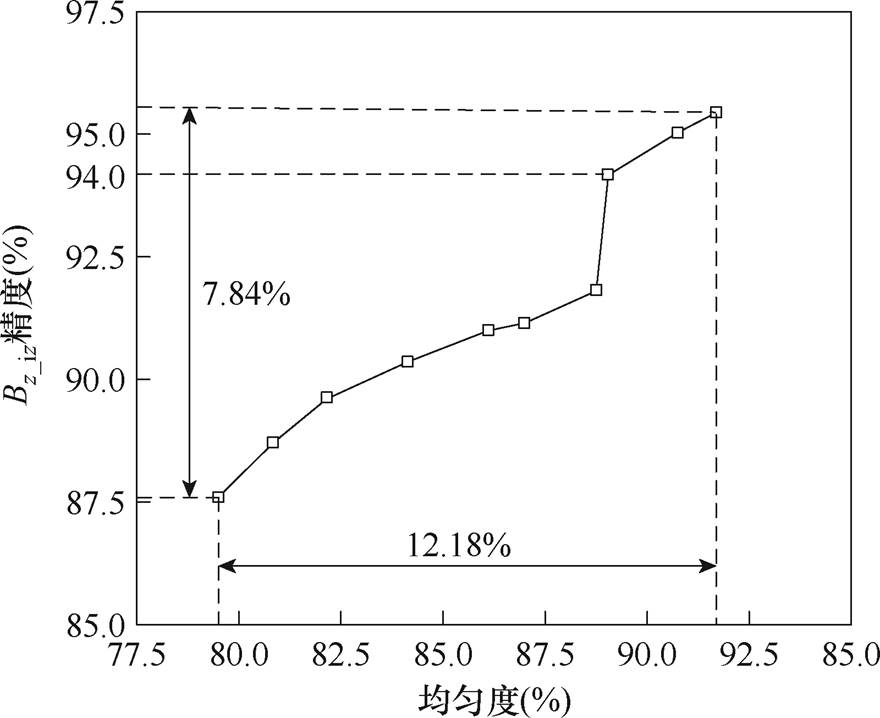
图2 龙骨测量点Bz_iz获取精度随均匀度变化曲线
Fig.2 Curve of Bz_iz with uniformity at keel measurement points
若不考虑工程可实施性及成本，当采用单个矩形线圈产生模拟磁场，线圈长度为1 400 m、宽度为1 000 m时，均匀度达到99.11%，接近完全均匀，Bz_iz获取精度高达97.61%。但是在工程实际中显然不可行，不可能最大限度地追求均匀度的提升而忽略成本的成倍增加。因此，在地磁模拟测量法的系统建设及线圈设计中，应以一定区域内模拟磁场均匀度为首要优化目标，根据船舶结构并结合实际工程环境的应用需求及可实施性要求，进行地磁模拟线圈的优化设计。
由于船舶结构特殊，长宽比较大，上层建筑复杂，若采用亥姆霍兹双层线圈结构来构建垂向地磁模拟系统，则搭建成本过高且实施性不强。因此，在实际工程中，如均匀度分析中构建的线圈系统，垂向模拟线圈通常设计成单层矩形线圈结构及其组合形式，即在单一矩形线圈的同一水平面内增加通以反向电流的局部调节线圈，减小线圈磁场的空间异变率，既可获得较大的均匀磁场空间，提高磁场均匀度，又能减小垂向线圈系统所占的空间，降低实施成本，提高工程适用性。
为了搭建多船型垂向地磁模拟系统，对线圈进行优化设计。垂向地磁模拟线圈优化设计总体示意图如图3所示。首先确定最大测量目标为尼米兹级航母船型，根据被测目标大小即可确定目标磁场均匀区域的大小，即由最大船型尺寸确定的目标均匀区为317 m×41 m×69 m的长方体域。然后，结合均匀度分析相关结论，确定首要设计指标为目标均匀区域内J≥89.05%，同时还要确定外层矩形线圈的尺寸范围及其内层调节线圈的具体结构。
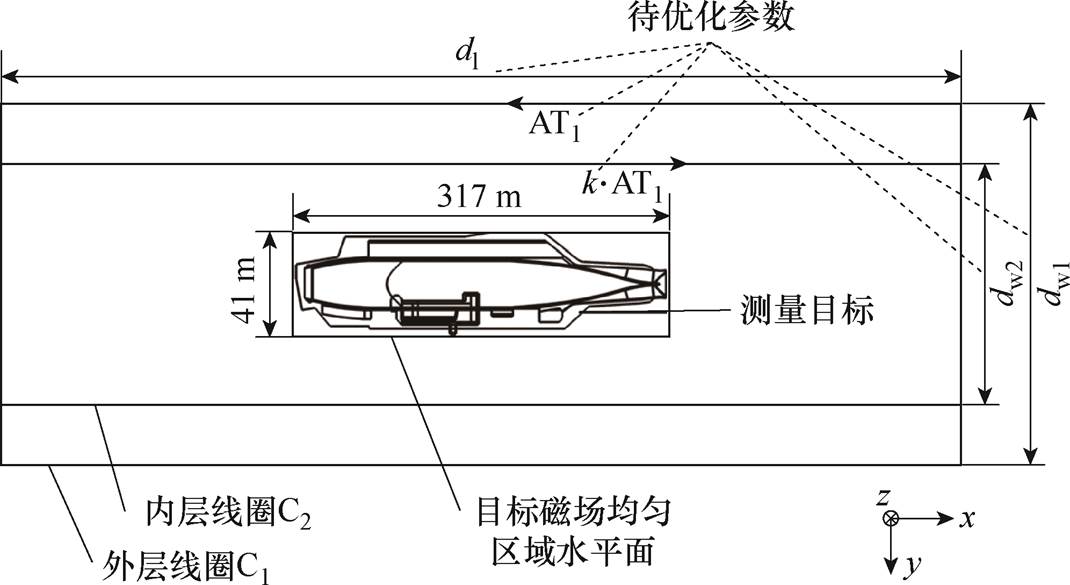
图3 垂向地磁模拟线圈优化设计总体示意图
Fig.3 General schematic diagram of optimization design of the vertical geomagnetic simulation coil
与横向多区段或纵向多区段内层结构相比，当内层采用单个矩形线圈结构时，虽然无法通过局部区域调节实现磁场均匀度的高度追求，但能够在满足均匀度设计指标的前提下，降低能量消耗和节约电缆敷设成本且提高施工便利性，更加适应工程实际的需要。另外，根据以往的实际线圈敷设经验，矩形线圈的长边一般设计成相同的敷设长度，不仅可以减少支架数量、降低耗材，而且可以提高模拟磁场的整体均匀度水平，因此，确定垂向模拟线圈为图3所示内外层矩形嵌套结构且内外层线圈长度相等。图3中还示出了该线圈结构可优化设计的几个参数，包括：内外层线圈长度dl、外层线圈宽度dw1、内层线圈宽度dw2、外层线圈安匝量AT1和安匝比k总共5个待优化参数。此外，k=-AT2/AT1，其中AT2为内层线圈的安匝量，通过变量k来调节AT2，可使参数优化过程中模拟磁场均匀度始终保持在较高的水平范围内。
除均匀度设计指标外，还需确定线圈尺寸、安匝量等指标，根据不同的优化设计指标建立合适的全局目标函数，并借助全局优化算法对目标函数进行迭代求解，获得满足指标要求的线圈最优设计方案。本文主要针对单目标和多目标优化问题对5个线圈参数进行优化求解，并给出相应的最优设计方案。单目标优化主要解决的是均匀度设计的最优化问题，在给定的参数范围内，追求均匀度的最大化；多目标优化解决的是线圈设计方案的工程适用性问题，在单目标优化的基础上，尽可能地实现节能减耗，能够同时满足均匀度、线圈长度和安匝量三个主要设计指标。在多目标优化问题中，不同目标之间相互制约，往往在改善其中一个目标性能的同时会造成其他目标性能的损失，很难求得一个使所有目标性能都达到最优的解，其解通常是一个非劣解的集合（Pareto最优解集），然后根据用户需求或工程实际需求选取一个或一组Pareto最优解，即多目标优化问题的满意解。在众多的多目标优化算法中，遗传算法的适用范围广，对目标函数的要求低，对于不连续不可微的目标函数依然可以求解，并且能够实现全局优化，可以充分满足本文进行多目标优化的需求，因此本文采用遗传算法进行优化求解[12]。最后，设计并搭建物理缩比实验平台对该线圈设计优化方案的有效性进行检验。
遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种自适应全局优化概率搜索算法[13]，自J. Holland和J. David Bagley首次提出这一算法后，其在工程中有着广泛的应用[14-15]。遗传算法的主要运算过程包括初始化群体、选择、交叉、变异和终止条件，通过运算过程的不断迭代、群体的不断优化，逐步搜索最优解、不断靠近满意值。
在进行遗传优化求解之前，要建立垂向地磁模拟线圈解析计算模型。在317 m×41 m×69 m的目标均匀区域中，以间距为1 m的等距截点作为该区域磁场均匀度考察点，设i点的磁感应强度垂向分量为Bz,i，外层线圈C1和内层线圈C2通电后对i点产生的磁场分别为Bz_C1,i和Bz_C2,i，则有
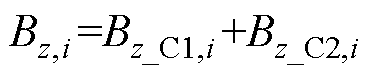（7）
以矩形线圈的几何中心为原点、线圈长度方向为x轴和宽度方向为y轴建立全局坐标系，由线圈尺度参数及均匀度考察区设置，可确定均匀度考察区内各点坐标，再根据Biot-Savart定律[16]，有
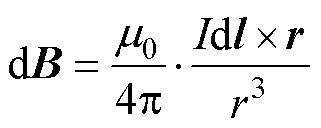（8）
可计算出内外矩形线圈的每根直线段单独通电对i点的作用，再对矩形线圈所有直线段的激励进行叠加，即可求得Bz,i。
3.2.1 以均匀度最优的单目标优化
以均匀度最优为线圈设计目标的单目标优化问题，是工程设计中常见的最优化问题，一般通过设置多个与设计目标（指标）直接相关的设计变量（也称为决策变量，或决策参数），在每个设计变量满足相应的约束条件下，使设计目标达到最优值（最大值或最小值）。对于该线圈设计的单目标优化问题，设置dl、dw1、dw2、k共4个参数为待优化参数，其中，根据第2节均匀度影响分析所得结论，将本文的均匀度设计指标确定为89.05%，采用遗传算法进行单目标优化求解。
遗传算法优化求解流程如图4所示。
1）编码和初始化种群。对4个待优化参数直接进行浮点数编码，再通过随机方式产生多个求解该适应度值函数的染色体编码，进而形成初始种群。结合实际场地条件及最大目标尺度，4个线圈参数对应的编码范围分别设定为：dl∈[500 m, 900 m]、dw1∈[100 m, 400 m]、dw2∈(100 m, 400 m)、k∈[-1, 0]，线圈长度大于宽度，外层线圈宽度大于内层线圈宽度。设定种群大小为10，则随机生成的初始化种群为一个维度为10×4的矩阵。
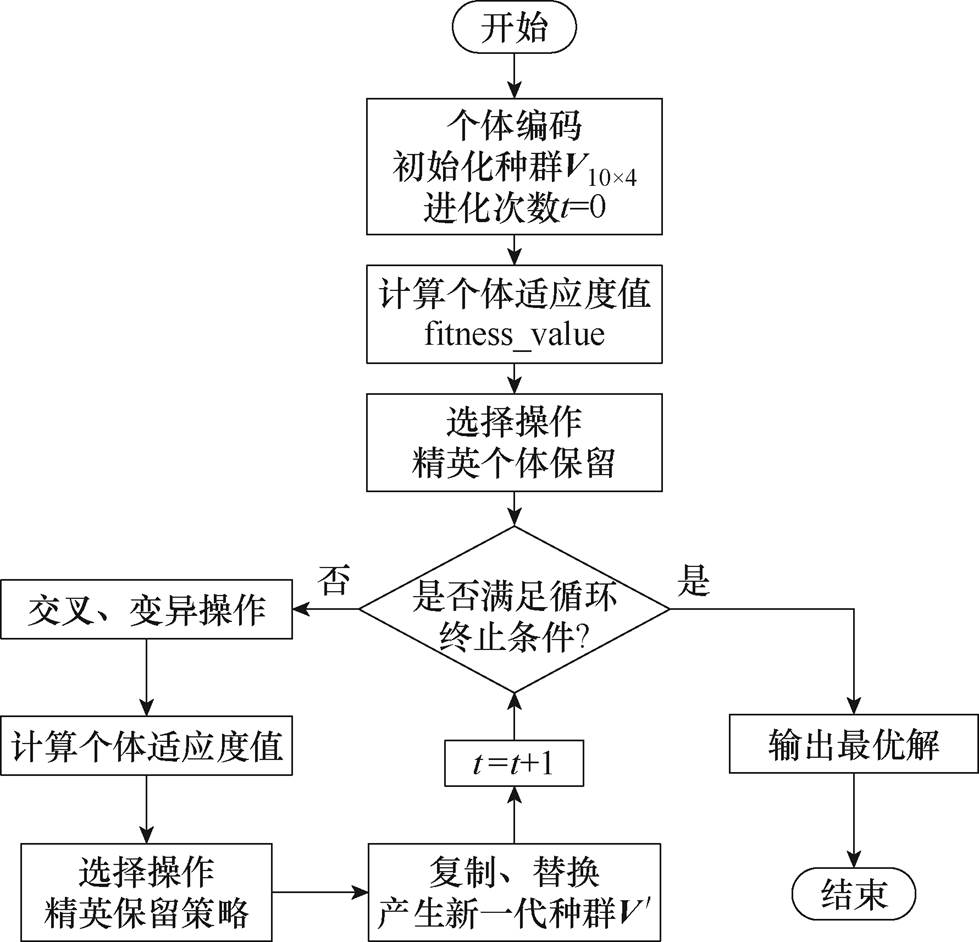
图4 遗传算法优化求解流程
Fig.4 Flow chart of genetic algorithm optimization solution
2）建立适应度值评价函数（目标函数）。由式（3）和式（4）定义可得该线圈模型的均匀度Jz为
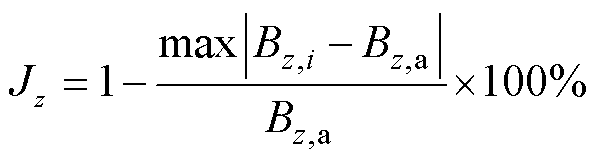（9）
由于是对Jz的单目标优化，不考虑安匝量的设计需求，则待优化参数可先忽略AT1。以模拟1倍左右地磁场垂向分量为参考，设定AT1= 22 000 A·N，此时适应度值函数确定为
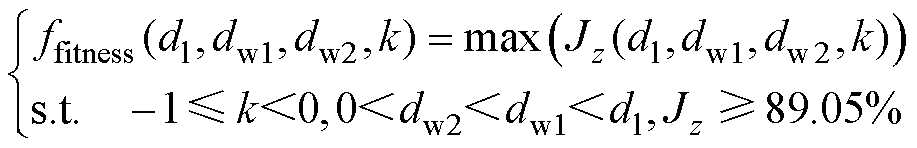（10）
3）选择、交叉和变异，该步骤为一循环迭代过程。在选择操作中引入精英保留策略，将每一代种群中的最优解所对应的精英个体复制到下一代中，防止进化过程中产生的精英个体被交叉和变异所破坏。在进行下一次交叉、变异前，筛选出当代种群中的最劣解对应的个体，用上一代中的精英个体进行替换，在加快整体收敛速度的同时，也提高了算法的稳定性。交叉操作使用适合浮点数编码的算术交叉算子，由初始种群中两个随机个体的线性组合产生两个新的个体，为提高算法的全局搜索能力，设定交叉概率pc为0.8。变异操作采用非均匀变异法，其中非均匀性参数设为1，变异概率pm设为0.1，有效提高了算法的进化能力。遗传进化的终止条件设置为Jz≥98%或t＞gmax，其中t表示进化次数，gmax表示最大遗传代数，当条件满足时循环终止。最后，设定gmax=100进行迭代求解，并输出最优解。
单目标优化适应度值收敛图如图5所示。图5示出了该单目标优化函数在100次迭代求解过程中适应度值的变化趋势。当t=41时，ffitness开始收敛，最终得到的最优解为Jz=96.70%，此时得到该线圈的最优参数为dl=899.821 m，dw1=294.027 m，dw2= 247.304 m，k=-0.628，满足该线圈优化的均匀度设计指标。但是，在获得高度均匀磁场的同时，线圈敷设长度达4 681.946 m、所需安匝量达35 816 A·N，线圈敷设长度及安匝量代价较高。为了进一步提高线圈优化设计方案的工程可行性，有必要对线圈磁场均匀度、线圈总长度、总安匝量等进行多目标优化设计。
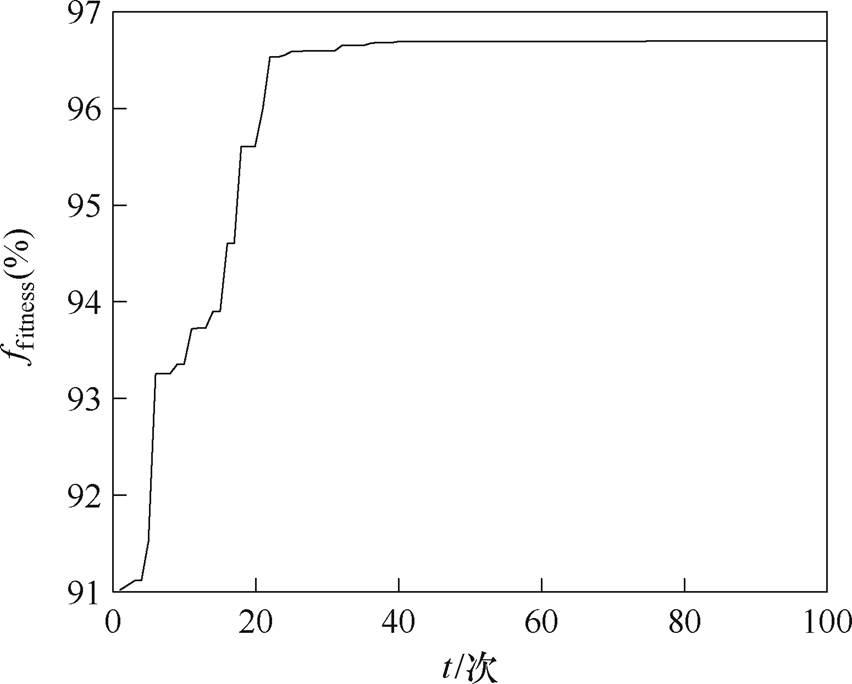
图5 单目标优化适应度值收敛图
Fig.5 Convergence graph of ffitness for single objective optimization
3.2.2 对均匀度、长度和安匝量的多目标优化
对于该线圈设计的多目标优化问题，由于工程环境比较明确，采取比较普遍的加权处理方法，将多目标问题转化为单目标优化问题，其求解过程就可以沿用3.2.1节中的几个优化求解步骤，主要区别在于适应度值函数的确立及遗传算法各参数的调整。
步骤1）中，添加第5个优化参数AT1，即外层线圈匝数与所加电流的乘积，同时适应度值评价函数引入线圈长度函数L和线圈安匝量函数AT，表达式为
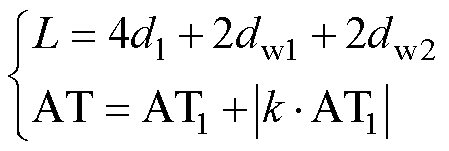（11）
根据目标均匀区域中心点的垂向磁场分量可以模拟1倍当地垂向地磁场的条件，设定其编码范围为AT1∈[18 000, 22 000] A·N，其他参数范围不变，种群大小仍设为10，初始种群为一个维度为10×5的矩阵。
步骤2）中，目标方向包括对线圈均匀度、长度及总安匝量的优化，建立多目标加权适应值评价函数为
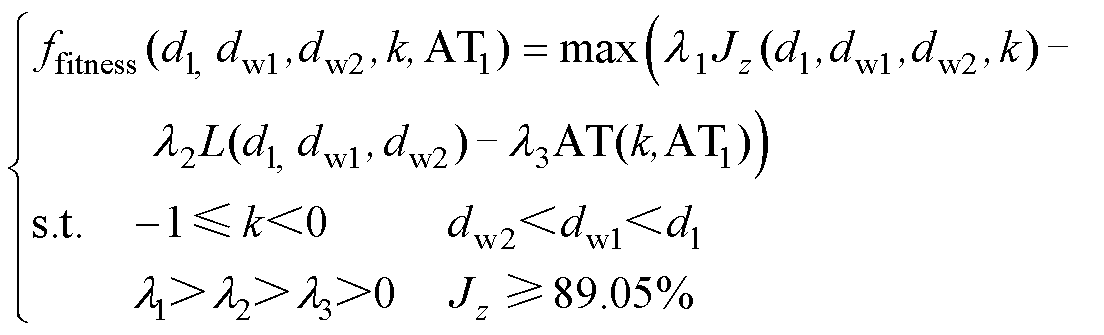（12）
式中，l1、l2、l3分别为3个优化目标的权重系数且均为正数。当ffitness在Pareto最优域内取得满意解时，既能满足该线圈模拟磁场均匀度设计指标，也能满足工程实际中线圈长度尽可能短、安匝量尽可能低的应用需求。根据3个目标值的关注度及其数值关系，按顺序确定适应度值评价函数的权重系数为[l1l2l3]=[4 500 0.7 0.000 1]。
步骤3）中，算法其他参数保持不变，gmax增加至500代，终止条件变为：Jz≥98%、L≤1 800和AT≤25 000 3个条件同时满足，或t＞gmax。该多目标问题优化求解过程与图4所示流程相似，结果如图6所示。
由图6所示结果可知，当t=244时，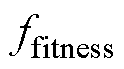
开始收敛，最终得到的一个满意解为Jz=90.98%、L= 3 291.716 m，AT=28 988.306 A·N，此时得到的最优线圈参数为dl=644.511 m，dw1=196.610 m，dw2= 160.226 m，k=-0.599，AT1=18 129.022 A·N，在满足均匀度设计目标的同时，另外两个目标的优化结果也符合预期，得到的满意解已经在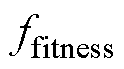的Pareto 最优域内。为直观地表征优化效果，图7和图8给出了线圈参数优化后其磁场有限元计算结果，分别以均匀度考察区过中心点的纵轴线为参考（纵剖图）和以均匀度考察区过中心点的横轴线为参考（横剖图），绘制内外线圈单独作用和内外线圈共同作用时产生的磁感应强度垂向分量分布。可以看出，当内外两层线圈共同作用时，线圈周围空间磁场的均匀度都得到改善，且纵向视角比横向更为明显。
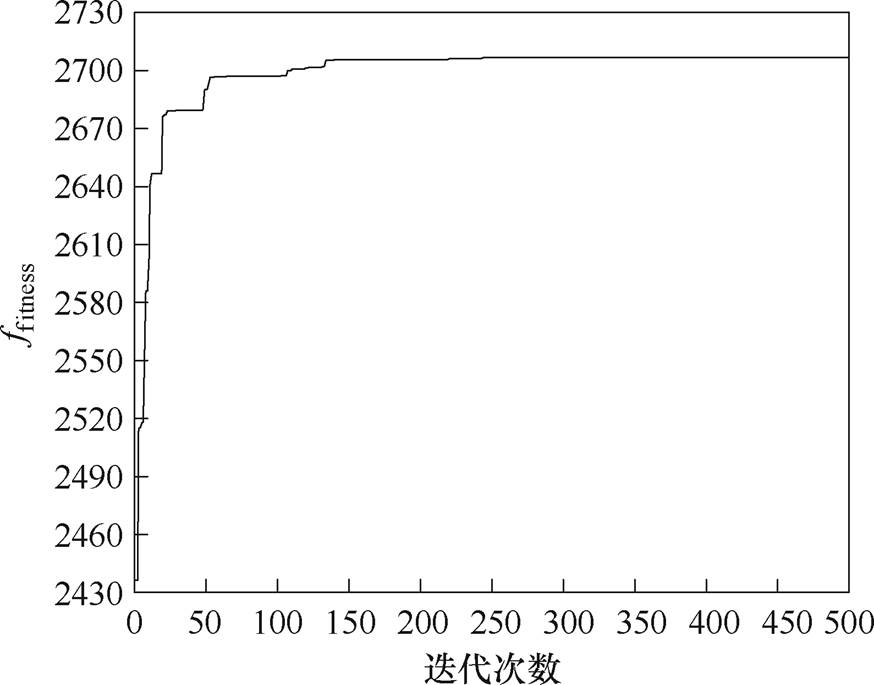
图6 多目标优化适应度值收敛图
Fig.6 Convergence graph of ffitness for multi-objective optimization
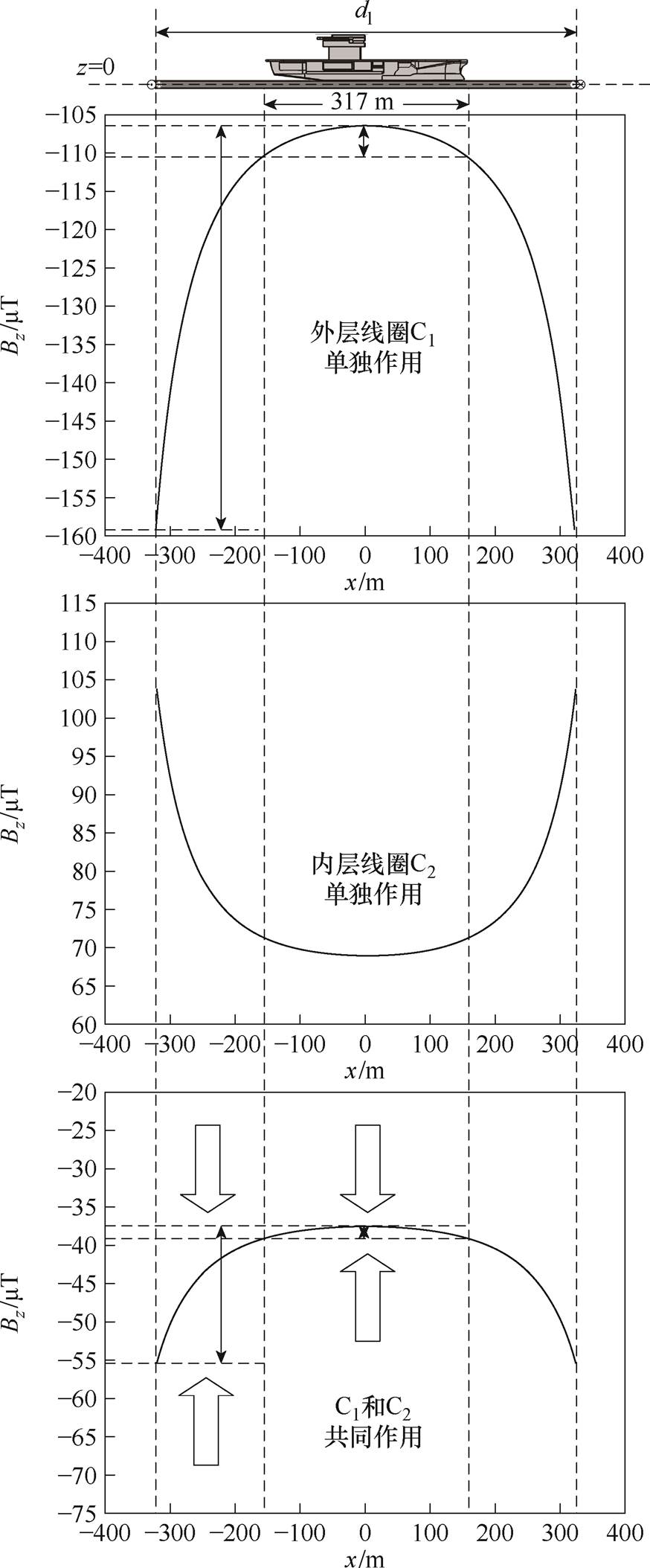
图7 纵剖面效果
Fig.7 Longitudinal-sectional renderings
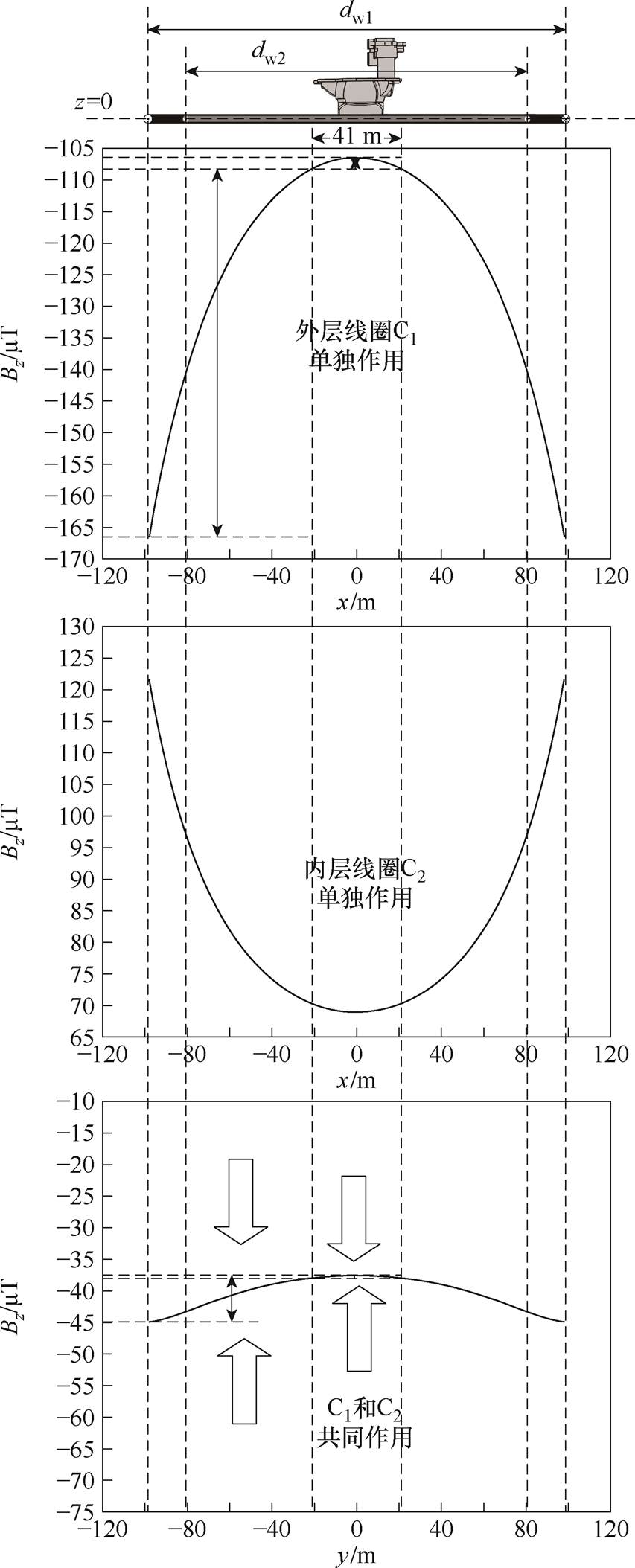
图8 横剖面效果
Fig.8 Cross section renderings
最后，对该组垂向地磁模拟线圈的两种不同优化方法设计效果进行比较，结果见表2。
分析表2中数据可知，单目标优化和多目标优化结果均达到了目标期望值。其中，单目标优化提供的线圈设计方案，通过优化线圈尺度和安匝比，在一定的线圈尺寸约束范围内取得了96.70%的高均匀度，可获得较为准确的感应磁场测量精度；与单目标优化结果相比，多目标优化提供的方案虽然取得的均匀度不及前者，但在满足均匀度设计指标的同时，很大程度地减小了线圈总长度及模拟地磁场所需的安匝量，同时满足了多个目标期望和设计指标。因此，当实际应用中对测量精度提出了更高的指标要求时，应当采取本文的单目标优化方法进行均匀度优化设计；当实际工程中对测量精度、施工难度及造价成本等多个方面均有要求时，应当采取本文的多目标优化方法对模拟线圈进行综合优化设计。总体来讲，虽然多目标优化方法优化参数多，目标函数复杂，求解过程难，但是其优化结果往往比单目标优化更加符合预期，满足工程实际的需求。接下来需要对线圈多目标优化方法的有效性进行实验验证，以利于进一步的推广应用。
表2 垂向线圈设计不同优化效果比较
Tab.2 Comparison of different optimization effects of the vertical coil design
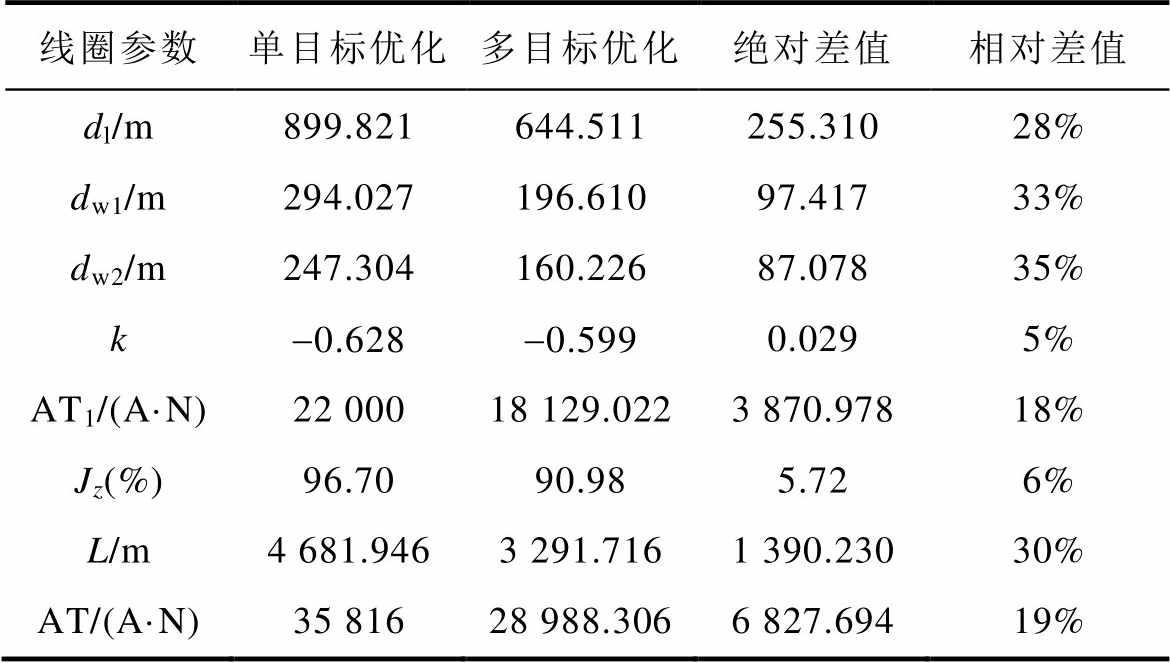
线圈参数单目标优化多目标优化绝对差值相对差值 dl/m899.821644.511255.31028% dw1/m294.027196.61097.41733% dw2/m247.304160.22687.07835% k-0.628-0.5990.0295% AT1/(A·N)22 00018 129.0223 870.97818% Jz(%)96.7090.985.726% L/m4 681.9463 291.7161 390.23030% AT/(A·N)35 81628 988.3066 827.69419%
为了验证本文线圈多目标优化设计方法的有效性，设计了图9所示的船舶缩比模型。
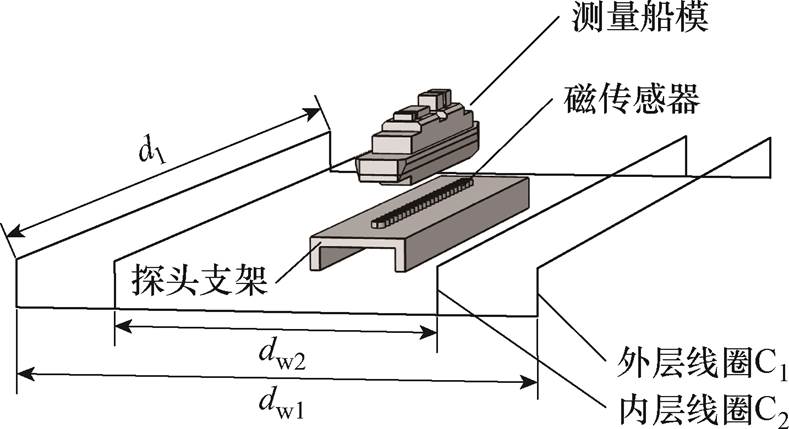
图9 船模实验模型
Fig.9 Schematic diagram of ship model experiment
均匀度设计指标不变，线圈参数dl、dw1、dw2、k和AT1根据磁性船模确定的均匀区域大小，借助3.2.2节垂向线圈多目标优化设计方法重新确立。其中，考虑到地磁模拟线圈通常固定敷设在水下，为方便船舶进出线圈均匀场区域，本文将单层水平矩形线圈架设成图9中的鞍形结构，产生磁场的方式和产生均匀场的条件与单层矩形线圈结构一致，基于该实际线圈结构所得实验结果可以验证本文垂向地磁模拟线圈优化设计的有效性。实验室船模实验平台及垂向线圈敷设实物如图10所示。
图10 实验线圈系统
Fig.10 Coil system in experiment
图10中被测船模通过无磁小车放置于磁场测量区的无磁轨道上，经优化设计的外层线圈C1和内层线圈C2组成垂向单层地磁模拟线圈组C12，归一化线圈尺寸参数为：dl=12.00，dw1=4.20，dw2=2.60，线圈平面与船模底面距离dz=0.22，在包裹船模的长方体空气域中，可产生均匀度达91.37%的磁场。磁传感器沿龙骨线布设在船模水线下方的1倍船宽深度上，龙骨测量线略长于1倍船长，共取23个等步长的点进行测量，将测得的Bz_iz作为该磁性船模的试验值。为了对试验值进行评估，尽可能地获得船舶垂向感应磁场真值，专门设计了垂向三层地磁模拟线圈组C3，由长度和宽度均大于C1的三层鞍形线圈组成，线圈几何中心与C12重合，产生模拟磁场的中心也重合，均匀度高达98.06%，测得的龙骨测量点船模Bz_iz可作为比对标准值。
图11分别给出了两组线圈作用下测得的船模龙骨Bz_iz试验值和标准值归一化分布图，可以看出Bz_iz试验值分布曲线与标准值非常接近，经计算可得当均匀度为91.37%时，Bz_iz测量精度达到95.91%，在满足均匀度J的设计指标的同时，Bz_iz测量精度Jd符合实际工程中的应用需求，线圈其他参数也均达到了最优状态，从而验证了本文垂向地磁模拟线圈多目标优化设计方法的有效性。
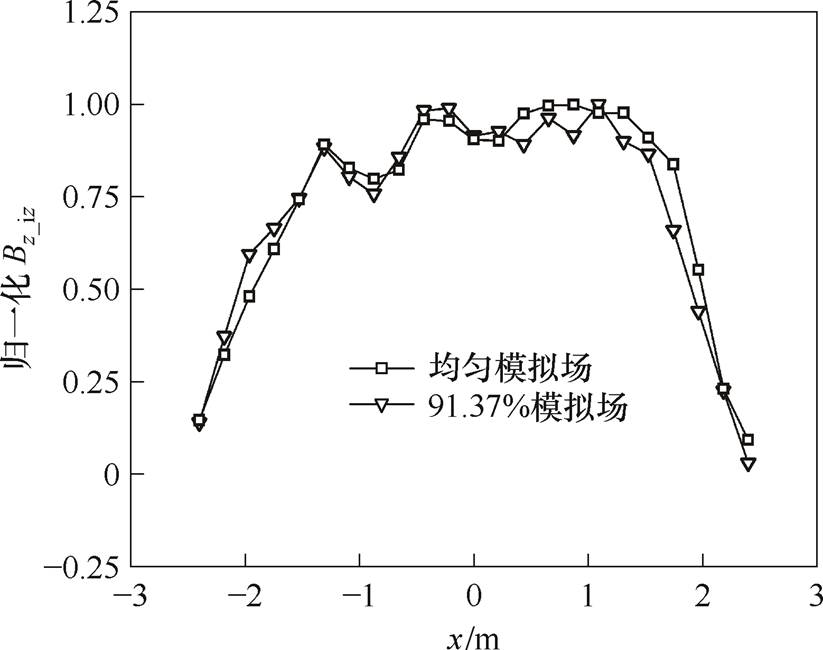
图11 船模实验归一化Bz_iz分布图
Fig.11 Normalized Bz_iz distribution diagram of ship model experiment
本文以船舶垂向感应磁场垂向分量Bz_iz为研究对象，先简述了垂向感应磁场测量原理，然后借助COMSOL Multiphysics有限元软件，通过数值算例定量研究了均匀度对地磁模拟法获取船舶Bz_iz精度的影响规律，得出当模拟磁场均匀度高达89.05%时，船舶垂向感应磁场获取精度优于94%的结论。再根据船舶结构并结合实际条件，建立了基于磁场均匀度与线圈尺寸的多目标优化模型，并采用遗传优化算法对线圈尺度及安匝量等参数进行优化求解，最后设计并开展了数值模拟验证与船模实验验证。结果表明，与单目标优化方法相比，本文提出的多目标优化方法，在满足均匀度设计指标的同时，显著减小了线圈总长度及所需安匝量，实现了多个目标期望和设计指标，从而提高了该测量方法在实际应用中的准确性与可行性。研究结论为地磁模拟线圈的设计提供了可靠的优化方法，也为地磁模拟法测量船舶感应磁场在实际应用中的推广提供了一定的参考。
参考文献
[1] 林春生, 龚沈光. 舰船物理场[M]. 2版. 北京: 兵器工业出版社, 2007.
[2] Kim D W, Lee S K, Kang B, et al. Efficient re- degaussing technique for a naval ship undergoing a breakdown in degaussing coils[J]. Journal of Magnetics, 2016, 21(2): 197-203.
[3] 王玉芬, 周国华, 吴轲娜, 等. 消磁站水下磁传感器定位方法[J]. 电工技术学报, 2024, 39(4): 956- 965.
Wang Yufen, Zhou Guohua, Wu Kena, et al. Loca- lization method for underwater magnetic sensors in the fixed deperming station[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 956-965.
[4] 何保委, 孙兆龙, 刘月林, 等. 一种舰船高精度感应磁场快速正演建模方法[J]. 电工技术学报, 2024, 39(6): 1589-1601.
He Baowei, Sun Zhaolong, Liu Yuelin, et al. A fast forward modeling method for high precision induced magnetic field of ships[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1589-1601.
[5] 汪永浩, 张国友. 基于两航向测量的船舶任意航向磁场计算方法[J]. 船电技术, 2014, 34(4): 76-80.
Wang Yonghao, Zhang Guoyou. Calculating method of ship magnetic field on any course based on two course measurements[J]. Ship Electrical Technology, 2014, 34(4): 76-80.
[6] 衣军, 张朝阳, 虞伟乔. 基于地磁模拟的潜艇感应磁场测量[J]. 上海海事大学学报, 2015, 36(1): 61-64.
Yi Jun, Zhang Zhaoyang, Yu Weiqiao. Measurement of submarines’ induced magnetic field based on geomagnetic simulation[J]. Journal of Shanghai Mari- time University, 2015, 36(1): 61-64.
[7] 唐申生, 周耀忠, 刘胜道, 等. 测量船舶垂向感应磁场的新方法[J]. 武汉理工大学学报(交通科学与工程版), 2005, 29(5): 659-662.
Tang Shensheng, Zhou Yaozhong, Liu Shengdao, et al. A new method of measuring vertical induced component of vessel’s magnetic field[J]. Journal of Wuhan University of Technology, 2005, 29(5): 659-662.
[8] 朱武兵, 赵文春, 庄劲武, 等. 一种均匀磁场线圈优化设计方法[J]. 海军工程大学学报, 2017, 29(5): 39-42.
Zhu Wubing, Zhao Wenchun, Zhuang Jinwu, et al. A new optimal design for coils of uniform magnetic field[J]. Journal of Naval University of Engineering, 2017, 29(5): 39-42.
[9] 郭成豹, 周炜昶. 舰船垂向感应磁场精确测量技术[J]. 中国舰船研究, 2018, 13(2): 135-139.
Guo Chengbao, Zhou Weichang. Precision measure- ment of ship’s induced vertical magnetic signatures[J]. Chinese Journal of Ship Research, 2018, 13(2): 135- 139.
[10] 何保委, 刘胜道, 周国华, 等. 基于多目标模拟退火法的垂向检测线圈改进[J]. 华中科技大学学报(自然科学版), 2021, 49(12): 46-50.
He Baowei, Liu Shengdao, Zhou Guohua, et al. Improvement of vertical detecting coil based on multi- objective simulated annealing method[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2021, 49(12): 46-50.
[11] 王锴松, 周国华, 刘月林, 等. 地磁模拟法测量舰船感应磁场的数值模拟[J]. 兵工学报, 2022, 43(3): 617-625.
Wang Kaisong, Zhou Guohua, Liu Yuelin, et al. numerical simulation of measuring ship’s induced magnetic field by geomagnetic field simulation method[J]. Journal of Ordnance Engineering, 2022, 43 (3): 617-625.
[12] 张缙, 刘智, 刘意, 等. 基于智能算法的双面散热SiC功率模块多目标优化设计[J]. 电工技术学报, 2023, 38(20): 5515-5529.
Zhang Jin, Liu Zhi, Liu Yi, et al. Research on multi-objective optimization design of double-sided cooling SiC power module based on intelligent algorithm[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5515-5529.
[13] 左超, 耿攀, 陈涛, 等. 基于遗传算法的消磁绕组优化设计[J]. 舰船科学技术, 2015, 37(2): 124-127.
Zuo Chao, Geng Pan, Chen Tao, et al. Optimization of degaussing winding design based on genetic algorithm[J]. Ship Science and Technology, 2015, 37(2): 124-127.
[14] 李水祥, 王桢. 基于有限元和遗传算法的厚壁线圈均匀梯度磁场优化设计[J]. 仪表技术与传感器, 2016(2): 95-98.
Li Shuixiang, Wang Zhen. Optimization of Maxwell coils with even grad magnetic field based on FEM and genetic algorithm[J]. Instrument Technique and Sensor, 2016(2): 95-98.
[15] 杜方鑫, 李玲, 吴震宇. 遗传算法与有限元相结合的高速电机转子优化[J]. 内蒙古师范大学学报(自然科学汉文版), 2019, 48(2): 129-133, 141.
Du Fangxin, Li Ling, Wu Zhenyu. Optimization on high-speed permanent magnet machine rotor based on genetic algorithm and finite element method[J]. Journal of Inner Mongolia Normal University (Natural Science Edition), 2019, 48(2): 129-133, 141.
[16] 冯慈璋, 马西奎. 工程电磁场导论[M]. 北京: 高等教育出版社, 2000.
Abstract The geomagnetic simulation method is an effective measurement technique for obtaining the vertical induced magnetic field of ships in degaussing applications. However, its measurement accuracy is constrained by the uniformity of the simulated geomagnetic field, while generating a highly uniform simulated geomagnetic field introduces challenges such as construction difficulties and significantly increased costs. To address this issue, this paper proposes a multi-objective optimization design method for geomagnetic simulation coils, considering practical engineering conditions, to achieve a highly uniform simulated geomagnetic field while simultaneously reducing the required coil length and ampere-turns.
First, based on the measurement principle of the geomagnetic simulation method, the influence of field uniformity on the accuracy of acquiring the ship’s vertical induced magnetic field was quantitatively analyzed using the finite element method. Subsequently, considering the ship’s structure and practical constraints, a multi-objective optimization model was established, targeting field uniformity, coil dimensions, and ampere-turns. The model was solved using a genetic optimization algorithm. Finally, an experimental platform was designed and constructed for validation. The proposed multi-objective optimization method significantly reduces the total coil length and required ampere-turns while meeting uniformity design specifications, thereby achieving multiple desired objectives and improving the accuracy and feasibility of this measurement method in practical applications.
Numerical simulations based on a specific ship model demonstrate that, compared with single-objective optimization results, the proposed multi-objective optimization solution reduces the total coil length by 30% and the required ampere-turns by 19% without significantly compromising field uniformity, while satisfying multiple design objectives.
Experimental results from a scaled ship model show that the redesigned geomagnetic simulation coil system, optimized using the proposed multi-objective method, achieves a field uniformity of 91.37%, with other parameters such as coil length also reaching optimal levels. The measured accuracy of the ship model’s induced magnetic field Bz_iz using the geomagnetic simulation method reaches 95.91%, meeting practical engineering requirements.
Both simulation and experimental results lead to the following conclusion: Compared with single-objective optimization, the proposed multi-objective optimization method effectively reduces the total coil length and required ampere-turns while maintaining field uniformity, fulfilling multiple design objectives and improving the accuracy and feasibility of the geomagnetic simulation method in real-world applications.
keywords：Geomagnetic simulation method, ship’s induced magnetic field, uniformity, finite element method, genetic optimization algorithm
中图分类号：TM 153+.1
DOI: 10.19595/j.cnki.1000-6753.tces.242121
国家自然科学基金资助项目（52207020）。
收稿日期 2024-11-25
改稿日期 2025-07-06
吴轲娜 女，1989年生，博士研究生，研究方向为电工理论与新技术、电磁环境与防护技术。E-mail: kenawu@163.com
周国华 男，1981年生，教授，博士生导师，研究方向为电磁环境与防护技术、电磁场数值计算等。E-mail: 0910021008@nue.edu.cn（通信作者）
（编辑 郭丽军）