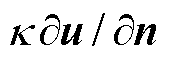 应当连续,即
应当连续,即摘要 基于深度神经网络的数据驱动算法已被广泛应用于电磁场快速求解,但其准确性高度依赖充足的样本数据,且在面对新数据时泛化能力较弱。相比之下,物理驱动算法通过引入物理先验知识,无需标注数据即可求解电磁场方程。然而在处理多介质场域问题时,介质间的交界条件需要额外添加损失函数约束,导致神经网络优化过程效率下降。同时,场域结构的复杂性又导致建模过程繁琐,限制了其广泛应用。深度里兹法(DRM)作为一种物理驱动算法,将里兹法与深度学习结合,构造基于能量泛函的损失函数,当其达到极值时,界面条件在泛函的意义上会自动得到满足,从而避免显式构造界面的损失。然而DRM采用神经网络输出作为试函数,尽管理论上界面条件得到满足,但由于神经网络试函数具有平滑拟合特性,实际计算中难以准确表征梯度剧烈变化的解,导致界面附近的误差增加。因此,该文提出一种改进的DRM架构,以增强其在训练过程中对界面特征的捕捉能力。通过对静电场和稳恒磁场的案例进行测试,与有限元计算结果进行对比,验证了该方法的有效性。
关键词:电磁场计算 物理驱动算法 深度里兹法 界面问题
在过去十年里,深度学习在处理文本和图像数据方面展现了显著的优势,并在计算机视觉和自然语言处理等领域取得了突破性进展。在工程领域,深度学习也成功应用于航空航天[1]、生物医学[2],尤其是电气和电子工程中[3-8]。深度神经网络能够有效处理高维参数空间,并从海量数据中提取关键特征,从而加速计算过程,推动了电磁场的快速计算[9]。
目前基于深度神经网络的数据驱动类算法,如U-net卷积神经网络,已经应用于快速求解各种物理场和工程问题[10-11],然而数据驱动算法计算结果的准确性与采集到的样本数量密切相关。实际中,无论是通过数值模拟还是实验测量得到的数据不可能无限多。在数据驱动的模式下,一方面,要在参数空间中加大样本数量以确保模型的准确性,从而大大增加了采样时间[9];另一方面,在许多物理和工程领域场景中,数据科学并没有结合已知的理论物理知识,如流体力学问题中的流场数据未结合质量守恒和动量守恒物理定律,即纳维-斯托克斯方程组(Navier-Stokes, N-S)方程,造成信息浪费,会出现模型收敛速度慢甚至是不收敛的情况,从而对计算精度产生影响[12-13],因此结合理论物理知识的物理驱动算法应运而生。
对于一个物理场过程或者系统的求解,实质上是求解基于这个物理场问题的参数化偏微分方程(Partial Differential Equations, PDEs)。物理驱动算法仅依赖物理规律来求解PDEs,无需标注数据。文献[14]提出的物理信息神经网络(Physics-Informed Neural Networks, PINNs),已广泛应用于单个和参数化PDEs的求解。文献[15]基于Petrov Galerkin方法与神经网络的相似性,提出了深度伽辽金方法(Deep Galerkin Method, DGM),通过将分片多项式基函数替换为神经网络空间,并在高维问题上进行了验证。文献[16]介绍了基于能量泛函的深度里兹法(Deep Ritz Method, DRM),旨在解决变分问题。与基于残差的PINNs相比,DRM通过降低微分算子的阶数实现了更快的收敛性,并降低了梯度消失或爆炸的可能。
物理驱动算法已经成功应用于温度场中的热传导问题[17]以及力学场中的线性弹性问题[18],但在电磁场计算中的应用仍较为有限。在电磁场中,涉及多种材料的界面问题增加了求解难度,现有网络结构在处理多区域高对比度系数的界面问题时,计算效率和精度均较低[19-20]。例如,在铸铁电机外壳与气隙之间,相对磁导率的差异可达200~400倍。在这些高对比度界面问题中,尽管函数是连续的,其梯度却剧烈变化,单一神经网络难以有效地表征这种变化[21]。文献[22-23]提出了处理介质不连续问题的分区域处理的方法,其实质是按照介质间的交界,将一个多介质边值问题转化为多个单一介质边值问题,再对界面条件进行处理。尽管采用多个神经网络可以在界面处逼近弱不连续解,但由此增加的损失函数数量使多目标优化过程极为复杂。此外,梯度下降算法需要同时更新多个神经网络的参数,导致反向传播次数增加,降低了计算效率[24]。并且对于如电机和变压器等具有复杂且不规则界面的模型,由于场域的结构复杂又导致了建模过程繁琐,构造界面损失函数条件的难度进一步增加,阻碍了物理驱动算法在电磁场计算中的深度应用。
本文基于深度里兹法,利用能量泛函描述物理系统,以解决电磁界面问题。针对神经网络试函数的平滑拟合特性,在网络结构中引入傅里叶特征,并采用自适应激活函数,增强了神经网络对界面特性的表征能力,并且结合硬边界条件和引入随机化低差异序列采样,进一步提高神经网络训练的稳定性。通过对静电场和稳恒磁场的案例进行测试,与有限元计算结果进行对比,验证了该方法的有效性。
设求解域G中包含有两种不同材料参数的介质,并且形成内部分界线L,如图1所示。在内部分界线处,材料参数k 是间断的。设分界线L把整个求解域分成Ga和Gb两个区域,L的外法线n规定为从Ga指向Gb,u表示场函数。根据电磁场的分界面条件,在L上u和切向分量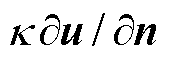 应当连续,即
应当连续,即
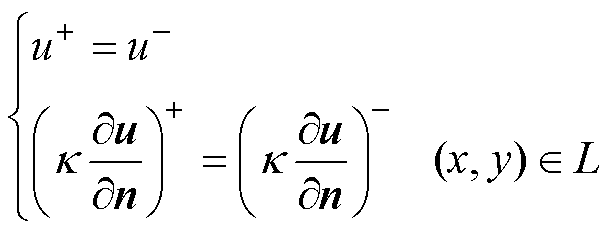 (1)
(1)
式中,上标+和-分别表示分面线L上某点的右极限和左极限。于是,当L上的材料参数k出现间断时,泊松方程的混合边值问题[25]写为
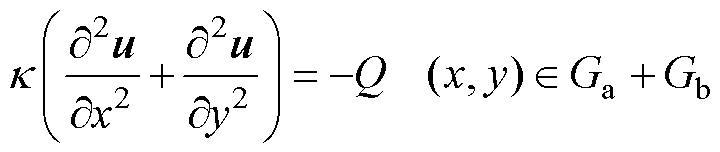 (2)
(2)
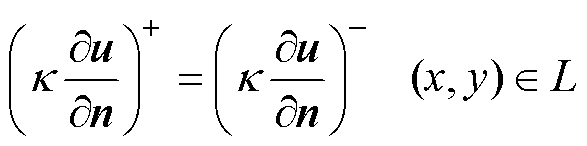 (3)
(3)
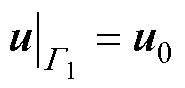 (4)
(4)
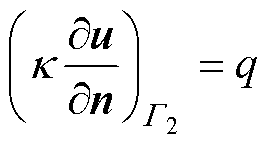 (5)
(5)
式中,Q为定义在区域内部的源项;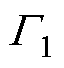 为具有第一类边界条件的边界,其中
为具有第一类边界条件的边界,其中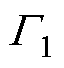 上给定边值u0,
上给定边值u0,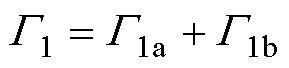 ,下角a和b分别表示属于Ga和Gb部分的边界;
,下角a和b分别表示属于Ga和Gb部分的边界;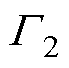 为具有第二类边界条件的边界,
为具有第二类边界条件的边界,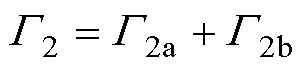 ,
, 上给定u的法向导数
上给定u的法向导数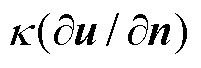 的值q。
的值q。
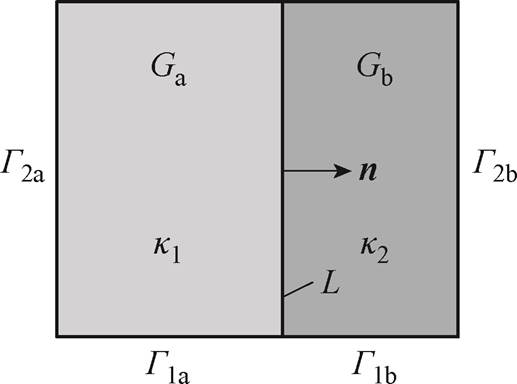
图1 电磁场界面问题
Fig.1 Electromagnetic interface problem
由于材料参数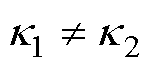 ,则根据式(2),可得
,则根据式(2),可得
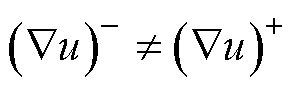 (6)
(6)
因此,u在材料界面L处不是连续可微的,其二阶偏导数不存在。
深度里兹法是基于深度神经网络(Deep Neural Network, DNN)的近似方法,适合于在变分偏微分方程公式引起的能量泛函最小化问题[16]。由变分原理可知,式(2)~式(5)的边值问题相应的泛函I(u)为
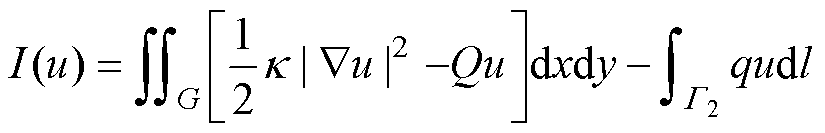 (7)
(7)
式(7)中的解u(x)可以用深度神经网络来近似,最常见的是使用多层感知器(Multilayer Perceptron, MLP),构造MLP需要神经元和网络层。神经元是深度神经网络的最小单位,其数学表达式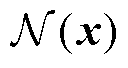 为
为
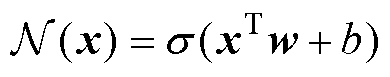 (8)
(8)
式中,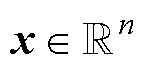 为输入向量;
为输入向量;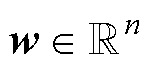 为权重向量;
为权重向量;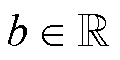 为偏置项;
为偏置项;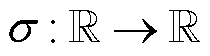 为被称为激活函数的非线性函数。接收相同输入的一组神经元形成一个层,该层的输出
为被称为激活函数的非线性函数。接收相同输入的一组神经元形成一个层,该层的输出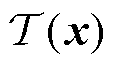 由式(9)给出。
由式(9)给出。
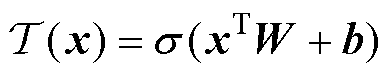 (9)
(9)
式中,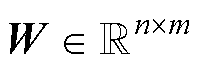 为连接各神经元权重的矩阵;
为连接各神经元权重的矩阵;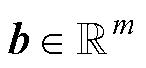 为相应的偏置向量;激活函数s以逐元素方式应用于该层的每个神经元。利用这些组件,可以通过一系列的线性变换和激活函数来构造一个连续的函数,即
为相应的偏置向量;激活函数s以逐元素方式应用于该层的每个神经元。利用这些组件,可以通过一系列的线性变换和激活函数来构造一个连续的函数,即
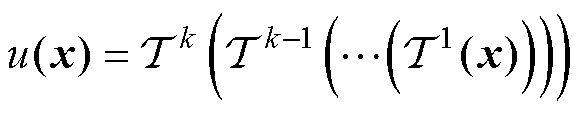 (10)
(10)
式中,k为神经网络的层数,其数量决定了神经网络的深度。该网络的权重与偏置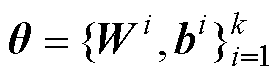 为可训练参数。
为可训练参数。
将神经网络的输出 作为试函数,其中u是Sobolev空间
作为试函数,其中u是Sobolev空间 中的试函数,将
中的试函数,将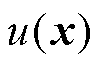 代入变分问题式(7),得到优化问题为
代入变分问题式(7),得到优化问题为
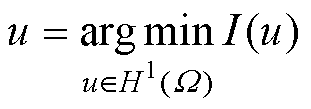 (11)
(11)
求边值问题式(2)~式(5),与在第一类边界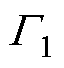 上满足
上满足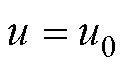 的条件下,求取泛函
的条件下,求取泛函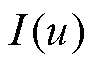 的极值等价,即等价于求解
的极值等价,即等价于求解
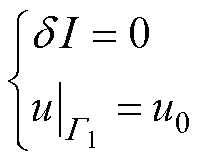 (12)
(12)
使u的容许函数在边界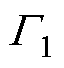 上满足
上满足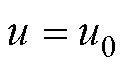 ,对u取变分
,对u取变分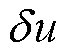 ,则有
,则有
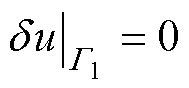 (13)
(13)
取泛函I的变分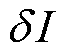 ,有
,有
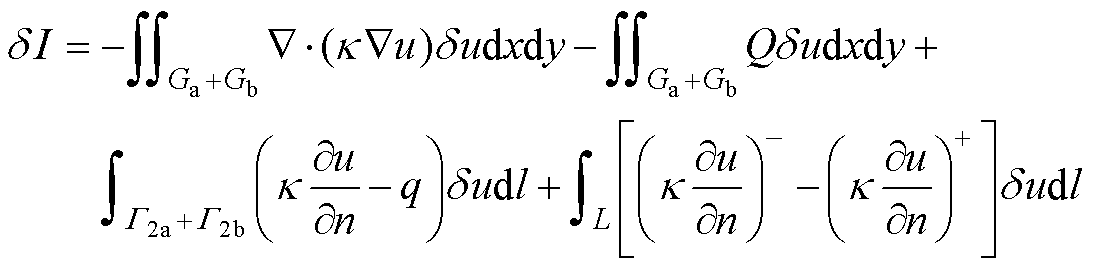 (14)
(14)
当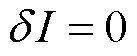 时,由于
时,由于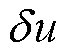 的任意性,故式(14)积分中的被积函数应分别为0,再加上第一类边界
的任意性,故式(14)积分中的被积函数应分别为0,再加上第一类边界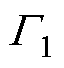 上的约束条件,即可得到式(2)~式(5)的边值问题。说明在优化问题中,当泛函达到极值时,极值函数
上的约束条件,即可得到式(2)~式(5)的边值问题。说明在优化问题中,当泛函达到极值时,极值函数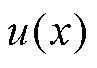 将是泊松方程混合边值问题的解,即变分问题式(7)与边值问题式(2)~式(5)等价。
将是泊松方程混合边值问题的解,即变分问题式(7)与边值问题式(2)~式(5)等价。
因此,通过式(7)定义损失函数,电磁界面问题的表达式(1)可以在优化器最小化损失函数的过程中自动得到满足,从而实现利用单一神经网络求解电磁界面问题,不需要额外构造界面损失,避免了多目标优化的复杂性。然而深度里兹法(DRM)采用神经网络输出作为试验函数,尽管理论上界面条件得到满足,但由于神经网络试函数具有平滑拟合特性,实际计算中难以准确表征梯度剧烈变化的解,导致界面附近的误差增加。
神经网络求解器的成功关键在于激活函数。几种激活函数的对比如图2所示。根据复合函数连续性定义,如果对位置信息进行编码并使用平滑激活函数,DNN的输出是平滑的,物理驱动算法中常用的激活函数为双曲正切(tanh),定义为
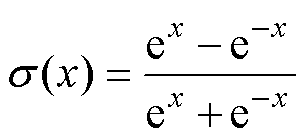 (15)
(15)
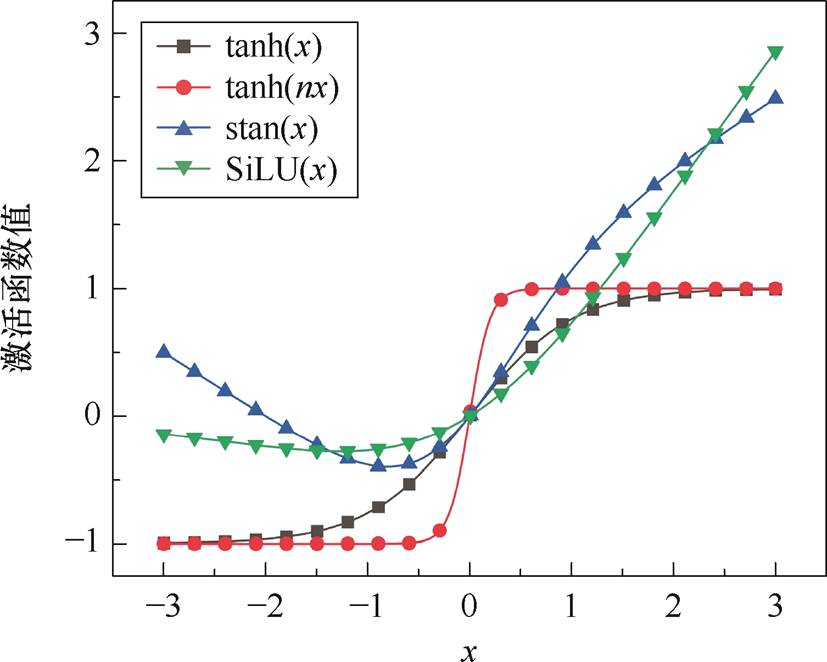
图2 激活函数对比
Fig.2 Comparison of activation functions
tanh导数范围为[0, 1],尤其位于饱和区时导数值非常小,这不利于表达电磁PDE解的特性,如弱不连续、高梯度等。在高梯度问题中,自适应tanh激活函数通过调节激活函数的斜率来提高网络捕获高频特征的能力。
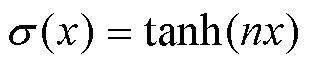 (16)
(16)
式中,n为一个可训练的参数。自适应tanh激活函数及其代理的微分特性如图3所示。图3a中,随着x的增加,tanh函数的斜率在零点附近变得更陡峭,使得激活函数在输入空间的小变化下产生更显著的输出差异。这种陡峭的特性使神经网络能够更精细地表示输出,从而提高了对高频或急剧变化特征的建模能力。
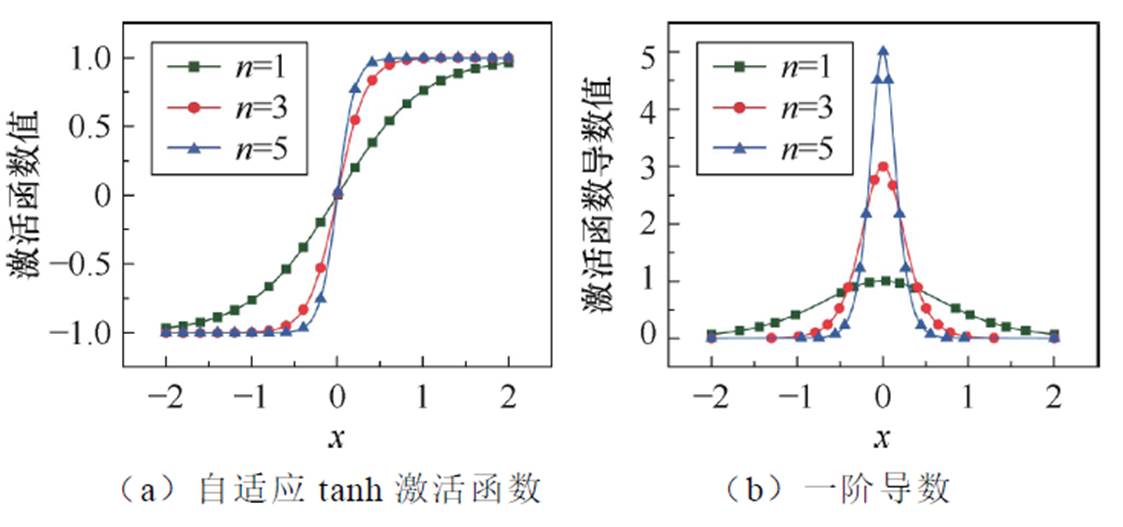
图3 自适应tanh激活函数及其代理的微分特性
Fig.3 Differential properties of adaptive tanh activation and its surrogate model
并且stan激活函数通过加入非线性项[26],也可以提高tanh激活函数的拟合能力,其表达式为
 (17)
(17)
式中,b为可学习参数,右端bx中x的引入增强了该激活函数的非线性,b的引入使得tanh斜率变大。stan激活函数及其代理的微分特性如图4所示。图4b表明,随着b的增大,代理的梯度也随之增大。自适应tanh与stan激活函数是对于弱不连续问题的光滑拟合,使得网络能够更好地适应界面条件,该特性适合拟合电磁PDE的解。
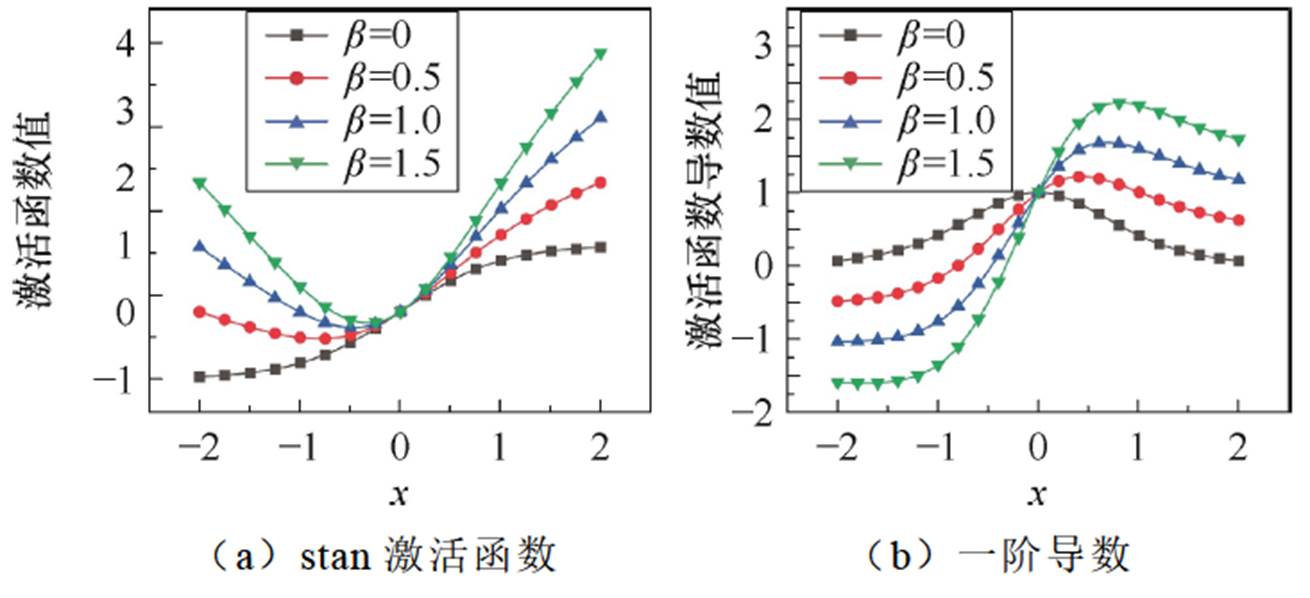
图4 stan激活函数及其代理的微分特性
Fig.4 Differential properties of stan activation and its surrogate model
在电磁场中,界面问题通常涉及不同材料之间的边界,这些边界处的电磁特性(如介电常数、电导率或磁导率)可能发生突变,导致电磁场在这些界面附近呈现显著的梯度或高频特征。
在神经网络的训练过程中,通常表现出一种频谱偏移特性,即优先学习低频信息。这些低频信息通常具有平滑且变化缓慢的特征。而高频信息,即快速变化的细节,往往在训练初期难以被有效捕获。这一特性使得神经网络在处理电磁界面问题时,可能无法充分学习界面处的高频变化细节,从而影响模型的精度和适用性。为了克服这一问题,神经网络的输入需经过一个编码层[27],以解决频谱偏移的“病”理现象,使得神经网络能够更有效地捕捉到电磁场界面上的高频特征。
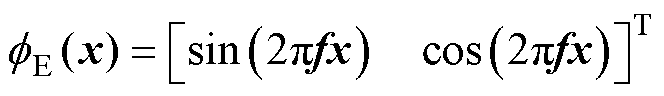 (18)
(18)
式中,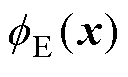 为对输入特征进行傅里叶特征映射;
为对输入特征进行傅里叶特征映射;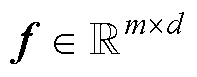 表示对将d维输入特征映射成m维,f服从均值为0、方差为s2的正态分布,f的作用为将神经网络的输入特征x在频域空间内映射成众多频域下的x,从而加快神经网络对于高频分量的捕捉能力和收敛速度。
表示对将d维输入特征映射成m维,f服从均值为0、方差为s2的正态分布,f的作用为将神经网络的输入特征x在频域空间内映射成众多频域下的x,从而加快神经网络对于高频分量的捕捉能力和收敛速度。
施加边界条件是物理驱动算法成功实现的关键。由式(14)可知,第二类边界条件可以在最小化能量泛函的过程中自动满足,因此不必单独考虑。而在第一类边界条件中,解决这一问题的一个常见方法是通过引入一个软约束。具体来说,这涉及在式(7)定义的函数中添加一个边界积分项,从而得到
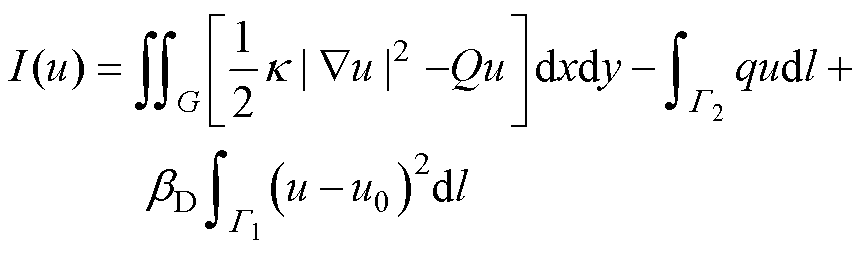 (19)
(19)
式中,bD为一个标量惩罚因子。
还有另外一种施加边界条件的方法就是硬边界条件[28]。其核心思想是将边界条件直接硬编码到神经网络中,通过将网络解作为插值函数和滤波函数的重新表达,精确边界条件成为预测解的一部分,具有精确边界条件的神经网络预测解可以表达为
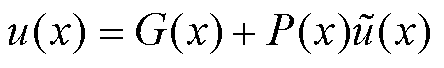 (20)
(20)
式中,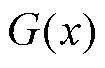 为插值函数;
为插值函数;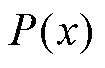 为波函数;
为波函数;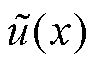 为施加硬边界条件之前的神经网络输出
为施加硬边界条件之前的神经网络输出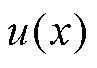 。
。
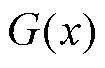 为插值边界条件的函数,在域中的任何位置,
为插值边界条件的函数,在域中的任何位置,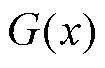 返回一个只基于域边界值的近似解,通过使用如逆距离加权(Inverse Distance Weighting, IDW)的插值方法,可以将边界条件的影响传递到域内部,该方法中权重随距离变化。IDW首先测量从边界点到领域内部的距离,然后根据距离计算每个边界点的加权值。
返回一个只基于域边界值的近似解,通过使用如逆距离加权(Inverse Distance Weighting, IDW)的插值方法,可以将边界条件的影响传递到域内部,该方法中权重随距离变化。IDW首先测量从边界点到领域内部的距离,然后根据距离计算每个边界点的加权值。
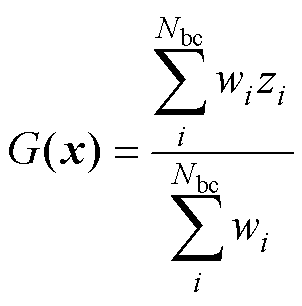 (21)
(21)
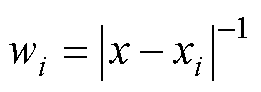 (22)
(22)
式中,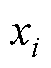 为第i个边界点坐标;
为第i个边界点坐标;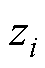 为边界条件值;Nbc为参与插值的点数。当配置点与边界条件点重合时,即
为边界条件值;Nbc为参与插值的点数。当配置点与边界条件点重合时,即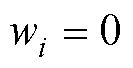 的情况下,需要通过在
的情况下,需要通过在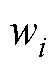 上加一个大于0的小值来避免除零错误。滤波函数
上加一个大于0的小值来避免除零错误。滤波函数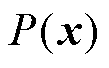 是精确施加边界条件的第二部分,其通过缩放网络输出并在靠近边界条件的区域减少输出贡献来发挥作用,
是精确施加边界条件的第二部分,其通过缩放网络输出并在靠近边界条件的区域减少输出贡献来发挥作用,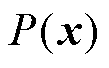 应平滑并且根据域的形状选择。根据域的形状和需要强制执行的边界条件,滤波函数可以采取不同的形状,对于正方形域,通常选择的滤波函数为
应平滑并且根据域的形状选择。根据域的形状和需要强制执行的边界条件,滤波函数可以采取不同的形状,对于正方形域,通常选择的滤波函数为
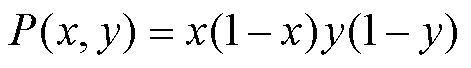 (23)
(23)
式中,x和y为域中的位置,其宽度和高度范围在[0, 1]之间。
通过数值积分离散能量函数式(7),得到了DNN训练过程中最小的损失函数。能量泛函是用伪随机样本进行离散化的,本文所选择的离散化方法是蒙特卡洛积分,引入一组在求解区域内部采样的训练点:选取M个域内点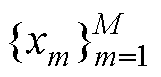 ,以及R个在边界
,以及R个在边界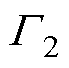 上采样的训练点
上采样的训练点 ,用神经网络的输出
,用神经网络的输出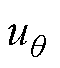 近似真实解u,因此离散化的能量泛函可表示为
近似真实解u,因此离散化的能量泛函可表示为
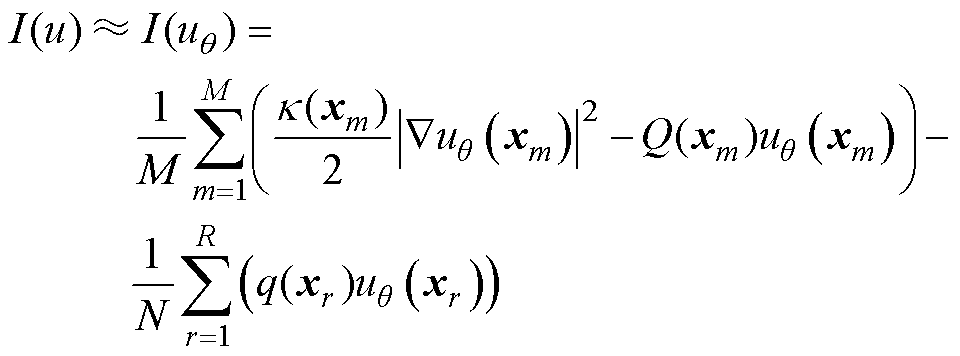 (24)
(24)
尽管该能量泛函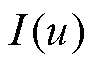 存在全局最小值,但在网络参数空间中可能存在局部最小值。此外,由于在每次迭代中重新选择训练点,每次迭代的损失情况将是不同的。因此,在本文中使用自适应矩估计(Adaptive Moment Estimation, Adam)算法[29],其可以处理稀疏梯度和非平稳目标,按照式(25)来迭代更新参数向量q。
存在全局最小值,但在网络参数空间中可能存在局部最小值。此外,由于在每次迭代中重新选择训练点,每次迭代的损失情况将是不同的。因此,在本文中使用自适应矩估计(Adaptive Moment Estimation, Adam)算法[29],其可以处理稀疏梯度和非平稳目标,按照式(25)来迭代更新参数向量q。
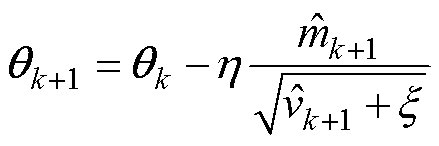 (25)
(25)
式中,h为学习率,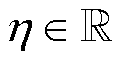 ;
;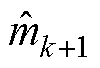 为偏置校正后的一阶矩估计;
为偏置校正后的一阶矩估计;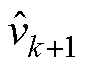 为偏置校正后的二阶矩估计;
为偏置校正后的二阶矩估计;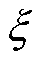 为一个小常数,用于防止出现除以零的情况。所有在式(25)中的运算都是逐元素进行的,DNN的参数向量q 的初始值通过Xavier初始化方法获得,关于空间坐标及可训练参数的导数计算,均使用自动微分技术得到。本文所采用的算法在电磁场求解中的应用过程如图5所示。
为一个小常数,用于防止出现除以零的情况。所有在式(25)中的运算都是逐元素进行的,DNN的参数向量q 的初始值通过Xavier初始化方法获得,关于空间坐标及可训练参数的导数计算,均使用自动微分技术得到。本文所采用的算法在电磁场求解中的应用过程如图5所示。
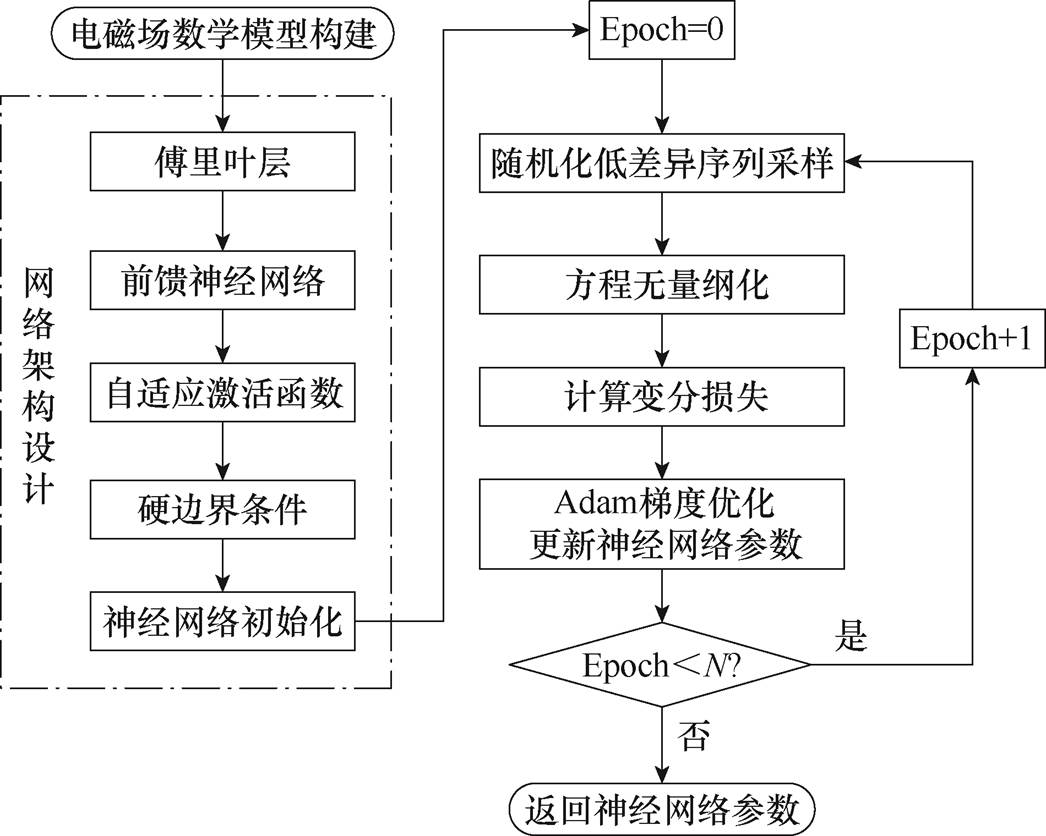
图5 算法流程
Fig.5 Algorithm flow chart
改进的DRM基于PyTorch框架实现,并采用一个全连接神经网络来逼近域内解。所使用的神经网络架构由三个隐藏层组成,每层包含100个神经元。
本节研究了电机齿槽结构导致的复杂界面问题,研究模型选取电机一个极距范围内的区域[30]。为简化建模,将定子内侧圆弧替换为直线处理。电机的轴向结构规则,可作为二维场进行分析;忽略磁饱和现象,铁磁介质的磁导率取自磁化曲线的直线部分;物理模型包括定子铁心、气隙、转子磁极、极间空气和励磁绕组区域。在空载情况下,磁场由励磁电流产生,不受电枢反应影响。
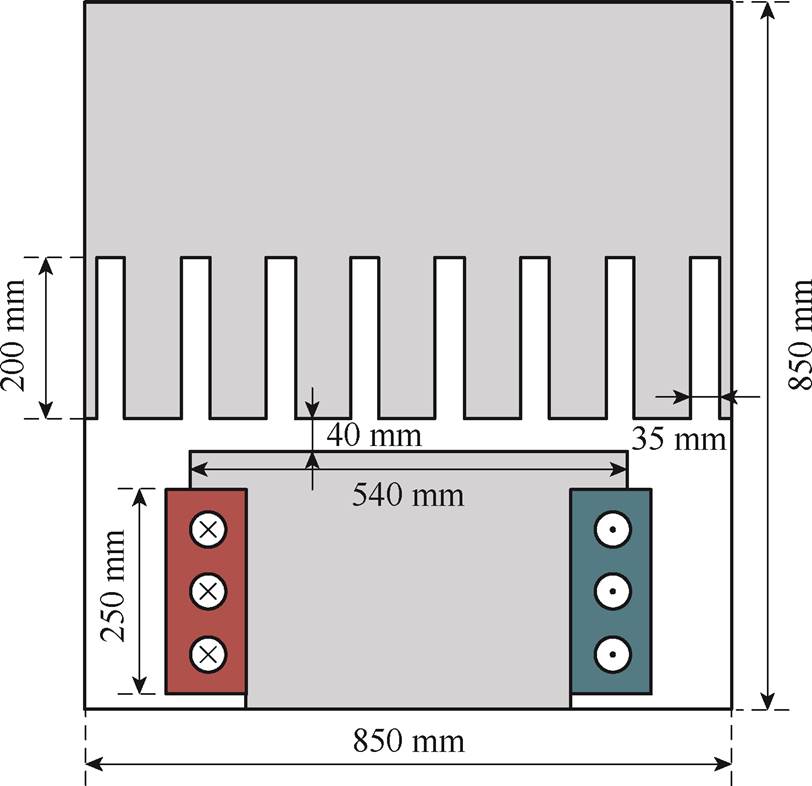
图6 简化电机模型
Fig.6 Simplified motor model
稳恒磁场的控制方程由式(26)给出。针对二维磁场,由于励磁绕组的电流密度J垂直于平面,这意味着只有z方向分量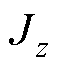 非零,磁矢势也将仅存在非零的z方向分量
非零,磁矢势也将仅存在非零的z方向分量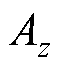 ,空气和导线的磁导率为
,空气和导线的磁导率为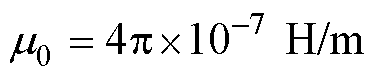 ,铁心的磁导率为
,铁心的磁导率为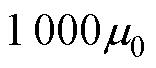 。空载励磁电流密度为
。空载励磁电流密度为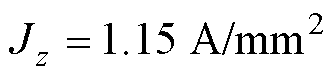 。
。
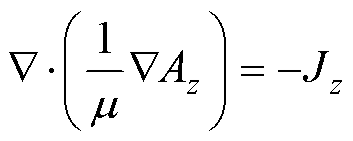 (26)
(26)
定子铁心侧边界施加第一类边界条件:
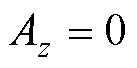 (27)
(27)
其余边界施加第二类边界条件:
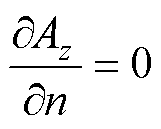 (28)
(28)
第二类边界条件在泛函方程中自动满足,不必处理,根据控制方程构造能量泛函,即
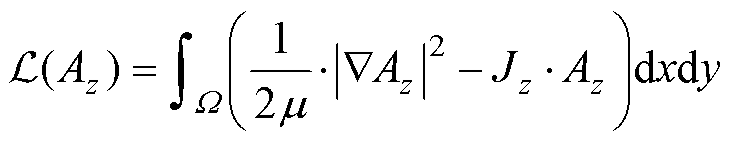 (29)
(29)
式中,积分区域W为整个电机的计算区域。
在神经网络训练过程中,恒定磁场的一个主要问题影响模型的收敛速度和稳定性:源项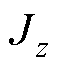 会导致初始权重参数的梯度增大异常,可能在训练初期引起梯度爆炸,阻碍网络的正常收敛。这一现象不同于DNN中常见的由激活函数引起的梯度爆炸,而是由PDEs本身的特性所致,往往导致训练不稳定,使得神经网络的训练过程变得缓慢且更容易受到数值误差的影响。数据驱动算法的解决方案通常采用归一化技术,但对x和y等参数的归一化可能导致梯度计算不准确,本文借鉴流体动力学中广泛应用的无量纲方程,以规避梯度爆炸问题。
会导致初始权重参数的梯度增大异常,可能在训练初期引起梯度爆炸,阻碍网络的正常收敛。这一现象不同于DNN中常见的由激活函数引起的梯度爆炸,而是由PDEs本身的特性所致,往往导致训练不稳定,使得神经网络的训练过程变得缓慢且更容易受到数值误差的影响。数据驱动算法的解决方案通常采用归一化技术,但对x和y等参数的归一化可能导致梯度计算不准确,本文借鉴流体动力学中广泛应用的无量纲方程,以规避梯度爆炸问题。
取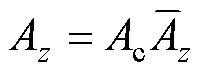 ,
, 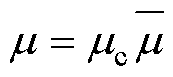 ,
, 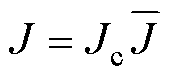 ,
, 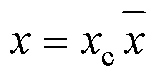 ,
, 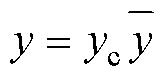 , 式中,上方加“-”表示无量纲化之后的物理量。其中
, 式中,上方加“-”表示无量纲化之后的物理量。其中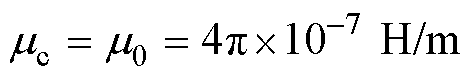 ,
, 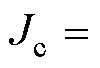
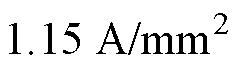 ,
,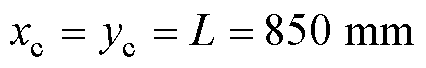 ,可以得到无量纲公式为
,可以得到无量纲公式为
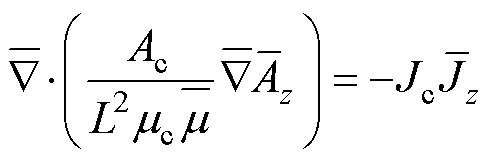 (30)
(30)
取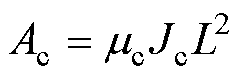 可得
可得
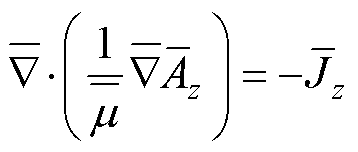 (31)
(31)
对式(31)求解后,通过伸缩变换返回到原变量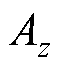 ,即
,即
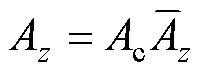 (32)
(32)
本文采用L2相对误差(L2 Relative Error, L2RE)来判断DRM的准确性,其是物理驱动算法中的一个标准误差度量,量化了总体误差[14],计算公式为
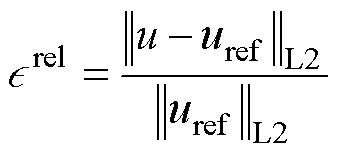 (33)
(33)
式中,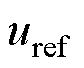 为参考解,例如有限元法解或解析解;
为参考解,例如有限元法解或解析解;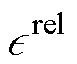 为L2相对误差。
为L2相对误差。
深度里兹法在解决物理问题时,对采样点的选择具有严格要求。本文中式(24)采用蒙特卡洛积分来估计损失函数,数值结果的准确性与采样方法密切相关。首先,低差异序列采样与传统随机采样在分布特性上存在显著区别,如图7所示,低差异序列(如Sobol序列)通过优化采样点的分布,使其在多维空间中尽可能均匀覆盖,从而减少数值积分的误差。相比之下,传统的随机采样方法生成的采样点往往存在聚集和空洞现象,导致积分估计的精度较低。理论上,拟蒙特卡罗积分,采用低差异序列时,其收敛速度可以达到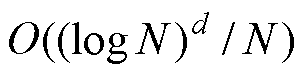 ,其中N为采样点数量,d为维度;而传统蒙特卡洛方法的收敛速度为
,其中N为采样点数量,d为维度;而传统蒙特卡洛方法的收敛速度为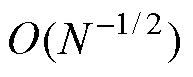 。这种更快的收敛速度意味着在相同的采样数量下,低差异序列能够提供更小的估计误差[31]。
。这种更快的收敛速度意味着在相同的采样数量下,低差异序列能够提供更小的估计误差[31]。

图7 不同采样序列对比
Fig.7 Comparison of different sampling sequences
本节在神经网络结构中嵌入傅里叶特征,并采用硬边界条件,激活函数使用自适应tanh激活函数,针对五种不同采样类别进行训练对比,如图8所示,当仅使用固定采样点进行训练时,尽管在训练初期模型的L2相对误差逐渐下降,但随着训练的深入,模型可能出现发散现象。这种现象称为过拟合,即模型过度拟合了训练数据中的细节,导致在新数据上的泛化性能下降。即便训练点数量远超模型参数的数量,过拟合问题仍有可能发生。
为了解决此问题,本文采用了在每次迭代中随机重新选择训练点的方法,由于在整个优化过程中训练集不断更新,每次迭代的损失评估基于新的采样点集合,从而有效避免了固有的过拟合问题。为了进一步增强低差异序列的适应性,本文引入随机化低差异序列(Owen scrambling),以增加序列的随机性,从而降低特定类型问题中的偏差和模式效应。随机化处理使得结果更加稳定,从图8可以看出,随机化低差异序列的收敛速度最快最稳定,这与理论结果相吻合。
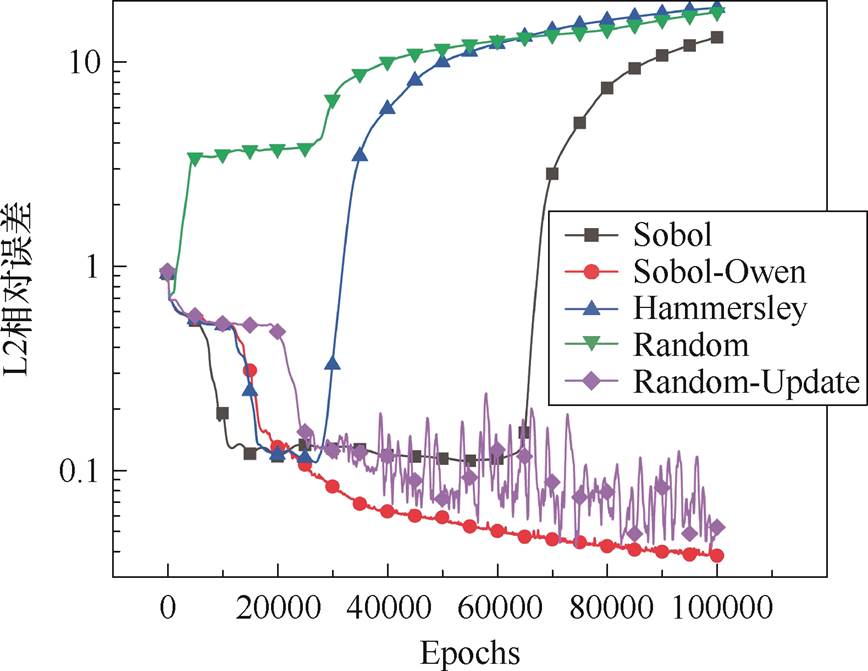
图8 不同采样序列训练对比
Fig.8 Comparison of training with different sampling sequences
为了验证激活函数对神经网络捕捉高频特征的效果,本小节分别选用了SiLU、tanh、tanh(nx)和stan激活函数进行实验比较。在神经网络结构中采用硬边界条件,采样方式选取随机化低差异序列,实验结果如图9所示。结果显示,SiLU激活函数的效果最差,而tanh(nx)和stan激活函数在捕获高频特征方面表现突出,特别是在训练初期L2相对误差下降速度更快,表明它们在适应高梯度区域和提升网络拟合能力方面具有优势。因此,在界面问题中,tanh(nx)和stan激活函数尤其有效,因为它们通过灵活调整斜率或加入非线性项,更好地适应了材料界面处的急剧变化,提高了神经网络对界面区域的拟合精度和稳定性。相比之下,标准tanh激活函数的表现略差。
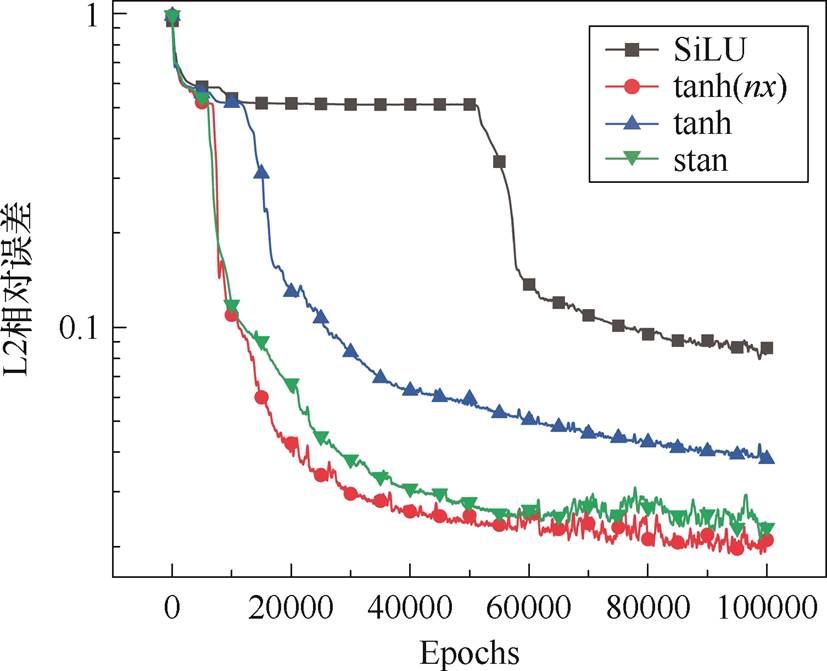
图9 不同激活函数训练对比
Fig.9 Comparison of training with different activation functions
在本小节中,通过比较四种不同配置,探讨傅里叶变换和硬边界条件对模型性能的影响。采样方式选取随机化低差异序列,激活函数使用tanh激活函数。具体的四种配置分别为:配置A(无傅里叶变换,无硬边界条件)、配置B(无傅里叶变换,应用硬边界条件)、配置C(应用傅里叶变换,无硬边界条件)、配置D(应用傅里叶变换,应用硬边界条件)。不同配置训练对比如图10所示。通过对不同配置下L2相对误差的分析,观察到傅里叶变换的应用,尤其是在配置C和配置D中,傅里叶特征成功捕捉了由于界面条件导致的高频特征,显著加快了模型在训练的收敛速度。此外,硬边界条件为模型提供了稳定的约束,有助于提高训练过程的稳定性和模型的泛化能力。配置C虽然在训练初期表现出快速误差下降,但由于缺乏硬边界条件,其后期的泛化能力略显不足,甚至训练误差有上升的趋势。整体趋势表明,配置D在所有配置中表现最佳,其误差迅速降低并维持在较低水平,表明在深度里兹法中,通过将傅里叶变换与硬边界条件的结合显著提升了模型的初期学习效率和长期性能的稳定性。
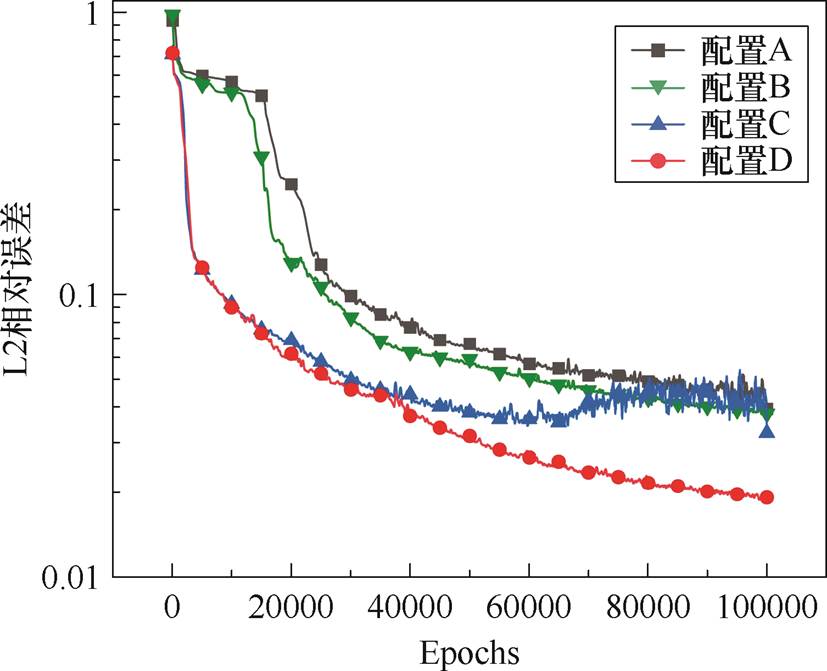
图10 不同配置训练对比
Fig.10 Comparison of training with different configurations
基于上述实验结果,为了提高DRM在界面问题中的识别能力,在神经网络结构中引入傅里叶特征变换,且采用自适应tanh激活函数。此外,使用硬边界条件,还通过随机化的低差异序列对模型中的2×104个点进行采样。经过1×105轮训练后,在计算域内生成了100×100个均匀采样点,最终得到了模型的磁势分布。与有限元解逐点对比误差如图11所示,L2相对误差为1.03%。进一步对磁势进行后处理得到磁通密度,与有限元解逐点对比误差如图12所示,L2相对误差为2.59%。
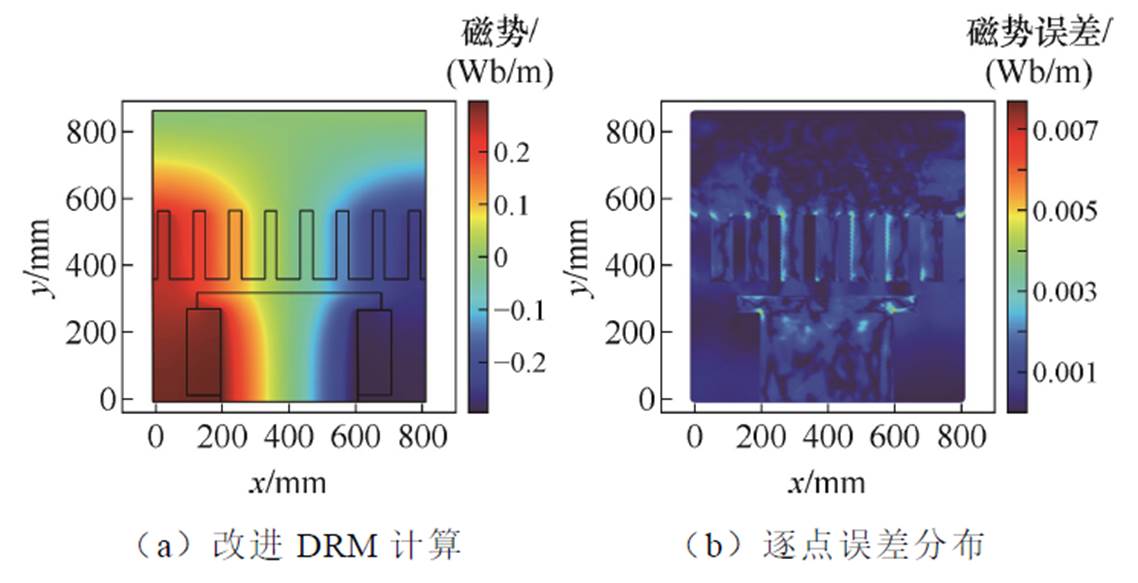
图11 磁势计算结果对比
Fig.11 Comparison of magnetic vector potential calculation results
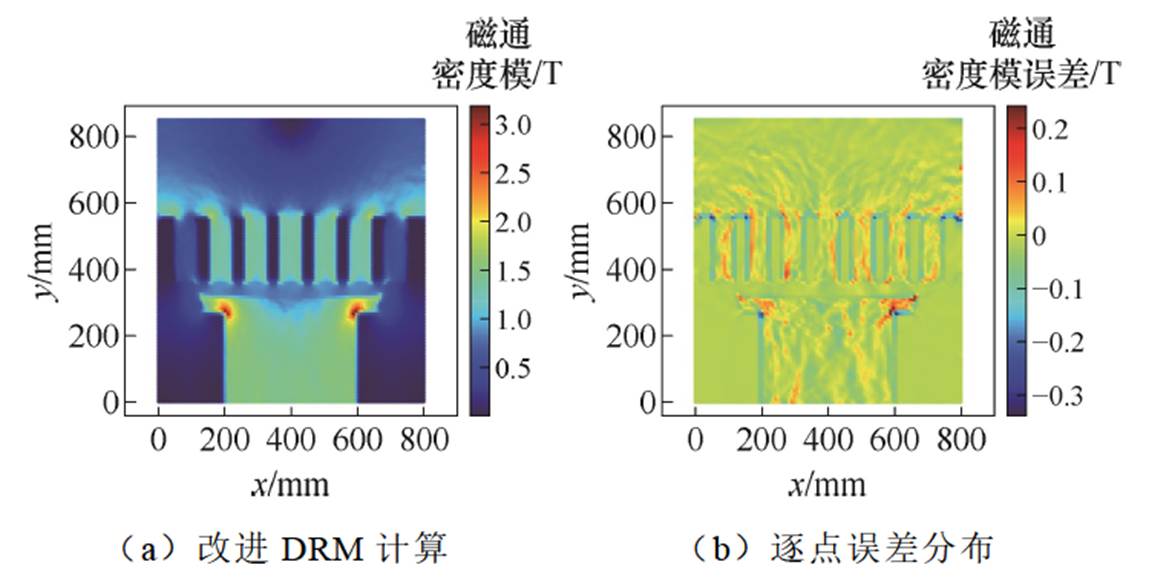
图12 磁通密度模值计算结果对比
Fig.12 Comparison of Magnetic flux density norm calculation results
改进后的DRM算法与原始DRM算法进行的对比分析结果如图13所示。结果表明,改进后的DRM算法在收敛速度和稳定性上都有显著提升。在相同轮次训练后,改进网络的磁势误差降低至1.03%,而未修改的网络误差则为5.46%。
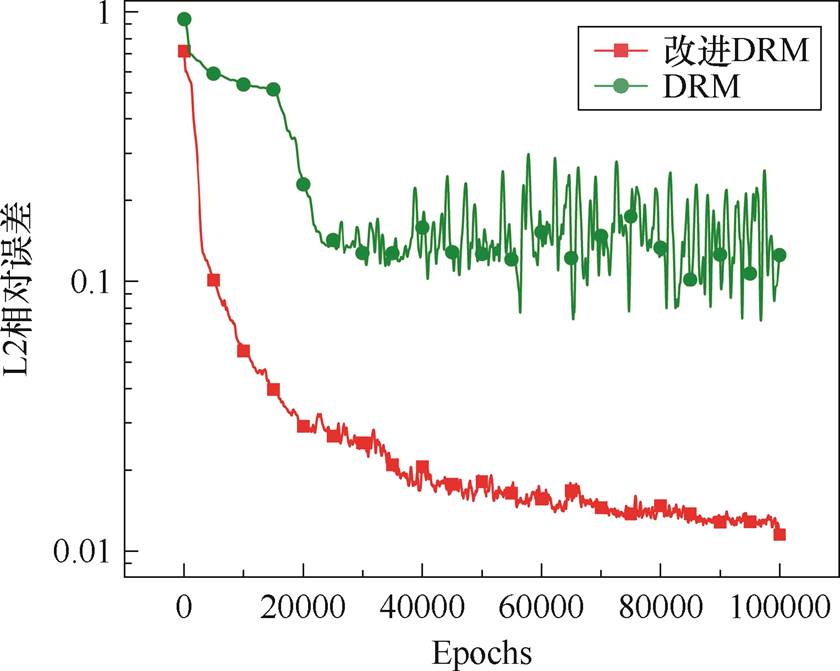
图13 磁场训练结果对比
Fig.13 Comparison of magnetic field training results
在平行平面场中,磁力线图就是矢量磁位的等位线图。改进后DRM和FEM计算的磁力线图如图14所示。从图14可知,空载磁场分布与实际情况基本符合。由于场域结构对称,磁力线沿中轴线对称分布,与有限元计算结果对比,可以看出两种算法的结果是一致的。
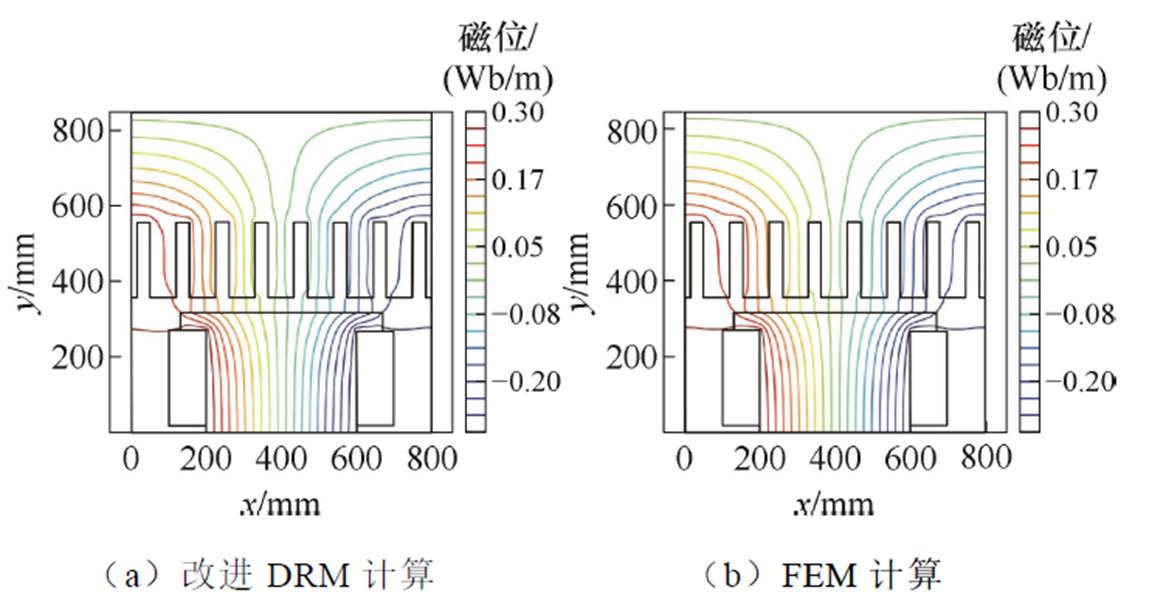
图14 磁力线对比
Fig.14 Comparison of magnetic field lines
为了展示改进的DRM算法对界面的处理效果,将其与有限元法以及原始DRM算法进行比较,选择在x=190 mm和y=500 mm处的磁势进行对比,结果如图15所示。从图15中可以看出,由于不同材料界面的存在,磁势在分界面处虽然保持连续性,但其一阶导数发生了跳跃,导致磁势表现出不平滑的特性。正是这种不光滑性增加了神经网络在学习过程中的难度,而改进的DRM方法所计算出的磁势与有限元法的结果几乎一致,成功地捕捉到了磁势一阶导数的跳跃特性,克服了由于不光滑性给学习过程带来的难度,而原始的DRM算法则很难准确捕捉到界面处的特性。
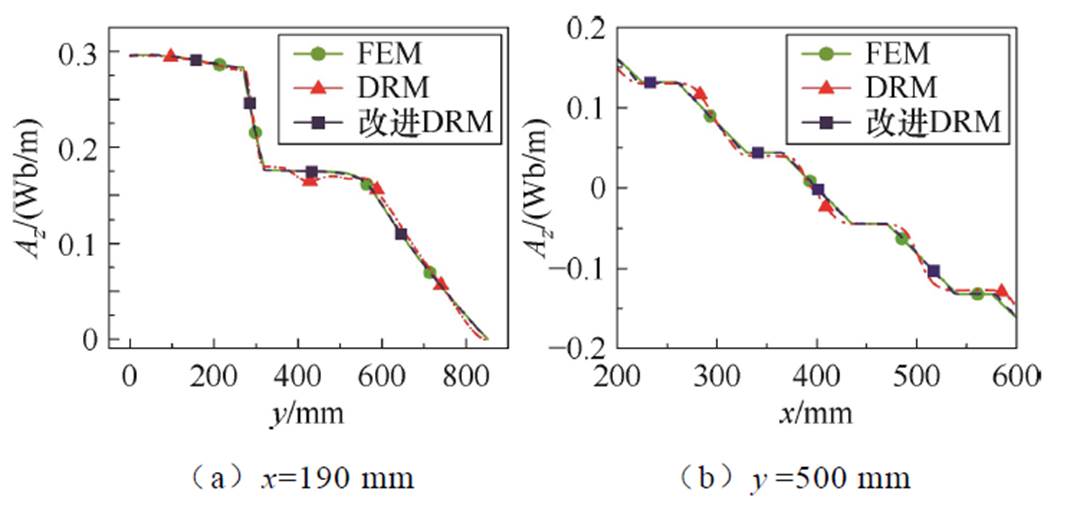
图15 界面处磁势计算结果对比
Fig.15 Comparison of magnetic potential calculation results at the interface
在介质阻挡放电(Dielectric Barrier Discharge,DBD)过程中,电场的计算至关重要。电场分布不仅受介电材料性质的影响,还与介质几何结构密切相关,例如,在DBD应用中,催化剂通常采用介电材料制成的催化剂球进行填充,从而调控空间中的电势分布。基于这一背景,文献[32]将DBD模型简化为三个介电球与一个介电板之间的电场,模型结构如图16所示。
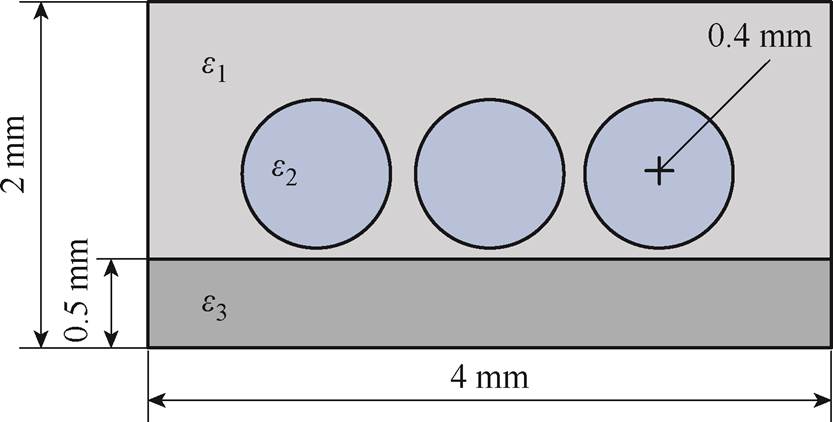
图16 介质阻挡放电模型
Fig.16 Dielectricbarrier discharge model
静电场的控制方程由式(34)给出,e为相对介电常数,j为电势。三种材料的相对介电常数分别选取为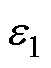 =1,
=1, 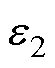 =4,
=4, 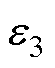 =0.1。对介电板的一边加100 V的电压,其他边接地,如式(35)所示。
=0.1。对介电板的一边加100 V的电压,其他边接地,如式(35)所示。
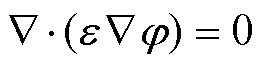 (34)
(34)
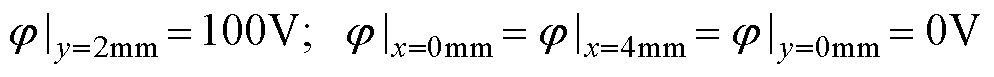 (35)
(35)
同样采取3.5节的训练方法进行训练。在经过6×104轮训练完成后,在计算域内生成了100×100个均匀采样点,最终得到该模型的电势分布以及和有限元解相比的逐点误差,结果如图17所示,与有限元结果相比,L2相对误差为1.49%。由于上边界附近左右两侧的电场梯度变化较大,中间的梯度变化较小,因此等势线为向下突出的对称弧,但在图17b中,相对误差在角点周围较大,经过统计得出最大的相对误差仅在上边界两个角点处,该位置是几乎所有数值计算错误的点,可忽略不计。因此为了更好地展示细节,截取了域的一部分进行电场强度模的计算,如图18所示,与有限元结果相比L2相对误差为2.35%。
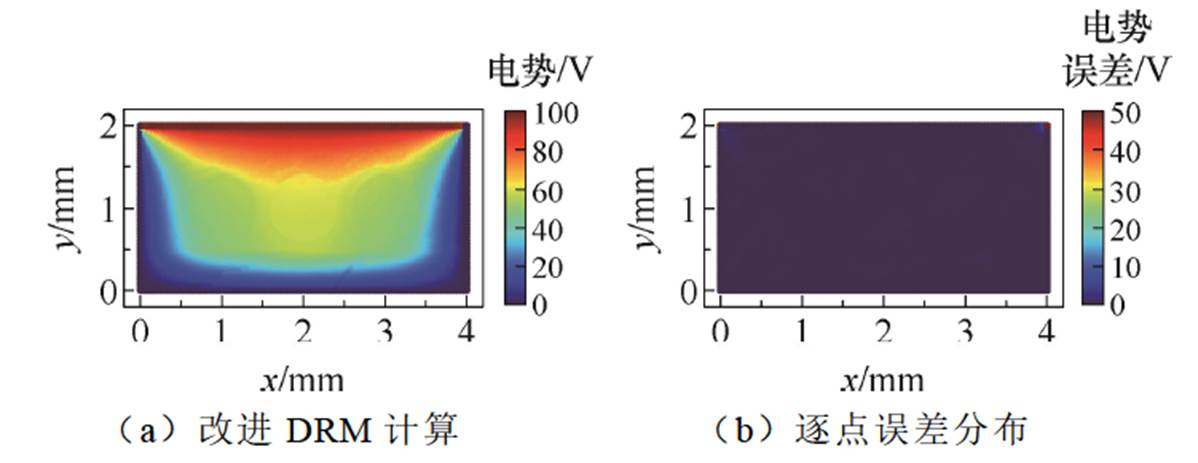
图17 电势计算结果对比
Fig.17 Comparison of electric potential calculation results
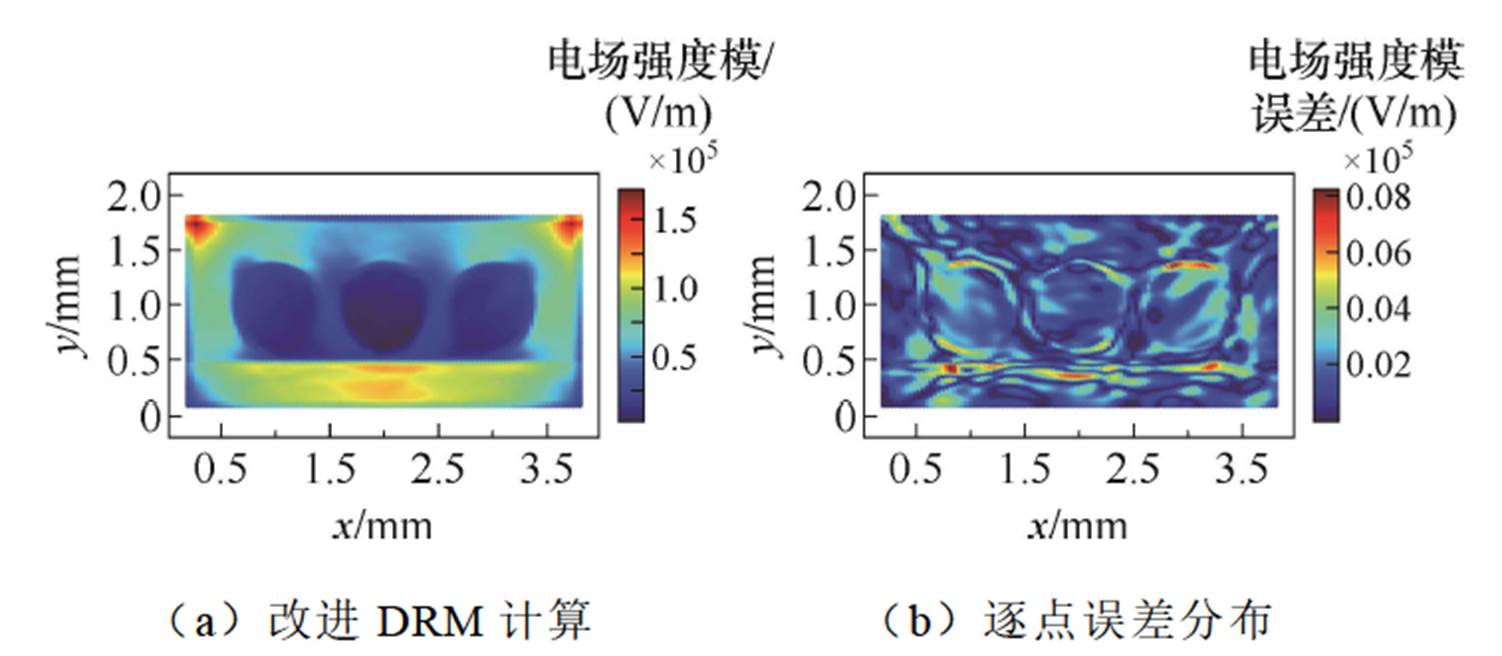
图18 电场强度模计算结果对比
Fig.18 Comparison of electric field norm calculation results
在相同轮次训练后L2相对误差对比如图19所示,改进DRM网络的电势误差降低至1.49%,而未修改的网络误差则为4.43%。
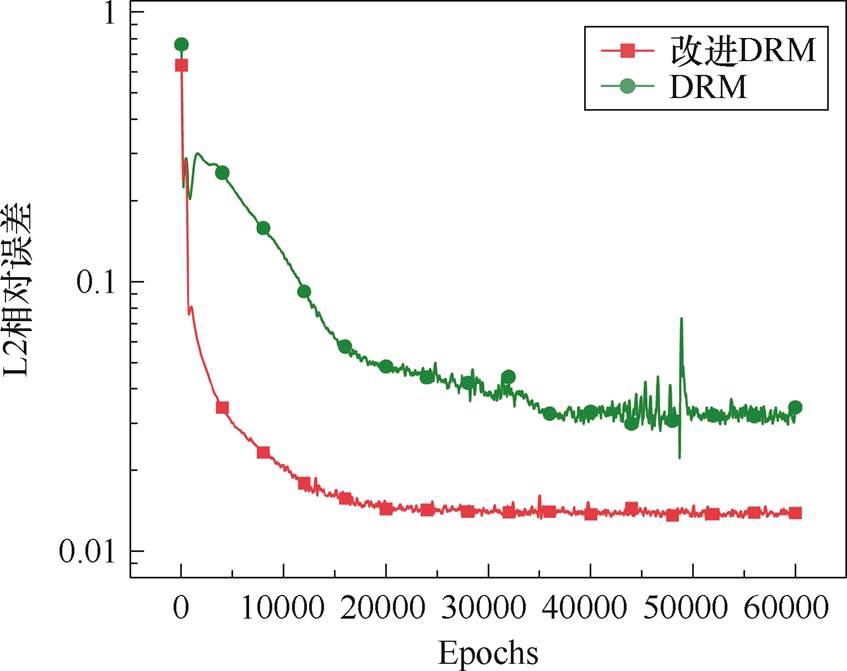
图19 电场训练结果对比
Fig.19 Comparison of electric field training results
同样地,比较有限元法与改进的DRM方法以及原始的DRM方法,选择在x=2 mm和y=1 mm处的电势进行对比,如图20所示,改进的DRM方法所计算出的电势与有限元法的结果几乎一致。原始的DRM算法则完全未捕捉到界面处的特性,偏差较大。
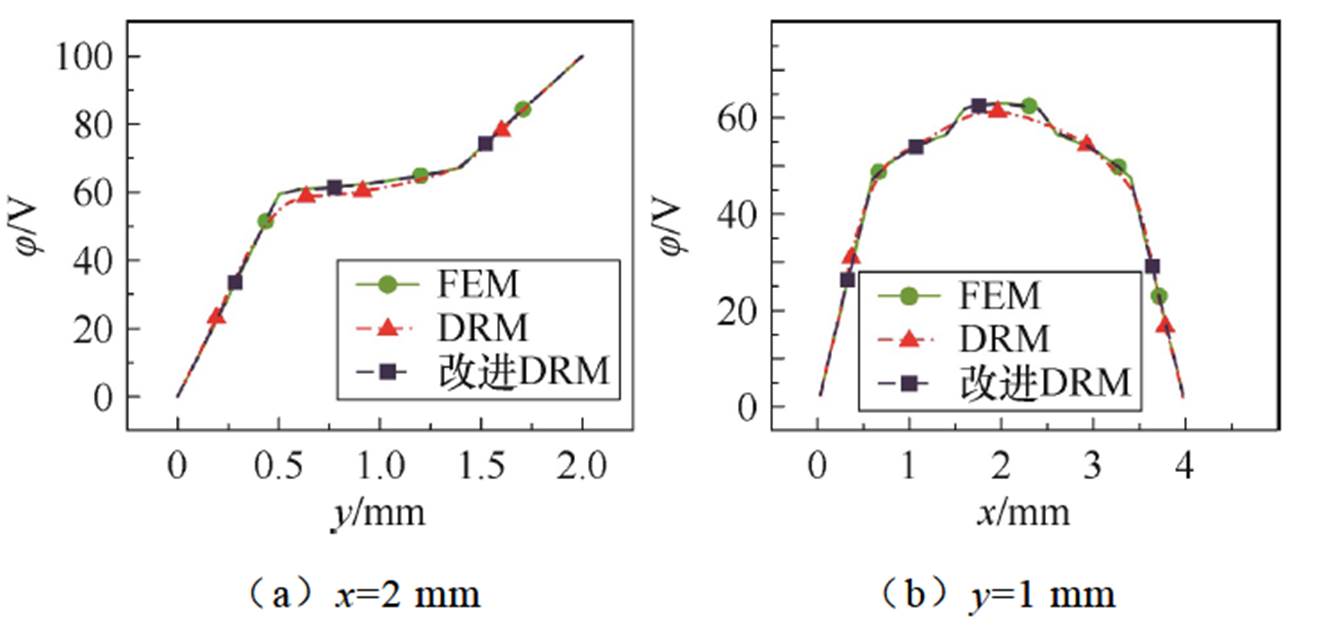
图20 界面处电势计算结果对比
Fig.20 Comparison of electric potential calculation results at the interface
针对物理驱动算法在复杂多介质场域中的应用,本文提出了一种基于深度里兹法的电磁场计算方法,主要结论如下:
1)改进的深度里兹法通过单一神经网络自动满足介质交界条件,简化了界面条件处理,充分训练后电磁场算例中的磁势和电势计算误差均控制在1.5%以内。
2)通过引入傅里叶特征变换和自适应tanh激活函数,改进后的神经网络能更有效地捕捉高频特征,提升了界面区域的拟合精度。经过相同轮次的训练,在磁场算例中,改进网络误差降至1.03%,而原网络误差为5.46%;在电场算例中,改进网络误差降至1.49%,而原网络误差为4.43%。
3)通过引入随机化低差异序列,提高了采样的随机性,降低了过拟合风险,并提升了训练收敛性。
本算法将在频域涡流场问题中继续研究,重点关注频域中实部和虚部的耦合计算,并考虑介质间趋肤效应的影响,以进一步扩展深度里兹法在复杂电磁场问题中的应用能力。
参考文献
[1] Kou Jiaqing, Zhang Weiwei. Data-driven modeling for unsteady aerodynamics and aeroelasticity[J]. Progress in Aerospace Sciences, 2021, 125: 100725.
[2] Wainberg M, Merico D, Delong A, et al. Deep learning in biomedicine[J]. Nature Biotechnology, 2018, 36(9): 829-838.
[3] 魏蓉, 陈锦培, 仲林林. 基于深度算子网络的电磁轨道发射速度趋肤效应的快速计算方法[J]. 电工技术学报, 2025, 40(5): 1344-1354.
Wei Rong, Chen Jinpei, Zhong Linlin. A fast computational method for velocity skin effect of electromagnetic rail launch based on deep operator network[J]. Transactions of China Electrotechnical Society, 2025, 40(5): 1344-1354.
[4] 仲林林, 吴冰钰, 吴奇. 基于元学习的气体放电等离子体电子Boltzmann方程数值求解[J]. 电工技术学报, 2024, 39(11): 3457-3466.
Zhong Linlin, Wu Bingyu, Wu Qi. numerical solution of electron Boltzmann equation in gas discharge plasmas based on meta learning[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3457- 3466.
[5] Qi Shutong, Wang Yinpeng, Li Yongzhong, et al. Two-dimensional electromagnetic solver based on deep learning technique[J]. IEEE Journal on Multiscale and Multiphysics Computational Techniques, 2020, 5: 83-88.
[6] 仲林林, 刘柯妤. 面向电力巡检图像目标检测的联邦学习激励机制[J]. 电工技术学报, 2024, 39(17): 5434-5449.
Zhong Linlin, Liu Keyu. Federated-learning incentive mechanism for object detection in power inspection images[J]. Transactions of China Electrotechnical Society, 2024, 39(17): 5434-5449.
[7] 张翼, 朱永利. 图信号与图卷积网络相结合的局部放电模式识别方法[J]. 中国电机工程学报, 2021, 41(18): 6472-6481.
Zhang Yi, Zhu Yongli, Liu Gang. A partial discharge pattern recognition method combining graph signal andgraph convolutional network[J]. Proceedings of the CSEE, 2021, 41(18): 6472-6481.
[8] 刘传洋, 吴一全, 刘景景. 无人机航拍图像中绝缘子缺陷检测的深度学习方法研究进展[J]. 电工技术学报, 2025, 40(9): 2897-2916.
Liu Chuanyang, Wu Yiquan, Liu Jingjing. Research progress of deep learning methods for insulator defect detection in UAV based aerial images[J]. Transactions of China Electrotechnical Society, 2025, 40(9): 2897- 2916.
[9] 张宇娇, 赵志涛, 徐斌, 等. 基于U-Net卷积神经网络的电磁场快速计算方法[J]. 电工技术学报, 2024, 39(9): 2730-2742.
Zhang Yujiao, Zhao Zhitao, Xu Bin, et al. Fast calculation method of electromagnetic field based on U-Net convolutional neural network[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2730- 2742.
[10] 金亮, 尹振豪, 刘璐, 等. 基于残差U-Net和自注意力Transformer编码器的磁场预测方法[J]. 电工技术学报, 2024, 39(10): 2937-2952.
Jin Liang, Yin Zhenhao, Liu Lu, et al. Magnetic field prediction method based on residual U-Net and self-attention transformer encoder[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 2937- 2952.
[11] 刘云鹏, 高艺倩, 刘刚, 等. 基于U-Net神经网络的油浸式变压器绕组流-热耦合快速计算[J]. 中国电机工程学报, 2024, 44(7): 2897-2910.
Liu Yunpeng, Gao Yiqian, Liu Gang, et al. Fast calculation of flow-thermal coupling model of oil-immersed transformer windings based on U-Net neural network[J]. Proceedings of the CSEE, 2024, 44(7): 2897-2910.
[12] Ibrahim I, Silva R, Mohammadi M H, et al. Surrogate models for design and optimization of inverter-fed synchronous motor drives[J]. IEEE Transactions on Magnetics, 2021, 57(6): 8203805.
[13] Tahkola M, Mukherjee V, Keränen J. Transient modeling of induction machine using artificial neural network surrogate models[J]. IEEE Transactions on Magnetics, 2022, 58(9): 7402204.
[14] Raissi M, Perdikaris P, Karniadakis G E. Physics- informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378: 686-707.
[15] Sirignano J, Spiliopoulos K. DGM: a deep learning algorithm for solving partial differential equations[J]. Journal of Computational Physics, 2018, 375: 1339- 1364.
[16] E Weinan, Yu Bing. The deep Ritz method: a deep learning-based numerical algorithm for solving varia- tional problems[J]. Communications in Mathematics and Statistics, 2018, 6(1): 1-12.
[17] Linghu Jiale, Dong Hao, Nie Yufeng, et al. Higher-order multi-scale deep Ritz method (HOMS- DRM) and its convergence analysis for solving thermal transfer problems of composite materials[J]. Computational Mechanics, 2025, 75(1): 71-95.
[18] Malekzadeh Fard K, Baghestani A M. Free vibration analysis of deep doubly curved open shells using the Ritz method[J]. Aerospace Science and Technology, 2017, 69: 136-148.
[19] He Cuiyu, Hu Xiaozhe, Mu Lin. A mesh-free method using piecewise deep neural network for elliptic interface problems[J]. Journal of Computational and Applied Mathematics, 2022, 412: 114358.
[20] Wang Zhongjian, Zhang Zhiwen. A mesh-free method for interface problems using the deep learning approach[J]. Journal of Computational Physics, 2020, 400: 108963.
[21] Chen Tianping, Chen Hong. Approximation capability to functions of several variables, nonlinear functionals, and operators by radial basis function neural networks[J]. IEEE Transactions on Neural Networks, 1995, 6(4): 904-910.
[22] Wu Sidi, Lu Benzhuo. INN: Interfaced neural networks as an accessible meshless approach for solving interface PDE problems[J]. Journal of Computational Physics, 2022, 470: 111588.
[23] Ying Jinyong, Liu Jiaxuan, Chen Jiaxin, et al. Multi- scale fusion network: a new deep learning structure for elliptic interface problems[J]. Applied Mathema- tical Modelling, 2023, 114: 252-269.
[24] Yao Yanzhong, Guo Jiawei, Gu Tongxiang. A deep learning method for multi-material diffusion problems based on physics-informed neural networks[J]. Computer Methods in Applied Mechanics and Engineering, 2023, 417: 116395.
[25] 汤蕴璆, 梁艳萍. 电机电磁场的分析与计算[M]. 北京: 机械工业出版社, 2010, 310-315.
[26] Gnanasambandam R, Shen Bo, Chung J, et al. Self- scalable tanh (stan): faster convergence and better generalization in physics-informed neural networks [J]. arXiv preprint arXiv: 2204. 12589, 2022.
[27] 张宇娇, 孙宏达, 赵志涛, 等. 基于物理信息神经网络的电磁场计算方法[J]. 电工技术学报, 2024, 39(17): 5251-5261.
Zhang Yujiao, Sun Hongda, Zhao Zhitao, et al. Electromagnetic field calculation method based on physical informed neural network[J]. Transactions of China Electrotechnical Society, 2024, 39(17): 5251- 5261.
[28] Sukumar N, Srivastava A. Exact imposition of boundary conditions with distance functions in physics- informed deep neural networks[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 389: 114333.
[29] Kingma D P, Ba J, Hammad M M. Adam: a method for stochastic optimization[J]. arXiv preprint arXiv: 1412. 6980, 2014.
[30] 王洪友, 杨光源, 邵可然. 基于无单元伽辽金法的电机电磁场计算[J]. 中国电机工程学报, 2012, 32(15): 148-154, 3.
Wang Hongyou, Yang Guangyuan, Shao Keran. Computations for electromagnetic field of synchro- nous generators based on the element-free Galerkin method[J]. Proceedings of the CSEE, 2012, 32(15): 148-154, 3.
[31] Owen A B. Scrambling sobol’ and niederreiter- xingpoints[J]. Journal of Complexity, 1998, 14(4): 466- 489.
[32] Zeng Xin, Zhang Shuai, Ren Chenhua, et al. Physics informed neural networks for electric field distribu- tion characteristics analysis[J]. Journal of Physics D Applied Physics, 2023, 56(16): 165202.
Abstract Data-driven algorithms based on deep neural networks have been widely used for rapid electromagnetic field solutions, but the accuracy of their calculation results is highly dependent on sufficient sample data. In the data-driven mode, on the one hand, the number of samples in the parameter space must be increased to ensure model accuracy, which greatly increases the sampling time. On the other hand, in many physical and engineering scenarios, data science does not combine known theoretical physics knowledge, resulting in information waste, slow model convergence or even non-convergence, which affects the calculation accuracy.
In contrast, physical-driven algorithms can solve electromagnetic field equations without annotating data by introducing physical prior knowledge. However, when dealing with multi-medium field problems, the boundary conditions between media require additional loss function constraints, resulting in a decrease in the efficiency of the neural network optimization process. At the same time, the complexity of the field structure leads to a cumbersome modeling process, and the difficulty of constructing interface loss function conditions is further increased, which hinders the in-depth application of physical-driven algorithms in electromagnetic field calculations. As a physics-driven algorithm, the deep Ritz method (DRM) combines the Ritz method with deep learning to construct a loss function based on energy functionals. When it reaches an extreme value, the interface conditions are automatically satisfied in the sense of functionals, thus avoiding the explicit construction of interface losses. The use of a single neural network to solve electromagnetic interface problems avoids the complexity of multi-objective optimization. However, DRM uses the output of a neural network as a test function. Although the interface conditions are theoretically satisfied, due to the smooth fitting characteristics of the neural network test function, it is difficult to accurately characterize the solution with drastic gradient changes in actual calculations, resulting in increased errors near the interface.
Therefore, this paper proposes an improved DRM architecture to enhance its ability to capture interface features during training. Considering that neural networks tend to give priority to low-frequency or large-scale features, this paper introduces embedded Fourier features to process network inputs. The input features of the neural network are mapped into many frequency domains in the frequency domain space, thereby accelerating the neural network’s ability to capture high-frequency components and the convergence speed. At the same time, an adaptive activation function is introduced to automatically adjust the slope of the activation function during the neural network training process to improve the network’s ability to capture high-frequency features. In order to use the improved DRM for stability training of electromagnetic fields, this paper adopts a fully connected neural network structure with hard boundaries. This method effectively eliminates the boundary loss in the total loss function. And by introducing randomized low-discrepancy sequences, the randomness of sampling is improved, the risk of overfitting is reduced, and the convergence of neural network training is improved.
By testing the cases of electrostatic fields and steady magnetic fields, the improved DRM and DRM are compared with the finite element calculation results respectively to verify the effectiveness of the method. The improved deep Ritz method captures high-frequency features more effectively and improves the fitting accuracy of the interface area. After the same round of training, in the magnetic field example, the error of the improved network is reduced to 1.03%, while the error of the original network is 5.46%; in the electric field example, the error of the improved network is reduced to 1.49%, while the error of the original network is 4.43%.
keywords:Electromagnetic field computation, physics-driven algorithms, deep Ritz method, interface problems
中图分类号:TM15
DOI: 10.19595/j.cnki.1000-6753.tces.242095
国家自然科学基金资助项目(52377005)。
收稿日期 2024-11-20
改稿日期 2024-12-26
张宇娇 女,1978年生,教授,博士生导师,研究方向为电气设备多物理场建模与仿真、电磁多物理场快速计算方法、基于数字孪生技术的电气设备故障诊断与健康寿命管理。E-mail: zhangyujiao@hfut.edu.cn
黄雄峰 男,1980年生,副教授,硕士生导师,研究方向为检测技术与自动化装置、人工智能新技术及应用。E-mail: hfut_huangxf@hfut.edu.cn(通信作者)
(编辑 郭丽军)