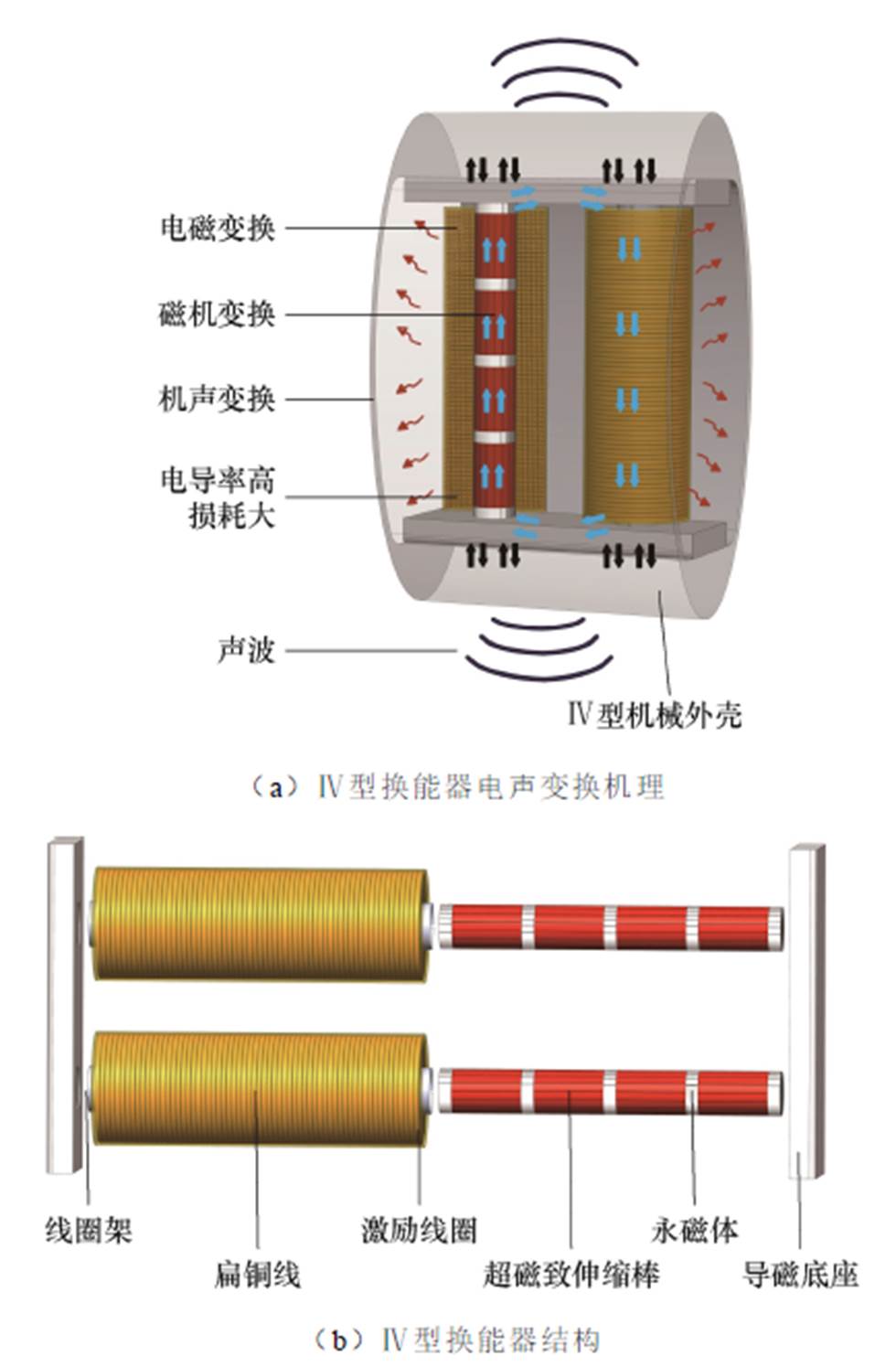
图1 超磁致伸缩电声换能器的结构
Fig.1 Structure of giant magnetostrictive electroacoustic transducer
摘要 大功率超磁致伸缩电声换能器（GMT）动态性能受制于复杂的非线性电-磁-机-声场耦合影响，传统频域方法难以真实反映其输入-输出关系，而准确地分析其时域特性是换能器优化设计的关键。尽管时域模型存在非线性、强耦合和计算效率低的问题，但是借助深度学习方法可以实现GMT时域特性的快速分析。为此，该文根据建立的GMT电-磁-机-声多物理场耦合时域模型，提出一种基于增强特征传递结构（EFTS）的GMT输出特性分析方法。首先，基于Jiles-Atherton模型建立考虑多物理场耦合的GMT时域有限元模型；其次，构建GMT的EFTS深度学习模型，通过Dense block结构使神经网络密集连接，实现特征信息在通道维度上的复用，从而提升模型收敛速度；最后，搭建实验平台并进行了验证。结果表明：所提EFTS深度学习模型显著提高了计算效率，单次计算时间仅为0.012 9 s；计算结果与实验数据吻合度良好，平均误差仅为0.26%，为GMT的快速、准确分析提供了新的解决方案。
关键词：超磁致伸缩电声换能器 多物理场耦合 增强特征传递结构 发射电流响应
超磁致伸缩电声换能器（Giant Magnetostrictive Electroacoustic Transducer, GMT）是一种利用稀土超磁致伸缩材料（Giant Magnetostrictive Material, GMM）在交变磁场条件下的磁致伸缩效应实现电声能量高效转换的水下精密装置。作为GMT的核心激励单元，GMM具有能量密度高、杨氏模量低的优点，被广泛应用于水下声呐、远距离探测、无损检测等领域[1-3]，尤其在研制低频大功率声源方面具有显著优势。
超磁致伸缩材料的输出特性由非线性电-磁-热-机多物理场耦合作用决定：一方面，在交变磁场的激励作用下，材料会产生磁滞和涡流现象；另一方面，在不同预应力作用下，会获取不同的应变和机械能量。这些因素导致GMT在电-磁-机-声能量转换过程中呈现复杂的非线性、强耦合、多变量的特点[4-5]。准确地分析GMT的输出特性是设计换能器的前提，也是研究换能器性能的重要手段。分析GMT输出特性的方法主要包括频域模型和时域模型，尽管频域模型已广泛应用于工程研究中[6-8]，但其无法全面反映系统的瞬态响应，因此无法准确地捕捉换能器在非线性和时变环境下的动态特性。相比之下，时域模型能够直接模拟系统的时间响应，能更有效地分析换能器的输出特性。例如，武汉理工大学从电路角度对制动器进行了时域分析，取得了较为理想的研究成果[9]，但对于Ⅳ型弯张换能器，构建其电路模型难度较大。而时域有限元分析法能够在结构复杂、材料特性不均匀及边界条件维数多的情况下，较为准确地获取换能器的输出特性。文献[10]从时域角度研究了换能器的瞬态性能，分析了宽带窄脉冲双匹配层换能器的时域特性。然而，在换能器的设计中，尤其是在具有多个设计参数的情况下，仅依赖时域模型进行计算会导致数据量庞大和计算过程复杂[11]，如何实现时域特性的快速计算是换能器优化设计的关键。
近年来，随着人工智能的迅猛发展，深度学习方法在解决多物理场耦合问题中的优势日益凸显，已被广泛应用于工程领域的优化设计中[12-13]。文献[14]对比了支持向量机和神经网络在变压器热点温度预测中的应用，证明了长短时记忆（Long Short- Term Memory, LSTM）深度学习模型在温度场快速预测中的优势；文献[15]则通过神经网络提高了变压器流-热耦合环境下绕组温升的计算精度和计算效率。然而，深度学习在GMT输出预测中的应用研究较少，尤其是GMT涉及电-磁-机-声多个物理场的强耦合，非线性问题更加复杂，亟须构建一种适用于换能器输出特性快速分析和优化设计的深度学习模型。
因此，本文利用增强特征传递结构（Enhanced Feature Transfer Structure, EFTS）深度学习模型对换能器的输入-输出关系进行研究。首先，计及GMM涡流效应及Jiles-Atherton磁滞过程，综合考虑GMT多物理场耦合因素，建立GMT时域瞬态模型，分析其时域输出特性；其次，由于该模型具有非线性、强耦合、多变量的特点，亟须解决其计算时间长、效率低的缺点；然后，提出一种基于EFTS的神经网络模型，实现换能器在多物理场耦合下不同工况、不同参数时输出响应的快速计算；最后，搭建GMT实验平台，将EFTS计算结果与实验结果进行对比，证明所提方法的有效性，进而可以快速准确地分析GMT在不同工况下的输出特性。
超磁致伸缩电声换能器的结构如图1所示，主要部件包括超磁致伸缩棒、永磁体、激励线圈、导磁底座和Ⅳ型机械外壳。其中，Ⅳ型机械外壳通过长轴方向的形变对棒材施加合适的轴向预应力；为了提高GMM棒内部磁场的均匀性，驱动振子部分由4根超磁致伸缩棒与5个永磁体以交替结构组成，棒材经径向切缝处理以削弱涡流影响；激励线圈为超磁致伸缩棒提供交变磁场，促使其周期性伸缩振动；永磁体为GMM棒提供合适的偏置磁场避免“倍频”现象；导磁底座由高磁导率的硅钢片压叠形成，与GMM棒、永磁体共同组成闭合磁路。GMM棒在线圈激励的交变磁场和永磁体提供的偏置磁场共同作用下产生磁致伸缩应变，从而迫使GMT的机械壳体发生周期性振动，实现位移输出和声波辐射。
图1 超磁致伸缩电声换能器的结构
Fig.1 Structure of giant magnetostrictive electroacoustic transducer
在外部交流磁场驱动下，GMM产生应变，但其输出会受到内部磁化过程和外部工况的影响，如非线性磁滞、涡流以及偏置磁场、预应力等因素，涉及电磁、磁机、机声能量的转换过程，具有非线性、强耦合的特点。因此，建立考虑电-磁-机-声多物理场耦合的GMT非线性动态时域模型，是准确表征换能器输入-输出特征的关键。虽然考虑GMM棒磁滞及磁致伸缩过程的动态模型可以精确描述换能器的输出特征，但该动态模型计算时间过长，用于换能器设计时效率过低。因此，基于时域动态特性建立GMT的EFTS神经网络深度学习模型，并结合换能器的实际输入工况可以实现对其输出特征的快速分析。
GMM棒在线圈激励的交变磁场下产生磁致伸缩应变，从而迫使GMT的机械壳体发生振动。当换能器工作在线圈激励的电磁场时，利用麦克斯韦方程组可以分析换能器的电磁场，如式（1）所示。
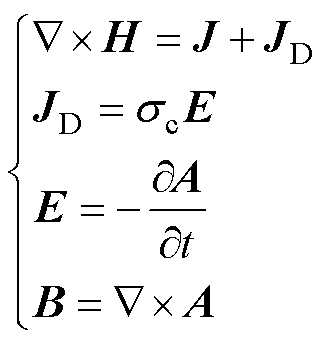（1）
式中，H为在GMM棒材中产生的磁场强度，kA/m；JD为与涡流项相关的电流密度，A/m2；J为激励线圈的电流密度，A/m2；sc为GMM棒材的电导率，S/m；E为电场强度，V/m；B为磁通密度，T；A为磁矢量势，V·s/m。
为表征GMM的不可逆磁化过程，使用Jiles- Atherton模型模拟磁化过程中的非线性环节，阐释其磁场强度和磁化强度间产生磁滞的原因。具体关系[16-17]为
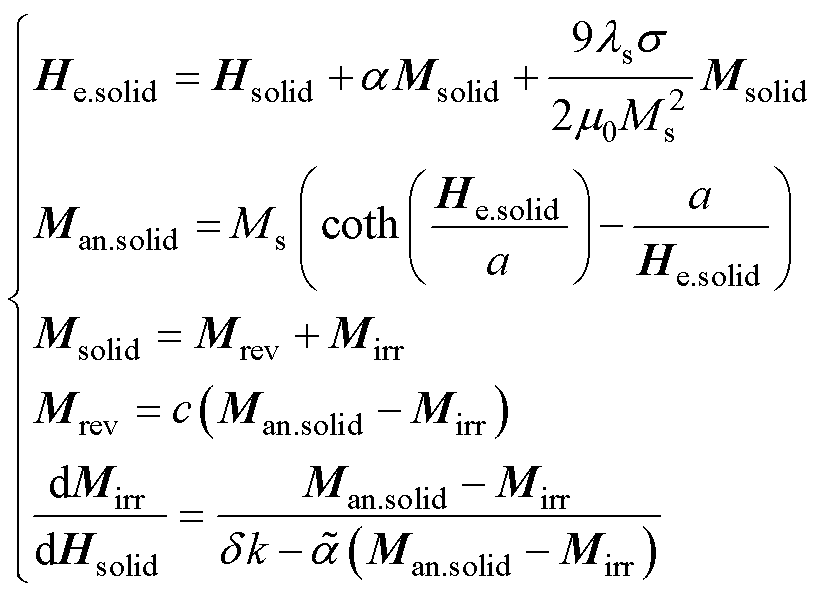（2）
式中，He.solid为有效磁场强度；Hsolid为外磁场强度；Msolid为磁化强度；a为畴壁相互作用系数；ls为饱和磁致伸缩系数；m0为真空磁导率；Ms为饱和磁化强度；Man.solid为无磁滞磁化强度；s为棒材预应力，9lssMsolid/(2m0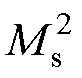
)表示由预应力s引发的磁场；a为无磁滞磁化强度形状系数；Mrev和Mirr分别为可逆和不可逆磁化强度；c为可逆系数；k为畴壁钉扎系数；
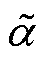=a+9lss/(2m0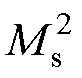)；d为方向系数，Hsolid增大时，d取+1，Hsolid减小时，d取-1。
GMM棒在偏置磁场Hbias和激励磁场Hac的共同作用下产生磁致伸缩应变lz。通过Jiles-Atherton模型反映磁致伸缩材料的磁滞特性，可以从本征意义上描述GMM的不可逆磁化过程。而Jiles- Atherton模型的参数a、Ms、a、c、k无法通过测量或计算获得，一般由准静态下的B-H曲线经群智能优化算法辨识得到。本文采用粒子群优化算法（Particle Swarm Optimization, PSO）对相关参数进行辨识[18]，结果见表1。
表1 Jiles-Atherton模型参数辨识结果
Tab.1 Parameter identification results of Jiles-Atherton model
参 数数 值 a1.01×10-2 Ms/(A/m)7.754×105 a/(A/m)9.171×103 c1.117×10-1 k/(A/m)1.426×104
GMM棒材是实现超磁致伸缩电声换能器电-磁-机多物理场耦合的核心部件，其内部应力平衡方程为
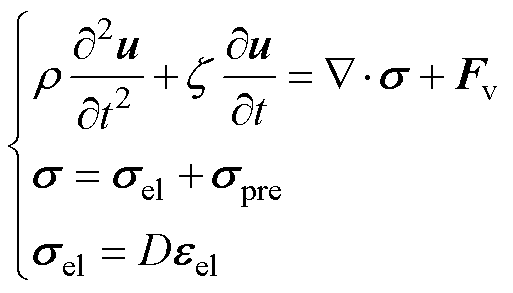（3）
式中，r为GMM棒材密度，kg/m3；z为棒材的机械阻尼，kg/s；u为GMM棒材的总输出位移，m；Fv为给定的机械体积力，N；s为应力张量，包括机械应力sel和预压应力spre，Pa；D为棒材的弹性系数；eel为棒材机械应变。
GMM棒材在线圈激励的交变磁场下产生磁致伸缩应变，磁场和机械场通过磁致伸缩效应相关联，其耦合关系如式（4）压磁方程所示。
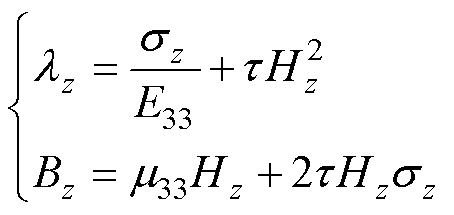（4）
式中，lz为棒材z轴方向的应变，引起壳体弯张振动；E33为z轴方向杨氏模量；t为棒材磁致伸缩耦合系数；sz为z轴方向的应力；Bz为z轴方向的磁通密度；Hz为z轴方向的磁场强度；m33为z轴方向的磁导率。
GMM棒材的磁致伸缩应变使换能器机械壳体发生形变振动，壳体表面会对周围的媒质产生激励作用从而产生声压。流体域中的声压满足声波动基本方程，表示为
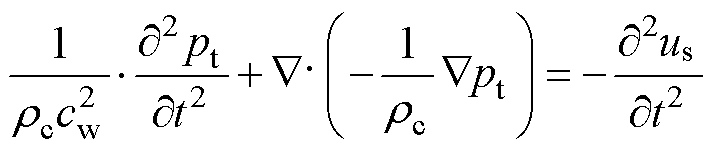（5）
式中，rc为水的密度，kg/m3；us为换能器壳体位移，m；cw为水中声速，m/s；pt为声压，Pa。
当GMT处于所辐射的声场中时，壳体表面会受到声场的反作用，因此其声-结构耦合边界需满足声压连续性和速度连续性两个声学边界条件，从而实现电声换能器机械壳体与声学传播介质水域之间的双向耦合。换能器壳体规律性弯张形变通过水域介质向外辐射声波，其单位发射电流响应（Transmit Current Response, TCR）为I0=1 A时在距离声轴中心1 m处的声源级大小[19]，表示为
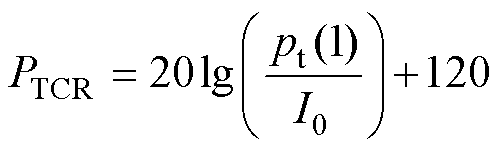（6）
式中，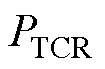
为单位发射电流响应；
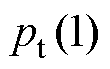为距离声轴1 m处的声压。
本文基于不同预应力和激励电流条件下的实测磁场数据分析表明：当预应力处于20～32 MPa范围内时，GMM棒材表现出较宽的线性响应区间；在此基础上，施加45～55 kA/m的激励磁场可有效发挥其性能优势。因此，在预应力为28 MPa、励磁频率为500 Hz、驱动电流为10 A的条件下，通过有限元仿真对GMT的输出性能进行验证。GMT动态模型的有限元声压仿真结果如图2所示，由其远场声压仿真结果结合式（6）即可得到GMT的单位发射电流响应约为182.72 dB。同时，基于实验室现有研究对其动态模型的磁场、磁致伸缩、声压等输出特征进行验证。
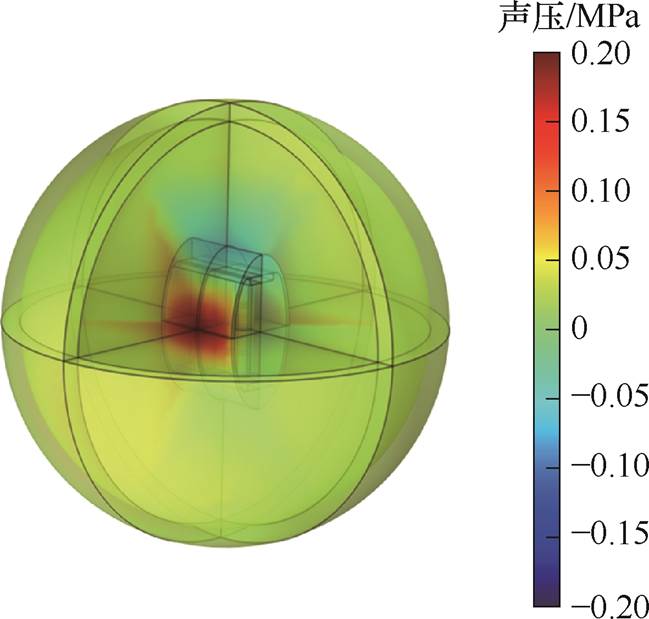
图2 GMT动态模型声压仿真结果
Fig.2 Sound pressure results of GMT dynamic model
在有限元仿真中充分考虑GMM棒的涡流效应，对棒材进行径向切缝，并通过优化切缝方式达到抑制涡流损耗的最佳效果。同时计及Jiles- Atherton磁滞模型，考虑GMM棒材的磁化过程，可以较为精准地模拟GMT时域动态磁场。GMT动态模型的磁场计算结果与实测磁场数据对比结果如图3所示。可知考虑多物理场耦合因素的超磁致伸缩电声换能器的动态磁场与实测磁场保持一致，动态模型的磁场计算结果与实测数据的平均误差为1.69%，误差较小，在误差范围内可以近似模拟GMT的磁场特性。
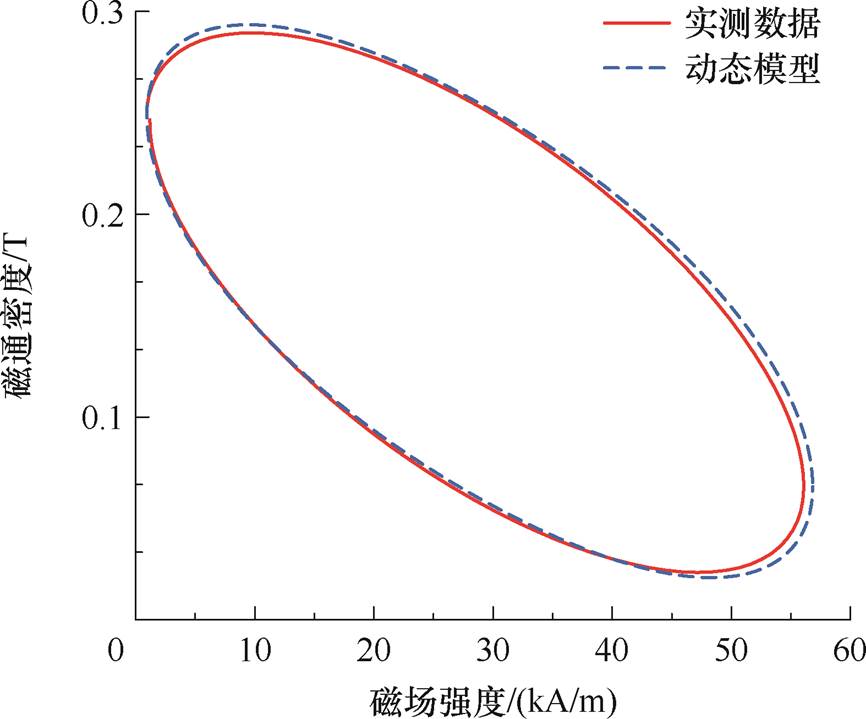
图3 GMT动态模型磁场曲线
Fig.3 GMT dynamic model magnetic field curve
在交流磁场激励下，GMM的磁致伸缩是换能器向外辐射声波的本质原因。因此，GMT的动态模型能否准确地模拟GMM的磁滞伸缩现象是其能否准确地表征换能器输出的关键。在相同激励条件下，GMT动态模型输出的磁致伸缩曲线与GMM实测数据的对比结果如图4所示。通过对比可知，GMT动态模型的磁致伸缩规律与GMM实测磁致伸缩规律保持一致，实测数据略大于动态模型输出结果，但误差较小，在磁场强度为55 kA/m时误差仅为3.30%。因此，在考虑多因素影响的超磁致伸缩电声换能器中，其动态模型的磁致伸缩曲线可以近似模拟换能器的磁致伸缩特性。
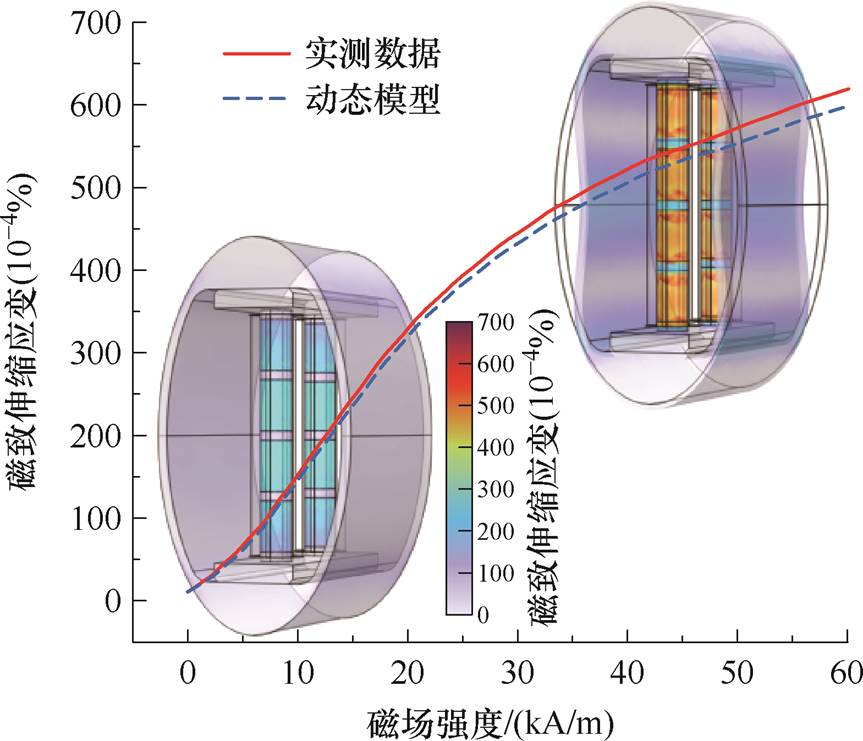
图4 GMT动态模型磁致伸缩曲线
Fig.4 GMT dynamic model magnetostriction curve
在额定工况下，超磁致伸缩电声换能器通过水域向外辐射声压，距离其声轴中心1 m处的声压输出结果如图5所示，声压幅值约为1.34 kPa，经计算可知换能器发射电流响应为182.54 dB。图5还对比了模型计算结果与实测结果的差异，可以明显发现，所提动态模型的声压曲线与实测声压结果吻合良好。因此，本文所提GMT动态模型可以有效地模拟换能器的声特性。
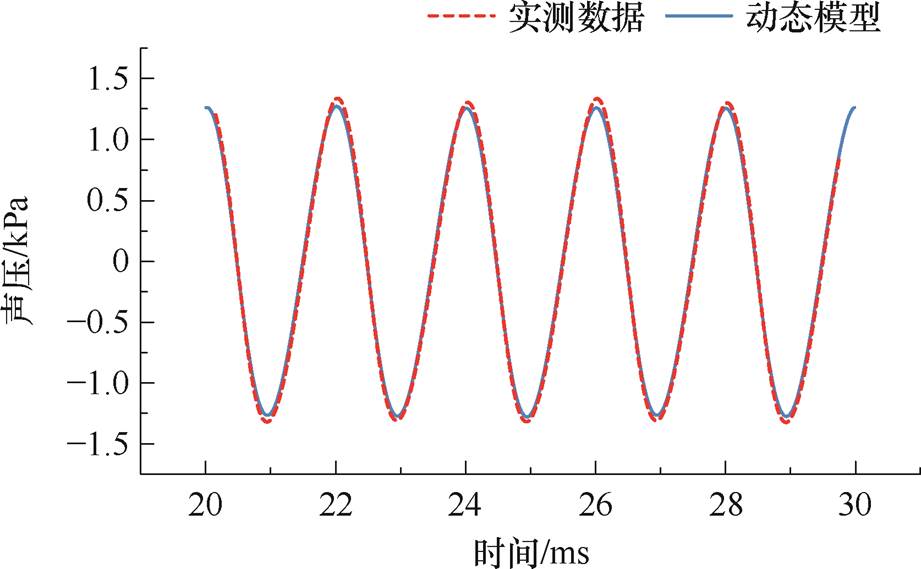
图5 GMT动态模型稳态声压曲线
Fig.5 Sound pressure curves of GMT dynamic model
综上可知，GMT的动态模型可以实现对GMT输出的精确模拟，但在有限元求解GMT多物理场耦合动态模型时，单次计算时间长达14 854 s，运行内存高达2.84 GB，不可避免地存在计算时间过长、效率过低的问题。而在基于GMT动态模型开展优化设计的过程中，由于换能器涉及电-磁-机-声多物理场相互耦合，需要优化的参数更多、计算时间更长。因此，亟须一种精度高、计算速度快的换能器输出特性分析方法。
针对换能器时域多物理场耦合动态模型计算效率低、计算资源消耗大的问题，本文建立了基于增强特征传递结构（EFTS）的神经网络，能够将GMT时域模型的样本数据作为神经网络的输入和标签，通过网络训练实现物理场的快速计算。
U-net神经网络是全卷积神经网络的一种改进，作为一种深度学习模型，其卷积操作能够有效地提取数据中的高维非线性特征。但卷积神经网络可能存在梯度消失和精度下降等问题，为了解决这一问题，本文提出一种EFTS神经网络，在U-net神经网络中引入Dense block和上采样与下采样之间的跳跃连接。EFTS神经网络结构如图6所示。图6中，跳跃连接可以使得更深层次的网络能够高效地训练，允许一个层的输出与网络中更下层的输出相结合，加强了前后层之间的信息流通，在一定程度上缓解了梯度消失现象，从而可以将神经网络搭建得很深。Dense block最大化了这种前后层的信息交流，通过建立前面所有层与后面层的密集连接，实现了特征在通道维度上的复用，不但减缓了梯度消失的现象，也使其可以在参数与计算量更少的情况下实现更优的性能[20]。
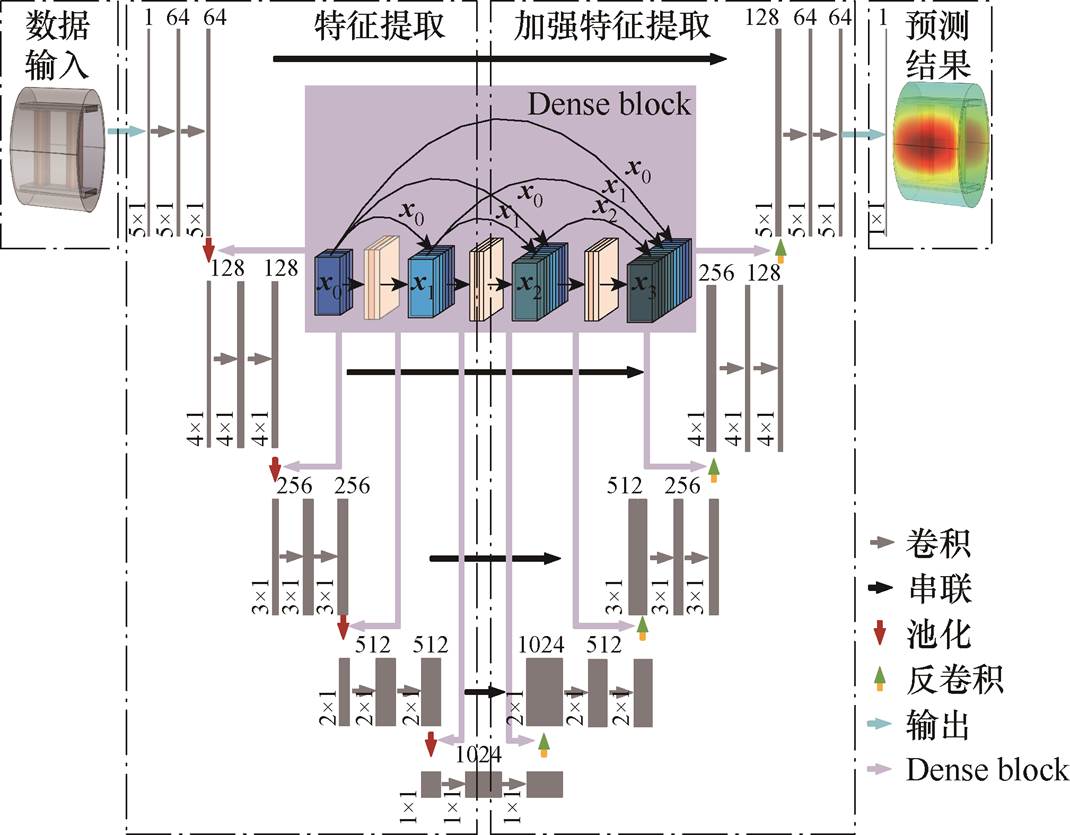
图6 EFTS神经网络结构
Fig.6 EFTS neural network structure
图6中，基于DenseNet架构的Dense block具有3层（L=3），增长率为3（d=3），特征图（x0）通过每个块的输出，经过批量归一化、ReLU激活以及使用卷积核大小K=3、步长S=1，以及填充P=1的卷积进行连接。在Dense block中，特征图的大小保持不变，而特征图的数量在每一层增加d个。因此，对于网络层l（l=1, 2,…, L），基于增长因子d，将添加dl个特征图。
EFTS神经网络主要由特征提取、加强特征提取密集模块、跳跃连接及预测等部分组成[21]。利用EFTS神经网络模型计算GMT输出特征的流程如图7所示，主要包括建立动态模型、生成样本数据、EFTS网络搭建和训练、特征预测。
1）建立动态模型：根据GMT多物理场耦合关系，建立其时域动态模型。主要包括三维几何建模、定义材料参数、设定控制方程和边界条件以及施加载荷等，最后进行求解。
2）样本数据生成：以激励电流的频率f，以及换能器壳体参数半长轴长度q、壳体厚度e、壳体高度h作为输入特征；分别以换能器辐射声压p、单位发射电流响应（TCR）作为输出特征。
3）EFTS网络搭建和训练：按照图7所示EFTS网络结构搭建深度学习模型，并将样本集进行归一化处理，设置优化函数类型、学习率、下降因子、下降周期、批量大小、迭代周期、损失函数等超参数，对GMT的EFTS深度学习神经网络进行训练。
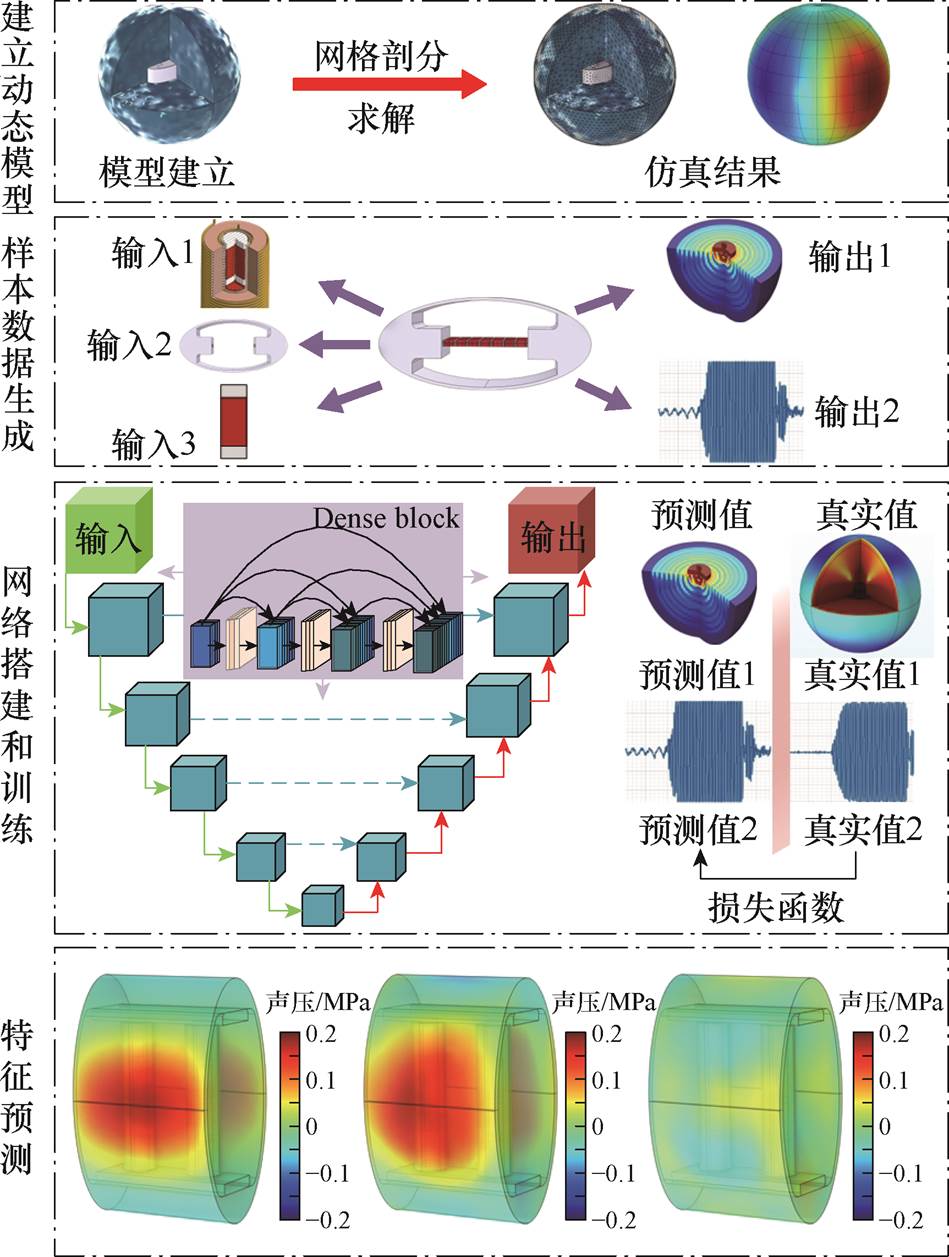
图7 EFTS神经网络快速计算流程
Fig.7 EFTS neural network fast computational flow
4）特征预测：将工况参数输入EFTS神经网络进行计算，并将计算结果与有限元计算结果进行对比。通过对预测结果进行评估，实现输出特征的快速计算。
EFTS神经网络计算结果的精度与超参数的不同取值密切相关[22]，本文以优化算法、学习率、衰减率作为深度学习模型的最佳超参数组合。其中，优化算法直接决定内部参数的更新方式。EFTS神经网络最佳超参数组合取值对比如图8所示。由图8a可知，随着迭代次数的增加，三种优化算法的误差和波动呈现不同的趋势，其中使用adam优化算法进行训练时效果最佳。此外，学习率决定了参数更新的速度。学习率越小，权重更新越慢，训练时间越长，甚至可能陷入局部最优；学习率越大，权重更新越快，但模型可能发散而无法准确地计算输出特征。学习率通常设定在10-6～0.1之间。如图8b所示，当学习率为0.001时，模型预测效果最好。而学习衰减率一般在0～1之间，如图8c所示，当衰减率取0.9时，误差波动起伏最小，收敛最快。
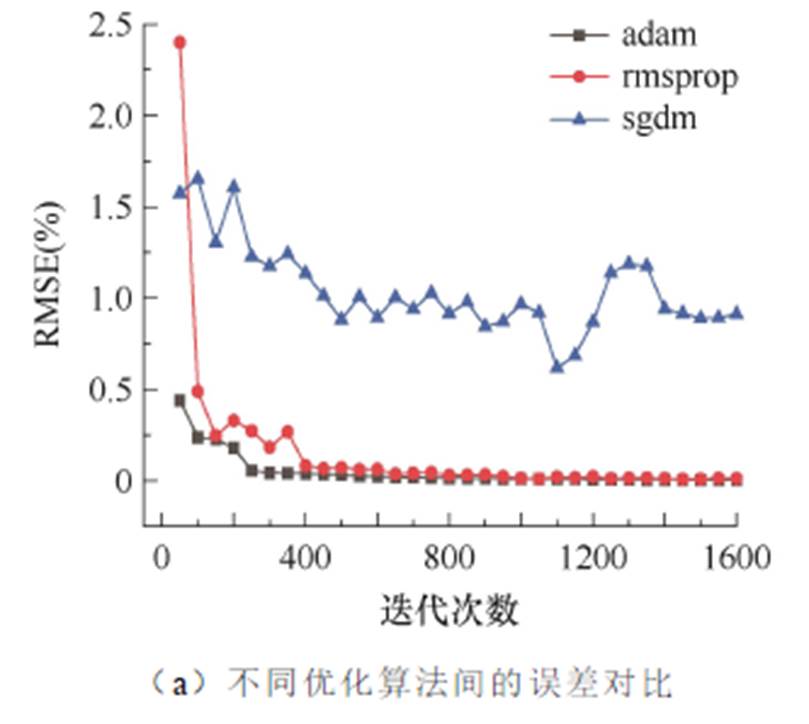
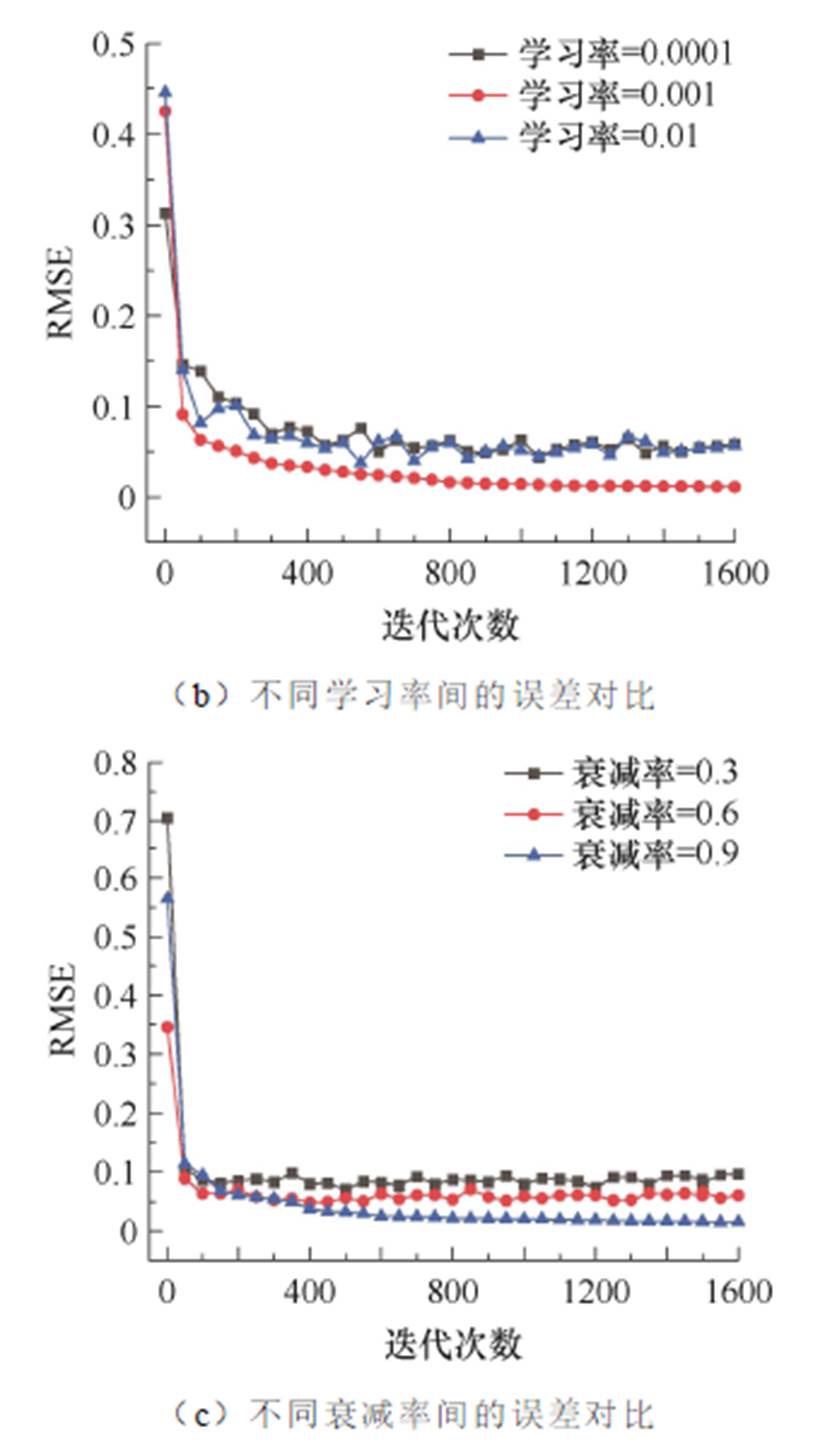
图8 EFTS神经网络最佳超参数组合取值对比
Fig.8 Comparison of the best hyperparameter combination values of EFTS neural network
不同的超参数对模型参数的更新有不同的影响。如图8a所示，sgdm算法相比其他算法更易在训练过程产生较大的波动。此外，学习率和学习衰减率设置过高或过低，都易导致训练过程中模型参数波动而出现振荡。
经上述分析可知，以优化算法、学习率、衰减率作为最佳超参数组合，并设置学习率为0.001、衰减率为0.9，且优化函数为adam时，超磁致伸缩电声换能器的EFTS神经网络训练效果最佳。
基于EFTS神经网络的深度学习模型的最佳超参数组合见表2。在最佳超参数组合下，对归一化后的样本数据进行训练，最后将计算结果进行反归一化操作，即可得到超磁致伸缩电声换能器与实际情况相符合的声学特征。
表2 最佳超参数组合
Tab.2 Optimal super parameter combination
超参数范围组合 优化算法adam/sgdm/rmspropadam 学习率0.000 1～0.010.001 衰减率0.3～0.90.9 单次计算时间/s0.012 9
换能器的可变几何结构包括半长轴长度q、壳体厚度e和壳体高度h，换能器的性能表征数据由壳体声压p表示。因此，换能器声压场的变化可以通过上述三个参数和频率的变化表征。此外，换能器声压场是由一系列点的等效声压构成，等效声压与节点位置密切相关，故采用各自的笛卡尔坐标(x, y, z)表示。最终确定换能器的输出变量为等效声压p，输入变量为x、y和z坐标，以及q、e、h和f的值。EFTS声压模型如图9所示。
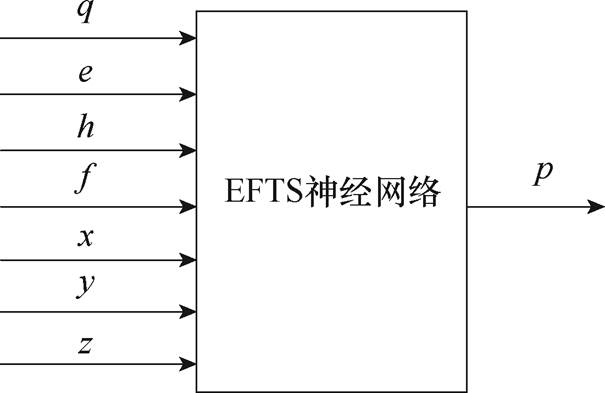
图9 EFTS声压模型
Fig.9 EFTS model of sound pressure
换能器EFTS声压模型的训练数据集由一组csv文件组成，这些文件描述了构成声压模型网格节点的x、y、z坐标和频率f，以及在这些节点上使用有限元软件计算得出的声压值p。数据结构如图10所示，换能器的几何参数包括：q、e和h。为进行换能器三维声压的计算，在有限元软件中共构建了81 个样本，如图10b所示。其中，每个样本包含的坐标数据点数量范围为1 600～1 800。来自不同csv文件的所有样本数据均被统一整理汇总至一个文件中，如图10c所示。
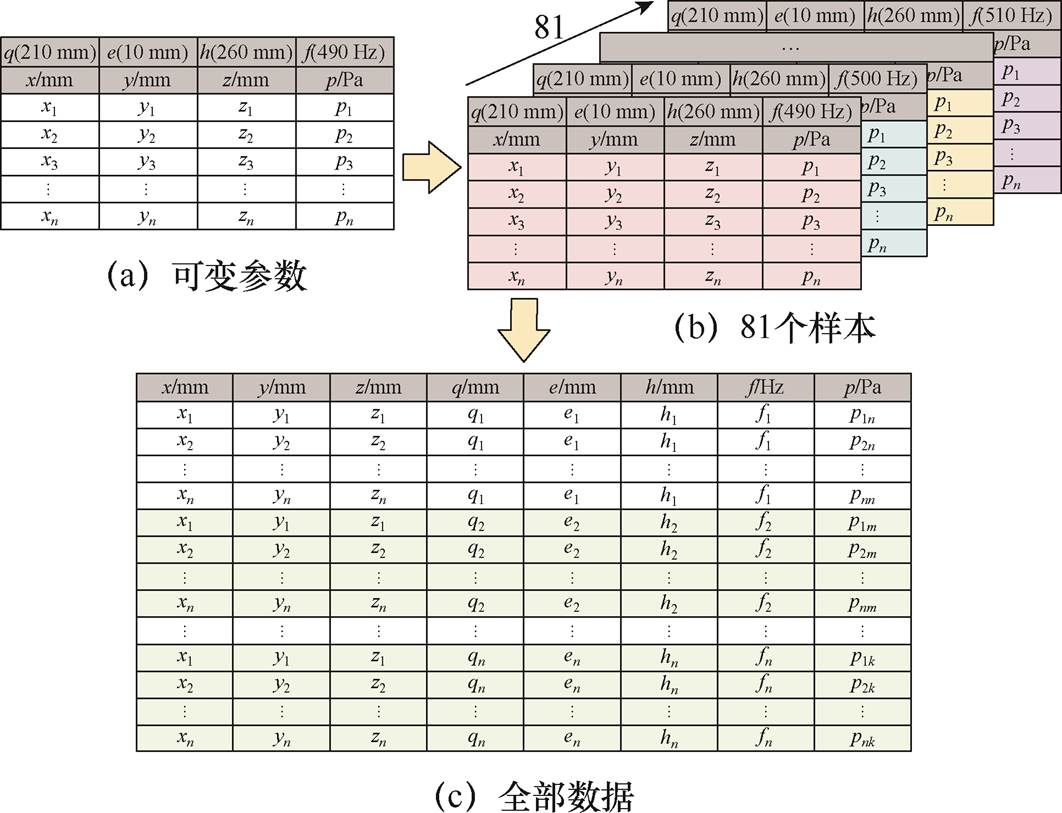
图10 数据结构
Fig.10 Data structure
将预处理数据中的70%作为训练数据，30%作为测试数据。为加快训练速度，设置最大训练轮数MaxEpochs取80，允许网络在给定数量的迭代中进行训练。miniBatchSize为每次用于梯度下降的批量数据的大小，取值为480。一次迭代表示将完整的数据集送入网络并完成前向计算和反向传播的过程。对于所研究的情况，训练周期共80轮，每轮迭代次数为229。
EFTS神经网络训练过程中的方均根误差（Root- Mean-Square Error, RMSE）和损失函数（Loss）在各轮训练中的分布情况如图11所示。由于损失函数为平均绝对误差（Mean Absolute Error, MAE），训练和验证过程的RMSE和Loss指标值均随着训练迭代次数的增加而减小。需要注意的是，模型在训练11轮后达到收敛，耗时3.85 h。经过训练，使用回归指标对模型进行评估，指标值为：Loss= 2.015 3×10-4，RMSE=0.020 1。可以得出，评估指标表现良好，RMSE指标具有可行性，适用于对不同尺寸结构换能器的输出声压进行预测。
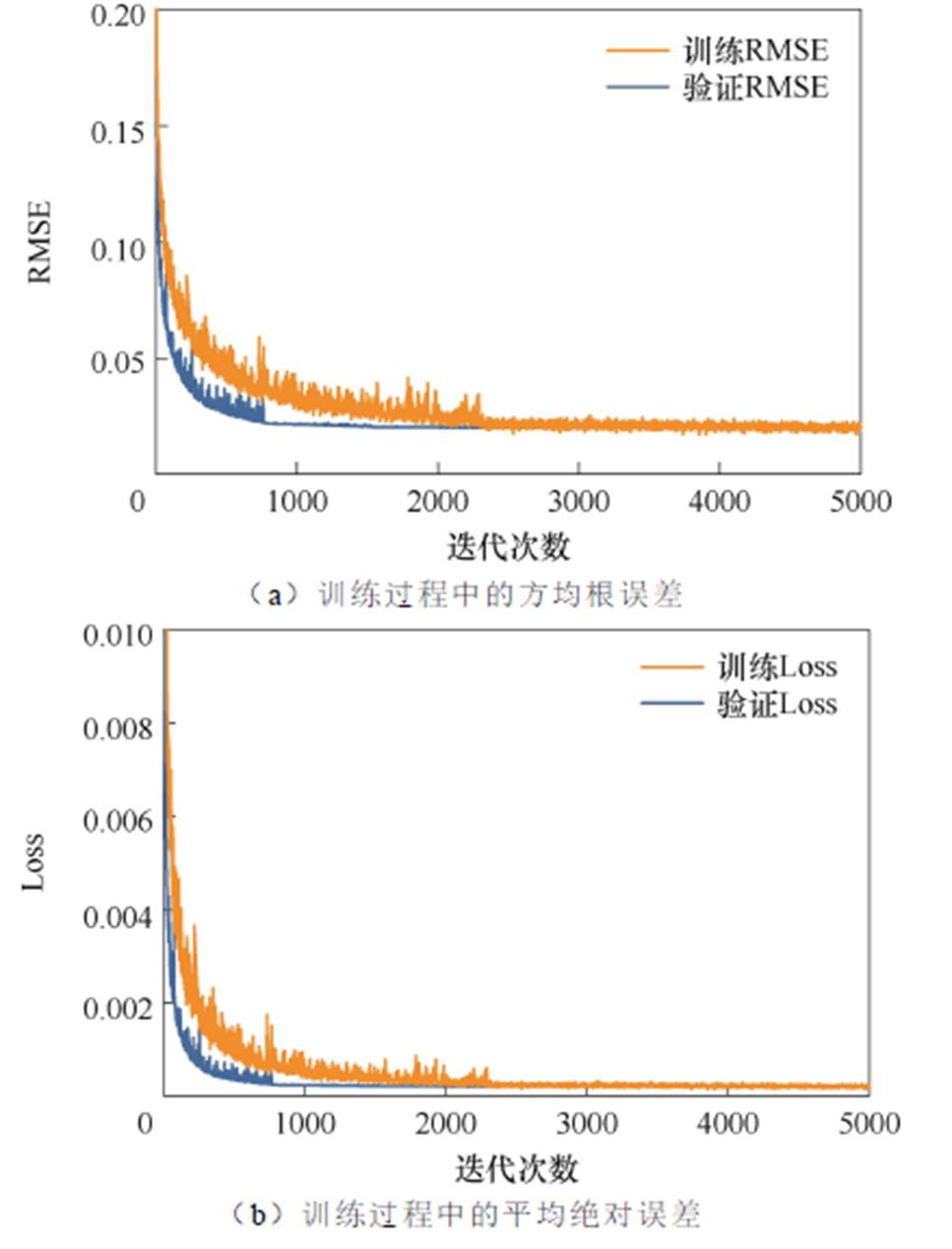
图11 评价指标随迭代次数的分布
Fig.11 Distribution of evaluation metrics with the iteration number
不同尺寸参数下换能器瞬时输出声压云图分布如图12所示。图12中分别对比了有限元软件计算、EFTS神经网络快速计算方法得出的声压云图，以及两者做差得到的误差云图。可以得出，表面声压场可视化后，其轮廓趋势相似，换能器输出声压的预测结果与有限元仿真结果一致。但由于超磁致伸缩电声换能器的几何模型具有复杂的三维结构，需要考虑几何结构的变化因素，并生成不同密集程度的网格，会导致基于EFTS神经网络预测的换能器声压值略高于仿真结果，这也是在某些区域预测分布存在误差的主要原因。
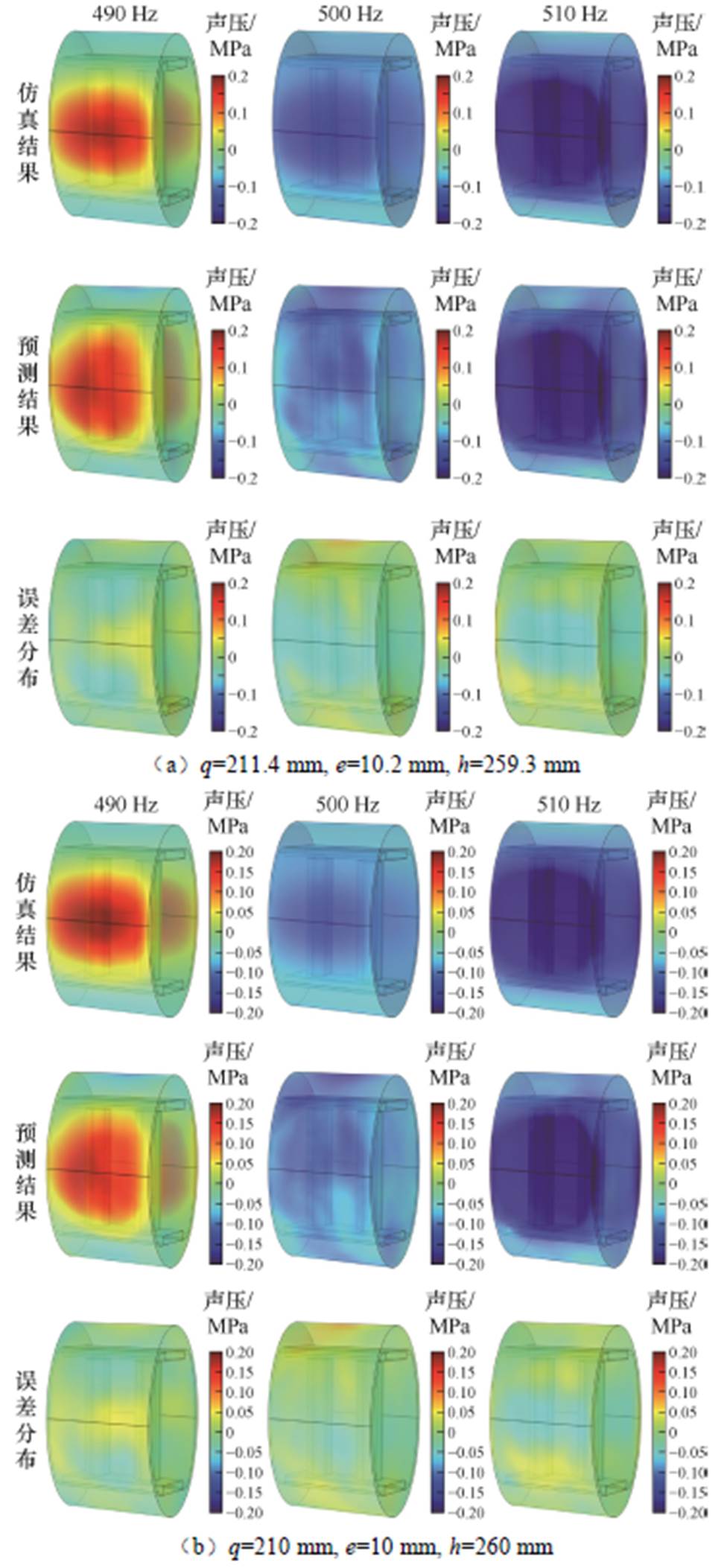
图12 换能器声压云图对比
Fig.12 Comparison of transducer sound pressure cloud images
由式（6）可知，换能器的输出声压与单位发射电流响应一一对应。因此，通过换能器的EFTS神经网络对其输出声压进行预测后，可以进一步得到换能器的输出响应。经数据重构后，建立了以换能器半长轴长度q、壳体厚度e、壳体高度h和激励频率f为输入变量，以单位发射电流响应（TCR）为输出性能指标的数据映射关系。
对上述81个样本进行计算，得到TCR预测曲线如图13所示。图中，横坐标表示样本编号，纵坐标表示超磁致伸缩电声换能器的TCR预测值、仿真值及误差结果。从图13中可以得出，EFTS神经网络对TCR预测值与仿真计算结果保持一致，方均根误差为0.017 2 dB，预测效果较好。此外，训练后的模型单次计算时间仅为0.012 9 s，说明该方法可以快速且较为准确地获取超磁致伸缩电声换能器的输出特性。
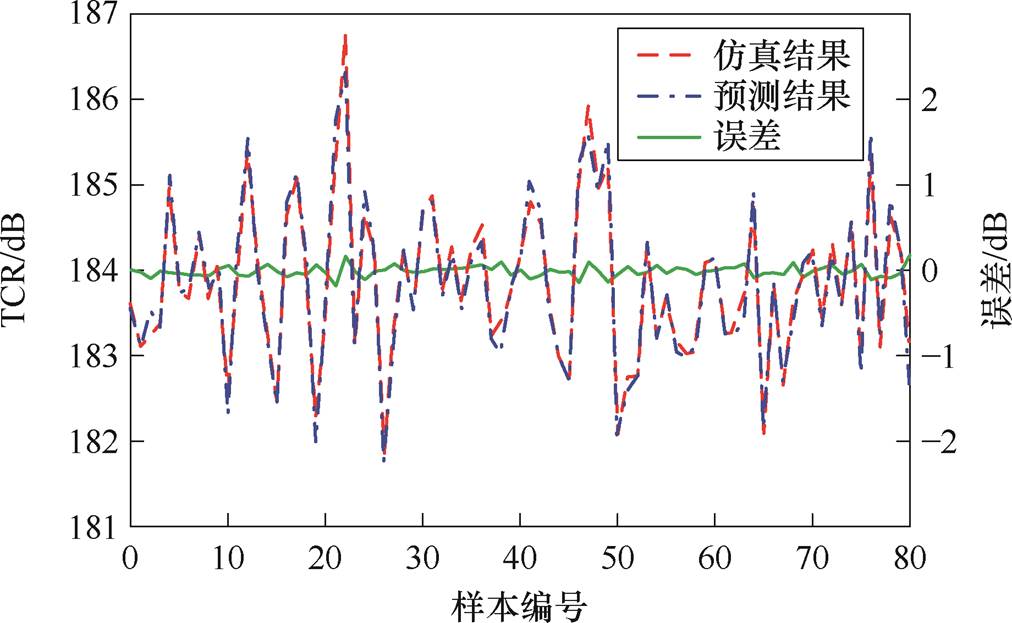
图13 TCR预测曲线（EFTS）
Fig.13 TCR prediction curve by EFTS
本文基于改进的EFTS神经网络模型实现复杂工况下换能器性能的快速分析，并结合粒子群算法对GMT的结构参数进行优化设计，从而实现换能器的高效设计。
GMT的输出声源级及谐振频率与其机械壳体密切相关，机械壳体参数示意图如图14所示，主要包括半长轴长度q、半短轴长度b、壳体厚度e、壳体高度h。由目标声源级可以计算磁路长度，从而确定半长轴长度q取值范围为200～220 mm。为简化设计流程，本文对GMT壳体长短轴比值施加约束，在半长轴长度q确定后，半短轴长度b随之确定。此外，根据GMT目标水深下的静水压，确定壳体厚度e取值范围为8～12 mm。壳体高度h则取决于磁路分布，最终取值范围为260～320 mm。通过上述结构参数的限制实现PSO中变量的约束，具体步骤参见文献[23]。使用GMT的EFTS神经网络对其输出特征进行快速计算，不同结构参数下换能器的单位发射电流响应差异较大。
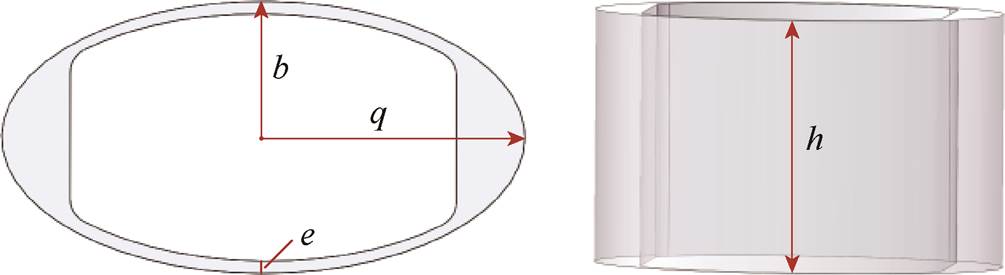
图14 机械壳体参数示意图
Fig.14 Housing parameters schematic diagram
借助PSO算法对换能器的TCR进行最大值寻优，其中效果最优的三组方案见表3。本文设计选取方案1作为换能器壳体参数，考虑实际受力及内部空间情况，取壳体厚度为10 mm，壳体高度为260 mm，半长轴长度为210 mm。
表3 换能器结构参数及输出响应（EFTS）
Tab.3 Structural parameters and output response of the transducer of EFTS
序号q/mme/mmh/mmTCR/dB 1211.39210.204259.291183.213 2209.389.123218.302183.185 3198.598.719209.925183.064
按照水声换能器测试国家标准，湖泊试验场地选择郴州东江湖水库，水最深达120 m，周围水域宽度大于500 m，测试天气晴朗，湖面无大波浪，湖流较小，回波干扰小，满足标准中的试验要求。按照图15所示结构搭建湖试平台。平台分为水下与水面两部分，其中，水上船舱主要由数据终端、功率放大器、阻抗匹配箱、示波器、功率分析仪等单元组成；水下部分主要由换能器样机、标准水听器、测深仪组成。由于换能器样机属于感性负载，需要为其进行阻抗匹配，而后由功率放大器提供不同频率的驱动电流。通过检测换能器的输入电压u、输入电流i以及两台水听器的输出电压u1、u2，可以计算换能器的发射电流响应并分析换能器的辐射声波质量。
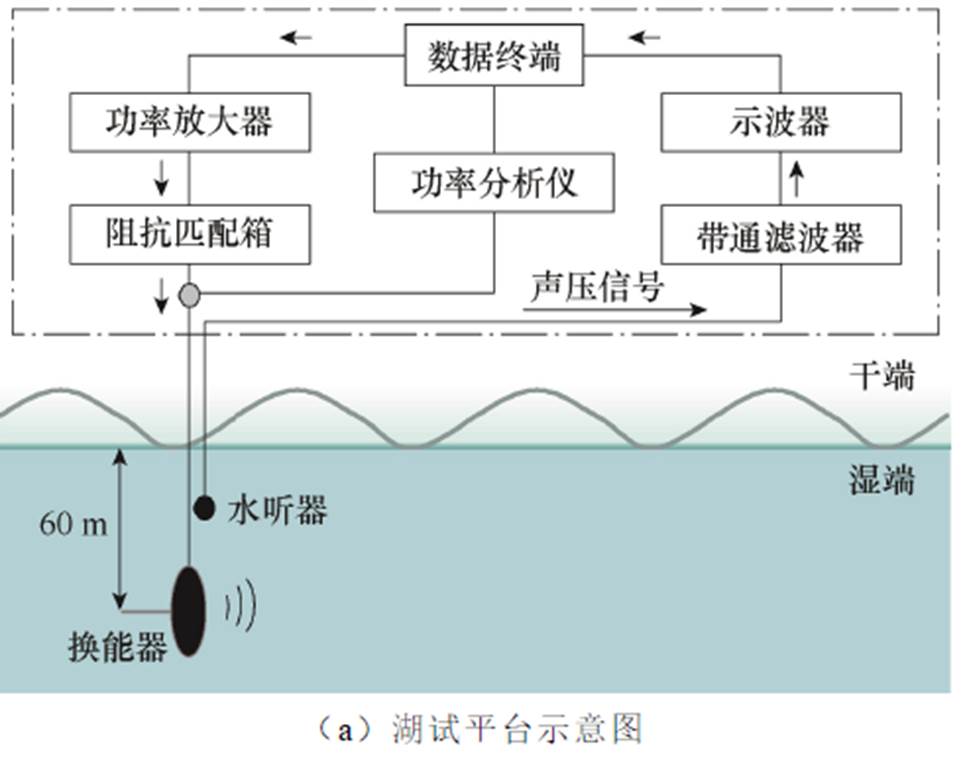
图15 湖试平台结构示意图
Fig.15 Structural diagram of the lake test platform
为避免湖底和周围环境反射波的影响，换能器声源级测试采用脉冲发射方式，脉冲波数量由换能器与湖底和湖面的测试距离以及测试频率确定，单次发射脉冲波数量取15。在测试脉冲波发射后，取波形稳定段内4～5个周期进行计算。
换能器样机在目标水深60 m、额定电流20 A、不同激励频率下（400～520 Hz）对GMT的输出进行测试。其中谐振点450 Hz频率下的输入电压、输入电流以及水听器输出电压波形如图16a所示。测试结果显示，交流450 Hz激励时，输入电压约为472.9 V，输入电流约为20.53 A，由于两台水听器灵敏度及悬挂位置不同，水听器电压分别为884.1 mV和876.3 mV。计算换能器在该工况下的单位发射电流响应约为182.79 dB，且波形状况良好，未出现倍频现象。
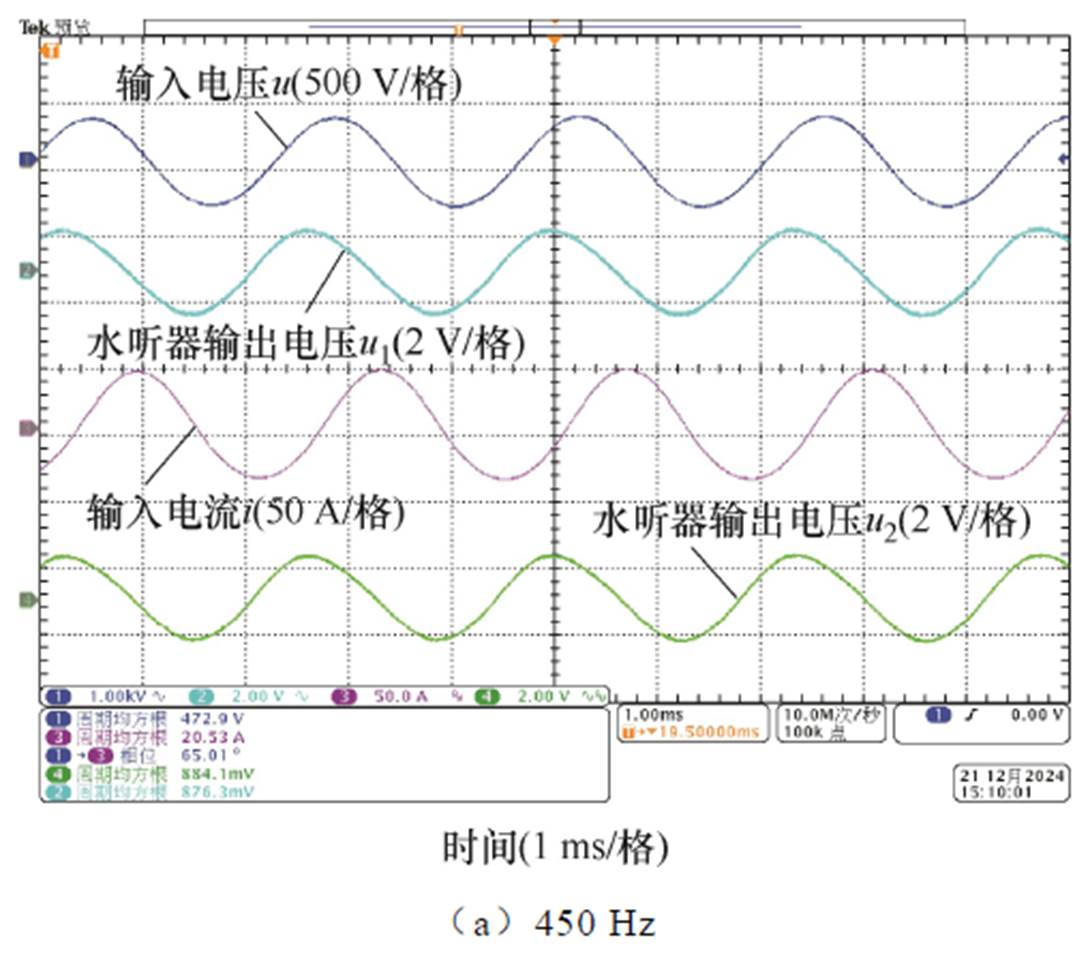
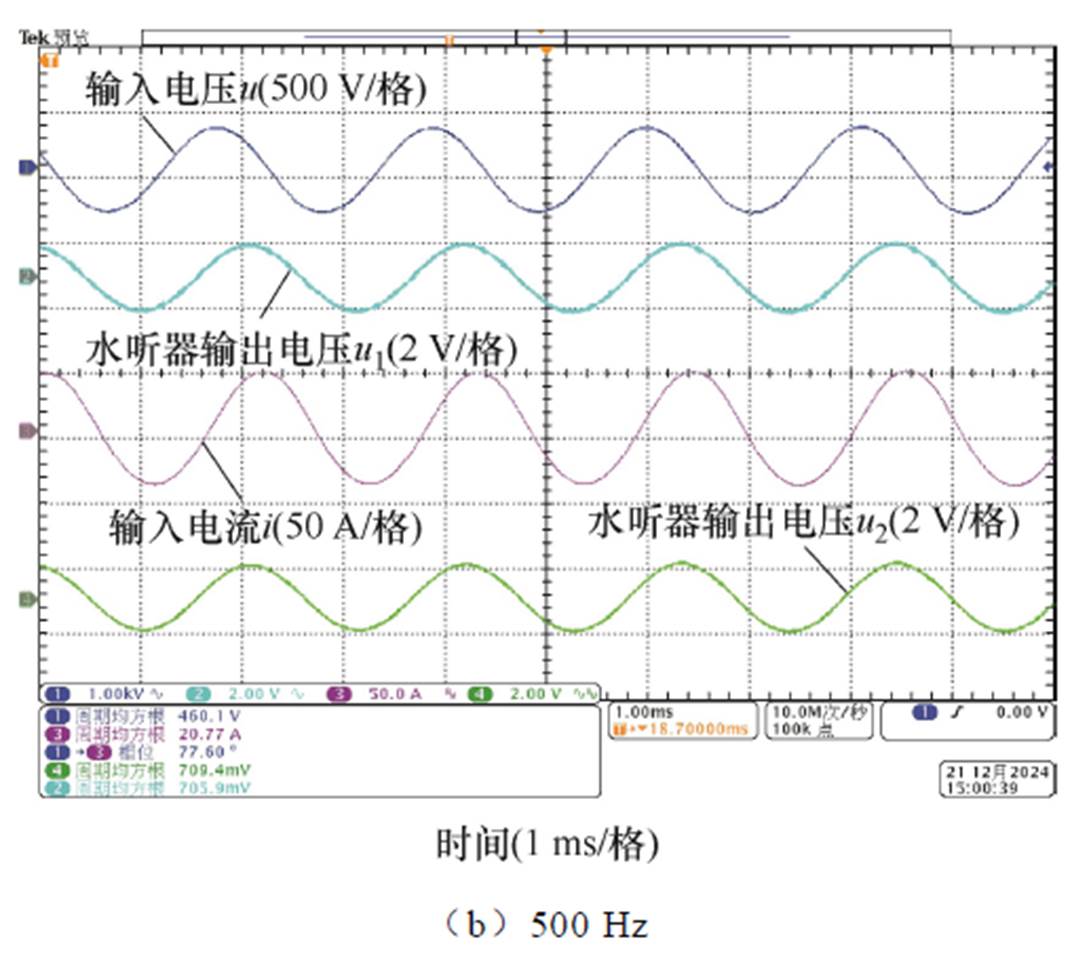
图16 换能器样机测试波形
Fig.16 Test waveforms of the transducer
根据式（6）和水听器输出电压，对不同频率下GMT的TCR进行计算。测试结果显示，在目标水深和额定工况下，换能器在不同频率激励电流驱动下的单位发射电流响应如图17所示，GMT的谐振频率为450 Hz，TCR误差对比见表4。由误差结果可知，使用EFTS神经网络计算得到的GMT谐振频率约为450 Hz，与实际测试值相同，且在不同频率下的TCR计算结果与实际分布规律一致。
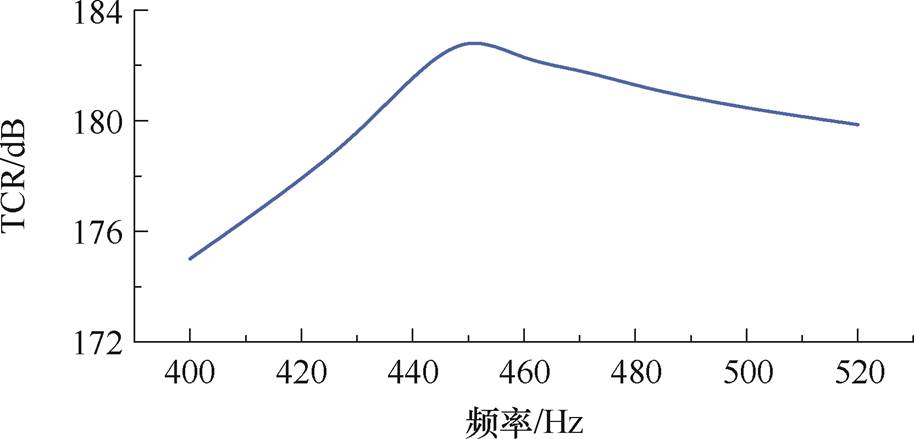
图17 单位发射电流响应
Fig.17 Unit transmit current response
表4 TCR误差对比
Tab.4 TCR error comparison
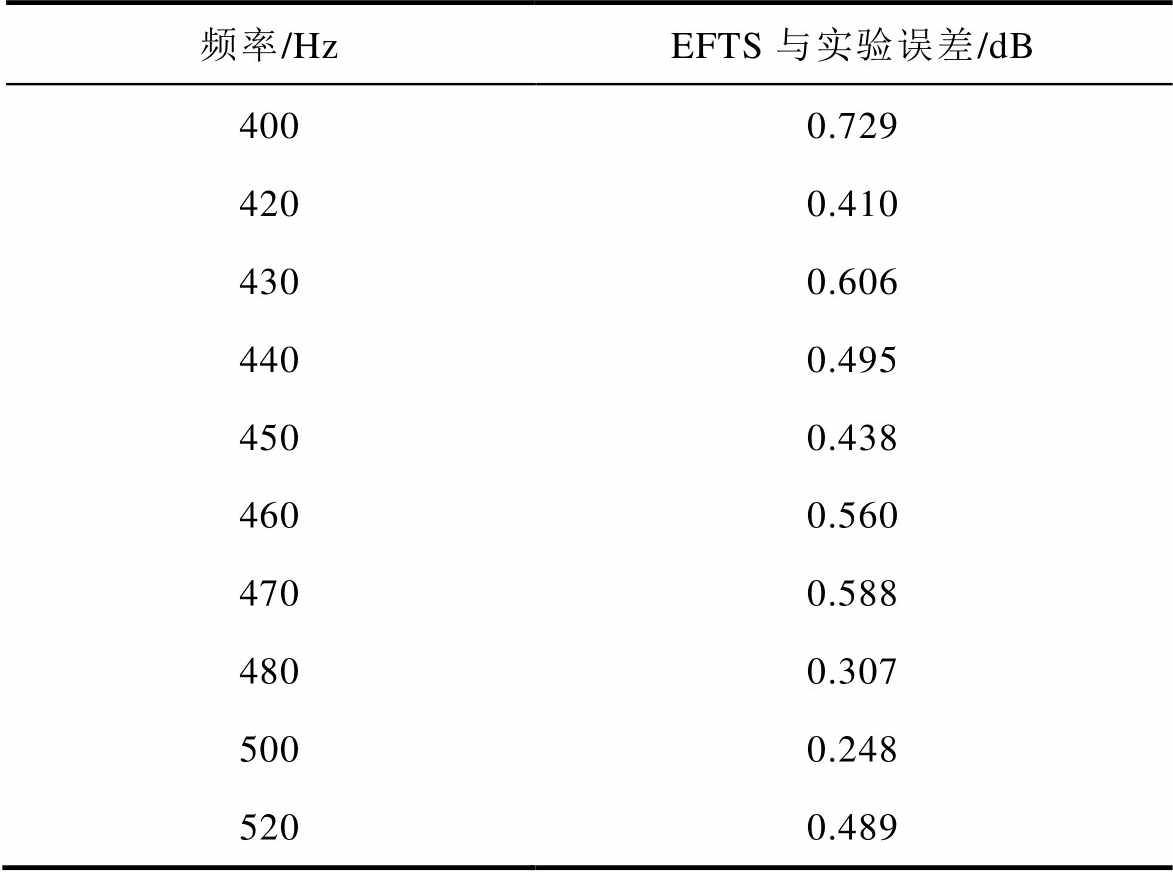
频率/HzEFTS与实验误差/dB 4000.729 4200.410 4300.606 4400.495 4500.438 4600.560 4700.588 4800.307 5000.248 5200.489
为了衡量不同频率下换能器的EFTS神经网络预测结果的准确性，采用相对误差表示EFTS预测值的偏差百分比，表达式为
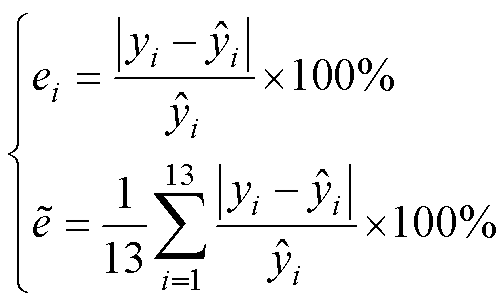（7）
式中，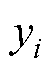
为第i个样本声源级实测值；
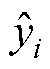为第i个样本EFTS神经网络的声源级预测值；
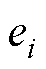为第i个样本误差；
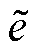为样本平均误差。
经计算，换能器的EFTS神经网络预测结果和实验结果最大误差为0.419%，平均误差为0.26%；而换能器的时域有限元模型计算结果与实验结果最大误差为0.541%，平均误差为0.271%。通过对比可知，GMT的EFTS神经网络快速计算结果与时域有限元模型计算结果相近，可信度较高。
本文以超磁致伸缩电声换能器为研究对象，基于有限元软件模拟了换能器的输出特性，分析了换能器电-磁-机-声多物理场耦合动态模型。并根据换能器动态模型，提出了一种基于改进EFTS神经网络的GMT输出特性分析方法。为了验证所提方法的准确性和有效性，研制了一款超磁致伸缩电声换能器样机，通过对比换能器深度学习模型与实验结果得到以下结论：
1）基于GMT电-磁-机-声多物理场耦合动态模型的输入-输出数据，构建了换能器的EFTS神经网络模型，可以快速、高效、准确地预测GMT的输出特性。
2）GMT的EFTS神经网络可以将单次计算时间从动态模型仿真时间的14 854 s减少到0.012 9 s，大大提高了计算效率。
3）GMT的EFTS神经网络预测结果与实验数据误差最大为0.419%，平均误差为0.26%，计算准确度较高。
参考文献
[1] 宁倩, 李桥, 高兵, 等. 电-磁-机-声多场边界下的超磁致伸缩Ⅳ型弯张换能器设计方法[J]. 电工技术学报, 2023, 38(12): 3112-3121.
Ning Qian, Li Qiao, Gao Bing, et al. Design of giant magnetostrictive class Ⅳ flextensional transducer under electrical-magnetic-mechanical-acoustic multi- field boundaries[J]. Transactions of China Electro- technical Society, 2023, 38(12): 3112-3121.
[2] 刘素贞, 杨圣哲, 张闯, 等. 基于非线性电磁超声表面波混频方法的金属疲劳裂纹检测[J]. 中国电机工程学报, 2021, 41(15): 5371-5381.
Liu Suzhen, Yang Shengzhe, Zhang Chuang, et al. Detection of metal fatigue cracks based on mixing method of nonlinear electromagnetic ultrasonic surface wave[J]. Proceedings of the CSEE, 2021, 41(15): 5371-5381.
[3] 黄文美, 郭万里, 郭萍萍, 等. 基于多目标遗传算法的高频磁致伸缩换能器优化设计[J]. 仪器仪表学报, 2022, 43(1): 111-119.
Huang Wenmei, Guo Wanli, Guo Pingping, et al. Optimization design of high frequency magnetos- trictive transducer based on the multi-objective genetic algorithm[J]. Chinese Journal of Scientific Instrument, 2022, 43(1): 111-119.
[4] 李姝汛, 杨鑫, 陈泽坤, 等. 计及漏磁的堆栈式超磁致伸缩制动器多物理场耦合建模研究[J]. 电工技术学报, 2023, 38(9): 2277-2288.
Li Shuxun, Yang Xin, Chen Zekun, et al. Multi-physics modeling research of stacked giant magnetostrictive actuator considering magnetic flux leakage[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2277-2288.
[5] Yang Mingzhi, Yang Xin, Wei Yanfei, et al. SPICE modeling of a high-power terfenol-D transducer considering losses and magnetic flux leakage[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2022, 69(2): 812-822.
[6] Zhang Xi, Li Hongguang, Zhao Xie, et al. Numerical analysis and experimental measurement on segmented ring transducer acoustic fields[J]. Applied Acoustics, 2023, 207: 109331.
[7] Guo Rongjing, Li Shiyang, Li Tangan, et al. Analysis and design of low frequency and high power flexten- sional transducer with double-grooves[J]. Applied Acoustics, 2019, 149: 25-31.
[8] Stachowiak D. Finite element analysis of the active element displacement in a giant magnetostrictive transducer[J]. COMPEL: the International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2016, 35(4): 1371-1381.
[9] 陈定方, 舒亮, 卢全国, 等. 超磁致伸缩致动器建模与控制仿真[J]. 机械工程学报, 2007, 43(8): 12-16.
Chen Dingfang, Shu Liang, Lu Quanguo, et al. Modeling and control simulation of giant magnetos- trictive actuator[J]. Chinese Journal of Mechanical Engineering, 2007, 43(8): 12-16.
[10] 夏飞, 许延峰, 胡青. 模拟海豚滴答声的仿生换能器设计[J]. 哈尔滨工程大学学报, 2023, 44(6): 962- 968.
Xia Fei, Xu Yanfeng, Hu Qing. Design of a bionic transducer that simulates the ticking sound of dolphins[J]. Journal of Harbin Engineering University, 2023, 44(6): 962-968.
[11] Teng Duo, Li Yatian. Finite element solutions for magnetic field problems in terfenol-D transducers[J]. Sensors, 2020, 20(10): 2808.
[12] 张宇娇, 赵志涛, 徐斌, 等. 基于U-net卷积神经网络的电磁场快速计算方法[J]. 电工技术学报, 2024, 39(9): 2730-2742.
Zhang Yujiao, Zhao Zhitao, Xu Bin, et al. Fast calculation method of electromagnetic field based on U-Net convolutional neural network[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2730-2742.
[13] 史冬岩, 王立夫, 张博洋, 等. 基于Pyramid- Attention-U-Net深度学习模型的实时拓扑优化设计[J]. 工程力学, 2024, 41(11): 217-224.
Shi Dongyan, Wang Lifu, Zhang Boyang, et al. Real- time topology optimization design upon Pyramid- Attention-U-Net deep learning model[J]. Engineering Mechanics, 2024, 41(11): 217-224.
[14] Guo Yi, Chang Yuan, Lu Bing. A review of temperature prediction methods for oil-immersed transformers[J]. Measurement, 2025, 239: 115383.
[15] 刘云鹏, 高艺倩, 刘刚, 等. 基于U-net神经网络的油浸式变压器绕组流-热耦合快速计算[J]. 中国电机工程学报, 2024, 44(7): 2897-2910.
Liu Yunpeng, Gao Yiqian, Liu Gang, et al. Fast calculation of flow-thermal coupling model of oil-immersed transformer windings based on U-net neural network[J]. Proceedings of the CSEE, 2024, 44(7): 2897-2910.
[16] Guo Pingping, Huang Wenmei, Feng Xiaobo, et al. Hysteresis measurement and generic modeling of magnetostrictive materials under high-frequency excitation and high-intensity bias field[J]. Measure- ment, 2024, 228: 114385.
[17] 黄文美, 薛胤龙, 王莉, 等. 考虑动态损耗的超磁致伸缩换能器的多场耦合模型[J]. 电工技术学报, 2016, 31(7): 173-178.
Huang Wenmei, Xue Yinlong, Wang Li, et al. Multi- field coupling model considering dynamic losses for giant magnetostrictive transducers[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 173-178.
[18] 高兵, 吴泽伟, 赵能桐, 等. 基于AFSA-eCS混合算法的超磁致伸缩换能器输出特性分析[J]. 电工技术学报, 2025, 40(2): 346-357.
Gao Bing, Wu Zewei, Zhao Nengtong, et al. Analysis of output characteristics of giant magnetostrictive transducers based on AFSA-eCS hybrid algorithm[J]. Transactions of China Electrotechnical Society, 2025, 40(2): 346-357.
[19] 滕舵, 杨虎. 水声换能器基础[M]. 2版. 西安: 西北工业大学出版社, 2020.
[20] Huang Gao, Liu Zhuang, Van Der Maaten L, et al. Densely connected convolutional networks[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 2017: 2261-2269.
[21] Hou Yuqing, Li Hui, Chen Hong, et al. A novel deep U-Net-LSTM framework for time-sequenced hydrodynamics prediction of the SUBOFF AFF-8[J]. Engineering Applications of Computational Fluid Mechanics, 2022, 16(1): 630-645.
[22] Gong Ruohan, Tang Zuqi. Investigation of convolutional neural network U-Net under small datasets in transformer magneto-thermal coupled analysis[J]. COMPEL-the International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2020, 39(4): 959-970.
[23] Zheng Jia, Li Shiyang, Wang Bin. Design of low-frequency broadband flextensional transducers based on combined particle swarm optimization and finite element method[J]. Smart Materials and Structures, 2021, 30(10): 105002.
Abstract The giant magnetostrictive electroacoustic transducer (GMT) represents a sophisticated underwater device that utilizes the magnetostrictive effect of rare earth giant magnetostrictive materials (GMM) under alternating magnetic fields to achieve efficient electroacoustic energy conversion. This technology demonstrates significant application potential in underwater sonar systems. However, the dynamic performance of GMT is substantially influenced by complex nonlinear electric-magnetic-mechanical-acoustic coupling effects. Traditional frequency-domain methods often fail to accurately represent the input-output relationships, making precise time-domain characteristic analysis crucial for optimal transducer design. Although the time-domain model has the problems of nonlinearity, strong coupling and low computational efficiency, the time-domain characteristics of GMT can be analyzed quickly with the help of deep learning methods. In this context, this paper proposes an enhanced feature transfer structure (EFTS) based on the time-domain model of GMT.
Firstly, based on the Jiles-Atherton hysteresis model of GMM, a time-domain finite element model (FEM) of GMT is established, incorporating the coupling of electromagnetic, mechanical, and acoustic multiple physical fields. The dynamic output characteristics of the transducer are analyzed by the FEM simulation results, and the accuracy of the dynamic model is validated based on existing research. Secondly, to address the issue of long computation time and low efficiency in the GMT FEM model, an EFTS deep learning model is constructed. The neural network is densely connected through a Dense block structure, enabling the reuse of feature information in the channel dimension, thereby accelerating the model’s convergence speed. Thirdly, the GMT EFTS deep learning model is trained to achieve rapid analysis of GMT output characteristics under multi-parameter nonlinear coupling, leveraging small-sample data from the FEM model. Comparative analysis demonstrates that the predicted values of TCR by the EFTS neural network align well with the simulation results, with an RMSE of 0.017, indicating that the proposed method can efficiently and accurately obtain the output characteristics of GMT. Finally, the structural parameters of GMT are optimized based on EFTS neural network and particle swarm optimization algorithm. The optimized structural parameters meet the design requirements and can be used as the final design scheme.
To further validate the feasibility of the proposed design method, a GMT prototype was developed based on the optimized design scheme, and a lake-based experimental platform was constructed. Experimental results demonstrate that at a target water depth of 60 meters, the transducer exhibits a resonant frequency of 450 Hz and achieves a maximum transmit current response (TCR) of 182.79 dB, accompanied by excellent waveform quality. Furthermore, the EFTS neural network prediction results show strong agreement with the experimental data. The feasibility of this method is verified, which provides a new solution for fast and accurate design of GMT.
In summary, the following conclusions can be drawn from the comparative analysis between the model and experimental results: (1) Based on the input and output data of GMT dynamic model, the EFTS neural network model of the transducer is constructed in this paper, which can predict the output characteristics of GMT quickly and accurately and obtain the corresponding design scheme. (2) The GMT EFTS neural network significantly enhances computational efficiency, reducing the single computation time from 14 854 seconds to merely 0.012 9 seconds. (3) The EFTS neural network exhibits high calculation accuracy, with a maximum error of 0.419% and an average error of 0.26% when validated against experimental data, confirming its reliability and precision.
keywords：Giant magnetostrictive electroacoustic transduction, multiple physical field coupling, enhanced feature transmission structure, transmit current response
中图分类号：TM271; TB565
DOI: 10.19595/j.cnki.1000-6753.tces.241953
国家自然科学基金项目（52377010）、国家自然科学基金重大科研仪器研制项目（52127901）和国家自然科学基金青年科学基金项目（52407203）资助。
收稿日期 2024-10-30
改稿日期 2025-01-18
徐修贤 男，1995年生，博士研究生，研究方向为大功率电声换能器系统。E-mail: xiuxian_xu@163.com
高 兵 男，1987年生，副教授，研究方向为多物理场计算和电声换能器等。E-mail: gbdnbh@hnu.edu.cn（通信作者）
（编辑 李 冰）