Tab.1 Comparison of regulation capabilities of ER, SOP and RPFC application scenarios

应用场景功率控制电压/功率因数控制相位差线路柔性合环频率差合环交直流配电网互联 RPFC√√√×× SOP√×√√√ ER√×√√√
摘要 为实现有源配电网馈线电压与功率因数的综合调控,该文提出一种基于线路阻抗调节原理的旋转潮流控制器(RPFC)电压/功率因数协调控制策略。首先,分析RPFC的拓扑结构与稳态特性,搭建了RPFC稳态输出阻抗的等效模型。其次,分析RPFC在阻性、容性、阻容性三种模式下的补偿特性。然后,提出RPFC的合环点电压/功率因数解耦控制方法,即根据电压、功率因数目标值计算得出RPFC需输出的等效阻抗,转化为旋转角设定值后,通过RPFC的转速内环完成无差控制。最后,通过仿真和实验对等效模型及控制方法进行了验证,实验中RPFC的调节误差控制在1.4%以内,验证了所提策略对线路电压及功率因数连续调节的有效性。
关键词:柔性互联配电网 旋转潮流控制器 电压调控 功率因数改善
随着国家大力支持新能源发电以及新能源发电技术的不断发展,分布式可再生能源在配电网的接入比例逐年升高,对系统的潮流分布、电压水平、短路容量等电气特性造成了一定影响,带来了功率因数恶化和过电压等问题[1-2]。现有配电网调压手段,如有载调压变压器[3]、就地配置无功补偿装 置[4-5]、配置储能系统[6-7]等均有其局限性。柔性互联装置可提供快速准确的失电支援及电能质量改善等功能,实现配电网间资源的柔性互动,解决分布式电源大规模接入带来的一系列电能质量问题[8-9]。
文献[10-12]开展了将柔性互联设备应用于配电网电压越限治理的研究。文献[10]提出了一种基于智能软开关(Soft Open Point, SOP)的主动配电网电压模型预测控制优化方法,可减小配电网节点电压偏差,应对配电网中新能源出力波动。文献[11]提出了利用配电网电力电子变压器对配电网进行电压调控的方案,引入无功电流反馈的无功补偿控制以提高配电网电压质量和稳定性。文献[12]提出了基于背靠背换流器的柔性互联微电网群分层协调控制策略,可在负载扰动时有效调控各微电网单元电压保持在额定值附近。在配电网功率因数治理方面,文献[13]提出了以柔性直流互联装置为核心的无功电压控制策略,通过置换柔性直流的无功出力,提高电网动态无功支撑能力,以应对稳态时局部电压或功率因数偏低及故障时的电压跌落;文献[14]提出了基于升压型功率因数校正变换器的控制方法,在保证线路功率因数的同时还有较强的抗外部干扰能力。
文献[10-14]所提方法均可有效实现配电网电压/功率因数调控,但电力电子设备存在成本较高、可靠性较差等缺点,可采用旋转潮流控制器(Rotary Power Flow Controller, RPFC)作为替代方案[15]。RPFC主体结构为旋转移相变压器(Rotary Phase Shift Transformer, RPST)[16],同时具备配电网网架内部与配电网台区之间的柔性互联能力,通过改变RPFC的移相角即可灵活控制串入线路的电压。为了清楚地将现有主要电力电子柔性互联设备与本文所提RPFC装置进行对比,通过调研和理论分析,形成了表1和表2的对比结果,表1列出了能量路由器(Energy Router, ER)、SOP和RPFC在多种配电网柔性互联场景的调控能力[10, 16-19],√表示适应此场景,×表示不适用,表2列出了三者的技术特征,包括无、弱、中、强、低、高的技术特点。根据表1和表2可知,RPFC的主要技术优势在于成本低、无谐波和抗冲击性强,在频繁扰动的有源配电网应用场景中具有一定优势。
表1 ER、SOP与RPFC应用场景调控能力对比
Tab.1 Comparison of regulation capabilities of ER, SOP and RPFC application scenarios

应用场景功率控制电压/功率因数控制相位差线路柔性合环频率差合环交直流配电网互联 RPFC√√√×× SOP√×√√√ ER√×√√√
表2 ER、SOP与RPFC的技术特征对比
Tab.2 Comparison of technical characteristics of ER, SOP and RPFC
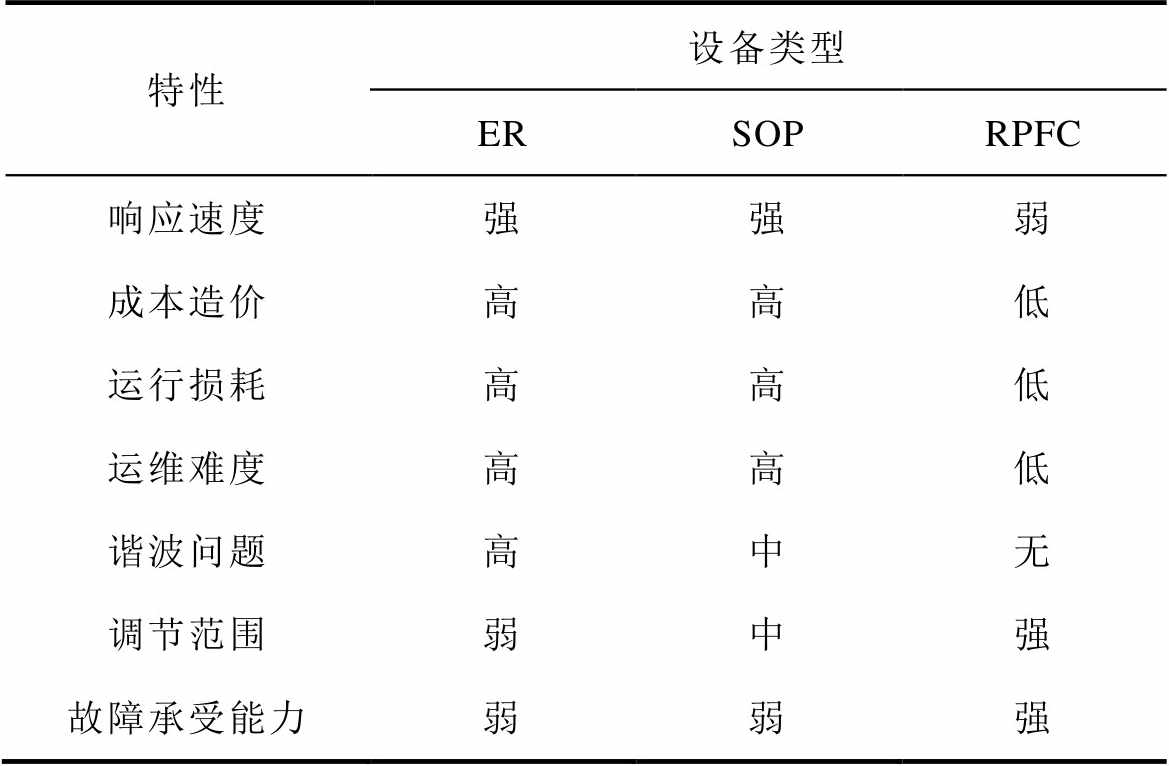
特性设备类型 ERSOPRPFC 响应速度强强弱 成本造价高高低 运行损耗高高低 运维难度高高低 谐波问题高中无 调节范围弱中强 故障承受能力弱弱强
现有文献已针对RPFC在无功补偿[20]、馈线电压控制[21]以及配电网功率控制[22]等方面开展了相关研究。文献[20]参考静止无功补偿器结构,提出了一种基于RPST的电压源型无功补偿器拓扑并设计了其控制策略,该装置可实现并网点无功功率的连续、双向调节,且具有成本低、易运维和抗冲击性强的优势。文献[21]研究了基于RPFC的馈线电压控制方法,能够对辐射型配电网的RPFC接入点下方电压进行有效控制。文献[22]针对一种花瓣型配电网,提出基于RPFC的两阶段转速功率控制策略,结果表明所提控制方案能够实现秒级调控,且控制精度保持在4%以内,具有良好的动、静态性能。然而,目前RPFC装置在配电网的应用中具有一定局限性,现有电压调节方法仅能对线路电压的幅值进行调节[21],并不能改善功率因数。因此亟须开展基于RPFC的电压/功率因数控制研究,以丰富其应用场景和提高配电网运行可靠性。
本文提出了采用RPFC的方式对合环点电压/功率因数进行有效控制。首先,分析了RPFC的拓扑结构与其稳态特性,搭建了RPFC稳态输出阻抗的等效模型。然后,分析了RPFC在三种模式下的补偿特性,提出了RPFC的合环点电压/功率因数解耦控制方法,即根据电压、功率因数目标值计算得到RPFC需输出的等效阻抗,转化为旋转角设定值后通过RPFC的转速内环完成无差控制。最后,开展了10 kV配电网的仿真验证,并搭建了380 V实验平台对所提控制策略进行了验证。结果表明,所提方法能够有效对合环点电压、功率因数进行有效控制,对配电网供电效率和安全性的提高具有积极 意义。
图1为RPFC的拓扑结构。根据图1,两台RPST的转子绕组并联连接于线路中用于设备励磁,定子绕组串联接入线路,可分别输出幅值一定、相位360°可调的电压相量,叠加后即可在线路中注入一个幅值、相位均可调的串联电压。
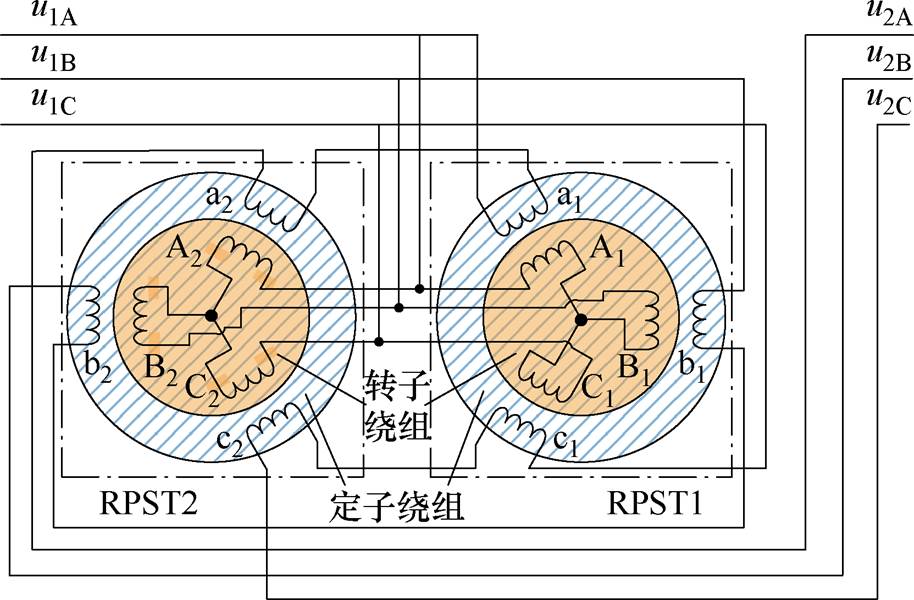
图1 RPFC拓扑结构
Fig.1 Topology structure of RPFC
RPFC的主电路如图2所示。u1和u2分别为RPFC接入点的首、末端电压;urt为转子绕组电压;ust1和ust2为两个定子绕组电压;user为RPFC向线路注入的串联电压;i为RPFC所在线路电流;ise和ish分别为RPFC串、并联侧电流;Zst为两台RPST定子阻抗;Zrt为RPFC转子阻抗;k为两台RPST的有效匝数比;a1和a2为两台RPST的移相角。
图2中,串联电压user可表示为[23]
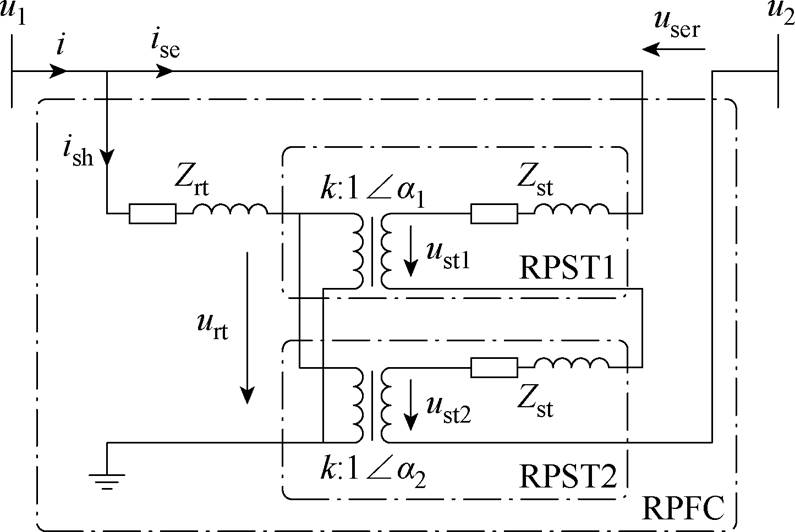
图2 RPFC的主电路示意图
Fig.2 Main circuit diagram of RPFC
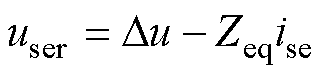 (1)
(1)
根据式(1)可将RPFC看作是受控输出电压源Du与等效阻抗Zeq串联,Du与Zeq的参数分别为
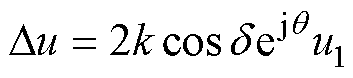 (2)
(2)
 (3)
(3)
式中,d为Du与定子电压的夹角;q为Du的相位。
此时,基于式(2)、式(3)可以得到RPFC电压相量图如图3所示。图中,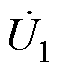 、
、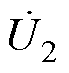 、
、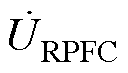 、
、 、
、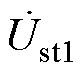 、
、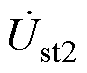 、
、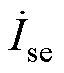 分别为u1、u2、user、Du、ust1、ust2、ise的相量形式。旋转角a1、a2与q、d的关系满足
分别为u1、u2、user、Du、ust1、ust2、ise的相量形式。旋转角a1、a2与q、d的关系满足
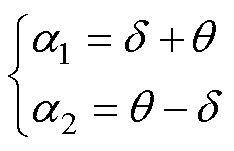 (4)
(4)
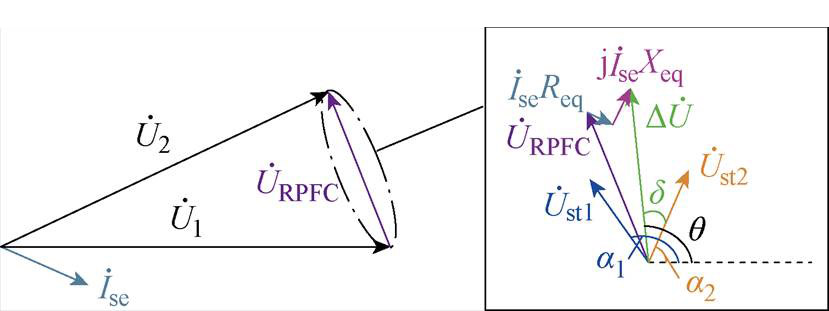
图3 RPFC输出电压相量图
Fig.3 Output voltage phasor diagram of RPFC
下面对RPFC的端口输出特性进行分析,根据图2可得线路电流i与串联电流ise满足
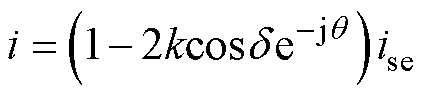 (5)
(5)
将式(5)代入式(1)得到串联电压user与线路电流i的关系为
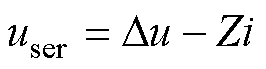 (6)
(6)
式中,Z为RPFC装置内阻抗,有
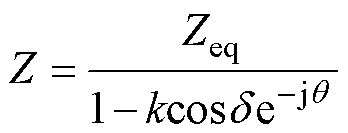 (7)
(7)
令式(6)的等式两边分别除以电流i得到
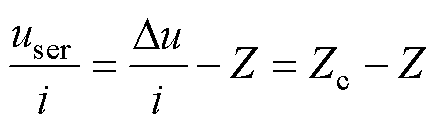 (8)
(8)
根据式(8),RPFC可等效为一个补偿阻抗Zc与内阻抗Z串联的阻抗模型,如图4所示。图中,us1为线路送端电压,uin为RPFC内阻抗压降,RL+jXL为线路阻抗。根据式(8)与图4可知,通过改变RPFC两移相角大小,可动态调节RPFC输出电压的阻抗约束关系,从而控制Rc+jXc的阻抗大小,实现对接入点末端电压u2的调节功能。
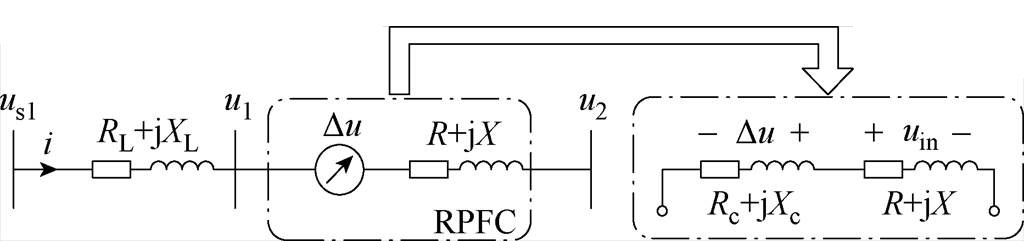
图4 RPFC阻抗模型
Fig.4 Impedance model of RPFC
根据输出电压和线路电流之间的相位关系,RPFC可采取阻性补偿、容性补偿和阻容性补偿三种阻抗方式,其对应相量如图5所示。图5中,j为线路功率因数角,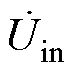 、
、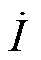 分别为uin、i的相量形式,
分别为uin、i的相量形式,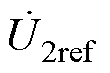 为
为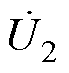 的设定值。
的设定值。
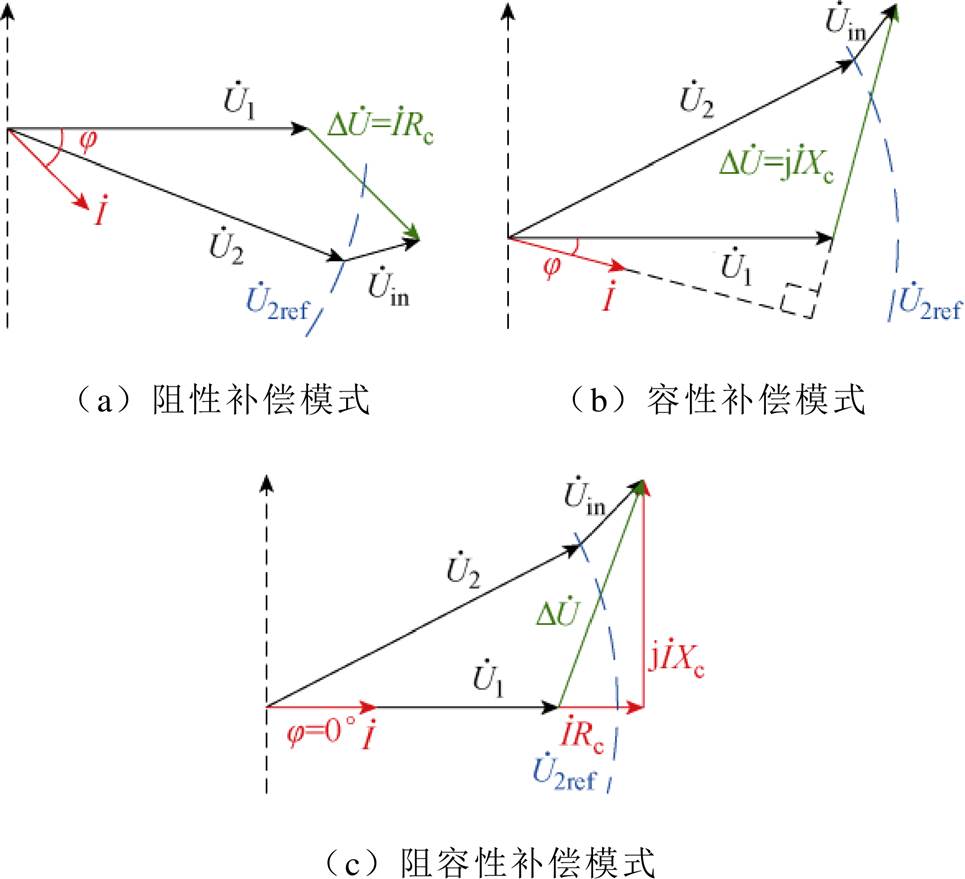
图5 RPFC阻抗模型相量图
Fig.5 Phasor diagram of RPFC impedance model
由图5可知,阻性补偿方式控制输出电压相位与电流相位保持一致,相当于在线路中串联一个正负和大小可调的补偿电阻Rc;容性补偿方式下输出电压Du与线路电流i互差90°,相当于在线路中串联一个正负和大小可调的补偿电抗Xc;阻容性补偿方式下,RPFC分别调节输出电压幅值和相位大小,即可等效为在线路中分别串入正负和大小均连续可调的Rc和Xc。
由图5可知,RPFC在不同补偿模式下对线路电压与功率因数的影响不同,有必要对RPFC的补偿特性进行分析。RPFC的补偿范围主要受两个因素制约,即线路受端电压幅值U2与线路功率因数角j。调节过程中二者需满足约束关系
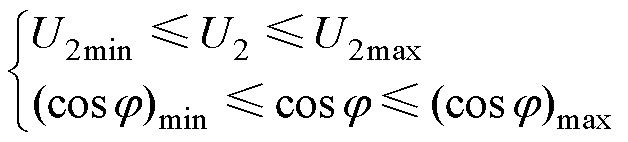 (9)
(9)
线路功率因数最大为1,因此(cosj)max=1,对应功率因数角最小值jmin=0;线路功率因数最小值(cosj)min对应功率因数角最大值jmax。
图6为RPFC阻性补偿模式相量图。图中,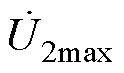 为
为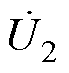 的最大值,
的最大值,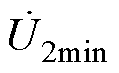 为
为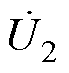 的最小值。
的最小值。

图6 阻性补偿模式相量图
Fig.6 Phasor diagram of resistive compensation mode
在阻性补偿模式下,Du与线路电流i同相位或反相位,补偿阻抗等效为一个电阻。通常情况下,RPFC内阻抗满足X R,根据电压相量关系和功率因数定义可得U2和cosj表达式为
R,根据电压相量关系和功率因数定义可得U2和cosj表达式为
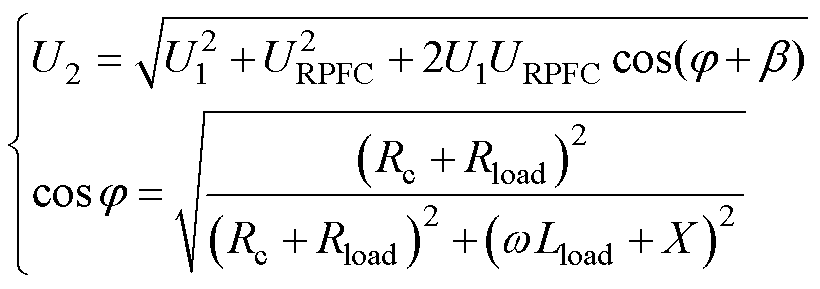 (10)
(10)
式中,Rload和wLload分别为负载的电阻与电抗分量;b为RPFC阻抗角,tanb=|Rc/X|;URPFC为RPFC总输出电压幅值,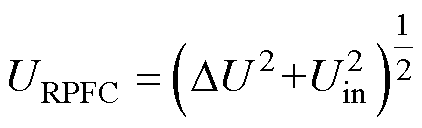 。由式(10)可知,阻性补偿模式下RPFC虽然可通过增大线路电阻的方式增大功率因数,但由于未对线路无功进行补偿,因此无法将cosj调节至较高水平,不能保证线路功率因数的完整治理。
。由式(10)可知,阻性补偿模式下RPFC虽然可通过增大线路电阻的方式增大功率因数,但由于未对线路无功进行补偿,因此无法将cosj调节至较高水平,不能保证线路功率因数的完整治理。
图7为RPFC容性补偿模式相量图。
在容性补偿模式下,RPFC输出电压Du超前/滞后于线路电流90°,补偿阻抗等效为一个电感/电容。RPFC内阻抗满足X R,则根据电压相量关系和功率因数定义可得U2和cosj表达式为
R,则根据电压相量关系和功率因数定义可得U2和cosj表达式为

图7 容性补偿模式相量图
Fig.7 Phasor diagram of capacitive compensation mode
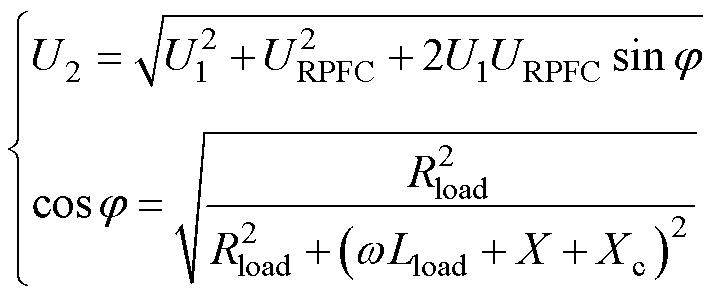 (11)
(11)
式中,Xc>0时,URPFC=DU-Uin;Xc<0时,URPFC= DU+Uin。根据图7,容性补偿模式下RPFC虽然可实现功率因数治理,但线路电压调节能力低于阻性补偿模式。
根据2.1与2.2节所述,阻性和容性补偿模式均存在一定的不足,因此可采取阻容性补偿模式,在满足调压的同时保证线路的功率因数。图8为RPFC阻容性补偿模式相量图。在阻容性补偿模式下,RPFC输出阻抗特性等效为一个正负和大小均连续可调的Rc和Xc。其电抗分量Xc对线路无功进行补偿,实现线路功率因数治理,电阻分量Rc根据电压调节需求,完成线路高/低电压治理。
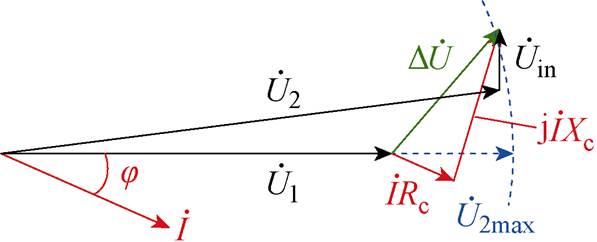
图8 阻容性补偿模式相量图
Fig.8 Phasor diagram of resistive and capacitive compensation mode
RPFC内阻抗满足X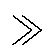 R,则根据电压相量关系和功率因数定义可得U2和cosj表达式为
R,则根据电压相量关系和功率因数定义可得U2和cosj表达式为
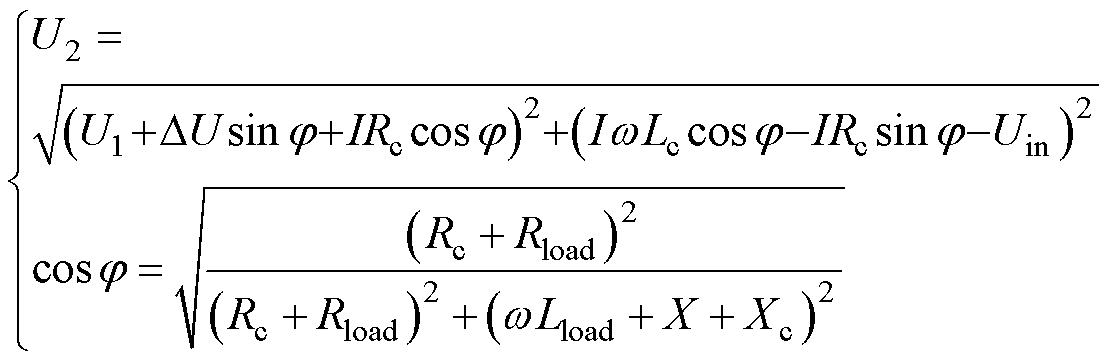 (12)
(12)
RPFC接入线路后,根据图4可得
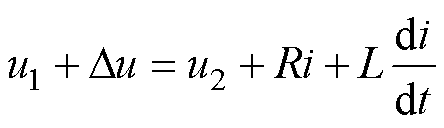 (13)
(13)
令u1定向于d轴,对式(13)进行Park变换可得
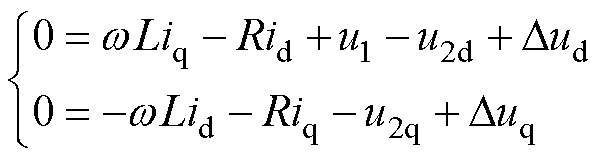 (14)
(14)
则根据式(14)得线路电流dq轴分量id和iq分别为
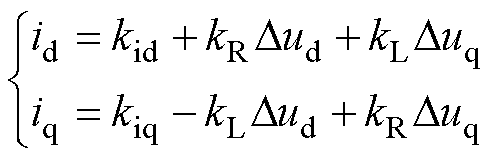 (15)
(15)
式中,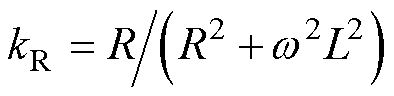 ,
,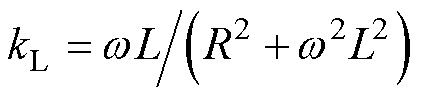 ;系数kid和kiq分别为
;系数kid和kiq分别为
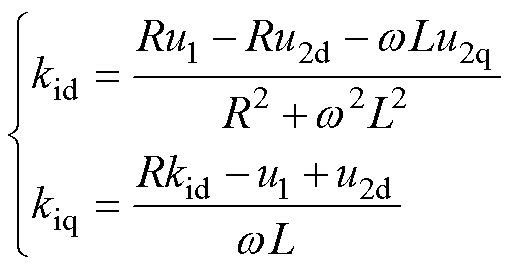 (16)
(16)
式中,u2d、u2q分别为u2的d轴、q轴分量。
通常RPFC的内电抗远大于内电阻,即wL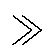 R,则式(15)可简化为
R,则式(15)可简化为
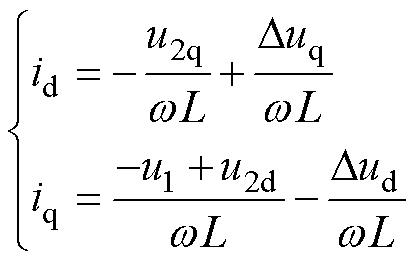 (17)
(17)
将Dud=iRc和Duq=jiwLc代入式(17)可得
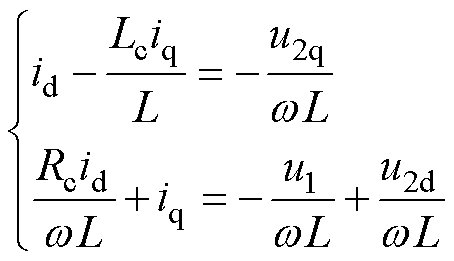 (18)
(18)
对式(18)求解可得
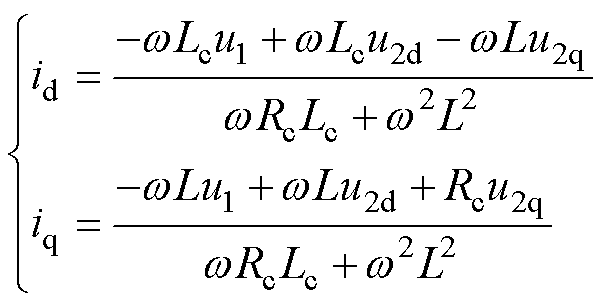 (19)
(19)
通常情况下,RPFC的内阻抗远小于装置的补偿阻抗,若忽略内电抗的大小,式(19)可化简为
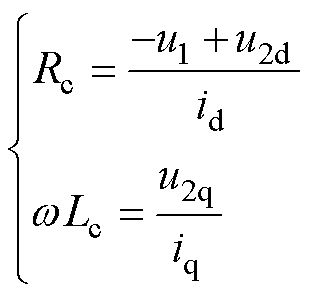 (20)
(20)
根据式(20),线路电流d轴分量id仅由补偿电阻Rc调节,线路电流q轴分量iq仅由补偿电抗wLc调节,能够实现RPFC补偿阻抗对线路电流的解耦控制。RPFC接入点下方电压幅值U2由补偿阻抗表示为
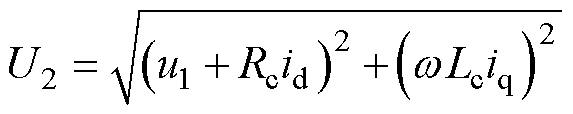 (21)
(21)
根据id和iq的关系可以得到RPFC接入点下方线路功率因数为
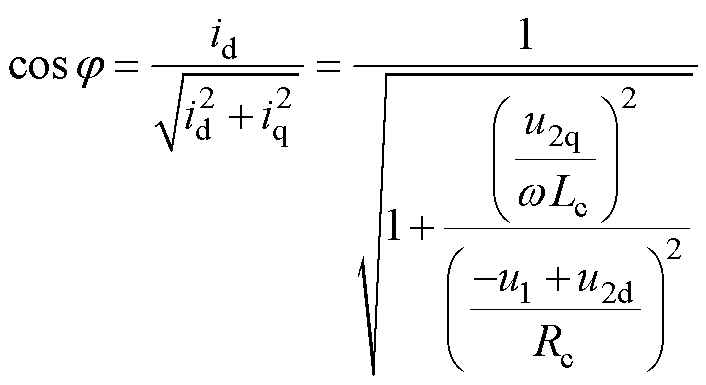 (22)
(22)
当系统要求用户侧电压幅值满足设定要求的同时优化线路功率因数,则需要通过增大补偿电抗wLc来降低线路电流q轴分量iq。当线路功率因数满足设定要求时,u2主要受线路电流d轴分量id影响。RPFC通过调节补偿电阻Rc的大小来改变id,从而将线路电压控制在设定范围内。
在Rc、wLc已知的情况下,由式(23)可计算得到RPFC串入线路矢量电压Du的大小,代入式(2)可求解得到q、d大小,最后基于式(4)求解得到a1和a2。
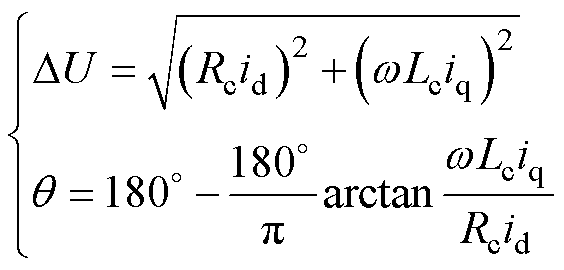 (23)
(23)
计及功率因数的RPFC电压调控策略框图如图9所示,主要包括三个模块:合环点电压/功率解耦控制、基于RPFC稳态电压源的a1和a2求解、RPFC转子角求解及控制。
(1)合环点电压/功率因数解耦控制。控制系统首先采集得到RPFC左端电压u1abc、右端电压u2abc以及线路电流iabc,计算得到线路功率因数、各电压幅值及dq变换后的dq轴分量。而后分别将合环点电压与功率因数经PI调节,根据式(21)和式(22)联立得到阻抗分量设定值Rcref和wLcref,再经PI调节后得到阻抗分量控制值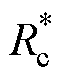 、
、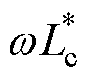 。
。

图9 RPFC控制策略框图
Fig.9 Block diagram of RPFC control strategy
(2)基于RPFC稳态电压源的a1和a2求解。在已知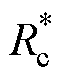 和
和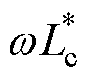 的前提下,通过式(23)即可求解得到Du的幅值及角度,并基于式(2)求解得到q和d大小。
的前提下,通过式(23)即可求解得到Du的幅值及角度,并基于式(2)求解得到q和d大小。
(3)RPFC转子角求解及控制。将q和d代入式(4)求解得到RPFC移相角设定值a1ref、a2ref。将RPFC移相角实际值与设定值作差后得到Da1和Da2,再经过基于位移规划的转速自适应控制方案得到伺服电动机的转速设定值w1ref、w2ref。该方案能够使两转子角同时达到目标,最终达到平稳控制的目的。而后控制系统通过生成PWM波控制伺服电动机驱动两台RPST旋转,使RPFC输出电压和相位达到设定要求,实现电压/功率因数的有效控制。
为验证本文所提控制模型的有效性,搭建了如图10所示的仿真模型,能够对RPFC接入点下方并网点电压和功率因数进行解耦调节,以实现台区的高质量供电,具体仿真数据见表3。图中,u1和u2分别为RPFC接入点首、末端电压,b和s分别为u1和u2的相位。
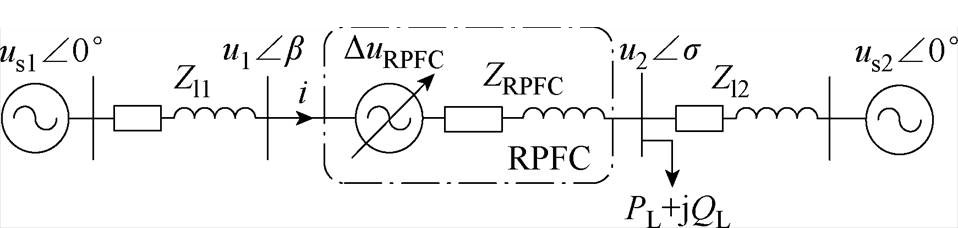
图10 基于RPFC的双电源供电仿真模型
Fig.10 Simulation model of dual-power supply system based on RPFC
表3 仿真模型参数
Tab.3 Parameters of simulation system
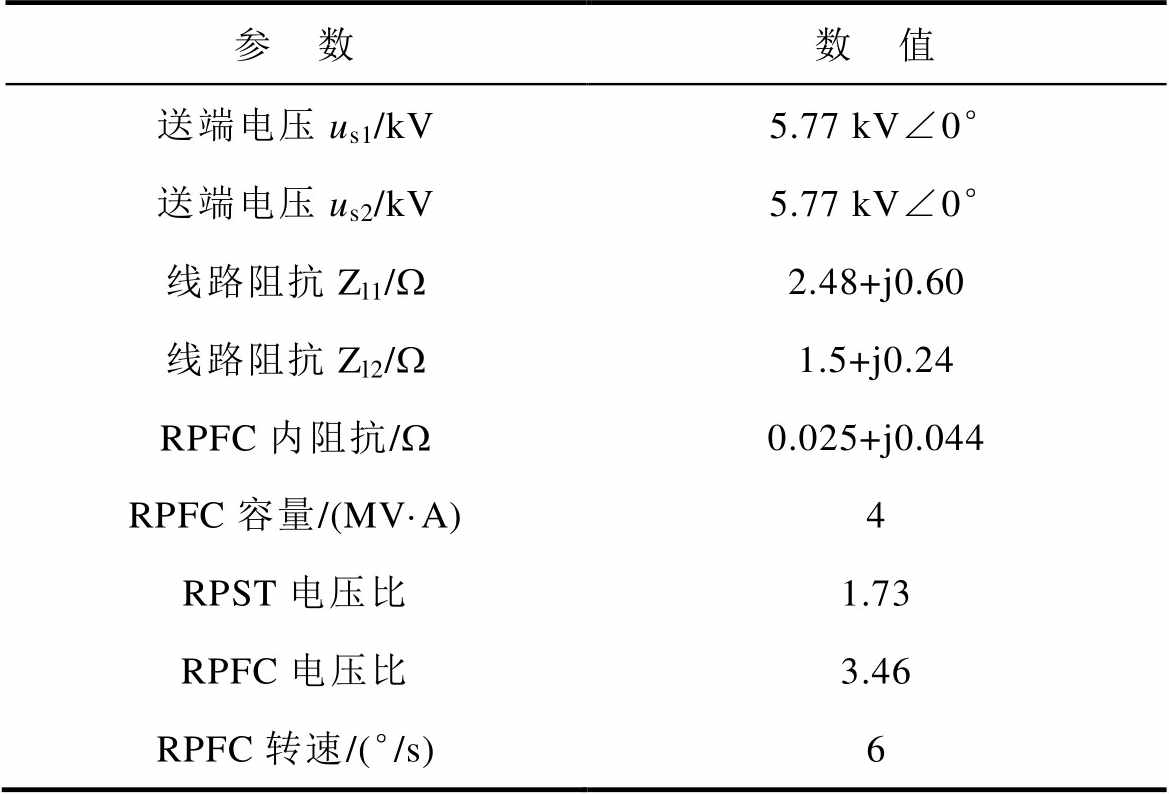
参 数数 值 送端电压us1/kV5.77 kV∠0° 送端电压us2/kV5.77 kV∠0° 线路阻抗Zl1/W2.48+j0.60 线路阻抗Zl2/W1.5+j0.24 RPFC内阻抗/W0.025+j0.044 RPFC容量/(MV·A)4 RPST电压比1.73 RPFC电压比3.46 RPFC转速/(°/s)6
4.1.1 阻性补偿特性分析
在阻性补偿模式下RPFC串入线路电压矢量与电流方向一致,在不考虑闭环无差控制时,RPFC阻性补偿模式的仿真结果如图11所示。
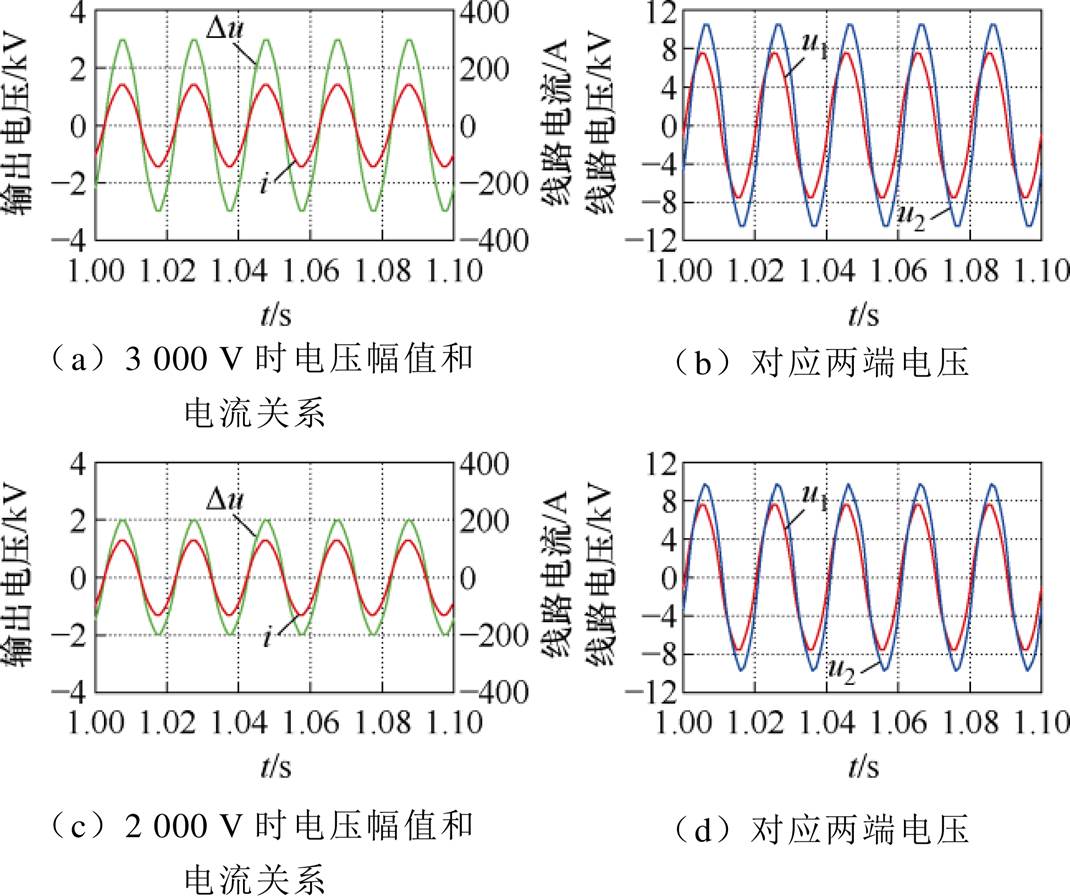
图11 RPFC阻性补偿仿真波形
Fig.11 RPFC resistance compensation simulation waveforms
可以看到,图11a和图11c的RPFC输出电压和电流相位基本相同,图11a中串入阻抗可等效为24.49 W,此时图11a中RPFC接入点上方电压有效值为5 367.01 V,RPFC接入点下方电压有效值为7 511.49 V;图11c中串入阻抗可等效为18.48 W,此时图11d中RPFC接入点上方电压有效值为5 393.58 V,RPFC接入点下方电压有效值为6 885.30 V。
4.1.2 容性补偿特性分析
在容性补偿模式下RPFC可以等效为补偿电抗Xc,此时的仿真波形如图12所示。
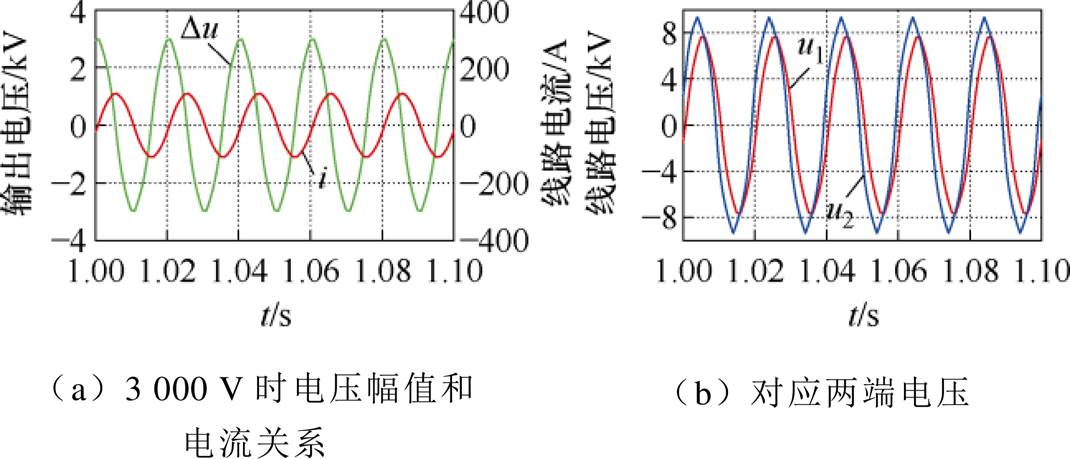
图12 RPFC容性补偿仿真波形
Fig.12 RPFC capacitive compensation simulation waveforms
参照图8,令PL+jQL=(1.452+j0.854) MV·A不变,通过解耦控制u2大小,而不影响合环点功率因数,验证RPFC调节功能,将仿真过程分为了三个阶段:阶段1:相电压有效值u2ref=5.80 kV;阶段2:相电压有效值u2ref=5.75 kV;阶段3:相电压有效值u2ref=5.70 kV。
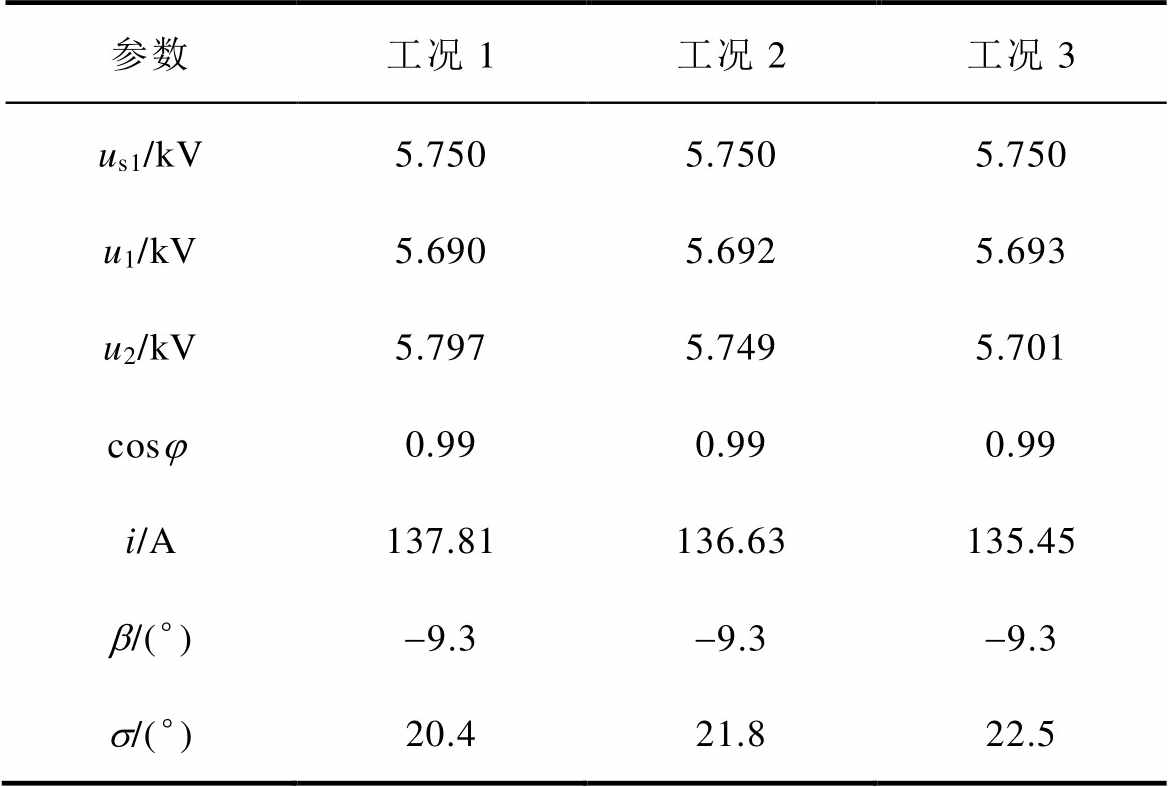
电压设定值变动下仿真波形如图13所示,仿真结果见附表1,可以看到,当设定值发生变动时,RPFC均能将用户侧电压控制在设定范围内,并能将线路功率因数进行优化(cosj=0.996)。u2在三种工况下的误差分别为0.052%、0.017%、0.018%。

图13 电压设定值变动下RPFC仿真波形
Fig.13 Simulation waveforms of RPFC under change of voltage settings
为了验证RPFC电压/功率因数解耦控制功能,设计了负载扰动功率对其控制效果进行验证,令用户侧电压设定值u2ref=5.75 kV不变,通过改变负载功率PL+jQL大小,将仿真过程分为了三个阶段:阶段1:负载功率PL+jQL=(1.452+j0.854) MV·A;阶段2:负载功率PL+jQL=(1.210+j0.610) MV·A;阶段3:负载功率PL+jQL=(1.694+j0.732) MV·A。
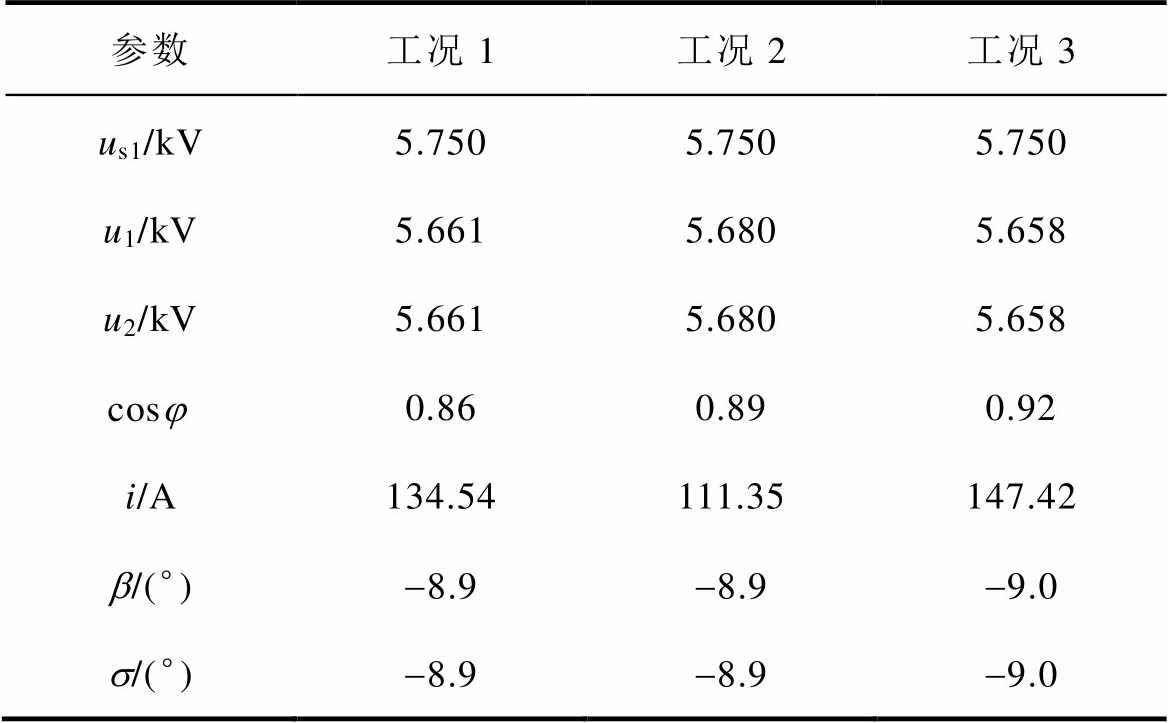
当RPFC旁路未投入运行时,仿真结果如附图1所示,具体仿真数据参照附表2。当RPFC未投运时,合环点(负载接入位置)的电压和功率因数随负载波动而变化。当RPFC投入运行后,分别采用文献[23]和本文方法进行仿真,结果如图14所示,具体仿真数据参照附表3。其中,图14a、图14b分别为本文方法和文献[23]方法得到的线路电压幅值,图14c、图14d是两种方法得到的线路电流幅值和线路电压相位,参数us1、u1、u2、i、b、s对应本文方法,参数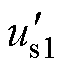 、
、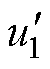 、
、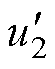 、
、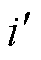 、
、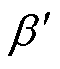 、
、 对应文献[23]方法;图14e和14f为分别采用本文方法和文献[23]方法调节后的线路功率因数。由图14和附表3可得,在负载发生扰动后,文献[23]所提方法仅能使电压u2的幅值满足设定要求,但并不能改变线路的功率因数;本文方法可在调节u2幅值的基础上,对线路功率因数进行优化,使其达到0.996,且u2在三种工况下的误差分别为0.035%、0.017%、0.017%。
对应文献[23]方法;图14e和14f为分别采用本文方法和文献[23]方法调节后的线路功率因数。由图14和附表3可得,在负载发生扰动后,文献[23]所提方法仅能使电压u2的幅值满足设定要求,但并不能改变线路的功率因数;本文方法可在调节u2幅值的基础上,对线路功率因数进行优化,使其达到0.996,且u2在三种工况下的误差分别为0.035%、0.017%、0.017%。

图14 负载扰动下RPFC调压仿真波形
Fig.14 RPFC voltage regulation simulation waveforms under load disturbance
为验证所提控制策略的有效性与正确性,搭建了如图15所示的380 V/40 kV·A RPFC实验平台开展实验验证,实验平台参数见表4。

图15 380 V/40 kV·A RPFC实验平台
Fig.15 Experimental platform of 380 V/40 kV·A RPFC
表4 实验平台参数
Tab.4 Parameters of experimental parameters
参 数数 值 RPFC容量/(kV·A)40 线路阻抗/W5.0+j5.0 RPST一次电压/V220 电源电压/V220 频率/Hz50 RPST转速/(°/s)6.0 RPST有效匝数比3.8 负载额定容量/(kV·A)9.9
RPFC在阻性补偿模式下的实验结果如图16所示。由图16可知,此时RPFC输出端口电压和电流相位基本一致,且u2侧电压幅值明显高于u1,u2的相位略滞后于u1。
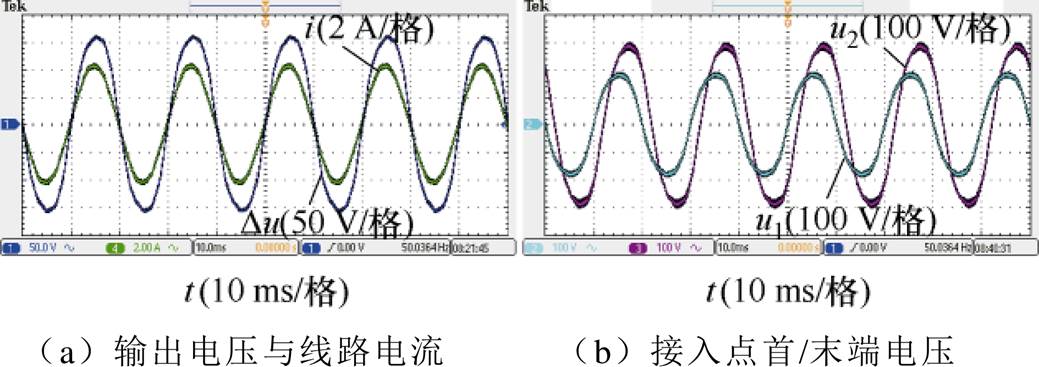
图16 RPFC阻性补偿模式验证
Fig.16 Verification of RPFC resistive compensation mode
RPFC在容性补偿模式下的实验结果如图17所示。由图17可知,此时RPFC输出电压超前于线路电流90°,补偿后的用户侧电压u2超前于RPFC左端电压u1,但未对幅值产生较大影响。

图17 RPFC容性补偿模式验证
Fig.17 Verification of RPFC capacitive compensation mode
根据图16、图17,RPFC可通过调节其输出电压,使输出端口表现为阻性或容性,与理论分析结果相符。
保持负载额定功率为PL+jQL=(6.0+j2.0) kV·A不变,在图15所示实验平台中进行电压/功率因数调控实验,并与文献[23]所提方法进行对比。图18为变设定值调压实验波形,表5为对应实验结果。其中,阶段A1~A5的电压设定值u2ref分别为220.0、225.0、230.0、235.0、240.0 V。由图18与表5可知,采用本文方法进行调控,当电压设定值发生变化时,RPFC可将u2调节至设定值附近,并保持功率因数在0.95附近。在各阶段调节过程中,电压和功率因数误差均控制在了0.5%以内,单次调节响应时间控制在了3s以内。而采用文献[23]方法时,RPFC仅能使u2达到设定值附近,无法将线路功率因数控制在某一设定值。
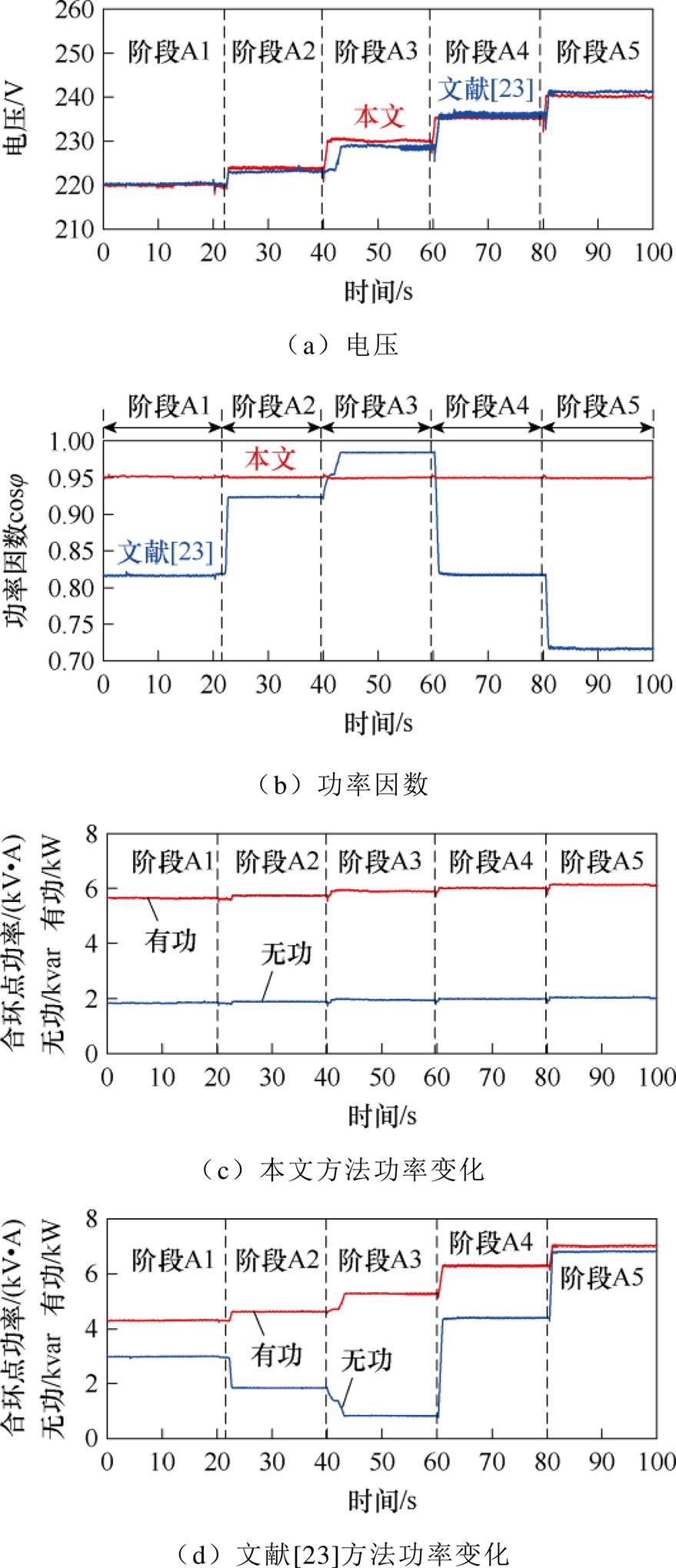
图18 变电压设定值实验波形
Fig.18 Experiment waveforms of variable voltage settings
表5 变电压设定值实验结果
Tab.5 Experiment results of variable voltage settings
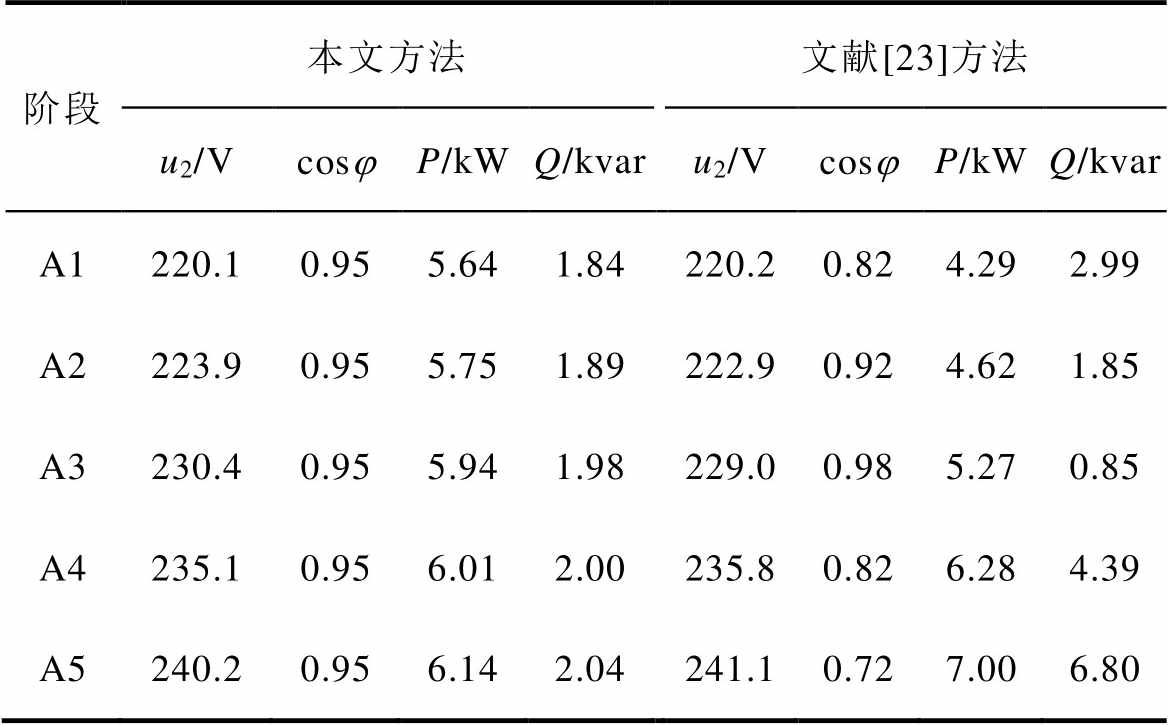
阶段本文方法文献[23]方法 u2/VcosjP/kWQ/kvaru2/VcosjP/kWQ/kvar A1220.10.955.641.84220.20.824.292.99 A2223.90.955.751.89222.90.924.621.85 A3230.40.955.941.98229.00.985.270.85 A4235.10.956.012.00235.80.826.284.39 A5240.20.956.142.04241.10.727.006.80
保持负载功率PL+jQL=(1.2+j0.3) kV·A与合环点电压u2=230.0 V不变,开展RPFC变功率因数调压实验。图19为变功率因数调压实验波形,表6为对应实验结果。其中,阶段B1~B5的合环点功率因数cosj分别为0.90、0.92、0.93、0.95、0.96。由图19与表6可知,功率因数设定值发生变化时,RPFC总能将用户侧电压u2稳定控制在230 V附近。在各阶段调节过程中,电压和功率因数误差均控制在了1.4%以内,单次调节响应时间控制在3.5 s以内。

图19 变功率因数设定值实验波形
Fig.19 Experiment waveforms of variable power factor settings
表6 变功率因数设定值实验结果
Tab.6 Experiment results of variable power factor settings
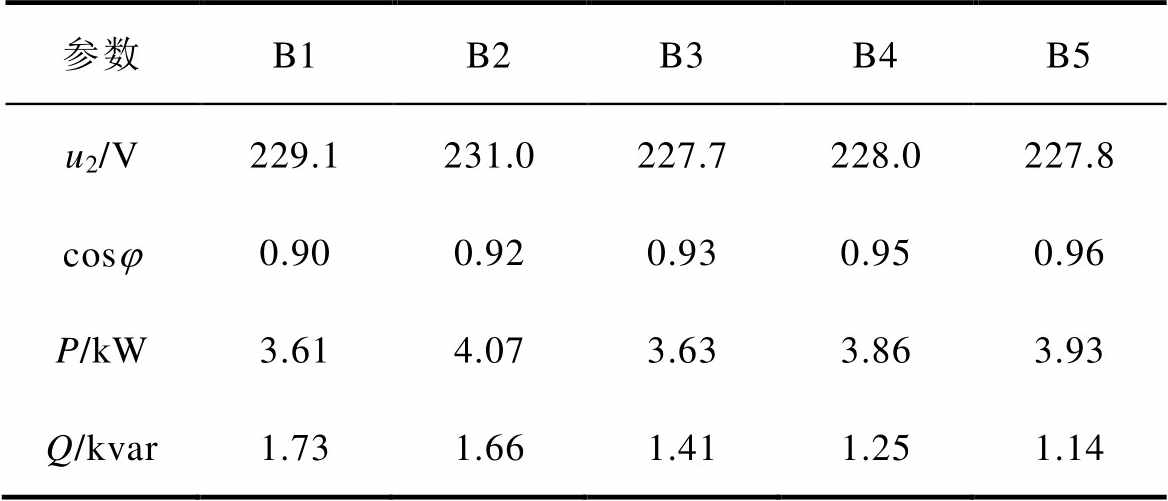
参数B1B2B3B4B5 u2/V229.1231.0227.7228.0227.8 cosj0.900.920.930.950.96 P/kW3.614.073.633.863.93 Q/kvar1.731.661.411.251.14
本文针对现有RPFC控制策略无法同时实现电压与功率因数调节的问题,提出了基于线路阻抗调节原理的RPFC电压/功率因数协调控制策略,并进行了仿真与实验验证,主要结论如下:
1)根据RPFC阻抗模型可知,改变RPFC两旋转角的大小可动态调节RPFC输出电压电流的阻抗约束关系,控制其输出端口的阻性/容性/阻容特性,从而实现接入点后方电压与功率因数的调节。
2)分析了RPFC的补偿特性,在阻性补偿模式下RPFC对功率因数的调控能力有限,在容性补偿模式下RPFC对线路电压的调控能力不足,采用阻容性补偿模式则可较好地实现电压与功率因数的共同调控。
3)在变电压和变功率因数设定值工况下,开展了RPFC电压/功率因数控制策略的仿真和实验验证,结果表明RPFC在变电压设定值和变功率因数设定值工况下,均有较好的解耦控制效果,且实验中电压和功率因数误差均控制在1.4%以内。
附录 部分仿真波形及结果
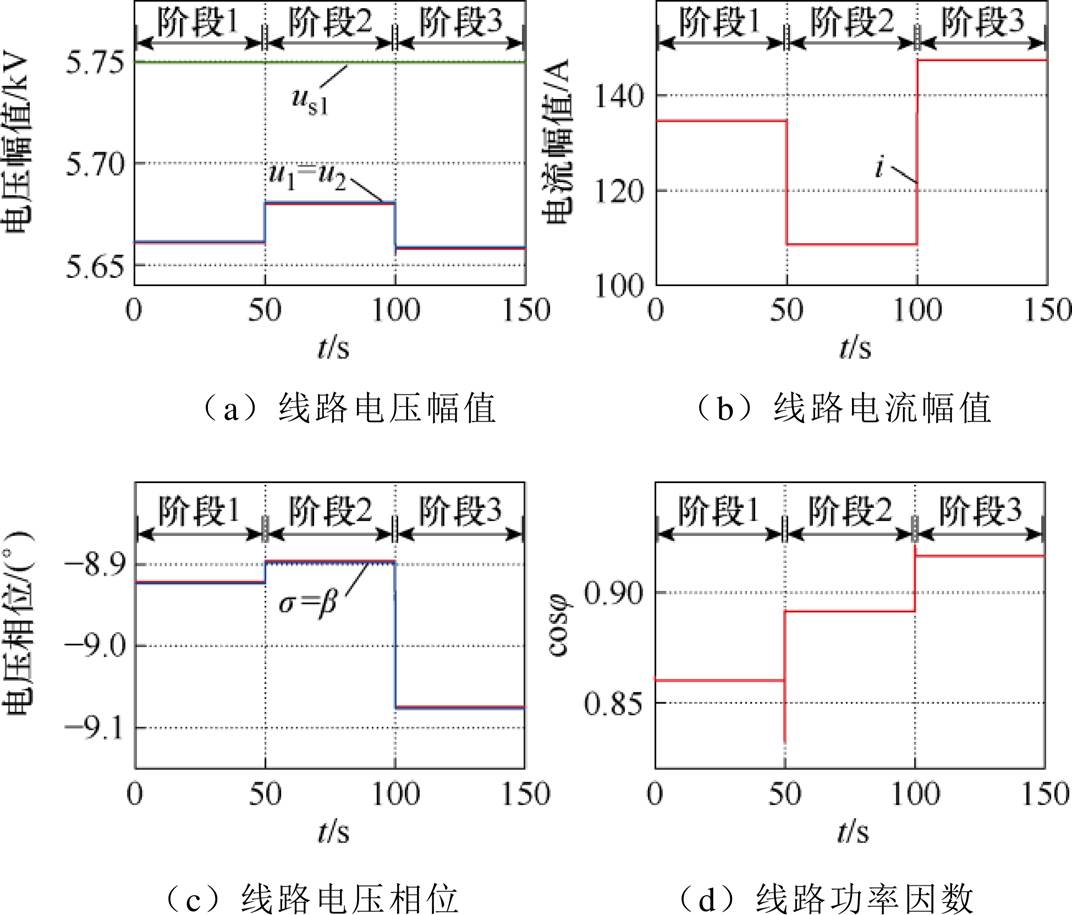
附图1 RPFC未投入时负载扰动仿真波形
App.Fig.1 Simulation waveforms of load disturbance when RPFC is not invested
附表1 变电压设定值仿真结果
App.Tab.1 Simulation results when voltage settings change
参数工况1工况2工况3 us1/kV5.7505.7505.750 u1/kV5.6905.6925.693 u2/kV5.7975.7495.701 cosj0.990.990.99 i/A137.81136.63135.45 b/(°)-9.3-9.3-9.3 s/(°)20.421.822.5
附表2 RPFC未投入时负载扰动仿真结果
App.Tab.2 Simulation results of load disturbance when RPFC is not invested
参数工况1工况2工况3 us1/kV5.7505.7505.750 u1/kV5.6615.6805.658 u2/kV5.6615.6805.658 cosj0.860.890.92 i/A134.54111.35147.42 b/(°)-8.9-8.9-9.0 s/(°)-8.9-8.9-9.0
附表3 RPFC投入后变负载仿真结果
App.Tab.3 Simulation results of transient load when RPFC is connected

参数本文方法文献[23]方法 工况1工况2工况3工况1工况2工况3 us1/kV5.7505.7505.7505.7505.7505.750 u1/kV5.6905.7025.6855.6605.6805.675 u2/kV5.7485.7495.7515.7525.7515.751 cosj0.990.990.990.860.890.92 i/A136.73110.08149.89136.74110.03149.86 b/(°)-9.3-9.2-9.4-8.9-8.9-9.1 s/(°)20.417.313.8-8.5-8.6-8.8
参考文献
[1] 黄大为, 王孝泉, 于娜, 等. 计及光伏出力不确定性的配电网混合时间尺度无功/电压控制策略[J]. 电工技术学报, 2022, 37(17): 4377-4389.
Huang Dawei, Wang Xiaoquan, Yu Na, et al. Hybrid timescale voltage/var control in distribution network considering PV power uncertainty[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4377- 4389.
[2] 张舒文, 郭春义, 赵薇, 等. 水光互补柔性直流外送系统的功率传输能力研究[J/OL]. 中国电机工程学报, 1-13[2025-05-22]. http://kns.cnki.net/kcms/ detail/11.2107.tm.20240829.1325.014.html.
Zhang Shuwen, Guo Chunyi, Zhao Wei, et al. Research on the power transmission capability of PV-Hydro complementary MMC-HVDC transmission system[J/OL]. Proceedings of the CSEE, 1-13[2025- 05-22]. http://kns.cnki.net/kcms/detail/11.2107.tm. 20240829.1325.014.html.
[3] 王子凌, 周金辉, 陈铭, 等. 计及有载调压的高光伏渗透率配电网储能优化配置[J]. 电力系统及其自动化学报, 2020, 32(8): 123-129, 137.
Wang Ziling, Zhou Jinhui, Chen Ming, et al. Optimal configuration of energy storage for high PV permeability distribution network with on-load voltage regulation[J]. Proceedings of the CSU-EPSA, 2020, 32(8): 123-129, 137.
[4] 张波, 高远, 王磊, 等. 考虑光伏电源可靠性的配电网无功电压调控策略[J]. 高电压技术, 2023, 49(7): 2775-2784.
Zhang Bo, Gao Yuan, Wang Lei, et al. Reactive voltage control strategy of distribution network considering the reliability of photovoltaic power supply[J]. High Voltage Engineering, 2023, 49(7): 2775-2784.
[5] 张波, 高远, 李铁成, 等. 考虑光伏电源可靠性的新能源配电网数据驱动无功电压优化控制[J]. 中国电机工程学报, 2024, 44(15): 5934-5947.
Zhang Bo, Gao Yuan, Li Tiecheng, et al. Data-driven voltage/var optimization control of active distribution network considering the reliability of photovoltaic power supply[J]. Proceedings of the CSEE, 2024, 44(15): 5934-5947.
[6] 杨婧颖, 王武林, 张明敏, 等. 考虑分布式光伏和储能参与的配电网电压分层控制方法[J]. 电力科学与技术学报, 2023, 38(5): 111-120, 215.
Yang Jingying, Wang Wulin, Zhang Mingmin, et al. Voltage hierarchical control method of distribution network considering distributed photovoltaic and energy storage[J]. Journal of Electric Power Science and Technology, 2023, 38(5): 111-120, 215.
[7] 李翠萍, 东哲民, 李军徽, 等. 配电网分布式储能集群调压控制策略[J]. 电力系统自动化, 2021, 45(4): 133-141.
Li Cuiping, Dong Zhemin, Li Junhui, et al. Control strategy of voltage regulation for distributed energy storage cluster in distribution network[J]. Automation of Electric Power Systems, 2021, 45(4): 133-141.
[8] 葛少云, 侯亭玉, 吴鸣, 等. 柔性互联配电网分布式电源承载能力分布鲁棒优化模型[J]. 电力系统自动化, 2023, 47(13): 140-148.
Ge Shaoyun, Hou Tingyu, Wu Ming, et al. Dis- tributionally robust optimization model of hosting capability for distributed generators in flexible interconnected distribution network[J]. Automation of Electric Power Systems, 2023, 47(13): 140-148.
[9] 朱建昆, 高红均, 贺帅佳, 等. 考虑供电能力提升的低压配电网柔性互联规划[J]. 高电压技术, 2024, 50(8): 3545-3559.
Zhu Jiankun, Gao Hongjun, He Shuaijia, et al. Flexible interconnection planning of low-voltage station area distribution network considering power supply capacity improvement[J]. High Voltage Engin- eering, 2024, 50(8): 3545-3559.
[10] 高聪哲, 黄文焘, 余墨多, 等. 基于智能软开关的主动配电网电压模型预测控制优化方法[J]. 电工技术学报, 2022, 37(13): 3263-3274.
Gao Congzhe, Huang Wentao, Yu Moduo, et al. A model predictive control method to optimize voltages for active distribution networks with soft open point[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3263-3274.
[11] 季振东, 王亚祥, 李东野, 等. 电力电子变压器参与配电网调压调频的应用研究[J]. 太阳能学报, 2024, 45(6): 182-190.
Ji Zhendong, Wang Yaxiang, Li Dongye, et al. Application research of power electronic transformers in frequency/voltage regulation of distribution net- works[J]. Acta Energiae Solaris Sinica, 2024, 45(6): 182-190.
[12] 孟潇潇, 邵冰冰, 韩平平, 等. 基于背靠背变流器柔性互联的微网群分层协同恢复控制策略[J]. 中国电机工程学报, 2023, 43(20): 7812-7827.
Meng Xiaoxiao, Shao Bingbing, Han Pingping, et al. hierarchical cooperative recovery control strategy for flexible interconnected microgrid cluster based on back-to-back converters[J]. Proceedings of the CSEE, 2023, 43(20): 7812-7827.
[13] 于汀, 蒲天骄, 刘广一, 等. 基于柔性直流分区互联的受端城市电网无功电压控制策略[J]. 高电压技术, 2017, 43(7): 2140-2145.
Yu Ting, Pu Tianjiao, Liu Guangyi, et al. Reactive power and voltage control strategy of receiving-end urban power grid with flexible DC interconnected between partitions[J]. High Voltage Engineering, 2017, 43(7): 2140-2145.
[14] 刘鑫磊, 张犁, 刘淇. 升压型功率因数校正变换器的改进线性自抗扰电压环控制[J]. 电网技术, 2023, 47(12): 5238-5247.
Liu Xinlei, Zhang Li, Liu Qi. Modified linear active disturbance rejection control-based voltage-loop control for boost PFC converter[J]. Power System Technology, 2023, 47(12): 5238-5247.
[15] Haddadi A M, Kazemi A. Optimal power flow control by rotary power flow controller[J]. Advances in Elec- trical and Computer Engineering, 2011, 11(2): 79- 86.
[16] 颜湘武, 邵晨, 彭维锋, 等. 基于旋转式潮流控制器的有源配电网柔性合环及紧急功率控制方法[J]. 中国电机工程学报, 2023, 43(16): 6192-6205.
Yan Xiangwu, Shao Chen, Peng Weifeng, et al. Flexible loop closing and emergency power control method for active distribution network based on the rotary power flow controller[J]. Proceedings of the CSEE, 2023, 43(16): 6192-6205.
[17] 李俊杰, 吴在军, 杨士慧, 等. 交直流混合微电网中电力电子变压器功率控制与模式切换方法[J]. 电力自动化设备, 2020, 40(8): 82-87,110.
Li Junjie, Wu Zaijun, Yang Shihui, et al. Power control and mode switching method of power electronic transformer in AC/DC hybrid microgrid[J]. Electric Power Automation Equipment, 2020, 40(8): 82-87, 110.
[18] 白迪, 张铁岩, 杨政. 基于可控等效阻抗的能量路由器无功电压控制策略研究[J]. 太阳能学报, 2022, 43(1): 329-334.
Bai Di, Zhang Tieyan, Yang Zheng. Research on reactive voltage control strategy of energy routers based on controllable equivalent impedance[J]. Acta Energiae Solaris Sinica, 2022, 43(1): 329-334.
[19] 姜昊, 孙毅超, 张艺凡, 等. 集群式岸电能量路由器供能精细化就地管控策略[J]. 电力系统保护与控制, 2024, 52(11): 31-41.
Jiang Hao, Sun Yichao, Zhang Yifan, et al. Refined local energy management strategy for clustered shore power energy routers[J]. Power System Protection and Control, 2024, 52(11): 31-41.
[20] 颜湘武, 郭燕, 彭维锋, 等. 基于旋转移相变压器的电压源型无功补偿器及其控制策略[J]. 电工技术学报, 2023, 38(16): 4448-4464.
Yan Xiangwu, Guo Yan, Peng Weifeng, et al. Voltage source var compensator based on rotary phase shifting transformer and its control strategy[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4448-4464.
[21] 颜湘武, 彭维锋, 邵晨, 等. 基于旋转潮流控制器的用户侧电压调控方法[J]. 电工技术学报, 2023, 38(增刊1): 70-79, 113.
Yan Xiangwu, Peng Weifeng, Shao Chen, et al. User side voltage control method based on rotating power flow controller[J]. Transactions of China Electro- technical Society, 2019, 38(S1): 70-79, 113.
[22] 邵晨, 颜湘武, 贾焦心, 等. 面向“花瓣型”配电网的旋转潮流控制器两阶段转速功率控制策略[J]. 电工技术学报, 2025, 40(1): 52-63.
Shao Chen, Yan Xiangwu, Jia Jiaoxin, et al. Two- stage rotational speed power control strategy of rotating Power flow controller for “petal type” distribution network[J]. Transactions of China Elec- trotechnical Society, 2025, 40(1): 52-63.
[23] 贾焦心, 彭维锋, 颜湘武, 等. 基于余弦定理的旋转潮流控制器功率解耦控制方法研究[J]. 电工技术学报, 2023, 38(13): 3425-3435.
Jia Jiaoxin, Peng Weifeng, Yan Xiangwu et al. Research on power decoupling control method rotary power flow controller based on cosine law[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3425-3435.
Abstract With strong national policy support and continuous advancements in renewable energy generation technologies, the integration of distributed renewable energy into distribution networks has been increasing annually. This trend has affected the electrical characteristics of the system, including power flow distribution, voltage levels, and short-circuit capacity, leading to power factor deterioration and overvoltage. To achieve integrated control of feeder voltage and power factor in active distribution networks, this paper proposes a coordinated voltage/power factor control strategy for the rotary power flow controller (RPFC) based on the principle of line impedance regulation.
Firstly, the topology and steady-state characteristics of the RPFC are analyzed. Based on the RPFC mathematical model, an equivalent model for its steady-state output impedance is developed, representing the RPFC as an impedance model composed of a compensating impedance in series with an internal impedance. By adjusting the phase angles of the RPFC, the impedance relationship between the output voltage and the compensation impedance can be dynamically controlled, allowing the regulation of the compensation impedance and thereby achieving the voltage control at the terminal of the connection point.
According to the phase relationship between the output voltage and the line current, the RPFC can operate in three modes of compensation: resistive, capacitive, and resistive-capacitive compensation. In resistive compensation mode, the output voltage phase aligns with the current phase, equivalent to inserting a compensating resistor with adjustable polarity and magnitude in series with the line. In capacitive compensation mode, the output voltage lags the line current by 90°, equivalent to inserting a compensating reactance with adjustable polarity and magnitude in series with the line. In resistive-capacitive compensation mode, the RPFC adjusts both the output voltage magnitude and phase, effectively inserting a compensating impedance with adjustable resistance and reactance.
Next, the compensation characteristics of the RPFC in the three modes-resistive, capacitive, and resistive-capacitive-are analyzed. Phasor diagrams for each mode are presented, and expressions for the voltage and power factor are derived. The advantages and disadvantages of each compensation mode are discussed.
Then, the mathematical model of the RPFC-connected line is analyzed using dq transformation, and a voltage/power factor control model based on the decoupling characteristics of the RPFC impedance is proposed. In this model, the d-axis component of the line current is regulated by the compensation resistance, while the q-axis component is controlled by the compensation reactance. Accordingly, the control of the line current is decoupled for independent regulation of each element through the RPFC’s compensation impedance. A voltage/power factor decoupling control method is designed. Herein, the equivalent impedance is calculated from the target voltage and power factor values. The impedance is then converted into a rotational angle set point, and zero-error control is achieved through the inner-loop speed control of the RPFC.
Finally, simulations and experiments are conducted. The results demonstrate that the RPFC can regulate its output voltage, enabling the output terminal to exhibit resistive or capacitive characteristics. Under varying voltage and power factor set points, the RPFC effectively adjusts the line voltage and power factor to maintain optimal performance. Furthermore, the control error of the RPFC is kept within 1.4%, validating the effectiveness of the proposed strategy for continuous voltage and power factor regulation in active distribution networks.
keywords:Flexible interconnected distribution grid, rotary power flow controller, voltage regulation, power factor improvement
DOI: 10.19595/j.cnki.1000-6753.tces.241967
中图分类号:TM761
国家自然科学基金青年基金(52207102)、中央高校基本科研业务费专项资金(2024MS110)、2023年度河北省高等学校科学研究(ZC2023047)、保定市科技计划项目任务书(2211ZG015)资助项目。
收稿日期 2024-11-02
改稿日期 2025-01-11
贾焦心 男,1991年生,博士,讲师,研究方向为新能源并网系统建模和控制、灵活交流配电系统等。E-mail: jiajx@163.com
吴炜林 男,2001年生,博士研究生,研究方向为灵活交流配电系统。E-mail: wuweilin0104@163.com(通信作者)
(编辑 郭丽军)