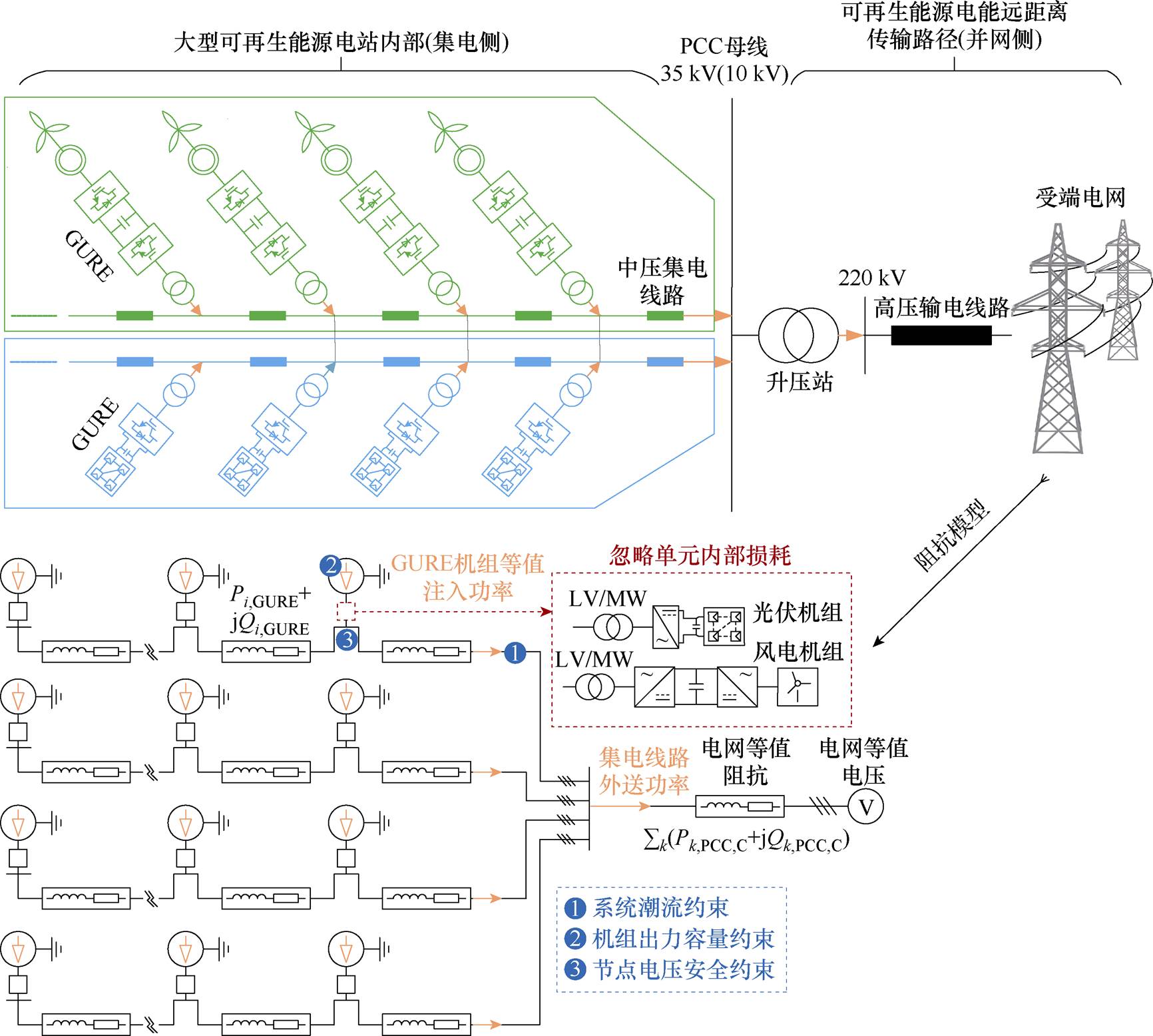
图1 大型可再生能源电站并网分析模型示意图
Fig.1 Grid integration analysis model of large-scale renewable energy power plant system
摘要 大型可再生能源电站因其“规模化拓扑、弱电网并入”特性,内部和外部的线路阻抗较大,易引发较高的线路电压差,增加系统过电压越限的风险。为优化电站系统电压分布,并避免传统集中式优化方法带来的通信负担,该文提出基于增广拉格朗日交替方向非精确牛顿法(ALADIN)的分布式非凸电压优化方法。首先,构建包含非线性潮流约束的非凸电压优化模型,并利用ALADIN进行分布式求解,实现可再生能源机组无功功率的最优调度,以改善电压分布。因此,对标准ALADIN算法步骤进行扩展,提出同步与异步更新机制,以应对实际通信中的信息延迟情况。算例分析表明,所提基于ALADIN的电压分布式非凸优化方法具有良好的收敛性和最优性,能有效优化电压分布至安全范围,且能灵活应对不同通信延迟场景。所提方法可降低大型可再生能源电站电压越限风险,提高电站安全稳定运行水平。
关键词:大型可再生能源电站 过电压越限 分布式非凸优化 增广拉格朗日交替方向非精确牛顿法
在“碳达峰、碳中和”目标下,电力系统中风、光等清洁能源的渗透率逐年提高,全球待建设与已投运的可再生能源电站数目剧增。然而,可再生能源电站的规模化扩建与高比例并网导致其系统自身面临的电压安全问题愈发凸显[1-2]。具体而言,大型可再生能源电站运行所遭遇的电压问题包括“外患”和“内忧”两个方面。电压的“外患”问题由可再生能源电站的外部并网环境导致[3]:我国风、光等可再生能源资源富集地区为西北部,而负荷中心为沿海东部地区,电能由西向东经过长距离输电线路外送,使得大型可再生能源电站普遍并入了弱电网环境中。由于弱电网环境的短路容量小、外部等值阻抗大,可再生能源电站与电力系统并网点(Point of Common Coupling, PCC)的电压将随外送功率的波动而显著变化。电压的“内忧”问题由可再生能源电站的内部线路环境导致[4]:大型可再生能源电站内部数目庞大的可再生能源发电单元(Generator Units of Renewable Energy, GURE)通过距离较远的集电线路连接。当经集电线路外送的可再生能源电能体量较大时,将导致集电线路首末端产生巨大的电压降落,从而增大了集电线路末端GURE接入点的过电压越限风险。因此,亟须有效的电压调控方法,以保障大型可再生能源电站系统的安全稳定运行。
电压优化方法通过求解最优潮流模型,以获得可控设备的最优动作指令,可有效地调控系统整体电压分布,适用于大型可再生能源电站系统[5-7]。现有系统电压优化方法可分为模型驱动和数据驱动方法两类。模型驱动方法适用于拓扑参数信息完备的电力系统运行场景,而数据驱动方法适用于系统信息感知度较低的配电网等运行场景[8-11]。大型可再生能源电站系统普遍集中建设,系统拓扑明晰,站内同步相量测量单元配置充分,因此系统整体信息感知度高、可观性强,适用于模型驱动法。此外,模型驱动法获得全系统电压控制最优解时,还具有避免参数过拟合和泛化能力缺失等问题的优势[12-13]。
对于模型驱动的电压优化方法,根据对通信的依赖程度,可进一步分为集中式电压优化和分布式电压优化两类。集中式电压优化方法需要一个中央控制器,该控制器可获取全系统信息并制定全系统最优的系统电压优化策略。例如,文献[14]的中央控制器考虑了PCC母线电压和风机端电压信息,制定了面向三种不同电压优化场景的最优决策方案。文献[15-16]的中央控制器分别考虑了光伏电站和光热混合电站的信息,提出了面向不同时间尺度的电压多阶段优化方法。集中式电压优化方法的执行方式直接有效,但需要中央控制器和各可控设备间的点对点通信,在可再生能源电站系统规模大型化的趋势下,系统的优化决策将遭遇巨大的通信压力。
相较而言,通信负担更小的分布式电压优化法更适用于大型可再生能源电站的系统电压优化。分布式电压优化方法的基本思想为,将原集中式电压优化问题拆分为多个各自独立的子优化问题并分别求解,依靠Agent控制器之间的相邻通信和分布式优化算法对局部优化变量进行更新迭代,从而逼近原集中式电压优化问题的全局最优解。在分布式电压优化模式中,全局优化问题被分解为多个局部子优化问题,被独立地进行求解。卡鲁需-库恩-塔克(Karush-Kuhn-Tucker, KKT)条件可被用来指导各局部子优化问题的优化过程,以使得各局部解最终能收敛至全局最优解。文献[17-18]分别采用交替方向乘子法(Alternating Direction of Multipliers Method, ADMM)和目标级联分析法(Analytical Target Cascading, ATC),实现了大型风电场站内的电压分布式优化。文献[19]将ADMM和ATC的分布式优化过程进行了嵌套结合,应用于集中式光伏电站系统电压优化中,同时添加了本地下垂控制,以响应光伏机组出力的短时波动。文献[20]将Benders分解算法嵌入列和约束生成算法中,有效地求解“max- min”内层问题包含整数变量的鲁棒优化模型,应用于大型电力系统的分布式随机规划模型中。
上述研究采用各类分布式优化算法,对所研究对象系统的电压进行了有效的控制,达到了满意的调控效果。然而,这些分布式优化算法的前提是求解的系统电压优化模型须为凸优化问题。例如文献[1, 17-20]中,采用忽略网损的线性化支路潮流(Linearzied DistFlow, LinDistFlow)约束以近似替代非线性的标准潮流约束,从而建立凸化的系统电压优化模型。这种处理方式未能充分考虑到可再生能源电站大型化后,并网环境和集电线路规模等因素对系统潮流分析的影响,因而未对大型可再生能源电站采用近似潮流约束的可行性作深入讨论。
根据前述,大型可再生能源电站运行具有“规模化拓扑、弱电网并入”的运行特征,其内、外部线路阻抗均较大,系统遭遇“内忧外患”电压问题。在此情况下,诸如LinDistFlow等线性化近似潮流约束将会导致较大的系统潮流计算误差,这将影响大型可再生能源电站系统电压优化决策的有效性。因此,采用非线性的标准潮流约束描述大型可再生能源电站整体潮流分布状态是尤为必要的。值得注意的是,标准潮流约束将导致电压优化模型具有非凸数学特征,此时KKT条件和全局最优解之间的“充分必要”关联不再成立,诸如ADMM等分布式优化算法的收敛性和最优性将无法得到严格保证。因此,亟须探寻新的分布式优化方法,以便有效地求解大型可再生能源电站系统电压调控所对应的非凸优化问题。
近期,有学者以ADMM算法的分布式优化过程为基础,提出了增广拉格朗日交替方向非精确牛顿法(Augmented Lagrangian Alternating Direction Inexact Newton, ALADIN),且尝试将其应用于各类非凸优化问题中[21-24],然而,目前鲜有学者将其用于系统电压优化领域。对于非凸优化问题的求解,相较于ADMM,ALADIN无论在迭代次数上还是收敛结果上,都更具优势。受此启发,本文考虑采用ALADIN算法,对大型可再生能源电站系统电压进行分布式非凸优化:首先,构建基于非线性标准潮流约束的系统电压优化模型;在此基础上,对构建的系统电压优化模型,以PCC母线为界,将其拆分为集电侧和并网侧的子优化模型,并构造出对应的电压优化共识问题,利用ALADIN算法作分布式优化求解;特别地,将ALADIN实现步骤扩展为同步更新和异步更新方式,以应对实际通信中的信息延迟情况。最后,通过算例仿真,说明构建非凸电压优化模型的必要性,验证ALADIN分布式优化结果的收敛性和最优性,探讨同步更新和异步更新方式应对通信延迟的可行性。
本节将首先阐述对大型可再生能源电站进行系统电压分析的模型基础;在此基础上,进一步构建该系统的非凸电压优化数学模型。
大型可再生能源电站系统的并网分析模型如图1所示。模型分为集电侧与并网侧。可再生能源电站系统内部称为集电侧,集电侧的多条中压集电线路并联于PCC母线处,各中压集电线路进一步并联了多个由风、光发电设备构成的GURE。可再生能源电站系统内部所有GURE生产的电能汇集于PCC母线。并网侧包括升压变电站、高压输电线路和受端交流电网。PCC母线处汇集的电能由变电站升压,通过高压输电线路最终远距离传送至受端交流电网。PCC母线为集电侧和并网侧的耦合环节。值得一提得是,本文并网分析模型未将升压站的分接头挡位调节纳入优化问题中,其原因为升压站挡位调节的响应速度远小于GURE的输出功率调节的响应速度,并且考虑到使用寿命因素的影响,其不应频繁地动作。因此,在本文所建系统并网分析模型中,升压站分接头挡位被视作定值。

图1 大型可再生能源电站并网分析模型示意图
Fig.1 Grid integration analysis model of large-scale renewable energy power plant system
上述大型可再生能源电站系统拓扑结构中,集电侧与并网侧的功率-电压稳态关系可采用阻抗模型进行分析。对于集电侧:①考虑各中压集电线路的阻抗参数;②在不失一般性与准确性的前提下,忽略GURE内部变换器损耗,因此各GURE与集电线路的耦合节点被视作PQ节点,对应节点注入功率即为GURE输出功率。对于并网侧:①升压变电站处理为理想变压器;②远距离输电线路和受端交流电网的相关参数通过戴维宁等效阻抗和电压表征;③在分析可再生能源电站系统内部的电压时,将远方受端交流电网视为平衡节点。
总结大型可再生能源电站“规模化拓扑、弱电网并入”的运行特征:对于系统外部并网侧,由于可再生能源电站远离负荷中心,电能外送的长距离输电线路使得系统普遍并入弱电网环境,并网侧戴维宁等效阻抗大;对于系统内部集电侧,大型可再生能源电站占地规模大,连接各GURE之间的中压集电线路较长,线路阻抗也较大。因此,当可再生能源电站进行规模化功率外送时,线路阻抗上的功率损耗较大,对系统电压分布的影响不可忽略。
本节将介绍大型可再生能源电站系统的非凸电压优化数学模型,涉及目标函数和约束条件两部分。
1.2.1 目标函数
1)大型可再生能源电站系统整体电压偏差
大型可再生能源电站系统应保证各节点电压具有尽量多的电压幅值安全裕度,从而在GURE出力波动导致系统节点电压偏移的情况下,避免出现过电压越限现象。对应的目标函数为
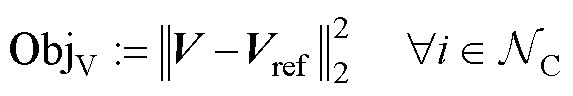 (1)
(1)
式中,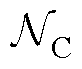 为集电侧节点集合;
为集电侧节点集合;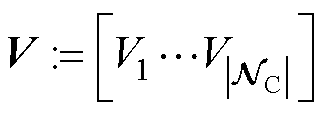 为节点电压幅值组成的列向量,
为节点电压幅值组成的列向量,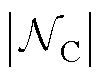 用于度量节点集合中的节点数;
用于度量节点集合中的节点数;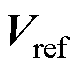 为节点参考电压幅值组成的列向量,向量中各元素设置为1(pu)标称值;
为节点参考电压幅值组成的列向量,向量中各元素设置为1(pu)标称值;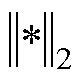 为向量2范数;“
为向量2范数;“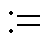 ”表示定义,以与等式约束公式中的“
”表示定义,以与等式约束公式中的“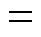 ”进行区别。
”进行区别。
2)大型可再生能源电站系统网损
为提升电能规模化外送的经济性,需保证大型可再生能源电站系统内部网损尽量小。对应的目标函数为
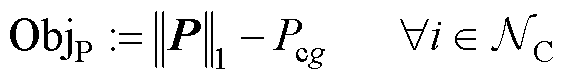 (2)
(2)
式中,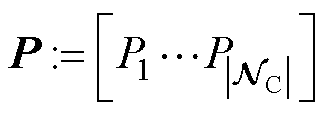 为集电侧各节点注入有功功率组成的列向量;
为集电侧各节点注入有功功率组成的列向量;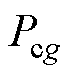 为由集电侧经PCC母线注入并网侧的有功功率;
为由集电侧经PCC母线注入并网侧的有功功率;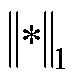 为向量1范数,
为向量1范数,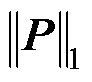 在数值上等于集电侧各节点注入有功功率之和,其与
在数值上等于集电侧各节点注入有功功率之和,其与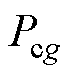 的差值即为大型可再生能源电站系统内部集电线路上消耗的网损。
的差值即为大型可再生能源电站系统内部集电线路上消耗的网损。
综上所述,本文考虑的总体目标函数为
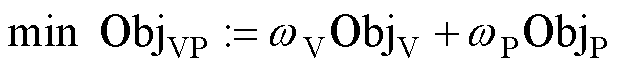 (3)
(3)
式中,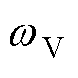 和
和 为权重系数,具体数值可根据调控需求自行设定。
为权重系数,具体数值可根据调控需求自行设定。
1.2.2 约束条件
本节所建非凸电压优化模型的约束包括以下三类:系统潮流约束作为等式约束、机组容量约束和节点电压安全约束作为关键不等式约束。
1)集电侧和并网侧潮流约束
如图1所示,大型可再生能源电站系统为辐射状结构,在可再生能源电站电压优化相关的工作中,常采用线性化的DistFlow模型,即LinDistFlow描述系统潮流[17-19]。该模型基于两项假设:①各节点电压偏差较小,各节点电压幅值均在1(pu)附近; ②忽略线路损耗。对于大型化的可再生能源电站而言,假设①依旧是合理的,这是因为减少电压偏差本身作为系统运行优化目标之一,优化后的系统电压幅值仍将处于1(pu)附近。然而,假设②不再合理。一方面,大型可再生能源电站可能并入弱电网环境中,该环境下的戴维宁等值阻抗大,若忽略线路损耗,将导致PCC母线处的电压幅值计算存在较大误差。另一方面,大型可再生能源电站内部为规模化集电线路系统,线路较长,线路阻抗也更大,忽略损耗也将对内部集电线路系统电压分布的计算产生较大影响。与以上阐述相关的定量分析将在后续4.1小节算例仿真中详细呈现。在这种情况下,基于LinDistFlow的线性化潮流约束所带来的潮流计算误差难以忽视,否则将显著降低电压优化决策的有效性。因此,为保证决策精度,本文仍基于非线性的标准潮流模型,构建集电侧和并网侧潮流约束为
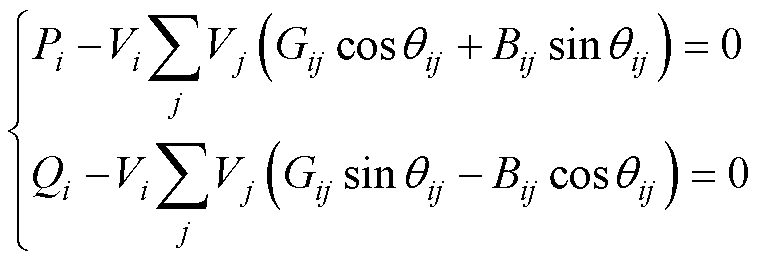
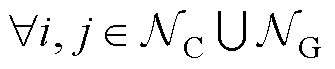 (4)
(4)
式中,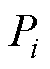 、
、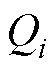 分别为节点i节点注入有功、无功功率;
分别为节点i节点注入有功、无功功率;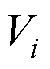 、
、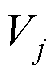 分别为节点i、j电压幅值;
分别为节点i、j电压幅值;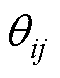 为节点i和j之间的相位差;
为节点i和j之间的相位差;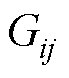 、
、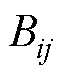 分别为节点导纳矩阵第i行和第j列元素的实部、虚部;
分别为节点导纳矩阵第i行和第j列元素的实部、虚部;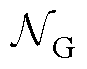 为并网侧节点集合。
为并网侧节点集合。
2)集电侧机组容量约束
大型可再生能源电站系统内部集电侧各节点的注入功率来自GURE。其中,GURE如图1所示采用了功率等值模型,忽略了可再生能源机组接入集电线路中的换流器损耗和变压器损耗。考虑GURE内部的光伏机组或风电机组普遍连接电压源型换流器,其损耗公式为与换流站交流侧相电压幅值相关的二次函数[25]。若考虑为光伏机组接入,在额定状态下,损耗约为1.1%。若考虑为风电机组接入,由于利用背靠背的换流站并网,在额定状态下,损耗会高于光伏机组,约为2.4%。对于变压器损耗,一台LV/MV的变压器,其有载损耗一般为额定容量的1%左右[26]。总结来看,光伏机组换流器和变压器损耗率之和约为2.2%,风电机组换流器和变压器损耗之和约为3.4%,均是相对较小的,因此忽略换流器和变压器损耗是可接受的。
考虑受到自身容量约束限制,机组有功和无功出力中,GURE的有功功率输出由可利用的最大功率点跟踪功率决定,无功功率输出由所构建的电压优化模型求解结果决定。对应约束条件为
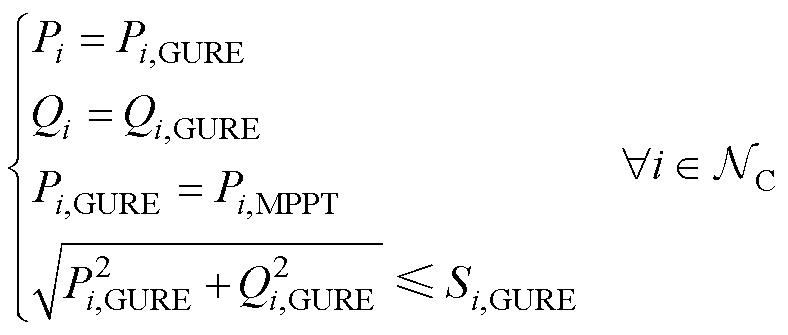 (5)
(5)
式中,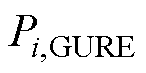 、
、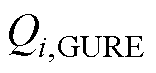 分别为节点i上GURE输出的有功、无功功率;
分别为节点i上GURE输出的有功、无功功率;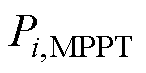 为节点i上GURE可利用的最大功率点跟踪功率,被视作定值;
为节点i上GURE可利用的最大功率点跟踪功率,被视作定值;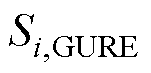 为GURE的视在功率最大额定值。
为GURE的视在功率最大额定值。
3)集电侧节点电压约束
集电侧节点电压的幅值和相位应满足相应约束为
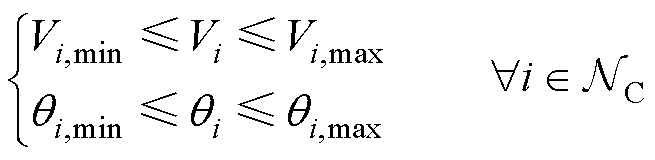 (6)
(6)
式中,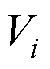 为节点i的电压幅值;
为节点i的电压幅值;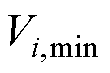 、
、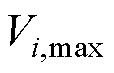 分别为系统安全运行时电压幅值的最小、最大值;
分别为系统安全运行时电压幅值的最小、最大值;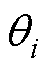 为节点i的电压相位;
为节点i的电压相位;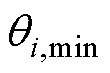 、
、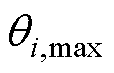 分别为系统安全运行时电压相位的最小、最大值。
分别为系统安全运行时电压相位的最小、最大值。
作为系统分布式电压优化的条件基础,本节将首先针对大型可再生能源电站的结构特征,构建适用于其特征需求的分布式通信架构。然后,结合该通信架构,将原集中式电压优化问题作拆分,构建分布式电压优化问题。
传统的集中式通信为“点对点”的通信方式。对于可再生能源电站而言,若采用集中式通信方式,则需要依靠中央控制器建立和每个GURE机组之间的通信连接。然而伴随着可再生能源电站系统规模的增大,装机规模迅速扩展,GURE机组的数量将大幅增加,中央控制器作为中心节点将面临巨大的信息处理压力,难以应对大量的GURE机组调控请求。考虑集中式通信存在的弊端和大型可再生能源电站的站内集群结构特征,将原系统拆分为多个子系统,仅在各子系统Agent控制器之间进行相邻分布式通信的方式,更适用于本文场景。
本文采用的支撑大型可再生能源电站系统分布式电压优化的分布式通信系统架构如图2所示。PCC母线、站外并网侧,以及站内各集电线路上均配置有分布式Agent控制器。特别地,集电线路上的各GURE受集电线路Agent控制器统一调控,各集电线路Agent与PCC母线Agent之间进行边界信息的相互传递。这种分布式通信方式将站内集电线路进行了分区调控,而非对每个GURE都配置单独的Agent进行调控,从而避免Agent配置过多所导致的计算收敛过慢的问题[27]。
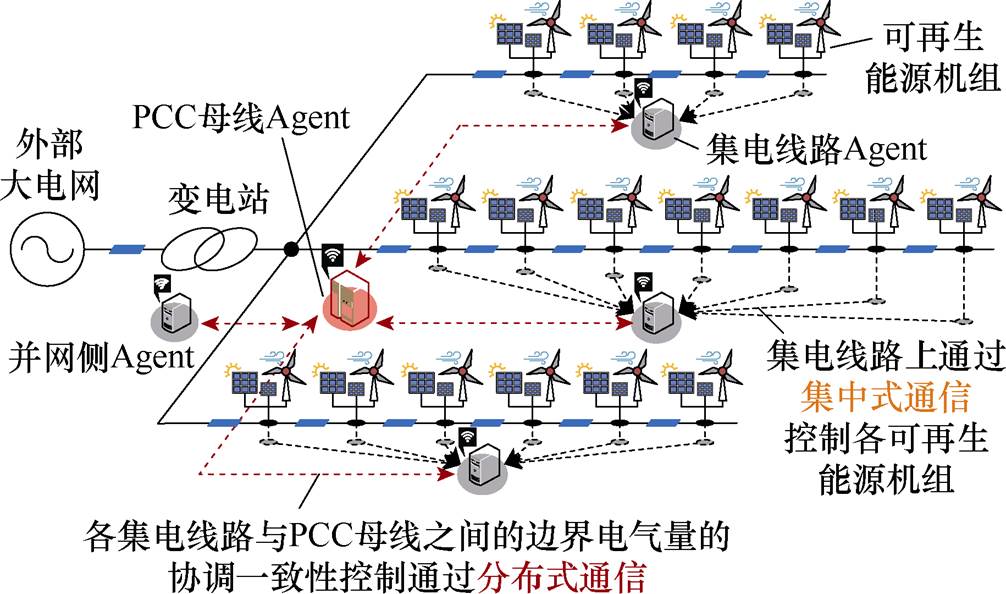
图2 支撑大型可再生能源电站系统分布式电压优化的分布式通信系统架构
Fig.2 Distributed communication system architecture supporting distributed voltage optimization for large-scale renewable energy power plants
根据图2所示分布式通信架构,对大型可再生能源电站按如图3所示的方式进行拆分。通过复制PCC母线,原系统被分解为一个并网侧子系统和若干集电侧系统。此时,需附加以下耦合约束。
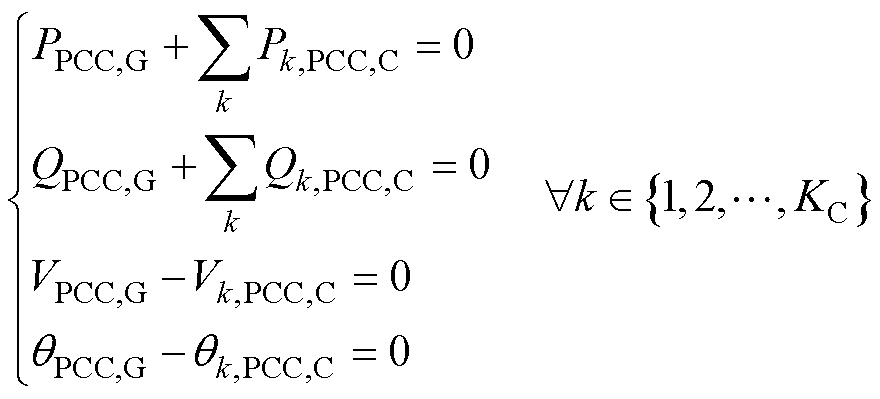 (7)
(7)
式中,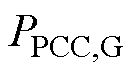 、
、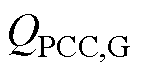 、
、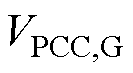 以及
以及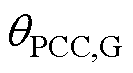 分别为并网侧PCC母线上的边界节点有功功率、无功功率、电压幅值以及相位;
分别为并网侧PCC母线上的边界节点有功功率、无功功率、电压幅值以及相位;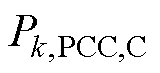 、
、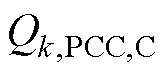 、
、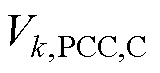 以及
以及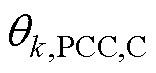 分别为与第k条集线路关联的PCC母线上的边界节点有功功率、无功功率、电压幅值以及相位;
分别为与第k条集线路关联的PCC母线上的边界节点有功功率、无功功率、电压幅值以及相位;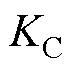 为可再生能源电站内部的集电线路条数;
为可再生能源电站内部的集电线路条数;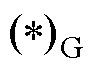 和
和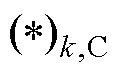 分别用于表示模型分解后与并网侧和集电系统侧第k条集电线路相关联的参数或变量。
分别用于表示模型分解后与并网侧和集电系统侧第k条集电线路相关联的参数或变量。
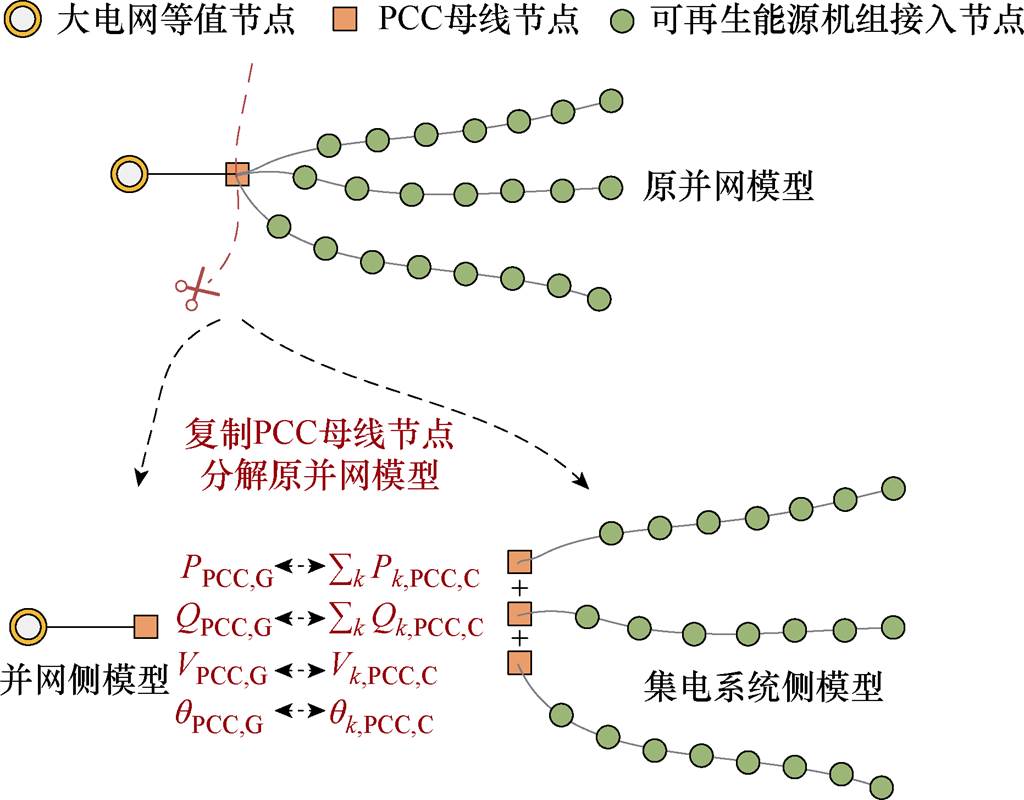
图3 大型可再生能源电站系统分解
Fig.3 System decomposition for large-scale renewable energy power plants
进一步地,式(3)~式(6)所对应的集中式优化模型可扩展为如下的分布式优化模型。
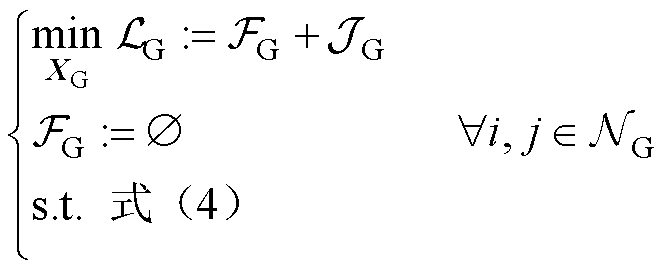 (8)
(8)
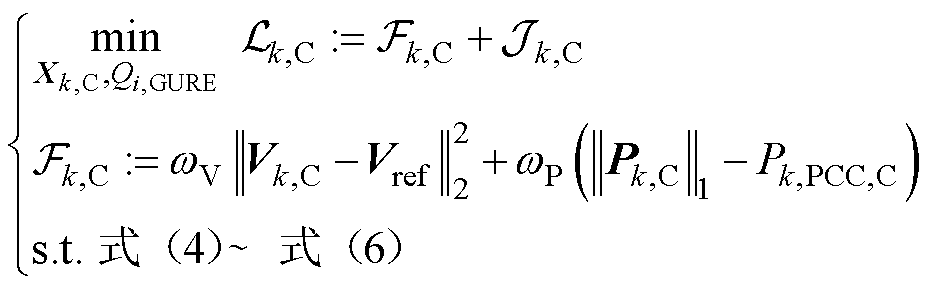
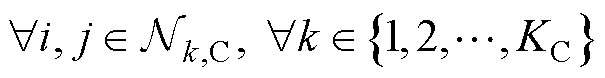 (9)
(9)
式(8)和式(9)分别为并网侧子系统和第k条集电线路侧子系统所对应的分布式电压优化问题;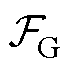 和
和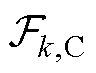 分别为分解后的优化目标函数,其中
分别为分解后的优化目标函数,其中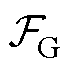 为
为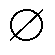 ,表示空集,式(8)的主要作用是为式(9)的优化计算提供边界电气量信息;
,表示空集,式(8)的主要作用是为式(9)的优化计算提供边界电气量信息;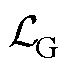 和
和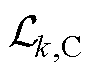 为与各子优化问题关联的增广拉格朗日函数,其中包含的增广项
为与各子优化问题关联的增广拉格朗日函数,其中包含的增广项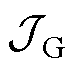 和
和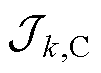 将在第3节作详细介绍。(*)G和(*)k,C分别表示与并网侧子系统和第k条集电线路侧子系统所关联的参数、变量,以及集合。
将在第3节作详细介绍。(*)G和(*)k,C分别表示与并网侧子系统和第k条集电线路侧子系统所关联的参数、变量,以及集合。
本节将对比新颖的ALADIN算法和经典ADMM算法的分布式优化求解过程,以便展现应用ALADIN算法对本文的非凸电压优化模型进行分布式优化时的关键要点。特别地,对ALADIN求解过程中的特殊步骤也将作强调说明。
ADMM和ALADIN拥有相似的分布式迭代过程,即通过交替方向的方式,迭代更新拉格朗日乘子,但两种方法在增广拉格朗日函数和共识问题的构造上有区别。为了更好地阐述ALADIN的特点和优势,首先对ADMM的分布式优化求解过程进行介绍,然后进一步阐述ALADIN的分布式优化求解过程。
3.1.1 ADMM分布式优化求解
ADMM下的并网侧和集电侧子优化问题按式(8)和式(9)进行构造。特别地,将ADMM下的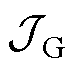 和
和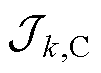 写作
写作
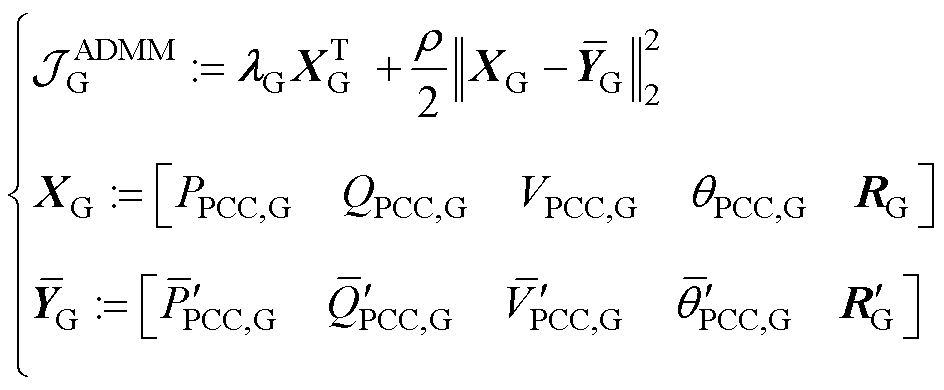 (10)
(10)
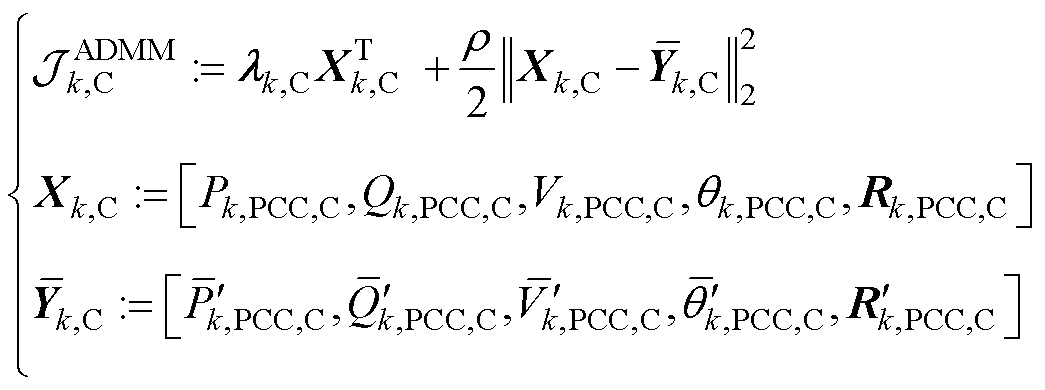 (11)
(11)
式中,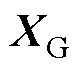 和
和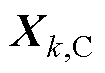 分别为并网侧子系统和集电线路侧子系统所包含的原集中式模型变量(向量);
分别为并网侧子系统和集电线路侧子系统所包含的原集中式模型变量(向量);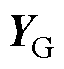 和
和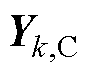 分别为通过复制边界节点后,在并网侧子系统和集电线路侧子系统中所产生的辅助变量(向量),其在求解并网侧和集电线路侧子系统时所对应的定值分别为
分别为通过复制边界节点后,在并网侧子系统和集电线路侧子系统中所产生的辅助变量(向量),其在求解并网侧和集电线路侧子系统时所对应的定值分别为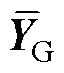 和
和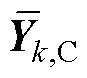 ;
;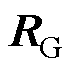 为子系统中除开在PCC母线处耦合的变量外,其余的所有变量组成的向量;
为子系统中除开在PCC母线处耦合的变量外,其余的所有变量组成的向量;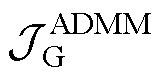 和
和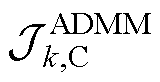 特指
特指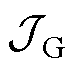 和
和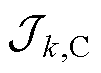 在ADMM下的表达式;
在ADMM下的表达式;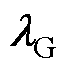 和
和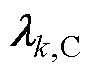 为对偶乘子项(向量);
为对偶乘子项(向量);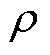 为罚函数项;
为罚函数项;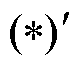 表示共识问题产生的复制变量;
表示共识问题产生的复制变量; 表示变量优化求解后的结果,为定值;
表示变量优化求解后的结果,为定值;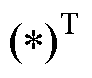 为向量转置符号。
为向量转置符号。
ADMM下的电压优化共识问题构造为
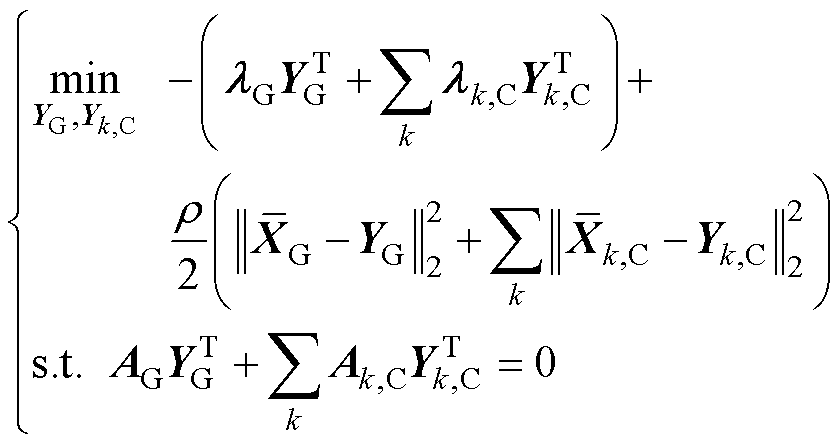
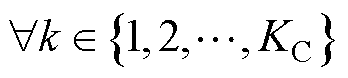 (12)
(12)
其中
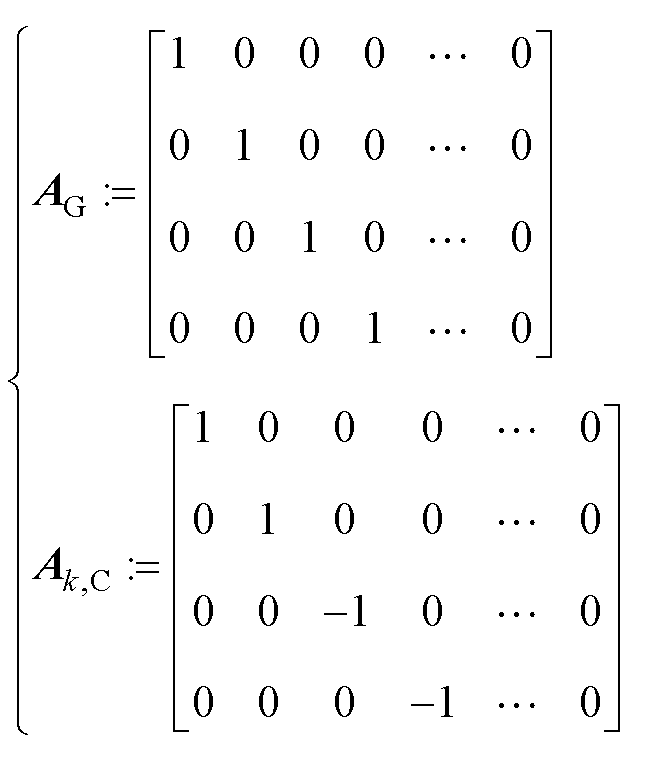 (13)
(13)
式(7)所示的耦合约束等价地转换为式(12)优化模型中所示的矩阵形式约束。
ADMM通过交替求解式(8)、式(9)和式(12)实现分布式优化,关键的对偶乘子项通过梯度上升法更新,迭代公式为
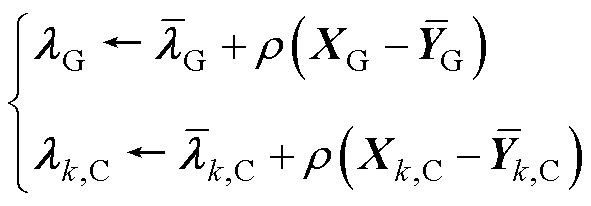 (14)
(14)
3.1.2 ALADIN分布式优化求解
ALADIN下的并网侧和集电侧子优化问题同样按式(8)和式(9)进行构造。但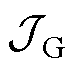 和
和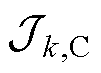 的表达式为
的表达式为
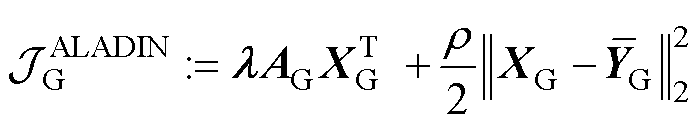 (15)
(15)
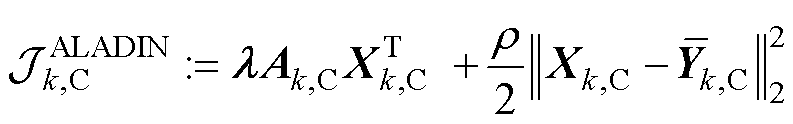 (16)
(16)
式中,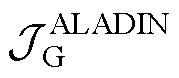 和
和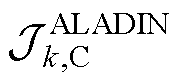 分别为
分别为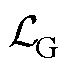 和
和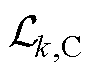 的增广项在ALADIN下的表达式。不同于ADMM,在ALADIN算法中,式(15)和式(16)所示的并网侧和集电线路侧子优化问题中的
的增广项在ALADIN下的表达式。不同于ADMM,在ALADIN算法中,式(15)和式(16)所示的并网侧和集电线路侧子优化问题中的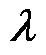 是统一的。
是统一的。
与ADMM类似,ALADIN中也有电压优化共识问题形成,即
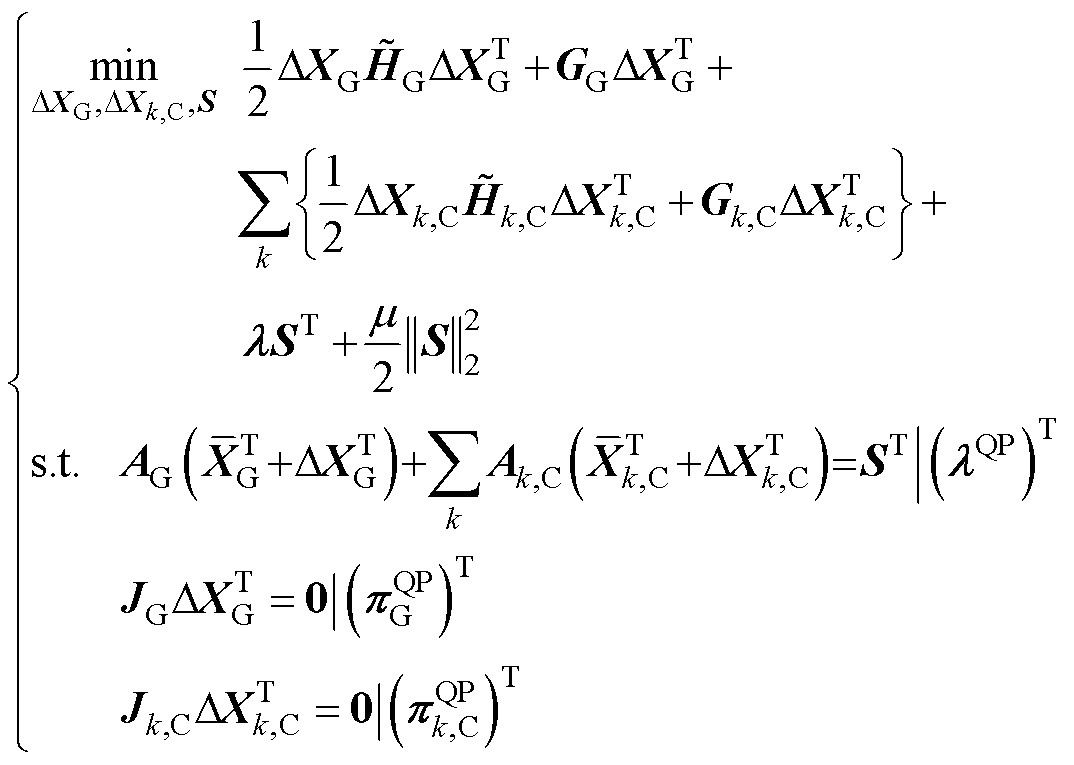
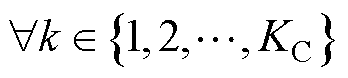 (17)
(17)
式中,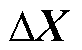 、
、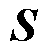 为原始变量,
为原始变量,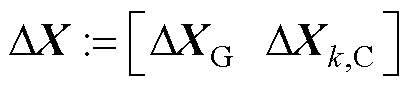 ;
;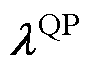 、
、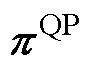 为对偶变量,
为对偶变量,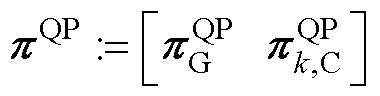 ;
;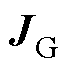 和
和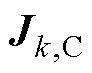 分别为与子优化问题约束关联的雅可比矩阵;
分别为与子优化问题约束关联的雅可比矩阵;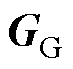 和
和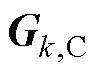 分别为与目标函数
分别为与目标函数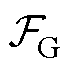 和
和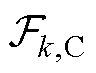 关联的梯度;
关联的梯度;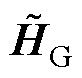 和
和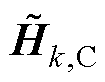 为海森矩阵近似计算结果,具体为
为海森矩阵近似计算结果,具体为
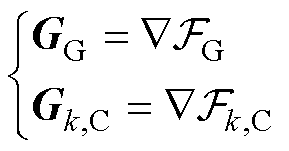 (18)
(18)
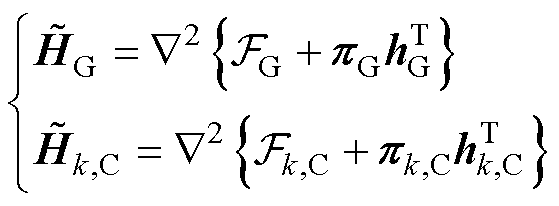 (19)
(19)
特别地,将式(8)和式(9)中的子优化问题约束分别表示为
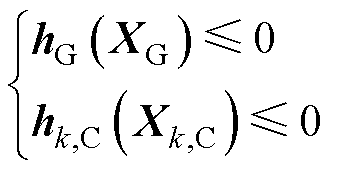 (20)
(20)
ALADIN通过交替求解式(8)、式(9)和式(17)实现分布式优化,关键的辅助变量与对偶乘子项通过线性搜索法更新[21]为
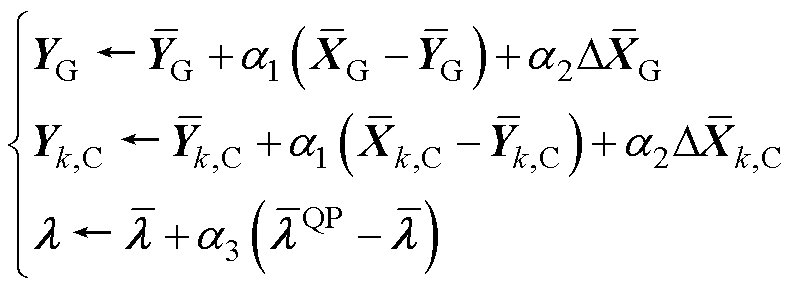 (21)
(21)
式中,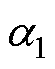 、
、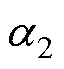 和
和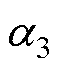 为线性搜索法中的相关参数,一般可设定为
为线性搜索法中的相关参数,一般可设定为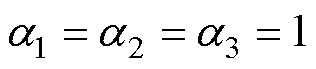 。
。
总结来看,应用ALADIN和ADMM进行分布式优化时,对原集中式电压优化问题拆分的思路是一致的,且两种方法都使用了增广项来处理原集中式电压优化问题中PCC母线处存在的边界耦合约束。不同的是,ADMM在每次迭代过程中需要求解原始问题的凸子问题,而ALADIN采用了不精确牛顿法来近似求解子问题,这使得ALADIN在处理非凸优化问题时,收敛性可以得到严格保证,其相关证明可详见文献[21]。ALADIN算法的迭代流程详见附录1。
(1)海森近似矩阵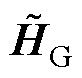 和
和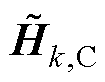 需保持正定以使得ALADIN算法收敛。然而,
需保持正定以使得ALADIN算法收敛。然而,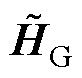 和
和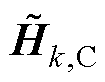 并不能严格保证其在每次迭代中都具备正定性,此时需要对其进行正定化处理。采取文献[21]中建议的方法,将非正定
并不能严格保证其在每次迭代中都具备正定性,此时需要对其进行正定化处理。采取文献[21]中建议的方法,将非正定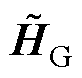 和
和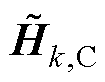 中的负特征值翻转为相反数,将零特征值替换为一个非常小的正数。
中的负特征值翻转为相反数,将零特征值替换为一个非常小的正数。
(2)式(17)所示的电压优化共识问题实际上对PCC母线上的边界耦合关系进行了缩放,即通过引入松弛的原始变量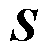 ,建立了如式(17)所示的包含等式约束的二次规划问题,其相较于含不等式约束的二次规划问题来说,更容易求解。但即便如此,式(17)的求解仍是相对复杂的,借助Cplex、Gurobi等凸规划求解器得到的优化结果很可能无法达到要求的精度,以至于影响ALADIN的整体迭代过程[21-24]。对此,根据文献[21]建议,可以直接列写式(17)所对应的KKT条件,再求解KKT条件所对应的线性方程组,以获得高质量的解析最优解。
,建立了如式(17)所示的包含等式约束的二次规划问题,其相较于含不等式约束的二次规划问题来说,更容易求解。但即便如此,式(17)的求解仍是相对复杂的,借助Cplex、Gurobi等凸规划求解器得到的优化结果很可能无法达到要求的精度,以至于影响ALADIN的整体迭代过程[21-24]。对此,根据文献[21]建议,可以直接列写式(17)所对应的KKT条件,再求解KKT条件所对应的线性方程组,以获得高质量的解析最优解。
对于式(17),其对应的拉格朗日函数为
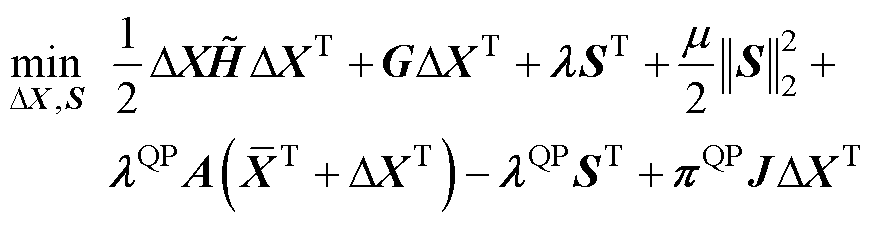 (22)
(22)
进一步可写出对应KKT条件为
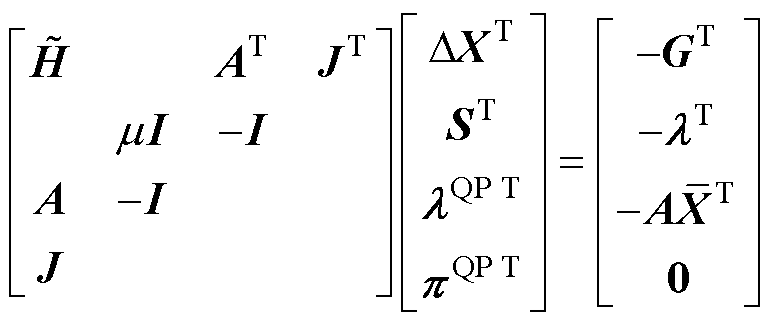 (23)
(23)
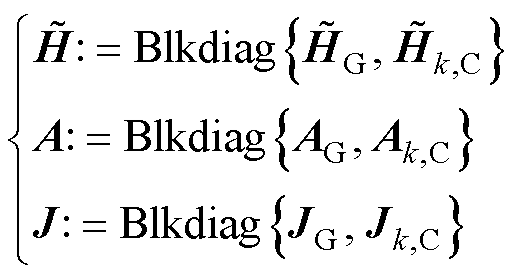 (24)
(24)
式中,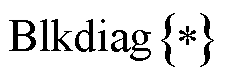 为矩阵块对角化的符号算子。
为矩阵块对角化的符号算子。
由以上论述可看出,对二次规划问题式(17)的优化求解可以等价地转换为对线性方程组式(23)的求解。鉴于式(23)包含的对称系数矩阵具有稀疏特征,可借助高性能的线性求解器获得高质量解。
(3)在求解非凸电压优化问题时,ADMM属于一阶算法[27]而ALADIN属于二阶算法[21],因此ALADIN具有更快收敛速度。ALADIN和ADMM在求解并网侧或集电侧子优化问题时均面临着非凸优化问题,在求解电压共识优化问题时均面临着求解凸二次规划问题,因此计算复杂度相同。然而,ADMM在每轮迭代中主要涉及拉格朗日乘子向量的信息传递,其复杂度为O(n)[27]。而ALADIN在每轮迭代中,需要全局协调来计算二阶海森矩阵信息,复杂度会更高,为O(n2)[21]。
(4)实际中,ALADIN算法的实现可能遭遇信息延迟问题。如前所述,ALADIN算法需要求解完并网侧和集电线路侧子优化问题后,才能进行电压共识优化问题的求解。换言之,在每轮迭代过程中,要求解电压共识优化问题,首先需要并网侧和集电侧子优化问题返回其边界电气量信息至PCC母线处。实际中,各分布式Agent控制器可能由于其自身电量不足等因素,计算能力和通信模块功率下降,导致并网侧或集电线路侧子优化问题在返回边界电气量的过程中存在信息延迟情况。
针对该问题,现有研究一般将信息更新方式分为同步更新和异步更新两种[28-29]。借助图4阐述两种更新方式:假定系统中存在3个分布式Agent控制器,其中Agnt-3相较于Agent-1和Agent-2存在明显信息延迟。在同步更新方式下,需要所有3个Agent返回信息后再执行下一次迭代,单次迭代时长取决于返回信息最慢的Agent。异步更新方式下,仅需部分Agent返回信息后(图中所用示例为至少2个Agent),就能执行下一次迭代。对比可看出,异步更新单次迭代耗时较同步更新更短,但是异步更新每次迭代返回的数据信息不如同步更新完整。为详细阐述两种更新方法,本文在附录1给出了标准的ALADIN算法,同步更新计算过程,并特别地构造了该算法的异步更新方案。
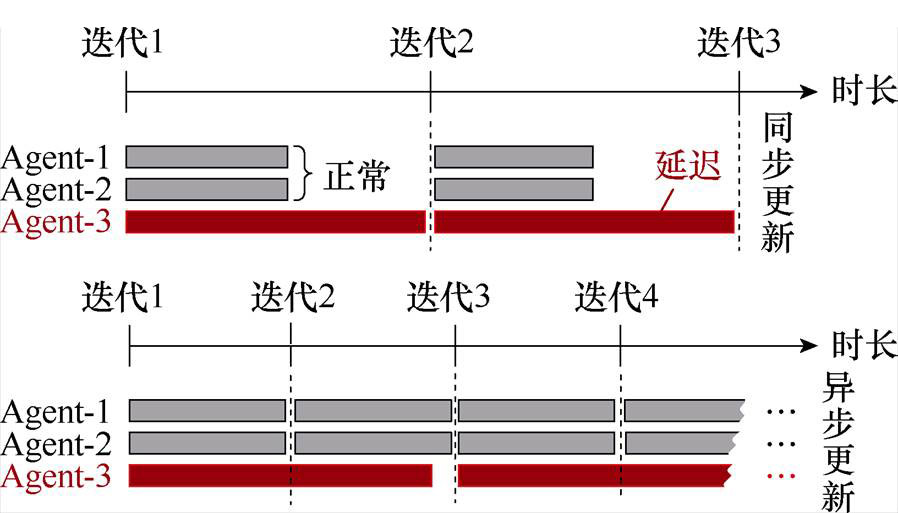
图4 分布式优化中的同步更新和异步更新示意图
Fig.4 Schematic diagram of information synchronization updates and asynchronous updates in distributed optimization
本文采用装机容量为8×12×2 MW的大型可再生能源电站系统进行算例分析,以验证所提方法的有效性,算例关键参数详见表1。大型可再生能源电站内部并联有8条集电线路,每条集电线路上等距离地依次接入12组GURE,站内为大规模集电系统;大型可再生能源电站外输电环境采用戴维宁模型进行等效,在设定的等值阻抗下,系统短路容量比为5.27,可被视作并入弱电网环境[30]。
表1 算例关键参数
Tab.1 The key parameters of case systems
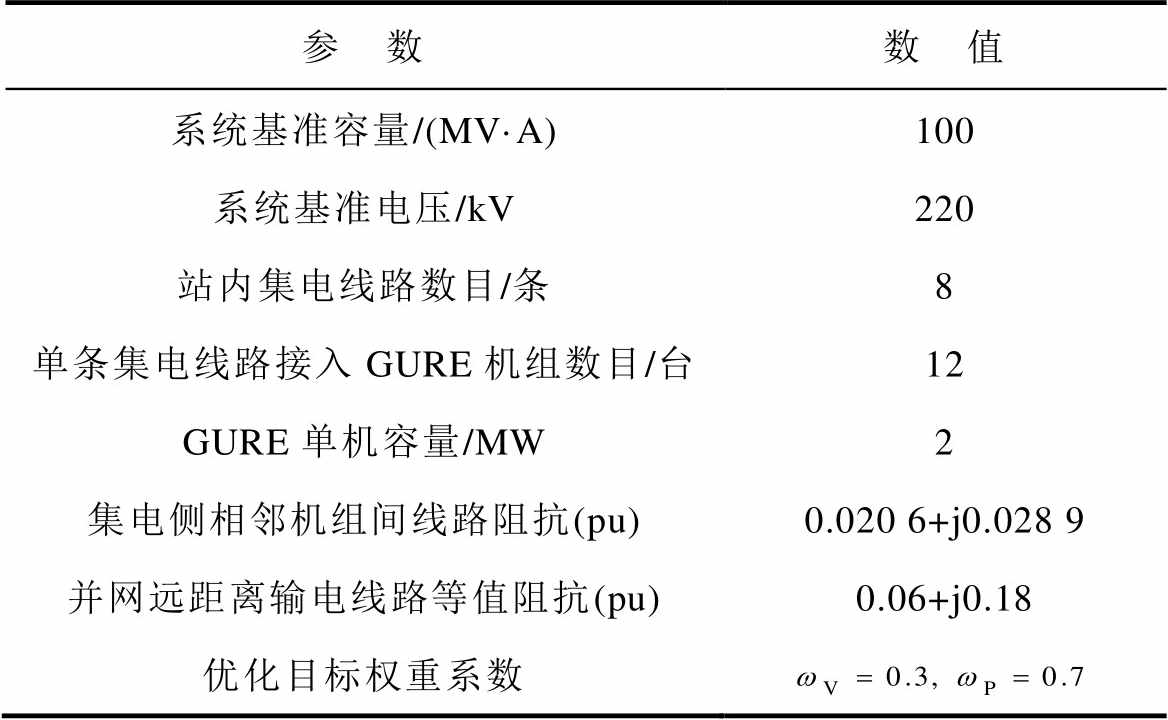
参 数数 值 系统基准容量/(MV·A)100 系统基准电压/kV220 站内集电线路数目/条8 单条集电线路接入GURE机组数目/台12 GURE单机容量/MW2 集电侧相邻机组间线路阻抗(pu)0.020 6+j0.028 9 并网远距离输电线路等值阻抗(pu)0.06+j0.18 优化目标权重系数
算例相关程序在Matlab环境下进行编译。基于ALADIN算法的大型可再生能源电站非凸电压优化数学模型借助CasADi框架实现[31];并网侧和集电侧的非凸子优化问题式(15)和式(16)采用IPOPT[32]求解器进行求解;电压优化共识问题式(17)转为线性方程式(23),利用MA57稀疏矩阵求解器[33]完成求解。算例分析中所涉及的牛-拉潮流计算利用MATPOWER[34]工具包实现,并视作潮流计算的基准结果。集中式优化结果通过直接求解式(3)~式(6)所示的非凸电压优化模型得出,视作电压优化的基准结果。上述涉及的所有程序利用配置为2.5-GHz CPU/16GB RAM的计算机执行,算法求解时间利用Matlab内置的tic/toc命令测量。
特别地,为方便后续对比叙述,定义三种分布式优化方案为:
方法A:利用ALADIN算法分布式求解基于非线性标准潮流约束的非凸电压优化模型,为本文所提方法。
方法B:利用ADMM算法分布式求解基于非线性标准潮流约束的非凸电压优化模型。
方法C:利用ADMM算法分布式求解基于线性LinDistFlow潮流约束的凸电压优化模型(LinDistFlow具体表达式详见附录第2节)。
本节中,4.1小节通过对比基于标准交流潮流模型与基于LinDistFlow潮流模型的潮流计算结果,验证对大型可再生能源电站系统建立非凸电压优化模型的必要性。4.2小节通过对比ADMM算法与ALADIN算法的分布式迭代次数,验证ALADIN求解非凸优化问题时在收敛性上的优势。4.3小节通过将ALADIN与ADMM得到的电压优化结果作对比,验证ALADIN求解非凸优化问题时的最优性;通过将ALADIN与集中式优化结果进行对比,展示ALADIN所得到的节点无功补偿决策结果和集中式优化所得结果基本一致。4.4小节通过对比ALADIN算法采用同步更新和异步更新时在收敛性和最优性上的差异,从而为应对信息延迟时选取合适的变量更新方式提供依据。
为验证大型可再生能源电站系统采用非线性标准潮流约束,从而建立非凸电压优化模型的必要性,本小节特别分析基于线性化潮流约束LinDistFlow的系统潮流计算误差。由于本文所提非凸电压优化模型采用的是非线性的标准潮流约束,潮流计算结果与基准值一致,因而无需特别比对。
首先,分析采用线性化潮流约束LinDistFlow替换非线性标准潮流约束时,可再生能源电站系统规模对站内集电线路潮流计算准确性的影响。算例分析中,将各GURE有功输出设定为1.6 MW,无功输出设定为0 Mvar。图5展示了基于线性化潮流约束LinDistFlow的站内潮流计算误差:由图5a可见,随着并联集电线路数量增加,集电线路节点电压和集电线路有功损耗的计算误差增大;由图5b可见,随着单条集电线路上GURE数量的增加,集电线路节点电压和集电线路有功损耗计算误差增大。
然后,分析采用线性化潮流约束LinDistFlow替换非线性标准潮流约束时,外部并网环境对站外PCC母线至受端电网段潮流计算准确性的影响。算例分析中,将PCC母线处的并网有功功率设定为50 MW,无功功率设定为20 Mvar,保持集电侧相邻机组间线路阻抗见表1,且大小不变,通过改变并网远距离输电线路等值阻抗大小来影响短路容量比,从而表征外部并网环境强弱变化。图6展示了基于线性化潮流约束下的站外潮流计算误差,由图6可知:随着短路容量比的减小,即外部并网环境由强变弱,PCC母线电压和外部等值电网的有功损耗计算误差增大。
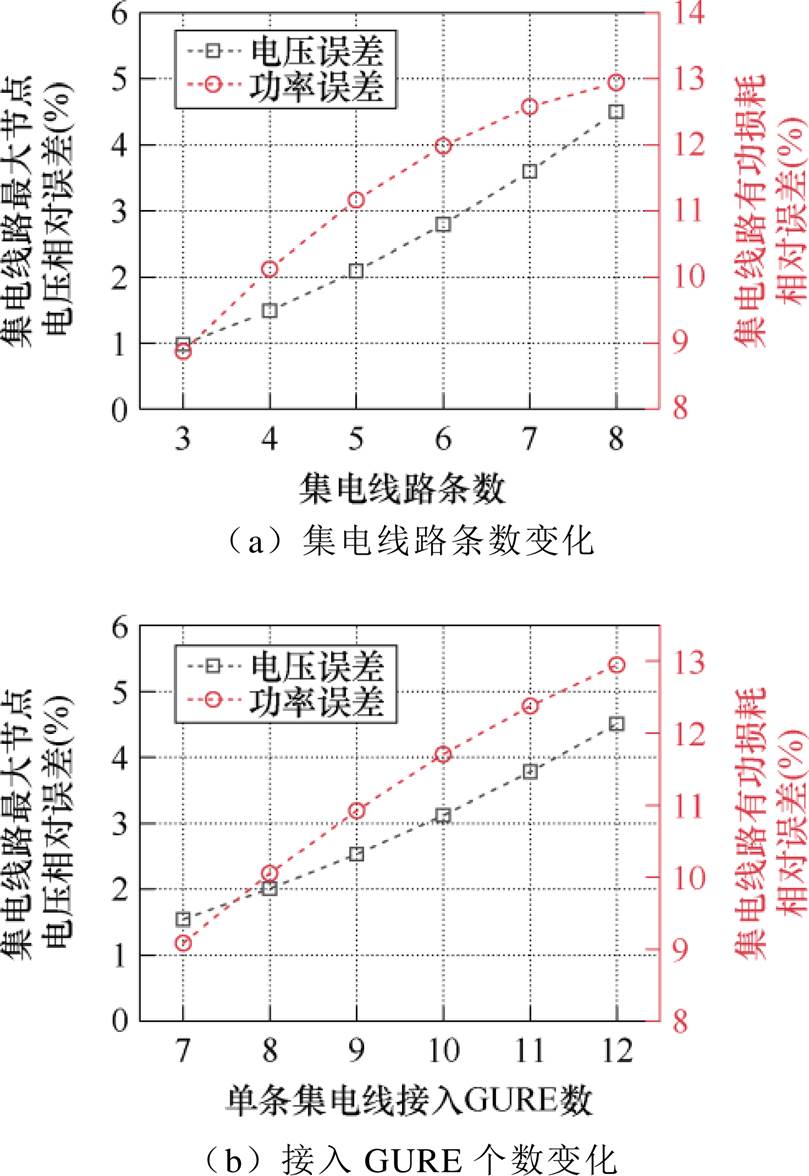
图5 LinDistFlow约束下的站内潮流计算误差
Fig.5 Calculation error of power flow inside the plant with the LinDistFlow constraints
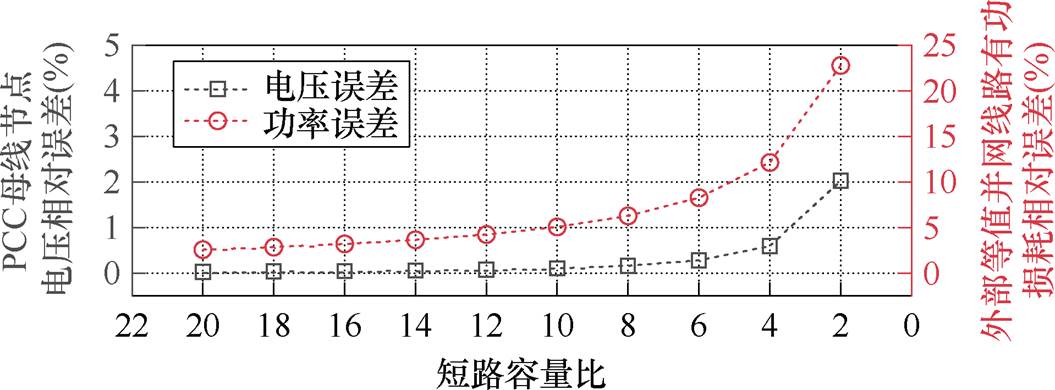
图6 LinDistFlow约束下的站外潮流计算误差
Fig.6 Calculation error of power flow outside the plant with the LinDistFlow constraints
总结如下:①伴随着可再生能源电站系统规模的增大,线性化潮流约束所导致的站内集电线路潮流计算误差也愈发明显;②由于大型可再生能源电站通常远离负荷中心,其并入弱电网环境时,线性化潮流约束所导致的外部等值电网潮流计算误差也难以忽视;③为有效地优化大型可再生能源电站系统电压,建立基于非线性标准潮流约束的非凸电压优化模型尤为必要。
本节对方法A和方法B在求解非凸电压优化模型时的收敛性进行分析。在作分布式优化时,涉及的边界耦合变量初值均统一为0,拉格朗日乘子初值设置为1,收敛条件为原始和对偶残差均小于1× 10-4(可认为边界电压项残差应小于0.000 1(pu),边界功率项残差应小于0.01 MW。考虑到±0.05(pu)的电压偏差范围和百MW级的系统装机总容量,此收敛条件是合理的)。
分析子优化问题中的罚函数参数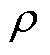 和电压优化共识问题中的参数
和电压优化共识问题中的参数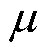 对方法A收敛性的影响。保持
对方法A收敛性的影响。保持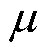 =50不变,设置
=50不变,设置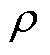 值从5~30变化,有残差收敛结果如图7所示。由图7可知,
值从5~30变化,有残差收敛结果如图7所示。由图7可知,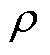 的取值并不会对ALADIN算法收敛性造成明显影响。不同
的取值并不会对ALADIN算法收敛性造成明显影响。不同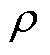 取值下,ALADIN算法均能在8次迭代左右达到收敛条件(残差小于1×10-4)。当迭代次数继续增加至12次,不同
取值下,ALADIN算法均能在8次迭代左右达到收敛条件(残差小于1×10-4)。当迭代次数继续增加至12次,不同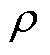 取值下的残差均跌至1×10-7以下,达到理想的收敛性。保持
取值下的残差均跌至1×10-7以下,达到理想的收敛性。保持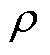 =10不变,设置
=10不变,设置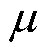 值从20~70变化,有残差收敛结果如图8所示。由图8可知,在绝大多数的
值从20~70变化,有残差收敛结果如图8所示。由图8可知,在绝大多数的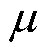 值取值下,ALADIN依然具有良好的收敛性;但当
值取值下,ALADIN依然具有良好的收敛性;但当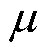 值取值过大(如
值取值过大(如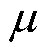 =70)时,会对算法收敛性产生负面作用。
=70)时,会对算法收敛性产生负面作用。
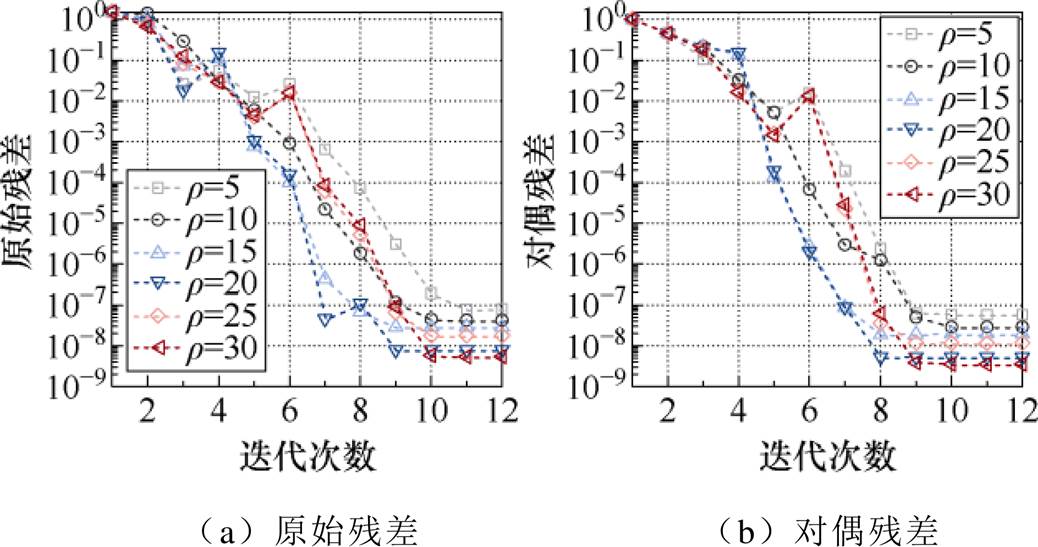
图7 不同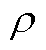 值下的方法A残差收敛情况(
值下的方法A残差收敛情况(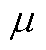 =50)
=50)
Fig.7 Convergence conditions of residuals for method A with different 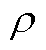 (
(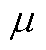 =50)
=50)
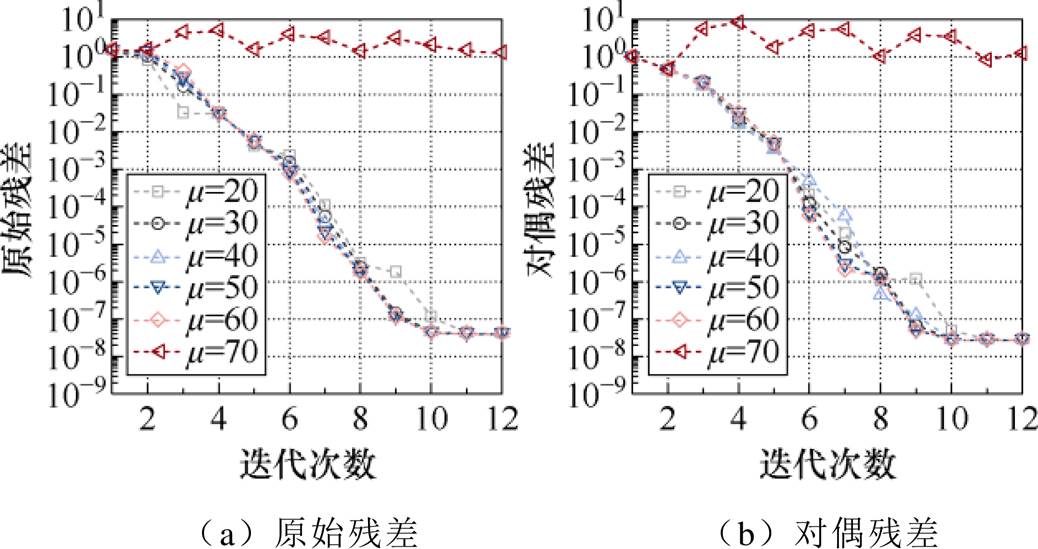
图8 不同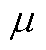 值下的方法A残差收敛情况(
值下的方法A残差收敛情况(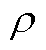 =10)
=10)
Fig.8 Convergence conditions of residuals for method A with different 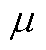 (
(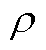 =10)
=10)
进一步地,对比方法A和方法B的收敛情况,以说明ALADIN算法相较于传统ADMM算法用分布式求解非凸优化问题时,在收敛性方面具有优势。由前所述,由于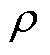 取值不会明显影响ALADIN的收敛性表现,这里选取
取值不会明显影响ALADIN的收敛性表现,这里选取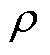 =10时的方法A用作对比分析。然而,
=10时的方法A用作对比分析。然而,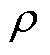 的取值会显著影响ADMM的收敛 性[22]。因此,为公平比较,这里列举多种
的取值会显著影响ADMM的收敛 性[22]。因此,为公平比较,这里列举多种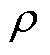 取值下的方法B用作对比分析。对比结果如图9所示:方法B的收敛性对
取值下的方法B用作对比分析。对比结果如图9所示:方法B的收敛性对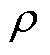 的取值非常敏感,过大或过小的
的取值非常敏感,过大或过小的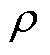 值均会造成方法B收敛速度过慢。
值均会造成方法B收敛速度过慢。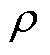 =15时的方法B具有相对最好的收敛性,然而其也需要在大约70次迭代后才能满足收敛条件。而方法A在大约10次迭代后,原始和对偶残差均已下降到1×10-7以下,收敛速率明显好于方法A。
=15时的方法B具有相对最好的收敛性,然而其也需要在大约70次迭代后才能满足收敛条件。而方法A在大约10次迭代后,原始和对偶残差均已下降到1×10-7以下,收敛速率明显好于方法A。
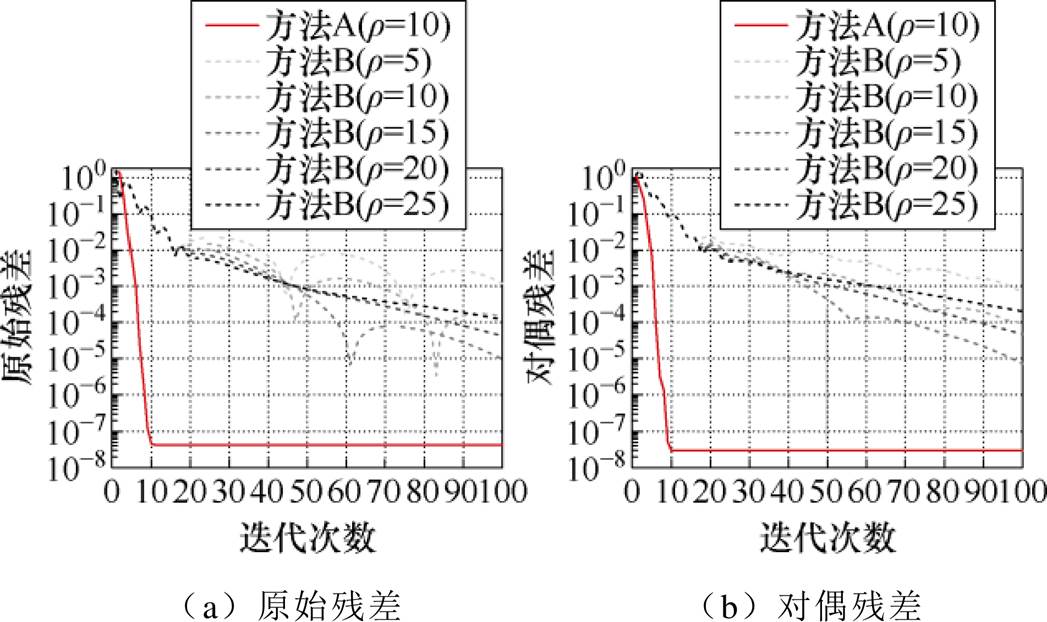
图9 方法A和方法B的残差收敛情况对比
Fig.9 Comparison of convergence conditions between method A and method B
最后,验证可再生能源电站规模对ALADIN算法收敛性的影响。通过增加集电线路并联条数和集电线路上接入的GURE机组数目,对方法A的收敛性展开分析(基于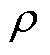 =10的情况),其情况如图10和图11所示:随着集电线路并联条数或集电线路上接入的GURE机组数目的增加,ALADIN始终保持良好的收敛性;在大约10次迭代后,不同系统规模下的原始和对偶残差均能跌落至到1×10-7附近,表现出理想的收敛性。特别地,图10和图11所示的各种情况下,并网侧模型和集电侧模型PCC母线耦合处的PCC母线电压幅值、有功功率、无功功率迭代情况详见附录第3节。
=10的情况),其情况如图10和图11所示:随着集电线路并联条数或集电线路上接入的GURE机组数目的增加,ALADIN始终保持良好的收敛性;在大约10次迭代后,不同系统规模下的原始和对偶残差均能跌落至到1×10-7附近,表现出理想的收敛性。特别地,图10和图11所示的各种情况下,并网侧模型和集电侧模型PCC母线耦合处的PCC母线电压幅值、有功功率、无功功率迭代情况详见附录第3节。
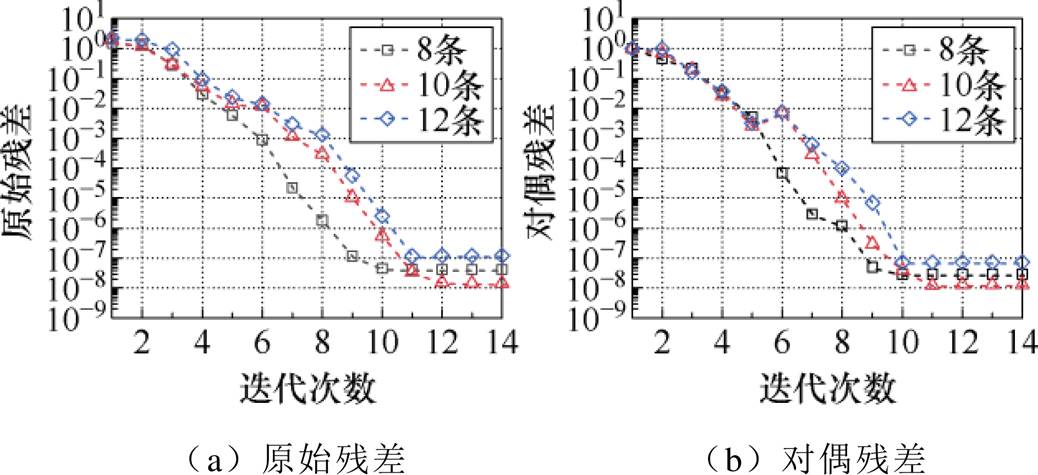
图10 不同集电线路数下的方法A残差情况
Fig.10 Convergence conditions for method A with different numbers of collecting power lines
总体而言:①ALADIN(方法A)算法的收敛性对参数变化拥有良好的鲁棒性,而ADMM(方法B)算法的收敛性对参数变化敏感;②无论参数如何取值,ALADIN算法仅需少量迭代即可收敛,而ADMM算法在合适的参数取值下,仍需大量迭代才能收敛;③随着可再生能源电站系统规模的扩展,ALADIN算法依旧具有良好的收敛性。
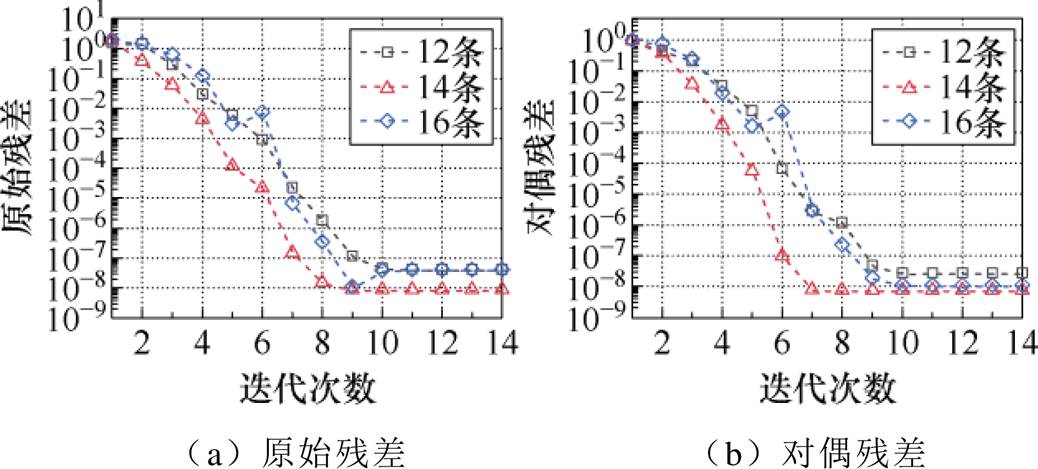
图11 不同GURE机组数下的方法A残差情况
Fig.11 Convergence conditions for method A with different numbers of GURE
首先,通过对比方法A、方法B、方法C对大型可再生能源电站系统电压的分布式优化结果,说明所提方法通过建立准确的优化模型和采用有效的优化算法,保障了大型可再生能源系统分布式电压优化决策的精度与速度。图12所示为基于本文所比较的各种方法,PCC母线至某集电线路末端节点的电压分布情况(其中0代表PCC母线节点编号,1~12代表集电线路上GURE的接入节点序号)。表2给出了各种方法作用下优化方法计算结果对比。
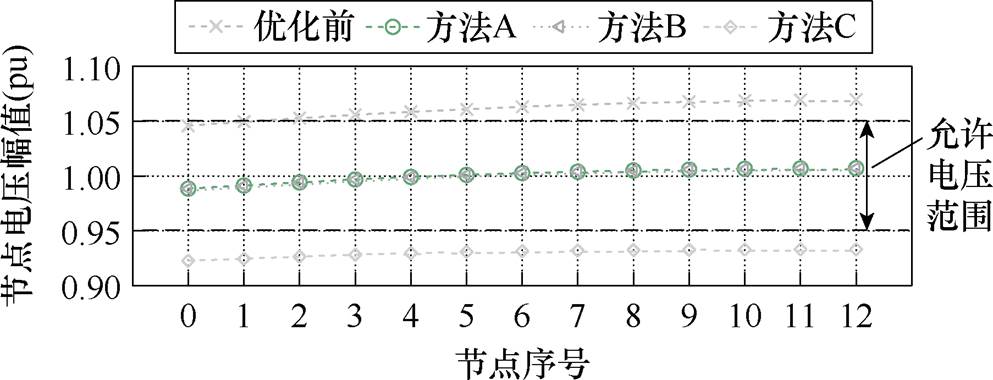
图12 电压分布优化结果对比
Fig.12 Comparison of voltage distribution optimization results
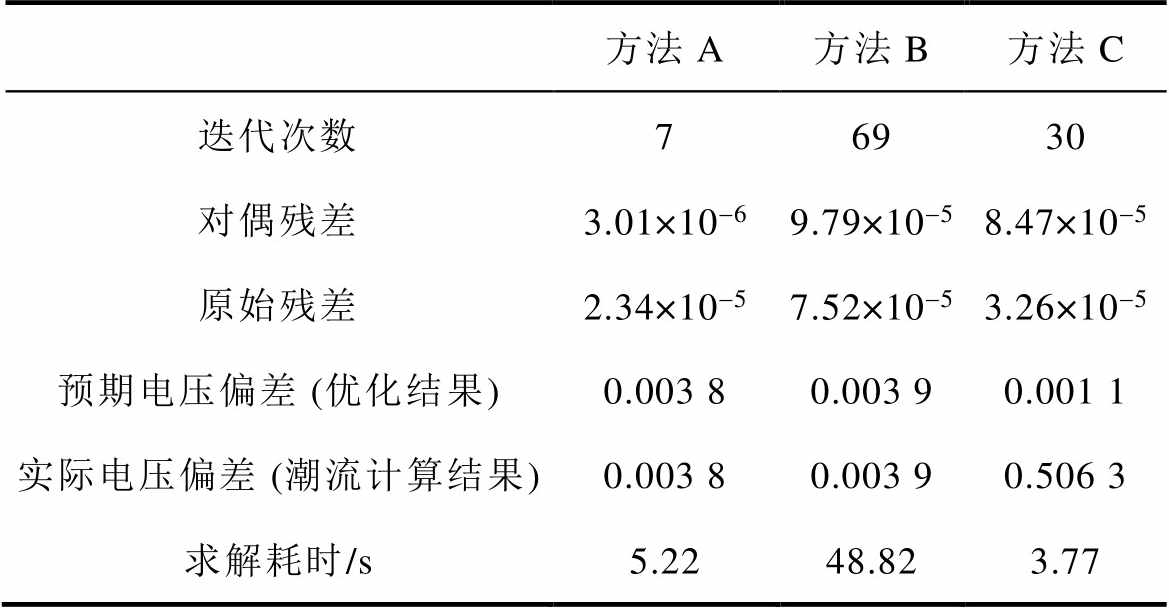
表2 各分布式优化方法计算结果对比
Tab.2 Comparison of distributed optimization results
方法A方法B方法C 迭代次数76930 对偶残差3.01×10-69.79×10-58.47×10-5 原始残差2.34×10-57.52×10-53.26×10-5 预期电压偏差 (优化结果)0.003 80.003 90.001 1 实际电压偏差 (潮流计算结果)0.003 80.003 90.506 3 求解耗时/s5.2248.823.77
结合图12与表2进行分析:在无任何电压优化方法作用时,可再生能源电站部分节点电压超过了允许上限;方法B可有效地使得系统各节点电压处于安全范围内,但是该方法下算法迭代总次数接近70次,总计算耗时接近49 s。方法C迭代次数较方法B少很多,30次即能完成收敛。且由于方法C在每次迭代时,求解的是一个线性规划问题,单次求解耗时也少,因此总的求解耗时仅约4 s左右。然而,由于方法C求解的电压优化模型是基于线性化LinDistFlow潮流约束,导致优化求解得到的预期电压结果与潮流计算所得的实际电压结果之间存在较大偏差,补偿的无功量多于实际需求,优化后的系统整体电压反而出现了低电压越限的情况;与前两种方法相比,方法A仅通过7次迭代,耗时约5 s,即完成了收敛。并且由于方法A求解的非凸电压优化模型采用非线性标准潮流约束,因此预期电压结果与实际电压结果是一致的。可以看到,方法A对应计算结果中,各节点电压均被优化至1(pu)附近,系统电压整体处于相当安全的范围内,电压越限风险得以消除。特别地,不同方法下,并网侧模型和集电侧模型PCC母线耦合处的母线电压幅值、有功功率、无功功率迭代情况详见附录第4节。
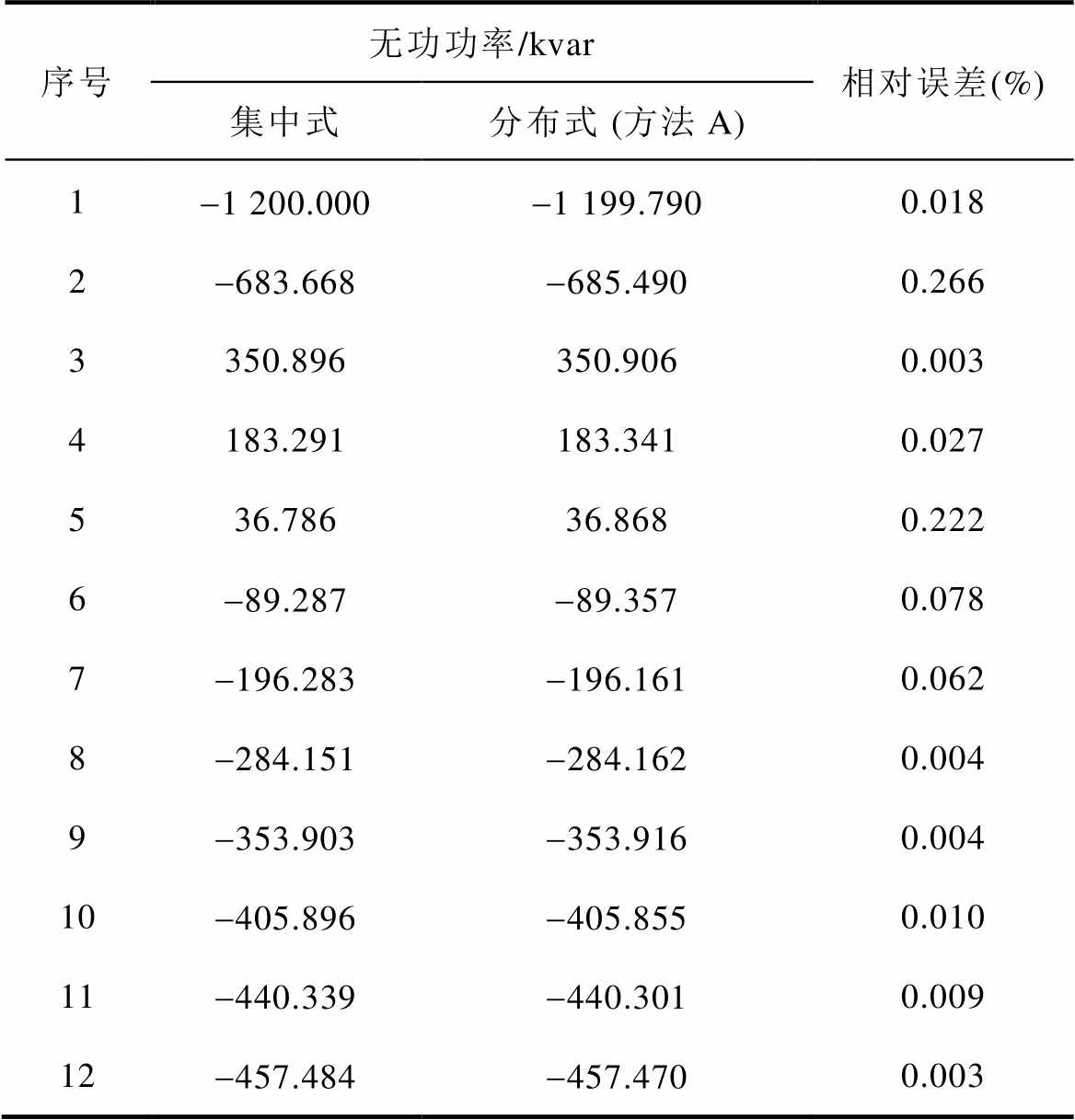
然后,考虑可再生能源电站系统的电压调控效果依赖集电线路上各GURE接入节点的无功补偿决策,将方法A和集中式优化下的节点无功补偿结果进行对比,以展现ALADIN优化决策的准确性。采用方法A和集中式优化的某集电线路节点无功补偿计算结果见表3。由表3可知:方法A采用ALADIN对非凸电压优化模型作分布式优化,得到的集电线路各节点无功补偿量和集中式优化下的结果基本一致,最大相对误差低于0.3%。
最后,将采用方法A补偿后的目标函数值和补偿前对应数值进行对比,以直观地展现ALADIN对大型可再生能源电站系统电压的调控作用。表4对比了节点无功补偿前后的目标函数。由表可知:通过方法A优化GURE无功输出进行系统节点无功补偿,使得目标函数值显著下降,其中电压偏差降低尤为明显。由于进行了额外的无功补偿,集电线路上的电流增大,优化后系统整体有功损耗相较于优化前的有所增加。然而,得益于考虑了最小化有功损耗作为优化目标之一,优化后的有功损耗结果仅略微增加。
总体看来:①利用ADMM求解非凸电压优化模型时(方法B),需要大量迭代次数才能完成收敛,求解耗时较长;②利用ADMM求解凸电压优化模型时(方法C),虽然所需迭代次数较非凸电压问题而言变少,求解耗时短,但受LinDistFlow线性化潮流约束所导致的潮流计算误差影响,系统实际电压分布和预期电压分布差距较大,系统整体电压偏差甚至比优化前更大;③利用ALADIN求解非凸电压优化模型时(方法A),仅需少量迭代即完成收敛,求解耗时短,分布式优化得到的节点无功补偿结果几乎与通过集中式优化得到的结果一致。在ALADIN的作用下,系统电压分布被优化至相当安全的范围内。
表3 优化后的集电线路节点无功补偿结果对比
Tab.3 Nodal reactive power optimization results on collecting power lines for large-scale renewable energy power plants
序号无功功率/kvar相对误差(%) 集中式分布式 (方法A) 1-1 200.000-1 199.7900.018 2-683.668-685.4900.266 3350.896350.9060.003 4183.291183.3410.027 536.78636.8680.222 6-89.287-89.3570.078 7-196.283-196.1610.062 8-284.151-284.1620.004 9-353.903-353.9160.004 10-405.896-405.8550.010 11-440.339-440.3010.009 12-457.484-457.4700.003
表4 系统无功补偿前后目标函数对比
Tab.4 Comparison of objective function results before and after system reactive power compensation
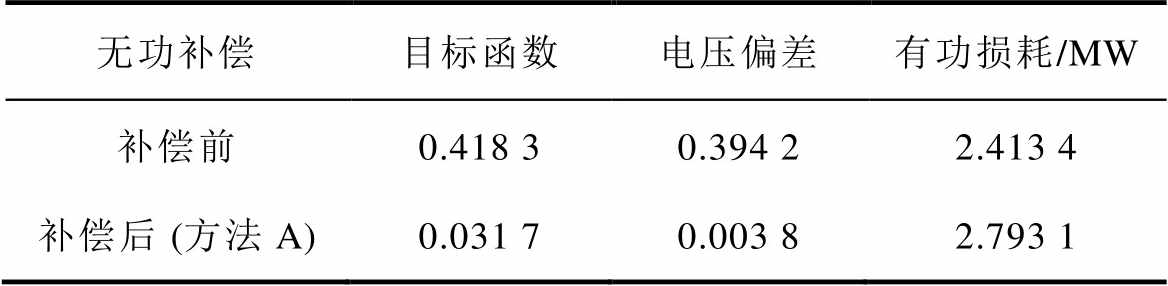
无功补偿目标函数电压偏差有功损耗/MW 补偿前0.418 30.394 22.413 4 补偿后 (方法A)0.031 70.003 82.793 1
为验证所提更新方案,接下来对ALADIN算法采用同步更新和异步更新分别应对信息延迟的效果进行对比。不失一般性,假设并网侧的分布式Agent存在信息延迟,因而返回边界电气量信息的速度较集电线路侧的分布式Agent慢。对此,考虑三种延迟情况给出算例仿真结果。延迟情况1:并网侧返还信息速度是集电线路侧的1.5倍;延迟情况2:并网侧返还信息速度是集电线路侧的2倍;延迟情况3:并网侧返还信息速度是集电线路侧的4倍。
图13和表5展示了不同通信延迟情况下的ALADIN算法异步更新情况。可以看出,正常情况、延迟情况1、延迟情况2和延迟情况3对应的迭代次数分别为7次、10次、15次和33次,说明信息延迟程度增加会导致迭代次数的增加。这是因为异步更新下,信息延迟程度的增加使得有延迟的并网侧Agent需要更多的迭代次数返还边界电气量信息才能实现收敛。此外,信息延迟程度较轻的情况(如延迟情况1)下,异步更新下的ALADIN算法可保持良好的最优性。随着信息延迟程度的增加,异步更新下的ALADIN算法最优性会受到不同程度的影响。而同步更新因为每次迭代均能接受所有Agent返还的信息,因而最优性不会受影响。
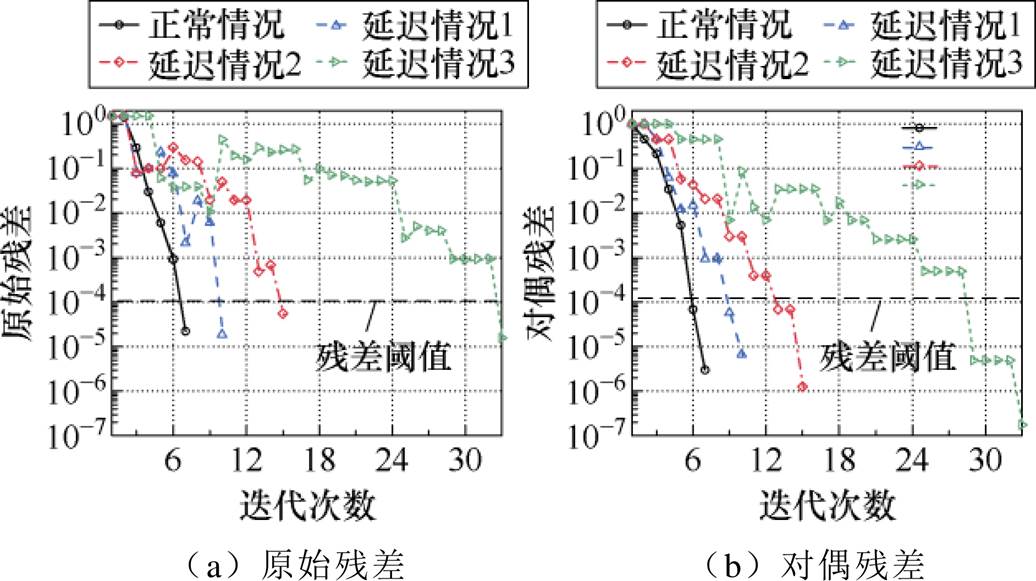
图13 不同通信延迟情况下的ALADIN算法采用异步更新方式的残差收敛情况
Fig.13 Residual convergence of ALADIN with asynchronous updates under different communication delays
表5 不同通信延迟情况下的ALADIN算法异步更新方式的优化情况对比
Tab.5 Comparison of ALADIN with asynchronous updates under different communication delays

对比情况收敛迭代/次目标函数相对误差(%) 正常情况79.9×10-5 延迟情况1105.1×10-5 延迟情况2151.1×10-2 延迟情况3334.2×10-3
表6对比了不同通信延迟情况下,ALADIN采用同步更新和异步更新的时间消耗,表中数值表示的是单位时间的倍数,定义1个单位时间为集电线路侧Agent(无延迟)每次迭代中返还边界电气量信息的耗时。可以看出,在无信息延迟时,异步更新过程和同步更新过程实质上没有区别,因此消耗时间相同;在信息延迟程度较轻时,异步更新下消耗的时间会相对较少;随着信息延迟程度的增加,同步更新下消耗的时间反而会更少。这是因为异步同步更新下,虽然每次迭代时间更短,但随着信息延迟程度的增加,其总迭代次数也会上升,从而导致总耗时反而比同步更新更长。
表6 不同通信延迟情况下采用不同信息更新方式的ALADIN算法计算用时对比
Tab.6 Comparison of computational time for ALADIN with different information update mechanisms under different communication delays

对比情况同步更新/单位时间异步更新/单位时间 正常情况77 延迟情况110.510 延迟情况21415 延迟情况32833
总结如下:①异步更新方式单次迭代耗时更短,同步更新方式收敛所需总迭代次数更少;②对于ALADIN算法而言,在应对信息延迟时究竟采用同步更新还是异步更新方式需要根据实际情况确定,在信息延迟较轻时优先考虑异步更新,在信息延迟较重时优先考虑同步更新。
为解决大型可再生能源电站规模化功率传输过程中面临的过电压越限风险,本文构建了面向大型可再生能源电站系统电压调控的非凸分布式优化模型,并通过ALADIN算法实现了模型的高效分布式优化求解。结合理论分析与算例测试,可得主要结论如下:
1)诸如LinDistFlow的线性化近似潮流约束会导致大型可再生能源电站系统电压计算存在较大误差。本文建立的基于非线性标准潮流约束的非凸电压分布式优化模型,能够提供准确的系统电压计算结果,对可再生能源电站系统规模化布局、长距离电能外送的运行场景有很好的适用性。
2)针对传统的ADMM等分布式优化算法在求解本文构建的非凸电压分布式优化模型时收敛性、最优性难以保障的问题,本文提出采用新颖的ALADIN分布式优化算法求解非凸电压分布式优化模型。ALADIN算法能够在极少次迭代后完成收敛,且取得与集中式优化几乎相同的电压优化结果。
3)通过ALADIN求解非凸电压优化模型得到的GURE无功输出,可以有效地将大型可再生能源电站系统的各节点电压优化至相当安全范围内。且ALADIN算法的实现,仅需要各分布式Agent控制器进行相邻通信即可,相较于常规的集中式电压优化方法,对电站造成的通信负担更小。
4)对于ALADIN算法,在应对信息延迟时究竟采用同步更新还是异步更新方式,可根据延迟程度的实际情况灵活地进行选择。
附 录
1.ALADIN算法实现步骤
附表1和附表2分别给出了标准ALADIN算法(也可视为基于同步更新的ALADIN算法)和基于异步更新的ALADIN算法的实现步骤(假设第n次迭代中,完成信息返回的并网或集电线路Agent集合为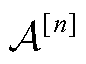 )。特别地,下表中
)。特别地,下表中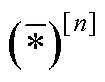 表示第n次分布式优化迭代中得到的变量确定值。
表示第n次分布式优化迭代中得到的变量确定值。
附表1 标准ALADIN算法伪码(同步更新)
App.Tab.1 Pseudocode of the standard ALADIN (synchronous updating)

1. 初始化初始化矩阵、,辅助变量、,惩罚项系数、初值;设置残差阈值;令; 2. 循环开始 /*求解并网侧子优化问题*/ 3. 求解含的,; /*求解集电侧子优化问题*/ 4. 求解含的,; /*更新灵敏度矩阵*/ 5. ;;; /*求解电压优化共识问题*/ 6. 求解稀疏线性方程组式(23); /*更新辅助变量和对偶乘子*/ 7. ; 8. 9. 直到原始残差和对偶残差均小于阈值;
附表2 基于异步更新的ALADIN算法伪码
App.Tab.2 Pseudocode of ALADIN (asynchronous updating)

1. 初始化初始化矩阵、,辅助变量、,惩罚项系数、初值;设置残差阈值;令; 2. 循环开始 /*求解并网侧子优化问题*/ 3.如果Agent属于 4. 求解含的,; 5.否则 6.不更新,; 7.结束 /*求解集电侧子优化问题*/ 8.如果Agent属于 9. 求解含的,; 10.否则 11.不更新,; 12.结束 /*更新灵敏度矩阵*/ 13. ;;; /*求解电压优化共识问题*/ 14.求解稀疏线性方程组式(23); /*更新并网子优化问题辅助变量和对偶乘子*/ 15.仅当 Agent属于 16.作更新,; 17.结束 /*更新并网子优化问题辅助变量和对偶乘子*/ 18.仅当 Agent属于 19.作更新,; 20.结束 21. ; 22. 直到原始残差和对偶残差均小于阈值;
2. LinDistFlow潮流模型
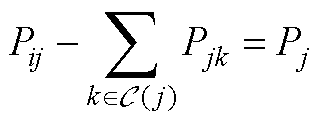 (A1)
(A1)
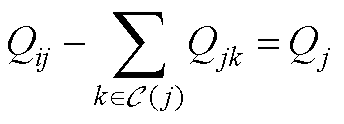 (A2)
(A2)
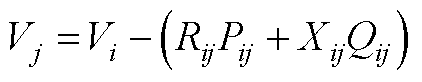 (A3)
(A3)
式中,Pj和Qj分别为节点注入有功和无功功率;Pij和Pjk分别为支路有功功率;Qij和Qjk分别为支路无功功率;Vi和Vj分别为节点电压幅值;Rij和Xij分别为线路电阻和电抗;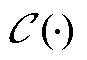 代表辐射型网路中与当前节点关联的下游节点。
代表辐射型网路中与当前节点关联的下游节点。
3.图10和图11所示各情况下,并网侧模型和集电侧模型在PCC母线耦合边界的电气量迭代情况
如附图1和附图2所示:在不同的集电线路条数和GURE机组数下,PCC母线耦合处无论是集电侧还是并网侧的电气量,均在少量迭代次数下即可重合一致。
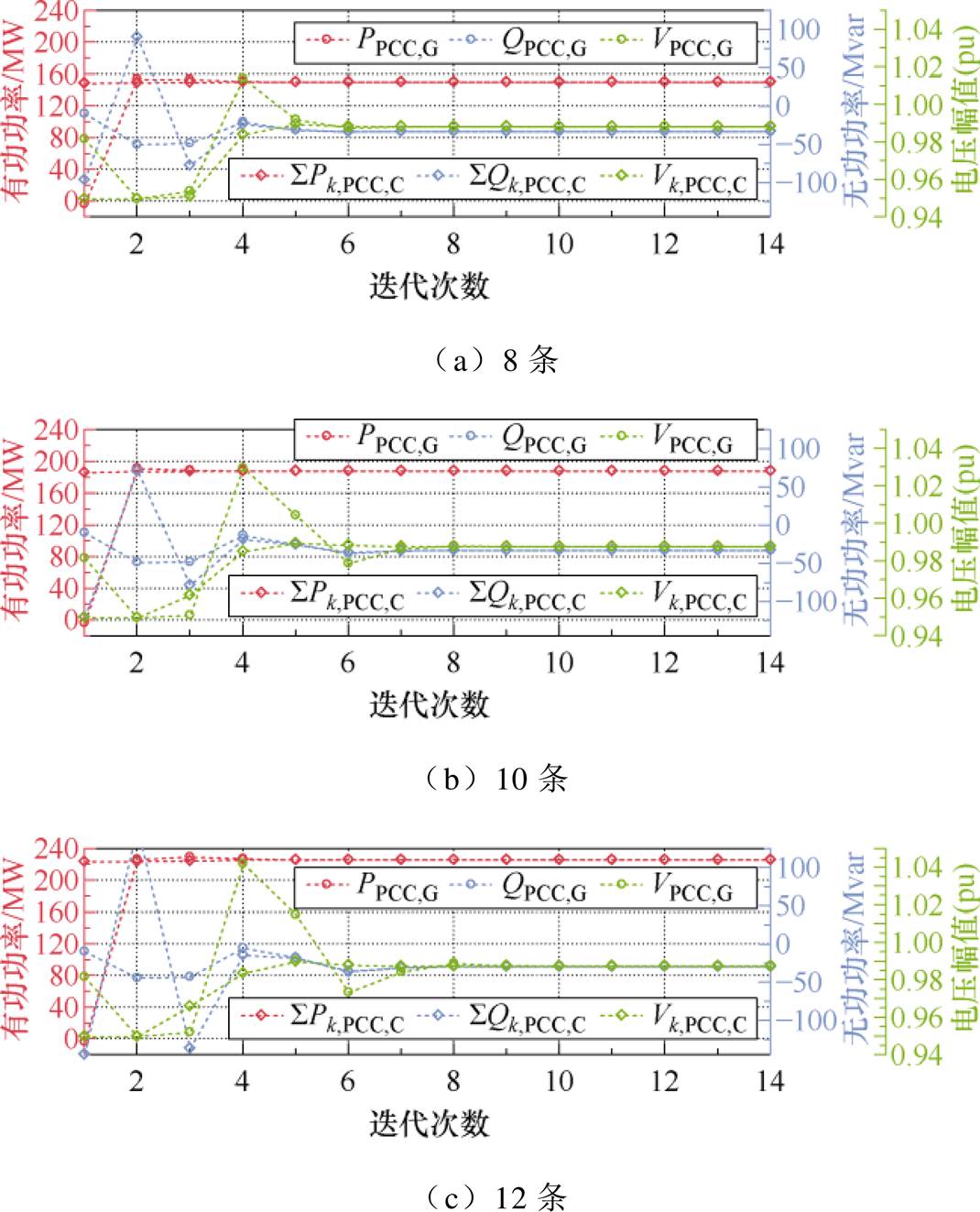
附图1 不同集电线路数下的PCC母线耦合边界电气量取值(方法A)
App.Fig.1 Iterative calculating process of coupling electrical variable values under different numbers of collecting power lines (method A)
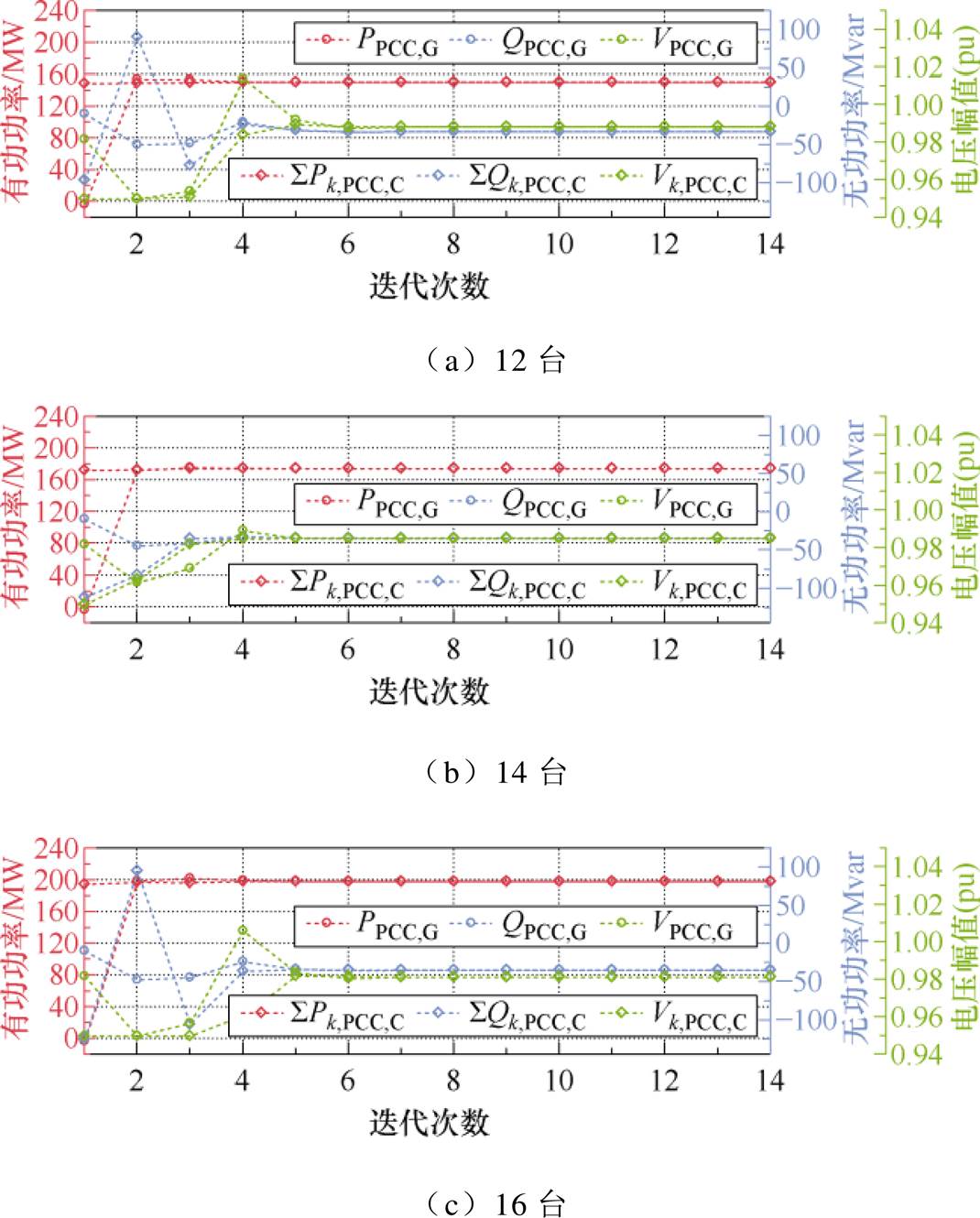
附图2 不同GURE机组数下的PCC母线耦合边界电气量迭代情况(方法A)
App.Fig.2 Iterative calculating process of coupling electrical variable values under different numbers of GURE units (method A)
特别地,相较于无功功率和电压幅值,有功功率的重合速度最快。这是因为各集电线路上的各GURE机组均按最大功率点跟踪数值输出有功功率,使得每次迭代中由集电侧子优化问题计算出的PCC母线有功功率变化幅度特别小,从而导致并网侧子优化问题计算出的PCC母线有功功率也在经历较少的迭代次数后迅速保持与其一致。
4.方法A、B、C分布式优化下的PCC母线处边界电气量迭代变化情况
附图3~附图5展现了利用不同方法进行电压优化时,由并网侧子优化问题和集电线路侧子优化问题计算得到的PCC母线边界电气量的变化情况。特别地,采用集中式优化方式求解非凸电压优化模型所得到的优化结果作为分析分布式电压优化结果最优性的基准参考值。由附图3~附图5可看出:方法A仅通过7次迭代完成了收敛,且各边界电气量数值基本和参考值结果一致,方法A具备良好的收敛性和最优性;方法B最终迭代收敛结果虽然和参考值结果基本一致,但需要通过接近70次迭代才完成收敛,不具备良好收敛性。方法C通过30次迭代完成了收敛,但有功功率、无功功率,以及电压幅值较参考结果数值均存在明显差别,不具备良好最优性。由此可看出,在求解非凸电压优化问题时,ALADIN较ADMM具备更好的收敛性和最优性。
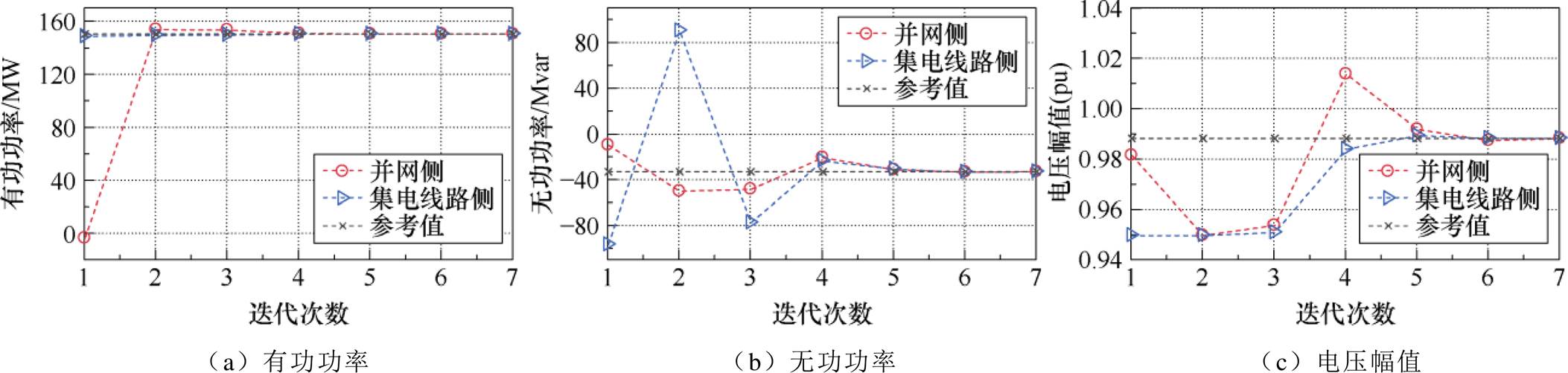
附图3 方法A的PCC母线耦合边界电气量迭代计算过程
App.Fig.3 Coupling electrical variable iterative calculating process of method A
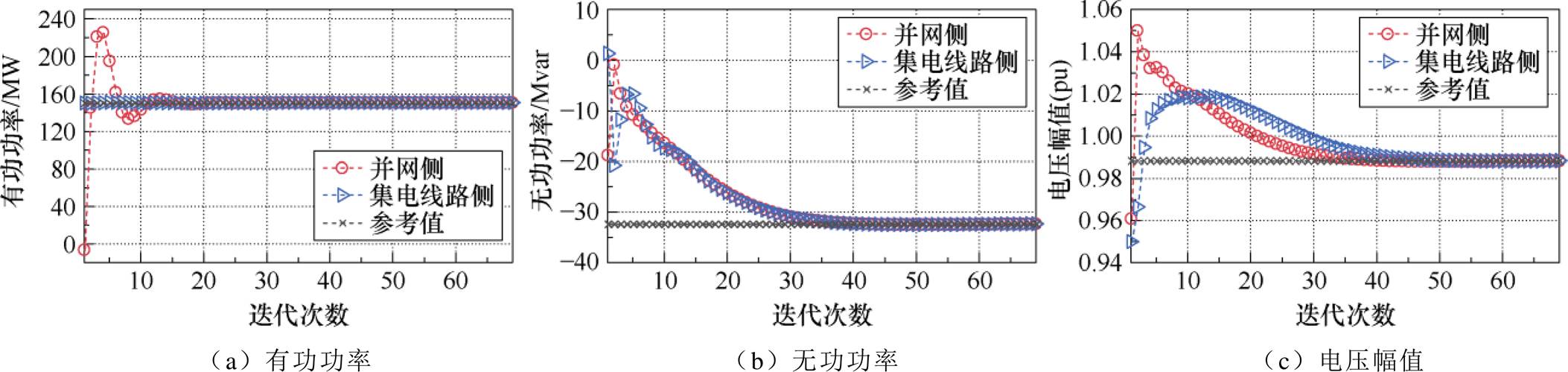
附图4 方法B的PCC母线耦合边界电气量迭代计算过程
App.Fig.4 Coupling electrical variable iterative calculating process of method B
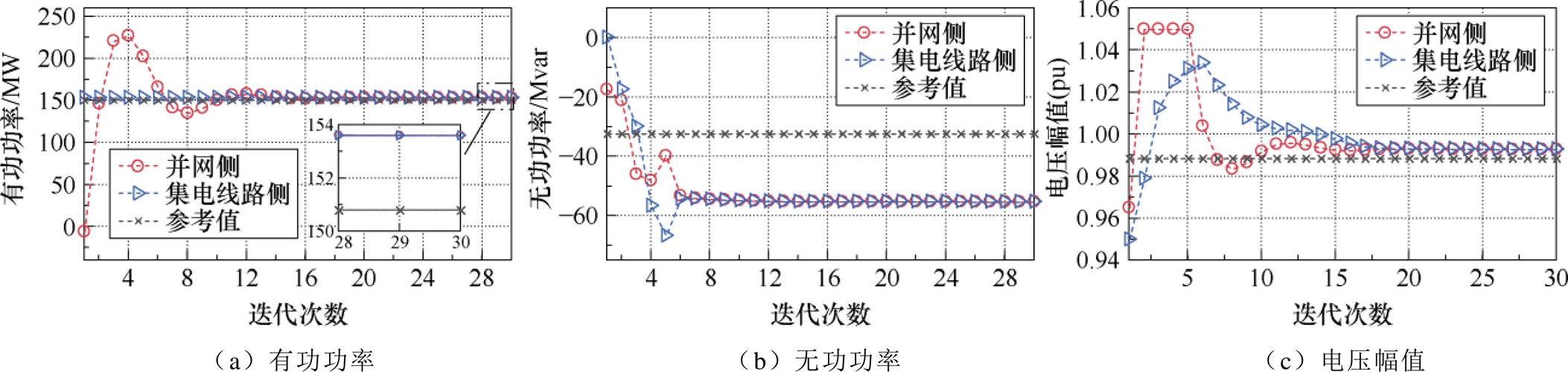
附图5 方法C的PCC母线耦合边界电气量迭代计算过程
App.Fig.5 Coupling electrical variable iterative calculating process of method C
参考文献
[1] 郭一飞. 交/直流并网风电场电压协调优化控制[D]. 济南: 山东大学, 2019.
Guo Yifei. Optimal coordinated voltage control of AC/DC connected wind farms[D]. Jinan: Shandong University, 2019.
[2] 张兆毅, 胡浩, 王子江, 等. 基于非线性仿射的风电场电压实时计算和优化方法[J]. 电工技术学报, 2024, 39(13): 3975-3989.
Zhang Zhaoyi, Hu Hao, Wang Zijiang, et al. Real- time voltage calculation and optimization method for wind farms based on nonlinear affine transfor- mation[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 3975-3989.
[3] 高本锋, 邓鹏程, 梁纪峰, 等. 光伏电站与弱交流电网间次同步交互作用路径及阻尼特性分析[J]. 电工技术学报, 2023, 38(24): 6679-6694.
Gao Benfeng, Deng Pengcheng, Liang Jifeng, et al. Analysis of path and damping characteristics of subsynchronous interaction between photovoltaic plant and weak AC grid [J]. Transactions of China Electrotechnical Society, 2023, 38(24):6679-669.
[4] 陈钊, 夏安俊, 汪宁渤, 等. 适用于低电压穿越仿真的风电场内集电线路等值方法[J]. 电力系统自动化, 2016, 40(8): 51-56.
Chen Zhao, Xia Anjun, Wang Ningbo, et al. Collector network equivalent method of wind farm for low voltage ride through simulation[J]. Automation of Electric Power Systems, 2016, 40(8): 51-56.
[5] 周林, 任伟, 廖波, 等. 并网型光伏电站无功电压控制[J]. 电工技术学报, 2015, 30(20): 168-175.
Zhou Lin, Ren Wei, Liao Bo, et al. Reactive power and voltage control for grid-connected PV power plants[J]. Transactions of China Electrotechnical Society, 2015, 30(20): 168-175.
[6] 杜红卫, 尉同正, 夏栋, 等. 基于集群动态划分的配电网无功电压自律-协同控制[J]. 电力系统自动化, 2024, 48(10): 171-181.
Du Hongwei, Wei Tongzheng, Xia Dong, et al. Reactive voltage self-regulation and coordination control in distribution networks based on cluster dynamic partition[J]. Automation of Electric Power Systems, 2024, 48(10): 171-181.
[7] 杨剑锋, 李婷, 杨爱民, 等. 含电能路由器的光伏配电网电压越限问题潮流优化研究[J]. 发电技术, 2025, 46(1): 113-125.
Yang Jianfeng, Li Ting, Yang Aimin, et al. Research on tidal optimization of voltage overrun problem in photovoltaic distribution network with electrical energy router[J]. Power Generation Technology, 2025, 46(1): 113-125.
[8] 张剑, 崔明建, 何怡刚. 结合数据驱动与物理模型的主动配电网双时间尺度电压协调优化控制[J]. 电工技术学报, 2024, 39(5): 1327-1339.
Zhang Jian, Cui Mingjian, He Yigang. Dual timescales coordinated and optimal voltages control in distribution systems using data-driven and physical optimization[J]. Transactions of China Electro- technical Society, 2024, 39(5): 1327-1339.
[9] 胡丹尔, 彭勇刚, 韦巍, 等. 多时间尺度的配电网深度强化学习无功优化策略[J]. 中国电机工程学报, 2022, 42(14): 5034-5045.
Hu Daner, Peng Yonggang, Wei Wei, et al. Multi- timescale deep reinforcement learning for reactive power optimization of distribution network[J]. Proceedings of the CSEE, 2022, 42(14): 5034-5045.
[10] 李鹏, 姜磊, 王加浩, 等. 基于深度强化学习的新能源配电网双时间尺度无功电压优化[J]. 中国电机工程学报, 2023, 43(16): 6255-6266.
Li Peng, Jiang Lei, Wang Jiahao, et al. Optimization of dual-time scale reactive voltage for distribution network with renewable energy based on deep reinforcement learning[J]. Proceedings of the CSEE, 2023, 43(16): 6255-6266.
[11] 路小俊, 吴在军, 李培帅, 等. 面向光伏集群的配电网模型-数据联合驱动无功/电压控制[J]. 电力系统自动化, 2024, 48(9): 97-106.
Lu Xiaojun, Wu Zaijun, Li Peishuai, et al. Combined model- and data-driven volt/var control for distri- bution network with photovoltaic clusters[J]. Auto- mation of Electric Power Systems, 2024, 48(9): 97-106.
[12] Rice L, Wong E, Kolter J Z. Overfitting in adversarially robust deep learning[EB/OL]. 2020: 2002. 11569. https://arxiv.org/abs/2002.11569v2.
[13] 陈明昊, 孙毅, 谢志远. 基于双层深度强化学习的园区综合能源系统多时间尺度优化管理[J]. 电工技术学报, 2023, 38(7):1864-1881.
Chen Minghao, Sun Yi, Xie Zhiyuan. The multi- time-scale management optimization method for park integrated energy system based on the bi-layer deep reinforcement learning[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1864-1881.
[14] Guo Qinglai, Sun Hongbin, Wang Bin, et al. Hierarchical automatic voltage control for integration of large-scale wind power: Design and imple- mentation[J]. Electric Power Systems Research, 2015, 120: 234-241.
[15] Li Haixiao, Zhou Lin, Mao Mingxuan, et al. Three- layer voltage/var control strategy for PV cluster considering steady-state voltage stability[J]. Journal of Cleaner Production, 2019, 217: 56-68.
[16] 李宗隆, 柏舸, 胡剑, 等. 考虑光热光伏混合电站内外双重电压安全的两阶段无功优化控制[J]. 电力系统保护与控制, 2023, 51(20): 170-179.
Li Zonglong, Bai Ge, Hu Jian, et al. Two-stage optimal reactive power control considering internal- external dual voltage security of a PV-CSP hybrid power station[J]. Power System Protection and Control, 2023, 51(20): 170-179.
[17] 王渝红, 廖逸犇, 宋雨妍, 等. 风电场内部分散式无功电压优化控制策略[J]. 高电压技术, 2022, 48(12): 5047-5056.
Wang Yuhong, Liao Yiben, Song Yuyan, et al. Distributed optimal control strategy of reactive power and voltage in wind farm[J]. High Voltage Engineering, 2022, 48(12): 5047-5056.
[18] Huang Sheng, Wu Qiuwei, Zhao Jin, et al. Distributed optimal voltage control for VSC-HVDC connected large-scale wind farm cluster based on analytical target cascading method[J]. IEEE Transactions on Sustainable Energy, 2020, 11(4): 2152-2161.
[19] Li Haixiao, Guo Ke, Hao Gaofeng, et al. Decent- ralized communication based two-tier volt-var control strategy for large-scale centralized photovoltaic power plant[J]. IEEE Transactions on Sustainable Energy, 2022, 13(1): 592-606.
[20] Huang Jinbo, Li Zhigang, Wu Q H. Fully decentralized multiarea reactive power optimization considering practical regulation constraints of devi- ces[J]. International Journal of Electrical Power & Energy Systems, 2019, 105: 351-364.
[21] Houska B, Frasch J, Diehl M. An augmented Lagrangian based algorithm for distributed NonConvex optimization[J]. SIAM Journal on Optimization, 2016, 26(2): 1101-1127.
[22] Engelmann A, Jiang Yuning, Mühlpfordt T, et al. Toward distributed OPF using ALADIN[J]. IEEE Transactions on Power Systems, 2019, 34(1): 584- 594.
[23] Jiang Yuning, Sauerteig P, Houska B, et al. Distributed optimization using ALADIN for MPC in smart grids[J]. IEEE Transactions on Control Systems Technology, 2021, 29(5): 2142-2152.
[24] Zhai Junyi, Dai Xinliang, Jiang Yuning, et al. Distributed optimal power flow for VSC-MTDC meshed AC/DC grids using ALADIN[J]. IEEE Transa- ctions on Power Systems, 2022, 37(6): 4861- 4873.
[25] Ergun H, Dave J, Van Hertem D, et al. Optimal power flow for AC-DC grids: formulation, convex relaxation, linear approximation, and implementation[J]. IEEE Transactions on Power Systems, 2019, 34(4): 2980- 2990.
[26] 黄伟煌, 胡书举, 许洪华. 中点钳位型中压三电平风电变流器的损耗分析[J]. 电力系统自动化, 2014, 38(15): 65-70.
Huang Weihuang, Hu Shuju, Xu Honghua. Power loss analysis of NPC medium-voltage three-level con- verters for wind power generation system[J]. Auto- mation of Electric Power Systems, 2014, 38(15): 65-70.
[27] Makhdoumi A, Ozdaglar A. Convergence rate of dis- tributed ADMM over networks[J]. IEEE Transactions on Automatic Control, 2017, 62(10): 5082-5095.
[28] Zhong Minyi, Cassandras C G. Asynchronous distributed optimization with event-driven com- munication[J]. IEEE Transactions on Automatic Control, 2010, 55(12): 2735-2750.
[29] Hong Mingyi. A distributed, asynchronous, and incremental algorithm for nonconvex optimization: an ADMM approach[J]. IEEE Transactions on Control of Network Systems, 2018, 5(3): 935-945.
[30] 曾祥辰, 刘青, 王嘉晨, 等. 弱电网下并网逆变器恒定带宽及稳定裕度的自适应控制策略[J]. 电工技术学报, 2024, 39(9): 2682-2695.
Zeng Xiangchen, Liu Qing, Wang Jiachen, et al. Adaptive control strategy of grid-connected inverters with constant bandwidth and stability margin in weak grids[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2682-2695.
[31] Andersson J A E, Gillis J, Horn G, et al. CasADi: a software framework for nonlinear optimization and optimal control[J]. Mathematical Programming Computation, 2019, 11(1): 1-36.
[32] Biegler L T, Zavala V M. Large-scale nonlinear programming using IPOPT: an integrating framework for enterprise-wide dynamic optimization[J]. Com- puters & Chemical Engineering, 2009, 33(3): 575- 582.
[33] Duff I S. MA57: -a code for the solution of sparse symmetric definite and indefinite systems[J]. ACM Transactions on Mathematical Software, 2004, 30(2): 118-144.
[34] Zimmerman R D, Murillo-Sánchez C E, Thomas R J. MATPOWER: steady-state operations, planning, and analysis tools for power systems research and education[J]. IEEE Transactions on Power Systems, 2011, 26(1): 12-19.
Abstract Large renewable energy power plants, characterized by “large-scale topology and integration into weak grids”, are susceptible to operational risks such as excessive voltage differentials and overvoltage. These challenges arise due to the high impedance of both internal and external transmission lines, posing significant threats to the plant’s safe and stable operation. This paper proposes a distributed nonconvex optimization framework for voltage regulation in large-scale renewable energy power plants, ensuring accurate voltage computation and mitigating communication overhead. Specifically, a nonconvex voltage optimization model is formulated based on nonlinear standard power flow constraints, and the augmented lagrangian-based alternating direction inexact newton (ALADIN) algorithm is employed to solve the problem in a distributed manner. This approach enables the optimal dispatch of reactive power from renewable energy units, effectively regulating the system-wide voltage profile, thereby enhancing the overall operational security and stability of the power plant.
Numerical experiments were conducted on a representative large-scale renewable energy power plant system. The necessity of employing a nonconvex voltage optimization model was analyzed. The numerical results demonstrate that the linearized voltage optimization model introduces significant errors in power flow calculations. The convergence performance of the ALADIN distributed optimization algorithm was validated. Compared to the traditional alternating direction method of multipliers (ADMM), ALADIN exhibits convergence behavior that is largely insensitive to the penalty parameter r. It achieves convergence within approximately 10 iterations, which is significantly fewer than the number of iterations required by ADMM. The optimality of the distributed optimization solution obtained via ALADIN was verified. The reactive power compensation results for each node in the collection lines closely matched those from centralized optimization, with a maximum relative error of less than0.3%. Moreover, the optimized voltage profile of the large-scale renewable energy power plant remained effectively constrained within the acceptable range of 0.95~1.05(pu). The flexibility of the ALADIN algorithm in handling communication delays in practical network environments was demonstrated. The algorithm supports both synchronous and asynchronous update strategies.
The following conclusions can be drawn. (1) Linearized approximation methods, such as LinDistFlow, introduce substantial errors in voltage calculations. The nonconvex distributed voltage optimization model based on nonlinear standard power flow constraints provides more accurate voltage calculations, making it suitable for large-scale layouts and long-distance power transmission scenarios. (2) The ALADIN distributed optimization algorithm is proposed. ALADIN converges quickly, producing results nearly identical to those of centralized optimization, thereby significantly improving optimization performance. (3) The reactive power output derived from ALADIN effectively optimizes node voltages within a safe range throughout the extensive enewable energy power plant system. (4) For the ALADIN algorithm, the choice between synchronous and asynchronous updates to handle information delays can be flexibly determined based on the actual degree of communication delay.
keywords:Large-scale renewable energy power stations, voltage limit violation, distributed non-convex optimization, augmented Lagrangian alternating direction non-exact Newton method
DOI: 10.19595/j.cnki.1000-6753.tces.241976
中图分类号:TM732
重庆市自然科学基金面上项目(CSTB2022NSCQ-MSX0997)和重庆市教委科学技术研究项目(KJQN202301166)资助。
收稿日期 2024-11-04
改稿日期 2025-01-11
李海啸 男,1993年生,博士,讲师,硕士生导师,研究方向为规模化可再生能源系统运行优化。E-mail: lihaixiao@cqut.edu.cn
包诗媛 女,1994年生,博士,讲师,硕士生导师,研究方向为综合能源系统运行优化。E-mail: baoshiyuan@cqut.edu.cn(通信作者)
(编辑 郭丽军)