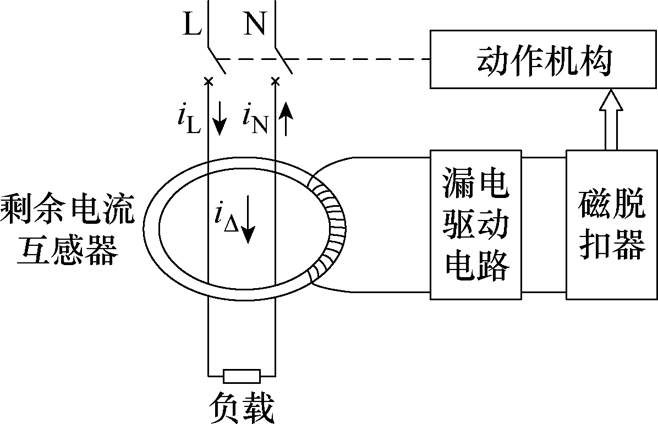
图1 电磁式漏电保护工作原理框图
Fig.1 Working principle diagram of electromagnetic residual current protection
摘要 电磁式漏电断路器无需辅助电源,在线路发生断相等故障后仍能进行漏电保护,广泛应用于漏电保护要求较高的场合。该文针对电磁式漏电断路器的漏电保护驱动电路与漏电保护特性稳健性开展研究。首先,分析电磁式漏电断路器的工作原理,研究串-并联电容补偿漏电驱动电路的拓扑结构与工作原理;其次,针对串-并联电容补偿漏电驱动电路,确定补偿电容匹配关系及其与漏电动作值的关系,分析剩余电流互感器磁滞特性与饱和特性对补偿电容匹配关系的影响;最后,研究补偿电容分散性和铁心磁参数分散性对漏电保护特性的影响,并对剩余电流互感器及补偿电容进行优化设计,提升了电磁式漏电断路器漏电保护特性的稳健性。
关键词:电磁式漏电断路器 漏电保护特性 电路拓扑分析 剩余电流互感器 稳健性设计
随着我国现代电力系统的发展和电气化进程的加速,漏电保护技术的应用已经深入到生产和生活的各个方面[1-5]。其中电磁式漏电断路器的结构简单、动作可靠,得到了广泛应用。电磁式漏电断路器中剩余电流互感器(Residual Current Transformer, RCT)采集漏电信号经漏电驱动电路驱动磁脱扣器,当流经磁脱扣器的电流达到磁脱扣器的释放电流时,磁脱扣器动作,实现漏电保护,因此对漏电驱动电路及剩余电流互感器、磁脱扣器的匹配设计均有较高要求。
围绕剩余电流互感器、漏电驱动电路和磁脱扣器三方面,众多学者展开了研究[6-9]。在剩余电流互感器方面,一些学者对其传输特性进行了分析。文献[10]推导了互感器取能功率与电路参数之间的匹配关系,确保在给定的电路条件下获得最大的输出功率。文献[11]建立了铁心动态磁滞损耗模型,分析了直流偏磁下的互感器传变特性。文献[12]提出了适用于自动重合闸期间的电流互感器剩磁快速抑制方法,通过二次侧的剩磁抑制电路来减小铁心的磁通。文献[13]考虑了剩余电流互感器铁心的磁滞特性及饱和特性并建立了仿真模型,能够在正弦形式和脉动直流形式的剩余电流下精确地模拟剩余电流互感器的传输特性,为电磁式漏电断路器在实际工作条件下的仿真分析提供了重要的理论和实践参考。
在漏电驱动电路方面,文献[14]研究了电磁式漏电断路器中抗扰型的漏电保护特性,分析了电路参数匹配关系与动作值的关系,为抗扰型漏电断路器的优化设计提供了参考。文献[15]提出了一种新型漏电检测方法,以消除使用常规检测方法时存在的漏电保护死区,提高了配电系统的可靠性。
在磁脱扣器方面,文献[16]建立了磁脱扣器的数学模型和有限元模型,深入探究了储能电容对磁脱扣器的衔铁释放响应状态的影响,并对电容匹配进行了优化设计。文献[17-18]建立了永磁接触器的联合仿真模型,能够反映动态过程中电磁磁场与永磁磁场的相互影响。文献[19-20]对漏电断路器内部导体结构进行了优化设计,有效降低了导体负荷电流产生的磁场对磁脱扣器的影响,同时设计了一种新的磁脱扣器屏蔽罩,大大降低了外界磁场和内部负荷电流对电磁式漏电断路器的影响,提高了其抗空间磁场干扰的能力。
由于剩余电流互感器一次电流为毫安级信号,二次电流信号更弱,且磁脱扣器为感性负载,因此要求漏电驱动电路简单、损耗小,能对感性负载进行补偿,以便提高二次输出电流和电压。另外,剩余电流互感器铁心磁特性分散性较大,会导致与漏电驱动电路、磁脱扣器的匹配发生变化,进而导致漏电断路器的保护特性不稳定,因此本文针对电磁式漏电断路器的漏电保护特性展开研究,研究了漏电驱动电路拓扑的工作原理,并分析了补偿电容、剩余电流互感器及磁脱扣器之间的匹配关系和参数分散性对漏电保护特性的影响,进而进行优化设计,最终提升了电磁式漏电断路器保护特性的稳健性。
电磁式漏电断路器的工作原理框图如图1所示。

图1 电磁式漏电保护工作原理框图
Fig.1 Working principle diagram of electromagnetic residual current protection
主回路L、N穿过剩余电流互感器铁心构成一次侧线圈回路。无漏电故障时,一次侧线圈回路电流相量和为零,漏电断路器不动作;发生漏电故障时,一次侧线圈回路电流相量和不为零,存在剩余电流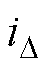 ,由电磁感应定律,剩余电流互感器二次侧产生感应电动势。当流经磁脱扣器的电流大于释放电流id时,磁脱扣器脱扣,动作机构断开主线路,实现漏电保护。
,由电磁感应定律,剩余电流互感器二次侧产生感应电动势。当流经磁脱扣器的电流大于释放电流id时,磁脱扣器脱扣,动作机构断开主线路,实现漏电保护。
剩余电流互感器的一、二次侧的线圈匝数较少,其阻抗低,为便于分析,在构建等效电路时,忽略一次侧和二次侧线圈的阻抗。将一次侧剩余电流折算到二次侧,作为电流源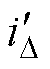 。设定剩余电流互感器工作在线性区,将励磁电感折算到二次侧为等效电感
。设定剩余电流互感器工作在线性区,将励磁电感折算到二次侧为等效电感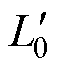 。磁脱扣器为感性元件,等效为Rr-Lr负载。剩余电流互感器经串-并联电容补偿后驱动磁脱扣器的等效电路如图2所示。
。磁脱扣器为感性元件,等效为Rr-Lr负载。剩余电流互感器经串-并联电容补偿后驱动磁脱扣器的等效电路如图2所示。
正弦剩余电流下,由电路定律,有
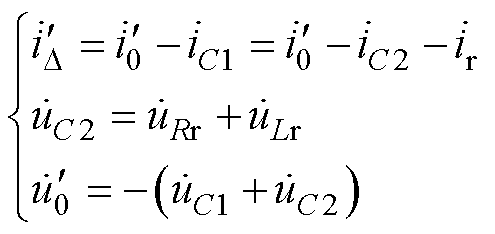 (1)
(1)
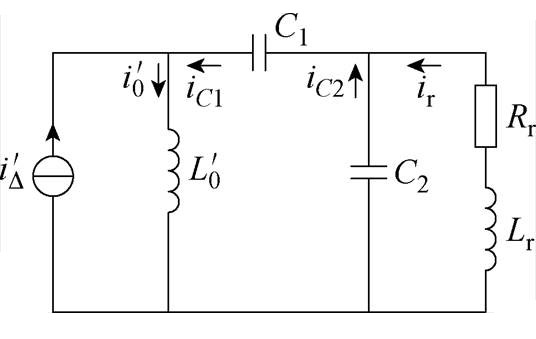
图2 串-并联电容补偿电路拓扑
Fig.2 Topology of compensation capacitor series-parallel circuit
式中,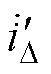 为折算到二次侧的剩余电流;
为折算到二次侧的剩余电流;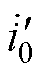 为折算到二次侧的励磁电流;
为折算到二次侧的励磁电流;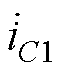 为流经电容C1的电流;
为流经电容C1的电流;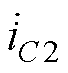 为流经电容C2的电流;
为流经电容C2的电流;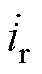 为流经磁脱扣器的电流;
为流经磁脱扣器的电流;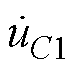 为电容C1两端电压;
为电容C1两端电压;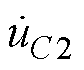 为电容C2两端电压;
为电容C2两端电压;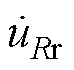 为磁脱扣器电阻电压;
为磁脱扣器电阻电压;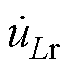 为磁脱扣器电感电压;
为磁脱扣器电感电压;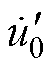 为折算到二次侧的励磁电压。
为折算到二次侧的励磁电压。
令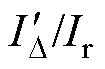 =k,有
=k,有
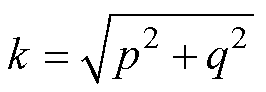 (2)
(2)
其中
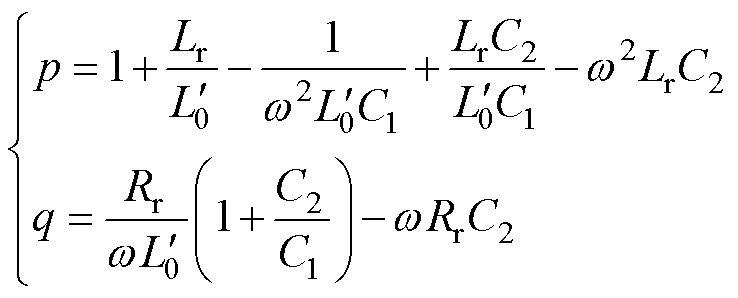 (3)
(3)
C1、C2分别取常见容值15、22、33、47、68、100 mF,得到幅值特性k与C1、C2的关系曲线如图3所示。图3a中,不同C2下不同曲线相交于一点,该点C1取值为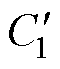 ,即
,即
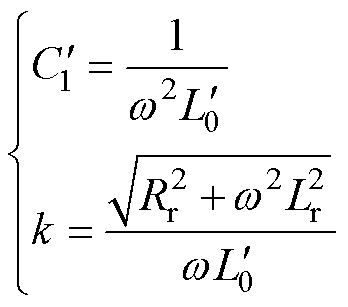 (4)
(4)
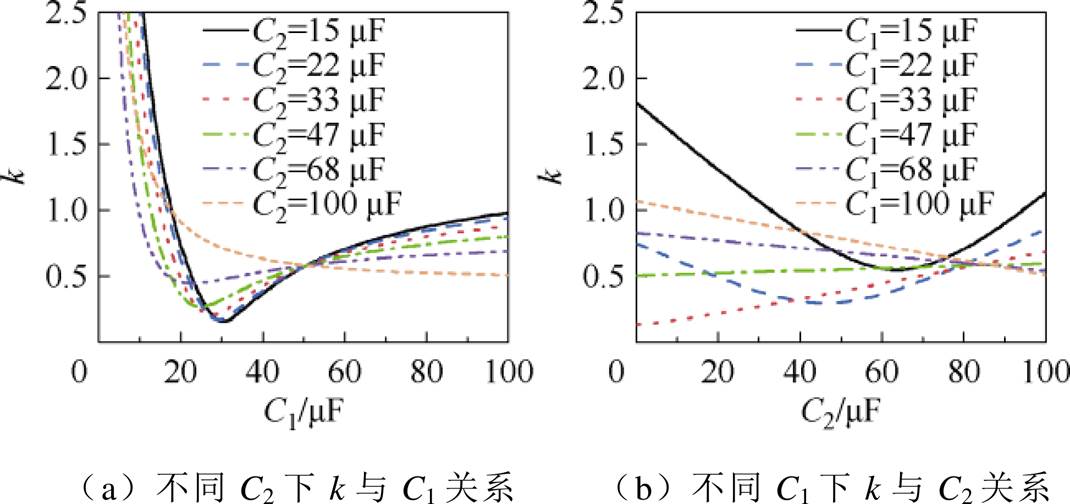
图3 k与补偿电容C1、C2的关系曲线
Fig.3 Relationship curves between k and compensation capacitors C1 and C2
由式(4)可知,串联补偿电容C1完全补偿剩余电流互感器励磁电感 时,k与C2无关。在补偿电容C2较小的情况下,随着C1增大,k先减小后增大。但随着C2增大,最优补偿点即k值的拐点向上偏移,甚至补偿电容C2超过一定值后,k呈现单调下降特征。
时,k与C2无关。在补偿电容C2较小的情况下,随着C1增大,k先减小后增大。但随着C2增大,最优补偿点即k值的拐点向上偏移,甚至补偿电容C2超过一定值后,k呈现单调下降特征。
图3b中,当C1取值47 mF和68 mF时,比较接近 ,因此k曲线变化幅度较小,动作值受C2的变化影响较小。串-并联电容补偿电路中各元件的电流电压相量关系如图4所示。
,因此k曲线变化幅度较小,动作值受C2的变化影响较小。串-并联电容补偿电路中各元件的电流电压相量关系如图4所示。
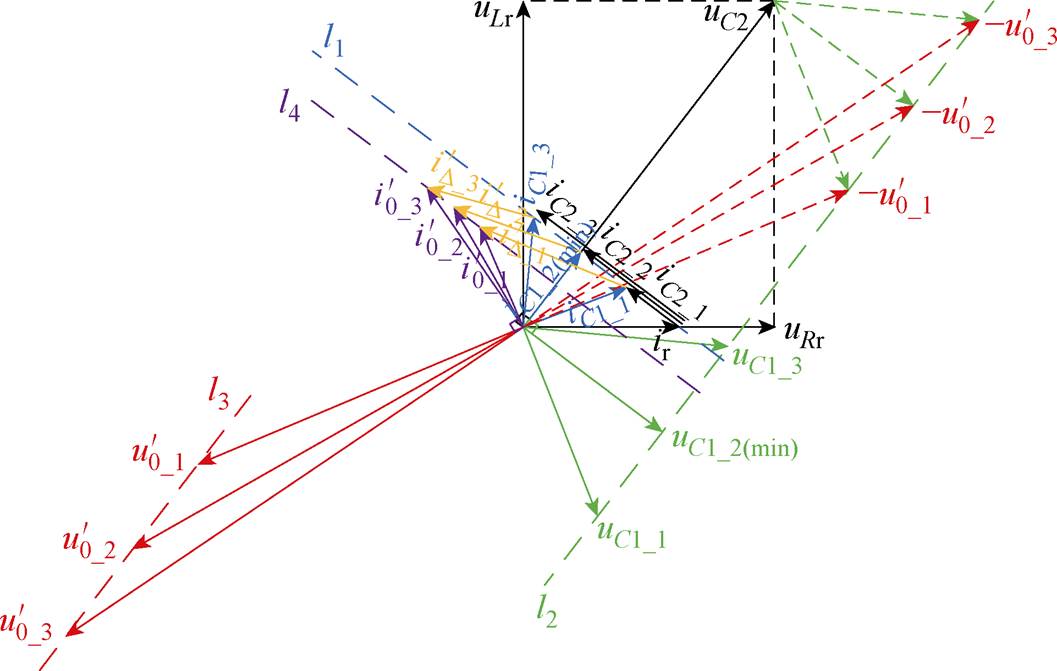
图4 串-并联电容补偿电路原理
Fig.4 The principle of compensating capacitors in series-parallel
已知流过磁脱扣器的电流ir,并联电容电压uC2与磁脱扣器线圈电压相等,则可以得到uC2。iC2_1、iC2_2和iC2_3为不同C2下的电容电流,其相位相同。C2容值越大,iC2也越大。串联电容电流iC1为并联电容电流iC2和流经脱扣器线圈电流ir的相量和,iC1末端轨迹均位于与iC2重合且与uC2垂直的蓝色虚线l1上。随着C2容值增大,iC1幅值先减小再增大,当iC1垂直于l1时,有最小值iC1_2(min)。串联电容电压uC1的相量末端轨迹位于与uC2平行的绿色虚线l2上,因此励磁电感电压 的相量末端轨迹位于红色虚线l3上,与uC2平行,因此励磁电流
的相量末端轨迹位于红色虚线l3上,与uC2平行,因此励磁电流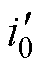 的相量末端轨迹与l3垂直,为紫色虚线l4,由此可以得到一次电流
的相量末端轨迹与l3垂直,为紫色虚线l4,由此可以得到一次电流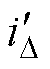 ,其始端位于虚线l1上,末端位于虚线l4上。
,其始端位于虚线l1上,末端位于虚线l4上。
当C1变化时,uC1的变化轨迹与uC2的距离发生变化,导致 的轨迹改变,从而使
的轨迹改变,从而使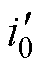 的轨迹变化,即l4和l1的距离发生变化。当C1容抗值与励磁感抗值相等时,电容完全补偿了励磁电感,因此
的轨迹变化,即l4和l1的距离发生变化。当C1容抗值与励磁感抗值相等时,电容完全补偿了励磁电感,因此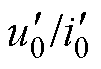 =uC1/iC1,iC1、
=uC1/iC1,iC1、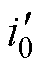 、
、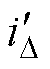 构成的三角形与uC1(虚线)、
构成的三角形与uC1(虚线)、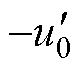 、uC2构成的三角形相似,所以uC2/
、uC2构成的三角形相似,所以uC2/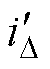 =
=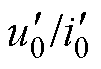 =uC1/iC1。改变C2时仅会改变iC2的大小,uC2为固定值,uC2/
=uC1/iC1。改变C2时仅会改变iC2的大小,uC2为固定值,uC2/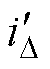 的比例不变,所以
的比例不变,所以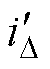 也就不会变化,即
也就不会变化,即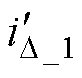 =
=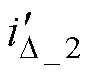 =
=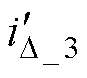 。
。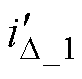 、
、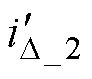 和
和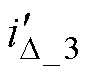 为对应不同C2下得到折算到二次侧的一次电流。且由于iC1_2与l1、l4垂直,所以l1和l4重合,串联补偿电容与励磁电感谐振状态如图5所示。该情况对应图4a中曲线的交点,即不同电容C2下,此时一次电流不变,电容C1完全补偿励磁电感,取值如式(4)所示。
为对应不同C2下得到折算到二次侧的一次电流。且由于iC1_2与l1、l4垂直,所以l1和l4重合,串联补偿电容与励磁电感谐振状态如图5所示。该情况对应图4a中曲线的交点,即不同电容C2下,此时一次电流不变,电容C1完全补偿励磁电感,取值如式(4)所示。
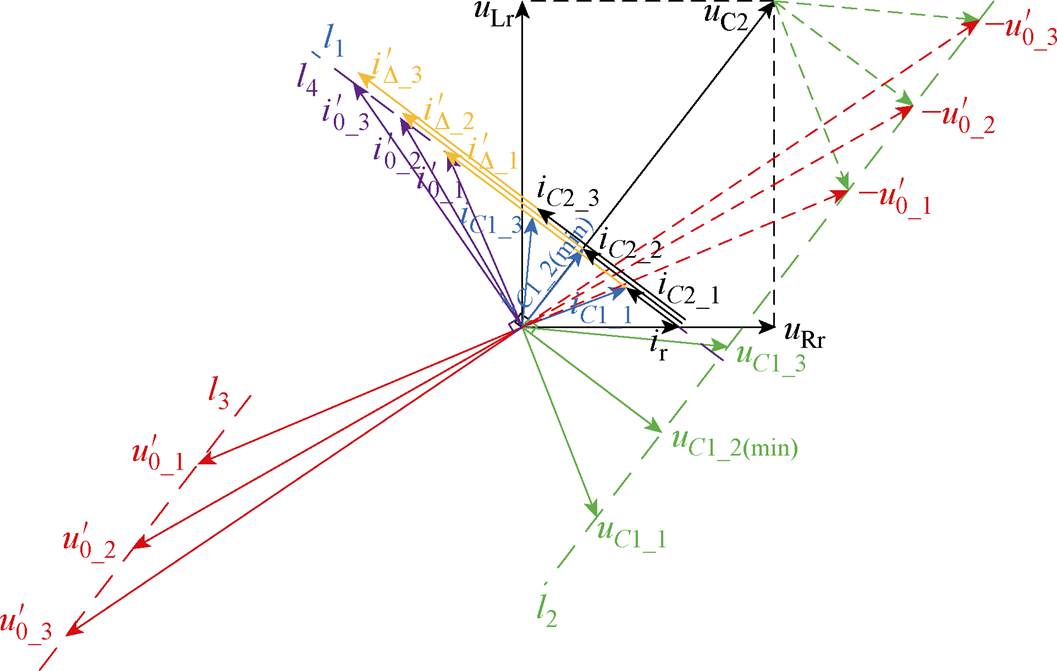
图5 串联补偿电容与励磁电感谐振状态
Fig.5 Resonance state of series compensation capacitor and excitation inductor
为满足标准要求[21],一般将漏电动作电流设计为0.75倍额定剩余动作电流。剩余电流互感器和磁脱扣器的相关参数见表1,若额定剩余动作电流为30 mA,则可确定k=0.798,从而确定补偿电容C1、C2的匹配关系为
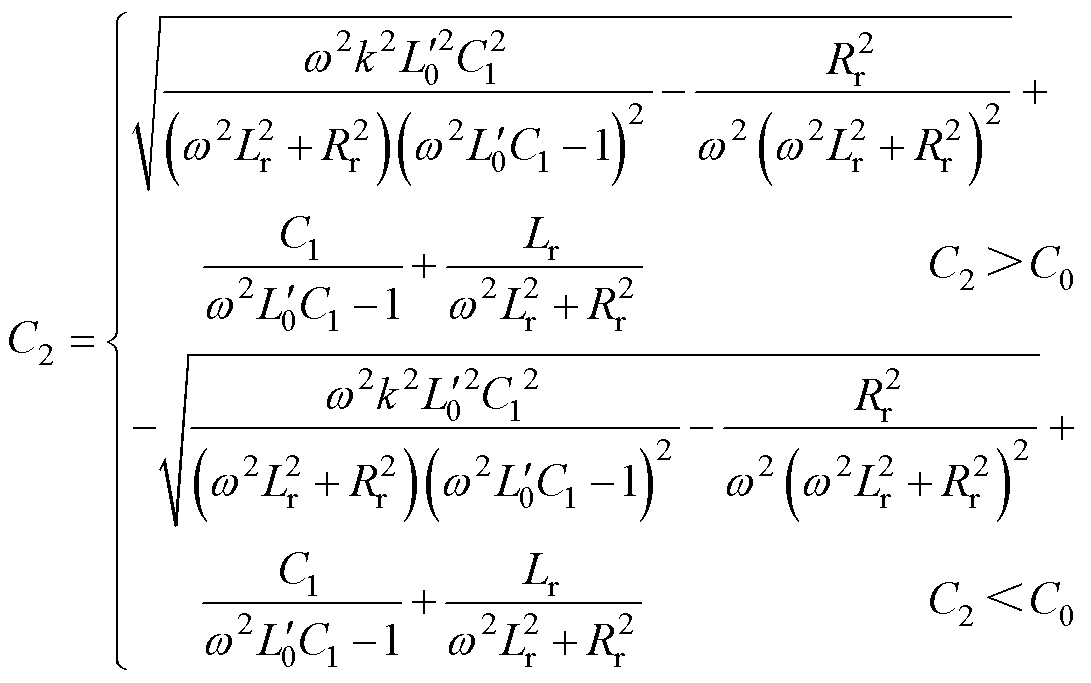 (5)
(5)
其中
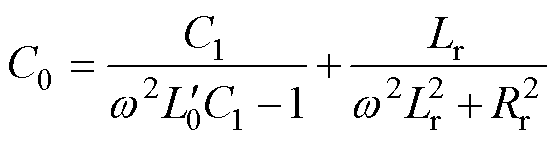
表1 剩余电流互感器与磁脱扣器参数
Tab.1 Parameters of RCT and magnetic release

参 数数 值 一次侧匝数N12 二次侧匝数N226 磁脱扣器电阻Rr/W8.4 磁脱扣器电感Lr/mH113 释放电流id/mA3
由式(5),补偿电容C1、C2的匹配关系还与剩余电流互感器的励磁电感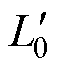 有关。分析励磁电感变化对C1、C2匹配关系的影响如图6所示。
有关。分析励磁电感变化对C1、C2匹配关系的影响如图6所示。
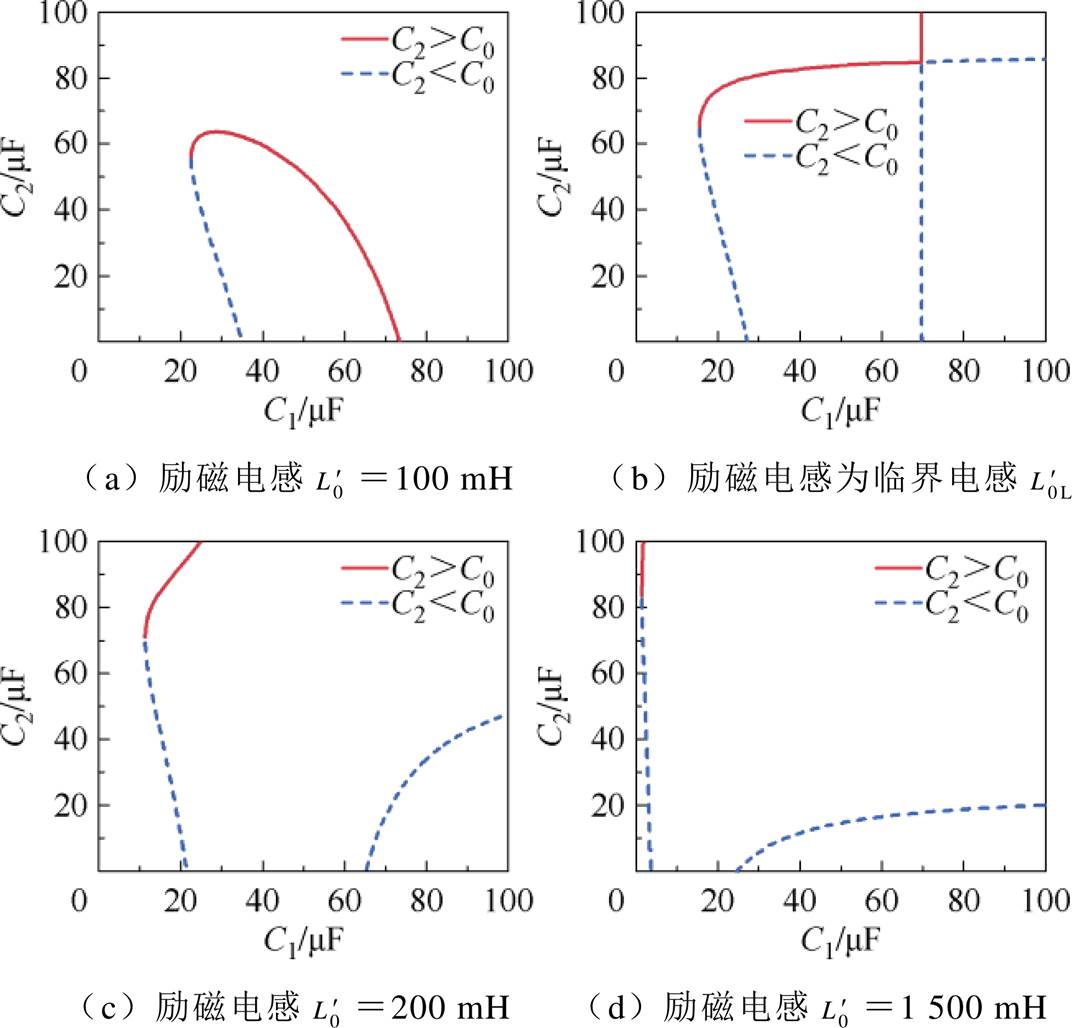
图6 不同励磁电感下的电容C1、C2匹配关系曲线
Fig.6 Matching relationship curves of capacitors C1 and C2 under different excitation inductors
当C1完全补偿剩余电流互感器励磁电感时,流过磁脱扣器电流与并联电容C2无关。因此,为使漏电动作值满足要求,即k为定值,在磁脱扣器参数一定的情况下,可由式(4)设计励磁电感的临界值为
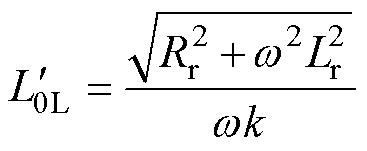 (6)
(6)
式中,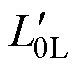 为匹配关系曲线形状完全发生变化的临界电感,不受补偿电容影响,主要取决于磁脱扣器及动作值。若励磁电感
为匹配关系曲线形状完全发生变化的临界电感,不受补偿电容影响,主要取决于磁脱扣器及动作值。若励磁电感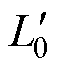 <
<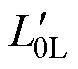 ,仍要求漏电动作值不变,则串联电容C1与并联电容C2匹配关系如图6a所示,此时曲线形状近似呈“倒V”形,匹配区间较为狭窄。若
,仍要求漏电动作值不变,则串联电容C1与并联电容C2匹配关系如图6a所示,此时曲线形状近似呈“倒V”形,匹配区间较为狭窄。若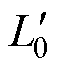 =
=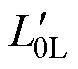 ,匹配关系如图6b所示曲线,图中垂直线为串联电容C1完全补偿剩余电流互感器励磁电感,此时动作值与C2容值无关。若
,匹配关系如图6b所示曲线,图中垂直线为串联电容C1完全补偿剩余电流互感器励磁电感,此时动作值与C2容值无关。若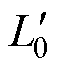 >
>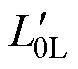 ,匹配关系为如图6c、图6d所示两支曲线,其中右半支曲线C1、C2呈正相关,容值需要同步增大或减小。右半支匹配关系曲线的水平渐近线为并联电容C2所能取到的最大值,满足
,匹配关系为如图6c、图6d所示两支曲线,其中右半支曲线C1、C2呈正相关,容值需要同步增大或减小。右半支匹配关系曲线的水平渐近线为并联电容C2所能取到的最大值,满足
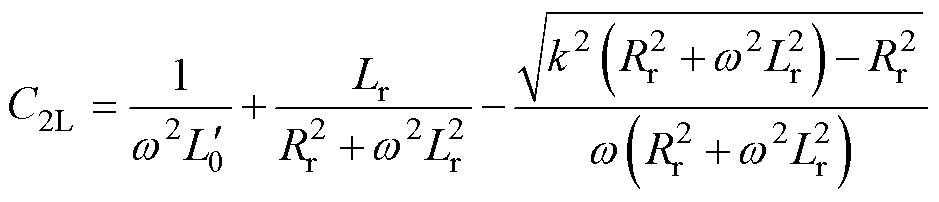 (7)
(7)
左半支匹配关系曲线的垂直渐近线为串联电容C1与励磁电感完全补偿,其值满足
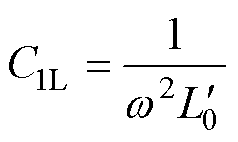 (8)
(8)
无论C1、C2匹配关系曲线走势如何变化,在10~100 mF的容值范围内,串联电容C1始终存在最小值为
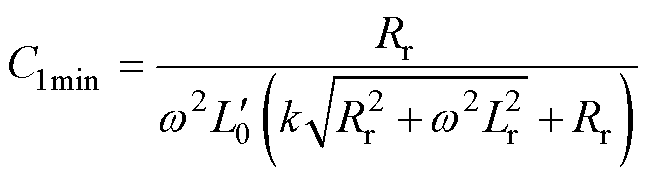 (9)
(9)
则在剩余电流互感器和磁脱扣器参数一定的情况下,串联电容C1≥C1min才能保证动作值满足要求,若小于该值,无论并联电容C2为多少,动作值均无法满足要求。
动作值为21、22、23和24 mA、励磁电感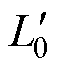 为100、200、1 500 mH的情况下,补偿电容C1、C2的匹配关系曲线如图7所示。
为100、200、1 500 mH的情况下,补偿电容C1、C2的匹配关系曲线如图7所示。
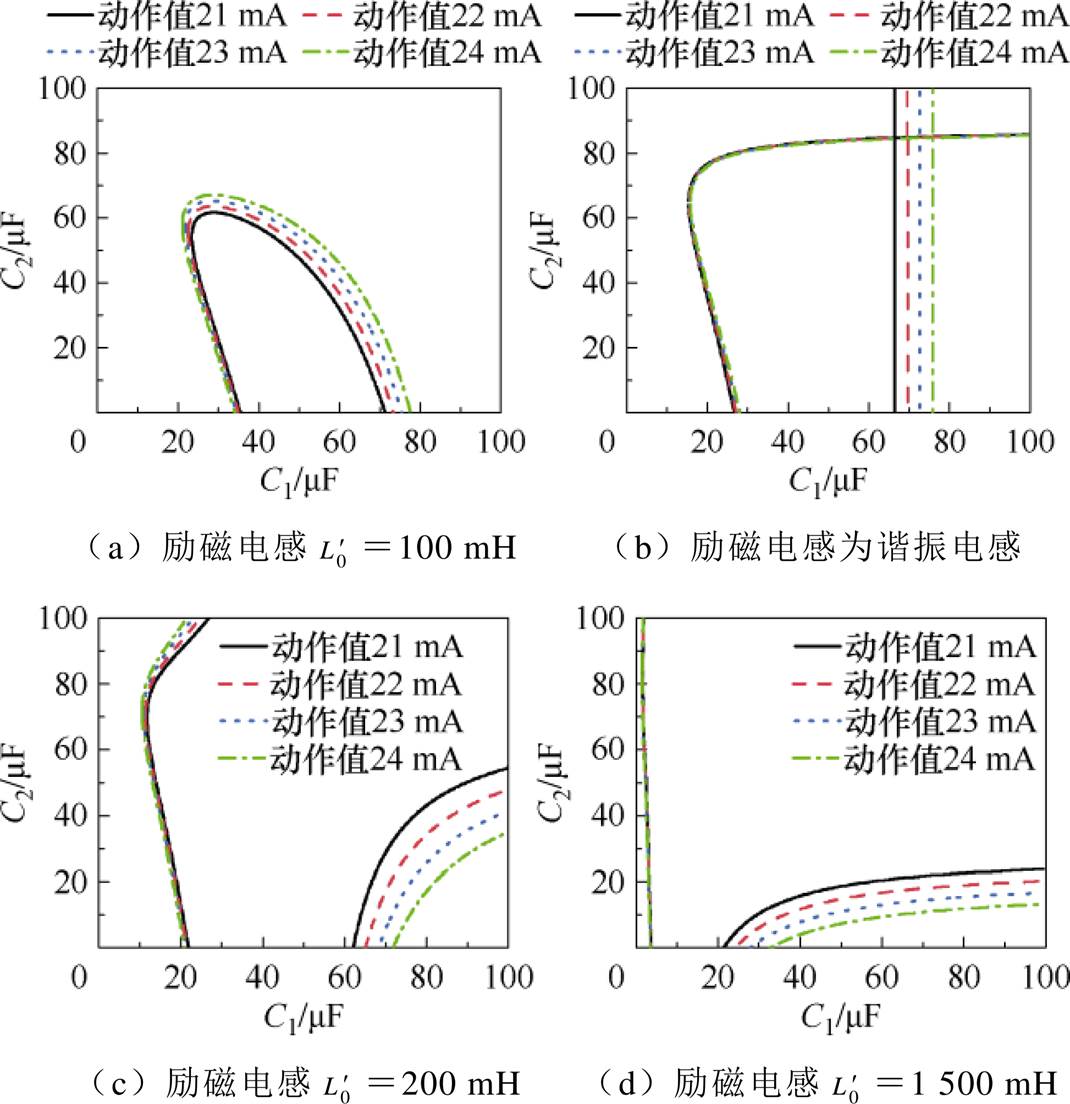
图7 不同动作值下的电容C1、C2的匹配关系曲线
Fig.7 Matching relationship curves of capacitors C1 and C2 under different action values
C1、C2匹配曲线越密集,则动作值受电容分散性的影响越大。
(1)当励磁电感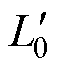 <
<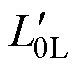 时,如图7a所示,电容设计范围较小,匹配曲线密集。
时,如图7a所示,电容设计范围较小,匹配曲线密集。
(2)当励磁电感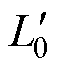 =
=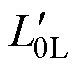 时,如图7b所示,匹配关系处于临界状态,此时漏电保护特性对L0的变化极为敏感,即使L0稍有变化,匹配曲线走势也完全不同。
时,如图7b所示,匹配关系处于临界状态,此时漏电保护特性对L0的变化极为敏感,即使L0稍有变化,匹配曲线走势也完全不同。
(3)当励磁电感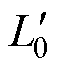 >
>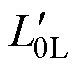 时,如图7c、图7d所示,左半支的匹配曲线非常密集,若C1容值稍有偏差,则动作值会发生较大变化,因此在设计中应参考右半支匹配曲线,对应的电容设计范围为
时,如图7c、图7d所示,左半支的匹配曲线非常密集,若C1容值稍有偏差,则动作值会发生较大变化,因此在设计中应参考右半支匹配曲线,对应的电容设计范围为
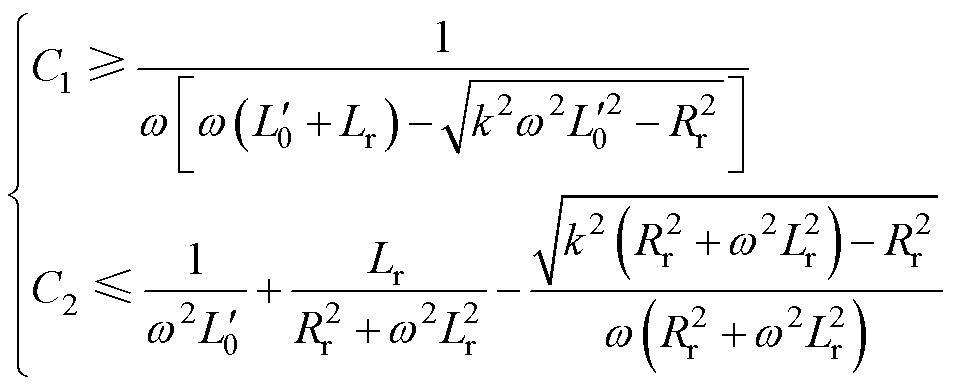 (10)
(10)
实际剩余电流互感器铁心是非线性磁材料,具有磁滞与饱和特性,会对补偿电容C1、C2的匹配产生影响,采用仿真方法来分析非线性励磁下C1、C2的匹配关系。剩余电流互感器磁参数见表2。动作值为21、22、23、24 mA,对应C1、C2的匹配关系曲线如图8所示。
表2 剩余电流互感器磁参数
Tab.2 RCT magnetic parameters

参 数数 值 饱和磁通密度Bs/T0.86 剩磁Br/T0.291 矫顽力Hc/(A/m)0.768
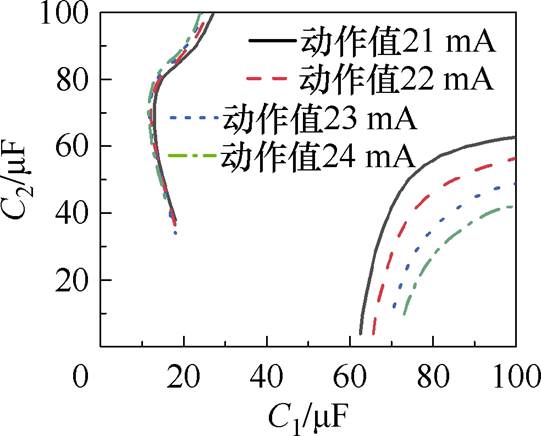
图8 不同动作值下的C1、C2的匹配关系曲线
Fig.8 Matching curves of C1 and C2 under different action values
剩余电流互感器铁心磁参数变化,补偿电容C1、C2的匹配关系随之变化。饱和磁通密度Bs为0.6~1.0 T、剩磁Br为0.1~0.5 T、矫顽力Hc为0.6~1.0 A/m的情况下,采用单因素轮换法对补偿电容C1、C2的匹配关系进行仿真分析,结果如图9所示。
不同磁参数下,C1、C2匹配关系曲线不完全相同,但仍与线性磁化特性下推导出的曲线变化规律一致。图9a中,Br、Hc不变,Bs增大时,铁心磁导率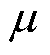 增大,励磁电感L0增大,左半支曲线向左偏移,右半支曲线向下偏移。图9b中,黑色曲线为Br较小时C1、C2的匹配关系曲线,此时在该电容范围内仅有一条曲线,这是由于Br较小时,磁导率
增大,励磁电感L0增大,左半支曲线向左偏移,右半支曲线向下偏移。图9b中,黑色曲线为Br较小时C1、C2的匹配关系曲线,此时在该电容范围内仅有一条曲线,这是由于Br较小时,磁导率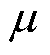 较小,励磁电感小于临界电感,匹配曲线形状发生变化,同图6a中所示。随着Br增大,励磁电感逐渐大于临界电感,右半支匹配曲线出现;剩磁进一步增大后,左半支曲线向左上偏移,右半支曲线向下偏移;剩磁过大后,磁滞回线畸变,励磁电感不再与其成正相关,因此在图9b中紫色曲线与绿色曲线近似重合,甚至部分范围内紫色曲线高于绿色曲线。图9c中,Br、Bs不变,Hc增大,磁导率
较小,励磁电感小于临界电感,匹配曲线形状发生变化,同图6a中所示。随着Br增大,励磁电感逐渐大于临界电感,右半支匹配曲线出现;剩磁进一步增大后,左半支曲线向左上偏移,右半支曲线向下偏移;剩磁过大后,磁滞回线畸变,励磁电感不再与其成正相关,因此在图9b中紫色曲线与绿色曲线近似重合,甚至部分范围内紫色曲线高于绿色曲线。图9c中,Br、Bs不变,Hc增大,磁导率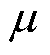 减小,励磁电感L0减小,从而左半支曲线向右偏移,右半支曲线向上偏移。从动作值及磁参数对补偿电容匹配关系的影响来看,饱和磁通密度Bs、剩磁Br增大会导致动作值减小,矫顽力Hc增大导致动作值增大。因此,考虑磁滞特性与饱和特性时,补偿电容C1、C2的匹配关系曲线与假设铁心磁化特性为线性情况下的匹配关系曲线形状、走势基本一致。
减小,励磁电感L0减小,从而左半支曲线向右偏移,右半支曲线向上偏移。从动作值及磁参数对补偿电容匹配关系的影响来看,饱和磁通密度Bs、剩磁Br增大会导致动作值减小,矫顽力Hc增大导致动作值增大。因此,考虑磁滞特性与饱和特性时,补偿电容C1、C2的匹配关系曲线与假设铁心磁化特性为线性情况下的匹配关系曲线形状、走势基本一致。
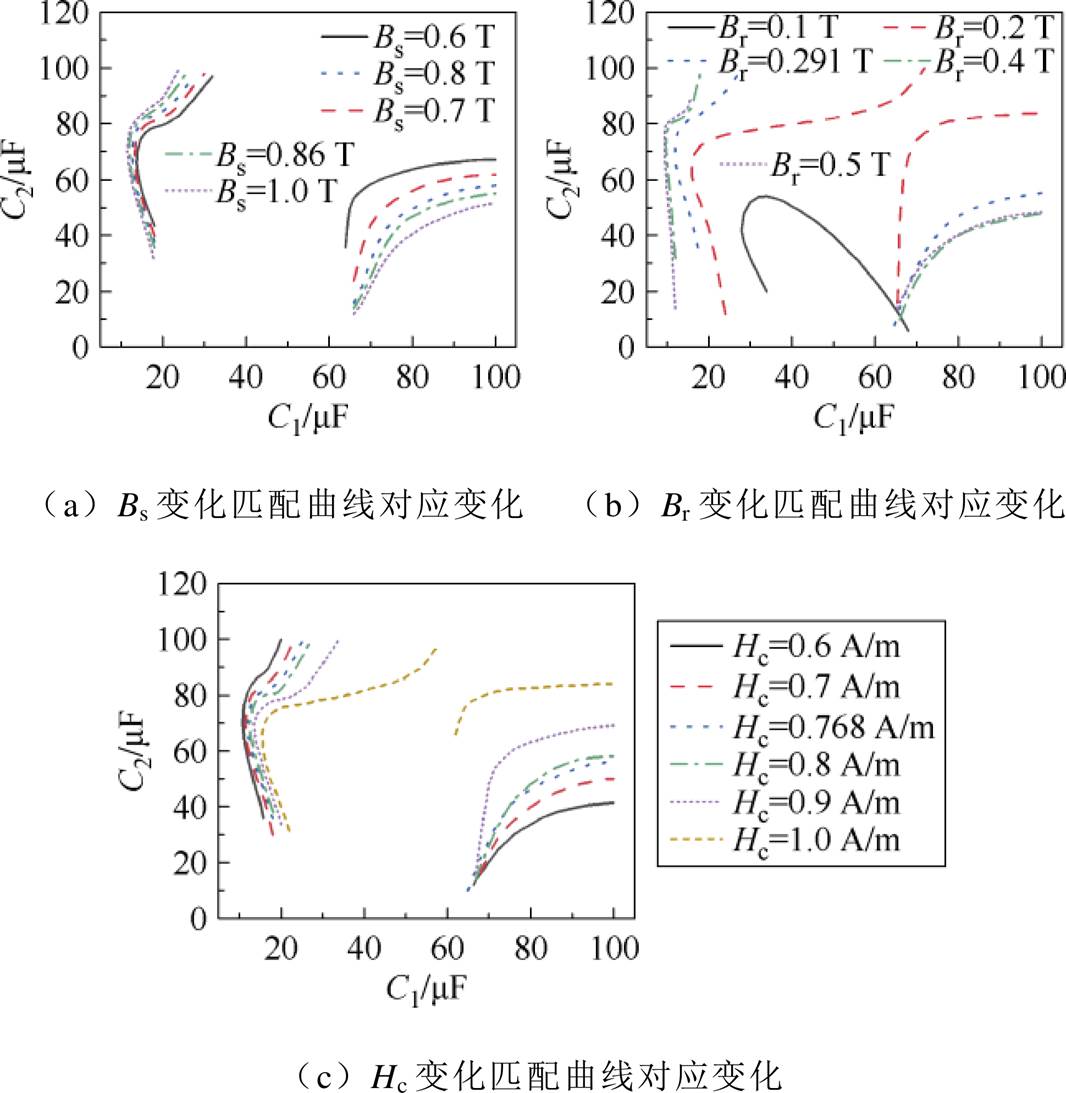
图9 磁参数变化对C1、C2匹配曲线的影响
Fig.9 The influence of magnetic parameter changes on the matching curves of C1 and C2
3.1.1 补偿电容分散性的影响
对串-并联电容补偿电路中的串联电容C1、并联电容C2进行灵敏度分析,在磁脱扣器不变的情况下,分析C2对C1灵敏度的影响,如图10所示。
当相对灵敏度S<1.0时,表明电路输出特性变化率低于元器件参数的偏移率,元器件参数的变化对电路性能的影响较小。图10中灵敏度曲线随着电容C1增大,先减小直至为零,之后增大,最后趋于0,与图3a中幅值特性k变化规律一致。随着电容C2增大,灵敏度曲线零点向左偏移,与k曲线拐点的变化规律相同,处于曲线拐点处动作值受C1容值变化的影响最小。当C2取值为100 mF时,灵敏度曲线无零点,对应k与C1的关系曲线无拐点。
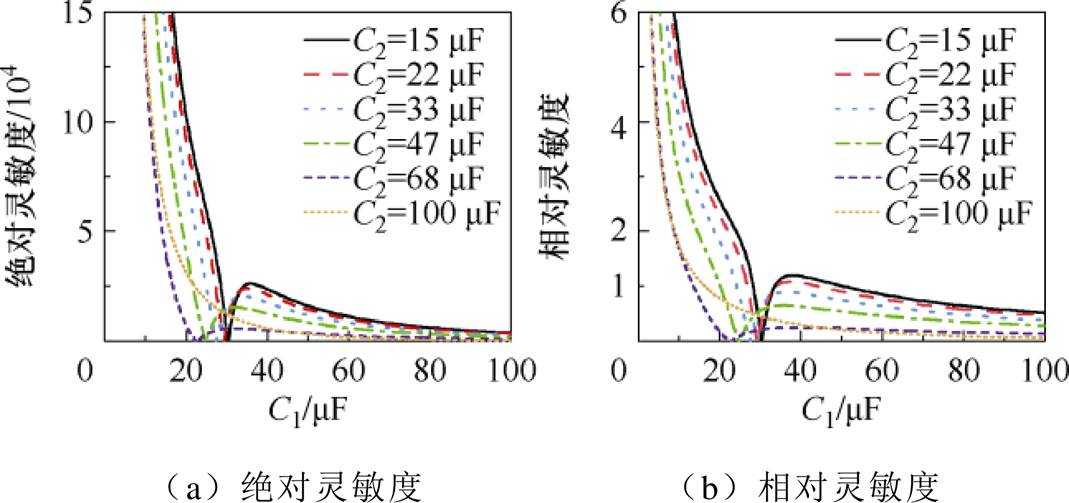
图10 不同电容C2下灵敏度随C1变化曲线
Fig.10 Sensitivity variation curves with C1 under different capacitors C2
同理,分析C1对C2灵敏度影响如图11所示。
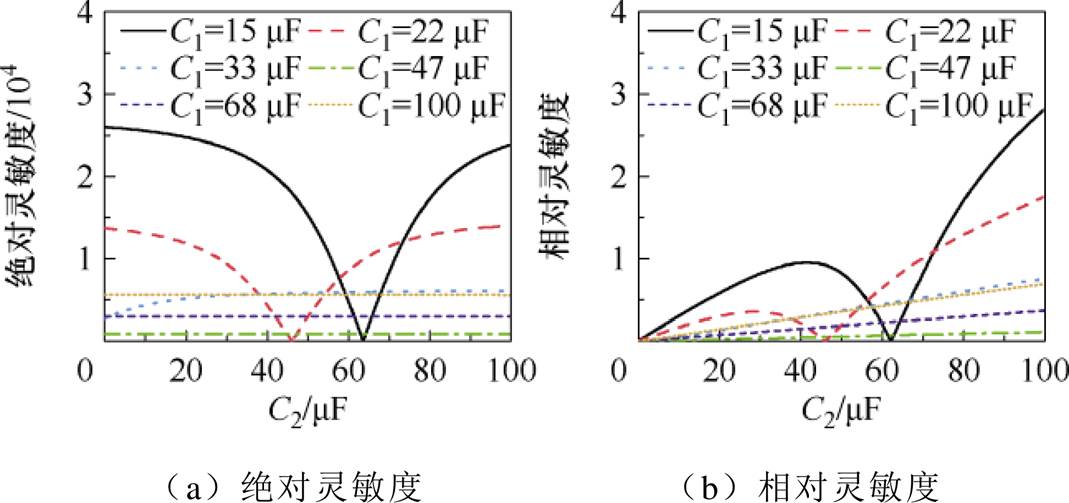
图11 不同电容C1下灵敏度随C2变化曲线
Fig.11 Sensitivity variation curves with C2 under different capacitors C1
图11中,不同电容C1下灵敏度随C2变化曲线与图3b中幅值特性k的变化规律相同。在零点处动作值受C2容值变化的影响最小,但整体上灵敏度曲线的变化幅度大,应将C1设计为较大容值,灵敏度曲线的变化幅度小且密集,漏电保护特性受C1、C2分散性的影响较小。设计C1、C2时,从灵敏度曲线来看,C1值常应位于60~100 mF,C2值常应位于10~70 mF。
3.1.2 磁参数分散性的影响
取C1、C2匹配关系曲线右半支五组补偿电容匹配参数见表3,设定磁参数变化范围为Bs:0.6~1.2 T,Br:0.1~0.5 T,Hc:0.6~1.2 A/m,仿真单一磁参数分散性对动作值的影响如图12所示。
表3 补偿电容匹配参数
Tab.3 Compensation capacitor matching parameters (单位: mF)
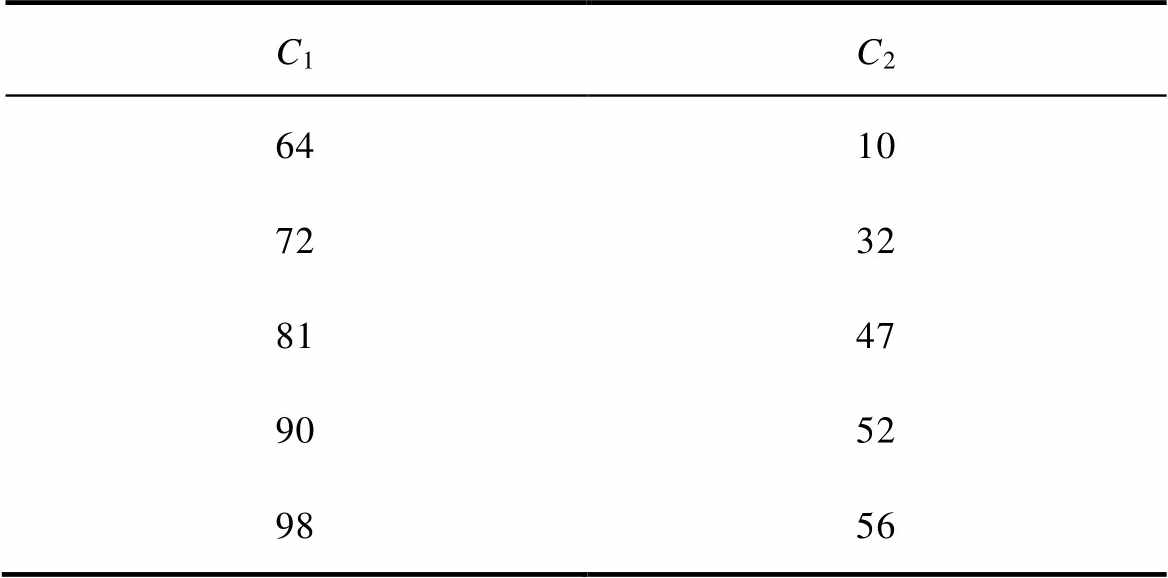
C1C2 6410 7232 8147 9052 9856
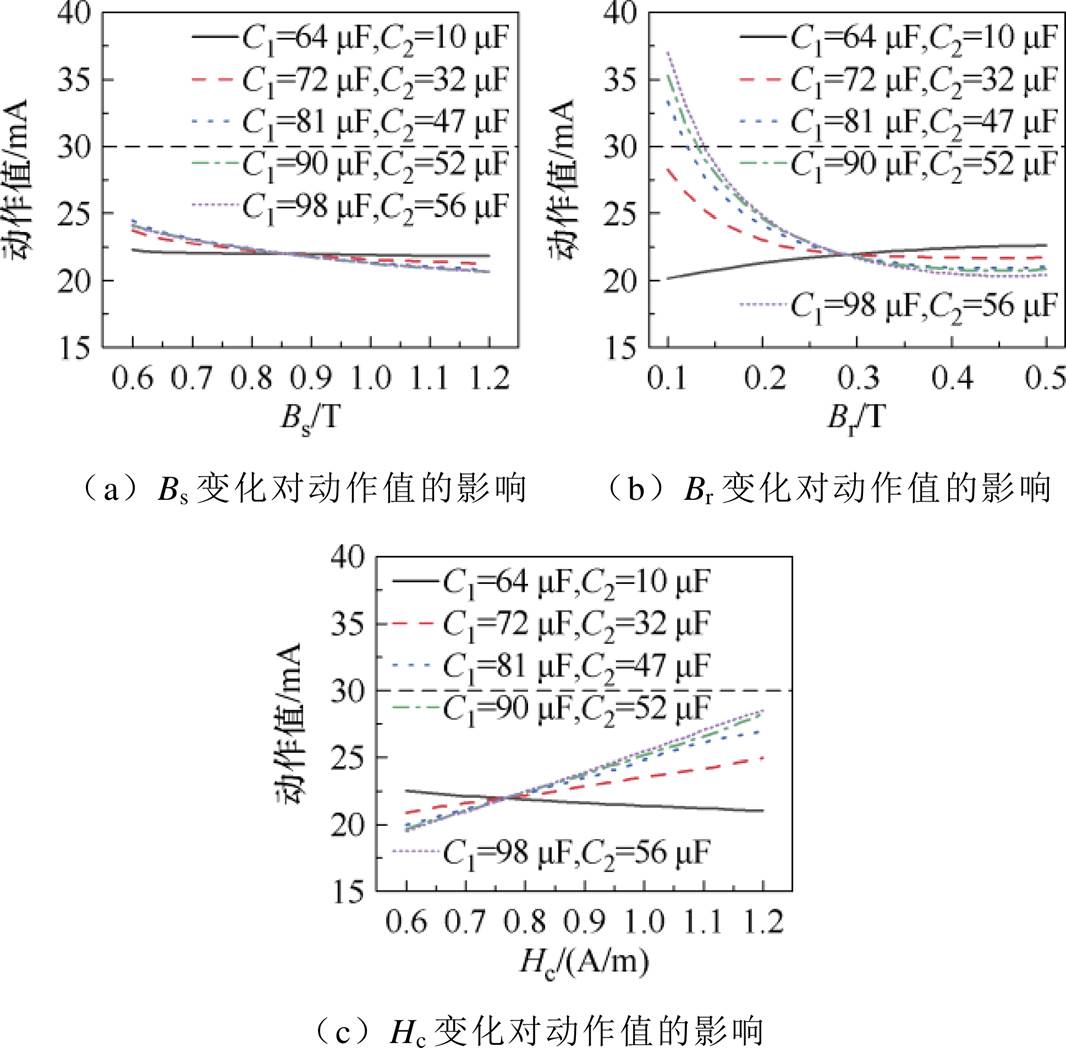
图12 磁参数分散性对动作值的影响
Fig.12 The influence of the dispersion of the magnetic parameters on the action value
图12中交点是根据表2铁心磁参数进行补偿电容匹配设计的。图中黑色曲线较平稳,在该组电容参数下动作值受磁参数的影响最小。根据仿真结果,Bs变化对动作值影响最小,在变化范围内动作值仍能保持在20~25 mA,相比之下,Br和Hc的变化导致动作值波动超出了这一范围,尤其Br的变化使得动作值甚至超过了额定剩余动作电流,因此剩余电流互感器磁参数中饱和磁通密度Bs对动作值影响最小,矫顽力Hc次之,剩磁Br对动作值影响最大。
右半支匹配曲线膝点左侧部分如图13所示。五组补偿电容参数中,当C1位于60~80 mF范围时,即右半支匹配曲线的膝点左侧范围(见图13左侧扇形部分),动作值受磁参数分散性的影响较小。此外结合图9,在该范围内,不同Bs、Br、Hc下C1、C2的匹配曲线较密集,进一步证实了这一结论。
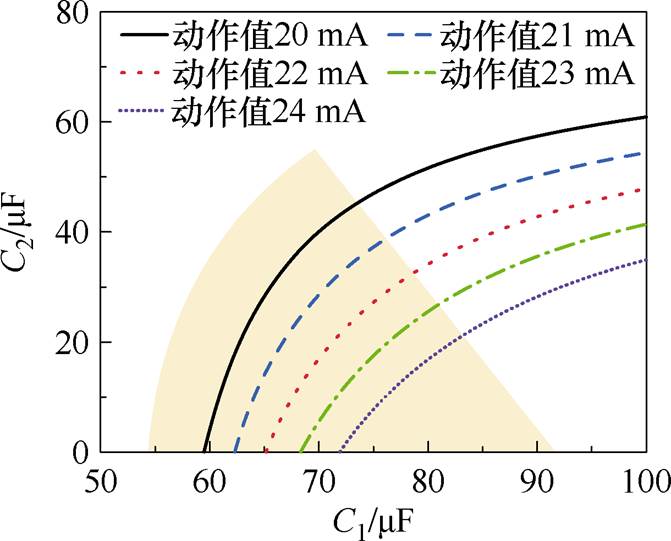
图13 右半支匹配曲线膝点左侧部分
Fig.13 The left part of the knee point of the matching curves of the right half branch
在设计剩余电流互感器磁参数时,可先确定饱和磁通密度Bs,Bs仅由材料决定,自身分散性小,且对动作值的影响较小,设定Bs=0.9 T;再分析动作值与Br、Hc的变化规律,确定Br、Hc的设计范围。在优化设计时,设定动作值为22 mA,选取三组补偿电容匹配参数,即C1=64 mF、C2=10 mF,C1=72 mF、C2=32 mF,C1=81 mF、C2=47 mF,在Bs=0.9 T情况下进行仿真分析,仿真结果如图14所示。
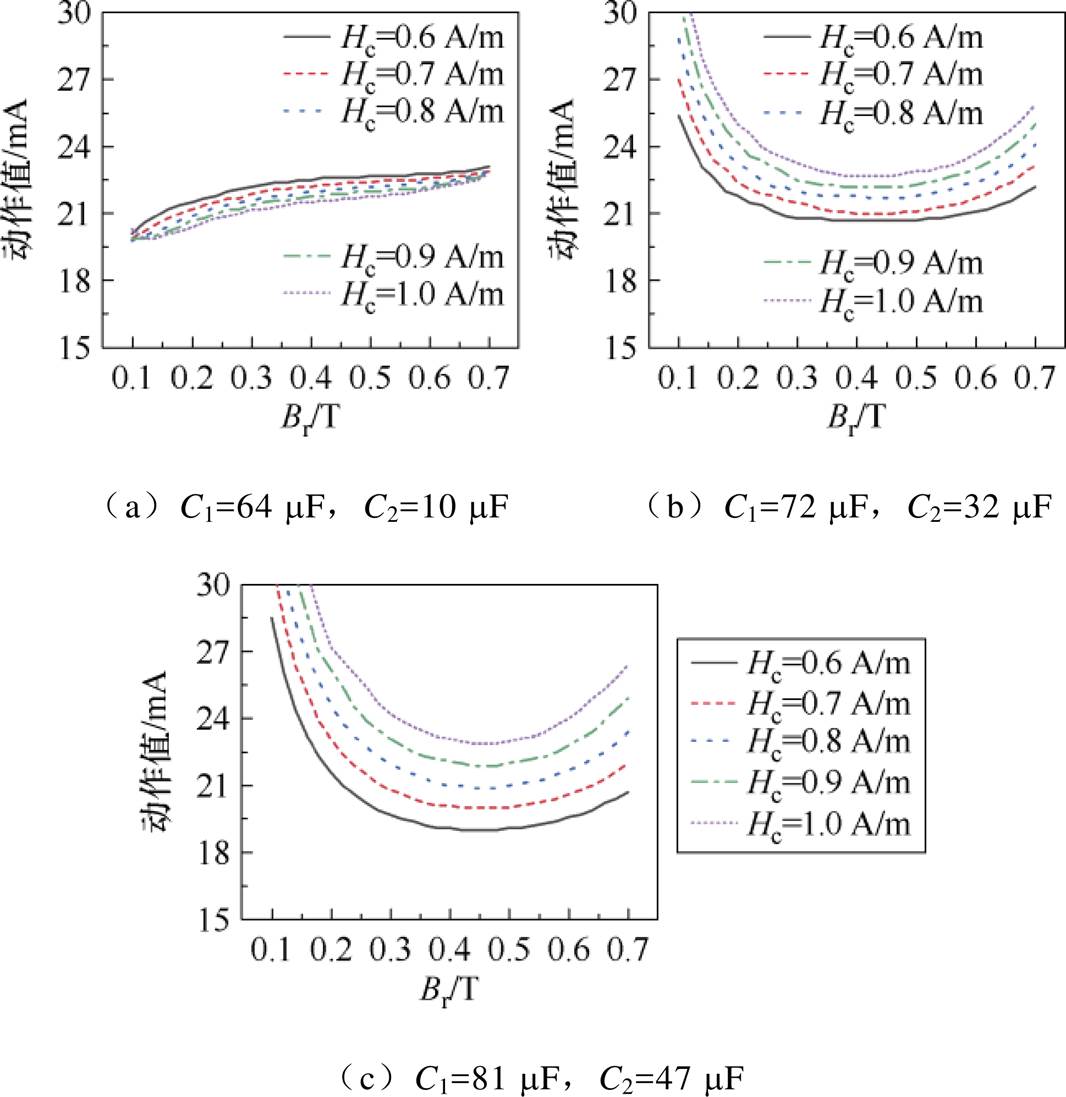
图14 不同Hc下Br与动作值的关系曲线
Fig.14 Relationship curves between Br and action values under different Hc
动作值曲线越平缓,漏电保护特性稳健性越好。图14a中,不同Hc下动作值曲线较为紧密,在该组电容参数下,Hc对动作值影响较小;Hc取值越小,平缓区间越大,Br分散性对动作值的影响越小;Br、Hc取值均比较大时,曲线有上翘趋势,这是由于Hc一定,Br过大导致磁滞回线畸变。图14b、图14c中,不同Hc下Br与动作值的关系曲线近似成“U”形,Hc不变时,动作值随着Br的增大先减小后增大,在“U”形曲线底部平缓区间较大,漏电保护特性稳健性较好。Hc越大,曲线的平缓区间越窄,动作值受Br分散性的影响较大。当Hc=0.6 A/m时,三幅图中平缓区间最大,稳健性最好。从仿真结果对比来看,选取第一组和第二组电容参数时,动作值受磁参数Br、Hc分散性的影响较小。
为提高电磁式漏电断路器漏电保护特性的稳健性,剩余电流互感器与漏电驱动电路的综合设计方法如下:
(1)确定剩余电流互感器铁心的饱和磁通密度Bs。本文选取Bs=0.9 T。
(2)确定补偿电容C1、C2的设计范围。根据磁心尺寸和磁脱扣器相关参数确定动作值后,可由式(6)得到临界电感值,设计剩余电流互感器的励磁电感大于临界电感,得到补偿电容C1、C2的匹配关系曲线。综合考虑容值变化及磁参数Br、Hc变化对动作值的影响,所选串联补偿电容C1应位于60~80 mF,并联补偿电容C2应位于10~30 mF,该范围内漏电保护特性受电容容差的影响较小,同时能降低磁参数分散性对动作值的影响。
(3)确定剩余电流互感器铁心的矫顽力Hc。由上述分析,在矫顽力Hc=0.6 A/m时,动作值与Br的曲线存在较大范围平缓区,与补偿电容参数相关性不大,因此选取0.6 A/m为Hc设计值。
(4)确定剩余电流互感器铁心的剩磁Br。由图14可知,剩磁为0.4 T时,位于不同电容、不同Hc的动作值曲线平缓区的中间部分,因此选取0.4 T为Br设计值。
根据以上方法,经仿真分析后可确定九种参数设计方案,见表4,方案0为原始参数,其余方案为新设计方案。
在补偿电容C1、C2容差±10%,磁参数Br、Hc分散性±20%下,取极限偏差对优化前后设计方案的保护特性进行仿真分析。C1、C2呈正相关的匹配关系,在取极限偏差时,C1、C2的偏差趋势应相反,因此每个方案共有(C1、C2)、Br、Hc三个因素,每个因素有正负两个偏差水平,采用L4(23)的正交表进行设计,见表5,并对结果进行统计分析。表中,C1+、C1-分别为C1容值偏差+10%和偏差-10%,C2+、C2-同理;Br+、Br-分别为剩磁偏差+20%和偏差-20%,Hc+、Hc-同理。根据表4对全部设计方案进行仿真分析,结果见附表1。
表4 参数设计方案
Tab.4 Parametric design scheme
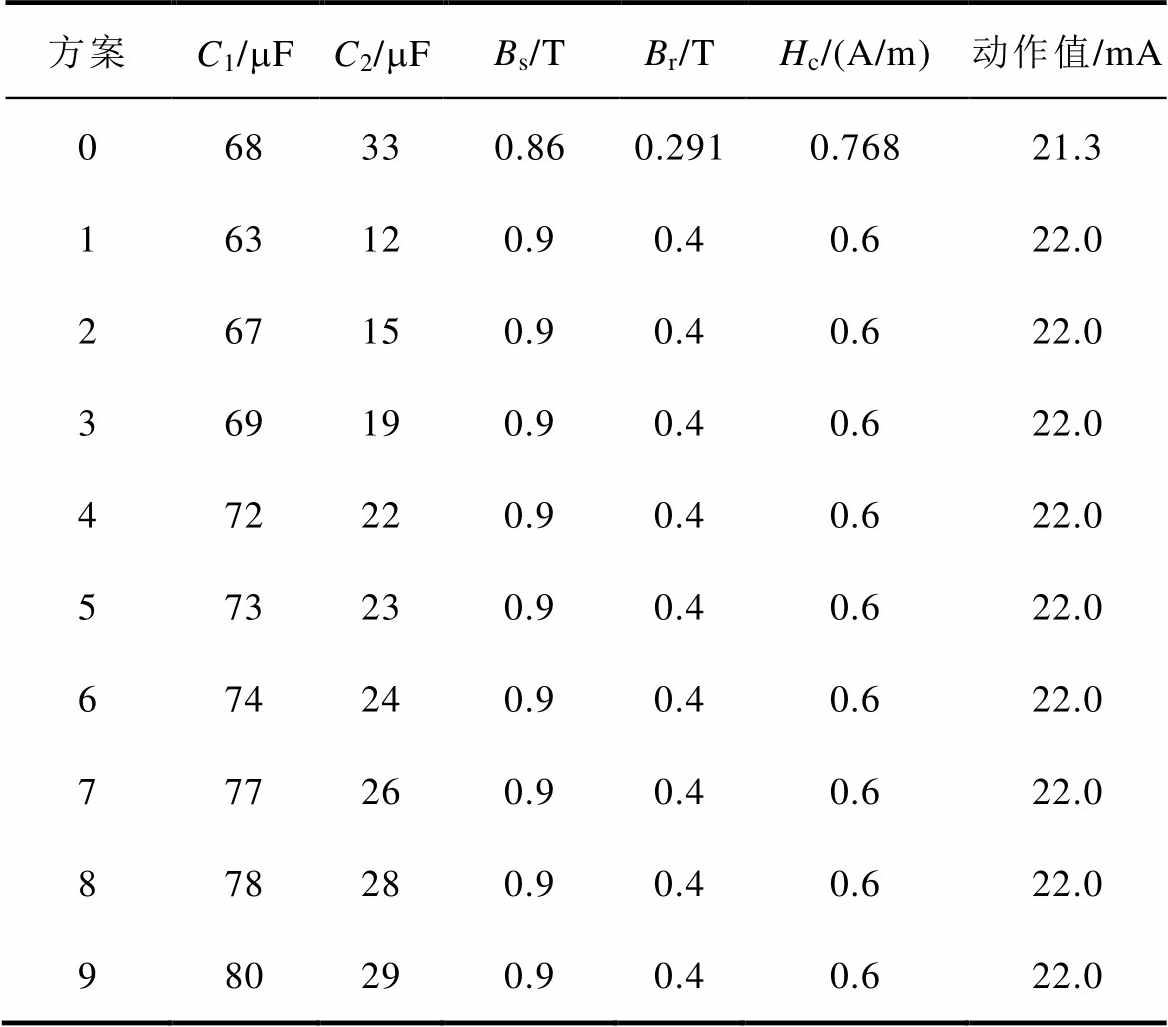
方案C1/mFC2/mFBs/TBr/THc/(A/m)动作值/mA 068330.860.2910.76821.3 163120.90.40.622.0 267150.90.40.622.0 369190.90.40.622.0 472220.90.40.622.0 573230.90.40.622.0 674240.90.40.622.0 777260.90.40.622.0 878280.90.40.622.0 980290.90.40.622.0
表5 L4(23)参数优化试验正交表
Tab.5 L4(23) orthogonal table for parameter optimization experiments

编号C1/mFC2/mFBr/THc/(A/m) 1C1+C2-Br+Hc+ 2C1+C2-Br-Hc- 3C1-C2+Br+Hc- 4C1-C2+Br-Hc+
原始方案在参数极限偏差下动作值能达到12.64%的偏差,新方案中方案3在所有方案中动作值的偏差最小,受参数分散性的影响最低,在参数极限偏差下动作值偏差在±6.82%以内,同比提高了46.04%,因此选择方案3为最佳参数组合,提高了漏电保护特性的稳健性。在脉动直流剩余电流下对方案3参数进行仿真,半波漏电动作值为31.0 mA,90°波漏电动作值为17.2 mA,135°波漏电动作值为17.6 mA,符合国标要求。
由于实际电容器的容值只有标准规定数值,并不是任意的,对C1、C2匹配关系曲线的验证存在一定难度,但可以对漏电驱动电路的幅值特性进行测试,并与仿真数据及理论曲线进行对比。C1、C2分别取15、22、33、47、68、100 mF容值,试验测试电路如图15所示,对比结果如附图1所示。
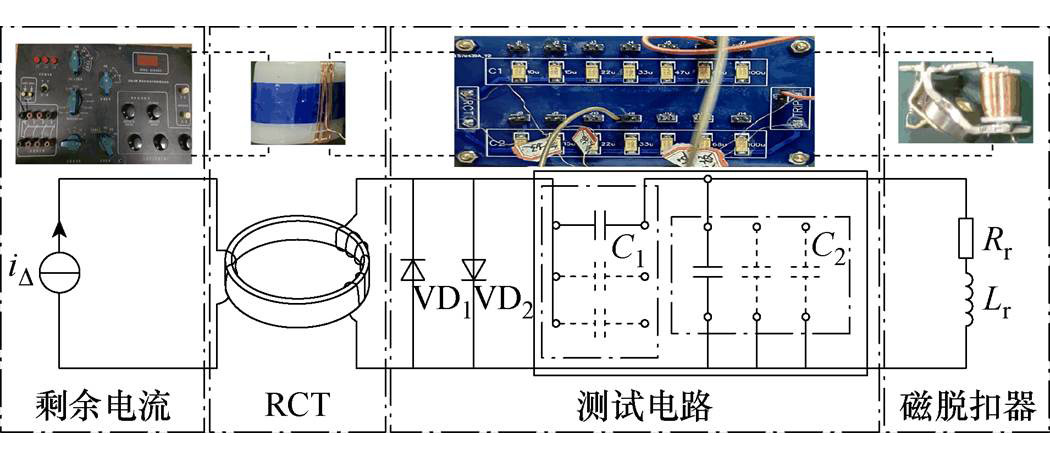
图15 幅值特性测试电路
Fig.15 Amplitude characteristic testing circuit
测得幅值特性k的试验数据与仿真数据及理论曲线基本一致。由于磁脱扣器释放电流设定值与实际值的误差及励磁电感L0、磁脱扣器电感Lr的测量误差,三者不会完全吻合,但总体差异较小,因此可证明本文理论分析与仿真模型正确,C1、C2的匹配关系曲线正确。
本文针对电磁式漏电断路器中剩余电流互感器与漏电驱动电路的匹配关系及其对漏电保护特性的影响进行了分析,并对补偿电容和剩余电流互感器进行了稳健性设计,主要结论如下:
1)分析了串-并联电容补偿漏电驱动电路拓扑的工作原理,探究了补偿电容与励磁电感、脱扣器电感的相互关系,确定了漏电驱动电路传输特性和一、二次电流电压的相量关系,为漏电保护特性分析与优化设计提供了理论依据。
2)分析了串-并联电容补偿电路中补偿电容及剩余电流互感器参数对漏电保护特性的影响。确定了串联补偿电容C1与并联补偿电容C2的匹配关系,C1、C2的匹配关系曲线随着励磁电感的变化,其形状会发生改变;分析了剩余电流互感器铁心磁参数对C1、C2匹配关系曲线的影响,当磁参数变化时,C1、C2的匹配曲线形状会发生变化,保护特性变化趋势不变。
3)分析了补偿电容分散性与剩余电流互感器铁心磁参数分散性对漏电保护特性的影响。进行了漏电保护特性的灵敏度分析,确定了补偿电容的优化设计范围,当补偿电容位于匹配曲线右半支的膝点左侧部分时,漏电保护特性稳健性好;明确了剩余电流互感器磁参数分散性对动作值的影响,确定了提高动作值稳健性的磁参数优化设计参考区间;提出了补偿电容参数与剩余电流互感器磁参数的综合设计方法,并确立了优化设计方案。在电容及磁参数相同波动条件下,动作值的波动量降低了46.04%。
附录 试验结果
附表1 正交试验结果
App.Tab.1 Orthogonal test results

方案C1/mFC2/mFBr/THc/(A/m)动作值/ mA动作值偏差(%) 074.829.70.3490.92223.5+10.33 74.829.70.2330.61422.1+3.76 61.236.30.3490.61418.6-12.68 61.236.30.2330.92221.1-0.94 169.310.80.480.7223.5+6.82 69.310.80.320.4823.4+6.36 56.713.20.480.4820.8-5.45 56.713.20.320.7219.5-11.36 273.713.50.480.7224.3+10.45 73.713.50.320.4823.4+6.36 60.316.50.480.4821.2-3.64 60.316.50.320.7220.1-8.64 375.917.10.480.7223.5+6.82 75.917.10.320.4823.0+4.55 62.120.90.480.4820.8-5.45 62.120.90.320.7220.5-6.82 479.219.80.480.7223.9+8.64 79.219.80.320.4823.0+4.55 64.824.20.480.4820.5-6.82 64.824.20.320.7220.8-5.45 580.320.70.480.7223.9+8.64 80.320.70.320.4823.0+4.55 65.725.30.480.4820.5-6.82 65.725.30.320.7220.8-5.45 681.421.60.480.7224.0+9.09 81.421.60.320.4822.9+4.09 66.626.40.480.4820.4-7.27 66.626.40.320.7221.0-4.55 784.723.40.480.7224.2+10 84.723.40.320.4823.0+4.55 69.328.60.480.4820.3-7.73 69.328.60.320.7221.2-3.64 885.825.20.480.7224.0+9.09 85.825.20.320.4822.6+2.73 70.230.80.480.4820.1-8.64 70.230.80.320.7221.3-3.18 98826.10.480.7224.1+9.55 8826.10.320.4822.7+3.18 7231.90.480.4820.1-8.64 7231.90.320.7221.5-2.27

附图1 幅值特性试验验证
App.Fig.1 Amplitude characteristic test verification
参考文献
[1] 孙荣可, 单玉凯, 薛永端, 等. 基于负荷电流闭锁的低压配电网漏电保护[J]. 电力系统及其自动化学报, 2023, 35(3): 21-28.
Sun Rongke, Shan Yukai, Xue Yongduan, et al. Leakage protection for low-voltage distribution network based on load current locking[J]. Proceedings of the CSU-EPSA, 2023, 35(3): 21-28.
[2] 高伟, 饶俊民, 全圣鑫, 等. 不均衡小样本下多特征优化选择的生命体触电故障识别方法[J]. 电工技术学报, 2024, 39(7): 2060-2071.
Gao Wei, Rao Junmin, Quan Shengxin, et al. Biological electric-shock fault identification method based on multi-feature optimization selection under unbalanced small sample[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2060-2071.
[3] Zhang Mingming, Qin Ping, Chen Yongjin, et al. Study on the detection method of leakage in TN-C area of low-voltage distribution network[C]//2021 International Conference on Power System Tech- nology (POWERCON), Haikou, China, 2021: 378- 381.
[4] 李奎, 郝运佥, 赵成晨, 等. 基于马尔可夫过程的漏电保护器服役状态及其可靠性分析[J]. 电工技术学报, 2023, 38(18): 5061-5076.
Li Kui, Hao Yunqian, Zhao Chengchen, et al. Service states and reliability analysis of residual current device based on Markov process[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 5061- 5076.
[5] Li Kui, Lin Jingyi, Niu Feng, et al. A novel fault leakage current detection method with protection deadzone elimination[J]. IEEE Transactions on Instru- mentation and Measurement, 2020, 70: 3505009.
[6] 沈泽亮, 汪金刚, 王谦, 等. 一种基于低频窄带扫描的电磁式电压互感器杂散电容测量与精确建模方法[J]. 电工技术学报, 2023, 38(8): 2211-2221.
Shen Zeliang, Wang Jingang, Wang Qian, et al. A method for stray capacitance measuring and refined modeling of potential transformer based on low frequency and narrow band scanning[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2211- 2221.
[7] 刘帼巾, 李想, 王泽, 等. 基于Wiener过程电子式漏电断路器的剩余寿命预测[J]. 电工技术学报, 2022, 37(2): 528-536.
Liu Guojin, Li Xiang, Wang Ze, et al. Remaining life prediction of electronic residual current circuit breaker based on Wiener process[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 528-536.
[8] 刘帼巾, 王泽, 李想, 等. 基于改进Bootstrap- Bayes的电子式剩余电流动作断路器可靠性评估[J]. 电工技术学报, 2022, 37(16): 4250-4258.
Liu Guojin, Wang Ze, Li Xiang, et al. Reliability evaluation of electronic residual current operated circuit breakers based on improved Bootstrap- Bayes[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4250-4258.
[9] Rui Li. Analysis and realization method of selective leakage protection technology of self-adaptive full compensation domain[C]//2020 5th International Con- ference on Power and Renewable Energy (ICPRE), Shanghai, China, 2020: 471-475.
[10] 司马文霞, 孙佳琪, |杨鸣, 等. 计及铁心非线性的变压器空间动态磁场加速计算方法[J]. 电工技术学报, 2025, 40(5): 1559-1574.
Sima Wenxia, Sun Jiaqi, Yang Ming, et al. Acce- lerated calculation method of space dynamic magnetic field of transformer considering core nonlinearity[J]. Transactions of China Electrotechnical Society, 2025, 40(5): 1559-1574.
[11] 王亮, 曾伟杰, 田娟, 等. 直流分量和谐波分量对电流互感器传输特性影响[J]. 电机与控制学报, 2023, 27(5): 1-8.
Wang Liang, Zeng Weijie, Tian Juan, et al. Influence of DC component and harmonic component on transmission characteristics of current transformer[J]. Electric Machines and Control, 2023, 27(5): 1-8.
[12] 段建东, 金转婷, 雷阳, 等. 自动重合闸期间电流互感器剩磁抑制研究[J]. 中国电机工程学报, 2019, 39(5): 1498-1505.
Duan Jiandong, Jin Zhuanting, Lei Yang, et al. Study on residual flux suppression of current transformer during automatic reclosing[J]. Proceedings of the CSEE, 2019, 39(5): 1498-1505.
[13] 李奎, 解晨雨, 牛峰, 等. 考虑非线性特性的剩余电流互感器建模及其输出调理电路参数设计[J]. 中国电机工程学报, 2022, 42(10): 3815-3826.
Li Kui, Xie Chenyu, Niu Feng, et al. Modeling of residual current transformer considering nonlinear characteristics and design of output conditioning circuit parameters[J]. Proceedings of the CSEE, 2022, 42(10): 3815-3826.
[14] 李奎, 徐子健, 卢志伟, 等. 电磁式漏电保护特性影响因素分析及其稳健性设计[J]. 电工技术学报, 2023, 38(14): 3930-3942.
Li Kui, Xu Zijian, Lu Zhiwei, et al. Factors analysis and robust design of electromagnetic leakage pro- tection characteristics[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3930-3942.
[15] Li Kui, Lin Jingyi, Niu Feng, et al. A novel fault leakage current detection method with protection deadzone elimination[J]. IEEE Transactions on Instru- mentation and Measurement, 2020, 70: 3505009.
[16] 李奎, 佟盟, 武一, 等. 磁脱扣器动作响应分析及储能电容匹配设计[J]. 电力自动化设备, 2024, 44(1): 167-173.
Li Kui, Tong Meng, Wu Yi, et al. Tripping response analysis and capacitor matching design of magnetic release[J]. Electric Power Automation Equipment, 2024, 44(1): 167-173.
[17] 汤龙飞, 柯昌辉, 许志红. 智能单稳态永磁接触器动作特性的联合仿真[J]. 中国电机工程学报, 2023, 43(4): 1641-1651.
Tang Longfei, Ke Changhui, Xu Zhihong. Co- simulation of action characteristics of intelligent monostable permanent magnet contactor[J]. Pro- ceedings of the CSEE, 2023, 43(4): 1641-1651.
[18] 吴敬轩, 许志红. 电磁接触器吸合过程无模型自适应控制策略[J]. 中国电机工程学报, 2020, 40(5): 1663-1673.
Wu Jingxuan, Xu Zhihong. A model-free adaptive control strategy for actuation of electromagnetic contactors[J]. Proceedings of the CSEE, 2020, 40(5): 1663-1673.
[19] 李奎, 李常宇, 牛峰, 等. 电磁式漏电断路器的空间磁场抗扰分析及屏蔽结构设计[J]. 电工技术学报, 2022, 37(9): 2161-2169.
Li Kui, Li Changyu, Niu Feng, et al. Anti-magnetic field interference analysis and shielding structure design of electromagnetic residual current circuit breaker[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2161-2169.
[20] Li Kui, Luo Chen, Niu Feng, et al. A new magnetic release design with high anti-interference capabi- lity[J]. IEEE Transactions on Magnetics, 2021, 57(5): 4001009.
[21] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. 剩余电流动作保护电器: GB/T 6829—2017[S]. 北京: 中国标准出版社, 2018.
Abstract Residual current devices (RCDs) are critical electrical safety devices that can quickly cut off the power supply when leakage faults occur in power lines or electrical equipment, thus preventing electrical fires and ensuring personal safety. Among them, electromagnetic RCDs are highly valued due to their stable leakage protection characteristics, excellent anti-interference capability, and rapid response time. This paper focuses on the series-parallel compensation capacitor in the leakage protection driving circuit of fast-acting electromagnetic RCDs and the robustness of leakage protection characteristics. The matching relationship between the series- parallel compensation capacitor and residual current transformer (RCT) is determined, and relevant parameters are optimized to enhance the robustness of electromagnetic leakage protection characteristics. The main research work and conclusions are as follows.
(1) The main components of electromagnetic RCD are analyzed. The transmission characteristics of RCT are affected by the excitation characteristics of the iron core and the driving circuit. The key factor for the reliable operation of the magnetic release is the excitation of ampere-turns, and the topology of the driving circuit determines the leakage protection characteristics. The working principle of the compensation circuit with a series-parallel capacitor is analyzed, and the relationship between circuit characteristics and element parameters is studied.
(2) The topology of the leakage driving circuit with a series-parallel compensation capacitor is investigated. The influence of compensation capacitors and RCT on leakage protection characteristics is explored. The matching principle of compensation capacitors and their relationship with leakage protection value are studied, and the variation characteristics of the capacitor matching curve under different protection values are determined. It is suggested that the exciting inductance of RCT should be designed to be greater than the critical inductance to reduce the influence of compensation capacitor dispersion on the leakage protection value. The impact of magnetic parameters of RCT on leakage protection characteristics is studied, and the influence of hysteresis and magnetic saturation characteristics on the matching principle of compensation capacitors is analyzed. The increase in saturation magnetic flux density Bs and remanence Br leads to a decrease in protection value. In contrast, the increase in coercive force Hc leads to an increase.
(3) The dispersion influence of compensation capacitors and RCT magnetic parameter on leakage protection characteristics is studied. The range of the compensation capacitor is determined through sensitivity analysis. Saturation magnetic flux density Bs shows the least influence on protection value, coercive force Hc shows the second least influence, and remanence Br shows the most significant influence. When the compensation capacitor is on the left side of the knee point of the right half of the matching curve, the leakage protection value is the least affected by the dispersion of magnetic parameters. A comprehensive design method for RCT and compensation capacitors is proposed, and the optimal design scheme is determined by an orthogonal method. Under the same component parameter fluctuation, the fluctuation range of leakage protection value is reduced by 46.04% after parameter optimization, enhancing the robustness of leakage protection characteristics.
keywords:Electromagnetic residual current device (RCD), leakage protection characteristics, circuit topology analysis, residual current transformer (RCT), robustness design
DOI: 10.19595/j.cnki.1000-6753.tces.241941
中图分类号:TM561
国家自然科学基金资助项目(51977059)。
收稿日期 2024-10-29
改稿日期 2024-12-09
李 奎 男,1965年生,教授,博士生导师,研究方向为电器可靠性与试验技术、电器智能化理论与技术等。E-mail: likui@hebut.edu.cn
牛 峰 男,1986年生,教授,博士生导师,研究方向为电机系统及控制。E-mail: niufeng@hebut.edu.cn(通信作者)
(编辑 崔文静)