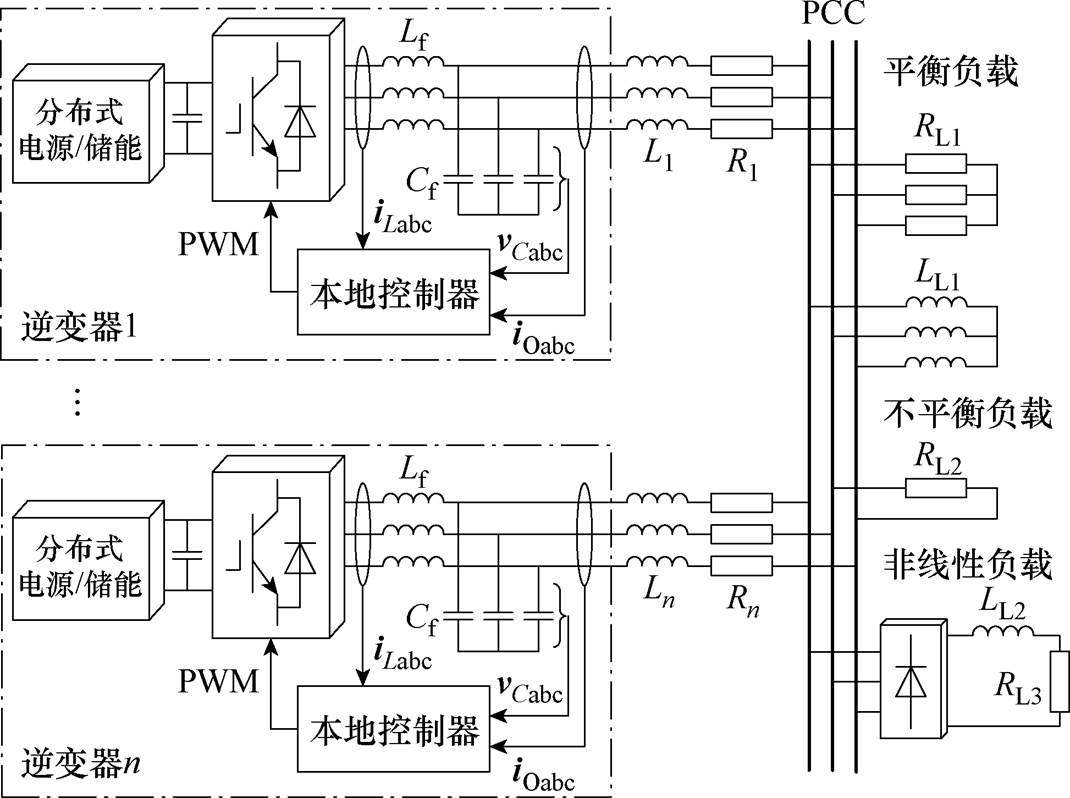
图1 典型逆变器并联系统拓扑
Fig.1 Topology of inverter-parallel systems
摘要 逆变器并联系统广泛应用于交流微电网、可再生能源发电、不间断电源和电动汽车等领域，实现负载功率在各台逆变器之间的合理分配是保证并联系统稳定可靠运行的关键技术。传统下垂控制仅能实现有功功率的均分，难以克服逆变器参数差异、线路阻抗差异等导致的非有功功率均分误差（包括无功功率、不平衡功率和谐波功率），易造成逆变器过载甚至系统失稳。针对该问题，该文提出一种基于双频率下垂控制的非有功功率均分策略：首先，沿用传统有功功率-基波频率下垂控制保证有功功率均分；其次，引入非有功功率-特定谐波频率下垂控制实现非有功功率均分；最后，该策略通过在逆变器输出电压中叠加特定谐波信号，利用该谐波信号的频率与非有功功率建立下垂机制，并通过谐波信号的有功功率变化自适应调整虚拟阻抗，最终实现非有功功率精确分配。该方法不依赖逆变器之间的通信和线路阻抗测量，可同时实现无功功率、不平衡功率及谐波功率的均分，仿真和实验结果验证了所提控制策略的有效性。
关键词：逆变器并联 下垂控制 功率均分 非有功功率 虚拟阻抗
在国家“双碳”目标和新型电力系统建设的战略背景下，微电网凭借其灵活性、可靠性和低碳特性，成为优化能源结构、提升电网韧性的关键技术。在微电网系统中，分布式能源一般通过逆变器等电力电子接口设备接入公共耦合点（Point of Common Coupling, PCC）[1-3]。因此，可将微电网简化为多台逆变器并联构成的系统以简化分析。此外，逆变器并联结构也广泛应用于可再生能源发电、不间断电源和电动汽车等领域，对实现低碳化能源转型、电动汽车普及以及关键基础设施的电力保障具有重要战略意义[4-5]。
逆变器并联系统中，功率均衡分配可优化整体运行效率，防止单一逆变器过载，并提高系统可靠性，因此功率均分是并联系统安全、高效、长期稳定工作的关键[6-8]。孤岛运行模式下为实现微电网逆变器之间的功率均衡，常采用下垂控制方法[9-11]，但由于各分布式电源间等效阻抗的差异，使受控于系统电压的无功功率无法实现精确均分，导致系统内产生无功环流，影响电能输送效率，严重时甚至引发系统不稳定[12-15]。与此同时，对于微电网中不可避免的一些单相负载和非线性负载，由于线路阻抗不同，也会使其产生的不平衡和谐波功率在几台并联逆变器之间不能均匀分配，距离负载较近的逆变器将会吸收大部分功率，可能会造成逆变器过 载[16-17]。无功功率、不平衡功率和谐波功率在物理本质上均反映了电流中的非有功分量，通过后文理论分析可说明，此三类功率的分配均受逆变器等效输出阻抗影响，可通过虚拟阻抗调节实现均分。根据IEEE 1459—2010标准[18]，非有功功率的定义中包含了无功功率、不平衡功率和谐波功率，因此本文将非有功功率视为控制对象以实现以上三种功率的协同均分。
针对微电网中非有功功率因线路阻抗不同而不能均分的问题，对其中某一单一功率均分进行了广泛研究。文献[19-20]在控制系统中添加虚拟阻抗，改善逆变器在全频段的等效阻抗特征，实现无功功率的均分。文献[22]设计了谐波下垂控制器和模型预测电压控制器，以替代传统的电压电流双闭环控制，使谐波功率在分布式发电机之间精确地按比例分配。文献[23-24]考虑了并联系统谐波功率均分精度与电能质量的折中，提出了一种基于通信的二次电压控制实现谐波功率均分。文献[16]提出一种基于小信号注入的控制方法，通过自动调整负序虚拟阻抗幅值的大小，以实现不平衡功率的均分。以上文献都只关注单一功率的均分，并未考虑多种功率的同时均分。为了实现不平衡与谐波功率的同时均分，文献[25]在文献[16]的基础上通过在每台逆变器输出电压中注入交流小信号调节虚拟阻抗的方法，实现了不平衡与谐波功率的自动均分。文献[26]利用保守功率理论和一致性算法自适应计算虚拟阻抗的大小，实现均分不平衡和谐波功率。还有一部分文献对非有功功率的同时均分进行了研究。文献[27]提出了一种基于一致性算法的分布式控制策略对无功功率、不平衡和谐波功率进行分配，但该方法中分布式发电机单元需与其相邻单元进行通信。综上所述，鲜有文献在无通信的基础上实现非有功功率的同时均分。
针对已有研究存在的问题，本文提出一种基于双频率下垂的非有功功率均分策略，通过在逆变器输出电压中注入特定谐波电压，并与非有功功率构建下垂关系，可在无通信的基础上实现非有功功率的自适应均分。
本文所研究的逆变器并联系统拓扑如图1所示，图中，Lf、Cf分别为滤波器的电感和电容，L1、R1分别为逆变器1支路的线路阻抗电感和电阻，Ln、Rn分别为逆变器n支路的线路阻抗电感和电阻，RL1为阻性平衡负载，LL1为感性平衡负载，RL2为不平衡负载，LL2、RL3分别为整流器所带的电感和电阻负载，iLabc为滤波器电感电流，iOabc为逆变器输出电流，vCabc为逆变器输出电压。各台逆变器通过线路阻抗连接到PCC，为简化分析，本文认为线路阻抗以感性为主。
图1 典型逆变器并联系统拓扑
Fig.1 Topology of inverter-parallel systems
考虑到实际中逆变器地理位置的不同，线路阻抗可能存在较大差异，因此图中线路阻抗各不相同。在不依赖逆变器之间通信的情况下，每台逆变器仅由本地控制器独立控制。负载侧接有阻性平衡负载RL1、感性平衡负载LL1、不平衡负载RL2及以整流器为代表的非线性负载。
采用下垂控制的逆变器可以等效成受控电压源，其频率和幅值会随输出功率的变化而变化，如图2所示为两台下垂控制逆变器在正序基波频率处并联的等效电路。
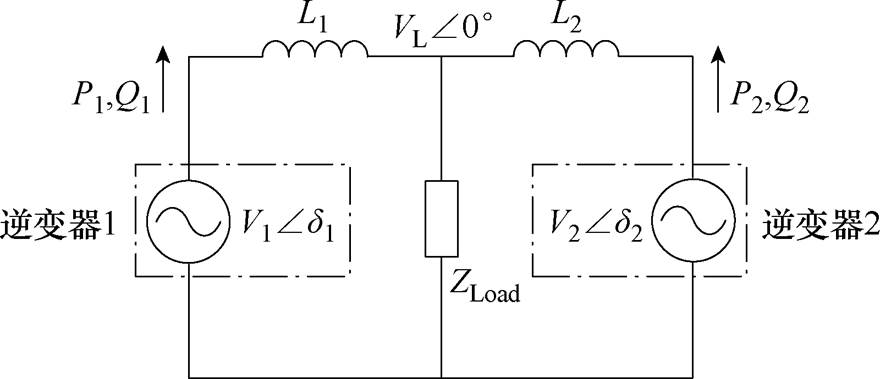
图2 正序基波频率处的等效电路
Fig.2 Equivalent circuit at positive-sequence fundamental frequency
在感性线路阻抗的情况下，第i台逆变器（i= 1, 2）的输出功率表示为
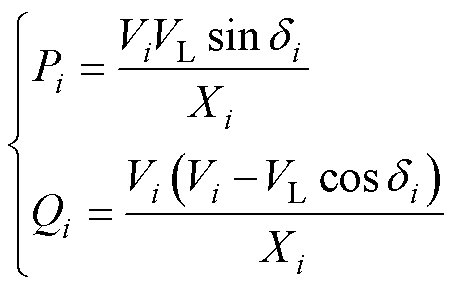（1）
式中，Vi为逆变器端口电压幅值；Xi为线路电感感抗；VL为PCC电压幅值；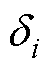
为逆变器端口电压和PCC电压的相位差。
实际情况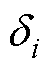足够小，可以忽略不记，则近似可得
，
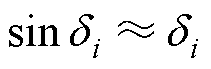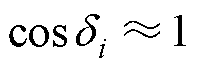，式（1）可简化为
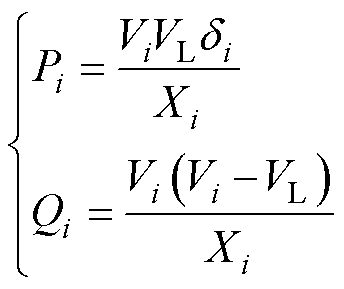（2）
从式（2）可以看出，输出有功功率和相位呈正相关，输出无功功率和电压幅值呈正相关，因此当线路阻抗以感性为主时，构建有功功率和频率下垂关系及无功功率和电压幅值下垂关系，即
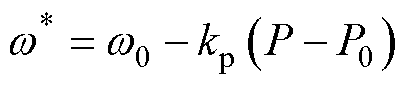（3）
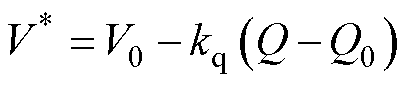（4）
式中，P、Q分别为逆变器实际输出有功功率和无功功率；P0、Q0分别为逆变器额定有功功率和额定无功功率；V*为实际电压幅值指令；w*为实际角频率；kq为无功功率下垂系数；kp为有功功率下垂系数；V0为额定电压幅值；w0为额定角频率。
由于频率是全局变量，系统达到稳态时，各逆变器的输出频率趋于一致。下垂控制提供的负反馈机制可保证有功功率会随着各台逆变器频率的自同步过程而达到均分。而输出电压幅值作为局部变量，受本地下垂控制和线路阻抗影响，线路阻抗差异会导致逆变器端电压不同，从而影响无功功率分配。
在本文所提控制策略中，将式（4）中的V*设定为额定值，取消了传统的Q-V下垂控制环节。这一设计基于以下考虑：首先，无功功率均分将由后文介绍的非有功功率-特定谐波频率下垂控制实现；其次，仍保留有功功率-频率下垂关系以确保有功功率的精确分配。此时V1=V2，那么由无功功率的计算公式（2）可知，逆变器输出无功功率与其线路阻抗成反比关系。这一特性表明，要实现并联逆变器间的无功功率均分，须保证各逆变器支路的等效线路阻抗相等。
对于图1所示的系统，由于下垂控制产生的参考电压是纯正弦的三相对称信号，不含负序和谐波分量，因此，在负序基波频率和谐波频率处逆变器呈现一个较小的输出阻抗特性。为简化分析，这里假设逆变器输出阻抗Zo远小于线路阻抗，可以忽略。
系统在负序基波频率处的简化等效电路如图3所示，其中不平衡负载表示为负序基波电流源In。由图3可知，不平衡功率QUi的分配与每条支路的等效阻抗成反比关系。
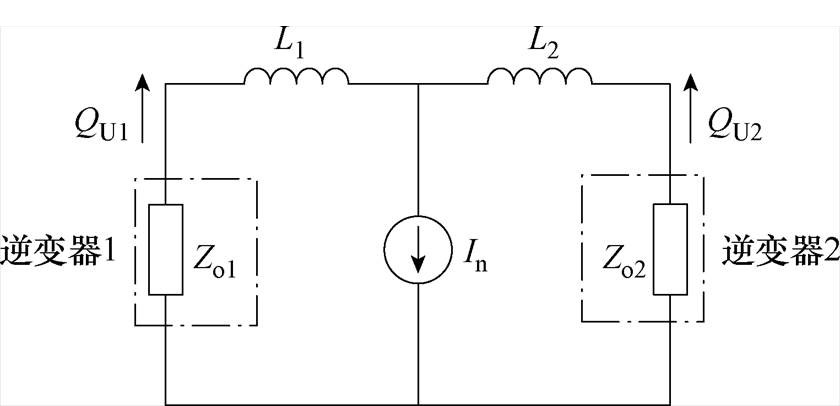
图3 负序基波频率处等效电路
Fig.3 Equivalent circuit at negative-sequence fundamental frequency
系统在谐波频率处等效电路如图4所示，其中非线性负载表示为谐波电流源Ih。由图4可知，谐波功率QHi的分配同样与每条支路的等效阻抗成反比关系。
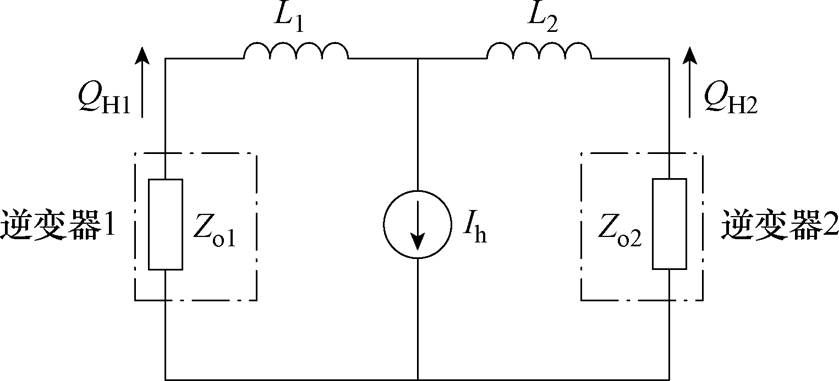
图4 谐波频率处等效电路
Fig.4 Equivalent circuit at harmonic frequencies
根据IEEE 1459—2010标准中给出的功率定 义[18]，对于一个电流中存在负序和谐波分量的三相系统，在不考虑电压不平衡及电压畸变的条件下，电压与谐波电流相互作用产生的谐波功率QH表示为
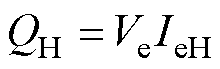（5）
式中，Ve为电压有效值；IeH为谐波电流有效值。
电压与负序基波电流相互作用产生的不平衡功率QU为
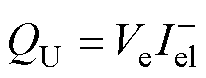（6）
式中，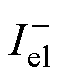
为基波电流负序分量。
电压与正序基波电流相互作用产生的基波正序视在功率S1为
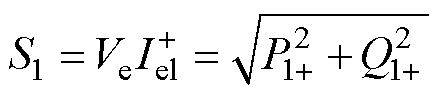（7）
式中，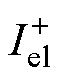
为基波电流正序分量；P1+为基波正序有功功率；Q1+为基波正序无功功率。
根据以上各式，有效视在功率S可表示为
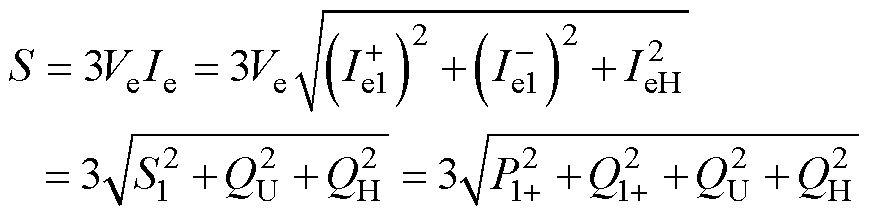（8）
式中，Ie为电流有效值。
综上所述，S由基波有功功率、基波无功功率、不平衡功率和谐波功率组成，则通过式（9）可求得非有功功率N，其包含无功功率、不平衡功率和谐波功率。
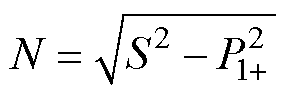（9）
通过式（9）求取非有功功率，可避免提取负序与各次谐波电流来计算不平衡功率与谐波功率，以简化计算量与实现难度。
为实现非有功功率的均分，本文采用注入特定谐波电压自适应地调节虚拟阻抗的方法[25]。该方法既不依赖通信，也不需要线路阻抗信息，其实现原理如下。
根据第1节的理论分析可知，为实现非有功功率的合理分配，可通过在逆变器控制回路中引入虚拟阻抗以调节各逆变器支路的等效阻抗。在线路阻抗为感性的前提下只需要加入虚拟电感即可，如此一来逆变器并联系统的简化等效电路如图5所示，其中Lv1和Lv2为虚拟电感，L1和L2为线路电感。显然虚拟电感同逆变器输出的N呈负相关，虚拟电感增加则N减小，当且仅当线路阻抗和虚拟阻抗满足式（10）中的关系时，N可在并联逆变器中实现均分。
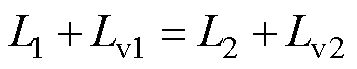（10）
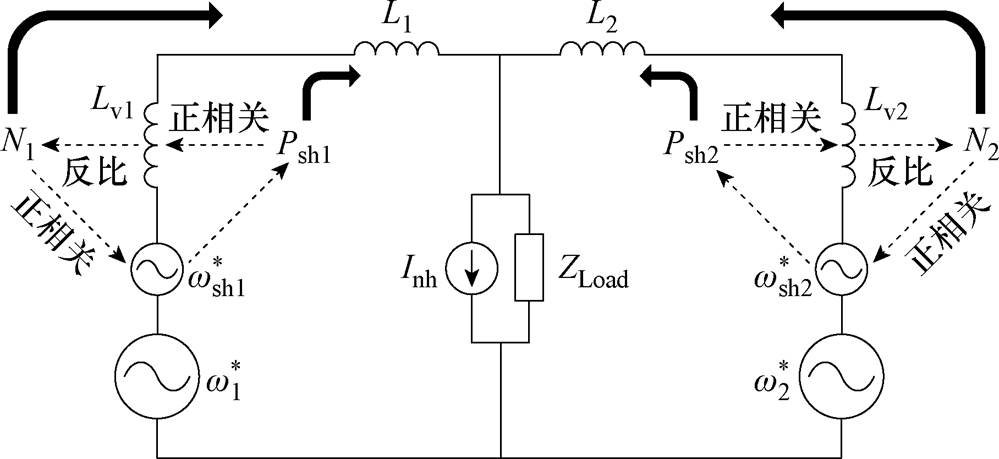
图5 调节过程示意图
Fig.5 Regulation process schematic diagram
受有功功率-频率下垂控制均分有功功率的启发，本文在逆变器输出电压中注入另一个高频的低幅值特定谐波电压，通过该电压的频率与控制目标N构建类似的下垂关系，称之为N-wsh下垂，则
（11）
式中，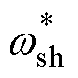
为特定谐波电压角频率实际指令值；wsh0为特定谐波电压角频率额定值（各逆变器设为同一值）；ksh为特定谐波电压下垂系数，为在图5的调节过程中形成负反馈回路，定义ksh为正。当各台逆变器容量相同时，ksh取相同值；当逆变器容量不同时，ksh应与其容量成反比，使N按照逆变器容量等比例均分。
在构建式（11）所示N-wsh下垂之后，控制环路仍是不完整的。特定谐波电压频率变化会引起特定谐波电压有功功率的变化，而N的调节变量是虚拟阻抗的大小，特定谐波电压有功功率和虚拟阻抗之间不存在任何关联，因此在控制环中人为构建两者之间的耦合关系，称之为Psh-Lv耦合关系，即
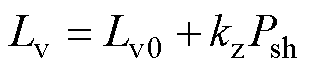（12）
式中，Lv为虚拟阻抗；Lv0为虚拟电感基准值（本文中设为0）；Psh为逆变器输出的特定谐波电压有功功率；kz为耦合系数，表示在Psh和Lv间形成正相关的关系，定义kz为正，文献[25]对其进行了类似的稳定性分析和方法设计，本文不作详细讨论。
图5展示了本方法的基本原理。假设系统中线路阻抗L1＞L2，则在开始调节前有N1＜N2。根据式（11）中的N-wsh下垂关系，有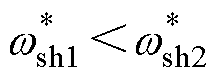
，即逆变器1的特定谐波电压相位减小，而逆变器2的特定谐波电压相位增加，进而导致Psh1减小，而Psh2增加。又根据式（12）中的Psh-Lv耦合关系，Lv1将会减小，Lv2将会增加，由此将使N1增加，而N2减小。这种负反馈机制可以自适应地调节虚拟阻抗以补偿线路阻抗的差异，使非有功功率的分配比例趋于均等。且由于特定谐波电压频率是全局变量，在系统进入稳态时各逆变器的特定谐波电压会达到频率同步，由式（10）可知此时的N是均分的。
图6为本文针对非有功功率均分提出的双频率下垂控制策略整体框图。控制策略主要由四个部分组成，分别为功率计算模块、N-wsh下垂控制模块、P-w下垂控制模块及虚拟阻抗压降合成模块。通过功率计算环节，求得逆变器输出的P、N和Psh；再由P-w下垂与N-wsh下垂环节得到基波参考电压与特定谐波参考电压，通过Psh-Lv耦合关系实现虚拟阻抗的自适应调节，并计算逆变器输出电流通过虚拟电感产生的压降；最后根据得到的基波参考电压、特定谐波参考电压和虚拟阻抗上的压降生成总参考电压。电压电流内环采用ab坐标系下的多谐振控制器以准确跟踪特定谐波参考电压。以下将对图6中关键的特定谐波电压参数选取、功率计算、电流信号提取及虚拟阻抗压降的计算的具体实现方法进行详细介绍。
2.2.1 特定谐波电压参数选取
在逆变器输出电压中注入特定谐波电压，需在控制架构中同时引入特定谐波参考电压指令和对应频率的谐振控制器，构建完整的谐波电压跟踪闭环。为尽量避免特定谐波电压带来的不利影响，其频率和幅值需要精心设计。
图6 总体控制框图
Fig.6 Overall control block diagram
1）特定谐波电压频率选取
文献[28]提出特定谐波电压频率的设计应避免(6k+3)f次谐波，k为整数，f为基波频率；否则，虚拟阻抗波形会因非线性和不平衡负载而产生波纹，也应避免(6k+4)f次谐波，否则将由于非线性负载和注入的特定谐波电压而产生波纹，并建议选择(6k+2)f或6kf次谐波，如300、400或100 Hz。本文采用300 Hz的特定谐波电压频率。
2）特定谐波电压幅值选取
本文特定谐波电压的幅值为固定常数，用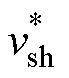
表示，幅值的选取需要同时考虑信号提取和电压质量问题。显然，特定谐波电压幅值越高越容易进行提取，但由此引入的电压畸变也会更加严重。考虑到IEEE 519标准中建议电压总谐波畸变率不高于8%，单次谐波电压畸变率不高于5%[29]，选取基波电压幅值的0.5%～2%作为特定谐波电压幅值。特定谐波电压频率和电压幅值确定后，则特定谐波参考电压在ab坐标系中表示为
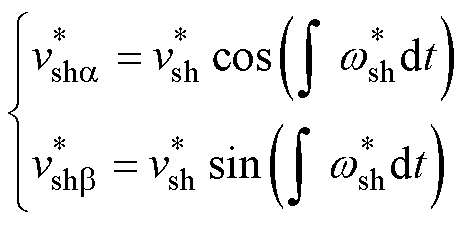（13）
式中，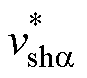
为特定谐波电压的a轴分量；
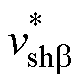为特定谐波电压的b轴分量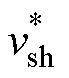；为特定谐波电压幅值。
2.2.2 功率计算
IEEE 1459—2010标准中使用了有效视在功率S的定义[18]，即保持系统有功功率损耗不变，将三相非平衡系统等效为三相平衡系统，得到等效变量Ue、Ie分别为
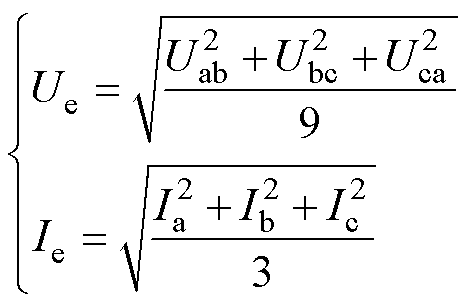（14）
式中，Ue为等效电压；Uab、Ubc、Uca为线电压；Ia、Ib、Ic为线电流。
则逆变器输出的S为
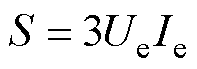（15）
有功功率P及特定谐波电压有功功率Psh分别为
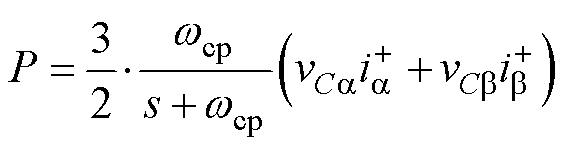（16）
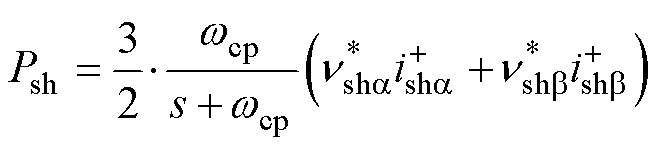（17）
式中，wcp为低通滤波器的截止频率；vCa和vCb分别为逆变器输出电压的a轴分量和b轴分量；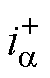
和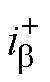
分别为基波电流的a轴正序分量和b轴正序分量；
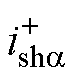和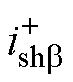
分别为特定谐波电流的a轴正序分量和b轴正序分量。低通滤波器用于滤除功率中的纹波和噪声，本文设置截止频率wcp=31 rad/s。
2.2.3 电流信号提取
为计算有功功率与特定谐波电压有功功率，需要对输出电流中的特定谐波分量进行分离提取。本文采用文献[30]提出的基于二阶广义积分器（Second Order Generalized Integrator, SOGI）的提取方法，该方法结构简单、提取准确、抗干扰能力强、动态响应速度快，其具体原理如图7所示。
图7 电流信号提取原理
Fig.7 Current signal extraction schematic diagram
首先通过基波电流和特定谐波电流的交叉反馈，形成谐波解耦网络（Harmonic Decoupling Net- work, HDN），以消除两电流分量之间的相互影响，之后通过分别工作在a轴和b轴的双SOGI正交信号发生器（Dual SOGI-Quadrature Signal Generator, DSOGI-QSG）提取不同频率的信号分量，其内部结构如图7b所示。为方便理解，可将SGGI-QSG看作一个带通滤波器，只有频率等于谐振频率ws的信号分量才能通过，系数k需在信号提取精度和提取速度之间折中考虑，本文取k=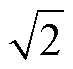
[30]。SGGI-QSG除可以提取谐振频率ws的分量外，还可以生成与该分量垂直并滞后90°的正交分量。在已知一个不平衡三相信号的a轴分量、b轴分量和对应的正交分量时，可以根据对称分量法将其正序分量和负序分量分离出来，图7c中所示的正负序计算（Positive- Negative-Sequence Calculation, PNSC）环节正是基于该原理。通过图7中的信号提取环节可以获得功率计算所需要的
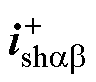及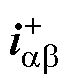
。
2.2.4 虚拟阻抗压降的计算
本文提出的自适应虚拟阻抗控制策略通过式（12）所示的耦合关系实现虚拟阻抗随特定谐波电压有功功率的实时调节。确定虚拟阻抗的大小后，需计算输出电流在虚拟阻抗上产生的压降，并在参考电压中减去该压降，以此来模拟真实阻抗的特性。若直接计算虚拟阻抗压降，则容易放大高频噪声，降低控制系统的暂态稳定性[31]。因此本文采用如图8所示的低通滤波微分环节计算虚拟阻抗压降[32]，其中，vzαβ为虚拟阻抗压降；iOab为逆变器输出电流；Rv为虚拟电阻（可提供有源阻尼，抑制系统谐振）；Lv为虚拟电感；wc为截止频率。该方法通过在传递函数中插入一个低通滤波器来衰减高频噪声，避免了高频噪声放大。通过设置合理的截止频率wc，可将频率高于wc的电流信号过滤，逆变器输出电流通过该低通滤波微分环节可等效成低于wc的电流信号在阻抗为Rv+jwLv的虚拟阻抗上产生的压降。
图8 低通滤波微分环节
Fig.8 Low-pass filter differential link
本节通过建立系统的小信号线性化模型，分析了系统的稳定性，并给出了ksh的设计方法。该模型中选择非有功功率在两台逆变器之间的分配误差作为控制闭环的被控对象。由于功率外环的控制带宽远低于电压内环的控制带宽，因此忽略电压内环的动态特性。通过在系统稳态工作点附近引入小的扰动，获得系统的小信号线性化模型，模型中带有符号“
”的变量表示扰动信号。
对注入的特定谐波信号分析，假设在稳态工作点附近引入很小的负载扰动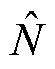
，由式（11）可得
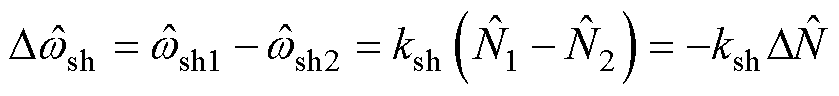（18）
式中，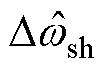
为逆变器间特定谐波电压频率差扰动；
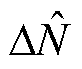为逆变器间非有功功率差扰动。
则两逆变器间的特定谐波电压相位差扰动为
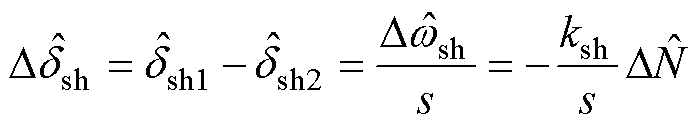（19）
式中，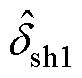
、
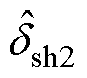分别为逆变器1、2的特定谐波电压相位扰动信号；
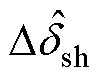为特定谐波电压相位差扰动信号。
每台逆变器输出的特定谐波有功功率之和应该等于负载上消耗的特定谐波有功功率，如式（20）所示，在负载不变的情况下可以认为是一个常数。
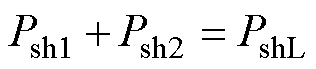（20）
式中，PshL为负载上消耗的特定谐波有功功率；Psh1、Psh2分别为逆变器1、2的特定谐波有功功率。由于PshL由PCC处特定谐波电压幅值决定，与两台逆变器特定谐波电压的相位变化无关，因此PshL可以近似看作常数，也就是说特定谐波有功功率扰动仅在逆变器之间流动，因此特定谐波有功功率扰动项为
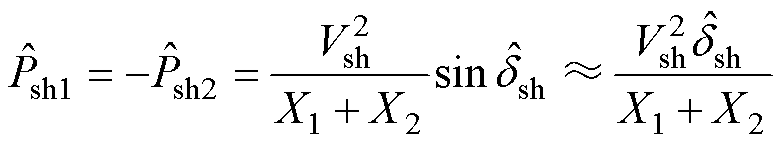（21）
则由式（12）和式（21）可得两台逆变器虚拟电感扰动项的关系为
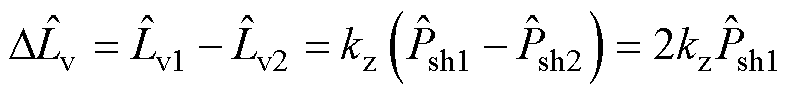（22）
对非有功功率进行分析，两逆变器间的非有功功率的分配误差扰动为
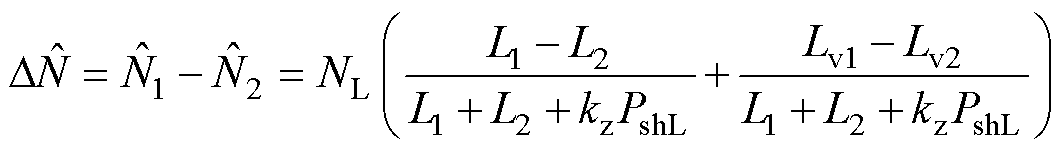（23）
式中，NL为负载吸收的总非有功功率功率，负载情况一定时为常数。
DN的小信号线性化表示式为
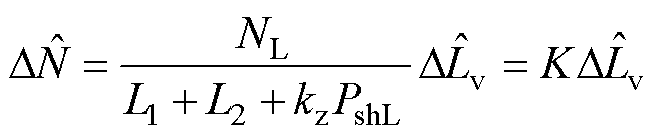（24）
式中，K=NL/(L1+L2+kzPshL)，kz确定后K为常数，结合式（18）、式（19）、式（21）、式（22）和式（24）可得完整的系统闭环模型如图9所示。
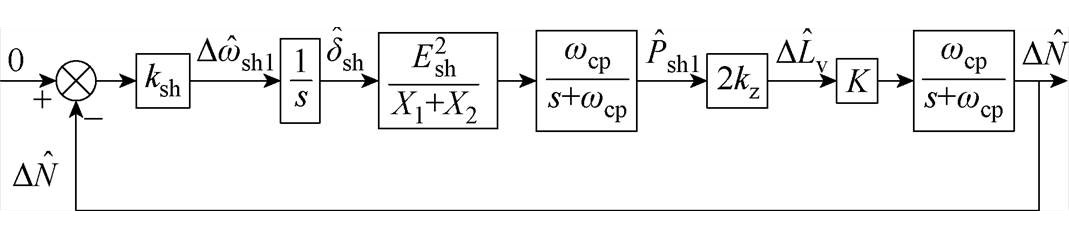
图9 系统小信号线性化模型
Fig.9 System small signal linearization model
这里将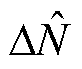作为闭环控制的被控对象，要实现功率均分，就要将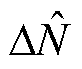控制为0。另外，该模型还需要考虑计算Psh和N时的低通滤波器，因其截止频率较低，对系统动态影响较大。
由上述推导得到的系统模型，可以写出其开环传递函数为
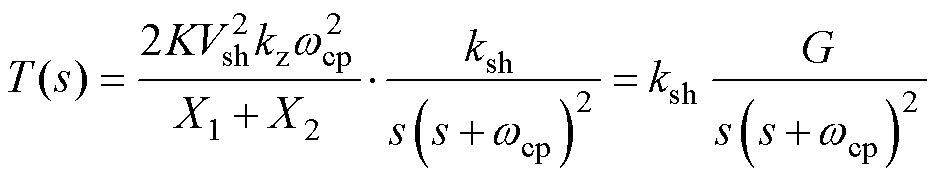（25）
式中，G=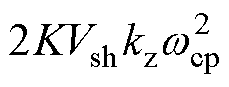
/(X1+X2)，在kz确定后G为常数。ksh可看作是增益，画出开环传递函数的伯德图如图10所示。图中给出了当ksh分别取0.000 01、0.000 5、0.001和0.002时的开环传递函数的伯德图，其相频特性曲线完全重合，幅频特性曲线随着ksh的增加而上移，也就是说，系统带宽增加但是稳定裕量减小。为了保证系统的稳定性，根据劳斯稳定性判据ksh需满足
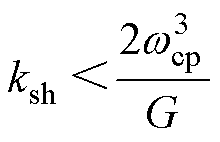（26）
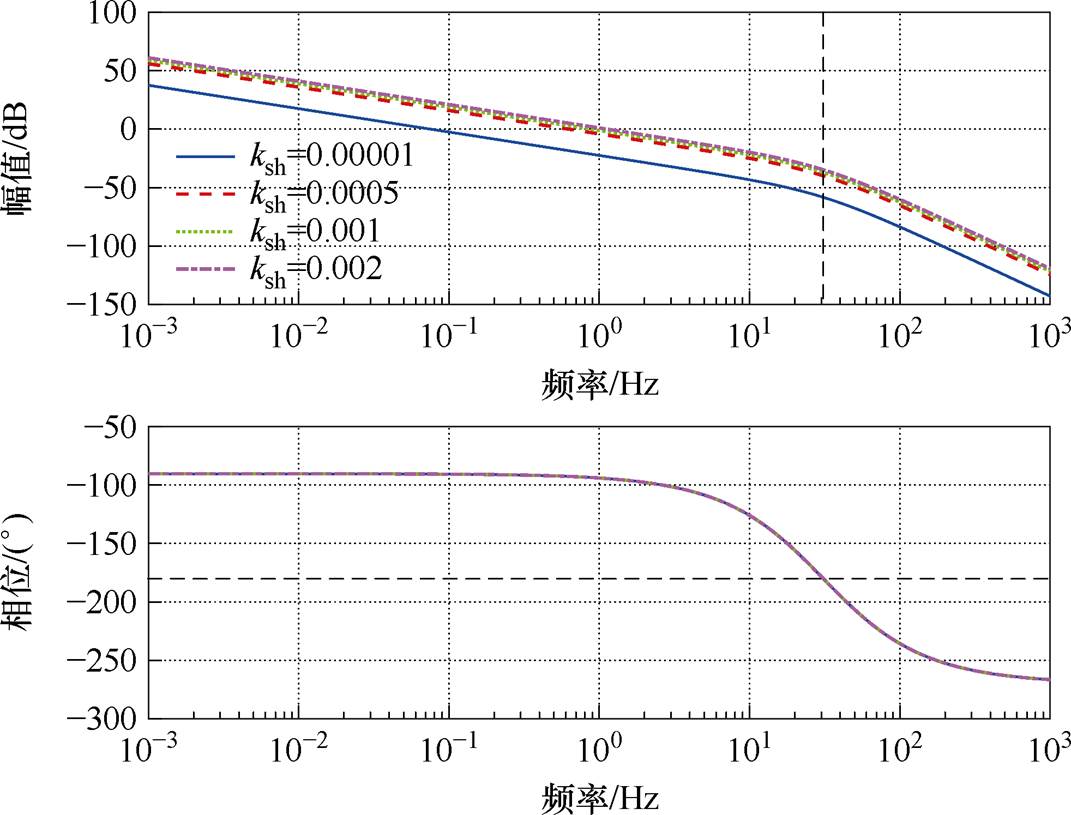
图10 系统开环传递函数的伯德图
Fig.10 Bode plot of open-loop transfer function in the system
为了验证本文所提出的非有功功率均分策略的可行性，在Matlab/Simulink平台中搭建图1所示的微电网系统仿真模型。该系统包含两台容量相同的逆变器，系统额定电压为380 V、频率为50 Hz、逆变器直流侧额定电压为700 V。负载侧包含电阻平衡负载、电感平衡负载、单相负载和非线性负载。系统仿真参数见表1。
表1 仿真和实验参数
Tab.1 Simulation and experimental parameters
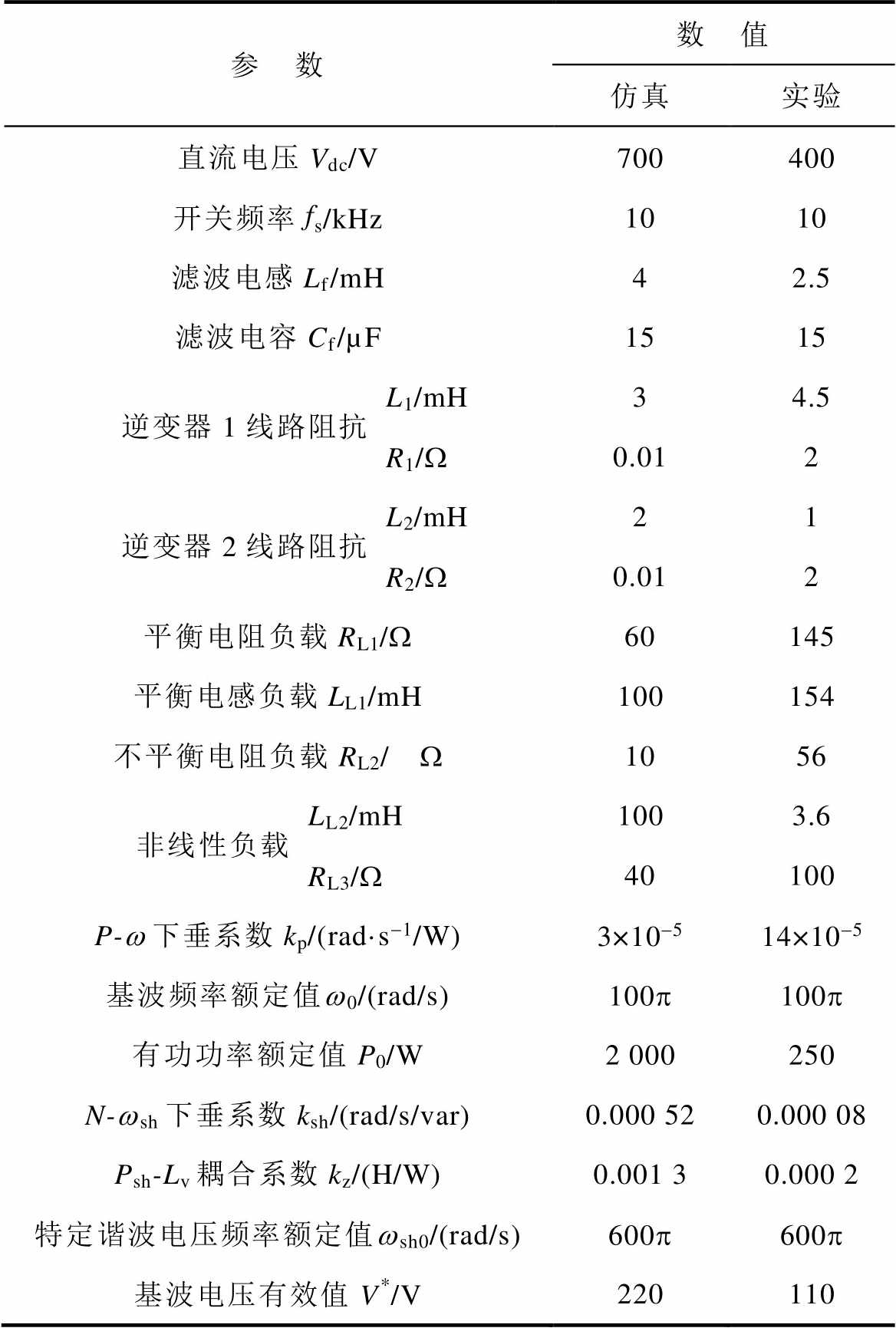
参 数数 值 仿真实验 直流电压Vdc/V700400 开关频率fs/kHz1010 滤波电感Lf/mH42.5 滤波电容Cf/µF1515 逆变器1线路阻抗L1/mH34.5 R1/W0.012 逆变器2线路阻抗L2/mH21 R2/W0.012 平衡电阻负载RL1/W60145 平衡电感负载LL1/mH100154 不平衡电阻负载RL2/W1056 非线性负载LL2/mH1003.6 RL3/W40100 P-w下垂系数kp/(rad·s-1/W)3×10-514×10-5 基波频率额定值w0/(rad/s)100p100p 有功功率额定值P0/W2 000250 N-wsh下垂系数ksh/(rad/s/var)0.000 520.000 08 Psh-Lv耦合系数kz/(H/W)0.001 30.000 2 特定谐波电压频率额定值wsh0/(rad/s)600p600p 基波电压有效值V*/V220110
为验证所提控制策略的有效性，仿真采用对比实验设计：在初始阶段（t＜2.5 s
，两台逆变器均采用传统下垂控制，此时特定谐波电压频率保持额定值且将虚拟电感置零，此时特定谐波电压不具备调节功能；在t=2.5 s时刻切换至本文提出的双频率下垂控制，观察切换后关键波形的变化。
图11展示了有功功率、非有功功率和虚拟电感三组波形的变化。从图11a可以观察到，当控制方法切换时，有功功率经历短暂暂态过程后重新恢复均分状态；图11b的波形对比清晰地展示了本文所提控制方法的效果，在传统控制阶段，非有功功率分配完全由线路阻抗自然决定，而采用本文方法后，非有功功率能平滑地实现精确均分；由图11c可以看出，由于线路阻抗不同，两台逆变器通过产生不同的虚拟电感，以补偿线路阻抗的差异，逆变器1虚拟电感约-0.2 mH，逆变器2虚拟电感约0.8 mH，以弥补1 mH的线路阻抗差异，近似满足式（10）的要求，可以保证每台逆变器的等效阻抗相等。
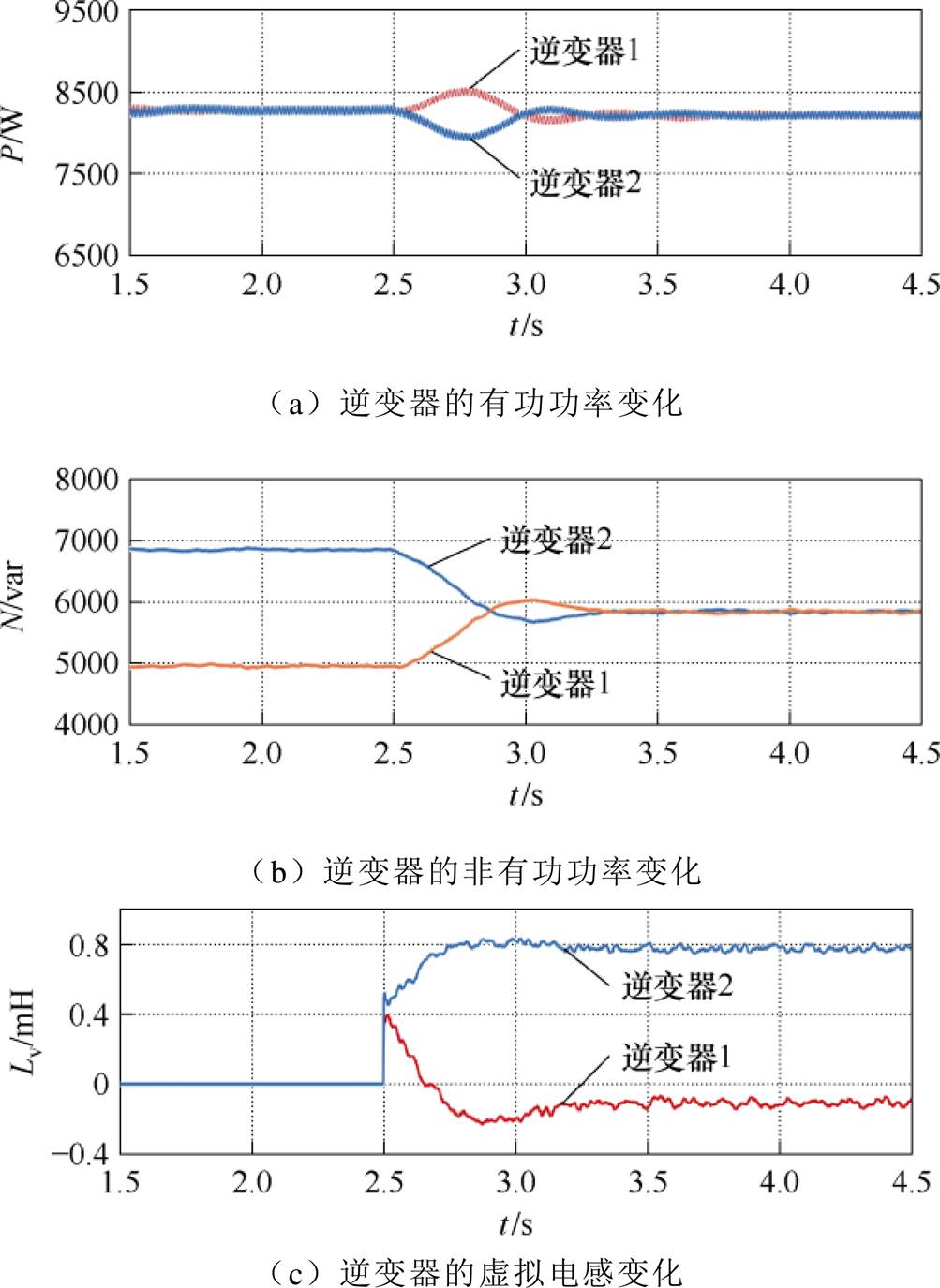
图11 从下垂控制切换到双频率下垂控制逆变器的有功功率、非有功功率及虚拟电感的变化
Fig.11 Transient characteristics of active power, nonactive power and virtual inductance during control mode transition from droop to dual-frequency droop
通过观察逆变器间的均流效果也能直观地反映非有功功率均分的效果。图12和图13分别展示了传统下垂控制与本文所提控制策略下两台逆变器的输出电流对比。
仿真结果表明：非有功功率不均分将会引起逆变器输出电流的差异，承担较大非有功功率的逆变器输出电流偏大，面临着输出过电流的风险以及潜在的散热不均衡问题。当切换本文方法后，两台逆变器各相输出电流基本重合，不仅验证了非有功功率均分效果，更从均流性能、波形质量等方面验证了该方法的工程实用价值。
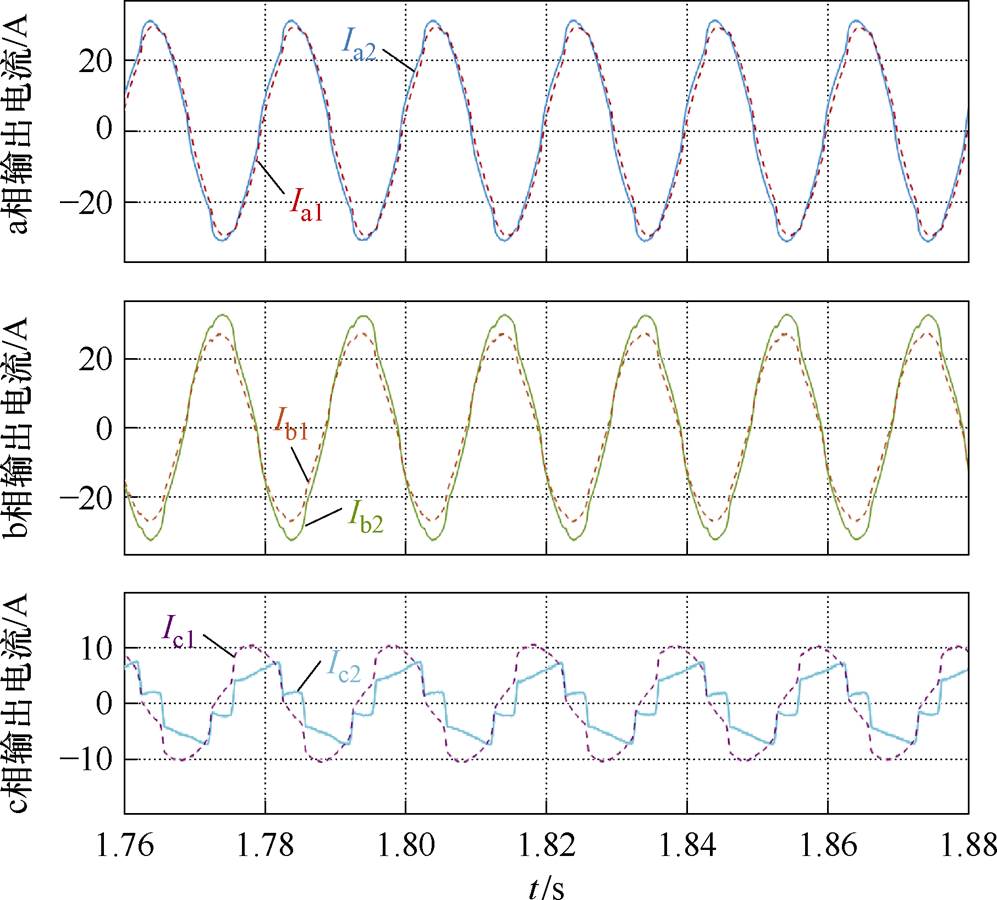
图12 逆变器采用下垂控制的输出电流
Fig.12 Output current of inverter with droop control
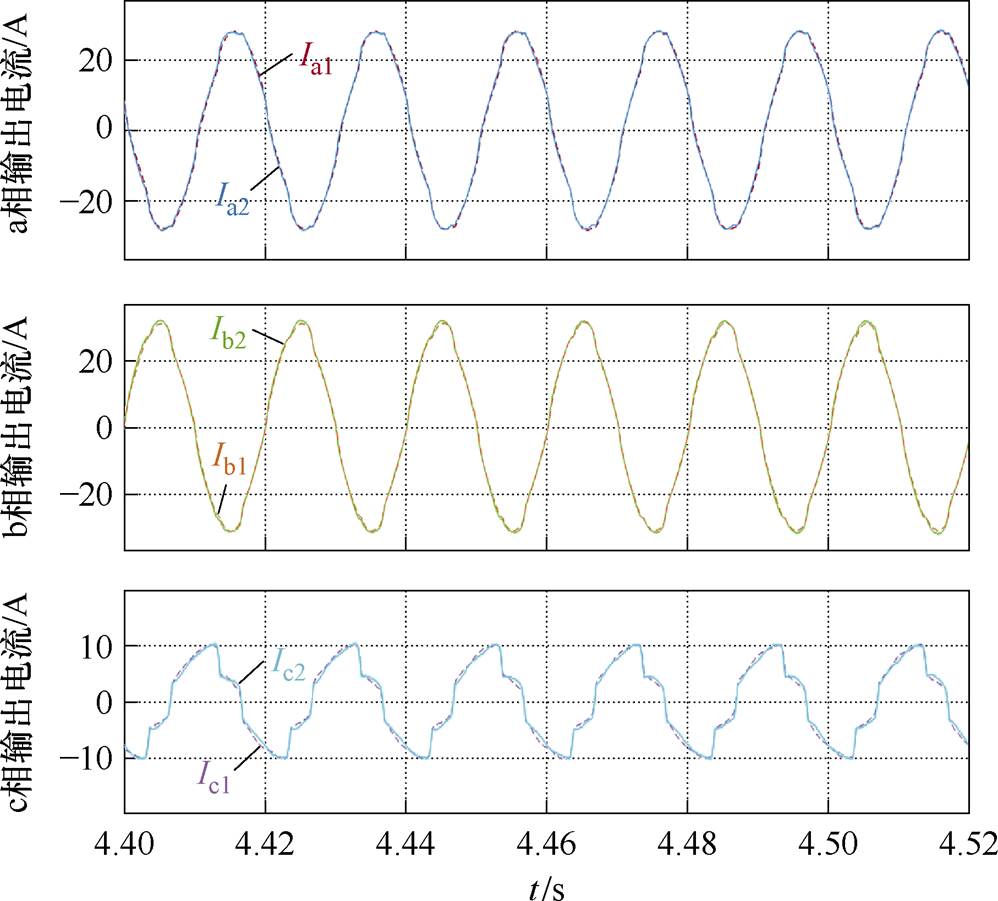
图13 逆变器采用双频率下垂控制的输出电流
Fig.13 Output current of inverter with dual-frequency-droop control
为验证本文所提方法的优越性，在相同仿真条件下，将双频率下垂控制方法与文献[25]中的小信号注入法进行对比，通过观察逆变器间的均流效果直观地反映非有功功率均分性能，结果如图14所示。
图14展示了采用小信号注入法时逆变器的输出电流波形，与图13所示双频率下垂控制的结果相比，在含无功负载的工况下，文献[25]方法的均流效果明显欠佳。仿真结果表明，本文提出的双频率下垂控制在负载的适应性范围里具有较好的优越性，能实现更好的功率均分效果。
为进一步验证本文提出策略的适用性，图15展示了双频率下垂控制下负载变化时非有功功率的动态响应过程。t1时刻前系统已稳定运行于双频率下垂控制，在t1时刻投入不平衡负载，t2时刻投入非线性负载，t3时刻投入无功负载，t4时刻切除对应的无功负载，t5时刻切除对应的非线性负载，t6时刻切除对应的不平衡负载。可以看出，系统在面对不同负载投入或切除时都能快速地恢复稳定运行，并实现非有功功率的均分。
图14 逆变器采用小交流信号注入法的输出电流
Fig.14 Output current of inverter with small-AC-signal injection control method
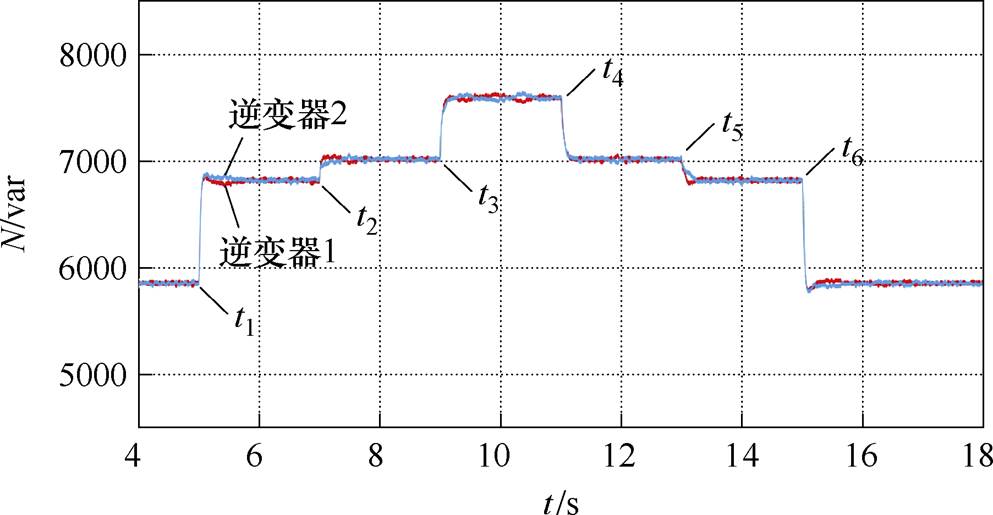
图15 双频率下垂控制负载变化时非有功功率变化
Fig.15 Nonactive power variation during dual-frequency droop control load changes
根据理论分析与仿真模型，搭建如图16所示的逆变器并联系统实验平台，验证本文所提的基于双频率下垂的非有功功率均分控制方法，参数见表1。
基于实验室现有环境，利用两台相同规格的逆变器搭建逆变器并联系统，通过不同线路阻抗并联在一起，直流侧由稳压直流电源提供400 V直流电压，考虑到实验安全性，逆变器端口相电压有效值为110 V。实验通过对比传统下垂控制与双频率下垂控制的输出特性验证所提方法的有效性。实验结果表明：传统下垂控制下，由于逆变器间线路阻抗的差异，有功功率虽能均分，但各逆变器输出的非有功功率有较大差异，两台逆变器输出的P、N波形如图17所示。切换到双频率下垂控制后N实现了均分，有功功率经历短暂暂态过程后重新恢复均分状态，与仿真结果相符。
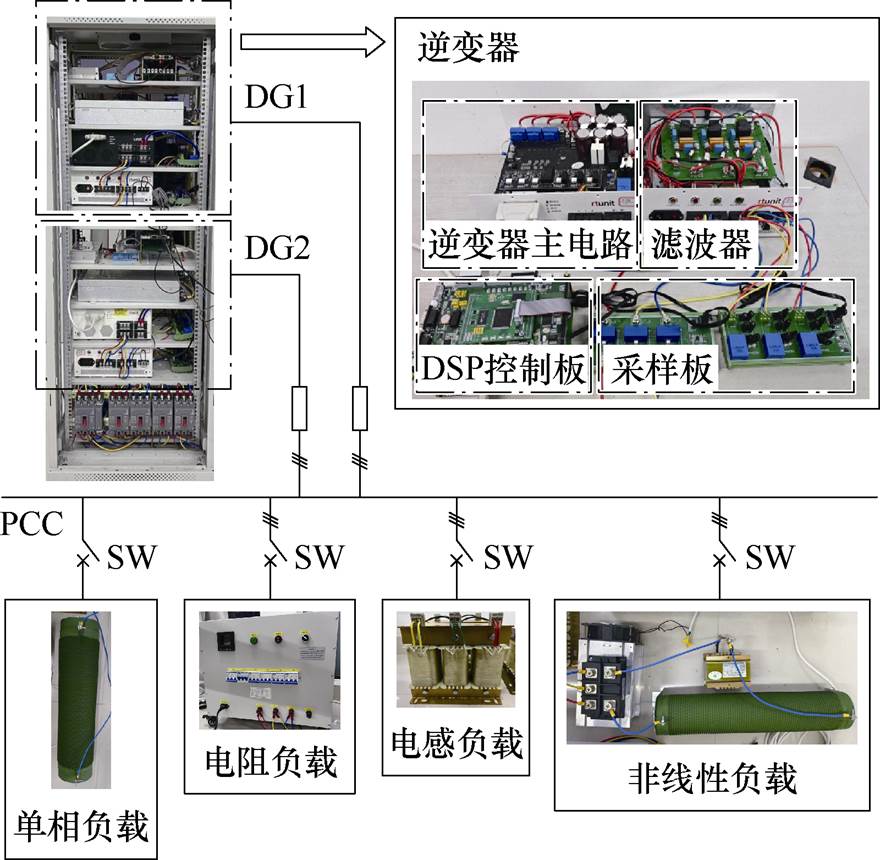
图16 实验平台
Fig.16 Experimental platform
图17 两台逆变器输出的P、N波形
Fig.17 Output waveforms of P and N under inverters
下垂控制下两逆变器各相输出电流对比如图18所示。从图18可以看出，在线路阻抗存在差异的工况下，传统下垂控制的两逆变器间的电流因无功功率不能均分存在一定的相位差，同时不平衡和谐波功率的不均分也使得逆变器间的电流幅值存在较大差异，容易存在逆变器过电流风险。
为更好地观察N的均分效果，从图19所示的两台逆变器各相输出电流的对比可以看出，采用本文方法后各相电流都实现了较好的均流效果，验证了本方法的有效性。综上所述，实验结果与仿真结果相吻合，与理论分析一致，验证了所提的控制策略能实现逆变器并联系统非有功功率均分。
为进一步验证本文提出策略的适用性，图20展示了在原实验基础上，采用双频率下垂控制时负载工况变化时非有功功率的动态响应过程。
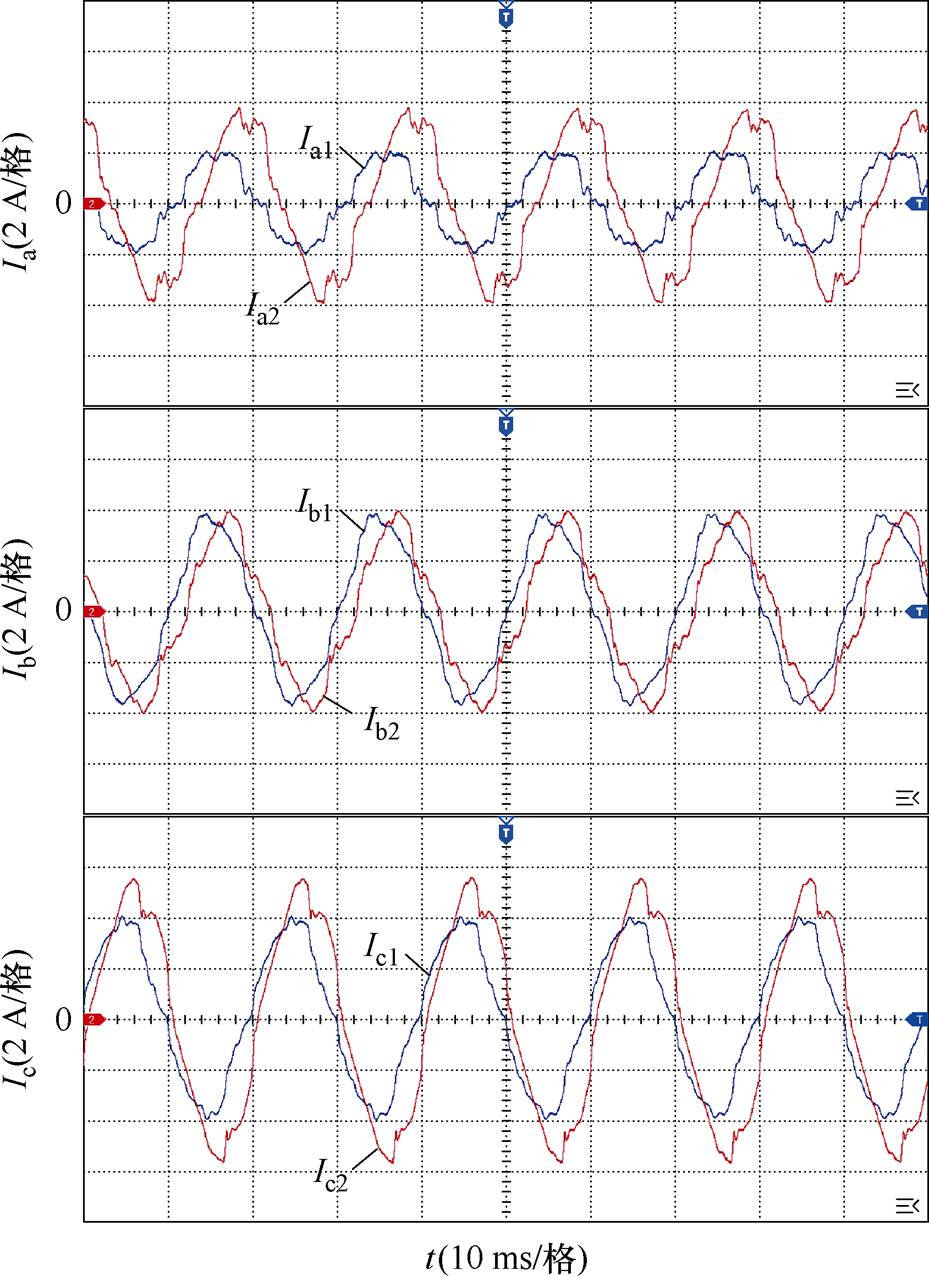
图18 下垂控制下两逆变器各相输出电流对比
Fig.18 Phase current comparison of dual inverters under droop control
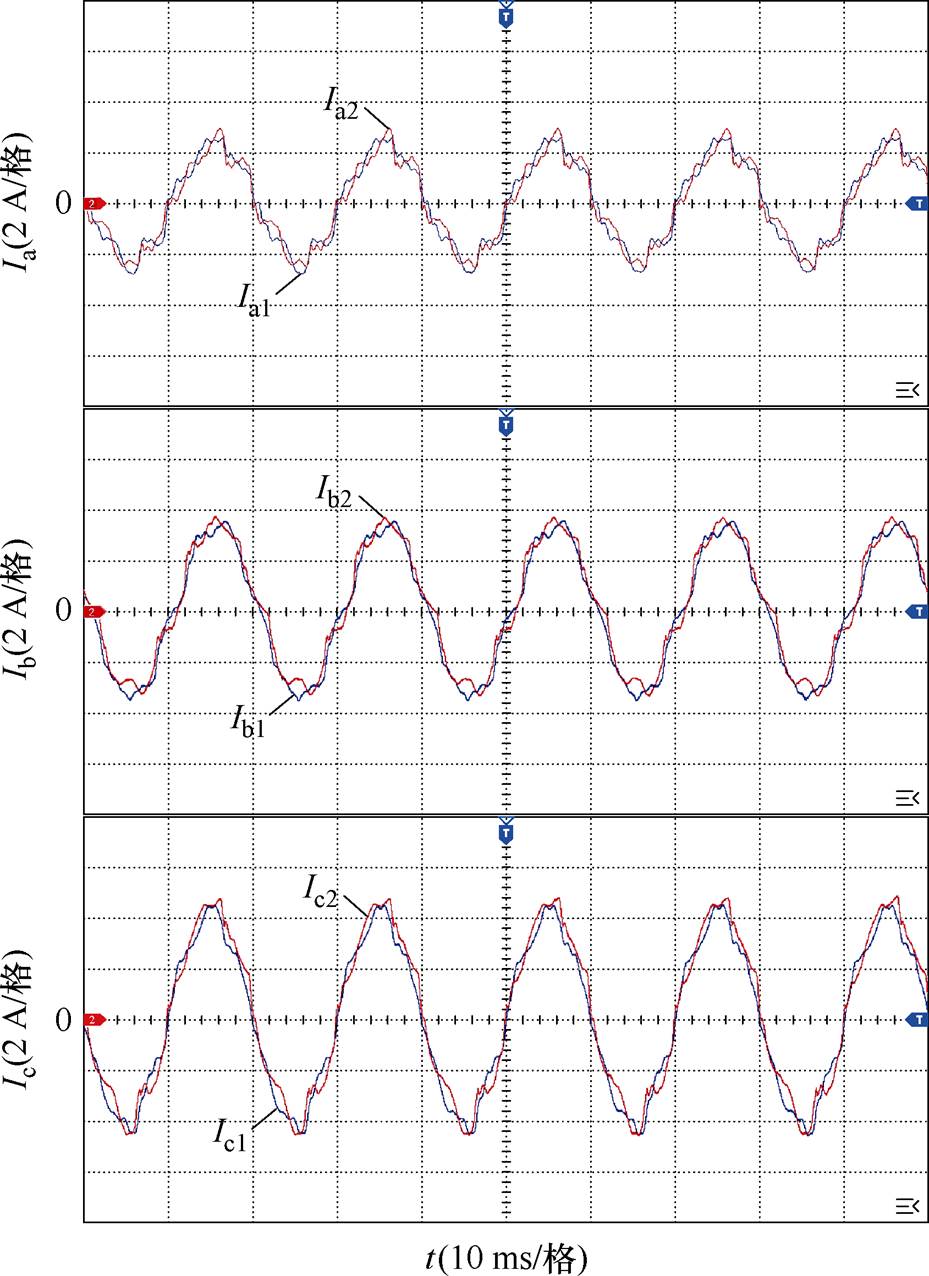
图19 双频率下垂控制下两逆变器各相输出电流对比
Fig.19 Phase current comparison of dual inverters under dual-frequency droop control
t1时刻前系统已稳定运行于双频率下垂控制，在t1时刻投入不平衡负载，t2时刻投入非线性负载，t3时刻投入无功负载，t4时刻切除对应的无功负载，t5时刻切除对应的非线性负载，t6时刻切除对应的不平衡负载。实验结果表明，所提控制策略在混合负载扰动下均能实现非有功功率的均分，验证了其在复杂微电网场景中的工程应用价值。
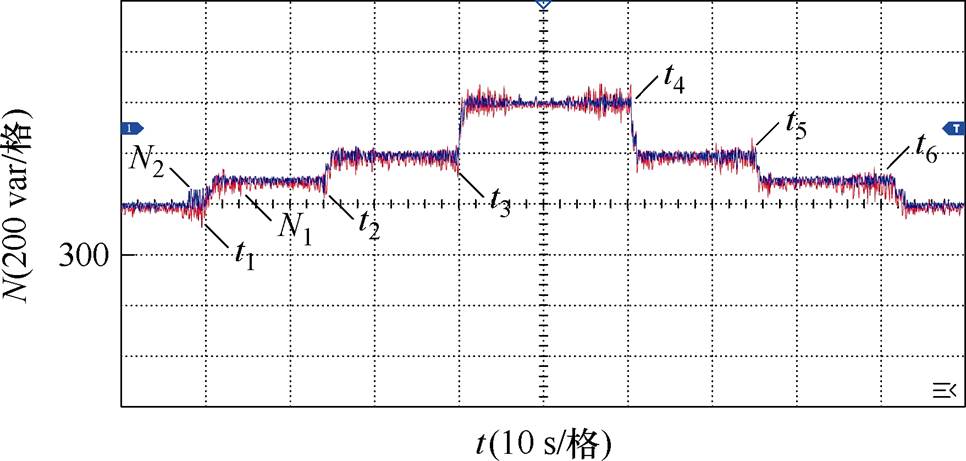
图20 双频率下垂控制负载变化时非有功功率变化
Fig.20 Nonactive power variation during dual-frequency droop control load changes
传统下垂控制适用于中小规模、以感性阻抗为主的低压微电网，特别适合三相负载基本平衡、谐波含量较低的线性负载场景，常见于工业阻感负载供电系统或对电能质量要求不高的备用电源系统。该控制方式在分布式发电单元容量差异较小、线路阻抗差异有限且无需通信的条件下，能够实现基本的有功、无功功率分配，但当系统出现高比例非线性负载、不平衡或大阻抗差异时，其控制性能将显著恶化。
本文提出的双频率下垂控制可适用于高比例新能源接入的复杂微电网场景，特别针对存在显著线路阻抗差异、谐波含量高和三相不平衡的电力系统。根据仿真与实验验证，该控制方法在包含混合线性负载、非线性负载、单三相混合供电以及多逆变器并联的现代微电网中表现优异，能够同步实现基波有功功率、无功功率以及谐波与不平衡功率的均分。典型应用场景包括：含有电动汽车充电站、变频驱动设备等非线性负载的工商业微电网；以及线路阻抗差异较大的分布式发电系统。相比传统下垂控制，双频率下垂控制在保持无通信优势的同时，拓展了对复杂负载工况的适应能力。
本文针对线路阻抗存在差异的逆变器并联系统，提出了一种基于双频率下垂的逆变器并联系统非有功功率均分控制策略。该策略引入特定谐波电压信号作为功率调节媒介，建立了非有功功率与虚拟阻抗之间的动态耦合关系，并利用非有功功率-特定谐波电压频率下垂控制实现虚拟阻抗自适应调节，有效地解决了传统控制方法中无功功率、不平衡与谐波功率不能同时均分的问题。仿真与实验结果充分证明了该方法的有效性。
该方法可实现逆变器并联系统的精确功率均分，无需并联逆变器之间的通信连接，无需获取线路阻抗信息，广泛适用于交流微电网、储能等多逆变器并联系统，使微电网在接入大量非线性负载与单相负载时维持系统的稳定运行，具有较好的工程应用价值。
参考文献
[1] 闫佳佳, 滕云, 邱实, 等. 计及供能可靠性动态约束与碳减排的充能型微电网互联系统优化模型[J]. 电工技术学报, 2022, 37(23): 5956-5975.
Yan Jiajia, Teng Yun, Qiu Shi, et al. Optimization model of charging microgrid interconnection system considering dynamic constraints of energy supply reliability and carbon emission reduction[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(23): 5956-5975.
[2] 盛万兴, 吴鸣, 季宇, 等. 分布式可再生能源发电集群并网消纳关键技术及工程实践[J]. 中国电机工程学报, 2019, 39(8): 2175-2186, 1.
Sheng Wanxing, Wu Ming, Ji Yu, et al. Key techniques and engineering practice of distributed renewable generation clusters integration[J]. Pro- ceedings of the CSEE, 2019, 39(8): 2175-2186, 1.
[3] 张基岳, 任洲洋, 姜云鹏, 等. 微电网定碳排运行域: 理论、构建与观测[J]. 电工技术学报, 2024, 39(8): 2342-2359.
Zhang Jiyue, Ren Zhouyang, Jiang Yunpeng, et al. Committed carbon emission operation region of microgrids: theory, construction and observation[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2342-2359.
[4] 范培潇, 杨军, 温裕鑫, 等. 考虑电动汽车与微电网参与的配电网双层协调控制策略[J]. 电力系统自动化, 2024, 48(19): 60-68.
Fan Peixiao, Yang Jun, Wen Yuxin, et al. Bi-layer coordinated control strategy of distribution network considering participation of electric vehicles and microgrid[J]. Automation of Electric Power Systems, 2024, 48(19): 60-68.
[5] 范培潇, 杨军, 温裕鑫, 等. 基于可进化模型预测控制的含电动汽车多微电网智能发电控制策略[J]. 电工技术学报, 2024, 39(3): 699-713.
Fan Peixiao, Yang Jun, Wen Yuxin, et al. A multi microgrid intelligent generation control strategy with electric vehicles based on evolutionary model predictive control[J]. Transactions of China Elec- trotechnical Society, 2024, 39(3): 699-713.
[6] 王浩, 仵哲, 康博阳, 等. 考虑电动汽车和蓄电池联合储能的交直流混合微电网功率协调控制策略[J].电工技术学报, 2024, 39(19): 6085-6103.
Wang Hao, Wu Zhe, Kang Boyang, et al. Power coordinated control strategy for AC/DC Hybrid microgrid considering combined energy storage of electric vehicles and batteries[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 6085- 6103.
[7] 何晋伟, 王坤放, 王瑞琪, 等. 电流源-电压源变流器混合并联独立供电系统的分布式功率控制[J]. 电力系统自动化, 2023, 47(23): 12-22.
He Jinwei, Wang Kunfang, Wang Ruiqi, et al. Distributed power control for hybrid parallel independent power supply system with current source and voltage source converters[J]. Automation of Electric Power Systems, 2023, 47(23): 12-22.
[8] 王力, 胡佳成, 曾祥君, 等. 基于混合储能的交直流混联微电网功率分级协调控制策略[J]. 电工技术学报, 2024, 39(8): 2311-2324.
Wang Li, Hu Jiacheng, Zeng Xiangjun, et al. Hierarchical coordinated power control strategy for AC-DC hybrid microgrid with hybrid energy storage[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2311-2324.
[9] Du Wenjuan, Fu Qiang, Wang H F. Power system small-signal angular stability affected by virtual synchronous generators[J]. IEEE Transactions on Power Systems, 2019, 34(4): 3209-3219.
[10] 于晶荣, 孙文, 于佳琪, 等. 基于惯性自适应的并网逆变器虚拟同步发电机控制[J]. 电力系统保护与控制, 2022, 50(4): 137-144.
Yu Jingrong, Sun Wen, Yu Jiaqi, et al. Virtual synchronous generator control of a grid-connected inverter based on adaptive inertia[J]. Power System Protection and Control, 2022, 50(4): 137-144.
[11] 刘勇, 刘鹏, 盘宏斌, 等. 基于改进下垂控制的多逆变器功率分配控制[J]. 电气传动, 2020, 50(12): 83-87.
Liu Yong, Liu Peng, Pan Hongbin, et al. Power distribution control of multi-inverter based on improved droop control[J]. Electric Drive, 2020, 50(12): 83-87.
[12] 许立, 董成哲. 基于虚拟阻抗的低压微网多逆变器环流抑制研究[J]. 电源学报, 2022, 20(5): 161- 168.
Xu Li, Dong Chengzhe. Research on circulating current suppression of multi-inverter in low-voltage microgrid based on virtual impedance[J]. Journal of Power Supply, 2022, 20(5): 161-168.
[13] 唐昆明, 王俊杰, 张太勤. 基于自适应下垂控制的微电网控制策略研究[J]. 电力系统保护与控制, 2016, 44(18): 68-74.
Tang Kunming, Wang Junjie, Zhang Taigin. Research on control strategy for microgrid based on adaptive droop control[J]. Power System Protection and Control, 2016, 44(18): 68-74.
[14] 周乐明, 罗安, 陈燕东, 等. 一种低延时鲁棒功率下垂控制方法[J]. 电工技术学报, 2016, 31(11): 1-12.
Zhou Leming, Luo An, Chen Yandong, et al. A low-delay robust droop control method[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(11): 1-12.
[15] 金国彬, 罗安, 陈燕东, 等. 基于P-V下垂系数修正的并联逆变器输出功率成比例分配实现[J]. 电工技术学报, 2016, 31(2): 112-120.
Jin Guobin, Luo An, Chen Yandong, et al. Pro- portional load sharing for parallel inverter systems based on modified P-V droop coefficient[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(2): 112-120.
[16] 刘宝谨, 刘进军, 刘增. 一种孤岛微网中均分不平衡功率的控制方法[J]. 电力电子技术, 2018, 52(10): 29-33.
Liu Baojin, Liu Jinjun, Liu Zeng. An unbalanced power sharing control method for islanded micro- grids[J]. Power Electronics, 2018, 52(10): 29-33.
[17] Adineh B, Keypour R, Davari P, et al. Review of harmonic mitigation methods in microgrid: from a hierarchical control perspective[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(3): 3044-3060.
[18] Definitions for the Measurement of Electric Power Quantities Under Sinusoidal, Nonsinusoidal, Balanced, or Unbalanced Conditions: IEEE 1459—2010[S]. IEEE, 2010.
[19] Fan Bishuang, Li Qikai, Wang Wen, et al. A novel droop control strategy of reactive power sharing based on adaptive virtual impedance in microgrids[J]. IEEE Transactions on Industrial Electronics, 2021, 69(11): 11335-11347.
[20] 陈宏志, 王旭, 刘建昌. 基于虚拟电阻匹配模式的逆变器并联方案[J]. 中国电机工程学报, 2012, 32(6): 24-32.
Chen Hongzhi, Wang Xu, Liu Jianchang. Current sharing method for parallel inverters based impedance matching mode[J]. Proceedings of the CSEE, 2012, 32(6): 24-32.
[21] 鲍薇, 胡学浩, 李光辉, 等. 独立型微电网中基于虚拟阻抗的改进下垂控制[J]. 电力系统保护与控制, 2013, 41(16): 7-13.
Bao Wei, Hu Xuehao, Li Guanghui, et al. An improved droop control strategy based on virtual impedance in islanded micro-grid[J]. Power System Protection and Control, 2013, 41(16): 7-13.
[22] 杨涛, 路晓庆, 董旭柱, 等. 交流微电网谐波功率分布式共享控制策略[J]. 高电压技术, 2024, 50(7): 3060-3069.
Yang Tao, Lu Xiaoqing, Dong Xuzhu, et al. Distributed control strategy for harmonic power sharing in AC microgrids[J]. High Voltage Engin- eering, 2024, 50(7): 3060-3069.
[23] Sreekumar P, Khadkikar V. A new virtual harmonic impedance scheme for harmonic power sharing in an islanded microgrid[J]. IEEE Transactions on Power Delivery, 2016, 31(3): 936-945.
[24] 吕志鹏, 盛万兴, 蒋雯倩, 等. 具备电压稳定和环流抑制能力的分频下垂控制器[J]. 中国电机工程学报, 2013, 33(36): 1-9, 239.
Lü Zhipeng, Sheng Wanxing, Jiang Wenqian, et al. Frequency dividing droop controllers with the function of voltage stabilization and circulation control[J]. Proceedings of the CSEE, 2013, 33(36): 1-9, 239.
[25] Liu Baojin, Liu Zeng, Liu Jinjun, et al. An adaptive virtual impedance control scheme based on small- AC-signal injection for unbalanced and harmonic power sharing in islanded microgrids[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 12333-12355.
[26] Burgos-Mellado C, Llanos J J, Cárdenas R, et al. Distributed control strategy based on a consensus algorithm and on the conservative power theory for imbalance and harmonic sharing in 4-wire micro- grids[J]. IEEE Transactions on Smart Grid, 2020, 11(2): 1604-1619.
[27] Yang Chunguang, Wu Xue, Song Qichao, et al. An enhanced power allocation strategy for microgrids considering frequency and voltage restoration[J]. Electronics, 2024, 13(10): 1966.
[28] An Ronghui, Liu Zeng, Liu Jinjun, et al. A com- prehensive solution to decentralized coordinative control of distributed generations in islanded micro- grid based on dual-frequency-droop[J]. IEEE Transa- ctions on Power Electronics, 2021, 37(3): 3583- 3598.
[29] Recommended Practice and Requirements for Harmonic Control in Electric Power Systems: IEEE 519[S]. IEEE, 2014.
[30] Guerrero J M, Matas J, Garcia de Vicuna L, et al. Decentralized control for parallel operation of distributed generation inverters using resistive output impedance[J]. IEEE Transactions on Industrial Electronics, 2007, 54(2): 994-1004.
[31] Zhu Yixin, Zhuo Fang, Wang Feng, et al. A virtual impedance optimization method for reactive power sharing in networked microgrid[J]. IEEE Transactions on Power Electronics, 2016, 31(4): 2890-2904.
[32] Wang Xiongfei, Li Yunwei, Blaabjerg F, et al. Virtual-impedance-based control for voltage-source and current-source converters[J]. IEEE Transactions on Power Electronics, 2015, 30(12): 7019-7037.
Abstract Parallel inverter systems are widely used in AC microgrids, renewable energy generation, UPS, and electric vehicles. Achieving reasonable power sharing among inverters is a key technology for the stable and reliable operation of parallel systems. Traditional droop control can achieve active power sharing but struggles to ensure equitable distribution of nonactive power (including reactive, unbalanced, and harmonic power) due to inverter parameter mismatches or line impedance differences, potentially leading to inverter overloading or system instability.
This paper proposes a dual-frequency-droop control strategy without communication or line impedance measurements. Reactive, unbalanced, and harmonic power all represent nonactive current components, and their distribution depends on the inverter output impedance. Equalizing the equivalent line impedance through virtual impedance enables simultaneous sharing of these power components. Following IEEE 1459-2010 standards that define nonactive power as encompassing reactive, unbalanced, and harmonic power, this strategy treats nonactive power as the unified control target. The dual-frequency-droop control includes conventional active power- fundamental frequency droop control for active power sharing and novel nonactive power-specific harmonic frequency droop control for nonactive power sharing. The method injects a specific harmonic signal (e.g., 300 Hz low-amplitude AC voltage) into the inverter output. Thus, a droop relationship between harmonic frequency and nonactive power, as well as a positive correlation between harmonic active power and virtual impedance, can be established. It forms a complete control loop for adaptive virtual impedance adjustment, compensating line impedance differences and ultimately achieving accurate nonactive power sharing.
A simulation model was developed in Matlab/Simulink featuring two parallel inverters with equal capacity connected to the PCC through different line impedances (predominantly inductive), supplying balanced, unbalanced, and nonlinear loads simultaneously. An identical experimental setup was constructed. In simulation, compared with conventional droop control and small-signal AC injection methods, the dual-frequency-droop control maintains accurate nonactive power distribution and improves current sharing among inverters. Dynamic response tests under various load disturbances show that the proposed method quickly restores stable operation while maintaining proper power sharing during balanced, unbalanced, and nonlinear load transients. The dual-frequency-droop control achieves effective nonactive power sharing and current distribution.
The following conclusion can be drawn.
(1) The proposed dual-frequency-droop control is suitable for complex microgrids with high renewable energy penetration, particularly in systems with significant line impedance variation, high harmonic distortion, and three-phase unbalance.
(2) In microgrids with mixed linear loads, nonlinear loads, single hybrid supply, three-phase hybrid supply, and multiple parallel inverters, this method simultaneously achieves accurate sharing of fundamental active power, reactive power, harmonic power, and unbalanced power. Compared to conventional droop control, it maintains communication-free operation while improving adaptability to complex load conditions.
keywords：Parallel inverter, droop control, power sharing, nonactive power, virtual impedance
DOI: 10.19595/j.cnki.1000-6753.tces.250972
中图分类号：TM464
福建省自然科学基金资助项目（2022J05026）。
收稿日期 2025-06-06
改稿日期 2025-07-19
刘宝谨 男，1992年生，讲师，硕士生导师，研究方向为基于分布式多变流器的微电网控制技术、可再生能源并网、构网型逆变器控制等。E-mail: lbj@fzu.edu.cn
郑 峰 男，1984年生，副教授，硕士生导师，研究方向为新型电力系统优化调度、微电网运行与控制、交直流电网限流技术。E-mail: zf_whu@163.com（通信作者）
（编辑 陈 诚）