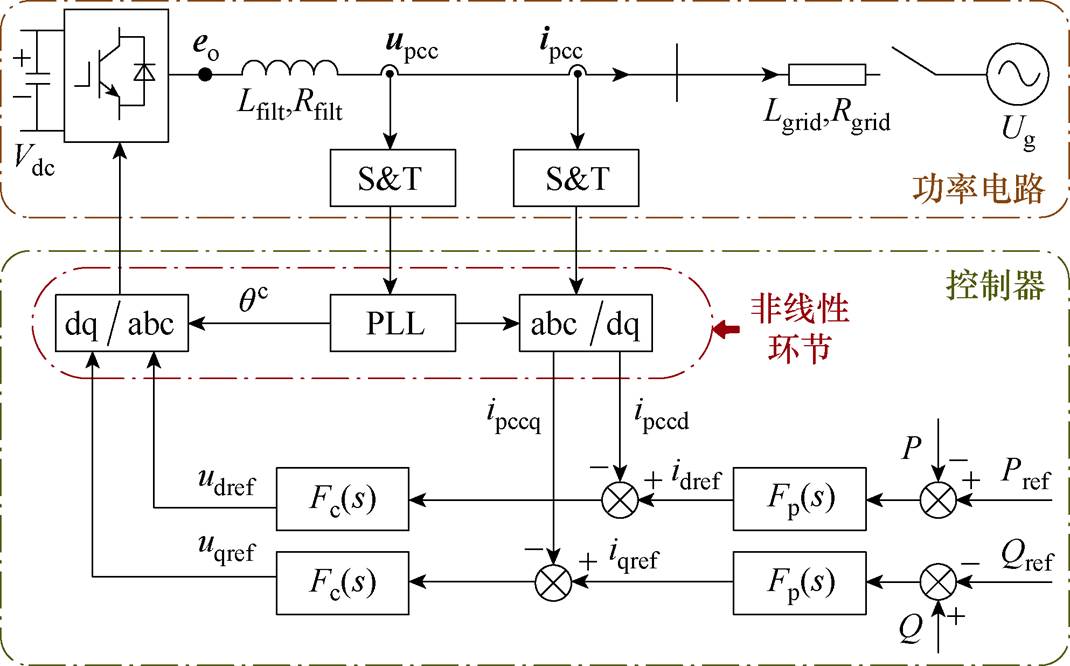
图1 PQ控制下的并网逆变系统结构
Fig.1 System structure diagram of GCI with PQ control
摘要 并网逆变器（GCI）是可再生能源并网的核心装置，其稳定性深刻地影响了现代电网的安全稳定运行。传统稳定性法已对GCI在特定工作点下的稳定性展开了大量讨论。然而，受新能源出力波动及负载随机投切的影响，GCI的工作点具有强时变性，不同工况的稳定性存在显著差异。PQ控制是常用的并网逆变器的控制策略，与单电流控制相比，具有多环路耦合、多时间尺度、强非线性等特性，为其动态特性分析带来了挑战。为了明确GCI在全工作区间内的动态特性，该文提出一种基于稳定域的PQ控制GCI稳定性分析方法，刻画系统的稳定边界。该文考虑锁相环（PLL）、功率环及电流环等控制环路间的相互耦合，建立内嵌工作点变量的GCI闭环传递函数模型。基于该模型，提出基于稳定域的稳定性图示方法，可同时分析多个变量对系统稳定性的影响。进一步地，研究电网阻抗、电网电压及PLL带宽等参数对稳定域的影响规律，并对比PQ控制并网逆变器与电流控制逆变器稳定边界的差异。仿真及实验验证了所提方法的正确性。
关键词：并网逆变器 PQ控制 工作点 稳定域 小信号模型
并网逆变器（Grid-Connected Inverter, GCI）是连接发电单元与电网的核心装置，承担着电能高效转换的重要任务[1-3]。在高比例可再生能源的现代电网中，GCI的动态特性影响电网安全稳定运行，因而受到广泛关注[4-6]。
受风电、光伏出力波动及负载投切的影响，GCI的输出功率不断改变，其工作点具有随机时变特性。工作点的随机时变将引起系统动态特性的改变进而影响稳定裕度[7-8]，严重时可能导致失稳。因此，研究并网逆变器时变工况下的稳定性具有重要意义。
为分析时变工作点下系统的稳定性，主要有以下三条技术路线：①基于离散工作点的方法，选取多个离散工作点分别建模分析，扩展系统稳定性分析范围；②采用概率小信号方法，通过研究系统关键特征值的概率密度函数（Probability Density Function, PDF）来分析系统失稳概率；③将工作点变量引入建模过程中，基于内嵌工作点变量的模型刻画系统稳定域，进而分析系统稳定性。
基于离散工作点的分析方法选取多个工作点分别代入分析模型中，进而分析不同工作点下的系统稳定性。文献[9]建立了光照强度与有功功率的关系式，将不同光照强度下的有功功率代入GCI阻抗模型（Impedance Model, IM），发现增加有功功率输出易恶化系统稳定性。文献[10]则采用状态空间模型分析了若干光照强度下光伏GCI稳定性的变化情况。在风力发电方面，文献[11-12]总结了风速对IM阻抗特性的影响规律，指出风速下降时，系统阻尼减小，因而更易失稳。相比基于单点分析方法，基于离散点的方法可更准确地描述系统动态特性。但其分析结论往往与工作点选取有关，选取不同组工作点分析后的结论可能存在差异。而且对于时变系统，随着运行时刻的无限延伸，系统工作点不断增加，基于离散点的方法无法遍历所有运行时刻，难以实现全工作区间的准确表征[7]。
概率分析法通常基于系统阻尼比[13-14]、特征 值[15-16]等关键参数的PDF来分析时变系统的失稳概率。文献[13-14]考虑光伏出力及负荷的随机波动，获取系统临界阻尼比的PDF后，可以评估在工作点随机改变时系统稳定及失稳的概率。类似地，文献[15]考虑了光伏发电出力的随机特性，通过关键特征值的PDF来分析光伏GCI的控制参数的影响。为提高稳定裕度，文献[16]在采用特征值的PDF分析系统失稳概率的同时，还以系统不稳定概率为性能指标，提出采用新型控制器或选择大容量负载等方法来降低失稳概率。然而，概率小信号法只能评估系统稳定与不稳定的概率，难以给出关于并网逆变系统稳定性的明确结论。
构建包含工作点参数的变系数模型，可直接分析不同工况下系统的稳定性。文献[17]将光照强度作为工作点变量引入GCI导纳建模过程，得到了光照强度-频率-相位/幅值的三维Bode图，从而分析光照强度对稳定性的影响。类似地，文献[18-19]建立了以风速为工作点变量的导纳模型，得到了风速-频率-相位/幅值三维Bode图，进而分析全风速区间系统的稳定性。除引入光照强度、风速等非电气量外，文献[20]则利用三维Bode图分析了以输出电流为工作点变量的系统的稳定性。然而，由于三维Bode图维数的限制，三维Bode图方法仅适用于单个工作点变量的分析，难以同时分析多个变量对稳定性的影响。
为同时分析多个变量对系统稳定性的影响，文献[21]将有功电流、电网电压作为工作点引入GCI建模，可以同时分析两个变量对系统稳定性影响。然而，其忽略了功率外环的影响，分析不够全面。功率外环是重要控制环节，功率外环对于系统稳定性有显著影响[22]，功率环的引入给系统带来多环路耦合、多时间尺度、强非线性等问题。现有研究表明：弱电网下，功率环会与锁相环（Phase-Locked Loop, PLL）[23]、电流内环[24]等环节产生耦合而影响系统稳定性。此外，有功环路与无功环路间也存在耦合[25]，当功率环参数不对称时又会引起频率耦合振荡，影响系统稳定性[26]。在时间尺度方面，各种控制回路具有不同时间尺度的控制带宽，导致不同频率范围的不稳定问题；电流内环控制容易引起高频不稳定问题[27]；而时间尺度更高的PLL和功率控制环路则易引起低频不稳定问题[28]。文献[21]以单电流环控制逆变器为分析对象，无法揭示多环路耦合、多时间尺度、强非线性下复杂控制环路对稳定性的影响，分析的结果不够准确。因此，分析时变工况下系统的稳定性时，考虑功率环的影响具有重要意义。
本文在参考文献[21]的基础上，分析了具有多环路耦合、多时间尺度、强非线性等复杂特性的PQ控制GCI的稳定性。首先，本文考虑了PLL、有功环、无功环和电流环等控制环路间的耦合特性，在PLL、功率计算环节均引入工作点变量，建立了内嵌工作点变量的PQ控制GCI模型，更全面、准确地表征逆变系统全工作区间的稳定性；其次，考虑物理电路的功率传输约束，通过数值分析，构建了GCI系统的三维稳定域，可直观获取工作区间内所有工作点的稳定性；再次，分析了系统外部参数（如电网阻抗、电网电压）和内部控制参数（PLL带宽）对稳定性的影响，并对比了PQ控制与电流控制逆变器稳定域的差异。最后，通过仿真和实验对理论分析进行了验证。本文涉及控制环路诸多复杂特性对稳定性的影响，所提方法可以为其他具备复杂控制策略的逆变器的稳定性分析提供参考。
本节对基于PQ控制的并网逆变系统进行小扰动建模，推导考虑电网强度和PLL影响的功率环控制表达式，获取可以表征并网逆变系统稳定性的闭环传递函数。
基于PQ控制的并网逆变系统结构如图1所 示[25-26]，控制系统由功率外环、电流内环、PLL构成。
图1 PQ控制下的并网逆变系统结构
Fig.1 System structure diagram of GCI with PQ control
图1中，Vdc为GCI直流侧电压，eo为GCI输出电压矢量，upcc、ipcc分别为并网电压、电流矢量，Lfilt、Rfilt分别为滤波电感及其寄生电阻；Lgrid和Rgrid分别为电网等效电感及等效电阻；P/Q、Pref/Qref分别为GCI有功/无功功率输出值及参考值；idref、iqref分别为GCI输出电流d轴、q轴电流参考值。本文采用dq轴去耦合控制，Fp(s)=Kps+Kis/s、Fc(s)=Kpc+ Kic/s分别为功率环、电流环的PI调节器。
本文使用基于同步坐标系的锁相环（Syn- chronous Reference Frame-PLL, SRF-PLL）跟踪电网电压，其基本模型及线性化模型分别如图2所示，为与实际PCC电压相位相区分，PLL输出相位添加上标c，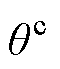
的表达式为
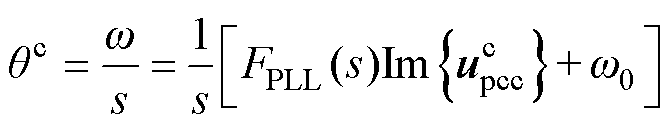（1）
式中，FPLL(s)为PLL的PI调节器，FPLL(s)=Kpp+Kip/s；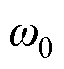
为额定角速度；
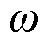为实际角速度。
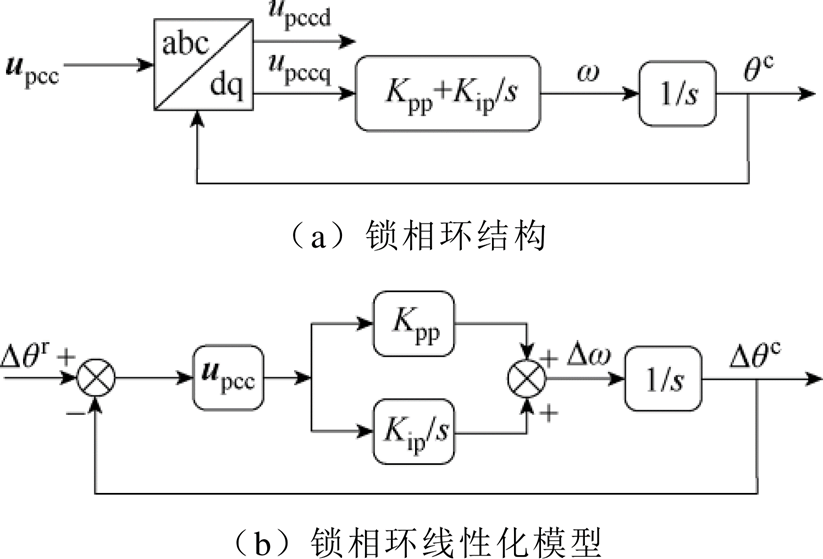
图2 锁相环及其线性化模型
Fig.2 Structure and linearized model of SRF-PLL
根据图3可知，由于PCC处电压波动，实际PCC电压相位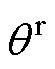
与PLL输出电压相位
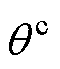存在偏差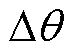
，其关系为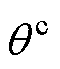=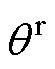+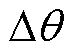，以此形成两种坐标系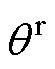；定义的同步坐标系和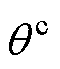对应的控制坐标系，控制坐标系下的量用上标“c”标注。
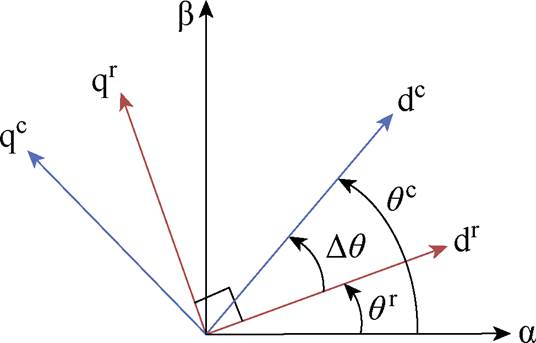
图3 同步dqr坐标系与控制dqc坐标系关系示意图
Fig.3 Diagram of the relationship between the actual dqr and the control dqc coordinate
变量x及其共轭量在不同控制坐标下小扰动之间的关系为
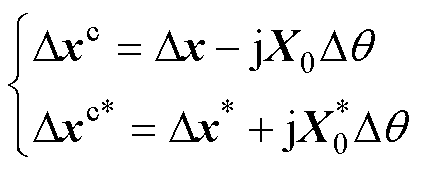（2）
式中，x为同步坐标系下的物理量，x=xd+jxq；上标“*”表示物理量的共轭量；X0为变量x的稳态值；xc为控制坐标系下对应的物理量。
功率电路在同步坐标系下的关系为
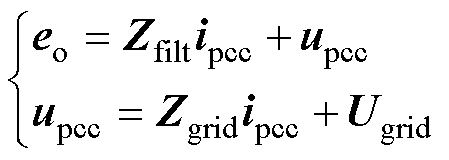（3）
式中，upcc、eo、ipcc分别为PCC电压矢量、GCI输出电压矢量、电网电流矢量，upcc=upccd+jupccq、eo= ed+jeq、ipcc=ipccd+jipccq；滤波电感及电网的阻抗分 别为
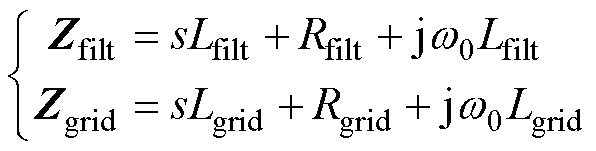（4）
GCI的调制电压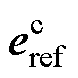
由电流环得到，功率环和电流环控制器在控制坐标系下可表示为
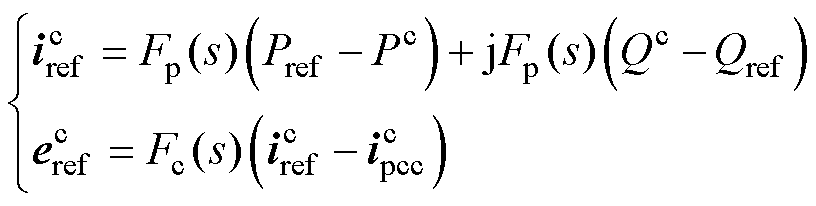（5）
电流内环的参考值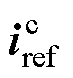
可进一步表示为
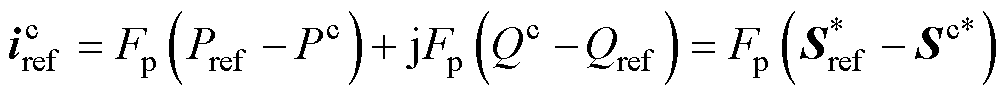（6）
式中，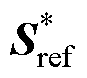
为参考功率的共轭量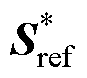，=Pref-jQref；
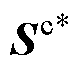为输出功率的共轭量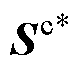，=Pc-jQc。
根据式（2）中不同坐标系下小扰动量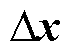
之间的转换关系，可得并网电流、电压及其共轭量小扰动之间关系为
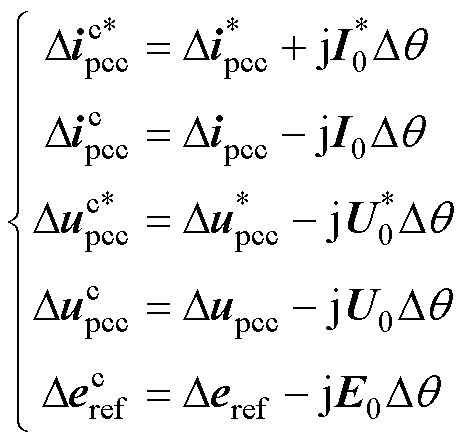（7）
式中，I0、E0和U0分别为GCI并网电流矢量稳态值、输出电压矢量稳态值和PCC电压矢量稳态值。
功率电路在同步坐标系下的小扰动关系式为
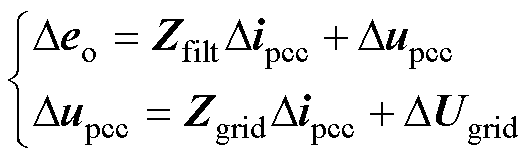（8）
对式（5）、式（6）进行小扰动分析可得
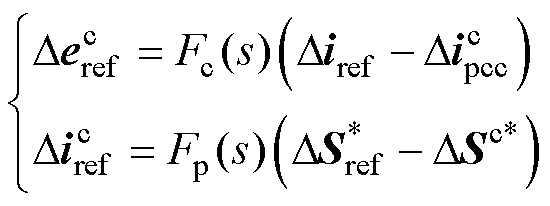（9）
功率在控制坐标系下的计算式为
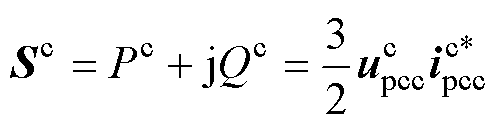（10）
则功率及其共轭量扰动关系式可分别表示为
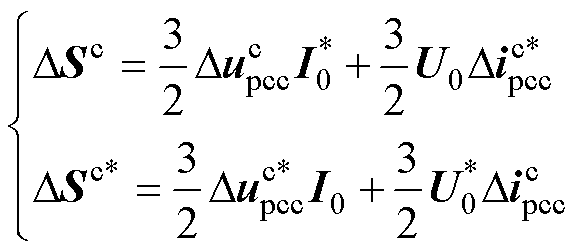（11）
PLL的扰动关系式为
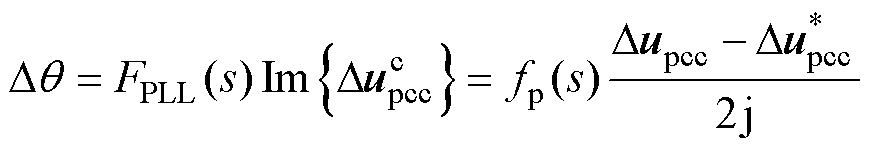（12）
其中
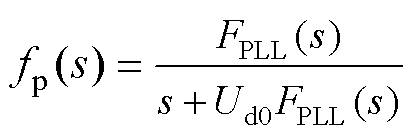
式中，Ud0为U0的d轴分量。将式（7）代入式（9），将控制器的输出电压从控制坐标系下的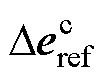
转换到同步坐标系下的
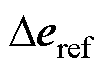得
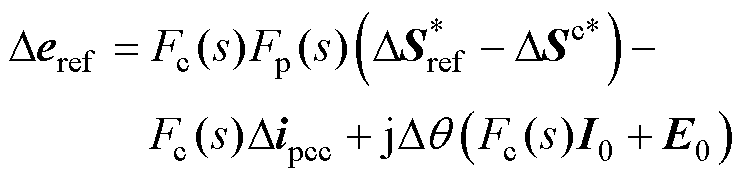（13）
同步坐标系下，GCI输出电压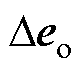
与控制器输出电压参考值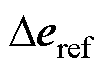间的关系为
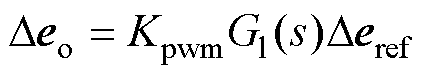（14）
式中，本文忽略调制Kpwm及延时环节G1(s)，即KpwmG1(s)=1。
联立式（8）与式（14）得
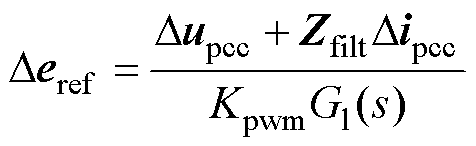（15）
联立式（4）、式（7）、式（11）、式（13）和式（15），简化可得并网电流的扰动表达式为
（16）
其中
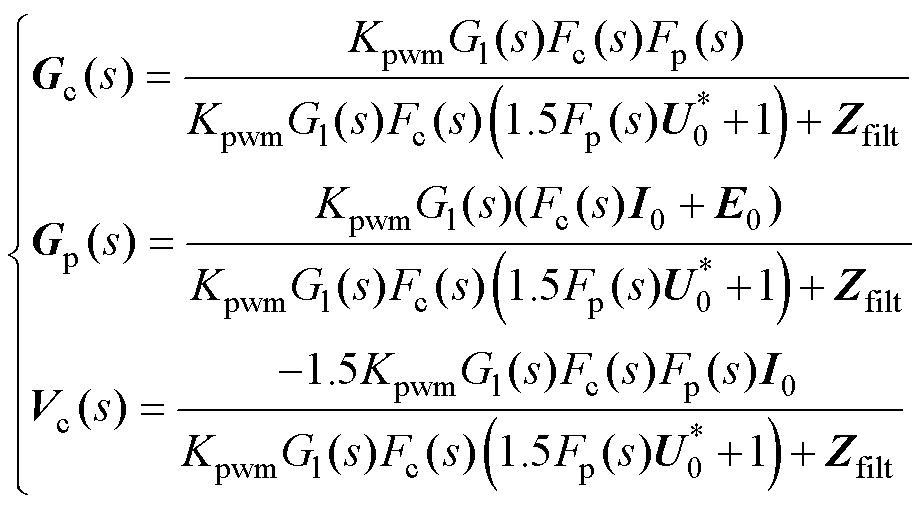
进一步地，先将PLL的扰动关系式（12）代入
式（16），消去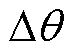，再将式（8）代入消去
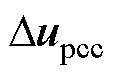及其共轭量，简化可得
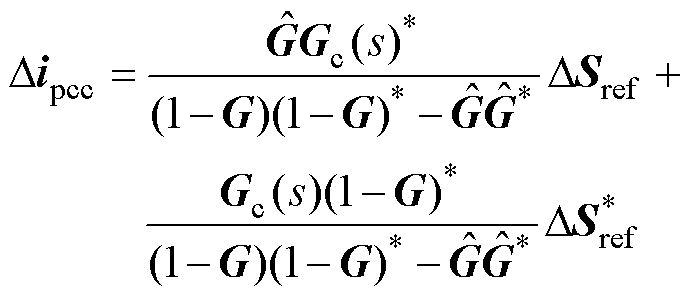（17）
其中
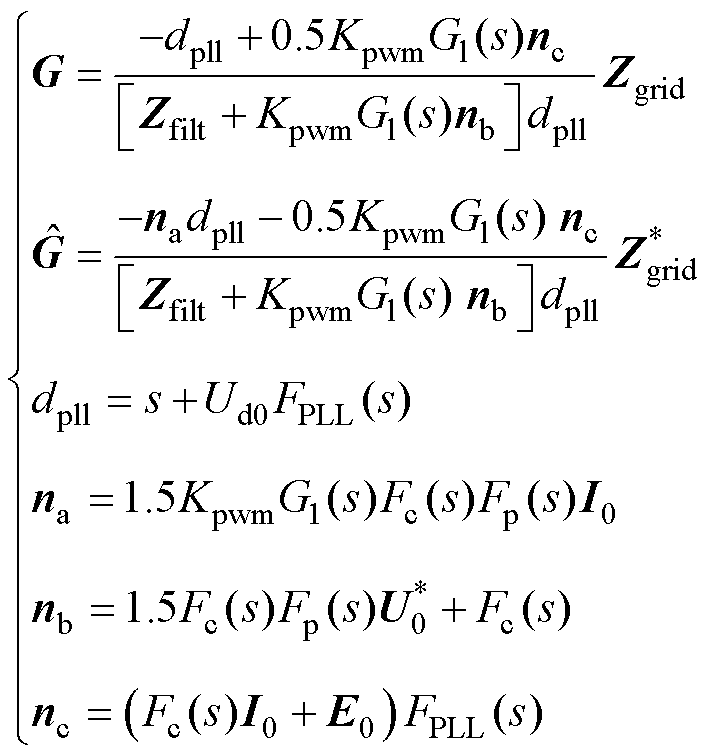
利用复数共轭关系，由式（17）分别推导出闭环系统dq轴电流扰动量与有功、无功功率参考值扰动量的关系式，如式（18）所示。图4给出了闭环系统的小信号模型结构。
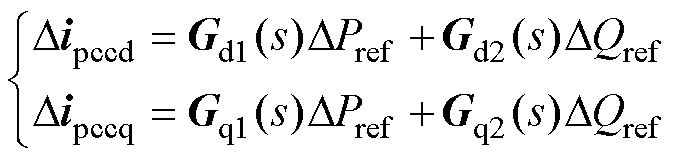（18）
其中
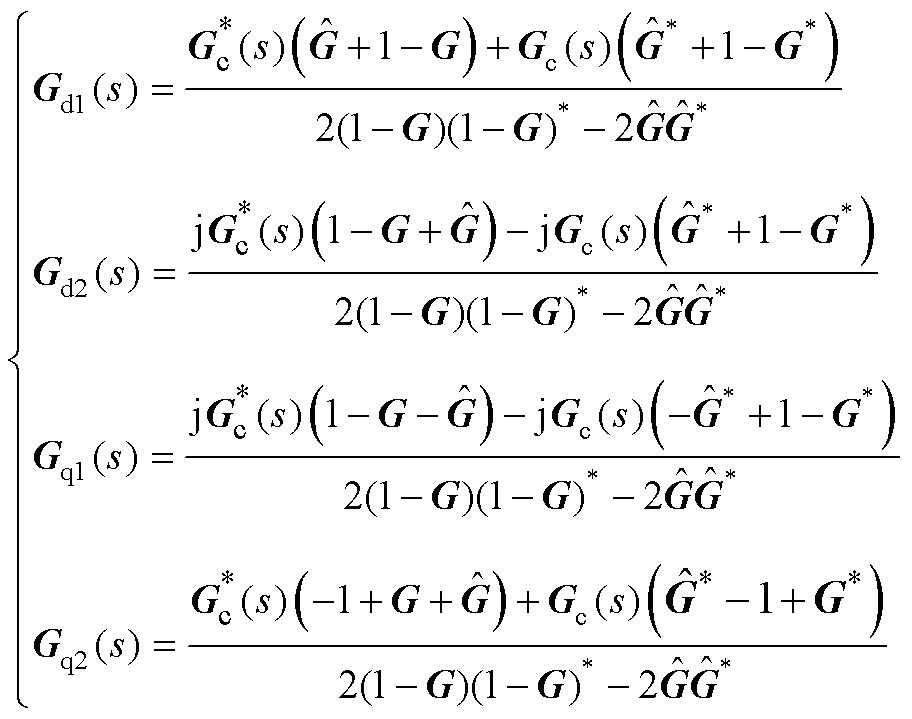
基于式（18），系统的稳定性可以通过4个单独的闭环传递函数Gd1、Gd2、Gq1和Gq2进行表征。4个闭环传递函数具有相同的分母多项式，若闭环传递函数的极点均在s平面的左半平面，则整个闭环系统稳定，图5为闭环系统的简化等效框图。
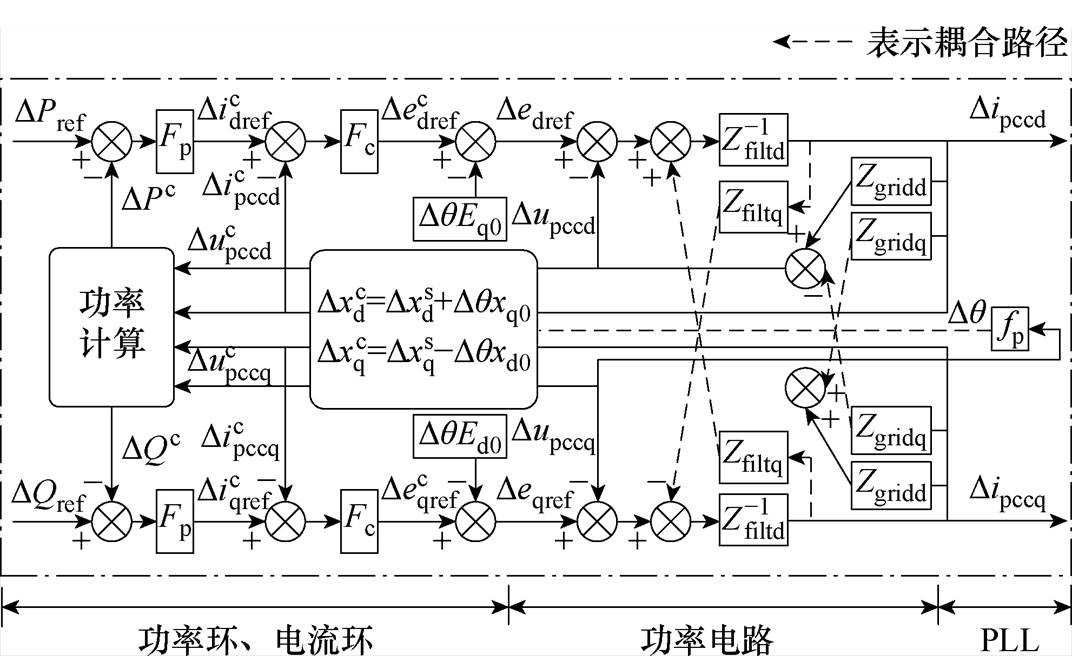
图4 闭环系统小信号模型结构
Fig.4 Small signal model structure of closed-loop system
图5 闭环系统简化等效框图
Fig.5 Block diagram of equivalent closed-loop system
第1节中，采用小信号稳定性分析法得到了并网逆变系统的闭环传递函数，可用于分析时变工作点下的稳定性问题。本节将通过数值分析，刻画系统全工作区间的稳定域，并进一步研究电网阻抗、电网电压、PLL带宽等对稳定域的影响规律。
2.1.1 稳定性分析范围
所分析的工作点需满足电路拓扑约束才可在其附近进行小信号分析，否则，无论采用任何控制策略以及控制参数均难以保证系统的稳定性。因此，在开展系统稳定域刻画之前，需筛选参与稳定性分析的工作点，即所分析的工作点应满足功率电路拓扑约束。将满足拓扑约束的工作点所构成的集合定义为拓扑约束域，记作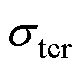
。
拓扑约束域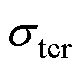的确定方法如下：稳态时，可认为输出功率值为给定参考值，公共耦合点（Point of Common Coupling, PCC）电压、电流及功率满足
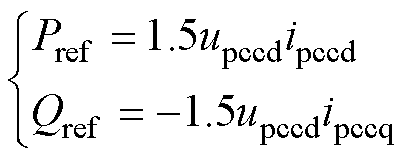（19）
由功率电路关系可得端电压、电网电压与输出电流间的表达式为
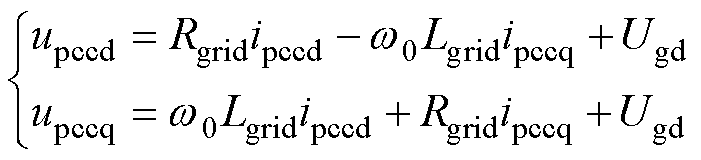（20）
联立式（19）和式（20）可得
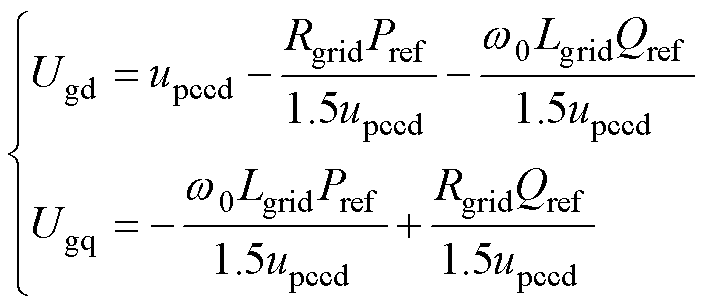（21）
又因为
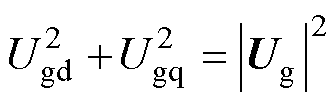（22）
联立式（19）、式（20）和式（22）可得到以PCC电压d轴分量为自变量的方程为
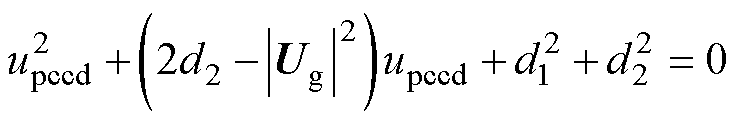（23）
其中
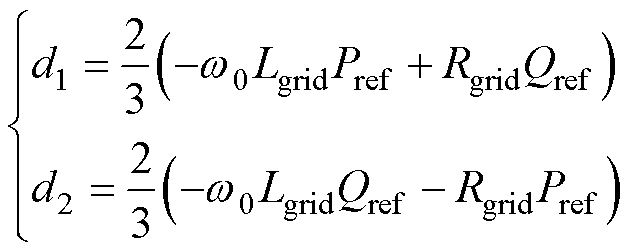
令a=1，b=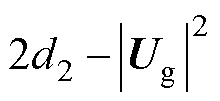
，c=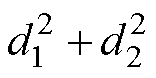
。在已知电网电压、GCI传输功率的条件下，可求解电压upccd。若方程式（23）存在正实数解，即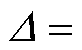
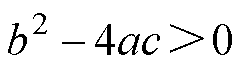，则说明给定功率满足电路拓扑约束，可参与稳定性分析。
2.1.2 稳定域的概念及刻画流程
所得闭环传递函数内嵌工作点变量，因此，闭环极点将随着工作点改变而变化，将第 (i, j) 个工作点 (Pi, Qj) 记作Fij。所有工作点组成的区间即为GCI的工作区间。在工作区间内，所有满足GCI功率电路约束条件的工作点构成系统的拓扑约束域。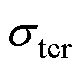
对于拓扑约束域stcr内的某一工作点Fij，基于式（1）～式（18）所提多变量建模方法，可得闭环传递函数G(s, Fij)。若G(s, Fij)所有极点均位于s左半平面，则在工作点Fij处系统稳定；反之，系统将难以稳定运行。在拓扑约束域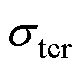内，所有小信号稳定的工作点组成的区间即为GCI的稳定域
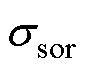，其他不稳定的工作点的集合即为失稳域，记作
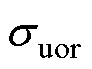。图6为GCI的稳定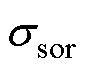域、失稳域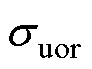及设定分析范围的示意图。
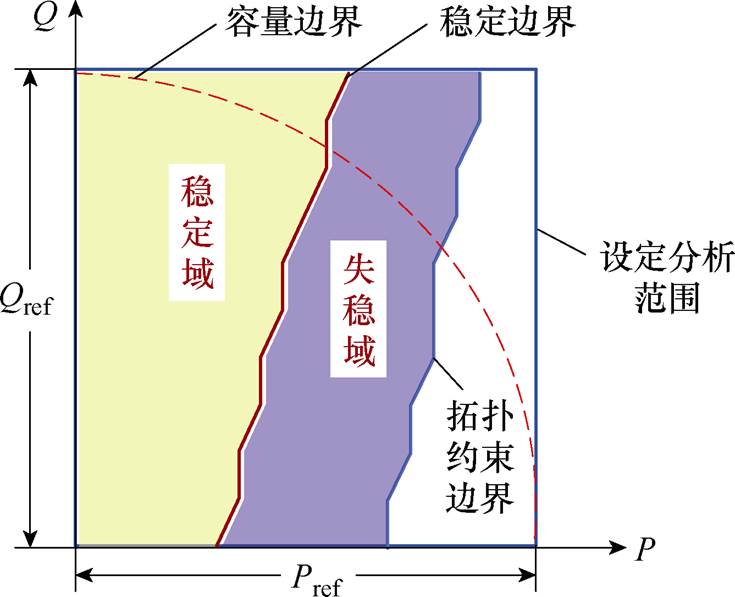
图6 稳定域示意图
Fig.6 Diagram of the stable operating region
根据上述分析，图7给出了PQ控制并网逆变系统稳定域刻画流程，主要步骤如下：
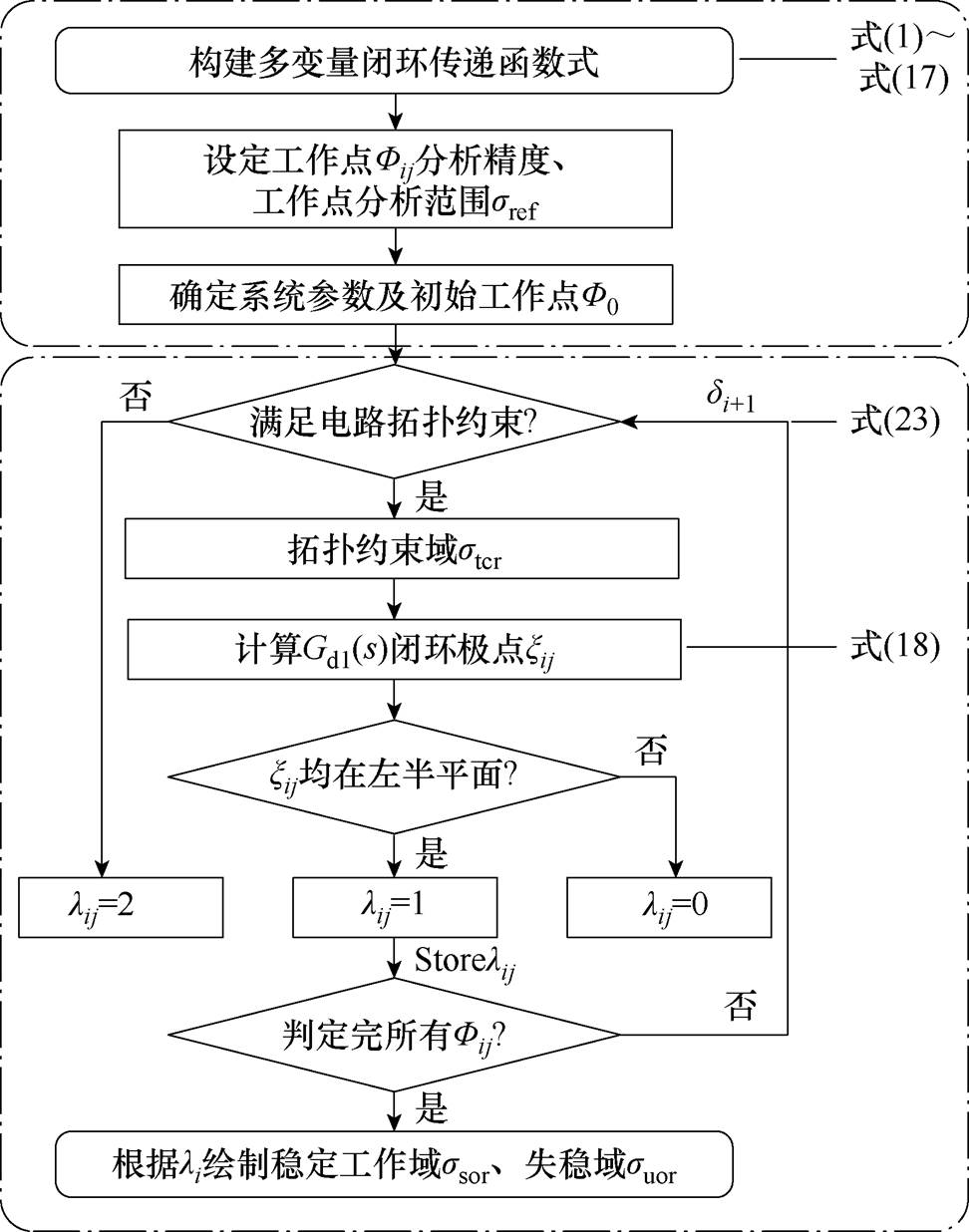
图7 稳定域刻画流程
Fig.7 Flow chart for stable operating region carving
（1）通过式（1）～式（18）所提方法，构建多变量闭环传递函数G(s, Fij)的关系式；确定系统电路参数；初始工作点F0(P0, Q0)、工作点分析范围sref(Pref, Qref)及分析精度 (DP, DQ)。
（2）根据式（19）～式（23）分析电路的拓扑约束边界，满足电路拓扑约束的Fij，组成拓扑约束域stcr。
（3）计算拓扑约束域stcr内工作点的G(s, Fij)的极点，根据G(s, Fij)极点分布情况分析稳定性，并储存判定结果lij。
（4）依据所得判定结果，刻画ssor。
2.2.1 系统额定参数下的稳定域
系统主要电路参数及控制参数见表1、表2。图8为额定参数下所得传递函数的闭环极点，由图8可知，系统的闭环极点均位于左半平面，因此并网系统能够保持稳定。
表1 主要电路参数
Tab.1 Main circuit parameters
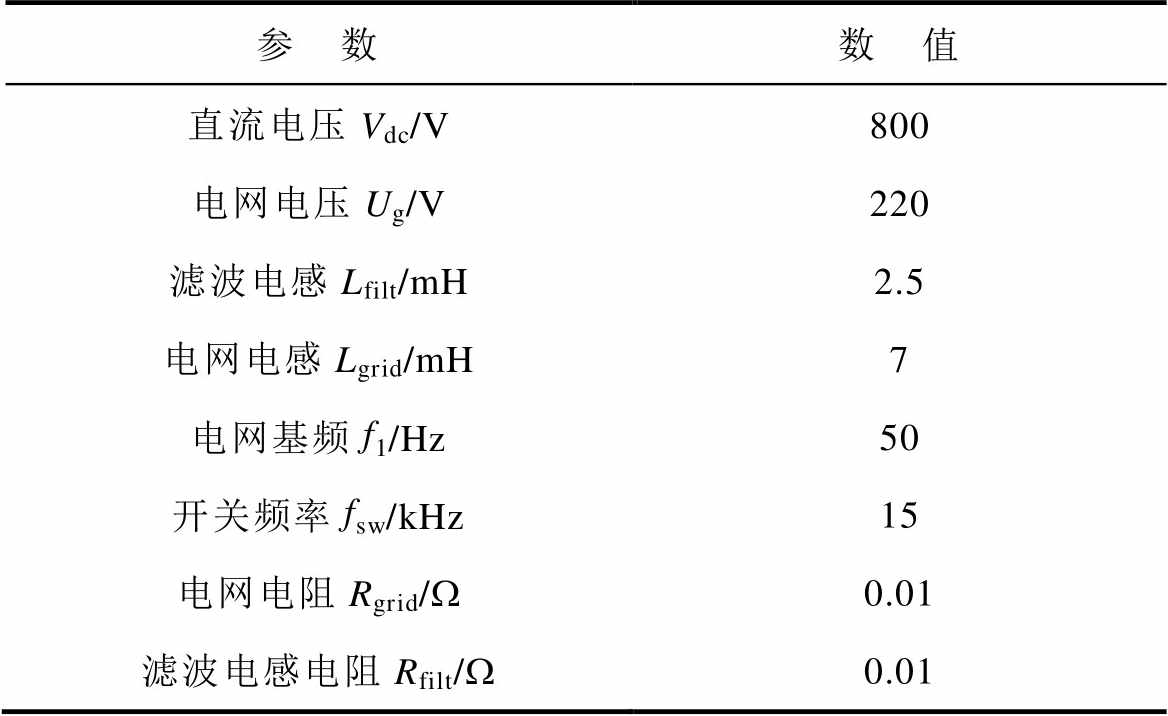
参 数数 值 直流电压Vdc/V800 电网电压Ug/V220 滤波电感Lfilt/mH2.5 电网电感Lgrid/mH7 电网基频f1/Hz50 开关频率fsw/kHz15 电网电阻Rgrid/W0.01 滤波电感电阻Rfilt/W0.01
表2 控制参数
Tab.2 Control parameters
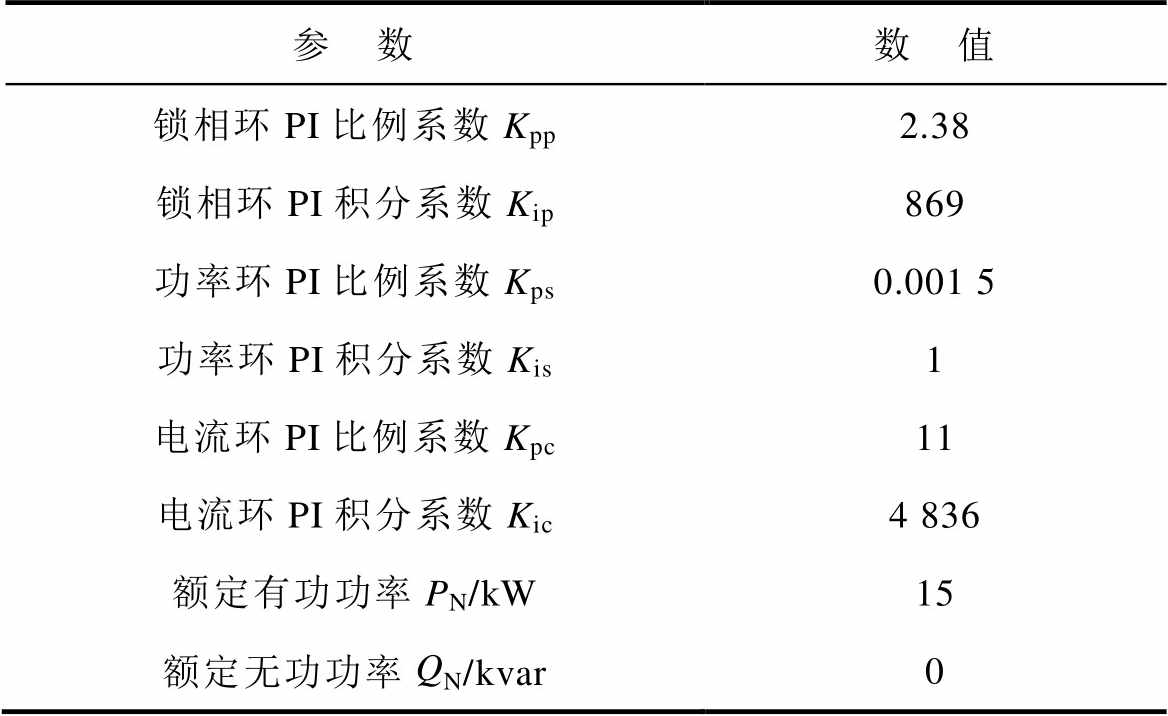
参 数数 值 锁相环PI比例系数Kpp2.38 锁相环PI积分系数Kip869 功率环PI比例系数Kps0.001 5 功率环PI积分系数Kis1 电流环PI比例系数Kpc11 电流环PI积分系数Kic4 836 额定有功功率PN/kW15 额定无功功率QN/kvar0
图8 闭环极点
Fig.8 Diagram of closed-loop pole
本文选取有功功率、无功功率为工作点变量，有功功率变化范围为0～22.5 kW，变化步长为1 kW；无功功率变化范围为0～22.5 kvar，变化步长为0.5 kvar。根据上述流程所刻画的稳定域及验证点如图9所示。
图9 稳定域及验证点
Fig.9 Stable operating region and verification points
图9中，左侧为稳定域，记作ssor；右侧为失稳域，记作suor。由图9可以看出，在给定参数下，当传输功率超过某一边界时，系统从稳定状态转变为不稳定状态。
2.2.2 阻抗参数对稳定域的影响分析
由于新能源长远距离输电的影响，电网阻抗不可忽略。将电网电感范围定为1～10 mH，变化步长为0.25 mH；电网电阻范围定为0.01～1 W，变化步长为0.01 W，其他参数保持不变；绘制的P-Q-Lgrid、P-Q-Rgrid三维图分别如图10、图11所示，求取不同Lgrid/Rgrid的等高线后，再对其进行投影即可获取不同Lgrid/Rgrid下的ssor边界。由图10可知，随着Lgrid取值的增大即电网强度降低，系统稳定边界逐渐左移，ssor不断缩小，这说明电网强度的降低易恶化系统稳定性。与电网电感相比，Rgrid增加反而可以增强系统稳定性。
图10 不同电网电感下系统稳定域及验证点
Fig.10 Stable operating region of the system with different Lgrid andverification point
图11 不同电网电阻下系统稳定域及验证点
Fig.11 Stable operating region of the system with different Rgrid and verification point
2.2.3 电网电压对稳定域的影响分析
除阻抗参数外，电网电压也影响系统稳定性，在正常工况下，由新能源波动或负载投切等因素的影响，电网电压在0.85～1.15(pu)内波动。为分析该波动区间内电网电压对稳定性的影响，利用所提方法刻画了不同电网电压下的稳定域，如图12所示，电网电压变化步长为0.01(pu)，其他参数保持不变。
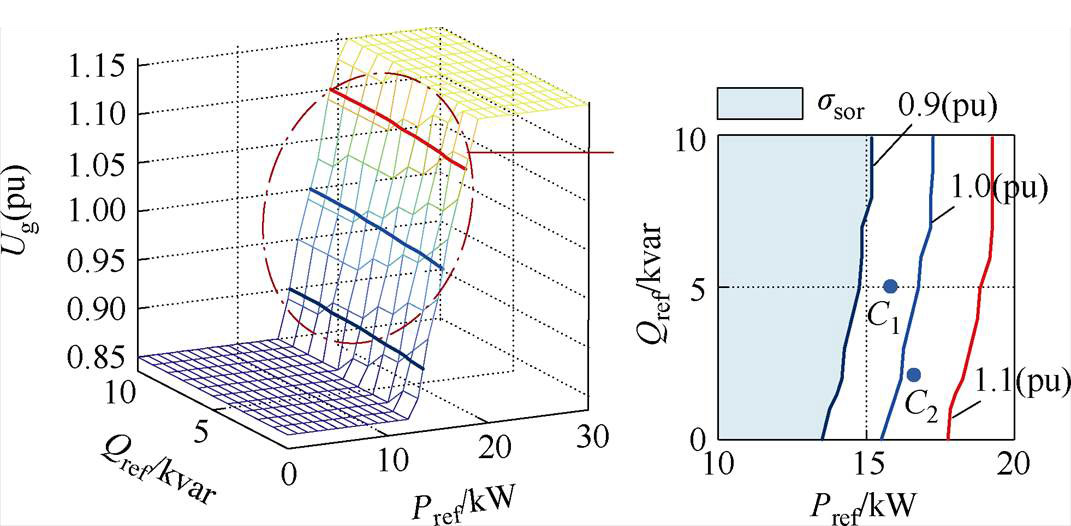
图12 不同电网电压下系统稳定域及验证点
Fig.12 Stable operating region of the system with different Ug andverification points
由图12可知，在0～10 kW的有功功率范围内，电网电压跌落0.1(pu)时，系统仍能稳定运行；当电网电压从1(pu)跌落至0.9(pu)时，系统稳定边界缩小，工作点C1从ssor过渡到suor。当电网电压从1(pu)抬升至1.1(pu)时，系统稳定性增强，工作点C2从suor迁移至ssor。此外，从二维图中不同电网电压对应的ssor边界可以看出，电网电压变化时，ssor改变的幅度较为均匀，说明在所分析范围内，ssor对电网电压变化的敏感度相近。
2.2.4 锁相环带宽对稳定域的影响分析
锁相环控制参数往往根据额定工况设计，当实际工作点偏离额定工况时，参数适用性难以确定。基于所得闭环传递函数，构建不同带宽下的ssor，可以直观获取当前带宽下系统的稳定性。分析思路如下：首先，建立锁相环带宽与PI控制器参数的关系式；其次，在式（18）所得闭环传递函数模型的基础上，将锁相环中的PI参数替换为以锁相环带宽为变量的表达式，推导得内嵌锁相环参数变量的稳定性分析模型；最后，根据所得模型，给定功率、锁相环带宽分析范围即可构建不同锁相环带宽下的ssor。
将锁相环的传递函数进行等效变换，写成典型二阶系统形式为
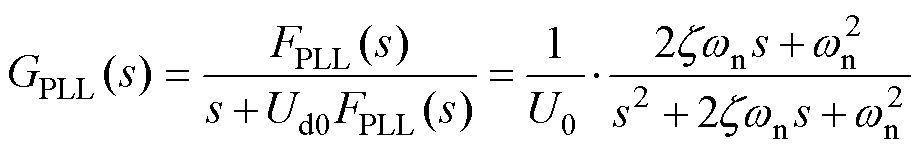（24）
式中，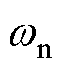
、
分别为系统的自然频率与阻尼比，其与锁相环PI调节器FPLL(s)=Kpp+Kip/s的关系可表示为
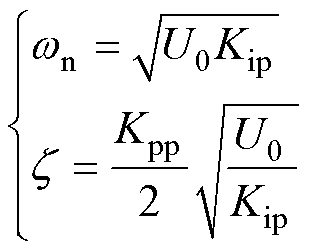（25）
根据锁相环带宽定义，可推得带宽fbw与自然频率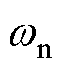的关系为
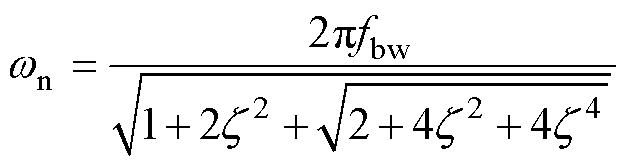（26）
考虑系统稳定性及动态性能的要求，阻尼比一般取0.707，因此，给定fbw后便可确定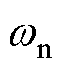，从而确定锁相环PI参数。由于式（25）中包含了PCC电压U0，本文分析额定工况下不同锁相环带宽对系统稳定性的影响，即U0为额定工况下的PCC电压，U0≈307.45 V。将fbw分析范围设置为10～80 Hz，变化步长为0.5 Hz，其他参数保持不变，绘制的P-Q-fbw三维图如图13所示。由图13的二维图可知，单位功率因数模式下，fbw为70、50、30 Hz时，ssor边界分别为9、12、19 kW。ssor与锁相环带宽呈负相关，且在较高功率范围内，带宽变化时，ssor改变的幅度更明显，说明较高功率下ssor对锁相环带宽变化的敏感度更高。
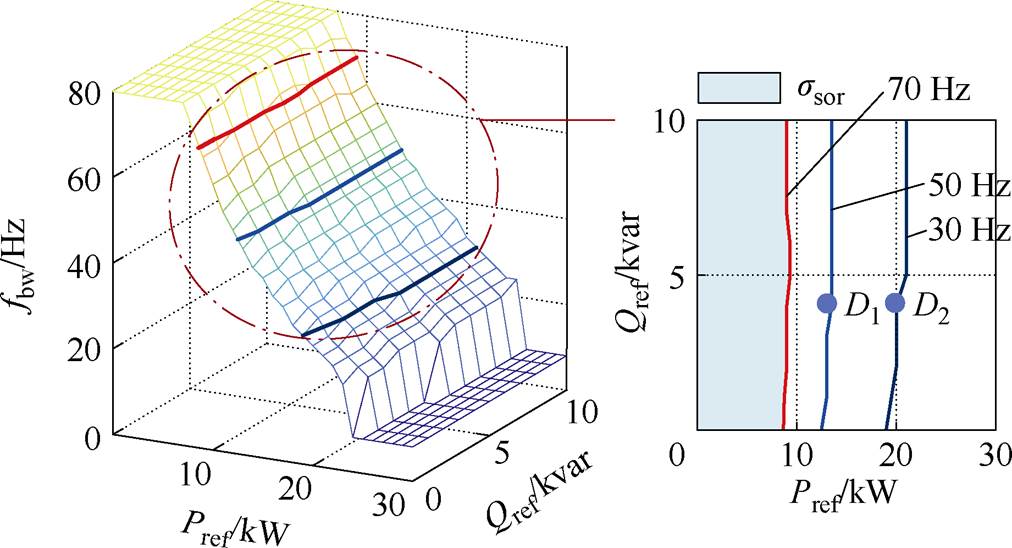
图13 不同PLL带宽下系统稳定域及验证点
Fig.13 Stable operating region of the system with different fbw and verification points
文献[21]中刻画了电流控制（Current Control, CC）GCI的稳定域，其中并网电流扰动量和电流参考值之间关系可表示为
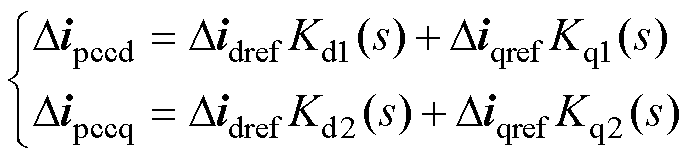（27）
同样地，电流控制GCI的系统的稳定性可由4个传递函数Kd1、Kd2、Kq1、Kq2进行表征。为对比电流控制GCI与PQ控制GCI稳定域的差异，本文基于功率计算式将其中的电流值等效替换为功率值，两种控制策略下的ssor对比结果如图14所示。除功率PI参数外，其余参数均保持一致。图14a、图14b和图14c分别为不同电网强度（SCR）、Ug、fbw下的ssor，实线、虚线分别表示PQ控制、电流控制下的ssor边界。其中，有功功率的基准值为15 kW，无功功率基准值为10 kvar。
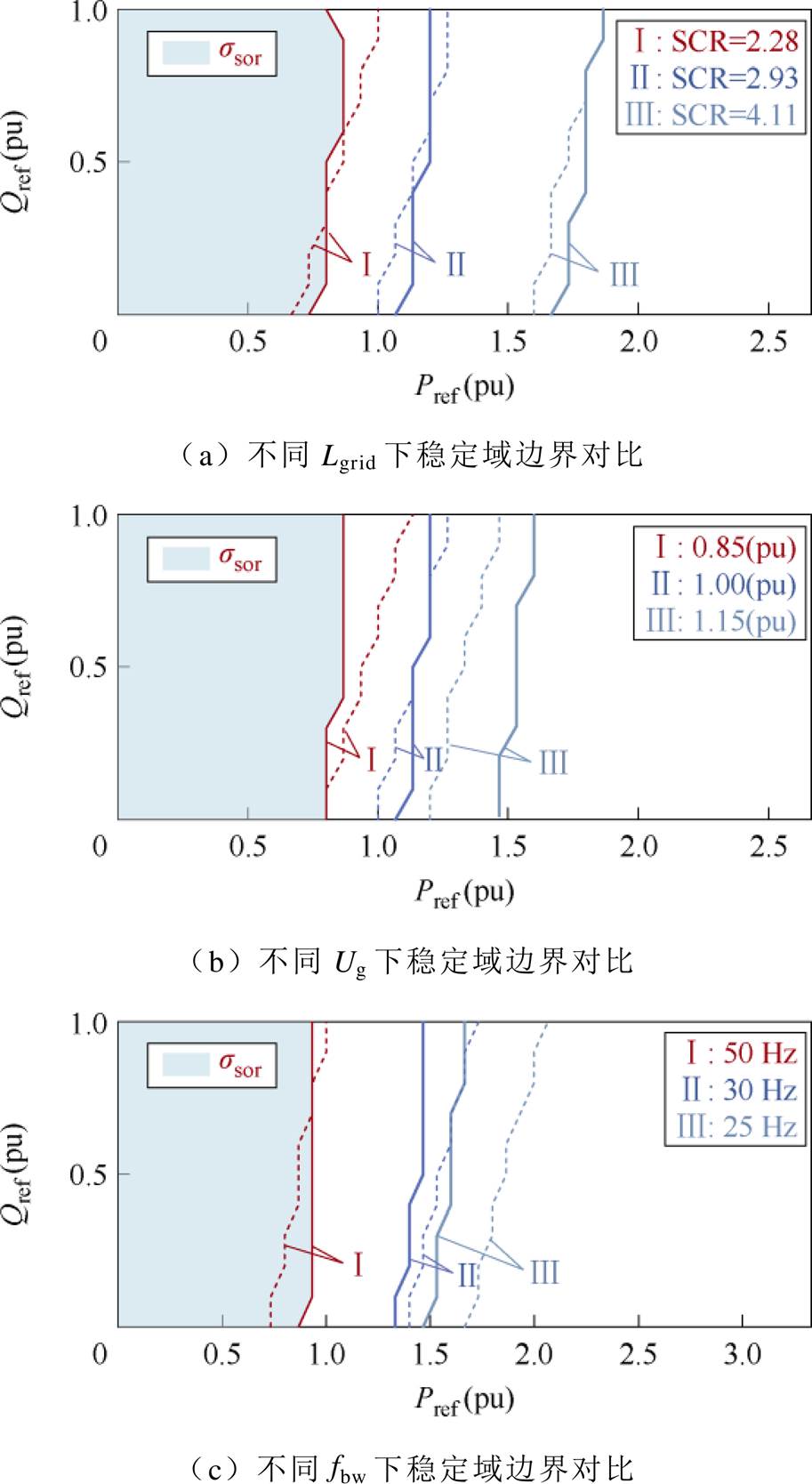
图14 电流控制GCI与PQ控制GCI稳定域对比
Fig.14 Comparison of the stable operating region of GCI with current control and GCI with PQ control
由图14可知，当电网强度、Ug、fbw等系统参数改变时，两种控制模式下的ssor变化趋势相同，即两者的ssor与电网强度、电网电压呈正相关，与锁相环带宽呈负相关。以单位功率因数工况为例，其稳定域边界的量化对比见表3。
表3 单位功率因数工况下稳定边界对比
Tab.3 Comparison of stability boundaries in unit power factor condition
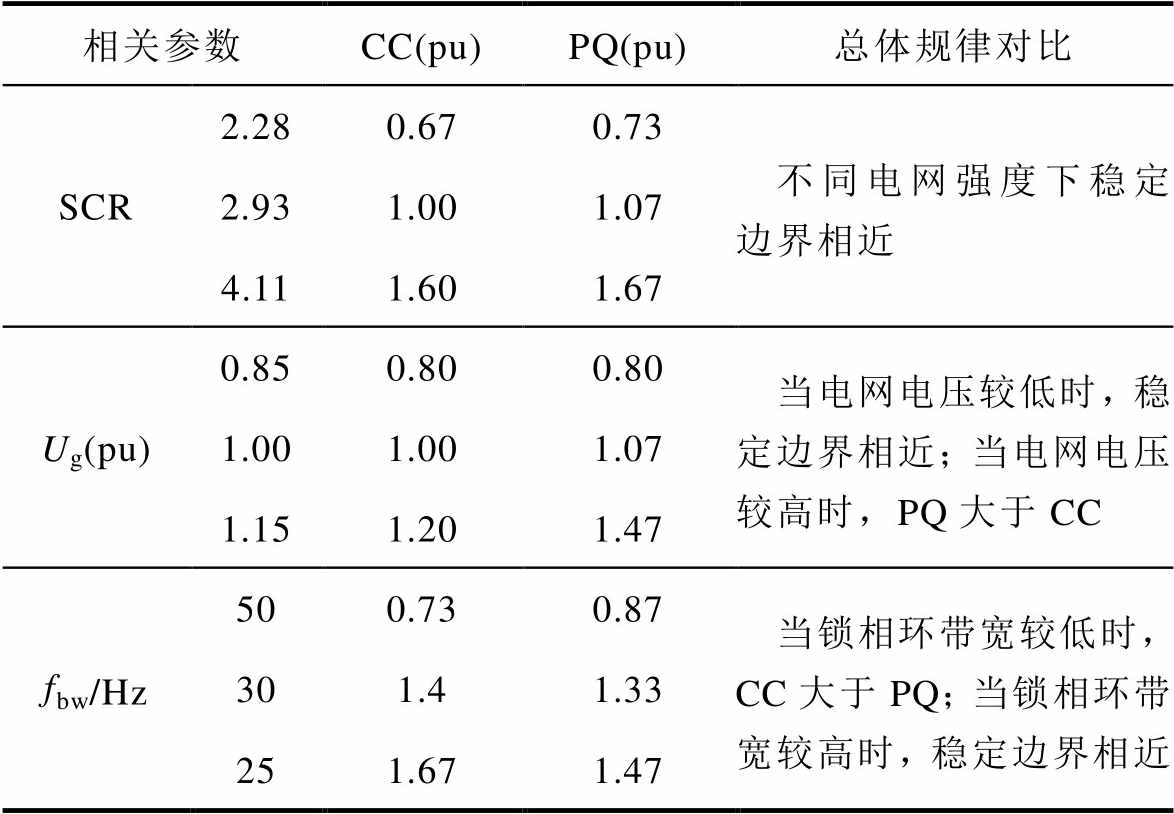
相关参数CC(pu)PQ(pu)总体规律对比 2.280.670.73不同电网强度下稳定边界相近 SCR2.931.001.07 4.111.601.67 0.850.800.80当电网电压较低时，稳定边界相近；当电网电压较高时，PQ大于CC Ug(pu)1.001.001.07 1.151.201.47 500.730.87当锁相环带宽较低时，CC大于PQ；当锁相环带宽较高时，稳定边界相近 fbw/Hz301.41.33 251.671.47
根据图14及表3，当其余参数保持一致时，单位功率因数工况下稳定边界对比结果如下：
（1）不同电网强度下，电流控制GCI与PQ控制GCI的稳定边界接近，PQ控制GCI的稳定边界高于电流控制约0.07(pu)。
（2）在不同电网电压下，当电网电压较低时，稳定边界相近，当电网电压较高时，PQ控制GCI的稳定边界高于电流控制。当Ug=1.15(pu)时，电流控制的稳定边界为1.20(pu)，PQ控制的稳定边界为1.47(pu)，相差约0.27(pu)。
（3）在不同锁相环带宽下，当锁相环带宽较低时，电流控制GCI的稳定边界高于PQ控制，当锁相环带宽较高时，两者稳定边界相近。当fbw=25 Hz时，PQ控制的稳定边界为1.47(pu)，而电流控制的稳定边界为1.67(pu)，电流控制逆变器的稳定边界高于PQ控制0.2(pu)。
在第3节中已经得到了并网逆变系统的额定参数下的稳定域ssor，研究了阻抗参数、电网电压及锁相环带宽对ssor的影响规律，本节搭建Matlab仿真模型，对分析结果进行验证。
为验证额定参数下ssor刻画的正确性，选取图9中A1、A2及A3 3个工作点进行仿真验证。A1（14 kW, 5 kvar）位于稳定域ssor，A2（17 kW, 7 kvar）位于稳定边界，A3（19 kW, 6 kvar）位于失稳域suor，三相并网电流及输出有功功率仿真波形如图15所示。工作点位于A1点时，三相并网电流波形对称，系统稳定，0.4 s时工作点从A1阶跃为A2，三相并网电流的总谐波畸变率（Total Harmonic Distortion, THD）有所提高，但此时仍处于稳定状态；0.6 s时工作点从A2阶跃为A3时，电流及功率出现振荡，系统失稳，与稳定域刻画结果吻合。
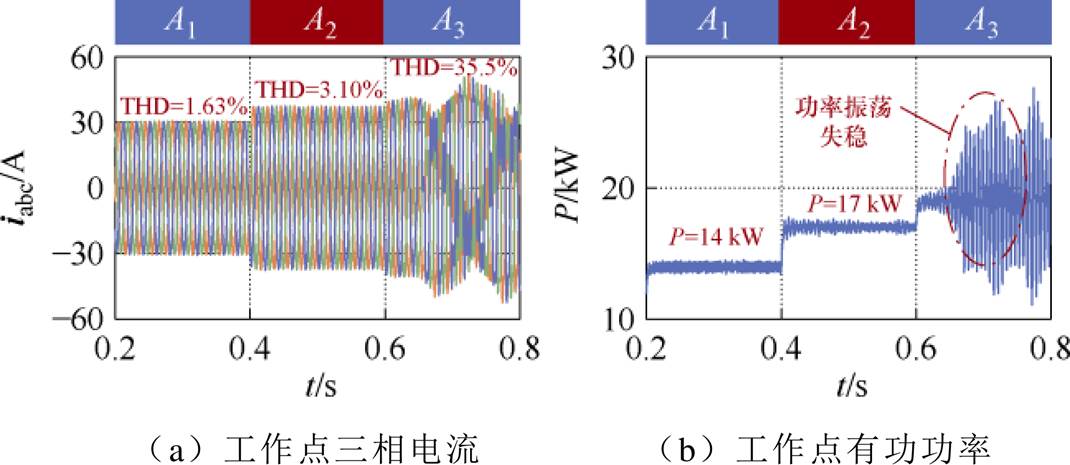
图15 稳定域验证点仿真波形
Fig.15 Simulation waveforms at the stable operating region verification points
对不同电网阻抗下的ssor验证结果如图16、图17所示，从图中可以看出，对于工作点B1（17 kW, 4 kvar），Lgrid=3 mH时，B1的三相并网电流对称，THD较低，保持稳定；0.5 s时将Lgrid切换为7 mH，此时，电流逐渐振荡，功率发散，系统失稳。相比之下，在工作点B2（15 kW, 2 kvar），随着Rgrid的增大，电流、功率始终保持稳定，THD从3.84%下降为1.45%，改善了系统稳定性，验证了基于稳定域分析方法的正确性。
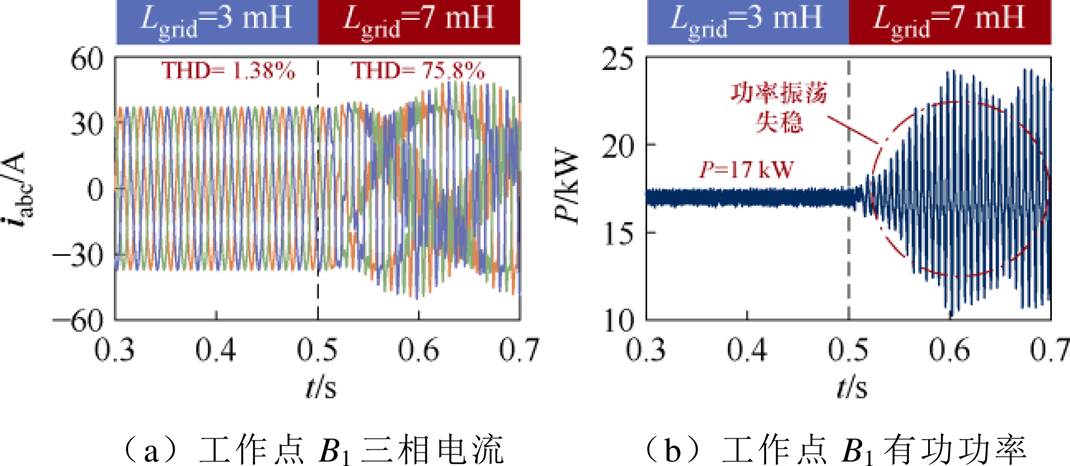
图16 阻抗参数验证点B1仿真波形
Fig.16 Simulation waveforms at impedance parameterverification point B1
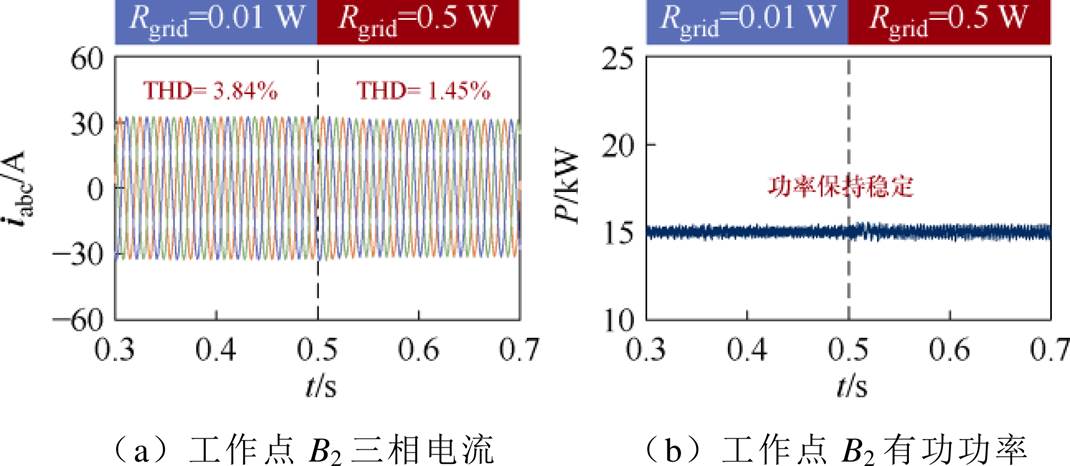
图17 阻抗参数验证点B2仿真波形
Fig.17 Simulation waveforms at impedance parameterverification point B2
选取图12中1.0(pu)、1.1(pu)电压对应的ssor边界上两点C1（16 kW, 5 kvar）、C2（17 kW, 2 kvar）进行变电压工况下的稳定性分析验证，其三相并网电流及输出有功功率仿真波形如图18、图19所示。
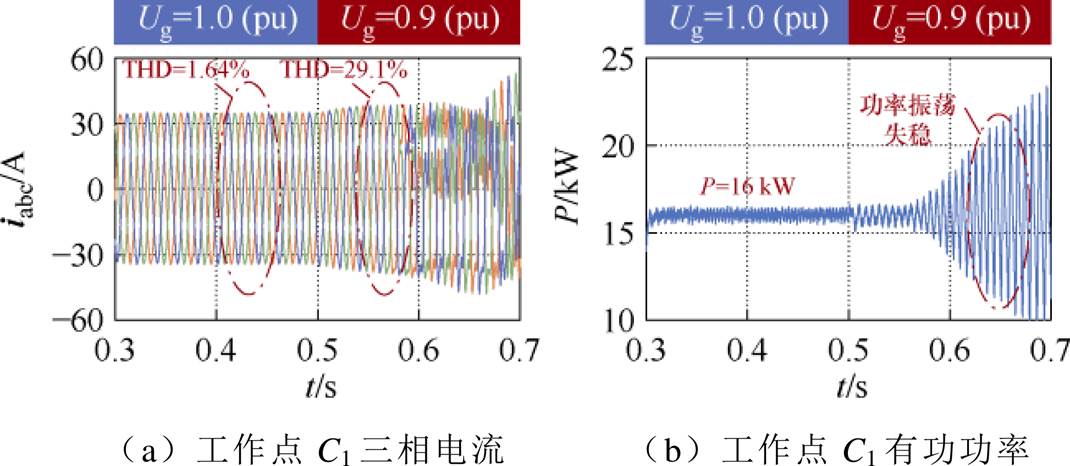
图18 电网电压跌落时验证点C1仿真波形
Fig.18 Simulation waveforms at the grid voltage drops verification point C1
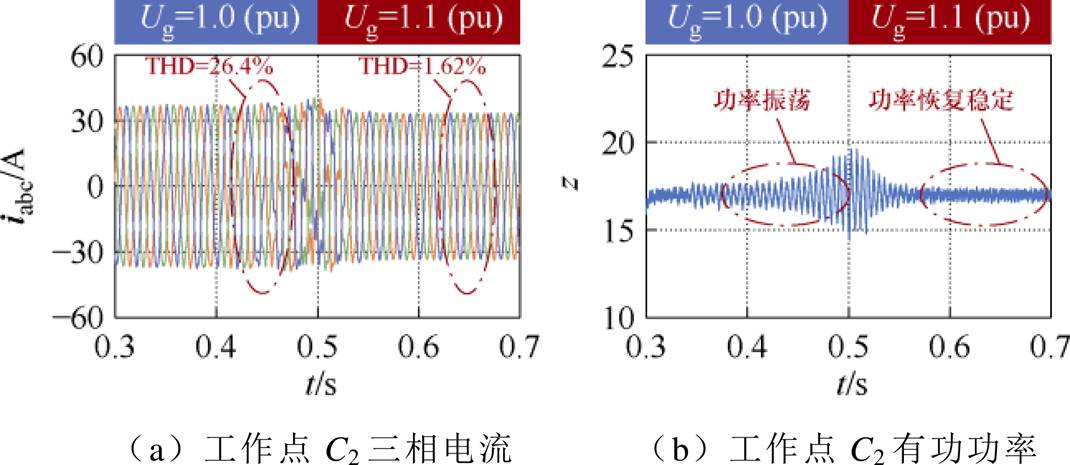
图19 波形电网电压抬升时验证点C2仿真波形
Fig.19 Simulation waveforms at the grid voltage rises verification point C2
在工作点C1，电网电压为1(pu)时，三相电网电流波形对称，功率保持稳定，THD为1.64%，系统稳定；0.5 s时电网电压跌落至0.9(pu)，电流出现振荡，THD大幅提高，功率振荡失稳。在工作点，0.3～0.5 s时系统功率振荡，处于失稳状态，0.5 s后，抬升电网电压，功率恢复稳定，三相电网电流THD从26.4%降低为1.62%，电网电压的提高，有助于增强系统的稳定性，仿真结果与理论分析一致。
最后，为验证锁相环参数改变时ssor构建的正确性，选取图13中点D1（14 kW, 4 kvar）、D2（20 kW, 4 kvar），其三相并网电流及输出有功功率仿真波形如图20、图21所示。
在工作点D1，随着fbw增加，系统从稳定运行至失稳，具体表现为：在0.3～0.5 s内，工作点D1位于ssor内，系统稳定，在0.5 s时fbw增加为52 Hz，此时D1迁移至suor，短暂运行一段时间后，并网电流波形振荡、发生严重畸变，THD从2.85%增加至62.4%，系统失稳。类似地，在0.3～0.5 s内，工作点D2的并网电流波形对称，THD仅为0.86%，具备良好的电能质量；但0.5 s后，fbw从26 Hz增加至34 Hz时，THD达35.5%，工作点D2从稳定转变为不稳定，与基于稳定域的分析结果相符。
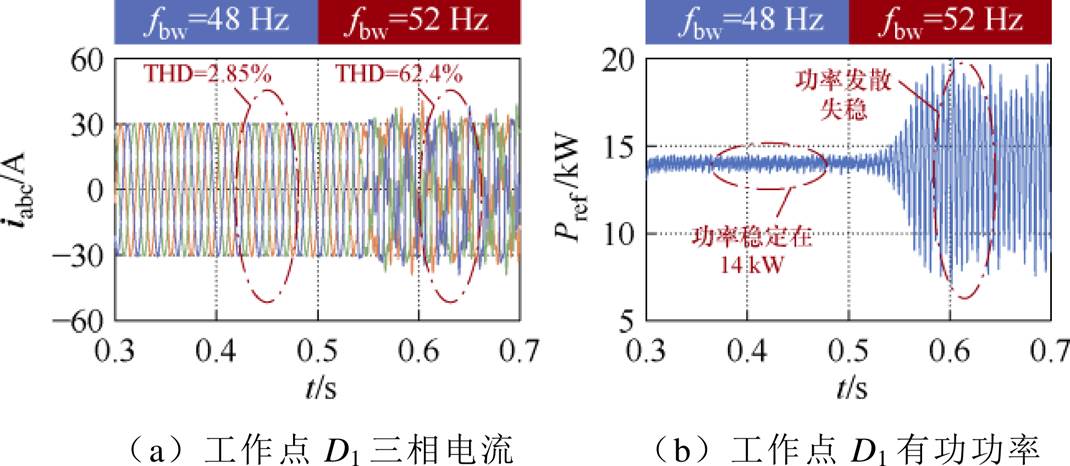
图20 PLL带宽验证点D1仿真波形
Fig.20 Simulation waveforms at PLL bandwidth verification point D1
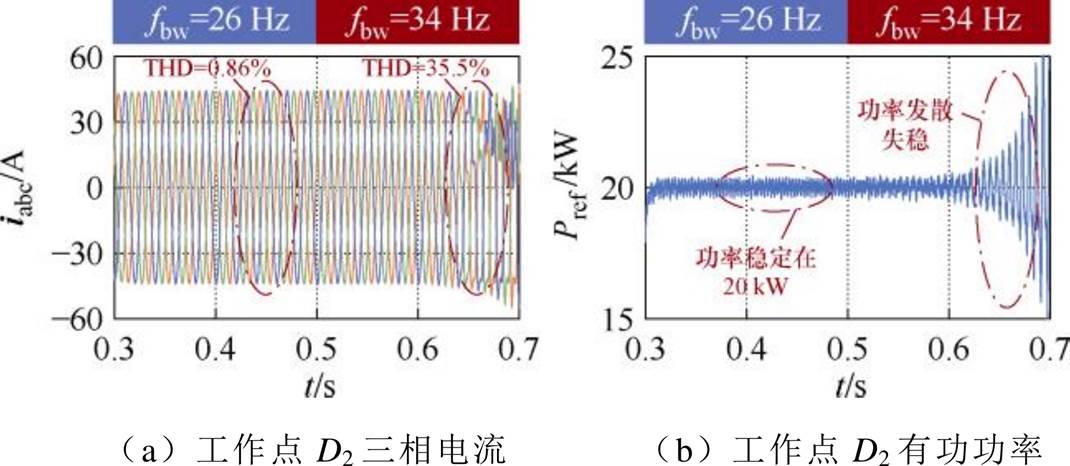
图21 PLL带宽验证点D2仿真波形
Fig.21 Simulation waveforms at PLL bandwidth verification point D2
在上述理论分析和仿真的基础上，进一步搭建实验平台来验证本文所提基于稳定域的GCI稳定性分析方法的正确性与有效性，其中控制参数部分与仿真部分一致。实验平台如图22所示。
图22 实验平台
Fig.22 Experimental platform
对图9中点A1、A4（15 kW, 4kvar）和suor中两点A3、A5（22 kW, 4 kvar）进行实验验证，图23给出了其三相电流及有功功率实验波形。从图23中可以看出，工作点处于稳定域时，系统能够保持稳定运行；当系统从稳定工作点迁移至不稳定工作点时，电流波形畸变，输出有功功率振荡，实验结果与理论分析一致。因此，所提方法可以有效判定不同工作点下系统稳定性。
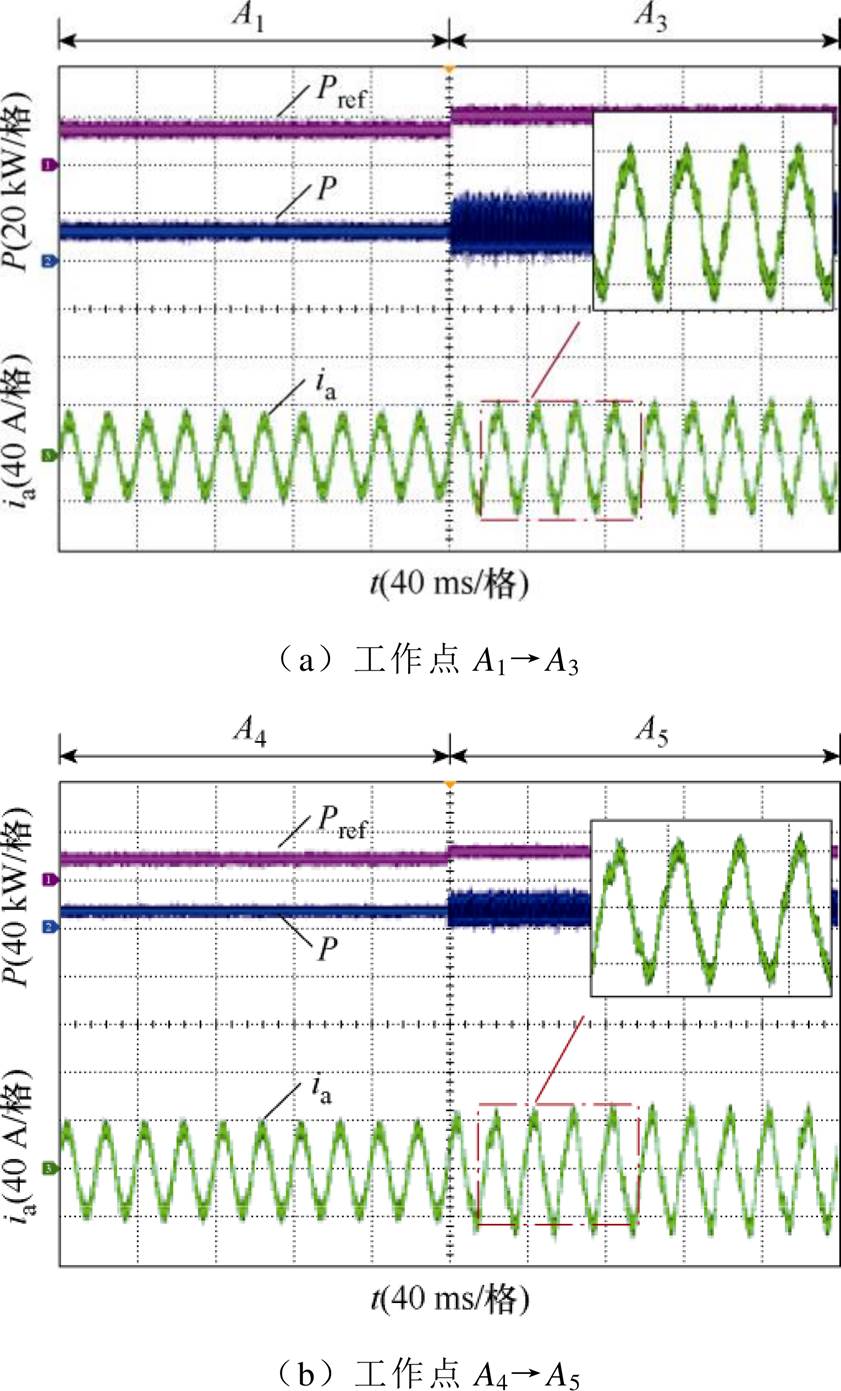
图23 稳定域验证点实验波形
Fig.23 Experimental waveforms at the stable operating region verification points
图24为电网电感改变验证点B1与电网电阻改变验证点B2的三相电流及有功功率实验波形。由图24可见，在同一工作点下，增加等效电感易恶化系统的稳定性；而等效电阻的增加时，影响不显著，稳定的工作点仍能保持稳定，实验结果与理论及仿真分析相符。
图25、图26分别为电网电压改变验证点C1与锁相环带宽改变验证点D1的实验波形，由图可见，在同一工作点下，锁相环带宽提高或电网电压跌落，系统从稳定运行过渡到不稳定运行状态，输出电流发生畸变，甚至振荡发散，实验结果与理论分析 一致。
图24 不同电网阻抗下实验波形
Fig.24 Experimental waveforms at different grid impedances
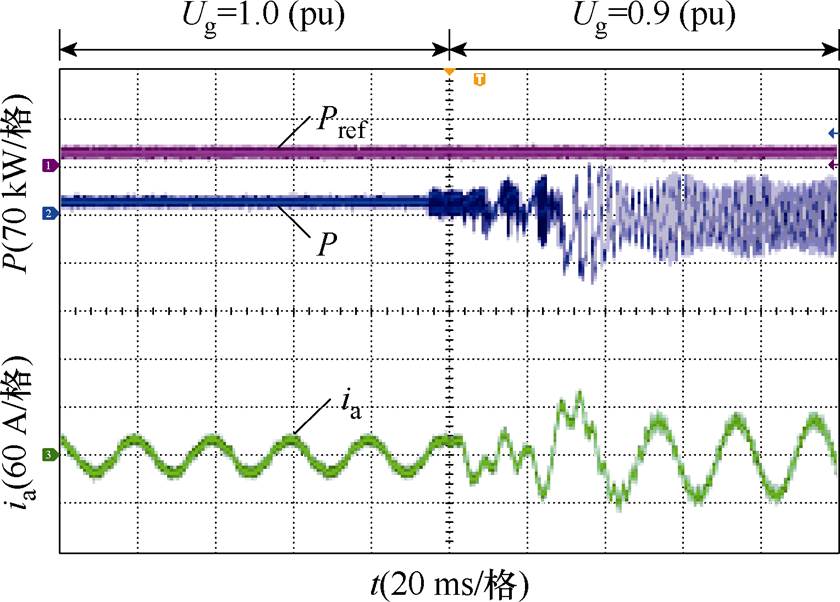
图25 不同电网电压下实验波形
Fig.25 Experimental waveforms under different grid voltages
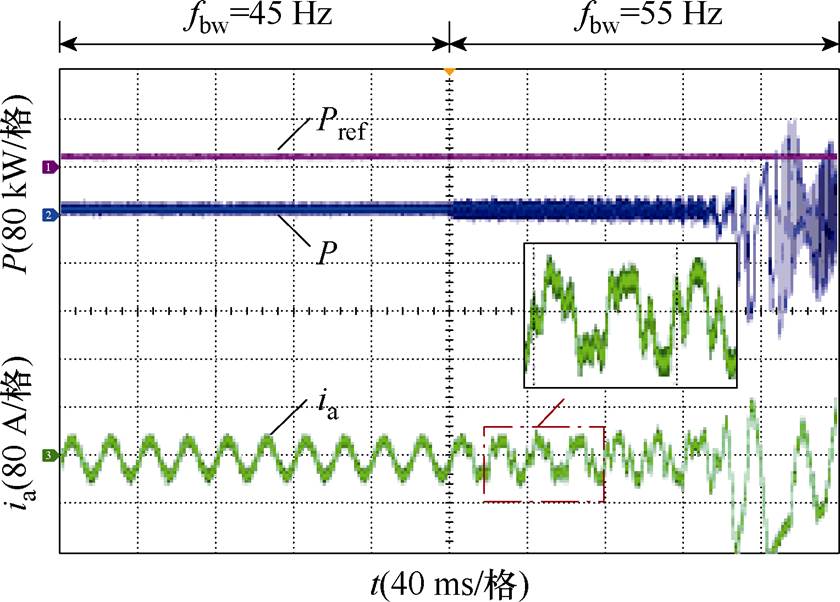
图26 不同PLL带宽下实验波形
Fig.26 Experimental waveforms at different PLL bandwidth
本文将工作点变量引入GCI的建模过程中，提出了一种基于稳定域的并网逆变系统的稳定性分析方法，主要工作及结论如下：
1）在建模方面：考虑了功率外环、电流环、锁相环动态特性及dq轴间的耦合效应，将工作点引入建模过程，推导了多变量的闭环传递函数模型，利用该模型可以直接分析时变工作点下系统的稳定性，避免了重复建模的复杂过程。
2）在稳定域构建方面：基于内嵌工作点变量的闭环传递函数模型，精确刻画了系统的稳定域，并进一步研究了电网阻抗、电网电压、锁相环带宽对稳定域的影响规律，并与电流控制进行了对比，两者在电网电压较高、锁相环带宽较低时，稳定域存在着显著差异。
3）在稳定性分析方面：基于所得稳定域，可以直观地获取时变工况下系统的稳定性信息。对稳定域分析结果表明，稳定域与电网电阻、电网电压呈正相关，与电网电感、锁相环带宽呈负相关。在所分析的功率范围，稳定域对电网电压变化的敏感度相近，但在较大功率范围内，稳定域对锁相环带宽变化的敏感度更高。
本文主要进行了PQ控制下逆变器的稳定性分析，尚未考虑其他控制策略及复杂的应用场景。然而，本文可以为其他控制策略提供理论基础，便于将小信号分析方法拓展至全工作域分析中。后续工作，将对其他控制方法下逆变系统的稳定性进行分析，并进一步研究多机并联等复杂场景下系统的稳定域的构建。
参考文献
[1] 谢小荣, 贺静波, 毛航银, 等. “双高”电力系统稳定性的新问题及分类探讨[J]. 中国电机工程学报, 2021, 41(2): 461-475.
Xie Xiaorong, He Jingbo, Mao Hangyin, et al. New issues and classification of power system stability with high shares of renewables and power elec- tronics[J]. Proceedings of the CSEE, 2021, 41(2): 461-475.
[2] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994.
Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[3] 张兴, 李明, 郭梓暄, 等. 新能源并网逆变器控制策略研究综述与展望[J]. 全球能源互联网, 2021, 4(5): 506-515.
Zhang Xing, Li Ming, Guo Zixuan, et al. Review and perspectives on control strategies for renewable energy grid-connected inverters[J]. Journal of Global Energy Interconnection, 2021, 4(5): 506-515.
[4] 高家元, 黄帅, 姜飞, 等. 弱电网下基于比例权重的控制环参数自适应调整并网逆变器稳定性提升方法[J]. 电工技术学报, 2024, 39(24): 7846-7859.
Gao Jiayuan, Huang Shuai, Jiang Fei, et al. Stability improvement method of grid-connected inverter based on proportional weight control loop parameters adaptive adjustment under weak grid[J]. Transactions of China Electrotechnical Society, 2024, 39(24): 7846-7859.
[5] 高磊, 吕敬, 马骏超, 等. 基于电路等效的并网逆变器失稳分析与稳定控制[J]. 电工技术学报, 2024, 39(8): 2325-2341.
Gao Lei, Lü Jing, Ma Junchao, et al. Instability analysis and stability control of grid-connected inverter based on impedance circuit equivalent[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2325-2341.
[6] 施松涛, 胡雪峰, 李金玉, 等. 扩大系统稳定分界频率和提升系统鲁棒性的LCL型逆变器控制策略[J/OL]. 电源学报, 1-14[2025-11-14].https://link.cnki. net/urlid/12.1420.TM.20250916.1522.005.
Shi Songtao, Hu Xuefeng, Li Jinyu, et al. Control strategy for LCL grid-connected inverter to expand system stability boundary frequency and enhance robustness[J]. Journal of Power Supply, 1-14[2025- 11-14]. https://link.cnki.net/urlid/12.1420.TM.20250916. 1522.005.
[7] 谢伟杰, 肖凡, 涂春鸣, 等. 考虑工作点时变特性的并网变流器全工作区间稳定性分析[J]. 中国电机工程学报, 2024, 44(7): 2801-2815.
Xie Weijie, Xiao Fan, Tu Chunming, et al. Full working area stability analysis of grid-connected converters considering time-varying characteristics of operating points[J]. Proceedings of the CSEE, 2024, 44(7): 2801-2815.
[8] 吴滨源, 李建文, 李永刚, 等. 并网逆变器dq阻抗灰箱辨识方法与应用[J]. 中国电机工程学报, 2022, 42(4): 1534-1546.
Wu Binyuan, Li Jianwen, Li Yonggang, et al. Gray- box identification method of grid-connected inverters dq impedance and its applications[J]. Proceedings of the CSEE, 2022, 42(4): 1534-1546.
[9] Tu Yiming, Liu Jinjun, Liu Teng, et al. Impedance- based stability analysis of large-scale PV station under weak grid condition considering solar radiation fluctuation[C]//2018 International Power Electronics Conference (IPEC-Niigata 2018 -ECCE Asia), Niigata, Japan, 2018: 3934-3939.
[10] Prakash S, Al Zaabi O, Behera R K, et al. Modeling and dynamic stability analysis of the grid-following inverter integrated with photovoltaics[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(4): 3788-3802.
[11] Liu Huakun, Xie Xiaorong, Gao Xiaodan, et al. Stability analysis of SSR in multiple wind farms connected to series-compensated systems using impedance network model[J]. IEEE Transactions on Power Systems, 2017, 33(3): 3118-3128.
[12] Sun Kun, Yao Wei, Fang Jiakun, et al. Impedance modeling and stability analysis of grid-connected DFIG-based wind farm with a VSC-HVDC[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1375-1390.
[13] Pepiciello A, Domínguez-García J L. Small-signal stability analysis of uncertain power systems: a comprehensive survey[J]. Renewable and Sustainable Energy Reviews, 2024, 200: 114576.
[14] Wang Guanzhong, Xin Huanhai, Wu Di, et al. Data-driven probabilistic small signal stability analysis for grid-connected PV systems[J]. Inter- national Journal of Electrical Power & Energy Systems, 2019, 113: 824-831.
[15] 齐宗强, 窦晓波, 卜强生, 等. 基于样本弱依赖多项式混沌展开式的电网小干扰概率分析[J]. 电力系统自动化, 2025, 49(6): 157-164.
Qi Zongqiang, Dou Xiaobo, Bu Qiangsheng, et al. Low-sample-dependent polynomial chaos expansion for probabilistic small signal stability analysis of power grids[J]. Automation of Electric Power Systems, 2025, 49(6): 157-164.
[16] Liu Shichao, Liu P X, Wang Xiaoyu. Stability analysis of grid-interfacing inverter control in distribution systems with multiple photovoltaic-based distributed generators[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12): 7339-7348.
[17] Shi Ying, Sun Yue, Liu Junliang, et al. Model and stability analysis of grid-connected PV system considering the variation of solar irradiance and cell temperature[J]. International Journal of Electrical Power & Energy Systems, 2021, 132: 107155.
[18] Zou Xiaoming, Du Xiong, Tai Hengming. Two- variable admittance model for D-PMSG-based wind turbine and stability criterion based on magnitude and phase contour plot[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 1484-1498.
[19] Du Chengmao, Du Xiong, Tong Chenghui, et al. Stability analysis for DFIG-based wind farm grid- connected system under all wind speed conditions[J]. IEEE Transactions on Industry Applications, 2023, 59(2): 2430-2445.
[20] Shi Ying, Sun Yue, Liu Junliang, et al. New analysis on two-variable converter impedance model in grid- connected systems[J]. IET Renewable Power Gen- eration, 2021, 15(15): 3704-3714.
[21] 涂春鸣, 郑宇婷, 肖凡, 等. 并网变流器全工作区间的稳定性分析方法研究[J]. 中国电机工程学报, 2023, 43(19): 7580-7592.
Tu Chunming, Zheng Yuting, Xiao Fan, et al. Study on the stability analysis method of grid-connected converters in full operating range[J]. Proceedings of the CSEE, 2023, 43(19): 7580-7592.
[22] 刘威, 谢小荣, 黄金魁, 等. 并网变流器的频率耦合阻抗模型及其稳定性分析[J]. 电力系统自动化, 2019, 43(3): 138-146.
Liu Wei, Xie Xiaorong, Huang Jinkui, et al. Frequency-coupled impedance model and stability analysis of grid-connected converter[J]. Automation of Electric Power Systems, 2019, 43(3): 138-146.
[23] Huang Linbin, Xin Huanhai, Li Zhiyi, et al. Grid- synchronization stability analysis and loop shaping for PLL-based power converters with different reactive power control[J]. IEEE Transactions on Smart Grid, 2019, 11(1): 501-516.
[24] Xue Danhong, Liu Jinjun, Liu Zeng, et al. Modeling and analysis of DC terminal impedance of voltage- source converters with different control modes[J]. IEEE Transactions on Power Electronics, 2019, 35(6): 5883-5896.
[25] 涂春鸣, 邹凯星, 高家元, 等. 基于不对称正负反馈效应的PQ功率控制并网逆变器稳定性分析[J]. 电工技术学报, 2023, 38(2): 496-509.
Tu Chunming, Zou Kaixing, Gao Jiayuan, et al. Stability analysis of grid-connected inverter under PQ power control based on asymmetric positive- negative-feedback effects[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 496-509.
[26] 唐欣, 李珍, 李勇, 等. 并网变流器频率耦合振荡分析及解耦控制设计[J]. 中国电机工程学报, 2023, 43(8): 3127-3137.
Tang Xin, Li Zhen, Li Yong, et al. Frequency coupling oscillation analysis and decoupling control design of grid connected converter[J]. Proceedings of the CSEE, 2023, 43(8): 3127-3137.
[27] 林鸿彬, 葛平娟, 徐海亮, 等. 异构逆变器并联系统改进Gershgorin圆稳定性判据及其多维谐振特性分析[J]. 电工技术学报, 2024, 39(8): 2265-2280.
Lin Hongbin, Ge Pingjuan, Xu Hailiang, et al. Improved Gershgorin-circle stability criterion and multi-dimensional resonance characteristics analysis for heterogeneous inverter paralleled system[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2265-2280.
[28] Zhou Weihua, Wang Yanbo, Torres-Olguin R E, et al. Effect of reactive power characteristic of offshore wind power plant on low-frequency stability[J]. IEEE Transactions on Energy Conversion, 2020, 35(2): 837-853.
Abstract Traditional stability methods have extensively discussed the stability of grid-connected inverters (GCI) at specific operating points. However, due to the fluctuation of new energy output and the randomness of load switching, the operating point of GCI exhibits significant time-varying characteristics. There are substantial differences in the stability of GCI under different working conditions. PQ control is a common control strategy for GCI, which has the characteristics of multi-loop coupling, multiple time scales, and strong nonlinearity compared to single-current control. To clarify the dynamic attributes of GCI, a stability analysis method of GCI with PQ control based on the stable operating region is proposed. The stable operating region can directly characterize the stability of the whole working range of the system.
Firstly, the mutual couples among the control loops, such as phase-locked loop (PLL), power loop, and current loop, are considered. The operating point variables are introduced into the small signal model of GCI by the PLL and power calculation sessions. The PQ control GCI model with embedded operating point variables is derived. It can comprehensively and accurately describe the stability of the inverter system over the full operating range. Secondly, considering the power circuit constraint, the stable operating region of GCI is constructed by numerical analysis. The stability of all operating points in the operating range can be visually obtained. Furthermore, the effects of external system parameters (e.g., grid impedance, grid voltage) and internal control parameters (PLL bandwidth) on stability are analyzed. The difference in the stable operating region between GCI with PQ control and GCI with current control is compared. Finally, the theoretical analysis is verified by simulation and experiment.
The following conclusions can be drawn from the simulation analysis. (1) The dynamic characteristics of the power outer loop, current loop, PLL, and the coupling effect between the dq-axis are considered. The working point is introduced for modeling, and the multivariable closed-loop transfer function model is derived. The model can directly analyze the system's stability under time-varying operating points, avoiding the complicated process of repeated modeling. (2) The closed-loop transfer function model based on embedded operating point variables can accurately characterize the stable operating region of the system. It can be used to analyze the trend of grid impedance, grid voltage, and phase-locked loop bandwidth in the stable operating region. A significant difference exists between the stable operating region of the GCI with PQ control and the GCI with current control at higher grid voltages and lower PLL bandwidths. (3) Based on the obtained stable operating region, the stability information of the system under time-varying operating conditions can be obtained intuitively. The stable operating region analysis shows that the stable operating region positively correlates with the grid resistance and voltage, while negatively correlating with the grid inductance and PLL bandwidth. In the analyzed power range, the sensitivity of stable operating region to grid voltage changes is similar. However, the sensitivity of stable operating region to PLL bandwidth variation is greater in higher power ranges.
keywords：Grid-connected inverter, PQ control, operating point, stable operating region, small-signal model
DOI: 10.19595/j.cnki.1000-6753.tces.241966
中图分类号：TM464
国家重点研发资助项目（2023YFB2407600）。
收稿日期 2024-11-03
改稿日期 2025-01-19
罗宇航 男，2001年生，硕士研究生，研究方向为分布式发电与电力电子技术。E-mail: yhl0869@hnu.edu.cn
郑宇婷 女，1999年生，博士研究生，研究方向为电力电子技术及其在电力系统中的应用。E-mail: yt0107yt@hnu.edu.cn（通信作者）
（编辑 陈 诚）