SiC逆变器驱动感应电机的高频脉振注入无速度传感器控制
卞小亮 原熙博 陈 硕 王 凯 赵传杰
(中国矿业大学电气工程学院 徐州 221116)
摘要 在基于高频脉振注入法的感应电机无速度传感器矢量控制系统中,凸极特性和转子位置估计误差是影响感应电机可靠稳定运行的关键因素。针对现有研究大多侧重于传统硅逆变器驱动的感应电机,该文以碳化硅(SiC)逆变器驱动的感应电机为研究对象,提出一种基于SiC逆变器高开关频率和高开关速度特性的感应电机无速度传感器控制方案。该方案分析不同注入频率对感应电机饱和凸极的影响,揭示SiC逆变器高注入频率增强饱和凸极的机理。在此基础上,分析逆变器死区时间设置对转子位置估计误差的影响,并采用二阶广义积分器抑制转子位置提取方法中的特定谐波,有效提高转子位置估计精度。实验结果表明,所提方案能够有效地提高基于高频脉振注入法的感应电机低速域无速度传感器矢量控制系统的可靠性和稳态性能。
关键词:碳化硅(SiC) 感应电机 饱和凸极 高频脉振注入 转子位置估计
0 引言
感应电机无速度传感器矢量控制系统省去了机械式的速度传感器,能够以低成本实现宽调速范围的机电能量转换,已经在工业领域广泛应用[1-2]。根据转子位置估计的原理,通常将无速度传感器控制方法分为基波模型法和高频注入法[3]。基波模型法是通过设计观测器,利用电压、电流信号来估计磁链和转子位置信号,在中、高速域,可以获得较高的估计精度。然而,在零、低速域,电机端口反电动势的幅值小,较低的信噪比难以准确估计磁链和转子位置信息,可能会导致较大的估计误差,使得基波模型法无法满足感应电机无速度传感器矢量控制系统对高性能运行的要求[4]。
高频注入法通过向电机定子中注入高频信号,利用电机凸极特性调制产生的高频响应信号,提取电机转速和转子位置信息,在零、低速域,可以获得较高的转子位置估计精度。根据高频信号在不同坐标轴系的注入,高频注入法可分为高频旋转注入法和高频脉振注入法[5]。其中,显著的凸极特性是使用高频注入法实现转子位置准确估计的前提,然而,感应电机三相绕组对称,不具备空间结构上的凸极特性。文献[6]通过向转子槽为闭口型的感应电机中注入高频电压信号诱发饱和凸极,然而在某些工作点,d、q轴饱和程度趋于一致,导致凸极特性消失。文献[7]设计感应电机的转子槽为开口型,并沿气隙方向改变开口槽的高度和宽度,通过向转子槽中注入高频电压信号,利用感应电机的空间凸极特性检测电机转速和转子位置信息。文献[8]基于有限元分析,研究了趋肤效应对感应电机转子电阻和电感参数的影响,通过注入电压信号使得电机d、q轴的参数产生差异而形成饱和凸极,但缺少实验验证。文献[9]提出了一种基于有限元计算的高频磁场等效电路,注入高频电压信号时,转子磁阻将影响高频磁场的分布,形成的多重凸极特性会降低转子位置估计精度。因此,凸极特性可以通过改造感应电机定、转子结构或利用饱和特性产生,且影响电机的运行性能。
高频脉振注入法是基于凸极特性,通过向估计同步旋转坐标系中的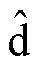 轴注入高频正弦电压信号,从
轴注入高频正弦电压信号,从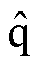 轴高频电流响应的幅值中提取转子位置信息。相比于高频旋转注入法,高频脉振注入算法结构简单,且转矩脉动较小。为了提高基于高频脉振注入法的转子位置估计精度,学者们进行了大量的研究。针对电机参数变化对转子位置估计的影响,文献[10]推导出含有电机变化参数的转子位置估计误差的解析表达式,从而指导系统参数的选择,减小估计误差,但未考虑动态工况。文献[11]针对逆变器输出谐波对转子位置估计误差的干扰问题,通过仿真和数值分析得出转子位置提取方法中多个电机参数对估计误差的影响规律,然而,只考虑了由数字控制器实现空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)时带来的离散化干扰。文献[12]针对滤波器的相位延时问题,提出一种基于双频陷波器级联低通滤波器(Low Pass Filter, LPF)的改进型位置误差信号提取策略,然而,陷波器较长的离散周期会导致幅值的失真,降低了转子位置估计精度。以上研究均是基于硅(Si)逆变器的高频脉振注入无速度传感器矢量控制系统。然而,近年来,以碳化硅(SiC)器件为代表的第三代宽禁带半导体飞速发展,其凭借高开关频率和低导通电阻等特性,在追求高功率密度、高效率的电机控制场合得到了广泛应用,且得到了学者们的广泛关注[13-15]。但迄今为止,很少有文献关注SiC器件的高开关频率和高开关速度特性对感应电机无速度传感器矢量控制系统性能的影响。
轴高频电流响应的幅值中提取转子位置信息。相比于高频旋转注入法,高频脉振注入算法结构简单,且转矩脉动较小。为了提高基于高频脉振注入法的转子位置估计精度,学者们进行了大量的研究。针对电机参数变化对转子位置估计的影响,文献[10]推导出含有电机变化参数的转子位置估计误差的解析表达式,从而指导系统参数的选择,减小估计误差,但未考虑动态工况。文献[11]针对逆变器输出谐波对转子位置估计误差的干扰问题,通过仿真和数值分析得出转子位置提取方法中多个电机参数对估计误差的影响规律,然而,只考虑了由数字控制器实现空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)时带来的离散化干扰。文献[12]针对滤波器的相位延时问题,提出一种基于双频陷波器级联低通滤波器(Low Pass Filter, LPF)的改进型位置误差信号提取策略,然而,陷波器较长的离散周期会导致幅值的失真,降低了转子位置估计精度。以上研究均是基于硅(Si)逆变器的高频脉振注入无速度传感器矢量控制系统。然而,近年来,以碳化硅(SiC)器件为代表的第三代宽禁带半导体飞速发展,其凭借高开关频率和低导通电阻等特性,在追求高功率密度、高效率的电机控制场合得到了广泛应用,且得到了学者们的广泛关注[13-15]。但迄今为止,很少有文献关注SiC器件的高开关频率和高开关速度特性对感应电机无速度传感器矢量控制系统性能的影响。
鉴于此,本文提出了一种基于SiC逆变器的感应电机高频脉振注入无速度传感器控制方案。该方案首先评估了不同注入频率对感应电机饱和凸极的影响,揭示了SiC逆变器高注入频率增强饱和凸极的机理;其次分析了SiC逆变器的高开关速度(短死区时间)特性对感应电机转子位置估计误差的影响,并推导出误差表达式;然后利用二阶广义积分器(Second-Order Generalized Integrator, SOGI),抑制传统转子位置提取方法中的特定谐波,提高转子位置估计精度;最后在基于SiC逆变器的感应电机无速度传感器控制实验平台上验证了所提方案的可行性。
1 基于高频脉振注入法的感应电机无速度传感器控制
1.1 高频脉振注入法原理
在同步旋转坐标系下,感应电机d、q轴的定子电压方程可表示为[16]
式中,usd, usq、isd, isq、λsd, λsq分别为沿d、q轴的定子电压分量、定子电流分量和定子磁链分量;Lm、Ls、Lr、Rs和Rr分别为互感、定子电感、转子电感、定子电阻和转子电阻;σ为漏感系数;ωe为电角频率;s为微分算子。
一般而言,基于高频脉振注入法,在零、低速域ωe较小,且Rr远小于jωhLr,其中,ωh为高频电压注入的角频率。此时d、q轴的定子高频电压方程可表示为
式中,usdh、usqh和isdh、isqh分别为沿d、q轴的定子高频电压分量和定子高频电流分量。
当注入频率较高时,可忽略电阻的影响,式(2)可以化简为
式中,Ld、Lq分别为d、q轴等效电感。
基于高频脉振注入法,向估计同步旋转坐标系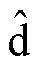 、
、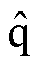 轴注入的高频电压信号可以表示为
轴注入的高频电压信号可以表示为
式中,Uh为注入高频信号的电压幅值。
估计同步旋转坐标系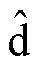 、
、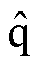 轴的高频响应电流可以表示为
轴的高频响应电流可以表示为
式中,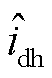 、
、 分别为估计同步坐标系
分别为估计同步坐标系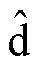 、
、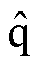 轴高频电流分量;
轴高频电流分量;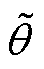 为参考同步旋转坐标系与估计同步旋转坐标系的角度误差;L为平均电感,L=(Ld+Lq)/2;ΔL为半差电感,ΔL=(Lq-Ld)/2。
为参考同步旋转坐标系与估计同步旋转坐标系的角度误差;L为平均电感,L=(Ld+Lq)/2;ΔL为半差电感,ΔL=(Lq-Ld)/2。
由式(5)可知,当ΔL≠0时,若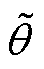 =0,则高频电流
=0,则高频电流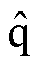 轴分量为0。
轴分量为0。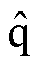 轴高频电流的幅值
轴高频电流的幅值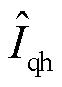 中含有转子位置误差信息,其表达式为
中含有转子位置误差信息,其表达式为
因此,通过对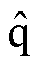 轴电流的处理,基于转子位置提取方法,可获得准确的转子位置估计信息。
轴电流的处理,基于转子位置提取方法,可获得准确的转子位置估计信息。
1.2 传统的转子位置提取方法
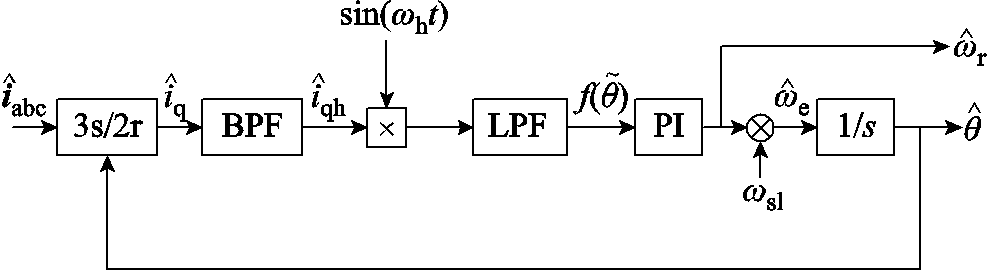
基于高频脉振电压注入法,电机转子位置提取方法的结构如图1所示。
首先使用带通滤波器(Bass Pass Filter, BPF)对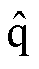 轴电流进行滤波,提取高频响应电流;其次对
轴电流进行滤波,提取高频响应电流;其次对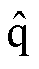 轴高频电流进行幅值调制,使用LPF滤除高频信息;最后经过锁相环(Phase Locked Loop, PLL)获得电机转子位置估计信息。具体的数学表达式为
轴高频电流进行幅值调制,使用LPF滤除高频信息;最后经过锁相环(Phase Locked Loop, PLL)获得电机转子位置估计信息。具体的数学表达式为
当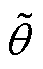 较小时,
较小时,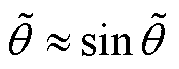 ,此时,将转子位置估计误差线性化可得
,此时,将转子位置估计误差线性化可得
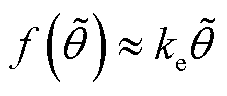 (8)
(8)
式中,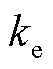 为转子位置误差系数,
为转子位置误差系数,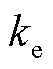 =
=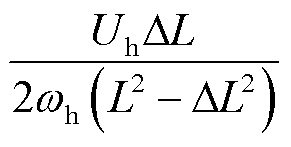 。
。
基于传统的转子位置提取方法,通过调节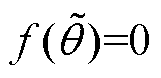 ,可以使转子位置角的估计值收敛于实际值,从而获得准确的转子位置信息。然而,在一般情况下,感应电机三相绕组对称,感应电机的d、q轴的等效电感相等,即Ld=Lq,半差电感ΔL=0,则无法通过式(7)获取转子位置信息。为了解决这一问题,通过向感应电机的
,可以使转子位置角的估计值收敛于实际值,从而获得准确的转子位置信息。然而,在一般情况下,感应电机三相绕组对称,感应电机的d、q轴的等效电感相等,即Ld=Lq,半差电感ΔL=0,则无法通过式(7)获取转子位置信息。为了解决这一问题,通过向感应电机的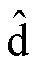 轴注入高频电压信号,利用磁饱和所引起的凸极效应,可以使得ΔL≠0,从而实现转子位置的辨识。因此一定的凸极特性是实现基于高频脉振注入法感应电机无速度传感器控制的前提条件。同时,由于非理想因素(如逆变器死区时间)的影响,转子位置估计误差
轴注入高频电压信号,利用磁饱和所引起的凸极效应,可以使得ΔL≠0,从而实现转子位置的辨识。因此一定的凸极特性是实现基于高频脉振注入法感应电机无速度传感器控制的前提条件。同时,由于非理想因素(如逆变器死区时间)的影响,转子位置估计误差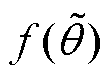 会产生误差,降低感应电机低速运行性能。
会产生误差,降低感应电机低速运行性能。
2 基于SiC逆变器的感应电机无速度传感器控制
2.1 SiC器件特性对感应电机饱和凸极的影响
在感应电机转子槽内放置由整块导体组成的线棒,在交流电的作用下,转子槽内导体的磁力线分布如图2所示。
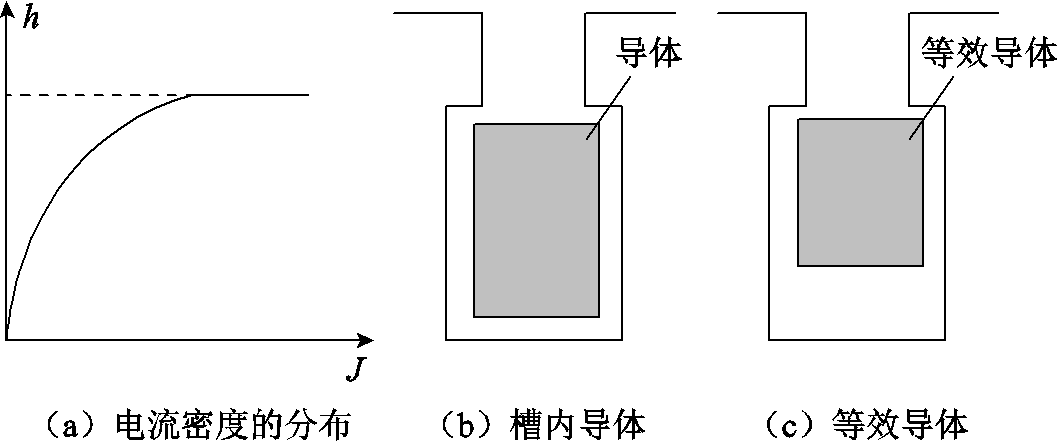
由于导体沿着槽高方向截面各部分的漏磁通匝链数不同,所以电流在导体上分布不均匀,电流密度随着槽高逐渐增大,使电流趋于线棒的表面[16],这种现象称为趋肤效应,如图3所示。图3a为电流密度随槽高变化的分布情况,其中h为导体距离槽底的高度,J为电流密度,同时假设槽内导体如图3b所示,在交流电的作用下,槽内等效导体如图3c所示。
在不同频率的交流电作用下,考虑趋肤效应的影响,等效导体的电阻值、漏电感值需要通过与注入频率相关的系数加以修正。假设槽内导体分为M层,当交流电压作用在槽内导体上时,它被均匀地分布在槽内导体的每一层。对于任意m层,电磁相量方程可以表示为
其中
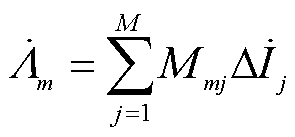 (10)
(10)
式中,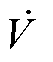 为电压相量;
为电压相量;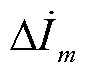 为m层电流相量;Rm为m层电阻;
为m层电流相量;Rm为m层电阻;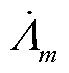 为m层磁链;Mmj为互感系数;m、j为层数(m>j)。
为m层磁链;Mmj为互感系数;m、j为层数(m>j)。
m层电流相量的表达式为
式中,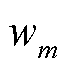 为m层截面的宽度;
为m层截面的宽度; ,
,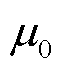 为真空磁导率,
为真空磁导率,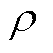 为电阻率。
为电阻率。
由式(11)可知,m层电流相量与其下层的电流相量均有关。假设第一层的电流相量为1+j0已知,可以通过递归的方法得到每一层的电流相量,槽内导体电流分布及相量图如图4所示。
由文献[17]可知,电阻的修正系数为
式中,Rac、Rdc分别为交、直流电阻;P为电阻损耗。
漏电感的修正系数为
式中,Lac、Ldc分别为交、直流电感;W为电感损耗;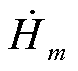 为第m层磁场强度相量。
为第m层磁场强度相量。
由式(12)、式(13)可知,在不同频率的交流电作用下,等效导体的电阻和漏电感均随着注入频率的不同而发生变化,且频率越高,电阻值越大、漏电感值越小。
文献[8]通过有限元分析了考虑磁场定向的感应电机转子棒的趋肤效应,量化分析了d、q轴高频电阻和高频电感与不同注入频率的关系。
首先,确定感应电机转子铁心的饱和水平。
其次,确定转子中的高频感应电流。定子由电流源激励,在d轴注入的情况下,给定子d、q轴施加的激励源为
式中,isd0、isq0 为初始基波电流;isdh为定子d轴高频电流;Ish为高频电流的幅值。
由于感应电机的d轴转子电压方程为
式中,λrd为转子d轴磁链;ird为转子d轴电流;Lsm、Lrm分别为定、转子磁化电感;Lrl,d为转子d轴漏感。
将式(14)代入式(15),可得转子d轴电流的幅值和相位分别为
同理,可以获得转子q轴电流。然后,向定、转子分别施加电流激励,可以得到不同注入频率下的转子高频电阻和高频电感。
其中,d、q轴的转子高频电感为
式中,λrq为转子q轴磁链;Irqh为q轴高频电流幅值。
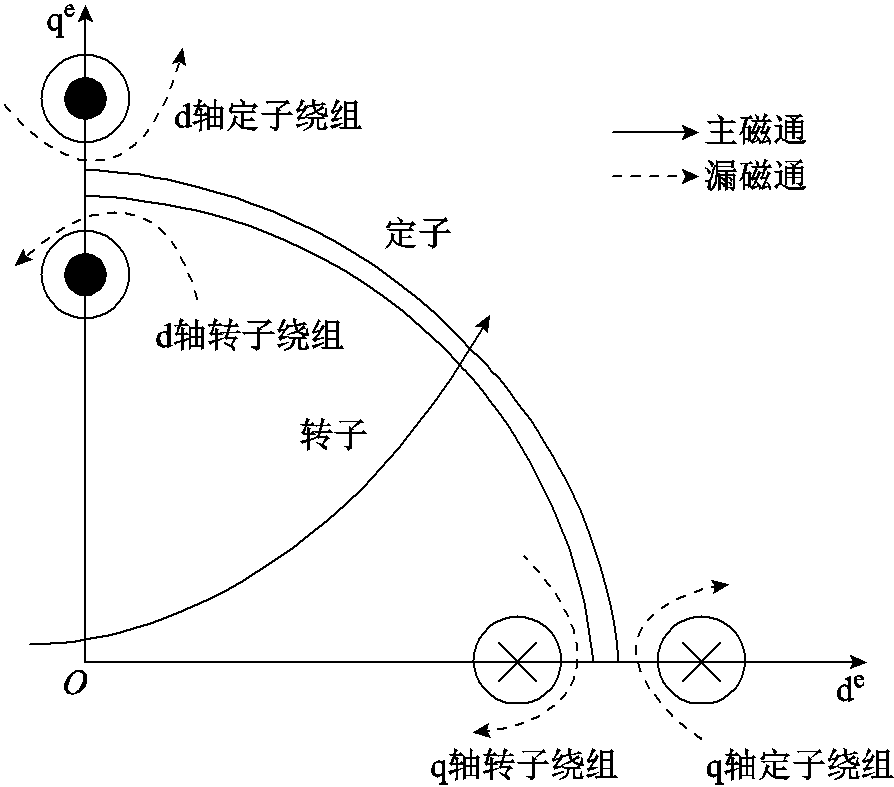
由式(17)可知,注入电压频率会导致高频电感的变化,从而影响饱和凸极的大小。通常,传统基于Si器件的高频脉振注入法受逆变器功率器件开关频率的限制,注入频率较低,通常为几百Hz,最高可达到PWM开关频率的1/6[18]。然而,SiC器件相比较于Si器件可工作在更高的开关频率范围,从而可以进一步提高注入电压的频率。值得注意的是,两极感应电机主磁通和漏磁通示意图如图5所示,在同步旋转坐标下,电机绕组与所对应的主磁链相互正交,即实际的d轴绕组位于q轴处,实际的q轴绕组位于d轴处[19]。故在主磁通所在d轴注入高频电压信号,则会因为d轴更加饱和,而导致d、q轴的饱和程度不同,使得感应电机的饱和凸极增强。
借鉴文献[20]的方法,可以量化不同注入电压的频率对感应电机饱和凸极的影响。由式(5)可以看出,高频电流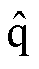 轴分量可以表示为
轴分量可以表示为
通过软件设置估计位置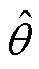 为0,则
为0,则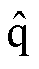 轴高频电流的幅值为
轴高频电流的幅值为
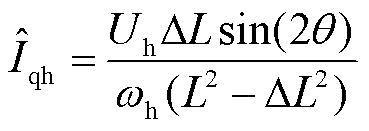 (19)
(19)
由式(19)可知,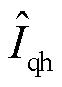 中含有ΔL,且随着2倍的同步旋转坐标系的速度
中含有ΔL,且随着2倍的同步旋转坐标系的速度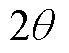 而变化。因此,感应电机的主凸极可以通过
而变化。因此,感应电机的主凸极可以通过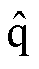 轴高频电流的幅值来刻画。
轴高频电流的幅值来刻画。
2.2 SiC器件特性对转子位置估计误差的影响
转子位置估计精度是衡量无速度传感器控制系统性能的重要指标。其中,逆变器非线性效应对转子位置估计精度有重要影响[21]。
相比于Si逆变器,SiC逆变器在非线性效应方面有所不同。尤其是SiC器件具有高开关速度特性,相比于Si器件可以设置更小的死区时间。同时,不同死区时间的设置,会造成电机相电流的畸变程度不同。
死区时间导致的电压畸变通常可以表示为
式中,Td为死区时间;Tc为PWM 开关周期;Udc为母线电压;is_p为电机定子p(p=a,b,c)相电流。
基于空间矢量表示法[22],式(20)可以表示为
其中,is为电机定子电流矢量,且
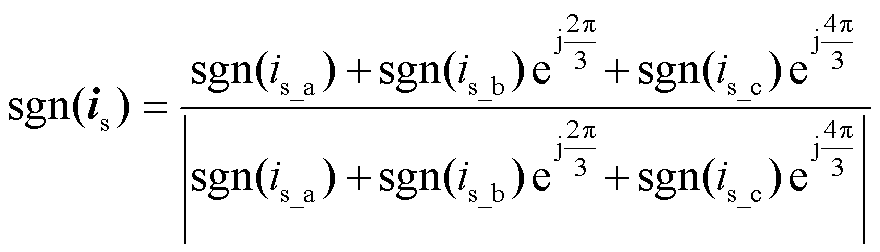
由式(21)可知,死区时间造成的电压畸变影响实际电压矢量的幅值和相位。因此,在d、q轴中,当同步旋转坐标系的速度为ωe、初始相位为0°时,电压畸变可以表示为[23]
由式(22)可知,d、q轴的电压畸变除了常数项以外,由6k次的谐波之和构成(k=1,2,3,···, +∞)。在dq轴坐标系中,将感应电机的定子电压方程的交叉耦合项看成扰动,则定子电压方程为
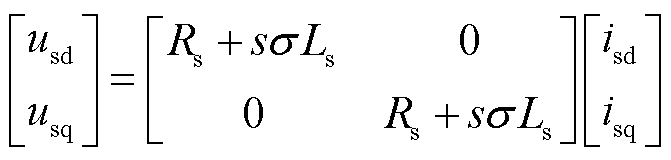 (23)
(23)
将式(22)代入式(23),可得相电流畸变的表达式为
因此,由式(22)和式(24)可知,相电流的畸变幅值中含有6k次谐波,且在相同的开关频率和母线电压下,电流畸变的幅值与死区时间成正比。
以a相为例,当a相电流的表达式为
式中,Im为基波幅值;φa为基频的初相位;φ6k为6k次谐波的初相位。
经过坐标变换,可得电机定子电流d、q轴分量为
其中
Isd=Imsinφa Isq=Imcosφa
Isd6k=Is6kcosφa Isq6k=-Is6ksinφa
由式(26)可知,死区时间导致d、q轴电流中存在6k次谐波。同理,死区时间也会使得d、q轴高频电流的幅值中叠加6k次谐波。因此,高频电流可表示为
经过坐标变换,可得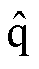 轴高频电流响应为
轴高频电流响应为
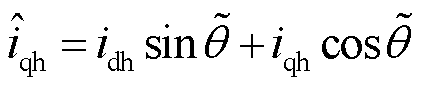 (28)
(28)
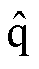 轴电流的幅值中含有的转子位置信息f(
轴电流的幅值中含有的转子位置信息f(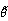 )为
)为
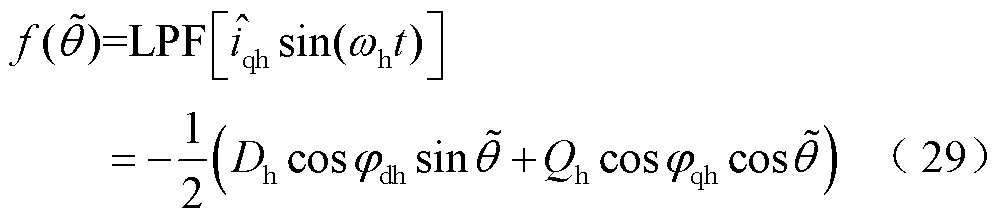
令f(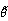 )=0,则转子位置估计误差为
)=0,则转子位置估计误差为
由式(30)可知,死区时间的设置会导致转子位置估计误差中含有基波的6k次谐波,这些谐波误差会降低感应电机无传感器控制的性能。其中,影响最大的为6次谐波。
2.3 基于特定谐波消除的转子位置提取方法
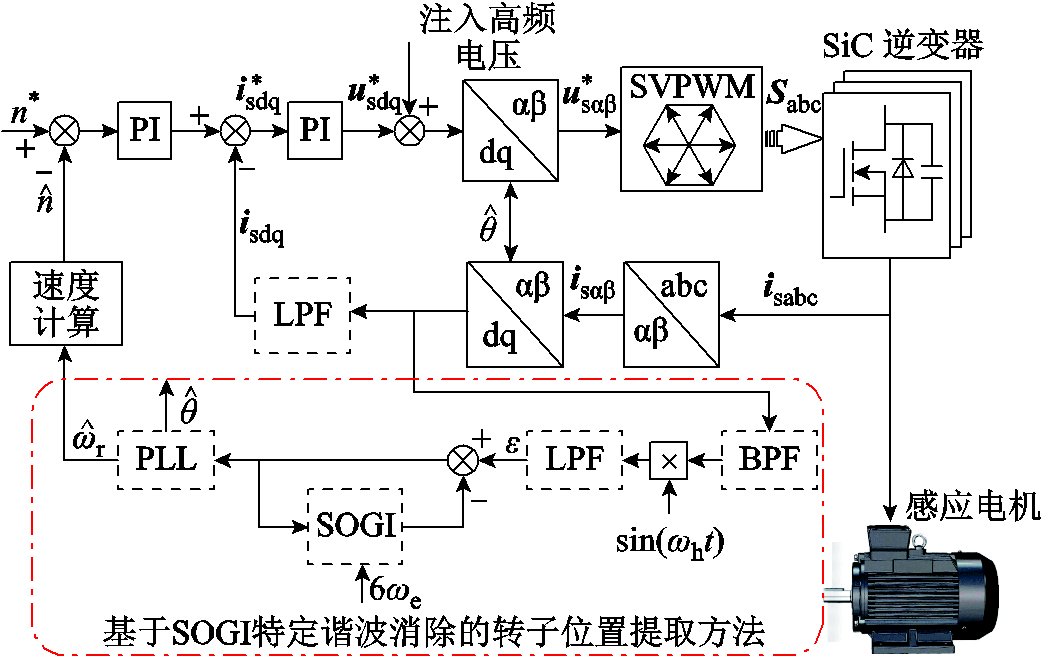
针对基于高频脉振注入法的感应电机转子位置估计存在误差的问题,本文提出了一种利用SOGI进行特定谐波消除的方法来提取转子位置信息。基于高频脉振注入法的感应电机无速度传感器控制框图如图6所示。
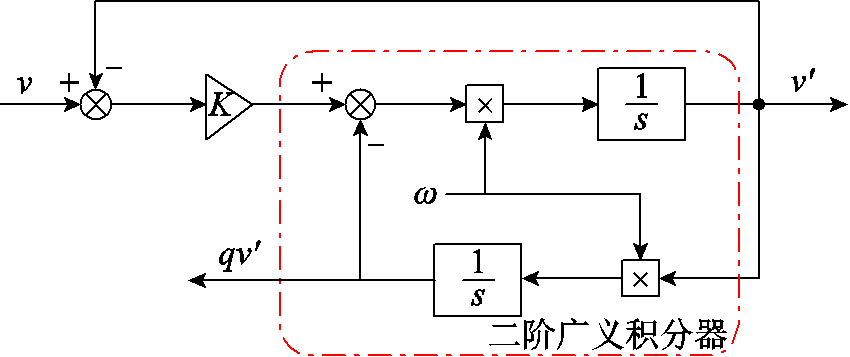
为了抑制转子位置估计误差中由于死区时间造成的6次谐波,首先利用SOGI提取转子位置误差中的6次谐波,然后用原始信号减去提取信号抑制转子位置估计误差。SOGI的结构框图如图7所示。
SOGI的传递函数为
式中,v为输入信号;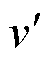 为输出信号,
为输出信号,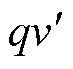 为正交输出信号;K为增益;ω为固有频率。
为正交输出信号;K为增益;ω为固有频率。
假设f=1 Hz,当增益K分别取K=0.1、K=0.5、K=1时,SOGI的Bode图如图8所示。K决定SOGI的通带带宽;ω决定SOGI通带的中心频率。当ω= 2p rad/s(f =1 Hz)时,则表示仅1 Hz附近的基波可以通过,而对其他频次的谐波有抑制作用,抑制谐波能力取决于K。
因此,假设SOGI的输入信号中含有6次谐波,即v=Vinsin(ωsht)。为了分析方便,取v=sin(ωsht),则SOGI的输出信号为
其中
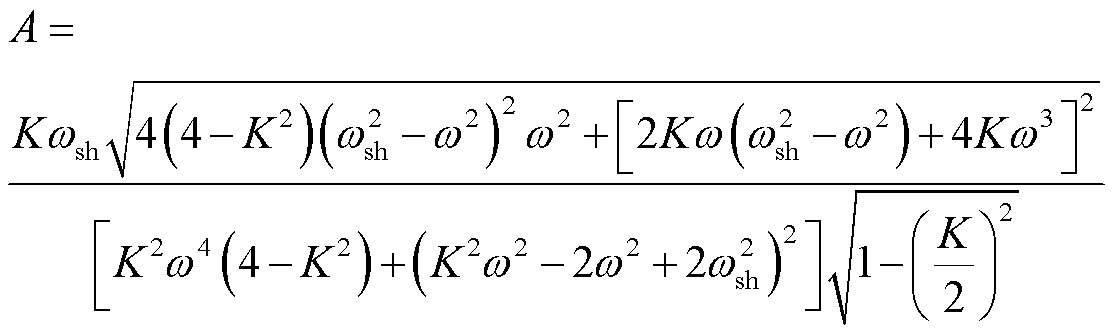
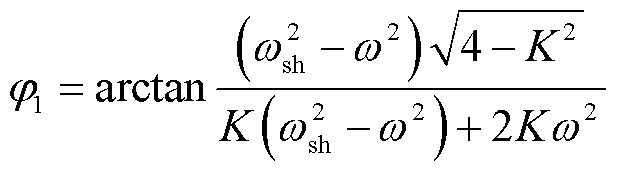
当固有频率ω=ωsh时,SOGI的输出信号为
图9a为ω无偏差时,不同K均可有效抑制6次谐波,但K越大,会增加与标准波的误差。图9b~图9d显示了当ω存在偏差时,不同K对谐波抑制的影响。K越大,对基波的影响越大,但抑制6次谐波能力增强。值得注意的是,在动态过程中,通常ω会出现较大偏差。因此,SOGI 参数选择需要考虑参数ω失配情况。
3 实验结果与分析
为验证SiC器件的高开关频率和高开关速度特性对基于高频脉振注入法的感应电机无速度传感器控制性能的影响,在如图10所示的基于SiC逆变器的7.5 kW感应电机实验对拖平台进行实验验证,采用德州仪器DSP(TMS320F28335)和赛灵思FPGA(XC3S400)作为控制板数字处理芯片,采用DA5725数模转换电路实现相关控制变量的观测,采用LEM的电压传感器(LV25-P)和电流传感器(LA55-P)测量电压和电流信息,采用KOYO增量式编码器(TRD-2T1000BF)检测实际的电机转子位置和转速。控制频率、采样频率与 PWM开关频率相同,所用感应电机的主要参数见表1。SiC MOSFET器件采用的是Wolfspeed(C2M0160120D,1 200 V/18 A)。
表1 感应电机主要参数
Tab.1 Main parameters of the IM

参数数值 额定功率/kW7.5 极对数2 额定转速/(r/min)1 500 定子电感/mH500 定子电阻/Ω0.66 转子电感/mH501 转子电阻/Ω0.90 互感/mH489
3.1 基于SiC逆变器的高开关频率特性对感应电机凸极效应的影响
图11为不同注入频率下,估计q轴高频电流的幅值及频谱分析的实验结果。由频谱分析的结果可见,随着注入频率从500 Hz提高到1 000 Hz,再到1 600 Hz,感应电机的主凸极(2fe)逐渐增强。此外,图11a中的主凸极在电流频谱中的幅值为 14.6 mA,图11b中的主凸极在电流频谱中的幅值为17.4 mA,图11c中主凸极在电流频谱中的幅值为20.1 mA,则1 600 Hz注入频率时相比于500 Hz,主凸极提高了37.67%。因此,基于SiC器件的高开关频率特性,提高注入电压的频率,有助于增强感应电机的饱和凸极,提高感应电机无速度传感器低速运行的可靠性。
3.2 基于SiC逆变器的高开关速度(短死区时间)对感应电机性能的影响
图12为注入频率在1 600 Hz时,不同死区时间下,估计转速(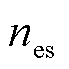 )、转速误差(Δn)和转速频谱幅值的实验结果。由转速频谱幅值发现不同死区时间的设置会导致不同程度的6次谐波。随着死区时间的减小,估计转速中的6次谐波降低。比较图12a和图12c中转速频谱中6次谐波的幅值发现,0.5 μs死区时间时的转速频谱幅值为1.2 r/min,相比较2 μs时的1.6 r/min,6次谐波的幅值降低了25%。因此,基于SiC器件的高开关速度特性,减少死区时间,有助于降低6次谐波,提高感应电机的转子位置估计精度。
)、转速误差(Δn)和转速频谱幅值的实验结果。由转速频谱幅值发现不同死区时间的设置会导致不同程度的6次谐波。随着死区时间的减小,估计转速中的6次谐波降低。比较图12a和图12c中转速频谱中6次谐波的幅值发现,0.5 μs死区时间时的转速频谱幅值为1.2 r/min,相比较2 μs时的1.6 r/min,6次谐波的幅值降低了25%。因此,基于SiC器件的高开关速度特性,减少死区时间,有助于降低6次谐波,提高感应电机的转子位置估计精度。
3.3 基于SOGI消除特定谐波的转子位置提取方法对感应电机性能的影响
图13为基于SOGI消除特定谐波的估计转速、转速误差和转速频谱幅值的实验结果。图13a为SOGI参数中K=0.1时的实验结果,与图12c中传统的转子位置误差提取方法相比,转速频谱中的2次、4次和6次谐波幅值均有所降低,尤其是6次谐波几乎被全部抑制。图13b为SOGI参数中K=1时的实验结果,相比于图13a,转速频谱幅值降低,平均转速误差从20 r/min降至14 r/min。因此,该方法在稳态工况下可以有效抑制特定谐波,提高稳态精度。
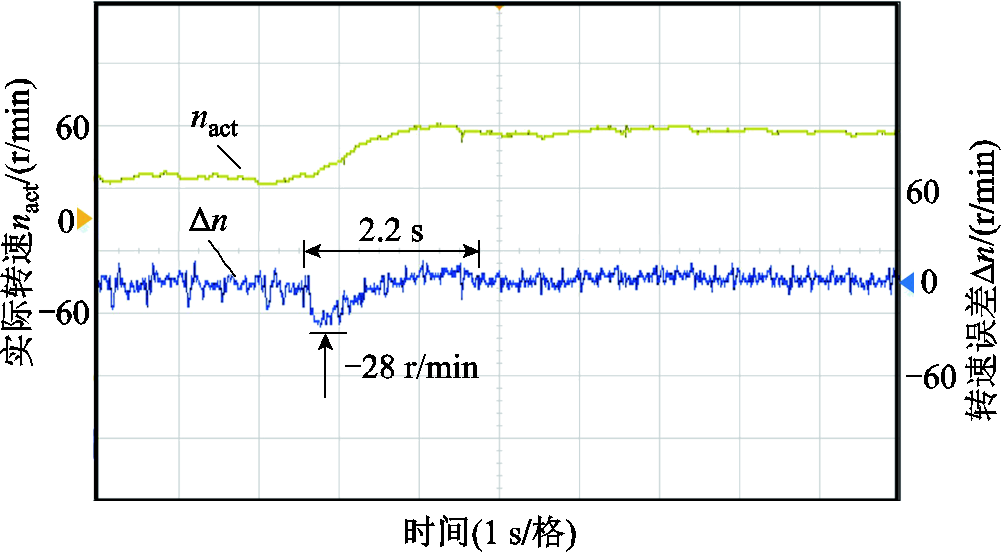
图14为基于SOGI消除特定谐波的实际转速nact和转速误差的实验结果。当SOGI参数为K=1时,将感应电机给定转速从30 r/min增加到60 r/min,在该动态过程中,转速误差最大为28 r/min,过渡时间为2.2 s,此时会导致SOGI参数ω失配。因此,SOGI参数的设计需权衡K和ω对谐波抑制效果的影响。
4 结论
本文以SiC逆变器驱动的感应电机为研究对象,提出一种基于高频脉振注入法的感应电机无速度传感器控制方案,利用SiC器件的高开关频率和高开关速度特性改善感应电机凸极特性不明显、转子位置估计误差大的问题,并与传统方法进行了对比实验。研究结论如下:
1)基于脉振注入法,根据SiC器件的高开关频率特性,提高注入电压的频率,可以有效增强感应电机的饱和凸极,注入频率为1 600 Hz的主凸极相比于500 Hz提高了37.67%,为感应电机无速度传感器控制的可靠运行提供了前提条件。
2)基于SiC器件的高开关速度特性,减少死区时间,可以有效降低6次谐波,在开关频率为 16 kHz时,死区时间为0.5 μs的6次谐波相比于 2 μs降低了25%,提高了转子位置估计精度。
3)基于SOGI特定谐波消除的转子位置提取方法,可以有效降低转子位置估计误差,同时需考虑SOGI参数K及ω失配的影响。
参考文献
[1] 杨凯, 王雨洁, 罗成, 等. 基于特征值分布的无传感器感应电机低速发电区域稳定性提升策略[J]. 电工技术学报, 2025, 40(18): 5907-5917. Yang Kai, Wang Yujie, Luo Cheng, et al. Eigenvalue-distribution-based stability enhancement strategy of speed-sensorless induction motor in low-speed regenerating region[J]. Transactions of China Electrotechnical Society, 2025, 40(18): 5907-5917.
[2] 赵琨, 宋宝, 唐小琦, 等. 基于扩张滑模-锁相环的感应电机无速度传感器矢量控制[J]. 中国电机工程学报, 2024, 44(20): 8270-8279. Zhao Kun, Song Bao, Tang Xiaoqi, et al. Senseless vector control method for induction motor based on extended sliding mode and phase locked loop[J]. Proceedings of the CSEE, 2024, 44(20): 8270-8279.
[3] 左运, 葛兴来, 李松涛, 等. 基于改进型q-PLL的牵引电机无速度传感器控制[J]. 中国电机工程学报, 2021, 41(1): 383-392, 427. Zuo Yun, Ge Xinglai, Li Songtao, et al. Speed sensorless control of traction motor based on the improved q-PLL[J]. Proceedings of the CSEE, 2021, 41(1): 383-392, 427.
[4] 杨凯, 李孺涵, 罗成, 等. 负载变化下无传感器感应电机主动零频穿越及脉动抑制策略[J]. 电工技术学报, 2023, 38(18): 4910-4920. Yang Kai, Li Ruhan, Luo Cheng, et al. Proactive low-frequency ride-through method and its ripple reduction for sensorless induction motor drives under load variations[J]. Transactions of China Electro-technical Society, 2023, 38(18): 4910-4920.
[5] 王建渊, 李英杰, 景航辉, 等. 基于静止轴系改进高频方波注入同步磁阻电机无传感器控制[J]. 电工技术学报, 2024, 39(12): 3658-3669. Wang Jianyuan, Li Yingjie, Jing Hanghui, et al. Sensorless control of high frequency square wave injection synchronous reluctance motor based on static axis system improvement[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3658-3669.
[6] Jansen P L, Lorenz R D. Transducerless field orientation concepts employing saturation-induced saliencies in induction machines[J]. IEEE Transa-ctions on Industry Applications, 1996, 32(6): 1380-1393.
[7] Mingardi D, Bianchi N, Alberti L, et al. Analysis and test of the sensorless capability of induction motors with created saliency[J]. IEEE Transactions on Industry Applications, 2016, 52(3): 2186-2193.
[8] Lee J H, Kwon Y C, Sul S K. Skin effect of squirrel cage induction motor under high-frequency signal injection[C]//2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 2021: 4737-4742.
[9] Zatocil H. Physical understanding of multiple saliencies in induction motors and their impact on sensorless control[C]//2008 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Ischia, Italy, 2008: 1503-1508.
[10] 刘海东, 周波, 郭鸿浩, 等. 脉振高频信号注入法误差分析[J]. 电工技术学报, 2015, 30(6): 38-44. Liu Haidong, Zhou Bo, Guo Honghao, et al. Error analysis of high frequency pulsating signal injection method[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 38-44.
[11] 魏海峰, 韦汉培, 张懿. 考虑逆变器输出谐波的永磁同步电机转子位置估计误差分析[J]. 电工技术学报, 2018, 33(4): 900-909. Wei Haifeng, Wei Hanpei, Zhang Yi. Error analysis of rotor position estimation for permanent magnet synchronous motor considering output harmonics of inverter[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 900-909.
[12] 刘计龙, 付康壮, 麦志勤, 等. 基于双频陷波器的改进型高频脉振电压注入无位置传感器控制策略[J]. 中国电机工程学报, 2021, 41(2): 749-759. Liu Jilong, Fu Kangzhuang, Mai Zhiqin, et al. Sensorless control strategy of improved HF pulsating voltage injection based on dual frequency notch filter [J]. Proceedings of the CSEE, 2021, 41(2): 749-759.
[13] 郑丹, 温旭辉, 范涛, 等. 高环境温度高功率密度SiC电机驱动控制器设计与实现[J]. 电工技术学报, 2025, 40(15): 4889-4904. Zheng Dan, Wen Xuhui, Fan Tao, et al. Design and implementation of SiC motor drive controller with high environmental temperature and high power density[J]. Transactions of China Electrotechnical Society, 2025, 40(15): 4889-4904.
[14] Lopez O, Guo Zhehui, Ordonez J, et al. A high power density SiC motor drive for a 6-phase PMSM[C]//2023 IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 2023: 3182-3187.
[15] 张少昆, 孙微, 范涛, 等. 基于分立器件并联的高功率密度碳化硅电机控制器研究[J]. 电工技术学报, 2023, 38(22): 5999-6014. Zhang Shaokun, Sun Wei, Fan Tao, et al. Research on high power density silicon carbide motor controller based on parallel connection of discrete devices[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 5999-6014.
[16] 王震宇, 孙伟, 蒋栋. 基于虚拟电压注入的闭环磁链观测器的感应电机无速度传感器矢量控制系统[J]. 电工技术学报, 2022, 37(2): 332-343. Wang Zhenyu, Sun Wei, Jiang Dong. Induction motor speed sensorless vector control system based on closed-loop flux observer with virtual voltage injection[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 332-343.
[17] Boglietti A, Cavagnino A, Lazzari M. Computational algorithms for induction motor equivalent circuit parameter determination: part II: skin effect and magnetizing characteristics[J]. IEEE Transactions on Industrial Electronics, 2010, 58(9): 3734-3740.
[18] 李浩源, 张兴, 杨淑英, 等. 基于高频信号注入的永磁同步电机无传感器控制技术综述[J]. 电工技术学报, 2018, 33(12): 2653-2664. Li Haoyuan, Zhang Xing, Yang Shuying, et al. Review on sensorless control of permanent magnet synchronous motor based on high-frequency signal injection[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2653-2664.
[19] Seung-Ki Sul. Control of Electric Machine Drive System[M]. lst ed. Hoboken, USA: Wiley Press, 2011.
[20] 麦志勤, 肖飞, 刘计龙, 等. 一种永磁同步电机凸极信号测量方法[J]. 电机与控制学报, 2022, 26(9): 18-29. Mai Zhiqin, Xiao Fei, Liu Jilong, et al. Measurement method for PMSM saliency signal[J]. Electric Machines and Control, 2022, 26(9): 18-29.
[21] Wang Gaolin, Ding Li, Li Zhuomin, et al. Enhanced position observer using second-order generalized integrator for sensorless interior permanent magnet synchronous motor drives[J]. IEEE Transactions on Energy Conversion, 2014, 29(2): 486-495.
[22] Bolognani S, Zigliotto M. Self-commissioning compensation of inverter non-idealities for sensorless AC drives applications[C]//2002 International Conference on Power Electronics, Machines and Drives (Conf. Publ. No. 487), Sante Fe, NM, USA, 2002: 30-37.
[23] Bolognani S, Peretti L, Zigliotto M. Repetitive-control-based self-commissioning procedure for inverter nonidealities compensation[J]. IEEE Transactions on Industry Applications, 2008, 44(5): 1587-1596.
Sensorless Control of SiC Inverter-Driven Induction Motors Using High-Frequency Pulsating Injection Method
Bian Xiaoliang Yuan Xibo Chen Shuo Wang Kai Zhao Chuanjie
(School of Electrical Engineering China University of Mining and Technology Xuzhou 221116 China)
Abstract The salient-pole characteristics and rotor position estimation error pose challenges in the sensor less control system of induction motors (IMs) based on the high-frequency pulsating injection (HFPI) method at low speeds, ultimately compromising the reliability and stability of motor operation. Based on the high switching frequency characteristic of the silicon carbide (SiC) inverter, increasing the frequency of the injection voltage thus enhances the saturated salient pole of the IM. To mitigate the rotor position estimation error caused by the deadtime of the inverter, this paper leverages the high switching speed of SiC devices and a harmonic suppression method based on a second-order generalized integrator (SOGI) to improve the accuracy of rotor position estimation.
According to the skin effect, the influence of different injection frequencies of the SiC inverter on the rotor bar of the IM is analyzed, where the high-frequency inductance varies with the injection frequency due to changes in the distribution of magnetic lines within the rotor bar. Then, based on this, the relationship between the high-frequency inductances of the d-q coordinate axis and different injection frequencies in the field-oriented control system of the IM is constructed by the finite element method. Finally, based on the improved measurement method of high-frequency inductance in the d-q coordinate axis, it effectively verified that the high injection frequency can enhance the saturated salient pole of the IM.
By the traditional method for extracting rotor position information, the relationship between the dead time and the rotor position estimation error is derived. Based on the high switching speed of the SiC inverter, setting a short dead time can reduce the 6k th harmonic in rotor position estimation. To mitigate the influence of the 6th harmonic, a specific harmonic elimination scheme based on SOGI is proposed toenhance theaccuracy of rotor position estimation. Additionally, to prevent the influence of SOGI parameter mismatch on the suppression effect, the parameter k needs to be selected reasonably to improve the low-speed performance under both dynamic and static conditions.
To validate the effectiveness of sensorless control using the HFPI method for IMs at low speeds based on SiC inverters, a 7.5 kW SiC inverter-based IM test platform was set up. Experimental results demonstrate that the HFPI method, implemented with SiC inverters, enhances the low-speed operational performance of the IM. The saturated salient-pole measurement tests were conducted to verify the effectiveness of high injection frequency in enhancing the saturated salient pole of the IM. As observed in the current spectrum, the main salient pole of the injection frequency of 1 600 Hz exhibits a 37.67% greater amplitude compared to that of 500 Hz. Additionally, to verify the impact of high switching speed on the rotor estimation error, the dead time of the SiC inverter was adjusted to test the accuracy of rotor position estimation. Analysis of the speed spectrum at a 16 kHz switching frequency reveals that a 0.5 μs dead time reduces the 6th harmonic component by 25% compared to a 2 μs dead time. Combining the specific harmonic suppression algorithm based on SOGI can further reduce the speed estimation error. These experimental results have confirmed that in the HFPI method, the IM driven by the SiC inverter can enhance the reliability and accuracy of rotor position estimation at low speeds.
Keywords: Silicon carbide (SiC), induction motor (IM), saturated salient pole, high-frequency pulsating injection, rotor position estimation
DOI: 10.19595/j.cnki.1000-6753.tces.250178
中图分类号:TM46; TM34
国家重点研发计划(2023YFE0115900)、国家自然科学基金(52177201,62503481)和江苏省自然科学基金(BK20220091)资助项目。
收稿日期 2025-01-31
改稿日期 2025-07-26
作者简介
卞小亮 男,1991年生,博士研究生,研究方向为宽禁带半导体的应用、交流电机无传感器控制。E-mail:xlbian@cumt.edu.cn
原熙博 男,1982年生,教授,博士生导师,研究方向为电力电子与电力传动。E-mail:yuanxibo@cumt.edu.cn(通信作者)
(编辑 郭丽军)
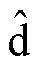 轴注入高频正弦电压信号,从
轴注入高频正弦电压信号,从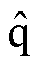 轴高频电流响应的幅值中提取转子位置信息。相比于高频旋转注入法,高频脉振注入算法结构简单,且转矩脉动较小。为了提高基于高频脉振注入法的转子位置估计精度,学者们进行了大量的研究。针对电机参数变化对转子位置估计的影响,文献[10]推导出含有电机变化参数的转子位置估计误差的解析表达式,从而指导系统参数的选择,减小估计误差,但未考虑动态工况。文献[11]针对逆变器输出谐波对转子位置估计误差的干扰问题,通过仿真和数值分析得出转子位置提取方法中多个电机参数对估计误差的影响规律,然而,只考虑了由数字控制器实现空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)时带来的离散化干扰。文献[12]针对滤波器的相位延时问题,提出一种基于双频陷波器级联低通滤波器(Low Pass Filter, LPF)的改进型位置误差信号提取策略,然而,陷波器较长的离散周期会导致幅值的失真,降低了转子位置估计精度。以上研究均是基于硅(Si)逆变器的高频脉振注入无速度传感器矢量控制系统。然而,近年来,以碳化硅(SiC)器件为代表的第三代宽禁带半导体飞速发展,其凭借高开关频率和低导通电阻等特性,在追求高功率密度、高效率的电机控制场合得到了广泛应用,且得到了学者们的广泛关注[13-15]。但迄今为止,很少有文献关注SiC器件的高开关频率和高开关速度特性对感应电机无速度传感器矢量控制系统性能的影响。
轴高频电流响应的幅值中提取转子位置信息。相比于高频旋转注入法,高频脉振注入算法结构简单,且转矩脉动较小。为了提高基于高频脉振注入法的转子位置估计精度,学者们进行了大量的研究。针对电机参数变化对转子位置估计的影响,文献[10]推导出含有电机变化参数的转子位置估计误差的解析表达式,从而指导系统参数的选择,减小估计误差,但未考虑动态工况。文献[11]针对逆变器输出谐波对转子位置估计误差的干扰问题,通过仿真和数值分析得出转子位置提取方法中多个电机参数对估计误差的影响规律,然而,只考虑了由数字控制器实现空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)时带来的离散化干扰。文献[12]针对滤波器的相位延时问题,提出一种基于双频陷波器级联低通滤波器(Low Pass Filter, LPF)的改进型位置误差信号提取策略,然而,陷波器较长的离散周期会导致幅值的失真,降低了转子位置估计精度。以上研究均是基于硅(Si)逆变器的高频脉振注入无速度传感器矢量控制系统。然而,近年来,以碳化硅(SiC)器件为代表的第三代宽禁带半导体飞速发展,其凭借高开关频率和低导通电阻等特性,在追求高功率密度、高效率的电机控制场合得到了广泛应用,且得到了学者们的广泛关注[13-15]。但迄今为止,很少有文献关注SiC器件的高开关频率和高开关速度特性对感应电机无速度传感器矢量控制系统性能的影响。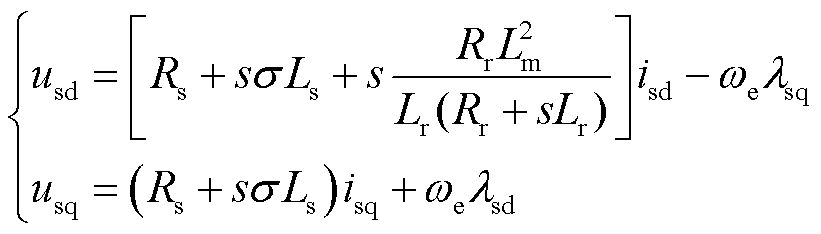 (1)
(1)
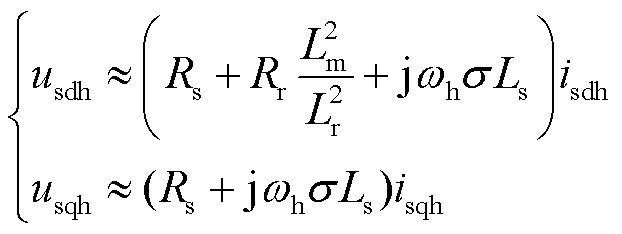 (2)
(2)
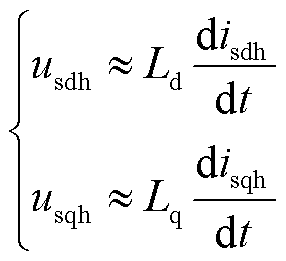 (3)
(3)
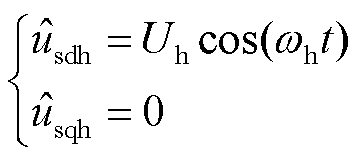 (4)
(4)
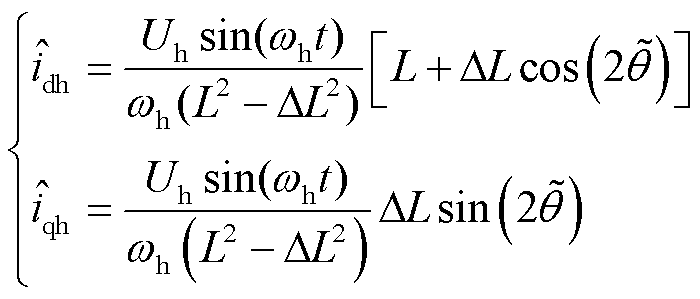 (5)
(5)
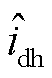 、
、 分别为估计同步坐标系
分别为估计同步坐标系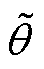 为参考同步旋转坐标系与估计同步旋转坐标系的角度误差;L为平均电感,L=(L
为参考同步旋转坐标系与估计同步旋转坐标系的角度误差;L为平均电感,L=(L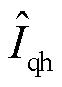 中含有转子位置误差信息,其表达式为
中含有转子位置误差信息,其表达式为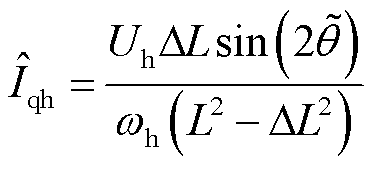 (6)
(6)
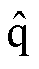 轴电流进行滤波,提取高频响应电流;其次对
轴电流进行滤波,提取高频响应电流;其次对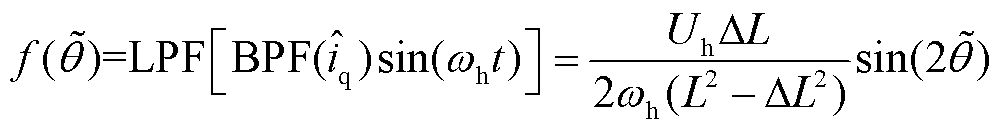 (7)
(7)
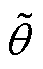 较小时,
较小时,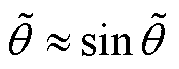 ,此时,将转子位置估计误差线性化可得
,此时,将转子位置估计误差线性化可得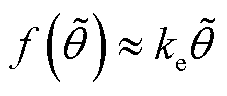 (8)
(8)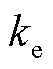 为转子位置误差系数,
为转子位置误差系数,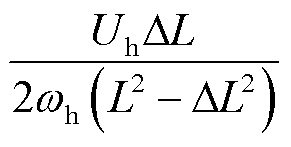 。
。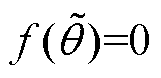 ,可以使转子位置角的估计值收敛于实际值,从而获得准确的转子位置信息。然而,在一般情况下,感应电机三相绕组对称,感应电机的d、q轴的等效电感相等,即L
,可以使转子位置角的估计值收敛于实际值,从而获得准确的转子位置信息。然而,在一般情况下,感应电机三相绕组对称,感应电机的d、q轴的等效电感相等,即L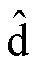 轴注入高频电压信号,利用磁饱和所引起的凸极效应,可以使得ΔL≠0,从而实现转子位置的辨识。因此一定的凸极特性是实现基于高频脉振注入法感应电机无速度传感器控制的前提条件。同时,由于非理想因素(如逆变器死区时间)的影响,转子位置估计误差
轴注入高频电压信号,利用磁饱和所引起的凸极效应,可以使得ΔL≠0,从而实现转子位置的辨识。因此一定的凸极特性是实现基于高频脉振注入法感应电机无速度传感器控制的前提条件。同时,由于非理想因素(如逆变器死区时间)的影响,转子位置估计误差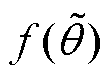 会产生误差,降低感应电机低速运行性能。
会产生误差,降低感应电机低速运行性能。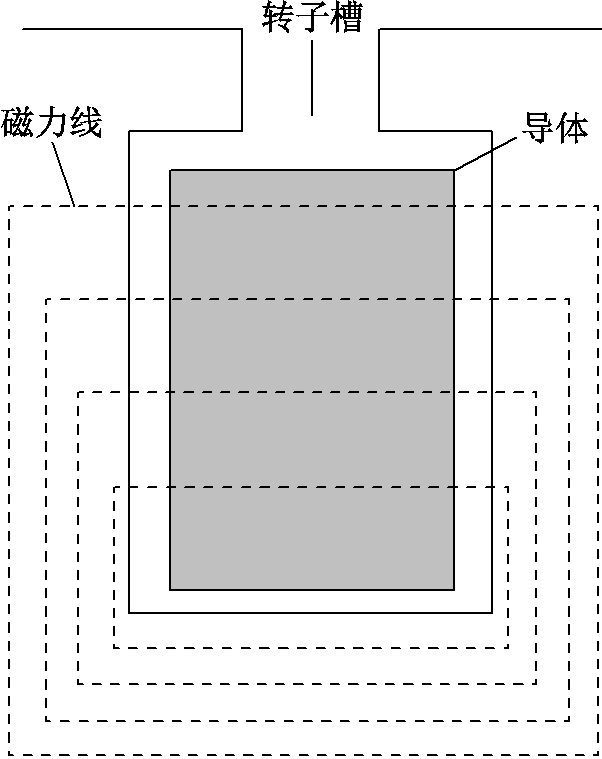
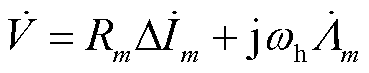 (9)
(9)
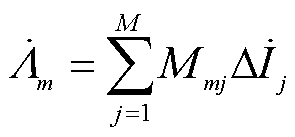 (10)
(10)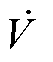 为电压相量;
为电压相量;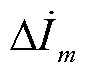 为m层电流相量;R
为m层电流相量;R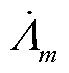 为m层磁链;M
为m层磁链;M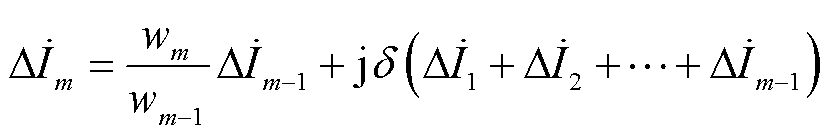 (11)
(11)
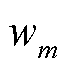 为m层截面的宽度;
为m层截面的宽度; ,
,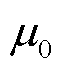 为真空磁导率,
为真空磁导率,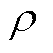 为电阻率。
为电阻率。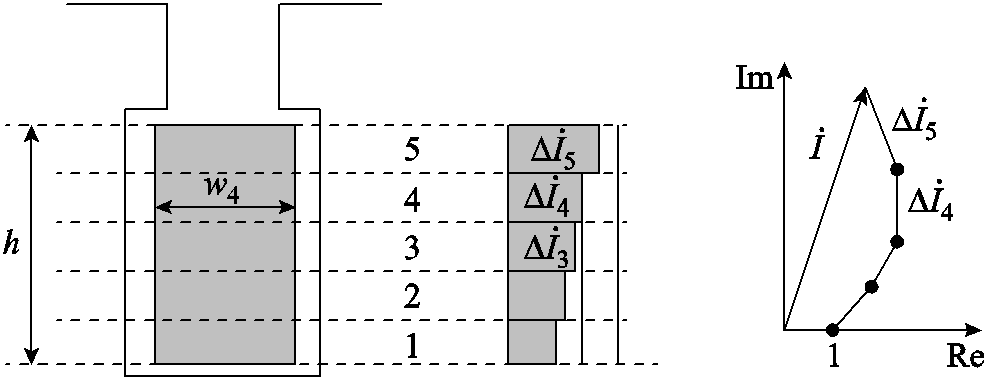
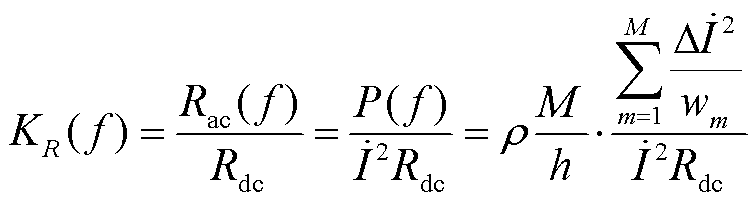 (12)
(12)
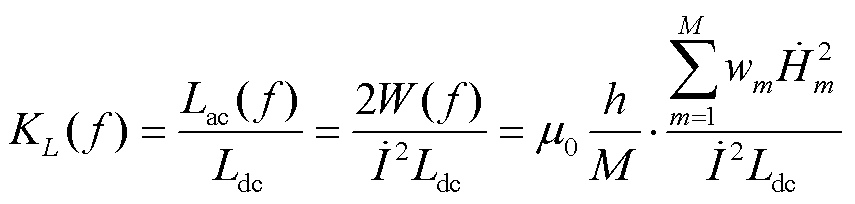 (13)
(13)
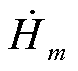 为第m层磁场强度相量。
为第m层磁场强度相量。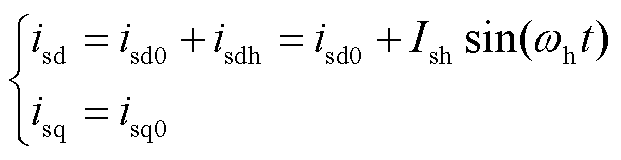 (14)
(14)
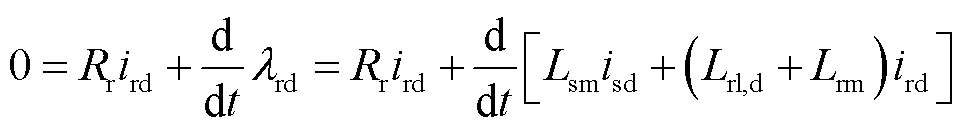 (15)
(15)
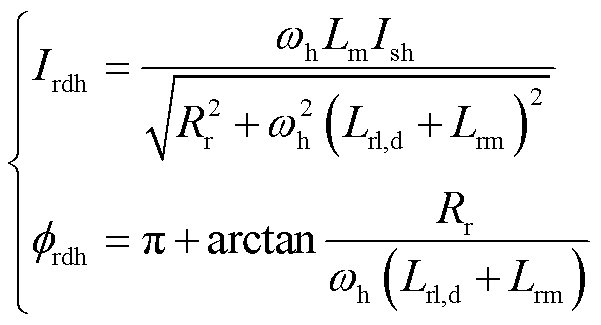 (16)
(16)
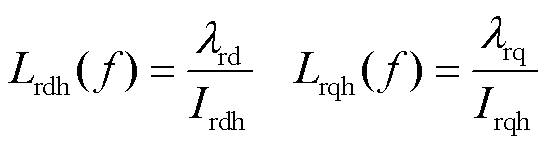 (17)
(17)
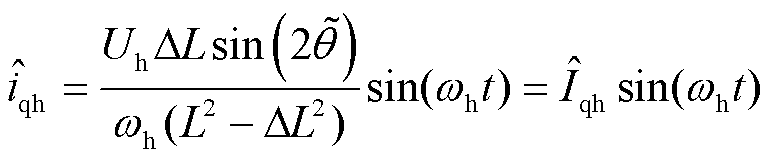 (18)
(18)
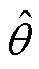 为0,则
为0,则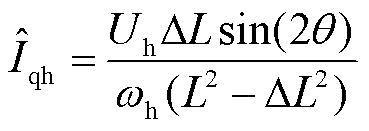 (19)
(19)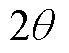 而变化。因此,感应电机的主凸极可以通过
而变化。因此,感应电机的主凸极可以通过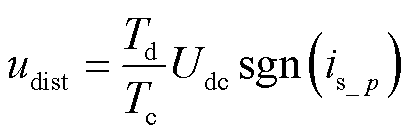 (20)
(20)
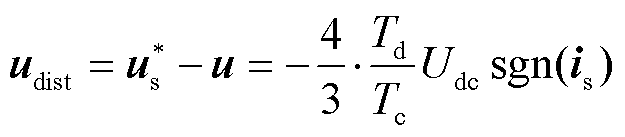 (21)
(21)
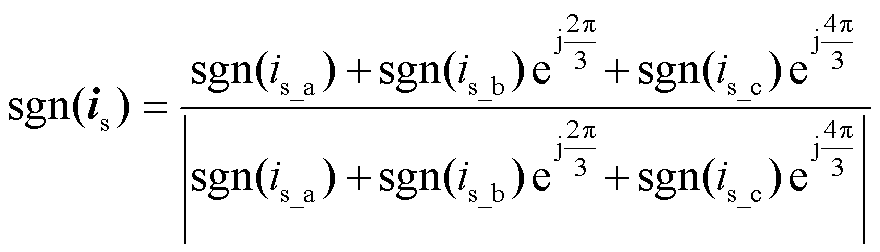
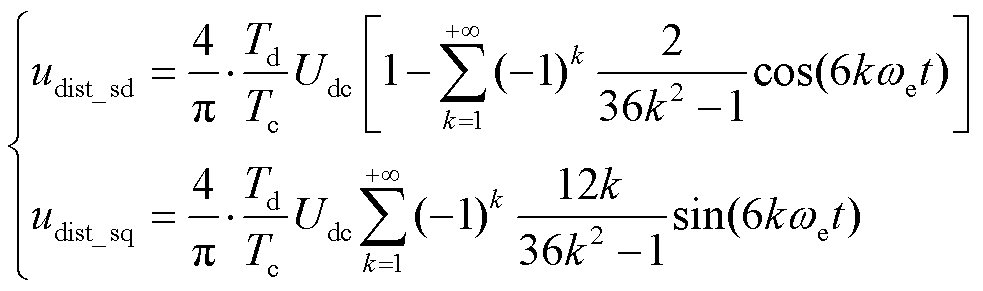 (22)
(22)
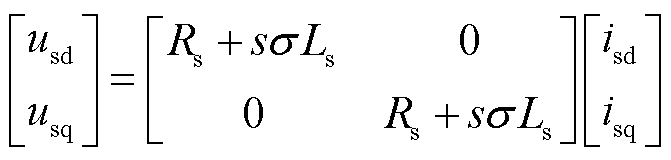 (23)
(23)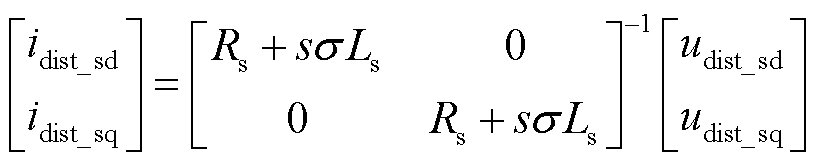 (24)
(24)
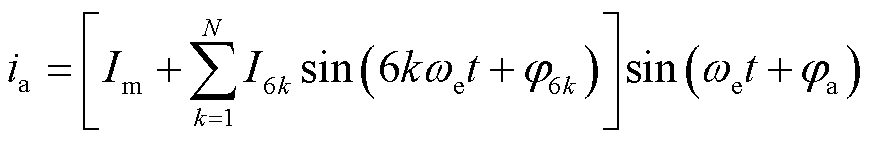 (25)
(25)
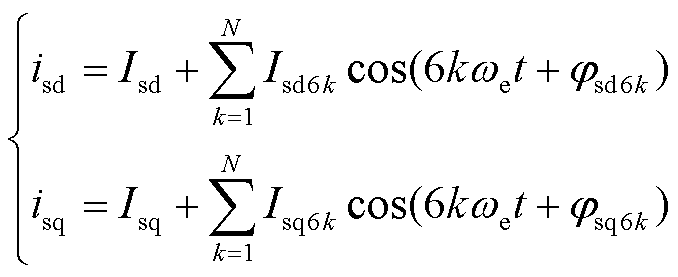 (26)
(26)
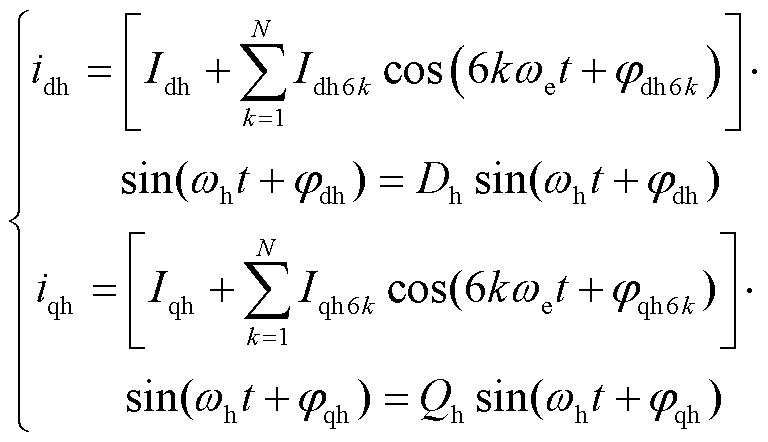 (27)
(27)
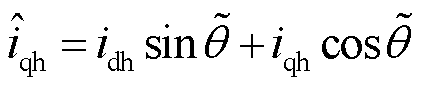 (28)
(28)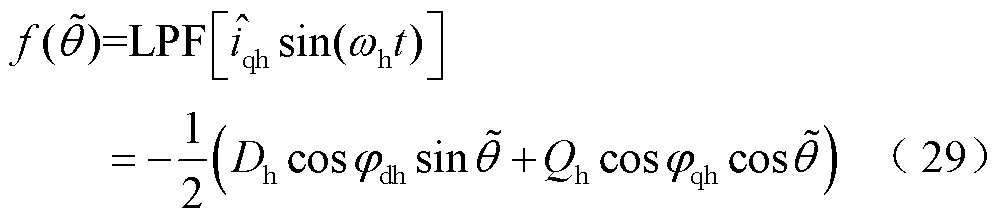
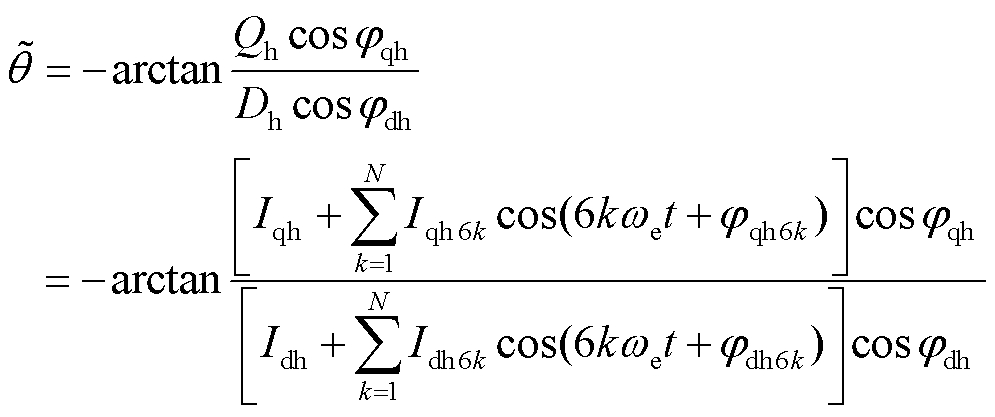 (30)
(30)
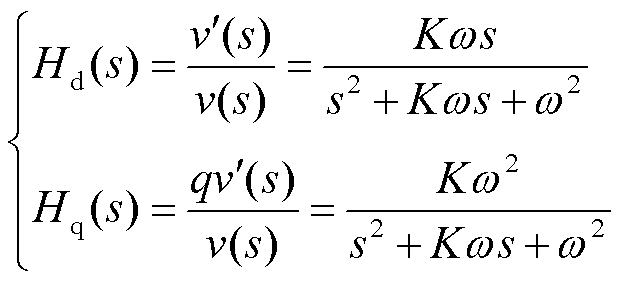 (31)
(31)
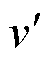 为输出信号,
为输出信号,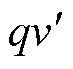 为正交输出信号;K为增益;ω为固有频率。
为正交输出信号;K为增益;ω为固有频率。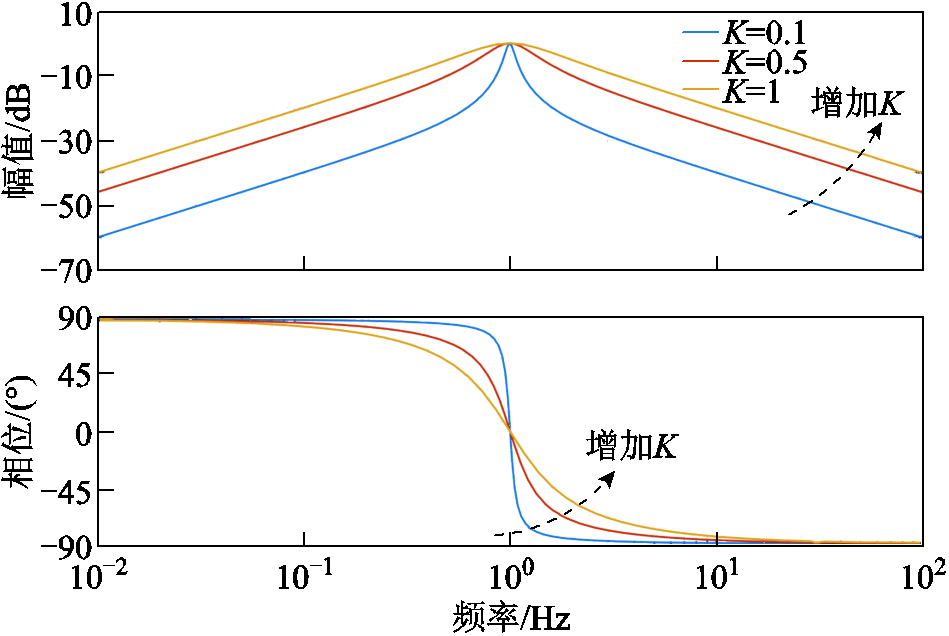
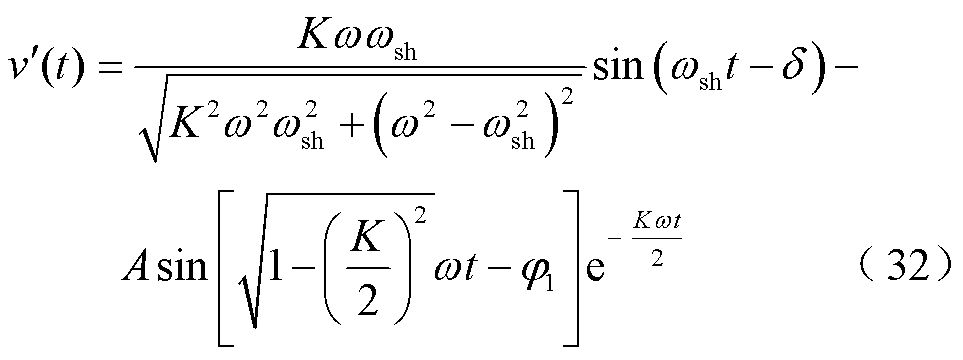
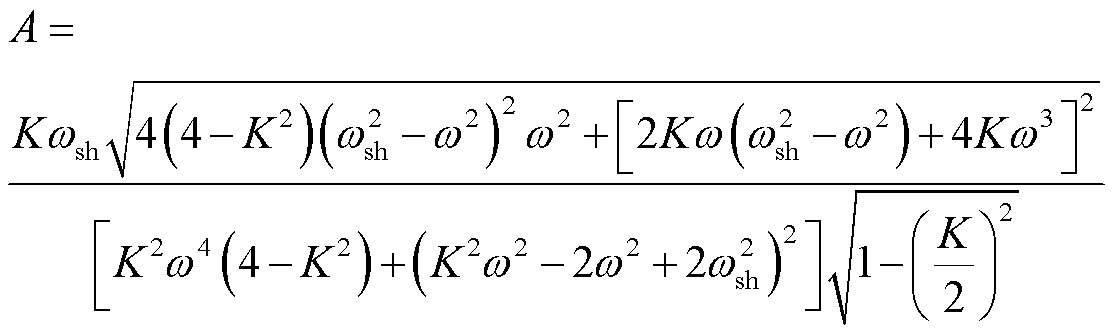
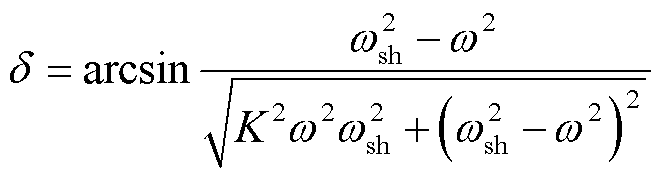
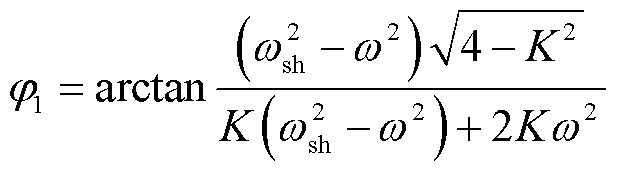
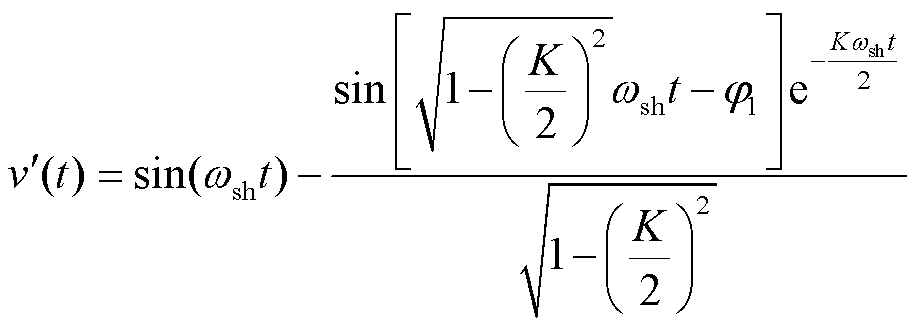 (33)
(33)




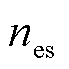 )、转速误差(Δn)和转速频谱幅值的实验结果。由转速频谱幅值发现不同死区时间的设置会导致不同程度的6次谐波。随着死区时间的减小,估计转速中的6次谐波降低。比较图12a和图12c中转速频谱中6次谐波的幅值发现,0.5 μs死区时间时的转速频谱幅值为1.2 r/min,相比较2 μs时的1.6 r/min,6次谐波的幅值降低了25%。因此,基于SiC器件的高开关速度特性,减少死区时间,有助于降低6次谐波,提高感应电机的转子位置估计精度。
)、转速误差(Δn)和转速频谱幅值的实验结果。由转速频谱幅值发现不同死区时间的设置会导致不同程度的6次谐波。随着死区时间的减小,估计转速中的6次谐波降低。比较图12a和图12c中转速频谱中6次谐波的幅值发现,0.5 μs死区时间时的转速频谱幅值为1.2 r/min,相比较2 μs时的1.6 r/min,6次谐波的幅值降低了25%。因此,基于SiC器件的高开关速度特性,减少死区时间,有助于降低6次谐波,提高感应电机的转子位置估计精度。