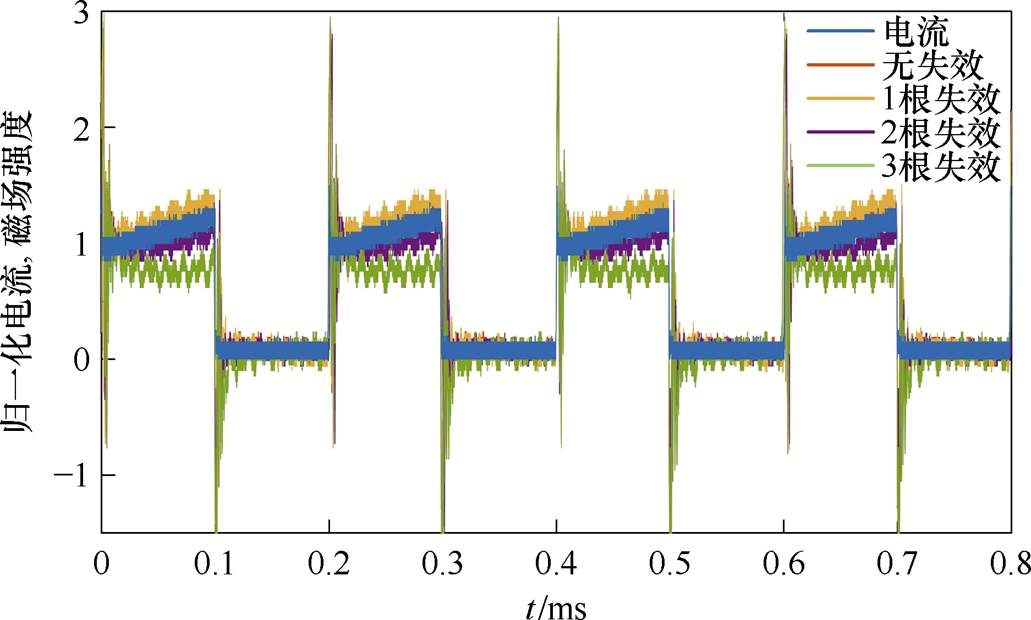
图1 键合线失效对电流与磁场分布的影响
Fig.1 Impact of bonding wire failure on current and magnetic field distribution
摘要 SiC功率模块因其高效率和高可靠性被广泛应用于电力电子领域,但其键合线在长期运行中可能发生失效,影响模块的稳定性和可靠性。现有研究中,磁阻传感器与Rogowski线圈的混合传感器已被用于键合线电流的监测,但在键合线失效时,测量稳定性仍有待提高。该文以提升混合传感器在键合线失效情况下的测量稳定性为目标,通过优化传感器设计与参数配置,包括印制电路板(PCB)厚度、Rogowski线圈匝数及磁阻传感器的放置位置,显著改善了传感器在键合线失效的情况下的抗干扰能力与测量精度。分析结果表明,当Rogowski线圈采用15匝绕组、PCB厚度为1.6 mm时,混合传感器的电流增益变化率在Microsemi公司的SiC模块键合线失效情况下能够保持稳定,不影响混合传感器对SiC芯片的电流测量。该文提出的优化方法为SiC功率模块的实时监测提供了一种更加高效、可靠的技术方案,对提升功率电子系统的长期运行稳定性具有重要意义。
关键词:碳化硅功率模块 混合电流传感器 Rogowski线圈 磁阻传感器 键合线失效
碳化硅(Silicon Carbide, SiC)功率模块因其在高温、高频条件下的卓越性能,被广泛应用于电动汽车、可再生能源发电和航空航天等领域[1-9]。因此,近年来SiC器件的可靠性受到学术界的关注,如低感封装设计[10]、器件结温等关键参数监测[11-12]、器件栅氧退化[13]等。功率模块通常集成多个半导体芯片,运行过程中会出现复杂的热、电、力多物理场耦合现象。这种多物理场的不均匀性会影响芯片间的电流分布,从而导致某些芯片出现过电流现 象[14-15]。因此,为了确保功率模块的可靠性,有必要对半导体芯片的电流进行分析与测量。
目前,键合线型封装功率模块的电流分析通常通过电路模拟和有限元方法(Finite Element Method, FEM)进行。王来利等[16]提出了一种基于人工神经网络(Artificial Neural Networks, ANN)的芯片级电热应力计算方法,通过建立动态电流分配和三维热耦合模型,解决了高功率IGBT模块中电流和热分配不均的问题。该方法通过自动化建模流程,在系统级仿真中实现了精确的芯片级电流、热量和应力计算,有效平衡了仿真精度与效率。时晓洁等[17]提出了一种基于PSpice、Matlab和COMSOL的自动化场-电路耦合仿真方法,通过自适应时间步调整和双向数据交换,对多芯片SiC功率模块的电流与热量实现高效精确分配和计算。该方法克服了传统仿真精度与效率的矛盾,验证了仿真与实验结果的误差在5%以内。
尽管有限元方法在多物理场分析中能高效地计算功率模块内部的电流分布,但仅适用于仿真分析,无法满足对功率模块电流进行在线实时测量的需求。针对这一需求,研究者们开发了多种电流传感方法。Gu Dazhong等[18]提出了一种集成栅极驱动和基于高带宽分流电阻的电流传感解决方案,采用飞跨拓扑电源设计,优化信号完整性,解决了SiC功率模块中的高精度电流测量需求,并降低了体积和复杂性。A. Q. Huang等[19]通过利用Si MOSFET作为传感器件,降低了成本并提高了高频和高温下的测量精度,适用于智能功率模块。此外,C. DiMarino等[20]设计了集成高频短路保护的栅极驱动器,通过印制电路板(Printed Circuit Board, PCB)嵌入场分级结构优化高压绝缘性能,并使用寄生电感电压检测实现高速电流传感。R. D. Lorenz等在2013年提出基于巨磁阻(Giant Magneto Resistance, GMR)点场探测器的电流测量方法,通过优化传感器位置解决了频率依赖性导致的测量精度问题;在此基础上,2020年设计了一种三相电流测量方法,采用单个3D磁场传感器结合交叉场解耦技术,从多相耦合磁场中提取电流信息,并通过导体结构布局优化提升了集成度和可靠性;2022年,进一步针对SiC模块的高频特性,提出相位误差减少和带宽扩展方法,通过实时相位补偿和布局优化解决了高频电流测量中的相位误差和带宽不足问题。这些研究系统性地解决了功率半导体模块中高精度、高频宽电流测量的技术挑战,同时提升了模块的集成度和性能[21-23]。
对于键合线型封装功率模块的电流测量,非侵入式、高带宽的电流传感方案是一个很好的选择。王来利等[24]提出了一种基于磁阻传感器和非环绕型Rogowski线圈的混合传感器方法,用于功率模块中键合线的非接触式电流测量,实现了芯片级电流监测。通过优化磁场集中设计和信号解耦矩阵计算,该方法能够在DC到100 MHz的带宽内精准测量单芯片和多芯片模块的电流分配,特别是在芯片开关过程中,解决了传统方法难以实现的精度和实时性问题。然而,Rogowski线圈和磁阻传感器都是基于磁场测量的电流传感器,其测量电流的输出值与键合线附近的磁场分布有关。当键合线发生失效时,键合线附近的磁场分布会发生变化,导致电流传感器的测量误差显著增加,如图1所示[25]。图1中磁场和电流波形已进行归一化,以便在同一坐标系下进行比较。蓝色波形为商用电流传感器在模块外部测得的总电流,受键合线失效影响较小;橙色波形为正常状态下键合线附近的磁场,与蓝色波形基本一致;其余颜色为键合线失效后的磁场波形,明显偏离蓝色参考曲线。基于此,本文提出了SiC功率模块键合线失效条件下的磁阻-Rogowski线圈电流传感器的抗干扰研究与设计。首先,本文利用解析方法推导出键合线与PCB型Rogowski线圈之间的互感公式,并进一步计算了线圈匝数、位置及PCB厚度变化对于抗键合线失效干扰能力的影响。其次,对键合线附近的磁场分布进行了理论分析,并根据分析的结果绘制出键合线未失效和失效时的磁场分布情况。找出了磁场不受键合线健康状态影响的位置,并以此作为磁阻传感器的放置位置。在此基础上,设计了磁阻-Rogowski线圈的信号处理电路。最后,模拟了SiC功率模块键合线失效情况下的电流检测。

图1 键合线失效对电流与磁场分布的影响
Fig.1 Impact of bonding wire failure on current and magnetic field distribution
本文选用的SiC功率模块为Microsemi公司生产的MSCSM120AM50CT1AG,其内部结构如图2所示。图2中明确标注了待监测的SiC芯片及相应的键合线位置。模块中的SiC芯片通过4根键合线连接实现电流传输。本节将介绍Rogowski线圈的基本原理,并基于MSCSM120AM50CT1AG模块的结构特点设计PCB型Rogowski线圈。

图2 SiC功率模块内部照片
Fig.2 Internal photo of SiC power module
如图2所示,SiC功率模块结构中SiC芯片的键合线布局非常紧凑,且芯片表面覆盖硅凝胶。在实际应用中,常规的商业柔性Rogowski线圈难以环绕键合线以测量电流,因此需要使用基于PCB的非环绕型Rogowski线圈。键合线与Rogowski线圈如图3所示。与传统环绕型Rogowski线圈相比,非环绕型设计能够更适应SiC功率模块的紧凑结构,并避免因封装空间受限导致的安装困难。该Rogowski线圈采用四层PCB设计,线圈绕组布置于PCB的顶层和底层,而返回线则布置于中间层。
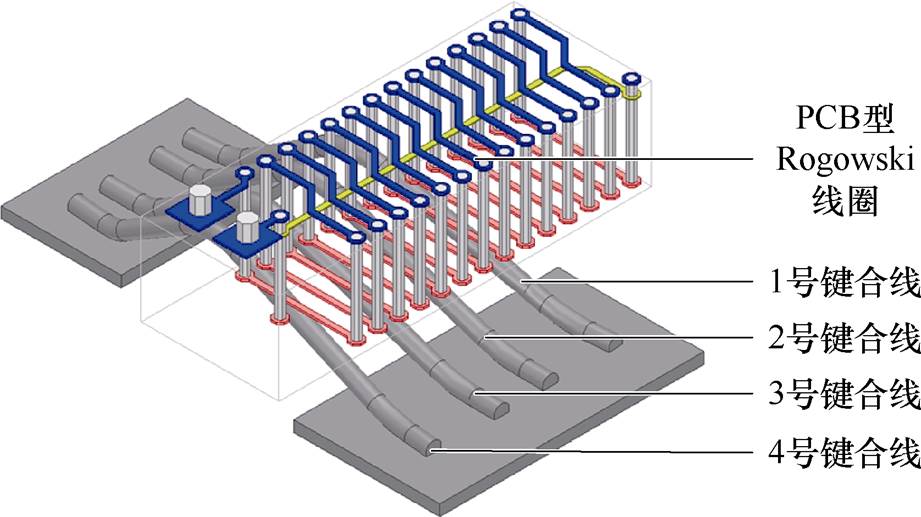
图3 键合线与Rogowski线圈
Fig.3 Bonding wires and Rogowski coil
Rogowski线圈是一种基于法拉第电磁感应定律的电流传感器,是测量交流电流和瞬态大电流的理想工具。与传统电流互感器相比,Rogowski线圈克服了因磁饱和导致无法测量大电流或高频电流的局限性。通过被测导体电流产生的磁场与线圈绕组的耦合作用,Rogowski线圈产生感应电动势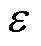 ,其大小可通过线圈与被测导体之间的互感M及电流i随时间t的变化率来表示,即
,其大小可通过线圈与被测导体之间的互感M及电流i随时间t的变化率来表示,即
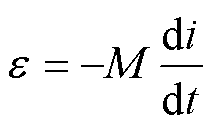 (1)
(1)
同时,感应电动势还可以通过穿过Rogowski线圈截面的磁通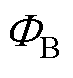 的变化率表示为
的变化率表示为
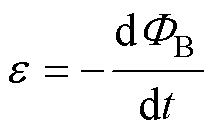 (2)
(2)
所以
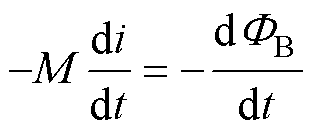 (3)
(3)
则被测导体与Rogowski线圈的互感为
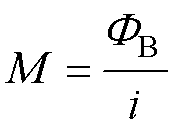 (4)
(4)
因此,要计算键合线与Rogowski线圈的互感,必须推导出通过线圈的磁通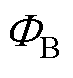 。当电流流经键合线时,其周围会产生磁场。在键合线之上布置单轴磁阻传感器,可用于测量键合线产生的磁场强度。如图4所示,根据安培环路定律,键合线附近的磁场强度
。当电流流经键合线时,其周围会产生磁场。在键合线之上布置单轴磁阻传感器,可用于测量键合线产生的磁场强度。如图4所示,根据安培环路定律,键合线附近的磁场强度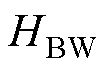 由其流过的电流iBW的大小决定。
由其流过的电流iBW的大小决定。
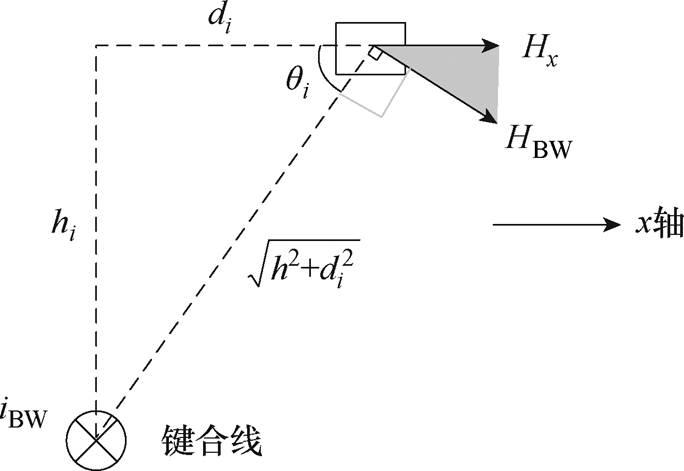
图4 单根键合线附近的磁场强度
Fig.4 Magnetic field intensity near a single bonding wire
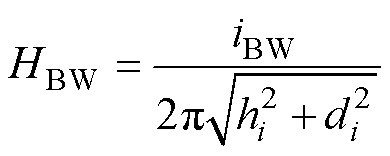 (5)
(5)
式中,iBW为单根键合线的电流;hi为空间某点到键合线i的垂直距离;di为空间某点到键合线i的水平距离。
对于单轴磁场传感器,只能测量沿x轴方向的磁场。因此,传感器沿x轴测得的磁场强度Hx为
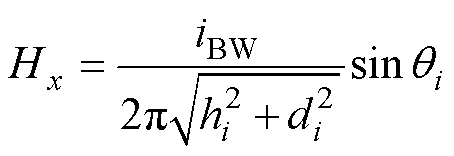 (6)
(6)
根据图4可知,式(6)可进一步写为
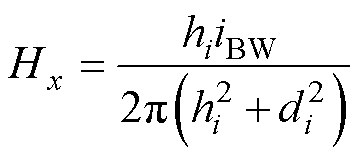 (7)
(7)
在计算键合线与线圈的互感时,可将键合线模型进行简化,单根键合线与单匝线圈的侧视图如图5所示。图5中,H为绕组高度,在PCB型Rogowski线圈中即为PCB厚度;h0为线圈到键合线前端的垂直距离;W为绕组的宽度;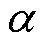 为键合线与水平面的夹角。
为键合线与水平面的夹角。
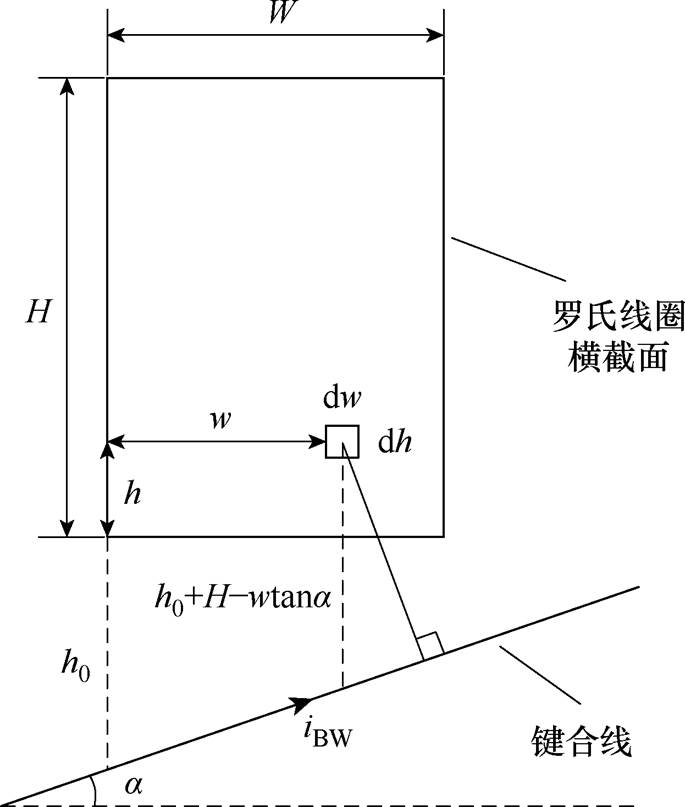
图5 单根键合线与单匝线圈(侧视图)
Fig.5 Single bonding wire and single turn coil (side view)
根据磁通的定义,通过单匝线圈的磁通可以通过对通过线圈截面A的磁通密度B做积分。
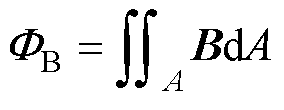 (8)
(8)
磁通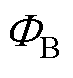 的定义式可以改写成垂直于线圈界面的磁场对线圈高度h和宽度w的二重积分,即
的定义式可以改写成垂直于线圈界面的磁场对线圈高度h和宽度w的二重积分,即
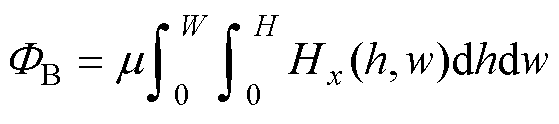 (9)
(9)
将式(7)代入二重积分,可得
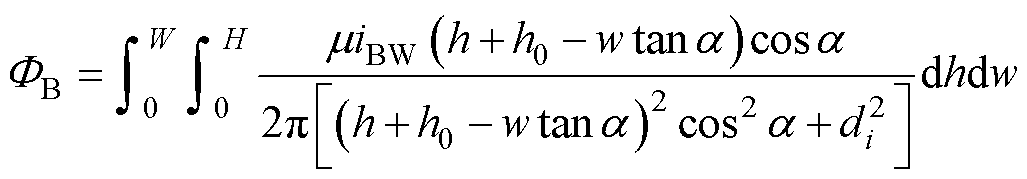 (10)
(10)
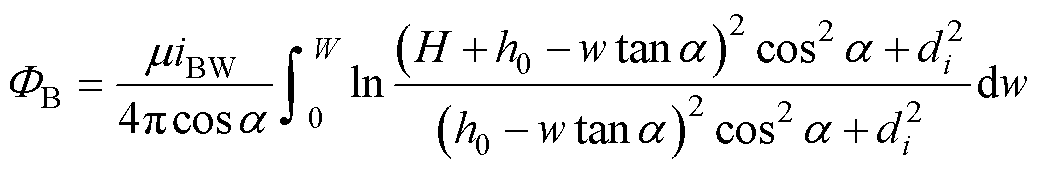 (11)
(11)
计算此积分,结合式(4),可以得出单根键合线与单匝线圈的互感为
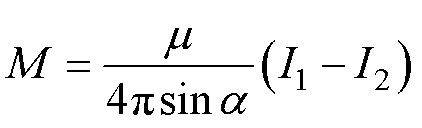 (12)
(12)
其中
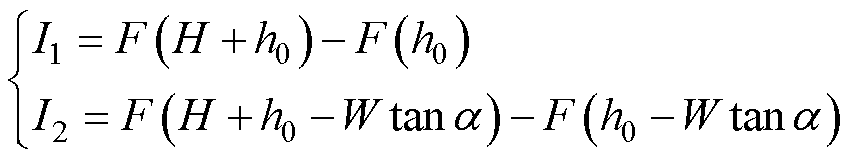 (13)
(13)
式中,F(x)表达式为
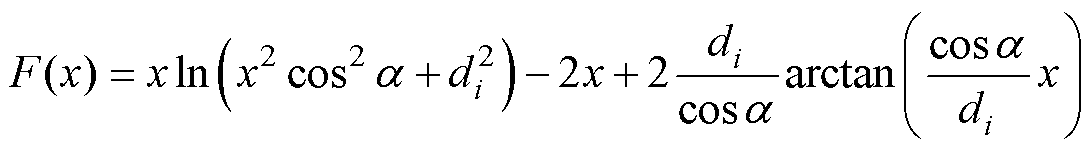 (14)
(14)
通过推导单匝线圈与键合线之间的互感公式,可以进一步分析匝数、线圈间距和相对位置对互感性能的影响。
前文已对单根键合线与单匝线圈的互感进行了分析。单键合线与Rogowski线圈的空间关系如图6所示,完整的Rogowski线圈由多个平行的单匝线圈组成。利用式(12)分别计算每个单匝线圈与单根键合线的互感,并将其相加,得出整个PCB型Rogowski线圈与单根键合线的互感。图6中,匝间距为0.34 mm。
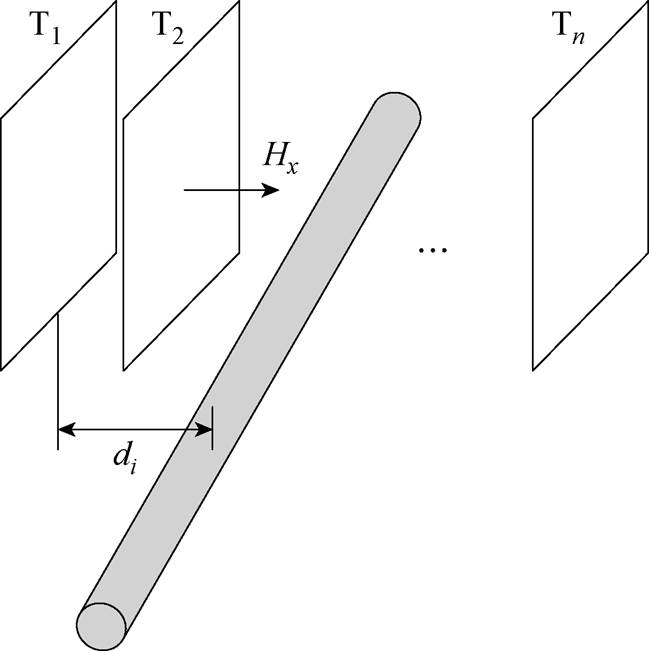
图6 单键合线与Rogowski线圈的空间关系
Fig.6 Spatial relationship between single bonding wire and Rogowski coil
为了避免多变量耦合带来的分析复杂性,本文采用先确定关键结构参数,再微调其他几何尺寸的逐步优化策略。首先固定PCB厚度H=1.6 mm,选取对互感与增益稳定性具有主导作用的匝数n,系统分析匝数为9~17区间内的性能变化,确定最优解并将其作为约束条件加以固定;随后,在匝数已确定的前提下,评估PCB厚度H单一变量对传感性能的具体影响。
分别取匝数n=9, 11, 13, 15, 17,沿着线圈截面的法线方向移动键合线,线圈高度为1.6 mm。并计算键合线在不同位置与Rogowski线圈的互感,结果如图7所示。图中纵轴表示键合线与线圈的互感;d表示键合线与Rogowski线圈中心的水平距离。五条曲线分别对应匝数为n时,在键合线距离线圈中心d的情况下,线圈与键合线的互感值。在实际应用中,键合线簇应对齐于Rogowski线圈的中心,使两者处于几何对称状态。此外,图7中标注了SiC功率模块四根键合线的位置及其与线圈的互感值。可以观察到,随着线圈匝数的增加,互感值逐渐增大;同时,靠近线圈中心的键合线,其互感值明显更高。
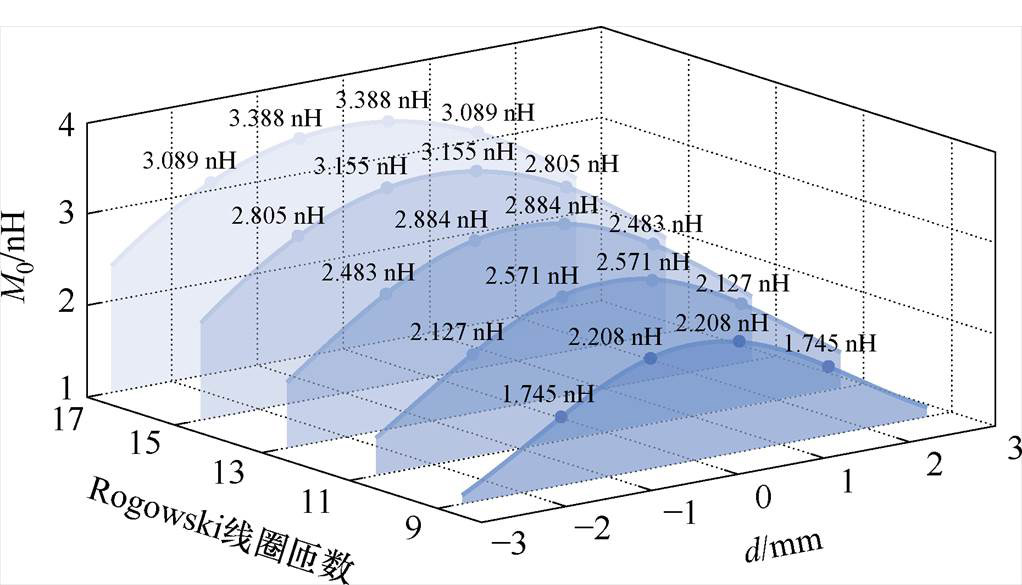
图7 Rogowski线圈互感M0与匝数和距离d的关系
Fig.7 Relationship between Rogowski coil mutual inductance M0, turns, and distance d
当SiC功率模块中出现键合线失效时,流经SiC芯片的总电流基本保持不变,但未失效的键合线电流会显著增加。因此,根据式(1),可以推导出每根键合线失效时Rogowski线圈电流增益的变化率。图8显示了键合线失效情况下,Rogowski线圈测量的电流增益变化率关系。图中纵轴表示电流放大变化率(以百分数表示),横轴表示Rogowski线圈的匝数n及失效键合线的编号。随着线圈匝数n的增加,键合线失效导致的电流增益变化率总体呈下降趋势。这表明增加线圈匝数能够提高键合线失效时线圈测量的稳定性。然而,匝数增加的Rogowski线圈也更容易与外部干扰磁场耦合。因此,在设计时应综合考虑稳定性与抗干扰性的平衡,避免盲目增加线圈匝数。根据图8的结果,当PCB型Rogowski线圈匝数为15时,键合线失效对线圈的增益影响控制在2%,能够在稳定性与抗干扰性之间取得平衡。
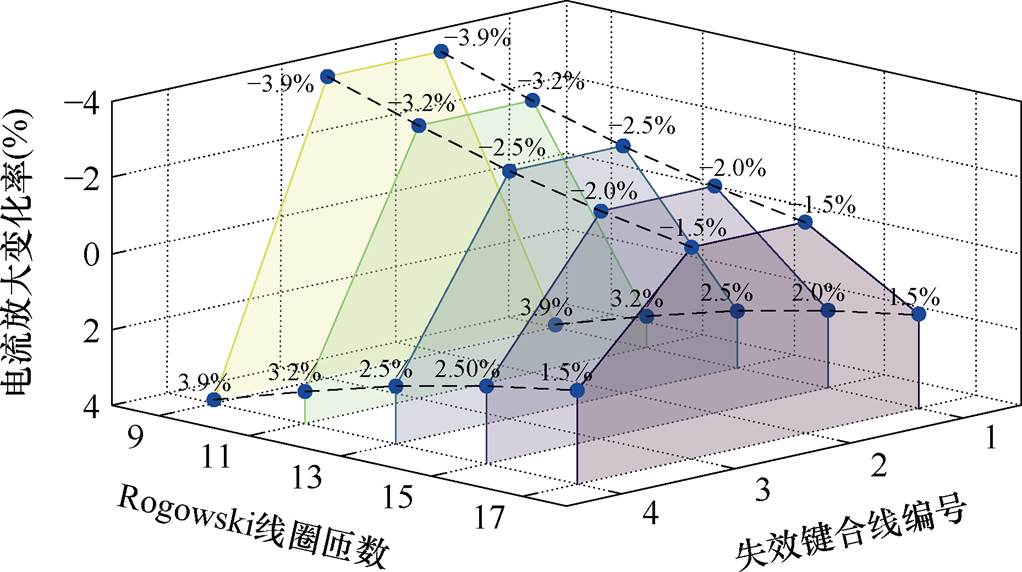
图8 Rogowski线圈匝数对键合线失效电流变化率的影响
Fig.8 Effect of Rogowski coil turns on current variation rate under bonding wire failure
在确定绕组匝数后,选取FR-4为材料的不同厚度PCB进行研究。通常,国内制造商提供的PCB厚度范围为0.4~2.0 mm。在本研究中,不考虑过薄的0.4 mm和0.6 mm板厚,而针对0.8、1.0、1.2、1.6和2.0 mm厚度的PCB型Rogowski线圈的键合线互感进行分析,结果如图9所示。表1显示了不同厚度PCB在不同键合线失效情况下的电流增益变化率。从结果中可以看出,随着PCB厚度的增加,Rogowski线圈与键合线的互感值显著增大。然而,不同厚度的PCB在键合线发生失效时,其电流增益变化率差异较小。需要注意的是,PCB厚度还会影响磁阻传感器的测量结果。因此,PCB厚度的最终选择需结合磁阻传感器抗干扰性能的研究结果确定。
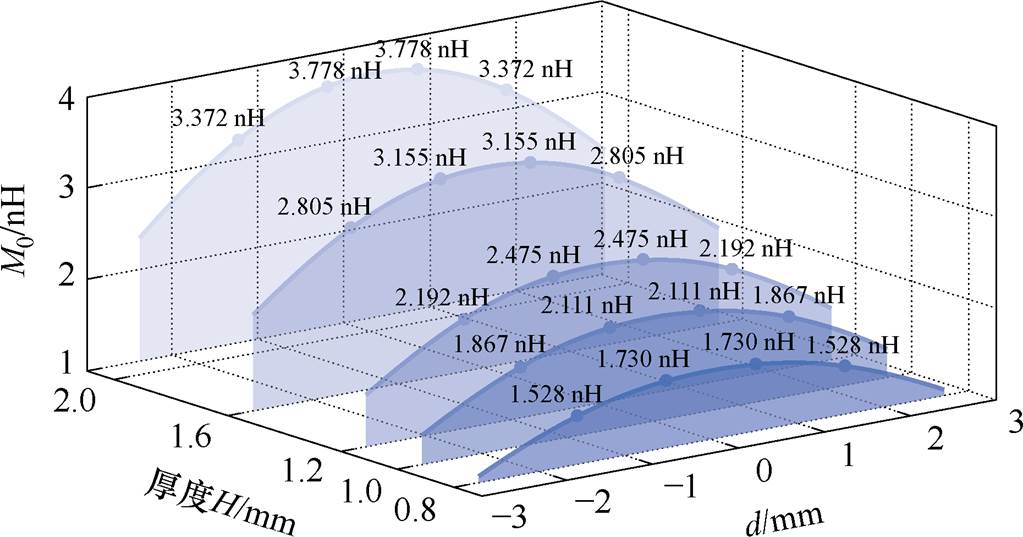
图9 Rogowski线圈互感M0与PCB厚度的关系
Fig.9 Relationship between Rogowski coil mutual and the thickness of PCB
表1 PCB厚度与电流增益变化率的关系
Tab.1 Relationship between PCB thickness and current gain variation
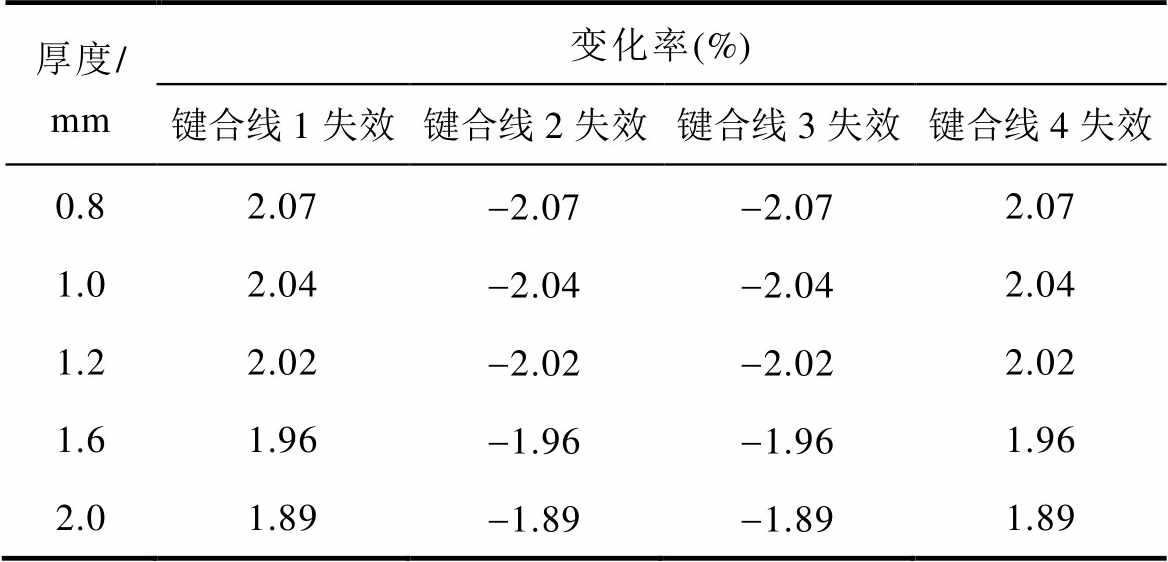
厚度/ mm变化率(%) 键合线1失效键合线2失效键合线3失效键合线4失效 0.82.07-2.07-2.072.07 1.02.04-2.04-2.042.04 1.22.02-2.02-2.022.02 1.61.96-1.96-1.961.96 2.01.89-1.89-1.891.89
磁阻(Magnetoresistor)传感器是一种点磁场传感器,其输出大小随磁阻所测得磁场大小而改变。由于通电导体会产生磁场,磁阻传感器常被用作电流传感器。磁阻传感器具有高灵敏度和非侵入式测量特点,适用于检测低频和直流信号。作为点磁场传感器,当SiC功率模块的键合线健康状态发生变化时,磁阻传感器测量键合线电流的增益可能发生改变,从而影响电流测量的准确性。因此,有必要研究键合线失效前后空间磁场的变化情况,以确定适合放置磁阻传感器的区域。本文使用的磁阻传感器为单轴磁场传感器。根据式(7),SiC功率模块的四根键合线在空间中产生的磁场可表示为
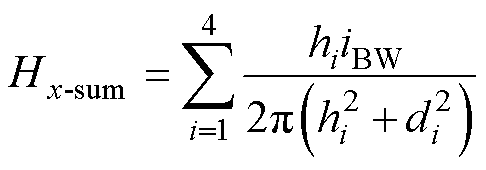 (15)
(15)
当一根键合线发生失效时,流经功率半导体芯片的总电流基本保持不变。因此,未失效的每根键合线中的电流会增加,从而导致空间中的磁场发生变化。以键合线1失效为例,此时空间中的磁场变化为
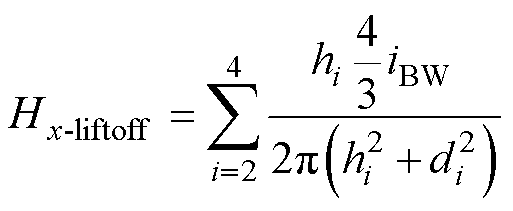 (16)
(16)
在SiC功率模块键合线失效时,PCB型Rogowski线圈的电流增益变化率已在第1节中计算得出。对于混合传感器的设计,应遵循5%的平坦带宽要求[22]。因此,当键合线发生失效时,磁阻传感器所测得的磁场变化率应满足
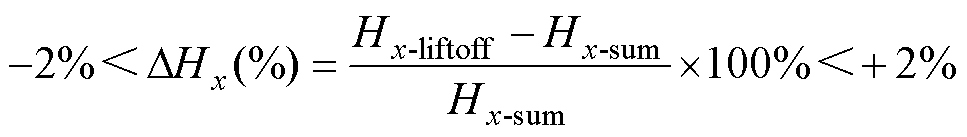 (17)
(17)
代入式(15)和式(16),并化简得
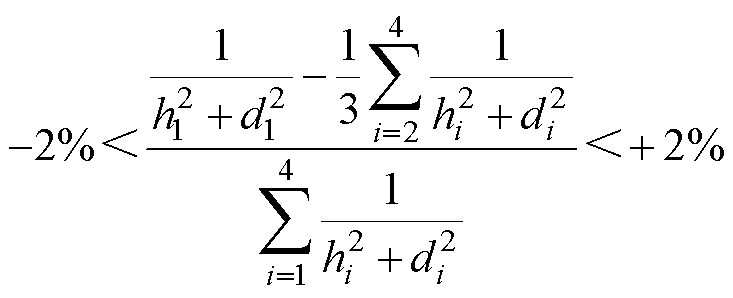 (18)
(18)
根据式(17),可以进行定性分析:当h di时,磁场变化率约为0。即当磁阻传感器相对于键合线的高度远大于其到键合线的水平距离时,键合线失效引起的磁场变化几乎可以忽略。这是因为无论四根键合线之间的电流如何分配,总电流保持不变,从远处观察可以将四根键合线视为一个整体。然而,随着高度h增加,一方面电流测量增益会变小;另一方面磁场传感器更容易受到外部磁场的干扰。因此,在满足式(17)的条件下,应尽可能地减小高度h。根据式(14),假设每根键合线电流为5 A,可以得到键合线附近的磁场分布,如图10所示。当键合线发生失效时,根据式(16),可以得出图11中的磁场分布。其中,图11a为键合线1失效时的磁场分布,图11b为键合线2失效时的情况。而键合线3和4失效时的磁场分布分别为图11a和图11b的水平翻转。显然,当键合线失效时,空间中的磁场分布发生了显著变化。
di时,磁场变化率约为0。即当磁阻传感器相对于键合线的高度远大于其到键合线的水平距离时,键合线失效引起的磁场变化几乎可以忽略。这是因为无论四根键合线之间的电流如何分配,总电流保持不变,从远处观察可以将四根键合线视为一个整体。然而,随着高度h增加,一方面电流测量增益会变小;另一方面磁场传感器更容易受到外部磁场的干扰。因此,在满足式(17)的条件下,应尽可能地减小高度h。根据式(14),假设每根键合线电流为5 A,可以得到键合线附近的磁场分布,如图10所示。当键合线发生失效时,根据式(16),可以得出图11中的磁场分布。其中,图11a为键合线1失效时的磁场分布,图11b为键合线2失效时的情况。而键合线3和4失效时的磁场分布分别为图11a和图11b的水平翻转。显然,当键合线失效时,空间中的磁场分布发生了显著变化。
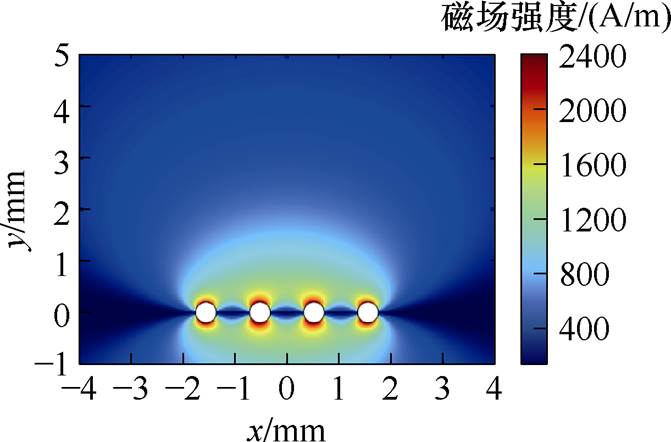
图10 键合线附近的磁场分布情况
Fig.10 Magnetic field distribution near bonding wires
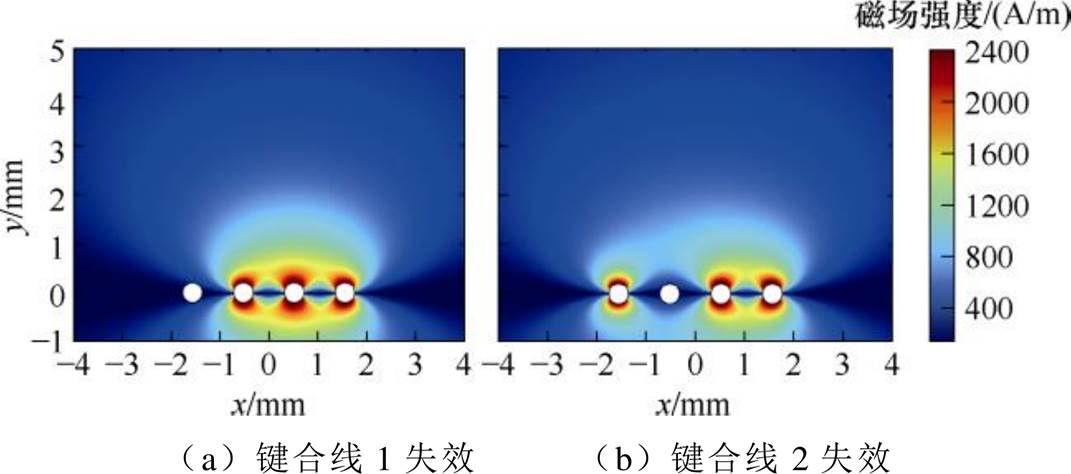
图11 键合线失效时的磁场分布
Fig.11 Magnetic field distribution during bonding failure
根据式(17),可以计算出当SiC功率模块的键合线失效时,空间中磁场的变化率,结果如图12所示。其中,图12a为键合线1失效时,键合线附近磁场变化率的分布;图12b为键合线2失效时的分布。同样地,键合线3和4失效时的情况分别为图12a和图12b的水平翻转。从图中可以看出,当键合线失效时,键合线相邻区域的磁场变化率发生剧烈波动,而远离键合线的区域磁场变化率则相对稳定。
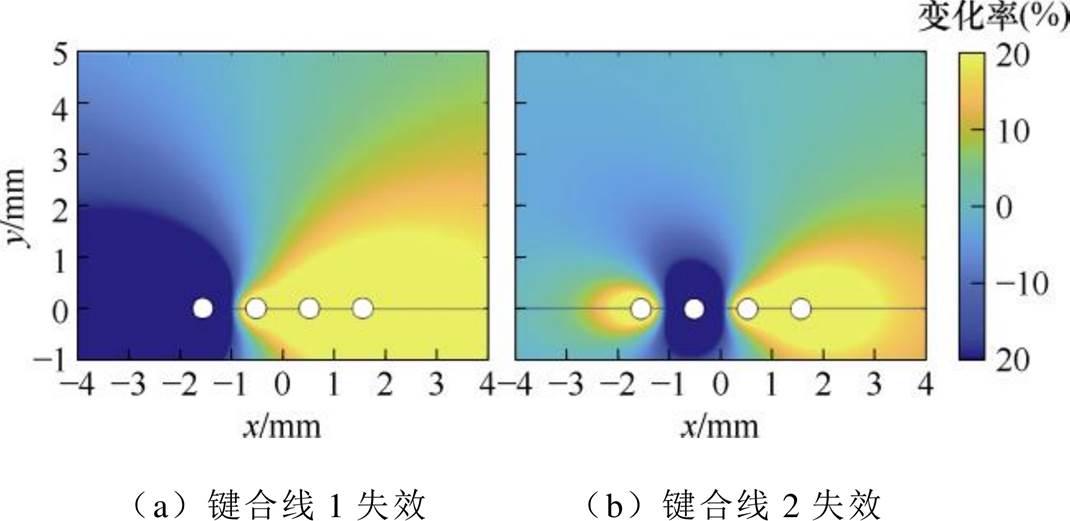
图12 键合线失效时的磁场变化率
Fig.12 Magnetic field change rate during bonding wire failure
根据式(17)所满足的条件,可以确定符合磁场变化率要求的区域。由于SiC功率模块包含四根键合线,每根键合线失效时,符合条件的区域有所不同。所以本文中求出了四根键合线分别失效时的符合条件区域,并将四个符合条件的区域合并成一幅图,如图13所示。图中显示了键合线失效时符合磁场变化率条件的区域分布。颜色由浅至深表示空间中满足条件的磁场变化个数,深蓝色区域的值为4,表示无论键合线1~键合线4中的任意一根失效,深蓝色区域的磁场变化率均符合式(17)。因此,图13中的深蓝色区域为磁阻传感器的最佳放置位置。图中深蓝色区域距离键合线中心3~5 mm。考虑到键合线在SiC功率模块封装中被硅凝胶灌封,其顶端距离硅凝胶表面约2 mm。结合第1节设计的厚度为1.6 mm的PCB型Rogowski线圈,将磁阻传感器放置在PCB顶层,并对齐键合线的中线即可确保传感器的输出不受键合线失效的影响。键合线中线上方4 mm处的磁场强度(A/m)和磁场变化率见表2,为键合线中线上方4.0 mm处的磁场强度及磁场变化率。从表中数据可以看出,在该点处键合线失效时,沿x轴方向的磁场强度及磁场变化率保持稳定。表中数据验证了在此位置放置磁阻传感器可以有效抑制因键合线失效导致的磁场变化。此外,深蓝色区域具有一定宽度,使磁阻传感器的放置位置具有较好的容错率。在上述分析中,假定某键合线失效后,其电流平均分配到剩余键合线中,本文所设计的磁阻传感器对电流分布不均匀时的情况也具有一定的容错能力。以键合线1失效为例,假设键合线2和键合线3总电流为3iBW,键合线4电流为iBW,通过计算可得磁阻传感器输出误差约为3.1%,即便在电流重新分布非理想的条件下,传感器依然能够保持较高的测量稳定性。
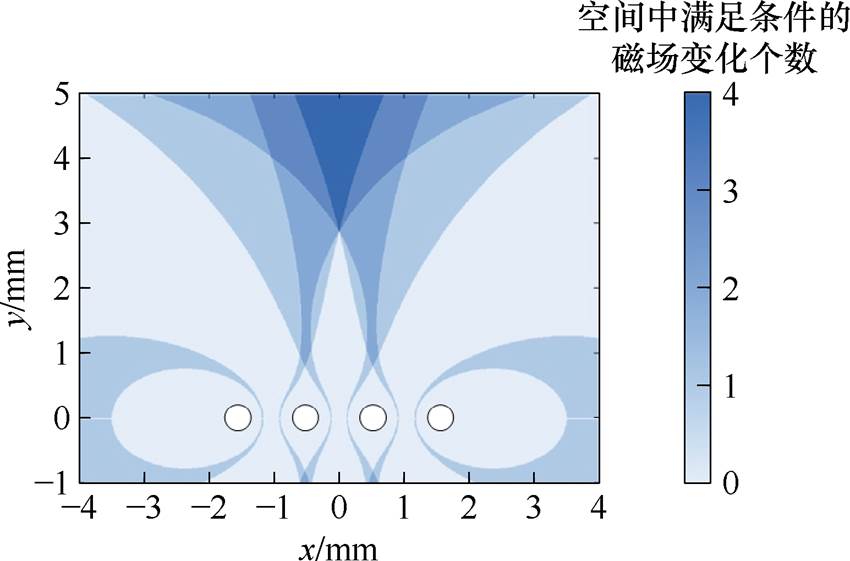
图13 磁阻传感器的最佳放置区域分布
Fig.13 Optimal placement distribution for magnetoresistive sensor
表2 键合线中线上方4 mm处的磁场强度(A/m)和磁场变化率
Tab.2 The magnetic field intensity (A/m) and magnetic field variation rate at 4 mm above the centerline of the bonding wires
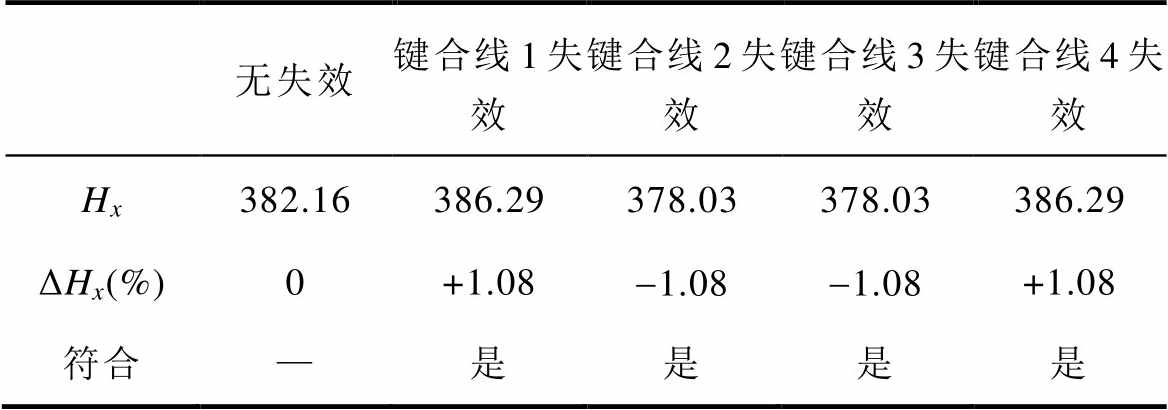
无失效键合线1失效键合线2失效键合线3失效键合线4失效 Hx382.16386.29378.03378.03386.29 ΔHx(%)0+1.08-1.08-1.08+1.08 符合—是是是是
将Rogowski线圈设计在1.6 mm厚的4层PCB上,如图14所示。由于磁阻-Rogowski线圈的电流测量会受到位置的影响,为避免传感器位置偏移造成测量误差,PCB的长宽设计与SiC功率模块内部尺寸一致。混合传感器的尺寸参数见表3。由于本文后续的实验中不涉及高温环境,故将所设计的PCB直接放置于模块硅凝胶之上。若在后续的实际应用中规避由于模块温度变化而影响传感器的测量结果,则可以将PCB悬空固定在硅凝胶之上,或采用热膨胀系数较小的PCB板材,以避免温升产生的PCB形变。另外,可以通过增加温度传感器的方法对磁阻传感器的温度漂移进行补偿[25]。
根据第1节分析,15匝的Rogowski线圈中心与键合线的中心对齐。利用Ansys Q3D提取Rogowski线圈的集总参数模型。Rogowski线圈的集总参数见表4,C0为线圈的寄生电容,L0为线圈的自感,R0为绕组电阻,M0为线圈和键合线的互感,该结果与图7中的计算结果接近,验证了设计的准确性。

图14 SiC功率模块与混合传感器
Fig.14 Photo of SiC power module and hybrid sensor
表3 混合传感器的尺寸参数
Tab.3 Design parameters of Rogowski coil

参 数数 值 绕组高度H/mm1.6 线圈到键合线前端的垂直距离h0/mm2.0 绕组宽度W/mm2.0 键合线与水平夹角a/(°)20 线圈匝间距离Dd/mm0.34
表4 Rogowski线圈的集总参数
Tab.4 The lumped parameters of Rogowski coil
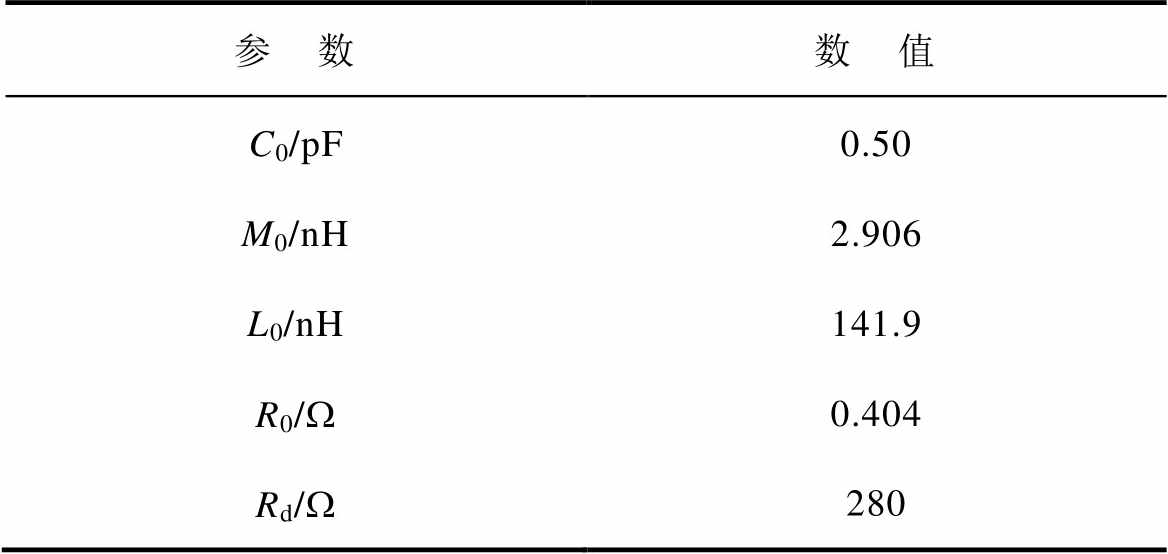
参 数数 值 C0/pF0.50 M0/nH2.906 L0/nH141.9 R0/W0.404 Rd/W280
根据磁阻传感器和Rogowski线圈的原理可知,磁阻传感器适用于低频和直流信号测量,需要配备仪表放大器;而Rogowski线圈适用于交流信号测量,需要配备积分器。由于两者的测量带宽存在交叠,需要通过滤波处理来消除带宽的重叠干扰。图15为混合传感器的信号处理电路,其中vIA为仪表放大器的输出,vcoil为Rogowski线圈的输出信号,vH为混合传感器的总输出。信号处理电路的传递函数为
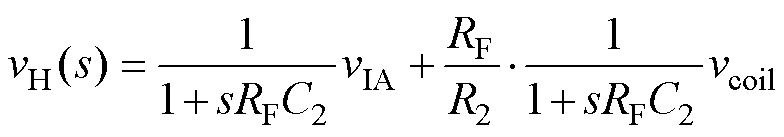 (19)
(19)
式中,R1=R2;C1=C2;RMR=RF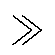 R1。
R1。
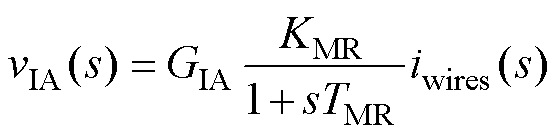 (20)
(20)
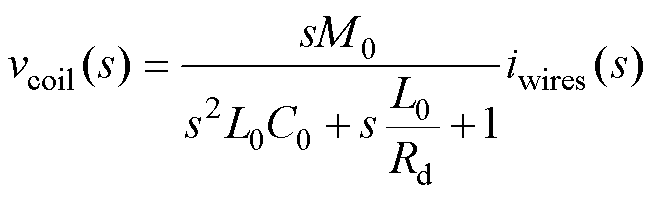 (21)
(21)
式中,KMR为磁阻传感器的测量系数;TMR为磁阻传感器的时间常数;GIA为仪表放大器的放大系数;iwires为键合线电流。根据磁阻传感器的数据手册以及表4中所计算的Rogowski线圈参数,可求得图15中各电阻和电容的具体值。通过LTspice软件模拟,可以得到混合传感器测量键合线电流的Bode图,如图16所示。从图中可以看出,在磁阻传感器与Rogowski线圈的测量带宽范围内,电流增益的差异仅为0.1 dB。混合传感器的整体测量带宽从直流扩展到100 MHz。图17为在键合线发生失效的情况下的混合传感器测量Bode图,图17a~图17d分别为键合线1~键合线4失效时的Bode图。从图17中可以看出,在单根键合线失效的情况下,电流测量增益的变化约为0.1 dB,变化率保持在2%以内。为降低分析复杂度,第1节采用理想二维模型进行初步设计,忽略了漏磁等细节,以便快速确定线圈参数;本小节则基于有限元仿真和实际结构提取参数,结果更贴近实测。尽管两者在电流增益变化率上存在一定差异,但数值上较接近,差异主要源自模型简化与制造偏差,验证了简化模型在趋势预测上的有效性。
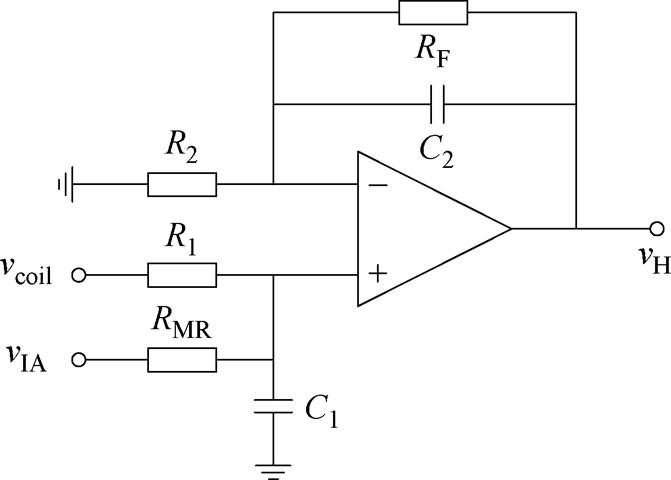
图15 混合传感器的信号处理电路
Fig.15 The signal processing circuit of hybrid sensor
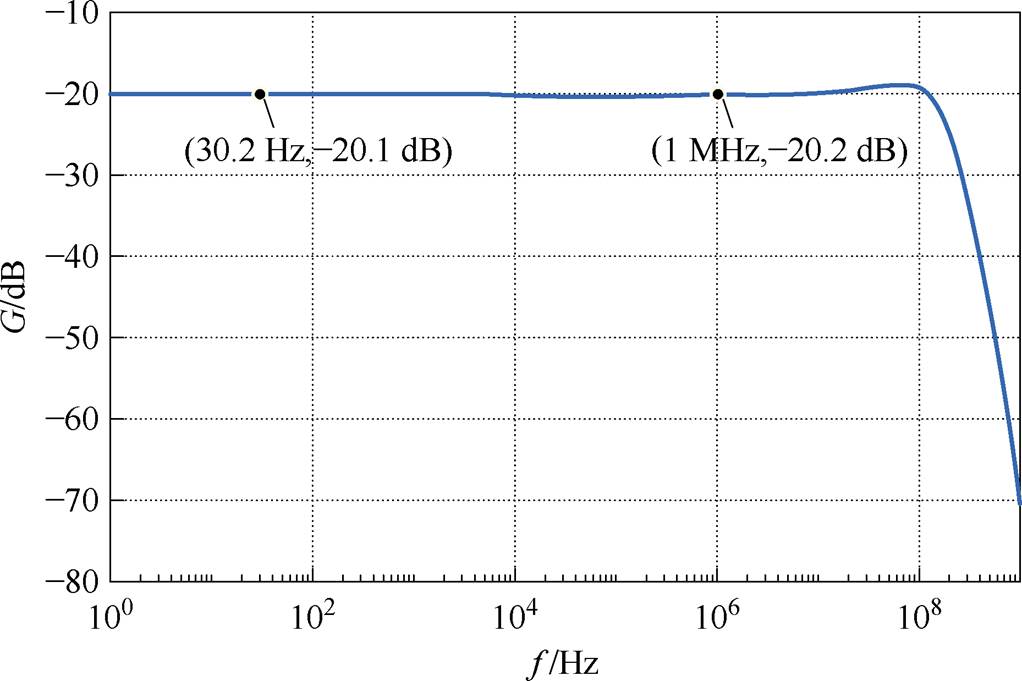
图16 混合传感器的Bode图
Fig.16 The Bode plot of hybrid sensor
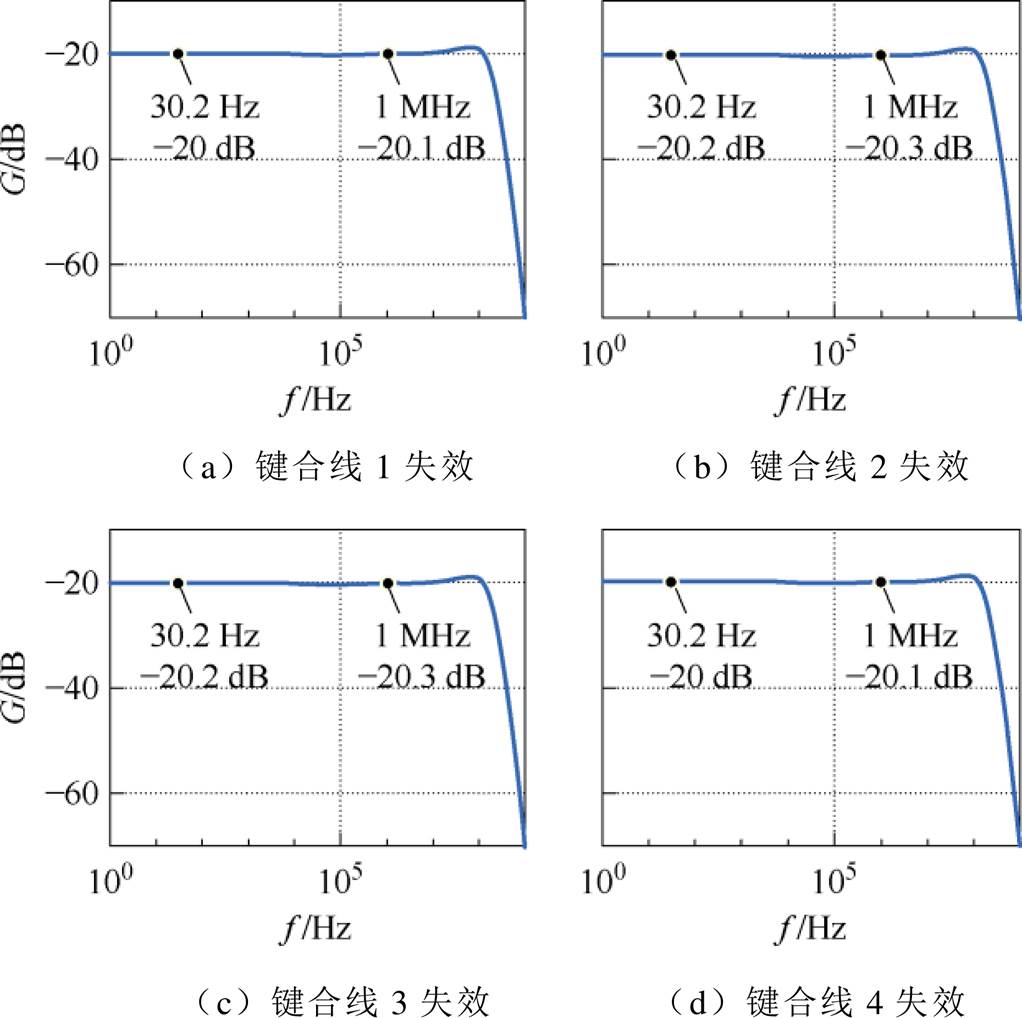
图17 键合线失效对混合传感器测量频率响应的影响
Fig.17 Impact of bonding wire failure on frequency response of hybrid sensor
已有研究表明,在高频电流作用下,趋肤效应和邻近效应对靠近键合线表面的磁场影响显著,但在远离键合线一定距离处,对磁场的影响则非常 小[24, 26]。在本文所设计的Rogowski线圈与磁阻传感器测量结构中,传感器远离键合线布置。因此,本文设计中趋肤效应与邻近效应不会对线圈互感及测量精度产生显著的影响。此外,在多芯片电流同时测量的场景中,磁场型电流传感器会存在磁场耦合的问题。对于该问题,已有文献提出磁场解耦方法可用于消除多导体间的交叉干扰。本文实验对象仅为单颗芯片,且线圈与栅极或功率端子无明显耦合关系,未表现出显著耦合干扰,因此实验中未设置解耦电路[26]。
本节设计了实验,用以验证磁阻-Rogowski线圈传感器在SiC功率模块键合线失效时的电流测量性能。实验中,将SiC功率模块集成在Buck变换器中,如图18所示。使用磁阻-Rogowski线圈对SiC功率模块的键合线电流进行监测,并通过剪断SiC功率模块的键合线来模拟键合线失效的情况。实验设置了不同的PCB厚度和Rogowski线圈匝数,以验证前文中的设计方案。实验平台的实物照片如图19所示。
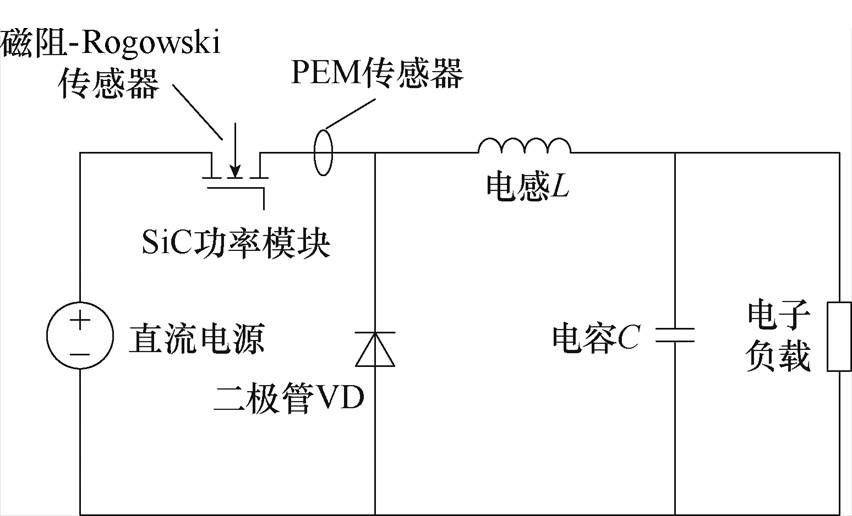
图18 Buck变换器示意图
Fig.18 The schematic diagram of the Buck converter

图19 实验平台照片
Fig.19 The photo of experiment platform
在SiC功率模块键合线未发生失效的情况下,使用磁阻-Rogowski线圈传感器对SiC芯片的键合线电流进行监测,并采用PEM商用电流传感器CWTUM06(测量带宽为34 Hz~30 MHz)对测量结果进行验证。如图20所示,展示了磁阻-Rogowski混合传感器与PEM商用电流传感器测量SiC功率模块键合线电流的对比结果。图20a为长时间范围内的电流波形。可以看出,两者在整体趋势上保持高度一致,验证了混合传感器的测量准确性。在器件开关过程的局部放大图中,图20b显示了SiC器件关断阶段,混合传感器能够捕捉到细微的振荡特征,并与商用传感器的波形高度吻合;图20c显示了SiC器件开通阶段,两者的测量结果仍然保持较高的一致性。
在键合线健康状态监测的实验中,对不同MSCSM120AM50CT1AG模块分别剪断了如图21所示的键合线1和键合线2。在不同实验条件下,磁阻- Rogowski混合传感器和PEM商用电流传感器在SiC功率模块键合线失效时的电流波形对比结果如图21所示。实验条件包括键合线失效位置、线圈匝数以及PCB厚度的变化。
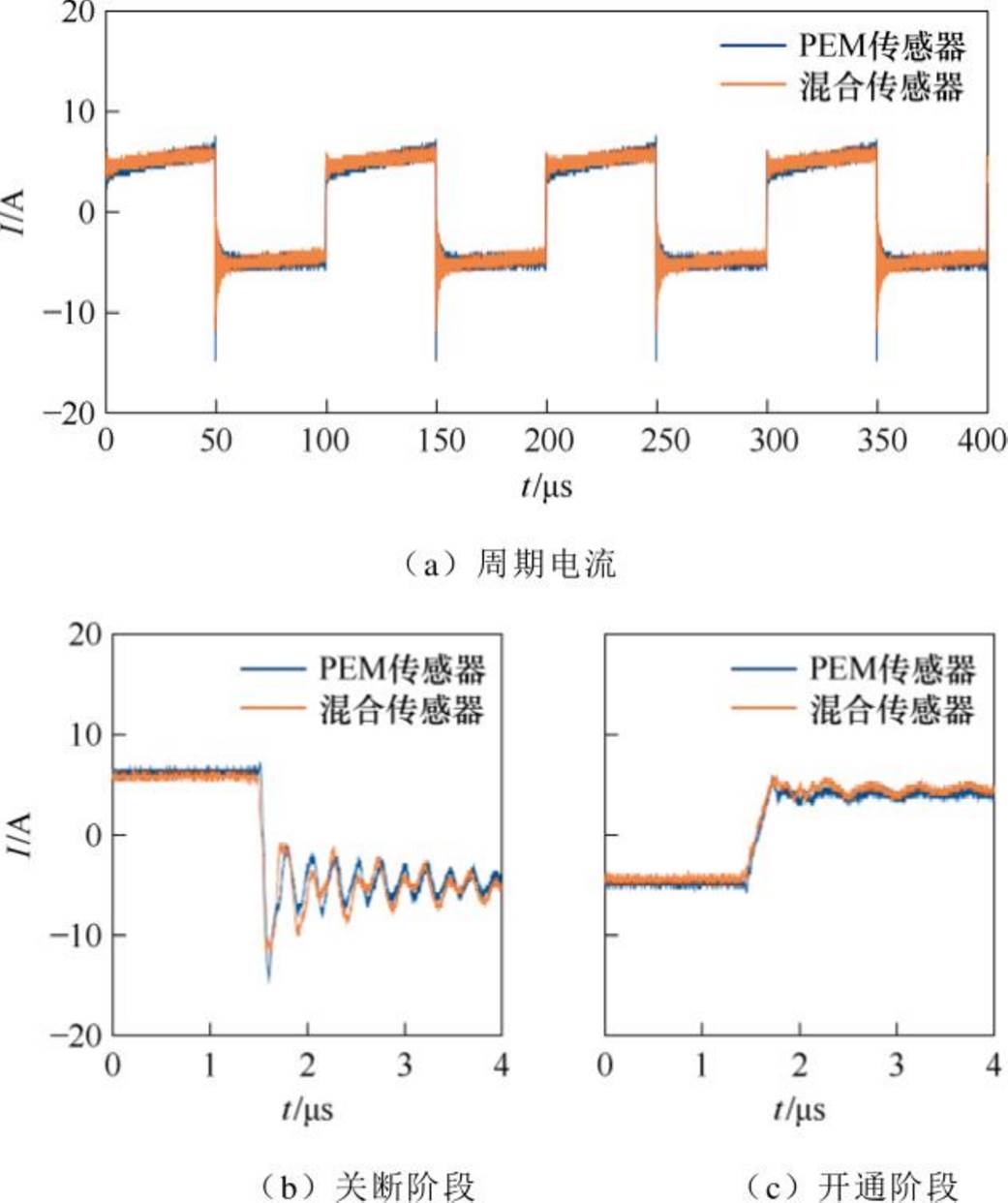
图20 未发生失效时的SiC功率模块键合线电流测量
Fig.20 Measured current waveforms without bonding wire failure
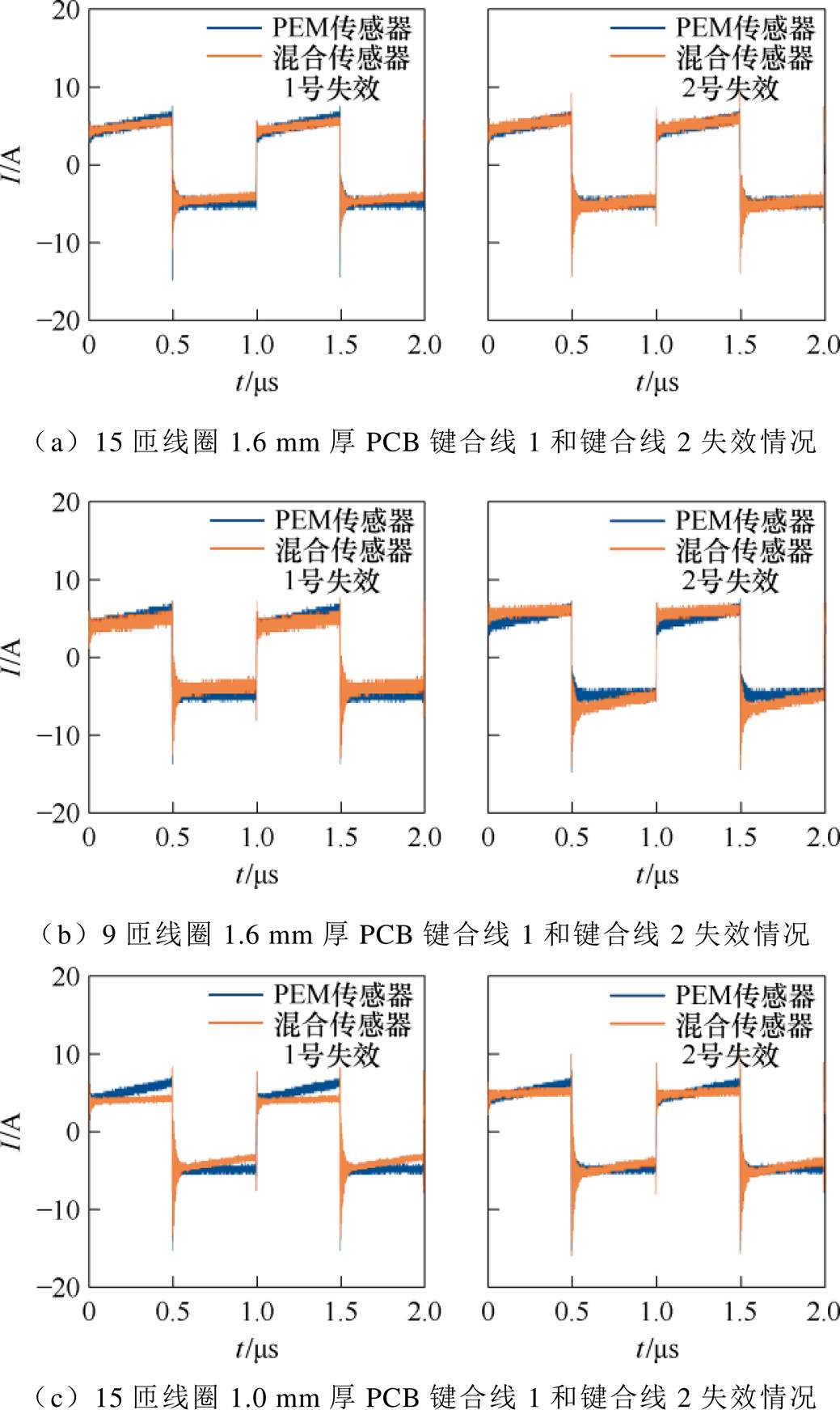
图21 发生键合线失效后的电流测量
Fig.21 Measured current waveforms after bonding wire failure
在图21a中,实验条件为15匝线圈和1.6 mm厚的PCB,无论键合线1或键合线2失效,混合传感器与商用传感器的测量结果基本一致,波形稳定无明显偏差,表现出良好的测量可靠性。
相比之下,在图21b的实验中,将线圈匝数减少为9匝,PCB厚度保持为1.6 mm,可以观察到混合传感器测量结果出现了微弱的波形偏差。这种情况下,偏差主要是由于Rogowski线圈的匝数减少,使得键合线发生失效时,键合线与线圈之间的互感明显变化所致。
在图21c中,虽然线圈匝数恢复到15匝,但PCB厚度减小为1.0 mm时,测量结果的波形偏差更为明显。这种情况下,造成混合传感器输出偏差的主要原因是磁阻传感器放置高度未处于图11所示的最佳区域内。所以在键合线发生失效时,磁阻传感器的电流测量增益会发生明显变化。
本文提出了一种融合磁阻传感器与Rogowski线圈的混合电流传感器,系统性地研究了其在SiC功率模块键合线失效条件下的抗干扰性能与测量精度。通过将磁阻传感器和Rogowski线圈的优势相结合,混合传感器实现了宽带覆盖,从直流到100 MHz的测量范围,同时具备对直流、低频以及高频信号的精准测量能力。实验结果表明,传感器的测量结果与商用传感器的测量结果高度一致,证明了其优异的测量精度和动态响应能力。
在研究过程中,本文分析了不同PCB厚度、Rogowski线圈匝数以及磁阻传感器放置位置对测量性能的影响。通过解析方法对PCB厚度、线圈匝数等参数进行了研究。在对SiC功率模块进行电流测量时,当Rogowski线圈采用15匝绕组、PCB厚度为1.6 mm,传感器的电流增益变化率能够保持在±2%的范围内。进一步,磁场分布分析确定了磁阻传感器的最佳放置区域,该区域的磁场变化率在键合线失效时保持稳定,显著降低了测量误差。最后,通过实验验证了混合传感器能够准确测量SiC功率模块芯片的电流。并且,所设计的15匝线圈、1.6 mm板厚的传感器能够在键合线失效的情况下依然保持准确的测量。
综上所述,本文对磁阻-Rogowski混合电流传感器的设计方法在实时性、测量精度、宽带能力和抗干扰性能方面具有显著优势,为SiC功率模块键合线电流测量提供了一种高效、可靠的解决方案,增强了混合电流传感器的抗干扰能力。未来的研究将进一步优化传感器的集成度,并探索其在其他功率电子模块中的应用潜力。
参考文献
[1] 张缙, 刘智, 刘意, 等. 基于智能算法的双面散热SiC功率模块多目标优化设计[J]. 电工技术学报, 2023, 38(20): 5515-5529.
Zhang Jin, Liu Zhi, Liu Yi, et al. Research on multi- objective optimization design of double-sided cooling SiC power module based on intelligent algorithm[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5515-5529.
[2] 王来利, 赵成, 张彤宇, 等. 碳化硅功率模块封装技术综述[J]. 电工技术学报, 2023, 38(18): 4947- 4962.
Wang Laili, Zhao Cheng, Zhang Tongyu, et al. Review of packaging technology for silicon carbide power modules[J]. Transactions of China Electro- technical Society, 2023, 38(18): 4947-4962.
[3] 孙培元, 孙立杰, 薛哲, 等. 高压SiC MOSFET研究现状与展望[J]. 电子与封装, 2023, 23(1): 115-126.
Sun Peiyuan, Sun Lijie, Xue Zhe, et al. Status and prospect of high-voltage SiC MOSFET[J]. Electronics & Packaging, 2023, 23(1): 115-126.
[4] 李锦, 党恩帅, 范雨顺, 等. 一种碳化硅与硅器件混合型三电平有源中点钳位零电压转换软开关变流器[J]. 电工技术学报, 2024, 39(8): 2496-2510.
Li Jin, Dang Enshuai, Fan Yushun, et al. A hybrid three-level active-neutral-point-clamped zero-voltage transition soft-switching converter with silicon carbide and silicon devices[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2496-2510.
[5] 朱远哲, 王玲, 吴争荣, 等. 基于Si和SiC器件混合的并网变流器及其调控策略研究[J].电气传动, 2025, 55(6): 36-44.
Zhu Yuanzhe, Wang Ling, Wu Zhengrong, et al. A grid-connected converter based on heterogeneous device hybrid and its control strategy[J]. Electric Drive, 2025, 55(6): 36-44.
[6] 荀博洋, 郝凤斌, 柏松, 等. 考虑损耗与应力下SiC模块的电路参数设计[J]. 电力电子技术, 2025, 59(4): 121-124.
Xun Boyang, Hao Fengbin, Bai Song, et al. Design of circuit parameters of SiC module considering loss and stress[J]. Power Electronics, 2025, 59(4): 121-124.
[7] 莫文逸, 张犁, 邹宇航. 一种SiC/Si混合五电平逆变器及其优化调制策略[J/OL]. 电源学报, 1-12[2025- 07-24]. http://kns.cnki.net/kcms/detail/12.1420.TM. 20250326.1521.006.html.
Mo Wenyi, Zhang Li, Zou Yuhang. A SiC/Si hybrid five-level inverter and its optimized modulation scheme[J/OL]. Journal of Power Supply, 1-12[2025- 07-24]. http://kns.cnki.net/kcms/detail/12.1420.TM.20250326.1521.006.html.
[8] 刘伟志. 基于SiC器件的三电平ANPC牵引变流器损耗分析[J]. 电气传动, 2023, 53(2): 16-23.
Liu Zhiwei. Design and loss analysis of three-level ANPC topology based on SiC device in traction drive system[J]. Electric Drive, 2023, 53(2): 16-23.
[9] 李鑫, 罗毅飞, 史泽南, 等. 一种基于物理的SiC MOSFET改进电路模型[J]. 电工技术学报, 2022, 37(20): 5214-5226.
Li Xin, Luo Yifei, Shi Zenan, et al. An improved physics-based circuit model for SiC MOSFET[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5214-5226.
[10] 张彤宇, 王来利, 苗昱, 等. 多芯片整体式Clip互连碳化硅功率模块反向耦合低感封装方法[J/OL]. 电工技术学报, 1-12[2025-07-24]. https://doi.org/ 10.19595/j.cnki.1000-6753.tces.250153.
Zhang Tongyu, Wang Laili, Miao Yu, et al. Multichip integral Clip bonding SiC power module reverse coupling low inductance packaging method[J/OL]. Transactions of China Electrotechnical Society, 1-12 [2025-07-24]. https://doi.org/10.19595/j.cnki.1000-6753. tces.250153.
[11] 张岩, 薛少鹏, 李阳, 等. 安全工作区外重复过电压硬开关下SiC MOSFET参数退化特性与机理[J]. 电工技术学报, 2025, 40(16): 5029-5043.
Zhang Yan, Xue Shaopeng, Li Yang, et al. Degra- dation of SiC MOSFETs under repetitive overvoltage and hard-switching stress outside the safe operating area[J]. Transactions of China Electrotechnical Society, 2025, 40(16): 5029-5043.
[12] 张擎昊, 郑大勇, 张品佳. SiC MOSFET结温监测与控制技术综述[J]. 中国电机工程学报, 2025, 45(3): 1034-1052.
Zhang Qinghao, Zheng Dayong, Zhang Pinjia. A review of junction temperature monitoring and control methods for SiC MOSFETs[J]. Proceedings of the CSEE, 2025, 45(3): 1034-1052.
[13] 胡嘉豪, 王英伦, 代豪豪, 等. SiC MOSFET器件栅氧可靠性研究综述[J]. 电源学报, 2024, 22(4): 1-11.
Hu Jiahao, Wang Yinglun, Dai Haohao, et al. Review on gate oxide reliability of SiC MOSFET devices[J]. Journal of Power Supply, 2024, 22(4): 1-11.
[14] 张瑜, 田鸿昌, 文阳. 基于动态栅极电阻的SiC MOSFET主动并联均流方法[J]. 高压电器, 2023, 59(9): 286-293.
Zhang Yu, Tian Hongchang, Wen Yang. Active parallel current sharing method of SiC MOSFET based on dynamic gate resistance[J]. High Voltage Apparatus, 2023, 59(9): 286-293.
[15] 宋玮琼, 郭帅, 韩柳, 等. 光伏逆变器中并联SiC器件电流失衡的监测技术研究[J]. 电气传动, 2024, 54(7): 16-21.
Song Weiqiong, Guo Shuai, Han Liu, et al. Monitoring technique research of current mismatch in parallel SiC devices for photovoltaic inverters[J]. Electric Drive, 2024, 54(7): 16-21.
[16] Wang Jianpeng, Chen Wenjie, Wu Yuwei, et al. Chip-level electrothermal stress calculation method of high-power IGBT modules in system-level simu- lation[J]. IEEE Transactions on Power Electronics, 2022, 37(9): 10546-10561.
[17] Yang Yayong, Wang Zhiqiang, Ge Yuxin, et al. An automated field-circuit coupling simulation method based on PSpice-MATLAB-COMSOL for SiC power module design[J]. IEEE Transactions on Power Electronics, 2023, 38(10): 12634-12647.
[18] Gu Dazhong, Kshirsagar P. Compact integrated gate drives and current sensing solution for SiC power modules[C]//2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 2017: 5139-5143.
[19] Liu Pengkun, Zhang Liqi, Huang A Q, et al. High bandwidth current sensing of SiC MOSFET with a Si current mirror[C]//2016 IEEE 4th Workshop on Wide Bandgap Power Devices and Applications (WiPDA), Fayetteville, AR, USA, 2016: 200-203.
[20] Cairnie M, DiMarino C. Gate driver for 10 kV SiC MOSFET power module with high-speed current sensing[C]//2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 2021: 5385-5392.
[21] Schneider P E, Horio M, Lorenz R D. Evaluation of point field sensing in IGBT modules for high- bandwidth current measurement[J]. IEEE Transa- ctions on Industry Applications, 2013, 49(3): 1430- 1437.
[22] Alvi M H, Sheng Minhao, Lorenz R D, et al. Power module design for integrated three-phase current sensing using a single 3-D point field detector[C]// 2020 IEEE Energy Conversion Congress and Expo- sition (ECCE), Detroit, MI, USA, 2020: 3328-3335.
[23] Sheng Minhao, Alvi M H, Lorenz R D. GMR-based integrated current sensing in SiC power modules with phase shift error reduction[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 10(3): 3477-3487.
[24] GuoW, Xiao G, Wang L. Non-contact power module current measurement based on bonding wire current sensing using hybrid sensor[J]. IEEE Transactions on Industrial Electronics.
[25] Guo Weili, Xiao Guochun, Wang Laili. Online condition monitoring of bonding wires lift-off in power modules based on magnetic field measu- rement[J]. IEEE Transactions on Power Electronics, 2025, 40(3): 4425-4436.
[26] Guo Weili, Xiao Guochun, Wang Laili. A compact magnetoresistance-Rogowski hybrid sensor for multi- chip online current sensing in press-pack power module[J]. IEEE Transactions on Industrial Elec- tronics, 2024, 71(9): 11529-11539.
Abstract SiC power modules are extensively utilized in power electronics owingwidely used in power electronics due to their exceptional performance in high-temperature and high-frequency conditions. However, the reliability and stability of these modules can be significantly compromised by bonding wire failures during prolonged operation. Such failures alter the magnetic field distribution around the bonding wires, negatively impacting the accuracy and stability of current measurement by magnetic-field-based sensors. To address this issue Therefore, this study proposes a hybrid current sensor integrating a magnetoresistive sensor and a PCB-based non-encircling Rogowski coil, focusing on optimizing its anti-interference performance under bonding wire failure conditions that integrates a magnetoresistive sensor and a PCB-based non-encircling Rogowski coil, focusing on optimizing its anti-interference performance under conditions of bonding wire failure.
The research begins by systematically analyzing the mutual inductance between the PCB-based Rogowski coil and the bonding wires of a Microsemi SiC power module is analyzed. Given the compact layout and the space limitations imposed by the module’s structure, traditional Rogowski coils are unsuitable. Therefore, a PCB-based non-encircling Rogowski coil design is adopted. The study employs theoretical derivation and finite element simulations to evaluate the impact influence of coil parameters such as turn number, coil spacing, and PCB thickness on mutual inductance and measurement stability, such as turn number, coil spacing, and PCB thickness, on mutual inductance and measurement stability is evaluated through theoretical derivations and finite element simulations. Results indicate that a coil design with 15 turns and a PCB thickness of 1.6 mm achieves optimal balance, maintaining the current gain variation within ±2% even under bonding wire failure scenarios an optimal balance, maintaining current gain variation within ±2% even under conditions of bonding wire failure.
Additionally, the spatial magnetic field distribution near the bonding wires is thoroughly analyzed, considering the conditions of both healthy and faulty bonding wires. The optimal placement for the magnetoresistive sensor is identified at 3~5 mm above the bonding wire centerline of the bonding wire, where the magnetic field intensity and its variation remain minimal during wire failures. The magnetoresistive sensor is strategically placed at the top layer of the PCB to ensure stable performance. The study further validates that even under uneven current redistribution among remaining functional wires, the measurement error remains minimal, demonstrating robust tolerance to non-ideal operating conditions.
Integration of the optimized magnetoresistive sensor and Rogowski coil into a unified hybrid current sensor system is described, detailing the integration of the optimized magnetoresistive sensor and Rogowski coil into a unified hybrid current sensor system is described, detailing a PCB-based design compatible with the SiC module's internal structure. The developed signal processing circuitry combines the strengths of both sensors—precision measurement of DC and low-frequency currents by the magnetoresistive sensor, and high-frequency current detection capabilities of the Rogowski coil—thereby achieving comprehensive coverage from DC to 100 MHz. The frequency response of this hybrid sensor is validated through LTspice simulations and experimental setups, confirming minimal variation in measurement accuracy under bonding wire failure.
Experimental verification is conducted using a Buck converter incorporating the SiC power module. Comparisons between the proposed hybrid sensor and a commercial current sensor confirm the high accuracy and reliability of the hybrid system across various scenarios, under including normal operation and multiple bonding wire failure conditions. Results demonstrate that the hybrid sensor reliably detects fine current fluctuations and maintains accurate measurements despite bonding wire faults, further validating the optimization strategy employed.
In conclusion, this study provides a robust and efficient technical solution for real-time monitoring and reliable current measurement in SiC power modules, particularly addressing the significant challenge of bonding wire failure-induced interference. The proposed hybrid current sensor significantly improves measurement stability and anti-interference capability, offering a promising approach for enhancing enhances measurement stability and anti-interference capability, offering a promising approach to improving the long-term reliability and operational stability of power electronic systems. Future work will aim to further improve sensor integration density strengthen sensor integration density and explore potential applications across a broader range of power electronic modules.
keywords:Silicon carbide power module, hybrid current senor, Rogowski coil, magnetoresistive sensor, bonding wire failure
DOI: 10.19595/j.cnki.1000-6753.tces.250177
中图分类号:TN306
国家电网科学技术项目(5400-202318549A-3-2-ZN)资助。
收稿日期 2025-02-03
改稿日期 2025-05-09
郭伟力 男,1996年生,博士研究生,研究方向宽禁带半导体封装及其可靠性。E-mail: gwl_bill@stu.xjtu.edu.cn
王来利 男,1982年生,教授,博士生导师,研究方向为宽禁带半导体器件封装集成及其应用技术。E-mail: llwang@mail.xjtu.edu.cn(通信作者)
(编辑 郭丽军)