亚阈值摆幅法解析表征SiC MOSFET陷阱电荷及其BTI机理分析应用
施 超1,2,3 李学宝2,3,4 王来利1 王 跃1 蒋馨玉2,3,4 陈中圆2,3 冉 立2,3,5
(1. 电工材料电气绝缘全国重点实验室(西安交通大学) 西安 710049 2. 北京怀柔实验室 北京 101499 3. 北京智慧能源研究院 北京 102209 4. 新能源电力系统全国重点实验室(华北电力大学) 北京 102206 5. 输变电装备技术全国重点实验室(重庆大学) 重庆 400044)
摘要 由于较高的界面态密度,温度偏置不稳定性(BTI)导致的SiC MOSFET阈值电压漂移问题严重影响了器件的栅氧可靠性,制约其进一步的应用与发展。界面态密度的表征是研究不同电热应力这些不稳定性对阈值电压漂移作用机理的关键,但传统表征方法不够便捷、准确。为此,该文根据基础理论导出一种新的采用亚阈值摆幅测定界面态密度的解析公式,并应用该解析公式研究了SiC MOSFET在不同电热应力条件下亚阈值摆幅、界面态密度、陷阱电荷量和阈值电压漂移的变化规律和作用机理。结果表明,在良性电热应力条件下,陷阱电荷量与初始电压应力幅值的变化近似成正比,当应力时间不小于系统最小测量时间的量级时,陷阱电荷量与之满足指数关系。此外,陷阱电荷量和阈值电压漂移的变化量在数量级和变化趋势上一致性较高,证明了通过亚阈值摆幅表征界面态密度以及计算陷阱电荷量的有效性。所提公式可为快捷检测器件的界面态密度提供指导,为加速工艺生产测试流程、提升器件的栅氧可靠性提供有效的工具。
关键词:SiC MOSFET 界面态密度 亚阈值摆幅 陷阱电荷 阈值电压 漂移
0 引言
近二十年来,随着硅基功率器件的性能逐渐逼近其材料极限,已难以满足日益增长的应用需求,以碳化硅(SiC)为代表的宽禁带半导体材料因此受到工业界的广泛关注[1-2]。得益于更高的阻断电压和工作温度、更快的开关速度以及更低的能量损耗等方面的优势,SiC金属氧化物半导体场效应晶体管(MOSFET)正逐渐在光伏、新能源汽车等领域取代硅(Si)基绝缘栅双极型晶体管(IGBT)[3-6]。尽管前景良好,但SiC MOSFET仍然存在许多尚未解决的坚固性和可靠性问题,尤其是栅氧可靠性问题。SiC-SiO2界面的界面态密度DIT可达1012 cm-2·eV-1甚至更高,较Si基器件高出2~3个数量级[7]。高密度的陷阱会降低器件的沟道迁移率,对其电学特性产生不利影响[8-9];也会导致并联器件阈值电压不一致,引发均流和均温问题,制约了SiC MOSFET在大容量电力电子系统中的应用与发展[10]。近来,为了研究由SiC MOSFET栅极氧化物陷阱造成的阈值电压不稳定问题,许多学者对陷阱的表征以及阈值电压随电热应力变化的规律展开了深入的研究。
常见的DIT表征方法包括高频法和电导法等。高频法最早由L. M. Terman[11]于1962年提出,因计算过程简单而应用较广,但该方法易受到杂质不完全离化的影响,导致提取的界面态密度偏离实际值。1967年E. H. Nicollian和A. Goetzberger提出了电导法[12],虽然能够提供更精确和可靠的结果,但测试周期较长,不满足实际生产需求。此外,还有C-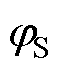 法[13]、深能级瞬态光谱(Deep Level Transient Spectroscopy, DLTS)法[14]、电荷泵法[15]等DIT的表征方法。这些方法尽管在特定条件下具有独特优势,但通常依赖C-V特性测量,而从实测电容中分离出界面陷阱电容存在较大的不精确性[16];或者需要专用设备,流程较为复杂,不具有便捷性。文献[17-18]提出了一种利用器件I-V特性亚阈值区域斜率的变化来表征SiC MOSFET界面态密度的方法。该方法测量简便、易于实施,适用于退化器件的界面态分析,然而该公式中的DIT是一个与亚阈值摆幅(Subthreshold Swing, SS)无关的量,研究人员难以利用SS便捷地评估DIT及器件的栅氧可靠性。文献[19]则将DIT表示为关于SS的函数,但该公式中仍涉及电容分量,同样面临难以精确分离界面陷阱电容的困难。此外,基于电容测量的DIT测定方法主要适用于简单的MOS电容结构,难以直接应用于复杂的MOSFET成品器件中。
法[13]、深能级瞬态光谱(Deep Level Transient Spectroscopy, DLTS)法[14]、电荷泵法[15]等DIT的表征方法。这些方法尽管在特定条件下具有独特优势,但通常依赖C-V特性测量,而从实测电容中分离出界面陷阱电容存在较大的不精确性[16];或者需要专用设备,流程较为复杂,不具有便捷性。文献[17-18]提出了一种利用器件I-V特性亚阈值区域斜率的变化来表征SiC MOSFET界面态密度的方法。该方法测量简便、易于实施,适用于退化器件的界面态分析,然而该公式中的DIT是一个与亚阈值摆幅(Subthreshold Swing, SS)无关的量,研究人员难以利用SS便捷地评估DIT及器件的栅氧可靠性。文献[19]则将DIT表示为关于SS的函数,但该公式中仍涉及电容分量,同样面临难以精确分离界面陷阱电容的困难。此外,基于电容测量的DIT测定方法主要适用于简单的MOS电容结构,难以直接应用于复杂的MOSFET成品器件中。
另一方面,不同的电热应力测试条件会导致获得不同的I-V曲线,从而造成DIT和阈值电压等测试结果的差异。关于电热应力的影响,现有的研究主要集中在阈值电压的温度偏置不稳定性(Bias Temperature Instability, BTI)上。当SiC MOSFET的栅极被施加正偏压时,禁带中部附近的受主型界面陷阱因捕获电子而带负电,导致阈值电压正向漂移,这种现象被称为“正偏压温度不稳定性(Positive Bias Temperature Instability, PBTI)”;反之,若栅极承受负压,靠近禁带中部的施主型界面陷阱失去电子而带正电,进而引起阈值电压负向漂移,被称为“负偏压温度不稳定性(Negative Bias Temperature Instability, NBTI)”[20]。阈值电压正漂移会导致器件导通电阻增加,降低变换器的效率;负漂移则可能引发器件误开通问题,威胁系统的稳定性和安全性。自2006年首次报道SiC MOSFET的阈值电压不稳定性以来[21],BTI问题已经成为制约SiC MOSFET商业化产品可靠性的关键挑战。文献[22]从阈值电压漂移和导通电阻退化的角度解释了PBTI下氧化物陷阱的捕获机理,但是缺乏对陷阱电荷的直观表征。文献[23]则分析了电应力幅值和时间等因素对陷阱电荷的影响,但并未通过量化陷阱电荷来解释阈值电压漂移的内在机理。文献[24-25]基于MOS器件内电荷转移的直接隧穿模型,提出陷阱电荷量与时间对数之间的数学关系,但受限于模型中待定系数的独特性和复杂性,该数学描述难以直接应用到实际器件的评价和工艺流程中。
综上所述,一方面,常见的界面态密度表征方法多依赖电容测量,不可避免地会带来难以从实测电容中分离出界面陷阱电容的难题,还常常需要专用测试设备,流程复杂、测量周期较长,且难以直接应用到成品MOSFET器件中,或者DIT表达式仅是一个与SS无关的函数,无法通过测量SS的变化来量化DIT的变化,不利于大批量评估MOSFET产品的栅氧可靠性。另一方面,关于BTI对SiC MOSFET的影响机理研究,现有文献大多集中在电热应力本身对阈值电压的影响规律上,鲜有文献量化不同电热应力下陷阱电荷的变化规律并将其应用到对阈值电压漂移的内在机理的解释中。鉴于上述问题,本文在传统I-V法基础上基于SS推导出了测定DIT的解析公式,并利用所提公式从I-V特性曲线中提取不同电热应力条件下的陷阱电荷,进而深入分析和解释初始电压应力幅值、应力时间和温度等影响因素对阈值电压漂移的作用规律和机理。本研究不仅能揭示电热应力作用下陷阱电荷的动态变化规律,还可为优化SiC MOSFET的设计与可靠性评估提供支持。
1 陷阱电荷的解析表征
1.1 陷阱电荷对阈值电压的影响
图1展示了SiC MOSFET在正栅压时MOS结构的能带分布情况,位于表面费米能级EFS,S下的部分受主型陷阱被电子占据而带负电——当栅压变化较快时,位于表面本征能级EiF,S与EFS,S之间的陷阱电荷由于恢复时间常数较长,来不及复合或隧穿到导带,导致残留的负电荷偏高,从而引起阈值电压正向漂移。图1中,VGS为栅-衬底电压降;VOX为氧化物两侧电压降;ECB,S为表面导带底能级;EVB,S为表面价带顶能级;Eg为禁带宽度;q为电荷常数;jB为体费米电势;jS为表面电势;ECB为导带底能级;EiF为本征费米能级;EFS为半导体费米能级;EVB为价带顶能级。
陷阱电荷捕获机理对阈值电压漂移的影响可由式(1)给出[26-27]。
式中,WMS为栅极与半导体的功函数差;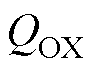 为氧化物中总的有效电荷;
为氧化物中总的有效电荷;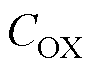 为单位面积的栅氧化层电容;
为单位面积的栅氧化层电容;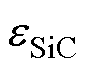 为SiC材料的介电常数;
为SiC材料的介电常数;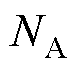 为掺杂浓度。
为掺杂浓度。
BTI效应主要是由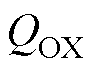 中的界面陷阱电荷
中的界面陷阱电荷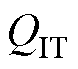 和靠近界面的氧化层电荷
和靠近界面的氧化层电荷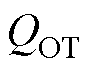 引起的,在可观测的时间尺度内不同电热应力导致了不一样的电荷交换,造成阈值电压漂移的差异[28-29]。后文将两者统称为陷阱电荷QTrap。本文不关注各个能级下陷阱的动力学特点,只分析总体电荷对阈值电压影响的行为。
引起的,在可观测的时间尺度内不同电热应力导致了不一样的电荷交换,造成阈值电压漂移的差异[28-29]。后文将两者统称为陷阱电荷QTrap。本文不关注各个能级下陷阱的动力学特点,只分析总体电荷对阈值电压影响的行为。
1.2 考虑亚阈值摆幅的界面态密度表征
SiC MOSFET的DIT在禁带中部的值较低,而在接近导带和价带的位置呈现指数型增大的趋势,整体分布形似“浴盆曲线”。高量级和大梯度的分布特点为从I-V曲线中提取DIT值提供了理论基础[17]。SiC MOSFET器件在弱反型区域中,漏源电流的近似解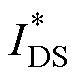 可表示为[16]
可表示为[16]
式中,VT为热电压;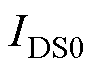 为与工艺相关的常数,可通过
为与工艺相关的常数,可通过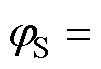
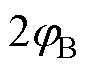 求得。
求得。
如图1所示,与陷阱能级有关的表面能级与导带底之间的能量距离由式(3)决定。
栅源电压VGS和表面电势jS的关系式可表示为
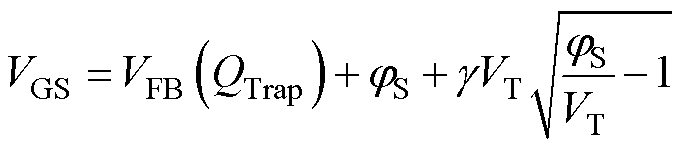 (4)
(4)
式中,VFB(QTrap)为考虑陷阱电荷的平带电压;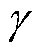 为与器件参数相关的量,
为与器件参数相关的量,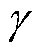 =(2qeSiCNA/VT)1/2/COX。
=(2qeSiCNA/VT)1/2/COX。
在器件I-V曲线上的亚阈值区域内任意找相邻的两点(VGS(jS), 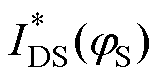 )和(VGS(jS+DjS),
)和(VGS(jS+DjS), 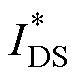 (jS+DjS)),代入式(2)得到这两点表面电势的值,再代入式(4)可获得各自的VFB(QTrap),分别记为VFB(QTrap, jS)和VFB(QTrap, jS+DjS),那么此时便可根据经典公式测定界面态密度[17-18, 30]为
(jS+DjS)),代入式(2)得到这两点表面电势的值,再代入式(4)可获得各自的VFB(QTrap),分别记为VFB(QTrap, jS)和VFB(QTrap, jS+DjS),那么此时便可根据经典公式测定界面态密度[17-18, 30]为
若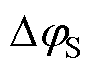 足够小,式(5)可表示为
足够小,式(5)可表示为
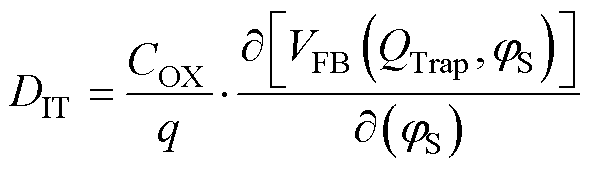 (6)
(6)
将式(4)看成VFB(QTrap)关于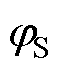 的函数,并求偏导,即
的函数,并求偏导,即
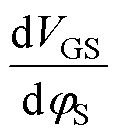 可由SS的定义[16]得到
可由SS的定义[16]得到
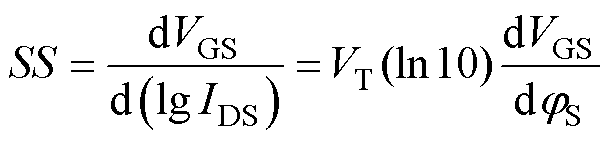 (8)
(8)
结合式(6)~式(8),得到本文所提的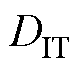 关于SS和
关于SS和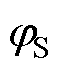 的解析公式为
的解析公式为
不同文献的DIT公式差异见表1。本文所提公式结合了文献[17-18]和文献[19]的优点,一方面将DIT表示为SS的函数,两者建立了直接联系,研究人员可以通过SS随陷阱能级分布的变化情况直接获取DIT在能带中的分布信息;另一方面新的表达式不包含电容分量,避免了难以精确分离特定电容的困难,且无需特殊的测试结构、特定的测试设备就可在常规MOSFET器件上完成产品栅氧特性的评估,非常适合大批量的分析和应用。本文所提公式可为快捷检测器件的界面态密度提供指导,为加速工艺生产测试流程、提升器件的栅氧可靠性提供高效工具。
表1 不同文献的DIT公式差异
Tab.1 Differences in DIT formulas from various literature

公式文献特点 [17-18]与SS无关 [19]DIT表示为SS的函数,但包含未知的电容分量 本文SS与DIT成正比,可用SS特性直接表征DIT特性;不包含电容分量
注:CDEP为耗尽层电容,k0为玻耳兹曼常数。
界面态密度和陷阱能级之间的关系[31]可总结为
式中,DIT,MID为中带界面陷阱密度;DIT,C为导带底界面陷阱密度;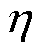 为衰减系数。
为衰减系数。
将式(10)中界面态密度对陷阱能级进行积分可以得到单位面积上陷阱电荷量[32]为
式中,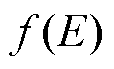 描述了电子占据位于能级E上陷阱的概率;DIT(E)为与能级有关的界面陷阱密度分布。
描述了电子占据位于能级E上陷阱的概率;DIT(E)为与能级有关的界面陷阱密度分布。
2 实验条件
本文的实验平台主要组成部分是Keysight B1505A、恒温箱(-60~150℃)、接地模组等,实验装置如图2a所示,图2b是简化原理。待测器件被自制夹具固定在靠近恒温箱内部热电偶的位置,使其所承受的温度最接近预设值。双绞导线用于夹具和接地模组、B1505A之间的电连接。在用接地模组完成器件的放电,并且恒温箱的温度稳定在预设值至少20 min之后再进行测试。另外,所有的电热应力测试条件均在器件手册推荐范围内,是良性的,防止对器件产生破坏性作用。
2.1 待测SiC MOSFET器件
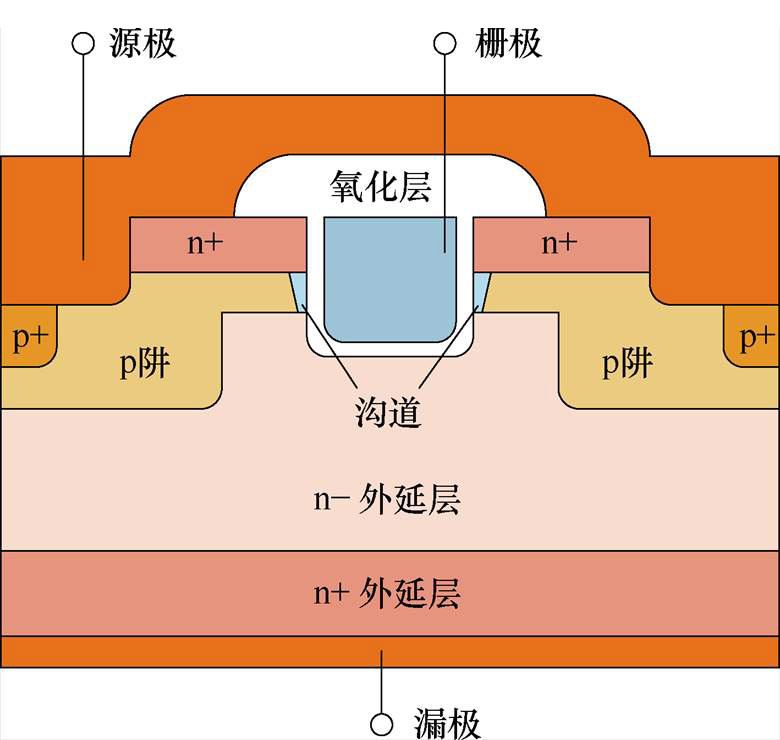
商用对称双沟槽SiC MOSFET器件简化结构如图3所示。沟槽栅SiC MOSFET结构独特,比平面栅型器件导通电阻更小,开关损耗更低,市场潜力巨大,然而其DIT更高,BTI下可能面临更为严重的阈值电压漂移问题[33]。因此本文以TO247-3封装的商用双沟槽器件SCT3080KL为实验对象,其典型参数见表2。表2中,栅氧厚度来源于器件的扫描电子显微镜(Scanning Electron Microscope, SEM)分析,如图4所示;p阱浓度为典型值[34-35]。
表2 待测器件典型参数
Tab.2 Typical parameters of devices under test
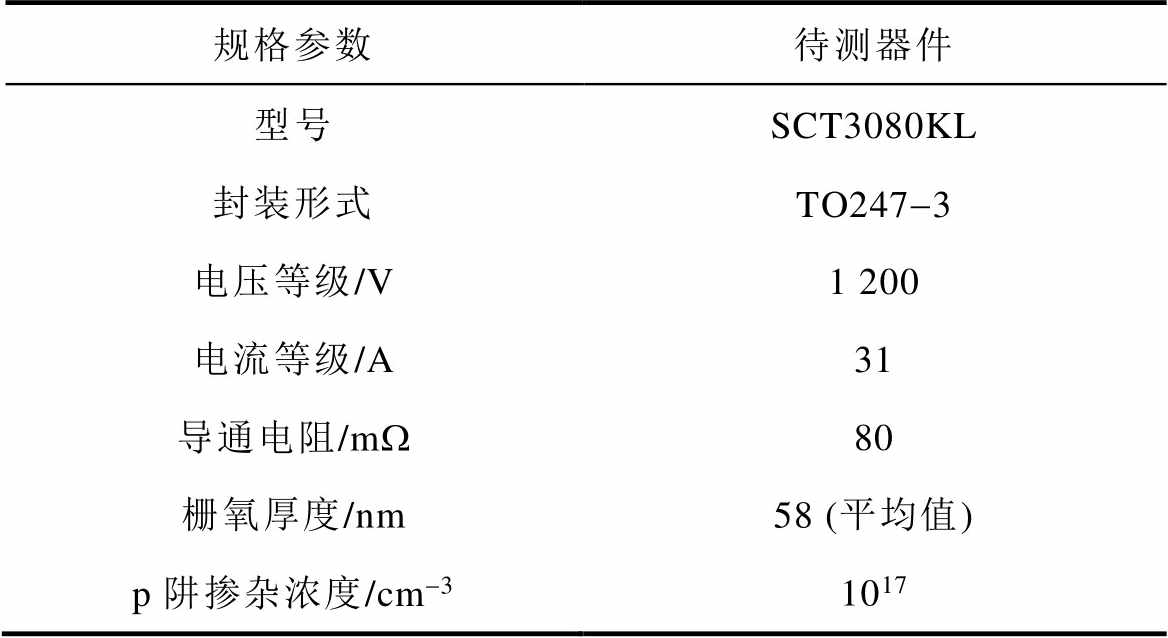
规格参数待测器件 型号SCT3080KL 封装形式TO247-3 电压等级/V1 200 电流等级/A31 导通电阻/mW80 栅氧厚度/nm58 (平均值) p阱掺杂浓度/cm-31017
2.2 器件电荷“清零”预处理
表3展示了相同电应力条件、不同温度等级下三端短接接地放电不同时间后的阈值电压测量结果。结果表明,随着三端短接接地放电时间的增加,陷阱捕获的电荷迅速被释放,电热应力引起的阈值电压漂移也迅速减小。尽管器件在低温环境下承受电应力后的阈值电压漂移量相较于高温环境下更大,但大部分电荷仍能在接地20 s左右被释放,320 s后电荷状态基本“清零”,阈值电压降至最低值。因此,为了保证后续实验的准确性,所有测试开始前均应将器件至少短接接地10 min,以尽可能地清除陷阱中的残留电荷。
表3 接地加速恢复时期阈值电压变化
Tab.3 Threshold voltage shift during ground accelerated recovery time
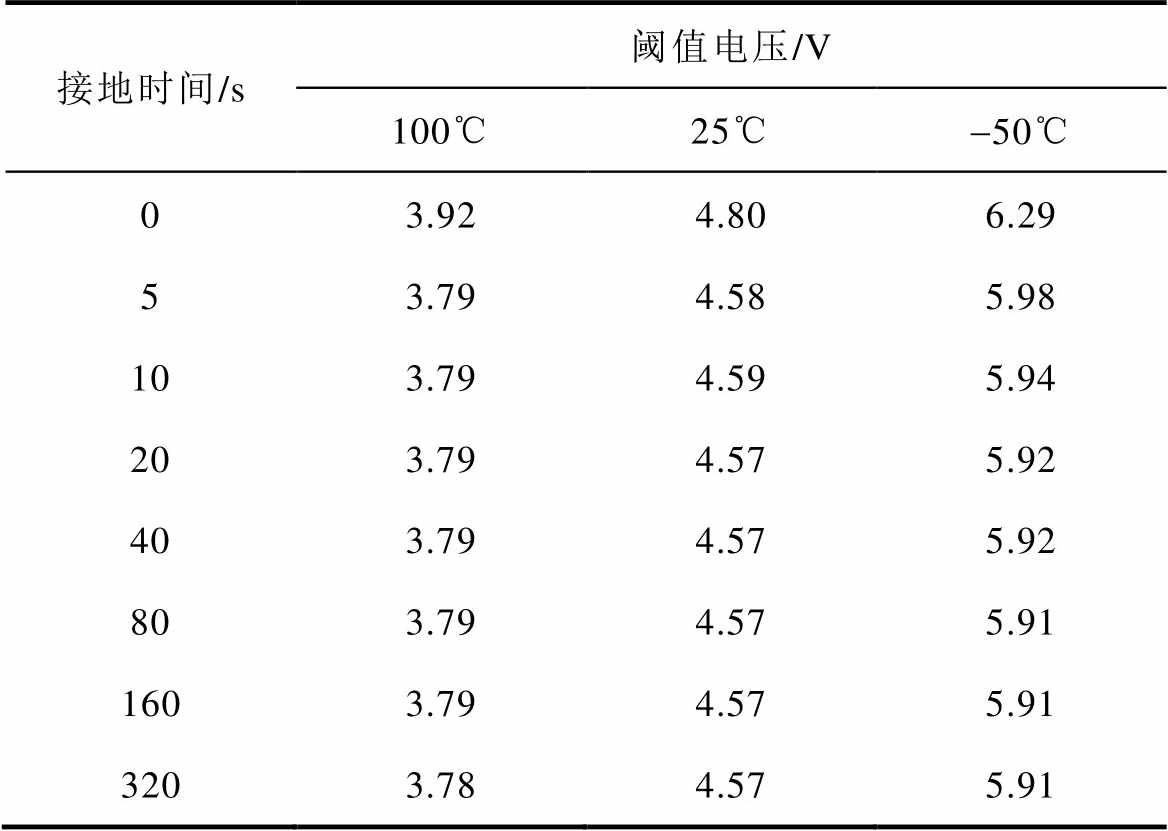
接地时间/s阈值电压/V 100℃25℃-50℃ 03.924.806.29 53.794.585.98 103.794.595.94 203.794.575.92 403.794.575.92 803.794.575.91 1603.794.575.91 3203.784.575.91
2.3 阶梯式电压波形的确定
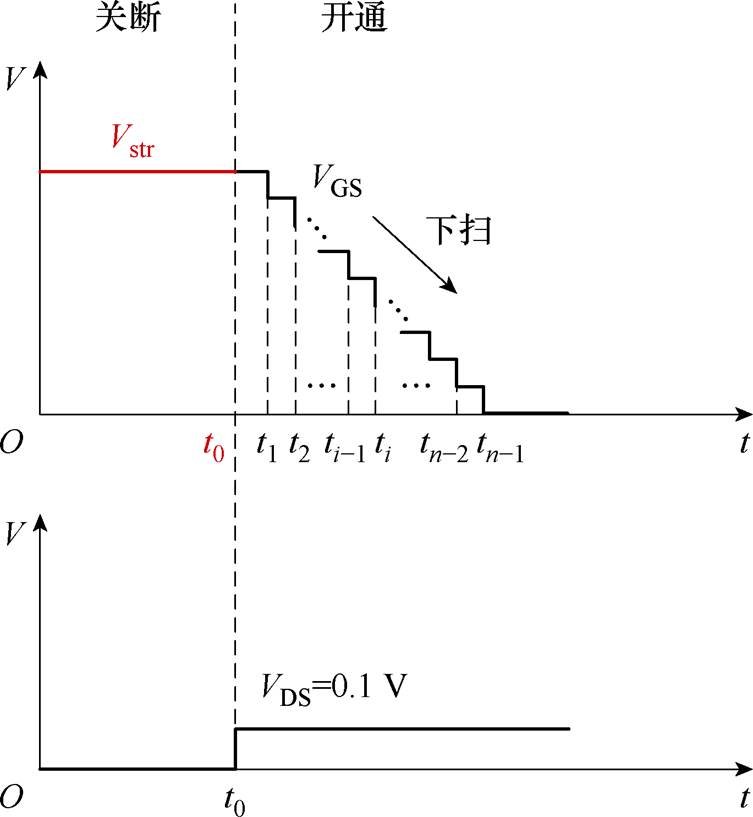
除了电压应力幅值和时间之外,扫描方向、扫描速度、扫描延迟时间以及测量温度等实验条件同样会影响界面态,从而造成阈值电压测量结果的差异[30]。本文主要研究前两个因素的影响。为降低其他变量的干扰,一方面,将扫描延迟时间设为0,并尽可能地提高扫描速度,以最大限度地保留应力期间捕获的陷阱电荷信息,从而提高测量的准确性;另一方面,由于NBTI测试中表面电势极性会发生变化,加上受到直流扫频速度的限制,在初始应力期间陷阱捕获的部分电荷会在测量期间逃逸,导致实际BTI效应被低估[36]。此外,文献[19]指出,扫描速度越快,测量的阈值电压漂移量越大。因此,本文采用0 s的延迟测量时间td、PBTI的扫描方向进行实验,以更准确地表征BTI中陷阱电荷的作用。PBTI测试时序图如图5所示。图5中,t0是初始电压应力时间。
2.4 系统最小测量时间的测定
由于设备在测试I-V静态特性时,需在每一个电压等级下经历“准静态”过程以获得电压-电流信息,即存在一个最小测量时间tmeas,min,它限制了电压扫频的速度,并将较大程度地影响短时应力对阈值电压的实际作用效果,因此有必要测定tmeas,min以更好地分析应力的作用。假设在扫频过程中各电压等级的准静态时间为tqs,延迟测量时间为td,则每一级阶梯式电压脉宽tw=td+tqs(见图5中的ti-ti-1),若下扫初始电压幅值为Vstr,终值为Vstop,步长为Vstep,则总测试时间tmeas为
在实际测试中,为了在兼顾实验速度的同时尽可能减小阈值电压提取误差,td为0 s,Vstep设为0.01 V。基于线性回归分析理论,得出本系统中tqs的估计值约为0.005 4 s。若Vstr为14 V,那么tmeas,min约为7.565 4 s。
3 陷阱电荷表征方法的有效性分析及应用
本节首先分析实验数据的有效性,在取得有效实验数据后提取阈值电压VTH并计算SS,然后应用本文所提式(9)测定DIT,最后利用式(11)获得|QTrap|。以此流程研究不同电热应力条件下DIT和SS的变化规律,并分析|QTrap|对VTH的影响机理。
3.1 陷阱电荷表征方法的有效性分析
图6是应用式(9)计算的常温下Vstr=14 V、t0= 300 s、td=0 s时DIT随陷阱能级变化的离散数据和拟合曲线分布示意图。从图中可知,能级越深时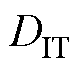 的计算值振荡越明显,且有发散的趋势(方框圈出),造成该现象的原因是B1505A测量微弱电流的精度不够,当测试的器件电流降低至nA以及更小的级别时,获取的电流结果出现了较大抖动。因此,考虑测量精度和实验误差,仅提取
的计算值振荡越明显,且有发散的趋势(方框圈出),造成该现象的原因是B1505A测量微弱电流的精度不够,当测试的器件电流降低至nA以及更小的级别时,获取的电流结果出现了较大抖动。因此,考虑测量精度和实验误差,仅提取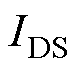 ≥100 nA的有效数据来计算DIT,更深能级(电流更小)的部分则利用式(10)进行曲线拟合来评估。
≥100 nA的有效数据来计算DIT,更深能级(电流更小)的部分则利用式(10)进行曲线拟合来评估。
接着应用本文所提公式计算当Vstr和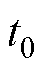 分别变化时陷阱电荷量大小的变化情况,并与相应的阈值电压变化量的值进行比较。常温下,若t0=300 s不变,当Vstr从14 V增大到22 V时,阈值电压及其陷阱电荷分量的变化量,DVTH和D|QTrap|/COX分别为0.07 V和0.045 8 V;当Vstr=14 V不变,t0从10 s变到300 s时,DVTH和D|QTrap|/COX分别为0.12 V和0.078 1 V。应用本文所提公式的分析计算结果表明,电热应力导致的阈值电压变化量与陷阱电荷对其的作用变化量数量级具有较好的一致性,初步证明了本文所提陷阱电荷表征解析式的有效性,其余电热应力条件下的变化情况将在下一小节详细展开讨论。
分别变化时陷阱电荷量大小的变化情况,并与相应的阈值电压变化量的值进行比较。常温下,若t0=300 s不变,当Vstr从14 V增大到22 V时,阈值电压及其陷阱电荷分量的变化量,DVTH和D|QTrap|/COX分别为0.07 V和0.045 8 V;当Vstr=14 V不变,t0从10 s变到300 s时,DVTH和D|QTrap|/COX分别为0.12 V和0.078 1 V。应用本文所提公式的分析计算结果表明,电热应力导致的阈值电压变化量与陷阱电荷对其的作用变化量数量级具有较好的一致性,初步证明了本文所提陷阱电荷表征解析式的有效性,其余电热应力条件下的变化情况将在下一小节详细展开讨论。
3.2 陷阱电荷表征方法的BTI机理分析应用
3.2.1 DIT和SS的关系
常温下,改变图6当前的电应力条件,利用前文所述的有效I-V曲线数据求得SS,再应用本文所提公式计算相应的DIT,获得如图7所示DIT与SS的关系曲线。不同电应力条件下DIT与SS的LRA拟合函数的决定系数R2均大于0.99,正线性相关程度很高。此外,三组数据拟合函数的斜率约为6.29×109,与式(9)中SS的系数在常温下的值6.28×109大小几乎一样,说明在当前实验数据范围内,由于式(9)中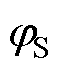 的作用很小,即使
的作用很小,即使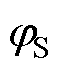 发生变化,也不会影响二者的线性关系,同时也证明了只需简单计算SS就能利用所提公式直接评估器件DIT的可行性。
发生变化,也不会影响二者的线性关系,同时也证明了只需简单计算SS就能利用所提公式直接评估器件DIT的可行性。
3.2.2 Vstr对陷阱电荷和阈值电压的影响
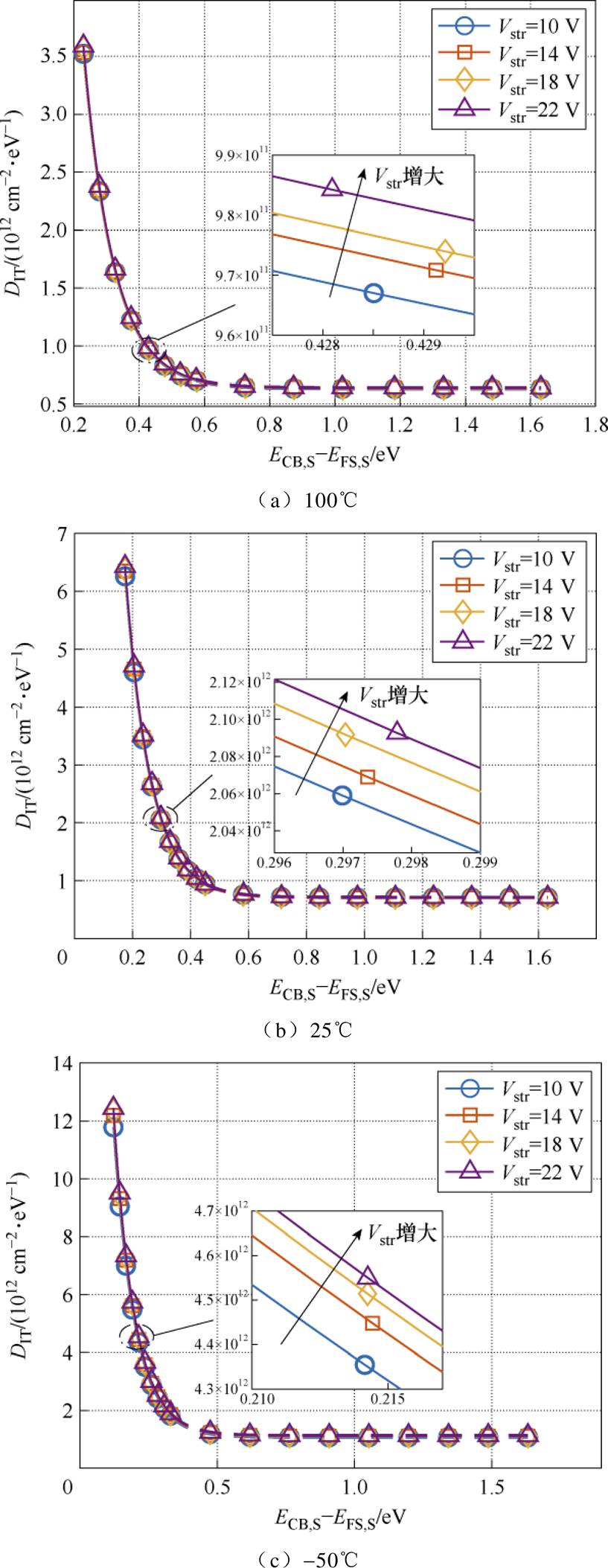
在三个温度等级下测试了t0=300 s、不同Vstr时器件的I-V特性曲线,获得如图8所示的界面态密度DIT分布曲线(除非另外说明,后文中的DIT曲线中实线部分均由实验数据拟合,虚线部分由拟合公式(10)推导)。当Vstr改变时,DIT分布曲线的整体趋势并不会发生变化,R2均大于0.99,拟合效果很好。随着Vstr的增长,DIT曲线逐渐向右上方漂移,从而使得DIT曲线下与陷阱电荷量有关的积分面积变大,|QTrap|总体呈现增加的趋势。对比图8a、图8b、图8c不同温度等级下的曲线可以发现,上述规律不会随着温度变化而改变。此外,随着温度从低温升到高温,DIT整体往左下方漂移,|QTrap|不断减小。图9表明SS(Ion/Ioff=5 mA/5 mA区间值)和DSS在当前测试条件下近似与Vstr呈线性关系。一方面,在同一温度等级下,Vstr越大,应力作用效果越深刻,DIT越大,SS也逐渐增大,规律与本文所提式(9)一致;另一方面,不同于DIT很小的理想器件温度越低SS越小的结论[16],高DIT的SiC MOSFET反而是低温加剧了SS的退化情况。这是因为随着温度的降低,给定自由电子密度的表面费米能级更加接近导带底,高DIT的SiC MOSFET的陷阱捕获载流子能力增强,有更多的界面态参与了电荷的捕获和发射过程,再加上低温下陷阱电荷的发射时间常数比较长[37],超过了tmeas,min,从而导致SS退化增大,I-V曲线更平缓,阈值电压正向漂移更加明显。
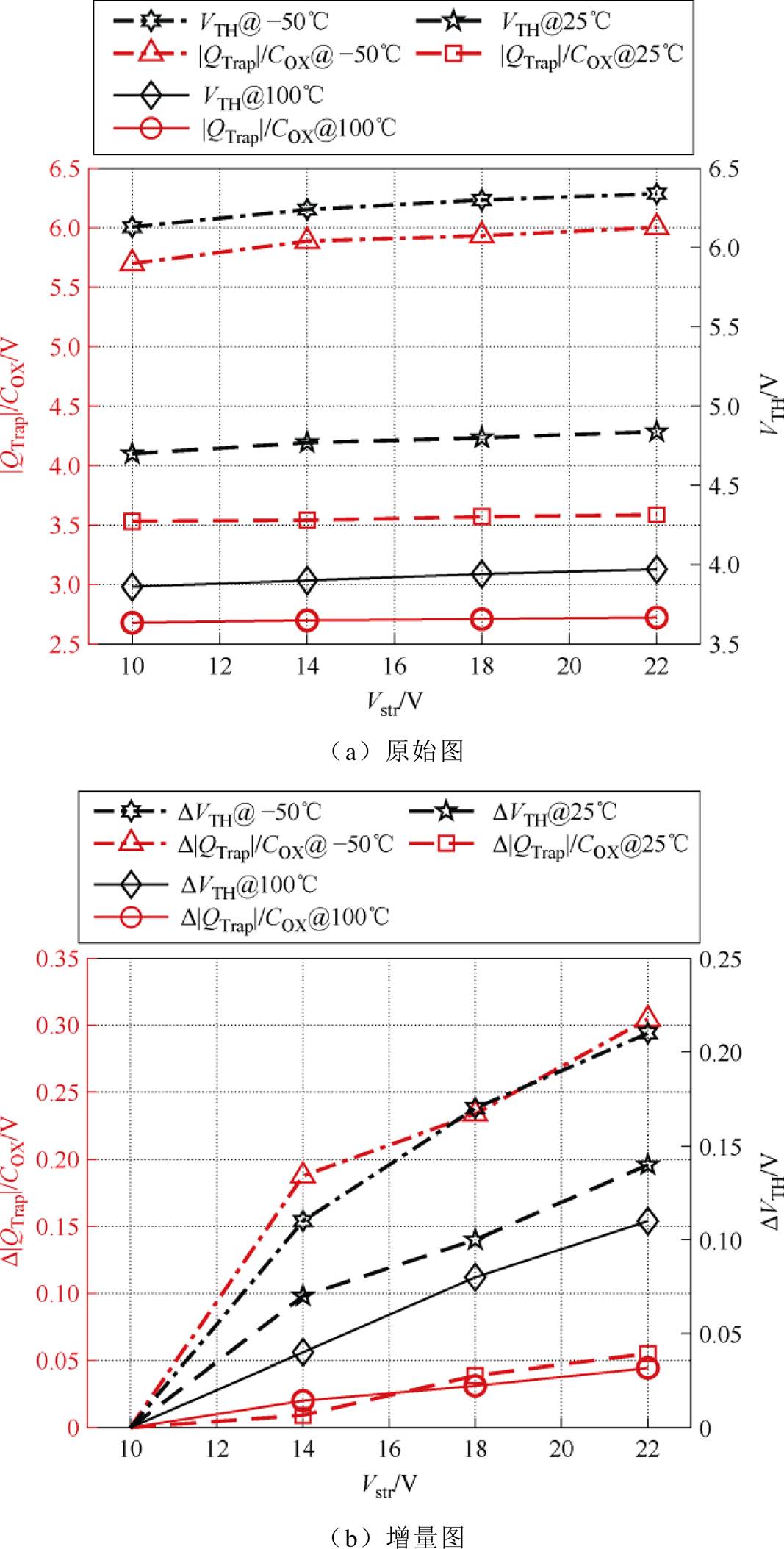
不同温度等级下|QTrap|/COX和VTH的原始值及其增量随Vstr变化如图10所示。从图10可知,在不同温度等级下,陷阱电荷量和阈值电压的变化趋势具有较好的一致性,两者都随着Vstr变化单调递增,可近似认为与Vstr成正比。温度越低、Vstr越大使陷阱捕获电荷的势垒更低[23, 37],陷阱状态更为饱满,阈值电压更大。此外,在各个温度等级下,发现D|QTrap|/COX的曲线略低于DVTH的曲线,这是由于受扫描速度的限制,初始电压应力阶段陷阱捕获的电荷在测量过程中有部分被中和,使得提取的陷阱电荷量被低估,但两者数量级具有较好的一致性,这证明了本文陷阱电荷表征方法的有效性。
3.2.3 t0对陷阱电荷和阈值电压的影响
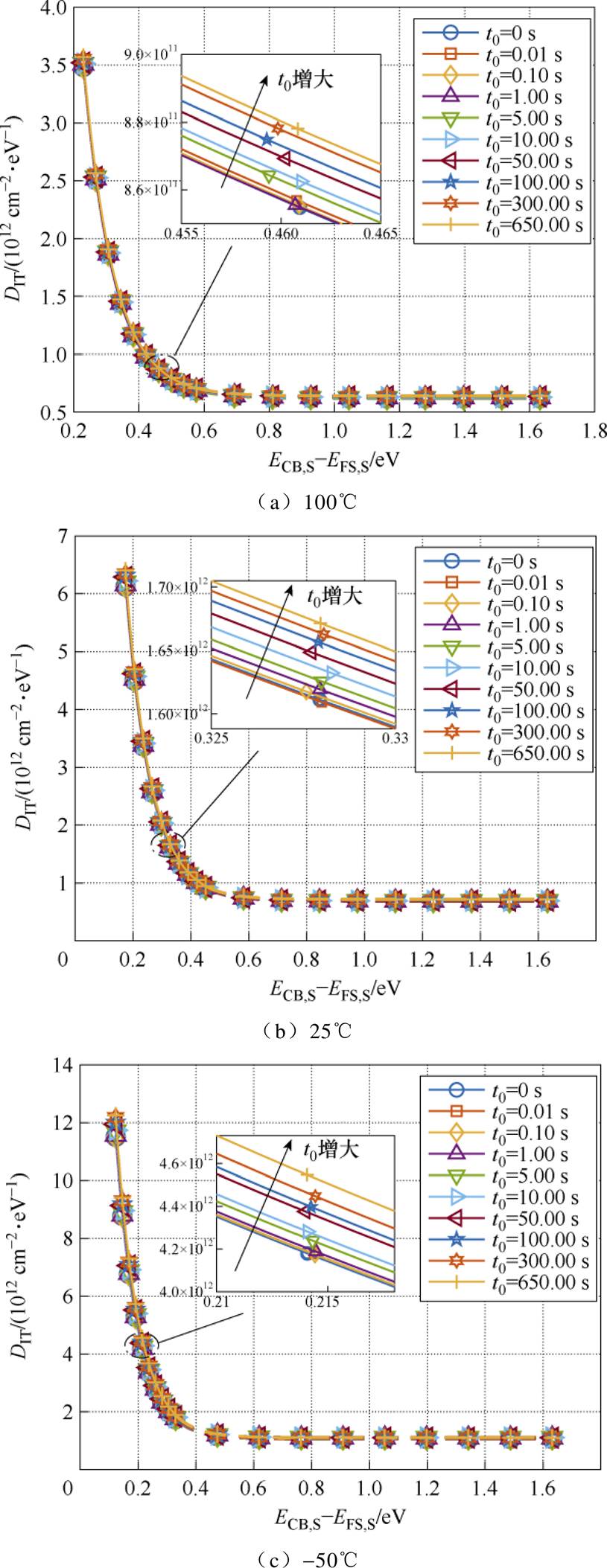
在不同温度等级下测试得到Vstr=14 V、不同t0时器件的I-V特性曲线,获得如图11所示的DIT分布曲线。可以看到,当应力时间t0<1.00 s时,由于远小于当前系统的tmeas,min,该电热应力对界面电荷的影响效果远小于测量应力本身,DIT曲线的漂移量较小且方向不稳定,可能造成陷阱电荷的异常波动。随着t0的增加,当其数量级与tmeas,min相当或更大时,器件捕获的电荷大幅增多,DIT曲线的漂移量明显增加,整体往右上方移动。
不同温度等级下SS随t0变化如图12所示。图12表明当t0≥tmeas,min时,由应力时间导致的SS的变化近似呈指数型增长,即在半对数坐标下为线性关系。此外,同图9的分析,应力效果的累积会加强器件SS的退化,且温度越低,退化越明显。
不同温度等级下|QTrap|/COX和VTH的原始值及其增量随t0变化如图13所示。从图13b可以看到,在t0较小时,由于阈值电压测量精度的限制,其值本身没有明显变化;陷阱电荷虽然有所波动但是总体上是逐渐增加的,温度越低,递增幅度越大。在同一应力幅值和时间下,DVTH和D|QTrap|/COX递增幅度随着温度的升高而降低,这可以解释为在当前VTH的测量系统中,温度越高,电子的热能越大,发射时间常数更小,陷阱释放电荷的速度更快,恢复热平衡的时间更短。图13表明在半对数坐标中,不同温度等级下,除了阈值电压随着t0变化单调递增,近似为线性关系外,陷阱电荷量也有同样的趋势,印证了陷阱电荷对阈值电压漂移的重要作用。
相较于传统直接分析不同电热应力对阈值电压漂移的影响,本节应用本文所提公式从亚阈值摆幅和陷阱电荷的角度深层次分析和解释了电热应力对阈值电压漂移的作用机理。由于界面及近界面陷阱的“忆荷性”,陷阱电荷状态很大程度上受到电热应力偏置历史的影响。实验结果表明,陷阱电荷是造成阈值电压漂移的主要原因,电热应力累计作用效果的差异导致阈值电压漂移量的差异。不同的电热应力条件会使得陷阱捕获不同量的电荷,造成亚阈值摆幅的退化情况和界面态密度分布曲线的不同。
4 结论
本文从SiC MOSFET阈值电压漂移的栅氧可靠性出发,针对界面态密度的表征方法和不同电热应力条件下界面态密度、亚阈值摆幅、陷阱电荷量和阈值电压的变化规律展开研究,主要结论如下:
1)基于微元思想将测定界面态密度的公式表示为关于亚阈值摆幅的函数解析式。所提公式表明可仅通过器件的I-V特性计算亚阈值摆幅进而直接表征界面态密度随能级分布的情况,再进行积分,求得陷阱电荷可评估器件关于阈值电压漂移的栅氧可靠性。相比于传统基于C-V特性的界面态密度表征方法,避免了从实测电容精确分离界面陷阱电容这一难题,使栅氧可靠性评估流程更加便捷。
2)考虑到陷阱的“忆荷性”特点,开展了器件承受一定电热应力条件后再三端短接接地不同时间的阈值电压测量实验。结果表明,尽管不同温度下阈值电压漂移量不同,温度越低漂移量越大,但均能在接地20 s左右释放大部分电荷,320 s后阈值电压降至最低值不再变化,电荷状态基本“清零”。因此,为了解耦不同电热应力条件下的作用以获得更准确的陷阱电荷表征结果,在所有的测试开始之前,需要进行电荷“清零”预处理工作,如将器件三端短接接地10 min以上以尽可能地清除陷阱中的残留电荷。
3)应用本文所提公式量化了不同电热应力条件下TO247-3封装、双沟槽结构SiC MOSFET陷阱电荷量的变化规律,分析了其对阈值电压漂移的作用机理。结果表明,SiC MOSFET较高的界面态密度使其在低温下的亚阈值摆幅更大,且随着电热应力作用效果的增强,亚阈值摆幅的退化情况更严重。在良性电热应力条件下,陷阱电荷量与初始电压应力幅值近似成正比,当应力时间不小于系统最小测量时间的量级时,与之满足指数关系。陷阱电荷的变化量与阈值电压漂移量的数量级和变化趋势一致性较高,证明了本文通过亚阈值摆幅的计算表征界面态密度及陷阱电荷的有效性。
参考文献
[1] 柯俊吉, 赵志斌, 谢宗奎, 等. 考虑寄生参数影响的碳化硅MOSFET开关暂态分析模型[J]. 电工技术学报, 2018, 33(8): 1762-1774.
Ke Junji, Zhao Zhibin, Xie Zongkui, et al. Analytical switching transient model for silicon carbide MOSFET under the influence of parasitic parameters[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(8): 1762-1774.
[2] 王来利, 赵成, 张彤宇, 等. 碳化硅功率模块封装技术综述[J]. 电工技术学报, 2023, 38(18): 4947- 4962.
Wang Laili, Zhao Cheng, Zhang Tongyu, et al. Review of packaging technology for silicon carbide power modules[J]. Transactions of China Electro- technical Society, 2023, 38(18): 4947-4962.
[3] 江芙蓉, 杨树, 盛况. 碳化硅MOSFET特征参数随温度变化的比较研究[J]. 电源学报, 2018, 16(6): 143-151.
Jiang Furong, Yang Shu, Sheng Kuang. Comparative study on temperature-dependent characteristic parameters of SiC MOSFET[J]. Journal of Power Supply, 2018, 16(6): 143-151.
[4] 张少昆, 孙微, 范涛, 等. 基于分立器件并联的高功率密度碳化硅电机控制器研究[J]. 电工技术学报, 2023, 38(22): 5999-6014.
Zhang Shaokun, Sun Wei, Fan Tao, et al. Research on high power density silicon carbide motor controller based on parallel connection of discrete devices[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 5999-6014.
[5] 李锦, 党恩帅, 范雨顺, 等. 一种碳化硅与硅器件混合型三电平有源中点钳位零电压转换软开关变流器[J]. 电工技术学报, 2024, 39(8): 2496-2510.
Li Jin, Dang Enshuai, Fan Yushun, et al. A hybrid three-level active-neutral-point-clamped zero-voltage transition soft-switching converter with silicon carbide and silicon devices[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2496-2510.
[6] 肖标, 郭祺, 涂春鸣, 等. 面向开关时序与驱动电压自主协同调控的SiC/Si混合开关驱动电路[J]. 电工技术学报, 2025, 40(4): 1117-1128.
Xiao Biao, Guo Qi, Tu Chunming, et al. SiC/Si hybrid switch drive circuit with autonomous and coordinated control of switching sequences and driving voltages[J]. Transactions of China Electrotechnical Society, 2025, 40(4): 1117-1128.
[7] Xie Minghang, Sun Pengju, Wang Kaihong, et al. Online gate-oxide degradation monitoring of planar SiC MOSFETs based on gate charge time[J]. IEEE Transactions on Power Electronics, 2022, 37(6): 7333-7343.
[8] Qi Jinwei, Yang Xu, Li Xin, et al. Temperature dependence of dynamic performance characterization of 1.2-kV SiC power MOSFETs compared with Si IGBTs for wide temperature applications[J]. IEEE Transactions on Power Electronics, 2018, 34(9): 9105-9117.
[9] Tanimoto Y, Saito A, Matsuura K, et al. Power-loss prediction of high-voltage SiC-mosfet circuits with compact model including carrier-trap influences[J]. IEEE Transactions on Power Electronics, 2016, 31(6): 4509-4516.
[10] Cai Yumeng, Chen Cong, Zhao Zhibin, et al. Characterization of gate-oxide degradation location for SiC MOSFETs based on the split C-V method under bias temperature instability conditions[J]. IEEE Transactions on Power Electronics, 2023, 38(5): 6081-6093.
[11] Terman L M. An investigation of surface states at a silicon/silicon oxide interface employing metal-oxide- silicon diodes[J]. Solid-State Electronics, 1962, 5(5): 285-299.
[12] Nicollian E H, Goetzberger A. The Si-SiO, interface– electrical properties as determined by the metal- insulator-silicon conductance technique[J]. The Bell System Technical Journal, 1967, 46(6): 1055-1033.
[13] Yoshioka H, Nakamura T, Kimoto T. Generation of very fast states by nitridation of the SiO2/SiC interface[J]. Journal of Applied Physics, 2012, 112(2): 024520.
[14] Hauck M, Weisse J, Lehmeyer J, et al. Quantitative investigation of near interface traps in 4H-SiC MOSFETs via drain current deep level transient spectroscopy[C]//2016 European Conference on Silicon Carbide & Related Materials (ECSCRM), Halkidiki, Greece, 2016: 1.
[15] Salinaro A, Pobegen G, Aichinger T, et al. Charge pumping measurements on differently passivated lateral 4H-SiC MOSFETs[J]. IEEE Transactions on Electron Devices, 2015, 62(1): 155-163.
[16] (美)施敏, 伍国珏. 半导体器件物理[M]. 耿莉, 张瑞智, 译. 西安: 西安交通大学出版社, 2023.
[17] DasGupta S, Brock, Kaplar R, et al. Extraction of trapped charge in 4H-SiC metal oxide semiconductor field effect transistors from subthreshold characteri- stics[J]. Applied Physics Letters, 2011, 99 (2): 023503.
[18] Hughart D R, Flicker J D, Atcitty S, et al. Sensitivity analysis of a technique for the extraction of interface trap density in SiC MOSFETs from subthreshold characteristics[C]//2014 IEEE International Reliabi- lity Physics Symposium, Waikoloa, HI, USA, 2014: 2C.2.1-2C.2.6.
[19] Schroder D K. Semiconductor material and device characterization[M]. New Jersey: John Wiley & Sons, 2005.
[20] Ortiz Gonzalez J A, Alatise O. A novel non-intrusive technique for BTI characterization in SiC MOSFETs[J]. IEEE Transactions on Power Electronics, 2018, 34(6): 5737-5747.
[21] Lelis A J, Habersat D, Lopez G, et al. Bias stress- induced threshold-voltage instability of SiC MOSFETs[J]. Materials Science Forum, 2006, 527-529: 1317-1320.
[22] Liang Ye, Zhang Yuanlei, Zhang Jingqun, et al. Characterization of oxide trapping in SiC MOSFETs under positive gate bias[J]. IEEE Journal of the Electron Devices Society, 2022, 10: 920-926.
[23] Guo Chunsheng, Cui Shaoxiong, Li Yumeng, et al. Study of the influence of different gate oxide traps on threshold voltage drift of SiC MOSFET based on transient current[J]. IEEE Transactions on Power Electronics, 2024, 39(8): 9629-9637.
[24] Karki U, González-SantiniN S, Peng F Z, et al. Effect of gate- oxide degradation on electrical parameters of silicon carbide MOSFETs[J]. IEEE Transactions on Electron Devices, 2020, 67(6): 2544-2552.
[25] LelisA J. Cause and effect of threshold-voltage instability on the reliability of silicon-carbide MOSFETs[D]. Maryland: University of Maryland, 2011.
[26] Kimoto T, Cooper J A. Fundamentals of Silicon Carbide Technology: Growth, Characterization, Devices, and Applications[M]. Singapore: John Wiley & Sons Singapore Pte. Ltd., 2014.
[27] Baliga B. Jayant. Fundamentals of Power Semicon- ductor Devices[M]. Cham: Springer International Publishing AG, 2019.
[28] Lelis A J, Habersat D, Green R, et al. Time depen- dence of bias-stress-induced SiC MOSFET threshold- voltage instability measurements[J]. IEEE Transa- ctions on Electron Devices, 2008, 55(8): 1835-1840.
[29] Rescher G, Pobegen G, Aichinger T, et al. Precon- ditioned BTI on 4H-SiC: proposal for a nearly delay time-independent measurement technique[J]. IEEE Transactions on Electron Devices, 2018, 65(4): 1419- 1426.
[30] Yang Chao, Wei Shengsheng, Wang Dejun. Bias temperature instability in SiC metal oxide semicon- ductor devices[J]. Journal of Physics D: Applied Physics, 2021, 54(12): 123002.
[31] Shintani M, Nakamura Y, Oishi K, et al. Surface- potential-based silicon carbide power MOSFET model for circuit simulation[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10774-10783.
[32] Albrecht M, Klupfel F J, Erlbacher T. An iterative surface potential algorithm including interface traps for compact modeling of SiC-MOSFETs[J]. IEEE Transactions on Electron Devices, 2020, 67(3): 855- 862.
[33] Wei Jiaxin, Wei Zhaoxiang, Hao Fu, et al. Review on the reliability mechanisms of SiC Power MOSFETs: a comparison between planar-gate and trench-gate structures[J]. IEEE Transactions on Power Electronics, 2023, 38(7): 8990-9005.
[34] Wang Ying, Lin Mao, Li Xingji, et al. Single-event burnout hardness for the 4H-SiC trench-gate MOSFETsbased on the multi-island buffer layer[J]. IEEE Transa- ctions on Electron Devices, 2019, 66(10): 4264-4272.
[35] Li Ping, Ma Rongyao, Shen Jingyu, et al. A novel SiC MOSFET with a fully depleted P-base MOS-channel diode for enhanced third quadrant performance[J]. IEEE Transactions on Electron Devices, 2022, 69(8): 4438-4443.
[36] Habersat D B, Lelis A J, Green R, et al. Comparison of test methods for proper characterization of VT in SiC MOSFETs[J]. Materials Science Forum, 2016, 858: 833-839.
[37] Vasilev A, Jech M, Grill A, et al. TCAD modeling of temperature activation of the hysteresis characteri- stics of lateral 4H-SiC MOSFETs[J]. IEEE Transa- ctions on Electron Devices, 2022, 69(6): 3290-3295.
Analytical Characterization of Trapped Charge in SiC MOSFETs Using Subthreshold Swing Method and Its Application in Bias Temperature Instability Mechanism Analysis
Shi Chao1,2,3 Li Xuebao2,3,4 Wang Laili1 Wang Yue1 Jiang Xinyu2,3,4 Chen Zhongyuan2,3 Ran Li2,3,5
(1. State Key Laboratory of Electrical Insulation and Power Equipment Xi’an Jiaotong University Xi’an 710049 China 2. Beijing Huairou Laboratory Beijing 101499 China 3. Beijing Institute of Smart Energy Beijing 102209 China 4. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources North China Electric Power University Beijing 102206 China 5. State Key Laboratory of Power Transmission Equipment Technology Chongqing University Chongqing 400044 China)
Abstract Owing to superior performance metrics in blocking voltage, operating temperature, switching speed, and switching loss, SiC MOSFETs are gradually replacing traditional silicon-based devices in fields such as photovoltaics and electric vehicles. Nevertheless, the widespread adoption of SiC MOSFETs is hindered by critical reliability challenges, particularly their exceptionally high interface state density (DIT), which induces threshold voltage drift under bias temperature instability (BTI) and severely compromises gate oxide reliability. Therefore, it is necessary to characterize the interface state density to analyze the degradation mechanism of devices under BTI.
Conventional DIT characterization methods predominantly rely on capacitance-voltage (C-V) measurements, which unavoidably face the challenge of decoupling the interface trap capacitance (CIT) from the total measured capacitance. Alternatively, some methods require specialized equipment, often involving complex protocols and time-consuming measurement cycles. In contrast, the method based on analyzing the slope change of the I-V characteristic in the subthreshold region is simple, rapid, and convenient, making it particularly suitable for characterizing degraded devices. In this work, the classical I-V method is further developed into an analytical expression of the subthreshold swing (SS) to DIT using the concept of infinitesimal analysis. On one hand, it circumvents the difficulty of precisely separating CIT, enabling measurements on conventional MOSFET devices without the need for special test structures. On the other hand, the proposed formula links DIT to SS, revealing an explicit linear proportionality between the two. Consequently, researchers can infer the distribution of DIT across the energy band by observing how the SS varies with energy level, which is crucial for understanding the impact of interface states and improving device performance.
Furthermore, to minimize the influence of factors other than initial voltage stress amplitude, stress time, and temperature, the paper discusses the roles of scan direction, scan speed, scan delay time, measurement time, and charge-clearing pretreatment. The results indicate that: (1) the device must be shorted to ground before every change of measurement condition to erase residual stress history; (2) I-V characteristics should be recorded with a descending step-voltage waveform rather than an ascending scan to prevent underestimation of trapped charge arising from surface-polarity reversal; and (3) reducing both scan delay and measurement time increases the effective scan rate, thus maximizing the retention of the effect of initial electrothermal stress on trapped charge.
Finally, the effects of different electrothermal stress conditions, including initial voltage stress amplitude, stress time, and temperature, are quantified. The results show that the variation of trapped charge correlates strongly with the magnitude of threshold voltage drift, demonstrating that trapped charge variation is the principal driver of this drift. Due to the charge-memory characteristic of traps, distinct electrothermal stress histories result in different amounts of charge captured in device traps, leading to non-uniform threshold voltage drift. The intrinsically high DIT of SiC MOSFETs produces a large SS at low temperature, which deteriorates further with increasing electrothermal stress. Under favorable electrothermal stress conditions, the initial voltage-stress amplitude scales approximately linearly with both trapped charge and threshold-voltage drift. In contrast, the initial voltage-stress time exhibits an exponential dependence on both of these quantities.
These findings provide rapid assessment guidance of DIT and offer efficient tools for accelerating the process production testing flow and enhancing the gate oxide reliability of SiC MOSFETs.
keywords:SiC MOSFET, interface state density, subthreshold swing, trapped charge, threshold voltage, drift
DOI: 10.19595/j.cnki.1000-6753.tces.242198
中图分类号:TN386
北京怀柔实验室资助项目(ZD2022004A)。
收稿日期 2024-12-06
改稿日期 2025-05-20
作者简介
施 超 男,1997年生,博士研究生,研究方向为大功率电力电子器件状态监测与可靠性评估。E-mail: shich.sch@stu.xjtu.edu.cn
李学宝 男,1988年生,副教授,博士生导师,研究方向为高压大功率电力电子器件封装。E-mail: lxb08357x@ncepu.edu.cn(通信作者)
(编辑 郭丽军)
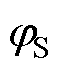 法[13]、深能级瞬态光谱(Deep Level Transient Spectroscopy, DLTS)法[14]、电荷泵法[15]等DIT的表征方法。这些方法尽管在特定条件下具有独特优势,但通常依赖C-V特性测量,而从实测电容中分离出界面陷阱电容存在较大的不精确性[16];或者需要专用设备,流程较为复杂,不具有便捷性。文献[17-18]提出了一种利用器件I-V特性亚阈值区域斜率的变化来表征SiC MOSFET界面态密度的方法。该方法测量简便、易于实施,适用于退化器件的界面态分析,然而该公式中的DIT是一个与亚阈值摆幅(Subthreshold Swing, SS)无关的量,研究人员难以利用SS便捷地评估DIT及器件的栅氧可靠性。文献[19]则将DIT表示为关于SS的函数,但该公式中仍涉及电容分量,同样面临难以精确分离界面陷阱电容的困难。此外,基于电容测量的DIT测定方法主要适用于简单的MOS电容结构,难以直接应用于复杂的MOSFET成品器件中。
法[13]、深能级瞬态光谱(Deep Level Transient Spectroscopy, DLTS)法[14]、电荷泵法[15]等DIT的表征方法。这些方法尽管在特定条件下具有独特优势,但通常依赖C-V特性测量,而从实测电容中分离出界面陷阱电容存在较大的不精确性[16];或者需要专用设备,流程较为复杂,不具有便捷性。文献[17-18]提出了一种利用器件I-V特性亚阈值区域斜率的变化来表征SiC MOSFET界面态密度的方法。该方法测量简便、易于实施,适用于退化器件的界面态分析,然而该公式中的DIT是一个与亚阈值摆幅(Subthreshold Swing, SS)无关的量,研究人员难以利用SS便捷地评估DIT及器件的栅氧可靠性。文献[19]则将DIT表示为关于SS的函数,但该公式中仍涉及电容分量,同样面临难以精确分离界面陷阱电容的困难。此外,基于电容测量的DIT测定方法主要适用于简单的MOS电容结构,难以直接应用于复杂的MOSFET成品器件中。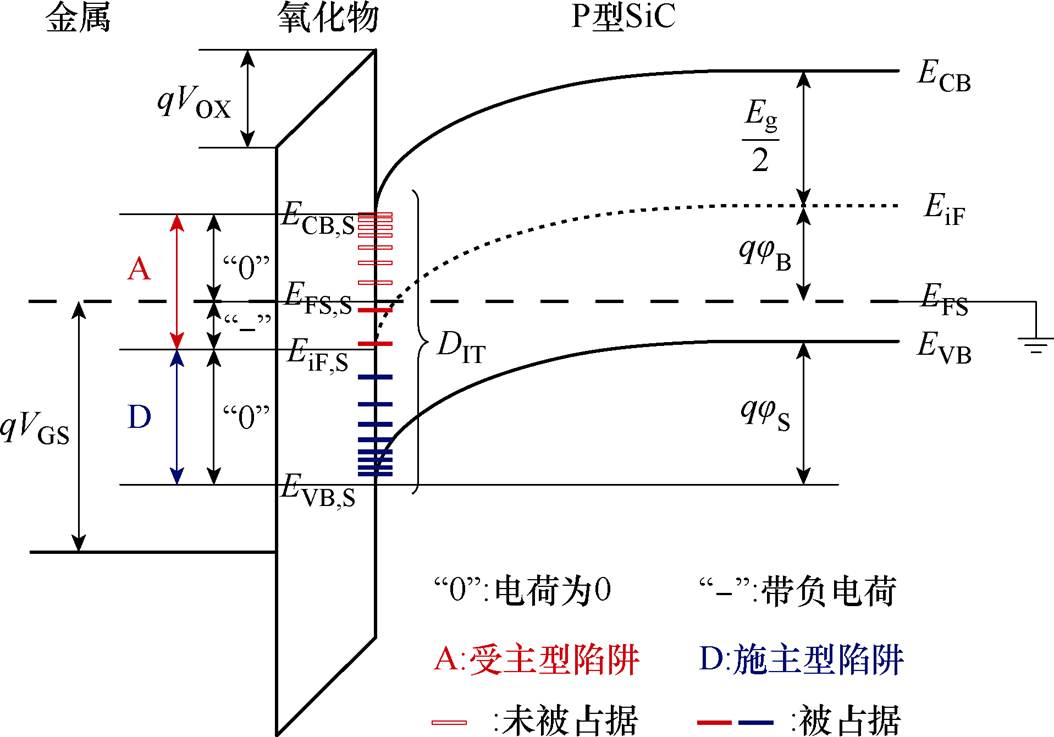
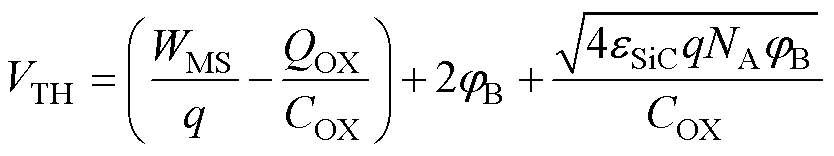 (1)
(1)
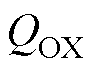 为氧化物中总的有效电荷;
为氧化物中总的有效电荷;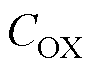 为单位面积的栅氧化层电容;
为单位面积的栅氧化层电容;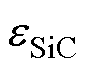 为SiC材料的介电常数;
为SiC材料的介电常数;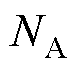 为掺杂浓度。
为掺杂浓度。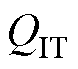 和靠近界面的氧化层电荷
和靠近界面的氧化层电荷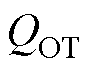 引起的,在可观测的时间尺度内不同电热应力导致了不一样的电荷交换,造成阈值电压漂移的差异
引起的,在可观测的时间尺度内不同电热应力导致了不一样的电荷交换,造成阈值电压漂移的差异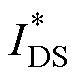 可表示为
可表示为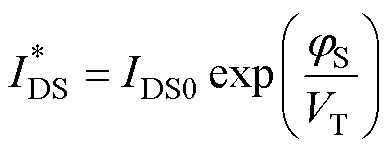 (2)
(2)
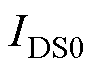 为与工艺相关的常数,可通过
为与工艺相关的常数,可通过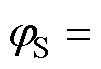
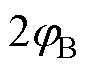 求得。
求得。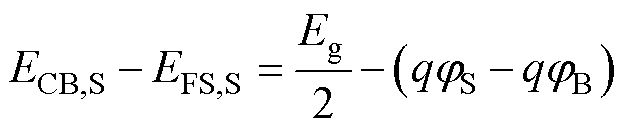 (3)
(3)
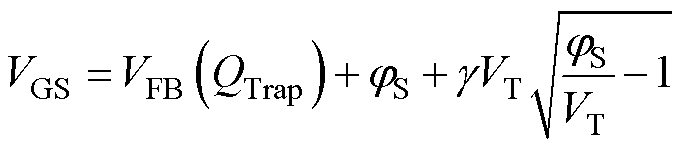 (4)
(4)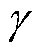 为与器件参数相关的量,
为与器件参数相关的量,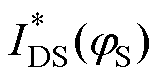 )和(V
)和(V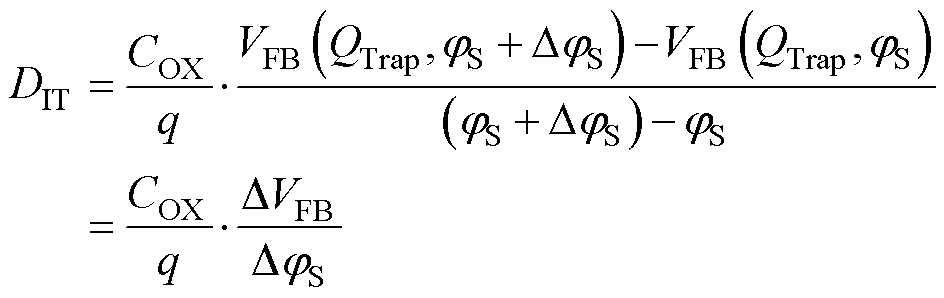 (5)
(5)
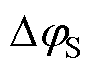 足够小,式(5)可表示为
足够小,式(5)可表示为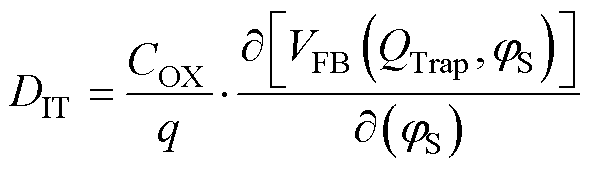 (6)
(6)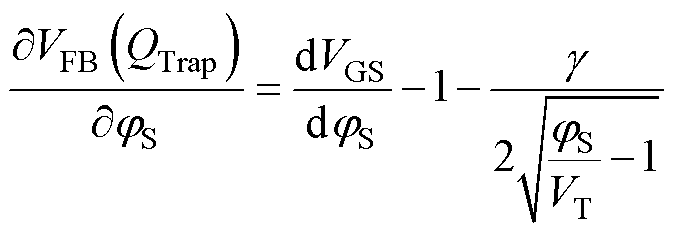 (7)
(7)
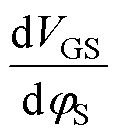 可由SS的定义
可由SS的定义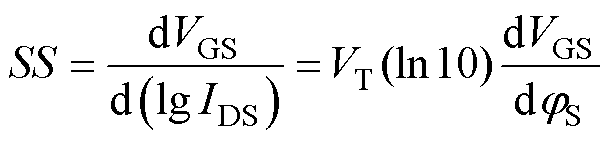 (8)
(8)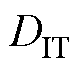 关于SS和
关于SS和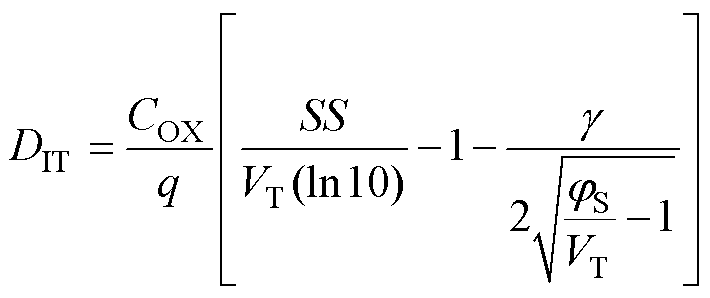 (9)
(9)

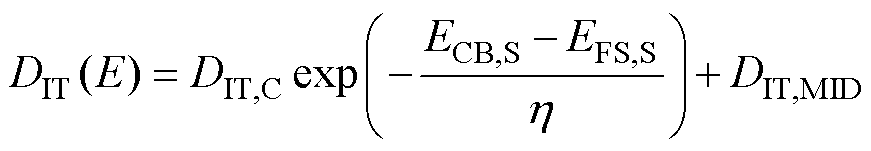 (10)
(10)
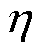 为衰减系数。
为衰减系数。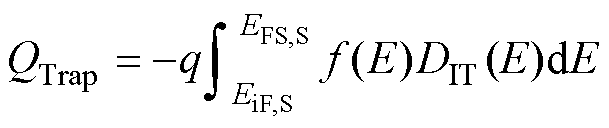 (11)
(11)
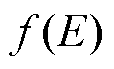 描述了电子占据位于能级E上陷阱的概率;D
描述了电子占据位于能级E上陷阱的概率;D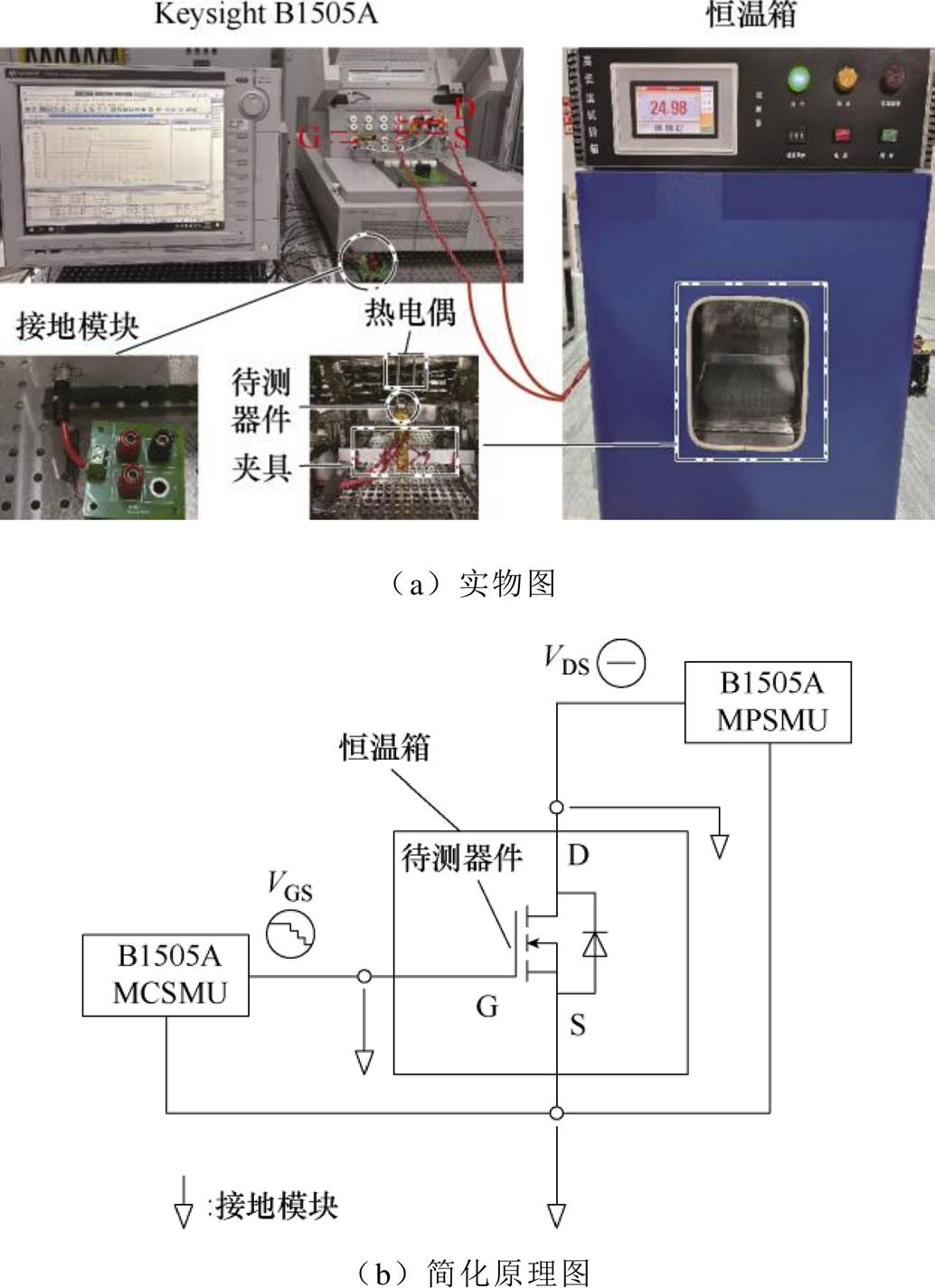



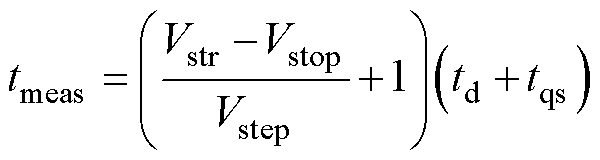 (12)
(12)
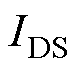 ≥100 nA的有效数据来计算D
≥100 nA的有效数据来计算D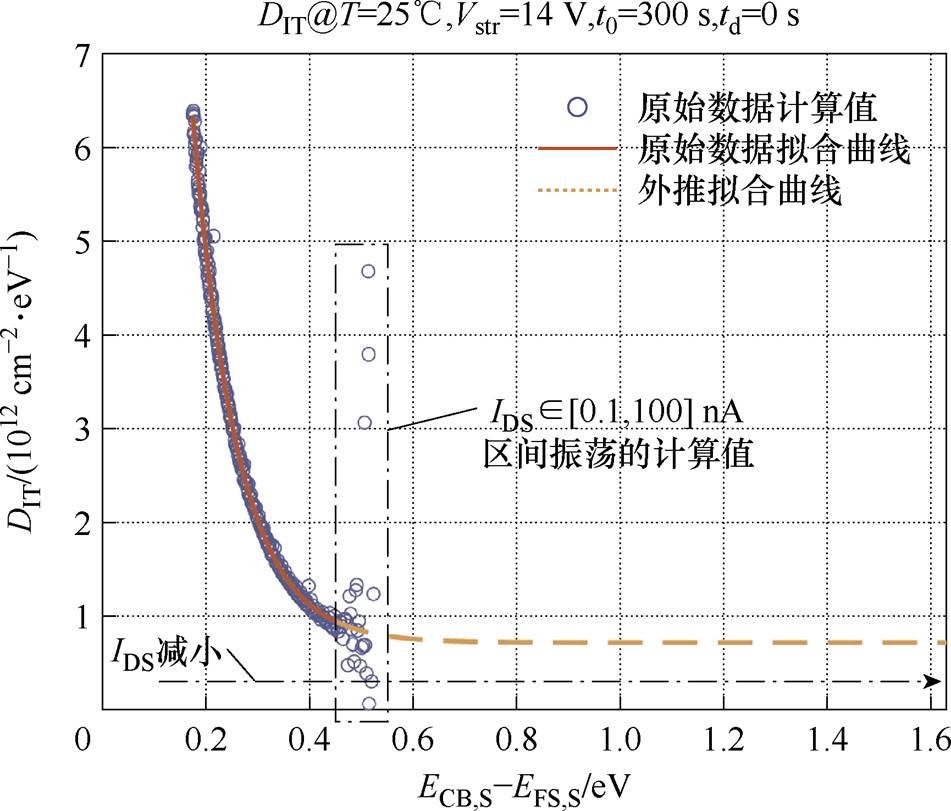
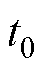 分别变化时陷阱电荷量大小的变化情况,并与相应的阈值电压变化量的值进行比较。常温下,若t
分别变化时陷阱电荷量大小的变化情况,并与相应的阈值电压变化量的值进行比较。常温下,若t