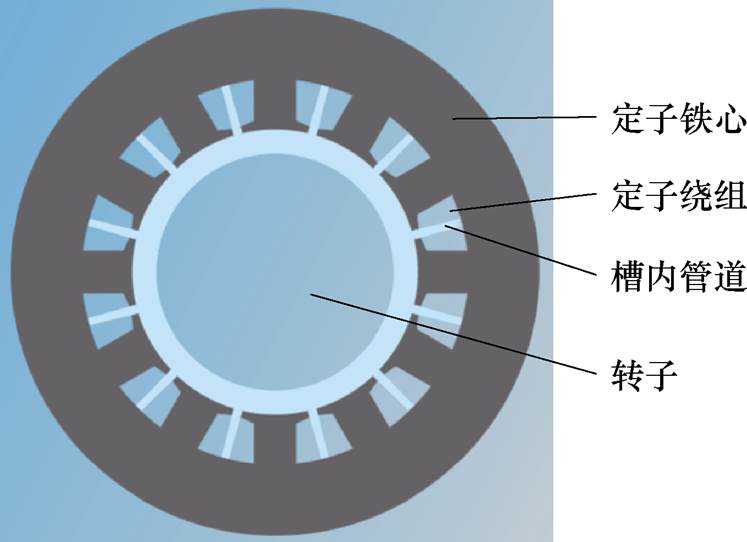
图1 电机定子槽内低温管道截面
Fig.1 Cross-sectional view of cryogenic pipe in the stator slot of the motor
摘要 液体火箭对电动泵驱动控制系统提出了轻量化、高可靠性和大功率的要求。然而,电机系统的输出功率受到多种因素的制约,难以进一步提升。为满足电动泵的需求,该文探讨了短时极限输出功率的概念。首先,在电压有限的条件下求解了电机的极限输出功率,确定了极限功率点,但这一工作点通常伴随着巨大的损耗。为有效带走较大铜损产生的热量,提出了一种新型冷却结构,在电机定子槽内构建低温流道。其次,在极限功率运行下基于槽的利用率和热量分布,探讨了散热量与流道形状参数之间的关系,并提出了多种流道拓扑设计。最后,由于定子电阻随温度变化会导致最大功率点的偏移,基于电磁-热耦合分析提出了一种基于热边界的起始极限功率点选择策略。同时,搭建了Y型流道的温升测试平台,通过实验验证了Y型流道下电机的极限功率,并证实了相关设计方法和冷却结构的可靠性与有效性。
关键词:极限输出功率 永磁同步电机 槽内管道蒸发冷却 Y型管道结构
国家发布多项商业发射行业相关的政策和规划,积极鼓励大众参与空间基础设施建设和应用开发,进而推动商业火箭发射行业的发展[1]。电动火箭具有快速响应、发射地点灵活、可回收、成本低等优势,适应商业发射市场,而为了满足电动火箭发动机的性能要求,世界各国普遍选择了污染小、成本低的推进燃料,如液态甲烷、液氧等。电动火箭发动机性能优异,被认为是未来火箭的发展方向[2]。区别于传统的气压涡轮泵,电动泵结构更加简单可靠,体积也更小。为降低火箭本身的质量,提高其有效载荷,可以选用功率密度更高、质量更轻的高速电机,作为火箭电动泵的发动机系统[3]。
电动火箭还有很大的发展空间。为了满足电动火箭应用于部分特殊环境的需求,火箭的电动泵系统也应该具有如下特点[4-6]:响应速度高、功率密度高、泵送介质温度低。而这些设计指标和要求是以往普通的永磁同步电机无法满足的。因此,泵送低温液体燃料的电动火箭的电机系统应运而生,与之匹配的高过载电机电磁设计、环境适应能力、新型材料以及电机冷却原理、结构和方法也在高速发展并逐步取得突破[7]。
为提高电机功率密度,国内外学者已尝试各种方法,集中体现在更高磁性能的转子磁路结构以及更优异的冷却系统等。日立公司、奥迪公司、比亚迪公司等,分别针对电动汽车领域开发了各自品牌的电机。奥迪公司开发的Q5混合动力汽车采用了最大转矩211 N·m、最大功率40 kW、额定转速2 300 r/min的永磁同步电机。日立公司采用了功率密度达到1.667 kW/kg的永磁同步电机。比亚迪的秦混合动力汽车采用了最大转矩200 N·m、额定转速10 000 r/min、最大功率20 kW的永磁同步电机[8]。文献[9]通过采用更优异的冷却系统,在定子槽中插入导热体,在槽中心和冷却装置之间直接建立高效的导热通路。文献[10]提出了一种新型电机冷却技术,将绕组换热器直接插入定子绕组相间,由于其较小的通道尺寸和微特性,能够产生较大的传热系数,并将这种冷却系统应用于实际电机,发现其显著地提高了电机的极限电负荷;但很少对电机极限输出功率进行探索,更少对其进行理论推导分析。
永磁同步电机在较小限制时输出功率在理论上存在着极值,但该极大值在实际应用中是无法实现的,并且实际值往往远小于该最大值[11]。而限制电机极限输出功率的因素众多,其中最重要的有两点:①当电压达到电压极限圆后,控制器无法向电机中注入更多的电流;②极限输出功率处电流取值往往较高,使电机温升过高造成绕组绝缘失效和永磁体不可逆退磁等问题[12-13]。
因此,本文以有限电压和温度场边界的双重限制为研究对象,探讨永磁电机的极限输出功率,旨在牺牲铜损以较小永磁体成本前提输出更大功率,并得到电机工作点,即能够在最小铜损条件下输出极限功率。为使电机可输出极限功率,需克服功率极值处铜损过高的弊端,因此本文提出了一种新型冷却结构,电机定子槽内低温管道截面如图1所示,在电机定子槽内构建低温管道,管道内放入火箭自有冷媒液氧,利用其气化潜热对绕组进行直接冷却,从而通过降低铜电阻率以降低铜损,并在该冷却系统边界条件下对铜损进行优化分析,为电机设计提供热约束条件,对高功率密度电机研发、电机极限输出功率研究具有指导性意义。

图1 电机定子槽内低温管道截面
Fig.1 Cross-sectional view of cryogenic pipe in the stator slot of the motor
对于id=0控制下的表贴式永磁电机,其电磁转矩T可表示为
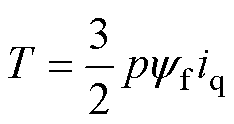 (1)
(1)
式中,p为极对数;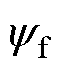 为磁链;iq为交轴电流。
为磁链;iq为交轴电流。
因此,在保证电机转速恒定的前提下,电机的输出功率应该和输入电流成正比,但实际却呈现如图2所示的变化趋势,对于特定样机,当电流增至一定程度后,输出功率上升幅度趋于平缓[14],意味着功率密度提升受限,因此研究输出功率制约因素成为提高功率密度的重要手段。
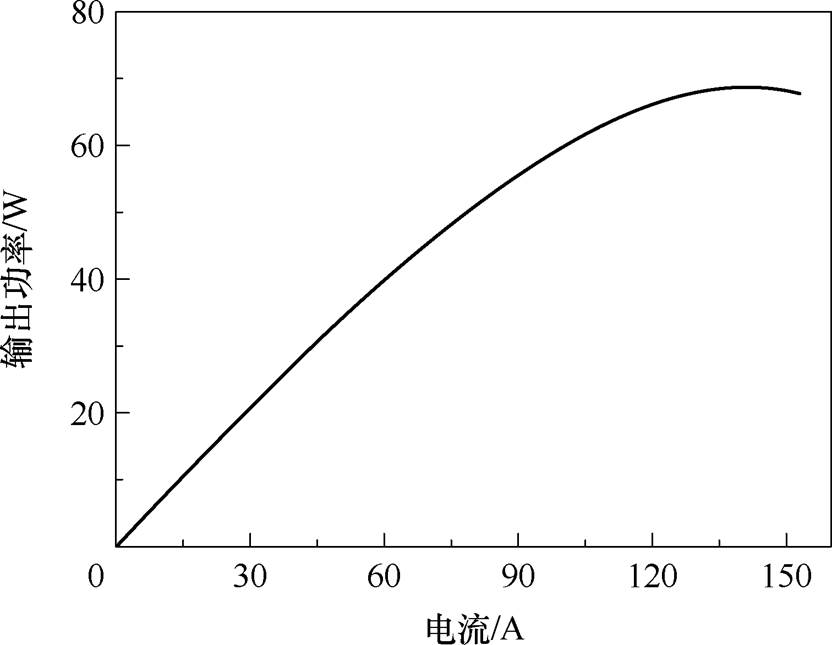
图2 样机输出功率随电流变化
Fig.2 The output power of the prototype varies with the current value
因此,本节从有限电压和温度场边界两方面入手,研究在其共同作用下电机所能输出的极限功率,电机技术指标为额定转速45 000 r/min、额定转矩13.5 N·m、母线电压600 V。
电机输入功率P1可分为三部分,损耗部分以是否随输入电流变化分为可变损耗和不变损耗。绕组铜损PCu是可变损耗[15];不变损耗包括铁损PFe和永磁体涡流损耗Py;其余则转换为电机输出功率P2。
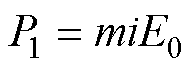 (2)
(2)
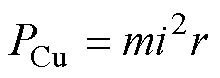 (3)
(3)
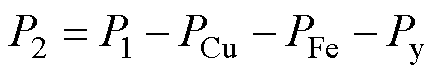 (4)
(4)
式中,i为电流;E0为空载反电动势;r为定子电阻;m为电机的相数。
为尽可能输出更高功率,应使电机达到电压极限圆[16],因此电机负载反电动势E表达式为
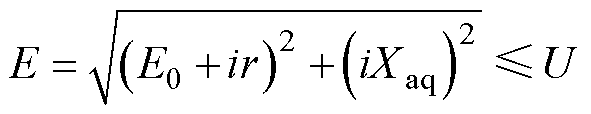 (5)
(5)
式中,Xaq为交轴电抗;U为母线电压。
式(6)为式(2)~式(5)联立所得的电机输出功率,有限电压限制下的输出功率随电流变化曲线如图3所示。可知,随电流的增加,电机的输出功率呈现先增加后减小的规律,存在极大值点1。功率减小的主要原因是电机电枢反应使负载反电动势达到有限电压后,控制器无法向电机中继续灌入电流。因此,如何在有限电压下合理设计电机空载反电动势和电流成为提高电机极限输出功率的有效手段。
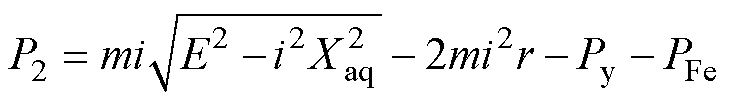 (6)
(6)
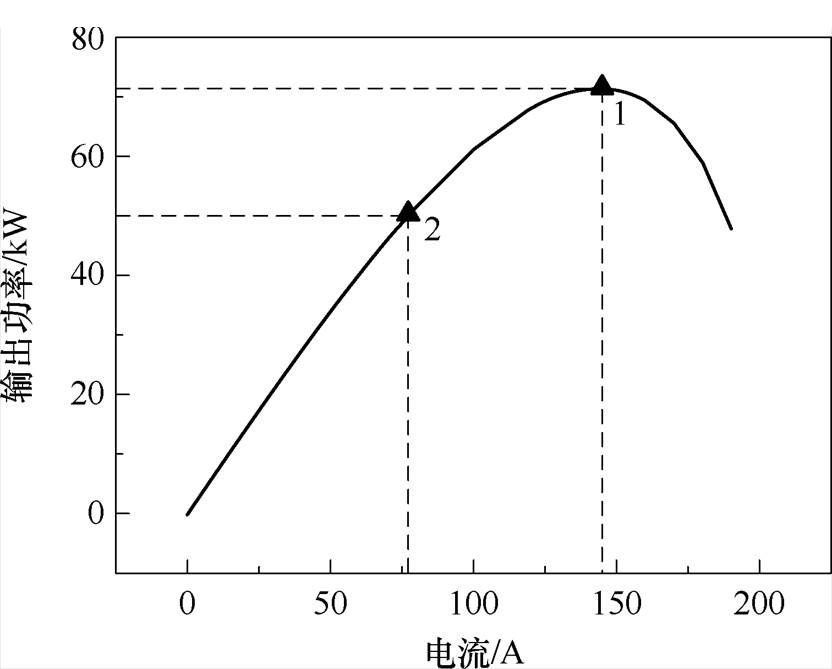
图3 有限电压限制下电机输出功率随电流的变化
Fig.3 Under limited voltage restrictions, the output power of the motor varies with the current value
对于特定尺寸电机,输出功率值决定其功率密度,因此对式(6)进行求导,因为两个偏导在合理范围内均为恒正,证明输出功率在电流上升和空载反电动势上升方向均为单调递增,此时极限功率输出点反电动势一定落在电压极限圆上。在此限制条件下,利用拉格朗日乘法求其极值。
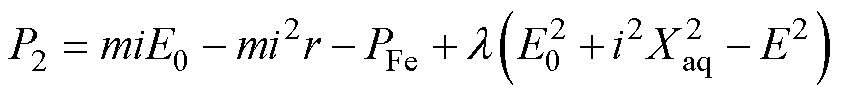 (7)
(7)
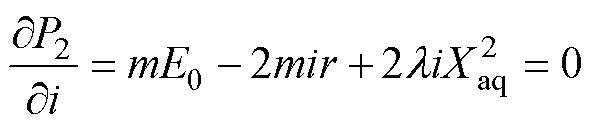 (8)
(8)
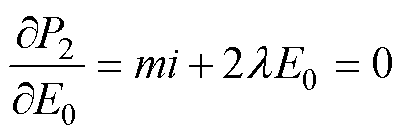 (9)
(9)
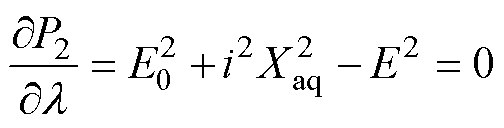 (10)
(10)
式中,l为拉格朗日乘子。
通过联立式(8)~式(10),得到最大功率点以及对应的电流为
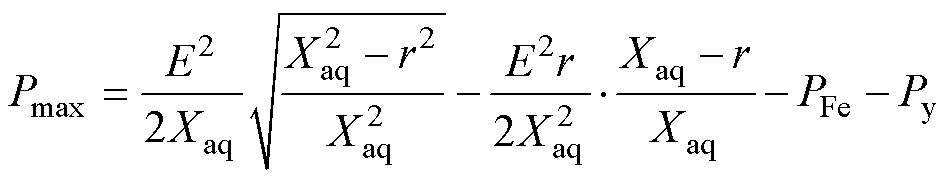 (11)
(11)
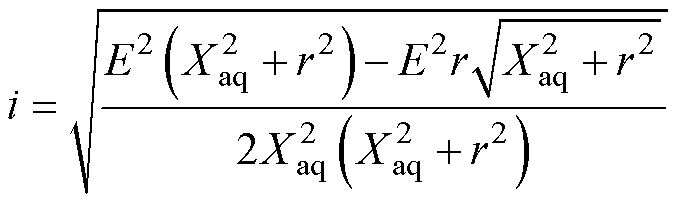 (12)
(12)
为了便于分析,可以认为电阻值r远远小于交轴电抗Xaq。最后,可得电机极限功率工作点及极限功率为其仅与负载反电动势和交轴电抗相关,因此可通过在设计时调整电机的电抗值来优化电机的极限输出功率。
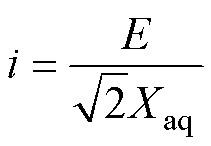 (13)
(13)
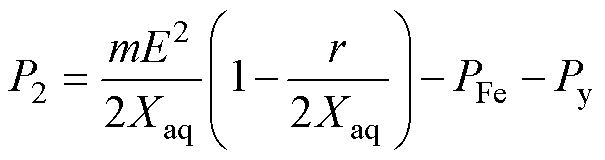 (14)
(14)
对于常规电机,负载反电动势约为空载反电动势的1.1倍较为合理,在此条件下电机输入电流和输出功率如图3中点2所示,电流值为77.2 A,此时输出功率为49.35 kW;而在极值点1取值处,输
入电流为141.0 A,极限功率为70.63 kW,可见功率密度可提升1.39倍。同时,由于极限功率处所需的电负荷较大,磁负荷较小,空载反电动势从221.5 V变为158.8 V,因此只需要更少的磁通量即可满足电机输出要求,大幅降低了永磁体成本。
但是在实际中点1处往往不可取,这是由损耗决定的,从点2到点1处,铜损需从1.39 kW增至4.65 kW,增加3.45倍,电机绕组绝缘材料无法承受如此高的损耗,因此在设计时往往根据实际情况平衡电磁负荷的选取来确定最终的电机设计方案。
依据电机技术指标进行初步设计,得到交轴电抗为1.041 W,定子电阻为0.054 W,此时铜损高达3.5 kW,显然电机绕组绝缘材料无法承受如此高的发热功率,为了使电机输出极限功率,可以通过增强冷却手段使得电机可承受铜损变大,或者应尽量降低铜损,但铜损限制下的电机极限输出功率的影响因素并不清晰。为降低铜损,需要减小定子电阻r或者增大交轴电抗Xaq,其关系为
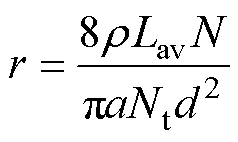 (15)
(15)
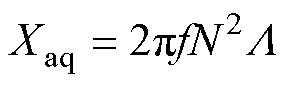 (16)
(16)
其中,主磁导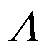 为永磁体内磁导、气隙磁导和铁心磁导的总和,有
为永磁体内磁导、气隙磁导和铁心磁导的总和,有
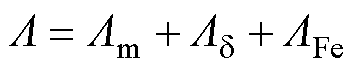
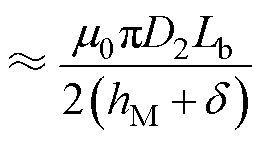 (17)
(17)
式中,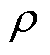 为铜电阻率;Nt为并绕根数;Lav为绕组半匝长;a为并联支路数;d为线径;f为频率;N为每相串联匝数;Lm为永磁体内磁导;Ld为气隙磁导;LFe为铁心磁导;m0为真空磁导率,D2为转子外径;Lb为铁心长度;hM为永磁体厚度;d为气隙长度。
为铜电阻率;Nt为并绕根数;Lav为绕组半匝长;a为并联支路数;d为线径;f为频率;N为每相串联匝数;Lm为永磁体内磁导;Ld为气隙磁导;LFe为铁心磁导;m0为真空磁导率,D2为转子外径;Lb为铁心长度;hM为永磁体厚度;d为气隙长度。
另外,需要指出,铁心磁通密度未饱和时,铁心磁导率极高,因此铁心磁导几乎为0。
综上所述,影响电机铜损限制下的电机极限输出功率的参数可分为三类:①仅影响Xaq的参数,为电机的主要尺寸,包括D2、Lb、hM和d,此外铁心磁通密度值也会因影响铁心磁导而对交轴电抗产生影响;②仅影响r的参数,集中在槽内绕组参数,包括r和Nt,与冷却方式相关;③同时影响两者的参数,主要为每相串联匝数N。本文主要以对定子电阻r的影响分析为主,同时在降低损耗的基础上,提出了一种新型冷却形式,在定子槽设置流道,引入低温冷却媒介,其槽内三维模型如图4所示。
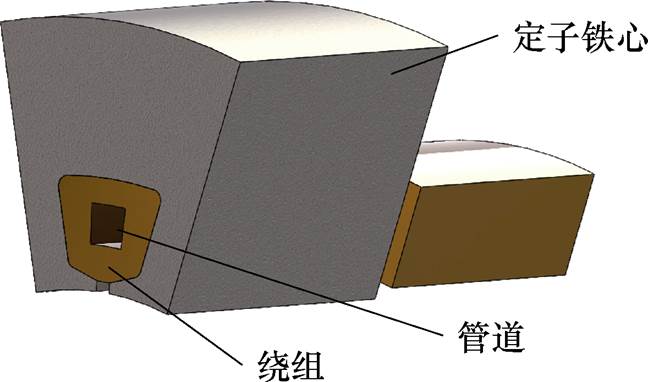
图4 电机槽内三维模型截面
Fig.4 Cross-section of the 3D model in the motor slot
在这种冷却形式下,首先需要分析其对电机参数的影响,槽内参数主要影响定子电阻。一方面,由于槽内流道的存在,电机的槽内铜线有效面积减少,从而导致定子电阻增大;另一方面,低温下电阻率变化较为敏感,如在常温下的电阻率约为液氮温度时的7.7倍。综合考虑这两个因素,定子电阻实际上会减小。接下来分析这种冷却形式对电机冷却能力的影响。由于冷却介质靠近电机绕组,设计了一条高效的热量传递路径,从而增强了冷却效果。因此,从电机参数和冷却能力的角度来看,这种冷却形式能够优化电机的极限功率输出。最终能否实现电机的理论最大功率点,取决于流道的设计,简而言之,就是依赖于冷却能力的提升。
对于槽内冷却,其冷却介质流量较大时,冷却介质足以带出电机产热,此时温升与壁面换热有关,即与管道形状散热面积相关。同时2.1节对于流道对定子电阻的影响分析引出了一个矛盾,当流道面积较大时,冷却效果较好,但同时由于电流密度升高,电机铜损也会变大;相反冷却效果会降低,但铜损相对较小。槽内流道的构建决定了最终的冷却效果,因此下面从槽内流道构建与最终温升来对槽内空间的分配进行研究。
电机槽内三维模型如图5所示,其流道截面积为Sc,流道周长为C。
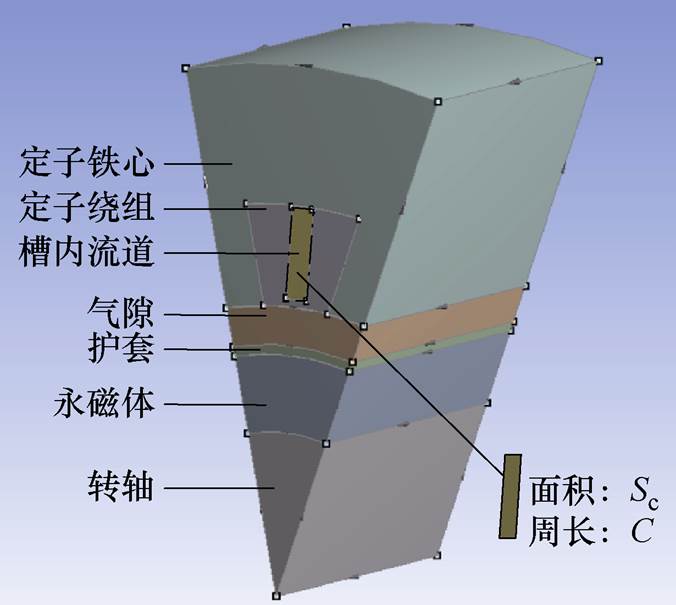
图5 电机槽内流道参数示意图
Fig.5 The parameters of the flow channel
分析流道散热能力,可以先求取流道的对流散热系数,有
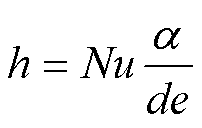 (18)
(18)
式中,h为流道对流散热系数;Nu为努塞尔数;a为冷却媒介的导热系数;de为流道当量直径。
流道努塞尔数计算为
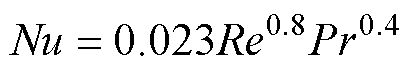 (19)
(19)
式中,Re为雷诺数;Pr为冷却媒介的普朗特常数。雷诺数计算为
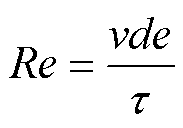 (20)
(20)
式中,v为油的流速;t为冷却媒介的运动黏滞系数。流道当量直径de是将冷却管道为非圆管形状等效为圆管形状的特征尺寸,有
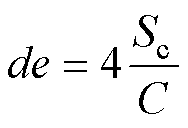 (21)
(21)
综上所述,经计算最后可以得到冷却流道的对流散热系数表达式为
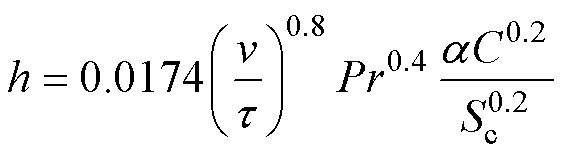 (22)
(22)
进一步得到电机冷却流道的散热量为
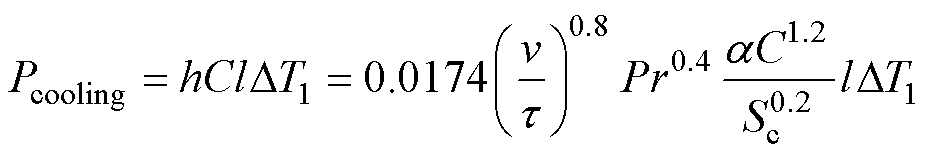 (23)
(23)
式中,l为流道长度;DT1为冷却介质与流道壁面的温差。式(23)揭示了影响流道冷却流道的关键因素,在确定冷却媒介后主要可以通过改变流速v、流道尺寸参数Sc和C来提升电机的散热量。需要注意的是,流道散热量Pcooling还与流道壁面的温差有关,在冷却流量充分的条件下可以将进出口的冷却媒介的温度变化忽略不计,故在预冷前提下温差DT1实际上与绕组的温升在数值上是相等的。
计算完电机冷却流道的散热量后,需要平衡其与电机所产生的铜损的关系。给出电机铜损值PCu为
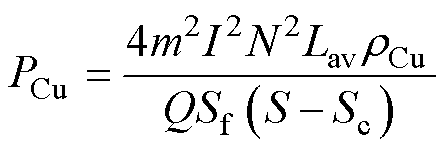 (24)
(24)
其中
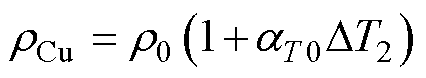 (25)
(25)
式中,I为电流有效值;Q为电机槽数;Sf为电机槽满率;S为电机槽面积;rCu为一个随着温度变化的量;r0为预冷下冷却媒介温度时的电阻率;aT0为绕组电阻率的温度系数;DT2为绕组温升。综合式(24)、式(25)可得
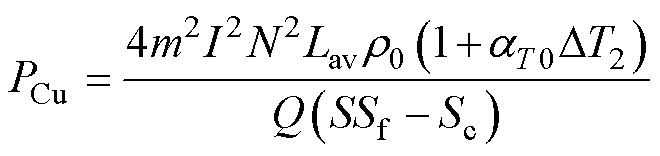 (26)
(26)
分析式(23)和式(26)即判断铜损量与冷却量之间的关系,这就涉及到选择怎样的冷却策略,一般情况下,设计时总是希望冷却流道所能带走的热量远远大于电机自身产生的损耗,包括铜损和铁损,满足散热量和发热量之间的差值最大。但显然在本文的背景下这种策略不适用于短时极限功率工作状态,在此工作状态下只需要保证电机在一定的工作时间、温升范围内稳定可靠运行即可。从式(23)和式(26)不难看出,散热量和铜损均与温升有关,即现行的冷却策略可以描述成式(27),铁损基本可以忽略不计。
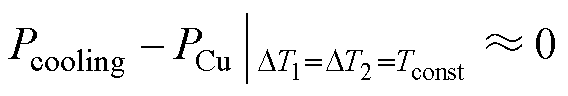 (27)
(27)
式中,Tconst为温升。
主要分析流道面积Sc、流道接触周长C、温升Tconst之间的关系,并且在分析过程中可以发现其他参数基本保持不变,简化冷却流道散热量和铜损的表达式为
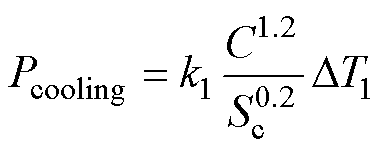 (28)
(28)
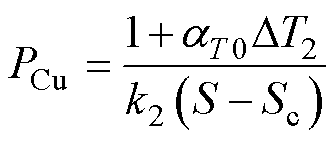 (29)
(29)
式中,k1、k2为常数。
综上所述,可以总结出电机流道构建的规律,表明在给定温升条件下,电机冷却流道的周长与面积之间存在一定关系。公式中的相关常数可以在一定范围内进行优化选择,但通常也需要考虑客观条件进行选取。在给定温升下,电机的散热量随着流道接触周长的增加而增加,而随着流道截面积的增加而减小。然而,对于流道形状的选择而言,接触周长和面积并不是两个独立的参数。在确定接触周长后,可以得到面积的上限;同样地,在确定面积后,可以得到接触周长的下限。进一步分析铜损,在给定温升下,铜损会随着流道截面积的增加而增加。这一规律为电机冷却流道的设计提供了重要的理论基础。
2.3.1 管道散热面积优化
根据以上推导出来的相关规律,为方便下绕组,且方便实验时液氮充满管道,管道结构需简单且不可分离,为使管道成型较明显且可使液氮通入管道中,限制厚度为1 mm,为得到最佳管道形状,分别构建T型、X型、Y型和V型四种结构,过程保证散热面积恒定,得到各结构温升分布如图6所示。需要注意的是,为了实验过程的安全,在实验中与后文的描述中均以液氮作为液体媒介,液氮沸点77 K,液氧的沸点为90 K,液氧的散热系数约为0.17 W/(m·K),优于液氮散热系数。
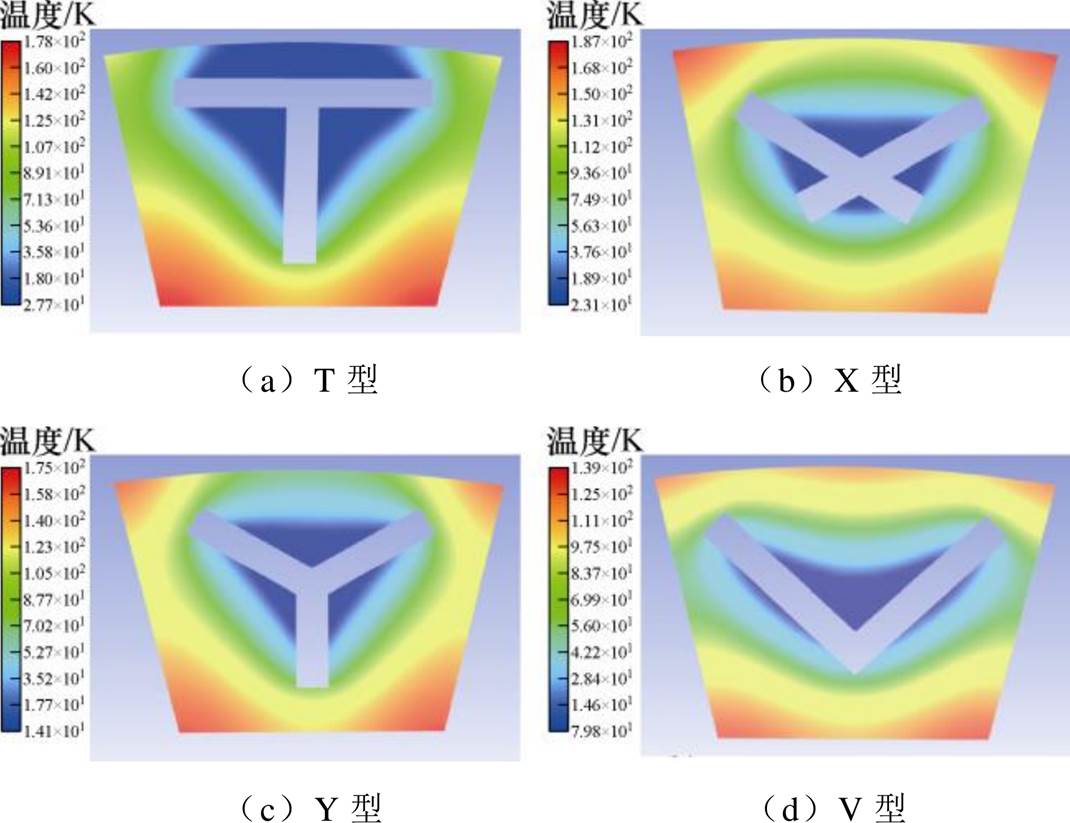
图6 不同管道形状下绕组温度分布
Fig.6 Temperature distribution of windings under different pipe shapes
可以发现,由于矩形结构上端拐角处温升较高,因此T型结构将过多的散热移到上方,导致下端热量积攒严重;由于管道厚度不能做到很薄,使得不能预留足够空间使X型和Y型结构的管道端部伸至绕组拐角处,形成中间温升低而各拐角处均产生较大温升的现象;而V型结构可以有效地将管道端部接近上端拐角处,又在下端保留了足够的液氮容量,相比而言,T型、X型和Y型管道结构最大温度分别为177.1、187.0和175.3 K,而V型结构最大温度仅为137.9 K,相比矩形结构温升降低61.7%。因此,在有限的管道空间内,V型结构冷却性能较好。
2.3.2 V型管道结构优化
当管道形状确定为V型后,其夹角a及管道下端距离端口处距离d1仍未确定,为使管道接近上端拐角处,应使上端拐点处于管道中心线上,以最大效益地对其冷却,因此a与d1呈一一对应关系,只需对d1进行优化分析。
分别取d1=1 mm、1.5 mm、2 mm和2.5 mm,得到不同位置绕组温度分布如图7所示。可以发现,当d1过小时,绕组上端部冷却效果较差,而当d1过大时,绕组下端部反而冷却效果较差,最终当d1取2 mm时,绕组内最大温度最小,为136.2 K,此时V型夹角为97.8°。
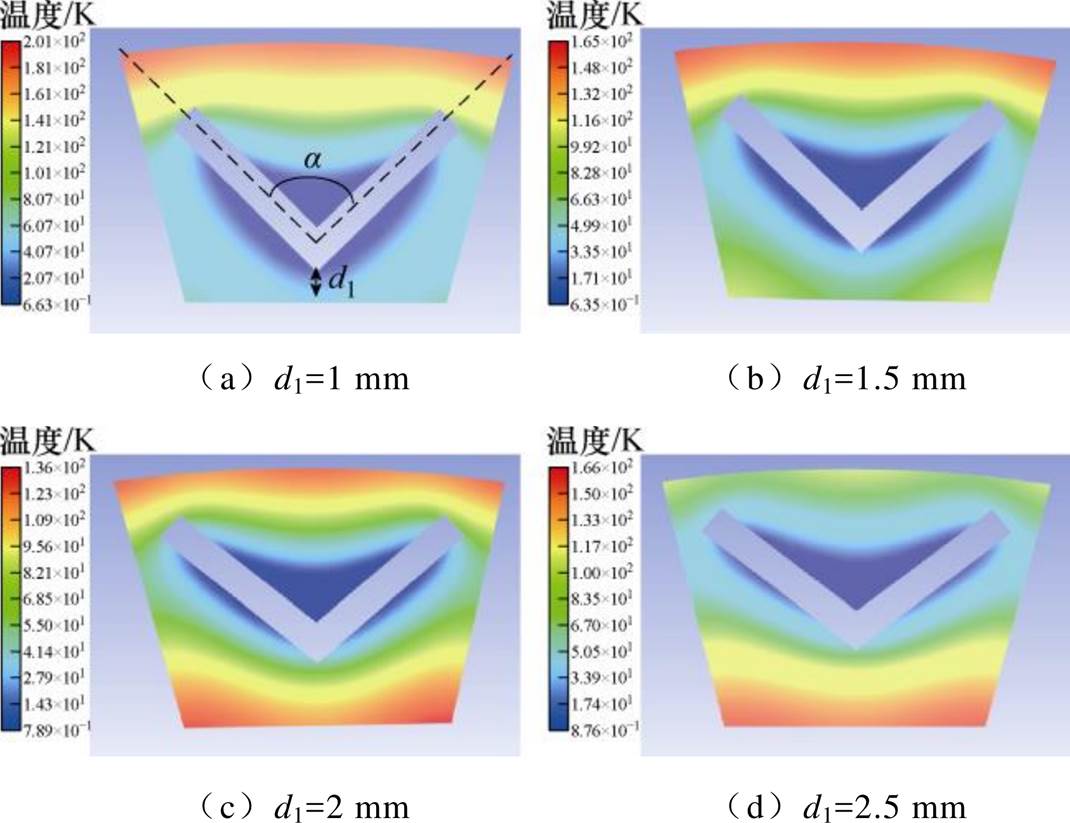
图7 不同d1下绕组温度分布
Fig.7 Temperature of windings under different d1
综上所述,为解决因铜损限制电机不可输出极限功率的问题,本节首先研究了流道参数与散热量之间的关系,然后分别构建T型、X型、Y型和V型四种结构,其最大温度分别为177.1、187.0、175.3和137.9 K,因此得到在有限的管道空间内V型结构冷却性能较好的结论,相比矩形结构温升降低61.7%。
对于火箭用电动泵类短时极限功率输出电机,冷却能力可以根据电机在限定时间、限定温升和有限元电压约束下所达到的最大功率来判断,此最大功率数值也就代表电机在此种形式下能够输出的极限功率。
在槽内冷却下,对于该种类的电机,由于铜的电阻率对温度敏感,低温介质初始工作温度较低,但随着温度的上升会导致电阻的上升,在铜损和绕组温升之间会形成恶性的正循环,这也就导致电机的工况随着电机的运行不断地发生变化。故需要一种电磁-热耦合的温度场分析方法,计算出在不同电流下一定时间内的电机温升情况,寻找出在电机允许温升内的最大电流值。同时,可以在电磁-热耦合场中提取出一些电机关键内在参数,研究其对有限电压和温度场边界共同约束下电机极限输出功率的影响。以此为基础,可以在短时超高功率密度电机设计之初给出相应的规律和路线。
电机热分析方法流程如图8所示,可以由电磁耦合不断根据瞬态温度得到当下的铜损,铜损计算式为
 (30)
(30)
从设计端考虑,电机铜损为
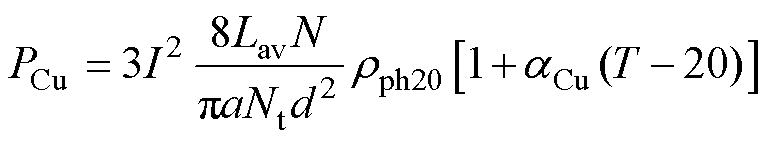 (31)
(31)
式中,aCu为电阻率温度系数,aCu=0.003 93,描述的是电阻率随温度变化的过程;Rph20为常温下的相电阻;rph20为常温下的铜电阻率。
综上所述,可以在电机尺寸参数确定后求得不同电流在工作时长内的温升,以表1所展示参数电机为例,电机槽内流道设计如图9所示。
计算其不同电流下对应的铜损和功率见表2。同时求出不同电流的温升曲线如图10所示,即可以确定电机的极限工作点以及极限功率,需要注意的是,此温升曲线是基于冷却介质流速为1.5 cm/s 求取。
从图10中不难看出,如若电机在200 s工作时间内,工作温度限制在0℃以内,此时极限功率点为i=210 A,此时的极限功率P2=60 004 W,也表明该种冷却形式下,电机工作最大容许铜损常温下数值为3 193.8 W。
为了验证上述分析的合理性,制作了一台带Y型槽内流道的液冷电机,具体参数见表1。在其工作过程中需保证冷却介质保持某一流速从入口流入,从出口流出,因此需要将其与液氮泵接出端相连,在固定的泵压下进行实验,实验电机定子如图11所示。由于实验采用三相交流源电流最大仅为10 A,采用绕组形式的方法对铜损进行等效设计,再加上低温下电阻率的改变,最终两流道结构铜损与电流对应见表3。

图8 电机热分析方法流程
Fig.8 Motor thermal analysis method flow chart
表1 电机参数
Tab.1 Motor parameters
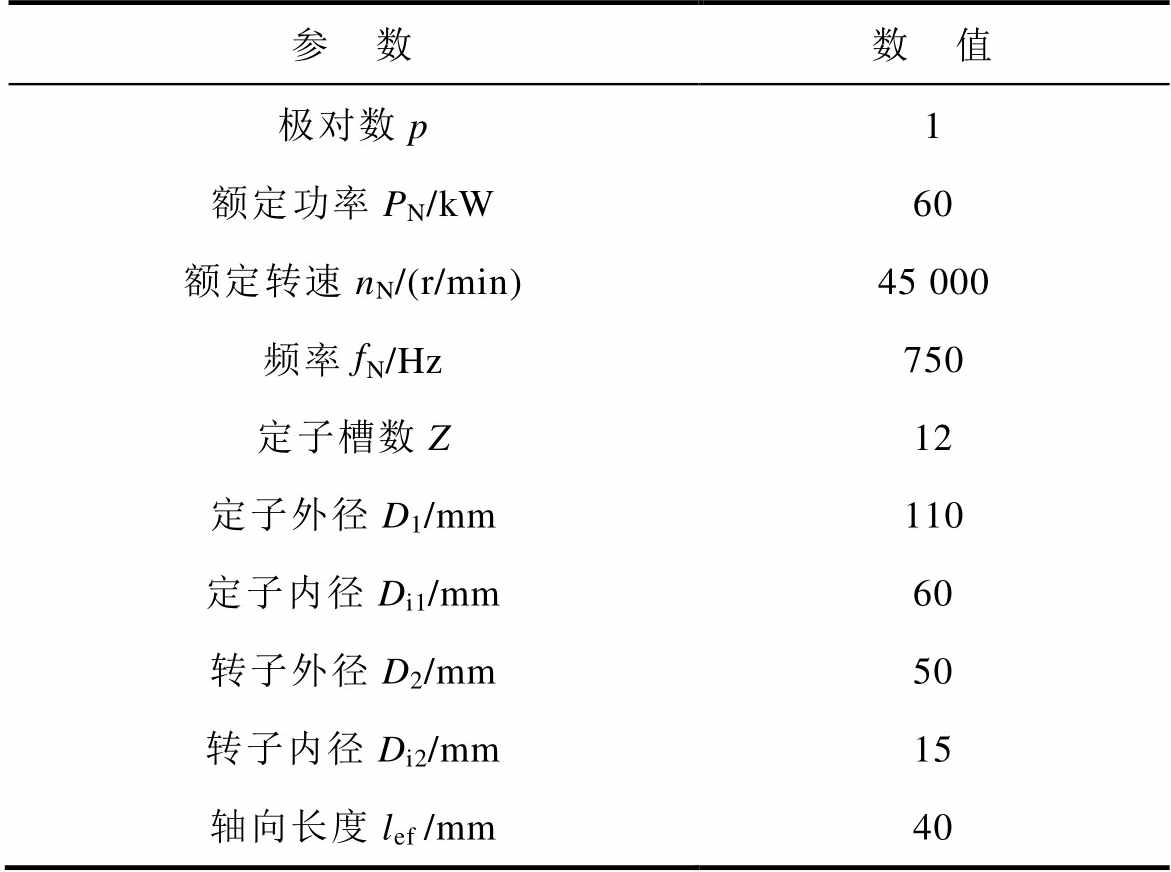
参 数数 值 极对数p1 额定功率PN/kW60 额定转速nN/(r/min)45 000 频率fN/Hz750 定子槽数Z12 定子外径D1/mm110 定子内径Di1/mm60 转子外径D2/mm50 转子内径Di2/mm15 轴向长度lef/mm40
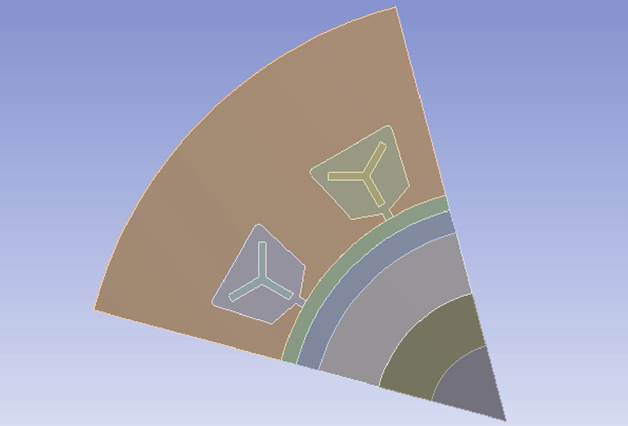
图9 电机槽内三维模型截面
Fig.9 Cross-section of the 3D model in the motor slot
表2 不同电流对应铜损与功率
Tab.2 Copper loss and power for different currents
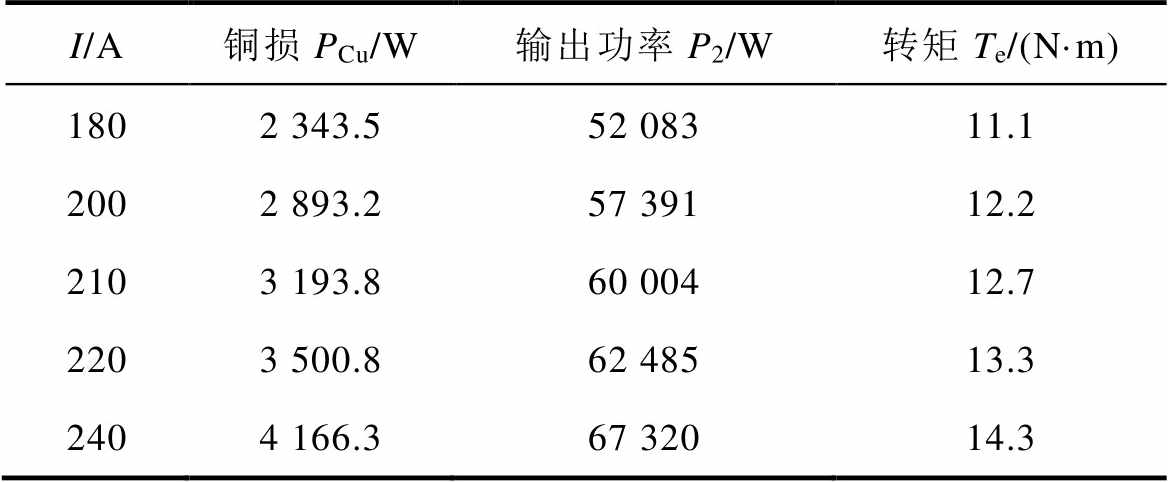
I/A铜损PCu/W输出功率P2/W转矩Te/(N·m) 1802 343.552 08311.1 2002 893.257 39112.2 2103 193.860 00412.7 2203 500.862 48513.3 2404 166.367 32014.3
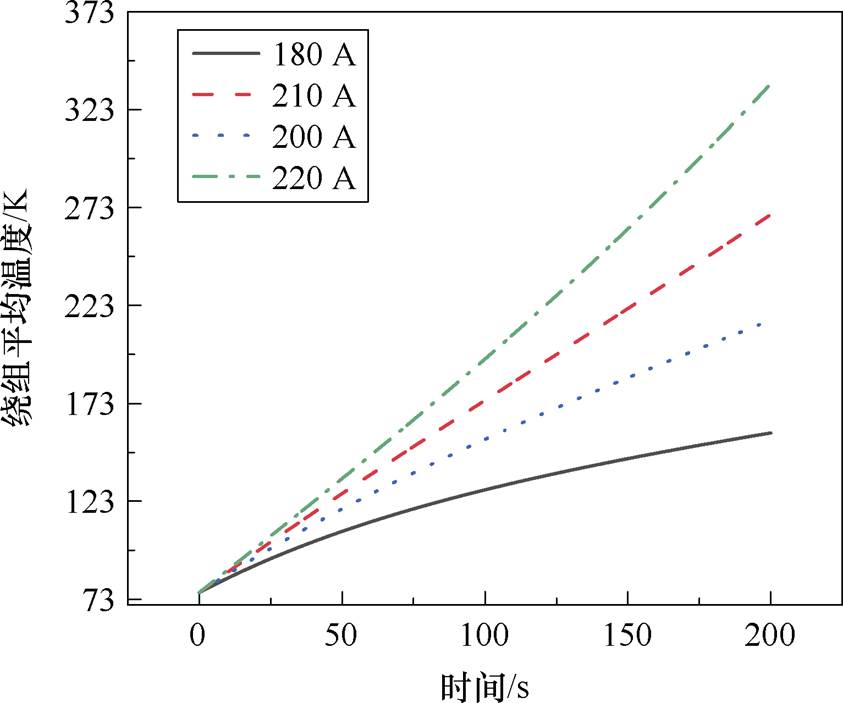
图10 电磁-热耦合模型不同电流的温升曲线
Fig.10 Electromagnetic-thermal coupling model temperature rise for different currents

图11 定子结构接线
Fig.11 Stator structure wiring diagram
表3 不同电流对应的发热功率
Tab.3 Corresponding heating power for different currents
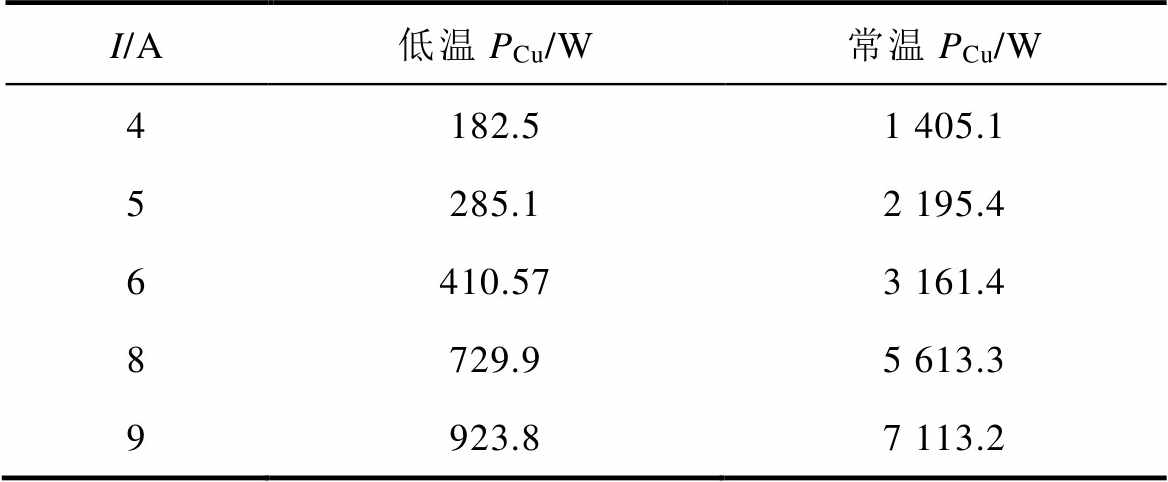
I/A低温PCu/W常温PCu/W 4182.51 405.1 5285.12 195.4 6410.573 161.4 8729.95 613.3 9923.87 113.2
在液氮流速为1.25 cm/s下,三相绕组通入恒流源5.9 A,在定子铜损为397 W情况下得到实验温升与电磁-热耦合仿真对比如图12所示。可见,200 s温升最终结果实验值相比仿真偏高约23.6%。可能的原因为仿真时粗略地使用上一个时间段的平均温度重新定义下一个仿真时间段的铜损值,导致局部过高点温升偏低。
保证液氮泵泵压不变,改变电流,得到不同电流下的绕组温升曲线如图13所示,可以发现,当工作时间设置为200 s、温升设置为273 K时,由图13可以得知,液氮流速为1.25 cm/s时,极限运行工作点为I1=5.9 A。又因为液体流速也会影响电机的散热能力,进而可得到200 s内温度场边界下绕组最大容许电流密度和电机最大容许铜损如图14所示,当液氮流速较低如0.58 cm/s时,电流密度允许达到43 A/mm2;当流速为3.83 cm/s时,甚至容许70 A/mm2的电流密度,冷却性能优越。
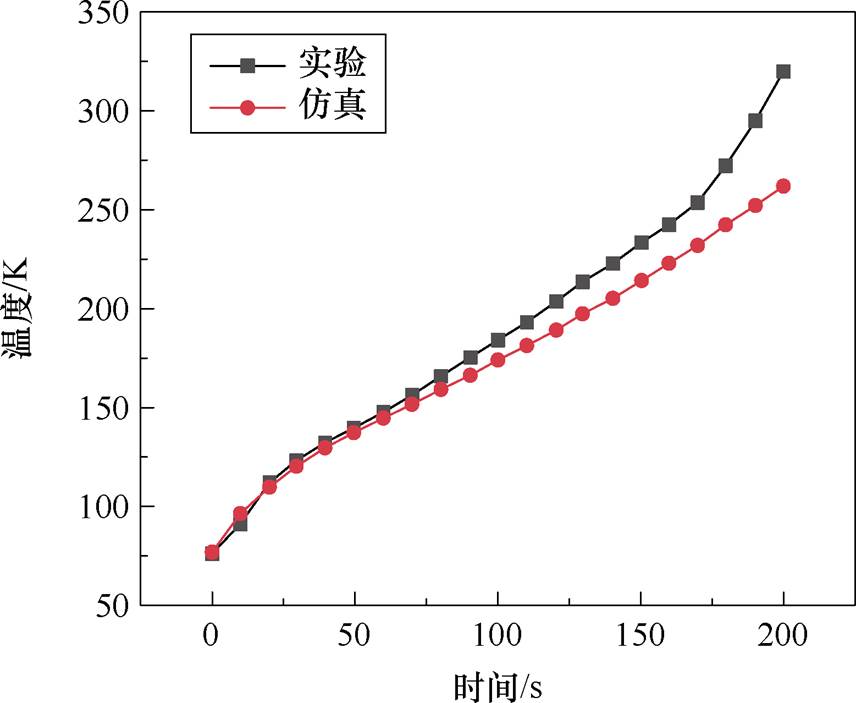
图12 仿真与实验的温升曲线
Fig.12 Simulated and experimental temperature rise curves
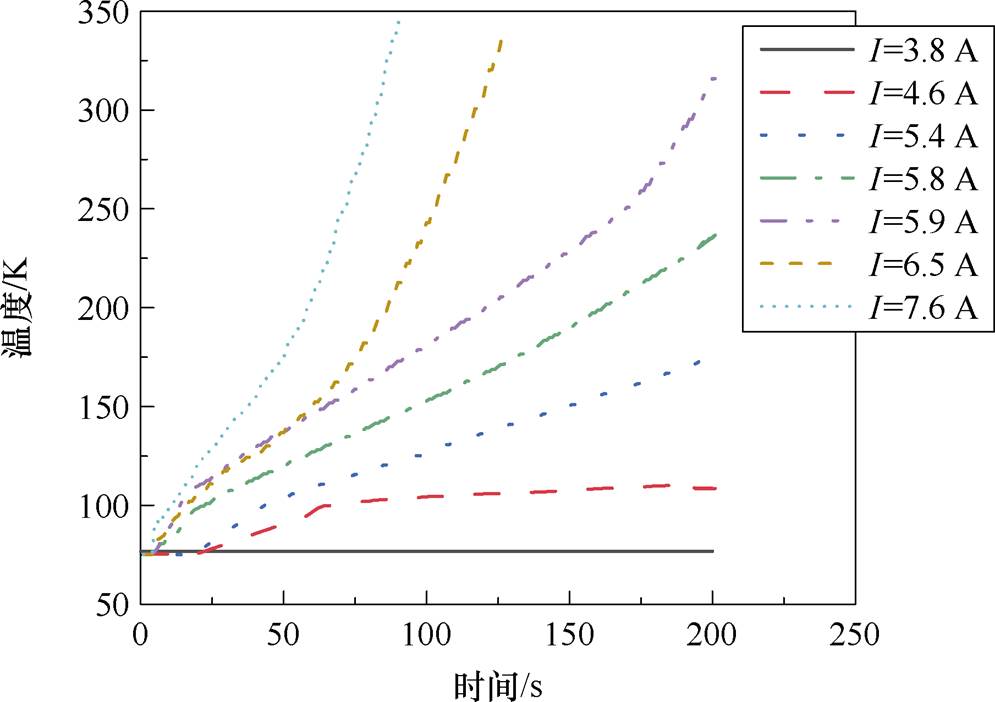
图13 v=1.25 cm/s时不同电流的温升曲线
Fig.13 Temperature rise curves for different current values at v=1.25 cm/s
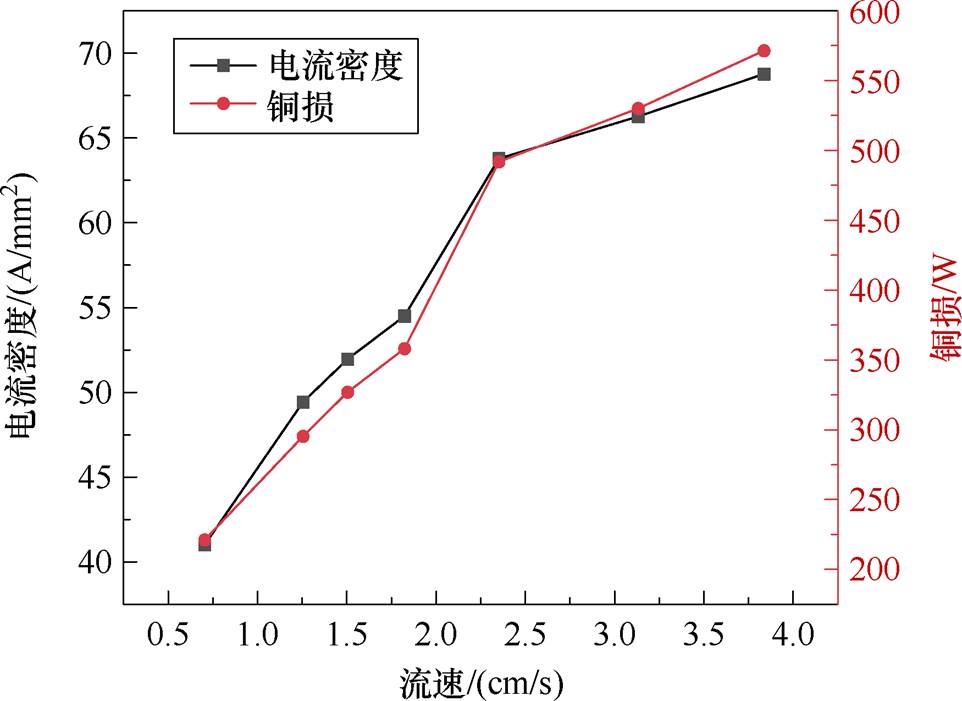
图14 不同液氮流速下所允许最大电流密度和铜损
Fig.14 Maximum current density and copper loss allowed at different liquid nitrogen flow rates
同时对比电磁模型的结果,实验中最大容许铜损数值为397 W,与电磁-热模型仿真结果414.88 W相比存在4.3%的误差。可能存在的原因是,在仿真中求取的是平均温度,而实验中温度传感器放置在绕组中心位置,可能测量的是绕组的热点温度,从而引起误差。
当电机以固定损耗产热使绕组温度升高时,由于低温时铜电阻率对温度较敏感,较小温升亦可引起铜损的成倍增加,其以最终温度分布上限时的铜损产热仍可被液氮气化潜热带出作为冷却边界。铜损等效原理如图15所示,当温度升高时,铜损亦增加,导致温度上升幅度加快,因此最终产生损耗正比于面积S1,而最终温度分布上限时的损耗正比于S2,因此以最恶劣情况时的铜损幅值的一半代替实际所产铜损来进行分析。
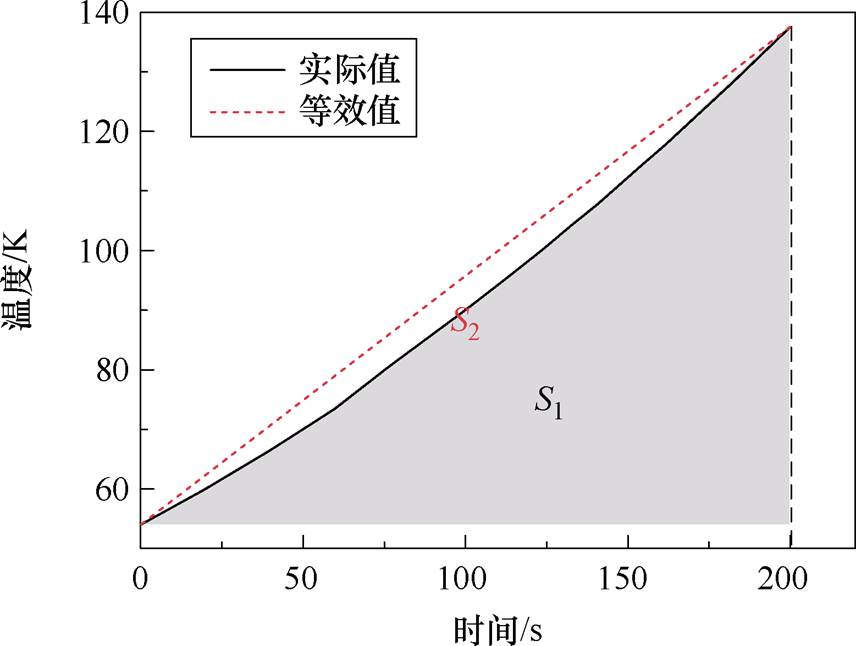
图15 铜损等效原理
Fig.15 Equivalent schematic diagram of copper loss
由3.2节可知,当液量较小不足以带出电机产热时的温升较高,其以负氮容体热密度是否超过单位体积液氧最大气化潜热带走热量为边界,因此冷却边界可转换为:当电机以最大温度铜损一半产热时,其等效负体热密度仍小于液氮气化潜热。
因此,可从以下两方面进行考量:①液氮气化潜热极值容许负体热密度增加的倍数k1;②由于绕组温度升高导致等效铜损增大的倍数k2,在不同初始温度铜损下,应使k2<k1,方可满足冷却边界条件。不同初始温度铜损下的k1和k2变化如图16所示,可以得到此冷却结构的冷却边界为PCu= 492.2 W,降低了铜损对输出功率极值的约束。
经优化后发现电机可容许最优铜损为492.2 W,电流为125.8 A,并将其作为冷却边界条件对电机进行设计优化,最终得到电机设计方案见表4。
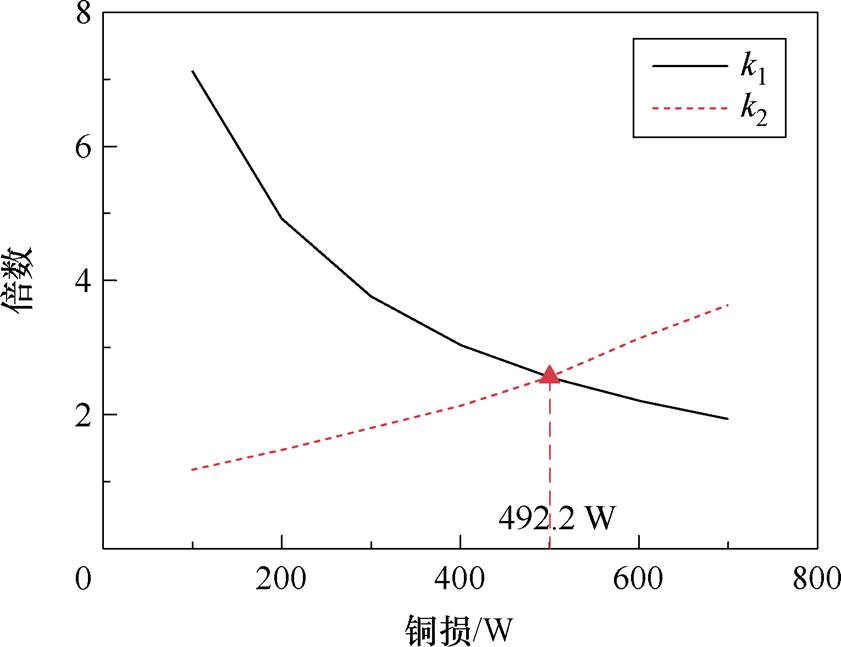
图16 冷却边界铜损确定
Fig.16 Cooling boundary copper loss determination
表4 电机设计方案
Tab.4 Motor design scheme

参 数数值 (型号) 定子外径/mm110 定子内径/mm60 铁心长度/mm40 气隙长度/mm5 永磁体厚度/mm8 槽数12 槽高/mm9.5 齿宽/mm8.2 管道形状Y型 管道截面积/mm212 管道厚度/mm1.0 空载反电动势/V171.7 负载反电动势/V233.0 电流/A127.0 电流密度/(A/mm2)49.9 转子涡流损耗/W117.8 铜损/W447.0 铁损/W101.7 效率(%)98.8 功率密度/(kW/kg)12.26
可见,电机铜损为447.0 W,小于最大铜损492.2 W,而相电流为127.0 A,与理论值125.8 A存在0.94%误差,因此验证了此分析方法的合理性。
在此Y型结构下得到冷却结构的冷却边界为PCu= 492.2 W。在此冷却边界,对电机进行优化设计,最终使电机功率密度高达12.26 kW/kg,同比常规电机提升119%。
1)针对电机往往无法输出极限功率而限制功率密度继续提高的问题,本文提出了在有限电压和温度场边界共同约束下的极限输出功率研究方法,可以得出以下结论:电机在有限电压约束下存在输出功率极大值,但电机往往不能取到极值点的根本原因归结为冷却条件无法达到铜损水平。
在引入了电机槽内冷却后既改善了电机的冷却条件也改变了电机的电阻。在定子槽内构建低温管道,利用火箭自有冷媒液氧气化潜热对绕组铜耗进行直接冷却的基础上,本文还进行了冷却边界下极限功率优化即对流道大小形状的研究。理论计算了低温介质所带走的热量和电机发热量,总结了流道构建相关规律。为抑制拐角处较大温升,提出了V型管道结构,相比传统矩形结构温升从219 K降至84 K,降低61.7%。
2)针对电机的工作状态,本文提出了一种电磁耦合的分析方法,计算电机在一定工作时间、固定温升下电机的极限功率。也通过实验验证了Y型流道电机在冷却介质不同流速下的极限功率,较常规水冷电机提升至少2.33倍;当流速为3.83 cm/s时,甚至可容许70 A/mm2的电流密度。最终得到该冷却系统边界为PCu=492.2 W。进而在冷却边界热约束下优化电机,最终电机功率密度高达12.26 kW/kg,同比增长119%。
本文采取Y型流道对该新型冷却结构进行实验验证,取得较好的效果。但对样机性能是否满足要求,液氮在蒸发后如何时刻充满V型槽内管道等有待下一步的探索。
参考文献
[1] 莫会成, 闵琳, 王健, 等. 现代高性能永磁交流伺服系统综述: 永磁电机篇[J]. 微电机, 2013, 46(9): 1-10, 40.
Mo Huicheng, Min Lin, Wang Jian, et al. Summa- rizing commentary on modern high-performance AC servo system-PM servo motor[J]. Micromotors, 2013, 46(9): 1-10, 40.
[2] 王浩明, 程诚, 李小芳, 等. 液体火箭发动机电动泵系统发展及性能研究[J]. 火箭推进, 2019, 45(5): 1-7.
Wang Haoming, Cheng Cheng, Li Xiaofang, et al. Development and performance study of electrically driven pump system for liquid rocket engine[J]. Journal of Rocket Propulsion, 2019, 45(5): 1-7.
[3] 刘洋, 付本帅, 杨建刚, 等. 电动泵压式液体火箭发动机系统建模与仿真[J]. 载人航天, 2019, 25(1): 107-115.
Liu Yang, Fu Benshuai, Yang Jiangang, et al. System modeling and simulation of electric pump feed liquid propellant rocket engine[J]. Manned Spaceflight, 2019, 25(1): 107-115.
[4] 佟文明, 侯明君, 孙鲁, 等. 基于精确子域模型的带护套转子高速永磁电机转子涡流损耗解析方法[J]. 电工技术学报, 2022, 37(16): 4047-4059.
Tong Wenming, Hou Mingjun, Sun Lu, et al. Analytical method of rotor eddy current loss for high-speed surface-mounted permanent magnet motor with rotor retaining sleeve[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4047-4059.
[5] 张书宽, 王发琛, 曲荣海, 等. 潜液式液化天然气泵用低温永磁同步电机研究现状综述[J]. 电工技术学报, 2024, 39(22): 6998-7018.
Zhang Shukuan, Wang Fachen, Qu Ronghai, et al. A review on cryogenic permanent magnet synchronous motor for submersible liquid natural gas pump[J]. Transactions of China Electrotechnical Society, 2024, 39(22): 6998-7018.
[6] Cao Jiwei, Zhang Chengming, Liu Jiaxi, et al. Investigation on maximum electromagnetic torque of permanent-magnet synchronous machines[J]. IEEE Access, 2019, 8: 113011-113020.
[7] Wan Yuan, Wu Shaopeng, Cui Shumei. Choice of pole spacer materials for a high-speed PMSM based on the temperature rise and thermal stress[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(7): 0608405.
[8] Lahne H C, Gerling D, Staton D, et al. Design of a 50 000 rpm high-speed high-power six-phase PMSM for use in aircraft applications[C]//2016 Eleventh International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 2016: 1-11.
[9] Galea M, Gerada C, Raminosoa T, et al. A thermal improvement technique for the phase windings of electrical machines[J]. IEEE Transactions on Industry Applications, 2012, 48(1): 79-87.
[10] Semidey S A, Mayor J R. Experimentation of an electric machine technology demonstrator incorpo- rating direct winding heat exchangers[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5771-5778.
[11] Zhang Fengyu, Gerada D, Xu Zeyuan, et al. Improved thermal modeling and experimental validation of oil-flooded high-performance machines with slot- channel cooling[J]. IEEE Transactions on Trans- portation Electrification, 2022, 8(1): 312-324.
[12] 张文校, 胡岩, 曹力, 等. 高速永磁屏蔽电机摩擦损耗分析与计算[J]. 电工技术学报, 2023, 38(12): 3122-3129.
Zhang Wenxiao, Hu Yan, Cao Li, et al. Analysis and calculation of friction loss of high-speed permanent magnetic shielding motor[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3122-3129.
[13] 史涔溦, 彭琳, 张振, 等. 电压源激励下表贴式永磁同步电机退磁故障建模与分析[J]. 电工技术学报, 2025, 40(8): 2430-2440.
Shi Cenwei, Peng Lin, Zhang Zhen, et al. Modeling and analysis of demagnetization fault in surface mounted permanent magnet synchronous motors with voltage source excitation[J]. Transactions of China Electrotechnical Society, 2025, 40(8): 2430-2440.
[14] 许光炜. 轻质化高速大功率永磁同步电机关键技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2020.
Xu Guangwei. Research on key technology of lightweight high speed high power permanent magnet synchronous motor[D]. Harbin: Harbin Institute of Technology, 2020.
[15] 骆凯传, 师蔚, 张舟云. 基于温度实验的永磁同步电机损耗分离方法[J]. 电工技术学报, 2022, 37(16): 4060-4073.
Luo Kaichuan, Shi Wei, Zhang Zhouyun. Method of loss separation of permanent magnet synchronous motor based on temperature experiment[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(16): 4060-4073.
[16] 李立毅, 张江鹏, 赵国平, 等. 考虑极限热负荷下高过载永磁同步电机的研究[J]. 中国电机工程学报, 2016, 36(3): 845-852.
Li Liyi, Zhang Jiangpeng, Zhao Guoping, et al. Research on the high overload permanent magnet synchronous motor considering extreme thermal load[J]. Proceedings of the CSEE, 2016, 36(3): 845-852.
Abstract With the advancement of pump-driven systems for liquid rockets, pump-driven motors are increasingly designed to be lightweight, highly reliable, and capable of short-term high-power output. However, the maximum power of these motor systems is constrained by voltage limitations and thermal boundaries, making significant power increases challenging. Traditional motor design methods often incorporate redundancy for maximum power rather than directly optimizing for the extreme power point. This paper introduces the concept of short-term extreme output power and establishes a design methodology for the extreme power point. Given the significant losses associated with this operating point, a novel cooling structure is proposed to effectively dissipate the heat generated by substantial copper losses. Through electromagnetic-thermal coupling analysis and experimental validation, the reliability and effectiveness of the proposed design methodology and cooling structure are demonstrated.
A mathematical model of the motor is first established to analyze the variation of output power with current under the voltage limit circle. As the current increases, the output power initially rises and then declines, exhibiting a maximum point. By employing the Lagrange multiplier method to solve for this maximum power point, it is found that only a minimal magnetic flux is required to meet the output requirements, significantly reducing the cost of permanent magnets. However, this extreme point is often impractical in real-world applications because, from the rated power point to the extreme power point, copper losses increase by 3.45 times, exceeding the thermal limits of the winding insulation materials. To adjust the extreme power point, the motor's tolerance to copper losses can be enhanced through improved cooling methods, or copper losses can be minimized. The primary factor influencing the motor's extreme output power under copper loss constraints is the stator resistance. This paper proposes a novel cooling configuration that incorporates flow channels in the stator slots and introduces a low-temperature cooling medium. This cooling approach not only reduces stator resistance but also designs an efficient heat transfer path by placing the cooling medium in close proximity to the windings, thereby enhancing cooling effectiveness. Consequently, from the perspectives of motor parameters and cooling capacity, this cooling configuration optimizes the motor's extreme power output. The ultimate realization of the theoretical maximum power point depends on the design of the flow channels.
A model for motor losses and cooling capacity is established, summarizing the principles of flow channel construction. Under a fixed temperature rise, the heat dissipation increases with the contact perimeter of the flow channel and decreases with the cross-sectional area. However, in the selection of flow channel shapes, the contact perimeter and area are not independent parameters. Once the contact perimeter is determined, an upper limit for the area can be derived, and vice versa. Cooling topologies of X, Y, Z, and V types are proposed. Among these, the maximum temperatures for T-type, X-type, and Y-type channel structures are 177.1 K, 187.0 K, and 175.3 K, respectively, while the V-type structure achieves a significantly lower maximum temperature of 137.9 K. Further optimization of the V-type structure reduces the maximum temperature to 136.2 K, with an optimal V-angle of 97.8°.
For short-term extreme power output motors, such as those used in rocket electric pumps, the cooling capacity can be evaluated by the maximum power achieved under constraints of limited time, temperature rise, and voltage. This maximum power represents the motor's extreme output capability. By establishing an electromagnetic-thermal coupling model, the temperature rise of the motor under different currents within a specified time is calculated to determine the maximum allowable current under the permitted temperature rise. Validation of the extreme power point and electromagnetic-thermal coupling model for a Y-type winding under specific parameters shows that, at a liquid nitrogen flow rate of 1.25 cm/s, a three-phase winding current of 5.9 A, and stator copper losses of 397 W, the experimental temperature rise is approximately 23.6% higher than the simulation results. This discrepancy may arise from the use of average temperatures from the previous time step to define copper losses in the simulation, leading to an underestimation of local high-temperature points. By maintaining constant liquid nitrogen pump pressure and varying the current, the temperature rise curves of the winding under different currents are obtained. At an operating time of 200 s and a temperature rise of 273 K, the extreme operating point at a liquid nitrogen flow rate of 1.25 cm/s is I1=5.9 A. The liquid flow rate significantly affects the cooling capacity, with the maximum allowable current density and copper losses under the temperature field boundary within 200 s varying with flow rate: at 0.58 cm/s, the current density can reach 43 A/mm2, while at 3.83 cm/s, it can reach 70 A/mm2, demonstrating superior cooling performance. The maximum allowable copper loss in the experiment is 397 W, with a 4.3% error compared to the simulation result of 414.88 W.
keywords:Extreme output power, permanent magnet synchronous motor (PMSM), evaporative cooling of pipes in the tank, Y-shaped pipe structure
DOI: 10.19595/j.cnki.1000-6753.tces.241910
中图分类号:TM614
国家自然科学基金(U2141224)专项资金资助项目。
收稿日期 2024-10-25
改稿日期 2025-01-20
陈博宇 男,2001年生,博士研究生,研究方向为高功率密度电机及低温冷却系统。E-mail: 2953464404@qq.com
曹继伟 男,1983年生,研究员,研究方向为高速、高效、高功率密度永磁电机设计,高温超导技术等。E-mail: caojiwei@hit.edu.cn(通信作者)
(编辑 崔文静)