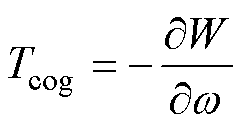 (1)
(1)
式中,Tcog为齿槽转矩;W为磁场能量。
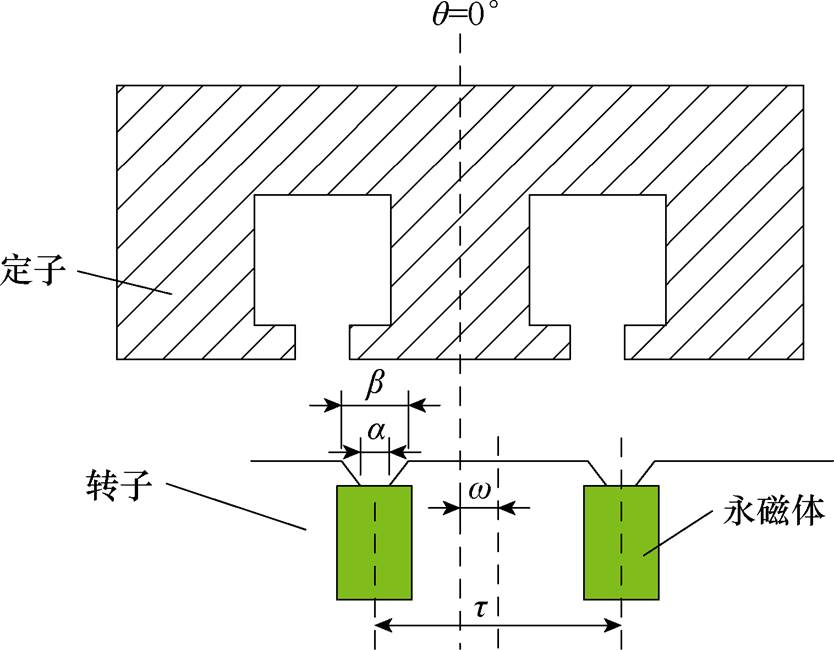
图1 内置切向式电机定、转子相对位置示意图
Fig.1 Schematic diagram of the relative position of stator and rotor of spoke motor
摘要 针对内置式永磁同步电机齿槽转矩大与转矩波动严重的问题,该文提出了一种转子铁心外圆开梯形槽结构的内置切向式永磁同步电机齿槽转矩抑制方法,该方法能有效降低电机的齿槽转矩和空载反电动势的谐波占比,同时有效降低电机的转矩波动。首先,利用解析法推导出考虑转子开槽来改变极弧系数的齿槽转矩计算公式,以一台14极12槽内置切向式永磁同步电机为例,利用有限元仿真计算,对比了无槽转子结构、矩形槽转子结构及梯形槽转子结构的齿槽转矩。同时,分析三种常用极槽配合下,梯形槽的短边开口角度与长边开口角度对齿槽转矩的影响,给出抑制齿槽转矩的梯形槽尺寸选取范围。对比分析无槽转子结构、矩形槽转子结构及优化后梯形槽转子结构永磁同步电机的空载反电动势、反电动势谐波占比、齿槽转矩与转矩波动,结果表明,开梯形槽结构能有效降低永磁电机的漏磁,提高电机的输出转矩性能,同时降低电机的齿槽转矩与转矩波动。最后,通过样机实验验证了仿真计算的准确性,为解决内置式永磁同步电机齿槽转矩大、转矩波动大的难题提供了一种有效的方法。
关键词:内置式永磁同步电机 切向式结构 梯形槽 齿槽转矩 转矩波动
内置式永磁同步电机(Interior Permanent Magnet Synchronous Motor, IPMSM)因其具有高功率密度、高转矩密度、弱磁能力强等优势,广泛地应用于电动汽车、电助力单车以及车用压缩机等领域[1-3]。相比于其他内置径向式结构,内置切向式转子结构能在同等转子体积下放置较多的永磁体,提供较高的转矩密度[4-5]。然而,内置切向式永磁电机也具有转子磁路复杂、齿槽转矩大及转矩波动大等缺点,会对电机平稳运行造成影响[6-7]。因此,如何降低内置切向式永磁同步电机的齿槽转矩及转矩波动已然成为近些年的研究热点[8-9]。
文献[10]通过在转子上加非磁性槽楔,合理地选用槽楔的形状和尺寸,可以有效削弱齿槽转矩。文献[11]分析了永磁体磁极分块个数及间隔对齿槽转矩的影响。结果表明,该方法能有效降低齿槽转矩的某些谐波。文献[12]提出了两种降低齿槽转矩的方法,分别是用最优斜角斜极转子和不等齿长的斜极转子,还研究了因制作工艺的公差所带来的影响。文献[13]采用不对称V字形转子结构来削弱齿槽转矩,该方法在工艺上产生难度,且磁极不对称会引起磁路不对称,对电机控制有一定影响。优化内置式电机转子结构能有效地降低齿槽转矩与转矩脉动,且不会降低电机输出转矩,也不会增加电机的成本[14-16]。文献[17]分析了转子动态偏心对电机的影响,指出转子动态偏心距增大到一定范围内能有效降低齿槽转矩。文献[18-19]推导出一种齿槽转矩解析方法。
以上降低齿槽转矩的方法多种多样,但大部分难以实现或者伴随其他负面影响,例如定子齿冠开辅助凹槽增加齿槽转矩周期数来降低齿槽转矩,但齿冠开辅助凹槽后会增大气隙中的谐波,对电机运行时的控制精度有一定的影响。不均匀气隙方法具有较容易实现、效果明显及能改善反电动势等优势。
本文针对内置切向式永磁电机,从齿槽转矩理论公式出发,提出一种改变极弧系数的转子铁心开梯形槽的方法,来降低齿槽转矩。
为了研究转子梯形槽尺寸对齿槽转矩的影响规律,本文利用有限元方法建立了内置切向式永磁电机参数化仿真模型,对比了无槽结构、矩形槽结构及梯形槽结构的齿槽转矩,并分析了梯形槽尺寸对齿槽转矩的影响。同时,对比了内置切向式无槽转子结构、矩形槽转子结构及优化后梯形槽转子结构的电机空载反电动势、静态下的齿槽转矩及额定负载时的转矩波动。最后结合实验结果论证了转子梯形槽新型结构能有效降低电机的齿槽转矩、反电动势谐波占比及转矩波动。
图1为内置切向式永磁电机定、转子相对位置示意图。图中,w为定转子间的相对角度,定子位置q=0°设定在特定定子齿中心轴线处,t为两极间宽度(角度表示),b为梯形槽长边开口角度,a为梯形槽短边开口角度。由齿槽转矩定义及能量法理论[19]可知
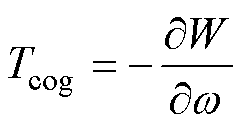 (1)
(1)
式中,Tcog为齿槽转矩;W为磁场能量。

图1 内置切向式电机定、转子相对位置示意图
Fig.1 Schematic diagram of the relative position of stator and rotor of spoke motor
忽略铁心饱和现象时,气隙磁场与永磁体中储存的能量可以近似看作整个电机磁场的储能,所以整个电机磁场储存的能量[18]可以表示为
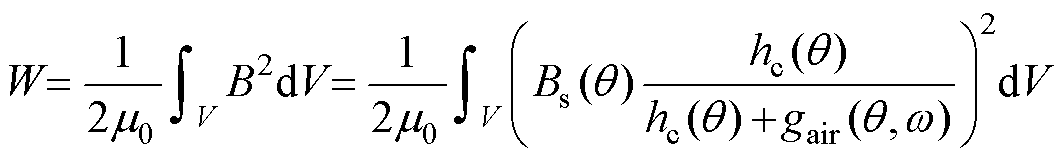 (2)
(2)
式中,m0为真空磁导率;B为气隙磁通密度幅值;V为气隙体积;Bs(q)为气隙磁通密度沿圆周的分布;hc(q)为永磁体充磁方向长度;gair(q,w)为有效气隙长度。
在得到电机磁场储能后,利用磁化密度和永磁体的磁化方向长度,通过傅里叶变换对电磁场储能表达式进行分解。
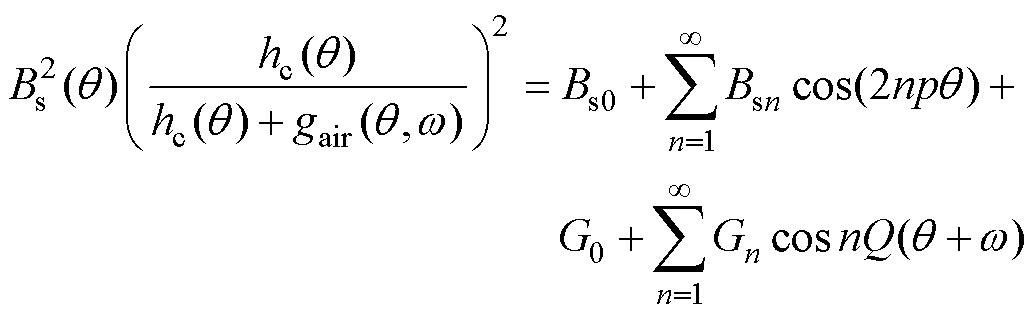 (3)
(3)
其中
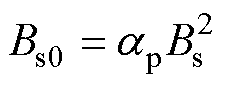 (4)
(4)
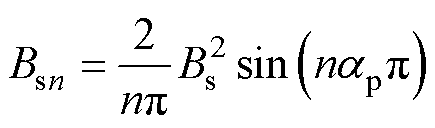 (5)
(5)
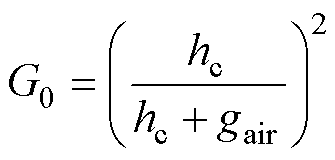 (6)
(6)
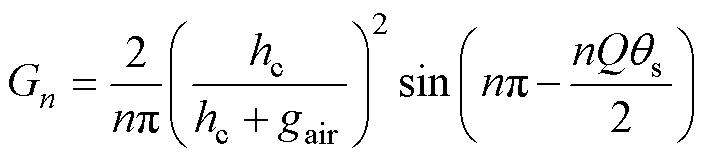 (7)
(7)
式中,Bs0、Bsn、G0、Gn为傅里叶变换后的未知变量;p为极对数;ap为永磁体极弧系数;Q为电机定子槽数;qs为槽口宽度(弧度表示);n为正整数,且能满足nQ/(2p)为整数,n的最小取值为2p/ GCD(2p,Q),GCD(2p,Q)为2p与Q的最大公约数[20]。
对于内置切向式电机来说,极弧系数定义为
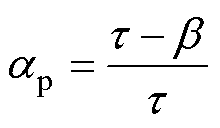 (8)
(8)
将式(2)~式(7)代入式(1),可得到齿槽转矩[18]为
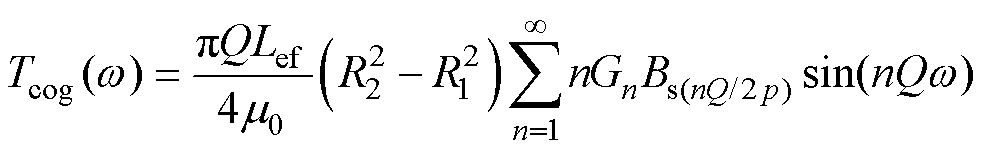 (9)
(9)
其中
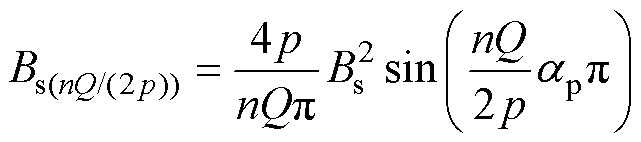 (10)
(10)
式中,Lef为铁心轴向长度;R2与R1分别为电机定子内径与转子外径。
由式(10)可知,选取合适极弧系数使Bs(nQ/2p)尽可能小能有效降低齿槽转矩,则需要满足
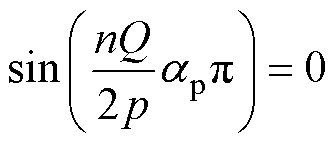 (11)
(11)
由式(11)可解得,ap=2kp/(nQ)(n为整数,且0<k<nQ/(2p)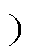 。
。
电机定子槽采用梯形槽结构,电机电枢绕组为分数槽集中绕组的形式,减小永磁电机端部绕组长度,降低铜耗。
转子结构为内置切向式转子结构,永磁同步电机的基本结构及dq轴如图2所示。
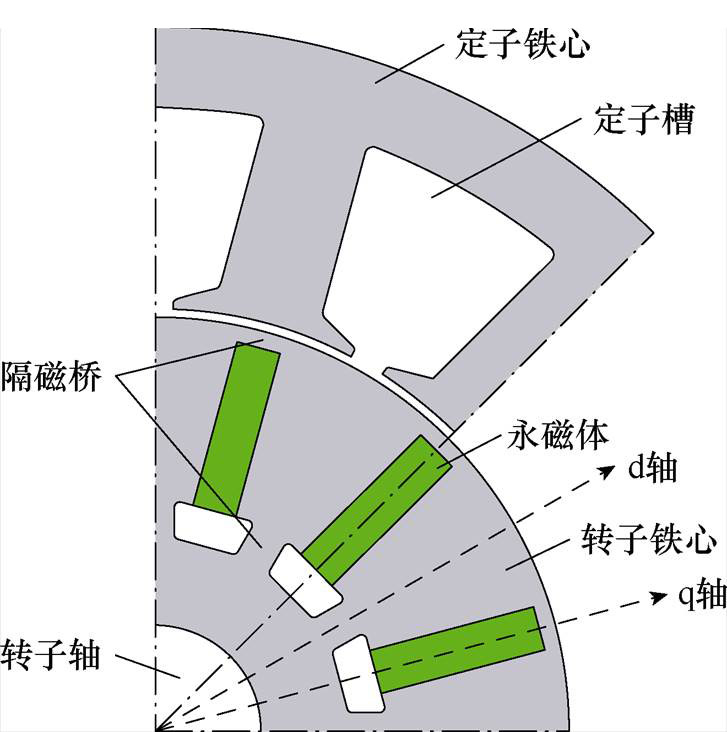
图2 内置切向式永磁同步电机基本结构1/4模型
Fig.2 Interior spoke-type permanent magnet synchronous motor basic structure 1/4 model
电机开矩形槽如图3所示,开槽宽度为do(mm)。电机开梯形槽如图4所示,假设靠近气隙一侧为梯形槽的长边,开口角度为电角度b(°),靠近永磁体一侧则为短边,开口角度为a (°),永磁体到气隙距离为h(mm)。
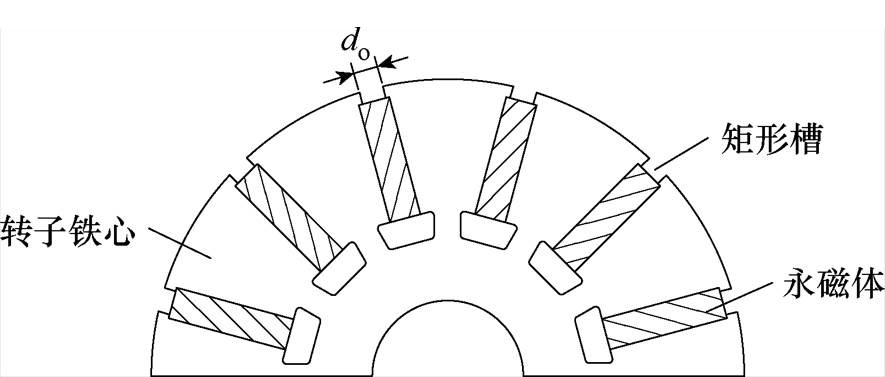
图3 矩形槽转子结构
Fig.3 Rectangular groove rotor structure diagram
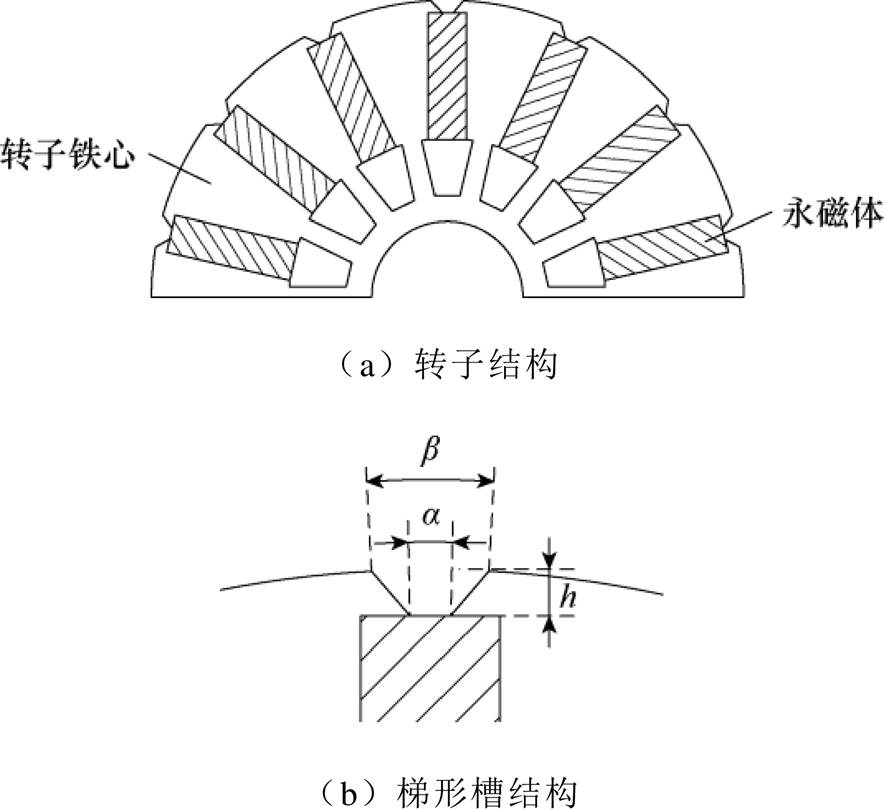
图4 电机转子示意图
Fig.4 Schematic diagram of the rotor of the motor
以一台12槽14极的永磁同步电机为研究对象,考虑三种槽结构对齿槽转矩的影响。电机参数见 表1,电机开梯形槽的模型示意图如图5所示。
表1 电机参数尺寸
Tab.1 Motor parameter dimensions
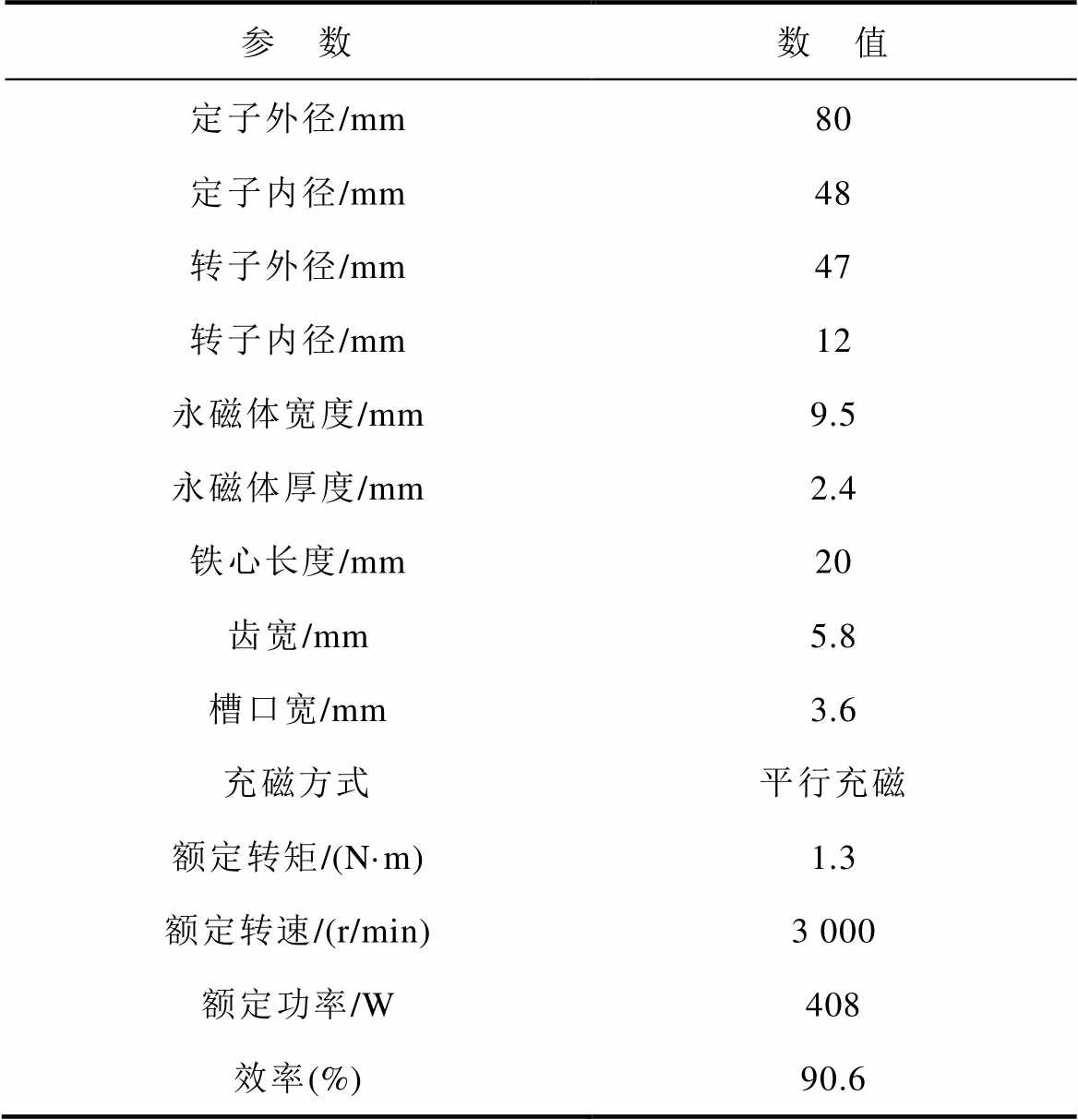
参 数数 值 定子外径/mm80 定子内径/mm48 转子外径/mm47 转子内径/mm12 永磁体宽度/mm9.5 永磁体厚度/mm2.4 铁心长度/mm20 齿宽/mm5.8 槽口宽/mm3.6 充磁方式平行充磁 额定转矩/(N·m)1.3 额定转速/(r/min)3 000 额定功率/W408 效率(%)90.6
对无槽转子结构、矩形槽转子结构及梯形槽转子结构进行有限元优化仿真。随着矩形槽开口变大,电机的漏磁降低,气隙磁通密度增大,电机的输出转矩增大,但齿槽转矩也较大,综合考虑输出转矩和齿槽转矩两种指标,矩形槽角度选取为4.8°,梯形槽长边开口角度为5°,短边开口角度为1°。三种转子结构齿槽转矩数据见表2。
图5 电机模型示意图
Fig.5 Schematic diagram of the motor model
表2 三种转子结构对应的齿槽转矩
Tab.2 The cogging torque corresponds to the three rotor configurations

转子结构齿槽转矩/(mN·m) 无槽转子37.28 矩形槽转子66.93 梯形槽转子13.17
转子结构开槽能降低电机漏磁,提高电机输出转矩。由仿真数据可知,转子结构开槽能影响电机的齿槽转矩,开矩形槽会增大电机的齿槽转矩,而开梯形槽能有效抑制齿槽转矩。
因此,本文接下来将研究梯形槽的高度、短边开口角度、长边开口角度对齿槽转矩的影响,以及不同极槽配合下梯形槽尺寸对齿槽转矩的影响。
梯形槽高度也表示为永磁体与转子外圆距离,随距离减小,电机的漏磁也有所降低,齿槽转矩也会发生变化。
针对梯形槽高度变化对齿槽转矩的影响规律进行研究分析,采用控制变量法,定义梯形槽长边开口角度b=6°,短边开口a=2°,取变量梯形槽高度h为0.6~1.1 mm,间隔0.1 mm,共6组数据进行仿真,结果见表3。
由表3中数据可知,齿槽转矩随槽口高度的增加而降低。此结果由于永磁体与气隙的距离增加,气隙磁场能量降低,齿槽转矩有所降低,因此同时考虑齿槽转矩与气隙磁通密度,梯形槽高度选取为1 mm,并且后续对不同极槽配合分析时,保持梯形槽高度为1 mm。
表3 不同梯形槽高度对应的齿槽转矩
Tab.3 Cogging torque corresponding to different trapezoidal groove heights
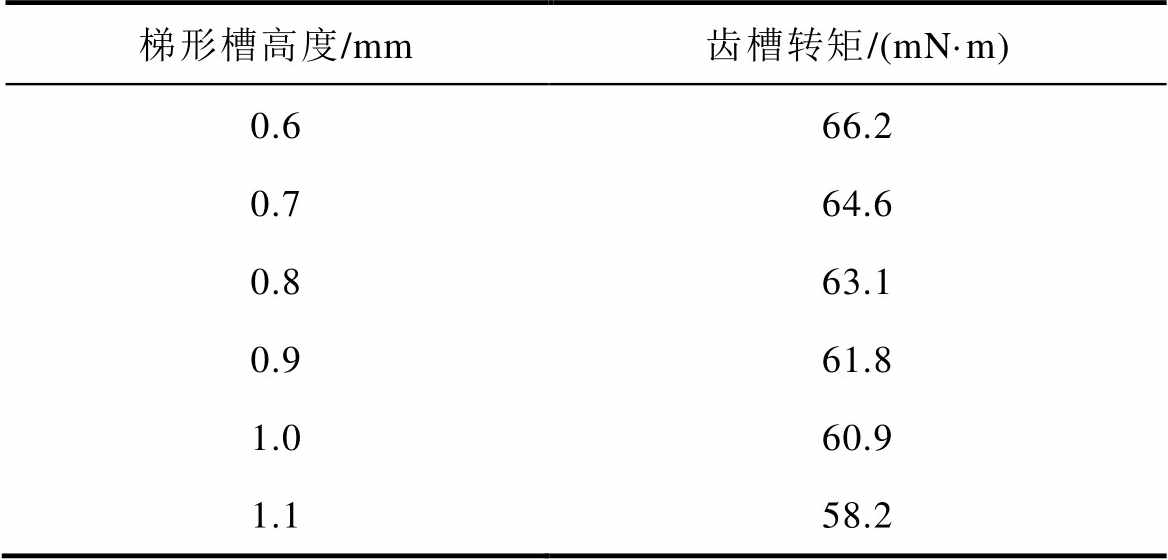
梯形槽高度/mm齿槽转矩/(mN·m) 0.666.2 0.764.6 0.863.1 0.961.8 1.060.9 1.158.2
当电机极槽配合为14极12槽时,根据式(11)可初步计算得ap=0.83、0.78,此时可得b为4.37°和5.66°,同时考虑梯形槽不同长边与短边开口角度的影响,选取梯形槽开口角度a、b为扫描参数,扫描范围与步长见表4。图6为不同梯形槽开口角度下的齿槽转矩数据。
表4 优化参数范围及步长
Tab.4 Optimization parameter range and step size (单位: °)

优化参数参数范围步长 a0.2~30.2 b3~60.2
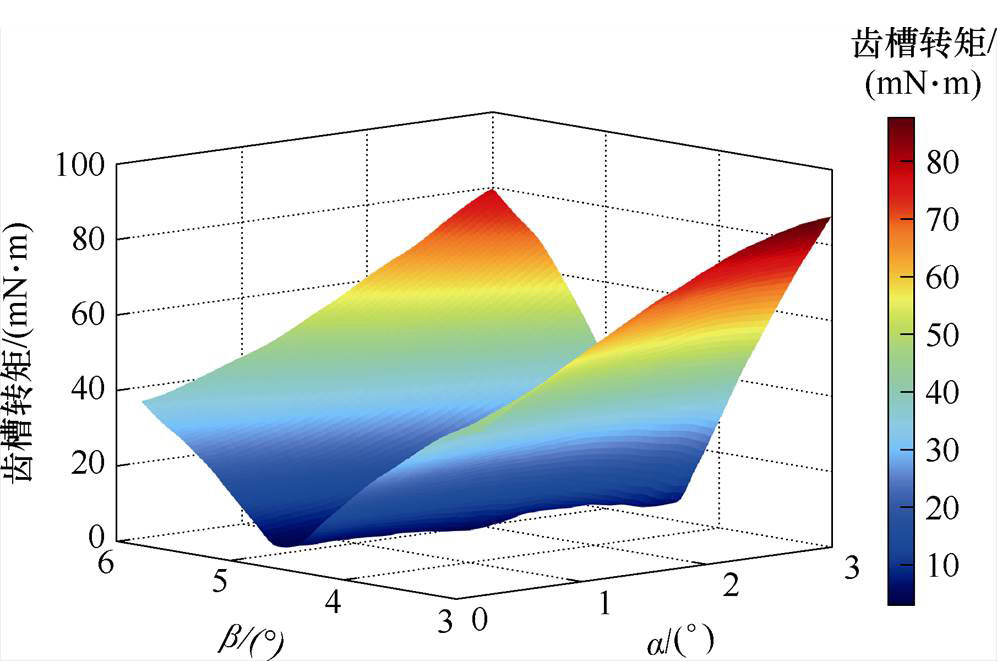
图6 14极12槽电机不同梯形槽开口角度齿槽转矩
Fig.6 14-poles 12-slots motor with different trapezoidal groove opening angles and cogging torque diagrams
分析数据,从图6中可以得出,随着梯形槽长边开口角度b的增加,电机齿槽转矩先降低后增加,在角度范围4.4°~5.6°时,相对较小;随着梯形槽短边开口角度a的增加,电机齿槽转矩为波动变化,在角度范围1.2°~1.4°时,相对较小。
考虑极数对尺寸系数的影响,更改极数为10极,其他参数保持不变。由式(11)可得,ap为0.80、0.83,此时可得b为7.2°和6.12°,将梯形槽长边开口角度扫描范围调整为5°~8°,仿真结果如图7所示。
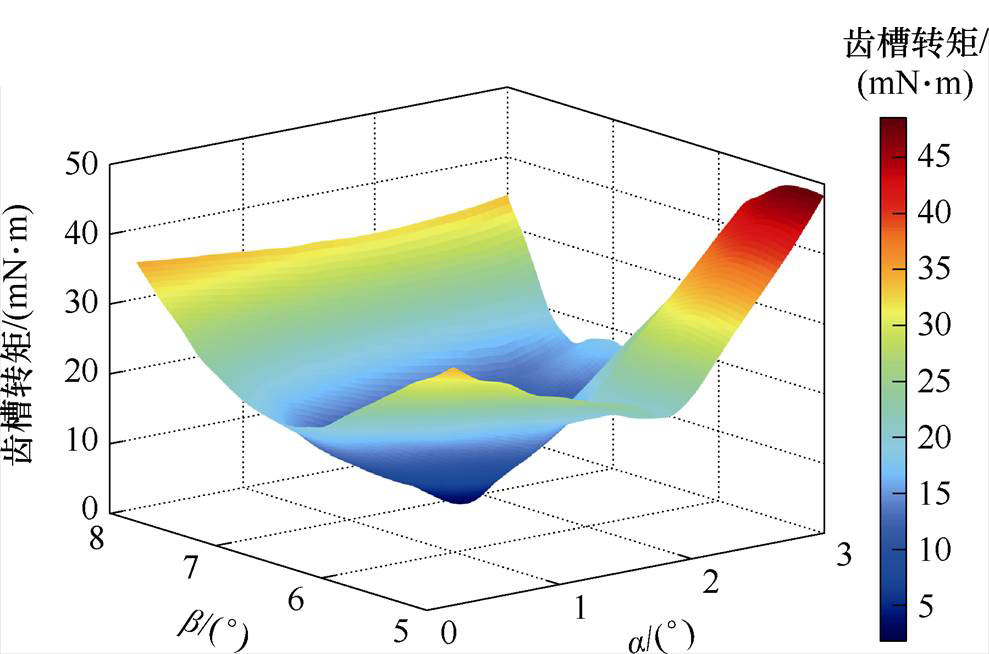
图7 10极12槽电机不同梯形槽开口角度齿槽转矩
Fig.7 10-poles 12-slots motor with different trapezoidal groove opening angles and cogging torque diagrams
由数据结果得出,梯形槽短边开口角度在1.4°~1.8°时,齿槽转矩相对较小;随着梯形槽长边开口角度的增加,电机齿槽转矩同样先降低后增加,梯形槽在长边开口角度b为6.2°~7.0°时,齿槽转矩相对较小。
考虑槽数对尺寸系数的影响,保持永磁体、定子及气隙等参数不变,将极槽配合调整为16极18槽。由式(11)可得ap为0.72、0.78,此时b为6.3°和4.95°,对电机静态齿槽转矩进行仿真,结果如图8所示。
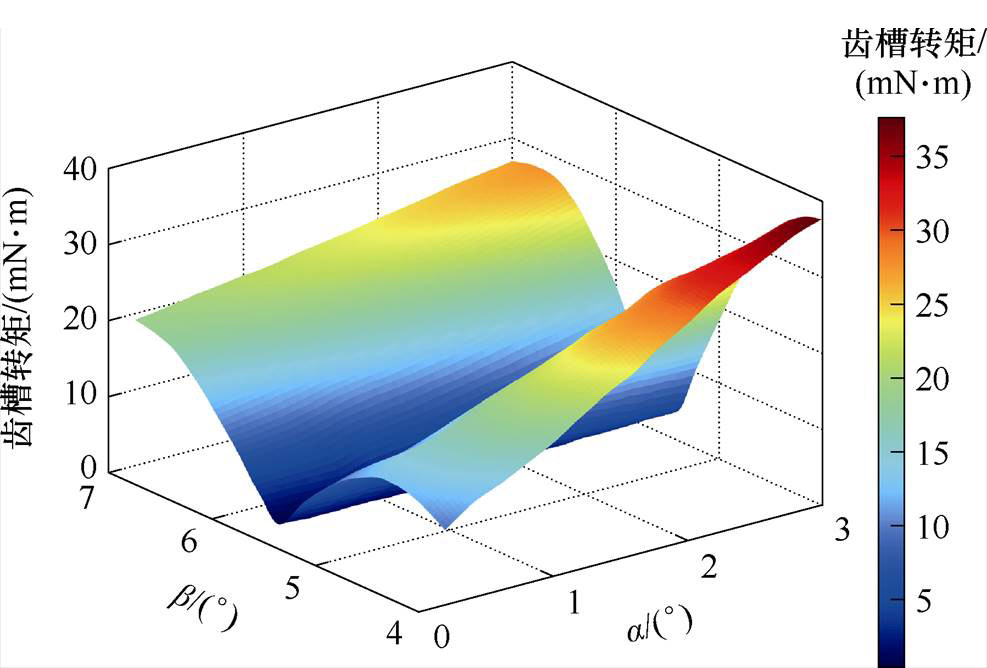
图8 16极18槽电机不同梯形槽开口角度齿槽转矩
Fig.8 16-poles 18-slots motor with different trapezoidal groove opening angles and cogging torque diagrams
由数据结果得出,随着梯形槽长边开口角度的增加,电机齿槽转矩同样先降低后增加,梯形槽在长边开口角度b为5.2°~6.0°时,齿槽转矩相对较小;梯形槽短边开口角度a在1.4°~1.6°时,齿槽转矩相对较小。
由此可知,针对内置切向式永磁同步电机,转子开梯形槽可降低电机齿槽转矩,当梯形槽长边开口角度b与短边开口角度a满足式(12)时,齿槽转矩抑制效果良好。
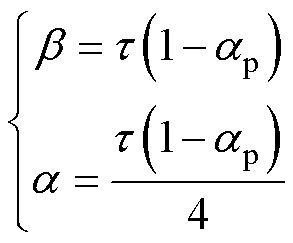 (12)
(12)
综合考虑电机的输出转矩与机械强度两种因素,极弧系数ap选取范围为0.7~0.9。
对电机电磁性能进行对比分析时采用表1数据,为满足转子机械强度,隔磁桥宽度选取为0.6 mm,对三种不同转子结构进一步仿真分析,转子无槽结构、矩形槽结构与梯形槽结构模型如图9所示。
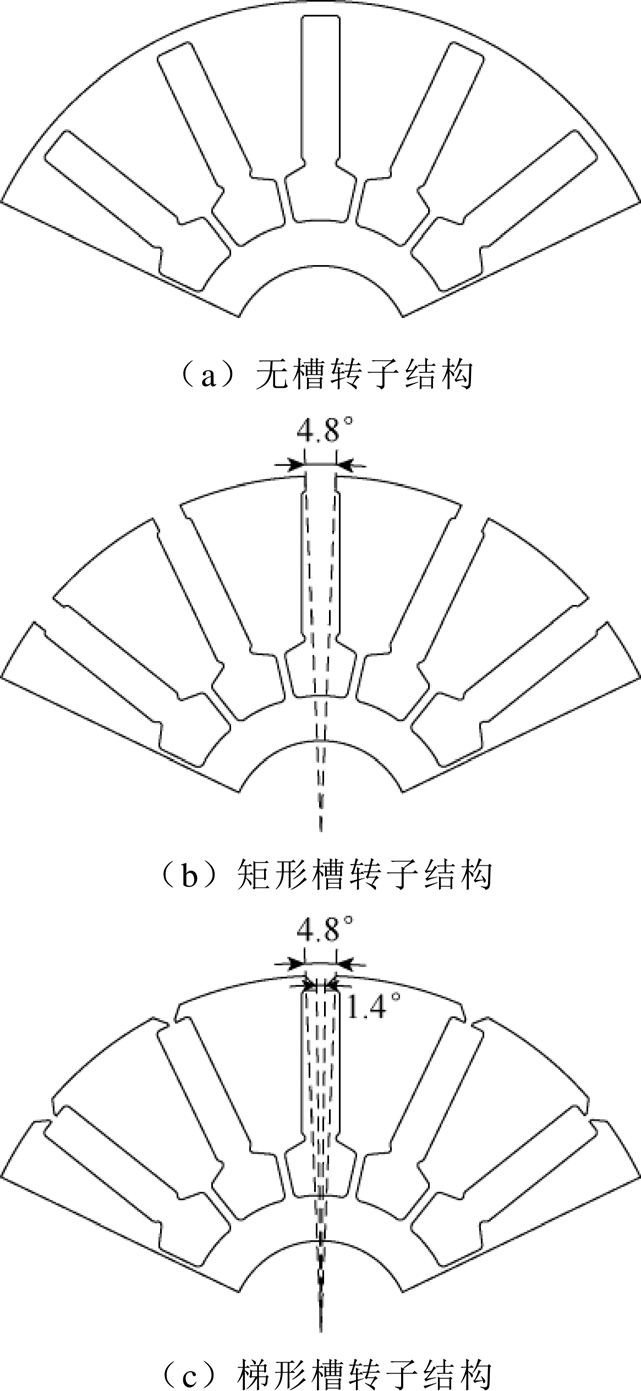
图9 电机转子结构模型对比
Fig.9 Comparison of motor rotor structure models
电机定、转子铁心硅钢片材料为A35-300,永磁体材料为N42H。电机绕组匝数为28,并联支路数为2。
图9a为无槽转子结构,图9b为矩形槽转子结构,极弧系数为0.81,计算后开口角度为4.8°,图9c为梯形槽转子结构,极弧系数为0.81,计算后梯形槽长边开口角度选取为4.8°,短边开口角度选取为1.4°。
空载反电动势为电机气隙磁场作用在电枢绕组上的表现,反电动势谐波畸变率对电机稳定运行具有一定影响。
对三种电机转子结构的空载反电动势进行有限元仿真,图10为三种电机在两个周期内的空载反电动势波形及其快速傅里叶变化分解结果。表5为三种转子结构空载反电动势数据。
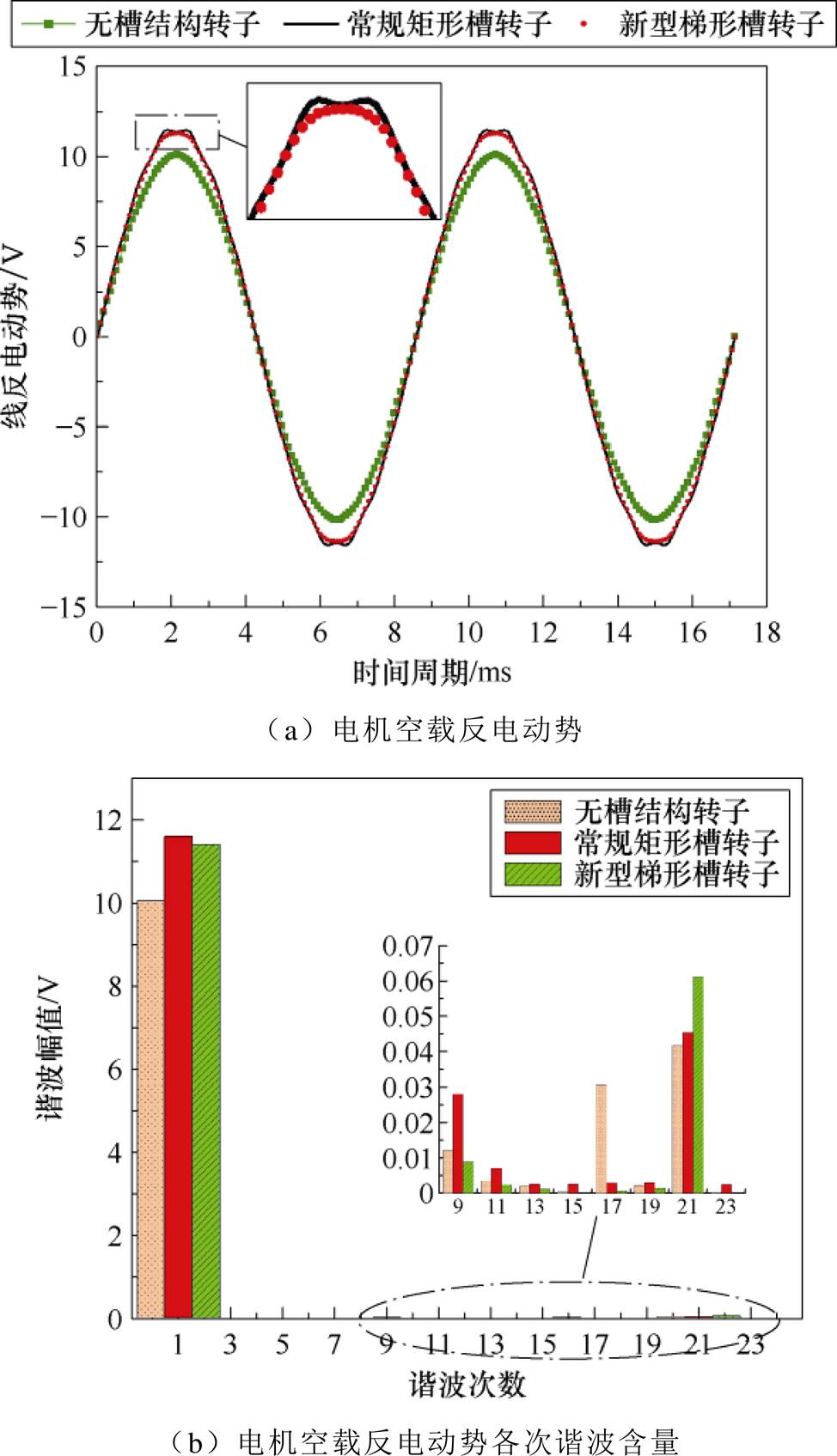
图10 空载反电动势及谐波含量
Fig.10 No-load back electromotive force and harmonic content diagram
表5 不同转子结构的空载反电动势
Tab.5 No-load back electromotive force for different rotor structures
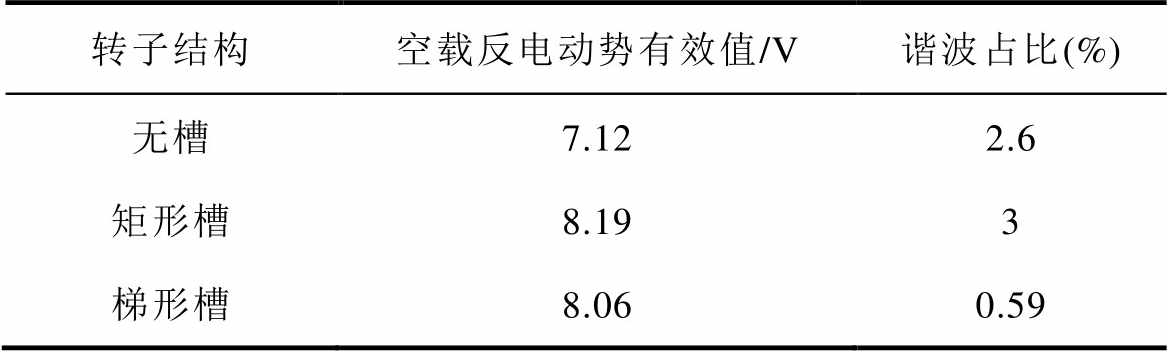
转子结构空载反电动势有效值/V谐波占比(%) 无槽7.122.6 矩形槽8.193 梯形槽8.060.59
无槽结构因漏磁较大,气隙磁通密度较低,空载反电动势低于开槽结构,两种开槽结构反电动势有效值较为接近。
对比反电动势谐波含量及幅值可知,新型梯形槽转子结构电机的21次谐波幅值略高于无槽结构电机与矩形槽电机,但由于其阶次较高且幅值很小,故可忽略,其余各阶次谐波幅值均低于矩形槽电机。
总谐波畸变率(Total Harmonic Distortion, THD)可表示[21]为
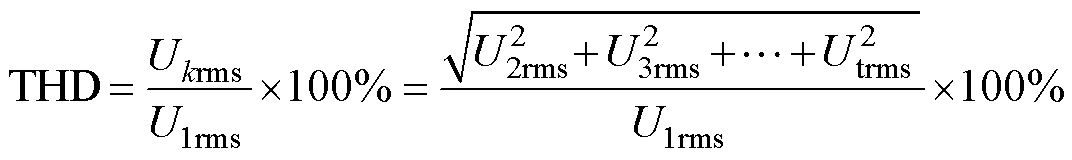 (13)
(13)
式中,Ukrms为各次谐波含量的方均根值(k=1, 2, 3,…, t);U1rms为基波的方均根值。
根据式(13)计算得到,无槽结构转子电机的空载反电动势谐波畸变率THD=2.6%,矩形槽转子结构电机的空载反电动势谐波畸变率THD=3%,而新型梯形槽转子结构电机的空载反电动势谐波畸变THD=0.59%。
分析数据,无槽结构反电动势有效值相对较低,电机转矩输出能力略低于开槽结构,开槽结构反电动势相对较高,但转子开矩形槽后,气隙磁阻发生变化,谐波畸变率较高,而梯形槽转子结构的电机反电动势谐波畸变率低,有利于电机稳定运行。
对三种转子结构进行齿槽转矩仿真分析,图11为三种结构电机在一个齿槽转矩周期内的齿槽转矩。
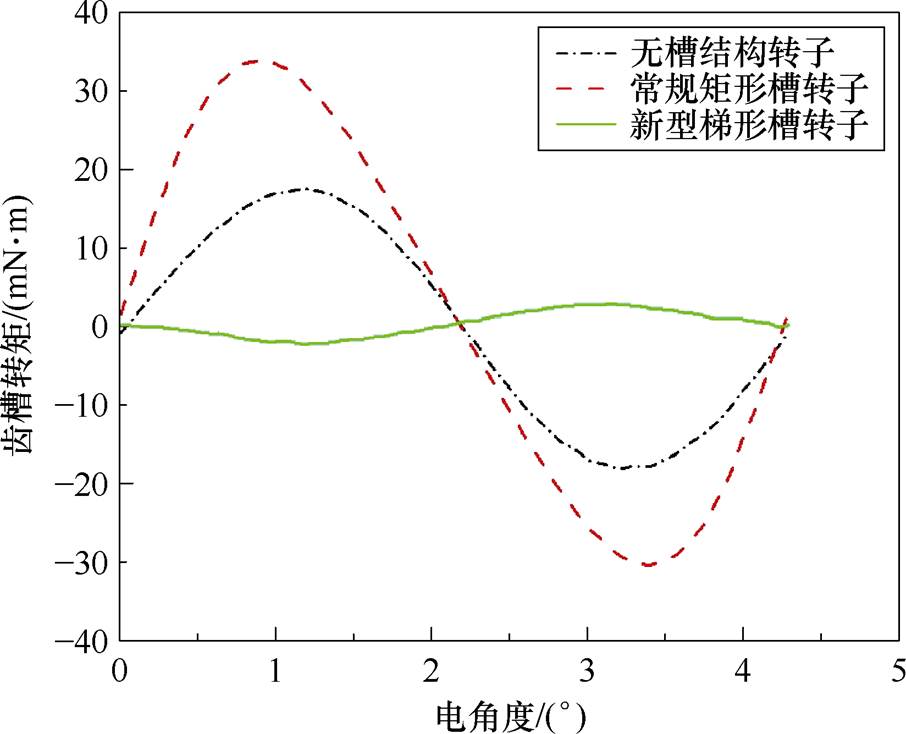
图11 三种结构齿槽转矩对比
Fig.11 Comparison of the cogging torque of the three structures
不同转子结构的齿槽转矩见表6,无槽结构和矩形槽结构转子齿槽转矩相对较高,将矩形槽改为梯形槽后,电机气隙磁通密度波形的形状接近正弦,谐波畸变率降低,电机的空载反电动势谐波占比降低80%,齿槽转矩抑制效果良好,相比于矩形槽转子,梯形槽转子的齿槽转矩降低90.9%,相比于无槽结构,梯形槽转子的齿槽转矩降低83.6%。
表6 不同转子结构的齿槽转矩
Tab.6 Cogging torque values for different rotor structures

转子结构齿槽转矩/(mN·m) 无槽35.65 矩形槽64.34 梯形槽5.83
电机的转矩波动和齿槽转矩原理相同,都是由于电机零阶切向电磁力所引起,在电机空载时表现为齿槽转矩,而在电机负载时表现为转矩波动,因此本方法可以有效降低转矩波动,图12为三种结构电机在额定工况下的转矩波形,转矩波动为
 (14)
(14)
式中,Tmax、Tmin、Tavg分别为输出转矩最大、最小、平均值。
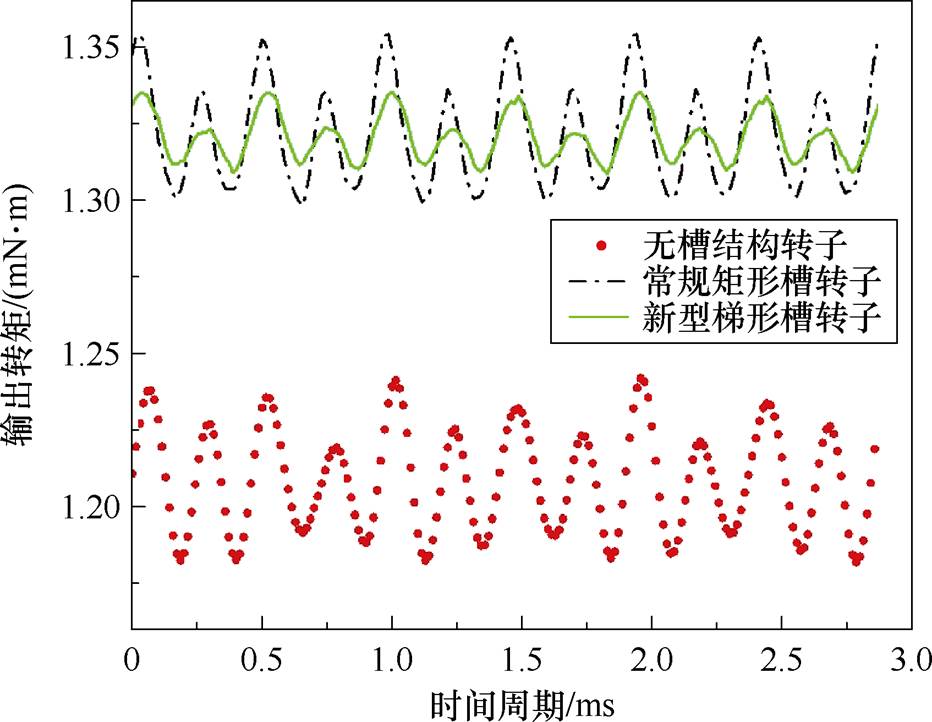
图12 额定工况下输出转矩
Fig.12 Torque diagram under rated operating conditions
不同电机转子结构转矩波动对比见表7,无槽结构电机的输出转矩为1.208 7 N·m,转矩波动经计算所得为4.96%,常规矩形槽电机的输出转矩为1.321 4 N·m,转矩波动经计算为5.34%,新型梯形槽电机的输出转矩为1.320 6 N·m,转矩波动为2.43%。无槽结构电机输出转矩较低,开槽结构电机在输出转矩接近的情况下,梯形槽电机转矩波动低于矩形槽电机54%,电机转矩输出性能更加稳定。
表7 不同电机转子结构转矩波动对比
Tab.7 Comparison of torque fluctuations of rotor structures of different motors
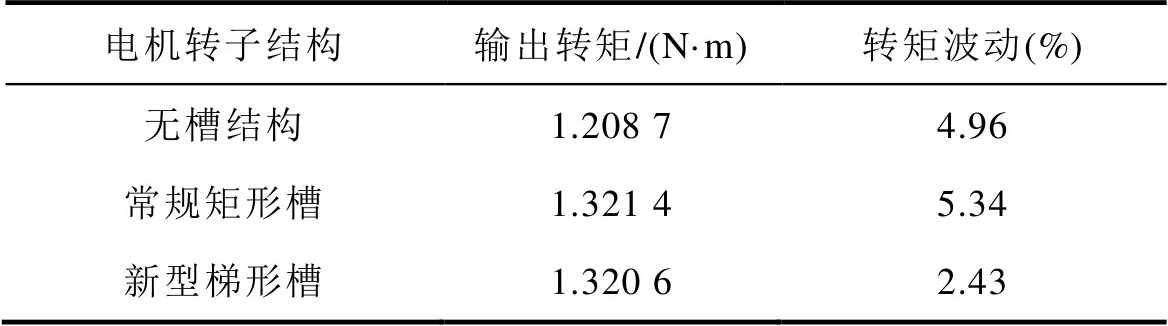
电机转子结构输出转矩/(N·m)转矩波动(%) 无槽结构1.208 74.96 常规矩形槽1.321 45.34 新型梯形槽1.320 62.43
为了验证仿真分析模型的正确性,将图9c转子结构制造成样机,并进行电机空载、静态齿槽转矩及负载性能实验。
图13为实验样机的定子铁心、转子铁心及样机整机,图14为样机整机与实验测试平台,其中测试平台包括转矩传感器与磁粉制动器,图15为样机空载实验反电动势波形。

图13 样机实物
Fig.13 Motor drawing

图14 样机整机及实验平台
Fig.14 Prototype machine and test platform
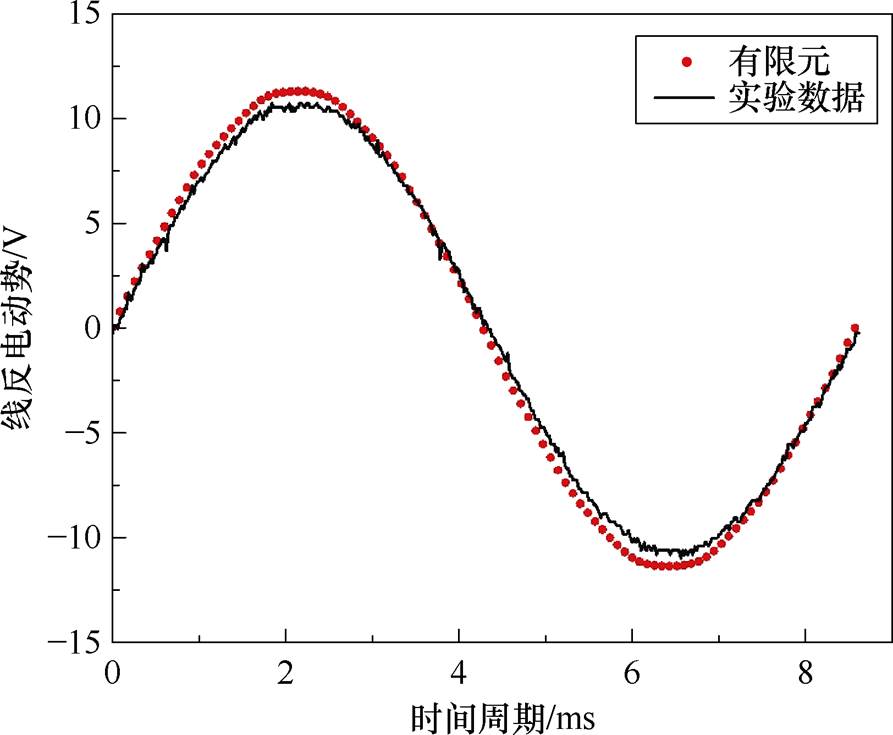
图15 空载反电动势波形
Fig.15 No-load back electromotive force waveforms
样机的空载反电动势有效值为7.75 V,对比有限元仿真8.06 V,误差为3.85%,这是由于工艺影响,定、转子真实气隙长度有所偏差以及实际永磁体尺寸略小于目标数据,该误差在允许范围内。
图16为齿槽转矩测试实验,用拉力计拉动联轴器所用的力与联轴器的力臂长度的乘积,即为电机空载时的齿槽转矩。

图16 齿槽转矩测试实验
Fig.16 Cogging torque test
由图16中拉力计数据可知,电机的静态阻力为0.03kg,齿槽转矩Tcog计算公式为
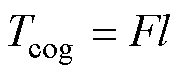 (15)
(15)
式中,F为拉力(N);l为力臂(m)。图16中,联轴器直径为45 mm。
由计算可得该样机齿槽转矩为6 mN·m,与有限元仿真对比误差为2.92%。因此,根据电机空载实验与齿槽转矩实验数据结果可知,空载反电动势计算误差为3.85%,齿槽转矩计算误差为2.92%,在误差允许范围内,因此实验结果验证了有限元仿真的有效性与实用性。
本文提出一种转子外圆开梯形槽结构来调整极弧系数抑制齿槽转矩的方法,并验证该方法的有效性,分析了转子开梯形槽高度、长边开口角度及短边开口角度对内置切向式永磁电机齿槽转矩的影响。由数据可得,随梯形槽高度增加,电机齿槽转矩减小,但减小幅度较小;随着梯形槽短边开口角度的增加,电机齿槽转矩为波动变化;随着梯形槽长边开口角度的增加,电机齿槽转矩先降低后增加。考虑两种开口角度对电机齿槽转矩的影响,给出抑制齿槽转矩的开口角度选取公式。同时,利用有限元软件仿真与计算,对比三种结构电机的空载反电动势、齿槽转矩与负载输出转矩,证明了新型梯形槽转子结构能降低电机漏磁、齿槽转矩及转矩波动,齿槽转矩降低90.9%,转矩波动降低54%。
对样机进行实验,实验结果表明,电机空载反电动势为7.75 V,误差为3.85%;齿槽转矩为6 mN·m,误差为2.92%,验证了新型梯形槽转子结构及开槽尺寸系数的有效性。因此,本文的主要研究工作对内置式永磁电机设计与生产具有重要意义。
参考文献
[1] 佟文明, 姚颖聪, 李世奇, 等. 考虑磁桥不均匀饱和的内置式永磁同步电机等效磁网络模型[J]. 电工技术学报, 2022, 37(12): 2961-2970.
Tong Wenming, Yao Yingcong, Li Shiqi, et al. Equivalent magnetic network model for interior permanent magnet machines considering non-uniform saturation of magnetic bridges[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 2961- 2970.
[2] Peng Chen, Wang Daohan, Feng Zhenkang, et al. A new segmented rotor to mitigate torque ripple and electromagnetic vibration of interior permanent mag- net machine[J]. IEEE Transactions on Industrial Elec- tronics, 2022, 69(2): 1367-1377.
[3] 高鹏, 任红兴, 王晓远, 等. 磁极径向组合式定子无磁轭模块化轴向磁通电机磁热特性分析[J/OL]. 电工技术学报, 2024: 1-15. (2024-10-30). https://link. cnki.net/doi/10.19595/j.cnki.1000-6753.tces.241230.
Gao Peng, Ren Hongxing, Wang Xiaoyuan, et al. Magnetic and thermal characteristics analysis of magnetic pole radial combination yokeless and segmented armature axial flux machine[J/OL]. Transa- ctions of China Electrotechnical Society, 2024: 1-15. (2024-10-30). https://link.cnki.net/doi/10.19595/j.cnki. 1000-6753.tces.241230.
[4] 李仕豪, 狄冲, 刘佶炜, 等. 考虑交叉耦合影响的内置式永磁同步电机电感计算及转矩分析[J]. 电工技术学报, 2023, 38(18): 4889-4899, 4931.
Li Shihao, Di Chong, Liu Jiwei, et al. Inductance calculation and torque analysis of interior permanent magnet synchronous machine considering cross- coupling effects[J]. Transactions of China Electro- technical Society, 2023, 38(18): 4889-4899, 4931.
[5] 孙玉华, 赵文祥, 吉敬华, 等. 高转矩性能多相组永磁电机及其关键技术综述[J]. 电工技术学报, 2023, 38(6): 1403-1420.
Sun Yuhua, Zhao Wenxiang, Ji Jinghua, et al. Overview of multi-star multi-phase permanent magnet machines with high torque performance and its key technologies[J]. Transactions of China Electro- technical Society, 2023, 38(6): 1403-1420.
[6] 王道涵, 彭晨, 王柄东, 等. 电动汽车新型转子内置式永磁同步电动机转矩脉动与电磁振动抑制研究[J]. 中国电机工程学报, 2022, 42(14): 5289-5300.
Wang Daohan, Peng Chen, Wang Bingdong, et al. Research on a novel interior permanent magnet machine with segmented rotor to mitigate torque ripple and electromagnetic vibration[J]. Proceedings of the CSEE, 2022, 42(14): 5289-5300.
[7] 王群京, 郑耀达, 刘先增. 基于结构参数优化的电机振动噪声的抑制研究[J]. 电气工程学报, 2023, 18(2): 16-25.
Wang Qunjing, Zheng Yaoda, Liu Xianzeng. Research on suppression of motor vibration and noise based on structural parameter optimization[J]. Journal of Elec- trical Engineering, 2023, 18(2): 16-25.
[8] 高锋阳, 齐晓东, 李晓峰, 等. 不等宽不等厚Halbach部分分段永磁同步电机电磁性能解析计算与优化分析[J]. 电工技术学报, 2022, 37(6): 1398- 1414.
Gao Fengyang, Qi Xiaodong, Li Xiaofeng, et al. Analytical calculation and optimization analysis of electromagnetic performance of halbach partially- segmented permanent magnet synchronous motors with unequal width and thickness[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1398- 1414.
[9] 高锋阳, 齐晓东, 李晓峰, 等. 部分分段Halbach永磁同步电机优化设计[J]. 电工技术学报, 2021, 36(4): 787-800.
Gao Fengyang, Qi Xiaodong, Li Xiaofeng, et al. Optimization design of partially-segmented halbach permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(4): 787-800.
[10] 杨玉波, 王秀和, 丁婷婷. 一种削弱永磁同步电动机齿槽转矩的方法[J]. 电机与控制学报, 2008, 12(5): 520-523.
Yang Yubo, Wang Xiuhe, Ding Tingting. Method of reducing cogging torque of solid-rotor permanent magnet synchronous motors[J]. Electric Machines and Control, 2008, 12(5): 520-523.
[11] 杨玉波, 王秀和, 朱常青. 基于分块永磁磁极的永磁电机齿槽转矩削弱方法[J]. 电工技术学报, 2012, 27(3): 73-78.
Yang Yubo, Wang Xiuhe, Zhu Changqing. Effect of permanent magnet segmentation on the cogging torque of surface mounted permanent magnet motors[J]. Transactions of China Electrotechnical Society, 2012, 27(3): 73-78.
[12] Ge Xiao, Zhu Z Q, Kemp G, et al. Optimal step-skew methods for cogging torque reduction accounting for three-dimensional effect of interior permanent magnet machines[J]. IEEE Transactions on Energy Con- version, 2017, 32(1): 222-232.
[13] Ren Wu, Xu Qiang, Li Qiong, et al. Reduction of cogging torque and torque ripple in interior PM machines with asymmetrical V-type rotor design[J]. IEEE Transactions on Magnetics, 2016, 52(7): 8104105.
[14] 王力新, 王晓远, 高鹏, 等. 电动汽车用内置式永磁同步电机转矩脉动分析及抑制[J]. 电工技术学报, 2024, 39(20): 6386-6396.
Wang Lixin, Wang Xiaoyuan, Gao Peng, et al. Torque ripple reduction analysis of interior permanent magnet synchronous motor for electric vehicle[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(20): 6386-6396.
[15] Song C H, Kim D H, Kim K C. Design of a novel IPMSM bridge for torque ripple reduction[J]. IEEE Transactions on Magnetics, 2021, 57(2): 8201004.
[16] Liu Chengcheng, Huang Xiaorui, Zhang Wenfeng, et al. Shape optimization and demagnetization analysis of interior permanent magnet synchronous machine with hybrid cores[J]. AIP Advances, 2023, 13(3): 035215.
[17] 韩雪岩, 王勇, 高俊. 低速永磁同步电机转子偏心的抑制措施[J]. 电机与控制学报, 2023, 27(11): 58-65.
Han Xueyan, Wang Yong, Gao Jun. Suppression of rotor eccentricity of low-speed permanent magnet synchronous motor[J]. Electric Machines and Control, 2023, 27(11): 58-65.
[18] 位海洋. 内置式永磁同步电机的转矩脉动优化研究[D]. 沈阳: 沈阳工业大学, 2021.
Wei Haiyang. Research on torque ripple optimization of interior permanent magnet synchronous machines[D]. Shenyang: Shenyang University of Technology, 2021.
[19] 卢志远, 王宇, 王锁. 基于磁导等效分离的无轴承永磁同步电机齿槽转矩解析[J/OL]. 电工技术学报, 2025: 1-14. (2025-01-24). https://link.cnki.net/doi/10. 19595/j.cnki.1000-6753.tces.241318.
Lu Zhiyuan, Wang Yu, Wang Suo. Analysis of cogging torque in a bearing-less permanent magnet synchronous motor based on magnetic permeability equivalent separation[J/OL]. Transactions of China Electrotechnical Society, 2025: 1-14. (2025-01-24). https://link.cnki.net/doi/10.19595/j.cnki.1000-6753. tces.241318.
[20] 邢泽智, 王秀和, 赵文良. 基于不同极弧系数组合分段倾斜磁极的表贴式永磁同步电机齿槽转矩削弱措施研究[J]. 中国电机工程学报, 2021, 41(16): 5737-5748.
Xing Zezhi, Wang Xiuhe, Zhao Wenliang. Research on reduction methods of cogging torque based on segmented skewing magnetic poles with different combinations of pole-arc coefficients in surface- mounted permanent magnet synchronous motors[J]. Proceedings of the CSEE, 2021, 41(16): 5737-5748.
[21] 谢颖, 黑亮声, 华邦杰, 等. 新型永磁游标电机的设计与研究[J]. 电机与控制学报, 2019, 23(2): 68-74.
Xie Ying, Hei Liangsheng, Hua Bangjie, et al. Design and analysis of a new vernier permanent-magnet motor[J]. Electric Machines and Control, 2019, 23(2): 68-74.
Abstract To solve the problems of ample cogging torque and severe torque fluctuation of interior permanent magnet synchronous motors (IPMSM), an interior spoke-type IPMSM cogging torque suppression method with a trapezoidal groove structure of the rotor core is proposed. This method can effectively reduce the harmonic proportion of cogging torque and no-load back electromotive force of the motor, as well as the torque fluctuation of the motor.
Firstly, the cogging torque calculation formula of the IPMSM with a semi-closed groove is derived by an analytical method. Changing the polar arc coefficient and air gap shape of the permanent magnet motor can effectively suppress cogging torque. For the interior spoke-type structure, a new method for reducing the cogging torque is proposed. A new expression for calculating the polar arc coefficient is proposed to change the shape of the air gap and the polar arc coefficient by changing the shape and size of the grooving.
Secondly, taking a 14-pole 12-slot interior spoke-type permanent magnet synchronous motor as an example, the influence of trapezoidal groove height on cogging torque is explored by finite element simulation. The cogging torque decreases with the increase in notch height. At the same time, the influence of the short-side opening angle and the long-side opening angle of the trapezoidal groove on the cogging torque is analyzed under the combination of three common pole grooves: 14-pole 12-slot, 10-pole 12-slot, and 16-pole 18-groove. Combined with the cogging torque calculation formula, polar arc coefficient calculation formula, and finite element simulation analysis, the trapezoidal groove selection formula is given. In addition, this paper compares the no-load back EMF, back EMF harmonic proportion, cogging torque, and torque fluctuation of the slot-less rotor, rectangular slot rotor structure, and the optimized trapezoidal slot rotor structure permanent magnet synchronous motor. The cogging torque of the trapezoidal rotor is reduced by 90.9% and 83.6% compared with the rectangular groove rotor and the slot-less structure. The output torque of the slot-less structure motor is low, and the torque fluctuation of the trapezoidal slot motor is 54% lower than that of the rectangular slot motor when the output torque of the slot-less structure motor is close. The torque output performance of the motor is stable.
Finally, the motor no-load test and static cogging torque test were carried out. The effective value of the no-load back electromotive force of the test prototype was 7.75 V. The cogging torque was 6 mN·m with an error of 2.92%. The experimental errors are all within the allowable range, verifying the effectiveness and practicability of the finite element simulation. This paper provides an effective method to solve the problem of significant cogging torque and torque fluctuation of IPMSM.
keywords:Interior permanent magnet synchronous motors (IPMSM), spoke-type, trapezoidal groove, cogging torque, torque ripple
DOI: 10.19595/j.cnki.1000-6753.tces.242114
中图分类号:TM351
中央军委装备发展部预研项目(31512040107)、国家优秀青年科学基金项目(52222702)、国家自然科学基金项目(52477059)和辽宁省教育厅面上项目(LJ212410142019)资助。
收稿日期 2024-11-26
改稿日期 2024-12-26
吴胜男 女,1985年生,副教授,硕士生导师,研究方向为特种电机及其控制。E-mail: imwushengnan@163.com
佟文明 男,1984年生,教授,博士生导师,研究方向为高性能电机及其控制。E-mail: twm822@126.com(通信作者)
(编辑 崔文静)