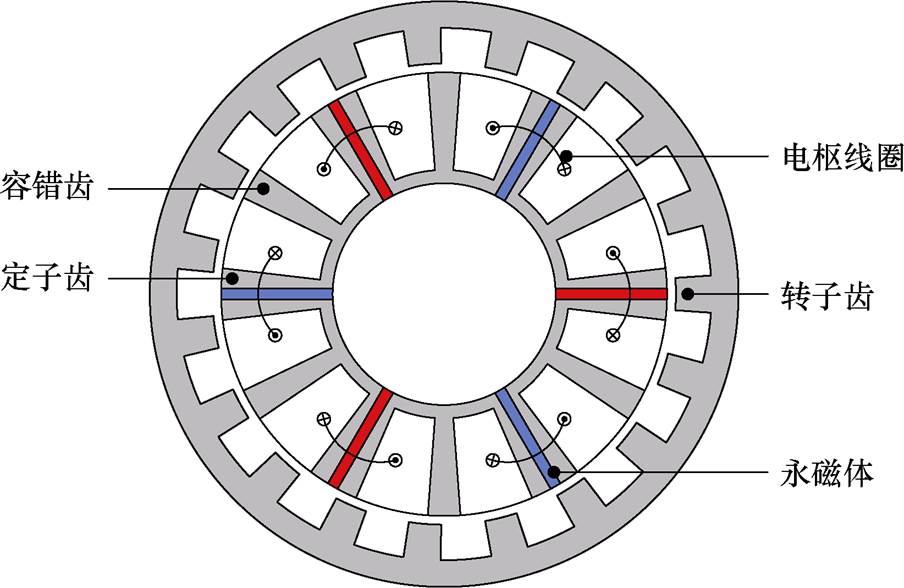
图1 磁通切换型永磁轮毂电机拓扑结构
Fig.1 Topology of the flux-switching permanent magnet in-wheel motor
摘要 凭借转矩密度较大、结构简单坚固、便于散热等优点,磁通切换型永磁轮毂电机在近年来得到广泛的研究。在其设计与优化过程中,大规模的电磁性能计算十分依赖求解耗时长、内存占用大的有限元软件,严重影响研发进度。针对上述问题,该文基于磁感原理,提出了一种矢量磁网络模型,旨在对电机性能进行快速准确的评估。除了考虑饱和现象和极间漏磁之外,该模型将涡流效应纳入考量,通过引入磁感元件实现对涡流效应的刻画。在此基础上,分别利用磁阻网络模型、矢量磁网络模型和有限元方法计算了一台磁通切换型永磁轮毂电机的电磁性能,并将计算结果与样机实验进行对比,验证所提模型的有效性。结果表明,相较于传统磁阻网络模型,矢量磁网络模型具有更高的电磁性能计算精度;相较于有限元模型,矢量磁网络模型具有更快的求解速度。
关键词:矢量磁路理论 磁通切换 磁感元件 轮毂电机 磁网络模型
近年来,随着电驱系统的技术水平快速提升,分布式轮毂驱动系统被视为未来电动汽车发展的必然方向[1]。虽然分布式轮毂驱动电动汽车的可操纵性更好[2]、安全性更高,但狭窄的轮内空间和恶劣的工作环境对轮毂电机的性能提出了更高的要求[3-4],如转矩密度高、容错性能好[5]等。针对上述要求,国内外学者对电动汽车用轮毂电机结构进行了诸多探索,提出了永磁辅助同步磁阻型轮毂电机[2]、多齿型双凸极永磁轮毂电机[3]、游标永磁轮毂电机[4]及磁通切换型永磁轮毂电机[5]等拓扑。
作为定子永磁型电机的典型代表,磁通切换型永磁轮毂(Flux Switching Permanent Magnet-In Wheel, FSPM-IW)电机的永磁体和绕组均安装于定子[6],转子仅由硅钢片叠压而成,不仅便于进行热管理[7-8],还极大地提升了转子的结构强度[9-10]。由于相邻永磁体之间的“聚磁效应”,FSPM-IW电机在额定工作点处具有更高的转矩密度[11-12]。因此,FSPM-IW电机在电动汽车用轮毂电机的应用中崭露头角,获得了广泛的关注。
为了满足轮毂电机的性能要求,在设计和优化阶段的大规模电磁性能计算通常依赖商用有限元软件展开,而有限元方法存在的内存占用大、计算耗时长等问题在所难免[13-15]。针对上述问题,等效磁网络模型从磁路分析法中衍生而来,能够很好地兼顾求解精度和求解速度,降低轮毂电机的研发难 度[15-17]。然而,即使目前国内外已有较多围绕磁网络模型建模方法的研究,仍有以下两个问题亟待解决。一方面,现有磁网络模型难以对电机铁耗进行准确计算[18-19]。现有方法通常在计算铁心磁通后,根据硅钢片材料的B-P曲线查表获得电机铁耗。由于磁网络模型采用集总磁路参数建模,不可避免地要对铁心中流过的磁通进行一定程度的简化,因此难以通过上述方法准确地计算电机铁耗[19]。另一方面,现有磁网络模型仅涉及磁阻元件,没有考虑铁心中涡流效应对磁通的反作用[20],由此导致计算所得磁通与铁心中流过磁通之间存在偏差,从而在评估电磁性能时产生误差。
最近提出的矢量磁路理论为解决上述两个问题提供了全新思路[20-21]。根据矢量磁路理论,电机铁心中的涡流反作用可以等效为闭合的导电线圈,进而通过等效磁感元件进行刻画[22]。此外,磁感元件的引入使涡流损耗的计算流程得到较大简化,计算精度也进一步提升[23-24],且不再依赖传统的铁耗经验计算公式,能够在电机初始设计阶段准确高效地评估涡流损耗。
综上所述,本文基于矢量磁路理论提出了一种全新的矢量磁网络模型。该方法将铁心中的涡流效应等效为磁感元件,然后利用“磁阻-磁感”串联支路建立矢量磁网络模型。相较于传统的磁阻网络模型,基于磁感原理的矢量磁网络模型在简化涡流损耗计算流程的同时,将涡流反作用纳入考量,从而更为准确地求解电磁性能。本文首先以一台磁通切换型永磁轮毂电机为研究对象,在介绍其拓扑结构后,从模型建立、迭代求解等角度提出了矢量磁网络模型。然后,分别采用传统磁阻网络模型、所提矢量磁网络模型以及有限元方法对电磁性能进行计算,并横向对比计算结果。最后,通过样机实验,进一步验证本文理论分析的正确性。
本文所研究的FSPM-IW电机结构如图1所示。该电机的定子由6个E形铁心单元和6块夹在其中的永磁体构成。其中,永磁体为切向磁化,并且相邻两块永磁体的磁化方向相反,由此产生的“聚磁效应”有利于增大FSPM-IW电机在额定点处的转矩密度。两个定子齿和一块永磁体共同组成一个定子极,6个集中式电枢线圈分别绕制在每一个定子极上,并相互连接构成三相电枢绕组。需要注意的是,相邻两个电枢线圈属于不同相绕组,且被容错齿隔开。这一设计有利于增强相间隔离,提升FSPM-IW电机的容错性能。此外,FSPM-IW电机的转子仅由硅钢片冲压而成,没有设置绕组和永磁体,其结构简单坚固,无需额外的保护措施,非常适合应用于轮毂直驱系统中。

图1 磁通切换型永磁轮毂电机拓扑结构
Fig.1 Topology of the flux-switching permanent magnet in-wheel motor
磁感元件可以定量地表征电机铁心中涡流效应对磁通的反作用[21, 23]。根据矢量磁路理论,除了传统磁网络模型中的磁阻元件外,还应引入磁感元件,从而更加准确地计算铁心中流过的磁通[22]。硅钢片矢量支路示意图如图2所示,在矢量磁网络模型中,FSPM-IW电机的每一片硅钢片均可等效为一条“磁阻-磁感”串联支路。图中,R、L分别为单片硅钢片的磁阻和磁感,下标x为第x片硅钢片,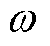 为铁心中磁通交变的角频率,
为铁心中磁通交变的角频率,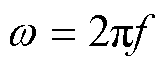 ,f为磁通频率。
,f为磁通频率。
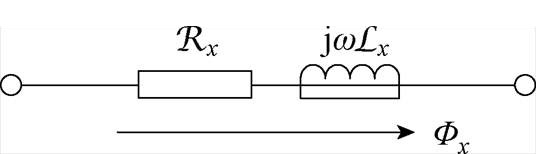
图2 硅钢片矢量支路示意图
Fig.2 Diagram of silicon steel sheet vector branch
结合图1,FSPM-IW电机的铁心可以划分为两类典型区域,分别为定转子轭部的弧形区域和定转子齿部的楔形区域,如图3所示。为了方便后续建立矢量磁网络模型,本节给出FSPM-IW电机中两种形状硅钢片的磁阻和磁感参数初值计算方法。图3中红色箭头所指为硅钢片中的磁通流动方向,且与图2中的红色箭头对应。
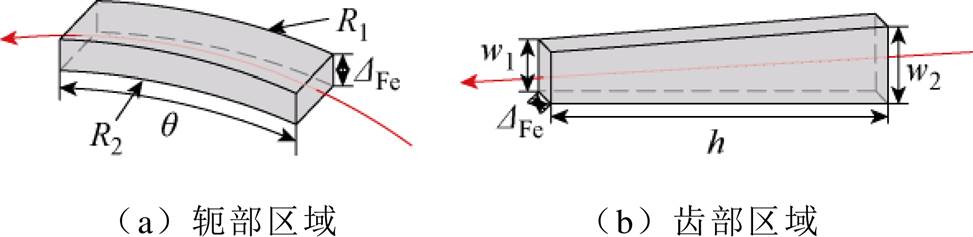
图3 铁心参数计算示意图
Fig.3 Calculation diagrams of iron core parameters
定转子轭部和齿部磁阻参数的计算方法为
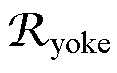
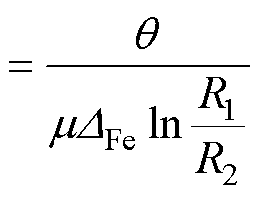 (1)
(1)
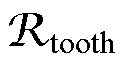
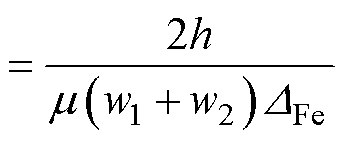 (2)
(2)
式中,R1、R2、h、q、w1、w2为尺寸参数,见图3标注;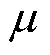 为硅钢片磁导率;
为硅钢片磁导率;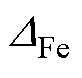 为硅钢片的厚度。
为硅钢片的厚度。
支路磁感参数计算式[21]为
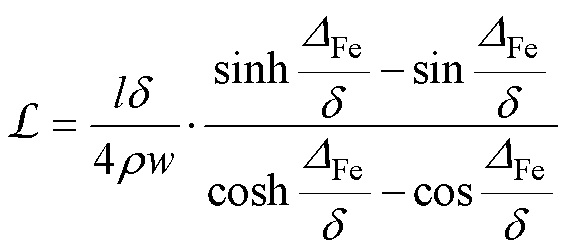 (3)
(3)
式中,l为硅钢片沿磁通方向的长度;w为硅钢片垂直磁通方向的宽度;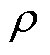 为铁心材料的电阻率;
为铁心材料的电阻率;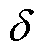 为计及趋肤效应时的趋肤深度。
为计及趋肤效应时的趋肤深度。
将式(3)中的三角函数与双曲函数按麦克劳林级数展开,并取前两项,可以推导出轭部区域的磁感参数计算方法为
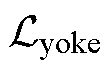
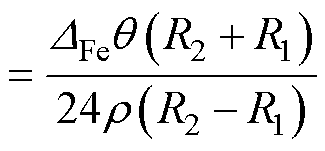 (4)
(4)
同理,定子齿、容错齿,以及转子齿部的楔形区域磁感参数计算方法为
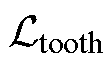
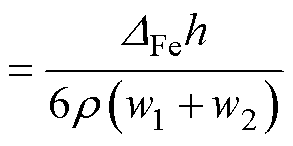 (5)
(5)
由此,硅钢片的磁阻抗参数可表示为
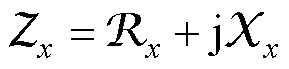 (6)
(6)
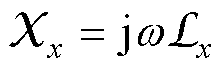 (7)
(7)
式中,j为虚数单位;Z、X分别为单片硅钢片的磁阻抗、磁抗。
对于磁通切换型电机,定、转子铁心中的磁通角频率并不相同,可分别计算为
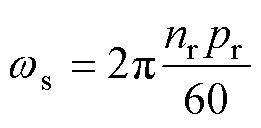 (8)
(8)
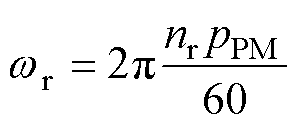 (9)
(9)
式中,nr为转子转速;pr和pPM分别为转子齿数和永磁体极对数。
FSPM-IW电机铁心支路可以视为每片硅钢片所对应支路的并联[20],即铁心支路参数为
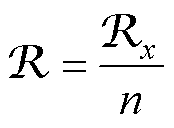 (10)
(10)
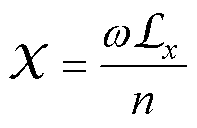 (11)
(11)
式中,n为FSPM-IW电机铁心所叠压的硅钢片片数。本文研究的FSPM-IW电机铁心采用硅钢片型号为50WW600,轴向长度为60 mm,共计叠压118片。
此外,铁心支路的磁导纳参数可计算为
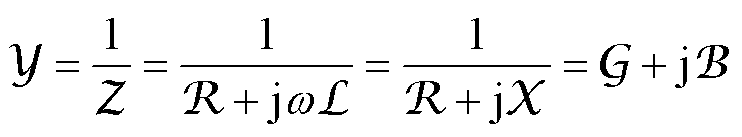 (12)
(12)
式中,Y、G、B分别为铁心支路的磁导纳、磁导、磁纳。
FSPM-IW电机定子铁心的建模方法如图4所示,FSPM-IW电机参数见表1。由于FSPM-IW电机的定子齿和容错齿均为楔形结构,靠近气隙一侧的齿宽较大,故沿径向将二者分别划分为两部分,并且将靠近气隙侧的齿一分为二,以此增加矢量磁网络模型的求解精度。此外,FSPM-IW电机中的永磁体和电枢绕组均以磁动势源的形式连接在定子轭部支路。
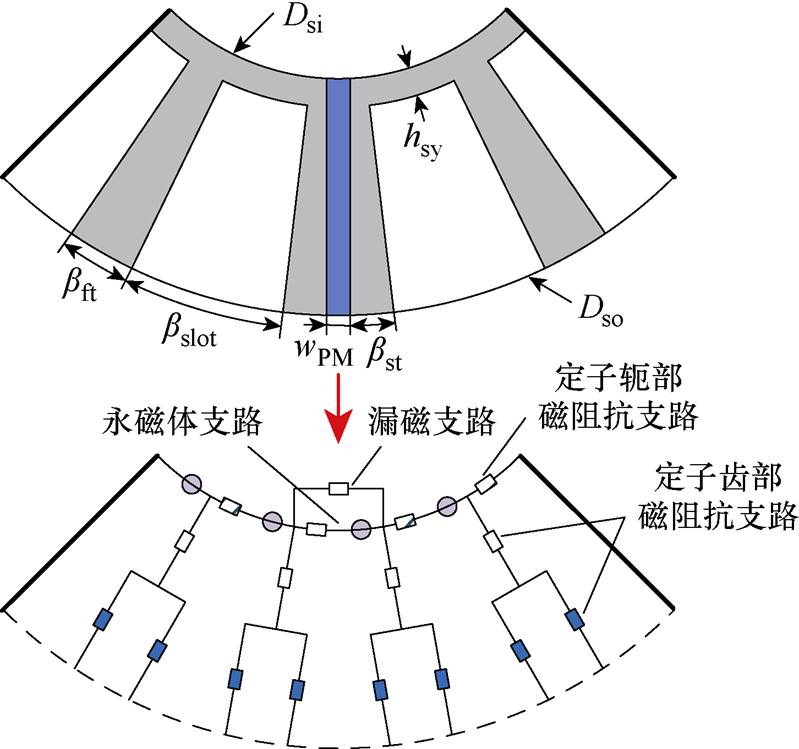
图4 定子铁心支路计算示意图
Fig.4 Calculation diagrams of stator core branches
表1 FSPM-IW电机参数
Tab.1 The parameters for FSPM-IW motor

参 数数值 (型号) 定子齿宽bst/(°)6.71 转子齿宽brt/(°)6.23 永磁体宽wPM/mm2.48 容错齿宽bft/(°)8.42 定子槽宽bslot/(°)17.66 定子轭高hsy/mm3.09 转子轭高hry/mm7.14 气隙长度g/mm0.4 轴向长度la/mm60 定子内径Dsi/mm50 定子外径Dso/mm100 转子外径Dro/mm130 永磁材料N35SH 铁心材料50WW600
永磁体可等效为“磁动势源-磁阻”串联,有
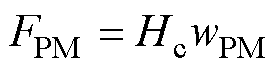 (13)
(13)
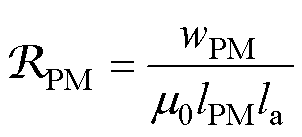 (14)
(14)
式中,Hc为永磁体的矫顽力;lPM为永磁体长度;FPM为磁动势源;RPM为磁阻参数;m0为真空磁导率。
电枢绕组对应的磁动势源为
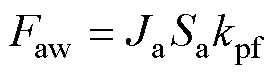 (15)
(15)
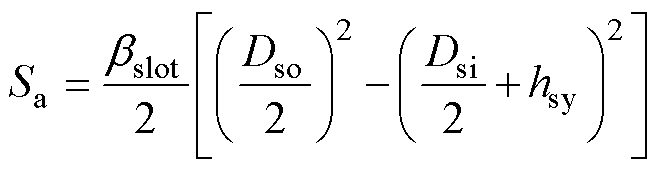 (16)
(16)
式中,Ja为电流密度;kpf为槽满率;Sa为槽面积。
FSPM-IW电机转子铁心的建模方法如图5所示。与定子铁心建模类似,转子齿近气隙的一侧同样划分为两条支路。FSPM-IW电机的气隙支路建模方法与磁阻网络模型保持一致,可以直接由图6给出的方法进行计算。图4和图5中的磁阻抗支路均为图2中的形式,为简单起见,建模示意图并未将其展开。
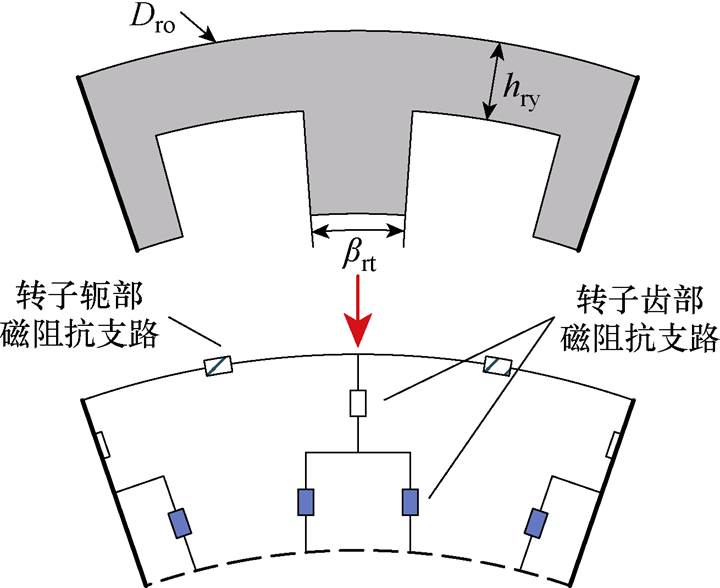
图5 转子铁心支路计算示意图
Fig.5 Calculation diagrams of rotor core branches
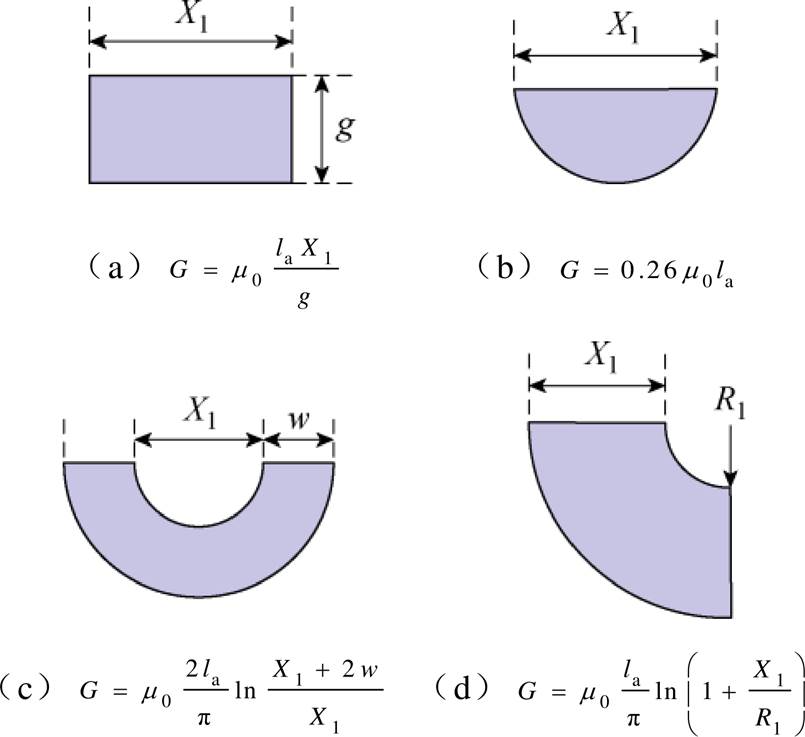
图6 气隙支路计算示意图
Fig.6 Calculation diagrams of air gap branches
将FSPM-IW电机的定子和转子分别建模后,经由气隙磁阻支路连接,即可得到FSPM-IW电机的矢量磁网络模型,如图7所示。方便起见,气隙磁阻支路仅由绿色虚线环标注。相较于有限元模型,本文提出的矢量磁网络模型极大地减少了节点数量,提升了计算效率。
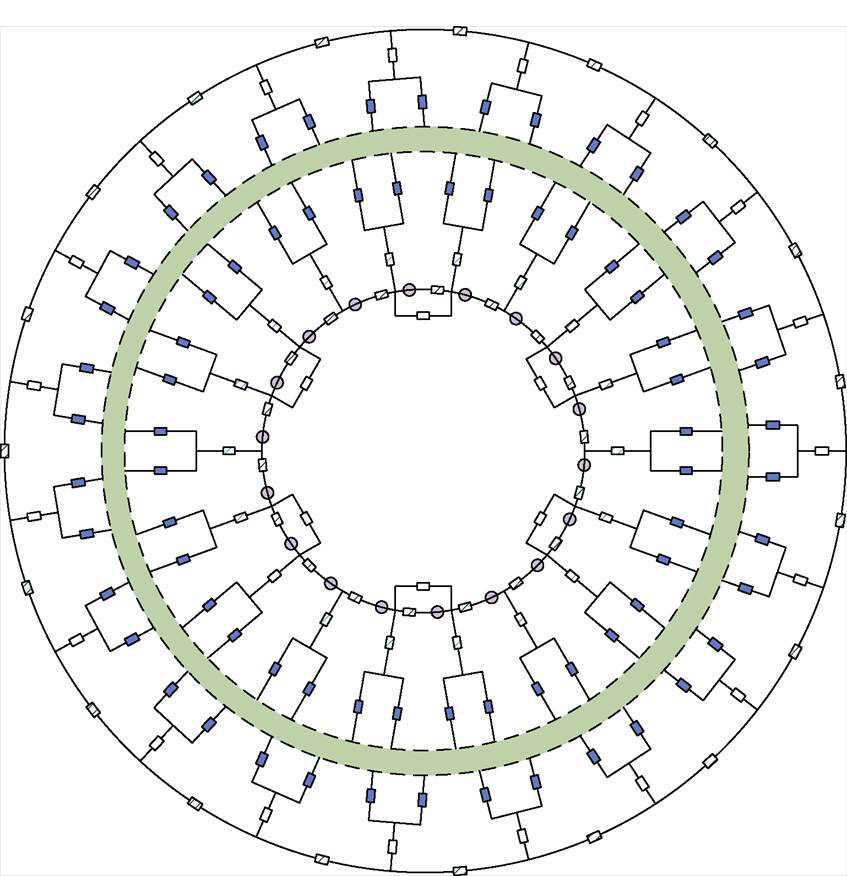
图7 基于矢量磁路理论的磁通切换型永磁轮毂电机矢量磁网络模型示意图
Fig.7 Diagrams of the equivalent magnetic network for the FSPM-IW motor based on the vector magnetic circuit theory
本文采用节点磁动势法列写方程组,并对矢量磁网络模型进行求解。分析FSPM-IW电机的电磁性能时,定转子铁心磁阻-磁感支路保持不变,当转子转动时,仅需对气隙磁阻支路进行调整。计算流程如图8所示。
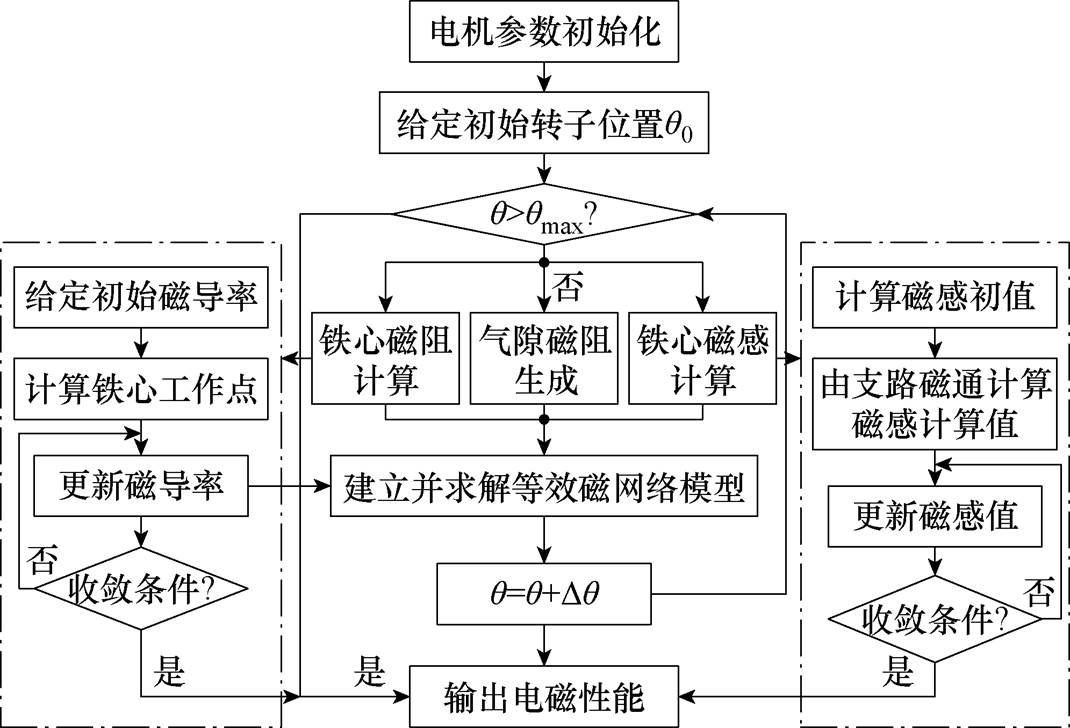
图8 矢量磁网络模型计算示意图
Fig.8 Calculation flow chart of vector magnetic network
首先,根据给定的转子初始位置对电机参数进行初始化。依据2.1节中给出的参数计算方法,计算FSPM-IW电机各条铁心支路的磁阻、磁感参数初值,生成当前转子位置的气隙磁阻支路,并建立节点磁动势方程组为
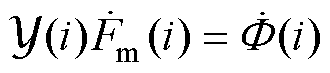 (17)
(17)
式中,i为矢量磁网络模型中的独立节点编号;Y(i)为与节点i相连的支路磁导纳;Fm(i)为节点i处的磁动势;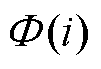 为流入该节点的磁通。
为流入该节点的磁通。
另外,式(17)中的磁导纳参数由铁心支路的磁阻抗推导而来。铁心支路的磁阻和反映涡流效应的磁抗均具有非线性,在求解过程中需要迭代更新。其中,对磁阻参数的迭代方法如下:
首先给定初始磁导率,在求解方程式(17)后,计算各铁心支路的磁通密度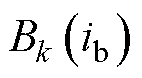 和磁场强度
和磁场强度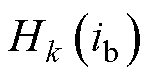 。其次,结合铁心材料的B-H曲线,基于求解出的磁通密度
。其次,结合铁心材料的B-H曲线,基于求解出的磁通密度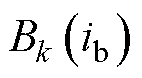 查找各支路对应的磁导率
查找各支路对应的磁导率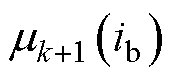 。此处,下标k为迭代次数,变量
。此处,下标k为迭代次数,变量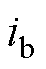 为支路编号。最后,由阻尼法对铁心磁导率进行更新,有
为支路编号。最后,由阻尼法对铁心磁导率进行更新,有
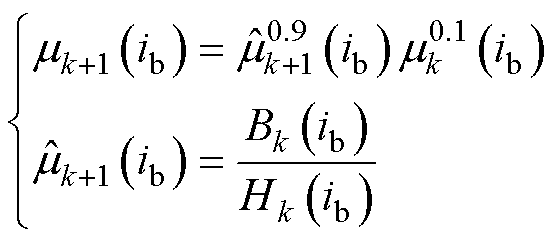 (18)
(18)
式中,上标 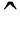 为由当前迭代结果计算所得参数,综合考虑求解速度和收敛性,阻尼系数取为0.9。利用更新后的磁导率重新计算铁心磁阻,并将计算结果回代至式(17),重新求解节点磁动势方程。至此,一次迭代完成,重复上述过程,直到满足收敛条件
为由当前迭代结果计算所得参数,综合考虑求解速度和收敛性,阻尼系数取为0.9。利用更新后的磁导率重新计算铁心磁阻,并将计算结果回代至式(17),重新求解节点磁动势方程。至此,一次迭代完成,重复上述过程,直到满足收敛条件
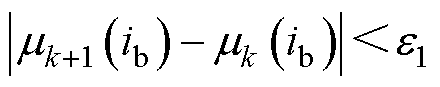 (19)
(19)
式中,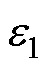 为预设的磁导率求解精度,此处选取为10-7。
为预设的磁导率求解精度,此处选取为10-7。
由于FSPM-IW电机铁心中磁通密度并非正弦,且存在较为明显的直流偏磁现象,需要对由式(4)~式(12)计算所得的磁感初值进行迭代,迭代方法如下:
首先,根据式(4)~式(12)计算铁心磁感初值,记为L0。求解节点磁动势方程,根据求解结果,计算铁心支路的磁通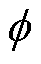 ,有效值
,有效值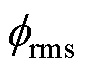 ,以及因电机铁心中涡流反作用产生的感应电压
,以及因电机铁心中涡流反作用产生的感应电压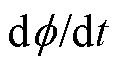 。基于上述结果,计算磁感的理论值Lk为
。基于上述结果,计算磁感的理论值Lk为
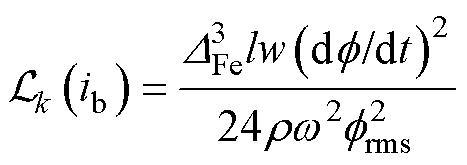 (20)
(20)
式中,下标k为式(17)的求解次数。
然后,同样采用阻尼法对磁感值进行更新,有
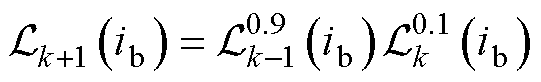 (21)
(21)
以第二次求解为例,根据式(4)和式(5)计算磁感初值L0,代入式(17)并完成第一次求解后,k取值为1,由式(20)计算的磁感理论值为L1,则第二次代入式(17)的磁感值为
 (22)
(22)
最后,将更新后的磁感值回代至式(17)并重新求解。重复上述过程,直到满足收敛条件
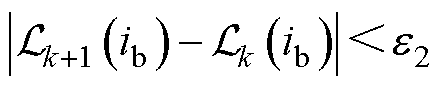 (23)
(23)
式中,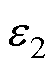 为支路磁感参数的求解精度,取值为10-3。
为支路磁感参数的求解精度,取值为10-3。
在完成上述迭代后,存储当前转子位置的计算结果。根据预设的转子运动步长,更新转子位置,重新生成气隙磁阻。在完成预设计算周期后,整理输出FSPM-IW电机的电磁性能。
本节将利用2.3节中建立的矢量磁网络模型对FSPM-IW电机的电磁性能进行计算,然后再将计算结果与有限元模型和样机实验结果进行对比。相较于磁阻网络模型,本节所提矢量磁网络模型引入了磁感元件,建模复杂性有所增加。为了进一步说明这种改进的必要性,本节将磁阻网络模型也纳入对比。此外,磁阻网络模型和矢量磁网络模型采用Visual Studio 2019进行编程计算,有限元模型采用JMAG-Designer 21.0建立,且计算机主要配置为CPU:i7-12700K,RAM:32 GB。
图9所示为FSPM-IW电机样机测试平台。样机的6个E形铁心单元由燕尾槽固定在定子内套筒上。为了方便安装永磁体和电枢绕组,在定子齿和容错齿的齿尖处分别加工了定位键和槽楔。样机转子共有19个转子齿,虽然会由此产生不平衡磁拉力,但其峰值远小于轴承的耐受能力,不会对电机运行产生明显的影响。本文选用一台他励直流电机作为负载,DSP控制器为TI-TMS320F28377D,控制频率为10 kHz,直流母线电压为12 V。

图9 样机与测试台架
Fig.9 The prototype and the testing rig
FSPM-IW电机的空载磁通密度云图如图10所示。右侧图例中标明的磁通密度数据由有限元模型获得,图中关键节点处(见红点标注)的磁通密度数据由本文所提出的矢量磁网络模型计算获得。由此可见,FSPM-IW电机铁心中的饱和效应主要发生于定转子的齿尖,以及靠近定子齿的轭部区域。
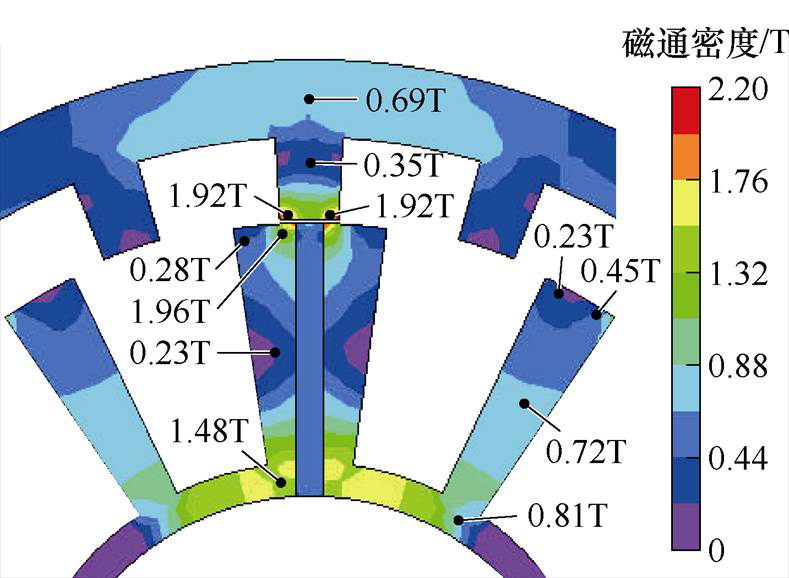
图10 q轴关键点磁通密度计算结果对比
Fig.10 Comparison of the flux density at q-axis
由磁阻网络模型、矢量磁网络模型以及有限元方法计算所得的FSPM-IW电机空载气隙磁通密度如图11所示,可以看出,三种方法的计算结果吻合度较好。两种磁网络模型在建模时均对漏磁现象进行了一定程度的简化,相较于有限元方法,对气隙磁通密度的细节刻画有所欠缺,见图中绿色点画线圈处的标注。此外,由于引入了磁感元件,并计及涡流反作用,在局部和全局峰值磁通密度处,矢量磁网络模型的计算结果与有限元结果更为接近。
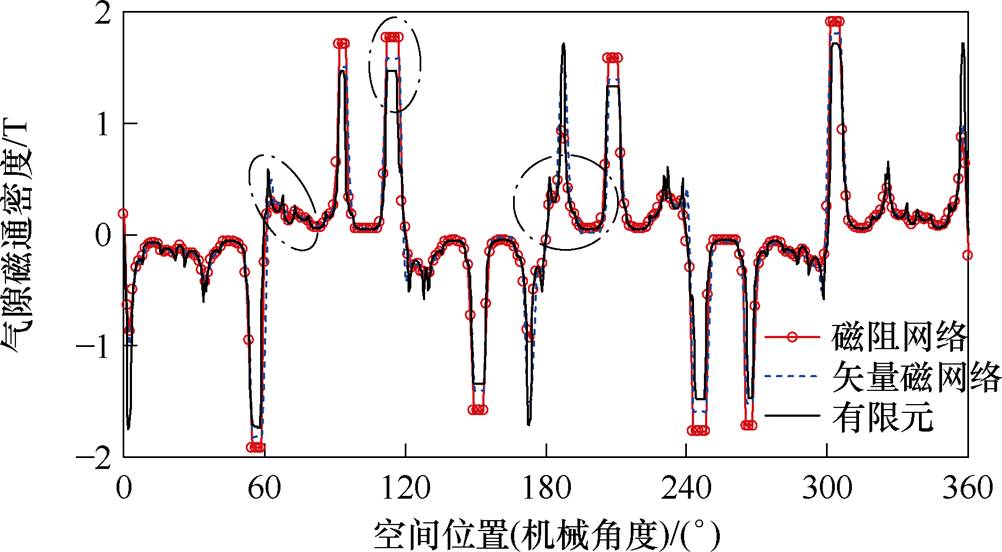
图11 气隙磁通密度波形对比
Fig.11 Comparison of the air gap flux density
结合图7所示的矢量磁网络模型,一个电枢线圈的包围区域中有4条定子齿支路。将4条支路中的磁链求和即可得到FSPM-IW电机每个线圈中的磁链,对应的计算方法为
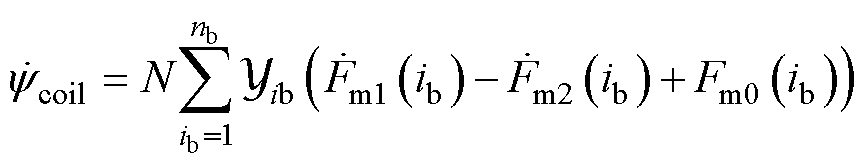 (24)
(24)
式中,N为线圈匝数;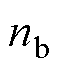 为线圈所包围的支路数量;
为线圈所包围的支路数量;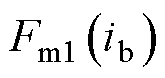 和
和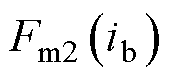 为该线圈所包围的n条支路中第
为该线圈所包围的n条支路中第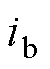 条支路两端的磁动势;
条支路两端的磁动势;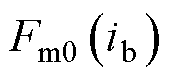 为支路
为支路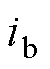 的初始磁动势。
的初始磁动势。
每相磁链的波形如图12所示,两种磁网络模型所求磁链波形与有限元计算结果十分相近。从150°~210°的波形局部放大图可见,由于未考虑涡流效应的影响,由磁阻网络模型计算所得的磁链幅值比矢量磁网络模型大,且与有限元结果相差更多。该现象进一步说明,矢量磁网络模型中添加的磁感元件能够很好地表征涡流效应,提高计算精度,有望在FSPM-IW电机的分析设计过程中代替有限元方法,从而提高计算效率。
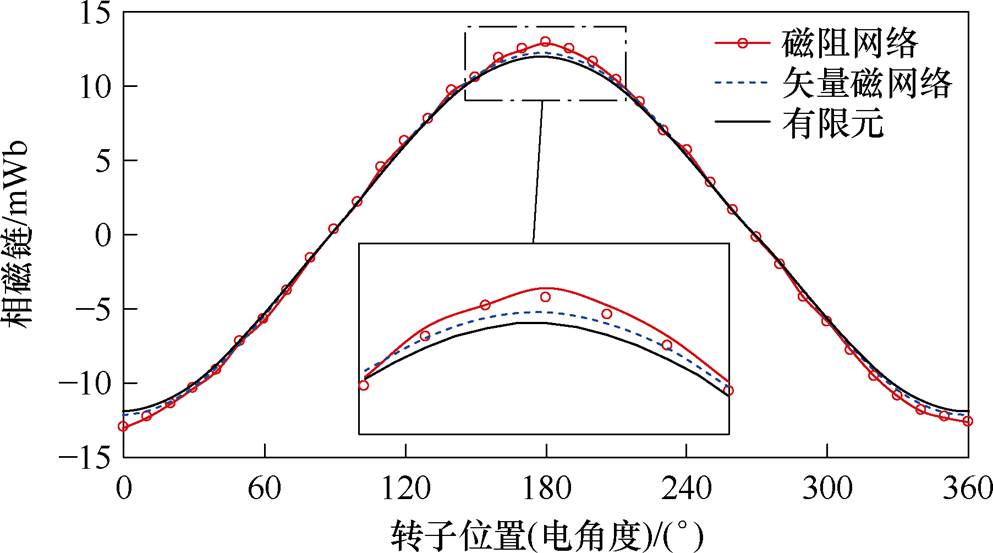
图12 相磁链波形对比
Fig.12 Comparison of the phase flux waveforms
在每相磁链的基础上,FSPM-IW电机的空载反电动势为
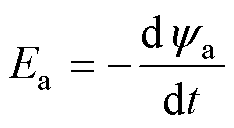 (25)
(25)
式中,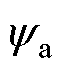 为A相磁链,波形如图12所示。
为A相磁链,波形如图12所示。
本文所研究的FSPM-IW电机额定转速为120 r/min,由磁阻网络模型、矢量磁网络模型和有限元方法计算,实测得到的反电动势波形如图13所示,括号中的数为波形畸变率。相较于有限元结果(2.83 V),矢量磁网络模型计算出的反电动势基波幅值为2.86 V,比磁阻网络模型(2.92 V)的计算精度更高。由于加工误差,实测的基波幅值为2.72 V,比有限元结果低3.9%,比矢量磁网络模型结果低5.1%。由于样机在加工时设置了极靴和定位槽,实测波形畸变率比矢量磁网络模型计算结果略低。
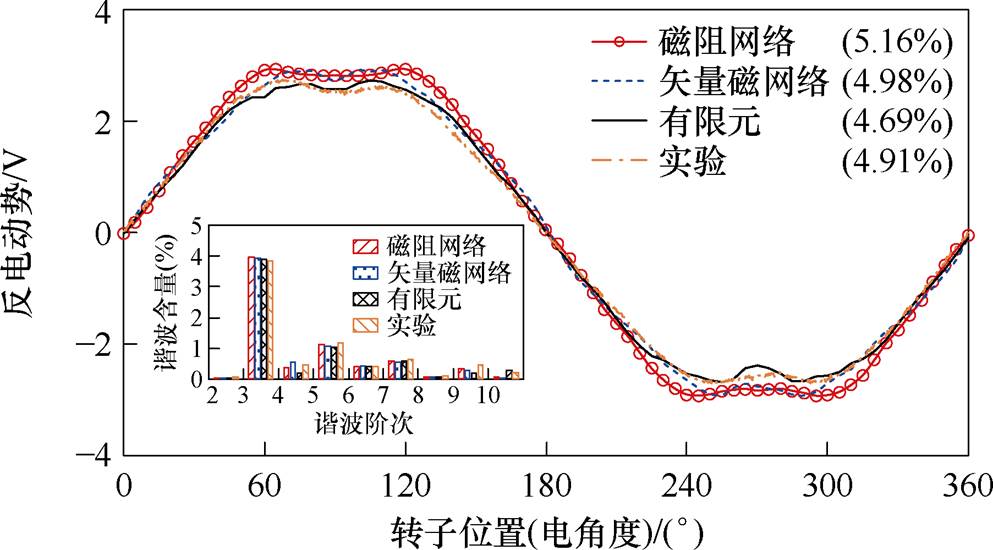
图13 反电动势对比
Fig.13 Comparison of the back electromotive force
FSPM-IW电机的电磁转矩可以由每相反电动势和注入电枢绕组的电流计算为
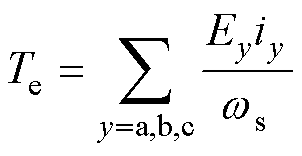 (26)
(26)
式中,Ey和iy分别为第y相的反电动势和电枢电流;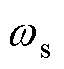 为转子转速。
为转子转速。
在额定转速下,计算和实测的输出转矩如图14所示,计算与实测转矩之间的误差由图右下角的柱状图予以标注。可以看出,两种磁网络模型都可以较好地预测输出转矩,但由于没有考虑涡流效应,磁阻网络模型的计算结果较大,与有限元方法和实测结果之间的误差也更大。在额定工作点(5 A/mm2)处,由磁阻网络模型计算的输出转矩为13.33 N·m,矢量磁网络模型的计算结果为12.87 N·m,有限元计算结果为12.66 N·m,实测转矩为11.92 N·m。
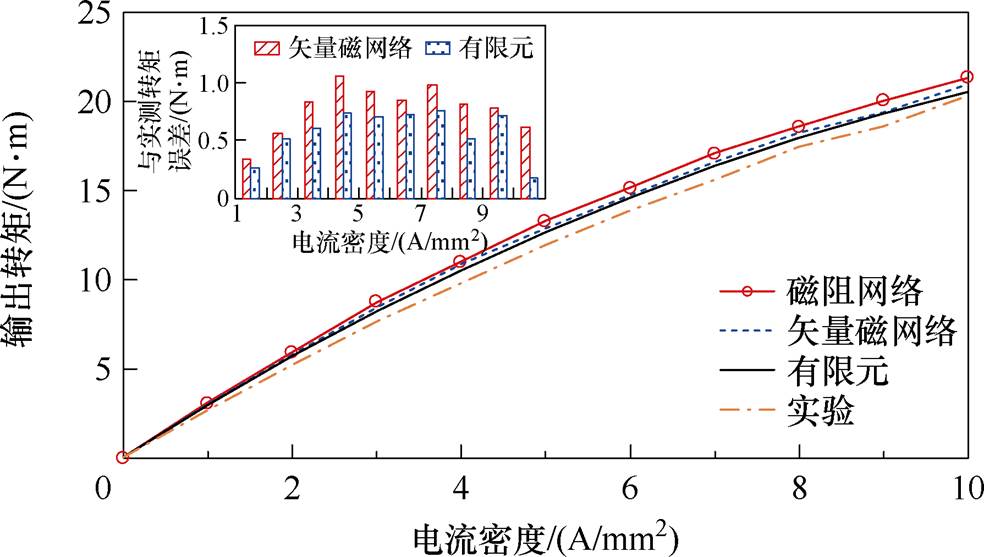
图14 电磁转矩对比
Fig.14 Comparison of the torque
对于磁阻网络模型,其空载磁滞和涡流损耗可计算[19]为
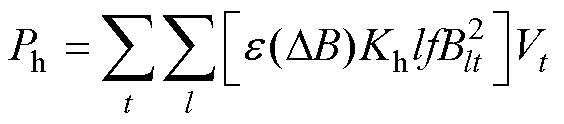 (27)
(27)
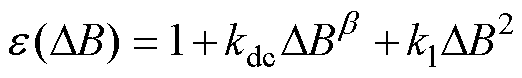 (28)
(28)
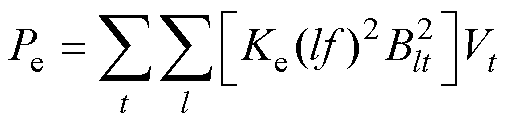 (29)
(29)
式中,Ph和Pe分别为磁滞和涡流损耗;Kh和Ke分别为磁滞和涡流损耗系数;Vt为第t条支路对应的铁心区域体积;Blt为第t条支路中第l次磁通密度谐波幅值;f为铁心磁通频率;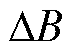 为直流偏置磁通密度;
为直流偏置磁通密度;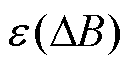 为修正系数;kdc、kl、
为修正系数;kdc、kl、 均为系数。
均为系数。
对于矢量磁网络模型而言,磁滞损耗的计算方法沿用式(27),而涡流损耗计算式[20]为
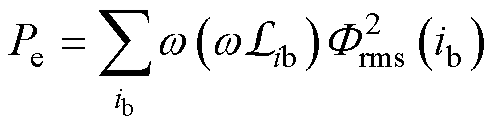 (30)
(30)
式中,Lib为迭代收敛后,第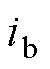 条铁心支路的磁感;
条铁心支路的磁感;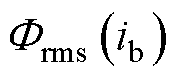 为流经支路
为流经支路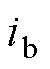 的磁通有效值。
的磁通有效值。
由于FSPM-IW电机的额定转速较低,功率等级和尺寸较小,其机械损耗较小,且在空载运行时永磁体涡流损耗可以忽略不计,因此可以认为实测的空载损耗仅由铁耗组成。在不同转速下,计算以及实测所得的空载损耗如图15所示。受限于集总参数模型对铁心支路的简化,两种磁网络模型的铁耗计算精度比有限元方法低。得益于磁感元件的引入,矢量磁网络模型可以直接计算涡流损耗,虽然铁耗计算结果与实测数据之间仍有误差,但计算结果已经与有限元方法十分接近,且该误差主要来源于磁滞损耗沿用了传统方法。由三种方法计算出的定转子铁心各部分的空载铁耗也在图15中对比。可以看出,FSPM-IW电机的铁耗中定子损耗占比较大,且主要集中在定子齿和容错齿中。
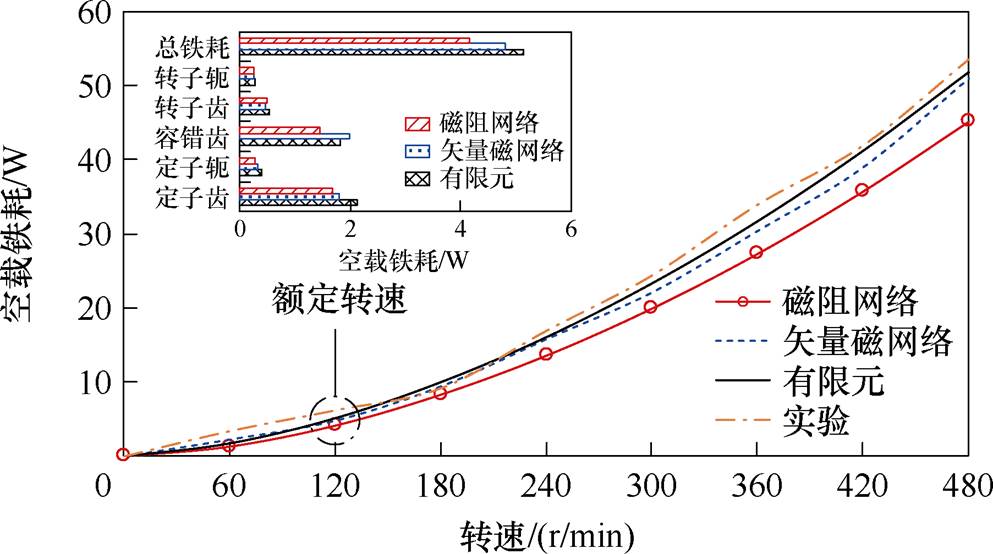
图15 空载损耗结果对比
Fig.15 Comparison of the open circuit loss
本文以一台FSPM-IW电机为研究对象,提出了一种基于磁感原理的矢量磁网络模型。为了计及涡流反作用,提升电磁性能的计算精度,并简化涡流损耗的计算流程,本文首次引入磁感元件定量表征定转子铁心中的涡流效应,建立基于“磁阻-磁感”串联支路的矢量磁网络模型。研究结果表明,相较于传统磁阻网络模型,本文所提的矢量磁网络模型考虑了涡流效应,在电磁性能计算精度,尤其是涡流损耗计算方面,有较大提升,与实验结果更为接近,有望成为电机设计阶段的方法支撑。
参考文献
[1] 关涛, 刘大猛, 何永勇. 永磁轮毂电机技术发展综述[J]. 电工技术学报, 2024, 39(2): 378-396.
Guan Tao, Liu Dameng, He Yongyong. Review on development of permanent magnet in-wheel motors[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 378-396.
[2] Nasiri-Zarandi R, Karami-Shahnani A, Toulabi M S, et al. Design and experimental performance assess- ment of an outer rotor PM-assisted SynRM for the electric bike propulsion[J]. IEEE Transactions on Transportation Electrification, 2023, 9(1): 727-736.
[3] Amirkhani M, Ali Ghanbari M, Kondelaji M A J, et al. Performance analysis of outer rotor multi-tooth biased flux permanent magnet motors[J]. IEEE Transactions on Energy Conversion, 2023, 38(3): 1738-1752.
[4] 樊英, 陈秋蒴, 陈俊磊, 等. 基于无人配送车辆运行工况的交替极游标轮毂电机优化设计[J]. 电工技术学报, 2023, 38(19): 5141-5151.
Fan Ying, Chen Qiushuo, Chen Junlei, et al. Opti- mization design of consequent pole vernier wheel motor based on operating conditions of unmanned delivery vehicles[J]. Transactions of China Elec- trotechnical Society, 2023, 38(19): 5141-5151.
[5] Chen Hao, Liu Xiangdong, Demerdash N A O, et al. Comparison and design optimization of a five-phase flux-switching PM machine for in-wheel traction applications[J]. IEEE Transactions on Energy Con- version, 2019, 34(4): 1805-1817.
[6] Zhao Wenxiang, Pan Xiaoyun, Ji Jinghua, et al. Analysis of PM eddy current loss in four-phase fault- tolerant flux-switching permanent-magnet machines by air-gap magnetic field modulation theory[J]. IEEE Transactions on Industrial Electronics, 2020, 67(7): 5369-5378.
[7] 李鑫宇, 孙天夫, 黄世军, 等. 永磁同步电机温度建模与热管理方法综述[J]. 电气工程学报, 2023, 18(4): 20-34.
Li Xinyu, Sun Tianfu, Huang Shijun, et al. Review and perspectives on thermal management methods for permanent magnet synchronous motors[J]. Journal of Electrical Engineering, 2023, 18(4): 20-34.
[8] Du Yi, Mao Yi, Xiao Feng, et al. Partitioned stator hybrid excited machine with DC-biased sinusoidal current[J]. IEEE Transactions on Industrial Electro- nics, 2022, 69(1): 236-248.
[9] Hua Wei, Su Peng, Tong Minghao, et al. Investigation of a five-phase E-core hybrid-excitation flux- switching machine for EV and HEV applications[J]. IEEE Transactions on Industry Applications, 2017, 53(1): 124-133.
[10] 李博, 朱建国, 刘成成, 等. 集成压缩机用双定子磁通切换电机的设计及优化[J]. 电机与控制学报, 2023, 27(1): 101-109.
Li Bo, Zhu Jianguo, Liu Chengcheng, et al. Design and optimization of dual-stator FSPMM for integrated compressor[J]. Electric Machines and Control, 2023, 27(1): 101-109.
[11] Wang Shuyou, Chen Fei, Tian Zuzhi, et al. An enhanced magnetic equivalent circuit model for a magnetorheological clutch including nonlinear per- meability, flux fringing, and leakage effects[J]. IEEE Transactions on Transportation Electrification, 2023, 9(1): 488-500.
[12] 杜爱赫, 解伟, 施振川, 等. 电动自行车用磁通切换电机研究[J]. 电机与控制应用, 2021, 48(8): 50-54.
Du Aihe, Xie Wei, Shi Zhenchuan, et al. Research on flux-switching machine for electric bicycle[J]. Elec- tric Machines & Control Application, 2021, 48(8): 50-54.
[13] 李世奇, 佟文明, 贾建国, 等. 考虑磁桥非线性的内置式永磁同步电机空载电磁性能通用解析模型[J]. 电工技术学报, 2023, 38(6): 1421-1432.
Li Shiqi, Tong Wenming, Jia Jianguo, et al. General analytical model of No-load electromagnetic per- formance of interior permanent magnet synchronous motors considering nonlinearity of magnetic bridges[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1421-1432.
[14] 胡岩, 王功臣. 航空用高速永磁发电机电磁设计研究[J]. 电气工程学报, 2015, 10(9): 22-29.
Hu Yan, Wang Gongchen. Electromagnetic design and research of high speed permanent magnet gen- erator for aviation[J]. Journal of Electrical Engin- eering, 2015, 10(9): 22-29.
[15] Cheng Ming, Chau K T, Chan C C, et al. Nonlinear varying-network magnetic circuit analysis for doubly salient permanent-magnet motors[J]. IEEE Transa- ctions on Magnetics, 2000, 36(1): 339-348.
[16] 徐伟, 张祎舒, 曹辰, 等. 定子不对称极混合励磁双凸极电机改进型非线性变磁网络模型构建方法研究[J]. 中国电机工程学报, 2023, 43(1): 304-318.
Xu Wei, Zhang Yishu, Cao Chen, et al. Improved construction method of nonlinear varying equivalent magnetic network model for hybrid excitation asymmetric stator pole double salient machine[J]. Proceedings of the CSEE, 2023, 43(1): 304-318.
[17] 夏云彦, 周洲, 邵远亮, 等. 基于动态磁网络法大型感应电机阻抗参数及起动特性计算[J]. 电工技术学报, 2024, 39(14): 4341-4352.
Xia Yunyan, Zhou Zhou, Shao Yuanliang, et al. Calculation of impedance parameters and starting characteristics of large induction motor based on dynamic magnetic network[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4341-4352.
[18] Cao Donghui, Zhao Wenxiang, Liu Tong, et al. Magneto-electric coupling network model for redu- ction of PM eddy current loss in flux-switching permanent magnet machine[J]. IEEE Transactions on Industrial Electronics, 2022, 69(2): 1189-1199.
[19] Tangudu J K, Jahns T M, EL-Refaie A. Core loss prediction using magnetic circuit model for fractional- slot concentrated-winding interior permanent magnet machines[C]//2010 IEEE Energy Conversion Con- gress and Exposition, Atlanta, GA, USA, 2010: 1004-1011.
[20] Cheng Ming, Qin Wei, Zhu Xinkai, et al. Magnetic- inductance: concept, definition, and applications[J]. IEEE Transactions on Power Electronics, 2022, 37(10): 12406-12414.
[21] 秦伟, 程明, 王政, 等. 矢量磁路及应用初探[J]. 中国电机工程学报, 2024, 44(18): 7381-7395.
Qin Wei, Cheng Ming, Wang Zheng, et al. Vector magnetic circuit and its preliminary applications[J]. Proceedings of the CSEE, 2024, 44(18): 7381-7395.
[22] 程明, 马钲洲, 王政, 等. 基于磁感的变压器和感应电机等效矢量磁路分析[J]. 电工技术学报, 2024, 39(15): 4697-4707.
Cheng Ming, Ma Zhengzhou, Wang Zheng, et al. Equivalent vector magnetic circuit analysis of trans- former and induction motor based on the magdu- ctance[J]. Transactions of China Electrotechnical Society, 2024, 39(15): 4697-4707.
[23] Qin Wei, Cheng Ming, Wang Zheng, et al. Vector magnetic circuit analysis of silicon steel sheet parameters under different frequencies for electrical machines[J]. IET Electric Power Applications, 2024, 18(9): 981-994.
[24] Li Chengbo, Cheng Ming, Qin Wei, et al. Analytical loss model for magnetic cores based on vector magnetic circuit theory[J]. IEEE Open Journal of Power Electronics, 2024, 5: 1659-1670.
Abstract In recent decades, the flux-switching permanent magnet in-wheel (FSPM-IW) motors have earned considerable attention, due to their inherent strengths in large torque density, robust rotor structure, and outstanding heat dissipation conditions. During its design and optimization stage, the large-scale electromagnetic performance calculation mainly relies on the finite element analysis (FEA), which requires unquantifiable time and memory consumption. Under such circumstances, the analytical methods, represented by magnetic network methods, are regarded as practical tools to balance evaluation accuracy and calculation time. However, the existing magnetic network methods only involve reluctance components, which cannot account for the eddy current effect. Therefore, this paper proposes the vector magnetic network (VMN) model based on the magductance principle.
Firstly, the topology and structural features of the FSPM-IW motor are introduced. Secondly, the calculation methods of reluctance and magductance parameters are deduced for iron cores based on the vector magnetic circuit theory. Accordingly, the “reluctance-magductance” branches can be formed for the VMN model considering the eddy current effect. The VMN models are established for the stator and the rotor, and the air gap reluctance branches then connect the two parts. The VMN model is built for the FSPM-IW motor. Through the nodal magneto-motive force method, the electromagnetic performance can be acquired by solving the equivalent equations. To improve the calculation accuracy, the nonlinear iteration process is employed in both the calculation of the branch’s reluctance and magductance components. Finally, the FSPM-IW motor is investigated, and the electromagnetic performance is compared using the proposed model, the traditional reluctance-based magnetic network model, and the FEA method.
The VMN model’s calculated air gap flux density and phase flux linkage waveforms are in superior consistency with the FEA result. The calculated back electro-motive force (back-EMF) waveform, average torque, and the open circuit loss align with the measured results from the prototype experiment. For the back-EMF, the fundamental amplitudes obtained by the VMN model, FEA method, and prototype experiment are 2.86 V, 2.83 V, and 2.72 V, respectively. Moreover, the average output torques are 12.87 N·m, 12.66 N·m, and 11.92 N·m for the three methods at the rated condition.
The following conclusions can be drawn. (1) Compared with the FEA method, the proposed VMN model significantly reduces the computational time-consumption and achieves satisfactory accuracy. (2) Compared with the traditional reluctance-based magnetic network model, the proposed VMN model exhibits higher precision in performance evaluation due to the introduction of magductance components. (3) The proposed VMN model provides a practical and convenient approach to the electromagnetic performance calculation. The result is close to the prototype experiment.
keywords:Vector magnetic circuit theory, flux-switching, magductance component, in-wheel motor, magnetic network model
DOI: 10.19595/j.cnki.1000-6753.tces.241971
中图分类号:TM351
国家自然科学基金(5245007, U24A20147)和江苏省研究生科研与实践创新计划(KYCX23_0250)资助项目。
收稿日期 2024-11-05
改稿日期 2024-11-25
许芷源 男,1998年生,博士研究生,研究方向为磁通切换型电机的分析、设计和控制。E-mail: zyxu@seu.edu.cn
程 明 男,1960年生,教授,博士生导师,IEEE Fellow和IET Fellow,研究方向为电动车驱动控制技术、新能源发电技术、微特电机及测控系统等。E-mail: mcheng@seu.edu.cn(通信作者)
(编辑 崔文静)