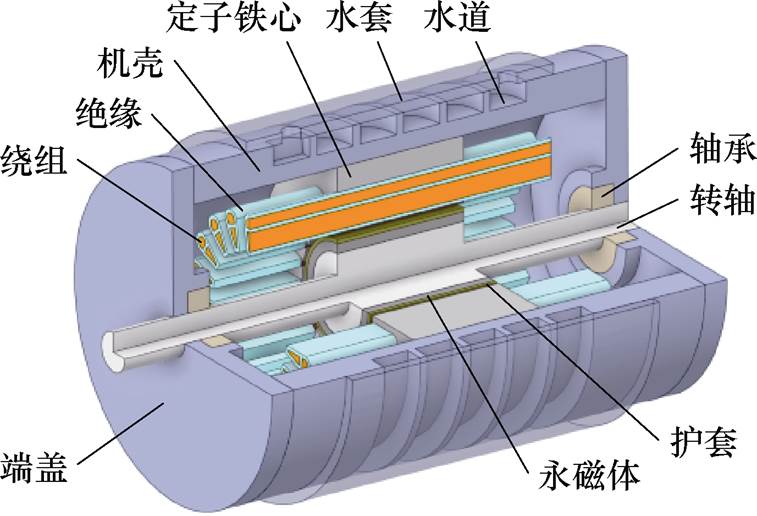
图1 高速永磁电机的物理模型
Fig.1 Physical model of the HSPMM
摘要 高速永磁电机(HSPMM)凭借高功率密度、良好的动态响应能力、可直接驱动负载等优点应用于许多工业设备,为预防温度过高引发故障,电机设计阶段温度评估问题的重要性日益凸显。当前,基于数值分析方法和集总参数热网络(LPTN)法的电机温升计算已得到了广泛应用,但是在保证计算精度的条件下提高温升计算效率仍是当前电机设计阶段面临的难题。该文提出一种三维集总参数热网络全模型,定子齿和槽部绕组之间的热量传递通过瓦片体网络拓扑搭建,电机内加载热源的空心圆柱体部件采用T型网络拓扑进行构建,无热源的空心圆柱体采用+型网络拓扑,装配间隙采用平板导热热阻。基于材料的温度特性采用电磁-热网络耦合求解方法对各节点的温度进行求解,通过一台7.5 kW、15 000 r/min的机壳水冷高速永磁电机的温升实验验证了所提三维LPTN的准确性。
关键词:高速永磁电机 三维集总参数热网络 磁热双向耦合 热分析
在航天航空、数控机床、电动汽车等行业中,高速永磁电机(High-Speed Permanent Magnet Machine, HSPMM)以其高效率、高功率密度、低维护需求等特点得到了广泛应用[1-2]。温度特性是HSPMM维持其性能、效率、可靠性和使用寿命的关键。然而,与相同功率的传统电机相比,HSPMM体积小与损耗密度大的特性更易引起电机温升的增加。温升过高容易造成永磁材料的不可逆退磁,恶化电机效率,同时也造成电机轴承的润滑失效[3-4]。由此可见,HSPMM温升的准确与快速计算对高速永磁电机设计具有重要意义。
近年来,针对永磁同步电机温度场计算问题,国内外学者采用有限体积法(Finite Volume Method, FVM)、有限元法(Finite Element Method, FEM)、集总参数热网络(Lumped Parameter Thermal Network, LPTN)等方法开展研究。文献[5]使用FVM研究永磁同步电机在变频供电下的温度分布规律。文献[6-7]对永磁电机提出了新型冷却结构,基于FVM的磁热单向耦合对电机温度场进行数值分析,并通过实验对比验证冷却效果。文献[8]基于FVM通过磁热双向耦合考虑绕组和永磁体的温变特性对高速永磁电机电磁损耗和热特性的影响。文献[9]采用FEM探讨了两种不同形状的内置式永磁体对电机其他部位温度的影响。文献[10]针对一台带有自循环轴向通风系统的MW级全封闭永磁同步电机采用FEM进行热敏感性分析,识别影响计算精度的最重要因素。文献[11]结合FEM和对流换热公式求解电机温度场,验证了周向水道冷却效果优于轴向水道。尽管FVM和FEM能更精细、更准确地预测热量在电机中的传递和分布,但这两种方法建模复杂,对计算机资源要求高,计算时间较长,不适用于电机初始设计与优化设计。
LPTN可基于电机设计参数快速建立温升计算模型,对计算资源要求较小,亦能快速实现HSPMM的热性能评估[12]。文献[13]搭建了简单的一维径向方向的LPTN评估电机温度。文献[14]利用平板导热热阻公式建立了基于径向和轴向的二维LPTN模型,而文献[15]利用空心圆柱体T型等效热网络构建电机的LPTN模型,进而求出电机各部件的平均温度,但二者都未考虑到转轴和端腔空气的对流换热,并不能完全适用于HSPMM。文献[16]将T型等效热网络简化为+型,仍然满足计算精度的要求,整体上可以有效地模拟热流,但并不能准确地反映传热的平均温度。文献[17]提出了基于轴向通风冷却系统的LPTN,将LPTN和FEM求解电磁损耗进行了双向耦合。虽然提高了计算准确度,但是在LPTN槽部绕组模型的建立中只考虑了槽内铜导体的轴向传热及等效绝缘部分的径向传热。文献[18]基于内置式永磁同步电机的轴向1/2的LPTN估计永磁体温升,但不能为有轴向气流的电机热网络的搭建提供依据。文献[19]的LPTN中考虑到表贴式高速永磁电机中钛合金护套涡流损耗和轴承损耗对电机温度的影响,以此对原电机设计方案进行优化,但该网络中未计及槽部绕组热量和气隙进行交换。
本文针对一台15 kW、30 000 r/min机壳水冷高速非晶合金永磁同步电机基于瓦片体网络拓扑、空心圆柱体的T型与+型网络拓扑、平板导热热阻、实心圆柱体网络拓扑搭建三维LPTN全域模型并进行求解。首先,通过二维时步有限元法和经验公式计算电机在变频供电下的电磁损耗和机械损耗,将损耗加载至LPTN对应热源处并求解各节点稳态温度。其次,考虑温度对永磁体、绕组、护套材料特性的影响重新计算电磁损耗,进而实现磁热双向耦合。然后,使用基于FVM的商业软件ANSYS Fluent验证本文提出的LPTN的可行性。最后,对一台7.5 kW、15 000 r/min水冷高速永磁电机进行温升实验,将实验结果和LPTN计算结果进行比较,验证该方法的准确性,为相似功率等级与冷却方式的HSPMM温升评估提供参考。
本文以一台15 kW、30 000 r/min机壳水冷高速非晶合金永磁电机为研究对象,电机绕组采用双层圆导线散下线形式,为方便电机建模对绕组端部平直化处理,即绕组端部伸出部分由等效直线段表示。此外,认为定子槽内浸渍状态良好,浸渍漆填充均匀且铜线绝缘漆分布均匀,槽绝缘和定子铁心接触紧密,槽内所有绝缘热性能相同[20]。高速永磁电机的物理模型如图1所示,机壳设有周向螺旋水道,永磁体材料为钕铁硼,转子由钛合金护套、永磁体和转轴构成,主要参数见表1。
高速永磁电机采用变频器供电,变频器供电在高速电机中引入大量高次时间谐波,定子铁心磁通密度是随时间变化的非标准正弦波,导致电机损耗增加,进而转化为热量影响电机温升,故准确地计算电机损耗十分重要。

图1 高速永磁电机的物理模型
Fig.1 Physical model of the HSPMM
表1 高速永磁电机的基本参数
Tab.1 Main parameters of the HSPMM
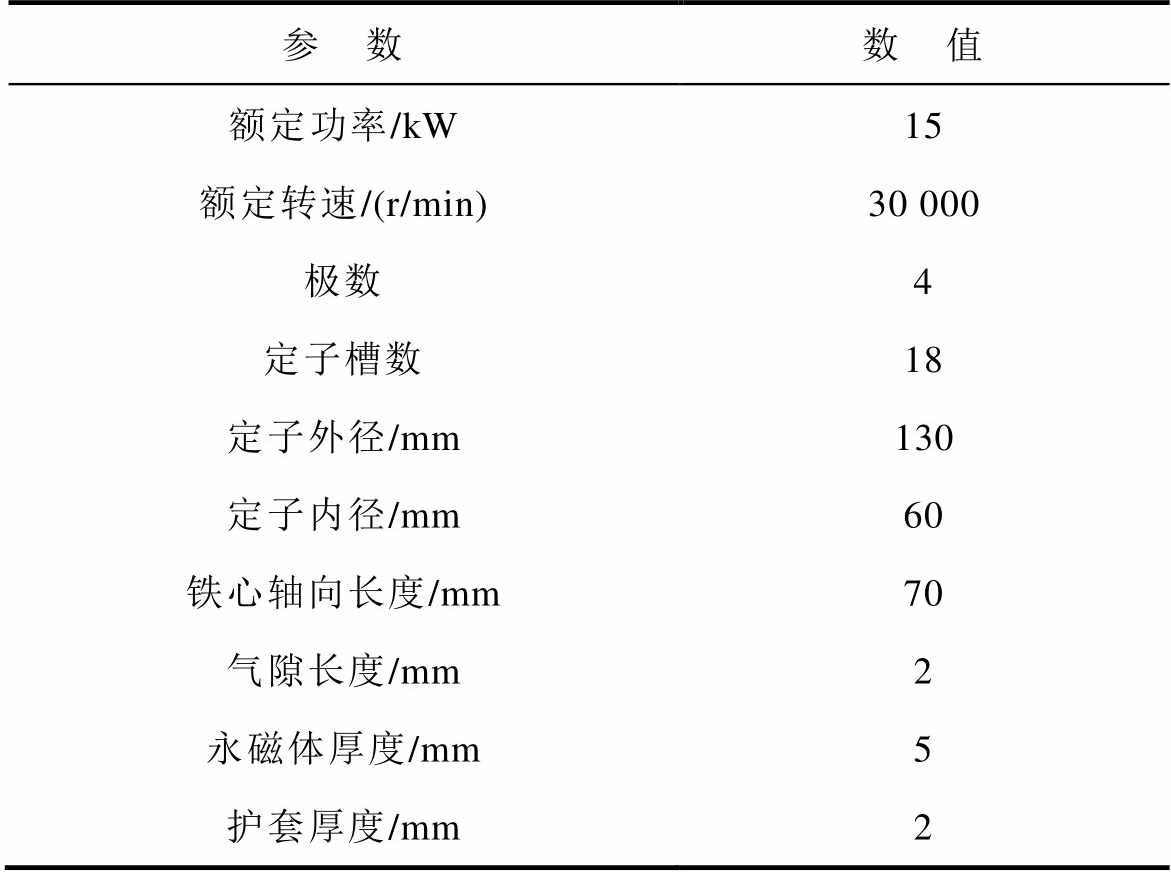
参 数数 值 额定功率/kW15 额定转速/(r/min)30 000 极数4 定子槽数18 定子外径/mm130 定子内径/mm60 铁心轴向长度/mm70 气隙长度/mm2 永磁体厚度/mm5 护套厚度/mm2
由于电机的工作频率为1 kHz,考虑导体的趋肤效应和邻近效应,交流铜耗Pac的计算方法如式(1)~式(3)所示。
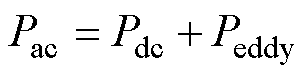 (1)
(1)
式中,Pdc为直流铜耗;Peddy为涡流铜耗。
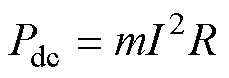 (2)
(2)
式中,m为绕组相数;I为相电流的有效值;R为一相的直流电阻。
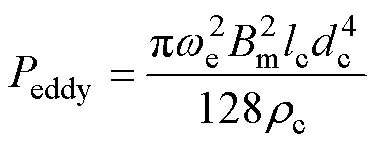 (3)
(3)
式中,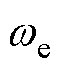 为磁通密度角频率;Bm为磁通密度幅值;lc为导体长度;dc为导体直径;
为磁通密度角频率;Bm为磁通密度幅值;lc为导体长度;dc为导体直径;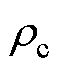 为导体的电阻率。
为导体的电阻率。
高速永磁电机定子铁耗不仅要考虑交变磁场的影响,还需考虑谐波与旋转磁场的影响。电机定子铁耗为铁心磁通密度基波及各次谐波分量产生的铁耗之和[21]。基于铁耗分离理论,定子铁心损耗PFe可表示为
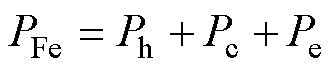 (4)
(4)
式中,Ph为磁滞损耗;Pc为经典涡流损耗;Pe为异常损耗。
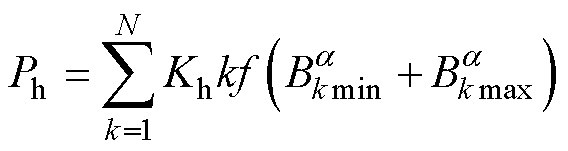 (5)
(5)
式中,Kh、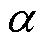 为铁心磁滞损耗系数;Bkmin、Bkmax分别为铁心第k次谐波磁通密度椭圆的短轴和长轴;f为频率。
为铁心磁滞损耗系数;Bkmin、Bkmax分别为铁心第k次谐波磁通密度椭圆的短轴和长轴;f为频率。
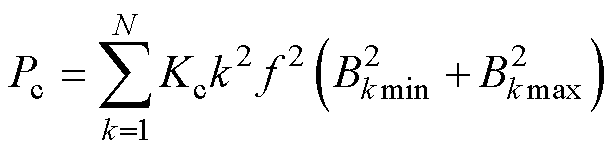 (6)
(6)
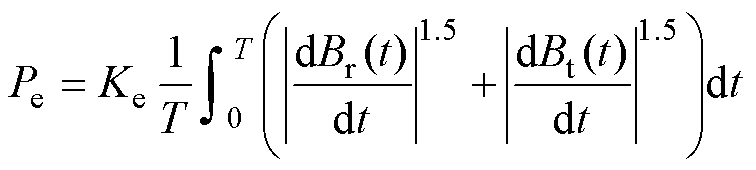 (7)
(7)
式中,Kc为经典涡流损耗系数;Ke为异常损耗系数;Br、Bt分别为铁心中径向和切向磁通密度。
先将定子铁心划分为如图2所示的五个区域,取齿顶区域中心点为P1s,齿部区域中心点为P2s,齿连轭区域中心点为P3s,齿对轭区域中心点为P4s,槽对轭区域中心点为P5s。然后基于FEM对各点进行磁场分析,并结合式(4)~式(7)计算定子齿部与轭部铁耗,损耗系数Kh、Kc、Ke、 通过对非晶合金定子铁心的损耗曲线进行非线性拟合求得。钛合金护套涡流损耗和永磁体涡流损耗直接通过FEM计算得出。
通过对非晶合金定子铁心的损耗曲线进行非线性拟合求得。钛合金护套涡流损耗和永磁体涡流损耗直接通过FEM计算得出。
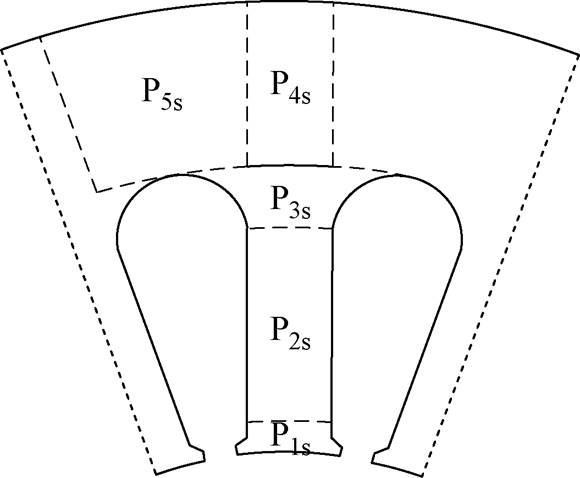
图2 定子铁心划分示意图
Fig.2 Schematic diagram of the division of stator core
高速电机中风摩损耗和轴承损耗不容忽视。由于转子旋转带动气隙内空气切向流动,达到额定转速时空气处于完全湍流的状态,在钛合金护套近壁面处的粘性底层中产生摩擦损耗。将转子模拟为一个封闭空间内的旋转圆柱体,表面摩擦系数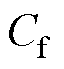 [22]为
[22]为
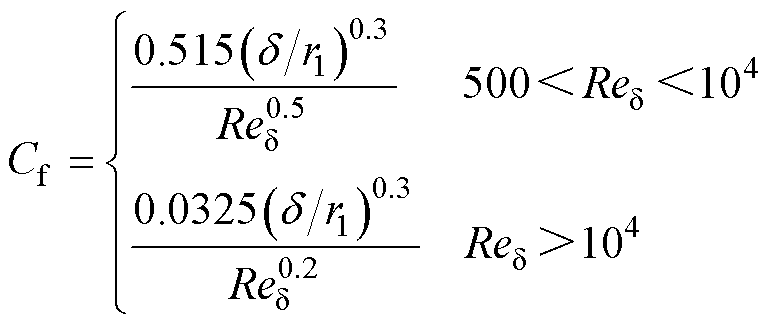 (8)
(8)
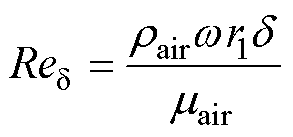 (9)
(9)
式中,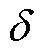 为气隙长度;
为气隙长度;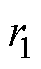 为转子表面外半径;
为转子表面外半径;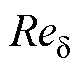 为气隙周向雷诺数;
为气隙周向雷诺数;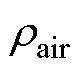 为空气密度;
为空气密度;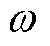 为转子机械角速度;
为转子机械角速度;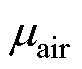 为空气的动力黏度。风摩损耗Pwind为
为空气的动力黏度。风摩损耗Pwind为
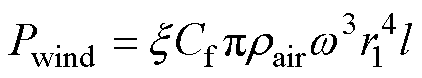 (10)
(10)
式中,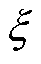 为转子表面粗糙度系数;l为气隙的轴向长度。经计算风摩损耗为33.7 W。
为转子表面粗糙度系数;l为气隙的轴向长度。经计算风摩损耗为33.7 W。
轴承损耗取决于轴的旋转速度、轴承类型、润滑剂的性质及轴承上的载荷,SKF轴承损耗Pb[23]为
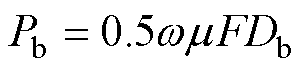 (11)
(11)
式中,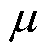 为轴承摩擦系数;F为轴承载荷;Db为轴承的内径。经计算轴承损耗为83.25 W。
为轴承摩擦系数;F为轴承载荷;Db为轴承的内径。经计算轴承损耗为83.25 W。
基于三维集总参数的热网络模型热计算需要根据电机实际情况对电机进行简化,因此,本文在建立高速永磁电机的LPTN模型之前做以下假设:
(1)电机内部热源均匀分布,且温度沿圆周方向对称分布。
(2)忽略电机内部热辐射作用。
(3)不考虑电机内温度对导热系数和对流散热系数的影响。
(4)径向、轴向、周向上的热流相互独立。
根据高速永磁电机实际结构特点建立图3所示的三维LPTN模型,①为定子轭部的温度节点,②为定子齿部的温度节点,③为槽部绕组的温度节点,④为端部绕组的温度节点,⑤为护套的温度节点,⑥为永磁体的温度节点,⑦~⑨为转轴的温度节点。基于集总参数思想,将定子轭、钛合金护套、永磁体、机壳、端盖、轴承近似为空心圆柱体,其中机壳离散为3个区域;将转轴离散为4个区域,中间部分视为空心圆柱体内嵌实心圆柱体,轴伸端近似为实心圆柱体;将定子齿和槽部绕组分别等效为瓦片体结构;将端部绕组等效为圆环体计算方法[24],该方法修正了端部绕组平均温度和最高温度的偏差;定子和机壳、永磁体和转轴之间的间隙用接触热阻模拟。用热压源模拟环境温度和冷却水温度。

图3 高速永磁电机的三维集总参数热网络
Fig.3 3D LPTN of the HSPMM
本文LPTN中的传导热阻使用了空心圆柱体热网络结构、实心圆柱体热网络结构、瓦片体热网络结构、平板导热热阻。
3.1.1 空心圆柱体热网络
空心圆柱体热网络可分为T型和+型网络拓扑,如图4所示。T型网络拓扑是基于径向和轴向的两个极坐标系一维常物性、稳态、无内热源导热微分方程推导出来的,并引入负热阻Rrm和Ram,将这两个三端口热网络相连以考虑热流源对平均温度的影响[25]。相比于传统的平板传热可以用较少的节点、较低的离散化水平获得电机各部件的平均温升。对于无内热源的部位,如机壳、端盖,可以将T型网络拓扑简化为+型。轴承在径向方向上的温度梯度远大于轴向方向,因此在建立热网络时只考虑其径向传热。

图4 空心圆柱体热网络
Fig.4 The thermal network of hollow cylinder
热网络中,Tro为外表面的温度,Tri为内表面温度,Ta1和Ta2为轴向两个端面温度。Tm为平均温度节点,从此处加载热流源。图4b中的径向上三个热阻计算如式(12)、式(13)所示,轴向上的三个热阻计算如式(14)~式(16)所示。
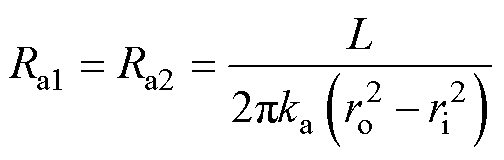 (12)
(12)
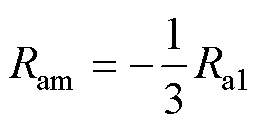 (13)
(13)
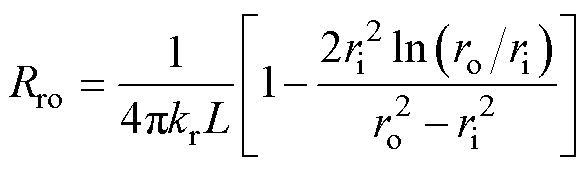 (14)
(14)
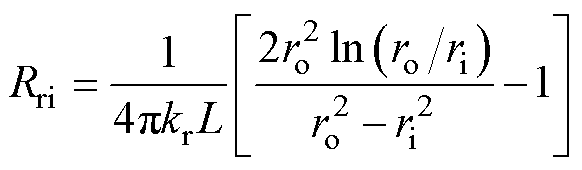 (15)
(15)
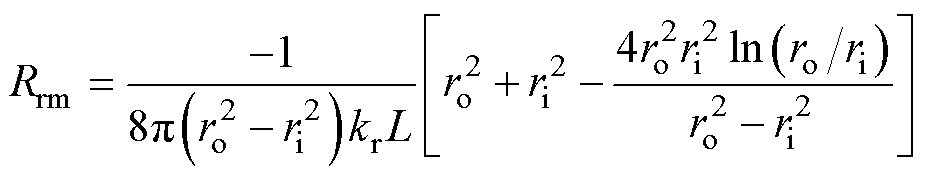 (16)
(16)
式中,L为空心圆柱体的轴向长度;ka为轴向导热系数;kr为径向导热系数;ro为空心圆柱体外半径;ri为空心圆柱体内半径。
对于+型网络,图4c中忽略了负热阻,轴向热阻不变,径向热阻简化为
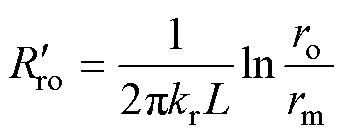 (17)
(17)
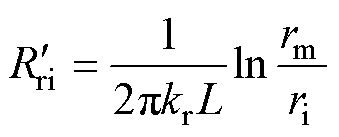 (18)
(18)
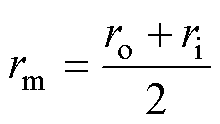 (19)
(19)
式中,rm为空心圆柱体的平均半径。
3.1.2 实心圆柱体热网络
实心圆柱体热网络如图5所示,设实心圆柱体半径为rsh,轴向长度为Lsh,任取一个径向截面,该面中有一距中心距离为r,宽度为dr的小圆环,对r处的热阻根据圆环占圆柱体径向截面积的比例进行积分,则从节点Tm至圆柱体外表面的径向热阻的计算式为
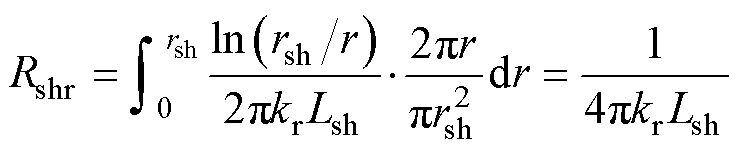 (20)
(20)
轴向上两个热阻的计算式为
 (21)
(21)
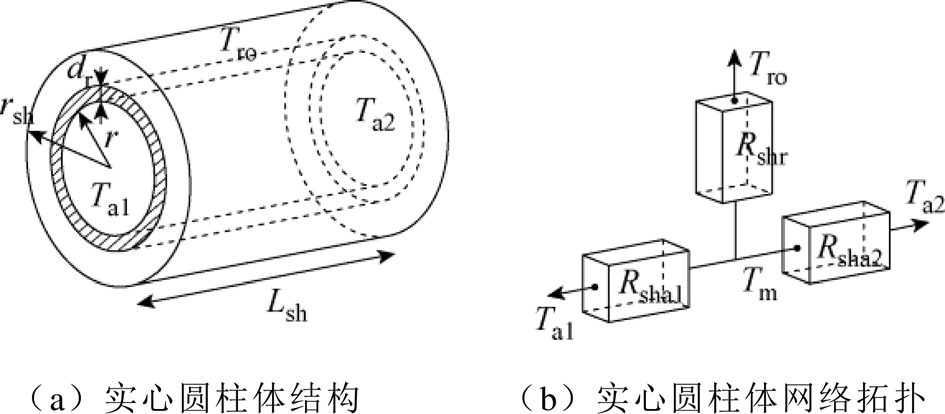
图5 实心圆柱体热网络
Fig.5 The thermal network of solid cylinder
3.1.3 瓦片体热网络
瓦片体热网络如图6所示,轴向上三个热阻Rwa1、Rwa2、Rwam和径向上三个热阻Rwro、Rwri、Rwrm在T型网络热阻计算式的基础上乘以2p/q,其中q为瓦片体所占圆周角度,并且从平均温度节点Tm处再连接一个三端口网络来描述周向热流的传递过程。
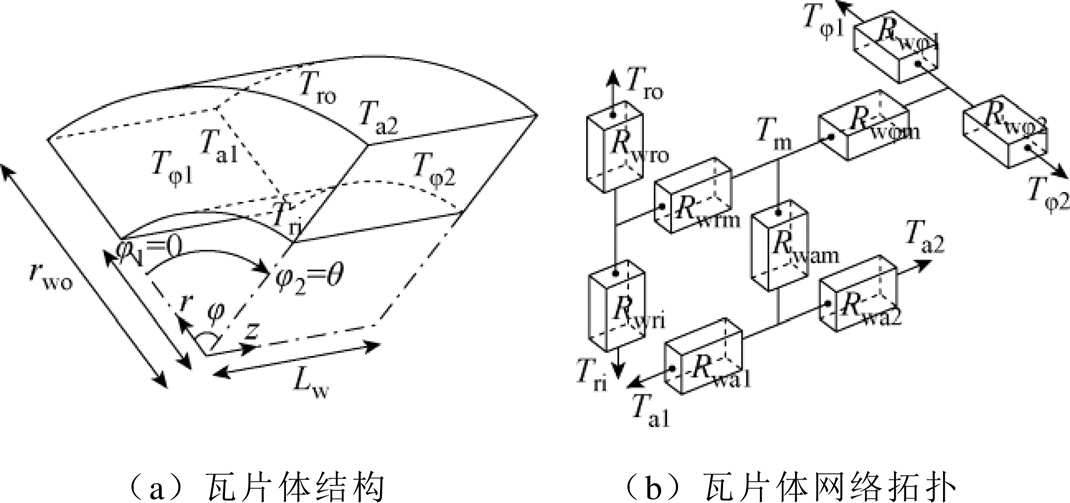
图6 瓦片体热网络
Fig.6 The thermal network of tile body
瓦片体周向上的三个热阻计算为
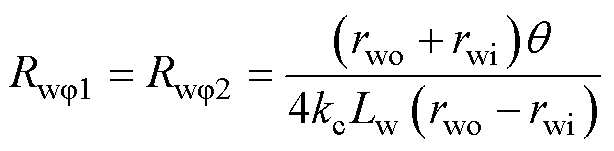 (22)
(22)
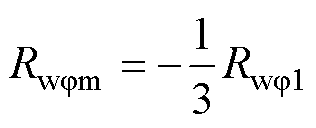 (23)
(23)
式中,rwo、rwi分别为瓦片体的外半径、内半径;Lw为瓦片体轴向长度;kc为瓦片体周向导热系数。
在该LPTN中定子槽部绕组和定子齿通过瓦片体结构等效。首先,针对槽内部件种类繁多、分部复杂的问题,将槽内所有部件视为单一实体,基于圆导线绕组的两阶段均匀化策略来估算等效实体的各向导热系数[26]。然后,从定子梨形槽底部将定子划分为轭部和多个齿段,依据齿段阴影面积相等的方法将槽形等效,如图7所示,这使得定子齿和槽部绕组为36个小瓦片体周向相连。又由于电机沿圆周方向温度对称分布,每个齿和每个槽部绕组的平均温度相同,因此最后可以将齿和槽部绕组分别视为1个等效瓦片体,每个等效瓦片体热阻均由18个小瓦片体对应热阻并联而成。
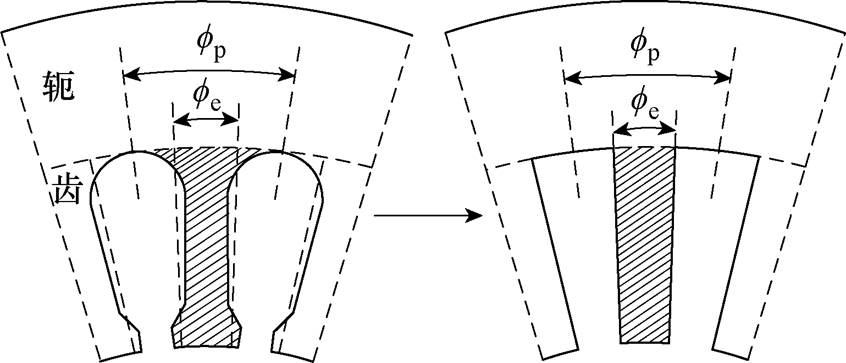
图7 定子槽形等效
Fig.7 Stator slot type equivalent
3.1.4 平板导热热阻
定子铁心和机壳、永磁体和转轴之间的接触热阻可依据平板导热热阻计算为
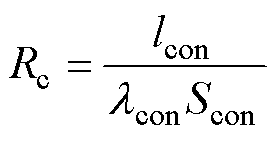 (24)
(24)
式中,lcon为间隙的长度;lcon为间隙材料的导热系数;Scon为接触面积。定子铁心和机壳装配间隙中为空气,长度为0.023 mm。永磁体和转轴间隙中为环氧树脂胶,长度为0.15 mm。
电机内外运动的流体与其流经的电机各零部件表面之间的对流传热常用对流热阻来模拟。
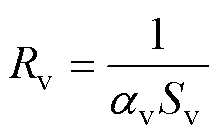 (25)
(25)
式中,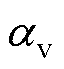 为对流散热系数;Sv为对流散热面积。
为对流散热系数;Sv为对流散热面积。
本文根据以下经验公式确定本台高速永磁电机中的对流散热系数[27-28]:
(1)气隙和定子内表面、转子外表面的对流散热系数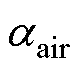 通过泰勒数Ta和努塞尔数Nu得到,有
通过泰勒数Ta和努塞尔数Nu得到,有
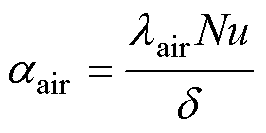 (26)
(26)
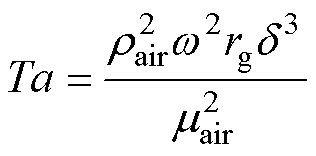 (27)
(27)
 (28)
(28)
式中,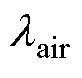 为空气导热系数;rg为气隙平均半径。
为空气导热系数;rg为气隙平均半径。
(2)定子端面对流散热系数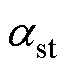 为
为
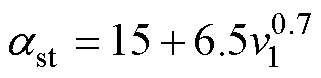 (29)
(29)
式中,v1为转子外表面线速度。
(3)绕组端部对流散热系数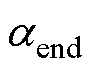 为
为
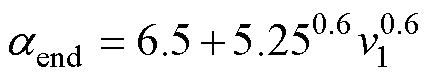 (30)
(30)
(4)转子端面对流散热系数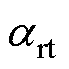 为
为
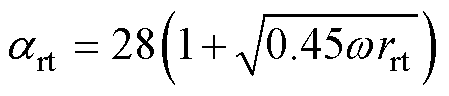 (31)
(31)
式中,rrt为转子端面平均半径。
(5)端腔空气和机壳、端盖对流散热系数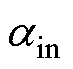 为
为
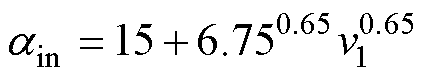 (32)
(32)
(6)端腔空气和轴伸段对流散热系数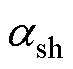 为
为
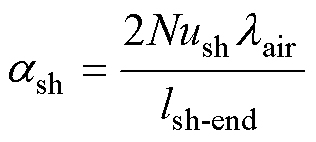 (33)
(33)
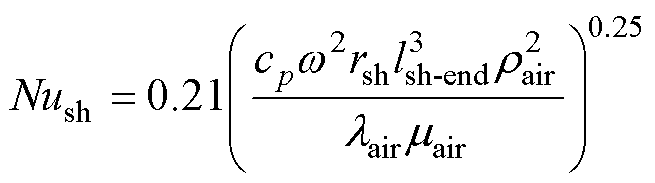 (34)
(34)
式中,Nush为轴伸段表面的努塞尔数;cp为空气的定压比热容;lsh-end为轴伸段至绕组的径向距离。
(7)机壳外表面对流散热系数为14 W/(m2·K)。
(8)螺旋水道对流散热系数计算详见文献[29]。
LPTN模型在Simulink中完成搭建,热源等效为电流源,环境温度和冷却水温度用电压源模拟,将热路求解转化为电路求解的形式。编写Matlab脚本文件计算各元件参数,并通过相关函数将参数输入至Simulink,以便于程序的模块化设计。
电磁-LPTN模型双向耦合计算流程如图8所示。首先,设定电机绕组、永磁体、钛合金护套的初始温度为20℃,在此温度下基于第2节的计算方法求解各部分损耗。其次,将损耗以电流源的形式加载至相应节点处,其中气隙风摩损耗的2/3加载至钛合金护套涡流损耗中,1/3气隙风摩损耗加载至定子齿部铁耗中,绕组铜耗按体积折算至槽部绕组和左右端部绕组。然后,求解LPTN各节点温度,得到绕组平均温度和永磁体平均温度。比较两者在计算前后的温度误差,若不满足收敛要求,则返回至第一步,重新设定新的初始温度并修改材料属性继续计算,直至温度误差达到精度要求时停止计算。
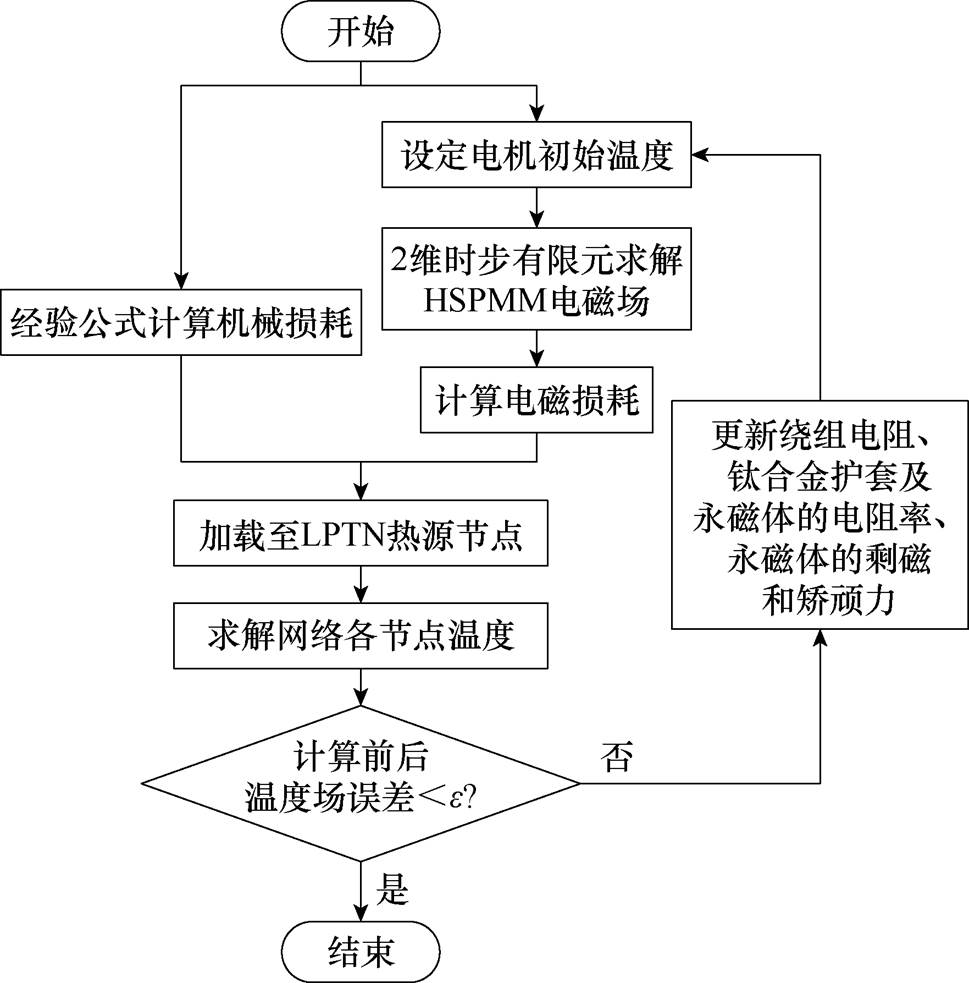
图8 电磁-热双向耦合计算流程
Fig.8 Computational flow of electromagnetic-thermal bidirectional coupling
绕组电阻和钛合金护套电阻率随温度的变化关系为
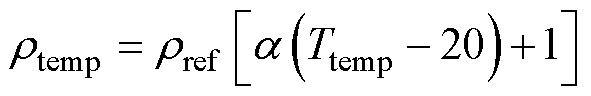 (35)
(35)
式中,Ttemp为工作温度;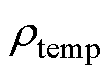 为Ttemp温度下的电阻率;
为Ttemp温度下的电阻率;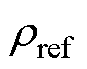 为20℃下电阻率;
为20℃下电阻率;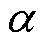 为温度系数。
为温度系数。
永磁体的温变特性为
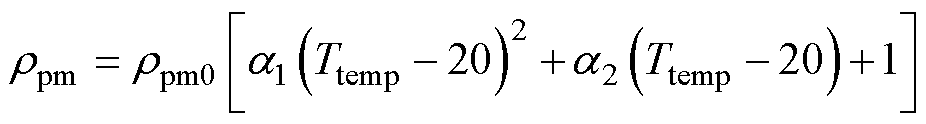 (36)
(36)
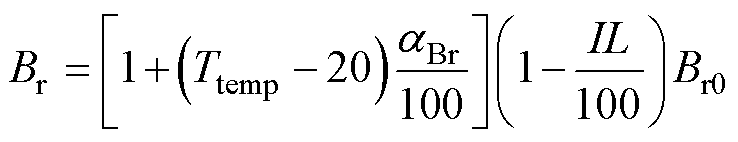 (37)
(37)
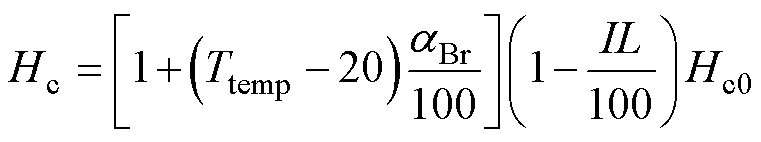 (38)
(38)
式中,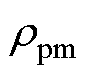 为永磁体Ttemp温度下的电阻率;
为永磁体Ttemp温度下的电阻率;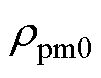 为永磁体20℃下的电阻率;
为永磁体20℃下的电阻率;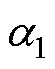 和
和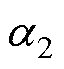 为永磁体电阻率温度系数;Br、Hc分别为永磁体Ttemp温度下的剩磁、矫顽力;Br0、Hc0分别为永磁体20℃下的剩磁、矫顽力;
为永磁体电阻率温度系数;Br、Hc分别为永磁体Ttemp温度下的剩磁、矫顽力;Br0、Hc0分别为永磁体20℃下的剩磁、矫顽力;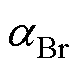 为永磁体剩磁的可逆温度系数;IL为永磁体剩磁的不可逆损失率。本文中高速永磁电机采用的永磁体牌号为N38UH。
为永磁体剩磁的可逆温度系数;IL为永磁体剩磁的不可逆损失率。本文中高速永磁电机采用的永磁体牌号为N38UH。
使用基于FVM的商业软件ANSYS Fluent对1/18的电机温度场进行仿真。各个电机部件被赋予特定的材料属性,对发热部件设置生热率。针对转子对内部空气的动态影响,采用多参考系模型策略。在保证网格质量的前提下,从气隙中心划分为静止和旋转两部分流体,确保旋转区域包含转子,设定旋转区域的转速为30 000 r/min。为了实现两个流体区域间的数据交换,将交界处的壁面设定为内部面。此外,运用壳热传导来模拟装配间隙的热传递。水道入口总进水流量为14 L/min,水温为24℃,进水口边界设为速度入口,出水口边界设为压力出口。
计及温度对电磁损耗的影响,LPTN的双向耦合迭代计算过程中绕组和永磁体电磁-热关系如图9所示。其中,第0次迭代中的损耗值为初始温度20℃下计算的,温度是基于初始温度下的损耗值计算得出的,此时绕组直流电阻值最小,铜耗最小,而永磁体的涡流损耗处于最大值。在经过4次迭代计算后,电机温度趋于稳定且误差达到精度要求,此时绕组铜耗为133.61 W,护套涡流损耗为142.58 W,永磁体涡流损耗为39.35 W。取最后一次迭代的损耗作为热源,基于FVM计算的高速永磁电机绕组和永磁体最终温度分布如图10所示,等效后的下层绕组温度比上层绕组高,最高温升出现在绕组端部,达到了71.17 K,永磁体的最高温升出现在轴向中心位置处,达到了134.42 K,由轴向中心向两侧温度逐渐递减。FVM和LPTN的双向耦合计算结果对比如图11所示,图中序号对应图3中热网络节点编号,其中①~⑥为对应热源节点,⑦~⑨为转轴上的节点,节点温度值处于FVM计算范围之间,证明了本文LPTN模型的正确性。
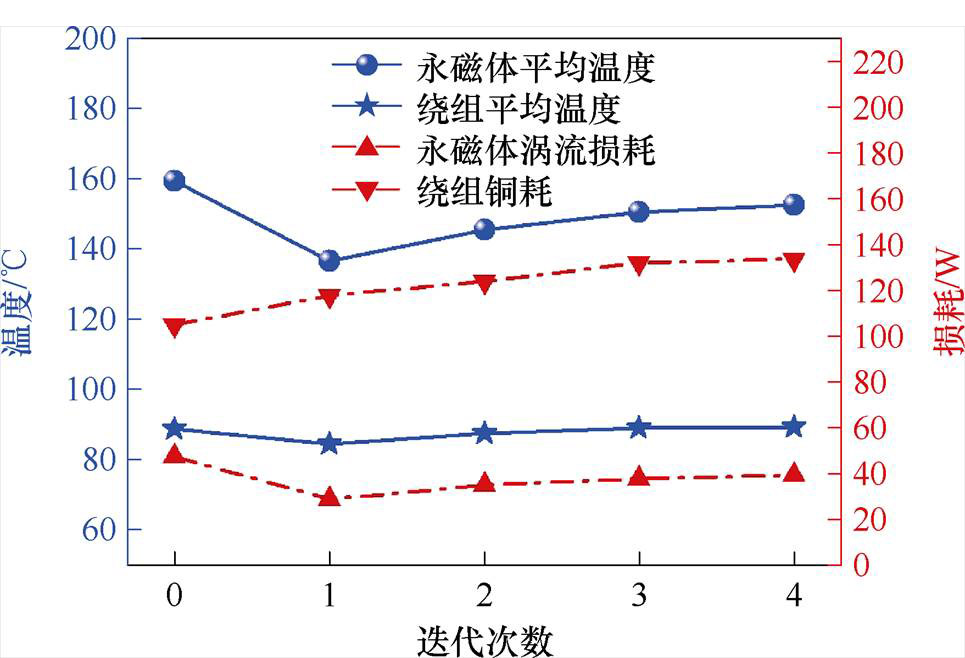
图9 LPTN迭代计算的损耗与温度曲线
Fig.9 The iterative computation curves of LPTN
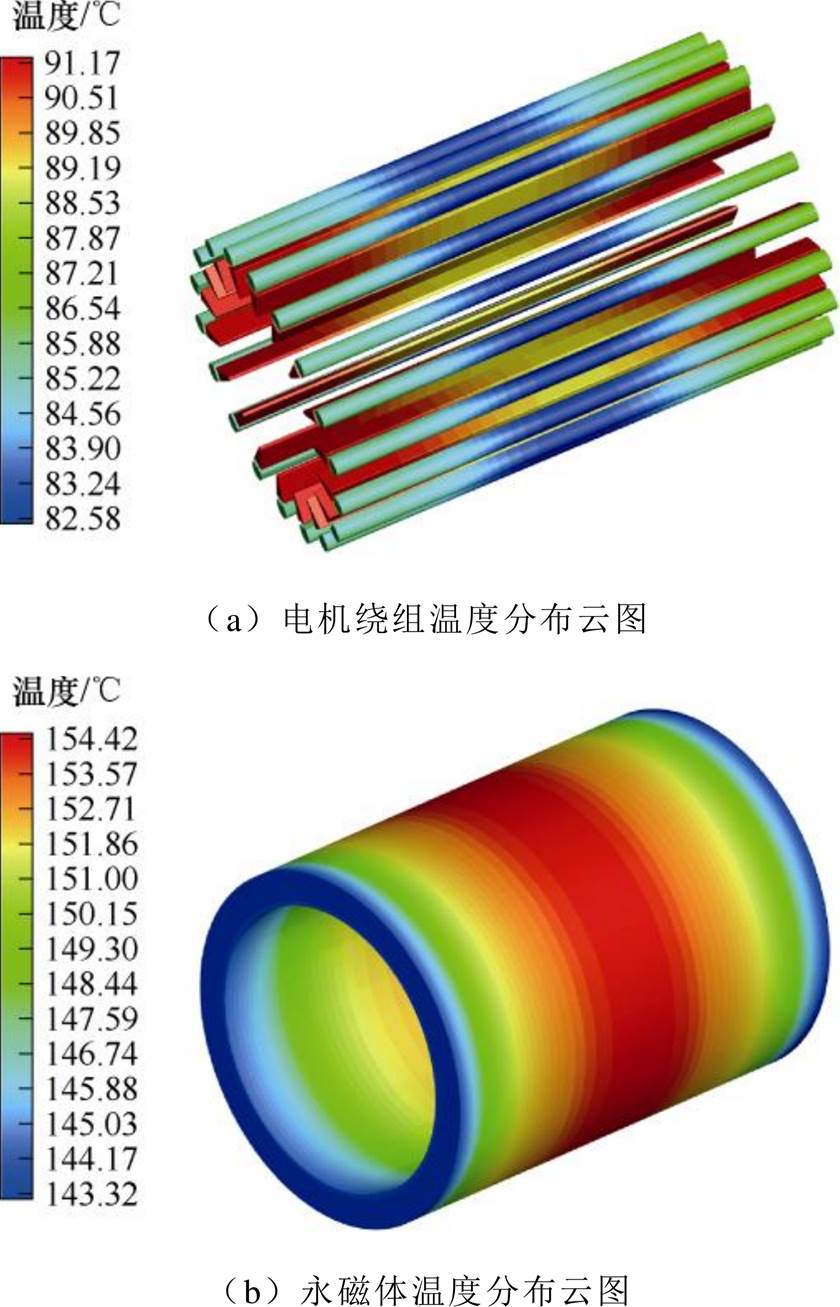
图10 FVM计算的电机关键发热部件温度分布
Fig.10 Temperature distribution of key heating components of the motor calculated by FVM
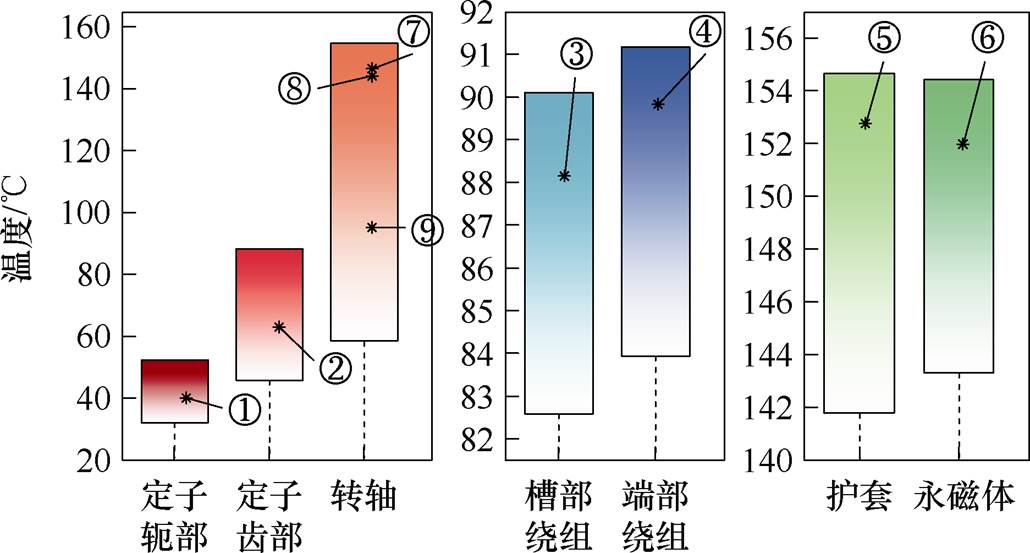
图11 LPTN与FVM计算结果对比
Fig.11 Comparison of the results of LPTN and FVM calculations
电磁-三维LPTN双向耦合与FVM求解所使用的计算机处理器为i5-12500H,内存为16 G。利用Fluent求解电机温度场所划的多面体网格数量为538 541,建模与计算总用时约5 h。利用Matlab求解三维LPTN的单次迭代计算用时0.89 s,极大地减少了计算量。
为验证三维热网络计算结果的准确性,受实验平台和轴承限制,本文对该样机转速为15 000 r/min、输出功率为7.5 kW、环境温度为26℃下进行温升实验,搭建如图12所示温升实验平台。两台参数性能完全相同的高速永磁电机处于对拖状态,左侧作为电动机,右侧作为发电机,中间通过轴联器将这两台电机连接在一起,在绕组端部和轴承处埋置热敏电阻以测量电机局部温升。

图12 样机温升实验平台
Fig.12 Prototype temperature rise test platform
实验平台的测量值和三维热网络的计算结果对比见表2。由此可见,三维热网络中的电机端部绕组和轴承的节点温升误差分别为5.22%和6.83%。该误差产生的一部分原因是由于对流散热系数是通过经验公式计算导致的,但在合理范围之内,满足工程实际要求,证明了本文提出的热网络的准确性。
表2 实验测量值和计算值对比
Tab.2 Comparison of experimental measurements and calculated values
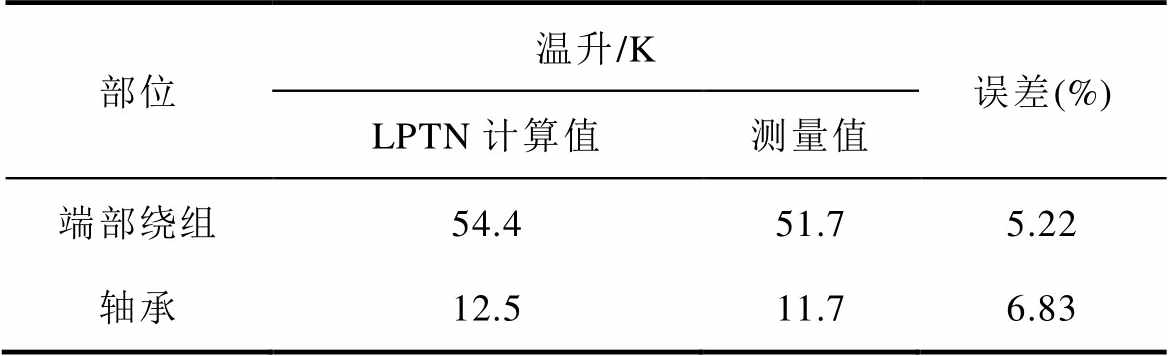
部位温升/K误差(%) LPTN计算值测量值 端部绕组54.451.75.22 轴承12.511.76.83
本文针对一台水冷高速永磁电机展开了热分析计算,建立了一种三维集总参数热网络全模型,该模型从径向、轴向、周向三个维度考虑了槽内绕组与定子齿部的传热,并计及槽内绕组与气隙之间的热交换,通过磁热双向耦合求解各节点温度,该热网络能够实现在较低的离散化水平下和较短的时间内计算电机温升且仍能保证计算精度,与实验值对比,端部绕组和轴承处的温升误差在7%以内。
本文编制的模块化三维热网络程序更便于移植,为具有类似转子结构和冷却方式的高速永磁电机的三维热网络的搭建和求解提供了重要参考。
参考文献
[1] 佟文明, 杨先凯, 鹿吉文, 等. 双层永磁体结构高速永磁电机转子涡流损耗解析模型[J]. 电工技术学报, 2024, 39(20): 6293-6304.
Tong Wenming, Yang Xiankai, Lu Jiwen, et al. Rotor eddy current loss analytical model for high-speed permanent magnet motor based on double layer permanent magnet structure[J]. Transactions of China Electrotechnical Society, 2024, 39(20): 6293-6304.
[2] 杨江涛, 王镇宇, 冯垚径, 等. 高速永磁电机转子过盈方式对转子应力的影响[J]. 电工技术学报, 2023, 38(16): 4263-4273.
Yang Jiangtao, Wang Zhenyu, Feng Yaojing, et al. Influence of shrink fitting modes on rotor stress of high speed permanent magnet machine[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(16): 4263-4273.
[3] 张文校, 胡岩, 曹力, 等. 高速永磁屏蔽电机摩擦损耗分析与计算[J]. 电工技术学报, 2023, 38(12): 3122-3129.
Zhang Wenxiao, Hu Yan, Cao Li, et al. Analysis and calculation of friction loss of high-speed permanent magnetic shielding motor[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3122-3129.
[4] 师蔚, 骆凯传, 张舟云. 基于热网络法的永磁电机温度在线估计[J]. 电工技术学报, 2023, 38(10): 2686-2697.
Shi Wei, Luo Kaichuan, Zhang Zhouyun. On-line temperature estimation of permanent magnet motor based on lumped parameter thermal network method[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2686-2697.
[5] 丁树业, 郭保成, 冯海军, 等. 变频控制下永磁同步电机温度场分析[J]. 中国电机工程学报, 2014, 34(9): 1368-1375.
Ding Shuye, Guo Baocheng, Feng Haijun, et al. Temperature field investigation of permanent magnet synchronous motors controlled by the frequency conversion control system[J]. Proceedings of the CSEE, 2014, 34(9): 1368-1375.
[6] Chen Wei, Ju Yuning, Yan Dong, et al. Design and optimization of dual-cycled cooling structure for fully-enclosed permanent magnet motor[J]. Applied Thermal Engineering, 2019, 152: 338-349.
[7] Kang Ming, Wang Huimin, Guo Liyan, et al. Self- circulation cooling structure design of permanent magnet machines for electric vehicle[J]. Applied Thermal Engineering, 2020, 165: 114593.
[8] Tong Wenming, Sun Ruolan, Li Shiqi, et al. Loss and thermal analysis for high-speed amorphous metal PMSMs using 3-D electromagnetic-thermal bi- directional coupling[J]. IEEE Transactions on Energy Conversion, 2021, 36(4): 2839-2849.
[9] Soualmi A, Zidat F, Lombard P, et al. Thermal study comparison of permanent magnets machines using finite element method (FEM) electric vehicles application[C]//2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Korea, 2018: 59-64.
[10] Tong Wenming, Wu Shengnan, Tang Renyuan. Research on the airflow and thermal performance in a large forced air-cooled permanent magnet syn- chronous machine[J]. IEEE Access, 2019, 7: 162343- 162352.
[11] Cheng Min, Ding Shichuan, Li Wei, et al. Cooling system design and thermal analysis of a PMSM for rail transit[C]//2020 15th IEEE Conference on Industrial Electronics and Applications (ICIEA), Kristiansand, Norway, 2020: 1912-1915.
[12] 张智贺, 杨鑫, 陈钰凯. 稀土超磁致伸缩换能器等效热网络建模研究[J]. 电工技术学报, 2022, 37(14): 3464-3474, 3565.
Zhang Zhihe, Yang Xin, Chen Yukai. Research on equivalent thermal network modeling for rare-earth giant magnetostrictive transducer[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3464- 3474, 3565.
[13] Kačenka A, Pop A C, Vintiloiu I, et al. Lumped parameter thermal modeling of permanent magnet synchronous motor[C]//2019 Electric Vehicles Inter- national Conference (EV), Bucharest, Romania, 2019: 1-6.
[14] 张兆宇, 于思洋, 张岳, 等. 永磁/磁阻混合转子双定子低速大转矩同步电机冷却及热管理技术研究[J]. 电机与控制学报, 2023, 27(11): 114-124.
Zhang Zhaoyu, Yu Siyang, Zhang Yue, et al. Cooling and thermal management technology for low speed and high torque synchronous motor with permanent magnet and reluctance hybrid rotor and double stator[J]. Electric Machines and Control, 2023, 27(11): 114-124.
[15] Liang Dawei, Zhu Z Q, Zhang Yafeng, et al. A hybrid lumped-parameter and two-dimensional analytical thermal model for electrical machines[J]. IEEE Transactions on Industry Applications, 2021, 57(1): 246-258.
[16] Chen Qixu, Wu Dechen, Li Guoli, et al. Development of a fast thermal model for calculating the tempera- ture of the interior PMSM[J]. Energies, 2021, 14(22): 7455.
[17] Wang Hanghang, Chen Junquan, Jiang Yapeng, et al. Coupled electromagnetic and thermal analysis of permanent magnet rectifier generator based on LPTN[J]. IEEE Transactions on Magnetics, 2022, 58(2): 8201705.
[18] Liang Dawei, Zhu Z Q, Shao Bo, et al. Estimation of two- and three-dimensional spatial magnet tempera- ture distributions for interior PMSMs based on hybrid analytical and lumped-parameter thermal model[J]. IEEE Transactions on Energy Conversion, 2022, 37(3): 2175-2189.
[19] Hu Kai, Zhang Guangming, Zhang Wenyi. Rotor design and optimization of high-speed surface- mounted permanent magnet motor based on the multi-physical field coupling method[J]. IEEE Access, 2023, 11: 69614-69625.
[20] 佟文明, 程雪斌, 孙静阳, 等. 转子风刺对高速永磁电机永磁体温升的抑制作用[J]. 中国电机工程学报, 2017, 37(5): 1526-1535.
Tong Wenming, Cheng Xuebin, Sun Jingyang, et al. Suppression effect of rotor wafters on permanent magnet temperature rise for high-speed permanent magnet motor[J]. Proceedings of the CSEE, 2017, 37(5): 1526-1535.
[21] Li Zheng, Che Shuai, Zhao Hui, et al. Loss analysis of high-speed permanent magnet motor based on energy saving and emission reduction[J]. Energy Reports, 2023, 9: 2379-2394.
[22] Huang Ziyuan, Fang Jiancheng. Multiphysics design and optimization of high-speed permanent-magnet electrical machines for air blower applications[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 2766-2774.
[23] Pyrhonen J, Jokinen T, Hrabovcova V. Design of Rotating Electrical Machines[M]. 2nd Ed, West Sussex: John Wiley & Sons Ltd, 2014.
[24] Saari J. Thermal analysis of high-speed induction machines[D]. Finland: Helsinki University of Tech- nology, 1998.
[25] Mellor P H, Roberts D, Turner D R. Lumped parameter thermal model for electrical machines of TEFC design[J]. IEE Proceedings B Electric Power Applications, 1991, 138(5): 205.
[26] 郭轩, 肖云昊, 李驰, 等. 综合考虑材料热各向异性与多种传热方式的磁性元件热阻网络精准模型[J]. 电工技术学报, 2024, 39(6): 1806-1817.
Guo Xuan, Xiao Yunhao, Li Chi, et al. An accurate thermal resistance network model for magnetic elements considering thermal anisotropy of materials and various heat transfer ways[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1806- 1817.
[27] Gronwald P O, Kern T A. Traction motor cooling systems: a literature review and comparative study[J]. IEEE Transactions on Transportation Electrification, 2021, 7(4): 2892-2913.
[28] 李鑫宇, 孙天夫, 黄世军, 等. 永磁同步电机温度建模与热管理方法综述[J]. 电气工程学报, 2023, 18(4): 20-34.
Li Xinyu, Sun Tianfu, Huang Shijun, et al. Review and perspectives on thermal management methods for permanent magnet synchronous motors[J]. Journal of Electrical Engineering, 2023, 18(4): 20-34.
[29] 钱洪. 高能量密度电机水冷系统设计与选用[J]. 电机与控制应用, 2013, 40(1): 9-12.
Qian Hong. Design and choose of cooling system for high-energy density motor[J]. Electric Machines & Control Application, 2013, 40(1): 9-12.
Abstract High-speed permanent magnet motors (HSPMMs) are increasingly applied in industrial fields, particularly in environments requiring high power density and rotational speeds. The issue of rising temperatures has become prominent. Excessive temperature rise can lead to a decline in the insulation performance of the motor, demagnetization of the magnetic materials, and even cause motor failure. Therefore, accurately predicting and assessing the rise in temperature during the design phase is crucial. Traditional methods for temperature rise calculation mostly rely on numerical analysis techniques. However, these methods face significant challenges in designing high-speed motors due to their low computational efficiency and high computational load. This paper proposes an efficient computational model based on a three-dimensional lumped parameter thermal network (LPTN) to improve the thermal network approach, ensuring accurate temperature rise predictions while reducing computational complexity.
The proposed LPTN model simplifies the complex heat transfer processes within the motor by establishing a rational topological structure. This model employs hollow cylindrical T-shaped and +-shaped topologies, solid cylindrical topologies, and tile-shaped topologies. Specifically, hollow cylinders represent the stator yoke, titanium alloy sheath, permanent magnets, motor housing, end caps, and bearings. At the same time, tile-shaped bodies are used to model the stator teeth and slot winding. The rotation shaft is treated as a combination of hollow and solid cylindrical bodies. The assembly gap is also modeled using a heat resistance representation based on flat-plate conduction. To better account for the impact of temperature on electromagnetic losses, the study also incorporates an electromagnetic-thermal network coupling solution method. This method achieves bidirectional coupling between magnetic and thermal fields through iterative calculations, enabling the consideration of the feedback effect of temperature variations on electromagnetic losses. Consequently, the accuracy of the temperature rise prediction is enhanced.
The finite volume method (FVM) calculates the motor's temperature field. It is found that the LPTN offers significant advantages in terms of setup and computational time. The time for a single iteration calculation is only 0.89 seconds, significantly improving computational efficiency, while the temperatures at all nodes in the thermal network are within the range of the FVM results. Additionally, a temperature rise experiment is conducted. Due to limitations imposed by the experimental platform and bearings, tests are carried out under operating conditions with an output power of 7.5 kW and a rotational speed of 15 000 r/min. The results show that the temperature rise errors at the end-winding and bearing locations are within 7%.
keywords:High-speed permanent magnet machines, three-dimensional lumped parameter thermal network, electromagnetic-thermal bi-directional coupling, thermal analysis
DOI: 10.19595/j.cnki.1000-6753.tces.241836
中图分类号:TM355
辽宁省科技厅联合基金项目面上资助计划项目(2023-MSLH-247)和辽宁省教育厅基本科研项目(JYTMS20231232)资助。
收稿日期 2024-10-21
改稿日期 2024-11-15
张 超 男,1988年生,副教授,硕士生导师,研究方向为特种电机及其控制。E-mail: zhchpm@163.com(通信作者)
司马秉奇 男,1999年生,硕士研究生,研究方向为永磁电机多物理场分析。E-mail: simabingqi@163.com
(编辑 崔文静)