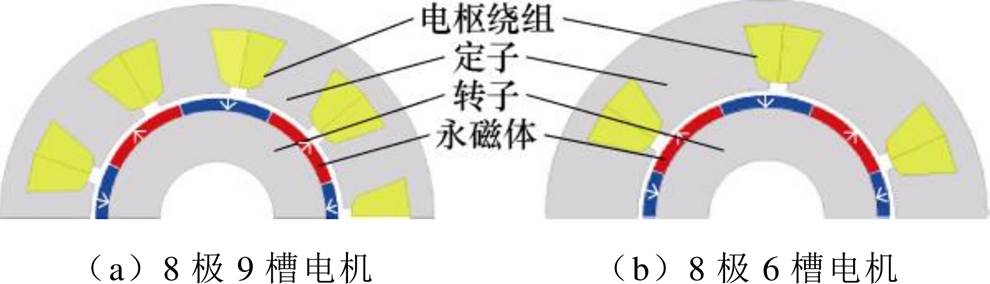
图1 不同槽极组合FSCW PMSM
Fig.1 FSCW PMSM with different slot-pole combination
摘要 为抑制槽极组合满足Ns=2pr±1的分数槽集中绕组（FSCW）永磁同步电机（PMSM）的不平衡磁拉力（UMF），并保持电磁转矩输出，提出一种基于气隙磁通密度谐波相位调节的UMF抑制方法。首先，基于磁场调制理论，分析气隙磁导对FSCW PMSM一阶电磁力波时间系数和空间系数的影响，确定产生UMF和电磁转矩的主要气隙磁通密度谐波阶次。其次，量化分解电机的UMF和电磁转矩，分析一阶电磁力波间的抵消关系。然后，通过优化定子槽口和辅助槽的结构参数，调节气隙磁通密度谐波相位，增强一阶电磁力波间的抵消效应，在有效抑制电机UMF的同时，保持电机电磁转矩输出。最后，对一台8极9槽FSCW PMSM进行仿真分析和样机实验，验证了基于气隙磁通密度谐波相位调节的UMF抑制与不降低电磁转矩输出设计方法的有效性。
关键词：分数槽集中绕组 不平衡磁拉力 电磁转矩 相位调节 一阶径向电磁力波
分数槽集中绕组（Fractional Slot Concentrated Winding, FSCW）永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）具有高转矩密度/功率密度、短绕组端部和高槽满率等优点，广泛应用于电动交通工具、家用电器、新能源发电领域、数控机床、机器人、国防军工等装备的动力来源和核心运动部件[1-4]。其中，4极/9槽、8极/9槽和10极/9槽等槽极组合电机具有更高的绕组基波系数和更低的绕组端部电阻，在电机设计中受到关注[5]。然而，采用这些槽极组合的FSCW PMSM，其转子存在较大不平衡磁拉力（Unbalanced Magnetic Force, UMF），导致电机产生振动和噪声，并降低轴承使用寿命。
UMF的产生主要涉及转子偏心和电机电磁结构不对称两个方面。前者是由于电机元件制造精度不足或安装误差较大，导致电机转子偏心产生UMF[6-7]。后者是由于电机电磁结构不对称导致电机产生非对称气隙磁通密度分布，从而在转子上形成时变UMF[8-10]。在实际运行中，电机电磁结构不对称产生的UMF会加剧转子偏心，进一步增加电机的UMF[11]。目前，一般采用麦克斯韦应力张量法计算电机的UMF。基于微扰理论，文献[12]提出了环形绕组无刷直流电机偏心所引起径向力解析模型，推导了偏心时气隙磁通密度函数和UMF。文献[13]将8极9槽FSCW PMSM的转子偏心情况沿轴向分割成多个均匀切片，通过计算每层切片的UMF，再轴向叠加计算总UMF。在电机电磁结构不对称产生UMF方面，槽极组合满足Ns=2pr±1（Ns为定子槽数，pr为电机极对数）的FSCW PMSM会产生更大的UMF。文献[14]提出了一种二维解析模型，推导了负载下切向电磁力波和轴向电磁力波。结果表明，径向电磁力波和切向电磁力波均会产生UMF。在此基础上，当2pr=3h-1（h为正整数）时，切向电磁力波产生的UMF与径向电磁力波产生的UMF为叠加关系；当2pr=3h+1时，切向电磁力波产生的UMF和径向电磁力波产生的UMF为抵消关系[15]。在FSCW PMSM的UMF抑制方面，一般采用如不等宽定子齿[16-17]、分段交错不等磁极[18]等非对称设计。该类方法在电机低速或轻载运行时抑制UMF较为有效，在电机高速运行时反而会增加UMF。随着有限元软件应用，一般采用多目标优化算法优化电机结构，实现UMF抑制效果。其中，优化设计定子铁心上的辅助槽[19-20]、转子铁心上设置虚齿结构[21]是UMF抑制常用方法。近年来，磁场调制理论广泛应用于电机设计的研究[22-23]。磁场调制理论将电机结构规格化为“励磁源”、“调制器”和“滤波器”三个基本要素的级联，在统一框架下分析了V型永磁电机[24]、反向磁通永磁电机[25]和磁通切换永磁电机[26-28]等电机电磁转矩和磁阻转矩的产生机理，并确定产生电磁转矩的主要磁通密度谐波阶次。电磁转矩输出减少将直接导致输出功率下降，尤其在电机起动和加速阶段易引发电机过热问题。但研究者一般通过多目标优化算法[29-30]、模态分析[31-32]优化电机“调制器”来抑制UMF，鲜有涉及UMF抑制与不降低电磁转矩相关设计方法的研究。
本文基于磁场调制理论，优化槽极组合满足Ns=2pr±1的FSCW PMSM“调制器”结构，通过调节气隙磁通密度谐波相位，增强一阶径向电磁力波间的抵消效应，在抑制电机UMF的同时，保持电机电磁转矩输出。首先，分析气隙磁导对电机一阶电磁力波时间系数和空间系数的影响，确定产生UMF和电磁转矩的主要气隙磁通密度谐波阶次。其次，量化分解电机UMF和电磁转矩，分析一阶电磁力波间的抵消关系。然后，通过优化定子槽口和辅助槽的结构参数，调节气隙磁通密度谐波相位，增强一阶电磁力波间的抵消效应，在有效抑制电机UMF的同时，保持电机电磁转矩输出。最后，对一台8极9槽FSCW PMSM进行仿真分析和样机实验，验证基于气隙磁通密度谐波相位调节UMF抑制与不降低电磁转矩输出设计方法的有效性。
以槽极组合满足Ns=2pr±1的8极9槽FSCW PMSM为例，同时选择8极6槽FSCW PMSM进行对比分析，两者有限元模型如图1所示。
为保证公平对比分析，两台电机具有相同的有效轴长和电枢电流。表1为两台FSCW PMSM的主要设计参数。
基于麦克斯韦应力张量法，在直角坐标系中对转子径向电磁力波和切向电磁力波进行分解，得到径向电磁力波、切向电磁力波分别产生的UMF以及电磁力波产生的总UMF[10]为
图1 不同槽极组合FSCW PMSM
Fig.1 FSCW PMSM with different slot-pole combination
表1 FSCW PMSM主要设计参数
Tab.1 Main design parameters of FSCW PMSM
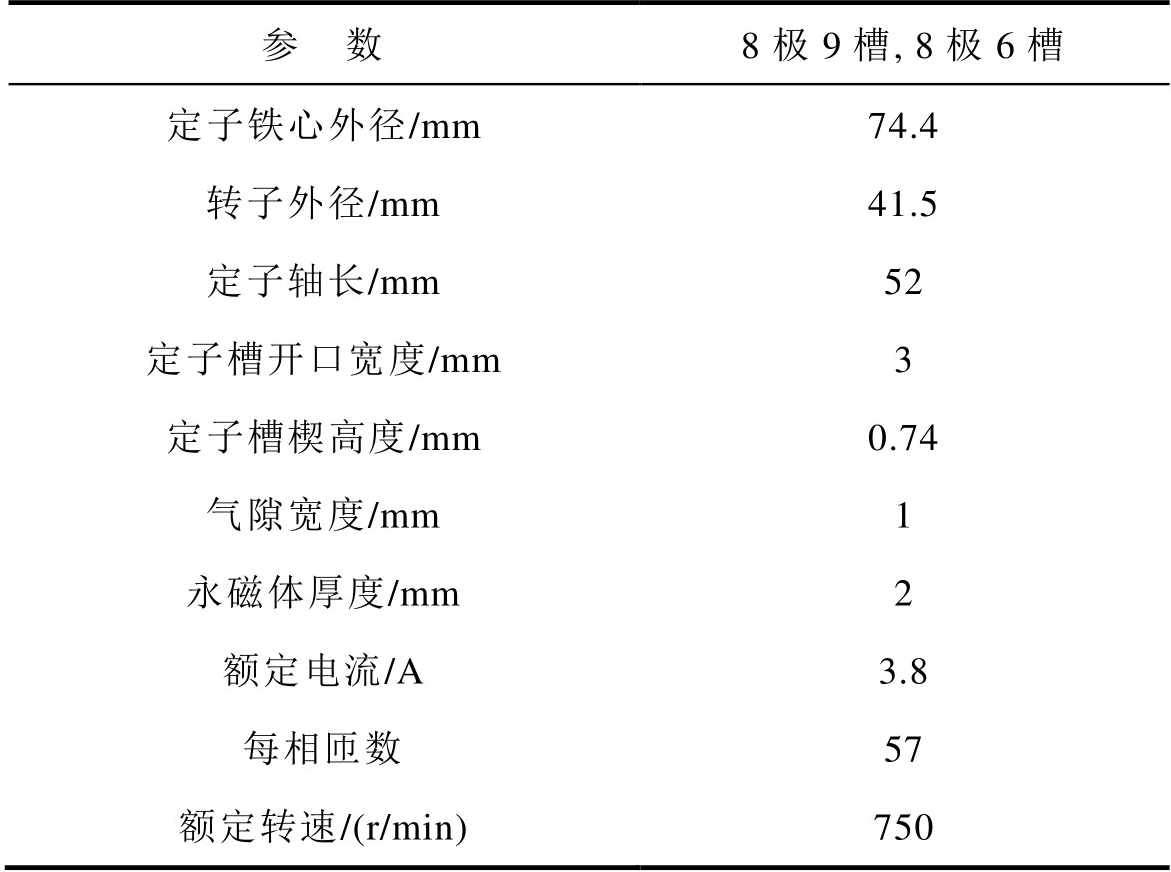
参 数8极9槽, 8极6槽 定子铁心外径/mm74.4 转子外径/mm41.5 定子轴长/mm52 定子槽开口宽度/mm3 定子槽楔高度/mm0.74 气隙宽度/mm1 永磁体厚度/mm2 额定电流/A3.8 每相匝数57 额定转速/(r/min)750
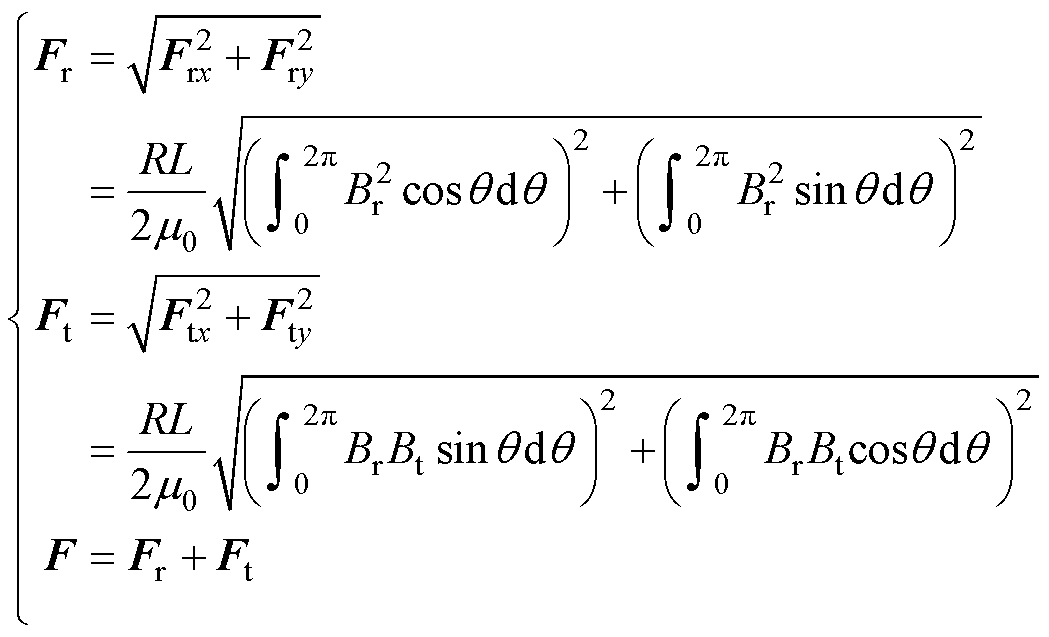（1）
式中，Br和Bt分别为径向和切向气隙磁通密度；Frx和Fry分别为径向电磁力波在x轴和y轴产生的UMF；Ftx和Fty分别为切向电磁力波在x轴和y轴产生的UMF；Fr和Ft分别为径向和切向电磁力波产生的UMF；R为转子半径；L为定子轴向长度；q为转子位置；m0为真空磁导率。
基于上述分析，一种8极9槽FSCW PMSM的径向UMF和切向UMF如图2所示，图中，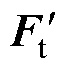
和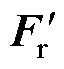
分别为8极6槽FSCW PMSM的径向UMF和切向UMF。经计算，8极6槽FSCW PMSM 的UMF极小，可忽略不计，8极9槽FSCW PMSM的总UMF为134 N，径向电磁力波和切向电磁力波产生的UMF分别占总UMF的60%和40%。根据式（1），径向电磁力波与切向电磁力波谐波分量相同，仅谐波幅值存在差异。因此，由径向电磁力波产生的UMF与由切向电磁力波产生的UMF具有相同的变化趋势和占比关系，以下将从径向电磁力波产生UMF的角度分析UMF产生机理。
图2 FSCW PMSM的径向UMF和切向UMF
Fig.2 Radial UMF and tangential UMF of FSCW PMSM
基于FSCW PMSM的磁动势和磁导，在忽略切向磁通密度分量的情况下，得到径向永磁磁通密度和径向电枢磁通密度分别[6]为
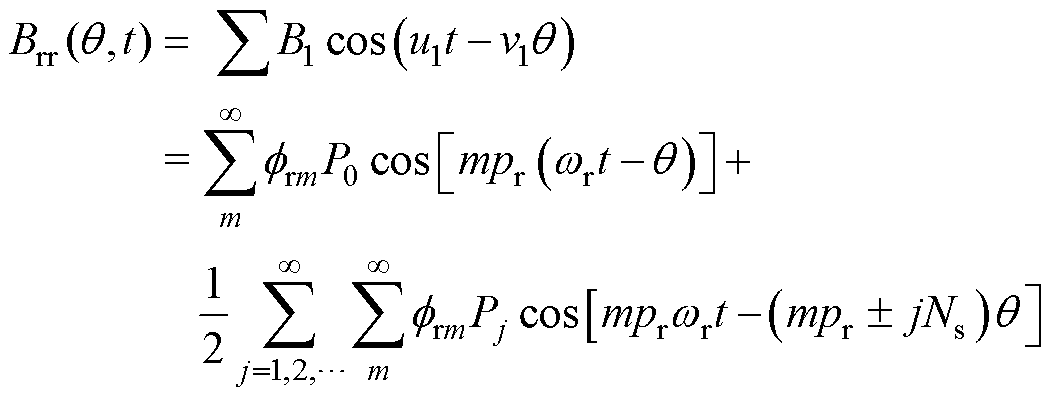（2）
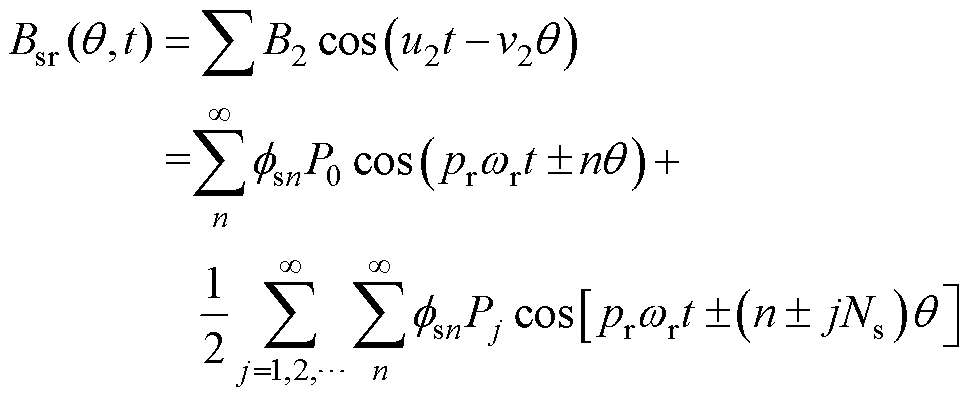（3）
式中，wr为机械角速度；m=1,3,5,…；mpr为永磁磁动势谐波阶次；n=1,2,3,…，由绕组分布决定；frm和fsn分别为m次和n次磁动势谐波幅值；P0为气隙磁导函数的直流分量；Pj为气隙磁导谐波幅值；j为正整数，表示气隙磁导谐波阶次；u1、v1分别为径向永磁磁通密度谐波时间系数和空间系数；u2、v2分别为径向电枢磁通密度谐波时间系数和空间系数；B1、B2分别为径向永磁磁通密度和径向电枢磁通密度谐波幅值。
由式（2）和式（3）可知，定子槽可改变径向永磁磁通密度谐波和电枢磁通密度谐波的空间系数，但不改变其时间系数。根据麦克斯韦应力张量法，第l次和第l+1次径向永磁磁通密度谐波和电枢磁通密度谐波合成的气隙磁通密度谐波所形成的径向电磁力波为
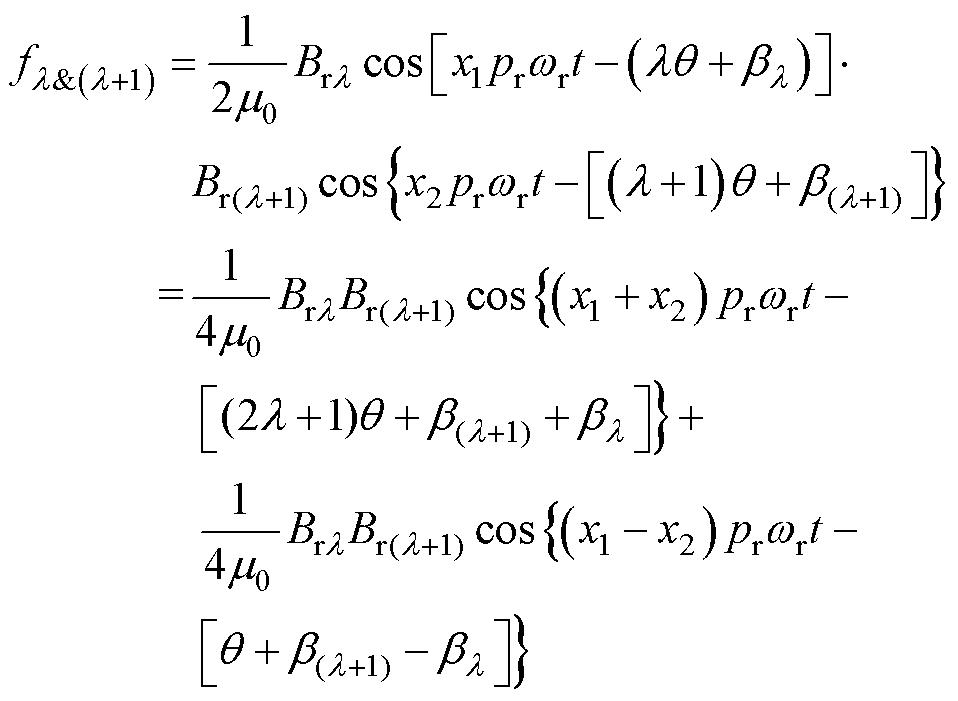（4）
式中，Brl、Br(l+1)分别为l、l+1次径向永磁磁通密度谐波和电枢磁通密度谐波合成的气隙磁通密度谐波幅值；bl和b(l+1)分别为l和l+1次径向永磁磁通密度谐波和电枢磁通密度谐波合成的气隙磁通密度谐波初始相位；x1pr和x2pr为永磁磁动势谐波阶次；x、s分别为径向电磁力波的时间系数、空间系数。
由式（4）可知，第l次和第l+1次气隙磁通密度谐波耦合形成一阶径向电磁力波和2l+1阶径向电磁力波。由调制产生的径向永磁磁通密度谐波与非调制产生的径向永磁磁通密度谐波相互耦合，形成的径向电磁力波时间系数和空间系数为
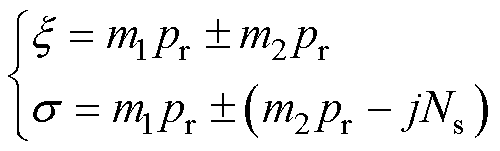（5）
式中，m1、m2为正奇数，采用m1、m2分别表示式（2）中由调制产生径向永磁磁通密度谐波与非调制产生径向永磁磁通密度谐波表达式中的m。
8极9槽FSCW PMSM和8极6槽FSCW PMSM的电枢磁动势和永磁磁动势在定子槽调制后的径向永磁磁通密度和电枢磁通密度如图3所示。图中，pr1和pr2分别为8极9槽FSCW PMSM和8极6槽FSCW PMSM的极对数。由图3可知，径向电枢磁通密度存在除3的倍数阶次谐波外的其他阶次谐波。相比径向永磁磁通密度，其幅值较小，而且非调制产生的径向永磁磁通密度谐波幅值远大于调制产生的径向永磁磁通密度谐波。
图3 径向永磁磁通密度和电枢磁通密度幅值
Fig.3 Amplitude of both radial permanent magnet flux density and radial armature flux density
根据径向永磁磁通密度谐波旋转方向，径向电磁力波的产生包括空间系数旋转方向相同径向永磁磁通密度谐波相互耦合和空间系数旋转方向相反径向永磁磁通密度谐波相互耦合两种方式。径向电磁力波空间系数见表2。表中，pr为极对数，Ns为槽数。针对径向永磁磁通密度谐波形成的径向电磁力波，将槽极组合满足Ns=2pr±1、Ns=2pr±2的两类FSCW PMSM的极对数与槽数代入式（5）中，可得径向电磁力波空间系数s。其中，当径向电磁力波空间系数(m3+m4±2j)pr±j、(m3-m4±2j)pr±j、(m5+m6±2j)pr±2j和(m5-m6±2j)pr±2j均为1时，表示为一阶径向电磁力波。此时，用m3、m4代替槽极组合满足Ns=2pr±1的FSCW PMSM在式（5）中的m1、m2；用m5、m6代替槽极组合满足Ns=2pr±2的FSCW PMSM在式（5）中的m1、m2。
表2 径向电磁力波空间系数
Fig.2 Spatial coefficients of radial electromagnetic force waves
槽极组合空间系数 旋转方向相反旋转方向相同 Ns=2pr±1(m3+m4±2j)pr±j(m3-m4±2j)pr±j Ns=2pr±2(m5+m6±2j)pr±2j(m5-m6±2j)pr±2j
槽极组合满足Ns=2pr±1的FSCW PMSM径向电磁力波的产生同样包括空间系数旋转方向相同径向永磁磁通密度谐波相互耦合和空间系数旋转方向相反径向永磁磁通密度谐波相互耦合两种方式。令表2中j=1，(m3+m4±2j)pr=0、(m3-m4±2j)pr=0，结合径向永磁磁通密度谐波产生一阶电磁力波条件，通过永磁磁动势谐波阶次进行约束，可得气隙磁导基波分量作用下的一阶径向电磁力波时间系数x，见表3。表中，e为自然数，(2e+1)pr和(2e-1)pr表示永磁磁动势谐波阶次。
表3 径向电磁力波时间系数
Fig.3 Time coefficient of radial electromagnetic force waves
旋转方向相反旋转方向相同 一阶电磁力波产生条件(m3+m4)±2×1=0(m3-m4)±2×1=0 时间系数(1×Pr+1×Pr)wr[(2e+1)pr-(2e-1)pr]wr
根据表2和表3，可得到如下结论：
（1）电机槽极组合满足Ns=2pr±1时，气隙磁导基波分量调制的永磁磁通密度谐波可产生一阶径向电磁力波，并且存在幅值较大的pr±1次径向永磁磁通密度谐波；电机槽极组合满足Ns=2pr±2时，气隙磁导基波分量调制的永磁磁通密度谐波不产生一阶径向电磁力波，并且不存在幅值较大的pr±1次径向永磁磁通密度谐波。
（2）电机槽极组合满足Ns=2pr±1时，由气隙磁导基波分量调制的径向永磁磁通密度谐波和非调制的永磁磁通密度谐波所产生一阶径向电磁力波具有相同的时间系数x=2pr。这使得一阶径向电磁力波间的相位差不变，从而在一个电周期中可实现一阶径向电磁力波间的抵消。
由图3可见，8极9槽FSCW PMSM径向气隙磁通密度谐波阶次主要为4次、12次。根据式（4），与4次、12次谐波产生UMF的径向气隙磁通密度谐波阶次为3次、5次和13次。不考虑漏磁，径向电枢磁通密度谐波的时间系数为pr，与4次、5次和13次永磁磁通密度谐波时间系数相同。3次、4次、5次、12次和13次径向气隙磁通密度谐波虽由永磁磁动势和电枢磁动势共同产生，但每阶径向气隙磁通密度谐波仅有唯一时间系数和空间系数。结合式（4），这些气隙磁通密度谐波产生的一阶径向电磁力波具有相同时间系数2pr，但其初始相位不同，存在抵消或增加关系。一阶径向电磁力波间的相位关系如图4所示。图中，f3&4、f4&5和f12&13分别为3次与4次气隙磁通密度谐波产生的一阶电磁力波、4次与5次气隙磁通密度谐波产生的一阶电磁力波、12次与13次气隙磁通密度谐波产生的一阶电磁力波，f4&5和f12&13的初始相位差为150°，两者为抵消关系；f4&5和f3&4的初始相位差为85°，两者为增加关系。
图4 一阶径向电磁力波间的相位关系
Fig.4 Phase relationship among the 1st radial electromagnetic force waves
根据式（1），由f3&4、f4&5和f12&13产生的不平衡磁拉力F3&4、F4&5和F12&13与总UMF对比如图5所示。由于f4&5的幅值远大于f3&4和f12&13的幅值，F4&5远大于F3&4和F12&13。同时，在只考虑主要阶次气隙磁通密度谐波的情况下，由于f3&4、f4&5和f12&13间的相位抵消关系，这使得F3&4、F4&5和F12&13的矢量和F3&4&F4&5&F12&13略小于总UMF。为有效抑制8极9槽FSCW PMSM的UMF，可通过削弱f3&4、f4&5和f12&13的幅值或增强f3&4、f4&5和f12&13间的相位抵消关系。
图5 f3&4、f4&5和f12&13产生的UMF与总UMF对比
Fig.5 Comparison of UMF produced by f3&4, f4&5 and f12&13 with the total UMF
基于麦克斯韦应力张量法，FSCW PMSM的电磁转矩[13]为
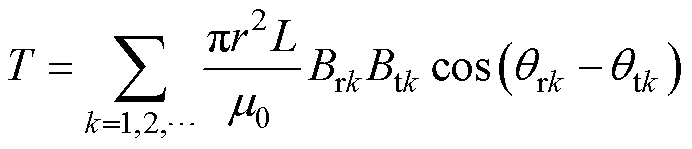（6）
式中，r为转子半径；Brk和Btk分别为第k次径向气隙磁通密度和切向气隙磁通密度幅值；qrk和qtk分别为第k次径向气隙磁通密度和切向气隙磁通密度初始相位。
对8极9槽FSCW PMSM气隙磁通密度进行傅里叶分解，其主要径向气隙磁通密度谐波和切向气隙磁通密度谐波相位差的余弦值如图6所示。由于4次径向气隙磁通密度谐波和切向气隙磁通密度谐波相位差的余弦值近似为0.5，其能够产生稳定电磁转矩，并且转矩脉动较小。在一个电周期中，其他阶次径向气隙磁通密度谐波和切向磁通密度相位差的余弦值近似按三角函数变化，无法产生稳定电磁转矩，且导致转矩脉动。
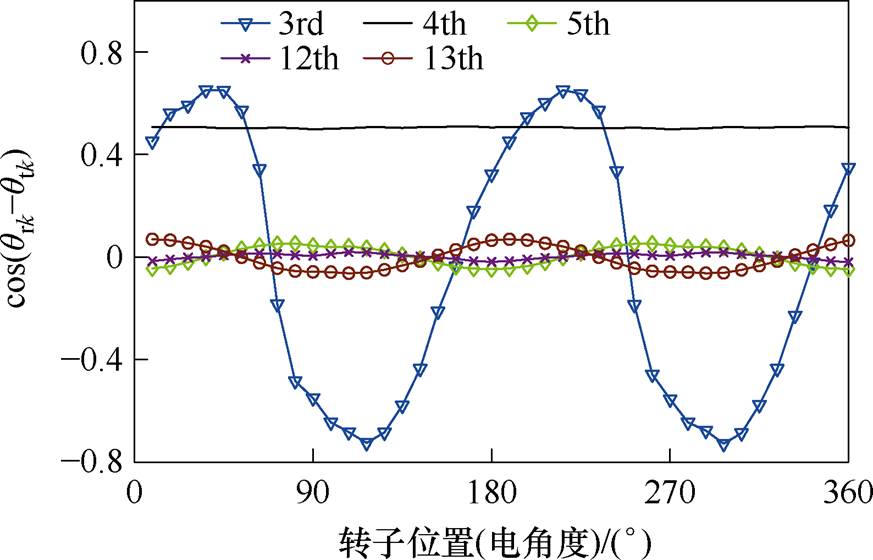
图6 径向气隙磁通密度和切向气隙磁通密度相位差的余弦值
Fig.6 Cosine of phase difference between the radial and tangential air-gap flux density
根据式（6），8极9槽FSCW PMSM的3次、4次、5次、12次和13次谐波产生的各阶次电磁转矩与总电磁转矩对比如图7所示。由图7计算可得，4次气隙磁通密度谐波产生的电磁转矩为2.48 N×m，占总电磁转矩2.55 N×m的97.3%，而其他气隙磁通密度谐波仅贡献2.7%的电磁转矩。
通过对8极9槽FSCW PMSM的UMF和电磁转矩进行量化分解可见，4次与5次径向气隙磁通密度是产生UMF的主要谐波阶次，而4次气隙磁通密度谐波对电磁转矩的贡献最大。为保持电机电磁转矩输出，不能削弱主要阶次气隙磁通密度谐波幅值，尤其是4次气隙磁通密度谐波幅值。但为有效抑制电机UMF，可通过调整主要气隙磁通密度谐波间的相位，增强一阶径向电磁力波间相位的抵消关系。
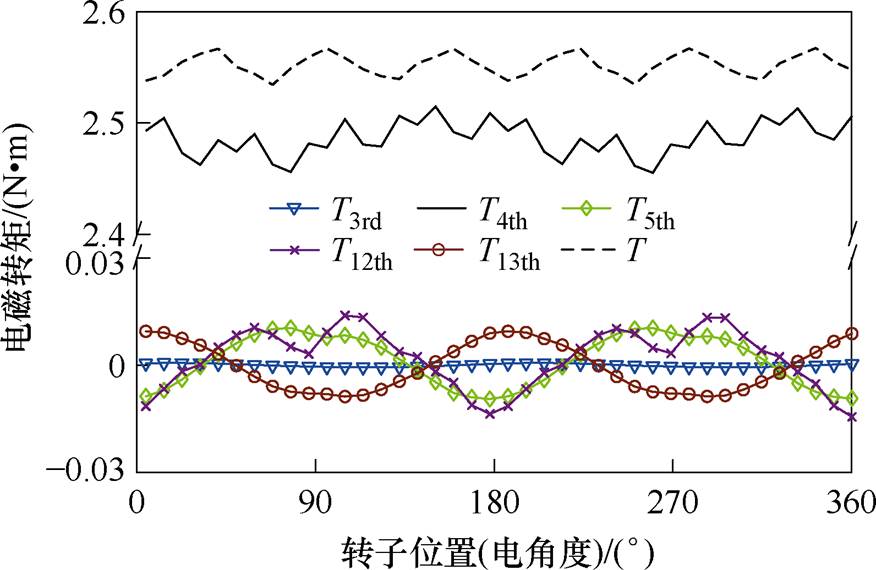
图7 各阶次电磁转矩与总电磁转矩对比
Fig.7 Comparison of each order electromagnetic torque with total electromagnetic torque
定子槽和辅助槽对FSCW PMSM的气隙磁通密度具有调制效应，可改变气隙磁通密度幅值和相 位[17, 26]。两者都是从电机“调制器”角度改善电机性能，前者通过调整定子槽结构参数，改善其对气隙磁通密度调制效应；在此基础上，后者对气隙磁通密度进行再调制。针对8极9槽FSCW PMSM，设计如图8所示定子槽和辅助槽。基于磁场调制理论，分析定子槽口和辅助槽对电磁转矩和UMF的影响，在有效抑制UMF的同时，保持电机电磁转矩输出。
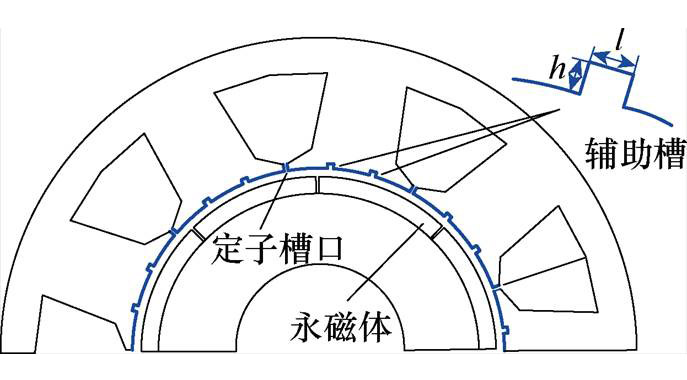
图8 定子槽口和辅助槽结构
Fig.8 Structure of stator slots and auxiliary slots
基于磁场调制理论，定子槽口对FSCW PMSM径向气隙磁通密度谐波幅值、电磁转矩和由径向电磁力波产生的UMF影响如图9所示。随定子槽口增加，受定子槽调制产生的3次、5次和13次径向气隙磁通密度谐波幅值越大，导致电机UMF增加；而4次和12次径向气隙磁通密度谐波幅值则先增大后减小。这使得电磁转矩同样先增加后减小，在定子槽口约为1.2 mm时达到最大。为不降低8极9槽FSCW PMSM的电磁转矩输出，同时有效抑制UMF，应设计较小的定子槽口。基于定子槽口对电磁转矩和UMF影响，设计的定子槽口为0.4 mm。
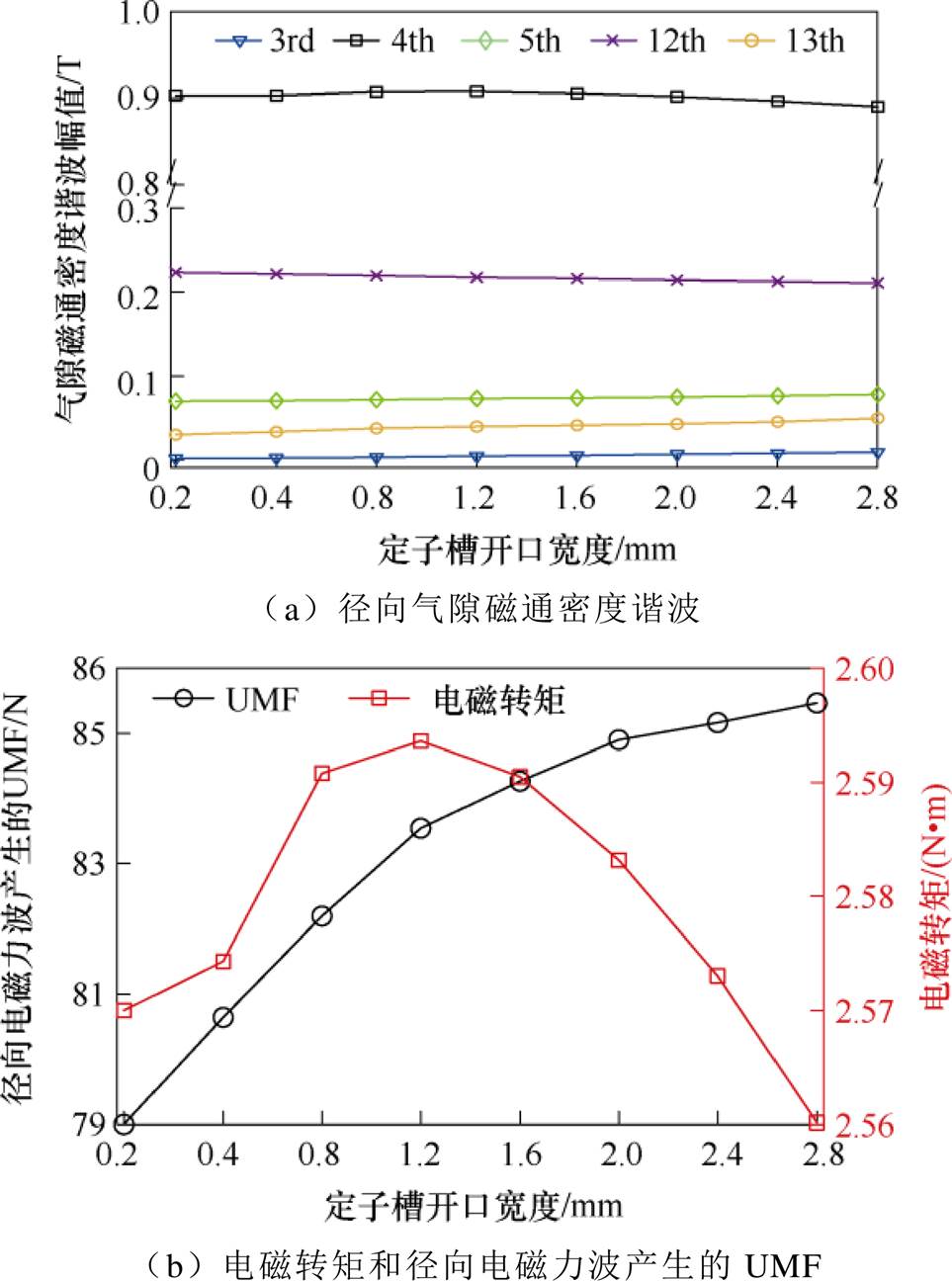
图9 定子槽口对电机性能的影响
Fig.9 The influence of stator slot on motor performance
在定子槽口设计基础上，增设辅助槽后的电机径向气隙磁通密度谐波相位如图10所示。可见，4次气隙磁通密度谐波与定子槽调制产生的5次和13次气隙磁通密度谐波具有相同的时间系数。12次气隙磁通密度谐波与定子槽调制产生的3次气隙磁通密度谐波具有相同的时间系数。由于辅助槽不改变气隙磁通密度谐波时间系数，在一个电周期中，不同径向气隙磁通密度谐波产生的一阶径向电磁力波间的相位关系一定。
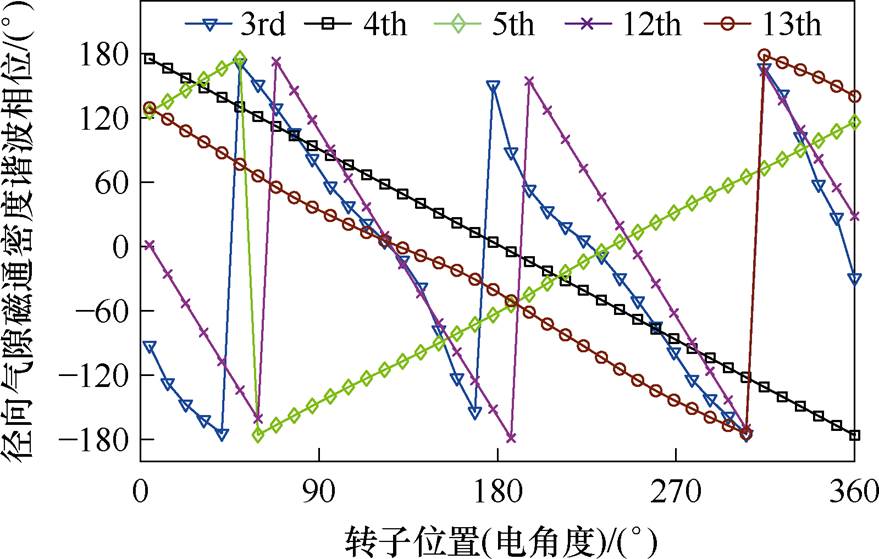
图10 径向气隙磁通密度谐波相位
Fig.10 Phase of the radial air-gap flux density harmonics
辅助槽结构参数对各次径向气隙磁通密度谐波幅值的影响如图11所示。可见，辅助槽深度和宽度的增加均会降低4次气隙磁通密度谐波幅值，降低电机电磁转矩输出。辅助槽深度在0.25～1.25 mm，辅助槽宽度在0.6～1.6 mm范围内，辅助槽深度和宽度对其他阶次气隙磁通密度谐波幅值影响不大。
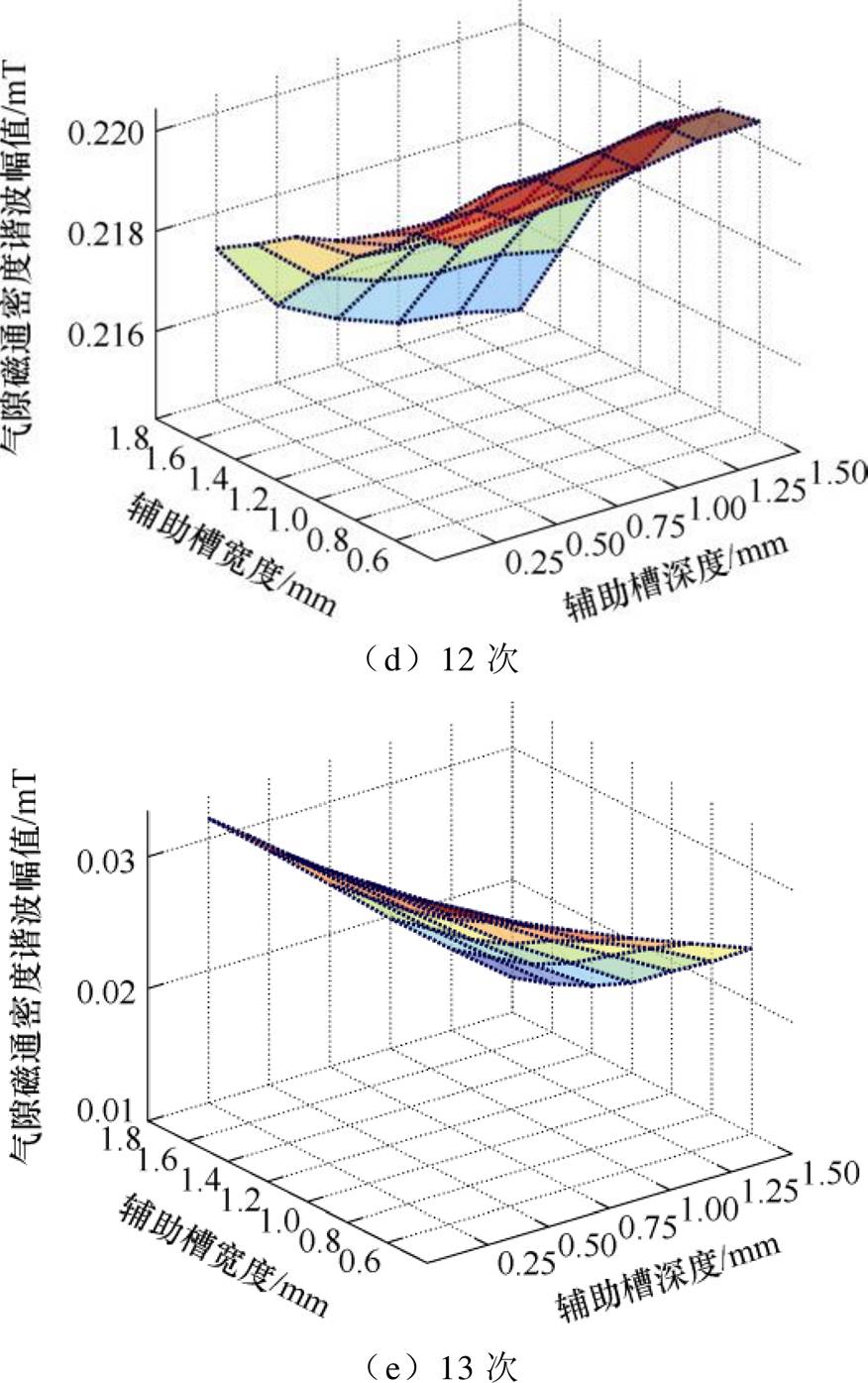
图11 辅助槽对各次气隙磁通密度谐波幅值影响
Fig.11 Influence of auxiliary slots on the amplitude of air-gap flux density harmonics
辅助槽结构参数对各次径向气隙磁通密度谐波相位影响如图12所示。可见，辅助槽深度和宽度对3次、5次、13次径向气隙磁通密度谐波相位影响较大，而对4次、12次径向气隙磁通密度谐波相位影响较小。这主要是由于辅助槽在定子槽调制的基础上进行再调制，对受调制效应产生的径向气隙磁通密度谐波相位影响大。
调节气隙磁通密度谐波相位可增加一阶径向电磁力波间相位的抵消效应，辅助槽结构参数对一阶径向电磁力波相位差的影响如图13所示。由图13a可见，随着辅助槽深度和宽度的增加，f4&5和f3&4的相位差增大并稳定在60°。由图13b可见，当设计的辅助槽深度和宽度适中时，f4&5和f12&13的相位差接近180°，此时一阶径向电磁力波间的抵消效应最强。
图12 辅助槽对各次气隙磁通密度谐波相位影响
Fig.12 Influence of auxiliary slots on the phase of air-gap flux density harmonics
基于上述分析，确定优化后定子槽口宽度为0.4 mm，辅助槽深度为0.75 mm，辅助槽宽度为1.2 mm。优化后一阶径向电磁力波间相位的关系和优化前后的UMF如图14所示。由图14a可见，f4&5与f12&13的相位差为178°，f3&4与f4&5的相位差在优化后有明显增大。由图14b可见，由于切向电磁力波与径向电磁力波谐波分量相同，仅幅值存在差异，优化后切向电磁力波产生的UMF与径向电磁力波产生的UMF抑制程度相近。
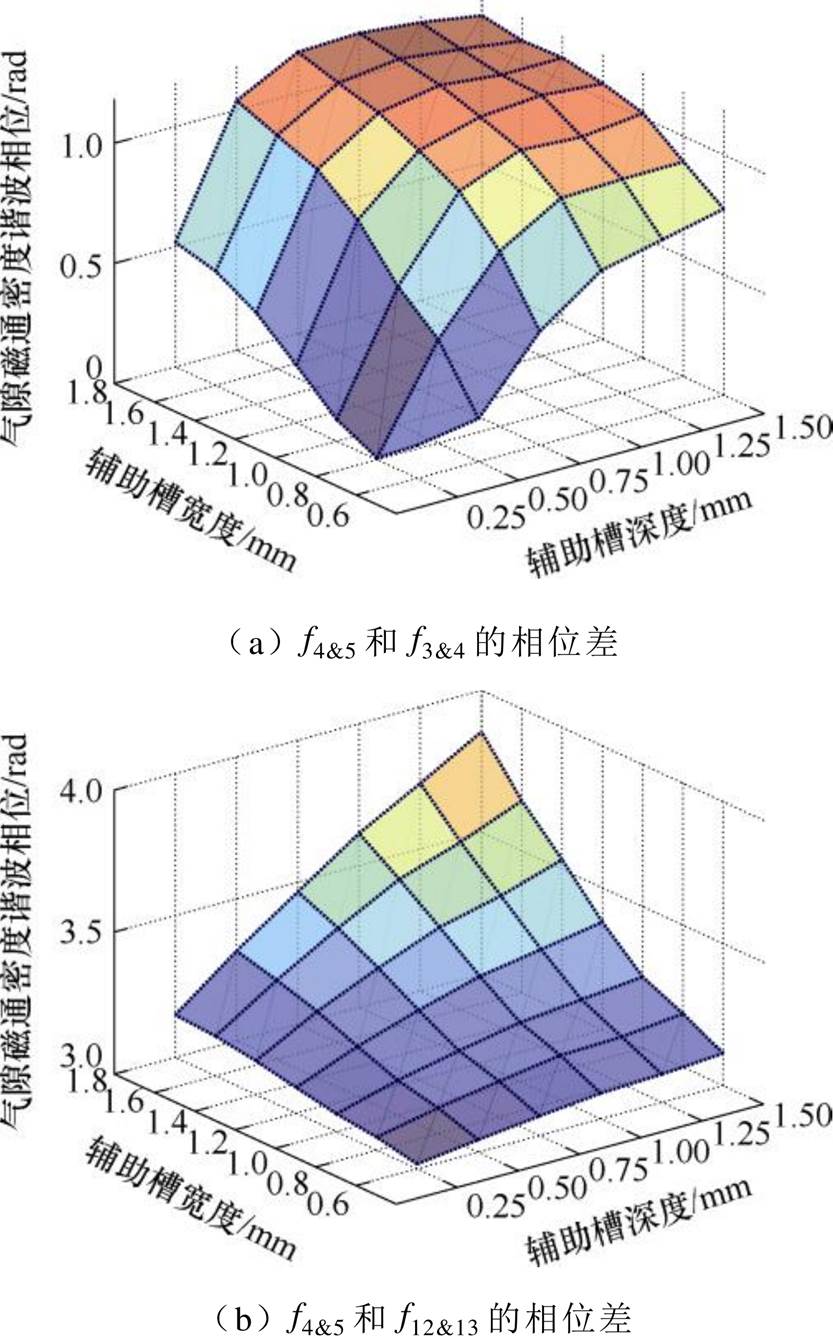
图13 辅助槽对一阶径向电磁力波间相位差的影响
Fig.13 Influence of auxiliary slots on the phase difference between 1st radial electromagnetic force waves
图14 一阶径向电磁力波和UMF
Fig.14 The 1st radial electromagnetic force waves and UMF
在不同电枢电流下，8极9槽FSCW PMSM优化前后的电磁转矩和UMF如图15所示。在额定状态下，电磁转矩由2.55 N×m降低至2.5 N×m，下降1.9%。总UMF由134 N降低至118 N，下降12%。综上所述，基于气隙磁通密度谐波相位调节UMF抑制与不降低电磁转矩输出的设计方法增强了一阶径向电磁力波间的相位抵消关系，在保持电机电磁转矩输出的同时，有效地抑制了电机的UMF。
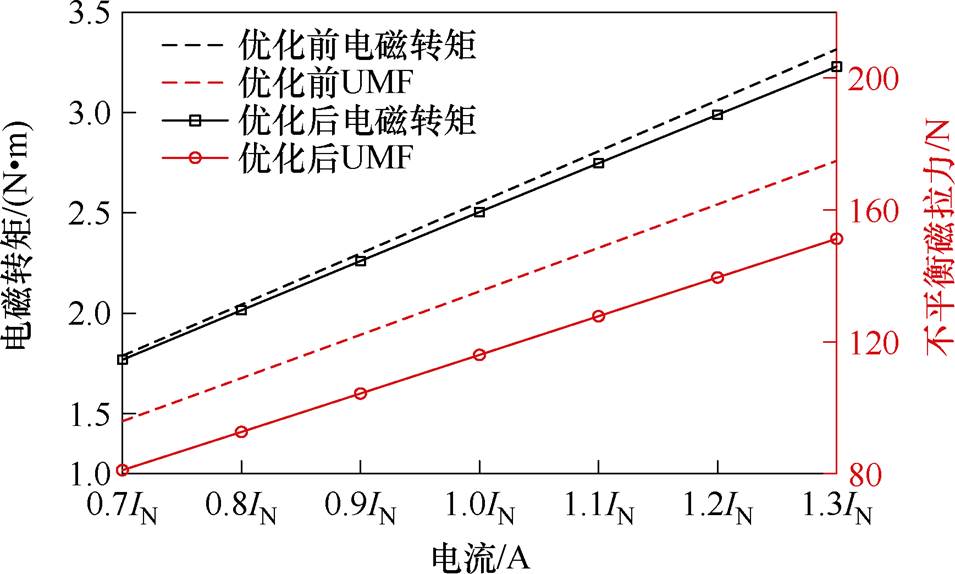
图15 电枢电流对电磁转矩和UMF影响
Fig.15 Influence of armature current on electromagnetic torque and UMF
为验证基于气隙磁通密度谐波相位调节UMF抑制与不降低电磁转矩输出设计方法的有效性，加工了一台如图16所示的8极9槽FSCW PMSM样机。图16a和图16b分别为样机的定子和转子，图16c为优化设计的定子槽口和辅助槽，定子槽口宽度、辅助槽宽度和深度与优化结果一致。为检测样机转子位置和转速，在转子轴端部安装了光电编码器。
图16 8极9槽FSCW PMSM样机
Fig.16 Prototype of 8-pole and 9-slot FSCW PMSM
基于如图17所示的实验平台，采用id=0控制，测试8极9槽FSCW PMSM样机电磁转矩。该实验平台包含直流电源、逆变器、RTU-BOX204半实物仿真控制器、上位机、PMSM样机、磁粉制动器、涡流制动器等。其中，磁粉制动器和涡流制动器为8极9槽FSCW PMSM样机提供可调负载。
图17 电磁转矩测试实验平台
Fig.17 Electromagnetic torque experimental platform
在电枢电流为3.8 A和转速为750 r/min的工况下，实验测得的8极9槽FSCW PMSM样机电磁转矩和三相电流如图18所示。由于二维有限元仿真未考虑机械制造公差和边缘效应，实验测得电磁转矩比有限元结果减少了约4%。
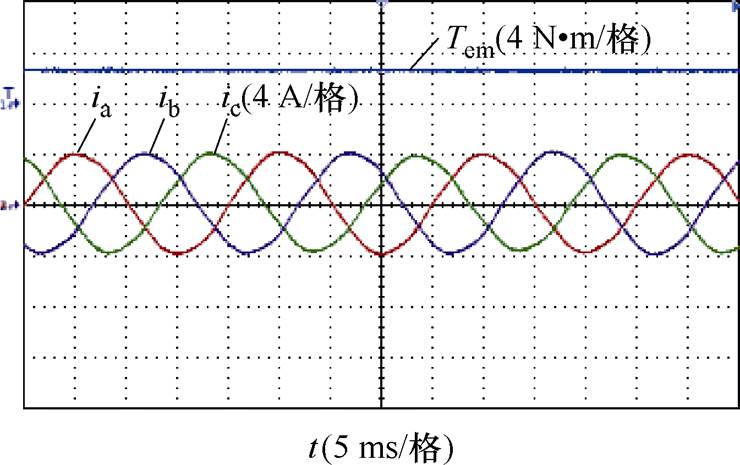
图18 电磁转矩和三相电流
Fig.18 Electromagnetic torque and three-phase currents
测试的电磁转矩和相电流关系如图19所示。由于仅考虑主要次谐波产生的电磁转矩，这使得解析结果略低于仿真结果。实验测量结果与优化后有限元仿真结果误差较小，额定工作点处误差值为4%，验证了通过优化设计定子槽口和辅助槽调节气隙磁通密度谐波相位，而不改变主要气隙磁通密度谐波幅值，保持了电机电磁转矩输出。
由于UMF是作用在转子上的径向力，其大小和方向随转子转动发生变化。在电机正常运行中，为防止UMF引起转子偏心，一般采用轴承固定转子。基于上述因素，目前鲜有在电机转子转动的过程中测试UMF的报道。为测试8极9槽FSCW PMSM样机的UMF，本文通过分离轴承外壳与电机外壳，设计了如图20所示的UMF测试实验平台。该实验平台包含加工的电机支架、压力传感器和压力显示仪等。在测试中，将轴承外壳与电机定子外壳分离，失去轴承到电机定子外壳间的固定作用后，表贴式转子的永磁体将吸附于定子内测的铜导体绕组一侧，造成转子偏心。为减小转子偏心对UMF测量精度影响，已知电机气隙为1 mm，采用两层厚度为0.3 mm的聚酯材料对电机气隙进行部分填充，剩下0.4 mm为空气气隙，然后，基于等高的轴承外壳与电机定子外壳设计，二次校正转子位置，并校正压力传感器归零，实现转子不偏心。通过电机控制系统输入特定的三相直流电使同步电机处于“初始位置矫正模式”，同时产生方向与压力传感器测量方向平行的UMF，测量静态UMF。
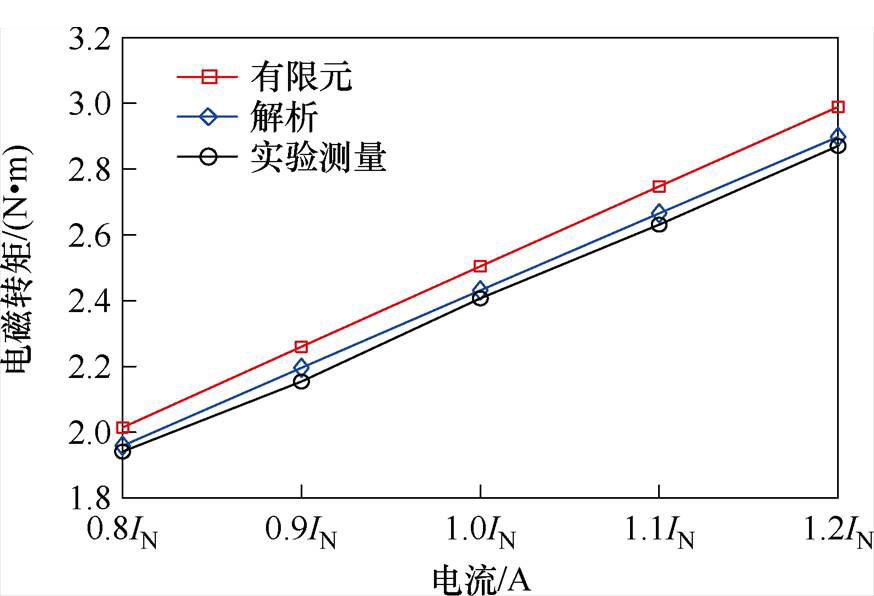
图19 电磁转矩和相电流关系
Fig.19 Relationship between electromagnetic torque and phase current
图20 UMF测量实验
Fig.20 UMF measurement experiment
本文开展采用和不采用聚酯材料填充电机气隙的UMF测量实验，在不同电流幅值下，UMF测量结果如图21所示。为使UMF的方向与压力计测量方向一致，在8极9槽FSCW PMSM的三相电枢绕组中通入如图21a所示的三相电流。由图21b可知，不采用聚酯材料填充电机气隙时，转子吸附于定子一侧，不仅无法确定UMF方向，UMF也小于表贴式永磁体对铜导体吸引力，导致压力传感器无法测量到力。
图21 UMF测量结果
Fig.21 Measurement results of UMF
在不同电枢电流幅值下，压力传感器测量结果与有限元仿真结果如图22所示。随着电枢电流幅值增加，压力传感器测量结果与有限元仿真结果比值为5.7%、6.23%、6.72%、7.08%和7.18%。压力传感器测量的是由连接装置传递过来的力，当电枢电流较小为4 A的时候，由于测量装置连接处精度不足，压力传感器测量的力偏小。当电枢电流较大时，UMF测量装置处于紧密连接状态，压力传感器测量结果可反映8极9槽FSCW PMSM的UMF幅值。
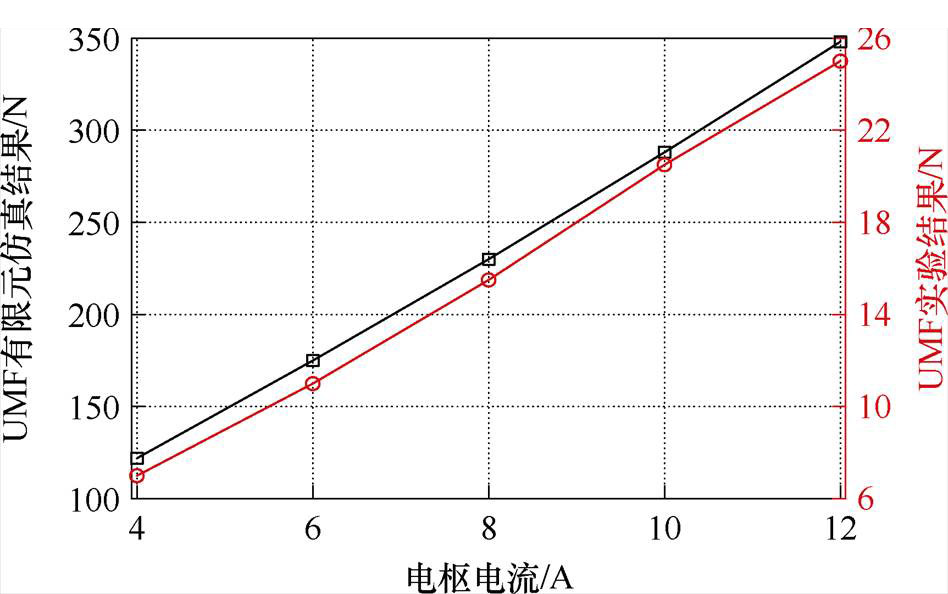
图22 UMF实验结果和有限元仿真结果
Fig.22 Measurement and simulation results of UMF
针对槽极组合满足Ns=2pr±1的FSCW PMSM在转子径向产生显著的UMF，导致电机的振动和噪声，并降低轴承使用寿命等问题，提出一种基于气隙磁通密度谐波相位调节UMF抑制与不降低电磁转矩输出的设计方法。仿真分析和样机实验验证了设计方法的有效性，并得到以下结论：
1）电机槽极组合满足Ns=2pr±1时，通过气隙磁导基波分量调制产生一阶径向电磁力波，且存在幅值较大的pr±1次径向永磁磁通密度谐波。由气隙磁导基波分量调制的径向永磁磁通密度谐波和非调制的永磁磁通密度谐波所产生一阶径向电磁力波具有相同的时间系数x=2pr，使得一阶径向电磁力波间的相位差不变，在一个电周期中实现了一阶径向电磁力波间的抵消。
2）8极9槽FSCW PMSM产生电磁转矩的主要气隙磁通密度谐波阶次为4次，产生UMF的主要气隙磁通密度谐波阶次为3次、4次、5次、12次和13次。为保持电机电磁转矩输出，不能削弱4次气隙磁通密度谐波幅值。但为有效抑制电机的UMF，可通过调整主要气隙磁通密度谐波相位，增强一阶径向电磁力波间的相位抵消关系。
3）减小定子槽口削弱了定子槽调制效应，增大了4次和12次气隙磁通密度谐波幅值，减小了由定子槽调制产生的气隙磁通密度谐波幅值。辅助槽对气隙磁通密度谐波进行再调制，其对气隙磁通密度谐波幅值影响较小，但改变了气隙磁通密度谐波相位，进而改变一阶电磁力波间的相位差，有效抑制了电机UMF。
4）为抑制槽极组合满足Ns=2pr±1的FSCW PMSM的UMF，并保持电磁转矩输出，在电机制造工艺方面，应采用较小定子槽开口宽度、面积适中且均匀分布的辅助槽。
参考文献
[1] Zhu Z Q, Azar Z, Ombach G. Influence of additional air gaps between stator segments on cogging torque of permanent-magnet machines having modular stators[J]. IEEE Transactions on Magnetics, 2012, 48(6): 2049- 2055.
[2] 陈浈斐, 邢宁, 马宏忠, 等. 分数槽永磁电机永磁体谐波涡流损耗建模与分析[J]. 电工技术学报, 2022, 37(14): 3514-3527.
Chen Zhenfei, Xing Ning, Ma Hongzhong, et al. Analytical modeling and analysis of magnet harmonic loss in fractional slot permanent-magnet machines[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3514-3527.
[3] 边旭, 纪毅, 梁艳萍. 外转子永磁同步电机径向电磁力分析与抑制[J]. 电机与控制学报, 2022, 26(10): 74-80.
Bian Xu, Ji Yi, Liang Yanping. Analysis and suppression of radial electromagnetic force of exter- nal rotor permanent magnet synchronous motor[J]. Electric Machines and Control, 2022, 26(10): 74-80.
[4] 许孝卓, 刘俊哲, 肖磊, 等. 基于磁-固耦合振动的永磁同步电机多目标优化设计[J]. 电气工程学报, 2024, 19(4): 149-158.
Xu Xiaozhuo, Liu Junzhe, Xiao Lei, et al. Multi- objective optimization design of permanent magnet synchronous motor based on magnetic-structural coupled vibration[J]. Journal of Electrical Engin- eering, 2024, 19(4): 149-158.
[5] 莫会成. 分数槽绕组与永磁无刷电动机[J]. 微电机, 2007, 40(11): 39-42, 81.
Mo Huicheng. Fractional-slot winding and PM brushless motor[J]. Micromotors Servo Technique, 2007, 40(11): 39-42, 81.
[6] Dorrell D G, Popescu M, Ionel D M. Unbalanced magnetic pull due to asymmetry and low-level static rotor eccentricity in fractional-slot brushless permanent- magnet motors with surface-magnet and consequent- pole rotors[J]. IEEE Transactions on Magnetics, 2010, 46(7): 2675-2685.
[7] 赵玫, 赵君, 左思承, 等. 横向磁通永磁直线电机电磁振动特性分析[J]. 电工技术学报, 2024, 39(1): 168-181.
Zhao Mei, Zhao Jun, Zuo Sicheng, et al. Analysis of electromagnetic vibration characteristics of transverse flux permanent magnet linear motor[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 168- 181.
[8] Ishak D, Zhu Z Q, Howe D. Permanent-magnet brushless machines with unequal tooth widths and similar slot and pole numbers[J]. IEEE Transactions on Industry Applications, 2005, 41(2): 584-590.
[9] Dorrell D G, Popescu M, Cossar C, et al. Unbalanced magnetic pull in fractional-slot brushless PM motors[C]//2008 IEEE Industry Applications Society Annual Meeting, Edmonton, AB, Canada, 2008: 1-8.
[10] Zhu Z Q, Ishak D, Howe D, et al. Unbalanced magnetic forces in permanent-magnet brushless machines with diametrically asymmetric phase windings[J]. IEEE Transactions on Industry Appli- cations, 2007, 43(6): 1544-1553.
[11] Sun Kai, He Yuling, Qiu Minghao, et al. Rotor unbalanced magnetic pull characteristics properties in synchronous generators due to dynamic air-gap eccentricity faults[C]//2021 IEEE 4th Student Con- ference on Electric Machines and Systems (SCEMS), Huzhou, China, 2021: 1-6.
[12] Kim D, Noh M D, Park Y W. Unbalanced magnetic forces due to rotor eccentricity in a toroidally wound BLDC motor[J]. IEEE Transactions on Magnetics, 2016, 52(7): 8203204.
[13] Li Y X, Zhu Z Q. Cogging torque and unbalanced magnetic force prediction in PM machines with axial-varying eccentricity by superposition method[J]. IEEE Transactions on Magnetics, 2017, 53(11): 1400404.
[14] Wu L J, Zhu Z Q, Chen J T, et al. An analytical model of unbalanced magnetic force in fractional-slot surface-mounted permanent magnet machines[J]. IEEE Transa- ctions on Magnetics, 2010, 46(7): 2686- 2700.
[15] Zhu Z Q, Mohd Jamil M L, Wu L J. Influence of slot and pole number combinations on unbalanced magnetic force in PM machines with diametrically asymmetric windings[J]. IEEE Transactions on Industry Applications, 2013, 49(1): 19-30.
[16] Lan Hua, Zou Jibin, Xu Yongxiang, et al. Investi- gation of unbalanced magnetic force in permanent magnet synchronous machines with asymmetric design[J]. IEEE Transactions on Magnetics, 2018, 54(11): 8203305.
[17] 薛东辉. 新能源汽车用不均匀齿(槽)距永磁同步电动机不平衡磁拉力、转矩脉动和电磁振动抑制研究[D]. 济南: 山东大学, 2020.
Xue Donghui. Research on unbalanced magnetic pull, torque ripple and electromagnetic vibration suppression of permanent magnet synchronous motor with uneven tooth(slot) pitch for new energy vehicles[D]. Jinan: Shandong University, 2020.
[18] 李泽星, 夏加宽, 刘铁法, 等. 基于分段交错不等磁极的表贴式永磁电机极频振动的削弱[J]. 电工技术学报, 2023, 38(4): 945-956.
Li Zexing, Xia Jiakuan, Liu Tiefa, et al. Reduction of pole-frequency vibration of surface-mounted per- manent magnet synchronous machines with piecewise stagger unequal poles[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 945-956.
[19] 韩雪岩, 王勇, 高俊. 低速永磁同步电机转子偏心的抑制措施[J]. 电机与控制学报, 2023, 27(11): 58-65.
Han Xueyan, Wang Yong, Gao Jun. Suppression of rotor eccentricity of low-speed permanent magnet synchronous motor[J]. Electric Machines and Control, 2023, 27(11): 58-65.
[20] 潘振芳, 李林. 基于辅助槽的永磁电机不平衡磁拉力抑制[J]. 微电机, 2021, 54(5): 9-13.
Pan Zhenfang, Li Lin. Unbalanced magnetic force reduction in PM machines by inserting auxiliary slots[J]. Micromotors, 2021, 54(5): 9-13.
[21] 李泽星, 夏加宽, 刘铁法, 等. 基于极间虚齿的表贴式永磁电机六倍频振动噪声的削弱[J]. 电工技术学报, 2023, 38(5): 1287-1298.
Li Zexing, Xia Jiakuan, Liu Tiefa, et al. Reduction of six times frequency vibration and noise of surface- mounted permanent magnet synchronous machines with interpolar virtual teeth[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1287-1298.
[22] Cheng Ming, Han Peng, Hua Wei. General airgap field modulation theory for electrical machines[J]. IEEE Transactions on Industrial Electronics, 2017, 64(8): 6063-6074.
[23] 程明, 文宏辉, 花为, 等. 电机气隙磁场调制统一理论及其典型应用[J]. 中国电机工程学报, 2021, 41(24): 8261-8283.
Cheng Ming, Wen Honghui, Hua Wei, et al. General airgap field modulation theory for electrical machines and its typical applications[J]. Proceedings of the CSEE, 2021, 41(24): 8261-8283.
[24] Li Ya, Yang Hui, Lin Heyun, et al. Torque generation mechanism and performance evaluation of a dual- sided PM machine with stator U-shaped magnets[J]. IEEE Transactions on Industry Applications, 2022, 58(1): 250-260.
[25] Yang Hui, Zhu Z Q, Lin Heyun, et al. Analysis of consequent-pole flux reversal permanent magnet machine with biased flux modulation theory[J]. IEEE Transactions on Industrial Electronics, 2020, 67(3): 2107-2121.
[26] Su Peng, Hua Wei, Wu Zhongze, et al. Analysis of the operation principle for rotor-permanent-magnet flux-switching machines[J]. IEEE Transactions on Industrial Electronics, 2018, 65(2): 1062-1073.
[27] Wang Peixin, Hua Wei, Zhang Gan, et al. Principle of flux-switching PM machine by magnetic field modulation theory part II: electromagnetic torque generation[J]. IEEE Transactions on Industrial Electronics, 2022, 69(3): 2437-2446.
[28] Zhu Z Q, Liu Yue. Analysis of air-gap field modu- lation and magnetic gearing effect in fractional-slot concentrated-winding permanent-magnet synchronous machines[J]. IEEE Transactions on Industrial Elec- tronics, 2018, 65(5): 3688-3698.
[29] 刘栋良, 詹成根, 屈峰, 等. 无人机17 kW电机振动噪声分析与巡航转速下尖端噪声优化[J]. 电工技术学报, 2024, 39(6): 1749-1763.
Liu Dongliang, Zhan Chenggen, Qu Feng, et al. Vibration noise analysis and tip noise optimization of unmanned aerial vehicle 17 kW motor at cruise speed[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1749-1763.
[30] 张玉峰, 高文韬, 史乔宁, 等. 基于改进迭代田口法的双余度永磁同步电机优化设计[J]. 电工技术学报, 2023, 38(10): 2637-2647, 2685.
Zhang Yufeng, Gao Wentao, Shi Qiaoning, et al. Optimization design of dual-redundancy permanent magnet synchronous motor based on improved iterations taguchi method[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2637-2647, 2685.
[31] 陈少先, 丁树业, 申淑锋, 等. 船舶用表贴式永磁同步电机的电磁振动分析与抑制[J]. 电工技术学报, 2023, 38(5): 1275-1286, 1298.
Chen Shaoxian, Ding Shuye, Shen Shufeng, et al. Analysis and suppression of electromagnetic vibration of surface mounted permanent magnet synchronous motor for ships[J]. Transactions of China Electro- technical Society, 2023, 38(5): 1275-1286, 1298.
[32] 刘凯, 张炳义, 冯桂宏. 基于电枢齿偏移法双面转子永磁同步电机振动噪声特性的研究[J]. 电工技术学报, 2021, 36(增刊1): 95-106.
Liu Kai, Zhang Bingyi, Feng Guihong. Research on electromagnetic vibration and noise characteristics of dual sided rotor permanent magnet synchronous motor based on armature offset approach[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(S1): 95-106.
Abstract The fractional slot concentrated winding (FSCW) permanent magnet synchronous motor (PMSM) with a slot pole combination satisfying Ns=2pr±1 has a high fundamental coefficient of winding and low end resistance, which has attracted attention in motor design. However, the FSCW PMSM has a significant unbalanced magnetic force (UMF) in its rotor, resulting in motor vibration and noise. Currently, most literature employs multi-objective optimization algorithms and modal analysis to optimize motor “modulators” for suppressing UMF. However, there is a lack of theoretical research on minimizing electromagnetic torque output reduction while achieving UMF suppression. Based on the theory of magnetic field modulation, this paper optimizes the slot pole combination. By adjusting the harmonic phase of the air gap magnetic density, the cancellation effect between the first-order radial electromagnetic force waves is enhanced, while suppressing the motor UMF and maintaining the motor electromagnetic torque output.
Firstly, the influence of air gap magnetic permeability on the time coefficient and spatial coefficient of the first-order electromagnetic force wave in PMSM is analyzed, and the main harmonic orders of air gap magnetic density that generate UMF and electromagnetic torque are determined. Secondly, the UMF and electromagnetic torque of the motor are quantitatively decomposed, and the cancellation relationship between first-order electromagnetic waves is analyzed. Then, the structural parameters of the stator slot and auxiliary slot are optimized, the harmonic phase of the air gap magnetic density is adjusted, and the cancellation effect between the first-order electromagnetic waves is enhanced. Finally, simulation analysis and prototype experiments were conducted on an 8-pole 9-slot FSCW PMSM.
The results show that the electromagnetic torque generated by the 4th air gap magnetic density harmonic is 2.48 N·m, accounting for 97.2% of the total electromagnetic torque (2.55 N·m). In comparison, other air gap magnetic density harmonics only contribute 2.8% of the electromagnetic torque. The phase cancellation relationship between the first-order radial electromagnetic force waves can be enhanced by adjusting the phase between the main air gap magnetic density harmonics. After optimization, the phase difference between the 8-pole 9-slot FSCW PMSM’s f4&5 and f12&13 is 178°, and the phase difference between f3&4 and f4&5 has significantly increased after optimization, resulting in an increased cancellation effect. At rated state, the electromagnetic torque decreases from 2.55 N·m to 2.5 N·m, representing a 1.9% decrease. The total UMF decreased from 134 N to 118 N, representing a 12% decrease. The error between the measurement and the simulation is small. The UMF change rate measured by the pressure sensor in the UMF measurement experiment is approximately equal to the UMF change rate in the finite element simulation.
The following conclusions can be drawn. (1) The main air gap magnetic density harmonic order for generating electromagnetic torque in an 8-pole 9-slot FSCW PMSM is 4th, and the main air gap magnetic density harmonic orders for generating UMF are 3rd, 4th, 5th, 12th, and 13th. To maintain the electromagnetic torque output of the motor, the amplitude of the 4th air gap magnetic resonance wave cannot be weakened. However, to effectively suppress the UMF of the motor, the phase cancellation relationship between the first-order radial electromagnetic force waves can be enhanced by adjusting the main air gap magnetic density harmonic phase. (2) Auxiliary slots with smaller stator slot opening width, moderate area, and uniform distribution should be used in the motor manufacturing process to suppress the UMF of FSCW PMSM with a slot pole combination that satisfies Ns=2pr±1 and maintain electromagnetic torque output.
keywords：Fractional slot concentrated winding, unbalanced magnetic forces, electromagnetic torque, phase regulation, 1st electromagnetic force waves
DOI: 10.19595/j.cnki.1000-6753.tces.241906
中图分类号：TM351
国家自然科学基金项目（52107039）、国家自然科学基金重点项目（51937002）和福建省自然科学基金项目（2021J05133）资助。
收稿日期 2024-10-25
改稿日期 2024-12-18
杨公德 男，1988年生，博士，副教授，研究方向为电力电子与电力传动技术、新型永磁电机设计与控制。E-mail: gdyang@fzu.edu.cn（通信作者）
陈宗孝 男，2001年生，硕士研究生，研究方向为新型永磁电机设计。E-mail: 1419063100@qq.com
（编辑 崔文静）